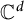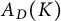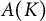1 Introduction
Let K be a compact subset of
![]() ${\mathbb C}^d$
,
${\mathbb C}^d$
,
![]() $d\geq 1$
. The classical function algebra
$d\geq 1$
. The classical function algebra
![]() $A(K)$
is defined to be
$A(K)$
is defined to be
![]() $C(K)\cap \mathcal {O} (K^{\circ })$
, where
$C(K)\cap \mathcal {O} (K^{\circ })$
, where
![]() $\mathcal {O}(K^{\circ })$
denotes the set of all holomorphic functions in the interior of K in
$\mathcal {O}(K^{\circ })$
denotes the set of all holomorphic functions in the interior of K in
![]() ${\mathbb C}^d$
. Note that if
${\mathbb C}^d$
. Note that if
![]() $K^{\circ }=\emptyset $
, then
$K^{\circ }=\emptyset $
, then
![]() $A(K)=C(K)$
. Denote by
$A(K)=C(K)$
. Denote by
![]() $P(K)$
the class of functions on K which are uniform limits of polynomials. In complex dimension
$P(K)$
the class of functions on K which are uniform limits of polynomials. In complex dimension
![]() $d=1,$
Mergelyan [Reference Mergelyan8] (see also [Reference Gaier3, p. 97]) gave the following complete characterization of compact sets on which polynomial approximation is possible.
$d=1,$
Mergelyan [Reference Mergelyan8] (see also [Reference Gaier3, p. 97]) gave the following complete characterization of compact sets on which polynomial approximation is possible.
Theorem 1.1 (Mergelyan theorem)
Let K be a compact subset of
![]() ${\mathbb C}.$
Then
${\mathbb C}.$
Then
![]() $P(K)=A(K)$
if and only if
$P(K)=A(K)$
if and only if
![]() ${\mathbb C}\setminus K$
is connected.
${\mathbb C}\setminus K$
is connected.
In [Reference Falcó, Gauthier, Manolaki and Nestoridis2], we constructed a counterexample to a Mergelyan-type statement given in [Reference Gamelin and Garnett4] concerning uniform approximation on compact sets K in
![]() ${\mathbb C}^d$
,
${\mathbb C}^d$
,
![]() $d\geq 1$
. In order to correct the statement in [Reference Gamelin and Garnett4], we introduced a natural function algebra
$d\geq 1$
. In order to correct the statement in [Reference Gamelin and Garnett4], we introduced a natural function algebra
![]() $A_D(K)$
, which is contained in the classical one
$A_D(K)$
, which is contained in the classical one
![]() $A(K)$
. The algebra
$A(K)$
. The algebra
![]() $A_D(K)$
is the algebra of all functions
$A_D(K)$
is the algebra of all functions
![]() $f\in A(K)$
which are holomorphic on every analytic disk contained in K, even meeting the boundary
$f\in A(K)$
which are holomorphic on every analytic disk contained in K, even meeting the boundary
![]() $\partial K$
of K. More precisely, a function
$\partial K$
of K. More precisely, a function
![]() $f:K\to {\mathbb C}$
belongs to
$f:K\to {\mathbb C}$
belongs to
![]() $A_D(K)$
if it is continuous on K and for every open disk
$A_D(K)$
if it is continuous on K and for every open disk
![]() $D \subseteq\mathbb {C}$
and every injective holomorphic mapping
$D \subseteq\mathbb {C}$
and every injective holomorphic mapping
![]() $\phi :D\to K$
the composition
$\phi :D\to K$
the composition
![]() $f\circ \phi $
is holomorphic on D.
$f\circ \phi $
is holomorphic on D.
In this paper, in addition to the family
![]() $P(K)$
of uniform limits on K of polynomials, we investigate the family
$P(K)$
of uniform limits on K of polynomials, we investigate the family
![]() $R(K)$
of uniform limits on K of rational functions which are holomorphic on a neighborhood of K. We also denote by
$R(K)$
of uniform limits on K of rational functions which are holomorphic on a neighborhood of K. We also denote by
![]() $\overline {\mathcal {O}}(K)$
the set of all functions
$\overline {\mathcal {O}}(K)$
the set of all functions
![]() $f:K\to {\mathbb C}$
such that there exists a sequence of open sets
$f:K\to {\mathbb C}$
such that there exists a sequence of open sets
![]() $(V_n)_{n=1}^{\infty }$
in
$(V_n)_{n=1}^{\infty }$
in
![]() $\mathbb {C}^d$
with
$\mathbb {C}^d$
with
![]() $K=\cap _{n=1}^{\infty } V_n$
and functions
$K=\cap _{n=1}^{\infty } V_n$
and functions
![]() $f_n:V_n\to {\mathbb C}$
holomorphic on
$f_n:V_n\to {\mathbb C}$
holomorphic on
![]() $V_n$
such that
$V_n$
such that
![]() $ {\sup _{z\in K}\vert f_n(z)-f(z)\vert \to 0}$
as n goes to infinity. It is easy to see that
$ {\sup _{z\in K}\vert f_n(z)-f(z)\vert \to 0}$
as n goes to infinity. It is easy to see that
![]() $P(K)\subseteq R(K)\subseteq \overline {\mathcal {O}}(K)\subseteq A_D(K)\subseteq A(K)$
. Moreover, when
$P(K)\subseteq R(K)\subseteq \overline {\mathcal {O}}(K)\subseteq A_D(K)\subseteq A(K)$
. Moreover, when
![]() $d=1$
, we have that
$d=1$
, we have that
![]() $A_D(K)= A(K)$
. One of the goals of this paper is to investigate when these classes coincide in higher dimensions, where the situation is far from being understood.
$A_D(K)= A(K)$
. One of the goals of this paper is to investigate when these classes coincide in higher dimensions, where the situation is far from being understood.
However, there are some known cases. For example, it is shown in [Reference Falcó, Gauthier, Manolaki and Nestoridis2] that if
![]() $K_1,K_2,\ldots ,K_d$
are planar compact sets and
$K_1,K_2,\ldots ,K_d$
are planar compact sets and
![]() $K=K_1\times \cdots \times K_d$
, then a function
$K=K_1\times \cdots \times K_d$
, then a function
![]() $f:K\to \mathbb {C}$
belongs to
$f:K\to \mathbb {C}$
belongs to
![]() $A_D(K)$
if and only if the slice functions belong to
$A_D(K)$
if and only if the slice functions belong to
![]() $A_D(K_i)$
for all
$A_D(K_i)$
for all
![]() $i=1,\ldots ,d$
; that is, for every
$i=1,\ldots ,d$
; that is, for every
![]() $i_0\in \{1,\ldots ,d\}$
and every choice of points
$i_0\in \{1,\ldots ,d\}$
and every choice of points
![]() $w_i\in K_i$
,
$w_i\in K_i$
,
![]() $i\in \{1,\ldots ,d\}\setminus \{i_0\}$
, the one-variable function,
$i\in \{1,\ldots ,d\}\setminus \{i_0\}$
, the one-variable function,
![]() $K_{i_0}\ni z\mapsto f(z_1,\ldots ,z_d)$
with
$K_{i_0}\ni z\mapsto f(z_1,\ldots ,z_d)$
with
![]() $z_{i_0}=z$
and
$z_{i_0}=z$
and
![]() $z_i=w_i$
for all
$z_i=w_i$
for all
![]() $i\in \{1,\ldots ,d\}\setminus \{i_0\}$
, belongs to
$i\in \{1,\ldots ,d\}\setminus \{i_0\}$
, belongs to
![]() $A_D(K_{i_0})$
. See also [Reference Chacrone, Gauthier and Nersessian1].
$A_D(K_{i_0})$
. See also [Reference Chacrone, Gauthier and Nersessian1].
A compact set
![]() $K\subseteq {\mathbb C}^d$
is called regular closed if every point in the boundary of K is the limit of a sequence of points in the interior of K. Thus, if K is regular closed and
$K\subseteq {\mathbb C}^d$
is called regular closed if every point in the boundary of K is the limit of a sequence of points in the interior of K. Thus, if K is regular closed and
![]() $K\ne \emptyset $
, then necessarily
$K\ne \emptyset $
, then necessarily
![]() $K^{\circ }\ne \emptyset $
. In [Reference Falcó, Gauthier, Manolaki and Nestoridis2], it was proved that, for nonvoid regular closed planar compact sets
$K^{\circ }\ne \emptyset $
. In [Reference Falcó, Gauthier, Manolaki and Nestoridis2], it was proved that, for nonvoid regular closed planar compact sets
![]() $K_1,\ldots , K_d$
and
$K_1,\ldots , K_d$
and
![]() $K=K_1\times \cdots \times K_d$
, we have
$K=K_1\times \cdots \times K_d$
, we have
![]() $A_D(K)=A(K)$
. In the second section of this note, we shall improve this result and characterize the equality of the two algebras when K is a product of planar compact sets (see Theorem 2.1). The third section includes the proof of this result and some corollaries. Sections 4 and 5 are devoted to investigating the equality of the two algebras on compact sets that are not necessarily product domains. In particular, polynomial, rational, and holomorphic approximation are considered.
$A_D(K)=A(K)$
. In the second section of this note, we shall improve this result and characterize the equality of the two algebras when K is a product of planar compact sets (see Theorem 2.1). The third section includes the proof of this result and some corollaries. Sections 4 and 5 are devoted to investigating the equality of the two algebras on compact sets that are not necessarily product domains. In particular, polynomial, rational, and holomorphic approximation are considered.
The sixth section of this note is devoted to the study of functions plausibly approximable by polynomials, rational functions, and holomorphic functions. More precisely, denoting by
![]() $\widehat {K}$
the polynomially convex hull of
$\widehat {K}$
the polynomially convex hull of
![]() $K,$
we show that a natural algebra containing
$K,$
we show that a natural algebra containing
![]() $P(K)$
is the algebra
$P(K)$
is the algebra
![]() $A_{D}(\widehat {K})$
; that is, the functions
$A_{D}(\widehat {K})$
; that is, the functions
![]() $f: K\to \mathbb {C}$
which admit a continuous extension
$f: K\to \mathbb {C}$
which admit a continuous extension
![]() $\widehat f$
to
$\widehat f$
to
![]() $\widehat {K}$
that belongs to
$\widehat {K}$
that belongs to
![]() $A_{D}(\widehat {K})$
are plausibly approximable, in the sense that every function that can be uniformly approximated on K by polynomials necessarily belongs to
$A_{D}(\widehat {K})$
are plausibly approximable, in the sense that every function that can be uniformly approximated on K by polynomials necessarily belongs to
![]() $A_{D}(\widehat {K})$
. If we replace polynomials by rational functions which are holomorphic on K, then the functions
$A_{D}(\widehat {K})$
. If we replace polynomials by rational functions which are holomorphic on K, then the functions
![]() $f: K\to \mathbb {C}$
which admit an extension to the rational convex hull
$f: K\to \mathbb {C}$
which admit an extension to the rational convex hull
![]() of K that belongs to
of K that belongs to
![]() are plausibly approximable.
are plausibly approximable.
Polynomially convex hulls and rationally convex hulls have played an extremely important role in approximation by polynomials and rational functions respectively. In order to replace polynomials and rational functions by functions holomorphic on some neighborhood of K, it is natural to seek an appropriate hull associated with such holomorphic approximation. There is no consensus in the literature as to the best way of defining such a hull for a compact set K and we shall introduce a new hull for this purpose, which we call an O-hull of K. We show that the functions
![]() $h: K\to \mathbb {C}$
which admit an extension to an O-hull X and belong to
$h: K\to \mathbb {C}$
which admit an extension to an O-hull X and belong to
![]() $A_{D}(X)$
are plausibly approximable. One can always choose as X the set K itself, but in general there are more choices of X, and, in some cases, there is no maximal O-hull for K.
$A_{D}(X)$
are plausibly approximable. One can always choose as X the set K itself, but in general there are more choices of X, and, in some cases, there is no maximal O-hull for K.
In Section 7, we strengthen a density result from [Reference Falcó, Gauthier, Manolaki and Nestoridis2], for compact sets of the form
![]() $K=K_1\times \cdots \times K_d$
. Finally, Section 8 contains some concluding remarks and problems for future research.
$K=K_1\times \cdots \times K_d$
. Finally, Section 8 contains some concluding remarks and problems for future research.
2 Main results
One of our main goals in this note is to prove the following theorem, which establishes conditions for the equality of the algebras
![]() $A_D(K)$
and
$A_D(K)$
and
![]() $A(K)$
when K is a product of nonvoid compact planar sets. We recall that a planar compact set F is called regular closed if
$A(K)$
when K is a product of nonvoid compact planar sets. We recall that a planar compact set F is called regular closed if
![]() $\overline {F^{\circ }}=F$
. We also recall that if
$\overline {F^{\circ }}=F$
. We also recall that if
![]() $K=K_1\times \dots \times K_{d}$
, where each
$K=K_1\times \dots \times K_{d}$
, where each
![]() $K_{i}$
is a compact set in
$K_{i}$
is a compact set in
![]() $\mathbb {C}$
, then a continuous function f belongs to
$\mathbb {C}$
, then a continuous function f belongs to
![]() $A_{D}(K)$
if and only if the slice functions belong to
$A_{D}(K)$
if and only if the slice functions belong to
![]() $A(K_{i})$
(see [Reference Falcó, Gauthier, Manolaki and Nestoridis2, Proposition 5.3]).
$A(K_{i})$
(see [Reference Falcó, Gauthier, Manolaki and Nestoridis2, Proposition 5.3]).
Theorem 2.1 Let
![]() $K_1,\ldots , K_d$
be nonvoid compact planar sets and
$K_1,\ldots , K_d$
be nonvoid compact planar sets and
![]() $K=K_1\times \cdots \times K_d$
. Then,
$K=K_1\times \cdots \times K_d$
. Then,
![]() $A_D(K)=A(K)$
if and only if one of the two following assertions holds:
$A_D(K)=A(K)$
if and only if one of the two following assertions holds:
-
(a)
 $K_1^{\circ }=K_2^{\circ }=\cdots =K_d^{\circ }=\emptyset $
,
$K_1^{\circ }=K_2^{\circ }=\cdots =K_d^{\circ }=\emptyset $
, -
(b)
 $K_i^{\circ }\ne \emptyset $
for all
$K_i^{\circ }\ne \emptyset $
for all
 $i\in \{1,\ldots ,d\}$
and all
$i\in \{1,\ldots ,d\}$
and all
 $K_i$
are regular closed sets for
$K_i$
are regular closed sets for
 $i\in \{1,\ldots ,d\}$
.
$i\in \{1,\ldots ,d\}$
.
In Section 3, we prove this result and provide some corollaries. Our other main results, that will be discussed in the subsequent sections, are Theorem 4.1, Example 5.1, Proposition 6.4, and Theorem 7.3.
3 Proof and corollaries of Theorem 2.1
Proof of Theorem 2.1
We distinguish four cases which cover the different scenarios of Theorem 2.1.
-
(i)
 $K_1^{\circ }=K_2^{\circ }=\cdots =K_d^{\circ }=\emptyset $
.
$K_1^{\circ }=K_2^{\circ }=\cdots =K_d^{\circ }=\emptyset $
. -
(ii) There exists
 $i_0,i_1\in \{1,2,\ldots ,d\}$
such that
$i_0,i_1\in \{1,2,\ldots ,d\}$
such that
 $K_{i_0}^{\circ }=\emptyset $
and
$K_{i_0}^{\circ }=\emptyset $
and
 $K_{i_1}^{\circ }\ne \emptyset $
.
$K_{i_1}^{\circ }\ne \emptyset $
. -
(iii)
 $K_i^{\circ }\ne \emptyset $
, for all
$K_i^{\circ }\ne \emptyset $
, for all
 $i\in \{1,2,\ldots ,d\}$
, and there is an
$i\in \{1,2,\ldots ,d\}$
, and there is an
 $i_0\in \{1,2,\ldots ,d\}$
such that
$i_0\in \{1,2,\ldots ,d\}$
such that
 $K_{i_0}$
is not regular closed.
$K_{i_0}$
is not regular closed. -
(iv)
 $K_i^{\circ }\ne \emptyset $
, for all
$K_i^{\circ }\ne \emptyset $
, for all
 $i \in \{1,2,\ldots ,d\}$
, and
$i \in \{1,2,\ldots ,d\}$
, and
 $K_i$
is regular closed for all
$K_i$
is regular closed for all
 $i\in \{1,2,\ldots ,d\}$
.
$i\in \{1,2,\ldots ,d\}$
.
We examine each case separately. For simplicity, we assume that if the interiors of
![]() $K_{i_1},\ldots ,K_{i_m}$
are not empty, then zero is in
$K_{i_1},\ldots ,K_{i_m}$
are not empty, then zero is in
![]() $(K_{i_1}\times \cdots \times K_{i_m})^{\circ }$
.
$(K_{i_1}\times \cdots \times K_{i_m})^{\circ }$
.
Case (i). In this case,
![]() $A(K_i)=A_D(K_i)=C(K_i)$
. It follows that for every
$A(K_i)=A_D(K_i)=C(K_i)$
. It follows that for every
![]() $f\in C(K)$
, the slice functions belong to
$f\in C(K)$
, the slice functions belong to
![]() $A_D(K_i)$
. Hence,
$A_D(K_i)$
. Hence,
![]() $f\in A_D(K)$
. Therefore,
$f\in A_D(K)$
. Therefore,
![]() $C(K)\subseteq A_D(K)$
. On the other hand,
$C(K)\subseteq A_D(K)$
. On the other hand,
![]() $K^{\circ }=\emptyset $
, which implies that
$K^{\circ }=\emptyset $
, which implies that
![]() $A(K)=C(K)$
. Thus, in Case (i), we have that
$A(K)=C(K)$
. Thus, in Case (i), we have that
![]() $A_D(K)\subseteq A(K)=C(K)\subseteq A_D(K)$
.
$A_D(K)\subseteq A(K)=C(K)\subseteq A_D(K)$
.
Case (ii). In this case,
![]() $K^{\circ }=\emptyset $
, so
$K^{\circ }=\emptyset $
, so
![]() $A(K)=C(K)$
. We shall show that
$A(K)=C(K)$
. We shall show that
![]() $A_D(K)\ne C(K)$
. Indeed, let
$A_D(K)\ne C(K)$
. Indeed, let
![]() $f(z_1,\ldots ,z_d)=\overline {z_{i_1}}$
. Then,
$f(z_1,\ldots ,z_d)=\overline {z_{i_1}}$
. Then,
![]() $f\in C(K)=A(K)$
, but the slice function corresponding to the coordinate
$f\in C(K)=A(K)$
, but the slice function corresponding to the coordinate
![]() $i_1$
is not holomorphic in
$i_1$
is not holomorphic in
![]() $K_{i_1}^{\circ }$
and does not belong to
$K_{i_1}^{\circ }$
and does not belong to
![]() $A(K_{i_1})=A_D(K_{i_1})$
. It follows that
$A(K_{i_1})=A_D(K_{i_1})$
. It follows that
![]() $f\notin A_D(K)$
. Thus,
$f\notin A_D(K)$
. Thus,
![]() $A_D(K)\ne C(K)=A(K)$
in this case.
$A_D(K)\ne C(K)=A(K)$
in this case.
Case (iii). Since
![]() $K_{i_0}$
is not regular closed, there exists
$K_{i_0}$
is not regular closed, there exists
![]() $w\in K_{i_0}\setminus \overline {K_{i_0}^{\circ }}$
. By the well-known Urysohn extension lemma, there exists a function
$w\in K_{i_0}\setminus \overline {K_{i_0}^{\circ }}$
. By the well-known Urysohn extension lemma, there exists a function
![]() $\phi \in C(K_{i_0})$
such that
$\phi \in C(K_{i_0})$
such that
![]() $\phi \equiv 0$
on
$\phi \equiv 0$
on
![]() $K_{i_0}^{\circ }$
and
$K_{i_0}^{\circ }$
and
![]() $\phi (w)=1$
. Since
$\phi (w)=1$
. Since
![]() $d>1$
, there exists
$d>1$
, there exists
![]() $i_1\in \{1,2,\ldots ,d\}\setminus \{i_0\}$
. We consider the function
$i_1\in \{1,2,\ldots ,d\}\setminus \{i_0\}$
. We consider the function
![]() $f(z_1,\ldots ,z_d)=\phi (z_{i_0})\cdot \overline {z_{i_1}}$
. Then,
$f(z_1,\ldots ,z_d)=\phi (z_{i_0})\cdot \overline {z_{i_1}}$
. Then,
![]() $f\in C(K)$
. Moreover, if
$f\in C(K)$
. Moreover, if
![]() $(z_1,\ldots ,z_d)\in K^{\circ }$
, then
$(z_1,\ldots ,z_d)\in K^{\circ }$
, then
![]() $z_{i_0}\in K_{i_0}^{\circ }$
, and thus
$z_{i_0}\in K_{i_0}^{\circ }$
, and thus
![]() $f(z_1,\ldots ,z_d)=\phi (z_{i_0})\cdot \overline {z_{i_1}}=0$
on
$f(z_1,\ldots ,z_d)=\phi (z_{i_0})\cdot \overline {z_{i_1}}=0$
on
![]() $K^{\circ }$
. It follows that
$K^{\circ }$
. It follows that
![]() $f\in \mathcal {O}(K^{\circ })$
. Hence,
$f\in \mathcal {O}(K^{\circ })$
. Hence,
![]() $f\in C(K)\cap \mathcal O(K^{\circ })=A(K)$
. Now, if
$f\in C(K)\cap \mathcal O(K^{\circ })=A(K)$
. Now, if
![]() $z_{i_0}=w$
, the slice function corresponding to the coordinate
$z_{i_0}=w$
, the slice function corresponding to the coordinate
![]() $i_1$
is
$i_1$
is
![]() $\phi (z_{i_0})\overline {z_{i_1}}=\phi (w)\overline {z_{i_1}}=\overline {z_{i_1}}$
and is not holomorphic in
$\phi (z_{i_0})\overline {z_{i_1}}=\phi (w)\overline {z_{i_1}}=\overline {z_{i_1}}$
and is not holomorphic in
![]() $K_{i_1}^{\circ }$
, and hence it does not belong to
$K_{i_1}^{\circ }$
, and hence it does not belong to
![]() $A_D(K_{i_1})=A(K_{i_1})$
. It follows that
$A_D(K_{i_1})=A(K_{i_1})$
. It follows that
![]() $f\notin A_D(K)$
. Therefore,
$f\notin A_D(K)$
. Therefore,
![]() $A_D(K)\ne A(K)$
in this case.
$A_D(K)\ne A(K)$
in this case.
Case (iv). In this case, we know from [Reference Falcó, Gauthier, Manolaki and Nestoridis2] that
![]() $A_D(K)=A(K)$
.
$A_D(K)=A(K)$
.
Since Cases (i)–(iv) cover the general case, the proof of Theorem 2.1 is complete.
In [Reference Falcó, Gauthier, Manolaki and Nestoridis2], it is also proved that, if for the planar compact sets
![]() $K_i$
,
$K_i$
,
![]() $i=1,\ldots ,d$
, we have
$i=1,\ldots ,d$
, we have
![]() $A_D(K_i)=\overline {\mathcal O}(K_i)$
for all
$A_D(K_i)=\overline {\mathcal O}(K_i)$
for all
![]() $i=1,\ldots ,d$
, then for the Cartesian product
$i=1,\ldots ,d$
, then for the Cartesian product
![]() $K=K_1\times \cdots \times K_d,$
we also have that
$K=K_1\times \cdots \times K_d,$
we also have that
![]() $A_D(K)=\overline {\mathcal O}(K)$
. One can easily see that the converse also holds. Combining results from [Reference Falcó, Gauthier, Manolaki and Nestoridis2] with Theorem 2.1, we obtain the following corollaries.
$A_D(K)=\overline {\mathcal O}(K)$
. One can easily see that the converse also holds. Combining results from [Reference Falcó, Gauthier, Manolaki and Nestoridis2] with Theorem 2.1, we obtain the following corollaries.
Corollary 3.1 Let
![]() $K_1,\ldots , K_d$
be nonvoid compact planar sets and
$K_1,\ldots , K_d$
be nonvoid compact planar sets and
![]() $K=K_1\times \cdots \times K_d$
. Then, polynomials are uniformly dense in
$K=K_1\times \cdots \times K_d$
. Then, polynomials are uniformly dense in
![]() $A_D(K)$
if and only if
$A_D(K)$
if and only if
![]() ${\mathbb C}\setminus K_i$
are connected for all
${\mathbb C}\setminus K_i$
are connected for all
![]() $i\in \{1,2,\ldots ,d\}$
.
$i\in \{1,2,\ldots ,d\}$
.
Proof For
![]() $d=1$
,
$d=1$
,
![]() $A(K_1)=A_D(K_1)$
, so this is just Mergelyan’s theorem (see Theorem 1.1).
$A(K_1)=A_D(K_1)$
, so this is just Mergelyan’s theorem (see Theorem 1.1).
Assume now that
![]() $d\geq 1$
. If polynomials are uniformly dense in
$d\geq 1$
. If polynomials are uniformly dense in
![]() $A_D(K)$
, it follows easily that polynomials are uniformly dense in
$A_D(K)$
, it follows easily that polynomials are uniformly dense in
![]() $A_D(K_i)$
for
$A_D(K_i)$
for
![]() $i=1,\ldots ,d$
. Therefore, according to the previous case,
$i=1,\ldots ,d$
. Therefore, according to the previous case,
![]() ${\mathbb C}\setminus K_i$
is connected. Suppose now that all
${\mathbb C}\setminus K_i$
is connected. Suppose now that all
![]() ${\mathbb C}\setminus K_i$
are connected for
${\mathbb C}\setminus K_i$
are connected for
![]() $i=1,\ldots ,d$
. Mergelyan’s theorem (Theorem 1.1) implies that polynomials are dense in each
$i=1,\ldots ,d$
. Mergelyan’s theorem (Theorem 1.1) implies that polynomials are dense in each
![]() $A(K_i)=A_D(K_i)$
. Hence,
$A(K_i)=A_D(K_i)$
. Hence,
![]() $\overline {\mathcal O}(K_i)=A_D(K_i)$
for all
$\overline {\mathcal O}(K_i)=A_D(K_i)$
for all
![]() $i=1,\ldots ,d$
. According to [Reference Falcó, Gauthier, Manolaki and Nestoridis2, Theorem 4.1], it follows that
$i=1,\ldots ,d$
. According to [Reference Falcó, Gauthier, Manolaki and Nestoridis2, Theorem 4.1], it follows that
![]() $\overline {\mathcal O}(K)=A_D(K)$
.
$\overline {\mathcal O}(K)=A_D(K)$
.
Since
![]() ${\mathbb C}\setminus K_i$
are connected, according to [Reference Falcó, Gauthier, Manolaki and Nestoridis2, Theorem 4.6], it follows that polynomials are uniformly dense on
${\mathbb C}\setminus K_i$
are connected, according to [Reference Falcó, Gauthier, Manolaki and Nestoridis2, Theorem 4.6], it follows that polynomials are uniformly dense on
![]() $\overline {\mathcal O}(K)$
. Thus, polynomials are uniformly dense in
$\overline {\mathcal O}(K)$
. Thus, polynomials are uniformly dense in
![]() $A_D(K)$
. See also [Reference Chacrone, Gauthier and Nersessian1, Reference Kioulafa, Kotsovolis and Nestoridis6, Reference Kotsovolis7].
$A_D(K)$
. See also [Reference Chacrone, Gauthier and Nersessian1, Reference Kioulafa, Kotsovolis and Nestoridis6, Reference Kotsovolis7].
Corollary 3.2 Let K be a countable compact set in
![]() ${\mathbb C}^d.$
Then,
${\mathbb C}^d.$
Then,
![]() $C(K)=P(K).$
$C(K)=P(K).$
Proof The projections of K are denumerable compact planar sets. Let F be their product. Then,
![]() $A(F)=P(F), \, A(F)=C(F)$
, and
$A(F)=P(F), \, A(F)=C(F)$
, and
![]() $A(K)=C(K).$
Now, if f is continuous on K, then, by Tietze’s theorem, it has a continuous extension h on F and h can be uniformly approximated on F (and on K) by polynomials.
$A(K)=C(K).$
Now, if f is continuous on K, then, by Tietze’s theorem, it has a continuous extension h on F and h can be uniformly approximated on F (and on K) by polynomials.
Corollary 3.3 Let
![]() $K_1,\ldots , K_d$
be nonvoid compact planar sets and
$K_1,\ldots , K_d$
be nonvoid compact planar sets and
![]() $K=K_1\times \cdots \times K_d$
. Then, polynomials are uniformly dense in
$K=K_1\times \cdots \times K_d$
. Then, polynomials are uniformly dense in
![]() $A(K)$
if and only if
$A(K)$
if and only if
![]() ${\mathbb C}\setminus K_i$
are connected for all
${\mathbb C}\setminus K_i$
are connected for all
![]() $i\in \{1,2,\ldots ,d\}$
and one of the conditions (a) or (b) of Theorem 2.1 holds.
$i\in \{1,2,\ldots ,d\}$
and one of the conditions (a) or (b) of Theorem 2.1 holds.
Proof Denote by
![]() $P(K)$
the set of uniform limits of polynomials on K. Then, we have
$P(K)$
the set of uniform limits of polynomials on K. Then, we have
Thus,
![]() $P(K)=A(K)$
is equivalent to
$P(K)=A(K)$
is equivalent to
![]() $P(K)=A_D(K)$
and
$P(K)=A_D(K)$
and
![]() $A_D(K)=A(K)$
. A combination of Theorem 2.1 and Corollary 3.1 completes the proof.
$A_D(K)=A(K)$
. A combination of Theorem 2.1 and Corollary 3.1 completes the proof.
Corollary 3.4 Let
![]() $K_1,\ldots , K_d$
be nonvoid compact planar sets and
$K_1,\ldots , K_d$
be nonvoid compact planar sets and
![]() $K=K_1\times \cdots \times K_d$
. Then,
$K=K_1\times \cdots \times K_d$
. Then,
![]() $A(K)=\overline {\mathcal O}(K)$
if and only if
$A(K)=\overline {\mathcal O}(K)$
if and only if
![]() $A(K_i)=\overline {\mathcal O}(K_i)$
, for all
$A(K_i)=\overline {\mathcal O}(K_i)$
, for all
![]() $i=1,2,\ldots ,d$
, and one of the conditions (a) or (b) of Theorem 2.1 holds.
$i=1,2,\ldots ,d$
, and one of the conditions (a) or (b) of Theorem 2.1 holds.
Proof Since
![]() $\overline {\mathcal O}(K)\subseteq A_D(K)\subseteq A(K)$
, it follows that
$\overline {\mathcal O}(K)\subseteq A_D(K)\subseteq A(K)$
, it follows that
![]() $\overline {\mathcal O}(K)= A(K)$
is equivalent to
$\overline {\mathcal O}(K)= A(K)$
is equivalent to
![]() $\overline {\mathcal O}(K)= A_D(K)$
and
$\overline {\mathcal O}(K)= A_D(K)$
and
![]() $A_D(K)= A(K)$
. According to [Reference Falcó, Gauthier, Manolaki and Nestoridis2],
$A_D(K)= A(K)$
. According to [Reference Falcó, Gauthier, Manolaki and Nestoridis2],
![]() $\overline {\mathcal O}(K)= A_D(K)$
is equivalent to
$\overline {\mathcal O}(K)= A_D(K)$
is equivalent to
![]() $\overline {\mathcal O}(K_i)= A_D(K_i)$
for all
$\overline {\mathcal O}(K_i)= A_D(K_i)$
for all
![]() $i=1,\ldots ,d$
. This combined with Theorem 2.1 completes the proof.
$i=1,\ldots ,d$
. This combined with Theorem 2.1 completes the proof.
Remark 3.5 Corollary 3.4 is in contradiction with [Reference Gamelin and Garnett4, Corollary 9.2], which implies the following: if
![]() $K_1,\ldots ,K_d$
are nonvoid planar compact sets,
$K_1,\ldots ,K_d$
are nonvoid planar compact sets,
![]() $K=K_1\times \cdots \times K_d$
and
$K=K_1\times \cdots \times K_d$
and
![]() $A(K_i)=\overline {\mathcal O}(K_i)$
for all
$A(K_i)=\overline {\mathcal O}(K_i)$
for all
![]() $i=1,\ldots ,d$
, then
$i=1,\ldots ,d$
, then
![]() $A(K)=\overline {\mathcal O}(K)$
. According to Corollary 3.4, it suffices to take
$A(K)=\overline {\mathcal O}(K)$
. According to Corollary 3.4, it suffices to take
![]() $d=2$
,
$d=2$
,
![]() $K_1$
a nonempty set with empty interior, and
$K_1$
a nonempty set with empty interior, and
![]() $K_2$
a set with nonempty interior with
$K_2$
a set with nonempty interior with
![]() $A(K_1)=\overline {\mathcal O}(K_1)$
and
$A(K_1)=\overline {\mathcal O}(K_1)$
and
![]() $A(K_2)=\overline {\mathcal O}(K_2)$
to obtain a contradiction. For instance, take
$A(K_2)=\overline {\mathcal O}(K_2)$
to obtain a contradiction. For instance, take
![]() $K_1=\{0\}$
and
$K_1=\{0\}$
and
![]() $K_2=\{w\in {\mathbb C}:\vert w\vert \leq 1\}$
. This was the counterexample given in [Reference Falcó, Gauthier, Manolaki and Nestoridis2], which led us to introduce the new natural function algebra
$K_2=\{w\in {\mathbb C}:\vert w\vert \leq 1\}$
. This was the counterexample given in [Reference Falcó, Gauthier, Manolaki and Nestoridis2], which led us to introduce the new natural function algebra
![]() $A_D(K)$
.
$A_D(K)$
.
4 The algebra
 $A_D(K)$
on general compact sets
$A_D(K)$
on general compact sets
We continue by studying compact sets which are not necessarily product domains. We start with a result which provides a simple necessary condition to ensure that the algebras
![]() $A_{D}(K)$
and
$A_{D}(K)$
and
![]() $A(K)$
coincide. This result was stated as a remark in the last section of [Reference Falcó, Gauthier, Manolaki and Nestoridis2].
$A(K)$
coincide. This result was stated as a remark in the last section of [Reference Falcó, Gauthier, Manolaki and Nestoridis2].
Theorem 4.1 Let
![]() $K\subseteq {\mathbb C}^d$
be a compact set. Then, if
$K\subseteq {\mathbb C}^d$
be a compact set. Then, if
![]() $A_D(K)=A(K)$
, we have that
$A_D(K)=A(K)$
, we have that
![]() $K\setminus \overline {K^{\circ }}$
contains no analytic disk.
$K\setminus \overline {K^{\circ }}$
contains no analytic disk.
Proof We shall prove the result by showing that if
![]() $K\setminus \overline {K^{\circ }}$
contains an analytic disk, then
$K\setminus \overline {K^{\circ }}$
contains an analytic disk, then
![]() $A_D(K)\ne A(K)$
. Since there is a holomorphic embedding of the open disk into
$A_D(K)\ne A(K)$
. Since there is a holomorphic embedding of the open disk into
![]() $K\setminus \overline {K^{\circ }},$
it is easy to see that there is also a holomorphic embedding
$K\setminus \overline {K^{\circ }},$
it is easy to see that there is also a holomorphic embedding
![]() $\varphi $
of the closed disk
$\varphi $
of the closed disk
![]() $\overline D$
into
$\overline D$
into
![]() $K\setminus \overline {K^{\circ }}$
. Consider g any function in
$K\setminus \overline {K^{\circ }}$
. Consider g any function in
![]() $A( \overline {K^{\circ }})$
. Then, since
$A( \overline {K^{\circ }})$
. Then, since
![]() $K\setminus \overline {K^{\circ }}$
has empty interior, any continuous extension of g belongs to the algebra
$K\setminus \overline {K^{\circ }}$
has empty interior, any continuous extension of g belongs to the algebra
![]() $A(K)$
. Consider the mapping
$A(K)$
. Consider the mapping
![]() $h:\varphi (\overline D)\to {\mathbb C}$
given by
$h:\varphi (\overline D)\to {\mathbb C}$
given by
![]() $h(z)=\overline {\varphi ^{-1}(z)}$
. Since
$h(z)=\overline {\varphi ^{-1}(z)}$
. Since
![]() $\varphi (\overline D)$
and
$\varphi (\overline D)$
and
![]() $ \overline {K^{\circ }}$
are disjoint compact sets, we can find a continuous mapping f on K which coincides with g on the set
$ \overline {K^{\circ }}$
are disjoint compact sets, we can find a continuous mapping f on K which coincides with g on the set
![]() $\overline {K^{\circ }}$
and coincides with h on
$\overline {K^{\circ }}$
and coincides with h on
![]() $\overline D$
. Then, the function f belongs to
$\overline D$
. Then, the function f belongs to
![]() $A(K)$
, but does not belong to
$A(K)$
, but does not belong to
![]() $A_D(K)$
. Thus, the algebras
$A_D(K)$
. Thus, the algebras
![]() $A(K)$
and
$A(K)$
and
![]() $A_D(K)$
must be different.
$A_D(K)$
must be different.
Corollary 4.2 Let
![]() $K\subseteq {\mathbb C}^d$
be a compact set. If
$K\subseteq {\mathbb C}^d$
be a compact set. If
![]() $K\setminus \overline {K^{\circ }}$
contains an analytic disk, then
$K\setminus \overline {K^{\circ }}$
contains an analytic disk, then
![]() $P(K)\subseteq R(K)\subseteq \overline {\mathcal O}(K)\subseteq A_D(K)\subsetneq A(K)$
. Thus,
$P(K)\subseteq R(K)\subseteq \overline {\mathcal O}(K)\subseteq A_D(K)\subsetneq A(K)$
. Thus,
![]() $P(K), R(K), \overline {\mathcal O}(K)$
, and
$P(K), R(K), \overline {\mathcal O}(K)$
, and
![]() $A_{D}(K)$
are different from
$A_{D}(K)$
are different from
![]() $A(K)$
.
$A(K)$
.
5 A counterexample to the converse statement of Theorem 4.1
It is natural to ask whether the converse statement of Theorem 4.1 holds; that is, if
![]() $A_D(K)\neq A(K)$
, then does
$A_D(K)\neq A(K)$
, then does
![]() $K\setminus \overline {K^{\circ }}$
always contain an analytic disk? As the following example demonstrates, the answer is negative.
$K\setminus \overline {K^{\circ }}$
always contain an analytic disk? As the following example demonstrates, the answer is negative.
Before showing the example, we recall that a compact set K is said to be regular closed if
![]() $K=\overline {K^{\circ }}.$
$K=\overline {K^{\circ }}.$
Example 5.1 There is a regular closed compact set
![]() $K\subseteq {\mathbb C}^2$
such that
$K\subseteq {\mathbb C}^2$
such that
![]() $K^{\circ }$
is connected and nonempty, and
$K^{\circ }$
is connected and nonempty, and
We remark that if we do not require that
![]() $K^{\circ }$
be connected and nonempty, it is easier to give such an example.
$K^{\circ }$
be connected and nonempty, it is easier to give such an example.
Details of the example:
Let
![]() $\overline D$
be the closed unit disk in
$\overline D$
be the closed unit disk in
![]() $\mathbb {C}$
and
$\mathbb {C}$
and
![]() $K_0=\{(z,w)\in {\mathbb C}^2:z\in \overline D, w=0\}.$
We will consider a sequence
$K_0=\{(z,w)\in {\mathbb C}^2:z\in \overline D, w=0\}.$
We will consider a sequence
![]() $P_n, \, n=1,2,\ldots $
, of polydomains, whose closures
$P_n, \, n=1,2,\ldots $
, of polydomains, whose closures
![]() $\overline P_n$
are disjoint from
$\overline P_n$
are disjoint from
![]() $K_0,$
such that
$K_0,$
such that
![]() $P_n\cap P_m\not =\emptyset $
if and only if
$P_n\cap P_m\not =\emptyset $
if and only if
![]() $|n-m|\le 1$
. We will also arrange that, for every
$|n-m|\le 1$
. We will also arrange that, for every
![]() $w\in K_0$
, there is a sequence
$w\in K_0$
, there is a sequence
![]() $w_n\in P_n$
converging to w, and conversely, if
$w_n\in P_n$
converging to w, and conversely, if
![]() $w_n\in P_n$
for all n and a subsequence of
$w_n\in P_n$
for all n and a subsequence of
![]() $w_n$
converges to a point s, then
$w_n$
converges to a point s, then
![]() $s \in K_0$
. Set
$s \in K_0$
. Set
Then,
![]() $K^{\circ }=\cup _nP_n$
is connected,
$K^{\circ }=\cup _nP_n$
is connected,
![]() $K=\overline {K^{\circ }}$
, and the disk
$K=\overline {K^{\circ }}$
, and the disk
![]() $K_0$
is contained in the boundary
$K_0$
is contained in the boundary
![]() $\partial K.$
We shall choose the polydomains
$\partial K.$
We shall choose the polydomains
![]() $P_n$
more carefully momentarily. For their construction, we shall make use of the following result (for its proof, see [Reference Gauthier and Kienzle5]).
$P_n$
more carefully momentarily. For their construction, we shall make use of the following result (for its proof, see [Reference Gauthier and Kienzle5]).
Lemma 5.2 Let
![]() $\varphi $
be continuously differentiable, and let
$\varphi $
be continuously differentiable, and let
![]() $\epsilon $
be positive and continuous on
$\epsilon $
be positive and continuous on
![]() $[0,1).$
Then, there is a function
$[0,1).$
Then, there is a function
![]() $\phi $
holomorphic in the unit disk, such that
$\phi $
holomorphic in the unit disk, such that
We note that, from [Reference Gauthier and Kienzle5, Theorem 1.3], we also have this result for
![]() $I=(-1,+1).$
$I=(-1,+1).$
Let
![]() $z: [0,1)\rightarrow D$
be an analytic curve whose “end” (cluster set) is
$z: [0,1)\rightarrow D$
be an analytic curve whose “end” (cluster set) is
![]() $\overline D$
and
$\overline D$
and
![]() $z'(t)\neq 0$
for each
$z'(t)\neq 0$
for each
![]() $t\in [0,1)$
. Moreover, let
$t\in [0,1)$
. Moreover, let
![]() $\epsilon : [0,1)\rightarrow (0,1]$
be a positive continuous function such that
$\epsilon : [0,1)\rightarrow (0,1]$
be a positive continuous function such that
![]() $\epsilon (t)\to 0$
as
$\epsilon (t)\to 0$
as
![]() $t\to 1.$
By Lemma 5.2, there is a nonconstant holomorphic function
$t\to 1.$
By Lemma 5.2, there is a nonconstant holomorphic function
![]() $\phi : D \to {\mathbb C},$
in the unit disk D, such that
$\phi : D \to {\mathbb C},$
in the unit disk D, such that
Since
![]() $z^{\prime }(t)\neq 0$
for all
$z^{\prime }(t)\neq 0$
for all
![]() $0\leq t <1$
, it follows that
$0\leq t <1$
, it follows that
![]() $\phi ^{\prime }(t)\neq 0$
for all
$\phi ^{\prime }(t)\neq 0$
for all
![]() $0\leq t <1$
. Invoking Lemma 5.2 again, there is a holomorphic function h in the unit disk D such that
$0\leq t <1$
. Invoking Lemma 5.2 again, there is a holomorphic function h in the unit disk D such that
We may choose a sequence
![]() $0<t_1<t_2<\cdots <t_n<\cdots , \, t_n\to 1,$
and positive numbers
$0<t_1<t_2<\cdots <t_n<\cdots , \, t_n\to 1,$
and positive numbers
![]() $r_n,$
such that the open disks
$r_n,$
such that the open disks
![]() $D_n=D(t_n,r_n)$
with centers
$D_n=D(t_n,r_n)$
with centers
![]() $t_n$
and radii
$t_n$
and radii
![]() $r_n$
form a chain in D (that is,
$r_n$
form a chain in D (that is,
![]() $D_n\cap D_m\not =\emptyset $
if and only if
$D_n\cap D_m\not =\emptyset $
if and only if
![]() $|n-m|\le 1$
) and the function
$|n-m|\le 1$
) and the function
![]() $\phi (\zeta )$
is invertible in a neighborhood of each
$\phi (\zeta )$
is invertible in a neighborhood of each
![]() $\overline D_n\cup \overline D_{n+1}.$
Moreover, since
$\overline D_n\cup \overline D_{n+1}.$
Moreover, since
![]() $h-\overline \phi $
is continuous on D and (5.2) holds, we may choose the
$h-\overline \phi $
is continuous on D and (5.2) holds, we may choose the
![]() $t_n$
and
$t_n$
and
![]() $r_n$
such that
$r_n$
such that
For
![]() $n=1,2,\ldots ,$
consider the open disks
$n=1,2,\ldots ,$
consider the open disks
![]() $W_n=D(2^{-n},2^{-n-1})$
and the polydomains
$W_n=D(2^{-n},2^{-n-1})$
and the polydomains
![]() $P_n\kern1.5pt{=}\kern1.5pt V_n\kern1.5pt{\times}\kern1.5pt W_n,$
where
$P_n\kern1.5pt{=}\kern1.5pt V_n\kern1.5pt{\times}\kern1.5pt W_n,$
where
![]() $V_n$
is the Jordan domain
$V_n$
is the Jordan domain
![]() ${V_n\kern1.5pt{=}\kern1.5pt\phi (D_n)\kern1.5pt{:=}\kern1.5pt\{z\kern1.5pt{\in}\kern1.5pt \mathbb {C}: z\kern1.5pt{=}\kern1.5pt\phi (\zeta ), \zeta \kern1.5pt{\in}\kern1.5pt D_n\}.}$
For these
${V_n\kern1.5pt{=}\kern1.5pt\phi (D_n)\kern1.5pt{:=}\kern1.5pt\{z\kern1.5pt{\in}\kern1.5pt \mathbb {C}: z\kern1.5pt{=}\kern1.5pt\phi (\zeta ), \zeta \kern1.5pt{\in}\kern1.5pt D_n\}.}$
For these
![]() $P_n,$
the set K defined by (5.1) has the required properties.
$P_n,$
the set K defined by (5.1) has the required properties.
We now define a function
![]() $f\in A(K),$
by setting
$f\in A(K),$
by setting
![]() $f(z,w)=\overline z,$
for
$f(z,w)=\overline z,$
for
![]() $(z,w)\in K_0$
and
$(z,w)\in K_0$
and
![]() $f(z,w)=h(\zeta _n(z)),$
for
$f(z,w)=h(\zeta _n(z)),$
for
![]() $(z,w)\in \overline P_n,$
where
$(z,w)\in \overline P_n,$
where
![]() $\zeta _n(z)$
is the inverse function of the restriction of the function
$\zeta _n(z)$
is the inverse function of the restriction of the function
![]() $\phi (\zeta )$
to
$\phi (\zeta )$
to
![]() $\overline D_n.$
The function f is well defined and continuous on
$\overline D_n.$
The function f is well defined and continuous on
![]() $K\setminus K^{\circ }$
because if
$K\setminus K^{\circ }$
because if
![]() $z\in \overline {D_n}\cap \overline {D_{n+1}}$
, then
$z\in \overline {D_n}\cap \overline {D_{n+1}}$
, then
![]() $\zeta _n(z)= \zeta _{n+1}(z)$
. It is easy to see that f is holomorphic on
$\zeta _n(z)= \zeta _{n+1}(z)$
. It is easy to see that f is holomorphic on
![]() $K^{\circ }$
.
$K^{\circ }$
.
There remains to show that f is continuous at points of
![]() $K^{\circ }.$
Since the restriction of f to
$K^{\circ }.$
Since the restriction of f to
![]() $K^{\circ }$
is continuous, it is sufficient to show that if
$K^{\circ }$
is continuous, it is sufficient to show that if
![]() $(z_k,w_k)$
is a sequence in
$(z_k,w_k)$
is a sequence in
![]() $K\setminus K^{\circ }$
converging to a point
$K\setminus K^{\circ }$
converging to a point
![]() $(z,0)\in K^{\circ },$
then
$(z,0)\in K^{\circ },$
then
![]() $f(z_k,w_k)\to f(z,0)=\overline z.$
We may assume that
$f(z_k,w_k)\to f(z,0)=\overline z.$
We may assume that
![]() $(z_k,w_k)\in P_{n(k)}, \, n(k)\to \infty .$
Moreover, if
$(z_k,w_k)\in P_{n(k)}, \, n(k)\to \infty .$
Moreover, if
![]() $(z_k,w_k)\in \overline P_{n(k)}$
, then
$(z_k,w_k)\in \overline P_{n(k)}$
, then
![]() $z_k\in \phi (\overline D_{n(k)})$
, and so there is
$z_k\in \phi (\overline D_{n(k)})$
, and so there is
![]() $y_k\in \overline D_{n(k)}$
such that
$y_k\in \overline D_{n(k)}$
such that
![]() $z_k=\phi (y_k)$
. Thus, using (5.3), we conclude that
$z_k=\phi (y_k)$
. Thus, using (5.3), we conclude that
which implies that
![]() $f\in C(K)$
since
$f\in C(K)$
since
![]() $\epsilon (t_n)\to 0$
as
$\epsilon (t_n)\to 0$
as
![]() $n\to \infty $
. Consequently,
$n\to \infty $
. Consequently,
![]() $f\in A(K)$
. Finally, it is easy to see that
$f\in A(K)$
. Finally, it is easy to see that
![]() $f\not \in A_D(K),$
since
$f\not \in A_D(K),$
since
![]() $f(z,w)= \overline z$
on the analytic disk
$f(z,w)= \overline z$
on the analytic disk
![]() $K_0.$
$K_0.$
6 Plausibly approximable functions
6.1 Polynomial approximation
Let K be a compact planar set, and let
![]() $P_n$
be a sequence of polynomials uniformly Cauchy on K. Then, by the maximum principle, it is uniformly Cauchy on every bounded component of the complement of K. Thus, if
$P_n$
be a sequence of polynomials uniformly Cauchy on K. Then, by the maximum principle, it is uniformly Cauchy on every bounded component of the complement of K. Thus, if
![]() $h \in C(K)$
is the uniform limit of
$h \in C(K)$
is the uniform limit of
![]() $P_n$
on K, then h has an extension f on the polynomially convex hull
$P_n$
on K, then h has an extension f on the polynomially convex hull
![]() $\widehat {K} $
of K, which is the union of K with all bounded components of the complement of K. Furthermore, f belongs to
$\widehat {K} $
of K, which is the union of K with all bounded components of the complement of K. Furthermore, f belongs to
![]() $A(K)$
. Conversely, if f belongs to
$A(K)$
. Conversely, if f belongs to
![]() $A(\widehat {K} )$
, since the complement of
$A(\widehat {K} )$
, since the complement of
![]() $\widehat {K} $
is connected, according to Mergelyan’s theorem in one variable, f belongs to
$\widehat {K} $
is connected, according to Mergelyan’s theorem in one variable, f belongs to
![]() $P(\widehat {K} )= P(K)$
. Thus, in one variable, the problem is solved: a function h on K belongs to
$P(\widehat {K} )= P(K)$
. Thus, in one variable, the problem is solved: a function h on K belongs to
![]() $P(K)$
if and only if it has an extension f belonging to
$P(K)$
if and only if it has an extension f belonging to
![]() $A(\widehat {K} )$
.
$A(\widehat {K} )$
.
If K is a compact subset of
![]() ${\mathbb C}^d$
,
${\mathbb C}^d$
,
![]() $d>1$
, then the polynomially convex hull
$d>1$
, then the polynomially convex hull
![]() $\widehat {K} $
of K is the set of
$\widehat {K} $
of K is the set of
![]() $z\in {\mathbb C}^d$
, such that for every polynomial P, the number
$z\in {\mathbb C}^d$
, such that for every polynomial P, the number
![]() $|P(z)|$
is less than or equal to the supremum on K of the modulus of P. It follows easily that if h belongs to
$|P(z)|$
is less than or equal to the supremum on K of the modulus of P. It follows easily that if h belongs to
![]() $P(K)$
, then it has an extension f in
$P(K)$
, then it has an extension f in
![]() $A_D(\widehat {K} ),$
so such functions are plausibly approximable by polynomials on K. Consider the following example.
$A_D(\widehat {K} ),$
so such functions are plausibly approximable by polynomials on K. Consider the following example.
Example 6.1 Let K be the unit sphere in
![]() ${\mathbb C}^d$
. Then,
${\mathbb C}^d$
. Then,
![]() $\widehat K$
is the closed unit ball
$\widehat K$
is the closed unit ball
![]() $\overline B$
and
$\overline B$
and
![]() $A_D(K)=C(K)$
,
$A_D(K)=C(K)$
,
![]() $A_D(\widehat {K} )= A(\overline B)=P(\overline B)$
. If
$A_D(\widehat {K} )= A(\overline B)=P(\overline B)$
. If
![]() $z=(z_1, \ldots ,z_d)$
, then the continuous function
$z=(z_1, \ldots ,z_d)$
, then the continuous function
![]() $h(z)= \overline {z_1}$
, the complex conjugate of
$h(z)= \overline {z_1}$
, the complex conjugate of
![]() $z_1$
, does not have an extension belonging to
$z_1$
, does not have an extension belonging to
![]() $A_D(\widehat {K} ),$
so it is not uniformly approximable by polynomials on
$A_D(\widehat {K} ),$
so it is not uniformly approximable by polynomials on
![]() $K.$
$K.$
It is easy to see that, for
![]() $d=1$
, if every h in
$d=1$
, if every h in
![]() $A_D(K)$
has an extension belonging to
$A_D(K)$
has an extension belonging to
![]() $A_D(\widehat {K} )$
, then K is polynomially convex. However, the result does not hold in general if
$A_D(\widehat {K} )$
, then K is polynomially convex. However, the result does not hold in general if
![]() $d>1$
as the following example shows. That is, there exists a set K that is not polynomially convex such that every function h in
$d>1$
as the following example shows. That is, there exists a set K that is not polynomially convex such that every function h in
![]() $A_D(K)$
has an extension belonging to
$A_D(K)$
has an extension belonging to
![]() $A_D(\widehat {K} )$
.
$A_D(\widehat {K} )$
.
Example 6.2 Let
![]() $d>1$
and
$d>1$
and
![]() $K_1:=\{z\in {\mathbb C}^d: 1/2\leq |z| \leq1\}$
, which is not polynomially convex. Then,
$K_1:=\{z\in {\mathbb C}^d: 1/2\leq |z| \leq1\}$
, which is not polynomially convex. Then,
![]() $\widehat K_1 $
is the closed unit ball B and every function h in
$\widehat K_1 $
is the closed unit ball B and every function h in
![]() $A_D(K_1)$
has an extension to
$A_D(K_1)$
has an extension to
![]() $A_D(\widehat {K_1})$
and can be approximated by polynomials.
$A_D(\widehat {K_1})$
and can be approximated by polynomials.
We shall show now that for every compact, convex set K with nonempty interior,
![]() $P(K)=A(K)$
, and for this, we shall invoke the following lemma. Although the lemma is well known, for the sake of completeness, we include the proof here.
$P(K)=A(K)$
, and for this, we shall invoke the following lemma. Although the lemma is well known, for the sake of completeness, we include the proof here.
Lemma 6.3 If
![]() $K\subseteq {\mathbb C}^d$
is a compact and convex set with
$K\subseteq {\mathbb C}^d$
is a compact and convex set with
![]() $K^{\circ }\ne \emptyset ,$
then for every
$K^{\circ }\ne \emptyset ,$
then for every
![]() $z_0\in K^{\circ }$
and every
$z_0\in K^{\circ }$
and every
![]() $z_1\in K,$
the segment
$z_1\in K,$
the segment
![]() $[z_0,z_1)$
is in
$[z_0,z_1)$
is in
![]() $K^{\circ }.$
Consequently, K is regular closed.
$K^{\circ }.$
Consequently, K is regular closed.
Proof Without loss of generality, we can assume that
![]() $z_0=0.$
Fix
$z_0=0.$
Fix
![]() $\epsilon>0$
such that the open ball of center zero and radius
$\epsilon>0$
such that the open ball of center zero and radius
![]() $\epsilon $
is in
$\epsilon $
is in
![]() $K^{\circ }$
,
$K^{\circ }$
,
![]() $B(0,\epsilon )\subseteq K^{\circ }$
. Consider z any fixed point in K. We claim that
$B(0,\epsilon )\subseteq K^{\circ }$
. Consider z any fixed point in K. We claim that
![]() $z\in \overline {K^{\circ }}$
. Indeed, for every
$z\in \overline {K^{\circ }}$
. Indeed, for every
![]() $r\in (0,1)$
and every
$r\in (0,1)$
and every
![]() ${y\in B(rz,(1-r)\epsilon )}$
, we have that
${y\in B(rz,(1-r)\epsilon )}$
, we have that
![]() $\frac {y-rz}{1-r}\in B(0,\epsilon )\subseteq K$
. By the convexity of K, we obtain that
$\frac {y-rz}{1-r}\in B(0,\epsilon )\subseteq K$
. By the convexity of K, we obtain that
![]() ${y=rz + (1-r) \frac {y-rz}{1-r}\in K}$
. Therefore,
${y=rz + (1-r) \frac {y-rz}{1-r}\in K}$
. Therefore,
![]() $ B(rz,(1-r)\epsilon )\subseteq K$
, and hence
$ B(rz,(1-r)\epsilon )\subseteq K$
, and hence
![]() $rz\in K^{\circ }$
. We have shown that
$rz\in K^{\circ }$
. We have shown that
![]() $[0,z)\subseteq K^{\circ }$
, and since
$[0,z)\subseteq K^{\circ }$
, and since
![]() $z=\lim _{r\to 1}rz$
, we obtain that
$z=\lim _{r\to 1}rz$
, we obtain that
![]() $K\subseteq \overline {K^{\circ }}$
.
$K\subseteq \overline {K^{\circ }}$
.
Proposition 6.4 If
![]() $K\subseteq {\mathbb C}^d$
is a compact, convex set with nonempty interior, then
$K\subseteq {\mathbb C}^d$
is a compact, convex set with nonempty interior, then
![]() $ P(K)=A(K)$
. In particular,
$ P(K)=A(K)$
. In particular,
![]() $P(K)=A_D(K)$
.
$P(K)=A_D(K)$
.
Proof We may assume that
![]() $0\in K^{\circ }$
, and by Lemma 6.3, we obtain that for each
$0\in K^{\circ }$
, and by Lemma 6.3, we obtain that for each
![]() $r<1$
and every
$r<1$
and every
![]() $z\in K$
, the point
$z\in K$
, the point
![]() $rz$
belongs to
$rz$
belongs to
![]() $K^{\circ }$
. Fix a function
$K^{\circ }$
. Fix a function
![]() $f\in A(K)$
. Then, the function
$f\in A(K)$
. Then, the function
![]() $f_r(z)=f(rz)$
is holomorphic on a neighborhood of K. Furthermore, for fixed
$f_r(z)=f(rz)$
is holomorphic on a neighborhood of K. Furthermore, for fixed
![]() $\epsilon>0$
, there exists
$\epsilon>0$
, there exists
![]() $r_\epsilon <1$
such that
$r_\epsilon <1$
such that
![]() $\vert f_{r_\epsilon }(z)-f(z)\vert <\epsilon /2$
for every
$\vert f_{r_\epsilon }(z)-f(z)\vert <\epsilon /2$
for every
![]() $z\in K$
. Since K is compact and convex, K is polynomially convex. By the Oka–Weil theorem, there exists a polynomial p such that
$z\in K$
. Since K is compact and convex, K is polynomially convex. By the Oka–Weil theorem, there exists a polynomial p such that
![]() $\vert p(z)-f_{r_\epsilon }(z)\vert <\epsilon /2$
for every
$\vert p(z)-f_{r_\epsilon }(z)\vert <\epsilon /2$
for every
![]() $z\in K$
. Thus,
$z\in K$
. Thus,
![]() $\vert p(z)-f(z)\vert <\epsilon $
for every
$\vert p(z)-f(z)\vert <\epsilon $
for every
![]() $z\in K$
. Hence, polynomials are dense in
$z\in K$
. Hence, polynomials are dense in
![]() $A_D(K)$
.
$A_D(K)$
.
6.2 Approximation by rational functions
Let K be a compact set in
![]() ${\mathbb C}^d$
,
${\mathbb C}^d$
,
![]() $d>1$
. The rationally convex hull
$d>1$
. The rationally convex hull
![]() of K is the set of z in
of K is the set of z in
![]() ${\mathbb C}^d$
such that for every rational function f holomorphic on an open set containing K, the number
${\mathbb C}^d$
such that for every rational function f holomorphic on an open set containing K, the number
![]() $|f(z)|$
is less than or equal to the supremum on K of the modulus of f. It follows easily that if a function h in
$|f(z)|$
is less than or equal to the supremum on K of the modulus of f. It follows easily that if a function h in
![]() $C(K)$
is in
$C(K)$
is in
![]() $R(K)$
, then h has an extension H in
$R(K)$
, then h has an extension H in
![]() . Thus, the functions h in
. Thus, the functions h in
![]() $C(K)$
admitting an extension H in
$C(K)$
admitting an extension H in
![]() are plausibly approximable by rational functions. In Examples 6.1 and 6.2, the rational convex hull and the polynomial convex hull coincide. Thus, Example 6.2 shows that there exists a set K that is not rationally convex such that every function h in
are plausibly approximable by rational functions. In Examples 6.1 and 6.2, the rational convex hull and the polynomial convex hull coincide. Thus, Example 6.2 shows that there exists a set K that is not rationally convex such that every function h in
![]() $A_D(K)$
has an extension belonging to
$A_D(K)$
has an extension belonging to
![]() .
.
If L is a rationally convex compact subset of
![]() $\mathbb {C}^d$
, then it is not always true that every function f in
$\mathbb {C}^d$
, then it is not always true that every function f in
![]() $A_D(L)$
can be approximated by rational functions. For example, let
$A_D(L)$
can be approximated by rational functions. For example, let
![]() $K_1$
be the Swiss cheese and put
$K_1$
be the Swiss cheese and put
![]() $L=K_1\times \{0\}.$
Then, L is rationally convex, but
$L=K_1\times \{0\}.$
Then, L is rationally convex, but
![]() $R(L)\not =A_D(L).$
$R(L)\not =A_D(L).$
6.3 Approximation by functions in
 $\mathcal {O}(K)$
$\mathcal {O}(K)$
Let us start with an example. Let K be the unit sphere in
![]() ${\mathbb C}^d$
,
${\mathbb C}^d$
,
![]() $d>1$
, and let f be a function holomorphic on a connected open set containing K. Then, f has an extension F holomorphic in an open set containing the closed unit ball
$d>1$
, and let f be a function holomorphic on a connected open set containing K. Then, f has an extension F holomorphic in an open set containing the closed unit ball
![]() $\overline B$
. Furthermore, for every z in
$\overline B$
. Furthermore, for every z in
![]() $\overline B$
,
$\overline B$
,
![]() $|F(z)|$
is less than or equal to the supremum of
$|F(z)|$
is less than or equal to the supremum of
![]() $|f|$
on K. It follows easily that if h is a function in
$|f|$
on K. It follows easily that if h is a function in
![]() $\overline {\mathcal {O}}(K)$
, then h has an extension in
$\overline {\mathcal {O}}(K)$
, then h has an extension in
![]() $A_D(\overline B)$
. As before, these functions are plausibly approximable by elements of
$A_D(\overline B)$
. As before, these functions are plausibly approximable by elements of
![]() $\mathcal {O}(K)$
. More generally, let K be a compact set in
$\mathcal {O}(K)$
. More generally, let K be a compact set in
![]() ${\mathbb C}^d$
,
${\mathbb C}^d$
,
![]() $d>1$
, and let X be a compact set in
$d>1$
, and let X be a compact set in
![]() ${\mathbb C}^d$
containing K and satisfying the following: for every open set V containing K so that every component of V meets K, and for every function f holomorphic on V, the function f has an extension F, to an open set containing X, that is holomorphic, and satisfies that for every
${\mathbb C}^d$
containing K and satisfying the following: for every open set V containing K so that every component of V meets K, and for every function f holomorphic on V, the function f has an extension F, to an open set containing X, that is holomorphic, and satisfies that for every
![]() $z\in X$
the number
$z\in X$
the number
![]() $|F(z)|$
is less than or equal to the supremum of
$|F(z)|$
is less than or equal to the supremum of
![]() $|f|$
on K.
$|f|$
on K.
We call such a compact set X an O-hull of K. Obviously,
![]() $X=K$
is always such a hull. We note that in general there is no maximal such hull. It follows that if K is rationally convex, then the only O-hull of K is K itself.
$X=K$
is always such a hull. We note that in general there is no maximal such hull. It follows that if K is rationally convex, then the only O-hull of K is K itself.
Example 6.5 Let
![]() $d>1$
and
$d>1$
and
![]() $K:=\{z\in {\mathbb C}^d: |z|=1/2 \text { or } |z|=1\}$
. Let r be a number in
$K:=\{z\in {\mathbb C}^d: |z|=1/2 \text { or } |z|=1\}$
. Let r be a number in
![]() $(1/2, 1)$
and let
$(1/2, 1)$
and let
![]() $X_r$
be the set of
$X_r$
be the set of
![]() $z \in {\mathbb C}^d$
such that
$z \in {\mathbb C}^d$
such that
![]() $|z|\in [0,1/2] \cup [r, 1]$
. Then
$|z|\in [0,1/2] \cup [r, 1]$
. Then
![]() $X_r$
is an O-hull of K and their union
$X_r$
is an O-hull of K and their union
![]() $\overline B$
too.
$\overline B$
too.
Example 6.6 Set
![]() $K=S\times \{0\}$
, where S is the Swiss cheese. Then, the only O-hull of K is K itself (since K is rationally convex), but
$K=S\times \{0\}$
, where S is the Swiss cheese. Then, the only O-hull of K is K itself (since K is rationally convex), but
![]() $A_D(K)$
and
$A_D(K)$
and
![]() $ \overline {\mathcal O}(K)$
are different from each other.
$ \overline {\mathcal O}(K)$
are different from each other.
7 A density result
We start by stating two of the main results which were proved in [Reference Falcó, Gauthier, Manolaki and Nestoridis2] (see Theorem 3.8 and Corollary 3.10, respectively).
Theorem 7.1 Let X be a compact subset of
![]() ${\mathbb C}$
such that
${\mathbb C}$
such that
![]() $\overline {\mathcal O}(X)=A_D(X)$
, and let Y be a compact subset of
$\overline {\mathcal O}(X)=A_D(X)$
, and let Y be a compact subset of
![]() ${\mathbb C}^m$
such that
${\mathbb C}^m$
such that
![]() $\overline {\mathcal O}(Y)=A_D(Y)$
. Then,
$\overline {\mathcal O}(Y)=A_D(Y)$
. Then,
![]() $\overline {\mathcal O}(X\times Y)=A_D(X\times Y)$
.
$\overline {\mathcal O}(X\times Y)=A_D(X\times Y)$
.
Corollary 7.2 Let
![]() $K_i, i=1,\ldots ,d$
, be compact subsets of
$K_i, i=1,\ldots ,d$
, be compact subsets of
![]() ${\mathbb C}$
, and let
${\mathbb C}$
, and let
![]() $L_i$
a subset of
$L_i$
a subset of
![]() ${\mathbb C} \cup \{\infty \}$
meeting every complementary component of
${\mathbb C} \cup \{\infty \}$
meeting every complementary component of
![]() $K_i$
. We also assume that
$K_i$
. We also assume that
![]() $ \overline {\mathcal O}(K_i)=A_D(K_i)$
. Then, every f in
$ \overline {\mathcal O}(K_i)=A_D(K_i)$
. Then, every f in
![]() $A_D(K_1\times \cdots \times K_d)$
can be uniformly approximated on
$A_D(K_1\times \cdots \times K_d)$
can be uniformly approximated on
![]() $K_1\times \cdots \times K_d$
by finite sums of finite products of rational functions of one variable
$K_1\times \cdots \times K_d$
by finite sums of finite products of rational functions of one variable
![]() $z_i$
with poles only in
$z_i$
with poles only in
![]() $L_i$
.
$L_i$
.
For
![]() $d=2$
, we have the following.
$d=2$
, we have the following.
Theorem 7.3 Let X be a compact subset of
![]() ${\mathbb C}$
such that
${\mathbb C}$
such that
![]() $\overline {\mathcal O}(X)=A_D(X)$
, and let Y be a compact subset of
$\overline {\mathcal O}(X)=A_D(X)$
, and let Y be a compact subset of
![]() ${\mathbb C}^m$
such that
${\mathbb C}^m$
such that
![]() $\overline {\mathcal O}(Y)=A_D(Y)$
. Let
$\overline {\mathcal O}(Y)=A_D(Y)$
. Let
![]() $L_X$
be a subset of
$L_X$
be a subset of
![]() ${\mathbb C} \cup \{\infty \}$
meeting every complementary component of X, and let S be a dense subset of
${\mathbb C} \cup \{\infty \}$
meeting every complementary component of X, and let S be a dense subset of
![]() $A_D(Y)$
. Then, every f in
$A_D(Y)$
. Then, every f in
![]() $A_D(X\times Y)$
can be uniformly approximated on
$A_D(X\times Y)$
can be uniformly approximated on
![]() $X\times Y$
by finite sums of products of the form
$X\times Y$
by finite sums of products of the form
![]() $g(z)h(w)$
, where g is a rational function of one variable z with poles only in
$g(z)h(w)$
, where g is a rational function of one variable z with poles only in
![]() $L_X$
and
$L_X$
and
![]() $h \in S$
.
$h \in S$
.
Remark 7.4 This strengthens Corollary 7.2 in case
![]() $d=2,$
for which we can take S to be the rational functions in
$d=2,$
for which we can take S to be the rational functions in
![]() $z_2$
with poles in
$z_2$
with poles in
![]() $L_2.$
$L_2.$
Proof According to Theorem 7.1, we can assume that f is holomorphic on a set
![]() ${V\times W}$
, where X is a subset of
${V\times W}$
, where X is a subset of
![]() $V\subseteq {\mathbb C}$
and Y is subset of
$V\subseteq {\mathbb C}$
and Y is subset of
![]() $W\subseteq {\mathbb C}^m$
and V and W are open sets. Let l be a cycle in
$W\subseteq {\mathbb C}^m$
and V and W are open sets. Let l be a cycle in
![]() $V\setminus X$
such that
$V\setminus X$
such that
![]() $Ind(l,z)=1$
for all
$Ind(l,z)=1$
for all
![]() $z \in X$
and
$z \in X$
and
![]() $Ind(l,z)=0$
for all
$Ind(l,z)=0$
for all
![]() $z \in \mathbb {C}\setminus V$
. Cauchy’s formula gives that, for
$z \in \mathbb {C}\setminus V$
. Cauchy’s formula gives that, for
![]() $z\in X$
and
$z\in X$
and
![]() $w \in Y$
, the number
$w \in Y$
, the number
![]() $f(z,w)$
is equal to an integral on l. The quantity to be integrated is uniformly continuous on
$f(z,w)$
is equal to an integral on l. The quantity to be integrated is uniformly continuous on
![]() $X\times Y\times l$
; therefore,
$X\times Y\times l$
; therefore,
![]() $f(z,w)$
can be uniformly approximated by Riemann sums of the integral on
$f(z,w)$
can be uniformly approximated by Riemann sums of the integral on
![]() $X\times Y$
; that is, linear combinations of products of the form
$X\times Y$
; that is, linear combinations of products of the form
![]() ${(\zeta _j-z)^{-1} f(\zeta _j,w)}$
. Each function
${(\zeta _j-z)^{-1} f(\zeta _j,w)}$
. Each function
![]() $f (\zeta _j,w)$
as a function of w can also be approximated by a function
$f (\zeta _j,w)$
as a function of w can also be approximated by a function
![]() $h_j(w) \in S$
, because
$h_j(w) \in S$
, because
![]() $\zeta _j$
is fixed and varies in a finite set. Similarly, the functions
$\zeta _j$
is fixed and varies in a finite set. Similarly, the functions
![]() $(\zeta _j-z)^{-1} $
can be approximated by rational functions
$(\zeta _j-z)^{-1} $
can be approximated by rational functions
![]() $g_j(z)$
with poles in
$g_j(z)$
with poles in
![]() $L_X$
.
$L_X$
.
Remark 7.5 In Theorem 7.3, in some scenarios, we can choose the functions g and h to belong to some specific families:
-
• If X is a compact subset of
 ${\mathbb C}$
with connected complement, then the functions g can be chosen to be polynomials.
${\mathbb C}$
with connected complement, then the functions g can be chosen to be polynomials. -
• If S is the set of polynomials of m variables, then of course the functions h are polynomials.
-
• If S is the set of rational functions of m variables holomorphic on Y, then of course the functions h are rational functions of m variables holomorphic on Y.
-
• If
 $S=\mathcal {O}(Y)$
, then of course the functions h are in
$S=\mathcal {O}(Y)$
, then of course the functions h are in
 $\mathcal {O}(Y)$
.
$\mathcal {O}(Y)$
.
8 Concluding remarks
We conclude with some remarks and lines of future research.
-
(1) It is natural to ask what happens if we replace the compact sets by closed sets, and require uniform approximation there, since our new algebra
 $A_{D}(K)$
can be defined for closed sets as well. Moreover, one can consider tangential (Carleman) approximation on closed (unbounded) sets. This problem was originally studied in [Reference Chacrone, Gauthier and Nersessian1] in the more general context of Riemann surfaces, where the authors avoided the error in [Reference Gamelin and Garnett4] by not using the standard definition for
$A_{D}(K)$
can be defined for closed sets as well. Moreover, one can consider tangential (Carleman) approximation on closed (unbounded) sets. This problem was originally studied in [Reference Chacrone, Gauthier and Nersessian1] in the more general context of Riemann surfaces, where the authors avoided the error in [Reference Gamelin and Garnett4] by not using the standard definition for
 $A.$
Instead, they gave a definition for A on products [Reference Chacrone, Gauthier and Nersessian1, p. 98], which is equivalent to
$A.$
Instead, they gave a definition for A on products [Reference Chacrone, Gauthier and Nersessian1, p. 98], which is equivalent to
 $A_D.$
In [Reference Falcó, Gauthier, Manolaki and Nestoridis2], a new original proof was written completely independently of [Reference Chacrone, Gauthier and Nersessian1] and new Mergelyan-type results were given for the algebra
$A_D.$
In [Reference Falcó, Gauthier, Manolaki and Nestoridis2], a new original proof was written completely independently of [Reference Chacrone, Gauthier and Nersessian1] and new Mergelyan-type results were given for the algebra
 $A_D$
, for example, for certain graphs as well as for Cartesian products of an arbitrary (possibly infinite) indexed family of planar compact sets. Thus, it would be interesting to investigate whether we can obtain analogous results for Carleman approximation on closed sets.
$A_D$
, for example, for certain graphs as well as for Cartesian products of an arbitrary (possibly infinite) indexed family of planar compact sets. Thus, it would be interesting to investigate whether we can obtain analogous results for Carleman approximation on closed sets. -
(2) There remains the open question of providing sufficient and necessary conditions for the existence of a maximal O-hull for a compact set K.
-
(3) Wu Jujie and the second author are presently investigating
 $A(K), \, A_D(K)$
and approximation, in the context of holomorphic motions.
$A(K), \, A_D(K)$
and approximation, in the context of holomorphic motions.