Introduction

Mountain glaciers are widely recognized as excellent indicators of climate change over recent centuries (Reference OerlemansOerlemans and Fortuin, 1992; Reference Haeberli, Maisch and PaulHaeberli and others, 2002; Reference ReynaudSolomon and others, 2007). As shown in numerous studies (Reference VincentVincent and others, 2004; Reference Oerlemans and FortuinOhmura and others, 2007), surface mass-balance change is closely related to climate change. Unfortunately, series of mass-balance observations are short (Reference Haeberli, Maisch and PaulHaeberli and others, 2002). Using ice-flow modelling, it is possible to reconstruct mass change from glacier extent fluctuations in the past. Conversely, ice-flow modelling is needed to simulate glacier fluctuations in the future from different mass-balance scenarios (Reference Vincent, Vallon, Reynaud and Le MeurWallinga and Van de Wal, 1998; Reference Le Meur, Gerbaux, Schäfer and VincentLe Meur and others, 2007). In both cases, the results depend on the reliability of these numerical modelling tools and thus on our understanding of ice-flow mechanisms.

Numerous ice-flow modelling studies have been carried out on glaciers with different degrees of complexity (Reference BindschadlerBindschadler, 1982; Reference Hubbard, Blatter, Nienow, Mair and HubbardHubbard and others, 1998; Reference Schäfer and Le MeurSpan and Kuhn, 2003; Reference Leysinger Vieli and GudmundssonLeysinger Vieli and Gudmundsson, 2004; Reference OerlemansOerlemans 2007; Schaefer and Le Meur, 2007). However, field observations on glaciers are generally not suitable for a thorough check of the results of these models over the entire glacier area. Field measurements are either available only for a small part of the glacier, or for the entire glacier area but with missing years. Except for some extensive field studies like the Unteraargletscher observations in Switzerland (Reference Huss, Sugiyama, Bauder and FunkHuss and others, 2007) or Hintereisferner observations in Austria (Reference Schäfer and Le MeurSpan and Kuhn, 2003), very few datasets are available for the entire area of a glacier over several decades. The main reason is that it is difficult to maintain field observations over long periods and to secure funding for such programmes.

As shown by several studies (Reference Lliboutry and ReynaudLliboutry and Reynaud, 1981; Reference VincentVincent and others, 2000; Reference Schäfer and Le MeurSpan and Kuhn, 2003), with the exception of surging glaciers, large dynamic changes are visible only over several decades of observations and are difficult to reproduce from glacier modelling.

The field observations of Glacier d’Argentière, France, relative to mass balance, thickness variations, ice-flow velocities and length fluctuations over 50 years are almost unique and provide a good opportunity to study the dynamics of this glacier. This glacier belongs to the French glacier-monitoring program GLACIOCLIM (http://www-lgge.obs.ujf-grenoble.fr/ServiceObs/index.htm), in which five French glaciers are investigated using mass balance, thickness changes, ice-flow velocities, snout fluctuations and meteorological measurements.

This paper first presents a long-term dataset for the purpose of future numerical modelling studies. For these studies, field measurements are needed either to constrain input data or to check model output results. The second topic of this paper is to study how glaciers such as Argentiére can respond to mass-balance change. For this purpose, the relationships between the surface mass balance and the ice-flow response are studied using measurements of surface mass balance, thickness change and ice-flow velocity. Similar to many alpine glaciers, Glacier d’Argentière reached maximum velocities and thicknesses in the early 1980s, followed by a sharp decrease in velocity over the subsequent two decades. Data collected from Glacier d’Argentière provide a good opportunity to study the relationships between surface mass balance and dynamic response over a period with changes in opposite directions. For this purpose, changes in ice-flow velocities, thickness and ice fluxes are compared and analyzed at three cross-sections of Glacier d’Argentière as a consequence of the surface mass-balance changes.

Study Site Description and Data

Glacier d'Argentière is located in the Mont Blanc range, French Alps (45°55' N, 6°57' E). Its surface area was 12.4 km² in 2003. The glacier extends from an altitude of ∽3400m at the upper bergschrund to 1600 m at the snout. The length of this glacier is ∽10 km. It faces north, except for a large part of the accumulation area (south-orientated tributaries). The annual mass balance ranges from about 2 mw.e. a^–1 in the accumulation area to about –10mw.e. a^–1 close to the snout. The equilibrium-line altitude (ELA) is close to 2800m on average over the last 20 years (Reference PatersonRabatel and others, 2005). This glacier is free of rock debris except for the tongue. The glacier has an icefall in its lower part between 2000 and 2400ma.s.l. (Fig. 1).

Fig. 1. Map of Glacier d’Argentière with measured transverse cross-sections.

The first topographic measurements were performed on the ablation area of Glacier d’Argentière in the beginning of the 20th century. In the 1970s, Emosson, a hydroelectric power company, intended to collect subglacial water. For this purpose, and for the installation of a cable car, information on glacier fluctuations was required. Consequently, regular field measurements have been carried out by the LGGE (Laboratoire de Glaciologie et Géophysique de l’Environnement, Grenoble) since 1975 along the three cross-sections shown in Figure 1. Except for 1986, at cross-sections 2 and 4, the measurements are continuous since 1976. Cross-section 7 is located at 2730 ma.s.l. close to the ELA. Cross-section 4 is located at 2400ma.s.l. close to the middle of the ablation area. Cross-section 2, at 1800 ma.s.l., is located on the lower part of the tongue. Note that the ice coming from the accumulation area of the Glacier des Rognons contributes to the ice flux of cross-section 4 but not to that of cross-section 7 (Fig. 1). The main goal was to assess the ice fluxes at each cross-section. For this purpose, the bedrock topography was determined using seismic soundings at cross-sections 2, 4 and 7. Moreover, 8 and 24 boreholes have been drilled on cross-sections 2 and 4, respectively, to check the seismic results (Reference Rabatel, Dedieu and VincentReynaud, 1959; Reference HantzHantz, 1981). The comparison shows differences which can reach 30m locally. However, the bedrock topography is relatively well known, with an average uncertainty of ±10m (Fig. 2).

Fig. 2. Cross-sections 7 (a), 4 (b) and 2 (c). The horizontal and vertical scales are the same for all cross-sections. The surface area values correspond to the year 1976. The cross-sections are seen from the downstream.

The first topographic measurements were performed on the ablation area of Glacier d’Argentière in the beginning of the 20th century. In the 1970s, Emosson, a hydroelectric power company, intended to collect subglacial water. For this purpose, and for the installation of a cable car, information on glacier fluctuations was required. Consequently, regular field measurements have been carried out by the LGGE (Laboratoire de Glaciologie et Géophysique de l’Environnement, Grenoble) since 1975 along the three cross-sections shown in Figure 1. Except for 1986, at cross-sections 2 and 4, the measurements are continuous since 1976. Cross-section 7 is located at 2730 ma.s.l. close to the ELA. Cross-section 4 is located at 2400ma.s.l. close to the middle of the ablation area. Cross-section 2, at 1800 ma.s.l., is located on the lower part of the tongue. Note that the ice coming from the accumulation area of the Glacier des Rognons contributes to the ice flux of cross-section 4 but not to that of cross-section 7 (Fig. 1). The main goal was to assess the ice fluxes at each cross-section. For this purpose, the bedrock topography was determined using seismic soundings at cross-sections 2, 4 and 7. Moreover, 8 and 24 boreholes have been drilled on cross-sections 2 and 4, respectively, to check the seismic results (Reference Rabatel, Dedieu and VincentReynaud, 1959; Reference HantzHantz, 1981). The comparison shows differences which can reach 30m locally. However, the bedrock topography is relatively well known, with an average uncertainty of ±10m (Fig. 2).

The surface ice-flow velocities are measured at the end of the ablation season (September) from stake displacements using topographic methods (theodolite surveys before 2000 and differential global positioning system (GPS) methods since 2000) and are known with an uncertainty of ±0.15ma^–1. Five to ten ablation stakes have been set on each cross-section for this purpose. In addition, painted stones have been used to complete the velocity network and to determine the ice velocities on the longitudinal flowline passing through the centre of each cross-section. For every cross-section, the values are interpolated at the middle of the flowline in order to determine for each year the annual ice-flow velocity at a fixed position. Velocity measurements on cross-section 2 are missing for 1986 and 1987. Thickness variation measurements have been carried out each year for each cross-section using geodetic methods with an uncertainty of ±0.20ma^–1.

In addition, surface annual mass balances were monitored in the ablation area between 1975 and 1993, from 20–30 ablation stakes. Since 1993, systematic winter and summer mass-balance measurements (May and September, respectively) have been performed on the entire surface of this glacier (Reference Span and KuhnVincent, 2002). About 40 sites have been selected at various elevations representative of the whole surface. Moreover, total cumulative mass balances have been calculated using an old map with elevation contours and repeated photogrammetric measurements. This map is of the Argentiére and Mer de Glace glaciers, published between 1900 and 1905 by Henri, Joseph and Charles Vallot at 1 : 20 000 scale. The accuracy of this map is unknown but it can be assumed that coordinates are accurate to within a few metres. Photogrammetric measurements have been performed by Laboratoire de Glaciologie et Géophysique de l’Environnement (LGGE) of the French Centre National de la Recherche Scientifique (Reference Span and KuhnVincent, 2002), using aerial photographs taken by IGN (French National Geographic Institute) in 1949, 1970, 1980 and 1994 and by LGGE in 1998 and 2003. Photogrammetric measurements are accurate to within several metres (vertical and horizontal accuracy) for aerial photographs taken prior to 1970 and down to 1 m for photographs taken later. According to the method used by Reference SolomonThibert and others (2008), we conclude that the uncertainties on volumetric changes of Glacier d’Argentière are of similar order. Consequently, a wealth of information is available for Glacier d’Argentière. This dataset offers a good opportunity to carry out a thorough analysis of glacier fluctuations over recent decades.

Mass-Balance Variations As The Origin of Ice-Flow Changes

Observed and reconstructed cumulative mean specific net balances are shown in Figure 3. Prior to the actual measurements, the annual mass balances were reconstructed using hypsometric and meteorological data (see Reference Span and KuhnVincent, 2002 for details). The overall trend between 1905 and 2007 is constrained by glacier volume variations deduced from map (1905) and aerial photographs (since 1949). As shown by Reference Span and KuhnVincent (2002), it would be illusive to reconstruct cumulative mass balance in the past without topographic or photogrammetric maps. For the purpose of our study, the goal is not to test model abilities to reconstruct mass balances, but to obtain realistic results. In this way, reconstructed and observed glaciological mass balances have been adjusted so that cumulative mass balances match volumetric mass balances from geodetic measurements. The glaciological mass balances have been adjusted over the 1980–2003 period, whereas the reconstructed mass balances have been adjusted over the 1905–2003 period. In the following analysis, both adjusted series have been used: reconstructed mass balance for the 1905–79 period and glaciological mass balance for the 1980–2007 period.

Fig. 3. Cumulative mean specific net balance (mw.e.) of Glacier d’Argentière from direct glaciological measurements (small triangles), from maps (large triangles) and from a reconstruction using meteorological parameters (dashed line).

Cumulative mean specific balance of Glacier d’Argentiére since 1905 is negative (loss of ∽22mw.e.) but with strong fluctuations. From Figure 3, it can be seen that Glacier d’Argentière lost mass over two main periods: 1942–53 and 1982–2007. As explained by Reference Span and KuhnVincent (2002),

the sharp mass-balance decline observed between 1942 and 1953 can be interpreted as the consequence of both increasing ablation and low accumulation. During this period, a significant part of the ablation may have been due to a low albedo value linked to low accumulation rates. Conversely, the glacier net balance rise observed between 1960 and 1981 is clearly related to low ablation values. For the more recent period (1982–2007), the decrease in net balance is connected to an ablation rise, and not to an accumulation decline. In addition, it has been shown that the increase in the summer melting rate corresponds roughly to a 24Wm^–2 rise in the energy flux at the glacier surface between the periods 1954–81 and 1982–2003 (Reference VincentVincent and others, 2004; Vincent, 2007).

Consequently, cumulative mean specific net balance reveals a strong change at the beginning of the 1980s, with a change in the mean specific net balance sign. Our study aims at investigating how Glacier d’Argentière can respond to this strong net balance change, in terms of ice-flow velocity, thickness and length changes.

Velocity and Thickness Changes Over The Last 50 Years

Figure 4 shows thickness variations and surface ice-flow velocities observed since 1950 on the cross-sections shown in Figure 1. Annual mass-balance and snout fluctuations have been plotted on the same graph. Figure 4 shows a striking difference between the upper and lower parts of the glacier. The ice-flow velocities and thicknesses show minor fluctuations in the upper part and very strong fluctuations in the lower part. Note that the vertical axis scales relative to ice-flow velocity and altitude are the same for each cross-section. For cross-section 7, at 2730ma.s.l., the thickness increased slightly by 8m between 1960 and 1985 and has since decreased by 23 m. The change in ice-flow velocity is also small: for the last period, 1985–2007, the surface ice-flow velocity has decreased by 10 ma^–1. As shown by Hintereisferner field data (Reference Schäfer and Le MeurSpan and Kuhn, 2003), the accumulation basin has the ability to restore original surface elevations after a mass-balance disturbance in a quick and direct way. Conversely, in the lower part of the glacier, at 1800ma.s.l., the thickness rose significantly by 40 m between 1960 and 1985 and has since declined sharply by 60 m. There, the ice-flow velocity has been reduced by a factor of 5, from 150 to 30ma^–1. Finally, the length of the glacier shows a very strong response with an amplitude of 600 m over the last 50 years.

Fig. 4. Thickness changes (dashed lines) and surface ice-flow velocities (solid lines) at cross-sections 7 (2730 m), 4 (2400 m) and 2 (1800 m). The observed (solid line) and reconstructed (dashed line) mean specific annual net balances of the glacier are plotted in the top part of the figure. The curve shows the 5 year running average. Snout fluctuations are shown in the bottom part of the figure (the origin of the vertical axis is arbitrary).

However, these changes are triggered by relatively small surface mass-balance changes. After reaching an average of +0.15mw.e. a^–1 during the 1954–81 period, the specific annual mass balance decreased to –0.70mw.e. a^–1 over the 1982–2007 period. As shown in previous studies, this mass-balance change is similar for other glaciers over the whole Alps and clearly connected to summer melting changes (Reference VincentVincent and others, 2004, Reference Vincent, Vallon, Reynaud and Le Meur2005; Reference Oerlemans and FortuinOhmura and others, 2007; Vincent, 2007).

The response of ice thickness to change in mass balance is instantaneous at 2730 and 2400ma.s.l. In addition, these thickness changes are similar to the cumulative mass-balance changes (see below). The general feature of the ice-flow velocity changes on these cross-sections is similar and synchronous with thickness changes. However, some irregularities in ice-flow velocities on a yearly scale are not visible on the thickness change curves. These could come from seasonal variations at the end of the ablation season, the measurements being performed each year between 15 August and 15 September. Although the velocities are presented as equivalent annual rates, the dates of measurements are not fixed and in general are not 365 days apart. The behaviour over cross-section 2, on the lower part of the glacier, is slightly different. In addition to the amplitude difference, the reaction time of the thickness change is delayed by ∽3 years. Although some measurements are missing, it seems that the same delay can be observed for the ice-velocity changes.

Finally, the global behaviour of the snout is similar to the thickness changes observed upstream. However, the response is delayed by ∽10–14 years following the mass-balance change. This delay seems to be similar following a positive change (advance in 1968 after positive mass balance from 1954) or following a negative change (retreat in 1991 after negative mass balance from 1981).

Analysis of Glacier Fluctuations

First, the ice fluxes have been calculated each year through the three cross-sections, using section areas and ice-flow velocity measurements:

where U is the depth-averaged horizontal ice-flow velocity (m a^–1) through the cross-section and S is the cross-section area (m²).

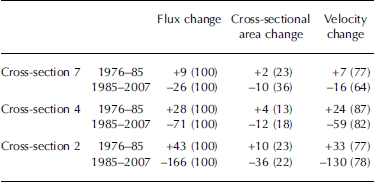
The depth-averaged horizontal ice-flow velocity through each cross-section is derived from the mean surface ice-flow velocity (Reference NyeNye, 1965). This approximation and variations in the fraction of the basal sliding lead to an uncertainty in the calculated flux of ∽10%, which lies within the range of uncertainty of the other variables, as discussed by Reference Huss, Sugiyama, Bauder and FunkHuss and others (2007). Furthermore, it should be noted that the following analysis is based on ice-flux changes and not on ice-flux values. Consequently, the influence of both basal sliding and Nye approximation uncertainties on ice-flux changes remains small. In addition, the uncertainty on the cross-section areas does not affect the calculations of ice-flux changes. The measured surface mass balance, thickness change, velocity change and ice-flux change were compared for each cross-section. Results are reported in Table 1. They reveal a straightforward relationship between annual thickness change and annual surface mass balance on cross-sections 7 and 4, with a correlation coefficient of 0.72 and 0.74, respectively. These relationships are strongly improved when data are compared over 3 year periods (with correlation coefficients >0.9). Over the tongue of the glacier, at cross-section 2, no relationship appears between surface mass balance and thickness change at the annual timescale. It is hardly improved with a 3 year timescale (with a correlation coefficient of 0.45). Conversely, Table 1 shows a striking correlation between flux change and velocity change over the whole area of the glacier. Provided that the ice fluxes have been calculated from ice-flow velocities and section areas, this reveals that the term S(∂U/∂t) is much larger than U(∂S/∂t), in which S and U are the section area and the mean velocity, respectively. In order to highlight the link between the flux change and velocity change, these parameters are compared over the whole thickening and decay periods in Table 2. For this purpose, the flux change, the cross-section area change and the velocity change have been calculated in percentage over the sub-periods 1976–85 and 1985–2007. These results show that 64–87% of flux changes can be explained by velocity changes. In cross-sections 2 and 4, the ice fluxes are much larger than that for cross-section 7, but in both cases they are strongly correlated with ice-flow velocities. In any case, this shows that the velocities are mainly responsible for the changes in ice fluxes.

Table 1. Correlation coefficients between thickness change, surface mass balance, velocity change and flux change (annual values) at the cross-sections over the period 1976–2007. The three reported values in each case correspond to cross-sections 7, 4 and 2, respectively. Velocity measurements on cross-section 2 are missing for two years (1986 and 1987)

Table 2. Variations in percent, relative to the 1976–85 and 1985–2007 periods. The flux change, the cross-section area change and the velocity change have been calculated in percentage over the sub-periods 1976–85 and 1985–2007. For instance, the variation in percent in velocity over the period 1976–85 has been calculated following (U ₁₉₈₅ –U ₁₉₇₆)/U _mean, where U ₁₉₈₅ is the measured velocity in 1985, U ₁₉₇₆ is the measured velocity in 1976 and U _mean is the average velocity between 1976 and 1985. The values in parentheses are the relative percentages of the flux changes

The flux change ranges from 7.5 to 10×10^–6m³ a^–1 at cross-section 7, from 8 to 14×10^–6m³ a^–1 at cross-section 4 and from 2 to 8×10^–6m³ a^–1 at cross-section 2 (Fig. 5a). The surface mass-balance changes upstream of each cross-section can be calculated from these ice-flux changes. Taking into account the surface area upstream of these cross-sections (5.8, 10.8 and 11.7 km², respectively), the mean surface mass-balance changes inferred from these flux changes are 0.43, 0.55 and 0.51 ma^–1 of ice, respectively. These values are similar for the three cross-sections, but are smaller than surface mass-balance changes resulting from observations mentioned in the previous section. The discrepancy could come from the response time of the ice fluxes to the change in the surface mass balance and suggests that the ice fluxes are not yet adjusted to the surface mass-balance change.

Fig. 5. Ice flux at cross-sections 7 (2730 m), 4 (2400 m) and 2 (1800 m). (b) Thickness variations at the same cross-sections. The thick line corresponds to the cumulative specific mass balance.

In Figure 5b, thickness changes are plotted together with the cumulative mass-balance changes of the glacier. The thickness changes are similar to the cumulative mass-balance changes at cross-sections 7 and 4, in the upper part of the glacier. At cross-section 2, the thickness changes are almost synchronous with those observed upstream, i.e. delayed by only 2 or 3 years, but the amplitude is far from the mass-balance change amplitude. This figure shows that thickness changes are mainly driven by surface mass-balance changes in the upper part of the glacier. For each cross-section, the thickness changes have been analyzed using the continuity equation which expresses the thickness change as a function of mass balance and ice-flux changes (Reference Ohmura, Bauder, Müller and KappenbergerPaterson, 1994, p. 256):

where b is the surface mass balance, b′ is the basal melting, ∂Q/∂x is the ice-flux change in the direction of x following a flowline and ∂Q/∂y is the ice-flux change perpendicular to the flowline direction. The basal melting b′ is negligible compared to the surface mass balance b. From this equation, it can be concluded that ∂Q/∂x and ∂Q/∂y are constant with time in the region of cross-section 7, that is, changes in extending/compressing flow in the horizontal directions of x and y are small. This conclusion is confirmed by ice-flow velocity and topographic measurements in the longitudinal and transversal directions. Indeed, the longitudinal and the transversal strain rates have been calculated using the annual ice-flow velocity measurements obtained from ablation stakes and painted stones. In the following analysis, it is assumed that the surface strain rates are representative of the whole section. At cross-section 7, the longitudinal strain rate ∂U/∂x and the transversal strain rate ∂V/∂y are close to zero and have not changed over the last three decades. The slope has not changed either; at cross-section 4, the longitudinal strain rate shows a slight extending flow of 0.01 a^–1 and a lateral strain rate of –0.015 a^–1. Both these strain rates as well as the surface slope have not changed significantly with time since the beginning of the measurements. These results show that thickness changes observed at cross-sections 7 and 4 are solely driven by surface mass-balance changes.

Cross-section 2 shows an opposite feature; Figure 5b reveals very large changes in thickness and that the influence of surface mass balance is small. The thickness changes are driven by the compressive flow changes. This conclusion is supported by ice-flow velocity measurements. In Figure 6, surface topography and surface ice-flow velocities have been plotted along the longitudinal direction in this region for two well-documented years, 1988 and 2003. These data point out significant changes over the last two decades. In 1988, in the vicinity of cross-section 2, the longitudinal strain rate varied from –0.20 to –0.04 a^–1, with an average of –0.11 a^–1 over a distance of 250m upstream of cross-section 2. This means that this longitudinal strain rate decreased by 0.03 a^–1 between 1988 and 2003, and is now 0.08 a^–1. Conversely, despite the large decrease of the thickness, the slope did not change significantly over the same period. The transverse strain rate is weak and also did not change significantly over

Fig. 6. Altitude (solid line) and surface ice-flow velocity (dashed line) observed along the flow direction of the glacier in the vicinity of cross-section 2, for the years 1988 and 2003. The origin of longitudinal distance is 155m upstream of cross-section 2.

the last 15 years. At the end of the 1980s, the negative surface mass balance in this area, close to –9.3ma^–1 of ice, was compensated by the horizontal compressive flow. In this region, the flow was very compressive in the direction of x in relation to the narrowing of the valley and the change in slope (Fig. 2). The walls prevent lateral extension, and the slowing down of the ice flow below the icefall must be compensated by extension in the vertical direction. Consequently, longitudinal compression was accompanied by vertical stretching. In 2003, this effect has decreased, as shown by the observed longitudinal strain rates.

Over the last 15 years, the influence of longitudinal strain-rate decrease on thickness change is 5 ma^–1, which is close to the observed thickness change over the last 5 years (4.4ma^–1). Although the uncertainty on longitudinal strain rate is large, its change is the only one to explain the thickness change observed over the last 15 years. The change in surface mass balance is <1ma^–1 of ice and cannot explain this strong thickness change. In addition, the glacier is covered by rock debris in this area and surface mass-balance fluctuations are weakly influenced by climate change. It results that the thickness changes at cross-section 2 are driven by longitudinal compression. In this region, changes in ice fluxes are similar to those observed at cross-section 4, but the valley shape is very different. The tongue of the glacier is confined in a narrow gorge downstream of icefall and changes in ice flux lead to large changes in ice thickness. The thickness changes on the tongue are clearly driven by the compressive flow changes and not by the surface mass-balance changes.

Conclusions

From the analysis of numerous data relative to the thickening and decay of Glacier d’Argentière over the last 50 years, it can be concluded that this glacier reacts very quickly to surface mass-balance change. The changes in ice flux are delayed by a maximum of 3 years relative to the changes in surface mass balance.

At each cross-section, the analysis of relationships between ice fluxes, thickness changes, ice-flow velocities and mass balance reveals that the ice-flux changes are driven by the ice-flow velocity changes. Our measurements show that velocity fluctuations are synchronous over the entire studied area. It seems that the glacier reacts as a whole. In the upper part of the glacier, the velocity and thickness changes easily accommodate the ice-flux changes because the section area is large. In this region, the term s(∂U/∂t) is much larger than u(∂S/∂t). The ice-flux changes can therefore be compensated by a small change in the cross-sectional areas. In addition, in the upper part of the glacier, the thickness changes are similar to cumulative mass-balance changes. The changes in compressing/extending flow are not significant in this area. We can conclude that thickness changes are mainly driven by surface mass-balance changes.

Conversely, the tongue of the glacier is located in a narrow gorge, and changes in ice flux lead to large changes in ice thickness and ice-flow velocity. As seen in the upper part of the glacier, the ice flux is accommodated by the velocity change but the ice flow is impeded by the valley walls. Consequently, the compressing flow does not remain constant with time. When the glacier is thickening, longitudinal compression increases and the rise in thickness becomes more pronounced. However, when the glacier is decreasing, the longitudinal compression also decreases. As shown from field data, the compressive strain rate has decreased over the last 15 years by 0.03 a^–1 in these areas. The thickness changes of the tongue are therefore clearly driven by the changes in compressing flow and not by those of surface mass-balance changes. This dataset will be useful to provide initial/boundary conditions and check the results of future ice-flow numerical modelling experiments.