Hostname: page-component-669899f699-qzcqf Total loading time: 0 Render date: 2025-04-24T19:34:32.213Z Has data issue: false hasContentIssue false
  • English
  • Français

A mathematical analysis of the Kakinuma model for interfacial gravity waves. Part II: justification as a shallow water approximation

Part of: Incompressible inviscid fluids Hyperbolic equations and systems Equations and systems of special type

Published online by Cambridge University Press:  18 March 2024

Vincent Duchêne  and
Tatsuo Iguchi
Vincent Duchêne
Affiliation:
Institut de Recherche Mathématique de Rennes, Univ Rennes, CNRS, IRMAR – UMR 6625, F-35000 Rennes, France (vincent.duchene@univ-rennes.fr)
Tatsuo Iguchi
Affiliation:
Department of Mathematics, Faculty of Science and Technology, Keio University, 3-14-1 Hiyoshi, Kohoku-ku, Yokohama 223-8522, Japan (iguchi@math.keio.ac.jp)
Get access Rights & Permissions [Opens in a new window]

Abstract

We consider the Kakinuma model for the motion of interfacial gravity waves. The Kakinuma model is a system of Euler–Lagrange equations for an approximate Lagrangian, which is obtained by approximating the velocity potentials in the Lagrangian of the full model. Structures of the Kakinuma model and the well-posedness of its initial value problem were analysed in the companion paper [14]. In this present paper, we show that the Kakinuma model is a higher order shallow water approximation to the full model for interfacial gravity waves with an error of order $O(\delta _1^{4N+2}+\delta _2^{4N+2})$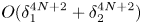 in the sense of consistency, where $\delta _1$ 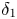and $\delta _2$ 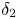are shallowness parameters, which are the ratios of the mean depths of the upper and the lower layers to the typical horizontal wavelength, respectively, and $N$ 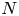is, roughly speaking, the size of the Kakinuma model and can be taken an arbitrarily large number. Moreover, under a hypothesis of the existence of the solution to the full model with a uniform bound, a rigorous justification of the Kakinuma model is proved by giving an error estimate between the solution to the Kakinuma model and that of the full model. An error estimate between the Hamiltonian of the Kakinuma model and that of the full model is also provided.

Keywords

interfacial wavesasymptotic modellingshallow water

MSC classification

Primary: 35L45: Initial value problems for first-order hyperbolic systems
Secondary: 35M31: Initial value problems for systems of mixed type 76B55: Internal waves
Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , First View , pp. 1 - 72
Check for updates
Copyright
Copyright © The Author(s), 2024. Published by Cambridge University Press on behalf of The Royal Society of Edinburgh

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Ambrose, D. M., Bona, J. L. and Nicholls, D. P.. On ill-posedness of truncated series models for water waves. Proc. R. Soc. A 470 (2014), 20130849.CrossRefGoogle Scholar
Athanassoulis, G. A. and Belibassakis, K. A.. A consistent coupled-mode theory for the propagation of small-amplitude water waves over variable bathymetry regions. J. Fluid Mech. 389 (1999), 275–301.CrossRefGoogle Scholar
Benjamin, T. B. and Bridges, T. J.. Reappraisal of the Kelvin–Helmholtz problem. Part 1. Hamiltonian structure. J. Fluid Mech. 333 (1997), 301–325.CrossRefGoogle Scholar
Boussinesq, J.. Addition au mémoire sur la théorie des ondes et des remous qui se propagent le long d'un canal rectangulaire, etc. J. Math. Pures Appl. 17 (1873), 47–52.Google Scholar
Bresch, D. and Renardy, M.. Well-posedness of two-layer shallow water flow between two horizontal rigid plates. Nonlinearity 24 (2011), 1081–1088.CrossRefGoogle Scholar
Choi, W.. On Rayleigh expansion for nonlinear long water waves. J. Hydrodyn. 31 (2019), 1115–1126.CrossRefGoogle Scholar
Choi, W.. High-order strongly nonlinear long wave approximation and solitary wave solution. J. Fluid Mech. 945 (2022), 38. Paper No. A15.CrossRefGoogle Scholar
Choi, W. and Camassa, R.. Fully nonlinear internal waves in a two-fluid system. J. Fluid Mech. 396 (1999), 1–36.CrossRefGoogle Scholar
Craig, W. and Sulem, C.. Numerical simulation of gravity waves. J. Comput. Phys. 108 (1993), 73–83.CrossRefGoogle Scholar
Dommermuth, D. G. and Yue, D. K.. A high-order spectral method for the study of nonlinear gravity waves. J. Fluid Mech. 184 (1987), 267–288.CrossRefGoogle Scholar
Duchêne, V.. Many models for water waves. Open math notes, OMN:202109.111309 (2021).Google Scholar
Duchêne, V.. Boussinesq/Boussinesq systems for internal waves with a free surface, and the KdV approximation. ESAIM Math. Model. Numer. Anal. 46 (2012), 145–185.CrossRefGoogle Scholar
Duchêne, V. and Iguchi, T.. A Hamiltonian structure of the Isobe–Kakinuma model for water waves. Water Waves 3 (2021), 193–211.CrossRefGoogle Scholar
Duchêne, V. and Iguchi, T.. A mathematical analysis of the Kakinuma model for interfacial gravity waves. Part I: Structures and well-posedness. To appear in Ann. Inst. H. Poincaré Anal. Non Linéaire.Google Scholar
Duchêne, V. and Melinand, B.. Rectification of a deep water model for surface gravity waves. To appear in Pure Appl. Anal.Google Scholar
Guyenne, P.. HOS simulations of nonlinear water waves in complex media. In Nonlinear Water Waves, Tutorials, Schools, and Workshops in the Mathematical Sciences, pp. 53–69 (Cham: Birkhäuser, 2019).CrossRefGoogle Scholar
Iguchi, T.. A shallow water approximation for water waves. J. Math. Kyoto Univ. 49 (2009), 13–55.Google Scholar
Iguchi, T.. Isobe–Kakinuma model for water waves as a higher order shallow water approximation. J. Differ. Equ. 265 (2018), 935–962.CrossRefGoogle Scholar
Iguchi, T.. A mathematical justification of the Isobe–Kakinuma model for water waves with and without bottom topography. J. Math. Fluid Mech. 20 (2018), 1985–2018.CrossRefGoogle Scholar
Iguchi, T., Tanaka, N. and Tani, A.. On the two-phase free boundary problem for two-dimensional water waves. Math. Ann. 309 (1997), 199–223.CrossRefGoogle Scholar
Isobe, M.. A proposal on a nonlinear gentle slope wave equation. In Proceedings of Coastal Engineering [Japanese], vol. 41, pp. 1–5 (Tokyo: Japan Society of Civil Engineers, 1994).Google Scholar
Isobe, M.. Time-dependent mild-slope equations for random waves. In Proceedings of 24th International Conference on Coastal Engineering, pp. 285–299 (New York, NY: ASCE, 1994).Google Scholar
Kakinuma, T.. Proceedings of Coastal Engineering [Japanese], vol. 47, pp. 1–5 (Tokyo: Japan Society of Civil Engineers, 2000).Google Scholar
Kakinuma, T.. A set of fully nonlinear equations for surface and internal gravity waves. In Coastal Engineering V: Computer Modelling of Seas and Coastal Regions, pp. 225–234 (Southampton, UK: WIT Press, 2001).Google Scholar
Kakinuma, T.. A nonlinear numerical model for surface and internal waves shoaling on a permeable beach. In Coastal engineering VI: Computer Modelling and Experimental Measurements of Seas and Coastal Regions, pp. 227–236 (Southampton, UK: WIT Press, 2003).Google Scholar
Kamotski, V. and Lebeau, G.. On 2D Rayleigh–Taylor instabilities. Asymptotic Anal. 42 (2005), 1–27.Google Scholar
Klopman, G., van Groesen, B. and Dingemans, M. W.. A variational approach to Boussinesq modelling of fully nonlinear water waves. J. Fluid Mech. 657 (2010), 36–63.CrossRefGoogle Scholar
Lannes, D.. A stability criterion for two-fluid interfaces and applications. Arch. Ration. Mech. Anal. 208 (2013), 481–567.CrossRefGoogle Scholar
Lannes, D.. The water waves problem: mathematical analysis and asymptotics. Math. Surveys Monogr., vol. 188 (Providence, RI: American Mathematical Society, 2013).Google Scholar
Lannes, D. and Ming, M.. The Kelvin–Helmholtz instabilities in two-fluids shallow water models. In Hamiltonian partial differential equations and applications. Fields Inst. Commun., vol. 75, pp. 185–234 (Toronto, ON: Fields Inst. Res. Math. Sci., 2015).CrossRefGoogle Scholar
Luke, J. C.. A variational principle for a fluid with a free surface. J. Fluid Mech. 27 (1967), 395–397.CrossRefGoogle Scholar
Matsuno, Y.. Hamiltonian formulation of the extended Green–Naghdi equations. Physica D 301/302 (2015), 1–7.CrossRefGoogle Scholar
Matsuno, Y.. Hamiltonian structure for two-dimensional extended Green–Naghdi equations. Proc. R. Soc. A 472 (2016), 20160127.CrossRefGoogle Scholar
Miyata, M.. An internal solitary wave of large amplitude. La Mer. 23 (1985), 43–48.Google Scholar
Murakami, Y. and Iguchi, T.. Solvability of the initial value problem to a model system for water waves. Kodai Math. J. 38 (2015), 470–491.CrossRefGoogle Scholar
Nemoto, R. and Iguchi, T.. Solvability of the initial value problem to the Isobe–Kakinuma model for water waves. J. Math. Fluid Mech. 20 (2018), 631–653.CrossRefGoogle Scholar
Nicholls, D. P.. High-order perturbation of surfaces short course: boundary value problems. In Lectures on the Theory of Water Waves. London Math. Soc. Lecture Note Ser., vol. 426, pp. 1–18 (Cambridge: Cambridge Univ. Press, 2016).Google Scholar
Papoutsellis, C. E. and Athanassoulis, G. A.. A new efficient Hamiltonian approach to the nonlinear water-wave problem over arbitrary bathymetry. ArXiv preprint:1704.03276.Google Scholar
Rayleigh, J. W. S.. On waves. Philos. Mag. 1 (1876), 251–271.Google Scholar
Stoker, J. J.. The formation of breakers and bores. The theory of nonlinear wave propagation in shallow water and open channels. Commun. Pure Appl. Math. 1 (1948), 1–87.CrossRefGoogle Scholar
West, B. J., Brueckner, K. A., Janda, R. S., Milder, D. M. and Milton, R. L.. A new numerical method for surface hydrodynamics. J. Geophys. Res. 92 (1987), 11803–11824.CrossRefGoogle Scholar
Wilkening, J. and Vasan, V.. Comparison of five methods of computing the Dirichlet-Neumann operator for the water wave problem. In Nonlinear Wave Equations: Analytic and Computational Techniques. Contemp. Math., vol. 635, pp. 175–210 (Providence, RI: Amer. Math. Soc., 2015).Google Scholar
Zakharov, V. E.. Stability of periodic waves of finite amplitude on the surface of a deep fluid. J. Appl. Mech. Tech. Phys. 9 (1968), 190–194.CrossRefGoogle Scholar