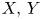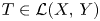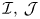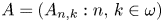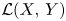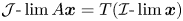1. Introduction
An infinite matrix with real entries $A=(a_{n,k})$![]() is said to be regular if it transforms convergent sequences into convergent sequences and preserves the corresponding limits (details will be given in § 2). A classical result due to Silverman–Toeplitz provides necessary and sufficient conditions, depending only on the entries of $A$
is said to be regular if it transforms convergent sequences into convergent sequences and preserves the corresponding limits (details will be given in § 2). A classical result due to Silverman–Toeplitz provides necessary and sufficient conditions, depending only on the entries of $A$![]() , which characterize the class of regular matrices, see e.g. [Reference Boos5, Theorem 2.3.7]:
, which characterize the class of regular matrices, see e.g. [Reference Boos5, Theorem 2.3.7]:
Theorem 1.1 An infinite real matrix $A=(a_{n,k})$![]() is regular if and only if:
is regular if and only if:
(i) $\sup _n \sum _k|a_{n,k}|<\infty$
 ;
;(ii) $\lim _n\sum _ka_{n,k}=1$
 ;
;(iii) $\lim _na_{n,k}=0$
 for all $k$
for all $k$ .
.
Several extensions and analogues of the characterization above can be found in the literature. First, a ‘ multidimensional” version of theorem 1.1 for double sequences has been proved by Robinson [Reference Robinson39] and Hugh J. Hamilton [Reference Hamilton19]. Second, in 1950 Abraham Robinson [Reference Robinson38] proved the operator analogue of theorem 1.1 replacing each $a_{n,k}$![]() with a (possibly unbounded) linear operator $A_{n,k}$
with a (possibly unbounded) linear operator $A_{n,k}$![]() acting on a given Banach space, cf. theorem 2.2. Third, in a different direction, the author and Connor [Reference Connor and Leonetti11] recently studied the ideal/filter version of the notion of regularity in the scalar case and proved that the analogue of theorem 1.1 holds in several, but not all, cases.
acting on a given Banach space, cf. theorem 2.2. Third, in a different direction, the author and Connor [Reference Connor and Leonetti11] recently studied the ideal/filter version of the notion of regularity in the scalar case and proved that the analogue of theorem 1.1 holds in several, but not all, cases.
The aim of this work is to provide a unifying framework which allows to shed light on the relationship between all the above results, to extend the latter ones, and to obtain, as a byproduct of the employed methods, several related characterizations. This will require us to deal with the theory of infinite matrices of linear operators and to prove a certain number of intermediate lemmas. Most results are formulated in the context of ideal convergence. We remark that this choice is not done for the sake of generality: indeed, for the above purposes, we exploit the simple facts that $c(\mathcal {I}) \cap \ell _\infty$![]() is $c$
is $c$![]() if $\mathcal {I}=\mathrm {Fin}$
if $\mathcal {I}=\mathrm {Fin}$![]() and equals to $\ell _\infty$
and equals to $\ell _\infty$![]() if $\mathcal {I}$
if $\mathcal {I}$![]() is maximal, that the Pringsheim convergence of double sequences coincides with $\mathcal {I}$
is maximal, that the Pringsheim convergence of double sequences coincides with $\mathcal {I}$![]() -convergence for a suitable ideal $\mathcal {I}$
-convergence for a suitable ideal $\mathcal {I}$![]() , etc. An additional motivation comes from the fact that the study of ideals on countable sets and their representability may have some relevant potential for the study of the geometry of Banach spaces, see e.g. [Reference Borodulin-Nadzieja and Farkas6, Reference Borodulin-Nadzieja, Farkas and Plebanek7, Reference Kadets, Leonov and Orhan23, Reference Kwela and Leonetti25, Reference Leonetti and Caprio29].
, etc. An additional motivation comes from the fact that the study of ideals on countable sets and their representability may have some relevant potential for the study of the geometry of Banach spaces, see e.g. [Reference Borodulin-Nadzieja and Farkas6, Reference Borodulin-Nadzieja, Farkas and Plebanek7, Reference Kadets, Leonov and Orhan23, Reference Kwela and Leonetti25, Reference Leonetti and Caprio29].
Informally, we provide an operator version of the characterization of regular matrices in the context of ideal convergence, together with some sufficient conditions which allow for several substantial simplifications. The results depend on the boundedness assumption on the sequence spaces in the domain and/or codomain of such matrices. In addition, we provide a characterization of the matrix classes $(\ell _\infty,\, c_0(\mathcal {J})\cap \ell _\infty )$![]() , $(c(\mathcal {I}),\, c_0(\mathcal {J})\cap \ell _\infty )$
, $(c(\mathcal {I}),\, c_0(\mathcal {J})\cap \ell _\infty )$![]() $(\ell _\infty,\, \ell _\infty (\mathcal {J}))$
$(\ell _\infty,\, \ell _\infty (\mathcal {J}))$![]() , and $(c,\,\ell _\infty (\mathcal {J}))$
, and $(c,\,\ell _\infty (\mathcal {J}))$![]() for certain ideals $\mathcal {I},\,\mathcal {J}$
for certain ideals $\mathcal {I},\,\mathcal {J}$![]() on $\omega$
on $\omega$![]() , see corollary 2.12, theorems 2.18, 3.8, and 3.10, respectively. Lastly, we obtain an ideal version of the Hahn–Schur theorem (which is used to prove that weak and norm convergence coincide on $\ell _1$
, see corollary 2.12, theorems 2.18, 3.8, and 3.10, respectively. Lastly, we obtain an ideal version of the Hahn–Schur theorem (which is used to prove that weak and norm convergence coincide on $\ell _1$![]() ), see theorem 4.6.
), see theorem 4.6.
The proofs of the main results are given in § 5.
2. Notations and main results
Let $\mathcal {I}$![]() be an ideal on the nonnegative integers $\omega$
be an ideal on the nonnegative integers $\omega$![]() , that is, a collection of subsets of $\omega$
, that is, a collection of subsets of $\omega$![]() which is closed under subsets and finite unions. Unless otherwise stated, it is assumed that it contains the collection $\mathrm {Fin}$
which is closed under subsets and finite unions. Unless otherwise stated, it is assumed that it contains the collection $\mathrm {Fin}$![]() of finite sets and it is different from the power set. Denote its dual filter by $\mathcal {I}^\star :=\{S\subseteq \omega : S^c \in \mathcal {I}\}$
of finite sets and it is different from the power set. Denote its dual filter by $\mathcal {I}^\star :=\{S\subseteq \omega : S^c \in \mathcal {I}\}$![]() and define $\mathcal {I}^+:=\{S\subseteq \omega : S\notin \mathcal {I}\}$
and define $\mathcal {I}^+:=\{S\subseteq \omega : S\notin \mathcal {I}\}$![]() . Among the most important ideals, we find the family of asymptotic density zero sets:
. Among the most important ideals, we find the family of asymptotic density zero sets:
We refer to [Reference Hrušák21] for a recent survey on ideals and associated filters.
Let $V$![]() be a real Banach space, and denote its closed unit ball by $B_V$
be a real Banach space, and denote its closed unit ball by $B_V$![]() and its unit sphere by $S_V$
and its unit sphere by $S_V$![]() . Given a sequence $\boldsymbol {x}=(x_n)$
. Given a sequence $\boldsymbol {x}=(x_n)$![]() taking values in $V$
taking values in $V$![]() and an ideal $\mathcal {I}$
and an ideal $\mathcal {I}$![]() on $\omega$
on $\omega$![]() , we say that $\boldsymbol {x}$
, we say that $\boldsymbol {x}$![]() is $\mathcal {I}$
is $\mathcal {I}$![]() -convergent to $\eta \in V$
-convergent to $\eta \in V$![]() , shortened as $\mathcal {I}\text {-}\lim \boldsymbol {x}=\eta$
, shortened as $\mathcal {I}\text {-}\lim \boldsymbol {x}=\eta$![]() or $\mathcal {I}\text {-}\lim _n x_n=\eta$
or $\mathcal {I}\text {-}\lim _n x_n=\eta$![]() , if $\{n \in \omega : x_n \notin U\} \in \mathcal {I}$
, if $\{n \in \omega : x_n \notin U\} \in \mathcal {I}$![]() for all neighbourhood $U$
for all neighbourhood $U$![]() of $\eta$
of $\eta$![]() ; for the clarify of exposition, all sequences taking values in $V$
; for the clarify of exposition, all sequences taking values in $V$![]() will be written in bold. Note that $\mathcal {Z}$
will be written in bold. Note that $\mathcal {Z}$![]() -convergence is usually called statistical convergence, see e.g. [Reference Fridy17]. As remarked in [Reference Drewnowski14, Example 3.4], the notion of $\mathcal {I}$
-convergence is usually called statistical convergence, see e.g. [Reference Fridy17]. As remarked in [Reference Drewnowski14, Example 3.4], the notion of $\mathcal {I}$![]() -convergence include the well-known uniform, Pringsheim, and Hardy convergences for double sequences. In addition, if $\boldsymbol {y}$
-convergence include the well-known uniform, Pringsheim, and Hardy convergences for double sequences. In addition, if $\boldsymbol {y}$![]() is a real nonnegative sequence, we write $\mathcal {I}\text {-}\limsup \boldsymbol {y}:=\inf \{r \in \mathbf {R}\cup \{\infty \}: \{n \in \omega : y_n\ge r\}\in \mathcal {I}\}$
is a real nonnegative sequence, we write $\mathcal {I}\text {-}\limsup \boldsymbol {y}:=\inf \{r \in \mathbf {R}\cup \{\infty \}: \{n \in \omega : y_n\ge r\}\in \mathcal {I}\}$![]() .
.
Now, define the following sequence spaces:

where $\|\boldsymbol {x}\|:=\sup _n\|x_n\|$![]() stands for the supremum norm and $\mathrm {supp}\,\boldsymbol {x}$
stands for the supremum norm and $\mathrm {supp}\,\boldsymbol {x}$![]() for the support $\{n \in \omega : x_n\neq 0\}$
for the support $\{n \in \omega : x_n\neq 0\}$![]() . Clearly, $\ell _\infty (V)=\ell _\infty (V,\, \mathrm {Fin})$
. Clearly, $\ell _\infty (V)=\ell _\infty (V,\, \mathrm {Fin})$![]() ; sequences in $\ell _\infty (V,\,\mathcal {I})$
; sequences in $\ell _\infty (V,\,\mathcal {I})$![]() are usually called $\mathcal {I}$
are usually called $\mathcal {I}$![]() -bounded. If $V=\mathbf {R}$
-bounded. If $V=\mathbf {R}$![]() and $\mathcal {I}=\mathrm {Fin}$
and $\mathcal {I}=\mathrm {Fin}$![]() , the above sequence spaces correspond to the usual $\ell _\infty$
, the above sequence spaces correspond to the usual $\ell _\infty$![]() , $c$
, $c$![]() , $c_0$
, $c_0$![]() , and $c_{00}$
, and $c_{00}$![]() , respectively. Every subspace of $\ell _\infty (V)$
, respectively. Every subspace of $\ell _\infty (V)$![]() will be endowed with the supremum norm. It is clear that $c_{00}(V,\,\mathcal {I})\subseteq c_{0}(V,\,\mathcal {I})\subseteq c(V,\,\mathcal {I})\subseteq \ell _\infty (V,\,\mathcal {I})$
will be endowed with the supremum norm. It is clear that $c_{00}(V,\,\mathcal {I})\subseteq c_{0}(V,\,\mathcal {I})\subseteq c(V,\,\mathcal {I})\subseteq \ell _\infty (V,\,\mathcal {I})$![]() . However, unless $\mathcal {I}=\mathrm {Fin}$
. However, unless $\mathcal {I}=\mathrm {Fin}$![]() or $V=\{0\}$
or $V=\{0\}$![]() , $c_{00}(V,\,\mathcal {I})$
, $c_{00}(V,\,\mathcal {I})$![]() is not contained in $\ell _\infty (V)$
is not contained in $\ell _\infty (V)$![]() . Hence it makes sense to define the subspace:
. Hence it makes sense to define the subspace:
and, similarly, $c_{0}^b(V,\,\mathcal {I})$![]() and $c_{00}^b(V,\,\mathcal {I})$
and $c_{00}^b(V,\,\mathcal {I})$![]() . The symbol $V$
. The symbol $V$![]() will be removed from the notation if it is understood from the context so that, e.g., $c_{00}(\mathcal {I})=c_{00}(V,\, \mathcal {I})$
will be removed from the notation if it is understood from the context so that, e.g., $c_{00}(\mathcal {I})=c_{00}(V,\, \mathcal {I})$![]() . Similarly, we may remove $\mathcal {I}$
. Similarly, we may remove $\mathcal {I}$![]() in the case $\mathcal {I}=\mathrm {Fin}$
in the case $\mathcal {I}=\mathrm {Fin}$![]() .
.
At this point, let $X,\,Y$![]() be two Banach space and denote by $\mathcal {L}(X,\,Y)$
be two Banach space and denote by $\mathcal {L}(X,\,Y)$![]() and $\mathcal {B}(X,\,Y)$
and $\mathcal {B}(X,\,Y)$![]() the vector spaces of linear operators from $X$
the vector spaces of linear operators from $X$![]() to $Y$
to $Y$![]() and its subspace of bounded linear operators, respectively. We assume that $\mathcal {L}(X,\,Y)$
and its subspace of bounded linear operators, respectively. We assume that $\mathcal {L}(X,\,Y)$![]() and all its subspaces are endowed with the strong operator topology so that a sequence $(T_n)$
and all its subspaces are endowed with the strong operator topology so that a sequence $(T_n)$![]() of linear operators in $\mathcal {L}(X,\,Y)$
of linear operators in $\mathcal {L}(X,\,Y)$![]() converges to $T \in \mathcal {L}(X,\,Y)$
converges to $T \in \mathcal {L}(X,\,Y)$![]() if and only if $(T_nx)$
if and only if $(T_nx)$![]() is convergent in the norm of $Y$
is convergent in the norm of $Y$![]() to $Tx$
to $Tx$![]() for all $x \in X$
for all $x \in X$![]() .
.
Let $A=(A_{n,k}: n,\,k \in \omega )$![]() be an infinite matrix of linear operators $A_{n,k}\in \mathcal {L}(X,\,Y)$
be an infinite matrix of linear operators $A_{n,k}\in \mathcal {L}(X,\,Y)$![]() . Moreover, for each $n \in \omega$
. Moreover, for each $n \in \omega$![]() and $E\subseteq \omega$
and $E\subseteq \omega$![]() , let us write
, let us write
and $A_{n,\ge k}:=A_{n,\{k,k+1,\ldots \}}$![]() for the $k$
for the $k$![]() th tail of the $n$
th tail of the $n$![]() th row of $A$
th row of $A$![]() . In particular, $A_{n,\omega }$
. In particular, $A_{n,\omega }$![]() is the $n$
is the $n$![]() th row of $A$
th row of $A$![]() (and use an analogue notation for a sequence $(T_k)$
(and use an analogue notation for a sequence $(T_k)$![]() of operators so that, for instance, $T_{\ge 2}=(T_2,\,T_3,\,\ldots )$
of operators so that, for instance, $T_{\ge 2}=(T_2,\,T_3,\,\ldots )$![]() ). For each $n \in \omega$
). For each $n \in \omega$![]() and $E\subseteq \omega$
and $E\subseteq \omega$![]() , define the the group norm:
, define the the group norm:
cf. [Reference Maddox33, Reference Maddox34] (in fact, every $x_k$![]() can be chosen on the unit sphere $S_X$
can be chosen on the unit sphere $S_X$![]() : this depends on the fact that, given distinct $a,\,b \in X$
: this depends on the fact that, given distinct $a,\,b \in X$![]() , the function $f: [0,\,1] \to \mathbf {R}$
, the function $f: [0,\,1] \to \mathbf {R}$![]() defined by $f(t):=\|a+t(b-a)\|$
defined by $f(t):=\|a+t(b-a)\|$![]() has a point of maximum in $t=0$
has a point of maximum in $t=0$![]() or in $t=1$
or in $t=1$![]() : indeed, the segment $\{a+t(b-a): t \in [0,\,1]\}$
: indeed, the segment $\{a+t(b-a): t \in [0,\,1]\}$![]() is contained in the closed ball with centre $0$
is contained in the closed ball with centre $0$![]() and radius $\max \{\|a\|,\,\|b\|\}$
and radius $\max \{\|a\|,\,\|b\|\}$![]() , which is convex). Note that the value $\|A_{n,E}\|$
, which is convex). Note that the value $\|A_{n,E}\|$![]() is possibly not finite. In addition, if $X=\mathbf {R}$
is possibly not finite. In addition, if $X=\mathbf {R}$![]() and $A_{n,E}$
and $A_{n,E}$![]() is represented by the real sequence $(a_{n,k}: k \in E)$
is represented by the real sequence $(a_{n,k}: k \in E)$![]() then $\|A_{n,E}\|=\sum _{k \in E}|a_{n,k}|$
then $\|A_{n,E}\|=\sum _{k \in E}|a_{n,k}|$![]() .
.
Given an $X$![]() -valued sequence $\boldsymbol {x}=(x_n)$
-valued sequence $\boldsymbol {x}=(x_n)$![]() , let $A\boldsymbol {x}$
, let $A\boldsymbol {x}$![]() be its $A$
be its $A$![]() -transform, that is, the sequence $A\boldsymbol {x}:=(A_n\boldsymbol {x}: n \in \omega )$
-transform, that is, the sequence $A\boldsymbol {x}:=(A_n\boldsymbol {x}: n \in \omega )$![]() where
where
provided that each series is convergent in the norm of $Y$![]() . Accordingly, let $\mathrm {dom}(A)$
. Accordingly, let $\mathrm {dom}(A)$![]() be the domain of $A$
be the domain of $A$![]() , that is, the family of those sequences $\boldsymbol {x}$
, that is, the family of those sequences $\boldsymbol {x}$![]() such that $A\boldsymbol {x}$
such that $A\boldsymbol {x}$![]() is well defined. For each sequence subspace $\mathscr {A}\subseteq X^\omega$
is well defined. For each sequence subspace $\mathscr {A}\subseteq X^\omega$![]() and $\mathscr {B}\subseteq Y^\omega$
and $\mathscr {B}\subseteq Y^\omega$![]() , let $(\mathscr {A},\, \mathscr {B})$
, let $(\mathscr {A},\, \mathscr {B})$![]() be the set of matrices $A=(A_{n,k})$
be the set of matrices $A=(A_{n,k})$![]() of (not necessarily bounded) linear operators in $\mathcal {L}(X,\,Y)$
of (not necessarily bounded) linear operators in $\mathcal {L}(X,\,Y)$![]() such that
such that
We refer to [Reference Maddox34] for the theory of infinite matrices of operators. In the scalar case, the relationship between summability and ideal convergence has been recently studied in [Reference Filipów and Tryba16].
2.1 Bounded to bounded case
The main definition of this work follows:
Definition 2.1 Let $\mathcal {I},\, \mathcal {J}$![]() be ideals on $\omega$
be ideals on $\omega$![]() and fix $T \in \mathcal {L}(X,\,Y)$
and fix $T \in \mathcal {L}(X,\,Y)$![]() . Then a matrix $A=(A_{n,k})$
. Then a matrix $A=(A_{n,k})$![]() of linear operators in $\mathcal {L}(X,\,Y)$
of linear operators in $\mathcal {L}(X,\,Y)$![]() is said to be $(\mathcal {I},\, \mathcal {J})$
is said to be $(\mathcal {I},\, \mathcal {J})$![]() -regular with respect to $T$
-regular with respect to $T$![]() if
if
If $T$![]() is the identity operator $I$
is the identity operator $I$![]() on $X$
on $X$![]() (namely, $Ix=x$
(namely, $Ix=x$![]() for all $x \in X$
for all $x \in X$![]() ), we simply say that $A$
), we simply say that $A$![]() is $(\mathcal {I},\,\mathcal {J})$
is $(\mathcal {I},\,\mathcal {J})$![]() -regular. Note that if $\mathcal {I}=\mathcal {J}=\mathrm {Fin}$
-regular. Note that if $\mathcal {I}=\mathcal {J}=\mathrm {Fin}$![]() , $X=Y=\mathbf {R}$
, $X=Y=\mathbf {R}$![]() , and $T=I$
, and $T=I$![]() , then definition 2.1 corresponds to the ordinary regular matrices.
, then definition 2.1 corresponds to the ordinary regular matrices.
The following result, essentially due to Robinson [Reference Robinson38, Theorem VII], is the (unbounded) operator version of theorem 1.1, cf. also [Reference Maddox32, Theorem 1].
Theorem 2.2 Fix a linear operator $T \in \mathcal {B}(X,\,Y)$![]() , where $X,\,Y$
, where $X,\,Y$![]() are Banach spaces. Then a matrix $A=(A_{n,k})$
are Banach spaces. Then a matrix $A=(A_{n,k})$![]() of linear operators in $\mathcal {L}(X,\,Y)$
of linear operators in $\mathcal {L}(X,\,Y)$![]() is $(\mathrm {Fin},\, \mathrm {Fin})$
is $(\mathrm {Fin},\, \mathrm {Fin})$![]() -regular with respect to $T$
-regular with respect to $T$![]() if and only if there exists $k_0 \in \omega$
if and only if there exists $k_0 \in \omega$![]() such that:
such that:
(S1) $\sup _n\|A_{n,\ge k_0}\|<\infty$
 ;
;(S2) $\lim _n \sum _{k}A_{n,k}=T$
 ;
;(S3) $\lim _n A_{n,k}=0$
 for all $k \in \omega$
for all $k \in \omega$ .
.
A variant for continuous linear operators between Fréchet spaces has been proved by Ramanujan in [Reference Ramanujan37], cf. also [Reference Li, Kang and Swartz30, Corollary 6].
Notice that (S3) can be rewritten as $\lim _n \sum _{k \in E}A_{n,k}x_k=0$![]() for all sequences $\boldsymbol {x} \in \ell _\infty (X)$
for all sequences $\boldsymbol {x} \in \ell _\infty (X)$![]() and $E \in \mathrm {Fin}$
and $E \in \mathrm {Fin}$![]() , which is also equivalent to $A \in (c_{00}(X),\, c_0(Y))$
, which is also equivalent to $A \in (c_{00}(X),\, c_0(Y))$![]() .
.
Remark 2.3 Condition (S3) may look equivalent also to:
(S4) $\lim _n \|A_{n,k}\|=0$
 for all $k \in \omega$
for all $k \in \omega$ .
.
This is correct if $X$![]() is finite dimensional, cf. lemma 3.4 below. However, (S4) is strictly stronger in general. For, set $X=\ell _2=\{x \in \ell _\infty : \sum _tx_t^2<\infty \}$
is finite dimensional, cf. lemma 3.4 below. However, (S4) is strictly stronger in general. For, set $X=\ell _2=\{x \in \ell _\infty : \sum _tx_t^2<\infty \}$![]() , and define $A_{n,0}x=(0,\,\ldots,\,0,\,x_{n+1},\,x_{n+2},\,\ldots )$
, and define $A_{n,0}x=(0,\,\ldots,\,0,\,x_{n+1},\,x_{n+2},\,\ldots )$![]() for all $n \in \omega$
for all $n \in \omega$![]() and $x \in \ell _2$
and $x \in \ell _2$![]() , and $A_{n,k}=0$
, and $A_{n,k}=0$![]() whenever $k>0$
whenever $k>0$![]() . Then $\|A_{n,0}\|=1$
. Then $\|A_{n,0}\|=1$![]() for all $n\in \omega$
for all $n\in \omega$![]() , and $\lim _n A_{n,0}x=0$
, and $\lim _n A_{n,0}x=0$![]() for all $x \in \ell _2$
for all $x \in \ell _2$![]() .
.
Remark 2.4 Another difference from the finite-dimensional case is that a $(\mathrm {Fin},\, \mathrm {Fin})$![]() -regular matrix does not necessarily belong to $(\ell _\infty (X),\,\ell _\infty (Y))$
-regular matrix does not necessarily belong to $(\ell _\infty (X),\,\ell _\infty (Y))$![]() . For, suppose that $X=Y=\ell _2$
. For, suppose that $X=Y=\ell _2$![]() , and let $e_k$
, and let $e_k$![]() be the $k$
be the $k$![]() th unit vector of $X$
th unit vector of $X$![]() for each $k \in \omega$
for each $k \in \omega$![]() . Building on the above example, consider the matrix $A=(A_{n,k})$
. Building on the above example, consider the matrix $A=(A_{n,k})$![]() of linear operators in $\mathcal {L}(\ell _2,\,\ell _2)$
of linear operators in $\mathcal {L}(\ell _2,\,\ell _2)$![]() such that $A=\mathrm {Id}+B$
such that $A=\mathrm {Id}+B$![]() , where $\mathrm {Id}$
, where $\mathrm {Id}$![]() is the identity matrix and
is the identity matrix and

Then $A$![]() satisfies conditions (S1)–(S3) with $T=I$
satisfies conditions (S1)–(S3) with $T=I$![]() and $k_0=0$
and $k_0=0$![]() , hence by theorem 1.1 $A$
, hence by theorem 1.1 $A$![]() is a $(\mathrm {Fin},\, \mathrm {Fin})$
is a $(\mathrm {Fin},\, \mathrm {Fin})$![]() -regular matrix. However, the sequence $\boldsymbol {x}:=(e_0,\,e_1,\,\ldots ) \in \ell _\infty (\ell _2)$
-regular matrix. However, the sequence $\boldsymbol {x}:=(e_0,\,e_1,\,\ldots ) \in \ell _\infty (\ell _2)$![]() does not belong to $\mathrm {dom}(A)$
does not belong to $\mathrm {dom}(A)$![]() , indeed $A_0\boldsymbol {x}=e_0-e_1-e_2-\cdots$
, indeed $A_0\boldsymbol {x}=e_0-e_1-e_2-\cdots$![]() is not norm convergent in $\ell _2$
is not norm convergent in $\ell _2$![]() . Therefore $A\notin (\ell _\infty (X),\,\ell _\infty (Y))$
. Therefore $A\notin (\ell _\infty (X),\,\ell _\infty (Y))$![]() , cf. theorem 3.8 below.
, cf. theorem 3.8 below.
Our first main result, which corresponds to the operator version of [Reference Connor and Leonetti11, Theorem 1.2], follows.
Theorem 2.5 Fix a linear operator $T \in \mathcal {L}(X,\,Y)$![]() , where $X,\,Y$
, where $X,\,Y$![]() are Banach spaces. Let also $\mathcal {I},\, \mathcal {J}$
are Banach spaces. Let also $\mathcal {I},\, \mathcal {J}$![]() be ideals on $\omega$
be ideals on $\omega$![]() . Then a matrix $A=(A_{n,k})$
. Then a matrix $A=(A_{n,k})$![]() of linear operators in $\mathcal {L}(X,\,Y)$
of linear operators in $\mathcal {L}(X,\,Y)$![]() is $(\mathcal {I},\, \mathcal {J})$
is $(\mathcal {I},\, \mathcal {J})$![]() -regular with respect to $T$
-regular with respect to $T$![]() if and only if there exists $k_0 \in \omega$
if and only if there exists $k_0 \in \omega$![]() such that:
such that:
(T1) $\sup _n\|A_{n,\ge k_0}\|<\infty$
 ;
;(T2) $\sup _n\|A_{n,k}x\|<\infty$
 for all $x \in X$
for all $x \in X$ and $k< k_0$
and $k< k_0$ ;
;(T3) $\sum _kA_{n,k}x_k$
 converges in the norm of $Y$
converges in the norm of $Y$ for all $\boldsymbol {x} \in c^b(X,\,\mathcal {I})$
for all $\boldsymbol {x} \in c^b(X,\,\mathcal {I})$ and $n \in \omega$
and $n \in \omega$ ;
;(T4) $\mathcal {J}\text {-}\lim _n \sum _{k}A_{n,k}=T$
 ;
;(T5) $A \in (c_{00}^b(X,\,\mathcal {I}),\, c_0(Y,\,\mathcal {J}))$
 .
.
In addition, if each $A_{n,k}$![]() is bounded, it is possible to choose $k_0=0$
is bounded, it is possible to choose $k_0=0$![]() .
.
For the sake of clarity, condition (T4) means that $A_n(x,\,x,\,\ldots )$![]() is norm convergent for all $n \in \omega$
is norm convergent for all $n \in \omega$![]() and $x \in X$
and $x \in X$![]() (which is weaker than (T3)) and, in addition, $\mathcal {J}\text {-}\lim _n A_n(x,\,x,\,\ldots )=Tx$
(which is weaker than (T3)) and, in addition, $\mathcal {J}\text {-}\lim _n A_n(x,\,x,\,\ldots )=Tx$![]() for all $x \in X$
for all $x \in X$![]() . Lastly, condition (T5) can be rephrased as: $A_n\boldsymbol {x}$
. Lastly, condition (T5) can be rephrased as: $A_n\boldsymbol {x}$![]() is norm convergent for all $n \in \omega$
is norm convergent for all $n \in \omega$![]() and all bounded sequences $\boldsymbol {x}$
and all bounded sequences $\boldsymbol {x}$![]() supported on $\mathcal {I}$
supported on $\mathcal {I}$![]() and, for such sequences, $\mathcal {J}\text {-}\lim A\boldsymbol {x}=0$
and, for such sequences, $\mathcal {J}\text {-}\lim A\boldsymbol {x}=0$![]() .
.
Remark 2.6 Note that (T5) could be replaced also with the stronger condition:
(T5′) $A \in (c_{00}^b(X,\,\mathcal {I}),\, c_0^b(Y,\,\mathcal {J}))$
 .
.
Indeed by definition 2.1 the transformed sequence $A\boldsymbol {x}$![]() is necessarily bounded for all $\boldsymbol {x} \in c^b(X,\,\mathcal {I})$
is necessarily bounded for all $\boldsymbol {x} \in c^b(X,\,\mathcal {I})$![]() . Also, the latter condition (T5$^\prime$
. Also, the latter condition (T5$^\prime$![]() ) would imply automatically (T2). Therefore, $A$
) would imply automatically (T2). Therefore, $A$![]() is $(\mathcal {I},\,\mathcal {J})$
is $(\mathcal {I},\,\mathcal {J})$![]() -regular with respect to $T$
-regular with respect to $T$![]() if and only if (T1), (T3), (T4), and (T5$^\prime$
if and only if (T1), (T3), (T4), and (T5$^\prime$![]() ) hold.
) hold.
However, we chose to state it in the former version for two reasons. First, if each $A_{n,k}$![]() is bounded, then (T2) is void so that our characterization holds with the weaker condition (T5). Second, most importantly, condition (T5) will be used also in the unbounded analogue given in theorem 2.14 below: this allows to highlight the differences between the two cases.
is bounded, then (T2) is void so that our characterization holds with the weaker condition (T5). Second, most importantly, condition (T5) will be used also in the unbounded analogue given in theorem 2.14 below: this allows to highlight the differences between the two cases.
Even if theorem 2.5 may look quite complicated, the reader should keep in mind that it deals with (possibly unbounded) linear operators and general ideal/filter convergence. We are going to see that, in some special circumstances, it may be considerably simplified because either some of conditions (T1)–(T5) are automatically satisfied or the latter ones collapse to simpler properties (in particular, recovering the classical ones). Several related results may be found in the literature in the case $X=Y$![]() equal to $\mathbf {R}$
equal to $\mathbf {R}$![]() or $\mathbf {C}$
or $\mathbf {C}$![]() , $T$
, $T$![]() equals to the identity operator $I$
equals to the identity operator $I$![]() or the zero operator, and $\mathcal {I},\,\mathcal {J}$
or the zero operator, and $\mathcal {I},\,\mathcal {J}$![]() being certain $F_{\sigma \delta }$
being certain $F_{\sigma \delta }$![]() -ideals (where ideals are regarded as subsets of the Cantor space $\{0,\,1\}^\omega$
-ideals (where ideals are regarded as subsets of the Cantor space $\{0,\,1\}^\omega$![]() ), see e.g. [Reference Connor and Gumus10, Reference Demirci, Khan and Orhan13, Reference Drewnowski14, Reference Kolk24, Reference Tripathy43].
), see e.g. [Reference Connor and Gumus10, Reference Demirci, Khan and Orhan13, Reference Drewnowski14, Reference Kolk24, Reference Tripathy43].
We remark also that, if $T$![]() is not bounded, then an $(\mathcal {I},\,\mathcal {J})$
is not bounded, then an $(\mathcal {I},\,\mathcal {J})$![]() -regular matrix $A$
-regular matrix $A$![]() with respect to $T$
with respect to $T$![]() may not exist: indeed, if each $A_{n,k}$
may not exist: indeed, if each $A_{n,k}$![]() is bounded and $\mathcal {J}=\mathrm {Fin}$
is bounded and $\mathcal {J}=\mathrm {Fin}$![]() , condition (T4) and the Banach–Steinhaus theorem imply that $T$
, condition (T4) and the Banach–Steinhaus theorem imply that $T$![]() is necessarily bounded.
is necessarily bounded.
In the case that $T=0$![]() , we obtain the following immediate consequence, cf. also corollary 2.12 below for the finite-dimensional case with $\mathcal {I}$
, we obtain the following immediate consequence, cf. also corollary 2.12 below for the finite-dimensional case with $\mathcal {I}$![]() maximal.
maximal.
Corollary 2.7 Let $X,\,Y$![]() be Banach spaces, and let also $\mathcal {I},\, \mathcal {J}$
be Banach spaces, and let also $\mathcal {I},\, \mathcal {J}$![]() be ideals on $\omega$
be ideals on $\omega$![]() . Then a matrix $A=(A_{n,k})$
. Then a matrix $A=(A_{n,k})$![]() of linear operators in $\mathcal {L}(X,\,Y)$
of linear operators in $\mathcal {L}(X,\,Y)$![]() belongs to $(c^b(X,\,\mathcal {I}),\, c^b_0(Y,\,\mathcal {J}))$
belongs to $(c^b(X,\,\mathcal {I}),\, c^b_0(Y,\,\mathcal {J}))$![]() if and only if there exists $k_0 \in \omega$
if and only if there exists $k_0 \in \omega$![]() such that (T1)–(T5) hold, with $T=0$
such that (T1)–(T5) hold, with $T=0$![]() .
.
In addition, if each $A_{n,k}$![]() is bounded, it is possible to choose $k_0=0$
is bounded, it is possible to choose $k_0=0$![]() .
.
It will be useful to define also the following properties:
(T3♮) $\lim _k \|A_{n,\ge k}\|=0$
 for all $n\in \omega$
for all $n\in \omega$ ;
;(T6♭) $\mathcal {J}\text {-}\lim _n \|A_{n,k}\|=0$
 for all $k\in \omega$
for all $k\in \omega$ .
.
It is clear that (S4) corresponds to (T6$^\flat$![]() ) in the case $\mathcal {J}=\mathrm {Fin}$
) in the case $\mathcal {J}=\mathrm {Fin}$![]() . Some implications between the above-mentioned conditions are collected below.
. Some implications between the above-mentioned conditions are collected below.
Proposition 2.8 With the same hypothesis of theorem 2.5, the following hold:
(i) If $\mathcal {I}=\mathrm {Fin}$
 then (T1) and (T4) imply (T3);
then (T1) and (T4) imply (T3);(ii) If $\mathcal {J}=\mathrm {Fin}$
 then (T5) implies (T2);
then (T5) implies (T2);(iii) (T1) and (T3$^{\natural }$
 ) imply (T3);
) imply (T3);(iv) If each $A_{n,k}$
 is bounded, it is possible to choose $k_0=0$
is bounded, it is possible to choose $k_0=0$ , hence (T2) holds;
, hence (T2) holds;(v) If $\mathrm {dim}(X)<\infty$
 each $A_{n,k}$
each $A_{n,k}$ is bounded. Moreover, (T1) implies (T3$^{\natural }$
is bounded. Moreover, (T1) implies (T3$^{\natural }$ );
);(vi) If $\mathrm {dim}(X)<\infty$
 and $A$
and $A$ is $(\mathcal {I},\, \mathcal {J})$
is $(\mathcal {I},\, \mathcal {J})$ -regular with respect to $T$
-regular with respect to $T$ , then (T6$^\flat$
, then (T6$^\flat$ ) holds;
) holds;(vii) If each $A_{n,k}$
 is a multiple of $A_0 \in \mathcal {L}(X,\,Y)$
is a multiple of $A_0 \in \mathcal {L}(X,\,Y)$ , then (T1) implies (T3$^{\natural }$
, then (T1) implies (T3$^{\natural }$ ) and $A_0\in \mathcal {B}(X,\,Y)$
) and $A_0\in \mathcal {B}(X,\,Y)$ ;
;(viii) If each $A_{n,k}$
 is a multiple of $A_0 \in \mathcal {L}(X,\,Y)$
is a multiple of $A_0 \in \mathcal {L}(X,\,Y)$ , then (T1) and (T5) imply (T6$^\flat$
, then (T1) and (T5) imply (T6$^\flat$ ).
).
It is immediate to check that theorem 2.2 comes as a corollary, putting together theorem 2.5 and proposition 2.8(i) and (ii).
However, the usefulness of a characterization of $(\mathcal {I},\, \mathcal {J})$![]() -regular matrices with respect to $T$
-regular matrices with respect to $T$![]() comes from the practical easiness to check whether conditions (T1)–(T5) hold together. Taking into account the implications given in proposition 2.8, it is evident that (T5) is the most demanding in this direction. Hence it makes sense to search for sufficient conditions which allow us to simplify it. In the same spirit of [Reference Connor and Leonetti11, Theorem 1.3], which studies the case $X=Y=\mathbf {R}$
comes from the practical easiness to check whether conditions (T1)–(T5) hold together. Taking into account the implications given in proposition 2.8, it is evident that (T5) is the most demanding in this direction. Hence it makes sense to search for sufficient conditions which allow us to simplify it. In the same spirit of [Reference Connor and Leonetti11, Theorem 1.3], which studies the case $X=Y=\mathbf {R}$![]() and $T=I$
and $T=I$![]() , we obtain characterizations of such matrices which avoid condition (T5). We need the new and much “easier” condition:
, we obtain characterizations of such matrices which avoid condition (T5). We need the new and much “easier” condition:
(T6) $\mathcal {J}\text {-}\lim _n \|A_{n,E}\|=0$
 for all $E \in \mathcal {I}$
for all $E \in \mathcal {I}$ .
.
Directly by the definition of group norm, it is clear that (T6) implies (T5) (and also (T6$^\flat$![]() )). This means that we are allowed to replace (T5) with the stronger condition (T6) provided that the latter is satisfied for matrices $A$
)). This means that we are allowed to replace (T5) with the stronger condition (T6) provided that the latter is satisfied for matrices $A$![]() which are $(\mathcal {I},\, \mathcal {J})$
which are $(\mathcal {I},\, \mathcal {J})$![]() -regular with respect to $T$
-regular with respect to $T$![]() , possibly under some additional constraints.
, possibly under some additional constraints.
Theorem 2.9 With the same hypotheses of theorem 2.5, suppose, in addition, that $\mathcal {J}$![]() is countably generated and that conditions (T3$^{\natural }$
is countably generated and that conditions (T3$^{\natural }$![]() ) and (T6$^\flat$
) and (T6$^\flat$![]() ) hold.
) hold.
Then $A$![]() is $(\mathcal {I},\, \mathcal {J})$
is $(\mathcal {I},\, \mathcal {J})$![]() -regular with respect to $T$
-regular with respect to $T$![]() if and only if there exists $k_0 \in \omega$
if and only if there exists $k_0 \in \omega$![]() such that (T1), (T4), and (T6) hold. In addition, if each $A_{n,k}$
such that (T1), (T4), and (T6) hold. In addition, if each $A_{n,k}$![]() is bounded, it is possible to choose $k_0=0$
is bounded, it is possible to choose $k_0=0$![]() .
.
On a similar direction, recall that, if $X,\,Y$![]() are vector lattices, then a linear operator $T \in \mathcal {L}(X,\,Y)$
are vector lattices, then a linear operator $T \in \mathcal {L}(X,\,Y)$![]() is said to be positive if $Tx\ge 0$
is said to be positive if $Tx\ge 0$![]() whenever $x\ge 0$
whenever $x\ge 0$![]() . In addition, a Banach space $V$
. In addition, a Banach space $V$![]() is called an AM-space if $V$
is called an AM-space if $V$![]() is also a vector lattice such that $0\le x\le y$
is also a vector lattice such that $0\le x\le y$![]() implies $\|x\| \le \|y\|$
implies $\|x\| \le \|y\|$![]() , and $\|x \vee y\|=\max \{\|x\|,\,\|y\|\}$
, and $\|x \vee y\|=\max \{\|x\|,\,\|y\|\}$![]() for all $x,\,y \ge 0$
for all $x,\,y \ge 0$![]() ; we say that $e \in V$
; we say that $e \in V$![]() is an order unit if, for all $x \in V$
is an order unit if, for all $x \in V$![]() there exists $n \in \omega$
there exists $n \in \omega$![]() such that $-ne \le x\le ne$
such that $-ne \le x\le ne$![]() . Accordingly, if $V\neq \{0\}$
. Accordingly, if $V\neq \{0\}$![]() , then necessarily $e>0$
, then necessarily $e>0$![]() . Examples of AM-spaces with order units include $\ell _\infty$
. Examples of AM-spaces with order units include $\ell _\infty$![]() and $C(K)$
and $C(K)$![]() spaces, for some compact Hausdorff space $K$
spaces, for some compact Hausdorff space $K$![]() . We refer to [Reference Aliprantis and Burkinshaw2, Reference Aliprantis and Burkinshaw3] for the underlying theory on vector lattices.
. We refer to [Reference Aliprantis and Burkinshaw2, Reference Aliprantis and Burkinshaw3] for the underlying theory on vector lattices.
Theorem 2.10 With the same hypotheses of theorem 2.5, suppose, in addition, that $X$![]() is an AM-space with order unit $e$
is an AM-space with order unit $e$![]() , $Y$
, $Y$![]() is a Banach lattice, each $A_{n,k}$
is a Banach lattice, each $A_{n,k}$![]() is a positive linear operator, and that condition (T3$^{\natural }$
is a positive linear operator, and that condition (T3$^{\natural }$![]() ) holds.
) holds.
Then $A$![]() is $(\mathcal {I},\, \mathcal {J})$
is $(\mathcal {I},\, \mathcal {J})$![]() -regular with respect to $T$
-regular with respect to $T$![]() if and only if (T1), (T4), and (T6) hold with $k_0=0$
if and only if (T1), (T4), and (T6) hold with $k_0=0$![]() .
.
In the finite-dimensional case, everything is simpler. Indeed, suppose that $X=\mathbf {R}^d$![]() and $Y=\mathbf {R}^m$
and $Y=\mathbf {R}^m$![]() , for some integers $d,\,m\ge 1$
, for some integers $d,\,m\ge 1$![]() . Then each linear operator $A_{n,k}$
. Then each linear operator $A_{n,k}$![]() is represented by the real matrix $[\,a_{n,k}(i,\,j): 1\le i\le m,\, 1\le j\le d\,]$
is represented by the real matrix $[\,a_{n,k}(i,\,j): 1\le i\le m,\, 1\le j\le d\,]$![]() and $T$
and $T$![]() is represented by the real matrix $[\,t(i,\,j): 1\le i\le m,\, 1\le j\le d\,]$
is represented by the real matrix $[\,t(i,\,j): 1\le i\le m,\, 1\le j\le d\,]$![]() .
.
Corollary 2.11 With the same hypotheses of theorem 2.5, suppose that $X=\mathbf {R}^d$![]() , $Y=\mathbf {R}^m$
, $Y=\mathbf {R}^m$![]() , and that $\mathcal {I}=\mathrm {Fin}$
, and that $\mathcal {I}=\mathrm {Fin}$![]() or $\mathcal {J}$
or $\mathcal {J}$![]() is countably generated or $a_{n,k}(i,\,j)\ge 0$
is countably generated or $a_{n,k}(i,\,j)\ge 0$![]() for all $1\le i \le m$
for all $1\le i \le m$![]() , $1\le j\le d$
, $1\le j\le d$![]() , and $n,\,k \in \omega$
, and $n,\,k \in \omega$![]() . Then $A$
. Then $A$![]() is $(\mathcal {I},\, \mathcal {J})$
is $(\mathcal {I},\, \mathcal {J})$![]() -regular with respect to $T$
-regular with respect to $T$![]() if and only if:
if and only if:
(F1) $\sup _n \sum _k\sum _{i,j}\left |a_{n,k}(i,\,j)\right |<\infty$
 ;
;(F2) $\mathcal {J}\text {-}\lim _n \sum _k a_{n,k}(i,\,j)=t(i,\,j)$
 for all $1\le i \le m$
for all $1\le i \le m$ and $1\le j\le d$
and $1\le j\le d$ ;
;(F3) $\mathcal {J}\text {-}\lim _n \sum _{k\in E}\sum _{i,j}\left |a_{n,k}(i,\,j)\right |=0$
 for all $E \in \mathcal {I}$
for all $E \in \mathcal {I}$ .
.
It is remarkable that the “easier” characterization with condition (F3) does not hold uniformly for all ideals $\mathcal {I},\, \mathcal {J}$![]() : indeed, it has been proved in [Reference Connor and Leonetti11, Theorem 1.4] that, even in the simplest case $X=Y=\mathbf {R}$
: indeed, it has been proved in [Reference Connor and Leonetti11, Theorem 1.4] that, even in the simplest case $X=Y=\mathbf {R}$![]() and $T=I$
and $T=I$![]() , there exists a $(\mathcal {Z},\, \mathcal {Z})$
, there exists a $(\mathcal {Z},\, \mathcal {Z})$![]() -regular matrix which does not satisfy (F3), where $\mathcal {Z}$
-regular matrix which does not satisfy (F3), where $\mathcal {Z}$![]() is the asymptotic density zero ideal defined in (2.1). In addition, condition (F3) can be simplified if $T$
is the asymptotic density zero ideal defined in (2.1). In addition, condition (F3) can be simplified if $T$![]() is the zero operator and $\mathcal {I}$
is the zero operator and $\mathcal {I}$![]() a maximal ideal:
a maximal ideal:
Corollary 2.12 With the same hypotheses of corollary 2.11, $A \in (\ell _\infty (\mathbf {R}^d),\, c_0^b (\mathbf {R}^m,\, \mathcal {J}))$![]() if and only if condition (F1) holds, together with:
if and only if condition (F1) holds, together with:
(F3′) $\mathcal {J}\text {-}\lim _n \sum _{k}\sum _{i,j}\left |a_{n,k}(i,\,j)\right |=0$
 .
.
This provides a generalization of [Reference Çakan and Altay8, Lemma 3.2] in the case $d=m=1$![]() , $T=0$
, $T=0$![]() , and $\mathcal {J}$
, and $\mathcal {J}$![]() equal to the countably generated ideal $\mathcal {I}_{\mathrm {P}}$
equal to the countably generated ideal $\mathcal {I}_{\mathrm {P}}$![]() defined below in (2.3).
defined below in (2.3).
A similar result can be obtained if each $A_{n,k}$![]() is a multiple of a given linear operator:
is a multiple of a given linear operator:
Corollary 2.13 With the same hypotheses of theorem 2.5, suppose that each $A_{n,k}$![]() is a multiple of a nonzero $A_0 \in \mathcal {L}(X,\,Y)$
is a multiple of a nonzero $A_0 \in \mathcal {L}(X,\,Y)$![]() , so that $A_{n,k}=a_{n,k}A_0$
, so that $A_{n,k}=a_{n,k}A_0$![]() for all $n,\,k \in \omega$
for all $n,\,k \in \omega$![]() . In addition, assume that $\mathcal {I}=\mathrm {Fin}$
. In addition, assume that $\mathcal {I}=\mathrm {Fin}$![]() , or $\mathcal {J}$
, or $\mathcal {J}$![]() is countably generated, or that $X$
is countably generated, or that $X$![]() is an AM-space with order unit $e$
is an AM-space with order unit $e$![]() , $Y$
, $Y$![]() is a Banach lattice, and $a_{n,k}\ge 0$
is a Banach lattice, and $a_{n,k}\ge 0$![]() for all $n,\,k \in \omega$
for all $n,\,k \in \omega$![]() .
.
Then $A$![]() is $(\mathcal {I},\, \mathcal {J})$
is $(\mathcal {I},\, \mathcal {J})$![]() -regular with respect to $T$
-regular with respect to $T$![]() if and only if:
if and only if:
(M1) $A_0 \in \mathcal {B}(X,\,Y)$
 ;
;(M2) $\sup _n \sum _k\left |a_{n,k}\right |<\infty$
 ;
;(M3) $T=\kappa A_0$
 , with $\kappa =\mathcal {J}\text {-}\lim _n \sum _k a_{n,k}$
, with $\kappa =\mathcal {J}\text {-}\lim _n \sum _k a_{n,k}$ ;
;(M4) $\mathcal {J}\text {-}\lim _n \sum _{k\in E}\left |a_{n,k}\right |=0$
 for all $E \in \mathcal {I}$
for all $E \in \mathcal {I}$ .
.
In particular, under the hypotheses of corollary 2.13, if $A$![]() is $(\mathcal {I},\,\mathcal {J})$
is $(\mathcal {I},\,\mathcal {J})$![]() -regular with respect to a linear operator $T$
-regular with respect to a linear operator $T$![]() , then $T$
, then $T$![]() is necessarily bounded.
is necessarily bounded.
In the following sections, we obtain the analogues of theorem 2.5 where we replace the bounded sequence spaces $c^b(X,\,\mathcal {I})$![]() and $c^b(Y,\,\mathcal {J})$
and $c^b(Y,\,\mathcal {J})$![]() of definition 2.1 with their unbounded versions $c(X,\,\mathcal {I})$
of definition 2.1 with their unbounded versions $c(X,\,\mathcal {I})$![]() and $c(Y,\,\mathcal {J})$
and $c(Y,\,\mathcal {J})$![]() .
.
2.2 Bounded to unbounded case
An ideal $\mathcal {J}$![]() on $\omega$
on $\omega$![]() is said to be a rapid $^+$
is said to be a rapid $^+$![]() -ideal if, for every $S \in \mathcal {J}^+$
-ideal if, for every $S \in \mathcal {J}^+$![]() and $F \in \mathrm {Fin}^+$
and $F \in \mathrm {Fin}^+$![]() , there exists $S^\prime \subseteq S$
, there exists $S^\prime \subseteq S$![]() such that $S^\prime \in \mathcal {J}^+$
such that $S^\prime \in \mathcal {J}^+$![]() and $|S^\prime \cap [0,\,n]|\le |F \cap [0,\,n]|$
and $|S^\prime \cap [0,\,n]|\le |F \cap [0,\,n]|$![]() for all $n\in \omega$
for all $n\in \omega$![]() . Moreover, $\mathcal {J}$
. Moreover, $\mathcal {J}$![]() is called a $P^+$
is called a $P^+$![]() -ideal if, for every decreasing sequence $(S_n)$
-ideal if, for every decreasing sequence $(S_n)$![]() in $\mathcal {J}^+$
in $\mathcal {J}^+$![]() , there exists $S \in \mathcal {J}^+$
, there exists $S \in \mathcal {J}^+$![]() such that $S\setminus S_n$
such that $S\setminus S_n$![]() is finite for all $n \in \omega$
is finite for all $n \in \omega$![]() . The class of rapid$^+$
. The class of rapid$^+$![]() and $P^+$
and $P^+$![]() -ideals have been studied also, e.g. in [Reference De Bondt and Vernaeve12, Reference García-Ferreira and Pino-Villela18, Reference Hrušák21, Reference Matet and Pawlikowski35]. The ideal $\mathcal {J}$
-ideals have been studied also, e.g. in [Reference De Bondt and Vernaeve12, Reference García-Ferreira and Pino-Villela18, Reference Hrušák21, Reference Matet and Pawlikowski35]. The ideal $\mathcal {J}$![]() is said to be countably generated if there exist a sequence $(Q_j)$
is said to be countably generated if there exist a sequence $(Q_j)$![]() of subsets of $\omega$
of subsets of $\omega$![]() such that $S \in \mathcal {J}$
such that $S \in \mathcal {J}$![]() if and only if $S\subseteq \bigcup _{j \in F}Q_j$
if and only if $S\subseteq \bigcup _{j \in F}Q_j$![]() for some $F \in \mathrm {Fin}$
for some $F \in \mathrm {Fin}$![]() .
.
Moreover, an ideal $\mathcal {J}$![]() on $\omega$
on $\omega$![]() is said to be selective if, for every decreasing sequence $(S_n)$
is said to be selective if, for every decreasing sequence $(S_n)$![]() in $\mathcal {J}^+$
in $\mathcal {J}^+$![]() , there exists $S \in \mathcal {J}^+$
, there exists $S \in \mathcal {J}^+$![]() such that $S\setminus [0,\,n] \subseteq S_n$
such that $S\setminus [0,\,n] \subseteq S_n$![]() for all $n \in \omega$
for all $n \in \omega$![]() , see e.g. [Reference Todorcevic42, Definition 7.3]. (They were introduced by Mathias in [Reference Mathias36] under the name of happy families.) It is easy to see, directly from the definitions, that every selective ideal is a rapid$^+$
, see e.g. [Reference Todorcevic42, Definition 7.3]. (They were introduced by Mathias in [Reference Mathias36] under the name of happy families.) It is easy to see, directly from the definitions, that every selective ideal is a rapid$^+$![]() $P^+$
$P^+$![]() -ideal. More precisely, it is known that an ideal $\mathcal {J}$
-ideal. More precisely, it is known that an ideal $\mathcal {J}$![]() on $\omega$
on $\omega$![]() is selective if and only if $\mathcal {J}$
is selective if and only if $\mathcal {J}$![]() is a $P^+$
is a $P^+$![]() -ideal and, in addition, for every sequence $(F_n)$
-ideal and, in addition, for every sequence $(F_n)$![]() of finite subsets of $\omega$
of finite subsets of $\omega$![]() with $F:=\bigcup _n F_n \in \mathcal {J}^+$
with $F:=\bigcup _n F_n \in \mathcal {J}^+$![]() , there exists $S \subseteq F$
, there exists $S \subseteq F$![]() such that $S \in \mathcal {J}^+$
such that $S \in \mathcal {J}^+$![]() and $|S \cap F_n|\le 1$
and $|S \cap F_n|\le 1$![]() for all $n \in \omega$
for all $n \in \omega$![]() , see e.g. [Reference Todorcevic42, Lemma 7.4]. We refer to [Reference Kwela and Zakrzewski26, Section 1] for a list of known examples of selective ideals. It is a folklore fact that every $F_\sigma$
, see e.g. [Reference Todorcevic42, Lemma 7.4]. We refer to [Reference Kwela and Zakrzewski26, Section 1] for a list of known examples of selective ideals. It is a folklore fact that every $F_\sigma$![]() -ideal is a $P^+$
-ideal is a $P^+$![]() -ideal, see e.g. [Reference Just and Krawczyk22]. However, the summable ideal $\mathcal {I}_{1/n}:=\{S\subseteq \omega : \sum _{n \in S}1/(n+1)<\infty \}$
-ideal, see e.g. [Reference Just and Krawczyk22]. However, the summable ideal $\mathcal {I}_{1/n}:=\{S\subseteq \omega : \sum _{n \in S}1/(n+1)<\infty \}$![]() is an $F_\sigma$
is an $F_\sigma$![]() -ideal which is not rapid$^+$
-ideal which is not rapid$^+$![]() , and $\mathcal {Z}$
, and $\mathcal {Z}$![]() is neither a rapid$^+$
is neither a rapid$^+$![]() nor $P^+$
nor $P^+$![]() -ideal (hence, they are not selective). This does not mean that the topological complexity of selective ideals is low: indeed, under Martin's axiom for countable posets, there exist uncountably many nonisomorphic maximal selective ideals (on the other hand, their existence is not provable in ZFC), see [Reference De Bondt and Vernaeve12, Section 5.1].
-ideal (hence, they are not selective). This does not mean that the topological complexity of selective ideals is low: indeed, under Martin's axiom for countable posets, there exist uncountably many nonisomorphic maximal selective ideals (on the other hand, their existence is not provable in ZFC), see [Reference De Bondt and Vernaeve12, Section 5.1].
For the next results, we need a slightly stronger version of selectivity: an ideal $\mathcal {J}$![]() on $\omega$
on $\omega$![]() is called strongly selective if, for every decreasing sequence $(S_n)$
is called strongly selective if, for every decreasing sequence $(S_n)$![]() in $\mathcal {J}^+$
in $\mathcal {J}^+$![]() , there exists $S=\{x_n: n \in \omega \} \in \mathcal {J}^+$
, there exists $S=\{x_n: n \in \omega \} \in \mathcal {J}^+$![]() such that $x_{n+1} \in S_{x_n}$
such that $x_{n+1} \in S_{x_n}$![]() for all $n \in \omega$
for all $n \in \omega$![]() . (Here, we are using $(x_n: n \in \omega )$
. (Here, we are using $(x_n: n \in \omega )$![]() for the canonical enumeration of $S$
for the canonical enumeration of $S$![]() . We are not aware whether this naming has been used somewhere else.) Of course, every strongly selective ideal is also selective. Note that every countably generated ideal is strongly selective (hence also rapid$^+$
. We are not aware whether this naming has been used somewhere else.) Of course, every strongly selective ideal is also selective. Note that every countably generated ideal is strongly selective (hence also rapid$^+$![]() and $P^+$
and $P^+$![]() ); in particular, $\mathrm {Fin}$
); in particular, $\mathrm {Fin}$![]() is a strongly selective ideal, cf. remark 2.16 below. More generally, it is easy to see that, if $\mathcal {J}$
is a strongly selective ideal, cf. remark 2.16 below. More generally, it is easy to see that, if $\mathcal {J}$![]() is an ideal on $\omega$
is an ideal on $\omega$![]() with the Baire property, then $\mathcal {J}$
with the Baire property, then $\mathcal {J}$![]() is selective if and only if it is strongly selective. Moreover, as pointed out by the referee, maximal strongly selective ideals coincide with maximal selective ideals, thanks to known characterizations of the latter ones (in particular, by the observations above, their existence can be shown under Martin's axiom).
is selective if and only if it is strongly selective. Moreover, as pointed out by the referee, maximal strongly selective ideals coincide with maximal selective ideals, thanks to known characterizations of the latter ones (in particular, by the observations above, their existence can be shown under Martin's axiom).
Lastly, we need the following weakening of condition (T1) (and they coincide if $\mathcal {J}=\mathrm {Fin}$![]() ):
):
(T1♭) There exists $J_0 \in \mathcal {J}^\star$
 for which $\sup _{n \in J_0}\|A_{n,\ge k_0}\|<\infty$
for which $\sup _{n \in J_0}\|A_{n,\ge k_0}\|<\infty$ and, for all $n \in \omega \setminus J_0$
and, for all $n \in \omega \setminus J_0$ , there exists $f(n) \in \omega$
, there exists $f(n) \in \omega$ such that $\|A_{n,\ge f(n)}\|<\infty$
such that $\|A_{n,\ge f(n)}\|<\infty$ .
.
This condition has been suggested by the example given in [Reference Connor and Leonetti11, Section 4].
With these premises, we state the analogue of theorem 2.5 for the unbounded codomain sequence spaces.
Theorem 2.14 Fix a linear operator $T \in \mathcal {L}(X,\,Y)$![]() , where $X,\,Y$
, where $X,\,Y$![]() are Banach spaces. Let also $\mathcal {I},\,\mathcal {J}$
are Banach spaces. Let also $\mathcal {I},\,\mathcal {J}$![]() be an ideal on $\omega$
be an ideal on $\omega$![]() such that $\mathcal {J}$
such that $\mathcal {J}$![]() is a strongly selective ideal.
is a strongly selective ideal.
Then a matrix $A=(A_{n,k})$![]() of linear operators in $\mathcal {L}(X,\,Y)$
of linear operators in $\mathcal {L}(X,\,Y)$![]() satisfies
satisfies
if and only if there exists $k_0 \in \omega$![]() such that (T1$^\flat$
such that (T1$^\flat$![]() ), (T3), (T4), and (T5) hold.
), (T3), (T4), and (T5) hold.
In addition, if each $A_{n,k}$![]() is bounded, it is possible to choose $k_0=f(n)=0$
is bounded, it is possible to choose $k_0=f(n)=0$![]() for all $n\in \omega \setminus J_0$
for all $n\in \omega \setminus J_0$![]() .
.
During the proof, need an ideal version of the Banach–Steinhaus theorem which has been recently proved in [Reference De Bondt and Vernaeve12], see theorem 3.5 below. Interestingly, the latter result provides a characterization of rapid$^+$![]() $P^+$
$P^+$![]() -ideals [Reference De Bondt and Vernaeve12, Theorem 5.1], which suggests that theorem 2.14 cannot be improved with the current techniques.
-ideals [Reference De Bondt and Vernaeve12, Theorem 5.1], which suggests that theorem 2.14 cannot be improved with the current techniques.
We remark that theorem 2.14 sheds light on the substantial difference between the classical Silverman–Toeplitz characterization stated in theorem 1.1 and its ‘ multidimensional” analogue proved by Robinson [Reference Robinson39] and Hamilton [Reference Hamilton19] for double sequences, namely, the weakening of (T1) to (T1$^\flat$![]() ). For, recall that a double sequence $(x_{m,n}: m,\,n \in \omega )$
). For, recall that a double sequence $(x_{m,n}: m,\,n \in \omega )$![]() has Pringsheim limit $\eta \in X$
has Pringsheim limit $\eta \in X$![]() , shortened as $\mathrm {P}\text {-}\lim _{m,n}x_{m,n}=\eta$
, shortened as $\mathrm {P}\text {-}\lim _{m,n}x_{m,n}=\eta$![]() , if for all $\varepsilon >0$
, if for all $\varepsilon >0$![]() there exists $k \in \omega$
there exists $k \in \omega$![]() such that $\|x_{m,n}-\eta \|<\varepsilon$
such that $\|x_{m,n}-\eta \|<\varepsilon$![]() for all $m,\,n \ge k$
for all $m,\,n \ge k$![]() . At this point, define the ideal:
. At this point, define the ideal:
where $\nu _2$![]() is the $2$
is the $2$![]() -adic valution defined by $\nu _2(0):=0$
-adic valution defined by $\nu _2(0):=0$![]() and $\nu _2(n):=\max \{k \in \omega : 2^k \text { divides }n\}$
and $\nu _2(n):=\max \{k \in \omega : 2^k \text { divides }n\}$![]() if $n>0$
if $n>0$![]() . Note that the ideal $\mathcal {I}_{\mathrm {P}}$
. Note that the ideal $\mathcal {I}_{\mathrm {P}}$![]() is countably generated by the sequence of sets $(Q_t: t \in \omega )$
is countably generated by the sequence of sets $(Q_t: t \in \omega )$![]() , where $Q_t:=\left \{S\subseteq \omega : \sup \nolimits _{n \in S}\nu _2(n)=t\right \}$
, where $Q_t:=\left \{S\subseteq \omega : \sup \nolimits _{n \in S}\nu _2(n)=t\right \}$![]() for all $t \in \omega$
for all $t \in \omega$![]() . Hence, $\mathcal {I}_{\mathrm {P}}$
. Hence, $\mathcal {I}_{\mathrm {P}}$![]() is a strongly selective ideal. Let also $h: \omega ^2\to \omega$
is a strongly selective ideal. Let also $h: \omega ^2\to \omega$![]() be an arbitrary bijection with the property that $h[\{(m,\,n) \in \omega ^2: \min \{m,\,n\}=k\}]=Q_k$
be an arbitrary bijection with the property that $h[\{(m,\,n) \in \omega ^2: \min \{m,\,n\}=k\}]=Q_k$![]() for all $k \in \omega$
for all $k \in \omega$![]() . Thus, we obtain
. Thus, we obtain
as it has been observed in [Reference Leonetti28, Section 4.2], cf. also [Reference Drewnowski14]. In other words, $\mathcal {I}_{\mathrm {P}}$![]() is an isomorphic copy on $\omega$
is an isomorphic copy on $\omega$![]() of the ideal on $\omega ^2$
of the ideal on $\omega ^2$![]() generated by vertical lines and horizontal lines, cf. remark 2.16 below. Relying on equivalence (2.4), the classical definition of RH-regular matrix $A$
generated by vertical lines and horizontal lines, cf. remark 2.16 below. Relying on equivalence (2.4), the classical definition of RH-regular matrix $A$![]() coincides with (2.2) in the case $X=Y=\mathbf {R}$
coincides with (2.2) in the case $X=Y=\mathbf {R}$![]() , $T=I$
, $T=I$![]() , and $\mathcal {I}=\mathcal {J}=\mathcal {I}_{\mathrm {P}}$
, and $\mathcal {I}=\mathcal {J}=\mathcal {I}_{\mathrm {P}}$![]() . With the same notations of corollary 2.11, we can state the following consequence in the finite-dimensional case.
. With the same notations of corollary 2.11, we can state the following consequence in the finite-dimensional case.
Corollary 2.15 Suppose that $X=\mathbf {R}^d$![]() , $Y=\mathbf {R}^m$
, $Y=\mathbf {R}^m$![]() , and let $\mathcal {I}$
, and let $\mathcal {I}$![]() , $\mathcal {J}$
, $\mathcal {J}$![]() be ideals on $\omega$
be ideals on $\omega$![]() such that $\mathcal {J}$
such that $\mathcal {J}$![]() is countably generated by a sequence of sets $(Q_t: t \in \omega )$
is countably generated by a sequence of sets $(Q_t: t \in \omega )$![]() .
.
Then a matrix $A$![]() satisfies (2.2) if and only if there exists $t_0 \in \omega$
satisfies (2.2) if and only if there exists $t_0 \in \omega$![]() such that:
such that:
(R1) $\sup _{n \in \omega \setminus Q_{t_0}} \sum _k\sum _{i,j}\left |a_{n,k}(i,\,j)\right |<\infty$
 ;
;(R2) $\sum _k\left |a_{n,k}(i,\,j)\right |<\infty$
 for all $n \in Q_{t_0}$
for all $n \in Q_{t_0}$ , $1\le i\le m$
, $1\le i\le m$ , and $1\le j\le d$
, and $1\le j\le d$ ;
;(R3) $\mathcal {J}\text {-}\lim _n \sum _k a_{n,k}(i,\,j)=t(i,\,j)$
 for all $1\le i \le m$
for all $1\le i \le m$ and $1\le j\le d$
and $1\le j\le d$ ;
;(R4) $\mathcal {J}\text {-}\lim _n \sum _{k\in E}\sum _{i,j}\left |a_{n,k}(i,\,j)\right |=0$
 for all $E \in \mathcal {I}$
for all $E \in \mathcal {I}$ .
.
It is clear that, if also $\mathcal {I}$![]() is countably generated by a sequence $(E_t: t \in \omega )$
is countably generated by a sequence $(E_t: t \in \omega )$![]() , which is the case of RH-regular matrices, then (R4) can be rewritten as:
, which is the case of RH-regular matrices, then (R4) can be rewritten as:
(R4′ ) $\mathcal {J}\text {-}\lim _n \sum _{k\in E_t}\sum _{i,j}\left |a_{n,k}(i,\,j)\right |=0$
 for all $t \in \omega$
for all $t \in \omega$ .
.
Another special instance of corollary 2.15 has been proved in [Reference Connor9, Theorem 5] for the case where $X=Y=\mathbf {R}$![]() , $T=I$
, $T=I$![]() , $A$
, $A$![]() is a RH-regular matrix with nonnegative real entries, $\mathcal {I}$
is a RH-regular matrix with nonnegative real entries, $\mathcal {I}$![]() is a $P$
is a $P$![]() -ideal (i.e. if $(S_n)$
-ideal (i.e. if $(S_n)$![]() is an increasing sequence in $\mathcal {I}$
is an increasing sequence in $\mathcal {I}$![]() , there exists $S \in \mathcal {I}$
, there exists $S \in \mathcal {I}$![]() such that $S_n\setminus S \in \mathrm {Fin}$
such that $S_n\setminus S \in \mathrm {Fin}$![]() for all $n$
for all $n$![]() ), and $\mathcal {J}=\mathrm {Fin}$
), and $\mathcal {J}=\mathrm {Fin}$![]() .
.
Other consequences of theorem 2.14, in the same vein of the ones given in § 2.1, may be obtained here, and they are left to the reader.
Remark 2.16 An ideal $\mathcal {I}$![]() on $\omega$
on $\omega$![]() is countably generated if and only if it is isomorphic to one of the following:
is countably generated if and only if it is isomorphic to one of the following:
(i) $\mathrm {Fin}$
 ;
;(ii) $\mathrm {Fin}\times \emptyset :=\{S\subseteq \omega ^2: \exists n \in \omega,\, S\subseteq [0,\,n]\times \omega \}$
 ;
;(iii) $\mathrm {Fin}\oplus \mathcal {P}(\omega ):=\{S\subseteq \{0,\,1\}\times \omega : |S\cap (\{0\}\times \omega )|<\infty \}$
 .
.
(Recall that two ideals $\mathcal {I}_1$![]() and $\mathcal {I}_2$
and $\mathcal {I}_2$![]() on countable sets $H_1$
on countable sets $H_1$![]() and $H_2$
and $H_2$![]() , respectively, are called isomorphic, written as $\mathcal {I}_1 \simeq \mathcal {I}_2$
, respectively, are called isomorphic, written as $\mathcal {I}_1 \simeq \mathcal {I}_2$![]() if there exists a bijection $h: H_1\to H_2$
if there exists a bijection $h: H_1\to H_2$![]() such that $h[S] \in \mathcal {I}_2$
such that $h[S] \in \mathcal {I}_2$![]() if and only if $S \in \mathcal {I}_1$
if and only if $S \in \mathcal {I}_1$![]() for all $S\subseteq H_1$
for all $S\subseteq H_1$![]() ; accordingly, it is easy to see that $\mathcal {I}_{\mathrm {P}} \simeq \mathrm {Fin}\times \emptyset$
; accordingly, it is easy to see that $\mathcal {I}_{\mathrm {P}} \simeq \mathrm {Fin}\times \emptyset$![]() , and that the ideals in (i)–(iii) are pairwise nonisomorphic.) This has been essentially proved in [Reference Farah15, Proposition 1.2.8], however the correct statement appears in [Reference Balcerzak, Głab and Swaczyna4, Section 2].
, and that the ideals in (i)–(iii) are pairwise nonisomorphic.) This has been essentially proved in [Reference Farah15, Proposition 1.2.8], however the correct statement appears in [Reference Balcerzak, Głab and Swaczyna4, Section 2].
We include its simple proof for the sake of completeness. Suppose that $\mathcal {I}$![]() is countably generated by a partition $\{Q_j: j \in \omega \}$
is countably generated by a partition $\{Q_j: j \in \omega \}$![]() of $\omega$
of $\omega$![]() , and define $J:=\{j \in \omega : Q_j \in \mathrm {Fin}\}$
, and define $J:=\{j \in \omega : Q_j \in \mathrm {Fin}\}$![]() . If $J$
. If $J$![]() is empty then every $Q_j$
is empty then every $Q_j$![]() is infinite, hence $\mathcal {I}\simeq \mathrm {Fin}\times \emptyset$
is infinite, hence $\mathcal {I}\simeq \mathrm {Fin}\times \emptyset$![]() . If $J$
. If $J$![]() is nonempty finite then $Q_j$
is nonempty finite then $Q_j$![]() is infinite for infinitely many $j\in \omega$
is infinite for infinitely many $j\in \omega$![]() , hence $\mathcal {I}\simeq \mathcal {J}$
, hence $\mathcal {I}\simeq \mathcal {J}$![]() , where
, where
However, $\mathcal {J}\simeq \mathrm {Fin}\times \emptyset$![]() , with the witnessing bijection $h: \omega \cup \omega ^2\to \omega ^2$
, with the witnessing bijection $h: \omega \cup \omega ^2\to \omega ^2$![]() defined by $h(a,\,b)=(a,\,b+1)$
defined by $h(a,\,b)=(a,\,b+1)$![]() and $h(a)=(a,\,0)$
and $h(a)=(a,\,0)$![]() for all $a,\,b \in \omega$
for all $a,\,b \in \omega$![]() . Hence, let us assume hereafter that $J$
. Hence, let us assume hereafter that $J$![]() is infinite. If $J^c$
is infinite. If $J^c$![]() is empty then $\mathcal {I}\simeq \mathrm {Fin}$
is empty then $\mathcal {I}\simeq \mathrm {Fin}$![]() . If $J^c$
. If $J^c$![]() is nonempty finite then $\mathcal {I}\simeq \mathrm {Fin}\oplus \mathcal {P}(\omega )$
is nonempty finite then $\mathcal {I}\simeq \mathrm {Fin}\oplus \mathcal {P}(\omega )$![]() . Lastly, if also $J^c$
. Lastly, if also $J^c$![]() is infinite, then $\mathcal {I}\simeq \mathcal {J}\simeq \mathrm {Fin}\times \emptyset$
is infinite, then $\mathcal {I}\simeq \mathcal {J}\simeq \mathrm {Fin}\times \emptyset$![]() .
.
2.3 Unbounded to bounded case
In this section, we may assume that $\mathcal {I}\neq \mathrm {Fin}$![]() , otherwise we go back in the previous cases. Differently from the other results, we are going to show that, quite often, there are no matrices $A$
, otherwise we go back in the previous cases. Differently from the other results, we are going to show that, quite often, there are no matrices $A$![]() which satisfy
which satisfy
unless $T$![]() is the zero operator. To this aim, recall that an ideal $\mathcal {I}$
is the zero operator. To this aim, recall that an ideal $\mathcal {I}$![]() is said to be tall if, for every infinite set $S\subseteq \omega$
is said to be tall if, for every infinite set $S\subseteq \omega$![]() , there exists an infinite subset $S^\prime \subseteq S$
, there exists an infinite subset $S^\prime \subseteq S$![]() which belongs to $\mathcal {I}$
which belongs to $\mathcal {I}$![]() (note that countably generated ideals, hence also $\mathrm {Fin}$
(note that countably generated ideals, hence also $\mathrm {Fin}$![]() , are not tall; for a necessary condition in the case of countably generated ideals $\mathcal {J}$
, are not tall; for a necessary condition in the case of countably generated ideals $\mathcal {J}$![]() and arbitrary $\mathcal {I}$
and arbitrary $\mathcal {I}$![]() , cf. remark 2.23 below).
, cf. remark 2.23 below).
Theorem 2.17 Fix a nonzero linear operator $T \in \mathcal {L}(X,\,Y)$![]() , where $X,\,Y$
, where $X,\,Y$![]() are Banach spaces. Let also $\mathcal {I},\,\mathcal {J}$
are Banach spaces. Let also $\mathcal {I},\,\mathcal {J}$![]() be an ideals on $\omega$
be an ideals on $\omega$![]() such that $\mathcal {I}$
such that $\mathcal {I}$![]() is tall.
is tall.
Then there are no matrices $A=(A_{n,k})$![]() of linear operators in $\mathcal {L}(X,\,Y)$
of linear operators in $\mathcal {L}(X,\,Y)$![]() which satisfy (2.5).
which satisfy (2.5).
Of course, if $T=0$![]() , then the zero matrix $A$
, then the zero matrix $A$![]() (namely, the matrix with $A_{n,k}=0$
(namely, the matrix with $A_{n,k}=0$![]() for all $n,\,k$
for all $n,\,k$![]() ) satisfies (2.5). However, this is essentially the unique possibility:
) satisfies (2.5). However, this is essentially the unique possibility:
Theorem 2.18 Let $X,\,Y$![]() be Banach spaces. Let also $\mathcal {I},\, \mathcal {J}$
be Banach spaces. Let also $\mathcal {I},\, \mathcal {J}$![]() be ideals on $\omega$
be ideals on $\omega$![]() such that $\mathcal {I}$
such that $\mathcal {I}$![]() is tall.
is tall.
Then a matrix $A=(A_{n,k})$![]() of linear operators in $\mathcal {L}(X,\,Y)$
of linear operators in $\mathcal {L}(X,\,Y)$![]() belongs to $(c(X,\,\mathcal {I}),\, c_0^b(Y,\,\mathcal {J}))$
belongs to $(c(X,\,\mathcal {I}),\, c_0^b(Y,\,\mathcal {J}))$![]() if and only if there exists $k_1 \in \omega$
if and only if there exists $k_1 \in \omega$![]() such that:
such that:
(B1) $A_{n,k}=0$
 for all $n \in \omega$
for all $n \in \omega$ and $k\ge k_1$
and $k\ge k_1$ ;
;(B2) $\sup _n \|A_{n,k}x\|<\infty$
 for all $x \in X$
for all $x \in X$ and $k< k_1$
and $k< k_1$ ;
;(B3) $\mathcal {J}\text {-}\lim _n A_{n,k}=0$
 for all $k< k_1$
for all $k< k_1$ .
.
As it will turn out, condition (B1) is satisfied also for all matrices in the larger class $(c_{00}(X,\,\mathcal {I}),\, \ell _\infty (Y))$![]() , provided that $\mathcal {I}$
, provided that $\mathcal {I}$![]() is tall.
is tall.
2.4 Unbounded to unbounded case
In this last section, we study the analogue condition for a matrix $A=(A_{n,k})$![]() of linear operators in $\mathcal {L}(X,\,Y)$
of linear operators in $\mathcal {L}(X,\,Y)$![]() to satisfy
to satisfy
Remark 2.19 In some cases, it is easy to provide examples of matrices which satisfy (2.6). Indeed, suppose that $T\in \mathcal {B}(X,\,Y)$![]() and $\mathcal {I}\subseteq \mathcal {J}$
and $\mathcal {I}\subseteq \mathcal {J}$![]() . We claim that the matrix $A=(A_{n,k})$
. We claim that the matrix $A=(A_{n,k})$![]() such that $A_{n,k}=T$
such that $A_{n,k}=T$![]() if $n=k$
if $n=k$![]() and $A_{n,k}=0$
and $A_{n,k}=0$![]() otherwise has this property. For, set $\boldsymbol {x} \in c(X,\,\mathcal {I})$
otherwise has this property. For, set $\boldsymbol {x} \in c(X,\,\mathcal {I})$![]() with $\mathcal {I}$
with $\mathcal {I}$![]() -limit $\eta$
-limit $\eta$![]() . Then $\mathcal {I}\text {-}\lim \nolimits _n A_n\boldsymbol {x}=\mathcal {I}\text {-}\lim \nolimits _n Tx_n=T(\mathcal {I}\text {-}\lim \boldsymbol {x})=T\eta,\,$
. Then $\mathcal {I}\text {-}\lim \nolimits _n A_n\boldsymbol {x}=\mathcal {I}\text {-}\lim \nolimits _n Tx_n=T(\mathcal {I}\text {-}\lim \boldsymbol {x})=T\eta,\,$![]() which implies $\mathcal {J}\text {-}\lim A\boldsymbol {x}=T\eta$
which implies $\mathcal {J}\text {-}\lim A\boldsymbol {x}=T\eta$![]() . Here, we used the fact the $T$
. Here, we used the fact the $T$![]() preserves $\mathcal {I}$
preserves $\mathcal {I}$![]() -convergence: this is clear if $T=0$
-convergence: this is clear if $T=0$![]() , otherwise $\{n \in \omega : \|Tx_n-T\eta \|<\varepsilon \} \supseteq \{n \in \omega : \|x_n-\eta \|<\varepsilon /\|T\|\} \in \mathcal {I}^\star$
, otherwise $\{n \in \omega : \|Tx_n-T\eta \|<\varepsilon \} \supseteq \{n \in \omega : \|x_n-\eta \|<\varepsilon /\|T\|\} \in \mathcal {I}^\star$![]() for all $\varepsilon >0$
for all $\varepsilon >0$![]() .
.
In the next results, we need a further weakening of (T1$^\flat$![]() ) and stronger versions of conditions (T3) and (T5), that is,
) and stronger versions of conditions (T3) and (T5), that is,
(T1♭♭) For all $n \in \omega$
 , there exists $f(n) \in \omega$
, there exists $f(n) \in \omega$ such that $\|A_{n,\ge f(n)}\|<\infty$
such that $\|A_{n,\ge f(n)}\|<\infty$ ;
;(T3♯) $\sum \nolimits _kA_{n,k}x_k$
 converges in the norm of $Y$
converges in the norm of $Y$ for all $\boldsymbol {x} \in c(X,\,\mathcal {I})$
for all $\boldsymbol {x} \in c(X,\,\mathcal {I})$ and $n \in \omega$
and $n \in \omega$ ;
;(T5♯) $A \in (c_{00}(X,\,\mathcal {I}),\,c_0(Y,\,\mathcal {J}))$
 .
.
Theorem 2.20 Fix a linear operator $T \in \mathcal {L}(X,\,Y)$![]() , where $X,\,Y$
, where $X,\,Y$![]() are Banach spaces. Let also $\mathcal {I},\,\mathcal {J}$
are Banach spaces. Let also $\mathcal {I},\,\mathcal {J}$![]() be an ideals on $\omega$
be an ideals on $\omega$![]() . Then a matrix $A=(A_{n,k})$
. Then a matrix $A=(A_{n,k})$![]() of linear operators in $\mathcal {L}(X,\,Y)$
of linear operators in $\mathcal {L}(X,\,Y)$![]() satisfies (2.6) if there exists $k_0 \in \omega$
satisfies (2.6) if there exists $k_0 \in \omega$![]() such that (T1$^\flat$
such that (T1$^\flat$![]() ), (T3$^{\sharp }$
), (T3$^{\sharp }$![]() ), (T4), and (T5$^{\sharp }$
), (T4), and (T5$^{\sharp }$![]() ) hold.
) hold.
Conversely, if $A$![]() satisfies (2.6) then (T1$^{\flat \flat }$
satisfies (2.6) then (T1$^{\flat \flat }$![]() ), (T3$^{\sharp }$
), (T3$^{\sharp }$![]() ), (T4), and (T5$^{\sharp }$
), (T4), and (T5$^{\sharp }$![]() ) hold.
) hold.
It turns out that we obtain a complete characterization if $\mathcal {J}$![]() is a strongly selective ideal:
is a strongly selective ideal:
Theorem 2.21 Fix a linear operator $T \in \mathcal {L}(X,\,Y)$![]() , where $X,\,Y$
, where $X,\,Y$![]() are Banach spaces. Let also $\mathcal {I},\,\mathcal {J}$
are Banach spaces. Let also $\mathcal {I},\,\mathcal {J}$![]() be an ideals on $\omega$
be an ideals on $\omega$![]() such that $\mathcal {J}$
such that $\mathcal {J}$![]() is a strongly selective ideal.
is a strongly selective ideal.
Then a matrix $A=(A_{n,k})$![]() of linear operators in $\mathcal {L}(X,\,Y)$
of linear operators in $\mathcal {L}(X,\,Y)$![]() satisfies (2.6) if and only if there exists $k_0 \in \omega$
satisfies (2.6) if and only if there exists $k_0 \in \omega$![]() such that (T1$^\flat$
such that (T1$^\flat$![]() ), (T3$^{\sharp }$
), (T3$^{\sharp }$![]() ), (T4), and (T5$^{\sharp }$
), (T4), and (T5$^{\sharp }$![]() ) hold.
) hold.
In addition, if each $A_{n,k}$![]() is bounded, it is possible to choose $k_0=f(n)=0$
is bounded, it is possible to choose $k_0=f(n)=0$![]() for all $n \in \omega \setminus J_0$
for all $n \in \omega \setminus J_0$![]() .
.
Some additional properties can be obtained in special cases:
Remark 2.22 Suppose that $\mathcal {I}$![]() is tall ideal. Then (T3$^{\sharp }$
is tall ideal. Then (T3$^{\sharp }$![]() ) implies, thanks to lemma 3.14, that $A$
) implies, thanks to lemma 3.14, that $A$![]() is row finite, namely, $\{k \in \omega : A_{n,k}\neq 0\} \in \mathrm {Fin}$
is row finite, namely, $\{k \in \omega : A_{n,k}\neq 0\} \in \mathrm {Fin}$![]() for all $n\in \omega$
for all $n\in \omega$![]() .
.
Remark 2.23 Suppose that $\mathcal {J}$![]() is a countably generated ideal. Then (T5$^{\sharp }$
is a countably generated ideal. Then (T5$^{\sharp }$![]() ) implies, thanks to theorem 3.15, that for every infinite $E \in \mathcal {I}$
) implies, thanks to theorem 3.15, that for every infinite $E \in \mathcal {I}$![]() there exists $J \in \mathcal {J}^\star$
there exists $J \in \mathcal {J}^\star$![]() such that $\{k \in E: A_{n,k}\neq 0 \text { for some }n \in J\}$
such that $\{k \in E: A_{n,k}\neq 0 \text { for some }n \in J\}$![]() is finite.
is finite.
3. Preliminaries
Unless otherwise stated, we assume that $X,\,Y$![]() are Banach spaces. We recall the following results on the so-called Köthe–Toeplitz $\beta$
are Banach spaces. We recall the following results on the so-called Köthe–Toeplitz $\beta$![]() -duals:
-duals:
Lemma 3.1 Let $(T_k)$![]() be a sequence of linear operators in $\mathcal {L}(X,\,Y)$
be a sequence of linear operators in $\mathcal {L}(X,\,Y)$![]() . Then $\sum _k T_kx_k$
. Then $\sum _k T_kx_k$![]() is convergent in the norm of $Y$
is convergent in the norm of $Y$![]() for all sequences $\boldsymbol {x} \in \ell _\infty (X)$
for all sequences $\boldsymbol {x} \in \ell _\infty (X)$![]() if and only if:
if and only if:
(N1) $\|T_{\ge k_0}\|<\infty$
 for some $k_0 \in \omega$
for some $k_0 \in \omega$ ;
;(N2) $\lim _k\|T_{\ge k}\|=0$
 .
.
In addition, if each $T_k$![]() is bounded, it is possible to choose $k_0=0$
is bounded, it is possible to choose $k_0=0$![]() .
.
Proof. See [Reference Maddox34, Proposition 3.1 and Proposition 3.3].
In particular, (N1) implies that $T_k$![]() is bounded for all $k\ge k_0$
is bounded for all $k\ge k_0$![]() . We remark that, if $X=\mathbf {R}$
. We remark that, if $X=\mathbf {R}$![]() and each linear operator $T_k$
and each linear operator $T_k$![]() can be written as $T_kx=xy_k$
can be written as $T_kx=xy_k$![]() , for some $y_k \in Y$
, for some $y_k \in Y$![]() , then the sequence $(T_k)$
, then the sequence $(T_k)$![]() of lemma 3.1 is also called “bounded multiplier convergent,” see e.g. [Reference Swartz41].
of lemma 3.1 is also called “bounded multiplier convergent,” see e.g. [Reference Swartz41].
Lemma 3.2 Let $(T_k)$![]() be a sequence of linear operators in $\mathcal {L}(X,\,Y)$
be a sequence of linear operators in $\mathcal {L}(X,\,Y)$![]() . Then $\sum _k T_kx_k$
. Then $\sum _k T_kx_k$![]() is norm convergent in $Y$
is norm convergent in $Y$![]() for all $\boldsymbol {x} \in c(X)$
for all $\boldsymbol {x} \in c(X)$![]() if and only if (N1) holds for some $k_0$
if and only if (N1) holds for some $k_0$![]() , together with:
, together with:
(N2′) $\sum _kT_k$
 converges in the strong operator topology.
converges in the strong operator topology.
In addition, if each $T_k$![]() is bounded, it is possible to choose $k_0=0$
is bounded, it is possible to choose $k_0=0$![]() .
.
Proof. See [Reference Maddox34, Proposition 3.2].
A characterization of the Köthe–Toeplitz $\beta$![]() -dual of a sequence space which is strictly related to $c(\mathcal {Z})$
-dual of a sequence space which is strictly related to $c(\mathcal {Z})$![]() can be found in [Reference Lascarides and Maddox27, Theorem 4].
can be found in [Reference Lascarides and Maddox27, Theorem 4].
However, if $X$![]() is finite dimensional, we have a simpler characterization:
is finite dimensional, we have a simpler characterization:
Corollary 3.3 Let $(T_k)$![]() be a sequence of linear operators in $\mathcal {L}(X,\,Y)$
be a sequence of linear operators in $\mathcal {L}(X,\,Y)$![]() and assume, in addition, that $X$
and assume, in addition, that $X$![]() is finite dimensional. Then the following are equivalent:
is finite dimensional. Then the following are equivalent:
(i) $\sum _kT_kx_k$
 is norm convergent in $Y$
is norm convergent in $Y$ for all sequences $\boldsymbol {x} \in \ell _\infty (X)$
for all sequences $\boldsymbol {x} \in \ell _\infty (X)$ ;
;(ii) $\sum _kT_kx_k$
 is norm convergent in $Y$
is norm convergent in $Y$ for all sequences $\boldsymbol {x} \in c(X)$
for all sequences $\boldsymbol {x} \in c(X)$ ;
;(iii) $\|T_\omega \|<\infty$
 .
.
Proof. The implication (i) $\implies$![]() (ii) is clear and (ii) $\implies$
(ii) is clear and (ii) $\implies$![]() (iii) follows by lemma 3.2. Indeed, since $d:=\mathrm {dim}(X)<\infty$
(iii) follows by lemma 3.2. Indeed, since $d:=\mathrm {dim}(X)<\infty$![]() , each $T_{k}$
, each $T_{k}$![]() is bounded.
is bounded.
(iii) $\implies$![]() (i) It follows by lemma 3.1 that it is enough to prove that condition (N2) holds, provided that $\|T_\omega \|<\infty$
(i) It follows by lemma 3.1 that it is enough to prove that condition (N2) holds, provided that $\|T_\omega \|<\infty$![]() . To this aim, suppose for the sake of contradiction that there exists $\varepsilon >0$
. To this aim, suppose for the sake of contradiction that there exists $\varepsilon >0$![]() such that $\limsup _k \|T_{\ge k}\|>\varepsilon$
such that $\limsup _k \|T_{\ge k}\|>\varepsilon$![]() . Then there exist a sequence $\boldsymbol {x}$
. Then there exist a sequence $\boldsymbol {x}$![]() taking values in the closed unit ball $B_X$
taking values in the closed unit ball $B_X$![]() and a partition $\{I_j: j \in \omega \}$
and a partition $\{I_j: j \in \omega \}$![]() of $\omega$
of $\omega$![]() in consecutive finite intervals such that
in consecutive finite intervals such that
Assume without loss of generality that $X=\mathbf {R}^d$![]() and, since every norm is equivalent, endow it with the $1$
and, since every norm is equivalent, endow it with the $1$![]() -norm $\|x\|:=\sum _i|x_i|$
-norm $\|x\|:=\sum _i|x_i|$![]() . Define the sequence $\boldsymbol {y}$
. Define the sequence $\boldsymbol {y}$![]() by $y_j:=\sum \nolimits _{k \in I_j}T_kx_k$
by $y_j:=\sum \nolimits _{k \in I_j}T_kx_k$![]() for all $j$
for all $j$![]() . Let $\{Q_1,\,\ldots,\,Q_{2^d}\}$
. Let $\{Q_1,\,\ldots,\,Q_{2^d}\}$![]() be the collection of all closed quadrants of $\mathbf {R}^d$
be the collection of all closed quadrants of $\mathbf {R}^d$![]() . Since $\bigcup _{i\le 2^d}Q_i=\mathbf {R}^d$
. Since $\bigcup _{i\le 2^d}Q_i=\mathbf {R}^d$![]() , there exist $i_0 \in [1,\,2^d]$
, there exist $i_0 \in [1,\,2^d]$![]() and an infinite set $J\subseteq \omega$
and an infinite set $J\subseteq \omega$![]() such that $y_j \in Q_{i_0}$
such that $y_j \in Q_{i_0}$![]() for all $j \in J$
for all $j \in J$![]() . It follows that
. It follows that

which contradicts the standing hypothesis.
Lemma 3.4 Let $(T_k)$![]() be a sequence of linear operators in $\mathcal {L}(X,\,Y)$
be a sequence of linear operators in $\mathcal {L}(X,\,Y)$![]() and assume, in addition, that $X$
and assume, in addition, that $X$![]() is finite dimensional and $\mathcal {J}\text {-}\lim _k \|T_kx\|=0$
is finite dimensional and $\mathcal {J}\text {-}\lim _k \|T_kx\|=0$![]() for all $x \in X$
for all $x \in X$![]() , where $\mathcal {J}$
, where $\mathcal {J}$![]() is an ideal on $\omega$
is an ideal on $\omega$![]() . Then $\mathcal {J}\text {-}\lim _k \|T_k\|=0$
. Then $\mathcal {J}\text {-}\lim _k \|T_k\|=0$![]() .
.
Proof. Since $d:=\mathrm {dim}(X)<\infty$![]() , each $T_k$
, each $T_k$![]() is bounded. Assume without loss of generality that $X=\mathbf {R}^d$
is bounded. Assume without loss of generality that $X=\mathbf {R}^d$![]() and endow it with the $1$
and endow it with the $1$![]() -norm as in the proof of corollary 3.3. Note that the set $\mathscr {E}$
-norm as in the proof of corollary 3.3. Note that the set $\mathscr {E}$![]() of extreme points of the closed unit ball is finite. Hence, for each $k \in \omega$
of extreme points of the closed unit ball is finite. Hence, for each $k \in \omega$![]() , there exists $e_k \in \mathscr {E}$
, there exists $e_k \in \mathscr {E}$![]() such that $\|T_k\|=\|T_ke_k\|$
such that $\|T_k\|=\|T_ke_k\|$![]() . It follows that
. It follows that
which completes the proof.
As anticipated, we need an ideal version of the Banach–Steinhaus theorem, which has been recently obtained in [Reference De Bondt and Vernaeve12].
Theorem 3.5 Let $\mathcal {J}$![]() be a rapid$^+$
be a rapid$^+$![]() $P^+$
$P^+$![]() -ideal on $\omega$
-ideal on $\omega$![]() . Also, let $(T_n)$
. Also, let $(T_n)$![]() be a sequence of linear operators in $B(X,\,Y)$
be a sequence of linear operators in $B(X,\,Y)$![]() and suppose that
and suppose that
Then $\mathcal {J}\text {-}\limsup _n\|T_n\|<\infty$![]() .
.
Proof. It follows by [Reference De Bondt and Vernaeve12, Theorem 3.1(b)].
The following result on unbounded operators is due to Lorentz and Macphail [Reference Lorentz and Macphail31] in the case $\mathcal {J}=\mathrm {Fin}$![]() , see also [Reference Maddox34, Theorem 4.1] for a textbook exposition.
, see also [Reference Maddox34, Theorem 4.1] for a textbook exposition.
Theorem 3.6 Let $(T_n)$![]() be a sequence of linear operators in $\mathcal {L}(X,\,Y)$
be a sequence of linear operators in $\mathcal {L}(X,\,Y)$![]() . Let also $(M_n)$
. Let also $(M_n)$![]() be a decreasing sequence of closed linear subspaces of $X$
be a decreasing sequence of closed linear subspaces of $X$![]() such that each $T_n$
such that each $T_n$![]() is bounded on $M_n$
is bounded on $M_n$![]() .
.
Lastly, fix a strongly selective ideal $\mathcal {J}$![]() on $\omega$
on $\omega$![]() and suppose that $(T_nx) \in \ell _\infty (Y,\,\mathcal {J})$
and suppose that $(T_nx) \in \ell _\infty (Y,\,\mathcal {J})$![]() for all $x \in X$
for all $x \in X$![]() . There there exist $n_0 \in \omega$
. There there exist $n_0 \in \omega$![]() and $J^\star \in \mathcal {J}^\star$
and $J^\star \in \mathcal {J}^\star$![]() such that $T_n$
such that $T_n$![]() is bounded on $M_{n_0}$
is bounded on $M_{n_0}$![]() for all $n \in J^\star$
for all $n \in J^\star$![]() .
.
Proof. For each $n \in \omega$![]() , define
, define
Note that $(S_n)$![]() is a decreasing sequence and $S_n \cap [0,\,n]=\emptyset$
is a decreasing sequence and $S_n \cap [0,\,n]=\emptyset$![]() for all $n \in \omega$
for all $n \in \omega$![]() . First, suppose that there exists $n_0 \in \omega$
. First, suppose that there exists $n_0 \in \omega$![]() such that $S_{n_0} \in \mathcal {J}$
such that $S_{n_0} \in \mathcal {J}$![]() . It follows that $T_k$
. It follows that $T_k$![]() is bounded on $M_{n_0}$
is bounded on $M_{n_0}$![]() for all $k \in J^\star :=\omega \setminus S_{n_0} \in \mathcal {J}^\star$
for all $k \in J^\star :=\omega \setminus S_{n_0} \in \mathcal {J}^\star$![]() . Hence, suppose hereafter that $(S_n)$
. Hence, suppose hereafter that $(S_n)$![]() is a decreasing sequence in $\mathcal {J}^+$
is a decreasing sequence in $\mathcal {J}^+$![]() . Since $\mathcal {J}$
. Since $\mathcal {J}$![]() is strongly selective, there exists $S \in \mathcal {J}^+$
is strongly selective, there exists $S \in \mathcal {J}^+$![]() with increasing enumeration $(k_n)$
with increasing enumeration $(k_n)$![]() with the property that $k_{n+1} \in S_{k_n}$
with the property that $k_{n+1} \in S_{k_n}$![]() for all $n \in \omega$
for all $n \in \omega$![]() . In other words, we have
. In other words, we have
It follows by the proof in [Reference Maddox34, Theorem 4.1] that there exists $x \in X$![]() such that $\|T_{k_{n+1}}x\|\ge n$
such that $\|T_{k_{n+1}}x\|\ge n$![]() for all $n\ge 2$
for all $n\ge 2$![]() . This contradicts the hypothesis that the sequence $(T_nx)$
. This contradicts the hypothesis that the sequence $(T_nx)$![]() is $\mathcal {J}$
is $\mathcal {J}$![]() -bounded.
-bounded.
Theorem 3.7 Let $A=(A_{n,k})$![]() be a matrix of linear operators in $\mathcal {L}(X,\,Y)$
be a matrix of linear operators in $\mathcal {L}(X,\,Y)$![]() . Let $\mathcal {J}$
. Let $\mathcal {J}$![]() be a strongly selective ideal on $\omega$
be a strongly selective ideal on $\omega$![]() . Then $A \in (c(X),\, \ell _\infty (Y,\, \mathcal {J}))$
. Then $A \in (c(X),\, \ell _\infty (Y,\, \mathcal {J}))$![]() only if there exists $k_0 \in \omega$
only if there exists $k_0 \in \omega$![]() which satisfies (T1$^\flat$
which satisfies (T1$^\flat$![]() ).
).
In addition, if each $A_{n,k}$![]() is bounded, it is possible to choose $k_0=f(n)=0$
is bounded, it is possible to choose $k_0=f(n)=0$![]() for all $n \in \omega \setminus J_0$
for all $n \in \omega \setminus J_0$![]() .
.
Proof. Thanks to lemma 3.2, for each $n \in \omega$![]() , there exists an integer $f(n) \in \omega$
, there exists an integer $f(n) \in \omega$![]() such that $\|A_{n,\ge f(n)}\|<\infty$
such that $\|A_{n,\ge f(n)}\|<\infty$![]() . Without loss of generality, we can suppose that the sequence $(f(n): n \in \omega )$
. Without loss of generality, we can suppose that the sequence $(f(n): n \in \omega )$![]() is weakly increasing. Now, for each $n \in \omega$
is weakly increasing. Now, for each $n \in \omega$![]() , define
, define
Then $(M_n)$![]() is a decreasing sequence of closed linear subspaces of the Banach space $c(X)$
is a decreasing sequence of closed linear subspaces of the Banach space $c(X)$![]() . In addition, for each $n \in \omega$
. In addition, for each $n \in \omega$![]() , the linear operator $A_n: c(X)\to Y$
, the linear operator $A_n: c(X)\to Y$![]() is well defined. Thanks to the Banach–Steinhaus theorem, $A_n$
is well defined. Thanks to the Banach–Steinhaus theorem, $A_n$![]() is bounded on $M_n$
is bounded on $M_n$![]() for all $n \in \omega$
for all $n \in \omega$![]() .
.
At this point, it follows by theorem 3.6 that there exist $n_0\in \omega$![]() and $J^\star \in \mathcal {J}^\star$
and $J^\star \in \mathcal {J}^\star$![]() such that $A_n$
such that $A_n$![]() is bounded on $M_{n_0}$
is bounded on $M_{n_0}$![]() for all $n \in J^\star$
for all $n \in J^\star$![]() . Thanks to theorem 3.5, we obtain that $\mathcal {J}\text {-}\limsup _n \|A_n\upharpoonright M_{n_0}\|<\infty$
. Thanks to theorem 3.5, we obtain that $\mathcal {J}\text {-}\limsup _n \|A_n\upharpoonright M_{n_0}\|<\infty$![]() , i.e., there exist a constant $\kappa >0$
, i.e., there exist a constant $\kappa >0$![]() and $J_0 \in \mathcal {J}^\star$
and $J_0 \in \mathcal {J}^\star$![]() , with $J_0=\omega$
, with $J_0=\omega$![]() if $\mathcal {J}=\mathrm {Fin}$
if $\mathcal {J}=\mathrm {Fin}$![]() , such that $\|A_n\boldsymbol {x}\|\le \kappa \|\boldsymbol {x}\|$
, such that $\|A_n\boldsymbol {x}\|\le \kappa \|\boldsymbol {x}\|$![]() for all $\boldsymbol {x} \in M_{n_0}$
for all $\boldsymbol {x} \in M_{n_0}$![]() and $n \in J_0$
and $n \in J_0$![]() . To complete the proof, observe that
. To complete the proof, observe that
which implies that $\|A_{n,\ge f(n_0)}\|\le \kappa$![]() . Since the upper bound is independent of $n\in J_0$
. Since the upper bound is independent of $n\in J_0$![]() , the claim follows by setting $k_0:=f(n_0)$
, the claim follows by setting $k_0:=f(n_0)$![]() .
.
The second part is clear once we observe that it is possible to choose $f(n)=0$![]() for all $n$
for all $n$![]() .
.
In the following results we need the following weakening of (T2), namely,
(T2♭) $\mathcal {J}\text {-}\limsup _n\|A_{n,k}x\|<\infty$
 for all $x \in X$
for all $x \in X$ and $k< k_0$
and $k< k_0$ .
.
It is clear that (T5) implies (T2$^\flat$![]() ), which is the reason why it does not appear in theorem 2.14, cf. remark 2.6.
), which is the reason why it does not appear in theorem 2.14, cf. remark 2.6.
Theorem 3.8 Let $A=(A_{n,k})$![]() be a matrix of linear operators in $\mathcal {L}(X,\,Y)$
be a matrix of linear operators in $\mathcal {L}(X,\,Y)$![]() . Also, let $\mathcal {J}$
. Also, let $\mathcal {J}$![]() be a strongly selective ideal on $\omega$
be a strongly selective ideal on $\omega$![]() . Then $A \in (\ell _\infty (X),\, \ell _\infty (Y,\, \mathcal {J}))$
. Then $A \in (\ell _\infty (X),\, \ell _\infty (Y,\, \mathcal {J}))$![]() if and only if there exists $k_0 \in \omega$
if and only if there exists $k_0 \in \omega$![]() such that (T1$^\flat$
such that (T1$^\flat$![]() ), (T2$^\flat$
), (T2$^\flat$![]() ), and (T3$^{\natural }$
), and (T3$^{\natural }$![]() ) hold.
) hold.
In addition, if each $A_{n,k}$![]() is bounded, it is possible to choose $k_0=0$
is bounded, it is possible to choose $k_0=0$![]() .
.
Proof. If part. Fix $\boldsymbol {x}\in \ell _\infty (X)$![]() . Thanks to lemma 3.1, for each $n$
. Thanks to lemma 3.1, for each $n$![]() , the sum $A_n\boldsymbol {x}=\sum _kA_{n,k}x_k$
, the sum $A_n\boldsymbol {x}=\sum _kA_{n,k}x_k$![]() is convergent in the norm of $Y$
is convergent in the norm of $Y$![]() , hence $A\boldsymbol {x}$
, hence $A\boldsymbol {x}$![]() is well defined. It follows by (T2$^\flat$
is well defined. It follows by (T2$^\flat$![]() ) that there exist $J_1 \in \mathcal {J}^\star$
) that there exist $J_1 \in \mathcal {J}^\star$![]() and $\kappa >0$
and $\kappa >0$![]() such that $\|A_{n,k}x_k\|\le \kappa$
such that $\|A_{n,k}x_k\|\le \kappa$![]() for all $k< k_0$
for all $k< k_0$![]() and $n \in J_1$
and $n \in J_1$![]() . Hence
. Hence
for all $n \in J_0\cap J_1 \in \mathcal {J}^\star$![]() , which proves that $A\boldsymbol {x} \in \ell _\infty (Y,\, \mathcal {J})$
, which proves that $A\boldsymbol {x} \in \ell _\infty (Y,\, \mathcal {J})$![]() .
.
Only If part. The necessity of (T1$^\flat$![]() ) follows by theorem 3.7, with $k_0=0$
) follows by theorem 3.7, with $k_0=0$![]() if each $A_{n,k}$
if each $A_{n,k}$![]() is bounded. Now, if (T2$^\flat$
is bounded. Now, if (T2$^\flat$![]() ) does not hold, there would exist $x \in X$
) does not hold, there would exist $x \in X$![]() and $k< k_0$
and $k< k_0$![]() such that $\mathcal {J}\text {-}\limsup _n\|A_{n,k}x\|=\infty$
such that $\mathcal {J}\text {-}\limsup _n\|A_{n,k}x\|=\infty$![]() . This contradicts the hypothesis that $A \in (\ell _\infty (X),\, \ell _\infty (Y,\,\mathcal {J}))$
. This contradicts the hypothesis that $A \in (\ell _\infty (X),\, \ell _\infty (Y,\,\mathcal {J}))$![]() by choosing $\boldsymbol {x} \in \ell _\infty (X)$
by choosing $\boldsymbol {x} \in \ell _\infty (X)$![]() such that $x_t=x$
such that $x_t=x$![]() if $t=k$
if $t=k$![]() and $x_t=0$
and $x_t=0$![]() otherwise. Lastly, the necessity of (T3$^{\natural }$
otherwise. Lastly, the necessity of (T3$^{\natural }$![]() ) follows by lemma 3.1.
) follows by lemma 3.1.
Remark 3.9 The same example given in remark 2.4 proves that, even if $X=Y$![]() , $\mathcal {J}=\mathrm {Fin}$
, $\mathcal {J}=\mathrm {Fin}$![]() , and each $A_{n,k}$
, and each $A_{n,k}$![]() is bounded (so that (T2$^\flat$
is bounded (so that (T2$^\flat$![]() ) is void), condition (T1$^\flat$
) is void), condition (T1$^\flat$![]() ) (as its stronger version (T1)) is not sufficient to characterize the matrix class $(\ell _\infty (X),\, \ell _\infty (Y,\,\mathcal {J}))$
) (as its stronger version (T1)) is not sufficient to characterize the matrix class $(\ell _\infty (X),\, \ell _\infty (Y,\,\mathcal {J}))$![]() ; cf. corollary 3.11 below for the finite-dimensional case.
; cf. corollary 3.11 below for the finite-dimensional case.
Theorem 3.10 Let $A=(A_{n,k})$![]() be a matrix of linear operators in $\mathcal {L}(X,\,Y)$
be a matrix of linear operators in $\mathcal {L}(X,\,Y)$![]() . Also, let $\mathcal {J}$
. Also, let $\mathcal {J}$![]() be a strongly selective ideal on $\omega$
be a strongly selective ideal on $\omega$![]() . Then $A \in (c(X),\, \ell _\infty (Y,\,\mathcal {J}))$
. Then $A \in (c(X),\, \ell _\infty (Y,\,\mathcal {J}))$![]() if and only if there exists $k_0 \in \omega$
if and only if there exists $k_0 \in \omega$![]() such that (T1$^\flat$
such that (T1$^\flat$![]() ) and (T2$^\flat$
) and (T2$^\flat$![]() ) hold, together with:
) hold, together with:
(T4♭) $\sum _{k}A_{n,k}$
 convergences in the strong operator topology for all $n$
convergences in the strong operator topology for all $n$ .
.
In addition, if each $A_{n,k}$![]() is bounded, it is possible to choose $k_0=0$
is bounded, it is possible to choose $k_0=0$![]() .
.
However, if $X$![]() is finite dimensional, it is possible to simplify the equivalences in theorems 3.8 and 3.10, namely, condition (T1$^\flat$
is finite dimensional, it is possible to simplify the equivalences in theorems 3.8 and 3.10, namely, condition (T1$^\flat$![]() ) is necessary and sufficient in both cases choosing $k_0=0$
) is necessary and sufficient in both cases choosing $k_0=0$![]()
Corollary 3.11 Let $A=(A_{n,k})$![]() be a matrix of linear operators in $\mathcal {L}(X,\,Y)$
be a matrix of linear operators in $\mathcal {L}(X,\,Y)$![]() and assume, in addition, that $X$
and assume, in addition, that $X$![]() is finite dimensional. Also, let $\mathcal {J}$
is finite dimensional. Also, let $\mathcal {J}$![]() be a strongly selective ideal on $\omega$
be a strongly selective ideal on $\omega$![]() .
.
Then the following are equivalent:
(i) $A \in (\ell _\infty (X),\, \ell _\infty (Y,\,\mathcal {J}))$
 ;
;(ii) $A \in (c(X),\, \ell _\infty (Y,\,\mathcal {J}))$
 ;
;(iii) (T1$^\flat$
 ) holds with $k_0=0$
) holds with $k_0=0$ .
.
Proof. (i) $\implies$![]() (ii) is clear, (ii) $\implies$
(ii) is clear, (ii) $\implies$![]() (iii) follows by theorem 3.7, and (iii) $\implies$
(iii) follows by theorem 3.7, and (iii) $\implies$![]() (i) follows by lemma 3.1, corollary 3.3, theorem 3.8, and the fact that each $A_{n,k}$
(i) follows by lemma 3.1, corollary 3.3, theorem 3.8, and the fact that each $A_{n,k}$![]() is bounded.
is bounded.
Lemma 3.12 Let $(T_k)$![]() be a sequence of nonzero linear operators in $\mathcal {L}(X,\,Y)$
be a sequence of nonzero linear operators in $\mathcal {L}(X,\,Y)$![]() . Then there exists a sequence $\boldsymbol {x} \in X^\omega$
. Then there exists a sequence $\boldsymbol {x} \in X^\omega$![]() such that $\sum _kT_kx_k$
such that $\sum _kT_kx_k$![]() is not convergent in the norm of $Y$
is not convergent in the norm of $Y$![]() .
.
Proof. For each $k\in \omega$![]() , pick $y_k \in X$
, pick $y_k \in X$![]() such that $T_ky_k\neq 0$
such that $T_ky_k\neq 0$![]() . Now define the sequence $\boldsymbol {x}$
. Now define the sequence $\boldsymbol {x}$![]() recursively as it follows: $x_0:=y_0$
recursively as it follows: $x_0:=y_0$![]() and, if $x_0,\,\ldots,\,x_{n-1}$
and, if $x_0,\,\ldots,\,x_{n-1}$![]() are defined for some $n\ge 1$
are defined for some $n\ge 1$![]() , then $x_n:=\kappa _n y_n$
, then $x_n:=\kappa _n y_n$![]() , where $\kappa _n:=(n+\|\sum _{k\le n-1}T_kx_k\|)/\|T_ny_n\|$
, where $\kappa _n:=(n+\|\sum _{k\le n-1}T_kx_k\|)/\|T_ny_n\|$![]() . Indeed, it follows that
. Indeed, it follows that
for all $n\ge 1$![]() , completing the proof.
, completing the proof.
Lemma 3.13 Let $\mathcal {I}$![]() be an ideal on $\omega$
be an ideal on $\omega$![]() which is tall. Then there exists a partition $\{E_n: n \in \omega \}$
which is tall. Then there exists a partition $\{E_n: n \in \omega \}$![]() of $\omega$
of $\omega$![]() such that $E_n \in \mathcal {I}\cap \mathrm {Fin}^+$
such that $E_n \in \mathcal {I}\cap \mathrm {Fin}^+$![]() for all $n$
for all $n$![]() .
.
Proof. We define such partition recursively, with the property that $\{0,\,\ldots,\,n\}\cup E_0\cup \cdots E_n$![]() for all $n$
for all $n$![]() . Since $\mathcal {I}$
. Since $\mathcal {I}$![]() is tall there exists an infinite set $S_0 \in \mathcal {I}$
is tall there exists an infinite set $S_0 \in \mathcal {I}$![]() , and set $E_0:=S_0\cup \{0\}$
, and set $E_0:=S_0\cup \{0\}$![]() . Now, suppose that $E_0,\,\ldots,\,E_{n-1}$
. Now, suppose that $E_0,\,\ldots,\,E_{n-1}$![]() have been defined, for some $n\ge 1$
have been defined, for some $n\ge 1$![]() , so that the set $G_n:=\omega \setminus \bigcup _{i< n}E_i$
, so that the set $G_n:=\omega \setminus \bigcup _{i< n}E_i$![]() belongs to $\mathcal {I}^\star$
belongs to $\mathcal {I}^\star$![]() . Since $\mathcal {I}$
. Since $\mathcal {I}$![]() is tall there exists an infinite set $S_n \in \mathcal {I}$
is tall there exists an infinite set $S_n \in \mathcal {I}$![]() contained in $G_n$
contained in $G_n$![]() . The claim follows defining $E_n:=S_n$
. The claim follows defining $E_n:=S_n$![]() if $n \notin G_n$
if $n \notin G_n$![]() and $E_n:=S_n\cup \{n\}$
and $E_n:=S_n\cup \{n\}$![]() otherwise.
otherwise.
Lemma 3.14 Let $(T_k)$![]() be a sequence of linear operators in $\mathcal {L}(X,\,Y)$
be a sequence of linear operators in $\mathcal {L}(X,\,Y)$![]() . Let also $\mathcal {I}$
. Let also $\mathcal {I}$![]() be a tall ideal on $\omega$
be a tall ideal on $\omega$![]() . Then $\sum _kT_kx_k$
. Then $\sum _kT_kx_k$![]() is convergent in the norm of $Y$
is convergent in the norm of $Y$![]() for all $\boldsymbol {x} \in c_{00}(X,\,\mathcal {I})$
for all $\boldsymbol {x} \in c_{00}(X,\,\mathcal {I})$![]() if and only if $\{k \in \omega : T_k \neq 0\}$
if and only if $\{k \in \omega : T_k \neq 0\}$![]() is finite.
is finite.
Proof. Thanks to lemma 3.13, there exists a partition $\{E_n: n \in \omega \}$![]() of $\omega$
of $\omega$![]() such that $E_n \in \mathcal {I}\cap \mathrm {Fin}^+$
such that $E_n \in \mathcal {I}\cap \mathrm {Fin}^+$![]() for all $n$
for all $n$![]() . Now, it follows by lemma 3.12 that $F_n:=\{k \in E_n: T_k\neq 0\} \in \mathrm {Fin}$
. Now, it follows by lemma 3.12 that $F_n:=\{k \in E_n: T_k\neq 0\} \in \mathrm {Fin}$![]() . Define $F:=\bigcup _n F_n$
. Define $F:=\bigcup _n F_n$![]() and suppose for the sake of contradiction that $F\notin \mathrm {Fin}$
and suppose for the sake of contradiction that $F\notin \mathrm {Fin}$![]() . Since $\mathcal {I}$
. Since $\mathcal {I}$![]() is tall, there exists an infinite subset $F^\prime \subseteq F$
is tall, there exists an infinite subset $F^\prime \subseteq F$![]() such that $F^\prime \in \mathcal {I}$
such that $F^\prime \in \mathcal {I}$![]() . However, by construction $\{k \in F^\prime : T_k\neq 0\}=F^\prime$
. However, by construction $\{k \in F^\prime : T_k\neq 0\}=F^\prime$![]() , which contradicts lemma 3.12.
, which contradicts lemma 3.12.
Recalling that a matrix $A$![]() is said to be row-finite if $\{k \in \omega : A_{n,k}\neq 0\} \in \mathrm {Fin}$
is said to be row-finite if $\{k \in \omega : A_{n,k}\neq 0\} \in \mathrm {Fin}$![]() for all $n\in \omega$
for all $n\in \omega$![]() , we provide strong necessary conditions on the entries of matrices in $(X^\omega,\, \ell _\infty (Y,\,\mathcal {J}))$
, we provide strong necessary conditions on the entries of matrices in $(X^\omega,\, \ell _\infty (Y,\,\mathcal {J}))$![]() and $(c_{00}(X,\,\mathcal {I}),\, \ell _\infty (Y))$
and $(c_{00}(X,\,\mathcal {I}),\, \ell _\infty (Y))$![]() , where $\mathcal {J}$
, where $\mathcal {J}$![]() is countably generated and $\mathcal {I}$
is countably generated and $\mathcal {I}$![]() is tall.
is tall.
Theorem 3.15 Let $A=(A_{n,k})$![]() be a matrix of linear operators in $\mathcal {L}(X,\,Y)$
be a matrix of linear operators in $\mathcal {L}(X,\,Y)$![]() such that $A \in (X^\omega,\, \ell _\infty (Y,\,\mathcal {J}))$
such that $A \in (X^\omega,\, \ell _\infty (Y,\,\mathcal {J}))$![]() , where $\mathcal {J}$
, where $\mathcal {J}$![]() is a countably generated ideal on $\omega$
is a countably generated ideal on $\omega$![]() . Then $A$
. Then $A$![]() is row finite and there exist $J \in \mathcal {J}^\star$
is row finite and there exist $J \in \mathcal {J}^\star$![]() and $k_1 \in \omega$
and $k_1 \in \omega$![]() such that $A_{n,k}=0$
such that $A_{n,k}=0$![]() for all $n \in J$
for all $n \in J$![]() and $k\ge k_1$
and $k\ge k_1$![]() .
.
Proof. First, suppose that $A \in (X^\omega,\, \ell _\infty (Y,\,\mathcal {J}))$![]() and that $\mathcal {J}$
and that $\mathcal {J}$![]() is generated by a sequence of increasing sets $(Q_j)$
is generated by a sequence of increasing sets $(Q_j)$![]() . Then $A$
. Then $A$![]() is row finite by lemma 3.12, so that $F_n:=\{k \in \omega : A_{n,k}\neq 0\} \in \mathrm {Fin}$
is row finite by lemma 3.12, so that $F_n:=\{k \in \omega : A_{n,k}\neq 0\} \in \mathrm {Fin}$![]() for all $n \in \omega$
for all $n \in \omega$![]() . Suppose for the sake of contradiction that
. Suppose for the sake of contradiction that
Define a strictly increasing sequence $(s_n)$![]() in $\omega$
in $\omega$![]() such that $s_0:=\min \{n \in \omega : F_n \neq \emptyset \}$
such that $s_0:=\min \{n \in \omega : F_n \neq \emptyset \}$![]() , and, recursively, $s_{n+1}:=\min (S_n\setminus Q_{j_n})$
, and, recursively, $s_{n+1}:=\min (S_n\setminus Q_{j_n})$![]() for all $n\in \omega$
for all $n\in \omega$![]() , where
, where
We claim that $S_n\setminus Q_{j_n}$![]() is nonempty, so that $s_{n+1}$
is nonempty, so that $s_{n+1}$![]() is well defined. Note that $S_n \in \mathcal {J}^+$
is well defined. Note that $S_n \in \mathcal {J}^+$![]() : indeed, in the opposite, we would contradict (3.2) by setting $J=S_n^c$
: indeed, in the opposite, we would contradict (3.2) by setting $J=S_n^c$![]() and $k_1=1+\max (F_{s_0}\cup \cdots \cup F_{s_n})$
and $k_1=1+\max (F_{s_0}\cup \cdots \cup F_{s_n})$![]() . In addition, since $Q_{j_n} \in \mathcal {J}$
. In addition, since $Q_{j_n} \in \mathcal {J}$![]() , it follows that $S_n\setminus Q_{j_n}\in \mathcal {J}^+$
, it follows that $S_n\setminus Q_{j_n}\in \mathcal {J}^+$![]() (in particular, it is nonempty).
(in particular, it is nonempty).
Since the set $S:=\{s_n: n \in \omega \}$![]() is not contained in any $Q_j$
is not contained in any $Q_j$![]() , it follows that $S \in \mathcal {J}^+$
, it follows that $S \in \mathcal {J}^+$![]() . In addition, set $k_{n}:=\max F_{s_n}$
. In addition, set $k_{n}:=\max F_{s_n}$![]() for all $n \in \omega$
for all $n \in \omega$![]() . Using a technique similar to the one used in lemma 3.12, we are going to construct a sequence $\boldsymbol {x}$
. Using a technique similar to the one used in lemma 3.12, we are going to construct a sequence $\boldsymbol {x}$![]() supported on $K:=\{k_n:n \in \omega \}$
supported on $K:=\{k_n:n \in \omega \}$![]() such that $\|A_n\boldsymbol {x}\|\ge n$
such that $\|A_n\boldsymbol {x}\|\ge n$![]() for all $n\in \omega$
for all $n\in \omega$![]() , so that $A\boldsymbol {x}\notin \ell _\infty (Y,\,\mathcal {J})$
, so that $A\boldsymbol {x}\notin \ell _\infty (Y,\,\mathcal {J})$![]() . To this aim, pick an arbitrary sequence $\boldsymbol {y} \in X^\omega$
. To this aim, pick an arbitrary sequence $\boldsymbol {y} \in X^\omega$![]() such that $A_{s_n,k_n}y_{n}\neq 0$
such that $A_{s_n,k_n}y_{n}\neq 0$![]() for all $n \in \omega$
for all $n \in \omega$![]() . Now define $\boldsymbol {x}$
. Now define $\boldsymbol {x}$![]() recursively so that $x_{k_0}:=y_0$
recursively so that $x_{k_0}:=y_0$![]() and, if $x_{k_0},\,\ldots,\,x_{k_{n-1}}$
and, if $x_{k_0},\,\ldots,\,x_{k_{n-1}}$![]() are given for some $n\ge 1$
are given for some $n\ge 1$![]() , then $x_{k_n}:=\kappa _n y_n$
, then $x_{k_n}:=\kappa _n y_n$![]() , where $\kappa _n:=(n+\|\sum _{i\le n-1}A_{s_n,k_i}x_{k_i}\|)/\|A_{s_n,k_n}y_n\|$
, where $\kappa _n:=(n+\|\sum _{i\le n-1}A_{s_n,k_i}x_{k_i}\|)/\|A_{s_n,k_n}y_n\|$![]() . Indeed, it follows that
. Indeed, it follows that

for all $n\ge 1$![]() . Since $S\in \mathcal {J}^+$
. Since $S\in \mathcal {J}^+$![]() , we conclude that $\mathcal {J}\text {-}\limsup _n\|A_n\boldsymbol {x}\|\neq 0$
, we conclude that $\mathcal {J}\text {-}\limsup _n\|A_n\boldsymbol {x}\|\neq 0$![]() .
.
Theorem 3.16 Let $A=(A_{n,k})$![]() be a matrix of linear operators in $\mathcal {L}(X,\,Y)$
be a matrix of linear operators in $\mathcal {L}(X,\,Y)$![]() such that $A \in (c_{00}(X,\,\mathcal {I}),\, \ell _\infty (Y))$
such that $A \in (c_{00}(X,\,\mathcal {I}),\, \ell _\infty (Y))$![]() , where $\mathcal {I}$
, where $\mathcal {I}$![]() is a tall ideal on $\omega$
is a tall ideal on $\omega$![]() . Then there exists $k_1 \in \omega$
. Then there exists $k_1 \in \omega$![]() such that $A_{n,k}=0$
such that $A_{n,k}=0$![]() for all $n \in \omega$
for all $n \in \omega$![]() and $k\ge k_1$
and $k\ge k_1$![]() .
.
4. Key tools
Let $A=(A_{n,k})$![]() be a matrix of linear operators in $\mathcal {L}(X,\,Y)$
be a matrix of linear operators in $\mathcal {L}(X,\,Y)$![]() and note that, for each $n \in \omega$
and note that, for each $n \in \omega$![]() and sequence $\boldsymbol {x}$
and sequence $\boldsymbol {x}$![]() taking values on the closed unit ball $B_X$
taking values on the closed unit ball $B_X$![]() , we have
, we have
In this section, we provide sufficient conditions on the matrix $A$![]() and on the ideal $\mathcal {J}$
and on the ideal $\mathcal {J}$![]() for the existence of a sequence $\boldsymbol {x}$
for the existence of a sequence $\boldsymbol {x}$![]() such that the above inequality is actually an equality. The following result is the operator version of the sliding jump argument contained in the proof of [Reference Connor and Leonetti11, Theorem 1.3] for the one-dimensional case $X=Y=\mathbf {R}$
such that the above inequality is actually an equality. The following result is the operator version of the sliding jump argument contained in the proof of [Reference Connor and Leonetti11, Theorem 1.3] for the one-dimensional case $X=Y=\mathbf {R}$![]() and $\mathcal {J}=\mathrm {Fin}$
and $\mathcal {J}=\mathrm {Fin}$![]() .
.
Theorem 4.1 Let $\mathcal {J}$![]() be an ideal on $\omega$
be an ideal on $\omega$![]() which is countably generated. Let also $A=(A_{n,k})$
which is countably generated. Let also $A=(A_{n,k})$![]() be a matrix of linear operators in $\mathcal {L}(X,\,Y)$
be a matrix of linear operators in $\mathcal {L}(X,\,Y)$![]() which satisfies conditions (T1$^\flat$
which satisfies conditions (T1$^\flat$![]() ) for some $k_0 \in \omega$
) for some $k_0 \in \omega$![]() , (T3$^{\natural }$
, (T3$^{\natural }$![]() ), and (T6$^\flat$
), and (T6$^\flat$![]() ). Then there exists a sequence $\boldsymbol {x}$
). Then there exists a sequence $\boldsymbol {x}$![]() with values on the unit sphere $S_X$
with values on the unit sphere $S_X$![]() such that
such that
Proof. Suppose that $\mathcal {J}$![]() is generated by an increasing sequence of sets $(Q_n)$
is generated by an increasing sequence of sets $(Q_n)$![]() , and define
, and define
It follows by (T6$^\flat$![]() ) that
) that
Hence there exists $J_1 \in \mathcal {J}^\star$![]() such that $\|A_{n, \le k_0}\|\le 1$
such that $\|A_{n, \le k_0}\|\le 1$![]() for all $n\in J_1$
for all $n\in J_1$![]() . Setting $J_2:=J_0\cap J_1 \in \mathcal {J}^\star$
. Setting $J_2:=J_0\cap J_1 \in \mathcal {J}^\star$![]() , it follows that
, it follows that
which is finite by condition (T1$^\flat$![]() ). This proves that $\eta _0 \neq \infty$
). This proves that $\eta _0 \neq \infty$![]() . Moreover, if $\eta _0=0$
. Moreover, if $\eta _0=0$![]() , it is enough to let $\boldsymbol {x}$
, it is enough to let $\boldsymbol {x}$![]() be an arbitrary sequence with values in $S_X$
be an arbitrary sequence with values in $S_X$![]() , thanks to (4.1). Hence, let us assume hereafter that $\eta _0 \in (0,\,\infty )$
, thanks to (4.1). Hence, let us assume hereafter that $\eta _0 \in (0,\,\infty )$![]() .
.
At this point, for each $n \in \omega$![]() , define the set
, define the set
and note that $(E_n)$![]() is a decreasing sequence of sets in $\mathcal {J}^+$
is a decreasing sequence of sets in $\mathcal {J}^+$![]() . Define also two strictly increasing sequences $(s_n)$
. Define also two strictly increasing sequences $(s_n)$![]() and $(m_n)$
and $(m_n)$![]() of nonnegative integers, a descreasing sequence $(H_n)$
of nonnegative integers, a descreasing sequence $(H_n)$![]() of sets of $\mathcal {J}^\star$
of sets of $\mathcal {J}^\star$![]() , and a decreasing sequence $(S_n)$
, and a decreasing sequence $(S_n)$![]() of sets in $\mathcal {J}^+$
of sets in $\mathcal {J}^+$![]() as it follows. Set $s_0:=\min S_0$
as it follows. Set $s_0:=\min S_0$![]() , with $S_0:=E_0$
, with $S_0:=E_0$![]() , $H_0:=\omega$
, $H_0:=\omega$![]() , and choose $m_0 \in \omega$
, and choose $m_0 \in \omega$![]() such that $\|A_{s_0, \ge m_0}\|\le \eta _0$
such that $\|A_{s_0, \ge m_0}\|\le \eta _0$![]() , which is possible by (T3$^{\natural }$
, which is possible by (T3$^{\natural }$![]() ). Now, suppose that $s_0,\,\ldots,\,s_{n-1},\,m_0,\,\ldots,\,m_{n-1} \in \omega$
). Now, suppose that $s_0,\,\ldots,\,s_{n-1},\,m_0,\,\ldots,\,m_{n-1} \in \omega$![]() and the sets $S_0,\,\ldots,\,S_{n-1}\in \mathcal {J}^+$
and the sets $S_0,\,\ldots,\,S_{n-1}\in \mathcal {J}^+$![]() and $H_0,\,\ldots,\,H_{n-1} \in \mathcal {J}^\star$
and $H_0,\,\ldots,\,H_{n-1} \in \mathcal {J}^\star$![]() have been defined for some $n\ge 1$
have been defined for some $n\ge 1$![]() .
.
(i) Set $H_n:=H_{n-1} \cap \left \{t \in \omega : \|A_{t,m_{n-1}}\|\le {\eta _0}/{2^n}\right \}$
 , so that $H_n \in \mathcal {J}^\star$
, so that $H_n \in \mathcal {J}^\star$ by (4.2);
by (4.2);(ii) Define $S_n:=E_n \cap H_n$
 , hence $S_n \in \mathcal {J}^+$
, hence $S_n \in \mathcal {J}^+$ and
(4.4)\begin{equation} \forall t\in S_n, \quad \|A_{t,\le m_{n-1}}\|\le \frac{\eta_0}{2^{n}}. \end{equation}
and
(4.4)\begin{equation} \forall t\in S_n, \quad \|A_{t,\le m_{n-1}}\|\le \frac{\eta_0}{2^{n}}. \end{equation}
(iii) Choose $s_n \in S_{n}\setminus Q_z$
 , where $k$
, where $k$ is an integer such that $s_{n-1} \in Q_k$
is an integer such that $s_{n-1} \in Q_k$ . In particular, $s_n>s_{n-1}$
. In particular, $s_n>s_{n-1}$ . Note that this is possible since $S_{n}\setminus Q_k \in \mathcal {J}^+$
. Note that this is possible since $S_{n}\setminus Q_k \in \mathcal {J}^+$ .
.(iv) Lastly, thanks to (T3$^{\natural }$
 ), choose $m_n>m_{n-1}$
), choose $m_n>m_{n-1}$ such that
(4.5)\begin{equation} \|A_{s_n, \ge m_n}\| \le \frac{\eta_0}{2^{n}}. \end{equation}
such that
(4.5)\begin{equation} \|A_{s_n, \ge m_n}\| \le \frac{\eta_0}{2^{n}}. \end{equation}
To conclude the proof, let $\boldsymbol {x}=(x_n)$![]() be a sequence taking values on the unit sphere $S_X$
be a sequence taking values on the unit sphere $S_X$![]() such that
such that
where $M_n:=\{k \in \omega : m_{n-1}< k\le m_n\}$![]() , and $x_n$
, and $x_n$![]() is arbitrarily chosen on the unit sphere $S_X$
is arbitrarily chosen on the unit sphere $S_X$![]() for all $n \in [0,\,m_0]$
for all $n \in [0,\,m_0]$![]() . It follows by (4.3)–(4.6) that
. It follows by (4.3)–(4.6) that

It follows by construction that we cannot find an integer $k$![]() such that $s_n \in Q_k$
such that $s_n \in Q_k$![]() for all $n \in \omega$
for all $n \in \omega$![]() . Therefore $\{s_n: n \in \omega \} \in \mathcal {J}^+$
. Therefore $\{s_n: n \in \omega \} \in \mathcal {J}^+$![]() and $\mathcal {J}\text {-}\limsup _n \|A_n\boldsymbol {x}\| \ge \eta _0$
and $\mathcal {J}\text {-}\limsup _n \|A_n\boldsymbol {x}\| \ge \eta _0$![]() .
.
The converse inequality follows by (4.1), completing the proof.
Related results (in the case $X=Y=\mathbf {R}$![]() and $\mathcal {J}=\mathrm {Fin}$
and $\mathcal {J}=\mathrm {Fin}$![]() ) can be found in [Reference Agnew1, Lemma 3.1] and [Reference Simons40, Corollary 12]. The following corollary is immediate (we omit details):
) can be found in [Reference Agnew1, Lemma 3.1] and [Reference Simons40, Corollary 12]. The following corollary is immediate (we omit details):
Corollary 4.2 With the same hypothesis of theorem 4.1, for each $E\subseteq \omega$![]() , there exists a sequence $\boldsymbol {x}$
, there exists a sequence $\boldsymbol {x}$![]() taking values on $S_X\cup \{0\}$
taking values on $S_X\cup \{0\}$![]() and supported on $E$
and supported on $E$![]() such that
such that
In the finite-dimensional case, the statement can be simplified:
Corollary 4.3 With the same notations of corollary 2.11, suppose that $X=\mathbf {R}^d$![]() , $Y=\mathbf {R}^m$
, $Y=\mathbf {R}^m$![]() , and that $\mathcal {J}$
, and that $\mathcal {J}$![]() is countably generated. Let also $A$
is countably generated. Let also $A$![]() be a matrix which satisfies:
be a matrix which satisfies:
(K1) $\sup _{n \in J_0} \sum _k\sum _{i,j}\left |a_{n,k}(i,\,j)\right |<\infty$
 for some $J_0 \in \mathcal {J}^\star$
for some $J_0 \in \mathcal {J}^\star$ ;
;(K2) $\sum _k\sum _{i,j}\left |a_{n,k}(i,\,j)\right |<\infty$
 for all $n \in \omega$
for all $n \in \omega$ ;
;(K3) $\mathcal {J}\text {-}\lim _n \sum _{i,j}\left |a_{n,k}(i,\,j)\right |=0$
 for all $k \in \omega$
for all $k \in \omega$ .
.
Then, for each $E\subseteq \omega$![]() , there exists a sequence $\boldsymbol {x}=(x^{(0)},\,x^{(1)},\,\ldots )$
, there exists a sequence $\boldsymbol {x}=(x^{(0)},\,x^{(1)},\,\ldots )$![]() taking values on $S_X\cup \{0\}$
taking values on $S_X\cup \{0\}$![]() and supported on $E$
and supported on $E$![]() such that
such that
Proof. Conditions (K1) and (K2) correspond to (T1$^\flat$![]() ), and (K3) corresponds to (T6$^\flat$
), and (K3) corresponds to (T6$^\flat$![]() ), cf. the proof of corollary 2.11. In addition, (T1$^\flat$
), cf. the proof of corollary 2.11. In addition, (T1$^\flat$![]() ) implies (T3$^{\natural }$
) implies (T3$^{\natural }$![]() ) by proposition 2.8(v) and remark 5.1 below. The claim follows by corollary 4.2.
) by proposition 2.8(v) and remark 5.1 below. The claim follows by corollary 4.2.
Remark 4.4 As it has been previously observed in remark 2.3, there exists a matrix $A$![]() which does not satisfy condition (T6$^\flat$
which does not satisfy condition (T6$^\flat$![]() ) with $\mathcal {J}=\mathrm {Fin}$
) with $\mathcal {J}=\mathrm {Fin}$![]() (which corresponds to (S4)) and, on other hand, it satisfies (T5) with $\mathcal {I}=\mathcal {J}=\mathrm {Fin}$
(which corresponds to (S4)) and, on other hand, it satisfies (T5) with $\mathcal {I}=\mathcal {J}=\mathrm {Fin}$![]() (which corresponds to (S3)). In addition, it is immediate to see that $A$
(which corresponds to (S3)). In addition, it is immediate to see that $A$![]() satisfies (T1) and (T3$^{\natural }$
satisfies (T1) and (T3$^{\natural }$![]() ) since $A_{n,k}=0$
) since $A_{n,k}=0$![]() for all $n\ge 0$
for all $n\ge 0$![]() and $k>0$
and $k>0$![]() . However, in this case, the conclusion of theorem 4.1 fails: indeed, if $\boldsymbol {x}=(x_0,\,x_1,\,\ldots )$
. However, in this case, the conclusion of theorem 4.1 fails: indeed, if $\boldsymbol {x}=(x_0,\,x_1,\,\ldots )$![]() is a sequence taking values on the closed unit ball of $\ell _2$
is a sequence taking values on the closed unit ball of $\ell _2$![]() then $\lim _n\|A_n\boldsymbol {x}\|=\lim _n\|A_{n,0}x_0\|= 0$
then $\lim _n\|A_n\boldsymbol {x}\|=\lim _n\|A_{n,0}x_0\|= 0$![]() , and $\|A_{n,\omega }\|=\|A_{n,0}\|=1$
, and $\|A_{n,\omega }\|=\|A_{n,0}\|=1$![]() for all $n\in \omega$
for all $n\in \omega$![]() . Hence we cannot replace (T6$^\flat$
. Hence we cannot replace (T6$^\flat$![]() ) in theorem 4.1 with the weaker pointwise condition $\mathcal {J}\text {-}\lim _nA_{n,k}=0$
) in theorem 4.1 with the weaker pointwise condition $\mathcal {J}\text {-}\lim _nA_{n,k}=0$![]() for all $k\in \omega$
for all $k\in \omega$![]() (namely, (T5) with $\mathcal {I}=\mathrm {Fin}$
(namely, (T5) with $\mathcal {I}=\mathrm {Fin}$![]() ).
).
However, the weaker condition above is sufficient to obtain the same claim if $\eta _0=\infty$![]() ; note that, as it has been shown above, this case is impossible with the hypotheses of theorem 4.1.
; note that, as it has been shown above, this case is impossible with the hypotheses of theorem 4.1.
Theorem 4.5 Let $\mathcal {J}$![]() be an ideal on $\omega$
be an ideal on $\omega$![]() which is countably generated. Let also $A=(A_{n,k})$
which is countably generated. Let also $A=(A_{n,k})$![]() be a matrix of linear operators in $\mathcal {L}(X,\,Y)$
be a matrix of linear operators in $\mathcal {L}(X,\,Y)$![]() which satisfies conditions (T3$^{\natural }$
which satisfies conditions (T3$^{\natural }$![]() ) and (T5) with $\mathcal {I}=\mathrm {Fin}$
) and (T5) with $\mathcal {I}=\mathrm {Fin}$![]() . In addition, assume that $\mathcal {J}\text {-}\limsup \nolimits _n \|A_{n,\ge f(n)}\|=\infty$
. In addition, assume that $\mathcal {J}\text {-}\limsup \nolimits _n \|A_{n,\ge f(n)}\|=\infty$![]() .
.
Then there exists a sequence $\boldsymbol {x}$![]() with values on $S_X$
with values on $S_X$![]() such that $\mathcal {J}\text {-}\limsup \nolimits _n \|A_n\boldsymbol {x}\|=\infty$
such that $\mathcal {J}\text {-}\limsup \nolimits _n \|A_n\boldsymbol {x}\|=\infty$![]() .
.
Proof. We proceed with the same strategy of the proof of theorem 4.1. Note that (T3$^{\natural }$![]() ) implies (T1$^{\flat \flat }$
) implies (T1$^{\flat \flat }$![]() ). Accordingly, define $E_n:=\{t \in \omega : \|A_{t,\ge f(t)}\| \ge n\}$
). Accordingly, define $E_n:=\{t \in \omega : \|A_{t,\ge f(t)}\| \ge n\}$![]() , which belongs to $\mathcal {J}^+$
, which belongs to $\mathcal {J}^+$![]() for each $n \in \omega$
for each $n \in \omega$![]() . Set $s_0:=\min S_0$
. Set $s_0:=\min S_0$![]() , with $S_0:=E_0$
, with $S_0:=E_0$![]() , $H_0:=\omega$
, $H_0:=\omega$![]() , choose $m_0 \in \omega$
, choose $m_0 \in \omega$![]() such that $\|A_{s_0,\ge m_0}\|\le 1$
such that $\|A_{s_0,\ge m_0}\|\le 1$![]() , which is possible by (T3$^{\natural }$
, which is possible by (T3$^{\natural }$![]() ), and pick some arbitrary vectors $x_0,\,\ldots,\,x_{m_0} \in S_X$
), and pick some arbitrary vectors $x_0,\,\ldots,\,x_{m_0} \in S_X$![]() .
.
Now, suppose that, for some $n\ge 1$![]() , all the integers $s_i,\, m_i$
, all the integers $s_i,\, m_i$![]() , sets $S_i,\, H_i\subseteq \omega$
, sets $S_i,\, H_i\subseteq \omega$![]() , and vectors $x_j$
, and vectors $x_j$![]() have been defined for all $i\le n-1$
have been defined for all $i\le n-1$![]() and $j\le m_{n-1}$
and $j\le m_{n-1}$![]() . Then, define recursively
. Then, define recursively
which belongs to $\mathcal {J}^\star$![]() thanks to (T5) with $\mathcal {I}=\mathrm {Fin}$
thanks to (T5) with $\mathcal {I}=\mathrm {Fin}$![]() . Define $S_n$
. Define $S_n$![]() and $s_n$
and $s_n$![]() as in the proof of theorem 4.1, and $m_n>m_{n-1}$
as in the proof of theorem 4.1, and $m_n>m_{n-1}$![]() such that $\|A_{s_n,\ge m_n}\|\le 1$
such that $\|A_{s_n,\ge m_n}\|\le 1$![]() , which is possible again by (T3$^{\natural }$
, which is possible again by (T3$^{\natural }$![]() ). Finally, we choose some vectors $\{x_k: k \in M_n\}$
). Finally, we choose some vectors $\{x_k: k \in M_n\}$![]() on the unit sphere $S_X$
on the unit sphere $S_X$![]() such that $\|\sum _{k \in M_n}A_{s_n,k}x_k\| \ge \|A_{s_n,M_n}\|-1$
such that $\|\sum _{k \in M_n}A_{s_n,k}x_k\| \ge \|A_{s_n,M_n}\|-1$![]() . (Here, differently from the previous proof, the sequence $\boldsymbol {x}$
. (Here, differently from the previous proof, the sequence $\boldsymbol {x}$![]() has been constructed recursively.) Reasoning as in (4.7), we conclude that
has been constructed recursively.) Reasoning as in (4.7), we conclude that
Therefore $\mathcal {J}\text {-}\limsup _n \|A_n\boldsymbol {x}\|=\infty$![]() .
.
As a consequence of the results above, we obtain an ideal version of the Hahn–Schur theorem (where the classical version corresponds to the case $\mathcal {J}=\mathrm {Fin}$![]() ):
):
Theorem 4.6 Let $\mathcal {J}$![]() be a countably generated ideal. Let also $A=(a_{n,k})$
be a countably generated ideal. Let also $A=(a_{n,k})$![]() be an infinite real matrix such that $\sum _k|a_{n,k}|<\infty$
be an infinite real matrix such that $\sum _k|a_{n,k}|<\infty$![]() for all $n \in \omega$
for all $n \in \omega$![]() and
and
Then $\mathcal {J}\text {-}\lim \nolimits _n \sum \nolimits _{k}|a_{n,k}|=0$![]() .
.
Proof. Set $\eta _0:=\mathcal {J}\text {-}\limsup \nolimits _n \sum _k|a_{n,k}| \in [0,\,\infty ]$![]() . Note also that the standing hypotheses imply (T3$^{\natural }$
. Note also that the standing hypotheses imply (T3$^{\natural }$![]() ) and (T6$^\flat$
) and (T6$^\flat$![]() ). In addition, if $\eta _0<\infty$
). In addition, if $\eta _0<\infty$![]() , then (T1) holds. It follows by theorems 4.1 and 4.5 that there exists a real sequence $\boldsymbol {x}$
, then (T1) holds. It follows by theorems 4.1 and 4.5 that there exists a real sequence $\boldsymbol {x}$![]() taking values in $\{1,\,-1\}$
taking values in $\{1,\,-1\}$![]() such that
such that
At this point, define $y_n:=(1+x_n)/2$![]() for all $n \in \omega$
for all $n \in \omega$![]() , so that $\boldsymbol {y}=\boldsymbol {1}_E$
, so that $\boldsymbol {y}=\boldsymbol {1}_E$![]() , where $E:=\{k \in \omega : x_k=1\}$
, where $E:=\{k \in \omega : x_k=1\}$![]() . It follows by (4.8) and (4.9) that
. It follows by (4.8) and (4.9) that

Therefore $\mathcal {J}\text {-}\lim \nolimits _n \sum \nolimits _{k}|a_{n,k}|=0$![]() .
.
Neither (T6$^\flat$![]() ) nor (T5) with $\mathcal {I}=\mathrm {Fin}$
) nor (T5) with $\mathcal {I}=\mathrm {Fin}$![]() will be required for a conclusion as in theorem 4.1 in the case of positive linear operators between certain Banach lattices.
will be required for a conclusion as in theorem 4.1 in the case of positive linear operators between certain Banach lattices.
Proposition 4.7 Let $X$![]() be an AM-space with order unit $e>0$
be an AM-space with order unit $e>0$![]() and let $Y$
and let $Y$![]() be a Banach lattice. Also, let $T=(T_k)$
be a Banach lattice. Also, let $T=(T_k)$![]() be a sequence of linear operators in $\mathcal {L}(X,\,Y)$
be a sequence of linear operators in $\mathcal {L}(X,\,Y)$![]() which are positive and such that $\sum _k T_kx_k$
which are positive and such that $\sum _k T_kx_k$![]() is convergent in the norm of $Y$
is convergent in the norm of $Y$![]() for all sequences $\boldsymbol {x} \in \ell _\infty (X)$
for all sequences $\boldsymbol {x} \in \ell _\infty (X)$![]() . Then
. Then
Proof. Thanks to [Reference Aliprantis and Burkinshaw2, Theorem 3.40], there exists a (unique, up to homeomorphism) compact Hausdorff space $K$![]() and a lattice isometry $h: X\to C(K)$
and a lattice isometry $h: X\to C(K)$![]() such that $h(e)$
such that $h(e)$![]() is the constant function $\boldsymbol {1}$
is the constant function $\boldsymbol {1}$![]() , where $C(K)$
, where $C(K)$![]() is the Banach lattice of continuous functions $f:K\to \mathbf {R}$
is the Banach lattice of continuous functions $f:K\to \mathbf {R}$![]() , endowed with the supremum norm. It follows that the closed unit ball $B_X$
, endowed with the supremum norm. It follows that the closed unit ball $B_X$![]() of $X$
of $X$![]() is simply the order interval $[-e,\,e]$
is simply the order interval $[-e,\,e]$![]() , indeed
, indeed
At this point, let us fix a nonempty $E\subseteq \omega$![]() , a positive integer $n$
, a positive integer $n$![]() with $n\le |E|$
with $n\le |E|$![]() , distinct integers $i_1,\,\ldots,\,i_n \in E$
, distinct integers $i_1,\,\ldots,\,i_n \in E$![]() , and vectors $x_1,\,\ldots,\,x_n \in X$
, and vectors $x_1,\,\ldots,\,x_n \in X$![]() such that $|x_k|\le e$
such that $|x_k|\le e$![]() for all $k \in \{1,\,\ldots,\,n\}$
for all $k \in \{1,\,\ldots,\,n\}$![]() . By the fact that each $T_{k}$
. By the fact that each $T_{k}$![]() is a positive linear operator and [Reference Aliprantis and Burkinshaw2, Theorem 1.7(2)], it follows that
is a positive linear operator and [Reference Aliprantis and Burkinshaw2, Theorem 1.7(2)], it follows that
By the definition of group norm and the compatibility between the norm and the order structure in $X$![]() , we obtain
, we obtain
which concludes the proof.
In the same spirit of corollary 4.2, we obtain the following consequence:
Corollary 4.8 Let $X$![]() be an AM-space with order unit $e>0$
be an AM-space with order unit $e>0$![]() and let $Y$
and let $Y$![]() be a Banach lattice. Also, let $\mathcal {J}$
be a Banach lattice. Also, let $\mathcal {J}$![]() be an ideal of $\omega$
be an ideal of $\omega$![]() , and $A=(A_{n,k})$
, and $A=(A_{n,k})$![]() be a matrix of positive linear operators such that $A \in (\ell _\infty (X),\, \ell _\infty (Y))$
be a matrix of positive linear operators such that $A \in (\ell _\infty (X),\, \ell _\infty (Y))$![]() . Then
. Then
where $x_n=e$![]() if $n \in E$
if $n \in E$![]() and $x_n=0$
and $x_n=0$![]() otherwise.
otherwise.
Proof. Proposition 4.7 implies that $\|A_{n,E}\|=\|\sum \nolimits _{k \in E}A_{n,k}e\|=\|A_n\boldsymbol {x}\|$![]() for all $n$
for all $n$![]() .
.
5. Main proofs
Proof Proof of theorem 2.5
If part. Suppose that (T1)–(T5) hold and fix a bounded sequence $\boldsymbol {x}$![]() which is $\mathcal {I}$
which is $\mathcal {I}$![]() -convergent to $\eta \in X$
-convergent to $\eta \in X$![]() . Thanks to (T3), $A_n\boldsymbol {x}$
. Thanks to (T3), $A_n\boldsymbol {x}$![]() is well defined for each $n \in \omega$
is well defined for each $n \in \omega$![]() . In addition, we obtain by (T1) and (T2) that inequality (3.1) holds for all $n$
. In addition, we obtain by (T1) and (T2) that inequality (3.1) holds for all $n$![]() (indeed, in our case $J_0=J_1=\omega$
(indeed, in our case $J_0=J_1=\omega$![]() ), proving that $A\boldsymbol {x} \in \ell _\infty (Y)$
), proving that $A\boldsymbol {x} \in \ell _\infty (Y)$![]() .
.
First, suppose that $\eta =0$![]() . Fix $\varepsilon >0$
. Fix $\varepsilon >0$![]() and define
and define
and $E:=\{n \in \omega : n< k_0 \text { or }\|x_n\|>\delta \}$![]() . Note that $E \in \mathcal {I}$
. Note that $E \in \mathcal {I}$![]() and that, again by (T3), $(\sum _{k \in E}A_{n,k}x_k: n \in \omega )$
and that, again by (T3), $(\sum _{k \in E}A_{n,k}x_k: n \in \omega )$![]() is a well-defined sequence in $Y$
is a well-defined sequence in $Y$![]() . In addition,
. In addition,
by (T5). Now, suppose that $\|A_n\boldsymbol {x}\|> \varepsilon$![]() for some $n \in \omega$
for some $n \in \omega$![]() . It follows that
. It follows that
By the definition of $\delta$![]() , this implies that
, this implies that
so that $n \in S$![]() . We conclude that $\{n \in \omega : \|A_n\boldsymbol {x}\|>\varepsilon \}\subseteq S \in \mathcal {J}$
. We conclude that $\{n \in \omega : \|A_n\boldsymbol {x}\|>\varepsilon \}\subseteq S \in \mathcal {J}$![]() . By the arbitrariness of $\varepsilon$
. By the arbitrariness of $\varepsilon$![]() , we obtain $\mathcal {J}\text {-}\lim A\boldsymbol {x}=0$
, we obtain $\mathcal {J}\text {-}\lim A\boldsymbol {x}=0$![]() .
.
At this point, suppose that $\eta \in X$![]() and define $\boldsymbol {y} \in X^\omega$
and define $\boldsymbol {y} \in X^\omega$![]() such that $y_n:=x_n-\eta$
such that $y_n:=x_n-\eta$![]() for all $n$
for all $n$![]() . Note that $\boldsymbol {y} \in c_0^b(X,\,\mathcal {I})$
. Note that $\boldsymbol {y} \in c_0^b(X,\,\mathcal {I})$![]() , hence by the previous case $A\boldsymbol {y}\in c_{0}^b(Y,\,\mathcal {J})$
, hence by the previous case $A\boldsymbol {y}\in c_{0}^b(Y,\,\mathcal {J})$![]() . It follows by (T4) that
. It follows by (T4) that
which proves that $A$![]() is $(\mathcal {I},\, \mathcal {J})$
is $(\mathcal {I},\, \mathcal {J})$![]() -regular with respect to $T$
-regular with respect to $T$![]() .
.
Only If part. Assume that $A$![]() is $(\mathcal {I},\, \mathcal {J})$
is $(\mathcal {I},\, \mathcal {J})$![]() -regular with respect to $T$
-regular with respect to $T$![]() . Hence, the matrix $A$
. Hence, the matrix $A$![]() belongs, in particular, to $(c(X),\, \ell _\infty (Y))$
belongs, in particular, to $(c(X),\, \ell _\infty (Y))$![]() . It follows by theorem 3.10 that conditions (T1) and (T2) hold. Also, for each $n \in \omega$
. It follows by theorem 3.10 that conditions (T1) and (T2) hold. Also, for each $n \in \omega$![]() , the sum $\sum _kA_{n,k}x_k$
, the sum $\sum _kA_{n,k}x_k$![]() is convergent in the norm of $Y$
is convergent in the norm of $Y$![]() for all sequences $\boldsymbol {x} \in c^b(X,\,\mathcal {I})$
for all sequences $\boldsymbol {x} \in c^b(X,\,\mathcal {I})$![]() , hence (T3) holds. Moreover, for each $x \in X$
, hence (T3) holds. Moreover, for each $x \in X$![]() , the constant sequence $(x,\,x,\,\ldots )$
, the constant sequence $(x,\,x,\,\ldots )$![]() has $\mathcal {I}$
has $\mathcal {I}$![]() -limit $x$
-limit $x$![]() , hence $\mathcal {J}\text {-}\lim _n\sum \nolimits _kA_{n,k}x=Tx$
, hence $\mathcal {J}\text {-}\lim _n\sum \nolimits _kA_{n,k}x=Tx$![]() , which is condition (T4).
, which is condition (T4).
Lastly, fix $\boldsymbol {x}\in c_{00}^b(X,\,\mathcal {I})$![]() , so that $\mathcal {I}\text {-}\lim \boldsymbol {x}=0$
, so that $\mathcal {I}\text {-}\lim \boldsymbol {x}=0$![]() . By the $(\mathcal {I},\, \mathcal {J})$
. By the $(\mathcal {I},\, \mathcal {J})$![]() -regularity of $A$
-regularity of $A$![]() with respect to $T$
with respect to $T$![]() , we obtain that $A\boldsymbol {x}$
, we obtain that $A\boldsymbol {x}$![]() is well defined and $\mathcal {J}\text {-}\lim A\boldsymbol {x}=T(0)=0$
is well defined and $\mathcal {J}\text {-}\lim A\boldsymbol {x}=T(0)=0$![]() . This proves (T5).
. This proves (T5).
The second part of the statement follows by proposition 2.8(iv).
Proof Proof of proposition 2.8
(i) Condition (T4) implies that $\sum _kA_{n,k}$![]() is convergent in strong operator topology for each $n \in \omega$
is convergent in strong operator topology for each $n \in \omega$![]() . The conclusion follows by lemma 3.2
. The conclusion follows by lemma 3.2
(ii) For all $k \in \omega$![]() and $x \in X$
and $x \in X$![]() , if $\lim _n A_{n,k}x=0$
, if $\lim _n A_{n,k}x=0$![]() then $\sup _n \|A_{n,k}x\|<\infty$
then $\sup _n \|A_{n,k}x\|<\infty$![]() .
.
(iii) It follows by lemma 3.1.
(iv) Since $A$![]() belongs to $(c(X),\, \ell _\infty (Y))$
belongs to $(c(X),\, \ell _\infty (Y))$![]() , the claim follows by theorem 3.7.
, the claim follows by theorem 3.7.
(v) It is known that each $A_{n,k}$![]() is bounded. The second part follows by lemma 3.1 and corollary 3.3. (Note that this is not necessarily true if $\mathrm {dim}(X)=\infty$
is bounded. The second part follows by lemma 3.1 and corollary 3.3. (Note that this is not necessarily true if $\mathrm {dim}(X)=\infty$![]() , cf. remark 3.9.)
, cf. remark 3.9.)
(vi) Given $k \in \omega$![]() and $x \in X$
and $x \in X$![]() , the sequence $\boldsymbol {x}$
, the sequence $\boldsymbol {x}$![]() defined by $x_n=x$
defined by $x_n=x$![]() if $n=k$
if $n=k$![]() and $x_n=0$
and $x_n=0$![]() otherwise has $\mathcal {I}$
otherwise has $\mathcal {I}$![]() -limit $0$
-limit $0$![]() , hence $\mathcal {J}\text {-}\lim _nA_{n,k}x=T(0)=0$
, hence $\mathcal {J}\text {-}\lim _nA_{n,k}x=T(0)=0$![]() . This claim follows by lemma 3.4.
. This claim follows by lemma 3.4.
(vii) For all $n,\,k \in \omega$![]() , there exists $a_{n,k} \in \mathbf {R}$
, there exists $a_{n,k} \in \mathbf {R}$![]() such that $A_{n,k}=a_{n,k}A_0$
such that $A_{n,k}=a_{n,k}A_0$![]() . Note also that
. Note also that
Hence condition (T1) implies that $A_0$![]() is necessarily bounded, $k_0=0$
is necessarily bounded, $k_0=0$![]() can be chosen by point (iv) above, and hence $\sup _n\sum \nolimits _k|a_{n,k}|<\infty$
can be chosen by point (iv) above, and hence $\sup _n\sum \nolimits _k|a_{n,k}|<\infty$![]() . Thanks to (5.2), it is immediate to conclude that $\lim _k\|A_{n,\ge k}\|=\|A_0\|\lim _k \sum _{t\ge k}|a_{n,t}|=0$
. Thanks to (5.2), it is immediate to conclude that $\lim _k\|A_{n,\ge k}\|=\|A_0\|\lim _k \sum _{t\ge k}|a_{n,t}|=0$![]() for all $n \in \omega$
for all $n \in \omega$![]() .
.
(viii) By point (vii) above, $A_0$![]() is bounded. Moreover, if $A_0=0$
is bounded. Moreover, if $A_0=0$![]() the claim is obvious. Otherwise, there exists $x \in X$
the claim is obvious. Otherwise, there exists $x \in X$![]() such that $A_0x\neq 0$
such that $A_0x\neq 0$![]() and by (T5) we obtain $\mathcal {J}\text {-}\lim _n A_{n,k}x=0$
and by (T5) we obtain $\mathcal {J}\text {-}\lim _n A_{n,k}x=0$![]() , so that $\|A_0x\|\cdot \mathcal {J}\text {-}\lim _n|a_{n,k}|=0$
, so that $\|A_0x\|\cdot \mathcal {J}\text {-}\lim _n|a_{n,k}|=0$![]() for all $k \in \omega$
for all $k \in \omega$![]() . It follows that $\mathcal {J}\text {-}\lim _n\|A_{n,k}\|=\|A_0\|\cdot \mathcal {J}\text {-}\lim _n|a_{n,k}|=0$
. It follows that $\mathcal {J}\text {-}\lim _n\|A_{n,k}\|=\|A_0\|\cdot \mathcal {J}\text {-}\lim _n|a_{n,k}|=0$![]() .
.
Remark 5.1 As it is evident from the above proofs, the statements of proposition 2.8(i), (iii), (v), (vii), and (viii) are correct also replacing (T1) with the weaker condition (T1$^{\flat \flat }$![]() ).
).
Proof Proof of theorem 2.9
First, assume that $A$![]() is $(\mathcal {I},\, \mathcal {J})$
is $(\mathcal {I},\, \mathcal {J})$![]() -regular with respect to $T$
-regular with respect to $T$![]() , with $\mathcal {J}$
, with $\mathcal {J}$![]() countably generated. Then (T1) and (T4) holds by theorem 2.5. Now, fix $\boldsymbol {x} \in c_{00}^b(X,\, \mathcal {I})$
countably generated. Then (T1) and (T4) holds by theorem 2.5. Now, fix $\boldsymbol {x} \in c_{00}^b(X,\, \mathcal {I})$![]() . Then $\mathcal {I}\text {-}\lim \boldsymbol {x}=0$
. Then $\mathcal {I}\text {-}\lim \boldsymbol {x}=0$![]() and, since $A$
and, since $A$![]() is $(\mathcal {I},\, \mathcal {J})$
is $(\mathcal {I},\, \mathcal {J})$![]() -regular, we obtain $\mathcal {J}\text {-}\lim A\boldsymbol {x}=0$
-regular, we obtain $\mathcal {J}\text {-}\lim A\boldsymbol {x}=0$![]() , namely, $\mathcal {J}\text {-}\lim _n \|A_n\boldsymbol {x}\|=0$
, namely, $\mathcal {J}\text {-}\lim _n \|A_n\boldsymbol {x}\|=0$![]() . Then (T6) holds by corollary 4.2.
. Then (T6) holds by corollary 4.2.
Conversely, assume that (T1), (T4), and (T6) hold. Then (T5) holds (since it is implied by (T6)), and conditions (T2) and (T3) hold by proposition 2.8(ii) and (iii), respectively. It follows by theorem 2.5 that $A$![]() is $(\mathcal {I},\, \mathcal {J})$
is $(\mathcal {I},\, \mathcal {J})$![]() -regular with respect to $T$
-regular with respect to $T$![]() .
.
Proof Proof of theorem 2.10
The first proof goes verbatim as in the proof of theorem 2.9, replacing corollary 4.2 with corollary 4.8. Also the second part proceeds similarly, with the difference that (T2) holds by proposition 2.8(iv): indeed, thanks to [Reference Aliprantis and Burkinshaw3, Theorem 4.3], each positive linear operator $A_{n,k}$![]() between Banach lattices is necessarily continuous.
between Banach lattices is necessarily continuous.
Proof Proof of corollary 2.11
Endow $\mathbf {R}^d$![]() and $\mathbf {R}^m$
and $\mathbf {R}^m$![]() with the corresponding $1$
with the corresponding $1$![]() -norm, as in the proof of corollary 3.3, so that $\|A_{n,k}\|=\max \nolimits _j\sum \nolimits _i|a_{n,k}(i,\,j)|$
-norm, as in the proof of corollary 3.3, so that $\|A_{n,k}\|=\max \nolimits _j\sum \nolimits _i|a_{n,k}(i,\,j)|$![]() , cf. e.g. [Reference Horn and Johnson20, Example 5.6.4]. Also, note that, for all $n \in \omega$
, cf. e.g. [Reference Horn and Johnson20, Example 5.6.4]. Also, note that, for all $n \in \omega$![]() and $E\subseteq \omega$
and $E\subseteq \omega$![]() ,
,
Accordingly, conditions (F1), (F2), and (F3) are simply a rewriting of (T1), (T4), and (T6), respectively, with $k_0=0$![]() (which can be chosen thanks to proposition 2.8(v) and (iv); in particular, in the following subcases, condition (T2) is void).
(which can be chosen thanks to proposition 2.8(v) and (iv); in particular, in the following subcases, condition (T2) is void).
Case $\mathcal {I}=\mathrm {Fin}$![]() : First, assume that $A$
: First, assume that $A$![]() is $(\mathcal {I},\,\mathcal {J})$
is $(\mathcal {I},\,\mathcal {J})$![]() -regular with respect to $T$
-regular with respect to $T$![]() . Then (T1) and (T4) hold by theorem 2.5. In addition, by proposition 2.8(vi) also (T6$^\flat$
. Then (T1) and (T4) hold by theorem 2.5. In addition, by proposition 2.8(vi) also (T6$^\flat$![]() ) holds. At this point, fix $E \in \mathrm {Fin}$
) holds. At this point, fix $E \in \mathrm {Fin}$![]() and note that $\|A_{n,E}\|\le \sum _{k \in E}\|A_{n,k}\|$
and note that $\|A_{n,E}\|\le \sum _{k \in E}\|A_{n,k}\|$![]() . Taking $\mathcal {J}$
. Taking $\mathcal {J}$![]() -limits on both sides, we obtain (T6). Conversely, assume that (T1), (T4) and (T6) hold. Then (T6) implies (T5). And (T3) holds by proposition 2.8(iii) and (v). Hence $A$
-limits on both sides, we obtain (T6). Conversely, assume that (T1), (T4) and (T6) hold. Then (T6) implies (T5). And (T3) holds by proposition 2.8(iii) and (v). Hence $A$![]() is $(\mathcal {I},\, \mathcal {J})$
is $(\mathcal {I},\, \mathcal {J})$![]() -regular with respect to $T$
-regular with respect to $T$![]() by theorem 2.5.
by theorem 2.5.
Case $\mathcal {J}$![]() is countably generated: If $A$
is countably generated: If $A$![]() is $(\mathcal {I},\,\mathcal {J})$
is $(\mathcal {I},\,\mathcal {J})$![]() -regular with respect to $T$
-regular with respect to $T$![]() , then (T1) and (T4) hold by theorem 2.5. In addition, (T3$^{\natural }$
, then (T1) and (T4) hold by theorem 2.5. In addition, (T3$^{\natural }$![]() ) and (T6$^\flat$
) and (T6$^\flat$![]() ) hold by proposition 2.8(v) and (vi). Then (T6) holds by theorem 2.9. The converse goes as in the previous case.
) hold by proposition 2.8(v) and (vi). Then (T6) holds by theorem 2.9. The converse goes as in the previous case.
Case $a_{n,k}(i,\,j)\ge 0$![]() for all $1\le i\le m$
for all $1\le i\le m$![]() , $1\le j\le d$
, $1\le j\le d$![]() , and $n,\,k \in \omega$
, and $n,\,k \in \omega$![]() : Note that $\mathbf {R}^d$
: Note that $\mathbf {R}^d$![]() is an AM-space with order unit $(1,\,\ldots,\,1)$
is an AM-space with order unit $(1,\,\ldots,\,1)$![]() . The proof goes on the same lines of the previous case replacing theorem 2.9 with theorem 2.10.
. The proof goes on the same lines of the previous case replacing theorem 2.9 with theorem 2.10.
Proof Proof of corollary 2.12
Let $\mathcal {I}$![]() and $\mathcal {I}^\prime$
and $\mathcal {I}^\prime$![]() be two maximal ideals such that $\{2\omega,\, 2\omega +1\} \subseteq \mathcal {I}\cup \mathcal {I}^\prime$
be two maximal ideals such that $\{2\omega,\, 2\omega +1\} \subseteq \mathcal {I}\cup \mathcal {I}^\prime$![]() . Since $c^b(\mathbf {R}^d,\,\mathcal {I})=c^b(\mathbf {R}^d,\,\mathcal {I}^\prime )=\ell _\infty (\mathbf {R}^d)$
. Since $c^b(\mathbf {R}^d,\,\mathcal {I})=c^b(\mathbf {R}^d,\,\mathcal {I}^\prime )=\ell _\infty (\mathbf {R}^d)$![]() , we obtain that (F3) holds with both $E=2\omega$
, we obtain that (F3) holds with both $E=2\omega$![]() and $E=2\omega +1$
and $E=2\omega +1$![]() , hence it is equivalent to (F3$^\prime$
, hence it is equivalent to (F3$^\prime$![]() ). In turn, (F3$^\prime$
). In turn, (F3$^\prime$![]() ) implies (F2) with $T=0$
) implies (F2) with $T=0$![]() . The claim follows by corollary 2.11.
. The claim follows by corollary 2.11.
Proof Proof of corollary 2.13
First, suppose that $A$![]() is $(\mathcal {I},\,\mathcal {J})$
is $(\mathcal {I},\,\mathcal {J})$![]() -regular with respect to $T$
-regular with respect to $T$![]() . It follows by theorem 2.5 that conditions (T1)–(T5) hold. Thanks to equation (5.2) above and (T1), there exists $k_0 \in \omega$
. It follows by theorem 2.5 that conditions (T1)–(T5) hold. Thanks to equation (5.2) above and (T1), there exists $k_0 \in \omega$![]() such that $\sup _{n}\|A_{n,\ge k_0}\|=\|A_0\|\sup _n\sum _{k\ge k_0}|a_{n,k}|<\infty$
such that $\sup _{n}\|A_{n,\ge k_0}\|=\|A_0\|\sup _n\sum _{k\ge k_0}|a_{n,k}|<\infty$![]() (since $A_0\neq 0$
(since $A_0\neq 0$![]() ), which implies (M1) and (M2). Condition (M3) is just a rewriting of (T4). In addition, conditions (T3$^{\natural }$
), which implies (M1) and (M2). Condition (M3) is just a rewriting of (T4). In addition, conditions (T3$^{\natural }$![]() ) and (T6$^\flat$
) and (T6$^\flat$![]() ) hold by proposition 2.8(vii)-(viii). It follows that (M4), which is just a rewriting of (T6), holds for the same reasons in the proof of corollary 2.11.
) hold by proposition 2.8(vii)-(viii). It follows that (M4), which is just a rewriting of (T6), holds for the same reasons in the proof of corollary 2.11.
Conversely, assume that conditions (M1)-(M4) hold. (M1) implies that each $A_{n,k}$![]() is bounded, hence it is possible to choose $k_0=0$
is bounded, hence it is possible to choose $k_0=0$![]() by proposition 2.8(iv), hence (T2) holds. Accordingly, (M2), (M3), and (M4) are just rewritings of (T1), (T4), and (T6), respectively. Lastly, (T3) follows by proposition 2.8(iii) and (vii), and (T5) is implied by (T6). To sum up, conditions (T1)–(T5) hold, and the conclusion follows by theorem 2.5.
by proposition 2.8(iv), hence (T2) holds. Accordingly, (M2), (M3), and (M4) are just rewritings of (T1), (T4), and (T6), respectively. Lastly, (T3) follows by proposition 2.8(iii) and (vii), and (T5) is implied by (T6). To sum up, conditions (T1)–(T5) hold, and the conclusion follows by theorem 2.5.
Proof Proof of theorem 2.14
It proceeds on the same lines of the proof of theorem 2.5 (recalling the (T5) implies (T2$^\flat$![]() )), with the only difference that it is not necessarily true that $J_0=J_1=\omega$
)), with the only difference that it is not necessarily true that $J_0=J_1=\omega$![]() but only $J_0,\,J_1 \in \mathcal {J}^\star$
but only $J_0,\,J_1 \in \mathcal {J}^\star$![]() .
.
Proof Proof of corollary 2.15
Proceeding as in the proof of corollary 2.11, note that conditions (R1) and (R2) are simply a rewriting of (T1$^\flat$![]() ), (R3) is a rewriting of (T4), and (R4) is a rewriting of (T6). Since each $A_{n,k}$
), (R3) is a rewriting of (T4), and (R4) is a rewriting of (T6). Since each $A_{n,k}$![]() is bounded, we choose $k_0=f(n)=0$
is bounded, we choose $k_0=f(n)=0$![]() for all $n \in Q_{t_0}$
for all $n \in Q_{t_0}$![]() in the statement of theorem 2.14.
in the statement of theorem 2.14.
First, assume that $A$![]() satisfies (2.2). It follows by theorem 2.14 that (T1$^\flat$
satisfies (2.2). It follows by theorem 2.14 that (T1$^\flat$![]() ), (T4), and (T5) hold. In addition, (T1$^\flat$
), (T4), and (T5) hold. In addition, (T1$^\flat$![]() ) implies (T3$^{\natural }$
) implies (T3$^{\natural }$![]() ) by lemma 3.1 and corollary 3.3; and condition (T6$^\flat$
) by lemma 3.1 and corollary 3.3; and condition (T6$^\flat$![]() ) holds by lemma 3.4. We conclude by corollary 4.2 that $A$
) holds by lemma 3.4. We conclude by corollary 4.2 that $A$![]() satisfies (T6).
satisfies (T6).
Conversely, assume that (T1$^\flat$![]() ), (T4), and (T6) hold. Then (T6) implies (T5). As before, (T1$^\flat$
), (T4), and (T6) hold. Then (T6) implies (T5). As before, (T1$^\flat$![]() ) implies (T3$^{\natural }$
) implies (T3$^{\natural }$![]() ), so that $A$
), so that $A$![]() satisfies (T3) by lemma 3.1. The conclusion follows by theorem 2.14.
satisfies (T3) by lemma 3.1. The conclusion follows by theorem 2.14.
Proof Proof of theorem 2.17
Suppose for the sake of contradiction that such a matrix $A$![]() exists. Since $A \in (c_{00}(X,\,\mathcal {I}),\, \ell _\infty (Y))$
exists. Since $A \in (c_{00}(X,\,\mathcal {I}),\, \ell _\infty (Y))$![]() , it follows by theorem 3.16 that
, it follows by theorem 3.16 that
At this point, since $A$![]() is also $(\mathcal {I},\,\mathcal {J})$
is also $(\mathcal {I},\,\mathcal {J})$![]() -regular with respect to $T$
-regular with respect to $T$![]() , then (T1)–(T5) hold by theorem 2.5. In addition, $T$
, then (T1)–(T5) hold by theorem 2.5. In addition, $T$![]() is a nonzero linear operator, hence there exists (a nonzero) $x \in X$
is a nonzero linear operator, hence there exists (a nonzero) $x \in X$![]() such that $y:=Tx\neq 0$
such that $y:=Tx\neq 0$![]() , and pick $\boldsymbol {x}:=(x,\,x,\,\ldots )$
, and pick $\boldsymbol {x}:=(x,\,x,\,\ldots )$![]() . Since $A$
. Since $A$![]() satisfies (2.5), we obtain that $\mathcal {J}\text {-}\lim A\boldsymbol {x}=y$
satisfies (2.5), we obtain that $\mathcal {J}\text {-}\lim A\boldsymbol {x}=y$![]() . However, it follows by condition (T5) that
. However, it follows by condition (T5) that
providing the desired contradiction.
Proof Proof of theorem 2.20
First, suppose that (T1$^\flat$![]() ), (T3$^{\sharp }$
), (T3$^{\sharp }$![]() ), (T4), and (T5$^{\sharp }$
), (T4), and (T5$^{\sharp }$![]() ) hold for some $k_0 \in \omega$
) hold for some $k_0 \in \omega$![]() . Fix a sequence $\boldsymbol {x}$
. Fix a sequence $\boldsymbol {x}$![]() such that $\mathcal {I}\text {-}\lim \boldsymbol {x}=\eta$
such that $\mathcal {I}\text {-}\lim \boldsymbol {x}=\eta$![]() . By (T3$^{\sharp }$
. By (T3$^{\sharp }$![]() ), $A\boldsymbol {x}$
), $A\boldsymbol {x}$![]() is well defined. Moreover, since (T5$^{\sharp }$
is well defined. Moreover, since (T5$^{\sharp }$![]() ) implies (T2$^\flat$
) implies (T2$^\flat$![]() ), we can pick $\kappa$
), we can pick $\kappa$![]() and $J_1 \in \mathcal {J}^\star$
and $J_1 \in \mathcal {J}^\star$![]() as in the proof of theorem 3.8, and define $E:=\{k \in \omega : \|x_k-\eta \|\ge 1\} \in \mathcal {I}$
as in the proof of theorem 3.8, and define $E:=\{k \in \omega : \|x_k-\eta \|\ge 1\} \in \mathcal {I}$![]() . Using (T5$^{\sharp }$
. Using (T5$^{\sharp }$![]() ), there exists $J_2 \in \mathcal {J}^\star$
), there exists $J_2 \in \mathcal {J}^\star$![]() such that $\left \|\sum _{k \in E, k\ge k_0}A_{n,k}x_k\right \|\le 1$
such that $\left \|\sum _{k \in E, k\ge k_0}A_{n,k}x_k\right \|\le 1$![]() for all $n \in J_2$
for all $n \in J_2$![]() . At this point, it follows by (T1$^\flat$
. At this point, it follows by (T1$^\flat$![]() ) that
) that

for all $n \in J$![]() , where $J:=J_0\cap J_1\cap J_2 \in \mathcal {J}^\star$
, where $J:=J_0\cap J_1\cap J_2 \in \mathcal {J}^\star$![]() . Therefore $A\boldsymbol {x} \in \ell _\infty (Y,\,\mathcal {J})$
. Therefore $A\boldsymbol {x} \in \ell _\infty (Y,\,\mathcal {J})$![]() .
.
We conclude as in the proof of theorem 2.5 that $A$![]() satisfies (2.6), with the only difference that Inequality (5.1) holds for all $n \in J_0$
satisfies (2.6), with the only difference that Inequality (5.1) holds for all $n \in J_0$![]() , once we replace $\sup _t\|A_{t,\ge k_0}\|$
, once we replace $\sup _t\|A_{t,\ge k_0}\|$![]() with $\sup _{t\in J_0}\|A_{t,\ge k_0}\|$
with $\sup _{t\in J_0}\|A_{t,\ge k_0}\|$![]() .
.
Conversely, if $A$![]() satisfies (2.6), then (T3$^{\sharp }$
satisfies (2.6), then (T3$^{\sharp }$![]() ) holds because the sequence $A\boldsymbol {x}$
) holds because the sequence $A\boldsymbol {x}$![]() is well defined for each $\boldsymbol {x} \in c(X,\,\mathcal {I})$
is well defined for each $\boldsymbol {x} \in c(X,\,\mathcal {I})$![]() ; moreover, $A\in (c^b(X,\,\mathcal {I}),\, c(Y,\,\mathcal {J}))$
; moreover, $A\in (c^b(X,\,\mathcal {I}),\, c(Y,\,\mathcal {J}))$![]() , and it follows by theorem 2.14 that conditions (T1$^\flat$
, and it follows by theorem 2.14 that conditions (T1$^\flat$![]() ) and (T4) hold. Lastly, if $\boldsymbol {x}$
) and (T4) hold. Lastly, if $\boldsymbol {x}$![]() is a sequence supported on $\mathcal {I}$
is a sequence supported on $\mathcal {I}$![]() , then $\mathcal {J}\text {-}\lim A\boldsymbol {x}=0$
, then $\mathcal {J}\text {-}\lim A\boldsymbol {x}=0$![]() , which proves (T5$^{\sharp }$
, which proves (T5$^{\sharp }$![]() ).
).
6. Closing remarks
We leave as open questions for the reader to check whether theorem 4.1 holds for the larger class of rapid$^+$![]() $P^+$
$P^+$![]() -ideals $\mathcal {J}$
-ideals $\mathcal {J}$![]() , and whether this condition characterizes the latter class of ideals in the same spirit of [Reference De Bondt and Vernaeve12, Theorem 5.1]. An analogue question could be asked for theorem 3.6. In addition, it would be interesting to obtain a characterization of the matrix class $(c(X,\,\mathcal {Z}),\, c(Y,\,\mathcal {Z}))$
, and whether this condition characterizes the latter class of ideals in the same spirit of [Reference De Bondt and Vernaeve12, Theorem 5.1]. An analogue question could be asked for theorem 3.6. In addition, it would be interesting to obtain a characterization of the matrix class $(c(X,\,\mathcal {Z}),\, c(Y,\,\mathcal {Z}))$![]() , analogously to theorem 2.21.
, analogously to theorem 2.21.
Acknowledgements
The author is grateful to PRIN 2017 (grant 2017CY2NCA) for financial support. He is very thankful to an anonymous referee for a careful and constructive reading of the manuscript.