1. Introduction
Transitional patterns in plane shear flows arise naturally from uniform turbulence at sufficiently low Reynolds number. These patterns feature a selected orientation of approximately ![]() $24^\circ$ when they emerge (Prigent et al. Reference Prigent, Grégoire, Chaté and Dauchot2003; Tsukahara et al. Reference Tsukahara, Seki, Kawamura and Tochio2005; Shimizu & Manneville Reference Shimizu and Manneville2019; Kashyap, Duguet & Dauchot Reference Kashyap, Duguet and Dauchot2020). When the Reynolds number is reduced further, these spatio-temporally intermittent structures display important features of non-equilibrium phase transitions; both experimental and numerical studies have demonstrated their membership in the directed percolation universality class in the case of plane Couette flow (Lemoult et al. Reference Lemoult, Shi, Avila, Jalikop, Avila and Hof2016; Chantry, Tuckerman & Barkley Reference Chantry, Tuckerman and Barkley2017; Klotz et al. Reference Klotz, Lemoult, Avila and Hof2022).
$24^\circ$ when they emerge (Prigent et al. Reference Prigent, Grégoire, Chaté and Dauchot2003; Tsukahara et al. Reference Tsukahara, Seki, Kawamura and Tochio2005; Shimizu & Manneville Reference Shimizu and Manneville2019; Kashyap, Duguet & Dauchot Reference Kashyap, Duguet and Dauchot2020). When the Reynolds number is reduced further, these spatio-temporally intermittent structures display important features of non-equilibrium phase transitions; both experimental and numerical studies have demonstrated their membership in the directed percolation universality class in the case of plane Couette flow (Lemoult et al. Reference Lemoult, Shi, Avila, Jalikop, Avila and Hof2016; Chantry, Tuckerman & Barkley Reference Chantry, Tuckerman and Barkley2017; Klotz et al. Reference Klotz, Lemoult, Avila and Hof2022).
Oblique patterns consist of turbulent regions (or bands) alternating with (quasi-)laminar gaps. An inherent feature of the coexistence of these two phases in planar shear flows is the large-scale flow along the laminar–turbulent interface. This along-band flow has been observed in both experimental and numerical configurations (Coles & van Atta Reference Coles and van Atta1966; Barkley & Tuckerman Reference Barkley and Tuckerman2007; Duguet & Schlatter Reference Duguet and Schlatter2013; Couliou & Monchaux Reference Couliou and Monchaux2015; Tuckerman, Chantry & Barkley Reference Tuckerman, Chantry and Barkley2020; Klotz, Pavlenko & Wesfreid Reference Klotz, Pavlenko and Wesfreid2021; Marensi, Yalnız & Hof Reference Marensi, Yalnız and Hof2023), and can be seen as a consequence of the breaking of spanwise symmetry and incompressibility (Duguet & Schlatter Reference Duguet and Schlatter2013).
Transitional turbulence presents a separation of scales: flow along the laminar–turbulent interface paves the large scales, while the streaks and rolls governed by the self-sustaining process of turbulence (Hamilton, Kim & Waleffe Reference Hamilton, Kim and Waleffe1995; Waleffe Reference Waleffe1997) are the basic ingredients of the small-scale flow. In channel flow, the spanwise streak spacing is commonly found to be ![]() $\lambda _{{span}}^+ \simeq 100$ (Kim, Moin & Moser Reference Kim, Moin and Moser1987), whereas it is found to be larger (
$\lambda _{{span}}^+ \simeq 100$ (Kim, Moin & Moser Reference Kim, Moin and Moser1987), whereas it is found to be larger (![]() $\lambda _{{span}}^+ \simeq 132$) in plane Couette flow at low enough Reynolds number (Komminaho, Lundbladh & Johansson Reference Komminaho, Lundbladh and Johansson1996; Jiménez Reference Jiménez1998; Tsukahara, Kawamura & Shingai Reference Tsukahara, Kawamura and Shingai2006). (The superscript
$\lambda _{{span}}^+ \simeq 132$) in plane Couette flow at low enough Reynolds number (Komminaho, Lundbladh & Johansson Reference Komminaho, Lundbladh and Johansson1996; Jiménez Reference Jiménez1998; Tsukahara, Kawamura & Shingai Reference Tsukahara, Kawamura and Shingai2006). (The superscript ![]() $+$ indicates non-dimensionalisation by wall variables, e.g.
$+$ indicates non-dimensionalisation by wall variables, e.g. ![]() $\lambda ^+= \lambda u_\tau / \nu$, where
$\lambda ^+= \lambda u_\tau / \nu$, where ![]() $\nu$ is the kinematic viscosity and
$\nu$ is the kinematic viscosity and ![]() $u_\tau$ is the wall-shear velocity. Subscripts
$u_\tau$ is the wall-shear velocity. Subscripts ![]() ${strm}$ and
${strm}$ and ![]() ${span}$ respectively denote streamwise and spanwise directions.)
${span}$ respectively denote streamwise and spanwise directions.)
In contrast, the wavelength of the large-scale patterns is much larger than that of the rolls and streaks, with a ratio of the order of 20 in patterned plane Couette flow. This scale separation is visible in the spectral analysis presented by several authors. We mention Tsukahara et al. (Reference Tsukahara, Seki, Kawamura and Tochio2005) in channel flow, Tuckerman & Barkley (Reference Tuckerman and Barkley2011) and Duguet & Schlatter (Reference Duguet and Schlatter2013) in Couette flow, and Ishida, Duguet & Tsukahara (Reference Ishida, Duguet and Tsukahara2017) in annular pipe flow. However, the exact contribution of the rolls and streaks in energising the large-scale patterns has never been investigated thoroughly.
In pipe flow, the energy distribution within turbulent structures was measured in the classic experiments of Wygnanski & Champagne (Reference Wygnanski and Champagne1973) and Wygnanski, Sokolov & Friedman (Reference Wygnanski, Sokolov and Friedman1975), and later in numerical simulations by Song et al. (Reference Song, Barkley, Hof and Avila2017). For localised turbulent structures known as puffs, turbulent production ![]() $P$ at the upstream side of a puff is larger than turbulent dissipation
$P$ at the upstream side of a puff is larger than turbulent dissipation ![]() $\epsilon$, whereas at the downstream side, dissipation dominates production, as it does throughout regions of quasi-laminar flow in general. No local balance between
$\epsilon$, whereas at the downstream side, dissipation dominates production, as it does throughout regions of quasi-laminar flow in general. No local balance between ![]() $P$ and
$P$ and ![]() $\epsilon$ is found within the puff. In contrast, in expanding or retracting turbulent zones, known as slugs, the flow in the turbulent core is locally in equilibrium, with production balancing dissipation (
$\epsilon$ is found within the puff. In contrast, in expanding or retracting turbulent zones, known as slugs, the flow in the turbulent core is locally in equilibrium, with production balancing dissipation (![]() $P \simeq \epsilon$). Theoretical efforts to model turbulent–laminar structures in pipe flow are based on these properties of the turbulent production and dissipation (Barkley Reference Barkley2011, Reference Barkley2016). We will report a similar out-of-equilibrium spatial distribution of energy in transitional plane Couette flow.
$P \simeq \epsilon$). Theoretical efforts to model turbulent–laminar structures in pipe flow are based on these properties of the turbulent production and dissipation (Barkley Reference Barkley2011, Reference Barkley2016). We will report a similar out-of-equilibrium spatial distribution of energy in transitional plane Couette flow.
Spectral energy budgets have been used extensively to quantify energy transfers and interactions between mean flow and turbulent kinetic energy (TKE) in high Reynolds number wall-bounded flows. This approach dates from Lumley (Reference Lumley1964), who conjectured that energy is transferred from small to large scales in shear flows as distance from the wall increases. This concept of inverse energy transfer was later investigated by Domaradzki et al. (Reference Domaradzki, Liu, Härtel and Kleiser1994), Bolotnov et al. (Reference Bolotnov, Lahey, Drew, Jansen and Oberai2010), Lee & Moser (Reference Lee and Moser2015, Reference Lee and Moser2019), Mizuno (Reference Mizuno2016), Cho, Hwang & Choi (Reference Cho, Hwang and Choi2018) and Kawata & Tsukahara (Reference Kawata and Tsukahara2021) (and references therein). However, only recently has the spectral energy budget been computed at low ![]() $Re_\tau$ by Symon, Illingworth & Marusic (Reference Symon, Illingworth and Marusic2021), in a turbulent channel of minimal size at
$Re_\tau$ by Symon, Illingworth & Marusic (Reference Symon, Illingworth and Marusic2021), in a turbulent channel of minimal size at ![]() $Re_\tau = u_\tau h /\nu = 180$ and for an exact coherent state of channel flow at
$Re_\tau = u_\tau h /\nu = 180$ and for an exact coherent state of channel flow at ![]() $Re_\tau =85$ found by Park & Graham (Reference Park and Graham2015) (where
$Re_\tau =85$ found by Park & Graham (Reference Park and Graham2015) (where ![]() $h$ denotes the channel half-gap). Currently, there is a lack of understanding of the spectral distribution of energy in transitional wall-bounded turbulence, especially regarding the role of energy transfers and triad interactions in the emergence of the large-scale flow.
$h$ denotes the channel half-gap). Currently, there is a lack of understanding of the spectral distribution of energy in transitional wall-bounded turbulence, especially regarding the role of energy transfers and triad interactions in the emergence of the large-scale flow.
This paper is devoted to the relationships between the inhomogeneous mean flow and turbulent fluctuations in transitional plane Couette flow, below ![]() $Re_\tau = u_\tau h /\nu = 66$. These are investigated through the computation of both physical (§ 4) and spectral (§ 5) energy balances in the regime where patterns emerge from uniform turbulence. We will survey the energy balance as a function of
$Re_\tau = u_\tau h /\nu = 66$. These are investigated through the computation of both physical (§ 4) and spectral (§ 5) energy balances in the regime where patterns emerge from uniform turbulence. We will survey the energy balance as a function of ![]() $Re$ in § 6. Turbulent production and nonlinear transfers at various wall-normal locations are included in Appendix A. The energy processes reported in this paper will be investigated further as a function of the pattern wavelength in our companion paper Gomé, Tuckerman & Barkley (Reference Gomé, Tuckerman and Barkley2023), where we will discuss their role in wavelength selection.
$Re$ in § 6. Turbulent production and nonlinear transfers at various wall-normal locations are included in Appendix A. The energy processes reported in this paper will be investigated further as a function of the pattern wavelength in our companion paper Gomé, Tuckerman & Barkley (Reference Gomé, Tuckerman and Barkley2023), where we will discuss their role in wavelength selection.
2. Numerical set-up
Plane Couette Flow is driven by two parallel rigid plates moving at opposite velocities ![]() $\pm U_{wall}$. Lengths are non-dimensionalised by the half-gap
$\pm U_{wall}$. Lengths are non-dimensionalised by the half-gap ![]() $h$ between the plates, velocities by
$h$ between the plates, velocities by ![]() $U_{wall}$, and time by
$U_{wall}$, and time by ![]() $h/U_{wall}$. The Reynolds number is defined to be
$h/U_{wall}$. The Reynolds number is defined to be ![]() $Re= U_{wall}\,h/\nu$. We will require one last dimensional quantity, the horizontal mean shear at the walls, which we denote by
$Re= U_{wall}\,h/\nu$. We will require one last dimensional quantity, the horizontal mean shear at the walls, which we denote by ![]() $U^\prime _{wall}$. We will use non-dimensional variables throughout. We use the pseudo-spectral parallel code Channelflow (Gibson Reference Gibson2012) to simulate the incompressible Navier–Stokes equations
$U^\prime _{wall}$. We will use non-dimensional variables throughout. We use the pseudo-spectral parallel code Channelflow (Gibson Reference Gibson2012) to simulate the incompressible Navier–Stokes equations
Since the bands are found to be oriented obliquely with respect to the streamwise direction, we use a periodic numerical domain that is tilted with respect to the streamwise direction of the flow, shown as the oblique rectangle in figure 1. This choice was introduced by Barkley & Tuckerman (Reference Barkley and Tuckerman2005) and has become common in studying turbulent bands (e.g. Reetz, Kreilos & Schneider Reference Reetz, Kreilos and Schneider2019; Paranjape, Duguet & Hof Reference Paranjape, Duguet and Hof2020; Tuckerman et al. Reference Tuckerman, Chantry and Barkley2020). The ![]() $x$ direction is chosen to be aligned with a typical turbulent band, and the
$x$ direction is chosen to be aligned with a typical turbulent band, and the ![]() $z$ direction to be orthogonal to the band. The relationship between streamwise–spanwise coordinates and tilted band-oriented
$z$ direction to be orthogonal to the band. The relationship between streamwise–spanwise coordinates and tilted band-oriented ![]() $(x,z)$ coordinates is
$(x,z)$ coordinates is
The domain is taken to be periodic in the x and z directions. The usual wall-normal coordinate is denoted by ![]() $y$, and the corresponding velocity by
$y$, and the corresponding velocity by ![]() $v$. The laminar base flow is
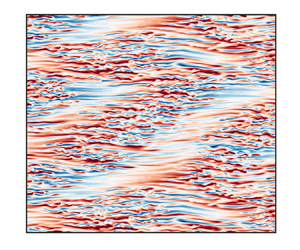
$v$. The laminar base flow is ![]() $\boldsymbol{U}_b \equiv y\boldsymbol{e}_{strm} = (U_b,0,W_b)$. The field visualised in figure 1 (black box) is obtained by concatenating four times a field resulting from a simulation in
$\boldsymbol{U}_b \equiv y\boldsymbol{e}_{strm} = (U_b,0,W_b)$. The field visualised in figure 1 (black box) is obtained by concatenating four times a field resulting from a simulation in ![]() $L_{{strm}}=200$,
$L_{{strm}}=200$, ![]() $L_{{span}}=100$.
$L_{{span}}=100$.

Figure 1. Visualisation of the numerically simulated flow at ![]() $Re=360$ and our numerical domains. Colours show
$Re=360$ and our numerical domains. Colours show ![]() $y$ velocity at
$y$ velocity at ![]() $y=0$ (blue
$y=0$ (blue ![]() $-0.2$, white 0, red 0.2) in a domain of size
$-0.2$, white 0, red 0.2) in a domain of size ![]() $L_{{strm}}=400$,
$L_{{strm}}=400$, ![]() $L_{{span}}=200$. Red and blue boxes show a minimal band unit and a long slender box, respectively.
$L_{{span}}=200$. Red and blue boxes show a minimal band unit and a long slender box, respectively.
The tilted box effectively reduces the dimensionality of the system by discarding large-scale variations along the short ![]() $x$ direction. This direction is considered homogeneous over large scales because it is determined only by small turbulent scales, and because the band is assumed to be infinite in
$x$ direction. This direction is considered homogeneous over large scales because it is determined only by small turbulent scales, and because the band is assumed to be infinite in ![]() $x$. The main underlying assumption is the angle of the pattern. In large non-tilted domains, turbulent bands in plane Couette flow exhibit two possible orientations (related by spanwise reflection; Prigent et al. Reference Prigent, Grégoire, Chaté, Dauchot and van Saarloos2002; Duguet, Schlatter & Henningson Reference Duguet, Schlatter and Henningson2010; Klotz et al. Reference Klotz, Lemoult, Avila and Hof2022), whereas only one orientation is permitted by our tilted box.
$x$. The main underlying assumption is the angle of the pattern. In large non-tilted domains, turbulent bands in plane Couette flow exhibit two possible orientations (related by spanwise reflection; Prigent et al. Reference Prigent, Grégoire, Chaté, Dauchot and van Saarloos2002; Duguet, Schlatter & Henningson Reference Duguet, Schlatter and Henningson2010; Klotz et al. Reference Klotz, Lemoult, Avila and Hof2022), whereas only one orientation is permitted by our tilted box.
In our simulations, we fix the angle ![]() $\theta = 24^{\circ }$, the number of grid points in the
$\theta = 24^{\circ }$, the number of grid points in the ![]() $y$ direction
$y$ direction ![]() $N_y=33$, the
$N_y=33$, the ![]() $x$ domain length
$x$ domain length ![]() $L_x=10$, the
$L_x=10$, the ![]() $x$ resolution
$x$ resolution ![]() $\Delta x = L_x/N_x=10/120$, and the
$\Delta x = L_x/N_x=10/120$, and the ![]() $z$ resolution
$z$ resolution ![]() $\Delta z = L_z/N_z = 0.08$ (similar to that used by Tsukahara et al. Reference Tsukahara, Kawamura and Shingai2006; Barkley & Tuckerman Reference Barkley and Tuckerman2007). The values of
$\Delta z = L_z/N_z = 0.08$ (similar to that used by Tsukahara et al. Reference Tsukahara, Kawamura and Shingai2006; Barkley & Tuckerman Reference Barkley and Tuckerman2007). The values of ![]() $N_x$ and
$N_x$ and ![]() $N_z$ include dealiasing in the
$N_z$ include dealiasing in the ![]() $x$ and
$x$ and ![]() $z$ directions. We will make extensive use of two numerical domains, with different domain sizes
$z$ directions. We will make extensive use of two numerical domains, with different domain sizes ![]() $L_z$, shown in figure 1.
$L_z$, shown in figure 1.
(i) Minimal band units, shown as the red box in figure 1, can accommodate a single turbulent band and associated quasi-laminar gap. This effectively restricts the flow to a perfectly periodic turbulent–laminar pattern of wavelength
 $\lambda =L_z$. The size
$\lambda =L_z$. The size  $L_z$ governing the periodicity of the pattern can be modified, as is investigated in the companion paper Gomé et al. (Reference Gomé, Tuckerman and Barkley2023). In the present paper, the minimal band unit is fixed at
$L_z$ governing the periodicity of the pattern can be modified, as is investigated in the companion paper Gomé et al. (Reference Gomé, Tuckerman and Barkley2023). In the present paper, the minimal band unit is fixed at  $L_z=40$, which corresponds to the natural spacing of bands observed experimentally and numerically.
$L_z=40$, which corresponds to the natural spacing of bands observed experimentally and numerically.(ii) Long slender boxes have a large
 $L_z$ direction that allows for a large number of gaps and bands in the system. The blue box in figure 1 is an example of such a domain with
$L_z$ direction that allows for a large number of gaps and bands in the system. The blue box in figure 1 is an example of such a domain with  $L_z = 240$, but a larger size
$L_z = 240$, but a larger size  $L_z=800$ is used in this paper and investigated in detail in Gomé et al. (Reference Gomé, Tuckerman and Barkley2023).
$L_z=800$ is used in this paper and investigated in detail in Gomé et al. (Reference Gomé, Tuckerman and Barkley2023).
Finally, for comparison with studies of uniform turbulence, we introduce the friction Reynolds number
Note that ![]() $Re_\tau = \sqrt {Re}$ in the laminar state. The values of
$Re_\tau = \sqrt {Re}$ in the laminar state. The values of ![]() $Re_\tau$ computed throughout this study are given in § A.1.
$Re_\tau$ computed throughout this study are given in § A.1.
3. Spectra in different configurations
We have carried out simulations in a long slender box of size ![]() $L_z=800$ for various
$L_z=800$ for various ![]() $Re$, with the uniform state at
$Re$, with the uniform state at ![]() $Re=500$ as an initial condition. Two such simulations are shown via spatio-temporal diagrams in figure 2 at
$Re=500$ as an initial condition. Two such simulations are shown via spatio-temporal diagrams in figure 2 at ![]() $Re=440$ and
$Re=440$ and ![]() $380$. With decreasing
$380$. With decreasing ![]() $Re$, the flow shows intermittent gaps (white spots in the figure) that emerge from the turbulent field at seemingly random locations. A gap is defined as a weakened turbulent structure, or a quasi-laminar zone, surrounded by turbulent flow. A gap is the opposite of a band, which is a turbulent core surrounded by quasi-laminar flow. In plane Couette flow, bands are observed at
$Re$, the flow shows intermittent gaps (white spots in the figure) that emerge from the turbulent field at seemingly random locations. A gap is defined as a weakened turbulent structure, or a quasi-laminar zone, surrounded by turbulent flow. A gap is the opposite of a band, which is a turbulent core surrounded by quasi-laminar flow. In plane Couette flow, bands are observed at ![]() $Re\in [300, 440]$ (Prigent et al. Reference Prigent, Grégoire, Chaté and Dauchot2003; Barkley & Tuckerman Reference Barkley and Tuckerman2007; Duguet et al. Reference Duguet, Schlatter and Henningson2010; Shi, Avila & Hof Reference Shi, Avila and Hof2013). Gaps and bands self-organise into patterns as
$Re\in [300, 440]$ (Prigent et al. Reference Prigent, Grégoire, Chaté and Dauchot2003; Barkley & Tuckerman Reference Barkley and Tuckerman2007; Duguet et al. Reference Duguet, Schlatter and Henningson2010; Shi, Avila & Hof Reference Shi, Avila and Hof2013). Gaps and bands self-organise into patterns as ![]() $Re$ is decreased. This is the situation observed in a long slender box in figure 2(b) (
$Re$ is decreased. This is the situation observed in a long slender box in figure 2(b) (![]() $Re=380$), where a regular alternation of gaps and turbulent bands is visible. In a minimal band unit, the system is constrained and the distinction between gaps and patterns is lost. While the system cannot exhibit the spatial intermittency seen in figure 2(a), temporal intermittency is possible and is seen as alternations between uniform turbulence and patterns, as illustrated in figure 2(c) at
$Re=380$), where a regular alternation of gaps and turbulent bands is visible. In a minimal band unit, the system is constrained and the distinction between gaps and patterns is lost. While the system cannot exhibit the spatial intermittency seen in figure 2(a), temporal intermittency is possible and is seen as alternations between uniform turbulence and patterns, as illustrated in figure 2(c) at ![]() $Re = 430$. Gomé et al. (Reference Gomé, Tuckerman and Barkley2023) investigate extensively the dynamical emergence of gap and patterns out of turbulent flow.
$Re = 430$. Gomé et al. (Reference Gomé, Tuckerman and Barkley2023) investigate extensively the dynamical emergence of gap and patterns out of turbulent flow.

Figure 2. Spatio-temporal visualisations of the emergence of gaps and patterns in a long slender box with ![]() $L_z=800$, for (a)
$L_z=800$, for (a) ![]() $Re=440$ and (b)
$Re=440$ and (b) ![]() $380$. Flow at
$380$. Flow at ![]() $t=0$ is initiated from uniform turbulence at
$t=0$ is initiated from uniform turbulence at ![]() $Re=500$. Colours show local cross-flow energy
$Re=500$. Colours show local cross-flow energy ![]() $(v^2 + u_{{span}}^2)/2$ at
$(v^2 + u_{{span}}^2)/2$ at ![]() $x=L_x/2$,
$x=L_x/2$, ![]() $y=0$ (white 0, dark orange 0.02). (c) Intermittent alternation between uniform and patterned turbulence at
$y=0$ (white 0, dark orange 0.02). (c) Intermittent alternation between uniform and patterned turbulence at ![]() $Re=430$ in a minimal band unit with
$Re=430$ in a minimal band unit with ![]() $L_z=40$.
$L_z=40$.
We define the total physical energy and total spectral energy of the flow as
where ![]() $\overline {(\cdot )}$ denotes the time and
$\overline {(\cdot )}$ denotes the time and ![]() $x$ average, and the Fourier transform is taken in the band-orthogonal direction
$x$ average, and the Fourier transform is taken in the band-orthogonal direction ![]() $z$:
$z$:
We will also use the turbulent kinetic energy (TKE) in both physical and spectral space,
where the flow has been decomposed into its mean and fluctuating components, ![]() $\boldsymbol {u} = \bar {\boldsymbol {u}} + \boldsymbol {u}^\prime$.
$\boldsymbol {u} = \bar {\boldsymbol {u}} + \boldsymbol {u}^\prime$.
Figure 3(a) shows ![]() $\hat {E}(y=0, k_z)$ for simulations in a long slender box at different values of
$\hat {E}(y=0, k_z)$ for simulations in a long slender box at different values of ![]() $Re$. The average has been carried out over a long period of time (
$Re$. The average has been carried out over a long period of time (![]() $t\in [100, 5000]$). The total energy spectra show two prominent energy-containing scales: one at small wavenumbers (approximately
$t\in [100, 5000]$). The total energy spectra show two prominent energy-containing scales: one at small wavenumbers (approximately ![]() $k_z=0.15$, i.e.
$k_z=0.15$, i.e. ![]() $\lambda _z \simeq 42$) corresponding to the alternation of turbulent bands and quasi-laminar gaps, and a second one at large wavenumbers (
$\lambda _z \simeq 42$) corresponding to the alternation of turbulent bands and quasi-laminar gaps, and a second one at large wavenumbers (![]() $k_z \simeq 1.41$,
$k_z \simeq 1.41$, ![]() $\lambda _z\simeq 4.45$), which we will denote
$\lambda _z\simeq 4.45$), which we will denote ![]() $k_{{rolls}}$. This small wavelength corresponds to a spanwise spacing
$k_{{rolls}}$. This small wavelength corresponds to a spanwise spacing ![]() $\lambda _{{span}} = 2{\rm \pi} \cos {\theta }/k_{{rolls}} = 4.06$, which is approximately the idealised periodicity of pairs of streaks and rolls in Couette flow (Waleffe Reference Waleffe1997), with individual rolls occupying the height
$\lambda _{{span}} = 2{\rm \pi} \cos {\theta }/k_{{rolls}} = 4.06$, which is approximately the idealised periodicity of pairs of streaks and rolls in Couette flow (Waleffe Reference Waleffe1997), with individual rolls occupying the height ![]() $L_y=2$ of the shear layer. In wall units, this peak corresponds to
$L_y=2$ of the shear layer. In wall units, this peak corresponds to ![]() $\lambda _{{span}}^+ = Re_\tau \,\lambda _{{span}} = 130$ at
$\lambda _{{span}}^+ = Re_\tau \,\lambda _{{span}} = 130$ at ![]() $Re=430$ (
$Re=430$ (![]() $Re_\tau = 31.9$). This is not far from the streak spacing
$Re_\tau = 31.9$). This is not far from the streak spacing ![]() $\lambda _{{span}}^+=136$ measured by Komminaho et al. (Reference Komminaho, Lundbladh and Johansson1996) in plane Couette flow at
$\lambda _{{span}}^+=136$ measured by Komminaho et al. (Reference Komminaho, Lundbladh and Johansson1996) in plane Couette flow at ![]() $Re_\tau = 52$. For
$Re_\tau = 52$. For ![]() $k_z>k_{{rolls}}$, the energy falls off rapidly with
$k_z>k_{{rolls}}$, the energy falls off rapidly with ![]() $k_z$ up to the resolution scale. The scale separation between the large-scale turbulent–laminar patterns and the small-scale streaks and rolls was already observed in the transitional regime by many authors (Tsukahara et al. Reference Tsukahara, Seki, Kawamura and Tochio2005; Tuckerman & Barkley Reference Tuckerman and Barkley2011; Ishida, Duguet & Tsukahara Reference Ishida, Duguet and Tsukahara2016). The spectrum varies with
$k_z$ up to the resolution scale. The scale separation between the large-scale turbulent–laminar patterns and the small-scale streaks and rolls was already observed in the transitional regime by many authors (Tsukahara et al. Reference Tsukahara, Seki, Kawamura and Tochio2005; Tuckerman & Barkley Reference Tuckerman and Barkley2011; Ishida, Duguet & Tsukahara Reference Ishida, Duguet and Tsukahara2016). The spectrum varies with ![]() $Re$, but mostly at large scales (low
$Re$, but mostly at large scales (low ![]() $k_z$): the large-scale peak is barely visible at
$k_z$): the large-scale peak is barely visible at ![]() $Re=500$, and grows in intensity with decreasing
$Re=500$, and grows in intensity with decreasing ![]() $Re$, becoming dominant for
$Re$, becoming dominant for ![]() $Re<440$. Meanwhile, the small-scale spectrum is only very weakly affected by the change in
$Re<440$. Meanwhile, the small-scale spectrum is only very weakly affected by the change in ![]() $Re$.
$Re$.

Figure 3. (a) Total energy spectra in a large long slender box ![]() $L_z=800$ (black line) at
$L_z=800$ (black line) at ![]() $y=0$, for different
$y=0$, for different ![]() $Re$. The spectra are averaged irrespective of the nature of the state (patterned or uniform). (b) Total energy spectra (continuous lines) in a minimal band unit of size
$Re$. The spectra are averaged irrespective of the nature of the state (patterned or uniform). (b) Total energy spectra (continuous lines) in a minimal band unit of size ![]() $L_z=40$. The spectra are computed individually in the uniform turbulence (red) and patterned states (blue), at
$L_z=40$. The spectra are computed individually in the uniform turbulence (red) and patterned states (blue), at ![]() $Re=430$. (c) Visualisations of the patterned mean flow in a minimal band unit: colours show the deviation of the along-band velocity from the laminar base flow
$Re=430$. (c) Visualisations of the patterned mean flow in a minimal band unit: colours show the deviation of the along-band velocity from the laminar base flow ![]() $\bar {U}-U_b$ (top plot) and the pressure
$\bar {U}-U_b$ (top plot) and the pressure ![]() $\bar {P}$ (bottom plot). Streamlines of the mean flow perpendicular to the bands are shown as grey curves. The laminar region is centered at
$\bar {P}$ (bottom plot). Streamlines of the mean flow perpendicular to the bands are shown as grey curves. The laminar region is centered at ![]() $z=0$.
$z=0$.
We now turn to the minimal band unit, which has exactly the periodicity of a single wavelength of the pattern. The flow in this configuration does not have localised gaps like those that appear in figure 2(a). Instead, the system fluctuates between patterned and uniform states as seen in figure 2(c), and each of the two states can be distinguished and consequently analysed separately. In particular, we can take means for patterned and uniform states independently.
The total energy spectrum in a minimal band unit at ![]() $Re=430$ is presented in figure 3(b). Contrary to figure 3(a), where unconditional averaging mixes uniform turbulence and localised gaps in the spectrum, here we have conditionally computed separately the spectrum for the patterned state (blue line) and the uniform state (red line). As expected, the spectrum for the uniform state lacks the peak at the pattern scale. The energy of the streak–roll structures
$Re=430$ is presented in figure 3(b). Contrary to figure 3(a), where unconditional averaging mixes uniform turbulence and localised gaps in the spectrum, here we have conditionally computed separately the spectrum for the patterned state (blue line) and the uniform state (red line). As expected, the spectrum for the uniform state lacks the peak at the pattern scale. The energy of the streak–roll structures ![]() $\hat {E}(k_{{rolls}})$ is higher in the uniform case than in the patterned case. This hints at a redistribution of the energy from small scales (near
$\hat {E}(k_{{rolls}})$ is higher in the uniform case than in the patterned case. This hints at a redistribution of the energy from small scales (near ![]() $k_{{rolls}}$) to large scales (
$k_{{rolls}}$) to large scales (![]() $\ll k _{{rolls}}$) when the flow changes from uniform to patterned turbulence. For
$\ll k _{{rolls}}$) when the flow changes from uniform to patterned turbulence. For ![]() $k_z > 2$, both spectra appear to collapse, suggesting that the small-scale energy distribution is the same in both cases.
$k_z > 2$, both spectra appear to collapse, suggesting that the small-scale energy distribution is the same in both cases.
We now consider the mean flow ![]() $\bar {\boldsymbol {u}}(y,z)$, computed from an
$\bar {\boldsymbol {u}}(y,z)$, computed from an ![]() $(x,t)$ average over long time intervals in either the patterned or the uniform state in the minimal band unit. The mean flow in this configuration was studied by Barkley & Tuckerman (Reference Barkley and Tuckerman2007). We visualise
$(x,t)$ average over long time intervals in either the patterned or the uniform state in the minimal band unit. The mean flow in this configuration was studied by Barkley & Tuckerman (Reference Barkley and Tuckerman2007). We visualise ![]() $\bar {\boldsymbol {u}} = (U(y,z), V(y,z), W(y,z))$ in figure 3(c), by showing
$\bar {\boldsymbol {u}} = (U(y,z), V(y,z), W(y,z))$ in figure 3(c), by showing ![]() $U-U_b$ and
$U-U_b$ and ![]() $\bar {P}$ (colours), and plotting the streamlines of
$\bar {P}$ (colours), and plotting the streamlines of ![]() $(V,W)$ (grey lines). (Figure 3(c) corrects the erroneous pressure displayed in Barkley & Tuckerman (Reference Barkley and Tuckerman2007, figure 5).) The flow is centred around the quasi-laminar region, and the total in-plane velocity
$(V,W)$ (grey lines). (Figure 3(c) corrects the erroneous pressure displayed in Barkley & Tuckerman (Reference Barkley and Tuckerman2007, figure 5).) The flow is centred around the quasi-laminar region, and the total in-plane velocity ![]() $(V,W)$ shows a circulation around this region of the flow. Here,
$(V,W)$ shows a circulation around this region of the flow. Here, ![]() $U-U_b$ shows two centro-symmetrically related zones of flow parallel to the band, localised in the upper layer (blue zone) and in the bottom layer (red zone).
$U-U_b$ shows two centro-symmetrically related zones of flow parallel to the band, localised in the upper layer (blue zone) and in the bottom layer (red zone).
The mean flow ![]() $\bar {\boldsymbol {u}}$ can be decomposed into Fourier modes:
$\bar {\boldsymbol {u}}$ can be decomposed into Fourier modes:
where ![]() $\mathcal {R}$ denotes real part,
$\mathcal {R}$ denotes real part, ![]() $\bar {\boldsymbol {u}}_0 \equiv \hat {\bar {\boldsymbol {u}}}(y, k_z=0)= (U_0(y), 0 , W_0(y))$ is the
$\bar {\boldsymbol {u}}_0 \equiv \hat {\bar {\boldsymbol {u}}}(y, k_z=0)= (U_0(y), 0 , W_0(y))$ is the ![]() $z$-independent (uniform) component of the mean flow,
$z$-independent (uniform) component of the mean flow, ![]() $\bar {\boldsymbol {u}}_1 = \hat {\bar {\boldsymbol {u}}}(y, k_z=2{\rm \pi} /L_z)$ is the Fourier coefficient corresponding to wavelength
$\bar {\boldsymbol {u}}_1 = \hat {\bar {\boldsymbol {u}}}(y, k_z=2{\rm \pi} /L_z)$ is the Fourier coefficient corresponding to wavelength ![]() $\lambda _z = L_z$, and
$\lambda _z = L_z$, and ![]() $\bar {\boldsymbol {u}}_{>1} \equiv \sum _{k_z>2{\rm \pi} /L_z} \hat {\bar {\boldsymbol {u}}}(y, k_z)$ is the remainder of the decomposition. (To lighten the notation, we omit the hats on
$\bar {\boldsymbol {u}}_{>1} \equiv \sum _{k_z>2{\rm \pi} /L_z} \hat {\bar {\boldsymbol {u}}}(y, k_z)$ is the remainder of the decomposition. (To lighten the notation, we omit the hats on ![]() $\bar {\boldsymbol {u}}$ when subscripts
$\bar {\boldsymbol {u}}$ when subscripts ![]() $0$,
$0$, ![]() $1$ and
$1$ and ![]() $>1$ are used to indicate the corresponding Fourier coefficients.) Most of the mean-flow energy lies in the uniform mode
$>1$ are used to indicate the corresponding Fourier coefficients.) Most of the mean-flow energy lies in the uniform mode ![]() $\bar {\boldsymbol {u}}_0$, with a few per cent in the trigonometric component
$\bar {\boldsymbol {u}}_0$, with a few per cent in the trigonometric component ![]() $\bar {\boldsymbol {u}}_1$. The energy in the remaining terms (
$\bar {\boldsymbol {u}}_1$. The energy in the remaining terms (![]() $\bar {\boldsymbol {u}}_{>1}$) is at least two orders of magnitude lower than that of
$\bar {\boldsymbol {u}}_{>1}$) is at least two orders of magnitude lower than that of ![]() $\bar {\boldsymbol {u}}_1$ (Barkley & Tuckerman Reference Barkley and Tuckerman2007).
$\bar {\boldsymbol {u}}_1$ (Barkley & Tuckerman Reference Barkley and Tuckerman2007).
The decomposition of ![]() $\bar {\boldsymbol {u}}$ into
$\bar {\boldsymbol {u}}$ into ![]() $\bar {\boldsymbol {u}}_0$ and
$\bar {\boldsymbol {u}}_0$ and ![]() $\bar {\boldsymbol {u}}_1$ is illustrated in figure 4. The mean flow and the TKE are visualised in the planes
$\bar {\boldsymbol {u}}_1$ is illustrated in figure 4. The mean flow and the TKE are visualised in the planes ![]() $y=\pm 0.47$. The most relevant scales involved in the mean flow and the fluctuations are illustrated in figure 5. Mode
$y=\pm 0.47$. The most relevant scales involved in the mean flow and the fluctuations are illustrated in figure 5. Mode ![]() $\bar {\boldsymbol {u}}_0$ has an S-shaped profile in
$\bar {\boldsymbol {u}}_0$ has an S-shaped profile in ![]() $y$ with small spanwise component. Mode
$y$ with small spanwise component. Mode ![]() $\bar {\boldsymbol {u}}_1$ contains the large-scale flow along laminar–turbulent interfaces.
$\bar {\boldsymbol {u}}_1$ contains the large-scale flow along laminar–turbulent interfaces.

Figure 4. Mean-flow decomposition in two Fourier modes ![]() $\bar {\boldsymbol {u}}_0$ and
$\bar {\boldsymbol {u}}_0$ and ![]() $\bar {\boldsymbol {u}}_1$ (3.4), visualised in the planes
$\bar {\boldsymbol {u}}_1$ (3.4), visualised in the planes ![]() $y=\pm 0.47$ at
$y=\pm 0.47$ at ![]() $Re=400$. Colours show TKE: turbulent and laminar zones are respectively in blue and white.
$Re=400$. Colours show TKE: turbulent and laminar zones are respectively in blue and white.

Figure 5. Illustration of the most relevant scales in transitional patterns. The upper part depicts the mean flow: ![]() $\bar {\boldsymbol {u}}_0$ is the uniform (
$\bar {\boldsymbol {u}}_0$ is the uniform (![]() $z$-independent) mean shear, illustrated by the mean streamwise velocity profile, while
$z$-independent) mean shear, illustrated by the mean streamwise velocity profile, while ![]() $\bar {\boldsymbol {u}}_1$ corresponds to scale
$\bar {\boldsymbol {u}}_1$ corresponds to scale ![]() $\lambda _z \sim 40$ and is dominated by the flow along the laminar–turbulent interfaces as illustrated in the streamwise–spanwise plane. The lower part depicts the fluctuations: scale
$\lambda _z \sim 40$ and is dominated by the flow along the laminar–turbulent interfaces as illustrated in the streamwise–spanwise plane. The lower part depicts the fluctuations: scale ![]() $\lambda _z \sim 40$ is illustrated by the periodic presence and absence of fluctuating cross-flow velocity. The scale
$\lambda _z \sim 40$ is illustrated by the periodic presence and absence of fluctuating cross-flow velocity. The scale ![]() $k_{{LS}}$ is that below which fluctuations receive energy by nonlinear interactions (via
$k_{{LS}}$ is that below which fluctuations receive energy by nonlinear interactions (via ![]() $\hat {T}_{nl}$, (5.3)), and
$\hat {T}_{nl}$, (5.3)), and ![]() $k_{{rolls}}$ is the scale of rolls and streaks, illustrated in the spanwise–
$k_{{rolls}}$ is the scale of rolls and streaks, illustrated in the spanwise–![]() $y$ plane.
$y$ plane.
4. Physical balance in a minimal band unit
The remainder of this paper will focus on the minimal band unit with fixed length ![]() $L_z=40$.
$L_z=40$.
Before turning to the energy balance in spectral space, we first consider the traditional turbulent energy decomposition in the physical-space representation (Pope Reference Pope2000), as carried out in transitional pipe flow by Wygnanski & Champagne (Reference Wygnanski and Champagne1973) and Song et al. (Reference Song, Barkley, Hof and Avila2017), and in bent pipe flow by Rinaldi, Canton & Schlatter (Reference Rinaldi, Canton and Schlatter2019). We write the balance equation for the TKE, ![]() $K(y,z)$, in the physical representation as
$K(y,z)$, in the physical representation as
where the production term, dissipation term and rate of strain are
Subscripts ![]() $i$ and
$i$ and ![]() $j$ range over
$j$ range over ![]() $\{1,2,3\}$ (or equivalently
$\{1,2,3\}$ (or equivalently ![]() $\{x,y,z\}$), and we use the Einstein summation convention. The transfer terms read
$\{x,y,z\}$), and we use the Einstein summation convention. The transfer terms read
which account, respectively, for nonlinear interactions, work by pressure and viscous diffusion. We also introduce the total transfer ![]() $T\equiv T_{nl} + T_{p} + T_{v}$. This TKE balance is accompanied by the energy balance of the mean flow,
$T\equiv T_{nl} + T_{p} + T_{v}$. This TKE balance is accompanied by the energy balance of the mean flow, ![]() $\bar {E} = \frac {1}{2}\bar {\boldsymbol {u}} \boldsymbol {\cdot } \bar {\boldsymbol {u}} = E - K$ (Pope Reference Pope2000, (5.131)):
$\bar {E} = \frac {1}{2}\bar {\boldsymbol {u}} \boldsymbol {\cdot } \bar {\boldsymbol {u}} = E - K$ (Pope Reference Pope2000, (5.131)):
where
and
In order to emphasise the derivation of (4.1) and (4.4) from the Navier–Stokes equations, we have retained temporal derivatives, despite the fact that these equations describe ![]() $t$ and
$t$ and ![]() $x$ averaged quantities. While turbulent–laminar banded patterns are statistically steady in plane Couette flow, there is in fact some slight motion of the band position. To gain in precision, we position the pattern at each time based on the phase of the
$x$ averaged quantities. While turbulent–laminar banded patterns are statistically steady in plane Couette flow, there is in fact some slight motion of the band position. To gain in precision, we position the pattern at each time based on the phase of the ![]() $z$-trigonometric Fourier coefficient of the along-band flow at the mid-plane:
$z$-trigonometric Fourier coefficient of the along-band flow at the mid-plane: ![]() $z_{{loc}}(t) = - \phi (t)\,L_z/2{\rm \pi}$, where
$z_{{loc}}(t) = - \phi (t)\,L_z/2{\rm \pi}$, where ![]() $\phi (t) = \arg \left \langle \hat {u}(x, 0, 2{\rm \pi} /L_z,t) \right \rangle _x$. Temporal averages are computed with this phase alignment, and we consider
$\phi (t) = \arg \left \langle \hat {u}(x, 0, 2{\rm \pi} /L_z,t) \right \rangle _x$. Temporal averages are computed with this phase alignment, and we consider ![]() $\partial K/\partial t = 0$ and
$\partial K/\partial t = 0$ and ![]() $\partial \bar {E}/\partial t = 0$. The results in this section are all presented in a frame centred around the quasi-laminar zone, as was done in Barkley & Tuckerman (Reference Barkley and Tuckerman2007).
$\partial \bar {E}/\partial t = 0$. The results in this section are all presented in a frame centred around the quasi-laminar zone, as was done in Barkley & Tuckerman (Reference Barkley and Tuckerman2007).
In figure 6(a) we represent the streamwise mean flow with arrows and the TKE ![]() $K(y,z)$ by colours. The centre of the turbulent region is at
$K(y,z)$ by colours. The centre of the turbulent region is at ![]() $z\pm 20$, while locations
$z\pm 20$, while locations ![]() $z=\pm10$ correspond to overhang regions (Lundbladh & Johansson Reference Lundbladh and Johansson1991; Duguet & Schlatter Reference Duguet and Schlatter2013), in which turbulence extends further towards positive z on the top and towards negative z on the bottom, and where the along-band large-scale flow is strongest (see figure 3c). Figures 6(b) and 6(c) display the terms in the energy budgets of (4.1) and (4.4). To better relate these results to those from pipe flow, we integrate the energy budgets over the upper half of the domain, where the
$z=\pm10$ correspond to overhang regions (Lundbladh & Johansson Reference Lundbladh and Johansson1991; Duguet & Schlatter Reference Duguet and Schlatter2013), in which turbulence extends further towards positive z on the top and towards negative z on the bottom, and where the along-band large-scale flow is strongest (see figure 3c). Figures 6(b) and 6(c) display the terms in the energy budgets of (4.1) and (4.4). To better relate these results to those from pipe flow, we integrate the energy budgets over the upper half of the domain, where the ![]() $z$ component of the mean flow is from left to right. We use the same symbols
$z$ component of the mean flow is from left to right. We use the same symbols ![]() $P$,
$P$, ![]() $\epsilon$, etc. to denote these half-height averages. (The lower half can be obtained from the upper half by symmetry and should be compared to pipe flow with the opposite streamwise direction.) All quantities depend strongly on
$\epsilon$, etc. to denote these half-height averages. (The lower half can be obtained from the upper half by symmetry and should be compared to pipe flow with the opposite streamwise direction.) All quantities depend strongly on ![]() $z$, and it is this dependence on which we will focus.
$z$, and it is this dependence on which we will focus.

Figure 6. (a) Mean profiles of the deviation from laminar flow (![]() $\bar {W} - W_b$) and the TKE (white 0, blue 0.08) in a turbulent–laminar pattern at
$\bar {W} - W_b$) and the TKE (white 0, blue 0.08) in a turbulent–laminar pattern at ![]() $Re=400$ centred around the laminar region at
$Re=400$ centred around the laminar region at ![]() $z=0$. (b) TKE and (c) mean-flow energy budgets for
$z=0$. (b) TKE and (c) mean-flow energy budgets for ![]() $Re=400$. Each term is integrated over the upper half of the domain,
$Re=400$. Each term is integrated over the upper half of the domain, ![]() $y\in [0, 1]$, where advection by the mean flow is towards the right. In (b), the regions where
$y\in [0, 1]$, where advection by the mean flow is towards the right. In (b), the regions where ![]() $P>\epsilon$ are shaded. There is a transfer of turbulent energy from shaded to non-shaded regions. In (c), the regions where
$P>\epsilon$ are shaded. There is a transfer of turbulent energy from shaded to non-shaded regions. In (c), the regions where ![]() $\bar {T}_{v} > P + \bar {\epsilon }$ are shaded. There is a transfer of mean-flow energy from shaded to non-shaded regions.
$\bar {T}_{v} > P + \bar {\epsilon }$ are shaded. There is a transfer of mean-flow energy from shaded to non-shaded regions.
Figure 6(b) shows the TKE budget. The energy balance is dominated by production and dissipation. Unsurprisingly, production is minimal in the quasi-laminar region where the fluctuations, and hence the Reynolds stresses, are small. The regions where production is larger than and smaller than dissipation are indicated in the figure with shading. This local disequilibrium between production and dissipation is accounted for by the transfers from advection and fluctuations, ![]() $\bar {\boldsymbol {u}} \boldsymbol {\cdot }\boldsymbol {\nabla } K$ and
$\bar {\boldsymbol {u}} \boldsymbol {\cdot }\boldsymbol {\nabla } K$ and ![]() $T$ (the former being of larger amplitude than the latter). The spatial transfer of energy goes from the shaded region (
$T$ (the former being of larger amplitude than the latter). The spatial transfer of energy goes from the shaded region (![]() $z\simeq 5$ to
$z\simeq 5$ to ![]() $z\simeq -12$, taking into account periodicity), to the unshaded region (
$z\simeq -12$, taking into account periodicity), to the unshaded region (![]() $z\simeq -12$ to
$z\simeq -12$ to ![]() $z\simeq 5$) in figure 6(b). Turbulent energy therefore goes from the turbulent zone to the quasi-laminar zone. These results are consistent with those in a band in plane Poiseuille flow (Brethouwer, Duguet & Schlatter Reference Brethouwer, Duguet and Schlatter2012, figure 5) and in a puff in pipe flow (Song et al. Reference Song, Barkley, Hof and Avila2017): when entering the turbulent region from upstream to downstream,
$z\simeq 5$) in figure 6(b). Turbulent energy therefore goes from the turbulent zone to the quasi-laminar zone. These results are consistent with those in a band in plane Poiseuille flow (Brethouwer, Duguet & Schlatter Reference Brethouwer, Duguet and Schlatter2012, figure 5) and in a puff in pipe flow (Song et al. Reference Song, Barkley, Hof and Avila2017): when entering the turbulent region from upstream to downstream, ![]() $P>\epsilon$ first, and then
$P>\epsilon$ first, and then ![]() $P<\epsilon$, which signifies a spatial flux of energy from upstream to downstream. (In the upper half of our Couette domain, increasing
$P<\epsilon$, which signifies a spatial flux of energy from upstream to downstream. (In the upper half of our Couette domain, increasing ![]() $z$ corresponds to going downstream in a pipe.)
$z$ corresponds to going downstream in a pipe.)
We now look at the energy budget of the mean flow, presented in figure 6(c), again centred around the laminar region and integrated over the upper half of the domain. Unlike pressure-driven channel or pipe flows, the energy is injected into the plane Couette flow by the imposed motion of the wall, and this is captured by the viscous diffusion term ![]() $\bar {T}_{v}$ in the mean-flow energy equation. The injected energy is mostly lost to mean-flow dissipation
$\bar {T}_{v}$ in the mean-flow energy equation. The injected energy is mostly lost to mean-flow dissipation ![]() $\bar {\epsilon }$ and TKE production
$\bar {\epsilon }$ and TKE production ![]() $P$, which extracts energy from the mean flow to fuel fluctuations. The remaining transport terms
$P$, which extracts energy from the mean flow to fuel fluctuations. The remaining transport terms ![]() $-\bar {\boldsymbol {u}}\boldsymbol {\cdot }\boldsymbol {\nabla }\bar {E} + \bar {T}_{nl} + \bar {T}_{p}$ account for the imbalance between injection, production and mean-flow dissipation:
$-\bar {\boldsymbol {u}}\boldsymbol {\cdot }\boldsymbol {\nabla }\bar {E} + \bar {T}_{nl} + \bar {T}_{p}$ account for the imbalance between injection, production and mean-flow dissipation: ![]() $\bar {T}_{v} - P - \bar {\epsilon } \ne 0$. We find that the overall transfer term appearing in the mean-flow equation behaves in the way opposite to the total transfer appearing in the TKE balance: mean-flow energy is transferred from the laminar region to the turbulent region, as illustrated by the shaded area in figure 6(c).
$\bar {T}_{v} - P - \bar {\epsilon } \ne 0$. We find that the overall transfer term appearing in the mean-flow equation behaves in the way opposite to the total transfer appearing in the TKE balance: mean-flow energy is transferred from the laminar region to the turbulent region, as illustrated by the shaded area in figure 6(c).
In pipe flow, Song et al. (Reference Song, Barkley, Hof and Avila2017) reported that the peak in TKE dissipation ![]() $\epsilon$ is shifted downstream from the peak in the production
$\epsilon$ is shifted downstream from the peak in the production ![]() $P$. Our data for the upper half of plane Couette flow does not support such a
$P$. Our data for the upper half of plane Couette flow does not support such a ![]() $z$-shift in the peaks in
$z$-shift in the peaks in ![]() $\epsilon$ and
$\epsilon$ and ![]() $P$. Meanwhile, unrelated to these considerations, we observe a considerable
$P$. Meanwhile, unrelated to these considerations, we observe a considerable ![]() $z$-shift between the peaks in mean-flow dissipation
$z$-shift between the peaks in mean-flow dissipation ![]() $\bar {\epsilon }$ at
$\bar {\epsilon }$ at ![]() $z=-15$ and production
$z=-15$ and production ![]() $P$ at
$P$ at ![]() $z=-20$, as shown in figure 6(c). This shift between
$z=-20$, as shown in figure 6(c). This shift between ![]() $P$ and
$P$ and ![]() $\bar {\epsilon }$ is consistent with overhangs in the mean flow located at the sides of turbulent regions where the TKE is maximal. We presume that some shift between
$\bar {\epsilon }$ is consistent with overhangs in the mean flow located at the sides of turbulent regions where the TKE is maximal. We presume that some shift between ![]() $P$ and
$P$ and ![]() $\bar {\epsilon }$ is also present in the pipe flow case, but this remains to be seen.
$\bar {\epsilon }$ is also present in the pipe flow case, but this remains to be seen.
5. Spectral decomposition
We now analyse the spectral balance of kinetic energy. In shear flows at higher ![]() $Re$, this analysis leads to a detailed understanding of the energy sources and transfers between scales. We refer the reader to Bolotnov et al. (Reference Bolotnov, Lahey, Drew, Jansen and Oberai2010), Lee & Moser (Reference Lee and Moser2015), Mizuno (Reference Mizuno2016) and Cho et al. (Reference Cho, Hwang and Choi2018) for studies at higher
$Re$, this analysis leads to a detailed understanding of the energy sources and transfers between scales. We refer the reader to Bolotnov et al. (Reference Bolotnov, Lahey, Drew, Jansen and Oberai2010), Lee & Moser (Reference Lee and Moser2015), Mizuno (Reference Mizuno2016) and Cho et al. (Reference Cho, Hwang and Choi2018) for studies at higher ![]() $Re_\tau$, and to Symon et al. (Reference Symon, Illingworth and Marusic2021) for a minimal channel study at
$Re_\tau$, and to Symon et al. (Reference Symon, Illingworth and Marusic2021) for a minimal channel study at ![]() $Re_\tau =180$. In a similar vein, Lee & Moser (Reference Lee and Moser2019) recently computed two-point correlations in channel flow.
$Re_\tau =180$. In a similar vein, Lee & Moser (Reference Lee and Moser2019) recently computed two-point correlations in channel flow.
5.1. Notation and governing equations
We begin by writing the Reynolds-averaged Navier–Stokes equations and the equation for fluctuations from the mean:
By taking the ![]() $z$ Fourier transform of (5.2) and multiplying by
$z$ Fourier transform of (5.2) and multiplying by ![]() $\widehat {u_j^\prime }^{*}$, followed by averaging over
$\widehat {u_j^\prime }^{*}$, followed by averaging over ![]() $x$ and
$x$ and ![]() $t$, we obtain a balance equation for the spectral kinetic energy
$t$, we obtain a balance equation for the spectral kinetic energy ![]() $\hat {K}(y,k_z) \equiv \frac {1}{2}\, \overline {\hat {\boldsymbol {u}}^{\prime ^{*}} \boldsymbol {\cdot } \hat {\boldsymbol {u}}^\prime }$:
$\hat {K}(y,k_z) \equiv \frac {1}{2}\, \overline {\hat {\boldsymbol {u}}^{\prime ^{*}} \boldsymbol {\cdot } \hat {\boldsymbol {u}}^\prime }$:
 \begin{align}
&\underbrace{
\vphantom{\mathcal{R}\left\{ \overline{\widehat{u_j^\prime}
\widehat{u^\prime_i \frac{\partial \bar{u}_j}{\partial
x_i}} } \right\}} \frac{\partial \hat{K}(y, k_z)}{\partial
t}}_0 + \underbrace{\mathcal{R}\left\{
\overline{{\widehat{u_j^\prime}^{*}}\,\widehat{
\bar{u}_i\,\frac{\partial u_j^\prime}{\partial x_i} }}
\right\} }_{-\hat{A}(y,k_z)} = \underbrace{-
\mathcal{R}\left\{
\overline{\widehat{u_j^\prime}^{*}\,\widehat{u^\prime_i\,\frac{\partial
\bar{u}_j}{\partial x_i}} } \right\}}_{\hat{\varPi}(y,
k_z)} - \underbrace{ \vphantom{\mathcal{R}\left\{
\overline{\widehat{u_j^\prime} \widehat{u^\prime_i
\frac{\partial \bar{u}_j}{\partial x_i}} } \right\}}
\frac{2}{Re}\,\overline{ \widehat{s_{ij}^\prime} \
\widehat{s_{ij}^\prime}^*}}_{\hat{D}(y,k_z)}\nonumber\\
& + \underbrace{\vphantom{- \mathcal{R}\left\{
\overline{\widehat{u_j^\prime}^{*} \widehat{ u_i^\prime
\frac{\partial u_j^\prime}{\partial x_i} }} \right\}}
\frac{2}{Re}\,\mathcal{R} \left\{
\overline{\frac{\partial}{\partial y}
(\widehat{u_j^\prime}^{*} \widehat{s_{yj}^\prime}) }
\right\}}_{\hat{T}_{v}(y,k_z)}\underbrace{\vphantom{\mathcal{R}\left\{
\overline{\widehat{u_j^\prime}^{*} \widehat{ u_i^\prime
\frac{\partial u_j^\prime}{\partial x_i} }} \right\}}
{} - \mathcal{R}\left\{
\overline{\frac{\partial}{\partial y}
(\widehat{u_y^{\prime}}^*\widehat{p^{\prime}})} \right\}
}_{\hat{T}_{p}(y,k_z)} \underbrace{{}-
\mathcal{R}\left\{ \overline{\widehat{u_j^\prime}^{*}
\widehat{ u_i^\prime\,\frac{\partial u_j^\prime}{\partial
x_i} }} \right\} }_{\hat{T}_{nl} (y,k_z)},
\end{align}
\begin{align}
&\underbrace{
\vphantom{\mathcal{R}\left\{ \overline{\widehat{u_j^\prime}
\widehat{u^\prime_i \frac{\partial \bar{u}_j}{\partial
x_i}} } \right\}} \frac{\partial \hat{K}(y, k_z)}{\partial
t}}_0 + \underbrace{\mathcal{R}\left\{
\overline{{\widehat{u_j^\prime}^{*}}\,\widehat{
\bar{u}_i\,\frac{\partial u_j^\prime}{\partial x_i} }}
\right\} }_{-\hat{A}(y,k_z)} = \underbrace{-
\mathcal{R}\left\{
\overline{\widehat{u_j^\prime}^{*}\,\widehat{u^\prime_i\,\frac{\partial
\bar{u}_j}{\partial x_i}} } \right\}}_{\hat{\varPi}(y,
k_z)} - \underbrace{ \vphantom{\mathcal{R}\left\{
\overline{\widehat{u_j^\prime} \widehat{u^\prime_i
\frac{\partial \bar{u}_j}{\partial x_i}} } \right\}}
\frac{2}{Re}\,\overline{ \widehat{s_{ij}^\prime} \
\widehat{s_{ij}^\prime}^*}}_{\hat{D}(y,k_z)}\nonumber\\
& + \underbrace{\vphantom{- \mathcal{R}\left\{
\overline{\widehat{u_j^\prime}^{*} \widehat{ u_i^\prime
\frac{\partial u_j^\prime}{\partial x_i} }} \right\}}
\frac{2}{Re}\,\mathcal{R} \left\{
\overline{\frac{\partial}{\partial y}
(\widehat{u_j^\prime}^{*} \widehat{s_{yj}^\prime}) }
\right\}}_{\hat{T}_{v}(y,k_z)}\underbrace{\vphantom{\mathcal{R}\left\{
\overline{\widehat{u_j^\prime}^{*} \widehat{ u_i^\prime
\frac{\partial u_j^\prime}{\partial x_i} }} \right\}}
{} - \mathcal{R}\left\{
\overline{\frac{\partial}{\partial y}
(\widehat{u_y^{\prime}}^*\widehat{p^{\prime}})} \right\}
}_{\hat{T}_{p}(y,k_z)} \underbrace{{}-
\mathcal{R}\left\{ \overline{\widehat{u_j^\prime}^{*}
\widehat{ u_i^\prime\,\frac{\partial u_j^\prime}{\partial
x_i} }} \right\} }_{\hat{T}_{nl} (y,k_z)},
\end{align}
where we revert from the general partial derivative ![]() $\partial /\partial x_i$ or subscript
$\partial /\partial x_i$ or subscript ![]() $i$ to the wall-normal coordinate
$i$ to the wall-normal coordinate ![]() $y$ when this is the only non-zero term. Here,
$y$ when this is the only non-zero term. Here,
(i)
 $\hat {A}$ is the interaction between mean velocity and gradient of fluctuations, corresponding to the spectral version of the advection term
$\hat {A}$ is the interaction between mean velocity and gradient of fluctuations, corresponding to the spectral version of the advection term  $\bar {\boldsymbol {u}} \boldsymbol {\cdot } \boldsymbol {\nabla } K$;
$\bar {\boldsymbol {u}} \boldsymbol {\cdot } \boldsymbol {\nabla } K$;(ii)
 $\hat {\varPi }$ is the spectral production term, which is an interaction between the mean gradient and fluctuations at scale
$\hat {\varPi }$ is the spectral production term, which is an interaction between the mean gradient and fluctuations at scale  $k_z$;
$k_z$;(iii)
 $\hat {D}$ is the viscous dissipation at mode
$\hat {D}$ is the viscous dissipation at mode  $k_z$;
$k_z$;(iv)
 $\hat {T}_{v}$,
$\hat {T}_{v}$,  $\hat {T}_p$ are transfer terms to mode
$\hat {T}_p$ are transfer terms to mode  $k_z$ due to strain–velocity and pressure–velocity correlations;
$k_z$ due to strain–velocity and pressure–velocity correlations;(v)
 $\hat {T}_{nl}$ is an inter-scale transfer to mode
$\hat {T}_{nl}$ is an inter-scale transfer to mode  $k_z$ due to triad interactions.
$k_z$ due to triad interactions.
When summed over ![]() $k_z$ and integrated over
$k_z$ and integrated over ![]() $y$,
$y$, ![]() $\hat {T}_{v}$,
$\hat {T}_{v}$, ![]() $\hat {T}_{p}$ and
$\hat {T}_{p}$ and ![]() $\hat {T}_{nl}$ are zero.
$\hat {T}_{nl}$ are zero.
The forms of the pressure, viscous diffusion, dissipation and triadic terms are the same as they would be if the flow were uniform in ![]() $z$. Only advection and production terms, which contain the inhomogeneous mean flow, do not simplify as in the uniform case, and instead require a convolution over wavenumbers. In the usual analysis of uniform turbulence in a non-tilted box (Bolotnov et al. Reference Bolotnov, Lahey, Drew, Jansen and Oberai2010; Cho et al. Reference Cho, Hwang and Choi2018; Lee & Moser Reference Lee and Moser2019),
$z$. Only advection and production terms, which contain the inhomogeneous mean flow, do not simplify as in the uniform case, and instead require a convolution over wavenumbers. In the usual analysis of uniform turbulence in a non-tilted box (Bolotnov et al. Reference Bolotnov, Lahey, Drew, Jansen and Oberai2010; Cho et al. Reference Cho, Hwang and Choi2018; Lee & Moser Reference Lee and Moser2019), ![]() $\bar {\boldsymbol {u}}$ reduces to
$\bar {\boldsymbol {u}}$ reduces to ![]() $(U(y),0,0)$ and
$(U(y),0,0)$ and ![]() $\hat {\bar {\boldsymbol {u}}}= (U(y), 0, 0)$ for
$\hat {\bar {\boldsymbol {u}}}= (U(y), 0, 0)$ for ![]() $k_z=0$, and is otherwise 0, which simplifies the spectral balance. In particular, the advection term
$k_z=0$, and is otherwise 0, which simplifies the spectral balance. In particular, the advection term ![]() $\hat {A}$ vanishes, because in such cases
$\hat {A}$ vanishes, because in such cases
 \begin{equation} \hat{A} (y, k_z) ={-}\mathcal{R}\left\{ \overline{\widehat{u_j^\prime}^{*}\,U(y)\,\widehat{ \frac{\partial u_j^\prime}{\partial x} }} \right\} ={-}\frac{1}{2}\, \mathcal{R}\left\{ U(y)\,\overline{ \frac{\partial}{\partial x} \widehat{u_j^\prime}^{*} \widehat{u_j^\prime}} \right\} = 0 \end{equation}
\begin{equation} \hat{A} (y, k_z) ={-}\mathcal{R}\left\{ \overline{\widehat{u_j^\prime}^{*}\,U(y)\,\widehat{ \frac{\partial u_j^\prime}{\partial x} }} \right\} ={-}\frac{1}{2}\, \mathcal{R}\left\{ U(y)\,\overline{ \frac{\partial}{\partial x} \widehat{u_j^\prime}^{*} \widehat{u_j^\prime}} \right\} = 0 \end{equation}
(due to averaging over the periodic ![]() $x$ direction). This is also true in the case of tilted uniform turbulence
$x$ direction). This is also true in the case of tilted uniform turbulence ![]() $\bar {\boldsymbol {u}}=(U(y), 0 , W(y))$. However, this is not true for a patterned mean flow
$\bar {\boldsymbol {u}}=(U(y), 0 , W(y))$. However, this is not true for a patterned mean flow ![]() $\bar {\boldsymbol {u}}=(U(y,z), V(y,z), W(y,z))$ like the one shown in figure 3(c).
$\bar {\boldsymbol {u}}=(U(y,z), V(y,z), W(y,z))$ like the one shown in figure 3(c).
Furthermore, we introduce the balance equation for the spectral energy of the mean flow ![]() $\hat {\bar {E}} \equiv \frac {1}{2} \hat {\bar {\boldsymbol {u}}}^* \boldsymbol {\cdot } \hat {\bar {\boldsymbol {u}}}$ at wavenumber
$\hat {\bar {E}} \equiv \frac {1}{2} \hat {\bar {\boldsymbol {u}}}^* \boldsymbol {\cdot } \hat {\bar {\boldsymbol {u}}}$ at wavenumber ![]() $k_z$:
$k_z$:
 \begin{align} &\underbrace{\vphantom{\mathcal{R}\left\{ \frac{\partial \hat{\bar{u}}_j^*}{\partial x_i} \widehat{\overline{u_i^\prime u_j^\prime}} \right\} } \frac{\partial \hat{\bar{E}}(y, k_z)}{\partial t} }_0 + \underbrace{\mathcal{R}\left\{ \hat{\bar{u}}_j^* \widehat{\bar{u}_i\,\frac{\partial \bar{u}_j}{\partial x_i} } \right\} }_{-\hat{\bar{A}}(y,k_z)} =\underbrace{\mathcal{R}\left\{ \frac{\partial \hat{\bar{u}}_j^*}{\partial x_i}\,\widehat{\overline{u_i^\prime u_j^\prime}} \right\} }_{-\hat{\bar{\varPi}}(y, k_z)} - \underbrace{\vphantom{\mathcal{R}\left\{ \frac{\partial \hat{\bar{u}}_j^*}{\partial x_i} \widehat{\overline{u_i^\prime u_j^\prime}} \right\} } ~ \frac{2}{Re}\, \hat{\bar{s}}_{ij} \hat{\bar{s}}_{ij}^*}_{\hat{\bar{D}}(y,k_z)} \nonumber\\ & + \underbrace{\frac{2}{Re}\, \mathcal{R}\left\{\frac{\partial}{\partial y} (\hat{\bar{u}}_j^* \hat{\bar{s}}_{yj} ) \right\}}_{\hat{\bar{T}}_{v}(y,k_z)} \underbrace{{}-\mathcal{R}\left\{ \frac{\partial}{\partial y} \hat{\bar{u}}_y^* \hat{\bar{p}} \right\} }_{\hat{\bar{T}}_{p}(y,k_z)} \underbrace{- \mathcal{R}\left\{ \frac{\partial}{\partial y}(\hat{\bar{u}}_j^* \widehat{\overline{u_y^\prime u_j^\prime}} ) \right\} }_{\hat{\bar{T}}_{nl} (y,k_z)}, \end{align}
\begin{align} &\underbrace{\vphantom{\mathcal{R}\left\{ \frac{\partial \hat{\bar{u}}_j^*}{\partial x_i} \widehat{\overline{u_i^\prime u_j^\prime}} \right\} } \frac{\partial \hat{\bar{E}}(y, k_z)}{\partial t} }_0 + \underbrace{\mathcal{R}\left\{ \hat{\bar{u}}_j^* \widehat{\bar{u}_i\,\frac{\partial \bar{u}_j}{\partial x_i} } \right\} }_{-\hat{\bar{A}}(y,k_z)} =\underbrace{\mathcal{R}\left\{ \frac{\partial \hat{\bar{u}}_j^*}{\partial x_i}\,\widehat{\overline{u_i^\prime u_j^\prime}} \right\} }_{-\hat{\bar{\varPi}}(y, k_z)} - \underbrace{\vphantom{\mathcal{R}\left\{ \frac{\partial \hat{\bar{u}}_j^*}{\partial x_i} \widehat{\overline{u_i^\prime u_j^\prime}} \right\} } ~ \frac{2}{Re}\, \hat{\bar{s}}_{ij} \hat{\bar{s}}_{ij}^*}_{\hat{\bar{D}}(y,k_z)} \nonumber\\ & + \underbrace{\frac{2}{Re}\, \mathcal{R}\left\{\frac{\partial}{\partial y} (\hat{\bar{u}}_j^* \hat{\bar{s}}_{yj} ) \right\}}_{\hat{\bar{T}}_{v}(y,k_z)} \underbrace{{}-\mathcal{R}\left\{ \frac{\partial}{\partial y} \hat{\bar{u}}_y^* \hat{\bar{p}} \right\} }_{\hat{\bar{T}}_{p}(y,k_z)} \underbrace{- \mathcal{R}\left\{ \frac{\partial}{\partial y}(\hat{\bar{u}}_j^* \widehat{\overline{u_y^\prime u_j^\prime}} ) \right\} }_{\hat{\bar{T}}_{nl} (y,k_z)}, \end{align}where
(i)
 $\hat {\bar {A}}$ is a nonlinear transfer term for the mean flow – this is a spectral version of the advection term
$\hat {\bar {A}}$ is a nonlinear transfer term for the mean flow – this is a spectral version of the advection term  $\bar {\boldsymbol {u}} \boldsymbol {\cdot } \boldsymbol {\nabla } \bar {E}$ appearing in the mean-flow balance equation (4.4);
$\bar {\boldsymbol {u}} \boldsymbol {\cdot } \boldsymbol {\nabla } \bar {E}$ appearing in the mean-flow balance equation (4.4);(ii)
 $\hat {\bar {\varPi }}$ is the interaction between Reynolds stress at scale
$\hat {\bar {\varPi }}$ is the interaction between Reynolds stress at scale  $k_z$ and the mean gradient at scale
$k_z$ and the mean gradient at scale  $k_z$, and hence is a production term;
$k_z$, and hence is a production term;(iii)
 $\hat {\bar {D}}$ is a dissipation term for the mean-flow energy;
$\hat {\bar {D}}$ is a dissipation term for the mean-flow energy;(iv)
 $\hat {\bar {T}}_{v}$,
$\hat {\bar {T}}_{v}$,  $\hat {\bar {T}}_{p}$ are transfer terms due to correlations between mean strain and velocity, and mean pressure and velocity;
$\hat {\bar {T}}_{p}$ are transfer terms due to correlations between mean strain and velocity, and mean pressure and velocity;(v)
 $\hat {\bar {T}}_{nl}$ is a flux term due to the interactions between the Reynolds stress and the mean flow.
$\hat {\bar {T}}_{nl}$ is a flux term due to the interactions between the Reynolds stress and the mean flow.
We have presented (5.3) and (5.5) with ![]() $y$ dependence to facilitate understanding the origin of the various terms. However, in the rest of this section, we will focus on
$y$ dependence to facilitate understanding the origin of the various terms. However, in the rest of this section, we will focus on ![]() $y$-integrated TKE and mean-flow balance to characterise the spectral distribution as a function of
$y$-integrated TKE and mean-flow balance to characterise the spectral distribution as a function of ![]() $k_z$. As the mean flow
$k_z$. As the mean flow ![]() $\bar {\boldsymbol {u}}$ is dominated by
$\bar {\boldsymbol {u}}$ is dominated by ![]() $\bar {\boldsymbol {u}}_0$ and
$\bar {\boldsymbol {u}}_0$ and ![]() $\bar {\boldsymbol {u}}_1$, we write (5.5) in
$\bar {\boldsymbol {u}}_1$, we write (5.5) in ![]() $y$-integrated form for
$y$-integrated form for ![]() $k_z=0$ and
$k_z=0$ and ![]() $k_z=2{\rm \pi} /L_z$ and obtain
$k_z=2{\rm \pi} /L_z$ and obtain
where we have introduced
with similar definitions for ![]() $\hat {\bar {A}}_0$,
$\hat {\bar {A}}_0$, ![]() $\hat {\bar {D}}_0$,
$\hat {\bar {D}}_0$, ![]() $\hat {\bar {A}}_1$ and
$\hat {\bar {A}}_1$ and ![]() $\hat {\bar {D}}_1$. We have also introduced the total energy injection due to the action of the walls:
$\hat {\bar {D}}_1$. We have also introduced the total energy injection due to the action of the walls:
 \begin{equation} I \equiv \sum_{k_z} \int_{{-}1}^1 \hat{\bar{T}}_{v}(y, k_z) \,\text{d} y = \frac{2}{Re} \left.\sum_{k_z} \hat{\bar{u}}_j^* (k_z) \ \hat{\bar{s}}_{yj} (k_z) \right\vert_{{-}1}^1. \end{equation}
\begin{equation} I \equiv \sum_{k_z} \int_{{-}1}^1 \hat{\bar{T}}_{v}(y, k_z) \,\text{d} y = \frac{2}{Re} \left.\sum_{k_z} \hat{\bar{u}}_j^* (k_z) \ \hat{\bar{s}}_{yj} (k_z) \right\vert_{{-}1}^1. \end{equation}
The only non-zero term in the final expression of (5.8) is mode ![]() $k_z=0$ (because the boundary condition dictates a fixed velocity everywhere on the wall), so that
$k_z=0$ (because the boundary condition dictates a fixed velocity everywhere on the wall), so that
 \begin{equation} I = \left.\frac{2}{Re}\,\hat{\bar{u}}_j^* (k_z=0)\ \hat{\bar{s}}_{yj} (k_z=0) \right\vert_{{-}1}^1 = 2\,\frac{u_\tau^2}{U_{wall}^2}. \end{equation}
\begin{equation} I = \left.\frac{2}{Re}\,\hat{\bar{u}}_j^* (k_z=0)\ \hat{\bar{s}}_{yj} (k_z=0) \right\vert_{{-}1}^1 = 2\,\frac{u_\tau^2}{U_{wall}^2}. \end{equation}
Note that ![]() $\hat {\bar {T}}_{p}$ and
$\hat {\bar {T}}_{p}$ and ![]() $\hat {\bar {T}}_{nl}$ integrate to zero, since both
$\hat {\bar {T}}_{nl}$ integrate to zero, since both ![]() $\bar {u}_y$ and the Reynolds stress vanish at the walls.
$\bar {u}_y$ and the Reynolds stress vanish at the walls.
Two important comments can be made at this stage. The first one starts from a word of caution: all terms in (5.5) are not the Fourier transforms of those in (4.4). (This is a generalisation of the fact that ![]() $\hat {E} (k_z)$ is defined to be
$\hat {E} (k_z)$ is defined to be ![]() $\hat {\boldsymbol {u}} (k_z)\boldsymbol {\cdot } \hat {\boldsymbol {u}} (k_z) /2$ and not
$\hat {\boldsymbol {u}} (k_z)\boldsymbol {\cdot } \hat {\boldsymbol {u}} (k_z) /2$ and not ![]() $\widehat {\boldsymbol {u} \boldsymbol {\cdot } \boldsymbol {u}}(k_z)/2$.) This means in particular that although energy is injected only in the balance of
$\widehat {\boldsymbol {u} \boldsymbol {\cdot } \boldsymbol {u}}(k_z)/2$.) This means in particular that although energy is injected only in the balance of ![]() $\bar {\boldsymbol {u}}_0$ via
$\bar {\boldsymbol {u}}_0$ via ![]() $I$, the energy is not injected uniformly within the flow, as
$I$, the energy is not injected uniformly within the flow, as ![]() $\bar {T}_{v}$ is not uniform in
$\bar {T}_{v}$ is not uniform in ![]() $z$ (see figure 6c). The connection with the physical injection of energy is indeed only through
$z$ (see figure 6c). The connection with the physical injection of energy is indeed only through ![]() $z$ averaging:
$z$ averaging:
The second comment is about the way in which this injected energy is communicated to the TKE spectral balance. Contrary to the physical-space version of the energy balance, where the same production ![]() $P$ appears in the TKE (4.1) and the mean flow (4.4) equations, the spectral production terms appearing in (5.3) and (5.5),
$P$ appears in the TKE (4.1) and the mean flow (4.4) equations, the spectral production terms appearing in (5.3) and (5.5), ![]() $\hat {\varPi }$ and
$\hat {\varPi }$ and ![]() $\hat {\bar {\varPi }}$, are different. However, the sum over
$\hat {\bar {\varPi }}$, are different. However, the sum over ![]() $k_z$ of these two terms agree, so we can write the total (
$k_z$ of these two terms agree, so we can write the total (![]() $y$-integrated) production
$y$-integrated) production ![]() $\varPi$ as
$\varPi$ as
 \begin{equation} \varPi \equiv \sum_{k_z} \int_{{-}1}^1 \hat{\varPi}(y, k_z) \,\text{d} y = \sum_{k_z} \int_{{-}1}^1 \hat{\bar{\varPi}}(y, k_z) \,\text{d} y . \end{equation}
\begin{equation} \varPi \equiv \sum_{k_z} \int_{{-}1}^1 \hat{\varPi}(y, k_z) \,\text{d} y = \sum_{k_z} \int_{{-}1}^1 \hat{\bar{\varPi}}(y, k_z) \,\text{d} y . \end{equation}Furthermore, in the physical-space representation,
where the last equality follows since all transfer terms integrate to zero. The equivalence (5.11) is key to understanding how TKE and mean-flow energy are connected. This will be developed further in § 5.2.
5.2. Results for the spectral energy balance
5.2.1. TKE balance
We examine the spectral balance of the TKE (5.3), integrated over the cross-channel direction. This balance is presented for the patterned state in figure 7(a) (![]() $Re=400$) and for the uniform state in figure 7(c) (
$Re=400$) and for the uniform state in figure 7(c) (![]() $Re=500$). The transfer terms
$Re=500$). The transfer terms ![]() $\hat {T}_{v}$ and
$\hat {T}_{v}$ and ![]() $\hat {T}_{p}$ are not shown as they integrate to zero. (The
$\hat {T}_{p}$ are not shown as they integrate to zero. (The ![]() $y$ dependence of energy transfer will be discussed in Appendix A.)
$y$ dependence of energy transfer will be discussed in Appendix A.)

Figure 7. (a) Spectral energy budget (5.3) for a pattern at ![]() $Re=400$, integrated over
$Re=400$, integrated over ![]() $y\in [-1, 1]$. Viscous and pressure transfers are not shown as they integrate to 0. The grey circles indicate
$y\in [-1, 1]$. Viscous and pressure transfers are not shown as they integrate to 0. The grey circles indicate ![]() $k_{{LS}}$ and
$k_{{LS}}$ and ![]() $k_{{SS}}$, which delimit the spectral region where transfer
$k_{{SS}}$, which delimit the spectral region where transfer ![]() $\hat {T}_{nl}$ is negative. (b) Spectral energy budget of the mean flow (5.5) for a pattern at
$\hat {T}_{nl}$ is negative. (b) Spectral energy budget of the mean flow (5.5) for a pattern at ![]() $Re=400$, integrated over
$Re=400$, integrated over ![]() $y\in [-1, 1]$, shown for
$y\in [-1, 1]$, shown for ![]() $k_z=0$,
$k_z=0$, ![]() $k_z=2{\rm \pi} /L_z$ and summed over
$k_z=2{\rm \pi} /L_z$ and summed over ![]() $k_z>2{\rm \pi} /L_z$. (c,d) Same as (a,b) for a uniform state at
$k_z>2{\rm \pi} /L_z$. (c,d) Same as (a,b) for a uniform state at ![]() $Re=500$. To convey both sign and order of magnitude, (b,d) show
$Re=500$. To convey both sign and order of magnitude, (b,d) show ![]() ${\rm sgn}(Q)\log |Q|$ for each quantity
${\rm sgn}(Q)\log |Q|$ for each quantity ![]() $Q$.
$Q$.
We first focus on the similarities between patterned and uniform states. We observe a peak in the production and dissipation terms near the energy-containing scale ![]() $k_{{rolls}} \simeq 1.41$, as we saw for the spectral energy in figures 3(a) and 3(b). At this scale, the nonlinear transfer
$k_{{rolls}} \simeq 1.41$, as we saw for the spectral energy in figures 3(a) and 3(b). At this scale, the nonlinear transfer ![]() $\hat {T}_{nl}$ is negative and of large amplitude: scale
$\hat {T}_{nl}$ is negative and of large amplitude: scale ![]() $k_{{rolls}}$ produces much more than it dissipates, and the remainder is transferred away from scale
$k_{{rolls}}$ produces much more than it dissipates, and the remainder is transferred away from scale ![]() $k_z$ to other scales. The nonlinear transfer becomes positive above a small-scale wavenumber that we denote
$k_z$ to other scales. The nonlinear transfer becomes positive above a small-scale wavenumber that we denote ![]() $k_{{SS}}$. (In both the patterned state at
$k_{{SS}}$. (In both the patterned state at ![]() $Re=400$ and the uniform state at
$Re=400$ and the uniform state at ![]() $Re=500$, we have
$Re=500$, we have ![]() $k_{{SS}} \simeq 3.6$.) This positive transfer at small scales is indicative of a direct energy cascade to small dissipative scales.
$k_{{SS}} \simeq 3.6$.) This positive transfer at small scales is indicative of a direct energy cascade to small dissipative scales.
The TKE balance for ![]() $k_z< k_{{rolls}}$ contrasts with that at large
$k_z< k_{{rolls}}$ contrasts with that at large ![]() $k_z$. First, production becomes negative for
$k_z$. First, production becomes negative for ![]() $k_z \lesssim 0.47$. This negative production at large scales appears in both patterned and uniform states. It corresponds to energy transfer from the fluctuations to the mean flow. We note that this unusual sign of part of the production term has also been reported by Symon et al. (Reference Symon, Illingworth and Marusic2021) in spanwise-constant modes of channel flow in a minimal domain that is too small to support laminar–turbulent patterns.
$k_z \lesssim 0.47$. This negative production at large scales appears in both patterned and uniform states. It corresponds to energy transfer from the fluctuations to the mean flow. We note that this unusual sign of part of the production term has also been reported by Symon et al. (Reference Symon, Illingworth and Marusic2021) in spanwise-constant modes of channel flow in a minimal domain that is too small to support laminar–turbulent patterns.
Second, energy in the range ![]() $k_z < 0.94$ is fuelled by a positive nonlinear transfer
$k_z < 0.94$ is fuelled by a positive nonlinear transfer ![]() $\hat {T}_{nl}$, which signifies a transfer from small to large scales. This is present in both patterned and uniform states. We denote the (large) scale at which this transfer becomes positive by
$\hat {T}_{nl}$, which signifies a transfer from small to large scales. This is present in both patterned and uniform states. We denote the (large) scale at which this transfer becomes positive by ![]() $k_{{LS}}$, as seen in figures 5, 7(a) and 7(c). In the part of the spectrum
$k_{{LS}}$, as seen in figures 5, 7(a) and 7(c). In the part of the spectrum ![]() $k_z< k_{{LS}}$, the influx of energy from smaller scales is mostly balanced by dissipation, while only a relatively small amount of energy is lost to the mean flow via negative production.
$k_z< k_{{LS}}$, the influx of energy from smaller scales is mostly balanced by dissipation, while only a relatively small amount of energy is lost to the mean flow via negative production.
Now considering the differences between the patterned (figure 7a) and uniform states (figure 7c), the advection term ![]() $\hat {A}$ plays a more significant role in redistributing energy between scales in the patterned state: it is positive for
$\hat {A}$ plays a more significant role in redistributing energy between scales in the patterned state: it is positive for ![]() $k_z<1.1 < k_{{rolls}}$, negative near
$k_z<1.1 < k_{{rolls}}$, negative near ![]() $k_{{rolls}}$, and negligible for
$k_{{rolls}}$, and negligible for ![]() $k_z>3$. This role is very similar to that of nonlinear transfers
$k_z>3$. This role is very similar to that of nonlinear transfers ![]() $\hat {T}_{nl}$, but with weaker amplitude. In the uniform state,
$\hat {T}_{nl}$, but with weaker amplitude. In the uniform state, ![]() $\hat {A}$ is nearly zero and would vanish if the mean flow were strictly uniform in
$\hat {A}$ is nearly zero and would vanish if the mean flow were strictly uniform in ![]() $z$; see (5.4). This is not exactly the case here, especially at
$z$; see (5.4). This is not exactly the case here, especially at ![]() $k_z \simeq k_{{rolls}}$, probably due to insufficiently long averaging. Other differences are visible between the uniform and patterned states, especially regarding the shape and intensity of each individual curve. For instance, near
$k_z \simeq k_{{rolls}}$, probably due to insufficiently long averaging. Other differences are visible between the uniform and patterned states, especially regarding the shape and intensity of each individual curve. For instance, near ![]() $k_{{rolls}}$ one sees that
$k_{{rolls}}$ one sees that ![]() $\hat {D} \simeq \hat {T}_{nl}$ in the uniform case, while
$\hat {D} \simeq \hat {T}_{nl}$ in the uniform case, while ![]() $\hat {D}$ exceeds
$\hat {D}$ exceeds ![]() $\hat {T}_{nl}$ in the patterned case.
$\hat {T}_{nl}$ in the patterned case.
5.2.2. Mean-flow balance
The spectral energy balance of the mean flow (5.6a,b) is presented in figures 7(b) and 7(d) for both patterned and uniform states. In the patterned case, the three plots correspond to modes ![]() $\bar {\boldsymbol {u}}_0$,
$\bar {\boldsymbol {u}}_0$, ![]() $\bar {\boldsymbol {u}}_1$ and
$\bar {\boldsymbol {u}}_1$ and ![]() $\bar {\boldsymbol {u}}_{>1}$. For the uniform state, the terms in the balance of
$\bar {\boldsymbol {u}}_{>1}$. For the uniform state, the terms in the balance of ![]() $\bar {\boldsymbol {u}}_1$ and
$\bar {\boldsymbol {u}}_1$ and ![]() $\bar {\boldsymbol {u}}_{>1}$ are zero up to numerical error, hence it is not meaningful to show them. In both the patterned and uniform cases,
$\bar {\boldsymbol {u}}_{>1}$ are zero up to numerical error, hence it is not meaningful to show them. In both the patterned and uniform cases, ![]() $\bar {\boldsymbol {u}}_0$ is fuelled by the mean strain via injection term
$\bar {\boldsymbol {u}}_0$ is fuelled by the mean strain via injection term ![]() $I$ (purple cross). This energy is dissipated (blue square) and also transferred to the fluctuations via the production
$I$ (purple cross). This energy is dissipated (blue square) and also transferred to the fluctuations via the production ![]() $\hat {\bar {\varPi }}_0$ (red circle). Note that
$\hat {\bar {\varPi }}_0$ (red circle). Note that ![]() $\hat {\bar {\varPi }} > 0$ corresponds to the usual positive TKE production and hence a sink of energy with respect to the mean flow: production appears as
$\hat {\bar {\varPi }} > 0$ corresponds to the usual positive TKE production and hence a sink of energy with respect to the mean flow: production appears as ![]() $-\hat {\bar {\varPi }}$ in the mean balance equation (5.5).
$-\hat {\bar {\varPi }}$ in the mean balance equation (5.5).
For ![]() $\bar {\boldsymbol {u}}_1$ in the patterned state (middle plot of figure 7b), the main source of energy is the advective term
$\bar {\boldsymbol {u}}_1$ in the patterned state (middle plot of figure 7b), the main source of energy is the advective term ![]() $\hat {\bar {A}}_1$, with some energy coming from the negative production
$\hat {\bar {A}}_1$, with some energy coming from the negative production ![]() $\hat {\bar {\varPi }}_1 < 0$. Thus the
$\hat {\bar {\varPi }}_1 < 0$. Thus the ![]() $\bar {\boldsymbol {u}}_1$ component of the mean flow is fuelled to some extent by a negative transfer from fluctuations back to mean flow, but the advective contribution dominates. The two sources are balanced by dissipation. The remaining scales in the mean spectral balance
$\bar {\boldsymbol {u}}_1$ component of the mean flow is fuelled to some extent by a negative transfer from fluctuations back to mean flow, but the advective contribution dominates. The two sources are balanced by dissipation. The remaining scales in the mean spectral balance ![]() $k_z>2{\rm \pi} /L_z$ (right-hand plot of figure 7b) are very weak compared to the first two components.
$k_z>2{\rm \pi} /L_z$ (right-hand plot of figure 7b) are very weak compared to the first two components.
Our results show that the advection term ![]() $\hat {\bar {A}}$ plays a crucial role in the mean-flow balance in the patterned state. Since this term represents a transfer due to nonlinearities, its sum over
$\hat {\bar {A}}$ plays a crucial role in the mean-flow balance in the patterned state. Since this term represents a transfer due to nonlinearities, its sum over ![]() $k_z$ and
$k_z$ and ![]() $y$ vanishes. At
$y$ vanishes. At ![]() $Re=400$, we find that
$Re=400$, we find that ![]() $\hat {\bar {A}}_0\simeq -1.77\times 10^{-4}$,
$\hat {\bar {A}}_0\simeq -1.77\times 10^{-4}$, ![]() $\hat {\bar {A}}_1\simeq 1.82\times 10^{-4}$ and
$\hat {\bar {A}}_1\simeq 1.82\times 10^{-4}$ and ![]() $\sum _{k_z>2{\rm \pi} /L_z} \int _{-1}^1 \hat {\bar {A}}(y, k_z) \,\text {d}y \simeq -5\times 10^{-6}$. Hence we have the approximate equality
$\sum _{k_z>2{\rm \pi} /L_z} \int _{-1}^1 \hat {\bar {A}}(y, k_z) \,\text {d}y \simeq -5\times 10^{-6}$. Hence we have the approximate equality
which holds for other values of ![]() $Re$ in the patterned regime. Even though the advection is negligible compared with the dominant terms in the
$Re$ in the patterned regime. Even though the advection is negligible compared with the dominant terms in the ![]() $\bar {\boldsymbol {u}}_0$ balance, it is the dominant source of energy at the pattern scale. In a perfectly uniform case,
$\bar {\boldsymbol {u}}_0$ balance, it is the dominant source of energy at the pattern scale. In a perfectly uniform case, ![]() $\hat {\bar {A}}_0$ would be zero.
$\hat {\bar {A}}_0$ would be zero.
We refer the reader to Appendix A for the ![]() $y$ dependence of the terms in the mean-flow budget (5.5).
$y$ dependence of the terms in the mean-flow budget (5.5).
5.2.3. Connection between TKE and mean flow
We now investigate the connection between the TKE and mean flow, focusing particularly on the spectral production terms ![]() $\hat {\bar {\varPi }}$ and
$\hat {\bar {\varPi }}$ and ![]() $\hat {\varPi }$. Recall that while these production terms take different forms in the TKE and mean-flow spectral balances (5.3) and (5.5), upon integration over
$\hat {\varPi }$. Recall that while these production terms take different forms in the TKE and mean-flow spectral balances (5.3) and (5.5), upon integration over ![]() $y$ and summation over
$y$ and summation over ![]() $k_z$ (5.11), they give the same total production
$k_z$ (5.11), they give the same total production ![]() $\varPi$.
$\varPi$.
We decompose the total production in two ways: first by writing the total TKE production ![]() $\varPi$ as a sum of its positive and negative parts, and second by considering the dominant contributions from
$\varPi$ as a sum of its positive and negative parts, and second by considering the dominant contributions from ![]() $\bar {\boldsymbol {u}}_0$ and
$\bar {\boldsymbol {u}}_0$ and ![]() $\bar {\boldsymbol {u}}_1$ in the mean-flow production
$\bar {\boldsymbol {u}}_1$ in the mean-flow production ![]() $\hat {\bar {\varPi }}$:
$\hat {\bar {\varPi }}$:
where
 \begin{equation} \hat{\varPi}^{{>}0} \equiv \sum_{k_z=0}^{\infty} \int_{{-}1}^1\hat{\varPi} (y,k_z) \,\text{d}y \varTheta \left( \int_{{-}1}^1 \hat{\varPi} (y, k_z) \,\text{d}y \right) \end{equation}
\begin{equation} \hat{\varPi}^{{>}0} \equiv \sum_{k_z=0}^{\infty} \int_{{-}1}^1\hat{\varPi} (y,k_z) \,\text{d}y \varTheta \left( \int_{{-}1}^1 \hat{\varPi} (y, k_z) \,\text{d}y \right) \end{equation}and
 \begin{equation} \hat{\varPi}^{{<}0} \equiv \sum_{k_z=0}^{\infty} \int_{{-}1}^1 \hat{\varPi} (y, k_z) \,\text{d}y \varTheta \left(- \int_{{-}1}^1 \hat{\varPi} (k_z)\,\text{d}y \right), \end{equation}
\begin{equation} \hat{\varPi}^{{<}0} \equiv \sum_{k_z=0}^{\infty} \int_{{-}1}^1 \hat{\varPi} (y, k_z) \,\text{d}y \varTheta \left(- \int_{{-}1}^1 \hat{\varPi} (k_z)\,\text{d}y \right), \end{equation}
with ![]() $\varTheta$ the Heaviside function. We recall that figure 7(a) shows that
$\varTheta$ the Heaviside function. We recall that figure 7(a) shows that ![]() $\int _{-1}^1 \hat {\varPi }(y, k_z) \,\text {d}y <0$ occurs mostly at large scales. Each term in (5.14) in the patterned and uniform states is displayed in table 1 for various values of
$\int _{-1}^1 \hat {\varPi }(y, k_z) \,\text {d}y <0$ occurs mostly at large scales. Each term in (5.14) in the patterned and uniform states is displayed in table 1 for various values of ![]() $Re$.
$Re$.
Table 1. Production terms appearing in the mean flow (5.5) and the TKE (5.3) balance, as decomposed in (5.14), for the flow regimes presented in figure 7.

We observe that in the patterned case, the positive production is very close to ![]() $\hat {\bar {\varPi }}_0$ and the negative production is very close to
$\hat {\bar {\varPi }}_0$ and the negative production is very close to ![]() $\hat {\bar {\varPi }}_1$, i.e.
$\hat {\bar {\varPi }}_1$, i.e. ![]() $\hat {\bar {\varPi }}_0 \simeq \hat {\varPi }^{>0}$ and
$\hat {\bar {\varPi }}_0 \simeq \hat {\varPi }^{>0}$ and ![]() $\hat {\bar {\varPi }}_1 \simeq \hat {\varPi }^{<0}$. In the uniform case,
$\hat {\bar {\varPi }}_1 \simeq \hat {\varPi }^{<0}$. In the uniform case, ![]() $\hat {\bar {\varPi }}_1$ is very small and
$\hat {\bar {\varPi }}_1$ is very small and ![]() $\hat {\bar {\varPi }}_0$ accounts for essentially all the production, so it is the sum of the positive and negative parts. In other words,
$\hat {\bar {\varPi }}_0$ accounts for essentially all the production, so it is the sum of the positive and negative parts. In other words,
 \begin{align} \hat{\bar{\varPi}}_0
\begin{cases} \simeq \hat{\varPi}^{{>}0} & \text{in
patterned state},\\ \simeq \hat{\varPi}^{{>}0} +
\varPi^{{<}0} & \text{in uniform state},
\end{cases} \quad \hat{\bar{\varPi}}_1 \begin{cases}
\simeq \varPi^{{<}0} & \text{in patterned state},
\\ \ll \varPi^{{<}0} & \text{in uniform state}.
\end{cases}
\end{align}
\begin{align} \hat{\bar{\varPi}}_0
\begin{cases} \simeq \hat{\varPi}^{{>}0} & \text{in
patterned state},\\ \simeq \hat{\varPi}^{{>}0} +
\varPi^{{<}0} & \text{in uniform state},
\end{cases} \quad \hat{\bar{\varPi}}_1 \begin{cases}
\simeq \varPi^{{<}0} & \text{in patterned state},
\\ \ll \varPi^{{<}0} & \text{in uniform state}.
\end{cases}
\end{align}
This supports an essential connection between the TKE and the mean-flow production terms: in the patterned state, almost all negative TKE production goes to ![]() $\bar {\boldsymbol {u}}_1$, and almost all positive TKE production comes from
$\bar {\boldsymbol {u}}_1$, and almost all positive TKE production comes from ![]() $\bar {\boldsymbol {u}}_0$; in the uniform state, the negative TKE production is absorbed by
$\bar {\boldsymbol {u}}_0$; in the uniform state, the negative TKE production is absorbed by ![]() $\bar {\boldsymbol {u}}=\bar {\boldsymbol {u}}_0$. (In all cases, the negative production,
$\bar {\boldsymbol {u}}=\bar {\boldsymbol {u}}_0$. (In all cases, the negative production, ![]() $\varPi ^{<0}$, represents less than
$\varPi ^{<0}$, represents less than ![]() $1.5\,\%$ of
$1.5\,\%$ of ![]() $\varPi$:
$\varPi$: ![]() $-\varPi ^{<0}/\varPi \simeq 1.46\,\%$ at
$-\varPi ^{<0}/\varPi \simeq 1.46\,\%$ at ![]() $Re=400$, and
$Re=400$, and ![]() $1.37\,\%$ at
$1.37\,\%$ at ![]() $Re=500$.)
$Re=500$.)
At this stage, we can draw the following conclusions, illustrated in figures 8(a) and 8(b).
(i) Most of the energy flows into the mean flow and then to TKE according to the usual picture from developed shear flows: energy is injected to
 $\bar {\boldsymbol {u}}_0$ by viscous stress, and is transferred to fluctuations via positive production. TKE is produced mostly at the scale of the energy-containing eddies (here, streaks and rolls) and is transferred to smaller scales, where it is dissipated.
$\bar {\boldsymbol {u}}_0$ by viscous stress, and is transferred to fluctuations via positive production. TKE is produced mostly at the scale of the energy-containing eddies (here, streaks and rolls) and is transferred to smaller scales, where it is dissipated.(ii) An important modification to this usual picture is the presence of an inverse transfer of some TKE to large scales via triad interactions
 $\hat {T}_{nl}$. This energy is not entirely dissipated and instead feeds back to the mean flow via negative production
$\hat {T}_{nl}$. This energy is not entirely dissipated and instead feeds back to the mean flow via negative production  $\hat {\varPi }^{<0}$.
$\hat {\varPi }^{<0}$.(iii) Although weak compared to total production
 $\varPi$, this negative production
$\varPi$, this negative production  $\hat {\varPi }^{<0}$ fuels
$\hat {\varPi }^{<0}$ fuels  $\bar {\boldsymbol {u}}_1$ in the patterned state.
$\bar {\boldsymbol {u}}_1$ in the patterned state.(iv) In the patterned state
 $\hat {\bar {A}}_1$ is the main source of energy of
$\hat {\bar {A}}_1$ is the main source of energy of  $\bar {\boldsymbol {u}}_1$: nonlinearities of the mean flow play a stronger role than negative production.
$\bar {\boldsymbol {u}}_1$: nonlinearities of the mean flow play a stronger role than negative production.

Figure 8. Illustration of the mean-flow–TKE interaction for (a) the uniformly turbulent state, and (b) the patterned state. In the uniform state, ![]() $\hat {\bar {\varPi }}_0 \simeq \hat {\varPi }^{<0} + \hat {\varPi }^{>0}$, while in the patterned state,
$\hat {\bar {\varPi }}_0 \simeq \hat {\varPi }^{<0} + \hat {\varPi }^{>0}$, while in the patterned state, ![]() $\hat {\bar {\varPi }}_0 \simeq \hat {\varPi }^{>0}$ and
$\hat {\bar {\varPi }}_0 \simeq \hat {\varPi }^{>0}$ and ![]() $\hat {\bar {\varPi }}_1 \simeq \hat {\varPi }^{<0}$.
$\hat {\bar {\varPi }}_1 \simeq \hat {\varPi }^{<0}$.
We have defined large scales as those for which the nonlinear transfer is negative: ![]() $k_z < k_{{LS}}$ in figures 7(a) and 7(c). This separates the large and small scales in figure 8. Note, however, that the scales at which production becomes negative are even larger:
$k_z < k_{{LS}}$ in figures 7(a) and 7(c). This separates the large and small scales in figure 8. Note, however, that the scales at which production becomes negative are even larger: ![]() $k_z \lesssim 0.5 < k_{{LS}}$ in figures 7(a) and 7(c). We do not distinguish these different notions of large scales in figure 8.
$k_z \lesssim 0.5 < k_{{LS}}$ in figures 7(a) and 7(c). We do not distinguish these different notions of large scales in figure 8.
We extend these considerations of transfers across scales by considering the quantities
 \begin{equation} \left.\begin{gathered} \hat{\varPi}_{{<}k}(k_z) \equiv \sum_{k_z^\prime < k_z }\int_{{-}1}^1 \hat{\varPi} (y, k_z^\prime) \,\text{d}y, \quad \hat{D}_{{<}k}(k_z) \equiv \sum_{k_z^\prime < k_z }\int_{{-}1}^1 \hat{D} (y, k_z^\prime) \, \text{d}y, \\ \hat{\varPhi}_{{<}k}(k_z) \equiv \sum_{k_z^\prime < k_z }\int_{{-}1}^1 \hat{T}_{nl} (y, k_z^\prime) \, \text{d}y, \quad \hat{A}_{{<}k}(k_z) \equiv \sum_{k_z^\prime < k_z }\int_{{-}1}^1 \hat{A} (y, k_z^\prime) \, \text{d}y. \end{gathered}\right\}\end{equation}
\begin{equation} \left.\begin{gathered} \hat{\varPi}_{{<}k}(k_z) \equiv \sum_{k_z^\prime < k_z }\int_{{-}1}^1 \hat{\varPi} (y, k_z^\prime) \,\text{d}y, \quad \hat{D}_{{<}k}(k_z) \equiv \sum_{k_z^\prime < k_z }\int_{{-}1}^1 \hat{D} (y, k_z^\prime) \, \text{d}y, \\ \hat{\varPhi}_{{<}k}(k_z) \equiv \sum_{k_z^\prime < k_z }\int_{{-}1}^1 \hat{T}_{nl} (y, k_z^\prime) \, \text{d}y, \quad \hat{A}_{{<}k}(k_z) \equiv \sum_{k_z^\prime < k_z }\int_{{-}1}^1 \hat{A} (y, k_z^\prime) \, \text{d}y. \end{gathered}\right\}\end{equation}
These scale-to-scale quantities are shown in figure 9, where ![]() $\hat {\varPhi }_{< k}$ is the nonlinear energy flux across a wavenumber
$\hat {\varPhi }_{< k}$ is the nonlinear energy flux across a wavenumber ![]() $k_z$. This integrated picture reveals a zone of inverse flux of energy to large scales (
$k_z$. This integrated picture reveals a zone of inverse flux of energy to large scales (![]() $\hat {\varPhi }_{< k} >0$ for
$\hat {\varPhi }_{< k} >0$ for ![]() $k_z<1.88$). For
$k_z<1.88$). For ![]() $k_z < O(1)$, this inverse transfer is the dominant source and is mostly balanced by dissipation. Starting at
$k_z < O(1)$, this inverse transfer is the dominant source and is mostly balanced by dissipation. Starting at ![]() $k_z > O(1)$, production comes into play and eventually is the only source.
$k_z > O(1)$, production comes into play and eventually is the only source.

Figure 9. Cumulative energy balance (5.18) integrated over ![]() $y\in [-1, 1]$ in the patterned case at
$y\in [-1, 1]$ in the patterned case at ![]() $Re=400$.
$Re=400$.
We emphasise that this strong inverse transfer does not correspond to an inverse cascade per se, because it does not lead to an accumulation of energy towards the largest available scale in the system. Rather, as presented in figure 3(a), simulations in large slender boxes show that energetic large scales are concentrated around ![]() $\lambda _z \simeq 40$, the scale of the turbulent–laminar patterns and not the domain scale.
$\lambda _z \simeq 40$, the scale of the turbulent–laminar patterns and not the domain scale.
6. Evolution with Reynolds number
We now address the dependence of the global energy balance on ![]() $Re$. Unlike previous studies (Rolland & Manneville Reference Rolland and Manneville2011; Tuckerman & Barkley Reference Tuckerman and Barkley2011), we do not focus on an order parameter for the transition between uniform turbulence and patterns, but rather compute the Reynolds decomposition for each of the two states throughout the transition. Recall that at intermediate
$Re$. Unlike previous studies (Rolland & Manneville Reference Rolland and Manneville2011; Tuckerman & Barkley Reference Tuckerman and Barkley2011), we do not focus on an order parameter for the transition between uniform turbulence and patterns, but rather compute the Reynolds decomposition for each of the two states throughout the transition. Recall that at intermediate ![]() $Re$ (e.g.
$Re$ (e.g. ![]() $Re=430$, as shown in figure 2c), the flow fluctuates between patterned and uniform states, similar to the dynamics of a fluctuating bistable system. With this in mind, conditional averaging has been carried out over selected time windows during which the state is either patterned or uniform. This results in discontinuities with
$Re=430$, as shown in figure 2c), the flow fluctuates between patterned and uniform states, similar to the dynamics of a fluctuating bistable system. With this in mind, conditional averaging has been carried out over selected time windows during which the state is either patterned or uniform. This results in discontinuities with ![]() $Re$ in most global measures, because the patterned and uniform states are different. Again, here we are not investigating the nature of the transition; rather, we are seeking to quantify properties of the patterned and uniform flows through it. In our companion paper Gomé et al. (Reference Gomé, Tuckerman and Barkley2023), we investigate the transition in a long slender box where the flow is not tightly constrained spatially as here, and show that the transition from uniform to patterned turbulence is in fact smooth.
$Re$ in most global measures, because the patterned and uniform states are different. Again, here we are not investigating the nature of the transition; rather, we are seeking to quantify properties of the patterned and uniform flows through it. In our companion paper Gomé et al. (Reference Gomé, Tuckerman and Barkley2023), we investigate the transition in a long slender box where the flow is not tightly constrained spatially as here, and show that the transition from uniform to patterned turbulence is in fact smooth.
Figure 10 presents the evolution of several quantities computed in a minimal band unit with ![]() $L_z=40$ for the uniform states at higher
$L_z=40$ for the uniform states at higher ![]() $Re$, and for the patterned states at lower
$Re$, and for the patterned states at lower ![]() $Re$. We first consider the terms appearing in the mean-flow balance, and show their evolution with
$Re$. We first consider the terms appearing in the mean-flow balance, and show their evolution with ![]() $Re$. We plot the injection
$Re$. We plot the injection ![]() $I$ along with total mean-flow dissipation
$I$ along with total mean-flow dissipation ![]() $\bar {D}$ and the total TKE production
$\bar {D}$ and the total TKE production ![]() $\varPi$, where
$\varPi$, where ![]() $\bar {D} \simeq \hat {\bar {D}}_0 + \hat {\bar {D}}_1$ since these terms dominate the dissipation (see figure 7b). Recall also that the total TKE production and dissipation are equal; see (5.12). As seen in figure 10, all quantities reach a maximum in the uniform state at
$\bar {D} \simeq \hat {\bar {D}}_0 + \hat {\bar {D}}_1$ since these terms dominate the dissipation (see figure 7b). Recall also that the total TKE production and dissipation are equal; see (5.12). As seen in figure 10, all quantities reach a maximum in the uniform state at ![]() $Re=430$, before dropping discontinuously to the patterned state as
$Re=430$, before dropping discontinuously to the patterned state as ![]() $Re$ is decreased. We also show the main source of energy of the large-scale flow,
$Re$ is decreased. We also show the main source of energy of the large-scale flow, ![]() $\hat {\bar {A}}_1\simeq -\hat {\bar {A}}_0$, which directs energy from
$\hat {\bar {A}}_1\simeq -\hat {\bar {A}}_0$, which directs energy from ![]() $\bar {\boldsymbol {u}}_0$ to
$\bar {\boldsymbol {u}}_0$ to ![]() $\bar {\boldsymbol {u}}_1$ via advection. Here,
$\bar {\boldsymbol {u}}_1$ via advection. Here, ![]() $\hat {\bar {A}}_1$ undergoes an especially dramatic increase when going from uniform turbulence to the patterned state. (We recall that
$\hat {\bar {A}}_1$ undergoes an especially dramatic increase when going from uniform turbulence to the patterned state. (We recall that ![]() $\hat {\bar {A}}_1$ vanishes in the uniform state up to numerical error.)
$\hat {\bar {A}}_1$ vanishes in the uniform state up to numerical error.)

Figure 10. Evolution with ![]() $Re$ of various energetic quantities defined throughout the text ((5.6a,b), (5.7a,b) and (5.8)). Open and filled symbols are used for the patterned and uniform states, respectively. In (h), circles and diamonds stand, respectively, for
$Re$ of various energetic quantities defined throughout the text ((5.6a,b), (5.7a,b) and (5.8)). Open and filled symbols are used for the patterned and uniform states, respectively. In (h), circles and diamonds stand, respectively, for ![]() $\hat {T}_{LS}/I$ and
$\hat {T}_{LS}/I$ and ![]() $\hat {T}_{SS}/I$.
$\hat {T}_{SS}/I$.
Figures 10(b,d,f,h) show quantities normalised by the injection rate ![]() $I$. We see that
$I$. We see that ![]() $\bar {D}/I$ increases with decreasing
$\bar {D}/I$ increases with decreasing ![]() $Re$ in figure 10, signifying that the mean-flow dissipation
$Re$ in figure 10, signifying that the mean-flow dissipation ![]() $\bar {D}$ increases more rapidly than the injection rate
$\bar {D}$ increases more rapidly than the injection rate ![]() $I$ with decreasing
$I$ with decreasing ![]() $Re$. As a consequence, relatively less energy is transferred to turbulence with decreasing
$Re$. As a consequence, relatively less energy is transferred to turbulence with decreasing ![]() $Re$. This is confirmed by the plot of normalised TKE production
$Re$. This is confirmed by the plot of normalised TKE production ![]() $\hat {\varPi }^{>0}/I \simeq \varPi /I$, which shows a decrease with decreasing
$\hat {\varPi }^{>0}/I \simeq \varPi /I$, which shows a decrease with decreasing ![]() $Re$. Meanwhile, while considerably smaller in magnitude, the normalised negative production,
$Re$. Meanwhile, while considerably smaller in magnitude, the normalised negative production, ![]() $\hat {\varPi }^{<0}/I$, decreases with decreasing
$\hat {\varPi }^{<0}/I$, decreases with decreasing ![]() $Re$ in the uniform regime, before switching to a value of lower intensity in the patterned state. Altogether, this shows that a larger fraction of the total energy is retained by the mean flow at lower
$Re$ in the uniform regime, before switching to a value of lower intensity in the patterned state. Altogether, this shows that a larger fraction of the total energy is retained by the mean flow at lower ![]() $Re$.
$Re$.
We finally turn to the evolution of transfer terms with ![]() $Re$. For this purpose, we focus only on the nonlinear transfers into large scales at
$Re$. For this purpose, we focus only on the nonlinear transfers into large scales at ![]() $k_z < k_{{LS}}$, and into small dissipative scales at
$k_z < k_{{LS}}$, and into small dissipative scales at ![]() $k_z > k_{{SS}}$ (see figure 7). We define the total nonlinear transfer to large scales
$k_z > k_{{SS}}$ (see figure 7). We define the total nonlinear transfer to large scales ![]() $\hat {T}_{LS}$ and to small scales
$\hat {T}_{LS}$ and to small scales ![]() $\hat {T}_{SS}$ by
$\hat {T}_{SS}$ by
 \begin{equation} \hat{T}_{LS} = \sum_{k_z \leqslant k_{{LS}}} \int_{{-}1}^1 \hat{T}_{nl}\,\text{d}y, \quad \hat{T}_{SS} = \sum_{k_z> k_{SS}} \int_{{-}1}^1 \hat{T}_{nl}\,\text{d}y . \end{equation}
\begin{equation} \hat{T}_{LS} = \sum_{k_z \leqslant k_{{LS}}} \int_{{-}1}^1 \hat{T}_{nl}\,\text{d}y, \quad \hat{T}_{SS} = \sum_{k_z> k_{SS}} \int_{{-}1}^1 \hat{T}_{nl}\,\text{d}y . \end{equation}
We plot both ![]() $\hat {T}_{LS}/I$ (circles) and
$\hat {T}_{LS}/I$ (circles) and ![]() $\hat {T}_{SS}/I$ (diamonds) in figure 10. For the uniform state, slightly more energy is transferred to large scales as
$\hat {T}_{SS}/I$ (diamonds) in figure 10. For the uniform state, slightly more energy is transferred to large scales as ![]() $Re$ decreases. Here,
$Re$ decreases. Here, ![]() $\hat {T}_{LS}/I$ undergoes a discontinuous drop at the transition to patterns, where relatively less transfer goes to large scales. On the other hand, the small-scale transfers decrease monotonically with decreasing
$\hat {T}_{LS}/I$ undergoes a discontinuous drop at the transition to patterns, where relatively less transfer goes to large scales. On the other hand, the small-scale transfers decrease monotonically with decreasing ![]() $Re$ and are barely impacted by the change in state. We find that
$Re$ and are barely impacted by the change in state. We find that ![]() $\hat {T}_{LS} \sim \hat {T}_{SS}$ in the patterned state, for unknown reasons.
$\hat {T}_{LS} \sim \hat {T}_{SS}$ in the patterned state, for unknown reasons.
Interestingly, the normalised quantities ![]() $\bar {D}/I$,
$\bar {D}/I$, ![]() $\varPi /I$ and
$\varPi /I$ and ![]() $\bar {T}_{SS}/I$ show a less abrupt transition from the uniform to the patterned state than their non-normalised counterparts, and could even be approximated as continuous as the system transitions from uniform to patterned flow (e.g. we find a difference of order
$\bar {T}_{SS}/I$ show a less abrupt transition from the uniform to the patterned state than their non-normalised counterparts, and could even be approximated as continuous as the system transitions from uniform to patterned flow (e.g. we find a difference of order ![]() $0.5\,\%$ in
$0.5\,\%$ in ![]() $\bar {D}/I$ in the uniform and patterned states at
$\bar {D}/I$ in the uniform and patterned states at ![]() $Re=430$, while it is
$Re=430$, while it is ![]() $7\,\%$ in
$7\,\%$ in ![]() $\bar {D}$). This signifies that the relative turbulent dissipation is approximately the same in the patterned and uniform states at fixed value of
$\bar {D}$). This signifies that the relative turbulent dissipation is approximately the same in the patterned and uniform states at fixed value of ![]() $Re$.
$Re$.
In summary, as ![]() $Re$ decreases, the mean flow dissipates its energy more rapidly than the fluctuations do, i.e. the flow is less turbulent and the mean flow retains more energy (this is due mostly to small turbulent scales dissipating less of the total energy, and secondly, because of greater fuelling of the mean flow by negative production
$Re$ decreases, the mean flow dissipates its energy more rapidly than the fluctuations do, i.e. the flow is less turbulent and the mean flow retains more energy (this is due mostly to small turbulent scales dissipating less of the total energy, and secondly, because of greater fuelling of the mean flow by negative production ![]() $\hat {\varPi }^{<0}$). It seems that there is a point at which the mean flow undergoes a sort of dissipation crisis, and diverts some of its energy from the uniform mode
$\hat {\varPi }^{<0}$). It seems that there is a point at which the mean flow undergoes a sort of dissipation crisis, and diverts some of its energy from the uniform mode ![]() $\bar {\boldsymbol {u}}_0$ to the large-scale mode
$\bar {\boldsymbol {u}}_0$ to the large-scale mode ![]() $\bar {\boldsymbol {u}}_1$, via the mean advection term. Therefore, the patterned state can be seen as more adapted to an increasingly dissipative environment when
$\bar {\boldsymbol {u}}_1$, via the mean advection term. Therefore, the patterned state can be seen as more adapted to an increasingly dissipative environment when ![]() $Re$ decreases.
$Re$ decreases.
7. Conclusion
Wall-bounded turbulence at low Reynolds numbers is marked by a strong scale separation between the streak/roll scale of the self-sustaining process that comprises the turbulence, and the large-scale flow associated with oblique laminar–turbulent patterns. In this paper, we have computed the spectral energy balances for both the mean flow and the turbulent fluctuations in a minimal band unit, thus revealing the energy transfers connecting the different scales in transitional plane Couette flow.
As expected, TKE production is maximal at the scale of streaks and rolls, and a direct cascade sends energy to smaller dissipative scales. However, part of the TKE is also transferred to large scales via nonlinear interaction. At large scales, this energy is sent partly to the mean flow, via negative production. The intense large-scale flow along laminar–turbulent bands appears in the trigonometric component of the mean flow ![]() $\bar {\boldsymbol {u}}_1$. The main energy source for
$\bar {\boldsymbol {u}}_1$. The main energy source for ![]() $\bar {\boldsymbol {u}}_1$ is its nonlinear interaction with the uniform component
$\bar {\boldsymbol {u}}_1$ is its nonlinear interaction with the uniform component ![]() $\bar {\boldsymbol {u}}_0$ (via the term called
$\bar {\boldsymbol {u}}_0$ (via the term called ![]() $\hat {\bar {A}}_1$ in this paper). This interaction is due to the mean advection, which plays a significant role in both spatial and spectral transfers of mean-flow energy. Interestingly, the
$\hat {\bar {A}}_1$ in this paper). This interaction is due to the mean advection, which plays a significant role in both spatial and spectral transfers of mean-flow energy. Interestingly, the ![]() $\bar {\boldsymbol {u}}_1$ component of the mean flow is also fuelled by negative production transferring energy from fluctuations to mean flow. However, this is only a secondary driver of
$\bar {\boldsymbol {u}}_1$ component of the mean flow is also fuelled by negative production transferring energy from fluctuations to mean flow. However, this is only a secondary driver of ![]() $\bar {\boldsymbol {u}}_1$, as negative production accounts for only approximately
$\bar {\boldsymbol {u}}_1$, as negative production accounts for only approximately ![]() $20\,\%$ of its energy sources (see figure 7b).
$20\,\%$ of its energy sources (see figure 7b).
Negative production has not received much attention, although it has been reported for spanwise-constant modes at ![]() $Re_\tau =180$ in a minimal channel by Symon et al. (Reference Symon, Illingworth and Marusic2021). We have found negative production at large scales in both patterned and uniform turbulence in plane Couette flow, in the region
$Re_\tau =180$ in a minimal channel by Symon et al. (Reference Symon, Illingworth and Marusic2021). We have found negative production at large scales in both patterned and uniform turbulence in plane Couette flow, in the region ![]() $Re_\tau \lesssim 66$ studied here. Altogether, the processes energising large-scale motions (inverse transfers and negative production), described here in both patterned and uniform turbulence at low
$Re_\tau \lesssim 66$ studied here. Altogether, the processes energising large-scale motions (inverse transfers and negative production), described here in both patterned and uniform turbulence at low ![]() $Re_\tau$, seem to be different from those reported in fully developed wall-bounded turbulence (Cimarelli, De Angelis & Casciola Reference Cimarelli, De Angelis and Casciola2013; Mizuno Reference Mizuno2016; Aulery et al. Reference Aulery, Dupuy, Toutant, Bataille and Zhou2017; Cho et al. Reference Cho, Hwang and Choi2018; Lee & Moser Reference Lee and Moser2019; Andreolli, Quadrio & Gatti Reference Andreolli, Quadrio and Gatti2021; Kawata & Tsukahara Reference Kawata and Tsukahara2021). See § A.2 for a more detailed analysis.
$Re_\tau$, seem to be different from those reported in fully developed wall-bounded turbulence (Cimarelli, De Angelis & Casciola Reference Cimarelli, De Angelis and Casciola2013; Mizuno Reference Mizuno2016; Aulery et al. Reference Aulery, Dupuy, Toutant, Bataille and Zhou2017; Cho et al. Reference Cho, Hwang and Choi2018; Lee & Moser Reference Lee and Moser2019; Andreolli, Quadrio & Gatti Reference Andreolli, Quadrio and Gatti2021; Kawata & Tsukahara Reference Kawata and Tsukahara2021). See § A.2 for a more detailed analysis.
Our results indicate that as the environment becomes more dissipative with decreasing ![]() $Re$, the mean flow in the uniform regime absorbs more and more energy, up to a most dissipative point where the flow transitions to the patterned state. The patterned state reorganises this energy between the uniform mean flow
$Re$, the mean flow in the uniform regime absorbs more and more energy, up to a most dissipative point where the flow transitions to the patterned state. The patterned state reorganises this energy between the uniform mean flow ![]() $\bar {\boldsymbol {u}}_0$ and the large-scale flow
$\bar {\boldsymbol {u}}_0$ and the large-scale flow ![]() $\bar {\boldsymbol {u}}_1$ through advection, in such a way that negative production is directed into the large-scale flow.
$\bar {\boldsymbol {u}}_1$ through advection, in such a way that negative production is directed into the large-scale flow.
In physical space, a possible equivalent picture is that nucleation of quasi-laminar gaps becomes necessary for turbulence to be sustained: with decreasing ![]() $Re$, the turbulent mean flow dissipates too much energy compared to what is injected in the flow, such that it needs additional fluxes from quasi-laminar regions, as those reported in § 4. This is essentially the physical argument put forward by Barkley (Reference Barkley2016) for the localisation of turbulent puffs in pipe flow. Further support for this effect can be found in our companion paper Gomé et al. (Reference Gomé, Tuckerman and Barkley2023), where we will show that in long slender boxes, as Re is decreased the total dissipation reaches a maximum just before laminar gaps become steady and patterns emerge.
$Re$, the turbulent mean flow dissipates too much energy compared to what is injected in the flow, such that it needs additional fluxes from quasi-laminar regions, as those reported in § 4. This is essentially the physical argument put forward by Barkley (Reference Barkley2016) for the localisation of turbulent puffs in pipe flow. Further support for this effect can be found in our companion paper Gomé et al. (Reference Gomé, Tuckerman and Barkley2023), where we will show that in long slender boxes, as Re is decreased the total dissipation reaches a maximum just before laminar gaps become steady and patterns emerge.
Our analysis of energy budgets does not invoke directly a dynamical mechanism, such as the self-sustaining process governing wall-bounded turbulence and related autonomous mechanisms describing large scales in developed turbulence (Hwang & Cossu Reference Hwang and Cossu2010; Hwang & Bengana Reference Hwang and Bengana2016; de Giovanetti, Sung & Hwang Reference de Giovanetti, Sung and Hwang2017; Cho et al. Reference Cho, Hwang and Choi2018). Further investigations are required to understand whether the inverse transfers and negative production that we observe are connected to the nonlinear regeneration of rolls in the self-sustaining process. Note that the energetic imprint of the self-sustaining process in developed wall-bounded turbulence was analysed recently by Cho et al. (Reference Cho, Hwang and Choi2018) and Kawata & Tsukahara (Reference Kawata and Tsukahara2021), the latter emphasising the role of nonlinear transfers.
Finally, although the oblique simulation domain is very useful for the study of inter-scale distribution of energy in patterned transitional turbulence, further confirmation via simulations in large streamwise–spanwise oriented domains is also required: our simulation domain restricts the flow in a number of ways, such as imposing an orientation as well as a mean streak spacing due to the restrained short size ![]() $L_x=10$. These features do not seem to alter the robust observations that we have made about mean-turbulent interaction and inverse transfers in uniform turbulence (see § A.4). However, it would be beneficial to disentangle the streamwise and spanwise directions in the energy budget, and to compute inter-component transfers, so as to better understand the role of the self-sustaining process in the generation of transitional large-scale structures.
$L_x=10$. These features do not seem to alter the robust observations that we have made about mean-turbulent interaction and inverse transfers in uniform turbulence (see § A.4). However, it would be beneficial to disentangle the streamwise and spanwise directions in the energy budget, and to compute inter-component transfers, so as to better understand the role of the self-sustaining process in the generation of transitional large-scale structures.
In Gomé et al. (Reference Gomé, Tuckerman and Barkley2023), the energy processes described above will be essential to understand the selection of a finite wavelength of transitional patterns.
Acknowledgements
The authors wish to thank Y. Duguet, S. Benavides, A. Frishman and T. Grafke for fruitful discussions, as well as the referees for their useful suggestions.
Funding
The calculations for this work were performed using high performance computing resources provided by the Grand Equipement National de Calcul Intensif at the Institut du Développement et des Ressources en Informatique Scientifique (IDRIS, CNRS) through grant no. A0102A01119. This work was supported by a grant from the Simons Foundation (grant no. 662985).
Declaration of interests
The authors report no conflict of interest.
Appendix A. Wall-normal dependence of spectral balance
A.1. Values of  $Re_\tau$ in a minimal band unit and a long slender box
$Re_\tau$ in a minimal band unit and a long slender box
In a minimal band unit at a transitional Reynolds number, the turbulence may be uniform or patterned during different time periods, i.e. it is temporally as well as spatially intermittent. For this reason, for each value of ![]() $Re$, we take the time average in (2.3) over a period during which the flow retains qualitatively the same state. This yields two slightly different values,
$Re$, we take the time average in (2.3) over a period during which the flow retains qualitatively the same state. This yields two slightly different values, ![]() $Re_\tau ^u$ for a uniform state and
$Re_\tau ^u$ for a uniform state and ![]() $Re_\tau ^p$ for a patterned state, as presented in table 2 for
$Re_\tau ^p$ for a patterned state, as presented in table 2 for ![]() $L_z=40$. In the non-dimensionalisations carried out in this paper, we use either
$L_z=40$. In the non-dimensionalisations carried out in this paper, we use either ![]() $Re_\tau ^u$ or
$Re_\tau ^u$ or ![]() $Re_\tau ^p$, as appropriate for the flow state.
$Re_\tau ^p$, as appropriate for the flow state.
Table 2. Values of ![]() $Re_\tau$ for various values of
$Re_\tau$ for various values of ![]() $Re$ in a minimal band unit (MBU) of size
$Re$ in a minimal band unit (MBU) of size ![]() $L_z=40$, and in a long slender box (LSB) of size
$L_z=40$, and in a long slender box (LSB) of size ![]() $L_z=800$. In the MBU,
$L_z=800$. In the MBU, ![]() $Re_\tau ^p$ and
$Re_\tau ^p$ and ![]() $Re_\tau ^u$ are obtained by averaging over the patterned or uniform state, respectively, while the time average is an LD. For
$Re_\tau ^u$ are obtained by averaging over the patterned or uniform state, respectively, while the time average is an LD. For ![]() $Re>500$, the patterned state does not occur.
$Re>500$, the patterned state does not occur.

In long slender boxes, we compute ![]() $Re_\tau$ by averaging unconditionally the flow state. This procedure does not resolve the local variability of the wall shear stress due to spatial intermittency; for this, we would need to omit
$Re_\tau$ by averaging unconditionally the flow state. This procedure does not resolve the local variability of the wall shear stress due to spatial intermittency; for this, we would need to omit ![]() $z$ averaging in (2.3) to produce
$z$ averaging in (2.3) to produce ![]() $z$-dependent values of
$z$-dependent values of ![]() $Re_\tau$; see Kashyap et al. (Reference Kashyap, Duguet and Dauchot2020) for a thorough analysis of fluctuations of
$Re_\tau$; see Kashyap et al. (Reference Kashyap, Duguet and Dauchot2020) for a thorough analysis of fluctuations of ![]() $Re_\tau$ within and outside turbulent bands.
$Re_\tau$ within and outside turbulent bands.
A.2. Energy balance at various  $y$ locations
$y$ locations
In the main part of the paper, nothing has been said about the location of the energy transfers in the wall-normal direction, and no distinction has been made between near-wall and bulk effects on the mean flow and turbulent energies. In this subsection, we present results on the TKE balance and subsequently the mean-flow balance for the patterned state at ![]() $Re=400$.
$Re=400$.
Figure 11 shows the spectral TKE balance at different ![]() $y$ locations: the mid-plane (
$y$ locations: the mid-plane (![]() $y=0$,
$y=0$, ![]() $y^+= 29.6$, figure 11a), the layer of maximal spectral production
$y^+= 29.6$, figure 11a), the layer of maximal spectral production ![]() $\hat {\varPi }$ (
$\hat {\varPi }$ (![]() $y=0.63$,
$y=0.63$, ![]() $y^+\simeq 11$, figure 11b), and the near-wall region (
$y^+\simeq 11$, figure 11b), and the near-wall region (![]() $y=0.92$,
$y=0.92$, ![]() $y^+\simeq 2.4$, figure 11c).
$y^+\simeq 2.4$, figure 11c).

Figure 11. TKE spectral balance (5.3) at different ![]() $y$ locations: (a) mid-plane,
$y$ locations: (a) mid-plane, ![]() $y=0$; (b)
$y=0$; (b) ![]() $y=0.63$; (c) near-wall,
$y=0.63$; (c) near-wall, ![]() $y=0.92$. Shown is a patterned case at
$y=0.92$. Shown is a patterned case at ![]() $Re=400$.
$Re=400$.
The balance in the near-wall region is simple because it is dominated by viscous effects, with injection of energy via the rate-of-strain compensated by dissipation. A small portion of the energy comes from a positive transfer ![]() $\hat {T}_{nl}$. In the plane
$\hat {T}_{nl}$. In the plane ![]() $y=0.63$, the production term
$y=0.63$, the production term ![]() $\hat {\varPi }$ is maximal (as will be shown in § A.3). Production peaks at the roll scale
$\hat {\varPi }$ is maximal (as will be shown in § A.3). Production peaks at the roll scale ![]() $k_{{rolls}}$, while the dissipation, viscous diffusion and nonlinear transfers are all negative with similar magnitudes near this scale. Production becomes negative and nonlinear transfers positive at long length scales (small
$k_{{rolls}}$, while the dissipation, viscous diffusion and nonlinear transfers are all negative with similar magnitudes near this scale. Production becomes negative and nonlinear transfers positive at long length scales (small ![]() $k_z$), similar to what we showed for
$k_z$), similar to what we showed for ![]() $y$-integrated quantities in § 5.2. The spectral balance at the mid-plane is qualitatively similar to that at the plane
$y$-integrated quantities in § 5.2. The spectral balance at the mid-plane is qualitatively similar to that at the plane ![]() $y=0.63$, with the notable exception that the viscous diffusion
$y=0.63$, with the notable exception that the viscous diffusion ![]() $\hat {T}_{v}$ vanishes due to reflection symmetry about the mid-plane. Here,
$\hat {T}_{v}$ vanishes due to reflection symmetry about the mid-plane. Here, ![]() $\hat {\varPi }$ and
$\hat {\varPi }$ and ![]() $T_{nl}$ are smaller in the mid-plane than in the plane
$T_{nl}$ are smaller in the mid-plane than in the plane ![]() $y=0.63$, while
$y=0.63$, while ![]() $\hat {D}$ and
$\hat {D}$ and ![]() $\hat {A}$ have nearly the same magnitude in both planes.
$\hat {A}$ have nearly the same magnitude in both planes.
The ![]() $y$ dependence of the mean-flow energy balance (5.5) is displayed in figure 12. In line with our previous observations on
$y$ dependence of the mean-flow energy balance (5.5) is displayed in figure 12. In line with our previous observations on ![]() $y$-integrated quantities (§ 5.2), figure 12 reveals a different phenomenology depending on the wavenumber (
$y$-integrated quantities (§ 5.2), figure 12 reveals a different phenomenology depending on the wavenumber (![]() $k_z=0$,
$k_z=0$, ![]() $k_z=2{\rm \pi} /L_z$ or
$k_z=2{\rm \pi} /L_z$ or ![]() $k_z>2{\rm \pi} /L_z$). The gain in energy in
$k_z>2{\rm \pi} /L_z$). The gain in energy in ![]() $\bar {\boldsymbol {u}}_0$ (figure 12a) due to the viscous transfer term
$\bar {\boldsymbol {u}}_0$ (figure 12a) due to the viscous transfer term ![]() $\hat {\bar {T}}_{v}$ is large near the wall, where energy is injected into the flow, whereas the two terms involving the Reynolds stress,
$\hat {\bar {T}}_{v}$ is large near the wall, where energy is injected into the flow, whereas the two terms involving the Reynolds stress, ![]() $\hat {\bar {\varPi }}$ and
$\hat {\bar {\varPi }}$ and ![]() $\hat {\bar {T}}_{nl}$, are dominant and in approximate balance at the mid-plane. Note that while
$\hat {\bar {T}}_{nl}$, are dominant and in approximate balance at the mid-plane. Note that while ![]() $\hat {\bar {T}}_{nl}$ integrates to zero, it has a local influence: flow above
$\hat {\bar {T}}_{nl}$ integrates to zero, it has a local influence: flow above ![]() $y=0.63$ transfers energy to flow below.
$y=0.63$ transfers energy to flow below.

Figure 12. Evolution of the mean-flow energy balance (5.5) with ![]() $y$, for
$y$, for ![]() $k_z=0$,
$k_z=0$, ![]() $k_z=2{\rm \pi} /L_z$, and summed over
$k_z=2{\rm \pi} /L_z$, and summed over ![]() $k_z>2{\rm \pi} /L_z$. (Values for
$k_z>2{\rm \pi} /L_z$. (Values for ![]() $y<0$ are obtained by reflection in
$y<0$ are obtained by reflection in ![]() $y=0$.) Shown is a patterned case at
$y=0$.) Shown is a patterned case at ![]() $Re=400$.
$Re=400$.
The balance of ![]() $\bar {\boldsymbol {u}}_1$ (figure 12b) presents a complex and interesting behaviour. We know from § 4 that when integrated over
$\bar {\boldsymbol {u}}_1$ (figure 12b) presents a complex and interesting behaviour. We know from § 4 that when integrated over ![]() $y$, the balance for mode
$y$, the balance for mode ![]() $\bar {\boldsymbol {u}}_1$ is such that
$\bar {\boldsymbol {u}}_1$ is such that ![]() $\hat {\bar {\varPi }}_1<0$, and that this mode extracts energy from TKE. However, the
$\hat {\bar {\varPi }}_1<0$, and that this mode extracts energy from TKE. However, the ![]() $y$ dependence of this term shows a change in sign: the production is negative (i.e.
$y$ dependence of this term shows a change in sign: the production is negative (i.e. ![]() $-\hat {\bar {\varPi }}_1>0$) only for
$-\hat {\bar {\varPi }}_1>0$) only for ![]() $-0.6 \lesssim y \lesssim 0.6$. This suggests the importance of turbulence in the bulk region for sustaining the bands. Here,
$-0.6 \lesssim y \lesssim 0.6$. This suggests the importance of turbulence in the bulk region for sustaining the bands. Here, ![]() $\hat {\bar {T}}_{nl}$ undergoes a change in sign at approximately the same
$\hat {\bar {T}}_{nl}$ undergoes a change in sign at approximately the same ![]() $y$ value, with similar behaviour, although their
$y$ value, with similar behaviour, although their ![]() $y$ integrals differ (the integral of
$y$ integrals differ (the integral of ![]() $\hat {\bar {T}}_{nl}$ vanishes, whereas that of
$\hat {\bar {T}}_{nl}$ vanishes, whereas that of ![]() $\hat {\bar {\varPi }}$ is negative). Also,
$\hat {\bar {\varPi }}$ is negative). Also, ![]() $\hat {\bar {T}}_{nl}$ dominates the energy source at
$\hat {\bar {T}}_{nl}$ dominates the energy source at ![]() $y\simeq 0.8$. At the wall (
$y\simeq 0.8$. At the wall (![]() $y=1$), the energy balance is between viscous diffusion and dissipation. The advection term
$y=1$), the energy balance is between viscous diffusion and dissipation. The advection term ![]() $\hat {\bar {A}}$ is always positive.
$\hat {\bar {A}}$ is always positive.
The situation at ![]() $k_z>2{\rm \pi} /L_z$ is perhaps of negligible importance because of the small amplitude of the energy at this scale. However, we note that the balance near the wall (i.e.
$k_z>2{\rm \pi} /L_z$ is perhaps of negligible importance because of the small amplitude of the energy at this scale. However, we note that the balance near the wall (i.e. ![]() $0.7 \lesssim y \lesssim 1$) is qualitatively similar to that of mode
$0.7 \lesssim y \lesssim 1$) is qualitatively similar to that of mode ![]() $\bar {\boldsymbol {u}}_1$, dominated by viscous diffusion, dissipation and triad interaction. In the bulk, energy comes from
$\bar {\boldsymbol {u}}_1$, dominated by viscous diffusion, dissipation and triad interaction. In the bulk, energy comes from ![]() $\hat {\bar {\varPi }}$ and is diverted towards the other terms.
$\hat {\bar {\varPi }}$ and is diverted towards the other terms.
A.3. Production and nonlinear transfers in the  $y$–
$y$– $k_z$ plane
$k_z$ plane
Figures 13 and 14 show, respectively, ![]() $\hat {\varPi }(y,k_z)$ and
$\hat {\varPi }(y,k_z)$ and ![]() $\hat {T}_{nl}(y,k_z)$ for different states and
$\hat {T}_{nl}(y,k_z)$ for different states and ![]() $Re$ ranging from 380 to 1000. We focus on these terms because of their unusual signs in the balance at large scales (small
$Re$ ranging from 380 to 1000. We focus on these terms because of their unusual signs in the balance at large scales (small ![]() $k_z$). The zone of negative production at large scales is encircled by the dashed contour. We note that negative production spans the range
$k_z$). The zone of negative production at large scales is encircled by the dashed contour. We note that negative production spans the range ![]() $y\in [0, 0.8]$ at low
$y\in [0, 0.8]$ at low ![]() $Re$, whereas it is more concentrated between
$Re$, whereas it is more concentrated between ![]() $y=0.6$ and 0.9 at
$y=0.6$ and 0.9 at ![]() $Re=1000$. In viscous units, it spans approximately from
$Re=1000$. In viscous units, it spans approximately from ![]() $y^+=5$ to
$y^+=5$ to ![]() $y^+ \simeq 30$ at all
$y^+ \simeq 30$ at all ![]() $Re$. Furthermore, the positive part of the spectrum is marked by a peak at
$Re$. Furthermore, the positive part of the spectrum is marked by a peak at ![]() $k_z=k_{{rolls}}$ corresponding to the most-producing streaks and rolls, whose wall-normal localisation increases with
$k_z=k_{{rolls}}$ corresponding to the most-producing streaks and rolls, whose wall-normal localisation increases with ![]() $Re$, from
$Re$, from ![]() $y=0.63$ (
$y=0.63$ (![]() $y^+\simeq 11$) at
$y^+\simeq 11$) at ![]() $Re=400$, to
$Re=400$, to ![]() $y=0.8$ (
$y=0.8$ (![]() $y^+\simeq 13$) at
$y^+\simeq 13$) at ![]() $Re=1000$.
$Re=1000$.

Figure 13. Visualisations of production ![]() $\hat {\varPi }(y, k_z)$ for different
$\hat {\varPi }(y, k_z)$ for different ![]() $Re$ and states. The cross-channel range is from the mid-plane (
$Re$ and states. The cross-channel range is from the mid-plane (![]() $y=0$,
$y=0$, ![]() $y^+=Re_\tau$, lower axis) to the wall (
$y^+=Re_\tau$, lower axis) to the wall (![]() $y=1$,
$y=1$, ![]() $y^+=0$, upper axis). The dashed line separates positive from negative values for small
$y^+=0$, upper axis). The dashed line separates positive from negative values for small ![]() $k_z$. (a) Pattern,
$k_z$. (a) Pattern, ![]() $Re=400$ (
$Re=400$ (![]() $Re_\tau = 29.7$). (b) Pattern,
$Re_\tau = 29.7$). (b) Pattern, ![]() $Re=430$ (
$Re=430$ (![]() $Re_\tau = 31.9$). (c) Uniform,
$Re_\tau = 31.9$). (c) Uniform, ![]() $Re=430$ (
$Re=430$ (![]() $Re_\tau = 33.0$). (d) Uniform,
$Re_\tau = 33.0$). (d) Uniform, ![]() $Re=1000$ (
$Re=1000$ (![]() $Re_\tau = 66.4$).
$Re_\tau = 66.4$).

Figure 14. Visualisations of nonlinear transfer ![]() $\hat {T}_{nl}(y, k_z)$ for different
$\hat {T}_{nl}(y, k_z)$ for different ![]() $Re$ and states. The cross-channel range is from the mid-plane (
$Re$ and states. The cross-channel range is from the mid-plane (![]() $y=0$,
$y=0$, ![]() $y^+=Re_\tau$, lower axis) to the wall (
$y^+=Re_\tau$, lower axis) to the wall (![]() $y=1$,
$y=1$, ![]() $y^+=0$, upper axis). (a) Pattern,
$y^+=0$, upper axis). (a) Pattern, ![]() $Re=400$ (
$Re=400$ (![]() $Re_\tau = 29.7$). (b) Pattern,
$Re_\tau = 29.7$). (b) Pattern, ![]() $Re=430$ (
$Re=430$ (![]() $Re_\tau = 31.9$). (c) Uniform,
$Re_\tau = 31.9$). (c) Uniform, ![]() $Re=430$ (
$Re=430$ (![]() $Re_\tau = 33.0$). (d) Uniform,
$Re_\tau = 33.0$). (d) Uniform, ![]() $Re=1000$ (
$Re=1000$ (![]() $Re_\tau = 66.4$).
$Re_\tau = 66.4$).

Figure 15. (a) Production and (b) nonlinear transfer spectra in a non-tilted domain with ![]() $(L_{{strm}}, L_{{span}})=(30,20)$ for
$(L_{{strm}}, L_{{span}})=(30,20)$ for ![]() $Re=1000$ (
$Re=1000$ (![]() $Re_\tau = 66$).
$Re_\tau = 66$).
The triadic interaction term ![]() $\hat {T}_{nl}$ is shown in figure 14. Inverse transfers are present from
$\hat {T}_{nl}$ is shown in figure 14. Inverse transfers are present from ![]() $k_z^+=0$ up to
$k_z^+=0$ up to ![]() $k_z^+ \simeq 0.07$ in the patterned cases, and
$k_z^+ \simeq 0.07$ in the patterned cases, and ![]() $k_z^+ \simeq 0.05$ in the uniform case at
$k_z^+ \simeq 0.05$ in the uniform case at ![]() $Re=1000$ (
$Re=1000$ (![]() $Re_\tau = 66.4$), i.e. scales smaller than that of rolls and streaks (
$Re_\tau = 66.4$), i.e. scales smaller than that of rolls and streaks (![]() $k_{{rolls}}\simeq 1.41$,
$k_{{rolls}}\simeq 1.41$, ![]() $k_{{rolls}}^+\simeq 0.04$ for
$k_{{rolls}}^+\simeq 0.04$ for ![]() $Re\leqslant 430$). However, this small-scale part of the inverse transfer is localised only near the wall (
$Re\leqslant 430$). However, this small-scale part of the inverse transfer is localised only near the wall (![]() $y^+<8$), while for
$y^+<8$), while for ![]() $k_z^+< 0.02$, the inverse transfer concerns the whole
$k_z^+< 0.02$, the inverse transfer concerns the whole ![]() $y$ domain.
$y$ domain.
We see two caveats that prevent further quantitative comparisons to other studies in non-tilted domains, for both transitional and non-transitional regimes. First, the imposition of an angle (![]() $\theta =24^\circ$) is completely arbitrary for uniform turbulence, and along with the short domain size
$\theta =24^\circ$) is completely arbitrary for uniform turbulence, and along with the short domain size ![]() $L_x$, the streak spacing is imposed in our numerical domain. In § A.4, we present results in a non-oblique flow unit
$L_x$, the streak spacing is imposed in our numerical domain. In § A.4, we present results in a non-oblique flow unit ![]() $(L_{{strm}}, L_{{span}})=(30,20)$ to confirm our observations in the minimal band unit in the non-transitional case
$(L_{{strm}}, L_{{span}})=(30,20)$ to confirm our observations in the minimal band unit in the non-transitional case ![]() $Re=1000$ (
$Re=1000$ (![]() $Re_\tau =66.2$). Second, the reduction to one dimension can miss the two-dimensionality of energy transfers: inter-scale transfers can actually be orientational, i.e. they may differ for wavenumbers
$Re_\tau =66.2$). Second, the reduction to one dimension can miss the two-dimensionality of energy transfers: inter-scale transfers can actually be orientational, i.e. they may differ for wavenumbers ![]() $(k_x, k_z)$ with the same modulus but different orientations. Therefore, inverse transfers in a one-dimensional spectrum can be misleading as they mix transfers between different orientations and transfers between different scales
$(k_x, k_z)$ with the same modulus but different orientations. Therefore, inverse transfers in a one-dimensional spectrum can be misleading as they mix transfers between different orientations and transfers between different scales ![]() $|\boldsymbol {k}|$.
$|\boldsymbol {k}|$.
These remarks aside, we can draw qualitative comparisons with the energetic large scales also present in high-![]() $Re$, developed wall-bounded turbulence (Jiménez Reference Jiménez1998; Smits, McKeon & Marusic Reference Smits, McKeon and Marusic2011; Lee & Moser Reference Lee and Moser2018, and references therein). The large-scale motions characterising our transitional regime are of a nature different to those observed in uniform shear flows at higher
$Re$, developed wall-bounded turbulence (Jiménez Reference Jiménez1998; Smits, McKeon & Marusic Reference Smits, McKeon and Marusic2011; Lee & Moser Reference Lee and Moser2018, and references therein). The large-scale motions characterising our transitional regime are of a nature different to those observed in uniform shear flows at higher ![]() $Re$, which are typically streamwise-elongated modes dictated by inertial effects far from the wall (in the outer zone). These large scales in fully developed turbulence can also be energised by inverse transfers from small scales (Cimarelli et al. Reference Cimarelli, De Angelis and Casciola2013; Mizuno Reference Mizuno2016; Aulery et al. Reference Aulery, Dupuy, Toutant, Bataille and Zhou2017; Cho et al. Reference Cho, Hwang and Choi2018; Lee & Moser Reference Lee and Moser2019; Andreolli et al. Reference Andreolli, Quadrio and Gatti2021; Kawata & Tsukahara Reference Kawata and Tsukahara2021). However, these inverse transfers are weaker than those reported here in transitional turbulence, and are essentially concentrated near the wall, while we observe inverse transfers over the whole shear layer that dominate the TKE budget at large scales. Furthermore, we recall that our large-scale transfers feed back on the mean flow via negative production, which, to the extent of our knowledge, has never been observed in developed turbulence.
$Re$, which are typically streamwise-elongated modes dictated by inertial effects far from the wall (in the outer zone). These large scales in fully developed turbulence can also be energised by inverse transfers from small scales (Cimarelli et al. Reference Cimarelli, De Angelis and Casciola2013; Mizuno Reference Mizuno2016; Aulery et al. Reference Aulery, Dupuy, Toutant, Bataille and Zhou2017; Cho et al. Reference Cho, Hwang and Choi2018; Lee & Moser Reference Lee and Moser2019; Andreolli et al. Reference Andreolli, Quadrio and Gatti2021; Kawata & Tsukahara Reference Kawata and Tsukahara2021). However, these inverse transfers are weaker than those reported here in transitional turbulence, and are essentially concentrated near the wall, while we observe inverse transfers over the whole shear layer that dominate the TKE budget at large scales. Furthermore, we recall that our large-scale transfers feed back on the mean flow via negative production, which, to the extent of our knowledge, has never been observed in developed turbulence.
A.4. Spectral balance in a streamwise–spanwise domain at  $Re_\tau = 66$
$Re_\tau = 66$
The use of a minimal band unit of size ![]() $(L_x, L_z) = (10,40)$ to study
$(L_x, L_z) = (10,40)$ to study ![]() $Re$ outside of the transitional regime can be misleading, mainly because the short size and the tilt angle impose a strict spacing for the streaks. This is certainly why the production and transfer spectra shown at
$Re$ outside of the transitional regime can be misleading, mainly because the short size and the tilt angle impose a strict spacing for the streaks. This is certainly why the production and transfer spectra shown at ![]() $Re=1000$ (figures 13d, 14d) present a sharp peak at
$Re=1000$ (figures 13d, 14d) present a sharp peak at ![]() $k_z = 1.41$ (
$k_z = 1.41$ (![]() $k_z^+ = 0.0214$,
$k_z^+ = 0.0214$, ![]() $\lambda _z^+ = 290$) along with a tenuous maximum at approximately
$\lambda _z^+ = 290$) along with a tenuous maximum at approximately ![]() $k_z^+ = 0.05$ (
$k_z^+ = 0.05$ (![]() $\lambda _z^+ = 126$,
$\lambda _z^+ = 126$, ![]() $\lambda _{{span}}^+ = 138$). In a streamwise–spanwise oriented domain of size
$\lambda _{{span}}^+ = 138$). In a streamwise–spanwise oriented domain of size ![]() $(L_{{strm}}, L_{{span}})=(30,20)$ and number of grid points
$(L_{{strm}}, L_{{span}})=(30,20)$ and number of grid points ![]() $(N_{{strm}}, N_{{span}})=(375,250)$, the streamwise-averaged spectrum is computed as a function of spanwise wavenumber
$(N_{{strm}}, N_{{span}})=(375,250)$, the streamwise-averaged spectrum is computed as a function of spanwise wavenumber ![]() $k_{{span}}$ in figure 15, and presents a peak located at approximately
$k_{{span}}$ in figure 15, and presents a peak located at approximately ![]() $k_{{span}}^+ = 0.05$,
$k_{{span}}^+ = 0.05$, ![]() $\lambda _{{span}}^+ \simeq 130$, and no peak below. This is also true for the transfer spectrum. However, the features observed in a minimal band unit are still present: negative production for
$\lambda _{{span}}^+ \simeq 130$, and no peak below. This is also true for the transfer spectrum. However, the features observed in a minimal band unit are still present: negative production for ![]() $k_{{span}}^+ < 0.01$, and inverse transfer occupying the whole shear layer for
$k_{{span}}^+ < 0.01$, and inverse transfer occupying the whole shear layer for ![]() $k_{{span}}^+ < 0.02$.
$k_{{span}}^+ < 0.02$.