I. INTRODUCTION
With the development of display technology and increased portable device screen resolution, the requirement of the high-definition video is increasing in today's world. In order to achieve better coding efficiency than H.264/AVC [Reference Wiegand, Sullivan, Bjøntegaard and Luthra1], some motion estimation algorithms are proposed to reduce the coding complexity while maintaining its high quality [Reference Al-Najdawi, Al-Najdawi and Tedmori2–Reference Cai and Pan4]. High efficiency video coding (HEVC) [Reference Sullivan, Ohm, Han and Wiegand5], also known as H.265, is developed by Joint Collaborative Team on Video Coding (JCT-VC) consisting of MPEG (Motion Picture Expert Group) and VCEG (Video Coding Experts Group). The structure of HEVC is similar to that of H.264/AVC, but it incorporates numerous advances, including quadtree structure, merge mode, sample adaptive offset, etc. Thanks to these advances, it achieves better video quality, or saves 50% bitrate compared with H.264/AVC. Many papers have been proposed to enhance the coding performance and applications of HEVC. Goswami et al. [Reference Goswami, Lee and Kim6] proposed a fast algorithm to reduce the encoding time of HEVC through texture-based analysis. In [Reference Fang, Gao, Xiong, Vasilakos and Fang7], a rate control mechanism is proposed to improve the bitrate accuracy and visual quality in HEVC. Usman et al. [Reference Usman, Jan and He8] proposed a secure, lightweight, energy-efficient and robust scheme which considers HEVC intra-encoded video streams as sources for data exchange between the mobile users and the media clouds.
HEVC defines three frame types, including I-, P-, and B-frames. I-frame plays an important role because the position of I-frame is the first encoded frame in a group of picture (GOP). It is encoded by using only intra coding and without using any other frame as reference. The B- and P-frames refer to the previous encoded frames to encode. In HEVC, the distance between two I-frames is called intra-period. HEVC encodes frames with a fixed intra-period. In HEVC, intra-period is set as 32 in common. However, using fixed intra-period to encode the sequence with the scene changes may require more bits. Figure 1 is the illustration of the above case.
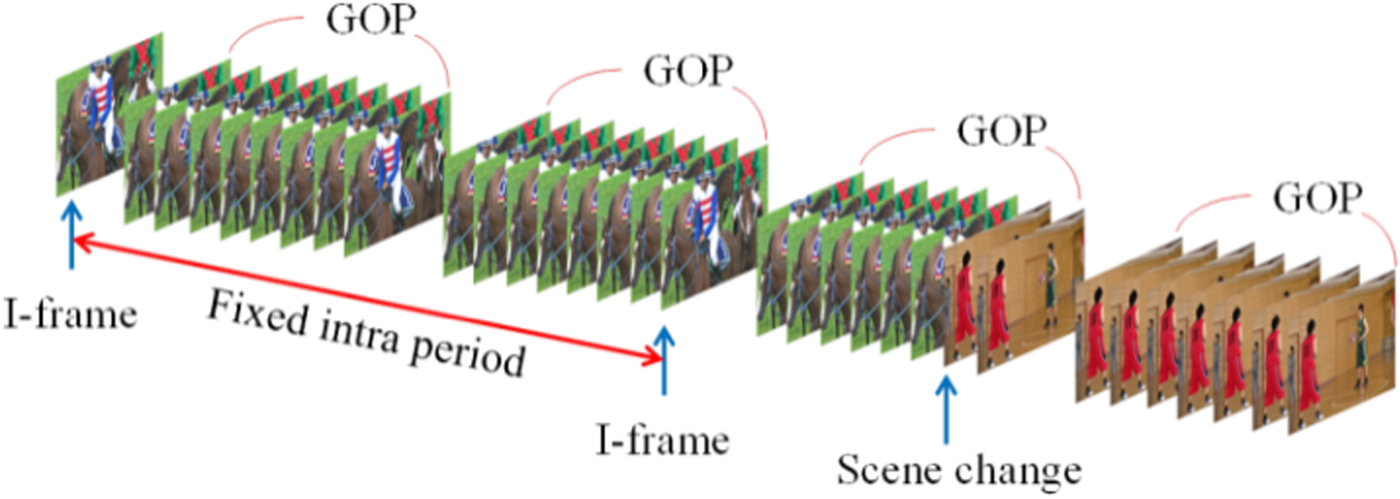
Fig. 1. Example of the fixed intra-period.
Figure 1 shows the position of scene change frame located behind of the frame that is encoded as I-frame, which causes the scene change frame not able to find a good reference block. The visual quality of the reconstructed scene change frame and those frames using scene change frame as a reference are lower. H.264/AVC also has this problem and some methods on this issue for H.264/AVC are proposed. Lee et al. [Reference Lee, Shin and Park9] proposed an I-frame decision method based on entropy of the block histogram. Ding et al. [Reference Ding and Yang10] employ the sum of transform difference to detect a scene change. These methods use different measurements to calculate the complexity of frames. When the value of measurement is larger or smaller than a predetermined threshold, the current frame is assigned as I-frame. However, these methods need to set a predetermined threshold to encode the sequences with different contents, and it is not guaranteed that the predetermined threshold is suitable for every sequence. For HEVC, research about the I-frame assignment method is lacking. Therefore, this paper proposes an I-frame assignment method based on Nash bargaining solution (NBS) in game theory for HEVC. Game theory [Reference Osborne and Rubinstein11] is the study about the interactive behavior of each player. Miranda et al. [Reference Miranda, Troffaes and Destercke12] present a study of the conjunction of possibility measures based on game theory. Moreover, game theory has been successfully applied to resource allocation problems solving and analyzing in the fields of bioinformatics application, channel coding, peer-to-peer system, sensor networks, and particle swarm optimization [Reference Moretti and Vasilakos13–Reference Leboucher, Shin, Siarry, Le Ménec, Chelouah and Tsourdos17]. In [Reference Ahmad and Luo18–Reference Yeh and Tseng20], game theory is applied to video coding. The pioneering work regarding game theory based rate control is proposed in [Reference Ahmad and Luo18]. The macroblocks of a frame compete for limited bits. The utility function is used to represent the preference of each macroblock. Based on NBS, a fair bit allocation is achieved. In [Reference Wang, Kwong and Zhang19], a frame level rate control for scalable video coding is proposed. It considers the quality dependency between different temporal levels, and bits are allocated for each frame based on NBS. Yeh et al. [Reference Yeh and Tseng20] proposed the largest coding unit (LCU) level bit allocation method for HEVC rate control. The structural similarity (SSIM) index is used to measure the distortion between the original frame and encoded frame. The R-SSIM is used to define the utility function for each LCU. Nash equilibrium is used to achieve the better bit allocation between the LCUs of a frame.
This paper regards the I-frame assignment problem as a resource allocation problem and formulates it by special game model, called as bargaining game. The bargaining game is a multiple-player game which is used to model the bargaining interactions. It is also regarded as a nonzero-sum two-player game. A two-player bargaining game is represented by a pair U, d, where the feasible utility set U ⊂ R 2 is a compact and convex set. For any u = (u 1, u 2) ∈ U, such that u > d, i.e. u 1 > d 1 and u 2 > d 2 [Reference Nash21]. Based on different assumptions, many solutions have been proposed such as NBS, generalized NBS, Kalai–Smorodinsky bargaining solution [Reference Kalai and Smorodinsky22], and Egalitarian bargaining solution. The generalized NBS is a unique bargaining solution that satisfied efficiency, linearity, independence of irrelevant alternatives axiom, which solves the generalized Nash product:
II. PROPOSED GAME THEORY BASED I-FRAME ASSIGNMENT METHOD
This section first describes the I-frame assignment problem. Suppose a sequence contains N f frames with the fixed intra-period and random access configuration; this sequence includes (N f − 1)/8 GOPs and only has (N f − 1)/32 intra-periods. The number of I-frames is equal to the number of intra-periods, so the I-frame assignment problem is which frame should be assigned as I-frame to maximize the overall coding efficiency. The first frame and the first GOP of the sequence are not considered in the game model. Here, we denote the number of the GOP and I frame used in the game model as N GOP and N I, respectively. The I-frame assignment problem is formulated as follows. Figure 2 shows the concept of the proposed method.
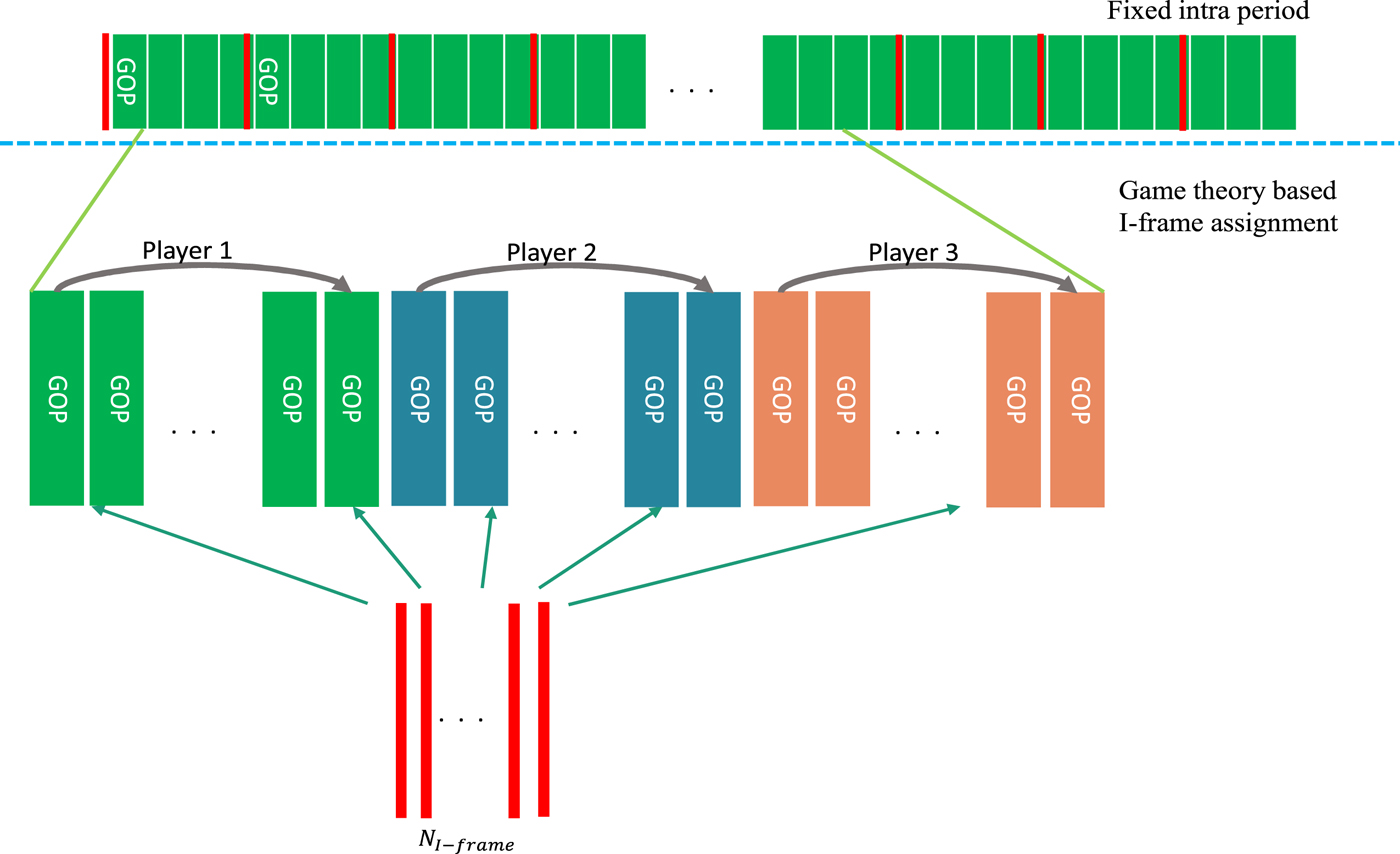
Fig. 2. Illustration of the proposed method.
A) Problem formulation
Player: The set of frames S contains the first frame of all GOPs in a sequence, i.e. S = {f i|i = 1, …, N GOP} where f i is the first frame of ith GOPs. S is averagely divided into N p subsets as ![]() $P_{1}\comma \; \ldots\comma \; P_{N_{p}}$ such that
$P_{1}\comma \; \ldots\comma \; P_{N_{p}}$ such that ![]() $P_{i} =\lcub f_{\lpar i-1\rpar \cdot \lpar \lpar N_{{GOP}}/N_{p}\rpar +1\rpar }\comma \; \ldots\comma \; f_{i\cdot \lpar N_{{GOP}}/N_{p} \rpar }\rcub $. Each subset P i is regarded as a player.
$P_{i} =\lcub f_{\lpar i-1\rpar \cdot \lpar \lpar N_{{GOP}}/N_{p}\rpar +1\rpar }\comma \; \ldots\comma \; f_{i\cdot \lpar N_{{GOP}}/N_{p} \rpar }\rcub $. Each subset P i is regarded as a player.
Strategies: The strategy represents the number of I-frames in the subset. Suppose the n i is the strategy of player i and the total number of I-frames is N I. An inequality constraint equation is formulated as follows:
 $$\sum_{i=1}^{N_p } n_i \le N_I. $$
$$\sum_{i=1}^{N_p } n_i \le N_I. $$Preference: Define that each player i has a mapping of a utility function u i to reflect its preference. The correlation coefficient of the two frames represents the similarity between the two frames. The correlation coefficient of two frames j and k is defined as:
where cov(f j, f k) is the covariance between the pixel values of the frame j and k, ![]() $\sigma_{f_{j} } $ and
$\sigma_{f_{j} } $ and ![]() $\sigma_{f_{k}} $ are the standard deviations of the pixel values of the frame j and k. For each player i has a list L i = {ω i,j|j = 1, …, N GOP/N p} where ω i, j is the frame index. The frame indexes in each list are arranged in ascending order of the correlation coefficient, i.e.
$\sigma_{f_{k}} $ are the standard deviations of the pixel values of the frame j and k. For each player i has a list L i = {ω i,j|j = 1, …, N GOP/N p} where ω i, j is the frame index. The frame indexes in each list are arranged in ascending order of the correlation coefficient, i.e. ![]() $C_{\omega_{i\comma j}\comma \omega_{i\comma j} -1} \le C_{\omega_{i\comma j+1}\comma \omega_{i\comma j+1} -1}$. For each player i, the frames
$C_{\omega_{i\comma j}\comma \omega_{i\comma j} -1} \le C_{\omega_{i\comma j+1}\comma \omega_{i\comma j+1} -1}$. For each player i, the frames ![]() $f_{\omega_{i\comma 1}}\comma \; \ldots\comma \; f_{\omega_{i\comma n_{i}}}$ may be assigned as I-frame.
$f_{\omega_{i\comma 1}}\comma \; \ldots\comma \; f_{\omega_{i\comma n_{i}}}$ may be assigned as I-frame.
In Fig. 3, suppose that the P i contains the frames j to l. The u i(1) is calculated as:
 $$u_i\lpar 1\rpar =\displaystyle{{\sum_{a=j}^{\omega_{i\comma 1} -2} C_{a\comma a+1} +\sum_{a=\omega_{i\comma 1} }^{l-1} C_{a\comma a+1}}\over{l-j}}. $$
$$u_i\lpar 1\rpar =\displaystyle{{\sum_{a=j}^{\omega_{i\comma 1} -2} C_{a\comma a+1} +\sum_{a=\omega_{i\comma 1} }^{l-1} C_{a\comma a+1}}\over{l-j}}. $$Only the correlation coefficient of the frames ω i,1 − 1 and ω i, 1 is not calculated, so equation (3) is also equal to
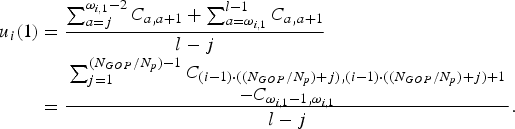 $$\eqalign{u_i \lpar 1\rpar &=\displaystyle{{\sum_{a=j}^{\omega_{i\comma 1} -2} C_{a\comma a+1} +\sum_{a=\omega_{i\comma 1} }^{l-1} C_{a\comma a+1}}\over{l-j}} \cr & =\displaystyle{{\matrix{\sum_{j=1}^{\lpar N_{GOP}/N_p \rpar -1} C_{\lpar i-1\rpar \cdot \lpar \lpar N_{GOP} /N_p \rpar +j\rpar \comma \lpar i-1\rpar \cdot \lpar \lpar N_{GOP} /N_p \rpar +j\rpar +1} \cr {-C_{\omega_{i\comma 1}-1\comma \omega_{i\comma 1}}}}}\over{l-j}}.} $$
$$\eqalign{u_i \lpar 1\rpar &=\displaystyle{{\sum_{a=j}^{\omega_{i\comma 1} -2} C_{a\comma a+1} +\sum_{a=\omega_{i\comma 1} }^{l-1} C_{a\comma a+1}}\over{l-j}} \cr & =\displaystyle{{\matrix{\sum_{j=1}^{\lpar N_{GOP}/N_p \rpar -1} C_{\lpar i-1\rpar \cdot \lpar \lpar N_{GOP} /N_p \rpar +j\rpar \comma \lpar i-1\rpar \cdot \lpar \lpar N_{GOP} /N_p \rpar +j\rpar +1} \cr {-C_{\omega_{i\comma 1}-1\comma \omega_{i\comma 1}}}}}\over{l-j}}.} $$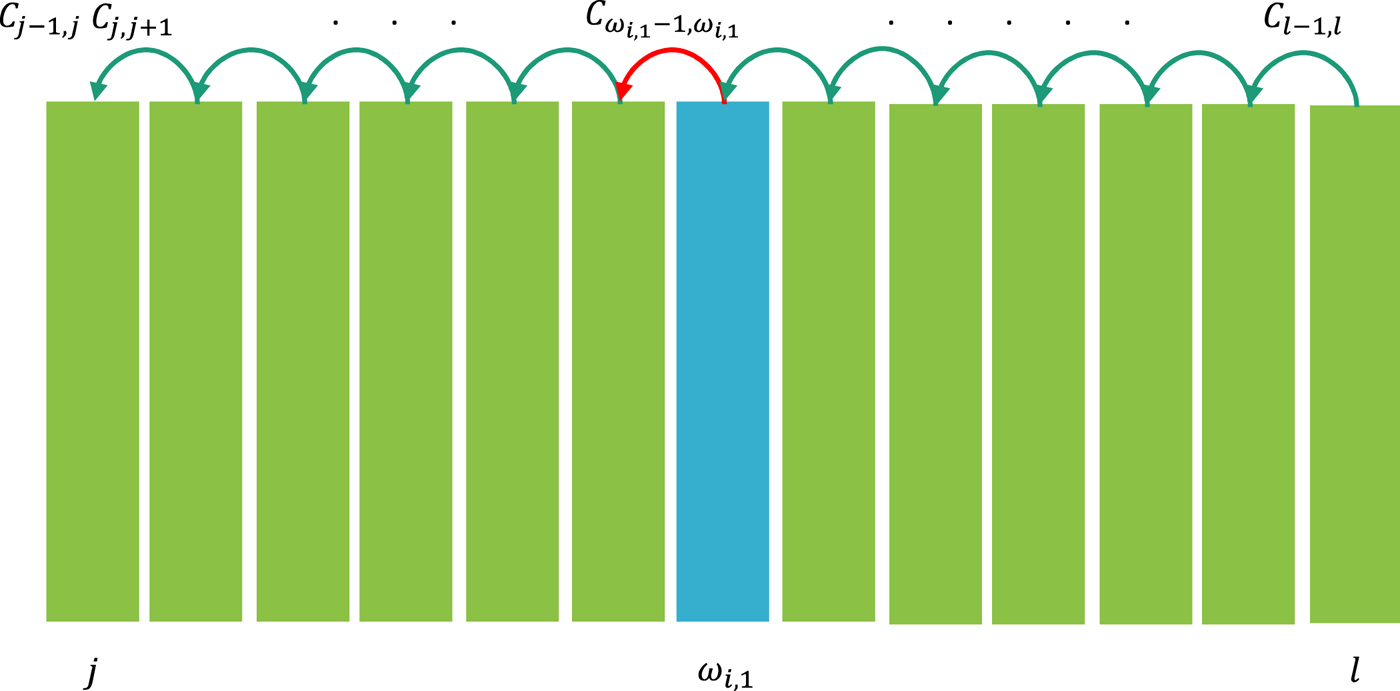
Fig. 3. Example of the calculation of the correlation coefficient.
Therefore, the general form of the utility function is defined as:
 $$u_i \lpar n_i\rpar =\displaystyle{{\matrix{\sum_{j=1}^{\lpar N_{GOP} /N_p \rpar -1}C_{\lpar i-1\rpar \cdot \lpar \lpar N_{GOP} /N_p \rpar +j\rpar \comma \lpar i-1\rpar \cdot \lpar \lpar N_{GOP} /N_p\rpar +j\rpar +1} \cr -\sum_{k=1}^{n_i} C_{\omega_{i\comma k-1}\comma \omega_{i\comma k}}}}\over{l-j+1-n_i}}. $$
$$u_i \lpar n_i\rpar =\displaystyle{{\matrix{\sum_{j=1}^{\lpar N_{GOP} /N_p \rpar -1}C_{\lpar i-1\rpar \cdot \lpar \lpar N_{GOP} /N_p \rpar +j\rpar \comma \lpar i-1\rpar \cdot \lpar \lpar N_{GOP} /N_p\rpar +j\rpar +1} \cr -\sum_{k=1}^{n_i} C_{\omega_{i\comma k-1}\comma \omega_{i\comma k}}}}\over{l-j+1-n_i}}. $$The utility function is defined as the average of correlation coefficients. When a player is assigned more I-frames, the utility of this player will increase.
Minimum utility: The minimum utility of the player i is denoted by d i which is used to guarantee the visual quality. Each player i requests ![]() $n_{i}^{min}$ to achieve the minimum utility, so
$n_{i}^{min}$ to achieve the minimum utility, so ![]() $n_{i} >n_{i}^{min}$.
$n_{i} >n_{i}^{min}$.
For example, a sequence is divided into several subsequences that contain 336 frames. Each subsequence is regarded as a game. Each game contains three players and 10 I-frames. Each player has 14 frames and competes for limit I-frames. Define that n i is ranged from 2 to 4. Figure 4 shows the curve of the utility function, which is an approximately linear function. The utility function is formulated as follows:
where a i and b i are the model parameters.
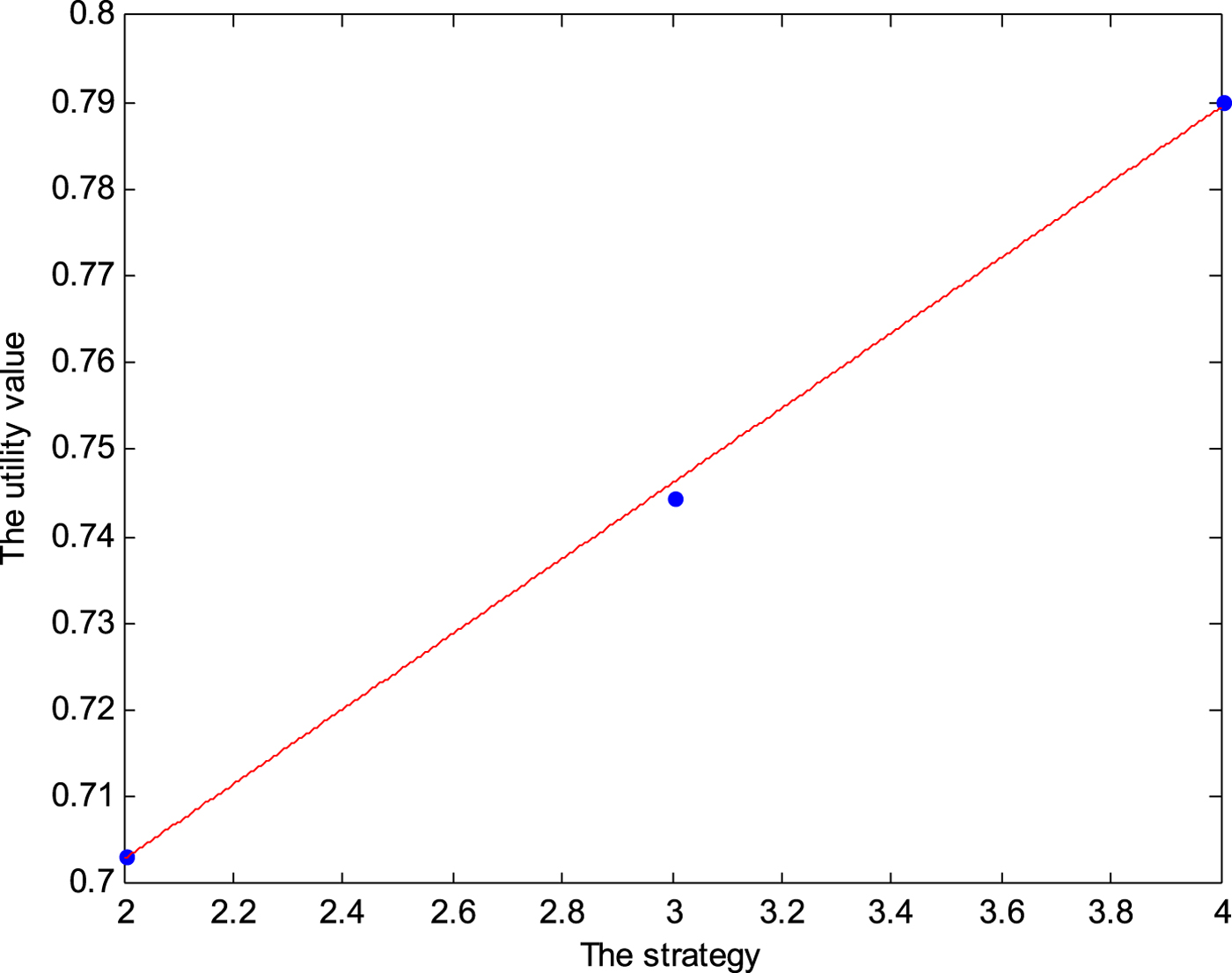
Fig. 4. The curve of the utility function.
B) I-frame assignment with Nash bargaining solution
Based on game theory, the optimal I-frame allocation can be solved as follows to obtain the NBS:
 $$\eqalign{{max} & \prod_{i=1}^3 \lpar {u_i \lpar {n_i } \rpar -u_i\lpar {n_i^{min}} \rpar } \rpar ^{p_i}\comma \; \cr \hbox{such that} & \sum_{i=1}^3 n_i \le 10\comma \; \quad n_i^{min} \lt n_i \lt n_i^{max}\comma \; } $$
$$\eqalign{{max} & \prod_{i=1}^3 \lpar {u_i \lpar {n_i } \rpar -u_i\lpar {n_i^{min}} \rpar } \rpar ^{p_i}\comma \; \cr \hbox{such that} & \sum_{i=1}^3 n_i \le 10\comma \; \quad n_i^{min} \lt n_i \lt n_i^{max}\comma \; } $$
where p i is the weight of each player i, so p i = 1/u i(0). Using equation (7) to formulate the I-frame assignment problem, it does not need to set the predetermined threshold. In addition, each player is assigned at least ![]() $n_{i}^{min}$ I-frames to keep the visual quality.
$n_{i}^{min}$ I-frames to keep the visual quality.
Because
for any x and y ∈ R, x ≠ y, α ∈ [0, 1], u i(n i) is concave.
Since u i is concave and injective, ln(u i) is strictly concave. Then equation (7) can be represented in the following form:
 $$\eqalign{{max} & \sum_{i=1}^3 p_i \cdot \ln \lpar u_i \lpar {n_i}\rpar -u_i \lpar {n_i^{min}}\rpar \rpar \comma \; \cr \hbox{such}\, \hbox{that} & \sum_{i=1}^3 n_i \le 10\comma \; \quad n_i^{min} \lt n_i \lt n_i^{max}.} $$
$$\eqalign{{max} & \sum_{i=1}^3 p_i \cdot \ln \lpar u_i \lpar {n_i}\rpar -u_i \lpar {n_i^{min}}\rpar \rpar \comma \; \cr \hbox{such}\, \hbox{that} & \sum_{i=1}^3 n_i \le 10\comma \; \quad n_i^{min} \lt n_i \lt n_i^{max}.} $$The above optimization problem can be solved by using Kuhn and Tucker theorem [Reference Kuhn and Tucker23,Reference Sundaram24]. This theorem is a generalized method of Lagrange multipliers. When some regularity conditions are satisfied, a solution in nonlinear programing can be optimized by adding Lagrange multipliers. Equation (8) can be reformulated as:
 $$\eqalign{J &= \sum_{i=1}^3 p_i \cdot \ln \lpar u_i \lpar {n_i }\rpar -u_i \lpar {n_i^{min}} \rpar \rpar +\lambda \left({10-\sum_{i=1}^3 n_i}\right)\cr & \quad +\sum_{i=1}^3 \theta_i \lpar {n_i -n_i^{min}} \rpar +\sum_{i=1}^3 \varepsilon_i \lpar {n_i^{max}-n_i}\rpar \comma \; } $$
$$\eqalign{J &= \sum_{i=1}^3 p_i \cdot \ln \lpar u_i \lpar {n_i }\rpar -u_i \lpar {n_i^{min}} \rpar \rpar +\lambda \left({10-\sum_{i=1}^3 n_i}\right)\cr & \quad +\sum_{i=1}^3 \theta_i \lpar {n_i -n_i^{min}} \rpar +\sum_{i=1}^3 \varepsilon_i \lpar {n_i^{max}-n_i}\rpar \comma \; } $$where λ, θ i, and ε i are the Lagrange multipliers. Then, the optimized solution can be obtained by solving equation (10):
 $$\left\{\matrix{\displaystyle{{\partial J}\over{\partial r_i}} = \displaystyle{{\partial p_i \cdot \ln\lpar {u_i \lpar {n_i } \rpar -u_i \lpar {n_i^{min}} \rpar }\rpar } \over{\partial n_i }}-\lambda +\theta_i -\varepsilon_i =0 \hfill \cr \displaystyle{{\partial J}\over{\partial \lambda }}=10-\mathop \sum \limits_{i=1}^3 n_i \ge 0 \hfill \cr \lambda \displaystyle{{\partial J}\over{\partial \lambda}} = \lambda \left({10-\sum_{i=1}^3 n_i} \right)= 0 \hfill \cr \theta_i \displaystyle{{\partial J}\over{\partial \theta_i}} = \theta_i \lpar {n_i-n_i^{min}}\rpar =0 \hfill \cr \varepsilon_i \displaystyle{{\partial J}\over{\partial \varepsilon_i}}=\varepsilon_i \lpar {n_i^{max}-n_i} \rpar =0\hfill }\right.\comma \; $$
$$\left\{\matrix{\displaystyle{{\partial J}\over{\partial r_i}} = \displaystyle{{\partial p_i \cdot \ln\lpar {u_i \lpar {n_i } \rpar -u_i \lpar {n_i^{min}} \rpar }\rpar } \over{\partial n_i }}-\lambda +\theta_i -\varepsilon_i =0 \hfill \cr \displaystyle{{\partial J}\over{\partial \lambda }}=10-\mathop \sum \limits_{i=1}^3 n_i \ge 0 \hfill \cr \lambda \displaystyle{{\partial J}\over{\partial \lambda}} = \lambda \left({10-\sum_{i=1}^3 n_i} \right)= 0 \hfill \cr \theta_i \displaystyle{{\partial J}\over{\partial \theta_i}} = \theta_i \lpar {n_i-n_i^{min}}\rpar =0 \hfill \cr \varepsilon_i \displaystyle{{\partial J}\over{\partial \varepsilon_i}}=\varepsilon_i \lpar {n_i^{max}-n_i} \rpar =0\hfill }\right.\comma \; $$where i ∈ 1, 2, …, N.
We assume that ![]() $n_{i} -n_{i}^{min}>0$,
$n_{i} -n_{i}^{min}>0$, ![]() $n_{i}^{max}-n_{i} >0$, and
$n_{i}^{max}-n_{i} >0$, and  $\sum_{i=1}^{3} {n_{i} =10} $, so θ i = 0, ε i = 0 and λ ≠ 0. Based on equation (10), ∂J/∂n i can be simplified as shown in equation (11):
$\sum_{i=1}^{3} {n_{i} =10} $, so θ i = 0, ε i = 0 and λ ≠ 0. Based on equation (10), ∂J/∂n i can be simplified as shown in equation (11):
 $$\eqalign{\displaystyle{{\partial J}\over{\partial n_i}} & = p_i \cdot \displaystyle{{\partial \ln \lpar {u_i \lpar {n_i } \rpar -u_i \lpar {n_i^{min}} \rpar }\rpar } \over{\partial n_i}}-\lambda \cr & = p_i \cdot \displaystyle{{\partial \ln \lpar {a_i \cdot n_i +b_i -a_i \cdot n_i^{min}-b_i } \rpar } \over {\partial n_i}}-\lambda \cr &= \displaystyle{{p_i}\over{\lpar n_i -n_i^{min}\rpar }}-\lambda =0.} $$
$$\eqalign{\displaystyle{{\partial J}\over{\partial n_i}} & = p_i \cdot \displaystyle{{\partial \ln \lpar {u_i \lpar {n_i } \rpar -u_i \lpar {n_i^{min}} \rpar }\rpar } \over{\partial n_i}}-\lambda \cr & = p_i \cdot \displaystyle{{\partial \ln \lpar {a_i \cdot n_i +b_i -a_i \cdot n_i^{min}-b_i } \rpar } \over {\partial n_i}}-\lambda \cr &= \displaystyle{{p_i}\over{\lpar n_i -n_i^{min}\rpar }}-\lambda =0.} $$n i can be represented as:
By substituting equation (12) into ![]() $\sum\nolimits_{i=1}^{3} {n_{i} =10}$, (1/λ) can be represented as
$\sum\nolimits_{i=1}^{3} {n_{i} =10}$, (1/λ) can be represented as
 $$\displaystyle{{1}\over{\lambda}} = \displaystyle{{1}\over{\sum_{i=1}^N p_i}}\left({10-\sum_{i=1}^3 n_i }\right). $$
$$\displaystyle{{1}\over{\lambda}} = \displaystyle{{1}\over{\sum_{i=1}^N p_i}}\left({10-\sum_{i=1}^3 n_i }\right). $$Therefore,
 $$n_i =min\left({\displaystyle{{p_i}\over{\sum_{j=1}^N p_j}}\left({10-\sum_{i=1}^3 n_i} \right)+n_i^{min}\comma \; n_i^{max}}\right)\comma \; $$
$$n_i =min\left({\displaystyle{{p_i}\over{\sum_{j=1}^N p_j}}\left({10-\sum_{i=1}^3 n_i} \right)+n_i^{min}\comma \; n_i^{max}}\right)\comma \; $$
where ![]() $n_{i}^{min}$ and
$n_{i}^{min}$ and ![]() $n_{i}^{max}$ are determined by experimental experience, in our experiment, the
$n_{i}^{max}$ are determined by experimental experience, in our experiment, the ![]() $n_{i}^{min}$ and
$n_{i}^{min}$ and ![]() $n_{i}^{max}$ are set as 2 and 4. The set of I-frame S I is defined as:
$n_{i}^{max}$ are set as 2 and 4. The set of I-frame S I is defined as:
For real-time applications, it is not acceptable that the proposed method needs a large frame recorder and an initial delay to storage enough sampling frames. However, it is acceptable for a video streaming service. Figure 5 shows the flowchart of the proposed method for a video streaming service. A buffer uses to store the frames accessed from the streaming server. In the initial stage, the first nine frames will be accessed to be stored in the buffer. In the first stage, the correlation coefficient of the first and the ninth frames in the buffer will be calculated and recorded. The first eight frames in the buffer will be removed, and the next eight frames will be stored in the buffer. The stage mentioned above is repeated until the number of the recorded correlation coefficient is enough. In the second stage, the I-frame assignment problem will be solved by using the proposed method. The third stage is to encode the subsequence. Repeat these three stages until the encode process is finished.
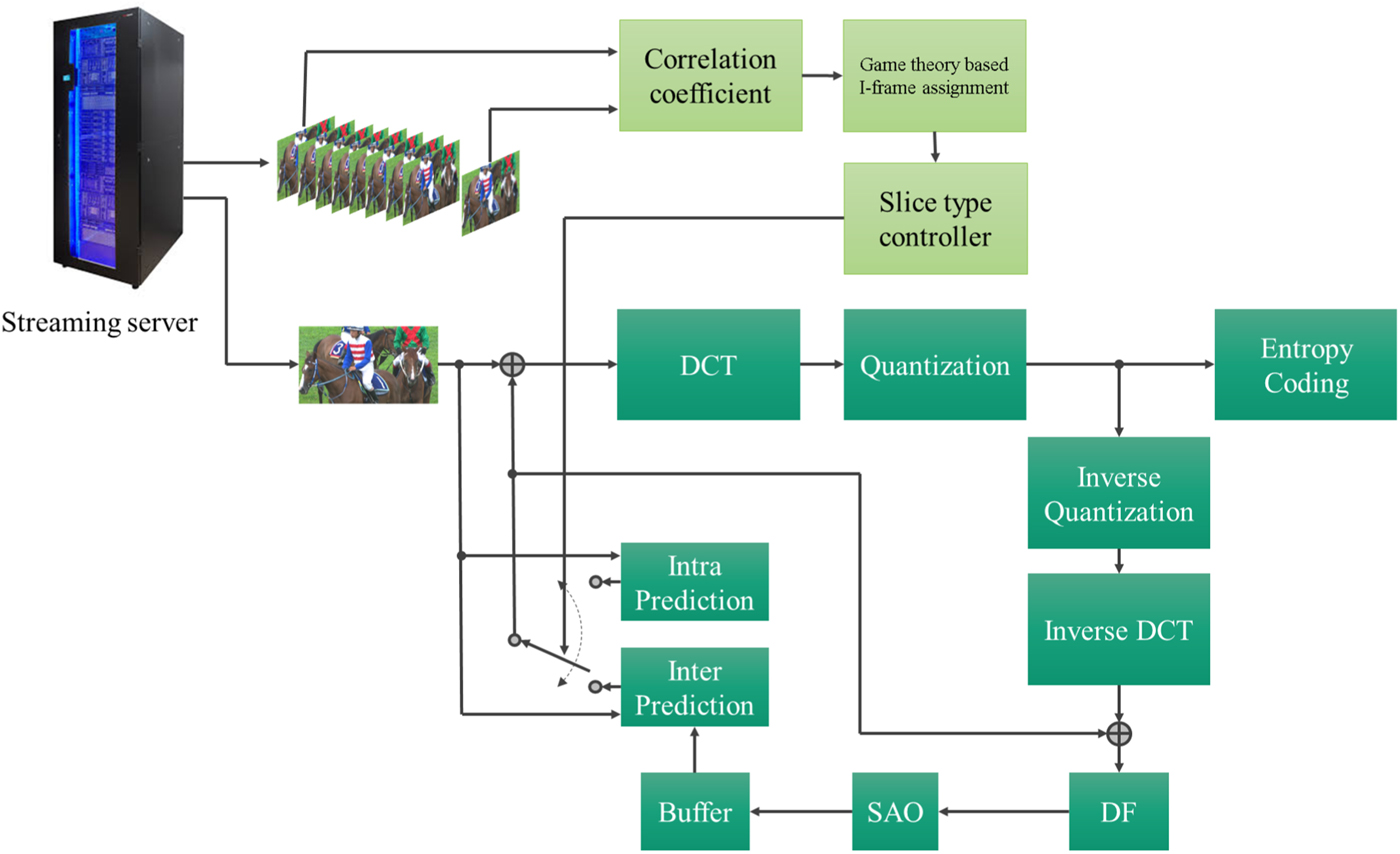
Fig. 5. Flowchart of the proposed method for video streaming service.
III. EXPERIMENTAL RESULTS
Experimental results are provided in this section to evaluate the performance of the proposed method. We combine different video sequences to generate six testing sequences. The components of each testing sequences are shown in Table 1. The test sequences D1, D2, and D3 are combined by different test sequences in class D, and the test sequences C1, C2, and C3 in class C. The resolution of the class D and class C is 416 × 240 and 832 × 480 pixels, respectively. The proposed method is implemented in HEVC reference software HM15.0 [25] and compared with the estimated I-frame assignment (EIFA) method and the fixed intra-period assignment (FIP). The EIFA method assigns the first frame of the current GOP as I-frame if the correlation coefficient of the first frames of the current GOP and the previous GOP is smaller than the predetermined threshold or the distance between the previous I-frame and the first frames of the current GOP is equal to 32. Other detailed simulation settings are shown in Table 2.
Table 1. Information on testing sequences.

Table 2. Simulation setting in HEVC.

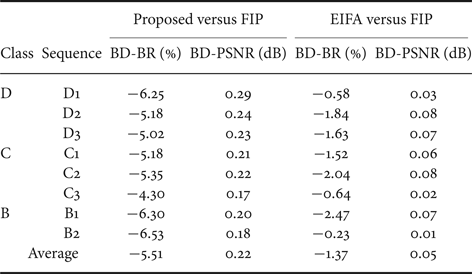
Table 3 shows the comparisons of the BD-BR and BD-PSNR [Reference Bjontegaard26] performance of the EIFA method and the proposed method with respect to the FIP method. Averagely, the proposed method shows 5.21% reductions on BD-BR, or 0.22 dB gain on BD-PSNR. The EIFA method shows 1.38% reduction on BD-BR, or 0.06 dB gain on BD-PSNR.
Table 3. Comparisons of BD-BR (%) and BD-PSNR (dB).
The rate-distortion (RD) curves of three methods with different testing sequences are shown in Fig. 6. By observing the RD curves in Fig. 6, the proposed method clearly achieves better coding performance when compared to the EIFA method and the FIP method.
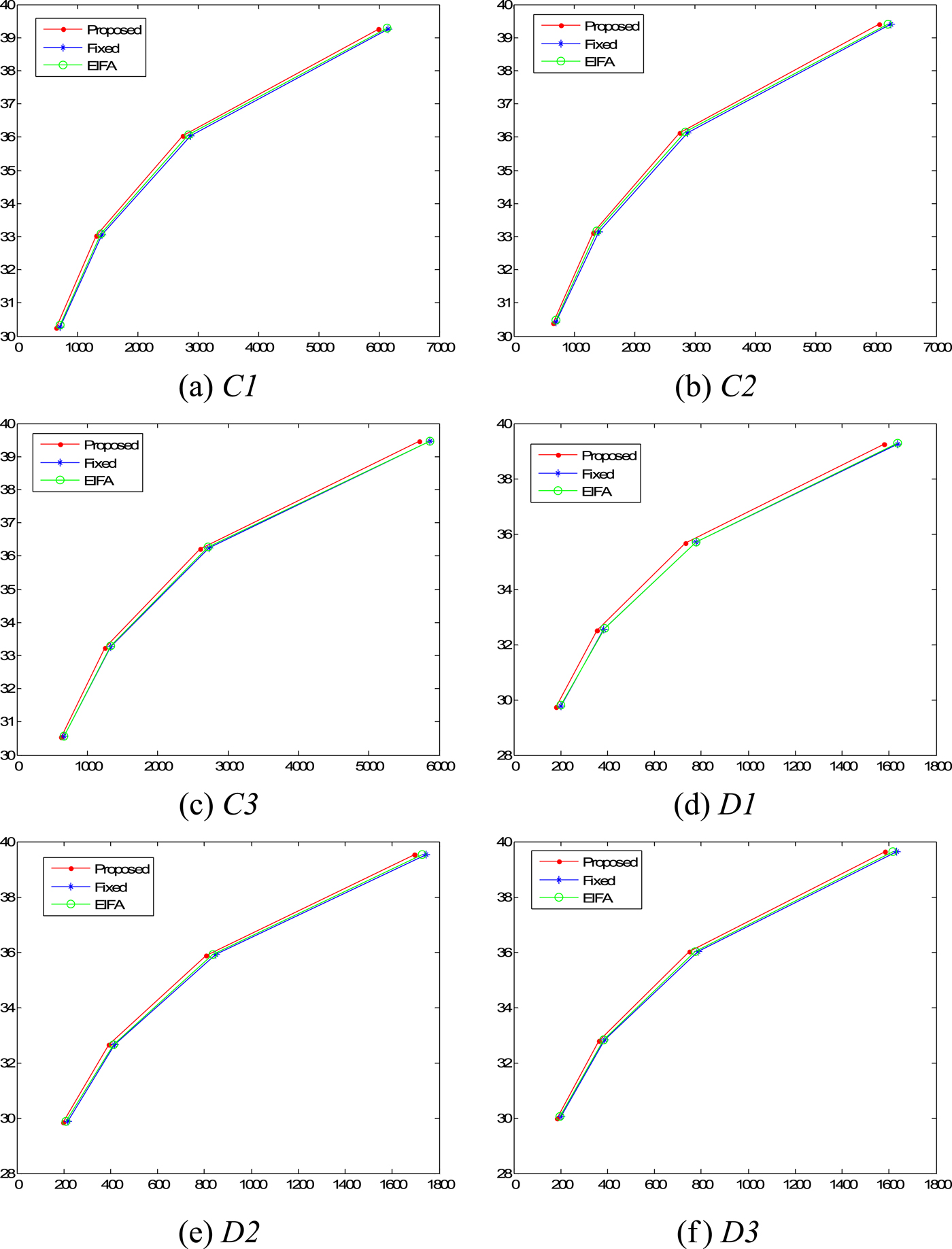
Fig. 6. Comparisons of RD curves.
IV. CONCLUSION
This paper proposes a new I-frame assignment method based on NBS in HEVC. In the proposed method, the encoded sequence is divided into several subsequences and each subsequence is regarded as a game. All GOPs in a subsequence is further divided into several sets of GOP. Each set of GOP is regarded as a player and competes for limit I-frames. The correlation coefficient of the two frames is used to calculate the utility function of each player. The optimal I-frame assignment is determined based on the generalized NBS. Experimental results show the proposed method outperforms HEVC by 5.21% bitrate saving.
ACKNOWLEDGEMENTS
The authors would like to thank the Ministry of Science and Technology, Taiwan, R.O.C. for financially supporting this research under contract no. MOST 107-2218-E-003-003-, MOST 106-2221-E-110-083-MY2, and MOST 105-2221-E-110-094-MY3. This work was financially supported by the “Intelligent Recognition Industry Service Center” from The Featured Areas Research Center Program within the frame-work of the Higher Education Sprout Project by the Ministry of Education (MOE) in Taiwan.
Chia-Hung Yeh received his B.S. and Ph.D. degrees from the Department of Electrical Engineering, National Chung Cheng University, Chiayi, Taiwan, in 1997 and 2002, respectively. He was an Assistant Professor from 2007 to 2010, an Associate Professor from 2010 to 2013, and a Professor from 2013 to 2017 with the Department of Electrical Engineering, National Sun Yat-sen University, Kaohsiung, Taiwan. He is currently a Distinguished Professor at National Taiwan Normal University, Taipei, Taiwan, and Vice Dean of College of Technology and Engineering. He has coauthored more than 250 technical international conferences and journal papers and held 47 patents in the USA, Taiwan, and China. He was the recipient of the 2013 IEEE MMSP Top 10% Paper Award, the 2014 IEEE GCCE Outstanding Poster Award, the 2015 APSIPA Distinguished Lecture, the 2017 IEEE SPS Tainan Section Chair, and the IEEE Outstanding Technical Achievement Award (IEEE Tainan Section). He became a Fellow of IET in 2017.
Ren-Fu Tseng received his M.S. degree from the Department of Applied Mathematics from National Sun Yat-sen University, Kaohsiung, Taiwan, in 2009 and a M.S. degree from the Department of Electrical Engineering from National Sun Yat-sen University, Kaohsiung, Taiwan, in 2015. His research interests are developing high efficiency video coding.
Mei-Juan Chen received her B.S., M.S., and Ph.D. degrees in Electrical Engineering from National Taiwan University, Taipei, in 1991, 1993, and 1997, respectively. She was an assistant professor (1997–2000) and an associate professor (2000–2005) in the Department of Electrical Engineering, National Dong Hwa University, Hualien, Taiwan. Since August 2005, she has been a professor of the Department of Electrical Engineering, National Dong Hwa University. She also served as the chair of her department from 2005–2006. Her research topics include image/video processing, video compression, motion estimation, error concealment, and video transcoding.
Chuan-Yu Chang received his M.S. degrees in electrical engineering from National Taiwan Ocean University, Keelung, Taiwan, in 1995, and a Ph.D. degree in electrical engineering from National Cheng Kung University, Tainan, Taiwan, in 2000. From 2001 to 2002, he was with the Department of Computer Science and Information Engineering, Shu-Te University, Kaohsiung, Taiwan. From 2002 to 2006, he was with the Department of Electronic Engineering, National Yunlin University of Science and Technology, Yunlin, Taiwan, where since 2007, he has been with the Department of Computer and Communication Engineering, where he is currently a Full Professor and Dean of Research & Development. He is the chair of IEEE Signal Processing Society Tainan Chapter, and an Associate Editor of the International Journal of Control Theory and Applications. His current research interests include neural networks and their application to medical image processing, wafer defect inspection, digital watermarking, and pattern recognition.











