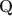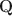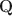1. Introduction
Cognitive diagnostic models (CDMs), or diagnostic classification models (Rupp et al., Reference Rupp, Templin and Henson2010; von Davier and Lee, Reference Davier and Lee2019), are powerful and popular discrete latent variable models in educational and psychological measurement. Based on subjects’ item responses, a CDM enables fine-grained diagnostic inference on multiple discrete latent attributes. Usually, each attribute is assumed to be binary and carries a specific meaning such as the mastery/deficiency of a skill, or the presence/absence of a mental disorder. In educational settings, the diagnostic feedback on the skill attributes provides details about students’ weaknesses and strengths, and can facilitate targeted instructions. In the past two decades, CDMs have attracted increasing research attention (e.g., Chen et al., Reference Chen, Liu, Xu and Ying2015; de la Torre, Reference de la Torre2011; Henson et al., Reference Henson, Templin and Willse2009; Junker and Sijtsma, Reference Junker and Sijtsma2001; Rupp et al., Reference Rupp, Templin and Henson2010; von Davier, Reference von Davier2008; von Davier and Lee, Reference Davier and Lee2019).
In the early years after the inception of CDMs, they were mostly applied to settings specifically designed for a diagnostic purpose, such as the celebrated fraction-subtraction data first collected and analyzed by Tatsuoka (Tatsuoka, Reference Tatsuoka1983). Recently, it is increasingly attractive to gear the diagnostic modeling methodology to large-scale modern educational assessments, such as the Trends in Mathematics and Science Study (TIMSS) or Programme for International Student Assessment (PISA) (e.g., see Chen and de la Torre, Reference Chen and de la Torre2014, George and Robitzsch, Reference George and Robitzsch2015, Gu and Xu, Reference Gu and Xu2023, von Davier, Reference von Davier2008). These applications create new opportunities and also bring about new challenges. For example, in the TIMSS 2019 eighth-grade math assessment, each item measures multiple granularities of skills: Content / Cognitive as the general ability domains, Number / Algebra / Geometry / Data and Probability as more specific skills under the Content domain, Knowing / Applying / Reasoning as more specific skills under the Cognitive domain, etc. These large-scale complex assessments call for new statistical and computational methods.
Reflecting on the current CDM (i.e., diagnostic modeling) literature, many studies adopt the saturated model for the latent attributes, in which every configuration of the attributes has a separate proportion parameter (e.g., Balamuta and Culpepper Reference Balamuta and Culpepper2022; Chen et al., Reference Chen, Liu, Xu and Ying2015, Reference Chen, Culpepper, Chen and Douglas2018, Reference Chen, Culpepper and Liang2020; Fang et al., Reference Fang, Liu and Ying2019; Gu and Xu, Reference Gu and Xu2019; Xu and Zhang, Reference Xu and Zhang2016, Reference Xu and Shang2018). Though being fully flexible, the saturated attribute model is not parsimonious, because it requires exponentially many parameters to describe the attribute distribution (
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$2^K-1$$\end{document}
![]() ones for K binary attributes). This lack of parsimony makes applying CDMs to modern high-dimensional-attribute settings very challenging, both statistically and computationally. There exist a few important exceptions to the saturated modeling practice, including the log-linear attribute model in Xu and von Davier (Reference Xu and von Davier2008), the higher-order IRT-based model in de la Torre and Douglas (Reference de la Torre and Douglas2004), and the multivariate probit model with one continuous factor in Templin et al. (Reference Templin, Henson, Templin and Roussos2008). These models either include parameters that are not straightforward to interpret (log-linear parameters in Xu and von Davier, Reference Xu and von Davier2008), or employ only a small number of continuous latent variables to model the attributes (de la Torre and Douglas, Reference de la Torre and Douglas2004; Templin et al., Reference Templin, Henson, Templin and Roussos2008).
ones for K binary attributes). This lack of parsimony makes applying CDMs to modern high-dimensional-attribute settings very challenging, both statistically and computationally. There exist a few important exceptions to the saturated modeling practice, including the log-linear attribute model in Xu and von Davier (Reference Xu and von Davier2008), the higher-order IRT-based model in de la Torre and Douglas (Reference de la Torre and Douglas2004), and the multivariate probit model with one continuous factor in Templin et al. (Reference Templin, Henson, Templin and Roussos2008). These models either include parameters that are not straightforward to interpret (log-linear parameters in Xu and von Davier, Reference Xu and von Davier2008), or employ only a small number of continuous latent variables to model the attributes (de la Torre and Douglas, Reference de la Torre and Douglas2004; Templin et al., Reference Templin, Henson, Templin and Roussos2008).
The questions motivating this work are: Is there an even more flexible, yet still parsimonious and interpretable way, to model the high-dimensional latent attributes? Is it possible to fully retain the power and goal of diagnostic modeling, and provide discrete diagnoses in multiple latent granularities (as desired in the aforementioned TIMSS application)? Is it possible to establish identifiability guarantees for such models with complex latent structures? To address these questions, we propose a deep generative modeling framework for cognitive diagnosis, which features multiple, potentially deep, entirely discrete latent layers. We name the new family of models Deep Cognitive Diagnostic Models (DeepCDMs), to reflect that they can serve as tools to hunt for deep diagnostic information. DeepCDMs enjoy several desirable properties simultaneously: parsimony and richness, interpretability, and identifiability. We elaborate on these advantages in the following.
First, DeepCDMs are statistically parsimonious yet have rich representational power. On the one hand, the parsimony comes from that a DeepCDM avoid the exponential complexity of parameters in the saturated attribute model. In fact, a DeepCDM requires only a quadratic or even linear number of parameters with respect to the number of latent variables. Such a reduction of parameter complexity does not come at the cost of a less suitable model. On the contrary, our model is well motivated by the fact that the fine-grained latent attributes often have structured dependence on each other due to some hidden mechanisms, for which the deep architecture is well suited to model. Indeed, the TIMSS assessment in which each item targets multiple skill granularities provides practical evidence for this argument. On the other hand, introducing multiple, potentially deep, latent layers can greatly enhance the expressive and representational power of a model, as widely recognized in the deep learning community (Bengio et al., Reference Bengio, Courville and Vincent2013; Goodfellow et al., Reference Goodfellow, Bengio and Courville2016; Ranganath et al., Reference Ranganath, Tang, Charlin, Blei and Gale2015).
Second, DeepCDMs are mathematically identifiable under intuitive conditions on the deep generative structure. Identifiability means that the parameters can be uniquely determined from the observed distribution. It is a highly desirable property and a prerequisite for valid statistical estimation. Recently, there have been an emerging literature addressing the identifiability issues of CDMs (Chen et al., Reference Chen, Culpepper and Liang2020; Culpepper, Reference Culpepper2019b; Fang et al., Reference Fang, Liu and Ying2019; Gu and Xu, Reference Gu and Xu2019, Reference Gu and Xu2020; Xu, Reference Xu2017; Xu and Zhang, Reference Xu and Zhang2016). However, all of these works focus on the saturated attribute model. It is unknown what conditions can ensure identifiability when higher-order latent structures are present in a CDM. We establish identifiability for various DeepCDMs with an arbitrary number of latent layers. Our identifiability conditions impose intuitive constraints on the between-layer graph structures captured by multiple “
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{Q}$$\end{document}
![]() -matrices”. These conditions directly inform how to design a DeepCDM—a ladder/pyramid shaped sparse graphical model, with the observed item responses occupying the bottom layer, and increasingly smaller sizes of latent layers when going deeper (see Fig. 1).
-matrices”. These conditions directly inform how to design a DeepCDM—a ladder/pyramid shaped sparse graphical model, with the observed item responses occupying the bottom layer, and increasingly smaller sizes of latent layers when going deeper (see Fig. 1).
Third, DeepCDMs are practically interpretable. The shrinking-ladder-shaped probabilistic graphical model can capture cognitive concepts and provide diagnostics from coarse to fine grained, and from high level to detailed. In a DeepCDM, when climbing up the ladder and going deeper, concepts become increasingly abstract and general, capturing the big picture of knowledge; when stepping down the ladder and going shallower, concepts become increasingly concrete and specific, capturing the fine-grained details of knowledge. Therefore, the proposed DeepCDM framework can characterize a complete picture of one’s knowledge structure and provide diagnostic feedback in multiple different resolutions, with each layer offering one particular resolution. Such diagnostic information can facilitate more effective multi-resolution interventions than traditional CDMs with a saturated attribute model.
In summary, this paper makes the following contributions in theory, methodology, and computation. First, we introduce a deep generative modeling framework for cognitive diagnosis for the first time, and propose a general class of interpretable and parsimonious DeepCDMs. Second, we develop identifiability theory for various DeepCDMs, applicable to both confirmatory and fully exploratory settings. Our identifiability conditions provide insights into what deep generative graph one can fundamentally uncover in a DeepCDM: a shrinking latent ladder when going deeper. Third, we propose Bayesian formulations and Gibbs sampling algorithms for various DeepCDMs. In this initial paper, our Bayesian inference methods are developed for the confirmatory setting with known and fixed
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{Q}$$\end{document}
![]() -matrices. Our algorithms enforce certain monotonicity constraints on parameters and produce interpretable estimation results.
-matrices. Our algorithms enforce certain monotonicity constraints on parameters and produce interpretable estimation results.
The rest of this paper is organized as follows. Section 2 reviews existing modeling approaches, proposes the general DeepCDM framework, and gives various specific examples. Section 3 proposes transparent identifiability conditions for various DeepCDMs and discusses their practical implications. Section 4 develops the Bayesian formulations of various DeepCDMs and their corresponding Gibbs sampling algorithms. Section 5 conducts simulations studies that corroborate the identifiability theory and demonstrate the performance of the proposed algorithms. Section 6 applies the DeepCDM methodology to data extracted from the TIMSS 2019 math assessment. Finally, Sect. 7 provides concluding remarks. The proofs of theorems and Gibbs sampling details are included in the Supplementary Material.
2. Deep Discrete Latent Variable Modeling for Diagnostic Purposes
2.1. Existing Approaches to Latent Attribute Modeling
A traditional CDM consists of two parts in the model: the measurement part and the latent part. The measurement part describes how the observed responses measure the latent attributes, and is closely related to the concept of the
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{Q}$$\end{document}
![]() -matrix (Tatsuoka, Reference Tatsuoka1983). Various diagnostic goals have led to different specific measurement models, including the Deterministic Input Noisy output “And” gate model (DINA; Junker and Sijtsma, Reference Junker and Sijtsma2001), the Deterministic Input Noisy output “Or” gate model (DINO; Templin and Henson, Reference Templin and Henson2006), the main-effect diagnostic models (de la Torre, Reference de la Torre2011; DiBello et al., Reference DiBello, Stout and Roussos1995; Maris, Reference Maris1999), and the all-effect general diagnostic models (de la Torre, Reference de la Torre2011; Henson et al., Reference Henson, Templin and Willse2009; von Davier, Reference von Davier2008). We defer introducing the details of these measurement models to Sect. 2.3. Next, we briefly review existing models for the latent part in a CDM; that is, models for the latent attributes.
-matrix (Tatsuoka, Reference Tatsuoka1983). Various diagnostic goals have led to different specific measurement models, including the Deterministic Input Noisy output “And” gate model (DINA; Junker and Sijtsma, Reference Junker and Sijtsma2001), the Deterministic Input Noisy output “Or” gate model (DINO; Templin and Henson, Reference Templin and Henson2006), the main-effect diagnostic models (de la Torre, Reference de la Torre2011; DiBello et al., Reference DiBello, Stout and Roussos1995; Maris, Reference Maris1999), and the all-effect general diagnostic models (de la Torre, Reference de la Torre2011; Henson et al., Reference Henson, Templin and Willse2009; von Davier, Reference von Davier2008). We defer introducing the details of these measurement models to Sect. 2.3. Next, we briefly review existing models for the latent part in a CDM; that is, models for the latent attributes.
We focus on the commonly considered case of binary attributes. Denote the ith subject’s latent attribute profile by
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{A}_i = (A_{i,1}, \ldots , A_{i,K})$$\end{document}
![]() , then each
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{A}_i$$\end{document}
, then each
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{A}_i$$\end{document}
![]() takes one of the
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$|\{0,1\}^K|=2^K$$\end{document}
takes one of the
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$|\{0,1\}^K|=2^K$$\end{document}
![]() possible configurations. In the current literature of CDMs, the most widely used model for the latent attributes is the saturated model (Chen et al., Reference Chen, Liu, Xu and Ying2015, Reference Chen, Culpepper, Chen and Douglas2018, Reference Chen, Culpepper and Liang2020; Fang et al., Reference Fang, Liu and Ying2019; Gu and Xu, Reference Gu and Xu2019; Xu and Zhang, Reference Xu and Zhang2016), which assumes that each binary pattern
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\varvec{\alpha }\in \{0,1\}^K$$\end{document}
possible configurations. In the current literature of CDMs, the most widely used model for the latent attributes is the saturated model (Chen et al., Reference Chen, Liu, Xu and Ying2015, Reference Chen, Culpepper, Chen and Douglas2018, Reference Chen, Culpepper and Liang2020; Fang et al., Reference Fang, Liu and Ying2019; Gu and Xu, Reference Gu and Xu2019; Xu and Zhang, Reference Xu and Zhang2016), which assumes that each binary pattern
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\varvec{\alpha }\in \{0,1\}^K$$\end{document}
![]() has its separate proportion parameter
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$p_{\varvec{\alpha }}$$\end{document}
has its separate proportion parameter
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$p_{\varvec{\alpha }}$$\end{document}
![]() with
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mathbb P(\textbf{A}_i = \varvec{\alpha }) = p_{\varvec{\alpha }}$$\end{document}
with
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mathbb P(\textbf{A}_i = \varvec{\alpha }) = p_{\varvec{\alpha }}$$\end{document}
![]() . These proportion parameters satisfy that
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$p_{\varvec{\alpha }}\ge 0$$\end{document}
. These proportion parameters satisfy that
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$p_{\varvec{\alpha }}\ge 0$$\end{document}
![]() and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\sum _{\varvec{\alpha }\in \{0,1\}^K} p_{\varvec{\alpha }} = 1$$\end{document}
and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\sum _{\varvec{\alpha }\in \{0,1\}^K} p_{\varvec{\alpha }} = 1$$\end{document}
![]() . Though being fully flexible and general, the saturated attribute model is not parsimonious, because it requires
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$2^K$$\end{document}
. Though being fully flexible and general, the saturated attribute model is not parsimonious, because it requires
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$2^K$$\end{document}
![]() proportion parameters in
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\varvec{\pi }$$\end{document}
proportion parameters in
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\varvec{\pi }$$\end{document}
![]() , an exponential parameter complexity.
, an exponential parameter complexity.
There exist two important approaches for modeling the binary attributes through a higher-order model. One approach is the higher-order latent trait model (HO-CDM) proposed by de la Torre and Douglas (Reference de la Torre and Douglas2004), which uses one or more continuous latent variables to explain the binary attributes through an IRT-type model. In the unidimensional case, each student is assumed to have a higher-order continuous ability
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\theta _i$$\end{document}
![]() , conditioned on which the attributes
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$A_{i1}, \ldots , A_{iK}$$\end{document}
, conditioned on which the attributes
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$A_{i1}, \ldots , A_{iK}$$\end{document}
![]() are independently generated through a Rasch, 1PL, or 2PL model (also see the GDINA R package and Ma and de la Torre, Reference Ma and de la Torre2020). See more discussions on the connections and differences between the HO-CDM and DeepCDMs in Sect. 5. Another approach proposed by Templin et al. (Reference Templin, Henson, Templin and Roussos2008) employs the multivariate probit model with a one-dimensional continuous factor. This approach assumes that each binary attribute
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$A_{i,k}$$\end{document}
are independently generated through a Rasch, 1PL, or 2PL model (also see the GDINA R package and Ma and de la Torre, Reference Ma and de la Torre2020). See more discussions on the connections and differences between the HO-CDM and DeepCDMs in Sect. 5. Another approach proposed by Templin et al. (Reference Templin, Henson, Templin and Roussos2008) employs the multivariate probit model with a one-dimensional continuous factor. This approach assumes that each binary attribute
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$A_{i,k}$$\end{document}
![]() is obtained via dichotomizing a Normal random variable
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\eta _{i,k}$$\end{document}
is obtained via dichotomizing a Normal random variable
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\eta _{i,k}$$\end{document}
![]() by a cut-off point, and the K Normal variables
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$(\eta _{i,1},\ldots ,\eta _{i,K})$$\end{document}
by a cut-off point, and the K Normal variables
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$(\eta _{i,1},\ldots ,\eta _{i,K})$$\end{document}
![]() are generated via a factor analysis model. Both of these two approaches use a small number of continuous latent variables to model the binary attributes.
are generated via a factor analysis model. Both of these two approaches use a small number of continuous latent variables to model the binary attributes.
Other than the higher-order latent variable models, the independence model and the log-linear model have also been considered for modeling the attributes (Maris, Reference Maris1999; Xu and von Davier, Reference Xu and von Davier2008). The independence attribute model is often overly simplistic in practice. The log-linear model in Xu and von Davier (Reference Xu and von Davier2008) is flexible, but employs parameters that are not straightforward to interpret. Another different model for the latent attributes is the attribute hierarchy method (AHM; Gierl et al., Reference Gierl, Leighton, Hunka and Cambridge2007, Templin and Bradshaw, Reference Templin and Bradshaw2014). The AHM assumes that the mastery of certain skill attributes is a prerequisite for that of others. As pointed out by Rupp et al. (Reference Rupp, Templin and Henson2010), the existing AHMs are pattern classification approaches rather than probabilistic measurement models.
2.2. The New DeepCDM Framework
Motivated by the appeal to perform diagnostic modeling at multiple granularities, we propose the deep cognitive diagnostic modeling framework. We adopt the probabilistic graphical model (Koller and Friedman, Reference Koller and Friedman2009; Wainwright et al., Reference Wainwright and Jordan2008) terminology, specifically, a directed graphical model, to rigorously define a DeepCDM. Graphical models use a graph as the basis for compactly encoding a complex joint distribution of high-dimensional random variables. In the graphical representation, the nodes correspond to the random variables, and the edges correspond to direct probabilistic interactions between them.
A general directed acyclic graph (DAG; also called a Bayesian network as in Pearl (Reference Pearl1988)) is defined as follows. In a DAG, every edge has a direction, and there are no directed cycles. DAGs are well suited to model the generative mechanism and causal relations involving latent variables; see the book Almond et al. (Reference Almond, Mislevy, Steinberg, Yan and Williamson2015) for using Bayesian networks in educational assessment. Consider M random variables
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$X_1,\ldots ,X_M$$\end{document}
![]() as M nodes in a DAG. If there is a directed edge from
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$X_\ell $$\end{document}
as M nodes in a DAG. If there is a directed edge from
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$X_\ell $$\end{document}
![]() to
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$X_m$$\end{document}
to
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$X_m$$\end{document}
![]() , then
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$X_\ell $$\end{document}
, then
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$X_\ell $$\end{document}
![]() is said to be a parent of
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$X_m$$\end{document}
is said to be a parent of
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$X_m$$\end{document}
![]() and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$X_m$$\end{document}
and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$X_m$$\end{document}
![]() a child of
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$X_\ell $$\end{document}
a child of
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$X_\ell $$\end{document}
![]() . Let
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\text { {pa}}(m)\subseteq \{1,\ldots ,M\}$$\end{document}
. Let
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\text { {pa}}(m)\subseteq \{1,\ldots ,M\}$$\end{document}
![]() be the set of indices of all parents of
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$X_m$$\end{document}
be the set of indices of all parents of
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$X_m$$\end{document}
![]() . Then, according to the general definition of a DAG, the joint distribution of the
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$X_1,\ldots ,X_M$$\end{document}
. Then, according to the general definition of a DAG, the joint distribution of the
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$X_1,\ldots ,X_M$$\end{document}
![]() factorizes as:
factorizes as:

where
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mathbb {P}(X_m \mid X_{\text { {pa}}(m)})$$\end{document}
![]() is the conditional distribution of
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$X_m$$\end{document}
is the conditional distribution of
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$X_m$$\end{document}
![]() given its parent variables
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$X_{\text { {pa}}(m)}$$\end{document}
given its parent variables
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$X_{\text { {pa}}(m)}$$\end{document}
![]() . The graph structure of a DAG encodes rich conditional dependence and independence relations among the node variables, as can be checked by examining (1). If a DAG consists of latent variables, then these latent variables need to be marginalized out in the joint distribution (1) in order to obtain the marginal distribution of the observed variables.
. The graph structure of a DAG encodes rich conditional dependence and independence relations among the node variables, as can be checked by examining (1). If a DAG consists of latent variables, then these latent variables need to be marginalized out in the joint distribution (1) in order to obtain the marginal distribution of the observed variables.
We next introduce the formulation and notation of a general DeepCDM. At the bottom layer of a DeepCDM are the observed response variables to the J items,
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{R}= (R_1, \ldots , R_J)$$\end{document}
![]() . The first (i.e., shallowest) latent layer adjacent to the bottom layer collects the most fine-grained latent attributes,
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{A}^{(1)} = (A^{(1)}_1, \ldots , A^{(1)}_{K_1})$$\end{document}
. The first (i.e., shallowest) latent layer adjacent to the bottom layer collects the most fine-grained latent attributes,
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{A}^{(1)} = (A^{(1)}_1, \ldots , A^{(1)}_{K_1})$$\end{document}
![]() . Note that a CDM with a saturated attribute model stops here and assumes the
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$K_1$$\end{document}
. Note that a CDM with a saturated attribute model stops here and assumes the
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$K_1$$\end{document}
![]() attributes can be arbitrarily dependent on each other. In contrast, we model the generating mechanism of the attributes through deeper latent layers. In a D-latent-layer DeepCDM, denote the dth latent layer (counting from the bottom) by
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{A}^{(d)} = (A^{(d)}_1, \ldots , A^{(d)}_{K_d})$$\end{document}
attributes can be arbitrarily dependent on each other. In contrast, we model the generating mechanism of the attributes through deeper latent layers. In a D-latent-layer DeepCDM, denote the dth latent layer (counting from the bottom) by
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{A}^{(d)} = (A^{(d)}_1, \ldots , A^{(d)}_{K_d})$$\end{document}
![]() for each
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$d=1,2,\ldots ,D$$\end{document}
for each
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$d=1,2,\ldots ,D$$\end{document}
![]() . All edges in a DeepCDM are pointing in the top-down direction, only potentially between two adjacent layers. See Fig. 1 for an example of a DeepCDM with
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$D=3$$\end{document}
. All edges in a DeepCDM are pointing in the top-down direction, only potentially between two adjacent layers. See Fig. 1 for an example of a DeepCDM with
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$D=3$$\end{document}
![]() . The definition in (1) also implies that all the variables in any specific layer of a DeepCDM are conditionally independent given the variables in the above layer. Such a graphical model intuitively describes how the more specific latent skills are successively generated by the more general higher-level latent “meta-skills”. To fully realize the diagnostic goal, a DeepCDM assumes all latent variables to be discrete. Later, our identifiability theory will reveal that there should be smaller and smaller latent layers when going deeper; that is,
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$K_1> K_2> \cdots > K_D$$\end{document}
. The definition in (1) also implies that all the variables in any specific layer of a DeepCDM are conditionally independent given the variables in the above layer. Such a graphical model intuitively describes how the more specific latent skills are successively generated by the more general higher-level latent “meta-skills”. To fully realize the diagnostic goal, a DeepCDM assumes all latent variables to be discrete. Later, our identifiability theory will reveal that there should be smaller and smaller latent layers when going deeper; that is,
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$K_1> K_2> \cdots > K_D$$\end{document}
![]() , another intuitive constraint.
, another intuitive constraint.

Figure. 1 A ladder-shaped three-latent-layer DeepCDM. Gray nodes are observed variables, and white nodes are latent ones. Multiple layers of binary latent variables
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{A}^{(1)}$$\end{document}
![]() ,
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{A}^{(2)}$$\end{document}
,
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{A}^{(2)}$$\end{document}
![]() , and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{A}^{(3)}$$\end{document}
, and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{A}^{(3)}$$\end{document}
![]() successively generate the observed binary responses
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{R}$$\end{document}
successively generate the observed binary responses
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{R}$$\end{document}
![]() . Binary matrices
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{Q}^{(1)}$$\end{document}
. Binary matrices
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{Q}^{(1)}$$\end{document}
![]() ,
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{Q}^{(2)}$$\end{document}
,
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{Q}^{(2)}$$\end{document}
![]() , and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{Q}^{(3)}$$\end{document}
, and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{Q}^{(3)}$$\end{document}
![]() encode the sparse connection patterns between adjacent layers in the graph.
encode the sparse connection patterns between adjacent layers in the graph.
A key feature of a DeepCDM is the multiple “
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{Q}$$\end{document}
![]() -matrices” at different depths of the graphical model, as in Fig. 1. In traditional cognitive diagnosis, the
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{Q}$$\end{document}
-matrices” at different depths of the graphical model, as in Fig. 1. In traditional cognitive diagnosis, the
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{Q}$$\end{document}
![]() -matrix (Tatsuoka, Reference Tatsuoka1983) is an important object that describes how the items measure the latent attributes. For example, if J items are designed to measure K latent attributes, then the
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{Q}$$\end{document}
-matrix (Tatsuoka, Reference Tatsuoka1983) is an important object that describes how the items measure the latent attributes. For example, if J items are designed to measure K latent attributes, then the
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{Q}$$\end{document}
![]() -matrix
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{Q}=(q_{j,k})$$\end{document}
-matrix
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{Q}=(q_{j,k})$$\end{document}
![]() has size
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$J\times K$$\end{document}
has size
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$J\times K$$\end{document}
![]() , in which
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$q_{j,k}=1$$\end{document}
, in which
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$q_{j,k}=1$$\end{document}
![]() or 0 indicates whether or not the jth item measures (i.e., directly depends on) the kth latent attribute. Recall that the edges in a graphical model exactly captures the direct dependence between variables, so
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$q_{j,k}=1$$\end{document}
or 0 indicates whether or not the jth item measures (i.e., directly depends on) the kth latent attribute. Recall that the edges in a graphical model exactly captures the direct dependence between variables, so
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$q_{j,k}=1$$\end{document}
![]() or 0 also reflects whether or not the kth latent node is a parent of the jth observed node in the graph. In other words, the traditional
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{Q}$$\end{document}
or 0 also reflects whether or not the kth latent node is a parent of the jth observed node in the graph. In other words, the traditional
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{Q}$$\end{document}
![]() -matrix summarize the sparse bipartite graph pattern between the latent attribute layer and the observed layer. This graphical perspective implies that a DeepCDM with D latent layers should require D matrices,
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{Q}^{(1)}$$\end{document}
-matrix summarize the sparse bipartite graph pattern between the latent attribute layer and the observed layer. This graphical perspective implies that a DeepCDM with D latent layers should require D matrices,
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{Q}^{(1)}$$\end{document}
![]() ,
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{Q}^{(2)}$$\end{document}
,
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{Q}^{(2)}$$\end{document}
![]() ,
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\ldots $$\end{document}
,
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\ldots $$\end{document}
![]() ,
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{Q}^{(D)}$$\end{document}
,
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{Q}^{(D)}$$\end{document}
![]() , to summarize the graph structure. In particular,
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{Q}^{(1)} = \left(q^{(1)}_{j,k}\right) $$\end{document}
, to summarize the graph structure. In particular,
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{Q}^{(1)} = \left(q^{(1)}_{j,k}\right) $$\end{document}
![]() has size
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$J\times K_1$$\end{document}
has size
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$J\times K_1$$\end{document}
![]() and resembles the traditional
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{Q}$$\end{document}
and resembles the traditional
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{Q}$$\end{document}
![]() -matrix; whereas for each
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$d=2,\ldots ,D$$\end{document}
-matrix; whereas for each
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$d=2,\ldots ,D$$\end{document}
![]() , the
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$K_{d-1}\times K_d$$\end{document}
, the
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$K_{d-1}\times K_d$$\end{document}
![]() matrix
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{Q}^{(d)} = \left(q^{(d)}_{k,\ell }\right) $$\end{document}
matrix
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{Q}^{(d)} = \left(q^{(d)}_{k,\ell }\right) $$\end{document}
![]() is similar in spirit to
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{Q}^{(1)}$$\end{document}
is similar in spirit to
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{Q}^{(1)}$$\end{document}
![]() , but describes how the variables in the
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$(d-1)$$\end{document}
, but describes how the variables in the
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$(d-1)$$\end{document}
![]() th latent layer depend on those in the layer above, the dth latent layer. Graphically, the entry
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$q^{(d)}_{k,\ell }=1$$\end{document}
th latent layer depend on those in the layer above, the dth latent layer. Graphically, the entry
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$q^{(d)}_{k,\ell }=1$$\end{document}
![]() or 0 indicates whether or not latent variable
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$A^{(d)}_{\ell }$$\end{document}
or 0 indicates whether or not latent variable
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$A^{(d)}_{\ell }$$\end{document}
![]() is a parent of latent variable
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$A^{(d-1)}_k$$\end{document}
is a parent of latent variable
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$A^{(d-1)}_k$$\end{document}
![]() . In this work, we will focus on developing estimation methods for the confirmatory DeepCDMs, where the
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{Q}$$\end{document}
. In this work, we will focus on developing estimation methods for the confirmatory DeepCDMs, where the
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{Q}$$\end{document}
![]() -matrices are assumed to be fixed and known.
-matrices are assumed to be fixed and known.
According to the general definition of DAGs in (1) and the DeepCDM setting specified in the last paragraph, the joint distribution of all the variables, including the latent ones, is



where we make explicit how the different
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{Q}$$\end{document}
![]() -matrices appear in different factors in the joint distribution. The generic superscript “CDM” in the conditional distributions in (3) and (4) means that the conditional distribution conforms to a cognitive diagnostic model, in each layer of the potentially deep generative process. Marginalizing out all the latent variables
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{A}^{(1)},\ldots ,\textbf{A}^{(D)}$$\end{document}
-matrices appear in different factors in the joint distribution. The generic superscript “CDM” in the conditional distributions in (3) and (4) means that the conditional distribution conforms to a cognitive diagnostic model, in each layer of the potentially deep generative process. Marginalizing out all the latent variables
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{A}^{(1)},\ldots ,\textbf{A}^{(D)}$$\end{document}
![]() in (2) gives the marginal distribution of the observed response vector
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{R}$$\end{document}
in (2) gives the marginal distribution of the observed response vector
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{R}$$\end{document}
![]() :
:
where
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\varvec{r}$$\end{document}
![]() is an observed response pattern, and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\varvec{\alpha }^{(d)}$$\end{document}
is an observed response pattern, and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\varvec{\alpha }^{(d)}$$\end{document}
![]() is a latent pattern for the dth latent layer. This work focuses on binary observed and latent variables with
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\varvec{r}\in \{0,1\}^J$$\end{document}
is a latent pattern for the dth latent layer. This work focuses on binary observed and latent variables with
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\varvec{r}\in \{0,1\}^J$$\end{document}
![]() and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\varvec{\alpha }^{(d)}\in \{0,1\}^{K_d}$$\end{document}
and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\varvec{\alpha }^{(d)}\in \{0,1\}^{K_d}$$\end{document}
![]() , where each observed variable denotes the correct/wrong response and each latent variable denotes the presence/absence of a skill or a meta-skill.
, where each observed variable denotes the correct/wrong response and each latent variable denotes the presence/absence of a skill or a meta-skill.
We model the latent variables
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{A}^{(D)}$$\end{document}
![]() in the deepest latent layer of a DeepCDM using a categorical distribution, similar to traditional CDMs. Specifically, we allow for two possible generating mechanisms for
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{A}^{(D)}$$\end{document}
in the deepest latent layer of a DeepCDM using a categorical distribution, similar to traditional CDMs. Specifically, we allow for two possible generating mechanisms for
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{A}^{(D)}$$\end{document}
![]() and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{A}^{(D-1)}\mid \textbf{A}^{(D)}$$\end{document}
and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{A}^{(D-1)}\mid \textbf{A}^{(D)}$$\end{document}
![]() : the pyramid mechanism and the ladder mechanism. In the pyramid case,
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{A}^{(D-1)}$$\end{document}
: the pyramid mechanism and the ladder mechanism. In the pyramid case,
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{A}^{(D-1)}$$\end{document}
![]() follows a latent class model (Goodman, Reference Goodman1974) with
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{A}^{(D)}$$\end{document}
follows a latent class model (Goodman, Reference Goodman1974) with
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{A}^{(D)}$$\end{document}
![]() serving as the latent class variable; in this case
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$K_D=1$$\end{document}
serving as the latent class variable; in this case
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$K_D=1$$\end{document}
![]() and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{A}^{(D)}$$\end{document}
and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{A}^{(D)}$$\end{document}
![]() ranges in
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\{1,\ldots ,B\}$$\end{document}
ranges in
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\{1,\ldots ,B\}$$\end{document}
![]() for some integer B. In the ladder case,
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{A}^{(D-1)}$$\end{document}
for some integer B. In the ladder case,
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{A}^{(D-1)}$$\end{document}
![]() follows yet another CDM with
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{A}^{(D)}$$\end{document}
follows yet another CDM with
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{A}^{(D)}$$\end{document}
![]() serving as the highest order latent traits; in this case
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$K_D>1$$\end{document}
serving as the highest order latent traits; in this case
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$K_D>1$$\end{document}
![]() and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{A}^{(D)}\in \{0,1\}^{K_D}$$\end{document}
and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{A}^{(D)}\in \{0,1\}^{K_D}$$\end{document}
![]() . Both mechanisms still use fully discrete latent variables and their corresponding distributions are:
. Both mechanisms still use fully discrete latent variables and their corresponding distributions are:
The proportion parameters satisfy
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\sum _{\varvec{\alpha }\in \{0,1\}^{K_D}} \pi ^{\textrm{ladder}}_{\varvec{\alpha }} = 1$$\end{document}
![]() or
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\sum _{b=1}^B \pi ^{\textrm{pyramid}}_b = 1$$\end{document}
or
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\sum _{b=1}^B \pi ^{\textrm{pyramid}}_b = 1$$\end{document}
![]() . Now we have completed specifying a general DeepCDM.
. Now we have completed specifying a general DeepCDM.
It is worth noting that in the literature of factor analysis of continuous data, hierarchical factor models (Schmid and Leiman, Reference Schmid and Leiman1957) or higher-order factor models (Yung et al., Reference Yung, Thissen and McLeod1999) are important and popular models that also contain multiple layers of factors. These models belong to the family of using continuous linear latent factors to model continuous responses, in which the statistical dependence among variables can be just summarized as covariance or correlation matrices. By contrast, the proposed DeepCDMs are a family of higher-order discrete latent variable models for discrete data. DeepCDMs can model various nonlinear and non-additive relationships among variables, e.g., DeepDINA with the interaction term of higher-order attributes and DeepLLM with the logistic link. These complex dependencies cannot be simply summarized by covariance or correlation matrices as in hierarchical continuous linear factor models in Schmid and Leiman (Reference Schmid and Leiman1957) and Yung et al. (Reference Yung, Thissen and McLeod1999).
2.3. Specific Examples of DeepCDMs
This subsection provides various specific examples of DeepCDMs under the general framework put forth in Sect. 2.2. Recall Equation (2) states that the joint distribution of all variables factorizes into the product of layerwise conditional distributions. As the superscript “CDM” in the conditional distributions in (3)–(4) implies, each conditional distribution conforms to a CDM. With a slight abuse of notation, we next also write the observed layer
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{R}$$\end{document}
![]() as
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{A}^{(0)}$$\end{document}
as
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{A}^{(0)}$$\end{document}
![]() , so that all of the layerwise conditionals can be written uniformly as
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mathbb {P}(\textbf{A}^{(d-1)}\mid \textbf{A}^{(d)},\textbf{Q}^{(d)})$$\end{document}
, so that all of the layerwise conditionals can be written uniformly as
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mathbb {P}(\textbf{A}^{(d-1)}\mid \textbf{A}^{(d)},\textbf{Q}^{(d)})$$\end{document}
![]() , for
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$d=1,\ldots ,D$$\end{document}
, for
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$d=1,\ldots ,D$$\end{document}
![]() . In the following, we define specific DeepCDMs based on which diagnostic model the layerwise conditionals follow.
. In the following, we define specific DeepCDMs based on which diagnostic model the layerwise conditionals follow.
Example 1
(DeepDINA) The DINA model proposed by Junker and Sijtsma (Reference Junker and Sijtsma2001) is a popular and fundamental model that adopts the conjunctive assumption. DINA assumes that students are expected to answer an item correctly only when they possess all required attributes of the item (i.e., the item’s parent attributes in the graphical model). Our DeepDINA model adopts the conjunctive assumption for each layer’s conditional distribution. In particular, the conditional distribution of
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$A^{(d-1)}_j$$\end{document}
![]() given its parent variables is
given its parent variables is

where the notation “
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\succeq $$\end{document}
![]() ” means “elementwisely greater than or equal to”, and “
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\nsucceq $$\end{document}
” means “elementwisely greater than or equal to”, and “
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\nsucceq $$\end{document}
![]() ” means otherwise. The
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mathbbm {1}(\cdot )$$\end{document}
” means otherwise. The
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mathbbm {1}(\cdot )$$\end{document}
![]() denotes a binary indicator function. The parameters
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\varvec{s}^{(d)} = (s^{(d)}_1,\ldots , s^{(d)}_{K_{d-1}})$$\end{document}
denotes a binary indicator function. The parameters
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\varvec{s}^{(d)} = (s^{(d)}_1,\ldots , s^{(d)}_{K_{d-1}})$$\end{document}
![]() and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\varvec{g}^{(d)} = (g^{(d)}_1,\ldots ,g^{(d)}_{K_{d-1}})$$\end{document}
and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\varvec{g}^{(d)} = (g^{(d)}_1,\ldots ,g^{(d)}_{K_{d-1}})$$\end{document}
![]() can be thought of as “quasi” slipping and guessing parameters, respectively. The interpretation of DeepDINA in an educational context is that, students are expected to master a skill (or a meta-skill) only when they possess all its higher-order parent skills in the probabilistic graphical model. Similar to Junker and Sijtsma (Reference Junker and Sijtsma2001), we assume
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$g^{(d)}_j < 1-s^{(d)}_j$$\end{document}
can be thought of as “quasi” slipping and guessing parameters, respectively. The interpretation of DeepDINA in an educational context is that, students are expected to master a skill (or a meta-skill) only when they possess all its higher-order parent skills in the probabilistic graphical model. Similar to Junker and Sijtsma (Reference Junker and Sijtsma2001), we assume
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$g^{(d)}_j < 1-s^{(d)}_j$$\end{document}
![]() for each j and d. This constraint can be interpreted as: comparing the subjects who master all the parent skills of an attribute
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$A_j^{(d-1)}$$\end{document}
for each j and d. This constraint can be interpreted as: comparing the subjects who master all the parent skills of an attribute
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$A_j^{(d-1)}$$\end{document}
![]() and the subjects who do not, the former ones have higher probability of mastering this skill
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$A_j^{(d-1)}$$\end{document}
and the subjects who do not, the former ones have higher probability of mastering this skill
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$A_j^{(d-1)}$$\end{document}
![]() itself.
itself.
The interpretation of DeepDINA in Example 1 that students are expected to master a skill when possessing all its higher-order parent skills may appear similar to the attribute hierarchy method (AHM; Gierl et al., Reference Gierl, Leighton, Hunka and Cambridge2007, Templin and Bradshaw, Reference Templin and Bradshaw2014). However, we point out that the AHM and DeepCDMs are not directly comparable, because the former assumes that the attributes can be directly connected to items whereas the latter assume high-order latent structures organized in multiple layers. Another modeling difference is that DeepDINA does not impose hard constraints on which attribute patterns are permissible as in AHMs. The quasi-guessing parameters
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\varvec{g}^{(d)}$$\end{document}
![]() in DeepDINA the probabilities that a student masters lower-level skills even when lacking their parent meta-skills.
in DeepDINA the probabilities that a student masters lower-level skills even when lacking their parent meta-skills.
Example 2
(DeepDINO) The DINO model proposed by Templin and Henson (Reference Templin and Henson2006) adopts a disjunctive assumption and assumes that subjects are expected to provide a positive response to an item as long as they possess at least one parent attribute. The DeepDINO model adopts the layerwise disjunctive assumption and has the following conditional:

As DINO is often applied to psychiatric diagnosis, the new DeepDINO can also be interpreted in this context as follows: patients are expected to exhibit a symptom (or meta-symptom) as long as they possess one of its higher-level “parent” symptoms or mental disorders.
Example 3
(Main-effect DeepCDMs) We use “Main-effect DeepCDMs” to generically refer to DeepCDMs in which the layerwise conditionals follow a main-effect diagnostic model. Specifically, a main-effect diagnostic model assumes that the probability of
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$A^{(d-1)}_j=1$$\end{document}
![]() depends on the main effects of those parent attributes through a link function
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$f(\cdot )$$\end{document}
depends on the main effects of those parent attributes through a link function
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$f(\cdot )$$\end{document}
![]() :
:
Note that not all the
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\beta _{j,k}^{(d)}$$\end{document}
![]() in the above equation are needed in the model specification. Only if
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$q_{j,k}^{(d)}=1$$\end{document}
in the above equation are needed in the model specification. Only if
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$q_{j,k}^{(d)}=1$$\end{document}
![]() will the corresponding
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\beta _{j,k}^{(d)}$$\end{document}
will the corresponding
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\beta _{j,k}^{(d)}$$\end{document}
![]() be incorporated in the model. When the link function f is the identity, (9) gives the additive cognitive diagnosis model (ACDM; de la Torre, Reference de la Torre2011); when f is the inverse logit function, (9) gives the Logistic Linear Model (LLM; Maris, Reference Maris1999); yet another parametrization of (9) gives rise to the reduced reparameterized unified model (R-RUM; DiBello et al., Reference DiBello, Stout and Roussos1995).
be incorporated in the model. When the link function f is the identity, (9) gives the additive cognitive diagnosis model (ACDM; de la Torre, Reference de la Torre2011); when f is the inverse logit function, (9) gives the Logistic Linear Model (LLM; Maris, Reference Maris1999); yet another parametrization of (9) gives rise to the reduced reparameterized unified model (R-RUM; DiBello et al., Reference DiBello, Stout and Roussos1995).
Example 4
(All-effect DeepCDMs) We use “All-effect DeepCDMs” to refer to DeepCDMs in which the layerwise conditionals follow an all-effect diagnostic model. An all-effect diagnostic model assumes that the probability of
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$A^{(d-1)}_j=1$$\end{document}
![]() depends on all of the possible main effects and interaction effects of the parent attributes:
depends on all of the possible main effects and interaction effects of the parent attributes:

Similar to Example (3), not all the
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\beta $$\end{document}
![]() -coefficients in the above equation are needed to specify the model. In particular, if
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\varvec{q}^{(d)}_j$$\end{document}
-coefficients in the above equation are needed to specify the model. In particular, if
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\varvec{q}^{(d)}_j$$\end{document}
![]() contains
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$K_j$$\end{document}
contains
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$K_j$$\end{document}
![]() ones, then
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$2^{K_j}$$\end{document}
ones, then
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$2^{K_j}$$\end{document}
![]() parameters are needed in (10). When the link function f is the identity, (9) gives the Generalized DINA model (GDINA; de la Torre, Reference de la Torre2011); when f is the inverse logit, (9) gives the log-linear CDM (LCDM; Henson et al., Reference Henson, Templin and Willse2009); see the general diagnostic model (GDM) framework in von Davier (Reference von Davier2008).
parameters are needed in (10). When the link function f is the identity, (9) gives the Generalized DINA model (GDINA; de la Torre, Reference de la Torre2011); when f is the inverse logit, (9) gives the log-linear CDM (LCDM; Henson et al., Reference Henson, Templin and Willse2009); see the general diagnostic model (GDM) framework in von Davier (Reference von Davier2008).
The parameters
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\varvec{c}^{(d)}$$\end{document}
![]() and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\varvec{g}^{(d)}$$\end{document}
and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\varvec{g}^{(d)}$$\end{document}
![]() ,
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$d=1,\ldots ,D$$\end{document}
,
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$d=1,\ldots ,D$$\end{document}
![]() in Examples 1–2 and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\varvec{\beta }^{(d)}$$\end{document}
in Examples 1–2 and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\varvec{\beta }^{(d)}$$\end{document}
![]() ,
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$d=1,\ldots ,D$$\end{document}
,
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$d=1,\ldots ,D$$\end{document}
![]() in Examples 3–4 are continuous parameters that help specify the conditional distribution of the binary variables in a DeepCDM. When
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$d=1$$\end{document}
in Examples 3–4 are continuous parameters that help specify the conditional distribution of the binary variables in a DeepCDM. When
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$d=1$$\end{document}
![]() , these parameters just resemble the item parameters in a traditional CDM. In a DeepDINA or DeepDINO, the number of continuous parameters required to model the latent attributes is
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$2\sum _{d=1}^{D-1} K_d + 2^{K_D}-1$$\end{document}
, these parameters just resemble the item parameters in a traditional CDM. In a DeepDINA or DeepDINO, the number of continuous parameters required to model the latent attributes is
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$2\sum _{d=1}^{D-1} K_d + 2^{K_D}-1$$\end{document}
![]() , while in a main-effect DeepCDM, this number is at most
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\sum _{d=1}^{D-1} K_d(K_{d+1}+1) + 2^{K_D}-1$$\end{document}
, while in a main-effect DeepCDM, this number is at most
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\sum _{d=1}^{D-1} K_d(K_{d+1}+1) + 2^{K_D}-1$$\end{document}
![]() . We will discuss more about the remarkable reduction of parameter complexity in a DeepCDM in the end of Sect. 3, after our identifiability conditions imply upper bounds for
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$K_1,\ldots ,K_D$$\end{document}
. We will discuss more about the remarkable reduction of parameter complexity in a DeepCDM in the end of Sect. 3, after our identifiability conditions imply upper bounds for
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$K_1,\ldots ,K_D$$\end{document}
![]() .
.
We emphasize that the most flexible feature of the DeepCDM framework is that different diagnostic models (including DINA, DINO, main-effect, and all-effect) can be flexibly combined in different layers of a DeepCDM. For example, in some practical applications, it may be desirable to adopt the most general all-effect diagnostic model for the bottom data layer for its flexibility in modeling the effects of the fine-grained attributes, whereas adopt the simpler main-effect or DINA model in the deeper latent layers for their parsimony and interpretability. We call such DeepCDMs the Hybrid DeepCDMs. Hybrid DeepCDMs allow to balance the expressivity and parsimony of a model, and offer a wide range of possibilities to construct a specific diagnostic model based on substantive considerations.
The proposed DeepCDMs cover the latent tree models (Mourad et al., Reference Mourad, Sinoquet, Zhang, Liu and Leray2013) as a special case. In a latent tree model, each variable has at most one parent in a tree graph; whereas a DeepCDM allows for a general DAG, in which each variable can have multiple parents (e.g., variable
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{A}^{(1)}_2$$\end{document}
![]() in Fig. 1). In terms of the generative model, a pyramid-shaped DeepCDM is closely related to the Bayesian Pyramid proposed in Gu and Dunson (Reference Gu and Dunson2023) and can be viewed as the latter adapted for diagnostic modeling goals. While the Bayesian Pyramid was implemented under the main-effect model and applied to extract genetic latent traits from DNA nucleotide sequences (Gu and Dunson, Reference Gu and Dunson2023), the DeepCDM framework is motivated by the need to hunt for deep diagnostic information and provides useful psychometric tools to this end. To better serve this goal, we develop a suite of methods and algorithms applicable to various layerwise diagnostic modeling assumptions; see Sect. 4 for details.
in Fig. 1). In terms of the generative model, a pyramid-shaped DeepCDM is closely related to the Bayesian Pyramid proposed in Gu and Dunson (Reference Gu and Dunson2023) and can be viewed as the latter adapted for diagnostic modeling goals. While the Bayesian Pyramid was implemented under the main-effect model and applied to extract genetic latent traits from DNA nucleotide sequences (Gu and Dunson, Reference Gu and Dunson2023), the DeepCDM framework is motivated by the need to hunt for deep diagnostic information and provides useful psychometric tools to this end. To better serve this goal, we develop a suite of methods and algorithms applicable to various layerwise diagnostic modeling assumptions; see Sect. 4 for details.
3. Identifiability Theory of DeepCDMs
Recently, there has been an emerging literature addressing the identifiability issues of CDMs (Chen et al., Reference Chen, Culpepper and Liang2020; Culpepper, Reference Culpepper2019b; Fang et al., Reference Fang, Liu and Ying2019; Gu and Xu, Reference Gu and Xu2019, Reference Gu and Xu2020, Reference Gu and Xu2021; Xu and Zhang, Reference Xu and Zhang2016; Xu, Reference Xu2017). However, all of the above works focus on the saturated attribute model. The only exception in the CDM literature is Gu and Xu (Reference Gu and Xu2022), which establishes identifiability of hierarchical CDMs under attribute hierarchies; but as aforementioned, a CDM with an attribute hierarchy is a not a fully probabilistic measurement model, so their corresponding identifiability conditions do not apply to DeepCDMs. In this section, we propose transparent identifiability conditions for various DeepCDMs. In the most general exploratory model settings, our theory guarantees the identifiability of all
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{Q}$$\end{document}
![]() -matrices
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{Q}^{(1)},\ldots ,\textbf{Q}^{(D)}$$\end{document}
-matrices
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{Q}^{(1)},\ldots ,\textbf{Q}^{(D)}$$\end{document}
![]() and all continuous parameters in the model. When the
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{Q}$$\end{document}
and all continuous parameters in the model. When the
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{Q}$$\end{document}
![]() -matrices are known as in the confirmatory settings, all of our identifiability conclusions still directly apply.
-matrices are known as in the confirmatory settings, all of our identifiability conclusions still directly apply.
3.1. Sharp Strict Identifiability Result for DeepDINA
DINA is one of the most basic and popular models in cognitive diagnosis. We establish sharp necessary and sufficient conditions for identifying the exploratory DeepDINA. Here, “exploratory” means that the
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{Q}$$\end{document}
![]() -matrices
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{Q}^{(1)},\ldots ,\textbf{Q}^{(D)}$$\end{document}
-matrices
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{Q}^{(1)},\ldots ,\textbf{Q}^{(D)}$$\end{document}
![]() are not assumed to be known and fixed. Such an identifiability notion will be the most flexible and useful one in practice; see identifiability results for exploratory diagnostic models with a saturated attribute model in Chen et al. (Reference Chen, Liu, Xu and Ying2015), Xu and Shang (Reference Xu and Shang2018), Culpepper (Reference Culpepper2019b), Chen et al. (Reference Chen, Culpepper and Liang2020), and Gu and Xu (Reference Gu and Xu2021). Denote the parameter space for the deep proportion parameters
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\varvec{\pi }^{\text { {deep}}}$$\end{document}
are not assumed to be known and fixed. Such an identifiability notion will be the most flexible and useful one in practice; see identifiability results for exploratory diagnostic models with a saturated attribute model in Chen et al. (Reference Chen, Liu, Xu and Ying2015), Xu and Shang (Reference Xu and Shang2018), Culpepper (Reference Culpepper2019b), Chen et al. (Reference Chen, Culpepper and Liang2020), and Gu and Xu (Reference Gu and Xu2021). Denote the parameter space for the deep proportion parameters
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\varvec{\pi }^{\text { {deep}}}$$\end{document}
![]() by
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\Delta ^{2^{K_D}-1} = \{\pi ^{\text { {deep}}}_{\varvec{\alpha }_\ell }:\, \sum _{\ell =1}^{2^{K_D}-1} \pi ^{\text { {deep}}}_{\varvec{\alpha }_\ell } = 1, \pi ^{\text { {deep}}}_{\varvec{\alpha }_\ell } >0\}$$\end{document}
by
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\Delta ^{2^{K_D}-1} = \{\pi ^{\text { {deep}}}_{\varvec{\alpha }_\ell }:\, \sum _{\ell =1}^{2^{K_D}-1} \pi ^{\text { {deep}}}_{\varvec{\alpha }_\ell } = 1, \pi ^{\text { {deep}}}_{\varvec{\alpha }_\ell } >0\}$$\end{document}
![]() ; throughout this work, we assume
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\pi ^{\text { {deep}}}_{\varvec{\alpha }_\ell } >0$$\end{document}
; throughout this work, we assume
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\pi ^{\text { {deep}}}_{\varvec{\alpha }_\ell } >0$$\end{document}
![]() holds for every deep latent pattern
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\varvec{\alpha }_\ell \in \{0,1\}^{K_D}$$\end{document}
holds for every deep latent pattern
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\varvec{\alpha }_\ell \in \{0,1\}^{K_D}$$\end{document}
![]() . This is a common assumption also adopted for single-latent-layer CDMs. We next define the strict identifiability.
. This is a common assumption also adopted for single-latent-layer CDMs. We next define the strict identifiability.
Definition 1
(Strict Identifiability) An exploratory DeepCDM model is said to be strictly identifiable, if the distribution of the observed vector
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{R}$$\end{document}
![]() in (5) uniquely determines all of the following: all continuous parameters in the layerwise conditional distributions, the deepest proportion parameters
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\varvec{\pi }^{\textrm{Deep}}$$\end{document}
in (5) uniquely determines all of the following: all continuous parameters in the layerwise conditional distributions, the deepest proportion parameters
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\varvec{\pi }^{\textrm{Deep}}$$\end{document}
![]() , and all
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{Q}$$\end{document}
, and all
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{Q}$$\end{document}
![]() -matrices at different depths
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{Q}^{(1)},\ldots ,\textbf{Q}^{(D)}$$\end{document}
-matrices at different depths
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{Q}^{(1)},\ldots ,\textbf{Q}^{(D)}$$\end{document}
![]() , up to some column/row permutation.
, up to some column/row permutation.
The identifiability notion in Definition 1 that each
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{Q}$$\end{document}
![]() -matrix is identifiable up to some column/row permutation is a trivial and inevitable phenomenon when there exist multiple latent variables; see Chen et al. (Reference Chen, Liu, Xu and Ying2015) and Xu and Shang (Reference Xu and Shang2018).
-matrix is identifiable up to some column/row permutation is a trivial and inevitable phenomenon when there exist multiple latent variables; see Chen et al. (Reference Chen, Liu, Xu and Ying2015) and Xu and Shang (Reference Xu and Shang2018).
Next, we summarize the existing necessary and sufficient identifiability conditions for the traditional DINA model with a saturated attribute model. These conditions will also play important roles in the identifiability of DeepDINA. Specifically, the following conditions (C), (R), and (D) are known to be necessary and sufficient for strict identifiability of DINA, both in the confirmatory case with a known
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{Q}$$\end{document}
![]() -matrix (Gu and Xu, Reference Gu and Xu2019) and in the exploratory case with an unknown
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{Q}$$\end{document}
-matrix (Gu and Xu, Reference Gu and Xu2019) and in the exploratory case with an unknown
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{Q}$$\end{document}
![]() -matrix (Gu and Xu, Reference Gu and Xu2021):
-matrix (Gu and Xu, Reference Gu and Xu2021):
Completeness. A \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$\textbf{Q}$$\end{document}
 -matrix with K columns contains an identity submatrix
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{I}_K$$\end{document}
-matrix with K columns contains an identity submatrix
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{I}_K$$\end{document}
 after some row permutation. That is, the
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{Q}$$\end{document}
after some row permutation. That is, the
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{Q}$$\end{document}
 can be row-permuted to be
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{Q}= [\textbf{I}_K, (\textbf{Q}^*)^\top ]^\top $$\end{document}
can be row-permuted to be
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{Q}= [\textbf{I}_K, (\textbf{Q}^*)^\top ]^\top $$\end{document}
 .
.Repeated-Measurement. Each of the K attributes is measured by at least three items.
Distinctness. Assuming Condition (C) holds, after removing the identity submatrix \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$\textbf{I}_K$$\end{document}
 from
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{Q}$$\end{document}
from
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{Q}$$\end{document}
 , the remaining submatrix
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{Q}^*$$\end{document}
, the remaining submatrix
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{Q}^*$$\end{document}
 contains K distinct column vectors.
contains K distinct column vectors.
We will call the above three conditions the C-R-D conditions for short. Our next theorem establishes sharp identifiability result for the exploratory DeepDINA with an arbitrary depth D, by providing the necessary and sufficient conditions on the multiple
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{Q}$$\end{document}
![]() -matrices.
-matrices.
Theorem 1
[DeepDINA] Consider a ladder-shaped exploratory DeepDINA model with D latent layers and D between-layer
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{Q}$$\end{document}
![]() -matrices
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{Q}^{(1)}, \ldots , \textbf{Q}^{(D)}$$\end{document}
-matrices
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{Q}^{(1)}, \ldots , \textbf{Q}^{(D)}$$\end{document}
![]() . The model is strictly identifiable if and only if each
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{Q}^{(d)}$$\end{document}
. The model is strictly identifiable if and only if each
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{Q}^{(d)}$$\end{document}
![]() ,
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$d=1,\ldots ,D$$\end{document}
,
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$d=1,\ldots ,D$$\end{document}
![]() , satisfies the C-R-D conditions.
, satisfies the C-R-D conditions.
The conditions in Theorem 1 are also necessary and sufficient for identifying the DeepDINO model introduced in Example 2, because of the duality between DINA and DINO (Chen et al., Reference Chen, Liu, Xu and Ying2015). The sharp identifiability conditions in Theorem 1 put transparent constraints on the
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{Q}$$\end{document}
![]() -matrices, and equivalently, transparent constraints on the between-layer graphical structures. In a graphical model, define
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$X_m$$\end{document}
-matrices, and equivalently, transparent constraints on the between-layer graphical structures. In a graphical model, define
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$X_m$$\end{document}
![]() to be an exclusive child of
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$X_\ell $$\end{document}
to be an exclusive child of
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$X_\ell $$\end{document}
![]() if the former has the latter has its only parent. The deep C-R-D conditions in Theorem 1 can be translated into graphical language as follows: each latent variable in the deep graphical model should have at least one exclusive child (Condition (C)) and at least three children in total (not necessarily all exclusive; Condition (R)) in the layer below; and after removing one exclusive child for each latent variable, the remaining sets of children of the
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$K_d$$\end{document}
if the former has the latter has its only parent. The deep C-R-D conditions in Theorem 1 can be translated into graphical language as follows: each latent variable in the deep graphical model should have at least one exclusive child (Condition (C)) and at least three children in total (not necessarily all exclusive; Condition (R)) in the layer below; and after removing one exclusive child for each latent variable, the remaining sets of children of the
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$K_d$$\end{document}
![]() latent variables in the dth latent layer should be mutually distinct (Condition (D)) for
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$d=1,\ldots ,D$$\end{document}
latent variables in the dth latent layer should be mutually distinct (Condition (D)) for
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$d=1,\ldots ,D$$\end{document}
![]() .
.
Example 5
Consider a DeepDINA model with
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$D=2$$\end{document}
![]() , and two
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{Q}$$\end{document}
, and two
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{Q}$$\end{document}
![]() -matrices
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{Q}^{(1)}$$\end{document}
-matrices
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{Q}^{(1)}$$\end{document}
![]() ,
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{Q}^{(2)}$$\end{document}
,
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{Q}^{(2)}$$\end{document}
![]() :
:

It is easy to verify that both
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{Q}^{(1)}$$\end{document}
![]() and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{Q}^{(2)}$$\end{document}
and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{Q}^{(2)}$$\end{document}
![]() satisfy the C-R-D conditions. Therefore, a ladder-shaped DeepDINA model with
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$J=9$$\end{document}
satisfy the C-R-D conditions. Therefore, a ladder-shaped DeepDINA model with
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$J=9$$\end{document}
![]() observed response variables,
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$K_1=5$$\end{document}
observed response variables,
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$K_1=5$$\end{document}
![]() finest-grained latent attributes, and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$K_2=2$$\end{document}
finest-grained latent attributes, and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$K_2=2$$\end{document}
![]() meta latent attributes in the deepest layer, is strictly identifiable. The identifiable quantities include
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{Q}$$\end{document}
meta latent attributes in the deepest layer, is strictly identifiable. The identifiable quantities include
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{Q}$$\end{document}
![]() -matrices
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{Q}^{(1)}$$\end{document}
-matrices
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{Q}^{(1)}$$\end{document}
![]() ,
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{Q}^{(2)}$$\end{document}
,
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{Q}^{(2)}$$\end{document}
![]() , deepest proportion parameters
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\varvec{\pi }^{\textrm{deep}}_{4\times 1}$$\end{document}
, deepest proportion parameters
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\varvec{\pi }^{\textrm{deep}}_{4\times 1}$$\end{document}
![]() , (quasi-)slipping and guessing parameters at both layers
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$(\varvec{s}^{(1)}_{9\times 1},\; \varvec{g}^{(1)}_{9\times 1})$$\end{document}
, (quasi-)slipping and guessing parameters at both layers
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$(\varvec{s}^{(1)}_{9\times 1},\; \varvec{g}^{(1)}_{9\times 1})$$\end{document}
![]() and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$(\varvec{s}^{(2)}_{5\times 1},\; \varvec{g}^{(2)}_{5\times 1})$$\end{document}
and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$(\varvec{s}^{(2)}_{5\times 1},\; \varvec{g}^{(2)}_{5\times 1})$$\end{document}
![]() .
.
As can be seen from the toy example in Example 5, we have
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$J>K_1>K_2$$\end{document}
![]() under the identifiable DeepDINA there. In general, if a
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{Q}$$\end{document}
under the identifiable DeepDINA there. In general, if a
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{Q}$$\end{document}
![]() -matrix of size
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$J\times K$$\end{document}
-matrix of size
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$J\times K$$\end{document}
![]() satisfies the C-R-D conditions, then there is a natural constraint on how large K can be with respect to J:
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$J > K + {\Big \lceil \log _2(K)\Big \rceil }$$\end{document}
satisfies the C-R-D conditions, then there is a natural constraint on how large K can be with respect to J:
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$J > K + {\Big \lceil \log _2(K)\Big \rceil }$$\end{document}
![]() (Gu and Xu, Reference Gu and Xu2021). This means in an identifiable DeepDINA, the sizes of the layers in the graphical model should satisfy
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$J > K_1 + {\Big \lceil \log _2(K_1)\Big \rceil }$$\end{document}
(Gu and Xu, Reference Gu and Xu2021). This means in an identifiable DeepDINA, the sizes of the layers in the graphical model should satisfy
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$J > K_1 + {\Big \lceil \log _2(K_1)\Big \rceil }$$\end{document}
![]() , and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$K_{d-1} > K_{d} + {\Big \lceil \log _2(K_d)\Big \rceil }$$\end{document}
, and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$K_{d-1} > K_{d} + {\Big \lceil \log _2(K_d)\Big \rceil }$$\end{document}
![]() for
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$d=2,\ldots ,D$$\end{document}
for
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$d=2,\ldots ,D$$\end{document}
![]() . This suggests an increasingly shrinking ladder architecture of the latent layers when going deeper.
. This suggests an increasingly shrinking ladder architecture of the latent layers when going deeper.
3.2. Strict Identifiability Result for General DeepCDMs
This subsection provides fully general strict identifiability conditions for an arbitrary DeepCDM. These conditions are also applicable to Hybrid DeepCDMs introduced in Sect. 2.3. From the identifiability result for DeepDINA in Theorem 1, one can see that it is those between-layer
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{Q}$$\end{document}
![]() -matrices that drive and deliver identifiability. In fact, this is correct intuition that applies much more broadly. Next, we formalize this intuition by establishing a general identifiability result for an arbitrary DeepCDM.
-matrices that drive and deliver identifiability. In fact, this is correct intuition that applies much more broadly. Next, we formalize this intuition by establishing a general identifiability result for an arbitrary DeepCDM.
Theorem 2
(General DeepCDM) Consider an exploratory general DeepCDM with D latent layers and D between-layer
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{Q}$$\end{document}
![]() -matrices
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{Q}^{(1)}, \ldots , \textbf{Q}^{(D)}$$\end{document}
-matrices
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{Q}^{(1)}, \ldots , \textbf{Q}^{(D)}$$\end{document}
![]() . Either Condition (S) or Condition (S
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\,^*$$\end{document}
. Either Condition (S) or Condition (S
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\,^*$$\end{document}
![]() ) below suffices for strict identifiability of the model.
) below suffices for strict identifiability of the model.
(S) Each \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$\textbf{Q}^{(d)}$$\end{document}
 can be written as
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{Q}^{(d)} = [\textbf{I}_{K_d},\; \textbf{I}_{K_d},\; \textbf{I}_{K_d},\; (\textbf{Q}^{(d)*})^\top ]^\top $$\end{document}
can be written as
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{Q}^{(d)} = [\textbf{I}_{K_d},\; \textbf{I}_{K_d},\; \textbf{I}_{K_d},\; (\textbf{Q}^{(d)*})^\top ]^\top $$\end{document}
 after some column/row permutation, where
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{Q}^{(d)*}$$\end{document}
after some column/row permutation, where
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{Q}^{(d)*}$$\end{document}
 is an arbitrary
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$(K_{d-1} - 3 K_d) \times K_d$$\end{document}
is an arbitrary
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$(K_{d-1} - 3 K_d) \times K_d$$\end{document}
 matrix (potentially empty).
matrix (potentially empty).(S \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$\,^*$$\end{document}
 ) This condition is the combination of both (S1
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\,^*$$\end{document}
) This condition is the combination of both (S1
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\,^*$$\end{document}
 ) and (S2
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\,^*$$\end{document}
) and (S2
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\,^*$$\end{document}
 ) below.
) below.(S1 \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$\,^*$$\end{document}
 ) Each
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{Q}^{(d)}$$\end{document}
) Each
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{Q}^{(d)}$$\end{document}
 can be written as
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{Q}^{(d)} = [\textbf{I}_{K_d},\; \textbf{I}_{K_d},\; (\textbf{Q}^{(d)*})^\top ]^\top $$\end{document}
can be written as
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{Q}^{(d)} = [\textbf{I}_{K_d},\; \textbf{I}_{K_d},\; (\textbf{Q}^{(d)*})^\top ]^\top $$\end{document}
 after some column/row permutation, where
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{Q}^{(d)*}$$\end{document}
after some column/row permutation, where
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{Q}^{(d)*}$$\end{document}
 is an arbitrary matrix (potentially empty).
is an arbitrary matrix (potentially empty).(S2 \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$\,^*$$\end{document}
 ) For any two different
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$K_d$$\end{document}
) For any two different
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$K_d$$\end{document}
 -dimensional latent patterns
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\varvec{\alpha }_c$$\end{document}
-dimensional latent patterns
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\varvec{\alpha }_c$$\end{document}
 ,
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\varvec{\alpha }_\ell \in \{0,1\}^{K_d}$$\end{document}
,
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\varvec{\alpha }_\ell \in \{0,1\}^{K_d}$$\end{document}
 , there exists some
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$j > 2K_d$$\end{document}
, there exists some
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$j > 2K_d$$\end{document}
 such that
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mathbb {P}(A_j^{(d-1)}=1\mid \textbf{A}^{(d)}=\varvec{\alpha }_c,\;\textbf{Q}^{(d)},\;\varvec{\theta }^{(d)}) \ne \mathbb {P}(A_j^{(d-1)}=1\mid \textbf{A}^{(d)}=\varvec{\alpha }_\ell ,\;\textbf{Q}^{(d)},\;\varvec{\theta }^{(d)})$$\end{document}
such that
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mathbb {P}(A_j^{(d-1)}=1\mid \textbf{A}^{(d)}=\varvec{\alpha }_c,\;\textbf{Q}^{(d)},\;\varvec{\theta }^{(d)}) \ne \mathbb {P}(A_j^{(d-1)}=1\mid \textbf{A}^{(d)}=\varvec{\alpha }_\ell ,\;\textbf{Q}^{(d)},\;\varvec{\theta }^{(d)})$$\end{document}
 , where
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\varvec{\theta }^{(d)}$$\end{document}
, where
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\varvec{\theta }^{(d)}$$\end{document}
 generically denotes continuous parameters required to fully specify the conditional distribution.
generically denotes continuous parameters required to fully specify the conditional distribution.
Remark 1
Condition (S) in Theorem 2 is similar to the conditions in Theorem 4 in Gu and Dunson (Reference Gu and Dunson2023) for identifying the Bayesian Pyramid model there. Condition (S
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$^*$$\end{document}
![]() ) in Theorem 2 relaxes the requirement on
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{Q}$$\end{document}
) in Theorem 2 relaxes the requirement on
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{Q}$$\end{document}
![]() -matrices compared to Condition (S), and impose an additional requirement on the conditional probabilities to establish identifiability. Condition (S
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$^*$$\end{document}
-matrices compared to Condition (S), and impose an additional requirement on the conditional probabilities to establish identifiability. Condition (S
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$^*$$\end{document}
![]() ) is similar to conditions (C1) and (C2) in Culpepper (Reference Culpepper2019b) imposed on the traditional
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{Q}$$\end{document}
) is similar to conditions (C1) and (C2) in Culpepper (Reference Culpepper2019b) imposed on the traditional
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{Q}$$\end{document}
![]() -matrix, which were proposed to identify an exploratory diagnostic model for ordinal responses with a one-latent-layer saturated attribute model.
-matrix, which were proposed to identify an exploratory diagnostic model for ordinal responses with a one-latent-layer saturated attribute model.
Theorem 2 is fully general and is applicable regardless of which specific diagnostic model each layer in a DeepCDM follows. According to the conditions in Theorem 2, the sizes of the layers in the graphical model should satisfy
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$J > 2K_1$$\end{document}
![]() , and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$K_{d-1} > 2K_d$$\end{document}
, and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$K_{d-1} > 2K_d$$\end{document}
![]() for
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$d=2,\ldots ,D$$\end{document}
for
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$d=2,\ldots ,D$$\end{document}
![]() , which also suggests an increasingly shrinking sparse latent ladder when going deeper.
, which also suggests an increasingly shrinking sparse latent ladder when going deeper.
Comparing the conditions in Theorems 1 and 2, one can see that the general sufficient conditions for an arbitrary DeepCDM are stronger than those needed for identifying the DeepDINA. The next proposition further guarantees that if a DeepCDM consists of a mix of DINA-layers and main-effect/all-effect layers, then those
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{Q}$$\end{document}
![]() -matrices corresponding to the DINA-layers only need to satisfy the weaker C-R-D conditions, instead of the stronger Conditions (S) or (S
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\,^*$$\end{document}
-matrices corresponding to the DINA-layers only need to satisfy the weaker C-R-D conditions, instead of the stronger Conditions (S) or (S
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\,^*$$\end{document}
![]() ) in Theorem 2.
) in Theorem 2.
Proposition 1
(Hybrid DeepCDM) Consider a Hybrid DeepCDM with D latent layers and D between-layer
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{Q}$$\end{document}
![]() -matrices
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{Q}^{(1)}, \ldots , \textbf{Q}^{(D)}$$\end{document}
-matrices
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{Q}^{(1)}, \ldots , \textbf{Q}^{(D)}$$\end{document}
![]() . If each
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{Q}^{(d)}$$\end{document}
. If each
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{Q}^{(d)}$$\end{document}
![]() satisfies the identifiability conditions for the specific diagnostic model that
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{A}^{(d-1)}\mid \textbf{A}^{(d)}$$\end{document}
satisfies the identifiability conditions for the specific diagnostic model that
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{A}^{(d-1)}\mid \textbf{A}^{(d)}$$\end{document}
![]() follows (i.e., C-R-D for DINA, (S) or (S
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\,^*$$\end{document}
follows (i.e., C-R-D for DINA, (S) or (S
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\,^*$$\end{document}
![]() ) for main-effect or all-effect model), then the entire DeepCDM is strictly identifiable.
) for main-effect or all-effect model), then the entire DeepCDM is strictly identifiable.
Proposition 1 reveals a key technical insight that our identifiability proofs leverage. That is, identifiability of DeepCDMs can be examined and established in a layer-by-layer manner, from the bottom up. This seemingly intuitive argument is rigorously true thanks to the probabilistic formulation of the directed graphical model and the discreteness nature of all the latent variables. See the proof of Theorem 1 in the Supplementary Material for details.
3.3. Generic Identifiability of Main-Effect and All-Effect DeepCDMs
Strict identifiability is the strongest possible identifiability notion, requiring parameters to be everywhere identifiable in their parameter space
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mathcal T$$\end{document}
![]() . A slightly weaker notion called generic identifiability (Allman et al., Reference Allman, Matias and Rhodes2009), instead requires parameters to be identifiable almost everywhere in
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mathcal T$$\end{document}
. A slightly weaker notion called generic identifiability (Allman et al., Reference Allman, Matias and Rhodes2009), instead requires parameters to be identifiable almost everywhere in
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mathcal T$$\end{document}
![]() , allowing identifiability to fail on a measure-zero subset
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mathcal N$$\end{document}
, allowing identifiability to fail on a measure-zero subset
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mathcal N$$\end{document}
![]() of
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mathcal T$$\end{document}
of
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mathcal T$$\end{document}
![]() . As pointed out by Allman et al. (Reference Allman, Matias and Rhodes2009), generic identifiability often suffices for real data analyses purposes and is a very useful identifiability notion in practice. In the CDM literature, Gu and Xu (Reference Gu and Xu2020) and Chen et al. (Reference Chen, Culpepper and Liang2020) proposed generic identifiability conditions for variants of CDMs with a saturated attribute model. Next, we build on the existing generic identifiability conditions to establish generic identifiability of main-effect and all-effect DeepCDMs. We define the main-effect-based DeepCDMs as follows.
. As pointed out by Allman et al. (Reference Allman, Matias and Rhodes2009), generic identifiability often suffices for real data analyses purposes and is a very useful identifiability notion in practice. In the CDM literature, Gu and Xu (Reference Gu and Xu2020) and Chen et al. (Reference Chen, Culpepper and Liang2020) proposed generic identifiability conditions for variants of CDMs with a saturated attribute model. Next, we build on the existing generic identifiability conditions to establish generic identifiability of main-effect and all-effect DeepCDMs. We define the main-effect-based DeepCDMs as follows.
Definition 2
(Main-effect-based DeepCDMs) A DeepCDM is said to be “main-effect-based”, if the layerwise conditional distribution can be written as:
where
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$f(\cdot )$$\end{document}
![]() is a link function, and the “
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\cdots $$\end{document}
is a link function, and the “
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\cdots $$\end{document}
![]() ” refers to potentially more terms such as the interaction-effects of the
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\alpha _k$$\end{document}
” refers to potentially more terms such as the interaction-effects of the
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\alpha _k$$\end{document}
![]() ’s and the intercept.
’s and the intercept.
Note that DeepDINA and DeepDINO are not main-effect-based DeepCDMs, because they do not contain the main-effect coefficients such as those
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\beta ^{(d)}_{j,k}$$\end{document}
![]() in Definition 2. These main-effect coefficients are essential to generic identifiability and allow for relaxing the condition that each
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{Q}^{(d)}$$\end{document}
in Definition 2. These main-effect coefficients are essential to generic identifiability and allow for relaxing the condition that each
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{Q}^{(d)}$$\end{document}
![]() should contain a submatrix
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{I}_{K_d}$$\end{document}
should contain a submatrix
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{I}_{K_d}$$\end{document}
![]() (Chen et al., Reference Chen, Culpepper and Liang2020; Gu and Xu, Reference Gu and Xu2020). We next formally define and establish generic identifiability of main-effect-based DeepCDMs.
(Chen et al., Reference Chen, Culpepper and Liang2020; Gu and Xu, Reference Gu and Xu2020). We next formally define and establish generic identifiability of main-effect-based DeepCDMs.
Definition 3
Define the allowable constrained parameter space for
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\varvec{\beta }^{(d)}$$\end{document}
![]() in Definition 2 under the binary matrix
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{Q}^{(d)}$$\end{document}
in Definition 2 under the binary matrix
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{Q}^{(d)}$$\end{document}
![]() as
as
The continuous parameters and the
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{Q}$$\end{document}
![]() -matrices are said to be generically identifiable if the set of unidentifiable continuous parameters has measure zero with respect to the Lebesgue measure on their parameter space
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\cup _{d=1}^D \Omega _{\textrm{main}}(\varvec{\beta }^{(d)};\, \textbf{Q}^{(d)}) \cup \Delta ^{2^{K_D}-1}$$\end{document}
-matrices are said to be generically identifiable if the set of unidentifiable continuous parameters has measure zero with respect to the Lebesgue measure on their parameter space
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\cup _{d=1}^D \Omega _{\textrm{main}}(\varvec{\beta }^{(d)};\, \textbf{Q}^{(d)}) \cup \Delta ^{2^{K_D}-1}$$\end{document}
![]() .
.
Theorem 3
Consider a main-effect-based DeepCDM. Suppose each
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{Q}^{(d)}$$\end{document}
![]() can be written as
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{Q}^{(d)}=[(\textbf{Q}^{(d)}_1)^\top , (\textbf{Q}^{(d)}_2)^\top , (\textbf{Q}^{{(d)}*})^\top ]^\top $$\end{document}
can be written as
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{Q}^{(d)}=[(\textbf{Q}^{(d)}_1)^\top , (\textbf{Q}^{(d)}_2)^\top , (\textbf{Q}^{{(d)}*})^\top ]^\top $$\end{document}
![]() after some column/row permutation and satisfies the following conditions. Then, the main-effect-based DeepCDM is generically identifiable.
after some column/row permutation and satisfies the following conditions. Then, the main-effect-based DeepCDM is generically identifiable.
Each \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$\textbf{Q}^{(d)}_m$$\end{document}
 (
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$m=1,2$$\end{document}
(
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$m=1,2$$\end{document}
 ) has size
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$K_d\times K_d$$\end{document}
) has size
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$K_d\times K_d$$\end{document}
 and takes the following form: \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$\begin{aligned} \textbf{Q}^{(d)}_m = \begin{pmatrix} 1 &{} * &{} \cdots &{} * \\ * &{} 1 &{} \cdots &{} * \\ \vdots &{} \vdots &{} \ddots &{} \vdots \\ * &{} * &{} \cdots &{} 1 \end{pmatrix}, \quad m=1,2;\quad d=1,\ldots ,D. \end{aligned}$$\end{document}That is, \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$\textbf{Q}^{(d)}_1$$\end{document}
and takes the following form: \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$\begin{aligned} \textbf{Q}^{(d)}_m = \begin{pmatrix} 1 &{} * &{} \cdots &{} * \\ * &{} 1 &{} \cdots &{} * \\ \vdots &{} \vdots &{} \ddots &{} \vdots \\ * &{} * &{} \cdots &{} 1 \end{pmatrix}, \quad m=1,2;\quad d=1,\ldots ,D. \end{aligned}$$\end{document}That is, \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$\textbf{Q}^{(d)}_1$$\end{document}
 and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{Q}^{(d)}_2$$\end{document}
and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{Q}^{(d)}_2$$\end{document}
 each has all the diagonal entries equal to one, whereas any off-diagonal entry is free to be either one or zero.
each has all the diagonal entries equal to one, whereas any off-diagonal entry is free to be either one or zero.The \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$(K_{d-1}-2K_d)\times K_d$$\end{document}
 submatrix
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{Q}^{{(d)}*}$$\end{document}
submatrix
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{Q}^{{(d)}*}$$\end{document}
 in
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{Q}^{(d)}$$\end{document}
in
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{Q}^{(d)}$$\end{document}
 ,
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$d=1,\ldots ,D$$\end{document}
,
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$d=1,\ldots ,D$$\end{document}
 , satisfies that each column contains at least one entry of “1”.
, satisfies that each column contains at least one entry of “1”.
Theorem 3 significantly relaxes the strict identifiability conditions in Theorem 2, by not requiring any
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{Q}^{(d)}$$\end{document}
![]() to contain an identity submatrix
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{I}_{K_d}$$\end{document}
to contain an identity submatrix
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{I}_{K_d}$$\end{document}
![]() . Note that these generic identifiability conditions in Theorem 3 also imply a shrinking latent ladder when going deeper, because (G1) and (G2) implicitly requires
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$J>2K_1$$\end{document}
. Note that these generic identifiability conditions in Theorem 3 also imply a shrinking latent ladder when going deeper, because (G1) and (G2) implicitly requires
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$J>2K_1$$\end{document}
![]() and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$K_d>2K_{d+1}$$\end{document}
and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$K_d>2K_{d+1}$$\end{document}
![]() for
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$d=1,\ldots ,D-1$$\end{document}
for
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$d=1,\ldots ,D-1$$\end{document}
![]() .
.
The natural upper bounds on the values of
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$K_1$$\end{document}
![]() ,
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$K_2$$\end{document}
,
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$K_2$$\end{document}
![]() ,
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\ldots $$\end{document}
,
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\ldots $$\end{document}
![]() given by all of our identifiability conditions further confirms the statistical parsimony of DeepCDMs. For example, in a two-latent-layer DeepCDM with
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$K_1=7$$\end{document}
given by all of our identifiability conditions further confirms the statistical parsimony of DeepCDMs. For example, in a two-latent-layer DeepCDM with
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$K_1=7$$\end{document}
![]() latent variables in the shallower latent layer and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$K_2=2$$\end{document}
latent variables in the shallower latent layer and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$K_2=2$$\end{document}
![]() ones in the deeper layer (which is the scenario in the real data analysis in Sect. 6), the number of parameters required by DeepLLM is
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\sum _{k=1}^{K_1} (\sum _{\ell =1}^{K_2} q^{(2)}_{k,\ell } + 1) + 2^{K_2}-1$$\end{document}
ones in the deeper layer (which is the scenario in the real data analysis in Sect. 6), the number of parameters required by DeepLLM is
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\sum _{k=1}^{K_1} (\sum _{\ell =1}^{K_2} q^{(2)}_{k,\ell } + 1) + 2^{K_2}-1$$\end{document}
![]() , which is at most 24, and that required by DeepDINA is
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$2K_1 + 2^{K_2}-1 = 17$$\end{document}
, which is at most 24, and that required by DeepDINA is
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$2K_1 + 2^{K_2}-1 = 17$$\end{document}
![]() , whereas the number of parameters required in a saturated attribute model would be
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$2^{K_1}-1 = 127$$\end{document}
, whereas the number of parameters required in a saturated attribute model would be
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$2^{K_1}-1 = 127$$\end{document}
![]() . Such a remarkable reduction of parameter complexity facilitates applying DeepCDMs when there is a large number of fine-grained latent attributes but a relatively small sample size.
. Such a remarkable reduction of parameter complexity facilitates applying DeepCDMs when there is a large number of fine-grained latent attributes but a relatively small sample size.
The easily understandable and intuitively interpretable identifiability conditions presented in this section are an appealing property of DeepCDMs. We next provide some insights into our proof strategy. The reason why we can establish identifiability in a layer-by-layer manner is two-fold. First, in a multilayer directed graphical model, when arrows are all top-down and only occur between adjacent layers, marginalizing out all the latent variables deeper than the shallowest layer result in a marginal restricted latent class model (RLCM; Gu and Xu, Reference Gu and Xu2020; Xu, Reference Xu2017). Once the proportion parameters for this RLCM are identifiable, this shallowest latent layer’s distribution is uniquely identified and can be theoretically treated as if observed when investigating identifiability of deeper layers. Second, we exploit one key property of existing identifiability theory of RLCMs – identifiability holds under conditions on the Q-matrix for arbitrary marginal distributions of the latent attributes. This property allows us to extend the identifiability conclusion to very flexible deep models since deeper layers could induce quite complex marginal dependencies among the latent attributes. Although proving identifiability is not technically very challenging upon realizing the above two key facts, we believe that uncovering these two facts to rigorously show identifiability still contributes to our understanding about CDMs and their potential.
On a related note, the HO-CDM proposed by de la Torre and Douglas (Reference de la Torre and Douglas2004) is a very popular and widely used high-order CDM. However, whether and when parameters in a general HO-CDM with multiple higher-order continuous latent traits are fully identifiable is still unknown. So there currently lacks a rigorous statistical justification for valid parameter estimation in that model. To our best knowledge, DeepCDMs are the first higher-order CDMs that are shown to be fully identifiable.
4. Bayesian Inference for DeepCDMs
Recently, Bayesian formulation and estimation of CDMs have gained increasing interest; see Culpepper (Reference Culpepper2015), Chen et al. (Reference Chen, Culpepper, Chen and Douglas2018), Fang et al. (Reference Fang, Liu and Ying2019), Chen et al. (Reference Chen, Culpepper and Liang2020), and Liu et al. (Reference Liu, Andersson and Skrondal2020), among others. Bayesian approaches can incorporate prior beliefs into the model formulation, and quantify the statistical uncertainty through the posterior distributions. Moreover, in the CDM context, Bayesian estimation algorithms can conveniently incorporate meaningful constraints into the posterior sampling process, including the monotonicity constraints on the model parameters (Culpepper, Reference Culpepper2015) and the identifiability constraints on the
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{Q}$$\end{document}
![]() -matrix (Chen et al., Reference Chen, Culpepper, Chen and Douglas2018).
-matrix (Chen et al., Reference Chen, Culpepper, Chen and Douglas2018).
In this section, we propose Bayesian formulations for several DeepCDMs and develop their corresponding efficient Gibbs sampling algorithms. As mentioned earlier, in this work we focus on developing Bayesian inference methods for the confirmatory setting with fixed and known
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{Q}$$\end{document}
![]() -matrices. For simplicity of presentation but without loss of generality, this section focuses on two-latent-layer DeepCDMs. We point out that all of our Bayesian inference procedures can be extended to a DeepCDM with more latent layers; this is the case thanks to both the conditional independence of non-adjacent layers in a DeepCDM and our layerwise Gibbs sampling steps. Now consider a two-latent-layer DeepCDM with
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$K_1$$\end{document}
-matrices. For simplicity of presentation but without loss of generality, this section focuses on two-latent-layer DeepCDMs. We point out that all of our Bayesian inference procedures can be extended to a DeepCDM with more latent layers; this is the case thanks to both the conditional independence of non-adjacent layers in a DeepCDM and our layerwise Gibbs sampling steps. Now consider a two-latent-layer DeepCDM with
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$K_1$$\end{document}
![]() fine-grained attributes and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$K_2$$\end{document}
fine-grained attributes and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$K_2$$\end{document}
![]() deeper meta attributes. With a sample of size N, denote the
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$N\times K_1$$\end{document}
deeper meta attributes. With a sample of size N, denote the
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$N\times K_1$$\end{document}
![]() first-layer latent attribute matrix by
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$(a^{(1)}_{ij})$$\end{document}
first-layer latent attribute matrix by
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$(a^{(1)}_{ij})$$\end{document}
![]() , and denote the
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$N\times K_2$$\end{document}
, and denote the
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$N\times K_2$$\end{document}
![]() second-layer latent variable matrix by
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$(a^{(2)}_{ij})$$\end{document}
second-layer latent variable matrix by
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$(a^{(2)}_{ij})$$\end{document}
![]() . Denote the ith row of these two matrices by
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\varvec{a}^{(1)}_i$$\end{document}
. Denote the ith row of these two matrices by
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\varvec{a}^{(1)}_i$$\end{document}
![]() and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\varvec{a}^{(2)}_i$$\end{document}
and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\varvec{a}^{(2)}_i$$\end{document}
![]() , respectively. Let
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\varvec{\theta }^{(d)}$$\end{document}
, respectively. Let
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\varvec{\theta }^{(d)}$$\end{document}
![]() generically denote the continuous parameters needed to specify the conditional distribution
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{A}^{(d-1)}\mid \textbf{A}^{(d)}$$\end{document}
generically denote the continuous parameters needed to specify the conditional distribution
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{A}^{(d-1)}\mid \textbf{A}^{(d)}$$\end{document}
![]() .
.
4.1. Bayesian Inference for DeepDINA
For any positive integer M, we denote
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$[M]=\{1,\ldots ,M\}$$\end{document}
![]() . The following continuous parameters are needed to specify a two-latent-layer DeepDINA: item parameters
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\varvec{\theta }^{(1)}=(\varvec{s}^{(1)}_{J\times 1}, ~\varvec{g}^{(1)}_{J\times 1})$$\end{document}
. The following continuous parameters are needed to specify a two-latent-layer DeepDINA: item parameters
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\varvec{\theta }^{(1)}=(\varvec{s}^{(1)}_{J\times 1}, ~\varvec{g}^{(1)}_{J\times 1})$$\end{document}
![]() , quasi-item parameters
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\varvec{\theta }^{(2)}=(\varvec{s}^{(2)}_{K_1\times 1},~ \varvec{g}^{(2)}_{K_1\times 1})$$\end{document}
, quasi-item parameters
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\varvec{\theta }^{(2)}=(\varvec{s}^{(2)}_{K_1\times 1},~ \varvec{g}^{(2)}_{K_1\times 1})$$\end{document}
![]() , and deep proportion parameters
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\varvec{\pi }^{\text { {deep}}}=(\pi _1,\ldots ,\pi _{2^{K_2}})$$\end{document}
, and deep proportion parameters
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\varvec{\pi }^{\text { {deep}}}=(\pi _1,\ldots ,\pi _{2^{K_2}})$$\end{document}
![]() . Consider a sample of size N and denote the observed
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$N\times J$$\end{document}
. Consider a sample of size N and denote the observed
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$N\times J$$\end{document}
![]() data matrix by
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mathcal R=(r_{ij})$$\end{document}
data matrix by
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mathcal R=(r_{ij})$$\end{document}
![]() . Define a
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$K_2$$\end{document}
. Define a
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$K_2$$\end{document}
![]() -dimensional vector
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\varvec{v}^{(2)}=(2^{K_2-1}, 2^{K_2-2}, \ldots , 2^0)^\top $$\end{document}
-dimensional vector
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\varvec{v}^{(2)}=(2^{K_2-1}, 2^{K_2-2}, \ldots , 2^0)^\top $$\end{document}
![]() , then
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\varvec{v}^{(2)}$$\end{document}
, then
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\varvec{v}^{(2)}$$\end{document}
![]() induces a bijection between the binary patterns and integers (Culpepper, Reference Culpepper2019a), and we define binary patterns
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\varvec{\alpha }_1,\ldots ,\varvec{\alpha }_{2^{K_2}} \in \{0,1\}^{K_2}$$\end{document}
induces a bijection between the binary patterns and integers (Culpepper, Reference Culpepper2019a), and we define binary patterns
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\varvec{\alpha }_1,\ldots ,\varvec{\alpha }_{2^{K_2}} \in \{0,1\}^{K_2}$$\end{document}
![]() such that
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\varvec{\alpha }_{\ell }^\top \varvec{v}^{(2)} = \ell -1$$\end{document}
such that
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\varvec{\alpha }_{\ell }^\top \varvec{v}^{(2)} = \ell -1$$\end{document}
![]() , for
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\ell =1,\ldots ,2^{K_2}$$\end{document}
, for
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\ell =1,\ldots ,2^{K_2}$$\end{document}
![]() .
.
When
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{Q}^{(1)}$$\end{document}
![]() and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{Q}^{(2)}$$\end{document}
and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{Q}^{(2)}$$\end{document}
![]() are fixed, DeepDINA has the following model formulation,
are fixed, DeepDINA has the following model formulation,


The prior for
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\varvec{\pi }^{\text { {deep}}}=(\pi _1,\ldots ,\pi _{2^{K_2}})$$\end{document}
![]() in (15) is the Dirichlet distribution with parameters
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\varvec{\delta }= (\delta _{1}, \ldots , \delta _{L})$$\end{document}
in (15) is the Dirichlet distribution with parameters
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\varvec{\delta }= (\delta _{1}, \ldots , \delta _{L})$$\end{document}
![]() . The prior for
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$s^{(d)}_j, g^{(d)}_j$$\end{document}
. The prior for
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$s^{(d)}_j, g^{(d)}_j$$\end{document}
![]() in (14) is a product of two truncated Beta densities with hyperparameters
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$(a_{s},b_{s})$$\end{document}
in (14) is a product of two truncated Beta densities with hyperparameters
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$(a_{s},b_{s})$$\end{document}
![]() and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$(a_{g}, b_{g})$$\end{document}
and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$(a_{g}, b_{g})$$\end{document}
![]() , respectively, similar to that in Culpepper (Reference Culpepper2015). The monotonicity constraint
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$g^{(d)}_j < 1-s^{(d)}_j$$\end{document}
, respectively, similar to that in Culpepper (Reference Culpepper2015). The monotonicity constraint
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$g^{(d)}_j < 1-s^{(d)}_j$$\end{document}
![]() in (14) ensures each item or attribute provides information to differentiate the capable and incapable subjects (Junker and Sijtsma, Reference Junker and Sijtsma2001).
in (14) ensures each item or attribute provides information to differentiate the capable and incapable subjects (Junker and Sijtsma, Reference Junker and Sijtsma2001).
The above Bayesian formulation of DeepDINA facilitates convenient posterior inference via a Gibbs sampler. Specifically, we sample each entry
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$a^{(1)}_{i,k}$$\end{document}
![]() individually to better leverage the multilayer generative process and to boost computational efficiency; this is different from sampling the entire latent vector
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\varvec{a}^{(1)}_{i}$$\end{document}
individually to better leverage the multilayer generative process and to boost computational efficiency; this is different from sampling the entire latent vector
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\varvec{a}^{(1)}_{i}$$\end{document}
![]() as in many previous Bayesian estimation approaches for CDMs. Define
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\varvec{a}^{(1)}_{i,-k}$$\end{document}
as in many previous Bayesian estimation approaches for CDMs. Define
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\varvec{a}^{(1)}_{i,-k}$$\end{document}
![]() to be the
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$(K_1-1)$$\end{document}
to be the
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$(K_1-1)$$\end{document}
![]() -dimensional subvector of
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\varvec{a}^{(1)}_{i}$$\end{document}
-dimensional subvector of
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\varvec{a}^{(1)}_{i}$$\end{document}
![]() containing entries other than
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$a^{(1)}_{i,k}$$\end{document}
containing entries other than
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$a^{(1)}_{i,k}$$\end{document}
![]() . The full conditional distribution of
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$a^{(1)}_{i,k}$$\end{document}
. The full conditional distribution of
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$a^{(1)}_{i,k}$$\end{document}
![]() is:
is:

In the above display, the “−” in the conditioning set for
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$a_{i,k}^{(1)}$$\end{document}
![]() generically summarizes all of the other quantities in the posterior, and the first equality is derived from the conditional independence properties of the graphical model. As for the second latent layer
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\varvec{a}_{i}^{(2)}$$\end{document}
generically summarizes all of the other quantities in the posterior, and the first equality is derived from the conditional independence properties of the graphical model. As for the second latent layer
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\varvec{a}_{i}^{(2)}$$\end{document}
![]() , we sample it from the categorical posterior with
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$2^{K_2}$$\end{document}
, we sample it from the categorical posterior with
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$2^{K_2}$$\end{document}
![]() components. The full conditional distribution of each element in
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\varvec{s}^{(1)}$$\end{document}
components. The full conditional distribution of each element in
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\varvec{s}^{(1)}$$\end{document}
![]() ,
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\varvec{g}^{(1)}$$\end{document}
,
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\varvec{g}^{(1)}$$\end{document}
![]() ,
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\varvec{s}^{(2)}$$\end{document}
,
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\varvec{s}^{(2)}$$\end{document}
![]() , and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\varvec{g}^{(2)}$$\end{document}
, and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\varvec{g}^{(2)}$$\end{document}
![]() is a truncated Beta, and that of
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\varvec{\pi }^{\text { {deep}}}$$\end{document}
is a truncated Beta, and that of
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\varvec{\pi }^{\text { {deep}}}$$\end{document}
![]() is a Dirichlet; we provide the detailed forms of these conditional distributions in the Supplementary Material.
is a Dirichlet; we provide the detailed forms of these conditional distributions in the Supplementary Material.
4.2. Bayesian Inference for Hybrid GDINA-DINA
A two-latent-layer Hybrid GDINA-DINA model features a GDINA layer for modeling
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{R}\mid \textbf{A}^{(1)}$$\end{document}
![]() and a DINA layer for modeling
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{A}^{(1)}\mid \textbf{A}^{(2)}$$\end{document}
and a DINA layer for modeling
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{A}^{(1)}\mid \textbf{A}^{(2)}$$\end{document}
![]() . Such a model may be useful in practical scenarios when it is desirable to adopt the general diagnostic model in the bottom layer for its flexibility and adopt a simpler DINA model in the deeper layer for its parsimony. The Hybrid GDINA-DINA model has the following generative process,
. Such a model may be useful in practical scenarios when it is desirable to adopt the general diagnostic model in the bottom layer for its flexibility and adopt a simpler DINA model in the deeper layer for its parsimony. The Hybrid GDINA-DINA model has the following generative process,

Since
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{A}^{(1)}\mid \textbf{A}^{(2)}$$\end{document}
![]() follows the DINA model, we adopt the same truncated Beta priors as that in (14) for the quasi-item parameters and enforce
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$g^{(2)}_k < 1- s^{(2)}_k$$\end{document}
follows the DINA model, we adopt the same truncated Beta priors as that in (14) for the quasi-item parameters and enforce
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$g^{(2)}_k < 1- s^{(2)}_k$$\end{document}
![]() . As for the model for
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{R}\mid \textbf{A}^{(1)}$$\end{document}
. As for the model for
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{R}\mid \textbf{A}^{(1)}$$\end{document}
![]() , we adopt the GDINA formulation proposed by de la Torre (Reference de la Torre2011) in (16) by using the identity link function
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$f(\cdot )$$\end{document}
, we adopt the GDINA formulation proposed by de la Torre (Reference de la Torre2011) in (16) by using the identity link function
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$f(\cdot )$$\end{document}
![]() in the all-effect general diagnostic model. A general diagnostic model with an identity link facilitates Gibbs sampling steps without data augmentation. Note that in order to perform Gibbs sampling directly, it is not convenient to directly work with the
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\beta $$\end{document}
in the all-effect general diagnostic model. A general diagnostic model with an identity link facilitates Gibbs sampling steps without data augmentation. Note that in order to perform Gibbs sampling directly, it is not convenient to directly work with the
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\beta $$\end{document}
![]() -coefficients in (16) and sample from their posteriors. Instead, similar to the existing GDINA EM algorithm in the literature, we adopt an invertible reparameterization of the
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\beta $$\end{document}
-coefficients in (16) and sample from their posteriors. Instead, similar to the existing GDINA EM algorithm in the literature, we adopt an invertible reparameterization of the
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\beta $$\end{document}
![]() -coefficients and define a set of
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\theta $$\end{document}
-coefficients and define a set of
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\theta $$\end{document}
![]() -coefficients that directly correspond to conditional correct response probabilities and are easy to sample from. Define
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mathcal K_j = \{k\in [K]:\; q^{(1)}_{j,k}=1\}$$\end{document}
-coefficients that directly correspond to conditional correct response probabilities and are easy to sample from. Define
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mathcal K_j = \{k\in [K]:\; q^{(1)}_{j,k}=1\}$$\end{document}
![]() , which is the set of indices of the latent attributes that item j measures. Then each
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\beta $$\end{document}
, which is the set of indices of the latent attributes that item j measures. Then each
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\beta $$\end{document}
![]() -coefficient in the GDINA layer in (16) can be equivalently written as
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\beta ^{(1)}_{j,S}$$\end{document}
-coefficient in the GDINA layer in (16) can be equivalently written as
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\beta ^{(1)}_{j,S}$$\end{document}
![]() , where S is a subset of
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mathcal K_j$$\end{document}
, where S is a subset of
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mathcal K_j$$\end{document}
![]() ; for example,
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\beta ^{(1)}_{j,\varnothing }=\beta ^{(1)}_{j,0}$$\end{document}
; for example,
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\beta ^{(1)}_{j,\varnothing }=\beta ^{(1)}_{j,0}$$\end{document}
![]() ,
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\beta ^{(1)}_{j,\{k\}} = \beta ^{(1)}_{j,k}$$\end{document}
,
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\beta ^{(1)}_{j,\{k\}} = \beta ^{(1)}_{j,k}$$\end{document}
![]() , and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\beta ^{(1)}_{j,\mathcal K_j}$$\end{document}
, and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\beta ^{(1)}_{j,\mathcal K_j}$$\end{document}
![]() corresponds to the parameter for highest order interaction effect of the required attributes. For any subset
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$S\subseteq \mathcal K_j$$\end{document}
corresponds to the parameter for highest order interaction effect of the required attributes. For any subset
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$S\subseteq \mathcal K_j$$\end{document}
![]() , denote by
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\varvec{q}^{(1)}_{j,S}:=(q^{(1)}_{j,k};\; k\in S)$$\end{document}
, denote by
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\varvec{q}^{(1)}_{j,S}:=(q^{(1)}_{j,k};\; k\in S)$$\end{document}
![]() the subvector of
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\varvec{q}_j$$\end{document}
the subvector of
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\varvec{q}_j$$\end{document}
![]() . We now define the
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\theta $$\end{document}
. We now define the
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\theta $$\end{document}
![]() -parameters as follows:
-parameters as follows:

where the equality indexed by “
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$(\star )$$\end{document}
![]() ” can be verified by simply following the definition of the
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\beta $$\end{document}
” can be verified by simply following the definition of the
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\beta $$\end{document}
![]() -parameters. For example,
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\theta ^{(1)}_{j,\{k\}} = \beta ^{(1)}_{j,\varnothing } + \beta ^{(1)}_{j,\{k\}}$$\end{document}
-parameters. For example,
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\theta ^{(1)}_{j,\{k\}} = \beta ^{(1)}_{j,\varnothing } + \beta ^{(1)}_{j,\{k\}}$$\end{document}
![]() represents the probability of providing positive response to item j given that the subject only masters the kth latent attribute
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$A_{k}^{(1)}$$\end{document}
represents the probability of providing positive response to item j given that the subject only masters the kth latent attribute
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$A_{k}^{(1)}$$\end{document}
![]() . With the above reparametrization and equality “
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$(\star )$$\end{document}
. With the above reparametrization and equality “
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$(\star )$$\end{document}
![]() ”, the
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\theta $$\end{document}
”, the
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\theta $$\end{document}
![]() -parameters directly represent positive response probabilities of certain clearly defined latent classes in the population. This structure implies that we can endow
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\theta _{j,S}$$\end{document}
-parameters directly represent positive response probabilities of certain clearly defined latent classes in the population. This structure implies that we can endow
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\theta _{j,S}$$\end{document}
![]() with a Beta prior and then have a Beta posterior. In particular, let the prior for
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\theta ^{(1)}_{j,S}$$\end{document}
with a Beta prior and then have a Beta posterior. In particular, let the prior for
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\theta ^{(1)}_{j,S}$$\end{document}
![]() be
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textrm{Beta}(a_\theta , b_\theta )$$\end{document}
be
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textrm{Beta}(a_\theta , b_\theta )$$\end{document}
![]() , then its posterior distribution is
, then its posterior distribution is

where S ranges in all the possible subsets of
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mathcal K_j$$\end{document}
![]() . This completes the description on how to sample the continuous parameters for the GDINA layer.
. This completes the description on how to sample the continuous parameters for the GDINA layer.
Interpretable monotonicity constraints can also be incorporated into the posterior sampling of the
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\theta ^{(1)}_{j,S}$$\end{document}
![]() parameters. For example, it may be reasonable to impose the constraint that the main-effect parameters of the attributes, i.e.,
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\beta _{j,k}^{(1)}$$\end{document}
parameters. For example, it may be reasonable to impose the constraint that the main-effect parameters of the attributes, i.e.,
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\beta _{j,k}^{(1)}$$\end{document}
![]() in (9), are positive (Culpepper, Reference Culpepper2019b). In our parametrization of
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\theta ^{(1)}_{j,S}$$\end{document}
in (9), are positive (Culpepper, Reference Culpepper2019b). In our parametrization of
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\theta ^{(1)}_{j,S}$$\end{document}
![]() , this constraint is equivalent to requiring
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\theta ^{(1)}_{j, \{k\}} > \theta ^{(1)}_{j,\varnothing }$$\end{document}
, this constraint is equivalent to requiring
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\theta ^{(1)}_{j, \{k\}} > \theta ^{(1)}_{j,\varnothing }$$\end{document}
![]() for each
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$k=1,\ldots ,K_1$$\end{document}
for each
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$k=1,\ldots ,K_1$$\end{document}
![]() . Such a constraint can be easily enforced by sampling
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\theta ^{(1)}_{j,\{k\}}$$\end{document}
. Such a constraint can be easily enforced by sampling
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\theta ^{(1)}_{j,\{k\}}$$\end{document}
![]() from a truncated Beta posterior as follows:
from a truncated Beta posterior as follows:

we provide the details of the Gibbs sampler for the Hybrid GDINA-DINA in the Supplementary Material.
4.3. Bayesian Inference for DeepLLM
In this subsection, we consider the two-latent-layer Deep Logistic Linear Model (DeepLLM). Let
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\sigma (x) = 1/(1+e^{-x})$$\end{document}
![]() denote the inverse logit function (i.e., sigmoid function). For
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\varvec{a}^{(i)}_2$$\end{document}
denote the inverse logit function (i.e., sigmoid function). For
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\varvec{a}^{(i)}_2$$\end{document}
![]() and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\varvec{\pi }^{\text { {deep}}}$$\end{document}
and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\varvec{\pi }^{\text { {deep}}}$$\end{document}
![]() , we adopt the same formulation and prior as (15). As for the additional parameters in a DeepLLM, we adopt the following formulation,
, we adopt the same formulation and prior as (15). As for the additional parameters in a DeepLLM, we adopt the following formulation,
The natural constraints imposed by the
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{Q}$$\end{document}
![]() -matrices
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$(\beta _{j,k}^{(1)} \mid q_{j,k}^{(1)}=0) \equiv 0$$\end{document}
-matrices
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$(\beta _{j,k}^{(1)} \mid q_{j,k}^{(1)}=0) \equiv 0$$\end{document}
![]() and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$(\beta _{k,m}^{(2)} \mid q_{k,m}^{(2)}=0) \equiv 0$$\end{document}
and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$(\beta _{k,m}^{(2)} \mid q_{k,m}^{(2)}=0) \equiv 0$$\end{document}
![]() can be readily enforced throughout the sampling process. In order to facilitate efficient Gibbs sampling steps based on full conditional distributions of all the parameters, we propose to use the Polya-Gamma data augmentation in Polson et al. (Reference Polson, Scott and Windle2013). This data augmentation strategy was also recently adopted for Bayesian Pyramids for multivariate categorical data in Gu and Dunson (Reference Gu and Dunson2023) and for saturated CDMs in Balamuta and Culpepper (Reference Balamuta and Culpepper2022). Different from these existing works, we apply Polya-Gamma augmentation not only for observed data layer
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{R}$$\end{document}
can be readily enforced throughout the sampling process. In order to facilitate efficient Gibbs sampling steps based on full conditional distributions of all the parameters, we propose to use the Polya-Gamma data augmentation in Polson et al. (Reference Polson, Scott and Windle2013). This data augmentation strategy was also recently adopted for Bayesian Pyramids for multivariate categorical data in Gu and Dunson (Reference Gu and Dunson2023) and for saturated CDMs in Balamuta and Culpepper (Reference Balamuta and Culpepper2022). Different from these existing works, we apply Polya-Gamma augmentation not only for observed data layer
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{R}$$\end{document}
![]() , but also for the latent layer
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{A}^{(1)}$$\end{document}
, but also for the latent layer
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{A}^{(1)}$$\end{document}
![]() , due to our multilayer logistic linear model assumption. Specifically, we introduce auxiliary variables
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$w^{(1)}_{i,j}$$\end{document}
, due to our multilayer logistic linear model assumption. Specifically, we introduce auxiliary variables
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$w^{(1)}_{i,j}$$\end{document}
![]() for
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$j\in [J]$$\end{document}
for
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$j\in [J]$$\end{document}
![]() ,
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$w^{(2)}_{i,k}$$\end{document}
,
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$w^{(2)}_{i,k}$$\end{document}
![]() for
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$k\in [K_1]$$\end{document}
for
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$k\in [K_1]$$\end{document}
![]() that follow the Polya-Gamma prior
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textrm{PG}\left(1, 0\right) $$\end{document}
that follow the Polya-Gamma prior
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textrm{PG}\left(1, 0\right) $$\end{document}
![]() . Introduce the following notation:
. Introduce the following notation:
Denote the probability density function of
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textrm{PG}(1,0)$$\end{document}
![]() by
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$p^{\textrm{PG}}(w\mid 1, 0)$$\end{document}
by
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$p^{\textrm{PG}}(w\mid 1, 0)$$\end{document}
![]() . By the property of the Polya-Gamma variables in Polson et al. (Reference Polson, Scott and Windle2013), we have the following identity for
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\phi ^{(1)}_{i,j}$$\end{document}
. By the property of the Polya-Gamma variables in Polson et al. (Reference Polson, Scott and Windle2013), we have the following identity for
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\phi ^{(1)}_{i,j}$$\end{document}
![]() :
:

and there is a similar identity for
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\phi ^{(2)}_{i,k}$$\end{document}
![]() . A nice consequence of the above equality is that the conditional posterior distributions for all the
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\beta ^{(1)}_{j,0}$$\end{document}
. A nice consequence of the above equality is that the conditional posterior distributions for all the
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\beta ^{(1)}_{j,0}$$\end{document}
![]() and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\beta ^{(1)}_{j,k}$$\end{document}
and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\beta ^{(1)}_{j,k}$$\end{document}
![]() are still Gaussian, and the conditional posterior distribution of each
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$w_{i,j}^{(1)}$$\end{document}
are still Gaussian, and the conditional posterior distribution of each
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$w_{i,j}^{(1)}$$\end{document}
![]() is still Polya-Gamma, with
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$(w_{i,j}^{(1)} \mid -) \sim \textrm{PG}(1,~ \phi ^{(1)}_{i,j})$$\end{document}
is still Polya-Gamma, with
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$(w_{i,j}^{(1)} \mid -) \sim \textrm{PG}(1,~ \phi ^{(1)}_{i,j})$$\end{document}
![]() . Similar posterior forms can be derived for
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\beta ^{(2)}_{k,m}$$\end{document}
. Similar posterior forms can be derived for
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\beta ^{(2)}_{k,m}$$\end{document}
![]() and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$w^{(2)}_{i,k}$$\end{document}
and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$w^{(2)}_{i,k}$$\end{document}
![]() , which are also Gaussian and Polya-Gamma, respectively. Such posterior distributions are easy to sample from and are the building blocks of our efficient Gibbs sampler for a DeepLLM. We provide the details of this Gibbs sampler for DeepLLM in the Supplementary Material.
, which are also Gaussian and Polya-Gamma, respectively. Such posterior distributions are easy to sample from and are the building blocks of our efficient Gibbs sampler for a DeepLLM. We provide the details of this Gibbs sampler for DeepLLM in the Supplementary Material.
We point out that our Gibbs samplers described in Sects. 4.1–4.3 can be readily extended to deeper models containing more than two latent layers. To see this, note that DeepCDMs have a nice property implied by the graphical model: given any layer
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{A}^{(d)}$$\end{document}
![]() , the layer above it
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{A}^{(d+1)}$$\end{document}
, the layer above it
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{A}^{(d+1)}$$\end{document}
![]() and the layer below it
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{A}^{(d-1)}$$\end{document}
and the layer below it
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{A}^{(d-1)}$$\end{document}
![]() are conditionally independent. This means in a DeepCDM with an arbitrary number of layers, when sampling parameters and latent structures for any specific layer, we only need to consider its two adjacent layers and derive the full conditional distributions based on these local model information. This fact allows straightforward extensions of our Gibbs sampling procedures to general hybrid DeepCDMs.
are conditionally independent. This means in a DeepCDM with an arbitrary number of layers, when sampling parameters and latent structures for any specific layer, we only need to consider its two adjacent layers and derive the full conditional distributions based on these local model information. This fact allows straightforward extensions of our Gibbs sampling procedures to general hybrid DeepCDMs.
5. Simulation Studies
We conduct simulation studies for the three two-latent-layer DeepCDMs considered in Sect. 4: DeepDINA in Sect. 4.1, Hybrid GDINA-DINA in Sect. 4.2, and DeepLLM in Sect. 4.3. We also conduct two additional simulation studies, one comparing a DeepCDM to a traditional CDM with a saturated attribute model, and one evaluating a DeepCDM’s robustness to deeper layer model misspecification. The following three different generative graphical structures (equivalently, forms of
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{Q}^{(1)}_{J\times K_1}$$\end{document}
![]() and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{Q}^{(2)}_{K_1\times K_2}$$\end{document}
and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{Q}^{(2)}_{K_1\times K_2}$$\end{document}
![]() ) are considered:
) are considered:



Denote the above three pairs of
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{Q}$$\end{document}
![]() -matrices by
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\{\textbf{Q}^{(1)}_a, \textbf{Q}^{(2)}_a\}$$\end{document}
-matrices by
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\{\textbf{Q}^{(1)}_a, \textbf{Q}^{(2)}_a\}$$\end{document}
![]() ,
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\{\textbf{Q}^{(1)}_b, \textbf{Q}^{(2)}_b\}$$\end{document}
,
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\{\textbf{Q}^{(1)}_b, \textbf{Q}^{(2)}_b\}$$\end{document}
![]() , and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\{\textbf{Q}^{(1)}_c, \textbf{Q}^{(2)}_c\}$$\end{document}
, and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\{\textbf{Q}^{(1)}_c, \textbf{Q}^{(2)}_c\}$$\end{document}
![]() , respectively. In all the simulation experiments, the Gibbs sampling algorithm is run for 15,000 iterations, with the first 10,000 iterations discarded as burn-in. Based on the last 5000 posterior samples, we calculate the posterior means of the continuous parameters as their point estimators. We observed sufficiently good convergence and mixing behaviors of all the Gibbs samplers through preliminary simulations.
, respectively. In all the simulation experiments, the Gibbs sampling algorithm is run for 15,000 iterations, with the first 10,000 iterations discarded as burn-in. Based on the last 5000 posterior samples, we calculate the posterior means of the continuous parameters as their point estimators. We observed sufficiently good convergence and mixing behaviors of all the Gibbs samplers through preliminary simulations.
Simulation Study I: Two-latent-layer DeepDINA.
Under each of the three pairs of
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{Q}$$\end{document}
![]() -matrices in (22)–(24), we specify the true item/quasi-item parameters to be
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$s_j^{(1)}=g_j^{(1)}=0.1$$\end{document}
-matrices in (22)–(24), we specify the true item/quasi-item parameters to be
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$s_j^{(1)}=g_j^{(1)}=0.1$$\end{document}
![]() for all
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$j\in [J]$$\end{document}
for all
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$j\in [J]$$\end{document}
![]() , and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$s_k^{(2)} = g_k^{(2)}=0.25$$\end{document}
, and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$s_k^{(2)} = g_k^{(2)}=0.25$$\end{document}
![]() for all
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$k\in [K_1]$$\end{document}
for all
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$k\in [K_1]$$\end{document}
![]() . We specify the true deep proportion parameters to be
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\varvec{\pi }^{\textrm{deep}} = (1/2^{K_2}, \ldots , 1/2^{K_2})$$\end{document}
. We specify the true deep proportion parameters to be
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\varvec{\pi }^{\textrm{deep}} = (1/2^{K_2}, \ldots , 1/2^{K_2})$$\end{document}
![]() , that is, uniform over the
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$2^{K_2}$$\end{document}
, that is, uniform over the
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$2^{K_2}$$\end{document}
![]() deep latent patterns. We consider three sample sizes
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$N=500, 1000, 2000$$\end{document}
deep latent patterns. We consider three sample sizes
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$N=500, 1000, 2000$$\end{document}
![]() , and carry out 100 independent simulation replicates in each of the nine resulting simulation settings. The
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{Q}$$\end{document}
, and carry out 100 independent simulation replicates in each of the nine resulting simulation settings. The
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{Q}$$\end{document}
![]() -matrices
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{Q}^{(1)}$$\end{document}
-matrices
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{Q}^{(1)}$$\end{document}
![]() and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{Q}^{(2)}$$\end{document}
and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{Q}^{(2)}$$\end{document}
![]() are fixed to the ground truths during estimation. We consider the posterior means of the model parameters as their point estimators, and calculate the mean root mean squared errors (RMSE) and mean absolute biases (aBias), each averaged across the 100 simulation replicates. Here, the mean absolute bias is a valid measure of the bias performance of an estimator, which is both broadly used in statistics (Morris et al., Reference Morris, White and Crowther2019) and also in previous studies about CDMs (Chen et al., Reference Chen, Culpepper and Liang2020; Xu and Shang, Reference Xu and Shang2018). Note that directly averaging the bias itself (instead of the absolute bias that we consider) across simulation replicates may give a misleading result, because positive and negative biases can cancel out each other. Table 1 presents the simulation results of the average RMSE and average aBias for the slipping and guessing parameters
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\varvec{\theta }^{(1)}_{\textrm{DINA}}$$\end{document}
are fixed to the ground truths during estimation. We consider the posterior means of the model parameters as their point estimators, and calculate the mean root mean squared errors (RMSE) and mean absolute biases (aBias), each averaged across the 100 simulation replicates. Here, the mean absolute bias is a valid measure of the bias performance of an estimator, which is both broadly used in statistics (Morris et al., Reference Morris, White and Crowther2019) and also in previous studies about CDMs (Chen et al., Reference Chen, Culpepper and Liang2020; Xu and Shang, Reference Xu and Shang2018). Note that directly averaging the bias itself (instead of the absolute bias that we consider) across simulation replicates may give a misleading result, because positive and negative biases can cancel out each other. Table 1 presents the simulation results of the average RMSE and average aBias for the slipping and guessing parameters
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\varvec{\theta }^{(1)}_{\textrm{DINA}}$$\end{document}
![]() , for the quasi-slipping and quasi-guessing parameters
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\varvec{\theta }^{(2)}_{\textrm{DINA}}$$\end{document}
, for the quasi-slipping and quasi-guessing parameters
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\varvec{\theta }^{(2)}_{\textrm{DINA}}$$\end{document}
![]() , and the deep proportion parameters
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\varvec{\pi }^{\text { {deep}}}$$\end{document}
, and the deep proportion parameters
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\varvec{\pi }^{\text { {deep}}}$$\end{document}
![]() .
.
Table 1 Two-latent-layer DeepDINA simulation results.

Note that the three generative graph structures in (22)–(24) all satisfy the strict identifiability conditions for the DeepDINA model. Specifically, all the
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{Q}^{(1)}$$\end{document}
![]() and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{Q}^{(2)}$$\end{document}
and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{Q}^{(2)}$$\end{document}
![]() satisfy the C-R-D conditions; therefore, Theorem 1 guarantees the strict identifiability of the parameters
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\varvec{\theta }^{(1)}_{\textrm{DINA}}$$\end{document}
satisfy the C-R-D conditions; therefore, Theorem 1 guarantees the strict identifiability of the parameters
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\varvec{\theta }^{(1)}_{\textrm{DINA}}$$\end{document}
![]() ,
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\varvec{\theta }^{(2)}_{\textrm{DINA}}$$\end{document}
,
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\varvec{\theta }^{(2)}_{\textrm{DINA}}$$\end{document}
![]() , and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\varvec{\pi }^{\text { {deep}}}$$\end{document}
, and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\varvec{\pi }^{\text { {deep}}}$$\end{document}
![]() . This identifiability conclusion is empirically confirmed by the simulation results in Table 1, where the estimation errors of these identifiable quantities measured through RMSE and aBias are all reasonably small.
. This identifiability conclusion is empirically confirmed by the simulation results in Table 1, where the estimation errors of these identifiable quantities measured through RMSE and aBias are all reasonably small.
Simulation Study II: Two-latent-layer Hybrid GDINA-DINA.
Under the two-latent-layer Hybrid GDINA-DINA model, we specify the deeper DINA-layer’s true parameters to be the same as that in the DeepDINA case with
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$s_k^{(2)} = g_k^{(2)}=0.25$$\end{document}
![]() for all
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$k\in [K_1]$$\end{document}
for all
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$k\in [K_1]$$\end{document}
![]() , and also specify the deep proportion parameters as
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\varvec{\pi }^{\textrm{deep}} = (1/2^{K_2}, \ldots , 1/2^{K_2})$$\end{document}
, and also specify the deep proportion parameters as
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\varvec{\pi }^{\textrm{deep}} = (1/2^{K_2}, \ldots , 1/2^{K_2})$$\end{document}
![]() . As for the GDINA-layer’s parameters, we specify them in the same way as the simulations in Xu and Shang (Reference Xu and Shang2018) and Chen et al. (Reference Chen, Culpepper and Liang2020); that is, for each item
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$j\in [J]$$\end{document}
. As for the GDINA-layer’s parameters, we specify them in the same way as the simulations in Xu and Shang (Reference Xu and Shang2018) and Chen et al. (Reference Chen, Culpepper and Liang2020); that is, for each item
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$j\in [J]$$\end{document}
![]() , set the lowest correct response probability to 0.2 for all-zero attribute profiles, set the highest correct response probability to 0.8 for all-one attribute profiles, and set all the main-effect and interaction-effect parameters under the GDINA model to be equal. The above true parameter specification can be equivalently written in the following mathematical form,
, set the lowest correct response probability to 0.2 for all-zero attribute profiles, set the highest correct response probability to 0.8 for all-one attribute profiles, and set all the main-effect and interaction-effect parameters under the GDINA model to be equal. The above true parameter specification can be equivalently written in the following mathematical form,

During the Bayesian posterior sampling process, we enforce the monotonicity constraint described in Sect. 4.2 by sampling the transformed parameters
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\theta _{j,\{k\}} = \beta ^{(1)}_{j,\varnothing } + \beta ^{(1)}_{j,\{k\}}$$\end{document}
![]() from the truncated Beta posteriors; this ensures the main-effect parameters
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\beta ^{(1)}_{j,\{k\}}$$\end{document}
from the truncated Beta posteriors; this ensures the main-effect parameters
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\beta ^{(1)}_{j,\{k\}}$$\end{document}
![]() to be positive. Table 2 presents the simulation results under the Hybrid GDINA-DINA model.
to be positive. Table 2 presents the simulation results under the Hybrid GDINA-DINA model.
Table 2 Two-latent-layer hybrid GDINA-DINA simulation results.

Table 2 shows that our method can accurately estimate all the parameters under the Hybrid GDINA-DINA model and the estimation accuracy improves as sample size grows. Indeed, all the
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{Q}^{(1)}_a$$\end{document}
![]() ,
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{Q}^{(1)}_b$$\end{document}
,
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{Q}^{(1)}_b$$\end{document}
![]() , and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{Q}^{(1)}_c$$\end{document}
, and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{Q}^{(1)}_c$$\end{document}
![]() satisfy the identifiability conditions for general diagnostic models (condition S in Theorem 2), and all the
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{Q}^{(2)}_a$$\end{document}
satisfy the identifiability conditions for general diagnostic models (condition S in Theorem 2), and all the
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{Q}^{(2)}_a$$\end{document}
![]() ,
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{Q}^{(2)}_b$$\end{document}
,
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{Q}^{(2)}_b$$\end{document}
![]() , and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{Q}^{(2)}_c$$\end{document}
, and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{Q}^{(2)}_c$$\end{document}
![]() satisfy the C-R-D conditions for identifying the DINA model. Therefore, Proposition 1 guarantees that all the parameters
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\varvec{\beta }^{(1)}_{\textrm{GDINA}}$$\end{document}
satisfy the C-R-D conditions for identifying the DINA model. Therefore, Proposition 1 guarantees that all the parameters
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\varvec{\beta }^{(1)}_{\textrm{GDINA}}$$\end{document}
![]() ,
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\varvec{\theta }^{(1)}_{\textrm{DINA}}$$\end{document}
,
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\varvec{\theta }^{(1)}_{\textrm{DINA}}$$\end{document}
![]() , and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\varvec{\pi }^{\text { {deep}}}$$\end{document}
, and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\varvec{\pi }^{\text { {deep}}}$$\end{document}
![]() in this Hybrid DeepCDM are fully identifiable, as supported by the numerical evidence in Table 2.
in this Hybrid DeepCDM are fully identifiable, as supported by the numerical evidence in Table 2.
Simulation Study III: Two-latent-layer DeepLLM. We conduct simulations for the DeepLLM, using the Gibbs sampler with the multilayer Polya-Gamma data augmentation strategy developed in Sect. 4.3. The true parameters in the two-latent-layer DeepLLM are specified as follows. Inside the inverse logit function, the intercept parameters for the two layers are set to
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\beta ^{(1)}_{j,0}=-3$$\end{document}
![]() for all
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$j\in [J]$$\end{document}
for all
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$j\in [J]$$\end{document}
![]() and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\beta ^{(2)}_{k,0}=-2$$\end{document}
and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\beta ^{(2)}_{k,0}=-2$$\end{document}
![]() for all
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$k\in [K_1]$$\end{document}
for all
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$k\in [K_1]$$\end{document}
![]() ; the shallower layer’s main-effect parameters are set to
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\beta ^{(1)}_{j,k} = 6/\left(\sum _{k'=1}^{K_1} q^{(1)}_{j,k'}\right) $$\end{document}
; the shallower layer’s main-effect parameters are set to
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\beta ^{(1)}_{j,k} = 6/\left(\sum _{k'=1}^{K_1} q^{(1)}_{j,k'}\right) $$\end{document}
![]() for which
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$q^{(1)}_{j,k}=1$$\end{document}
for which
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$q^{(1)}_{j,k}=1$$\end{document}
![]() , and the deeper layer’s main-effect parameters are set to
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\beta ^{(2)}_{k,m} = 4/\left(\sum _{m'=1}^{K_2} q^{(2)}_{k,m'}\right) $$\end{document}
, and the deeper layer’s main-effect parameters are set to
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\beta ^{(2)}_{k,m} = 4/\left(\sum _{m'=1}^{K_2} q^{(2)}_{k,m'}\right) $$\end{document}
![]() for which
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$q^{(2)}_{k,m}=1$$\end{document}
for which
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$q^{(2)}_{k,m}=1$$\end{document}
![]() . Note that these
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\beta $$\end{document}
. Note that these
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\beta $$\end{document}
![]() -parameters in a DeepLLM are all inside the inverse logit function
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$f(x) = e^x/(1+e^x)$$\end{document}
-parameters in a DeepLLM are all inside the inverse logit function
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$f(x) = e^x/(1+e^x)$$\end{document}
![]() to generate the correct response probability, so they are on a different scale than those probability parameters under the DINA or GDINA model. Table 3 presents the estimation accuracy results for the two-latent-layer DeepLLM model.
to generate the correct response probability, so they are on a different scale than those probability parameters under the DINA or GDINA model. Table 3 presents the estimation accuracy results for the two-latent-layer DeepLLM model.
Table 3 Two-latent-layer DeepLLM simulation results.

The simulation results in Table 2 also show decreasing estimation errors with growing sample sizes. We point out that the “RMSE” and “aBias” values in different tables are not directly comparable, because the logistic-scale parameters
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\varvec{\beta }^{(2)}_{\textrm{LLM}}$$\end{document}
![]() and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\varvec{\beta }^{(2)}_{\textrm{LLM}}$$\end{document}
and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\varvec{\beta }^{(2)}_{\textrm{LLM}}$$\end{document}
![]() in Table 3 have larger magnitudes than DINA/GDINA parameters in the previous Tables 1 and 2. The three first-layer
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{Q}$$\end{document}
in Table 3 have larger magnitudes than DINA/GDINA parameters in the previous Tables 1 and 2. The three first-layer
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{Q}$$\end{document}
![]() -matrix
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{Q}^{(1)}_a$$\end{document}
-matrix
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{Q}^{(1)}_a$$\end{document}
![]() ,
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{Q}^{(1)}_b$$\end{document}
,
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{Q}^{(1)}_b$$\end{document}
![]() , and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{Q}^{(1)}_c$$\end{document}
, and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{Q}^{(1)}_c$$\end{document}
![]() all satisfy the identifiability conditions under general diagnostic models which cover the LLM as a special case, so the
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\varvec{\beta }^{(1)}_{\textrm{LLM}}$$\end{document}
all satisfy the identifiability conditions under general diagnostic models which cover the LLM as a special case, so the
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\varvec{\beta }^{(1)}_{\textrm{LLM}}$$\end{document}
![]() are always identifiable across structures (a), (b), and (c) (see the layerwise identifiability argument in Proposition 1). As for the second-layer
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{Q}$$\end{document}
are always identifiable across structures (a), (b), and (c) (see the layerwise identifiability argument in Proposition 1). As for the second-layer
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{Q}$$\end{document}
![]() -matrix in the three settings,
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{Q}^{(2)}_a$$\end{document}
-matrix in the three settings,
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{Q}^{(2)}_a$$\end{document}
![]() and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{Q}^{(2)}_c$$\end{document}
and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{Q}^{(2)}_c$$\end{document}
![]() satisfy the strict identifiability conditions for LLM while
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{Q}^{(2)}_c$$\end{document}
satisfy the strict identifiability conditions for LLM while
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{Q}^{(2)}_c$$\end{document}
![]() satisfies the generic identifiability conditions for LLM. For quantities
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\varvec{\beta }^{(2)}_{\textrm{LLM}}$$\end{document}
satisfies the generic identifiability conditions for LLM. For quantities
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\varvec{\beta }^{(2)}_{\textrm{LLM}}$$\end{document}
![]() and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\varvec{\pi }^{\text { {deep}}}$$\end{document}
and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\varvec{\pi }^{\text { {deep}}}$$\end{document}
![]() associated with
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{Q}^{(2)}$$\end{document}
associated with
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{Q}^{(2)}$$\end{document}
![]() , Table 3 shows that their estimation errors in the generic identifiability case (b) are still reasonably small, though slightly worse than those in the strictly identifiable cases (a) and (c). Overall, all the above simulation results corroborate the identifiability conclusions about DeepCDMs and also provide evidence that our Bayesian estimation algorithms have good empirical performance.
, Table 3 shows that their estimation errors in the generic identifiability case (b) are still reasonably small, though slightly worse than those in the strictly identifiable cases (a) and (c). Overall, all the above simulation results corroborate the identifiability conclusions about DeepCDMs and also provide evidence that our Bayesian estimation algorithms have good empirical performance.
In addition to the estimation performance of the population parameters, we also present the attribute classification accuracy for different layers of attributes in Table 4. The numbers in this table are calculated as follows: in each simulation replicate, we obtain the posterior modes of each subject’s each attribute entry in the shallower-layer
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{A}^{(1)}$$\end{document}
![]() (similarly for the deeper-layer
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{A}^{(2)}$$\end{document}
(similarly for the deeper-layer
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{A}^{(2)}$$\end{document}
![]() ), and then average them across the 100 simulation replicates to get the attribute classification accuracy. For all three DeepCDMs and all three
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{Q}$$\end{document}
), and then average them across the 100 simulation replicates to get the attribute classification accuracy. For all three DeepCDMs and all three
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{Q}$$\end{document}
![]() -matrices structures (a), (b), and (c), the attribute classification accuracy numbers remain reasonably high, basically exceeding 90% for the shallower
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{A}^{(1)}$$\end{document}
-matrices structures (a), (b), and (c), the attribute classification accuracy numbers remain reasonably high, basically exceeding 90% for the shallower
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{A}^{(1)}$$\end{document}
![]() and exceeding 70% for the deeper
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{A}^{(2)}$$\end{document}
and exceeding 70% for the deeper
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{A}^{(2)}$$\end{document}
![]() . The classification accuracy for deeper attributes is lower than that for shallower ones, which is an inevitable characteristic shared by all higher-order latent variable models widely used in statistics. Despite this, the fact that the deeper attributes still have classification accuracies beyond 70%, and even beyond 90% for DeepLLM, demonstrates that the estimation quality of deeper attributes in our model does not degrade too much and is still acceptable. Furthermore, Table 4 indicates that the DeepLLM has the best performance in classifying the deeper
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{A}^{(2)}$$\end{document}
. The classification accuracy for deeper attributes is lower than that for shallower ones, which is an inevitable characteristic shared by all higher-order latent variable models widely used in statistics. Despite this, the fact that the deeper attributes still have classification accuracies beyond 70%, and even beyond 90% for DeepLLM, demonstrates that the estimation quality of deeper attributes in our model does not degrade too much and is still acceptable. Furthermore, Table 4 indicates that the DeepLLM has the best performance in classifying the deeper
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{A}^{(2)}$$\end{document}
![]() and the smallest gap between the classification accuracies of
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{A}^{(1)}$$\end{document}
and the smallest gap between the classification accuracies of
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{A}^{(1)}$$\end{document}
![]() and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{A}^{(2)}$$\end{document}
and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{A}^{(2)}$$\end{document}
![]() . This observation suggests that in the considered settings, DeepLLM may be a more preferable model among the DeepCDM family in terms of estimating the deeper latent attributes.
. This observation suggests that in the considered settings, DeepLLM may be a more preferable model among the DeepCDM family in terms of estimating the deeper latent attributes.
Table 4 Attribute classification accuracy across all of the simulation settings.

Simulation Study IV: Comparison to the saturated attribute model. In this simulation study, we generate data using a DeepCDM (DeepDINA here) but estimate parameters using both the DeepCDM and the traditional one-layer CDM (DINA here) with a saturated attribute model. We compare (a) the computation time of the two models, and also (b) their accuracy in recovering the proportions
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\varvec{\pi }^{(1)}$$\end{document}
![]() of the latent attributes
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{A}^{(1)}$$\end{document}
of the latent attributes
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{A}^{(1)}$$\end{document}
![]() . The distribution of
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{A}^{(1)}$$\end{document}
. The distribution of
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{A}^{(1)}$$\end{document}
![]() can be parameterized by
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\varvec{\pi }^{(1)} = (\pi ^{(1)}_{\varvec{\alpha }}; \varvec{\alpha }\in \{0,1\}^{K_1})$$\end{document}
can be parameterized by
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\varvec{\pi }^{(1)} = (\pi ^{(1)}_{\varvec{\alpha }}; \varvec{\alpha }\in \{0,1\}^{K_1})$$\end{document}
![]() where
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\pi ^{(1)}_{\varvec{\alpha }} = \mathbb P(\textbf{A}^{(1)} = \varvec{\alpha })$$\end{document}
where
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\pi ^{(1)}_{\varvec{\alpha }} = \mathbb P(\textbf{A}^{(1)} = \varvec{\alpha })$$\end{document}
![]() . Under DINA with a traditional saturated attribute model,
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\varvec{\pi }^{(1)}$$\end{document}
. Under DINA with a traditional saturated attribute model,
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\varvec{\pi }^{(1)}$$\end{document}
![]() are directly treated as parameters and estimated, while in the DeepDINA model,
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\varvec{\pi }^{(1)}$$\end{document}
are directly treated as parameters and estimated, while in the DeepDINA model,
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\varvec{\pi }^{(1)}$$\end{document}
![]() follows another higher-order DINA model and can be calculated after estimating these higher-order parameters. Here we focus on comparing the accuracy of recovering the distribution of
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{A}^{(1)}$$\end{document}
follows another higher-order DINA model and can be calculated after estimating these higher-order parameters. Here we focus on comparing the accuracy of recovering the distribution of
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{A}^{(1)}$$\end{document}
![]() via
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\varvec{\pi }^{(1)}$$\end{document}
via
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\varvec{\pi }^{(1)}$$\end{document}
![]() because this is the key difference between the two models. Table 5 displays the average RMSEs of
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\varvec{\pi }^{(1)}$$\end{document}
because this is the key difference between the two models. Table 5 displays the average RMSEs of
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\varvec{\pi }^{(1)}$$\end{document}
![]() and the average computation time under the two models. In particular, the 6th column “Ratio” in Table 5 displays the ratios of RMSEs under the deep and the saturated model (i.e., ratios of numbers in the 4th and 5th columns in the table), and the 9th column “Ratio” displays the ratio of computation time under the two models (i.e., ratios of numbers in the 7th and 8th columns in the table). Compared to the traditional estimation method for the one-layer DINA model, our DeepDINA method yields 20-60% of the RMSE in estimating
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\varvec{\pi }^{(1)}$$\end{document}
and the average computation time under the two models. In particular, the 6th column “Ratio” in Table 5 displays the ratios of RMSEs under the deep and the saturated model (i.e., ratios of numbers in the 4th and 5th columns in the table), and the 9th column “Ratio” displays the ratio of computation time under the two models (i.e., ratios of numbers in the 7th and 8th columns in the table). Compared to the traditional estimation method for the one-layer DINA model, our DeepDINA method yields 20-60% of the RMSE in estimating
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\varvec{\pi }^{(1)}$$\end{document}
![]() and takes 9–25% of the computation time. These comparisons imply that appropriately taking into account higher-order discrete structures will lead to both more accurate estimation and more efficient computation. Here, more accurate estimation is thanks to the suitable modeling of the latent attribute dependence, and more efficient computation is thanks to the statistical parsimony and our efficient Gibbs sampling steps of a fewer number of parameters.
and takes 9–25% of the computation time. These comparisons imply that appropriately taking into account higher-order discrete structures will lead to both more accurate estimation and more efficient computation. Here, more accurate estimation is thanks to the suitable modeling of the latent attribute dependence, and more efficient computation is thanks to the statistical parsimony and our efficient Gibbs sampling steps of a fewer number of parameters.
Simulation Study V: Robustness of DeepCDM to Deep Layer Misspecification.
We perform a simulation study to evaluate our method’s performance under a misspecified higher-order model. Here we generate data from the HO-CDM in de la Torre and Douglas (Reference de la Torre and Douglas2004) that have higher-order continuous latent traits behind the binary latent attributes. Consider structure (c) in (24) with
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$J=30$$\end{document}
![]() items,
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$K_1=8$$\end{document}
items,
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$K_1=8$$\end{document}
![]() attributes, and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$K_2=3$$\end{document}
attributes, and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$K_2=3$$\end{document}
![]() higher-order continuous latent traits
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$(\theta ^{(2)}_1, \theta ^{(2)}_2, \theta ^{(2)}_3) =: \varvec{\theta }^{(2)}$$\end{document}
higher-order continuous latent traits
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$(\theta ^{(2)}_1, \theta ^{(2)}_2, \theta ^{(2)}_3) =: \varvec{\theta }^{(2)}$$\end{document}
![]() . Let
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\theta ^{(2)}_1, \theta ^{(2)}_2, \theta ^{(2)}_3$$\end{document}
. Let
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\theta ^{(2)}_1, \theta ^{(2)}_2, \theta ^{(2)}_3$$\end{document}
![]() follow independent standard normal distributions. Given
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\varvec{\theta }^{(2)}$$\end{document}
follow independent standard normal distributions. Given
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\varvec{\theta }^{(2)}$$\end{document}
![]() , the first-layer CDM parameters are set to be the same in the previous DeepLLM simulation setting. Then we fit the data using our Gibbs sampler developed for DeepLLM, and then examine the estimated shallower-layer item parameters
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\varvec{\beta }^{(1)}$$\end{document}
, the first-layer CDM parameters are set to be the same in the previous DeepLLM simulation setting. Then we fit the data using our Gibbs sampler developed for DeepLLM, and then examine the estimated shallower-layer item parameters
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\varvec{\beta }^{(1)}$$\end{document}
![]() under this misspecified model. For better visualization, for a randomly generated dataset, in Fig. 2 we plot the heatmap of the estimated
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\varvec{\beta }^{(1)}$$\end{document}
under this misspecified model. For better visualization, for a randomly generated dataset, in Fig. 2 we plot the heatmap of the estimated
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\varvec{\beta }^{(1)}$$\end{document}
![]() in the form of
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$J\times K_1$$\end{document}
in the form of
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$J\times K_1$$\end{document}
![]() matrix whose sparsity pattern is given by the
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{Q}$$\end{document}
matrix whose sparsity pattern is given by the
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{Q}$$\end{document}
![]() -matrix
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{Q}^{(1)}\in \{0,1\}^{J\times K_1}$$\end{document}
-matrix
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{Q}^{(1)}\in \{0,1\}^{J\times K_1}$$\end{document}
![]() . We can see that the estimated coefficients
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\widehat{\varvec{\beta }}^{(1)}$$\end{document}
. We can see that the estimated coefficients
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\widehat{\varvec{\beta }}^{(1)}$$\end{document}
![]() under a misspecified higher-order model is still close to the ground truth, even for a relatively small sample size
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$N=500$$\end{document}
under a misspecified higher-order model is still close to the ground truth, even for a relatively small sample size
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$N=500$$\end{document}
![]() . For a larger sample size
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$N=2000$$\end{document}
. For a larger sample size
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$N=2000$$\end{document}
![]() , the estimated
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\widehat{\varvec{\beta }}^{(1)}$$\end{document}
, the estimated
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\widehat{\varvec{\beta }}^{(1)}$$\end{document}
![]() matrix becomes closer to the truth.
matrix becomes closer to the truth.
Furthermore, we also look beyond a single simulation trial and carry out 100 independent simulation replicates to assess our method’s average performance under model misspecification. Figure 3 presents the boxplots of root mean squared errors (RMSEs) of the estimated shallower-layer
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\varvec{\beta }^{(1)}$$\end{document}
![]() parameters based on the 100 replicates. This figure clearly shows a decreasing trend of estimation errors of
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\varvec{\beta }^{(1)}$$\end{document}
parameters based on the 100 replicates. This figure clearly shows a decreasing trend of estimation errors of
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\varvec{\beta }^{(1)}$$\end{document}
![]() as sample size increases. Together with the previous Fig. 2, we have empirically demonstrated that our DeepCDM methodology has some robustness to model misspecification of the deeper-layers.
as sample size increases. Together with the previous Fig. 2, we have empirically demonstrated that our DeepCDM methodology has some robustness to model misspecification of the deeper-layers.
Table 5 Comparisons between the two-latent-layer DeepDINA and the saturated DINA model in terms of the RMSE of the proportions
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\varvec{\pi }^{(1)}$$\end{document}
![]() of the fine-grained latent attributes
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{A}^{(1)}$$\end{document}
of the fine-grained latent attributes
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{A}^{(1)}$$\end{document}
![]() and the computation time.
and the computation time.


Figure. 2 Estimated first-layer parameters
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\varvec{\beta }^{(1)}$$\end{document}
![]() under a misspecified latent attribute model. The data are generated from a continuous higher-order latent trait model but estimated using our DeepLLM method.
under a misspecified latent attribute model. The data are generated from a continuous higher-order latent trait model but estimated using our DeepLLM method.

Figure. 3 RMSE boxplots for the estimated first-layer parameters
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\varvec{\beta }^{(1)}$$\end{document}
![]() under a misspecified latent attribute model. Results are based on 100 independent simulation replications for each sample size.
under a misspecified latent attribute model. Results are based on 100 independent simulation replications for each sample size.
We next offer more discussions between the connections and differences between the very popular HO-CDM and the proposed DeepCDMs. As described in de la Torre and Douglas (Reference de la Torre and Douglas2004), the motivation for proposing the HO-CDM includes parsimony and interpretability. For the HO-CDM, the parsimony comes from using an IRT model with continuous latent traits to model the binary attributes, and the interpretability comes from defining a plausible model for the relationship between general ability and specific knowledge. On one hand, as mentioned in Sect. 1, DeepCDMs also similarly have the advantages of parsimony and interpretability. On the other hand, there are also several key differences between the HO-CDM and DeepCDMs. First, DeepCDMs use fully discrete latent layers, which offer a different interpretation of multi-granularity skill diagnosis. Second, the above simulation study implies that a special member in the DeepCDM family – DeepLLM – can serve as an approximation to HO-CDM; our DeepLLM method can robustly estimate the item parameters for data generated from HO-CDM. It is then worth emphasizing that DeepLLM is just a special member of the DeepCDM family, and that other members in this family can flexibly model structures well beyond the logistic linear form used in DeepLLM and HO-CDM. For example, DeepDINA or Hybrid GDINA-DINA can model the nonlinear conjunctive relationship or interaction effects of higher-order discrete attributes, and they are still identifiable and easy to estimate via Gibbs sampling (see Sect. 4). However, there currently do not exist extensions of HO-CDM to nonlinear higher-order latent variable settings.
6. Application to the TIMSS Assessment Data
We demonstrate the DeepCDM methodology by applying it to data extracted from the TIMSS 2019 math assessment mentioned in Sect. 1; the data are accessed from the TIMSS 2019 International Database (Fishbein et al., Reference Fishbein, Foy and Yin2021). We use two-latent-layer DeepCDMs to analyze the US student response data to item block No.2 in the eighth grade math assessment. Prior to our analysis, the original student response data are converted into binary correct/wrong responses as follows, based on the TIMSS 2019 Item Information available in the online database (Fishbein et al., Reference Fishbein, Foy and Yin2021). For multiple-choice items, a student response is coded as one if the response matches the correct answer key, and coded as zero otherwise; for constructed response items, a student response is coded as one if the number of scores received is equal to the maximal score of the item, and coded as zero otherwise.
Among the US eighth grade participants, we consider students that took the math item block No.2 and give responses to all the
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$J=28$$\end{document}
![]() items in this block. This results in a binary observed data matrix containing responses from
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$N=972$$\end{document}
items in this block. This results in a binary observed data matrix containing responses from
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$N=972$$\end{document}
![]() students. The online TIMSS 2019 Item Information—Grade 8 provides details about which specific skills each test item is measuring, and we use these information to construct the
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{Q}$$\end{document}
students. The online TIMSS 2019 Item Information—Grade 8 provides details about which specific skills each test item is measuring, and we use these information to construct the
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{Q}$$\end{document}
![]() -matrices. There are four content skills:
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\alpha ^{(1)}_1$$\end{document}
-matrices. There are four content skills:
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\alpha ^{(1)}_1$$\end{document}
![]() : Number;
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\alpha ^{(1)}_2$$\end{document}
: Number;
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\alpha ^{(1)}_2$$\end{document}
![]() : Algebra;
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\alpha ^{(1)}_3$$\end{document}
: Algebra;
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\alpha ^{(1)}_3$$\end{document}
![]() : Geometry; and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\alpha ^{(1)}_4$$\end{document}
: Geometry; and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\alpha ^{(1)}_4$$\end{document}
![]() : Data and Probability; and three cognitive skills:
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\alpha ^{(1)}_5$$\end{document}
: Data and Probability; and three cognitive skills:
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\alpha ^{(1)}_5$$\end{document}
![]() : Knowing;
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\alpha ^{(1)}_6$$\end{document}
: Knowing;
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\alpha ^{(1)}_6$$\end{document}
![]() : Applying; and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\alpha ^{(1)}_7$$\end{document}
: Applying; and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\alpha ^{(1)}_7$$\end{document}
![]() : Reasoning. These content and cognitive skills can be viewed as subcompetences for which it is desirable to provide fine-grained diagnoses. Therefore, we model these seven skills as
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$K_1=7$$\end{document}
: Reasoning. These content and cognitive skills can be viewed as subcompetences for which it is desirable to provide fine-grained diagnoses. Therefore, we model these seven skills as
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$K_1=7$$\end{document}
![]() fine-grained attributes in the shallower latent layer in a DeepCDM. In fact, each test item is listed as measuring one content skill and one cognitive skill; for example, the first item in block No.2 measures
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\alpha ^{(1)}_1$$\end{document}
fine-grained attributes in the shallower latent layer in a DeepCDM. In fact, each test item is listed as measuring one content skill and one cognitive skill; for example, the first item in block No.2 measures
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\alpha ^{(1)}_1$$\end{document}
![]() : Number, and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\alpha ^{(1)}_5$$\end{document}
: Number, and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\alpha ^{(1)}_5$$\end{document}
![]() : Knowing. We use such available item information to obtain the first-layer
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$J\times K_1$$\end{document}
: Knowing. We use such available item information to obtain the first-layer
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$J\times K_1$$\end{document}
![]() \documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{Q}$$\end{document}
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{Q}$$\end{document}
![]() -matrix
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{Q}^{(1)}_{28\times 7}$$\end{document}
-matrix
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{Q}^{(1)}_{28\times 7}$$\end{document}
![]() in Table 6. Further, as already implied by the above skill descriptions, the seven specific skills naturally belong to two general domains: the content domain and the cognitive domain. Here, the wordings of naming “content” and “cognitive” as two “domains” are official terms defined by and provided in the online TIMSS 2019 Assessment Frameworks. Diagnosing a student’s states on these latent domains can reflect their general strengths/weaknesses on these two broad aspects. So the deeper latent layer in our DeepCDM has two domain attributes:
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\alpha ^{(2)}_1$$\end{document}
in Table 6. Further, as already implied by the above skill descriptions, the seven specific skills naturally belong to two general domains: the content domain and the cognitive domain. Here, the wordings of naming “content” and “cognitive” as two “domains” are official terms defined by and provided in the online TIMSS 2019 Assessment Frameworks. Diagnosing a student’s states on these latent domains can reflect their general strengths/weaknesses on these two broad aspects. So the deeper latent layer in our DeepCDM has two domain attributes:
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\alpha ^{(2)}_1$$\end{document}
![]() : Content and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\alpha ^{(2)}_2$$\end{document}
: Content and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\alpha ^{(2)}_2$$\end{document}
![]() : Cognitive. According to the equivalence between the direct dependencies among variables and the
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{Q}$$\end{document}
: Cognitive. According to the equivalence between the direct dependencies among variables and the
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{Q}$$\end{document}
![]() -matrix entries, we can use the above attribute information to construct a
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$K_1\times K_2$$\end{document}
-matrix entries, we can use the above attribute information to construct a
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$K_1\times K_2$$\end{document}
![]() matrix
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{Q}^{(2)}_{7\times 2} = (q^{(2)}_{k,m})$$\end{document}
matrix
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{Q}^{(2)}_{7\times 2} = (q^{(2)}_{k,m})$$\end{document}
![]() , shown in Table 7.
, shown in Table 7.
Table 6 First-layer
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{Q}$$\end{document}
![]() -matrix
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{Q}^{(1)}_{28\times 7}$$\end{document}
-matrix
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{Q}^{(1)}_{28\times 7}$$\end{document}
![]() for item block No.2 in TIMSS 2019 eighth grade math assessment.
for item block No.2 in TIMSS 2019 eighth grade math assessment.

Table 7 Second-layer
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{Q}$$\end{document}
![]() -matrix
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{Q}^{(2)}_{7\times 2}$$\end{document}
-matrix
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{Q}^{(2)}_{7\times 2}$$\end{document}
![]() for TIMSS 2019 eighth grade math assessment.
for TIMSS 2019 eighth grade math assessment.

We then apply our Bayesian estimation method to the TIMSS data. DeepDINA is not used here because
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{Q}^{(1)}$$\end{document}
![]() does not satisfy the C-R-D conditions (i.e., does not contain an identity submatrix
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{I}_{K_1}$$\end{document}
does not satisfy the C-R-D conditions (i.e., does not contain an identity submatrix
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{I}_{K_1}$$\end{document}
![]() ), and hence does not give an identifiable DeepDINA model. As for DeepLLM and Hybrid GDINA-DINA (abbreviated as Hybrid G-D hereafter), it is not difficult to verify that
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{Q}^{(1)}_{28\times 7}$$\end{document}
), and hence does not give an identifiable DeepDINA model. As for DeepLLM and Hybrid GDINA-DINA (abbreviated as Hybrid G-D hereafter), it is not difficult to verify that
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{Q}^{(1)}_{28\times 7}$$\end{document}
![]() in Table 6 satisfies the generic identifiability conditions (G1) and (G2) in Theorem 3 for main-effect-based models, and that
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{Q}^{(2)}_{7\times 2}$$\end{document}
in Table 6 satisfies the generic identifiability conditions (G1) and (G2) in Theorem 3 for main-effect-based models, and that
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{Q}^{(2)}_{7\times 2}$$\end{document}
![]() in Table 7 satisfies the strict identifiability condition (S) in Theorem 2 for general diagnostic models. This means all the parameters in DeepLLM and Hybrid G-D are all strictly or generically identifiable. Note that
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{Q}^{(2)}$$\end{document}
in Table 7 satisfies the strict identifiability condition (S) in Theorem 2 for general diagnostic models. This means all the parameters in DeepLLM and Hybrid G-D are all strictly or generically identifiable. Note that
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{Q}^{(2)}$$\end{document}
![]() has all the rows each being either (1, 0) or (0, 1), in which case the Hybrid G-D model in fact covers both DeepDINA and DeepLLM as special cases and offers a more general alternative. Therefore, we focus on the more general Hybrid G-D model next.
has all the rows each being either (1, 0) or (0, 1), in which case the Hybrid G-D model in fact covers both DeepDINA and DeepLLM as special cases and offers a more general alternative. Therefore, we focus on the more general Hybrid G-D model next.
We run the Gibbs sampler for Hybrid G-D for 15,000 iterations and retain the last 5000 as our posterior samples, the same as in the simulation studies. Based on these samples, the posterior means are calculated for all the continuous parameters in the model. The deep proportion parameters’ posterior means are
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\overline{\varvec{\pi }}^{\text { {deep}}} = (0.477,~ 0.033, ~ 0.059, ~ 0.430)$$\end{document}
![]() , which correspond to deep latent patterns
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{A}^{(2)} = (0,0)$$\end{document}
, which correspond to deep latent patterns
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{A}^{(2)} = (0,0)$$\end{document}
![]() , (0, 1), (1, 0), (1, 1), respectively. This estimated
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\overline{\varvec{\pi }}^{\text { {deep}}}$$\end{document}
, (0, 1), (1, 0), (1, 1), respectively. This estimated
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\overline{\varvec{\pi }}^{\text { {deep}}}$$\end{document}
![]() implies that the two domain attributes exhibit a relatively high correlation. As for the quasi-item parameters characterizing
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mathbb {P}(A^{(1)}_k\mid \textbf{A}^{(2)}, \textbf{Q}^{(2)})$$\end{document}
implies that the two domain attributes exhibit a relatively high correlation. As for the quasi-item parameters characterizing
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mathbb {P}(A^{(1)}_k\mid \textbf{A}^{(2)}, \textbf{Q}^{(2)})$$\end{document}
![]() and item parameters characterizing
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mathbb {P}(R^{(1)}_j\mid \textbf{A}^{(1)}, \textbf{Q}^{(1)})$$\end{document}
and item parameters characterizing
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mathbb {P}(R^{(1)}_j\mid \textbf{A}^{(1)}, \textbf{Q}^{(1)})$$\end{document}
![]() , we plot their posterior means in Fig. 4. Specifically, Fig. 4a shows the conditional attribute mastery probabilities given the domain attributes, with its left column showing the quasi-guessing parameters
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\varvec{g}^{(2)} = (g^{(2)}_1, \ldots , g^{(2)}_7)^\top $$\end{document}
, we plot their posterior means in Fig. 4. Specifically, Fig. 4a shows the conditional attribute mastery probabilities given the domain attributes, with its left column showing the quasi-guessing parameters
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\varvec{g}^{(2)} = (g^{(2)}_1, \ldots , g^{(2)}_7)^\top $$\end{document}
![]() , and right column showing one minus the quasi-slipping parameters
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{1}_{7\times 1} - \varvec{s}^{(2)} = (1-s^{(2)}_1, \ldots , 1-s^{(2)}_7)^\top $$\end{document}
, and right column showing one minus the quasi-slipping parameters
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{1}_{7\times 1} - \varvec{s}^{(2)} = (1-s^{(2)}_1, \ldots , 1-s^{(2)}_7)^\top $$\end{document}
![]() . Figure 4b shows the conditional correct response probabilities given the fine-grained attributes, that is, the
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\theta $$\end{document}
. Figure 4b shows the conditional correct response probabilities given the fine-grained attributes, that is, the
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\theta $$\end{document}
![]() -parameters in (18). For each item j, the column
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\theta _0$$\end{document}
-parameters in (18). For each item j, the column
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\theta _0$$\end{document}
![]() refers to
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\theta ^{(1)}_{j,\varnothing }$$\end{document}
refers to
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\theta ^{(1)}_{j,\varnothing }$$\end{document}
![]() ; column
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\theta _k$$\end{document}
; column
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\theta _k$$\end{document}
![]() refers to
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\theta ^{(1)}_{j,\{k\}}$$\end{document}
refers to
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\theta ^{(1)}_{j,\{k\}}$$\end{document}
![]() for
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$k=1,\ldots ,7$$\end{document}
for
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$k=1,\ldots ,7$$\end{document}
![]() ; column
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\theta _{15}$$\end{document}
; column
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\theta _{15}$$\end{document}
![]() refers to the
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\theta ^{(1)}_{j,\{1,5\}}$$\end{document}
refers to the
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\theta ^{(1)}_{j,\{1,5\}}$$\end{document}
![]() , etc. For an item
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$j\in \{1,\ldots ,28\}$$\end{document}
, etc. For an item
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$j\in \{1,\ldots ,28\}$$\end{document}
![]() , only those “effective”
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\theta $$\end{document}
, only those “effective”
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\theta $$\end{document}
![]() -parameters are plotted in Fig. 4. For example, the first item requires the first and the fifth attributes (i.e., Number and Knowing), so only four
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\theta $$\end{document}
-parameters are plotted in Fig. 4. For example, the first item requires the first and the fifth attributes (i.e., Number and Knowing), so only four
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\theta $$\end{document}
![]() -parameters are “effective” and shown in the first line in Fig. 4b:
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\theta _{0}$$\end{document}
-parameters are “effective” and shown in the first line in Fig. 4b:
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\theta _{0}$$\end{document}
![]() ,
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\theta _1$$\end{document}
,
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\theta _1$$\end{document}
![]() ,
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\theta _5$$\end{document}
,
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\theta _5$$\end{document}
![]() , and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\theta _{15}$$\end{document}
, and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\theta _{15}$$\end{document}
![]() .
.

Figure. 4 TIMSS 2019 eighth-grade math assessment US data, item block No.2, estimated parameters from the Hybrid-GDINA-DINA model. Plot (a): deeper DINA-layer parameters, with the left column being
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\varvec{g}^{(2)}$$\end{document}
![]() and the right column being
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{1}_{7\times 1} - \varvec{s}^{(2)}$$\end{document}
and the right column being
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{1}_{7\times 1} - \varvec{s}^{(2)}$$\end{document}
![]() ; plot (b): conditional correct response probabilities under GDINA.
; plot (b): conditional correct response probabilities under GDINA.

Figure. 5 TIMSS 2019 eighth-grade math assessment US data, item block No.2, estimated latent profiles. In plots (b) and (d), the sample data points are jittered from zero/one.
To further inspect the latent attributes’ mutual dependence, we calculate the element-wise posterior modes of the discrete latent profiles and obtain the
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$N\times K_1$$\end{document}
![]() binary matrix
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\bar{\textbf{A}}^{(1)} = (\bar{a}^{(1)}_{i,k})$$\end{document}
binary matrix
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\bar{\textbf{A}}^{(1)} = (\bar{a}^{(1)}_{i,k})$$\end{document}
![]() and the
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$N\times K_2$$\end{document}
and the
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$N\times K_2$$\end{document}
![]() binary matrix
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\bar{\textbf{A}}^{(2)} = (\bar{a}^{(1)}_{i,m})$$\end{document}
binary matrix
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\bar{\textbf{A}}^{(2)} = (\bar{a}^{(1)}_{i,m})$$\end{document}
![]() . Specifically, each binary entry
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\bar{a}^{(1)}_{i,k}$$\end{document}
. Specifically, each binary entry
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\bar{a}^{(1)}_{i,k}$$\end{document}
![]() is the posterior mode of
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$a^{(1)}_{i,k}$$\end{document}
is the posterior mode of
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$a^{(1)}_{i,k}$$\end{document}
![]() based on the retained posterior samples, and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\bar{a}^{(2)}_{i,m}$$\end{document}
based on the retained posterior samples, and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\bar{a}^{(2)}_{i,m}$$\end{document}
![]() is similarly obtained. Based on the
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$K_1=7$$\end{document}
is similarly obtained. Based on the
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$K_1=7$$\end{document}
![]() columns of
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\bar{\textbf{A}}^{(1)}$$\end{document}
columns of
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\bar{\textbf{A}}^{(1)}$$\end{document}
![]() and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$K_2=2$$\end{document}
and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$K_2=2$$\end{document}
![]() columns of
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\bar{\textbf{A}}^{(2)}$$\end{document}
columns of
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\bar{\textbf{A}}^{(2)}$$\end{document}
![]() , we generate the scatterplot matrices in Fig. 5. In this figure, the two plots on the left show the correlation between the second-layer domain attributes (Fig. 5a) and those between pairs of the first-layer fine-grained attributes (Fig. 5c). The two plots on the right panel of Fig. 5 show the jittered versions of the scatterplot matrices, which more explicitly visualize the pairwise joint distributions of latent variables. As expected, the seven fine-grained latent skills show relatively high positive dependencies on each other, which supports using the DeepCDM modeling framework. Moreover, the estimated posterior mode matrices
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\bar{\textbf{A}}^{(1)}$$\end{document}
, we generate the scatterplot matrices in Fig. 5. In this figure, the two plots on the left show the correlation between the second-layer domain attributes (Fig. 5a) and those between pairs of the first-layer fine-grained attributes (Fig. 5c). The two plots on the right panel of Fig. 5 show the jittered versions of the scatterplot matrices, which more explicitly visualize the pairwise joint distributions of latent variables. As expected, the seven fine-grained latent skills show relatively high positive dependencies on each other, which supports using the DeepCDM modeling framework. Moreover, the estimated posterior mode matrices
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\bar{\textbf{A}}^{(1)}$$\end{document}
![]() and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\bar{\textbf{A}}^{(2)}$$\end{document}
and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\bar{\textbf{A}}^{(2)}$$\end{document}
![]() provide multi-granularity diagnoses of students’ strengths/weaknesses on both the two broader domain attributes and the seven more fine-grained attributes.
provide multi-granularity diagnoses of students’ strengths/weaknesses on both the two broader domain attributes and the seven more fine-grained attributes.
Next, we also perform a comparative analysis of a TIMSS 2019 fourth-grade math assessment dataset (item block No. 7) using both a DeepCDM and a traditional CDM to see their difference. Specifically, we consider both the Hybrid G-D model (which is GDINA with a higher-order DINA layer), and GDINA with a saturated latent attribute model. In terms of statistical parsimony, our Hybrid G-D requires much fewer parameters than GDINA with a saturated latent layer. In particular, to model
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$K_1=6$$\end{document}
![]() fine-grained latent attributes, the Hybrid G-D model uses only
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$3 + 6\times 2 = 15$$\end{document}
fine-grained latent attributes, the Hybrid G-D model uses only
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$3 + 6\times 2 = 15$$\end{document}
![]() parameters while the traditional saturated attribute model uses a large number of
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$2^6-1 = 63$$\end{document}
parameters while the traditional saturated attribute model uses a large number of
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$2^6-1 = 63$$\end{document}
![]() parameters. Such statistical parsimony implies that our DeepCDM would require a smaller sample size to reach the same level of parameter estimation precision. In terms of substantive interpretations, the correlation plots in Fig. 6 show that the Hybrid G-D model gives a much more interpretable correlation structure among the fine-grained latent attributes (in the left panel) than GDINA with a saturated attribute model (in the right panel). Specifically, recall that the first three attributes fall in the “Content” domain and the last three attributes fall in the “Cognitive” domain. The nearly block diagonal heatmap in Fig. 6a shows that our DeepCDM induces much higher correlations among attributes within a same domain than those across two different domains. On the other hand, for the GDINA model with a saturated attribute model, Fig. 6b shows a somewhat counter-intuitive pattern: “Data” has a relatively small correlation with all other attributes and there are no clear separation between the content-related attributes and the cognitive-related ones.
parameters. Such statistical parsimony implies that our DeepCDM would require a smaller sample size to reach the same level of parameter estimation precision. In terms of substantive interpretations, the correlation plots in Fig. 6 show that the Hybrid G-D model gives a much more interpretable correlation structure among the fine-grained latent attributes (in the left panel) than GDINA with a saturated attribute model (in the right panel). Specifically, recall that the first three attributes fall in the “Content” domain and the last three attributes fall in the “Cognitive” domain. The nearly block diagonal heatmap in Fig. 6a shows that our DeepCDM induces much higher correlations among attributes within a same domain than those across two different domains. On the other hand, for the GDINA model with a saturated attribute model, Fig. 6b shows a somewhat counter-intuitive pattern: “Data” has a relatively small correlation with all other attributes and there are no clear separation between the content-related attributes and the cognitive-related ones.

Figure. 6 Estimated attribute correlation plots given by the proposed Hybrid GDINA-DINA model (i.e., GDINA model with a higher-order DINA layer) in (a) and GDINA with a saturated attribute model in b for the TIMSS 2019 4th grade math booklet 7 dataset.
7. Discussion
In this work, we have proposed a new family of interpretable diagnostic models called DeepCDMs, established transparent identifiability conditions and general identifiability theory, and developed Bayesian estimation methods for them. On one hand, DeepCDMs are well motivated by the applied goal of uncovering rich and structured diagnostic information from educational and behavioral data. Through the estimated multilayer latent profiles, DeepCDMs enable multi-granularity diagnoses of latent attributes from coarse to fine grained and from high level to detailed. On the other hand, in terms of discrete latent structures, DeepCDMs share similarities with powerful deep learning models such as deep belief networks (Hinton et al., Reference Hinton, Osindero and Teh2006) and deep Boltzmann machines (Salakhutdinov and Larochelle, Reference Salakhutdinov and Larochelle2010), and are expressive modeling tools. Distinctively, DeepCDMs are fully identifiable under our conditions, which is a desirable property lacked by most deep learning models. In a nutshell, our identifiability conditions can be summarized as: as long as each
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{Q}^{(d)}$$\end{document}
![]() satisfies the identifiability condition under the CDM to which the shallower layer
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{A}^{(d-1)}$$\end{document}
satisfies the identifiability condition under the CDM to which the shallower layer
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{A}^{(d-1)}$$\end{document}
![]() (or
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{R}$$\end{document}
(or
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{R}$$\end{document}
![]() if
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$d=1$$\end{document}
if
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$d=1$$\end{document}
![]() ) conforms, then the entire DeepCDM is identifiable. Our identifiability guarantees form the very foundation for deriving interpretable and reliable insights in practical applications, and offer the very guidelines on adopting a shrinking-ladder-shaped generative graph structure. Simulation results empirically corroborate the identifiability conclusions, and also demonstrate the good practical performance of our Bayesian estimation algorithms.
) conforms, then the entire DeepCDM is identifiable. Our identifiability guarantees form the very foundation for deriving interpretable and reliable insights in practical applications, and offer the very guidelines on adopting a shrinking-ladder-shaped generative graph structure. Simulation results empirically corroborate the identifiability conclusions, and also demonstrate the good practical performance of our Bayesian estimation algorithms.
In our real data example in Sect. 6 and other potential future applications, the deeper-layer binary variables are not used in order to capture the person’s continuous variability in the coarse-grained higher-order skills as in the HO-CDM in de la Torre and Douglas (Reference de la Torre and Douglas2004). Instead, the higher-order meta attributes provide an additional layer of discrete diagnoses of the persons’ higher-order skills. Such a diagnostic modeling goal shares a similar motivation with originally using CDMs as an alternative modeling tool to the classical (multi-dimensional) IRT models with continuous latent traits. Historically, IRT has been the dominating modeling methodology in educational and psychological measurement, thanks to their excellent ability of capturing subjects’ latent variability. Nonetheless, in the recent two decades, CDMs have also emerged as powerful alternative tools that provide fine-grained discrete diagnoses of skills, instead of capturing the continuous variability. In this sense, we view the proposed DeepCDMs as going further down the road of diagnostic classification, by providing skill diagnoses with multiple layers of granularity. To fully realize the applied potential of the proposed new framework, our far-reaching goal is for practitioners to design new cognitive diagnostic assessments directly inspired by the DeepCDM identifiability theory.
DeepCDMs suppose that the latent variables follow a multilayer generative structure. In practice, admittedly, it may not always be the case that attributes follow multiple neat layers as in a DeepCDM. On the other hand, however, we believe that in a number of CDM modeling and application scenarios, the advantages of DeepCDMs in terms of statistical parsimony, practical interpretability, and identifiability outweigh the induced limitation. Our motivation for proposing DeepCDMs is not to replace, but to complement, other latent structural models (including attribute hierarchy methods, higher-order continuous latent trait models) in the CDM literature as an alternative family of interpretable and identifiable models. Specifically, we expect DeepCDMs will be suitable for those applications where multi-resolution discrete diagnoses of latent attributes are of interest. We hope this work contributes a useful first step toward a versatile toolbox of providing statistically justified multi-granularity diagnostic classification.
The proposed DeepCDM framework unlocks many interesting future research possibilities. First, this paper has focused on binary responses and binary latent variables in all the layers, but the DeepCDM framework can be readily extended to polytomous responses and polytomous attributes (Chen and de la Torre, Reference Chen and de la Torre2013; Gao et al., Reference Gao, Ma, Wang, Cai and Tu2021). Similar identifiability conditions on the between-layer
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{Q}$$\end{document}
![]() -matrices may be obtained, and corresponding Bayesian estimation methods can also be developed. To this end, the Bayesian Pyramid model and its corresponding Bayesian estimation method in Gu and Dunson (Reference Gu and Dunson2023) is an example, which deals with multivariate unordered categorical data with binary latent layers. Second, this paper develops Markov Chain Monte Carlo algorithms for estimation. In the future, it would also be useful to develop more scalable variational Bayesian inference algorithms or EM algorithms for DeepCDMs to enhance computational efficiency.
-matrices may be obtained, and corresponding Bayesian estimation methods can also be developed. To this end, the Bayesian Pyramid model and its corresponding Bayesian estimation method in Gu and Dunson (Reference Gu and Dunson2023) is an example, which deals with multivariate unordered categorical data with binary latent layers. Second, this paper develops Markov Chain Monte Carlo algorithms for estimation. In the future, it would also be useful to develop more scalable variational Bayesian inference algorithms or EM algorithms for DeepCDMs to enhance computational efficiency.
Another interesting future direction is to perform exploratory DeepCDM analysis and estimate the
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{Q}$$\end{document}
![]() -matrices from data. This initial work has focused on confirmatory scenarios in which multi-granularity design information are available and can be directly translated into the
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{Q}$$\end{document}
-matrices from data. This initial work has focused on confirmatory scenarios in which multi-granularity design information are available and can be directly translated into the
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{Q}$$\end{document}
![]() -matrices. Nevertheless, all of our identifiability results are fully general and applicable to the exploratory settings with unknown
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{Q}$$\end{document}
-matrices. Nevertheless, all of our identifiability results are fully general and applicable to the exploratory settings with unknown
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{Q}$$\end{document}
![]() -matrices. This means we have also obtained identifiability guarantees for directly estimating all the
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{Q}$$\end{document}
-matrices. This means we have also obtained identifiability guarantees for directly estimating all the
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{Q}$$\end{document}
![]() -matrices in a DeepCDM. In recent years, there has been an increasing interest in exploratory estimation of CDMs, including those using Bayesian approaches (Balamuta and Culpepper, Reference Balamuta and Culpepper2022; Chen et al., Reference Chen, Culpepper and Liang2020; Culpepper, Reference Culpepper2019b) and those using frequentist ones (Chen et al., Reference Chen, Liu, Xu and Ying2015; Gu and Xu, Reference Gu and Xu2023; Xu and Shang, Reference Xu and Shang2018). Developing efficient methods to estimate the multiple
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{Q}$$\end{document}
-matrices in a DeepCDM. In recent years, there has been an increasing interest in exploratory estimation of CDMs, including those using Bayesian approaches (Balamuta and Culpepper, Reference Balamuta and Culpepper2022; Chen et al., Reference Chen, Culpepper and Liang2020; Culpepper, Reference Culpepper2019b) and those using frequentist ones (Chen et al., Reference Chen, Liu, Xu and Ying2015; Gu and Xu, Reference Gu and Xu2023; Xu and Shang, Reference Xu and Shang2018). Developing efficient methods to estimate the multiple
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\textbf{Q}$$\end{document}
![]() -matrices in a DeepCDM is important future work. Furthermore, in an even more exploratory setting, it would also be interesting to study how to select the number of latent variables
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$K_1$$\end{document}
-matrices in a DeepCDM is important future work. Furthermore, in an even more exploratory setting, it would also be interesting to study how to select the number of latent variables
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$K_1$$\end{document}
![]() ,
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$K_2$$\end{document}
,
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$K_2$$\end{document}
![]() , etc., in each layer in a DeepCDM. Nonparametric Bayesian approaches can be useful tools toward this end (e.g., Chen et al., Reference Chen, Liu, Culpepper and Chen2021, Fang et al., Reference Fang, Liu and Ying2019, Gu and Dunson, Reference Gu and Dunson2023).
, etc., in each layer in a DeepCDM. Nonparametric Bayesian approaches can be useful tools toward this end (e.g., Chen et al., Reference Chen, Liu, Culpepper and Chen2021, Fang et al., Reference Fang, Liu and Ying2019, Gu and Dunson, Reference Gu and Dunson2023).
On the application front, for modern large-scale educational assessments such as TIMSS and PISA, we believe there is a promising future potential of using the DeepCDM methodology to model and analyze high-dimensional response data, to generate new insights into student achievement, and to enhance multi-granularity instruction and intervention. Indeed, the TIMSS 2019 eighth grade math assessment offers more levels of item information than are used in our current data analysis. For example, under the “Number” skill, there are still four different topic areas: Integers/Fractions and decimals/Ratio, proportion, and percent, which are candidates for more fine-grained attributes. In the future, advancing and refining the computational techniques for DeepCDMs with more layers can help extract even more nuanced diagnoses about student subcompetences from large-scale assessment data.
On a final note, we would like to give a broader discussion on DeepCDMs’ implications. In applied cognitive psychology, the concept of “higher-order thinking skills” was put forward (Brookhart, Reference Brookhart2010; Schraw and Robinson, Reference Schraw and Robinson2011) which includes problem solving, critical thinking, creativity, and so on; in linguistics, the “ladder of abstraction” idea was proposed (Hayakawa, Reference Hayakawa1947; Munson et al., Reference Munson, Edwards, Beckman, Cohn, Fougeron, Huffman, Cohn, Fougeron and Huffman2011) to describe the way humans think and communicate in varying degrees of abstraction through languages; and in deep learning, an influential review article Bengio et al. (Reference Bengio, Courville and Vincent2013) pointed out that using deep architectures can potentially lead to progressively more abstract features at higher layers of representations. Our shrinking-ladder-shaped DeepCDMs attempt to offer principled and identifiable statistical models to back up such substantive theory and deep learning heuristics. We hope the DeepCDM framework will be useful for practitioners, illuminating for theoreticians, and triggering fruitful future research on using rigorous statistical methods to cross-fertilize the fields of (deep) machine learning and psychometrics.
Supplementary Material.
The Supplementary Material contains the proofs of the identifiability theorems and the details of the Gibbs sampling algorithms for posterior computation.
Acknowledgements
This work is partially supported by NSF Grant DMS-2210796. The author thanks the editor Prof. Matthias von Davier and two anonymous reviewers for their many helpful and constructive comments that helped improve this paper’s quality.