1. Introduction
In the present paper, we consider the problem describing two-dimensional gravity waves travelling on a flow of finite depth. For an ideal fluid of constant density, say water, the effects of surface tension are neglected, whereas the flow is assumed to be rotational with a constant vorticity; this, according to observations, is a type of motion commonly occurring in nature (see, for example, Swan, Cummings & James (Reference Swan, Cummings and James2001), Thomas (Reference Thomas1981) and references therein). Also, it is assumed that the reference frame is moving with the wave so that the relative velocity field is stationary. Our aim is to consider a new class of solitary waves each having a cat's-eye – a region of closed streamlines surrounding a stagnation point. To the best of the authors’ knowledge, there are no results concerning solitary waves having such a pattern of streamlines; so far, this kind of behaviour has been known only for periodic waves with vorticity.
The mathematical theory of two-dimensional solitary waves on irrotational flows goes back to the discovery of John Scott Russell, who was the first to observe in 1834 and subsequently to analyse a solitary wave of elevation (see Russell Reference Russell1844). The existence of the latter was justified mathematically by Boussinesq in 1877 and rediscovered by Korteweg and de Vries in 1895. The existence of solitary waves in the framework of the full water wave problem is far more complicated and the first proofs were obtained much later (Lavrentiev Reference Lavrentiev1954; Friedrichs & Hyers Reference Friedrichs and Hyers1954). Modern proofs by Thomas (Reference Thomas1977) and Mielke (Reference Mielke1988) use the Nash–Moser implicit function theorem and a dynamical system approach, respectively. All these papers deal only with waves of small amplitude, whereas Amick & Toland (Reference Amick and Toland1981b) constructed large-amplitude solitary waves using global bifurcation theory and then proved the existence of a limiting wave of the extreme form, that is, having an angled crest (see Amick, Fraenkel & Toland Reference Amick, Fraenkel and Toland1982). All solitary waves considered in these papers are of positive elevation, symmetric and monotone on each side of the crest (see Craig & Sternberg Reference Craig and Sternberg1988; McLeod Reference McLeod1984). The corresponding flows, being irrotatonal, have a simple structure of streamlines (see Constantin & Escher Reference Constantin and Escher2007; Constantin Reference Constantin2010): they are unbounded curves similar (diffeomorphic) to the free surface profile. For all unidirectional waves with vorticity (when the horizontal component ![]() $u$ of the relative velocity field has a constant sign everywhere in the fluid), the latter property is also true. Essentially, this forbids the presence of critical layers and stagnation points.
$u$ of the relative velocity field has a constant sign everywhere in the fluid), the latter property is also true. Essentially, this forbids the presence of critical layers and stagnation points.
The first construction of unidirectional small-amplitude solitary waves with vorticity was given by Ter-Krikorov (Reference Ter-Krikorov1962), whereas Benjamin (Reference Benjamin1962) obtained an approximate form of the wave profile which is the same as in the irrotational case. However, relationships between the wave amplitude, the length scale and the propagation velocities depend on the primary velocity distribution in a complicated way. Much later, Groves & Wahlén (Reference Groves and Wahlén2008) and Hur (Reference Hur2008) obtained new results for this topic. The latter authors also considered solitary waves with vorticity in the presence of surface tension (Groves & Wahlén Reference Groves and Wahlén2007). The method used in Groves & Wahlén (Reference Groves and Wahlén2007, Reference Groves and Wahlén2008), known as spatial dynamics, is essentially an infinite-dimensional version of the centre-manifold reduction which is known as spatial dynamics because it is applied to a Hamiltonian system with the horizontal spatial coordinate playing the role of time. The first use of this method in the water-wave theory is due to Kirchgässner (Reference Kirchgässner1982, Reference Kirchgässner1988) (see also Mielke Reference Mielke1986, Reference Mielke1988, Reference Mielke1991), whereas an application of spatial dynamics to three-dimensional waves is given in Groves & Nilsson (Reference Groves and Nilsson2018) (see also references therein). So far, use of spatial dynamics has been restricted exclusively to small-amplitude waves. Recently, Wheeler (Reference Wheeler2013) examined waves of large amplitude, but, like in the irrotational case, all solitary-wave solutions have the same structure of streamlines, that is, are symmetric and of positive elevation (see Hur Reference Hur2008; Wheeler Reference Wheeler2015; Kozlov, Kuznetsov & Lokharu Reference Kozlov, Kuznetsov and Lokharu2015, Reference Kozlov, Kuznetsov and Lokharu2017). Thus, looking for a more complicated geometry of solitary waves, it is natural to consider flows with stagnation points and critical levels within the fluid domain. As in Wahlén (Reference Wahlén2009), by a critical level we mean a curve for which the horizontal component of velocity vanishes.
The simplest case of flows with critical levels is that of constant negative vorticity, and there are several advantages of studying this case. Flows with constant vorticity are more easily tractable mathematically (see Ehrnström Reference Ehrnström2008; Wahlén Reference Wahlén2009; Constantin, Strauss & Vărvărucă Reference Constantin, Strauss and Vărvărucă2016; Hur & Wheeler Reference Hur and Wheeler2020). Moreover, these flows are of substantial practical importance being pertinent to a wide range of hydrodynamic phenomena (see Constantin et al. Reference Constantin, Strauss and Vărvărucă2016, p. 196); an important example are currents producing shear near the sea bed. A new feature of laminar flows with constant vorticity (compared with irrotational ones) is that there are flows with critical levels. Moreover, it was shown by Wahlén (Reference Wahlén2009) that small perturbations of these parallel flows are periodic waves with arrays of cat's-eye vortices – regions where closed streamlines surround stagnation points. An extension to periodic waves of large amplitude with critical layers is given in Constantin et al. (Reference Constantin, Strauss and Vărvărucă2016) (it includes overhanging waves). Despite the fact that waves considered in Wahlén (Reference Wahlén2009) and Constantin et al. (Reference Constantin, Strauss and Vărvărucă2016) have critical layers, the geometry of free-surface profiles is still simple; it is symmetric about every crest and trough, whereas monotone in between (just like that of the classical Stokes waves). Examples of more complicated wave profiles are known (see Ehrnström, Escher & Wahlén Reference Ehrnström, Escher and Wahlén2011; Aasen & Varholm Reference Aasen and Varholm2017; Kozlov & Lokharu Reference Kozlov and Lokharu2017, Reference Kozlov and Lokharu2019). However, the vorticity distribution must be at least linear in order to construct them. It should be emphasized that all theoretical studies of waves with critical layers have been restricted so far to the periodic setting.
In the 1980s and 1990s, much attention was devoted to numerical computation of various solitary waves on flows with constant vorticity; see the papers by Vanden-Broeck (Reference Vanden-Broeck1994, Reference Vanden-Broeck1995) and references therein. In particular, an interesting family of solitary-wave profiles was obtained in the second of these papers; it approaches a singular one with trapped circular bulb at the crest which happens as the gravity acceleration tends to zero. However, no attempt was made to find bottom or interior stagnation points for solitary waves. On the other hand, Teles da Silva & Peregrine (Reference Teles da Silva and Peregrine1988) were the first who numerically observed eddies surrounding interior stagnation points beneath wave crests of periodic waves on water of finite depth with constant vorticity (see also Ribeiro, Milewski & Nachbin Reference Ribeiro, Milewski and Nachbin2017).
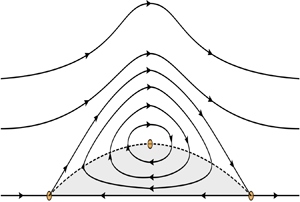
In the present paper, a new family of solitary waves is constructed for large negative values of the constant vorticity. All these waves have a remarkable property: the corresponding flow is unidirectional at both infinities, but there is a cat's-eye vortex centred below the wave crest (see figure 1). (The term was coined by Kelvin in his considerations of a shear flow having this pattern of streamlines; see Majda & Bertozzi Reference Majda and Bertozzi2002, pp. 53–54.) The vortex is bottom-adjacent and separated from the unidirectional flow above it by a critical streamline connecting two stagnation points on the bottom. Every solitary wave under consideration is obtained as a long-wave limit of Stokes wave-trains; in this aspect, our result is similar to that of Amick & Toland (Reference Amick and Toland1981a), who dealt with the irrotational case. However, Stokes waves have a cat's-eye vortex centred below each crest in our case. For a sketch of the corresponding streamline pattern, see the top part of figure 4, whereas examples computed numerically are presented in Ribeiro et al. (Reference Ribeiro, Milewski and Nachbin2017, pp. 803–804). As the wavelength goes to infinity, these vortices do not shrink, which differs from the case of small-amplitude waves, a sketch of which is plotted by Wahlén (Reference Wahlén2009) in his figure 1. A sketch of streamlines corresponding to our solitary wave is plotted in figure 1, where the circles denote stagnation points. Moreover, the dashed line shows the critical level along which the horizontal component of velocity vanishes and the critical streamline located above the critical level also connects the two bottom stagnation points; the direction of streaming is indicated by arrows.
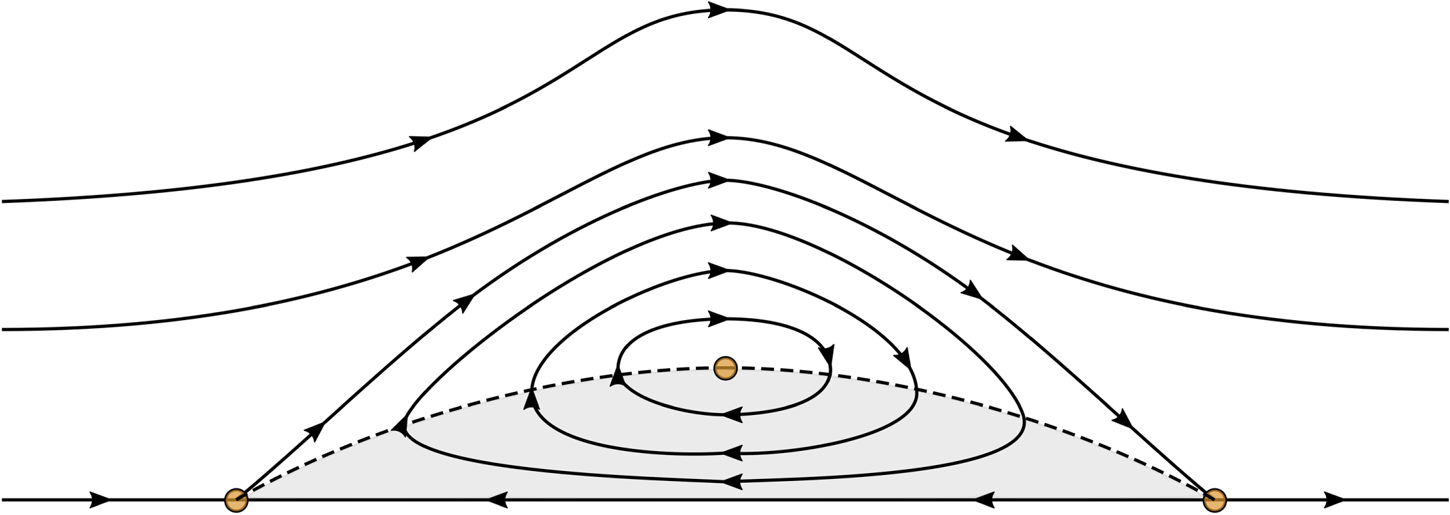
Figure 1. A sketch of a streamline pattern. Solid lines are streamlines and the direction of the flow (in the moving frame) is denoted by arrows. The dashed curve is a critical layer, where the horizontal component of the velocity field vanishes, while circles are stagnation points. The direction of the flow below the critical layer (grey region) is opposite to the direction of the flow above it.
It should be emphasized that small-amplitude solitary waves constructed in this paper cannot be captured by applying spatial dynamics directly because the problem turns, in some sense, into a singular one as the vorticity tends to infinity. Thus, an appropriate scaling and a careful analysis are required before spatial dynamics can be used.
The plan of the paper is as follows. Statement of the problem and formulation of the main results are given in § 1.1. Then, in § 2, the problem is scaled and reformulated in a suitable way. After that, in § 3, it is reduced to a finite-dimensional Hamiltonian system and theorem 3.2 provides the existence of solitary waves. Then the main theorem 1.1 is proved in § 4. A discussion of the presented results is given in § 5.
1.1. Statement of the problem and formulation of the main result
Let an open channel of uniform rectangular cross-section be bounded from below by a horizontal rigid bottom and let water occupying the channel be bounded from above by a free surface not touching the bottom. The surface tension is neglected and the pressure is assumed to be constant on the free surface. In appropriate Cartesian coordinates ![]() $(X,Y)$, the bottom coincides with the
$(X,Y)$, the bottom coincides with the ![]() $X$ axis and gravity acts in the negative
$X$ axis and gravity acts in the negative ![]() $Y$ direction. The frame of reference is chosen so that the velocity field is time-independent as well as the unknown free-surface profile. The latter is assumed to be the graph of
$Y$ direction. The frame of reference is chosen so that the velocity field is time-independent as well as the unknown free-surface profile. The latter is assumed to be the graph of ![]() $Y = \eta (X)$,
$Y = \eta (X)$, ![]() $X\in \mathbb {R}$, where
$X\in \mathbb {R}$, where ![]() $\eta$ is a positive function; we note that for irrotational waves this is always true (see Varvaruca Reference Varvaruca2008). The water motion is supposed to be two-dimensional and rotational, where the vorticity distribution is a constant; combining this and the incompressibility of water, we seek the velocity field in the form
$\eta$ is a positive function; we note that for irrotational waves this is always true (see Varvaruca Reference Varvaruca2008). The water motion is supposed to be two-dimensional and rotational, where the vorticity distribution is a constant; combining this and the incompressibility of water, we seek the velocity field in the form ![]() $(\psi _Y, -\psi _X)$, in which case
$(\psi _Y, -\psi _X)$, in which case ![]() $\psi (X,Y)$ is referred to as the stream function.
$\psi (X,Y)$ is referred to as the stream function.
It is convenient to use the non-dimensional variables proposed by Keady & Norbury (Reference Keady and Norbury1978). Namely, lengths and velocities are scaled to ![]() $(Q^2/g)^{1/3}$ and
$(Q^2/g)^{1/3}$ and ![]() $(Q g)^{1/3}$, respectively, where
$(Q g)^{1/3}$, respectively, where ![]() $Q$ is the mass flux and
$Q$ is the mass flux and ![]() $g$ is the acceleration due to gravity. Thus,
$g$ is the acceleration due to gravity. Thus, ![]() $Q$ and
$Q$ and ![]() $g$ are equal to unity in this case. Since the surface tension is neglected, the pair
$g$ are equal to unity in this case. Since the surface tension is neglected, the pair ![]() $(\psi , \eta )$ must satisfy the following free-boundary problem:
$(\psi , \eta )$ must satisfy the following free-boundary problem:
Here ![]() $b > 0$ is the vorticity constant, while constant
$b > 0$ is the vorticity constant, while constant ![]() $R$ is considered as a parameter of the problem; it is referred to as the total head or the Bernoulli constant (e.g. Keady & Norbury Reference Keady and Norbury1978). This statement (with a general vorticity distribution) has long been known and its derivation from the governing equations and the assumptions about the boundary behaviour of water particles can be found in Constantin & Strauss (Reference Constantin and Strauss2004).
$R$ is considered as a parameter of the problem; it is referred to as the total head or the Bernoulli constant (e.g. Keady & Norbury Reference Keady and Norbury1978). This statement (with a general vorticity distribution) has long been known and its derivation from the governing equations and the assumptions about the boundary behaviour of water particles can be found in Constantin & Strauss (Reference Constantin and Strauss2004).
A solution of problem (1.1a)–(1.1d) defines a solitary wave provided the following relations hold:
Here ![]() $h$ is a constant, which coincides with the depth of a certain laminar flow at infinity. A sketch of the profile, which is typical for a solitary wave, is shown in figure 2. It should be noted that the flow at infinity is not uniform as it is in the irrotational case.
$h$ is a constant, which coincides with the depth of a certain laminar flow at infinity. A sketch of the profile, which is typical for a solitary wave, is shown in figure 2. It should be noted that the flow at infinity is not uniform as it is in the irrotational case.
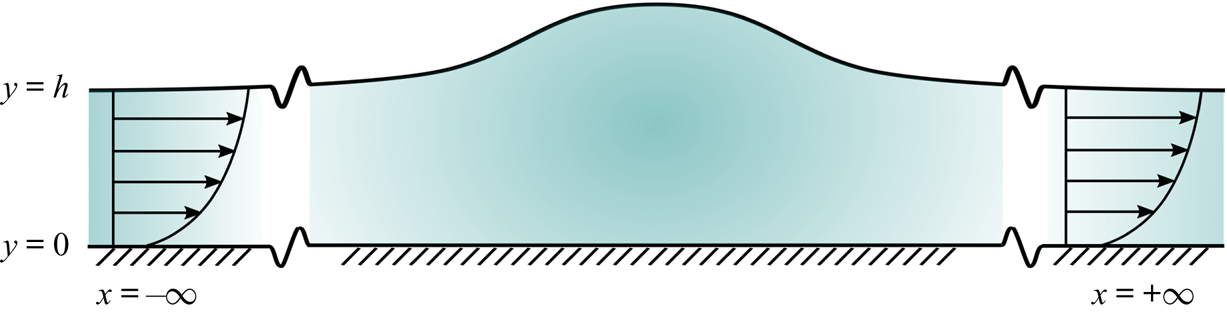
Figure 2. A sketch of the solitary wave profile on a unidirectional flow.
Now we are in a position to formulate our main result concerning the existence of solitary waves of elevation.
Theorem 1.1 For every sufficiently large ![]() $b > 0$, problem (1.1a)–(1.1d), (1.2) has a solution
$b > 0$, problem (1.1a)–(1.1d), (1.2) has a solution ![]() $(\psi , \eta )$ with the following properties:
$(\psi , \eta )$ with the following properties:
(i)
 $\eta (X) > h$ for all
$\eta (X) > h$ for all  $X \in \mathbb {R}$, that is,
$X \in \mathbb {R}$, that is,  $\eta$ describes a solitary wave of elevation;
$\eta$ describes a solitary wave of elevation;(ii) there are two stagnation points on the bottom and two streamlines within the fluid domain connect these points (see figure 1); the critical level corresponds to the upper streamline, whereas the other one is on the bottom;
(iii) the critical streamline surrounds a region of streamlines around an interior stagnation point on the vertical line through the crest;
(iv) all streamlines above the critical one are diffeomorphic to the free-surface profile.
An equivalent formulation of this assertion and its proof are given in the next two sections. Our approach is based on a carefully chosen scaling of the original problem. Then we apply the spatial dynamics method to the scaled problem in the same way as in Kozlov & Lokharu (Reference Kozlov and Lokharu2019). This allows us to reduce the problem to a finite-dimensional Hamiltonian system; it has one degree of freedom and admits a homoclinic orbit describing a solitary wave of elevation in the original coordinates. The orbit goes around an equilibrium point representing a shear flow of constant depth with a counter-current and this guarantees the presence of a stagnation point and a critical streamline as is illustrated in figure 1.
2. Reformulation of the problem
To avoid difficulties arising from the fact that ![]() $b$ is large, it is convenient to scale variables as follows:
$b$ is large, it is convenient to scale variables as follows:
This transforms (1.1a)–(1.1d) into
where ![]() $\gamma = b^{-3/2}$ and
$\gamma = b^{-3/2}$ and ![]() $\bar {R} = R b^{-1}$. This problem describes two-dimensional waves with vorticity (the latter is equal to one) and weak gravity because
$\bar {R} = R b^{-1}$. This problem describes two-dimensional waves with vorticity (the latter is equal to one) and weak gravity because ![]() $\gamma$ is a small parameter provided
$\gamma$ is a small parameter provided ![]() $b$ is large.
$b$ is large.
Let us consider the stream solution ![]() $\bar {\psi } = u(\bar {y};s)$ and
$\bar {\psi } = u(\bar {y};s)$ and ![]() $\bar {\eta } = h(s)$ such that
$\bar {\eta } = h(s)$ such that ![]() $u'(0)=s$. From (2.2a)–(2.2c) one obtains the unique pair
$u'(0)=s$. From (2.2a)–(2.2c) one obtains the unique pair
and (2.2d) yields the corresponding Bernoulli constant:
If ![]() $s<0$, then the laminar flow defined by (2.3a,b) has a near-bottom counter-current, whereas the corresponding flow is unidirectional when
$s<0$, then the laminar flow defined by (2.3a,b) has a near-bottom counter-current, whereas the corresponding flow is unidirectional when ![]() $s > 0$. In what follows we assume that
$s > 0$. In what follows we assume that ![]() $s<0$.
$s<0$.
2.1. Flattening transformation
Changing the coordinates ![]() $(\bar {x}, \bar {y})$ to
$(\bar {x}, \bar {y})$ to
we map the water domain onto the strip ![]() $\mathbb {R} \times (0, h(s))$. Let
$\mathbb {R} \times (0, h(s))$. Let
be a new unknown function, for which problem (2.2) with ![]() $\bar {R} = \bar {R}(s)$ takes the form
$\bar {R} = \bar {R}(s)$ takes the form
Note that ![]() $\hat {\varPhi } = u(y;s)$ and
$\hat {\varPhi } = u(y;s)$ and ![]() $\bar {\eta } = h(s)$ is a solution of this system. Let us write (2.7) as a first-order system, for which purpose it is convenient to introduce the variable
$\bar {\eta } = h(s)$ is a solution of this system. Let us write (2.7) as a first-order system, for which purpose it is convenient to introduce the variable ![]() $\hat {\varPsi }$ conjugate to
$\hat {\varPsi }$ conjugate to ![]() $\hat \varPhi$ (cf. Kozlov & Kuznetsov Reference Kozlov and Kuznetsov2013):
$\hat \varPhi$ (cf. Kozlov & Kuznetsov Reference Kozlov and Kuznetsov2013):
This allows us to write (2.7) as follows:
Furthermore, we have that
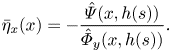 \begin{equation} \bar{\eta}_x(x) = - \frac{\hat{\varPsi}(x,h(s))}{\hat{\varPhi}_y(x,h(s))}. \end{equation}
\begin{equation} \bar{\eta}_x(x) = - \frac{\hat{\varPsi}(x,h(s))}{\hat{\varPhi}_y(x,h(s))}. \end{equation} Relations (2.9) can be considered as an infinite-dimensional dynamical system for ![]() $\hat {\varPhi }$ and
$\hat {\varPhi }$ and ![]() $\hat {\varPsi }$ only. Indeed,
$\hat {\varPsi }$ only. Indeed, ![]() $\bar {\eta }$ and
$\bar {\eta }$ and ![]() $\bar {\eta }_x$ can be eliminated with the help of (2.9e) and (2.10), which will be formalized in the next section.
$\bar {\eta }_x$ can be eliminated with the help of (2.9e) and (2.10), which will be formalized in the next section.
2.2. Linearization around a laminar flow
Let us linearize relations (2.9) around the stream solution ![]() $\hat {\varPhi } = u(y;s), \hat {\varPsi } = 0, \bar {\eta }=h(s)$, for which purpose we introduce
$\hat {\varPhi } = u(y;s), \hat {\varPsi } = 0, \bar {\eta }=h(s)$, for which purpose we introduce
Then we obtain from (2.9):
Here
whereas the nonlinear operators in (2.12a), (2.12b) and (2.12c) have the form
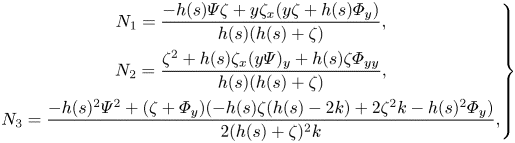 \begin{equation} \left.\begin{array}{c@{}} N_1 = \dfrac{-h(s) \varPsi \zeta + y \zeta_x(y\zeta + h(s) \varPhi_y)}{h(s)(h(s)+\zeta)},\\ N_2 = \dfrac{\zeta^2 + h(s)\zeta_x(y\varPsi)_y + h(s)\zeta \varPhi_{yy}}{h(s)(h(s)+\zeta)},\\ N_3 = \dfrac{-h(s)^2\varPsi^2 + (\zeta+\varPhi_y)(-h(s)\zeta(h(s)-2k) +2\zeta^2 k-h(s)^2\varPhi_y)}{2(h(s)+\zeta)^2 k} , \end{array}\right\} \end{equation}
\begin{equation} \left.\begin{array}{c@{}} N_1 = \dfrac{-h(s) \varPsi \zeta + y \zeta_x(y\zeta + h(s) \varPhi_y)}{h(s)(h(s)+\zeta)},\\ N_2 = \dfrac{\zeta^2 + h(s)\zeta_x(y\varPsi)_y + h(s)\zeta \varPhi_{yy}}{h(s)(h(s)+\zeta)},\\ N_3 = \dfrac{-h(s)^2\varPsi^2 + (\zeta+\varPhi_y)(-h(s)\zeta(h(s)-2k) +2\zeta^2 k-h(s)^2\varPhi_y)}{2(h(s)+\zeta)^2 k} , \end{array}\right\} \end{equation}respectively. Moreover, we find that
Substituting these expressions into formulae for ![]() $N_1$,
$N_1$, ![]() $N_2$ and
$N_2$ and ![]() $N_3$, we see that (2.12a) and (2.12b) form an infinite-dimensional reversible dynamical system on the manifold defined by (2.12c) and (2.12d); the mapping
$N_3$, we see that (2.12a) and (2.12b) form an infinite-dimensional reversible dynamical system on the manifold defined by (2.12c) and (2.12d); the mapping ![]() $(\varPhi ,\varPsi ) \mapsto (\varPhi ,-\varPsi )$ is the reverser. Nonlinearity of the boundary condition (2.12d) is inessential in view of its reducibility to a homogeneous one by a proper change of variables; see Groves & Wahlén (Reference Groves and Wahlén2008) and Kozlov & Lokharu (Reference Kozlov and Lokharu2019) for details.
$(\varPhi ,\varPsi ) \mapsto (\varPhi ,-\varPsi )$ is the reverser. Nonlinearity of the boundary condition (2.12d) is inessential in view of its reducibility to a homogeneous one by a proper change of variables; see Groves & Wahlén (Reference Groves and Wahlén2008) and Kozlov & Lokharu (Reference Kozlov and Lokharu2019) for details.
Let us assume that ![]() $\varPsi \in C(\mathbb {R}; X_1)$ and
$\varPsi \in C(\mathbb {R}; X_1)$ and ![]() $\varPhi \in C(\mathbb {R};X_2)$, where
$\varPhi \in C(\mathbb {R};X_2)$, where ![]() $X_m = \{\, f \in H^m(0,1): f(0) =0 \}$,
$X_m = \{\, f \in H^m(0,1): f(0) =0 \}$, ![]() $m=1,2$, and
$m=1,2$, and ![]() $H^m(0,1)$ stands for the corresponding Sobolev space. Since
$H^m(0,1)$ stands for the corresponding Sobolev space. Since ![]() $k$ and
$k$ and ![]() $\kappa$ depend analytically on
$\kappa$ depend analytically on ![]() $s$ and
$s$ and ![]() $\gamma$ belonging to a small neighbourhood of the origin, the same is true for the operators
$\gamma$ belonging to a small neighbourhood of the origin, the same is true for the operators ![]() $N_1$,
$N_1$, ![]() $N_2$ and
$N_2$ and ![]() $N_3$. More precisely, let
$N_3$. More precisely, let
be a small neighbourhood of the origin in the parameter space, then
whereas ![]() $N_3 \in C^{\infty } (X_1 \times X_2 \times \varLambda _\epsilon; \mathbb {R})$. Moreover, all derivatives of these operators are bounded and uniformly continuous in
$N_3 \in C^{\infty } (X_1 \times X_2 \times \varLambda _\epsilon; \mathbb {R})$. Moreover, all derivatives of these operators are bounded and uniformly continuous in ![]() $\varLambda _\epsilon$.
$\varLambda _\epsilon$.
2.3. A linear eigenvalue problem
The centre subspace of system (2.12) is determined by the imaginary spectrum of the linear operator ![]() $\mathcal {L} (\varPsi , \varPhi )=(- \varPhi _{yy}, \varPsi )$ defined on a subspace of
$\mathcal {L} (\varPsi , \varPhi )=(- \varPhi _{yy}, \varPsi )$ defined on a subspace of ![]() $X_1 \times X_2$ and subject to the homogeneous condition
$X_1 \times X_2$ and subject to the homogeneous condition
It is straightforward to establish that the spectrum of ![]() $\mathcal {L}$ is discrete and consists of all
$\mathcal {L}$ is discrete and consists of all ![]() $\hat {\tau } \in {\mathbb {C}}$ such that
$\hat {\tau } \in {\mathbb {C}}$ such that ![]() $\mu = \hat {\tau }^2$ is an eigenvalue of the following Sturm–Liouville problem:
$\mu = \hat {\tau }^2$ is an eigenvalue of the following Sturm–Liouville problem:
(Basic facts about Sturm–Liouville problems can be found in Teschl (Reference Teschl2012).) Thus, the imaginary spectrum of ![]() $\mathcal {L}$ corresponds to the negative eigenvalues of (2.19a,b).
$\mathcal {L}$ corresponds to the negative eigenvalues of (2.19a,b).
The spectrum of (2.19a,b) is discrete and consists of real simple eigenvalues, say
accumulating at infinity, whereas the corresponding eigenfunctions ![]() $\varphi _j$ can be rescaled to form an orthonormal basis in
$\varphi _j$ can be rescaled to form an orthonormal basis in ![]() $L^2(0,h(s))$.
$L^2(0,h(s))$.
2.4. On the existence of a negative eigenvalue
Let us investigate the spectral problem (2.19a,b) for negative ![]() $s$ and positive
$s$ and positive ![]() $\gamma$ such that
$\gamma$ such that ![]() $\lambda = (s, \gamma ) \in \varLambda _\epsilon$ and
$\lambda = (s, \gamma ) \in \varLambda _\epsilon$ and ![]() $\epsilon$ is sufficiently small. Solving (2.19a,b) explicitly, we find that
$\epsilon$ is sufficiently small. Solving (2.19a,b) explicitly, we find that ![]() $\mu _1$ is the unique negative eigenvalue equal to, say
$\mu _1$ is the unique negative eigenvalue equal to, say ![]() $- \tau ^2$, provided
$- \tau ^2$, provided ![]() $\tau$ is defined by the dispersion equation:
$\tau$ is defined by the dispersion equation:
Using the definition of ![]() $\kappa$, we see that
$\kappa$, we see that
Therefore, ![]() $\kappa h(s) > 1$ for all
$\kappa h(s) > 1$ for all ![]() $s < 0$ and
$s < 0$ and ![]() $\gamma > 0$ such that
$\gamma > 0$ such that ![]() $(s, \gamma ) \in \varLambda _\epsilon$, and so the dispersion equation has a unique root
$(s, \gamma ) \in \varLambda _\epsilon$, and so the dispersion equation has a unique root ![]() $\tau > 0$ such that
$\tau > 0$ such that
Since ![]() $[h(s)]^2 = 2 + O (s)$ as
$[h(s)]^2 = 2 + O (s)$ as ![]() $s \to 0$, we see that
$s \to 0$, we see that ![]() $\tau$ tends to zero as
$\tau$ tends to zero as ![]() $s,\gamma \to 0$. Therefore, some asymptotic formulae below will be written in terms of the small parameter
$s,\gamma \to 0$. Therefore, some asymptotic formulae below will be written in terms of the small parameter ![]() $\tau$. Let us summarize.
$\tau$. Let us summarize.
If ![]() $\gamma -s$ is positive, which is the case when
$\gamma -s$ is positive, which is the case when ![]() $s < 0$, then (2.19a,b) has a negative eigenvalue
$s < 0$, then (2.19a,b) has a negative eigenvalue ![]() $\mu _1 = -\tau ^2$. Moreover, there exists only one such eigenvalue and
$\mu _1 = -\tau ^2$. Moreover, there exists only one such eigenvalue and ![]() $\tau \to 0$ as
$\tau \to 0$ as ![]() $s,\gamma \to 0;$ the corresponding normalized eigenfunction has the asymptotic formula
$s,\gamma \to 0;$ the corresponding normalized eigenfunction has the asymptotic formula
and (2.24) is uniform with respect to ![]() $y \in [0,h(s)]$ and
$y \in [0,h(s)]$ and ![]() $\lambda = (s,\gamma ) \in \varLambda _\epsilon$. The positive spectrum of
$\lambda = (s,\gamma ) \in \varLambda _\epsilon$. The positive spectrum of ![]() $\mathcal {L}$ is separated from zero, because
$\mathcal {L}$ is separated from zero, because ![]() $\mu _2 > {\rm \pi}^2/h^2(s)> {\rm \pi}^2/2$ for small negative
$\mu _2 > {\rm \pi}^2/h^2(s)> {\rm \pi}^2/2$ for small negative ![]() $s$.
$s$.
3. Reduction to a finite-dimensional system
Let us reduce system (2.12) to a finite-dimensional Hamiltonian one, for which purpose the centre-manifold technique of Mielke (Reference Mielke1988) (he considered quasilinear elliptic problems in cylinders) is used. For this purpose we apply a result obtained by Kozlov & Lokharu (Reference Kozlov and Lokharu2019); namely, their theorem 3.1 provides a convenient way for obtaining a reduced problem. Prior to that, the so-called spectral splitting is applied to decompose the system.
3.1. Spectral decomposition and reduction
Following the method proposed by Kozlov & Lokharu (Reference Kozlov and Lokharu2019), we seek ![]() $(\varPhi , \varPsi )$ in the form
$(\varPhi , \varPsi )$ in the form
where ![]() $\tilde {\varPhi }$ and
$\tilde {\varPhi }$ and ![]() $\tilde {\varPsi }$ are orthogonal to
$\tilde {\varPsi }$ are orthogonal to ![]() $\varphi _1$ in
$\varphi _1$ in ![]() $L^2(0,h(s))$; that is,
$L^2(0,h(s))$; that is,
For ![]() $\lambda \in \varLambda _\epsilon$ we define projectors
$\lambda \in \varLambda _\epsilon$ we define projectors ![]() ${\mathcal {P}}_{\lambda } \phi = \alpha \varphi _1$ and
${\mathcal {P}}_{\lambda } \phi = \alpha \varphi _1$ and ![]() $\tilde {\mathcal {P}}_{\lambda } = \textrm {id} - {\mathcal {P}}_{\lambda }$, which are well defined on
$\tilde {\mathcal {P}}_{\lambda } = \textrm {id} - {\mathcal {P}}_{\lambda }$, which are well defined on ![]() $H^1 (0,h(s))$ and orthogonal in
$H^1 (0,h(s))$ and orthogonal in ![]() $L^2 (0,h(s))$. Multiplying (2.12a) and (2.12b) by
$L^2 (0,h(s))$. Multiplying (2.12a) and (2.12b) by ![]() $\varphi _1$ and integrating over
$\varphi _1$ and integrating over ![]() $(0,h(s))$, we obtain
$(0,h(s))$, we obtain
where
 \begin{equation} \left.\begin{array}{c@{}} F_{1}(\varPsi,\varPhi; \lambda) = \displaystyle\int_0^{h(s)} N_1(\varPsi,\varPhi; \lambda) \varphi_1 \, \textrm{d} y , \\ F_{2}(\varPsi,\varPhi; \lambda) = \displaystyle\int_0^{h(s)} N_2(\varPsi,\varPhi; \lambda) \varphi_1 \, \textrm{d} y - N_3(\varPsi,\varPhi; \lambda) \varphi_1 (h(s)) . \end{array}\right\} \end{equation}
\begin{equation} \left.\begin{array}{c@{}} F_{1}(\varPsi,\varPhi; \lambda) = \displaystyle\int_0^{h(s)} N_1(\varPsi,\varPhi; \lambda) \varphi_1 \, \textrm{d} y , \\ F_{2}(\varPsi,\varPhi; \lambda) = \displaystyle\int_0^{h(s)} N_2(\varPsi,\varPhi; \lambda) \varphi_1 \, \textrm{d} y - N_3(\varPsi,\varPhi; \lambda) \varphi_1 (h(s)) . \end{array}\right\} \end{equation}
The system for ![]() $\tilde {\varPhi }$ and
$\tilde {\varPhi }$ and ![]() $\tilde {\varPsi }$ is as follows:
$\tilde {\varPsi }$ is as follows:
and these functions satisfy the following boundary conditions:
Let ![]() $\tilde {X}_{j}^{(\lambda )}$ denote
$\tilde {X}_{j}^{(\lambda )}$ denote ![]() $\tilde {\mathcal {P}}_{\lambda }(X_j)$,
$\tilde {\mathcal {P}}_{\lambda }(X_j)$, ![]() $j=0,1,2$, where
$j=0,1,2$, where ![]() $\lambda \in \varLambda _\epsilon$, and so
$\lambda \in \varLambda _\epsilon$, and so ![]() $\tilde {\varPsi } \in \tilde {X}_{1}^{(\lambda )}$ and
$\tilde {\varPsi } \in \tilde {X}_{1}^{(\lambda )}$ and ![]() $\tilde {\varPhi } \in \tilde {X}_{2}^{(\lambda )}$ for all
$\tilde {\varPhi } \in \tilde {X}_{2}^{(\lambda )}$ for all ![]() $x \in \mathbb {R}$ and
$x \in \mathbb {R}$ and ![]() $\lambda \in \varLambda _\epsilon$. Then theorem 3.1 proved in Kozlov & Lokharu (Reference Kozlov and Lokharu2019) yields the following assertion for the decomposed system (3.3)–(3.8a,b).
$\lambda \in \varLambda _\epsilon$. Then theorem 3.1 proved in Kozlov & Lokharu (Reference Kozlov and Lokharu2019) yields the following assertion for the decomposed system (3.3)–(3.8a,b).
Theorem 3.1 For any ![]() $m \geq 2$ there exist
$m \geq 2$ there exist ![]() $\epsilon > 0$, neighbourhoods
$\epsilon > 0$, neighbourhoods ![]() $W \subset \mathbb {R}^2,$
$W \subset \mathbb {R}^2,$![]() $W_1 \subset X_1, W_2 \subset X_2$ and the vector-functions
$W_1 \subset X_1, W_2 \subset X_2$ and the vector-functions ![]() $r_j : W \times \varLambda _\epsilon \to W_j,$
$r_j : W \times \varLambda _\epsilon \to W_j,$![]() $j=1,2,$ of the class
$j=1,2,$ of the class ![]() $C^m (W \times \varLambda _\epsilon )$ with the following properties.
$C^m (W \times \varLambda _\epsilon )$ with the following properties.
(i) The derivatives of
 $r_1$ and
$r_1$ and  $r_2$ are bounded and uniformly continuous, and the estimate
(3.9)holds uniformly with respect to
$r_2$ are bounded and uniformly continuous, and the estimate
(3.9)holds uniformly with respect to \begin{equation} \|r_1;H^1\|+\|r_2;H^2\|=O(|\alpha|^2+|\beta|^2), \quad where \ (\alpha,\beta) \in W, \end{equation}
\begin{equation} \|r_1;H^1\|+\|r_2;H^2\|=O(|\alpha|^2+|\beta|^2), \quad where \ (\alpha,\beta) \in W, \end{equation} $\lambda \in \varLambda _\epsilon$.
$\lambda \in \varLambda _\epsilon$.(ii)
 $r_j(\alpha ,\beta ,\lambda ) \in \tilde {X}_{j}^{(\lambda )}$,
$r_j(\alpha ,\beta ,\lambda ) \in \tilde {X}_{j}^{(\lambda )}$,  $j=1,2,$ for all
$j=1,2,$ for all  $\lambda \in \varLambda _\epsilon$ and all
$\lambda \in \varLambda _\epsilon$ and all  $(\alpha ,\beta ) \in W$.
$(\alpha ,\beta ) \in W$.(iii) The set
 $M^\lambda = \{ (\varPsi ^r[\alpha ,\beta; \lambda ], \varPhi ^r[\alpha ,\beta; \lambda ]):(\alpha ,\beta )\in W, \ \lambda \in \varLambda _\epsilon \} \subset X_1 \times X_2$, where
(3.10)is a locally invariant manifold for (2.12), that is, through every point of
$M^\lambda = \{ (\varPsi ^r[\alpha ,\beta; \lambda ], \varPhi ^r[\alpha ,\beta; \lambda ]):(\alpha ,\beta )\in W, \ \lambda \in \varLambda _\epsilon \} \subset X_1 \times X_2$, where
(3.10)is a locally invariant manifold for (2.12), that is, through every point of \begin{equation} \varPsi^r[\alpha,\beta; \lambda]=\beta\varphi_1+r_1(\alpha,\beta;\lambda) \quad and \quad \varPhi^r[\alpha,\beta; \lambda]=\alpha\varphi_1+r_2(\alpha,\beta;\lambda), \end{equation}
\begin{equation} \varPsi^r[\alpha,\beta; \lambda]=\beta\varphi_1+r_1(\alpha,\beta;\lambda) \quad and \quad \varPhi^r[\alpha,\beta; \lambda]=\alpha\varphi_1+r_2(\alpha,\beta;\lambda), \end{equation} $M^\lambda$ goes only one solution of (2.12) and it belongs to
$M^\lambda$ goes only one solution of (2.12) and it belongs to  $M^\lambda$ as long as
$M^\lambda$ as long as  $(r_1, r_2) \in W_1 \times W_2$.
$(r_1, r_2) \in W_1 \times W_2$.(iv) Every global solution
 $(\alpha ,\beta ) \in C(\mathbb {R};W)$ of the reduced system
(3.11)where
$(\alpha ,\beta ) \in C(\mathbb {R};W)$ of the reduced system
(3.11)where \begin{equation} \begin{gathered} \alpha_x = \beta + F_{1}(\varPsi^r[\alpha,\beta; \lambda],\varPhi^r[\alpha,\beta; \lambda]; \lambda), \\ \beta_x = \mu_1 \alpha + F_{2}(\varPsi^r[\alpha,\beta; \lambda],\varPhi^r[\alpha,\beta; \lambda]; \lambda) , \end{gathered} \end{equation}
\begin{equation} \begin{gathered} \alpha_x = \beta + F_{1}(\varPsi^r[\alpha,\beta; \lambda],\varPhi^r[\alpha,\beta; \lambda]; \lambda), \\ \beta_x = \mu_1 \alpha + F_{2}(\varPsi^r[\alpha,\beta; \lambda],\varPhi^r[\alpha,\beta; \lambda]; \lambda) , \end{gathered} \end{equation} $\lambda \in \varLambda _\epsilon ,$ generates the solution
$\lambda \in \varLambda _\epsilon ,$ generates the solution  $(\varPsi ,\varPhi )$ of (2.12) with
(3.12a,b)Moreover, the reduced system (3.11) is reversible.
$(\varPsi ,\varPhi )$ of (2.12) with
(3.12a,b)Moreover, the reduced system (3.11) is reversible. \begin{equation} \varPsi(x,y) = \varPsi^r[\alpha(x),\beta(x); \lambda](y), \quad \varPhi(x,y) = \varPhi^r[\alpha(x),\beta(x); \lambda](y). \end{equation}
\begin{equation} \varPsi(x,y) = \varPsi^r[\alpha(x),\beta(x); \lambda](y), \quad \varPhi(x,y) = \varPhi^r[\alpha(x),\beta(x); \lambda](y). \end{equation}
A direct calculation shows that the reduced system (3.11) has the following structure:
 \begin{equation} \begin{gathered} \alpha_x = \beta [ 1 + O(|\alpha|+|\alpha|^2+|\beta|^2) ], \\ \beta_x = -\tau^2 \alpha + A \alpha^2 + O(|\alpha|^3+|\beta|^2), \end{gathered} \end{equation}
\begin{equation} \begin{gathered} \alpha_x = \beta [ 1 + O(|\alpha|+|\alpha|^2+|\beta|^2) ], \\ \beta_x = -\tau^2 \alpha + A \alpha^2 + O(|\alpha|^3+|\beta|^2), \end{gathered} \end{equation}
where ![]() $A = \tfrac 12 c_0^3+O(|s|^2 + |\gamma |^2)$ as
$A = \tfrac 12 c_0^3+O(|s|^2 + |\gamma |^2)$ as ![]() $s,\gamma \to 0$ and
$s,\gamma \to 0$ and ![]() $c_0$ is the constant defined in (2.24); hence
$c_0$ is the constant defined in (2.24); hence ![]() $A = \sqrt {3^3 / 2^{13/2}}+O(|s|^2 + |\gamma |^2)$. Now, we are in a position to formulate and prove the following.
$A = \sqrt {3^3 / 2^{13/2}}+O(|s|^2 + |\gamma |^2)$. Now, we are in a position to formulate and prove the following.
Theorem 3.2 Problem (3.13) has a homoclinic solution such that
whereas ![]() $\beta _h$ is defined implicitly by the first formula (3.13). Here
$\beta _h$ is defined implicitly by the first formula (3.13). Here ![]() $\alpha ^\star _+ = A^{-1} + O(\tau ^2)$ is a constant independent of
$\alpha ^\star _+ = A^{-1} + O(\tau ^2)$ is a constant independent of ![]() $x$.
$x$.
Proof. It is known (see Groves & Stylianou Reference Groves and Stylianou2014; Kozlov & Kuznetsov Reference Kozlov and Kuznetsov2013) that problem (1.1a)–(1.1d) has a Hamiltonian structure (even for arbitrary vorticity) with the horizontal coordinate playing the role of time. The corresponding Hamiltonian is the flow force invariant; in the original coordinates ![]() $(X, Y)$, it has the following form:
$(X, Y)$, it has the following form:
 \begin{equation} {\mathcal{S}} = \left[ \tfrac 12 R - b \right] \eta (X) - \tfrac 12 \left\{ \eta^2 (X) - \int_0^{\eta (X)} \tfrac 12 (\psi_Y^2 - \psi_X^2) + b \psi \, \textrm{d} Y \right\}. \end{equation}
\begin{equation} {\mathcal{S}} = \left[ \tfrac 12 R - b \right] \eta (X) - \tfrac 12 \left\{ \eta^2 (X) - \int_0^{\eta (X)} \tfrac 12 (\psi_Y^2 - \psi_X^2) + b \psi \, \textrm{d} Y \right\}. \end{equation}
Thus, the reduced system (3.13) has a constant of motion ![]() ${\mathcal {H}}(\alpha ,\beta )$; to obtain an expression for it one has to subject
${\mathcal {H}}(\alpha ,\beta )$; to obtain an expression for it one has to subject ![]() $b^{-1}{\mathcal {S}}$ to all changes of variables described above. A direct calculation yields that
$b^{-1}{\mathcal {S}}$ to all changes of variables described above. A direct calculation yields that
where ![]() $A$ is the coefficient in the second equation (3.13). It should be noted that
$A$ is the coefficient in the second equation (3.13). It should be noted that ![]() $\mathcal {H} (\alpha , \beta )$ is an even function of
$\mathcal {H} (\alpha , \beta )$ is an even function of ![]() $\beta$ which follows from reversibility of this system. The form of
$\beta$ which follows from reversibility of this system. The form of ![]() $\mathcal {H} (\alpha , \beta )$ suggests that variables must be scaled as follows:
$\mathcal {H} (\alpha , \beta )$ suggests that variables must be scaled as follows:
where
and so the scaled equations are
 \begin{equation} \begin{gathered} {[}\alpha_1]_{x_1} = \beta_1+ \tau^2 \beta_1 O \left( |\alpha_1|+|\beta_1|^2 \right) , \\ [\beta_1]_{x_1} = -\alpha_1 + A \alpha_1^2 + \tau^2 O \left( |\alpha_1|^3+|\beta_1|^2 \right) . \end{gathered} \end{equation}
\begin{equation} \begin{gathered} {[}\alpha_1]_{x_1} = \beta_1+ \tau^2 \beta_1 O \left( |\alpha_1|+|\beta_1|^2 \right) , \\ [\beta_1]_{x_1} = -\alpha_1 + A \alpha_1^2 + \tau^2 O \left( |\alpha_1|^3+|\beta_1|^2 \right) . \end{gathered} \end{equation} The graph of ![]() ${\mathcal {H}}_1(\alpha ,0)$ in a neighbourhood of the origin is sketched in figure 3(a). It is clear that the local maximum of this function close to the origin is attained at
${\mathcal {H}}_1(\alpha ,0)$ in a neighbourhood of the origin is sketched in figure 3(a). It is clear that the local maximum of this function close to the origin is attained at ![]() $\alpha =\alpha ^\star _+$ and
$\alpha =\alpha ^\star _+$ and ![]() $L = {\mathcal {H}}_1(\alpha ^\star _+,0)$ is its value. Then the level line
$L = {\mathcal {H}}_1(\alpha ^\star _+,0)$ is its value. Then the level line
is a closed curve for every ![]() $\ell \in (0, L)$ and it corresponds to a periodic solution. The contour
$\ell \in (0, L)$ and it corresponds to a periodic solution. The contour
defines the homoclinic orbit; see a sketch of level lines in figure 3(b). The values ![]() $\alpha _-^\star$ and
$\alpha _-^\star$ and ![]() $\alpha _+^\star$ correspond to the ‘crest’ level and the limiting depth, respectively. An essential feature of the homoclinic orbit is that
$\alpha _+^\star$ correspond to the ‘crest’ level and the limiting depth, respectively. An essential feature of the homoclinic orbit is that ![]() $\alpha _1$ attains negative values on its left-hand part; this implies that there is a stagnation point as will be shown below.
$\alpha _1$ attains negative values on its left-hand part; this implies that there is a stagnation point as will be shown below.
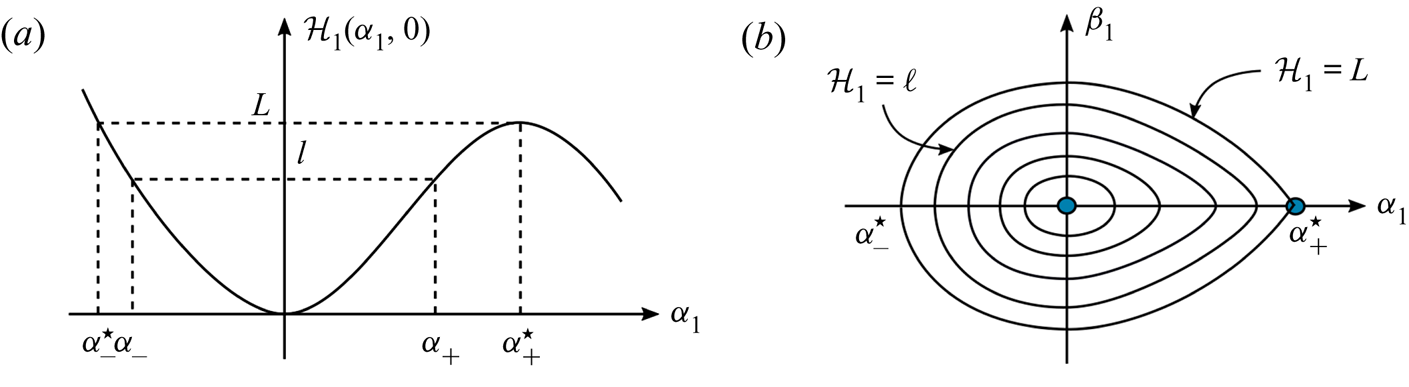
Figure 3. The behaviour of the Hamiltonian near the origin (a) and its level curves (b). (a) Graph of the function ![]() ${\mathcal {H}}_1(\alpha _1,0)$. (b) Phase portrait.
${\mathcal {H}}_1(\alpha _1,0)$. (b) Phase portrait.
Let us turn to proving (3.14). By ![]() $\alpha _1^h$ we denote a homoclinic solution to (3.19). It is easy to see that it is monotone on each side of the crest which corresponds to the value
$\alpha _1^h$ we denote a homoclinic solution to (3.19). It is easy to see that it is monotone on each side of the crest which corresponds to the value ![]() $\alpha _1^h(0) = \alpha _-^\star$. Then we have
$\alpha _1^h(0) = \alpha _-^\star$. Then we have
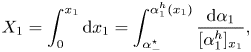 \begin{equation} X_1 = \int_0^{x_1} \textrm{d}x_1 = \int_{\alpha_-^\star}^{\alpha_1^h(x_1)} \frac{\textrm{d} \alpha_1}{[\alpha_1^h]_{x_1}} , \end{equation}
\begin{equation} X_1 = \int_0^{x_1} \textrm{d}x_1 = \int_{\alpha_-^\star}^{\alpha_1^h(x_1)} \frac{\textrm{d} \alpha_1}{[\alpha_1^h]_{x_1}} , \end{equation}
where ![]() $[\alpha _1^h]_{x_1} = \beta _1^h [ 1+O(\tau ^2) ]$; see the first equation (3.19). On the other hand,
$[\alpha _1^h]_{x_1} = \beta _1^h [ 1+O(\tau ^2) ]$; see the first equation (3.19). On the other hand,
where the system's reversibility is used. Expressing ![]() $[\beta _1^h]^2$ from the last formula and taking into account the fact that it is positive on the interval of the integration, we obtain
$[\beta _1^h]^2$ from the last formula and taking into account the fact that it is positive on the interval of the integration, we obtain
 \begin{equation} x_1 = \int_{\alpha_-^\star}^{\alpha_1^h(x_1)} \frac{\textrm{d} \alpha_1} {[\alpha_1^h]_{x_1}} = [1+O(\tau^2)] \int_{\alpha_-^\star}^{\alpha_1^h(x_1)} \frac{\textrm{d} \alpha_1}{\sqrt{2 [L-{\mathcal{H}}_1(\alpha_1^h,0)]}} . \end{equation}
\begin{equation} x_1 = \int_{\alpha_-^\star}^{\alpha_1^h(x_1)} \frac{\textrm{d} \alpha_1} {[\alpha_1^h]_{x_1}} = [1+O(\tau^2)] \int_{\alpha_-^\star}^{\alpha_1^h(x_1)} \frac{\textrm{d} \alpha_1}{\sqrt{2 [L-{\mathcal{H}}_1(\alpha_1^h,0)]}} . \end{equation}Let us find an approximation of the integral using a third-degree polynomial for the expression under the square root; more precisely, let us show that
where
It should be emphasized that (3.25) is used as a representation of ![]() $L-{\mathcal {H}}_1(\alpha _1,0)$ only on the interval
$L-{\mathcal {H}}_1(\alpha _1,0)$ only on the interval ![]() $[\alpha _-^\star , \alpha _+^\star ]$. To prove (3.25) we note that
$[\alpha _-^\star , \alpha _+^\star ]$. To prove (3.25) we note that
A direct calculation yields that the estimate ![]() $O(\tau ^2)$ holds for
$O(\tau ^2)$ holds for
Therefore, solving a linear system, one obtains that up to ![]() $O(\tau ^2)$ the coefficients of
$O(\tau ^2)$ the coefficients of
are the same as those of ![]() $Q_1$. This shows that the error in (3.25) has the same estimate
$Q_1$. This shows that the error in (3.25) has the same estimate ![]() $O(\tau ^2)$. It remains to use the fact that
$O(\tau ^2)$. It remains to use the fact that ![]() $L-{\mathcal {H}}_1(\alpha _1,0)$ has a simple zero at
$L-{\mathcal {H}}_1(\alpha _1,0)$ has a simple zero at ![]() $\alpha _-^\star$ and a double zero at
$\alpha _-^\star$ and a double zero at ![]() $\alpha _+^\star$ which proves (3.25).
$\alpha _+^\star$ which proves (3.25).
Now we have
 \begin{align} \int_{\alpha_-^\star}^{\alpha_1^h(x_1)} \frac{\textrm{d} \alpha_1}{\sqrt{2(L-{\mathcal{H}}_1(\alpha_1,0))}} &= [1+O(\tau^2)] \int_{\alpha_-^\star}^{\alpha_1^h(x_1)} \frac{\textrm{d} \alpha_1}{\sqrt{2a(\alpha_1- \alpha_-^\star)(\alpha_1-\alpha_+^\star)^2}}\nonumber\\ &= \frac{1+O(\tau^2)}{a_0\sqrt{2a}} \left[ \ln\left| \frac{a_0+\sqrt{\alpha_1-\alpha_-^\star}}{a_0-\sqrt{\alpha_1-\alpha_-^\star}} \right| \right]_{\alpha_1=\alpha_-^\star}^{\alpha_1=\alpha_1^h(x_1)} \nonumber\\ &= \frac{1+O(\tau^2)}{a_0\sqrt{2a}} \left( \ln\left[ \frac{\left(a_0+\sqrt{\alpha_1^h(x_1)-\alpha_-^\star}\right)^2}{\alpha_+^\star -\alpha_1^h(x_1) }\right] \right), \end{align}
\begin{align} \int_{\alpha_-^\star}^{\alpha_1^h(x_1)} \frac{\textrm{d} \alpha_1}{\sqrt{2(L-{\mathcal{H}}_1(\alpha_1,0))}} &= [1+O(\tau^2)] \int_{\alpha_-^\star}^{\alpha_1^h(x_1)} \frac{\textrm{d} \alpha_1}{\sqrt{2a(\alpha_1- \alpha_-^\star)(\alpha_1-\alpha_+^\star)^2}}\nonumber\\ &= \frac{1+O(\tau^2)}{a_0\sqrt{2a}} \left[ \ln\left| \frac{a_0+\sqrt{\alpha_1-\alpha_-^\star}}{a_0-\sqrt{\alpha_1-\alpha_-^\star}} \right| \right]_{\alpha_1=\alpha_-^\star}^{\alpha_1=\alpha_1^h(x_1)} \nonumber\\ &= \frac{1+O(\tau^2)}{a_0\sqrt{2a}} \left( \ln\left[ \frac{\left(a_0+\sqrt{\alpha_1^h(x_1)-\alpha_-^\star}\right)^2}{\alpha_+^\star -\alpha_1^h(x_1) }\right] \right), \end{align}
where ![]() $a_0 = \sqrt {\alpha _+^\star -\alpha _-^\star }$. Comparing this and (3.24), one obtains the following asymptotic formula for the solitary-wave solution:
$a_0 = \sqrt {\alpha _+^\star -\alpha _-^\star }$. Comparing this and (3.24), one obtains the following asymptotic formula for the solitary-wave solution:
where the formulae ![]() $\alpha _-^\star = - \alpha _+^\star /2 + O (\tau ^2)$ and
$\alpha _-^\star = - \alpha _+^\star /2 + O (\tau ^2)$ and ![]() $\alpha _+^\star = A^{-1} + O (\tau ^2)$ are taken into account. Furthermore, it is straightforward to show that
$\alpha _+^\star = A^{-1} + O (\tau ^2)$ are taken into account. Furthermore, it is straightforward to show that
where
The latter is a homoclinic solution of (3.19) with ![]() $\tau =0$, in which case
$\tau =0$, in which case ![]() $\beta _1 = [\alpha _1^{h,\star }]_{x_1}$. Combining this and the asymptotic formula (3.31), one arrives at (3.14) by rescaling variables to the original ones.
$\beta _1 = [\alpha _1^{h,\star }]_{x_1}$. Combining this and the asymptotic formula (3.31), one arrives at (3.14) by rescaling variables to the original ones.
3.2. Periodic waves
The streamline pattern for periodic solutions was studied in Wahlén (Reference Wahlén2009). It was shown that below every crest there is a cat's-eye region adjacent to the bottom as in figure 4. Our aim is to show that this region stays bounded as ![]() $\ell \to L$, so that the solitary wave has a similar streamline pattern.
$\ell \to L$, so that the solitary wave has a similar streamline pattern.
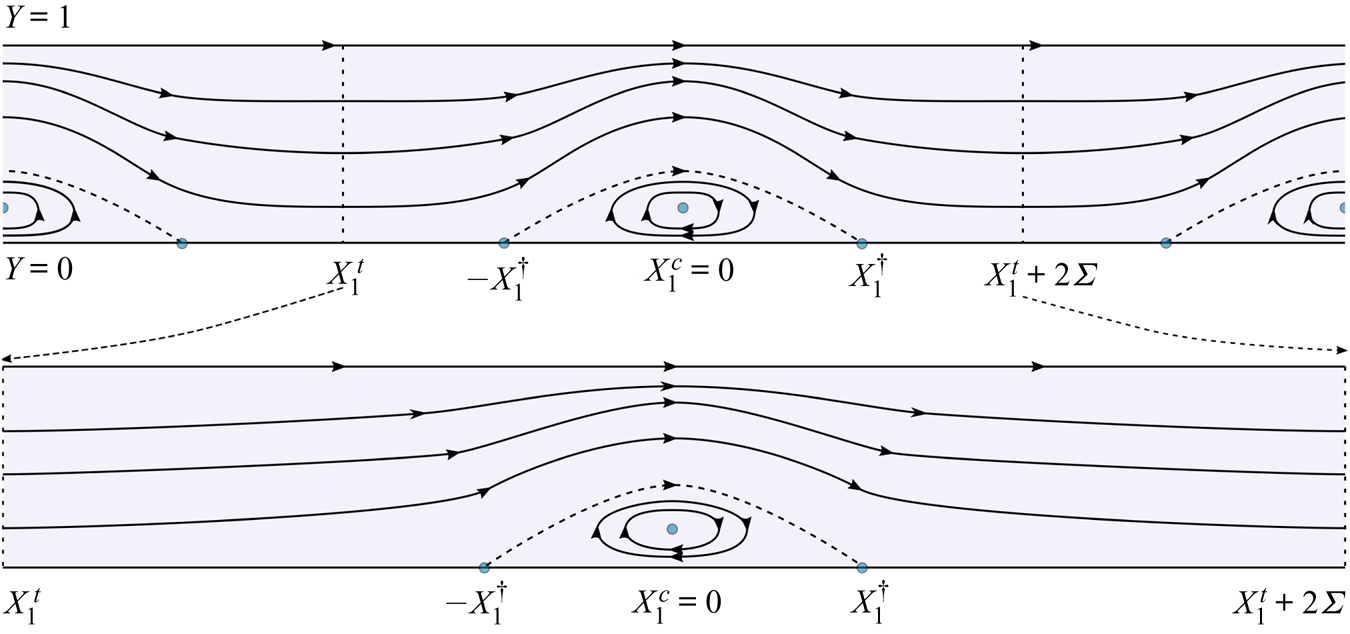
Figure 4. Two Stokes waves corresponding to different values of ![]() $\ell$ plotted in
$\ell$ plotted in ![]() $(X_1,Y)$ variables.
$(X_1,Y)$ variables.
An approximation of solutions for periodic waves can be found in the same way as for solitary waves. Indeed, let us consider the periodic solution ![]() $\alpha _1^\ell$ corresponding to some energy
$\alpha _1^\ell$ corresponding to some energy ![]() ${\mathcal {H}}_1=\ell$. Let a trough of this wave be located at
${\mathcal {H}}_1=\ell$. Let a trough of this wave be located at ![]() $x_1^c = 0$ and let the nearest crest to the left be at
$x_1^c = 0$ and let the nearest crest to the left be at ![]() $x_1^t < x_1^c$ (see figure 4). Then for every
$x_1^t < x_1^c$ (see figure 4). Then for every ![]() $x_1 \in (x_1^t x_1^c]$ we have
$x_1 \in (x_1^t x_1^c]$ we have
 \begin{equation} x_1 - x_1^t = \int_{\alpha_-}^{\alpha_1^\ell(x_1)} \frac{\textrm{d} \alpha_1}{[\alpha_1^\ell]_{x_1}} = [1+O(\tau^2)] \int_{\alpha_-}^{\alpha_1^\ell(x_1)} \frac{\textrm{d} \alpha_1}{\sqrt{2 [\ell-{\mathcal{H}}_1(\alpha_1,0)]}} . \end{equation}
\begin{equation} x_1 - x_1^t = \int_{\alpha_-}^{\alpha_1^\ell(x_1)} \frac{\textrm{d} \alpha_1}{[\alpha_1^\ell]_{x_1}} = [1+O(\tau^2)] \int_{\alpha_-}^{\alpha_1^\ell(x_1)} \frac{\textrm{d} \alpha_1}{\sqrt{2 [\ell-{\mathcal{H}}_1(\alpha_1,0)]}} . \end{equation}In particular, the half-period of this solution is equal to
and so ![]() $\varSigma _\ell \to +\infty$ as
$\varSigma _\ell \to +\infty$ as ![]() $\ell \to L$. Let us estimate the bottom width of a cat's-eye vortex (in figure 4, it is bounded above by the dashed streamline). On every interval symmetric about the crest and having the length
$\ell \to L$. Let us estimate the bottom width of a cat's-eye vortex (in figure 4, it is bounded above by the dashed streamline). On every interval symmetric about the crest and having the length ![]() $2 \varSigma _\ell$, there are exactly two stagnation points on the bottom that bound the bottom-attached vortex (these points are plotted as dots in figure 4), and
$2 \varSigma _\ell$, there are exactly two stagnation points on the bottom that bound the bottom-attached vortex (these points are plotted as dots in figure 4), and ![]() $\alpha _1^\ell (\pm x_1^\dagger ) = 0$ at these points nearest to the origin. From (3.34) the approximate formula follows:
$\alpha _1^\ell (\pm x_1^\dagger ) = 0$ at these points nearest to the origin. From (3.34) the approximate formula follows:
 \begin{equation} -x_1^\dagger-x_1^t = [1+O(\tau^2)] \int_{\alpha_-}^{0} \frac{\textrm{d} \alpha_1}{\sqrt{2 [\ell - {\mathcal{H}}_1 (\alpha_1, 0) ]}} , \end{equation}
\begin{equation} -x_1^\dagger-x_1^t = [1+O(\tau^2)] \int_{\alpha_-}^{0} \frac{\textrm{d} \alpha_1}{\sqrt{2 [\ell - {\mathcal{H}}_1 (\alpha_1, 0) ]}} , \end{equation}
which yields that ![]() $x_1^\dagger = O(1)$ as
$x_1^\dagger = O(1)$ as ![]() $\ell \to L$ in view that the integral
$\ell \to L$ in view that the integral
 \begin{equation} \int_{\alpha_-}^{0} \frac{\textrm{d} \alpha_1}{\sqrt{2 [L - {\mathcal{H}}_1 (\alpha_1, 0) ]}} \end{equation}
\begin{equation} \int_{\alpha_-}^{0} \frac{\textrm{d} \alpha_1}{\sqrt{2 [L - {\mathcal{H}}_1 (\alpha_1, 0) ]}} \end{equation}
is finite. Indeed, the function ![]() $L - {\mathcal {H}}_1 (\alpha _1, 0)$ has only one simple zero
$L - {\mathcal {H}}_1 (\alpha _1, 0)$ has only one simple zero ![]() $\alpha _1=\alpha _-^\star$ on the interval of integration. Thus,
$\alpha _1=\alpha _-^\star$ on the interval of integration. Thus, ![]() $x_1^\dagger$ remains bounded when the wavelength goes to infinity, and the same is true for the domain occupied by cat's-eye vortex. Therefore, the pattern of streamlines remains the same for the limiting solitary wave (see figure 1).
$x_1^\dagger$ remains bounded when the wavelength goes to infinity, and the same is true for the domain occupied by cat's-eye vortex. Therefore, the pattern of streamlines remains the same for the limiting solitary wave (see figure 1).
4. Proof of theorem 1.1
From (3.31), it is straightforward to recover the asymptotics of the free-surface profile in the original non-dimensional coordinates; it looks as follows:
and so describes a solitary wave of elevation. Here, the depth at infinity is ![]() $h_- = h(s) + 2s$, which coincides with that of the unidirectional laminar flow conjugate to (2.3a,b). (Thus, this flow supports solitary waves similarly to the irrotational case.) Furthermore,
$h_- = h(s) + 2s$, which coincides with that of the unidirectional laminar flow conjugate to (2.3a,b). (Thus, this flow supports solitary waves similarly to the irrotational case.) Furthermore, ![]() $c_0$ is the constant defined in (2.24) and
$c_0$ is the constant defined in (2.24) and ![]() $\tau$ is the unique positive root of the dispersion equation (2.21), which, according to (2.23), tends to zero as
$\tau$ is the unique positive root of the dispersion equation (2.21), which, according to (2.23), tends to zero as ![]() $s \to 0$ and
$s \to 0$ and ![]() $b \to \infty$ simultaneously (indeed,
$b \to \infty$ simultaneously (indeed, ![]() $\gamma = b^{-3/2}$).
$\gamma = b^{-3/2}$).
To show that the flow supporting this wave has a bottom-attached cat's-eye vortex, let us track back the changes of coordinates made above and find that
Here ![]() $\varPhi (x,y) = \alpha (x) \varphi _1 (y) + y O (\tau ^4) = c_0 y [\alpha (x) + O(\tau ^4)]$ as
$\varPhi (x,y) = \alpha (x) \varphi _1 (y) + y O (\tau ^4) = c_0 y [\alpha (x) + O(\tau ^4)]$ as ![]() $\tau \to 0$, where the second equality is a consequence of (2.24). Hence we see that
$\tau \to 0$, where the second equality is a consequence of (2.24). Hence we see that
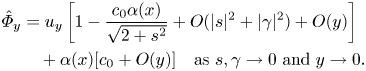 \begin{align} \hat{\varPhi}_y &= u_y \left[ 1- \frac{c_0 \alpha (x)}{\sqrt{2+s^2}} + O (|s|^2 + |\gamma|^2) + O(y) \right]\nonumber\\ &\quad+ \alpha (x) [c_0 + O(y)] \quad \mbox{as} \ s,\gamma \to 0 \ \mbox{and} \ y \to 0 . \end{align}
\begin{align} \hat{\varPhi}_y &= u_y \left[ 1- \frac{c_0 \alpha (x)}{\sqrt{2+s^2}} + O (|s|^2 + |\gamma|^2) + O(y) \right]\nonumber\\ &\quad+ \alpha (x) [c_0 + O(y)] \quad \mbox{as} \ s,\gamma \to 0 \ \mbox{and} \ y \to 0 . \end{align}
The first term is negative near the bottom because ![]() $u_y < 0$ according to formula (2.3a,b) and the assumption that
$u_y < 0$ according to formula (2.3a,b) and the assumption that ![]() $s<0$, whereas the expression in the square brackets is positive. Moreover, it was established in the proof of theorem 3.2 that
$s<0$, whereas the expression in the square brackets is positive. Moreover, it was established in the proof of theorem 3.2 that ![]() $\alpha (x)$ is negative on some interval. Taking this into account, the second term in the last formula also attains negative values near the bottom which shows that the same is true for
$\alpha (x)$ is negative on some interval. Taking this into account, the second term in the last formula also attains negative values near the bottom which shows that the same is true for ![]() $\hat {\varPhi }_y$.
$\hat {\varPhi }_y$.
It follows from considerations in § 3.2 that the cat's-eye region shown in figure 4 remains bounded as ![]() $\ell \to L$. This yields that the pattern of streamlines of
$\ell \to L$. This yields that the pattern of streamlines of ![]() $\hat {\varPhi }$ has the structure plotted in figure 1. Since the pattern of streamlines of
$\hat {\varPhi }$ has the structure plotted in figure 1. Since the pattern of streamlines of ![]() $\psi$ is essentially the same, this completes the proof of theorem 1.1.
$\psi$ is essentially the same, this completes the proof of theorem 1.1.
5. Concluding remarks
We have considered the problem describing water waves in a rotational flow of finite depth when the corresponding unperturbed shear flow has a near-bottom counter-current. The latter flow exists, in particular, when the vorticity is a negative constant; its value is assumed to be large which simplifies the analysis as to whether this flow supports a solitary wave. It was emphasized by Benjamin (Reference Benjamin1962) that investigating propagation of waves, it is essential to avoid the artificial assumption of irrotational motion because it ignores the effects of friction and current. In the model presented here, the latter is taken into account directly by the vorticity distribution, whereas the former is treated as diffused over the whole cross-section of an infinitely long channel.
Our approach combines scaling and the spatial dynamics technique. By scaling, the problem is shown to be equivalent to another one, in which the vorticity is equal to ![]() $-1$, whereas the gravity constant
$-1$, whereas the gravity constant ![]() $\gamma > 0$ is treated as a small parameter depending on the original vorticity. Moreover, an extra parameter is involved in our construction, namely the velocity
$\gamma > 0$ is treated as a small parameter depending on the original vorticity. Moreover, an extra parameter is involved in our construction, namely the velocity ![]() $s < 0$ of the unperturbed flow at the bottom. The main results are that this flow supports a solitary wave provided
$s < 0$ of the unperturbed flow at the bottom. The main results are that this flow supports a solitary wave provided ![]() $\gamma$ and
$\gamma$ and ![]() $s$ are sufficiently small, whereas the pattern of streamlines contains a bottom-attached region below the crest, where they are closed and surround an interior stagnation point. This extends previous results on solitary waves concerning unidirectional flows only to the more complicated flow.
$s$ are sufficiently small, whereas the pattern of streamlines contains a bottom-attached region below the crest, where they are closed and surround an interior stagnation point. This extends previous results on solitary waves concerning unidirectional flows only to the more complicated flow.
It occurs that the presence of two parameters even simplifies tackling the problem despite neither of them being suitable for use in the spatial dynamics method in the same way as in Groves & Wahlén (Reference Groves and Wahlén2008). Nevertheless, this method is applicable, because there is another natural small parameter. Indeed, the centre subspace of the spatial dynamics method is determined by the imaginary spectrum of the linearized operator defined by a nonlinear system. We linearize our system depending on the parameter ![]() $\gamma$ (it arises after a flattening transformation which is a standard procedure when the partial hodograph transform cannot be used) around the stream solution involving the second parameter
$\gamma$ (it arises after a flattening transformation which is a standard procedure when the partial hodograph transform cannot be used) around the stream solution involving the second parameter ![]() $s$ and this leads to a Sturm–Liouville problem. If both
$s$ and this leads to a Sturm–Liouville problem. If both ![]() $\gamma$ and
$\gamma$ and ![]() $s$ are small, then it has only one negative eigenvalue,
$s$ are small, then it has only one negative eigenvalue, ![]() $- \tau ^2$, where
$- \tau ^2$, where ![]() $\tau$ is a unique positive root of the dispersion equation. Moreover,
$\tau$ is a unique positive root of the dispersion equation. Moreover, ![]() $\tau \to 0$ as
$\tau \to 0$ as ![]() $\gamma$ and
$\gamma$ and ![]() $s$ go to zero, and so it is convenient to use
$s$ go to zero, and so it is convenient to use ![]() $\tau$ as a small parameter while analysing a finite-dimensional Hamiltonian system to which the original one reduces.
$\tau$ as a small parameter while analysing a finite-dimensional Hamiltonian system to which the original one reduces.
As in the simpler case studied by Groves & Wahlén (Reference Groves and Wahlén2008), there exists a homoclinic solution of the finite-dimensional system, and it is expressed in terms of the hyperbolic secant, but in a more complicated way. Moreover, the asymptotic formula (4.1) recovered from the homoclinic solution expresses the free-surface profile of a solitary wave in the original coordinates. Presumably, this formula is suitable for numerical computation of the profile. Indeed, if proper values of ![]() $\gamma$ and
$\gamma$ and ![]() $s$ are taken, then the root
$s$ are taken, then the root ![]() $\tau$ can be found numerically from the dispersion equation (2.21) and used for evaluating (4.1). Computation of the corresponding streamlines is a more sophisticated task, as a paper by Ribeiro et al. (Reference Ribeiro, Milewski and Nachbin2017) dealing with periodic waves demonstrates. Adaptation of their method to solitary waves is a challenge to be investigated. Another question related to the latter paper is to find out whether the pressure on the bottom boundary is different from that in the irrotational case.
$\tau$ can be found numerically from the dispersion equation (2.21) and used for evaluating (4.1). Computation of the corresponding streamlines is a more sophisticated task, as a paper by Ribeiro et al. (Reference Ribeiro, Milewski and Nachbin2017) dealing with periodic waves demonstrates. Adaptation of their method to solitary waves is a challenge to be investigated. Another question related to the latter paper is to find out whether the pressure on the bottom boundary is different from that in the irrotational case.
Acknowledgements
V.K. was supported by the Swedish Research Council (VR), 2017-03837. N.K. acknowledges support from Linköping University.
Declaration of interests
The authors report no conflict of interest.