Article contents
Nonlinear elasticity with vanishing nonlocal self-repulsion
Published online by Cambridge University Press: 28 September 2023
Abstract
We prove that for nonlinear elastic energies with strong enough energetic control of the outer distortion of admissible deformations, almost everywhere global invertibility as constraint can be obtained in the $\Gamma$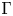 -limit of the elastic energy with an added nonlocal self-repulsion term with asymptocially vanishing coefficient. The self-repulsion term considered here formally coincides with a Sobolev–Slobodeckiĭ seminorm of the inverse deformation. Variants near the boundary or on the surface of the domain are also studied.
-limit of the elastic energy with an added nonlocal self-repulsion term with asymptocially vanishing coefficient. The self-repulsion term considered here formally coincides with a Sobolev–Slobodeckiĭ seminorm of the inverse deformation. Variants near the boundary or on the surface of the domain are also studied.
Keywords
MSC classification
- Type
- Research Article
- Information
- Copyright
- Copyright © The Author(s), 2023. Published by Cambridge University Press on behalf of The Royal Society of Edinburgh
References
- 1
- Cited by



