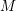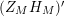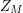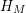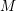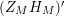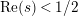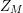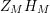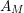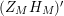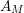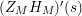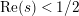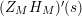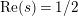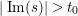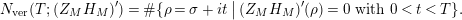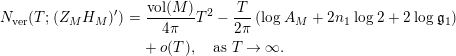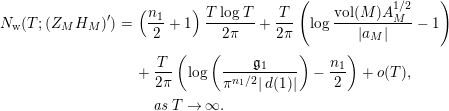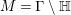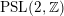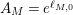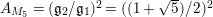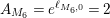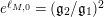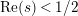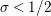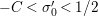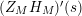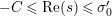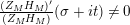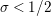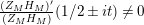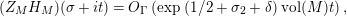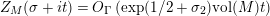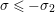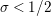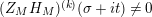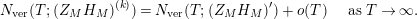1 Introduction
1.1 Selberg zeta functions for compact Riemann surfaces
In [Reference Luo22], Luo initiated the study of the nontrivial zeros of the derivative
![]() $Z_{M}^{\prime }$
of the Selberg zeta function
$Z_{M}^{\prime }$
of the Selberg zeta function
![]() $Z_{M}$
associated to a compact, hyperbolic Riemann surface
$Z_{M}$
associated to a compact, hyperbolic Riemann surface
![]() $M$
, proving analogues of results obtained by Spira [Reference Speiser27] and Berndt [Reference Berndt4] for the Riemann zeta function. Further refinements of results by Luo were established in [Reference Garunkŝtis11] and [Reference Garunkŝtis12]. As is standard in analytic number theory, the nontrivial zeros of
$M$
, proving analogues of results obtained by Spira [Reference Speiser27] and Berndt [Reference Berndt4] for the Riemann zeta function. Further refinements of results by Luo were established in [Reference Garunkŝtis11] and [Reference Garunkŝtis12]. As is standard in analytic number theory, the nontrivial zeros of
![]() $Z_{M}$
, or
$Z_{M}$
, or
![]() $Z_{M}^{\prime }$
, are its zeros which do not arise from the poles of the multiplicative factor of the functional equation. In the case of a compact Riemann surface, the nontrivial zeros of
$Z_{M}^{\prime }$
, are its zeros which do not arise from the poles of the multiplicative factor of the functional equation. In the case of a compact Riemann surface, the nontrivial zeros of
![]() $Z_{M}$
and
$Z_{M}$
and
![]() $Z_{M}^{\prime }$
are zeros different from negative integers. Let us summarize the three main results stemming from the aforementioned articles, which are location, vertical distribution, and an asymptotic count for the weighted vertical distribution of the nontrivial zeros of
$Z_{M}^{\prime }$
are zeros different from negative integers. Let us summarize the three main results stemming from the aforementioned articles, which are location, vertical distribution, and an asymptotic count for the weighted vertical distribution of the nontrivial zeros of
![]() $Z_{M}^{\prime }$
.
$Z_{M}^{\prime }$
.
In [Reference Luo22] it is shown that
![]() $Z_{M}^{\prime }(s)$
has at most a finite number of nontrivial zeros in the half-plane
$Z_{M}^{\prime }(s)$
has at most a finite number of nontrivial zeros in the half-plane
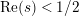 $\text{Re}(s)<1/2$
. This result was strengthened in [Reference Minamide24] and [Reference Minamide25] where it is proved that
$\text{Re}(s)<1/2$
. This result was strengthened in [Reference Minamide24] and [Reference Minamide25] where it is proved that
![]() $Z_{M}^{\prime }(s)$
has no nontrivial zeros in the half-plane
$Z_{M}^{\prime }(s)$
has no nontrivial zeros in the half-plane
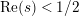 $\text{Re}(s)<1/2$
.
$\text{Re}(s)<1/2$
.
Let
![]() $\text{vol}(M)$
denote the hyperbolic volume of
$\text{vol}(M)$
denote the hyperbolic volume of
![]() $M$
. Let
$M$
. Let
![]() $\ell _{M,0}$
be the length of the shortest closed geodesic on
$\ell _{M,0}$
be the length of the shortest closed geodesic on
![]() $M$
. Let
$M$
. Let
![]() $m_{M,0}$
denote the number of inconjugate geodesics whose length is
$m_{M,0}$
denote the number of inconjugate geodesics whose length is
![]() $\ell _{M,0}$
. Let
$\ell _{M,0}$
. Let
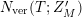 $N_{\text{ver}}(T;Z_{M}^{\prime })$
be the number of nontrivial zeros of
$N_{\text{ver}}(T;Z_{M}^{\prime })$
be the number of nontrivial zeros of
![]() $Z_{M}^{\prime }(s)$
where
$Z_{M}^{\prime }(s)$
where
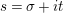 $s=\unicode[STIX]{x1D70E}+it$
with
$s=\unicode[STIX]{x1D70E}+it$
with
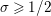 $\unicode[STIX]{x1D70E}\geqslant 1/2$
and
$\unicode[STIX]{x1D70E}\geqslant 1/2$
and
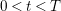 $0<t<T$
, and let
$0<t<T$
, and let
 $$\begin{eqnarray}N_{\text{w}}(T;Z_{M}^{\prime })=\mathop{\sum }_{{Z_{M}^{\prime }(\unicode[STIX]{x1D70E}+it)=0\atop 0<t<T,\unicode[STIX]{x1D70E}>1/2}}(\unicode[STIX]{x1D70E}-1/2)\end{eqnarray}$$
$$\begin{eqnarray}N_{\text{w}}(T;Z_{M}^{\prime })=\mathop{\sum }_{{Z_{M}^{\prime }(\unicode[STIX]{x1D70E}+it)=0\atop 0<t<T,\unicode[STIX]{x1D70E}>1/2}}(\unicode[STIX]{x1D70E}-1/2)\end{eqnarray}$$
be the weighted vertical distribution with weights equal to distances of zeros to the critical line. Then, building on the results form [Reference Luo22], it is proved in [Reference Garunkŝtis11] and [Reference Garunkŝtis12] that
 $$\begin{eqnarray}N_{\text{ver}}(T;Z_{M}^{\prime })=\frac{\text{vol}(M)}{4\unicode[STIX]{x1D70B}}T^{2}-\frac{\ell _{M,0}}{2\unicode[STIX]{x1D70B}}T+o(T)\quad \text{as }T\rightarrow \infty ,\end{eqnarray}$$
$$\begin{eqnarray}N_{\text{ver}}(T;Z_{M}^{\prime })=\frac{\text{vol}(M)}{4\unicode[STIX]{x1D70B}}T^{2}-\frac{\ell _{M,0}}{2\unicode[STIX]{x1D70B}}T+o(T)\quad \text{as }T\rightarrow \infty ,\end{eqnarray}$$
and
 $$\begin{eqnarray}\displaystyle N_{\text{w}}(T;Z_{M}^{\prime }) & = & \displaystyle \frac{T}{2\unicode[STIX]{x1D70B}}\log T+\frac{T}{2\unicode[STIX]{x1D70B}}\left(\frac{1}{2}\ell _{M,0}+\log \left(\frac{\text{vol}(M)(1-e^{-\ell _{M,0}})}{m_{M,0}\ell _{M,0}}\right)-1\right)\nonumber\\ \displaystyle & & \displaystyle +\,o(T)\quad \text{as }T\rightarrow \infty .\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle N_{\text{w}}(T;Z_{M}^{\prime }) & = & \displaystyle \frac{T}{2\unicode[STIX]{x1D70B}}\log T+\frac{T}{2\unicode[STIX]{x1D70B}}\left(\frac{1}{2}\ell _{M,0}+\log \left(\frac{\text{vol}(M)(1-e^{-\ell _{M,0}})}{m_{M,0}\ell _{M,0}}\right)-1\right)\nonumber\\ \displaystyle & & \displaystyle +\,o(T)\quad \text{as }T\rightarrow \infty .\end{eqnarray}$$
The study of the zeros of
![]() $Z_{M}^{\prime }$
is of particular interest because of the connection with spectral analysis. Recall that if
$Z_{M}^{\prime }$
is of particular interest because of the connection with spectral analysis. Recall that if
![]() $s$
is a nontrivial zero of
$s$
is a nontrivial zero of
![]() $Z_{M}(s)$
, then
$Z_{M}(s)$
, then
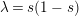 $\unicode[STIX]{x1D706}=s(1-s)$
is an eigenvalue of an
$\unicode[STIX]{x1D706}=s(1-s)$
is an eigenvalue of an
![]() $L^{2}$
-eigenfunction of the hyperbolic Laplacian which acts on the space of smooth functions on
$L^{2}$
-eigenfunction of the hyperbolic Laplacian which acts on the space of smooth functions on
![]() $M$
. Common zeros of
$M$
. Common zeros of
![]() $Z_{M}$
and
$Z_{M}$
and
![]() $Z_{M}^{\prime }$
are, in fact, zeros of
$Z_{M}^{\prime }$
are, in fact, zeros of
![]() $Z_{M}(s)$
with multiplicity greater than one. Such zeros of
$Z_{M}(s)$
with multiplicity greater than one. Such zeros of
![]() $Z_{M}$
correspond to multi-dimensional eigenspaces of the Laplacian. As shown in [Reference Luo22, p. 1143], all zeros of
$Z_{M}$
correspond to multi-dimensional eigenspaces of the Laplacian. As shown in [Reference Luo22, p. 1143], all zeros of
![]() $Z_{M}^{\prime }(s)$
on the line
$Z_{M}^{\prime }(s)$
on the line
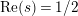 $\text{Re}(s)=1/2$
, except possibly at
$\text{Re}(s)=1/2$
, except possibly at
![]() $s=1/2$
, correspond to multiple zeros of
$s=1/2$
, correspond to multiple zeros of
![]() $Z_{M}$
. The problem of obtaining nontrivial bounds for the dimension of eigenspaces of the Laplacian is very difficult; see [Reference Iwaniec17, p. 160]. Thus, it is possible that refined information regarding (1) possibly could shed light on this important, outstanding question.
$Z_{M}$
. The problem of obtaining nontrivial bounds for the dimension of eigenspaces of the Laplacian is very difficult; see [Reference Iwaniec17, p. 160]. Thus, it is possible that refined information regarding (1) possibly could shed light on this important, outstanding question.
1.2 Noncompact Riemann surfaces
Let
![]() $\mathbb{H}$
denote the hyperbolic upper half-plane. Let
$\mathbb{H}$
denote the hyperbolic upper half-plane. Let
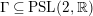 $\unicode[STIX]{x1D6E4}\subseteq \text{PSL}(2,\mathbb{R})$
be any Fuchsian group of the first kind acting by fractional linear transformations on
$\unicode[STIX]{x1D6E4}\subseteq \text{PSL}(2,\mathbb{R})$
be any Fuchsian group of the first kind acting by fractional linear transformations on
![]() $\mathbb{H}$
, and let
$\mathbb{H}$
, and let
![]() $M$
be the quotient space
$M$
be the quotient space
![]() $\unicode[STIX]{x1D6E4}\backslash \mathbb{H}$
.
$\unicode[STIX]{x1D6E4}\backslash \mathbb{H}$
.
One realization of the spectral analysis of the Laplacian on the surface
![]() $M$
is the location of nontrivial zeros of the associated Selberg zeta function
$M$
is the location of nontrivial zeros of the associated Selberg zeta function
![]() $Z_{M}$
, defined for
$Z_{M}$
, defined for
![]() $s\in \mathbb{C}$
with
$s\in \mathbb{C}$
with
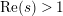 $\text{Re}(s)>1$
by the Euler product
$\text{Re}(s)>1$
by the Euler product
 $$\begin{eqnarray}\displaystyle Z_{M}(s)=\mathop{\prod }_{n=0}^{\infty }\mathop{\prod }_{P_{0}\in {\mathcal{H}}(\unicode[STIX]{x1D6E4})}\big(1-e^{-(s+n)\ell _{P_{0}}}\big)=\mathop{\prod }_{n=0}^{\infty }\mathop{\prod }_{P_{0}\in {\mathcal{H}}(\unicode[STIX]{x1D6E4})}\big(1-N(P_{0})^{-(s+n)}\big). & & \displaystyle \nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle Z_{M}(s)=\mathop{\prod }_{n=0}^{\infty }\mathop{\prod }_{P_{0}\in {\mathcal{H}}(\unicode[STIX]{x1D6E4})}\big(1-e^{-(s+n)\ell _{P_{0}}}\big)=\mathop{\prod }_{n=0}^{\infty }\mathop{\prod }_{P_{0}\in {\mathcal{H}}(\unicode[STIX]{x1D6E4})}\big(1-N(P_{0})^{-(s+n)}\big). & & \displaystyle \nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
Here
![]() ${\mathcal{H}}(\unicode[STIX]{x1D6E4})$
denotes a complete set of representatives of inconjugate, primitive hyperbolic elements of
${\mathcal{H}}(\unicode[STIX]{x1D6E4})$
denotes a complete set of representatives of inconjugate, primitive hyperbolic elements of
![]() $\unicode[STIX]{x1D6E4}$
,
$\unicode[STIX]{x1D6E4}$
,
![]() $P_{0}$
is a primitive hyperbolic element,
$P_{0}$
is a primitive hyperbolic element,
![]() $\ell _{P_{0}}$
is the hyperbolic length of the geodesic path in the homotopy class determined by
$\ell _{P_{0}}$
is the hyperbolic length of the geodesic path in the homotopy class determined by
![]() $P_{0}$
and the norm
$P_{0}$
and the norm
![]() $N(P_{0})$
is equal to
$N(P_{0})$
is equal to
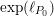 $\exp (\ell _{P_{0}})$
.
$\exp (\ell _{P_{0}})$
.
The function
![]() $Z_{M}$
possesses a meromorphic continuation to the whole complex plane and satisfies the functional equation
$Z_{M}$
possesses a meromorphic continuation to the whole complex plane and satisfies the functional equation
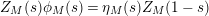 $Z_{M}(s)\unicode[STIX]{x1D719}_{M}(s)=\unicode[STIX]{x1D702}_{M}(s)Z_{M}(1-s)$
, where
$Z_{M}(s)\unicode[STIX]{x1D719}_{M}(s)=\unicode[STIX]{x1D702}_{M}(s)Z_{M}(1-s)$
, where
![]() $\unicode[STIX]{x1D719}_{M}(s)$
denotes the determinant of the scattering matrix
$\unicode[STIX]{x1D719}_{M}(s)$
denotes the determinant of the scattering matrix
![]() $\unicode[STIX]{x1D6F7}_{M}(s)$
,
$\unicode[STIX]{x1D6F7}_{M}(s)$
,
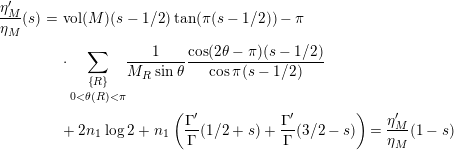 $$\begin{eqnarray}\displaystyle \frac{\unicode[STIX]{x1D702}_{M}^{\prime }}{\unicode[STIX]{x1D702}_{M}}(s) & = & \displaystyle \text{vol}(M)(s-1/2)\tan (\unicode[STIX]{x1D70B}(s-1/2))-\unicode[STIX]{x1D70B}\nonumber\\ \displaystyle & & \displaystyle \cdot \,\underset{0<\unicode[STIX]{x1D703}(R)<\unicode[STIX]{x1D70B}}{\underset{\left\{R\right\}}{\sum }}\frac{1}{M_{R}\sin \unicode[STIX]{x1D703}}\frac{\cos (2\unicode[STIX]{x1D703}-\unicode[STIX]{x1D70B})(s-1/2)}{\cos \unicode[STIX]{x1D70B}(s-1/2)}\nonumber\\ \displaystyle & & \displaystyle +\,2n_{1}\log 2+n_{1}\left(\frac{\unicode[STIX]{x1D6E4}^{\prime }}{\unicode[STIX]{x1D6E4}}(1/2+s)+\frac{\unicode[STIX]{x1D6E4}^{\prime }}{\unicode[STIX]{x1D6E4}}(3/2-s)\right)=\frac{\unicode[STIX]{x1D702}_{M}^{\prime }}{\unicode[STIX]{x1D702}_{M}}(1-s)\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \frac{\unicode[STIX]{x1D702}_{M}^{\prime }}{\unicode[STIX]{x1D702}_{M}}(s) & = & \displaystyle \text{vol}(M)(s-1/2)\tan (\unicode[STIX]{x1D70B}(s-1/2))-\unicode[STIX]{x1D70B}\nonumber\\ \displaystyle & & \displaystyle \cdot \,\underset{0<\unicode[STIX]{x1D703}(R)<\unicode[STIX]{x1D70B}}{\underset{\left\{R\right\}}{\sum }}\frac{1}{M_{R}\sin \unicode[STIX]{x1D703}}\frac{\cos (2\unicode[STIX]{x1D703}-\unicode[STIX]{x1D70B})(s-1/2)}{\cos \unicode[STIX]{x1D70B}(s-1/2)}\nonumber\\ \displaystyle & & \displaystyle +\,2n_{1}\log 2+n_{1}\left(\frac{\unicode[STIX]{x1D6E4}^{\prime }}{\unicode[STIX]{x1D6E4}}(1/2+s)+\frac{\unicode[STIX]{x1D6E4}^{\prime }}{\unicode[STIX]{x1D6E4}}(3/2-s)\right)=\frac{\unicode[STIX]{x1D702}_{M}^{\prime }}{\unicode[STIX]{x1D702}_{M}}(1-s)\end{eqnarray}$$
and where
![]() $\{R\}$
denotes a complete, finite set of inconjugate elliptic elements of
$\{R\}$
denotes a complete, finite set of inconjugate elliptic elements of
![]() $\unicode[STIX]{x1D6E4}$
so that
$\unicode[STIX]{x1D6E4}$
so that
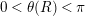 $0<\unicode[STIX]{x1D703}(R)<\unicode[STIX]{x1D70B}$
is the uniquely determined real number such that
$0<\unicode[STIX]{x1D703}(R)<\unicode[STIX]{x1D70B}$
is the uniquely determined real number such that
![]() $R$
is conjugate to the matrix
$R$
is conjugate to the matrix
 $$\begin{eqnarray}\left(\begin{array}{@{}cc@{}}\cos \unicode[STIX]{x1D703}(R) & -\sin \unicode[STIX]{x1D703}(R)\\ \sin \unicode[STIX]{x1D703}(R) & \cos \unicode[STIX]{x1D703}(R)\\ \end{array}\right).\end{eqnarray}$$
$$\begin{eqnarray}\left(\begin{array}{@{}cc@{}}\cos \unicode[STIX]{x1D703}(R) & -\sin \unicode[STIX]{x1D703}(R)\\ \sin \unicode[STIX]{x1D703}(R) & \cos \unicode[STIX]{x1D703}(R)\\ \end{array}\right).\end{eqnarray}$$
The scattering determinant
![]() $\unicode[STIX]{x1D719}_{M}(s)$
has a decomposition into a product of a general Dirichlet series and Gamma functions. Specifically, we can write
$\unicode[STIX]{x1D719}_{M}(s)$
has a decomposition into a product of a general Dirichlet series and Gamma functions. Specifically, we can write
 $$\begin{eqnarray}\unicode[STIX]{x1D719}_{M}(s)=\unicode[STIX]{x1D70B}^{n_{1}/2}\left(\frac{\unicode[STIX]{x1D6E4}\left(s-\frac{1}{2}\right)}{\unicode[STIX]{x1D6E4}(s)}\right)^{n_{1}}\overset{\infty }{\underset{n=1}{\sum }}\frac{d(n)}{\mathfrak{g}_{n}^{2s}}\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D719}_{M}(s)=\unicode[STIX]{x1D70B}^{n_{1}/2}\left(\frac{\unicode[STIX]{x1D6E4}\left(s-\frac{1}{2}\right)}{\unicode[STIX]{x1D6E4}(s)}\right)^{n_{1}}\overset{\infty }{\underset{n=1}{\sum }}\frac{d(n)}{\mathfrak{g}_{n}^{2s}}\end{eqnarray}$$
where
![]() $n_{1}$
is the number of cusps of
$n_{1}$
is the number of cusps of
![]() $M$
, and
$M$
, and
![]() $\{d(n)\}$
and
$\{d(n)\}$
and
![]() $\{\mathfrak{g}_{n}\}$
are sequences of real numbers with
$\{\mathfrak{g}_{n}\}$
are sequences of real numbers with
 $$\begin{eqnarray}0<\mathfrak{g}_{1}<\cdots <\mathfrak{g}_{n}<\mathfrak{g}_{n+1}<\cdots \,;\end{eqnarray}$$
$$\begin{eqnarray}0<\mathfrak{g}_{1}<\cdots <\mathfrak{g}_{n}<\mathfrak{g}_{n+1}<\cdots \,;\end{eqnarray}$$
given in terms of Kloosterman sums (see [Reference Iwaniec17, p. 160]). Let us write
 $\unicode[STIX]{x1D719}_{M}(s)=K_{M}(s)\cdot H_{M}(s)$
where
$\unicode[STIX]{x1D719}_{M}(s)=K_{M}(s)\cdot H_{M}(s)$
where
 $$\begin{eqnarray}\displaystyle K_{M}(s) & = & \displaystyle \unicode[STIX]{x1D70B}^{n_{1}/2}\left(\frac{\unicode[STIX]{x1D6E4}\left(s-\frac{1}{2}\right)}{\unicode[STIX]{x1D6E4}(s)}\right)^{n_{1}}e^{c_{1}s+c_{2}},\quad \text{with }\nonumber\\ \displaystyle & & \displaystyle c_{1}=-2\log \mathfrak{g}_{1}\qquad \text{and}\qquad c_{2}=\log d(1),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle K_{M}(s) & = & \displaystyle \unicode[STIX]{x1D70B}^{n_{1}/2}\left(\frac{\unicode[STIX]{x1D6E4}\left(s-\frac{1}{2}\right)}{\unicode[STIX]{x1D6E4}(s)}\right)^{n_{1}}e^{c_{1}s+c_{2}},\quad \text{with }\nonumber\\ \displaystyle & & \displaystyle c_{1}=-2\log \mathfrak{g}_{1}\qquad \text{and}\qquad c_{2}=\log d(1),\end{eqnarray}$$
and
 $$\begin{eqnarray}\displaystyle H_{M}(s)=1+\overset{\infty }{\underset{n=2}{\sum }}\frac{a(n)}{r_{n}^{2s}}\quad \text{with }r_{n}=\mathfrak{g}_{n}/\mathfrak{g}_{1}>1\qquad \text{and}\qquad a(n)=d(n)/d(1). & & \displaystyle \nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle H_{M}(s)=1+\overset{\infty }{\underset{n=2}{\sum }}\frac{a(n)}{r_{n}^{2s}}\quad \text{with }r_{n}=\mathfrak{g}_{n}/\mathfrak{g}_{1}>1\qquad \text{and}\qquad a(n)=d(n)/d(1). & & \displaystyle \nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
The Dirichlet series expansion for
![]() $H_{M}(s)$
converges for all
$H_{M}(s)$
converges for all
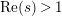 $\text{Re}(s)>1$
. We call the function
$\text{Re}(s)>1$
. We call the function
![]() $H_{M}$
the Dirichlet series portion of the scattering determinant
$H_{M}$
the Dirichlet series portion of the scattering determinant
![]() $\unicode[STIX]{x1D719}_{M}$
. In general, the function
$\unicode[STIX]{x1D719}_{M}$
. In general, the function
![]() $H_{M}$
can be expressed as the determinant of a matrix whose entries are general Kloosterman sums; see [Reference Iwaniec17, Theorem 3.4]. The constants
$H_{M}$
can be expressed as the determinant of a matrix whose entries are general Kloosterman sums; see [Reference Iwaniec17, Theorem 3.4]. The constants
![]() $\mathfrak{g}_{1}$
and
$\mathfrak{g}_{1}$
and
![]() $\mathfrak{g}_{2}$
are explained in terms of the left lower entries of the matrices appearing in the double coset decomposition of
$\mathfrak{g}_{2}$
are explained in terms of the left lower entries of the matrices appearing in the double coset decomposition of
![]() $\unicode[STIX]{x1D6E4}$
. Therefore, the constants
$\unicode[STIX]{x1D6E4}$
. Therefore, the constants
![]() $\mathfrak{g}_{1}$
and
$\mathfrak{g}_{1}$
and
![]() $\mathfrak{g}_{2}$
are precisely connected to the Fuchsian group
$\mathfrak{g}_{2}$
are precisely connected to the Fuchsian group
![]() $\unicode[STIX]{x1D6E4}$
and
$\unicode[STIX]{x1D6E4}$
and
![]() $H_{M}(s)$
is a Dirichlet series carrying the information related to parabolic subgroups of
$H_{M}(s)$
is a Dirichlet series carrying the information related to parabolic subgroups of
![]() $\unicode[STIX]{x1D6E4}$
.
$\unicode[STIX]{x1D6E4}$
.
By nontrivial zeros of
![]() $Z_{M}(s)$
we mean all nonreal zeros and real zeros at points
$Z_{M}(s)$
we mean all nonreal zeros and real zeros at points
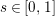 $s\in [0,1]$
such that
$s\in [0,1]$
such that
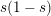 $s(1-s)$
is equal to an eigenvalue of the Laplacian that is less than or equal to
$s(1-s)$
is equal to an eigenvalue of the Laplacian that is less than or equal to
![]() $1/4$
. The nontrivial zeros are related to the spectrum of the Laplacian in the sense that, according to [Reference Hejhal14, Theorem 5.3], the nontrivial zeros of
$1/4$
. The nontrivial zeros are related to the spectrum of the Laplacian in the sense that, according to [Reference Hejhal14, Theorem 5.3], the nontrivial zeros of
![]() $Z_{M}$
are located at points of the form
$Z_{M}$
are located at points of the form
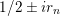 $1/2\pm ir_{n}$
where
$1/2\pm ir_{n}$
where
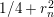 $1/4+r_{n}^{2}$
is a discrete eigenvalue of the Laplacian and at points
$1/4+r_{n}^{2}$
is a discrete eigenvalue of the Laplacian and at points
![]() $1-\unicode[STIX]{x1D70C}$
in the half-plane
$1-\unicode[STIX]{x1D70C}$
in the half-plane
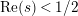 $\text{Re}(s)<1/2$
which are poles of the determinant
$\text{Re}(s)<1/2$
which are poles of the determinant
![]() $\unicode[STIX]{x1D719}_{M}$
of the scattering matrix.
$\unicode[STIX]{x1D719}_{M}$
of the scattering matrix.
We may conclude that the function
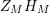 $Z_{M}H_{M}$
is “spectrally equivalent” to
$Z_{M}H_{M}$
is “spectrally equivalent” to
![]() $Z_{M}$
in the following sense: The function
$Z_{M}$
in the following sense: The function
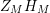 $Z_{M}H_{M}$
can be represented as a general Dirichlet series converging in the half-plane
$Z_{M}H_{M}$
can be represented as a general Dirichlet series converging in the half-plane
 $\text{Re}(s)>1$
and carrying information about the underlying group
$\text{Re}(s)>1$
and carrying information about the underlying group
![]() $\unicode[STIX]{x1D6E4}$
; it possesses a meromorphic continuation to the entire complex plane satisfying the functional equation
$\unicode[STIX]{x1D6E4}$
; it possesses a meromorphic continuation to the entire complex plane satisfying the functional equation
 $$\begin{eqnarray}(Z_{M}H_{M})(s)=\unicode[STIX]{x1D702}_{M}(s)K_{M}^{-1}(s)Z_{M}(1-s);\end{eqnarray}$$
$$\begin{eqnarray}(Z_{M}H_{M})(s)=\unicode[STIX]{x1D702}_{M}(s)K_{M}^{-1}(s)Z_{M}(1-s);\end{eqnarray}$$
and its nontrivial zeros are at points
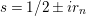 $s=1/2\pm ir_{n}$
, where
$s=1/2\pm ir_{n}$
, where
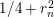 $1/4+r_{n}^{2}$
is a discrete eigenvalue of the Laplacian and at points
$1/4+r_{n}^{2}$
is a discrete eigenvalue of the Laplacian and at points
![]() $s=\unicode[STIX]{x1D70C}$
in the half-plane
$s=\unicode[STIX]{x1D70C}$
in the half-plane
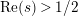 $\text{Re}(s)>1/2$
which are zeros of the determinant
$\text{Re}(s)>1/2$
which are zeros of the determinant
![]() $\unicode[STIX]{x1D719}_{M}$
of the scattering matrix. Based on this argument, we may, loosely speaking, say that
$\unicode[STIX]{x1D719}_{M}$
of the scattering matrix. Based on this argument, we may, loosely speaking, say that
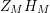 $Z_{M}H_{M}$
carries the same amount of spectral information as
$Z_{M}H_{M}$
carries the same amount of spectral information as
![]() $Z_{M}$
does. Besides that, the function
$Z_{M}$
does. Besides that, the function
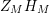 $Z_{M}H_{M}$
has no nontrivial zeros in the half-plane
$Z_{M}H_{M}$
has no nontrivial zeros in the half-plane
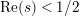 $\text{Re}(s)<1/2$
.
$\text{Re}(s)<1/2$
.
The question of studying the zeros of
![]() $Z_{M}^{\prime }$
when
$Z_{M}^{\prime }$
when
![]() $M$
is not compact by applying methods presented in this paper begins with one possible technical difficulty stemming from the fact that the function
$M$
is not compact by applying methods presented in this paper begins with one possible technical difficulty stemming from the fact that the function
![]() $Z_{M}$
has an infinite number of zeros in the half-plane
$Z_{M}$
has an infinite number of zeros in the half-plane
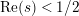 $\text{Re}(s)<1/2$
, each one of which would produce a negative weight in the weighted counting function
$\text{Re}(s)<1/2$
, each one of which would produce a negative weight in the weighted counting function
![]() $N_{\text{w}}$
. On the other hand, the function
$N_{\text{w}}$
. On the other hand, the function
 $Z_{M}H_{M}$
has no nontrivial zeros in the half-plane
$Z_{M}H_{M}$
has no nontrivial zeros in the half-plane
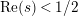 $\text{ Re}(s)<1/2$
and carries the same spectral information as
$\text{ Re}(s)<1/2$
and carries the same spectral information as
![]() $Z_{M}$
does. Therefore, as a result we shall study the zeros of
$Z_{M}$
does. Therefore, as a result we shall study the zeros of
 $(Z_{M}H_{M})^{\prime }$
.
$(Z_{M}H_{M})^{\prime }$
.
As we shall see below, the choice of
 $Z_{M}H_{M}$
instead of
$Z_{M}H_{M}$
instead of
![]() $Z_{M}$
is further justified by the fact that, according to the statement (a) of the Main Theorem, the only zeros of
$Z_{M}$
is further justified by the fact that, according to the statement (a) of the Main Theorem, the only zeros of
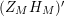 $(Z_{M}H_{M})^{\prime }$
on the critical line (with imaginary part greater than some constant depending upon the group) are the multiple zeros of
$(Z_{M}H_{M})^{\prime }$
on the critical line (with imaginary part greater than some constant depending upon the group) are the multiple zeros of
![]() $Z_{M}$
; therefore, the study of zeros of
$Z_{M}$
; therefore, the study of zeros of
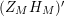 $(Z_{M}H_{M})^{\prime }$
is related to the problem of obtaining bounds for the dimension of eigenspaces of discrete eigenvalues of the Laplacian on
$(Z_{M}H_{M})^{\prime }$
is related to the problem of obtaining bounds for the dimension of eigenspaces of discrete eigenvalues of the Laplacian on
![]() $M$
.
$M$
.
In conclusion, we followed the guide provided by the technical issues we faced and chose to study the zeros of
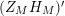 $(Z_{M}H_{M})^{\prime }$
. To be specific, we viewed the positivity issues described above as important, thus we focused our attention on the zeros of
$(Z_{M}H_{M})^{\prime }$
. To be specific, we viewed the positivity issues described above as important, thus we focused our attention on the zeros of
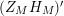 $(Z_{M}H_{M})^{\prime }$
. Nonetheless, the problem of studying the zeros of
$(Z_{M}H_{M})^{\prime }$
. Nonetheless, the problem of studying the zeros of
![]() $Z_{M}^{\prime }$
is both well-posed and remains open. It is quite possible that a successful study of the zeros of
$Z_{M}^{\prime }$
is both well-posed and remains open. It is quite possible that a successful study of the zeros of
![]() $Z_{M}^{\prime }$
when combined with the results of the present paper would yield interesting results. We leave such a study to a motivated reader.
$Z_{M}^{\prime }$
when combined with the results of the present paper would yield interesting results. We leave such a study to a motivated reader.
1.3 The main result
The function
 $H_{M}^{\prime }/H_{M}$
admits the general Dirichlet series expansion
$H_{M}^{\prime }/H_{M}$
admits the general Dirichlet series expansion
 $$\begin{eqnarray}\frac{H_{M}^{\prime }}{H_{M}}(s)=\mathop{\sum }_{i=1}^{\infty }\frac{b(q_{i})}{q_{i}^{s}},\end{eqnarray}$$
$$\begin{eqnarray}\frac{H_{M}^{\prime }}{H_{M}}(s)=\mathop{\sum }_{i=1}^{\infty }\frac{b(q_{i})}{q_{i}^{s}},\end{eqnarray}$$
where the series on the right converges absolutely and uniformly for
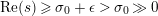 $\text{Re}(s)\geqslant \unicode[STIX]{x1D70E}_{0}+\unicode[STIX]{x1D716}>\unicode[STIX]{x1D70E}_{0}\gg 0$
, and where
$\text{Re}(s)\geqslant \unicode[STIX]{x1D70E}_{0}+\unicode[STIX]{x1D716}>\unicode[STIX]{x1D70E}_{0}\gg 0$
, and where
![]() $\{q_{i}\}$
is a nondecreasing sequence of positive real numbers consisting of all finite products of numbers
$\{q_{i}\}$
is a nondecreasing sequence of positive real numbers consisting of all finite products of numbers
![]() $r_{n}^{2}>1$
. Obviously,
$r_{n}^{2}>1$
. Obviously,
 $q_{2}>q_{1}=\inf q_{i}=(\mathfrak{g}_{2}/\mathfrak{g}_{1})^{2}$
. Furthermore,
$q_{2}>q_{1}=\inf q_{i}=(\mathfrak{g}_{2}/\mathfrak{g}_{1})^{2}$
. Furthermore,
 $$\begin{eqnarray}b(q_{1})=-a(2)\log q_{1}=-2(d(2)/d(1))\log (\mathfrak{g}_{2}/\mathfrak{g}_{1}).\end{eqnarray}$$
$$\begin{eqnarray}b(q_{1})=-a(2)\log q_{1}=-2(d(2)/d(1))\log (\mathfrak{g}_{2}/\mathfrak{g}_{1}).\end{eqnarray}$$
Let
![]() $\ell _{M,0}$
be the length of a shortest closed geodesic, or systole, on
$\ell _{M,0}$
be the length of a shortest closed geodesic, or systole, on
![]() $M$
. With our notation from above, let
$M$
. With our notation from above, let
 $$\begin{eqnarray}A_{M}=\min \big\{e^{\ell _{M,0}},\left(\mathfrak{g}_{2}/\mathfrak{g}_{1}\right)^{2}\big\}.\end{eqnarray}$$
$$\begin{eqnarray}A_{M}=\min \big\{e^{\ell _{M,0}},\left(\mathfrak{g}_{2}/\mathfrak{g}_{1}\right)^{2}\big\}.\end{eqnarray}$$
Here, we have dropped the subscript
![]() $M$
on
$M$
on
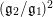 $(\mathfrak{g}_{2}/\mathfrak{g}_{1})^{2}$
in order to ease the notation; however, it is clear that
$(\mathfrak{g}_{2}/\mathfrak{g}_{1})^{2}$
in order to ease the notation; however, it is clear that
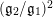 $(\mathfrak{g}_{2}/\mathfrak{g}_{1})^{2}$
depends on
$(\mathfrak{g}_{2}/\mathfrak{g}_{1})^{2}$
depends on
![]() $M$
. Let
$M$
. Let
![]() $m_{M,0}$
denote the number of inconjugate closed geodesics on
$m_{M,0}$
denote the number of inconjugate closed geodesics on
![]() $M$
with length
$M$
with length
![]() $\ell _{M,0}$
. If
$\ell _{M,0}$
. If
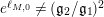 $e^{\ell _{M,0}}\neq (\mathfrak{g}_{2}/\mathfrak{g}_{1})^{2}$
, let
$e^{\ell _{M,0}}\neq (\mathfrak{g}_{2}/\mathfrak{g}_{1})^{2}$
, let
 $$\begin{eqnarray}a_{M}=\left\{\begin{array}{@{}cc@{}}\displaystyle \frac{m_{M,0}\ell _{M,0}}{1-e^{-\ell _{M,0}}}; & \text{if }e^{\ell _{M,0}}<\left(\mathfrak{g}_{2}/\mathfrak{g}_{1}\right)^{2}\\ b(\left(\mathfrak{g}_{2}/\mathfrak{g}_{1}\right)^{2}); & \text{if }e^{\ell _{M,0}}>\left(\mathfrak{g}_{2}/\mathfrak{g}_{1}\right)^{2}\end{array}\right\}.\end{eqnarray}$$
$$\begin{eqnarray}a_{M}=\left\{\begin{array}{@{}cc@{}}\displaystyle \frac{m_{M,0}\ell _{M,0}}{1-e^{-\ell _{M,0}}}; & \text{if }e^{\ell _{M,0}}<\left(\mathfrak{g}_{2}/\mathfrak{g}_{1}\right)^{2}\\ b(\left(\mathfrak{g}_{2}/\mathfrak{g}_{1}\right)^{2}); & \text{if }e^{\ell _{M,0}}>\left(\mathfrak{g}_{2}/\mathfrak{g}_{1}\right)^{2}\end{array}\right\}.\end{eqnarray}$$
If
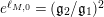 $e^{\ell _{M,0}}=(\mathfrak{g}_{2}/\mathfrak{g}_{1})^{2}$
, let
$e^{\ell _{M,0}}=(\mathfrak{g}_{2}/\mathfrak{g}_{1})^{2}$
, let
 $$\begin{eqnarray}a_{M}=\frac{m_{M,0}\ell _{M,0}}{1-e^{-\ell _{M,0}}}+b(\left(\mathfrak{g}_{2}/\mathfrak{g}_{1}\right)^{2}).\end{eqnarray}$$
$$\begin{eqnarray}a_{M}=\frac{m_{M,0}\ell _{M,0}}{1-e^{-\ell _{M,0}}}+b(\left(\mathfrak{g}_{2}/\mathfrak{g}_{1}\right)^{2}).\end{eqnarray}$$
Observe that
![]() $a_{M}$
is the sum of the two terms which appear in the two cases in (10), not the arithmetic average as one would expect from elementary Fourier analysis.
$a_{M}$
is the sum of the two terms which appear in the two cases in (10), not the arithmetic average as one would expect from elementary Fourier analysis.
With all this, the main result of this article is the following.
Main Theorem.
Let
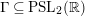 $\unicode[STIX]{x1D6E4}\subseteq \text{PSL}_{2}(\mathbb{R})$
be any Fuchsian group of the first kind acting by fractional linear transformations on
$\unicode[STIX]{x1D6E4}\subseteq \text{PSL}_{2}(\mathbb{R})$
be any Fuchsian group of the first kind acting by fractional linear transformations on
![]() $\mathbb{H}$
, and let
$\mathbb{H}$
, and let
![]() $M$
be the quotient space
$M$
be the quotient space
![]() $\unicode[STIX]{x1D6E4}\backslash \mathbb{H}$
. Let
$\unicode[STIX]{x1D6E4}\backslash \mathbb{H}$
. Let
![]() $Z_{M}(s)$
be the associated Selberg zeta function, and
$Z_{M}(s)$
be the associated Selberg zeta function, and
![]() $H_{M}(s)$
be the Dirichlet series portion of the determinant of the associated scattering matrix.
$H_{M}(s)$
be the Dirichlet series portion of the determinant of the associated scattering matrix.
-
(a) There are a finite number of nontrivial zeros of
 $(Z_{M}H_{M})^{\prime }(s)$
in the half-plane
$(Z_{M}H_{M})^{\prime }(s)$
in the half-plane
 $\text{Re}(s)<1/2$
. In addition, there exist some
$\text{Re}(s)<1/2$
. In addition, there exist some
 $t_{0}>0$
such that any zero of
$t_{0}>0$
such that any zero of
 $(Z_{M}H_{M})^{\prime }(s)$
on the line
$(Z_{M}H_{M})^{\prime }(s)$
on the line
 $\operatorname{Re}(s)=1/2$
with property
$\operatorname{Re}(s)=1/2$
with property
 $|\operatorname{Im}(s)|>t_{0}$
arises from a multiple zero of
$|\operatorname{Im}(s)|>t_{0}$
arises from a multiple zero of
 $Z_{M}(s)$
.
$Z_{M}(s)$
. -
(b) Let us define the vertical counting function
Then $$\begin{eqnarray}N_{\text{ver}}(T;(Z_{M}H_{M})^{\prime })=\#\{\unicode[STIX]{x1D70C}=\unicode[STIX]{x1D70E}+it\,\big|\,(Z_{M}H_{M})^{\prime }(\unicode[STIX]{x1D70C})=0\text{ with }0<t<T\}.\end{eqnarray}$$
In particular, if
$$\begin{eqnarray}N_{\text{ver}}(T;(Z_{M}H_{M})^{\prime })=\#\{\unicode[STIX]{x1D70C}=\unicode[STIX]{x1D70E}+it\,\big|\,(Z_{M}H_{M})^{\prime }(\unicode[STIX]{x1D70C})=0\text{ with }0<t<T\}.\end{eqnarray}$$
In particular, if $$\begin{eqnarray}\displaystyle N_{\text{ver}}(T;(Z_{M}H_{M})^{\prime }) & = & \displaystyle \frac{\text{ vol}(M)}{4\unicode[STIX]{x1D70B}}T^{2}-\frac{T}{2\unicode[STIX]{x1D70B}}\left(\log A_{M}+2n_{1}\log 2+2\log \mathfrak{g}_{1}\right)\nonumber\\ \displaystyle & & \displaystyle +\,o(T),\quad \text{as }T\rightarrow \infty .\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle N_{\text{ver}}(T;(Z_{M}H_{M})^{\prime }) & = & \displaystyle \frac{\text{ vol}(M)}{4\unicode[STIX]{x1D70B}}T^{2}-\frac{T}{2\unicode[STIX]{x1D70B}}\left(\log A_{M}+2n_{1}\log 2+2\log \mathfrak{g}_{1}\right)\nonumber\\ \displaystyle & & \displaystyle +\,o(T),\quad \text{as }T\rightarrow \infty .\nonumber\end{eqnarray}$$
 $M$
is co-compact, then (1) holds true.
$M$
is co-compact, then (1) holds true.
-
(c) Let us define the weighted vertical counting function
Then $$\begin{eqnarray}N_{\text{w}}(T;(Z_{M}H_{M})^{\prime })=\mathop{\sum }_{{(Z_{M}H_{M})^{\prime }(\unicode[STIX]{x1D70E}+it)=0\atop 0<t<T\,\,\text{ and}\,\,\unicode[STIX]{x1D70E}>1/2}}(\unicode[STIX]{x1D70E}-1/2).\end{eqnarray}$$
In particular, if
$$\begin{eqnarray}N_{\text{w}}(T;(Z_{M}H_{M})^{\prime })=\mathop{\sum }_{{(Z_{M}H_{M})^{\prime }(\unicode[STIX]{x1D70E}+it)=0\atop 0<t<T\,\,\text{ and}\,\,\unicode[STIX]{x1D70E}>1/2}}(\unicode[STIX]{x1D70E}-1/2).\end{eqnarray}$$
In particular, if $$\begin{eqnarray}\displaystyle N_{\text{w}}(T;(Z_{M}H_{M})^{\prime }) & = & \displaystyle \left(\frac{n_{1}}{2}+1\right)\frac{T\log T}{2\unicode[STIX]{x1D70B}}+\frac{T}{2\unicode[STIX]{x1D70B}}\left(\log \frac{\text{ vol}(M)A_{M}^{1/2}}{|a_{M}|}-1\right)\nonumber\\ \displaystyle & & \displaystyle +\,\frac{T}{2\unicode[STIX]{x1D70B}}\left(\log \left(\frac{\mathfrak{g}_{1}}{\unicode[STIX]{x1D70B}^{n_{1}/2}|\,d(1)|}\right)-\frac{n_{1}}{2}\right)+o(T),\nonumber\\ \displaystyle & & \displaystyle \quad \text{as }T\rightarrow \infty .\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle N_{\text{w}}(T;(Z_{M}H_{M})^{\prime }) & = & \displaystyle \left(\frac{n_{1}}{2}+1\right)\frac{T\log T}{2\unicode[STIX]{x1D70B}}+\frac{T}{2\unicode[STIX]{x1D70B}}\left(\log \frac{\text{ vol}(M)A_{M}^{1/2}}{|a_{M}|}-1\right)\nonumber\\ \displaystyle & & \displaystyle +\,\frac{T}{2\unicode[STIX]{x1D70B}}\left(\log \left(\frac{\mathfrak{g}_{1}}{\unicode[STIX]{x1D70B}^{n_{1}/2}|\,d(1)|}\right)-\frac{n_{1}}{2}\right)+o(T),\nonumber\\ \displaystyle & & \displaystyle \quad \text{as }T\rightarrow \infty .\nonumber\end{eqnarray}$$
 $M$
is co-compact, then (2) holds true.
$M$
is co-compact, then (2) holds true.
As stated in the Main Theorem, the above asymptotic formulas specialize in the case
![]() $M$
is compact to give the main results in [Reference Garunkŝtis11, Reference Garunkŝtis12, Reference Luo22, Reference Minamide24] and [Reference Minamide25]. More precisely, in [Reference Minamide24] and [Reference Minamide25] it is proved that
$M$
is compact to give the main results in [Reference Garunkŝtis11, Reference Garunkŝtis12, Reference Luo22, Reference Minamide24] and [Reference Minamide25]. More precisely, in [Reference Minamide24] and [Reference Minamide25] it is proved that
![]() $Z_{M}^{\prime }$
in the compact case possesses no nonreal zeros in the half-plane
$Z_{M}^{\prime }$
in the compact case possesses no nonreal zeros in the half-plane
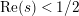 $\text{Re}(s)<1/2$
, a statement which we believe to hold true for
$\text{Re}(s)<1/2$
, a statement which we believe to hold true for
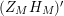 $(Z_{M}H_{M})^{\prime }$
.
$(Z_{M}H_{M})^{\prime }$
.
Similar results for the zeros of higher derivatives of
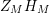 $Z_{M}H_{M}$
are presented in a later section. In addition, corollaries of the main theorem, analogous to results from [Reference Levinson and Montgomery21], are derived.
$Z_{M}H_{M}$
are presented in a later section. In addition, corollaries of the main theorem, analogous to results from [Reference Levinson and Montgomery21], are derived.
Since the proof of the Main Theorem is rather technical, let us present here a summary of the ideas involved in its proof.
Part (a) of the Main Theorem is proved in two parts. First, we employ the functional equation for the Selberg zeta function together with a bound for the growth of the logarithmic derivative
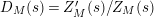 $D_{M}(s)=Z_{M}^{\prime }(s)/Z_{M}(s)$
in the right half of the critical strip in order to deduce that
$D_{M}(s)=Z_{M}^{\prime }(s)/Z_{M}(s)$
in the right half of the critical strip in order to deduce that
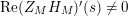 $\text{Re}(Z_{M}H_{M})^{\prime }(s)\neq 0$
for sufficiently large
$\text{Re}(Z_{M}H_{M})^{\prime }(s)\neq 0$
for sufficiently large
![]() $\text{Im}(s)$
in the half-plane
$\text{Im}(s)$
in the half-plane
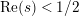 $\text{Re}(s)<1/2$
. However, this method has a critical line as its boundary. Therefore, in order to show that all (but eventually finitely many) multiple zeros of
$\text{Re}(s)<1/2$
. However, this method has a critical line as its boundary. Therefore, in order to show that all (but eventually finitely many) multiple zeros of
![]() $Z_{M}$
on the critical line are also zeros of
$Z_{M}$
on the critical line are also zeros of
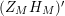 $(Z_{M}H_{M})^{\prime }$
, we employ the Hadamard product representation of the completed Selberg zeta function, which was proved in [Reference Fischer7], and conduct careful analysis of the imaginary part of the logarithmic derivative of
$(Z_{M}H_{M})^{\prime }$
, we employ the Hadamard product representation of the completed Selberg zeta function, which was proved in [Reference Fischer7], and conduct careful analysis of the imaginary part of the logarithmic derivative of
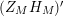 $(Z_{M}H_{M})^{\prime }$
.
$(Z_{M}H_{M})^{\prime }$
.
Parts (b) and (c) of the Main Theorem are proved by an application of Littlewood’s theorem [Reference Titchmarsh29, p. 132] to the function
 $$\begin{eqnarray}X_{M}(s):=\frac{A_{M}^{s}}{a_{M}}(Z_{M}H_{M})^{\prime }(s)\end{eqnarray}$$
$$\begin{eqnarray}X_{M}(s):=\frac{A_{M}^{s}}{a_{M}}(Z_{M}H_{M})^{\prime }(s)\end{eqnarray}$$
followed by a careful technical analysis of the integrals obtained. There are two main difficulties appearing in the noncompact case. The first one is to control the growth of
![]() $D_{M}(s)$
inside the critical strip, which is resolved by an application of Theorem 5 below. What remains is the second technical point, which is to study the growth of
$D_{M}(s)$
inside the critical strip, which is resolved by an application of Theorem 5 below. What remains is the second technical point, which is to study the growth of
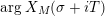 $\arg X_{M}(\unicode[STIX]{x1D70E}+iT)$
, for large
$\arg X_{M}(\unicode[STIX]{x1D70E}+iT)$
, for large
![]() $T$
and
$T$
and
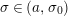 $\unicode[STIX]{x1D70E}\in (a,\unicode[STIX]{x1D70E}_{0})$
, where
$\unicode[STIX]{x1D70E}\in (a,\unicode[STIX]{x1D70E}_{0})$
, where
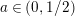 $a\in (0,1/2)$
is an arbitrary constant. In order to address this problem, we prove a Phragmen–Lindelöf type bound for
$a\in (0,1/2)$
is an arbitrary constant. In order to address this problem, we prove a Phragmen–Lindelöf type bound for
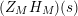 $(Z_{M}H_{M})(s)$
inside the strip
$(Z_{M}H_{M})(s)$
inside the strip
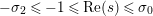 $-\unicode[STIX]{x1D70E}_{2}\leqslant -1\leqslant \text{Re}(s)\leqslant \unicode[STIX]{x1D70E}_{0}$
and the Lindelöf type bound for
$-\unicode[STIX]{x1D70E}_{2}\leqslant -1\leqslant \text{Re}(s)\leqslant \unicode[STIX]{x1D70E}_{0}$
and the Lindelöf type bound for
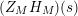 $(Z_{M}H_{M})(s)$
for
$(Z_{M}H_{M})(s)$
for
![]() $\text{Re}(s)$
close to
$\text{Re}(s)$
close to
![]() $1/2$
. These bounds are necessary in order to apply the generalized Backlund equivalent for the Lindelöf hypothesis (see § 2.5) which will yield a sharp bound for
$1/2$
. These bounds are necessary in order to apply the generalized Backlund equivalent for the Lindelöf hypothesis (see § 2.5) which will yield a sharp bound for
 $(Z_{M}H_{M})^{\prime }(s)$
near the critical line. The resulting estimate enables one to apply Jensen’s theorem and deduce that
$(Z_{M}H_{M})^{\prime }(s)$
near the critical line. The resulting estimate enables one to apply Jensen’s theorem and deduce that
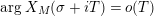 $\arg X_{M}(\unicode[STIX]{x1D70E}+iT)=o(T)$
, as
$\arg X_{M}(\unicode[STIX]{x1D70E}+iT)=o(T)$
, as
![]() $T\rightarrow \infty$
.
$T\rightarrow \infty$
.
1.4 Properties of the invariant
 $A_{M}$
$A_{M}$
Aspects of the spectral analysis of the Laplacian acting on smooth functions on a hyperbolic Riemann surface can be measured by studying the zeros of the Selberg zeta function. As discussed above, one equivalently can study the zeros of
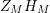 $Z_{M}H_{M}$
. Therefore, by slight extension, the zeros of
$Z_{M}H_{M}$
. Therefore, by slight extension, the zeros of
 $(Z_{M}H_{M})^{\prime }$
provide another measure of the spectral analysis of the Laplacian. In this regard, the quantity
$(Z_{M}H_{M})^{\prime }$
provide another measure of the spectral analysis of the Laplacian. In this regard, the quantity
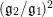 $(\mathfrak{g}_{2}/\mathfrak{g}_{1})^{2}$
is a new spectral invariant. In addition, our Main Theorem asserts that for any given surface, the spectral analysis depends on the comparison of
$(\mathfrak{g}_{2}/\mathfrak{g}_{1})^{2}$
is a new spectral invariant. In addition, our Main Theorem asserts that for any given surface, the spectral analysis depends on the comparison of
![]() $e^{\ell _{M,0}}$
and
$e^{\ell _{M,0}}$
and
 $(\mathfrak{g}_{2}/\mathfrak{g}_{1})^{2}$
.
$(\mathfrak{g}_{2}/\mathfrak{g}_{1})^{2}$
.
In § 7, we consider various arithmetic groups and compare
![]() $e^{\ell _{M,0}}$
to
$e^{\ell _{M,0}}$
to
 $(\mathfrak{g}_{2}/\mathfrak{g}_{1})^{2}$
. More precisely, we prove the following proposition.
$(\mathfrak{g}_{2}/\mathfrak{g}_{1})^{2}$
. More precisely, we prove the following proposition.
Proposition 1.
-
(i) For all surfaces
 $M=\unicode[STIX]{x1D6E4}\setminus \mathbb{H}$
, where
$M=\unicode[STIX]{x1D6E4}\setminus \mathbb{H}$
, where
 $\unicode[STIX]{x1D6E4}$
is a congruence subgroup or principal congruence subgroup of the group
$\unicode[STIX]{x1D6E4}$
is a congruence subgroup or principal congruence subgroup of the group
 $\text{PSL}(2,\mathbb{Z})$
we have that
$\text{PSL}(2,\mathbb{Z})$
we have that
 $A_{M}=e^{\ell _{M,0}}$
.
$A_{M}=e^{\ell _{M,0}}$
. -
(ii) For the surface
 $M_{5}$
corresponding to the arithmetic group
$M_{5}$
corresponding to the arithmetic group
 $\unicode[STIX]{x1D6E4}_{0}^{+}(5)$
we have that
$\unicode[STIX]{x1D6E4}_{0}^{+}(5)$
we have that
 $A_{M_{5}}=(\mathfrak{g}_{2}/\mathfrak{g}_{1})^{2}=((1+\sqrt{5})/2)^{2}$
. For the surface
$A_{M_{5}}=(\mathfrak{g}_{2}/\mathfrak{g}_{1})^{2}=((1+\sqrt{5})/2)^{2}$
. For the surface
 $M_{6}$
corresponding to the arithmetic group
$M_{6}$
corresponding to the arithmetic group
 $\unicode[STIX]{x1D6E4}_{0}^{+}(6)$
, which has the same signature as
$\unicode[STIX]{x1D6E4}_{0}^{+}(6)$
, which has the same signature as
 $\unicode[STIX]{x1D6E4}_{0}^{+}(5)$
, we have that
$\unicode[STIX]{x1D6E4}_{0}^{+}(5)$
, we have that
 $A_{M_{6}}=e^{\ell _{M_{6},0}}=2$
.
$A_{M_{6}}=e^{\ell _{M_{6},0}}=2$
. -
(iii) There exists a surface
 $M$
where
$M$
where
 $e^{\ell _{M,0}}=(\mathfrak{g}_{2}/\mathfrak{g}_{1})^{2}$
.
$e^{\ell _{M,0}}=(\mathfrak{g}_{2}/\mathfrak{g}_{1})^{2}$
.
With respect to statements (i) and (ii) of the above proposition we find it very interesting that, in the sense of our Main Theorem, not all arithmetic surfaces, even those with the same topological signature, have the same behavior.
Also in § 7, in order to prove statement (iii) of Proposition 1 we argue that if one considers a degenerating family of hyperbolic Riemann surfaces within the moduli space of surfaces of fixed topological type, one eventually has the inequality
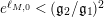 $e^{\ell _{M,0}}<(\mathfrak{g}_{2}/\mathfrak{g}_{1})^{2}$
near the boundary. As a result, if one begins with congruence group and degenerates the corresponding surface, one will ultimately encounter a surface where
$e^{\ell _{M,0}}<(\mathfrak{g}_{2}/\mathfrak{g}_{1})^{2}$
near the boundary. As a result, if one begins with congruence group and degenerates the corresponding surface, one will ultimately encounter a surface where
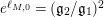 $e^{\ell _{M,0}}=(\mathfrak{g}_{2}/\mathfrak{g}_{1})^{2}$
. More generally, however, it seems as if moduli space can be separated into sets defined by the sign of
$e^{\ell _{M,0}}=(\mathfrak{g}_{2}/\mathfrak{g}_{1})^{2}$
. More generally, however, it seems as if moduli space can be separated into sets defined by the sign of
 $e^{\ell _{M,0}}-(\mathfrak{g}_{2}/\mathfrak{g}_{1})^{2}$
where most, but not all, arithmetic surfaces are in the component where
$e^{\ell _{M,0}}-(\mathfrak{g}_{2}/\mathfrak{g}_{1})^{2}$
where most, but not all, arithmetic surfaces are in the component where
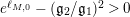 $e^{\ell _{M,0}}-(\mathfrak{g}_{2}/\mathfrak{g}_{1})^{2}>0$
, and the Deligne–Mumford boundary lies in the component where
$e^{\ell _{M,0}}-(\mathfrak{g}_{2}/\mathfrak{g}_{1})^{2}>0$
, and the Deligne–Mumford boundary lies in the component where
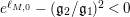 $e^{\ell _{M,0}}-(\mathfrak{g}_{2}/\mathfrak{g}_{1})^{2}<0$
.
$e^{\ell _{M,0}}-(\mathfrak{g}_{2}/\mathfrak{g}_{1})^{2}<0$
.
We could not explicitly construct a surface where
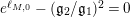 $e^{\ell _{M,0}}-(\mathfrak{g}_{2}/\mathfrak{g}_{1})^{2}=0$
, even though we prove that such surfaces exist.
$e^{\ell _{M,0}}-(\mathfrak{g}_{2}/\mathfrak{g}_{1})^{2}=0$
, even though we prove that such surfaces exist.
1.5 A comparison of counting functions
In [Reference Hejhal14, Theorem 2.22], D. Hejhal establishes the asymptotic behavior of the weighted vertical distribution of zeros of
![]() $\unicode[STIX]{x1D719}_{M}$
within the critical strip. In our notation, the zeros of
$\unicode[STIX]{x1D719}_{M}$
within the critical strip. In our notation, the zeros of
![]() $\unicode[STIX]{x1D719}_{M}$
within the critical strip coincide with the zeros of the Dirichlet series
$\unicode[STIX]{x1D719}_{M}$
within the critical strip coincide with the zeros of the Dirichlet series
![]() $H_{M}$
, so then [Reference Hejhal14, Theorem 2.22] establishes the asymptotic behavior of the weighted vertical counting function
$H_{M}$
, so then [Reference Hejhal14, Theorem 2.22] establishes the asymptotic behavior of the weighted vertical counting function
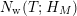 $N_{\text{w}}(T;H_{M})$
.
$N_{\text{w}}(T;H_{M})$
.
Let
![]() $M$
be any finite volume hyperbolic Riemann surface. We claim there exists a co-compact hyperbolic Riemann surface
$M$
be any finite volume hyperbolic Riemann surface. We claim there exists a co-compact hyperbolic Riemann surface
![]() $\widetilde{M}$
such that
$\widetilde{M}$
such that
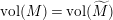 $\text{vol}(M)=\text{vol}(\widetilde{M})$
,
$\text{vol}(M)=\text{vol}(\widetilde{M})$
,
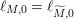 $\ell _{M,0}=\ell _{\widetilde{M},0}$
and
$\ell _{M,0}=\ell _{\widetilde{M},0}$
and
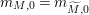 $m_{M,0}=m_{\widetilde{M},0}$
, which we argue as follows. In the case when the number
$m_{M,0}=m_{\widetilde{M},0}$
, which we argue as follows. In the case when the number
![]() $n_{1}$
of cusps of the surface
$n_{1}$
of cusps of the surface
![]() $M$
is even, we choose the surface
$M$
is even, we choose the surface
![]() $\widetilde{M}_{1}$
to be any co-compact surface with genus
$\widetilde{M}_{1}$
to be any co-compact surface with genus
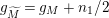 $g_{\widetilde{M}}=g_{M}+n_{1}/2$
and the same structure of elliptic points as
$g_{\widetilde{M}}=g_{M}+n_{1}/2$
and the same structure of elliptic points as
![]() $M$
, hence
$M$
, hence
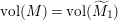 $\text{vol}(M)=\text{vol}(\widetilde{M}_{1})$
. If the number of cusps of the surface
$\text{vol}(M)=\text{vol}(\widetilde{M}_{1})$
. If the number of cusps of the surface
![]() $M$
is odd, we choose the surface
$M$
is odd, we choose the surface
![]() $\widetilde{M}_{1}$
to be any co-compact surface with genus
$\widetilde{M}_{1}$
to be any co-compact surface with genus
 $g_{\widetilde{M}}=g_{M}+(n_{1}-1)/2$
such that it has the same structure of elliptic points as
$g_{\widetilde{M}}=g_{M}+(n_{1}-1)/2$
such that it has the same structure of elliptic points as
![]() $M$
, plus one additional elliptic point of order 2. By the Gauss–Bonnet formula,
$M$
, plus one additional elliptic point of order 2. By the Gauss–Bonnet formula,
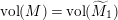 $\text{vol}(M)=\text{vol}(\widetilde{M}_{1})$
. We then deform the surface
$\text{vol}(M)=\text{vol}(\widetilde{M}_{1})$
. We then deform the surface
![]() $\widetilde{M}_{1}$
in moduli space so that its shortest geodesic has the length equal to
$\widetilde{M}_{1}$
in moduli space so that its shortest geodesic has the length equal to
![]() $\ell _{M,0}$
and the number of inconjugate geodesics of length
$\ell _{M,0}$
and the number of inconjugate geodesics of length
![]() $\ell _{M,0}$
is
$\ell _{M,0}$
is
![]() $m_{M,0}$
.
$m_{M,0}$
.
In § 9.2, we show that one can compare [Reference Hejhal14, Theorem 2.22] with generalization of the part (c) of the Main Theorem to higher derivatives in order to establish a simple asymptotic relation between
 $N_{\text{w}}(T;(Z_{M}H_{M})^{(k)})$
,
$N_{\text{w}}(T;(Z_{M}H_{M})^{(k)})$
,
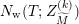 $N_{\text{w}}(T;Z_{\widetilde{M}}^{(k)})$
for
$N_{\text{w}}(T;Z_{\widetilde{M}}^{(k)})$
for
![]() $k\geqslant 1$
and
$k\geqslant 1$
and
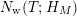 $N_{\text{w}}(T;H_{M})$
. Namely, we prove the following theorem.
$N_{\text{w}}(T;H_{M})$
. Namely, we prove the following theorem.
Theorem 2. Let
![]() $M$
be a finite volume hyperbolic Riemann surface such that, in the notation of (9),
$M$
be a finite volume hyperbolic Riemann surface such that, in the notation of (9),
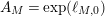 $A_{M}=\exp (\ell _{M,0})$
. Then, for all integers
$A_{M}=\exp (\ell _{M,0})$
. Then, for all integers
![]() $k\geqslant 1$
$k\geqslant 1$
 $$\begin{eqnarray}N_{\text{w}}(T;(Z_{M}H_{M})^{(k)})=N_{\text{w}}(T;Z_{\widetilde{M}}^{(k)})+N_{\text{w}}(T;H_{M})+o(T)\quad \text{as }T\rightarrow \infty .\end{eqnarray}$$
$$\begin{eqnarray}N_{\text{w}}(T;(Z_{M}H_{M})^{(k)})=N_{\text{w}}(T;Z_{\widetilde{M}}^{(k)})+N_{\text{w}}(T;H_{M})+o(T)\quad \text{as }T\rightarrow \infty .\end{eqnarray}$$
We find it very interesting that, in the case when
![]() $M$
is such that
$M$
is such that
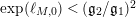 $\exp (\ell _{M,0})<(\mathfrak{g}_{2}/\mathfrak{g}_{1})^{2}$
, the coefficients of the first two terms, namely
$\exp (\ell _{M,0})<(\mathfrak{g}_{2}/\mathfrak{g}_{1})^{2}$
, the coefficients of the first two terms, namely
![]() $T\log T$
and
$T\log T$
and
![]() $T$
, in the asymptotic development of the counting function
$T$
, in the asymptotic development of the counting function
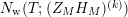 $N_{\text{w}}(T;(Z_{M}H_{M})^{(k)})$
for all
$N_{\text{w}}(T;(Z_{M}H_{M})^{(k)})$
for all
![]() $k\geqslant 1$
coincide with known results, namely Hejhal’s theorem and (2).
$k\geqslant 1$
coincide with known results, namely Hejhal’s theorem and (2).
1.6 Further comments
Weyl’s law in its classical form evaluates the lead asymptotic behavior of the vertical counting function
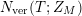 $N_{\text{ver}}(T;Z_{M})$
for compact
$N_{\text{ver}}(T;Z_{M})$
for compact
![]() $M$
. As far as is known, the expansion in
$M$
. As far as is known, the expansion in
![]() $T$
involves
$T$
involves
![]() $\text{vol}(M)$
and no other information associated to the uniformizing group
$\text{vol}(M)$
and no other information associated to the uniformizing group
![]() $\unicode[STIX]{x1D6E4}$
. If
$\unicode[STIX]{x1D6E4}$
. If
![]() $M$
is noncompact, the generalization of Weyl’s law addresses the asymptotic behavior of
$M$
is noncompact, the generalization of Weyl’s law addresses the asymptotic behavior of
 $$\begin{eqnarray}\#\{\unicode[STIX]{x1D706}_{j,M}<1/4+T^{2}\}-\frac{1}{4\unicode[STIX]{x1D70B}}\int _{-T}^{T}\unicode[STIX]{x1D719}_{M}^{\prime }/\unicode[STIX]{x1D719}_{M}(1/2+ir)\,dr\end{eqnarray}$$
$$\begin{eqnarray}\#\{\unicode[STIX]{x1D706}_{j,M}<1/4+T^{2}\}-\frac{1}{4\unicode[STIX]{x1D70B}}\int _{-T}^{T}\unicode[STIX]{x1D719}_{M}^{\prime }/\unicode[STIX]{x1D719}_{M}(1/2+ir)\,dr\end{eqnarray}$$
where
![]() $\unicode[STIX]{x1D706}_{j,M}$
is the eigenvalue of an
$\unicode[STIX]{x1D706}_{j,M}$
is the eigenvalue of an
![]() $L^{2}$
eigenfunction of the Laplacian on
$L^{2}$
eigenfunction of the Laplacian on
![]() $M$
. The asymptotic expansion of (14) is recalled below (see (68)) and, as in the compact case, all terms in the expansion involve elementary quantities associated to the uniformizing group
$M$
. The asymptotic expansion of (14) is recalled below (see (68)) and, as in the compact case, all terms in the expansion involve elementary quantities associated to the uniformizing group
![]() $\unicode[STIX]{x1D6E4}$
.
$\unicode[STIX]{x1D6E4}$
.
In § 9.1, we express the function in (14) in terms of
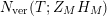 $N_{\text{ver}}(T;Z_{M}H_{M})$
, obtaining an expression which involves the constant
$N_{\text{ver}}(T;Z_{M}H_{M})$
, obtaining an expression which involves the constant
![]() $\mathfrak{g}_{1}$
. As a result, we accept the appearance of the term
$\mathfrak{g}_{1}$
. As a result, we accept the appearance of the term
![]() $\mathfrak{g}_{2}/\mathfrak{g}_{1}$
in our Main Theorem as being an appropriate generalization of a version of Weyl’s law.
$\mathfrak{g}_{2}/\mathfrak{g}_{1}$
in our Main Theorem as being an appropriate generalization of a version of Weyl’s law.
In a different direction, if one considers a degenerating family of finite volume hyperbolic Riemann surfaces, then it was shown in [Reference Huntley, Jorgenson and Lundelius15] that the asymptotic behavior of the associated sequence of vertical counting functions
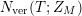 $N_{\text{ver}}(T;Z_{M})$
has lead asymptotic behavior, for fixed
$N_{\text{ver}}(T;Z_{M})$
has lead asymptotic behavior, for fixed
![]() $T$
, which involves the lengths of the pinching geodesics; see [Reference Huntley, Jorgenson and Lundelius15, Theorem 5.5]. As a result, we do not view the appearance of the invariant
$T$
, which involves the lengths of the pinching geodesics; see [Reference Huntley, Jorgenson and Lundelius15, Theorem 5.5]. As a result, we do not view the appearance of the invariant
![]() $\ell _{M,0}$
in (1) and (2) as a new feature when using Weyl’s laws to understand refined information associated to the uniformizing group
$\ell _{M,0}$
in (1) and (2) as a new feature when using Weyl’s laws to understand refined information associated to the uniformizing group
![]() $\unicode[STIX]{x1D6E4}$
.
$\unicode[STIX]{x1D6E4}$
.
However, we find the appearance of the constants
![]() $A_{M}$
and
$A_{M}$
and
![]() $a_{M}$
, as defined in (9), (10) and (11) to be intriguing, specially since values of
$a_{M}$
, as defined in (9), (10) and (11) to be intriguing, specially since values of
![]() $A_{M}$
and
$A_{M}$
and
![]() $a_{M}$
are different for certain arithmetic groups of the same signature. In particular, for any given surface
$a_{M}$
are different for certain arithmetic groups of the same signature. In particular, for any given surface
![]() $M$
, we do not know if there are conditions which determine the value taken by
$M$
, we do not know if there are conditions which determine the value taken by
![]() $A_{M}$
. Consequently, we conclude that the study of the vertical counting function
$A_{M}$
. Consequently, we conclude that the study of the vertical counting function
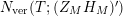 $N_{\text{ver}}(T;(Z_{M}H_{M})^{\prime })$
contains a term which provides new information associated to
$N_{\text{ver}}(T;(Z_{M}H_{M})^{\prime })$
contains a term which provides new information associated to
![]() $\unicode[STIX]{x1D6E4}$
which we do not see as being previously detected. In other words, if we are allowed to view the vertical counting function
$\unicode[STIX]{x1D6E4}$
which we do not see as being previously detected. In other words, if we are allowed to view the vertical counting function
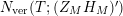 $N_{\text{ver}}(T;(Z_{M}H_{M})^{\prime })$
as another measure of the spectral analysis of the Laplacian on
$N_{\text{ver}}(T;(Z_{M}H_{M})^{\prime })$
as another measure of the spectral analysis of the Laplacian on
![]() $M$
, then our Main Theorem shows the existence of refined information, namely
$M$
, then our Main Theorem shows the existence of refined information, namely
![]() $A_{M}$
with its conditional definition (9), about the uniformizing group
$A_{M}$
with its conditional definition (9), about the uniformizing group
![]() $\unicode[STIX]{x1D6E4}$
.
$\unicode[STIX]{x1D6E4}$
.
1.7 Computations for the modular group
After the completion of this article, W. Luo brought to our attention the unpublished article [Reference Minamide23] from 2008 in which the author undertakes a related study in the case when
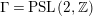 $\unicode[STIX]{x1D6E4}=\text{ PSL}(2,\mathbb{Z})$
. There are a number of important differences between the results in the present paper and those in [Reference Minamide23], which we now discuss.
$\unicode[STIX]{x1D6E4}=\text{ PSL}(2,\mathbb{Z})$
. There are a number of important differences between the results in the present paper and those in [Reference Minamide23], which we now discuss.
In [Reference Minamide23], as the title of the article states, the author studies the zeros of the derivative of the zeta function
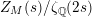 $Z_{M}(s)/\unicode[STIX]{x1D701}_{\mathbb{Q}}(2s)$
where
$Z_{M}(s)/\unicode[STIX]{x1D701}_{\mathbb{Q}}(2s)$
where
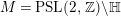 $M=\text{ PSL}(2,\mathbb{Z})\backslash \mathbb{H}$
. If we restrict our analysis to the case when
$M=\text{ PSL}(2,\mathbb{Z})\backslash \mathbb{H}$
. If we restrict our analysis to the case when
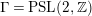 $\unicode[STIX]{x1D6E4}=\text{ PSL}(2,\mathbb{Z})$
, then the function whose derivative we study is
$\unicode[STIX]{x1D6E4}=\text{ PSL}(2,\mathbb{Z})$
, then the function whose derivative we study is
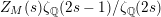 $Z_{M}(s)\unicode[STIX]{x1D701}_{\mathbb{Q}}(2s-1)/\unicode[STIX]{x1D701}_{\mathbb{Q}}(2s)$
. Since the article [Reference Minamide23] studies a different function than in the present article, one would expect that the statements of the main results are different, as, indeed, is the case. More importantly, however, the asymptotic expansions obtained in [Reference Minamide23] has an error term of
$Z_{M}(s)\unicode[STIX]{x1D701}_{\mathbb{Q}}(2s-1)/\unicode[STIX]{x1D701}_{\mathbb{Q}}(2s)$
. Since the article [Reference Minamide23] studies a different function than in the present article, one would expect that the statements of the main results are different, as, indeed, is the case. More importantly, however, the asymptotic expansions obtained in [Reference Minamide23] has an error term of
![]() $O(T)$
, whereas our error term is
$O(T)$
, whereas our error term is
![]() $o(T)$
, which is significant since the coefficient of the
$o(T)$
, which is significant since the coefficient of the
![]() $T$
term contains the quantity
$T$
term contains the quantity
![]() $A_{M}$
, which we view as a new spectral invariant. Finally, we note that the article [Reference Minamide23] studies the single group
$A_{M}$
, which we view as a new spectral invariant. Finally, we note that the article [Reference Minamide23] studies the single group
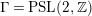 $\unicode[STIX]{x1D6E4}=\text{ PSL}(2,\mathbb{Z})$
.
$\unicode[STIX]{x1D6E4}=\text{ PSL}(2,\mathbb{Z})$
.
The approach presented in [Reference Minamide23] raise the question if a similar modification of the Selberg zeta function
![]() $Z_{M}$
can occur in the general setting of the present paper. To do so, one can write the function
$Z_{M}$
can occur in the general setting of the present paper. To do so, one can write the function
![]() $H_{M}(s)$
as a ratio
$H_{M}(s)$
as a ratio
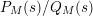 $P_{M}(s)/Q_{M}(s)$
of two entire functions of order at most two and then consider
$P_{M}(s)/Q_{M}(s)$
of two entire functions of order at most two and then consider
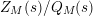 $Z_{M}(s)/Q_{M}(s)$
. It is true that the function
$Z_{M}(s)/Q_{M}(s)$
. It is true that the function
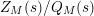 $Z_{M}(s)/Q_{M}(s)$
has nontrivial zeros only at zeros of
$Z_{M}(s)/Q_{M}(s)$
has nontrivial zeros only at zeros of
![]() $Z_{M}$
stemming from the discrete eigenvalues of the Laplacian. However, the Phillips–Sarnak conjecture/philosophy then asserts that for generic
$Z_{M}$
stemming from the discrete eigenvalues of the Laplacian. However, the Phillips–Sarnak conjecture/philosophy then asserts that for generic
![]() $M$
, the quotient
$M$
, the quotient
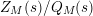 $Z_{M}(s)/Q_{M}(s)$
would have a finite number of nontrivial zeros, hence can be written as a polynomial times Gamma-type functions. Aside from this assertion, while focusing solely from the point of view of application of techniques developed in this paper, the function
$Z_{M}(s)/Q_{M}(s)$
would have a finite number of nontrivial zeros, hence can be written as a polynomial times Gamma-type functions. Aside from this assertion, while focusing solely from the point of view of application of techniques developed in this paper, the function
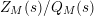 $Z_{M}(s)/Q_{M}(s)$
is suitable in the sense that it possesses no nonreal zeros in the half-plane
$Z_{M}(s)/Q_{M}(s)$
is suitable in the sense that it possesses no nonreal zeros in the half-plane
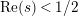 $\text{Re}(s)<1/2$
. However, there are two reasons why the investigation of
$\text{Re}(s)<1/2$
. However, there are two reasons why the investigation of
 $Z_{M}(s)H_{M}(s)$
is more natural. Firstly, the spectral information carried by
$Z_{M}(s)H_{M}(s)$
is more natural. Firstly, the spectral information carried by
![]() $P_{M}(s)$
, namely, the zeros of the scattering determinant, is lost when considering
$P_{M}(s)$
, namely, the zeros of the scattering determinant, is lost when considering
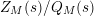 $Z_{M}(s)/Q_{M}(s)$
. More importantly, unless the explicit expression for the scattering determinant is known, it is very difficult to determine
$Z_{M}(s)/Q_{M}(s)$
. More importantly, unless the explicit expression for the scattering determinant is known, it is very difficult to determine
![]() $Q_{M}(s)$
explicitly and hence express
$Q_{M}(s)$
explicitly and hence express
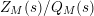 $Z_{M}(s)/Q_{M}(s)$
in terms of the information related to the underlying group
$Z_{M}(s)/Q_{M}(s)$
in terms of the information related to the underlying group
![]() $\unicode[STIX]{x1D6E4}$
, whereas
$\unicode[STIX]{x1D6E4}$
, whereas
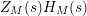 $Z_{M}(s)H_{M}(s)$
has a general Dirichlet series representation in terms of the group information.
$Z_{M}(s)H_{M}(s)$
has a general Dirichlet series representation in terms of the group information.
1.8 Outline of the paper
This article is organized as follows. In § 2, we establish notation and recall necessary results from the literature. The zero-free region for
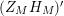 $(Z_{M}H_{M})^{\prime }$
, as stated in part (a) of the Main Theorem, will be proved in § 3. Various lemmas leading up to the proof of parts (b) and (c) of the main Theorem will be given in § 4, the proof of parts (b) and (c) will be completed in § 5, and in § 6 we state and prove several corollaries of the Main Theorem. The examples of congruence groups and “moonshine” groups will be given in § 7. In § 8, we prove results analogous to our Main Theorem for higher derivatives of
$(Z_{M}H_{M})^{\prime }$
, as stated in part (a) of the Main Theorem, will be proved in § 3. Various lemmas leading up to the proof of parts (b) and (c) of the main Theorem will be given in § 4, the proof of parts (b) and (c) will be completed in § 5, and in § 6 we state and prove several corollaries of the Main Theorem. The examples of congruence groups and “moonshine” groups will be given in § 7. In § 8, we prove results analogous to our Main Theorem for higher derivatives of
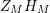 $Z_{M}H_{M}$
. Finally, in § 9, we give various concluding remarks.
$Z_{M}H_{M}$
. Finally, in § 9, we give various concluding remarks.
2 Background material
2.1 Counting functions
Let
![]() $F$
denote either a general Dirichlet series with a critical line;
$F$
denote either a general Dirichlet series with a critical line;
![]() $F$
itself may be the derivative of another general Dirichlet series. We assume that
$F$
itself may be the derivative of another general Dirichlet series. We assume that
![]() $F$
is normalized to be convergent in the half-plane
$F$
is normalized to be convergent in the half-plane
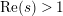 $\text{Re}(s)>1$
with critical line
$\text{Re}(s)>1$
with critical line
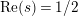 $\text{Re}(s)=1/2$
. We define the vertical counting function of
$\text{Re}(s)=1/2$
. We define the vertical counting function of
![]() $F$
as
$F$
as
 $$\begin{eqnarray}N_{\text{ver}}(T;F)=\mathop{\sum }_{{F(\unicode[STIX]{x1D70E}+it)=0\atop 0<t<T,0<\unicode[STIX]{x1D70E}<1}}1\end{eqnarray}$$
$$\begin{eqnarray}N_{\text{ver}}(T;F)=\mathop{\sum }_{{F(\unicode[STIX]{x1D70E}+it)=0\atop 0<t<T,0<\unicode[STIX]{x1D70E}<1}}1\end{eqnarray}$$
and the weighted vertical counting function of
![]() $F$
as
$F$
as
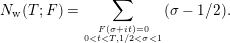 $$\begin{eqnarray}N_{\text{w}}(T;F)=\mathop{\sum }_{{F(\unicode[STIX]{x1D70E}+it)=0\atop 0<t<T,1/2<\unicode[STIX]{x1D70E}<1}}(\unicode[STIX]{x1D70E}-1/2).\end{eqnarray}$$
$$\begin{eqnarray}N_{\text{w}}(T;F)=\mathop{\sum }_{{F(\unicode[STIX]{x1D70E}+it)=0\atop 0<t<T,1/2<\unicode[STIX]{x1D70E}<1}}(\unicode[STIX]{x1D70E}-1/2).\end{eqnarray}$$
2.2 Additional identities
The logarithmic derivative
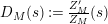 $D_{M}(s):=\frac{Z_{M}^{\prime }}{Z_{M}}(s)$
of the Selberg zeta function may be expressed, for
$D_{M}(s):=\frac{Z_{M}^{\prime }}{Z_{M}}(s)$
of the Selberg zeta function may be expressed, for
 $\operatorname{Re}(s)>1$
as the absolutely convergent series
$\operatorname{Re}(s)>1$
as the absolutely convergent series
 $$\begin{eqnarray}D_{M}(s)=\mathop{\sum }_{P\in {\mathcal{H}}(\unicode[STIX]{x1D6E4})}\frac{\unicode[STIX]{x1D6EC}(P)}{N(P)^{s}},\quad \text{where }\unicode[STIX]{x1D6EC}(P):=\frac{\log N(P_{0})}{1-N(P)^{-1}}.\end{eqnarray}$$
$$\begin{eqnarray}D_{M}(s)=\mathop{\sum }_{P\in {\mathcal{H}}(\unicode[STIX]{x1D6E4})}\frac{\unicode[STIX]{x1D6EC}(P)}{N(P)^{s}},\quad \text{where }\unicode[STIX]{x1D6EC}(P):=\frac{\log N(P_{0})}{1-N(P)^{-1}}.\end{eqnarray}$$
Dirichlet series representation of the logarithmic derivative of the function
 $Z_{M}H_{M}$
is given by the following lemma.
$Z_{M}H_{M}$
is given by the following lemma.
Lemma 3. There exists a constant
![]() $\unicode[STIX]{x1D70E}_{0}^{\prime }\geqslant 1$
such that for all
$\unicode[STIX]{x1D70E}_{0}^{\prime }\geqslant 1$
such that for all
![]() $s\in \mathbb{C}$
with
$s\in \mathbb{C}$
with
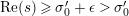 $\operatorname{Re}(s)\geqslant \unicode[STIX]{x1D70E}_{0}^{\prime }+\unicode[STIX]{x1D716}>\unicode[STIX]{x1D70E}_{0}^{\prime }$
, we have that
$\operatorname{Re}(s)\geqslant \unicode[STIX]{x1D70E}_{0}^{\prime }+\unicode[STIX]{x1D716}>\unicode[STIX]{x1D70E}_{0}^{\prime }$
, we have that
 $$\begin{eqnarray}\frac{(Z_{M}H_{M})^{\prime }}{(Z_{M}H_{M})}(s)=\underset{P\in {\mathcal{H}}(\unicode[STIX]{x1D6E4})}{\sum }\frac{\unicode[STIX]{x1D6EC}(P)}{N(P)^{s}}+\mathop{\sum }_{i=1}^{\infty }\frac{b\left(q_{i}\right)}{\mathop{q}_{i}^{s}}.\end{eqnarray}$$
$$\begin{eqnarray}\frac{(Z_{M}H_{M})^{\prime }}{(Z_{M}H_{M})}(s)=\underset{P\in {\mathcal{H}}(\unicode[STIX]{x1D6E4})}{\sum }\frac{\unicode[STIX]{x1D6EC}(P)}{N(P)^{s}}+\mathop{\sum }_{i=1}^{\infty }\frac{b\left(q_{i}\right)}{\mathop{q}_{i}^{s}}.\end{eqnarray}$$
In addition, the series converge absolutely and uniformly on every compact subset of the half-plane
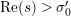 $\operatorname{Re}(s)>\unicode[STIX]{x1D70E}_{0}^{\prime }$
.
$\operatorname{Re}(s)>\unicode[STIX]{x1D70E}_{0}^{\prime }$
.
Proof. Equation (16) follows immediately from (8) and (15). We may take
![]() $\unicode[STIX]{x1D70E}_{0}^{\prime }$
to be equal to
$\unicode[STIX]{x1D70E}_{0}^{\prime }$
to be equal to
![]() $\unicode[STIX]{x1D70E}_{0}$
, which was defined in § 1.4.◻
$\unicode[STIX]{x1D70E}_{0}$
, which was defined in § 1.4.◻
Lemma 4. The derivative of the function
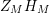 $Z_{M}H_{M}$
satisfies the functional equation
$Z_{M}H_{M}$
satisfies the functional equation
 $$\begin{eqnarray}(Z_{M}H_{M})^{\prime }(s)=f_{M}(s)\unicode[STIX]{x1D702}_{M}(s)K_{M}^{-1}(s)\widetilde{Z}_{M}(1-s)Z_{M}(1-s),\end{eqnarray}$$
$$\begin{eqnarray}(Z_{M}H_{M})^{\prime }(s)=f_{M}(s)\unicode[STIX]{x1D702}_{M}(s)K_{M}^{-1}(s)\widetilde{Z}_{M}(1-s)Z_{M}(1-s),\end{eqnarray}$$
where
 $$\begin{eqnarray}f_{M}(s):=\text{vol}(M)(1/2-s)\left(\tan \unicode[STIX]{x1D70B}(1/2-s)\right)\end{eqnarray}$$
$$\begin{eqnarray}f_{M}(s):=\text{vol}(M)(1/2-s)\left(\tan \unicode[STIX]{x1D70B}(1/2-s)\right)\end{eqnarray}$$
and
 $$\begin{eqnarray}\widetilde{Z}_{M}(s):=\frac{1}{f_{M}(s)}\left(\frac{\unicode[STIX]{x1D702}_{M}^{\prime }}{\unicode[STIX]{x1D702}_{M}}(s)-\frac{K_{M}^{\prime }}{K_{M}}(1-s)-\frac{Z_{M}^{\prime }}{Z_{M}}(s)\right).\end{eqnarray}$$
$$\begin{eqnarray}\widetilde{Z}_{M}(s):=\frac{1}{f_{M}(s)}\left(\frac{\unicode[STIX]{x1D702}_{M}^{\prime }}{\unicode[STIX]{x1D702}_{M}}(s)-\frac{K_{M}^{\prime }}{K_{M}}(1-s)-\frac{Z_{M}^{\prime }}{Z_{M}}(s)\right).\end{eqnarray}$$
Proof. Straightforward computation stemming from (7).◻
2.3 An integral representation for
 $D_{M}(s)$
$D_{M}(s)$
In this section, we recall results from [Reference Avdispahić and Smajlović3] on the growth of the logarithmic derivative
![]() $D_{M}(s)$
and its derivatives
$D_{M}(s)$
and its derivatives
![]() $D_{M}^{(k)}(s)$
for
$D_{M}^{(k)}(s)$
for
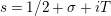 $s=1/2+\unicode[STIX]{x1D70E}+iT$
, as
$s=1/2+\unicode[STIX]{x1D70E}+iT$
, as
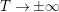 $T\rightarrow \pm \infty$
, for
$T\rightarrow \pm \infty$
, for
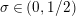 $\unicode[STIX]{x1D70E}\in (0,1/2)$
.
$\unicode[STIX]{x1D70E}\in (0,1/2)$
.
Theorem 5. [Reference Avdispahić and Smajlović3]
For
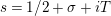 $s=1/2+\unicode[STIX]{x1D70E}+iT$
,
$s=1/2+\unicode[STIX]{x1D70E}+iT$
,
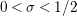 $0<\unicode[STIX]{x1D70E}<1/2$
and every nonnegative integer
$0<\unicode[STIX]{x1D70E}<1/2$
and every nonnegative integer
![]() $k$
, we have the asymptotic bound
$k$
, we have the asymptotic bound
 $$\begin{eqnarray}\displaystyle D_{M}^{(k)}(s) & = & \displaystyle O\left(\min \left\{\frac{|T|}{\unicode[STIX]{x1D70E}^{k+1}\log |T|},|T|^{1-2\unicode[STIX]{x1D70E}}\log ^{k-2\unicode[STIX]{x1D70E}}|T|\right.\right.\nonumber\\ \displaystyle & & \displaystyle \left.\left.\cdot \,\,\underset{j=0,\ldots ,k}{\max }\left\{\frac{1}{\unicode[STIX]{x1D70E}^{j+1}\log ^{j+1}|T|},\log \left|\frac{T}{\unicode[STIX]{x1D70E}}\right|\right\}\right\}\right),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle D_{M}^{(k)}(s) & = & \displaystyle O\left(\min \left\{\frac{|T|}{\unicode[STIX]{x1D70E}^{k+1}\log |T|},|T|^{1-2\unicode[STIX]{x1D70E}}\log ^{k-2\unicode[STIX]{x1D70E}}|T|\right.\right.\nonumber\\ \displaystyle & & \displaystyle \left.\left.\cdot \,\,\underset{j=0,\ldots ,k}{\max }\left\{\frac{1}{\unicode[STIX]{x1D70E}^{j+1}\log ^{j+1}|T|},\log \left|\frac{T}{\unicode[STIX]{x1D70E}}\right|\right\}\right\}\right),\end{eqnarray}$$
as
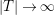 $|T|\rightarrow \infty$
.
$|T|\rightarrow \infty$
.
2.4 The completed function
 $\unicode[STIX]{x1D6EF}_{M}$
$\unicode[STIX]{x1D6EF}_{M}$
In this section, we recall the notation and results from [Reference Fischer7]. The notation of [Reference Fischer7] is adjusted to our setting; we take
![]() $k=0$
, dimension
$k=0$
, dimension
![]() $d=1$
and
$d=1$
and
![]() $\unicode[STIX]{x1D70F}^{\ast }=n_{1}$
.
$\unicode[STIX]{x1D70F}^{\ast }=n_{1}$
.
The completed function
![]() $\unicode[STIX]{x1D6EF}_{M}$
associated to the Selberg zeta function is defined by
$\unicode[STIX]{x1D6EF}_{M}$
associated to the Selberg zeta function is defined by
 $$\begin{eqnarray}\unicode[STIX]{x1D6EF}_{M}(s)=\unicode[STIX]{x1D6EF}_{I}(s)\unicode[STIX]{x1D6EF}_{M,\text{hyp}}(s)\unicode[STIX]{x1D6EF}_{M,\text{par}}(s)\unicode[STIX]{x1D6EF}_{M,\text{ell}}(s)\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6EF}_{M}(s)=\unicode[STIX]{x1D6EF}_{I}(s)\unicode[STIX]{x1D6EF}_{M,\text{hyp}}(s)\unicode[STIX]{x1D6EF}_{M,\text{par}}(s)\unicode[STIX]{x1D6EF}_{M,\text{ell}}(s)\end{eqnarray}$$
where
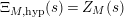 $\unicode[STIX]{x1D6EF}_{M,\text{hyp}}(s)=Z_{M}(s)$
is the Selberg zeta function and the remaining functions are associated to the identity, parabolic, and elliptic elements in the underlying uniformizing group. The logarithmic derivative of the identity term
$\unicode[STIX]{x1D6EF}_{M,\text{hyp}}(s)=Z_{M}(s)$
is the Selberg zeta function and the remaining functions are associated to the identity, parabolic, and elliptic elements in the underlying uniformizing group. The logarithmic derivative of the identity term
![]() $\unicode[STIX]{x1D6EF}_{I}$
is given by
$\unicode[STIX]{x1D6EF}_{I}$
is given by
 $$\begin{eqnarray}-\frac{1}{2s-1}\frac{\unicode[STIX]{x1D6EF}_{I}^{\prime }(s)}{\unicode[STIX]{x1D6EF}_{I}(s)}=\frac{\text{vol}(M)}{2\unicode[STIX]{x1D70B}}\frac{\unicode[STIX]{x1D6E4}^{\prime }}{\unicode[STIX]{x1D6E4}}(s);\end{eqnarray}$$
$$\begin{eqnarray}-\frac{1}{2s-1}\frac{\unicode[STIX]{x1D6EF}_{I}^{\prime }(s)}{\unicode[STIX]{x1D6EF}_{I}(s)}=\frac{\text{vol}(M)}{2\unicode[STIX]{x1D70B}}\frac{\unicode[STIX]{x1D6E4}^{\prime }}{\unicode[STIX]{x1D6E4}}(s);\end{eqnarray}$$
see [Reference Fischer7, Remark 3.1.3]. The function
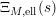 $\unicode[STIX]{x1D6EF}_{M,\text{ell}}(s)$
is computed in [Reference Fischer7, Corollary 2.3.5]; using Stirling’s formula, one can show that
$\unicode[STIX]{x1D6EF}_{M,\text{ell}}(s)$
is computed in [Reference Fischer7, Corollary 2.3.5]; using Stirling’s formula, one can show that
 $$\begin{eqnarray}\frac{1}{2s-1}\frac{\unicode[STIX]{x1D6EF}_{M,\text{ell}}^{\prime }(s)}{\unicode[STIX]{x1D6EF}_{M,\text{ell}}(s)}=O\left(\frac{1}{\left|t\right|}\log \left|t\right|\right)\end{eqnarray}$$
$$\begin{eqnarray}\frac{1}{2s-1}\frac{\unicode[STIX]{x1D6EF}_{M,\text{ell}}^{\prime }(s)}{\unicode[STIX]{x1D6EF}_{M,\text{ell}}(s)}=O\left(\frac{1}{\left|t\right|}\log \left|t\right|\right)\end{eqnarray}$$
for any
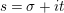 $s=\unicode[STIX]{x1D70E}+it$
,
$s=\unicode[STIX]{x1D70E}+it$
,
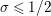 $\unicode[STIX]{x1D70E}\leqslant 1/2$
, as
$\unicode[STIX]{x1D70E}\leqslant 1/2$
, as
![]() $|t|\rightarrow \infty$
.
$|t|\rightarrow \infty$
.
The function
 $\unicode[STIX]{x1D6EF}_{M,\text{par}}(s)$
is described in [Reference Fischer7, Definition 3.1.4]. For our purposes, it suffices to relate
$\unicode[STIX]{x1D6EF}_{M,\text{par}}(s)$
is described in [Reference Fischer7, Definition 3.1.4]. For our purposes, it suffices to relate
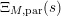 $\unicode[STIX]{x1D6EF}_{M,\text{par}}(s)$
to the scattering determinant
$\unicode[STIX]{x1D6EF}_{M,\text{par}}(s)$
to the scattering determinant
![]() $\unicode[STIX]{x1D719}_{M}(s)$
, so that we obtain an expression for
$\unicode[STIX]{x1D719}_{M}(s)$
, so that we obtain an expression for
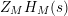 $Z_{M}H_{M}(s)$
. The following computations derive such an expression for
$Z_{M}H_{M}(s)$
. The following computations derive such an expression for
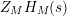 $Z_{M}H_{M}(s)$
.
$Z_{M}H_{M}(s)$
.
Let
 $\{p_{1},\ldots ,p_{N_{0}}\}$
denote the set of poles of
$\{p_{1},\ldots ,p_{N_{0}}\}$
denote the set of poles of
![]() $\unicode[STIX]{x1D719}_{M}$
lying in
$\unicode[STIX]{x1D719}_{M}$
lying in
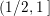 $(\!1/2,1]$
, counted with multiplicities; let
$(\!1/2,1]$
, counted with multiplicities; let
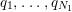 $q_{1},\ldots ,q_{N_{1}}$
denote the set of real zeros of
$q_{1},\ldots ,q_{N_{1}}$
denote the set of real zeros of
![]() $\unicode[STIX]{x1D719}_{M}$
larger than
$\unicode[STIX]{x1D719}_{M}$
larger than
![]() $1/2$
and let
$1/2$
and let
 $\{q_{n}\}_{n>N_{1}}$
denote the set of zeros of
$\{q_{n}\}_{n>N_{1}}$
denote the set of zeros of
![]() $\unicode[STIX]{x1D719}_{M}$
with positive imaginary parts, counted with multiplicities. In the notation of [Reference Fischer7, Definition 3.2.2], we set
$\unicode[STIX]{x1D719}_{M}$
with positive imaginary parts, counted with multiplicities. In the notation of [Reference Fischer7, Definition 3.2.2], we set
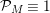 ${\mathcal{P}}_{M}\equiv 1$
if
${\mathcal{P}}_{M}\equiv 1$
if
![]() $n_{1}=0$
, otherwise we define
$n_{1}=0$
, otherwise we define
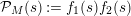 ${\mathcal{P}}_{M}(s):=f_{1}(s)f_{2}(s)$
where
${\mathcal{P}}_{M}(s):=f_{1}(s)f_{2}(s)$
where
 $$\begin{eqnarray}f_{1}(s):=\mathop{\prod }_{n=1}^{N_{1}}\left(1+\frac{s-1/2}{q_{n}-1/2}\right)\exp \left[\frac{1}{2}\left(\frac{s-1/2}{q_{n}-1/2}\right)^{2}\right]\end{eqnarray}$$
$$\begin{eqnarray}f_{1}(s):=\mathop{\prod }_{n=1}^{N_{1}}\left(1+\frac{s-1/2}{q_{n}-1/2}\right)\exp \left[\frac{1}{2}\left(\frac{s-1/2}{q_{n}-1/2}\right)^{2}\right]\end{eqnarray}$$
and
 $$\begin{eqnarray}\displaystyle f_{2}(s) & := & \displaystyle \mathop{\prod }_{n\geqslant N_{1}+1}\left(1+\frac{s-1/2}{q_{n}-1/2}\right)\left(1+\frac{s-1/2}{\overline{q_{n}}-1/2}\right)\nonumber\\ \displaystyle & & \displaystyle \times \,\exp \left[\frac{1}{2}\left(\frac{s-1/2}{q_{n}-1/2}\right)^{2}+\frac{1}{2}\left(\frac{s-1/2}{\overline{q_{n}}-1/2}\right)^{2}\right].\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle f_{2}(s) & := & \displaystyle \mathop{\prod }_{n\geqslant N_{1}+1}\left(1+\frac{s-1/2}{q_{n}-1/2}\right)\left(1+\frac{s-1/2}{\overline{q_{n}}-1/2}\right)\nonumber\\ \displaystyle & & \displaystyle \times \,\exp \left[\frac{1}{2}\left(\frac{s-1/2}{q_{n}-1/2}\right)^{2}+\frac{1}{2}\left(\frac{s-1/2}{\overline{q_{n}}-1/2}\right)^{2}\right].\nonumber\end{eqnarray}$$
The infinite product which defines
![]() $f_{2}$
converges uniformly on compact subsets of
$f_{2}$
converges uniformly on compact subsets of
![]() $\mathbb{C}$
and defines an entire function of finite order.
$\mathbb{C}$
and defines an entire function of finite order.
Lemma 6. For all
![]() $s\in \mathbb{C}$
, the product
$s\in \mathbb{C}$
, the product
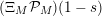 $(\unicode[STIX]{x1D6EF}_{M}{\mathcal{P}}_{M})(1-s)$
can be expressed as
$(\unicode[STIX]{x1D6EF}_{M}{\mathcal{P}}_{M})(1-s)$
can be expressed as
 $$\begin{eqnarray}\displaystyle \left(\unicode[STIX]{x1D6EF}_{M}{\mathcal{P}}_{M}\right)(1-s) & = & \displaystyle (Z_{M}H_{M})(s)\cdot \unicode[STIX]{x1D6EF}_{I}(s)\cdot \unicode[STIX]{x1D6EF}_{M,\text{ell}}(s)\cdot \frac{\unicode[STIX]{x1D70B}^{n_{1/2}}d(1)}{\unicode[STIX]{x1D719}_{M}(1/2)}\mathfrak{g}_{1}^{-s-1}\nonumber\\ \displaystyle & & \displaystyle \cdot \,\left(s-\frac{1}{2}\right)^{(1/2)\text{ Tr}(I_{n_{1}}-\unicode[STIX]{x1D6F7}_{M}(1/2))-n_{1}}\nonumber\\ \displaystyle & & \displaystyle \cdot \,\,\unicode[STIX]{x1D6E4}(s)^{-n_{1}}\overset{N_{0}}{\underset{m=1}{\prod }}\left(\frac{s-p_{m}}{1/2-p_{m}}\right)\!.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \left(\unicode[STIX]{x1D6EF}_{M}{\mathcal{P}}_{M}\right)(1-s) & = & \displaystyle (Z_{M}H_{M})(s)\cdot \unicode[STIX]{x1D6EF}_{I}(s)\cdot \unicode[STIX]{x1D6EF}_{M,\text{ell}}(s)\cdot \frac{\unicode[STIX]{x1D70B}^{n_{1/2}}d(1)}{\unicode[STIX]{x1D719}_{M}(1/2)}\mathfrak{g}_{1}^{-s-1}\nonumber\\ \displaystyle & & \displaystyle \cdot \,\left(s-\frac{1}{2}\right)^{(1/2)\text{ Tr}(I_{n_{1}}-\unicode[STIX]{x1D6F7}_{M}(1/2))-n_{1}}\nonumber\\ \displaystyle & & \displaystyle \cdot \,\,\unicode[STIX]{x1D6E4}(s)^{-n_{1}}\overset{N_{0}}{\underset{m=1}{\prod }}\left(\frac{s-p_{m}}{1/2-p_{m}}\right)\!.\end{eqnarray}$$
Proof. From the functional equation [Reference Fischer7, (3.2.4), p. 123], we have, for all
![]() $s\in \mathbb{C}$
$s\in \mathbb{C}$
 $$\begin{eqnarray}\left(\unicode[STIX]{x1D6EF}_{M}{\mathcal{P}}_{M}\right)(1-s)=\left(\unicode[STIX]{x1D6EF}_{M}{\mathcal{P}}_{M}\right)(s)\mathfrak{g}_{1}^{2s-1}\overset{N_{0}}{\underset{m=1}{\prod }}\left(\frac{s-p_{m}}{1-s-p_{m}}\right)\frac{1}{\unicode[STIX]{x1D719}_{M}(1/2)}\unicode[STIX]{x1D719}_{M}(s).\end{eqnarray}$$
$$\begin{eqnarray}\left(\unicode[STIX]{x1D6EF}_{M}{\mathcal{P}}_{M}\right)(1-s)=\left(\unicode[STIX]{x1D6EF}_{M}{\mathcal{P}}_{M}\right)(s)\mathfrak{g}_{1}^{2s-1}\overset{N_{0}}{\underset{m=1}{\prod }}\left(\frac{s-p_{m}}{1-s-p_{m}}\right)\frac{1}{\unicode[STIX]{x1D719}_{M}(1/2)}\unicode[STIX]{x1D719}_{M}(s).\end{eqnarray}$$
On the other hand, by [Reference Fischer7, Corollary 2.4.22] it is easy to see that
 $$\begin{eqnarray}\displaystyle \left(\unicode[STIX]{x1D6EF}_{M,\text{par}}{\mathcal{P}}_{M}\right)(s) & = & \displaystyle (s-1/2)^{(1/2)\text{ Tr}I_{n_{1}}-\unicode[STIX]{x1D6F7}_{M}(1/2)}\mathfrak{g}_{1}^{-s}\left(\frac{1}{\unicode[STIX]{x1D6E4}(s+1/2)}\right)^{n_{1}}\nonumber\\ \displaystyle & & \displaystyle \cdot \,\overset{N_{0}}{\underset{m=1}{\prod }}\left(1+\frac{s-1/2}{p_{m}-1/2}\right).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \left(\unicode[STIX]{x1D6EF}_{M,\text{par}}{\mathcal{P}}_{M}\right)(s) & = & \displaystyle (s-1/2)^{(1/2)\text{ Tr}I_{n_{1}}-\unicode[STIX]{x1D6F7}_{M}(1/2)}\mathfrak{g}_{1}^{-s}\left(\frac{1}{\unicode[STIX]{x1D6E4}(s+1/2)}\right)^{n_{1}}\nonumber\\ \displaystyle & & \displaystyle \cdot \,\overset{N_{0}}{\underset{m=1}{\prod }}\left(1+\frac{s-1/2}{p_{m}-1/2}\right).\nonumber\end{eqnarray}$$
We now write
![]() $\unicode[STIX]{x1D719}_{M}$
as
$\unicode[STIX]{x1D719}_{M}$
as
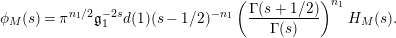 $$\begin{eqnarray}\unicode[STIX]{x1D719}_{M}(s)=\unicode[STIX]{x1D70B}^{n_{1}/2}\mathfrak{g}_{1}^{-2s}d(1)(s-1/2)^{-n_{1}}\left(\frac{\unicode[STIX]{x1D6E4}(s+1/2)}{\unicode[STIX]{x1D6E4}(s)}\right)^{n_{1}}H_{M}(s).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D719}_{M}(s)=\unicode[STIX]{x1D70B}^{n_{1}/2}\mathfrak{g}_{1}^{-2s}d(1)(s-1/2)^{-n_{1}}\left(\frac{\unicode[STIX]{x1D6E4}(s+1/2)}{\unicode[STIX]{x1D6E4}(s)}\right)^{n_{1}}H_{M}(s).\end{eqnarray}$$
The result follows through direct and straightforward computations involving the definition of
![]() $\unicode[STIX]{x1D6EF}_{M}$
together with (24).◻
$\unicode[STIX]{x1D6EF}_{M}$
together with (24).◻
2.5 On generalized Backlund equivalent for the Lindelöf hypothesis
An important ingredient in the proof of the Main Theorem is a bound on the growth of the function
 $Z_{M}H_{M}$
on the critical line
$Z_{M}H_{M}$
on the critical line
 $\text{ Re}(s)=1/2$
. We obtain the bound using a slight modification of [Reference Garunkŝtis10, Proposition 2], which we now state.
$\text{ Re}(s)=1/2$
. We obtain the bound using a slight modification of [Reference Garunkŝtis10, Proposition 2], which we now state.
Proposition 7. Let
![]() $f(s)$
be a meromorphic function for all
$f(s)$
be a meromorphic function for all
![]() $s\in \mathbb{C}$
which is holomorphic in the region
$s\in \mathbb{C}$
which is holomorphic in the region
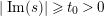 $|\operatorname{Im}(s)|\geqslant t_{0}>0$
, for some fixed
$|\operatorname{Im}(s)|\geqslant t_{0}>0$
, for some fixed
![]() $t_{0}$
. Let
$t_{0}$
. Let
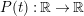 $P(t):\mathbb{R}\rightarrow \mathbb{R}$
be nondecreasing function such that
$P(t):\mathbb{R}\rightarrow \mathbb{R}$
be nondecreasing function such that
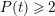 $P(t)\geqslant 2$
. Let
$P(t)\geqslant 2$
. Let
 $N(\unicode[STIX]{x1D70E},f,T)$
denote the number of zeros
$N(\unicode[STIX]{x1D70E},f,T)$
denote the number of zeros
![]() $\unicode[STIX]{x1D70C}$
of
$\unicode[STIX]{x1D70C}$
of
![]() $f$
in the region
$f$
in the region
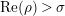 $\operatorname{Re}(\unicode[STIX]{x1D70C})>\unicode[STIX]{x1D70E}$
;
$\operatorname{Re}(\unicode[STIX]{x1D70C})>\unicode[STIX]{x1D70E}$
;
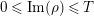 $0\leqslant \operatorname{Im}(\unicode[STIX]{x1D70C})\leqslant T$
.
$0\leqslant \operatorname{Im}(\unicode[STIX]{x1D70C})\leqslant T$
.
Assume there exist constants
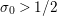 $\unicode[STIX]{x1D70E}_{0}>1/2$
and
$\unicode[STIX]{x1D70E}_{0}>1/2$
and
![]() $\unicode[STIX]{x1D714}>0$
such that for
$\unicode[STIX]{x1D714}>0$
such that for
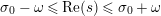 $\unicode[STIX]{x1D70E}_{0}-\unicode[STIX]{x1D714}\leqslant \operatorname{Re}(s)\leqslant \unicode[STIX]{x1D70E}_{0}+\unicode[STIX]{x1D714}$
we have
$\unicode[STIX]{x1D70E}_{0}-\unicode[STIX]{x1D714}\leqslant \operatorname{Re}(s)\leqslant \unicode[STIX]{x1D70E}_{0}+\unicode[STIX]{x1D714}$
we have
 $$\begin{eqnarray}|f(s)|\geqslant c>0\qquad \text{and},\qquad (f^{\prime }/f)(s)=o(P(t))\quad \text{as}\quad t=\text{Im}(s)\rightarrow \infty .\end{eqnarray}$$
$$\begin{eqnarray}|f(s)|\geqslant c>0\qquad \text{and},\qquad (f^{\prime }/f)(s)=o(P(t))\quad \text{as}\quad t=\text{Im}(s)\rightarrow \infty .\end{eqnarray}$$
Furthermore, assume that
 $|f(s)|>0$
for
$|f(s)|>0$
for
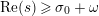 $\operatorname{Re}(s)\geqslant \unicode[STIX]{x1D70E}_{0}+\unicode[STIX]{x1D714}$
and that for some fixed number
$\operatorname{Re}(s)\geqslant \unicode[STIX]{x1D70E}_{0}+\unicode[STIX]{x1D714}$
and that for some fixed number
![]() $D>0$
we have
$D>0$
we have
 $$\begin{eqnarray}f(s)=O((P(t))^{D})\quad \text{ as }t=\text{ Im}(s)\rightarrow \infty ,\text{ uniformly for }\operatorname{Re}(s)\geqslant 2-3\unicode[STIX]{x1D70E}_{0}.\end{eqnarray}$$
$$\begin{eqnarray}f(s)=O((P(t))^{D})\quad \text{ as }t=\text{ Im}(s)\rightarrow \infty ,\text{ uniformly for }\operatorname{Re}(s)\geqslant 2-3\unicode[STIX]{x1D70E}_{0}.\end{eqnarray}$$
Then if the estimate
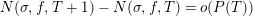 $N(\unicode[STIX]{x1D70E},f,T+1)-N(\unicode[STIX]{x1D70E},f,T)=o(P(T))$
holds true for all
$N(\unicode[STIX]{x1D70E},f,T+1)-N(\unicode[STIX]{x1D70E},f,T)=o(P(T))$
holds true for all
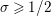 $\unicode[STIX]{x1D70E}\geqslant 1/2$
as
$\unicode[STIX]{x1D70E}\geqslant 1/2$
as
![]() $T\rightarrow \infty$
, then
$T\rightarrow \infty$
, then
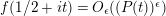 $f(1/2+it)=O_{\unicode[STIX]{x1D716}}((P(t))^{\unicode[STIX]{x1D716}})$
as
$f(1/2+it)=O_{\unicode[STIX]{x1D716}}((P(t))^{\unicode[STIX]{x1D716}})$
as
![]() $t\rightarrow \infty$
.
$t\rightarrow \infty$
.
There are slight differences between our statement above and [Reference Garunkŝtis10, Proposition 2]. Firstly, we assume the function
![]() $f$
depends on a single complex variable
$f$
depends on a single complex variable
![]() $s$
, not necessarily a member of a family of meromorphic functions. Secondly, the author of [Reference Garunkŝtis10] assumes that
$s$
, not necessarily a member of a family of meromorphic functions. Secondly, the author of [Reference Garunkŝtis10] assumes that
![]() $f$
has a finite number of poles which lie in a compact set. A review of the proof [Reference Garunkŝtis10, Proposition 2] reveals that the argument is based on Landau’s theorem (see [Reference Garunkŝtis10, Lemma 8]) and Hadamard’s three circles theorem (see [Reference Garunkŝtis10, Lemma 9]). These classical results are applied to the function
$f$
has a finite number of poles which lie in a compact set. A review of the proof [Reference Garunkŝtis10, Proposition 2] reveals that the argument is based on Landau’s theorem (see [Reference Garunkŝtis10, Lemma 8]) and Hadamard’s three circles theorem (see [Reference Garunkŝtis10, Lemma 9]). These classical results are applied to the function
![]() $f(s)$
in the neighborhood
$f(s)$
in the neighborhood
 $|s-s_{0}|\leqslant 2(\unicode[STIX]{x1D70E}_{0}-1/2-\unicode[STIX]{x1D6FF})$
of the point
$|s-s_{0}|\leqslant 2(\unicode[STIX]{x1D70E}_{0}-1/2-\unicode[STIX]{x1D6FF})$
of the point
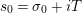 $s_{0}=\unicode[STIX]{x1D70E}_{0}+iT$
for sufficiently large
$s_{0}=\unicode[STIX]{x1D70E}_{0}+iT$
for sufficiently large
![]() $T$
. The proof given in [Reference Garunkŝtis10] carries through without any changes whatsoever under the assumptions we state above.
$T$
. The proof given in [Reference Garunkŝtis10] carries through without any changes whatsoever under the assumptions we state above.
We refer the reader to [Reference Garunkŝtis10] for the proof and various interesting generalizations of Proposition 7.
3 Zeros in a half-plane
 $\operatorname{Re}(s)<1/2$
$\operatorname{Re}(s)<1/2$
In this section, we prove part (a) of the Main Theorem. In fact, we prove more than stated, since our analysis will yield regions where each of the functions
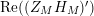 $\text{Re}((Z_{M}H_{M})^{\prime })$
and
$\text{Re}((Z_{M}H_{M})^{\prime })$
and
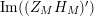 $\text{Im}((Z_{M}H_{M})^{\prime })$
are nonvanishing.
$\text{Im}((Z_{M}H_{M})^{\prime })$
are nonvanishing.
Proposition 8.
-
(a) For
 $\unicode[STIX]{x1D70E}<1/2$
, there exists
$\unicode[STIX]{x1D70E}<1/2$
, there exists
 $t_{0}>0$
, which may depend on
$t_{0}>0$
, which may depend on
 $\unicode[STIX]{x1D70E}$
, such that
$\unicode[STIX]{x1D70E}$
, such that  $$\begin{eqnarray}\operatorname{Re}((Z_{M}H_{M})^{\prime }(\unicode[STIX]{x1D70E}+it))\neq 0\quad \text{ for all }t\text{ such that }|t|>t_{0}.\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Re}((Z_{M}H_{M})^{\prime }(\unicode[STIX]{x1D70E}+it))\neq 0\quad \text{ for all }t\text{ such that }|t|>t_{0}.\end{eqnarray}$$
-
(b) For every constant
 $C>0$
and arbitrary
$C>0$
and arbitrary
 $-C<\unicode[STIX]{x1D70E}_{0}^{\prime }<1/2$
there are at most finitely many zeros of
$-C<\unicode[STIX]{x1D70E}_{0}^{\prime }<1/2$
there are at most finitely many zeros of
 $(Z_{M}H_{M})^{\prime }(s)$
inside the strip
$(Z_{M}H_{M})^{\prime }(s)$
inside the strip
 $-C\leqslant \operatorname{Re}(s)\leqslant \unicode[STIX]{x1D70E}_{0}^{\prime }$
.
$-C\leqslant \operatorname{Re}(s)\leqslant \unicode[STIX]{x1D70E}_{0}^{\prime }$
.
Proof. We first present the proof of part (a). By taking the logarithmic derivative of the functional equation (7) we get for
 $s=\unicode[STIX]{x1D70E}+it$
with
$s=\unicode[STIX]{x1D70E}+it$
with
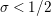 $\unicode[STIX]{x1D70E}<1/2$
, the equation
$\unicode[STIX]{x1D70E}<1/2$
, the equation
 $$\begin{eqnarray}\frac{(Z_{M}H_{M})^{\prime }}{(Z_{M}H_{M})}(\unicode[STIX]{x1D70E}+it)=\frac{\unicode[STIX]{x1D702}_{M}^{\prime }}{\unicode[STIX]{x1D702}_{M}}(\unicode[STIX]{x1D70E}+it)-\frac{K_{M}^{\prime }}{K_{M}}(\unicode[STIX]{x1D70E}+it)-\frac{Z_{M}^{\prime }}{Z_{M}}(1-\unicode[STIX]{x1D70E}-it).\end{eqnarray}$$
$$\begin{eqnarray}\frac{(Z_{M}H_{M})^{\prime }}{(Z_{M}H_{M})}(\unicode[STIX]{x1D70E}+it)=\frac{\unicode[STIX]{x1D702}_{M}^{\prime }}{\unicode[STIX]{x1D702}_{M}}(\unicode[STIX]{x1D70E}+it)-\frac{K_{M}^{\prime }}{K_{M}}(\unicode[STIX]{x1D70E}+it)-\frac{Z_{M}^{\prime }}{Z_{M}}(1-\unicode[STIX]{x1D70E}-it).\end{eqnarray}$$
From the definition (4) of
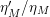 $\unicode[STIX]{x1D702}_{M}^{\prime }/\unicode[STIX]{x1D702}_{M}$
and
$\unicode[STIX]{x1D702}_{M}^{\prime }/\unicode[STIX]{x1D702}_{M}$
and
![]() $K_{M}$
, one can use Stirling’s formula, together with the bound
$K_{M}$
, one can use Stirling’s formula, together with the bound
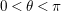 $0<\unicode[STIX]{x1D703}<\unicode[STIX]{x1D70B}$
, to show that
$0<\unicode[STIX]{x1D703}<\unicode[STIX]{x1D70B}$
, to show that
 $$\begin{eqnarray}\displaystyle \text{Re}\left(\frac{\unicode[STIX]{x1D702}_{M}^{\prime }}{\unicode[STIX]{x1D702}_{M}}(\unicode[STIX]{x1D70E}+it)\right) & = & \displaystyle -\text{vol}(M)t+O(\log |t|)\qquad \text{and}\nonumber\\ \displaystyle \frac{K_{M}^{\prime }}{K_{M}}(\unicode[STIX]{x1D70E}+it) & = & \displaystyle O(\log |t|),\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \text{Re}\left(\frac{\unicode[STIX]{x1D702}_{M}^{\prime }}{\unicode[STIX]{x1D702}_{M}}(\unicode[STIX]{x1D70E}+it)\right) & = & \displaystyle -\text{vol}(M)t+O(\log |t|)\qquad \text{and}\nonumber\\ \displaystyle \frac{K_{M}^{\prime }}{K_{M}}(\unicode[STIX]{x1D70E}+it) & = & \displaystyle O(\log |t|),\nonumber\end{eqnarray}$$
for
 $\unicode[STIX]{x1D70E}<1/2$
and as
$\unicode[STIX]{x1D70E}<1/2$
and as
![]() $|t|\rightarrow \infty$
. Therefore,
$|t|\rightarrow \infty$
. Therefore,
 $$\begin{eqnarray}\text{Re}\left(-\frac{(Z_{M}H_{M})^{\prime }}{(Z_{M}H_{M})}(\unicode[STIX]{x1D70E}+it)\right)=\text{vol}(M)t+O(\log |t|)+\text{Re}\left(\frac{Z_{M}^{\prime }}{Z_{M}}(1-\unicode[STIX]{x1D70E}-it)\right)\!.\end{eqnarray}$$
$$\begin{eqnarray}\text{Re}\left(-\frac{(Z_{M}H_{M})^{\prime }}{(Z_{M}H_{M})}(\unicode[STIX]{x1D70E}+it)\right)=\text{vol}(M)t+O(\log |t|)+\text{Re}\left(\frac{Z_{M}^{\prime }}{Z_{M}}(1-\unicode[STIX]{x1D70E}-it)\right)\!.\end{eqnarray}$$
Replacing
![]() $\unicode[STIX]{x1D70E}$
by
$\unicode[STIX]{x1D70E}$
by
![]() $1/2-\unicode[STIX]{x1D70E}$
in (20) we get, for
$1/2-\unicode[STIX]{x1D70E}$
in (20) we get, for
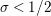 $\unicode[STIX]{x1D70E}<1/2$
$\unicode[STIX]{x1D70E}<1/2$
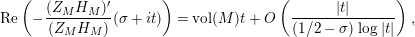 $$\begin{eqnarray}\operatorname{Re}\left(-\frac{(Z_{M}H_{M})^{\prime }}{\left(Z_{M}H_{M}\right)}(\unicode[STIX]{x1D70E}+it)\right)=\text{vol}(M)t+O\left(\frac{|t|}{(1/2-\unicode[STIX]{x1D70E})\log |t|}\right),\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Re}\left(-\frac{(Z_{M}H_{M})^{\prime }}{\left(Z_{M}H_{M}\right)}(\unicode[STIX]{x1D70E}+it)\right)=\text{vol}(M)t+O\left(\frac{|t|}{(1/2-\unicode[STIX]{x1D70E})\log |t|}\right),\end{eqnarray}$$
as
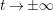 $t\rightarrow \pm \infty$
. Therefore, there exists
$t\rightarrow \pm \infty$
. Therefore, there exists
![]() $t_{0}>0$
such that
$t_{0}>0$
such that
 $$\begin{eqnarray}\operatorname{Re}\left(\frac{(Z_{M}H_{M})^{\prime }}{(Z_{M}H_{M})}(\unicode[STIX]{x1D70E}+it)\right)\neq 0\quad \text{ for all }s=\unicode[STIX]{x1D70E}+it,\text{ with }|t|>t_{0}.\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Re}\left(\frac{(Z_{M}H_{M})^{\prime }}{(Z_{M}H_{M})}(\unicode[STIX]{x1D70E}+it)\right)\neq 0\quad \text{ for all }s=\unicode[STIX]{x1D70E}+it,\text{ with }|t|>t_{0}.\end{eqnarray}$$
On the other hand, the nontrivial zeros of the function
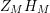 $Z_{M}H_{M}$
are either nontrivial zeros
$Z_{M}H_{M}$
are either nontrivial zeros
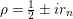 $\unicode[STIX]{x1D70C}=\frac{1}{2}\pm ir_{n}$
of
$\unicode[STIX]{x1D70C}=\frac{1}{2}\pm ir_{n}$
of
![]() $Z_{M}$
or zeros
$Z_{M}$
or zeros
![]() $\unicode[STIX]{x1D70C}$
of
$\unicode[STIX]{x1D70C}$
of
![]() $\unicode[STIX]{x1D719}_{M}$
. All except finitely many zeros of
$\unicode[STIX]{x1D719}_{M}$
. All except finitely many zeros of
![]() $\unicode[STIX]{x1D719}_{M}$
have real part bigger than
$\unicode[STIX]{x1D719}_{M}$
have real part bigger than
![]() $1/2$
; therefore,
$1/2$
; therefore,
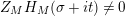 $Z_{M}H_{M}(\unicode[STIX]{x1D70E}+it)\neq 0$
for
$Z_{M}H_{M}(\unicode[STIX]{x1D70E}+it)\neq 0$
for
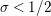 $\unicode[STIX]{x1D70E}<1/2$
and
$\unicode[STIX]{x1D70E}<1/2$
and
![]() $t>t_{0}$
. Therefore, we conclude that
$t>t_{0}$
. Therefore, we conclude that
 $\operatorname{Re}((Z_{M}H_{M})^{\prime }(\unicode[STIX]{x1D70E}+it))\neq 0$
for all
$\operatorname{Re}((Z_{M}H_{M})^{\prime }(\unicode[STIX]{x1D70E}+it))\neq 0$
for all
![]() $t>t_{0}$
. With all this, the proof of part (a) is complete.
$t>t_{0}$
. With all this, the proof of part (a) is complete.
To prove part (b), we employ Lemma 4. Recall the function
![]() $\widetilde{Z}_{M}(s)$
which is defined in (19). Let us write
$\widetilde{Z}_{M}(s)$
which is defined in (19). Let us write
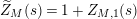 $\widetilde{Z}_{M}(s)=1+Z_{M,1}(s)$
. Then
$\widetilde{Z}_{M}(s)=1+Z_{M,1}(s)$
. Then
 $$\begin{eqnarray}\displaystyle -f_{M}(s)Z_{M,1}(s) & = & \displaystyle \unicode[STIX]{x1D70B}\underset{0<\unicode[STIX]{x1D703}(R)<\unicode[STIX]{x1D70B}}{\underset{\left\{R\right\}}{\sum }}\frac{1}{M_{R}\sin \unicode[STIX]{x1D703}}\frac{\cos (2\unicode[STIX]{x1D703}-\unicode[STIX]{x1D70B})(s-1/2)}{\cos \unicode[STIX]{x1D70B}(s-1/2)}-2n_{1}\log 2\nonumber\\ \displaystyle & & \displaystyle -\,n_{1}\left(\frac{\unicode[STIX]{x1D6E4}^{\prime }}{\unicode[STIX]{x1D6E4}}(1/2+s)+\frac{\unicode[STIX]{x1D6E4}^{\prime }}{\unicode[STIX]{x1D6E4}}(3/2-s)\right.\nonumber\\ \displaystyle & & \displaystyle -\,\left.\frac{\unicode[STIX]{x1D6E4}^{\prime }}{\unicode[STIX]{x1D6E4}}(1/2-s)+\frac{\unicode[STIX]{x1D6E4}^{\prime }}{\unicode[STIX]{x1D6E4}}(1-s)\right)+\frac{Z_{M}^{\prime }}{Z_{M}}(s),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle -f_{M}(s)Z_{M,1}(s) & = & \displaystyle \unicode[STIX]{x1D70B}\underset{0<\unicode[STIX]{x1D703}(R)<\unicode[STIX]{x1D70B}}{\underset{\left\{R\right\}}{\sum }}\frac{1}{M_{R}\sin \unicode[STIX]{x1D703}}\frac{\cos (2\unicode[STIX]{x1D703}-\unicode[STIX]{x1D70B})(s-1/2)}{\cos \unicode[STIX]{x1D70B}(s-1/2)}-2n_{1}\log 2\nonumber\\ \displaystyle & & \displaystyle -\,n_{1}\left(\frac{\unicode[STIX]{x1D6E4}^{\prime }}{\unicode[STIX]{x1D6E4}}(1/2+s)+\frac{\unicode[STIX]{x1D6E4}^{\prime }}{\unicode[STIX]{x1D6E4}}(3/2-s)\right.\nonumber\\ \displaystyle & & \displaystyle -\,\left.\frac{\unicode[STIX]{x1D6E4}^{\prime }}{\unicode[STIX]{x1D6E4}}(1/2-s)+\frac{\unicode[STIX]{x1D6E4}^{\prime }}{\unicode[STIX]{x1D6E4}}(1-s)\right)+\frac{Z_{M}^{\prime }}{Z_{M}}(s),\end{eqnarray}$$
where
![]() $f_{M}$
is defined in (18).
$f_{M}$
is defined in (18).
As in the proof of part (a), we can use Stirling’s formula and (20) to arrive at the bound
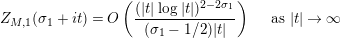 $$\begin{eqnarray}Z_{M,1}(\unicode[STIX]{x1D70E}_{1}+it)=O\left(\frac{(|t|\log |t|)^{2-2\unicode[STIX]{x1D70E}_{1}}}{(\unicode[STIX]{x1D70E}_{1}-1/2)|t|}\right)\quad \text{as }|t|\rightarrow \infty\end{eqnarray}$$
$$\begin{eqnarray}Z_{M,1}(\unicode[STIX]{x1D70E}_{1}+it)=O\left(\frac{(|t|\log |t|)^{2-2\unicode[STIX]{x1D70E}_{1}}}{(\unicode[STIX]{x1D70E}_{1}-1/2)|t|}\right)\quad \text{as }|t|\rightarrow \infty\end{eqnarray}$$
for
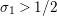 $\unicode[STIX]{x1D70E}_{1}>1/2$
and
$\unicode[STIX]{x1D70E}_{1}>1/2$
and
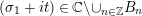 $(\unicode[STIX]{x1D70E}_{1}+it)\in \mathbb{C}\backslash \cup _{n\in \mathbb{Z}}B_{n}$
where
$(\unicode[STIX]{x1D70E}_{1}+it)\in \mathbb{C}\backslash \cup _{n\in \mathbb{Z}}B_{n}$
where
![]() $B_{n}$
are small circles of fixed radius centered at integers. In particular, for
$B_{n}$
are small circles of fixed radius centered at integers. In particular, for
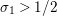 $\unicode[STIX]{x1D70E}_{1}>1/2$
and
$\unicode[STIX]{x1D70E}_{1}>1/2$
and
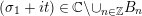 $(\unicode[STIX]{x1D70E}_{1}+it)\in \mathbb{C}\backslash \cup _{n\in \mathbb{Z}}B_{n}$
, function
$(\unicode[STIX]{x1D70E}_{1}+it)\in \mathbb{C}\backslash \cup _{n\in \mathbb{Z}}B_{n}$
, function
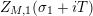 $Z_{M,1}(\unicode[STIX]{x1D70E}_{1}+iT)$
is uniformly bounded in
$Z_{M,1}(\unicode[STIX]{x1D70E}_{1}+iT)$
is uniformly bounded in
![]() $T$
. Therefore,
$T$
. Therefore,
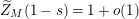 $\widetilde{Z}_{M}(1-s)=1+o(1)$
, as
$\widetilde{Z}_{M}(1-s)=1+o(1)$
, as
 $\operatorname{Im}(s)\rightarrow \pm \infty$
in the strip
$\operatorname{Im}(s)\rightarrow \pm \infty$
in the strip
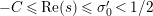 $-C\leqslant \operatorname{Re}(s)\leqslant \unicode[STIX]{x1D70E}_{0}^{\prime }<1/2$
, hence
$-C\leqslant \operatorname{Re}(s)\leqslant \unicode[STIX]{x1D70E}_{0}^{\prime }<1/2$
, hence
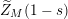 $\widetilde{Z}_{M}(1-s)$
has finitely many zeros in this strip.
$\widetilde{Z}_{M}(1-s)$
has finitely many zeros in this strip.
Since
![]() $Z_{M}(s)$
has only finitely many zeros for
$Z_{M}(s)$
has only finitely many zeros for
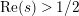 $\operatorname{Re}(s)>1/2$
, the function
$\operatorname{Re}(s)>1/2$
, the function
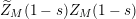 $\widetilde{Z}_{M}(1-s)Z_{M}(1-s)$
will have finitely many zeros in the strip
$\widetilde{Z}_{M}(1-s)Z_{M}(1-s)$
will have finitely many zeros in the strip
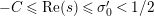 $-C\leqslant \operatorname{Re}(s)\leqslant \unicode[STIX]{x1D70E}_{0}^{\prime }<1/2$
. Equation (17) then implies that the set of zeros of
$-C\leqslant \operatorname{Re}(s)\leqslant \unicode[STIX]{x1D70E}_{0}^{\prime }<1/2$
. Equation (17) then implies that the set of zeros of
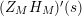 $(Z_{M}H_{M})^{\prime }(s)$
in the strip
$(Z_{M}H_{M})^{\prime }(s)$
in the strip
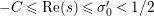 $-C\leqslant \operatorname{Re}(s)\leqslant \unicode[STIX]{x1D70E}_{0}^{\prime }<1/2$
is finite since the factor
$-C\leqslant \operatorname{Re}(s)\leqslant \unicode[STIX]{x1D70E}_{0}^{\prime }<1/2$
is finite since the factor
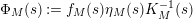 $\unicode[STIX]{x1D6F7}_{M}(s):=f_{M}(s)\unicode[STIX]{x1D702}_{M}(s)K_{M}^{-1}(s)$
of the functional equation (17) also has at most finitely many zeros in this strip.◻
$\unicode[STIX]{x1D6F7}_{M}(s):=f_{M}(s)\unicode[STIX]{x1D702}_{M}(s)K_{M}^{-1}(s)$
of the functional equation (17) also has at most finitely many zeros in this strip.◻
We note that the zeros of
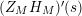 $(Z_{M}H_{M})^{\prime }(s)$
which arise from zeros of
$(Z_{M}H_{M})^{\prime }(s)$
which arise from zeros of
![]() $\unicode[STIX]{x1D6F7}_{M}$
are viewed as trivial zeros. They are located in the region
$\unicode[STIX]{x1D6F7}_{M}$
are viewed as trivial zeros. They are located in the region
 $\operatorname{Re}(s)<1/2$
and arise at all negative integers.
$\operatorname{Re}(s)<1/2$
and arise at all negative integers.
The above method of examining zeros of the function
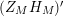 $(Z_{M}H_{M})^{\prime }$
has the critical line as its limitation, since the bounds for the logarithmic derivative (20) hold true only in the half-plane
$(Z_{M}H_{M})^{\prime }$
has the critical line as its limitation, since the bounds for the logarithmic derivative (20) hold true only in the half-plane
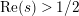 $\operatorname{Re}(s)>1/2$
. In order to derive results valid on the critical line we need a representation on the critical line. Such a representation exists for the complete zeta function
$\operatorname{Re}(s)>1/2$
. In order to derive results valid on the critical line we need a representation on the critical line. Such a representation exists for the complete zeta function
![]() $\unicode[STIX]{x1D6EF}_{M}(s)$
(see § 2.4).
$\unicode[STIX]{x1D6EF}_{M}(s)$
(see § 2.4).
Proposition 9. There exists a number
![]() $t_{0}>0$
such that the following statements hold:
$t_{0}>0$
such that the following statements hold:
-
(a)
 $\frac{(Z_{M}H_{M})^{\prime }}{(Z_{M}H_{M})}(\unicode[STIX]{x1D70E}+it)\neq 0$
for all
$\frac{(Z_{M}H_{M})^{\prime }}{(Z_{M}H_{M})}(\unicode[STIX]{x1D70E}+it)\neq 0$
for all
 $\unicode[STIX]{x1D70E}<1/2$
and all
$\unicode[STIX]{x1D70E}<1/2$
and all
 $|t|>t_{0}$
;
$|t|>t_{0}$
; -
(b)
 $\frac{(Z_{M}H_{M})^{\prime }}{(Z_{M}H_{M})}(1/2\pm it)\neq 0$
for all
$\frac{(Z_{M}H_{M})^{\prime }}{(Z_{M}H_{M})}(1/2\pm it)\neq 0$
for all
 $|t|>t_{0}$
,
$|t|>t_{0}$
,
 $t\neq r_{n}$
for all
$t\neq r_{n}$
for all
 $n\geqslant 0$
.
$n\geqslant 0$
.
Proof. Let
![]() $\unicode[STIX]{x1D70E}<0$
. By Proposition 8, there exists a constant
$\unicode[STIX]{x1D70E}<0$
. By Proposition 8, there exists a constant
![]() $t_{0}^{\prime }>0$
such that for all
$t_{0}^{\prime }>0$
such that for all
![]() $\unicode[STIX]{x1D70E}<0$
and all
$\unicode[STIX]{x1D70E}<0$
and all
![]() $|t|>t_{0}^{\prime }$
we have
$|t|>t_{0}^{\prime }$
we have
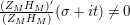 $\frac{(Z_{M}H_{M})^{\prime }}{(Z_{M}H_{M})}(\unicode[STIX]{x1D70E}+it)\neq 0$
. Therefore, it is enough to prove the statement when
$\frac{(Z_{M}H_{M})^{\prime }}{(Z_{M}H_{M})}(\unicode[STIX]{x1D70E}+it)\neq 0$
. Therefore, it is enough to prove the statement when
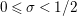 $0\leqslant \unicode[STIX]{x1D70E}<1/2$
. Without loss of generality, we assume that
$0\leqslant \unicode[STIX]{x1D70E}<1/2$
. Without loss of generality, we assume that
![]() $t>0$
.
$t>0$
.
Taking the logarithmic derivatives of the both sides of the equation (23), we get
 $$\begin{eqnarray}\displaystyle \frac{1}{2s-1}\frac{(Z_{M}H_{M})^{\prime }}{(Z_{M}H_{M})}(s) & = & \displaystyle -\frac{1}{2s-1}\frac{\unicode[STIX]{x1D6EF}_{I}^{\prime }(s)}{\unicode[STIX]{x1D6EF}_{I}(s)}-\frac{1}{2s-1}\frac{\unicode[STIX]{x1D6EF}_{M,\text{ell}}^{\prime }(s)}{\unicode[STIX]{x1D6EF}_{M,\text{ell}}(s)}\nonumber\\ \displaystyle & & \displaystyle +\,\frac{\log \mathfrak{g}_{1}}{2s-1}+\frac{n_{1}}{2s-1}\frac{\unicode[STIX]{x1D6E4}^{\prime }}{\unicode[STIX]{x1D6E4}}(s)\nonumber\\ \displaystyle & & \displaystyle +\,\frac{n_{1}-\frac{1}{2}\text{ Tr}\left(I_{n_{1}}-\unicode[STIX]{x1D6F7}(\frac{1}{2})\right)}{2(s-1/2)^{2}}-\frac{1}{2s-1}\mathop{\sum }_{m=1}^{N_{0}}\frac{1}{s-p_{m}}\nonumber\\ \displaystyle & & \displaystyle -\,\frac{1}{2s-1}\frac{\left(\unicode[STIX]{x1D6EF}_{M}{\mathcal{P}}_{M}\right)^{\prime }}{\left(\unicode[STIX]{x1D6EF}_{M}{\mathcal{P}}_{M}\right)}(1-s),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \frac{1}{2s-1}\frac{(Z_{M}H_{M})^{\prime }}{(Z_{M}H_{M})}(s) & = & \displaystyle -\frac{1}{2s-1}\frac{\unicode[STIX]{x1D6EF}_{I}^{\prime }(s)}{\unicode[STIX]{x1D6EF}_{I}(s)}-\frac{1}{2s-1}\frac{\unicode[STIX]{x1D6EF}_{M,\text{ell}}^{\prime }(s)}{\unicode[STIX]{x1D6EF}_{M,\text{ell}}(s)}\nonumber\\ \displaystyle & & \displaystyle +\,\frac{\log \mathfrak{g}_{1}}{2s-1}+\frac{n_{1}}{2s-1}\frac{\unicode[STIX]{x1D6E4}^{\prime }}{\unicode[STIX]{x1D6E4}}(s)\nonumber\\ \displaystyle & & \displaystyle +\,\frac{n_{1}-\frac{1}{2}\text{ Tr}\left(I_{n_{1}}-\unicode[STIX]{x1D6F7}(\frac{1}{2})\right)}{2(s-1/2)^{2}}-\frac{1}{2s-1}\mathop{\sum }_{m=1}^{N_{0}}\frac{1}{s-p_{m}}\nonumber\\ \displaystyle & & \displaystyle -\,\frac{1}{2s-1}\frac{\left(\unicode[STIX]{x1D6EF}_{M}{\mathcal{P}}_{M}\right)^{\prime }}{\left(\unicode[STIX]{x1D6EF}_{M}{\mathcal{P}}_{M}\right)}(1-s),\end{eqnarray}$$
for all
![]() $s\in \mathbb{C}$
different from zeros and poles of
$s\in \mathbb{C}$
different from zeros and poles of
![]() $Z_{M}$
and
$Z_{M}$
and
![]() $\unicode[STIX]{x1D719}_{M}$
. Applying [Reference Fischer7, formula (3.4.1)] yields
$\unicode[STIX]{x1D719}_{M}$
. Applying [Reference Fischer7, formula (3.4.1)] yields
 $$\begin{eqnarray}\displaystyle \left(\unicode[STIX]{x1D6EF}_{M}{\mathcal{P}}_{M}\right)(s) & = & \displaystyle e^{Q(s)}(s-1/2)^{2d_{1/4}}\nonumber\\ \displaystyle & & \displaystyle \cdot \,\underset{n\geqslant 0\text{, }r_{n}\neq 0}{\prod }\left(1+\frac{(s-1/2)^{2}}{\mathop{r}_{n}^{2}}\right)\exp \left(-\frac{(s-1/2)^{2}}{\mathop{r}_{n}^{2}}\right)\nonumber\\ \displaystyle & & \displaystyle \cdot \,\,\overset{N_{1}}{\underset{n=1}{\prod }}\left(1-\frac{s-1/2}{\unicode[STIX]{x1D702}_{n}}\right)\exp \left(-\frac{s-1/2}{\unicode[STIX]{x1D702}_{n}}+\frac{(s-1/2)^{2}}{2\unicode[STIX]{x1D702}_{n}^{2}}\right)\nonumber\\ \displaystyle & & \displaystyle \cdot \,\underset{n\geqslant N_{1}+1}{\prod }\left(1+\frac{s-1/2}{\unicode[STIX]{x1D702}_{n}+i\unicode[STIX]{x1D6FE}_{n}}\right)\left(1+\frac{s-1/2}{\unicode[STIX]{x1D702}_{n}-i\unicode[STIX]{x1D6FE}_{n}}\right)\nonumber\\ \displaystyle & & \displaystyle \cdot \,\exp \left(-\frac{2\unicode[STIX]{x1D702}_{n}\left(s-\frac{1}{2}\right)}{\unicode[STIX]{x1D702}_{n}^{2}+\unicode[STIX]{x1D6FE}_{n}^{2}}+\left(s-\frac{1}{2}\right)^{2}\frac{\unicode[STIX]{x1D702}_{n}^{2}-\unicode[STIX]{x1D6FE}_{n}^{2}}{\left(\unicode[STIX]{x1D702}_{n}^{2}+\unicode[STIX]{x1D6FE}_{n}^{2}\right)^{2}}\right),\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \left(\unicode[STIX]{x1D6EF}_{M}{\mathcal{P}}_{M}\right)(s) & = & \displaystyle e^{Q(s)}(s-1/2)^{2d_{1/4}}\nonumber\\ \displaystyle & & \displaystyle \cdot \,\underset{n\geqslant 0\text{, }r_{n}\neq 0}{\prod }\left(1+\frac{(s-1/2)^{2}}{\mathop{r}_{n}^{2}}\right)\exp \left(-\frac{(s-1/2)^{2}}{\mathop{r}_{n}^{2}}\right)\nonumber\\ \displaystyle & & \displaystyle \cdot \,\,\overset{N_{1}}{\underset{n=1}{\prod }}\left(1-\frac{s-1/2}{\unicode[STIX]{x1D702}_{n}}\right)\exp \left(-\frac{s-1/2}{\unicode[STIX]{x1D702}_{n}}+\frac{(s-1/2)^{2}}{2\unicode[STIX]{x1D702}_{n}^{2}}\right)\nonumber\\ \displaystyle & & \displaystyle \cdot \,\underset{n\geqslant N_{1}+1}{\prod }\left(1+\frac{s-1/2}{\unicode[STIX]{x1D702}_{n}+i\unicode[STIX]{x1D6FE}_{n}}\right)\left(1+\frac{s-1/2}{\unicode[STIX]{x1D702}_{n}-i\unicode[STIX]{x1D6FE}_{n}}\right)\nonumber\\ \displaystyle & & \displaystyle \cdot \,\exp \left(-\frac{2\unicode[STIX]{x1D702}_{n}\left(s-\frac{1}{2}\right)}{\unicode[STIX]{x1D702}_{n}^{2}+\unicode[STIX]{x1D6FE}_{n}^{2}}+\left(s-\frac{1}{2}\right)^{2}\frac{\unicode[STIX]{x1D702}_{n}^{2}-\unicode[STIX]{x1D6FE}_{n}^{2}}{\left(\unicode[STIX]{x1D702}_{n}^{2}+\unicode[STIX]{x1D6FE}_{n}^{2}\right)^{2}}\right),\nonumber\end{eqnarray}$$
for all
![]() $s\in \mathbb{C}$
and where the notation is as follows:
$s\in \mathbb{C}$
and where the notation is as follows:
 $\unicode[STIX]{x1D702}_{n}:=\operatorname{Re}(q_{n})$
;
$\unicode[STIX]{x1D702}_{n}:=\operatorname{Re}(q_{n})$
;
 $\unicode[STIX]{x1D6FE}_{n}:=\operatorname{Im}(q_{n})$
,
$\unicode[STIX]{x1D6FE}_{n}:=\operatorname{Im}(q_{n})$
,
![]() $d_{1/4}$
is the multiplicity of
$d_{1/4}$
is the multiplicity of
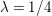 $\unicode[STIX]{x1D706}=1/4$
as an eigenvalue; and
$\unicode[STIX]{x1D706}=1/4$
as an eigenvalue; and
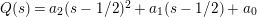 $Q(s)=a_{2}(s-1/2)^{2}+a_{1}(s-1/2)+a_{0}$
for some constants
$Q(s)=a_{2}(s-1/2)^{2}+a_{1}(s-1/2)+a_{0}$
for some constants
![]() $a_{i}$
,
$a_{i}$
,
 $i=0,1,2$
computed in [Reference Fischer7]. The constants
$i=0,1,2$
computed in [Reference Fischer7]. The constants
![]() $a_{1}$
and
$a_{1}$
and
![]() $a_{2}$
are defined by [Reference Fischer7, formulas (3.4.8) and (3.4.9)]. For our purposes it is important to know that
$a_{2}$
are defined by [Reference Fischer7, formulas (3.4.8) and (3.4.9)]. For our purposes it is important to know that
![]() $a_{1}$
and
$a_{1}$
and
![]() $a_{2}$
are real.
$a_{2}$
are real.
We now compute the logarithmic derivative of
 $(\unicode[STIX]{x1D6EF}_{M}{\mathcal{P}}_{M})(s)$
and substitute the expression into (27). After some elementary calculations, employing the Stirling formula and having in mind (21) and (22) we end up with
$(\unicode[STIX]{x1D6EF}_{M}{\mathcal{P}}_{M})(s)$
and substitute the expression into (27). After some elementary calculations, employing the Stirling formula and having in mind (21) and (22) we end up with
 $$\begin{eqnarray}\displaystyle \frac{1}{2s-1}\frac{(Z_{M}H_{M})^{\prime }}{(Z_{M}H_{M})}(s) & = & \displaystyle \frac{\text{vol}(M)}{2\unicode[STIX]{x1D70B}}\frac{\unicode[STIX]{x1D6E4}^{\prime }}{\unicode[STIX]{x1D6E4}}(s)+\underset{n\geqslant 0\text{, }r_{n}\neq 0}{\sum }\left(\frac{1}{(s-\frac{1}{2})^{2}+r_{n}^{2}}-\frac{1}{\mathop{r}_{n}^{2}}\right)\nonumber\\ \displaystyle & & \displaystyle +\,a_{2}+\underset{n\geqslant N_{1}+1}{\sum }\left[\frac{\mathop{\unicode[STIX]{x1D702}}_{n}^{2}-\unicode[STIX]{x1D6FE}_{n}^{2}}{\left(\mathop{\unicode[STIX]{x1D702}}_{n}^{2}+\unicode[STIX]{x1D6FE}_{n}^{2}\right)^{2}}\right.\nonumber\\ \displaystyle & & \displaystyle \left.+\,\frac{\unicode[STIX]{x1D6FE}_{n}^{2}-\unicode[STIX]{x1D702}_{n}^{2}+\unicode[STIX]{x1D702}_{n}(s-1/2)}{\big(\big(\unicode[STIX]{x1D702}_{n}-s+1/2\big)^{2}+\unicode[STIX]{x1D6FE}_{n}^{2}\big)\left(\unicode[STIX]{x1D702}_{n}^{2}+\unicode[STIX]{x1D6FE}_{n}^{2}\right)}\right]\nonumber\\ \displaystyle & & \displaystyle +\,\frac{1}{2}\underset{n=1}{\overset{N_{1}}{\sum }}\left(\frac{1}{\unicode[STIX]{x1D702}_{n}^{2}}-\frac{1}{\unicode[STIX]{x1D702}_{n}(\unicode[STIX]{x1D702}_{n}-s+1/2)}\right)+O\left(\frac{\log t}{t}\right),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \frac{1}{2s-1}\frac{(Z_{M}H_{M})^{\prime }}{(Z_{M}H_{M})}(s) & = & \displaystyle \frac{\text{vol}(M)}{2\unicode[STIX]{x1D70B}}\frac{\unicode[STIX]{x1D6E4}^{\prime }}{\unicode[STIX]{x1D6E4}}(s)+\underset{n\geqslant 0\text{, }r_{n}\neq 0}{\sum }\left(\frac{1}{(s-\frac{1}{2})^{2}+r_{n}^{2}}-\frac{1}{\mathop{r}_{n}^{2}}\right)\nonumber\\ \displaystyle & & \displaystyle +\,a_{2}+\underset{n\geqslant N_{1}+1}{\sum }\left[\frac{\mathop{\unicode[STIX]{x1D702}}_{n}^{2}-\unicode[STIX]{x1D6FE}_{n}^{2}}{\left(\mathop{\unicode[STIX]{x1D702}}_{n}^{2}+\unicode[STIX]{x1D6FE}_{n}^{2}\right)^{2}}\right.\nonumber\\ \displaystyle & & \displaystyle \left.+\,\frac{\unicode[STIX]{x1D6FE}_{n}^{2}-\unicode[STIX]{x1D702}_{n}^{2}+\unicode[STIX]{x1D702}_{n}(s-1/2)}{\big(\big(\unicode[STIX]{x1D702}_{n}-s+1/2\big)^{2}+\unicode[STIX]{x1D6FE}_{n}^{2}\big)\left(\unicode[STIX]{x1D702}_{n}^{2}+\unicode[STIX]{x1D6FE}_{n}^{2}\right)}\right]\nonumber\\ \displaystyle & & \displaystyle +\,\frac{1}{2}\underset{n=1}{\overset{N_{1}}{\sum }}\left(\frac{1}{\unicode[STIX]{x1D702}_{n}^{2}}-\frac{1}{\unicode[STIX]{x1D702}_{n}(\unicode[STIX]{x1D702}_{n}-s+1/2)}\right)+O\left(\frac{\log t}{t}\right),\end{eqnarray}$$
as
 $t=\operatorname{Im}(s)\rightarrow \infty$
. We now set
$t=\operatorname{Im}(s)\rightarrow \infty$
. We now set
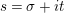 $s=\unicode[STIX]{x1D70E}+it$
with
$s=\unicode[STIX]{x1D70E}+it$
with
![]() $t>0$
and
$t>0$
and
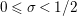 $0\leqslant \unicode[STIX]{x1D70E}<1/2$
. By computing the imaginary parts of both sides (28) we get
$0\leqslant \unicode[STIX]{x1D70E}<1/2$
. By computing the imaginary parts of both sides (28) we get
 $$\begin{eqnarray}\displaystyle & & \displaystyle \hspace{-3.99994pt}\text{Im}\left(\frac{1}{2\unicode[STIX]{x1D70E}-1+2it}\frac{(Z_{M}H_{M})^{\prime }}{(Z_{M}H_{M})}(\unicode[STIX]{x1D70E}+it)\right)\nonumber\\ \displaystyle & & \displaystyle \hspace{-3.99994pt}\quad =\frac{\text{vol}(M)}{2\unicode[STIX]{x1D70B}}\cdot \left[\frac{t}{\unicode[STIX]{x1D70E}^{2}+t^{2}}+\mathop{\sum }_{n=1}^{\infty }\frac{t}{(n+\unicode[STIX]{x1D70E})^{2}+t^{2}}\right]\nonumber\\ \displaystyle & & \displaystyle \hspace{-3.99994pt}\qquad +\,\underset{n\geqslant 0\text{, }r_{n}\neq 0}{\sum }\frac{t(1/2-\unicode[STIX]{x1D70E})}{\left((\unicode[STIX]{x1D70E}-1/2)^{2}-t^{2}+r_{n}^{2}\right)^{2}+4t^{2}(\unicode[STIX]{x1D70E}-1/2)^{2}}\nonumber\\ \displaystyle & & \displaystyle \hspace{-3.99994pt}\qquad +\,O\left(\frac{1}{t}\right)+O\left(\frac{\log t}{t}\right)\nonumber\\ \displaystyle & & \displaystyle \hspace{-3.99994pt}\qquad +\,\underset{n\geqslant N_{1}+1}{\sum }\frac{t\unicode[STIX]{x1D702}_{n}(3\unicode[STIX]{x1D6FE}_{n}^{2}-t^{2})-t\unicode[STIX]{x1D702}_{n}^{3}+t(1/2-\unicode[STIX]{x1D70E})(2\unicode[STIX]{x1D6FE}_{n}^{2}-2\unicode[STIX]{x1D702}_{n}^{2}-\unicode[STIX]{x1D702}_{n}(1/2-\unicode[STIX]{x1D70E}))}{\left[((\unicode[STIX]{x1D702}_{n}-\unicode[STIX]{x1D70E}+1/2)^{2}+\unicode[STIX]{x1D6FE}_{n}^{2}-t^{2})^{2}+4t^{2}(\unicode[STIX]{x1D702}_{n}+1/2-\unicode[STIX]{x1D70E})^{2}\right](\mathop{\unicode[STIX]{x1D702}}_{n}^{2}+\unicode[STIX]{x1D6FE}_{n}^{2})}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \hspace{-3.99994pt}\text{Im}\left(\frac{1}{2\unicode[STIX]{x1D70E}-1+2it}\frac{(Z_{M}H_{M})^{\prime }}{(Z_{M}H_{M})}(\unicode[STIX]{x1D70E}+it)\right)\nonumber\\ \displaystyle & & \displaystyle \hspace{-3.99994pt}\quad =\frac{\text{vol}(M)}{2\unicode[STIX]{x1D70B}}\cdot \left[\frac{t}{\unicode[STIX]{x1D70E}^{2}+t^{2}}+\mathop{\sum }_{n=1}^{\infty }\frac{t}{(n+\unicode[STIX]{x1D70E})^{2}+t^{2}}\right]\nonumber\\ \displaystyle & & \displaystyle \hspace{-3.99994pt}\qquad +\,\underset{n\geqslant 0\text{, }r_{n}\neq 0}{\sum }\frac{t(1/2-\unicode[STIX]{x1D70E})}{\left((\unicode[STIX]{x1D70E}-1/2)^{2}-t^{2}+r_{n}^{2}\right)^{2}+4t^{2}(\unicode[STIX]{x1D70E}-1/2)^{2}}\nonumber\\ \displaystyle & & \displaystyle \hspace{-3.99994pt}\qquad +\,O\left(\frac{1}{t}\right)+O\left(\frac{\log t}{t}\right)\nonumber\\ \displaystyle & & \displaystyle \hspace{-3.99994pt}\qquad +\,\underset{n\geqslant N_{1}+1}{\sum }\frac{t\unicode[STIX]{x1D702}_{n}(3\unicode[STIX]{x1D6FE}_{n}^{2}-t^{2})-t\unicode[STIX]{x1D702}_{n}^{3}+t(1/2-\unicode[STIX]{x1D70E})(2\unicode[STIX]{x1D6FE}_{n}^{2}-2\unicode[STIX]{x1D702}_{n}^{2}-\unicode[STIX]{x1D702}_{n}(1/2-\unicode[STIX]{x1D70E}))}{\left[((\unicode[STIX]{x1D702}_{n}-\unicode[STIX]{x1D70E}+1/2)^{2}+\unicode[STIX]{x1D6FE}_{n}^{2}-t^{2})^{2}+4t^{2}(\unicode[STIX]{x1D702}_{n}+1/2-\unicode[STIX]{x1D70E})^{2}\right](\mathop{\unicode[STIX]{x1D702}}_{n}^{2}+\unicode[STIX]{x1D6FE}_{n}^{2})}.\end{eqnarray}$$
Since
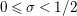 $0\leqslant \unicode[STIX]{x1D70E}<1/2$
we have that
$0\leqslant \unicode[STIX]{x1D70E}<1/2$
we have that
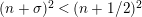 $(n+\unicode[STIX]{x1D70E})^{2}<(n+1/2)^{2}$
, for all
$(n+\unicode[STIX]{x1D70E})^{2}<(n+1/2)^{2}$
, for all
![]() $n\geqslant 0$
. Therefore
$n\geqslant 0$
. Therefore
 $$\begin{eqnarray}\frac{t}{\unicode[STIX]{x1D70E}^{2}+t^{2}}+\!\mathop{\sum }_{n=1}^{\infty }\frac{t}{(n+\unicode[STIX]{x1D70E})^{2}+t^{2}}>\frac{t}{1/4+t^{2}}+\!\mathop{\sum }_{n=1}^{\infty }\frac{t}{(n+1/2)^{2}+t^{2}}=\frac{\unicode[STIX]{x1D70B}}{2}\tanh (\unicode[STIX]{x1D70B}t).\end{eqnarray}$$
$$\begin{eqnarray}\frac{t}{\unicode[STIX]{x1D70E}^{2}+t^{2}}+\!\mathop{\sum }_{n=1}^{\infty }\frac{t}{(n+\unicode[STIX]{x1D70E})^{2}+t^{2}}>\frac{t}{1/4+t^{2}}+\!\mathop{\sum }_{n=1}^{\infty }\frac{t}{(n+1/2)^{2}+t^{2}}=\frac{\unicode[STIX]{x1D70B}}{2}\tanh (\unicode[STIX]{x1D70B}t).\end{eqnarray}$$
Furthermore, since
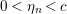 $0<\unicode[STIX]{x1D702}_{n}<c$
, for some positive constant
$0<\unicode[STIX]{x1D702}_{n}<c$
, for some positive constant
![]() $c$
and all
$c$
and all
![]() $n\geqslant 1$
and
$n\geqslant 1$
and
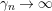 $\unicode[STIX]{x1D6FE}_{n}\rightarrow \infty$
, as
$\unicode[STIX]{x1D6FE}_{n}\rightarrow \infty$
, as
![]() $n\rightarrow \infty$
, by the choice of
$n\rightarrow \infty$
, by the choice of
![]() $\unicode[STIX]{x1D70E}$
we have that
$\unicode[STIX]{x1D70E}$
we have that
 $$\begin{eqnarray}(1/2-\unicode[STIX]{x1D70E})(2\unicode[STIX]{x1D6FE}_{n}^{2}-2\unicode[STIX]{x1D702}_{n}^{2}-\unicode[STIX]{x1D702}_{n}(1/2-\unicode[STIX]{x1D70E}))\geqslant 2\unicode[STIX]{x1D6FE}_{n}^{2}-2\unicode[STIX]{x1D702}_{n}^{2}-\unicode[STIX]{x1D702}_{n}\geqslant 0\end{eqnarray}$$
$$\begin{eqnarray}(1/2-\unicode[STIX]{x1D70E})(2\unicode[STIX]{x1D6FE}_{n}^{2}-2\unicode[STIX]{x1D702}_{n}^{2}-\unicode[STIX]{x1D702}_{n}(1/2-\unicode[STIX]{x1D70E}))\geqslant 2\unicode[STIX]{x1D6FE}_{n}^{2}-2\unicode[STIX]{x1D702}_{n}^{2}-\unicode[STIX]{x1D702}_{n}\geqslant 0\end{eqnarray}$$
for all but finitely many
 $n\geqslant (N_{1}+1)$
. Let
$n\geqslant (N_{1}+1)$
. Let
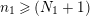 $n_{1}\geqslant (N_{1}+1)$
be an integer such that
$n_{1}\geqslant (N_{1}+1)$
be an integer such that
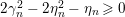 $2\unicode[STIX]{x1D6FE}_{n}^{2}-2\unicode[STIX]{x1D702}_{n}^{2}-\unicode[STIX]{x1D702}_{n}\geqslant 0$
for all
$2\unicode[STIX]{x1D6FE}_{n}^{2}-2\unicode[STIX]{x1D702}_{n}^{2}-\unicode[STIX]{x1D702}_{n}\geqslant 0$
for all
![]() $n\geqslant n_{1}$
. For simplicity, we introduce the notation
$n\geqslant n_{1}$
. For simplicity, we introduce the notation
 $$\begin{eqnarray}D(n,\unicode[STIX]{x1D70E},t)=\left((\unicode[STIX]{x1D702}_{n}-\unicode[STIX]{x1D70E}+1/2)^{2}+\unicode[STIX]{x1D6FE}_{n}^{2}-t^{2}\right)^{2}+4t^{2}(\unicode[STIX]{x1D702}_{n}+1/2-\unicode[STIX]{x1D70E})^{2}.\end{eqnarray}$$
$$\begin{eqnarray}D(n,\unicode[STIX]{x1D70E},t)=\left((\unicode[STIX]{x1D702}_{n}-\unicode[STIX]{x1D70E}+1/2)^{2}+\unicode[STIX]{x1D6FE}_{n}^{2}-t^{2}\right)^{2}+4t^{2}(\unicode[STIX]{x1D702}_{n}+1/2-\unicode[STIX]{x1D70E})^{2}.\end{eqnarray}$$
From (29), we conclude the existence a constant
![]() $C_{1}>0$
and a positive number
$C_{1}>0$
and a positive number
![]() $t_{0}>t_{0}^{\prime }$
such that for all
$t_{0}>t_{0}^{\prime }$
such that for all
![]() $t>t_{0}$
,
$t>t_{0}$
,
 $$\begin{eqnarray}\displaystyle & & \displaystyle \displaystyle \text{Im}\!\left(\frac{1}{2\unicode[STIX]{x1D70E}-1+2it}\frac{(Z_{M}H_{M})^{\prime }}{(Z_{M}H_{M})}(\unicode[STIX]{x1D70E}+it)\!\right)\nonumber\\ \displaystyle & & \displaystyle ~\displaystyle \quad \geqslant \frac{\text{vol}(M)}{4}\tanh (\unicode[STIX]{x1D70B}t)-C_{1}\frac{\log t}{t}+\underset{|\unicode[STIX]{x1D6FE}_{n}|<t/\sqrt{3}}{\sum }\frac{t\unicode[STIX]{x1D702}_{n}(3\unicode[STIX]{x1D6FE}_{n}^{2}-t^{2})}{D(n,\unicode[STIX]{x1D70E},t)(\mathop{\unicode[STIX]{x1D702}}_{n}^{2}+\unicode[STIX]{x1D6FE}_{n}^{2})}\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\underset{N_{1}+1\leqslant n\leqslant n_{1}}{\sum }\frac{(1/2\,-\unicode[STIX]{x1D70E})t(2\mathop{\unicode[STIX]{x1D6FE}}_{n}^{2}\,-\,2\unicode[STIX]{x1D702}_{n}^{2}\,-\,\unicode[STIX]{x1D702}_{n})}{D(n,\unicode[STIX]{x1D70E},t)(\mathop{\unicode[STIX]{x1D702}}_{n}^{2}+\unicode[STIX]{x1D6FE}_{n}^{2})}+\underset{n\geqslant N_{1}+1}{\sum }\frac{-t\mathop{\unicode[STIX]{x1D702}}_{n}^{3}}{D(n,\unicode[STIX]{x1D70E},t)\left(\mathop{\unicode[STIX]{x1D702}}_{n}^{2}+\unicode[STIX]{x1D6FE}_{n}^{2}\right)}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \displaystyle \text{Im}\!\left(\frac{1}{2\unicode[STIX]{x1D70E}-1+2it}\frac{(Z_{M}H_{M})^{\prime }}{(Z_{M}H_{M})}(\unicode[STIX]{x1D70E}+it)\!\right)\nonumber\\ \displaystyle & & \displaystyle ~\displaystyle \quad \geqslant \frac{\text{vol}(M)}{4}\tanh (\unicode[STIX]{x1D70B}t)-C_{1}\frac{\log t}{t}+\underset{|\unicode[STIX]{x1D6FE}_{n}|<t/\sqrt{3}}{\sum }\frac{t\unicode[STIX]{x1D702}_{n}(3\unicode[STIX]{x1D6FE}_{n}^{2}-t^{2})}{D(n,\unicode[STIX]{x1D70E},t)(\mathop{\unicode[STIX]{x1D702}}_{n}^{2}+\unicode[STIX]{x1D6FE}_{n}^{2})}\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\underset{N_{1}+1\leqslant n\leqslant n_{1}}{\sum }\frac{(1/2\,-\unicode[STIX]{x1D70E})t(2\mathop{\unicode[STIX]{x1D6FE}}_{n}^{2}\,-\,2\unicode[STIX]{x1D702}_{n}^{2}\,-\,\unicode[STIX]{x1D702}_{n})}{D(n,\unicode[STIX]{x1D70E},t)(\mathop{\unicode[STIX]{x1D702}}_{n}^{2}+\unicode[STIX]{x1D6FE}_{n}^{2})}+\underset{n\geqslant N_{1}+1}{\sum }\frac{-t\mathop{\unicode[STIX]{x1D702}}_{n}^{3}}{D(n,\unicode[STIX]{x1D70E},t)\left(\mathop{\unicode[STIX]{x1D702}}_{n}^{2}+\unicode[STIX]{x1D6FE}_{n}^{2}\right)}.\end{eqnarray}$$
Observe that each term in each summand in (30) is negative. We investigate separately each of the three sums on the right-hand side of (30).
Since
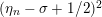 $(\unicode[STIX]{x1D702}_{n}-\unicode[STIX]{x1D70E}+1/2)^{2}$
is bounded by some constant, by enlarging
$(\unicode[STIX]{x1D702}_{n}-\unicode[STIX]{x1D70E}+1/2)^{2}$
is bounded by some constant, by enlarging
![]() $t_{0}$
if necessary, we get that
$t_{0}$
if necessary, we get that
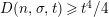 $D(n,\unicode[STIX]{x1D70E},t)\geqslant t^{4}/4$
for all
$D(n,\unicode[STIX]{x1D70E},t)\geqslant t^{4}/4$
for all
![]() $n$
such that
$n$
such that
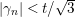 $|\unicode[STIX]{x1D6FE}_{n}|<t/\sqrt{3}$
and all
$|\unicode[STIX]{x1D6FE}_{n}|<t/\sqrt{3}$
and all
![]() $t>t_{0}$
. Therefore
$t>t_{0}$
. Therefore
 $$\begin{eqnarray}\displaystyle 0\leqslant \underset{|\unicode[STIX]{x1D6FE}_{n}|<t/\sqrt{3}}{\sum }\frac{t\unicode[STIX]{x1D702}_{n}(t^{2}-3\unicode[STIX]{x1D6FE}_{n}^{2})}{D(n,\unicode[STIX]{x1D70E},t)\left(\mathop{\unicode[STIX]{x1D702}}_{n}^{2}+\unicode[STIX]{x1D6FE}_{n}^{2}\right)}\leqslant \frac{2}{t}\underset{|\unicode[STIX]{x1D6FE}_{n}|<t/\sqrt{3}}{\sum }\frac{2\unicode[STIX]{x1D702}_{n}}{\left(\mathop{\unicode[STIX]{x1D702}}_{n}^{2}+\unicode[STIX]{x1D6FE}_{n}^{2}\right)}=O(1/t), & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle 0\leqslant \underset{|\unicode[STIX]{x1D6FE}_{n}|<t/\sqrt{3}}{\sum }\frac{t\unicode[STIX]{x1D702}_{n}(t^{2}-3\unicode[STIX]{x1D6FE}_{n}^{2})}{D(n,\unicode[STIX]{x1D70E},t)\left(\mathop{\unicode[STIX]{x1D702}}_{n}^{2}+\unicode[STIX]{x1D6FE}_{n}^{2}\right)}\leqslant \frac{2}{t}\underset{|\unicode[STIX]{x1D6FE}_{n}|<t/\sqrt{3}}{\sum }\frac{2\unicode[STIX]{x1D702}_{n}}{\left(\mathop{\unicode[STIX]{x1D702}}_{n}^{2}+\unicode[STIX]{x1D6FE}_{n}^{2}\right)}=O(1/t), & & \displaystyle \nonumber\end{eqnarray}$$
as
![]() $t\rightarrow \infty$
because the series
$t\rightarrow \infty$
because the series
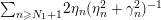 $\sum _{n\geqslant N_{1}+1}2\unicode[STIX]{x1D702}_{n}(\unicode[STIX]{x1D702}_{n}^{2}+\unicode[STIX]{x1D6FE}_{n}^{2})^{-1}$
converges; see [Reference Fischer7, Corollary 2.4.17].
$\sum _{n\geqslant N_{1}+1}2\unicode[STIX]{x1D702}_{n}(\unicode[STIX]{x1D702}_{n}^{2}+\unicode[STIX]{x1D6FE}_{n}^{2})^{-1}$
converges; see [Reference Fischer7, Corollary 2.4.17].
For the second and the third sum in (30) we use the elementary inequality
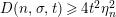 $D(n,\unicode[STIX]{x1D70E},t)\geqslant 4t^{2}\unicode[STIX]{x1D702}_{n}^{2}$
to deduce that both sums are
$D(n,\unicode[STIX]{x1D70E},t)\geqslant 4t^{2}\unicode[STIX]{x1D702}_{n}^{2}$
to deduce that both sums are
![]() $O(1/t)$
as
$O(1/t)$
as
![]() $t\rightarrow \infty$
, hence all sums on the right-hand side of (30) are
$t\rightarrow \infty$
, hence all sums on the right-hand side of (30) are
![]() $O(1/t)$
, as
$O(1/t)$
, as
![]() $t\rightarrow \infty$
. Therefore, there exists a constant
$t\rightarrow \infty$
. Therefore, there exists a constant
![]() $C_{2}>0$
, such that for all
$C_{2}>0$
, such that for all
![]() $t>t_{0}$
,
$t>t_{0}$
,
![]() $t\neq r_{n}$
and
$t\neq r_{n}$
and
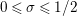 $0\leqslant \unicode[STIX]{x1D70E}\leqslant 1/2$
one has
$0\leqslant \unicode[STIX]{x1D70E}\leqslant 1/2$
one has
 $$\begin{eqnarray}\displaystyle \text{Im}\left(\frac{1}{2\unicode[STIX]{x1D70E}-1+2it}\frac{(Z_{M}H_{M})^{\prime }}{(Z_{M}H_{M})}(\unicode[STIX]{x1D70E}+it)\right)\geqslant \frac{\text{vol}(M)}{4}\cdot \tanh \unicode[STIX]{x1D70B}t-\frac{C_{1}\log t+C_{2}}{t}. & & \displaystyle \nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \text{Im}\left(\frac{1}{2\unicode[STIX]{x1D70E}-1+2it}\frac{(Z_{M}H_{M})^{\prime }}{(Z_{M}H_{M})}(\unicode[STIX]{x1D70E}+it)\right)\geqslant \frac{\text{vol}(M)}{4}\cdot \tanh \unicode[STIX]{x1D70B}t-\frac{C_{1}\log t+C_{2}}{t}. & & \displaystyle \nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
Since
 $\tanh \unicode[STIX]{x1D70B}t=1+O(e^{-\unicode[STIX]{x1D70B}t})$
, as
$\tanh \unicode[STIX]{x1D70B}t=1+O(e^{-\unicode[STIX]{x1D70B}t})$
, as
![]() $t\rightarrow \infty$
we conclude that statement (a) holds true.
$t\rightarrow \infty$
we conclude that statement (a) holds true.
We now prove part (b). We put
 $s=1/2+it$
for
$s=1/2+it$
for
![]() $t>0$
with
$t>0$
with
![]() $t\neq r_{n}$
in (29) to get
$t\neq r_{n}$
in (29) to get
 $$\begin{eqnarray}\displaystyle \text{Im}\left(\frac{1}{2it}\frac{\left(Z_{M}H_{M}\right)^{\prime }}{(Z_{M}H_{M})}\left(\frac{1}{2}+it\right)\right) & = & \displaystyle \frac{\text{vol}(M)}{4}\tanh (\unicode[STIX]{x1D70B}t)+O\left(\frac{\log t}{t}\right)\nonumber\\ \displaystyle & & \displaystyle +\,\underset{n\geqslant N_{1}+1}{\sum }\frac{t\unicode[STIX]{x1D702}_{n}(3\unicode[STIX]{x1D6FE}_{n}^{2}-t^{2})-t\unicode[STIX]{x1D702}_{n}^{3}}{D(n,1/2,t)\left(\mathop{\unicode[STIX]{x1D702}}_{n}^{2}+\unicode[STIX]{x1D6FE}_{n}^{2}\right)}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \text{Im}\left(\frac{1}{2it}\frac{\left(Z_{M}H_{M}\right)^{\prime }}{(Z_{M}H_{M})}\left(\frac{1}{2}+it\right)\right) & = & \displaystyle \frac{\text{vol}(M)}{4}\tanh (\unicode[STIX]{x1D70B}t)+O\left(\frac{\log t}{t}\right)\nonumber\\ \displaystyle & & \displaystyle +\,\underset{n\geqslant N_{1}+1}{\sum }\frac{t\unicode[STIX]{x1D702}_{n}(3\unicode[STIX]{x1D6FE}_{n}^{2}-t^{2})-t\unicode[STIX]{x1D702}_{n}^{3}}{D(n,1/2,t)\left(\mathop{\unicode[STIX]{x1D702}}_{n}^{2}+\unicode[STIX]{x1D6FE}_{n}^{2}\right)}.\nonumber\end{eqnarray}$$
Analogously as in the proof of part (a) we deduce that there exist a constant
![]() $t_{1}>0$
such that (31) holds true with
$t_{1}>0$
such that (31) holds true with
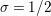 $\unicode[STIX]{x1D70E}=1/2$
and some constants
$\unicode[STIX]{x1D70E}=1/2$
and some constants
![]() $C_{1}$
and
$C_{1}$
and
![]() $C_{2}$
, for all
$C_{2}$
, for all
![]() $t>t_{1}$
,
$t>t_{1}$
,
![]() $t\neq r_{n}$
. The proof of part (b) is complete.◻
$t\neq r_{n}$
. The proof of part (b) is complete.◻
We can now give a proof of part (a) of the Main Theorem.
The function
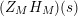 $(Z_{M}H_{M})(s)$
has finitely many nontrivial zeros in the region
$(Z_{M}H_{M})(s)$
has finitely many nontrivial zeros in the region
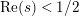 $\operatorname{Re}(s)<1/2$
. Combining this statement with Proposition 9(a) immediately implies the existence a of constant
$\operatorname{Re}(s)<1/2$
. Combining this statement with Proposition 9(a) immediately implies the existence a of constant
![]() $t_{0}$
such that
$t_{0}$
such that
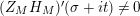 $(Z_{M}H_{M})^{\prime }(\unicode[STIX]{x1D70E}+it)\neq 0$
for
$(Z_{M}H_{M})^{\prime }(\unicode[STIX]{x1D70E}+it)\neq 0$
for
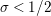 $\unicode[STIX]{x1D70E}<1/2$
and
$\unicode[STIX]{x1D70E}<1/2$
and
![]() $|t|>t_{0}$
.
$|t|>t_{0}$
.
Proposition 9(b) yields that
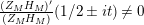 $\frac{(Z_{M}H_{M})^{\prime }}{(Z_{M}H_{M})}(1/2\pm it)\neq 0$
for
$\frac{(Z_{M}H_{M})^{\prime }}{(Z_{M}H_{M})}(1/2\pm it)\neq 0$
for
![]() $|t|>t_{0}$
,
$|t|>t_{0}$
,
![]() $t\neq r_{n}$
for all
$t\neq r_{n}$
for all
![]() $n\geqslant 1$
. Therefore, the only zeros of
$n\geqslant 1$
. Therefore, the only zeros of
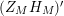 $(Z_{M}H_{M})^{\prime }$
on the line
$(Z_{M}H_{M})^{\prime }$
on the line
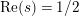 $\text{Re}(s)=1/2$
, with at most a finite number of exceptions, are multiple zeros of
$\text{Re}(s)=1/2$
, with at most a finite number of exceptions, are multiple zeros of
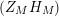 $(Z_{M}H_{M})$
, or, equivalently, multiple zeros of
$(Z_{M}H_{M})$
, or, equivalently, multiple zeros of
![]() $Z_{M}$
.
$Z_{M}$
.
4 Preliminary lemmas
In this section, we prove some preliminary results needed in the proof of the Main Theorem. Let quantity
![]() $A_{M}$
, respectively
$A_{M}$
, respectively
![]() $a_{M}$
, be defined by (9) and (10), respectively (11) and let
$a_{M}$
, be defined by (9) and (10), respectively (11) and let
![]() $X_{M}(s)$
be defined by (12). Let
$X_{M}(s)$
be defined by (12). Let
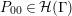 $P_{00}\in {\mathcal{H}}(\unicode[STIX]{x1D6E4})$
denote the primitive hyperbolic element of
$P_{00}\in {\mathcal{H}}(\unicode[STIX]{x1D6E4})$
denote the primitive hyperbolic element of
![]() $\unicode[STIX]{x1D6E4}$
with the property that
$\unicode[STIX]{x1D6E4}$
with the property that
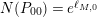 $N(P_{00})=e^{\ell _{M,0}}$
; or equivalently, with the property that
$N(P_{00})=e^{\ell _{M,0}}$
; or equivalently, with the property that
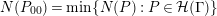 $N(P_{00})=\min \{N(P):P\in {\mathcal{H}}(\unicode[STIX]{x1D6E4})\}$
. In the case when
$N(P_{00})=\min \{N(P):P\in {\mathcal{H}}(\unicode[STIX]{x1D6E4})\}$
. In the case when
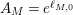 $A_{M}=e^{\ell _{M,0}}$
we may write
$A_{M}=e^{\ell _{M,0}}$
we may write
![]() $a_{M}$
in terms of the norm of
$a_{M}$
in terms of the norm of
![]() $P_{00}$
, namely
$P_{00}$
, namely
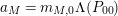 $a_{M}=m_{M,0}\unicode[STIX]{x1D6EC}(P_{00})$
.
$a_{M}=m_{M,0}\unicode[STIX]{x1D6EC}(P_{00})$
.
Lemma 10. There exist
![]() $\unicode[STIX]{x1D70E}_{1}>1$
and a constant
$\unicode[STIX]{x1D70E}_{1}>1$
and a constant
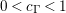 $0<c_{\unicode[STIX]{x1D6E4}}<1$
such that for
$0<c_{\unicode[STIX]{x1D6E4}}<1$
such that for
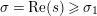 $\unicode[STIX]{x1D70E}=\operatorname{Re}(s)\geqslant \unicode[STIX]{x1D70E}_{1}$
, we have the asymptotic formula
$\unicode[STIX]{x1D70E}=\operatorname{Re}(s)\geqslant \unicode[STIX]{x1D70E}_{1}$
, we have the asymptotic formula
 $$\begin{eqnarray}X_{M}(s)=1+O(c_{\unicode[STIX]{x1D6E4}}^{\unicode[STIX]{x1D70E}})\neq 0,\quad \text{as }\unicode[STIX]{x1D70E}\rightarrow +\infty .\end{eqnarray}$$
$$\begin{eqnarray}X_{M}(s)=1+O(c_{\unicode[STIX]{x1D6E4}}^{\unicode[STIX]{x1D70E}})\neq 0,\quad \text{as }\unicode[STIX]{x1D70E}\rightarrow +\infty .\end{eqnarray}$$
Proof. From the Euler product definition (3) of
![]() $Z_{M}$
and from (6), we have that
$Z_{M}$
and from (6), we have that
 $$\begin{eqnarray}Z_{M}(s)=1+O(N(P_{00})^{-\operatorname{Re}(s)})\qquad \text{and}\qquad H_{M}(s)=1+O(r_{2}^{-2\operatorname{Re}(s)})\end{eqnarray}$$
$$\begin{eqnarray}Z_{M}(s)=1+O(N(P_{00})^{-\operatorname{Re}(s)})\qquad \text{and}\qquad H_{M}(s)=1+O(r_{2}^{-2\operatorname{Re}(s)})\end{eqnarray}$$
as
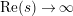 $\operatorname{Re}(s)\rightarrow \infty$
. Furthermore, by the definition of
$\operatorname{Re}(s)\rightarrow \infty$
. Furthermore, by the definition of
![]() $A_{M}$
and
$A_{M}$
and
![]() $a_{M}$
$a_{M}$
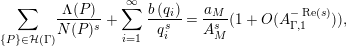 $$\begin{eqnarray}\underset{\{P\}\in {\mathcal{H}}(\unicode[STIX]{x1D6E4})}{\sum }\frac{\unicode[STIX]{x1D6EC}(P)}{N(P)^{s}}+\mathop{\sum }_{i=1}^{\infty }\frac{b\left(q_{i}\right)}{\mathop{q}_{i}^{s}}=\frac{a_{M}}{\mathop{A}_{M}^{s}}(1+O(\mathop{A}_{\unicode[STIX]{x1D6E4},1}^{-\operatorname{Re}(s)})),\end{eqnarray}$$
$$\begin{eqnarray}\underset{\{P\}\in {\mathcal{H}}(\unicode[STIX]{x1D6E4})}{\sum }\frac{\unicode[STIX]{x1D6EC}(P)}{N(P)^{s}}+\mathop{\sum }_{i=1}^{\infty }\frac{b\left(q_{i}\right)}{\mathop{q}_{i}^{s}}=\frac{a_{M}}{\mathop{A}_{M}^{s}}(1+O(\mathop{A}_{\unicode[STIX]{x1D6E4},1}^{-\operatorname{Re}(s)})),\end{eqnarray}$$
as
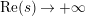 $\operatorname{Re}(s)\rightarrow +\infty$
, for some constant
$\operatorname{Re}(s)\rightarrow +\infty$
, for some constant
 $A_{\unicode[STIX]{x1D6E4},1}>1$
. Multiplying the formula (16) by
$A_{\unicode[STIX]{x1D6E4},1}>1$
. Multiplying the formula (16) by
 $(Z_{M}H_{M})(s)$
and employing the equation (32) we complete the proof.◻
$(Z_{M}H_{M})(s)$
and employing the equation (32) we complete the proof.◻
The following lemma provides the bound for the growth of the function
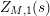 $Z_{M,1}(s)$
; recall that
$Z_{M,1}(s)$
; recall that
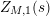 $Z_{M,1}(s)$
is defined by (26).
$Z_{M,1}(s)$
is defined by (26).
Lemma 11. Let
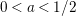 $0<a<1/2$
be an arbitrary real number and let
$0<a<1/2$
be an arbitrary real number and let
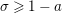 $\unicode[STIX]{x1D70E}\geqslant 1-a$
. Then
$\unicode[STIX]{x1D70E}\geqslant 1-a$
. Then
 $$\begin{eqnarray}\displaystyle \log \left|1+Z_{M,1}(\unicode[STIX]{x1D70E}\pm iT)\right| & = & \displaystyle O(|Z_{M,1}(\unicode[STIX]{x1D70E}\pm iT)|)=O(T^{2a-1}\log ^{2a}T),\nonumber\\ \displaystyle & & \displaystyle \text{as }T\rightarrow \infty .\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \log \left|1+Z_{M,1}(\unicode[STIX]{x1D70E}\pm iT)\right| & = & \displaystyle O(|Z_{M,1}(\unicode[STIX]{x1D70E}\pm iT)|)=O(T^{2a-1}\log ^{2a}T),\nonumber\\ \displaystyle & & \displaystyle \text{as }T\rightarrow \infty .\end{eqnarray}$$
Proof. From the bound (20) with
![]() $k=0$
and
$k=0$
and
 $\unicode[STIX]{x1D70E}\geqslant 1-a$
, we get
$\unicode[STIX]{x1D70E}\geqslant 1-a$
, we get
 $$\begin{eqnarray}\frac{Z_{M}^{\prime }}{Z_{M}}(\unicode[STIX]{x1D70E}\pm iT)=O((T\log T)^{1-2(\unicode[STIX]{x1D70E}-1/2)})=O((T\log T)^{2a}),\quad \text{as }T\rightarrow \infty ,\end{eqnarray}$$
$$\begin{eqnarray}\frac{Z_{M}^{\prime }}{Z_{M}}(\unicode[STIX]{x1D70E}\pm iT)=O((T\log T)^{1-2(\unicode[STIX]{x1D70E}-1/2)})=O((T\log T)^{2a}),\quad \text{as }T\rightarrow \infty ,\end{eqnarray}$$
where the implied constant depends only upon
![]() $M$
and
$M$
and
![]() $a$
. We can then argue in the same manner as in the proof of Proposition 8(b). Namely, applying Stirling’s formula and the above estimate, we get, for
$a$
. We can then argue in the same manner as in the proof of Proposition 8(b). Namely, applying Stirling’s formula and the above estimate, we get, for
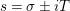 $s=\unicode[STIX]{x1D70E}\pm iT$
and
$s=\unicode[STIX]{x1D70E}\pm iT$
and
![]() $T\geqslant 1$
, the estimate
$T\geqslant 1$
, the estimate
 $$\begin{eqnarray}\left|\frac{1}{f_{M}(s)}\!\left(\frac{\unicode[STIX]{x1D702}_{M}^{\prime }}{\unicode[STIX]{x1D702}_{M}}(s)-\frac{K_{M}^{\prime }}{K_{M}}(1-s)-\frac{Z_{M}^{\prime }}{Z_{M}}(s)\right)-1\right|=O\left(\frac{\log T}{T}+\frac{(T\log T)^{2a}}{T}\right)\!,\end{eqnarray}$$
$$\begin{eqnarray}\left|\frac{1}{f_{M}(s)}\!\left(\frac{\unicode[STIX]{x1D702}_{M}^{\prime }}{\unicode[STIX]{x1D702}_{M}}(s)-\frac{K_{M}^{\prime }}{K_{M}}(1-s)-\frac{Z_{M}^{\prime }}{Z_{M}}(s)\right)-1\right|=O\left(\frac{\log T}{T}+\frac{(T\log T)^{2a}}{T}\right)\!,\end{eqnarray}$$
as
![]() $T\rightarrow \infty$
. This implies the bound (33) as claimed.◻
$T\rightarrow \infty$
. This implies the bound (33) as claimed.◻
The following lemma is a Phragmén–Lindelöf type bound for
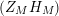 $(Z_{M}H_{M})$
. The bound will be used to derive a similar bound for
$(Z_{M}H_{M})$
. The bound will be used to derive a similar bound for
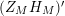 $(Z_{M}H_{M})^{\prime }$
using the Cauchy formula.
$(Z_{M}H_{M})^{\prime }$
using the Cauchy formula.
Lemma 12. Let
![]() $\unicode[STIX]{x1D70E}_{2}\geqslant 1$
be a fixed real number, such that
$\unicode[STIX]{x1D70E}_{2}\geqslant 1$
be a fixed real number, such that
![]() $-\unicode[STIX]{x1D70E}_{2}$
is not a pole of
$-\unicode[STIX]{x1D70E}_{2}$
is not a pole of
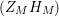 $(Z_{M}H_{M})$
. Then, for an arbitrary
$(Z_{M}H_{M})$
. Then, for an arbitrary
![]() $\unicode[STIX]{x1D6FF}>0$
$\unicode[STIX]{x1D6FF}>0$
-
(a)
 $$\begin{eqnarray}(Z_{M}H_{M})(\unicode[STIX]{x1D70E}+it)=O_{\unicode[STIX]{x1D6E4}}\left(\exp \left(1/2+\unicode[STIX]{x1D70E}_{2}+\unicode[STIX]{x1D6FF}\right)\text{vol}(M)t\right),\end{eqnarray}$$
$$\begin{eqnarray}(Z_{M}H_{M})(\unicode[STIX]{x1D70E}+it)=O_{\unicode[STIX]{x1D6E4}}\left(\exp \left(1/2+\unicode[STIX]{x1D70E}_{2}+\unicode[STIX]{x1D6FF}\right)\text{vol}(M)t\right),\end{eqnarray}$$
-
(b)
for $$\begin{eqnarray}Z_{M}(\unicode[STIX]{x1D70E}+it)=O_{\unicode[STIX]{x1D6E4}}\left(\exp (1/2+\unicode[STIX]{x1D70E}_{2})\text{vol}(M)t\right)\end{eqnarray}$$
$$\begin{eqnarray}Z_{M}(\unicode[STIX]{x1D70E}+it)=O_{\unicode[STIX]{x1D6E4}}\left(\exp (1/2+\unicode[STIX]{x1D70E}_{2})\text{vol}(M)t\right)\end{eqnarray}$$
 $t\geqslant 1$
, uniformly in
$t\geqslant 1$
, uniformly in
 $\unicode[STIX]{x1D70E}\leqslant -\unicode[STIX]{x1D70E}_{2}$
.
$\unicode[STIX]{x1D70E}\leqslant -\unicode[STIX]{x1D70E}_{2}$
.
Proof. To prove part (a), we apply the Phragmen–Lindelöf theorem to the function
 $$\begin{eqnarray}F(s)=(Z_{M}H_{M})(s)\exp \left[\text{vol}(M)(1/2+\unicode[STIX]{x1D70E}_{2}+\unicode[STIX]{x1D6FF})is\right]\end{eqnarray}$$
$$\begin{eqnarray}F(s)=(Z_{M}H_{M})(s)\exp \left[\text{vol}(M)(1/2+\unicode[STIX]{x1D70E}_{2}+\unicode[STIX]{x1D6FF})is\right]\end{eqnarray}$$
which is an entire function of finite order at most two in the sector
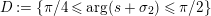 $D:=\{\unicode[STIX]{x1D70B}/4\leqslant \arg (s+\unicode[STIX]{x1D70E}_{2})\leqslant \unicode[STIX]{x1D70B}/2\}$
. Obviously,
$D:=\{\unicode[STIX]{x1D70B}/4\leqslant \arg (s+\unicode[STIX]{x1D70E}_{2})\leqslant \unicode[STIX]{x1D70B}/2\}$
. Obviously,
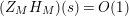 $(Z_{M}H_{M})(s)=O(1)$
along the line
$(Z_{M}H_{M})(s)=O(1)$
along the line
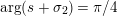 $\arg (s+\unicode[STIX]{x1D70E}_{2})=\unicode[STIX]{x1D70B}/4$
, since
$\arg (s+\unicode[STIX]{x1D70E}_{2})=\unicode[STIX]{x1D70B}/4$
, since
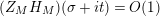 $(Z_{M}H_{M})(\unicode[STIX]{x1D70E}+it)=O(1)$
, for
$(Z_{M}H_{M})(\unicode[STIX]{x1D70E}+it)=O(1)$
, for
![]() $\unicode[STIX]{x1D70E}>\unicode[STIX]{x1D70E}_{1}$
and
$\unicode[STIX]{x1D70E}>\unicode[STIX]{x1D70E}_{1}$
and
![]() $t\geqslant 1$
; see the proof of Lemma 10. Therefore,
$t\geqslant 1$
; see the proof of Lemma 10. Therefore,
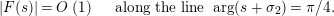 $$\begin{eqnarray}\left|F(s)\right|=O\left(1\right)\quad \text{ along the line }\arg (s+\unicode[STIX]{x1D70E}_{2})=\unicode[STIX]{x1D70B}/4.\end{eqnarray}$$
$$\begin{eqnarray}\left|F(s)\right|=O\left(1\right)\quad \text{ along the line }\arg (s+\unicode[STIX]{x1D70E}_{2})=\unicode[STIX]{x1D70B}/4.\end{eqnarray}$$
To determine the behavior of the function
![]() $F(s)$
along the vertical line
$F(s)$
along the vertical line
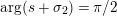 $\arg (s+\unicode[STIX]{x1D70E}_{2})=\unicode[STIX]{x1D70B}/2$
, that is, for
$\arg (s+\unicode[STIX]{x1D70E}_{2})=\unicode[STIX]{x1D70B}/2$
, that is, for
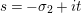 $s=-\unicode[STIX]{x1D70E}_{2}+it$
,
$s=-\unicode[STIX]{x1D70E}_{2}+it$
,
![]() $t\geqslant 0$
, we use the functional equation (7) to get
$t\geqslant 0$
, we use the functional equation (7) to get
 $$\begin{eqnarray}\displaystyle \left|F(-\unicode[STIX]{x1D70E}_{2}+it)\right| & = & \displaystyle \exp \left(-\left(1/2+\unicode[STIX]{x1D70E}_{2}+\unicode[STIX]{x1D6FF}\right)\text{vol}(M)t\right)\left|\unicode[STIX]{x1D702}(-\unicode[STIX]{x1D70E}_{2}+it)\right|\nonumber\\ \displaystyle & & \displaystyle \times \,\left|K_{M}^{-1}\left(-\unicode[STIX]{x1D70E}_{2}+it\right)\right|\cdot O(1),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \left|F(-\unicode[STIX]{x1D70E}_{2}+it)\right| & = & \displaystyle \exp \left(-\left(1/2+\unicode[STIX]{x1D70E}_{2}+\unicode[STIX]{x1D6FF}\right)\text{vol}(M)t\right)\left|\unicode[STIX]{x1D702}(-\unicode[STIX]{x1D70E}_{2}+it)\right|\nonumber\\ \displaystyle & & \displaystyle \times \,\left|K_{M}^{-1}\left(-\unicode[STIX]{x1D70E}_{2}+it\right)\right|\cdot O(1),\end{eqnarray}$$
since
 $1+\unicode[STIX]{x1D70E}_{2}\geqslant 2$
. It remains to estimate
$1+\unicode[STIX]{x1D70E}_{2}\geqslant 2$
. It remains to estimate
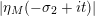 $|\unicode[STIX]{x1D702}_{M}(-\unicode[STIX]{x1D70E}_{2}+it)|$
. Applying (4), [Reference Hejhal13, formula (4.4), p. 76], Stirling’s formula and the bound
$|\unicode[STIX]{x1D702}_{M}(-\unicode[STIX]{x1D70E}_{2}+it)|$
. Applying (4), [Reference Hejhal13, formula (4.4), p. 76], Stirling’s formula and the bound
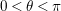 $0<\unicode[STIX]{x1D703}<\unicode[STIX]{x1D70B}$
, elementary computations show that
$0<\unicode[STIX]{x1D703}<\unicode[STIX]{x1D70B}$
, elementary computations show that
 $$\begin{eqnarray}\left|\unicode[STIX]{x1D702}_{M}(-\unicode[STIX]{x1D70E}_{2}+it)\right|=O\left(\exp \left(\text{vol}(M)(1/2+\unicode[STIX]{x1D70E}_{2})t+O(1)\right)\right)\quad \text{as }t\rightarrow +\infty .\end{eqnarray}$$
$$\begin{eqnarray}\left|\unicode[STIX]{x1D702}_{M}(-\unicode[STIX]{x1D70E}_{2}+it)\right|=O\left(\exp \left(\text{vol}(M)(1/2+\unicode[STIX]{x1D70E}_{2})t+O(1)\right)\right)\quad \text{as }t\rightarrow +\infty .\end{eqnarray}$$
Formula (6.1.45) from [Reference Abramowitz and Stegun1], which itself is an application of Stirling’s formula, yields
 $$\begin{eqnarray}\left|K_{M}^{-1}\left(-\unicode[STIX]{x1D70E}_{2}+it\right)\right|=O\left(\exp \left(\frac{n_{1}}{2}\log t\right)\right)\quad \text{as }t\rightarrow +\infty .\end{eqnarray}$$
$$\begin{eqnarray}\left|K_{M}^{-1}\left(-\unicode[STIX]{x1D70E}_{2}+it\right)\right|=O\left(\exp \left(\frac{n_{1}}{2}\log t\right)\right)\quad \text{as }t\rightarrow +\infty .\end{eqnarray}$$
Substituting the bound (36) together with (35) into (34) we get
 $$\begin{eqnarray}\left|F(-\unicode[STIX]{x1D70E}_{2}+it)\right|=O\left(\exp \left(-\text{vol}(M)\unicode[STIX]{x1D6FF}t+\frac{n_{1}}{2}\log t+O(\log (t))\right)\right)=o(1),\end{eqnarray}$$
$$\begin{eqnarray}\left|F(-\unicode[STIX]{x1D70E}_{2}+it)\right|=O\left(\exp \left(-\text{vol}(M)\unicode[STIX]{x1D6FF}t+\frac{n_{1}}{2}\log t+O(\log (t))\right)\right)=o(1),\end{eqnarray}$$
as
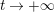 $t\rightarrow +\infty$
. One now can apply the Phragmen–Lindelöf theorem, which implies that
$t\rightarrow +\infty$
. One now can apply the Phragmen–Lindelöf theorem, which implies that
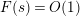 $F(s)=O(1)$
in the sector
$F(s)=O(1)$
in the sector
 $D:=\{\unicode[STIX]{x1D70B}/4\leqslant \arg (s+\unicode[STIX]{x1D70E}_{2})\leqslant \unicode[STIX]{x1D70B}/2\}$
and the proof of (a) is complete.
$D:=\{\unicode[STIX]{x1D70B}/4\leqslant \arg (s+\unicode[STIX]{x1D70E}_{2})\leqslant \unicode[STIX]{x1D70B}/2\}$
and the proof of (a) is complete.
To prove (b), we repeat the proof given above for the function
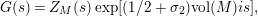 $G(s)=Z_{M}(s)\exp [(1/2+\unicode[STIX]{x1D70E}_{2})\text{vol}(M)is],$
which is an entire function of finite order in the sector
$G(s)=Z_{M}(s)\exp [(1/2+\unicode[STIX]{x1D70E}_{2})\text{vol}(M)is],$
which is an entire function of finite order in the sector
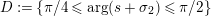 $D:=\{\unicode[STIX]{x1D70B}/4\leqslant \arg (s+\unicode[STIX]{x1D70E}_{2})\leqslant \unicode[STIX]{x1D70B}/2\}$
. We omit the details.◻
$D:=\{\unicode[STIX]{x1D70B}/4\leqslant \arg (s+\unicode[STIX]{x1D70E}_{2})\leqslant \unicode[STIX]{x1D70B}/2\}$
. We omit the details.◻
The following lemma is a Lindelöf type bound for the function
 $Z_{M}H_{M}$
which will be used to deduce a sharper bound for the function
$Z_{M}H_{M}$
which will be used to deduce a sharper bound for the function
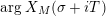 $\arg X_{M}(\unicode[STIX]{x1D70E}+iT)$
, when
$\arg X_{M}(\unicode[STIX]{x1D70E}+iT)$
, when
![]() $\unicode[STIX]{x1D70E}$
is close to
$\unicode[STIX]{x1D70E}$
is close to
![]() $1/2$
.
$1/2$
.
Lemma 13. For
![]() $\unicode[STIX]{x1D716}>0$
and
$\unicode[STIX]{x1D716}>0$
and
![]() $t\geqslant 1$
$t\geqslant 1$
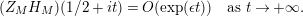 $$\begin{eqnarray}(Z_{M}H_{M})(1/2+it)=O(\exp (\unicode[STIX]{x1D716}t))\quad \text{as }t\rightarrow +\infty .\end{eqnarray}$$
$$\begin{eqnarray}(Z_{M}H_{M})(1/2+it)=O(\exp (\unicode[STIX]{x1D716}t))\quad \text{as }t\rightarrow +\infty .\end{eqnarray}$$
Proof. Since
 $$\begin{eqnarray}|H_{M}(1/2+it)|=|\unicode[STIX]{x1D719}_{M}(1/2+it)||K_{M}^{-1}(1/2+it)|=O(\exp (n_{1}\log t/2)),\end{eqnarray}$$
$$\begin{eqnarray}|H_{M}(1/2+it)|=|\unicode[STIX]{x1D719}_{M}(1/2+it)||K_{M}^{-1}(1/2+it)|=O(\exp (n_{1}\log t/2)),\end{eqnarray}$$
as
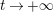 $t\rightarrow +\infty$
, it is enough to prove that
$t\rightarrow +\infty$
, it is enough to prove that
 $Z_{M}(1/2+it)=O(\exp (\unicode[STIX]{x1D716}t))$
as
$Z_{M}(1/2+it)=O(\exp (\unicode[STIX]{x1D716}t))$
as
![]() $t\rightarrow \infty$
.
$t\rightarrow \infty$
.
We apply Proposition 7. In the notation of Proposition 7 we take
 $$\begin{eqnarray}f(s)=Z_{M}(s)\quad \text{with }\unicode[STIX]{x1D70E}_{0}=\unicode[STIX]{x1D70E}_{1}+\unicode[STIX]{x1D714}>\unicode[STIX]{x1D70E}_{1}\qquad \text{and}\qquad P(t)=2\exp (t),\end{eqnarray}$$
$$\begin{eqnarray}f(s)=Z_{M}(s)\quad \text{with }\unicode[STIX]{x1D70E}_{0}=\unicode[STIX]{x1D70E}_{1}+\unicode[STIX]{x1D714}>\unicode[STIX]{x1D70E}_{1}\qquad \text{and}\qquad P(t)=2\exp (t),\end{eqnarray}$$
where
![]() $\unicode[STIX]{x1D70E}_{1}$
is defined in Lemma 10. Let us verify that all assumptions of Proposition 7 are fulfilled.
$\unicode[STIX]{x1D70E}_{1}$
is defined in Lemma 10. Let us verify that all assumptions of Proposition 7 are fulfilled.
The function
![]() $Z_{M}$
is meromorphic function of finite order, with poles at points on the real line; see [Reference Hejhal14, p. 498]. Hence
$Z_{M}$
is meromorphic function of finite order, with poles at points on the real line; see [Reference Hejhal14, p. 498]. Hence
![]() $Z_{M}(s)$
is holomorphic function for
$Z_{M}(s)$
is holomorphic function for
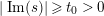 $|\operatorname{Im}(s)|\geqslant t_{0}>0$
, for any
$|\operatorname{Im}(s)|\geqslant t_{0}>0$
, for any
![]() $t_{0}>0$
.
$t_{0}>0$
.
From the proof of Lemma 10 it is obvious that
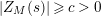 $|Z_{M}(s)|\geqslant c>0$
and
$|Z_{M}(s)|\geqslant c>0$
and
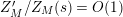 $Z_{M}^{\prime }/Z_{M}(s)=O(1)$
as
$Z_{M}^{\prime }/Z_{M}(s)=O(1)$
as
![]() $t\rightarrow \infty$
, for
$t\rightarrow \infty$
, for
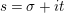 $s=\unicode[STIX]{x1D70E}+it$
and with
$s=\unicode[STIX]{x1D70E}+it$
and with
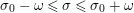 $\unicode[STIX]{x1D70E}_{0}-\unicode[STIX]{x1D714}\leqslant \unicode[STIX]{x1D70E}\leqslant \unicode[STIX]{x1D70E}_{0}+\unicode[STIX]{x1D714}$
. Furthermore,
$\unicode[STIX]{x1D70E}_{0}-\unicode[STIX]{x1D714}\leqslant \unicode[STIX]{x1D70E}\leqslant \unicode[STIX]{x1D70E}_{0}+\unicode[STIX]{x1D714}$
. Furthermore,
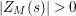 $|Z_{M}(s)|>0$
for
$|Z_{M}(s)|>0$
for
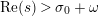 $\text{ Re}(s)>\unicode[STIX]{x1D70E}_{0}+\unicode[STIX]{x1D714}$
.
$\text{ Re}(s)>\unicode[STIX]{x1D70E}_{0}+\unicode[STIX]{x1D714}$
.
From Lemma 12(b), we have that
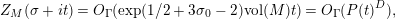 $$\begin{eqnarray}Z_{M}(\unicode[STIX]{x1D70E}+it)=O_{\unicode[STIX]{x1D6E4}}(\exp (1/2+3\unicode[STIX]{x1D70E}_{0}-2)\text{vol}(M)t)=O_{\unicode[STIX]{x1D6E4}}(P(t)^{D}),\end{eqnarray}$$
$$\begin{eqnarray}Z_{M}(\unicode[STIX]{x1D70E}+it)=O_{\unicode[STIX]{x1D6E4}}(\exp (1/2+3\unicode[STIX]{x1D70E}_{0}-2)\text{vol}(M)t)=O_{\unicode[STIX]{x1D6E4}}(P(t)^{D}),\end{eqnarray}$$
for a fixed
 $D=(3\unicode[STIX]{x1D70E}_{0}-3/2)\text{vol}(M)$
, uniformly in
$D=(3\unicode[STIX]{x1D70E}_{0}-3/2)\text{vol}(M)$
, uniformly in
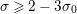 $\unicode[STIX]{x1D70E}\geqslant 2-3\unicode[STIX]{x1D70E}_{0}$
.
$\unicode[STIX]{x1D70E}\geqslant 2-3\unicode[STIX]{x1D70E}_{0}$
.
Since
![]() $Z_{M}$
has no zeros in the half-plane
$Z_{M}$
has no zeros in the half-plane
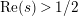 $\text{ Re}(s)>1/2$
, the Lindelöf condition on the vertical distribution of zeros of
$\text{ Re}(s)>1/2$
, the Lindelöf condition on the vertical distribution of zeros of
![]() $Z_{M}(s)$
in the half-plane
$Z_{M}(s)$
in the half-plane
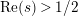 $\text{ Re}(s)>1/2$
, as required in Proposition 7, is trivially fulfilled.
$\text{ Re}(s)>1/2$
, as required in Proposition 7, is trivially fulfilled.
Therefore, all the assumptions of Proposition 7 are satisfied, hence
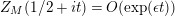 $Z_{M}(1/2+it)=O(\exp (\unicode[STIX]{x1D716}t))$
as
$Z_{M}(1/2+it)=O(\exp (\unicode[STIX]{x1D716}t))$
as
![]() $t\rightarrow \infty$
.◻
$t\rightarrow \infty$
.◻
Lemma 14. For an arbitrary
![]() $\unicode[STIX]{x1D716}>0$
,
$\unicode[STIX]{x1D716}>0$
,
![]() $t\geqslant 1$
and
$t\geqslant 1$
and
![]() $\unicode[STIX]{x1D70E}_{2}$
defined in Lemma 12 we have
$\unicode[STIX]{x1D70E}_{2}$
defined in Lemma 12 we have
 $$\begin{eqnarray}(Z_{M}H_{M})^{\prime }(\unicode[STIX]{x1D70E}+it)=\left\{\begin{array}{@{}ll@{}}O(\exp \unicode[STIX]{x1D716}t) & \quad \text{for }\frac{1}{2}\leqslant \unicode[STIX]{x1D70E}\leqslant \unicode[STIX]{x1D70E}_{0}\\ O(\exp (1/2-\unicode[STIX]{x1D70E}+\unicode[STIX]{x1D716})t) & \quad \text{for }-\unicode[STIX]{x1D70E}_{2}\leqslant \unicode[STIX]{x1D70E}<1/2,\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}(Z_{M}H_{M})^{\prime }(\unicode[STIX]{x1D70E}+it)=\left\{\begin{array}{@{}ll@{}}O(\exp \unicode[STIX]{x1D716}t) & \quad \text{for }\frac{1}{2}\leqslant \unicode[STIX]{x1D70E}\leqslant \unicode[STIX]{x1D70E}_{0}\\ O(\exp (1/2-\unicode[STIX]{x1D70E}+\unicode[STIX]{x1D716})t) & \quad \text{for }-\unicode[STIX]{x1D70E}_{2}\leqslant \unicode[STIX]{x1D70E}<1/2,\end{array}\right.\end{eqnarray}$$
as
![]() $t\rightarrow \infty$
.
$t\rightarrow \infty$
.
Proof. The proof involves an application of the Phragmen–Lindelöf theorem to the open sector bounded by the lines
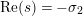 $\text{Re}(s)=-\unicode[STIX]{x1D70E}_{2}$
,
$\text{Re}(s)=-\unicode[STIX]{x1D70E}_{2}$
,
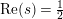 $\text{ Re}(s)=\frac{1}{2}$
and
$\text{ Re}(s)=\frac{1}{2}$
and
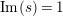 $\text{ Im}(s)=1$
. The bounds to be used come from Lemma 12, with
$\text{ Im}(s)=1$
. The bounds to be used come from Lemma 12, with
![]() $\unicode[STIX]{x1D6FF}=\unicode[STIX]{x1D716}$
, and from Lemma 13. A direct application of the Phragmen–Lindelöf theorem yields the bound
$\unicode[STIX]{x1D6FF}=\unicode[STIX]{x1D716}$
, and from Lemma 13. A direct application of the Phragmen–Lindelöf theorem yields the bound
 $$\begin{eqnarray}(Z_{M}H_{M})(\unicode[STIX]{x1D70E}+it)=O(\exp (1/2-\unicode[STIX]{x1D70E}+\unicode[STIX]{x1D716})t),\end{eqnarray}$$
$$\begin{eqnarray}(Z_{M}H_{M})(\unicode[STIX]{x1D70E}+it)=O(\exp (1/2-\unicode[STIX]{x1D70E}+\unicode[STIX]{x1D716})t),\end{eqnarray}$$
for
![]() $t\geqslant 1$
and
$t\geqslant 1$
and
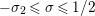 $-\unicode[STIX]{x1D70E}_{2}\leqslant \unicode[STIX]{x1D70E}\leqslant 1/2$
. Similarly, for
$-\unicode[STIX]{x1D70E}_{2}\leqslant \unicode[STIX]{x1D70E}\leqslant 1/2$
. Similarly, for
![]() $\unicode[STIX]{x1D70E}_{0}$
defined as in Lemma 12, one can apply the Phragmen–Lindelöf theorem in the open sector bounded by the lines
$\unicode[STIX]{x1D70E}_{0}$
defined as in Lemma 12, one can apply the Phragmen–Lindelöf theorem in the open sector bounded by the lines
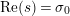 $\text{Re}(s)=\unicode[STIX]{x1D70E}_{0}$
,
$\text{Re}(s)=\unicode[STIX]{x1D70E}_{0}$
,
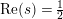 $\text{Re}(s)=\frac{1}{2}$
and
$\text{Re}(s)=\frac{1}{2}$
and
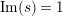 $\text{ Im}(s)=1$
, from which one gets
$\text{ Im}(s)=1$
, from which one gets
 $$\begin{eqnarray}(Z_{M}H_{M})(\unicode[STIX]{x1D70E}+it)=O(\exp \unicode[STIX]{x1D716}t),\end{eqnarray}$$
$$\begin{eqnarray}(Z_{M}H_{M})(\unicode[STIX]{x1D70E}+it)=O(\exp \unicode[STIX]{x1D716}t),\end{eqnarray}$$
for
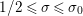 $1/2\leqslant \unicode[STIX]{x1D70E}\leqslant \unicode[STIX]{x1D70E}_{0}$
. The Cauchy integral formula can be applied, from which we have the equation
$1/2\leqslant \unicode[STIX]{x1D70E}\leqslant \unicode[STIX]{x1D70E}_{0}$
. The Cauchy integral formula can be applied, from which we have the equation
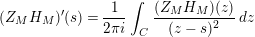 $$\begin{eqnarray}(Z_{M}H_{M})^{\prime }(s)=\frac{1}{2\unicode[STIX]{x1D70B}i}\int _{C}\frac{(Z_{M}H_{M})(z)}{(z-s)^{2}}\,dz\end{eqnarray}$$
$$\begin{eqnarray}(Z_{M}H_{M})^{\prime }(s)=\frac{1}{2\unicode[STIX]{x1D70B}i}\int _{C}\frac{(Z_{M}H_{M})(z)}{(z-s)^{2}}\,dz\end{eqnarray}$$
where
![]() $C$
is a circle of a small, fixed radius
$C$
is a circle of a small, fixed radius
![]() $r<\unicode[STIX]{x1D716}$
, centered at
$r<\unicode[STIX]{x1D716}$
, centered at
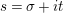 $s=\unicode[STIX]{x1D70E}+it$
. Applying (38) to
$s=\unicode[STIX]{x1D70E}+it$
. Applying (38) to
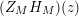 $(Z_{M}H_{M})(z)$
, when
$(Z_{M}H_{M})(z)$
, when
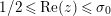 $1/2\leqslant \operatorname{Re}(z)\leqslant \unicode[STIX]{x1D70E}_{0}$
and (37) when
$1/2\leqslant \operatorname{Re}(z)\leqslant \unicode[STIX]{x1D70E}_{0}$
and (37) when
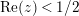 $\operatorname{Re}(z)<1/2$
, we deduce that
$\operatorname{Re}(z)<1/2$
, we deduce that
 $$\begin{eqnarray}(Z_{M}H_{M})^{\prime }(\unicode[STIX]{x1D70E}+it)=O\left(\exp ((r+\unicode[STIX]{x1D716})t)/r\right)=O(\exp (2\unicode[STIX]{x1D716}t))\end{eqnarray}$$
$$\begin{eqnarray}(Z_{M}H_{M})^{\prime }(\unicode[STIX]{x1D70E}+it)=O\left(\exp ((r+\unicode[STIX]{x1D716})t)/r\right)=O(\exp (2\unicode[STIX]{x1D716}t))\end{eqnarray}$$
for
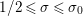 $1/2\leqslant \unicode[STIX]{x1D70E}\leqslant \unicode[STIX]{x1D70E}_{0}$
and
$1/2\leqslant \unicode[STIX]{x1D70E}\leqslant \unicode[STIX]{x1D70E}_{0}$
and
![]() $t\geqslant 1$
. This proves the first part of the Lemma when replacing
$t\geqslant 1$
. This proves the first part of the Lemma when replacing
![]() $\unicode[STIX]{x1D700}$
by
$\unicode[STIX]{x1D700}$
by
![]() $\unicode[STIX]{x1D700}/2$
.
$\unicode[STIX]{x1D700}/2$
.
In the case when
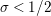 $\unicode[STIX]{x1D70E}<1/2$
, we can use the functional equation for
$\unicode[STIX]{x1D70E}<1/2$
, we can use the functional equation for
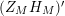 $(Z_{M}H_{M})^{\prime }$
to arrive at the expression
$(Z_{M}H_{M})^{\prime }$
to arrive at the expression
 $$\begin{eqnarray}\displaystyle |(Z_{M}H_{M})^{\prime }(-\unicode[STIX]{x1D70E}_{2}+it)| & = & \displaystyle |\unicode[STIX]{x1D702}_{M}(-\unicode[STIX]{x1D70E}_{2}+it)||K_{M}^{-1}(-\unicode[STIX]{x1D70E}_{2}+it)||Z_{M}(1+\unicode[STIX]{x1D70E}_{2}-it)|\nonumber\\ \displaystyle & & \displaystyle \cdot \left|\frac{\unicode[STIX]{x1D702}_{M}^{\prime }}{\unicode[STIX]{x1D702}_{M}}(-\unicode[STIX]{x1D70E}_{2}+it)-\frac{K_{M}^{\prime }}{K_{M}}(-\unicode[STIX]{x1D70E}_{2}+it)\right.\nonumber\\ \displaystyle & & \displaystyle -\,\left.\frac{Z_{M}^{\prime }}{Z_{M}}(1+\unicode[STIX]{x1D70E}_{2}-it)\right|.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle |(Z_{M}H_{M})^{\prime }(-\unicode[STIX]{x1D70E}_{2}+it)| & = & \displaystyle |\unicode[STIX]{x1D702}_{M}(-\unicode[STIX]{x1D70E}_{2}+it)||K_{M}^{-1}(-\unicode[STIX]{x1D70E}_{2}+it)||Z_{M}(1+\unicode[STIX]{x1D70E}_{2}-it)|\nonumber\\ \displaystyle & & \displaystyle \cdot \left|\frac{\unicode[STIX]{x1D702}_{M}^{\prime }}{\unicode[STIX]{x1D702}_{M}}(-\unicode[STIX]{x1D70E}_{2}+it)-\frac{K_{M}^{\prime }}{K_{M}}(-\unicode[STIX]{x1D70E}_{2}+it)\right.\nonumber\\ \displaystyle & & \displaystyle -\,\left.\frac{Z_{M}^{\prime }}{Z_{M}}(1+\unicode[STIX]{x1D70E}_{2}-it)\right|.\nonumber\end{eqnarray}$$
Since
![]() $\unicode[STIX]{x1D70E}_{2}\geqslant 1$
, we have
$\unicode[STIX]{x1D70E}_{2}\geqslant 1$
, we have
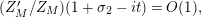 $(Z_{M}^{\prime }/Z_{M})(1+\unicode[STIX]{x1D70E}_{2}-it)=O(1),$
as
$(Z_{M}^{\prime }/Z_{M})(1+\unicode[STIX]{x1D70E}_{2}-it)=O(1),$
as
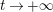 $t\rightarrow +\infty$
. Elementary computations involving the definition of the function
$t\rightarrow +\infty$
. Elementary computations involving the definition of the function
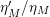 $\unicode[STIX]{x1D702}_{M}^{\prime }/\unicode[STIX]{x1D702}_{M}$
and the Stirling formula imply that
$\unicode[STIX]{x1D702}_{M}^{\prime }/\unicode[STIX]{x1D702}_{M}$
and the Stirling formula imply that
 $$\begin{eqnarray}\frac{\unicode[STIX]{x1D702}_{M}^{\prime }}{\unicode[STIX]{x1D702}_{M}}(-\unicode[STIX]{x1D70E}_{2}+it)-\frac{K_{M}^{\prime }}{K_{M}}(-\unicode[STIX]{x1D70E}_{2}+it)-\frac{Z^{\prime }}{Z}(1+\unicode[STIX]{x1D70E}_{2}-it)=O(t)\quad \text{ as }t\rightarrow \infty ;\end{eqnarray}$$
$$\begin{eqnarray}\frac{\unicode[STIX]{x1D702}_{M}^{\prime }}{\unicode[STIX]{x1D702}_{M}}(-\unicode[STIX]{x1D70E}_{2}+it)-\frac{K_{M}^{\prime }}{K_{M}}(-\unicode[STIX]{x1D70E}_{2}+it)-\frac{Z^{\prime }}{Z}(1+\unicode[STIX]{x1D70E}_{2}-it)=O(t)\quad \text{ as }t\rightarrow \infty ;\end{eqnarray}$$
in brief, one sees the asymptotic bound by observing that the leading term in the above expression is
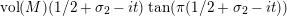 $\text{vol}(M)(1/2+\unicode[STIX]{x1D70E}_{2}-it)\tan (\unicode[STIX]{x1D70B}(1/2+\unicode[STIX]{x1D70E}_{2}-it))$
. From the bounds (35) and (36) obtained in the proof of Lemma 12, we arrive at the bound
$\text{vol}(M)(1/2+\unicode[STIX]{x1D70E}_{2}-it)\tan (\unicode[STIX]{x1D70B}(1/2+\unicode[STIX]{x1D70E}_{2}-it))$
. From the bounds (35) and (36) obtained in the proof of Lemma 12, we arrive at the bound
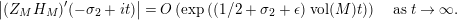 $$\begin{eqnarray}\left|(Z_{M}H_{M})^{\prime }(-\unicode[STIX]{x1D70E}_{2}+it)\right|=O\left(\exp \left(\left(1/2+\unicode[STIX]{x1D70E}_{2}+\unicode[STIX]{x1D716}\right)\text{vol}(M)t\right)\right)\quad \text{as }t\rightarrow \infty .\end{eqnarray}$$
$$\begin{eqnarray}\left|(Z_{M}H_{M})^{\prime }(-\unicode[STIX]{x1D70E}_{2}+it)\right|=O\left(\exp \left(\left(1/2+\unicode[STIX]{x1D70E}_{2}+\unicode[STIX]{x1D716}\right)\text{vol}(M)t\right)\right)\quad \text{as }t\rightarrow \infty .\end{eqnarray}$$
The bound claimed in the statement of the Lemma follows by applying the Phragmen–Lindelöf theorem to the function
 $(Z_{M}H_{M})^{\prime }$
in the open sector bounded by the lines
$(Z_{M}H_{M})^{\prime }$
in the open sector bounded by the lines
 $\operatorname{Im}(s)=1$
,
$\operatorname{Im}(s)=1$
,
 $\operatorname{Re}(s)=-\unicode[STIX]{x1D70E}_{2}$
and
$\operatorname{Re}(s)=-\unicode[STIX]{x1D70E}_{2}$
and
 $\operatorname{Re}(s)=1/2$
, keeping in mind that
$\operatorname{Re}(s)=1/2$
, keeping in mind that
 $-\unicode[STIX]{x1D70E}_{2}\leqslant \unicode[STIX]{x1D70E}<1/2$
.◻
$-\unicode[STIX]{x1D70E}_{2}\leqslant \unicode[STIX]{x1D70E}<1/2$
.◻
5 Vertical and weighted vertical distribution of zeros
In this section, we prove parts (b) and (c) of the Main Theorem.
We fix a large positive number
![]() $T$
and choose number
$T$
and choose number
![]() $T^{\prime }$
such that
$T^{\prime }$
such that
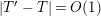 $|T^{\prime }-T|=O(1)$
independently of
$|T^{\prime }-T|=O(1)$
independently of
![]() $T$
where no zero of
$T$
where no zero of
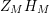 $Z_{M}H_{M}$
has imaginary part equal to
$Z_{M}H_{M}$
has imaginary part equal to
![]() $T^{\prime }$
. Let
$T^{\prime }$
. Let
![]() $t_{0}>0$
be a number such that
$t_{0}>0$
be a number such that
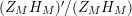 $(Z_{M}H_{M})^{\prime }/(Z_{M}H_{M})$
$(Z_{M}H_{M})^{\prime }/(Z_{M}H_{M})$
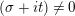 $(\unicode[STIX]{x1D70E}+it)\neq 0$
for all
$(\unicode[STIX]{x1D70E}+it)\neq 0$
for all
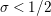 $\unicode[STIX]{x1D70E}<1/2$
and
$\unicode[STIX]{x1D70E}<1/2$
and
![]() $|t|>t_{0}$
; the existence of such
$|t|>t_{0}$
; the existence of such
![]() $t_{0}$
is established by Proposition 9. Let
$t_{0}$
is established by Proposition 9. Let
![]() $\unicode[STIX]{x1D70E}_{0}\geqslant 1$
be a constant chosen so that
$\unicode[STIX]{x1D70E}_{0}\geqslant 1$
be a constant chosen so that
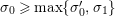 $\unicode[STIX]{x1D70E}_{0}\geqslant \max \{\unicode[STIX]{x1D70E}_{0}^{\prime },\unicode[STIX]{x1D70E}_{1}\}$
, where
$\unicode[STIX]{x1D70E}_{0}\geqslant \max \{\unicode[STIX]{x1D70E}_{0}^{\prime },\unicode[STIX]{x1D70E}_{1}\}$
, where
![]() $\unicode[STIX]{x1D70E}_{0}^{\prime }$
is defined in Lemma 3 and
$\unicode[STIX]{x1D70E}_{0}^{\prime }$
is defined in Lemma 3 and
![]() $\unicode[STIX]{x1D70E}_{1}$
is defined in Lemma 10. Let
$\unicode[STIX]{x1D70E}_{1}$
is defined in Lemma 10. Let
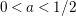 $0<a<1/2$
be arbitrary.
$0<a<1/2$
be arbitrary.
The function
![]() $X_{M}(s)$
, which was defined in (12), is holomorphic in the rectangle
$X_{M}(s)$
, which was defined in (12), is holomorphic in the rectangle
 $R(a,T^{\prime })$
with vertices
$R(a,T^{\prime })$
with vertices
![]() $a+it_{0}$
,
$a+it_{0}$
,
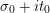 $\unicode[STIX]{x1D70E}_{0}+it_{0}$
,
$\unicode[STIX]{x1D70E}_{0}+it_{0}$
,
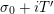 $\unicode[STIX]{x1D70E}_{0}+iT^{\prime }$
and
$\unicode[STIX]{x1D70E}_{0}+iT^{\prime }$
and
![]() $a+iT^{\prime }$
. As in [Reference Luo22], we use Littlewood’s theorem from which we get the formula
$a+iT^{\prime }$
. As in [Reference Luo22], we use Littlewood’s theorem from which we get the formula
 $$\begin{eqnarray}\displaystyle 2\unicode[STIX]{x1D70B}\!\underset{t_{0}<\unicode[STIX]{x1D6FE}<T^{\prime },\unicode[STIX]{x1D6FD}^{\prime }>a}{\underset{\unicode[STIX]{x1D70C}^{\prime }=\unicode[STIX]{x1D6FD}^{\prime }+i\unicode[STIX]{x1D6FE}}{\sum }}\!\!(\unicode[STIX]{x1D6FD}^{\prime }-a) & = & \displaystyle \int _{t_{0}}^{T^{\prime }}\!\!\log |X_{M}(a+it)|dt-\!\int _{t_{0}}^{T^{\prime }}\log |X_{M}(\unicode[STIX]{x1D70E}_{0}+it)|dt\nonumber\\ \displaystyle & & \displaystyle -\!\int _{a}^{\unicode[STIX]{x1D70E}_{0}}\!\arg X_{M}(\unicode[STIX]{x1D70E}+it_{0})\,d\unicode[STIX]{x1D70E}+\!\int _{a}^{\unicode[STIX]{x1D70E}_{0}}\!\arg X_{M}(\unicode[STIX]{x1D70E}+iT^{\prime })\,d\unicode[STIX]{x1D70E}\nonumber\\ \displaystyle & = & \displaystyle I_{1}-I_{2}-I_{3}+I_{4}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle 2\unicode[STIX]{x1D70B}\!\underset{t_{0}<\unicode[STIX]{x1D6FE}<T^{\prime },\unicode[STIX]{x1D6FD}^{\prime }>a}{\underset{\unicode[STIX]{x1D70C}^{\prime }=\unicode[STIX]{x1D6FD}^{\prime }+i\unicode[STIX]{x1D6FE}}{\sum }}\!\!(\unicode[STIX]{x1D6FD}^{\prime }-a) & = & \displaystyle \int _{t_{0}}^{T^{\prime }}\!\!\log |X_{M}(a+it)|dt-\!\int _{t_{0}}^{T^{\prime }}\log |X_{M}(\unicode[STIX]{x1D70E}_{0}+it)|dt\nonumber\\ \displaystyle & & \displaystyle -\!\int _{a}^{\unicode[STIX]{x1D70E}_{0}}\!\arg X_{M}(\unicode[STIX]{x1D70E}+it_{0})\,d\unicode[STIX]{x1D70E}+\!\int _{a}^{\unicode[STIX]{x1D70E}_{0}}\!\arg X_{M}(\unicode[STIX]{x1D70E}+iT^{\prime })\,d\unicode[STIX]{x1D70E}\nonumber\\ \displaystyle & = & \displaystyle I_{1}-I_{2}-I_{3}+I_{4}.\end{eqnarray}$$
The variable
![]() $\unicode[STIX]{x1D70C}^{\prime }$
denotes a zero of
$\unicode[STIX]{x1D70C}^{\prime }$
denotes a zero of
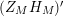 $(Z_{M}H_{M})^{\prime }$
, and the integrals
$(Z_{M}H_{M})^{\prime }$
, and the integrals
![]() $I_{1}$
,
$I_{1}$
,
![]() $I_{2}$
,
$I_{2}$
,
![]() $I_{3}$
and
$I_{3}$
and
![]() $I_{4}$
are defined to be the four integrals in (39), in obvious notation. By Proposition 9, the condition that
$I_{4}$
are defined to be the four integrals in (39), in obvious notation. By Proposition 9, the condition that
 $\operatorname{Im}(\unicode[STIX]{x1D70C}^{\prime })>t_{0}$
implies that
$\operatorname{Im}(\unicode[STIX]{x1D70C}^{\prime })>t_{0}$
implies that
 $\operatorname{Re}(\unicode[STIX]{x1D70C}^{\prime })\geqslant 1/2$
, hence the sum on the left-hand side of (39) is actually taken over all zeros of
$\operatorname{Re}(\unicode[STIX]{x1D70C}^{\prime })\geqslant 1/2$
, hence the sum on the left-hand side of (39) is actually taken over all zeros of
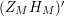 $(Z_{M}H_{M})^{\prime }$
with imaginary part in the interval
$(Z_{M}H_{M})^{\prime }$
with imaginary part in the interval
![]() $(t_{0},T^{\prime })$
.
$(t_{0},T^{\prime })$
.
We investigate integrals
![]() $I_{1}$
,
$I_{1}$
,
![]() $I_{2}$
,
$I_{2}$
,
![]() $I_{3}$
and
$I_{3}$
and
![]() $I_{4}$
separately.
$I_{4}$
separately.
Obviously,
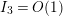 $I_{3}=O(1)$
as
$I_{3}=O(1)$
as
![]() $T\rightarrow \infty$
since, in fact,
$T\rightarrow \infty$
since, in fact,
![]() $I_{3}$
is independent of
$I_{3}$
is independent of
![]() $T$
. As for
$T$
. As for
![]() $I_{2}$
, the function
$I_{2}$
, the function
![]() $\log X_{M}$
is holomorphic and bounded in the infinite strip
$\log X_{M}$
is holomorphic and bounded in the infinite strip
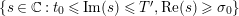 $\{s\in \mathbb{C}:t_{0}\leqslant \operatorname{Im}(s)\leqslant T^{\prime },\operatorname{Re}(s)\geqslant \unicode[STIX]{x1D70E}_{0}\}$
, hence following the argument from [Reference Luo22] we get that
$\{s\in \mathbb{C}:t_{0}\leqslant \operatorname{Im}(s)\leqslant T^{\prime },\operatorname{Re}(s)\geqslant \unicode[STIX]{x1D70E}_{0}\}$
, hence following the argument from [Reference Luo22] we get that
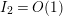 $I_{2}=O(1)$
as
$I_{2}=O(1)$
as
![]() $T\rightarrow \infty$
.
$T\rightarrow \infty$
.
The evaluation of
![]() $I_{4}$
closely follows the lines of the proof treating the analogous integral in the compact case considered by Garunkštis in [Reference Garunkŝtis11], the new input being our Lemma 14. In order to show that
$I_{4}$
closely follows the lines of the proof treating the analogous integral in the compact case considered by Garunkštis in [Reference Garunkŝtis11], the new input being our Lemma 14. In order to show that
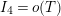 $I_{4}=o(T)$
, it is sufficient to prove that
$I_{4}=o(T)$
, it is sufficient to prove that
 $$\begin{eqnarray}\arg X(\unicode[STIX]{x1D70E}+iT^{\prime })=o(T)\quad \text{ for }a\leqslant \unicode[STIX]{x1D70E}\leqslant \unicode[STIX]{x1D70E}_{0}\quad \text{and}\quad \text{as }T\rightarrow \infty .\end{eqnarray}$$
$$\begin{eqnarray}\arg X(\unicode[STIX]{x1D70E}+iT^{\prime })=o(T)\quad \text{ for }a\leqslant \unicode[STIX]{x1D70E}\leqslant \unicode[STIX]{x1D70E}_{0}\quad \text{and}\quad \text{as }T\rightarrow \infty .\end{eqnarray}$$
The proof of (40) is very similar to the proof of [Reference Garunkŝtis11, formula (3.4)], hence we omit the details. It remains to evaluate
![]() $I_{1}$
.
$I_{1}$
.
5.1 Evaluation of
 $I_{1}$
$I_{1}$
We shall break apart further
![]() $I_{1}$
by using the functional equation (17) for
$I_{1}$
by using the functional equation (17) for
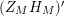 $(Z_{M}H_{M})^{\prime }$
, the definition (12) of
$(Z_{M}H_{M})^{\prime }$
, the definition (12) of
![]() $X_{M}$
, and representation of
$X_{M}$
, and representation of
 $\widetilde{Z}_{M}(s)=1+Z_{M,1}(s)$
which was used in the proof of Proposition 8(b). By doing so, we arrive at the expression
$\widetilde{Z}_{M}(s)=1+Z_{M,1}(s)$
which was used in the proof of Proposition 8(b). By doing so, we arrive at the expression
 $$\begin{eqnarray}\displaystyle I_{1} & = & \displaystyle -\int _{t_{0}}^{T^{\prime }}\log \left|a_{M}A_{M}^{-(a+it)}\right|dt\nonumber\\ \displaystyle & & \displaystyle +\,\int _{t_{0}}^{T^{\prime }}\log |f_{M}(a+it)\unicode[STIX]{x1D702}_{M}(a+it)K_{M}^{-1}(a+it)|dt\nonumber\\ \displaystyle & & \displaystyle +\,\int _{t_{0}}^{T^{\prime }}\log \left|Z_{M}\left(1-(a+it)\right)\right|dt+\int _{t_{0}}^{T^{\prime }}\log \left|1+Z_{M,1}\left(1-(a+it)\right)\right|dt\nonumber\\ \displaystyle & & \displaystyle \qquad =I_{11}+I_{12}+I_{13}+I_{14},\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle I_{1} & = & \displaystyle -\int _{t_{0}}^{T^{\prime }}\log \left|a_{M}A_{M}^{-(a+it)}\right|dt\nonumber\\ \displaystyle & & \displaystyle +\,\int _{t_{0}}^{T^{\prime }}\log |f_{M}(a+it)\unicode[STIX]{x1D702}_{M}(a+it)K_{M}^{-1}(a+it)|dt\nonumber\\ \displaystyle & & \displaystyle +\,\int _{t_{0}}^{T^{\prime }}\log \left|Z_{M}\left(1-(a+it)\right)\right|dt+\int _{t_{0}}^{T^{\prime }}\log \left|1+Z_{M,1}\left(1-(a+it)\right)\right|dt\nonumber\\ \displaystyle & & \displaystyle \qquad =I_{11}+I_{12}+I_{13}+I_{14},\nonumber\end{eqnarray}$$
with the obvious notation for the integrals
![]() $I_{11}$
,
$I_{11}$
,
![]() $I_{12}$
,
$I_{12}$
,
![]() $I_{13}$
and
$I_{13}$
and
![]() $I_{14}$
. Clearly, we have that
$I_{14}$
. Clearly, we have that
 $$\begin{eqnarray}I_{11}=-T\left(\log |a_{M}|-a\log A_{M}\right)+O(1)\quad \text{ as }T\rightarrow \infty .\end{eqnarray}$$
$$\begin{eqnarray}I_{11}=-T\left(\log |a_{M}|-a\log A_{M}\right)+O(1)\quad \text{ as }T\rightarrow \infty .\end{eqnarray}$$
From the computations on the bottom of [Reference Luo22, p. 1146], we have that
 $$\begin{eqnarray}\int _{t_{0}}^{T^{\prime }}\!\!\log |f_{M}(a+it)|dt=T\log T+T(\log \text{vol}(M)-1)+O(\log T)\quad \text{as }T\rightarrow \infty ,\end{eqnarray}$$
$$\begin{eqnarray}\int _{t_{0}}^{T^{\prime }}\!\!\log |f_{M}(a+it)|dt=T\log T+T(\log \text{vol}(M)-1)+O(\log T)\quad \text{as }T\rightarrow \infty ,\end{eqnarray}$$
hence
 $$\begin{eqnarray}\displaystyle I_{12} & = & \displaystyle T\log T+T\left(\log \text{vol}(M)-1\right)+\int _{t_{0}}^{T^{\prime }}\log \left|\unicode[STIX]{x1D702}_{M}(a+it)\right|dt\nonumber\\ \displaystyle & & \displaystyle +\,\int _{t_{0}}^{T^{\prime }}\log \left|K_{M}^{-1}(a+it)\right|dt+O(\log T)\nonumber\\ \displaystyle & = & \displaystyle T\log T+T(\log \text{vol}(M)-1)+I_{121}+I_{122}+O(\log T)\quad \text{as }T\rightarrow \infty ,\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle I_{12} & = & \displaystyle T\log T+T\left(\log \text{vol}(M)-1\right)+\int _{t_{0}}^{T^{\prime }}\log \left|\unicode[STIX]{x1D702}_{M}(a+it)\right|dt\nonumber\\ \displaystyle & & \displaystyle +\,\int _{t_{0}}^{T^{\prime }}\log \left|K_{M}^{-1}(a+it)\right|dt+O(\log T)\nonumber\\ \displaystyle & = & \displaystyle T\log T+T(\log \text{vol}(M)-1)+I_{121}+I_{122}+O(\log T)\quad \text{as }T\rightarrow \infty ,\end{eqnarray}$$
with obvious notation for
![]() $I_{121}$
and
$I_{121}$
and
![]() $I_{122}$
. Stirling’s formula implies that
$I_{122}$
. Stirling’s formula implies that
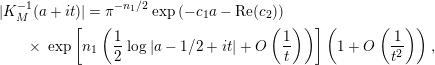 $$\begin{eqnarray}\displaystyle & & \displaystyle |K_{M}^{-1}(a+it)|=\unicode[STIX]{x1D70B}^{-n_{1}/2}\exp \left(-c_{1}a-\text{Re}(c_{2})\right)\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\exp \left[n_{1}\left(\frac{1}{2}\log \left|a-1/2+it\right|+O\left(\frac{1}{t}\right)\right)\right]\left(1+O\left(\frac{1}{t^{2}}\right)\right),\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle |K_{M}^{-1}(a+it)|=\unicode[STIX]{x1D70B}^{-n_{1}/2}\exp \left(-c_{1}a-\text{Re}(c_{2})\right)\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\exp \left[n_{1}\left(\frac{1}{2}\log \left|a-1/2+it\right|+O\left(\frac{1}{t}\right)\right)\right]\left(1+O\left(\frac{1}{t^{2}}\right)\right),\nonumber\end{eqnarray}$$
as
![]() $t\rightarrow \infty$
, where
$t\rightarrow \infty$
, where
![]() $c_{1}$
and
$c_{1}$
and
![]() $c_{2}$
are constants defined in (5). Therefore,
$c_{2}$
are constants defined in (5). Therefore,
 $$\begin{eqnarray}\displaystyle I_{122} & = & \displaystyle \left(-c_{1}a-\text{Re}(c_{2})-\frac{n_{1}}{2}\log \unicode[STIX]{x1D70B}\right)T+\frac{n_{1}}{2}\int _{t_{0}}^{T^{\prime }}\!\!\log |a-1/2+it|+O(\log T)\nonumber\\ \displaystyle & = & \displaystyle \frac{n_{1}}{2}T\log T-T\left(c_{1}a+\text{Re}(c_{2})+\frac{n_{1}}{2}\log \unicode[STIX]{x1D70B}+\frac{n_{1}}{2}\right)+O(\log T)\nonumber\\ \displaystyle & & \displaystyle \quad \text{as }T\rightarrow \infty .\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle I_{122} & = & \displaystyle \left(-c_{1}a-\text{Re}(c_{2})-\frac{n_{1}}{2}\log \unicode[STIX]{x1D70B}\right)T+\frac{n_{1}}{2}\int _{t_{0}}^{T^{\prime }}\!\!\log |a-1/2+it|+O(\log T)\nonumber\\ \displaystyle & = & \displaystyle \frac{n_{1}}{2}T\log T-T\left(c_{1}a+\text{Re}(c_{2})+\frac{n_{1}}{2}\log \unicode[STIX]{x1D70B}+\frac{n_{1}}{2}\right)+O(\log T)\nonumber\\ \displaystyle & & \displaystyle \quad \text{as }T\rightarrow \infty .\end{eqnarray}$$
As in the proof of Lemma 12, one can use (4) and Stirling’s formula to get
 $$\begin{eqnarray}I_{121}=\left(\frac{1}{2}-a\right)\frac{\text{vol}(M)}{2}T^{2}+2n_{1}(\log 2)(a-1/2)T+O(\log T)\quad \text{as }T\rightarrow \infty .\end{eqnarray}$$
$$\begin{eqnarray}I_{121}=\left(\frac{1}{2}-a\right)\frac{\text{vol}(M)}{2}T^{2}+2n_{1}(\log 2)(a-1/2)T+O(\log T)\quad \text{as }T\rightarrow \infty .\end{eqnarray}$$
By substituting (45) and (44) into (43), we arrive at
 $$\begin{eqnarray}\displaystyle I_{12} & = & \displaystyle \left(\frac{1}{2}-a\right)\frac{\text{vol}(M)}{2}T^{2}+\left(\frac{n_{1}}{2}+1\right)T\log T+O(\log T)\nonumber\\ \displaystyle & & \displaystyle +\,T\bigg[2n_{1}\log 2(a-1/2)-c_{1}a+\log \text{vol}(M)-1-\text{Re}(c_{2})\nonumber\\ \displaystyle & & \displaystyle \qquad -\,\frac{n_{1}}{2}\log \unicode[STIX]{x1D70B}-\frac{n_{1}}{2}\bigg]\quad \text{as }T\rightarrow \infty .\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle I_{12} & = & \displaystyle \left(\frac{1}{2}-a\right)\frac{\text{vol}(M)}{2}T^{2}+\left(\frac{n_{1}}{2}+1\right)T\log T+O(\log T)\nonumber\\ \displaystyle & & \displaystyle +\,T\bigg[2n_{1}\log 2(a-1/2)-c_{1}a+\log \text{vol}(M)-1-\text{Re}(c_{2})\nonumber\\ \displaystyle & & \displaystyle \qquad -\,\frac{n_{1}}{2}\log \unicode[STIX]{x1D70B}-\frac{n_{1}}{2}\bigg]\quad \text{as }T\rightarrow \infty .\end{eqnarray}$$
The integral
![]() $I_{13}$
is estimated by applying the Cauchy’s theorem to the function
$I_{13}$
is estimated by applying the Cauchy’s theorem to the function
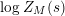 $\log Z_{M}(s)$
within in the rectangle with vertices
$\log Z_{M}(s)$
within in the rectangle with vertices
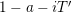 $1-a-iT^{\prime }$
,
$1-a-iT^{\prime }$
,
![]() $2-iT^{\prime }$
,
$2-iT^{\prime }$
,
![]() $2-it_{0}$
and
$2-it_{0}$
and
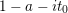 $1-a-it_{0}$
. As in [Reference Luo22], it is easily shown that
$1-a-it_{0}$
. As in [Reference Luo22], it is easily shown that
 $$\begin{eqnarray}I_{13}=-\int _{1-a}^{2}\arg Z_{M}(\unicode[STIX]{x1D70E}-iT^{\prime })\,d\unicode[STIX]{x1D70E}+O(1)=O\left(\underset{1-a\leqslant \unicode[STIX]{x1D70E}\leqslant 2}{\max }\left|\log Z_{M}(\unicode[STIX]{x1D70E}-iT^{\prime })\right|\right).\end{eqnarray}$$
$$\begin{eqnarray}I_{13}=-\int _{1-a}^{2}\arg Z_{M}(\unicode[STIX]{x1D70E}-iT^{\prime })\,d\unicode[STIX]{x1D70E}+O(1)=O\left(\underset{1-a\leqslant \unicode[STIX]{x1D70E}\leqslant 2}{\max }\left|\log Z_{M}(\unicode[STIX]{x1D70E}-iT^{\prime })\right|\right).\end{eqnarray}$$
From
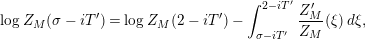 $$\begin{eqnarray}\log Z_{M}(\unicode[STIX]{x1D70E}-iT^{\prime })=\log Z_{M}(2-iT^{\prime })-\int _{\unicode[STIX]{x1D70E}-iT^{\prime }}^{2-iT^{\prime }}\frac{Z_{M}^{\prime }}{Z_{M}}(\unicode[STIX]{x1D709})\,d\unicode[STIX]{x1D709},\end{eqnarray}$$
$$\begin{eqnarray}\log Z_{M}(\unicode[STIX]{x1D70E}-iT^{\prime })=\log Z_{M}(2-iT^{\prime })-\int _{\unicode[STIX]{x1D70E}-iT^{\prime }}^{2-iT^{\prime }}\frac{Z_{M}^{\prime }}{Z_{M}}(\unicode[STIX]{x1D709})\,d\unicode[STIX]{x1D709},\end{eqnarray}$$
and the bound in (20) we obtain the expression
 $$\begin{eqnarray}\displaystyle I_{13} & = & \displaystyle \int _{t_{0}}^{T^{\prime }}\log |Z_{M}(1-a-it)|dt=O((T\log T)^{2-2(1-a)})=O((T\log T)^{2a})\nonumber\\ \displaystyle & & \displaystyle \qquad \text{as }T\rightarrow \infty .\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle I_{13} & = & \displaystyle \int _{t_{0}}^{T^{\prime }}\log |Z_{M}(1-a-it)|dt=O((T\log T)^{2-2(1-a)})=O((T\log T)^{2a})\nonumber\\ \displaystyle & & \displaystyle \qquad \text{as }T\rightarrow \infty .\end{eqnarray}$$
Directly from Lemma 11, we have the estimate
 $$\begin{eqnarray}\displaystyle I_{14}=\int _{t_{0}}^{T^{\prime }}\log \left|1+Z_{M,1}\left(1-(a+it)\right)\right|dt=O\left((T\log T)^{2a}\right)\quad \text{ as }T\rightarrow \infty . & & \displaystyle \nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle I_{14}=\int _{t_{0}}^{T^{\prime }}\log \left|1+Z_{M,1}\left(1-(a+it)\right)\right|dt=O\left((T\log T)^{2a}\right)\quad \text{ as }T\rightarrow \infty . & & \displaystyle \nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
Combining (41), (46), (47) and (48) yields
 $$\begin{eqnarray}\displaystyle I_{1} & = & \displaystyle \left(\frac{1}{2}-a\right)\frac{\text{vol}(M)}{2}T^{2}+\left(\frac{n_{1}}{2}+1\right)T\log T+O((T\log T)^{2a})+TC_{M,a}\nonumber\\ \displaystyle & & \displaystyle \quad \text{as }T\rightarrow \infty ,\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle I_{1} & = & \displaystyle \left(\frac{1}{2}-a\right)\frac{\text{vol}(M)}{2}T^{2}+\left(\frac{n_{1}}{2}+1\right)T\log T+O((T\log T)^{2a})+TC_{M,a}\nonumber\\ \displaystyle & & \displaystyle \quad \text{as }T\rightarrow \infty ,\end{eqnarray}$$
where
 $$\begin{eqnarray}\displaystyle C_{M,a} & = & \displaystyle (a-1/2)\cdot 2n_{1}\log 2+a(\log A_{M}-c_{1})-\log |a_{M}|\nonumber\\ \displaystyle & & \displaystyle +\,\log \text{vol}(M)-1-\text{Re}(c_{2})-\frac{n_{1}}{2}\log \unicode[STIX]{x1D70B}-\frac{n_{1}}{2}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle C_{M,a} & = & \displaystyle (a-1/2)\cdot 2n_{1}\log 2+a(\log A_{M}-c_{1})-\log |a_{M}|\nonumber\\ \displaystyle & & \displaystyle +\,\log \text{vol}(M)-1-\text{Re}(c_{2})-\frac{n_{1}}{2}\log \unicode[STIX]{x1D70B}-\frac{n_{1}}{2}.\nonumber\end{eqnarray}$$
Finally, we have arrived at our estimate for
![]() $I_{1}$
.
$I_{1}$
.
5.2 Proof of the Main Theorem
Since
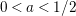 $0<a<1/2$
, we have that
$0<a<1/2$
, we have that
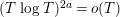 $(T\log T)^{2a}=o(T)$
. We have shown that
$(T\log T)^{2a}=o(T)$
. We have shown that
![]() $I_{2}$
and
$I_{2}$
and
![]() $I_{3}$
are
$I_{3}$
are
![]() $O(1)$
as
$O(1)$
as
![]() $T\rightarrow \infty$
and that
$T\rightarrow \infty$
and that
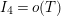 $I_{4}=o(T)$
as
$I_{4}=o(T)$
as
![]() $T\rightarrow \infty$
. Hence, by substituting equation (49) into (39) we get
$T\rightarrow \infty$
. Hence, by substituting equation (49) into (39) we get
 $$\begin{eqnarray}\displaystyle 2\unicode[STIX]{x1D70B}\underset{t_{0}<\unicode[STIX]{x1D6FE}<T^{\prime }}{\underset{\unicode[STIX]{x1D70C}^{\prime }=\unicode[STIX]{x1D6FD}^{\prime }+i\unicode[STIX]{x1D6FE}}{\sum }}(\unicode[STIX]{x1D6FD}^{\prime }-a) & = & \displaystyle \left(\frac{1}{2}-a\right)\frac{\text{vol}(M)}{2}T^{2}\nonumber\\ \displaystyle & & \displaystyle +\,\left(\frac{n_{1}}{2}+1\right)T\log T+TC_{M,a}+o(T)\quad \text{ as }T\rightarrow \infty ,\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle 2\unicode[STIX]{x1D70B}\underset{t_{0}<\unicode[STIX]{x1D6FE}<T^{\prime }}{\underset{\unicode[STIX]{x1D70C}^{\prime }=\unicode[STIX]{x1D6FD}^{\prime }+i\unicode[STIX]{x1D6FE}}{\sum }}(\unicode[STIX]{x1D6FD}^{\prime }-a) & = & \displaystyle \left(\frac{1}{2}-a\right)\frac{\text{vol}(M)}{2}T^{2}\nonumber\\ \displaystyle & & \displaystyle +\,\left(\frac{n_{1}}{2}+1\right)T\log T+TC_{M,a}+o(T)\quad \text{ as }T\rightarrow \infty ,\end{eqnarray}$$
where
![]() $C_{M,a}$
is defined above.
$C_{M,a}$
is defined above.
Substituting
![]() $a/2$
instead of
$a/2$
instead of
![]() $a$
into (50), subtracting the obtained formulas, and then dividing by
$a$
into (50), subtracting the obtained formulas, and then dividing by
![]() $a/2$
yields the statement (b) of the Main Theorem.
$a/2$
yields the statement (b) of the Main Theorem.
As for part (c) of the Main Theorem, we begin with the formula
 $$\begin{eqnarray}\underset{0<\unicode[STIX]{x1D6FE}\leqslant T}{\underset{\unicode[STIX]{x1D70C}^{\prime }=\unicode[STIX]{x1D6FD}^{\prime }+i\unicode[STIX]{x1D6FE}}{\sum }}(\unicode[STIX]{x1D6FD}^{\prime }-1/2)=\underset{0<\unicode[STIX]{x1D6FE}<T^{\prime }}{\underset{\unicode[STIX]{x1D70C}^{\prime }=\unicode[STIX]{x1D6FD}^{\prime }+i\unicode[STIX]{x1D6FE}}{\sum }}(\unicode[STIX]{x1D6FD}^{\prime }-a)+(a-1/2)\underset{0<\unicode[STIX]{x1D6FE}<T^{\prime }}{\underset{\unicode[STIX]{x1D70C}^{\prime }=\unicode[STIX]{x1D6FD}^{\prime }+i\unicode[STIX]{x1D6FE}}{\sum }}1\text{.}\end{eqnarray}$$
$$\begin{eqnarray}\underset{0<\unicode[STIX]{x1D6FE}\leqslant T}{\underset{\unicode[STIX]{x1D70C}^{\prime }=\unicode[STIX]{x1D6FD}^{\prime }+i\unicode[STIX]{x1D6FE}}{\sum }}(\unicode[STIX]{x1D6FD}^{\prime }-1/2)=\underset{0<\unicode[STIX]{x1D6FE}<T^{\prime }}{\underset{\unicode[STIX]{x1D70C}^{\prime }=\unicode[STIX]{x1D6FD}^{\prime }+i\unicode[STIX]{x1D6FE}}{\sum }}(\unicode[STIX]{x1D6FD}^{\prime }-a)+(a-1/2)\underset{0<\unicode[STIX]{x1D6FE}<T^{\prime }}{\underset{\unicode[STIX]{x1D70C}^{\prime }=\unicode[STIX]{x1D6FD}^{\prime }+i\unicode[STIX]{x1D6FE}}{\sum }}1\text{.}\end{eqnarray}$$
The first sum on the right-hand side of (51) is estimated by (50). The second sum on the right-hand side of (51) is estimated by part (b) of the Main Theorem, keeping in mind that the difference between the second sum in (51) and the sum in part (b) is the finite number of zeros in the half-plane
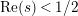 $\text{ Re}(s)<1/2$
.
$\text{ Re}(s)<1/2$
.
With all this, the proof of the Main Theorem is complete.
In the case when the surface is co-compact the statement of the Main Theorem is easily deduced, since, in that case
 $n_{1}=c_{1}=c_{2}=0$
,
$n_{1}=c_{1}=c_{2}=0$
,
 $H_{M}=1$
,
$H_{M}=1$
,
 $A_{M}=\exp (\ell _{M,0})$
and
$A_{M}=\exp (\ell _{M,0})$
and
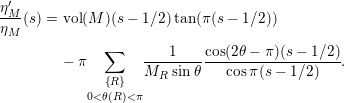 $$\begin{eqnarray}\displaystyle \frac{\unicode[STIX]{x1D702}_{M}^{\prime }}{\unicode[STIX]{x1D702}_{M}}(s) & = & \displaystyle \text{vol}(M)(s-1/2)\tan (\unicode[STIX]{x1D70B}(s-1/2))\nonumber\\ \displaystyle & & \displaystyle -\,\unicode[STIX]{x1D70B}\underset{0<\unicode[STIX]{x1D703}(R)<\unicode[STIX]{x1D70B}}{\underset{\left\{R\right\}}{\sum }}\frac{1}{M_{R}\sin \unicode[STIX]{x1D703}}\frac{\cos (2\unicode[STIX]{x1D703}-\unicode[STIX]{x1D70B})(s-1/2)}{\cos \unicode[STIX]{x1D70B}(s-1/2)}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \frac{\unicode[STIX]{x1D702}_{M}^{\prime }}{\unicode[STIX]{x1D702}_{M}}(s) & = & \displaystyle \text{vol}(M)(s-1/2)\tan (\unicode[STIX]{x1D70B}(s-1/2))\nonumber\\ \displaystyle & & \displaystyle -\,\unicode[STIX]{x1D70B}\underset{0<\unicode[STIX]{x1D703}(R)<\unicode[STIX]{x1D70B}}{\underset{\left\{R\right\}}{\sum }}\frac{1}{M_{R}\sin \unicode[STIX]{x1D703}}\frac{\cos (2\unicode[STIX]{x1D703}-\unicode[STIX]{x1D70B})(s-1/2)}{\cos \unicode[STIX]{x1D70B}(s-1/2)}.\nonumber\end{eqnarray}$$
6 Corollaries of the Main Theorem
In this section, we deduce three corollaries of our Main Theorem. The results we prove are analogous to [Reference Levinson and Montgomery21, Theorem 2 and Theorem 3], with, in their notation,
![]() $k=1$
. Similar results may be deduced for the weighted vertical distribution of zeros of the
$k=1$
. Similar results may be deduced for the weighted vertical distribution of zeros of the
![]() $k$
th derivative, based on the results of § 8, with suitably replaced constants.
$k$
th derivative, based on the results of § 8, with suitably replaced constants.
Corollary 15. For
![]() $\unicode[STIX]{x1D6FF}>1/2$
, let
$\unicode[STIX]{x1D6FF}>1/2$
, let
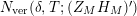 $N_{\text{ver}}(\unicode[STIX]{x1D6FF},T;(Z_{M}H_{M})^{\prime })$
denote the number of zeros
$N_{\text{ver}}(\unicode[STIX]{x1D6FF},T;(Z_{M}H_{M})^{\prime })$
denote the number of zeros
![]() $\unicode[STIX]{x1D70C}^{\prime }$
of
$\unicode[STIX]{x1D70C}^{\prime }$
of
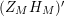 $(Z_{M}H_{M})^{\prime }$
such that
$(Z_{M}H_{M})^{\prime }$
such that
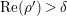 $\operatorname{Re}(\unicode[STIX]{x1D70C}^{\prime })>\unicode[STIX]{x1D6FF}$
and
$\operatorname{Re}(\unicode[STIX]{x1D70C}^{\prime })>\unicode[STIX]{x1D6FF}$
and
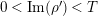 $0<\operatorname{Im}(\unicode[STIX]{x1D70C}^{\prime })<T$
. Then, for an arbitrary
$0<\operatorname{Im}(\unicode[STIX]{x1D70C}^{\prime })<T$
. Then, for an arbitrary
![]() $\unicode[STIX]{x1D716}>0$
$\unicode[STIX]{x1D716}>0$
 $$\begin{eqnarray}N_{\text{ver}}\left(\frac{1}{2}+\unicode[STIX]{x1D716},T;(Z_{M}H_{M})^{\prime }\right)<\frac{1}{\unicode[STIX]{x1D716}}N_{\text{w}}(T;(Z_{M}H_{M})^{\prime }).\end{eqnarray}$$
$$\begin{eqnarray}N_{\text{ver}}\left(\frac{1}{2}+\unicode[STIX]{x1D716},T;(Z_{M}H_{M})^{\prime }\right)<\frac{1}{\unicode[STIX]{x1D716}}N_{\text{w}}(T;(Z_{M}H_{M})^{\prime }).\end{eqnarray}$$
Proof. Trivially, we have the bounds
 $$\begin{eqnarray}\displaystyle N_{\text{ver}}\left(\frac{1}{2}+\unicode[STIX]{x1D716},T;(Z_{M}H_{M})^{\prime }\right) & {<} & \displaystyle \frac{1}{1/2+\unicode[STIX]{x1D716}}\underset{\unicode[STIX]{x1D70E}>1/2+\unicode[STIX]{x1D716}\text{, }0<t<T}{\underset{(Z_{M}H_{M})^{\prime }(\unicode[STIX]{x1D70E}+it)=0}{\sum }}\unicode[STIX]{x1D70E}\nonumber\\ \displaystyle & = & \displaystyle \frac{1}{1/2+\unicode[STIX]{x1D716}}\underset{\unicode[STIX]{x1D70E}>1/2+\unicode[STIX]{x1D716}\text{, }0<t<T}{\underset{(Z_{M}H_{M})^{\prime }(\unicode[STIX]{x1D70E}+it)=0}{\sum }}\left(\unicode[STIX]{x1D70E}-\frac{1}{2}\right)\nonumber\\ \displaystyle & & \displaystyle +\,\frac{1/2}{1/2+\unicode[STIX]{x1D716}}N_{\text{ver}}\left(\frac{1}{2}+\unicode[STIX]{x1D716},T;(Z_{M}H_{M})^{\prime }\right)\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle N_{\text{ver}}\left(\frac{1}{2}+\unicode[STIX]{x1D716},T;(Z_{M}H_{M})^{\prime }\right) & {<} & \displaystyle \frac{1}{1/2+\unicode[STIX]{x1D716}}\underset{\unicode[STIX]{x1D70E}>1/2+\unicode[STIX]{x1D716}\text{, }0<t<T}{\underset{(Z_{M}H_{M})^{\prime }(\unicode[STIX]{x1D70E}+it)=0}{\sum }}\unicode[STIX]{x1D70E}\nonumber\\ \displaystyle & = & \displaystyle \frac{1}{1/2+\unicode[STIX]{x1D716}}\underset{\unicode[STIX]{x1D70E}>1/2+\unicode[STIX]{x1D716}\text{, }0<t<T}{\underset{(Z_{M}H_{M})^{\prime }(\unicode[STIX]{x1D70E}+it)=0}{\sum }}\left(\unicode[STIX]{x1D70E}-\frac{1}{2}\right)\nonumber\\ \displaystyle & & \displaystyle +\,\frac{1/2}{1/2+\unicode[STIX]{x1D716}}N_{\text{ver}}\left(\frac{1}{2}+\unicode[STIX]{x1D716},T;(Z_{M}H_{M})^{\prime }\right)\end{eqnarray}$$
Therefore,
 $$\begin{eqnarray}\frac{2\unicode[STIX]{x1D716}}{1+2\unicode[STIX]{x1D716}}N_{\text{ver}}\left(\frac{1}{2}+\unicode[STIX]{x1D716},T;(Z_{M}H_{M})^{\prime }\right)<\frac{2}{1+2\unicode[STIX]{x1D716}}N_{\text{w}}(T;(Z_{M}H_{M})^{\prime }),\end{eqnarray}$$
$$\begin{eqnarray}\frac{2\unicode[STIX]{x1D716}}{1+2\unicode[STIX]{x1D716}}N_{\text{ver}}\left(\frac{1}{2}+\unicode[STIX]{x1D716},T;(Z_{M}H_{M})^{\prime }\right)<\frac{2}{1+2\unicode[STIX]{x1D716}}N_{\text{w}}(T;(Z_{M}H_{M})^{\prime }),\end{eqnarray}$$
from which the result immediately follows.◻
Observe that the lead term in the asymptotic expansion in part (b) of the Main Theorem is
![]() $O(T^{2})$
, whereas the lead term in the asymptotic expansion in part (c) of the Main Theorem is
$O(T^{2})$
, whereas the lead term in the asymptotic expansion in part (c) of the Main Theorem is
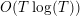 $O(T\log (T))$
. Consequently, Corollary 15 shows that zeros of
$O(T\log (T))$
. Consequently, Corollary 15 shows that zeros of
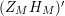 $(Z_{M}H_{M})^{\prime }$
are concentrated very close the critical line
$(Z_{M}H_{M})^{\prime }$
are concentrated very close the critical line
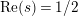 $\operatorname{Re}(s)=1/2$
. The following corollary further quantifies this observation.
$\operatorname{Re}(s)=1/2$
. The following corollary further quantifies this observation.
Corollary 16. For any
![]() $\unicode[STIX]{x1D6FF}>1/2$
, let
$\unicode[STIX]{x1D6FF}>1/2$
, let
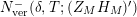 $N_{\text{ver}}^{-}(\unicode[STIX]{x1D6FF},T;(Z_{M}H_{M})^{\prime })$
denote the number of nontrivial zeros
$N_{\text{ver}}^{-}(\unicode[STIX]{x1D6FF},T;(Z_{M}H_{M})^{\prime })$
denote the number of nontrivial zeros
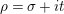 $\unicode[STIX]{x1D70C}=\unicode[STIX]{x1D70E}+it$
of
$\unicode[STIX]{x1D70C}=\unicode[STIX]{x1D70E}+it$
of
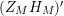 $(Z_{M}H_{M})^{\prime }$
with
$(Z_{M}H_{M})^{\prime }$
with
![]() $\unicode[STIX]{x1D70E}<\unicode[STIX]{x1D6FF}$
and
$\unicode[STIX]{x1D70E}<\unicode[STIX]{x1D6FF}$
and
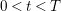 $0<t<T$
. Then, for any constant
$0<t<T$
. Then, for any constant
![]() $\unicode[STIX]{x1D716}>0$
,
$\unicode[STIX]{x1D716}>0$
,
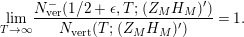 $$\begin{eqnarray}\underset{T\rightarrow \infty }{\lim }\frac{N_{\text{ver}}^{-}(1/2+\unicode[STIX]{x1D716},T;(Z_{M}H_{M})^{\prime })}{N_{\text{vert}}(T;(Z_{M}H_{M})^{\prime })}=1.\end{eqnarray}$$
$$\begin{eqnarray}\underset{T\rightarrow \infty }{\lim }\frac{N_{\text{ver}}^{-}(1/2+\unicode[STIX]{x1D716},T;(Z_{M}H_{M})^{\prime })}{N_{\text{vert}}(T;(Z_{M}H_{M})^{\prime })}=1.\end{eqnarray}$$
Proof. Corollary 15 implies that
 $$\begin{eqnarray}1\geqslant \frac{N_{\text{ver}}^{-}(1/2+\unicode[STIX]{x1D716},T;(Z_{M}H_{M})^{\prime })}{N_{\text{vert}}(T;(Z_{M}H_{M})^{\prime })}>1-\frac{1}{\unicode[STIX]{x1D716}}\frac{N_{\text{w}}(T;(Z_{M}H_{M})^{\prime })}{N_{\text{vert}}(T;(Z_{M}H_{M})^{\prime })}.\end{eqnarray}$$
$$\begin{eqnarray}1\geqslant \frac{N_{\text{ver}}^{-}(1/2+\unicode[STIX]{x1D716},T;(Z_{M}H_{M})^{\prime })}{N_{\text{vert}}(T;(Z_{M}H_{M})^{\prime })}>1-\frac{1}{\unicode[STIX]{x1D716}}\frac{N_{\text{w}}(T;(Z_{M}H_{M})^{\prime })}{N_{\text{vert}}(T;(Z_{M}H_{M})^{\prime })}.\end{eqnarray}$$
From the Main Theorem (b) and (c) we deduce that
 $$\begin{eqnarray}\frac{N_{\text{w}}(T;(Z_{M}H_{M})^{\prime })}{N_{\text{vert}}(T;(Z_{M}H_{M})^{\prime })}\rightarrow 0\quad \text{ as }T\rightarrow \infty .\end{eqnarray}$$
$$\begin{eqnarray}\frac{N_{\text{w}}(T;(Z_{M}H_{M})^{\prime })}{N_{\text{vert}}(T;(Z_{M}H_{M})^{\prime })}\rightarrow 0\quad \text{ as }T\rightarrow \infty .\end{eqnarray}$$
Therefore, by passing to the limit as
![]() $T\rightarrow \infty$
in (53), the claimed result follows.◻
$T\rightarrow \infty$
in (53), the claimed result follows.◻
The following corollary gives estimates of short sums of distances
 $(\unicode[STIX]{x1D70E}-1/2)$
.
$(\unicode[STIX]{x1D70E}-1/2)$
.
Corollary 17. Let
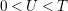 $0<U<T$
. Then,
$0<U<T$
. Then,
 $$\begin{eqnarray}\displaystyle 2\unicode[STIX]{x1D70B}\underset{\unicode[STIX]{x1D70E}>1/2,T<t\leqslant T+U}{\underset{(Z_{M}H_{M})^{\prime }(\unicode[STIX]{x1D70E}+it)=0}{\sum }}\left(\unicode[STIX]{x1D70E}-\frac{1}{2}\right) & = & \displaystyle \left(\frac{n_{1}}{2}+1\right)U\log (T+U)\nonumber\\ \displaystyle & & \displaystyle +\,\left(\log \frac{\mathfrak{g}_{1}\text{vol}(M)A_{M}^{1/2}}{\unicode[STIX]{x1D70B}^{n_{1}/2}|d(1)a_{M}|}\right)U\nonumber\\ \displaystyle & & \displaystyle +\,o(T)+O(U^{2}/T)\quad \text{ as }T\rightarrow \infty .\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle 2\unicode[STIX]{x1D70B}\underset{\unicode[STIX]{x1D70E}>1/2,T<t\leqslant T+U}{\underset{(Z_{M}H_{M})^{\prime }(\unicode[STIX]{x1D70E}+it)=0}{\sum }}\left(\unicode[STIX]{x1D70E}-\frac{1}{2}\right) & = & \displaystyle \left(\frac{n_{1}}{2}+1\right)U\log (T+U)\nonumber\\ \displaystyle & & \displaystyle +\,\left(\log \frac{\mathfrak{g}_{1}\text{vol}(M)A_{M}^{1/2}}{\unicode[STIX]{x1D70B}^{n_{1}/2}|d(1)a_{M}|}\right)U\nonumber\\ \displaystyle & & \displaystyle +\,o(T)+O(U^{2}/T)\quad \text{ as }T\rightarrow \infty .\end{eqnarray}$$
Proof. The left-hand side of the (54) is equal to
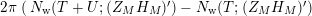 $2\unicode[STIX]{x1D70B}(N_{\text{w}}(T+U;(Z_{M}H_{M})^{\prime })-N_{\text{w}}(T;(Z_{M}H_{M})^{\prime })$
, hence part (c) of the Main Theorem yields
$2\unicode[STIX]{x1D70B}(N_{\text{w}}(T+U;(Z_{M}H_{M})^{\prime })-N_{\text{w}}(T;(Z_{M}H_{M})^{\prime })$
, hence part (c) of the Main Theorem yields
 $$\begin{eqnarray}\displaystyle 2\unicode[STIX]{x1D70B}\!\underset{\unicode[STIX]{x1D70E}>1/2,T<t\leqslant T+U}{\underset{(Z_{M}H_{M})^{\prime }(\unicode[STIX]{x1D70E}+it)=0}{\sum }}\!\!\left(\!\unicode[STIX]{x1D70E}-\frac{1}{2}\right) & = & \displaystyle \left(\frac{n_{1}}{2}+1\right)\!\!\left(\!T\,\text{log}\!\left(\!1+\frac{U}{T}\right)-U+U\log (T+U)\!\right)\nonumber\\ \displaystyle & & \displaystyle +\!\left(\log \frac{\mathfrak{g}_{1}\text{vol}(M)A_{M}^{1/2}}{\unicode[STIX]{x1D70B}^{n_{1}/2}|d(1)a_{M}|}\right)\!U+o(T)\quad \text{as }T\rightarrow \infty .\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle 2\unicode[STIX]{x1D70B}\!\underset{\unicode[STIX]{x1D70E}>1/2,T<t\leqslant T+U}{\underset{(Z_{M}H_{M})^{\prime }(\unicode[STIX]{x1D70E}+it)=0}{\sum }}\!\!\left(\!\unicode[STIX]{x1D70E}-\frac{1}{2}\right) & = & \displaystyle \left(\frac{n_{1}}{2}+1\right)\!\!\left(\!T\,\text{log}\!\left(\!1+\frac{U}{T}\right)-U+U\log (T+U)\!\right)\nonumber\\ \displaystyle & & \displaystyle +\!\left(\log \frac{\mathfrak{g}_{1}\text{vol}(M)A_{M}^{1/2}}{\unicode[STIX]{x1D70B}^{n_{1}/2}|d(1)a_{M}|}\right)\!U+o(T)\quad \text{as }T\rightarrow \infty .\end{eqnarray}$$
The elementary observation that
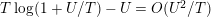 $T\log (1+U/T)-U=O(U^{2}/T)$
completes the proof.◻
$T\log (1+U/T)-U=O(U^{2}/T)$
completes the proof.◻
7 Examples
The Main Theorem naturally leads to the following question: Are there examples of groups
![]() $\unicode[STIX]{x1D6E4}$
where
$\unicode[STIX]{x1D6E4}$
where
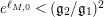 $e^{\ell _{M,0}}<(\mathfrak{g}_{2}/\mathfrak{g}_{1})^{2}$
as well as groups where
$e^{\ell _{M,0}}<(\mathfrak{g}_{2}/\mathfrak{g}_{1})^{2}$
as well as groups where
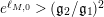 $e^{\ell _{M,0}}>(\mathfrak{g}_{2}/\mathfrak{g}_{1})^{2}$
? The purpose of this section is to prove Proposition 1 and present examples of groups in each category. In fact, there are examples of both arithmetic and nonarithmetic groups in each category.
$e^{\ell _{M,0}}>(\mathfrak{g}_{2}/\mathfrak{g}_{1})^{2}$
? The purpose of this section is to prove Proposition 1 and present examples of groups in each category. In fact, there are examples of both arithmetic and nonarithmetic groups in each category.
7.1 Congruence subgroups
In this subsection we prove part (i) of Proposition 1.
Let
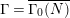 $\unicode[STIX]{x1D6E4}=\overline{\unicode[STIX]{x1D6E4}_{0}(N)}$
be the congruence subgroup defined by the arithmetic condition
$\unicode[STIX]{x1D6E4}=\overline{\unicode[STIX]{x1D6E4}_{0}(N)}$
be the congruence subgroup defined by the arithmetic condition
 $$\begin{eqnarray}\overline{\unicode[STIX]{x1D6E4}_{0}(N)}:=\left\{\left(\begin{array}{@{}cc@{}}a & b\\ c & d\end{array}\right)\in \text{SL}(2,\mathbb{Z}):c\equiv 0\,(\text{mod }N)\right\}\Big/\pm I,\end{eqnarray}$$
$$\begin{eqnarray}\overline{\unicode[STIX]{x1D6E4}_{0}(N)}:=\left\{\left(\begin{array}{@{}cc@{}}a & b\\ c & d\end{array}\right)\in \text{SL}(2,\mathbb{Z}):c\equiv 0\,(\text{mod }N)\right\}\Big/\pm I,\end{eqnarray}$$
where
![]() $I$
denotes the identity matrix and
$I$
denotes the identity matrix and
![]() $N$
is a positive integer. If
$N$
is a positive integer. If
 $N=p_{1}\cdots p_{r}$
, for distinct primes
$N=p_{1}\cdots p_{r}$
, for distinct primes
 $p_{1},\ldots ,p_{r}$
; then, it is proved in [Reference Huxley16], that the corresponding surface has
$p_{1},\ldots ,p_{r}$
; then, it is proved in [Reference Huxley16], that the corresponding surface has
![]() $n_{1}=2^{r}$
cusps and the scattering determinant is given by the formula
$n_{1}=2^{r}$
cusps and the scattering determinant is given by the formula
 $$\begin{eqnarray}\unicode[STIX]{x1D711}_{N}(s)=\left[\sqrt{\unicode[STIX]{x1D70B}}\frac{\unicode[STIX]{x1D6E4}(s-1/2)}{\unicode[STIX]{x1D6E4}(s)}\right]^{n_{1}}\left[\frac{\unicode[STIX]{x1D701}_{\mathbb{Q}}(2s-1)}{\unicode[STIX]{x1D701}_{\mathbb{Q}}(2s)}\right]^{n_{1}}\mathop{\prod }_{p\mid N}\left(\frac{1-p^{2-2s}}{1-p^{2s}}\right)^{n_{1}/2},\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D711}_{N}(s)=\left[\sqrt{\unicode[STIX]{x1D70B}}\frac{\unicode[STIX]{x1D6E4}(s-1/2)}{\unicode[STIX]{x1D6E4}(s)}\right]^{n_{1}}\left[\frac{\unicode[STIX]{x1D701}_{\mathbb{Q}}(2s-1)}{\unicode[STIX]{x1D701}_{\mathbb{Q}}(2s)}\right]^{n_{1}}\mathop{\prod }_{p\mid N}\left(\frac{1-p^{2-2s}}{1-p^{2s}}\right)^{n_{1}/2},\end{eqnarray}$$
where
![]() $\unicode[STIX]{x1D701}_{\mathbb{Q}}$
is the Riemann zeta function. Now, it is easy to show that
$\unicode[STIX]{x1D701}_{\mathbb{Q}}$
is the Riemann zeta function. Now, it is easy to show that
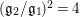 $(\mathfrak{g}_{2}/\mathfrak{g}_{1})^{2}=4$
. In the case
$(\mathfrak{g}_{2}/\mathfrak{g}_{1})^{2}=4$
. In the case
![]() $N$
is not square-free, an application of [Reference Hejhal14], formula (4.2), page 536 yields the same conclusion.
$N$
is not square-free, an application of [Reference Hejhal14], formula (4.2), page 536 yields the same conclusion.
All elements of
![]() $\overline{\unicode[STIX]{x1D6E4}_{0}(N)}$
have integer entries, so any hyperbolic element has trace whose absolute value is at least equal to 3. Therefore,
$\overline{\unicode[STIX]{x1D6E4}_{0}(N)}$
have integer entries, so any hyperbolic element has trace whose absolute value is at least equal to 3. Therefore,
 $e^{\ell _{M,0}}\geqslant u$
where
$e^{\ell _{M,0}}\geqslant u$
where
![]() $u$
is a solution to
$u$
is a solution to
 $u^{1/2}+u^{-1/2}=3$
. Solving, we get that
$u^{1/2}+u^{-1/2}=3$
. Solving, we get that
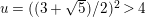 $u=((3+\sqrt{5})/2)^{2}>4$
. Therefore, for any such group
$u=((3+\sqrt{5})/2)^{2}>4$
. Therefore, for any such group
![]() $\overline{\unicode[STIX]{x1D6E4}_{0}(N)}$
, one has that
$\overline{\unicode[STIX]{x1D6E4}_{0}(N)}$
, one has that
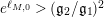 $e^{\ell _{M,0}}>(\mathfrak{g}_{2}/\mathfrak{g}_{1})^{2}$
.
$e^{\ell _{M,0}}>(\mathfrak{g}_{2}/\mathfrak{g}_{1})^{2}$
.
In the case of the principal congruence subgroups
![]() $\overline{\unicode[STIX]{x1D6E4}(N)}$
the scattering determinant can be computed using the analysis presented in [Reference Hejhal14] and [Reference Huxley16]. As above, one shows that
$\overline{\unicode[STIX]{x1D6E4}(N)}$
the scattering determinant can be computed using the analysis presented in [Reference Hejhal14] and [Reference Huxley16]. As above, one shows that
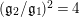 $(\mathfrak{g}_{2}/\mathfrak{g}_{1})^{2}=4$
because the Dirichlet series portion of the scattering determinant is shown to be given by ratios of classical Dirichlet series. Furthermore, the matrices in
$(\mathfrak{g}_{2}/\mathfrak{g}_{1})^{2}=4$
because the Dirichlet series portion of the scattering determinant is shown to be given by ratios of classical Dirichlet series. Furthermore, the matrices in
![]() $\overline{\unicode[STIX]{x1D6E4}(N)}$
also have integral entries, so
$\overline{\unicode[STIX]{x1D6E4}(N)}$
also have integral entries, so
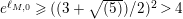 $e^{\ell _{M,0}}\geqslant ((3+\sqrt{(5)})/2)^{2}>4$
.
$e^{\ell _{M,0}}\geqslant ((3+\sqrt{(5)})/2)^{2}>4$
.
7.2 Moonshine subgroups
We now prove part (ii) of Proposition 1.
Following [Reference Gannon8], we use the term “moonshine group” for any subgroup
![]() $\unicode[STIX]{x1D6E4}$
of
$\unicode[STIX]{x1D6E4}$
of
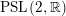 $\text{PSL}(2,\mathbb{R})$
which satisfies the following two conditions. First, there exists an integer
$\text{PSL}(2,\mathbb{R})$
which satisfies the following two conditions. First, there exists an integer
![]() $N\geqslant 1$
such that
$N\geqslant 1$
such that
![]() $\unicode[STIX]{x1D6E4}$
contains
$\unicode[STIX]{x1D6E4}$
contains
![]() $\overline{\unicode[STIX]{x1D6E4}_{0}(N)}$
. Second,
$\overline{\unicode[STIX]{x1D6E4}_{0}(N)}$
. Second,
![]() $\unicode[STIX]{x1D6E4}$
contains the element
$\unicode[STIX]{x1D6E4}$
contains the element
![]() $(\begin{smallmatrix}1 & k\\ 0 & 1\end{smallmatrix})$
if and only if
$(\begin{smallmatrix}1 & k\\ 0 & 1\end{smallmatrix})$
if and only if
![]() $k\in \mathbb{Z}$
.
$k\in \mathbb{Z}$
.
Following [Reference Cummins6, p. 363], let
![]() $f$
be a square-free, nonnegative integer, and consider the group
$f$
be a square-free, nonnegative integer, and consider the group
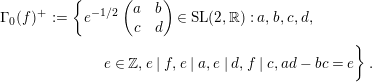 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6E4}_{0}(f)^{+} & := & \displaystyle \left\{e^{-1/2}\left(\begin{array}{@{}cc@{}}a & b\\ c & d\end{array}\right)\in \text{SL}(2,\mathbb{R}):a,b,c,d,\right.\nonumber\\ \displaystyle & & \displaystyle \left.\qquad e\in \mathbb{Z},e\mid f,e\mid a,e\mid d,f\mid c,ad-bc=e\vphantom{\frac{1}{2}}\right\}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6E4}_{0}(f)^{+} & := & \displaystyle \left\{e^{-1/2}\left(\begin{array}{@{}cc@{}}a & b\\ c & d\end{array}\right)\in \text{SL}(2,\mathbb{R}):a,b,c,d,\right.\nonumber\\ \displaystyle & & \displaystyle \left.\qquad e\in \mathbb{Z},e\mid f,e\mid a,e\mid d,f\mid c,ad-bc=e\vphantom{\frac{1}{2}}\right\}.\nonumber\end{eqnarray}$$
In [Reference Cummins6, Lemma 2.20] it is proved that the parabolic elements of
![]() $\unicode[STIX]{x1D6E4}_{0}(f)^{+}$
have integral entries. Therefore,
$\unicode[STIX]{x1D6E4}_{0}(f)^{+}$
have integral entries. Therefore,
![]() $\unicode[STIX]{x1D6E4}_{0}(f)^{+}$
is a moonshine group. Let
$\unicode[STIX]{x1D6E4}_{0}(f)^{+}$
is a moonshine group. Let
 $\overline{\unicode[STIX]{x1D6E4}_{0}(f)^{+}}=\unicode[STIX]{x1D6E4}_{0}(f)^{+}/\pm I$
. In [Reference Jorgenson, Smajlović and Then20] it is proved that the Riemann surface
$\overline{\unicode[STIX]{x1D6E4}_{0}(f)^{+}}=\unicode[STIX]{x1D6E4}_{0}(f)^{+}/\pm I$
. In [Reference Jorgenson, Smajlović and Then20] it is proved that the Riemann surface
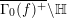 $\overline{\unicode[STIX]{x1D6E4}_{0}(f)^{+}}\backslash \mathbb{H}$
for all square-free
$\overline{\unicode[STIX]{x1D6E4}_{0}(f)^{+}}\backslash \mathbb{H}$
for all square-free
![]() $f$
has finite volume and one cusp at infinity.
$f$
has finite volume and one cusp at infinity.
Consider the case when
![]() $f=5$
. The scattering matrix in this case has a single entry which, as proved in [Reference Jorgenson, Smajlović and Then20] is given by
$f=5$
. The scattering matrix in this case has a single entry which, as proved in [Reference Jorgenson, Smajlović and Then20] is given by
 $$\begin{eqnarray}\unicode[STIX]{x1D6F7}_{5}(s)=\sqrt{\unicode[STIX]{x1D70B}}\frac{\unicode[STIX]{x1D6E4}(s-1/2)}{\unicode[STIX]{x1D6E4}(s)}\left(\frac{5^{s}+5}{5^{s}(5^{s}+1)}\right)\cdot \frac{\unicode[STIX]{x1D701}_{\mathbb{Q}}(2s-1)}{\unicode[STIX]{x1D701}_{\mathbb{Q}}(2s)},\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6F7}_{5}(s)=\sqrt{\unicode[STIX]{x1D70B}}\frac{\unicode[STIX]{x1D6E4}(s-1/2)}{\unicode[STIX]{x1D6E4}(s)}\left(\frac{5^{s}+5}{5^{s}(5^{s}+1)}\right)\cdot \frac{\unicode[STIX]{x1D701}_{\mathbb{Q}}(2s-1)}{\unicode[STIX]{x1D701}_{\mathbb{Q}}(2s)},\end{eqnarray}$$
hence, one immediately can show that
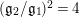 $(\mathfrak{g}_{2}/\mathfrak{g}_{1})^{2}=4$
.
$(\mathfrak{g}_{2}/\mathfrak{g}_{1})^{2}=4$
.
It is easy to confirm that
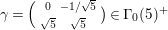 $\unicode[STIX]{x1D6FE}=\Bigl(\begin{smallmatrix}0 & -1/\sqrt{5}\\ \sqrt{5} & \sqrt{5}\end{smallmatrix})\in \unicode[STIX]{x1D6E4}_{0}(5)^{+}$
. The trace of
$\unicode[STIX]{x1D6FE}=\Bigl(\begin{smallmatrix}0 & -1/\sqrt{5}\\ \sqrt{5} & \sqrt{5}\end{smallmatrix})\in \unicode[STIX]{x1D6E4}_{0}(5)^{+}$
. The trace of
![]() $\unicode[STIX]{x1D6FE}$
is
$\unicode[STIX]{x1D6FE}$
is
![]() $\sqrt{5}>2$
, hence
$\sqrt{5}>2$
, hence
![]() $\unicode[STIX]{x1D6FE}$
is hyperbolic. Therefore,
$\unicode[STIX]{x1D6FE}$
is hyperbolic. Therefore,
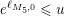 $e^{\ell _{M_{5},0}}\leqslant u$
where
$e^{\ell _{M_{5},0}}\leqslant u$
where
![]() $u$
is a positive solution of
$u$
is a positive solution of
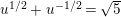 $u^{1/2}+u^{-1/2}=\sqrt{5}$
. Solving, we have that
$u^{1/2}+u^{-1/2}=\sqrt{5}$
. Solving, we have that
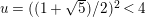 $u=((1+\sqrt{5})/2)^{2}<4$
.
$u=((1+\sqrt{5})/2)^{2}<4$
.
With all this, we have proved that
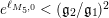 $e^{\ell _{M_{5},0}}<(\mathfrak{g}_{2}/\mathfrak{g}_{1})^{2}$
.
$e^{\ell _{M_{5},0}}<(\mathfrak{g}_{2}/\mathfrak{g}_{1})^{2}$
.
The surface
 $\overline{\unicode[STIX]{x1D6E4}_{0}(5)^{+}}\backslash \mathbb{H}$
has a signature (0;2,2,2;1) meaning that its genus is zero, it has three inequivalent elliptic points of order two and one cusp. The surface
$\overline{\unicode[STIX]{x1D6E4}_{0}(5)^{+}}\backslash \mathbb{H}$
has a signature (0;2,2,2;1) meaning that its genus is zero, it has three inequivalent elliptic points of order two and one cusp. The surface
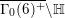 $\overline{\unicode[STIX]{x1D6E4}_{0}(6)^{+}}\backslash \mathbb{H}$
has the same signature, as shown in [Reference Cummins6, Table C]. The scattering matrix in this case has a single entry which is given by
$\overline{\unicode[STIX]{x1D6E4}_{0}(6)^{+}}\backslash \mathbb{H}$
has the same signature, as shown in [Reference Cummins6, Table C]. The scattering matrix in this case has a single entry which is given by
 $$\begin{eqnarray}\unicode[STIX]{x1D6F7}_{6}(s)=\sqrt{\unicode[STIX]{x1D70B}}\frac{\unicode[STIX]{x1D6E4}(s-1/2)}{\unicode[STIX]{x1D6E4}(s)}\left(\frac{(2^{s}+2)(3^{s}+3)}{6^{s}(2^{s}+1)(3^{s}+1)}\right)\cdot \frac{\unicode[STIX]{x1D701}_{\mathbb{Q}}(2s-1)}{\unicode[STIX]{x1D701}_{\mathbb{Q}}(2s)}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6F7}_{6}(s)=\sqrt{\unicode[STIX]{x1D70B}}\frac{\unicode[STIX]{x1D6E4}(s-1/2)}{\unicode[STIX]{x1D6E4}(s)}\left(\frac{(2^{s}+2)(3^{s}+3)}{6^{s}(2^{s}+1)(3^{s}+1)}\right)\cdot \frac{\unicode[STIX]{x1D701}_{\mathbb{Q}}(2s-1)}{\unicode[STIX]{x1D701}_{\mathbb{Q}}(2s)}.\end{eqnarray}$$
Obviously,
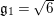 $\mathfrak{g}_{1}=\sqrt{6}$
,
$\mathfrak{g}_{1}=\sqrt{6}$
,
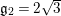 $\mathfrak{g}_{2}=2\sqrt{3}$
, hence
$\mathfrak{g}_{2}=2\sqrt{3}$
, hence
 $(\mathfrak{g}_{2}/\mathfrak{g}_{1})^{2}=2$
.
$(\mathfrak{g}_{2}/\mathfrak{g}_{1})^{2}=2$
.
On the other hand,
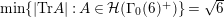 $\min \{|\text{Tr}A|:A\in {\mathcal{H}}(\unicode[STIX]{x1D6E4}_{0}(6)^{+})\}=\sqrt{6}$
, hence
$\min \{|\text{Tr}A|:A\in {\mathcal{H}}(\unicode[STIX]{x1D6E4}_{0}(6)^{+})\}=\sqrt{6}$
, hence
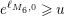 $e^{\ell _{M_{6},0}}\geqslant u$
where
$e^{\ell _{M_{6},0}}\geqslant u$
where
![]() $u>1$
is a solution of the equation
$u>1$
is a solution of the equation
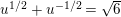 $u^{1/2}+u^{-1/2}=\sqrt{6}$
. Since
$u^{1/2}+u^{-1/2}=\sqrt{6}$
. Since
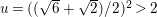 $u=((\sqrt{6}+\sqrt{2})/2)^{2}>2$
, we see that
$u=((\sqrt{6}+\sqrt{2})/2)^{2}>2$
, we see that
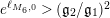 $e^{\ell _{M_{6},0}}>(\mathfrak{g}_{2}/\mathfrak{g}_{1})^{2}$
. This completes the proof of Proposition 1(ii).
$e^{\ell _{M_{6},0}}>(\mathfrak{g}_{2}/\mathfrak{g}_{1})^{2}$
. This completes the proof of Proposition 1(ii).
7.3 On existence of surfaces where
 $e^{\ell _{M,0}}=(\mathfrak{g}_{2}/\mathfrak{g}_{1})^{2}$
$e^{\ell _{M,0}}=(\mathfrak{g}_{2}/\mathfrak{g}_{1})^{2}$
We now argue the existence of an abundance of surfaces for which
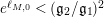 $e^{\ell _{M,0}}<(\mathfrak{g}_{2}/\mathfrak{g}_{1})^{2}$
and prove part (iii) of Proposition 1.
$e^{\ell _{M,0}}<(\mathfrak{g}_{2}/\mathfrak{g}_{1})^{2}$
and prove part (iii) of Proposition 1.
Let
![]() $M_{\unicode[STIX]{x1D70F}}$
denote a degenerating family of Riemann surfaces, parameterized by the holomorphic parameter
$M_{\unicode[STIX]{x1D70F}}$
denote a degenerating family of Riemann surfaces, parameterized by the holomorphic parameter
![]() $\unicode[STIX]{x1D70F}$
, which approach the Deligne–Mumford boundary of moduli space when
$\unicode[STIX]{x1D70F}$
, which approach the Deligne–Mumford boundary of moduli space when
![]() $\unicode[STIX]{x1D70F}$
approaches zero. One can select distinguished points of
$\unicode[STIX]{x1D70F}$
approaches zero. One can select distinguished points of
![]() $M_{\unicode[STIX]{x1D70F}}$
which are either removed or whose local coordinates
$M_{\unicode[STIX]{x1D70F}}$
which are either removed or whose local coordinates
![]() $z$
are replaced by fractional powers
$z$
are replaced by fractional powers
![]() $z^{1/n}$
. By doing so, one obtains a degenerating sequence of hyperbolic Riemann surfaces of any signature; we refer the reader to [Reference Huntley, Jorgenson and Lundelius15] and references therein for further details regarding the construction of the sequence of degenerating hyperbolic Riemann surfaces.
$z^{1/n}$
. By doing so, one obtains a degenerating sequence of hyperbolic Riemann surfaces of any signature; we refer the reader to [Reference Huntley, Jorgenson and Lundelius15] and references therein for further details regarding the construction of the sequence of degenerating hyperbolic Riemann surfaces.
By construction, the length of the smallest geodesic on
![]() $M_{\ell }$
approaches zero, so then
$M_{\ell }$
approaches zero, so then
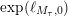 $\exp (\ell _{M_{\unicode[STIX]{x1D70F}},0})$
approaches one as
$\exp (\ell _{M_{\unicode[STIX]{x1D70F}},0})$
approaches one as
![]() $\unicode[STIX]{x1D70F}$
approaches zero. In [Reference Garbin, Jorgenson and Munn9], the authors prove that through degeneration, parabolic Eisenstein series on
$\unicode[STIX]{x1D70F}$
approaches zero. In [Reference Garbin, Jorgenson and Munn9], the authors prove that through degeneration, parabolic Eisenstein series on
![]() $M_{\unicode[STIX]{x1D70F}}$
converge to parabolic Eisenstein series on the limit surface; see part (ii) of the Main Theorem of [Reference Garbin, Jorgenson and Munn9]. To be precise, one needs that the holomorphic parameter
$M_{\unicode[STIX]{x1D70F}}$
converge to parabolic Eisenstein series on the limit surface; see part (ii) of the Main Theorem of [Reference Garbin, Jorgenson and Munn9]. To be precise, one needs that the holomorphic parameter
![]() $s$
of the parabolic Eisenstein series lies in the half-plane
$s$
of the parabolic Eisenstein series lies in the half-plane
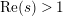 $\text{Re}(s)>1$
and the spatial parameter
$\text{Re}(s)>1$
and the spatial parameter
![]() $z$
to lie in a bounded region of
$z$
to lie in a bounded region of
![]() $M_{\unicode[STIX]{x1D70F}}$
. However, in these ranges, one can compute the scattering matrix by computing the zeroth Fourier coefficient of the parabolic Eisenstein series, and, subsequently, compute the ratio
$M_{\unicode[STIX]{x1D70F}}$
. However, in these ranges, one can compute the scattering matrix by computing the zeroth Fourier coefficient of the parabolic Eisenstein series, and, subsequently, compute the ratio
![]() $\mathfrak{g}_{2}/\mathfrak{g}_{1}$
on
$\mathfrak{g}_{2}/\mathfrak{g}_{1}$
on
![]() $M_{\unicode[STIX]{x1D70F}}$
. Since the parabolic Eisenstein series converge through degeneration to the parabolic Eisenstein series on the limit surface, the associated scattering matrix converges to a submatrix
$M_{\unicode[STIX]{x1D70F}}$
. Since the parabolic Eisenstein series converge through degeneration to the parabolic Eisenstein series on the limit surface, the associated scattering matrix converges to a submatrix
![]() $\unicode[STIX]{x1D6F7}$
of the full scattering matrix on the limit surface. Clearly, the determinant of
$\unicode[STIX]{x1D6F7}$
of the full scattering matrix on the limit surface. Clearly, the determinant of
![]() $\unicode[STIX]{x1D6F7}$
can be decomposed into a product of Gamma functions and a Dirichlet series, where the Dirichlet series is such that
$\unicode[STIX]{x1D6F7}$
can be decomposed into a product of Gamma functions and a Dirichlet series, where the Dirichlet series is such that
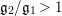 $\mathfrak{g}_{2}/\mathfrak{g}_{1}>1$
.
$\mathfrak{g}_{2}/\mathfrak{g}_{1}>1$
.
Therefore, we conclude that for all
![]() $\unicode[STIX]{x1D70F}$
sufficiently close to zero, we have that
$\unicode[STIX]{x1D70F}$
sufficiently close to zero, we have that
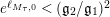 $e^{\ell _{M_{\unicode[STIX]{x1D70F}},0}}<(\mathfrak{g}_{2}/\mathfrak{g}_{1})^{2}$
. In fact, all surfaces near the Deligne–Mumford boundary of any given moduli space satisfy the inequality
$e^{\ell _{M_{\unicode[STIX]{x1D70F}},0}}<(\mathfrak{g}_{2}/\mathfrak{g}_{1})^{2}$
. In fact, all surfaces near the Deligne–Mumford boundary of any given moduli space satisfy the inequality
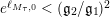 $e^{\ell _{M_{\unicode[STIX]{x1D70F}},0}}<(\mathfrak{g}_{2}/\mathfrak{g}_{1})^{2}$
.
$e^{\ell _{M_{\unicode[STIX]{x1D70F}},0}}<(\mathfrak{g}_{2}/\mathfrak{g}_{1})^{2}$
.
In addition, let us assume that one is considering a moduli space which contains a congruence subgroup so then there exists a surface where
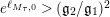 $e^{\ell _{M_{\unicode[STIX]{x1D70F}},0}}>(\mathfrak{g}_{2}/\mathfrak{g}_{1})^{2}$
. Then by combining the above argument with the computations from § 7.1, there exists surfaces for which
$e^{\ell _{M_{\unicode[STIX]{x1D70F}},0}}>(\mathfrak{g}_{2}/\mathfrak{g}_{1})^{2}$
. Then by combining the above argument with the computations from § 7.1, there exists surfaces for which
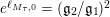 $e^{\ell _{M_{\unicode[STIX]{x1D70F}},0}}=(\mathfrak{g}_{2}/\mathfrak{g}_{1})^{2}$
. However, we have not been successful in our attempts to explicitly construct such a surface. In a sense, our Main Theorem shows that surfaces for which
$e^{\ell _{M_{\unicode[STIX]{x1D70F}},0}}=(\mathfrak{g}_{2}/\mathfrak{g}_{1})^{2}$
. However, we have not been successful in our attempts to explicitly construct such a surface. In a sense, our Main Theorem shows that surfaces for which
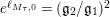 $e^{\ell _{M_{\unicode[STIX]{x1D70F}},0}}=(\mathfrak{g}_{2}/\mathfrak{g}_{1})^{2}$
have a larger number of zeros of
$e^{\ell _{M_{\unicode[STIX]{x1D70F}},0}}=(\mathfrak{g}_{2}/\mathfrak{g}_{1})^{2}$
have a larger number of zeros of
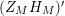 $(Z_{M}H_{M})^{\prime }$
than nearby surfaces for which the inequality holds.
$(Z_{M}H_{M})^{\prime }$
than nearby surfaces for which the inequality holds.
8 Higher derivatives
In this section, we outline the proof of the Main Theorem for higher order derivatives of
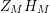 $Z_{M}H_{M}$
. The results are analogous to theorems proved for the zeros of the higher order derivatives of the Riemann zeta function; see [Reference Berndt4] and [Reference Levinson and Montgomery21].
$Z_{M}H_{M}$
. The results are analogous to theorems proved for the zeros of the higher order derivatives of the Riemann zeta function; see [Reference Berndt4] and [Reference Levinson and Montgomery21].
8.1 Preliminary lemmas on higher derivatives
In order to deduce the vertical and weighted vertical distribution of zeros of the higher order derivatives of
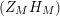 $(Z_{M}H_{M})$
we prove some preliminary lemmas, analogous to lemmas in § 4.
$(Z_{M}H_{M})$
we prove some preliminary lemmas, analogous to lemmas in § 4.
Lemma 18. Let
![]() $f_{M}(s)$
be defined by (18) and
$f_{M}(s)$
be defined by (18) and
![]() $\widetilde{Z}_{M}(s)$
defined by (19). Let us define, inductively, the functions
$\widetilde{Z}_{M}(s)$
defined by (19). Let us define, inductively, the functions
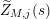 $\widetilde{Z}_{M,j}(s)$
as
$\widetilde{Z}_{M,j}(s)$
as
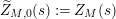 $\widetilde{Z}_{M,0}(s):=Z_{M}(s)$
,
$\widetilde{Z}_{M,0}(s):=Z_{M}(s)$
,
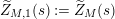 $\widetilde{Z}_{M,1}(s):=\widetilde{Z}_{M}(s)$
and, for
$\widetilde{Z}_{M,1}(s):=\widetilde{Z}_{M}(s)$
and, for
![]() $j\geqslant 2$
,
$j\geqslant 2$
,
 $$\begin{eqnarray}\displaystyle \widetilde{Z}_{M,j}(1-s)=\frac{1}{f_{M}(s)}\!\left(\!(j-1)\frac{f_{M}^{\prime }}{f_{M}}(s)+\frac{\unicode[STIX]{x1D702}_{M}^{\prime }}{\unicode[STIX]{x1D702}_{M}}(s)-\frac{K_{M}^{\prime }}{K_{M}}(s)-\!\overset{j-1}{\underset{i=0}{\sum }}\frac{\widetilde{Z}_{M,i}^{\prime }}{\widetilde{Z}_{M,i}}(1-s)\!\right)\!. & & \displaystyle \nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \widetilde{Z}_{M,j}(1-s)=\frac{1}{f_{M}(s)}\!\left(\!(j-1)\frac{f_{M}^{\prime }}{f_{M}}(s)+\frac{\unicode[STIX]{x1D702}_{M}^{\prime }}{\unicode[STIX]{x1D702}_{M}}(s)-\frac{K_{M}^{\prime }}{K_{M}}(s)-\!\overset{j-1}{\underset{i=0}{\sum }}\frac{\widetilde{Z}_{M,i}^{\prime }}{\widetilde{Z}_{M,i}}(1-s)\!\right)\!. & & \displaystyle \nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
Then for every positive integer
![]() $k$
the
$k$
the
![]() $k$
th derivative of the function
$k$
th derivative of the function
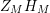 $Z_{M}H_{M}$
can be represented as
$Z_{M}H_{M}$
can be represented as
 $$\begin{eqnarray}(Z_{M}H_{M})^{(k)}(s)=\left(f_{M}(s)\right)^{k}\unicode[STIX]{x1D702}_{M}(s)K_{M}^{-1}(s)Z_{M}(1-s)\overset{k}{\underset{i=1}{\prod }}\widetilde{Z}_{M,i}(1-s).\end{eqnarray}$$
$$\begin{eqnarray}(Z_{M}H_{M})^{(k)}(s)=\left(f_{M}(s)\right)^{k}\unicode[STIX]{x1D702}_{M}(s)K_{M}^{-1}(s)Z_{M}(1-s)\overset{k}{\underset{i=1}{\prod }}\widetilde{Z}_{M,i}(1-s).\end{eqnarray}$$
Proof. The proof is based on a rather obvious induction argument.◻
Lemma 19. For
![]() $j\geqslant 1$
, let
$j\geqslant 1$
, let
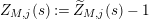 $Z_{M,j}(s):=\widetilde{Z}_{M,j}(s)-1$
. For small
$Z_{M,j}(s):=\widetilde{Z}_{M,j}(s)-1$
. For small
![]() $\unicode[STIX]{x1D6FF}>0$
and
$\unicode[STIX]{x1D6FF}>0$
and
![]() $\unicode[STIX]{x1D6FF}_{1}>0$
, let
$\unicode[STIX]{x1D6FF}_{1}>0$
, let
![]() $\unicode[STIX]{x1D70E}_{1}$
be a real number such that
$\unicode[STIX]{x1D70E}_{1}$
be a real number such that
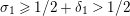 $\unicode[STIX]{x1D70E}_{1}\geqslant 1/2+\unicode[STIX]{x1D6FF}_{1}>1/2$
and
$\unicode[STIX]{x1D70E}_{1}\geqslant 1/2+\unicode[STIX]{x1D6FF}_{1}>1/2$
and
 $(\unicode[STIX]{x1D70E}_{1}\pm iT)$
is away from circles of a fixed, small radius
$(\unicode[STIX]{x1D70E}_{1}\pm iT)$
is away from circles of a fixed, small radius
![]() $\unicode[STIX]{x1D6FF}>0$
, centered at integers. Then for
$\unicode[STIX]{x1D6FF}>0$
, centered at integers. Then for
![]() $k=0,1$
$k=0,1$
 $$\begin{eqnarray}Z_{M,j}^{(k)}(\unicode[STIX]{x1D70E}_{1}\pm iT)=O\left(\frac{(T\log T)^{2-2\unicode[STIX]{x1D70E}_{1}}\log ^{k}T}{(\unicode[STIX]{x1D70E}_{1}-1/2)T}\right)\quad \text{as }T\rightarrow \infty ,\end{eqnarray}$$
$$\begin{eqnarray}Z_{M,j}^{(k)}(\unicode[STIX]{x1D70E}_{1}\pm iT)=O\left(\frac{(T\log T)^{2-2\unicode[STIX]{x1D70E}_{1}}\log ^{k}T}{(\unicode[STIX]{x1D70E}_{1}-1/2)T}\right)\quad \text{as }T\rightarrow \infty ,\end{eqnarray}$$
and
 $$\begin{eqnarray}\frac{\widetilde{Z}_{M,j}^{\prime }}{\widetilde{Z}_{M,j}}(\unicode[STIX]{x1D70E}_{1}\pm iT)=O\left(\frac{(T\log T)^{2-2\unicode[STIX]{x1D70E}_{1}}\log T}{(\unicode[STIX]{x1D70E}_{1}-1/2)T}\right)\quad \text{as }T\rightarrow \infty .\end{eqnarray}$$
$$\begin{eqnarray}\frac{\widetilde{Z}_{M,j}^{\prime }}{\widetilde{Z}_{M,j}}(\unicode[STIX]{x1D70E}_{1}\pm iT)=O\left(\frac{(T\log T)^{2-2\unicode[STIX]{x1D70E}_{1}}\log T}{(\unicode[STIX]{x1D70E}_{1}-1/2)T}\right)\quad \text{as }T\rightarrow \infty .\end{eqnarray}$$
Proof. We prove the statement by induction in
![]() $j\geqslant 1$
. When
$j\geqslant 1$
. When
![]() $j=1$
, we use formula (26), which we differentiate, use the bound on the growth of the derivative of the digamma function (see [Reference Abramowitz and Stegun1, formula 6.4.12.]) and the bound (20) with
$j=1$
, we use formula (26), which we differentiate, use the bound on the growth of the derivative of the digamma function (see [Reference Abramowitz and Stegun1, formula 6.4.12.]) and the bound (20) with
![]() $k=0$
or
$k=0$
or
![]() $k=1$
. These computations, which are elementary, allow one to prove (58) for
$k=1$
. These computations, which are elementary, allow one to prove (58) for
 $\unicode[STIX]{x1D70E}_{1}\geqslant 1/2+\unicode[STIX]{x1D6FF}_{1}>1/2$
in the case when
$\unicode[STIX]{x1D70E}_{1}\geqslant 1/2+\unicode[STIX]{x1D6FF}_{1}>1/2$
in the case when
![]() $j=1$
. In addition,
$j=1$
. In addition,
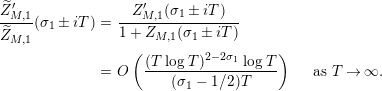 $$\begin{eqnarray}\displaystyle \frac{\widetilde{Z}_{M,1}^{\prime }}{\widetilde{Z}_{M,1}}(\unicode[STIX]{x1D70E}_{1}\pm iT) & = & \displaystyle \frac{Z_{M,1}^{\prime }(\unicode[STIX]{x1D70E}_{1}\pm iT)}{1+Z_{M,1}(\unicode[STIX]{x1D70E}_{1}\pm iT)}\nonumber\\ \displaystyle & = & \displaystyle O\left(\frac{(T\log T)^{2-2\unicode[STIX]{x1D70E}_{1}}\log T}{(\unicode[STIX]{x1D70E}_{1}-1/2)T}\right)\quad \text{ as }T\rightarrow \infty .\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \frac{\widetilde{Z}_{M,1}^{\prime }}{\widetilde{Z}_{M,1}}(\unicode[STIX]{x1D70E}_{1}\pm iT) & = & \displaystyle \frac{Z_{M,1}^{\prime }(\unicode[STIX]{x1D70E}_{1}\pm iT)}{1+Z_{M,1}(\unicode[STIX]{x1D70E}_{1}\pm iT)}\nonumber\\ \displaystyle & = & \displaystyle O\left(\frac{(T\log T)^{2-2\unicode[STIX]{x1D70E}_{1}}\log T}{(\unicode[STIX]{x1D70E}_{1}-1/2)T}\right)\quad \text{ as }T\rightarrow \infty .\nonumber\end{eqnarray}$$
With all this, we have proved (59) for
![]() $j=1$
.
$j=1$
.
Assume now that (58) and (59) hold true for all
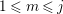 $1\leqslant m\leqslant j$
. Then, by (56) we get
$1\leqslant m\leqslant j$
. Then, by (56) we get
 $$\begin{eqnarray}1+Z_{M,j+1}(s)=\widetilde{Z}_{M,j+1}(s)=1+Z_{M,j}(s)+\frac{1}{f_{M}(s)}\left(\frac{f_{M}^{\prime }}{f_{M}}(s)-\frac{\widetilde{Z}_{M,k,j}^{\prime }}{\widetilde{Z}_{M,j}}(s)\right).\end{eqnarray}$$
$$\begin{eqnarray}1+Z_{M,j+1}(s)=\widetilde{Z}_{M,j+1}(s)=1+Z_{M,j}(s)+\frac{1}{f_{M}(s)}\left(\frac{f_{M}^{\prime }}{f_{M}}(s)-\frac{\widetilde{Z}_{M,k,j}^{\prime }}{\widetilde{Z}_{M,j}}(s)\right).\end{eqnarray}$$
Therefore, by the inductive assumption on
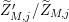 $\widetilde{Z}_{M,j}^{\prime }/\widetilde{Z}_{M,j}$
and
$\widetilde{Z}_{M,j}^{\prime }/\widetilde{Z}_{M,j}$
and
![]() $Z_{M,j}$
, we have for
$Z_{M,j}$
, we have for
![]() $k=0,1$
,
$k=0,1$
,
 $$\begin{eqnarray}Z_{M,j+1}^{(k)}(\unicode[STIX]{x1D70E}_{1}\pm iT)=O\left(\frac{(T\log T)^{2-2\unicode[STIX]{x1D70E}_{1}}\log ^{k}T}{(\unicode[STIX]{x1D70E}_{1}-1/2)T}\right)\quad \text{ as }T\rightarrow \infty .\end{eqnarray}$$
$$\begin{eqnarray}Z_{M,j+1}^{(k)}(\unicode[STIX]{x1D70E}_{1}\pm iT)=O\left(\frac{(T\log T)^{2-2\unicode[STIX]{x1D70E}_{1}}\log ^{k}T}{(\unicode[STIX]{x1D70E}_{1}-1/2)T}\right)\quad \text{ as }T\rightarrow \infty .\end{eqnarray}$$
In other words, (58) holds true with
 $m=j+1$
. In addition,
$m=j+1$
. In addition,
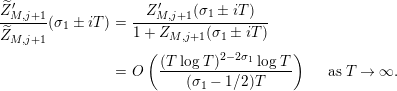 $$\begin{eqnarray}\displaystyle \frac{\widetilde{Z}_{M,j+1}^{\prime }}{\widetilde{Z}_{M,j+1}}(\unicode[STIX]{x1D70E}_{1}\pm iT) & = & \displaystyle \frac{Z_{M,j+1}^{\prime }(\unicode[STIX]{x1D70E}_{1}\pm iT)}{1+Z_{M,j+1}(\unicode[STIX]{x1D70E}_{1}\pm iT)}\nonumber\\ \displaystyle & = & \displaystyle O\left(\frac{(T\log T)^{2-2\unicode[STIX]{x1D70E}_{1}}\log T}{(\unicode[STIX]{x1D70E}_{1}-1/2)T}\right)\quad \text{ as }T\rightarrow \infty .\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \frac{\widetilde{Z}_{M,j+1}^{\prime }}{\widetilde{Z}_{M,j+1}}(\unicode[STIX]{x1D70E}_{1}\pm iT) & = & \displaystyle \frac{Z_{M,j+1}^{\prime }(\unicode[STIX]{x1D70E}_{1}\pm iT)}{1+Z_{M,j+1}(\unicode[STIX]{x1D70E}_{1}\pm iT)}\nonumber\\ \displaystyle & = & \displaystyle O\left(\frac{(T\log T)^{2-2\unicode[STIX]{x1D70E}_{1}}\log T}{(\unicode[STIX]{x1D70E}_{1}-1/2)T}\right)\quad \text{ as }T\rightarrow \infty .\nonumber\end{eqnarray}$$
The proof is complete.◻
For any integer
![]() $k\geqslant 2$
, let us define
$k\geqslant 2$
, let us define
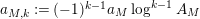 $a_{M,k}:=(-1)^{k-1}a_{M}\log ^{k-1}A_{M}$
, where we set
$a_{M,k}:=(-1)^{k-1}a_{M}\log ^{k-1}A_{M}$
, where we set
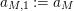 $a_{M,1}:=a_{M}$
. The analogue of the function
$a_{M,1}:=a_{M}$
. The analogue of the function
![]() $X_{M}(s)$
, defined by (12), is
$X_{M}(s)$
, defined by (12), is
 $$\begin{eqnarray}X_{M,k}(s):=\frac{A_{M}^{s}}{a_{M,k}}(Z_{M}H_{M})^{(k)}(s),\end{eqnarray}$$
$$\begin{eqnarray}X_{M,k}(s):=\frac{A_{M}^{s}}{a_{M,k}}(Z_{M}H_{M})^{(k)}(s),\end{eqnarray}$$
where, of course,
 $X_{M,1}(s)=X_{M}(s)$
.
$X_{M,1}(s)=X_{M}(s)$
.
Lemma 20. For any integer
![]() $k\geqslant 1$
, there exists constants
$k\geqslant 1$
, there exists constants
![]() $\unicode[STIX]{x1D70E}_{k}>1$
and
$\unicode[STIX]{x1D70E}_{k}>1$
and
 $0<c_{\unicode[STIX]{x1D6E4},k}<1$
such that for all
$0<c_{\unicode[STIX]{x1D6E4},k}<1$
such that for all
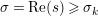 $\unicode[STIX]{x1D70E}=\operatorname{Re}(s)\geqslant \unicode[STIX]{x1D70E}_{k}$
,
$\unicode[STIX]{x1D70E}=\operatorname{Re}(s)\geqslant \unicode[STIX]{x1D70E}_{k}$
,
 $$\begin{eqnarray}X_{M,k}(s)=1+O(c_{\unicode[STIX]{x1D6E4},k}^{\unicode[STIX]{x1D70E}})\neq 0\quad \text{ as }\unicode[STIX]{x1D70E}\rightarrow +\infty .\end{eqnarray}$$
$$\begin{eqnarray}X_{M,k}(s)=1+O(c_{\unicode[STIX]{x1D6E4},k}^{\unicode[STIX]{x1D70E}})\neq 0\quad \text{ as }\unicode[STIX]{x1D70E}\rightarrow +\infty .\end{eqnarray}$$
Proof. For
![]() $k=1$
, the statement is Lemma 10. Furthermore, from the proof of Lemma 10 and the definition of constants
$k=1$
, the statement is Lemma 10. Furthermore, from the proof of Lemma 10 and the definition of constants
![]() $A_{M}$
and
$A_{M}$
and
![]() $a_{M,1}$
, we see that
$a_{M,1}$
, we see that
 $$\begin{eqnarray}(Z_{M}H_{M})^{\prime }(s)=Z_{M}(s)H_{M}(s){\mathcal{D}}_{1}(s),\end{eqnarray}$$
$$\begin{eqnarray}(Z_{M}H_{M})^{\prime }(s)=Z_{M}(s)H_{M}(s){\mathcal{D}}_{1}(s),\end{eqnarray}$$
where
![]() ${\mathcal{D}}_{1}(s)$
is a Dirichlet series, converging absolutely for
${\mathcal{D}}_{1}(s)$
is a Dirichlet series, converging absolutely for
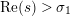 $\text{Re}(s)>\unicode[STIX]{x1D70E}_{1}$
, for sufficiently large
$\text{Re}(s)>\unicode[STIX]{x1D70E}_{1}$
, for sufficiently large
![]() $\unicode[STIX]{x1D70E}_{1}$
, with the leading term equal to
$\unicode[STIX]{x1D70E}_{1}$
, with the leading term equal to
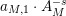 $a_{M,1}\cdot A_{M}^{-s}$
as
$a_{M,1}\cdot A_{M}^{-s}$
as
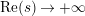 $\operatorname{Re}(s)\rightarrow +\infty$
.
$\operatorname{Re}(s)\rightarrow +\infty$
.
Let us define, for
![]() $k\geqslant 1$
and
$k\geqslant 1$
and
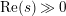 $\operatorname{Re}(s)\gg 0$
$\operatorname{Re}(s)\gg 0$
 $$\begin{eqnarray}(Z_{M}H_{M})^{(k)}(s)=Z_{M}(s)H_{M}(s){\mathcal{D}}_{k}(s).\end{eqnarray}$$
$$\begin{eqnarray}(Z_{M}H_{M})^{(k)}(s)=Z_{M}(s)H_{M}(s){\mathcal{D}}_{k}(s).\end{eqnarray}$$
We claim that
![]() ${\mathcal{D}}_{k}(s)$
is a Dirichlet series with the leading term equal to
${\mathcal{D}}_{k}(s)$
is a Dirichlet series with the leading term equal to
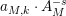 $a_{M,k}\cdot A_{M}^{-s}$
as
$a_{M,k}\cdot A_{M}^{-s}$
as
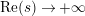 $\operatorname{Re}(s)\rightarrow +\infty$
. The statement is obviously true for
$\operatorname{Re}(s)\rightarrow +\infty$
. The statement is obviously true for
![]() $k=1$
. A simple inductive argument shows that the statement is true for all
$k=1$
. A simple inductive argument shows that the statement is true for all
![]() $k\geqslant 1$
. Therefore, for
$k\geqslant 1$
. Therefore, for
 $\operatorname{Re}(s)=\unicode[STIX]{x1D70E}\gg 0$
, we may write
$\operatorname{Re}(s)=\unicode[STIX]{x1D70E}\gg 0$
, we may write
 $$\begin{eqnarray}(Z_{M}H_{M})^{(k)}(s)=Z_{M}(s)H_{M}(s)\frac{a_{M,k}}{A_{M}^{s}}\left(1+O(A_{\unicode[STIX]{x1D6E4},k}^{-\unicode[STIX]{x1D70E}})\right)\quad \text{ as }\operatorname{Re}(s)\rightarrow \infty .\end{eqnarray}$$
$$\begin{eqnarray}(Z_{M}H_{M})^{(k)}(s)=Z_{M}(s)H_{M}(s)\frac{a_{M,k}}{A_{M}^{s}}\left(1+O(A_{\unicode[STIX]{x1D6E4},k}^{-\unicode[STIX]{x1D70E}})\right)\quad \text{ as }\operatorname{Re}(s)\rightarrow \infty .\end{eqnarray}$$
Equation (32) implies that there exists
![]() $\unicode[STIX]{x1D70E}_{k}\geqslant 1$
and a constant
$\unicode[STIX]{x1D70E}_{k}\geqslant 1$
and a constant
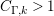 $C_{\unicode[STIX]{x1D6E4},k}>1$
such that for
$C_{\unicode[STIX]{x1D6E4},k}>1$
such that for
 $\operatorname{Re}s>\unicode[STIX]{x1D70E}_{k}$
, we have
$\operatorname{Re}s>\unicode[STIX]{x1D70E}_{k}$
, we have
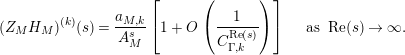 $$\begin{eqnarray}(Z_{M}H_{M})^{(k)}(s)=\frac{a_{M,k}}{A_{M}^{s}}\left[1+O\left(\frac{1}{C_{\unicode[STIX]{x1D6E4},k}^{\operatorname{Re}(s)}}\right)\right]\quad \text{ as }\operatorname{Re}(s)\rightarrow \infty .\end{eqnarray}$$
$$\begin{eqnarray}(Z_{M}H_{M})^{(k)}(s)=\frac{a_{M,k}}{A_{M}^{s}}\left[1+O\left(\frac{1}{C_{\unicode[STIX]{x1D6E4},k}^{\operatorname{Re}(s)}}\right)\right]\quad \text{ as }\operatorname{Re}(s)\rightarrow \infty .\end{eqnarray}$$
Setting
 $c_{\unicode[STIX]{x1D6E4},k}=1/C_{\unicode[STIX]{x1D6E4},k}$
completes the proof.◻
$c_{\unicode[STIX]{x1D6E4},k}=1/C_{\unicode[STIX]{x1D6E4},k}$
completes the proof.◻
Lemma 21. For arbitrary
![]() $\unicode[STIX]{x1D716}>0$
,
$\unicode[STIX]{x1D716}>0$
,
![]() $t\geqslant 1$
and
$t\geqslant 1$
and
![]() $\unicode[STIX]{x1D70E}_{2}\geqslant 1$
such that
$\unicode[STIX]{x1D70E}_{2}\geqslant 1$
such that
![]() $-\unicode[STIX]{x1D70E}_{2}$
is not a pole of
$-\unicode[STIX]{x1D70E}_{2}$
is not a pole of
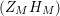 $(Z_{M}H_{M})$
we have, for any positive integer
$(Z_{M}H_{M})$
we have, for any positive integer
![]() $k$
$k$
 $$\begin{eqnarray}(Z_{M}H_{M})^{(k)}(\unicode[STIX]{x1D70E}+it)=\left\{\begin{array}{@{}ll@{}}O(\exp \unicode[STIX]{x1D716}t) & \text{ for }\frac{1}{2}\leqslant \unicode[STIX]{x1D70E}\leqslant \unicode[STIX]{x1D70E}_{0},\\ O\left(\exp (1/2-\unicode[STIX]{x1D70E}+\unicode[STIX]{x1D716})t\right) & \text{ for }-\unicode[STIX]{x1D70E}_{2}\leqslant \unicode[STIX]{x1D70E}<1/2,\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}(Z_{M}H_{M})^{(k)}(\unicode[STIX]{x1D70E}+it)=\left\{\begin{array}{@{}ll@{}}O(\exp \unicode[STIX]{x1D716}t) & \text{ for }\frac{1}{2}\leqslant \unicode[STIX]{x1D70E}\leqslant \unicode[STIX]{x1D70E}_{0},\\ O\left(\exp (1/2-\unicode[STIX]{x1D70E}+\unicode[STIX]{x1D716})t\right) & \text{ for }-\unicode[STIX]{x1D70E}_{2}\leqslant \unicode[STIX]{x1D70E}<1/2,\end{array}\right.\end{eqnarray}$$
as
![]() $t\rightarrow \infty$
.
$t\rightarrow \infty$
.
Proof. When
![]() $k=1$
, the statement is proved in Lemma 14. Assume that the statement of Lemma holds for an integer
$k=1$
, the statement is proved in Lemma 14. Assume that the statement of Lemma holds for an integer
![]() $k\geqslant 1$
. Then for
$k\geqslant 1$
. Then for
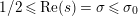 $1/2\leqslant \operatorname{Re}(s)=\unicode[STIX]{x1D70E}\leqslant \unicode[STIX]{x1D70E}_{0}$
the Cauchy integral formula yields
$1/2\leqslant \operatorname{Re}(s)=\unicode[STIX]{x1D70E}\leqslant \unicode[STIX]{x1D70E}_{0}$
the Cauchy integral formula yields
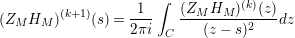 $$\begin{eqnarray}(Z_{M}H_{M})^{(k+1)}(s)=\frac{1}{2\unicode[STIX]{x1D70B}i}\int _{C}\frac{(Z_{M}H_{M})^{(k)}(z)}{(z-s)^{2}}dz\end{eqnarray}$$
$$\begin{eqnarray}(Z_{M}H_{M})^{(k+1)}(s)=\frac{1}{2\unicode[STIX]{x1D70B}i}\int _{C}\frac{(Z_{M}H_{M})^{(k)}(z)}{(z-s)^{2}}dz\end{eqnarray}$$
where
![]() $C$
is a circle of a small, fixed radius
$C$
is a circle of a small, fixed radius
![]() $r<\unicode[STIX]{x1D716}$
, centered at
$r<\unicode[STIX]{x1D716}$
, centered at
![]() $s$
. Using the inductive assumption on
$s$
. Using the inductive assumption on
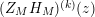 $(Z_{M}H_{M})^{(k)}(z)$
, we then get the bounds
$(Z_{M}H_{M})^{(k)}(z)$
, we then get the bounds
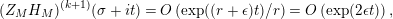 $$\begin{eqnarray}(Z_{M}H_{M})^{(k+1)}(\unicode[STIX]{x1D70E}+it)=O\left(\exp ((r+\unicode[STIX]{x1D716})t)/r\right)=O\left(\exp (2\unicode[STIX]{x1D716}t)\right),\end{eqnarray}$$
$$\begin{eqnarray}(Z_{M}H_{M})^{(k+1)}(\unicode[STIX]{x1D70E}+it)=O\left(\exp ((r+\unicode[STIX]{x1D716})t)/r\right)=O\left(\exp (2\unicode[STIX]{x1D716}t)\right),\end{eqnarray}$$
for
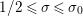 $1/2\leqslant \unicode[STIX]{x1D70E}\leqslant \unicode[STIX]{x1D70E}_{0}$
and
$1/2\leqslant \unicode[STIX]{x1D70E}\leqslant \unicode[STIX]{x1D70E}_{0}$
and
![]() $t\geqslant 1$
. This proves the first part of Lemma for
$t\geqslant 1$
. This proves the first part of Lemma for
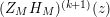 $(Z_{M}H_{M})^{(k+1)}(z)$
, hence, the first part of the Lemma holds true for all
$(Z_{M}H_{M})^{(k+1)}(z)$
, hence, the first part of the Lemma holds true for all
![]() $k\geqslant 1$
.
$k\geqslant 1$
.
In the case when
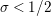 $\unicode[STIX]{x1D70E}<1/2$
, we employ the functional equation (57) for
$\unicode[STIX]{x1D70E}<1/2$
, we employ the functional equation (57) for
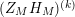 $(Z_{M}H_{M})^{(k)}$
to deduce that
$(Z_{M}H_{M})^{(k)}$
to deduce that
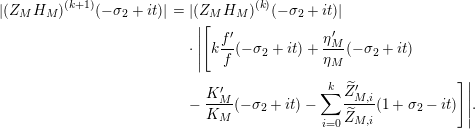 $$\begin{eqnarray}\displaystyle |(Z_{M}H_{M})^{(k+1)}(-\unicode[STIX]{x1D70E}_{2}+it)| & = & \displaystyle |(Z_{M}H_{M})^{(k)}(-\unicode[STIX]{x1D70E}_{2}+it)|\nonumber\\ \displaystyle & & \displaystyle \cdot \,\Bigg|\Bigg[k\frac{f^{\prime }}{f}(-\unicode[STIX]{x1D70E}_{2}+it)+\frac{\unicode[STIX]{x1D702}_{M}^{\prime }}{\unicode[STIX]{x1D702}_{M}}(-\unicode[STIX]{x1D70E}_{2}+it)\nonumber\\ \displaystyle & & \displaystyle -\,\frac{K_{M}^{\prime }}{K_{M}}(-\unicode[STIX]{x1D70E}_{2}+it)-\overset{k}{\underset{i=0}{\sum }}\frac{\widetilde{Z}_{M,i}^{\prime }}{\widetilde{Z}_{M,i}}(1+\unicode[STIX]{x1D70E}_{2}-it)\Bigg]\Bigg|.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle |(Z_{M}H_{M})^{(k+1)}(-\unicode[STIX]{x1D70E}_{2}+it)| & = & \displaystyle |(Z_{M}H_{M})^{(k)}(-\unicode[STIX]{x1D70E}_{2}+it)|\nonumber\\ \displaystyle & & \displaystyle \cdot \,\Bigg|\Bigg[k\frac{f^{\prime }}{f}(-\unicode[STIX]{x1D70E}_{2}+it)+\frac{\unicode[STIX]{x1D702}_{M}^{\prime }}{\unicode[STIX]{x1D702}_{M}}(-\unicode[STIX]{x1D70E}_{2}+it)\nonumber\\ \displaystyle & & \displaystyle -\,\frac{K_{M}^{\prime }}{K_{M}}(-\unicode[STIX]{x1D70E}_{2}+it)-\overset{k}{\underset{i=0}{\sum }}\frac{\widetilde{Z}_{M,i}^{\prime }}{\widetilde{Z}_{M,i}}(1+\unicode[STIX]{x1D70E}_{2}-it)\Bigg]\Bigg|.\nonumber\end{eqnarray}$$
Since
![]() $\unicode[STIX]{x1D70E}_{2}\geqslant 1$
, we have
$\unicode[STIX]{x1D70E}_{2}\geqslant 1$
, we have
 $Z_{M}^{\prime }/Z_{M}(1+\unicode[STIX]{x1D70E}_{2}-it)=O(1)$
as
$Z_{M}^{\prime }/Z_{M}(1+\unicode[STIX]{x1D70E}_{2}-it)=O(1)$
as
 $t\rightarrow +\infty$
. Furthermore, formula (59) and the same computations as in the proof of Lemma 14 imply that
$t\rightarrow +\infty$
. Furthermore, formula (59) and the same computations as in the proof of Lemma 14 imply that
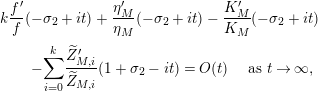 $$\begin{eqnarray}\displaystyle & & \displaystyle k\frac{f^{\prime }}{f}(-\unicode[STIX]{x1D70E}_{2}+it)+\frac{\unicode[STIX]{x1D702}_{M}^{\prime }}{\unicode[STIX]{x1D702}_{M}}(-\unicode[STIX]{x1D70E}_{2}+it)-\frac{K_{M}^{\prime }}{K_{M}}(-\unicode[STIX]{x1D70E}_{2}+it)\nonumber\\ \displaystyle & & \displaystyle \qquad -\overset{k}{\underset{i=0}{\sum }}\frac{\widetilde{Z}_{M,i}^{\prime }}{\widetilde{Z}_{M,i}}(1+\unicode[STIX]{x1D70E}_{2}-it)=O(t)\quad \text{ as }t\rightarrow \infty ,\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle k\frac{f^{\prime }}{f}(-\unicode[STIX]{x1D70E}_{2}+it)+\frac{\unicode[STIX]{x1D702}_{M}^{\prime }}{\unicode[STIX]{x1D702}_{M}}(-\unicode[STIX]{x1D70E}_{2}+it)-\frac{K_{M}^{\prime }}{K_{M}}(-\unicode[STIX]{x1D70E}_{2}+it)\nonumber\\ \displaystyle & & \displaystyle \qquad -\overset{k}{\underset{i=0}{\sum }}\frac{\widetilde{Z}_{M,i}^{\prime }}{\widetilde{Z}_{M,i}}(1+\unicode[STIX]{x1D70E}_{2}-it)=O(t)\quad \text{ as }t\rightarrow \infty ,\nonumber\end{eqnarray}$$
since the leading term in the above expression is
 $\text{vol}(M)(1/2+\unicode[STIX]{x1D70E}_{2}-it)$
$\text{vol}(M)(1/2+\unicode[STIX]{x1D70E}_{2}-it)$
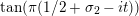 $\tan (\unicode[STIX]{x1D70B}(1/2+\unicode[STIX]{x1D70E}_{2}-it))$
. By the inductive assumption on
$\tan (\unicode[STIX]{x1D70B}(1/2+\unicode[STIX]{x1D70E}_{2}-it))$
. By the inductive assumption on
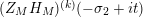 $(Z_{M}H_{M})^{(k)}(-\unicode[STIX]{x1D70E}_{2}+it)$
, we get
$(Z_{M}H_{M})^{(k)}(-\unicode[STIX]{x1D70E}_{2}+it)$
, we get
 $$\begin{eqnarray}\displaystyle |(Z_{M}H_{M})^{(k+1)}(-\unicode[STIX]{x1D70E}_{2}+it)| & = & \displaystyle O\left(\exp \left(\left(\frac{1}{2}+\unicode[STIX]{x1D70E}_{2}+\unicode[STIX]{x1D716}\right)\text{vol}(M)t\right)\right),\nonumber\\ \displaystyle & & \displaystyle \text{as }t\rightarrow \infty .\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle |(Z_{M}H_{M})^{(k+1)}(-\unicode[STIX]{x1D70E}_{2}+it)| & = & \displaystyle O\left(\exp \left(\left(\frac{1}{2}+\unicode[STIX]{x1D70E}_{2}+\unicode[STIX]{x1D716}\right)\text{vol}(M)t\right)\right),\nonumber\\ \displaystyle & & \displaystyle \text{as }t\rightarrow \infty .\nonumber\end{eqnarray}$$
As in the proof of Lemma 14, one applies the Phragmen–Lindelöf theorem to the function
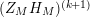 $(Z_{M}H_{M})^{(k+1)}$
in the open sector bounded by the lines
$(Z_{M}H_{M})^{(k+1)}$
in the open sector bounded by the lines
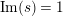 $\operatorname{Im}(s)=1$
,
$\operatorname{Im}(s)=1$
,
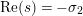 $\operatorname{Re}(s)=-\unicode[STIX]{x1D70E}_{2}$
and
$\operatorname{Re}(s)=-\unicode[STIX]{x1D70E}_{2}$
and
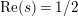 $\operatorname{Re}(s)=1/2$
. As a result, the proof of the second part of the Lemma is complete for
$\operatorname{Re}(s)=1/2$
. As a result, the proof of the second part of the Lemma is complete for
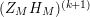 $(Z_{M}H_{M})^{(k+1)}$
.◻
$(Z_{M}H_{M})^{(k+1)}$
.◻
8.2 Distribution of zeros of
 $(Z_{M}H_{M})^{(k)}$
$(Z_{M}H_{M})^{(k)}$
The following theorem is the analogue of the Main Theorem for zeros of higher derivatives of
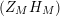 $(Z_{M}H_{M})$
.
$(Z_{M}H_{M})$
.
Theorem 22. With the notation as above, the following statements are true for any integer
![]() $k\geqslant 2$
.
$k\geqslant 2$
.
-
(a) For
 $\unicode[STIX]{x1D70E}<1/2$
, there exist
$\unicode[STIX]{x1D70E}<1/2$
, there exist
 $t_{0}>0$
such that
$t_{0}>0$
such that
 $(Z_{M}H_{M})^{(k)}(\unicode[STIX]{x1D70E}+it)\neq 0$
for all
$(Z_{M}H_{M})^{(k)}(\unicode[STIX]{x1D70E}+it)\neq 0$
for all
 $|t|>t_{0}$
.
$|t|>t_{0}$
. -
(b)
(62) $$\begin{eqnarray}N_{\text{ver}}(T;(Z_{M}H_{M})^{(k)})=N_{\text{ver}}(T;(Z_{M}H_{M})^{\prime })+o(T)\quad \text{ as }T\rightarrow \infty .\end{eqnarray}$$
$$\begin{eqnarray}N_{\text{ver}}(T;(Z_{M}H_{M})^{(k)})=N_{\text{ver}}(T;(Z_{M}H_{M})^{\prime })+o(T)\quad \text{ as }T\rightarrow \infty .\end{eqnarray}$$
-
(c)
(63) $$\begin{eqnarray}\displaystyle \hspace{-10.00002pt}N_{\text{w}}(T;(Z_{M}H_{M})^{(k)}) & = & \displaystyle N_{\text{w}}(T;(Z_{M}H_{M})^{\prime })+\frac{(k-1)T}{2\unicode[STIX]{x1D70B}}[\log (T\cdot \text{vol}(M))-1]\nonumber\\ \displaystyle & & \displaystyle -\,\frac{T}{2\unicode[STIX]{x1D70B}}\log ((k-1)\log A_{M})+o(T)\quad \text{as }T\rightarrow \infty .\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \hspace{-10.00002pt}N_{\text{w}}(T;(Z_{M}H_{M})^{(k)}) & = & \displaystyle N_{\text{w}}(T;(Z_{M}H_{M})^{\prime })+\frac{(k-1)T}{2\unicode[STIX]{x1D70B}}[\log (T\cdot \text{vol}(M))-1]\nonumber\\ \displaystyle & & \displaystyle -\,\frac{T}{2\unicode[STIX]{x1D70B}}\log ((k-1)\log A_{M})+o(T)\quad \text{as }T\rightarrow \infty .\end{eqnarray}$$
Proof. We first outline the proof of part (a). For
![]() $k\geqslant 2$
,
$k\geqslant 2$
,
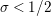 $\unicode[STIX]{x1D70E}<1/2$
and
$\unicode[STIX]{x1D70E}<1/2$
and
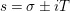 $s=\unicode[STIX]{x1D70E}\pm iT$
equation (57) yields
$s=\unicode[STIX]{x1D70E}\pm iT$
equation (57) yields
 $$\begin{eqnarray}\displaystyle \frac{(Z_{M}H_{M})^{(k)}}{(Z_{M}H_{M})^{(k-1)}}(s) & = & \displaystyle \log \left((Z_{M}H_{M})^{(k-1)}(s)\right)^{\prime }\nonumber\\ \displaystyle & = & \displaystyle (k-1)\frac{f^{\prime }}{f}(s)+\frac{\unicode[STIX]{x1D702}_{M}^{\prime }}{\unicode[STIX]{x1D702}_{M}}(s)-\frac{K_{M}^{\prime }}{K_{M}}(s)-\frac{Z_{M}^{\prime }}{Z_{M}}(1-s)\nonumber\\ \displaystyle & & \displaystyle -\,\overset{k-1}{\underset{i=1}{\sum }}\frac{\widetilde{Z}_{M,i}^{\prime }}{\widetilde{Z}_{M,i}}(1-s).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \frac{(Z_{M}H_{M})^{(k)}}{(Z_{M}H_{M})^{(k-1)}}(s) & = & \displaystyle \log \left((Z_{M}H_{M})^{(k-1)}(s)\right)^{\prime }\nonumber\\ \displaystyle & = & \displaystyle (k-1)\frac{f^{\prime }}{f}(s)+\frac{\unicode[STIX]{x1D702}_{M}^{\prime }}{\unicode[STIX]{x1D702}_{M}}(s)-\frac{K_{M}^{\prime }}{K_{M}}(s)-\frac{Z_{M}^{\prime }}{Z_{M}}(1-s)\nonumber\\ \displaystyle & & \displaystyle -\,\overset{k-1}{\underset{i=1}{\sum }}\frac{\widetilde{Z}_{M,i}^{\prime }}{\widetilde{Z}_{M,i}}(1-s).\end{eqnarray}$$
We now apply (59) with
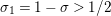 $\unicode[STIX]{x1D70E}_{1}=1-\unicode[STIX]{x1D70E}>1/2$
and (20) to deduce that
$\unicode[STIX]{x1D70E}_{1}=1-\unicode[STIX]{x1D70E}>1/2$
and (20) to deduce that
 $$\begin{eqnarray}\frac{Z_{M}^{\prime }}{Z_{M}}(1-s)+\overset{k-1}{\underset{i=1}{\sum }}\frac{\widetilde{Z}_{M,i}^{\prime }}{\widetilde{Z}_{M,i}}(1-s)=O\left(\frac{(T\log T)^{2\unicode[STIX]{x1D70E}}\log T}{(1/2-\unicode[STIX]{x1D70E})}\right)\quad \text{as }T\rightarrow \infty .\end{eqnarray}$$
$$\begin{eqnarray}\frac{Z_{M}^{\prime }}{Z_{M}}(1-s)+\overset{k-1}{\underset{i=1}{\sum }}\frac{\widetilde{Z}_{M,i}^{\prime }}{\widetilde{Z}_{M,i}}(1-s)=O\left(\frac{(T\log T)^{2\unicode[STIX]{x1D70E}}\log T}{(1/2-\unicode[STIX]{x1D70E})}\right)\quad \text{as }T\rightarrow \infty .\end{eqnarray}$$
Since
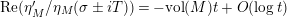 $\operatorname{Re}(\unicode[STIX]{x1D702}_{M}^{\prime }/\unicode[STIX]{x1D702}_{M}(\unicode[STIX]{x1D70E}\pm iT))=-\text{vol}(M)t+O(\log t)$
and
$\operatorname{Re}(\unicode[STIX]{x1D702}_{M}^{\prime }/\unicode[STIX]{x1D702}_{M}(\unicode[STIX]{x1D70E}\pm iT))=-\text{vol}(M)t+O(\log t)$
and
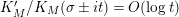 $K_{M}^{\prime }/K_{M}(\unicode[STIX]{x1D70E}\pm it)=O(\log t)$
as
$K_{M}^{\prime }/K_{M}(\unicode[STIX]{x1D70E}\pm it)=O(\log t)$
as
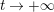 $t\rightarrow +\infty$
, we immediately deduce from (64) that
$t\rightarrow +\infty$
, we immediately deduce from (64) that
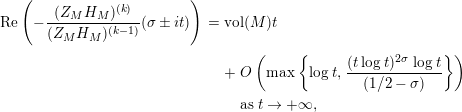 $$\begin{eqnarray}\displaystyle \text{Re}\left(-\frac{(Z_{M}H_{M})^{(k)}}{(Z_{M}H_{M})^{(k-1)}}(\unicode[STIX]{x1D70E}\pm it)\right) & = & \displaystyle \text{vol}(M)t\nonumber\\ \displaystyle & & \displaystyle +\,O\left(\max \left\{\log t,\frac{(t\log t)^{2\unicode[STIX]{x1D70E}}\log t}{(1/2-\unicode[STIX]{x1D70E})}\right\}\right)\nonumber\\ \displaystyle & & \displaystyle \quad \text{as }t\rightarrow +\infty ,\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \text{Re}\left(-\frac{(Z_{M}H_{M})^{(k)}}{(Z_{M}H_{M})^{(k-1)}}(\unicode[STIX]{x1D70E}\pm it)\right) & = & \displaystyle \text{vol}(M)t\nonumber\\ \displaystyle & & \displaystyle +\,O\left(\max \left\{\log t,\frac{(t\log t)^{2\unicode[STIX]{x1D70E}}\log t}{(1/2-\unicode[STIX]{x1D70E})}\right\}\right)\nonumber\\ \displaystyle & & \displaystyle \quad \text{as }t\rightarrow +\infty ,\nonumber\end{eqnarray}$$
for any
 $\unicode[STIX]{x1D70E}<1/2$
. This proves part (a).
$\unicode[STIX]{x1D70E}<1/2$
. This proves part (a).
The proof of parts (b) and (c) closely follows lines of the proof of parts (b) and (c) of the Main Theorem. We fix a large positive number
![]() $T$
and choose number
$T$
and choose number
![]() $T^{\prime }$
to be a bounded distance from
$T^{\prime }$
to be a bounded distance from
![]() $T$
such that
$T$
such that
![]() $T^{\prime }$
is distinct from the imaginary part of any zero of
$T^{\prime }$
is distinct from the imaginary part of any zero of
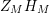 $Z_{M}H_{M}$
. We fix a number
$Z_{M}H_{M}$
. We fix a number
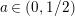 $a\in (0,1/2)$
and use part (a) of the Theorem to choose
$a\in (0,1/2)$
and use part (a) of the Theorem to choose
![]() $t_{0}>0$
to be the number such that
$t_{0}>0$
to be the number such that
 $(Z_{M}H_{M})^{(k)}(\unicode[STIX]{x1D70E}+it)\neq 0$
for all
$(Z_{M}H_{M})^{(k)}(\unicode[STIX]{x1D70E}+it)\neq 0$
for all
![]() $\unicode[STIX]{x1D70E}\leqslant a$
and
$\unicode[STIX]{x1D70E}\leqslant a$
and
![]() $|t|>t_{0}$
. Let
$|t|>t_{0}$
. Let
![]() $\unicode[STIX]{x1D70E}_{0}$
be a constant such that
$\unicode[STIX]{x1D70E}_{0}$
be a constant such that
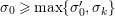 $\unicode[STIX]{x1D70E}_{0}\geqslant \max \{\unicode[STIX]{x1D70E}_{0}^{\prime },\unicode[STIX]{x1D70E}_{k}\}$
, where
$\unicode[STIX]{x1D70E}_{0}\geqslant \max \{\unicode[STIX]{x1D70E}_{0}^{\prime },\unicode[STIX]{x1D70E}_{k}\}$
, where
![]() $\unicode[STIX]{x1D70E}_{0}^{\prime }$
is defined in Lemma 3 and
$\unicode[STIX]{x1D70E}_{0}^{\prime }$
is defined in Lemma 3 and
![]() $\unicode[STIX]{x1D70E}_{k}$
is defined in Lemma 20.
$\unicode[STIX]{x1D70E}_{k}$
is defined in Lemma 20.
We apply Littlewood’s theorem to the function
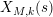 $X_{M,k}(s)$
, defined by (60) which is holomorphic in the rectangle
$X_{M,k}(s)$
, defined by (60) which is holomorphic in the rectangle
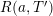 $R(a,T^{\prime })$
with vertices
$R(a,T^{\prime })$
with vertices
![]() $a+it_{0}$
,
$a+it_{0}$
,
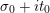 $\unicode[STIX]{x1D70E}_{0}+it_{0}$
,
$\unicode[STIX]{x1D70E}_{0}+it_{0}$
,
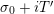 $\unicode[STIX]{x1D70E}_{0}+iT^{\prime }$
,
$\unicode[STIX]{x1D70E}_{0}+iT^{\prime }$
,
![]() $a+iT^{\prime }$
. The resulting formula is
$a+iT^{\prime }$
. The resulting formula is
 $$\begin{eqnarray}\displaystyle 2\unicode[STIX]{x1D70B}\underset{t_{0}<\unicode[STIX]{x1D6FE}^{(k)}<T^{\prime },\unicode[STIX]{x1D6FD}^{(k)}>a}{\underset{\unicode[STIX]{x1D70C}^{(k)}=\unicode[STIX]{x1D6FD}^{(k)}+i\unicode[STIX]{x1D6FE}^{(k)}}{\sum }}\left(\unicode[STIX]{x1D6FD}^{(k)}-a\right) & = & \displaystyle \int _{t_{0}}^{T^{\prime }}\log \left|X_{M,k}(a+it)\right|dt\nonumber\\ \displaystyle & & \displaystyle -\,\int _{t_{0}}^{T^{\prime }}\log \left|X_{M,k}(\unicode[STIX]{x1D70E}_{0}+it)\right|dt\nonumber\\ \displaystyle & & \displaystyle -\,\int _{a}^{\unicode[STIX]{x1D70E}_{0}}\arg X_{M,k}(\unicode[STIX]{x1D70E}+it_{0})\,d\unicode[STIX]{x1D70E}\nonumber\\ \displaystyle & & \displaystyle +\,\int _{a}^{\unicode[STIX]{x1D70E}_{0}}\arg X_{M,k}(\unicode[STIX]{x1D70E}+iT^{\prime })\,d\unicode[STIX]{x1D70E}\nonumber\\ \displaystyle & = & \displaystyle I_{1,k}+I_{2,k}+I_{3,k}+I_{4,k},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle 2\unicode[STIX]{x1D70B}\underset{t_{0}<\unicode[STIX]{x1D6FE}^{(k)}<T^{\prime },\unicode[STIX]{x1D6FD}^{(k)}>a}{\underset{\unicode[STIX]{x1D70C}^{(k)}=\unicode[STIX]{x1D6FD}^{(k)}+i\unicode[STIX]{x1D6FE}^{(k)}}{\sum }}\left(\unicode[STIX]{x1D6FD}^{(k)}-a\right) & = & \displaystyle \int _{t_{0}}^{T^{\prime }}\log \left|X_{M,k}(a+it)\right|dt\nonumber\\ \displaystyle & & \displaystyle -\,\int _{t_{0}}^{T^{\prime }}\log \left|X_{M,k}(\unicode[STIX]{x1D70E}_{0}+it)\right|dt\nonumber\\ \displaystyle & & \displaystyle -\,\int _{a}^{\unicode[STIX]{x1D70E}_{0}}\arg X_{M,k}(\unicode[STIX]{x1D70E}+it_{0})\,d\unicode[STIX]{x1D70E}\nonumber\\ \displaystyle & & \displaystyle +\,\int _{a}^{\unicode[STIX]{x1D70E}_{0}}\arg X_{M,k}(\unicode[STIX]{x1D70E}+iT^{\prime })\,d\unicode[STIX]{x1D70E}\nonumber\\ \displaystyle & = & \displaystyle I_{1,k}+I_{2,k}+I_{3,k}+I_{4,k},\end{eqnarray}$$
where
![]() $\unicode[STIX]{x1D70C}^{(k)}$
denotes the zero of
$\unicode[STIX]{x1D70C}^{(k)}$
denotes the zero of
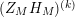 $(Z_{M}H_{M})^{(k)}$
. By the choice of
$(Z_{M}H_{M})^{(k)}$
. By the choice of
![]() $t_{0}$
, the sum on the left-hand side of (65) is actually taken over all zeros
$t_{0}$
, the sum on the left-hand side of (65) is actually taken over all zeros
![]() $\unicode[STIX]{x1D70C}^{(k)}$
of
$\unicode[STIX]{x1D70C}^{(k)}$
of
 $(Z_{M}H_{M})^{(k)}$
with imaginary part in the interval
$(Z_{M}H_{M})^{(k)}$
with imaginary part in the interval
![]() $(t_{0},T^{\prime })$
.
$(t_{0},T^{\prime })$
.
Trivially,
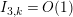 $I_{3,k}=O(1)$
as
$I_{3,k}=O(1)$
as
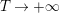 $T\rightarrow +\infty$
. The application of Lemma 20 immediately yields that
$T\rightarrow +\infty$
. The application of Lemma 20 immediately yields that
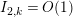 $I_{2,k}=O(1)$
as
$I_{2,k}=O(1)$
as
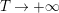 $T\rightarrow +\infty$
, once we apply the same method as in evaluation of
$T\rightarrow +\infty$
, once we apply the same method as in evaluation of
![]() $I_{2}$
.
$I_{2}$
.
One can follow the steps of the proof that
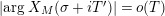 $|\!\arg X_{M}(\unicode[STIX]{x1D70E}+iT^{\prime })|=o(T)$
as
$|\!\arg X_{M}(\unicode[STIX]{x1D70E}+iT^{\prime })|=o(T)$
as
 $T\rightarrow +\infty$
in the present setting. One uses function
$T\rightarrow +\infty$
in the present setting. One uses function
![]() $X_{M,k}$
instead of
$X_{M,k}$
instead of
![]() $X_{M}$
and Lemma 21 instead of Lemma 14. From this, we deduce that
$X_{M}$
and Lemma 21 instead of Lemma 14. From this, we deduce that
 $|\!\arg X_{M,k}(\unicode[STIX]{x1D70E}+iT^{\prime })|=o(T)$
as
$|\!\arg X_{M,k}(\unicode[STIX]{x1D70E}+iT^{\prime })|=o(T)$
as
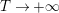 $T\rightarrow +\infty$
. Therefore, it is left to evaluate
$T\rightarrow +\infty$
. Therefore, it is left to evaluate
![]() $I_{1,k}$
.
$I_{1,k}$
.
From definition of
![]() $X_{M,k}$
, using the functional equation (57) for
$X_{M,k}$
, using the functional equation (57) for
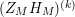 $(Z_{M}H_{M})^{(k)}$
, we get for
$(Z_{M}H_{M})^{(k)}$
, we get for
![]() $k\geqslant 2$
, the expression
$k\geqslant 2$
, the expression
 $$\begin{eqnarray}\displaystyle I_{1,k} & = & \displaystyle \int _{t_{0}}^{T^{\prime }}\log \left|A_{M}^{(a+it)}a_{M,k}^{-1}\right|dt+k\int _{t_{0}}^{T^{\prime }}\log |f_{M}(a+it)|dt\nonumber\\ \displaystyle & & \displaystyle +\,\!\int _{t_{0}}^{T^{\prime }}\log |\unicode[STIX]{x1D702}_{M}(a+it)|dt\nonumber\\ \displaystyle & & \displaystyle +\,\int _{t_{0}}^{T^{\prime }}\log |K_{M}^{-1}(a+it)|dt+\int _{t_{0}}^{T^{\prime }}\log |Z_{M}(1-a-it)|dt\nonumber\\ \displaystyle & & \displaystyle +\,\mathop{\sum }_{i=1}^{k-1}\int _{t_{0}}^{T^{\prime }}\log |1+Z_{M,i}(1-a-it)|dt.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle I_{1,k} & = & \displaystyle \int _{t_{0}}^{T^{\prime }}\log \left|A_{M}^{(a+it)}a_{M,k}^{-1}\right|dt+k\int _{t_{0}}^{T^{\prime }}\log |f_{M}(a+it)|dt\nonumber\\ \displaystyle & & \displaystyle +\,\!\int _{t_{0}}^{T^{\prime }}\log |\unicode[STIX]{x1D702}_{M}(a+it)|dt\nonumber\\ \displaystyle & & \displaystyle +\,\int _{t_{0}}^{T^{\prime }}\log |K_{M}^{-1}(a+it)|dt+\int _{t_{0}}^{T^{\prime }}\log |Z_{M}(1-a-it)|dt\nonumber\\ \displaystyle & & \displaystyle +\,\mathop{\sum }_{i=1}^{k-1}\int _{t_{0}}^{T^{\prime }}\log |1+Z_{M,i}(1-a-it)|dt.\end{eqnarray}$$
By employing equation (58) with
![]() $k=0$
, we get
$k=0$
, we get
 $$\begin{eqnarray}\int _{t_{0}}^{T^{\prime }}\log |1+Z_{M,i}(1-a-it)|dt=O((T\log T)^{2a})\quad \text{as }T\rightarrow \infty\end{eqnarray}$$
$$\begin{eqnarray}\int _{t_{0}}^{T^{\prime }}\log |1+Z_{M,i}(1-a-it)|dt=O((T\log T)^{2a})\quad \text{as }T\rightarrow \infty\end{eqnarray}$$
for all
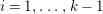 $i=1,\ldots ,k-1$
. Substituting this equation, together with (42), (44), (45) and (47) into (66), we immediately deduce that
$i=1,\ldots ,k-1$
. Substituting this equation, together with (42), (44), (45) and (47) into (66), we immediately deduce that
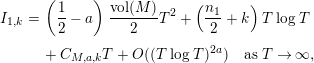 $$\begin{eqnarray}\displaystyle I_{1,k} & = & \displaystyle \left(\frac{1}{2}-a\right)\frac{\text{vol}(M)}{2}T^{2}+\left(\frac{n_{1}}{2}+k\right)T\log T\nonumber\\ \displaystyle & & \displaystyle +\,C_{M,a,k}T+O((T\log T)^{2a})\quad \text{as }T\rightarrow \infty ,\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle I_{1,k} & = & \displaystyle \left(\frac{1}{2}-a\right)\frac{\text{vol}(M)}{2}T^{2}+\left(\frac{n_{1}}{2}+k\right)T\log T\nonumber\\ \displaystyle & & \displaystyle +\,C_{M,a,k}T+O((T\log T)^{2a})\quad \text{as }T\rightarrow \infty ,\nonumber\end{eqnarray}$$
where
 $$\begin{eqnarray}\displaystyle C_{M,a,k} & = & \displaystyle 2\left(a-\frac{1}{2}\right)n_{1}\log 2+a\log A_{M}-\log |a_{M,k}|\nonumber\\ \displaystyle & & \displaystyle +\,k(\log (\text{vol}(M))-1)+2a\log \mathfrak{g}_{1}-\log |d(1)|-\frac{n_{1}}{2}(\log \unicode[STIX]{x1D70B}+1).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle C_{M,a,k} & = & \displaystyle 2\left(a-\frac{1}{2}\right)n_{1}\log 2+a\log A_{M}-\log |a_{M,k}|\nonumber\\ \displaystyle & & \displaystyle +\,k(\log (\text{vol}(M))-1)+2a\log \mathfrak{g}_{1}-\log |d(1)|-\frac{n_{1}}{2}(\log \unicode[STIX]{x1D70B}+1).\nonumber\end{eqnarray}$$
Combining this equation with the bounds on
![]() $I_{2,k}$
,
$I_{2,k}$
,
![]() $I_{3,k}$
and
$I_{3,k}$
and
![]() $I_{4,k}$
and (65), we get
$I_{4,k}$
and (65), we get
 $$\begin{eqnarray}\displaystyle 2\unicode[STIX]{x1D70B}\underset{t_{0}<\unicode[STIX]{x1D6FE}^{(k)}<T^{\prime }}{\underset{\unicode[STIX]{x1D70C}^{(k)}=\unicode[STIX]{x1D6FD}^{(k)}+i\unicode[STIX]{x1D6FE}^{(k)}}{\sum }}\left(\unicode[STIX]{x1D6FD}^{(k)}-a\right) & = & \displaystyle \left(\frac{1}{2}-a\right)\frac{\text{vol}(M)}{2}T^{2}+\left(\frac{n_{1}}{2}+k\right)T\log T\nonumber\\ \displaystyle & & \displaystyle +\,C_{M,a,k}T+o(T)\quad \text{as }T\rightarrow \infty .\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle 2\unicode[STIX]{x1D70B}\underset{t_{0}<\unicode[STIX]{x1D6FE}^{(k)}<T^{\prime }}{\underset{\unicode[STIX]{x1D70C}^{(k)}=\unicode[STIX]{x1D6FD}^{(k)}+i\unicode[STIX]{x1D6FE}^{(k)}}{\sum }}\left(\unicode[STIX]{x1D6FD}^{(k)}-a\right) & = & \displaystyle \left(\frac{1}{2}-a\right)\frac{\text{vol}(M)}{2}T^{2}+\left(\frac{n_{1}}{2}+k\right)T\log T\nonumber\\ \displaystyle & & \displaystyle +\,C_{M,a,k}T+o(T)\quad \text{as }T\rightarrow \infty .\end{eqnarray}$$
Replacing
![]() $a$
by
$a$
by
![]() $a/2$
in (67) and subtracting proves part (b). Part (c) is proved by employing an analogue of equation (51), with
$a/2$
in (67) and subtracting proves part (b). Part (c) is proved by employing an analogue of equation (51), with
![]() $\unicode[STIX]{x1D6FD}^{\prime }$
and
$\unicode[STIX]{x1D6FD}^{\prime }$
and
![]() $\unicode[STIX]{x1D70C}^{\prime }$
replaced by
$\unicode[STIX]{x1D70C}^{\prime }$
replaced by
![]() $\unicode[STIX]{x1D6FD}^{(k)}$
and
$\unicode[STIX]{x1D6FD}^{(k)}$
and
![]() $\unicode[STIX]{x1D70C}^{(k)}$
.◻
$\unicode[STIX]{x1D70C}^{(k)}$
.◻
Remark 23. The statement of Theorem 22 is true in the case of co-compact Riemann surfaces
![]() $\unicode[STIX]{x1D6E4}\setminus \mathbb{H}$
when taking
$\unicode[STIX]{x1D6E4}\setminus \mathbb{H}$
when taking
 $H_{M}=1$
and
$H_{M}=1$
and
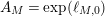 $A_{M}=\exp (\ell _{M,0})$
in (62) and (63).
$A_{M}=\exp (\ell _{M,0})$
in (62) and (63).
In the case when
![]() $\unicode[STIX]{x1D6E4}\setminus \mathbb{H}$
is compact the statement (b) of Theorem 22 was announced by Luo in [Reference Luo22], with the weaker error term
$\unicode[STIX]{x1D6E4}\setminus \mathbb{H}$
is compact the statement (b) of Theorem 22 was announced by Luo in [Reference Luo22], with the weaker error term
![]() $O(T)$
. As one can see, we put considerable effort into the analysis yielding the error term
$O(T)$
. As one can see, we put considerable effort into the analysis yielding the error term
![]() $o(T)$
, and the structure of the constant
$o(T)$
, and the structure of the constant
![]() $C_{M,a,k}$
is, in our opinion, fascinating.
$C_{M,a,k}$
is, in our opinion, fascinating.
Remark 24. From the formula (63) for the weighted vertical distribution of zeros of
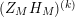 $(Z_{M}H_{M})^{(k)}$
, we see that the differentiation of
$(Z_{M}H_{M})^{(k)}$
, we see that the differentiation of
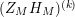 $(Z_{M}H_{M})^{(k)}$
increases the sum
$(Z_{M}H_{M})^{(k)}$
increases the sum
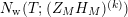 $N_{\text{w}}(T;(Z_{M}H_{M})^{(k)})$
by the quantity
$N_{\text{w}}(T;(Z_{M}H_{M})^{(k)})$
by the quantity
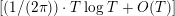 $[(1/(2\unicode[STIX]{x1D70B}))\cdot T\log T+O(T)]$
as
$[(1/(2\unicode[STIX]{x1D70B}))\cdot T\log T+O(T)]$
as
![]() $T\rightarrow \infty$
. Hence, after each differentiation, zeros of
$T\rightarrow \infty$
. Hence, after each differentiation, zeros of
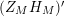 $(Z_{M}H_{M})^{\prime }$
move further to the right of
$(Z_{M}H_{M})^{\prime }$
move further to the right of
![]() $1/2$
. Since every zero of
$1/2$
. Since every zero of
 $(Z_{M}H_{M})^{\prime }$
on the line
$(Z_{M}H_{M})^{\prime }$
on the line
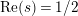 $\operatorname{Re}(s)=1/2$
(up to finitely many of them) is a multiple zero of
$\operatorname{Re}(s)=1/2$
(up to finitely many of them) is a multiple zero of
![]() $Z_{M}$
, this result fully supports the “bounded multiplicities conjecture”. To recall, the “bounded multiplicities conjecture” asserts that the order of every multiple zero of
$Z_{M}$
, this result fully supports the “bounded multiplicities conjecture”. To recall, the “bounded multiplicities conjecture” asserts that the order of every multiple zero of
![]() $Z_{M}$
is uniformly bounded, or, equivalently, that the dimension of every eigenspace associated to the discrete eigenvalue of the Laplacian on
$Z_{M}$
is uniformly bounded, or, equivalently, that the dimension of every eigenspace associated to the discrete eigenvalue of the Laplacian on
![]() $M$
is uniformly bounded, with a bound depending solely upon
$M$
is uniformly bounded, with a bound depending solely upon
![]() $M$
.
$M$
.
9 Concluding remarks
9.1 Revisiting Weyl’s law
Weyl’s law for an arbitrary finite volume hyperbolic Riemann surface
![]() $M$
is the following asymptotic formula, which we quote from [Reference Hejhal14, p. 466]:
$M$
is the following asymptotic formula, which we quote from [Reference Hejhal14, p. 466]:
 $$\begin{eqnarray}\displaystyle N_{M,\text{dis}}(T)+N_{M,\text{con}}(T) & = & \displaystyle \frac{\text{vol}(M)}{4\unicode[STIX]{x1D70B}}T^{2}-\frac{n_{1}}{\unicode[STIX]{x1D70B}}T\log T+\frac{n_{1}T}{\unicode[STIX]{x1D70B}}(1-\log 2)\nonumber\\ \displaystyle & & \displaystyle +\,O\,(T/\log T)\quad \text{as }T\rightarrow \infty ,\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle N_{M,\text{dis}}(T)+N_{M,\text{con}}(T) & = & \displaystyle \frac{\text{vol}(M)}{4\unicode[STIX]{x1D70B}}T^{2}-\frac{n_{1}}{\unicode[STIX]{x1D70B}}T\log T+\frac{n_{1}T}{\unicode[STIX]{x1D70B}}(1-\log 2)\nonumber\\ \displaystyle & & \displaystyle +\,O\,(T/\log T)\quad \text{as }T\rightarrow \infty ,\end{eqnarray}$$
where
 $$\begin{eqnarray}N_{M,\text{dis}}(T)=\#\{s=1/2+it|Z_{M}(s)=0\text{ and }0\leqslant t\leqslant T\}\end{eqnarray}$$
$$\begin{eqnarray}N_{M,\text{dis}}(T)=\#\{s=1/2+it|Z_{M}(s)=0\text{ and }0\leqslant t\leqslant T\}\end{eqnarray}$$
and
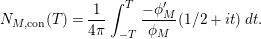 $$\begin{eqnarray}N_{M,\text{con}}(T)=\frac{1}{4\unicode[STIX]{x1D70B}}\int _{-T}^{T}\frac{-\unicode[STIX]{x1D719}_{M}^{\prime }}{\unicode[STIX]{x1D719}_{M}}(1/2+it)\,dt.\end{eqnarray}$$
$$\begin{eqnarray}N_{M,\text{con}}(T)=\frac{1}{4\unicode[STIX]{x1D70B}}\int _{-T}^{T}\frac{-\unicode[STIX]{x1D719}_{M}^{\prime }}{\unicode[STIX]{x1D719}_{M}}(1/2+it)\,dt.\end{eqnarray}$$
The term
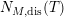 $N_{M,\text{dis}}(T)$
counts the number of zeros of the Selberg zeta function
$N_{M,\text{dis}}(T)$
counts the number of zeros of the Selberg zeta function
![]() $Z_{M}(s)$
on the critical line
$Z_{M}(s)$
on the critical line
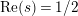 $\text{Re}(s)=1/2$
, whereas the term
$\text{Re}(s)=1/2$
, whereas the term
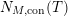 $N_{M,\text{con}}(T)$
is related to the number of zeros of
$N_{M,\text{con}}(T)$
is related to the number of zeros of
![]() $Z_{M}(s)$
off the critical line but within the critical strip. In the following proposition, we relate the counting function
$Z_{M}(s)$
off the critical line but within the critical strip. In the following proposition, we relate the counting function
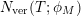 $N_{\text{ver}}(T;\unicode[STIX]{x1D719}_{M})$
with the function
$N_{\text{ver}}(T;\unicode[STIX]{x1D719}_{M})$
with the function
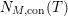 $N_{M,\text{con}}(T)$
, showing that the constant
$N_{M,\text{con}}(T)$
, showing that the constant
![]() $\mathfrak{g}_{1}$
appears in the resulting asymptotic formula.
$\mathfrak{g}_{1}$
appears in the resulting asymptotic formula.
Proposition 25. There exists a sequence
![]() $\{T_{n}\}$
of positive numbers tending toward infinity such that, with the notation as above, we have the asymptotic formula
$\{T_{n}\}$
of positive numbers tending toward infinity such that, with the notation as above, we have the asymptotic formula
 $$\begin{eqnarray}N_{\text{ver}}(T_{n};\unicode[STIX]{x1D719}_{M})=N_{M,\text{con}}(T_{n})-\frac{\log \mathfrak{g}_{1}}{\unicode[STIX]{x1D70B}}T_{n}+O\left(\log T_{n}\right)\quad \text{as }n\rightarrow \infty .\end{eqnarray}$$
$$\begin{eqnarray}N_{\text{ver}}(T_{n};\unicode[STIX]{x1D719}_{M})=N_{M,\text{con}}(T_{n})-\frac{\log \mathfrak{g}_{1}}{\unicode[STIX]{x1D70B}}T_{n}+O\left(\log T_{n}\right)\quad \text{as }n\rightarrow \infty .\end{eqnarray}$$
Proof. Let
![]() $R(T)$
denote the rectangle with vertexes
$R(T)$
denote the rectangle with vertexes
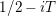 $1/2-iT$
,
$1/2-iT$
,
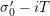 $\unicode[STIX]{x1D70E}_{0}^{\prime }-iT$
,
$\unicode[STIX]{x1D70E}_{0}^{\prime }-iT$
,
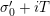 $\unicode[STIX]{x1D70E}_{0}^{\prime }+iT$
,
$\unicode[STIX]{x1D70E}_{0}^{\prime }+iT$
,
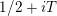 $1/2+iT$
, where
$1/2+iT$
, where
![]() $\unicode[STIX]{x1D70E}_{0}^{\prime }>\unicode[STIX]{x1D70E}_{0}$
, where
$\unicode[STIX]{x1D70E}_{0}^{\prime }>\unicode[STIX]{x1D70E}_{0}$
, where
![]() $\unicode[STIX]{x1D70E}_{0}$
is defined in § 1.3. Therefore, the series (8) converges uniformly and absolutely for Re
$\unicode[STIX]{x1D70E}_{0}$
is defined in § 1.3. Therefore, the series (8) converges uniformly and absolutely for Re
![]() $s\geqslant \unicode[STIX]{x1D70E}_{0}^{\prime }$
, and all zeros of
$s\geqslant \unicode[STIX]{x1D70E}_{0}^{\prime }$
, and all zeros of
![]() $\unicode[STIX]{x1D719}_{M}$
with real part greater than 1/2 lie inside
$\unicode[STIX]{x1D719}_{M}$
with real part greater than 1/2 lie inside
![]() $R(T)$
. Recall that the zeros of
$R(T)$
. Recall that the zeros of
![]() $\unicode[STIX]{x1D719}_{M}$
appear in pairs of the form
$\unicode[STIX]{x1D719}_{M}$
appear in pairs of the form
![]() $\unicode[STIX]{x1D70C}$
and
$\unicode[STIX]{x1D70C}$
and
![]() $\overline{\unicode[STIX]{x1D70C}}$
. As a result, the proposition follow by studying the expression
$\overline{\unicode[STIX]{x1D70C}}$
. As a result, the proposition follow by studying the expression
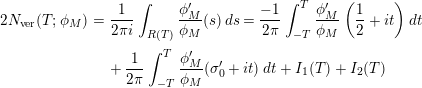 $$\begin{eqnarray}\displaystyle 2N_{\text{ver}}(T;\unicode[STIX]{x1D719}_{M}) & = & \displaystyle \frac{1}{2\unicode[STIX]{x1D70B}i}\int _{R(T)}\frac{\unicode[STIX]{x1D719}_{M}^{\prime }}{\unicode[STIX]{x1D719}_{M}}(s)\,ds=\frac{-1}{2\unicode[STIX]{x1D70B}}\int _{-T}^{T}\frac{\unicode[STIX]{x1D719}_{M}^{\prime }}{\unicode[STIX]{x1D719}_{M}}\left(\frac{1}{2}+it\right)dt\nonumber\\ \displaystyle & & \displaystyle +\,\frac{1}{2\unicode[STIX]{x1D70B}}\int _{-T}^{T}\frac{\unicode[STIX]{x1D719}_{M}^{\prime }}{\unicode[STIX]{x1D719}_{M}}(\unicode[STIX]{x1D70E}_{0}^{\prime }+it)\,dt+I_{1}(T)+I_{2}(T)\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle 2N_{\text{ver}}(T;\unicode[STIX]{x1D719}_{M}) & = & \displaystyle \frac{1}{2\unicode[STIX]{x1D70B}i}\int _{R(T)}\frac{\unicode[STIX]{x1D719}_{M}^{\prime }}{\unicode[STIX]{x1D719}_{M}}(s)\,ds=\frac{-1}{2\unicode[STIX]{x1D70B}}\int _{-T}^{T}\frac{\unicode[STIX]{x1D719}_{M}^{\prime }}{\unicode[STIX]{x1D719}_{M}}\left(\frac{1}{2}+it\right)dt\nonumber\\ \displaystyle & & \displaystyle +\,\frac{1}{2\unicode[STIX]{x1D70B}}\int _{-T}^{T}\frac{\unicode[STIX]{x1D719}_{M}^{\prime }}{\unicode[STIX]{x1D719}_{M}}(\unicode[STIX]{x1D70E}_{0}^{\prime }+it)\,dt+I_{1}(T)+I_{2}(T)\nonumber\end{eqnarray}$$
where
![]() $I_{1}$
and
$I_{1}$
and
![]() $I_{2}$
denote the integrals along the horizontal lines which bound
$I_{2}$
denote the integrals along the horizontal lines which bound
![]() $R(T)$
. In [Reference Jorgenson and Lang18, Theorem 7.1] it is proved that
$R(T)$
. In [Reference Jorgenson and Lang18, Theorem 7.1] it is proved that
![]() $\unicode[STIX]{x1D719}_{M}$
is of regularized product type with order
$\unicode[STIX]{x1D719}_{M}$
is of regularized product type with order
![]() $M=0$
. As a result, from [Reference Jorgenson and Lang19, Chapter 1], we have the existence of a sequence of real numbers
$M=0$
. As a result, from [Reference Jorgenson and Lang19, Chapter 1], we have the existence of a sequence of real numbers
![]() $\{T_{n}\}$
tending to infinity such that
$\{T_{n}\}$
tending to infinity such that
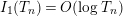 $I_{1}(T_{n})=O(\log T_{n})$
and
$I_{1}(T_{n})=O(\log T_{n})$
and
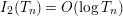 $I_{2}(T_{n})=O(\log T_{n})$
when
$I_{2}(T_{n})=O(\log T_{n})$
when
![]() $n\rightarrow \infty$
, so then
$n\rightarrow \infty$
, so then
 $$\begin{eqnarray}\displaystyle 2N_{\text{ver}}(T_{n};\unicode[STIX]{x1D719}_{M}) & = & \displaystyle -\frac{1}{2\unicode[STIX]{x1D70B}}\int _{-T_{n}}^{T_{n}}\frac{\unicode[STIX]{x1D719}_{M}^{\prime }}{\unicode[STIX]{x1D719}_{M}}\left(\frac{1}{2}+it\right)dt\nonumber\\ \displaystyle & & \displaystyle +\,\frac{1}{2\unicode[STIX]{x1D70B}}\int _{-T_{n}}^{T_{n}}\frac{\unicode[STIX]{x1D719}_{M}^{\prime }}{\unicode[STIX]{x1D719}_{M}}(\unicode[STIX]{x1D70E}_{0}^{\prime }+it)\,dt+O(\log T_{n})\quad \text{when }n\rightarrow \infty .\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle 2N_{\text{ver}}(T_{n};\unicode[STIX]{x1D719}_{M}) & = & \displaystyle -\frac{1}{2\unicode[STIX]{x1D70B}}\int _{-T_{n}}^{T_{n}}\frac{\unicode[STIX]{x1D719}_{M}^{\prime }}{\unicode[STIX]{x1D719}_{M}}\left(\frac{1}{2}+it\right)dt\nonumber\\ \displaystyle & & \displaystyle +\,\frac{1}{2\unicode[STIX]{x1D70B}}\int _{-T_{n}}^{T_{n}}\frac{\unicode[STIX]{x1D719}_{M}^{\prime }}{\unicode[STIX]{x1D719}_{M}}(\unicode[STIX]{x1D70E}_{0}^{\prime }+it)\,dt+O(\log T_{n})\quad \text{when }n\rightarrow \infty .\nonumber\end{eqnarray}$$
Using the notation as above, we now write
 $$\begin{eqnarray}\displaystyle \int _{-T_{n}}^{T_{n}}\frac{\unicode[STIX]{x1D719}_{M}^{\prime }}{\unicode[STIX]{x1D719}_{M}}(\unicode[STIX]{x1D70E}_{0}^{\prime }+it)\,dt & = & \displaystyle \mathop{\sum }_{i=1}^{\infty }\frac{b\left(q_{i}\right)}{q_{i}^{\unicode[STIX]{x1D70E}_{0}^{\prime }}}\int _{-T_{n}}^{T_{n}}\frac{dt}{q_{i}^{it}}-4T\log \mathfrak{g}_{1}\nonumber\\ \displaystyle & & \displaystyle +\,n_{1}\int _{-T_{n}}^{T_{n}}\left(\frac{\unicode[STIX]{x1D6E4}^{\prime }}{\unicode[STIX]{x1D6E4}}\left(\unicode[STIX]{x1D70E}_{0}^{\prime }+it-\frac{1}{2}\right)-\frac{\unicode[STIX]{x1D6E4}^{\prime }}{\unicode[STIX]{x1D6E4}}(\unicode[STIX]{x1D70E}_{0}^{\prime }+it)\right)dt.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \int _{-T_{n}}^{T_{n}}\frac{\unicode[STIX]{x1D719}_{M}^{\prime }}{\unicode[STIX]{x1D719}_{M}}(\unicode[STIX]{x1D70E}_{0}^{\prime }+it)\,dt & = & \displaystyle \mathop{\sum }_{i=1}^{\infty }\frac{b\left(q_{i}\right)}{q_{i}^{\unicode[STIX]{x1D70E}_{0}^{\prime }}}\int _{-T_{n}}^{T_{n}}\frac{dt}{q_{i}^{it}}-4T\log \mathfrak{g}_{1}\nonumber\\ \displaystyle & & \displaystyle +\,n_{1}\int _{-T_{n}}^{T_{n}}\left(\frac{\unicode[STIX]{x1D6E4}^{\prime }}{\unicode[STIX]{x1D6E4}}\left(\unicode[STIX]{x1D70E}_{0}^{\prime }+it-\frac{1}{2}\right)-\frac{\unicode[STIX]{x1D6E4}^{\prime }}{\unicode[STIX]{x1D6E4}}(\unicode[STIX]{x1D70E}_{0}^{\prime }+it)\right)dt.\nonumber\end{eqnarray}$$
Interchanging the sum and the integral above is justified by the fact that the series defining
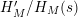 $H_{M}^{\prime }/H_{M}(s)$
converges absolutely and uniformly for
$H_{M}^{\prime }/H_{M}(s)$
converges absolutely and uniformly for
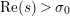 $\operatorname{Re}(s)>\unicode[STIX]{x1D70E}_{0}$
. Furthermore, we also have that
$\operatorname{Re}(s)>\unicode[STIX]{x1D70E}_{0}$
. Furthermore, we also have that
 $$\begin{eqnarray}\mathop{\sum }_{i=1}^{\infty }\frac{b\left(q_{i}\right)}{q_{i}^{\unicode[STIX]{x1D70E}_{0}^{\prime }}}\int _{-T_{n}}^{T_{n}}\frac{dt}{q_{i}^{it}}=O\left(1\right)\quad \text{as }n\rightarrow \infty ,\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{i=1}^{\infty }\frac{b\left(q_{i}\right)}{q_{i}^{\unicode[STIX]{x1D70E}_{0}^{\prime }}}\int _{-T_{n}}^{T_{n}}\frac{dt}{q_{i}^{it}}=O\left(1\right)\quad \text{as }n\rightarrow \infty ,\end{eqnarray}$$
Using the series representation of the digamma function we get that
 $$\begin{eqnarray}\int _{-T_{n}}^{T_{n}}\left(\frac{\unicode[STIX]{x1D6E4}^{\prime }}{\unicode[STIX]{x1D6E4}}\left(\unicode[STIX]{x1D70E}_{0}^{\prime }+it-\frac{1}{2}\right)-\frac{\unicode[STIX]{x1D6E4}^{\prime }}{\unicode[STIX]{x1D6E4}}\left(\unicode[STIX]{x1D70E}_{0}^{\prime }+it\right)\right)dt=O(1)\quad \text{ as }n\rightarrow \infty .\end{eqnarray}$$
$$\begin{eqnarray}\int _{-T_{n}}^{T_{n}}\left(\frac{\unicode[STIX]{x1D6E4}^{\prime }}{\unicode[STIX]{x1D6E4}}\left(\unicode[STIX]{x1D70E}_{0}^{\prime }+it-\frac{1}{2}\right)-\frac{\unicode[STIX]{x1D6E4}^{\prime }}{\unicode[STIX]{x1D6E4}}\left(\unicode[STIX]{x1D70E}_{0}^{\prime }+it\right)\right)dt=O(1)\quad \text{ as }n\rightarrow \infty .\end{eqnarray}$$
With all this, the proof of the Proposition is complete.◻
Remark 26. The above proposition shows that the term
 $-(\log \mathfrak{g}_{1}/\unicode[STIX]{x1D70B})T$
measures the discrepancy between the number of zeros of
$-(\log \mathfrak{g}_{1}/\unicode[STIX]{x1D70B})T$
measures the discrepancy between the number of zeros of
![]() $\unicode[STIX]{x1D719}_{M}$
with real part greater that
$\unicode[STIX]{x1D719}_{M}$
with real part greater that
![]() $1/2$
, meaning
$1/2$
, meaning
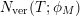 $N_{\text{ver}}(T;\unicode[STIX]{x1D719}_{M})$
, and the quantity
$N_{\text{ver}}(T;\unicode[STIX]{x1D719}_{M})$
, and the quantity
 $N_{M,\text{con}}(T)$
, appearing in the classical version of the Weyl’s law.
$N_{M,\text{con}}(T)$
, appearing in the classical version of the Weyl’s law.
Furthermore, one can restate Proposition 25 as the relation representing Weyl’s law
 $$\begin{eqnarray}\displaystyle N_{\text{ver}}(T_{n};Z_{M}H_{M}) & = & \displaystyle \frac{\text{vol}(M)}{4\unicode[STIX]{x1D70B}}T_{n}^{2}-\frac{n_{1}}{\unicode[STIX]{x1D70B}}T_{n}\log T_{n}+\frac{T_{n}}{\unicode[STIX]{x1D70B}}\left(n_{1}(1-\log 2)-\log \mathfrak{g}_{1}\right)\nonumber\\ \displaystyle & & \displaystyle +\,O\left(T_{n}/\log T_{n}\right),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle N_{\text{ver}}(T_{n};Z_{M}H_{M}) & = & \displaystyle \frac{\text{vol}(M)}{4\unicode[STIX]{x1D70B}}T_{n}^{2}-\frac{n_{1}}{\unicode[STIX]{x1D70B}}T_{n}\log T_{n}+\frac{T_{n}}{\unicode[STIX]{x1D70B}}\left(n_{1}(1-\log 2)-\log \mathfrak{g}_{1}\right)\nonumber\\ \displaystyle & & \displaystyle +\,O\left(T_{n}/\log T_{n}\right),\end{eqnarray}$$
as
![]() $n\rightarrow \infty$
.
$n\rightarrow \infty$
.
A direct consequence of the relation (69), Main Theorem and Theorem 22 is the following reformulation of the Weyl’s law:
Corollary 27. There exist a sequence
![]() $\{T_{n}\}$
of positive real numbers tending to infinity such that, for every positive integer
$\{T_{n}\}$
of positive real numbers tending to infinity such that, for every positive integer
![]() $k$
$k$
 $$\begin{eqnarray}\displaystyle N_{\text{ver}}(T_{n};Z_{M}H_{M}) & = & \displaystyle N_{\text{ver}}(T_{n};(Z_{M}H_{M})^{(k)})-\frac{n_{1}}{\unicode[STIX]{x1D70B}}T_{n}\log T_{n}\nonumber\\ \displaystyle & & \displaystyle +\,\frac{T_{n}}{2\unicode[STIX]{x1D70B}}(2n_{1}+\log A_{M})+o(T_{n})\quad \text{as }n\rightarrow \infty .\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle N_{\text{ver}}(T_{n};Z_{M}H_{M}) & = & \displaystyle N_{\text{ver}}(T_{n};(Z_{M}H_{M})^{(k)})-\frac{n_{1}}{\unicode[STIX]{x1D70B}}T_{n}\log T_{n}\nonumber\\ \displaystyle & & \displaystyle +\,\frac{T_{n}}{2\unicode[STIX]{x1D70B}}(2n_{1}+\log A_{M})+o(T_{n})\quad \text{as }n\rightarrow \infty .\nonumber\end{eqnarray}$$
Remark 28. An interpretation of the constant
![]() $\log \mathfrak{g}_{1}$
, similar to the one derived in Proposition 25 is obtained in [Reference Fischer7, formula (3.4.15)], where it is shown, in our notation, that
$\log \mathfrak{g}_{1}$
, similar to the one derived in Proposition 25 is obtained in [Reference Fischer7, formula (3.4.15)], where it is shown, in our notation, that
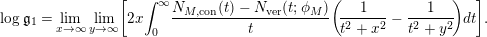 $$\begin{eqnarray}\log \mathfrak{g}_{1}=\lim _{x\rightarrow \infty }\lim _{y\rightarrow \infty }\!\left[2x\!\int _{0}^{\infty }\!\frac{N_{M,\text{con}}(t)-N_{\text{ver}}(t;\unicode[STIX]{x1D719}_{M})}{t}\!\left(\!\frac{1}{t^{2}+x^{2}}-\frac{1}{t^{2}+y^{2}}\!\right)\!dt\right]\!.\end{eqnarray}$$
$$\begin{eqnarray}\log \mathfrak{g}_{1}=\lim _{x\rightarrow \infty }\lim _{y\rightarrow \infty }\!\left[2x\!\int _{0}^{\infty }\!\frac{N_{M,\text{con}}(t)-N_{\text{ver}}(t;\unicode[STIX]{x1D719}_{M})}{t}\!\left(\!\frac{1}{t^{2}+x^{2}}-\frac{1}{t^{2}+y^{2}}\!\right)\!dt\right]\!.\end{eqnarray}$$
A geometric interpretation of the constant
![]() $\mathfrak{g}_{1}$
, in the case when the surface has one cusp
$\mathfrak{g}_{1}$
, in the case when the surface has one cusp
![]() $\mathfrak{a}$
is derived in [Reference Iwaniec17]. In that case,
$\mathfrak{a}$
is derived in [Reference Iwaniec17]. In that case,
![]() $\mathfrak{g}_{1}^{-1}$
is the radius of the largest isometric circle arising in the construction of the standard polygon for the group
$\mathfrak{g}_{1}^{-1}$
is the radius of the largest isometric circle arising in the construction of the standard polygon for the group
![]() $\unicode[STIX]{x1D70E}_{\mathfrak{a}}^{-1}\unicode[STIX]{x1D6E4}\unicode[STIX]{x1D70E}_{\mathfrak{a}}$
, where
$\unicode[STIX]{x1D70E}_{\mathfrak{a}}^{-1}\unicode[STIX]{x1D6E4}\unicode[STIX]{x1D70E}_{\mathfrak{a}}$
, where
![]() $\unicode[STIX]{x1D70E}_{\mathfrak{a}}$
denotes the scaling matrix of the cusp
$\unicode[STIX]{x1D70E}_{\mathfrak{a}}$
denotes the scaling matrix of the cusp
![]() $\mathfrak{a}$
.
$\mathfrak{a}$
.
As stated in the introduction, we do not know of a spectral or geometric interpretation of the constant
![]() $\mathfrak{g}_{2}$
, besides the trivial one which realizes
$\mathfrak{g}_{2}$
, besides the trivial one which realizes
![]() $\mathfrak{g}_{2}$
as the second largest denominator of the Dirichlet series portion of the scattering determinant. Therefore, we view Corollary 27 as giving rise to a new spectral invariant.
$\mathfrak{g}_{2}$
as the second largest denominator of the Dirichlet series portion of the scattering determinant. Therefore, we view Corollary 27 as giving rise to a new spectral invariant.
9.2 A comparison of counting functions
In this section, we will prove Theorem 2. In effect, it is necessary to recall results from [Reference Hejhal14], translate the notation in [Reference Hejhal14] to the notation in the present paper, then combine the result with (2) and parts (c) of the Main Theorem and Theorem 22.
From [Reference Hejhal14, Theorem 2.22] we have the asymptotic relation
 $$\begin{eqnarray}\displaystyle N_{\text{w}}(T;H_{M}) & = & \displaystyle \frac{n_{1}}{2}\cdot \frac{T\log T}{2\unicode[STIX]{x1D70B}}+\frac{T}{2}\left(-\frac{n_{1}}{2\unicode[STIX]{x1D70B}}-\frac{1}{\unicode[STIX]{x1D70B}}\log \left|b_{2}\right|\right)+O(\log T)\nonumber\\ \displaystyle & & \displaystyle \qquad \text{as }T\rightarrow \infty .\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle N_{\text{w}}(T;H_{M}) & = & \displaystyle \frac{n_{1}}{2}\cdot \frac{T\log T}{2\unicode[STIX]{x1D70B}}+\frac{T}{2}\left(-\frac{n_{1}}{2\unicode[STIX]{x1D70B}}-\frac{1}{\unicode[STIX]{x1D70B}}\log \left|b_{2}\right|\right)+O(\log T)\nonumber\\ \displaystyle & & \displaystyle \qquad \text{as }T\rightarrow \infty .\end{eqnarray}$$
Note that in [Reference Hejhal14], the author counts the zeros of
![]() $H_{M}$
in both the upper and lower half-planes, whereas the counting function
$H_{M}$
in both the upper and lower half-planes, whereas the counting function
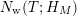 $N_{\text{w}}(T;H_{M})$
only considers those zeros in the upper half-plane. Recall that the zeros and poles of
$N_{\text{w}}(T;H_{M})$
only considers those zeros in the upper half-plane. Recall that the zeros and poles of
![]() $H$
appear symmetrically about the real axis. As a result, the relation (70) differs from [Reference Hejhal14, Theorem 2.22] by a factor of two. Comparing [Reference Hejhal14, eq. (2.15) on p. 445] with our notation we deduce that
$H$
appear symmetrically about the real axis. As a result, the relation (70) differs from [Reference Hejhal14, Theorem 2.22] by a factor of two. Comparing [Reference Hejhal14, eq. (2.15) on p. 445] with our notation we deduce that
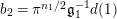 $b_{2}=\unicode[STIX]{x1D70B}^{n_{1}/2}\mathfrak{g}_{1}^{-1}d(1)$
, hence, we are able to rewrite [Reference Hejhal14, Theorem 2.22] as
$b_{2}=\unicode[STIX]{x1D70B}^{n_{1}/2}\mathfrak{g}_{1}^{-1}d(1)$
, hence, we are able to rewrite [Reference Hejhal14, Theorem 2.22] as
 $$\begin{eqnarray}\displaystyle N_{\text{w}}(T;H_{M}) & = & \displaystyle \frac{n_{1}}{2}\cdot \frac{T\log T}{2\unicode[STIX]{x1D70B}}-\frac{T}{2\unicode[STIX]{x1D70B}}\left(\frac{n_{1}}{2}+\frac{n_{1}}{2}\log \unicode[STIX]{x1D70B}+\log \left|d(1)\right|-\log \mathfrak{g}_{1}\right)\nonumber\\ \displaystyle & & \displaystyle +\,O(\log T)\quad \text{as }T\rightarrow \infty .\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle N_{\text{w}}(T;H_{M}) & = & \displaystyle \frac{n_{1}}{2}\cdot \frac{T\log T}{2\unicode[STIX]{x1D70B}}-\frac{T}{2\unicode[STIX]{x1D70B}}\left(\frac{n_{1}}{2}+\frac{n_{1}}{2}\log \unicode[STIX]{x1D70B}+\log \left|d(1)\right|-\log \mathfrak{g}_{1}\right)\nonumber\\ \displaystyle & & \displaystyle +\,O(\log T)\quad \text{as }T\rightarrow \infty .\end{eqnarray}$$
Comparing (71) with part (c) of Main Theorem we deduce that
 $$\begin{eqnarray}N_{\text{w}}(T;(Z_{M}H_{M})^{\prime })-N_{\text{w}}(T;H_{M})\displaystyle =\frac{T\log T}{2\unicode[STIX]{x1D70B}}+\frac{T}{2\unicode[STIX]{x1D70B}}C+o(T)\quad \text{as }T\rightarrow \infty\end{eqnarray}$$
$$\begin{eqnarray}N_{\text{w}}(T;(Z_{M}H_{M})^{\prime })-N_{\text{w}}(T;H_{M})\displaystyle =\frac{T\log T}{2\unicode[STIX]{x1D70B}}+\frac{T}{2\unicode[STIX]{x1D70B}}C+o(T)\quad \text{as }T\rightarrow \infty\end{eqnarray}$$
with
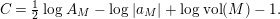 $C=\frac{1}{2}\log A_{M}-\log |a_{M}|+\log \text{vol}(M)-1.$
$C=\frac{1}{2}\log A_{M}-\log |a_{M}|+\log \text{vol}(M)-1.$
Assume that
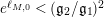 $e^{\ell _{M,0}}<(\mathfrak{g}_{2}/\mathfrak{g}_{1})^{2}$
, so then
$e^{\ell _{M,0}}<(\mathfrak{g}_{2}/\mathfrak{g}_{1})^{2}$
, so then
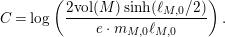 $$\begin{eqnarray}C=\log \left(\frac{2\text{vol}(M)\sinh (\ell _{M,0}/2)}{e\cdot m_{M,0}\ell _{M,0}}\right).\end{eqnarray}$$
$$\begin{eqnarray}C=\log \left(\frac{2\text{vol}(M)\sinh (\ell _{M,0}/2)}{e\cdot m_{M,0}\ell _{M,0}}\right).\end{eqnarray}$$
Let
![]() $\widetilde{M}$
be any co-compact hyperbolic Riemann surface such that
$\widetilde{M}$
be any co-compact hyperbolic Riemann surface such that
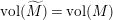 $\text{vol}(\widetilde{M})=\text{vol}(M)$
. Assume that
$\text{vol}(\widetilde{M})=\text{vol}(M)$
. Assume that
![]() $M$
and
$M$
and
![]() $\widetilde{M}$
have systoles of equal length, and the same number of inconjugate classes of systoles. Then, using (2), we arrive at the conclusion that
$\widetilde{M}$
have systoles of equal length, and the same number of inconjugate classes of systoles. Then, using (2), we arrive at the conclusion that
 $$\begin{eqnarray}N_{\text{w}}(T;(Z_{M}H_{M})^{\prime })-N_{\text{w}}(T;H_{M})=N_{\text{w}}(T;Z_{\widetilde{M}}^{\prime })+o(T)\quad \text{as }T\rightarrow \infty .\end{eqnarray}$$
$$\begin{eqnarray}N_{\text{w}}(T;(Z_{M}H_{M})^{\prime })-N_{\text{w}}(T;H_{M})=N_{\text{w}}(T;Z_{\widetilde{M}}^{\prime })+o(T)\quad \text{as }T\rightarrow \infty .\end{eqnarray}$$
Furthermore, when
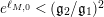 $e^{\ell _{M,0}}<(\mathfrak{g}_{2}/\mathfrak{g}_{1})^{2}$
, comparing (72) with part (c) of Theorem 22, for
$e^{\ell _{M,0}}<(\mathfrak{g}_{2}/\mathfrak{g}_{1})^{2}$
, comparing (72) with part (c) of Theorem 22, for
![]() $k\geqslant 2$
we arrive at
$k\geqslant 2$
we arrive at
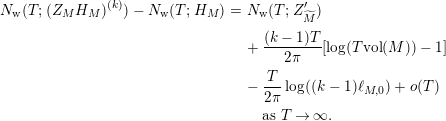 $$\begin{eqnarray}\displaystyle N_{\text{w}}(T;(Z_{M}H_{M})^{(k)})-N_{\text{w}}(T;H_{M}) & = & \displaystyle N_{\text{w}}(T;Z_{\widetilde{M}}^{\prime })\nonumber\\ \displaystyle & & \displaystyle +\,\frac{(k-1)T}{2\unicode[STIX]{x1D70B}}[\log (T\text{vol}(M))-1]\nonumber\\ \displaystyle & & \displaystyle -\,\frac{T}{2\unicode[STIX]{x1D70B}}\log ((k-1)\ell _{M,0})+o(T)\nonumber\\ \displaystyle & & \displaystyle \quad \text{as }T\rightarrow \infty .\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle N_{\text{w}}(T;(Z_{M}H_{M})^{(k)})-N_{\text{w}}(T;H_{M}) & = & \displaystyle N_{\text{w}}(T;Z_{\widetilde{M}}^{\prime })\nonumber\\ \displaystyle & & \displaystyle +\,\frac{(k-1)T}{2\unicode[STIX]{x1D70B}}[\log (T\text{vol}(M))-1]\nonumber\\ \displaystyle & & \displaystyle -\,\frac{T}{2\unicode[STIX]{x1D70B}}\log ((k-1)\ell _{M,0})+o(T)\nonumber\\ \displaystyle & & \displaystyle \quad \text{as }T\rightarrow \infty .\nonumber\end{eqnarray}$$
Then, from part (c) of Theorem 22 applied to the zeta function
![]() $Z_{\widetilde{M}}$
we deduce
$Z_{\widetilde{M}}$
we deduce
 $$\begin{eqnarray}N_{\text{w}}(T;(Z_{M}H_{M})^{(k)})-N_{\text{w}}(T;H_{M})\displaystyle =N_{\text{w}}(T;(Z_{\widetilde{M}})^{(k)})+o(T)\quad \text{as }T\rightarrow \infty .\end{eqnarray}$$
$$\begin{eqnarray}N_{\text{w}}(T;(Z_{M}H_{M})^{(k)})-N_{\text{w}}(T;H_{M})\displaystyle =N_{\text{w}}(T;(Z_{\widetilde{M}})^{(k)})+o(T)\quad \text{as }T\rightarrow \infty .\end{eqnarray}$$
This proves Theorem 2.
We find the comparison of counting functions, as summarized in (13) very interesting, especially since the coefficients in the asymptotic expansions in (70) and part (c) of the Main Theorem are somewhat involved and dissimilar from other known asymptotic expansions.
9.3 Concluding remarks
In [Reference Conway, McKay and Sebbar5] the authors defined
![]() $213$
genus zero subgroups of which
$213$
genus zero subgroups of which
![]() $171$
are associated to “Moonshine”. It would be interesting to compute the invariant
$171$
are associated to “Moonshine”. It would be interesting to compute the invariant
![]() $A_{M}$
for each of these groups to see if further information regarding the groups, possibly related to “moonshine”, is uncovered.
$A_{M}$
for each of these groups to see if further information regarding the groups, possibly related to “moonshine”, is uncovered.
Is it possible to explicitly determine an example of a surface where
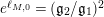 $e^{\ell _{M,0}}=(\mathfrak{g}_{2}/\mathfrak{g}_{1})^{2}$
? More generally, one could study the set of such surfaces, as a subset of moduli space. Is the set of surfaces where
$e^{\ell _{M,0}}=(\mathfrak{g}_{2}/\mathfrak{g}_{1})^{2}$
? More generally, one could study the set of such surfaces, as a subset of moduli space. Is the set of surfaces where
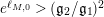 $e^{\ell _{M,0}}>(\mathfrak{g}_{2}/\mathfrak{g}_{1})^{2}$
a connected subset of moduli space, or are there several components? Is there another characterization of surfaces where
$e^{\ell _{M,0}}>(\mathfrak{g}_{2}/\mathfrak{g}_{1})^{2}$
a connected subset of moduli space, or are there several components? Is there another characterization of surfaces where
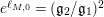 $e^{\ell _{M,0}}=(\mathfrak{g}_{2}/\mathfrak{g}_{1})^{2}$
? Many other basic questions can be easily posed, and we find these problems very interesting.
$e^{\ell _{M,0}}=(\mathfrak{g}_{2}/\mathfrak{g}_{1})^{2}$
? Many other basic questions can be easily posed, and we find these problems very interesting.
In [Reference Avdispahić, Jorgenson and Smajlović2], the authors determined the asymptotic behavior of Selberg’s zeta function through degeneration up to the critical line. It would be interesting to study the asymptotic behavior of the zeros of the derivative of Selberg’s zeta function through degeneration, either in moduli space or through elliptic degeneration.
To come full circle, we return to the setting of the Riemann zeta function and speculate if one can attempt to mimic results which follow from the Levinson–Montgomery article [Reference Levinson and Montgomery21]. Specifically, we recall, that Levinson used results from the distribution of zeros of
![]() $\unicode[STIX]{x1D701}_{\mathbb{Q}}^{\prime }$
to prove that more than
$\unicode[STIX]{x1D701}_{\mathbb{Q}}^{\prime }$
to prove that more than
![]() $1/3$
of the zeros of the Riemann zeta function lie on the critical line. Can one follow a similar investigation in the setting of the Selberg zeta function associated to a noncompact, finite volume surface? To do so, we note that a starting point would be to establish an analogue of the approximate functional equation for the Selberg zeta function. Results in this direction would be very significant, and we plan to undertake the project in the near future.
$1/3$
of the zeros of the Riemann zeta function lie on the critical line. Can one follow a similar investigation in the setting of the Selberg zeta function associated to a noncompact, finite volume surface? To do so, we note that a starting point would be to establish an analogue of the approximate functional equation for the Selberg zeta function. Results in this direction would be very significant, and we plan to undertake the project in the near future.
Acknowledgments
We thank the referee for the numerous comments and invaluable assistance. Their efforts greatly assisted in improving the exposition of the article.