Published online by Cambridge University Press: 02 March 2023
The aim of this paper is to study the dimension reduction analysis of an elastic plate with small thickness reinforced with increasing number of thin ribbons developing fractal geometry. We prove the 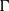 $\Gamma $-convergence of the energy functionals to a two-dimensional effective energy including singular terms supported within the Sierpinski carpet.
$\Gamma $-convergence of the energy functionals to a two-dimensional effective energy including singular terms supported within the Sierpinski carpet.