Introduction
Stroke is a prominent cause of long-term disability affecting over seven million people in the United States alone (Benjamin et al., Reference Benjamin, Muntner, Alonso, Bittencourt, Callaway, Carson, Chamberlain, Chang, Cheng, Das, Delling, Djousse, MSV, Ferguson, Fornage, Jordan, Khan, Kissela, Knutson, Kwan, Lackland, Lewis, Lichtman, Longenecker, Loop, Lutsey, Martin, Matsushita, Moran, Mussolino, O’Flaherty, Pandey, Perak, Rosamond, Roth, Sampson, Satou, Schroeder, Shah, Spartano, Stokes, Tirschwell, Tsao, Turakhia, VanWagner, Wilkins, Wong and Virani2019), many of whom suffer from hemiparesis. Though the impact of hemiparesis is wide-ranging, its effects are particularly apparent in gait; hemiparetic gait is typically slow, asymmetric, and inefficient (Olney and Richards, Reference Olney and Richards1996), posing an increased risk of fall. These impairments can limit community ambulation in a way that significantly affects participation in activities of daily living (ADLs), often leading to isolation, depression, and even secondary strokes (Do Lee et al., Reference Do Lee, Folsom and Blair2003; Linden et al., Reference Linden, Blomstrand and Skoog2007).
Rehabilitation after stroke plays a crucial role in restoring gait. Comprising an iterative process alternating between gait assessment and intervention such as motor recovery training, extensive literature demonstrates that effective gait training after stroke is functional, task-specific, intensive, and repetitive (Eng and Tang, Reference Eng and Tang2007; Langhorne et al., Reference Langhorne, Coupar and Pollock2009; Winstein et al., Reference Winstein, Stein, Arena, Bates, Cherney, Cramer, Deruyter, Eng, Fisher, Harvey and Lang2016). Furthermore, deterioration in regained mobility after inpatient care is a major challenge for effective rehabilitation, emphasizing the importance of continued, postdischarge training throughout the chronic stages of stroke recovery (Paolucci, Reference Paolucci2008).
Gait Monitoring and Wearable Devices in Poststroke Rehabilitation
To encourage such training paradigms in and beyond the clinic, our group develops wearable robots called soft exosuits (see Figure 1) that deliver mechanical power to the paretic (P) ankle via functional apparel and cable-based actuation systems, in step with a patient’s natural gait cycle (Awad et al., Reference Awad, Bae, O’Donnell, De Rossi, Hendron, Sloot, Kudzia, Allen, Holt, Ellis and Walsh2017; Bae et al., Reference Bae, Siviy, Rouleau, Menard, Odonnell, Geliana, Athanassiu, Ryan, Bibeau, Sloot, Kudzia, Ellis, Awad and Walsh2018). During activities typical to rehabilitation, soft exosuits have been found to reduce common gait compensations such as hip hiking, circumduction, and propulsion asymmetry (Awad et al., Reference Awad, Bae, O’Donnell, De Rossi, Hendron, Sloot, Kudzia, Allen, Holt, Ellis and Walsh2017)—locomotor improvements that may amplify benefits from conventional training (Awad et al., Reference Awad, Kudzia, Revi, Ellis and Walsh2020). Moreover, a unique characteristic of soft exosuits is their ability to switch quickly from applying assistance to no assistance (while minimally restricting gait), potentially enabling new approaches for gait rehabilitation. Beyond soft exosuits, other lightweight wearable robots have improved ankle power production (McCain et al., Reference McCain, Dick, Giest, Nuckols, Lewek, Saul and Sawicki2019) and walking speed (Jayaraman et al., Reference Jayaraman, O’Brien, Madhavan, Mummidisetty, Roth, Hohl, Tapp, Brennan, Kocherginsky, Williams, Takahashi and Rymer2019) in people poststroke.
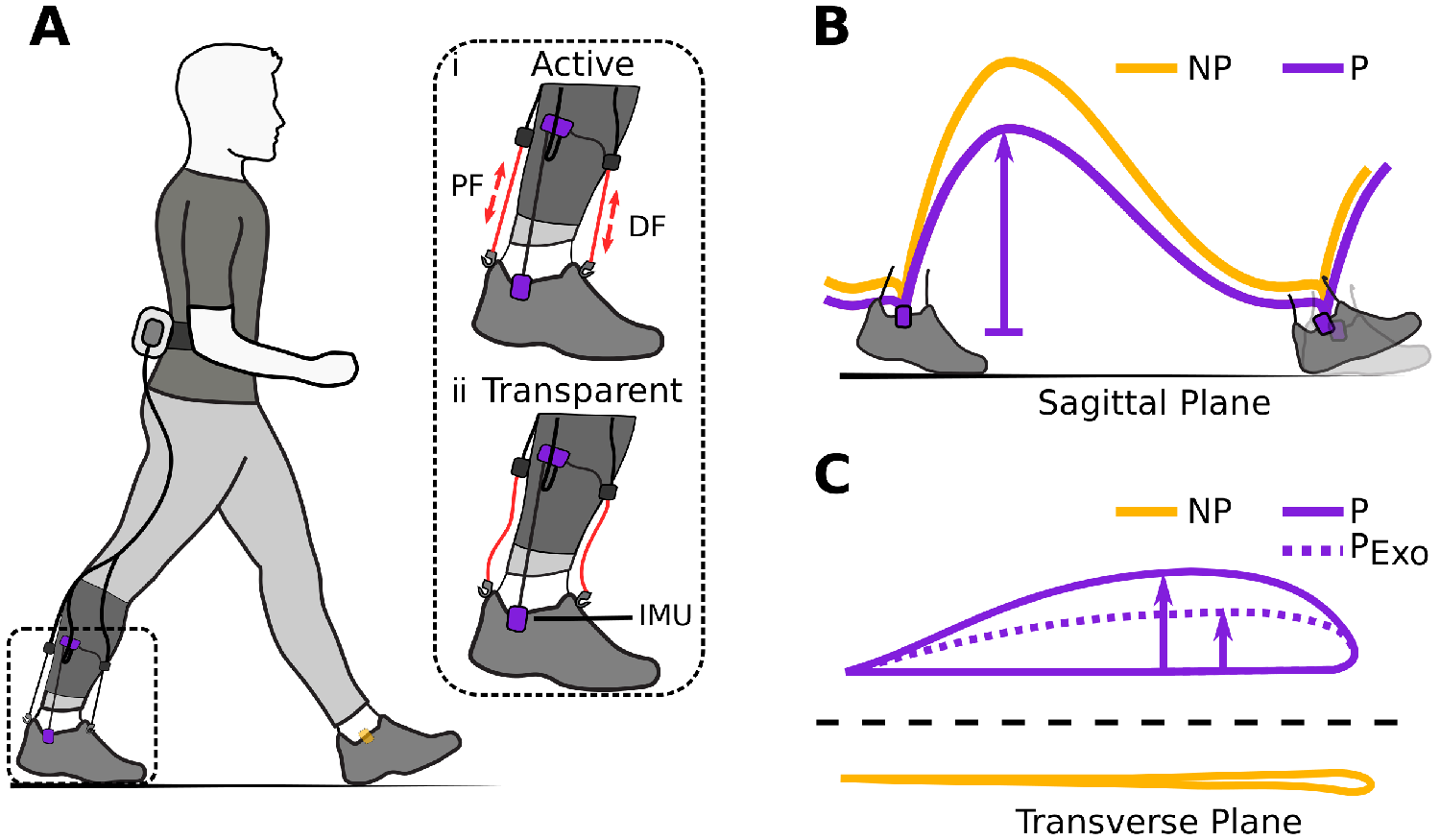
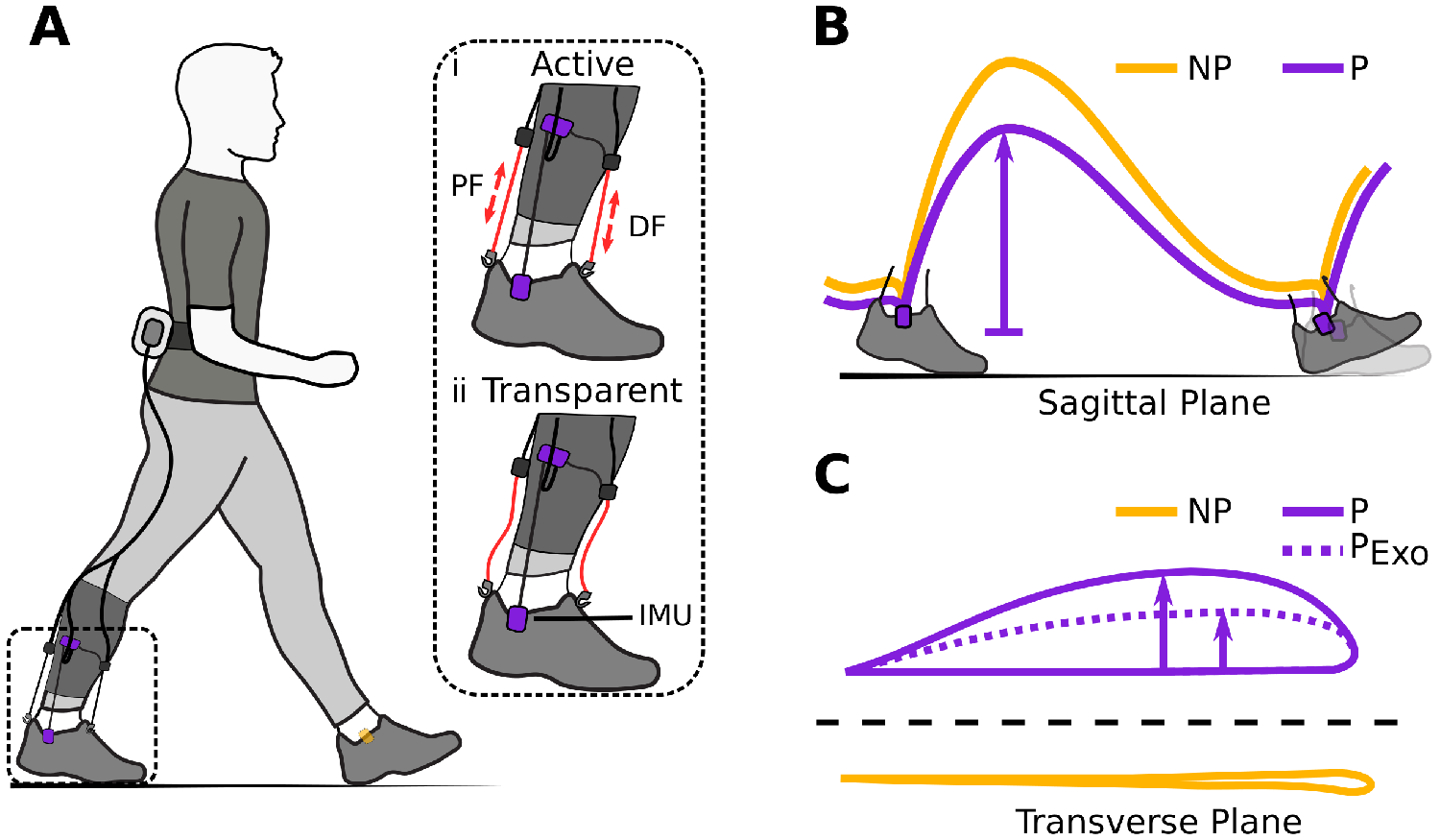
Figure 1. (a) Hardware setup for ambulatory gait monitoring in exosuit-assisted walking. The integrated foot inertial measurement units analyze the gait cycle to inform the exosuit controller when to correctly provide plantarflexion (PF) and dorsiflexion (DF) assistance (i). The exosuit can quickly switch from active to transparent mode (ii) allowing a person to walk without assistance and hence their natural walking pattern if desired. Typical impairments in poststroke gait include reduced ground clearance (b), often causing individuals to compensate with increased lateral displacement during swing (c). Awad et al. (Reference Awad, Bae, O’Donnell, De Rossi, Hendron, Sloot, Kudzia, Allen, Holt, Ellis and Walsh2017) showed that exosuit assistance can help reduce such compensatory mechanisms.
While these outcomes are promising, monitoring gait improvements after stroke can be challenging, particularly in outpatient or community-based rehabilitation environments. Clinical tools, like mobility scales and outcome measures that support therapists in assessing ADL-related improvements, are reliable in classifying functional abilities. Still, they may lack the precision and frequency required to reflect subtle changes in mobility (Toro et al., Reference Toro, Nester and Farren2007), such as those induced by an exosuit. Similarly, even highly trained clinicians may have difficulty visually detecting stride-by-stride or between-session improvements (Paolucci et al., Reference Paolucci, Grasso, Antonucci, Bragoni, Troisi, Morelli, Coiro, De Angelis and Rizzi2001; Walker et al.,Reference Walker, Sunnerhagen and Fisher2013). Moreover, in community or at-home rehabilitation, insurance status, restricted patient mobility, or remote living conditions may constrain access to regular physical therapy assessment altogether (Hickey et al., Reference Hickey, Horgan, O’Neill and McGee2012).
Instrumented ambulatory monitoring may help overcome some of these barriers by allowing clinicians to assess gait remotely, objectively, and continually. In particular, integration with new rehabilitation approaches such as telemedicine could help extend clinical gait training to the community on a broader scale. Furthermore, in combination with new wearable robot technologies such as soft exosuits, quantitatively monitoring the immediate impact of provided assistance may allow clinicians to adjust training routines and tune assistance parameters effectively within an in-person or remote training session. Similarly, recent studies suggest that wearable robots can tune assistance based on physiological data (Zhang et al., Reference Zhang, Hol, Slot and Luinge2011). Likewise, future iterations of soft exosuits could automatically tune assistance based on an individual’s gait metric response by integrating ambulatory gait metrics directly into the exosuit’s control loop.
Indeed, being small, lightweight, and unobtrusive, inertial measurement units (IMUs) in particular have proven attractive for estimating spatiotemporal gait metrics in various clinical and nonclinical applications. Soft exosuits, for instance, use IMUs as a high-level control input for temporal gait segmentation. Necessarily, this has enabled exosuits to export a variety of clinically important temporal gait metrics such as stance-swing ratios and P and nonparetic (NP) step time (Awad et al., Reference Awad, Bae, O’Donnell, De Rossi, Hendron, Sloot, Kudzia, Allen, Holt, Ellis and Walsh2017). Outside the field of wearable robotics, a number of studies investigating IMUs for gait metric reconstruction over the last decade have shown promising outcomes both in healthy (Sabatini et al., Reference Sabatini, Martelloni, Scapellato and Cavallo2005; Schepers et al., Reference Schepers, van Asseldonk, Baten and Veltink2010; Mariani et al., Reference Mariani, Hoskovec, Rochat, Büla, Penders and Aminian2010; Köse et al., Reference Köse, Cereatti and Della Croce2012; Rebula et al., Reference Rebula, Ojeda, Adamczyk and Kuo2013; Benoussaad et al., Reference Benoussaad, Sijobert, Mombaur and Coste2016) and impaired (Trojaniello et al., Reference Trojaniello, Cereatti, Pelosin, Avanzino, Mirelman, Hausdorff and Della Croce2014; Rampp et al., Reference Rampp, Barth, Schülein, Gaßmann, Klucken and Eskofier2015; Ferrari et al., Reference Ferrari, Ginis, Hardegger, Casamassima, Rocchi and Chiari2016; Visi et al., Reference Visi, Georgiou, Holland, Pinzone, Donaldson and Tetley2017; Porciuncula et al., Reference Porciuncula, Roto, Kumar, Davis, Roy, Walsh and Awad2018) populations. Though work relying solely on IMUs in people poststroke has been more limited, some studies have also explored approaches complementing IMUs with additional sensors such as foot switches and ultrasound sensors (Meulen et al., Reference van Meulen, Weenk, Buurke, van Beijnum and Veltink2016) that can directly provide inter-limb measures such as step length. Yet other studies incorporate kinematic models combined with IMUs spread across the lower limbs to compute gait metrics (Moore et al., Reference Moore, Hickey, Lord, Del Din, Godfrey and Rochester2017; Wang et al., Reference Wang, Sun, Li and Liu2018). Please see the section “Correcting Sensor Drift” for a more detailed explanation of the methods used in the literature. Broadly, though encouraging, existing methods often rely on manual tuning that may not be adaptable across highly heterogeneous populations such as people poststroke. A requirement of manual tuning may limit these methods’ usability for control in wearable robots such as exosuits. Motivated by these factors, our goal was to update exosuit gait detection algorithms developed for poststroke populations without adding additional hardware requirements. Moreover, it is to date unclear if IMU-based gait monitoring is accurate even in the presence of potential motion artifacts from exosuit assistance.
In this paper, we present an accurate and robust method of computing gait metrics in poststroke walking with IMUs attached bilaterally to the paretic and nonparetic foot. As a secondary objective, we show a proof of concept for using gait monitoring integrated with an exosuit in the community. Though we anticipate this method is effective with or without an assistive device, to avoid imposing additional burdens on clinicians wishing to monitor gait in their patients wearing exosuits, we use IMUs already integrated into an exosuit system.
Algorithm for Robust Zero-Velocity Update Detection
Estimating spatial gait metrics relies on reconstructing foot trajectories. As IMUs measure linear accelerations (and angular velocities), measuring changes in position typically requires numerical integration of sensor signals. However, due to sensor inaccuracies, estimation error (i.e., drift) accumulates during numerical integration, rendering the estimated metrics unusable within seconds if not accounted for. Canonically, these inaccuracies manifest themselves in the form of bias (![]() $ \beta $; poor estimates in the signal mean) and noise (
$ \beta $; poor estimates in the signal mean) and noise (![]() $ \epsilon $; zero-mean inaccuracies) (Woodman, Reference Woodman2007).
$ \epsilon $; zero-mean inaccuracies) (Woodman, Reference Woodman2007).
Correcting Sensor Drift
State-of-the art ambulatory gait monitoring systems correct this drift by discarding estimation error using zero-velocity updates (ZUPTs); recurring instances or periods in the gait cycle during which foot motion is known to be zero (Foxlin, Reference Foxlin2005). Conventionally, approaches look at either linear accelerations, angular velocities, or combinations of both signals to detect ZUPTs (Skog et al., Reference Skog, Händel, Nilsson and Rantakokko2010). That is, researchers use empirically tuned thresholds to determine when the designated ZUPT detection signals fall reasonably close to zero. Additional constraints such as mandatory ZUPT window lengths are also common to improve detection accuracy and increase robustness (Jim, Reference Jim2009; Rampp et al., Reference Rampp, Barth, Schülein, Gaßmann, Klucken and Eskofier2015; Rebula et al., Reference Rebula, Ojeda, Adamczyk and Kuo2013). Typically, when the ipsilateral detection signals approach zero—suggesting the (ipsilateral) foot is stationary—algorithms restart the integration. This constrains the time period in which error can accumulate and, by modeling the error propagation over time, discards already accumulated drift from the faulty position estimate. Such approaches have successfully estimated gait parameters in unimpaired individuals (Sabatini et al., Reference Sabatini, Martelloni, Scapellato and Cavallo2005) as well as in various populations with gait pathologies (Mariani et al., Reference Mariani, Jiménez, Vingerhoets and Aminian2013; Trojaniello et al., Reference Trojaniello, Cereatti, Pelosin, Avanzino, Mirelman, Hausdorff and Della Croce2014; Ferrari et al., Reference Ferrari, Ginis, Hardegger, Casamassima, Rocchi and Chiari2016).
While promising, variability in stroke induced hemiparetic gait, especially on the paretic side (Kempski et al., Reference Kempski, Awad, Buchanan, Higginson and Knarr2018), can make it difficult to generalize thresholds for inter- and even intra-patient use; unexpected or irregular foot motion may lead to missed or unwarranted ZUPT detections if thresholds are not optimally tuned, a complication that may result in highly inaccurate gait metric estimates (Rebula et al., Reference Rebula, Ojeda, Adamczyk and Kuo2013). Other studies (Schepers et al., Reference Schepers, Koopman and Veltink2007; Schepers et al. Reference Schepers, van Asseldonk, Baten and Veltink2010) rely on additional sensors such as foot switches to segment gait and define ZUPTs. Furthermore, there is no work to our knowledge demonstrating that IMU-based gait monitoring can resolve small improvements in walking on an intra-person basis in community environments.
Zero-Velocity Update Detection Using Contralateral Foot Information
We implemented our ZUPT detection method using a strap-down double integration algorithm with linear drift compensation similar to Sabatini et al. (Reference Sabatini, Martelloni, Scapellato and Cavallo2005). The gait segmentation uses information from both feet to identify paretic toe-off and nonparetic toe-off. As the toe-off event on the contralateral side indicates early single limb support on the ipsilateral side, biomechanically this event is likely to coincide with a foot-flat instance of the ipsilateral foot, assuming the person is not running. Commonly, paretic-foot instability can introduce local minima around the sharp negative peaks in Figure 2 that correspond with toe-off. For real-time applications, waiting until angular velocity switches from negative to positive helps avoid these local minima. As this zero crossing follows the actual (peak) toe-off event in the gait cycle by approximately 4–6%, it should be noted that the ZUPT instance will show the same degree of latency compared to the actual (biomechanical) toe-off event, resulting in a slight shift from early stance toward mid-stance (see Figure 2). Confirming contralateral toe-off with the zero crossing of contralateral angular velocity, we leverage this biomechanical constraint to reliably define ZUPT instances on the opposite, ipsilateral foot.
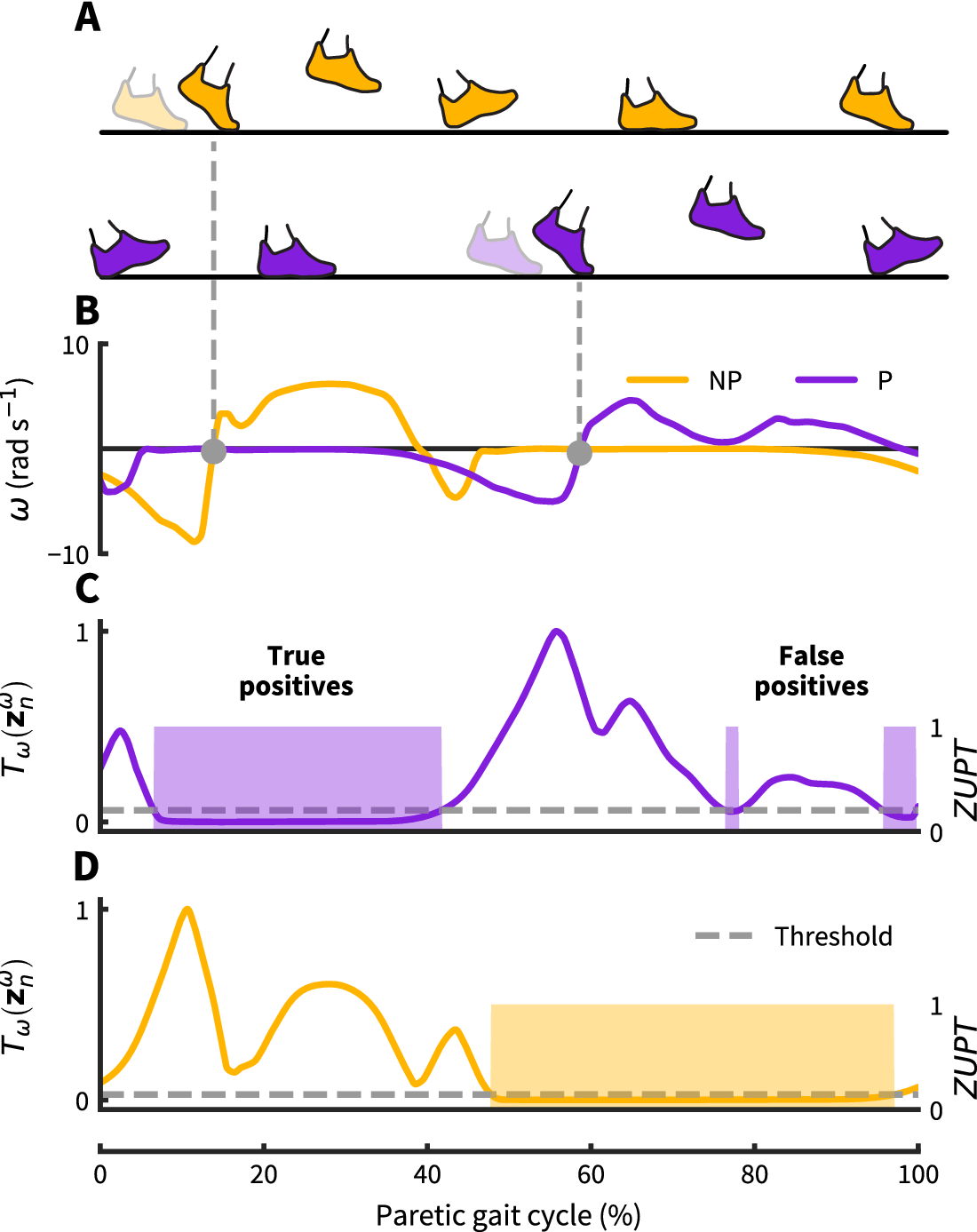
Figure 2. Zero-velocity update detection approach: (a) Nonparetic and paretic gait cycle. (b) Our approach uses contralateral angular velocity zero crossings to detect ZUPT instances on the ipsilateral foot (grey dots). (c–d) Threshold based ZUPT detection shown for an angular rate energy detector as in Skog et al. (Reference Skog, Händel, Nilsson and Rantakokko2010). This method defines a ZUPT as any time the decision metric ![]() $ {T}_{\omega } $(normalized as shown here) falls below a predetermined threshold. For this particular detector, the decision metric
$ {T}_{\omega } $(normalized as shown here) falls below a predetermined threshold. For this particular detector, the decision metric ![]() $ {T}_{\omega } $ broadly measures foot rotational energy normalized to vary between 0 and 1. For the demonstrated threshold, the paretic side shows two falsely identified ZUPT phases caused by unanticipated low angular velocity during swing. The same threshold works correctly for the nonparetic side. Both thresholds are normalized to the respective maximum detector signal value.
$ {T}_{\omega } $ broadly measures foot rotational energy normalized to vary between 0 and 1. For the demonstrated threshold, the paretic side shows two falsely identified ZUPT phases caused by unanticipated low angular velocity during swing. The same threshold works correctly for the nonparetic side. Both thresholds are normalized to the respective maximum detector signal value.
Double Integration Framework
Figure 3 illustrates the general algorithm framework. All input signals utilized by the algorithm—comprising three-axis accelerations in the local (or sensor) frame, three-axis orientation expressed as unit quaternions computed directly by the onboard IMU Kalman Filter as well as angular velocity in the sagittal plane—are obtained from the exosuit-integrated foot IMUs.

Figure 3. General algorithm pipeline. The exosuit-integrated foot inertial measurement units provide three-dimensional linear, sensor frame acceleration as well as angular velocity. After transforming the acceleration signal to a fixed world frame and removing gravity, the resulting acceleration signal ![]() $ {a}_w(t) $ is integrated twice to obtain position estimates. The angular velocity is used by the gait detection algorithm to segment the gait cycle—providing temporal gait features—and detect ZUPT instances that allow us to compensate drift from the computed position trajectories. Based on the resulting three-dimensional foot trajectories, spatial gait metrics for both feet can be computed.
$ {a}_w(t) $ is integrated twice to obtain position estimates. The angular velocity is used by the gait detection algorithm to segment the gait cycle—providing temporal gait features—and detect ZUPT instances that allow us to compensate drift from the computed position trajectories. Based on the resulting three-dimensional foot trajectories, spatial gait metrics for both feet can be computed.
For each time sample, the local acceleration signal is transformed into world frame coordinates based on the current IMU-provided orientation estimate. After removing gravity, the resulting acceleration signal is integrated twice using trapezoidal integration to obtain position estimates. Once the algorithm receives a ZUPT confirmation flag, the integration is re-initialized, and after subtracting the accumulated sensor drift from the uncorrected position estimate we obtain drift compensated position trajectories in each world frame direction. That is, assuming (quasi) constant bias ![]() $ \beta $ and zero-mean noise
$ \beta $ and zero-mean noise ![]() $ \epsilon $, we can model the measured acceleration as
$ \epsilon $, we can model the measured acceleration as ![]() $ \hat{a}(t)=a(t)+\beta +\epsilon (t) $, where
$ \hat{a}(t)=a(t)+\beta +\epsilon (t) $, where ![]() $ a(t) $ refers to the actual acceleration. Consequently, integrating the bias term twice results in position error growing quadratically over time. Knowing the true velocity at each ZUPT event to be zero, the position error
$ a(t) $ refers to the actual acceleration. Consequently, integrating the bias term twice results in position error growing quadratically over time. Knowing the true velocity at each ZUPT event to be zero, the position error ![]() $ {e}_p $ accumulated over the stride interval
$ {e}_p $ accumulated over the stride interval ![]() $ {T}_s $ can be modelled as:
$ {T}_s $ can be modelled as:
 $$ {e}_p=\underset{0}{\overset{\ {T}_s}{\iint }}\beta\ \mathrm{d}t\mathrm{d}t=\frac{1}{2}\ {v}_{\mathrm{ZUPT}}\ {T}_s, $$
$$ {e}_p=\underset{0}{\overset{\ {T}_s}{\iint }}\beta\ \mathrm{d}t\mathrm{d}t=\frac{1}{2}\ {v}_{\mathrm{ZUPT}}\ {T}_s, $$where ![]() $ {v}_{\mathsf{ZUPT}} $ refers to the velocity error (i.e., the estimated velocity) at each ZUPT event.
$ {v}_{\mathsf{ZUPT}} $ refers to the velocity error (i.e., the estimated velocity) at each ZUPT event.
Gait Metric Computation
Based on the drift-corrected position trajectories, we computed gait metrics between subsequent ZUPTs. Stride Length (SL) was defined as the transverse-plane distance between two successive ZUPT events of the same foot (i.e., the magnitude of a vector pointing in the direction of progression):
where ![]() $ {d}_x(i) $ and
$ {d}_x(i) $ and ![]() $ {d}_y(i) $ refer to the overall displacements within the current (
$ {d}_y(i) $ refer to the overall displacements within the current (![]() $ i $th) stride in
$ i $th) stride in ![]() $ x $ and
$ x $ and ![]() $ y $ directions, respectively. Maximum lateral displacement (MLD) was computed as:
$ y $ directions, respectively. Maximum lateral displacement (MLD) was computed as:
where ![]() $ {D}_{xy,i}(k) $ marks the perpendicular distance at every sample point
$ {D}_{xy,i}(k) $ marks the perpendicular distance at every sample point ![]() $ k $ between the direction of progression and the transverse-plane foot trajectory. Similarly, maximum vertical displacement (MVD) was defined as the maximum value of the vertical (z-direction) trajectory. Ground truth motion capture measurements were computed in the same way, using markers rigidly attached to each IMU.
$ k $ between the direction of progression and the transverse-plane foot trajectory. Similarly, maximum vertical displacement (MVD) was defined as the maximum value of the vertical (z-direction) trajectory. Ground truth motion capture measurements were computed in the same way, using markers rigidly attached to each IMU.
Experimental Validation with a Soft Exosuit
To determine algorithm performance in terms of accuracy and robustness, we conducted an overground, in-lab study with eight participants in the chronic phase of poststroke recovery. Figure 4 shows the experimental setup. The soft exosuit’s design is detailed in Bae et al. (Reference Bae, Siviy, Rouleau, Menard, Odonnell, Geliana, Athanassiu, Ryan, Bibeau, Sloot, Kudzia, Ellis, Awad and Walsh2018), but briefly it consists of a proximally mounted actuation unit connected to a distally mounted textile component at the shank with a pair of Bowden cables, one each for plantarflexion (PF) and dorsiflexion (DF). The Bowden cables’ outer sheaths anchor on the shank while their inner cables extend to the foot, generating either PF or DF moments when the respective cable retracts. An IMU (MTi-3; XSens; Netherlands; 100 Hz) mounted on either shoe detects the events described in section “Double Integration Framework.”
Figure 4. (a) Experimental setup for in-lab validation. Participants wearing an exosuit walked continuously with and without exosuit assistance for 4 min each on an overground track in the motion capture laboratory at Harvard University with a total length of 36.9 m. The inertial measurement units (IMUs) were rigidly attached to marker clusters mounted laterally to both feet to minimize relative movement between the IMU and optical markers (see close-up image). The IMU coordinate frame origin was approximated as the center of the four optical markers. Optical motion capture data were collected during the straight path section that fully lies within the capture volume of the cameras (b).
Experimental Overview
Participants (N = 8; age: 48.9 ± 10.0 years; 4 male; Table 1) wearing the exosuit as described previously, were asked to perform two 4 min bouts on an overground track instrumented with nine force plates (FP4060-15; Bertec; Columbus, OH; 2,000 Hz) and a total length of 36.9 m, one bout with the suit active and one bout with the suit inactive at a comfortable walking speed. The order of the two conditions was randomized and exosuit assistance was set as in Bae et al. (Reference Bae, Siviy, Rouleau, Menard, Odonnell, Geliana, Athanassiu, Ryan, Bibeau, Sloot, Kudzia, Ellis, Awad and Walsh2018), with a peak PF cable force of 25% body weight and peak DF cable position held constant after tuning by an experienced clinician. Accuracy was determined with respect to a 14-camera optical motion capture system (Oqus; Qualisys; Sweden; 200 Hz). For synchronization purposes, data were streamed via Bluetooth connection to a nearby computer and analyzed through postprocessing. Medical clearance and signed informed consent forms approved by the Harvard University Human Subjects Review Board were obtained for all participants.
Table 1. Demographic and clinical information of the participants for the present study, including the paretic side, gender, age, time since stroke (TSS), type of stroke, 10-m walk test speed at a self-selected comfortable pace (10MWS CWS), and the number of usable strides from each participant on the P and NP sides

Abbreviations: NP, nonparetic; P, paretic.
Outcome Metrics
Gait metrics were computed as defined above. Accuracy and precision were evaluated in terms of mean (absolute) errors between motion capture and estimated metrics and their respective standard deviations. We further computed inter-rater reliability based on intraclass correlation analysis (![]() $ ICC $) according to the convention by McGraw and Wong (Reference McGraw and Wong1996), evaluating agreement
$ ICC $) according to the convention by McGraw and Wong (Reference McGraw and Wong1996), evaluating agreement ![]() $ ICC\left(A,1\right) $ and consistency
$ ICC\left(A,1\right) $ and consistency ![]() $ ICC\left(C,1\right) $ between both measurement systems. We also computed Pearson’s correlation coefficient between motion capture and estimated metrics, along with the 95% limits of agreement (LoA) between the two metrics. Lastly, we defined robustness in terms of detected versus actual ZUPT events. A ZUPT event was considered correctly detected if it fell within a ground truth window defined based on optical motion capture trajectories. That is, a ground truth ZUPT instance was defined as long as the direction of progression trajectory remained (quasi) stationary, which was considered to be the case if the difference between subsequent sample values remained below a threshold value of 1 mm.
$ ICC\left(C,1\right) $ between both measurement systems. We also computed Pearson’s correlation coefficient between motion capture and estimated metrics, along with the 95% limits of agreement (LoA) between the two metrics. Lastly, we defined robustness in terms of detected versus actual ZUPT events. A ZUPT event was considered correctly detected if it fell within a ground truth window defined based on optical motion capture trajectories. That is, a ground truth ZUPT instance was defined as long as the direction of progression trajectory remained (quasi) stationary, which was considered to be the case if the difference between subsequent sample values remained below a threshold value of 1 mm.
Results
Figure 5 and Table 2 illustrate the results for the three computed gait metrics, separated by paretic and nonparetic sides. Furthermore, Table 3 summarizes the statistical outcome metrics based on a total of 227 (P) and 220 (NP) usable strides for which our approach correctly detected ZUPTs in all cases for both sides. Following the interpretation guidelines from Cicchetti (Reference Cicchetti1994), we observed excellent inter-rater reliability both in terms of agreement ![]() $ \left(0.84< ICC\left(A,1\right)<1.00\right) $ and consistency
$ \left(0.84< ICC\left(A,1\right)<1.00\right) $ and consistency ![]() $ \left(0.86< ICC\left(C,1\right)<1.00\right) $ across all metrics (Table 3). Following, we list the main outcomes for each gait metric in more detail.
$ \left(0.86< ICC\left(C,1\right)<1.00\right) $ across all metrics (Table 3). Following, we list the main outcomes for each gait metric in more detail.

Figure 5. Regression Plots for three gait metrics, stride length (SL), maximum lateral displacement (MLD), and maximum vertical displacement (MVD), shown for the paretic (P) and nonparetic (NP) sides. Each point is the average data from one participant during either the Active (red) or Transparent (grey) condition. Regression plots show Pearson’s correlation (![]() $ r $) between reference and algorithm estimates, with *** indicating p < .001. Plots show linear fit (blue) as well as identity line (grey dashed) representing perfect estimation.
$ r $) between reference and algorithm estimates, with *** indicating p < .001. Plots show linear fit (blue) as well as identity line (grey dashed) representing perfect estimation.
Table 2. Summary of average ± std motion capture (mocap) and inertial measurement unit (IMU) values for each metric in both the active (A) and transparent (T) modes, along with the mean and percent error for between ground truth motion capture and IMU-estimated values

Abbreviations: MLD, maximum lateral displacement; MVD, maximum vertical displacement; NP, nonparetic; P, paretic; SL, stride length.
Table 3. Summary of statistical differences between motion capture ground truth and inertial measurement unit (IMU)-based estimates for the Active (A) and Transparent (T) conditions, including Pearson’s correlation coefficient (r; **p < .01, ***p < .001), limits of agreement (![]() $ LoA;95\% LoA $), and inter-class correlation coefficients for both agreement (
$ LoA;95\% LoA $), and inter-class correlation coefficients for both agreement (![]() $ ICC\left(A,1\right) $) and consistency (
$ ICC\left(A,1\right) $) and consistency (![]() $ ICC\left(A,1\right) $)
$ ICC\left(A,1\right) $)

Abbreviations: MLD, maximum lateral displacement; MVD, maximum vertical displacement; NP, nonparetic; P, paretic; SL, stride length.
Stride length
Among the metrics reported in this study, stride length was most accurately reconstructed, with mean estimation errors less than 2.6 ± 1.1 cm (P) and 3.8 ± 2.3 cm (NP) corresponding to 2.1 ± 0.6% (P) and 3.5 ± 1.9% (NP).
Maximum lateral displacement
Mean estimation errors for MLD were smaller than 0.11 ± 0.38 cm (P) and 0.24 ± 0.43 cm (NP), corresponding to 3.31 ± 6.38% (P) and 10.9 ± 14.5% (NP).
Maximum vertical displacement
Mean estimation errors for MVD were smaller than −0.43 ± 0.51 cm (P) and −0.64 ± 0.60 cm (NP), corresponding to −2.68 ± 3.07% (P) and − 3.46 ± 3.36% (NP).
Real-Time Gait Metric Response to Exosuit Assistance
While the previous validation experiment demonstrated our method’s robustness and accuracy, the feasibility of monitoring gait outside the lab would enable our long-term goal of deploying community-based rehabilitation technologies. As exosuits can instantaneously switch between providing assistance and being transparent to the wearer, monitoring gait reliably and continuously could make exosuits more versatile. Allowing them to provide assistance only when needed by the wearer could enable training with higher intensity while maintaining gait of a certain quality. To demonstrate how monitoring the efficacy of exosuit assistance might shape such training scenarios in the future, we conducted a case study (![]() $ N=1 $) mimicking more real-world conditions. To this end, we asked participant S3 to return for an additional visit during which we monitored gait metric response to exosuit assistance in a community environment.
$ N=1 $) mimicking more real-world conditions. To this end, we asked participant S3 to return for an additional visit during which we monitored gait metric response to exosuit assistance in a community environment.
Experimental Overview
The participant walked five laps around a predetermined 150 m circuit in a well-trafficked plaza near Harvard University (Figure 6). For the first two laps, the participant walked wearing an exosuit without obtaining assistance (transparent). Previous studies have shown that walking with an exosuit in the transparent condition is a close representation of a person’s natural, baseline walking capability (Awad et al., Reference Awad, Kudzia, Revi, Ellis and Walsh2020). At the beginning of the third lap, a researcher activated assistance. The participant then underwent one lap allowing adaptation to the assistance, and two more laps walking with the exosuit active. Performing this experiment as a loop rather than as a timed walk over straight pathways ensured that the active and inactive conditions took place over identical terrain. The participant was instructed to walk at a comfortable speed she could maintain over the entire trial. Medical clearance and a signed informed consent form approved by the Harvard University Human Subjects Review Board were obtained for this participant.

Figure 6. Experimental setup for collecting gait metric data during community-based walking. The participant was guided by a physical therapist for a total of five laps around a well-trafficked plaza at Harvard University. Sensor data were streamed via Bluetooth to a nearby computer, carried by a researcher following the participant.
Outcome Metrics
An indicator of walking impairment poststroke (Von Schroeder et al., Reference Von Schroeder, Coutts, Lyden, Billings and Nickel1995), we chose stride length as an outcome metric to compare the effect of walking with exosuit assistance (active) to no exosuit assistance (transparent). To test for statistical significance in stride length between the two suit conditions, we performed nonparametric analysis of variance (Wilcoxon Rank Sum test) as the obtained results were partially non-normally distributed.
Results
We collected a total of 498 strides. Significant differences comparing exosuit assistance (active) to no assistance (transparent) were captured by the algorithm during our in-lab validation experiment, showing an increase of 13.9 cm (P) and 13.7 cm (NP) for stride length (both ![]() $ p<.001 $). Similarly, during outdoor testing, after adaptation to exosuit assistance, we saw a significant increase of 7.9 cm (P) and 7.3 cm (NP) for stride length compared to no suit assistance (both
$ p<.001 $). Similarly, during outdoor testing, after adaptation to exosuit assistance, we saw a significant increase of 7.9 cm (P) and 7.3 cm (NP) for stride length compared to no suit assistance (both ![]() $ p<.001 $). Figure 7 shows the effect of exosuit assistance on poststroke gait, illustrated for stride length.
$ p<.001 $). Figure 7 shows the effect of exosuit assistance on poststroke gait, illustrated for stride length.

Figure 7. Gait metric response in poststroke overground walking with and without exosuit assistance shown for P and NP stride lengths. The inertial measurement unit-based monitoring algorithm presented here detected significant differences between active and transparent modes (***p < .001).
Discussion
In this work, we used exosuit-integrated inertial sensors for gait metric estimation in chronic poststroke overground walking. To this end, we implemented a double integration algorithm with linear drift compensation. The main contribution of this work lies within a new form of ZUPT detection approach that informs the algorithm when to perform integration resets and correct sensor drift. That is, instead of relying on ipsilateral detection thresholds, our method defines ZUPT instances contralaterally, utilizing information from both feet. Confirming our hypothesis, we demonstrated this approach to be highly robust to irregular walking conditions poststroke.
Our in-lab validation showed excellent agreement between estimation and ground truth optical motion capture. In comparison, being among the most accurate methods found in the literature, Trojaniello et al. (Reference Trojaniello, Cereatti, Pelosin, Avanzino, Mirelman, Hausdorff and Della Croce2014) reported stride length in hemiparetic walking with comparable mean absolute errors of 3%. Visi et al. (Reference Visi, Georgiou, Holland, Pinzone, Donaldson and Tetley2017) showed similar outcomes for stride length in hemiparetic gait, reporting comparable to higher mean errors of 2.3 ± 1.7% (NP) and 5.7 ± 2.0% (P), respectively, however considering only a small sample size of ![]() $ N=1 $. Though data on stroke populations are limited, outcomes reported for other impaired populations may allow more extended comparisons. Hannink et al. (Reference Hannink, Kautz, Pasluosta, Barth, Schülein, Gaßmann, Klucken and Eskofier2016) reviewed multiple studies estimating stride length in elderly and impaired populations, reporting (relative) precisions between 6.1 cm and 8.4 cm (5–11%), with mean errors close to zero.
$ N=1 $. Though data on stroke populations are limited, outcomes reported for other impaired populations may allow more extended comparisons. Hannink et al. (Reference Hannink, Kautz, Pasluosta, Barth, Schülein, Gaßmann, Klucken and Eskofier2016) reviewed multiple studies estimating stride length in elderly and impaired populations, reporting (relative) precisions between 6.1 cm and 8.4 cm (5–11%), with mean errors close to zero.
Regarding MLD, the relatively high percentage errors we observed—particularly on the NP side—can be explained by the very small absolute lateral displacements of 5 cm (P) and 2 cm (NP), which mean even small errors appear quite substantial. Moreover, errors of a few mm are approaching the smallest distance resolvable with the 9 mm reflective markers used for this study. Still, comparing these outcomes to swing width errors in Parkinsonian gait (0.15 ± 2.13 cm) (Mariani et al., Reference Mariani, Jiménez, Vingerhoets and Aminian2013), we observe comparable mean estimation errors with noticeably improved precision for both sides.
Lastly, estimation errors for MVD are lower than Hannink et al. (Reference Hannink, Ollenschläger, Kluge and Roth2017), who tested various reconstruction methods on a clinical benchmark dataset with accuracies of −0.84 ± 3.98 cm. Moreover, our errors are comparable to Kitagawa and Ogihara (Reference Kitagawa and Ogihara2016) (0.2 ± 0.7 cm) and substantially lower than Mariani et al. (Reference Mariani, Rochat, Büla and Aminian2012) (4.2 ± 2.2 cm), both reported for healthy populations.
In summary, we found improvements on previously reported precisions, suggested by smaller error variance across metrics. Mean estimation errors were comparable or lower than reported for MLD and MVD, while showing slightly biased error distributions for stride length. A comparison to the method published in Skog et al. (Reference Skog, Händel, Nilsson and Rantakokko2010) on the data set presented here (Supplementary Table S1) indicates the same. While difficult to confirm without an extended analysis, the small error variance may potentially come from a difference in reliability in detecting ZUPTs between our method and others. False positives (i.e., ZUPTs during swing) would likely result in underestimated positions by cutting the integration period artificially short. Conversely, false negatives (i.e., missed ZUPTs) could lead to overestimated positions by letting the integration accumulate for too long. Combined, these inaccuracies may result in mean error distributions centered around zero, but with increased variability compared to a method that misses no ZUPTs. A future analysis retuning both the window size and detection threshold from Skog et al. (Reference Skog, Händel, Nilsson and Rantakokko2010) to poststroke walking may provide further insight regarding this hypothesized relationship between missed or false ZUPTs and estimation errors. Considering that we enforce ZUPTs at single instances as opposed to over periods of time could explain the slightly biased errors distributions observed in some cases, as this allows drift to accumulate for longer periods of time. While in theory accounted for by the drift compensation, this can become more problematic if bias instabilities—potentially caused by inaccurate orientation estimates or genuine IMU bias fluctuations—invalidate the assumption of linear velocity drift (Woodman, Reference Woodman2007). Incorporating higher-order drift functions that potentially better capture these effects may increase accuracy in future work. In addition, we expect a certain degree of residual error due to factors such as misalignment between the IMU coordinate frame origin and the coordinate frame origin approximated by the optical markers (see Figure 4), soft tissue artifacts or maximum achievable resolutions given optical marker sizes of up to 9 mm.
Gait training is an integral component of recovery after a stroke. While effective, current clinical standards may lack the precision and frequency to monitor small improvements in walking during and after therapy. As wearable devices such as soft exosuits encourage community or at-home rehabilitation, and as the field of gait therapy continues to encourage telemedicine, monitoring gait quality becomes even more important. Devices capable of measuring both short- and long-term changes in walking will inform not only the development and application of exoskeletons, but also help expand current therapeutic practices out of the clinic.
With respect to clinical applicability, an important assessment criterion is a method’s sensitivity to changes in gait characteristics over time. Assessing long-term gait changes may provide insights to rehabilitation progression or general mobility declines, while monitoring the immediate response to intervention approaches such as exosuit assistance may help inform treatment implementations. As particularly within a session such differences can be small, gait monitoring systems require measurement precision high enough to resolve subtle but clinically meaningful outcomes reliably. In this context, Hannink et al. (Reference Hannink, Kautz, Pasluosta, Barth, Schülein, Gaßmann, Klucken and Eskofier2016) argued that for sufficient resolution, error standard deviations need to be less than half the true effect magnitude. Moreover, a reasonable evaluation benchmark could be an algorithm’s capability of resolving minimally detectable changes (MDCs), representing important reference values in everyday clinical assessment. Kesar et al. (Reference Kesar, Binder-Macleod, Hicks and Reisman2011) for example, reported paretic within-session step length MDCs of 2.62 cm in poststroke (treadmill) walking. For stride length, though not explicitly reported, this could suggest standard deviation requirements in ranges lower than ±2.6 cm, if we assume stride length to be about twice step length. Notably, people poststroke typically exhibit less variability on a treadmill than overground, shrinking treadmill-derived MDCs and making them more difficult to resolve. For between-session assessment, recent work by Geiger et al. (Reference Geiger, Supiot, Pradon, Do, Zory and Roche2019) found stride length MDCs of around 11.96 cm in poststroke gait which—by the same reasoning—would require standard deviations in ranges lower than 6 cm. Standard deviations of less than 1.3 cm (P) and 2.3 cm (NP) achieved in this work would be sufficiently small to meet these requirements in both cases.
As a complement to our in-lab validation, our use-case experiment further demonstrated our algorithm’s robustness in conditions typical to more pedestrian situations, such as negotiating small obstacles in the walkway and navigating around passersby. The ability to reliably monitor wearer response to exosuit assistance in such community-like settings could help establish new exosuit-assisted gait training paradigms. Indeed, recent work on control individualization (Siviy et al., Reference Siviy, Bae, Baker, Porciuncula, Baker, Ellis, Awad and Walsh2020) underscores how people poststroke can be sensitive to changes in exosuit assistance. Future work in this domain could explore gait metrics as objective functions to automatically tune assistance parameters based on individual wearer response. By closing the loop between assessment of gait and intervention, exosuits may thereby assist throughout the whole spectrum of poststroke rehabilitation. Still, the feasibility study presented here contains data from only a single participant. Analyses of how well the exosuit improves gait in people poststroke with more statistical power have been conducted in the lab (Awad et al., Reference Awad, Bae, O’Donnell, De Rossi, Hendron, Sloot, Kudzia, Allen, Holt, Ellis and Walsh2017; Reference Awad, Kudzia, Revi, Ellis and Walsh2020), but future work may wish to repeat those analyses in the community.
Limitations of this study may guide further directions for future work. To that end, incorporating a simple model of the foot in swing could provide more granular information about foot clearance, instead of ankle clearance only. Minimal toe clearance is particularly interesting to clinicians, as it is an indicator of tripping risk in stroke survivors (Begg et al., Reference Begg, Tirosh, Said, Sparrow, Steinberg, Levinger and Galea2014). In addition, measures such as step length asymmetry are clinically relevant, but require more information about the relative position of either foot than is available from the present pair of foot-mounted IMUs. In prior work, this has been addressed by using different sets of IMUs (Moore et al., Reference Moore, Hickey, Lord, Del Din, Godfrey and Rochester2017; Wang et al., Reference Wang, Sun, Li and Liu2018), mounting an IMU to the pelvis (Köse et al., Reference Köse, Cereatti and Della Croce2012), or by using additional sensors (Meulen et al., Reference van Meulen, Weenk, Buurke, van Beijnum and Veltink2016). Moreover, while estimation error was small on both sides, accuracy differences between the paretic and nonparetic side could be subject to further investigation in the future. That we saw higher estimation errors on the NP side may be the result of higher variation in P side toe-off detection due to P side walking instability. More specifically, as nonparetic ZUPTs require information from the contralateral (paretic) side, paretic side instability may manifest as slightly poorer ZUPT estimates on the nonparetic side. This is a primary distinction from methods such as Visi et al. (Reference Visi, Georgiou, Holland, Pinzone, Donaldson and Tetley2017), which rely on purely ipsilateral information for ZUPT detection. Exploring error sensitivity to nonlinear drift functions, as indicated previously, may provide more conclusive information in this regard. Lastly, the method presented here requires IMUs that can provide orientation estimates in order to calculate accelerations in the global frame. Future work exploring how orientation estimates from lower-cost IMUs influence performance would be valuable in assessing our method’s applicability across different hardware setups.
Acknowledgments
We would like to thank Mr Jonathan Foster, Mr Jack Eiel, and Ms Lauren Bizarro for their contributions to data collection. We would also like to thank the participants who donated their time to this study.
Funding Statement
Research reported in this publication was supported by the National Institutes of Health under award number BRG R01HD088619. This material is based upon work supported by the National Science Foundation Graduate Research Fellowship under Grant No. DGE1144152. This material is based upon work supported by the National Science Foundation under Grant No. CMMI-1925085. This work was supported by American Heart Association grant AHA 18TPA34170171.
Competing Interests
Patents describing the exosuit components documented in this article have been filed with the U.S. Patent Office. C.S., J.B, N.K., and C.J.W. are authors on one or more of those patents or patent applications. Harvard University has entered into a licensing and collaboration agreement with ReWalk Robotics. C.J.W. is a paid consultant for ReWalk Robotics. The other authors declare that they have no competing interests.
Authorship Contributions
P.A., C.S., and C.J.W. designed the study. P.A. and J.B. designed the double integration framework. J.B., N.K., and C.S. provided feedback on the double integration framework. P.A, C.S., and D.K.C. collected and processed data. P.A., C.S. wrote the first draft, and approved the final version of the manuscript. T.D.E., L.N.A., and C.J.W. revised the manuscript and approved the final version.
Data Availability Statement
The data supporting the main conclusions of this manuscript are located within the manuscript. Additional data are available upon request (C.J.W., [email protected]).
Ethical Standards
The authors assert that all procedures contributing to this work comply with the ethical standards of the relevant national and institutional committees on human experimentation and with the Helsinki Declaration of 1975, as revised in 2008.
Supplementary Materials
To view supplementary material for this article, please visit http://doi.org/10.1017/wtc.2020.11.