1. Introduction
When examined on a fine enough scale any medium appears to be discontinuous. However the study of deformable media have shown, on the whole, that it is always possible to adopt a sufficiently large scale to be allowed to take into account macroscopic behavioural parameters and to reason within the framework of continuum mechanics. Of course, this macroscopic behaviour is directly determined by the microscopic structure of the medium: frequently, a microscopic study, even a qualitative one, reveals the correct procedure to be taken in continuum mechanics.
For example, in soil mechanics, the study of the deformations of a sand mass (an essentially discontinuous medium to the human eye), is normally carried out within the framework of continuum mechanics. It is thus within this framework that the study of the deformation of a snow mass should be situated.
In order to solve a problem of deformable media, three sorts of equations are required. First the fundamental laws of conversation must be stated: the conservation of momentum, mass, and energy. These equations are valid, whatever the medium may be. On the other hand, the second group of equations, which consists of the constitutive equations or the stress–strain relationship enables the specifity of a given medium to be taken into consideration.
It should be noted that a constitutive equation is not completely arbitrary and must conform to the principle of objectivity (which states the invariance of the law in any continuous change of referential frame) and also the second law of thermodynamics. Finally the third group of equations which are constructed from the boundary conditions depends on the problem under consideration.
Taking account of the boundary conditions in cases where they are complex, requires the use of computing codes based, for example, on the finite-element method. This means that the constitutive equation used must be tri-dimensional in general cases, or bi-dimensional in the case of a plane state of deformation, and, furthermore, they must be written in incremental form in order to be able to describe the considerable non-linearity of snow behaviour. This article is above all concerned with the formulation of the constitutive equation of a snow sample.
The following points are considered in turn: first the experimental study is described and a first elementary rheological formulation of the snow sample under study is arrived at. Then the proposed constitutive equations are presented, this being done in an incremental form. Finally the parameters are calculated and the validity of the equation is checked on a different class of tests.
2. Experiment and discussion
(i) Experimental study
The tests took place in the laboratory of the Centre d’Étude de la Neige at la Croix de Chamrousse (altitude 2250 m).
Snow type
The test samples were gathered directly within the near vicinity of the laboratory. This procedure implies certain scatter in the snow characteristics (temperature, density, structure, etc.) since all the material for testing was not gathered simultaneously; however this scatter is convenient for our purpose.
The tests were performed on freshly fallen snow with visible particles, which was dry, or very slightly damp, the density range being between 150–200 kg/m3. The temperature ranged from —10°C to —2°C.
Equipment and testing procedures
The equipment used was a cylindrical triaxial apparatus, with measurement of the sample volume change. Isotropic pressure on the cell was exerted by means of an anti-freeze circuit linked to a variable height system of pots. A double burette (cf. Bishop) in the circuit enabled the volume change of the sample to be determined. The tests were carried out in a cold room, regulated to the temperature of the snow being tested.
The tests were in two parts:
-
(i) A creep phase under isotropic compression: one or several load stages of successive isotropic stresses being applied to the sample. The deformation of the sample volume was monitored during the test.
-
(ii) After this initial phase the sample was compressed at constant deformation-rates by an electromechanical press (6.45, 2.30, 0.91 mm/min); the lateral pressure being maintained constant.
Experimental results. A remarkable feature of snow is its creep behaviour when it is in a state of isotropic stress (Reference SalmSalm, 1971; Reference SalmSalm, [1975]). The tests corroborated these findings.
Creep tests. Figures I and 2 are isotropic creep curves in which ΔV/V o (relative volume change) is plotted against t (time) for σi = 5 X 103 Pa and σi = 13 X 103 Pa (σi being the applied isotropic stress). In the initial phase of the test there is a decrease in the creep-rate which then becomes stable. Initial creep-rate increases when σi increases. Figure 3 shows the evolution of the relative volume change with time in the case of a test in which increasing isotropic pressures σi were applied. The sample became markedly denser, with a volume decrease at the end of the test of as much as 50% of the initial volume. It can be seen from Figure 3 that despite the preliminary increase in the density caused by the previous loadings, an increase in the isotropic stress always has as a result a sharp acceleration in the volume change.

Fig. 1. Isotropic creep, σi = 5 kPa.

Fig. 2. Isotropic creep, σi = 13kPa.

Fig. 3. Isotropic creep, σi increasing by stages: 5, 13, 33, 60 kPa.
Triaxial tests. Two types of curves are obtained by these tests. The curve of axial stress variation with axial deformation (σ1, ε1) and the curve of relative volume change with this deformation (εv, ε1). Axial strain is ε1 defined from the experimental data as Δl / l 0. The curves (σ1, ε1) are characterized by two features (Fig. 4): (i) OA is concave downwards; (ii) AB shows slight concavity upwards or even linearity. This profile is also to be found in curves of simple compression.

Fig. 4. Triaxial test, axial compression rate 2.77 mm/mim; σ3 = 13kPa.
The rate at which the sample is compressed affects its response as has been frequently reported (Reference Kinosita [i.e. Kinoshita], and ŌuraKinosita, 1967; Reference Shinojima and ŌuraShinojima, 1967) and at high rates the curve does reveal severe irregularities (saw tooth). Reference SalmSalm (1971) has shown that when the sample has, prior to testing, undergone a preliminary loading, this “saw-tooth” phenomenon does not occur. It is caused by local structure collapse, that is to say, to the appearance of heterogeneous features which prevent, a priori, this behaviour being interpreted by means of a rheological model essentially designed for homogeneous samples.
In so far as the curves of the volume change are concerned, Figure 5 shows an example of the results obtained. Volume change and axial strain are plotted, starting from the application of the deviatoric loading (not from the preliminary application of the isotropic compression σ3).

Fig. 5. Volumetric strain versus axial strain during a triaxial test.
The curves obtained are nearly linear. This stems from the fact that the variations of volume evolve proportionally to axial deformation. It should be noted however that the volume deformations change less rapidly than axial deformations, which implies a slight lateral expansion of the sample. Calculating a value of Poisson’s ratio from these data would provide a value of v = 0.13; however, this is the ratio of lateral to axial strain-rate, not the classical elastic parameter in Hooke’s equations. In other words, this ratio is not necessarily a rheological parameter, but can be the result of the superposition of several rheological behaviours (elasticity, plasticity, viscosity). These findings may be compared to the results obtained by Reference Shinojima and ŌuraShinojima (1967), who suggests a Poisson’s ratio of 0.03 under compression.
(ii) Elementary rheological features
After certain considerations of a qualitative nature on the fine-grained structure of deposited snow, the question of how the behaviour of the latter can be accounted for within the framework of continuum mechanics is examined.
Structure
Deposited snow has a dispersed structure; it consists of:
-
(i) Particles which can be either monocrystals or crystal aggregates. It may be assumed that these particles are not compressible, at least in so far as common snows that have not reached a very high degree of compactness are concerned.
-
(ii) Gas which is a mixture of air and water vapour.
-
(iii) Intergranular bonds. These bonds may evolve considerably during the history of the material. We do not intend to deal here with this evolution in the snow cover under the influence of factors such as temperature gradient within it. Suffice it to say that under the effect of mechanical stress these bonds undergo physico-chemical evolution. This evolution is accompanied by the appearance, disappearance, and displacement of bonds. It is doubtless the interplay of these different evolutions that makes time the fundamental parameter in the response of snow to mechanical stress.
Snow as a continuous medium
Isotropy. The way in which snow is naturally deposited necessarily creates a certain degree of anisotropy in deposited snow. The tests carried out however demonstrate that this is negligible in the case of naturally deposited snow. The triaxial behaviour of core samples, one vertical and the other horizontal within the same layer, were shown to reveal no perceptible difference. Thus the hypothesis of isotropic behaviour will be made in relation to a norm of undeformed naturally deposited snow.
Isotropic creep. The tests reveal a considerable degree of creep under isotropic compression. This fundamental feature of behaviour has to be taken into consideration in formulating laws governing snow.
Limit surface. At no stage during our tests was there any plastic rupture of the sample, such a phenomenon being assumed to be characterized by an evident rupture surface and/or by an asymptotic limit on the stress–strain curve. Different paths were taken in a bisecting plane of the space of principal stresses without meeting any limit surface of plasticity. Figure 6 shows the paths taken within this space.

Fig. 6. Stress paths in stress space.
Path 1 is isotropic, thus plasticity must be excluded.
Path 2. σ1 increases, σ3 remains constant. If there is a limit surface of plasticity then this path must intersect it.
Path 3. σ1 increasing, σ3 decreasing. Pot descent during the tests. This path must intersect the limit surface of plasticity.
Path 4. Uniaxial compression, σ3 ═ 0. This path must intersect the limit surface. It must be noted that further continuation of the path to higher-order stresses leads, not to rupture, but to the compression of the core sample 15 cm high into an ice galette of 2 cm (Reference Kinosita [i.e. Kinoshita], and ŌuraKinosita, 1967).
This does not exclude the possibility of the existence of brittle ruptures at relatively higher speeds of loading.
Viscous and elastic behaviour. A typical experimental curve of the triaxial test is shown on Figure 4. The beginning of the curve, a field of very small deformation, can be interpreted as an elasticity stage. The second part of the curve corresponds to a viscous (irreversible) flow of the material.
The memory effect. Examination of the experimental results of creep under successive loadings shows that the history of the stresses has an important influence. The examples shown below, which are extreme examples, illustrate this influence. Two stress histories leading to the same total stress at time t 1 are shown in Figures 7a and b. The responses in viscous deformation (non-instantaneous) are shown respectively in Figures 7c and d. It is clear that the creep rates at t 1 are quite different, depending on whether the major stress stage was applied before or after the minor one. The fact that if the later stress history is σ ═ ct for a time t great in comparison to t 1, one has a coincidence in the creep curves, in no way alters the importance of the factor of the “history” when the behaviour of materials during the phases of stress evolution is to be studied.

Fig. 7. Stress histories and corresponding strain responses.
Lateral deformation. During the tests lateral deformation of the sample was truly negligible. Thus, from these test results it is possible to give a rheological description of deposited snow as a visco-elastic material with memory, being predominantly viscous. It is upon this basis that the following incremental formulation of the constitutive equations was elaborated.
3. Constitutive equations for deposited snow
(i) The incremental formulation of constitutive equations
Under a given mechanical loading applied during a given time (this is termed a “stress path”) a homogeneous sample has a defined unique response, which depends on the material, the response covering a certain time span. (This is termed the “response path”.) The constitutive equations, or rheological law governing the material, supplies a determined and unique response path corresponding to a stress path graduated in time.
In the case of simple constitutive equations this relationship between stress path and response path degenerates. For elastic materials (loaded in isothermically) stresses and deformations are linked by a simple function: f (σ, ε) ═ 0. If the approximation is made of a perfectly plastic rigid solid, then the constitutive equations are reduced to a plasticity criterion and a flow rule. And for pure viscosity without any memory effect, the existence of a function linking the stress to the pure deformation-rate is assumed.
For deposited snow these different approximations are very crude. Snow, as has been shown above can be considered as a visco-elastic material. Moreover, experience shows that snow belongs to that class of viscous materials having a significant memory effect: that is to say that the deformation rate depends not only on the stress which is being applied at the time, but also on the history of stresses that has already been applied to the material. As a reasonable approximation, deposited snow can be said to follow Boltzmann’s superposition principle. This states that the response to the sum of multiple loading histories is equal to the sum of the response of each loading history.
The rheological law of deposited snow must therefore be studied within the general framework of a functional relationship between states of stress and deformation: knowledge of the totality of the stress path is necessary to determine the response path. Accounting for this function, that is to say the global formulation of the soil law, is therefore highly complex.
Let us take a homogeneous sample with a defined loading history. If a small load is applied to it (for example the small pure deformation dε) for the time increment dt, the small response of the sample (dσ, being the variation in the state of the stress which is being applied in co-rotational axes) will be found to be unique. This statement, which is no more than the principle of determinism applied at an incremental level, implies the existence of a function f, depending on the total history of the sample, thus:
This is the general incremental formulation of rheological laws.
This function f applies to infinitely small quantities. If it is assumed to be regular at the origin it will be possible to get a limited development to the first order which will be valid within a given region around the origin.
Thus
Taking into the account the symmetry of the tensors dε and dσ we get dε α ═ Mαβ dσ β +Cα dt which allows us to represent them as six-component vectors. In this relation Mαβ dσ β stands for the elasto-plastic part of the small deformation while the vector C is the creep-rate. It will thus be feasible to describe a visco-elastic behaviour (Reference Darve, Darve, Boulon and ChambonDarve and others, 1978).
The mathematical description used henceforth is the Hencky strain tensor, defined as
L being the pure strain after rotationFootnote * . This description is convenient with large strains and displacements.
The incremental formulation is particularly well adapted for incorporation within numerical calculus programmes based on the finite-element method, for the behaviour of the material does have a high degree of non-linearity and is moreover influenced by memory effects. These mechanical properties, thus, vary profoundly during loading. If this evolution is to be described, it will be necessary to monitor step by step (increment by increment), at each point of the field under consideration, the loading brought to bear by the boundary conditions. The necessity of decomposing the exterior load into successive increments is thus reflected, at a rheological level, by an incremental formulation of the equation.
(ii) Elasticity
As a first approximation snow may be considered to be isotropic. It can then be shown that the matrix, M, may be expressed in terms of only two quantities: Young’s modulus and Poisson’s ratio.
The value of this modulus is, in the adopted formulation, linked to the average stress:
and the proposed relation between E and σm can be written:
Poisson’s ratio is considered as constant.
The matrix M finally has the form:
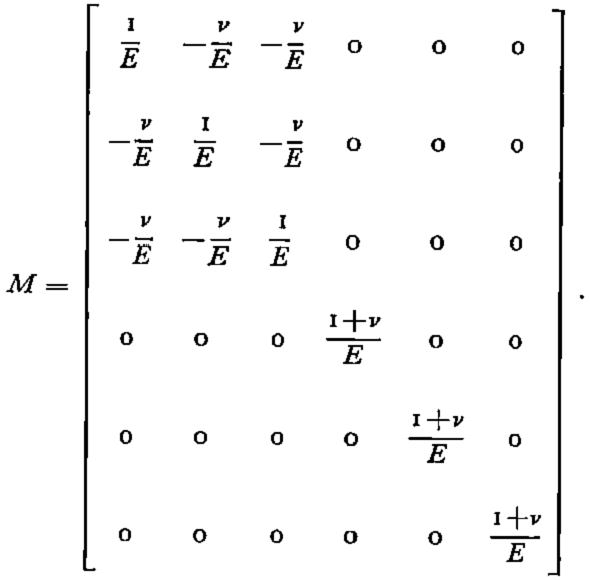
Within the framework of the problem under consideration (the study of snow cover) it is natural to make the hypothesis of plane deformation; in this case the formulation is restricted to four components for the vectors dε and dσ as in plane deformation we have

The non-linear elastic part of the deformation increment is formulated thus:

(iii) Viscosity
a. General discussion
The viscous part of the equations is represented in the formulation by the vector C, which is the creep-rate vector. This is viewed from the principal axes of deformation increments

If {C} is expressed in axes related to the principal axes by a rotation of angle ø

The values C I, C II, C III are the principal creep-rates. When the material is put in a state of stress consisting of several non-zero elements σI ≠ 0, σII ≠ 0, σIII ≠ 0 the problem of the coupling of creep mechanisms in these different directions is posed: independence between C I, C II, and C III, although kinematically possible, is not physically apparent. To assume it would be restrictive.
C I represents the creep deformation-rate in the direction I at moment t in a state of ongoing stress and deformation, at the end of the material’s history.
A further notion is now introduced; that of uniaxial creep-rate. This would be the deformation rate C I⋆, should coupling not occur: that is to say that only εI, εI, and their respective histories are taken into account in the calculation of C I⋆. The same applies for C II⋆ and C III⋆.
b. Detailed formulation
Coupling. Taking into account the interdirectional coupling of the proposed incremental formulation requires the introduction of a “pseudo Poisson’s ratio of viscosity” referred to as χ and defined by

within the framework of a test under the following conditions:

The values of the principal creep-rates are expressed therefore as a function of the “uniaxial creep-rates” defined in paragraph (iii)a as follows:

Formulation of uniaxial creep rates
—Guiding principles
In the adopted formulation the fictitious creep-rate as defined above and symbolized C I⋆ is made to depend on:
-
1. The present level of the total stress in the principal direction under consideration.
-
2. The stress history, that is to say the manner in which the present level if stress has been obtained.
-
3. The present level of total viscous deformation.
The influence of factors (1) and (2) has been examined in the preceding paragraphs on the analysis of the experimental results.
In so far as the third factor is concerned, the introduction of the current value of total viscous deformation as a parameter enables the following experimental data to be accounted for in the formulation: if a sample is made to undergo a stress history consisting of equal increments applied at constant time intervals (cf. Fig. 8) the answer in viscous deformation is not one of identical, juxtaposed truncated curves, but, on the contrary, of non-identical ones, each differing from the previous one by having a decreased creep-rate.
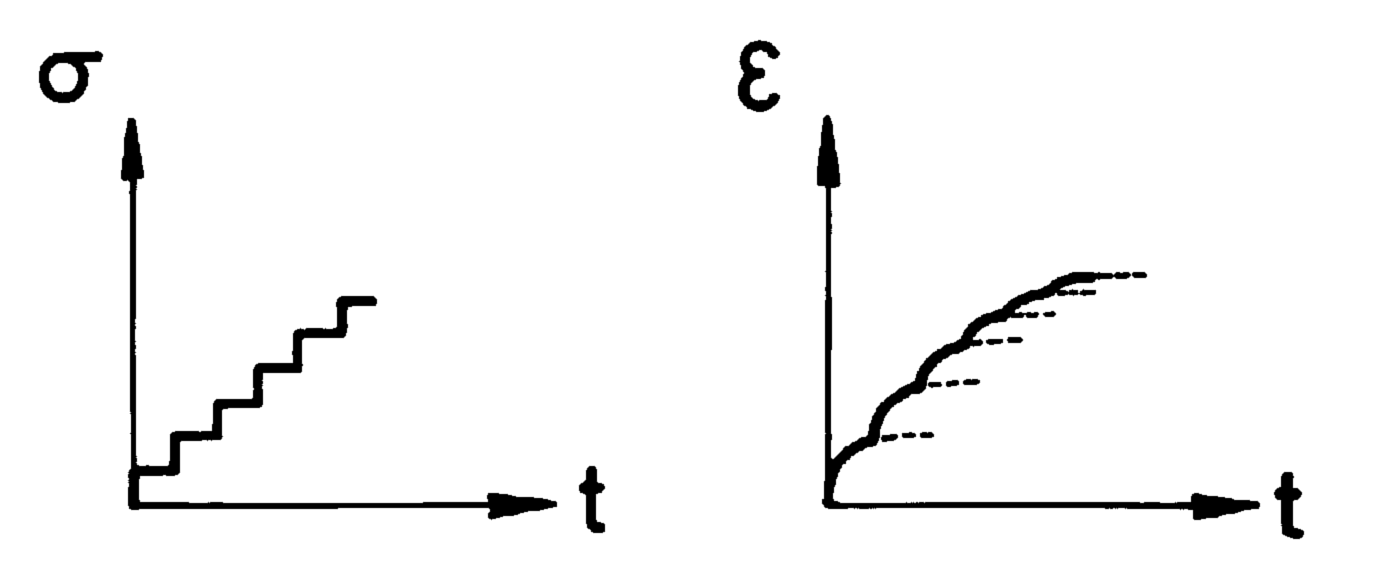
Fig. 8. Incremental stress history and corresponding strain response.
Such tests were performed; an example is given in Figure 3. It should be underlined that here the stress increments, far from being equal, are increasing, and this helps to make the phenomenon less obvious.
It is thus necessary to introduce a parameter which takes into account the fact that creep depends on the state of total deformation.
—Analytic formulation of uniaxial creep under constant stress.
The following formulation is proposed for uniaxial creep under constant stress: it is assumed that it is possible to approach the experimental curve with a sufficient degree of approximation by an analytic curve obtained as the sum of two terms:
-
a hyperbolic term (short term)
and
-
a linear term (long term)

The corresponding creep-rate is then:

The choice of the value C requires some comment. This is the long-term element of the creep-rate. The element B/(At+B)2 represents the short term. When t approaches zero (the onset of loading) this hyperbolic element tends towards I/B. In so far as C is concerned, we have not at our disposition sufficient experimental results covering a large enough range of long-term creep tests. From results obtained at Chamrousse by J. P. Navarre and P. Blaix of the Centre d’Étude de la Neige of Grenoble, during the winter 1975–76 it has seemed to us possible to take a long-term rate (oblique incline of the asymptote) equal to one-hundredth of the initial rate.
Doubtless this approximation could be improved upon: however in order to determine satisfactorily parameters which account for actual behaviour, access would be required to a wide experimental basis in the area of long-term creep. In the absence of such a basis, the hypothesis of one-hundredth seem to be acceptable.

produces

The influence of the level of stress (uniaxial in the principal direction under study) is introduced in the following way: coefficients A and B of the above-mentioned relationship are expressed as functions of principal stress σ (σ ═ σI, σII, σIII):

The result of this option is that the uniaxial creep-rate, all other things being equal, has a linear variation with the applied stress:

This relation gives the proposed formulation for uniaxial creep under constant stress. In cases where there is an evolution in stress this relation must be applicable, not to the total stress but to the stress increments. This is the problem that will now be considered in the following paragraph.
—Formulation of monoaxial creep under successive stages of stress.
The problem is that of determining the current creep-rate at the end of the stress history represented by the values of σ as a function of time.
We have seen the necessity of taking into account the history if errors are to be avoided.
The Boltzmann principle which applies to visco-elastic materials assumes that the response to a complex history is equal to the sum of the separate responses. This means that if to a history σ1(τ) [― ∞ < τ ≤ t] there is a response ε1(t) and if to σ2(τ) there is ε2(t) then to a history σ1(τ) + σ2(τ) the corresponding response will be ε1(t)+ε2(t).
By reasoning on incremental lines we can determine the stress history by a finite number of data which are: Δσi the stress increments, and τi the loading time of the stress increments [τi — τi–I]being the time increments.
Applying the superposition principle to creep-rates, the suggested formulation expresses the current uniaxial creep-rate as a sum of the current elementary uniaxial rates, each being relative to a part of the stress history; that is to say to a pair (Δσi, τi) which summarizes the history of stress increments in two terms: Δσi being the amplitude of increment and τi the moment at which the increment is applied.
We thus have:

The partial rates, symbolized

One further aspect of the problem remains to be taken into account. It is that of the influence of the current value of the total viscous deformation, the importance of which, has been outlined above.
—Influence of the total current viscosity deformation.
This value is introduced in the terms B′ and A′, the formulation coefficients. The notation being ε0 k (value of the total viscosity deformation at τ k ), Δσk being the moment of application af the stress increment.
Calculated on such experimental basis as we at the moment have at our disposition, the expressions A′ and B′ can be formulated in the following way:

The current uniaxial creep-rate may therefore be obtained by the sum of the terms
that is to say that at step l the real uniaxial creep-rate is expressed by the relation:

In non-discrete form, this would be:

The uniaxial creep-rate at time t is then expressed as a function of strain, stress-rate, and time from a very remote time (—∞) to the instant t.Footnote *
Now if this is seen from the standpoint of the general framework of the study of the vector C, the value
After this detailed account of the non-linear elastic elements and viscous elements of the proposed formulation, we shall now describe its implementation.
4. Application
(i) Parameters of the equation
The proposed equation, in its incremental form described in the first part of this paper, has a certain number of parameters which are features of the type of snow studied.
These parameters (their manner of appearance has been discussed above), total nine altogether.
-
E 0, K, n, v for the elastic element;
-
a, α, b, β, χ for the viscous element.
-
It is by means of laboratory tests that these parameters are determined.
The determination of E 0, K, and n requires triaxial tests at different rates each one carried out at a constant compression rate. The initial gradient for a curve E ⋆ for a single, average stress σm (equal to σ3 as this is the beginning of the test) varies with the compression rate but tends to a terminal value E when this rate has increasing values. It is from the curve of the variations of E with the stress that E, K, and N may be determined. The Poisson's ratio, which has little influence, is assigned a small value (v = 0.1).
In order to determine the viscosity parameters, creep tests (uniaxial and isotropic) are required. Creep tests of a single stress value enable α and β to be determined. To determine the parameters a and b it is necessary to have creep tests with several stress stages successively applied. The parameter χ which is the pseudo-viscous Poisson's ratio can be measured as the ratio of lateral deformation to axial deformation of a cylindrical sample during a test in uniaxial creep.
Table I shows the parameters which have been determined experimentally and introduced into the formulation. The values were determined on the “parameter-determining paths” (p.d. paths).
Table I. Parameters used in the formulation

In the following paragraphs ((ii) and (iii)) the integration of the constitutive equations along particular stress paths is described. The first paragraph deals with “parameter-determining paths”. These are the paths monitored in the stress area during the laboratory tests from the results of which the numerical values of the parameters were determined. The second paragraphs show the results obtained on verification paths. These paths are, by definition, stress paths which are not in the vicinity of the “p.d. paths” and for which there are experimental results which allow the validity of the proposed formulation to be estimated.
(ii) Parameter-determining paths
These are of two types.
-
(a) σI = σII = σIII = constrant,
-
(b) σI = σII = σIII = s(t)
with

There is a perfect correspondence here to loading paths that were applied experimentally in the laboratory of the Centre d'Étude de la Neige at la Croix de Chamrousse. It is on the basis of these tests that the parameters were calculated. The comparison of the experimental findings and the response curves derived from the equations substantiates the choice that was made in establishing the formulation.
Type (a) paths.
The tests that were carried out supply experimental data for two cases of applied stress.
-
σiso = 5 x 103 Pa for the first four.
-
σiso = 13 X 103 Pa for the last two.
The calculated curves and the experimental points may be compared on Figures 9 and 10. The history of the applied stress is shown in the inset. The extreme dispersion of the experimental results, in particular in Figure 9, should be noted. This is a reminder, should such a thing be necessary, that the problem is one of correctly taking qualitative phenomena into account within the framework of a suitable formulation.

Fig. 9. Experimental points and calculated curves for type (a) parameter-determining path shown in inset.

Fig. 10. Experimental points and calculated curves for type (a) parameter-determining path shown in inset.
Type (b) paths.
Figure 11 shows the comparison between results obtained using the constitutive equations and the figures for creep deformation obtained during an isotropic test with several stress stages.

Fig. 11. Experimental points and calculated curve for type (b) parameter-determining path shown in inset.
The successive stresses are as follows:
It is the parameters of current total deformation which bring into play coefficients a and b which are tested along this path.
(iii) Verification paths
The verification paths chosen are of particular complexity, and are a rigorous test of the applicability of the constitutive equations.
They are paths which were monitored experimentally during the constant-rate triaxial tests preceded by a phase of isotropic creep.
These paths are complex (stresses and deformations both being applied); furthermore they have two stages:
-
stage I, t < t 1, isotropic compression: σI = σII = σIII = constant,
-
stage II, t ≥ t 1, axial crushing:
= constant; σII = σIII = constant.
Figures 12 and 13 shows the paths monitored for stress and deformation. These figures show:
-
The applied path (a continuous line) (unvarying stress or deformation rate).
-
The response path (dotted line).
-
The test results supply a great deal of data. In Table II a selection of the results can be found for comparison.

Fig. 12. Stress history for a verification path.

Fig. 13. Deformation path for a verification path.
Table II. Selection of results from verification paths

The evolution of stress in the experimental results and the calculated results can be compared by referring to the figures corresponding to each test (the figure numbers are indicated on the table).
Figures 14, 15, 16, which relate to tests performed under the same confining stress σ3, show that despite a considerable variation in the compression rates (0.91, 2.7, and 6.45 mm/min), the proposed formulation makes it possible to obtain very satisfactory results.

Fig. 14. Results of a verification path test. The solid curve shows the prediction from the formulation and the points show actual test results.

Fig. 15. Results of a verification path test. The solid curve shows the prediction from the formulation and the points show actual test results.

Fig. 16. Results of a verification path test. The solid curve shows the prediction from the formulation and the points show actual test results.
The disparity to be seen on Figure 15 between the crush starting point of the experimental and calculated crush curves is due to the fact that for this test isotropic creep was relatively less than for the average of the tests at σ3 = 5 X 103 Pa. Figure 10 clearly shows the considerable scatter of the results. Thus the calculated curve can, at best, only show a mean of the cluster of the experimental curves. The same reasoning applies, but to a lesser degree, for Figures 14 and 16.
The test results of simple compression (σ3 = 0) are shown on Figures 17 and 18. In Figure 18 which compares the calculated curve to two curves obtained in the same test conditions on two different samples, a high level of agreement can be seen. On the other hand this level of agreement is not so high in Figure 17.

Fig. 17. Results of a verification path test. The solid curve shows the prediction from the formulation and the points show actual test results.

Fig. 18. Results of a verification path test. The solid curve shows the prediction from the formulation and the points show actual test results.
Finally, Figure 19 shows a test under lateral stress of 13 X 103 Pa with a relatively long isotropic compression phase (23 min). The level of agreement is satisfactory.

Fig. 19. Results of a verification path test. The solid curve shows the prediction from the formulation and the points show actual test results.
These results, obtained as they were, on verification paths at a considerable distance from the parameter-determining paths would seem to be very encouraging as, it should not be forgotten, the conditions for testing the constitutive equations are, in so far as they bring into play high rates of deformation, very exacting.
Conclusion
The constitutive equations whose features have been described above make it possible to describe non-linear visco-elastic behaviour incorporating memory effects of the snow sample under consideration. The tests required for calculating the parameters have been stated and the validity of the equation has been verified against other tests.
The full scope of these constitutive equations however, will only be fully revealed once it is introduced into numerical calculation programmes based on the finite-element method (Reference Boulon, Boulon, Chambon and DarveBoulon and others, 1977). The calculation of the stability of the snow cover on a slope and of the stresses imposed on snow fences will then be feasible. Soil–snow slip or slip between different layers of snow could be accounted for by an algorithm which has already been tested for problems of soil mechanics (Reference Boulon, Boulon, Darve, Desrues and ForayBoulon and others, 1978).
Acknowledgements
Thanks are due to the Centre d'Étude de la Neige who have, both by financing this work and by putting the laboratory of La Croix de Chamrousse at our disposal, made this study possible.
























