Introduction
Marine ice sheets rest on beds that lie below sea level and their drainage takes place through surrounding ice shelves. Grounded ice-sheet flowis dominated by horizontal shearing while the ice-shelf flow is dominated by longitudinal stretching and lateral shearing. The two types of flow couple together across a transition zone near the grounding line, where longitudinal and shear stresses are of the same order of magnitude. A long debate on the dynamics of such ice sheets was initiated in the 1970s, when Reference WeertmanWeertman (1974) proposed that a marine ice sheet which lies on an upward-sloping bed is unstable. Recently, the instability hypothesis has been strongly reinforced, based on a boundary-layer theory due to Reference SchoofSchoof (2007b). Moreover, Reference Vieli and PayneVieli and Payne (2005) showed the poor ability of marine ice-sheet models to give consistent prognostic results and, more particularly, they highlighted the influence of the grid size on model results. One of their main conclusions was that no reliable model was able to predict grounding-line dynamics at the time of their study.
As a consequence, there is an urgent need to improve marine ice-sheet models in order to (1) corroborate recent theoretical predictions, and (2) obtain confident simulations of the grounding-line dynamics. We recently proposed a full Stokes resolution of the ice-sheet/ice-shelf transition (Reference Durand, Gagliardini, de Fleurian, Zwinger and Le MeurDurand and others, in press). This approach has been built on abundant literature dealing with the coupling between a grounded ice sheet and a floating ice shelf and identifying this transition zone as a crucial control of the marine ice-sheet dynamics (e.g. Reference WeertmanWeertman, 1974; Reference Van der VeenVan der Veen, 1985; Reference Chugunov and WilchinskyChugunov and Wilchinsky, 1996; Reference HindmarshHindmarsh, 1996; Reference Vieli and PayneVieli and Payne, 2005; Reference SchoofSchoof, 2007a,Reference Schoofb). The main equations developed by Reference Durand, Gagliardini, de Fleurian, Zwinger and Le MeurDurand and others (in press) are recalled here. We then emphasize the impact of the mesh resolution on the calculated steady state with the proposed method. Finally, we show that consistent results can only be obtained if a small grid mesh is prescribed in the vicinity of the grounding line.
Equations
Notations and main hypothesis
The problem to be solved consists of the gravity-driven flow of isothermal, incompressible and non-linear viscous ice. The geometry is restricted to a two-dimensional plane flow perpendicular to the y direction. Ice flows along the x direction, and the z axis is the vertical upward-pointing axis. Notation is detailed in Figure 1. The ice sheet flows over a rigid bedrock, z = b(x), assuming a non-linear friction law for the grounded part, and extends further as an ice shelf over the ocean. In the case of the ice shelf, the ice slides perfectly over the sea. The last grounded point defines the grounding line and is denoted x G hereafter. The left-hand side of the domain is assumed to be symmetric and the shelf ends at the right-hand side of the domain.

Fig. 1. Notation for the problem to be solved.
The constitutive law for the ice behavior is a Norton–Hoff type law (Glen’s flow law in glaciology):
where S is the deviatoric stress tensor, Dij = (ui ,j +uj ,i )/2 are the components of the strain-rate tensor and u is the velocity. The effective viscosity, η, can be expressed as
where the strain-rate invariant, γ e, is defined as
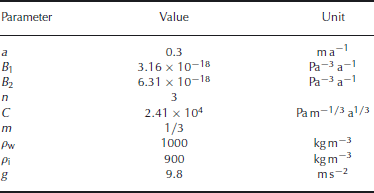
In the following applications, n is set to 3 and ice is assumed isothermal, such that the fluidity parameter, B, remains constant (see values in Table 1).
Table 1. Values of the parameters used in this study, which correspond to steps 5 and 6 of the Marine Ice-Sheet Intercomparison Project (MISMIP) benchmark, but are expressed differently, as here the fluidity parameter is B = 2A. However, numerically the constitutive relations are rigorously the same.
State equations and boundary conditions
The ice flow is computed by solving the Stokes problem, expressed by the mass-conservation equation in the case of incompressibility
and the momentum conservation equations
where σ = S − pI is the Cauchy stress with p the isotropic pressure; ρ i is the ice density and g the gravity vector.
In the present problem, the lateral boundaries of the domain are a dome and a calving front. The dome is assumed to be axisymmetric for the flow problem, which implies that ux(0,z) = 0. The calving front is an artificial cutting of the shelf, which can be seen as the point where icebergs are calved. The exact position of the calving front is not relevant to our problem because it does not influence the upstream flow. This surface undergoes the sea-ice pressure, p w(z,t), which evolves vertically as
where ρ w is the sea-water density and l w the sea level.
In addition to the lateral boundaries, the ice body is bounded by two free surfaces, namely the stress-free upper surface, z = z s(x, t), and the bottom surface, z = z b(x, t), at the interface between the bed or sea and the ice. The evolution of the two free surfaces is determined by solving a local transport equation. Note also that the length of the sea/ice interface, starting from the grounding line, x G(t), is not known in advance and is part of the solution.
The upper surface is a stress-free surface, which implies that n · (σ · n)| s = p atm ≈ 0, where n is the unit normal vector of the surface pointing outward and the subscript ‘s’ denotes the value taken at the ice/air interface. The equation governing the upper stress-free surface evolution reads:
where ui (x, z s) denotes the upper surface velocity in the horizontal (i = x) and vertical (i = z) directions and a(x, t) is the accumulation/ablation function given as a vertical flux at the upper surface. In what follows, the accumulation is supposed constant both in space and in time (see Table 1).
The bottom sea stress-free surface obeys the following equation:
Table 1. Values of the parameters used in this study, which correspond to steps 5 and 6 of the Marine Ice-Sheet Intercomparison Project (MISMIP) benchmark, but are expressed differently, as here the fluidity parameter is B = 2A. However, numerically the constitutive relations are rigorously the same
where accretion of sea water by refreezing or melt of bottom ice is neglected. Note that this equation is still valid for the points on the bottom surface which are in contact with the bedrock. Assuming a rigid, impenetrable bedrock, z = b(x), the following topological conditions must be fulfilled by z s and z b:
As a consequence, the unilateral link between the ice and the bedrock can be treated as a contact problem: the ice cannot penetrate the bedrock but is allowed to move away from it (Reference LestringantLestringant, 1994). Resolutions of the contact problem have been inspired by previous studies on subglacial cavities, namely the works of Reference SchoofSchoof (2005) and Reference Gagliardini, Cohen, Råaback and ZwingerGagliardini and others (2007). At a given point, x, ice is assumed to be in ‘true’ contact with the bedrock (and corresponding boundary conditions are applied; see below) if the ice touches the bed and the stress exerted by the ice is larger than the sea-water pressure. Conversely, the ice is assumed to be in contact with the sea if the bottom surface is above the bed or if the ice touches the bed and the sea-water pressure remains larger than the normal stress, σ nn. In other words:
(1) the ice/bedrock boundary condition applies if
(2) the ice/sea boundary condition applies if
where the subscript | b denotes the value taken at the bottom surface. For the flow problem, two different boundary conditions have to be applied, depending on whether the ice is in contact with the bedrock or with the sea. For the ice/bedrock boundary condition (i.e. condition (1) above), a non-linear friction law is applied:
where τ b is the basal shear stress, u b = u · t is the sliding velocity at the base and t is the tangent vector to the surface z b. The parameters C and m entering the friction law are given in Table 1. For the ice/sea boundary condition (i.e. condition (2) above), the ice is sliding perfectly over the sea, i.e. t · (σ · n)b = 0, and the normal stress is equal to the buoyancy sea-water pressure (Equation (6)).
The equations presented above have been implemented in the finite-element code Elmer (http://www.csc.fi/elmer/). For gravity-driven ice flow we solve the set of the Stokes equations neglecting inertia terms. More details on the numerics are given by Reference Durand, Gagliardini, de Fleurian, Zwinger and Le MeurDurand and others (in press). Note that a similar approach, i.e. full Stokes finite-element modeling of marine ice sheets, was initiated by Reference LestringantLestringant (1994) and used more recently by Reference Nowicki and WinghamNowicki and Wingham (2008).
Set-Up of the Simulations
Numerical experiments were carried out using the overdeepening bed presented by Reference SchoofSchoof (2007a) which, expressed in our reference frame, is given by:
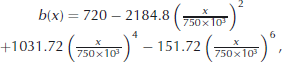
where x and b are in meters. The values of the different parameters used in this study are detailed in Table 1. Note that the set-up of the experiments corresponds to steps 5 and 6 of the Marine Ice-Sheet Intercomparison Project (MISMIP, http://homepages.ulb.ac.be//fpattyn/mismip/). We used a constant accumulation, a =0.3ma − 1, over the whole domain, whereas accretion–melting is neglected below the ice shelf. Initial simulations start with an initial 10 m layer of ice resting on land up to the position where this layer begins to float (x G = 482.4 km for the prescribed ρ i and ρ w; see Table 1). Downstream of x G, a 10 m thick ice shelf extends the grounded part. The vertical extension of the domain is discretized using N by = 30 equal thickness layers, whereas the number of elements in the horizontal direction N bx is adjusted for the different simulations and given below, for each case. Transient simulations are run until steady state is reached (once the relative variation of volume is <1×10 − 6 between two successive time-steps).
Sensitivity to the Horizontal Mesh Resolution
Using the settings described in the previous section, different simulations for fluidity, B 1 (see Table 1), were driven for a regular horizontal mesh with horizontal grid sizes of 20, 15, 10, 7.5, 5 and 2.5 km. Steady state was reached (for durations of 26.9, 30.0, 24.2, 21.2, 20.1 and 21.2 ka, respectively), and the corresponding ice-sheet and ice-shelf surface profiles are plotted in Figure 2 (neglecting grid sizes 20 and 5 km for the sake of clarity). Evolution of x G through time is shown in Figure 3.

Fig. 2. Steady-state surface profiles for different grid resolutions. Filled areas correspond to simulations with a constant horizontal grid size over the whole domain: 15, 10, 7.5 and 2.5 km (from black to light gray). Black thin curve depicts results obtained using the adaptive mesh refinement method with Δx0 = 2.5 km (light gray). The inset shows an enlargement near the grounding line of the upper surface. Black curve with symbols corresponds to the local steady surface profile obtained using the adaptive mesh refinement method with Δx0 = 2.5 km; the gray curve with symbols to that with Δx0 = 200 m.

Fig. 3. Evolution of x G through time for runs with various constant horizontal grid size over the whole domain: 20 km (thick black curve), 15 km (thick gray curve), 10 km (thick gray dashed curve), 7.5 km (thin gray dashed curve) and 2.5 km (thick light gray curve). The fine black line indicates results using the adaptive mesh refinement method (Δx0 = 2.5 km). Horizontal dotted line corresponds to the result obtained with the boundary layer theory developed by Reference SchoofSchoof (2007a) for the same prescribed fluidity, B 1. This latter is insensitive to grid resolution.
As shown by Reference Vieli and PayneVieli and Payne (2005), marine ice-sheet models are highly sensitive to their horizontal grid size. The results of the present experiments clearly demonstrate that the method described above does not derogate from the Vieli and Payne conclusions, in the sense that important sensitivity to the grid resolution is clearly highlighted as x G decreases significantly with increasing horizontal resolution (see Figs 2 and 3). Predictions of themodel can be dramatically affected, particularly in the presence of an overdeepening bed, as the grounding line is not stable on reverse bed slope (Reference SchoofSchoof, 2007a; Reference Durand, Gagliardini, de Fleurian, Zwinger and Le MeurDurand and others, in press). Indeed, in a reverse-slope region, surrounded by two areas of normal slopes that are two branches of stable solutions, for large grid size, the branch corresponding to the larger solution is sometimes selected (probably erroneously). Such a situation is illustrated in Figure 2, as the larger grid sizes (>15 km) lead to steady positions of the grounding line beyond the unstable area. In practice, typical grid resolutions used for ice-sheet modeling (>10 km) are unable to predict a steady position for the grounding line. It should be noted that computing times increase from 2 to 20 days for 20 and 2.5 km grid resolutions, respectively, using a 2.6GHz processor. This severely constrains further investigations of the model behavior with high-resolution grid sizes.
Adaptive Mesh Refinement Around x G
A crucial validation of the present model would be to find a maximal horizontal grid size below which grounding-line dynamics are no longer mesh-dependent. As mentioned above, accessing fine grid resolutions (<1 km) would require large computational facilities and rapidly becomes unmanageable. Therefore, we developed a method that allows an adaptive refinement of the mesh around the grounding line. A constant grid size, Δx0, is set over a distance, L f, centered around x G. Upstream of x G − L f /2 and downstream of x G + L f /2, a geometric progression of the horizontal extension of the mesh is prescribed. The total number of elements in the horizontal direction is adjusted to obtain reasonable increases (i.e. <10% increase from one element to the next). Readjustment of the mesh is repeated after each displacement of the grounding line. Note that with this method, the total number of nodes is constant; only the horizontal distribution of the nodes is modified. Sensitivity tests have shown very similar behavior of the grounding-line dynamics whatever the value of L f. Despite the limited impact of L f, the horizontal mesh extension around x G was kept constant, as this allows regular displacement of the grounding line during the simulation (i.e. a multiple of Δx0 at each time-step).
In Figure 2, the steady surface profile for a simulation with Δx0 = 2.5km over a L f = 10 km range around x G is shown. A good match between this last surface profile and that obtained with a 2.5 km regular mesh is observed. Relative differences between the two simulations in terms of steady-state grounding-line position and volume are <2%. Note also that the two simulations show very similar transient behavior, as illustrated by the evolutions of x G versus time plotted in Figure 3. Some conclusions can already be drawn from the comparison of these two simulations. First, this fully validates the adaptive mesh refinement method used here, which then allows for exploration of the model behavior for further refinements of the grid around the grounding line. Second, this shows that the state of a marine ice sheet is strongly influenced by the behavior of a narrow column centered over x G, confirming the theoretical assertion of Reference SchoofSchoof (2007b).
Simulations were performed for Δx0 ranging from 100 to 2500 m. For each run, the steady-state position of the grounding line is plotted versus Δx0 in Figure 4. Results from simulations with a regular mesh size are also shown. As observed in Figure 2, horizontal extension of the ice sheet significantly decreases with increasing grid resolution. However, for Δx0 ≤ 5 km there is not such a clear trend. Unfortunately, because the computing resources required for simulations with Δx0 ≤ 100m are huge (>2weeks), we were unable to establish whether the model converges toward a unique value of x G when Δx0 tends to 0. If such convergence exists, it is obviously not monotonic. Despite this limitation, the model seems to give consistent results for resolution finer than 5 km as in this case, the standard deviation of x G at steady state being 5.5 km. A similar exercise with grid resolutions ranging from 2.5 to 20 km was performed using a vertically integrated stress approximation model with a differentiated margin condition to calculate the margin velocity (Hindmarsh, unpublished information). These results are also plotted in Figure 4. Sensitivity to grid resolution appears to be less important than with the full Stokes finite-element model; for example, although x G does not converge to a particular value with a smaller grid, it never crosses the upward-sloping area for large grid sizes in that case. Variability from one model to the other is large; in particular, the full Stokes finite-element approach presents a difference of ∼100 km in the grounding-line steady position with the boundary layer results. Note that this discrepancy decreases to ∼40 km when x G at steady state moves away from the unstable region (Reference Durand, Gagliardini, de Fleurian, Zwinger and Le MeurDurand and others, in press).

Fig. 4. Steady-state grounding-line position as a function of the horizontal extension of the grid, Δx0, used for the simulations. Filled circles indicate results from the constant-grid mesh simulations, and empty circles those from the adaptive mesh refinement method described in the text. Crosses depict results obtained with a vertically integrated model (Hindmarsh, unpublished data), and the horizontal dotted line represents the result obtained with the semi-analytical formula due to Reference SchoofSchoof (2007a).
Further validation of the model requires us to test whether, for a given grid size, the steady state is influenced by the way the ice sheet has been built. Following Reference SchoofSchoof (2007a), we chose to vary the fluidity rather than other parameters (e.g. sea level). In what follows, we chose to use Δx0 = 200 m. This is a compromise between reasonable calculation times and fine enough resolution to properly describe surface oscillations induced by changes in basal conditions in the vicinity of the grounding line (see inset of Fig. 2 and Reference Durand, Gagliardini, de Fleurian, Zwinger and Le MeurDurand and others, in press, for more details). A first steady state is obtained starting from a 10mthick ice layer with a prescribed fluidity of B 2 (see Table 1). Starting from the obtained steady state with fluidity B 2 at t = 0, three simulations were run with different variations of the fluidity from B 2 to B 1: (1) a steady decrease from t = 0 to t = 30 ka followed by 5 ka of relaxation with B 1; (2) ten regular step changes every 3 ka followed by 5 ka of relaxation; and (3) fluidity set to B 1 at t = 0 and kept constant during the 35 ka of the simulation. Evolution of the fluidity with time is plotted in Figure 5a for each run. The corresponding evolutions of x G with time for the three simulations are plotted in Figure 5b. A notable feature is the ability of the model to react after even a small perturbation. Indeed, following values given by Reference PatersonPaterson (1994), each small step of the fluidity in run (2) corresponds to a temperature shift of ∼0.5 ◦ C. Such sensitivity to small perturbations has also been observed for small modifications in sea level, basal sliding or accumulation. For example, a perturbation of the steady state obtained with B 2 with a 1 m sea-level drop leads to a 1.8 km advance of x G before a new steady state is found (data not shown). This is a very important result as some marine ice-sheet models have shown very poor sensitivity to much more dramatic perturbations (e.g. a few kilometers of grounding-line retreat after a sea-level rise of 125 m; see Reference Vieli and PayneVieli and Payne, 2005). Also note that all the simulations have reached their steady state after the 35 ka of the run. Notably, the positions of the grounding line after 35 ka are exactly the same: x G = 822.8 km. This is also the steady position reached if the simulation starts from a 10 m thick ice layer with B 1.

Fig. 5. (a) Evolution of the fluidity versus time for run (1) in light gray, run (2) in dark gray and run (3) in black. All simulations start from the steady state obtained with fluidity B 2 (see text and Table 1 for details). (b) Evolution of the grounding line versus time for the different runs. For a given run, gray tones are the same in (a) and (b).
The sensitivity of the model to perturbations as well as the reproducibility of the grounding-line positions, whatever the rate of decrease of fluidity, gives confidence in the model results.
Conclusions
We recently proposed a new approach to solve the contact problem at the interface between the grounded part of an ice mass and its extension over the sea (Reference Durand, Gagliardini, de Fleurian, Zwinger and Le MeurDurand and others, in press). In the proposed approach, the ice flow is determined by solving the full Stokes problem implemented in the finite-element code Elmer. Here we have shown that the proposed method, despite its high sensitivity to the horizontal mesh resolution, can give consistent results as long as the horizontal extension of the element is small enough (<5 km) in the vicinity of the grounding line. Indeed, standard deviation of the grounding-line positions at the steady state for simulations with Δx0 < 5km is ∼6km. This value is small in comparison with the previous similar experiments of Reference Vieli and PayneVieli and Payne (2005) (40 km is a classical grid size for models using the shallow-ice approximation; Reference Ritz, Rommelaere and DumasRitz and others, 2001). However, this shows that full Stokes finite-element modeling of marine ice sheets should be handled with care, and that intensive grid sensitivity tests should be conducted. Furthermore, steady-state solutions are independent of the applied perturbation in fluidity, provided this perturbation remains monotonic. It is also worth noting that the model is sensitive to small variations of fluidity which correspond to a perturbation of <1◦C.
Acknowledgements
This research is a part of the DACOTA project (ANR-06-VULN-016-01) funded by the Agence National de la Recherche, France. Most of the computations presented in this paper were performed at the Service Commun de Calcul Intensif de l’Observatoire de Grenoble.




