Introduction
Callaway (1959) showed that the thermal conductivity coefficient λ of a dielectric crystal can be expressed as:

where x = hω/kT, k is Boltzmann's constant, T is the absolute temperature, 2πh is Planck's constant, ω is the phonon frequency, and Θ is the Debye temperature. The total relaxation time τ is obtained by using the equation
where the τi are the relaxation times corresponding to different phonon interaction mechanisms.
As Klinger (1975) pointed out, the correction term λ2 can be neglected for ice samples, and the relaxation time due to phonon interaction with crystal imperfections can be written as:
where R takes the values 2 or 3 depending on the origin of the sample.
In order to describe phonon-phonon interactions it is sufficient to use a relaxation time for umklapp processes given by
According to Casimir (1938) the thermal conductivity coefficient depends on a constant relaxation time
at sufficiently low temperatures at which the phonons are scattered at the boundaries of the sample. Here Lc is the Casimir length given by:
with a and b the sides of the crystal parallelepiped perpendicular to the heat flow. H is a coefficient near to one due to the finite length of the sample.
In this case the thermal conductivity coefficient can be approximated by:

As the temperature region where Equation (7) is valid could not be attained in his experiments, Klinger (1975) used a Casimir length calculated from Equation (6) with H = 1 in order to fit his experimental results. This method is only valid if the chosen mean value of the sound velocity is the most appropriate one. On the other hand if there are small-angle grain boundaries present in the crystal, the “apparent Casimir length”, will be smaller than that calculated from the macroscopic crystal. As an incorrect value for τC can lead to erroneous parameters in Equation (3), it is necessary to measure the heat conduction directly in the temperature region where Equation (7) is valid in order to give a more reliable interpretation of the influence of lattice defects on low-temperature heat conduction data for ice. This is the purpose of the present work.

Fig. 1. Simplified view of the sample holder used in our experiments.
Experimental Procedure
Heat conduction experiments have been done between 0.58 K and 4.01 K on a 3He-apparatus at the Service des Basses Températures, Centre d'Études Nucléaires de Grenoble.
The major difficulty was to ensure a good thermal contact between the sample and the cooling bath. As ice is very fragile, it was not possible to ensure a sufficiently good contact by pressing the sample between copper plates as Klinger (1975) did at higher temperatures.
As the thermal dilatation coefficient of ice is very much higher than that of copper it is not possible to freeze the crystal on a compact copper block.
We developed the sample holder shown in Figure 1 which gave good results: a small Plexiglas (polymethylmelhacrylate) vessel contained a loose bundle of 340 tinned copper wires each 0.15 mm in diameter. These wires were related to the 3He bath.
The sample mounting was done in a cold room at 257 K. We introduced supercooled water into the vessel and froze the sample to the copper wires. The cooling down of the sample from cold-room temperature to liquid-nitrogen temperature was done at a rate of about 0.6 K/min.
We applied the steady-state heat-flow method and computed the thermal conductivity coefficient from Fourier's law:
where P is the power applied to the sample, a and b the section of the sample, l is the distance between thermometers, and ΔT the measured temperature difference.
We used two Allen Bradley carbon resistors as thermometers. The carbon resistor at the “hot” side of the sample was calibrated by comparing it to a “Cryo Resistor” germanium resistance of known characteristics. On the basis of this calibration the absolute temperature of the carbon resistor was computed using an empirical law. The heater delivering the power P was a strain gauge of 110 Ω. Another heating device fixed on the sample holder allowed us to elevate the temperature of the sample without applying power to it. In order to eliminate errors due to radiation and conduction in the heating wires, we used the double heating method.
We apply a known power to the sample and read the values of the two resistance thermometers. Then we heat the sample holder without applying power to the sample until the temperature of the thermometer near to the heat sink is at the same value. ΔT is given by the difference of the temperatures indicated by the calibrated carbon resistor near to the heat source and the absolute temperature by the mean value indicated by the calibrated thermometer in the two cases.
The dimensions of the sample used were:
The distance between thermometers was:
This gives us a form factor:
Experimental Errors
The error on the form factor given by Equation (9) affects only the absolute value of λ. The systematic error due to the variation of λ in the temperature interval ΔT can be neglected if we take care to satisfy the condition Δ?/? < 5%.
Accidental errors are essentially due to the measurement of ΔT. It is not possible to evaluate these errors in a general manner as errors in ΔT depend simultaneously on the sensitivities of the carbon resistors and on the fact that the power dissipated in the resistors has to be negligible compared to the power applied to the sample. This fact limits the sensitivity of the detection device. In general we can say that these errors are situated between 6 and 20%. In one exceptional case it was as large as 60%. Error bars are given for all results in Figure 2.
Results
Five runs of the thermal conductivity measurements have been done on one sample cut perpendicular to the c-axis within the temperature range from 0.58 to 4.01 K. The results are indicated in Figure 2. Qualitatively the interactions of phonons with crystal imperfections seem to become ineffective at temperatures as low as 1.5 to 1.2 K. For still lower temperatures a law ![]() seems to be verified.
seems to be verified.

Fig. 2. Heat conduction of an ice sample cut perpendicular to c-axis between 0.58 and 4.01 K. Full line: theoretical low- temperature law.
The points of run 4 are slightly displaced to lower values compared to the points of runs 1, 2, 3, and 5.
The extrapolation of our values to higher temperatures using thermal conductivity values from Klinger (1975) obtained on crystals with comparable crystallographic orientation suggests the existence of a maximum of thermal conductivity between 2 and 9 K.
Discussion
The value of the integral in Equation (7) is ![]() . If we take H = 1 since the sample length is much greater than a and b,
Equation (6) gives us the Casimir length Lc = 0.65 cm, and if we use as mean value of the sound velocity v = 2.5 × 105 cm/s, Equation (7) gives us a low-temperature law of thermal conductivity of the form
. If we take H = 1 since the sample length is much greater than a and b,
Equation (6) gives us the Casimir length Lc = 0.65 cm, and if we use as mean value of the sound velocity v = 2.5 × 105 cm/s, Equation (7) gives us a low-temperature law of thermal conductivity of the form
This is not too far from our experimental results as shown in Figure 2 if we take into account that we took a mean value of the sound velocity for the computation of the factor in Equation (10).
We were not able to explain in a satisfying manner the slight systematic displacement of run 4 relative to the other runs. A loss of power due to incomplete pumping of the exchange gas seems to be excluded as it would result in higher apparent λ values. Further the apparent λ values would depend on the applied power. In run 3 we repeated the measurements with different applied powers, but there was no important change in λ. It seems more plausible to explain the systematic deviation by a slight overheating of the calibrated carbon resistor due to a higher measuring current suggesting in this way a higher apparent Δ?.
A definite answer whether or not we attained the region of constant mean free path can only be given if we are able to extend our measurements to still lower temperatures. Those measurements will give us at the same time information concerning which conditions of sample preparation lead to specular reflection of the phonons at the boundaries of the sample. A definitive interpretation of the type of interaction of phonons with defects in ice would seem possible when we have extended the range of heat conduction measurements on one sample from say 0. 1 K to 20 K (the temperature where the influence of phonon scattering on defects becomes negligible compared to phonon-phonon interactions of the “umklapp” type (see Klinger, 1975). This work is in progress in our laboratory.
Acknowledgements
We would like to thank M. Bochirol, the head of the Service des Basses Températures du Centre d'Etudes Nucléaires de Grenoble for giving us the possibility of making the measurements reported here in his laboratory. Discussions with Mme de Goёr and M. de Combarieu are gratefully acknowledged. We are greatly indebted to M. Bedin and M. Favre for technical aid during the experiments.


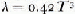 . Measurements at still lower temperatures are necessary to confirm our results.
. Measurements at still lower temperatures are necessary to confirm our results.

