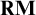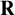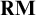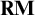1 Informal introduction
The notion of structural completeness (
![]() $\mathbf {SC}$
) was introduced by W. A. Pogorzelski in [Reference Pogorzelski24]. A consequence relation is
$\mathbf {SC}$
) was introduced by W. A. Pogorzelski in [Reference Pogorzelski24]. A consequence relation is
![]() $\mathbf {SC}$
if all of its admissible rules are derivable. The distinction between the admissibility and derivability of a rule lies in the extent of its applicability within a given consequence relation. An admissible rule is one that “works” on the theorems of a given logic, meaning it guarantees that its conclusion is a theorem whenever all its premises are theorems. A derivable rule, on the other hand, is a rule in the “standard sense,” meaning it can be applied to an arbitrary set of formulas. Thus, roughly speaking, in a given consequence relation,
$\mathbf {SC}$
if all of its admissible rules are derivable. The distinction between the admissibility and derivability of a rule lies in the extent of its applicability within a given consequence relation. An admissible rule is one that “works” on the theorems of a given logic, meaning it guarantees that its conclusion is a theorem whenever all its premises are theorems. A derivable rule, on the other hand, is a rule in the “standard sense,” meaning it can be applied to an arbitrary set of formulas. Thus, roughly speaking, in a given consequence relation,
![]() $\varphi $
follows from a set of premises
$\varphi $
follows from a set of premises
![]() $\Sigma $
if there exists a finite subset
$\Sigma $
if there exists a finite subset
![]() $\Gamma $
of
$\Gamma $
of
![]() $\Sigma $
such that
$\Sigma $
such that
![]() $\Gamma /\varphi $
is a derivable rule in the system. Clearly, if we are working within a fixed deductive system, every derivable rule is also admissible. However, numerous counterexamples demonstrate that the converse is not generally true. Two paradigmatic examples of non-derivable admissible rules are the Harrop’s rule
$\Gamma /\varphi $
is a derivable rule in the system. Clearly, if we are working within a fixed deductive system, every derivable rule is also admissible. However, numerous counterexamples demonstrate that the converse is not generally true. Two paradigmatic examples of non-derivable admissible rules are the Harrop’s rule
 $$\begin{align*}\dfrac{\neg\varphi\to(\psi\lor\chi)}{(\neg\varphi\to\psi)\lor(\neg\varphi\to\chi)} \end{align*}$$
$$\begin{align*}\dfrac{\neg\varphi\to(\psi\lor\chi)}{(\neg\varphi\to\psi)\lor(\neg\varphi\to\chi)} \end{align*}$$
for intuitionistic logic
![]() $\mathbf {Int}$
and the disjunctive syllogism rule
$\mathbf {Int}$
and the disjunctive syllogism rule
![]() $\mathtt {DS}$
$\mathtt {DS}$
for the system of relevance logic
![]() $\mathbf {R}$
. Adding these rules to their respective systems does not affect the sets of theorems but alters the consequence relations. Thus, neither of these two logics is structurally complete (
$\mathbf {R}$
. Adding these rules to their respective systems does not affect the sets of theorems but alters the consequence relations. Thus, neither of these two logics is structurally complete (
![]() $\mathbf {SC}$
).
$\mathbf {SC}$
).
To emphasize the importance of the
![]() $\mathbf {SC}$
property, let us recall two major formal definitions of the notion of “a logic.” The first treats it as a mere set of theorems, usually generated from an initial set of axioms via certain rules. In this approach, there is no distinction between derivable and admissible rules, as these rules are applied only to theorems. The second definition views a logic as a consequence relation—a binary relation between sets of formulas (premises) and single formulas (conclusions). In a sense, the phenomenon of structural incompleteness underscores the superiority of the second approach, as two logics can share identical sets of theorems but differ when viewed as consequence relations.Footnote
1
The distinction between derivable and admissible rules, which is only possible within the framework of consequence relations, is precisely why the second definition is more nuanced.
$\mathbf {SC}$
property, let us recall two major formal definitions of the notion of “a logic.” The first treats it as a mere set of theorems, usually generated from an initial set of axioms via certain rules. In this approach, there is no distinction between derivable and admissible rules, as these rules are applied only to theorems. The second definition views a logic as a consequence relation—a binary relation between sets of formulas (premises) and single formulas (conclusions). In a sense, the phenomenon of structural incompleteness underscores the superiority of the second approach, as two logics can share identical sets of theorems but differ when viewed as consequence relations.Footnote
1
The distinction between derivable and admissible rules, which is only possible within the framework of consequence relations, is precisely why the second definition is more nuanced.
Hereditary structural completeness (
![]() $\mathbf {HSC}$
) is a stronger form of the standard structural completeness (
$\mathbf {HSC}$
) is a stronger form of the standard structural completeness (
![]() $\mathbf {SC}$
). A consequence relation is said to be
$\mathbf {SC}$
). A consequence relation is said to be
![]() $\mathbf {HSC}$
if and only if it is
$\mathbf {HSC}$
if and only if it is
![]() $\mathbf {SC}$
and all of its extensions are also
$\mathbf {SC}$
and all of its extensions are also
![]() $\mathbf {SC}$
. In this paper, we will investigate the problem of hereditary structural completeness within extensions of the logic
$\mathbf {SC}$
. In this paper, we will investigate the problem of hereditary structural completeness within extensions of the logic
![]() $\mathbf {R}$
-mingle (
$\mathbf {R}$
-mingle (
![]() $\mathbf {RM}$
), which is the most well-known and widely studied extension of Belnap and Anderson’s system of relevance logic
$\mathbf {RM}$
), which is the most well-known and widely studied extension of Belnap and Anderson’s system of relevance logic
![]() $\mathbf {R}$
.
$\mathbf {R}$
.
The system
![]() $\mathbf {RM}$
is obtained by adding the “mingle” axiom
$\mathbf {RM}$
is obtained by adding the “mingle” axiom
![]() $p \to (p \to p)$
to
$p \to (p \to p)$
to
![]() $\mathbf {R}$
. Dunn established in [Reference Dunn12] that Sugihara algebras provide an adequate algebraic semantics for
$\mathbf {R}$
. Dunn established in [Reference Dunn12] that Sugihara algebras provide an adequate algebraic semantics for
![]() $\mathbf {RM}$
. The theory of Sugihara algebras will be crucial to our investigation, as we approach the problem using the powerful framework of abstract algebraic logic. Our final theorem will demonstrate that the structure of the poset of all hereditarily structurally complete extensions of
$\mathbf {RM}$
. The theory of Sugihara algebras will be crucial to our investigation, as we approach the problem using the powerful framework of abstract algebraic logic. Our final theorem will demonstrate that the structure of the poset of all hereditarily structurally complete extensions of
![]() $\mathbf {RM}$
is the converse of the well-ordering
$\mathbf {RM}$
is the converse of the well-ordering
![]() $\omega ^+$
with an additional element adjoined above 1:
$\omega ^+$
with an additional element adjoined above 1:
The problem of (hereditary) structural completeness has often been explored in the context of non-classical logics. So far, results regarding
![]() $\mathbf {SC}$
have been confined to axiomatic systems. A well-known theorem proven by Citkin in [Reference Citkin10] characterizes
$\mathbf {SC}$
have been confined to axiomatic systems. A well-known theorem proven by Citkin in [Reference Citkin10] characterizes
![]() $\mathbf {HSC}$
superintuitionistic logics (axiomatic extensions of
$\mathbf {HSC}$
superintuitionistic logics (axiomatic extensions of
![]() $\mathbf {Int}$
) in the following manner: a given variety of Heyting algebras is
$\mathbf {Int}$
) in the following manner: a given variety of Heyting algebras is
![]() $\mathbf {HSC}$
if and only if it omits five specific algebras; this is further equivalent to the statement that there are exactly five maximal non-
$\mathbf {HSC}$
if and only if it omits five specific algebras; this is further equivalent to the statement that there are exactly five maximal non-
![]() $\mathbf {HSC}$
superintuitionistic logics. Similarly, Rybakov’s theorem from [Reference Rybakov27] indicates that, in the case of axiomatic extensions of modal logic
$\mathbf {HSC}$
superintuitionistic logics. Similarly, Rybakov’s theorem from [Reference Rybakov27] indicates that, in the case of axiomatic extensions of modal logic
![]() $\mathbf {K4}$
, there are twenty such algebras.
$\mathbf {K4}$
, there are twenty such algebras.
While these characterizations are sophisticated and undoubtedly elegant, they can be seen as somewhat roundabout; they do not directly identify the
![]() $\mathbf {HSC}$
extensions themselves but rather highlight the algebras that must be omitted.Footnote
2
In the current work, we will provide a direct characterization of the
$\mathbf {HSC}$
extensions themselves but rather highlight the algebras that must be omitted.Footnote
2
In the current work, we will provide a direct characterization of the
![]() $\mathbf {HSC}$
extensions of
$\mathbf {HSC}$
extensions of
![]() $\mathbf {RM}$
: we will construct the poset of the respective quasivarieties and describe the algebras that generate them. In the final part of the paper, we will also examine a weaker version of
$\mathbf {RM}$
: we will construct the poset of the respective quasivarieties and describe the algebras that generate them. In the final part of the paper, we will also examine a weaker version of
![]() $\mathbf {SC}$
—passive structural completeness—and obtain a Citkin-style characterization for passively structurally complete quasivarieties of Sugihara algebras. In this case, only two algebras will need to be omitted.
$\mathbf {SC}$
—passive structural completeness—and obtain a Citkin-style characterization for passively structurally complete quasivarieties of Sugihara algebras. In this case, only two algebras will need to be omitted.
Structural completeness has been widely investigated among substructural logics [Reference Cintula and Metcalfe9, Reference Kowalski20, Reference Olson, Raftery and van Alten23]. In particular, the problem of
![]() $\mathbf {SC}$
has been addressed for certain fragments of
$\mathbf {SC}$
has been addressed for certain fragments of
![]() $\mathbf {RM}$
with Ackermann’s constant
$\mathbf {RM}$
with Ackermann’s constant
![]() $\mathbf {t}$
added to the original signature (
$\mathbf {t}$
added to the original signature (
![]() $\mathbf {RM}^{\mathbf {t}}$
) in [Reference Olson and Raftery22, Reference Olson, Raftery and van Alten23]. The positive (negation-free) fragment of
$\mathbf {RM}^{\mathbf {t}}$
) in [Reference Olson and Raftery22, Reference Olson, Raftery and van Alten23]. The positive (negation-free) fragment of
![]() $\mathbf {RM}^{\mathbf {t}}$
is
$\mathbf {RM}^{\mathbf {t}}$
is
![]() $\mathbf {HSC}$
[Reference Olson and Raftery22], while the purely implicational fragment of
$\mathbf {HSC}$
[Reference Olson and Raftery22], while the purely implicational fragment of
![]() $\mathbf {RM}$
is not
$\mathbf {RM}$
is not
![]() $\mathbf {SC}$
(see [Reference Olson, Raftery and van Alten23]). However, we will consider
$\mathbf {SC}$
(see [Reference Olson, Raftery and van Alten23]). However, we will consider
![]() $\mathbf {RM}$
in its original signature.
$\mathbf {RM}$
in its original signature.
The most pertinent result related to our inquiry is the theorem proven by Raftery and Świrydowicz in [Reference Świrydowicz and Raftery19], which states that there are no
![]() $\mathbf {SC}$
axiomatic extensions of
$\mathbf {SC}$
axiomatic extensions of
![]() $\mathbf {R}$
other than classical propositional logic (
$\mathbf {R}$
other than classical propositional logic (
![]() $\mathbf {CPL}$
) and inconsistent logic. Since
$\mathbf {CPL}$
) and inconsistent logic. Since
![]() $\mathbf {RM}$
is an axiomatic extension of
$\mathbf {RM}$
is an axiomatic extension of
![]() $\mathbf {R}$
, it follows that neither
$\mathbf {R}$
, it follows that neither
![]() $\mathbf {RM}$
nor any of its axiomatic extensions—excluding
$\mathbf {RM}$
nor any of its axiomatic extensions—excluding
![]() $\mathbf {CPL}$
and inconsistent logic—is
$\mathbf {CPL}$
and inconsistent logic—is
![]() $\mathbf {SC}$
. In this paper, we will tackle a more general problem: we will investigate arbitrary extensions of
$\mathbf {SC}$
. In this paper, we will tackle a more general problem: we will investigate arbitrary extensions of
![]() $\mathbf {RM}$
, not limited to axiomatic ones.
$\mathbf {RM}$
, not limited to axiomatic ones.
2 Preliminaries
We assume a countably infinite set of propositional variables, denoted by
![]() $\mathsf {Var} = \{p_1, p_2, p_3, \ldots \}$
(in practice, we will use letters
$\mathsf {Var} = \{p_1, p_2, p_3, \ldots \}$
(in practice, we will use letters
![]() $p, q, r, \ldots $
). A language
$p, q, r, \ldots $
). A language
![]() $\mathcal {L}$
is a set of symbols; specifically,
$\mathcal {L}$
is a set of symbols; specifically,
![]() $\mathcal {L} = \mathsf {Var} \cup \mathsf {Con}$
, where
$\mathcal {L} = \mathsf {Var} \cup \mathsf {Con}$
, where
![]() $\mathsf {Con}$
is the set of logical connectives
$\mathsf {Con}$
is the set of logical connectives
![]() $\{\neg , \lor , \wedge , \to , \leftrightarrow \}$
. As usual,
$\{\neg , \lor , \wedge , \to , \leftrightarrow \}$
. As usual,
![]() $\neg $
is unary and the rest of the connectives are binary. The set of formulas
$\neg $
is unary and the rest of the connectives are binary. The set of formulas
![]() $\mathcal {F}$
consists of properly constructed finite strings of symbols from
$\mathcal {F}$
consists of properly constructed finite strings of symbols from
![]() $\mathcal {L}$
; that is,
$\mathcal {L}$
; that is,
![]() $p, \neg \varphi , \varphi \ast \psi $
, where
$p, \neg \varphi , \varphi \ast \psi $
, where
![]() $\ast $
is any binary connective. A uniform substitution is a map from
$\ast $
is any binary connective. A uniform substitution is a map from
![]() $\mathcal {F}$
to
$\mathcal {F}$
to
![]() $\mathcal {F}$
that preserves logical operations, i.e., an endomorphism of the absolutely free formula algebra. We define
$\mathcal {F}$
that preserves logical operations, i.e., an endomorphism of the absolutely free formula algebra. We define
![]() $\vdash \subseteq 2^{\mathcal {F}} \times \mathcal {F}$
as a consequence relation if it satisfies the following properties:
$\vdash \subseteq 2^{\mathcal {F}} \times \mathcal {F}$
as a consequence relation if it satisfies the following properties:
-
• reflexive:
 $\Sigma \vdash \sigma $
for any
$\Sigma \vdash \sigma $
for any
 $\sigma \in \Sigma $
;
$\sigma \in \Sigma $
; -
• monotonic: if
 $\Sigma \vdash \sigma $
, then
$\Sigma \vdash \sigma $
, then
 $\Sigma \cup \Gamma \vdash \sigma $
;
$\Sigma \cup \Gamma \vdash \sigma $
; -
• transitive: if
 $\Gamma \vdash \varphi $
and for any
$\Gamma \vdash \varphi $
and for any
 $\gamma \in \Gamma $
we have
$\gamma \in \Gamma $
we have
 $\Sigma \vdash \gamma $
, then
$\Sigma \vdash \gamma $
, then
 $\Sigma \vdash \varphi $
;
$\Sigma \vdash \varphi $
; -
• structural: if
 $\Sigma \vdash \varphi $
, then
$\Sigma \vdash \varphi $
, then
 $s(\Sigma ) \vdash s(\varphi )$
for any uniform substitution s;
$s(\Sigma ) \vdash s(\varphi )$
for any uniform substitution s; -
• finitary:
 $\Sigma \vdash \varphi $
if and only if
$\Sigma \vdash \varphi $
if and only if
 $\Sigma ' \vdash \varphi $
for some finite subset
$\Sigma ' \vdash \varphi $
for some finite subset
 $\Sigma '$
of
$\Sigma '$
of
 $\Sigma $
.
$\Sigma $
.
Elements of
![]() $2^{\mathcal {F}} \times \mathcal {F}$
whose first component is finite will be called rules. Instead of writing
$2^{\mathcal {F}} \times \mathcal {F}$
whose first component is finite will be called rules. Instead of writing
![]() $\langle \Gamma , \varphi \rangle $
, we will adopt the following notation:
$\langle \Gamma , \varphi \rangle $
, we will adopt the following notation:
![]() $\Gamma / \varphi $
, where
$\Gamma / \varphi $
, where
![]() $\Gamma \cup \{\varphi \}$
is a finite subset of
$\Gamma \cup \{\varphi \}$
is a finite subset of
![]() $\mathcal {F}$
. If a given rule
$\mathcal {F}$
. If a given rule
![]() $\Gamma / \varphi $
is a member of a consequence relation
$\Gamma / \varphi $
is a member of a consequence relation
![]() $\vdash $
, then we say that
$\vdash $
, then we say that
![]() $\Gamma / \varphi $
is a derivable rule of
$\Gamma / \varphi $
is a derivable rule of
![]() $\vdash $
. According to our definition, all consequence relations are finitary, so we can identify a given consequence relation with the set of its derivable rules. A derivable rule of a given consequence relation
$\vdash $
. According to our definition, all consequence relations are finitary, so we can identify a given consequence relation with the set of its derivable rules. A derivable rule of a given consequence relation
![]() $\vdash $
of the form
$\vdash $
of the form
![]() $\emptyset / \varphi $
is called a theorem of
$\emptyset / \varphi $
is called a theorem of
![]() $\vdash $
and is shortly denoted by
$\vdash $
and is shortly denoted by
![]() $\varphi $
. Each consequence relation is a set of rules, some of which may be theorems. For two consequence relations
$\varphi $
. Each consequence relation is a set of rules, some of which may be theorems. For two consequence relations
![]() $\vdash _0,\,\vdash _1\, \subseteq 2^{\mathcal {F}} \times \mathcal {F}$
, we say that
$\vdash _0,\,\vdash _1\, \subseteq 2^{\mathcal {F}} \times \mathcal {F}$
, we say that
![]() $\vdash _1$
is an extension of
$\vdash _1$
is an extension of
![]() $\vdash _0$
if
$\vdash _0$
if
![]() $\vdash _0 \,\,\subseteq \,\, \vdash _1$
. It is easy to see that the intersection of an arbitrary set of consequence relations is also a consequence relation:
$\vdash _0 \,\,\subseteq \,\, \vdash _1$
. It is easy to see that the intersection of an arbitrary set of consequence relations is also a consequence relation:
![]() $\bigcap _{i \in I} \vdash _i$
is reflexive, monotonic, transitive, structural, and finitary, given that each
$\bigcap _{i \in I} \vdash _i$
is reflexive, monotonic, transitive, structural, and finitary, given that each
![]() $\vdash _i$
has these properties. Thus, for any set of rules X, there exists a least consequence relation
$\vdash _i$
has these properties. Thus, for any set of rules X, there exists a least consequence relation
![]() $\vdash $
that contains X. In such cases, we will say that X defines
$\vdash $
that contains X. In such cases, we will say that X defines
![]() $\vdash $
. A rule
$\vdash $
. A rule
![]() $\Gamma / \varphi $
is admissible in
$\Gamma / \varphi $
is admissible in
![]() $\vdash $
if and only if, for any substitution
$\vdash $
if and only if, for any substitution
![]() $\sigma $
,
$\sigma $
,
![]() $\sigma (\varphi )$
is a theorem of
$\sigma (\varphi )$
is a theorem of
![]() $\vdash $
whenever
$\vdash $
whenever
![]() $\sigma (\Gamma )$
is a set of theorems of
$\sigma (\Gamma )$
is a set of theorems of
![]() $\vdash $
. Furthermore, a rule
$\vdash $
. Furthermore, a rule
![]() $\Gamma / \varphi $
is passive in
$\Gamma / \varphi $
is passive in
![]() $\vdash $
iff there is no uniform substitution
$\vdash $
iff there is no uniform substitution
![]() $\sigma $
, such that
$\sigma $
, such that
![]() $\sigma (\Gamma )$
is a set of theorems of
$\sigma (\Gamma )$
is a set of theorems of
![]() $\vdash $
. Thus, each passive rule of
$\vdash $
. Thus, each passive rule of
![]() $\vdash $
is vacuously admissible. A given consequence relation
$\vdash $
is vacuously admissible. A given consequence relation
![]() $\vdash $
is structurally complete (
$\vdash $
is structurally complete (
![]() $\mathbf {SC}$
) iff each admissible rule in
$\mathbf {SC}$
) iff each admissible rule in
![]() $\vdash $
is derivable. Furthermore, a consequence relation is hereditarily structurally complete (
$\vdash $
is derivable. Furthermore, a consequence relation is hereditarily structurally complete (
![]() $\mathbf {HSC}$
) when all of its extensions are
$\mathbf {HSC}$
) when all of its extensions are
![]() $\mathbf {SC}$
. Consequence relations that are
$\mathbf {SC}$
. Consequence relations that are
![]() $\mathbf {SC}$
but not
$\mathbf {SC}$
but not
![]() $\mathbf {HSC}$
(i.e., those that have at least one extension that is not
$\mathbf {HSC}$
(i.e., those that have at least one extension that is not
![]() $\mathbf {SC}$
) will be called non-hereditarily structurally complete (
$\mathbf {SC}$
) will be called non-hereditarily structurally complete (
![]() $\mathbf {nHSC}$
).
$\mathbf {nHSC}$
).
It is natural to associate a closure operator C with a given consequence relation
![]() $\vdash $
in the following way:
$\vdash $
in the following way:
![]() $\varphi \in C(X)$
if and only if
$\varphi \in C(X)$
if and only if
![]() $X \vdash \varphi $
for any
$X \vdash \varphi $
for any
![]() $X \subseteq \mathcal {F}$
. It has also been common to first define a structural and finitary closure operator as a primitive notion and then treat the consequence operation as a secondary entity. However, it seems more natural to talk about derivable rules in the context of consequence relations (simply as their members). Since the notions of consequence operator and consequence relation are two sides of the same coin, we decide to stick to the latter, treating it as the fundamental notion that captures the meaning of the term ‘logic’.
$X \subseteq \mathcal {F}$
. It has also been common to first define a structural and finitary closure operator as a primitive notion and then treat the consequence operation as a secondary entity. However, it seems more natural to talk about derivable rules in the context of consequence relations (simply as their members). Since the notions of consequence operator and consequence relation are two sides of the same coin, we decide to stick to the latter, treating it as the fundamental notion that captures the meaning of the term ‘logic’.
A Horn formula, or quasi-identity as it is also called, is a first-order sentence of the form
![]() $\forall _{x_1, \ldots , x_l}(\varphi _1(x_1, \ldots , x_l) \approx \psi _1(x_1, \ldots , x_l) \& \ldots \& \varphi _n(x_1, \ldots , x_l) \approx \psi _n(x_1, \ldots , x_l) \Longrightarrow \varphi (x_1, \ldots , x_l) \approx \psi (x_1, \ldots , x_l)$
. In practice, we will omit the quantifiers. Identities are quasi-identities with an empty antecedent. Let
$\forall _{x_1, \ldots , x_l}(\varphi _1(x_1, \ldots , x_l) \approx \psi _1(x_1, \ldots , x_l) \& \ldots \& \varphi _n(x_1, \ldots , x_l) \approx \psi _n(x_1, \ldots , x_l) \Longrightarrow \varphi (x_1, \ldots , x_l) \approx \psi (x_1, \ldots , x_l)$
. In practice, we will omit the quantifiers. Identities are quasi-identities with an empty antecedent. Let
![]() $\Phi $
be a quasi-equation and
$\Phi $
be a quasi-equation and
![]() $\mathfrak {A}$
be an algebra.
$\mathfrak {A}$
be an algebra.
![]() $\mathfrak {A} \vDash \Phi $
means that
$\mathfrak {A} \vDash \Phi $
means that
![]() $\Phi $
holds in
$\Phi $
holds in
![]() $\mathfrak {A}$
. For a class of algebras, we write
$\mathfrak {A}$
. For a class of algebras, we write
![]() $\mathsf {K} \vDash \Phi $
to indicate that
$\mathsf {K} \vDash \Phi $
to indicate that
![]() $\Phi $
holds in each member of
$\Phi $
holds in each member of
![]() $\mathsf {K}$
. We will use standard notation
$\mathsf {K}$
. We will use standard notation
![]() $\mathsf {H}, \mathsf {I}, \mathsf {S}, \mathsf {P}$
, and
$\mathsf {H}, \mathsf {I}, \mathsf {S}, \mathsf {P}$
, and
![]() $\mathsf {P}_{\mathsf {U}}$
for the well-known algebraic closure operators defined on arbitrary classes of algebras. Thus, given a class of algebras
$\mathsf {P}_{\mathsf {U}}$
for the well-known algebraic closure operators defined on arbitrary classes of algebras. Thus, given a class of algebras
![]() $\mathsf {K}$
,
$\mathsf {K}$
,
![]() $\mathsf {H}(\mathsf {K}), \mathsf {I}(\mathsf {K}), \mathsf {S}(\mathsf {K}), \mathsf {P}(\mathsf {K}), \mathsf {P}_{\mathsf {U}}(\mathsf {K})$
are
$\mathsf {H}(\mathsf {K}), \mathsf {I}(\mathsf {K}), \mathsf {S}(\mathsf {K}), \mathsf {P}(\mathsf {K}), \mathsf {P}_{\mathsf {U}}(\mathsf {K})$
are
![]() $\mathsf {K}$
’s closures under homomorphic images, isomorphic copies, subalgebras, direct products, and ultraproducts, respectively. For two algebras
$\mathsf {K}$
’s closures under homomorphic images, isomorphic copies, subalgebras, direct products, and ultraproducts, respectively. For two algebras
![]() $\mathfrak {A}$
and
$\mathfrak {A}$
and
![]() $\mathfrak {B}$
, we will write
$\mathfrak {B}$
, we will write
![]() $\mathfrak {A} \cong \mathfrak {B}$
when
$\mathfrak {A} \cong \mathfrak {B}$
when
![]() $\mathfrak {A} \in \mathsf {I}(\mathfrak {B})$
. Given a class of algebras
$\mathfrak {A} \in \mathsf {I}(\mathfrak {B})$
. Given a class of algebras
![]() $\mathsf {K}$
,
$\mathsf {K}$
,
![]() $\mathbf {F}_{\mathsf {K}}(\kappa )$
will denote the
$\mathbf {F}_{\mathsf {K}}(\kappa )$
will denote the
![]() $\kappa $
-generated algebra that is free in
$\kappa $
-generated algebra that is free in
![]() $\mathsf {I}\mathsf {S}\mathsf {P}(\mathsf {K})$
. We will also write
$\mathsf {I}\mathsf {S}\mathsf {P}(\mathsf {K})$
. We will also write
![]() $\mathsf {V}(\mathsf {K})$
for
$\mathsf {V}(\mathsf {K})$
for
![]() $\mathsf {H}\mathsf {S}\mathsf {P}(\mathsf {K})$
and
$\mathsf {H}\mathsf {S}\mathsf {P}(\mathsf {K})$
and
![]() $\mathsf {Q}(\mathsf {K})$
for
$\mathsf {Q}(\mathsf {K})$
for
![]() $\mathsf {I}\mathsf {S}\mathsf {P}\mathsf {P}_{\mathsf {U}}(\mathsf {K})$
. We will use obvious notation for finite direct powers:
$\mathsf {I}\mathsf {S}\mathsf {P}\mathsf {P}_{\mathsf {U}}(\mathsf {K})$
. We will use obvious notation for finite direct powers:
![]() $\mathfrak {A}^1 = \mathfrak {A}$
, and
$\mathfrak {A}^1 = \mathfrak {A}$
, and
![]() $\mathfrak {A}^{n+1} = \mathfrak {A}^n \times \mathfrak {A}$
. To indicate that an algebra
$\mathfrak {A}^{n+1} = \mathfrak {A}^n \times \mathfrak {A}$
. To indicate that an algebra
![]() $\mathfrak {A}$
is embeddable in (isomorphic to a subalgebra of)
$\mathfrak {A}$
is embeddable in (isomorphic to a subalgebra of)
![]() $\mathfrak {B}$
, i.e.,
$\mathfrak {B}$
, i.e.,
![]() $\mathfrak {A} \in \mathsf {I}\mathsf {S}(\mathfrak {B})$
, we will use the following notation:
$\mathfrak {A} \in \mathsf {I}\mathsf {S}(\mathfrak {B})$
, we will use the following notation:
![]() $\mathfrak {A} \preceq \mathfrak {B}$
. We will also write
$\mathfrak {A} \preceq \mathfrak {B}$
. We will also write
![]() $\mathfrak {A} \prec \mathfrak {B}$
when
$\mathfrak {A} \prec \mathfrak {B}$
when
![]() $\mathfrak {A} \preceq \mathfrak {B}$
and
$\mathfrak {A} \preceq \mathfrak {B}$
and
![]() $\mathfrak {A} \not \cong \mathfrak {B}$
. If
$\mathfrak {A} \not \cong \mathfrak {B}$
. If
![]() $\mathsf {K} = \mathsf {V}(\mathsf {K})$
, then it is called a variety; if
$\mathsf {K} = \mathsf {V}(\mathsf {K})$
, then it is called a variety; if
![]() $\mathsf {K} = \mathsf {Q}(\mathsf {K})$
, then it is a quasivariety. Arbitrary varieties will be referred to as
$\mathsf {K} = \mathsf {Q}(\mathsf {K})$
, then it is a quasivariety. Arbitrary varieties will be referred to as
![]() $\mathcal {V}$
and quasivarieties as
$\mathcal {V}$
and quasivarieties as
![]() $\mathcal {Q}$
.Footnote
3
Varieties are definable by identities, and quasivarieties by quasi-identities.
$\mathcal {Q}$
.Footnote
3
Varieties are definable by identities, and quasivarieties by quasi-identities.
Now, we will recall some results concerning the algebraic counterpart of the structural completeness property, which were first formulated by Bergman in [Reference Bergman5].Footnote
4
For a consequence relation, being structurally complete is equivalent to having no proper extensions with the same set of theorems. To see that, let
![]() $\vdash _0\,\, \subsetneq \,\, \vdash _1$
be two consequence relations, where the second properly extends the first, with the additional property that they have the same theorems, i.e.,
$\vdash _0\,\, \subsetneq \,\, \vdash _1$
be two consequence relations, where the second properly extends the first, with the additional property that they have the same theorems, i.e.,
![]() $\vdash _0 \varphi $
if and only if
$\vdash _0 \varphi $
if and only if
![]() $\vdash _1 \varphi $
for any
$\vdash _1 \varphi $
for any
![]() $\varphi \in \mathcal {F}$
. Hence, there is a rule
$\varphi \in \mathcal {F}$
. Hence, there is a rule
![]() $\Gamma / \psi $
in
$\Gamma / \psi $
in
![]() $\vdash _1$
that does not belong to
$\vdash _1$
that does not belong to
![]() $\vdash _0$
. However,
$\vdash _0$
. However,
![]() $\Gamma / \psi $
is admissible in
$\Gamma / \psi $
is admissible in
![]() $\vdash _0$
(otherwise, the set of theorems would be different). Hence,
$\vdash _0$
(otherwise, the set of theorems would be different). Hence,
![]() $\vdash _0$
is not
$\vdash _0$
is not
![]() $\mathbf {SC}$
. For the other direction, let
$\mathbf {SC}$
. For the other direction, let
![]() $\vdash _0$
be such that each of its proper extensions also properly extends the set of its theorems. If there is a rule
$\vdash _0$
be such that each of its proper extensions also properly extends the set of its theorems. If there is a rule
![]() $\Gamma / \psi $
that is an admissible but non-derivable rule of
$\Gamma / \psi $
that is an admissible but non-derivable rule of
![]() $\vdash _0$
, then it is easy to see that
$\vdash _0$
, then it is easy to see that
![]() $\vdash _1$
, defined by the set of rules
$\vdash _1$
, defined by the set of rules
![]() $\vdash \cup \{\langle \Gamma , \psi \rangle \}$
, properly extends
$\vdash \cup \{\langle \Gamma , \psi \rangle \}$
, properly extends
![]() $\vdash _0$
and has exactly the same theorems, contradicting the initial assumption. Thus, in algebraic terms—assuming Blok–Pigozzi algebraizability, which ‘reverses the order’—we have the following:
$\vdash _0$
and has exactly the same theorems, contradicting the initial assumption. Thus, in algebraic terms—assuming Blok–Pigozzi algebraizability, which ‘reverses the order’—we have the following:
Fact 2.1. A given quasivariety
![]() $\mathcal {Q}$
is
$\mathcal {Q}$
is
![]() $\mathbf {SC}$
if and only if, for any quasivariety
$\mathbf {SC}$
if and only if, for any quasivariety
![]() $\mathcal {Q}' \subsetneq \mathcal {Q}$
, it is the case that
$\mathcal {Q}' \subsetneq \mathcal {Q}$
, it is the case that
![]() $\mathsf {H} \mathcal {Q}' \subsetneq \mathsf {H} \mathcal {Q}$
.
$\mathsf {H} \mathcal {Q}' \subsetneq \mathsf {H} \mathcal {Q}$
.
Thus, the
![]() $\mathbf {SC}$
quasivarieties are precisely those that are generated by their
$\mathbf {SC}$
quasivarieties are precisely those that are generated by their
![]() $\omega $
-generated free algebras. A given quasivariety is
$\omega $
-generated free algebras. A given quasivariety is
![]() $\mathbf {HSC}$
if and only if all of its subquasivarieties are
$\mathbf {HSC}$
if and only if all of its subquasivarieties are
![]() $\mathbf {SC}$
—analogously, a consequence relation is
$\mathbf {SC}$
—analogously, a consequence relation is
![]() $\mathbf {HSC}$
if and only if it has only
$\mathbf {HSC}$
if and only if it has only
![]() $\mathbf {SC}$
extensions. Not surprisingly, a given
$\mathbf {SC}$
extensions. Not surprisingly, a given
![]() $\mathbf {SC}$
quasivariety is
$\mathbf {SC}$
quasivariety is
![]() $\mathbf {nHSC}$
when it has at least one subquasivariety that is not
$\mathbf {nHSC}$
when it has at least one subquasivariety that is not
![]() $\mathbf {SC}$
.
$\mathbf {SC}$
.
3
 $\mathbf {RM}$
and Sugihara algebras
$\mathbf {RM}$
and Sugihara algebras
Let
![]() $\mathfrak {A}_\omega =\langle \mathbb {Z};\wedge ,\lor ,\neg ,\to \rangle $
, where
$\mathfrak {A}_\omega =\langle \mathbb {Z};\wedge ,\lor ,\neg ,\to \rangle $
, where
![]() $\mathbb {Z}$
is the set of integers,
$\mathbb {Z}$
is the set of integers,
![]() $x\wedge y=\min (x,y),x\lor y=\max (x,y)$
,
$x\wedge y=\min (x,y),x\lor y=\max (x,y)$
,
![]() $\neg k=-k$
and for
$\neg k=-k$
and for
![]() $\to $
we have
$\to $
we have
 $$ \begin{align*} k\to l &= \begin{cases} -k\lor l, & \text{if }k\leq l;\\ -k\wedge l, & \text{otherwise. } \end{cases} \ \end{align*} $$
$$ \begin{align*} k\to l &= \begin{cases} -k\lor l, & \text{if }k\leq l;\\ -k\wedge l, & \text{otherwise. } \end{cases} \ \end{align*} $$
It is evident that there are two types of finite subalgebras of
![]() $\mathfrak {A}_\omega $
: those that contain
$\mathfrak {A}_\omega $
: those that contain
![]() $0$
and those that do not. The former will be termed “odd,” while the latter will be referred to as “even.” Consequently, we introduce the following notation for
$0$
and those that do not. The former will be termed “odd,” while the latter will be referred to as “even.” Consequently, we introduce the following notation for
![]() $n\geq 1$
:
$n\geq 1$
:
 $$ \begin{align*} \mathfrak{A}_{2n} & =\langle\{-n,\dots,-1,1,\dots,n\};\wedge,\lor,\neg,\to\rangle,\\ \mathfrak{A}_{2n+1} & =\langle\{-n,\dots,-1,0,1,\dots,n\};\wedge,\lor,\neg,\to\rangle. \end{align*} $$
$$ \begin{align*} \mathfrak{A}_{2n} & =\langle\{-n,\dots,-1,1,\dots,n\};\wedge,\lor,\neg,\to\rangle,\\ \mathfrak{A}_{2n+1} & =\langle\{-n,\dots,-1,0,1,\dots,n\};\wedge,\lor,\neg,\to\rangle. \end{align*} $$
![]() $\mathfrak {A}_1$
is the trivial one element algebra.
$\mathfrak {A}_1$
is the trivial one element algebra.
![]() $\mathfrak {A}_2$
is a two element boolean algebra. An infinite proper subalgebra of
$\mathfrak {A}_2$
is a two element boolean algebra. An infinite proper subalgebra of
![]() $\mathfrak {A}_\omega $
will be denoted by
$\mathfrak {A}_\omega $
will be denoted by
![]() $\mathfrak {A}_{\omega \setminus \{0\}}=\langle \mathbb {Z}\setminus \{0\};\wedge ,\lor ,\neg ,\to \rangle $
. An algebra
$\mathfrak {A}_{\omega \setminus \{0\}}=\langle \mathbb {Z}\setminus \{0\};\wedge ,\lor ,\neg ,\to \rangle $
. An algebra
![]() $\mathfrak {A}$
will be referred to as Sugihara algebra when
$\mathfrak {A}$
will be referred to as Sugihara algebra when
![]() $\mathfrak {A}\in \mathsf {V}(\mathfrak {A}_\omega )=\mathsf {Q}(\mathfrak {A}_\omega )$
.
$\mathfrak {A}\in \mathsf {V}(\mathfrak {A}_\omega )=\mathsf {Q}(\mathfrak {A}_\omega )$
.
Anderson and Belnap’s [Reference Anderson and Belnap4, p. 341] system of relevance logic
![]() $\mathbf {R}$
is defined by 13 axioms and two rules:
$\mathbf {R}$
is defined by 13 axioms and two rules:
-
A1
 $p\to p$
$p\to p$
-
A2
 $(p\to q)\to ((q\to r)\to (p\to r))$
$(p\to q)\to ((q\to r)\to (p\to r))$
-
A3
 $p\to ((p\to q)\to q)$
$p\to ((p\to q)\to q)$
-
A4
 $(p\to (p\to q))\to (p\to q)$
$(p\to (p\to q))\to (p\to q)$
-
A5
 $p\wedge q\to p$
$p\wedge q\to p$
-
A6
 $p\wedge q\to q$
$p\wedge q\to q$
-
A7
 $((p\to q)\wedge (p\to r))\to (p\to q\wedge r)$
$((p\to q)\wedge (p\to r))\to (p\to q\wedge r)$
-
A8
 $p\to p\lor q$
$p\to p\lor q$
-
A9
 $p\to q\lor p$
$p\to q\lor p$
-
A10
 $((q\to p)\wedge (r\to p))\to (q\lor r \to p)$
$((q\to p)\wedge (r\to p))\to (q\lor r \to p)$
-
A11
 $p\wedge (q\lor r)\to (p\wedge q)\lor r$
$p\wedge (q\lor r)\to (p\wedge q)\lor r$
-
A12
 $(p\to \neg q)\to (q\to \neg p)$
$(p\to \neg q)\to (q\to \neg p)$
-
A13
 $\neg \neg p\to p$
$\neg \neg p\to p$
The two rules of the system is modus ponens MP
![]() $\{p,p\to q\}/q$
and the adjunction rule AD
$\{p,p\to q\}/q$
and the adjunction rule AD
![]() $\{p,q\}/p\wedge q$
.
$\{p,q\}/p\wedge q$
.
The logic
![]() $\mathbf {R}$
–mingle (
$\mathbf {R}$
–mingle (
![]() $\mathbf {RM}$
) is obtained by adding the “mingle axiom”
$\mathbf {RM}$
) is obtained by adding the “mingle axiom”
![]() $p\to (p\to p)$
to the axiomatic system of relevant logic
$p\to (p\to p)$
to the axiomatic system of relevant logic
![]() $\mathbf {R}$
. We will consider
$\mathbf {R}$
. We will consider
![]() $\mathbf {RM}$
as a consequence relation rather than merely as a set of theorems. The logic
$\mathbf {RM}$
as a consequence relation rather than merely as a set of theorems. The logic
![]() $\mathbf {RM}$
is algebraizable in the sense of [Reference Blok and Pigozzi7] with respect to the quasivariety of Sugihara algebras, using the set of formulas
$\mathbf {RM}$
is algebraizable in the sense of [Reference Blok and Pigozzi7] with respect to the quasivariety of Sugihara algebras, using the set of formulas
![]() $\{p\to q, q\to p\}$
and the equation
$\{p\to q, q\to p\}$
and the equation
![]() $p\approx p\to p$
. For a given finitary rule
$p\approx p\to p$
. For a given finitary rule
![]() $R=\Gamma /\varphi $
, where
$R=\Gamma /\varphi $
, where
![]() $\Gamma =\{\gamma _1,\gamma _2,\dots ,\gamma _n\}$
we can say that Sugihara algebra
$\Gamma =\{\gamma _1,\gamma _2,\dots ,\gamma _n\}$
we can say that Sugihara algebra
![]() $\mathfrak {A}$
satisfies R if
$\mathfrak {A}$
satisfies R if
![]() $\mathfrak {A}\vDash \gamma _1\approx \gamma _1\to \gamma _1 \& \cdots \&\gamma _n\approx \gamma _n\to \gamma _n\Longrightarrow \varphi \approx \varphi \to \varphi $
. In such cases, we will use the abbreviated notation
$\mathfrak {A}\vDash \gamma _1\approx \gamma _1\to \gamma _1 \& \cdots \&\gamma _n\approx \gamma _n\to \gamma _n\Longrightarrow \varphi \approx \varphi \to \varphi $
. In such cases, we will use the abbreviated notation
![]() $\mathfrak {A}\vDash R$
and say that
$\mathfrak {A}\vDash R$
and say that
![]() $\mathfrak {A}$
satisfies the rule R. It is straightforward to observe that, to check whether R holds in
$\mathfrak {A}$
satisfies the rule R. It is straightforward to observe that, to check whether R holds in
![]() $\mathfrak {A}$
, we do not need to translate R into a quasi-equation; instead, we can treat
$\mathfrak {A}$
, we do not need to translate R into a quasi-equation; instead, we can treat
![]() $\mathfrak {A}$
as a logical matrix with the set of designated elements
$\mathfrak {A}$
as a logical matrix with the set of designated elements
![]() $\{a\in \mathsf {A}:a=a\to a\}$
. We naturally define an absolute value of an element
$\{a\in \mathsf {A}:a=a\to a\}$
. We naturally define an absolute value of an element
![]() $a\in \mathfrak {A}$
as
$a\in \mathfrak {A}$
as
![]() $|a|:=a\to a$
. We define deductive filters
$|a|:=a\to a$
. We define deductive filters
![]() $F\subseteq \mathsf {A}$
as standard lattice filters such that the set of designated values is included in F; that is,
$F\subseteq \mathsf {A}$
as standard lattice filters such that the set of designated values is included in F; that is,
![]() $\{a\in \mathsf {A}: a= |a|\}\subseteq F$
. Thus, as a consequence of algebraizability, we have an order isomorphism between the lattices of deductive filters and congruences for a given Sugihara algebra.
$\{a\in \mathsf {A}: a= |a|\}\subseteq F$
. Thus, as a consequence of algebraizability, we have an order isomorphism between the lattices of deductive filters and congruences for a given Sugihara algebra.
Now, we will gather results on Sugihara algebras from [Reference Blok and Dziobiak6, Reference Czelakowski and Dziobiak11, Reference Dunn12, Reference Krawczyk21], which will be crucial in the proof of the theorem.
Let us start with two important results that can be found in [Reference Blok and Dziobiak6, p. 275]
Theorem 3.1 (Blok and Dziobiak, 1985).
Sugihara algebras are locally finite, i.e., each Sugihara subalgebra generated by a finite set is finite.
Theorem 3.2 (Blok and Dziobiak, 1985).
Algebras of the form
![]() $\mathfrak {A}_n$
,
$\mathfrak {A}_n$
,
![]() $n<\omega $
are the only—up to isomorphism—finite subdirectly irreducible algebras.
$n<\omega $
are the only—up to isomorphism—finite subdirectly irreducible algebras.
As a consequence of these, we can restate the theorem of Dunn [Reference Dunn12, Theorem 9, p. 9] in its purely algebraic version:
Theorem 3.3 (Dunn, 1970).
![]() $\mathsf {V}(\mathfrak {A}_1)\subseteq \mathsf {V}(\mathfrak {A}_2)\subseteq \mathsf {V}(\mathfrak {A}_3)\subseteq \mathsf {V}(\mathfrak {A}_4)\subseteq \cdots \subseteq \mathsf {V}(\mathfrak {A}_\omega )=\mathsf {V}(\{\mathfrak {A}_n:n\in \omega \})$
.
$\mathsf {V}(\mathfrak {A}_1)\subseteq \mathsf {V}(\mathfrak {A}_2)\subseteq \mathsf {V}(\mathfrak {A}_3)\subseteq \mathsf {V}(\mathfrak {A}_4)\subseteq \cdots \subseteq \mathsf {V}(\mathfrak {A}_\omega )=\mathsf {V}(\{\mathfrak {A}_n:n\in \omega \})$
.
We can already observe that Sugihara algebras enjoy some nice properties. They are locally finite, their finite subdirectly irreducibles are chains, and the lattice of subvarieties of Sugihara algebras form an
![]() $\omega ^+$
well ordering. Consequently, due to the Blok–Pigozzi algebraizability, the lattice of axiomatic extensions of
$\omega ^+$
well ordering. Consequently, due to the Blok–Pigozzi algebraizability, the lattice of axiomatic extensions of
![]() $\mathbf {RM}$
is the converse of
$\mathbf {RM}$
is the converse of
![]() $\omega ^+$
well-ordering. As will become evident below, there is also an elegant characterization of directly indecomposable Sugihara algebras.
$\omega ^+$
well-ordering. As will become evident below, there is also an elegant characterization of directly indecomposable Sugihara algebras.
Definition 3.4. Let
![]() $\mathfrak {A}=\langle \mathsf {A};\wedge ,\lor ,\neg ,\to \rangle $
be a Sugihara algebra.
$\mathfrak {A}=\langle \mathsf {A};\wedge ,\lor ,\neg ,\to \rangle $
be a Sugihara algebra.
![]() $\bot \mathfrak {A}\top =\langle \mathsf {A}\cup \{\bot ,\top \};\wedge ,\lor ,\neg ,\to \rangle $
, where
$\bot \mathfrak {A}\top =\langle \mathsf {A}\cup \{\bot ,\top \};\wedge ,\lor ,\neg ,\to \rangle $
, where
![]() $\bot $
and
$\bot $
and
![]() $\top $
are added as lower and upper bounds,
$\top $
are added as lower and upper bounds,
![]() $\wedge $
and
$\wedge $
and
![]() $\lor $
are interpreted standardly in the resulting lattice,
$\lor $
are interpreted standardly in the resulting lattice,
![]() $\neg a=\neg ^{\mathfrak {A}} a$
for
$\neg a=\neg ^{\mathfrak {A}} a$
for
![]() $a\in \mathsf {A}$
,
$a\in \mathsf {A}$
,
![]() $\neg \top =\bot $
,
$\neg \top =\bot $
,
![]() $\neg \bot =\top $
and:
$\neg \bot =\top $
and:
 $$ \begin{align*} a\to b = \begin{cases} a\to^{\mathfrak{A}} b, & \text{if }a,b\in\mathsf{A},\\ \top, & \text{if }a=\bot\text{ or }b=\top,\\ \bot, & \text{otherwise}. \end{cases} \end{align*} $$
$$ \begin{align*} a\to b = \begin{cases} a\to^{\mathfrak{A}} b, & \text{if }a,b\in\mathsf{A},\\ \top, & \text{if }a=\bot\text{ or }b=\top,\\ \bot, & \text{otherwise}. \end{cases} \end{align*} $$
We also write
![]() $\bot ^{n+1}\mathfrak {A}\top ^{n+1}$
to indicate
$\bot ^{n+1}\mathfrak {A}\top ^{n+1}$
to indicate
![]() $\bot \bot ^n\mathfrak {A}\top ^n\top $
. Note that
$\bot \bot ^n\mathfrak {A}\top ^n\top $
. Note that
![]() ${\top , \bot }$
is assumed to be disjoint from
${\top , \bot }$
is assumed to be disjoint from
![]() $\mathsf {A}$
in
$\mathsf {A}$
in
![]() $\bot \mathfrak {A}\top $
, so we must distinguish between the different ‘tops’ and ‘bottoms’ in algebras of the form
$\bot \mathfrak {A}\top $
, so we must distinguish between the different ‘tops’ and ‘bottoms’ in algebras of the form
![]() $\bot ^n\mathfrak {A}\top ^n$
where
$\bot ^n\mathfrak {A}\top ^n$
where
![]() $n \geq 2$
. To clarify, we will use
$n \geq 2$
. To clarify, we will use
![]() $\bot _i$
and
$\bot _i$
and
![]() $\top _i$
to denote the ith bottom and top, respectively. Following this notation,
$\top _i$
to denote the ith bottom and top, respectively. Following this notation,
![]() $\bot ^n\mathfrak {A}\top ^n$
becomes
$\bot ^n\mathfrak {A}\top ^n$
becomes
![]() $\bot _n \dots \bot _2\bot _1\mathfrak {A}\top _1\top _2 \dots \top _n$
, where
$\bot _n \dots \bot _2\bot _1\mathfrak {A}\top _1\top _2 \dots \top _n$
, where
![]() $\top _i \leq \top _j$
and
$\top _i \leq \top _j$
and
![]() $\bot _j \leq \bot _i$
in terms of lattice ordering for
$\bot _j \leq \bot _i$
in terms of lattice ordering for
![]() $i \leq j$
.
$i \leq j$
.
It is immediate to see that for any subdirectly irreducible finite Sugihara algebra
![]() $\mathfrak {A}$
,
$\mathfrak {A}$
,
![]() $\bot \mathfrak {A}\top $
is also subdirectly irreducible, i.e.,
$\bot \mathfrak {A}\top $
is also subdirectly irreducible, i.e.,
![]() $\bot \mathfrak {A}_n\top \cong \mathfrak {A}_{n+2}$
. Next, we will recall a characterization of DI Sugihara algebras [Reference Blok and Dziobiak6, Corollary 2.5, p. 278].
$\bot \mathfrak {A}_n\top \cong \mathfrak {A}_{n+2}$
. Next, we will recall a characterization of DI Sugihara algebras [Reference Blok and Dziobiak6, Corollary 2.5, p. 278].
Theorem 3.5 (Blok and Dziobiak, 1985).
A finite Sugihara algebra
![]() $\mathfrak {A}$
is directly indecomposable iff
$\mathfrak {A}$
is directly indecomposable iff
![]() $\mathfrak {A}\cong \mathfrak {A}_2$
or
$\mathfrak {A}\cong \mathfrak {A}_2$
or
![]() $\mathfrak {A}\cong \bot \mathfrak {B}\top $
, where
$\mathfrak {A}\cong \bot \mathfrak {B}\top $
, where
![]() $\mathfrak {B}$
is a finite Sugihara algebra.
$\mathfrak {B}$
is a finite Sugihara algebra.
Thus, DI Sugihara algebras are simply arbitrary Sugihara algebras extended with disjoint top and bottom elements. However, the most important tool for our investigations will be critical algebras. A finite algebra
![]() $\mathfrak {A}$
is said to be critical if and only if
$\mathfrak {A}$
is said to be critical if and only if
![]() $\mathfrak {A} \notin \mathsf {I}\mathsf {S}\mathsf {P}({\mathfrak {B} : \mathfrak {B} \prec \mathfrak {A}})$
. It is well known that every locally finite quasivariety is generated by its critical algebras (cf. [Reference Hyndman and Nation18]). Since Sugihara algebras are locally finite, we will use critical algebras as fundamental building blocks for quasivarieties. A specific description of critical Sugihara algebras was provided in [Reference Czelakowski and Dziobiak11, p. 285], and this will serve as a crucial tool in our investigations.
$\mathfrak {A} \notin \mathsf {I}\mathsf {S}\mathsf {P}({\mathfrak {B} : \mathfrak {B} \prec \mathfrak {A}})$
. It is well known that every locally finite quasivariety is generated by its critical algebras (cf. [Reference Hyndman and Nation18]). Since Sugihara algebras are locally finite, we will use critical algebras as fundamental building blocks for quasivarieties. A specific description of critical Sugihara algebras was provided in [Reference Czelakowski and Dziobiak11, p. 285], and this will serve as a crucial tool in our investigations.
Theorem 3.6 (Czelakowski and Dziobiak, 1999).
If a Sugihara algebra
![]() $\mathfrak {A}$
is critical, then it is isomorphic to an algebra of one of the following four types:
$\mathfrak {A}$
is critical, then it is isomorphic to an algebra of one of the following four types:
-
1.
 $\mathfrak {A}_k$
;
$\mathfrak {A}_k$
; -
2.
 $\mathfrak {A}_{2i}\times \mathfrak {A}_k$
, where
$\mathfrak {A}_{2i}\times \mathfrak {A}_k$
, where
 $2_i\neq k$
;
$2_i\neq k$
; -
3.
 $\bot ^{p_1}\mathfrak {A}_{2k_1}\times \dots \bot ^{p_n}\mathfrak {A}_{2k_n}\times \mathfrak {A}_k\top ^{p_n}\ldots \top ^{p_1}$
, where
$\bot ^{p_1}\mathfrak {A}_{2k_1}\times \dots \bot ^{p_n}\mathfrak {A}_{2k_n}\times \mathfrak {A}_k\top ^{p_n}\ldots \top ^{p_1}$
, where
 $2k_n< k$
if k is even, and
$2k_n< k$
if k is even, and
 $k_n<k$
and
$k_n<k$
and
 $k_i<k_{i+1}+p_{i+1}$
for all
$k_i<k_{i+1}+p_{i+1}$
for all
 $1\leq i\leq n-1$
whenever
$1\leq i\leq n-1$
whenever
 $2\leq n$
;
$2\leq n$
; -
4.
 $\mathfrak {A}_{2k_0}\times \mathfrak {B}$
where
$\mathfrak {A}_{2k_0}\times \mathfrak {B}$
where
 $\mathfrak {B}$
is of type 3 and
$\mathfrak {B}$
is of type 3 and
 $k_0<k_1 + p_1$
.
$k_0<k_1 + p_1$
.
It is easy to see that algebras of the third type take the form
![]() $\bot ^m\mathfrak {A}\top ^m$
, where
$\bot ^m\mathfrak {A}\top ^m$
, where
![]() $\mathfrak {A}$
is of the fourth type. To familiarize the reader with these types, we provide several examples:
$\mathfrak {A}$
is of the fourth type. To familiarize the reader with these types, we provide several examples:
![]() $\bot ^2\mathfrak {A}_4\times \mathfrak {A}_6\top ^2$
is an algebra of the third type, while
$\bot ^2\mathfrak {A}_4\times \mathfrak {A}_6\top ^2$
is an algebra of the third type, while
![]() $\mathfrak {A}_6\times \bot \mathfrak {A}_8\times \mathfrak {A}_5\top $
and
$\mathfrak {A}_6\times \bot \mathfrak {A}_8\times \mathfrak {A}_5\top $
and
![]() $\mathfrak {A}_8\times \bot ^2\mathfrak {A}_6\times \mathfrak {A}_5\top ^2$
are of the fourth type. Additionally,
$\mathfrak {A}_8\times \bot ^2\mathfrak {A}_6\times \mathfrak {A}_5\top ^2$
are of the fourth type. Additionally,
![]() $\bot ^{11}(\mathfrak {A}_6\times \bot \mathfrak {A}_8\times \mathfrak {A}_5\top )\top ^{11}$
is of the third type.
$\bot ^{11}(\mathfrak {A}_6\times \bot \mathfrak {A}_8\times \mathfrak {A}_5\top )\top ^{11}$
is of the third type.
On the other hand, the following algebras do not satisfy this description:
![]() $\bot ^3\mathfrak {A}_3\times \mathfrak {A}_5\top ^3$
—at most one algebra in the construction can be odd;
$\bot ^3\mathfrak {A}_3\times \mathfrak {A}_5\top ^3$
—at most one algebra in the construction can be odd;
![]() $\bot \mathfrak {A}_4\times \mathfrak {A}_4\top $
—algebras within the construction cannot be the same; and
$\bot \mathfrak {A}_4\times \mathfrak {A}_4\top $
—algebras within the construction cannot be the same; and
![]() $\mathfrak {A}_8\times \bot ^2\mathfrak {A}_2\times \mathfrak {A}_3\top ^2$
—here,
$\mathfrak {A}_8\times \bot ^2\mathfrak {A}_2\times \mathfrak {A}_3\top ^2$
—here,
![]() $4\not <1+2$
, contrary to the description.
$4\not <1+2$
, contrary to the description.
Furthermore, in the context of nested product operations, the “horizontal” notation used in third- and fourth-type algebras quickly becomes difficult to read. It is hard to determine which algebras are extended by the respective tops and bottoms. Parentheses provide some clarification, but we argue that the vertical “quasi-Hasse” notation is easier to read. For example, consider the algebra
![]() $\bot (\mathfrak {A}_6\times (\bot ^3(\mathfrak {A}_4\times (\bot ^2\mathfrak {A}_2\times \mathfrak {A}_3\top ^2))\top ^3))\top $
. Let us present this in a vertical notation, somewhat resembling a Hasse diagram:
$\bot (\mathfrak {A}_6\times (\bot ^3(\mathfrak {A}_4\times (\bot ^2\mathfrak {A}_2\times \mathfrak {A}_3\top ^2))\top ^3))\top $
. Let us present this in a vertical notation, somewhat resembling a Hasse diagram:

The scope of the extending tops and bottoms is indicated by the nearest ellipse. Fortunately, we will later introduce a method that simplifies these nested algebras, eliminating some notational problems in the subsequent sections.
One can observe that in algebras of the third and fourth type, for any
![]() $i<n$
, we have
$i<n$
, we have
![]() $\mathfrak {A}_{2k_i}\preceq \bot ^{p_{i+1}}\mathfrak {A}_{2k_{i+1}}\times \dots \bot ^{p_n}\mathfrak {A}_{2k_n}\times \mathfrak {A}_k\top ^{p_n}\ldots \top ^{p_{i+1}}$
. While this is straightforward to verify directly, the observation also follows from three key facts:
$\mathfrak {A}_{2k_i}\preceq \bot ^{p_{i+1}}\mathfrak {A}_{2k_{i+1}}\times \dots \bot ^{p_n}\mathfrak {A}_{2k_n}\times \mathfrak {A}_k\top ^{p_n}\ldots \top ^{p_{i+1}}$
. While this is straightforward to verify directly, the observation also follows from three key facts:
-
• if
 $\bot \mathfrak {B}\top $
is critical, then
$\bot \mathfrak {B}\top $
is critical, then
 $\mathfrak {B}$
is critical,
$\mathfrak {B}$
is critical, -
• if
 $\mathfrak {A}\times \mathfrak {B}$
is critical, then both
$\mathfrak {A}\times \mathfrak {B}$
is critical, then both
 $\mathfrak {A}$
and
$\mathfrak {A}$
and
 $\mathfrak {B}$
are critical, and
$\mathfrak {B}$
are critical, and -
• the Lemma 3.4 from [Reference Czelakowski and Dziobiak11] which states that if
 $\mathfrak {A}\times \mathfrak {B}$
is critical, then it is isomorphic to
$\mathfrak {A}\times \mathfrak {B}$
is critical, then it is isomorphic to
 $\mathfrak {A}_{2n}\times \bot \mathfrak {C}\top $
where
$\mathfrak {A}_{2n}\times \bot \mathfrak {C}\top $
where
 $\mathfrak {A}_{2n}$
is embeddable in
$\mathfrak {A}_{2n}$
is embeddable in
 $\bot \mathfrak {C}\top $
under assumption that
$\bot \mathfrak {C}\top $
under assumption that
 $\bot \mathfrak {C}\top $
is not subdirectly irreducible.
$\bot \mathfrak {C}\top $
is not subdirectly irreducible.
We will also use the following result from [Reference Krawczyk21, p. 1250]:
Theorem 3.7 (Krawczyk, 2022).
![]() $\mathsf {Q}(\mathfrak {A}_2\times \mathfrak {A}_3)$
and
$\mathsf {Q}(\mathfrak {A}_2\times \mathfrak {A}_3)$
and
![]() $\mathsf {Q}(\mathfrak {A}_2\times \mathfrak {A}_4)$
are the only covers of
$\mathsf {Q}(\mathfrak {A}_2\times \mathfrak {A}_4)$
are the only covers of
![]() $\mathsf {Q}(\mathfrak {A}_2)$
(the variety of Boolean algebras) in the lattice of subquasivarieties of
$\mathsf {Q}(\mathfrak {A}_2)$
(the variety of Boolean algebras) in the lattice of subquasivarieties of
![]() $\mathsf {Q}(\mathfrak {A}_\omega )$
and
$\mathsf {Q}(\mathfrak {A}_\omega )$
and
![]() $\mathsf {Q}(\mathfrak {A}_2\times \mathfrak {A}_3)\neq \mathsf {Q}(\mathfrak {A}_2\times \mathfrak {A}_4)$
.
$\mathsf {Q}(\mathfrak {A}_2\times \mathfrak {A}_3)\neq \mathsf {Q}(\mathfrak {A}_2\times \mathfrak {A}_4)$
.
Thus, we know that the lattice of quasivarieties of Sugihara algebras is more complex than that of varieties: it does not form a chain, as it contains incomparable elements. As the theorem shows, such elements already appear at the very bottom of the lattice.
4 The theorem and its proof
Our ultimate goal is to isolate the poset of all
![]() $\mathbf {HSC}$
consequence relations extending
$\mathbf {HSC}$
consequence relations extending
![]() $\mathbf {RM}$
. To achieve this, we begin by describing all structurally complete quasivarieties of Sugihara algebras. Next, within the set of
$\mathbf {RM}$
. To achieve this, we begin by describing all structurally complete quasivarieties of Sugihara algebras. Next, within the set of
![]() $\mathbf {SC}$
quasivarieties, we distinguish the
$\mathbf {SC}$
quasivarieties, we distinguish the
![]() $\mathbf {SC}$
quasivarieties that possess the additional property of hereditariness from those that do not. The fundamental theorem we aim to prove takes the following form:
$\mathbf {SC}$
quasivarieties that possess the additional property of hereditariness from those that do not. The fundamental theorem we aim to prove takes the following form:
Theorem 4.1. The set of all
![]() $\mathbf {HSC}$
subquasivarieties of Sugihara algebras is
$\mathbf {HSC}$
subquasivarieties of Sugihara algebras is
In the general algebraic setting, an approach to the problem of (hereditary) structural completeness based on projectivity has proven to be fruitful [Reference Aglianò and Citkin2, Reference Aglianò and Ugolini3]. However, as has already become apparent, we have a rather rich theory of Sugihara algebras at our disposal, and thus our strategy will differ. In one way or another, most of the proofs that follow will rely on the algebras from Theorem 3.6, since locally finite quasivarieties are known to be generated by their critical members [Reference Hyndman and Nation18]. However, the algebras of the third and fourth types in Theorem 3.6 are rather complex and difficult to handle. To ease the process, we will simplify certain instances of these algebras by providing their
![]() $\mathcal {Q}$
-equivalent descriptions. As will become apparent later, this simplification reveals that Theorem 3.6 cannot be strengthened into a full characterization (note that it presents only a necessary condition for criticality, as it is framed as an implication).
$\mathcal {Q}$
-equivalent descriptions. As will become apparent later, this simplification reveals that Theorem 3.6 cannot be strengthened into a full characterization (note that it presents only a necessary condition for criticality, as it is framed as an implication).
![]() $\mathcal {Q}$
-equivalence, or Horn equivalence, as we will also refer to it, is a weaker version of the standard model-theoretic notion of elementary equivalence. As the reader likely knows, or suspects, two algebras are Horn equivalent if they satisfy the same quasi-identities, rendering them indistinguishable from one another from the perspective of quasivarieties. To make things precise: by a quasi-identical theory of a given algebra
$\mathcal {Q}$
-equivalence, or Horn equivalence, as we will also refer to it, is a weaker version of the standard model-theoretic notion of elementary equivalence. As the reader likely knows, or suspects, two algebras are Horn equivalent if they satisfy the same quasi-identities, rendering them indistinguishable from one another from the perspective of quasivarieties. To make things precise: by a quasi-identical theory of a given algebra
![]() $\mathfrak {A}$
, we understand the set
$\mathfrak {A}$
, we understand the set
![]() $\mathsf {Th}_{\mathsf {q}}(\mathfrak {A}):=\{\varphi :\mathfrak {A}\vDash \varphi ,\,\,\varphi \text { is a Horn formula}\}$
. The definition of Horn-equivalence has the following form:
$\mathsf {Th}_{\mathsf {q}}(\mathfrak {A}):=\{\varphi :\mathfrak {A}\vDash \varphi ,\,\,\varphi \text { is a Horn formula}\}$
. The definition of Horn-equivalence has the following form:
Definition 4.2 (
 $\mathcal {Q}$
-equivalence).
$\mathcal {Q}$
-equivalence).
Let
![]() $\mathfrak {A},\mathfrak {B}$
be algebras of the same similarity type. We say that
$\mathfrak {A},\mathfrak {B}$
be algebras of the same similarity type. We say that
![]() $\mathfrak {A}$
and
$\mathfrak {A}$
and
![]() $\mathfrak {B}$
are
$\mathfrak {B}$
are
![]() $\mathcal {Q}$
-equivalent (symbolically:
$\mathcal {Q}$
-equivalent (symbolically:
![]() $\mathfrak {A}\approx _{\mathsf {q}}\mathfrak {B}$
) iff
$\mathfrak {A}\approx _{\mathsf {q}}\mathfrak {B}$
) iff
![]() $\mathsf {Th}_{\mathsf {q}}(\mathfrak {A})=\mathsf {Th}_{\mathsf {q}}(\mathfrak {B})$
.
$\mathsf {Th}_{\mathsf {q}}(\mathfrak {A})=\mathsf {Th}_{\mathsf {q}}(\mathfrak {B})$
.
We start with a simple observation.
Fact 4.3. For any algebras
![]() $\mathfrak {A},\mathfrak {B}$
of the same type, the following statements are equivalent:
$\mathfrak {A},\mathfrak {B}$
of the same type, the following statements are equivalent:
-
1.
 $\mathfrak {A}\approx _{\mathsf {q}}\mathfrak {B}$
.
$\mathfrak {A}\approx _{\mathsf {q}}\mathfrak {B}$
. -
2.
 $\mathsf {I}\mathsf {S}\mathsf {P}\mathsf {P}_{\mathsf {U}}(\mathfrak {A})=\mathsf {I}\mathsf {S}\mathsf {P}\mathsf {P}_{\mathsf {U}}(\mathfrak {B})$
.
$\mathsf {I}\mathsf {S}\mathsf {P}\mathsf {P}_{\mathsf {U}}(\mathfrak {A})=\mathsf {I}\mathsf {S}\mathsf {P}\mathsf {P}_{\mathsf {U}}(\mathfrak {B})$
. -
3. For any quasivariety
 $\mathcal {Q}$
, we have
$\mathcal {Q}$
, we have
 $\mathfrak {A}\in \mathcal {Q}$
iff
$\mathfrak {A}\in \mathcal {Q}$
iff
 $\mathfrak {B}\in \mathcal {Q}$
.
$\mathfrak {B}\in \mathcal {Q}$
.
The equivalence of the three statements follows directly from the fact that quasivarieties are defined by quasi-identities. In the case where both algebras are finite, we can modify the second statement to
![]() $\mathsf {I}\mathsf {S}\mathsf {P}(\mathfrak {A}) = \mathsf {I}\mathsf {S}\mathsf {P}(\mathfrak {B})$
. We are now ready to prove the key “simplification” lemma. This lemma will be used to show that certain algebras of the third type are Horn-equivalent to a product of two Sugihara chains.
$\mathsf {I}\mathsf {S}\mathsf {P}(\mathfrak {A}) = \mathsf {I}\mathsf {S}\mathsf {P}(\mathfrak {B})$
. We are now ready to prove the key “simplification” lemma. This lemma will be used to show that certain algebras of the third type are Horn-equivalent to a product of two Sugihara chains.
Lemma 4.4. Let
![]() $n\in \omega $
and
$n\in \omega $
and
![]() $\mathfrak {A},\mathfrak {B},\mathfrak {C}$
all be Sugihara algebras such that
$\mathfrak {A},\mathfrak {B},\mathfrak {C}$
all be Sugihara algebras such that
![]() $\mathfrak {A}\preceq \mathfrak {B}\preceq \mathfrak {C}$
. Then
$\mathfrak {A}\preceq \mathfrak {B}\preceq \mathfrak {C}$
. Then
![]() $\mathfrak {A}\times \bot ^n\mathfrak {B}\times \mathfrak {C}\top ^n\approx _{\mathsf {q}}\mathfrak {A}\times \bot ^n\mathfrak {C}\top ^n$
.
$\mathfrak {A}\times \bot ^n\mathfrak {B}\times \mathfrak {C}\top ^n\approx _{\mathsf {q}}\mathfrak {A}\times \bot ^n\mathfrak {C}\top ^n$
.
Proof. Without the loss of generality, we assume that
![]() $\mathsf {A}\subseteq \mathsf {B}\subseteq \mathsf {C}$
. We will show that
$\mathsf {A}\subseteq \mathsf {B}\subseteq \mathsf {C}$
. We will show that
![]() $\mathsf {Q}(\mathfrak {A}\times \bot ^n\mathfrak {C}\top ^n)=\mathsf {Q}(\mathfrak {A}\times \bot ^n\mathfrak {B}\times \mathfrak {C}\top ^n)$
.
$\mathsf {Q}(\mathfrak {A}\times \bot ^n\mathfrak {C}\top ^n)=\mathsf {Q}(\mathfrak {A}\times \bot ^n\mathfrak {B}\times \mathfrak {C}\top ^n)$
.
For the left-to-right inclusion we prove that
![]() $\mathfrak {A}\times \bot ^n\mathfrak {C}\top ^n\preceq \mathfrak {A}\times \bot ^n\mathfrak {B}\times \mathfrak {C}\top ^n$
. The embedding e is given simply by
$\mathfrak {A}\times \bot ^n\mathfrak {C}\top ^n\preceq \mathfrak {A}\times \bot ^n\mathfrak {B}\times \mathfrak {C}\top ^n$
. The embedding e is given simply by
 $$ \begin{align*} (a,c) &\mapsto (a,(a,c)) &\text{ for } (a,c)\in\mathsf{A}\times\mathsf{C};\\ (a,x_i) &\mapsto (a,x_i) &\text{ for } (a,x_i)\in\mathsf{A}\times\{\bot_i,\top_i\}, 1\leq i\leq n. \end{align*} $$
$$ \begin{align*} (a,c) &\mapsto (a,(a,c)) &\text{ for } (a,c)\in\mathsf{A}\times\mathsf{C};\\ (a,x_i) &\mapsto (a,x_i) &\text{ for } (a,x_i)\in\mathsf{A}\times\{\bot_i,\top_i\}, 1\leq i\leq n. \end{align*} $$
Is is easy to see that such a function is indeed an injective homomorphism. Thus
![]() $\mathfrak {A}\times \bot ^n\mathfrak {C}\top ^n\in \mathsf {S}(\mathfrak {A}\times \bot ^n\mathfrak {B}\times \mathfrak {C}\top ^n)\subseteq \mathsf {Q}(\mathfrak {A}\times \bot ^n\mathfrak {B}\times \mathfrak {C}\top ^n)$
, which implies
$\mathfrak {A}\times \bot ^n\mathfrak {C}\top ^n\in \mathsf {S}(\mathfrak {A}\times \bot ^n\mathfrak {B}\times \mathfrak {C}\top ^n)\subseteq \mathsf {Q}(\mathfrak {A}\times \bot ^n\mathfrak {B}\times \mathfrak {C}\top ^n)$
, which implies
![]() $\mathsf {Q}(\mathfrak {A}\times \bot ^n\mathfrak {C}\top ^n)\subseteq \mathsf {Q}(\mathfrak {A}\times \bot ^n\mathfrak {B}\times \mathfrak {C}\top ^n)$
.
$\mathsf {Q}(\mathfrak {A}\times \bot ^n\mathfrak {C}\top ^n)\subseteq \mathsf {Q}(\mathfrak {A}\times \bot ^n\mathfrak {B}\times \mathfrak {C}\top ^n)$
.
For the opposite inclusion, we will show that
![]() $\mathfrak {A}\times \bot ^n\mathfrak {B}\times \mathfrak {C}\top ^n\preceq \mathfrak {A}^2\times (\bot ^n\mathfrak {C}\top ^n)^2\cong (\mathfrak {A}\times \bot ^n\mathfrak {C}\top ^n)^2$
. Now the embedding e is defined by
$\mathfrak {A}\times \bot ^n\mathfrak {B}\times \mathfrak {C}\top ^n\preceq \mathfrak {A}^2\times (\bot ^n\mathfrak {C}\top ^n)^2\cong (\mathfrak {A}\times \bot ^n\mathfrak {C}\top ^n)^2$
. Now the embedding e is defined by
 $$ \begin{align*} (a,(b,c)) &\mapsto ((a,a),(b,c)) &\text{ for } (a,b,c)\in\mathsf{A}\times\mathsf{B}\times\mathsf{C};\\ (a,x_i) &\mapsto ((a,a),(x_i,x_i)) &\text{ for } (a,x_i)\in\mathsf{A}\times\{\bot_i,\top_i\}, 1\leq i\leq n. \end{align*} $$
$$ \begin{align*} (a,(b,c)) &\mapsto ((a,a),(b,c)) &\text{ for } (a,b,c)\in\mathsf{A}\times\mathsf{B}\times\mathsf{C};\\ (a,x_i) &\mapsto ((a,a),(x_i,x_i)) &\text{ for } (a,x_i)\in\mathsf{A}\times\{\bot_i,\top_i\}, 1\leq i\leq n. \end{align*} $$
It is obvious that e is injective. To see that e preserves
![]() $\neg $
, let
$\neg $
, let
![]() $(a,b,c)\in \mathsf {A}\times \mathsf {B}\times \mathsf {C}$
.
$(a,b,c)\in \mathsf {A}\times \mathsf {B}\times \mathsf {C}$
.
![]() $e(\neg (a,{\kern1.5pt}(b,c))){\kern1.5pt}={\kern1.5pt}e((\neg a,{\kern1.5pt}(\neg b, \neg c))){\kern1.5pt}={\kern1.5pt}((\neg a,\neg a),{\kern1.5pt} (\neg b,\neg c)){\kern1.5pt}={\kern1.5pt} \neg ((a,a),{\kern1.5pt}(b,c)){\kern1.5pt}=\neg e((a,(b,c)))$
. The case when
$e(\neg (a,{\kern1.5pt}(b,c))){\kern1.5pt}={\kern1.5pt}e((\neg a,{\kern1.5pt}(\neg b, \neg c))){\kern1.5pt}={\kern1.5pt}((\neg a,\neg a),{\kern1.5pt} (\neg b,\neg c)){\kern1.5pt}={\kern1.5pt} \neg ((a,a),{\kern1.5pt}(b,c)){\kern1.5pt}=\neg e((a,(b,c)))$
. The case when
![]() $(a,x_i)\in \mathsf {A}\times \{\bot _i,\top _i\}$
is equally trivial by the fact that
$(a,x_i)\in \mathsf {A}\times \{\bot _i,\top _i\}$
is equally trivial by the fact that
![]() $\neg \bot _i=\top _i$
and
$\neg \bot _i=\top _i$
and
![]() $\neg \top _i=\bot _i$
. For binary operations we check only
$\neg \top _i=\bot _i$
. For binary operations we check only
![]() $\to $
since
$\to $
since
![]() $\lor ,\wedge $
are trivial. Let
$\lor ,\wedge $
are trivial. Let
![]() $(a,b,c), (a',b',c')\in \mathsf {A}\times \mathsf {B}\times \mathsf {C}$
. We will show two cases as examples and leave the rest for the reader since they can be shown in the same manner.
$(a,b,c), (a',b',c')\in \mathsf {A}\times \mathsf {B}\times \mathsf {C}$
. We will show two cases as examples and leave the rest for the reader since they can be shown in the same manner.
For the first example let:
![]() $e((a,(b,c)))\to e((a',(b',c')))=((a,a),(b,c))\to ((a',a'),{\kern1pt}(b',c')){\kern1pt}={\kern1pt}((a\to a',a\to a'),{\kern1pt}(b{\kern1pt}\to{\kern1pt} b',c{\kern1pt}\to{\kern1pt} c')){\kern1pt}={\kern1pt}e((a,(b,c))){\kern1pt}\to{\kern1pt} (a', (b', c')))$
.
$e((a,(b,c)))\to e((a',(b',c')))=((a,a),(b,c))\to ((a',a'),{\kern1pt}(b',c')){\kern1pt}={\kern1pt}((a\to a',a\to a'),{\kern1pt}(b{\kern1pt}\to{\kern1pt} b',c{\kern1pt}\to{\kern1pt} c')){\kern1pt}={\kern1pt}e((a,(b,c))){\kern1pt}\to{\kern1pt} (a', (b', c')))$
.
To prove one more case:
![]() $e((a',\bot _i))\to e((a,(b,c)))=((a',a'),(\bot _i,\bot _i))\to ((a,a),(b,c))=((a'\to a,a'\to a),(\top _i,\top _i))\ =\ e((a'\to a,\top _i))\ =\ e((a',\bot _i)\to (a,(b,c)))$
.
$e((a',\bot _i))\to e((a,(b,c)))=((a',a'),(\bot _i,\bot _i))\to ((a,a),(b,c))=((a'\to a,a'\to a),(\top _i,\top _i))\ =\ e((a'\to a,\top _i))\ =\ e((a',\bot _i)\to (a,(b,c)))$
.
Thus, we have shown
![]() $\mathfrak {A}\times \bot ^n\mathfrak {B}\times \mathfrak {C}\top ^n\in \mathsf {S}\mathsf {P}(\mathfrak {A}\times \bot ^n\mathfrak {C}\top ^n)\subseteq \mathsf {Q}(\mathfrak {A}\times \bot ^n\mathfrak {C}\top ^n)$
. This proves the right-to-left inclusion.
$\mathfrak {A}\times \bot ^n\mathfrak {B}\times \mathfrak {C}\top ^n\in \mathsf {S}\mathsf {P}(\mathfrak {A}\times \bot ^n\mathfrak {C}\top ^n)\subseteq \mathsf {Q}(\mathfrak {A}\times \bot ^n\mathfrak {C}\top ^n)$
. This proves the right-to-left inclusion.
As we have proven the equality of the two quasivarieties, the statement from the lemma follows immediately by the Fact 4.3.
As a consequence of the above lemma, we can assert that Theorem 3.6 cannot be strengthened to an equivalence. Given the assumption of Lemma 4.4, we have
![]() $\mathfrak {A} \times \bot ^n \mathfrak {B} \times \mathfrak {C} \top ^n \in \mathsf {Q}(\mathfrak {A} \times \bot ^n \mathfrak {C} \top ^n)$
, which implies that
$\mathfrak {A} \times \bot ^n \mathfrak {B} \times \mathfrak {C} \top ^n \in \mathsf {Q}(\mathfrak {A} \times \bot ^n \mathfrak {C} \top ^n)$
, which implies that
![]() $\mathfrak {A} \times \bot ^n \mathfrak {B} \times \mathfrak {C} \top ^n$
is not critical. For a concrete example, consider
$\mathfrak {A} \times \bot ^n \mathfrak {B} \times \mathfrak {C} \top ^n$
is not critical. For a concrete example, consider
![]() $\mathfrak {A}_4 \times \bot \mathfrak {A}_6 \times \mathfrak {A}_8 \top $
, which is clearly an algebra of the fourth type. Yet, by Lemma 4.4, we have
$\mathfrak {A}_4 \times \bot \mathfrak {A}_6 \times \mathfrak {A}_8 \top $
, which is clearly an algebra of the fourth type. Yet, by Lemma 4.4, we have
![]() $\mathfrak {A}_4 \times \bot \mathfrak {A}_6 \times \mathfrak {A}_8 \top \in \mathsf {Q}(\mathfrak {A}_4 \times \mathfrak {A}_{10})$
, and
$\mathfrak {A}_4 \times \bot \mathfrak {A}_6 \times \mathfrak {A}_8 \top \in \mathsf {Q}(\mathfrak {A}_4 \times \mathfrak {A}_{10})$
, and
![]() $\mathfrak {A}_4 \times \mathfrak {A}_{10}$
is a proper subalgebra of
$\mathfrak {A}_4 \times \mathfrak {A}_{10}$
is a proper subalgebra of
![]() $\mathfrak {A}_4 \times \bot \mathfrak {A}_6 \times \mathfrak {A}_8 \top $
. This shows that
$\mathfrak {A}_4 \times \bot \mathfrak {A}_6 \times \mathfrak {A}_8 \top $
. This shows that
![]() $\mathfrak {A}_4 \times \bot \mathfrak {A}_6 \times \mathfrak {A}_8 \top $
is not critical.
$\mathfrak {A}_4 \times \bot \mathfrak {A}_6 \times \mathfrak {A}_8 \top $
is not critical.
However, the authors seem to acknowledge the potential incompleteness of their description, referring to it as “a certain, satisfactory-for-our-purpose description” [Reference Czelakowski and Dziobiak11, p. 281]. This description remains satisfactory for our purposes as well, as it will suffice to prove the main theorem.
It is known that for every
![]() $\mathbf {SC}$
quasivariety
$\mathbf {SC}$
quasivariety
![]() $\mathcal {Q}$
, we have
$\mathcal {Q}$
, we have
![]() $\mathcal {Q} = \mathsf {Q}(\mathbf {F}_{\mathcal {Q}}(\omega ))$
. However, free algebras on finite generators are usually complicated, and
$\mathcal {Q} = \mathsf {Q}(\mathbf {F}_{\mathcal {Q}}(\omega ))$
. However, free algebras on finite generators are usually complicated, and
![]() $\omega $
-generated ones are even more so. Therefore, we seek an alternative description of
$\omega $
-generated ones are even more so. Therefore, we seek an alternative description of
![]() $\mathbf {SC}$
Sugihara quasivarieties—specifically, simpler, possibly finite algebras that generate them. By Theorem 3.3, there are countably infinitely many varieties of Sugihara algebras, each generated by a single algebra of the form
$\mathbf {SC}$
Sugihara quasivarieties—specifically, simpler, possibly finite algebras that generate them. By Theorem 3.3, there are countably infinitely many varieties of Sugihara algebras, each generated by a single algebra of the form
![]() $\mathfrak {A}_\alpha $
, where
$\mathfrak {A}_\alpha $
, where
![]() $\alpha \leq \omega $
. Thus, we can partition the lattice of subquasivarieties of Sugihara algebras into a countable set of equivalence classes, with each class corresponding to the algebras that generate the same variety. In this framework,
$\alpha \leq \omega $
. Thus, we can partition the lattice of subquasivarieties of Sugihara algebras into a countable set of equivalence classes, with each class corresponding to the algebras that generate the same variety. In this framework,
![]() $\mathbf {SC}$
quasivarieties are precisely the minimal elements of each equivalence class, represented by
$\mathbf {SC}$
quasivarieties are precisely the minimal elements of each equivalence class, represented by
![]() $\mathsf {V}(\mathfrak {A}_\alpha )$
for
$\mathsf {V}(\mathfrak {A}_\alpha )$
for
![]() $\alpha \leq \omega $
.
$\alpha \leq \omega $
.
In practice, the case where
![]() $\alpha = \omega $
turns out to be special, so we will first address the finite cases, where
$\alpha = \omega $
turns out to be special, so we will first address the finite cases, where
![]() $n < \omega $
, and then move on to the remaining infinite case.
$n < \omega $
, and then move on to the remaining infinite case.
Definition 4.5. Let
![]() $\mathcal {Q}_1$
,
$\mathcal {Q}_1$
,
![]() $\mathcal {Q}_2$
be quasivarieties of Sugihara algebras. We define an equivalence relation on quasivarieties of Sugihara algebras putting:
$\mathcal {Q}_2$
be quasivarieties of Sugihara algebras. We define an equivalence relation on quasivarieties of Sugihara algebras putting:
![]() $\mathcal {Q}_1\sim \mathcal {Q}_2$
iff
$\mathcal {Q}_1\sim \mathcal {Q}_2$
iff
![]() $\mathsf {H}(\mathcal {Q}_1)=\mathsf {H}(\mathcal {Q}_2)$
.
$\mathsf {H}(\mathcal {Q}_1)=\mathsf {H}(\mathcal {Q}_2)$
.
In order to determine the equivalence class of a given quasivariety, we introduce the notion of the degree of a given critical Sugihara algebra.
Definition 4.6. Let
![]() $\mathfrak {A}$
be isomorphic to one of the four types of algebras from Theorem 3.6. We define the degree of
$\mathfrak {A}$
be isomorphic to one of the four types of algebras from Theorem 3.6. We define the degree of
![]() $\mathfrak {A}$
,
$\mathfrak {A}$
,
![]() $deg(\mathfrak {A})$
to be:
$deg(\mathfrak {A})$
to be:
 $$ \begin{align*} deg(\mathfrak{A}) = \begin{cases} n, & \text{if }\mathfrak{A}\cong\mathfrak{A}_n,\\ max(\{2i,k\}), & \text{if }\mathfrak{A}\cong\mathfrak{A}_{2i}\times\mathfrak{A}_k,\\ max(\{2k_n,k\}) + 2(p_n +\cdots +p_1), & \text{if }\mathfrak{A}\cong\mathfrak{B},\\ max(\{2k_n,k\}) + 2(p_n +\cdots +p_1), & \text{if }\mathfrak{A}\cong\mathfrak{A}_{2k_0}\times\mathfrak{B}, \end{cases} \end{align*} $$
$$ \begin{align*} deg(\mathfrak{A}) = \begin{cases} n, & \text{if }\mathfrak{A}\cong\mathfrak{A}_n,\\ max(\{2i,k\}), & \text{if }\mathfrak{A}\cong\mathfrak{A}_{2i}\times\mathfrak{A}_k,\\ max(\{2k_n,k\}) + 2(p_n +\cdots +p_1), & \text{if }\mathfrak{A}\cong\mathfrak{B},\\ max(\{2k_n,k\}) + 2(p_n +\cdots +p_1), & \text{if }\mathfrak{A}\cong\mathfrak{A}_{2k_0}\times\mathfrak{B}, \end{cases} \end{align*} $$
where
![]() $\mathfrak {B}=\bot ^{p_1}\mathfrak {A}_{2k_1}\times \dots \bot ^{p_n}\mathfrak {A}_{2k_n}\times \mathfrak {A}_k\top ^{p_n}\ldots \top ^{p_1}$
.
$\mathfrak {B}=\bot ^{p_1}\mathfrak {A}_{2k_1}\times \dots \bot ^{p_n}\mathfrak {A}_{2k_n}\times \mathfrak {A}_k\top ^{p_n}\ldots \top ^{p_1}$
.
Observe that the notion of the degree of a given Sugihara algebra does not coincide with the standard lattice-theoretic notion of height (i.e., the cardinality of the longest chain in a lattice). To illustrate this, consider
![]() $\mathfrak {B}=\bot \mathfrak {A}_2\times \mathfrak {A}_3\top $
. By definition 4.6,
$\mathfrak {B}=\bot \mathfrak {A}_2\times \mathfrak {A}_3\top $
. By definition 4.6,
![]() $deg(\mathfrak {B})=5$
. However, the set
$deg(\mathfrak {B})=5$
. However, the set
![]() $\{\bot ,(-1,0),(0,0),(1,0),(1,1),\top \}\subseteq \mathsf {B}$
forms a six-element subchain of
$\{\bot ,(-1,0),(0,0),(1,0),(1,1),\top \}\subseteq \mathsf {B}$
forms a six-element subchain of
![]() $\mathfrak {B}$
.
$\mathfrak {B}$
.
By local finiteness of Sugihara algebras, we have the following:
Lemma 4.7. Let
![]() $m\in \omega $
. Let
$m\in \omega $
. Let
![]() $\mathsf {K}$
be a class of critical algebras.
$\mathsf {K}$
be a class of critical algebras.
![]() $\mathsf {Q}(\mathsf {K})\in [\mathsf {V}(\mathfrak {A}_m)]_{/\sim }$
iff there is a critical algebra
$\mathsf {Q}(\mathsf {K})\in [\mathsf {V}(\mathfrak {A}_m)]_{/\sim }$
iff there is a critical algebra
![]() $\mathfrak {A}\in \mathsf {K}$
such that
$\mathfrak {A}\in \mathsf {K}$
such that
![]() $deg(\mathfrak {A})=m$
and there is no critical algebra
$deg(\mathfrak {A})=m$
and there is no critical algebra
![]() $\mathfrak {B}$
in
$\mathfrak {B}$
in
![]() $\mathsf {K}$
such that
$\mathsf {K}$
such that
![]() $deg(\mathfrak {B})>m$
.
$deg(\mathfrak {B})>m$
.
Proof. First we will show that for any critical algebra
![]() $\mathfrak {A}$
s.t.
$\mathfrak {A}$
s.t.
![]() $deg(\mathfrak {A})=m$
, we have
$deg(\mathfrak {A})=m$
, we have
![]() $\mathsf {V}(\mathfrak {A})=\mathsf {V}(\mathfrak {A}_m)$
. The cases when
$\mathsf {V}(\mathfrak {A})=\mathsf {V}(\mathfrak {A}_m)$
. The cases when
![]() $\mathfrak {A}$
is of the first and second type (see Theorem 3.6) are trivial. Hence assume that
$\mathfrak {A}$
is of the first and second type (see Theorem 3.6) are trivial. Hence assume that
![]() $\mathfrak {A}\cong \bot ^{p_1}\mathfrak {A}_{2k_1}\times \ldots \bot ^{p_n}\mathfrak {A}_{2k_n}\times \mathfrak {A}_k\top ^{p_n}\ldots \top ^{p_1}$
. We will show that 1)
$\mathfrak {A}\cong \bot ^{p_1}\mathfrak {A}_{2k_1}\times \ldots \bot ^{p_n}\mathfrak {A}_{2k_n}\times \mathfrak {A}_k\top ^{p_n}\ldots \top ^{p_1}$
. We will show that 1)
![]() $\mathfrak {A}_m\in \mathsf {H}(\mathfrak {A})$
and 2)
$\mathfrak {A}_m\in \mathsf {H}(\mathfrak {A})$
and 2)
![]() $\mathfrak {A}\in \mathsf {V}(\mathfrak {A}_m)$
.
$\mathfrak {A}\in \mathsf {V}(\mathfrak {A}_m)$
.
For 1) we will proceed inductively. Let
![]() $n=1$
. Thus
$n=1$
. Thus
![]() $\mathfrak {A}\cong \bot ^{p_1}\mathfrak {A}_{2k_0}\times \mathfrak {A}_k\top ^{p_1}$
. Let
$\mathfrak {A}\cong \bot ^{p_1}\mathfrak {A}_{2k_0}\times \mathfrak {A}_k\top ^{p_1}$
. Let
![]() $z=max\{2k_0,k\}$
. Obviously
$z=max\{2k_0,k\}$
. Obviously
![]() $\mathfrak {A}_z\in \mathsf {H}(\mathfrak {A}_{2k_0}\times \mathfrak {A}_k)$
. It is equally easy to see that
$\mathfrak {A}_z\in \mathsf {H}(\mathfrak {A}_{2k_0}\times \mathfrak {A}_k)$
. It is equally easy to see that
![]() $\mathfrak {A}_m\cong \bot ^{p_1}\mathfrak {A}_z\top ^{p_1}\in \mathsf {H}(\bot ^{p_1}\mathfrak {A}_{2k_0}\times \mathfrak {A}_k\top ^{p_1})$
. Now let
$\mathfrak {A}_m\cong \bot ^{p_1}\mathfrak {A}_z\top ^{p_1}\in \mathsf {H}(\bot ^{p_1}\mathfrak {A}_{2k_0}\times \mathfrak {A}_k\top ^{p_1})$
. Now let
![]() $\mathfrak {A}\cong \bot ^{p_1}\mathfrak {A}_{2k_1}\times \ldots \bot ^{p_n}\mathfrak {A}_{2k_n}\times \mathfrak {A}_k\top ^{p_n}\ldots \top ^{p_1}$
, where
$\mathfrak {A}\cong \bot ^{p_1}\mathfrak {A}_{2k_1}\times \ldots \bot ^{p_n}\mathfrak {A}_{2k_n}\times \mathfrak {A}_k\top ^{p_n}\ldots \top ^{p_1}$
, where
![]() $n\geq 2$
. By inductive hypothesis
$n\geq 2$
. By inductive hypothesis
![]() $\mathfrak {A}_{m-p_1}\in \mathsf {H}(\bot ^{p_2}\mathfrak {A}_{2k_2}\times \ldots \bot ^{p_n}\mathfrak {A}_{2k_n}\times \mathfrak {A}_k\top ^{p_n}\ldots \top ^{p_2})$
. Thus
$\mathfrak {A}_{m-p_1}\in \mathsf {H}(\bot ^{p_2}\mathfrak {A}_{2k_2}\times \ldots \bot ^{p_n}\mathfrak {A}_{2k_n}\times \mathfrak {A}_k\top ^{p_n}\ldots \top ^{p_2})$
. Thus
![]() $\mathfrak {A}_{m-p_1}\in \mathsf {H}(\mathfrak {A}_{2k_1}\times \bot ^{p_2}\mathfrak {A}_{2k_2}\times \ldots \bot ^{p_n}\mathfrak {A}_{2k_n}\times \mathfrak {A}_k\top ^{p_n}\ldots \top ^{p_2})$
, since
$\mathfrak {A}_{m-p_1}\in \mathsf {H}(\mathfrak {A}_{2k_1}\times \bot ^{p_2}\mathfrak {A}_{2k_2}\times \ldots \bot ^{p_n}\mathfrak {A}_{2k_n}\times \mathfrak {A}_k\top ^{p_n}\ldots \top ^{p_2})$
, since
![]() $\mathfrak {A}_{2k_1}$
is embeddable in
$\mathfrak {A}_{2k_1}$
is embeddable in
![]() $\bot ^{p_2}\mathfrak {A}_{2k_2}\times \ldots \bot ^{p_n}\mathfrak {A}_{2k_n}\times \mathfrak {A}_k\top ^{p_n}\ldots \top ^{p_2}$
. But then it is easy to see that
$\bot ^{p_2}\mathfrak {A}_{2k_2}\times \ldots \bot ^{p_n}\mathfrak {A}_{2k_n}\times \mathfrak {A}_k\top ^{p_n}\ldots \top ^{p_2}$
. But then it is easy to see that
![]() $\mathfrak {A}_m\cong \bot ^{p_1}\mathfrak {A}_{m-p_1}\top ^{p_n}\in \mathsf {H}(\bot ^{p_1}\mathfrak {A}_{2k_1}\times \ldots \bot ^{p_n}\mathfrak {A}_{2k_n}\times \mathfrak {A}_k\top ^{p_n}\ldots \top ^{p_1})$
.
$\mathfrak {A}_m\cong \bot ^{p_1}\mathfrak {A}_{m-p_1}\top ^{p_n}\in \mathsf {H}(\bot ^{p_1}\mathfrak {A}_{2k_1}\times \ldots \bot ^{p_n}\mathfrak {A}_{2k_n}\times \mathfrak {A}_k\top ^{p_n}\ldots \top ^{p_1})$
.
For 2) notice that for any
![]() $\mathfrak {B}\in \mathsf {V}(\mathfrak {A}_l)$
it is the case that
$\mathfrak {B}\in \mathsf {V}(\mathfrak {A}_l)$
it is the case that
![]() $\bot \mathfrak {B}\top \in \mathsf {V}(\bot \mathfrak {A}_l\top )$
, because if
$\bot \mathfrak {B}\top \in \mathsf {V}(\bot \mathfrak {A}_l\top )$
, because if
![]() $\mathfrak {B}$
is a subdirect product of
$\mathfrak {B}$
is a subdirect product of
![]() $\{\mathfrak {A}_{l_i}:i\in I,l_i\leq l\}$
, then
$\{\mathfrak {A}_{l_i}:i\in I,l_i\leq l\}$
, then
![]() $\bot \mathfrak {B}\top $
is a subdirect product of
$\bot \mathfrak {B}\top $
is a subdirect product of
![]() $\{\bot \mathfrak {A}_{l_i}\top :i\in I,l_i\leq l\}$
. Also, if
$\{\bot \mathfrak {A}_{l_i}\top :i\in I,l_i\leq l\}$
. Also, if
![]() $\mathfrak {B}\in \mathsf {V}(\mathfrak {A}_l)$
and
$\mathfrak {B}\in \mathsf {V}(\mathfrak {A}_l)$
and
![]() $\mathfrak {C}\preceq \mathfrak {B}$
, then
$\mathfrak {C}\preceq \mathfrak {B}$
, then
![]() $\mathfrak {B}\times \mathfrak {C}\in \mathsf {V}(\mathfrak {A}_l)$
. We start from the fact that
$\mathfrak {B}\times \mathfrak {C}\in \mathsf {V}(\mathfrak {A}_l)$
. We start from the fact that
![]() $\mathfrak {A}_{2k_n}\times \mathfrak {A}_k\in \mathsf {V}(\mathfrak {A}_z)$
, where
$\mathfrak {A}_{2k_n}\times \mathfrak {A}_k\in \mathsf {V}(\mathfrak {A}_z)$
, where
![]() $z=max(\{2k_n,k\})$
. Then we combine two previous observations using them alternately to get 2).
$z=max(\{2k_n,k\})$
. Then we combine two previous observations using them alternately to get 2).
The result for the remaining fourth type of algebras follows immediately from the previous case.
Now, to prove the lemma, let
![]() $\mathsf {K}$
be a class of critical algebras, and
$\mathsf {K}$
be a class of critical algebras, and
![]() $\mathsf {Q}(\mathsf {K})\in [\mathsf {V}(\mathfrak {A}_m)]_{/\sim }$
. Hence
$\mathsf {Q}(\mathsf {K})\in [\mathsf {V}(\mathfrak {A}_m)]_{/\sim }$
. Hence
![]() $\mathsf {K}\subseteq \mathsf {Q}(\mathsf {K})\subseteq \mathsf {H}\mathsf {Q}(\mathsf {K})=\mathsf {V}(\mathfrak {A}_m)$
. If there is
$\mathsf {K}\subseteq \mathsf {Q}(\mathsf {K})\subseteq \mathsf {H}\mathsf {Q}(\mathsf {K})=\mathsf {V}(\mathfrak {A}_m)$
. If there is
![]() $k>m$
,
$k>m$
,
![]() $\mathfrak {B}\in \mathsf {K}$
such that
$\mathfrak {B}\in \mathsf {K}$
such that
![]() $deg(\mathfrak {B})=k$
, then
$deg(\mathfrak {B})=k$
, then
![]() $\mathfrak {A}_k\in \mathsf {H}(\mathfrak {B})\subseteq \mathsf {V}(\mathfrak {A}_m)$
which cannot be the case, since it contradicts Theorem 3.3. If, on the other hand, for each
$\mathfrak {A}_k\in \mathsf {H}(\mathfrak {B})\subseteq \mathsf {V}(\mathfrak {A}_m)$
which cannot be the case, since it contradicts Theorem 3.3. If, on the other hand, for each
![]() $\mathfrak {B}\in \mathsf {K}$
,
$\mathfrak {B}\in \mathsf {K}$
,
![]() $deg(\mathfrak {B})<m$
, then let
$deg(\mathfrak {B})<m$
, then let
![]() $z=max(\{deg(\mathfrak {B}):\mathfrak {B}\in \mathsf {K}\})$
. Obviously
$z=max(\{deg(\mathfrak {B}):\mathfrak {B}\in \mathsf {K}\})$
. Obviously
![]() $z<m$
, so
$z<m$
, so
![]() $\mathsf {Q}(\mathsf {K})\sim \mathsf {V}(\mathfrak {A}_z)$
which contradicts the assumption. This gives us the right-hand side of the equivalence from the lemma.
$\mathsf {Q}(\mathsf {K})\sim \mathsf {V}(\mathfrak {A}_z)$
which contradicts the assumption. This gives us the right-hand side of the equivalence from the lemma.
For the other direction, assume that there is a critical algebra
![]() $\mathfrak {A}\in \mathsf {K}$
such that
$\mathfrak {A}\in \mathsf {K}$
such that
![]() $deg(\mathfrak {A})=m$
and there is no critical algebra
$deg(\mathfrak {A})=m$
and there is no critical algebra
![]() $\mathfrak {B}$
in
$\mathfrak {B}$
in
![]() $\mathsf {K}$
such that
$\mathsf {K}$
such that
![]() $deg(\mathfrak {B})>m$
. From the first conjunct we know that
$deg(\mathfrak {B})>m$
. From the first conjunct we know that
![]() $\mathsf {V}(\mathfrak {A}_m)\subseteq \mathsf {H}\mathsf {Q}(\mathsf {K})$
. From the second conjunct we get
$\mathsf {V}(\mathfrak {A}_m)\subseteq \mathsf {H}\mathsf {Q}(\mathsf {K})$
. From the second conjunct we get
![]() $\mathsf {K}\subseteq \mathsf {V}(\mathfrak {A}_m)$
. Thus
$\mathsf {K}\subseteq \mathsf {V}(\mathfrak {A}_m)$
. Thus
![]() $\mathsf {Q}(\mathsf {K})\sim \mathsf {V}(\mathfrak {A}_m)$
.
$\mathsf {Q}(\mathsf {K})\sim \mathsf {V}(\mathfrak {A}_m)$
.
In Lemma 4.7, we addressed all finite cases, i.e., the members of the equivalence classes
![]() $[\mathsf {V}(\mathfrak {A}_m)]{/\sim }$
for
$[\mathsf {V}(\mathfrak {A}_m)]{/\sim }$
for
![]() $m \in \omega $
. We now turn to the infinite case, involving the members of
$m \in \omega $
. We now turn to the infinite case, involving the members of
![]() $[\mathfrak {A}_\omega ]{/\sim }$
.
$[\mathfrak {A}_\omega ]{/\sim }$
.
Lemma 4.8. Let
![]() $\mathsf {K}$
be a class of critical algebras.
$\mathsf {K}$
be a class of critical algebras.
![]() $\mathsf {Q}(\mathsf {K})\in [\mathsf {V}(\mathfrak {A}_\omega )]_{/\sim }$
iff for each
$\mathsf {Q}(\mathsf {K})\in [\mathsf {V}(\mathfrak {A}_\omega )]_{/\sim }$
iff for each
![]() $n\in \omega $
there is a critical algebra
$n\in \omega $
there is a critical algebra
![]() $\mathfrak {A}\in \mathsf {K}$
such that
$\mathfrak {A}\in \mathsf {K}$
such that
![]() $deg(\mathfrak {A})\geq n$
.
$deg(\mathfrak {A})\geq n$
.
Proof. For the left to right direction assume that there is
![]() $n\in \omega $
s.t. there is no
$n\in \omega $
s.t. there is no
![]() $m\geq n$
, s.t.
$m\geq n$
, s.t.
![]() $deg(\mathfrak {A})=m$
and
$deg(\mathfrak {A})=m$
and
![]() $\mathfrak {A}\in \mathsf {K}$
. But then by Lemma 4.7, we get
$\mathfrak {A}\in \mathsf {K}$
. But then by Lemma 4.7, we get
![]() $\mathsf {Q}(\mathsf {K})\subseteq \mathsf {V}(\mathfrak {A}_m)$
which means that
$\mathsf {Q}(\mathsf {K})\subseteq \mathsf {V}(\mathfrak {A}_m)$
which means that
![]() $\mathsf {Q}(\mathsf {K})\notin [\mathsf {V}(\mathfrak {A}_\omega )]_{/\sim }$
.
$\mathsf {Q}(\mathsf {K})\notin [\mathsf {V}(\mathfrak {A}_\omega )]_{/\sim }$
.
For the right to left assume that for each
![]() $n\in \omega $
there is a critical algebra
$n\in \omega $
there is a critical algebra
![]() $\mathfrak {A}\in \mathsf {K}$
such that
$\mathfrak {A}\in \mathsf {K}$
such that
![]() $deg(\mathfrak {A})\geq n$
. Then, using the fact that for each critical
$deg(\mathfrak {A})\geq n$
. Then, using the fact that for each critical
![]() $\mathfrak {B}$
, s.t.
$\mathfrak {B}$
, s.t.
![]() $deg(\mathfrak {B})=m$
we have
$deg(\mathfrak {B})=m$
we have
![]() $\mathfrak {A}_m\in \mathsf {H}(\mathfrak {B})$
, we obtain that for each n there is
$\mathfrak {A}_m\in \mathsf {H}(\mathfrak {B})$
, we obtain that for each n there is
![]() $m\geq n$
s.t.
$m\geq n$
s.t.
![]() $\mathfrak {A}_m\in \mathsf {H}(\mathsf {K})$
. But also
$\mathfrak {A}_m\in \mathsf {H}(\mathsf {K})$
. But also
![]() $\mathfrak {A}_n\in \mathsf {H}\mathsf {S}(\mathfrak {A}_m)$
for each
$\mathfrak {A}_n\in \mathsf {H}\mathsf {S}(\mathfrak {A}_m)$
for each
![]() $n\leq m$
. This way we have shown that for each n,
$n\leq m$
. This way we have shown that for each n,
![]() $\mathfrak {A}_n\in \mathsf {V}(\mathsf {K})$
, which proves the Lemma.
$\mathfrak {A}_n\in \mathsf {V}(\mathsf {K})$
, which proves the Lemma.
Lemmas 4.7 and 4.8 establish an equivalent condition for membership in a given equivalence class, which ultimately depends on the degree of critical algebras. Based on this result, we will characterize each
![]() $\mathbf {SC}$
quasivariety as being generated by a single (in most cases finite) algebra.
$\mathbf {SC}$
quasivariety as being generated by a single (in most cases finite) algebra.
Lemma 4.9. For any
![]() $m\geq 2$
,
$m\geq 2$
,
![]() $\mathsf {Q}(\mathfrak {A}_2\times \mathfrak {A}_m)$
is
$\mathsf {Q}(\mathfrak {A}_2\times \mathfrak {A}_m)$
is
![]() $\mathbf {SC}$
.
$\mathbf {SC}$
.
Proof. It is enough to show that for any non-trivial quasivariety
![]() $\mathcal {Q}$
of Sugihara algebras such that:
$\mathcal {Q}$
of Sugihara algebras such that:
![]() $\mathcal {Q}\in [\mathsf {V}(\mathfrak {A}_m)]_{/\sim }$
, (
$\mathcal {Q}\in [\mathsf {V}(\mathfrak {A}_m)]_{/\sim }$
, (
![]() $m\geq 2$
), we have
$m\geq 2$
), we have
![]() $\mathsf {Q}(\mathfrak {A}_2\times \mathfrak {A}_m)\subseteq \mathcal {Q}$
. By Lemma 4.7, there is a critical
$\mathsf {Q}(\mathfrak {A}_2\times \mathfrak {A}_m)\subseteq \mathcal {Q}$
. By Lemma 4.7, there is a critical
![]() $\mathfrak {A}\in \mathcal {Q}$
s.t.
$\mathfrak {A}\in \mathcal {Q}$
s.t.
![]() $deg(\mathfrak {A})=m$
. Obviously
$deg(\mathfrak {A})=m$
. Obviously
![]() $\mathfrak {A}_2\in \mathcal {Q}$
. By Theorem 3.6, there are four cases to consider.
$\mathfrak {A}_2\in \mathcal {Q}$
. By Theorem 3.6, there are four cases to consider.
If
![]() $\mathfrak {A}\cong \mathfrak {A}_m$
, then obviously
$\mathfrak {A}\cong \mathfrak {A}_m$
, then obviously
![]() $\mathfrak {A}_2\times \mathfrak {A}_m\in \mathcal {Q}$
.
$\mathfrak {A}_2\times \mathfrak {A}_m\in \mathcal {Q}$
.
If
![]() $\mathfrak {A}\cong \mathfrak {A}_{j}\times \mathfrak {A}_m$
where
$\mathfrak {A}\cong \mathfrak {A}_{j}\times \mathfrak {A}_m$
where
![]() $j<m$
and at least one of these numbers is even, then
$j<m$
and at least one of these numbers is even, then
![]() $\mathfrak {A}_2\times \mathfrak {A}_m\preceq \mathfrak {A}_{j}\times \mathfrak {A}_m$
, so
$\mathfrak {A}_2\times \mathfrak {A}_m\preceq \mathfrak {A}_{j}\times \mathfrak {A}_m$
, so
![]() $\mathfrak {A}_2\times \mathfrak {A}_m\in \mathcal {Q}$
.
$\mathfrak {A}_2\times \mathfrak {A}_m\in \mathcal {Q}$
.
Let
![]() $\mathfrak {A}\cong \bot ^{p_1}\mathfrak {A}_{2k_1}\times \ldots \bot ^{p_n}\mathfrak {A}_{2k_n}\times \mathfrak {A}_k\top ^{p_n}\ldots \top ^{p_1}$
. Obviously
$\mathfrak {A}\cong \bot ^{p_1}\mathfrak {A}_{2k_1}\times \ldots \bot ^{p_n}\mathfrak {A}_{2k_n}\times \mathfrak {A}_k\top ^{p_n}\ldots \top ^{p_1}$
. Obviously
![]() $\mathfrak {A}_2\times \mathfrak {A}\in \mathcal {Q}$
. We have
$\mathfrak {A}_2\times \mathfrak {A}\in \mathcal {Q}$
. We have
![]() $\mathfrak {A}_2\preceq \mathfrak {A}_{2k_1}$
and
$\mathfrak {A}_2\preceq \mathfrak {A}_{2k_1}$
and
![]() $\mathfrak {A}_{2k_i}\preceq \bot ^{p_{i+1}}\mathfrak {A}_{2k_{i+1}}\times \ldots \bot ^{p_n}\mathfrak {A}_{2k_n}\times \mathfrak {A}_k\top ^{p_n}\ldots \top ^{p_{i+1}}$
for each
$\mathfrak {A}_{2k_i}\preceq \bot ^{p_{i+1}}\mathfrak {A}_{2k_{i+1}}\times \ldots \bot ^{p_n}\mathfrak {A}_{2k_n}\times \mathfrak {A}_k\top ^{p_n}\ldots \top ^{p_{i+1}}$
for each
![]() $i<n$
, so we can apply Lemma 4.4
$i<n$
, so we can apply Lemma 4.4
![]() $n-1$
times and get
$n-1$
times and get
![]() $\mathfrak {A}_2\times \mathfrak {A}\approx _{\mathsf {q}} \mathfrak {A}_2\times \bot ^{l}\mathfrak {A}_{2k_n}\times \mathfrak {A}_k\top ^{l}$
, where
$\mathfrak {A}_2\times \mathfrak {A}\approx _{\mathsf {q}} \mathfrak {A}_2\times \bot ^{l}\mathfrak {A}_{2k_n}\times \mathfrak {A}_k\top ^{l}$
, where
![]() $l=p_1+\dots +p_n$
. Obviously
$l=p_1+\dots +p_n$
. Obviously
![]() $\mathfrak {A}_2$
is embeddable in both
$\mathfrak {A}_2$
is embeddable in both
![]() $\mathfrak {A}_{2k_n}$
and
$\mathfrak {A}_{2k_n}$
and
![]() $\mathfrak {A}_k$
. If
$\mathfrak {A}_k$
. If
![]() $2k_n>k$
, then
$2k_n>k$
, then
![]() $m=2(k_n+l)$
and
$m=2(k_n+l)$
and
![]() $\mathfrak {A}_2\times \bot ^{l}\mathfrak {A}_2\times \mathfrak {A}_{2k_n}\top ^{l}\preceq \mathfrak {A}_2\times \bot ^{l}\mathfrak {A}_{2k_n}\times \mathfrak {A}_k\top ^{l}$
, so
$\mathfrak {A}_2\times \bot ^{l}\mathfrak {A}_2\times \mathfrak {A}_{2k_n}\top ^{l}\preceq \mathfrak {A}_2\times \bot ^{l}\mathfrak {A}_{2k_n}\times \mathfrak {A}_k\top ^{l}$
, so
![]() $\mathfrak {A}_2\times \bot ^{l}\mathfrak {A}_2\times \mathfrak {A}_{2k_n}\top ^{l}\in \mathcal {Q}$
and we can apply Lemma 4.4 one more time:
$\mathfrak {A}_2\times \bot ^{l}\mathfrak {A}_2\times \mathfrak {A}_{2k_n}\top ^{l}\in \mathcal {Q}$
and we can apply Lemma 4.4 one more time:
![]() $\mathfrak {A}_2\times \bot ^{l}\mathfrak {A}_2\times \mathfrak {A}_{2k_n}\top ^{l}\approx _{\mathsf {q}}\mathfrak {A}_2\times \bot ^{l}\mathfrak {A}_{2k_n}\top ^{l}\cong \mathfrak {A}_2\times \mathfrak {A}_m$
. Hence,
$\mathfrak {A}_2\times \bot ^{l}\mathfrak {A}_2\times \mathfrak {A}_{2k_n}\top ^{l}\approx _{\mathsf {q}}\mathfrak {A}_2\times \bot ^{l}\mathfrak {A}_{2k_n}\top ^{l}\cong \mathfrak {A}_2\times \mathfrak {A}_m$
. Hence,
![]() $\mathfrak {A}_2\times \mathfrak {A}_m\in \mathcal {Q}$
. If, on the other hand,
$\mathfrak {A}_2\times \mathfrak {A}_m\in \mathcal {Q}$
. If, on the other hand,
![]() $2k_n<k$
, then 4.4 can be applied immediately, since
$2k_n<k$
, then 4.4 can be applied immediately, since
![]() $\mathfrak {A}_{2k_n}\preceq \mathfrak {A}_k$
, and thus we get
$\mathfrak {A}_{2k_n}\preceq \mathfrak {A}_k$
, and thus we get
![]() $\mathfrak {A}_2\times \mathfrak {A}\approx _{\mathsf {q}}\mathfrak {A}_2\times \bot ^l\mathfrak {A}_k\top ^l\cong \mathfrak {A}_2\times \mathfrak {A}_m$
. Again, we obtain
$\mathfrak {A}_2\times \mathfrak {A}\approx _{\mathsf {q}}\mathfrak {A}_2\times \bot ^l\mathfrak {A}_k\top ^l\cong \mathfrak {A}_2\times \mathfrak {A}_m$
. Again, we obtain
![]() $\mathfrak {A}_2\times \mathfrak {A}_m\in \mathcal {Q}$
.
$\mathfrak {A}_2\times \mathfrak {A}_m\in \mathcal {Q}$
.
Finally, if
![]() $\mathfrak {A}$
is of the fourth type, that is
$\mathfrak {A}$
is of the fourth type, that is
![]() $\mathfrak {A}\cong \mathfrak {A}_{2k_0}\times \mathfrak {B}$
, where
$\mathfrak {A}\cong \mathfrak {A}_{2k_0}\times \mathfrak {B}$
, where
![]() $\mathfrak {B}$
is of the third type, then
$\mathfrak {B}$
is of the third type, then
![]() $\mathfrak {A}_2\times \mathfrak {B}\preceq \mathfrak {A}$
and we can repeat the reasoning from the previous case.
$\mathfrak {A}_2\times \mathfrak {B}\preceq \mathfrak {A}$
and we can repeat the reasoning from the previous case.
Once again, we address the infinite case separately.
Lemma 4.10.
![]() $\mathsf {Q}(\{\mathfrak {A}_2\times \mathfrak {A}_{2m}:m\in \omega \})=\mathsf {Q}(\mathfrak {A}_2\times \mathfrak {A}_{\omega \setminus \{0\}})$
is
$\mathsf {Q}(\{\mathfrak {A}_2\times \mathfrak {A}_{2m}:m\in \omega \})=\mathsf {Q}(\mathfrak {A}_2\times \mathfrak {A}_{\omega \setminus \{0\}})$
is
![]() $\mathbf {SC}$
.
$\mathbf {SC}$
.
Proof. First we prove equality, then we will move on to structural completeness. Inclusion from the left to right is trivial. To see that
![]() $\mathsf {Q}(\mathfrak {A}_2\times \mathfrak {A}_{\omega \setminus \{0\}})\subseteq \mathsf {Q}(\{\mathfrak {A}_2\times \mathfrak {A}_{2m}:m\in \omega \})$
let U be a non-principal ultrafilter over
$\mathsf {Q}(\mathfrak {A}_2\times \mathfrak {A}_{\omega \setminus \{0\}})\subseteq \mathsf {Q}(\{\mathfrak {A}_2\times \mathfrak {A}_{2m}:m\in \omega \})$
let U be a non-principal ultrafilter over
![]() $\omega $
. It can be proven that
$\omega $
. It can be proven that
![]() $\mathfrak {A}_2\times \mathfrak {A}_{\omega \setminus \{0\}}$
is embeddable in
$\mathfrak {A}_2\times \mathfrak {A}_{\omega \setminus \{0\}}$
is embeddable in
![]() $(\Pi _{n\in \omega }(\mathfrak {A}_2\times \mathfrak {A}_{2n}))_{/_U}$
. To see that, first define a function f from
$(\Pi _{n\in \omega }(\mathfrak {A}_2\times \mathfrak {A}_{2n}))_{/_U}$
. To see that, first define a function f from
![]() $\{-1,1\}\times \mathbb {Z}\setminus \{0\}$
into the direct product:
$\{-1,1\}\times \mathbb {Z}\setminus \{0\}$
into the direct product:
![]() $\Pi _{n\in \omega }(\{-1,1\}\times \{-n,\dots ,-1,1,\dots ,n\})$
by
$\Pi _{n\in \omega }(\{-1,1\}\times \{-n,\dots ,-1,1,\dots ,n\})$
by
 $$ \begin{align*} f((x,n))(m)= \begin{cases} (1,1), &\text{ if }m<n,\\ (x,n), &\text{ otherwise.} \end{cases} \end{align*} $$
$$ \begin{align*} f((x,n))(m)= \begin{cases} (1,1), &\text{ if }m<n,\\ (x,n), &\text{ otherwise.} \end{cases} \end{align*} $$
Now e given by
![]() $e((x,n))=[f((x,n))]_{/_U}$
can be easily seen to be an embedding of
$e((x,n))=[f((x,n))]_{/_U}$
can be easily seen to be an embedding of
![]() $\mathfrak {A}_2\times \mathfrak {A}_{\omega \setminus \{0\}}$
into
$\mathfrak {A}_2\times \mathfrak {A}_{\omega \setminus \{0\}}$
into
![]() $\Pi _{n\in \omega }(\mathfrak {A}_2\times \mathfrak {A}_{2n})_{/_U}$
.
$\Pi _{n\in \omega }(\mathfrak {A}_2\times \mathfrak {A}_{2n})_{/_U}$
.
Let
![]() $\mathsf {Q}(\mathsf {K})\in [\mathsf {V}(\mathfrak {A}_\omega )]_{/\sim }$
, where
$\mathsf {Q}(\mathsf {K})\in [\mathsf {V}(\mathfrak {A}_\omega )]_{/\sim }$
, where
![]() $\mathsf {K}$
is a class of critical algebras. By Lemma 4.8 for each n there is
$\mathsf {K}$
is a class of critical algebras. By Lemma 4.8 for each n there is
![]() $\mathfrak {A}\in \mathsf {K}$
such that
$\mathfrak {A}\in \mathsf {K}$
such that
![]() $deg(\mathfrak {A})\geq n$
. By the reasoning from 4.9 we know that there is
$deg(\mathfrak {A})\geq n$
. By the reasoning from 4.9 we know that there is
![]() $\mathfrak {A}_2\times \mathfrak {A}_m\in \mathsf {Q}(\mathfrak {A})$
, where
$\mathfrak {A}_2\times \mathfrak {A}_m\in \mathsf {Q}(\mathfrak {A})$
, where
![]() $n\leq m=deg(\mathfrak {A})$
. Thus
$n\leq m=deg(\mathfrak {A})$
. Thus
![]() $\mathfrak {A}_2\times \mathfrak {A}_m\in \mathsf {Q}(\mathsf {K})$
. Also for any
$\mathfrak {A}_2\times \mathfrak {A}_m\in \mathsf {Q}(\mathsf {K})$
. Also for any
![]() $2j=l\leq m$
,
$2j=l\leq m$
,
![]() $\mathfrak {A}_2\times \mathfrak {A}_l\preceq \mathfrak {A}_2\times \mathfrak {A}_m$
, which means that
$\mathfrak {A}_2\times \mathfrak {A}_l\preceq \mathfrak {A}_2\times \mathfrak {A}_m$
, which means that
![]() $\mathsf {Q}(\{\mathfrak {A}_2\times \mathfrak {A}_{2m}:m\in \omega \})\subseteq \mathsf {Q}(\mathsf {K})$
.
$\mathsf {Q}(\{\mathfrak {A}_2\times \mathfrak {A}_{2m}:m\in \omega \})\subseteq \mathsf {Q}(\mathsf {K})$
.
By combining Lemmas 4.9 and 4.10, we can now state that the set of all
![]() $\mathbf {SC}$
quasivarieties of Sugihara algebras is
$\mathbf {SC}$
quasivarieties of Sugihara algebras is
![]() $\{\mathsf {Q}(\mathfrak {A}_1), \mathsf {Q}(\mathfrak {A}_2 \times \mathfrak {A}_{\omega \setminus \{0\}})\} \cup \{\mathsf {Q}(\mathfrak {A}_2 \times \mathfrak {A}_n) : 2 \leq n \in \omega \}$
. As will become apparent later, this subposet of the entire lattice of quasivarieties of Sugihara algebras is illustrated in Figure 1. We are now ready to eliminate some of the
$\{\mathsf {Q}(\mathfrak {A}_1), \mathsf {Q}(\mathfrak {A}_2 \times \mathfrak {A}_{\omega \setminus \{0\}})\} \cup \{\mathsf {Q}(\mathfrak {A}_2 \times \mathfrak {A}_n) : 2 \leq n \in \omega \}$
. As will become apparent later, this subposet of the entire lattice of quasivarieties of Sugihara algebras is illustrated in Figure 1. We are now ready to eliminate some of the
![]() $\mathbf {SC}$
quasivarieties from Figure 1 as non-hereditary.
$\mathbf {SC}$
quasivarieties from Figure 1 as non-hereditary.

Figure 1 Structurally complete quasivarieties of Sugihara algebras.
Lemma 4.11. For each
![]() $n\geq 2$
, it is the case that
$n\geq 2$
, it is the case that
![]() $\mathsf {Q}(\mathfrak {A}_2\times \mathfrak {A}_{2n+1})$
is not
$\mathsf {Q}(\mathfrak {A}_2\times \mathfrak {A}_{2n+1})$
is not
![]() $\mathbf {HSC}$
.
$\mathbf {HSC}$
.
Proof. By Theorem 3.7, we know that
![]() $\mathsf {Q}(\mathfrak {A}_2\times \mathfrak {A}_3,\mathfrak {A}_2\times \mathfrak {A}_4)$
is not
$\mathsf {Q}(\mathfrak {A}_2\times \mathfrak {A}_3,\mathfrak {A}_2\times \mathfrak {A}_4)$
is not
![]() $\mathbf {SC}$
, since
$\mathbf {SC}$
, since
![]() $\mathsf {Q}(\mathfrak {A}_2\times \mathfrak {A}_3,\mathfrak {A}_2\times \mathfrak {A}_4)\supsetneq \mathsf {Q}(\mathfrak {A}_2\times \mathfrak {A}_4)$
and
$\mathsf {Q}(\mathfrak {A}_2\times \mathfrak {A}_3,\mathfrak {A}_2\times \mathfrak {A}_4)\supsetneq \mathsf {Q}(\mathfrak {A}_2\times \mathfrak {A}_4)$
and
![]() $\mathsf {Q}(\mathfrak {A}_2\times \mathfrak {A}_3,\mathfrak {A}_2\times \mathfrak {A}_4)\sim \mathsf {Q}(\mathfrak {A}_2\times \mathfrak {A}_4)$
. Also,
$\mathsf {Q}(\mathfrak {A}_2\times \mathfrak {A}_3,\mathfrak {A}_2\times \mathfrak {A}_4)\sim \mathsf {Q}(\mathfrak {A}_2\times \mathfrak {A}_4)$
. Also,
![]() $\mathfrak {A}_2\times \mathfrak {A}_3,\mathfrak {A}_2\times \mathfrak {A}_4\preceq \mathfrak {A}_2\times \mathfrak {A}_{2n+1}$
for
$\mathfrak {A}_2\times \mathfrak {A}_3,\mathfrak {A}_2\times \mathfrak {A}_4\preceq \mathfrak {A}_2\times \mathfrak {A}_{2n+1}$
for
![]() $n\geq 2$
which means that
$n\geq 2$
which means that
![]() $\mathsf {Q}(\mathfrak {A}_2\times \mathfrak {A}_3,\mathfrak {A}_2\times \mathfrak {A}_4)\subsetneq \mathsf {Q}(\mathfrak {A}_2\times \mathfrak {A}_{2n+1})$
and consequently falsifies the heredity of
$\mathsf {Q}(\mathfrak {A}_2\times \mathfrak {A}_3,\mathfrak {A}_2\times \mathfrak {A}_4)\subsetneq \mathsf {Q}(\mathfrak {A}_2\times \mathfrak {A}_{2n+1})$
and consequently falsifies the heredity of
![]() $\mathbf {SC}$
for
$\mathbf {SC}$
for
![]() $\mathsf {Q}(\mathfrak {A}_2\times \mathfrak {A}_{2n+1})$
.
$\mathsf {Q}(\mathfrak {A}_2\times \mathfrak {A}_{2n+1})$
.
We have spotted infinitely many quasivarieties which are
![]() $\mathbf {nHSC}$
. To prove that the remaining
$\mathbf {nHSC}$
. To prove that the remaining
![]() $\mathbf {SC}$
extensions are hereditary, let us define three special rules.
$\mathbf {SC}$
extensions are hereditary, let us define three special rules.
We have a non-paraconsistency rule
![]() $\mathtt {NP}$
, disjunctive syllogism
$\mathtt {NP}$
, disjunctive syllogism
![]() $\mathtt {DS}$
and a special rule
$\mathtt {DS}$
and a special rule
![]() $\mathtt {R}$
. Due to algebraizability, these rules are equivalent to respective quasi-identities—here, we chose the ‘logical notation’ over the ‘algebraic’ one for the sake of readability.
$\mathtt {R}$
. Due to algebraizability, these rules are equivalent to respective quasi-identities—here, we chose the ‘logical notation’ over the ‘algebraic’ one for the sake of readability.
Lemma 4.12. It is the case that:
 $$ \begin{align*} \mathfrak{A}_2\times\mathfrak{A}_{\omega\setminus\{0\}}&\vDash\mathtt{NP},\mathtt{DS},\mathtt{R}\\ \mathfrak{A}_3&\nvDash\mathtt{NP}\\ \mathfrak{A}_4&\nvDash\mathtt{R}\\ \mathfrak{A}_2\times\mathfrak{A}_3&\nvDash\mathtt{DS} \end{align*} $$
$$ \begin{align*} \mathfrak{A}_2\times\mathfrak{A}_{\omega\setminus\{0\}}&\vDash\mathtt{NP},\mathtt{DS},\mathtt{R}\\ \mathfrak{A}_3&\nvDash\mathtt{NP}\\ \mathfrak{A}_4&\nvDash\mathtt{R}\\ \mathfrak{A}_2\times\mathfrak{A}_3&\nvDash\mathtt{DS} \end{align*} $$
Proof. Designated values (positive elements) on
![]() $\mathfrak {A}_2\times \mathfrak {A}_{\omega \setminus \{0\}}$
are elements of the form
$\mathfrak {A}_2\times \mathfrak {A}_{\omega \setminus \{0\}}$
are elements of the form
![]() $(1,k)$
where
$(1,k)$
where
![]() $k\geq 1$
. It is easy to see that for any interpretation i s.t.
$k\geq 1$
. It is easy to see that for any interpretation i s.t.
![]() $i(p)=(1,k)$
, it must be that case that
$i(p)=(1,k)$
, it must be that case that
![]() $i(\neg p)=(-1,-k)$
and thus the premises of
$i(\neg p)=(-1,-k)$
and thus the premises of
![]() $\mathtt {NP}$
are not satisfiable, which means
$\mathtt {NP}$
are not satisfiable, which means
![]() $\mathfrak {A}_2\times \mathfrak {A}_{\omega \setminus \{0\}}\vDash \mathtt {NP}$
. On the other hand, if we take the interpretation i s.t.
$\mathfrak {A}_2\times \mathfrak {A}_{\omega \setminus \{0\}}\vDash \mathtt {NP}$
. On the other hand, if we take the interpretation i s.t.
![]() $i(p)=0$
and
$i(p)=0$
and
![]() $i(q)=-1$
on
$i(q)=-1$
on
![]() $\mathfrak {A}_3$
, we see that
$\mathfrak {A}_3$
, we see that
![]() $\mathfrak {A}_3\nvDash \mathtt {NP}$
.
$\mathfrak {A}_3\nvDash \mathtt {NP}$
.
Now, if we take any interpretation such that
![]() $i(p)=(1,j)$
and
$i(p)=(1,j)$
and
![]() $i(q)=(1,j)$
, for
$i(q)=(1,j)$
, for
![]() $j,k\geq 1$
, we immediately see that
$j,k\geq 1$
, we immediately see that
![]() $i(p\to q)=(1,j\to k)$
and thus
$i(p\to q)=(1,j\to k)$
and thus
![]() $i(\neg (p\to q))=(-1,\neg (j\to k))$
, which shows that the set of premises of
$i(\neg (p\to q))=(-1,\neg (j\to k))$
, which shows that the set of premises of
![]() $\mathtt {R}$
are not satisfiable in
$\mathtt {R}$
are not satisfiable in
![]() $\mathfrak {A}_2\times \mathfrak {A}_{\omega \setminus \{0\}}$
and consequently
$\mathfrak {A}_2\times \mathfrak {A}_{\omega \setminus \{0\}}$
and consequently
![]() $\mathfrak {A}_2\times \mathfrak {A}_{\omega \setminus \{0\}}\vDash \mathtt {R}$
. Now let
$\mathfrak {A}_2\times \mathfrak {A}_{\omega \setminus \{0\}}\vDash \mathtt {R}$
. Now let
![]() $i(p)=2$
,
$i(p)=2$
,
![]() $i(q)=1$
,
$i(q)=1$
,
![]() $i(r)=-1$
in
$i(r)=-1$
in
![]() $\mathfrak {A}_4$
. Hence
$\mathfrak {A}_4$
. Hence
![]() $i(\neg (p\to q))=-(2\to 1)=--2=2$
. This interpretation falsifies
$i(\neg (p\to q))=-(2\to 1)=--2=2$
. This interpretation falsifies
![]() $\mathtt {R}$
in
$\mathtt {R}$
in
![]() $\mathfrak {A}_4$
, i.e.,
$\mathfrak {A}_4$
, i.e.,
![]() $\mathfrak {A}_4\nvDash \mathtt {R}$
.
$\mathfrak {A}_4\nvDash \mathtt {R}$
.
Finally, let
![]() $i(p)=(1,k)$
where
$i(p)=(1,k)$
where
![]() $k\geq 1$
. Hence
$k\geq 1$
. Hence
![]() $i(\neg p)=(-1,-k)$
which means that in order for
$i(\neg p)=(-1,-k)$
which means that in order for
![]() $i(\neg p\lor q)$
to be positive, it must be the case that
$i(\neg p\lor q)$
to be positive, it must be the case that
![]() $i(q)=(1,j)$
for some
$i(q)=(1,j)$
for some
![]() $j\geq 1$
. This gives us
$j\geq 1$
. This gives us
![]() $\mathfrak {A}_2\times \mathfrak {A}_{\omega \setminus \{0\}}\vDash \mathtt {DS}$
. Lastly we show that
$\mathfrak {A}_2\times \mathfrak {A}_{\omega \setminus \{0\}}\vDash \mathtt {DS}$
. Lastly we show that
![]() $\mathfrak {A}_2\times \mathfrak {A}_3\nvDash \mathtt {DS}$
: take i s.t.
$\mathfrak {A}_2\times \mathfrak {A}_3\nvDash \mathtt {DS}$
: take i s.t.
![]() $i(p)=(1,0)$
,
$i(p)=(1,0)$
,
![]() $i(q)=(1,-1)$
.
$i(q)=(1,-1)$
.
Lemma 4.13. Let
![]() $\mathcal {Q}$
be a quasivariety of Sugihara algebras and
$\mathcal {Q}$
be a quasivariety of Sugihara algebras and
![]() $n\in \omega $
. If
$n\in \omega $
. If
![]() $\mathcal {Q}\subseteq \mathsf {Q}(\mathfrak {A}_2\times \mathfrak {A}_{2n})$
and
$\mathcal {Q}\subseteq \mathsf {Q}(\mathfrak {A}_2\times \mathfrak {A}_{2n})$
and
![]() $\mathcal {Q}\neq \mathsf {Q}(\mathfrak {A}_1)$
, then
$\mathcal {Q}\neq \mathsf {Q}(\mathfrak {A}_1)$
, then
![]() $\mathcal {Q}=\mathsf {Q}(\mathfrak {A}_2\times \mathfrak {A}_{2m})$
, where
$\mathcal {Q}=\mathsf {Q}(\mathfrak {A}_2\times \mathfrak {A}_{2m})$
, where
![]() $m\leq n$
.
$m\leq n$
.
Proof. First observe that
![]() $\mathfrak {A}_2\times \mathfrak {A}_{2n}\preceq \mathfrak {A}_2\times \mathfrak {A}_{\omega \setminus \{0\}}$
, so
$\mathfrak {A}_2\times \mathfrak {A}_{2n}\preceq \mathfrak {A}_2\times \mathfrak {A}_{\omega \setminus \{0\}}$
, so
![]() $\mathfrak {A}_2\times \mathfrak {A}_{2n}\vDash \mathtt {NP}, \mathtt {DS}, \mathtt {R}$
. Let
$\mathfrak {A}_2\times \mathfrak {A}_{2n}\vDash \mathtt {NP}, \mathtt {DS}, \mathtt {R}$
. Let
![]() $\mathfrak {A}\in \mathcal {Q}\subseteq \mathsf {Q}(\mathfrak {A}_2\times \mathfrak {A}_{2n})$
be critical. We can assume that
$\mathfrak {A}\in \mathcal {Q}\subseteq \mathsf {Q}(\mathfrak {A}_2\times \mathfrak {A}_{2n})$
be critical. We can assume that
![]() $\mathfrak {A}$
is not a Boolean algebra, since
$\mathfrak {A}$
is not a Boolean algebra, since
![]() $\mathsf {Q}(\mathfrak {A}_2)=\mathsf {Q}(\mathfrak {A}_2\times \mathfrak {A}_2)$
. If
$\mathsf {Q}(\mathfrak {A}_2)=\mathsf {Q}(\mathfrak {A}_2\times \mathfrak {A}_2)$
. If
![]() $\mathfrak {A}\cong \mathfrak {A}_k$
, then either
$\mathfrak {A}\cong \mathfrak {A}_k$
, then either
![]() $\mathfrak {A}_3\preceq \mathfrak {A}$
or
$\mathfrak {A}_3\preceq \mathfrak {A}$
or
![]() $\mathfrak {A}_4\preceq \mathfrak {A}$
. By Lemma 4.12, it means that either
$\mathfrak {A}_4\preceq \mathfrak {A}$
. By Lemma 4.12, it means that either
![]() $\mathfrak {A}\nvDash \mathtt {NP}$
or
$\mathfrak {A}\nvDash \mathtt {NP}$
or
![]() $\mathfrak {A}\nvDash \mathtt {R}$
. Hence
$\mathfrak {A}\nvDash \mathtt {R}$
. Hence
![]() $\mathfrak {A}\notin \mathsf {Q}(\mathfrak {A}_2\times \mathfrak {A}_{2n})$
, so it must be the case that
$\mathfrak {A}\notin \mathsf {Q}(\mathfrak {A}_2\times \mathfrak {A}_{2n})$
, so it must be the case that
![]() $\mathfrak {A}\not \cong \mathfrak {A}_k$
for any k. If
$\mathfrak {A}\not \cong \mathfrak {A}_k$
for any k. If
![]() $\mathfrak {A}\cong \mathfrak {A}_{2k}\times \mathfrak {A}_m$
and
$\mathfrak {A}\cong \mathfrak {A}_{2k}\times \mathfrak {A}_m$
and
![]() $\mathfrak {A}\not \cong \mathfrak {A}_2\times \mathfrak {A}_j$
for any j, then
$\mathfrak {A}\not \cong \mathfrak {A}_2\times \mathfrak {A}_j$
for any j, then
![]() $m>2$
and
$m>2$
and
![]() $k>1$
, so either
$k>1$
, so either
![]() $\mathfrak {A}_4\preceq \mathfrak {A}$
(when m is even) or
$\mathfrak {A}_4\preceq \mathfrak {A}$
(when m is even) or
![]() $\mathfrak {A}_2\times \mathfrak {A}_3\preceq \mathfrak {A}$
(when m is odd), hence either
$\mathfrak {A}_2\times \mathfrak {A}_3\preceq \mathfrak {A}$
(when m is odd), hence either
![]() $\mathfrak {A}\nvDash \mathtt {R}$
or
$\mathfrak {A}\nvDash \mathtt {R}$
or
![]() $\mathfrak {A}\nvDash \mathtt {NP}$
which by Lemma 4.12 cannot be the case. If
$\mathfrak {A}\nvDash \mathtt {NP}$
which by Lemma 4.12 cannot be the case. If
![]() $\mathfrak {A}\cong \bot ^{p_1}\mathfrak {A}_{2k_1}\times \ldots \bot ^{p_n}\mathfrak {A}_{2k_n}\times \mathfrak {A}_k\top ^{p_n}\ldots \top ^{p_1}$
, then—due to the fact that for any non-trivial finite
$\mathfrak {A}\cong \bot ^{p_1}\mathfrak {A}_{2k_1}\times \ldots \bot ^{p_n}\mathfrak {A}_{2k_n}\times \mathfrak {A}_k\top ^{p_n}\ldots \top ^{p_1}$
, then—due to the fact that for any non-trivial finite
![]() $\mathfrak {B}$
, it is the case that
$\mathfrak {B}$
, it is the case that
![]() $\mathfrak {A}_4\preceq \bot \mathfrak {B}\top $
—we get
$\mathfrak {A}_4\preceq \bot \mathfrak {B}\top $
—we get
![]() $\mathfrak {A}_4\preceq \mathfrak {A}$
which, as we have previously showed, cannot be the case. If
$\mathfrak {A}_4\preceq \mathfrak {A}$
which, as we have previously showed, cannot be the case. If
![]() $\mathfrak {A}\cong \mathfrak {A}_{2k_0}\times \bot ^{p_1}\mathfrak {A}_{2k_1}\times \ldots \bot ^{p_n}\mathfrak {A}_{2k_n}\times \mathfrak {A}_k\top ^{p_n}\ldots \top ^{p_1}$
, then either
$\mathfrak {A}\cong \mathfrak {A}_{2k_0}\times \bot ^{p_1}\mathfrak {A}_{2k_1}\times \ldots \bot ^{p_n}\mathfrak {A}_{2k_n}\times \mathfrak {A}_k\top ^{p_n}\ldots \top ^{p_1}$
, then either
![]() $k_0>1$
, or
$k_0>1$
, or
![]() $k_0=1$
. If
$k_0=1$
. If
![]() $k_0>1$
, then
$k_0>1$
, then
![]() $\mathfrak {A}_4\preceq \mathfrak {A}$
—contradiction. If
$\mathfrak {A}_4\preceq \mathfrak {A}$
—contradiction. If
![]() $k_0=1$
, then by Lemma 4.4,
$k_0=1$
, then by Lemma 4.4,
![]() $\mathfrak {A}\approx _{\mathsf {q}}\mathfrak {A}_2\times \bot ^l\mathfrak {A}_{2k_n}\times \mathfrak {A}_n\top ^l$
, where
$\mathfrak {A}\approx _{\mathsf {q}}\mathfrak {A}_2\times \bot ^l\mathfrak {A}_{2k_n}\times \mathfrak {A}_n\top ^l$
, where
![]() $l=p_1+\dots +p_n$
. If n is odd, then it can be easily seen that
$l=p_1+\dots +p_n$
. If n is odd, then it can be easily seen that
![]() $\mathfrak {A}_2\times \mathfrak {A}_3\preceq \mathfrak {A}_2\times \bot ^l\mathfrak {A}_{2}\times \mathfrak {A}_3\top ^l\preceq \mathfrak {A}_2\times \bot ^l\mathfrak {A}_{2k_n}\times \mathfrak {A}_n\top ^l$
, hence again
$\mathfrak {A}_2\times \mathfrak {A}_3\preceq \mathfrak {A}_2\times \bot ^l\mathfrak {A}_{2}\times \mathfrak {A}_3\top ^l\preceq \mathfrak {A}_2\times \bot ^l\mathfrak {A}_{2k_n}\times \mathfrak {A}_n\top ^l$
, hence again
![]() $\mathfrak {A}\nvDash \mathtt {DS}$
—contradiction. If
$\mathfrak {A}\nvDash \mathtt {DS}$
—contradiction. If
![]() $n=2m$
, then
$n=2m$
, then
![]() $\mathfrak {A}_2\preceq \mathfrak {A}_{2k_0}\preceq \mathfrak {A}_n$
which by Lemma 4.4 gives us
$\mathfrak {A}_2\preceq \mathfrak {A}_{2k_0}\preceq \mathfrak {A}_n$
which by Lemma 4.4 gives us
![]() $\mathfrak {A}\approx _{\mathsf {q}}\mathfrak {A}_2\times \mathfrak {A}_{2(m+l)}$
.
$\mathfrak {A}\approx _{\mathsf {q}}\mathfrak {A}_2\times \mathfrak {A}_{2(m+l)}$
.
This way, we have shown that all critical Sugihara algebras from
![]() $\mathsf {Q}(\mathfrak {A}_2\times \mathfrak {A}_n)$
are Horn-equivalent to algebras of the form
$\mathsf {Q}(\mathfrak {A}_2\times \mathfrak {A}_n)$
are Horn-equivalent to algebras of the form
![]() $\mathfrak {A}_2\times \mathfrak {A}_{2m}$
, which proves the lemma.
$\mathfrak {A}_2\times \mathfrak {A}_{2m}$
, which proves the lemma.
Lemma 4.14. If
![]() $\mathcal {Q}$
is a non-trivial quasivariety of Sugihara algebras and
$\mathcal {Q}$
is a non-trivial quasivariety of Sugihara algebras and
![]() $\mathcal {Q}\subsetneq \mathsf {Q}(\mathfrak {A}_2\times \mathfrak {A}_{\omega \setminus \{0\}})$
, then
$\mathcal {Q}\subsetneq \mathsf {Q}(\mathfrak {A}_2\times \mathfrak {A}_{\omega \setminus \{0\}})$
, then
![]() $\mathcal {Q}=\mathsf {Q}(\mathfrak {A}_2\times \mathfrak {A}_{2n})$
for some
$\mathcal {Q}=\mathsf {Q}(\mathfrak {A}_2\times \mathfrak {A}_{2n})$
for some
![]() $n\in \omega $
.
$n\in \omega $
.
Proof. Let
![]() $\mathcal {Q}\subseteq \mathsf {Q}(\mathfrak {A}_2\times \mathfrak {A}_{\omega \setminus \{0\}})$
be a quasivariety and
$\mathcal {Q}\subseteq \mathsf {Q}(\mathfrak {A}_2\times \mathfrak {A}_{\omega \setminus \{0\}})$
be a quasivariety and
![]() $\mathcal {Q}\supseteq \mathsf {K}$
be its class of critical algebras. Obviously
$\mathcal {Q}\supseteq \mathsf {K}$
be its class of critical algebras. Obviously
![]() $\mathcal {Q}=\mathsf {Q}(\mathsf {K})$
. By previous reasoning, it must be the case that members of
$\mathcal {Q}=\mathsf {Q}(\mathsf {K})$
. By previous reasoning, it must be the case that members of
![]() $\mathsf {K}$
are of the form
$\mathsf {K}$
are of the form
![]() $\mathfrak {A}_2\times \mathfrak {A}_{2n}$
. Since
$\mathfrak {A}_2\times \mathfrak {A}_{2n}$
. Since
![]() $\mathcal {Q}$
is properly included in
$\mathcal {Q}$
is properly included in
![]() $\mathsf {Q}(\mathfrak {A}_2\times \mathfrak {A}_{\omega \setminus \{0\}})$
it must be the case that
$\mathsf {Q}(\mathfrak {A}_2\times \mathfrak {A}_{\omega \setminus \{0\}})$
it must be the case that
![]() $\mathfrak {A}_2\times \mathfrak {A}_{\omega \setminus \{0\}}\notin \mathcal {Q}$
, which proves the Lemma.
$\mathfrak {A}_2\times \mathfrak {A}_{\omega \setminus \{0\}}\notin \mathcal {Q}$
, which proves the Lemma.
The only remaining step for the main result to follow is to prove the following:
Lemma 4.15.
![]() $\mathsf {Q}(\mathfrak {A}_2\times \mathfrak {A}_3)$
is
$\mathsf {Q}(\mathfrak {A}_2\times \mathfrak {A}_3)$
is
![]() $\mathbf {HSC}$
.
$\mathbf {HSC}$
.
Proof. By Lemma 4.9, we already know that
![]() $\mathsf {Q}(\mathfrak {A}_2\times \mathfrak {A}_3)$
is
$\mathsf {Q}(\mathfrak {A}_2\times \mathfrak {A}_3)$
is
![]() $\mathbf {SC}$
. By Theorem 3.7, we know that it is
$\mathbf {SC}$
. By Theorem 3.7, we know that it is
![]() $\mathbf {HSC}$
as its only subquasivarieties are the Boolean algebras and the trivial class.
$\mathbf {HSC}$
as its only subquasivarieties are the Boolean algebras and the trivial class.
The fundamental Theorem 4.1 follows from Lemmas 4.9–4.11 and 4.13–4.15. Additionally, we have an immediate corollary stating that the quasivarieties from Lemma 4.11 are the only ones that are
![]() $\mathbf {nHSC}$
. Formally, from Lemmas 4.9–4.11, and Theorem 4.1, we derive the following corollary:
$\mathbf {nHSC}$
. Formally, from Lemmas 4.9–4.11, and Theorem 4.1, we derive the following corollary:
Corollary 4.16. The set of all
![]() $\mathbf {nHSC}$
quasivarieties of Sugihara algebras is
$\mathbf {nHSC}$
quasivarieties of Sugihara algebras is
![]() $\{\mathsf {Q}(\mathfrak {A}_2\times \mathfrak {A}_{2k+1}):k\geq 2\}$
.
$\{\mathsf {Q}(\mathfrak {A}_2\times \mathfrak {A}_{2k+1}):k\geq 2\}$
.
The content of Theorem 4.1, along with Corollary 4.16, is depicted in Figure 2.

Figure 2 Structurally complete quasivarieties of Sugihara algebras.
5 Passive structural completeness
Finally, let us note that there is a weaker version of the
![]() $\mathbf {SC}$
property discussed in the literature. This is the concept of overflow, or passive structural completeness, as formulated in [Reference Wroński30]. A logical system (or a quasivariety) is said to be overflow complete if all of its passive admissible rules are derivable. It has been shown that a quasivariety is overflow complete if and only if all of its non-trivial members satisfy exactly the same positive sentences [Reference Wroński30, Fact 2, p. 68]. Recall that a positive first-order sentence is one constructed using the existential quantifier
$\mathbf {SC}$
property discussed in the literature. This is the concept of overflow, or passive structural completeness, as formulated in [Reference Wroński30]. A logical system (or a quasivariety) is said to be overflow complete if all of its passive admissible rules are derivable. It has been shown that a quasivariety is overflow complete if and only if all of its non-trivial members satisfy exactly the same positive sentences [Reference Wroński30, Fact 2, p. 68]. Recall that a positive first-order sentence is one constructed using the existential quantifier
![]() $\exists $
, the falsum constant
$\exists $
, the falsum constant
![]() $\mathbf {f}$
, and the connectives of conjunction
$\mathbf {f}$
, and the connectives of conjunction
![]() $\&$
and disjunction
$\&$
and disjunction
![]() $\veebar $
. Using the previously proven lemmas, along with some new ones, we can provide a Citkin-style characterization of overflow complete extensions of
$\veebar $
. Using the previously proven lemmas, along with some new ones, we can provide a Citkin-style characterization of overflow complete extensions of
![]() $\mathbf {RM}$
in terms of two ‘omitting’ algebras.
$\mathbf {RM}$
in terms of two ‘omitting’ algebras.
In order to prove the theorem, we shall first recall the original Wroński characterization of overflow completeness, and then modify it for our purposes. Standardly, by
![]() $\mathsf {Th}(\mathsf {K})$
we will understand a first-order theory of a class of structures
$\mathsf {Th}(\mathsf {K})$
we will understand a first-order theory of a class of structures
![]() $\mathsf {K}$
.
$\mathsf {K}$
.
Fact 5.1 (Wroński, 2009).
Let
![]() $\mathcal {Q}^+$
be a class of all non-trivial members of a quasivariety
$\mathcal {Q}^+$
be a class of all non-trivial members of a quasivariety
![]() $\mathcal {Q}$
. The following conditions are equivalent:
$\mathcal {Q}$
. The following conditions are equivalent:
-
1.
 $\mathcal {Q}$
is overflow complete.
$\mathcal {Q}$
is overflow complete. -
2.
 $\mathsf {Th}(\mathcal {Q}^+)\cap \{\varphi ,\neg \varphi \}\neq \emptyset $
, for every positive sentence
$\mathsf {Th}(\mathcal {Q}^+)\cap \{\varphi ,\neg \varphi \}\neq \emptyset $
, for every positive sentence
 $\varphi $
.
$\varphi $
.
We can slightly weaken the assumption of the above characterization.
Fact 5.2. Let
![]() $\mathcal {Q}=\mathsf {Q}(\mathsf {K})$
, where
$\mathcal {Q}=\mathsf {Q}(\mathsf {K})$
, where
![]() $\mathsf {K}$
does not contain a trivial algebra. Let
$\mathsf {K}$
does not contain a trivial algebra. Let
![]() $\mathsf {K}^*=\mathsf {K}\cup \{\mathbf {F}_{\mathcal {Q}}(\omega )\}$
. The following conditions are equivalent:
$\mathsf {K}^*=\mathsf {K}\cup \{\mathbf {F}_{\mathcal {Q}}(\omega )\}$
. The following conditions are equivalent:
-
1.
 $\mathcal {Q}$
is overflow complete.
$\mathcal {Q}$
is overflow complete. -
2.
 $\mathsf {Th}(\mathsf {K}^*)\cap \{\varphi ,\neg \varphi \}\neq \emptyset $
, for every positive sentence
$\mathsf {Th}(\mathsf {K}^*)\cap \{\varphi ,\neg \varphi \}\neq \emptyset $
, for every positive sentence
 $\varphi $
.
$\varphi $
.
Proof. One direction follows immediately from the original characterization. The second implication is just a matter of rewriting Wroński’s original proof—the weaker assumption is just enough. For the sake of self-containment let us include it here. Assume 2. Let R be a passive rule which is equivalent to a quasi-identity
![]() $\varphi _1\approx \psi _1 \,\&\, \dots \,\&\,\varphi _n\approx \psi _n\Longrightarrow x\approx y$
. Further, let R be admissible for
$\varphi _1\approx \psi _1 \,\&\, \dots \,\&\,\varphi _n\approx \psi _n\Longrightarrow x\approx y$
. Further, let R be admissible for
![]() $\mathcal {Q}=\mathsf {Q}(\mathsf {K})$
. This means that
$\mathcal {Q}=\mathsf {Q}(\mathsf {K})$
. This means that
![]() $\mathbf {F}_{\mathcal {Q}}(\omega )\nvDash \exists _{x_1,\dots ,x_k}(\varphi _1\approx \psi _1 \,\&\, \dots \,\&\,\varphi _n\approx \psi _n)$
, where
$\mathbf {F}_{\mathcal {Q}}(\omega )\nvDash \exists _{x_1,\dots ,x_k}(\varphi _1\approx \psi _1 \,\&\, \dots \,\&\,\varphi _n\approx \psi _n)$
, where
![]() $x_1,\dots ,x_k$
exhaust all of the variables from the conjunction of identities. From assumption, we get
$x_1,\dots ,x_k$
exhaust all of the variables from the conjunction of identities. From assumption, we get
![]() $\mathsf {K}\nvDash \exists _{x_1,\dots ,x_k}(\varphi _1\approx \psi _1 \,\&\, \dots \,\&\,\varphi _n\approx \psi _n)$
which means that R is derivable.
$\mathsf {K}\nvDash \exists _{x_1,\dots ,x_k}(\varphi _1\approx \psi _1 \,\&\, \dots \,\&\,\varphi _n\approx \psi _n)$
which means that R is derivable.
In the first formulation, proving overflow completeness comes down to showing positive equivalence of all non-trivial members of a given quasivariety. In the second variant, we can restrict ourselves to the generating class plus the free algebra on infinitely many free generators.
Lemma 5.3. For any
![]() $n,m\in \omega $
,
$n,m\in \omega $
,
![]() $\mathfrak {A}_2\times \mathfrak {A}_n$
is positively equivalent to
$\mathfrak {A}_2\times \mathfrak {A}_n$
is positively equivalent to
![]() $\mathfrak {A}_2\times \mathfrak {A}_m$
.
$\mathfrak {A}_2\times \mathfrak {A}_m$
.
Proof. Without the loss of generality assume that
![]() $n\leq m$
. If both n and m are even or if m is odd, then
$n\leq m$
. If both n and m are even or if m is odd, then
![]() $\mathfrak {A}_2\times \mathfrak {A}_n\in \mathsf {Q}(\mathfrak {A}_2\times \mathfrak {A}_m)$
. But by Lemma 4.9
$\mathfrak {A}_2\times \mathfrak {A}_n\in \mathsf {Q}(\mathfrak {A}_2\times \mathfrak {A}_m)$
. But by Lemma 4.9
![]() $\mathsf {Q}(\mathfrak {A}_2\times \mathfrak {A}_m)$
is
$\mathsf {Q}(\mathfrak {A}_2\times \mathfrak {A}_m)$
is
![]() $\mathbf {SC}$
. Thus, it is also overflow complete which by Fact 5.1 means that all of its non-trivial members are positively equivalent. The remaining case is when n is odd and m is even. But then
$\mathbf {SC}$
. Thus, it is also overflow complete which by Fact 5.1 means that all of its non-trivial members are positively equivalent. The remaining case is when n is odd and m is even. But then
![]() $\mathfrak {A}_2\times \mathfrak {A}_n, \mathfrak {A}_2\times \mathfrak {A}_m\in \mathsf {Q}(\mathfrak {A}_2\times \mathfrak {A}_{m+1})$
and we can repeat the reasoning.
$\mathfrak {A}_2\times \mathfrak {A}_n, \mathfrak {A}_2\times \mathfrak {A}_m\in \mathsf {Q}(\mathfrak {A}_2\times \mathfrak {A}_{m+1})$
and we can repeat the reasoning.
Lemma 5.4. Let
![]() $\mathcal {Q}$
be a quasivariety of Sugihara algebras, n a natural number.
$\mathcal {Q}$
be a quasivariety of Sugihara algebras, n a natural number.
![]() $\mathbf {F}_{\mathcal {Q}}(\omega )$
is positively equivalent to
$\mathbf {F}_{\mathcal {Q}}(\omega )$
is positively equivalent to
![]() $\mathfrak {A}_2\times \mathfrak {A}_n$
.
$\mathfrak {A}_2\times \mathfrak {A}_n$
.
Proof. Since
![]() $\mathcal {Q} \sim \mathcal {V}=\mathsf {V}(\mathfrak {A}_\alpha )$
for some ordinal
$\mathcal {Q} \sim \mathcal {V}=\mathsf {V}(\mathfrak {A}_\alpha )$
for some ordinal
![]() $\alpha \leq \omega $
, it must be the case that
$\alpha \leq \omega $
, it must be the case that
![]() $\mathbf {F}_{\mathcal {Q}}(\omega )=\mathbf {F}_{\mathcal {V}}(\omega )$
. If
$\mathbf {F}_{\mathcal {Q}}(\omega )=\mathbf {F}_{\mathcal {V}}(\omega )$
. If
![]() $\alpha $
is a natural number k, then
$\alpha $
is a natural number k, then
![]() $\mathbf {F}_{\mathcal {V}}(\omega )\in \mathsf {Q}(\mathfrak {A}_2\times \mathfrak {A}_k)$
and
$\mathbf {F}_{\mathcal {V}}(\omega )\in \mathsf {Q}(\mathfrak {A}_2\times \mathfrak {A}_k)$
and
![]() $\mathsf {Q}(\mathfrak {A}_2\times \mathfrak {A}_k)$
is
$\mathsf {Q}(\mathfrak {A}_2\times \mathfrak {A}_k)$
is
![]() $\mathbf {SC}$
, so also overflow complete and thus by Fact 5.1
$\mathbf {SC}$
, so also overflow complete and thus by Fact 5.1
![]() $\mathfrak {A}_2\times \mathfrak {A}_k$
is positively equivalent to
$\mathfrak {A}_2\times \mathfrak {A}_k$
is positively equivalent to
![]() $\mathbf {F}_{\mathcal {V}}(\omega )$
. But by Lemma 5.3
$\mathbf {F}_{\mathcal {V}}(\omega )$
. But by Lemma 5.3
![]() $\mathfrak {A}_2\times \mathfrak {A}_k$
is positively equivalent to
$\mathfrak {A}_2\times \mathfrak {A}_k$
is positively equivalent to
![]() $\mathfrak {A}_2\times \mathfrak {A}_n$
, so the result follows. If, on the other hand,
$\mathfrak {A}_2\times \mathfrak {A}_n$
, so the result follows. If, on the other hand,
![]() $\alpha =\omega $
, then
$\alpha =\omega $
, then
![]() $\mathbf {F}_{\mathcal {V}}(\omega )\in \mathsf {Q}(\mathfrak {A}_2\times \mathfrak {A}_{\omega \setminus \{0\}})=\mathsf {Q}(\{\mathfrak {A}_2\times \mathfrak {A}_{2n}:n\geq 0\})$
which is
$\mathbf {F}_{\mathcal {V}}(\omega )\in \mathsf {Q}(\mathfrak {A}_2\times \mathfrak {A}_{\omega \setminus \{0\}})=\mathsf {Q}(\{\mathfrak {A}_2\times \mathfrak {A}_{2n}:n\geq 0\})$
which is
![]() $\mathbf {SC}$
and we repeat the reasoning.
$\mathbf {SC}$
and we repeat the reasoning.
Now we can move on to the proof of the theorem:
Theorem 5.5. A subquasivariety of Sugihara algebras
![]() $\mathcal {Q}$
is overflow complete iff
$\mathcal {Q}$
is overflow complete iff
![]() $\mathfrak {A}_3\notin \mathcal {Q}$
and
$\mathfrak {A}_3\notin \mathcal {Q}$
and
![]() $\mathfrak {A}_4\notin \mathcal {Q}$
.
$\mathfrak {A}_4\notin \mathcal {Q}$
.
Proof. For the left to right direction assume that either
![]() $\mathfrak {A}_4$
or
$\mathfrak {A}_4$
or
![]() $\mathfrak {A}_3$
belong to
$\mathfrak {A}_3$
belong to
![]() $\mathcal {Q}$
. By the Lemma 4.10 it must be the case that
$\mathcal {Q}$
. By the Lemma 4.10 it must be the case that
![]() $\mathfrak {A}_2\times \mathfrak {A}_n\in \mathcal {Q}$
for some
$\mathfrak {A}_2\times \mathfrak {A}_n\in \mathcal {Q}$
for some
![]() $n\leq \omega $
. If
$n\leq \omega $
. If
![]() $\mathfrak {A}_3\in \mathcal {Q}$
, then define
$\mathfrak {A}_3\in \mathcal {Q}$
, then define
![]() $\varphi := \exists x (x=\neg x)$
andFootnote
5
note that
$\varphi := \exists x (x=\neg x)$
andFootnote
5
note that
![]() $\mathfrak {A}_3\Vdash \varphi $
while
$\mathfrak {A}_3\Vdash \varphi $
while
![]() $\mathfrak {A}_2\times \mathfrak {A}_n\nVdash \varphi $
. If
$\mathfrak {A}_2\times \mathfrak {A}_n\nVdash \varphi $
. If
![]() $\mathfrak {A}_4\in \mathcal {Q}$
, then let
$\mathfrak {A}_4\in \mathcal {Q}$
, then let
![]() $\psi :=\exists x\exists y \,(|x|\approx x \,\,\&\,\, |y|\approx y \,\,\&\,\, |\neg (x\to y)|=\neg (x\to y))$
. Observe that
$\psi :=\exists x\exists y \,(|x|\approx x \,\,\&\,\, |y|\approx y \,\,\&\,\, |\neg (x\to y)|=\neg (x\to y))$
. Observe that
![]() $\mathfrak {A}_4\Vdash \psi $
and
$\mathfrak {A}_4\Vdash \psi $
and
![]() $\mathfrak {A}_2\times \mathfrak {A}_n\nVdash \psi $
. This means that
$\mathfrak {A}_2\times \mathfrak {A}_n\nVdash \psi $
. This means that
![]() $\mathcal {Q}$
is not overflow complete.
$\mathcal {Q}$
is not overflow complete.
For the opposite direction assume that
![]() $\mathfrak {A}_3\notin \mathcal {Q}$
and
$\mathfrak {A}_3\notin \mathcal {Q}$
and
![]() $\mathfrak {A}_4\notin \mathcal {Q}$
. We will show that all of its critical algebras are of the form
$\mathfrak {A}_4\notin \mathcal {Q}$
. We will show that all of its critical algebras are of the form
![]() $\mathfrak {A}_2\times \mathfrak {A}_n$
for some
$\mathfrak {A}_2\times \mathfrak {A}_n$
for some
![]() $n\in \omega $
. Obviously
$n\in \omega $
. Obviously
![]() $\mathcal {Q}$
cannot contain any chains longer than
$\mathcal {Q}$
cannot contain any chains longer than
![]() $\mathfrak {A}_2$
. Any algebra of the second type from the Theorem 3.6 must be of the form
$\mathfrak {A}_2$
. Any algebra of the second type from the Theorem 3.6 must be of the form
![]() $\mathfrak {A}_2\times \mathfrak {A}_n$
(otherwise
$\mathfrak {A}_2\times \mathfrak {A}_n$
(otherwise
![]() $\mathfrak {A}_4\in \mathcal {Q}$
). If
$\mathfrak {A}_4\in \mathcal {Q}$
). If
![]() $\mathfrak {B}$
is a non-trivial finite algebra, then
$\mathfrak {B}$
is a non-trivial finite algebra, then
![]() $\mathfrak {A}_4\preceq \bot \mathfrak {B}\top $
, so any algebra of the third type cannot be included in
$\mathfrak {A}_4\preceq \bot \mathfrak {B}\top $
, so any algebra of the third type cannot be included in
![]() $\mathcal {Q}$
. If an algebra is of the fourth type, then by the already established reasoning (Lemmas 4.4 and 4.9) it has to be Horn-equivalent to an algebra of the form
$\mathcal {Q}$
. If an algebra is of the fourth type, then by the already established reasoning (Lemmas 4.4 and 4.9) it has to be Horn-equivalent to an algebra of the form
![]() $\mathfrak {A}_2\times \bot ^l\mathfrak {A}_{2k}\times \mathfrak {A}_j\top ^l$
(otherwise
$\mathfrak {A}_2\times \bot ^l\mathfrak {A}_{2k}\times \mathfrak {A}_j\top ^l$
(otherwise
![]() $\mathfrak {A}_4\in \mathcal {Q}$
). If
$\mathfrak {A}_4\in \mathcal {Q}$
). If
![]() $2k\leq j$
, then Lemma 4.4 applies again and we get an equivalent algebra
$2k\leq j$
, then Lemma 4.4 applies again and we get an equivalent algebra
![]() $\mathfrak {A}_2\times \mathfrak {A}_{j+2l}$
. If
$\mathfrak {A}_2\times \mathfrak {A}_{j+2l}$
. If
![]() $j<2l$
and j is even, then the situation is completely analogous. Lastly, if j is odd and
$j<2l$
and j is even, then the situation is completely analogous. Lastly, if j is odd and
![]() $j<2k$
, then both
$j<2k$
, then both
![]() $\mathfrak {A}_2\times \bot ^l\mathfrak {A}_{2k}\top ^l$
and
$\mathfrak {A}_2\times \bot ^l\mathfrak {A}_{2k}\top ^l$
and
![]() $\mathfrak {A}_2\times \bot ^l\mathfrak {A}_j\top ^l$
are subalgebras of
$\mathfrak {A}_2\times \bot ^l\mathfrak {A}_j\top ^l$
are subalgebras of
![]() $\mathfrak {A}_2\times \bot ^l\mathfrak {A}_{2k}\times \mathfrak {A}_j\top ^l$
. For the first embedding take
$\mathfrak {A}_2\times \bot ^l\mathfrak {A}_{2k}\times \mathfrak {A}_j\top ^l$
. For the first embedding take
![]() $e_1(i,a)=(i,(a,0))$
, if
$e_1(i,a)=(i,(a,0))$
, if
![]() $a\in \mathfrak {A}_{2k}$
and
$a\in \mathfrak {A}_{2k}$
and
![]() $e_1(i,x)=(i,x)$
, if
$e_1(i,x)=(i,x)$
, if
![]() $x\in \{\bot _1,\dots ,\bot _l,\top _1,\dots ,\top _l\}$
. For the embeddability of the second algebra observe that by Lemma 4.4
$x\in \{\bot _1,\dots ,\bot _l,\top _1,\dots ,\top _l\}$
. For the embeddability of the second algebra observe that by Lemma 4.4
![]() $\mathfrak {A}_2\times \bot ^l\mathfrak {A}_j\top ^l\preceq \mathfrak {A}_2\times \bot ^l\mathfrak {A}_2\times \mathfrak {A}_j\top ^l\preceq \mathfrak {A}_2\times \bot ^l\mathfrak {A}_{2k}\times \mathfrak {A}_j\top ^l$
. But then
$\mathfrak {A}_2\times \bot ^l\mathfrak {A}_j\top ^l\preceq \mathfrak {A}_2\times \bot ^l\mathfrak {A}_2\times \mathfrak {A}_j\top ^l\preceq \mathfrak {A}_2\times \bot ^l\mathfrak {A}_{2k}\times \mathfrak {A}_j\top ^l$
. But then
 $\mathfrak {A}_2\times \bot ^l\mathfrak {A}_{2k}\times \mathfrak {A}_j\top ^l\preceq \mathfrak {A}_2\times \mathfrak {A}_2\times \bot ^l\mathfrak {A}_{2k}\top ^l\times \bot ^l\mathfrak {A}_j\top ^l\cong \mathfrak {A}_2\times \bot ^l\mathfrak {A}_{2k}\top ^l\times \mathfrak {A}_2\times \bot ^l\mathfrak {A}_j\top ^l$
Thus
$\mathfrak {A}_2\times \bot ^l\mathfrak {A}_{2k}\times \mathfrak {A}_j\top ^l\preceq \mathfrak {A}_2\times \mathfrak {A}_2\times \bot ^l\mathfrak {A}_{2k}\top ^l\times \bot ^l\mathfrak {A}_j\top ^l\cong \mathfrak {A}_2\times \bot ^l\mathfrak {A}_{2k}\top ^l\times \mathfrak {A}_2\times \bot ^l\mathfrak {A}_j\top ^l$
Thus
![]() $\mathcal {Q}$
is generated by the algebras of the form
$\mathcal {Q}$
is generated by the algebras of the form
![]() $\mathfrak {A}_2\times \mathfrak {A}_n$
, so we can apply Lemmas 5.3 and 5.4 and Fact 5.2 to conclude the proof.
$\mathfrak {A}_2\times \mathfrak {A}_n$
, so we can apply Lemmas 5.3 and 5.4 and Fact 5.2 to conclude the proof.
On the basis of our main Theorems 4.1 and 5.5, we can characterize those quasivarieties of Sugihara algebras which are overflow complete but not
![]() $\mathbf {SC}$
.
$\mathbf {SC}$
.
Corollary 5.6. A quasivariety
![]() $\mathcal {Q}$
of Sugihara algebras is overflow complete but not
$\mathcal {Q}$
of Sugihara algebras is overflow complete but not
![]() $\mathbf {SC}$
iff either:
$\mathbf {SC}$
iff either:
-
(i)
 $\mathcal {Q}=\mathsf {Q}(\mathfrak {A}_2\times \mathfrak {A}_{2n+1},\mathfrak {A}_2\times \mathfrak {A}_{2m})$
for some
$\mathcal {Q}=\mathsf {Q}(\mathfrak {A}_2\times \mathfrak {A}_{2n+1},\mathfrak {A}_2\times \mathfrak {A}_{2m})$
for some
 $m>n$
, or
$m>n$
, or -
(ii)
 $\mathcal {Q}=\mathsf {Q}(\mathfrak {A}_2\times \mathfrak {A}_{\omega \setminus \{0\}}, \mathfrak {A}_2\times \mathfrak {A}_{2n+1})$
for some n, or
$\mathcal {Q}=\mathsf {Q}(\mathfrak {A}_2\times \mathfrak {A}_{\omega \setminus \{0\}}, \mathfrak {A}_2\times \mathfrak {A}_{2n+1})$
for some n, or -
(iii)
 $\mathcal {Q}=\mathsf {Q}(\mathfrak {A}_2\times \mathfrak {A}_{\omega })$
.
$\mathcal {Q}=\mathsf {Q}(\mathfrak {A}_2\times \mathfrak {A}_{\omega })$
.
6 Active structural completeness
Another variant of
![]() $\mathbf {SC}$
is active or almost structural completeness (
$\mathbf {SC}$
is active or almost structural completeness (
![]() $\mathbf {ASC}$
), a concept recently introduced and algebraically developed in [Reference Dzik and Stronkowski13]. This notion can be seen as complementary to
$\mathbf {ASC}$
), a concept recently introduced and algebraically developed in [Reference Dzik and Stronkowski13]. This notion can be seen as complementary to
![]() $\mathbf {PSC}$
. A consequence relation is said to be
$\mathbf {PSC}$
. A consequence relation is said to be
![]() $\mathbf {ASC}$
if its only admissible non-derivable rules are passive.
$\mathbf {ASC}$
if its only admissible non-derivable rules are passive.
We will adopt a strategy similar to the one used previously: first, we will modify the original algebraic characterization of
![]() $\mathbf {ASC}$
to align with the techniques established in the proof of the main theorem. Then, we will apply these methods to characterize all
$\mathbf {ASC}$
to align with the techniques established in the proof of the main theorem. Then, we will apply these methods to characterize all
![]() $\mathbf {ASC}$
subquasivarieties of Sugihara algebras and, subsequently, to isolate those that are
$\mathbf {ASC}$
subquasivarieties of Sugihara algebras and, subsequently, to isolate those that are
![]() $\mathbf {ASC}$
but not
$\mathbf {ASC}$
but not
![]() $\mathbf {SC}$
.
$\mathbf {SC}$
.
Among the many equivalent algebraic properties for a quasivariety to be
![]() $\mathbf {ASC}$
, we recall the condition most useful for our purposes [Reference Dzik and Stronkowski13, Theorem 3.1, p. 532]:
$\mathbf {ASC}$
, we recall the condition most useful for our purposes [Reference Dzik and Stronkowski13, Theorem 3.1, p. 532]:
Theorem 6.1 (Dzik and Stronkowski, 2016).
A quasivariety
![]() $\mathcal {Q}$
is
$\mathcal {Q}$
is
![]() $\mathbf {ASC}$
iff for any
$\mathbf {ASC}$
iff for any
![]() $\mathfrak {A}\in \mathcal {Q}$
,
$\mathfrak {A}\in \mathcal {Q}$
,
![]() $\mathfrak {A}\times \mathbf {F}_{\mathcal {Q}}(\omega )\in \mathsf {I}\mathsf {S}\mathsf {P}\mathsf {P}_{\mathsf {U}}(\mathbf {F}_{\mathcal {Q}}(\omega ))$
.
$\mathfrak {A}\times \mathbf {F}_{\mathcal {Q}}(\omega )\in \mathsf {I}\mathsf {S}\mathsf {P}\mathsf {P}_{\mathsf {U}}(\mathbf {F}_{\mathcal {Q}}(\omega ))$
.
Once again, we will modify the theorem in a manner similar to the approach taken for
![]() $\mathbf {PSC}$
: restricting
$\mathbf {PSC}$
: restricting
![]() $\mathfrak {A}$
to be a critical algebra and replacing the free algebra with the product of a two-element Boolean algebra and a characteristic chain. This leads to the following modified version:
$\mathfrak {A}$
to be a critical algebra and replacing the free algebra with the product of a two-element Boolean algebra and a characteristic chain. This leads to the following modified version:
Lemma 6.2. Let
![]() $\mathcal {Q}$
be a quasivariety of Sugihara algebras such that
$\mathcal {Q}$
be a quasivariety of Sugihara algebras such that
![]() $\mathcal {Q}\sim \mathsf {V}(\mathfrak {A}_n)$
for some
$\mathcal {Q}\sim \mathsf {V}(\mathfrak {A}_n)$
for some
![]() $n\in \omega $
. Then
$n\in \omega $
. Then
![]() $\mathcal {Q}$
is
$\mathcal {Q}$
is
![]() $\mathbf {ASC}$
iff for any critical
$\mathbf {ASC}$
iff for any critical
![]() $\mathfrak {B}\in \mathcal {Q}$
,
$\mathfrak {B}\in \mathcal {Q}$
,
![]() $\mathfrak {B}\times \mathfrak {A}_2\times \mathfrak {A}_n\in \mathsf {I}\mathsf {S}\mathsf {P}\mathsf {P}_{\mathsf {U}}(\mathfrak {A}_2\times \mathfrak {A}_n)$
. If
$\mathfrak {B}\times \mathfrak {A}_2\times \mathfrak {A}_n\in \mathsf {I}\mathsf {S}\mathsf {P}\mathsf {P}_{\mathsf {U}}(\mathfrak {A}_2\times \mathfrak {A}_n)$
. If
![]() $\mathcal {Q}\sim \mathsf {V}(\mathfrak {A}_\omega )$
, then
$\mathcal {Q}\sim \mathsf {V}(\mathfrak {A}_\omega )$
, then
![]() $\mathcal {Q}$
is
$\mathcal {Q}$
is
![]() $\mathbf {ASC}$
iff for any critical
$\mathbf {ASC}$
iff for any critical
![]() $\mathfrak {B}\in \mathcal {Q}$
,
$\mathfrak {B}\in \mathcal {Q}$
,
![]() $\mathfrak {B}\times \mathfrak {A}_2\times \mathfrak {A}_{\omega \setminus \{0\}}\in \mathsf {I}\mathsf {S}\mathsf {P}\mathsf {P}_{\mathsf {U}}(\mathfrak {A}_2\times \mathfrak {A}_{\omega \setminus \{0\}})$
.
$\mathfrak {B}\times \mathfrak {A}_2\times \mathfrak {A}_{\omega \setminus \{0\}}\in \mathsf {I}\mathsf {S}\mathsf {P}\mathsf {P}_{\mathsf {U}}(\mathfrak {A}_2\times \mathfrak {A}_{\omega \setminus \{0\}})$
.
Proof. Let
![]() $\mathcal {Q}\sim \mathsf {V}(\mathfrak {A}_n)$
.
$\mathcal {Q}\sim \mathsf {V}(\mathfrak {A}_n)$
.
Assume that
![]() $\mathcal {Q}$
is
$\mathcal {Q}$
is
![]() $\mathbf {ASC}$
. Let
$\mathbf {ASC}$
. Let
![]() $q:=\varphi \Rightarrow s(x_1,\dots ,x_n)\approx t(x_1,\dots ,x_n)$
where
$q:=\varphi \Rightarrow s(x_1,\dots ,x_n)\approx t(x_1,\dots ,x_n)$
where
![]() $\varphi :=s_0(x_1,\dots ,x_n)\approx t_0(x_1,\dots ,x_n)\,\&\ldots \&\,s_k(x_1,\dots ,x_n)\approx t_k(x_1,\dots ,x_n)$
be such that
$\varphi :=s_0(x_1,\dots ,x_n)\approx t_0(x_1,\dots ,x_n)\,\&\ldots \&\,s_k(x_1,\dots ,x_n)\approx t_k(x_1,\dots ,x_n)$
be such that
![]() $\mathbf {F}_{\mathcal {Q}}(\omega )\vDash q$
. Let
$\mathbf {F}_{\mathcal {Q}}(\omega )\vDash q$
. Let
![]() $\mathfrak {B}\in \mathcal {Q}$
. If q is passive, then
$\mathfrak {B}\in \mathcal {Q}$
. If q is passive, then
![]() $\mathbf {F}_{\mathcal {Q}}(\omega )\nvDash \exists x_1,\dots ,x_n\varphi $
. By Lemmas 5.3 and 5.4 we get
$\mathbf {F}_{\mathcal {Q}}(\omega )\nvDash \exists x_1,\dots ,x_n\varphi $
. By Lemmas 5.3 and 5.4 we get
![]() $\mathfrak {A}_2\times \mathfrak {A}_n\nvDash \exists x_1,\dots ,x_n\varphi $
. But then also
$\mathfrak {A}_2\times \mathfrak {A}_n\nvDash \exists x_1,\dots ,x_n\varphi $
. But then also
![]() $\mathfrak {B}\times \mathfrak {A}_2\times \mathfrak {A}_n\nvDash \exists x_1,\dots ,x_n\varphi $
which vacuously means
$\mathfrak {B}\times \mathfrak {A}_2\times \mathfrak {A}_n\nvDash \exists x_1,\dots ,x_n\varphi $
which vacuously means
![]() $\mathfrak {B}\times \mathfrak {A}_2\times \mathfrak {A}_n\vDash q$
. Now, assume that q is not passive. But then q is derivable in
$\mathfrak {B}\times \mathfrak {A}_2\times \mathfrak {A}_n\vDash q$
. Now, assume that q is not passive. But then q is derivable in
![]() $\mathcal {Q}$
, so
$\mathcal {Q}$
, so
![]() $\mathfrak {B}\vDash q$
and also
$\mathfrak {B}\vDash q$
and also
![]() $\mathfrak {B}\times \mathfrak {A}_2\times \mathfrak {A}_n\vDash q$
.
$\mathfrak {B}\times \mathfrak {A}_2\times \mathfrak {A}_n\vDash q$
.
For the other direction, let
![]() $q:=(s_0(\overline {x})\approx t_0(\overline {x})\,\&\ldots \&\, s_k(\overline {x})\approx t_k(\overline {x}))\Rightarrow s(\overline {x})\approx t(\overline {x})$
where
$q:=(s_0(\overline {x})\approx t_0(\overline {x})\,\&\ldots \&\, s_k(\overline {x})\approx t_k(\overline {x}))\Rightarrow s(\overline {x})\approx t(\overline {x})$
where
![]() $\overline {x}=x_1,\ldots , x_n$
be an admissible rule in
$\overline {x}=x_1,\ldots , x_n$
be an admissible rule in
![]() $\mathcal {Q}$
. Thus,
$\mathcal {Q}$
. Thus,
![]() $\mathbf {F}_{\mathcal {Q}}(\omega )\vDash q$
. By Lemma 4.9, this means that
$\mathbf {F}_{\mathcal {Q}}(\omega )\vDash q$
. By Lemma 4.9, this means that
![]() $\mathfrak {A}_2\times \mathfrak {A}_n\vDash q$
. Suppose further that there is a critical
$\mathfrak {A}_2\times \mathfrak {A}_n\vDash q$
. Suppose further that there is a critical
![]() $\mathfrak {B}\in \mathcal {Q}$
such that
$\mathfrak {B}\in \mathcal {Q}$
such that
![]() $\mathfrak {B}\nvDash q$
. Then there are
$\mathfrak {B}\nvDash q$
. Then there are
![]() $b_1,\dots ,b_n\in \mathsf {B}$
such that
$b_1,\dots ,b_n\in \mathsf {B}$
such that
![]() $s_0(b_1,\dots ,b_n)=t_0(b_1,\dots ,b_n)$
,…,
$s_0(b_1,\dots ,b_n)=t_0(b_1,\dots ,b_n)$
,…,
![]() $s_k(b_1,\dots ,b_n)= t_k(b_1,\dots ,b_n)$
and
$s_k(b_1,\dots ,b_n)= t_k(b_1,\dots ,b_n)$
and
![]() $s(b_1,\dots ,b_n)\neq t(b_1,\dots ,b_n)$
. Let
$s(b_1,\dots ,b_n)\neq t(b_1,\dots ,b_n)$
. Let
![]() $\varphi :=(s_0(\overline {x})\approx t_0(\overline {x})\,\&\ldots \&\,s_k(\overline {x})\approx t_k(\overline {x}))$
. Assume for reductio that
$\varphi :=(s_0(\overline {x})\approx t_0(\overline {x})\,\&\ldots \&\,s_k(\overline {x})\approx t_k(\overline {x}))$
. Assume for reductio that
![]() $\mathbf {F}_{\mathcal {Q}}(\omega )\vDash \exists \overline {x}\varphi $
. By Lemmas 5.3 and 5.4 we get that
$\mathbf {F}_{\mathcal {Q}}(\omega )\vDash \exists \overline {x}\varphi $
. By Lemmas 5.3 and 5.4 we get that
![]() $\mathfrak {A}_2\times \mathfrak {A}_n\vDash \exists \overline {x}\varphi $
. Let
$\mathfrak {A}_2\times \mathfrak {A}_n\vDash \exists \overline {x}\varphi $
. Let
![]() $a_1,\dots ,a_n\in \mathfrak {A}_2\times \mathfrak {A}_n$
be such that
$a_1,\dots ,a_n\in \mathfrak {A}_2\times \mathfrak {A}_n$
be such that
![]() $s_0(a_1,\dots ,a_n)=t_0(a_1,\dots ,a_n)$
,…,
$s_0(a_1,\dots ,a_n)=t_0(a_1,\dots ,a_n)$
,…,
![]() $s_k(a_1,\dots ,a_n)= t_k(a_1,\dots ,a_n)$
. But then
$s_k(a_1,\dots ,a_n)= t_k(a_1,\dots ,a_n)$
. But then
![]() $s_0((a_1,b_1),\dots ,(a_n,b_n))=t_0((a_1,b_1),\dots ,(a_n,b_n))$
,…,
$s_0((a_1,b_1),\dots ,(a_n,b_n))=t_0((a_1,b_1),\dots ,(a_n,b_n))$
,…,
![]() $s_k((a_1,b_1),\dots ,(a_n,b_n))= t_k((a_1,b_1),\dots ,(a_n,b_n))$
, but
$s_k((a_1,b_1),\dots ,(a_n,b_n))= t_k((a_1,b_1),\dots ,(a_n,b_n))$
, but
![]() $s((a_1,b_1),\dots ,(a_n,b_n))$
$s((a_1,b_1),\dots ,(a_n,b_n))$
![]() $\neq t((a_1,b_1),\dots ,(a_n,b_n))$
. This means that
$\neq t((a_1,b_1),\dots ,(a_n,b_n))$
. This means that
![]() $\mathfrak {A}\times \mathfrak {A}_2\times \mathfrak {A}_n\nvDash q$
—contradiction. Thus
$\mathfrak {A}\times \mathfrak {A}_2\times \mathfrak {A}_n\nvDash q$
—contradiction. Thus
![]() $\mathbf {F}_{\mathcal {Q}}(\omega )\nvDash \exists \overline {x}\varphi $
which means that q is passive, so
$\mathbf {F}_{\mathcal {Q}}(\omega )\nvDash \exists \overline {x}\varphi $
which means that q is passive, so
![]() $\mathcal {Q}$
is
$\mathcal {Q}$
is
![]() $\mathbf {ASC}$
.
$\mathbf {ASC}$
.
The case where
![]() $\mathcal {Q}\sim \mathsf {V}(\mathfrak {A}_\omega )$
is covered similarly—just substitute
$\mathcal {Q}\sim \mathsf {V}(\mathfrak {A}_\omega )$
is covered similarly—just substitute
![]() $\mathfrak {A}_2\times \mathfrak {A}_{\omega \setminus \{0\}}$
for
$\mathfrak {A}_2\times \mathfrak {A}_{\omega \setminus \{0\}}$
for
![]() $\mathfrak {A}_2\times \mathfrak {A}_n$
in the above proof.
$\mathfrak {A}_2\times \mathfrak {A}_n$
in the above proof.
Theorem 6.3. Let
![]() $\mathcal {Q}$
be a quasivariety of Sugihara algebras.
$\mathcal {Q}$
be a quasivariety of Sugihara algebras.
![]() $\mathcal {Q}$
is
$\mathcal {Q}$
is
![]() $\mathbf {ASC}$
iff either:
$\mathbf {ASC}$
iff either:
![]() $\mathfrak {A}_2\times \mathfrak {A}_3\notin \mathcal {Q}$
or
$\mathfrak {A}_2\times \mathfrak {A}_3\notin \mathcal {Q}$
or
![]() $\mathcal {Q}\sim \mathsf {V}(\mathfrak {A}_{2n+1})$
for some
$\mathcal {Q}\sim \mathsf {V}(\mathfrak {A}_{2n+1})$
for some
![]() $n\in \omega $
.
$n\in \omega $
.
Proof. For one direction, assume that
![]() $\mathcal {Q}\not \sim (\mathfrak {A}_{2n+1})$
and
$\mathcal {Q}\not \sim (\mathfrak {A}_{2n+1})$
and
![]() $\mathfrak {A}_2\times \mathfrak {A}_3\in \mathcal {Q}$
. Thus, either i)
$\mathfrak {A}_2\times \mathfrak {A}_3\in \mathcal {Q}$
. Thus, either i)
![]() $\mathcal {Q}\sim \mathsf {V}(\mathfrak {A}_{2n})$
, where
$\mathcal {Q}\sim \mathsf {V}(\mathfrak {A}_{2n})$
, where
![]() $n\geq 2$
(if
$n\geq 2$
(if
![]() $n=1$
, then it must be the case that
$n=1$
, then it must be the case that
![]() $\mathfrak {A}_2\times \mathfrak {A}_3\notin \mathcal {Q}$
), or ii)
$\mathfrak {A}_2\times \mathfrak {A}_3\notin \mathcal {Q}$
), or ii)
![]() $\mathcal {Q}\sim \mathsf {V}(\mathfrak {A}_\omega )$
. But then
$\mathcal {Q}\sim \mathsf {V}(\mathfrak {A}_\omega )$
. But then
![]() $\mathfrak {A}_2\times \mathfrak {A}_3\preceq \mathfrak {A}_2\times \mathfrak {A}_3\times \mathfrak {A}_2\times \mathfrak {A}_{2n}\notin \mathcal {Q}(\mathfrak {A}_2\times \mathfrak {A}_{2n})$
which by Lemma 6.2 means that
$\mathfrak {A}_2\times \mathfrak {A}_3\preceq \mathfrak {A}_2\times \mathfrak {A}_3\times \mathfrak {A}_2\times \mathfrak {A}_{2n}\notin \mathcal {Q}(\mathfrak {A}_2\times \mathfrak {A}_{2n})$
which by Lemma 6.2 means that
![]() $\mathcal {Q}$
is not
$\mathcal {Q}$
is not
![]() $\mathbf {ASC}$
. If
$\mathbf {ASC}$
. If
![]() $\mathcal {Q}\sim \mathsf {V}(\mathfrak {A}_\omega )$
, then
$\mathcal {Q}\sim \mathsf {V}(\mathfrak {A}_\omega )$
, then
![]() $\mathfrak {A}_2\times \mathfrak {A}_3\preceq \mathfrak {A}_2\times \mathfrak {A}_3\times \mathfrak {A}_2\times \mathfrak {A}_{\omega \setminus \{0\}}\notin \mathcal {Q}(\mathfrak {A}_2\times \mathfrak {A}_{\omega \setminus \{0\}})$
.
$\mathfrak {A}_2\times \mathfrak {A}_3\preceq \mathfrak {A}_2\times \mathfrak {A}_3\times \mathfrak {A}_2\times \mathfrak {A}_{\omega \setminus \{0\}}\notin \mathcal {Q}(\mathfrak {A}_2\times \mathfrak {A}_{\omega \setminus \{0\}})$
.
For the opposite direction, first assume that
![]() $\mathcal {Q}\sim \mathsf {V}(\mathfrak {A}_{2n+1})$
. We will show that for any critical algebra
$\mathcal {Q}\sim \mathsf {V}(\mathfrak {A}_{2n+1})$
. We will show that for any critical algebra
![]() $\mathfrak {B}$
of
$\mathfrak {B}$
of
![]() $\mathcal {Q}$
it is the case that
$\mathcal {Q}$
it is the case that
![]() $\mathfrak {A}_2\times \mathfrak {B}\times \mathfrak {A}_{2n+1}\approx _{\mathsf {q}}\mathfrak {A}_2\times \mathfrak {A}_{2n+1}$
. By Lemma 6.2, this will be enough to show that
$\mathfrak {A}_2\times \mathfrak {B}\times \mathfrak {A}_{2n+1}\approx _{\mathsf {q}}\mathfrak {A}_2\times \mathfrak {A}_{2n+1}$
. By Lemma 6.2, this will be enough to show that
![]() $\mathcal {Q}$
is
$\mathcal {Q}$
is
![]() $\mathbf {ASC}$
. Let
$\mathbf {ASC}$
. Let
![]() $\mathfrak {B}\in \mathcal {Q}$
be critical. By Lemma 4.7, its degree must be less or equal to
$\mathfrak {B}\in \mathcal {Q}$
be critical. By Lemma 4.7, its degree must be less or equal to
![]() $2n+1$
. Thus we can keep applying the reasoning from the simplification Lemma 4.4 to obtain Horn equivalence.
$2n+1$
. Thus we can keep applying the reasoning from the simplification Lemma 4.4 to obtain Horn equivalence.
In case
![]() $\mathcal {Q}\not \sim \mathsf {V}(\mathfrak {A}_{2n+1})$
, we have that
$\mathcal {Q}\not \sim \mathsf {V}(\mathfrak {A}_{2n+1})$
, we have that
![]() $\mathfrak {A}_2\times \mathfrak {A}_3\notin \mathcal {Q}$
. But this means that for any critical
$\mathfrak {A}_2\times \mathfrak {A}_3\notin \mathcal {Q}$
. But this means that for any critical
![]() $\mathfrak {B}\in \mathcal {Q}$
it must be the case that
$\mathfrak {B}\in \mathcal {Q}$
it must be the case that
![]() $deg(\mathfrak {B})$
is even (otherwise
$deg(\mathfrak {B})$
is even (otherwise
![]() $\mathfrak {A}_2\times \mathfrak {A}_3\preceq \mathfrak {A}_2\times \mathfrak {B}$
). But then by our key simplification Lemma 4.4 we have
$\mathfrak {A}_2\times \mathfrak {A}_3\preceq \mathfrak {A}_2\times \mathfrak {B}$
). But then by our key simplification Lemma 4.4 we have
![]() $\mathfrak {A}_2\times \mathfrak {B}\approx _{\mathsf {q}}\mathfrak {A}_2\times \mathfrak {A}_{2m}$
for some m. Furthermore,
$\mathfrak {A}_2\times \mathfrak {B}\approx _{\mathsf {q}}\mathfrak {A}_2\times \mathfrak {A}_{2m}$
for some m. Furthermore,
![]() $\mathfrak {A}_2\times \mathfrak {B}\times \mathfrak {A}_{2n}\approx _{\mathsf {q}}\mathfrak {A}_2\times \mathfrak {A}_{2n}$
for any
$\mathfrak {A}_2\times \mathfrak {B}\times \mathfrak {A}_{2n}\approx _{\mathsf {q}}\mathfrak {A}_2\times \mathfrak {A}_{2n}$
for any
![]() $n>m$
which proves the theorem.
$n>m$
which proves the theorem.
We have an immediate corollary:
Corollary 6.4.
![]() $\mathcal {Q}$
is
$\mathcal {Q}$
is
![]() $\mathbf {ASC}$
but not
$\mathbf {ASC}$
but not
![]() $\mathbf {SC}$
iff either:
$\mathbf {SC}$
iff either:
-
(i)
 $\mathfrak {A}_3\in \mathcal {Q}\sim \mathsf {V}(\mathfrak {A}_{2n+1})$
for some
$\mathfrak {A}_3\in \mathcal {Q}\sim \mathsf {V}(\mathfrak {A}_{2n+1})$
for some
 $n\in \omega $
, or
$n\in \omega $
, or -
(ii)
 $\mathfrak {A}_4\in \mathcal {Q}\sim \mathsf {V}(\mathfrak {A}_{2n+1})$
for some
$\mathfrak {A}_4\in \mathcal {Q}\sim \mathsf {V}(\mathfrak {A}_{2n+1})$
for some
 $n\in \omega $
, or
$n\in \omega $
, or -
(iii)
 $\mathfrak {A}_4\in \mathcal {Q}$
and
$\mathfrak {A}_4\in \mathcal {Q}$
and
 $\mathfrak {A}_2\times \mathfrak {A}_3\notin \mathcal {Q}$
.
$\mathfrak {A}_2\times \mathfrak {A}_3\notin \mathcal {Q}$
.
7 Conclusion
Let us conclude with several remarks. First, observe that if it were not for
![]() $\mathsf {Q}(\mathfrak {A}_2\times \mathfrak {A}_3)$
, the poset of
$\mathsf {Q}(\mathfrak {A}_2\times \mathfrak {A}_3)$
, the poset of
![]() $\mathbf {RM}$
’s
$\mathbf {RM}$
’s
![]() $\mathbf {HSC}$
extensions would be a chain—a chain isomorphic to
$\mathbf {HSC}$
extensions would be a chain—a chain isomorphic to
![]() $\mathbf {RM}$
’s axiomatic extensions. The covering relation in the
$\mathbf {RM}$
’s axiomatic extensions. The covering relation in the
![]() $\mathbf {HSC}$
poset of Figure 2a is the restricted covering relation within the entire lattice of Sugihara quasivarieties. In contrast, the
$\mathbf {HSC}$
poset of Figure 2a is the restricted covering relation within the entire lattice of Sugihara quasivarieties. In contrast, the
![]() $\mathbf {nHSC}$
quasivarieties form a chain; however, the covering relation in its lattice, shown in Figure 2b, is not a restriction of the covering relation in the entire lattice of Sugihara quasivarieties. To see this, note that we have
$\mathbf {nHSC}$
quasivarieties form a chain; however, the covering relation in its lattice, shown in Figure 2b, is not a restriction of the covering relation in the entire lattice of Sugihara quasivarieties. To see this, note that we have
![]() $\mathsf {Q}(\mathfrak {A}_2\times \mathfrak {A}_{2n+1})\supsetneq \mathsf {Q}(\mathfrak {A}_2\times \mathfrak {A}_{2n},\mathfrak {A}_2\times \mathfrak {A}_{2n-1})\supsetneq \mathsf {Q}(\mathfrak {A}_2\times \mathfrak {A}_{2n-1})$
.
$\mathsf {Q}(\mathfrak {A}_2\times \mathfrak {A}_{2n+1})\supsetneq \mathsf {Q}(\mathfrak {A}_2\times \mathfrak {A}_{2n},\mathfrak {A}_2\times \mathfrak {A}_{2n-1})\supsetneq \mathsf {Q}(\mathfrak {A}_2\times \mathfrak {A}_{2n-1})$
.
Next, let us examine the three rules from Lemma 4.12 more closely. All of these rules are admissible in
![]() $\mathbf {RM}$
—we have shown that they are derivable for
$\mathbf {RM}$
—we have shown that they are derivable for
![]() $\mathsf {I}\mathsf {S}\mathsf {P}\mathsf {P}_{\mathsf {U}}(\mathfrak {A}_2\times \mathfrak {A}_{\omega \setminus \{0\}})$
, and the logic associated with this quasivariety is
$\mathsf {I}\mathsf {S}\mathsf {P}\mathsf {P}_{\mathsf {U}}(\mathfrak {A}_2\times \mathfrak {A}_{\omega \setminus \{0\}})$
, and the logic associated with this quasivariety is
![]() $\mathbf {RM}$
’s
$\mathbf {RM}$
’s
![]() $\mathbf {SC}$
extension with the same set of theorems (admissible rules).Footnote
6
The first and third rules are similar in a certain way: arbitrary formulas follow from their premises, so proving their non-derivability in a given Sugihara matrix involves finding an interpretation under which the set of premises is satisfiable. Failure of
$\mathbf {SC}$
extension with the same set of theorems (admissible rules).Footnote
6
The first and third rules are similar in a certain way: arbitrary formulas follow from their premises, so proving their non-derivability in a given Sugihara matrix involves finding an interpretation under which the set of premises is satisfiable. Failure of
![]() $\mathtt {NP}$
satisfaction has commonly been adopted as a definition of paraconsistency. The
$\mathtt {NP}$
satisfaction has commonly been adopted as a definition of paraconsistency. The
![]() $\mathtt {R}$
rule, on the other hand, is a new rule introduced specifically to separate algebras containing the 4-element Sugihara subchain from the
$\mathtt {R}$
rule, on the other hand, is a new rule introduced specifically to separate algebras containing the 4-element Sugihara subchain from the
![]() $\mathbf {HSC}$
quasivarieties. A somewhat similar rule can be found in Tokarz’s work [Reference Tokarz28, p. 66]. Tokarz’s rule takes the form
$\mathbf {HSC}$
quasivarieties. A somewhat similar rule can be found in Tokarz’s work [Reference Tokarz28, p. 66]. Tokarz’s rule takes the form
![]() ${\neg ((p\to p)\leftrightarrow (q\to q)}/r$
. This rule can also be observed to hold in
${\neg ((p\to p)\leftrightarrow (q\to q)}/r$
. This rule can also be observed to hold in
![]() $\mathfrak {A}_2\times \mathfrak {A}_{\omega \setminus {0}}$
but not in
$\mathfrak {A}_2\times \mathfrak {A}_{\omega \setminus {0}}$
but not in
![]() $\mathfrak {A}_4$
. Lastly, the only non-passive rule from Lemma 4.12 is the disjunctive syllogism
$\mathfrak {A}_4$
. Lastly, the only non-passive rule from Lemma 4.12 is the disjunctive syllogism
![]() $\mathtt {DS}$
, also referred to as the
$\mathtt {DS}$
, also referred to as the
![]() $(\gamma )$
rule in [Reference Anderson and Belnap4]. The structural incompleteness of
$(\gamma )$
rule in [Reference Anderson and Belnap4]. The structural incompleteness of
![]() $\mathbf {R}$
has long been known, stemming from the nonderivability of
$\mathbf {R}$
has long been known, stemming from the nonderivability of
![]() $\mathtt {DS}$
.
$\mathtt {DS}$
.
Finally, to put our result in a broader context, let us once again mention
![]() $\mathbf {RM}^{\mathbf {t}}$
and its positive fragment. As it turns out, odd Sugihara monoids, which serve as adequate semantics for
$\mathbf {RM}^{\mathbf {t}}$
and its positive fragment. As it turns out, odd Sugihara monoids, which serve as adequate semantics for
![]() $\mathbf {RM}^{\mathbf {t}}$
, are categorically equivalent to relative Stone algebras, which, in turn, provide adequate algebraic semantics for positive fragment Gödel–Dummett logic (for representation theorems for Sugihara monoids, see [Reference Fussner and Galatos15–Reference Galatos and Raftery17]). The lattice of subvarieties of linear Stone algebras forms an
$\mathbf {RM}^{\mathbf {t}}$
, are categorically equivalent to relative Stone algebras, which, in turn, provide adequate algebraic semantics for positive fragment Gödel–Dummett logic (for representation theorems for Sugihara monoids, see [Reference Fussner and Galatos15–Reference Galatos and Raftery17]). The lattice of subvarieties of linear Stone algebras forms an
![]() $\omega ^+$
well-ordering, just like the subvarieties of Sugihara algebras. Gödel–Dummett logic is known to be hereditarily structurally complete (HSC) [Reference Dzik and Wroński14, Reference Prucnal25], which, in algebraic terms, implies that any subquasivariety of Stone algebras is, in fact, a variety. By categorical equivalence, this property also holds for odd Sugihara monoids.
$\omega ^+$
well-ordering, just like the subvarieties of Sugihara algebras. Gödel–Dummett logic is known to be hereditarily structurally complete (HSC) [Reference Dzik and Wroński14, Reference Prucnal25], which, in algebraic terms, implies that any subquasivariety of Stone algebras is, in fact, a variety. By categorical equivalence, this property also holds for odd Sugihara monoids.
More generally, it is interesting to note that having isomorphic lattices of subvarieties does not necessarily yield any similarity in the structure of respective lattices of subquasivarieties. It is known that the structure of subvarieties of p-algebras (implication-free reducts of Heyting algebras with intuitionistic negation) is also that of
![]() $\omega ^+$
well-ordering, yet the lattice of its subquasivarieties is uncountable [Reference Adams1, Reference Wroński29]. The cardinality of the set of subquasivarieties of Sugihara algebras remain unknown. It has been established that the number of subquasivarieties of a quasivariety generated by a finite set of finite Sugihara algebras has to be finite [Reference Blok and Dziobiak6]. Thus, the cardinality of the whole lattice must be determined by the size of the class
$\omega ^+$
well-ordering, yet the lattice of its subquasivarieties is uncountable [Reference Adams1, Reference Wroński29]. The cardinality of the set of subquasivarieties of Sugihara algebras remain unknown. It has been established that the number of subquasivarieties of a quasivariety generated by a finite set of finite Sugihara algebras has to be finite [Reference Blok and Dziobiak6]. Thus, the cardinality of the whole lattice must be determined by the size of the class
![]() $[\mathsf {V}(\mathfrak {A}_\omega )]_\sim $
.
$[\mathsf {V}(\mathfrak {A}_\omega )]_\sim $
.
There are two clear conclusions to be drawn from these final remarks. First, modifying the original signature of the logic or its corresponding algebras (as in this case, by adding the constant
![]() $\mathbf {t}$
or removing negation) can significantly alter the structure of the extensions of a given logic. Secondly, an isomorphism between the lattices of subvarieties of two classes of algebras does not necessarily imply any similarity in the structure of their lattices of subquasivarieties.
$\mathbf {t}$
or removing negation) can significantly alter the structure of the extensions of a given logic. Secondly, an isomorphism between the lattices of subvarieties of two classes of algebras does not necessarily imply any similarity in the structure of their lattices of subquasivarieties.
Funding
This research has been funded by the National Science Center (Poland), grant number 2022/45/B/HS1/00606.