Hostname: page-component-f554764f5-246sw Total loading time: 0 Render date: 2025-04-14T15:09:45.227Z Has data issue: false hasContentIssue false
  • English
  • Français

A NOTE ON THE NON-EXISTENCE OF PRIME MODELS OF THEORIES OF PSEUDO-FINITE FIELDS

Part of: Connections with logic Model theory

Published online by Cambridge University Press:  03 March 2025

ZOÉ CHATZIDAKIS Open the ORCID record for ZOÉ CHATZIDAKIS [Opens in a new window]
ZOÉ CHATZIDAKIS*
Affiliation:
CNRS (IMJ-PRG) SORBONNE UNIVERSITÉ UNIVERSITÉ PARIS CITÉ PARIS, FRANCE
*
Email: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We show that if a field A is not pseudo-finite, then there is no prime model of the theory of pseudo-finite fields over A. Assuming GCH, we extend this result to 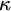$\kappa $-prime models, for 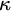$\kappa $ an uncountable cardinal or 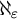$\aleph _\varepsilon $.

Keywords

pseudo-finite fieldsprime models

MSC classification

Primary: 03C60: Model-theoretic algebra 12L12: Model theory
Type
Article
Information
The Journal of Symbolic Logic , Volume 90 , Issue 1 , March 2025 , pp. 52 - 67
Check for updates
Copyright
© The Author(s), 2025. Published by Cambridge University Press on behalf of The Association for Symbolic Logic

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

Footnotes

†

Editor’s note: Sadly, Zoé Chatzidakis passed away on January 22 this year. The last revision of the present paper was prepared by her on November 2024 and only a few typos have been corrected. The files were recovered thanks to Tamara Servi. We thank her and also the anonymous referee for their help in making possible the publication.

References

REFERENCES

Ax, J., The elementary theory of finite fields . Annals of Mathematics , vol. 88 (1968), pp. 239–271.Google Scholar
Chatzidakis, Z., Remarks around the non-existence of difference closure . Model Theory , vol. 2 (2023), no 2. pp. 405–427.Google Scholar
Chatzidakis, Z. and Pillay, A., Generic structures and simple theories . Annals of Pure and Applied Logic , vol. 95 (1998), pp. 71–92.Google Scholar
Fried, M. and Jarden, M., Field Arithmetic , second ed., Ergebnisse, 11, Springer, Berlin, 2005.Google Scholar
Hrushovski, E., Pseudo-finite fields and related structures, Model Theory and Applications (Bélair et al., editors), Quaderni di Matematica, 11, Aracne, Rome, 2005, pp. 151–212.Google Scholar
Lang, S., Introduction to Algebraic Geometry , Addison-Wesley Pub. Co., Menlo Park, 1973.Google Scholar