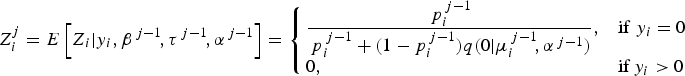1. INTRODUCTION
The shipping industry has witnessed a rapid growth in the last three decades because of the significant increase in transportation demands. Shipping movements are operated in complex and high-risk envolutions, and many shipping accidents occur at sea as well as in restricted waters (Akten, Reference Akten2004). Factors such as collision, contact, fire/explosion, grounding, material/hull damage, sinking, darkness and adverse weather conditions affect the seriousness of a shipping accidents in many different ways.
Shipping lines have shown an increasing tendency to use larger sized ships because of their scale advantages. However, a large ship has reduced manoeuvrability, which ultimately increases its accident risk (Chapman and Akten, Reference Chapman and Akten1998). Since a bigger size generates a corresponding increase in cargo and passengers, this may lead to catastrophic consequences in terms of loss of human life. It is incumbent upon policy-makers to implement efficient navigational safety strategies with the objective of decreasing the loss of human life if an accident does occur. Considering the limited available resources and budgets, policy-makers have to prioritise safety strategies. This can be achieved with the help of a comprehensive understanding of the contributory factors that affect the loss of human life.
Numerous studies have been carried out to analyse past shipping accidents. A major focus was placed on fishing accidents in these studies (e.g., Jin et al., Reference Jin, Kite-Powell and Talley2001; Jin and Thunberg, Reference Jin and Thunberg2005; Perez-Labajos et al., Reference Perez-Labajos, Azofra, Blanco, Achutegui and Gonzalez2006; Perez-Labajos et al., Reference Perez-Labajos, Blanco, Azofra, Achutegui and Eguia2009; Roberts et al., Reference Roberts, Jaremin and Marlow2010). However, it should be noted that these results were only applicable to fishing vessels. Considering all ship types, some other researchers (e.g., Birpinar et al., Reference Birpinar, Talu and Gonencgil2009; Aydogdu et al., Reference Aydogdu, Yurtoren, Park and Park2012) also investigated the relationship between the contributory factors and the risk of shipping accidents. Nevertheless, the data sources used for the analysis were for specific water areas. The results and findings may not be the same for other water areas.
The South China Sea is one of the world's busiest international sea-lanes. More than half of the world's tanker traffic and merchant fleet sail through the South China Sea every year (Rosenberg and Chung, Reference Rosenberg and Chung2008). Shipping safety in the South China Sea can affect the global economy. There are extreme weather events and navigational hazards in this sea area, resulting in serious maritime casualties in terms of human life loss (Wang et al., Reference Wang, Li, Liu, Zhang, Zou and Cheng2014). Although some researchers (e.g., Rosenberg and Chung, Reference Rosenberg and Chung2008; Rosenberg, Reference Rosenberg2009; Wang et al., Reference Wang, Li, Liu, Zhang, Zou and Cheng2014) have investigated maritime safety and security in the South China Sea, the effects of contributory factors (e.g., ship type, accident type, operation conditions, etc) on human life loss resulting from shipping accidents have not been fully quantified. Therefore, the objective of this study is to explore the contributory factors influencing human life loss caused by shipping accidents occurring in the South China Sea using the Zero-Inflated Negative Binomial (ZINB) regression technique.
2. LITERATURE REVIEW
Many researchers (e.g., Jin et al., Reference Jin, Kite-Powell and Talley2001; Jin and Thunberg, Reference Jin and Thunberg2005; Perez-Labajos et al., Reference Perez-Labajos, Azofra, Blanco, Achutegui and Gonzalez2006; Roberts et al., Reference Roberts, Jaremin and Marlow2010) have focused their attention on fishing vessel accidents. For example, Jin et al. (Reference Jin, Kite-Powell and Talley2001) examined the determinants of the total losses and number of fatal and non-fatal crew injuries resulting from commercial fishing vessel accidents. It was found that the probability of a total loss of the vessel was the highest in a capsizing, followed by a sinking accident. In addition, fire/explosions and capsizings were expected to incur the greatest number of crew fatalities. In addition, some researchers also examined ship accidents involving tankers (Eliopoulou and Papanikolaou, Reference Eliopoulou and Papanikolaou2007), passenger ships (Talley et al., Reference Talley, Jin and Kite-Powell2006) and cellular type containerships (e.g., Eliopoulou et al., Reference Eliopoulou, Hamann, Papanikolaou and Golyshev2013).
It should be pointed out that the results from the aforementioned studies were based on the specific ship type. In other words, these studies do not provide information on the effects of ship type on the shipping accident consequences. On another hand, many other studies have been conducted to investigate the relationship between the contributory factors and shipping accident risks considering all ship types. For example, some researchers (e.g., Akten, Reference Akten2004; Ozsoysal and Ozsoysal, Reference Ozsoysal and Ozsoysal2006; Birpinar et al., Reference Birpinar, Talu and Gonencgil2009; Uluscu et al., Reference Uluscu, Ozbas, Altiok and Or2009; Aydogdu et al., Reference Aydogdu, Yurtoren, Park and Park2012) analysed shipping accidents and proposed many navigation safety enhancement strategies in the Istanbul Strait. Debnath and Chin (Reference Debnath and Chin2010) explored the influencing factors of shipping collision risks in the Singapore Port waters. Weng et al. (Reference Weng, Meng and Qu2012) examined the effects of time and traffic directions on shipping accident frequency in the Singapore Strait.
Nevertheless, these studies were limited to specific water areas (e.g., the Istanbul Strait). The results and findings from these studies may not be applicable for other water areas. Although the South China Sea is an important region for international trade (Wang et al., Reference Wang, Li, Liu, Zhang, Zou and Cheng2014), there has not been a great deal of literature on the analysis of shipping accident risk in such an important sea area. Furthermore, the limited work related to the South China Sea was merely focused on maritime safety and security (e.g., Rosenberg and Chung, Reference Rosenberg and Chung2008; Rosenberg, Reference Rosenberg2009; Wang et al., Reference Wang, Li, Liu, Zhang, Zou and Cheng2014). Few efforts have been made to quantitatively evaluate the shipping accident consequence in terms of human life loss and the corresponding influencing factors (e.g., ship type, accident type, operation conditions) in this strategic water area.
So far, many statistical methods have been applied to evaluate the shipping accident consequences. Jin et al. (Reference Jin, Kite-Powell and Talley2001) estimated total losses and crew injuries in commercial fishing vessel accidents using Probit and negative binomial regression methods. Talley et al. (Reference Talley, Jin and Kite-Powell2006) applied the Tobit, negative binomial and Poisson regression techniques to determine the total loss, injuries and deaths/missing people in passenger vessel accidents, respectively. Talley et al. (Reference Talley, Jin and Kite-Powell2008) modelled the severity of cruise vessel accidents using the Tobit regression method. Yip (2008) employed the negative binomial regression technique to describe the injuries and fatalities caused by ship accidents in Hong Kong Waters. Jin (Reference Jin2014) developed an ordered Probit model to evaluate the vessel damage and crew injury severity in fishing vessel accidents. However, it should be pointed out that the majority of shipping accidents may cause no fatalities or injuries. In other words, the count data (e.g., the human life loss) often have a large number of zero outcomes in maritime safety analysis. To deal with the problem of excess zeros, one of the commonly used methods is the zero-inflated distribution. To the best of our knowledge, there are few studies utilising the zero-inflated regression technique in shipping accident consequence analysis.
3. ZERO-INFLATED NEGATIVE BINOMIAL REGRESSION MODEL
A zero-inflated distribution is actually a mixture of two distributions including a delta distribution on zero (“perfect state”) and a distribution on the non-negative integers (“imperfect state”). In general, a data record is in the perfect state with probability p and in the imperfect state with probability 1-p. If the data record is in the perfect state, it takes only the value zero. If the record is in the imperfect state, it follows a distribution on non-negative integers (including the value of zero). Lambert (Reference Lambert1992) proposed a Zero-Inflated Poisson (ZIP) regression model in which the probability p was related to covariates using a logistic regression model, and a log-linear regression model was developed to relate the Poisson mean to covariates in the imperfect state. As an alternative to ZIP regression, one may consider negative binomial (ZINB) regression if the count data continue to suggest additional over-dispersion (Minami et al., Reference Minami, Lennert-Cody, Gao and Roman-Verdesoto2007). In a ZINB regression model, the negative binomial model is used for the imperfect state.
For the zero-inflated model specification, a natural set of starting values for the covariates is provided by the Probit or Logit and independent Poisson or negative binomial estimates. To determine the probability of p for the perfect state, another efficient method is to use the Poisson or negative binomial estimates which are multiplied by a value of τ. More specifically, the probability function of a ZINB regression model can be expressed by
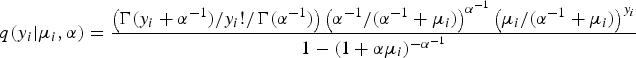 $$q(y_i \vert \mu _i, \alpha ) = \displaystyle{{\left( {\Gamma (y_i + \alpha ^{ - 1} )/y_i !/\Gamma (\alpha ^{ - 1} )} \right)\left( {\alpha ^{ - 1} /(\alpha ^{ - 1} + \mu _i )} \right)^{\alpha ^{ - 1}} \left( {\mu _i /(\alpha ^{ - 1} + \mu _i )} \right)^{y_i}} \over {1 - (1 + \alpha \mu _i )^{ - \alpha ^{ - 1}}}} $$
$$q(y_i \vert \mu _i, \alpha ) = \displaystyle{{\left( {\Gamma (y_i + \alpha ^{ - 1} )/y_i !/\Gamma (\alpha ^{ - 1} )} \right)\left( {\alpha ^{ - 1} /(\alpha ^{ - 1} + \mu _i )} \right)^{\alpha ^{ - 1}} \left( {\mu _i /(\alpha ^{ - 1} + \mu _i )} \right)^{y_i}} \over {1 - (1 + \alpha \mu _i )^{ - \alpha ^{ - 1}}}} $$where Xi is the vector of the explanatory variables for the negative binomial regression model, β is the vector of coefficients, p i is the probability of perfect state, α is the dispersion parameter, τ is the adjustment parameter, Φ denotes the cumulative distribution function of a standard normal random variable.
The estimates of β, τ and α can be determined by maximising the log-likelihood function ![]() $\ln L({\bi \beta}, \tau, \alpha \vert y,X) = \sum\nolimits_{i = 1}^N {\ln f\left( {y_i \vert {\bi X}_i, {\bi \beta}, \tau, \alpha} \right)} $ with respect to β, τ and α. Note that it is unknown which state the zero-valued observations belong to. Hence, the procedures for estimating the coefficients of the generalised linear models and generalised additive models are not applicable for the ZINB regression models. We can use the Expectation-Maximisation (EM) algorithm (Dempster et al., Reference Dempster, Larid. and Rubin1977) that is similar to the quasi-Newton methods to determine the maximum likelihood estimates. In the EM algorithm, a new random variable Z is introduced. Note that the random variable Z is only partially observable. If y is strictly greater than zero, the value of Z is known (i.e., zero) while it is unknown otherwise. More specifically, the EM algorithm at the j th iteration includes the following three steps:
$\ln L({\bi \beta}, \tau, \alpha \vert y,X) = \sum\nolimits_{i = 1}^N {\ln f\left( {y_i \vert {\bi X}_i, {\bi \beta}, \tau, \alpha} \right)} $ with respect to β, τ and α. Note that it is unknown which state the zero-valued observations belong to. Hence, the procedures for estimating the coefficients of the generalised linear models and generalised additive models are not applicable for the ZINB regression models. We can use the Expectation-Maximisation (EM) algorithm (Dempster et al., Reference Dempster, Larid. and Rubin1977) that is similar to the quasi-Newton methods to determine the maximum likelihood estimates. In the EM algorithm, a new random variable Z is introduced. Note that the random variable Z is only partially observable. If y is strictly greater than zero, the value of Z is known (i.e., zero) while it is unknown otherwise. More specifically, the EM algorithm at the j th iteration includes the following three steps:
(1) E-step: Compute
 $$Z_i^j = E\left[ {Z_i \vert y_i, {\bi \beta} ^{\,j - 1}\!, \tau ^{\,j - 1}\!, \alpha ^{\,j - 1}} \right] = \left\{ {\matrix{ {\displaystyle{{\,p_i^{\,j - 1}} \over {\,p_i^{\,j - 1} + (1 - p_i^{\,j - 1} )q(0 \vert \mu _i^{\,j - 1}\!, \alpha ^{\,j - 1} )}},} \hfill & {{\rm if}\;y_i = 0} \hfill \cr {0,} \hfill & {{\rm if}\,y_i \gt 0} \hfill \cr}} \right.$$
$$Z_i^j = E\left[ {Z_i \vert y_i, {\bi \beta} ^{\,j - 1}\!, \tau ^{\,j - 1}\!, \alpha ^{\,j - 1}} \right] = \left\{ {\matrix{ {\displaystyle{{\,p_i^{\,j - 1}} \over {\,p_i^{\,j - 1} + (1 - p_i^{\,j - 1} )q(0 \vert \mu _i^{\,j - 1}\!, \alpha ^{\,j - 1} )}},} \hfill & {{\rm if}\;y_i = 0} \hfill \cr {0,} \hfill & {{\rm if}\,y_i \gt 0} \hfill \cr}} \right.$$(2) M-step for β and α: Determine the estimates β j and α j by fitting the negative binomial regression model using the weights (
 $1 - Z_i^j $) and the response variable y i.
$1 - Z_i^j $) and the response variable y i.(3) M-step for τ: Determine the estimate τ j by fitting the Probit regression model using the β j and response variable
 $Z_i^j $.
$Z_i^j $.
The details of the EM algorithm can be found in Lambert (Reference Lambert1992) and Hall (Reference Hall2000). Minami et al. (Reference Minami, Lennert-Cody, Gao and Roman-Verdesoto2007) also explained how to implement the EM algorithm for the ZINB regression model.
4. DATA
Shipping accident casualty data were collected from the shipping accident database managed by Lloyd's List Intelligence Company. The shipping casualty data used for this study were of accidents occurring in the South China Sea between 2001 and 2010. The South China Sea is a marginal sea that is a part of the Pacific Ocean, encompassing an area from the Singapore and Malacca Straits to the Strait of Taiwan and is around 3,500,000 square kilometres. The area's importance largely results from one-third of the world's shipping transiting through its waters. It is located to the south of China, east of Vietnam and Cambodia, west of the Philippines, east of the Malay peninsula and Sumatra and north of the Banka-Belitung Islands and Borneo, as shown in Figure 1.

Figure 1. Location of South China Sea.
In the shipping accident database, each recorded data element includes the following information: (i) ship type; (ii) accident type; (iii) operating conditions; (iv) accident location and, (v) the loss of human life, including passengers and crew members who died or went missing in the accident. The operating conditions include detailed information regarding weather condition, the operating time and dock condition. In this study, the operating time was divided into two categories: daytime and night time periods. Hereafter, the daytime period is defined as the period from the local time of sunrise to the time of sunset. It should be pointed out that the times of sunrise and sunset vary with the time of year. We classified the accident location based on the distance to the harbour or port. The optimum number of categories can be determined using the Centroid Clustering (CC) algorithm. In the CC algorithm, the objective function is to minimise the sum of the squared distances from the category means. The algorithm terminates when the number of iterations arrives at the preset maximum value. The optimum number of categories was found to be two: Category 1 (0, 20 km) and Category 2 (20 km, ∞). Hence, the accident location was divided into two categories: “near the coastal area/harbour/port” (i.e., Category 1) and “far away from the coastal area/harbour/port” (i.e., Category 2). Using the same method, the ship type was classified into three groups: (i) cruise ships; (ii) ferry/RO-RO (roll-on/roll-off) ships; and (iii) other ship types (e.g., container carriers, cargo ships).
The accident types include collision, fire/explosion, machinery damage/failure (e.g., lost rudder, fouled propeller), hull damage (holed, cracks, structural failure), contact, grounding, sinking, capsizing, and accidents due to miscellaneous non-classified reasons. Hereafter, a collision is defined as a situation where a ship struck or was struck by another ship on the water surface. Contact refers to the situation where the ship struck any fixed or floating objects other than those included under collision or grounding. Grounding refers to a situation where a ship is in contact with the sea bottom or a bottom obstacle, struck object on the sea floor, or struck or touched the bottom. Capsizing refers to a situation where a ship is turned on its side or she is upside down. Note that capsizing does not mean that the ship will sink in the end. In addition, capsizing is not the only prerequisite of sinking. The occurrence of collision, contact and grounding might also lead to the occurrence of ship sinking.
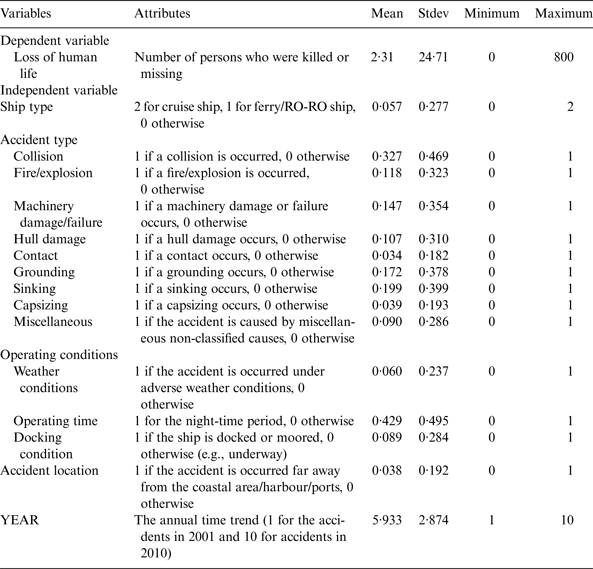
A total of 1,671 shipping accidents occurring in the South China Sea were recorded from 2001 to 2010. Of these accidents, there are at least one death and/or missing people in 201 ship accidents. Table 1 presents the variables and their descriptive statistics. The mean statistics reveal that 32·7%, 11·8%, 14·7%, 10·7%, 3·4%, 17·2%, 19·9%, 3·9% and 9·0% shipping accidents were collision, fire/explosion, machinery damage/failure, contact, grounding, sinking, capsizing and accidents caused by miscellaneous reasons in the South China Sea. The proportions of ships involved in shipping accidents were approximately 1·1% for cruise ships, 3·5% for ferry/RO-RO ships and 95·4% for other ship types. The majority of shipping accidents occurred in good weather conditions (94·0%), and 42·9% of accidents occurred at night. 8·9% of shipping accidents occurred when the ship was docked or moored. In addition, a relatively small proportion of accidents occurred far away from the coastal area/harbour/ports (3·8%). The loss of human life resulting from shipping accidents ranges from 0 to 800, with an average value of 2·31 fatalities or missing persons.
Table 1. Variable descriptions.

5. RESULTS AND DISCUSSIONS
In this study, a univariate statistical analysis has also been performed to compare with the ZINB regression model, which aims to show the potential limitations of the univariate statistical technique.
5.1. Univariate statistical analysis results
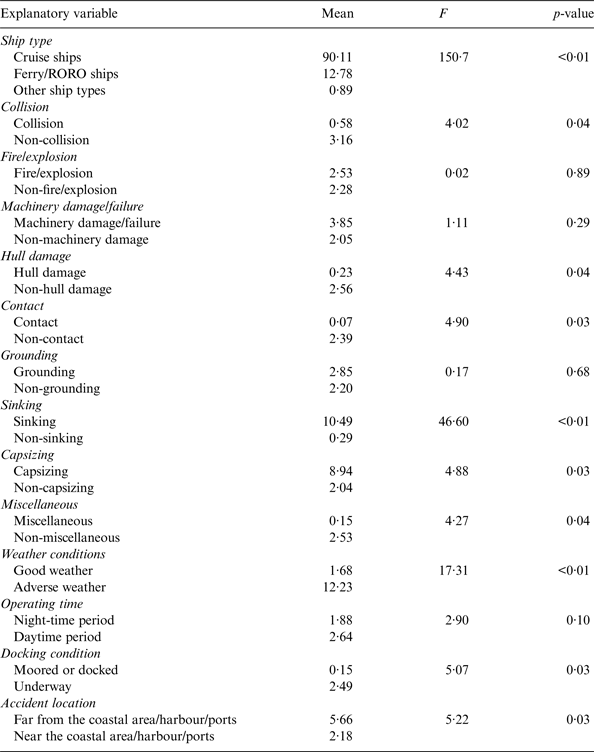
As a widely-used univariate statistical analysis technique, a one-way Analysis of Variance (ANOVA) analysis was carried out to determine whether the mean loss of human life in shipping accidents is significantly influenced by the contributory factors. Table 2 reports the ANOVA analysis results for the loss of life resulting from shipping accidents in the South China Sea. According to the table, the mean loss of life is bigger for fire/explosion, machinery damage/failure, grounding, sinking and capsizing accidents occurring in adverse weather conditions. A bigger mean of human life loss is associated with the shipping accidents occurring far away from the coastal area/harbour/ports. Surprisingly, Table 2 shows that the occurrence of collision, contact and hull damage accidents decreases the loss of human life, which is inconsistent with our expectation.
Table 2. ANOVA test results for the human life loss in shipping accidents.

One possible reason for the inconsistency might be that the above univariate statistical technique only allows the analysis of a single factor at a time. However, the consequence of a shipping accident is influenced by multiple factors at the same time. Therefore, it may give rise to biased or incorrect results by isolating a single factor for analysis while treating other factors as fixed. It is thus more appropriate to employ multivariate analysis, for example, ZINB regression technique, which takes multiple factors into account simultaneously for analysing shipping accident casualties.
5.2. ZINB regression model results
The zero-inflated regression procedure in the Limdep software (Version 9, Econometric Software Inc., NY, USA) was performed to calibrate the proposed ZINB regression model using the collected 1,671 shipping accident records. In order to demonstrate that the ZINB model provides the best fit to these data, another three regression models are also tested, namely the Poisson regression model, negative binomial regression model and ZIP regression model. When several models are available, one can compare the model performance using the most regularly used measures such as the Akaike Information Criterion (AIC), the Bayesian Information Criterion (BIC) and the Deviance Information Criterion (DIC). The AIC penalises a model with a larger number of parameters and is defined as AIC = −2 ln L + 2q, where ln L represents the fitted log-likelihood and q is the number of parameters for the model. The BIC penalises a model with a larger number of parameters and a larger sample size, and is defined as BIC = −2 ln L + q ln(N), where N is the sample size. The DIC is a hierarchical modelling generalisation of the AIC and BIC, and is defined ![]() $DIC = - 2\ln L + \displaystyle{{{\rm Var}\left( { - 2\ln (p(y \vert \theta )} \right)} \over 2}$, where p(y|θ) is the likelihood function and θ are the parameters for the model. In general, lower values of the AIC and BIC statistics are preferable. Table 3 gives the measures of fit comparison results of different regression models. It can be seen from the table that the ZINB regression model provides the best fit to the shipping accident data owing to the smallest AIC, BIC and DIC statistics. These results confirm the appropriateness of using the ZINB regression technique to model the loss of human life resulting from shipping accidents.
$DIC = - 2\ln L + \displaystyle{{{\rm Var}\left( { - 2\ln (p(y \vert \theta )} \right)} \over 2}$, where p(y|θ) is the likelihood function and θ are the parameters for the model. In general, lower values of the AIC and BIC statistics are preferable. Table 3 gives the measures of fit comparison results of different regression models. It can be seen from the table that the ZINB regression model provides the best fit to the shipping accident data owing to the smallest AIC, BIC and DIC statistics. These results confirm the appropriateness of using the ZINB regression technique to model the loss of human life resulting from shipping accidents.
Table 3. Comparison results of different regression models.

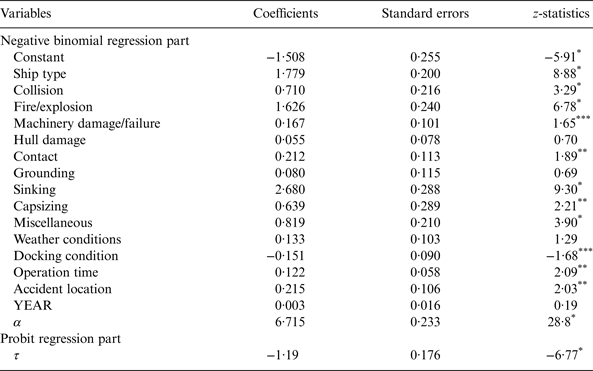
Table 4 gives the ZINB regression model results for shipping accidents in the South China Sea. From the table, it can be seen that the coefficient for collisions is positive and statistically significant at a 0·01 level, indicating that collisions are strongly associated with a large number of deaths and missing people in a shipping accident. The over-dispersion parameter α in the model is positive and statistically significant at a 0·01 confidence level, suggesting that the data in the imperfect state is still over-dispersed. The model results also show that the loss of human life in shipping accidents is significantly influenced (at a significance level of 0·01) by the following explanatory variables: fire/explosion, sinking and miscellaneous causes. The coefficients associated with the contact, capsizing, operating time and accident location are statistically significant at a significance level of 0·05 while two variables, machinery damage/failure and docking condition can affect the loss of human life at a significance level of 0·10. Table 4 also shows that the weather condition has a minor effect on the loss of human life caused by shipping accidents occurring in the South China Sea.
Table 4. Estimated coefficients of the variables used for the ZINB regression model.

Note: * denotes a significance level of 0·01; ** represents a significance level of 0·05; *** represents a significance level of 0·10.
With the exception of docking condition, the other explanatory variables (e.g., collision, fire/explosion) have positive signs. This implies that the number of deaths and missing people is expected to be greater for collision, fire/explosion, contact, sinking, capsizing, hull damage, machinery damage/failure and accidents caused by miscellaneous reasons. In addition, the loss of human life will increase if the shipping accident occurs under adverse weather conditions (e.g., strong winds, waves). The negative sign of the docking condition indicates that the loss of human life is less when the ship is docking or moored. Although the coefficient associated with the annual time trend variable (i.e., YEAR) is positive, it is close to zero and not statistically significant at the level of 0·05. This indicates that the temporal effect on the human life loss is very marginal during the 10-year period.
5.3. Marginal effects
Although the signs of the estimated coefficients for the ZINB regression model could provide information on whether changes in given explanatory variables increase or decrease the loss of human life resulting from shipping accidents, they cannot provide further information on the extent to how much the loss of human life is changed. In general, the marginal effect is defined as the relative change in the average human life loss resulting from one unit increase for an explanatory variable. More specifically, the marginal effect of the explanatory variable x i in the ZINB regression model can be expressed by
where u is the expected value of the estimates from the negative binomial model, φ is the standard normal density function, and β i is the coefficient of the explanatory variable x i used in the ZINB regression model. Figure 2 depicts the marginal effects of explanatory variables on the human life loss in shipping accidents. More detailed discussions are shown below.

Figure 2. Marginal effects on the loss of human life in shipping accidents.
5.3.1. Effects of ship type
One interesting finding from Figure 2 is that the loss of human life in shipping accidents is significantly affected by the ship type. More specifically, on average, the loss of human life for ferry/RO-RO ships is larger than for other ship types (e.g., container ships) by 3·79 fatalities. This result may be attributed to the fact that ferry/RO-RO ships capsize very quickly (Montewka et al., Reference Montewka, Ehlers, Goerlandt, Hinz, Tabri and Kujala2014). Clearly, the quick capsizing event may result in a high number of fatalities. Another possible reason might be that the emergency evacuation efficiency is low on a ship carrying a large number of passengers (Lois et al., Reference Lois, Wang, Wall and Ruxton2004).In particular, a large number of people finding themselves in the confines of a ship at sea can also expect to experience panic when a fire is present. This result provides evidence to support the argument of House (Reference House2014) that passenger ships have the potential to incur high casualty rates in the event of major shipping accidents. To enhance the passenger ship safety level, all passenger ships are required to be fitted with emergency towing arrangements fore and aft, pre-rigged and capable of easy deployment.
5.3.2. Effects of operation conditions
Consistent with previous studies (e.g., Talley et al., Reference Talley, Jin and Kite-Powell2006), the ship operating time is strongly correlated with the human life loss. Figure 2 highlights that the mean of human life loss in night time accidents is generally higher than for daytime accidents (by 0·26 fatalities), which is quite close to the finding from the study of Akten (Reference Akten2004). The higher human life loss at night might be attributed to the fact that people require longer evacuation time at night compared to during the daytime period, especially as most people would be asleep at this time (Boulougouris and Papanikolaou, Reference Boulougouris and Papanikolaou2002; IMO, 2007).
Consistent with our expectations, adverse weather conditions are associated with increased human life loss. It can be seen from Figure 2 that the expected human life loss is 0·28 fatalities higher for shipping accidents occurring under adverse weather conditions. This implies that for every 100 shipping accidents occuring under adverse weather conditions, 28 more fatalities and missing people are expected. Figure 2 also shows a marginal effect of −0·32 for the docking condition, suggesting that there are 32 fewer fatalities or missing persons for every 100 shipping accidents when ships are moored or docked.
5.3.3. Effects of accident location
Similar to the study of Jin (Reference Jin2014), the distance to the shore is also a significant factor influencing the shipping accident consequence in terms of human life loss in this study. Figure 2 shows that a shipping accident occurring far away from the shore can cause 0·46 more fatalities, as compared with a shipping accident close to the shore. This result is consistent with what we expected because there will be a long response time and a poor rescuing efficiency for the shipping accidents occuring far away from the coastal area/harbour/ports.
5.3.4. Effects of accident type
From Figure 2, we can see that the highest loss of life is strongly associated with the sinking accident. The loss of human life will dramatically increase by 5·71 fatalities if a ship eventually sinks into the sea. To prevent the occurrence of sinking, one efficient method is to enhance ship structural safety. Another method is to maintain stability during damage. The extreme case of sinking does not occur as long as the ship has stability even if the ship is structurally damaged (Lee et al., Reference Lee, Lee, Park and Kim2005). Compared to sinking, capsizing has a smaller effect in increasing loss of life. It is found that this will increase by 1·36 fatalities. The smaller effect of capsizing on loss of life can be explained by the fact that sinking is often the final outcome of capsizing. Our historical shipping accident data show that 93·8% (61 out of 65) of ships involved in capsizing accidents in the South China Sea eventually sank between 2001 and 2010. Therefore, the data on capsizing has been at least partially captured by the sinking data.
Figure 2 shows that the human life loss in fire/explosion accidents is, on average, 3·46 fatalities higher than in shipping accidents where no fire/explosions are involved. This might be explained by the fact that sudden and overwhelming events provide little evacuation time for the passengers or crew members (National Research Council, 1991). Another possible reason is that there is only a small survival chance for people who get caught in fires on a ship. To prevent the occurrence of fire/explosion accidents, ship owners are encouraged to equip their vessels with an efficient flame arrestor, back fire arrester or other similar devices on the injectors of each inboard engine and efficiently ventilate enclosed spaces so as to remove explosive and flammable gases (Jin et al., Reference Jin, Kite-Powell and Talley2001). In addition, training is extremely important because there are no fire departments to call upon at sea. Crew members and passengers would have to extinguish a fire by themselves.
In Figure 2, it can be seen that collision has less effect than fire/explosion. More specifically, the occurrence of collision accidents could increase the human life loss by 1·51 fatalities. Figure 2 also shows that the occurrence of contact and grounding accidents could increase the human life loss by 0·45 fatalities and 0·17 fatalities, respectively. As argued by Ziarati and Ziarati (Reference Ziarati and Ziarati2007), poor communications between personnel, ineffective use of charts and inadequate manning levels are the three primary causes of grounding accidents. To reduce the occurrence likelihood of grounding accidents, ship masters should be well trained to understand what is expected of them. Although machinery damage/failure has a small effect in increasing human life loss (by 0·36 fatalities) in this study, it continues to be the cause of the majority of losses in marine insurance. Statistics from the International Union of Marine Insurance (IUMI, 2013) reported that 40% of hull claims by number are machinery damage, accounting for 20% of costs.
5.4. Underreporting effect
Underreporting of maritime accidents is a problem not only for the authorities endeavouring to improve maritime safety through legislation, but also for the entities that use maritime casualty statistics in risk and accident analysis (Psarros et al., Reference Psarros, Skjong and Eide2010; Hassel et al., Reference Hassel, Asbjornslett and Hole2011). It is known that a certain number of unreported maritime accidents are confirmed by first-hand reports from ship operators. There could be several possible reasons for this, including local reporting procedures not being understood by the crew or ship-owner. In general, the reliability of accident analysis results may be affected by the proportion of missing data. In this study, no other database was collected to confirm how many accident reports were missing. Nevertheless, we can evaluate the effects of the missing data by randomly excluding a part of data for the model development.
Figure 3 shows the effects of missing (excluded) data on the stability of coefficients for the developed ZINB regression model. It can be seen that the coefficients of the majority variables would be slightly altered if only a small proportion of data (e.g., 5% of data) was excluded from the model development. However, the coefficient of docking condition is very sensitive to the missing data. It can be seen that there will be a 60% change in the coefficient of docking condition when 5% of data are missing. The relatively big change in the coefficient of docking condition might be due to the small weight of this variable in the developed model. Note that all coefficients would change significantly if there were a large proportion of missing data (e.g., 30% of data), as shown in Figure 3. Figure 4 further presents the marginal effects for different proportions of missing data. It can be seen that there would be relatively big changes in the marginal effects of explanatory variables (e.g., sinking, collision, year) if there were a large proportion of missing data (e.g., 30% of data). In addition, some variables (e.g., contact, grounding, docking condition) may even yield opposing effects when a large number of data were missing, as shown in Figure 4.

Figure 3. Effects of missing data on the stability of variable coefficients.

Figure 4. Effects of missing data on the marginal effects.
6. CONCLUSIONS
The South China Sea is considered to be a hot spot due to the high loss of human life resulting from shipping accidents occurring in this water area. This study employed the ZINB regression technique to evaluate shipping accident casualties (i.e., human life loss) and the corresponding contributory factors in the South China Sea. With ten years of historical shipping accident data, a ZINB regression model has been developed in this study.
The ZINB regression model results show that the high human life loss is associated with collision, fire/explosion, grounding, contact, sinking, capsizing, machinery damage/failure and miscellaneous shipping accidents occurring under bad weather conditions during the night time periods. Furthermore, the marginal effect analysis results show that the increase of the expected human life loss is the largest for sinking accidents, followed by fire/explosion accidents, collisions, capsizing accidents, contact and grounding accidents. Machinery damage/failure and hull damage are found to have smaller effects in the increase of human life loss. Consistent with our expectation, there will be more human life loss for the accidents occurring under adverse weather conditions and/or far away from the coastal area/harbour/port. In addition, the fatalities could be less when the ship is moored or docked.
One implication of this study is that it is essential to prevent ships from capsizing or sinking once an accident occurs so that the resulting loss can be reduced significantly in the South China Sea. Government agencies and shipping companies could employ the developed ZINB regression model to assess various safety enhancing measures and strategies. The developed model in this study can also help insurance companies to evaluate the possible loss of human life and damage to ships. It should be pointed out that the ZINB regression technique is only applicable when there are excess zeros and the distribution of the observed counts is over-dispersed. However, if there is no apparent reason to suspect that two states (i.e., perfect and imperfect states) might be present, the use of a ZINB model may be simply capturing model mis-specification that could result from factors such as unobserved effects (heterogeneity) in the data (Lord et al., Reference Lord, Washington and Ivan2005).
One limitation of this study is that shipping traffic information was not included in the collected shipping accident database. In future, we will compare our accident results to traffic properties after collecting shipping traffic data. Due to data limitations, the injuries resulting from shipping accidents were not analysed in this study. In addition, the number of people onboard has not been considered as an explanatory variable because the majority of collected shipping accident records did not contain the values of this variable. Future studies will be conducted to examine the injuries resulting from shipping accidents and take into account the number of people on board. It is also interesting to investigate whether the dusk/dawn time period can exhibit different effects on the human life loss compared with the night time period in the future.
ACKNOWLEDGEMENTS
The authors sincerely thank the Editor-in-Chief and three anonymous referees for their helpful comments and valuable suggestions, which considerably improved the exposition of this work. This study is supported by the National Natural Science Foundation of China (Grant no. 51308037).