Introduction
The region between the grounded part of an ice sheet and the part where the ice begins to float [grounding zone) is of crucial importance when discussing the potential instability of the West Antarctic ice sheet (WAIS) (Weertman, 1974; Hughes, 1977; Thomas and Bentley, 1978). The grounding line, which is where the glacier detaches from its bed and becomes afloat, may advance seaward as a result of an increase in glacier thickness, a decrease in sea level or an isostatic uprise of the seabed. Where the bedrock slopes down toward the center of the ice sheet, as is true of most of the WAIS, the ice sheet may be prone to an irreversible collapse if the grounding line starts to retreat (Hughes, 1977; Thomas, 1979).
Observational data are sparse at the grounding line. Tiltmeters have been used to detect the limit of tidal flexing (Stephenson, 1984), but the method is time-consuming, affected by model assumptions (Smith, 1991) and limited to point measurements. Kinematic global positioning system (GPS) is a more effective and accurate technique for locating the limit of tidal flexing (Vaughan, 1994), but spatial sampling is also limited. Satellite visible imagery and radar al time try offer a larger-scale view of the possible location of the grounding line, but at a much coarser spatial resolution. Similarly, radio-echo sounding can be used to locate grounding zones, but changes in radio-echo associated with the presence of sea water underneath the glacier are not always easy to interpret (Drewry and others, 1980). As a result of these limitations, there is considerable uncertainty about most grounding lines in the Antarctic.
Recent advances in satellite synthetic aperture radar interferometry suggest that this technique may be able to map the limit of tidal flexing, or glacier hinge line (Holds-worth, 1969), with better precision than any oilier technique, simultaneously over the entire glacier width, with a uniform sampling scheme (Rignot, 1996). Because the technique is re-peatablc, it may help detect hinge-line migration and thereby provide an early warning of the location and magnitude of glacier changes over the wide areas covered by the satellite.
Here, we employ the radar interferometry technique to map the hinge line of Rutford Ice Stream (RIS) and Carlson Inlet (CI), Antarctica, using data collected in 1992 and 1996 by the European remote-sensing satellites ERS-1 and ERS-2 (Fig. 1). These two glaciers dra in the Ellsworth Land portion of the WAIS into theWeddell Sea, but their flow is restrained by the presence of the Filrhnrr-Ronne Ice Shelf, the world's largest ice-shelf system.
The ERS radar data are analyzed here to locate the glacier hinge line, detect its migration between 1992 and 1996, compare the hinge-line ice-volume flux with mass accumulation in the interior, and conclude on the state of balance and stability of the glaciers.
2. Study Area
RIS is a fast-flowing outlet glacier which flows imo the Rlchner—Ronne Ice Shelf (Crabtree and Doake, 1982). Two major ground surveys of RIS were conducted in 1978-80 and 1984-86 (Doake and others, 1987). The surveys showed that the ice-stream grounding line has a complex morphology, with several thick ice tongues running along the flow separated by thinner narrow troughs (Stephenson and Doake, 1982). A prominent bedrock knoll is present at the center of the glacier, at the grounding line (Stephenson and Doake, 1982; Vaughan, 1994).
The first radar interferogram of RIS was obtained by Goldstein and others (1993). The deformation signal re-corded over the 6 day time interval which separated successive data acquisitions of the ERS satellite was analyzed in terms of its contributions from creep How, tidal motion and surface topography. The grounding line of RIS was subsequently mapped with a precision of 500m. Comparison of this result with Stephenson's (1984) map suggested a 2 km retreat of the grounding line between 1980 and 1992. The authors, however, judged the comparison inconclusive because of large uncertainties in registration of the ERS data and in Stephenson's method (Smith, 1991).
Fig. 1. Radar amplitude image (120 × 220 km) in a PS grid of RIS and CI acquired by ERS-1 on 1 January 1996. © ESA 1996. (b) Magnitude of the ice velocity (50ma−1 contours) of RIS andCIin 1992 derivedfrorn a combination of interferometry data (across-track velocity) and image speckle tracking (along-track velocity). Ice velocity in (b) is not valid on floating ice, because of tidal contamination of the radar signal. Comparison between (a) and (b) indicates that the ice flow of CI is confined along its northern flank, in between two (radar-bright) zones ofcrevassing. The hinge-line positions of CI and RIS are indicated as white continuous lines in (a) and (b) for reference.
CI, northern of RIS, Hows at only 7 m a−1 , compared to 400 m a−1 for RLS (Frölich and Doake, 1988). The large contrast in ice velocity was attributed to differences in basal conditions by Frolich and others (1989).
3. Method
The premise of using a single radar interferogram to detect the limit of tidal flexing of a glacier was presented by Goldstein and others (1993). The approach is limited in precision to several hundred meters, because the location of the limit of tidal Hexing is contaminated by Glaciol creep flow. To separate Glaciol creep flow from tidal motion, multiple interferograms are necessary (Hartl and others, 1994). With multiple interferograms, the limil of tidal flexing may then be mapped with a precision of a few tens of meters (Rignot, 1996; Rignot and others, 1997).
The hinge line is located upstream of the grounding line (Smith, 1991). Downstream of the grounding line is the line of first hydrostatic equilibrium of the ice, where ice thickness may be inferred from surface elevation. On RIS, the hinge line is separated from the line of first hydrostatic equilibrium by about 2 km, according to Vaughan (1994).
4. Interferogram Generation
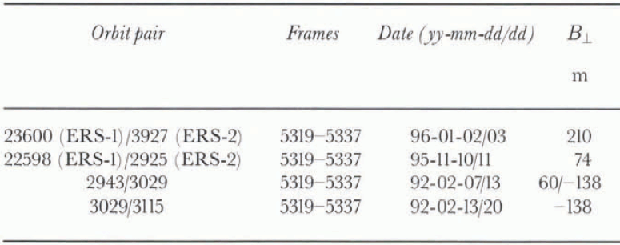
Fourteen ERS scenes acquired in 1992 and 1996 (table 1) were utilized to generate four interferograms of RIS and CI. The interferograms were subsequently projected onto a polar Stereographic (PS) grid with a 50 m sample spacing (Fig. 1). The two 1996 interferograms were combined t4o estimate both the topography and the line-of-sight velocity of grounded ice using a standard approach (e.g. Zebker and others, 1994).
Ground control for the generation of the interferomelric topography was provided by an altimetric digital elevation model (DEM) of Antarctica assembled from ERS radar al-timetry data and distributed on a PS grid at a 5 km spacing
Table 1. ERS orbit pairs used in this study. B ‖ is the inter-feromelric baseline in the direction perpendicular to the line of sight of the radar. Frame 5337 corresponds to RIS. Frame 5319 corresponds to CI. ERS is a sun-synchronous satellite orbiting at about 800 km altitude, illuminating the surface at 23° away from the vertical, with a 100 km swath, at a spatial resolution of 4 m in the along-track direction (azimuth) and 20 m in the cross-track direction (range)
(Bambcr and Bindschadlcr, 1997). The DEM was converted from ellipsoid height into orthometric height using the OSU91 geoid model. The DEM provides a coarse resolution of the local topography, mostly reliable on flat terrain (e.g. ice shelf), which is used to remove the effect of topography in the differential interferograms (see below) and estimate ice thickness at the grounding line assuming hydrostatic equilibrium of the ice.
The interferometrically derived topography is more detailed (40 m spatial resolution) and more accurate (10-20 m precision in height) on grounded ice terrain than the altimetric DEM (5 km spacing and local errors in height of several tens of meters). On floating ice, however, the altimetric DEM is more precise (1 m precision in elevation), whereas the radar signal is contaminated by tide which is difficult to remove. As a result, to infer the glacier tidal displacements on floating ice (Eig. 2), we removed the glacier topography using the altimetric DEM. Conversely, to infer the ice velocity on grounded ice, we utilized the interferometrically derived topography (fig. 1b).
Tide-only interferograms were formed by calculating the difference between two interferograms which had been corrected for surface topography using the Antarctic DEM and which spanned the same time interval between data acquisitions (so the creep deformation signal was the same in both interferograms). We assumed that the glacier creep flow was steady and continuous over the time period of observation. If that assumption were violated, we would see deformation fringes on grounded ice which are not due to topographic errors (which are, for instance, visible on Fletcher Promontory and on the main trunk of RIS in Figure 2). We do not see such an unexplained signal.
One tide intcrfcrogram was created from the three scenes acquired in 1992 (fig. 2a), and another was made from the four scenes acquired in 1996 (fig. 2b). The 1992 interferogram, which is much noisier than the 1996 intcrfcrogram, was filtered prior to phase unwrapping (which is the process of adding multiples of 360° to the phase, starting from a reference point at zero phase). The 1992 and 1996 tide interferograms were projected onto a PS grid, and co-registered automatically by using the cross-correlation of the radar image intensity. Areas of significant ice motion were excluded from the registration process. The rms noise of the registration fit was 0.5 pixels (20 m) in both the along- and across-track directions.
The uncertainly in absolute registration of the imagery is much larger and typically about 200-500 m. The error in absolute location of the imagery, however, does not affect the estimation of glacier changes since the multi-date data are co-registered independently ofthat information.
Fig. 2. Tidal motion of RIS and CI in (a) 1992 and (b) 1996 after removal of the ice-sheet topography using a 5 km altimetric DEM of Antarctica (Rarnber and Rindschadler. 1997). Residual fringes on grounded ice (e.g. on Fletcher Promontory) are caused by artefacts in the 5 km DEM. Each full cycle of grey-tone variation represents a 100mm vertical displacement of the glacier surface induced by tidal motion. Black squares delineate the locations of Figure 3. White areas indicate no data because phase noise was too high to perform phase unwrapping.
Fig. 3. High-resolution details of the tidal motion of RIS in (a) 1992 and (b) 1996; and CI in (c) 1992 end (d) 1996 on a PS grid at 50 m sample spacing. The profiles, Pi's, refer to Table 3 and Figures 4-6. Each full cycle of grey-tone variation represents a 62 mm vertical displacement of the glacier surface. To facilitate the comparison between the 1992 and 1996 displacements, the 1996 tidal displacements were multiplied by 3.505 to approximate the amplitude of the 1992 tidal displacements. The tidal displacements recorded on grounded ice near the hinge line average zero.
5. Results
5.1. Tidal displacements
Tidal flexure zones stand out in the tide interferograms (figs 2 and 3).Thcy correspond to transition regions of high fringe rate which indicate that the glacier surface is vertically displaced over relatively short (a few km) horizontal distances in order to bring the ice into hydrostatic equilibrium. The hinge line is the inward limit of tidal flexing (Holdsworth, 1969). A few km downstream of the hinge line, the fringe rate decreases, which indicates that the glacier surface undergoes less deformation as the ice reaches more stable hydrostatic equilibrium conditions. The flexure zone extends smoothly along the ice margin, confirming that the glacier margins are fully coupled with the grounded ice, as noted by Vaughan (1994).
The shape of the RIS hinge is consistent with, but probably more accurate than, that inferred by Stephenson (1984) and discussed by Smith (1991). The grounded zone of CI exhibits a comparatively sinuous geometry. Both grounding zones differ from straight lines or elevation contour lines. The complexity of the grounding zone is expected from the known rough character of the bedrock topography in this area (Smith and Doake, 1994). On CI, the interferometric data reveal the presence of two bedrock knolls several tens of meters high and several km in diameter at the hinge line. One knoll is located on the southern part of the glacier, which is almost stagnant (ice velocity 10-20m a−1; fig. 1b). The other runs across the northern, fast-moving section of the glacier (ice velocity 100 m a−1; fig. 1b). These features suggesl (hat the position of the hinge line of CI is also pinned down by the local bedrock topography.
Areas of local grounding of the ice shelf are identified downstream of the hinge line in the differential interfero-grams (Fig. 2). They correspond to zones of concentrated fringes, located away from the shear margins, on the ice shelf proper. On RIS, one such area of local grounding appears about 41 km seaward from the hinge line, along the glacier southern margin; another appears about 17 km from the hinge line, near the glacier center. The latter is not visible in the 1996 data. Since the 1996 ocean tides were less negative (Table 2 shows that the largest negative tide correspondcd to orbit ERS-1 2943 acquired in 1992), this grounding zone is probably partially grounded and undergoes tidal flexure only at very low tides. Although we did not perform a detailed comparison of these interferograms with the predictions of areas of local grounding (Doake and others, 1987) based on radio-echo sounding data, our data confirm the presence of numerous areas of partial grounding on the ice shelf in the mouth of RIS.
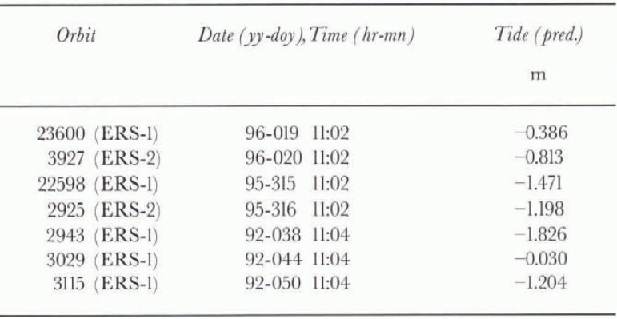
Table 2. Tide predictions for RIS at the location of the bedrock knoll (personal communication from D. G. Vaughan, 1997)
On CI, a prominent (10 km wide) area of grounded ice appears 60km downstream from the hinge line (Fig. 2). The radar brightness of the ice shelf at that location is high and textured (Fig. 1), which suggests the presence of surface crevasses and significant obstruction to ice flow.
5.2. Comparison with predicted tides
Tidal amplitudes calculated at the bedrock knoll in the center of RIS from four main tidal constituents (Vaughan, 1994) are shown in Table 2 (personal communication from D. G. Vaughan, 1997). The scene-to-scene variation in tidal amplitude for the 1992 data is three times larger than that calculated for the 1996 data. Indeed, the 1996 scenes are separated by 24 hours, which is close to the repeat cycle of diurnal tides and twice that of semi-diurnal lides, whereas the 1992 data are separated by 6 days, which amplifies differences in diurnal and semi-diurnal tides.
The change in tidal amplitude, δz between different epochs may also be obtained from the tide interferograms by multiplying the phase values, δφ, recorded across the zone of tidal flexure by 
where λ is the radar wavelength (0.0566 m) and θ = 23° is the angle of the radar illumination from the vertical. A single interferogram measures the difference in tidal deformation between two epochs. A tide interferogram measures flow that difference varies between two interferograms, meaning that it measures a quadruple difference in tide. The interferometric results may therefore be directly compared to quadruple differences in predicted tide.
From the 1992 tide interferogram, we measure a 3.25 m vertical uplift vs 2.97 m predicted. Similarly, the 1996 tide interferogram indicates a -0.96 m vertical uplift vs -0.7 m predicted. The interferograms are therefore in good agreement with the first-order tide predictions.
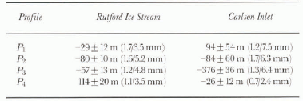
5.3. Hinge-line detection For each glacier, we selected four profiles that cross the zone of tidal flexure (Fig. 3). To locate the point of hinging, we utilized a model lit of the profiles based on an clastic-beam the
Table 3. Hinge-line migration (m) determined from four profiles by model fitting of the interferometrically determined tidal displacements. The measurement precision (±) is determined by varying the position of the profile by ±250 m along the north axis. The rms difference (mm) between the model fit and the data is indicated in parentheses (first number isfor the 1996 profile, second number is for the 1992 profile)
ory (Holdsworth, 1969). The predicted flexure of an elastic beam, w(x), is written as
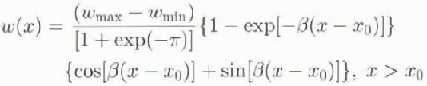
where β is the flexural rigidity of the ice (m−1), x is the abscissa along the profile (m) and x=x0 at the hinge line. For each tidal profile, we estimated lour parameters in the least-squares sense: the flexural rigidity of the ice β, the maximum and minimum height of the profile wmax and wmin. and the position of the hinge line x0. A measure of the goodness of fit was provided by the rms difference between the model and the interferometric data. The hinge-line migration was then measured as the shift in position of x0 along the profile between 1992 and 1996.
The results, shown in Table 3, indicate a rms noise of the model lit of only a few mm (see also figs 4 and 5). This low noise level is remarkable given the model simplicity. Model fitting was, howev er, performed only on the segment of the tidal profile closest to the hinge line (meaning extending from 1-2 km upstream of the hinge line to 4-5 km below the hinge line). Model fitting of longer profiles would ob\iously not perform as well since the pattern of tidal flexure exhibited by the glacier is nol one-dimensional (figs 2 and 3).
5.4. Comparison with GPS data
A profile Ρ0 was extracted on RIS at the location of a kinematic GPS profile collected in 1993 (A-Α' in Vaughan, 1995). The GPS and ERS profiles compare well, although the GPS data exhibit considerably more noise (Fig. 6). A model fit of the GPS data yields a rms noise of 20 mm, one order of magnitude larger than that achieved with interferometry (3 mm). The comparison suggests that radar interferometry measures tidal displacements better than GPS, and thereby oilers a level of precision in mapping of the glacier hinge line which is totally unprecedented.
Ίο obtain a good overlap between the GPS and ERS curves, we had to shift our interferogram 350 m to the west on the PS grid. The GPS data are geolocated with 5 m precision (personal communication from D. G. Vaughan, 1997). We would nol expect the hinge line to migrate 350 m in 3years based on the results discussed in the next section. The shift is therefore due to an error in absolute geolocation of the ERS imagery.
Fig. 4. (a) Modelfitting (continuous line) rifthe ERS interferometric displacements (dotted line) acquired along prrifile PI rif RIS (Fig. 3a and b) in 1992 (black dots) and 1996 (grry dots ); ( b) difference between the model fit and the 1996 ( diamonds) and 1992 da ta (crosses). No data are available in the middle rif the prqfile, because rif high phase noise in the 1992 data. The rms noise rif the model fit is 1.3mmJor the 1996 data and 3.5 mmJor the 1992 data. The inferred flexural rigidity rif the ice, /3, is 0.24 km - I in both cases. Black and grry arrows indicate the 1992 and 1996 hinge-line positions, respective(y. The detected hinge-line migration is - 29 _ 12 m in 4 years.
5.5. Hinge-line migration
To determine the precision with which wc measure hinge-line migration, the model-lit comparison was extended on both sides of the selected profiles, Pi's, over an area 500 m wide (or one-third of the glacier thickness), which means that live parallel profiles were examined on each side of the main profile. The values of x0 were calculated for each one of the 11 profiles, and the results were averaged to calculate a mean offset and a standard deviation. The standard deviation of the offsets, which indicates the precision of detection of hinge-line migration, was typically < 70 m (table 3).
Profile P1 of RIS exhibits no hinge-line migration (table 3). Pi runs across the bedrock knoll at the glacier center (fig. 3a). The glacier slope at that location is 0.03 (personal communication from D. G. Vaughan, 1997) compared to 0.002 over the rest of the glacier. A hinge-line migration is therefore least likely to be observed over that part of the glacier. Profiles Ρ 3 and P4, located along the sides of the knoll where the glacier slope is only 0.002, also show no hinge-line migration in 4 years. The only hingc-linc migration above noise level may be the 114 m advance of the hinge-line position along P4. Overall, these values are relatively small and suggest that the hinge line of RIS did not migrate between 1992 and 1996. Converted to ice-thickness changes using a mean slope of 0.002, the measured hinge-line migration suggests that the thickness of RIS has not changed by more than 5 cm aH.
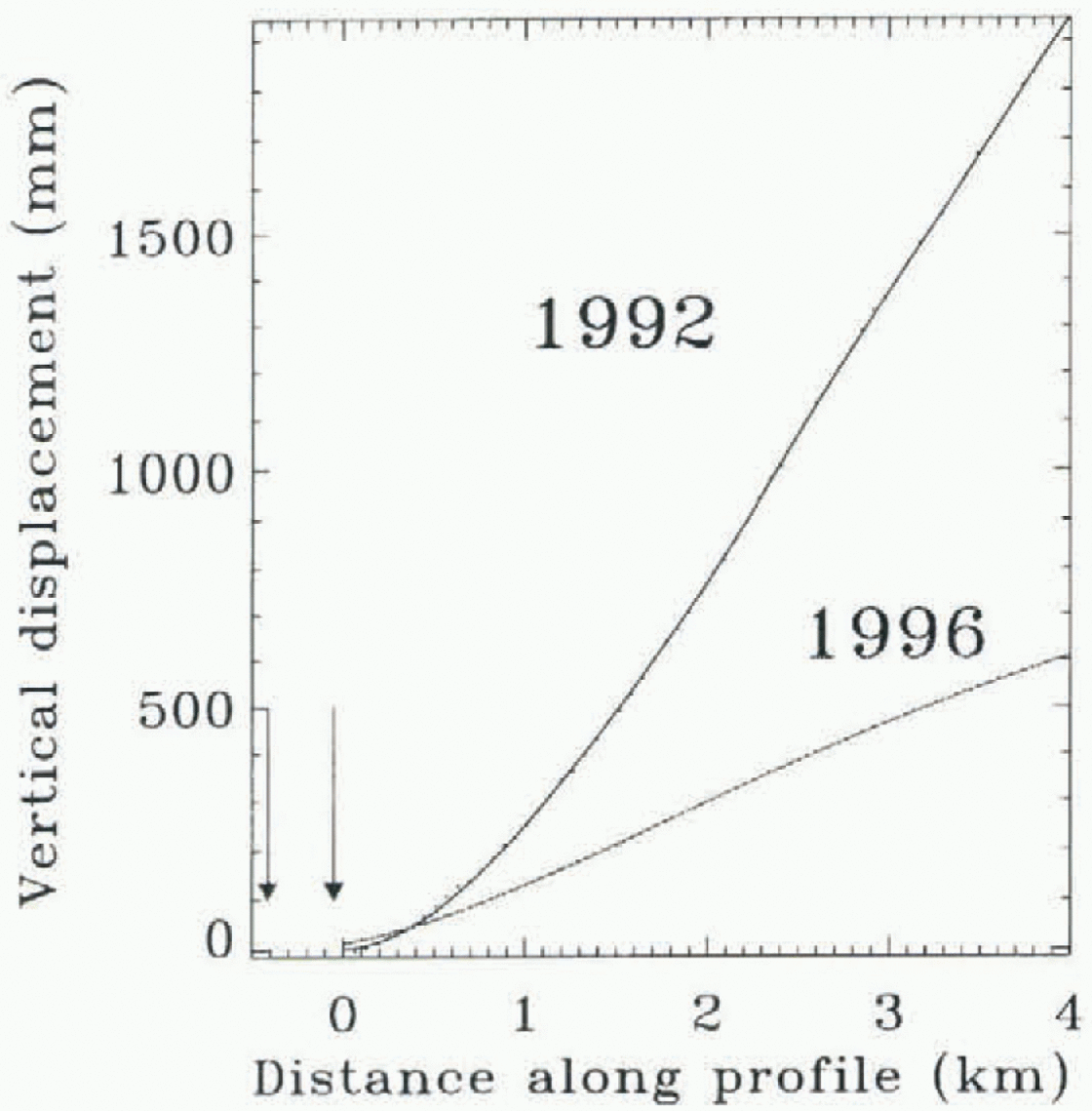
Fig. 5. Model fitting (continuous lines) of the radar interferometry data acquired in 1992 (black dots) and 1996 (grey dots) along profile Ρ3 of CI (fig. 3c). The rms noise of the model fit is 1.3 nini fir the 1996 data and 6.4 mm for the 1992 data. The inferred flexural rigidity of the ice, β, is 0.28 km. Black and grey arrows indicate the 1992 and 1996 hinge-line positions, respectively. The hinge-line migration is -376±36 m in 4years.
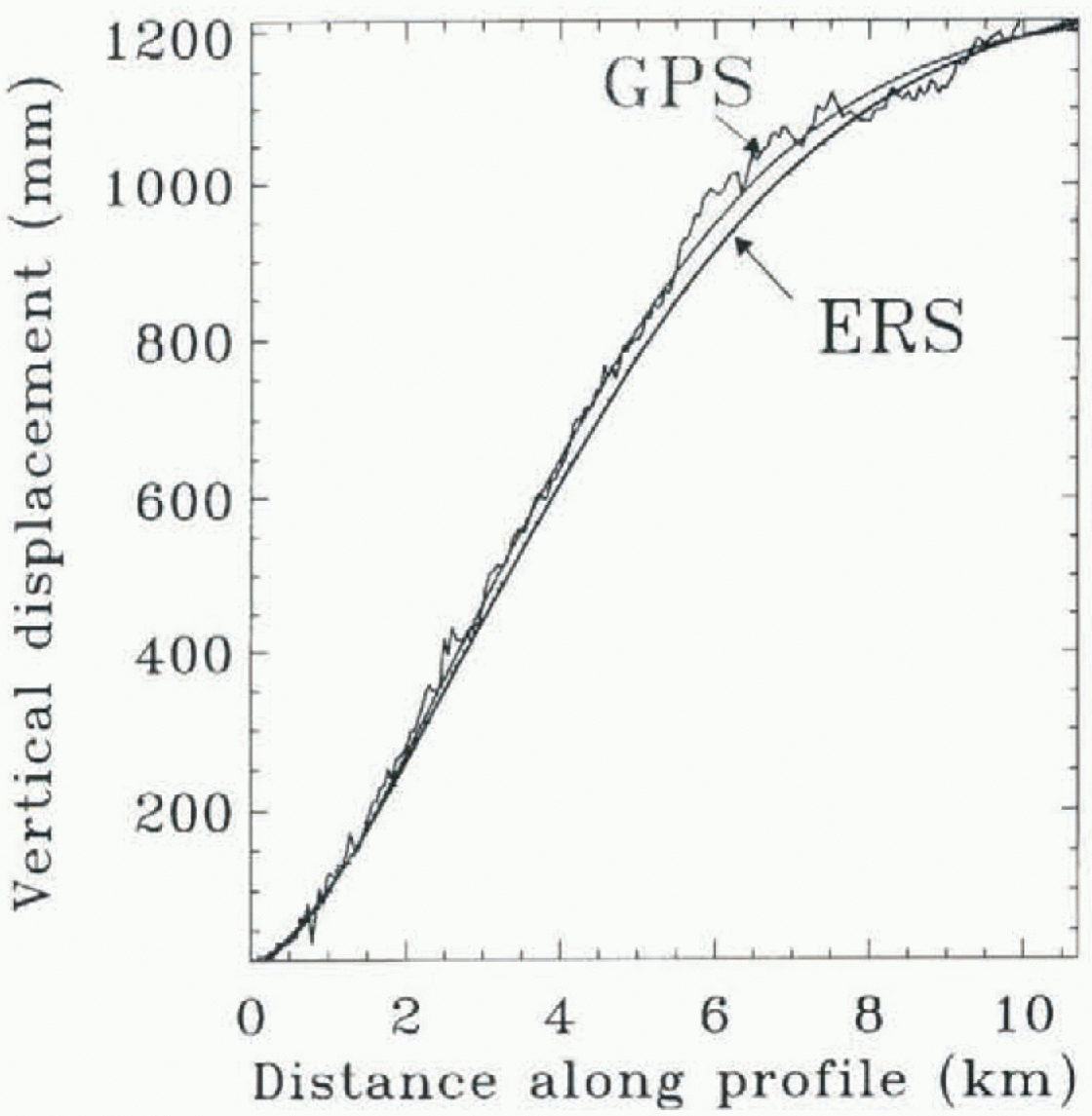
Fig. 6. Comparison of a GPS profile acquired in 1993 (personal communication from D. G. Vaughan, 1997) along profile P0 in figure 3a with the displacement measured in 1996 by ERS. The rms of the model fit (continuous lines) is 20 mm for GPS and 3 mm for ERS.(a) Modelfitting (continuous line) of the ERS interferometric displacements (dotted line) acquired along profile P1 of RIS (fig. 3a and b) in 1992 (black dots) and 1996 (grey dots); (b) difference between the model fit and the 1996 (diamonds) and 1992 data (crosses). No data are available in the middle of the profile, because of high phase noise in the 1992 data. The rms noise of the model fit is 1.3 mm for the 1996 data and 3.5 mm for the 1992 data. The inferred flexural rigidity of the ice, β, is 0.24 km−1 in both cases. Black and grey arrows indicate the 1992 and 1996 hinge-line positions, respectively. The detected hinge-line migration is -29 ± 12 m in 4years.
On CI, the hinge-line position remained stable along P1 P2 and P4, but retreated 374 m along P3. Profile P3 runs across the presumed location of a bedrock knoll, where the ice appears to be stagnant (10 m a−1 vs 100 m a−1 in the active part of CI). Since changes in ocean tide are not expected to produce that level of migration (see below), the ice must be thinning in this area. This region of CI may be changing at present. This possibility is supported by the fact that morphological features present in the 1992 and 1996 radar imagery suggest a position of the ice-stream margin which is displaced by 10 km from the dynamic margin revealed by radar interferometry (fig. 1b).
5.6. Influence of tide
The hinge-line position migrates back and forth with changes in ocean tide. The magnitude of hinge-line migra-tion, δx, depends on the change in tide, δz, the density of ice, ρW the density of sea water, 
surface slope, 
, and bedrock slope, αs
at the hinge line, according to
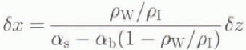
where αs
and αb
are counted positive upwards (Thomas and Bentley, 1978). Using 
, 
(Jenkins and Doake, 1991), and αb (which is unknown) equal to αs ± 0.002 (errors in αb
weight 10 times less than errors in αs
in Equation (2)), we find 
. The negative sign means t hat a positive change in sea-level height 
, displaces the hinge line inland 
.
Using this relation and the tide values in Table 2, we calculated δz
and δx and predicted the glacier tidal flexure w(x) at different epochs using 
in Equation (1). The resulting tidal displacements were then differenced in the same order as for the generation of the tide interferograms. The hinge-line position which resulted from this calculation was found to be displaced from its mean-sea-level position 
in Equation (2)) by a quantity 
in 1992 and 
in 1996. Hence, the effect of tide on the 1992-96 hinge-line migration is to induce a 60 m advance of the hinge line, which is comparable to our precision of detection of hinge-line migration. At the location of the bedrock knoll (
), the hinge-line migration due to tide is less than 10 m.
If these predictions of the effect of tide on hinge-line migration are correct, it means that the apparent stability of the hinge-line positions of both glaciers inferred from radar interferometry is real and not due to ocean tide. The conclusion is that the glacier thickness of both ice streams has remained stable at the hinge line between 1992 and 1996.
Mass balance of RIS
Radar interferometry only measures the ice velocity in the line of sight of the radar, which is in the across-track direction of the satellite. in the absence of data collected along both an ascending and a descending track of the ERS satellite, we combined our interferometric velocities with image displacements measured along track using a novel feature-tracking technique (Michel, 1997). Spatial resolution is I m along track in the ERS data (vs 20 m across track) and the recorded displacements' are independent of tide. in this manner, we obtained ice velocities in the along-track direction with a precision of 8 m a−1 from one of the 1992 6 day pair. The across-track velocities are known from radar interferometry with a precision of 1 m a−1. Tο obtain a three-dimensional flow vector, we further assumed that the flow verlor is parallel to the glacier surface given by the Antarctic DEM (Fig. 7).
Ice thickness was estimated at the hinge line (which was drawn on the interferograms based on a regular set of profiles Pi's) assuming hydrostatic equilibrium of the ice, and using an ice density of 
and a sea-water density of pw = 1028 kg m−3 (Jenkins and Doake, 1991). Ice elevation is in principle known with a precision better than 1 m from the altimetric DEM.
Fig. 7. Icevetory Ir (m a−1) in lile horizontal plane (continuous line with diamonds), ice velocity normal to the hinge-line position shoh m πι Figure 1 (dotted, line with diamonds), and ice thickness at the hinge line (continuous grey line with triangles) deduced from hydrostatic equilibrium of the ice using a 5 km altimetric DEAt of Antarctica on (a) RIS and (b) CI, obtained from ERS data acquired in 1992.
The glacier fluxes were calculated as discrete sums (40 points across glacier) of the ice-veloeity component normal to the hinge-line position multiplied by the ice thickness at that location. Increasing the number of points did not change the results. Uncertainties in the absolute position of the hinge line of ±300 m did nol change the ice fluxes by more than 5%. overall, we estimate the precision of the calculated fluxes to be 10%, assuming that the altimetric of M is indeed accurate at the meter level. For RIS, the calculated ice discharge is 17.6 km ice a−1 at the hinge line. For CI, the hinge-line discharge is 2.9 km ice a−1.
The calculated ice discharge of RIS is close to that calculated by Lindstrom and Hughes (1984) (17.4km w.e. a or 19.4km3icea−1) and Crabtree and Doake 1982) (18.5km1 w.e. a−1), but is probably more precise since il is based on a complete cross-glacier profile of velocity and thickness data.
The drainage basins of RIS and CI, estimated starting from the end points of the hinge-line profile used to cal-culate ice discharge, were drawn on the computer using an automatic procedure based on surface slope and The Antarctic DEM interpolated to a 1 km spacing (Fig. 8). The accumulation area of CI is 9200 + 100 km2, with a 100 km2 uncertainly associated with a +500 m uncertainty in the position of the periphery of the drainage basin. The accumulation area of RIS is 62500 ± 1000 km2, with a higher uncertainty due to unknown topography of the Ellsworth Mountains. The value obtained for RIS is larger than earlier estimates (40500 km2 by Crabtree and Doake 1982); 28683 km2 by Lindstrom and Hughes (1984); and 36000 km2 by Doake and others (1987)), but our value is based on more precise elevation data.
Fig. 8. Drainage basins (dotted line) of CI and RIS, deduced from the 5 km altimetric DEM of Antarctica interpolated to 1 km spacing (contour levels in thin black lines). Ice shelves are shown in shaded grey. Grounded ice is white. Ellsworth Mountains are colored black.
Mass accumulation over Antarctica regridded onto a 100 km PS grid (personal communication from M. Giovinetto, 1998) was employed to calculate a mass input to the hinge line from the interior regions of 18.3 km3 w.e. a for RIS (20.0 ±2 km3 ice a−1), and 2.6 km3 w.e. a−1 for CI (2.9 ± 0.1 km ice a). If the above results are correct, it means than CI is in equilibrium conditions. RIS exhibits a slightly positive mass budget (+3±4 km3 ice a−1) which suggests that the ice may be thickening.
Conclusions
The example discussed in this study illustrates the usefulness of radar interferometry in providing essential information on glacier grounding-line stability and mass balance in the AntarctiC. The technique provides a complete mapping of the glacier hinge line with unprecedented precision (a few tens of meters). Radar interferometry may also be used to detect hinge-line migration in response to glacier changes and/or changes in ocean tide.
On RIS and CI, the precision of detection of hinge-line migration was about ± 70 m in 4 years. We found no hinge-line migration on these ice streams between 1992 and 1996. Calculations of the effect of changes in ocean tide on the hinge-line position indicated that the inlerferametry results were biased by no more than 60 m. Hence, we conclude that RIS and CI exhibit no change in ice thickness at the grounding line at present. A revision of their mass budget also suggests equilibrium conditions at the grounding line.
Other examples of this approach to the determination of the state of balance and stability of large outlet glaciers are given in Rignot (in press a, b) in the cases of Pine Island Glacier, West Antarctica (for which the grounding line retreated 5 km in 4 years), and Petermann Gletscher, Greenland (for which the grounding line retreated 270 m in 4 years).
Acknowledgements
I would like to thank R. Dietrich and D. Vaughan for their thoughtful review of the manuscript. I thank D. Vaughan for providing tide predictions and GPS profiles for RIS which helped constitute an invaluable set of ground-truth data for this study. I thank J. Bamber for providing a DEM of Antarctica without which this study would have been considerably more difficult. I thank the European Space Agency (ESA) for making the ERS data available to us. This work was performed at thejet Propulsion Laboratory, California Institute of Technology, under a contract with the Polar Program of the National Aeronautics and Space Administration.
