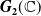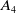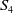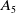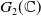1. Introduction
Cartan classified inner automorphisms of finite order of simple Lie algebras
![]() $\mathfrak g$
over the complex numbers, up to conjugation [Reference Cartan2]. See Reeder [Reference Reeder21] for a modern recollection. Motivated by developments in the theory of automorphic Lie algebras (see e.g. [Reference Lombardo and Mikhailov19, Reference Lombardo and Sanders20, Reference Knibbeler, Lombardo and Sanders15, Reference Knibbeler, Lombardo and Sanders16, Reference Knibbeler, Lombardo and Veselov17]), we would like to extend this classification of embeddings of cyclic groups to all finite subgroups of
$\mathfrak g$
over the complex numbers, up to conjugation [Reference Cartan2]. See Reeder [Reference Reeder21] for a modern recollection. Motivated by developments in the theory of automorphic Lie algebras (see e.g. [Reference Lombardo and Mikhailov19, Reference Lombardo and Sanders20, Reference Knibbeler, Lombardo and Sanders15, Reference Knibbeler, Lombardo and Sanders16, Reference Knibbeler, Lombardo and Veselov17]), we would like to extend this classification of embeddings of cyclic groups to all finite subgroups of
![]() $\mathrm{PSL}(2,\mathbb C)$
, which we will call polyhedral groups, consisting of cyclic groups of order n, dihedral groups of order 2n, the tetrahedral group, the octahedral group and the icosahedral group, denoted respectively
$\mathrm{PSL}(2,\mathbb C)$
, which we will call polyhedral groups, consisting of cyclic groups of order n, dihedral groups of order 2n, the tetrahedral group, the octahedral group and the icosahedral group, denoted respectively
The groups
![]() $\mathsf{T}$
,
$\mathsf{T}$
,
![]() $\mathsf{O}$
and
$\mathsf{O}$
and
![]() $\mathsf{I}$
are isomorphic to
$\mathsf{I}$
are isomorphic to
![]() $A_4$
,
$A_4$
,
![]() $S_4$
and
$S_4$
and
![]() $A_5,$
respectively.
$A_5,$
respectively.
If
![]() $\mathfrak{g}$
is one of the classical simple Lie algebras, one can find a satisfying classification using character theory for finite groups. For the exceptional Lie algebras, the full solution to this problem is still out of reach. The important case of embedding the icosahedral group and its double cover into
$\mathfrak{g}$
is one of the classical simple Lie algebras, one can find a satisfying classification using character theory for finite groups. For the exceptional Lie algebras, the full solution to this problem is still out of reach. The important case of embedding the icosahedral group and its double cover into
![]() $E_8({\mathbb C})$
was first solved by Frey [Reference Frey8]. Recently, Frey and Rudelius [Reference Frey and Rudelius10] completed the classification of homomorphisms of (binary) polyhedral groups into
$E_8({\mathbb C})$
was first solved by Frey [Reference Frey8]. Recently, Frey and Rudelius [Reference Frey and Rudelius10] completed the classification of homomorphisms of (binary) polyhedral groups into
![]() $E_8({\mathbb C})$
and further refined its connection to 6-dimensional superconformal field theories. Moreover, they corrected some errors in the physics and mathematics literature on this topic and thus (almost) reconciled their results.
$E_8({\mathbb C})$
and further refined its connection to 6-dimensional superconformal field theories. Moreover, they corrected some errors in the physics and mathematics literature on this topic and thus (almost) reconciled their results.
Throughout, let V be the 7-dimensional faithful representation of
![]() $\mathfrak g_2(\mathbb C)$
. Its exponents generate a Lie group
$\mathfrak g_2(\mathbb C)$
. Its exponents generate a Lie group
![]() $G_2(\mathbb C)$
in
$G_2(\mathbb C)$
in
![]() $\mathrm{SO}(V)$
. The centre of
$\mathrm{SO}(V)$
. The centre of
![]() $G_2(\mathbb C)$
is trivial, and all automorphisms of
$G_2(\mathbb C)$
is trivial, and all automorphisms of
![]() $\mathfrak g_2(\mathbb C)$
are inner, which implies an isomorphism
$\mathfrak g_2(\mathbb C)$
are inner, which implies an isomorphism
given by the adjoint representation. We will use this isomorphism without further mention and refer to Draper [Reference Draper Fontanals6] for a comprehensive and accessible discussion of concrete models for groups of type
![]() $G_2$
.
$G_2$
.
Finite subgroups of
![]() $G_2(\mathbb C)$
have been classified by Cohen and Wales in [Reference Cohen and Wales4], but the conjugacy classes of polyhedral groups are not listed in this paper. We are able to obtain this list for the groups
$G_2(\mathbb C)$
have been classified by Cohen and Wales in [Reference Cohen and Wales4], but the conjugacy classes of polyhedral groups are not listed in this paper. We are able to obtain this list for the groups
![]() $\mathsf{T}$
,
$\mathsf{T}$
,
![]() $\mathsf{O}$
and
$\mathsf{O}$
and
![]() $\mathsf{I}$
with elementary methods because finite subgroups of
$\mathsf{I}$
with elementary methods because finite subgroups of
![]() $G_2(\mathbb C)$
are conjugate if and only if they are conjugate in
$G_2(\mathbb C)$
are conjugate if and only if they are conjugate in
![]() $\mathrm{GL}(V)$
, the latter being decidable by character theory. This powerful theorem was obtained independently by Larsen in [Reference Larsen18] and Griess in [Reference Griess11].
$\mathrm{GL}(V)$
, the latter being decidable by character theory. This powerful theorem was obtained independently by Larsen in [Reference Larsen18] and Griess in [Reference Griess11].
Cohen and Griess [Reference Cohen and Griess3] initiated a flurry of research into embeddings of simple and quasisimple groups, such as the icosahedral group
![]() $\mathsf{I}$
and its double cover, into all exceptional Lie groups. See Frey and Ryba [Reference Frey and Ryba7] for a recent overview of the history and current state of the art. The classification of subgroups was finished in 2002 by Griess and Ryba [Reference Griess12], who also settled the classification of conjugacy classes of embeddings in particular cases. They proved that there are precisely four conjugacy classes of monomorphisms
$\mathsf{I}$
and its double cover, into all exceptional Lie groups. See Frey and Ryba [Reference Frey and Ryba7] for a recent overview of the history and current state of the art. The classification of subgroups was finished in 2002 by Griess and Ryba [Reference Griess12], who also settled the classification of conjugacy classes of embeddings in particular cases. They proved that there are precisely four conjugacy classes of monomorphisms
![]() $\mathsf{I}\hookrightarrow G_2(\mathbb C)$
which realise two conjugacy classes of icosahedral subgroups of
$\mathsf{I}\hookrightarrow G_2(\mathbb C)$
which realise two conjugacy classes of icosahedral subgroups of
![]() $G_2(\mathbb C)$
(the latter fact also obtained by Frey in [Reference Frey9]).
$G_2(\mathbb C)$
(the latter fact also obtained by Frey in [Reference Frey9]).
In this paper, we classify monomorphisms from the tetrahedral and octahedral group into
![]() $G_2(\mathbb C)$
up to conjugation and recover this classification for the icosahedral group obtained by Griess and Ryba with a different proof. The classification of dihedral groups in
$G_2(\mathbb C)$
up to conjugation and recover this classification for the icosahedral group obtained by Griess and Ryba with a different proof. The classification of dihedral groups in
![]() $G_2(\mathbb C)$
remains open.
$G_2(\mathbb C)$
remains open.
2. Cyclic groups in
 $\textbf{G}_{\textbf{2}}(\mathbb C)$
$\textbf{G}_{\textbf{2}}(\mathbb C)$
Elements of finite order in the connected Lie group
![]() $G=\mathrm{Aut}\!\left({\mathfrak{g}} \right)^0$
for a simple complex Lie algebra
$G=\mathrm{Aut}\!\left({\mathfrak{g}} \right)^0$
for a simple complex Lie algebra
![]() $\mathfrak g$
are classified using the geometry of affine Weyl groups. The very short explanation is that any diagonalisable element of G is conjugate to an element of a Cartan subgroup T, and two elements in a T are conjugate in G if and only if they are conjugate by the Weyl group
$\mathfrak g$
are classified using the geometry of affine Weyl groups. The very short explanation is that any diagonalisable element of G is conjugate to an element of a Cartan subgroup T, and two elements in a T are conjugate in G if and only if they are conjugate by the Weyl group
![]() $N_G(T)/T$
. If an element of G has also finite order, it is a rational point in a (compact) maximal torus in G. A maximal torus is isomorphic, through the exponential map, with a real Cartan subalgebra (CSA) up to translations by the co-weight lattice. Thus, the conjugacy classes of elements of finite order in G are identified with rational linear combinations of simple co-weights in the CSA, modulo the action of the Weyl group and the co-weight lattice. This latter group is known as the extended affine Weyl group.
$N_G(T)/T$
. If an element of G has also finite order, it is a rational point in a (compact) maximal torus in G. A maximal torus is isomorphic, through the exponential map, with a real Cartan subalgebra (CSA) up to translations by the co-weight lattice. Thus, the conjugacy classes of elements of finite order in G are identified with rational linear combinations of simple co-weights in the CSA, modulo the action of the Weyl group and the co-weight lattice. This latter group is known as the extended affine Weyl group.
One of the great insights of Cartan was to work modulo the affine Weyl group instead (the semidirect product of the Weyl group and the co-root lattice, rather than the co-weight lattice), which has a simplex as fundamental domain in the CSA, and handle the remaining symmetry using Dynkin diagrams. Determining the vertices of this simplex then yields
Theorem 2.1 (Cartan) Let
![]() $\mathfrak{g}$
be a simple complex Lie algebra and
$\mathfrak{g}$
be a simple complex Lie algebra and
![]() $\{\alpha_1,\ldots,\alpha_\ell\}$
a base for its root system with highest root
$\{\alpha_1,\ldots,\alpha_\ell\}$
a base for its root system with highest root
![]() $\sum_{i=1}^\ell a_i\alpha_i$
. Set
$\sum_{i=1}^\ell a_i\alpha_i$
. Set
![]() $a_0=1$
.
$a_0=1$
.
Elements of order n in
![]() $\mathrm{Aut}\!\left({\mathfrak g} \right)^0$
, up to conjugation, are in one-to-one correspondence with sequences of nonnegative relative prime integers
$\mathrm{Aut}\!\left({\mathfrak g} \right)^0$
, up to conjugation, are in one-to-one correspondence with sequences of nonnegative relative prime integers
![]() $\{s_0,\ldots,s_\ell\}$
such that
$\{s_0,\ldots,s_\ell\}$
such that
up to symmetry of the affine Dynkin diagram. The conjugacy class associated with
![]() $\{s_0,\ldots,s_\ell\}$
is represented by the automorphism sending the Chevalley generator
$\{s_0,\ldots,s_\ell\}$
is represented by the automorphism sending the Chevalley generator
![]() $E_j$
of the Lie algebra to
$E_j$
of the Lie algebra to
![]() $\zeta^{s_j} E_j$
, where
$\zeta^{s_j} E_j$
, where
![]() $j=0,\ldots,\ell$
and
$j=0,\ldots,\ell$
and
![]() $\zeta=\exp\!\frac{2\pi i}{n}$
.
$\zeta=\exp\!\frac{2\pi i}{n}$
.
The sequence
![]() $\{s_0,\ldots,s_\ell\}$
lists the coordinates for the class of automorphisms. For the full story, we refer to the original work of Cartan [Reference Cartan2] and Kac (who extended the result to all automorphisms of finite order) [Reference Kac13, Reference Kac14] and the enlightening treatment of Reeder [Reference Reeder21]. See Bourbaki [Reference Bourbaki1] for a thorough study of (extended) affine Weyl groups.
$\{s_0,\ldots,s_\ell\}$
lists the coordinates for the class of automorphisms. For the full story, we refer to the original work of Cartan [Reference Cartan2] and Kac (who extended the result to all automorphisms of finite order) [Reference Kac13, Reference Kac14] and the enlightening treatment of Reeder [Reference Reeder21]. See Bourbaki [Reference Bourbaki1] for a thorough study of (extended) affine Weyl groups.
Example 2.2 The affine Dynkin diagram of Lie type
![]() $G_2$
is given by
$G_2$
is given by
![]()
with weights
![]() $a_i$
written above the nodes. If we look for automorphisms g of order 3, we find two conjugacy classes. With coordinates
$a_i$
written above the nodes. If we look for automorphisms g of order 3, we find two conjugacy classes. With coordinates
![]() $s_i$
written in the diagram,Footnote
1
they are 0
$s_i$
written in the diagram,Footnote
1
they are 0![]() 1 — 1 and 1
1 — 1 and 1![]() 0 — 0. The automorphism g can be presented by extending these coordinates to the root system additively, modulo
0 — 0. The automorphism g can be presented by extending these coordinates to the root system additively, modulo
![]() $n=3$
, yielding a diagram of the eigenvalues of g at the root spaces of
$n=3$
, yielding a diagram of the eigenvalues of g at the root spaces of
![]() $\mathfrak g_2(\mathbb C)$
, cf. Figure 1. The weights of the representation V correspond to the short roots together with zero. Therefore, one can easily obtain the trace of g on V from the diagram in Figure 1.
$\mathfrak g_2(\mathbb C)$
, cf. Figure 1. The weights of the representation V correspond to the short roots together with zero. Therefore, one can easily obtain the trace of g on V from the diagram in Figure 1.
We present all conjugacy classes of automorphisms of order
![]() $\le 5$
in Table 1.
$\le 5$
in Table 1.

Figure 1. Order 3 elements in
![]() $G_2(\mathbb C)$
diagonalised by a Cartan Weyl basis. Thick lines indicate simple roots. The number s at a root indicates an eigenvalue
$G_2(\mathbb C)$
diagonalised by a Cartan Weyl basis. Thick lines indicate simple roots. The number s at a root indicates an eigenvalue
![]() $e^{\frac{2\pi i s}{3}}$
at the root space.
$e^{\frac{2\pi i s}{3}}$
at the root space.
Table 1. Elements of
![]() $G_2(\mathbb C)$
of order
$G_2(\mathbb C)$
of order
![]() $\le 5$
(with
$\le 5$
(with
![]() $\phi^{\pm}=\frac{1\pm\sqrt{5}}{2}$
).
$\phi^{\pm}=\frac{1\pm\sqrt{5}}{2}$
).

Two more lemmas are needed in preparation for the next section.
Lemma 2.3. If
![]() $\mathrm{PSL}(2,\mathbb{C})\hookrightarrow G_2(\mathbb C)$
is a monomorphism, then the conjugacy class of order 3 elements in
$\mathrm{PSL}(2,\mathbb{C})\hookrightarrow G_2(\mathbb C)$
is a monomorphism, then the conjugacy class of order 3 elements in
![]() $\mathrm{PSL}(2,\mathbb{C})$
is mapped into the conjugacy class of 0
$\mathrm{PSL}(2,\mathbb{C})$
is mapped into the conjugacy class of 0![]() 1—1 in
1—1 in
![]() $G_2(\mathbb C)$
.
$G_2(\mathbb C)$
.
Proof. An element g of order 3 in
![]() $\mathrm{PSL}(2,\mathbb C)$
is conjugate to
$\mathrm{PSL}(2,\mathbb C)$
is conjugate to
![]() $\pm\mathrm{diag}\big(e^\frac{2\pi i}{6},e^{-\frac{2\pi i}{6}}\big)=\pm\ e^{\frac{2\pi i}{6}H}$
where
$\pm\mathrm{diag}\big(e^\frac{2\pi i}{6},e^{-\frac{2\pi i}{6}}\big)=\pm\ e^{\frac{2\pi i}{6}H}$
where
![]() $H=\mathrm{diag}(1,-1)$
belongs to the Lie algebra
$H=\mathrm{diag}(1,-1)$
belongs to the Lie algebra
![]() $\mathfrak{sl}({2},\mathbb{C})$
of
$\mathfrak{sl}({2},\mathbb{C})$
of
![]() $\mathrm{PSL}(2,\mathbb C)$
. Suppose g is mapped to the conjugacy class of 1
$\mathrm{PSL}(2,\mathbb C)$
. Suppose g is mapped to the conjugacy class of 1![]() 0—0 in
0—0 in
![]() $G_2(\mathbb C)$
. Then, H acts on the simple root spaces with weights 2
$G_2(\mathbb C)$
. Then, H acts on the simple root spaces with weights 2![]() 0. By linear extension over the root system, we find all weights of
0. By linear extension over the root system, we find all weights of
![]() $\mathfrak g_2(\mathbb C)$
as representation of
$\mathfrak g_2(\mathbb C)$
as representation of
![]() $\mathfrak{sl}({2},\mathbb{C})$
, and see weight 6 has multiplicity two and weight 4 has multiplicity one. Such a representation of
$\mathfrak{sl}({2},\mathbb{C})$
, and see weight 6 has multiplicity two and weight 4 has multiplicity one. Such a representation of
![]() $\mathfrak{sl}({2},\mathbb{C})$
does not exist. Hence, g is mapped to the other conjugacy class of order 3 elements in
$\mathfrak{sl}({2},\mathbb{C})$
does not exist. Hence, g is mapped to the other conjugacy class of order 3 elements in
![]() $G_2(\mathbb C)$
.
$G_2(\mathbb C)$
.
Lemma 2.4. Let g be a diagonalisable element of
![]() $G_2(\mathbb C)$
with trace
$G_2(\mathbb C)$
with trace
![]() $\chi_V(g)$
and denote the trace of its action on
$\chi_V(g)$
and denote the trace of its action on
![]() $\mathfrak g_2(\mathbb C)$
by
$\mathfrak g_2(\mathbb C)$
by
![]() $\chi_{\mathfrak g_2(\mathbb C)}(g)$
. Then
$\chi_{\mathfrak g_2(\mathbb C)}(g)$
. Then

Proof. The Lie group
![]() $G_2(\mathbb C)$
is realised as a Lie subgroup of
$G_2(\mathbb C)$
is realised as a Lie subgroup of
![]() $\mathrm{SO}(V)$
. This turns
$\mathrm{SO}(V)$
. This turns
![]() $\mathfrak{so}(V)$
into a 21-dimensional representation of
$\mathfrak{so}(V)$
into a 21-dimensional representation of
![]() $\mathfrak g_2(\mathbb C)$
, which has
$\mathfrak g_2(\mathbb C)$
, which has
![]() $\mathfrak g_2(\mathbb C)$
as 14-dimensional subrepresentation. By complete reducibility, there must be a 7-dimensional representation U such that
$\mathfrak g_2(\mathbb C)$
as 14-dimensional subrepresentation. By complete reducibility, there must be a 7-dimensional representation U such that
![]() $\mathfrak{so}(V)=\mathfrak g_2(\mathbb C)\oplus U$
as
$\mathfrak{so}(V)=\mathfrak g_2(\mathbb C)\oplus U$
as
![]() $\mathfrak g_2(\mathbb C)$
representation. It follows from the classification of representations of
$\mathfrak g_2(\mathbb C)$
representation. It follows from the classification of representations of
![]() $\mathfrak g_2(\mathbb C)$
that U is either trivial or
$\mathfrak g_2(\mathbb C)$
that U is either trivial or
![]() $U=V$
. If U is trivial, then
$U=V$
. If U is trivial, then
![]() $\mathfrak g_2(\mathbb C)$
is a nontrivial ideal in
$\mathfrak g_2(\mathbb C)$
is a nontrivial ideal in
![]() $\mathfrak{so}(V)$
, contradicting the simplicity of the latter. Hence,
$\mathfrak{so}(V)$
, contradicting the simplicity of the latter. Hence,
![]() $\mathfrak{so}(V)=\mathfrak g_2(\mathbb C)\oplus V.$
$\mathfrak{so}(V)=\mathfrak g_2(\mathbb C)\oplus V.$
If we consider the trace of g on the left- and right-hand side and observe that the trace of g on
![]() $\mathfrak{so}(V)$
is related to
$\mathfrak{so}(V)$
is related to
![]() $\chi_V(g)$
by
$\chi_V(g)$
by
![]() $\chi_{\mathfrak{so}(V)}(g)=(\chi_V(g)^2-\chi_V(g^2))/2,$
we obtain the desired result.
$\chi_{\mathfrak{so}(V)}(g)=(\chi_V(g)^2-\chi_V(g^2))/2,$
we obtain the desired result.
3.
 $\mathsf{TOI}$
groups in
$\mathsf{TOI}$
groups in
 $\textbf{G}_{\textbf{2}}(\mathbb C)$
$\textbf{G}_{\textbf{2}}(\mathbb C)$
The
![]() $\mathsf{T}\mathsf{O}\mathsf{I}$
groups have presentation
$\mathsf{T}\mathsf{O}\mathsf{I}$
groups have presentation
Taking
![]() $n=3, 4$
or 5 results in
$n=3, 4$
or 5 results in
![]() $\mathsf{T}, \mathsf{O}$
or
$\mathsf{T}, \mathsf{O}$
or
![]() $\mathsf{I},$
respectively. Their character tables are provided in Table 2.
$\mathsf{I},$
respectively. Their character tables are provided in Table 2.
Table 2. Irreducible characters of
![]() $\mathsf{T}$
, with
$\mathsf{T}$
, with
![]() $\zeta=e^{\frac{2\pi i}{3}}$
, of
$\zeta=e^{\frac{2\pi i}{3}}$
, of
![]() $\mathsf{O}$
and
$\mathsf{O}$
and
![]() $\mathsf{I}$
, with
$\mathsf{I}$
, with
![]() $\phi^{\pm}=\frac{1\pm\sqrt{5}}{2}$
.
$\phi^{\pm}=\frac{1\pm\sqrt{5}}{2}$
.

Lemma 3.1 If
![]() $\Gamma$
is a
$\Gamma$
is a
![]() $\mathsf{T}\mathsf{O}\mathsf{I}$
group and
$\mathsf{T}\mathsf{O}\mathsf{I}$
group and
![]() $\Gamma\hookrightarrow G_2(\mathbb C)$
a monomorphism, then any element
$\Gamma\hookrightarrow G_2(\mathbb C)$
a monomorphism, then any element
![]() $\gamma\in\Gamma$
of order 3 is mapped to the class of 0
$\gamma\in\Gamma$
of order 3 is mapped to the class of 0![]() 1—1 in
1—1 in
![]() $G_2(\mathbb C)$
.
$G_2(\mathbb C)$
.
Proof. In Table 1, we see that
![]() $G_2(\mathbb C)$
only has one class of involutions, which has trace
$G_2(\mathbb C)$
only has one class of involutions, which has trace
![]() $-1$
, and two classes of elements of order 3, with traces 1 (at the class of 0
$-1$
, and two classes of elements of order 3, with traces 1 (at the class of 0![]() 1—1) and
1—1) and
![]() $-2$
. The claim follows by observing that the
$-2$
. The claim follows by observing that the
![]() $\mathsf{T}\mathsf{O}\mathsf{I}$
groups do not have a seven dimensional character with values
$\mathsf{T}\mathsf{O}\mathsf{I}$
groups do not have a seven dimensional character with values
![]() $-1$
and
$-1$
and
![]() $-2$
at the elements of order 2 and 3, respectively.
$-2$
at the elements of order 2 and 3, respectively.
In Table 3, we list all 7-dimensional characters of
![]() $\mathsf{T}\mathsf{O}\mathsf{I}$
groups with value
$\mathsf{T}\mathsf{O}\mathsf{I}$
groups with value
![]() $-1$
and 1 at elements of order 2 and 3, respectively, and irrational value at elements of order 5. Due to Lemma 3.1 and Table 1, we know that these conditions are necessary for the character of a monomorphism of a
$-1$
and 1 at elements of order 2 and 3, respectively, and irrational value at elements of order 5. Due to Lemma 3.1 and Table 1, we know that these conditions are necessary for the character of a monomorphism of a
![]() $\mathsf{T}\mathsf{O}\mathsf{I}$
group into
$\mathsf{T}\mathsf{O}\mathsf{I}$
group into
![]() $G_2(\mathbb{C})$
.
$G_2(\mathbb{C})$
.
Table 3. Characters of
![]() $\mathsf{T}\mathsf{O}\mathsf{I}$
groups in
$\mathsf{T}\mathsf{O}\mathsf{I}$
groups in
![]() $G_2(\mathbb C)$
.
$G_2(\mathbb C)$
.

One way to construct embeddings of polyhedral groups is through a composition
There is one embedding
![]() $\mathsf{T}\hookrightarrow\mathrm{PSL}(2,\mathbb C)$
, two embeddings
$\mathsf{T}\hookrightarrow\mathrm{PSL}(2,\mathbb C)$
, two embeddings
![]() $\mathsf{O}\hookrightarrow\mathrm{PSL}(2,\mathbb C)$
and also two embeddings
$\mathsf{O}\hookrightarrow\mathrm{PSL}(2,\mathbb C)$
and also two embeddings
![]() $\mathsf{I}\hookrightarrow\mathrm{PSL}(2,\mathbb C)$
, up to conjugation. Moreover, there are precisely two embeddings
$\mathsf{I}\hookrightarrow\mathrm{PSL}(2,\mathbb C)$
, up to conjugation. Moreover, there are precisely two embeddings
![]() $\mathrm{PSL}(2,\mathbb C)\hookrightarrow G_2(\mathbb C)$
up to conjugation [Reference Collingwood and McGovern5]. They are represented by the weighted Dynkin diagrams 2
$\mathrm{PSL}(2,\mathbb C)\hookrightarrow G_2(\mathbb C)$
up to conjugation [Reference Collingwood and McGovern5]. They are represented by the weighted Dynkin diagrams 2![]() 2 and 2
2 and 2![]() 0. The linear extension of these weights to the root system yields the weights of
0. The linear extension of these weights to the root system yields the weights of
![]() $\mathfrak g_2(\mathbb C)$
as a representation of
$\mathfrak g_2(\mathbb C)$
as a representation of
![]() $\mathfrak{sl}({2},\mathbb{C})$
.
$\mathfrak{sl}({2},\mathbb{C})$
.
The characters of the various compositions realise all options from Table 3. From character theory, we know that this classifies the embeddings in
![]() $G_2(\mathbb C)$
up to conjugation in
$G_2(\mathbb C)$
up to conjugation in
![]() $\mathrm{GL}(V)$
. Thanks to the work of Larsen and Griess [Reference Larsen18, Reference Griess11], we can conclude that these conjugation classes correspond to the conjugation classes in
$\mathrm{GL}(V)$
. Thanks to the work of Larsen and Griess [Reference Larsen18, Reference Griess11], we can conclude that these conjugation classes correspond to the conjugation classes in
![]() $G_2(\mathbb C)$
. Thus we arrive at our main results.
$G_2(\mathbb C)$
. Thus we arrive at our main results.
Theorem 3.2 The conjugation classes of monomorphisms of
![]() $\mathsf{T}$
,
$\mathsf{T}$
,
![]() $\mathsf{O}$
and
$\mathsf{O}$
and
![]() $\mathsf{I}$
into
$\mathsf{I}$
into
![]() $G_2(\mathbb C)$
are classified by the characters in Table 3.
$G_2(\mathbb C)$
are classified by the characters in Table 3.
The part of this theorem concerning the icosahedral group can also be found in [Reference Griess12, Section 4] where a different proof is given.
There is an automorphism of
![]() $\mathsf{I}$
sending
$\mathsf{I}$
sending
![]() $\gamma_a$
to
$\gamma_a$
to
![]() $\gamma_a^2$
. The conjugacy classes of monomorphisms
$\gamma_a^2$
. The conjugacy classes of monomorphisms
![]() $\mathsf{I}\hookrightarrow G_2(\mathbb C)$
with the first two and last two icosahedral characters of Table 3 are interchanged when precomposed with this automorphism. Thus, we see that there are only two conjugacy classes of images of monomorphisms
$\mathsf{I}\hookrightarrow G_2(\mathbb C)$
with the first two and last two icosahedral characters of Table 3 are interchanged when precomposed with this automorphism. Thus, we see that there are only two conjugacy classes of images of monomorphisms
![]() $\mathsf{I}\hookrightarrow G_2(\mathbb C)$
, and recover [Reference Frey9, Theorem 4.11].
$\mathsf{I}\hookrightarrow G_2(\mathbb C)$
, and recover [Reference Frey9, Theorem 4.11].
Theorem 3.3 Each monomorphism of
![]() $\mathsf{T}$
,
$\mathsf{T}$
,
![]() $\mathsf{O}$
and
$\mathsf{O}$
and
![]() $\mathsf{I}$
into
$\mathsf{I}$
into
![]() $G_2(\mathbb C)$
factors through
$G_2(\mathbb C)$
factors through
![]() $\mathrm{PSL}(2,\mathbb C)$
.
$\mathrm{PSL}(2,\mathbb C)$
.
This result provides a practical construction, since monomorphisms
![]() $\Gamma\hookrightarrow\mathrm{PSL}(2,\mathbb C)$
and
$\Gamma\hookrightarrow\mathrm{PSL}(2,\mathbb C)$
and
![]() $\mathrm{PSL}(2,\mathbb C)\hookrightarrow G_2(\mathbb C)$
can be found in the literature.
$\mathrm{PSL}(2,\mathbb C)\hookrightarrow G_2(\mathbb C)$
can be found in the literature.
Theorem 3.4 If
![]() $\Gamma$
is a
$\Gamma$
is a
![]() $\mathsf{T}\mathsf{O}\mathsf{I}$
group embedded in
$\mathsf{T}\mathsf{O}\mathsf{I}$
group embedded in
![]() $\mathrm{Aut}\!\left({\mathfrak g_2(\mathbb C)} \right)$
, then the only element in
$\mathrm{Aut}\!\left({\mathfrak g_2(\mathbb C)} \right)$
, then the only element in
![]() $\mathfrak g_2(\mathbb C)$
fixed by all
$\mathfrak g_2(\mathbb C)$
fixed by all
![]() $\gamma\in\Gamma$
is 0.
$\gamma\in\Gamma$
is 0.
Proof. Using Lemma 2.4 and Theorem 3.2, we can compute all characters of
![]() $\Gamma$
-actions on
$\Gamma$
-actions on
![]() $\mathfrak g_2(\mathbb C)$
and observe that none of them has a trivial component.
$\mathfrak g_2(\mathbb C)$
and observe that none of them has a trivial component.
We have not classified embeddings of the dihedral groups in
![]() $G_2(\mathbb C)$
. The following example shows why this task cannot be completed with the same approach.
$G_2(\mathbb C)$
. The following example shows why this task cannot be completed with the same approach.
Example 3.5 We construct a monomorphism
![]() $\mathsf{D}_{3}\hookrightarrow G_2(\mathbb C)$
which shows that Lemma 3.1, Theorems 3.3 and 3.4 all fail for dihedral groups. We do so with a concrete model L of
$\mathsf{D}_{3}\hookrightarrow G_2(\mathbb C)$
which shows that Lemma 3.1, Theorems 3.3 and 3.4 all fail for dihedral groups. We do so with a concrete model L of
![]() $\mathfrak g_2(\mathbb C)$
in
$\mathfrak g_2(\mathbb C)$
in
![]() $\mathfrak{gl}(7,\mathbb C)$
. Let
$\mathfrak{gl}(7,\mathbb C)$
. Let
![]() $x=(x_1, x_2, x_3)^t$
and let
$x=(x_1, x_2, x_3)^t$
and let
 \begin{equation*}L=\left\{\left(\begin{array}{c@{\quad}c@{\quad}c}0&-\sqrt{2}y^t&-\sqrt{2}x^t\\ \\[-8pt]\sqrt{2}x&a&l_y\\ \\[-8pt]\sqrt{2}y&l_x&-a^t\end{array}\right)\,|\,a\in\mathfrak{sl}({3},\mathbb{C}),\,x,y\in\mathbb{C}^3\right\},\quad l_{x}=\left(\begin{array}{c@{\quad}c@{\quad}c}0&-x_3&x_2\\ \\[-8pt]x_3&0&-x_1\\ \\[-8pt]-x_2&x_1&0\end{array}\right).\end{equation*}
\begin{equation*}L=\left\{\left(\begin{array}{c@{\quad}c@{\quad}c}0&-\sqrt{2}y^t&-\sqrt{2}x^t\\ \\[-8pt]\sqrt{2}x&a&l_y\\ \\[-8pt]\sqrt{2}y&l_x&-a^t\end{array}\right)\,|\,a\in\mathfrak{sl}({3},\mathbb{C}),\,x,y\in\mathbb{C}^3\right\},\quad l_{x}=\left(\begin{array}{c@{\quad}c@{\quad}c}0&-x_3&x_2\\ \\[-8pt]x_3&0&-x_1\\ \\[-8pt]-x_2&x_1&0\end{array}\right).\end{equation*}
See [Reference Draper Fontanals6] for a proof that (a conjugate of) L is indeed a simple Lie subalgebra of
![]() $\mathfrak{gl}(7,\mathbb C)$
of type
$\mathfrak{gl}(7,\mathbb C)$
of type
![]() $G_2$
, so that we can identify L with
$G_2$
, so that we can identify L with
![]() $\mathfrak g_2(\mathbb C)$
and
$\mathfrak g_2(\mathbb C)$
and
![]() $\mathrm{Aut}\!\left({L} \right)$
with
$\mathrm{Aut}\!\left({L} \right)$
with
![]() $G_2(\mathbb C)$
.
$G_2(\mathbb C)$
.
Conjugation with the diagonal matrix
![]() $\mathrm{diag}(1,\zeta,\zeta,\zeta,\zeta^2,\zeta^2,\zeta^2)$
,
$\mathrm{diag}(1,\zeta,\zeta,\zeta,\zeta^2,\zeta^2,\zeta^2)$
,
![]() $\zeta=e^{\frac{2\pi i}{3}}$
, defines an automorphism of
$\zeta=e^{\frac{2\pi i}{3}}$
, defines an automorphism of
![]() $\mathfrak{gl}(7,\mathbb C)$
which preserves L. Let r be its restriction to L. Then, r is an order 3 automorphism of L. The elements of L fixed by r form a Lie subalgebra isomorphic to
$\mathfrak{gl}(7,\mathbb C)$
which preserves L. Let r be its restriction to L. Then, r is an order 3 automorphism of L. The elements of L fixed by r form a Lie subalgebra isomorphic to
![]() $\mathfrak{sl}({3},\mathbb{C})$
; hence, r belongs to the conjugacy class of 1
$\mathfrak{sl}({3},\mathbb{C})$
; hence, r belongs to the conjugacy class of 1![]() 0—0 in
0—0 in
![]() $G_2(\mathbb C)$
(cf. Figure 1).
$G_2(\mathbb C)$
(cf. Figure 1).
The map
![]() $M\mapsto -M^t$
also defines an automorphism of
$M\mapsto -M^t$
also defines an automorphism of
![]() $\mathfrak{gl}(7,\mathbb C)$
which preserves L. Let s be its restriction to L, an automorphism of order 2. Then,
$\mathfrak{gl}(7,\mathbb C)$
which preserves L. Let s be its restriction to L, an automorphism of order 2. Then,
![]() $rs=sr^{-1}$
; hence, r and s generate a dihedral group of order 6 in
$rs=sr^{-1}$
; hence, r and s generate a dihedral group of order 6 in
![]() $G_2(\mathbb C)$
.
$G_2(\mathbb C)$
.
Contrary to the case of the
![]() $\mathsf{T}\mathsf{O}\mathsf{I}$
groups, the map
$\mathsf{T}\mathsf{O}\mathsf{I}$
groups, the map
![]() $\mathsf{D}_{3}\hookrightarrow G_2(\mathbb C)$
we have constructed does not factor through
$\mathsf{D}_{3}\hookrightarrow G_2(\mathbb C)$
we have constructed does not factor through
![]() $\mathrm{PSL}(2,\mathbb C)$
because of Lemma 2.3 and the fact that its image has nontrivial intersection with the conjugacy class of 1
$\mathrm{PSL}(2,\mathbb C)$
because of Lemma 2.3 and the fact that its image has nontrivial intersection with the conjugacy class of 1![]() 0—0. Moreover, we compute that the elements fixed by
0—0. Moreover, we compute that the elements fixed by
![]() $\mathsf{D}_{3}$
form a subalgebra of
$\mathsf{D}_{3}$
form a subalgebra of
![]() $\mathfrak g_2(\mathbb C)$
isomorphic to
$\mathfrak g_2(\mathbb C)$
isomorphic to
![]() $\mathfrak{sl}({2},\mathbb{C})$
.
$\mathfrak{sl}({2},\mathbb{C})$
.
Acknowledgements
We are grateful to Jan Sanders for very helpful and stimulating discussions. We thank the anonymous reviewer for interesting historical remarks.
Funding
This work is supported by the Engineering and Physical Sciences Research Council (EPSRC): the work of SL and VK is supported by the grant EP/V048546/1; the work of CO is supported by the grant EP/W522569/1.