Hostname: page-component-6bf8c574d5-mcfzb Total loading time: 0 Render date: 2025-03-07T04:11:00.893Z Has data issue: false hasContentIssue false
  • English
  • Français

SUBSHIFTS OF FINITE TYPE WITH A HOLE

Part of: Topological dynamics Discrete mathematics in relation to computer science

Published online by Cambridge University Press:  22 March 2022

HARITHA CHERIYATH  and
NIKITA AGARWAL
HARITHA CHERIYATH
Affiliation:
Department of Mathematics, Indian Institute of Science Education and Research Bhopal, Bhopal Bypass Road, Bhauri, Bhopal 462 066, Madhya Pradesh, India e-mail: [email protected]
NIKITA AGARWAL*
Affiliation:
Department of Mathematics, Indian Institute of Science Education and and Research Bhopal, Bhopal Bypass Road, Bhauri, Bhopal 462 066, Madhya Pradesh, India
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We consider a subshift of finite type on q symbols with a union of t cylinders based at words of identical length p as the hole. We explore the relationship between the escape rate into the hole and a rational function, 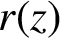$r(z)$, of correlations between forbidden words in the subshift with the hole. In particular, we prove that there exists a constant 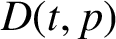$D(t,p)$ such that if 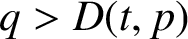$q>D(t,p)$, then the escape rate is faster into the hole when the value of the corresponding rational function 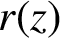$r(z)$ evaluated at 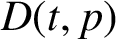$D(t,p)$ is larger. Further, we consider holes which are unions of cylinders based at words of identical length, having zero cross-correlations, and prove that the escape rate is faster into the hole with larger Poincaré recurrence time. Our results are more general than the existing ones known for maps conjugate to a full shift with a single cylinder as the hole.

Keywords

subshifts of finite typeopen dynamical systemssymbolic dynamicsescape ratecombinatoricscorrelation polynomial of words

MSC classification

Primary: 37B10: Symbolic dynamics
Secondary: 68R15: Combinatorics on words
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 115 , Issue 1 , August 2023 , pp. 73 - 98
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Communicated by Dmitry Badziahin

The research of the first author is supported by the Council of Scientific & Industrial Research (CSIR), India (file no. 09/1020(0133)/2018-EMR-I), and the second author is supported by the Science Engineering Research Board, Department of Science and Technology, India (file no. CRG/2019/003823) and the Center for Research on Environment and Sustainable Technologies (CREST), IISER Bhopal, CoE funded by the Ministry of Human Resource Development (MHRD), India.

References

Attarchi, H. and Bunimovich, L. A, ‘Why escape is faster than expected’, J. Phys. A 53(43) (2020), 435002.CrossRefGoogle Scholar
Bolding, M. and Bunimovich, L. A., ‘Where and when orbits of chaotic systems prefer to go’, Nonlinearity 32(5) (2019), 1731–1771.CrossRefGoogle Scholar
Bruin, H., Demers, M. F. and Todd, M., ‘Hitting and escaping statistics: mixing, targets and holes’, Adv. Math. 328 (2018), 1263–1298.CrossRefGoogle Scholar
Bunimovich, L. A. and Vela-Arevalo, L. V., ‘Some new surprises in chaos’, Chaos 25(9) (2015), 097614, 11 pages.CrossRefGoogle ScholarPubMed
Bunimovich, L. A. and Yurchenko, A., ‘Where to place a hole to achieve a maximal escape rate’, Israel J. Math. 182 (2011), 229–252.CrossRefGoogle Scholar
Demers, M., Wright, P. and Young, L. S., ‘Escape rates and physically relevant measures for billiards with small holes’, Comm. Math. Phys. 294(2) (2010), 353–388.CrossRefGoogle Scholar
Froyland, G. and Stancevic, O., ‘Escape rates and Perron–Frobenius operators: open and closed dynamical systems’, Discrete Contin. Dyn. Syst. Ser. B 14(2) (2010), 457–472.Google Scholar
Guibas, L. J. and Odlyzko, A. M., ‘Maximal prefix-synchronized codes’, SIAM J. Appl. Math. 35(2) (1978), 401–418.CrossRefGoogle Scholar
Guibas, L. J. and Odlyzko, A. M., ‘String overlaps, pattern matching, and nontransitive games’, J. Combin. Theory Ser. A 30(2) (1981), 183–208.10.1016/0097-3165(81)90005-4CrossRefGoogle Scholar
Hao, B., Xie, H., Yu, Z. and Chen, G., ‘Avoided strings in bacterial complete genomes and a related combinatorial problem’, Ann. Comb. 4(3–4) (2000), 247–255.CrossRefGoogle Scholar
Haritha, C. and Agarwal, N., ‘Product of expansive Markov maps with hole’, Discrete Contin. Dyn. Syst. 39(10) (2019), 5743–5774.Google Scholar
Haritha, C. and Agarwal, N., ‘On the Perron root and eigenvectors associated with a subshift of finite type’, Linear Algebra Appl. 633 (2022), 42–70.Google Scholar
Lind, D. and Marcus, B., An Introduction to Symbolic Dynamics and Coding (Cambridge University Press, Cambridge, 1995).CrossRefGoogle Scholar
Odlyzko, A. M., ‘Enumeration of strings’, in: Combinatorial Algorithms on Words, NATO ASI Series F, 12 (eds. A. Apostolico and Z. Galil) (Springer, Berlin, 1985), 205–228.10.1007/978-3-642-82456-2_14CrossRefGoogle Scholar
Parry, W., ‘Intrinsic Markov chains’, Trans. Amer. Math. Soc. 112 (1964), 55–66.CrossRefGoogle Scholar
Pianigiani, G. and Yorke, J. A., ‘Expanding maps on sets which are almost invariant: decay and chaos’, Trans. Amer. Math. Soc. 252 (1979), 351–366.Google Scholar