1. INTRODUCTION
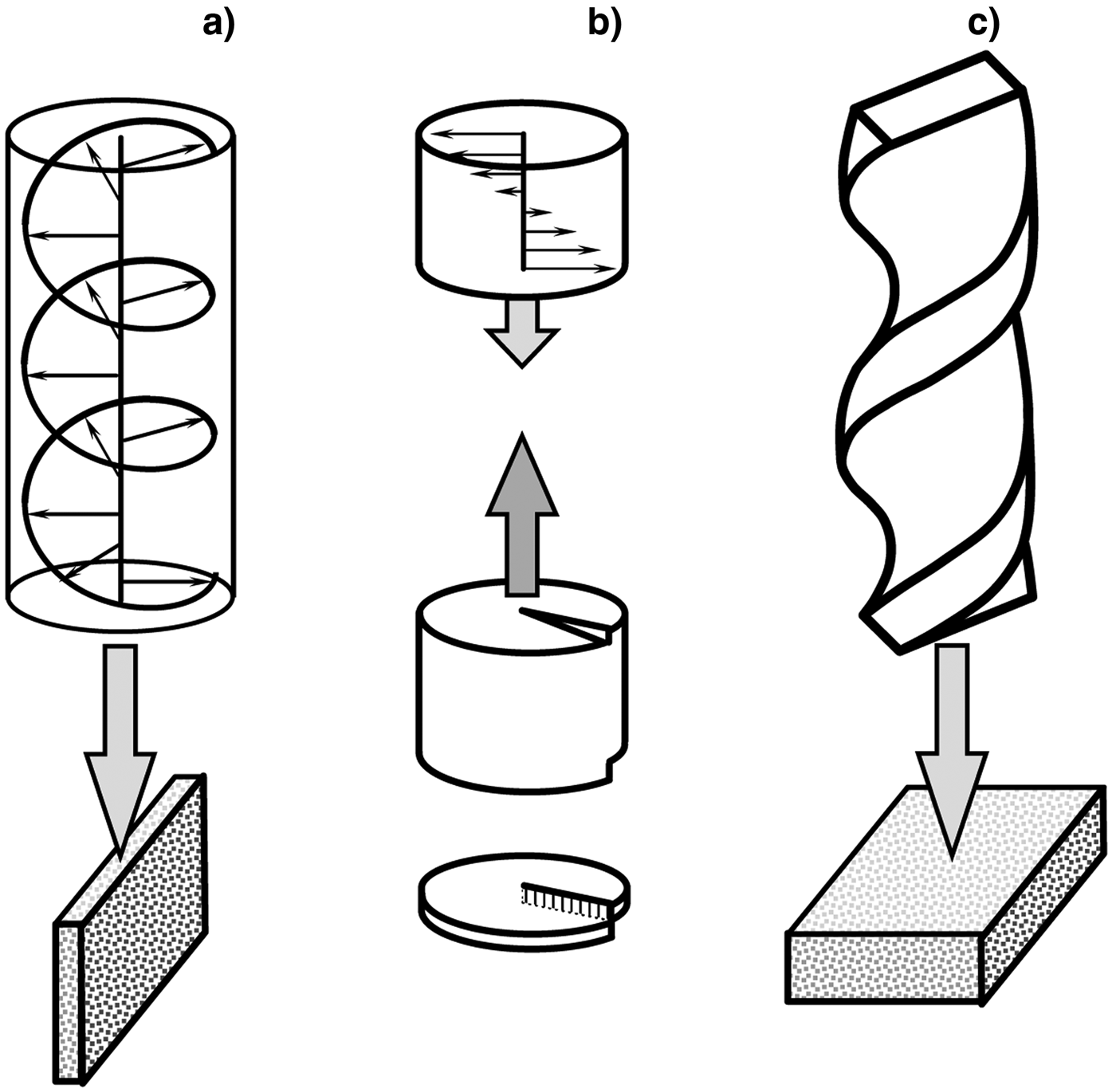
The efficient transfer of orbital angular momentum (OAM) from laser pulses to particles becomes possible with sufficient light intensity. At low intensities, the mechanical torque of Laguerre–Gaussian (LG) pulses (Allen et al., Reference Allen, Beijersbergen, Spreeuw and Woerdman1992) and the transformation fundamental modes into higher order LG modes (Beijersbergen et al., Reference Beijersbergen, Coerwinkel, Kristensen and Woerdman1994) have been investigated using optical plates. At relativistic intensities, there are three possible ways of inducing ion rotation in an overdense plasma and are illustrated schematically in Figure 1: using a circularly polarized (CP) light interacting with a flat foil, so that the axis of propagation is in the plane of the target; a simple linearly polarized (LP) pulse and a thin (light) spiral foil (Yin et al., Reference Yin, Baifei, Lingang, Xiaomei, Wenpeng and Zhizhan2014) or using a spiral-shaped laser pulse (Seryi, Reference Seryi2014). The first scenario is based upon the circular motion of electrons in the CP light resulting in a torque in the target due to the charge-separation perpendicular to the radius. In the second case, the reflected light will also contain some OAM in the opposite direction to the induced OAM in the target (conservation of momentum). The third method is currently being investigated and will be reported elsewhere. This paper only considers the first and second cases using CP pulses.
Fig. 1. Schematic view of different methods for inducing rotation of electrons and ions in overdense plasma: (a) CP pulse shining on a thin foil, (b) LP plane wave interacting with a spiral surface and (c) spiral (or cork-screw) laser pulse interaction with flat foil.
Laser pulses, besides reproducing exotic astrophysical phenomena in laboratory plasma (Bulanov et al., Reference Bulanov, Esirkepov, Habs, Pegoraro and Tajima2009) and plasma vorticity diagnosis (Mendonca et al., Reference Mendonca, Thidé and Then2009), could have an important application in the generation of higher-order harmonics with finite OAM (Hernandez-Gracia et al., Reference Hernandez-Gracia, Picón, Plaja and Román2013). The investigation of a rotating light ion beam propagation in plasmas is also an interesting topic (Takayuki & Keishiro, Reference Takayuki and Keishiro1987). The rectification of magnetic fields in intense laser–plasma interactions, known as the inverse Faraday effect (Takayuki & Keishiro, Reference Takayuki and Keishiro1988), could be realized in underdense plasma using pulses with high OAM. The circular motion of electrons can generate very strong (up to 109 or 106 G in underdense plasma) (Naseri et al., Reference Naseri, Bychenkov and Rozmus2010) longitudinal magnetic fields, which could lead to better electron collimation in laser wakefield acceleration (Jha et al., Reference Jha, Saroch, Mishra and Upadhyay2012) and preservation of beam emittance, in a similar way as emittance compensation solenoids are used in radio frequency (RF) guns.
Laser pulse duration is an important parameter because the electron heating process results in an omnidirectional plasma expansion. If the plasma density is near critical, the partial removal of electrons often results in a strong Coulomb explosion in the region used to generate rotating ions. These effects can ruin and decrease the total OAM of the target plasma; therefore, shorter pulses are preferable for these investigations. However, the optimal pulse length, which depends on the plasma parameters, has to be determined. In this paper, we concentrate on very short pulses interacting with mass limited plasma slabs and the dependence of final OAM on the laser intensity is investigated.
2. FLAT TARGETS
All simulations were performed using VORPAL (VSim) 3D (Nieter & Cary, Reference Nieter and Cary2004) plasma simulation code. The simplest setup is illustrated in Figure 2. The target is made of solid hydrogen with a density n 0 = 28n cr. The foil (height, h = 0.1 μm in the z-direction) is placed in the middle of the simulation domain with transversal width (y-direction) of 6 µm (R t = 3 μm) and with longitudinal length (x-direction) of 2 µm. The target plasma slab starts at 
$x = 3\, {\rm \mu} {\rm m}$. The laser pulse is CP with Gaussian intensity profile transversally and longitudinally with peak intensity I L. It is produced by combining two orthogonal LP (in the y- and z-directions) pulses shifted by one quarter period (π/2 phase shift). The pulse duration is defined by t L = 20 fs [full-width at half-maximum (FWHM)] and the spot radius is R L = 1 μm (FWHM). The peak intensity is I L = 1020 W/cm2 and the corresponding normalized electric field amplitude 
$a_0 = (I_{\rm L} [10^{18} {\rm W}/{\rm cm}^2 ]{\rm \lambda} _{\rm L}^2 [{\rm \mu} {\rm m}^2 ]/1.37)^{1/2} = 6.83$, where λL = 0.8 μm is the laser wavelength. The laser propagates in the x-direction with axis at (y 0, z 0) = (3, 3) μm, which is the axis of symmetry of the target as well.
Fig. 2. Sketch of the simulation setup (a).
The left and right boundaries (in the x-direction) absorb electromagnetic (EM) waves and reflect particles. The EM fields are absorbed by perfectly matched layer (PML) regions, which are 0.5 µm thick at both ends of the simulation box and electrons are specularly reflected, with the same velocity, where the layers start. Even if the electrons have relativistic velocities (≈ c), they return to the target around 35 fs (20–25 fs after generation from the target front side), which is close to the end of the interaction. The density of reflected electrons is very low and thus will not significantly influence the rotation. With this setup, unrealistic back-reflected waves in the system can be avoided and the total charge conserved. The number of macroparticles per cell is 50 and the simulation box has the dimensions 
$7 \times 6 \times 6 \,{\rm \mu} {\rm m}^3 $, which corresponds 350 × 300 × 300 grid cells. Transversally periodic boundaries are used due the very small amount of energy in waves propagating in this direction.
The total OAM transferred to the protons be measured from the simulation by summing 
$L_{_x} = ({\rm \bf r} \times {\rm \bf p})_x $ for all protons, where 
$r = \sqrt {(y - y_0 )^2 + (z - z_0 )^2} $ is the modulus of position vector of the proton with respect to the axis of symmetry of the system. The final value of OAM, the maximum value achieved at the end of the laser–plasma interaction (t e ≈ 40 fs) is defined as:
$$L_{{\rm i}x} (t_{\rm e} ) = \sum\limits_{\matrix{\,j}} ({\rm \bf r}_j \times {\rm \bf p}_j )_x, $$where j denotes the proton numbering.
Electronic OAM is measured in the same way but the symbol L ex (
$L_x^{\rm e} $ for a single electron) is used. The total OAM of the laser pulse can be estimated: L Lx ≈ εL/ωL, where εL is the laser energy (Yin et al., Reference Yin, Baifei, Lingang, Xiaomei, Wenpeng and Zhizhan2014). For a pulse energy around 100 mJ, The OAM value is of the order of L 0 = 10−17 kg m2 s−1, thus we introduce the dimensionless quantity: Λx = L x/L 0. It can be measured numerically in space and time from the simulation data using the electric and magnetic field components:
$$L_{{\rm L}x} (x_0, x_1 ) = \displaystyle{1 \over {c^2}} \int_{x_0} ^{x_1} \int_0^{2y_0} \int_0^{2z_0} ({\rm \bf r} \times {\rm \bf S})_x dz dy dx,$$
where 
${\rm \bf S} = ({\rm \bf E} \times {\rm \bf B})/{\rm \mu} _0 $ is the Poynting vector and x 0, x 1 are the borders of the longitudinal interval where the OAM of EM fields is determined. According to the law of conservation of momentum, the OAM of incoming laser pulse has to be equal to the measured OAM of particles and EM waves in the system, which is shown in the Appendix.
Figure 3a shows the time evolution of L Lx (0, Δx left) and L Lx (x sim − Δx right, x sim), where Δx left = Δx right = 1 μm is the length of laser pulse propagation during the time between two consecutive dumping of the output data and x sim = 7 μm is the total length of the simulation box. The total OAM entering and leaving the simulation domain can be found by integrating these curves with respect to time. This is shown in the Appendix. Initially the laser pulse entering the simulation box contains only positive OAM, but the reflected and transmitted light also contains negative OAM. This means that the flat rectangular obstacle (foil target) breaks the circular symmetry of the laser pulse and the fields generated during the interaction will be LP. The pulse reaches the end of the simulation domain at t = 20 fs and it leaves the domain at t = 60 fs, when the OAM at both boundaries is once more nearly zero. We can also measure the total power (VORPAL calculates the integrated Poynting vector over the transversal plane for each time step) passing through the left and right boundaries (before the PML regions). This is plotted in Figure 3b and can be used to calculate that about 23% of the laser energy is absorbed by the particles. The oscillating structure in the transmitted light (green curve) indicates that the flat target partially transforms the light from CP into LP, confirming the existence of the negative OAM observed in Figure 3a. This oscillation is also visible in the reflected light as measured at the left boundary (blue curve).
Fig. 3. Evolution of L Lx (a) in a 1 μm thick layer at the left (blue) and right (green) boundary. The dashed and dotted lines show the negative and positive components, respectively. In the right (b), the total power is shown in time on the left and right boundaries. The red line corresponds to the incoming pulse.
2.1. Electron dynamics
The flat foil is placed in the xy-plane and in a half-period of the laser pulse, when E z is negative, then electrons are accelerated in the positive z-direction (Fig. 4). In the second half of the period, the same thing happens on the opposite side of the target. In this way, the flat target mainly absorbs energy from the z-component of the laser E-field, thus transforms it into an LP light, in the vicinity of the overdense plasma. From the energy history of the electrons shown in Figure 4, we see that the electrons initially gain the kinetic energy, which is higher in the z-direction, and slowly transfer it to the protons. In the early stage of the interaction, the OAM of electrons is also much greater than the protonic OAM (see the Appendix for more details). As a result of the partly linear polarization, the ponderomotive force will oscillate and the remaining electrons in the target feel a strong longitudinal force generating density oscillations with a wavelength equal to half of the laser wavelength.
Fig. 4. Time evolution of electron (blue and magenta) and proton (green) transversal energy and the E z (red) field component of the laser pulse.
The longitudinal electric fields are generated by the density modulations in the plasma and by the electron bunches rotating around the plasma surface. Figure 5a shows that electron density oscillations have different periodicity inside and outside the plasma. The E x field (Figs 5b and 5c) has the same structure as the density in Figure 5a, showing that the fields are induced by the space charge of the electrons. This periodic structure is also observed in the OAM distribution around the target.
Fig. 5. Electron density distribution (macroparticles) is shown inside and outside (above at z = 3.2 μm) of the target (a) integrated in the y direction at t = 27 fs. In the middle (b) and right (c) pictures, the longitudinal electric fields are shown at the same time inside and outside, respectively. The plasma is placed between x = 3.5 and 5.5 μm.
By definition, the OAM of an electron is calculated as 
$L_x^{\rm e} = (y - y_0 )p_z - (z - z_0 )p_y $. The electrons can have positive or negative OAM depending on the position and momentum. It is known that in the half laser period, when E z < 0, the y-component of the E-field changes sign and becomes maximum when E z = 0. Therefore the electrons OAM can change sign at one side of the target.
Figures 6a and 6b show that the electrons are not fully bunched by the ponderomotive pressure, but some components fall behind the leading front, which travels almost with the speed of light. Those backward spreading electrons are still attracted by the protons in the target and obtain negative OAM, because the electric field changes its sign in this half-period (Figs 6c and 6d). As the electrons are still located above the target (E z is still negative), they drag the protons azimuthally since the charge separation field points in the same direction as in the other half laser period. On the other side of the target (y > y 0), the electrons will have the same momentum distribution but with lower density, because initially all are accelerated in the negative y-direction. It means that the electrons spend more time in the left side of the above the target as they do in the right side below it. This mechanism is very similar to the generation of electron nano-bunches and attopulses with p-polarized pules (Naumova et al., Reference Naumova, Hou, Mourou, Nees and Sokolov2004a, Reference Naumova, Maksimchuk, Mourou, Nees, Sokolov and Yanovskyb and Andreev & Platonov, Reference Andreev and Platonov2013), but here an s-polarized component is also included and 90° incident angle is considered.
Fig. 6. Density distribution of electrons (a,b) for 
$y \lt 3\, {\rm \mu} {\rm m}$ at times: 7.5 fs (left), 8.5 fs (right). The corresponding average 
$L_x^{\rm e} $ distribution (c,d) normalized to m ecR L.
The final OAM of electrons, averaged in time and space, can be estimated as:
$$L^{\prime}_{{\rm ex}} = N_{{\rm eh}} \lt L_x^{\rm e} \gt = N_{{\rm eh}} \displaystyle{{m_{\rm e} c^2 a_0^2} \over {{\rm \omega} _{\rm L}}} = N_{{\rm eh}} \displaystyle{{{\rm \varepsilon} _{{\rm eh}}} \over {{\rm \omega} _{\rm L}}} = {\rm \eta} _{\rm e} {\rm \varepsilon} _{\rm L} /{\rm \omega} _{\rm L}, $$where N eh = ηeεL/εeh is the number of electrons dragged by the CP laser pulse; εeh, ηe are the electron energy and absorption efficiency, which we measured from the simulation. Here we assumed that all electrons have relativistic energy, which leads to overestimated momentum conversion as it is shown in the next section.
Longitudinal magnetic fields are also induced by the strong electric current generated by the rotating electrons. The x- and y-components of the B-field are shown in Figure 7 in the xz-plane at y = 3 μm. The longitudinal magnetic field is generated by the transverse current of electrons (motion in the y-direction) and these fields propagate away from the target with large divergence. In Figure 7b, the phase compression (Naumova et al., Reference Naumova, Hou, Mourou, Nees and Sokolov2004a, Reference Naumova, Maksimchuk, Mourou, Nees, Sokolov and Yanovskyb) is clearly visible, where the laser field (B y) is compressed and propagates in forward direction in attopulses. As the electrons are extracted from the plasma by the laser field, they form an overdense wall near the surface which is swept by the ponderomotive force with velocity close to the speed of light. This relativistic mirror will not reflect, but rather emit radiation in the forward direction which is highly compressed in the laboratory frame due to the Doppler effect. This phenomenon can be also interpreted as coherent synchrotron radiation and will be reported in details elsewhere. The negative B-field undergoes the same transformation below the target.
Fig. 7. The x (b) and y (b) components of the magnetic field above the target at t = 27 fs. The field amplitude in the laser pulse is B L = 105 T.
The theoretical estimation of the OAM transferred to the protons formulated in Eq. (3) is not accurate because the majority of the electrons are non-relativistic. The time evolution of particle and laser OAM is compared to Eqs. (A1) and (A2) in the Appendix, where a conservation law is formulated proving the accuracy of the simulation.
2.2. Ion dynamics
The total energy of the laser pulse is about εL = 0.12 J which corresponds to ΛLx = 5.08. This means that there is around 40% OAM conversion efficiency of laser light energy to the protons because Λix (t e) = 2.1 (see Fig. A14 in the Appendix) calculated by Eq. (1). The theoretical value of OAM of electrons is calculated according to Eq. (3) which yields Λ′ex = 1.1 but the ions can gain about twice this value. It follows from the non-relativistic relation between energy and momentum: 
$ \lt L_x^{\rm e} \gt = r \lt p_{{\rm e} \bot} \gt = 2 \lt {\rm \varepsilon} _{{\rm eh}} \gt /{\rm \omega} _{\rm L} $. This factor of 2 difference between L ix and L′ex is measured in simulations.
L x is not the same for all protons contributing to the total OAM of the target and some part of the target could rotate with higher azimuthal velocity. This anisotropy is the main difference between the OAM of a rigid body and of a plasma. Plasma expansion as well as rotation occurs simultaneously which modifies the OAM distribution within the target. This process results in a radial symmetric distribution of the momentum vectors of protons in the transversal plane which, of course, does not generate rotation. In order to remove this transverse momentum contribution, the summation of L x is performed using one half of the plasma in conjunction with the other mirrored half of the plasma. In this way, the OAM contribution coming from the plasma expansion cancels out and the resultant OAM only appears in one quarter of the transversal plane.
The color plot in Figure 8 is generated by the process described above and only shows the upper left part of the simulation domain because the lower right section has the same structure. The blue line in Figure 8 represents the OAM spectrum of all protons. In the bottom pictures, we see that the L x distribution is almost symmetric due to the plasma expansion. The resultant spectrum (green line) is produced by subtracting the values in the negative and positive intervals of the spectrum of all protons (blue line). Later, when the plasma expansion evolves, negative OAM also appears in the spatial distribution and in the spectra as well (Fig. 8, right). The overall OAM remains positive and it is entirely induced by the laser pulse, the OAM associated with the plasma expansion cancels out due to symmetry.
Fig. 8. The L x spectrum and color plot of proton OAM distribution at t = 27 fs (a,c) and at t = 54 fs (b,d). One macro-particle contains 142.8 n 0/n cr real particles. The green curve (resultant OAM) is obtained by the subtraction of counted particle number (blue curve) lying in the positive and negative intervals.
The electric sheath field on the target surface can only interact with protons in a thin layer, which explains the spatial OAM distribution shown in Figure 8. The OAM of a single electron is 
$L_x^{\rm e} = rp_{{\rm e} \bot} {\rm \sim} r\;exp\;( - r^2 /R_{\rm L}^2 )$, which is zero in the center and far from the center (r ≫ R L) and in the intermediate regions, it is transferred to the protons. Thus, the proton OAM has a maximum value near the edge of the laser focal spot (FWHM).
2.3. OAM scaling with laser intensity
The final angular momentum for different laser spot size and intensity is shown in Table 1. We could expect that the plasma areal density has an optimal value depending on the laser intensity, which in the RPA regime is formulated as (Macchi et al., Reference Macchi, Veghini and Pegoraro2009): n 0h/n crλL = a 0/π. If the areal density is too high, then the laser pulse cannot accelerate the ions to high velocity, or only a small fraction is accelerated (the target is too heavy). If this value is low, then the laser can pass through the plasma due to relativistic transparency without developing the charge separation field needed for acceleration. The same argument can be formulated for the case of plasma rotation (azimuthal acceleration). In the second row of Table 1, the parameters are obtained for this optimal condition. Plasma densities above and below this optimal value are called overdense and underdense, respectively. The overall results show that a larger laser spot size increases more the OAM than higher laser intensity. By maintaining the target density, the plasma becomes more transparent when higher peak intensity is applied and thus lowers OAM conversion efficiency. When the areal density is higher (or the intensity is lower) than the optimal one the rotation is still strong and the gained OAM remains proportional to the laser power.
Table 1. Simulation parameters and the measured OAM at the end of the pulse. 
$h = 0.1\, {\rm \mu} {\rm m}$, Rt = 3 μm
In later simulations, the laser spot size is larger R L = 1.5 μm and is equal to the half width of the target, R t = 1.5 μm. The height of the target is h = 0.2 μm. In this scenario, the laser pulse can propagate along the sides, in the lateral vacuum regions as well as above and below the plasma slab. The simulation box has the same size and boundaries. The advantage of this setup is that the angle of rotation can be visualized by plotting the density distribution of protons. Table 2 shows the results for t = 40 fs. The percentage of protons that contribute to the positive OAM of the target is shown in the last column and is obtained by integrating the resultant spectrum (green line in Fig. 8).
Table 2. Simulation parameters and the measured OAM at the end of the pulse. h = 0.2 μm, Rt = 1.5 μm
In Figure 9a, values from Table 2 are shown by the dashed lines, while the full lines show the calculated values using ηe from the simulation and Eq. (3). It is evident that the overdense regime (n 0h/n crλL > a 0/π) is more efficient at generating OAM, yielding a two times higher final OAM then the theoretical model given by Eq. (3). In this case, the measured energy conversion was 
${\rm \eta} _{\rm e} = 15\% $, while for the lower density it was smaller and inversely proportional to a 0. The optimal parameters for RPA (I L = 2.59 · 1020 W/cm2 and n 0 = 14n cr) are not optimal for the OAM. This effect is connected to the forward electron drift with respect to the ions, because momentum transfer requires electrons close to the target surface, where charge separation is initiated. The maximum L ix is obtained for a 0 = 13.66, which is very close to the lower boundary of the transparent regime. Figure 9b shows the time evolution of L ix and L ex. The electron OAM is close to zero, because the oscillating high amplitude is averaged in space but protons simultaneously gain OAM from positive and negative electronic OAM (Fig. 6). Here, with higher intensity, there is a slightly higher OAM of electrons also means weaker conversion efficiency as the parameters approach the transparent regime.
The final L x spectra of protons in Figure 10 show that there are a large proportion of protons with higher momentum in strongly overdense plasma. If the target is only partially heated, then the charge-separation electric field cannot penetrate deeply into the plasma, due to the shielding cold electrons. Thus the majority of protons from the plasma surface are accelerated to high velocity. In the underdense regime, more protons are accelerated, because the electrostatic force acts deeper in the plasma, but to lower velocity, because the electron energy is finite and the plasma expansion strongly modifies the target shape. This can be seen in Figure 11a, where the plasma density is relatively low; the original shape is not maintained and the target explodes.
Fig. 10. The L x spectrum of protons at t = 50 fs. The red and blue curves correspond to the overdense conditions, while the green curve is measured in the underdense regime. One macro-particle contains 142.8 n 0/n cr real particles.
Fig. 11. Density distribution (macroparticles) of the protons at t = 50 fs within a 0.5 μm thin layer at the target front side for n 0 = 28 n cr (a) and n 0 = 56 n cr (b). The normalized laser amplitude is a 0 = 9.66, the color is in logarithmic scale.
The simulation corresponding to Figure 11b shows a slight angle (≈ 4−5°) between the horizontal line and the plasma edge. This is a clear hallmark of rotation. It can be seen that the protons rotate anticlockwise (the direction of laser propagation is toward the reader and thus the circular motion is clockwise) and the final OAM is Λix (t e) = 6.76, but only 1.5% of the total protons take part in the rotation forming a low-density cloud surrounding the bulk target.
The azimuthal velocity component (v φ) has to be calculated in order to characterize the plasma rotation. The angular momentum of the target can be written as:
$$L_{{\rm i}x} = 0.5R_{\rm t} N_{\rm i} m_{\rm i} \lt v_{\rm \varphi} \gt, $$The plasma can be modeled as a rotating disc due to the strong radial expansion and N i = πR 2n il, where n i represents the density of rotating ions. Now the average azimuthal velocity can be expressed:
$$\lt v_{\rm \varphi} \gt = \displaystyle{{2L_{{\rm i}x}} \over {{\rm \pi} R^3 ln_{\rm i} m_{\rm i}}}. $$After substituting the values measured from the simulation (n i, L ix) one obtains v φ ≈ 0.01 c, where c is the speed of light. The radial expansion velocity is about 0.11 c, thus the angle of rotation is about 5°, which is close to the model's result of 4° (Fig. 11). Actually, the simulations' slightly smaller value is expected due to the Gaussian intensity distribution of the laser pulse. The simulation was repeated with plane wave (transversally uniform intensity in the whole simulation domain) but the clear signature of the rotation is not visible due to the stronger radial expansion of the plasma.
3. SPIRAL TARGETS
Proton rotation can be induced in flat targets by the circular motion of the hot electron cloud, which creates a Debye sheath perpendicular to the target, in the azimuthal direction. Twisted targets, with a spiral shape (Fig. 12a), in conjunction with the longitudinal radiation pressure and the OAM of the laser pulse can increase the OAM of protons. Such targets are generated, in simulations, by defining a plasma slab in each grid cell (along the x-direction) tilted with an angle which depends on position: α = 2π(x − x 0)/λsp, where x 0 is the starting position of the target. In this case, the charge separation field generated by the ponderomotive pressure, has an azimuthal component, which further accelerates the protons in this direction. In this case, the shape of the target also defines the maximal OAM.
Fig. 12. Spiral target for 2 μm step size (a). The color denotes the longitudinal position (in x) of the protons. (b) The proton density distribution is shown for the same target at two different cross-section positions and at two time instances: at the beginning (10 fs) and at the end (40 fs) of the interaction.
Figure 12b shows the superposition of the proton density distribution for a 2 µm spiral step at early (10 fs) and late (40 fs) times measured at two positions (x = 4 and 5 μm) within 0.1 µm thin layers. This clearly shows the rotation. The red part (higher density) of the color plot shows the initial cross-section of the plasma and the yellow part (lower density) shows the expanded and rotated plasma seen at the end of the laser–plasma interaction. The x-coordinate axis (direction of laser propagation) points toward the reader; thus, the direction of the rotation is anticlockwise.
Table 3 shows simulation results with the same target mass and with laser intensity 2 × 1020 W/cm2. The width of the laser pulse and target is 3 µm (R L = R t = 1.5 μm). The crucial parameter is the spiral step (λsp), which has an optimal value around 2 λL. If the step size is increased, most of the laser energy would be absorbed in the front of the target, which flattens as λsp goes to infinity and thus the results presented in the previous section are reproduced. The rotation of the electric field vector in the laser pulse has the same orientation as the spiral target.
Table 3. Simulation parameters and the measured OAM at the end of the pulse. Here a 0 = 9.66 and Rt = RL = 1.5 μm
In the case of simulation with λsp = 1.5 λL, the direction of the circular polarization was changed to be opposite to the spiral orientation. This results in a higher OAM, because the electrons now circulate in the negative direction (anticlockwise). The similar value for OAM obtained for both cases shows that the circular motion of the electrons has a small effect on the rotation in spiral targets and the ponderomotive force generates the majority of the OAM. Another important observation was that the percentage of the rotating protons is much higher compared with the flat targets, as indicated in Figure 13.
Fig. 13. Comparison of the filtered spectra from the simulations presented in Table 3. The absolute value of L x is shown and the numbers mean the percentage of rotating protons.
In the simulations presented in this section, the total OAM of the laser pulse was ΛLx = 21.2 meaning that the conversion efficiency is much higher. In the optimal case (third row in Table 3), it can be up to 60–70%, depending on the direction of circular polarization. The 60% conversion efficiency was also observed by Yin et al. (Reference Yin, Baifei, Lingang, Xiaomei, Wenpeng and Zhizhan2014), where linear polarization and planar wave was used. Here we observe that the circular motion of electrons can enhance the OAM of ions by 16%. The better OAM conversion efficiency in the case of spiral target can be attributed to the reflected light carrying an OAM with opposite sign to the induced OAM in the target.
4. CONCLUSIONS
It has been shown that in the case of flat mass-limited target and CP pulse, only a few percent of the protons contribute to the final OAM measured in the simulations. If the plasma density is reduced, then more protons rotate in the same direction, but with lower velocity while with higher plasma densities, less particles rotate with higher velocity. For the maximal OAM, the target areal density has to be higher than the optimal areal density for RPA. In this overdense regime, the final OAM is linearly proportional to the laser pulse energy and decreasing the density increase the number of rotating protons but the total OAM decreases. If the density is even lower, then the target plasma becomes relativistically transparent and the rotation becomes very inefficient.
The spiral shape of the target exploits the longitudinal ponderomotive force and in this case the direction of the OAM depends on the spiral orientation. In this case, the maximum OAM of individual protons is smaller by a factor of 2 than in the case of a flat foil, but the number of accelerated protons is much higher (factor of 10), as shown in Figure 13 and Table 2. By applying a CP pulse with opposite polarization, the absolute OAM value is increased, but the ponderomotive pressure contribution dominants to the final OAM. The optimal step size of the spiral is about λsp ≈ 2 λL and by changing the size, the spectral shape of the OAM distribution can be changed.
Due to numerical and computational restrictions, we could not simulate the plasma behavior on a longer time scale. For the scope of this paper, the physics during the interaction provides enough information regarding the momentum transfer. However, some simulations were prolonged up to 60 fs that showed that after the laser pulse leaves the plasma region, the electron rotation is insignificant and the electrons become thermalized and form a hot cloud surrounding the rotating ions. These ions feel a significant expansion in all directions, but their finite OAM is preserved and they drift in the forward direction. Some momentum transfer occurs from the ions back to electrons, which needs further future investigation. The plasma corona, which is formed by these ions and the accompanying thermal electrons, leaves the bulk target and propagates as a quasi-neutral rotating beam.
ACKNOWLEDGEMENT
The authors would like to thank Tech-X Corp and specifically Dr. J. Smith for technical support and advice with VSim simulations. We also thank Ivan Konoplev and Faissal Bakkali Taheri for their help and support. The ELI-ALPS project (GOP-1.1.1.-12/B-2012-0001) is supported by the European Union and co-financed by the European Regional Development Fund.
Supplementary Material
To view supplementary material for this artilce, please visit http://dx.doi.org/10.1017/S0263034615000853.
APPENDIX: A. MOMENTUM CONSERVATION
The momentum conservation equation, which has to be fulfilled at any time, is the following:
$${\rm OAM}_{{\rm in}} = L_{ix} + L_{{\rm e}x} + {\rm OAM}_{{\rm out}} + L_{{\rm L}x} (0,x_{{\rm sim}} ),$$
where 
${\rm OAM}_{{\rm in}} (t) = \sum\nolimits_{N_{\rm d} (t)} L_{{\rm L}x} (0,{\rm \Delta} x_{{\rm left}} )$ is the angular momentum of the incoming laser pulse, N d(t) is the number of data output corresponding at the time instance t. OAMout is measured in the same way, summing L Lx (x sim − Δx right, x sim). These operations are basically the integration of blue and green lines in Figure 3, from which the curves shown with the same color in Figure A14 is obtained. For the electrons, this value is very small Λex ≈ 0.1, because it is only the averaged value. In (Yin et al., Reference Yin, Baifei, Lingang, Xiaomei, Wenpeng and Zhizhan2014), it is shown that with LP laser pulse, the OAM of electrons oscillate around zero with an amplitude comparable with L ix (t e). Here the positive and negative OAM cancel out each other but both contribute locally to the final OAM of protons. The blue dashed line in Figure A14 is the summation of momenta given in the right-hand side of Eq. (A1), which should be equal to OAMin, which is represented by the full blue line. The agreement is very good over the time interval of interest. At later times due to the periodic boundaries and numerical errors, this equality is not fulfilled.
Fig. A14. The total angular momentum of protons and EM fields measured in the simulation domain. Here OAMEM = L Lx (0, x sim), is measured at each dumping time and OAMin, OAMout are defined in the text [see Eq. (A1)].
We performed another simulation with much greater time resolution in order to follow what happens to the particle OAM within one laser cycle. Five measurements can be done during one laser period. In order to save time, the pulse duration FWHM was reduced to 10 fs and the target starts at x = 1 μm.
In Figure A15, the time evolution of different OAMs in the system are shown. It can be seen that the measured OAM of particles (≈41% of laser OAM) follows the shape of an error function and this can be used to reconstruct the torque of the laser pulse acting on the particles, because it follows the time dependence of the laser intensity:
$$T = 0.41{\rm \varepsilon} _{\rm L} /(\sqrt {2{\rm \pi}} {\rm \sigma} _{\rm L} {\rm \omega} _{\rm L} )\;exp\;( - (t - t_0 )^2 /2{\rm \sigma} _{\rm L}^2 ),$$
where σL = t L/2.355, t 0 is the time when the laser reaches the target and 
$1/\sqrt {2{\rm \pi}} $ is a normalization factor. After integrating this function, we obtain the dashed red line Figure A15, which accurately describes the generated OAM of particles. After the peak intensity reaches the target, the electron OAM oscillates around a constant value showing that the plasma expansion, driven by the hot electrons, has a significant influence over the laser-driven rotation. An OM exchange between the electrons and ions is observable, because the proton OAM also contains small fluctuations.
Fig. A15. Time evolution of the total (positive plus negative) OAM of electrons and protons. The red line shows the laser torque [Eq. (A2)] according to 41% laser OAM and the dashed line is its integral in time. The laser–plasma interaction starts at 
$t_0 \approx 4.5 \,{\rm fs}$.
The very quick energy transfer from electrons to protons can be attributed to the large interaction surface between the species. The measured kinetic energy of protons is two times smaller in the longitudinal direction than in the transversal one, while for the electrons we measured two times higher energy in the longitudinal motion at t = 18 fs. It also shows that the energy transfer in the longitudinal direction is much weaker than in the transversal plane.
In Figure A16, the total OAM of the third electron bunch (appearing when the third laser cycle reaches the plasma front) is shown in time as it propagates on the target surface. The selected region is one wavelength long (0.8 µm) moving window and it follows the bunch, moving along the x-axis with the speed of light. The bunch appears at 9.5 fs and overall contains more positive than negative OAM. As it flies above the target surface, it leaves some electrons, which will have negative OAM because E y changes its sign. Meanwhile below the target, another bunch appears in the second half of the laser period, which also has positive OAM. When the upper third bunch reaches the end of the target, most of the electrons are in the negative OAM phase and they counterbalance the positive OAM carried by the lower bunch, thus the total OAM is once more zero. The momentum transfer to protons continues although the average (total) OAM of electrons is zero.
Fig. A16. The positive (green) and total (blue) OAM of electrons within one wavelength longitudinal interval moving with speed of light.
Open access
