1. Introduction
Bacteria are prokaryotic microorganisms forced to live in a zero Reynolds number environment. Due to the kinematic reversibility of viscous flows, some bacteria have developed a non-reciprocal propulsion mechanism for locomotion, the rotation of flagella. The bacterium body and the flagella are rotated in opposite directions by molecular motors. Under rotation the flagella adopt a helical shape and propel the bacterium by working as a screw. Some bacteria can move both forward or backwards, in a push or pull mode, depending on the direction of rotation of the molecular motors and on the chirality of their flagella. As bacteria are often found in confined environments they have developed different strategies to swim while foraging in those conditions. One example is a swimming mode used by some monotrichous and bipolar bacteria, where bacteria wrap their flagella around their own bodies, resembling an Archimedes’ screw (Kühn et al. Reference Kühn, Schmidt, Eckhardt and Thormann2017; Thormann, Beta & Kühn Reference Thormann, Beta and Kühn2022; Tian et al. Reference Tian, Wu, Zhang and Yuan2022). These bacteria swim alternating between two different modes, the wrapped mode and the extended mode, where in the latter the flagella extend away from their bodies.
The wrapped mode emerges when a bacterium encounters highly viscous or strongly confined environments (Kühn et al. Reference Kühn, Schmidt, Eckhardt and Thormann2017). When a bacterium gets trapped during its forward pushing mode a buckling instability occurs in the flagellar hook that triggers the flagellum wrapped mode (Kühn et al. Reference Kühn, Schmidt, Eckhardt and Thormann2017; Park et al. Reference Park, Kim, Lee and Lim2022). The number of known bacterial species showcasing a wrapped mode under confinement is growing (Thormann et al. Reference Thormann, Beta and Kühn2022). Thus, a natural question arises: Is the wrapped mode a mere accident or is it selected due to some advantage to the bacteria? Some studies suggest that the wrapped mode confers advantages to the motion in confinement environments. Kühn et al. observed experimentally that the wrapped mode can enhance the motion in highly viscous and structured environments (Kühn et al. Reference Kühn, Schmidt, Farthing, Rossmann, Helm, Wilson, Eckhardt and Thormann2018). Kinosita et al. studied the motion of bacteria with the wrapped mode in very tight confinements and concluded that the wrapped mode can allow the bacteria to glide over the substrate (Kinosita et al. Reference Kinosita, Kikuchi, Mikami, Nakane and Nishizaka2018). Along this line of work we investigate how the flagellum motion in the wrapped mode favours the motion of bacteria under strong confinement by hydrodynamic interactions only. To this end we investigate the swimming of a bacterium inside circular pipes by means of computational fluid dynamics (CFD) simulations. We model the bacterium as a rigid ellipsoidal body with a single rigid flagellum attached to one of its poles, as done in previous works (Higdon Reference Higdon1979; Lauga et al. Reference Lauga, DiLuzio, Whitesides and Stone2006). The hydrodynamic interactions between the bacterium and pipe are computed by solving the Stokes equations with the rigid multiblob method, a regularized boundary integral method (Balboa Usabiaga et al. Reference Balboa Usabiaga, Kallemov, Delmotte, Bhalla, Griffith and Donev2016; Balboa Usabiaga & Delmotte Reference Balboa Usabiaga and Delmotte2022). We show that the extended mode is more efficient in bulk and wide pipes while the wrapped mode can be more efficient in tight pipes. The flow fields around the bacterium reveal that the wrapped mode works as an Archimedes’ screw, pulling the fluid along the pipe. The scheme of the paper is the following, in § 2 we describe our numerical method and present some validations, then we describe our results in § 3 and conclude in § 4.
2. Numerical method
We model a monotrichous bacterium as a rigid ellipsoid with an helical flagellum attached to one of its poles. The flagellum is also modelled as a rigid object since it reaches an equilibrium configuration during steady-state swimming (Higdon Reference Higdon1979; Das & Lauga Reference Das and Lauga2018). The body and the flagellum are connected by inextensible links that allow the flagellum to rotate freely around its main axis but otherwise it is forced to move concomitant to the rigid ellipsoid. Therefore, the bacterium's configuration is completely specified by seven degrees of freedom, the position and orientation of the body and the flagellum rotation, or phase angle, around its axis (Higdon Reference Higdon1979; Pimponi et al. Reference Pimponi, Chinappi, Gualtieri and Casciola2016). The rigid objects, ![]() $\mathcal {B}_n$, move with linear and angular velocities,
$\mathcal {B}_n$, move with linear and angular velocities, ![]() $\boldsymbol {u}_n$ and
$\boldsymbol {u}_n$ and ![]() $\boldsymbol {\omega }_n$, where we use the subindex
$\boldsymbol {\omega }_n$, where we use the subindex ![]() $n$ to denote either the bacterium body or the flagellum. Due to the small bacterium size, the flow Reynolds number is vanishingly small,
$n$ to denote either the bacterium body or the flagellum. Due to the small bacterium size, the flow Reynolds number is vanishingly small, ![]() ${Re} \sim 10^{-5}$. Thus, the flow can be modelled with the Stokes equations
${Re} \sim 10^{-5}$. Thus, the flow can be modelled with the Stokes equations
where ![]() $p$ and
$p$ and ![]() $\boldsymbol {v}$ are the fluid pressure and velocity and
$\boldsymbol {v}$ are the fluid pressure and velocity and ![]() $\eta$ its viscosity. A no-slip boundary condition is imposed on the surface of the bacterium body and its flagellum
$\eta$ its viscosity. A no-slip boundary condition is imposed on the surface of the bacterium body and its flagellum
where ![]() $\boldsymbol {q}_n$ is the tracking point of the rigid bodies (e.g. the bacterium body centre and the flagellum attachment point, respectively).
$\boldsymbol {q}_n$ is the tracking point of the rigid bodies (e.g. the bacterium body centre and the flagellum attachment point, respectively).
To solve the coupled fluid–structure interaction problem we use the rigid multiblob method for articulated bodies. We summarize the numerical method while a detailed description can be found elsewhere (Balboa Usabiaga & Delmotte Reference Balboa Usabiaga and Delmotte2022). The rigid bodies are discretized with a finite number of blobs with position ![]() $\boldsymbol {r}_i$, as shown in figure 1. As the inertia is negligible the conservation of momentum reduces to the balance of force and torque. The discrete force and torque balance for the rigid object
$\boldsymbol {r}_i$, as shown in figure 1. As the inertia is negligible the conservation of momentum reduces to the balance of force and torque. The discrete force and torque balance for the rigid object ![]() $n$ can be written as
$n$ can be written as
where ![]() $\boldsymbol {f}_n$ and
$\boldsymbol {f}_n$ and ![]() $\boldsymbol {\tau }_n$ are the external forces and torques acting on the rigid objects while
$\boldsymbol {\tau }_n$ are the external forces and torques acting on the rigid objects while ![]() $\boldsymbol {\lambda }_i$ are the constrained forces acting on the blobs that ensure the rigid motion of the bacterium body and the flagellum. The second sums in (2.4)–(2.5) run over the links,
$\boldsymbol {\lambda }_i$ are the constrained forces acting on the blobs that ensure the rigid motion of the bacterium body and the flagellum. The second sums in (2.4)–(2.5) run over the links, ![]() $\mathcal {L}_n$, attached to the rigid object
$\mathcal {L}_n$, attached to the rigid object ![]() $n$ and
$n$ and ![]() $\boldsymbol {\phi }_{n}$ is the force exerted by the link
$\boldsymbol {\phi }_{n}$ is the force exerted by the link ![]() $n$ to keep the rigid bodies connected while
$n$ to keep the rigid bodies connected while ![]() $|\Delta \boldsymbol {l}_{np}|$ is the link length.
$|\Delta \boldsymbol {l}_{np}|$ is the link length.

Figure 1. Bacterium, ![]() $2.04\ {\mathrm {\mu }}{\rm m}$ long and
$2.04\ {\mathrm {\mu }}{\rm m}$ long and ![]() $0.49\ {\mathrm {\mu }}{\rm m}$ wide, inside a pipe with inner radius
$0.49\ {\mathrm {\mu }}{\rm m}$ wide, inside a pipe with inner radius ![]() $r_{0} = 0.4125\ {\mathrm {\mu }}{\rm m}$ with its flagellum in the extended and wrapped configuration. In both cases the flagellum has the same amplitude
$r_{0} = 0.4125\ {\mathrm {\mu }}{\rm m}$ with its flagellum in the extended and wrapped configuration. In both cases the flagellum has the same amplitude ![]() $\alpha = 0.32\ {\mathrm {\mu }}{\rm m}$ and the same number of waves along its axis
$\alpha = 0.32\ {\mathrm {\mu }}{\rm m}$ and the same number of waves along its axis ![]() $N_{\lambda } = 1.1$. Here, we show a dissected section of the pipe to make the bacterium visible.
$N_{\lambda } = 1.1$. Here, we show a dissected section of the pipe to make the bacterium visible.
The discrete no-slip condition evaluated at each blob ![]() $i$ is
$i$ is
The mobility matrix ![]() $\boldsymbol {M}_{ij}$ gives the hydrodynamic interaction between any two blobs,
$\boldsymbol {M}_{ij}$ gives the hydrodynamic interaction between any two blobs, ![]() $i$ and
$i$ and ![]() $j$, of radii
$j$, of radii ![]() $a_i$ and
$a_i$ and ![]() $a_j$. We use a regularized version of the Oseen tensor, the Rotne–Prager tensor (Wajnryb et al. Reference Wajnryb, Mizerski, Zuk and Szymczak2013)
$a_j$. We use a regularized version of the Oseen tensor, the Rotne–Prager tensor (Wajnryb et al. Reference Wajnryb, Mizerski, Zuk and Szymczak2013)
where ![]() $\boldsymbol {G}(\boldsymbol {r},\boldsymbol {r}')$ is the Green's function of the Stokes equations and
$\boldsymbol {G}(\boldsymbol {r},\boldsymbol {r}')$ is the Green's function of the Stokes equations and ![]() $\delta (r)$ is the Dirac delta function. The advantage of this formulation is that the regularized mobility has no divergence even when blobs get close and it is not necessary to use special quadrature rules. Equations (2.4)–(2.6) form a linear system for the unknown velocities,
$\delta (r)$ is the Dirac delta function. The advantage of this formulation is that the regularized mobility has no divergence even when blobs get close and it is not necessary to use special quadrature rules. Equations (2.4)–(2.6) form a linear system for the unknown velocities, ![]() $\boldsymbol {u}_n$ and
$\boldsymbol {u}_n$ and ![]() $\boldsymbol {\omega }_n$, and constraint forces,
$\boldsymbol {\omega }_n$, and constraint forces, ![]() $\boldsymbol {\lambda }_j$ and
$\boldsymbol {\lambda }_j$ and ![]() $\boldsymbol {\phi }_n$, that can be solved efficiently with iterative methods such as the generalized minimal residual method (GMRES) (Balboa Usabiaga et al. Reference Balboa Usabiaga, Kallemov, Delmotte, Bhalla, Griffith and Donev2016; Balboa Usabiaga & Delmotte Reference Balboa Usabiaga and Delmotte2022).
$\boldsymbol {\phi }_n$, that can be solved efficiently with iterative methods such as the generalized minimal residual method (GMRES) (Balboa Usabiaga et al. Reference Balboa Usabiaga, Kallemov, Delmotte, Bhalla, Griffith and Donev2016; Balboa Usabiaga & Delmotte Reference Balboa Usabiaga and Delmotte2022).
2.1. Validation
Here, we test our computational model against previous theoretical and computational works on helical flagellar swimming. As first validation, we compute the swimming speed, in bulk, of a bacterium formed by a spherical body of radius ![]() $c=1$ and an helical flagellum of length
$c=1$ and an helical flagellum of length ![]() $L$ and compare our results against those of Higdon (Reference Higdon1979). Following Higdon, we use flagella of helical shape with wavenumber
$L$ and compare our results against those of Higdon (Reference Higdon1979). Following Higdon, we use flagella of helical shape with wavenumber ![]() $k$, amplitude
$k$, amplitude ![]() $\alpha =1/k$ and thickness radius
$\alpha =1/k$ and thickness radius ![]() $\rho / c = 0.02$. We discretize the bacterium body with
$\rho / c = 0.02$. We discretize the bacterium body with ![]() $162$ blobs and the flagella with
$162$ blobs and the flagella with ![]() $125$,
$125$, ![]() $250$ and
$250$ and ![]() $500$ blobs for the flagellum lengths,
$500$ blobs for the flagellum lengths, ![]() $L = 5, 10, 20$, respectively. We present in figure 2(a) the dimensionless velocity,
$L = 5, 10, 20$, respectively. We present in figure 2(a) the dimensionless velocity, ![]() $U k / \omega$, where
$U k / \omega$, where ![]() $\omega$ is the relative angular velocity between the bacterium body and flagellum vs the number of waves in the flagellum,
$\omega$ is the relative angular velocity between the bacterium body and flagellum vs the number of waves in the flagellum, ![]() $N_{\lambda }$. The agreement with the results of Higdon is good for all the flagella considered.
$N_{\lambda }$. The agreement with the results of Higdon is good for all the flagella considered.

Figure 2. (a) Non-dimensional swimming speed, ![]() $Uk/\omega _{motor}$, plotted against the flagellum number of waves,
$Uk/\omega _{motor}$, plotted against the flagellum number of waves, ![]() $N_{\lambda }=z_{max}/k$, for bacteria with a spherical body of radius
$N_{\lambda }=z_{max}/k$, for bacteria with a spherical body of radius ![]() $c=1$ and different flagellum lengths
$c=1$ and different flagellum lengths ![]() $L$. The flagellum thickness,
$L$. The flagellum thickness, ![]() $\rho / c=0.02$, amplitude
$\rho / c=0.02$, amplitude ![]() $\alpha$ and wavenumber
$\alpha$ and wavenumber ![]() $k=1 / \alpha$ are set to compare with the results of Higdon (Reference Higdon1979). Dashed lines represent Higdon's results while symbols represent our simulation results. (b) Circular trajectory comparison between a bacterium swimming above a no-slip surface and a free surface. The arrows on the curves represent the direction of swimming.
$k=1 / \alpha$ are set to compare with the results of Higdon (Reference Higdon1979). Dashed lines represent Higdon's results while symbols represent our simulation results. (b) Circular trajectory comparison between a bacterium swimming above a no-slip surface and a free surface. The arrows on the curves represent the direction of swimming.
As a second validation we compute the trajectory of a bacterium above a no-slip and a free-slip surface. The equations of motion are integrated with a midpoint scheme which requires solving two mobility problems per time step to find the bacterium body and flagellum velocities (Balboa Usabiaga & Delmotte Reference Balboa Usabiaga and Delmotte2022). The bacterium body is modelled as an ellipsoid with major axis length ![]() $4$ and aspect ratio
$4$ and aspect ratio ![]() $\gamma = 2$, discretized with
$\gamma = 2$, discretized with ![]() $287$ blobs. The flagellum of length
$287$ blobs. The flagellum of length ![]() $L=11.91$ and
$L=11.91$ and ![]() $N_{\lambda } = 2$ is discretized with
$N_{\lambda } = 2$ is discretized with ![]() $154$ blobs. We also incorporate a short-range steric repulsion between the blobs and the surface to avoid possible overlaps. We use a steric repulsion of strength
$154$ blobs. We also incorporate a short-range steric repulsion between the blobs and the surface to avoid possible overlaps. We use a steric repulsion of strength ![]() $f=0.01 \ {\rm pN}$ for overlapping blobs with the surface and with an exponential decay with a characteristic length
$f=0.01 \ {\rm pN}$ for overlapping blobs with the surface and with an exponential decay with a characteristic length ![]() $\xi =0.01\ {\mathrm {\mu }}{\rm m}$ for non-overlapping blobs. It is well known from previous studies that flagellated bacteria move in circular trajectories, of opposite directions, when swimming close to a no-slip or a free-slip surface (Lauga et al. Reference Lauga, DiLuzio, Whitesides and Stone2006; Shum, Gaffney & Smith Reference Shum, Gaffney and Smith2010; Pimponi et al. Reference Pimponi, Chinappi, Gualtieri and Casciola2016). In addition, Pimponi et al. (Reference Pimponi, Chinappi, Gualtieri and Casciola2016) reported that the radius of the trajectory is small in the free-slip case in comparison with the no-slip case. Our results capture the previously observed features, the bacterium is hydrodynamically attracted to the surface and swims in circles, see figure 2(b).
$\xi =0.01\ {\mathrm {\mu }}{\rm m}$ for non-overlapping blobs. It is well known from previous studies that flagellated bacteria move in circular trajectories, of opposite directions, when swimming close to a no-slip or a free-slip surface (Lauga et al. Reference Lauga, DiLuzio, Whitesides and Stone2006; Shum, Gaffney & Smith Reference Shum, Gaffney and Smith2010; Pimponi et al. Reference Pimponi, Chinappi, Gualtieri and Casciola2016). In addition, Pimponi et al. (Reference Pimponi, Chinappi, Gualtieri and Casciola2016) reported that the radius of the trajectory is small in the free-slip case in comparison with the no-slip case. Our results capture the previously observed features, the bacterium is hydrodynamically attracted to the surface and swims in circles, see figure 2(b).
3. Results and discussion
In this section we study the swimming of a bacterium inside circular pipes of radius ![]() $r_0$ and length
$r_0$ and length ![]() $L_0 \approx 21 r_0$ aligned along
$L_0 \approx 21 r_0$ aligned along ![]() $z$. Keeping the aspect ratio constant ensures that the flow disturbance created by the bacterium decays to negligible values at the pipes ends (Liron & Shahar Reference Liron and Shahar1978). We model the pipes as immobile rigid objects discretized with blobs just like the bacterium (Balboa Usabiaga et al. Reference Balboa Usabiaga, Kallemov, Delmotte, Bhalla, Griffith and Donev2016). We place the bacterium in the middle of the pipes and we use that configuration to compute the bacterium velocity. Since the Stokes equations assume steady-state flows, the velocity in a given configuration can be obtained by solving the mobility problem one single time. Later, we will consider the case where the bacterium freely swims inside a periodic pipe.
$z$. Keeping the aspect ratio constant ensures that the flow disturbance created by the bacterium decays to negligible values at the pipes ends (Liron & Shahar Reference Liron and Shahar1978). We model the pipes as immobile rigid objects discretized with blobs just like the bacterium (Balboa Usabiaga et al. Reference Balboa Usabiaga, Kallemov, Delmotte, Bhalla, Griffith and Donev2016). We place the bacterium in the middle of the pipes and we use that configuration to compute the bacterium velocity. Since the Stokes equations assume steady-state flows, the velocity in a given configuration can be obtained by solving the mobility problem one single time. Later, we will consider the case where the bacterium freely swims inside a periodic pipe.
We consider two different swimming modes. First, the extended mode where the flagellum is attached to the body front part and it extends away from it. In the second mode the flagellum is wrapped around the bacterium body, see figure 1. In both cases we apply constant and opposite torques, of magnitude ![]() $\tau _m=0.46\ {\rm pN}\ {\mathrm {\mu }}{\rm m}$, to the body and the flagellum to model the work exerted by a molecular motor. Thus, we assume that the molecular motor always works in the constant torque (low frequency) regime (Xing et al. Reference Xing, Bai, Berry and Oster2006). In most numerical experiments the flagellum extends along its main axis a length similar to the bacterium body. Thus, in the wrapped mode, the body is fully covered by the flagellum. The bacterium body, always
$\tau _m=0.46\ {\rm pN}\ {\mathrm {\mu }}{\rm m}$, to the body and the flagellum to model the work exerted by a molecular motor. Thus, we assume that the molecular motor always works in the constant torque (low frequency) regime (Xing et al. Reference Xing, Bai, Berry and Oster2006). In most numerical experiments the flagellum extends along its main axis a length similar to the bacterium body. Thus, in the wrapped mode, the body is fully covered by the flagellum. The bacterium body, always ![]() $2.04 {\mathrm {\mu }}{\rm m}$ long and
$2.04 {\mathrm {\mu }}{\rm m}$ long and ![]() $0.49\ {\mathrm {\mu }}{\rm m}$ wide, is discretized with 292 blobs of radius
$0.49\ {\mathrm {\mu }}{\rm m}$ wide, is discretized with 292 blobs of radius ![]() $a=0.0425\ {\mathrm {\mu }}{\rm m}$. The geometric details of the helical flagella and pipes used in this work are presented in tables 1 and 2.
$a=0.0425\ {\mathrm {\mu }}{\rm m}$. The geometric details of the helical flagella and pipes used in this work are presented in tables 1 and 2.
Table 1. Flagellum model parameters. Flagellum length, ![]() $L$, amplitude,
$L$, amplitude, ![]() $\alpha$, wavenumber,
$\alpha$, wavenumber, ![]() $k$, maximum extension along its axis,
$k$, maximum extension along its axis, ![]() $L_z$, number of waves along its axis,
$L_z$, number of waves along its axis, ![]() $N_{\lambda }=L_{z} / \lambda = L_z k / (2{\rm \pi} )$, blob radius,
$N_{\lambda }=L_{z} / \lambda = L_z k / (2{\rm \pi} )$, blob radius, ![]() $a$, and number of blobs
$a$, and number of blobs ![]() $N_b$. The amplitude of the wave was exponentially damped near the attachment point with a damping factor
$N_b$. The amplitude of the wave was exponentially damped near the attachment point with a damping factor ![]() $k_E=k$, as in Higdon (Reference Higdon1979).
$k_E=k$, as in Higdon (Reference Higdon1979).

Table 2. Pipe model dimensions. Length ![]() $L$, inner radius
$L$, inner radius ![]() $r_0$ and number of blobs
$r_0$ and number of blobs ![]() $N_b$. The blob radius is
$N_b$. The blob radius is ![]() $a=0.1\ {\mathrm {\mu }}{\rm m}$ in all cases.
$a=0.1\ {\mathrm {\mu }}{\rm m}$ in all cases.

All the motion is driven by the rotation of the flagellum. Therefore, we start looking at its angular velocity, ![]() $\omega _z$, see figure 3(a). In bulk the flagellum rotates two times faster in the extended mode than in the wrapped mode. The slower rotation can be explained by the additional drag experienced by the flagellum in the wrapped mode, which is caused by the proximity of the flagellum to the bacterium body. Both modes reduce their angular velocities as
$\omega _z$, see figure 3(a). In bulk the flagellum rotates two times faster in the extended mode than in the wrapped mode. The slower rotation can be explained by the additional drag experienced by the flagellum in the wrapped mode, which is caused by the proximity of the flagellum to the bacterium body. Both modes reduce their angular velocities as ![]() $r_0$ decreases due to the additional hydrodynamic drag generated by the pipe walls. However, the decrease is proportionally less important in the wrapped mode as its initial drag was larger. Thus, the ratio between the angular frequencies of the two modes falls from a factor
$r_0$ decreases due to the additional hydrodynamic drag generated by the pipe walls. However, the decrease is proportionally less important in the wrapped mode as its initial drag was larger. Thus, the ratio between the angular frequencies of the two modes falls from a factor ![]() ${\sim }2$ in bulk to a factor
${\sim }2$ in bulk to a factor ![]() ${\sim }1.6$ in the smallest pipe considered.
${\sim }1.6$ in the smallest pipe considered.

Figure 3. Flagellum angular velocity, ![]() $\omega _z$, (a) and bacterium swimming speed along the pipe,
$\omega _z$, (a) and bacterium swimming speed along the pipe, ![]() $u_z$, (b) vs pipe radius
$u_z$, (b) vs pipe radius ![]() $r_0$. Results for the extended and wrapped mode using the same flagellum (model II) with length
$r_0$. Results for the extended and wrapped mode using the same flagellum (model II) with length ![]() $L=3.6\ {\mathrm {\mu }}{\rm m}$ and amplitude
$L=3.6\ {\mathrm {\mu }}{\rm m}$ and amplitude ![]() $\alpha =0.32 {\mathrm {\mu }}{\rm m}$. The dashed lines depict bulk values. The inset in (a) shows the swimming speed against the flagellum angular frequency for all of the pipe radii used. The inset in (b) shows the swimming speed calculated with a minimal model, (3.2).
$\alpha =0.32 {\mathrm {\mu }}{\rm m}$. The dashed lines depict bulk values. The inset in (a) shows the swimming speed against the flagellum angular frequency for all of the pipe radii used. The inset in (b) shows the swimming speed calculated with a minimal model, (3.2).
Next, we look at the swimming speed along the pipe axis, ![]() $u_z$, see figure 3(b). We observe that in bulk the wrapped mode swims approximately twice slower than in the extended mode. This result is consistent with experimental observations (Kühn et al. Reference Kühn, Schmidt, Eckhardt and Thormann2017; Grognot & Taute Reference Grognot and Taute2021; Thormann et al. Reference Thormann, Beta and Kühn2022; Tian et al. Reference Tian, Wu, Zhang and Yuan2022). The slower swimming speed in the wrapped mode is a consequence of the slower rotation of its flagellum. Under confinement the swimming speed,
$u_z$, see figure 3(b). We observe that in bulk the wrapped mode swims approximately twice slower than in the extended mode. This result is consistent with experimental observations (Kühn et al. Reference Kühn, Schmidt, Eckhardt and Thormann2017; Grognot & Taute Reference Grognot and Taute2021; Thormann et al. Reference Thormann, Beta and Kühn2022; Tian et al. Reference Tian, Wu, Zhang and Yuan2022). The slower swimming speed in the wrapped mode is a consequence of the slower rotation of its flagellum. Under confinement the swimming speed, ![]() $u_z$, decreases for the extended mode as the pipe radius is decreased. Again, the additional hydrodynamic drag generated by the pipe walls is responsible for this effect. In contrast, the wrapped mode exhibits a non-monotonic trend in its swimming speed. As the pipe radius is decreased the bacterium swims faster, up to the point where the ratio between the pipe radius and the flagellum amplitude is
$u_z$, decreases for the extended mode as the pipe radius is decreased. Again, the additional hydrodynamic drag generated by the pipe walls is responsible for this effect. In contrast, the wrapped mode exhibits a non-monotonic trend in its swimming speed. As the pipe radius is decreased the bacterium swims faster, up to the point where the ratio between the pipe radius and the flagellum amplitude is ![]() $r_0 / \alpha \approx 1.5$. Beyond that point the swimming speed decreases with
$r_0 / \alpha \approx 1.5$. Beyond that point the swimming speed decreases with ![]() $r_0$. The striking difference between both swimmer modes is also shown in the inset of figure 3(a), which shows the swimming velocity vs the flagellum angular velocity for all pipe radii. Because the Stokes equations are linear the linear and angular velocity are proportional when keeping all geometric parameters constant. However, changing the pipe radius affects the proportionality constant dramatically for the wrapped mode and only weakly for the extended mode. A resolution study shows that these results are maintained after increasing the resolution of our discretization by factors 4 and 16, see the Appendix and figure 10.
$r_0$. The striking difference between both swimmer modes is also shown in the inset of figure 3(a), which shows the swimming velocity vs the flagellum angular velocity for all pipe radii. Because the Stokes equations are linear the linear and angular velocity are proportional when keeping all geometric parameters constant. However, changing the pipe radius affects the proportionality constant dramatically for the wrapped mode and only weakly for the extended mode. A resolution study shows that these results are maintained after increasing the resolution of our discretization by factors 4 and 16, see the Appendix and figure 10.
We seek a physical mechanism that explains the difference between swimming modes and the speed enhancement in the wrapped case. We start by considering the motion of a single helical flagellum inside a pipe. We apply a constant torque on the helical flagellum and measure its translational and rotational speeds. Note that, in this case, the flagellum is not a torque-free swimmer, as there is no body to which to apply an opposite torque. Nonetheless, this numerical experiment is useful to understand the more complex wrapped mode. We observe an increase in the swimming speed for decreasing pipe radius with respect to the bulk value above a critical pipe radius, see figure 4, similar to the wrapped mode results. For the single flagellum, its swimming speed can be written as ![]() $u_z = M_{tr} \tau _z$. For moderate confinements the hydrodynamic interactions with the wall increase the value of the mobility coupling term,
$u_z = M_{tr} \tau _z$. For moderate confinements the hydrodynamic interactions with the wall increase the value of the mobility coupling term, ![]() $M_{tr}$, with respect to the bulk values, thus, the swimming speed is increased. For very tight confinements the lubrication interactions dominate the interactions with the wall and
$M_{tr}$, with respect to the bulk values, thus, the swimming speed is increased. For very tight confinements the lubrication interactions dominate the interactions with the wall and ![]() $M_{tr}$ decreases below the bulk values. These effects were already reported by Liu, Breuer & Powers (Reference Liu, Breuer and Powers2014) for an infinite flagellum within an infinite pipe. This speed increase is observed despite the reduction in the flagellum angular velocity,
$M_{tr}$ decreases below the bulk values. These effects were already reported by Liu, Breuer & Powers (Reference Liu, Breuer and Powers2014) for an infinite flagellum within an infinite pipe. This speed increase is observed despite the reduction in the flagellum angular velocity, ![]() $\omega _z$, with
$\omega _z$, with ![]() $r_0$, see figure 4 inset.
$r_0$, see figure 4 inset.

Figure 4. Swimming speed, ![]() $u_z$, and
$u_z$, and ![]() $z$-component of the angular velocity (inset),
$z$-component of the angular velocity (inset), ![]() $\omega _z$, of a single helical flagellum with amplitude
$\omega _z$, of a single helical flagellum with amplitude ![]() $\alpha =0.32\ {\mathrm {\mu }}{\rm m}$ (model II) inside a pipe of radius
$\alpha =0.32\ {\mathrm {\mu }}{\rm m}$ (model II) inside a pipe of radius ![]() $r_0$. The dashed lines depicts the bulk values and a snapshot of the flagellum in a pipe is shown in the inset.
$r_0$. The dashed lines depicts the bulk values and a snapshot of the flagellum in a pipe is shown in the inset.
For the whole bacterium the situation is more complex because, at the same time that the flagellum thrust is enhanced, an additional drag on the bacterium body tends to reduce the swimming speed. This interplay between the enhanced thrust and the additional drag has been observed in a recent experimental study with E. coli (Vizsnyiczai et al. Reference Vizsnyiczai, Frangipane, Bianchi, Saglimbeni, Dell'Arciprete and Di Leonardo2020). Vizsnyiczai et al. observed that a bacterium swimming in an extended mode inside a pipe swims slower than a bacterium in a channel. However, when the bacterium is exiting the pipe and only its flagellum remains inside, the swimming speed is larger than in a channel, showing the increased translation–rotational coupling experienced by the flagellum and the lack of an additional drag acting on the bacterium body (Vizsnyiczai et al. Reference Vizsnyiczai, Frangipane, Bianchi, Saglimbeni, Dell'Arciprete and Di Leonardo2020). Our numerical results agree with the experimental work of Vizsnyiczai et al. for the extended mode while they suggest that, for the wrapped mode, the enhanced thrust is the dominant effect.
To explore in more detail the difference between the two swimming configurations we introduce a minimal model in which we treat the bacterium body and flagellum as two connected rigid bodies that move exactly along the pipe axis and are free to rotate along their axes (Vizsnyiczai et al. Reference Vizsnyiczai, Frangipane, Bianchi, Saglimbeni, Dell'Arciprete and Di Leonardo2020). Thus, in the minimal model the velocities perpendicular to the pipe axis are assumed to be zero, unlike in the previous simulations. Taking into account that the bacterium is a free-force-torque swimmer we can write the linear system
 \begin{equation} \begin{bmatrix} u_z \\ \omega^{body}_z \\ u_z \\ \omega^{flag}_z \end{bmatrix} = \begin{bmatrix} M_{tt} & 0 & C_{tt} & C_{tr} \\ 0 & M_{rr} & C_{rt} & C_{rr} \\ C_{tt} & C_{rt} & N_{tt} & N_{tr} \\ C_{tr} & C_{rr} & N_{tr} & N_{rr} \\ \end{bmatrix} \begin{bmatrix} f_z \\ \tau_z \\ -f_z \\ -\tau_z \end{bmatrix}.\end{equation}
\begin{equation} \begin{bmatrix} u_z \\ \omega^{body}_z \\ u_z \\ \omega^{flag}_z \end{bmatrix} = \begin{bmatrix} M_{tt} & 0 & C_{tt} & C_{tr} \\ 0 & M_{rr} & C_{rt} & C_{rr} \\ C_{tt} & C_{rt} & N_{tt} & N_{tr} \\ C_{tr} & C_{rr} & N_{tr} & N_{rr} \\ \end{bmatrix} \begin{bmatrix} f_z \\ \tau_z \\ -f_z \\ -\tau_z \end{bmatrix}.\end{equation}
All the mobility components in (3.1) depend on the pipe radius and the bacterium mode (extended or wrapped) due to the hydrodynamic interactions. The unknowns in the linear system are the swimming velocity, ![]() $u_z$, the angular velocities of body and flagellum,
$u_z$, the angular velocities of body and flagellum, ![]() $\omega ^{body}_{z}$ and
$\omega ^{body}_{z}$ and ![]() $\omega ^{flag}_{z}$, and the force acting on each of them
$\omega ^{flag}_{z}$, and the force acting on each of them ![]() $f_z$. Solving these equations for the swimming velocity we obtain
$f_z$. Solving these equations for the swimming velocity we obtain
We compute numerically all the mobility components and plot the contribution of the first and second terms of (3.2) in figure 5. Panel (a) shows that the first term in (3.2) is the dominant one. It also shows that the decay in the speed is more pronounced for the extended mode, which occurs due to a stronger decay of ![]() $M_{tt}$ and
$M_{tt}$ and ![]() $N_{tr}$ due to the hydrodynamic drag generated by the pipe. The contribution of the second term of (3.2) is qualitatively different for both modes, as shown in figure 5(b). The mobility component
$N_{tr}$ due to the hydrodynamic drag generated by the pipe. The contribution of the second term of (3.2) is qualitatively different for both modes, as shown in figure 5(b). The mobility component ![]() $C_{tr}$ decays to almost zero for the wrapped mode but not for the extended mode. For the wrapped mode that term was a negative contribution, thus, when it vanishes it leads to an overall speed increase. The minimal model, including both the first and second terms of (3.2), explains the full numerical result reasonably well, as shown in figure 5(c). Thus, the main difference between the two swimming modes is a lower decrease of the coefficients
$C_{tr}$ decays to almost zero for the wrapped mode but not for the extended mode. For the wrapped mode that term was a negative contribution, thus, when it vanishes it leads to an overall speed increase. The minimal model, including both the first and second terms of (3.2), explains the full numerical result reasonably well, as shown in figure 5(c). Thus, the main difference between the two swimming modes is a lower decrease of the coefficients ![]() $M_{tt}$ and
$M_{tt}$ and ![]() $N_{tr}$ in the wrapped mode.
$N_{tr}$ in the wrapped mode.
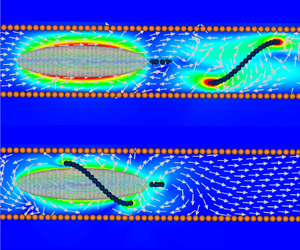
To further understand the difference between the two swimming modes we compute the flow around the bacterium in a tight pipe, with ![]() $r_0/\alpha = 1.56$, using the highest resolution model, with
$r_0/\alpha = 1.56$, using the highest resolution model, with ![]() ${\sim }16$ times the number of blobs than the original simulations, see the Appendix. For the extended mode we show the instantaneous and the average flow field during one flagellum rotation in figure 6(a,b). The same flows for the wrapped mode are shown in figure 6(c,d). As the bacterium moves along the pipe an equivalent volume of fluid is displaced to make room for the bacterium, after all, the fluid is incompressible. The fluid can be pushed further along the pipe or transported to the back of the bacterium but, interestingly, flow perturbations decay exponentially fast along the pipe (Liron & Shahar Reference Liron and Shahar1978), therefore, it follows that, in long enough pipes, all the fluid displaced would be moved to the back of the bacterium. We can see in figure 6(b) a counter-flow close to the pipe wall. However, the high velocity gradients suggest a large drag that we observed as a reduction in the bacterium swimming speed. In the wrapped mode the flagellum works as an Archimedes’ screw, helping to push fluid to the back of the bacterium, see figure 6(d). The effect of the flagellum pushing the fluid is observed more clearly in supplementary movie 1. This is the ultimate mechanism that differentiates the two swimming modes and makes the additional drag on the body the dominant effect for the extended mode and the enhanced rotation–translation coupling the dominant one for the wrapped mode.
${\sim }16$ times the number of blobs than the original simulations, see the Appendix. For the extended mode we show the instantaneous and the average flow field during one flagellum rotation in figure 6(a,b). The same flows for the wrapped mode are shown in figure 6(c,d). As the bacterium moves along the pipe an equivalent volume of fluid is displaced to make room for the bacterium, after all, the fluid is incompressible. The fluid can be pushed further along the pipe or transported to the back of the bacterium but, interestingly, flow perturbations decay exponentially fast along the pipe (Liron & Shahar Reference Liron and Shahar1978), therefore, it follows that, in long enough pipes, all the fluid displaced would be moved to the back of the bacterium. We can see in figure 6(b) a counter-flow close to the pipe wall. However, the high velocity gradients suggest a large drag that we observed as a reduction in the bacterium swimming speed. In the wrapped mode the flagellum works as an Archimedes’ screw, helping to push fluid to the back of the bacterium, see figure 6(d). The effect of the flagellum pushing the fluid is observed more clearly in supplementary movie 1. This is the ultimate mechanism that differentiates the two swimming modes and makes the additional drag on the body the dominant effect for the extended mode and the enhanced rotation–translation coupling the dominant one for the wrapped mode.

Figure 6. In-plane velocity fields around a bacterium inside a pipe with inner radius ![]() $r_0/\alpha = 1.56$. Instantaneous and average flow fields during one flagellum rotation for the extended mode, (a,b), respectively, and for the wrapped mode (c,d). The flagellum is not shown in the panels with the average flows (b,d). See also supplementary movie 1 available at https://doi.org/10.1017/jfm.2024.594.
$r_0/\alpha = 1.56$. Instantaneous and average flow fields during one flagellum rotation for the extended mode, (a,b), respectively, and for the wrapped mode (c,d). The flagellum is not shown in the panels with the average flows (b,d). See also supplementary movie 1 available at https://doi.org/10.1017/jfm.2024.594.
3.1. Power and efficiency
The power consumption is an important quantity for a microswimmer propelling in a viscous environment and the efficiency can be more important than the absolute swimming speed. Thus, we measure these quantities. Considering that the chemical energy used within the cell is beyond the scope of our work, we limit ourselves to studying the power dissipated by the Stokes flow and the microswimmers hydrodynamic efficiency. The power exerted by a microswimmer on the medium and dissipated by the flow is
where the sum is over rigid bodies, in our case the bacterium body and its flagellum. As the power is generated by the motor, the power consumed by a bacterium during its swimming can be rewritten as ![]() $P_m = \boldsymbol {\tau }_m \boldsymbol {\cdot } \boldsymbol {\omega }_m = \boldsymbol {\tau }_m \boldsymbol {\cdot } (\boldsymbol {\omega }_{flag} - \boldsymbol {\omega }_{body})$. In the absence of elastic or soft steric interactions the two expressions are equivalent. We will always use (3.3) to account for the soft steric interactions used in § 3.3.
$P_m = \boldsymbol {\tau }_m \boldsymbol {\cdot } \boldsymbol {\omega }_m = \boldsymbol {\tau }_m \boldsymbol {\cdot } (\boldsymbol {\omega }_{flag} - \boldsymbol {\omega }_{body})$. In the absence of elastic or soft steric interactions the two expressions are equivalent. We will always use (3.3) to account for the soft steric interactions used in § 3.3.
The wrapped mode consumes less power for all pipe radii owing to the slower rotation of its flagellum, see figure 7 inset. Under confinement the power exerted by the motor decays for both swimming modes. Of more interest is the hydrodynamic efficiency of the swimmers in propelling themselves. There are several approaches to defining the hydrodynamic efficiency (Childress Reference Childress2012). We follow a classical approach and define the inverse efficiency as the power normalized with the power necessary to pull the bacterium body with the same speed (Higdon Reference Higdon1979; Lauga & Eloy Reference Lauga and Eloy2013)
where ![]() $M_{zz}=u_{z}/f_{z}$ is body mobility (without flagellum) along the pipe axis and
$M_{zz}=u_{z}/f_{z}$ is body mobility (without flagellum) along the pipe axis and ![]() $u_z$ the velocity. Figure 7 shows the inverse efficiency as a function of the pipe radius. In bulk and wide pipes the extended mode is more efficient. However, there is a cross-over and for tight confinements the wrapped mode becomes more efficient. This is a result of the lower power consumption of the wrapped mode and, importantly, its enhanced velocity within the pipe. This result suggests that the wrapped mode has an advantage for propulsion in confined spaces. To verify the accuracy of the results we perform a resolution study by increasing the resolution by factors of 4 and 16 and we obtain essentially the same results as shown in the Appendix and figure 10. So far we have only used one flagellum, model II, and a bacterium placed exactly on the middle of the pipe. In the next two sections we explore whether these results are robust under a change in these conditions.
$u_z$ the velocity. Figure 7 shows the inverse efficiency as a function of the pipe radius. In bulk and wide pipes the extended mode is more efficient. However, there is a cross-over and for tight confinements the wrapped mode becomes more efficient. This is a result of the lower power consumption of the wrapped mode and, importantly, its enhanced velocity within the pipe. This result suggests that the wrapped mode has an advantage for propulsion in confined spaces. To verify the accuracy of the results we perform a resolution study by increasing the resolution by factors of 4 and 16 and we obtain essentially the same results as shown in the Appendix and figure 10. So far we have only used one flagellum, model II, and a bacterium placed exactly on the middle of the pipe. In the next two sections we explore whether these results are robust under a change in these conditions.

Figure 7. Inverse of the efficiency vs radius of the pipe (![]() $r_0$). The inset shows the swimming power and the dashed lines depict the bulk values.
$r_0$). The inset shows the swimming power and the dashed lines depict the bulk values.
3.2. Robustness of results: effect of  $N_{\lambda }$ and L
$N_{\lambda }$ and L
Bacterial species present flagella of different lengths, amplitudes and pitch angles which affect the bacterium bulk speeds and efficiencies (Higdon Reference Higdon1979; Lauga & Eloy Reference Lauga and Eloy2013). Here, we explore if the wrapped mode is a more efficient swimming style in confined environments for a wide variety of flagellum models. We build five flagellum models by varying simultaneously the flagellum length, ![]() $L$, and the number of waves along its length,
$L$, and the number of waves along its length, ![]() $N_{\lambda }=L_z / \lambda$, where
$N_{\lambda }=L_z / \lambda$, where ![]() $L_z$ is the flagellum extension along its axis and
$L_z$ is the flagellum extension along its axis and ![]() $\lambda$ the wavelength of the helical wave, see figure 8(a,b) and table 1. We present the inverse efficiency for all flagellum models and pipe radii in figure 8(c,d).
$\lambda$ the wavelength of the helical wave, see figure 8(a,b) and table 1. We present the inverse efficiency for all flagellum models and pipe radii in figure 8(c,d).

Figure 8. Shapes of extended (a) and wrapped (b) bacterium modes with different ![]() $N_{\lambda }$ values. Inverse of the swimming efficiency vs radius of the pipe (
$N_{\lambda }$ values. Inverse of the swimming efficiency vs radius of the pipe (![]() $r_0$) for different values of
$r_0$) for different values of ![]() $N_{\lambda }$ for the extended mode (c) and the wrapped mode (d).
$N_{\lambda }$ for the extended mode (c) and the wrapped mode (d).
The general trend is the same as before. For wide pipes the extended mode is more efficient than the wrapped mode for all flagellum models except one (![]() $N_{\lambda }=2.5$). Under confinement both swimmers increase their efficiency but the improvement is stronger for the wrapped mode, which becomes the most efficient for pipes with
$N_{\lambda }=2.5$). Under confinement both swimmers increase their efficiency but the improvement is stronger for the wrapped mode, which becomes the most efficient for pipes with ![]() $r_0 / \alpha \lessapprox 1.7$. In those situations the wrapped mode is approximately two times more efficient than the extended mode. The efficiency, for both swimming modes, is non-monotonic in
$r_0 / \alpha \lessapprox 1.7$. In those situations the wrapped mode is approximately two times more efficient than the extended mode. The efficiency, for both swimming modes, is non-monotonic in ![]() $N_{\lambda }$. When
$N_{\lambda }$. When ![]() $N_{\lambda } \,{\ll}\,1$ the flagellum is almost straight, thus, it cannot propel the bacterium. Therefore, the swimming speed and the efficiency initially grow with
$N_{\lambda } \,{\ll}\,1$ the flagellum is almost straight, thus, it cannot propel the bacterium. Therefore, the swimming speed and the efficiency initially grow with ![]() $N_{\lambda }$. Beyond a certain value of
$N_{\lambda }$. Beyond a certain value of ![]() $N_{\lambda }$ the flagellum tangent forms a large angle with the direction of motion, which again reduces the propulsion efficiency. For intermediate values of
$N_{\lambda }$ the flagellum tangent forms a large angle with the direction of motion, which again reduces the propulsion efficiency. For intermediate values of ![]() $N_{\lambda }$ the flagellum is helical shaped, which allows propulsion. For both modes the flagellum with
$N_{\lambda }$ the flagellum is helical shaped, which allows propulsion. For both modes the flagellum with ![]() $N_{\lambda }=1.5$ is the most efficient under confinement for the flagellum lengths considered. For bacteria swimming in bulk the optimum is also close to
$N_{\lambda }=1.5$ is the most efficient under confinement for the flagellum lengths considered. For bacteria swimming in bulk the optimum is also close to ![]() $N_{\lambda }=1.5$, although the exact optimum
$N_{\lambda }=1.5$, although the exact optimum ![]() $N_{\lambda }$ depends on the flagellum length (Higdon Reference Higdon1979). For the extended mode, optimal swimming occurs around the non-dimensional pipe radius,
$N_{\lambda }$ depends on the flagellum length (Higdon Reference Higdon1979). For the extended mode, optimal swimming occurs around the non-dimensional pipe radius, ![]() $r_{0}/\alpha$ = 1.5 for all values of
$r_{0}/\alpha$ = 1.5 for all values of ![]() $N_{\lambda }$. For the wrapped mode the optimal swimming occurs for lower values of
$N_{\lambda }$. For the wrapped mode the optimal swimming occurs for lower values of ![]() $r_{0}/\alpha$.
$r_{0}/\alpha$.
3.3. Robustness of results: dynamical simulations
So far we have computed the swimming speed when the bacterium is located in the middle of the pipe and aligned along it. However, freely swimming bacteria can tilt and move towards the pipe wall. To verify if the results reported so far are robust, we perform dynamic simulations where the bacterium is free to displace away from the pipe centreline and to change orientations. We use the same pipe models as before but impose periodic boundary conditions along the pipe. To solve the Stokes equations with these boundary conditions we use a periodic fast multipole method implemented in the library STKFMM (Yan & Shelley Reference Yan and Shelley2018). To avoid the overlap of the bacterium with the pipe we include a steric repulsion interaction between the blobs of pipe and bacterium with a repulsion strength of ![]() $f=0.05 \ {\rm pN}$ for overlapping blobs and with an exponential decay with a characteristic length
$f=0.05 \ {\rm pN}$ for overlapping blobs and with an exponential decay with a characteristic length ![]() $\xi =0.01\ {\mathrm {\mu }}{\rm m}$ for non-overlapping blobs. As in § 2.1 we use a midpoint integrator to integrate the equations of motion (Balboa Usabiaga & Delmotte Reference Balboa Usabiaga and Delmotte2022). In all simulations we use the same time step size,
$\xi =0.01\ {\mathrm {\mu }}{\rm m}$ for non-overlapping blobs. As in § 2.1 we use a midpoint integrator to integrate the equations of motion (Balboa Usabiaga & Delmotte Reference Balboa Usabiaga and Delmotte2022). In all simulations we use the same time step size, ![]() $\Delta t=10^{-3} {\rm s}$, so a full flagellum rotation takes around 12 (36) time steps for the fastest (slowest) rotating flagella. For all models considered in this section we simulate the bacterium for
$\Delta t=10^{-3} {\rm s}$, so a full flagellum rotation takes around 12 (36) time steps for the fastest (slowest) rotating flagella. For all models considered in this section we simulate the bacterium for ![]() $10\ {\rm s}$ so the bacterium can swim at least
$10\ {\rm s}$ so the bacterium can swim at least ![]() $70\ {\mathrm {\mu }}{\rm m}$. We use the last
$70\ {\mathrm {\mu }}{\rm m}$. We use the last ![]() $8\ {\rm s}$ to extract the swimming speed and the power consumption.
$8\ {\rm s}$ to extract the swimming speed and the power consumption.
We observe that the bacterium swimming in the extended mode swims near the pipe walls while bacterium swimming in the wrapped mode tries to remain away from them. This lateral displacement is more evident in wide pipes where the bacterium has more space to move, see supplementary movie 2, and it is reminiscent of the hydrodynamic attraction to walls by the extended mode mentioned in § 2.1 and the hydrodynamic repulsion from walls experienced by the wrapped mode (not shown). The swimming speed and efficiency, for the bacterium with flagellum model II, are shown in figure 9. The same general trend as for the static simulations is observed. However, the efficiency curves do not cross-over. The cross-over is not observed because this time the wrapped swimming speed along the pipe, ![]() $u_z$, barely increases with confinement, and the efficiency depends strongly on
$u_z$, barely increases with confinement, and the efficiency depends strongly on ![]() $u_z$. The magnitude of
$u_z$. The magnitude of ![]() $u_z$ does not increase because the bacterium swims with a tilt towards the wall, see figure 9(c) and supplementary movie 3. In contrast, the extended mode cannot tilt significantly in small pipes as that is prevented by its rigid flagellum, which favours the motion along the pipe.
$u_z$ does not increase because the bacterium swims with a tilt towards the wall, see figure 9(c) and supplementary movie 3. In contrast, the extended mode cannot tilt significantly in small pipes as that is prevented by its rigid flagellum, which favours the motion along the pipe.

Figure 9. Swimming speed (a) and hydrodynamic efficiency (b) of wrapped and extended modes swimming along a periodic pipe extracted from ![]() $10\ {\rm s}$ long dynamic simulations. Full symbols use flagellum model II, which extends the same length as the body, and open symbols use model flagellum VI, which extends longer. The longer flagellum prevents the tilt of the wrapped mode, which results in higher speeds and better efficiencies. (c) Two bacteria inside a pipe. A bacterium with a short flagellum performs a precession motion around the pipe axis while a bacterium with a long flagellum is forced to swim straight. The swimming direction is shown with a large arrow and the pipe axis with a dashed line.
$10\ {\rm s}$ long dynamic simulations. Full symbols use flagellum model II, which extends the same length as the body, and open symbols use model flagellum VI, which extends longer. The longer flagellum prevents the tilt of the wrapped mode, which results in higher speeds and better efficiencies. (c) Two bacteria inside a pipe. A bacterium with a short flagellum performs a precession motion around the pipe axis while a bacterium with a long flagellum is forced to swim straight. The swimming direction is shown with a large arrow and the pipe axis with a dashed line.
To verify if the whole extension of the swimmers affects the result we run another set of simulations using a longer flagellum, model VI, that extends beyond the bacterium body, see figure 9(c) and supplementary movie 4. The results are presented as open symbols in figure 9. In this case the speed of the wrapped mode is approximately independent on the confinement but larger than with the shorter flagellum. As a result we observe a cross-over between the efficiencies of the wrapped and extended modes. Overall, these results show that (i) the swimming speed is less sensitive to confinement for the wrapped mode than for the extended mode, (ii), the efficiency improves strongly for the wrapped mode and (iii), depending on the flagellum details, the wrapped mode can be the most efficient way to swim under confinement.
4. Conclusions
In this paper we have presented the dynamics of two different swimming modes, namely the extended and wrapped modes of monotrichous-type bacteria. Under bulk conditions the extended mode swims faster and more efficiently than the wrapped mode. However, under strong confinement the efficiency of the wrapped mode improves faster than for the extended mode. For a wide number of flagellum shapes, with different lengths and wavelengths, the bacterium in the wrapped mode swims more efficiently. For both swimming modes the flagellum rotation–translation coupling is enhanced by the pipe confinement (Liu et al. Reference Liu, Breuer and Powers2014; Vizsnyiczai et al. Reference Vizsnyiczai, Frangipane, Bianchi, Saglimbeni, Dell'Arciprete and Di Leonardo2020). However, the drag on the bacterium body is also increased and only for the wrapped mode is the enhanced flagellum coupling the dominant effect. The flow fields around the bacterium suggest that the wrapped mode works as an Archimedes’ screw helping to transport the fluid displaced by the motion of the bacterium. Such a screw-like configuration improves the swimming efficiency.
These results are complementary to the experimental work of Kinosita et al. where the bacterium Burkholderia adopting the wrapped mode was observed to glide in very narrow ducts (Kinosita et al. Reference Kinosita, Kikuchi, Mikami, Nakane and Nishizaka2018). It seems that, either by gliding over a substrate or by means of hydrodynamic interactions, the wrapped mode promotes the motion of bacteria in tight confinements. It is interesting to note that some bipolar flagellated bacteria can display a wrapped and an extended mode simultaneously, where the flagellum at the front pole wraps around the body and the rear one remains extended (Murat et al. Reference Murat, Hérisse, Espinosa, Bossa, Alberto and Wu2015; Constantino et al. Reference Constantino, Jabbarzadeh, Fu, Shen, Fox, Haesebrouck, Linden and Bansil2018; Thormann et al. Reference Thormann, Beta and Kühn2022; Bansil et al. Reference Bansil, Constantino, Su-Arcaro, Liao, Shen and Fox2023). Such a mixed mode could present some advantages under confinement that should be investigated.
Supplementary movies
Supplementary movies are available at https://doi.org/10.1017/jfm.2024.594.
Funding
The project that gave rise to these results received the support of a fellowship from ‘la Caixa’ Foundation (ID 100010434), fellowship LCF/BQ/PI20/11760014 and from the European Union's Horizon 2020 research and innovation programme under the Marie Skłodowska-Curie grant agreement no. 847648. Funding provided by the Basque Government through the BERC 2022-2025 program and by the Ministry of Science and Innovation: BCAM Severo Ochoa accreditation CEX2021-001142-S/MICIN/AEI/10.13039/501100011033 and the project PID2020-117080RB-C55 ‘Microscopic foundations of soft matter experiments: computational nano-hydrodynamics (Compu-Nano-Hydro)’ is also acknowledged.
Declaration of interests
The authors report no conflict of interest.
Appendix. Resolution study
Here, we conduct a resolution study to verify the robustness of our results. We reduce the blob radius used to discretize the bacterium body and the pipes from ![]() $a$ to
$a$ to ![]() $a/2$ and
$a/2$ and ![]() $a/4$ while at the same time increasing the resolution so the numbers of blobs are
$a/4$ while at the same time increasing the resolution so the numbers of blobs are ![]() ${\sim }4$ and
${\sim }4$ and ![]() ${\sim }16$ larger than in the original model, respectively. We do not refine the flagellum as its thickness, proportional to the blob radius, should remain constant during the resolution study.
${\sim }16$ larger than in the original model, respectively. We do not refine the flagellum as its thickness, proportional to the blob radius, should remain constant during the resolution study.
For these three resolutions we measure the swimming speed (![]() $u_z$), flagellum rotational speed (
$u_z$), flagellum rotational speed (![]() $\omega _z$), swimming power (
$\omega _z$), swimming power (![]() $P$) and inverse efficiency (
$P$) and inverse efficiency (![]() $\eta ^{-1}$). The results are presented in figure 10. There are some differences in the swimming speed, see figure 10(a). However, the other quantities only show a small deviation with respect to the original resolution. The cross-over in the inverse of the efficiency between the wrapped and the extended mode is more pronounced for the highest resolution considered, see figure 10(d). More important, the overall trends observed for all the magnitudes measured remain unchanged for all resolutions, and thus, the results are robust against the resolution of the model.
$\eta ^{-1}$). The results are presented in figure 10. There are some differences in the swimming speed, see figure 10(a). However, the other quantities only show a small deviation with respect to the original resolution. The cross-over in the inverse of the efficiency between the wrapped and the extended mode is more pronounced for the highest resolution considered, see figure 10(d). More important, the overall trends observed for all the magnitudes measured remain unchanged for all resolutions, and thus, the results are robust against the resolution of the model.

Figure 10. (a) Swimming speed, (b) flagellum angular speed, (c) swimming power and (d) inverse of the efficiency vs pipe radius for three different resolutions with blob radii ![]() $a$,
$a$, ![]() $a/2$ and
$a/2$ and ![]() $a/4$. Red curve symbols extended mode and blue curve symbols wrapped mode.
$a/4$. Red curve symbols extended mode and blue curve symbols wrapped mode.