FFQ can produce unreliable energetic and nutrient estimates, leading some critics to deem self-report dietary assessment ‘a failed research paradigm’ and even ‘pseudoscientific’( Reference Archer, Pavela and Lavie 1 ). Dietary assessments’ flaws are often attributed to limitations in memory and self-report( Reference Archer, Pavela and Lavie 1 ). There has long been a concerted effort to improve such assessments, including use of novel technologies( Reference Thompson, Subar and Loria 2 ), cognitive interviewing( Reference Subar, Thompson and Smith 3 ), measures at multiple time points( Reference Moshfegh, Rhodes and Baer 4 ), integration of objective (e.g. biomarkers( Reference Freedman, Kipnis and Schatzkin 5 )) and subjective (e.g. social desirability) supplemental measures with reported diet, as well as novel approaches towards scoring( Reference Drewnowski, Maillot and Darmon 6 , Reference Schulze, Hoffmann and Kroke 7 ) and analysing( Reference DiBello, Kraft and McGarvey 8 – Reference Newby and Tucker 10 ) the raw data such methods produce. However, psychometric methodologies have been almost entirely overlooked. This is concerning for two reasons: First, survey psychometrics was largely developed in order to account for the limitations of self-reported behaviours( Reference Devellis 11 ). Second, advances in psychometrics are constantly improving assessments in many fields, the most noticeable being the use of item response theory (IRT) in the Patient Reported Outcomes Measurement Information System (PROMIS)( Reference Chang and Reeve 12 ). The present commentary is intended to make a case for the broader use of psychometric modelling to hone and refine FFQ.
Many areas of medicine and epidemiology have undergone strides in measurement, as epitomised by PROMIS( Reference Chang and Reeve 12 ). PROMIS scales use an IRT framework to optimise item properties. PROMIS users also have the option of leveraging computer-adaptive testing, which customises the items as an individual responds in real-time, based on his/her previous responses. It is reasonable to ask why such measurement advances have not yet been applied to FFQ. One possible answer, albeit a fairly dismissive one, is that diet is different and harder to assess. Another possibility is that some fields arbitrarily develop in different directions, and do not respond quickly to some methodological advances. One glaring contrast is that FFQ are often used to produce a host of different variables, whereas psychometrically validated tools typically hone in on one underlying construct.
There are many different kinds of FFQ. Some attempt to measure the entire diet, whereas others are restricted to individual nutrients or focus on particular aspects of diet most salient to overall health. There are also many ways to analyse results from a single FFQ: one can look at the intake of an individual nutrient, food selections, dietary patterns derived from factor analysis, or an index of overall diet quality based on an a priori scoring system. All of these techniques show some promise in standardising dietary assessment, but they are open to debate. Factor analyses of FFQ consistently derive a range of informative factors, which typically classify FFQ items as Western/unhealthy foods, non-Western/prudent foods, and/or based on a type of food (e.g. fruit, meat, dessert, etc.)( Reference Newby and Tucker 10 ). But factor analysis can be difficult to replicate across samples and/or FFQ. Diet indexes, on the other hand, do not necessarily produce more robust relations with disease outcomes( Reference Kourlaba and Panagiotakos 13 ). They are also commonly calculated using nutritional estimates rather than item responses (i.e. food choices), which is problematic (for reasons discussed below). Shorter FFQ (or screeners) more closely resemble PROMIS scales, however they are frequently derived from longer FFQ, and almost never have undergone psychometric validation( Reference Gebremariam, Vaque-Crusellas and Andersen 14 ), at least of the sort common in other fields.
One problem with factor analytic approaches is that they are more typically used for exploratory rather than for measurement purposes. Within psychometrics, factor analysis is conducted with the goal of determining which items belong on a certain scale( Reference Reise, Waller and Comrey 15 ). This process is important regardless of the number of items on a scale. As demonstrated below, it is even important for very brief diet scales. This validation procedure is conducted under the assumption that items which load on the same dimension(s) will best capture the latent construct the scale is measuring. It is necessary to review what is meant by a ‘latent construct’.
Latent constructs
A construct is ‘an abstract, possibly hypothetical entity that is inferred from a set of similar … or directly observed behaviours’( Reference Raykov and Marcoulides 16 ). Constructs are latent as they cannot be directly observed and are indirectly assessed through items that represent the latent construct( Reference Devellis 11 , Reference Raykov and Marcoulides 16 ). Examples of latent constructs in psychology include depression, extroversion, intelligence, etc. Such latent constructs are manifest in an infinite number of ways. It is often assumed that a latent construct causes its manifestation, and not the other way around. That is, someone is talkative because she is extroverted. This assumption is also reflected in structural equation models that use latent variables. In these models, as seen in Fig. 1 model A, path arrows tend to point from the latent construct to the observed variable( Reference Kline 17 , Reference Nunnally and Bernstein 18 ). Typically in such models, the latent construct is the variable of substantive interest, whereas the observed variable is a mere indicator of the latent construct. For any given scale, no indicator is a perfect measure of the latent construct. But indicator errors, that is, the extent to which indicators do not reflect the latent construct, are assumed to be independent and unsystematic. Under these assumptions, the error associated with each individual indicator washes out. Any psychological scale developed with psychometrics is built around its latent construct. This is distinctly not the case with FFQ, and it is worth speculating about why.

Fig. 1 Conceptual model for most psychometric scales (model A) and for FFQ (model B).
FFQ are intended to estimate what people eat, how much they eat, and how often they eat foods from defined lists over a specified time. They may be scored in various ways, often using nutritional databases to estimate total energetic intake, macronutrients, etc. This process is depicted in Fig. 1 model B. Unlike psychological and behavioural scales, FFQ are intended to estimate nutrient intakes, not latent constructs. But that does not mean that responses to FFQ are uninfluenced by latent constructs – most likely, as demonstrated in the consistency of FFQ-derived factors( Reference Newby and Tucker 10 ), they are. That is, someone reaches for a cookie because he likes sweets. By ignoring the effects of one or multiple latent constructs that underlie a pattern of responses, FFQ are not protected from error in the same way that most psychometric scales are. This problem is likely compounded by running item responses through an external database in order to derive nutrient intake estimates.
Fig. 1 model B demonstrates how far removed the nutritional estimates are from the latent constructs that inevitably underlie them. For example, consider a hypothetical FFQ that assessed consumption of hamburgers, mayonnaise and many other foods. Further, imagine that after running an exploratory factor analysis, hamburgers and mayonnaise (along with a variety of other foods) are found to load on the same ‘unhealthy eating’ factor, and that mayonnaise has a stronger item loading than hamburger. Psychometrically, this result means that mayonnaise may be a better surrogate marker for an ‘unhealthy food’ latent construct than hamburger. However, consuming one serving of a hamburger will be associated with four times the energetic intake of a serving of mayonnaise. That is, mayonnaise would be a better indicator of the latent construct, but hamburger would contribute more towards the estimate of energetic intake. This point, of course, applies to all the other items on the same FFQ, and to all the nutrient estimates that it produces.
This is one explanation for why, as Schulze( Reference Schulze, Hoffmann and Kroke 7 ) noted, factor analyses on responses to FFQ (i.e. food choices) are preferable than factor analyses on derived nutrient estimates. Schulze also proposed using exploratory factor analysis on FFQ to derive weighted standardised factor scores, which could be applied across different sampled populations( Reference Schulze, Hoffmann and Kroke 7 ). This application of factor analysis is perhaps the closest in spirit to psychometric applications. However, the use of factor analysis to determine which items to select in a dietary assessment – that is, as an intermediary step in scale development – is curiously lacking, even in Schulze’s work. As our empirical example below demonstrates, this is even important for brief screeners, before applying additional IRT modelling. First, however, we provide a description of our data.
Motivating example
Our adoption of psychometric tools was motivated by data collected using the Global Assessment Tool (GAT), a survey completed annually by all US Army personnel( Reference Peterson, Park and Castro 19 ). The GAT consists mostly of psychological scales, although in 2012 items were added to measure nutrition, sleep, and physical activity( Reference Lentino, Purvis and Murphy 20 , Reference Purvis, Lentino and Jackson 21 ). A five-item Healthy Eating Scale (HES-5) was used to assess compliance with public health nutrition recommendations, based loosely on the Healthy Eating Index( Reference Guenther, Reedy and Krebs-Smith 22 ). The HES-5 asks about consumption of fruits, vegetables, whole grains, dairy products and fish. Each item has six response categories, although response categories for fish (‘4 or more times/week’; ‘2 or 3 times/week’; ‘1 time/week’; ‘2 times/month’; ‘1 time/month’; ‘rarely or never’) differ from the other four items (‘3 or more times/d’; ‘2 times/d’; ‘1 time/d’; ‘3–6 times/week’; ‘1 or 2 times/week’; ‘rarely or never’). As with most food consumption questions, these response options were intended to relate to public health recommendations, and are similar to those used in other research, including the Health Related Behaviours Survey of military personnel( Reference Bray, Pemberton and Hourani 23 ). Six additional nutrition questions asked about frequency of snack, water, soda and sports drink consumption; days per week of breakfast consumption; and consumption of recovery snacks after exercise. The exact wording for these items can be found in the online Supplementary Appendix.
Our study used data from participants who completed the GAT during 2 weeks in July 2012, and consented to have their responses used for future research. After concluding that a full review was not required for this investigation because the Army provided data stripped of identification elements to the Consortium for Health and Military Performance per an established data use agreement, the Uniformed Services University of the Health Sciences Institutional Review Board approved analysis of data provided by participants who agreed that their responses could be used for research.
The HES-5 is much shorter than a standard FFQ, or even most dietary screeners. However, its items are similar to those used in FFQ. More importantly, focusing on a few items allows us to demonstrate the sorts of measurement decisions, and their granularity, that IRT can inform, with regard to item selection and response category wording. Analysing HES-5 data on a large heterogeneous sample also allows for differential item functioning (DIF) analysis, which can help to determine scale validity across different sub-samples.
Descriptive and correlational analyses using these data have already been published( Reference Purvis, Lentino and Jackson 21 ). We developed IRT models from the original data set to examine scale validation, a standard in many fields but not previously explored in the field of nutrition. From an initial sample of 14 580 participants, 1886 were excluded from these analyses due to missing demographic data, and 594 due to extreme responses (i.e. all responses were in the highest response category or all responses were in the lowest response category). The remaining 12 370 participants were on average 28 years of age (sd 8·3), 83 % male and 84 % enlisted, serving in either Active Duty (53 %) or Reserve/National Guard (47 %). Analyses were conducted in flexMIRT® version 3.03 by using the default settings (e.g. cross-product standard errors, Bock–Aitkin estimation algorithm, etc.)( Reference Cai 24 ). Results from the IRT models were illuminating and unexpected. But when we looked for dietary assessment literature employing IRT models for guidance, we found none.
Below we provide a brief description of IRT, and then proceed with the role of confirmatory factor analysis in item selection, because unidimensionality is an assumption for most IRT models.
Item response theory
IRT is a measurement paradigm that avails a set of psychometric models common in survey and test development( Reference de Ayala 25 ). IRT analyses can be useful to optimise scale accuracy and reliability. They allow for fine-grained analysis on the ability of an item’s response options to discriminate between various levels of the latent trait. IRT analyses can be used to score surveys and elucidate scale properties. They are particularly powerful in scale development, as they can be used iteratively to hone, improve, and eliminate items( Reference Reise, Waller and Comrey 15 ).
At their core, all IRT models aim to estimate the probability that a respondent will provide a particular response to a given survey (or test) item; these probabilities, furthermore, are conditional on where the respondent is located on a latent trait’s continuum (which here is healthy eating)( Reference de Ayala 25 – Reference Steinberg and Thissen 27 ). For example, take an item that assesses one component of healthy eating: fruit consumption. As healthy eating increases, an individual has a higher probability of endorsing a higher response option (e.g. ‘four per d’) than a lower response option (e.g. ‘one per d’) for the fruit consumption item. Given a set of items measuring the same latent trait (e.g. healthy eating), IRT models aim to pinpoint those probabilities, for each response option within each respective item. Further, IRT models often use iterative maximum likelihood procedures to simultaneously estimate both (a) the probability that someone will provide a particular answer to a survey question, conditional on his or her underlying level of the latent trait, and (b) an individual’s level of the latent trait based on his or her responses. IRT surveys are scored by applying complicated algorithms, based on an individual’s pattern of responses.
For readers who are less familiar with IRT, some of these principles will become clearer when applied below, and a number of excellent resources are available: from introductory articles( Reference Chang and Reeve 12 , Reference Bock 28 , Reference Edelen and Reeve 29 ) to comprehensive books( Reference de Ayala 25 , Reference Linden and Hambleton 30 , Reference Thissen and Steinberg 31 ). A core assumption for IRT-derived scales is that all of the items within the scale are measuring the same latent construct (or the intended multiple constructs in multidimensional models). Therefore, this assumption is tested next, by using confirmatory factor analysis.
Analytic techniques
Factor analysis
In our analysis of the HES-5 data set, the latent construct was healthy eating. In addition to the scale’s original five items, six items relating to healthy diet practices were also administered. Therefore, we conducted confirmatory factor analysis to determine which of the eleven items would load on a single dimension. Healthy eating could be multidimensional, but most brief scales are aimed at measuring unidimensional constructs; for those scales, unidimensionality is a fundamental assumption. Items were selected based on factor loadings that were strong (e.g. above 0·3), homogeneous (e.g. generally similar factor loadings) and on the same factor( Reference Reise, Waller and Comrey 15 ).
Based on the results, we selected five items. Four were from the original HES-5: fruit (factor loading: 0·81), vegetables (0·85), whole grains (0·75), dairy products (0·58). The fifth, from the additional items, was water consumption (0·45). Four items with moderate factor loadings (breakfast, 0·38; fish, 0·32; recovery, 0·32 and snacks, 0·28) were excluded because their loadings varied too much from the five items that should be included. The remaining items had low (sports drinks, 0·05) or negative (soda, −0·23) loadings.
Item response theory calibration
The next step was to fit IRT models to the five selected items. There are many IRT models to choose from, based on survey item formats, theoretical assumptions, dimensionality, and other considerations( Reference de Ayala 25 ). We used the Graded Response Model (GRM)( Reference Samejima 32 ). The GRM is common in similar surveys with ordered categories, although there are also other less common options( Reference Thissen and Steinberg 33 ). The GRM is based on the probability that a participant (x) at a certain level of the latent trait (θ, with a standardised distribution around 0) will endorse a particular response category (or any higher response category):
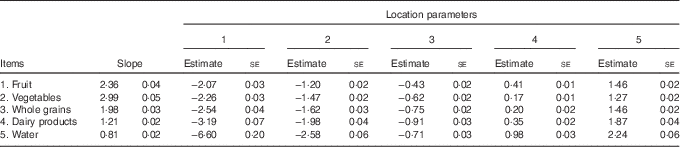
Analysing the response data with the GRM provides a discrimination parameter for each item (α i ) and location parameters for each item’s response categories (β ij ). The resulting probability curves are examined in item characteristic curves (Fig. 2) that graph the probability that a participant will endorse a particular response option as a function of her level of θ. Items with high discrimination parameter values have a greater ability to differentiate people along θ than items with low discrimination parameters; but parameters that are too high may indicate assumption violations (such as items being locally dependent). Ideal discrimination parameters range from about 0·8 to 2·5( Reference de Ayala 25 ). Response options with extreme location parameters (e.g. above 3) are only likely to be endorsed by individuals with extreme levels of θ. Lastly, the term item/test information indicates the degree of certainty in an individual’s estimated level of θ. Item information is conceptually similar to other reliability metrics (e.g. Cronbach’s α), however it varies over levels of θ, indicating the precision of scores across different levels of the latent trait. The concept of item information is important in IRT because it allows individual items and scales to be honed for a particular population (e.g. unhealthy eaters, chronic disease patients, etc.).

Fig. 2 Item characteristic curves for item 3, whole grains, based on the six response categories (0=‘rarely or never’; 1=‘1 or 2 times/week’; 2=‘3–6 times/week’; 3=‘1 time/d’; 4=‘2 times/d’; 5=‘3 or more times/d’), based on the nominal model (a, which does not impose a response category order) and the Graded Response Model (b, which does impose a response category order).
The GRM assumes that each item’s response categories are in the correct order – that is, as the probability of endorsing a higher response category (e.g. going from eating fruit ‘2 or 3 times/week’ to ‘4 or more times/week’) increases, so will the underlying level of healthy eating. Therefore, before applying the GRM, this assumption was tested using Bock’s nominal model( Reference Bock 34 ), which, unlike the GRM, imposes no order on the response categories.
The nominal model
Bock’s nominal model demonstrated problems with the order of the response categories. These issues can be seen by inspecting the item characteristic curves, which depict the estimated probability of endorsing a response category as a function of θ. For the four food categories, item characteristic curves overlapped for the three lowest response categories (0, 1, 2), as exemplified in Fig. 2, left panel, for whole grains. Results indicate that these response categories were not adequately discriminating participants along the latent trait. Such a pattern is concerning, because it shows that, as healthy eating (or θ) decreases, participants become increasingly more likely to endorse the third response option (‘3 to 6 times/week’), and less likely to endorse the lower response options (‘1 or 2 times/week’, ‘rarely or never’).
As the GRM imposes an order on the item categories, evidence that the response categories do not follow their expected order is disconcerting. Analytically, it is not always clear how to handle item categories that do not align in the expected order( Reference Garcia-Perez 35 ). Analysts who use such scales often collapse overlapping response categories to force the remaining categories into the correct order. But collapsing response categories entails a loss of information and may bias scores( Reference Garcia-Perez 35 ). Such findings do provide valuable insights for improving the scale. Here, the three highest response options refer to food consumption in terms of days (e.g. ‘4 or more times/d’; ‘2 or 3 times/d’; ‘1 time/d’); the problematic response options refer to food consumption in terms of weeks (‘3–6 times/week’; ‘1 or 2 times/week’), followed by the lowest response option, ‘rarely or never’. A possible explanation, discussed further below, is that these response options were confusing to respondents, particularly the distinction between days and weeks.
Graded Response Model
Next, the GRM was applied to the items (with their original response categories). The model’s fit was moderate (based on a root mean squared error of approximation, M2, of 0·07( Reference Maydeu-Olivares and Joe 36 )). The GRM imposes an order onto the response categories; the effect of this on the estimated probabilities of endorsing each whole grain response category can be seen in Fig. 2. GRM item parameters are provided in Table 1. All of the item-slopes are within the normal expected ranges, although water (0·81) was much lower, indicating that it may not discriminate as well as the other items over levels of healthy eating. Water’s lowest response option, ‘never or rarely’, also had an extreme location, likely because few people ‘never or rarely’ drink water. Using testlet models( Reference Steinberg and Thissen 37 ), which allow for multiple item-factors, the possibility that vegetables exhibited local dependence with fruit was ruled out.
Table 1 Item parameters(Item parameter estimates with their standard errors)
Information can be quantified for the scale as a whole (Fig. 3, left panel) or for individual items (fruit: centre and water: right panels). Inspection of the overall information curve shows a sharp peak at the centre of θ, and declines on each side as θ increased and decreased. This indicates the scale was most reliable when characterising healthy eating at the centre of the distribution. Conversely, the scale may be less suited for individuals who are moderately above or moderately below average healthy eaters. Information curves for most of the items are similar to that of the total scale (as seen in the fruit item, Fig. 3, centre panel), with the exception of the information curve for the water item (right panel). Water’s information curve was relatively low and flat, indicating its limited role in characterising healthy eating. Marginal reliability for the entire scale was 0·85, which is considered moderately acceptable.

Fig. 3 Test information as a function of healthy eating (θ) for the entire scale (left), the fruit item (middle) and the water item (right).
Judged by common IRT standards, these items were suboptimal and need improvement, although the four food items may provide a foundation for future work. The water item was the poorest performing of the five items and its inclusion could be a judgment call, depending on the uses of the scale and the importance of water intake. Rewording the lower response categories for the food items, and the lowest response category for the water item, would likely improve the scale. For the food items, a better set of response categories might have been formed by not intermixing days and weeks. For example, ‘3–6 times/week’ could be replaced with ‘about every other day’.
Differential item functioning
Next, DIF analyses were conducted to determine scale validity( Reference Thissen, Steinberg and Wainer 38 ) and whether an item’s parameters vary across populations, when controlling for levels of the latent construct. This amounts to testing whether the connection between an item and a latent construct differs across two populations. For example, if males and females with the same level of ‘healthy eating’ respond to the fruit item differently, then the fruit item may not characterise healthy eating well for one of the groups (i.e. demonstrate sex bias). This is of particular concern in dietary assessment where FFQ are tailored to different demographic groups( Reference Sharma 39 ).
In the present example, the survey was given to a large Army sample, with the intention of summarising healthy eating status across potentially disparate sub-populations. The US Army has many heterogeneous groups. In particular, as women are integrated into combat roles, they will be monitored more closely, due to increased risk of injury( Reference Tepe, Yarnell and Nindl 40 ). Active Duty and Reserve/National Guard soldiers are expected to maintain similar levels of fitness( 41 ), but have differences in health status( Reference Kazman, de la Motte and Bramhall 42 , Reference Warr, Alvar and Dodd 43 ). Therefore, DIF comparisons were made for the following groups: males v. females; Active Duty v. Reserve/National Guard; and Officer v. Enlisted.
There are nuanced ways to empirically quantify DIF, but these are best considered as screens to flag items for further review( Reference Hambleton 44 ). In our example, DIF analyses were conducted by allowing one item’s slope parameter to vary across groups, while holding the other four items constant. This was conducted, first, using the ‘sweep’ procedure in flexMirt( Reference Cai 24 , Reference Woods, Cai and Wang 45 ), and second by examining the percentage change in the model log likelihood when an item’s parameters were constrained to be equal v. when they were allowed to differ across groups. Although this is a common approach( Reference Thissen, Steinberg and Wainer 38 ), it assumes that most of the items do not exhibit DIF. Still, it provides an empirical approach to test item-equivalence across groups.
DIF results indicated that the items functioned similarly across sex, service component, and officer status. The largest differences were observed in the sex comparisons, as females had a smaller slope for the whole grain (female: 1·69 (se 0·07); male: 2·24 (se 0·04); χ 2=49·2, P<0·001) and dairy products (female: 1·10 (se 0·05); male: 1·33 (se 0·03), χ 2=15·1, P<0·001) items than males. This indicates that the whole grain and dairy product items were slightly less discriminating for women than for men. For Enlisted v. Officer comparisons, differences were noted for the slopes for the vegetable (Enlisted: 2·62 (se 0·05); Officer: 3·61 (se 0·22), χ 2=18·7, P<0·001) and whole grain (Enlisted: 1·85 (se 0·03); Officer: 1·53 (se 0·07); χ 2=18·3, P<0·001) items. These differences in item parameters, although statistically significant, could likely be considered minor, as they were associated with minimal improvements in model fit (<0·01 % change in log likelihood).
Items that exhibit DIF are not necessarily bad, but they need to be more carefully considered (both quantitatively and qualitatively) for future use( Reference Hambleton 44 ). Judging the magnitude of DIF is field-specific, and it depends on a how a scale is used and interpreted. For instance, it may be the case that vegetables are less related to healthy eating (e.g. due to lack of availability) for Enlisted than for Officer personnel. Alternatively, if there is no scientific rationale for this finding, then inclusion of the vegetable item should be scrutinised further, particularly if using the scale to make comparisons between Enlisted and Officers. Examining DIF becomes particularly important when scales are linked to high-stakes decisions, such as the allocation of resources or the effectiveness of interventions.
Conclusions
On the surface, the results above can inform some very practical decisions faced by those who develop FFQ. The findings with regard to the response options should be particularly useful, and imply an easy fix of attending to the time-spans used in response categories. The DIF analysis provides some comfort that other brief screeners may be valid across the types of sub-populations compared above. And the four core food items appear to comprise a workable albeit imperfect scale from which to build future screeners. All of these recommendations rest on modelling the response options along the latent construct, which itself was created using only select items. This analytic approach is standard in many disciplines, and is most useful as an iterative step in scale development to check and rectify statistical assumptions (e.g. for item selection, wording, etc.). At the same time, it should not be underestimated how very different this approach is from those used in dietary assessments.
The motivating example consisted of a very brief scale, but diet consumption questions in brief scales and screeners are often derived from those in longer FFQ. Although longer FFQ could certainly be subjected to IRT calibration, the sample size requirements for longer scales increases substantially. More importantly, latent constructs can often be adequately assessed with a limited number of items, typically under ten items depending on the topic, especially if the items are well-constructed( Reference Devellis 11 ). FFQ are intended to produce nutrient estimates; brief screeners are often intended to quantify compliance with public health dietary recommendations. Users of both of these sorts of scales are more interested in properties of consumed food, and less interested in latent constructs. But when measuring behaviours, which are almost certainly influenced by latent constructs or traits, the user’s interest in modelling food does not matter; the estimated properties of dietary patterns will be subordinate to the nature of behaviour. Further consideration about how behaviours work provides a plausible explanation for the results above.
Behaviours have a temporal aspect, which may account for findings with regard to the response categories and the confirmatory factor analysis. Just as it may be important to include descriptors with the same denominator (e.g. days or weeks), it may also be important to ask about foods that are eaten at roughly the same frequency. Fish, although generally included in public health guidelines, is eaten less frequently than other healthy foods. Regardless of the health value of different foods, foods consumed at similar frequencies are more likely to be part of the same construct (or load on the same dimension) than foods consumed in different frequencies. Latent constructs, and their respective behaviours, can be targeted at various levels of generality (e.g. depression, v. a specific aspect of depression)( Reference Hampson, John and Goldberg 46 ). For diet, it is likely that some specific dietary tendencies function more like stable traits (e.g. consumption of salt, fat, sugar), and thus are more amendable to psychometric techniques, than others (e.g. consumption of Fe, vitamin D).
A scale’s validity is not black or white, and many lines of evidence contribute to it( Reference Messick 47 ). FFQ developed using IRT methodologies might be validated by using more ‘objective’ techniques, such as nutritional biomarker panels. These sorts of objective measures might be used in a number of ways, such as providing a measure of convergent validity or providing ‘anchor points’ that can be used for interpreting FFQ scores. It is particularly important, however, to ensure a strong theoretical connection between the latent construct being measured and the objective criterion that is used for validation (or interpretation). For example, it is likely that healthy eating – even if it could be measured perfectly – would only moderately correlate with lipid profiles. Lessons from other fields would suggest that ‘objective’ or non-self-reported measures are not automatically better than self-reported measures( Reference Freedman, Kipnis and Schatzkin 5 , Reference Buysse 48 – Reference Weldring and Smith 50 ).
Summary
This commentary was intended to introduce IRT and to highlight aspects of IRT that may be particularly crucial for FFQ and related scales. To keep the manuscript concise, a number of IRT fundamentals were not discussed, including local dependence( Reference Chen and Thissen 51 ), more subtle examinations of DIF (e.g. non-uniform DIF, factorial invariance( Reference Hambleton 44 , Reference Teresi 52 )), and powerful extensions of IRT, such as multidimensional models( Reference Reckase 53 ) and computer-adaptive testing( Reference Chang and Reeve 12 , Reference Lawrence 54 ).
If dietary assessments were modelled off of scales that assess behavioural traits, then psychometric and IRT models could be leveraged to further optimise them. Such scales are aimed at assessing latent constructs or traits, which can not only be quantified, but also subjected to extensive statistical tests to gauge measurement error and scale reliability. Their mechanics are depicted in model A in Fig. 1. Model A describes both a conceptual and a statistical model, which lies at the roots of psychometrics. As individual indicators are merely meant to reflect the latent construct, they do not have to be measured with the same precision that foods are measured in dietary assessments. In part, that is why behavioural scales use Likert-type scales (e.g. with anchors such as ‘sometimes’, ‘agree’, etc.) more often than precise response categories (e.g. ‘1 time/week’). Model B describes a conceptual model, but its statistical model remains ambiguous. In theory, Model B is more desirable for dietary assessment; in practice, it is less attainable.
That said, short of creating a whole new FFQ and iteratively using IRT models in the decision process (which was beyond the scope of our work), it is difficult to prove that IRT enhances dietary assessment, largely because psychometric scales have different aims and standards than dietary assessments. It is our hope that the aims and standards commonly seen in psychometric scales are more widely adopted, in some form or another, in dietary assessment.
Acknowledgements
The authors would like to acknowledge Drs Ji Seung Yang and Tracy Sweet of the University of Maryland Educational Department of Measurement and Statistics for their instruction in the fundamentals of IRT and their valuable feedback. The authors would also like to acknowledge Mr Jeffery Galecki also for his in-depth statistical guidance, feedback and notes. These individuals have provided consent to be acknowledged.
This study was funded by a grant from Comprehensive Soldier and Family Fitness (HT9404-12-1-0017; F191GJ). Comprehensive Soldier and Family Fitness had no role in the design, analysis or writing of this article.
J. B. K. performed the analysis and interpretation of data, and drafted the manuscript. J. M. S provided input with regard to the conception and design of the paper, and assisted with critical manuscript revisions. P. A. D. assisted with the acquisition of the data; the conception and design of the survey; obtained funding; and oversaw the project.
No financial disclosures were reported by the authors of this paper.
Supplementary material
For supplementary material/s referred to in this article, please visit https://doi.org/10.1017/S0007114517002215






