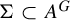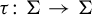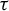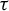1 Introduction
The main goal of the present paper is to extend and generalize well-known results about limit sets and nilpotency of classical cellular automata, that is, cellular automata with finite alphabets, to the setting of algebraic cellular automata over algebraic sofic subshifts, where the alphabet is the set of rational points of an algebraic variety.
Since the pioneering work of John von Neumann in the 1940s [Reference von Neumann58], the mathematical theory of cellular automata has led to very interesting questions, with deep connections to areas such as theoretical computer science, decidability, dynamical systems, ergodic theory, harmonic analysis, and geometric group theory. In his empirical classification of the long-term behavior of classical cellular automata, Wolfram [Reference Wolfram60] introduced the notion of a limit set. For classical cellular automata, properties of limit sets and their relations with various notions of nilpotency were subsequently investigated by several authors (see [Reference Culik, Pachl and Yu18, Reference Guillon, Richard, Ochmański and Tyszkiewicz24, Reference Kari25, Reference Milnor34, Reference Salo, Dennunzio, Formenti, Manzoni and Porreca51]). In particular, Aanderaa and Lewis [Reference Aanderaa and Lewis1] and, independently, Kari [Reference Kari25] proved undecidability of nilpotency for classical cellular automata over
![]() $\mathbb {Z}$
: this undecidability result constitutes one of the most influential results in the theory of cellular automata and one of the main motivations for the study of nilpotency in the symbolic dynamics setting. In general, these properties of limit sets become false when the alphabet is allowed to be infinite. A major problem arising when working with infinite alphabets is that images of subshifts of finite type may fail to be closed (e.g. [Reference Ceccherini-Silberstein and Coornaert10, Example 3.3.3]). Nevertheless, infinite alphabet subshifts and their dynamics are not only intrinsically interesting but also fundamental to the study of smooth dynamical systems (cf. e.g. [Reference Boyle, Buzzi and Gómez8], [Reference Kitchens28, Ch. 7], [Reference Lima and Sarig29, Reference Sarig52, Reference Sarig53] and the references therein).
$\mathbb {Z}$
: this undecidability result constitutes one of the most influential results in the theory of cellular automata and one of the main motivations for the study of nilpotency in the symbolic dynamics setting. In general, these properties of limit sets become false when the alphabet is allowed to be infinite. A major problem arising when working with infinite alphabets is that images of subshifts of finite type may fail to be closed (e.g. [Reference Ceccherini-Silberstein and Coornaert10, Example 3.3.3]). Nevertheless, infinite alphabet subshifts and their dynamics are not only intrinsically interesting but also fundamental to the study of smooth dynamical systems (cf. e.g. [Reference Boyle, Buzzi and Gómez8], [Reference Kitchens28, Ch. 7], [Reference Lima and Sarig29, Reference Sarig52, Reference Sarig53] and the references therein).
After Gromov [Reference Gromov20], the study of injectivity and surjectivity of algebraic cellular automata was pursued in [Reference Ceccherini-Silberstein and Coornaert11, Reference Ceccherini-Silberstein, Coornaert and Picardello12, Reference Ceccherini-Silberstein, Coornaert and Phung14, Reference Ceccherini-Silberstein, Coornaert and Phung15, Reference Phung39] to obtain generalizations of the Ax–Grothendieck theorem [Reference Ax3], [Reference Grothendieck23, Proposition 10.4.11] and of the Moore–Myhill Garden of Eden theorem [Reference Moore35, Reference Myhill36]. Nilpotency is in the opposite direction since a nilpotent map is never injective nor surjective when the underlying set has at least two elements.
To state our results, let us first introduce some terminology and notation. Let
![]() $f \colon X \to X$
be a map from a set X into itself. Given an integer
$f \colon X \to X$
be a map from a set X into itself. Given an integer
![]() $n \geq 1$
, the nth iterate of f is the map
$n \geq 1$
, the nth iterate of f is the map
![]() $f^n \colon X \to X$
defined by
$f^n \colon X \to X$
defined by ![]() (n times). The sets
(n times). The sets
![]() $f^n(X)$
,
$f^n(X)$
,
![]() $n \geq 1$
, form a decreasing sequence of subsets of X. The limit set
$n \geq 1$
, form a decreasing sequence of subsets of X. The limit set ![]() of f is the set of points that occur after iterating f arbitrarily many times.
of f is the set of points that occur after iterating f arbitrarily many times.
Observe that
![]() $f(\Omega (f)) \subset \Omega (f)$
. The inclusion may be strict, and equality holds if and only if every
$f(\Omega (f)) \subset \Omega (f)$
. The inclusion may be strict, and equality holds if and only if every
![]() $x \in \Omega (f)$
admits a backward orbit, that is, a sequence
$x \in \Omega (f)$
admits a backward orbit, that is, a sequence
![]() $(x_i)_{i \geq 0}$
of points of X such that
$(x_i)_{i \geq 0}$
of points of X such that
![]() $x_0 = x$
and
$x_0 = x$
and
![]() $f(x_{i + 1}) = x_i$
for all
$f(x_{i + 1}) = x_i$
for all
![]() $i \geq 0$
. Clearly, f is surjective if and only if
$i \geq 0$
. Clearly, f is surjective if and only if
![]() $\Omega (f) = X$
. Note also that
$\Omega (f) = X$
. Note also that ![]() and that
and that
![]() $\Omega (f^n) = \Omega (f)$
for every
$\Omega (f^n) = \Omega (f)$
for every
![]() $n \geq 1$
. The map f is stable if
$n \geq 1$
. The map f is stable if
![]() $f^{n+1}(X)=f^n(X)$
for some
$f^{n+1}(X)=f^n(X)$
for some
![]() $n \geq 1$
. If f is stable, then
$n \geq 1$
. If f is stable, then
![]() $\Omega (f) \not = \varnothing $
unless
$\Omega (f) \not = \varnothing $
unless
![]() $X = \varnothing $
. Clearly, f is stable whenever X is finite. If X is infinite, there always exist maps
$X = \varnothing $
. Clearly, f is stable whenever X is finite. If X is infinite, there always exist maps
![]() $f \colon X \to X$
with
$f \colon X \to X$
with
![]() $\Omega (f) = \varnothing $
(cf. Lemma A.1).
$\Omega (f) = \varnothing $
(cf. Lemma A.1).
Assume that X is a topological space and
![]() $f \colon X \to X$
is a continuous map. One says that
$f \colon X \to X$
is a continuous map. One says that
![]() $x \in X$
is a recurrent (respectively non-wandering) point of f if for every neighborhood U of x, there exists
$x \in X$
is a recurrent (respectively non-wandering) point of f if for every neighborhood U of x, there exists
![]() $n \geq 1$
such that
$n \geq 1$
such that
![]() $f^n(x) \in U$
(respectively
$f^n(x) \in U$
(respectively
![]() $f^n(U)$
meets U). Let
$f^n(U)$
meets U). Let
![]() $\operatorname {\mathrm {R}}(f)$
(respectively
$\operatorname {\mathrm {R}}(f)$
(respectively
![]() $\operatorname {\mathrm {NW}}(f)$
) denote the set of recurrent (respectively non-wandering) points of f. It is immediate that
$\operatorname {\mathrm {NW}}(f)$
) denote the set of recurrent (respectively non-wandering) points of f. It is immediate that
![]() $\operatorname {\mathrm {Per}}(f) \subset \operatorname {\mathrm {R}}(f) \subset \operatorname {\mathrm {NW}}(f)$
and that
$\operatorname {\mathrm {Per}}(f) \subset \operatorname {\mathrm {R}}(f) \subset \operatorname {\mathrm {NW}}(f)$
and that
![]() $\operatorname {\mathrm {NW}}(f)$
is a closed subset of X. In general, neither
$\operatorname {\mathrm {NW}}(f)$
is a closed subset of X. In general, neither
![]() $\operatorname {\mathrm {Per}}(f)$
, nor
$\operatorname {\mathrm {Per}}(f)$
, nor
![]() $\operatorname {\mathrm {R}}(f)$
, nor
$\operatorname {\mathrm {R}}(f)$
, nor
![]() $\Omega (f)$
are closed in X (see Example 15.1).
$\Omega (f)$
are closed in X (see Example 15.1).
Suppose now that X is a uniform space and
![]() $f \colon X \to X$
is a uniformly continuous map. One says that a point
$f \colon X \to X$
is a uniformly continuous map. One says that a point
![]() $x \in X$
is chain-recurrent if for every entourage E of X, there exist an integer
$x \in X$
is chain-recurrent if for every entourage E of X, there exist an integer
![]() $n \geq 1$
and a sequence of points
$n \geq 1$
and a sequence of points
![]() $x_0,x_1,\ldots ,x_n \in X$
such that
$x_0,x_1,\ldots ,x_n \in X$
such that
![]() $x = x_0 =~x_n$
and
$x = x_0 =~x_n$
and
![]() $(f(x_i),x_{i + 1}) \in E$
for all
$(f(x_i),x_{i + 1}) \in E$
for all
![]() $0 \leq i \leq n - 1$
. We shall denote by
$0 \leq i \leq n - 1$
. We shall denote by
![]() $\operatorname {\mathrm {CR}}(f)$
the set of chain-recurrent points of f. Observe that
$\operatorname {\mathrm {CR}}(f)$
the set of chain-recurrent points of f. Observe that
![]() $\operatorname {\mathrm {CR}}(f)$
is always closed in X.
$\operatorname {\mathrm {CR}}(f)$
is always closed in X.
Let G be a group and let A be a set, called the alphabet. The set ![]() , consisting of all maps from G to A, is called the set of configurations over the group G and the alphabet A. We equip
, consisting of all maps from G to A, is called the set of configurations over the group G and the alphabet A. We equip
![]() $A^G = \prod _{g \in G} A$
with its prodiscrete uniform structure, that is, the product uniform structure obtained by taking the discrete uniform structure on each factor A of
$A^G = \prod _{g \in G} A$
with its prodiscrete uniform structure, that is, the product uniform structure obtained by taking the discrete uniform structure on each factor A of
![]() $A^G$
. Note that
$A^G$
. Note that
![]() $A^G$
is a totally disconnected Hausdorff space and that
$A^G$
is a totally disconnected Hausdorff space and that
![]() $A^G$
is compact if and only if A is finite. The shift action of the group G on
$A^G$
is compact if and only if A is finite. The shift action of the group G on
![]() $A^G$
is the action defined by
$A^G$
is the action defined by
![]() $(g,x) \mapsto g x$
, where
$(g,x) \mapsto g x$
, where ![]() for all
for all
![]() $g,h \in G$
and
$g,h \in G$
and
![]() $x \in A^G$
. This action is uniformly continuous with respect to the prodiscrete uniform structure.
$x \in A^G$
. This action is uniformly continuous with respect to the prodiscrete uniform structure.
For a subgroup
![]() $H \subset G$
, define
$H \subset G$
, define ![]() . Then
. Then
![]() $\operatorname {\mathrm {Fix}}(G)$
is the set of constant configurations while
$\operatorname {\mathrm {Fix}}(G)$
is the set of constant configurations while
![]() $\operatorname {\mathrm {Fix}}(\{1_G\}) = A^G$
. A configuration
$\operatorname {\mathrm {Fix}}(\{1_G\}) = A^G$
. A configuration
![]() $x \in A^G$
is said to be periodic if its G-orbit is finite, that is, there is a finite index subgroup H of G such that
$x \in A^G$
is said to be periodic if its G-orbit is finite, that is, there is a finite index subgroup H of G such that
![]() $x \in \operatorname {\mathrm {Fix}}(H)$
.
$x \in \operatorname {\mathrm {Fix}}(H)$
.
A G-invariant subset
![]() $\Sigma \subset A^G$
is called a subshift of
$\Sigma \subset A^G$
is called a subshift of
![]() $A^G$
. Note that we do not require closedness in
$A^G$
. Note that we do not require closedness in
![]() $A^G$
in our definition of a subshift.
$A^G$
in our definition of a subshift.
Given a finite subset
![]() $D \subset G$
and a (finite or infinite) subset
$D \subset G$
and a (finite or infinite) subset
![]() $P \subset A^D$
, the set
$P \subset A^D$
, the set
is a closed subshift of
![]() $A^G$
(here
$A^G$
(here
![]() $(g^{-1}x)\vert _D \in A^D$
denotes the restriction of the configuration
$(g^{-1}x)\vert _D \in A^D$
denotes the restriction of the configuration
![]() $g^{-1}x$
to D). One says that
$g^{-1}x$
to D). One says that
![]() $ \Sigma (D,P)$
is the subshift of finite type associated with
$ \Sigma (D,P)$
is the subshift of finite type associated with
![]() $(D,P)$
and that D is a defining memory set for
$(D,P)$
and that D is a defining memory set for
![]() $\Sigma $
.
$\Sigma $
.
Let B be another alphabet set. A map
![]() $\tau \colon B^G \to A^G$
is called a cellular automaton if there exist a finite subset
$\tau \colon B^G \to A^G$
is called a cellular automaton if there exist a finite subset
![]() $M \subset G$
and a map
$M \subset G$
and a map
![]() $\mu \colon B^M \to A$
such that
$\mu \colon B^M \to A$
such that
Such a set M is then called a memory set and
![]() $\mu $
is called a local defining map for
$\mu $
is called a local defining map for
![]() $\tau $
. It is clear from the definition that every cellular automaton
$\tau $
. It is clear from the definition that every cellular automaton
![]() $\tau \colon B^G \to A^G$
is uniformly continuous and G-equivariant (see [Reference Ceccherini-Silberstein and Coornaert10]).
$\tau \colon B^G \to A^G$
is uniformly continuous and G-equivariant (see [Reference Ceccherini-Silberstein and Coornaert10]).
More generally, if
![]() $\Sigma _1 \subset B^G$
and
$\Sigma _1 \subset B^G$
and
![]() $\Sigma _2 \subset A^G$
are subshifts, a map
$\Sigma _2 \subset A^G$
are subshifts, a map
![]() $\tau \colon \Sigma _1 \to \Sigma _2$
is a cellular automaton if it can be extended to a cellular automaton
$\tau \colon \Sigma _1 \to \Sigma _2$
is a cellular automaton if it can be extended to a cellular automaton
![]() $B^G \to A^G$
.
$B^G \to A^G$
.
Suppose now that
![]() $U, V$
are algebraic varieties (respectively algebraic groups) over a field K, and let
$U, V$
are algebraic varieties (respectively algebraic groups) over a field K, and let ![]() ,
, ![]() denote the sets of K-points of V and U, that is, the set consisting of all K-scheme morphisms
denote the sets of K-points of V and U, that is, the set consisting of all K-scheme morphisms
![]() $\operatorname {\mathrm {Spec}}(K) \to V$
and
$\operatorname {\mathrm {Spec}}(K) \to V$
and
![]() $\operatorname {\mathrm {Spec}}(K) \to U$
, respectively. See [Reference Ceccherini-Silberstein, Coornaert and Phung14, Appendix A], [Reference Ceccherini-Silberstein, Coornaert and Phung15, §2] for basic definitions and properties of algebraic varieties. The following definition was introduced in the case
$\operatorname {\mathrm {Spec}}(K) \to U$
, respectively. See [Reference Ceccherini-Silberstein, Coornaert and Phung14, Appendix A], [Reference Ceccherini-Silberstein, Coornaert and Phung15, §2] for basic definitions and properties of algebraic varieties. The following definition was introduced in the case
![]() $U=V$
in [Reference Ceccherini-Silberstein, Coornaert and Phung14, Definition 1.1] and [Reference Phung39] after Gromov [Reference Gromov20]. A cellular automaton
$U=V$
in [Reference Ceccherini-Silberstein, Coornaert and Phung14, Definition 1.1] and [Reference Phung39] after Gromov [Reference Gromov20]. A cellular automaton
![]() $\tau \colon B^G \to A^G$
is an algebraic (respectively algebraic group) cellular automaton if
$\tau \colon B^G \to A^G$
is an algebraic (respectively algebraic group) cellular automaton if
![]() $\tau $
admits a memory set M with local defining map
$\tau $
admits a memory set M with local defining map
![]() $\mu \colon B^M \to A$
induced by some algebraic morphism (respectively homomorphism of algebraic groups)
$\mu \colon B^M \to A$
induced by some algebraic morphism (respectively homomorphism of algebraic groups)
![]() $f \colon U^M \to V$
(here
$f \colon U^M \to V$
(here
![]() $U^M$
denotes the K-fibered product of a family of copies of U indexed by M). More generally, given subshifts
$U^M$
denotes the K-fibered product of a family of copies of U indexed by M). More generally, given subshifts
![]() $\Sigma _1 \subset B^G$
and
$\Sigma _1 \subset B^G$
and
![]() $\Sigma _2 \subset A^G$
, a map
$\Sigma _2 \subset A^G$
, a map
![]() $\tau \colon \Sigma _1 \to \Sigma _2$
is called an algebraic (respectively algebraic group) cellular automaton if it is the restriction of some algebraic (resp. algebraic group) cellular automaton
$\tau \colon \Sigma _1 \to \Sigma _2$
is called an algebraic (respectively algebraic group) cellular automaton if it is the restriction of some algebraic (resp. algebraic group) cellular automaton
![]() ${\tilde {\tau } \colon B^G \to A^G}$
(see §16 for an example).
${\tilde {\tau } \colon B^G \to A^G}$
(see §16 for an example).
Every cellular automaton with finite alphabet A is an algebraic cellular automaton over any field K (see [Reference Ceccherini-Silberstein, Coornaert and Phung14, remarks after Definition 1]). Indeed, it suffices to embed A as a subset of K and then observe that, if M is a finite set, any map
![]() $\mu \colon A^M \to A$
is the restriction of some polynomial map
$\mu \colon A^M \to A$
is the restriction of some polynomial map
![]() $P \colon K^M \to K$
(which can be made explicit by using Lagrange interpolation formula). Similarly, any linear cellular automaton (cf. [Reference Ceccherini-Silberstein and Coornaert10, Ch. 8], [Reference Ceccherini-Silberstein, Coornaert and Phung16]) is an algebraic cellular automaton: if A is a finite-dimensional vector space over a field K and M is a finite set, then any linear map
$P \colon K^M \to K$
(which can be made explicit by using Lagrange interpolation formula). Similarly, any linear cellular automaton (cf. [Reference Ceccherini-Silberstein and Coornaert10, Ch. 8], [Reference Ceccherini-Silberstein, Coornaert and Phung16]) is an algebraic cellular automaton: if A is a finite-dimensional vector space over a field K and M is a finite set, then any linear map
![]() $\mu \colon A^M \to A$
is clearly a polynomial.
$\mu \colon A^M \to A$
is clearly a polynomial.
Definition 1.1. One says that
![]() $\Sigma \subset A^G$
is an algebraic (respectively algebraic group) subshift of finite type if there exist a finite subset
$\Sigma \subset A^G$
is an algebraic (respectively algebraic group) subshift of finite type if there exist a finite subset
![]() $D \subset G$
and an algebraic subvariety (respectively algebraic subgroup)
$D \subset G$
and an algebraic subvariety (respectively algebraic subgroup)
![]() $W \subset V^D$
such that, with the notation introduced in (1.1), one has
$W \subset V^D$
such that, with the notation introduced in (1.1), one has
![]() $\Sigma = \Sigma (D,W(K))$
.
$\Sigma = \Sigma (D,W(K))$
.
By analogy with the definition of sofic subshifts in the classical setting, we define algebraic sofic subshifts and algebraic group sofic subshifts as follows (see Definition 16.4 for more general notions).
Definition 1.2. Let G be a group and let V be an algebraic variety (respectively algebraic group) over a field K. Let ![]() . A subset
. A subset
![]() $\Sigma \subset A^G$
is called an algebraic (respectively algebraic group) sofic subshift if it is the image of an algebraic (respectively algebraic group) subshift of finite type
$\Sigma \subset A^G$
is called an algebraic (respectively algebraic group) sofic subshift if it is the image of an algebraic (respectively algebraic group) subshift of finite type
![]() $\Sigma ' \subset B^G$
, where
$\Sigma ' \subset B^G$
, where
![]() $B=U(K)$
and U is a K-algebraic variety (respectively K-algebraic group), under an algebraic (respectively algebraic group) cellular automaton
$B=U(K)$
and U is a K-algebraic variety (respectively K-algebraic group), under an algebraic (respectively algebraic group) cellular automaton
![]() $\tau ' \colon B^G \to A^G$
.
$\tau ' \colon B^G \to A^G$
.
Every algebraic sofic subshift
![]() $\Sigma \subset A^G$
is indeed a subshift but it may fail to be closed in
$\Sigma \subset A^G$
is indeed a subshift but it may fail to be closed in
![]() $A^G$
(cf. Example 15.1). However, it turns out that, under suitable natural conditions (see hypotheses (H1), (H2), (H3) below), all algebraic sofic subshifts
$A^G$
(cf. Example 15.1). However, it turns out that, under suitable natural conditions (see hypotheses (H1), (H2), (H3) below), all algebraic sofic subshifts
![]() $\Sigma \subset A^G$
are closed in
$\Sigma \subset A^G$
are closed in
![]() $A^G$
(cf. Corollary 8.2). Moreover, we establish a fundamental characterization of algebraic subshifts of finite type by the descending chain property (cf. Theorem 10.1).
$A^G$
(cf. Corollary 8.2). Moreover, we establish a fundamental characterization of algebraic subshifts of finite type by the descending chain property (cf. Theorem 10.1).
With the notation as in Definition 1.2, we shall investigate in this paper various dynamical aspects of an algebraic cellular automaton
![]() $\tau \colon \Sigma \to \Sigma $
over an algebraic sofic subshift
$\tau \colon \Sigma \to \Sigma $
over an algebraic sofic subshift
![]() $\Sigma \subset A^G$
satisfying one of the following hypotheses (with the same notation throughout the paper):
$\Sigma \subset A^G$
satisfying one of the following hypotheses (with the same notation throughout the paper):
-
(H1) K is an uncountable algebraically closed field (e.g.
 $K = \mathbb {C}$
);
$K = \mathbb {C}$
); -
(H2) K is algebraically closed and
 $U, V$
are complete (e.g. projective) algebraic varieties over K;
$U, V$
are complete (e.g. projective) algebraic varieties over K; -
(H3) K is algebraically closed, V is an algebraic group over K,
 $\Sigma \subset A^G$
is an algebraic group sofic subshift, and
$\Sigma \subset A^G$
is an algebraic group sofic subshift, and
 $\tau \colon \Sigma \to \Sigma $
is an algebraic group cellular automaton.
$\tau \colon \Sigma \to \Sigma $
is an algebraic group cellular automaton.
We shall establish the following result.
Theorem 1.3. Let G be a group and let V be an algebraic variety over a field K. Let ![]() and let
and let
![]() $\Sigma \subset A^G$
be an algebraic sofic subshift. Let
$\Sigma \subset A^G$
be an algebraic sofic subshift. Let
![]() $\tau \colon \Sigma \to \Sigma $
be an algebraic cellular automaton and assume that one of the conditions
$\tau \colon \Sigma \to \Sigma $
be an algebraic cellular automaton and assume that one of the conditions
![]() $(\mathrm {H1})$
,
$(\mathrm {H1})$
,
![]() $(\mathrm {H2})$
,
$(\mathrm {H2})$
,
![]() $(\mathrm {H3})$
is satisfied. Then the following hold:
$(\mathrm {H3})$
is satisfied. Then the following hold:
-
(i)
 $\Omega (\tau )$
is a closed subshift of
$\Omega (\tau )$
is a closed subshift of
 $A^G$
;
$A^G$
; -
(ii)
 $\tau (\Omega (\tau )) = \Omega (\tau )$
;
$\tau (\Omega (\tau )) = \Omega (\tau )$
; -
(iii)
 $\operatorname {\mathrm {Per}}(\tau ) \subset \operatorname {\mathrm {R}}(\tau ) \subset \operatorname {\mathrm {NW}}(\tau ) \subset \operatorname {\mathrm {CR}}(\tau ) \subset \Omega (\tau )$
;
$\operatorname {\mathrm {Per}}(\tau ) \subset \operatorname {\mathrm {R}}(\tau ) \subset \operatorname {\mathrm {NW}}(\tau ) \subset \operatorname {\mathrm {CR}}(\tau ) \subset \Omega (\tau )$
; -
(iv) if
 $(\mathrm {H2})$
or
$(\mathrm {H2})$
or
 $(\mathrm {H3})$
is satisfied and
$(\mathrm {H3})$
is satisfied and
 $\Omega (\tau )$
is a subshift of finite type, then
$\Omega (\tau )$
is a subshift of finite type, then
 $\tau $
is stable;
$\tau $
is stable; -
(v) for every subgroup
 $H \subset G$
, if
$H \subset G$
, if
 $\Sigma \cap \operatorname {\mathrm {Fix}}(H) \neq \varnothing $
, then
$\Sigma \cap \operatorname {\mathrm {Fix}}(H) \neq \varnothing $
, then
 $\Omega (\tau ) \cap \operatorname {\mathrm {Fix}}(H) \neq \varnothing $
.
$\Omega (\tau ) \cap \operatorname {\mathrm {Fix}}(H) \neq \varnothing $
.
See [Reference Ceccherini-Silberstein, Coornaert and Phung16, Theorem 1.5] for a linear version of the above theorem.
One says that a map
![]() $f \colon X \to X$
from a set X into itself is nilpotent if there exist a constant map
$f \colon X \to X$
from a set X into itself is nilpotent if there exist a constant map
![]() $c \colon X \to X$
and an integer
$c \colon X \to X$
and an integer
![]() $n_0 \geq 1$
such that
$n_0 \geq 1$
such that
![]() $f^{n_0} = c$
. This implies
$f^{n_0} = c$
. This implies
![]() $f^n = c$
for all
$f^n = c$
for all
![]() $n \geq n_0$
. Such a constant map c is then unique and we say that the unique point
$n \geq n_0$
. Such a constant map c is then unique and we say that the unique point
![]() $x_0 \in X$
such that
$x_0 \in X$
such that
![]() $c(x) = x_0$
for all
$c(x) = x_0$
for all
![]() $x \in X$
is the terminal point of f. The terminal point of a nilpotent map is its unique fixed point.
$x \in X$
is the terminal point of f. The terminal point of a nilpotent map is its unique fixed point.
Observe that if
![]() $f \colon X \to X$
is nilpotent with terminal point
$f \colon X \to X$
is nilpotent with terminal point
![]() $x_0$
, then
$x_0$
, then
![]() $\Omega (f) = \{x_0\}$
is a singleton. The converse is not true in general. Actually, as soon as the set X is infinite, there exist non-nilpotent maps
$\Omega (f) = \{x_0\}$
is a singleton. The converse is not true in general. Actually, as soon as the set X is infinite, there exist non-nilpotent maps
![]() $f \colon X \to X$
whose limit set is reduced to a single point (cf. Lemma A.1). However, in the algebraic setting, we obtain the following result.
$f \colon X \to X$
whose limit set is reduced to a single point (cf. Lemma A.1). However, in the algebraic setting, we obtain the following result.
Theorem 1.4. If we keep the same notation and hypotheses as in Theorem 1.3, then the following conditions are equivalent:
-
(a)
 $\tau $
is nilpotent;
$\tau $
is nilpotent; -
(b) the limit set
 $\Omega (\tau )$
is reduced to a single configuration.
$\Omega (\tau )$
is reduced to a single configuration.
The analog of Theorem 1.4 for classical cellular automata follows from [Reference Culik, Pachl and Yu18, Theorem 3.5]. However, Theorem 1.4 can be seen as a generalization of an interesting and non-trivial property of endomorphisms of algebraic varieties (by taking
![]() $G = \{1_G\}$
).
$G = \{1_G\}$
).
Both Theorems 1.3 and 1.4 become false if we remove the hypothesis that the ground field K is algebraically closed (see Examples 15.1, 15.8, and 15.9). To illustrate the significance of our results, note that for a group G and a finite set A, the space
![]() $A^G$
is compact by Tychonoff’s theorem. Consequently, if
$A^G$
is compact by Tychonoff’s theorem. Consequently, if
![]() $\Sigma \subset A^G$
is a closed subshift and
$\Sigma \subset A^G$
is a closed subshift and
![]() $\tau \colon A^G \to A^G$
is a cellular automaton, then
$\tau \colon A^G \to A^G$
is a cellular automaton, then
![]() $\tau ^n(\Sigma )$
is closed in
$\tau ^n(\Sigma )$
is closed in
![]() $A^G$
for every
$A^G$
for every
![]() $n \geq 1$
and it follows that
$n \geq 1$
and it follows that
![]() $\Omega (\tau )$
is a closed subshift of
$\Omega (\tau )$
is a closed subshift of
![]() $A^G$
. A standard compactness argument shows also that
$A^G$
. A standard compactness argument shows also that
![]() $\Omega (\tau ) \not = \varnothing $
if
$\Omega (\tau ) \not = \varnothing $
if
![]() $\Sigma \neq \varnothing $
(cf. [Reference Culik, Pachl and Yu18]). When A is infinite,
$\Sigma \neq \varnothing $
(cf. [Reference Culik, Pachl and Yu18]). When A is infinite,
![]() $A^G$
is no longer compact and, given a closed subshift
$A^G$
is no longer compact and, given a closed subshift
![]() $\Sigma \subset A^G$
, the limit set of a cellular automaton
$\Sigma \subset A^G$
, the limit set of a cellular automaton
![]() $\tau \colon \Sigma \to \Sigma $
is, in general, no longer closed in
$\tau \colon \Sigma \to \Sigma $
is, in general, no longer closed in
![]() $A^G$
(cf. Example 15.1). Also, when A is infinite, it may happen that
$A^G$
(cf. Example 15.1). Also, when A is infinite, it may happen that
![]() $\Omega (\tau ) = \varnothing $
while
$\Omega (\tau ) = \varnothing $
while
![]() $\Sigma \neq \varnothing $
or even
$\Sigma \neq \varnothing $
or even
![]() $\tau (\Omega (\tau )) \subsetneqq \Omega (\tau )$
(cf. Proposition A.2 and Example 15.8).
$\tau (\Omega (\tau )) \subsetneqq \Omega (\tau )$
(cf. Proposition A.2 and Example 15.8).
A self-map
![]() $f \colon X \to X$
on a set X is said to be pointwise nilpotent if there exists a point
$f \colon X \to X$
on a set X is said to be pointwise nilpotent if there exists a point
![]() $x_0 \in X$
such that for every
$x_0 \in X$
such that for every
![]() $x \in X$
, there exists an integer
$x \in X$
, there exists an integer
![]() $n_0 \geq 1$
such that
$n_0 \geq 1$
such that
![]() $f^n(x)=x_0$
for all
$f^n(x)=x_0$
for all
![]() $n \geq n_0$
.
$n \geq n_0$
.
Consider a group G with the following property: for every finite alphabet A, any cellular automaton
![]() $\tau \colon A^G \to A^G$
with
$\tau \colon A^G \to A^G$
with
![]() $\Omega (\tau )$
finite is nilpotent. Such a group G cannot be finite. Indeed, for G finite and
$\Omega (\tau )$
finite is nilpotent. Such a group G cannot be finite. Indeed, for G finite and ![]() , the identity cellular automaton map
, the identity cellular automaton map
![]() $\tau \colon A^G \to A^G$
has a finite limit set
$\tau \colon A^G \to A^G$
has a finite limit set
![]() $\Omega (\tau ) = A^G$
without being nilpotent. By [Reference Guillon, Richard, Ochmański and Tyszkiewicz24, Corollary 4] or [Reference Culik, Pachl and Yu18], we know that
$\Omega (\tau ) = A^G$
without being nilpotent. By [Reference Guillon, Richard, Ochmański and Tyszkiewicz24, Corollary 4] or [Reference Culik, Pachl and Yu18], we know that
![]() $G=\mathbb {Z}$
satisfies the above property. In Theorem 13.1, we show that actually it is satisfied by all infinite groups.
$G=\mathbb {Z}$
satisfies the above property. In Theorem 13.1, we show that actually it is satisfied by all infinite groups.
More generally, we obtain the following various characterizations of nilpotent algebraic cellular automata.
Theorem 1.5. Let G be an infinite group and let V be an algebraic variety over a field K. Let
![]() $A=V(K)$
and let
$A=V(K)$
and let
![]() $\Sigma \subset A^G$
be a non-empty topologically mixing algebraic sofic subshift (e.g.
$\Sigma \subset A^G$
be a non-empty topologically mixing algebraic sofic subshift (e.g.
![]() $A^G$
for
$A^G$
for
![]() $A \not = \varnothing $
). Let
$A \not = \varnothing $
). Let
![]() $\tau \colon \Sigma \to \Sigma $
be an algebraic cellular automaton. Assume that one of the conditions
$\tau \colon \Sigma \to \Sigma $
be an algebraic cellular automaton. Assume that one of the conditions
![]() $(\mathrm {H1})$
,
$(\mathrm {H1})$
,
![]() $(\mathrm {H2})$
,
$(\mathrm {H2})$
,
![]() $(\mathrm {H3})$
is satisfied. Then the following are equivalent:
$(\mathrm {H3})$
is satisfied. Then the following are equivalent:
-
(a)
 $\tau $
is nilpotent;
$\tau $
is nilpotent; -
(b)
 $\tau $
is pointwise nilpotent;
$\tau $
is pointwise nilpotent; -
(c) the limit set
 $\Omega (\tau )$
is finite.
$\Omega (\tau )$
is finite.
If G is finitely generated, then the above conditions are equivalent to
-
(d) each
 $x \in \Omega (\tau )$
is periodic and the set
$x \in \Omega (\tau )$
is periodic and the set
 $\{x(1_G) \colon x \in \Omega (\tau )\}$
of alphabet values of
$\{x(1_G) \colon x \in \Omega (\tau )\}$
of alphabet values of
 $\Omega (\tau )$
is finite.
$\Omega (\tau )$
is finite.
Note that for classical cellular automata, the equivalence of items (a) and (b) does not require neither the topological mixing nor the soficity conditions on the subshift
![]() ${\Sigma \subset A^G}$
(this is a result going back to Kari, [Reference Salo50]). We do not know whether or not, in our more general setting, the above-mentioned conditions can be dropped. For classical cellular automata, the equivalence of items (b) and (c) is given in Theorem 13.1. Note that, however, if the alphabet A is infinite, for any group G, there exist non-nilpotent cellular automata whose limit set is reduced to a single configuration and therefore is finite (cf. Proposition A.2).
${\Sigma \subset A^G}$
(this is a result going back to Kari, [Reference Salo50]). We do not know whether or not, in our more general setting, the above-mentioned conditions can be dropped. For classical cellular automata, the equivalence of items (b) and (c) is given in Theorem 13.1. Note that, however, if the alphabet A is infinite, for any group G, there exist non-nilpotent cellular automata whose limit set is reduced to a single configuration and therefore is finite (cf. Proposition A.2).
A linear version of the above theorem was given in [Reference Ceccherini-Silberstein, Coornaert and Phung16, Theorem 1.9 and Corollary 1.10]. Our general strategy evolves around the analysis of the so-called space-time inverse system associated with a cellular automaton (cf. §4). Such inverse systems and their variants as constructed in the proofs of the main theorems allow us to first conduct a local analysis of the dynamical system as in Theorems 7.1 and 9.1. We can then pass to the inverse limit, by means of the key technical algebro-geometric tools Lemmas 3.1 and 3.3, to obtain global properties such as a closed mapping property in Theorem 8.1 and a characterization of algebraic subshifts of finite type in Theorem 10.1. Variants of space-time inverse systems also allow us to reduce Theorem 1.5 to the finite alphabet case studied in Theorem 13.1.
We remark that by a similar strategy, it is shown in [Reference Phung42] that for a polycyclic-by-finite group G and an algebraic group V over an algebraically closed field K, all algebraic group sofic subshifts of
![]() $A^G$
, where
$A^G$
, where
![]() $A=V(K)$
, are in fact algebraic group subshifts of finite type. Moreover, our techniques and results, notably the closed mapping property (Theorem 8.1) and the Noetherianity of algebraic subshifts of finite type (Theorem 10.1), admit a wide range of applications including the shadowing property of algebraic group cellular automata [Reference Phung43, Reference Phung44], the Garden of Eden theorem for algebraic group cellular automata [Reference Phung47], a dynamical characterization of the Noetherianity of group rings in terms of the Markov properties [Reference Ceccherini-Silberstein, Coornaert and Phung16], properties of images of algebraic subshifts under embeddings of symbolic varieties [Reference Phung45], and extensions of the direct finiteness conjecture of Kaplansky [Reference Ceccherini-Silberstein, Coornaert and Phung17, Reference Phung40, Reference Phung41, Reference Phung46, Reference Phung48]. Finally, for interested readers, we would like to mention the connections of our results and their applications with some finiteness results in difference algebras and proalgebraic groups obtained in, e.g., [Reference Ovchinnikov, Pogudin and Scanlon38, Reference Tomašić and Wibmer56, Reference Wibmer59].
$A=V(K)$
, are in fact algebraic group subshifts of finite type. Moreover, our techniques and results, notably the closed mapping property (Theorem 8.1) and the Noetherianity of algebraic subshifts of finite type (Theorem 10.1), admit a wide range of applications including the shadowing property of algebraic group cellular automata [Reference Phung43, Reference Phung44], the Garden of Eden theorem for algebraic group cellular automata [Reference Phung47], a dynamical characterization of the Noetherianity of group rings in terms of the Markov properties [Reference Ceccherini-Silberstein, Coornaert and Phung16], properties of images of algebraic subshifts under embeddings of symbolic varieties [Reference Phung45], and extensions of the direct finiteness conjecture of Kaplansky [Reference Ceccherini-Silberstein, Coornaert and Phung17, Reference Phung40, Reference Phung41, Reference Phung46, Reference Phung48]. Finally, for interested readers, we would like to mention the connections of our results and their applications with some finiteness results in difference algebras and proalgebraic groups obtained in, e.g., [Reference Ovchinnikov, Pogudin and Scanlon38, Reference Tomašić and Wibmer56, Reference Wibmer59].
Most of our results for arbitrary groups are inferred from the results for finitely generated groups by the restriction technique applied to cellular automata over subshifts of sub-finite-type (cf. §§2.4, 2.5, 2.6).
A detailed analysis is given in Example 15.1 to provide a non-trivial counter-example to Theorems 1.3 and 8.1. Some generalizations of our results are given in §16. In the Appendix, we study pointwise nilpotency over infinite groups and arbitrary alphabets (cf. Proposition A.5).
2 Preliminaries
2.1 Notation
We use the symbols
![]() $\mathbb {Z}$
for the integers,
$\mathbb {Z}$
for the integers,
![]() $\mathbb {N}$
for the non-negative integers,
$\mathbb {N}$
for the non-negative integers,
![]() $\mathbb {R}$
for the reals, and
$\mathbb {R}$
for the reals, and
![]() $\mathbb {C}$
for the complex numbers.
$\mathbb {C}$
for the complex numbers.
We write
![]() $A^B$
for the set consisting of all maps from a set B into a set A. Let
$A^B$
for the set consisting of all maps from a set B into a set A. Let
![]() $C \subset B$
. If
$C \subset B$
. If
![]() $x \in A^B$
, we denote by
$x \in A^B$
, we denote by
![]() $x\vert _C$
the restriction of x to C, that is, the map
$x\vert _C$
the restriction of x to C, that is, the map
![]() $x\vert _C \colon C \to A$
given by
$x\vert _C \colon C \to A$
given by
![]() $x\vert _C(c) = x(c)$
for all
$x\vert _C(c) = x(c)$
for all
![]() $c \in C$
. If
$c \in C$
. If
![]() $X \subset A^B$
, we denote
$X \subset A^B$
, we denote ![]() . Let
. Let
![]() $E,F$
be subsets of a group G. We write
$E,F$
be subsets of a group G. We write ![]() and define inductively
and define inductively
![]() $E^n$
for all
$E^n$
for all
![]() $n \in \mathbb {N}$
by setting
$n \in \mathbb {N}$
by setting ![]() and
and ![]() .
.
Let A be a set and let E be a subset of a group G. Given
![]() $x \in A^E$
, we define
$x \in A^E$
, we define
![]() $gx \in A^{gE}$
by
$gx \in A^{gE}$
by ![]() for all
for all
![]() $h \in g E$
.
$h \in g E$
.
2.2 Algebraic varieties
Let V be an algebraic variety over a field K, that is, a reduced K-scheme of finite type. We equip V with its Zariski topology. Every subset
![]() $Z \subset V$
is equipped with the induced topology and we denote by
$Z \subset V$
is equipped with the induced topology and we denote by
![]() $Z(K)$
the subset of K-points of V lying in Z. Subvarieties of V mean closed subsets with the reduced induced scheme structure.
$Z(K)$
the subset of K-points of V lying in Z. Subvarieties of V mean closed subsets with the reduced induced scheme structure.
Remark 2.1. Every subvariety of a complete (that is, proper) algebraic variety is also complete. Images of morphisms of complete algebraic varieties are complete subvarieties (cf. [Reference Liu31, §3.3.2]). Likewise, kernels and images of homomorphisms of algebraic groups are also algebraic subgroups and are thus Zariski closed (cf. [Reference Milne33, Proposition 1.41, Theorems 5.80, 5.81]).
Suppose now that the base field K is algebraically closed. Then we can identify the set of K-points
![]() $A=V(K)$
of a K-algebraic variety V with the set of closed points of V (cf. [Reference Grothendieck21, Proposition 6.4.2]). By a common abuse, we regard A as an algebraic variety. Similarly, induced maps on closed points by morphisms of K-algebraic varieties are also called algebraic morphisms.
$A=V(K)$
of a K-algebraic variety V with the set of closed points of V (cf. [Reference Grothendieck21, Proposition 6.4.2]). By a common abuse, we regard A as an algebraic variety. Similarly, induced maps on closed points by morphisms of K-algebraic varieties are also called algebraic morphisms.
2.3 Chain-recurrent points
Proposition 2.2. Let X be a uniform space and let
![]() $f \colon X \to X$
be a continuous map. Then
$f \colon X \to X$
be a continuous map. Then
![]() $\operatorname {\mathrm {NW}}(f) \subset \operatorname {\mathrm {CR}}(f)$
.
$\operatorname {\mathrm {NW}}(f) \subset \operatorname {\mathrm {CR}}(f)$
.
Proof. (Cf. [Reference Shub55, Proposition 1.7] in the metrizable case) Let
![]() $x \in \operatorname {\mathrm {NW}}(f)$
and let E be an entourage of X. Choose a symmetric entourage S of X such that
$x \in \operatorname {\mathrm {NW}}(f)$
and let E be an entourage of X. Choose a symmetric entourage S of X such that
![]() $S\circ S\subset E$
. By the continuity of f at x, there exists a symmetric entourage T of X with
$S\circ S\subset E$
. By the continuity of f at x, there exists a symmetric entourage T of X with
![]() $T \subset S$
such that
$T \subset S$
such that
![]() $(f(x),f(z)) \in S$
whenever
$(f(x),f(z)) \in S$
whenever
![]() $(x,z) \in T$
. The set
$(x,z) \in T$
. The set
![]() $U \subset X$
, consisting of all
$U \subset X$
, consisting of all
![]() $z \in X$
such that
$z \in X$
such that
![]() $(x,z) \in T$
, is a neighborhood of x. Since x is non-wandering, there exist an integer
$(x,z) \in T$
, is a neighborhood of x. Since x is non-wandering, there exist an integer
![]() $n \geq 1$
and a point
$n \geq 1$
and a point
![]() $y \in U$
such that
$y \in U$
such that
![]() $f^n(y) \in U$
. Let us show that there is a sequence of points
$f^n(y) \in U$
. Let us show that there is a sequence of points
![]() $x_0,x_1,\ldots ,x_n \in X$
such that
$x_0,x_1,\ldots ,x_n \in X$
such that
![]() $x= x_0 = x_n$
and
$x= x_0 = x_n$
and
![]() $(f(x_i),x_{i + 1}) \in E$
for all
$(f(x_i),x_{i + 1}) \in E$
for all
![]() $0 \leq i \leq n - 1$
. First observe that since
$0 \leq i \leq n - 1$
. First observe that since
![]() $y \in U$
, we have
$y \in U$
, we have
![]() $(x,y) \in T$
and therefore
$(x,y) \in T$
and therefore
![]() $(f(x), f(y)) \in S$
. If
$(f(x), f(y)) \in S$
. If
![]() $n=1$
, we can take
$n=1$
, we can take
![]() $x_0 = x_1 = x$
. Indeed, we then have
$x_0 = x_1 = x$
. Indeed, we then have
![]() $f(y) = f^n(y) \in U$
and hence
$f(y) = f^n(y) \in U$
and hence
![]() $(f(y),x) {\kern-1pt}\in{\kern-1pt} T \subset S$
. Therefore,
$(f(y),x) {\kern-1pt}\in{\kern-1pt} T \subset S$
. Therefore,
![]() $(f(x_0),x_1) = (f(x),x) {\kern-1pt}\in{\kern-1pt} S \circ S \subset E$
. If
$(f(x_0),x_1) = (f(x),x) {\kern-1pt}\in{\kern-1pt} S \circ S \subset E$
. If
![]() $n \geq 2$
, we can take the points
$n \geq 2$
, we can take the points
![]() $x_0,x_1,\ldots ,x_n$
defined by
$x_0,x_1,\ldots ,x_n$
defined by
![]() $x = x_0 = x_n$
and
$x = x_0 = x_n$
and
![]() $x_i = f^i(y)$
for all
$x_i = f^i(y)$
for all
![]() $1 \leq i \leq n -1$
. Indeed, we then have
$1 \leq i \leq n -1$
. Indeed, we then have
![]() $(f(x_0),x_1) = (f(x),f(y)) \in S \subset S \circ S \subset E$
. However, we have
$(f(x_0),x_1) = (f(x),f(y)) \in S \subset S \circ S \subset E$
. However, we have
![]() $(f(x_i),x_{i+1}) = (f^{i + 1}(y),f^{i + 1}(y)) \in E$
for all
$(f(x_i),x_{i+1}) = (f^{i + 1}(y),f^{i + 1}(y)) \in E$
for all
![]() $1 \leq i \leq n -2$
. Finally, as
$1 \leq i \leq n -2$
. Finally, as
![]() $f^n(y) \in U$
, we have
$f^n(y) \in U$
, we have
![]() $(f(x_{n - 1}),x_n) = (f^n(y),x) \in T \subset S \subset S \circ S \subset E$
. This shows that
$(f(x_{n - 1}),x_n) = (f^n(y),x) \in T \subset S \subset S \circ S \subset E$
. This shows that
![]() ${x \in \operatorname {\mathrm {CR}}(f)}$
.
${x \in \operatorname {\mathrm {CR}}(f)}$
.
Proposition 2.3. Let X be a Hausdorff uniform space and let
![]() $f \colon X \to X$
be a uniformly continuous map. Suppose that
$f \colon X \to X$
be a uniformly continuous map. Suppose that
![]() $f^n(X)$
is closed in X for all
$f^n(X)$
is closed in X for all
![]() $n \in \mathbb {N}$
. Then
$n \in \mathbb {N}$
. Then
![]() $\operatorname {\mathrm {CR}}(f) \subset \Omega (f)$
.
$\operatorname {\mathrm {CR}}(f) \subset \Omega (f)$
.
Proof. Denote by
![]() $\mathcal {E}$
the set of entourages of X. Let
$\mathcal {E}$
the set of entourages of X. Let
![]() $x \in \operatorname {\mathrm {CR}}(f)$
. Given
$x \in \operatorname {\mathrm {CR}}(f)$
. Given
![]() $E \in \mathcal {E}$
, we define
$E \in \mathcal {E}$
, we define
![]() $\nu (E) \in \mathbb {N} \setminus \{0\}$
to be the least
$\nu (E) \in \mathbb {N} \setminus \{0\}$
to be the least
![]() $n \in \mathbb {N}$
such that there exists a sequence of points
$n \in \mathbb {N}$
such that there exists a sequence of points
![]() $x_0,x_1,\ldots ,x_n \in X$
satisfying that
$x_0,x_1,\ldots ,x_n \in X$
satisfying that
![]() $x = x_0 = x_n$
and
$x = x_0 = x_n$
and
![]() $(f(x_i), x_{i + 1}) \in E$
for all
$(f(x_i), x_{i + 1}) \in E$
for all
![]() $0 \leq i \leq n - 1$
. Note that the map
$0 \leq i \leq n - 1$
. Note that the map
![]() $\nu \colon \mathcal {E} \to \mathbb {N} \setminus \{0\}$
is decreasing in the sense that if
$\nu \colon \mathcal {E} \to \mathbb {N} \setminus \{0\}$
is decreasing in the sense that if
![]() $E,E' \in \mathcal {E}$
and
$E,E' \in \mathcal {E}$
and
![]() $E \subset E'$
, then
$E \subset E'$
, then
![]() $\nu (E') \leq \nu (E)$
. We distinguish two cases according to whether the map
$\nu (E') \leq \nu (E)$
. We distinguish two cases according to whether the map
![]() $\nu $
is bounded or not.
$\nu $
is bounded or not.
In the first case, let ![]() . Take
. Take
![]() $E_0 \in \mathcal {E}$
such that
$E_0 \in \mathcal {E}$
such that
![]() $\nu (E_0) = k$
. Let
$\nu (E_0) = k$
. Let
![]() $E \in \mathcal {E}$
. Choose a symmetric entourage
$E \in \mathcal {E}$
. Choose a symmetric entourage
![]() $S \in \mathcal {E}$
such that
$S \in \mathcal {E}$
such that
Since f is uniformly continuous, so are
![]() $f^{2}, \ldots , f^{k}$
. Thus, we can find a symmetric entourage
$f^{2}, \ldots , f^{k}$
. Thus, we can find a symmetric entourage
![]() $T \subset E_0$
such that
$T \subset E_0$
such that
![]() $(f^p(y),f^p(z)) \in S$
whenever
$(f^p(y),f^p(z)) \in S$
whenever
![]() $(y,z) \in T$
and
$(y,z) \in T$
and
![]() ${0 \leq p \leq k}$
. By the maximality of k and the fact that
${0 \leq p \leq k}$
. By the maximality of k and the fact that
![]() $T \subset E_0$
, we have
$T \subset E_0$
, we have
![]() $\nu (T) = k$
. Therefore, we can find a sequence of points
$\nu (T) = k$
. Therefore, we can find a sequence of points
![]() $x_0, x_1, \ldots , x_k \in X$
such that
$x_0, x_1, \ldots , x_k \in X$
such that
![]() $x =x_0=x_k$
and
$x =x_0=x_k$
and
![]() $(f(x_i), x_{i+1}) \in T$
for all
$(f(x_i), x_{i+1}) \in T$
for all
![]() $0 \leq i \leq k - 1$
. Looking at the sequence of points
$0 \leq i \leq k - 1$
. Looking at the sequence of points
![]() $f^k(x) = f^k(x_0), f^{k - 1}(x_{1}), f^{k - 2}(x_{2}), \ldots , f^{1}(x_{k - 1}), x_k = x$
and using the fact that, for all
$f^k(x) = f^k(x_0), f^{k - 1}(x_{1}), f^{k - 2}(x_{2}), \ldots , f^{1}(x_{k - 1}), x_k = x$
and using the fact that, for all
![]() ${0 \leq i \leq k -1}$
,
${0 \leq i \leq k -1}$
,
since
![]() $(f(x_{i }), x_{i + 1}) \in T$
, we see that
$(f(x_{i }), x_{i + 1}) \in T$
, we see that
As the entourage
![]() $E \in \mathcal {E}$
was arbitrary and X is Hausdorff, it follows that
$E \in \mathcal {E}$
was arbitrary and X is Hausdorff, it follows that
![]() $x = f^k(x)$
. Hence, the point x is periodic and therefore belongs to
$x = f^k(x)$
. Hence, the point x is periodic and therefore belongs to
![]() $\Omega (f)$
.
$\Omega (f)$
.
Consider now the second case, where
![]() $\nu $
is unbounded. Let
$\nu $
is unbounded. Let
![]() $m \geq 1$
be an integer. We will show that
$m \geq 1$
be an integer. We will show that
![]() $x \in f^m(X)$
. Take
$x \in f^m(X)$
. Take
![]() $E_0 \in \mathcal {E}$
so that
$E_0 \in \mathcal {E}$
so that
![]() $\nu (E_0) \geq m$
. Let
$\nu (E_0) \geq m$
. Let
![]() $E \in \mathcal {E}$
. Choose a symmetric entourage
$E \in \mathcal {E}$
. Choose a symmetric entourage
![]() $S \in \mathcal {E}$
such that
$S \in \mathcal {E}$
such that
As in the first case, we can find a symmetric entourage
![]() $T \in \mathcal {E}$
such that
$T \in \mathcal {E}$
such that
![]() $T \subset E_0$
and
$T \subset E_0$
and
![]() $(f^p(y),f^p(z)) \in S$
whenever
$(f^p(y),f^p(z)) \in S$
whenever
![]() $(y,z) \in T$
and
$(y,z) \in T$
and
![]() $0 \leq p \leq m$
. Observe that
$0 \leq p \leq m$
. Observe that ![]() since
since
![]() $T \subset E_0$
. By definition of
$T \subset E_0$
. By definition of
![]() $\nu $
, we can find a sequence of points
$\nu $
, we can find a sequence of points
![]() $x_0, x_1, \ldots , x_{n} \in X$
such that
$x_0, x_1, \ldots , x_{n} \in X$
such that
![]() $x =x_0=x_n$
and
$x =x_0=x_n$
and
![]() $(f(x_i), x_{i+1}) \in T$
for all
$(f(x_i), x_{i+1}) \in T$
for all
![]() $0 \leq i \leq n -1$
. Looking now at the sequence of points
$0 \leq i \leq n -1$
. Looking now at the sequence of points
![]() $f^m(x_{n - m}),f^{m - 1}(x_{n - m + 1}), \ldots , f(x_{n - 1}), x_n = x$
, and using the fact that, for all
$f^m(x_{n - m}),f^{m - 1}(x_{n - m + 1}), \ldots , f(x_{n - 1}), x_n = x$
, and using the fact that, for all
![]() $0 \leq i \leq m -1$
, we have
$0 \leq i \leq m -1$
, we have
 $$ \begin{align*} & (f^{m - i}(x_{n - m + i}), f^{m - i - 1}(x_{n - m + i + 1})) \\ &\quad = (f^{m - i - 1}(f(x_{n - m + i})), f^{m - i - 1}(x_{n - m + i + 1})) \in S \end{align*} $$
$$ \begin{align*} & (f^{m - i}(x_{n - m + i}), f^{m - i - 1}(x_{n - m + i + 1})) \\ &\quad = (f^{m - i - 1}(f(x_{n - m + i})), f^{m - i - 1}(x_{n - m + i + 1})) \in S \end{align*} $$
since
![]() $(f(x_{n - m + i})),x_{n - m + i + 1}) \in T$
, we see that
$(f(x_{n - m + i})),x_{n - m + i + 1}) \in T$
, we see that
As the entourage
![]() $E \in \mathcal {E}$
was arbitrary, it follows that x belongs to the closure of
$E \in \mathcal {E}$
was arbitrary, it follows that x belongs to the closure of
![]() $f^m(X)$
. Since
$f^m(X)$
. Since
![]() $f^m(X)$
is closed in X by our hypothesis, we conclude that
$f^m(X)$
is closed in X by our hypothesis, we conclude that
![]() $x \in f^m(X)$
for every
$x \in f^m(X)$
for every
![]() $m \geq 1$
. This shows that
$m \geq 1$
. This shows that
![]() $x \in \Omega (f)$
.
$x \in \Omega (f)$
.
Using the fact that the topology of any compact Hausdorff space is induced by a unique uniform structure, an immediate consequence of Proposition 2.3 is the following well-known result (see e.g. [Reference Osipenko37, Ch. 6]).
Corollary 2.4. Let X be a compact Hausdorff space and let
![]() $f \colon X \to X$
be a continuous map. Then
$f \colon X \to X$
be a continuous map. Then
![]() $\operatorname {\mathrm {CR}}(f) \subset \Omega (f)$
.
$\operatorname {\mathrm {CR}}(f) \subset \Omega (f)$
.
2.4 Subshifts of sub-finite-type
Let G be a group and let A be a set. A subshift
![]() $\Sigma \subset A^G$
is called a subshift of sub-finite-type if it is a factor of a subshift of finite type (cf. (1.1)), namely, there exist a set B, a cellular automaton
$\Sigma \subset A^G$
is called a subshift of sub-finite-type if it is a factor of a subshift of finite type (cf. (1.1)), namely, there exist a set B, a cellular automaton
![]() $\tau ' \colon B^G \to A^G$
, and a subshift of finite type
$\tau ' \colon B^G \to A^G$
, and a subshift of finite type
![]() $\Sigma ' \subset B^G$
such that
$\Sigma ' \subset B^G$
such that
![]() $\Sigma = \tau '(\Sigma ')$
. Note that we do not require
$\Sigma = \tau '(\Sigma ')$
. Note that we do not require
![]() $\Sigma $
to be closed in
$\Sigma $
to be closed in
![]() $A^G$
. In the following, every finite subset D of G containing a defining memory set of
$A^G$
. In the following, every finite subset D of G containing a defining memory set of
![]() $\Sigma '$
as well as a memory set of
$\Sigma '$
as well as a memory set of
![]() $\tau '$
will be called a memory set of the subshift of sub-finite-type
$\tau '$
will be called a memory set of the subshift of sub-finite-type
![]() $\Sigma $
. The existence of such a memory set will be necessary for the restriction technique (cf. §§2.5 and 2.6) when the group G is not finitely generated.
$\Sigma $
. The existence of such a memory set will be necessary for the restriction technique (cf. §§2.5 and 2.6) when the group G is not finitely generated.
Example 2.5. If G is a group, V is an algebraic variety over a field K, and ![]() , then it immediately follows from Definition 1.2 in §1 that every algebraic sofic subshift
, then it immediately follows from Definition 1.2 in §1 that every algebraic sofic subshift
![]() $\Sigma \subset A^G$
is a subshift of sub-finite-type of
$\Sigma \subset A^G$
is a subshift of sub-finite-type of
![]() $A^G$
.
$A^G$
.
In the rest of the paper, a memory set of an algebraic sofic subshift
![]() $\Sigma $
will mean any memory set of
$\Sigma $
will mean any memory set of
![]() $\Sigma $
regarded as a subshift of sub-finite-type.
$\Sigma $
regarded as a subshift of sub-finite-type.
Example 2.6. Let A be a set and let
![]() $\Gamma $
be an A-labeled directed graph. This means that
$\Gamma $
be an A-labeled directed graph. This means that
![]() $\Gamma $
is a quintuple
$\Gamma $
is a quintuple
![]() $\Gamma = (V,E,\alpha ,\omega ,\unicode{x3bb} )$
, where
$\Gamma = (V,E,\alpha ,\omega ,\unicode{x3bb} )$
, where
![]() $V,E$
are sets, and
$V,E$
are sets, and
![]() $\alpha ,\omega \colon E \to V$
,
$\alpha ,\omega \colon E \to V$
,
![]() $\unicode{x3bb} \colon E \to A$
are maps. The elements of V are called the vertices of
$\unicode{x3bb} \colon E \to A$
are maps. The elements of V are called the vertices of
![]() $\Gamma $
, those of E are called its edges, and, for every edge
$\Gamma $
, those of E are called its edges, and, for every edge
![]() $e \in E$
, the vertex
$e \in E$
, the vertex
![]() $\alpha (e)$
(respectively
$\alpha (e)$
(respectively
![]() $\omega (e))$
is called the initial (respectively terminal) vertex of e while
$\omega (e))$
is called the initial (respectively terminal) vertex of e while
![]() $\unicode{x3bb} (e)$
is called its label. The label of a configuration
$\unicode{x3bb} (e)$
is called its label. The label of a configuration
![]() $x \in E^{\mathbb {Z}}$
is the configuration
$x \in E^{\mathbb {Z}}$
is the configuration
![]() $\Lambda (x) \in A^{\mathbb {Z}}$
defined by
$\Lambda (x) \in A^{\mathbb {Z}}$
defined by
![]() $\Lambda (x)(n) = \unicode{x3bb} (x(n))$
for all
$\Lambda (x)(n) = \unicode{x3bb} (x(n))$
for all
![]() $n \in \mathbb {Z}$
. Observe that
$n \in \mathbb {Z}$
. Observe that
![]() $\Lambda \colon E^{\mathbb {Z}} \to A^{\mathbb {Z}}$
is a cellular automaton admitting
$\Lambda \colon E^{\mathbb {Z}} \to A^{\mathbb {Z}}$
is a cellular automaton admitting ![]() as a memory set and
as a memory set and
![]() $\unicode{x3bb} \colon E^M = E \to A$
as the associated local defining map. An element
$\unicode{x3bb} \colon E^M = E \to A$
as the associated local defining map. An element
![]() $x \in E^{\mathbb {Z}}$
is called a path of
$x \in E^{\mathbb {Z}}$
is called a path of
![]() $\Gamma $
if it satisfies
$\Gamma $
if it satisfies
![]() $\omega (x(n)) = \alpha (x(n+1))$
for all
$\omega (x(n)) = \alpha (x(n+1))$
for all
![]() $n \in \mathbb {Z}$
. Clearly, the subset
$n \in \mathbb {Z}$
. Clearly, the subset
![]() $\Sigma ' \subset E^{\mathbb {Z}}$
consisting of all paths of
$\Sigma ' \subset E^{\mathbb {Z}}$
consisting of all paths of
![]() $\Gamma $
is the subshift of finite type
$\Gamma $
is the subshift of finite type
![]() $\Sigma (D,P)$
of
$\Sigma (D,P)$
of
![]() $E^{\mathbb {Z}}$
, where
$E^{\mathbb {Z}}$
, where ![]() and
and ![]() . One says that
. One says that
![]() $\Sigma '$
is the Markov shift associated with the unlabeled graph
$\Sigma '$
is the Markov shift associated with the unlabeled graph
![]() $(V,E,\alpha ,\omega )$
(cf. [Reference Kitchens28, Ch. 7]). We deduce that
$(V,E,\alpha ,\omega )$
(cf. [Reference Kitchens28, Ch. 7]). We deduce that ![]() is a subshift of sub-finite-type of
is a subshift of sub-finite-type of
![]() $A^{\mathbb {Z}}$
. Conversely, it can be shown that every subshift of sub-finite-type of
$A^{\mathbb {Z}}$
. Conversely, it can be shown that every subshift of sub-finite-type of
![]() $A^{\mathbb {Z}}$
can be obtained, up to topological conjugacy, as the set of labels of the paths of a suitably chosen A-labeled graph. The proof of this last result is, mutatis mutandis, the one used in the classical setting for showing that every sofic finite alphabet subshift over
$A^{\mathbb {Z}}$
can be obtained, up to topological conjugacy, as the set of labels of the paths of a suitably chosen A-labeled graph. The proof of this last result is, mutatis mutandis, the one used in the classical setting for showing that every sofic finite alphabet subshift over
![]() $\mathbb {Z}$
can be presented by a finite labeled graph (see e.g. [Reference Lind and Marcus30, Theorem 3.2.1]).
$\mathbb {Z}$
can be presented by a finite labeled graph (see e.g. [Reference Lind and Marcus30, Theorem 3.2.1]).
The following result says that the notion of subshifts of sub-finite-type is only interesting when G is not finitely generated.
Proposition 2.7. Let G be a finitely generated group and let A be a set. Then every subshift
![]() $\Sigma \subset A^G$
is a subshift of sub-finite-type.
$\Sigma \subset A^G$
is a subshift of sub-finite-type.
Proof. Let D be a finite generating subset of G such that
![]() $1_G \in D$
and
$1_G \in D$
and
![]() $D=D^{-1}$
. Let
$D=D^{-1}$
. Let
![]() ${\Sigma \subset A^G}$
be a subshift. Let
${\Sigma \subset A^G}$
be a subshift. Let ![]() and define
and define ![]() . Consider the subshift of finite type
. Consider the subshift of finite type ![]() of
of
![]() $B^G$
. Since
$B^G$
. Since
![]() $D=D^{-1}$
generates G and contains
$D=D^{-1}$
generates G and contains
![]() $1_G$
, the map
$1_G$
, the map
![]() $\mathfrak {X} \mapsto \mathfrak {X}(1_G)$
is a bijection from
$\mathfrak {X} \mapsto \mathfrak {X}(1_G)$
is a bijection from
![]() $\Sigma '$
onto
$\Sigma '$
onto
![]() $\Sigma $
. Indeed, for every
$\Sigma $
. Indeed, for every
![]() $g \in G$
and
$g \in G$
and
![]() $\mathfrak {X} \in \Sigma '$
, by writing
$\mathfrak {X} \in \Sigma '$
, by writing
![]() $g= s_1 \cdots s_n$
for some
$g= s_1 \cdots s_n$
for some
![]() $s_1, \ldots , s_n \in D$
, we find that
$s_1, \ldots , s_n \in D$
, we find that
Let
![]() $\tau \colon B^G \to A^G$
be the cellular automaton with memory set
$\tau \colon B^G \to A^G$
be the cellular automaton with memory set
![]() $\{1_G\}$
and associated local defining map
$\{1_G\}$
and associated local defining map
![]() $\mu \colon B \to A$
given by
$\mu \colon B \to A$
given by
![]() $x \mapsto x(1_G)$
. In other words,
$x \mapsto x(1_G)$
. In other words,
![]() $\tau (\mathfrak {X})(g) = (\mathfrak {X}(g))(1_G)$
for every
$\tau (\mathfrak {X})(g) = (\mathfrak {X}(g))(1_G)$
for every
![]() $\mathfrak {X} \in B^G$
and
$\mathfrak {X} \in B^G$
and
![]() $g \in G$
. Hence, for every
$g \in G$
. Hence, for every
![]() $\mathfrak {X} \in \Sigma '$
, we have
$\mathfrak {X} \in \Sigma '$
, we have
![]() $\tau (\mathfrak {X}) = \mathfrak {X}(1_G)$
since for all
$\tau (\mathfrak {X}) = \mathfrak {X}(1_G)$
since for all
![]() $g \in G$
,
$g \in G$
,
As
![]() $\mathfrak {X}(1_G) \in B= \Sigma $
is arbitrary, we conclude that
$\mathfrak {X}(1_G) \in B= \Sigma $
is arbitrary, we conclude that
![]() $\Sigma =\tau (\Sigma ')$
is a subshift of sub- finite-type.
$\Sigma =\tau (\Sigma ')$
is a subshift of sub- finite-type.
2.5 Restriction of cellular automata and of subshifts of sub-finite-type
Let G be a group and let A be a set. Let
![]() $\Sigma \subset A^G$
be a subshift of sub-finite-type. Hence, there exist a set B, a cellular automaton
$\Sigma \subset A^G$
be a subshift of sub-finite-type. Hence, there exist a set B, a cellular automaton
![]() $\tau ' \colon B^G \to A^G$
, and a subshift of finite type
$\tau ' \colon B^G \to A^G$
, and a subshift of finite type
![]() $\Sigma ' \subset B^G$
such that
$\Sigma ' \subset B^G$
such that
![]() $\Sigma = \tau '(\Sigma ')$
. Let
$\Sigma = \tau '(\Sigma ')$
. Let
![]() $D \subset G$
be a finite subset such that D is a defining memory set of
$D \subset G$
be a finite subset such that D is a defining memory set of
![]() $\Sigma '$
as well as a memory set of
$\Sigma '$
as well as a memory set of
![]() $\tau '$
. Let
$\tau '$
. Let
![]() $H\subset G$
be a subgroup of G containing D. Denote by
$H\subset G$
be a subgroup of G containing D. Denote by ![]() the set of all right cosets of H in G. As the right cosets of H in G form a partition of G, we have natural factorizations
the set of all right cosets of H in G. As the right cosets of H in G form a partition of G, we have natural factorizations
 $$ \begin{align*} A^G = \prod_{c \in G/H} A^c, \quad B^G = \prod_{c \in G/H} B^c \end{align*} $$
$$ \begin{align*} A^G = \prod_{c \in G/H} A^c, \quad B^G = \prod_{c \in G/H} B^c \end{align*} $$
in which each
![]() $x \in A^G$
(respectively
$x \in A^G$
(respectively
![]() $x \in B^G$
) is identified with
$x \in B^G$
) is identified with
![]() $ (x\vert _c)_{c \in G/H} \in \prod _{c \in G/H} A^c$
(respectively
$ (x\vert _c)_{c \in G/H} \in \prod _{c \in G/H} A^c$
(respectively
![]() $(x\vert _c)_{c \in G/H} \in \prod _{c \in G/H} B^c$
). Since
$(x\vert _c)_{c \in G/H} \in \prod _{c \in G/H} B^c$
). Since
![]() $g D \subset gH$
for every
$g D \subset gH$
for every
![]() $g \in G$
, the above factorization of
$g \in G$
, the above factorization of
![]() $B^G$
induces a factorization
$B^G$
induces a factorization
 $$ \begin{align*} \Sigma' = \prod_{c \in G/H} \Sigma^{\prime}_c, \end{align*} $$
$$ \begin{align*} \Sigma' = \prod_{c \in G/H} \Sigma^{\prime}_c, \end{align*} $$
where
![]() $\Sigma ^{\prime }_c = \{x\vert _c \colon x \in \Sigma '\}$
for all
$\Sigma ^{\prime }_c = \{x\vert _c \colon x \in \Sigma '\}$
for all
![]() $c \in G/H$
. Likewise, for each
$c \in G/H$
. Likewise, for each
![]() $c \in G/H$
, let
$c \in G/H$
, let
![]() ${\Sigma _c = \{x\vert _c \colon x \in ~\Sigma \}}$
.
${\Sigma _c = \{x\vert _c \colon x \in ~\Sigma \}}$
.
Lemma 2.8. The factorization
![]() $A^G = \prod _{c \in G/H} A^c$
induces a factorization
$A^G = \prod _{c \in G/H} A^c$
induces a factorization
 $$ \begin{align*} \Sigma = \prod_{c \in G/H} \Sigma_c. \end{align*} $$
$$ \begin{align*} \Sigma = \prod_{c \in G/H} \Sigma_c. \end{align*} $$
Proof. Since H contains a memory set of
![]() $\tau '$
, we have
$\tau '$
, we have
![]() $\tau ' = \prod _{c \in G/H} \tau ^{\prime }_c$
, where
$\tau ' = \prod _{c \in G/H} \tau ^{\prime }_c$
, where
![]() ${\tau ^{\prime }_c \colon B^c \to A^c}$
is given by
${\tau ^{\prime }_c \colon B^c \to A^c}$
is given by ![]() for all
for all
![]() $y \in B^c$
, where
$y \in B^c$
, where
![]() $x \in B^G$
is any configuration extending y. We deduce that
$x \in B^G$
is any configuration extending y. We deduce that
![]() $\Sigma _c = (\tau '( \Sigma '))_c = \tau ^{\prime }_c(\Sigma ^{\prime }_c)$
for every
$\Sigma _c = (\tau '( \Sigma '))_c = \tau ^{\prime }_c(\Sigma ^{\prime }_c)$
for every
![]() $c \in G/H$
. Hence,
$c \in G/H$
. Hence,
 $$ \begin{align*} \Sigma = \tau'(\Sigma') = \tau' \bigg( \prod_{c \in G/H} \Sigma^{\prime}_c \bigg) = \prod_{c \in G/H} \tau^{\prime}_c(\Sigma^{\prime}_c) = \prod_{c \in G/H} \Sigma_c.\\[-48pt] \end{align*} $$
$$ \begin{align*} \Sigma = \tau'(\Sigma') = \tau' \bigg( \prod_{c \in G/H} \Sigma^{\prime}_c \bigg) = \prod_{c \in G/H} \tau^{\prime}_c(\Sigma^{\prime}_c) = \prod_{c \in G/H} \Sigma_c.\\[-48pt] \end{align*} $$
Let
![]() $T \subset G$
be a complete set of representatives for the right cosets of H in G such that
$T \subset G$
be a complete set of representatives for the right cosets of H in G such that
![]() $1_G \in T$
. Then, for each
$1_G \in T$
. Then, for each
![]() $c \in G/H$
, we have a uniform homeomorphism
$c \in G/H$
, we have a uniform homeomorphism
![]() $\phi _c \colon \Sigma _c \to \Sigma _H$
given by
$\phi _c \colon \Sigma _c \to \Sigma _H$
given by
![]() $\phi _c(y)(h) = y(gh)$
for all
$\phi _c(y)(h) = y(gh)$
for all
![]() $y \in \Sigma _c$
, where
$y \in \Sigma _c$
, where
![]() $g \in T$
represents c. In particular,
$g \in T$
represents c. In particular,
![]() $\Sigma \neq \varnothing $
if and only if
$\Sigma \neq \varnothing $
if and only if
![]() $\Sigma _H \neq \varnothing $
.
$\Sigma _H \neq \varnothing $
.
Now suppose in addition that
![]() $\tau \colon \Sigma \to \Sigma $
is a cellular automaton which admits a memory set contained in H. Then we have
$\tau \colon \Sigma \to \Sigma $
is a cellular automaton which admits a memory set contained in H. Then we have
![]() $\tau = \prod _{c \in G/H} \tau _c$
, where
$\tau = \prod _{c \in G/H} \tau _c$
, where
![]() $\tau _c \colon \Sigma _c \to \Sigma _c$
is defined by setting
$\tau _c \colon \Sigma _c \to \Sigma _c$
is defined by setting ![]() for all
for all
![]() $y \in \Sigma _c$
, where
$y \in \Sigma _c$
, where
![]() $x \in \Sigma $
is any configuration extending y. Note that for each
$x \in \Sigma $
is any configuration extending y. Note that for each
![]() $c \in G/ H$
, the maps
$c \in G/ H$
, the maps
![]() $\tau _c$
and
$\tau _c$
and
![]() $\tau _H$
are conjugate by
$\tau _H$
are conjugate by
![]() $\phi _c$
, that is, we have
$\phi _c$
, that is, we have
![]() $\tau _c = \phi _c^{-1} \circ \tau _H \circ \phi _c$
. This allows us to identify the action of
$\tau _c = \phi _c^{-1} \circ \tau _H \circ \phi _c$
. This allows us to identify the action of
![]() $\tau _c$
on
$\tau _c$
on
![]() $\Sigma _c$
with that of the restriction cellular automaton
$\Sigma _c$
with that of the restriction cellular automaton
![]() $\tau _H$
on
$\tau _H$
on
![]() $\Sigma _H$
. See Reference Ceccherini-Silberstein and Coornaert9 and [Reference Ceccherini-Silberstein and Coornaert10, Section 1.7].
$\Sigma _H$
. See Reference Ceccherini-Silberstein and Coornaert9 and [Reference Ceccherini-Silberstein and Coornaert10, Section 1.7].
Lemma 2.9. The following hold:
-
(i)
 $\Omega (\tau ) = \Omega (\tau _H)^{G/H}$
;
$\Omega (\tau ) = \Omega (\tau _H)^{G/H}$
; -
(ii)
 $\tau $
is nilpotent if and only if
$\tau $
is nilpotent if and only if
 $\tau _H$
is nilpotent.
$\tau _H$
is nilpotent.
Proof. Observe that the map
![]() $x \mapsto (\phi _c(x\vert _c))_{c \in G/H}$
yields a bijection
$x \mapsto (\phi _c(x\vert _c))_{c \in G/H}$
yields a bijection
![]() $\Omega (\tau ) \to \prod _{c \in G/H} \Omega (\tau _H) = \Omega (\tau _H)^{G/H}$
, and this proves point (i). Point (ii) is clear by the above discussion.
$\Omega (\tau ) \to \prod _{c \in G/H} \Omega (\tau _H) = \Omega (\tau _H)^{G/H}$
, and this proves point (i). Point (ii) is clear by the above discussion.
2.6 Restriction and the closed image property
Let G be a group and let
![]() $A, B$
be sets. Let
$A, B$
be sets. Let
![]() $\Sigma \subset A^G$
be a subshift of sub-finite-type and let now
$\Sigma \subset A^G$
be a subshift of sub-finite-type and let now
![]() $\tau \colon A^G \to B^G$
be a cellular automaton whose source and domain are the full shifts
$\tau \colon A^G \to B^G$
be a cellular automaton whose source and domain are the full shifts
![]() $A^G$
and
$A^G$
and
![]() $B^G$
, respectively. Let
$B^G$
, respectively. Let
![]() $H\subset G$
be a subgroup of G containing a memory set of
$H\subset G$
be a subgroup of G containing a memory set of
![]() $\Sigma $
and a memory set of
$\Sigma $
and a memory set of
![]() $\tau $
. As in §2.5, we have the factorizations
$\tau $
. As in §2.5, we have the factorizations
![]() $\Sigma = \prod _{c \in G/H} \Sigma _c$
(cf. Lemma 2.8) and
$\Sigma = \prod _{c \in G/H} \Sigma _c$
(cf. Lemma 2.8) and
![]() $\tau = \prod _{c \in G/H} \tau _c$
, with
$\tau = \prod _{c \in G/H} \tau _c$
, with
![]() $\tau _c \colon A^c \to B^c$
defined by
$\tau _c \colon A^c \to B^c$
defined by ![]() for all
for all
![]() $y \in A^c$
, where
$y \in A^c$
, where
![]() $x \in A^G$
is any configuration extending y.
$x \in A^G$
is any configuration extending y.
Lemma 2.10. The set
![]() $\tau (\Sigma )$
is closed in
$\tau (\Sigma )$
is closed in
![]() $B^G$
if and only if
$B^G$
if and only if
![]() $\tau _H(\Sigma _H)$
is closed in
$\tau _H(\Sigma _H)$
is closed in
![]() $B^H$
.
$B^H$
.
Proof. We have
![]() $\tau (\Sigma )= \prod _{c \in G/H} \tau _c(\Sigma _c)$
. It is immediate that
$\tau (\Sigma )= \prod _{c \in G/H} \tau _c(\Sigma _c)$
. It is immediate that
![]() $\tau _H(\Sigma _H)$
is closed in
$\tau _H(\Sigma _H)$
is closed in
![]() $B^H$
if
$B^H$
if
![]() $\tau (\Sigma )$
is closed in
$\tau (\Sigma )$
is closed in
![]() $B^G$
. For the converse implication, we have for every
$B^G$
. For the converse implication, we have for every
![]() $c \in G/H$
a uniform homeomorphism
$c \in G/H$
a uniform homeomorphism
![]() $\psi _c \colon B^c \to B^H$
by fixing a complete set containing
$\psi _c \colon B^c \to B^H$
by fixing a complete set containing
![]() $1_G$
of representatives for the right cosets of H in G (cf. §2.5). Thus, if
$1_G$
of representatives for the right cosets of H in G (cf. §2.5). Thus, if
![]() $\tau _H(\Sigma _H)$
is closed, then so is
$\tau _H(\Sigma _H)$
is closed, then so is
![]() ${\tau _c(\Sigma _c) = \psi _c^{-1}(\tau _H(\Sigma _H))}$
. Consequently,
${\tau _c(\Sigma _c) = \psi _c^{-1}(\tau _H(\Sigma _H))}$
. Consequently,
![]() $\tau (\Sigma )$
is closed in
$\tau (\Sigma )$
is closed in
![]() $B^G$
whenever
$B^G$
whenever
![]() $\tau _H(\Sigma _H)$
is closed in
$\tau _H(\Sigma _H)$
is closed in
![]() $B^H$
since the product of closed subspaces is closed in the product topology.
$B^H$
since the product of closed subspaces is closed in the product topology.
3 Inverse limits of countably pro-constructible sets
Let I be a directed set, that is, a partially ordered set in which every pair of elements admits an upper bound. An inverse system of sets indexed by I consists of the following data: (1) a set
![]() $Z_i$
for each
$Z_i$
for each
![]() $i \in I$
; (2) a transition map
$i \in I$
; (2) a transition map
![]() $\varphi _{ij} \colon Z_j \to Z_i$
for all
$\varphi _{ij} \colon Z_j \to Z_i$
for all
![]() $i,j \in I$
such that
$i,j \in I$
such that
![]() $i \prec j$
. Furthermore, the transition maps must satisfy the following conditions:
$i \prec j$
. Furthermore, the transition maps must satisfy the following conditions:
 $$ \begin{align*} \varphi_{ii} &= \operatorname{\mathrm{Id}}_{Z_i}\quad \text{(the identity map on}\ Z_i)\ \text{for all } i \in I, \\\varphi_{ij} \circ \varphi_{jk} &= \varphi_{ik}\quad \text{for all}\ i,j,k \in I\ \text{such that } i \prec j \prec k. \end{align*} $$
$$ \begin{align*} \varphi_{ii} &= \operatorname{\mathrm{Id}}_{Z_i}\quad \text{(the identity map on}\ Z_i)\ \text{for all } i \in I, \\\varphi_{ij} \circ \varphi_{jk} &= \varphi_{ik}\quad \text{for all}\ i,j,k \in I\ \text{such that } i \prec j \prec k. \end{align*} $$
One then speaks of the inverse system
![]() $(Z_i,\varphi _{ij})$
, or simply
$(Z_i,\varphi _{ij})$
, or simply
![]() $(Z_i)$
if the index set and the transition maps are clear from the context.
$(Z_i)$
if the index set and the transition maps are clear from the context.
The inverse limit of an inverse system
![]() $(Z_i,\varphi _{i j})$
is the subset
$(Z_i,\varphi _{i j})$
is the subset
consisting of all
![]() $(z_i)_{i \in I}$
such that
$(z_i)_{i \in I}$
such that
![]() $\varphi _{i j}(z_j)= z_i$
for all
$\varphi _{i j}(z_j)= z_i$
for all
![]() $i \prec j$
.
$i \prec j$
.
A subset of a topological space X is said to be locally closed if it is the intersection of a closed subset and an open subset of X. It is said to be constructible if it is a finite union of locally closed subsets of X. It is said to be proconstructible if it is the intersection of a family of constructible subsets [Reference Grothendieck22, Définition I.9.4]. We shall say that a subset of X is countably proconstructible if it is the intersection of a countable family of constructible subsets. It is clear that every countably proconstructible subset can be written as the intersection of a decreasing sequence of constructible subsets.
The following lemma is analogous to [Reference Phung39, Lemma 4.1].
Lemma 3.1. Let K be an uncountable algebraically closed field and let
![]() $f \colon X \to Y$
be an algebraic morphism of algebraic varieties over K. If
$f \colon X \to Y$
be an algebraic morphism of algebraic varieties over K. If
![]() $(C_k)_{k \in \mathbb {N}}$
is a decreasing sequence of constructible subsets of X, then
$(C_k)_{k \in \mathbb {N}}$
is a decreasing sequence of constructible subsets of X, then
 $$ \begin{align*} f \bigg( \bigcap_{k \in \mathbb{N}} C_k(K) \bigg) = \bigcap_{k \in \mathbb{N}} f(C_k(K)) = \bigcap_{k \in \mathbb{N}} f(C_k)(K). \end{align*} $$
$$ \begin{align*} f \bigg( \bigcap_{k \in \mathbb{N}} C_k(K) \bigg) = \bigcap_{k \in \mathbb{N}} f(C_k(K)) = \bigcap_{k \in \mathbb{N}} f(C_k)(K). \end{align*} $$
Proof. Since for each
![]() $k \in \mathbb {N}$
we have
$k \in \mathbb {N}$
we have
![]() $f(C_k(K))= f(C_k)(K)$
(cf. for example [Reference Ceccherini-Silberstein, Coornaert and Phung14, Lemma A.22(v)]), the second equality is verified. For the first equality, we have trivially
$f(C_k(K))= f(C_k)(K)$
(cf. for example [Reference Ceccherini-Silberstein, Coornaert and Phung14, Lemma A.22(v)]), the second equality is verified. For the first equality, we have trivially
![]() $f ( \bigcap _{k \in \mathbb {N}} C_k(K) ) \subset \bigcap _{k \in \mathbb {N}} f(C_k(K))$
. Conversely, assume that
$f ( \bigcap _{k \in \mathbb {N}} C_k(K) ) \subset \bigcap _{k \in \mathbb {N}} f(C_k(K))$
. Conversely, assume that
![]() $y \in \bigcap _{k \in \mathbb {N}} f(C_k(K))$
. For each
$y \in \bigcap _{k \in \mathbb {N}} f(C_k(K))$
. For each
![]() $k \in \mathbb {N}$
, set
$k \in \mathbb {N}$
, set
Note that
![]() $F_k$
is the set of closed points of a constructible subset of X. Remark also that, for every
$F_k$
is the set of closed points of a constructible subset of X. Remark also that, for every
![]() $k \in \mathbb {N}$
, we have
$k \in \mathbb {N}$
, we have
![]() $F_{k+1} \subset F_k$
and
$F_{k+1} \subset F_k$
and
![]() $F_k \not = \varnothing $
. Hence, by [Reference Ceccherini-Silberstein, Coornaert and Phung14, Lemma B.3], there exists
$F_k \not = \varnothing $
. Hence, by [Reference Ceccherini-Silberstein, Coornaert and Phung14, Lemma B.3], there exists
![]() $x \in \bigcap _{k \in \mathbb {N}} F_k$
. Clearly,
$x \in \bigcap _{k \in \mathbb {N}} F_k$
. Clearly,
![]() $f(x)=y$
and
$f(x)=y$
and
![]() $x \in \bigcap _{k \in \mathbb {N}} C_k(K)$
. Therefore,
$x \in \bigcap _{k \in \mathbb {N}} C_k(K)$
. Therefore,
![]() $ \bigcap _{k \in \mathbb {N}} f(C_k(K)) \subset f ( \bigcap _{k \in \mathbb {N}} C_k(K) )$
and the proof is completed.
$ \bigcap _{k \in \mathbb {N}} f(C_k(K)) \subset f ( \bigcap _{k \in \mathbb {N}} C_k(K) )$
and the proof is completed.
In case (H1), we shall make use of the following generalization of [Reference Ceccherini-Silberstein, Coornaert and Phung14, Lemma B.2] to countable inverse systems of countably proconstructible subsets.
Lemma 3.2. Let K be an uncountable algebraically closed field. Let
![]() $(X_i, f_{ij})$
be an inverse system indexed by a countable directed set I, where each
$(X_i, f_{ij})$
be an inverse system indexed by a countable directed set I, where each
![]() $X_i$
is a K-algebraic variety and each transition map
$X_i$
is a K-algebraic variety and each transition map
![]() $f_{i j} \colon X_j \to X_i$
is an algebraic morphism. Suppose given, for each
$f_{i j} \colon X_j \to X_i$
is an algebraic morphism. Suppose given, for each
![]() $i \in I$
, a non-empty countably proconstructible subset
$i \in I$
, a non-empty countably proconstructible subset
![]() $C_i \subset X_i$
. Let
$C_i \subset X_i$
. Let
![]() $Z_i= C_i(K)$
and assume that
$Z_i= C_i(K)$
and assume that
![]() $f_{ij}(Z_j)\subset Z_i$
for all
$f_{ij}(Z_j)\subset Z_i$
for all
![]() $i\prec j$
in I. Then the inverse system
$i\prec j$
in I. Then the inverse system
![]() $(Z_i,\varphi _{i j})_I$
, where
$(Z_i,\varphi _{i j})_I$
, where
![]() $\varphi _{i j} \colon Z_j \to Z_i$
is the restriction of
$\varphi _{i j} \colon Z_j \to Z_i$
is the restriction of
![]() $f_{i j}$
to
$f_{i j}$
to
![]() $Z_j$
, verifies
$Z_j$
, verifies
![]() $\varprojlim _{i \in I} Z_i \neq \varnothing $
.
$\varprojlim _{i \in I} Z_i \neq \varnothing $
.
Proof. Since I is a countable directed set, we can find a totally ordered cofinal subset
![]() ${\{i_n : n \in \mathbb {N}\} \subset I}$
. As
${\{i_n : n \in \mathbb {N}\} \subset I}$
. As
![]() $\varprojlim _{n \in \mathbb {N}} Z_{i_n} = \varprojlim _{i \in I} Z_i$
, we can suppose, without any loss of generality, that
$\varprojlim _{n \in \mathbb {N}} Z_{i_n} = \varprojlim _{i \in I} Z_i$
, we can suppose, without any loss of generality, that
![]() $I= \mathbb {N}$
.
$I= \mathbb {N}$
.
For each
![]() $i \in \mathbb {N}$
, we can find a decreasing sequence of constructible subsets
$i \in \mathbb {N}$
, we can find a decreasing sequence of constructible subsets
![]() $(C_{ik})_{k \in \mathbb {N}}$
of
$(C_{ik})_{k \in \mathbb {N}}$
of
![]() $X_i$
such that
$X_i$
such that
![]() $C_i= \bigcap _{k \in \mathbb {N}} C_{ik}$
. For
$C_i= \bigcap _{k \in \mathbb {N}} C_{ik}$
. For
![]() $k \in \mathbb {N}$
, let
$k \in \mathbb {N}$
, let
![]() $Z_{ik}= C_{ik}(K)$
. By Lemma 3.1, we have for every
$Z_{ik}= C_{ik}(K)$
. By Lemma 3.1, we have for every
![]() $i \leq j$
:
$i \leq j$
:
 $$ \begin{align} Z_i= \bigcap_{k = 0}^{\infty} Z_{ik} \neq \varnothing, \quad f_{ij}(Z_j) = \bigcap_{k=0}^{\infty} f_{ij} (Z_{jk}). \end{align} $$
$$ \begin{align} Z_i= \bigcap_{k = 0}^{\infty} Z_{ik} \neq \varnothing, \quad f_{ij}(Z_j) = \bigcap_{k=0}^{\infty} f_{ij} (Z_{jk}). \end{align} $$
Consider the universal inverse system
![]() $(Z^{\prime }_i, \varphi ^{\prime }_{ij})_{i,j \in \mathbb {N}}$
of the system
$(Z^{\prime }_i, \varphi ^{\prime }_{ij})_{i,j \in \mathbb {N}}$
of the system
![]() $(Z_i, \varphi _{ij})_{i,j \in \mathbb {N}}$
, that is, for every
$(Z_i, \varphi _{ij})_{i,j \in \mathbb {N}}$
, that is, for every
![]() $i \in \mathbb {N}$
, let
$i \in \mathbb {N}$
, let

and let the maps
![]() $\varphi ^{\prime }_{ij} \colon Z^{\prime }_{j} \to Z^{\prime }_i$
be the restrictions of
$\varphi ^{\prime }_{ij} \colon Z^{\prime }_{j} \to Z^{\prime }_i$
be the restrictions of
![]() $\varphi _{ij} \colon Z_j \to Z_i$
.
$\varphi _{ij} \colon Z_j \to Z_i$
.
Remark that
![]() $\varprojlim _{i \in \mathbb {N}} Z^{\prime }_i= \varprojlim _{i \in \mathbb {N}} Z_i$
. Hence, it suffices to check that the sets
$\varprojlim _{i \in \mathbb {N}} Z^{\prime }_i= \varprojlim _{i \in \mathbb {N}} Z_i$
. Hence, it suffices to check that the sets
![]() $Z^{\prime }_i$
are non-empty and the transition maps
$Z^{\prime }_i$
are non-empty and the transition maps
![]() $\varphi ^{\prime }_{ij}$
are surjective for all
$\varphi ^{\prime }_{ij}$
are surjective for all
![]() $i \leq j$
. By equation (3.1), Chevalley’s theorem (see for example [Reference Vakil57, Theorem 7.4.2], [Reference Grothendieck22, Théorème I.8.4]) implies that each
$i \leq j$
. By equation (3.1), Chevalley’s theorem (see for example [Reference Vakil57, Theorem 7.4.2], [Reference Grothendieck22, Théorème I.8.4]) implies that each
![]() $Z^{\prime }_i$
is a countable intersection of constructible sets:
$Z^{\prime }_i$
is a countable intersection of constructible sets:
 $$ \begin{align*} Z^{\prime}_i = \bigcap_{j=i}^\infty f_{ij}(Z_{j}) = \bigcap_{j = i}^\infty \bigcap_{k=0}^\infty f_{ij} (Z_{jk}). \end{align*} $$
$$ \begin{align*} Z^{\prime}_i = \bigcap_{j=i}^\infty f_{ij}(Z_{j}) = \bigcap_{j = i}^\infty \bigcap_{k=0}^\infty f_{ij} (Z_{jk}). \end{align*} $$
For each
![]() $n \geq i$
, consider the diagonal set
$n \geq i$
, consider the diagonal set

By Chevalley’s theorem,
![]() $Y_n$
is a constructible subset of
$Y_n$
is a constructible subset of
![]() $X_i(K)$
. For every
$X_i(K)$
. For every
![]() $n \geq i$
, we have
$n \geq i$
, we have
![]() $Y_{n+1} \subset Y_n$
and since
$Y_{n+1} \subset Y_n$
and since
![]() $Z_n \ne \varnothing $
,
$Z_n \ne \varnothing $
,
 $$ \begin{align} Y_n \supset \bigcap_{j=i}^n \bigcap_{k = 0}^\infty f_{ij}(Z_{jk}) = \bigcap_{j=i}^n f_{ij} (Z_j) \supset f_{in}(Z_n) = \varphi_{in}(Z_n) \neq \varnothing. \end{align} $$
$$ \begin{align} Y_n \supset \bigcap_{j=i}^n \bigcap_{k = 0}^\infty f_{ij}(Z_{jk}) = \bigcap_{j=i}^n f_{ij} (Z_j) \supset f_{in}(Z_n) = \varphi_{in}(Z_n) \neq \varnothing. \end{align} $$
As
![]() $Z^{\prime }_i = \bigcap _{n=i}^\infty Y_n$
, [Reference Ceccherini-Silberstein, Coornaert and Phung14, Lemma B.2] implies that
$Z^{\prime }_i = \bigcap _{n=i}^\infty Y_n$
, [Reference Ceccherini-Silberstein, Coornaert and Phung14, Lemma B.2] implies that
![]() $Z^{\prime }_i \neq \varnothing $
for
$Z^{\prime }_i \neq \varnothing $
for
![]() $i \in \mathbb {N}$
. Now let
$i \in \mathbb {N}$
. Now let
![]() $k, i \in \mathbb {N}$
with
$k, i \in \mathbb {N}$
with
![]() $k \leq i$
and let
$k \leq i$
and let
![]() $z \in Z^{\prime }_k$
. For each
$z \in Z^{\prime }_k$
. For each
![]() $n \geq i$
, by definition of
$n \geq i$
, by definition of
![]() $Z^{\prime }_k$
, there exists
$Z^{\prime }_k$
, there exists
![]() $y \in Z_n$
such that
$y \in Z_n$
such that
![]() $\varphi _{k n}(y)=z$
and thus
$\varphi _{k n}(y)=z$
and thus
By equations (3.2), (3.3), and for
![]() $n \geq i$
, the constructible subset
$n \geq i$
, the constructible subset
is non-empty and
![]() $T_{n+1} \subset T_n$
as
$T_{n+1} \subset T_n$
as
![]() $Y_{n+1} \subset Y_n$
. Finally, we find that
$Y_{n+1} \subset Y_n$
. Finally, we find that
 $$ \begin{align*} (\varphi_{k i}')^{-1} (z) & = \varphi_{k i}^{-1} (z) \cap Z^{\prime}_i = \bigcap_{n=i}^\infty \varphi_{k i}^{-1} (z) \cap Y_n = \bigcap_{n=i}^\infty T_n \end{align*} $$
$$ \begin{align*} (\varphi_{k i}')^{-1} (z) & = \varphi_{k i}^{-1} (z) \cap Z^{\prime}_i = \bigcap_{n=i}^\infty \varphi_{k i}^{-1} (z) \cap Y_n = \bigcap_{n=i}^\infty T_n \end{align*} $$
is non-empty by [Reference Ceccherini-Silberstein, Coornaert and Phung14, Lemma B.2]. The proof is thus completed.
We shall apply repeatedly the following result in cases (H2)–(H3).
Lemma 3.3. Let K be an algebraically closed field. Let
![]() $(X_i, f_{ij})$
be an inverse system indexed by a countable index set I, where each
$(X_i, f_{ij})$
be an inverse system indexed by a countable index set I, where each
![]() $X_i$
is a non-empty K-algebraic variety and each transition map
$X_i$
is a non-empty K-algebraic variety and each transition map
![]() $f_{i j} \colon X_j \to X_i$
is an algebraic morphism such that
$f_{i j} \colon X_j \to X_i$
is an algebraic morphism such that
![]() $f_{ij}(X_j) \subset X_i$
is a closed subset for all
$f_{ij}(X_j) \subset X_i$
is a closed subset for all
![]() $i \prec j$
. Then
$i \prec j$
. Then
![]() $\varprojlim _{i \in I} X_i(K) \neq \varnothing $
.
$\varprojlim _{i \in I} X_i(K) \neq \varnothing $
.
Proof. The statement is proved in [Reference Phung39, Proposition 4.2].
4 Space-time inverse systems
Let G be a finitely generated group and let A be a set. Let
![]() $\Sigma \subset A^G$
be a closed subshift and assume that
$\Sigma \subset A^G$
be a closed subshift and assume that
![]() $\tau \colon \Sigma \to \Sigma $
is a cellular automaton. Let
$\tau \colon \Sigma \to \Sigma $
is a cellular automaton. Let
![]() $\widetilde {\tau } \colon A^G \to A^G$
be a cellular automaton extending
$\widetilde {\tau } \colon A^G \to A^G$
be a cellular automaton extending
![]() $\tau $
.
$\tau $
.
Let
![]() $M\subset G$
be a memory set of
$M\subset G$
be a memory set of
![]() $\widetilde {\tau }$
. Since every finite subset of G containing a memory set of
$\widetilde {\tau }$
. Since every finite subset of G containing a memory set of
![]() $\widetilde {\tau }$
is itself a memory set of
$\widetilde {\tau }$
is itself a memory set of
![]() $\widetilde {\tau }$
, we can choose M such that
$\widetilde {\tau }$
, we can choose M such that
![]() $1_G \in M$
,
$1_G \in M$
,
![]() $M = M^{-1}$
, and M generates G. Note that this implies in particular that the sequence
$M = M^{-1}$
, and M generates G. Note that this implies in particular that the sequence
![]() $(M^n)_{n \in \mathbb {N}}$
is an exhaustion of G, that is:
$(M^n)_{n \in \mathbb {N}}$
is an exhaustion of G, that is:
-
(Mem1)
 $M^{n+1} \supset M^n$
for all
$M^{n+1} \supset M^n$
for all
 $n \in \mathbb {N}$
; and
$n \in \mathbb {N}$
; and -
(Mem2)
 $\bigcup _{n \in \mathbb {N}} M^n = G$
.
$\bigcup _{n \in \mathbb {N}} M^n = G$
.
Equip
![]() $\mathbb {N}^2$
with the product ordering
$\mathbb {N}^2$
with the product ordering
![]() $\prec $
. Thus, given
$\prec $
. Thus, given
![]() $i,j,k,l \in \mathbb {N}$
, we have
$i,j,k,l \in \mathbb {N}$
, we have
![]() $(i,j) \prec (k,l)$
if and only if
$(i,j) \prec (k,l)$
if and only if
![]() $i \leq k$
and
$i \leq k$
and
![]() $j \leq l$
.
$j \leq l$
.
We construct an inverse system
![]() $(\Sigma _{i j})_{i,j \in \mathbb {N}}$
indexed by the directed set
$(\Sigma _{i j})_{i,j \in \mathbb {N}}$
indexed by the directed set
![]() $(\mathbb {N}^2, \prec )$
in the following way.
$(\mathbb {N}^2, \prec )$
in the following way.
First, given
![]() $i,j \in \mathbb {N}$
, we define
$i,j \in \mathbb {N}$
, we define
![]() $\Sigma _{i j}$
as being the set consisting of the restrictions to
$\Sigma _{i j}$
as being the set consisting of the restrictions to
![]() $M^{i + j}$
of all the configurations that belong to
$M^{i + j}$
of all the configurations that belong to
![]() $\Sigma $
, that is,
$\Sigma $
, that is,
To define the transition maps
![]() $\Sigma _{k l} \to \Sigma _{i j}$
(
$\Sigma _{k l} \to \Sigma _{i j}$
(
![]() $(i,j) \prec (k,l)$
) of the inverse system
$(i,j) \prec (k,l)$
) of the inverse system
![]() $(\Sigma _{ij})_{i,j \in \mathbb {N}}$
, it is clearly enough to define, for all
$(\Sigma _{ij})_{i,j \in \mathbb {N}}$
, it is clearly enough to define, for all
![]() $i,j \in \mathbb {N}$
, the unit-horizontal transition map
$i,j \in \mathbb {N}$
, the unit-horizontal transition map
![]() $p_{i j} \colon \Sigma _{i+1, j} \to \Sigma _{i j}$
, the unit-vertical transition map
$p_{i j} \colon \Sigma _{i+1, j} \to \Sigma _{i j}$
, the unit-vertical transition map
![]() $q_{i j} \colon \Sigma _{i,j+1} \to \Sigma _{i j}$
, and verify that the diagram
$q_{i j} \colon \Sigma _{i,j+1} \to \Sigma _{i j}$
, and verify that the diagram

is commutative, that is,
We define
![]() $p_{i j}$
as being the map obtained by restriction to
$p_{i j}$
as being the map obtained by restriction to
![]() $M^{i + j} \subset M^{i + j + 1}$
. Thus for all
$M^{i + j} \subset M^{i + j + 1}$
. Thus for all
![]() $\sigma \in \Sigma _{i + 1,j}$
, we have
$\sigma \in \Sigma _{i + 1,j}$
, we have
To define
![]() $q_{i j}$
, we first observe that, given
$q_{i j}$
, we first observe that, given
![]() $x \in \Sigma $
and
$x \in \Sigma $
and
![]() $g \in G$
, it follows from equation (1.2) applied to
$g \in G$
, it follows from equation (1.2) applied to
![]() $\widetilde {\tau }$
that
$\widetilde {\tau }$
that
![]() $\tau (x)(g)$
only depends on the restriction of x to
$\tau (x)(g)$
only depends on the restriction of x to
![]() $gM$
. As
$gM$
. As
![]() $gM \subset M^{i + j + 1}$
for all
$gM \subset M^{i + j + 1}$
for all
![]() $g \in M^{i + j}$
, we deduce from this observation that, given
$g \in M^{i + j}$
, we deduce from this observation that, given
![]() $\sigma \in \Sigma _{i,j + 1}$
and
$\sigma \in \Sigma _{i,j + 1}$
and
![]() $x \in \Sigma $
extending
$x \in \Sigma $
extending
![]() $\sigma $
, the formula
$\sigma $
, the formula
yields a well-defined element
![]() $q_{i j}(\sigma ) \in \Sigma _{i j}$
and hence a map
$q_{i j}(\sigma ) \in \Sigma _{i j}$
and hence a map
![]() $q_{i j} \colon \Sigma _{i,j+1} \to \Sigma _{i j}$
.
$q_{i j} \colon \Sigma _{i,j+1} \to \Sigma _{i j}$
.
To check that equation (4.1) is satisfied, let
![]() $\sigma \in \Sigma _{i+1,j+1}$
and choose a configuration
$\sigma \in \Sigma _{i+1,j+1}$
and choose a configuration
![]() ${x \in \Sigma }$
extending
${x \in \Sigma }$
extending
![]() $\sigma $
. By applying equation (4.2), we see that
$\sigma $
. By applying equation (4.2), we see that
![]() $p_{i,j+1}(\sigma ) = x\vert _{M^{i + j + 1}}$
. Therefore, using equation (4.3), we get
$p_{i,j+1}(\sigma ) = x\vert _{M^{i + j + 1}}$
. Therefore, using equation (4.3), we get
However, by applying again equation (4.3), we see that
![]() $q_{i+1,j} (\sigma ) = (\tau (x))\vert _{M^{i + j + 1}}$
. Therefore, using equation (4.2), we get
$q_{i+1,j} (\sigma ) = (\tau (x))\vert _{M^{i + j + 1}}$
. Therefore, using equation (4.2), we get
We deduce from equations (4.4) and (4.5) that
![]() $q_{i j} \circ p_{i,j+1} (\sigma ) = p_{i j} \circ q_{i+1,j} (\sigma ) $
for all
$q_{i j} \circ p_{i,j+1} (\sigma ) = p_{i j} \circ q_{i+1,j} (\sigma ) $
for all
![]() $\sigma \in \Sigma _{i + 1,j + 1}$
. This shows equation (4.1).
$\sigma \in \Sigma _{i + 1,j + 1}$
. This shows equation (4.1).
Definition 4.1. The inverse system
![]() $(\Sigma _{ij})_{i,j \in \mathbb {N}}$
is called the space-time inverse system associated with the triple
$(\Sigma _{ij})_{i,j \in \mathbb {N}}$
is called the space-time inverse system associated with the triple
![]() $(\Sigma ,\tau ,M)$
.
$(\Sigma ,\tau ,M)$
.
It might be useful to consider the inverse system
![]() $(\Sigma _{ij})_{i,j \in \mathbb {N}}$
as a refined diagram of the space-time evolution of the cellular automaton
$(\Sigma _{ij})_{i,j \in \mathbb {N}}$
as a refined diagram of the space-time evolution of the cellular automaton
![]() $\tau $
that in addition keeps track of the local dynamics. Comparing to the usual space-time diagram of a classical cellular automaton introduced in [Reference Wolfram61], in [Reference Milnor34], or recently in [Reference Cyr, Franks and Kra19], the main difference of our construction is the following. First, the horizontal direction indexed by
$\tau $
that in addition keeps track of the local dynamics. Comparing to the usual space-time diagram of a classical cellular automaton introduced in [Reference Wolfram61], in [Reference Milnor34], or recently in [Reference Cyr, Franks and Kra19], the main difference of our construction is the following. First, the horizontal direction indexed by
![]() $i \in \mathbb {N}$
in our space-time inverse system represents the extension of the ambient spaces of
$i \in \mathbb {N}$
in our space-time inverse system represents the extension of the ambient spaces of
![]() $1_G$
instead of the exact position in the universe G as in the classical diagram. Second, the vertical direction indexed by
$1_G$
instead of the exact position in the universe G as in the classical diagram. Second, the vertical direction indexed by
![]() $j \in \mathbb {N}$
represents the past instead of the future. More precisely, let us fix
$j \in \mathbb {N}$
represents the past instead of the future. More precisely, let us fix
![]() $i \in \mathbb {N}$
and consider the induced inverse subsystem
$i \in \mathbb {N}$
and consider the induced inverse subsystem
![]() $(\Sigma _{ij})_{j \in \mathbb {N}}$
lying above
$(\Sigma _{ij})_{j \in \mathbb {N}}$
lying above
![]() $\Sigma _{i0}= \Sigma _{M^i}$
. Then each
$\Sigma _{i0}= \Sigma _{M^i}$
. Then each
![]() $(\Sigma _{ij})_{j \in \mathbb {N}}$
should be regarded as an approximation of the past light cone of the events happening in
$(\Sigma _{ij})_{j \in \mathbb {N}}$
should be regarded as an approximation of the past light cone of the events happening in
![]() $M^i$
, that is, of configurations
$M^i$
, that is, of configurations
![]() $\sigma \in \Sigma _{M^i}$
.
$\sigma \in \Sigma _{M^i}$
.
Remark 4.2. Observe that the inverse system
![]() $(\Sigma _{i j})_{i,j \in \mathbb {N}}$
is a subsystem of the full inverse system
$(\Sigma _{i j})_{i,j \in \mathbb {N}}$
is a subsystem of the full inverse system
![]() $(A^{M^{i + j}})_{i,j \in \mathbb {N}}$
associated with the triple
$(A^{M^{i + j}})_{i,j \in \mathbb {N}}$
associated with the triple
![]() $(A^G,\widetilde {\tau },M)$
. In the following, we shall denote by
$(A^G,\widetilde {\tau },M)$
. In the following, we shall denote by
![]() $\widetilde {p} _{ij}\colon A^{M^{i+j+1}} \to A^{M^{i+j}}$
(respectively
$\widetilde {p} _{ij}\colon A^{M^{i+j+1}} \to A^{M^{i+j}}$
(respectively
![]() $\widetilde {q}_{ij} \colon A^{M^{i+j+1}} \to A^{M^{i+j}}$
) the unit horizontal (respectively vertical) transition maps of the full inverse system
$\widetilde {q}_{ij} \colon A^{M^{i+j+1}} \to A^{M^{i+j}}$
) the unit horizontal (respectively vertical) transition maps of the full inverse system
![]() $(A^{M^{i + j}})_{i,j \in \mathbb {N}}$
.
$(A^{M^{i + j}})_{i,j \in \mathbb {N}}$
.
Remark 4.3. For the hypotheses (H1), (H2), and (H3) in §1, we have the following easy but useful remark. If
![]() $A=V(K)$
for some algebraic variety V over an algebraically closed field K and if
$A=V(K)$
for some algebraic variety V over an algebraically closed field K and if
![]() $\widetilde {\tau } \colon A^G \to A^G$
is an algebraic (respectively algebraic group) cellular automaton, then the transition maps of the full inverse system
$\widetilde {\tau } \colon A^G \to A^G$
is an algebraic (respectively algebraic group) cellular automaton, then the transition maps of the full inverse system
![]() $(A^{M^{i + j}})_{i,j \in \mathbb {N}}$
are algebraic morphisms (respectively homomorphisms of algebraic groups).
$(A^{M^{i + j}})_{i,j \in \mathbb {N}}$
are algebraic morphisms (respectively homomorphisms of algebraic groups).
If we fix
![]() $j \in \mathbb {N}$
in our space-time inverse system, we get a horizontal inverse system
$j \in \mathbb {N}$
in our space-time inverse system, we get a horizontal inverse system
![]() $(\Sigma _{i j})_{i \in \mathbb {N}}$
indexed by
$(\Sigma _{i j})_{i \in \mathbb {N}}$
indexed by
![]() $\mathbb {N}$
whose transition maps are the restriction maps
$\mathbb {N}$
whose transition maps are the restriction maps
![]() $p_{i j} \colon \Sigma _{i + 1,j} \to ~\Sigma _{i j}$
,
$p_{i j} \colon \Sigma _{i + 1,j} \to ~\Sigma _{i j}$
,
![]() $i \in \mathbb {N}$
. It immediately follows from the closedness of
$i \in \mathbb {N}$
. It immediately follows from the closedness of
![]() $\Sigma $
in
$\Sigma $
in
![]() $A^G$
and properties (Mem1)–(Mem2) that the limit
$A^G$
and properties (Mem1)–(Mem2) that the limit
can be identified with
![]() $\Sigma $
in a canonical way. Moreover, the maps
$\Sigma $
in a canonical way. Moreover, the maps
![]() $q_{i j} \colon \Sigma _{i, j + 1} \to \Sigma _{i j}$
define an inverse system morphism from the inverse system
$q_{i j} \colon \Sigma _{i, j + 1} \to \Sigma _{i j}$
define an inverse system morphism from the inverse system
![]() $(\Sigma _{i, j + 1})_{i \in \mathbb {N}}$
to the inverse system
$(\Sigma _{i, j + 1})_{i \in \mathbb {N}}$
to the inverse system
![]() $(\Sigma _{i j})_{i \in \mathbb {N}}$
. This yields a limit map
$(\Sigma _{i j})_{i \in \mathbb {N}}$
. This yields a limit map
![]() $\tau _j \colon \Sigma _{j + 1} \to \Sigma _j$
. Using the identifications
$\tau _j \colon \Sigma _{j + 1} \to \Sigma _j$
. Using the identifications
![]() $\Sigma _{j + 1} = \Sigma _j = \Sigma $
, we have
$\Sigma _{j + 1} = \Sigma _j = \Sigma $
, we have
![]() $\tau _j = \tau $
for all
$\tau _j = \tau $
for all
![]() $j \in \mathbb {N}$
. We deduce that the limit
$j \in \mathbb {N}$
. We deduce that the limit
is the set of backward orbits (or complete histories [Reference Milnor34]) of
![]() $\tau $
, that is, the set consisting of all sequences
$\tau $
, that is, the set consisting of all sequences
![]() $(x_j)_{j \in \mathbb {N}}$
such that
$(x_j)_{j \in \mathbb {N}}$
such that
![]() $x_j \in \Sigma $
and
$x_j \in \Sigma $
and
![]() $x_j = \tau (x_{j+1})$
for all
$x_j = \tau (x_{j+1})$
for all
![]() $j \in \mathbb {N}$
. Such a sequence satisfies
$j \in \mathbb {N}$
. Such a sequence satisfies
![]() $x_0 = \tau ^n(x_n)$
for all
$x_0 = \tau ^n(x_n)$
for all
![]() $n \in \mathbb {N}$
and hence
$n \in \mathbb {N}$
and hence
![]() $x_0 \in \Omega (\tau )$
. Thus, we obtain the following result.
$x_0 \in \Omega (\tau )$
. Thus, we obtain the following result.
Lemma 4.4. We have a canonical map
![]() $\Phi \colon \varprojlim _{i,j \in \mathbb {N}} \Sigma _{ij} \to \Omega (\tau )$
. In particular, we have that
$\Phi \colon \varprojlim _{i,j \in \mathbb {N}} \Sigma _{ij} \to \Omega (\tau )$
. In particular, we have that
We will see that the map
![]() $\Phi \colon \varprojlim _{i,j \in \mathbb {N}} \Sigma _{ij} \to \Omega (\tau )$
is surjective in the algebraic setting (cf. Theorem 9.1). Therefore, in this case, every limit configuration
$\Phi \colon \varprojlim _{i,j \in \mathbb {N}} \Sigma _{ij} \to \Omega (\tau )$
is surjective in the algebraic setting (cf. Theorem 9.1). Therefore, in this case, every limit configuration
![]() $x \in \Omega (\tau )$
admits a backward orbit and
$x \in \Omega (\tau )$
admits a backward orbit and
![]() $\tau (\Omega (\tau )) = \Omega (\tau )$
.
$\tau (\Omega (\tau )) = \Omega (\tau )$
.
5 Approximation of subshifts of finite type
In this section, keeping all the notation and hypotheses introduced in the previous section, we assume in addition that
![]() $\Sigma $
is a subshift of finite type. We fix a finite subset
$\Sigma $
is a subshift of finite type. We fix a finite subset
![]() $D \subset G$
and a subset
$D \subset G$
and a subset
![]() $P \subset A^D$
such that
$P \subset A^D$
such that
![]() $\Sigma = \Sigma (D, P)$
(cf. equation (1.1)). We begin with a useful observation.
$\Sigma = \Sigma (D, P)$
(cf. equation (1.1)). We begin with a useful observation.
Lemma 5.1. For every finite subset
![]() $E \subset G$
such that
$E \subset G$
such that
![]() $D \subset E$
, we have
$D \subset E$
, we have
![]() $\Sigma = \Sigma (D, P) = \Sigma (E, \Sigma _E)$
.
$\Sigma = \Sigma (D, P) = \Sigma (E, \Sigma _E)$
.
Proof. Let
![]() $x \in \Sigma $
and
$x \in \Sigma $
and
![]() $g \in G$
, then clearly
$g \in G$
, then clearly
![]() $(g^{-1}x) \vert _E \in \Sigma _E$
. Thus,
$(g^{-1}x) \vert _E \in \Sigma _E$
. Thus,
![]() $\Sigma \subset \Sigma (E, \Sigma _E)$
. Conversely, let
$\Sigma \subset \Sigma (E, \Sigma _E)$
. Conversely, let
![]() $x \in \Sigma (E, \Sigma _E)$
and
$x \in \Sigma (E, \Sigma _E)$
and
![]() $g \in G$
, then
$g \in G$
, then
![]() $(g^{-1}x)\vert _D = ((g^{-1}x)\vert _E)\vert _D\in (\Sigma _E)_D \subset P$
since
$(g^{-1}x)\vert _D = ((g^{-1}x)\vert _E)\vert _D\in (\Sigma _E)_D \subset P$
since
![]() $D \subset E$
. Therefore,
$D \subset E$
. Therefore,
![]() $x \in \Sigma (D,P)=\Sigma $
and the conclusion follows.
$x \in \Sigma (D,P)=\Sigma $
and the conclusion follows.
For all
![]() $i, j \in \mathbb {N}$
, we define
$i, j \in \mathbb {N}$
, we define ![]() and
and
Remark that
![]() $\Sigma _{ij} \subset A_{ij}$
. Indeed, we have
$\Sigma _{ij} \subset A_{ij}$
. Indeed, we have
 $$ \begin{align*} \Sigma_{ij} & = \{ x \in A^{M^{i+j}} \colon \text{ there exists } y \in A^G, x = y \vert_{M^{i+j}}, (g^{-1} y)\vert_{D} \in P \text{ for all } g \in G\} \\ & \subset \{ x \in A^{M^{i+j}} \colon \text{ there exists } y \in A^G, x = y \vert_{M^{i+j}}, (g^{-1} y)\vert_{D} \in P \text{ for all } g \in D_{ij}\} \\ &= \{ x \in A^{M^{i+j}} \colon (g^{-1} x)\vert_D \in P \text{ for all } g\in D_{ij} \} \\ & = A_{ij}. \end{align*} $$
$$ \begin{align*} \Sigma_{ij} & = \{ x \in A^{M^{i+j}} \colon \text{ there exists } y \in A^G, x = y \vert_{M^{i+j}}, (g^{-1} y)\vert_{D} \in P \text{ for all } g \in G\} \\ & \subset \{ x \in A^{M^{i+j}} \colon \text{ there exists } y \in A^G, x = y \vert_{M^{i+j}}, (g^{-1} y)\vert_{D} \in P \text{ for all } g \in D_{ij}\} \\ &= \{ x \in A^{M^{i+j}} \colon (g^{-1} x)\vert_D \in P \text{ for all } g\in D_{ij} \} \\ & = A_{ij}. \end{align*} $$
Remark also that for all
![]() $(i, j) \prec (k, l)$
in
$(i, j) \prec (k, l)$
in
![]() $\mathbb {N}^2$
, we have
$\mathbb {N}^2$
, we have
![]() $D_{ij} \subset D_{kl}$
because
$D_{ij} \subset D_{kl}$
because
![]() $M^{i+j} \subset M^{k+l}$
by property (Mem1).
$M^{i+j} \subset M^{k+l}$
by property (Mem1).
For
![]() $i,j,k \in \mathbb {N}$
such that
$i,j,k \in \mathbb {N}$
such that
![]() $i \leq k$
, consider the canonical projection
$i \leq k$
, consider the canonical projection
Clearly,
![]() $\widetilde {p}_{ijk}(A_{k j}) \subset A_{ij}$
since
$\widetilde {p}_{ijk}(A_{k j}) \subset A_{ij}$
since
![]() $D_{ij} \subset D_{k+j}$
. We thus obtain well-defined projection maps
$D_{ij} \subset D_{k+j}$
. We thus obtain well-defined projection maps
which extend the horizontal transition maps
![]() $\Sigma _{k j} \to \Sigma _{ij}$
of the space-time inverse system
$\Sigma _{k j} \to \Sigma _{ij}$
of the space-time inverse system
![]() $(\Sigma _{ij})_{i,j \in \mathbb {N}}$
associated with
$(\Sigma _{ij})_{i,j \in \mathbb {N}}$
associated with
![]() $\tau \colon \Sigma \to \Sigma $
and the memory set M.
$\tau \colon \Sigma \to \Sigma $
and the memory set M.
Remark 5.2. In general,
![]() $(A_{ij})_{i,j \in \mathbb {N}}$
is not a subsystem of the space-time inverse system
$(A_{ij})_{i,j \in \mathbb {N}}$
is not a subsystem of the space-time inverse system
![]() $(A^{M^{i+j}})_{i, j \in \mathbb {N}}$
associated with
$(A^{M^{i+j}})_{i, j \in \mathbb {N}}$
associated with
![]() $(A^G,\widetilde {\tau },M)$
(cf. Remark 4.2). There is no trivial reason for
$(A^G,\widetilde {\tau },M)$
(cf. Remark 4.2). There is no trivial reason for
![]() $\widetilde {q}_{ij}(A_{i,j+1}) \subset A_{ij}$
unless
$\widetilde {q}_{ij}(A_{i,j+1}) \subset A_{ij}$
unless
![]() $\Sigma $
is the full shift.
$\Sigma $
is the full shift.
The following lemma says that each row of the system
![]() $(A_{ij}, p_{ijk})_{i,j,k \in \mathbb {N}}$
gives us an approximation of
$(A_{ij}, p_{ijk})_{i,j,k \in \mathbb {N}}$
gives us an approximation of
![]() $\Sigma $
.
$\Sigma $
.
Lemma 5.3. For every
![]() $j \in \mathbb {N}$
, there is a canonical bijection
$j \in \mathbb {N}$
, there is a canonical bijection
Proof. Since
![]() $\Sigma _{i j} \subset A_{ij}$
for all
$\Sigma _{i j} \subset A_{ij}$
for all
![]() $i, j\in \mathbb {N}$
, each
$i, j\in \mathbb {N}$
, each
![]() $x \in \Sigma $
defines naturally an element
$x \in \Sigma $
defines naturally an element
![]() $\Psi _j(x) = (x\vert _{M^{i+j}})_{i \in \mathbb {N}}\in \varprojlim _{i \in \mathbb {N}} (A_{ij}, p_{ijk})$
. Conversely, let
$\Psi _j(x) = (x\vert _{M^{i+j}})_{i \in \mathbb {N}}\in \varprojlim _{i \in \mathbb {N}} (A_{ij}, p_{ijk})$
. Conversely, let
![]() $(x_i)_{i \in \mathbb {N}} \in \varprojlim _{i \in \mathbb {N}} (A_{ij}, p_{ijk})$
. Define
$(x_i)_{i \in \mathbb {N}} \in \varprojlim _{i \in \mathbb {N}} (A_{ij}, p_{ijk})$
. Define
![]() $x \in ~A^G$
by setting, for each
$x \in ~A^G$
by setting, for each
![]() $g \in G$
,
$g \in G$
, ![]() for any
for any
![]() $i \in \mathbb {N}$
large enough such that
$i \in \mathbb {N}$
large enough such that
![]() $g \in M^{i + j}$
. The fact that the configuration
$g \in M^{i + j}$
. The fact that the configuration
![]() $x \in A^G$
is well defined follows from properties (Mem1) and (Mem2). Let
$x \in A^G$
is well defined follows from properties (Mem1) and (Mem2). Let
![]() $g \in G$
. Take i large enough so that
$g \in G$
. Take i large enough so that
![]() $g D \subset M^{i + j}$
. Then
$g D \subset M^{i + j}$
. Then
![]() $g \in D_{i j}$
and
$g \in D_{i j}$
and
![]() $(g^{-1} x)\vert _D = (g^{-1} x_i)\vert _D \in P$
since
$(g^{-1} x)\vert _D = (g^{-1} x_i)\vert _D \in P$
since
![]() $x_i \in A_{i j}$
. This shows that
$x_i \in A_{i j}$
. This shows that
![]() $x \in \Sigma $
.
$x \in \Sigma $
.
Lemma 5.4. For all
![]() $i, j \in \mathbb {N}$
, we have
$i, j \in \mathbb {N}$
, we have
Proof. Let
![]() $y \in \Sigma $
and let
$y \in \Sigma $
and let
![]() $x= y\vert _{M^{i+j}} \in \Sigma _{ij}$
. Let
$x= y\vert _{M^{i+j}} \in \Sigma _{ij}$
. Let
![]() $k \geq i$
. Since
$k \geq i$
. Since
![]() $y\vert _{M^{k+j}} \in \Sigma _{M^{k+j}} \subset A_{k j}$
, it follows that
$y\vert _{M^{k+j}} \in \Sigma _{M^{k+j}} \subset A_{k j}$
, it follows that
As y is arbitrary, the proof is finished.
6 Algebraic subshifts of finite type
Keeping the notation and hypotheses of §5, we assume in this section that
![]() $A=V(K)$
and
$A=V(K)$
and
![]() $P=W(K)$
, where V is an algebraic variety over an algebraically closed field K and
$P=W(K)$
, where V is an algebraic variety over an algebraically closed field K and
![]() $W \subset V^D$
is an algebraic subvariety. Thus,
$W \subset V^D$
is an algebraic subvariety. Thus,
![]() $\Sigma =\Sigma (D, P) \subset A^G$
is an algebraic subshift of finite type.
$\Sigma =\Sigma (D, P) \subset A^G$
is an algebraic subshift of finite type.
For all
![]() $i, j \in \mathbb {N}$
, it is clear that
$i, j \in \mathbb {N}$
, it is clear that
![]() $A_{ij}$
is a closed algebraic subset of
$A_{ij}$
is a closed algebraic subset of
![]() $A^{M^{i+j}}$
since it is a finite intersection of sets of closed points of closed subvarieties of
$A^{M^{i+j}}$
since it is a finite intersection of sets of closed points of closed subvarieties of
![]() $V^{M^{i+j}}$
:
$V^{M^{i+j}}$
:
 $$ \begin{align} A_{ij} = \bigcap_{g \in D_{ij}} \pi_{ij,g}^{-1} (gW) (K). \end{align} $$
$$ \begin{align} A_{ij} = \bigcap_{g \in D_{ij}} \pi_{ij,g}^{-1} (gW) (K). \end{align} $$
Here,
![]() $\pi _{ij,g} \colon V^{M^{i+j}} \to V^{gD}$
is the projection induced by the inclusion
$\pi _{ij,g} \colon V^{M^{i+j}} \to V^{gD}$
is the projection induced by the inclusion
![]() $gD \subset M^{i+j}$
for
$gD \subset M^{i+j}$
for
![]() $g \in D_{ij}$
. The subset
$g \in D_{ij}$
. The subset
![]() $gW \subset V^{gD}$
is defined as the image of W under the isomorphism
$gW \subset V^{gD}$
is defined as the image of W under the isomorphism
![]() $V^D \simeq V^{gD}$
induced by the bijection
$V^D \simeq V^{gD}$
induced by the bijection
![]() $D \simeq gD$
given by
$D \simeq gD$
given by
![]() $h \mapsto gh$
for every
$h \mapsto gh$
for every
![]() $h \in D$
.
$h \in D$
.
Observe that the maps
![]() $\pi _{ij,g}$
above and the transition maps of the inverse system
$\pi _{ij,g}$
above and the transition maps of the inverse system
![]() $(\Sigma _{ij})_{i,j \in \mathbb {N}}$
are induced by morphisms of algebraic varieties.
$(\Sigma _{ij})_{i,j \in \mathbb {N}}$
are induced by morphisms of algebraic varieties.
In this section, we consider the following conditions:
-
(C2) V is a complete K-algebraic variety;
-
(C3) V is a K-algebraic group and
 $W \subset V$
is an algebraic subgroup.
$W \subset V$
is an algebraic subgroup.
Remark 6.1. In case (C3), note that the projections
![]() $p_{ijk} \colon A_{k j} \to A_{ij}$
(cf. equation (5.2)) are homomorphisms of algebraic groups.
$p_{ijk} \colon A_{k j} \to A_{ij}$
(cf. equation (5.2)) are homomorphisms of algebraic groups.
Proposition 6.2. With the above notation and hypotheses, suppose in addition that one of the conditions
![]() $(\mathrm {H1})$
,
$(\mathrm {H1})$
,
![]() $(\mathrm {C2})$
,
$(\mathrm {C2})$
,
![]() $(\mathrm {C3})$
is satisfied. Then, for each
$(\mathrm {C3})$
is satisfied. Then, for each
![]() $i, j \in \mathbb {N}$
, we have
$i, j \in \mathbb {N}$
, we have
and
![]() $\Sigma _{i j}$
is a countably proconstructible subset of
$\Sigma _{i j}$
is a countably proconstructible subset of
![]() $A^{M^{i+j}}$
. Moreover, in case
$A^{M^{i+j}}$
. Moreover, in case
![]() $(\mathrm {C2})$
(respectively
$(\mathrm {C2})$
(respectively
![]() $(\mathrm {C3})$
),
$(\mathrm {C3})$
),
![]() $\Sigma _{ij}$
is a complete subvariety (respectively an algebraic subgroup) of
$\Sigma _{ij}$
is a complete subvariety (respectively an algebraic subgroup) of
![]() $A^{M^{i+j}}$
.
$A^{M^{i+j}}$
.
Proof. The inclusion
![]() $\Sigma _{ij} \subset \bigcap _{k \geq i} p_{ijk}(A_{k j})$
follows from Lemma 5.4.
$\Sigma _{ij} \subset \bigcap _{k \geq i} p_{ijk}(A_{k j})$
follows from Lemma 5.4.
Let
![]() $x \in \bigcap _{k \geq i} p_{ijk}(A_{k j}) \subset A^{M^{i+j}}$
. We must show that x can be extended to an element of
$x \in \bigcap _{k \geq i} p_{ijk}(A_{k j}) \subset A^{M^{i+j}}$
. We must show that x can be extended to an element of
![]() $\Sigma $
. Consider the following inverse system lying above x. Let
$\Sigma $
. Consider the following inverse system lying above x. Let
![]() $B_i=\{x\}$
and for each
$B_i=\{x\}$
and for each
![]() $k \geq i$
, we set
$k \geq i$
, we set
which is a closed algebraic subset of
![]() $A^{M^{k+j}}$
. Since
$A^{M^{k+j}}$
. Since
![]() $x \in p_{ijk}(A_{k j})$
, each set
$x \in p_{ijk}(A_{k j})$
, each set
![]() $B_{k}$
is non-empty. From equation (6.3), it is clear that for every
$B_{k}$
is non-empty. From equation (6.3), it is clear that for every
![]() $k \geq i$
, we have
$k \geq i$
, we have
By restricting the map
![]() $\widetilde {p}_{kj}$
to
$\widetilde {p}_{kj}$
to
![]() $B_{k+1}$
, we have for each
$B_{k+1}$
, we have for each
![]() $k \geq i$
a well-defined algebraic map
$k \geq i$
a well-defined algebraic map
![]() $\pi _k \colon B_{k+1} \to B_k$
. Thus, we obtain an inverse subsystem
$\pi _k \colon B_{k+1} \to B_k$
. Thus, we obtain an inverse subsystem
![]() $(B_k)_{k \geq i}$
with transition maps
$(B_k)_{k \geq i}$
with transition maps
![]() $\pi _{nm} \colon B_m \to B_n$
, where
$\pi _{nm} \colon B_m \to B_n$
, where
![]() $m \geq n \geq i$
, as compositions of the maps
$m \geq n \geq i$
, as compositions of the maps
![]() $\pi _k$
.
$\pi _k$
.
We claim that
![]() $\varprojlim _{k \geq i} B_k \neq \varnothing $
. Indeed, this follows from Lemma 3.2 if case (H1) is satisfied and from Lemma 3.3 and Remark 2.1 in case (C2). Suppose now that case (C3) is satisfied. Since
$\varprojlim _{k \geq i} B_k \neq \varnothing $
. Indeed, this follows from Lemma 3.2 if case (H1) is satisfied and from Lemma 3.3 and Remark 2.1 in case (C2). Suppose now that case (C3) is satisfied. Since
![]() $x \in \bigcap _{k \geq i} p_{ijk}(A_{k j})$
, there exists for each
$x \in \bigcap _{k \geq i} p_{ijk}(A_{k j})$
, there exists for each
![]() $k~\geq ~i$
a point
$k~\geq ~i$
a point
![]() $z_k \in B_k$
such that
$z_k \in B_k$
such that
![]() $p_{ijk}(z_k)=x$
. Let
$p_{ijk}(z_k)=x$
. Let
![]() $V_k = \ker p_{ijk}$
be an algebraic subgroup of
$V_k = \ker p_{ijk}$
be an algebraic subgroup of
![]() $A^{M^{k+j}}$
, then clearly
$A^{M^{k+j}}$
, then clearly
![]() ${B_k = z_k V_k}$
where the group law is written multiplicatively. For all integers
${B_k = z_k V_k}$
where the group law is written multiplicatively. For all integers
![]() $m \geq n \geq i$
, the map
$m \geq n \geq i$
, the map
![]() $\pi _{mn}$
is the restriction of a homomorphism of algebraic groups (cf. Remark 4.3). Therefore,
$\pi _{mn}$
is the restriction of a homomorphism of algebraic groups (cf. Remark 4.3). Therefore,
![]() $\pi _{nm}(B_m)$
is a translate of an algebraic subgroup of
$\pi _{nm}(B_m)$
is a translate of an algebraic subgroup of
![]() $A^{M^{n+j}}$
and thus is Zariski closed in
$A^{M^{n+j}}$
and thus is Zariski closed in
![]() $B_n$
(cf. Remark 2.1). Hence, the claim follows, also in case (C3), from Lemma 3.3.
$B_n$
(cf. Remark 2.1). Hence, the claim follows, also in case (C3), from Lemma 3.3.
Therefore, we can find
![]() $(y_k)_{k \geq i} \in \varprojlim _{k \geq i} B_k$
. Let
$(y_k)_{k \geq i} \in \varprojlim _{k \geq i} B_k$
. Let
![]() $y \in A^{G}$
be defined as follows. Given
$y \in A^{G}$
be defined as follows. Given
![]() $g \in G$
, set
$g \in G$
, set
![]() $y(g)= y_k(g)$
for any
$y(g)= y_k(g)$
for any
![]() $k \geq i$
such that
$k \geq i$
such that
![]() $g \in M^{k+j}$
. Then y is well defined by property (Mem2). For each
$g \in M^{k+j}$
. Then y is well defined by property (Mem2). For each
![]() $g \in G$
, choose
$g \in G$
, choose
![]() $k \geq i$
so that
$k \geq i$
so that
![]() $gD \subset M^{k+j}$
. Then
$gD \subset M^{k+j}$
. Then
![]() $(g^{-1}y)\vert _D = y_k\vert _{gD} \in W(K)$
which follows from the definition of
$(g^{-1}y)\vert _D = y_k\vert _{gD} \in W(K)$
which follows from the definition of
![]() $A_{kj}$
and since
$A_{kj}$
and since
![]() $y_k \in B_{kj} \subset A_{kj}$
. Hence,
$y_k \in B_{kj} \subset A_{kj}$
. Hence,
![]() $y \in \Sigma $
. By construction,
$y \in \Sigma $
. By construction,
![]() $x= y \vert _{M^{i+j}}$
and we deduce that
$x= y \vert _{M^{i+j}}$
and we deduce that
![]() $\bigcap _{k \geq i} q_{ijk}(A_{k j}) \subset \Sigma _{M^{i+j}}$
. The proof of equation (6.2) is completed. Thus, by Chevalley’s theorem,
$\bigcap _{k \geq i} q_{ijk}(A_{k j}) \subset \Sigma _{M^{i+j}}$
. The proof of equation (6.2) is completed. Thus, by Chevalley’s theorem,
![]() $\Sigma _{i j}$
is a countably proconstructible subset of
$\Sigma _{i j}$
is a countably proconstructible subset of
![]() $A^{M^{i+j}}$
.
$A^{M^{i+j}}$
.
Finally, the last statement follows from equation (6.2) and Remark 2.1 and Noetherianity of the Zariski topology of
![]() $A^{M^{i+j}}$
. Note that the sequence
$A^{M^{i+j}}$
. Note that the sequence
![]() $(q_{ijk}(A_{k j}))_{k \geq i}$
is trivially a descending sequence.
$(q_{ijk}(A_{k j}))_{k \geq i}$
is trivially a descending sequence.
Corollary 6.3. With the above notation and hypotheses, suppose that condition
![]() $(\mathrm {H1})$
(respectively
$(\mathrm {H1})$
(respectively
![]() $(\mathrm {C2})$
, respectively
$(\mathrm {C2})$
, respectively
![]() $(\mathrm {C3})$
) is satisfied for
$(\mathrm {C3})$
) is satisfied for
![]() $\Sigma $
. Then, for each finite subset
$\Sigma $
. Then, for each finite subset
![]() $E \subset G$
, the restriction
$E \subset G$
, the restriction
![]() $\Sigma _E $
is a countably proconstructible subset (respectively a complete subvariety, respectively an algebraic subgroup) of
$\Sigma _E $
is a countably proconstructible subset (respectively a complete subvariety, respectively an algebraic subgroup) of
![]() $A^E$
.
$A^E$
.
Proof. Let
![]() $i, j \in \mathbb {N}$
be large enough so that
$i, j \in \mathbb {N}$
be large enough so that
![]() $E \subset M^{i+j}$
. Let
$E \subset M^{i+j}$
. Let
![]() $\pi \colon A^{M^{i+j}} \to A^E$
be the induced projection. It follows that
$\pi \colon A^{M^{i+j}} \to A^E$
be the induced projection. It follows that
![]() $\Sigma _E = \pi (\Sigma _{ij})$
. In cases (C2) and (C3), Proposition 6.2 and Remark 2.1 imply that
$\Sigma _E = \pi (\Sigma _{ij})$
. In cases (C2) and (C3), Proposition 6.2 and Remark 2.1 imply that
![]() $\Sigma _E$
is respectively a complete subvariety and an algebraic subgroup of
$\Sigma _E$
is respectively a complete subvariety and an algebraic subgroup of
![]() $A^E$
. In case (H1), we find by Lemma 3.1 that
$A^E$
. In case (H1), we find by Lemma 3.1 that
 $$ \begin{align} \Sigma_E = \pi (\Sigma_{ij}) = \pi \bigg(\bigcap_{k \geq i} p_{ijk} (A_{kj}) \bigg) = \bigcap_{n \in \mathbb{N}} \pi (p_{ijk} (A_{kj}) ). \end{align} $$
$$ \begin{align} \Sigma_E = \pi (\Sigma_{ij}) = \pi \bigg(\bigcap_{k \geq i} p_{ijk} (A_{kj}) \bigg) = \bigcap_{n \in \mathbb{N}} \pi (p_{ijk} (A_{kj}) ). \end{align} $$
Hence,
![]() $\Sigma _E$
is countably proconstructible by Chevalley’s theorem. The proof is completed.
$\Sigma _E$
is countably proconstructible by Chevalley’s theorem. The proof is completed.
7 Algebraic sofic subshifts
Consider the following hypothesis without condition on cellular automata:
![]() $(\mathrm {\widehat {H3}})\quad K$
is algebraically closed, V is a K-algebraic group, and
$(\mathrm {\widehat {H3}})\quad K$
is algebraically closed, V is a K-algebraic group, and
![]() $\Sigma \subset A^G$
is an algebraic group sofic subshift.
$\Sigma \subset A^G$
is an algebraic group sofic subshift.
We can now state the main local result for algebraic sofic subshifts.
Theorem 7.1. Let V be an algebraic variety over a field K and let
![]() $A= V(K)$
. Let G be a finitely generated group and let
$A= V(K)$
. Let G be a finitely generated group and let
![]() $\Sigma \subset A^G$
be an algebraic sofic subshift. Let E be a finite subset of G. Suppose that condition
$\Sigma \subset A^G$
be an algebraic sofic subshift. Let E be a finite subset of G. Suppose that condition
![]() $(\mathrm {H1})$
(respectively
$(\mathrm {H1})$
(respectively
![]() $(\mathrm {H2})$
, respectively
$(\mathrm {H2})$
, respectively
![]() $(\mathrm {\widehat {H3}})$
) is satisfied. Then the restriction
$(\mathrm {\widehat {H3}})$
) is satisfied. Then the restriction
![]() $\Sigma _E \subset A^E$
is a countably proconstructible subset (respectively a complete subvariety, respectively an algebraic subgroup) of
$\Sigma _E \subset A^E$
is a countably proconstructible subset (respectively a complete subvariety, respectively an algebraic subgroup) of
![]() $A^E$
.
$A^E$
.
Proof. By hypothesis, there exist in cases (H1) and (H2) an algebraic variety (respectively in case
![]() $(\mathrm {\widehat {H3}})$
an algebraic group) U over K, an algebraic (respectively algebraic group) cellular automaton
$(\mathrm {\widehat {H3}})$
an algebraic group) U over K, an algebraic (respectively algebraic group) cellular automaton
![]() $\tau ' \colon B^G \to A^G$
where
$\tau ' \colon B^G \to A^G$
where
![]() $B= U(K)$
, and an algebraic (respectively algebraic group) subshift of finite type
$B= U(K)$
, and an algebraic (respectively algebraic group) subshift of finite type
![]() $\Sigma ' \subset B^G$
such that
$\Sigma ' \subset B^G$
such that
![]() $\Sigma = \tau ' (\Sigma ')$
. Note that
$\Sigma = \tau ' (\Sigma ')$
. Note that
![]() $U,V$
are complete varieties in case (H2). Let M be a memory set of
$U,V$
are complete varieties in case (H2). Let M be a memory set of
![]() $\tau '$
. By Corollary 6.3, the set
$\tau '$
. By Corollary 6.3, the set
![]() $\Sigma ^{\prime }_{ME}$
is countably proconstructible. Hence,
$\Sigma ^{\prime }_{ME}$
is countably proconstructible. Hence,
![]() $\Sigma ^{\prime }_{ME} = \bigcap _{n \in \mathbb {N}} C_n$
where
$\Sigma ^{\prime }_{ME} = \bigcap _{n \in \mathbb {N}} C_n$
where
![]() $(C_n)_{n \in \mathbb {N}}$
is some decreasing sequence of constructible subsets of
$(C_n)_{n \in \mathbb {N}}$
is some decreasing sequence of constructible subsets of
![]() $A^{ME}$
. Let
$A^{ME}$
. Let
![]() $\varphi \colon B^{ME} \to A^E$
be given by
$\varphi \colon B^{ME} \to A^E$
be given by
![]() $\varphi (x)(g)= \tau '(y)(g)$
for every
$\varphi (x)(g)= \tau '(y)(g)$
for every
![]() $x \in B^{ME}$
,
$x \in B^{ME}$
,
![]() $g \in E$
and every
$g \in E$
and every
![]() $y \in B^G$
extending x. Then
$y \in B^G$
extending x. Then
![]() $\varphi $
is algebraic (cf. [Reference Ceccherini-Silberstein, Coornaert and Phung14, Lemma 3.2]) and in case
$\varphi $
is algebraic (cf. [Reference Ceccherini-Silberstein, Coornaert and Phung14, Lemma 3.2]) and in case
![]() $(\mathrm {\widehat {H3}})$
, it is a homomorphism of algebraic groups (cf. [Reference Phung39, Lemma 3.4]). In case (H1), we can conclude by Chevalley’s theorem since
$(\mathrm {\widehat {H3}})$
, it is a homomorphism of algebraic groups (cf. [Reference Phung39, Lemma 3.4]). In case (H1), we can conclude by Chevalley’s theorem since
 $$ \begin{align} \Sigma_E = (\tau'(\Sigma'))_E = \varphi(\Sigma^{\prime}_{ME}) = \varphi \bigg(\bigcap_{n \in \mathbb{N}} C_n \bigg) = \bigcap_{n \in \mathbb{N}} \varphi (C_n), \end{align} $$
$$ \begin{align} \Sigma_E = (\tau'(\Sigma'))_E = \varphi(\Sigma^{\prime}_{ME}) = \varphi \bigg(\bigcap_{n \in \mathbb{N}} C_n \bigg) = \bigcap_{n \in \mathbb{N}} \varphi (C_n), \end{align} $$
where the last equality follows from Lemma 3.1. Finally, in cases (H2) and
![]() $(\mathrm {\widehat {H3}})$
, Corollary 6.3 implies that
$(\mathrm {\widehat {H3}})$
, Corollary 6.3 implies that
![]() $\Sigma _E = \varphi (\Sigma ^{\prime }_{ME})$
is respectively a complete subvariety and an algebraic subgroup of
$\Sigma _E = \varphi (\Sigma ^{\prime }_{ME})$
is respectively a complete subvariety and an algebraic subgroup of
![]() $A^E$
.
$A^E$
.
8 A closed mapping property and chain recurrent sets
Using the space-time inverse system, we give a short proof of the following result saying that the image of an algebraic sofic subshift under an algebraic cellular automaton is closed. It extends the linear case in [Reference Ceccherini-Silberstein, Coornaert and Phung16, Theorem 4.1].
Let G be a group. Let
![]() $V_0, V_1$
be algebraic varieties over an algebraically field K. Let
$V_0, V_1$
be algebraic varieties over an algebraically field K. Let
![]() $A_0 = V_0(K)$
and let
$A_0 = V_0(K)$
and let
![]() $A_1=V_1(K)$
. Let
$A_1=V_1(K)$
. Let
![]() $\tau \colon A_0^G \to A_1^G$
be an algebraic cellular automaton and let
$\tau \colon A_0^G \to A_1^G$
be an algebraic cellular automaton and let
![]() $\Sigma \subset A_0^G$
be an algebraic sofic subshift.
$\Sigma \subset A_0^G$
be an algebraic sofic subshift.
Then
![]() $\Sigma $
is the image of some algebraic subshift of finite type
$\Sigma $
is the image of some algebraic subshift of finite type
![]() $\Sigma ' \subset B^G$
under an algebraic cellular automaton
$\Sigma ' \subset B^G$
under an algebraic cellular automaton
![]() $\tau ' \colon B^G \to A_0^G$
, where B is the set of K-points of a K-algebraic variety U.
$\tau ' \colon B^G \to A_0^G$
, where B is the set of K-points of a K-algebraic variety U.
To avoid notational confusion, we introduce in this section the following hypotheses similar to hypotheses (H1), (H2), and (H3),
![]() $(\mathrm {\widehat {H3}})$
:
$(\mathrm {\widehat {H3}})$
:
-
 $(\mathrm {\widetilde {H1}})$
K is uncountable;
$(\mathrm {\widetilde {H1}})$
K is uncountable; -
 $(\mathrm {\widetilde {H2}})$
$(\mathrm {\widetilde {H2}})$
 $U, V_0$
are complete K-algebraic varieties;
$U, V_0$
are complete K-algebraic varieties; -
 $(\mathrm {\widetilde {H3}})$
$(\mathrm {\widetilde {H3}})$
 $U, V_0$
, and
$U, V_0$
, and
 $V_1$
are K-algebraic groups,
$V_1$
are K-algebraic groups,
 $\Sigma ' \subset B^G$
is an algebraic group subshift of finite type, and
$\Sigma ' \subset B^G$
is an algebraic group subshift of finite type, and
 $\tau ' \colon B^G \to A_0^G$
and
$\tau ' \colon B^G \to A_0^G$
and
 $\tau \colon A_0^G \to A_1^G$
are algebraic group cellular automata.
$\tau \colon A_0^G \to A_1^G$
are algebraic group cellular automata.
Theorem 8.1. With the above notation, if one of the conditions
![]() $(\mathrm {\widetilde {H1}})$
,
$(\mathrm {\widetilde {H1}})$
,
![]() $(\mathrm {\widetilde {H2}})$
,
$(\mathrm {\widetilde {H2}})$
,
![]() $(\mathrm {\widetilde {H3}})$
is satisfied, then
$(\mathrm {\widetilde {H3}})$
is satisfied, then
![]() $\tau (\Sigma )$
is closed in
$\tau (\Sigma )$
is closed in
![]() $A_1^G$
.
$A_1^G$
.
Proof. It is clear that, up to replacing
![]() $\tau $
by the composition
$\tau $
by the composition
![]() $\tau \circ \tau '$
and
$\tau \circ \tau '$
and
![]() $\Sigma $
by
$\Sigma $
by
![]() $\Sigma '$
, we can suppose without loss of generality that
$\Sigma '$
, we can suppose without loss of generality that
![]() $\Sigma $
is an algebraic subshift of finite type. The hypotheses
$\Sigma $
is an algebraic subshift of finite type. The hypotheses
![]() $(\mathrm {\widetilde {H2}})$
,
$(\mathrm {\widetilde {H2}})$
,
![]() $(\mathrm {\widetilde {H3}})$
now become respectively:
$(\mathrm {\widetilde {H3}})$
now become respectively:
-
(P2)
 $V_0$
is a complete K-algebraic variety;
$V_0$
is a complete K-algebraic variety; -
(P3)
 $V_0$
and
$V_0$
and
 $V_1$
are K-algebraic groups,
$V_1$
are K-algebraic groups,
 $\Sigma \subset A_0^G$
is an algebraic group subshift of finite type, and
$\Sigma \subset A_0^G$
is an algebraic group subshift of finite type, and
 $\tau \colon A_0^G \to A_1^G$
is an algebraic group cellular automaton.
$\tau \colon A_0^G \to A_1^G$
is an algebraic group cellular automaton.
Let
![]() $D \subset G$
be a defining memory set of
$D \subset G$
be a defining memory set of
![]() $\Sigma $
. Let
$\Sigma $
. Let
![]() $d \in A_1^G$
be in the closure of
$d \in A_1^G$
be in the closure of
![]() $\tau (\Sigma )$
. We must show that
$\tau (\Sigma )$
. We must show that
![]() $d \in \tau (\Sigma )$
.
$d \in \tau (\Sigma )$
.
Suppose first that G is finitely generated. Let
![]() $M \subset G$
be a finite memory subset of
$M \subset G$
be a finite memory subset of
![]() $\tau $
containing
$\tau $
containing
![]() $\{1_G\} \cup D$
which generates G and satisfies
$\{1_G\} \cup D$
which generates G and satisfies
![]() $M=M^{-1}$
. Consider the inverse system
$M=M^{-1}$
. Consider the inverse system
![]() $(A_0^{M^i})_{i\in \mathbb {N}}$
whose transition maps
$(A_0^{M^i})_{i\in \mathbb {N}}$
whose transition maps
![]() $p _{ij}\colon A_0^{M^j} \to A_0^{M^i}$
, where
$p _{ij}\colon A_0^{M^j} \to A_0^{M^i}$
, where
![]() $0 \leq i \leq j$
, are defined as the canonical projections induced by the inclusions
$0 \leq i \leq j$
, are defined as the canonical projections induced by the inclusions
![]() $M^i \subset M^j$
. For every
$M^i \subset M^j$
. For every
![]() $i \geq 1$
, the induced map
$i \geq 1$
, the induced map
![]() $q_i \colon A_0^{M^i} \to A_1^{M^{i-1}}$
is given as follows. For every
$q_i \colon A_0^{M^i} \to A_1^{M^{i-1}}$
is given as follows. For every
![]() $\sigma \in A_0^{M^i}$
, we set
$\sigma \in A_0^{M^i}$
, we set ![]() , where
, where
![]() $x \in A_0^G$
is any configuration that extends
$x \in A_0^G$
is any configuration that extends
![]() $\sigma $
. For every
$\sigma $
. For every
![]() $i \geq 1$
, we define
$i \geq 1$
, we define
Since d belongs to the closure of
![]() $\tau (\Sigma )$
in
$\tau (\Sigma )$
in
![]() $A_1^G$
, it follows that
$A_1^G$
, it follows that
![]() $Z_i \neq \varnothing $
for every
$Z_i \neq \varnothing $
for every
![]() $i \geq 1$
. By restricting the projections
$i \geq 1$
. By restricting the projections
![]() $p_{ij} \colon A^{M^j} \to A^{M^i}$
to
$p_{ij} \colon A^{M^j} \to A^{M^i}$
to
![]() $Z_j$
, we obtain well-defined transition maps
$Z_j$
, we obtain well-defined transition maps
![]() $\pi _{ij} \colon Z_j \to Z_i$
, where
$\pi _{ij} \colon Z_j \to Z_i$
, where
![]() $j \geq i \geq 1$
, of the inverse system
$j \geq i \geq 1$
, of the inverse system
![]() $(Z_i)_{i \geq 1}$
.
$(Z_i)_{i \geq 1}$
.
It suffices to show that
![]() $\varprojlim _{i \geq 1} Z_i \neq \varnothing $
since, by construction of
$\varprojlim _{i \geq 1} Z_i \neq \varnothing $
since, by construction of
![]() $Z_i$
and
$Z_i$
and
![]() $\Sigma _{ij}$
(see also [Reference Ceccherini-Silberstein, Coornaert and Phung14, Lemma 2.1]), we have
$\Sigma _{ij}$
(see also [Reference Ceccherini-Silberstein, Coornaert and Phung14, Lemma 2.1]), we have
![]() $\tau (c) = d$
for every
$\tau (c) = d$
for every
![]() $c \in \varprojlim _{i \geq 1} Z_i \subset \varprojlim _{i \geq 1} \Sigma _{M^{i+1}} = \Sigma $
(by equation (4.6) since
$c \in \varprojlim _{i \geq 1} Z_i \subset \varprojlim _{i \geq 1} \Sigma _{M^{i+1}} = \Sigma $
(by equation (4.6) since
![]() $\Sigma $
is closed as it is a subshift of finite type).
$\Sigma $
is closed as it is a subshift of finite type).
Thanks to Theorem 7.1, the conclusion follows by a direct application of Lemma 3.2, respectively Lemma 3.3, to the inverse system
![]() $(Z_i)_{i \in \mathbb {N}}$
if case
$(Z_i)_{i \in \mathbb {N}}$
if case
![]() $(\mathrm {\widetilde {H1}})$
, respectively case (P2), is satisfied. Assume now that case (P3) is satisfied. For each
$(\mathrm {\widetilde {H1}})$
, respectively case (P2), is satisfied. Assume now that case (P3) is satisfied. For each
![]() $i \geq 1$
, choose
$i \geq 1$
, choose
![]() $z_i \in Z_i$
and let
$z_i \in Z_i$
and let ![]() be an algebraic subgroup of
be an algebraic subgroup of
![]() $\Sigma _{M^i}$
(by Theorem 7.1). We have
$\Sigma _{M^i}$
(by Theorem 7.1). We have
![]() $Z_i= z_i V_i$
. Hence (by Remark 4.3), for
$Z_i= z_i V_i$
. Hence (by Remark 4.3), for
![]() $j \geq i \geq 1$
,
$j \geq i \geq 1$
,
![]() $\pi _{ij}(Z_j) $
is a translate of an algebraic subgroup of
$\pi _{ij}(Z_j) $
is a translate of an algebraic subgroup of
![]() $\Sigma _{M^i}$
and thus is Zariski closed in
$\Sigma _{M^i}$
and thus is Zariski closed in
![]() $Z_i$
. Therefore, case (P3) follows from Lemma 3.3.
$Z_i$
. Therefore, case (P3) follows from Lemma 3.3.
For a general group G, consider a finite memory set M of
![]() $\tau $
containing
$\tau $
containing
![]() $\{1_G\} \cup D$
and such that
$\{1_G\} \cup D$
and such that
![]() $M=M^{-1}$
. Let
$M=M^{-1}$
. Let
![]() $H \subset G$
be the subgroup generated by M. As
$H \subset G$
be the subgroup generated by M. As
![]() $\Sigma _H$
is clearly an algebraic (respectively in case
$\Sigma _H$
is clearly an algebraic (respectively in case
![]() $(\mathrm {\widetilde {H3}})$
an algebraic group) subshift of finite type, the above discussion shows that
$(\mathrm {\widetilde {H3}})$
an algebraic group) subshift of finite type, the above discussion shows that
![]() $\tau _H(\Sigma _H)$
is closed in
$\tau _H(\Sigma _H)$
is closed in
![]() $A_1^G$
and so is
$A_1^G$
and so is
![]() $\tau (\Sigma )$
by Lemma 2.10.
$\tau (\Sigma )$
by Lemma 2.10.
Corollary 8.2. Let G be a group. Let V be an algebraic variety over a field K and let ![]() . Let
. Let
![]() $\Sigma \subset A^G$
be an algebraic sofic subshift. If one of the conditions
$\Sigma \subset A^G$
be an algebraic sofic subshift. If one of the conditions
![]() $(\mathrm {H1})$
,
$(\mathrm {H1})$
,
![]() $(\mathrm {H2})$
,
$(\mathrm {H2})$
,
![]() $(\mathrm {\widehat {H3}})$
is satisfied, then
$(\mathrm {\widehat {H3}})$
is satisfied, then
![]() $\Sigma $
is closed in
$\Sigma $
is closed in
![]() $A^G$
.
$A^G$
.
Proof. It suffices to apply Theorem 8.1 in the case
![]() $V_0=V_1$
to the identity map
$V_0=V_1$
to the identity map
![]() $\tau = \operatorname {\mathrm {Id}}_{A^G}$
, where
$\tau = \operatorname {\mathrm {Id}}_{A^G}$
, where
![]() $A = V_0(K) = V_1(K)$
.
$A = V_0(K) = V_1(K)$
.
Corollary 8.3. With the notation and hypotheses as in Theorem 1.3, we have
![]() ${\operatorname {\mathrm {CR}} (\tau ) \subset \Omega (\tau )}$
.
${\operatorname {\mathrm {CR}} (\tau ) \subset \Omega (\tau )}$
.
9 Applications to backward orbits and limit sets
Thanks to the closedness property of algebraic sofic subshifts, we can establish the following key relation among inverse space-time systems, backward orbits, and limit sets.
Theorem 9.1. Let V be an algebraic variety over a field K and let
![]() $A= V(K)$
. Let G be a finitely generated group and let
$A= V(K)$
. Let G be a finitely generated group and let
![]() $\Sigma \subset A^G$
be an algebraic sofic subshift. Let
$\Sigma \subset A^G$
be an algebraic sofic subshift. Let
![]() $\tau \colon \Sigma \to \Sigma $
be an algebraic cellular automaton. Assume that one of the conditions
$\tau \colon \Sigma \to \Sigma $
be an algebraic cellular automaton. Assume that one of the conditions
![]() $(\mathrm {H1})$
,
$(\mathrm {H1})$
,
![]() $(\mathrm {H2})$
,
$(\mathrm {H2})$
,
![]() $(\mathrm {H3})$
is satisfied. Then, with the notation as in §4, we have a surjective map
$(\mathrm {H3})$
is satisfied. Then, with the notation as in §4, we have a surjective map
![]() $\Phi \colon \varprojlim _{i,j \in \mathbb {N}} \Sigma _{ij}~\to ~\Omega (\tau )$
.
$\Phi \colon \varprojlim _{i,j \in \mathbb {N}} \Sigma _{ij}~\to ~\Omega (\tau )$
.
Proof. By Corollary 8.2, the subshift
![]() $\Sigma $
is closed in
$\Sigma $
is closed in
![]() $A^G$
. Hence,
$A^G$
. Hence,
![]() $\varprojlim _{i,j \in \mathbb {N}} \Sigma _{ij}$
is the set of backward orbits of
$\varprojlim _{i,j \in \mathbb {N}} \Sigma _{ij}$
is the set of backward orbits of
![]() $\tau $
and we have a canonical map
$\tau $
and we have a canonical map
![]() $\Phi \colon \varprojlim _{i,j \in \mathbb {N}} \Sigma _{ij} \to \Omega (\tau )$
given in Lemma 4.4. Now let
$\Phi \colon \varprojlim _{i,j \in \mathbb {N}} \Sigma _{ij} \to \Omega (\tau )$
given in Lemma 4.4. Now let
![]() $y_0 \in \Omega (\tau ) \subset \Sigma $
. We must show that there exists
$y_0 \in \Omega (\tau ) \subset \Sigma $
. We must show that there exists
![]() $x \in \varprojlim _{i,j \in \mathbb {N}} \Sigma _{ij} $
such that
$x \in \varprojlim _{i,j \in \mathbb {N}} \Sigma _{ij} $
such that
![]() $\Phi (x)=y_0$
. For every
$\Phi (x)=y_0$
. For every
![]() $i, j \in \mathbb {N}$
, define a closed subset
$i, j \in \mathbb {N}$
, define a closed subset
By definition of
![]() $\Omega (\tau )$
, there exists for every
$\Omega (\tau )$
, there exists for every
![]() $j \in \mathbb {N}$
an element
$j \in \mathbb {N}$
an element
![]() $y_j \in \Sigma $
such that
$y_j \in \Sigma $
such that
![]() ${\tau ^j (y_j)=y_0}$
. Hence, it follows from the definition of the transition maps
${\tau ^j (y_j)=y_0}$
. Hence, it follows from the definition of the transition maps
![]() $q_{ik}$
and of
$q_{ik}$
and of
![]() $\Sigma _{ij}$
that
$\Sigma _{ij}$
that
![]() $y_j\vert _{M^{i+j}} \in B_{ij}$
. In particular,
$y_j\vert _{M^{i+j}} \in B_{ij}$
. In particular,
![]() $B_{ij} \neq \varnothing $
for every
$B_{ij} \neq \varnothing $
for every
![]() $i, j \in \mathbb {N}$
. By restricting the transition maps of the space-time inverse system
$i, j \in \mathbb {N}$
. By restricting the transition maps of the space-time inverse system
![]() $(\Sigma _{ij})_{i, j \in \mathbb {N}}$
to the sets
$(\Sigma _{ij})_{i, j \in \mathbb {N}}$
to the sets
![]() $B_{ij}$
, we obtain a well-defined inverse subsystem
$B_{ij}$
, we obtain a well-defined inverse subsystem
![]() $(B_{ij})_{i, j \in \mathbb {N}}$
.
$(B_{ij})_{i, j \in \mathbb {N}}$
.
We claim that
![]() $\varprojlim _{i, j \in \mathbb {N}} B_{ij} \neq \varnothing $
. Indeed, by Theorem 7.1, case (H1) is implied by Lemma 3.2. In case (H2), Theorem 7.1 implies that
$\varprojlim _{i, j \in \mathbb {N}} B_{ij} \neq \varnothing $
. Indeed, by Theorem 7.1, case (H1) is implied by Lemma 3.2. In case (H2), Theorem 7.1 implies that
![]() $B_{ij}$
is a complete algebraic subvariety of
$B_{ij}$
is a complete algebraic subvariety of
![]() $\Sigma _{ij}$
and thus of
$\Sigma _{ij}$
and thus of
![]() $A^{M^{i+j}}$
. Hence, case (H2) follows from Lemma 3.3 and Remark 2.1. In case (H3), a similar argument as in the proof of Proposition 6.2 shows that the transition maps of the system
$A^{M^{i+j}}$
. Hence, case (H2) follows from Lemma 3.3 and Remark 2.1. In case (H3), a similar argument as in the proof of Proposition 6.2 shows that the transition maps of the system
![]() $(B_{ij})_{i, j \in \mathbb {N}}$
have Zariski closed images. Therefore, case (H3) follows immediately from Lemma 3.3. Thus, we can find
$(B_{ij})_{i, j \in \mathbb {N}}$
have Zariski closed images. Therefore, case (H3) follows immediately from Lemma 3.3. Thus, we can find
It is clear from the constructions of the inverse system
![]() $(B_{ij})_{i, j \in \mathbb {N}}$
and of the map
$(B_{ij})_{i, j \in \mathbb {N}}$
and of the map
![]() $\Phi $
(see the proof of Lemma 4.4) that
$\Phi $
(see the proof of Lemma 4.4) that
![]() $\Phi (x)= y_0$
. The proof of the lemma is completed.
$\Phi (x)= y_0$
. The proof of the lemma is completed.
Corollary 9.2. With the notation and hypotheses as in Theorem 1.3, we have
![]() $\tau (\Omega (\tau ))= \Omega (\tau )$
.
$\tau (\Omega (\tau ))= \Omega (\tau )$
.
Proof. Let
![]() $M\subset G$
be a finite subset containing
$M\subset G$
be a finite subset containing
![]() $1_G$
, a memory set of
$1_G$
, a memory set of
![]() $\tau $
, and a memory set of
$\tau $
, and a memory set of
![]() $\Sigma $
and such that
$\Sigma $
and such that
![]() $M=M^{-1}$
. Let
$M=M^{-1}$
. Let
![]() $H \subset G$
be the subgroup generated by M. Since
$H \subset G$
be the subgroup generated by M. Since
![]() $\tau = \prod _{c \in G/H} \tau _c$
and
$\tau = \prod _{c \in G/H} \tau _c$
and
![]() $\Omega (\tau )= \prod _{c \in G /H} \Omega (\tau _c)$
(cf. Lemma 2.9), we can suppose without loss of generality that
$\Omega (\tau )= \prod _{c \in G /H} \Omega (\tau _c)$
(cf. Lemma 2.9), we can suppose without loss of generality that
![]() $G=H$
. Let
$G=H$
. Let
![]() $x {\kern-1pt}\in{\kern-1pt} \Omega (\tau )$
, then
$x {\kern-1pt}\in{\kern-1pt} \Omega (\tau )$
, then
![]() $x \in \tau ^n(X)$
for every
$x \in \tau ^n(X)$
for every
![]() $n {\kern-1pt}\geq{\kern-1pt} 0$
. Thus,
$n {\kern-1pt}\geq{\kern-1pt} 0$
. Thus,
![]() $\tau (x) \in \tau ^{n+1}(X)$
for every
$\tau (x) \in \tau ^{n+1}(X)$
for every
![]() $n \geq 0$
and it follows that
$n \geq 0$
and it follows that
![]() $\tau (x) \in \Omega (\tau )$
. Therefore,
$\tau (x) \in \Omega (\tau )$
. Therefore,
![]() $\tau (\Omega (\tau )) \subset \Omega (\tau )$
. For the converse inclusion, let
$\tau (\Omega (\tau )) \subset \Omega (\tau )$
. For the converse inclusion, let
![]() $y \in \Omega (\tau )$
. By Theorem 9.1, there exists
$y \in \Omega (\tau )$
. By Theorem 9.1, there exists
![]() ${x = (x_{ij}) \in \varprojlim _{i,j \in \mathbb {N}} \Sigma _{ij}}$
such that
${x = (x_{ij}) \in \varprojlim _{i,j \in \mathbb {N}} \Sigma _{ij}}$
such that
![]() $ \Phi (x)=y$
. However, equation (4.7) tells us that
$ \Phi (x)=y$
. However, equation (4.7) tells us that
![]() $\Phi ^{-1}(y) \subset \varprojlim _{i,j \in \mathbb {N}} \Sigma _{ij}$
is the set of backward orbits of y under
$\Phi ^{-1}(y) \subset \varprojlim _{i,j \in \mathbb {N}} \Sigma _{ij}$
is the set of backward orbits of y under
![]() $\tau $
. Hence, we can find
$\tau $
. Hence, we can find
![]() $z \in \Omega (\tau )$
such that
$z \in \Omega (\tau )$
such that
![]() $\tau (z)= y$
. Thus,
$\tau (z)= y$
. Thus,
![]() $\Omega (\tau ) \subset \tau (\Omega (\tau ))$
and the conclusion follows.
$\Omega (\tau ) \subset \tau (\Omega (\tau ))$
and the conclusion follows.
10 Noetherianity of algebraic subshifts of finite type
The goal of this section is to establish the following characterization of algebraic subshifts of finite type by the descending chain property. It extends the linear version in [Reference Ceccherini-Silberstein, Coornaert and Phung16, Theorem 1.1 and Corollary 1.2]. The proof is an application of Theorem 7.1 combined with the construction of an inverse system analogous to the space-time inverse system. More precisely, we obtain the following theorem.
Theorem 10.1. Let G be a finitely generated group and let V be an algebraic variety (respectively an algebraic group) over an algebraically closed field K. Let
![]() $A=V(K)$
and let
$A=V(K)$
and let
![]() $\Sigma \subset A^G$
be a subshift. Consider the following properties:
$\Sigma \subset A^G$
be a subshift. Consider the following properties:
-
(a)
 $\Sigma $
is a subshift of finite type;
$\Sigma $
is a subshift of finite type; -
(b)
 $\Sigma $
is an algebraic (respectively algebraic group) subshift of finite type;
$\Sigma $
is an algebraic (respectively algebraic group) subshift of finite type; -
(c) every descending sequence of algebraic (respectively algebraic group) sofic subshifts of
 $A^G$
such that
$A^G$
such that $$ \begin{align*} \Sigma_0 \supset \Sigma_1 \supset \cdots \supset \Sigma_n \supset \Sigma_{n+1} \supset \cdots \end{align*} $$
$$ \begin{align*} \Sigma_0 \supset \Sigma_1 \supset \cdots \supset \Sigma_n \supset \Sigma_{n+1} \supset \cdots \end{align*} $$
 $\bigcap _{n \geq 0} \Sigma _n = \Sigma $
eventually stabilizes.
$\bigcap _{n \geq 0} \Sigma _n = \Sigma $
eventually stabilizes.
Then we have
![]() $(\mathrm{b}) \implies (\mathrm{a}) \implies (\mathrm{c})$
. Moreover, if
$(\mathrm{b}) \implies (\mathrm{a}) \implies (\mathrm{c})$
. Moreover, if
![]() $\Sigma \subset A^G$
is an algebraic (respectively algebraic group) sofic subshift, then
$\Sigma \subset A^G$
is an algebraic (respectively algebraic group) sofic subshift, then
![]() $(\mathrm{a}) \iff (\mathrm{b}) \iff (\mathrm{c})$
.
$(\mathrm{a}) \iff (\mathrm{b}) \iff (\mathrm{c})$
.
Proof. It is trivial that (b)
![]() $\implies $
(a). Assume that
$\implies $
(a). Assume that
![]() $\Sigma $
is a subshift of finite type. Hence,
$\Sigma $
is a subshift of finite type. Hence,
![]() $\Sigma = \Sigma (D, W)$
, where
$\Sigma = \Sigma (D, W)$
, where
![]() $D \subset G$
is finite and
$D \subset G$
is finite and
![]() $W \subset A^D$
is some subset. Let
$W \subset A^D$
is some subset. Let
![]() $\Sigma _0 \supset \Sigma _1 \supset \cdots $
be a descending sequence of algebraic (respectively algebraic group) sofic subshifts of
$\Sigma _0 \supset \Sigma _1 \supset \cdots $
be a descending sequence of algebraic (respectively algebraic group) sofic subshifts of
![]() $A^G$
whose intersection is
$A^G$
whose intersection is
![]() $\Sigma $
. Let
$\Sigma $
. Let
![]() $M \subset G$
be a finite generating subset containing
$M \subset G$
be a finite generating subset containing
![]() ${\{1_G\} \cup D}$
and such that
${\{1_G\} \cup D}$
and such that
![]() $M=M^{-1}$
. Consider the inverse system
$M=M^{-1}$
. Consider the inverse system
![]() $(X_{ij})_{i,j \in \mathbb {N}}$
defined by
$(X_{ij})_{i,j \in \mathbb {N}}$
defined by ![]() . Remark that
. Remark that
![]() $X_{i,j+1} \subset X_{ij}$
since
$X_{i,j+1} \subset X_{ij}$
since
![]() $\Sigma _{j+1} \subset \Sigma _j$
for all
$\Sigma _{j+1} \subset \Sigma _j$
for all
![]() $i, j \in \mathbb {N}$
. We define the unit transition maps
$i, j \in \mathbb {N}$
. We define the unit transition maps
![]() $p_{ij} \colon X_{i+1, j} \to X_{ij}$
by
$p_{ij} \colon X_{i+1, j} \to X_{ij}$
by
![]() $p_{ij}(x)= x\vert _{M^{i}}$
for every
$p_{ij}(x)= x\vert _{M^{i}}$
for every
![]() $x \in X_{i+1, j}$
and
$x \in X_{i+1, j}$
and
![]() $q_{ij} \colon X_{i, j+1} \to X_{ij}$
simply as the inclusion maps.
$q_{ij} \colon X_{i, j+1} \to X_{ij}$
simply as the inclusion maps.
For all
![]() $i, j \in \mathbb {N}$
, Theorem 7.1 implies that every
$i, j \in \mathbb {N}$
, Theorem 7.1 implies that every
![]() $X_{ij}$
is a complete variety (respectively an algebraic group) over K. By Noetherianity of the Zariski topology, the decreasing sequence
$X_{ij}$
is a complete variety (respectively an algebraic group) over K. By Noetherianity of the Zariski topology, the decreasing sequence
![]() $(X_{0j})_{j \in ~\mathbb {N}}$
of algebraic closed subsets of
$(X_{0j})_{j \in ~\mathbb {N}}$
of algebraic closed subsets of
![]() $A^{M}$
eventually stabilizes, say,
$A^{M}$
eventually stabilizes, say,
![]() ${X_{0j}= X_{0m}}$
for all
${X_{0j}= X_{0m}}$
for all
![]() $j \in \mathbb {N}$
for some
$j \in \mathbb {N}$
for some
![]() $m \in \mathbb {N}$
. Let
$m \in \mathbb {N}$
. Let ![]() , then
, then ![]() is an algebraic (respectively algebraic group) subshift of finite type. It is clear that
is an algebraic (respectively algebraic group) subshift of finite type. It is clear that
![]() $\Sigma _m \subset \Sigma '$
and hence
$\Sigma _m \subset \Sigma '$
and hence
![]() $\Sigma \subset \Sigma '$
. We shall prove the converse inclusion.
$\Sigma \subset \Sigma '$
. We shall prove the converse inclusion.
Let
![]() $w \in W'$
. We construct an inverse subsystem
$w \in W'$
. We construct an inverse subsystem
![]() $(Z_{ij})_{i \geq m, j \geq 0}$
of
$(Z_{ij})_{i \geq m, j \geq 0}$
of
![]() $(X_{ij})_{i \geq m, j \geq 0}$
as follows. For
$(X_{ij})_{i \geq m, j \geq 0}$
as follows. For
![]() $i \geq m$
, let
$i \geq m$
, let ![]() which is clearly an algebraic closed subvariety (respectively a translate of an algebraic subgroup) of
which is clearly an algebraic closed subvariety (respectively a translate of an algebraic subgroup) of
![]() $X_{i0}$
. For
$X_{i0}$
. For
![]() $i \geq m, j \geq 0$
, we define an algebraic closed subvariety (respectively a translate of an algebraic subgroup (by Theorem 7.1)) of
$i \geq m, j \geq 0$
, we define an algebraic closed subvariety (respectively a translate of an algebraic subgroup (by Theorem 7.1)) of
![]() $X_{ij}$
as follows:
$X_{ij}$
as follows:
The transition maps of
![]() $(Z_{ij})_{i \geq m, j \geq 0}$
are well defined as the restrictions of the transition maps of the system
$(Z_{ij})_{i \geq m, j \geq 0}$
are well defined as the restrictions of the transition maps of the system
![]() $(X_{ij})_{i \geq m, j \geq 0}$
. These transition maps have Zariski closed images (by Remark 2.1).
$(X_{ij})_{i \geq m, j \geq 0}$
. These transition maps have Zariski closed images (by Remark 2.1).
By our construction, each
![]() $Z_{ij}$
is clearly non-empty. Hence, Lemma 3.3 implies that there exists
$Z_{ij}$
is clearly non-empty. Hence, Lemma 3.3 implies that there exists
![]() $x = (x_{ij})_{i \geq m,j \geq 0} \in \varprojlim Z_{ij}$
. Let
$x = (x_{ij})_{i \geq m,j \geq 0} \in \varprojlim Z_{ij}$
. Let
![]() $y \in A^G$
be defined by
$y \in A^G$
be defined by
![]() $y(g)= x_{i0}(g)$
for every
$y(g)= x_{i0}(g)$
for every
![]() $g \in G$
and any large enough
$g \in G$
and any large enough
![]() $i\geq m$
such that
$i\geq m$
such that
![]() $g \in M^{i}$
. Observe that
$g \in M^{i}$
. Observe that
![]() $x_{ij} = x_{ik}$
for every
$x_{ij} = x_{ik}$
for every
![]() $i \geq m$
and
$i \geq m$
and
![]() $0 \leq j \leq k$
since the vertical transition maps
$0 \leq j \leq k$
since the vertical transition maps
![]() $X_{ik} \to X_{ij}$
are simply inclusions. Consequently, for every
$X_{ik} \to X_{ij}$
are simply inclusions. Consequently, for every
![]() $n \in \mathbb {N}$
, we have
$n \in \mathbb {N}$
, we have
![]() $y \in \Sigma _n$
by equation (4.6) since
$y \in \Sigma _n$
by equation (4.6) since
![]() $\Sigma _n$
is closed in
$\Sigma _n$
is closed in
![]() $A^G$
(cf. Corollary 8.2). Hence,
$A^G$
(cf. Corollary 8.2). Hence,
![]() $y \in \Sigma $
. By construction,
$y \in \Sigma $
. By construction,
![]() $y\vert _{M^m} = w$
. Since w was arbitrary, this shows that
$y\vert _{M^m} = w$
. Since w was arbitrary, this shows that
![]() $W' \subset \Sigma _{M^m}$
. Hence,
$W' \subset \Sigma _{M^m}$
. Hence,
![]() $\Sigma ' = \Sigma (M^m, W') \subset \Sigma (M^m, \Sigma _{M^m}) = \Sigma $
. The last equality follows from Lemma 5.1 as
$\Sigma ' = \Sigma (M^m, W') \subset \Sigma (M^m, \Sigma _{M^m}) = \Sigma $
. The last equality follows from Lemma 5.1 as
![]() $D \subset M^m$
. Therefore,
$D \subset M^m$
. Therefore,
![]() $\Sigma ' = \Sigma $
and
$\Sigma ' = \Sigma $
and
![]() $\Sigma _n= \Sigma $
for all
$\Sigma _n= \Sigma $
for all
![]() $n \geq m$
. This proves that (a)
$n \geq m$
. This proves that (a)
![]() $\implies $
(c).
$\implies $
(c).
Suppose now that
![]() $\Sigma \subset A^G$
is an algebraic (respectively algebraic group) sofic subshift which is not a subshift of finite type. Let
$\Sigma \subset A^G$
is an algebraic (respectively algebraic group) sofic subshift which is not a subshift of finite type. Let
![]() $M \subset G$
be a finite generating subset containing
$M \subset G$
be a finite generating subset containing
![]() $\{1_G\}$
such that
$\{1_G\}$
such that
![]() $M=M^{-1}$
. For every
$M=M^{-1}$
. For every
![]() $n \in \mathbb {N}$
, consider
$n \in \mathbb {N}$
, consider ![]() (as in §4). Theorem 7.1 tells us that
(as in §4). Theorem 7.1 tells us that
![]() $W_n$
is a complete algebraic subvariety (respectively an algebraic subgroup) of
$W_n$
is a complete algebraic subvariety (respectively an algebraic subgroup) of
![]() $A^{M^n}$
. Set
$A^{M^n}$
. Set ![]() for every
for every
![]() $n \in \mathbb {N}$
, then
$n \in \mathbb {N}$
, then
![]() $\Sigma _n$
is an algebraic (respectively algebraic group) subshift of finite type. As
$\Sigma _n$
is an algebraic (respectively algebraic group) subshift of finite type. As
![]() $(\Sigma _{M^{n+1}})_{M^n} = \Sigma _{M^n}$
, it is clear that
$(\Sigma _{M^{n+1}})_{M^n} = \Sigma _{M^n}$
, it is clear that
![]() ${\Sigma \subset \Sigma _{n+1} \subset \Sigma _n}$
for every
${\Sigma \subset \Sigma _{n+1} \subset \Sigma _n}$
for every
![]() $n \in \mathbb {N}$
. We claim that
$n \in \mathbb {N}$
. We claim that
![]() $\Sigma = \bigcap _{n \in \mathbb {N}} \Sigma _n$
. Indeed, we only need to prove that
$\Sigma = \bigcap _{n \in \mathbb {N}} \Sigma _n$
. Indeed, we only need to prove that
![]() $\bigcap _{n \in \mathbb {N}} \Sigma _n \subset \Sigma $
. Let
$\bigcap _{n \in \mathbb {N}} \Sigma _n \subset \Sigma $
. Let
![]() $x \in \bigcap _{n \in \mathbb {N}} \Sigma _n$
. Then by definition of
$x \in \bigcap _{n \in \mathbb {N}} \Sigma _n$
. Then by definition of
![]() $\Sigma _n$
, we find that
$\Sigma _n$
, we find that
![]() $x\vert _{M^n} \in W_n= \Sigma _{M^n}$
for every
$x\vert _{M^n} \in W_n= \Sigma _{M^n}$
for every
![]() $n \in \mathbb {N}$
. Thus, since
$n \in \mathbb {N}$
. Thus, since
![]() $\Sigma $
is closed (cf. Corollary 8.2),
$\Sigma $
is closed (cf. Corollary 8.2),
![]() ${x \in \varprojlim _{n \in \mathbb {N}} \Sigma _{M^n} =\Sigma }$
(cf. equation (4.6)) and hence
${x \in \varprojlim _{n \in \mathbb {N}} \Sigma _{M^n} =\Sigma }$
(cf. equation (4.6)) and hence
![]() $\bigcap _{n \in \mathbb {N}} \Sigma _n \subset \Sigma $
. However, the descending sequence
$\bigcap _{n \in \mathbb {N}} \Sigma _n \subset \Sigma $
. However, the descending sequence
![]() $(\Sigma _n)_{n \in \mathbb {N}}$
cannot stabilize since otherwise the subshift
$(\Sigma _n)_{n \in \mathbb {N}}$
cannot stabilize since otherwise the subshift
![]() $\Sigma $
would be of finite type. This shows that (c)
$\Sigma $
would be of finite type. This shows that (c)
![]() $\implies $
(a) if
$\implies $
(a) if
![]() $\Sigma $
is an algebraic (respectively algebraic group) sofic subshift. The proof is complete.
$\Sigma $
is an algebraic (respectively algebraic group) sofic subshift. The proof is complete.
Examples 10.2. (Markov properties)
The examples below provide the original sources and motivations for our main result in this section (Theorem 10.1).
(a) Let G be a group and let A be a finite group. Equip the configuration space
![]() $A^G$
with the product group structure (thus, given two configurations
$A^G$
with the product group structure (thus, given two configurations
![]() $x,y \in A^G$
, their product is defined as the configuration
$x,y \in A^G$
, their product is defined as the configuration
![]() $xy \in A^G$
given by
$xy \in A^G$
given by ![]() for all
for all
![]() $g \in G$
). A closed subshift
$g \in G$
). A closed subshift
![]() $X \subset A^G$
which is also a subgroup of
$X \subset A^G$
which is also a subgroup of
![]() $A^G$
is called a group subshift. Group subshifts
$A^G$
is called a group subshift. Group subshifts
![]() $X \subset A^{\mathbb {Z}}$
are called Markov subgroups in [Reference Kitchens28, §6.3], and were studied and classified up to topological conjugacy by Kitchens in [Reference Kitchens27] (see also [Reference Kitchens28, Theorem 6.3.3]).
$X \subset A^{\mathbb {Z}}$
are called Markov subgroups in [Reference Kitchens28, §6.3], and were studied and classified up to topological conjugacy by Kitchens in [Reference Kitchens27] (see also [Reference Kitchens28, Theorem 6.3.3]).
One says that a group G is of finite Markov type if for any finite group A, every group subshift
![]() $\Sigma \subset A^G$
is of finite type. The finite Markov type property is a weakening of the Markov type property introduced by Schmidt in [Reference Schmidt54, Definition 4.1].
$\Sigma \subset A^G$
is of finite type. The finite Markov type property is a weakening of the Markov type property introduced by Schmidt in [Reference Schmidt54, Definition 4.1].
The following hold:
-
(i) every finite group is of finite Markov type;
-
(ii) the additive group
 $\mathbb {Z}$
is of finite Markov type. This result was established by Kitchens in [Reference Kitchens27, Proposition 4] (see also [Reference Kitchens28, Lemma 6.3.5], [Reference Lind and Marcus30, Exercise 2.1.11], and [Reference Ceccherini-Silberstein and Coornaert13, Exercise 1.114]);
$\mathbb {Z}$
is of finite Markov type. This result was established by Kitchens in [Reference Kitchens27, Proposition 4] (see also [Reference Kitchens28, Lemma 6.3.5], [Reference Lind and Marcus30, Exercise 2.1.11], and [Reference Ceccherini-Silberstein and Coornaert13, Exercise 1.114]); -
(iii) every subgroup of a group of finite Markov type is finitely generated (this is also expressed by saying that groups of finite Markov type are Noetherian). As a consequence, every group of finite Markov type is countable and contains no non-abelian free subgroups;
-
(iv) every quotient of a group of finite Markov type is of finite Markov type;
-
(v) every group containing a finite index subgroup of finite Markov type is itself of finite Markov type;
-
(vi) a group G is of finite Markov type if and only if G is countable and, for any finite group A, every descending sequence of group subshifts of
 $A^G$
eventually stabilizes, that is, there exists
$A^G$
eventually stabilizes, that is, there exists $$ \begin{align*} X_0 \supset X_1 \supset X_2 \supset \cdots \supset X_n \supset X_{n+1} \supset \cdots \end{align*} $$
$$ \begin{align*} X_0 \supset X_1 \supset X_2 \supset \cdots \supset X_n \supset X_{n+1} \supset \cdots \end{align*} $$
 $n_0 \in \mathbb {N}$
such that
$n_0 \in \mathbb {N}$
such that
 $X_n = X_{n_0}$
for all
$X_n = X_{n_0}$
for all
 ${n \geq n_0}$
(cf. [Reference Ceccherini-Silberstein and Coornaert13, Exercise 1.112]).
${n \geq n_0}$
(cf. [Reference Ceccherini-Silberstein and Coornaert13, Exercise 1.112]).
In other words, the class of groups of finite Markov type is closed under the operations of taking subgroups, quotients, and extensions by finite or cyclic groups. As a consequence, all finitely generated abelian groups are of finite Markov type (a result observed by Kitchens and Schmidt [Reference Kitchens and Schmidt26, Remark 3.10(2)]). In fact, more generally, the class of groups of finite Markov type contains all polycyclic-by-finite groups (cf. [Reference Ceccherini-Silberstein and Coornaert13, Exercise 4.37]), a particular case of [Reference Schmidt54, Theorem I.4.2]. The question whether or not every group of finite Markov type is polycyclic-by-finite remains, at our present knowledge, open.
(b) Let G be a group, let K be a field, and let A be a finite-dimensional vector space over K. Equip the configuration space
![]() $A^G$
with the product vector space structure (thus, given a scalar
$A^G$
with the product vector space structure (thus, given a scalar
![]() $\unicode{x3bb} \in K$
and two configurations
$\unicode{x3bb} \in K$
and two configurations
![]() $x,y \in A^G$
, one defines the configuration
$x,y \in A^G$
, one defines the configuration
![]() ${\unicode{x3bb} x \in A^G}$
(respectively
${\unicode{x3bb} x \in A^G}$
(respectively
![]() $x + y \in A^G$
) by setting
$x + y \in A^G$
) by setting ![]() (respectively
(respectively ![]() ) for all
) for all
![]() $g \in G$
. A closed subshift
$g \in G$
. A closed subshift
![]() $\Sigma \subset A^G$
which is also a vector subspace of
$\Sigma \subset A^G$
which is also a vector subspace of
![]() $A^G$
is called a linear subshift. One says that a group G is of K-linear Markov type if for any finite-dimensional vector space A over K, every linear subshift
$A^G$
is called a linear subshift. One says that a group G is of K-linear Markov type if for any finite-dimensional vector space A over K, every linear subshift
![]() $\Sigma \subset A^G$
is of finite type. Analogous properties to items (i)–(vi) in point (a), for groups of K-linear Markov type, are shown in [Reference Ceccherini-Silberstein, Coornaert and Phung16, §6] (see also [Reference Phung42] for some more general results). In other words, the class of K-linear Markov groups is closed under the operations of taking subgroups, quotients, and extensions by finite or cyclic groups, and contains all polycyclic-by-finite groups (cf. [Reference Ceccherini-Silberstein, Coornaert and Phung16, Corollary 1.4]). In addition, one has the following characterization: a group G is of K-linear Markov type if and only if its group ring
$\Sigma \subset A^G$
is of finite type. Analogous properties to items (i)–(vi) in point (a), for groups of K-linear Markov type, are shown in [Reference Ceccherini-Silberstein, Coornaert and Phung16, §6] (see also [Reference Phung42] for some more general results). In other words, the class of K-linear Markov groups is closed under the operations of taking subgroups, quotients, and extensions by finite or cyclic groups, and contains all polycyclic-by-finite groups (cf. [Reference Ceccherini-Silberstein, Coornaert and Phung16, Corollary 1.4]). In addition, one has the following characterization: a group G is of K-linear Markov type if and only if its group ring
![]() $K[G]$
is one-sided Noetherian [Reference Ceccherini-Silberstein, Coornaert and Phung16, Theorem 1.3].
$K[G]$
is one-sided Noetherian [Reference Ceccherini-Silberstein, Coornaert and Phung16, Theorem 1.3].
11 Proof of Theorem 1.3
For item (i), we know that
![]() $\Omega (\tau )$
is G-invariant by the G-equivariance of
$\Omega (\tau )$
is G-invariant by the G-equivariance of
![]() $\tau $
. However, as the set of algebraic cellular automata over
$\tau $
. However, as the set of algebraic cellular automata over
![]() $\Sigma $
is closed under the composition of maps (cf. [Reference Ceccherini-Silberstein, Coornaert and Phung14, Proposition 3.3] for the case of full shifts, the general case is proved similarly), the map
$\Sigma $
is closed under the composition of maps (cf. [Reference Ceccherini-Silberstein, Coornaert and Phung14, Proposition 3.3] for the case of full shifts, the general case is proved similarly), the map
![]() $\tau ^n \colon \Sigma \to \Sigma $
is an algebraic cellular automaton for every
$\tau ^n \colon \Sigma \to \Sigma $
is an algebraic cellular automaton for every
![]() $n \geq 1$
. It then follows from Theorem 8.1 that
$n \geq 1$
. It then follows from Theorem 8.1 that
![]() $\tau ^n(\Sigma )$
is closed in
$\tau ^n(\Sigma )$
is closed in
![]() $A^G$
for every
$A^G$
for every
![]() $n \geq 1$
and thus
$n \geq 1$
and thus
![]() $\Omega (\tau ) = \bigcap _{n \geq 1} \tau ^n(\Sigma )$
is also closed in
$\Omega (\tau ) = \bigcap _{n \geq 1} \tau ^n(\Sigma )$
is also closed in
![]() $A^G$
. This shows that
$A^G$
. This shows that
![]() $\Omega (\tau )$
is a closed subshift of
$\Omega (\tau )$
is a closed subshift of
![]() $A^G$
and item (i) is proved.
$A^G$
and item (i) is proved.
For item (v), let
![]() $z \in \Sigma \cap \operatorname {\mathrm {Fix}}(H)$
for some subgroup
$z \in \Sigma \cap \operatorname {\mathrm {Fix}}(H)$
for some subgroup
![]() $H \subset G$
. Let
$H \subset G$
. Let
![]() $F \subset G$
be the subgroup generated by a finite subset M containing
$F \subset G$
be the subgroup generated by a finite subset M containing
![]() $\{1_G\}$
and memory sets of
$\{1_G\}$
and memory sets of
![]() $\tau $
,
$\tau $
,
![]() $\Sigma $
, and such that
$\Sigma $
, and such that
![]() $M=M^{-1}$
. Note that
$M=M^{-1}$
. Note that
![]() $z\vert _F$
is fixed by the subgroup
$z\vert _F$
is fixed by the subgroup ![]() of F. Consider the space-time inverse system
of F. Consider the space-time inverse system
![]() $(\Sigma _{ij})_{i, j \in \mathbb {N}}$
associated with the restriction
$(\Sigma _{ij})_{i, j \in \mathbb {N}}$
associated with the restriction
![]() $\tau _F$
and M as in Definition 4.1. Keep the notation in §4. For all
$\tau _F$
and M as in Definition 4.1. Keep the notation in §4. For all
![]() $i, j \in \mathbb {N}$
, let
$i, j \in \mathbb {N}$
, let
be the restriction to
![]() $M^{i+j}$
of R-fixed points in
$M^{i+j}$
of R-fixed points in
![]() $A^H$
. Clearly,
$A^H$
. Clearly,
![]() $\Delta _{ij}$
is respectively a closed subvariety, a complete algebraic subvariety, and an algebraic subgroup of
$\Delta _{ij}$
is respectively a closed subvariety, a complete algebraic subvariety, and an algebraic subgroup of
![]() $A^{M^{i+j}}$
in cases (H1), (H2), and (H3). Define also
$A^{M^{i+j}}$
in cases (H1), (H2), and (H3). Define also ![]() .
.
Note that
![]() $\tau _F$
sends R-fixed points to R-fixed points. Hence, by restricting the transition maps to the sets
$\tau _F$
sends R-fixed points to R-fixed points. Hence, by restricting the transition maps to the sets
![]() $Z_{ij}$
, we obtain a well-defined inverse subsystem of
$Z_{ij}$
, we obtain a well-defined inverse subsystem of
![]() $(\Sigma _{ij})_{i,j \in \mathbb {N}}$
. Theorem 7.1 implies that respectively in each case (H1), (H2), and (H3), the set
$(\Sigma _{ij})_{i,j \in \mathbb {N}}$
. Theorem 7.1 implies that respectively in each case (H1), (H2), and (H3), the set
![]() $Z_{ij} \subset A^{M^{i+j}}$
is a countably proconstructible subset, a complete algebraic subvariety, and an algebraic subgroup. Each
$Z_{ij} \subset A^{M^{i+j}}$
is a countably proconstructible subset, a complete algebraic subvariety, and an algebraic subgroup. Each
![]() $Z_{ij}$
is non-empty since it contains
$Z_{ij}$
is non-empty since it contains
![]() $z\vert _{M^{i+j}}$
. Hence, Lemmas 3.2 and 3.3 imply that there exists
$z\vert _{M^{i+j}}$
. Hence, Lemmas 3.2 and 3.3 imply that there exists
![]() $x \in \varprojlim _{i,j \in \mathbb {N}} Z_{ij} \subset \varprojlim _{i,j \in \mathbb {N}} \Sigma _{ij}$
. By Lemma 4.4, we obtain
$x \in \varprojlim _{i,j \in \mathbb {N}} Z_{ij} \subset \varprojlim _{i,j \in \mathbb {N}} \Sigma _{ij}$
. By Lemma 4.4, we obtain
![]() $y= \Phi (x) \in \Omega (\tau _F) \subset A^H$
. By our construction, y is fixed by R. By Lemma 2.9(i),
$y= \Phi (x) \in \Omega (\tau _F) \subset A^H$
. By our construction, y is fixed by R. By Lemma 2.9(i),
![]() ${\Omega (\tau ) = \Omega (\tau _F)^{G/F}}$
. Thus, y induces a configuration of
${\Omega (\tau ) = \Omega (\tau _F)^{G/F}}$
. Thus, y induces a configuration of
![]() $\Omega (\tau )$
fixed by H. This proves item (v).
$\Omega (\tau )$
fixed by H. This proves item (v).
To finish the proof of Theorem 1.3, note that item (ii) follows from Corollary 9.2 and item (iii) follows from the general property
![]() $\operatorname {\mathrm {Per}}(\tau ) \subset \operatorname {\mathrm {R}}(\tau ) \subset \operatorname {\mathrm {NW}}(\tau ) \subset \operatorname {\mathrm {CR}}(\tau )$
and from the inclusion
$\operatorname {\mathrm {Per}}(\tau ) \subset \operatorname {\mathrm {R}}(\tau ) \subset \operatorname {\mathrm {NW}}(\tau ) \subset \operatorname {\mathrm {CR}}(\tau )$
and from the inclusion
![]() $\operatorname {\mathrm {CR}}(\tau ) \subset \Omega (\tau ) $
proved in Corollary 8.3. Finally, in case (H2) (respectively in case (H3)), item (iv) is a direct consequence of the implication (a)
$\operatorname {\mathrm {CR}}(\tau ) \subset \Omega (\tau ) $
proved in Corollary 8.3. Finally, in case (H2) (respectively in case (H3)), item (iv) is a direct consequence of the implication (a)
![]() $\implies $
(c) in Theorem 10.1 applied to
$\implies $
(c) in Theorem 10.1 applied to
![]() $\Omega (\tau )$
and the decreasing sequence of algebraic (respectively algebraic group) sofic subshifts
$\Omega (\tau )$
and the decreasing sequence of algebraic (respectively algebraic group) sofic subshifts
![]() $\tau (\Sigma ) \supset \tau ^2(\Sigma ) \supset \cdots \supset \tau ^n(\Sigma ) \supset \tau ^{n+1}(\Sigma ) \supset \cdots $
which satisfies
$\tau (\Sigma ) \supset \tau ^2(\Sigma ) \supset \cdots \supset \tau ^n(\Sigma ) \supset \tau ^{n+1}(\Sigma ) \supset \cdots $
which satisfies ![]() by definition.
by definition.
12 Proof of Theorem 1.4
It is clear that (a)
![]() $\implies $
(b). For the converse implication, suppose that
$\implies $
(b). For the converse implication, suppose that
![]() $\Omega (\tau )= \{x_0\}$
for some
$\Omega (\tau )= \{x_0\}$
for some
![]() $x_0 \in \Sigma $
. As
$x_0 \in \Sigma $
. As
![]() $\Omega (\tau )$
is G-invariant, there exists an element denoted by
$\Omega (\tau )$
is G-invariant, there exists an element denoted by
![]() $0 \in A$
such that
$0 \in A$
such that
![]() $x_0(g)= 0$
for every
$x_0(g)= 0$
for every
![]() $g \in G$
, that is,
$g \in G$
, that is,
![]() $x_0=0^G$
. Let
$x_0=0^G$
. Let
![]() $M\subset G$
be a finite subset containing a memory set of
$M\subset G$
be a finite subset containing a memory set of
![]() $\tau $
and a memory set of
$\tau $
and a memory set of
![]() $\Sigma $
such that
$\Sigma $
such that
![]() $1_G \in M$
and
$1_G \in M$
and
![]() $M=M^{-1}$
. Let H be the subgroup generated by M and consider the restriction
$M=M^{-1}$
. Let H be the subgroup generated by M and consider the restriction
![]() $\tau _H$
. By Lemma 2.9, we deduce that
$\tau _H$
. By Lemma 2.9, we deduce that
![]() $\Omega (\tau _H)$
must be a singleton as well and
$\Omega (\tau _H)$
must be a singleton as well and
![]() $\tau $
is nilpotent if
$\tau $
is nilpotent if
![]() $\tau _H$
is. Thus, up to replacing G by H, we can suppose that G is generated by M.
$\tau _H$
is. Thus, up to replacing G by H, we can suppose that G is generated by M.
We construct an inverse subsystem
![]() $(\Sigma ^*_{ij})_{i, j \in \mathbb {N}}$
of the space-time inverse system
$(\Sigma ^*_{ij})_{i, j \in \mathbb {N}}$
of the space-time inverse system
![]() $(\Sigma _{ij})_{i, j \in \mathbb {N}}$
associated with
$(\Sigma _{ij})_{i, j \in \mathbb {N}}$
associated with
![]() $\tau $
and the memory set M (cf. Definition 4.1) as follows. Let
$\tau $
and the memory set M (cf. Definition 4.1) as follows. Let ![]() for every
for every
![]() $i \geq 0$
. For all
$i \geq 0$
. For all
![]() $i \geq 0$
and
$i \geq 0$
and
![]() $j \geq 1$
, we define
$j \geq 1$
, we define
The unit transition maps
![]() $q^*_{ij} \colon \Sigma ^*_{i, j+1} \to \Sigma ^*_{i j}$
and
$q^*_{ij} \colon \Sigma ^*_{i, j+1} \to \Sigma ^*_{i j}$
and
![]() $p^*_{ij} \colon \Sigma ^*_{i+1, j} \to \Sigma ^*_{ij}$
of the inverse subsystem
$p^*_{ij} \colon \Sigma ^*_{i+1, j} \to \Sigma ^*_{ij}$
of the inverse subsystem
![]() $(\Sigma ^*_{ij})_{i, j \in \mathbb {N}}$
are defined respectively by the restrictions of the transition maps
$(\Sigma ^*_{ij})_{i, j \in \mathbb {N}}$
are defined respectively by the restrictions of the transition maps
![]() $q_{ij}$
and
$q_{ij}$
and
![]() $p_{ij}$
of
$p_{ij}$
of
![]() $(\Sigma _{ij})_{i, j \in \mathbb {N}}$
.
$(\Sigma _{ij})_{i, j \in \mathbb {N}}$
.
Assume in contrast that
![]() $\tau $
is not nilpotent. We claim that
$\tau $
is not nilpotent. We claim that
![]() $\Sigma ^*_{ij} \neq \varnothing $
for all
$\Sigma ^*_{ij} \neq \varnothing $
for all
![]() $i, j \in \mathbb {N}$
. Otherwise,
$i, j \in \mathbb {N}$
. Otherwise,
![]() $\Sigma ^*_{ij}= \varnothing $
for some
$\Sigma ^*_{ij}= \varnothing $
for some
![]() $i, j \in \mathbb {N}$
. If
$i, j \in \mathbb {N}$
. If
![]() $j=0$
, then
$j=0$
, then
![]() $\Sigma ^*_{i0}= \varnothing $
, that is,
$\Sigma ^*_{i0}= \varnothing $
, that is,
![]() $x(1_G) = 0$
for all
$x(1_G) = 0$
for all
![]() $x \in \Sigma _{i0}$
, and since
$x \in \Sigma _{i0}$
, and since
![]() $\Sigma $
is G-invariant and
$\Sigma $
is G-invariant and
![]() $1_G \in M^{i+j}$
, we deduce that
$1_G \in M^{i+j}$
, we deduce that
![]() $\Sigma = \{0^G\}$
. Hence,
$\Sigma = \{0^G\}$
. Hence,
![]() $\tau $
is trivially nilpotent and we arrive at a contradiction. Thus,
$\tau $
is trivially nilpotent and we arrive at a contradiction. Thus,
![]() $j \geq 1$
and by definition of
$j \geq 1$
and by definition of
![]() $\Sigma _{ij}$
, we have for every
$\Sigma _{ij}$
, we have for every
![]() $x \in \Sigma _{ij}$
that
$x \in \Sigma _{ij}$
that
Since
![]() $\tau ^{i+j}$
is G-equivariant, it follows that
$\tau ^{i+j}$
is G-equivariant, it follows that
![]() $\tau ^{i+j}(x)=0^G$
for every
$\tau ^{i+j}(x)=0^G$
for every
![]() $x \in \Sigma $
, which contradicts the assumption that
$x \in \Sigma $
, which contradicts the assumption that
![]() $\tau $
is not nilpotent. This proves the claim, that is,
$\tau $
is not nilpotent. This proves the claim, that is,
![]() $\Sigma ^*_{ij} \neq \varnothing $
for all
$\Sigma ^*_{ij} \neq \varnothing $
for all
![]() $i, j \in \mathbb {N}$
. We are going to show that
$i, j \in \mathbb {N}$
. We are going to show that
Indeed, equation (12.1) is a direct application of Theorem 7.1 and Lemma 3.2 to the inverse system
![]() $(\Sigma ^*_{ij})_{i, j \in \mathbb {N}}$
in case (H1). For cases (H2) and (H3), observe that for every
$(\Sigma ^*_{ij})_{i, j \in \mathbb {N}}$
in case (H1). For cases (H2) and (H3), observe that for every
![]() $(i, j) \prec (k, l)$
in
$(i, j) \prec (k, l)$
in
![]() $\mathbb {N}^2$
, we have
$\mathbb {N}^2$
, we have
where
![]() $F_{(i,j), (k,l)} \colon \Sigma _{kl} \to \Sigma _{ij}$
is the transition map of the inverse system
$F_{(i,j), (k,l)} \colon \Sigma _{kl} \to \Sigma _{ij}$
is the transition map of the inverse system
![]() $(\Sigma _{ij})_{i, j \in \mathbb {N}}$
. Indeed, by definition of
$(\Sigma _{ij})_{i, j \in \mathbb {N}}$
. Indeed, by definition of
![]() $\Sigma ^*_{kl}$
and
$\Sigma ^*_{kl}$
and
![]() $\Sigma ^*_{ij}$
, and using the equality
$\Sigma ^*_{ij}$
, and using the equality
![]() $F_{(i,0),(k,l)} = F_{(i,0),(i,j)} \circ F_{(i,j), (k,l)}$
, we see that
$F_{(i,0),(k,l)} = F_{(i,0),(i,j)} \circ F_{(i,j), (k,l)}$
, we see that
 $$ \begin{align*} F_{(i,j), (k,l)} (\Sigma^*_{k,l}) & = F_{(i,j), (k,l)} (\Sigma_{k,l} \setminus F^{-1}_{(i,0),(k,l)}(\Sigma_{i,0} \setminus \Sigma^*_{i,0}) ) \\ & \supset F_{(i,j), (k,l)} (\Sigma_{kl}) \setminus F_{(i,j), (k,l)}(F^{-1}_{(i,0),(k,l)}(\Sigma_{i0} \setminus A^*_{i0}) ) \\ & \supset F_{(i,j), (k,l)} (\Sigma_{kl}) \setminus F^{-1}_{(i,0),(i,j)}(\Sigma_{i0} \setminus \Sigma^*_{i0}) \\ & = F_{(i,j), (k,l)} (\Sigma_{kl}) \setminus (\Sigma_{ij} \setminus \Sigma^*_{ij}) \\ & = F_{(i,j), (k,l)} (\Sigma_{kl}) \cap \Sigma^*_{ij}. \end{align*} $$
$$ \begin{align*} F_{(i,j), (k,l)} (\Sigma^*_{k,l}) & = F_{(i,j), (k,l)} (\Sigma_{k,l} \setminus F^{-1}_{(i,0),(k,l)}(\Sigma_{i,0} \setminus \Sigma^*_{i,0}) ) \\ & \supset F_{(i,j), (k,l)} (\Sigma_{kl}) \setminus F_{(i,j), (k,l)}(F^{-1}_{(i,0),(k,l)}(\Sigma_{i0} \setminus A^*_{i0}) ) \\ & \supset F_{(i,j), (k,l)} (\Sigma_{kl}) \setminus F^{-1}_{(i,0),(i,j)}(\Sigma_{i0} \setminus \Sigma^*_{i0}) \\ & = F_{(i,j), (k,l)} (\Sigma_{kl}) \setminus (\Sigma_{ij} \setminus \Sigma^*_{ij}) \\ & = F_{(i,j), (k,l)} (\Sigma_{kl}) \cap \Sigma^*_{ij}. \end{align*} $$
However, clearly
![]() $F_{(i,j), (k,l)} (\Sigma ^*_{kl}) \subset F_{(i,j), (k,l)} (\Sigma _{kl}) \cap \Sigma ^*_{ij}$
, and equation (12.2) is proved.
$F_{(i,j), (k,l)} (\Sigma ^*_{kl}) \subset F_{(i,j), (k,l)} (\Sigma _{kl}) \cap \Sigma ^*_{ij}$
, and equation (12.2) is proved.
In cases (H2) and (H3), the set
![]() $F_{(i,j), (k,l)}(\Sigma _{kl})$
is closed in
$F_{(i,j), (k,l)}(\Sigma _{kl})$
is closed in
![]() $\Sigma _{ij}$
by Remarks 2.1, 4.3, and Theorem 7.1. We infer from equation (12.2) that
$\Sigma _{ij}$
by Remarks 2.1, 4.3, and Theorem 7.1. We infer from equation (12.2) that
![]() $F_{(i,j), (k,l)} (\Sigma ^*_{kl})$
is a Zariski closed subset of
$F_{(i,j), (k,l)} (\Sigma ^*_{kl})$
is a Zariski closed subset of
![]() $\Sigma ^*_{ij}$
. Therefore,
$\Sigma ^*_{ij}$
. Therefore,
![]() $\varprojlim _{i, j \in \mathbb {N}} \Sigma ^{*}_{ij} \neq \varnothing $
results from Lemma 3.3 and equation (12.1) is proved in all cases.
$\varprojlim _{i, j \in \mathbb {N}} \Sigma ^{*}_{ij} \neq \varnothing $
results from Lemma 3.3 and equation (12.1) is proved in all cases.
We can thus choose
![]() $x =(x_{ij})_{i, j \in \mathbb {N}} \in \varprojlim _{i,j \in \mathbb {N}} \Sigma ^{*}_{ij}$
. Let
$x =(x_{ij})_{i, j \in \mathbb {N}} \in \varprojlim _{i,j \in \mathbb {N}} \Sigma ^{*}_{ij}$
. Let
![]() $\Phi \colon \varprojlim _{i,j \in \mathbb {N}} \Sigma _{ij} \to \Omega (\tau )$
be the map given in Theorem 9.1. As
$\Phi \colon \varprojlim _{i,j \in \mathbb {N}} \Sigma _{ij} \to \Omega (\tau )$
be the map given in Theorem 9.1. As
![]() $\varprojlim _{i,j \in \mathbb {N}} \Sigma ^{*}_{ij} \subset \varprojlim _{i,j \in \mathbb {N}} \Sigma _{ij}$
, we obtain
$\varprojlim _{i,j \in \mathbb {N}} \Sigma ^{*}_{ij} \subset \varprojlim _{i,j \in \mathbb {N}} \Sigma _{ij}$
, we obtain
![]() ${y_0= \Phi (x) \in \Omega (\tau )}$
. As
${y_0= \Phi (x) \in \Omega (\tau )}$
. As
![]() $y_0(1_G) = x_{00}(1_G)$
by definition of
$y_0(1_G) = x_{00}(1_G)$
by definition of
![]() $\Phi $
and as
$\Phi $
and as
![]() $x_{00}(1_G) \neq 0$
since
$x_{00}(1_G) \neq 0$
since
![]() $x_{00} \in \Sigma ^*_{00}$
, we deduce that
$x_{00} \in \Sigma ^*_{00}$
, we deduce that
![]() $\Omega (\tau ) \neq \{0^G\}$
. This contradiction shows that (b)
$\Omega (\tau ) \neq \{0^G\}$
. This contradiction shows that (b)
![]() $\implies $
(a).
$\implies $
(a).
13 Nilpotency over finite alphabets
The following theorem strengthens and extends to any infinite group some results established for full shifts over
![]() $G = \mathbb {Z}$
by Culik, Pachl, and Yu [Reference Culik, Pachl and Yu18, Theorem 3.5] and by Guillon and Richard [Reference Guillon, Richard, Ochmański and Tyszkiewicz24, Corollary 4].
$G = \mathbb {Z}$
by Culik, Pachl, and Yu [Reference Culik, Pachl and Yu18, Theorem 3.5] and by Guillon and Richard [Reference Guillon, Richard, Ochmański and Tyszkiewicz24, Corollary 4].
Suppose that X is a topological space equipped with a continuous action of a group G. One says that the dynamical system
![]() $(X,G)$
is topologically mixing if for each pair of non-empty open subsets U and V of X, there exists a finite subset
$(X,G)$
is topologically mixing if for each pair of non-empty open subsets U and V of X, there exists a finite subset
![]() $F \subset G$
such that
$F \subset G$
such that
![]() $U \cap gV \neq ~\varnothing $
for all
$U \cap gV \neq ~\varnothing $
for all
![]() $g \in G \setminus F$
. Given a group G and a finite set A, a closed subshift
$g \in G \setminus F$
. Given a group G and a finite set A, a closed subshift
![]() ${\Sigma \subset A^G}$
is said to be topologically mixing provided
${\Sigma \subset A^G}$
is said to be topologically mixing provided
![]() $(\Sigma ,G)$
is topologically mixing. If
$(\Sigma ,G)$
is topologically mixing. If
![]() $(X,G)$
is a topologically mixing dynamical system and
$(X,G)$
is a topologically mixing dynamical system and
![]() $f \colon X \to X$
is a continuous G-equivariant map, then the factor system
$f \colon X \to X$
is a continuous G-equivariant map, then the factor system
![]() $(f(X), G)$
is also topologically mixing.
$(f(X), G)$
is also topologically mixing.
Theorem 13.1. Let G be an infinite group, let A be a finite set, and let
![]() $\Sigma \subset A^G$
be a non-empty topologically mixing subshift of sub-finite-type (e.g.
$\Sigma \subset A^G$
be a non-empty topologically mixing subshift of sub-finite-type (e.g.
![]() $\Sigma = A^G$
, or, if G is finitely generated,
$\Sigma = A^G$
, or, if G is finitely generated,
![]() $\Sigma $
is of finite type). Let
$\Sigma $
is of finite type). Let
![]() $\tau \colon \Sigma \to \Sigma $
be a cellular automaton. Then the following conditions are equivalent:
$\tau \colon \Sigma \to \Sigma $
be a cellular automaton. Then the following conditions are equivalent:
-
(a)
 $\tau $
is nilpotent;
$\tau $
is nilpotent; -
(b) the limit set
 $\Omega (\tau )$
is reduced to a single configuration;
$\Omega (\tau )$
is reduced to a single configuration; -
(c) the limit set
 $\Omega (\tau )$
is finite.
$\Omega (\tau )$
is finite.
If G is finitely generated, then the above conditions are equivalent to
-
(d) the limit set
 $\Omega (\tau )$
consists only of periodic configurations.
$\Omega (\tau )$
consists only of periodic configurations.
Before starting the proof of the above theorem, we present a preliminary lemma. The result is probably well known, but since we could not find any reference, we include a proof for the sake of completeness.
Lemma 13.2. Let G be a finitely generated group, let A be a set, and let
![]() $\Sigma \subset A^G$
be a finite subshift. Then
$\Sigma \subset A^G$
be a finite subshift. Then
![]() $\Sigma $
is of finite type.
$\Sigma $
is of finite type.
Roughly, the idea is simple. Every configuration
![]() $x \in \Sigma $
has a finite orbit, equivalently, its stabilizer
$x \in \Sigma $
has a finite orbit, equivalently, its stabilizer
![]() $H_x = \operatorname {\mathrm {Stab}}_G(x)$
is of finite index in G. Since the intersection of finitely many finite-index subgroups is of finite index, the group
$H_x = \operatorname {\mathrm {Stab}}_G(x)$
is of finite index in G. Since the intersection of finitely many finite-index subgroups is of finite index, the group ![]() is of finite index in G. Moreover, by the Poincaré lemma, there exists a finite index normal subgroup
is of finite index in G. Moreover, by the Poincaré lemma, there exists a finite index normal subgroup
![]() $K\!\subset H$
. This way, we can embed
$K\!\subset H$
. This way, we can embed
![]() $\Sigma $
into
$\Sigma $
into
![]() $A^{G/K}$
(cf. [Reference Ceccherini-Silberstein and Coornaert10, Proposition 1.3.7]). As
$A^{G/K}$
(cf. [Reference Ceccherini-Silberstein and Coornaert10, Proposition 1.3.7]). As
![]() $G/K$
is finite, it follows that
$G/K$
is finite, it follows that
![]() $\Sigma $
is of finite type. The proof below is a detailed and self-contained version of the above idea. See [Reference Ceccherini-Silberstein, Coornaert and Phung16, Proposition 2.4] for a linear version (where ‘finite’ becomes ‘finite-dimensional’).
$\Sigma $
is of finite type. The proof below is a detailed and self-contained version of the above idea. See [Reference Ceccherini-Silberstein, Coornaert and Phung16, Proposition 2.4] for a linear version (where ‘finite’ becomes ‘finite-dimensional’).
Proof of Lemma 13.2
Let
![]() $S \subset G$
be a finite generating subset of G. After replacing S by
$S \subset G$
be a finite generating subset of G. After replacing S by
![]() $S \cup S^{-1} \cup \{1_G\}$
, we can assume that
$S \cup S^{-1} \cup \{1_G\}$
, we can assume that
![]() $S = S^{-1}$
and
$S = S^{-1}$
and
![]() $1_G \in S$
. Then, given any element
$1_G \in S$
. Then, given any element
![]() $g \in G$
, there exist
$g \in G$
, there exist
![]() $n \in \mathbb {N}$
and
$n \in \mathbb {N}$
and
![]() $s_1, s_2, \ldots , s_n \in S$
such that
$s_1, s_2, \ldots , s_n \in S$
such that
![]() $g = s_1s_2 \cdots s_n$
. The minimal
$g = s_1s_2 \cdots s_n$
. The minimal
![]() $n \in \mathbb {N}$
in such an expression of g is the S-length of g, denoted by
$n \in \mathbb {N}$
in such an expression of g is the S-length of g, denoted by
![]() $\ell _S(g)$
.
$\ell _S(g)$
.
For all distinct
![]() $x,y \in \Sigma $
, we can find
$x,y \in \Sigma $
, we can find
![]() $g = g_{x,y} \in G$
such that
$g = g_{x,y} \in G$
such that
![]() $x(g) \neq y(g)$
. Then the finite set
$x(g) \neq y(g)$
. Then the finite set ![]() satisfies
satisfies
Let us show that
![]() $\Sigma = \Sigma (D,P)$
for
$\Sigma = \Sigma (D,P)$
for
![]() $D = SD_0$
and
$D = SD_0$
and ![]() . By definition, we have
. By definition, we have
 $$ \begin{align} \Sigma(D,P) &= \{x \in A^G : \mbox{ for all } g \in G \mbox{ there exists } x_g \in \Sigma \mbox{ such that }\notag \\ &\qquad (g^{-1} x)(d) = x_g(d) \text{ for all } d \in D \}. \end{align} $$
$$ \begin{align} \Sigma(D,P) &= \{x \in A^G : \mbox{ for all } g \in G \mbox{ there exists } x_g \in \Sigma \mbox{ such that }\notag \\ &\qquad (g^{-1} x)(d) = x_g(d) \text{ for all } d \in D \}. \end{align} $$
Note that the element
![]() $x_g \in \Sigma $
in equation (13.2) is uniquely defined by
$x_g \in \Sigma $
in equation (13.2) is uniquely defined by
![]() $x \in \Sigma (D,P)$
and
$x \in \Sigma (D,P)$
and
![]() $g \in G$
, since
$g \in G$
, since
![]() $D \supset D_0$
so that
$D \supset D_0$
so that
![]() $x_g\vert _D = x_g'\vert _D$
infers
$x_g\vert _D = x_g'\vert _D$
infers
![]() $x_g = x_g'$
by equation (13.1).
$x_g = x_g'$
by equation (13.1).
We clearly have
![]() $\Sigma \subset \Sigma (D,P)$
, since
$\Sigma \subset \Sigma (D,P)$
, since
![]() $\Sigma $
is G-invariant.
$\Sigma $
is G-invariant.
For the converse inclusion, suppose that
![]() $x \in \Sigma (D,P)$
and let us show that
$x \in \Sigma (D,P)$
and let us show that
![]() ${x = x_{1_G} \in \Sigma }$
. We prove by induction on the S-length of g that
${x = x_{1_G} \in \Sigma }$
. We prove by induction on the S-length of g that
for all
![]() $g \in G$
. If
$g \in G$
. If
![]() $\ell _S(g) = 0$
, then
$\ell _S(g) = 0$
, then
![]() $g = 1_G$
and equation (13.3) holds trivially. Suppose now that
$g = 1_G$
and equation (13.3) holds trivially. Suppose now that
![]() $\ell _S(g) = n$
and let
$\ell _S(g) = n$
and let
![]() $s \in S$
. Given
$s \in S$
. Given
![]() $d_0 \in D_0$
we have, on the one hand,
$d_0 \in D_0$
we have, on the one hand,
![]() $x(gsd_0) = (g^{-1}x)(sd_0) = x_g(sd_0) = s^{-1}x_g(d_0)$
, and, on the other hand,
$x(gsd_0) = (g^{-1}x)(sd_0) = x_g(sd_0) = s^{-1}x_g(d_0)$
, and, on the other hand,
![]() $x(gsd_0) = ((gs)^{-1}x)(d_0) = x_{gs}(d_0)$
. This shows that
$x(gsd_0) = ((gs)^{-1}x)(d_0) = x_{gs}(d_0)$
. This shows that
![]() $(s^{-1}x_g)\vert _{D_0} = x_{gs}\vert _{D_0}$
. Since
$(s^{-1}x_g)\vert _{D_0} = x_{gs}\vert _{D_0}$
. Since
![]() $s^{-1}x_g$
and
$s^{-1}x_g$
and
![]() $x_{gs}$
both belong to
$x_{gs}$
both belong to
![]() $\Sigma $
, we deduce from equation (13.1) that
$\Sigma $
, we deduce from equation (13.1) that
![]() $s^{-1}x_g = x_{gs}$
. By induction, we have
$s^{-1}x_g = x_{gs}$
. By induction, we have
![]() $x_g = g^{-1}x_{1_G}$
so that
$x_g = g^{-1}x_{1_G}$
so that
![]() $x_{gs} = (gs)^{-1}x_{1_G}$
. This proves equation (13.3). From equation (13.3) we obtain, for every
$x_{gs} = (gs)^{-1}x_{1_G}$
. This proves equation (13.3). From equation (13.3) we obtain, for every
![]() $g \in G$
,
$g \in G$
,
This shows that
![]() $x = x_{1_G} \in \Sigma $
.
$x = x_{1_G} \in \Sigma $
.
Proof of Theorem 13.1
The equivalence (a)
![]() $\iff $
(b) follows from Theorem 1.4. The implication (b)
$\iff $
(b) follows from Theorem 1.4. The implication (b)
![]() $\implies $
(c) is obvious.
$\implies $
(c) is obvious.
Suppose now that
![]() $\Omega (\tau )$
is finite. Let
$\Omega (\tau )$
is finite. Let
![]() $M \subset G$
be a finite subset which serves as a memory set for both
$M \subset G$
be a finite subset which serves as a memory set for both
![]() $\tau $
and
$\tau $
and
![]() $\Sigma $
, and denote by
$\Sigma $
, and denote by
![]() $H \subset G$
the subgroup it generates. Let
$H \subset G$
the subgroup it generates. Let
![]() $\tau _H \colon \Sigma _H \to \Sigma _H$
denote the corresponding restriction cellular automaton. It follows from Lemma 2.9 that
$\tau _H \colon \Sigma _H \to \Sigma _H$
denote the corresponding restriction cellular automaton. It follows from Lemma 2.9 that
![]() $\Omega (\tau ) = \Omega (\tau _H)^{G/H}$
. If G is not finitely generated, then
$\Omega (\tau ) = \Omega (\tau _H)^{G/H}$
. If G is not finitely generated, then
![]() $G/H$
is infinite and necessarily
$G/H$
is infinite and necessarily
![]() $\Omega (\tau _H)$
and therefore
$\Omega (\tau _H)$
and therefore
![]() $\Omega (\tau )$
must consist of a single element, as
$\Omega (\tau )$
must consist of a single element, as
![]() $\Omega (\tau )$
is non-empty (cf. Theorem 1.3). This proves the implication (c)
$\Omega (\tau )$
is non-empty (cf. Theorem 1.3). This proves the implication (c)
![]() $\implies $
(b) for G not finitely generated.
$\implies $
(b) for G not finitely generated.
If G is finitely generated, it follows from Lemma 13.2 that
![]() $\Omega (\tau )$
is a subshift of finite type. Since A is finite, the characterization of subshifts of finite type in Theorem 10.1 can be applied to the sequence
$\Omega (\tau )$
is a subshift of finite type. Since A is finite, the characterization of subshifts of finite type in Theorem 10.1 can be applied to the sequence
and implies that there exists
![]() $n_0 \in \mathbb {N}$
such that
$n_0 \in \mathbb {N}$
such that
![]() $\Omega (\tau ) = \tau ^{n_0}(\Sigma )$
. Therefore,
$\Omega (\tau ) = \tau ^{n_0}(\Sigma )$
. Therefore,
![]() $\Omega (\tau )$
is a factor of
$\Omega (\tau )$
is a factor of
![]() $\Sigma $
. Since
$\Sigma $
. Since
![]() $\Sigma $
is topologically mixing, so is
$\Sigma $
is topologically mixing, so is
![]() $\Omega (\tau )$
. Now let
$\Omega (\tau )$
. Now let
![]() $x, y \in \Omega (\tau )$
. As
$x, y \in \Omega (\tau )$
. As
![]() $\Omega (\tau )$
is finite and Hausdorff,
$\Omega (\tau )$
is finite and Hausdorff,
![]() $\{x\}$
and
$\{x\}$
and
![]() $\{y\}$
are open in
$\{y\}$
are open in
![]() $\Omega (\tau )$
. Thus, by topological mixing of
$\Omega (\tau )$
. Thus, by topological mixing of
![]() $\Omega (\tau )$
, there exists a finite subset
$\Omega (\tau )$
, there exists a finite subset
![]() $F \subset G$
such that
$F \subset G$
such that
![]() $x = gy$
for all
$x = gy$
for all
![]() $g \in G \setminus F$
. Since
$g \in G \setminus F$
. Since
![]() $\Omega (\tau )$
is finite, the stabilizer H of y in G is an infinite subgroup of G. It follows that
$\Omega (\tau )$
is finite, the stabilizer H of y in G is an infinite subgroup of G. It follows that
![]() $H \cap (G \setminus F) \neq \varnothing $
. Taking
$H \cap (G \setminus F) \neq \varnothing $
. Taking
![]() $g \in H \cap (G \setminus F)$
yields
$g \in H \cap (G \setminus F)$
yields
![]() $x = gy = y$
. Hence,
$x = gy = y$
. Hence,
![]() $\Omega (\tau )$
is a singleton and this concludes the proof of the implication (c)
$\Omega (\tau )$
is a singleton and this concludes the proof of the implication (c)
![]() $\implies $
(b).
$\implies $
(b).
Finally, suppose that G is finitely generated. As any finite G-invariant subset of
![]() $A^G$
necessarily consists only of periodic configurations, we have (c)
$A^G$
necessarily consists only of periodic configurations, we have (c)
![]() $\implies $
(d). The reverse implication follows from the finiteness of closed subshifts containing only periodic configurations proved in [Reference Ballier4, Theorem 5.8] and in [Reference Meyerovitch and Salo32, Theorem 1.4] (see also [Reference Ballier, Durand and Jeandel5, Theorem 3.8] for the case
$\implies $
(d). The reverse implication follows from the finiteness of closed subshifts containing only periodic configurations proved in [Reference Ballier4, Theorem 5.8] and in [Reference Meyerovitch and Salo32, Theorem 1.4] (see also [Reference Ballier, Durand and Jeandel5, Theorem 3.8] for the case
![]() $G= \mathbb {Z}^2$
). Note that since
$G= \mathbb {Z}^2$
). Note that since
![]() $A^G$
is compact and
$A^G$
is compact and
![]() $\tau $
is continuous,
$\tau $
is continuous,
![]() $\Omega (\tau )$
is closed in
$\Omega (\tau )$
is closed in
![]() $A^G$
.
$A^G$
.
14 Proof of Theorem 1.5
By Corollary 8.2, we know that
![]() $\Sigma $
is closed in
$\Sigma $
is closed in
![]() $A^G$
. The equivalence (a)
$A^G$
. The equivalence (a)
![]() $\iff $
(b) thus results from Proposition A.5. It is trivial that (a)
$\iff $
(b) thus results from Proposition A.5. It is trivial that (a)
![]() $\implies $
(c)
$\implies $
(c)
![]() $\implies $
(d). For the implications (d)
$\implies $
(d). For the implications (d)
![]() $\implies $
(a) and (c)
$\implies $
(a) and (c)
![]() $\implies $
(a), let
$\implies $
(a), let
![]() $M \subset G$
be a finite subset containing the memory sets of both
$M \subset G$
be a finite subset containing the memory sets of both
![]() $\tau $
and
$\tau $
and
![]() $\Sigma $
such that
$\Sigma $
such that
![]() $1_G \in M$
and
$1_G \in M$
and
![]() $M=M^{-1}$
. Let H be the subgroup of G generated by M. Let
$M=M^{-1}$
. Let H be the subgroup of G generated by M. Let
![]() $\tau _H \colon \Sigma _H \to \Sigma _H$
denote the restriction cellular automaton. By Lemma 2.9(i), we have
$\tau _H \colon \Sigma _H \to \Sigma _H$
denote the restriction cellular automaton. By Lemma 2.9(i), we have
![]() $\Omega (\tau ) = \Omega (\tau _H)^{G/H}$
. Thus, if
$\Omega (\tau ) = \Omega (\tau _H)^{G/H}$
. Thus, if
![]() $\Omega (\tau )$
is finite, then so is
$\Omega (\tau )$
is finite, then so is
![]() $\tau (\tau _H)$
. Likewise, if item (d) holds for
$\tau (\tau _H)$
. Likewise, if item (d) holds for
![]() $\tau $
, then
$\tau $
, then
![]() $\{ x(1_G) \colon x \in \Omega (\tau _H) \}$
is finite and
$\{ x(1_G) \colon x \in \Omega (\tau _H) \}$
is finite and
![]() $\Omega (\tau _H)$
consists of periodic configurations as well. However,
$\Omega (\tau _H)$
consists of periodic configurations as well. However,
![]() $\tau $
is nilpotent if
$\tau $
is nilpotent if
![]() $\tau _H$
is nilpotent by Lemma 2.9(ii). Therefore, up to replacing G by H, we can assume that G is finitely generated by M. It then suffices to show that (d)
$\tau _H$
is nilpotent by Lemma 2.9(ii). Therefore, up to replacing G by H, we can assume that G is finitely generated by M. It then suffices to show that (d)
![]() $\implies $
(a) as we already know that (c)
$\implies $
(a) as we already know that (c)
![]() $\implies $
(d).
$\implies $
(d).
Assume that item (d) holds. Then ![]() is finite. As
is finite. As
![]() $\Omega (\tau )$
is G-invariant,
$\Omega (\tau )$
is G-invariant,
![]() $x(g)\in T$
for every
$x(g)\in T$
for every
![]() $x \in \Omega (\tau )$
and
$x \in \Omega (\tau )$
and
![]() $g \in G$
.
$g \in G$
.
Let
![]() $(\Sigma _{ij})_{i, j \in \mathbb {N}}$
be the space-time inverse system associated with
$(\Sigma _{ij})_{i, j \in \mathbb {N}}$
be the space-time inverse system associated with
![]() $\tau $
and the memory set M. We set
$\tau $
and the memory set M. We set ![]() for every
for every
![]() $i \geq 0$
, and define for every
$i \geq 0$
, and define for every
![]() $i \geq 0$
and
$i \geq 0$
and
![]() $j \geq 1$
:
$j \geq 1$
:
The unit transition maps
![]() $p^*_{ij} \colon \Sigma ^*_{i+1, j} \to \Sigma ^*_{ij}$
and
$p^*_{ij} \colon \Sigma ^*_{i+1, j} \to \Sigma ^*_{ij}$
and
![]() $q^*_{ij} \colon \Sigma ^*_{i, j+1} \to \Sigma ^*_{i j}$
are respectively the restrictions of the transition maps
$q^*_{ij} \colon \Sigma ^*_{i, j+1} \to \Sigma ^*_{i j}$
are respectively the restrictions of the transition maps
![]() $p_{ij}$
and
$p_{ij}$
and
![]() $q_{ij}$
of the system
$q_{ij}$
of the system
![]() $(\Sigma _{ij})_{i, j \in \mathbb {N}}$
.
$(\Sigma _{ij})_{i, j \in \mathbb {N}}$
.
Suppose first that
![]() $\Sigma ^*_{ij} \neq \varnothing $
for all
$\Sigma ^*_{ij} \neq \varnothing $
for all
![]() $i, j \in \mathbb {N}$
. Then exactly as in the proof of Theorem 1.4, there exists
$i, j \in \mathbb {N}$
. Then exactly as in the proof of Theorem 1.4, there exists
![]() $x =(x_{ij})_{i, j \in \mathbb {N}} \in \varprojlim _{i,j \in \mathbb {N}} \Sigma ^{*}_{ij}$
and we obtain
$x =(x_{ij})_{i, j \in \mathbb {N}} \in \varprojlim _{i,j \in \mathbb {N}} \Sigma ^{*}_{ij}$
and we obtain
![]() $y_0 = \Phi (x) \in \Omega (\tau )$
with
$y_0 = \Phi (x) \in \Omega (\tau )$
with
![]() $y_0(1_G) = x_{00}(1_G)$
. However,
$y_0(1_G) = x_{00}(1_G)$
. However,
![]() $x_{00}(1_G) \notin T$
because
$x_{00}(1_G) \notin T$
because
![]() $x_{00} \in \Sigma ^*_{00}$
, we find that
$x_{00} \in \Sigma ^*_{00}$
, we find that
![]() $\Omega (\tau ) \not \subset T^G$
, which is a contradiction.
$\Omega (\tau ) \not \subset T^G$
, which is a contradiction.
Therefore, we must have
![]() $\Sigma ^*_{ij}= \varnothing $
for some
$\Sigma ^*_{ij}= \varnothing $
for some
![]() $i, j \in \mathbb {N}$
. If
$i, j \in \mathbb {N}$
. If
![]() $j=0$
, then
$j=0$
, then
![]() $\Sigma ^*_{i0}= \varnothing $
and
$\Sigma ^*_{i0}= \varnothing $
and
![]() $x(1_G) \in T$
for all
$x(1_G) \in T$
for all
![]() $x \in \Sigma _{i0}$
. We deduce that
$x \in \Sigma _{i0}$
. We deduce that
![]() $A^G \subset T^G$
and thus
$A^G \subset T^G$
and thus
![]() $A \subset T$
is finite. As G is infinite and
$A \subset T$
is finite. As G is infinite and
![]() $\Omega (\tau )$
contains only periodic configurations, Theorem 13.1 implies that
$\Omega (\tau )$
contains only periodic configurations, Theorem 13.1 implies that
![]() $\tau $
is nilpotent. If
$\tau $
is nilpotent. If
![]() $j \geq 1$
, then by definition of
$j \geq 1$
, then by definition of
![]() $\Sigma _{ij}$
, we have for every
$\Sigma _{ij}$
, we have for every
![]() $x \in \Sigma _{ij}$
that
$x \in \Sigma _{ij}$
that
Hence, as
![]() $\tau ^{j}$
is G-equivariant, we deduce that
$\tau ^{j}$
is G-equivariant, we deduce that
![]() $\tau ^{j}(x) \in T^G$
for every
$\tau ^{j}(x) \in T^G$
for every
![]() $x \in A^G$
. Thus, the restriction
$x \in A^G$
. Thus, the restriction ![]() is a well-defined cellular automaton. As a subset of
is a well-defined cellular automaton. As a subset of
![]() $\Omega (\tau )$
, the set
$\Omega (\tau )$
, the set
![]() $\Omega (\sigma )$
also consists of periodic configurations. We deduce from Theorem 13.1 that
$\Omega (\sigma )$
also consists of periodic configurations. We deduce from Theorem 13.1 that
![]() $\sigma $
is nilpotent, say,
$\sigma $
is nilpotent, say,
![]() $\sigma ^m(x) = x_0$
for all
$\sigma ^m(x) = x_0$
for all
![]() $x \in T^G$
for some
$x \in T^G$
for some
![]() $m \in \mathbb {N}$
and
$m \in \mathbb {N}$
and
![]() $x_0 \in A^G$
. It follows that
$x_0 \in A^G$
. It follows that
![]() $\tau ^{(m+1)j}(x)= \sigma ^m(\tau ^{j} (x) ) =x_0$
for all
$\tau ^{(m+1)j}(x)= \sigma ^m(\tau ^{j} (x) ) =x_0$
for all
![]() $x \in A^G$
. We conclude that
$x \in A^G$
. We conclude that
![]() $\tau $
is nilpotent. The proof of the theorem is completed.
$\tau $
is nilpotent. The proof of the theorem is completed.
15 Counter-examples
The following example (cf. [Reference Ceccherini-Silberstein and Coornaert11, Example 5.1] and [Reference Ceccherini-Silberstein, Coornaert and Phung14, Example 8.1]) shows that Theorem 8.1 and assertions (i) and (iii) of Theorem 1.3 become false if we remove the hypothesis that the ground field K is algebraically closed.
Example 15.1. Let ![]() be the additive group of integers and let
be the additive group of integers and let ![]() denote the affine line over
denote the affine line over
![]() $\mathbb {R}$
. Then
$\mathbb {R}$
. Then ![]() . Consider the cellular automaton
. Consider the cellular automaton
![]() $\tau \colon \mathbb {R}^{\mathbb {Z}} \to \mathbb {R}^{\mathbb {Z}}$
with memory set
$\tau \colon \mathbb {R}^{\mathbb {Z}} \to \mathbb {R}^{\mathbb {Z}}$
with memory set ![]() and associated local defining map
and associated local defining map
![]() $\mu \colon \mathbb {R}^M \to \mathbb {R}$
defined by
$\mu \colon \mathbb {R}^M \to \mathbb {R}$
defined by
![]() $\mu (p) = p(1) - p(0)^2$
for all
$\mu (p) = p(1) - p(0)^2$
for all
![]() $p \in \mathbb {R}^M$
. Clearly,
$p \in \mathbb {R}^M$
. Clearly,
![]() $\tau $
is an algebraic cellular automaton over
$\tau $
is an algebraic cellular automaton over
![]() $(G,V,\mathbb {R})$
. Indeed,
$(G,V,\mathbb {R})$
. Indeed,
![]() $\mu $
is induced by the algebraic morphism
$\mu $
is induced by the algebraic morphism
![]() $f\colon V^2 \to V$
associated with the morphism of
$f\colon V^2 \to V$
associated with the morphism of
![]() $\mathbb {R}$
-algebras
$\mathbb {R}$
-algebras
 $$ \begin{align*} \mathbb{R}[t] & \to \mathbb{R}[t_0,t_1] \\ t & \mapsto t_1-t_0^2. \end{align*} $$
$$ \begin{align*} \mathbb{R}[t] & \to \mathbb{R}[t_0,t_1] \\ t & \mapsto t_1-t_0^2. \end{align*} $$
Note that
![]() $\tau \colon \mathbb {R}^{\mathbb {Z}}\to \mathbb {R}^{\mathbb {Z}}$
is given by
$\tau \colon \mathbb {R}^{\mathbb {Z}}\to \mathbb {R}^{\mathbb {Z}}$
is given by
Claim 15.2. The limit set
![]() $\Omega (\tau )$
is a dense non-closed subset of
$\Omega (\tau )$
is a dense non-closed subset of
![]() $\mathbb {R}^{\mathbb {Z}}$
. In particular,
$\mathbb {R}^{\mathbb {Z}}$
. In particular,
![]() $\Omega (\tau )$
is not a closed subshift of
$\Omega (\tau )$
is not a closed subshift of
![]() $\mathbb {R}^{\mathbb {Z}}$
.
$\mathbb {R}^{\mathbb {Z}}$
.
Proof. Let
![]() $c \in \mathbb {R}^{\mathbb {Z}}$
and let
$c \in \mathbb {R}^{\mathbb {Z}}$
and let
![]() $F \subset \mathbb {Z}$
be a finite subset. Choose an integer
$F \subset \mathbb {Z}$
be a finite subset. Choose an integer
![]() $m \in \mathbb {Z}$
such that
$m \in \mathbb {Z}$
such that
![]() $F\subset [m,\infty )$
and consider the configuration
$F\subset [m,\infty )$
and consider the configuration
![]() $d \in \mathbb {R}^{\mathbb {Z}}$
defined by
$d \in \mathbb {R}^{\mathbb {Z}}$
defined by ![]() if
if
![]() $n < m$
and
$n < m$
and ![]() if
if
![]() $n \geq m$
. For each
$n \geq m$
. For each
![]() $k \in \mathbb {N}$
, define by induction on k a configuration
$k \in \mathbb {N}$
, define by induction on k a configuration
![]() $d_k \in \mathbb {R}^{\mathbb {Z}}$
in the following way. We first take
$d_k \in \mathbb {R}^{\mathbb {Z}}$
in the following way. We first take
![]() $d_0 = d$
. Then, assuming that the configuration
$d_0 = d$
. Then, assuming that the configuration
![]() $d_k$
has been defined, we define the configuration
$d_k$
has been defined, we define the configuration
![]() $d_{k + 1}$
, using induction on n, by
$d_{k + 1}$
, using induction on n, by ![]() if
if
![]() $n \leq m$
and
$n \leq m$
and ![]() if
if
![]() $n \geq m$
. Clearly,
$n \geq m$
. Clearly,
![]() $\tau (d_{k + 1}) = d_k$
so that
$\tau (d_{k + 1}) = d_k$
so that
![]() $d = d_0 = \tau ^k(d_k)$
for all
$d = d_0 = \tau ^k(d_k)$
for all
![]() $k \in \mathbb {N}$
. Therefore,
$k \in \mathbb {N}$
. Therefore,
![]() $d \in \Omega (\tau )$
. Since c and d coincide on
$d \in \Omega (\tau )$
. Since c and d coincide on
![]() $[m,\infty )$
and hence on F, this shows that c is in the closure of
$[m,\infty )$
and hence on F, this shows that c is in the closure of
![]() $\Omega (\tau )$
. Thus,
$\Omega (\tau )$
. Thus,
![]() $\Omega (\tau )$
is dense in
$\Omega (\tau )$
is dense in
![]() $\mathbb {R}^{\mathbb {Z}}$
.
$\mathbb {R}^{\mathbb {Z}}$
.
In [Reference Ceccherini-Silberstein and Coornaert11, Example 5.1] and [Reference Ceccherini-Silberstein, Coornaert and Phung14, Example 8.1], it is shown that
![]() $\operatorname {\mathrm {Im}}(\tau )$
is not closed of
$\operatorname {\mathrm {Im}}(\tau )$
is not closed of
![]() $R^{\mathbb {Z}}$
and the constant configuration
$R^{\mathbb {Z}}$
and the constant configuration
![]() $e\in \mathbb {R}^{\mathbb {Z}}$
, defined by
$e\in \mathbb {R}^{\mathbb {Z}}$
, defined by ![]() for all
for all
![]() $n\in \mathbb {Z}$
, does not belong to
$n\in \mathbb {Z}$
, does not belong to
![]() $\operatorname {\mathrm {Im}}(\tau )$
. This implies that
$\operatorname {\mathrm {Im}}(\tau )$
. This implies that
![]() $e \notin \Omega (\tau )$
. As
$e \notin \Omega (\tau )$
. As
![]() $\Omega (\tau )$
is dense in
$\Omega (\tau )$
is dense in
![]() $\mathbb {R}^{\mathbb {Z}}$
, we deduce that
$\mathbb {R}^{\mathbb {Z}}$
, we deduce that
![]() $\Omega (\tau )$
is not closed in
$\Omega (\tau )$
is not closed in
![]() $\mathbb {R}^{\mathbb {Z}}$
.
$\mathbb {R}^{\mathbb {Z}}$
.
Remark that
![]() $\operatorname {\mathrm {Im}}(\tau )$
is an algebraic sofic subshift of
$\operatorname {\mathrm {Im}}(\tau )$
is an algebraic sofic subshift of
![]() $\mathbb {R}^{\mathbb {Z}}$
since it is the image of the full shift
$\mathbb {R}^{\mathbb {Z}}$
since it is the image of the full shift
![]() $\mathbb {R}^{\mathbb {Z}}$
under the algebraic cellular automaton
$\mathbb {R}^{\mathbb {Z}}$
under the algebraic cellular automaton
![]() $\tau $
. Thus, an algebraic sofic subshift may fail to be closed in the ambient full shift.
$\tau $
. Thus, an algebraic sofic subshift may fail to be closed in the ambient full shift.
For every integer
![]() $n \geq 1$
, the set
$n \geq 1$
, the set ![]() is a memory set for
is a memory set for
![]() $\tau ^n$
. Let
$\tau ^n$
. Let
![]() $\mu _n \colon \mathbb {R}^{M_n} \to \mathbb {R}$
denote the associated local defining map. We shall use the fact that for each
$\mu _n \colon \mathbb {R}^{M_n} \to \mathbb {R}$
denote the associated local defining map. We shall use the fact that for each
![]() $n \geq 1$
, there exists a polynomial
$n \geq 1$
, there exists a polynomial
![]() $\nu _n \in \mathbb {R}[t_0, \ldots , t_{n-1}]$
such that for every
$\nu _n \in \mathbb {R}[t_0, \ldots , t_{n-1}]$
such that for every
![]() $p \in \mathbb {R}^{M_n}$
,
$p \in \mathbb {R}^{M_n}$
,
This fact can be proved by an easy induction. For
![]() $n=1$
, we have
$n=1$
, we have
![]() $\mu _1(p) = \mu (p) = p(1) - p(0)^2$
for every
$\mu _1(p) = \mu (p) = p(1) - p(0)^2$
for every
![]() $p \in \mathbb {R}^{M_1}$
so that we can take
$p \in \mathbb {R}^{M_1}$
so that we can take
![]() $\nu _1(t_0)= - t_0^2$
. Suppose now that the assertion holds for some
$\nu _1(t_0)= - t_0^2$
. Suppose now that the assertion holds for some
![]() $n\geq 1$
. Let
$n\geq 1$
. Let
![]() $c \in \mathbb {R}^{\mathbb {Z}}$
and let
$c \in \mathbb {R}^{\mathbb {Z}}$
and let
![]() $d = \tau ^{n}(c)$
. By the induction hypothesis, we have that
$d = \tau ^{n}(c)$
. By the induction hypothesis, we have that
![]() $d(0)= \mu _n(c(0), \ldots , c(n))$
and
$d(0)= \mu _n(c(0), \ldots , c(n))$
and
Therefore, we get
 $$ \begin{align*} \tau^{n+1}(c)(0) & = \tau(\tau^{n}(c))(0) = \tau(d)(0) = d(1) - d(0)^2 \\ & = c(n+1) + \nu_k(c(1), \ldots, c(n)) - \mu_n(c(0), \ldots, c(k))^2 \\ & = c(n+1) + \nu_{n+1}(c(0), \ldots, c(n)), \end{align*} $$
$$ \begin{align*} \tau^{n+1}(c)(0) & = \tau(\tau^{n}(c))(0) = \tau(d)(0) = d(1) - d(0)^2 \\ & = c(n+1) + \nu_k(c(1), \ldots, c(n)) - \mu_n(c(0), \ldots, c(k))^2 \\ & = c(n+1) + \nu_{n+1}(c(0), \ldots, c(n)), \end{align*} $$
where
![]() $\nu _{n+1} \in \mathbb {R}[t_0, \ldots , t_{n}]$
is given by the formula
$\nu _{n+1} \in \mathbb {R}[t_0, \ldots , t_{n}]$
is given by the formula
Thus, for every
![]() $p \in \mathbb {R}^{M_{n+1}}$
,
$p \in \mathbb {R}^{M_{n+1}}$
,
and the assertion follows by induction.
Claim 15.3. For every configuration
![]() $c \in \mathbb {R}^{\mathbb {Z}}$
and any integer
$c \in \mathbb {R}^{\mathbb {Z}}$
and any integer
![]() $n \geq 1$
, there exists
$n \geq 1$
, there exists
![]() $d \in \mathbb {R}^{\mathbb {Z}}$
such that
$d \in \mathbb {R}^{\mathbb {Z}}$
such that
![]() $d(k) = c(k)$
for all
$d(k) = c(k)$
for all
![]() $k \leq 0$
and
$k \leq 0$
and
![]() $\tau ^{n}(d)(k)=c(k)$
for all
$\tau ^{n}(d)(k)=c(k)$
for all
![]() $k \geq -n+1$
.
$k \geq -n+1$
.
Proof. Let
![]() $c \in \mathbb {R}^{\mathbb {Z}}$
. We define
$c \in \mathbb {R}^{\mathbb {Z}}$
. We define
![]() $d \in \mathbb {R}^{\mathbb {Z}}$
by
$d \in \mathbb {R}^{\mathbb {Z}}$
by
and inductively for
![]() $k \geq 1$
by
$k \geq 1$
by
By applying equations (15.1) and (15.2), we obtain, for every
![]() $k \geq -n+1$
,
$k \geq -n+1$
,
 $$ \begin{align*} \tau^{n}(d)(k) & = \mu_{n}(d(k), \ldots, d(n+k)) \\ & = d(n+k) + \nu_{n}(d(k), \ldots, d(k+n-1)) \\ & = c(k), \end{align*} $$
$$ \begin{align*} \tau^{n}(d)(k) & = \mu_{n}(d(k), \ldots, d(n+k)) \\ & = d(n+k) + \nu_{n}(d(k), \ldots, d(k+n-1)) \\ & = c(k), \end{align*} $$
and the claim is proved.
Claim 15.4. The set
![]() $\operatorname {\mathrm {R}}(\tau )$
is a dense non-closed subset of
$\operatorname {\mathrm {R}}(\tau )$
is a dense non-closed subset of
![]() $\mathbb {R}^{\mathbb {Z}}$
. In particular,
$\mathbb {R}^{\mathbb {Z}}$
. In particular,
![]() $\operatorname {\mathrm {R}}(\tau )$
is not a closed subshift of
$\operatorname {\mathrm {R}}(\tau )$
is not a closed subshift of
![]() $\mathbb {R}^{\mathbb {Z}}$
.
$\mathbb {R}^{\mathbb {Z}}$
.
Proof. Let
![]() $c \in \mathbb {R}^{\mathbb {Z}}$
. For each
$c \in \mathbb {R}^{\mathbb {Z}}$
. For each
![]() $n_0 \geq 1$
, define by induction on
$n_0 \geq 1$
, define by induction on
![]() $n \geq n_0$
a configuration
$n \geq n_0$
a configuration
![]() ${d_n \in \mathbb {R}^{\mathbb {Z}}}$
in the following way. Let
${d_n \in \mathbb {R}^{\mathbb {Z}}}$
in the following way. Let
![]() $d_{n_0} = c$
. Then, assuming that the configuration
$d_{n_0} = c$
. Then, assuming that the configuration
![]() $d_n$
has been defined, we can choose by Claim 15.3 and the
$d_n$
has been defined, we can choose by Claim 15.3 and the
![]() $\mathbb {Z}$
-equivariance of
$\mathbb {Z}$
-equivariance of
![]() $\tau $
a configuration
$\tau $
a configuration
![]() $d_{n + 1}$
satisfying
$d_{n + 1}$
satisfying
![]() $d_{n+1}(k) = d_n(k)$
for
$d_{n+1}(k) = d_n(k)$
for
![]() $k \leq 2 \cdot 3^{n}$
and
$k \leq 2 \cdot 3^{n}$
and
![]() $\tau ^{3^{n+1}}(d_{n+1})(k) = d_n(k)$
for
$\tau ^{3^{n+1}}(d_{n+1})(k) = d_n(k)$
for
![]() $k \geq -3^n+1$
.
$k \geq -3^n+1$
.
Hence, we can define
![]() $d \in \mathbb {R}^{\mathbb {Z}}$
by setting
$d \in \mathbb {R}^{\mathbb {Z}}$
by setting
![]() $d(k)= d_n(k)$
for any
$d(k)= d_n(k)$
for any
![]() $n \geq n_0$
such that
$n \geq n_0$
such that
![]() ${k \leq 2 \cdot 3^{n}}$
. Let
${k \leq 2 \cdot 3^{n}}$
. Let
![]() $n \geq n_0$
. Remark that
$n \geq n_0$
. Remark that
![]() $M_{3^{n+1}}$
is a memory set of
$M_{3^{n+1}}$
is a memory set of
![]() $\tau ^{3^{n+1}}$
and
$\tau ^{3^{n+1}}$
and
![]() $d(k)= d_{n+1}(k)$
for
$d(k)= d_{n+1}(k)$
for
![]() $k \leq 2 \cdot 3^{n+1}$
. Hence, for
$k \leq 2 \cdot 3^{n+1}$
. Hence, for
![]() $-3^n +1 \leq k \leq 3^n$
so that in particular
$-3^n +1 \leq k \leq 3^n$
so that in particular
![]() $3^{n+1} + k \leq 2 \cdot 3^{n+1}$
, we have
$3^{n+1} + k \leq 2 \cdot 3^{n+1}$
, we have
Since this holds for all
![]() $n \geq n_0$
and as every finite subset is contained in
$n \geq n_0$
and as every finite subset is contained in
![]() $\{ -3^n+1 , \ldots , 3^n\}$
for any large enough n, we deduce that
$\{ -3^n+1 , \ldots , 3^n\}$
for any large enough n, we deduce that
![]() $d \in \operatorname {\mathrm {R}}(\tau )$
.
$d \in \operatorname {\mathrm {R}}(\tau )$
.
It is clear from the construction that
![]() $d_n(k)= c(k)$
for every
$d_n(k)= c(k)$
for every
![]() $n \geq n_0$
and
$n \geq n_0$
and
![]() $k \leq 2 \cdot 3^{n_0}$
. Thus,
$k \leq 2 \cdot 3^{n_0}$
. Thus,
![]() $d(k) = c(k)$
for every
$d(k) = c(k)$
for every
![]() $k \leq 2 \cdot 3^{n_0}$
. As
$k \leq 2 \cdot 3^{n_0}$
. As
![]() $n_0 \geq 1$
is arbitrary, it follows that every
$n_0 \geq 1$
is arbitrary, it follows that every
![]() $c \in \mathbb {R}^{\mathbb {Z}}$
belongs to the closure of
$c \in \mathbb {R}^{\mathbb {Z}}$
belongs to the closure of
![]() $\operatorname {\mathrm {R}}(\tau )$
. In other words,
$\operatorname {\mathrm {R}}(\tau )$
. In other words,
![]() $\operatorname {\mathrm {R}}(\tau )$
is dense in
$\operatorname {\mathrm {R}}(\tau )$
is dense in
![]() $\mathbb {R}^{\mathbb {Z}}$
.
$\mathbb {R}^{\mathbb {Z}}$
.
The set
![]() $\operatorname {\mathrm {R}}(\tau )$
is not closed in
$\operatorname {\mathrm {R}}(\tau )$
is not closed in
![]() $\mathbb {R}^{\mathbb {Z}}$
. Indeed, the configuration
$\mathbb {R}^{\mathbb {Z}}$
. Indeed, the configuration
![]() $e \in \mathbb {R}^{\mathbb {Z}}$
, given by
$e \in \mathbb {R}^{\mathbb {Z}}$
, given by
![]() $e(k) = 1$
for all
$e(k) = 1$
for all
![]() $k \in \mathbb {Z}$
, does not belong to
$k \in \mathbb {Z}$
, does not belong to
![]() $\operatorname {\mathrm {R}}(\tau )$
since
$\operatorname {\mathrm {R}}(\tau )$
since
![]() $\tau ^n(e)(0) = 0 \not = c(0)$
for all
$\tau ^n(e)(0) = 0 \not = c(0)$
for all
![]() $n \geq 1$
.
$n \geq 1$
.
Claim 15.5. One has
![]() $\operatorname {\mathrm {NW}}(\tau ) = \operatorname {\mathrm {CR}}(\tau ) = \mathbb {R}^{\mathbb {Z}}$
.
$\operatorname {\mathrm {NW}}(\tau ) = \operatorname {\mathrm {CR}}(\tau ) = \mathbb {R}^{\mathbb {Z}}$
.
Proof. By Claim 15.4, the set
![]() $\operatorname {\mathrm {R}}(\tau )$
is dense in
$\operatorname {\mathrm {R}}(\tau )$
is dense in
![]() $\mathbb {R}^{\mathbb {Z}}$
. Since
$\mathbb {R}^{\mathbb {Z}}$
. Since
![]() $\operatorname {\mathrm {NW}}(\tau )$
and
$\operatorname {\mathrm {NW}}(\tau )$
and
![]() $\operatorname {\mathrm {CR}}(\tau )$
are closed in
$\operatorname {\mathrm {CR}}(\tau )$
are closed in
![]() $\mathbb {R}^{\mathbb {Z}}$
and contain
$\mathbb {R}^{\mathbb {Z}}$
and contain
![]() $\operatorname {\mathrm {R}}(\tau )$
, we deduce that
$\operatorname {\mathrm {R}}(\tau )$
, we deduce that
![]() $\operatorname {\mathrm {NW}}(\tau ) = \operatorname {\mathrm {CR}}(\tau ) = \mathbb {R}^{\mathbb {Z}}$
.
$\operatorname {\mathrm {NW}}(\tau ) = \operatorname {\mathrm {CR}}(\tau ) = \mathbb {R}^{\mathbb {Z}}$
.
Claim 15.6. One has
![]() $\operatorname {\mathrm {R}}(\tau ) \not \subset \Omega (\tau )$
and
$\operatorname {\mathrm {R}}(\tau ) \not \subset \Omega (\tau )$
and
![]() $\Omega (\tau ) \not \subset \operatorname {\mathrm {R}}(\tau )$
.
$\Omega (\tau ) \not \subset \operatorname {\mathrm {R}}(\tau )$
.
Proof. By the proof of Claim 15.2, we know that the configuration
![]() $c \in \mathbb {R}^{\mathbb {Z}}$
, given by
$c \in \mathbb {R}^{\mathbb {Z}}$
, given by
![]() $c(k)=0$
if
$c(k)=0$
if
![]() $k \leq - 1$
and
$k \leq - 1$
and
![]() $c(k)=1$
if
$c(k)=1$
if
![]() $k \geq 0$
, belongs to
$k \geq 0$
, belongs to
![]() $\Omega (\tau )$
. However, as
$\Omega (\tau )$
. However, as
![]() $\tau ^n(c)(0)=0 \neq c(0)$
for every
$\tau ^n(c)(0)=0 \neq c(0)$
for every
![]() $n \geq 1$
, it follows that
$n \geq 1$
, it follows that
![]() $c \notin \operatorname {\mathrm {R}}(\tau )$
.
$c \notin \operatorname {\mathrm {R}}(\tau )$
.
However, reconsider the configuration
![]() $e \in \mathbb {R}^{\mathbb {Z}}$
given by
$e \in \mathbb {R}^{\mathbb {Z}}$
given by
![]() $e(k)=1$
for every
$e(k)=1$
for every
![]() $k \in \mathbb {Z}$
. The proof of Claim 15.4 actually shows that there exists
$k \in \mathbb {Z}$
. The proof of Claim 15.4 actually shows that there exists
![]() $d \in \operatorname {\mathrm {R}}(\tau )$
such that
$d \in \operatorname {\mathrm {R}}(\tau )$
such that
![]() ${d(k)= e(k)=1}$
for all
${d(k)= e(k)=1}$
for all
![]() $k \leq 0$
. Suppose that there exists
$k \leq 0$
. Suppose that there exists
![]() $b \in \mathbb {R}^{\mathbb {Z}}$
such that
$b \in \mathbb {R}^{\mathbb {Z}}$
such that
![]() $\tau (b)= d$
. Then
$\tau (b)= d$
. Then
![]() $b(k+1) = 1 + b(k)^2$
for all
$b(k+1) = 1 + b(k)^2$
for all
![]() $k \leq 0$
. Thus,
$k \leq 0$
. Thus,
![]() $1 \leq b(k) \leq b(k+1)$
for all
$1 \leq b(k) \leq b(k+1)$
for all
![]() $k \leq 0$
, so that the limit
$k \leq 0$
, so that the limit ![]() exists and is finite. By passing to the limit in the relation
exists and is finite. By passing to the limit in the relation
![]() $b(k+1) = 1 + b(k)^2$
, we find that
$b(k+1) = 1 + b(k)^2$
, we find that
![]() $t=1+t^2$
, which is a contradiction as t must be real. This shows that
$t=1+t^2$
, which is a contradiction as t must be real. This shows that
![]() $d \notin \tau (\mathbb {R}^{\mathbb {Z}})$
and thus
$d \notin \tau (\mathbb {R}^{\mathbb {Z}})$
and thus
![]() $d \notin \Omega (\tau )$
. The proof is completed.
$d \notin \Omega (\tau )$
. The proof is completed.
Remark 15.7. Consider the complex version of Example 15.1, that is, let
![]() $\tau _{\mathbb {C}} \colon \mathbb {C}^{\mathbb {Z}} \to \mathbb {C}^{\mathbb {Z}}$
be the algebraic cellular automaton over
$\tau _{\mathbb {C}} \colon \mathbb {C}^{\mathbb {Z}} \to \mathbb {C}^{\mathbb {Z}}$
be the algebraic cellular automaton over
![]() $(\mathbb {Z}, {\mathbb {A}}^1_{\mathbb {C}},\mathbb {C})$
with memory set
$(\mathbb {Z}, {\mathbb {A}}^1_{\mathbb {C}},\mathbb {C})$
with memory set
![]() $M = \{0,1\}\subset \mathbb {Z}$
and associated local defining map
$M = \{0,1\}\subset \mathbb {Z}$
and associated local defining map
![]() $\mu _{\mathbb {C}} \colon \mathbb {C}^M \to \mathbb {C}$
defined by
$\mu _{\mathbb {C}} \colon \mathbb {C}^M \to \mathbb {C}$
defined by
![]() $\mu _{\mathbb {C}}(p) = p(1) - p(0)^2$
for all
$\mu _{\mathbb {C}}(p) = p(1) - p(0)^2$
for all
![]() $p \in \mathbb {C}^M$
.
$p \in \mathbb {C}^M$
.
Then the same proofs as in Claims 15.4 and 15.5 show that
![]() $\operatorname {\mathrm {R}}(\tau _{\mathbb {C}})$
is a dense non-closed subset of
$\operatorname {\mathrm {R}}(\tau _{\mathbb {C}})$
is a dense non-closed subset of
![]() $\mathbb {C}^{\mathbb {Z}}$
and that
$\mathbb {C}^{\mathbb {Z}}$
and that
![]() $\operatorname {\mathrm {NW}}(\tau _{\mathbb {C}}) = \operatorname {\mathrm {CR}}(\tau _{\mathbb {C}}) = \mathbb {C}^{\mathbb {Z}}$
. By applying Theorem 1.3(ii), we deduce that
$\operatorname {\mathrm {NW}}(\tau _{\mathbb {C}}) = \operatorname {\mathrm {CR}}(\tau _{\mathbb {C}}) = \mathbb {C}^{\mathbb {Z}}$
. By applying Theorem 1.3(ii), we deduce that
![]() $\Omega (\tau _{\mathbb {C}}) = \mathbb {C}^{\mathbb {Z}}$
, that is,
$\Omega (\tau _{\mathbb {C}}) = \mathbb {C}^{\mathbb {Z}}$
, that is,
![]() $\tau _{\mathbb {C}}$
is surjective, which can also be easily checked by a direct verification.
$\tau _{\mathbb {C}}$
is surjective, which can also be easily checked by a direct verification.
The following example shows that assertion (v) of Theorem 1.3 becomes false if we remove the hypothesis that the ground field K is algebraically closed.
Example 15.8. Let G be a group and let ![]() denote the affine line over
denote the affine line over
![]() $\mathbb {R}$
. Consider the algebraic morphism
$\mathbb {R}$
. Consider the algebraic morphism
![]() $f \colon V \to V$
given by
$f \colon V \to V$
given by
![]() $t \mapsto t^2 + 1$
. Take
$t \mapsto t^2 + 1$
. Take ![]() and let
and let
![]() $\tau \colon A^G \to A^G$
denote the cellular automaton with memory set
$\tau \colon A^G \to A^G$
denote the cellular automaton with memory set ![]() and associated local defining map
and associated local defining map
![]() $\mu \colon A^M = A \to A$
given by
$\mu \colon A^M = A \to A$
given by
![]() $a \mapsto a^2 + 1$
. The cellular automaton
$a \mapsto a^2 + 1$
. The cellular automaton
![]() $\tau $
is algebraic since
$\tau $
is algebraic since
![]() $\mu $
is induced by f but its limit set
$\mu $
is induced by f but its limit set
![]() $\Omega (\tau )$
is clearly empty. Remark also that
$\Omega (\tau )$
is clearly empty. Remark also that
![]() $\tau $
is not stable since otherwise,
$\tau $
is not stable since otherwise,
![]() $\Omega (\tau )$
would be non-empty.
$\Omega (\tau )$
would be non-empty.
The following example shows that Theorem 1.4 becomes false if we remove the hypothesis that the ground field K is algebraically closed.
Example 15.9. Let G be a group and let ![]() denote the projective line over
denote the projective line over
![]() $\mathbb {R}$
. Consider the algebraic morphism
$\mathbb {R}$
. Consider the algebraic morphism
![]() $f \colon V \to V$
given by
$f \colon V \to V$
given by
![]() $(x \colon y) \mapsto (x^2 + y^2 \colon y^2)$
. Take
$(x \colon y) \mapsto (x^2 + y^2 \colon y^2)$
. Take ![]() and let
and let
![]() $\tau \colon A^G \to A^G$
denote the cellular automaton with memory set
$\tau \colon A^G \to A^G$
denote the cellular automaton with memory set ![]() and associated local defining map
and associated local defining map
![]() $\mu \colon A^M = A \to A$
given by
$\mu \colon A^M = A \to A$
given by
![]() $a \mapsto a^2 + 1$
. The cellular automaton
$a \mapsto a^2 + 1$
. The cellular automaton
![]() $\tau $
is algebraic since
$\tau $
is algebraic since
![]() $\mu $
is induced by f. Clearly, the limit set
$\mu $
is induced by f. Clearly, the limit set
![]() $\Omega (\tau )$
is reduced to the constant configuration
$\Omega (\tau )$
is reduced to the constant configuration
![]() $g \mapsto \infty $
but
$g \mapsto \infty $
but
![]() $\tau $
is not nilpotent.
$\tau $
is not nilpotent.
16 Generalizations
Using basic properties of proper morphisms, it is not hard to see that all the results for case (H2) (respectively for case
![]() $(\mathrm {\widetilde {H2}})$
in Theorem 8.1) remain valid if V (respectively
$(\mathrm {\widetilde {H2}})$
in Theorem 8.1) remain valid if V (respectively
![]() $V_0$
) is assumed to be separated (and not necessarily complete). For this, it suffices to remark that images of morphisms from a complete algebraic variety to a separated algebraic variety (cf. [Reference Liu31, §3.3.1]) are Zariski closed complete subvarieties (cf. [Reference Liu31, §3.3.2]). This leads us to the following definition.
$V_0$
) is assumed to be separated (and not necessarily complete). For this, it suffices to remark that images of morphisms from a complete algebraic variety to a separated algebraic variety (cf. [Reference Liu31, §3.3.1]) are Zariski closed complete subvarieties (cf. [Reference Liu31, §3.3.2]). This leads us to the following definition.
Definition 16.1. Let G be a group and let V be a separated algebraic variety over a field K. Let ![]() . A subset
. A subset
![]() $\Sigma \subset A^G$
is called a complete algebraic sofic subshift if it is the image of an algebraic subshift of finite type
$\Sigma \subset A^G$
is called a complete algebraic sofic subshift if it is the image of an algebraic subshift of finite type
![]() $\Sigma ' \subset B^G$
, where
$\Sigma ' \subset B^G$
, where
![]() $B=U(K)$
and U is a complete K-algebraic variety, under an algebraic cellular automaton
$B=U(K)$
and U is a complete K-algebraic variety, under an algebraic cellular automaton
![]() $\tau ' \colon B^G \to A^G$
.
$\tau ' \colon B^G \to A^G$
.
With the above definition, Theorem 10.1 can also be extended as follows without any changes in the proof.
Theorem 16.2. Let G be a finitely generated group. Let V be a separated algebraic variety over an algebraically closed field K. Let
![]() $A=V(K)$
and let
$A=V(K)$
and let
![]() $\Sigma \subset A^G$
be a complete algebraic sofic subshift. Then following are equivalent:
$\Sigma \subset A^G$
be a complete algebraic sofic subshift. Then following are equivalent:
-
(a)
 $\Sigma $
is a subshift of finite type;
$\Sigma $
is a subshift of finite type; -
(b)
 $\Sigma $
is an algebraic subshift of finite type;
$\Sigma $
is an algebraic subshift of finite type; -
(c) every descending sequence of algebraic sofic subshifts of
 $A^G$
such that
$A^G$
such that $$ \begin{align*} \Sigma_0 \supset \Sigma_1 \supset \cdots \supset \Sigma_n \supset \Sigma_{n+1} \supset \cdots \end{align*} $$
$$ \begin{align*} \Sigma_0 \supset \Sigma_1 \supset \cdots \supset \Sigma_n \supset \Sigma_{n+1} \supset \cdots \end{align*} $$
 $\bigcap _{n \geq 0} \Sigma _n = \Sigma $
eventually stabilizes.
$\bigcap _{n \geq 0} \Sigma _n = \Sigma $
eventually stabilizes.
Now, let G be a group and let V be an algebraic variety over a field K. Let
![]() $A=V(K)$
and let
$A=V(K)$
and let
![]() $\Sigma \subset A^G$
be a subset.
$\Sigma \subset A^G$
be a subset.
Definition 16.3.
![]() $\Sigma \subset A^G$
is called a countably proconstructible subshift of finite type (CPSFT) if there exist a finite subset
$\Sigma \subset A^G$
is called a countably proconstructible subshift of finite type (CPSFT) if there exist a finite subset
![]() $D \subset G$
and a subset
$D \subset G$
and a subset
![]() $W \subset V^D$
which is the complement in
$W \subset V^D$
which is the complement in
![]() $V^D$
of a countable number of constructible subsets (cf. §3), such that
$V^D$
of a countable number of constructible subsets (cf. §3), such that
![]() $\Sigma = \Sigma (D,W(K))$
. Similarly,
$\Sigma = \Sigma (D,W(K))$
. Similarly,
![]() $\Sigma \subset A^G$
is a countably proconstructible sofic subshift (CPS subshift) if it is the image of a CPSFT under an algebraic cellular automaton with range
$\Sigma \subset A^G$
is a countably proconstructible sofic subshift (CPS subshift) if it is the image of a CPSFT under an algebraic cellular automaton with range
![]() $A^G$
.
$A^G$
.
Our proofs actually show that Theorem 1.3 (except point (iv)), Theorem 1.4 (respectively Theorem 1.5) still hold if we replace hypotheses (H1), (H2), and (H3) and the assumption
![]() $\Sigma \subset A^G$
being an algebraic sofic subshift (respectively a topologically mixing algebraic sofic subshift) by a more general hypothesis:
$\Sigma \subset A^G$
being an algebraic sofic subshift (respectively a topologically mixing algebraic sofic subshift) by a more general hypothesis:
-
(H) K is an uncountable algebraically closed field and
 $\Sigma \subset A^G$
is a
$\Sigma \subset A^G$
is a
 $\operatorname {\mathrm {CPS}}$
subshift (respectively topologically mixing
$\operatorname {\mathrm {CPS}}$
subshift (respectively topologically mixing
 $\operatorname {\mathrm {CPS}}$
subshift) and
$\operatorname {\mathrm {CPS}}$
subshift) and
 $\tau \colon \Sigma \to \Sigma $
is an algebraic cellular automaton.
$\tau \colon \Sigma \to \Sigma $
is an algebraic cellular automaton.
In fact, it can be directly checked from our proofs that results for case (H1) in §6 (respectively §§7 and 8) remain valid if we assume that K is an uncountable algebraically closed field and
![]() $\Sigma $
is a
$\Sigma $
is a
![]() $\operatorname {\mathrm {CPSFT}}$
(respectively a
$\operatorname {\mathrm {CPSFT}}$
(respectively a
![]() $\operatorname {\mathrm {CPS}}$
subshift).
$\operatorname {\mathrm {CPS}}$
subshift).
We now introduce a non-trivial class of non-empty
![]() $\operatorname {\mathrm {CPSFT}}$
(cf. Theorem 16.6).
$\operatorname {\mathrm {CPSFT}}$
(cf. Theorem 16.6).
Definition 16.4. Let G be a group. Let V be an algebraic variety over a field K and let
![]() $A= V(K)$
. A subshift
$A= V(K)$
. A subshift
![]() $\Sigma \subset A^G$
is called a full
$\Sigma \subset A^G$
is called a full
![]() $\operatorname {\mathrm {CPSFT}}$
if there exist a finite subset
$\operatorname {\mathrm {CPSFT}}$
if there exist a finite subset
![]() ${D \subset G}$
and a subset
${D \subset G}$
and a subset
![]() $W = V^D \setminus ( \bigcup _{n \in \mathbb {N}} U_n)$
where each
$W = V^D \setminus ( \bigcup _{n \in \mathbb {N}} U_n)$
where each
![]() $U_n \subset V^D$
is a constructible subset satisfying
$U_n \subset V^D$
is a constructible subset satisfying
![]() $\dim U_n < \dim V^D$
, such that
$\dim U_n < \dim V^D$
, such that
![]() $\Sigma = \Sigma (D, W(K))$
. Here,
$\Sigma = \Sigma (D, W(K))$
. Here,
![]() $\dim Z$
denotes the Krull dimension of a constructible subset Z (see for example [Reference Ceccherini-Silberstein, Coornaert and Phung15]).
$\dim Z$
denotes the Krull dimension of a constructible subset Z (see for example [Reference Ceccherini-Silberstein, Coornaert and Phung15]).
Remark that if V is finite, that is,
![]() $\dim V=0$
, the conditions
$\dim V=0$
, the conditions
![]() $\dim U_n < \dim V^D$
imply that
$\dim U_n < \dim V^D$
imply that
![]() $U_n = \varnothing $
for every
$U_n = \varnothing $
for every
![]() $n \in \mathbb {N}$
, thus
$n \in \mathbb {N}$
, thus
![]() $W=V^D$
. Hence, when the alphabet is finite, the only full
$W=V^D$
. Hence, when the alphabet is finite, the only full
![]() $\operatorname {\mathrm {CPSFT}}$
is the full shift.
$\operatorname {\mathrm {CPSFT}}$
is the full shift.
Example 16.5. If
![]() $G= \mathbb {Z}$
,
$G= \mathbb {Z}$
,
![]() $A = \mathbb {C}$
,
$A = \mathbb {C}$
,
![]() $D= \{0, 1\} \subset \mathbb {Z}$
,
$D= \{0, 1\} \subset \mathbb {Z}$
,
![]() $W = \mathbb {C}^D \setminus E$
, where
$W = \mathbb {C}^D \setminus E$
, where
![]() $E \subset \mathbb {C}^D \simeq \mathbb {C}^2$
is any countable union of complex algebraic curves and points, then
$E \subset \mathbb {C}^D \simeq \mathbb {C}^2$
is any countable union of complex algebraic curves and points, then
![]() $\Sigma ' = \Sigma (D, W) \subset \mathbb {C}^{\mathbb {Z}}$
is a non-empty full CPSFT (by Theorem 16.6). Let
$\Sigma ' = \Sigma (D, W) \subset \mathbb {C}^{\mathbb {Z}}$
is a non-empty full CPSFT (by Theorem 16.6). Let
![]() $\tau ' \colon \mathbb {C}^{\mathbb {Z}} \to \mathbb {C}^{\mathbb {Z}}$
be given by
$\tau ' \colon \mathbb {C}^{\mathbb {Z}} \to \mathbb {C}^{\mathbb {Z}}$
be given by
![]() $\tau '(x)(n) = x(n)^2 - x(n+1) +1$
for every
$\tau '(x)(n) = x(n)^2 - x(n+1) +1$
for every
![]() $x \in \mathbb {C}^{\mathbb {Z}}, n \in \mathbb {Z}$
, then
$x \in \mathbb {C}^{\mathbb {Z}}, n \in \mathbb {Z}$
, then ![]() is a non-empty closed CPS subshift of
is a non-empty closed CPS subshift of
![]() $\mathbb {C}^{\mathbb {Z}}$
(by Theorem 8.1 which is true under the condition (H)). Note that
$\mathbb {C}^{\mathbb {Z}}$
(by Theorem 8.1 which is true under the condition (H)). Note that ![]() is an algebraic cellular automaton.
is an algebraic cellular automaton.
Theorem 16.6. Let G be a group. Let V be a non-empty algebraic variety over an uncountable algebraically closed field K and let
![]() $A= V(K)$
. Then every full
$A= V(K)$
. Then every full
![]() $\operatorname {\mathrm {CPSFT}} \Sigma \subset A^G$
is non-empty.
$\operatorname {\mathrm {CPSFT}} \Sigma \subset A^G$
is non-empty.
Proof. We write
![]() $\Sigma = \Sigma (D, W(K))$
for some finite subset
$\Sigma = \Sigma (D, W(K))$
for some finite subset
![]() $D \subset G$
and
$D \subset G$
and
![]() $W = V^D \setminus ( \bigcup _{n \in \mathbb {N}} U_n)$
, where
$W = V^D \setminus ( \bigcup _{n \in \mathbb {N}} U_n)$
, where
![]() $U_n \subset V^D$
,
$U_n \subset V^D$
,
![]() $n \in \mathbb {N}$
, is a constructible subset such that
$n \in \mathbb {N}$
, is a constructible subset such that
![]() $\dim U_n < \dim V^D$
. In particular, W is a countably proconstructible subset of
$\dim U_n < \dim V^D$
. In particular, W is a countably proconstructible subset of
![]() $V^D$
. Suppose first that G is finitely generated and let the notation be as in §5. Then the same proof for case (H1) of Proposition 6.2 actually implies that
$V^D$
. Suppose first that G is finitely generated and let the notation be as in §5. Then the same proof for case (H1) of Proposition 6.2 actually implies that
![]() $\Sigma _{ij} = \bigcap _{k \geq i} p_{ijk}(A_{kj})$
for
$\Sigma _{ij} = \bigcap _{k \geq i} p_{ijk}(A_{kj})$
for
![]() $i, j \in \mathbb {N}$
, where
$i, j \in \mathbb {N}$
, where
![]() $ A_{ij} = \bigcap _{g \in D_{ij}} \pi _{ij,g}^{-1} (gW) (K) \subset A^{M^{i+j}} $
(cf. equation (6.1)). Note that
$ A_{ij} = \bigcap _{g \in D_{ij}} \pi _{ij,g}^{-1} (gW) (K) \subset A^{M^{i+j}} $
(cf. equation (6.1)). Note that
![]() $D_{ij}$
is finite and
$D_{ij}$
is finite and
![]() $g W \simeq W$
for all
$g W \simeq W$
for all
![]() $g \in G$
. It follows immediately that
$g \in G$
. It follows immediately that
![]() $A_{ij}$
is also a complement of a countable number of constructible subsets
$A_{ij}$
is also a complement of a countable number of constructible subsets
![]() $Z_n$
such that
$Z_n$
such that
![]() $\dim Z_n < \dim A^{M^{i+j}}$
for every
$\dim Z_n < \dim A^{M^{i+j}}$
for every
![]() $n \in \mathbb {N}$
. Hence, for every finite subset
$n \in \mathbb {N}$
. Hence, for every finite subset
![]() $I \subset \mathbb {N}$
, the constructible set
$I \subset \mathbb {N}$
, the constructible set
![]() $\bigcap _{n \in I} (A^{M^{i+j}} \setminus Z_n) \neq \varnothing $
by the dimensional reason. By Lemma 3.2, we deduce that
$\bigcap _{n \in I} (A^{M^{i+j}} \setminus Z_n) \neq \varnothing $
by the dimensional reason. By Lemma 3.2, we deduce that
![]() $A_{ij} = \bigcap _{n \in \mathbb {N}} (A^{M^{i+j}} \setminus Z_n) \neq \varnothing $
for every
$A_{ij} = \bigcap _{n \in \mathbb {N}} (A^{M^{i+j}} \setminus Z_n) \neq \varnothing $
for every
![]() $i, j \in \mathbb {N}$
. Always by Lemma 3.2,
$i, j \in \mathbb {N}$
. Always by Lemma 3.2,
![]() $\Sigma _{ij} = \bigcap _{k \geq i} p_{ijk}(A_{kj}) \neq \varnothing $
for all
$\Sigma _{ij} = \bigcap _{k \geq i} p_{ijk}(A_{kj}) \neq \varnothing $
for all
![]() $i, j \in \mathbb {N}$
and thus
$i, j \in \mathbb {N}$
and thus
![]() $ \varprojlim _{i \in \mathbb {N}} \Sigma _{ij} \neq \varnothing $
. Finally, the bijection
$ \varprojlim _{i \in \mathbb {N}} \Sigma _{ij} \neq \varnothing $
. Finally, the bijection
![]() $\Sigma \simeq \varprojlim _{i \in \mathbb {N}} \Sigma _{ij}$
(cf. equation (4.6)) implies that
$\Sigma \simeq \varprojlim _{i \in \mathbb {N}} \Sigma _{ij}$
(cf. equation (4.6)) implies that
![]() $\Sigma \neq \varnothing $
.
$\Sigma \neq \varnothing $
.
For an arbitrary group G, let H be the subgroup generated by D. Then by Lemma 2.8, we have a factorization
![]() $\Sigma = \prod _{c \in G/H} \Sigma _c$
where the sets
$\Sigma = \prod _{c \in G/H} \Sigma _c$
where the sets
![]() $\Sigma _c$
are pairwise homeomorphic. By the above paragraph, we know that
$\Sigma _c$
are pairwise homeomorphic. By the above paragraph, we know that
![]() $\Sigma _H \neq \varnothing $
and therefore
$\Sigma _H \neq \varnothing $
and therefore
![]() $\Sigma \neq \varnothing $
.
$\Sigma \neq \varnothing $
.
Theorem 16.6 serves as a motivation for the notion of full CPSFT as we see in the following comparison with the finite alphabet case. It is well known that for
![]() $G= \mathbb {Z}^d$
,
$G= \mathbb {Z}^d$
,
![]() $d \geq 2$
, and for a finite set A of cardinality at least 2, it is algorithmically undecidable whether the subshift of finite type
$d \geq 2$
, and for a finite set A of cardinality at least 2, it is algorithmically undecidable whether the subshift of finite type
![]() $\Sigma (D,P) \subset A^G$
is non-empty for a given finite subset
$\Sigma (D,P) \subset A^G$
is non-empty for a given finite subset
![]() $D \in G$
and a given subset
$D \in G$
and a given subset
![]() $ P \subset A^D$
. This is known as the domino problem (cf. [Reference Aubrun, Barbieri and Sablik2, Reference Berger7, Reference Robinson49]; see also the recent [Reference Bartholdi and Salo6], where a notion of ‘simulation’ for labeled graphs is introduced and applied to the domino problem for the Cayley graph of the lamplighter group and, more generally, to Diestel–Leader graphs).
$ P \subset A^D$
. This is known as the domino problem (cf. [Reference Aubrun, Barbieri and Sablik2, Reference Berger7, Reference Robinson49]; see also the recent [Reference Bartholdi and Salo6], where a notion of ‘simulation’ for labeled graphs is introduced and applied to the domino problem for the Cayley graph of the lamplighter group and, more generally, to Diestel–Leader graphs).
A Appendix
A.1 Limit sets and nilpotency of general maps
Given a set X, recall that a map
![]() ${f \colon X \to X}$
is pointwise nilpotent if there exists
${f \colon X \to X}$
is pointwise nilpotent if there exists
![]() $x_0 \in X$
such that for every
$x_0 \in X$
such that for every
![]() $x \in X$
, there exists an integer
$x \in X$
, there exists an integer
![]() $n_0 \geq 1$
such that
$n_0 \geq 1$
such that
![]() $f^n(x) = x_0$
for all
$f^n(x) = x_0$
for all
![]() $n \geq n_0$
. Such an
$n \geq n_0$
. Such an
![]() $x_0$
is then the unique fixed point of f and is called the terminal point of the pointwise nilpotent map f. Clearly, if f is nilpotent, then it is pointwise nilpotent and the terminal point of f as a nilpotent map coincides with its terminal point as a pointwise nilpotent map. Moreover, if f is pointwise nilpotent, then its limit set is reduced to its terminal point. When the set X is finite, the three conditions: (i) f is nilpotent; (ii) f is pointwise nilpotent; and (iii) the limit set of f is a singleton, are all equivalent. This becomes false when X is infinite. Actually, we have the following lemma.
$x_0$
is then the unique fixed point of f and is called the terminal point of the pointwise nilpotent map f. Clearly, if f is nilpotent, then it is pointwise nilpotent and the terminal point of f as a nilpotent map coincides with its terminal point as a pointwise nilpotent map. Moreover, if f is pointwise nilpotent, then its limit set is reduced to its terminal point. When the set X is finite, the three conditions: (i) f is nilpotent; (ii) f is pointwise nilpotent; and (iii) the limit set of f is a singleton, are all equivalent. This becomes false when X is infinite. Actually, we have the following lemma.
Lemma A.1. Let X be an infinite set. Then the following hold:
-
(i) there exists a map
 $f \colon X \to X$
such that
$f \colon X \to X$
such that
 $\Omega (f) = \varnothing $
;
$\Omega (f) = \varnothing $
; -
(ii) there exists a map
 $f \colon X \to X$
which is not pointwise nilpotent (and hence not nilpotent) such that
$f \colon X \to X$
which is not pointwise nilpotent (and hence not nilpotent) such that
 $\Omega (f)$
is a singleton;
$\Omega (f)$
is a singleton; -
(iii) there exists a map
 $f \colon X \to X$
such that
$f \colon X \to X$
such that
 $f(\Omega (f)) \subsetneqq \Omega (f)$
;
$f(\Omega (f)) \subsetneqq \Omega (f)$
; -
(iv) there exists a surjective (and hence non-nilpotent) pointwise nilpotent map
 ${f \colon X \to X}$
.
${f \colon X \to X}$
.
Proof. (i) Since X is infinite, there exists a bijective map
![]() $\psi \colon \mathbb {N} \times X \to X$
. Then the map
$\psi \colon \mathbb {N} \times X \to X$
. Then the map
![]() $f \colon X \to X$
defined by
$f \colon X \to X$
defined by ![]() , where
, where
![]() $g \colon \mathbb {N} \times X \to \mathbb {N} \times X$
is given by
$g \colon \mathbb {N} \times X \to \mathbb {N} \times X$
is given by
![]() $g(n,x) = (n + 1,x)$
for all
$g(n,x) = (n + 1,x)$
for all
![]() $(n,x) \in \mathbb {N} \times X$
, satisfies
$(n,x) \in \mathbb {N} \times X$
, satisfies
![]() $\Omega (f) = \Omega (g) = \varnothing $
. This shows item (i).
$\Omega (f) = \Omega (g) = \varnothing $
. This shows item (i).
(ii) Let ![]() . Since X is infinite, there exists an injective map
. Since X is infinite, there exists an injective map
![]() $\varphi \colon \widehat {\mathbb {N}} \to X$
that is not surjective. Then the map
$\varphi \colon \widehat {\mathbb {N}} \to X$
that is not surjective. Then the map
![]() $f \colon X \to X$
defined by
$f \colon X \to X$
defined by
![]() $f(\varphi (n)) = \varphi (n + 1)$
for all
$f(\varphi (n)) = \varphi (n + 1)$
for all
![]() $n \in \mathbb {N}$
and
$n \in \mathbb {N}$
and
![]() $f(x) = \varphi (\infty )$
for all
$f(x) = \varphi (\infty )$
for all
![]() $x \in X \setminus \varphi (\mathbb {N})$
satisfies
$x \in X \setminus \varphi (\mathbb {N})$
satisfies
![]() $\Omega (f) = \{\varphi (\infty )\}$
but is clearly not pointwise nilpotent.
$\Omega (f) = \{\varphi (\infty )\}$
but is clearly not pointwise nilpotent.
(iii) Consider, for each
![]() $n \geq 1$
, the set
$n \geq 1$
, the set ![]() and the map
and the map
![]() $g_n \colon I_n \to I_n$
given by
$g_n \colon I_n \to I_n$
given by ![]() if
if
![]() $k \geq 1$
and
$k \geq 1$
and
![]() $g_n(0) = 0$
. Let Y be the set obtained by taking disjoint copies of the sets
$g_n(0) = 0$
. Let Y be the set obtained by taking disjoint copies of the sets
![]() $I_n$
,
$I_n$
,
![]() $n \geq 1$
, and identifying all copies of
$n \geq 1$
, and identifying all copies of
![]() $0$
in a single point
$0$
in a single point
![]() $y_0$
and all copies of
$y_0$
and all copies of
![]() $1$
in a single point
$1$
in a single point
![]() $y_1 \not = y_0$
. Then the maps
$y_1 \not = y_0$
. Then the maps
![]() $g_n$
induce a well-defined quotient map
$g_n$
induce a well-defined quotient map
![]() $g \colon Y \to Y$
. Clearly,
$g \colon Y \to Y$
. Clearly,
![]() $\Omega (g) = \{y_0,y_1\}$
while
$\Omega (g) = \{y_0,y_1\}$
while
![]() $g(\Omega (g)) = \{y_0\}$
. As X is infinite, the set Y can be regarded as a subset of X. Then the map
$g(\Omega (g)) = \{y_0\}$
. As X is infinite, the set Y can be regarded as a subset of X. Then the map
![]() $f \colon X \to X$
, defined by
$f \colon X \to X$
, defined by
![]() $f(x) = g(x)$
if
$f(x) = g(x)$
if
![]() $x \in Y$
and
$x \in Y$
and
![]() $f(x) = x$
otherwise, satisfies
$f(x) = x$
otherwise, satisfies
![]() $\Omega (f) = \{y_0,y_1\} \cup (X \setminus Y)$
while
$\Omega (f) = \{y_0,y_1\} \cup (X \setminus Y)$
while
![]() $f(\Omega (f)) = \{y_0\} \cup (X \setminus Y) \subsetneqq \Omega (f)$
.
$f(\Omega (f)) = \{y_0\} \cup (X \setminus Y) \subsetneqq \Omega (f)$
.
(iv) Choose a point
![]() $x_0 \in X$
and a bijective map
$x_0 \in X$
and a bijective map
![]() $\xi \colon \mathbb {N} \times X \to X \setminus \{x_0\}$
. Then the map
$\xi \colon \mathbb {N} \times X \to X \setminus \{x_0\}$
. Then the map
![]() $f \colon X \to X$
, defined by
$f \colon X \to X$
, defined by
![]() $f(\xi (n,x)) = \xi (n - 1,x)$
if
$f(\xi (n,x)) = \xi (n - 1,x)$
if
![]() $n \geq 1$
and
$n \geq 1$
and
![]() $f(x_0) = f(\xi (0,x)) = x_0$
for all
$f(x_0) = f(\xi (0,x)) = x_0$
for all
![]() $x \in X$
, is clearly surjective and pointwise nilpotent (with terminal point
$x \in X$
, is clearly surjective and pointwise nilpotent (with terminal point
![]() $x_0$
).
$x_0$
).
A.2 Limit sets and nilpotency of general cellular automata
Proposition A.2. Let A be an infinite set and let G be a group. Then the following hold:
-
(i) there exists a cellular automaton
 $\tau \colon A^G \to A^G$
with
$\tau \colon A^G \to A^G$
with
 $\Omega (\tau ) = \varnothing $
;
$\Omega (\tau ) = \varnothing $
; -
(ii) there exists a non-nilpotent cellular automaton
 $\tau \colon A^G \to A^G$
such that
$\tau \colon A^G \to A^G$
such that
 $\Omega (\tau )$
is reduced to a single configuration;
$\Omega (\tau )$
is reduced to a single configuration; -
(iii) there exists a cellular automaton
 $\tau \colon A^G \to A^G$
which satisfies
$\tau \colon A^G \to A^G$
which satisfies
 $\tau (\Omega (\tau )) \subsetneqq \Omega (\tau )$
;
$\tau (\Omega (\tau )) \subsetneqq \Omega (\tau )$
; -
(iv) if the group G is finite, then there exists a pointwise nilpotent cellular automaton
 $\tau \colon A^G \to A^G$
which is not nilpotent.
$\tau \colon A^G \to A^G$
which is not nilpotent.
Proof. Given a map
![]() $f \colon A \to A$
, we consider the cellular automaton
$f \colon A \to A$
, we consider the cellular automaton
![]() $\tau \colon A^G \to A^G$
with memory set
$\tau \colon A^G \to A^G$
with memory set ![]() and associated local defining map
and associated local defining map ![]() , that is,
, that is,
![]() $\tau = \prod _{g \in G} f$
.
$\tau = \prod _{g \in G} f$
.
By Lemma A.1(i), there exists
![]() $f \colon A \to A$
whose limit set is empty. Clearly, the associated cellular automaton
$f \colon A \to A$
whose limit set is empty. Clearly, the associated cellular automaton
![]() $\tau \colon A^G \to A^G$
has also empty limit set, showing item (i).
$\tau \colon A^G \to A^G$
has also empty limit set, showing item (i).
By Lemma A.1(ii), there exists a non-nilpotent map
![]() $f \colon A \to A$
such that
$f \colon A \to A$
such that
![]() $\Omega (f) = \{a_0\}$
for some
$\Omega (f) = \{a_0\}$
for some
![]() $a_0 \in A$
. Then, for such a choice of f, the cellular automaton
$a_0 \in A$
. Then, for such a choice of f, the cellular automaton
![]() $\tau \colon A^G \to A^G$
is not nilpotent and
$\tau \colon A^G \to A^G$
is not nilpotent and
![]() $\Omega (\tau ) = \{x_0\}$
, where
$\Omega (\tau ) = \{x_0\}$
, where
![]() $x_0 \in A^G$
is the constant configuration defined by
$x_0 \in A^G$
is the constant configuration defined by ![]() for all
for all
![]() $g \in G$
. This shows item (ii).
$g \in G$
. This shows item (ii).
By Lemma A.1(iii), we can find a map
![]() $f \colon A \to A$
which satisfies
$f \colon A \to A$
which satisfies
![]() $f(\Omega (f)) \subsetneqq \Omega (f)$
. Then, for such a choice of f, the cellular automaton
$f(\Omega (f)) \subsetneqq \Omega (f)$
. Then, for such a choice of f, the cellular automaton
![]() $\tau \colon A^G \to A^G$
clearly satisfies
$\tau \colon A^G \to A^G$
clearly satisfies
![]() $\tau (\Omega (\tau )) \subsetneqq \Omega (\tau )$
. This shows item (iii).
$\tau (\Omega (\tau )) \subsetneqq \Omega (\tau )$
. This shows item (iii).
Finally, by Lemma A.1(iv), there exists a surjective map
![]() $f \colon A \to A$
which is pointwise nilpotent. The associated cellular automaton
$f \colon A \to A$
which is pointwise nilpotent. The associated cellular automaton
![]() $\tau \colon A^G \to A^G$
is surjective and hence not nilpotent. For G finite,
$\tau \colon A^G \to A^G$
is surjective and hence not nilpotent. For G finite,
![]() $\tau $
is clearly pointwise nilpotent. This shows item (iv).
$\tau $
is clearly pointwise nilpotent. This shows item (iv).
A.3 Nilpotency and pointwise nilpotency of general cellular automata
Lemma A.3. Let A be a set and let G be a group. Let
![]() $\Sigma \subset A^G$
be a topologically transitive closed subshift. Suppose that
$\Sigma \subset A^G$
be a topologically transitive closed subshift. Suppose that
![]() $X \subset \Sigma $
is a closed subshift of
$X \subset \Sigma $
is a closed subshift of
![]() $A^G$
with non-empty interior in
$A^G$
with non-empty interior in
![]() $\Sigma $
. Then one has
$\Sigma $
. Then one has
![]() $X = \Sigma $
.
$X = \Sigma $
.
Proof. Let
![]() $U \subset \Sigma $
be a non-empty open subset of
$U \subset \Sigma $
be a non-empty open subset of
![]() $\Sigma $
. Let V denote the interior of X in
$\Sigma $
. Let V denote the interior of X in
![]() $\Sigma $
. Note that V is G-invariant. By topological transitivity, there exists
$\Sigma $
. Note that V is G-invariant. By topological transitivity, there exists
![]() $g \in G$
such that
$g \in G$
such that
![]() $U \cap gV \neq \varnothing $
. As
$U \cap gV \neq \varnothing $
. As
![]() $U \cap g V = U \cap V \subset U \cap X$
, we deduce that
$U \cap g V = U \cap V \subset U \cap X$
, we deduce that
![]() $U \cap X \neq \varnothing $
. Hence, X is dense in
$U \cap X \neq \varnothing $
. Hence, X is dense in
![]() $\Sigma $
. Since X is also closed in
$\Sigma $
. Since X is also closed in
![]() $\Sigma $
, we conclude that
$\Sigma $
, we conclude that
![]() $X= \Sigma $
.
$X= \Sigma $
.
Lemma A.4. Let A be a set and let G be an infinite group. Let
![]() $\Sigma \subset A^G$
be a topologically mixing closed subshift of sub-finite-type. Suppose that
$\Sigma \subset A^G$
be a topologically mixing closed subshift of sub-finite-type. Suppose that
![]() $\tau \colon \Sigma \to \Sigma $
is a cellular automaton satisfying the following property: there exists a constant configuration
$\tau \colon \Sigma \to \Sigma $
is a cellular automaton satisfying the following property: there exists a constant configuration
![]() $x_0 \in \Sigma $
such that, for every
$x_0 \in \Sigma $
such that, for every
![]() $x \in \Sigma $
, there is an integer
$x \in \Sigma $
, there is an integer
![]() $n \geq 1$
such that
$n \geq 1$
such that
![]() $\tau ^n(x) = x_0$
. Then
$\tau ^n(x) = x_0$
. Then
![]() $\tau $
is nilpotent with terminal point
$\tau $
is nilpotent with terminal point
![]() $x_0$
.
$x_0$
.
Proof. Suppose first that G is countable. As
![]() $A^G$
is a countable product of discrete spaces, it admits a complete metric compatible with its topology. Since
$A^G$
is a countable product of discrete spaces, it admits a complete metric compatible with its topology. Since
![]() $\Sigma $
is closed in
$\Sigma $
is closed in
![]() $A^G$
, it follows that the topology induced on
$A^G$
, it follows that the topology induced on
![]() $\Sigma $
is completely metrizable and hence that
$\Sigma $
is completely metrizable and hence that
![]() $\Sigma $
is a Baire space. For each integer
$\Sigma $
is a Baire space. For each integer
![]() $n \geq 1$
, the set
$n \geq 1$
, the set
is a closed subshift of
![]() $A^G$
. We have
$A^G$
. We have
![]() $\Sigma = \bigcup _{n \geq 1} X_n$
by our hypothesis on
$\Sigma = \bigcup _{n \geq 1} X_n$
by our hypothesis on
![]() $\tau $
. By the Baire category theorem, there is an integer
$\tau $
. By the Baire category theorem, there is an integer
![]() $n_0 \geq 1$
such that
$n_0 \geq 1$
such that
![]() $X_{n_0}$
has a non-empty interior. The subshift
$X_{n_0}$
has a non-empty interior. The subshift
![]() $\Sigma $
is topologically mixing and therefore topologically transitive since G is infinite. It follows that
$\Sigma $
is topologically mixing and therefore topologically transitive since G is infinite. It follows that
![]() $X_{n_0} = \Sigma $
by Lemma A.3. Thus,
$X_{n_0} = \Sigma $
by Lemma A.3. Thus,
![]() $\tau ^{n_0}(x) = x_0$
for all
$\tau ^{n_0}(x) = x_0$
for all
![]() $x \in \Sigma $
. This shows that
$x \in \Sigma $
. This shows that
![]() $\tau $
is nilpotent with terminal point
$\tau $
is nilpotent with terminal point
![]() $x_0$
. Note that we have not used the hypothesis that
$x_0$
. Note that we have not used the hypothesis that
![]() $\Sigma $
is of sub-finite-type in this part of the proof.
$\Sigma $
is of sub-finite-type in this part of the proof.
Let us treat now the general case. Suppose that G is an infinite (possibly uncountable) group. Let
![]() $M \subset G$
be a finite memory set for both
$M \subset G$
be a finite memory set for both
![]() $\tau $
and
$\tau $
and
![]() $\Sigma $
. As G is infinite, there exists an infinite countable subgroup
$\Sigma $
. As G is infinite, there exists an infinite countable subgroup
![]() $H \subset G$
containing M. Let
$H \subset G$
containing M. Let
![]() $\tau _H \colon \Sigma _H \to \Sigma _H$
denote the restriction cellular automaton (cf. §2.5). Thanks to the decompositions
$\tau _H \colon \Sigma _H \to \Sigma _H$
denote the restriction cellular automaton (cf. §2.5). Thanks to the decompositions
![]() $\tau = \prod _{c \in G/H} \tau _c$
and
$\tau = \prod _{c \in G/H} \tau _c$
and
![]() $\Sigma = \prod _{c \in G/H} \Sigma _c$
where
$\Sigma = \prod _{c \in G/H} \Sigma _c$
where
![]() $\tau _c \colon \Sigma _c \to \Sigma _c$
(cf. §2.5), it is not hard to see that
$\tau _c \colon \Sigma _c \to \Sigma _c$
(cf. §2.5), it is not hard to see that
![]() $\Sigma _H$
and
$\Sigma _H$
and
![]() $\tau _H$
satisfy similar hypotheses as
$\tau _H$
satisfy similar hypotheses as
![]() $\Sigma $
and
$\Sigma $
and
![]() $\tau $
with the constant terminal point
$\tau $
with the constant terminal point
![]() $x_0\vert _H$
. Remark that
$x_0\vert _H$
. Remark that
![]() $\Sigma _H$
is topologically mixing since H is infinite and
$\Sigma _H$
is topologically mixing since H is infinite and
![]() $\Sigma $
is topologically mixing. Hence,
$\Sigma $
is topologically mixing. Hence,
![]() $\tau _H$
is nilpotent by the above paragraph. Therefore,
$\tau _H$
is nilpotent by the above paragraph. Therefore,
![]() $\tau $
is itself nilpotent by Lemma 2.9(ii).
$\tau $
is itself nilpotent by Lemma 2.9(ii).
The following result is well known, at least in the case of full shifts with finite alphabets (cf. [Reference Guillon, Richard, Ochmański and Tyszkiewicz24, Proposition 2], [Reference Salo50, Proposition 1], [Reference Meyerovitch and Salo32]).
Proposition A.5. Let A be a set and let G be an infinite group. Let
![]() $\Sigma \subset A^G$
be a topologically mixing closed subshift of sub-finite-type. Suppose that
$\Sigma \subset A^G$
be a topologically mixing closed subshift of sub-finite-type. Suppose that
![]() $\tau \colon \Sigma \to \Sigma $
is a cellular automaton. Then the following conditions are equivalent:
$\tau \colon \Sigma \to \Sigma $
is a cellular automaton. Then the following conditions are equivalent:
-
(i)
 $\tau $
is nilpotent;
$\tau $
is nilpotent; -
(ii)
 $\tau $
is pointwise nilpotent;
$\tau $
is pointwise nilpotent; -
(iii) there exists a constant configuration
 $x_0 \in \Sigma $
such that, for every
$x_0 \in \Sigma $
such that, for every
 $x \in \Sigma $
, there is an integer
$x \in \Sigma $
, there is an integer
 $n \geq 1$
such that
$n \geq 1$
such that
 $\tau ^n(x) = x_0$
.
$\tau ^n(x) = x_0$
.
Proof. The implication (i)
![]() $\implies $
(ii) is obvious and (ii)
$\implies $
(ii) is obvious and (ii)
![]() $\implies $
(iii) immediately follows from G-equivariance of
$\implies $
(iii) immediately follows from G-equivariance of
![]() $\tau $
. The implication (iii)
$\tau $
. The implication (iii)
![]() $\implies $
(i) follows from Lemma A.4.
$\implies $
(i) follows from Lemma A.4.
Remark A.6. The equivalences (i)
![]() $\iff $
(ii)
$\iff $
(ii)
![]() $\iff $
(iii) hold trivially true when A and G are both finite. The implication (i)
$\iff $
(iii) hold trivially true when A and G are both finite. The implication (i)
![]() $\implies $
(ii) and the equivalence (ii)
$\implies $
(ii) and the equivalence (ii)
![]() $\iff $
(iii) remain valid for G finite. However, it follows from Proposition A.2(iv) that the implication (ii)
$\iff $
(iii) remain valid for G finite. However, it follows from Proposition A.2(iv) that the implication (ii)
![]() $\implies $
(i) becomes false for A infinite and G finite.
$\implies $
(i) becomes false for A infinite and G finite.