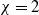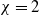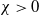1. Introduction and main results
This paper is concerned with a class of chemotaxis systems with singular sensitivity of the following form
in a bounded and smooth spatial domain
![]() $\Omega \subset \mathbb{R}^n$
, with the parameters
$\Omega \subset \mathbb{R}^n$
, with the parameters
![]() $\chi \gt 0$
and
$\chi \gt 0$
and
![]() $\kappa \gt 0$
, which is proposed in [Reference Short, D’Orsogna, Pasour, Tita, Brantingham, Bertozzi and Chayes33] to describe the propagation of urban criminal activities with the particular value
$\kappa \gt 0$
, which is proposed in [Reference Short, D’Orsogna, Pasour, Tita, Brantingham, Bertozzi and Chayes33] to describe the propagation of urban criminal activities with the particular value
![]() $\chi =2$
. Here,
$\chi =2$
. Here,
![]() $u(x,t)$
and
$u(x,t)$
and
![]() $v(x,t)$
represent the density of criminals and an abstract so-called attractiveness value at location
$v(x,t)$
represent the density of criminals and an abstract so-called attractiveness value at location
![]() $x$
and time
$x$
and time
![]() $t$
, respectively; the given source function
$t$
, respectively; the given source function
![]() $h_1$
denotes the introduction of criminal agents into the system, and the given function
$h_1$
denotes the introduction of criminal agents into the system, and the given function
![]() $h_2$
describes the density of additional criminals, which may exist even in the absence of any criminal agents. We refer to [Reference Short, Bertozzi and Brantingham32, Reference Short, Brantingham, Bertozzi and Tita34] for more details on (1), to [Reference Bellomo, Colasuonno, Knopoff and Soler3, Reference Berestycki and Nadal5, Reference Gu, Wang and Yi13, Reference Pitcher26, Reference Short, Mohler, Brantingham and Tita35, Reference Tse and Ward38, Reference Zipkin, Short and Bertozzi49] for further developments of crime models and to [Reference Bellomo, Outada, Soler, Tao and Winkler4, Reference D’Orsogna and Perc9] for more comprehensive reviews of related works.
$h_2$
describes the density of additional criminals, which may exist even in the absence of any criminal agents. We refer to [Reference Short, Bertozzi and Brantingham32, Reference Short, Brantingham, Bertozzi and Tita34] for more details on (1), to [Reference Bellomo, Colasuonno, Knopoff and Soler3, Reference Berestycki and Nadal5, Reference Gu, Wang and Yi13, Reference Pitcher26, Reference Short, Mohler, Brantingham and Tita35, Reference Tse and Ward38, Reference Zipkin, Short and Bertozzi49] for further developments of crime models and to [Reference Bellomo, Outada, Soler, Tao and Winkler4, Reference D’Orsogna and Perc9] for more comprehensive reviews of related works.
To elucidate our motivation, we first recall some analytical progress related to the system (1). For the classical solvability of the initial-boundary value problem, the local existence and uniqueness of solutions has been obtained in [Reference Rodríguez and Bertozzi28] and the global existence of solutions has been established provided that either
![]() $n=1$
[Reference Rodríguez and Winkler29, Reference Wang, Wang and Feng41] or
$n=1$
[Reference Rodríguez and Winkler29, Reference Wang, Wang and Feng41] or
![]() $n\geq 2$
with the additional condition that
$n\geq 2$
with the additional condition that
![]() $\chi \lt \frac 2n$
[Reference Freitag11, Reference Shen and Li31], or the initial data and the given functions
$\chi \lt \frac 2n$
[Reference Freitag11, Reference Shen and Li31], or the initial data and the given functions
![]() $h_1$
and
$h_1$
and
![]() $h_2$
are assumed to be small [Reference Ahn, Kang and Lee1, Reference Tao and Winkler37]. It has been shown that these restrictions can be relaxed to
$h_2$
are assumed to be small [Reference Ahn, Kang and Lee1, Reference Tao and Winkler37]. It has been shown that these restrictions can be relaxed to
![]() $\chi \gt 0$
when
$\chi \gt 0$
when
![]() $n=2$
[Reference Winkler44] or to
$n=2$
[Reference Winkler44] or to
![]() $\chi \in (0,\sqrt{3})$
when
$\chi \in (0,\sqrt{3})$
when
![]() $n=3$
[Reference Jiang and Yang15], in the sense of radial renormalised solvability. In addition, considering interacting individuals may have attempted to avoid competition, the model corresponding to (1) with the linear criminal diffusion (i.e.
$n=3$
[Reference Jiang and Yang15], in the sense of radial renormalised solvability. In addition, considering interacting individuals may have attempted to avoid competition, the model corresponding to (1) with the linear criminal diffusion (i.e.
![]() $\Delta u$
) replaced by the nonlinear criminal diffusion (i.e.
$\Delta u$
) replaced by the nonlinear criminal diffusion (i.e.
![]() $\nabla \cdot \left (u^{m-1}\nabla u\right )$
with some
$\nabla \cdot \left (u^{m-1}\nabla u\right )$
with some
![]() $m\gt 0$
) also has been studied by researchers. For this nonlinear model, it is known that its two-dimensional initial-boundary value problem admits a global bounded weak solution provided that either
$m\gt 0$
) also has been studied by researchers. For this nonlinear model, it is known that its two-dimensional initial-boundary value problem admits a global bounded weak solution provided that either
![]() $m\gt \frac 32$
[Reference Rodríguez and Winkler30] or
$m\gt \frac 32$
[Reference Rodríguez and Winkler30] or
![]() $m\gt 1$
and
$m\gt 1$
and
![]() $\chi \lt \frac{\sqrt{3}}{2}$
[Reference Yang and Yang47]. On the other hand, if the logistic source term, that is,
$\chi \lt \frac{\sqrt{3}}{2}$
[Reference Yang and Yang47]. On the other hand, if the logistic source term, that is,
![]() $au-bu^\alpha$
with
$au-bu^\alpha$
with
![]() $a\in \mathbb{R}$
and
$a\in \mathbb{R}$
and
![]() $b\gt 0$
, is incorporated into (1), then, the resulting system has a global generalised solution for
$b\gt 0$
, is incorporated into (1), then, the resulting system has a global generalised solution for
![]() $n=2$
and
$n=2$
and
![]() $\alpha =2$
[Reference Heihoff14], which is eventually smooth ( [Reference Qiu and Li27]), and possesses a global classical solution for either
$\alpha =2$
[Reference Heihoff14], which is eventually smooth ( [Reference Qiu and Li27]), and possesses a global classical solution for either
![]() $n=2,3$
and
$n=2,3$
and
![]() $\alpha \gt 2$
[Reference Heihoff14, Reference Wang and Feng40] or
$\alpha \gt 2$
[Reference Heihoff14, Reference Wang and Feng40] or
![]() $n\geq 4$
and
$n\geq 4$
and
![]() $\alpha \gt \frac{n}{4}+1$
[Reference Wang and Feng40]. When
$\alpha \gt \frac{n}{4}+1$
[Reference Wang and Feng40]. When
![]() $\kappa =0$
,
$\kappa =0$
,
![]() $h_1\equiv 0$
,
$h_1\equiv 0$
,
![]() $h_2\equiv 0$
and
$h_2\equiv 0$
and
![]() $u_t$
is replaced by
$u_t$
is replaced by
![]() $\tau u_t$
with
$\tau u_t$
with
![]() $\tau \in (0,1)$
, the model (1) arrives at a reduced crime model considered in [Reference Fuest and Heihoff12], where a statement on spontaneous emergence of arbitrarily large values of
$\tau \in (0,1)$
, the model (1) arrives at a reduced crime model considered in [Reference Fuest and Heihoff12], where a statement on spontaneous emergence of arbitrarily large values of
![]() $\|u(\cdot,t)\|_{L^q}$
with
$\|u(\cdot,t)\|_{L^q}$
with
![]() $q\gt \frac n2$
has been derived for
$q\gt \frac n2$
has been derived for
![]() $\chi \gt 0$
and
$\chi \gt 0$
and
![]() $n\geq 3$
. As to long-time behaviours of solutions of (1), for
$n\geq 3$
. As to long-time behaviours of solutions of (1), for
![]() $\chi \lt \frac 2n$
with
$\chi \lt \frac 2n$
with
![]() $n\geq 2$
the asymptotic stability of constant steady states has been considered in [Reference Shen and Li31], provided that
$n\geq 2$
the asymptotic stability of constant steady states has been considered in [Reference Shen and Li31], provided that
![]() $h_1\equiv \textit{const.}$
and
$h_1\equiv \textit{const.}$
and
![]() $h_2\equiv \textit{const.}$
with certain smallness; under the assumptions that
$h_2\equiv \textit{const.}$
with certain smallness; under the assumptions that
![]() $h_1\rightarrow 0$
and
$h_1\rightarrow 0$
and
![]() $h_2\rightarrow h_{2,\infty }$
in some sense as
$h_2\rightarrow h_{2,\infty }$
in some sense as
![]() $t\rightarrow \infty$
, the convergence results
$t\rightarrow \infty$
, the convergence results
![]() $(u,v)\rightarrow (0,v_\infty )$
have been studied in some appropriate senses in [Reference Ahn, Kang and Lee1, Reference Jiang and Yang15, Reference Rodríguez and Winkler29, Reference Tao and Winkler37, Reference Winkler44], where
$(u,v)\rightarrow (0,v_\infty )$
have been studied in some appropriate senses in [Reference Ahn, Kang and Lee1, Reference Jiang and Yang15, Reference Rodríguez and Winkler29, Reference Tao and Winkler37, Reference Winkler44], where
![]() $v_\infty$
denotes the solution to the boundary value problem
$v_\infty$
denotes the solution to the boundary value problem
Furthermore, we refer to [Reference Berestycki, Wei and Winter6, Reference Cantrell, Cosner and Manásevich8, Reference Kolokolnikov, Ward and Wei16, Reference Lloyd and O’Farrell23–Reference Mei and Wei25, Reference Short, Bertozzi and Brantingham32, Reference Tse and Ward39] for the mathematical analytical work on related stationary problems, which reveal the possibility of stably spatial heterogeneous behaviour resembling crime hotspot formation and support that the system (1) is adequate to describe the formation of crime hotspots encountered in reality.
Compared the analytical results on (1) mentioned above, we find that the range of the parameter
![]() $\chi$
which guarantees the global existence of classical solutions of the system (1) seems to become larger when either the spatial domain is one or in multidimensional settings, the initial data and the source functions satisfy some smallness or radial symmetric assumption, or the solution concept is considered under proper generalised frameworks. Thus, we are wondering whether or not there exists an appropriate generalised framework within which for any
$\chi$
which guarantees the global existence of classical solutions of the system (1) seems to become larger when either the spatial domain is one or in multidimensional settings, the initial data and the source functions satisfy some smallness or radial symmetric assumption, or the solution concept is considered under proper generalised frameworks. Thus, we are wondering whether or not there exists an appropriate generalised framework within which for any
![]() $\chi \gt 0$
the corresponding
$\chi \gt 0$
the corresponding
![]() $n(\geq 2)$
-dimensional initial-boundary value problem of (1) is solvable without imposing these additional conditions on both the initial data and the source functions
$n(\geq 2)$
-dimensional initial-boundary value problem of (1) is solvable without imposing these additional conditions on both the initial data and the source functions
![]() $h_1$
and
$h_1$
and
![]() $h_2$
.
$h_2$
.
Motivated by this, the first purpose of the present work is to present that for arbitrary
![]() $\chi \gt 0$
, the following initial-boundary value problem:
$\chi \gt 0$
, the following initial-boundary value problem:
 \begin{equation} \left \{ \begin{split} &u_t= \Delta u-\chi \nabla \cdot \left (u\nabla \ln v\right )-\kappa uv+h_1,&\ x\in \Omega,\ t\gt 0, \\ &v_t=\Delta v-v+uv+h_2, &\ x\in \Omega,\ t\gt 0,\\ &\nabla u\cdot \nu =\nabla v\cdot \nu =0,&\ x\in \partial \Omega,\ t\gt 0,\\ &u(x,0)=u_0(x),\ v(x,0)=v_0(x),&\ x\in \Omega, \end{split} \right . \end{equation}
\begin{equation} \left \{ \begin{split} &u_t= \Delta u-\chi \nabla \cdot \left (u\nabla \ln v\right )-\kappa uv+h_1,&\ x\in \Omega,\ t\gt 0, \\ &v_t=\Delta v-v+uv+h_2, &\ x\in \Omega,\ t\gt 0,\\ &\nabla u\cdot \nu =\nabla v\cdot \nu =0,&\ x\in \partial \Omega,\ t\gt 0,\\ &u(x,0)=u_0(x),\ v(x,0)=v_0(x),&\ x\in \Omega, \end{split} \right . \end{equation}
where
![]() $\nu$
denotes the exterior normal vector to the boundary
$\nu$
denotes the exterior normal vector to the boundary
![]() $\partial \Omega$
, possesses solutions in an appropriate generalised framework in the two-dimensional setting, without imposing any assumption of smallness and radial symmetry of both the initial data and the source functions
$\partial \Omega$
, possesses solutions in an appropriate generalised framework in the two-dimensional setting, without imposing any assumption of smallness and radial symmetry of both the initial data and the source functions
![]() $h_1$
and
$h_1$
and
![]() $h_2$
.
$h_2$
.
Before going further, we shall be precise about the notion of generalised solutions to the initial-boundary value problem (3) considered in this work.
Definition 1. A pair
![]() $(u,v)$
is called a global generalised solution to the initial-boundary value problem (3) if for any
$(u,v)$
is called a global generalised solution to the initial-boundary value problem (3) if for any
![]() $T\gt 0$
,
$T\gt 0$
,
(1) it holds that
 \begin{equation} \left \{ \begin{split} &u\in L^1(\Omega \times (0,T)),\,\,\,\nabla \ln (1+u)\in L^2(\Omega \times (0,T)),\\ &v\in L^1(\Omega \times (0,T)),\,\,\,\nabla \ln v\in L^2(\Omega \times (0,T)),\\ &uv\in L^1(\Omega \times (0,T)),\\ &u(x,t)\geq 0,\,\,\, v(x,t)\gt 0,\,\,\, a.e.\,\, \mathrm{in}\,\,\Omega \times [0,T]; \end{split} \right . \end{equation}
\begin{equation} \left \{ \begin{split} &u\in L^1(\Omega \times (0,T)),\,\,\,\nabla \ln (1+u)\in L^2(\Omega \times (0,T)),\\ &v\in L^1(\Omega \times (0,T)),\,\,\,\nabla \ln v\in L^2(\Omega \times (0,T)),\\ &uv\in L^1(\Omega \times (0,T)),\\ &u(x,t)\geq 0,\,\,\, v(x,t)\gt 0,\,\,\, a.e.\,\, \mathrm{in}\,\,\Omega \times [0,T]; \end{split} \right . \end{equation}
(2) it holds that
(3) it holds that for some
![]() $p,q\gt 0$
and each non-negative
$p,q\gt 0$
and each non-negative
![]() $\varphi (x,t)\in C_0^\infty (\overline{\Omega }\times [0,T))$
$\varphi (x,t)\in C_0^\infty (\overline{\Omega }\times [0,T))$
 \begin{align} &-\int _\Omega (u_0+1)^{-p}v_0^{-q}\varphi |_{t=0} dx-\int _0^T\int _\Omega (u+1)^{-p}v^{-q}\varphi _tdxdt \nonumber \\ & \quad\le -p(p+1)\int _0^T\int _\Omega (u+1)^{-p-2}v^{-q}\varphi |\nabla u|^2dxdt\nonumber \\ &\qquad+\int _0^T\int _\Omega \left (p(p+1)\chi \frac{u}{u+1}-2pq\right )(u+1)^{-p-1}v^{-q-1}\varphi \nabla u\cdot \nabla v dxdt\nonumber \\ &\qquad+\int _0^T\int _\Omega \left (\chi pq\frac{u}{u+1}-q(q+1)\right )(u+1)^{-p}v^{-q-2}\varphi |\nabla v|^2dxdt\nonumber \\ &\qquad-p\int _0^T\int _\Omega (u+1)^{-p-1}v^{-q}\left (-\kappa uv+h_1\right )\varphi dxdt-q\int _0^T\int _\Omega (u+1)^{-p}v^{-q-1}\left (- v+u v+h_2 \right )\varphi dxdt\nonumber \\ &\qquad+p\int _0^T\int _\Omega (u+1)^{-p-1}v^{-q}\nabla u \cdot \nabla \varphi dxdt-p\chi \int _0^T\int _\Omega (u+1)^{-p-1}v^{-q-1}u\nabla v\cdot \nabla \varphi dxdt\nonumber \\ &\qquad+q\int _0^T\int _\Omega (u+1)^{-p}v^{-q-1}\nabla v\cdot \nabla \varphi dxdt; \end{align}
\begin{align} &-\int _\Omega (u_0+1)^{-p}v_0^{-q}\varphi |_{t=0} dx-\int _0^T\int _\Omega (u+1)^{-p}v^{-q}\varphi _tdxdt \nonumber \\ & \quad\le -p(p+1)\int _0^T\int _\Omega (u+1)^{-p-2}v^{-q}\varphi |\nabla u|^2dxdt\nonumber \\ &\qquad+\int _0^T\int _\Omega \left (p(p+1)\chi \frac{u}{u+1}-2pq\right )(u+1)^{-p-1}v^{-q-1}\varphi \nabla u\cdot \nabla v dxdt\nonumber \\ &\qquad+\int _0^T\int _\Omega \left (\chi pq\frac{u}{u+1}-q(q+1)\right )(u+1)^{-p}v^{-q-2}\varphi |\nabla v|^2dxdt\nonumber \\ &\qquad-p\int _0^T\int _\Omega (u+1)^{-p-1}v^{-q}\left (-\kappa uv+h_1\right )\varphi dxdt-q\int _0^T\int _\Omega (u+1)^{-p}v^{-q-1}\left (- v+u v+h_2 \right )\varphi dxdt\nonumber \\ &\qquad+p\int _0^T\int _\Omega (u+1)^{-p-1}v^{-q}\nabla u \cdot \nabla \varphi dxdt-p\chi \int _0^T\int _\Omega (u+1)^{-p-1}v^{-q-1}u\nabla v\cdot \nabla \varphi dxdt\nonumber \\ &\qquad+q\int _0^T\int _\Omega (u+1)^{-p}v^{-q-1}\nabla v\cdot \nabla \varphi dxdt; \end{align}
(4) it holds that for each non-negative
![]() $\varphi (x,t)\in C_0^\infty (\overline{\Omega }\times [0,T))$
$\varphi (x,t)\in C_0^\infty (\overline{\Omega }\times [0,T))$
We here give a remark on the constants
![]() $p$
and
$p$
and
![]() $q$
appeared in (7).
$q$
appeared in (7).
Remark 1. For given
![]() $\chi \gt 0$
, the admissible
$\chi \gt 0$
, the admissible
![]() $(p,q)$
is that
$(p,q)$
is that
![]() $p\geq 1$
and
$p\geq 1$
and
![]() $q\geq 2$
, fulfilling that
$q\geq 2$
, fulfilling that
in our subsequent analyses (see Lemma 3.6 below).
To state the first result on the global existence of such generalised solutions, the initial data
![]() $(u_0,v_0)$
are throughout assumed to satisfy
$(u_0,v_0)$
are throughout assumed to satisfy
 \begin{equation} \left \{ \begin{split} &u_0\in C^0(\overline{\Omega })\,\,\,\, \mathrm{with}\,\,\,\, u_0\geq 0\,\,\,\,\mathrm{and}\,\,\,\,u_0\not \equiv 0,\\ &v_0\in W^{1,\infty }(\overline{\Omega })\,\,\,\, \mathrm{with}\,\,\,\, \inf \limits _{x\in \overline{\Omega }}v_0\gt 0, \end{split} \right . \end{equation}
\begin{equation} \left \{ \begin{split} &u_0\in C^0(\overline{\Omega })\,\,\,\, \mathrm{with}\,\,\,\, u_0\geq 0\,\,\,\,\mathrm{and}\,\,\,\,u_0\not \equiv 0,\\ &v_0\in W^{1,\infty }(\overline{\Omega })\,\,\,\, \mathrm{with}\,\,\,\, \inf \limits _{x\in \overline{\Omega }}v_0\gt 0, \end{split} \right . \end{equation}
and the source functions
![]() $h_1$
and
$h_1$
and
![]() $h_2$
are supposed to fulfil
$h_2$
are supposed to fulfil
With Definition 1 and the assumptions (10)–(11) at hand, the first result reads as follows.
Theorem 1.1.
Let
![]() $\Omega \subset \mathbb{R}^2$
be a bounded and smooth spatial domain, and (10)–(11) hold. Then, for any
$\Omega \subset \mathbb{R}^2$
be a bounded and smooth spatial domain, and (10)–(11) hold. Then, for any
![]() $\chi \gt 0$
, the initial-boundary value problem (3) possesses at least one global generalised solution in the sense of Definition 1.
$\chi \gt 0$
, the initial-boundary value problem (3) possesses at least one global generalised solution in the sense of Definition 1.
Remark 2. By a slight adaptation of [Reference Winkler45, Lemma 2.1], we can show that if
such that
![]() $u\geq 0$
and
$u\geq 0$
and
![]() $v\gt 0$
in
$v\gt 0$
in
![]() $\overline{\Omega }\times (0,T)$
and
$\overline{\Omega }\times (0,T)$
and
![]() $(u,v)$
is a solution of (3) in the sense of Definition 1, then
$(u,v)$
is a solution of (3) in the sense of Definition 1, then
![]() $(u,v)$
also solves (3) in the classical sense. This also supports the interest in our concept of generalised solutions.
$(u,v)$
also solves (3) in the classical sense. This also supports the interest in our concept of generalised solutions.
Going beyond the global existence statement, we naturally focus on the large-time behaviour of generalised solutions. To achieve it, we additionally assume that
with some
![]() $h_{2,\infty }\in C^1(\overline{\Omega })$
. The second result on the asymptotic behaviour of the generalised solution established in Theorem 1.1 can be stated as follows.
$h_{2,\infty }\in C^1(\overline{\Omega })$
. The second result on the asymptotic behaviour of the generalised solution established in Theorem 1.1 can be stated as follows.
Theorem 1.2.
Let all assumptions in Theorem 1.1 be satisfied, and let (12)–(14) be fulfilled. Under the additional assumption that
![]() $\Omega$
is convex, for the global generalised solution of the initial-boundary value problem (3) taken from Theorem 1.1, there exists a null set
$\Omega$
is convex, for the global generalised solution of the initial-boundary value problem (3) taken from Theorem 1.1, there exists a null set
![]() $\mathcal{N}\subset (0,\infty )$
such that
$\mathcal{N}\subset (0,\infty )$
such that
where
![]() $v_\infty$
denotes the solution of the boundary value problem (2).
$v_\infty$
denotes the solution of the boundary value problem (2).
Remark 3. In comparison with [Reference Li and Xie20, Theorem 1.2] and [Reference Li, Wang and Xie22, Theorem 1.3], where the long-time behaviour of generalised solution to the system that with
![]() $u$
instead of
$u$
instead of
![]() $uv$
in the second equation of (3) was obtained in two-dimensional setting and higher dimensional settings, respectively, our result in Theorem 1.2 is weaker due to the presence of the nonlinear production
$uv$
in the second equation of (3) was obtained in two-dimensional setting and higher dimensional settings, respectively, our result in Theorem 1.2 is weaker due to the presence of the nonlinear production
![]() $+uv$
; especially, we do not know how to prove the eventual smoothness of the generalised solution established in Theorem 1.1.
$+uv$
; especially, we do not know how to prove the eventual smoothness of the generalised solution established in Theorem 1.1.
1.1. Technical strategy and structure of the article
The first objective of this paper is to present that the initial-boundary value problem (3) possesses a global generalised solution. Usually, to this end, one should seek an appropriate generalised framework and thereby obtain the global existence of generalised solutions via an approximation procedure. Here, our novelty of analysis consists of structuring an appropriate generalised framework, in which the difficulty is to define the solution component
![]() $v$
adequately. Although our definition of the solution component
$v$
adequately. Although our definition of the solution component
![]() $u$
is inspired by the generalised framework introduced in [Reference Lankeit and Winkler18, Reference Zhigun48] for the logarithmic Keller-Segel system with linear production, our definition of the solution component
$u$
is inspired by the generalised framework introduced in [Reference Lankeit and Winkler18, Reference Zhigun48] for the logarithmic Keller-Segel system with linear production, our definition of the solution component
![]() $v$
is completely different from that in [Reference Lankeit and Winkler18, Reference Zhigun48] due to the presence of the nonlinear production
$v$
is completely different from that in [Reference Lankeit and Winkler18, Reference Zhigun48] due to the presence of the nonlinear production
![]() $+uv$
in the second equation in (3), or, more precisely, we structure the generalised definition of the solution component
$+uv$
in the second equation in (3), or, more precisely, we structure the generalised definition of the solution component
![]() $v$
by respectively defining the generalised subsolution and supersolution, see (6) and (8) in Definition 1. After this, to get the generalised solution via an appropriate approximation procedure, the key steps are to establish a series of uniform a priori estimates, see Lemmas 3.1 and 3.2.
$v$
by respectively defining the generalised subsolution and supersolution, see (6) and (8) in Definition 1. After this, to get the generalised solution via an appropriate approximation procedure, the key steps are to establish a series of uniform a priori estimates, see Lemmas 3.1 and 3.2.
The second objective of this paper is to perform the large-time behaviour of the generalised solution
![]() $(u,v)$
determined in Theorem 1.1, under the additional assumptions (12)–(14). To achieve this, we start to present that for any
$(u,v)$
determined in Theorem 1.1, under the additional assumptions (12)–(14). To achieve this, we start to present that for any
![]() $\varepsilon \in (0,1)$
$\varepsilon \in (0,1)$
see Lemma 4.4. Taking advantage of this and an appropriate approximation procedure invoking the Beppo Levi theorem, for any
![]() $t\gt 0$
we get the key estimate:
$t\gt 0$
we get the key estimate:
 \begin{align*} &\int _\Omega |v_\varepsilon -v_\infty |(\cdot,t+1)dx-\int _\Omega |v_\varepsilon -v_\infty |(\cdot,t)dx+\int _t^{t+1}\int _\Omega |v_\varepsilon -v_\infty | dxds\\ & \quad\leq \int _t^{t+1}\int _\Omega u_\varepsilon v_\varepsilon dxds+\int _t^{t+1}\int _\Omega |h_2-h_{2,\infty }|dxds, \end{align*}
\begin{align*} &\int _\Omega |v_\varepsilon -v_\infty |(\cdot,t+1)dx-\int _\Omega |v_\varepsilon -v_\infty |(\cdot,t)dx+\int _t^{t+1}\int _\Omega |v_\varepsilon -v_\infty | dxds\\ & \quad\leq \int _t^{t+1}\int _\Omega u_\varepsilon v_\varepsilon dxds+\int _t^{t+1}\int _\Omega |h_2-h_{2,\infty }|dxds, \end{align*}
where
![]() $v_\infty$
denotes the solution of the boundary value problem (2), see the proof of Lemma 4.5 for details. In terms of it, setting
$v_\infty$
denotes the solution of the boundary value problem (2), see the proof of Lemma 4.5 for details. In terms of it, setting
![]() $z_\varepsilon (t)\;:\!=\;\int _t^{t+1}\int _\Omega |v_\varepsilon -v_\infty | dxds$
we have
$z_\varepsilon (t)\;:\!=\;\int _t^{t+1}\int _\Omega |v_\varepsilon -v_\infty | dxds$
we have
by which an application of the ODE techniques (see Lemma 4.2) invoking (16) presents the desired decay in Theorem 1.2.
The rest of this paper is arranged as follows. In the following section, we present the global well-posedness for the approximate problem (17). In Section 3, the global existence of generalised solutions to the initial-boundary value problem (3) is established. Section 4 is devoted to showing the large-time behaviour desired in Theorem 1.2 via an appropriate approximation procedure invoking the Beppo Levi theorem.
2. Preliminaries
To construct a generalised solution of the initial-boundary value problem (3) by an approximation procedure, for each
![]() $\varepsilon \in (0, 1)$
we shall consider the following approximate problem
$\varepsilon \in (0, 1)$
we shall consider the following approximate problem
 \begin{equation} \left \{ \begin{split} &u_{\varepsilon t}=\Delta u_{\varepsilon }-\chi \nabla \cdot \left (u_{\varepsilon }\nabla \ln v_{\varepsilon }\right )-\kappa u_\varepsilon v_\varepsilon +h_1, & x \in \Omega, \,t\gt 0,\\ &v_{\varepsilon t}=\Delta v_{\varepsilon }-v_\varepsilon +\frac{u_\varepsilon v_\varepsilon }{1+\varepsilon u_\varepsilon v_\varepsilon }+h_2, & x \in \Omega,\, t\gt 0,\\ &\frac{\partial u_{\varepsilon }}{\partial \nu }=\frac{\partial v_{\varepsilon }}{\partial \nu }=0, & x \in \partial \Omega, \,t\gt 0,\\ &u_{\varepsilon }(x, 0)=u_{0}(x), \quad v_{\varepsilon }(x, 0)=v_{0}(x), & x \in \Omega . \end{split} \right . \end{equation}
\begin{equation} \left \{ \begin{split} &u_{\varepsilon t}=\Delta u_{\varepsilon }-\chi \nabla \cdot \left (u_{\varepsilon }\nabla \ln v_{\varepsilon }\right )-\kappa u_\varepsilon v_\varepsilon +h_1, & x \in \Omega, \,t\gt 0,\\ &v_{\varepsilon t}=\Delta v_{\varepsilon }-v_\varepsilon +\frac{u_\varepsilon v_\varepsilon }{1+\varepsilon u_\varepsilon v_\varepsilon }+h_2, & x \in \Omega,\, t\gt 0,\\ &\frac{\partial u_{\varepsilon }}{\partial \nu }=\frac{\partial v_{\varepsilon }}{\partial \nu }=0, & x \in \partial \Omega, \,t\gt 0,\\ &u_{\varepsilon }(x, 0)=u_{0}(x), \quad v_{\varepsilon }(x, 0)=v_{0}(x), & x \in \Omega . \end{split} \right . \end{equation}
An application of the well-known strategy harnessing the contraction mapping principle and the well-known pointwise positivity property of the Neumann heat semigroup, as in [Reference Aida, Osaka, Tsujikawa and Mimura2, Reference Freitag11, Reference Rodríguez and Bertozzi28, Reference Winkler43], ensures the global existence of classical solution to the approximate problems (17).
Lemma 2.1. Let the assumptions (10)–(11) hold. For each
![]() $\varepsilon \in (0,1)$
and any
$\varepsilon \in (0,1)$
and any
![]() $\chi \gt 0$
, there exists a unique pair
$\chi \gt 0$
, there exists a unique pair
![]() $(u_\varepsilon,v_\varepsilon )$
of positive functions with the properties that for any
$(u_\varepsilon,v_\varepsilon )$
of positive functions with the properties that for any
![]() $T\gt 0$
$T\gt 0$
 \begin{equation*} \left \{ \begin {split} &u_\varepsilon \in C^0\big (\overline {\Omega }\times [0,T]\big )\cap C^{2,1}\big (\overline {\Omega }\times (0,T]\big ),\\ &v_\varepsilon \in \bigcap \limits _{p\gt 2}C^0\big ([0,T];\; W^{1,p}(\overline {\Omega })\big )\cap C^{2,1}\big (\overline {\Omega }\times (0,T]\big ), \end {split} \right . \end{equation*}
\begin{equation*} \left \{ \begin {split} &u_\varepsilon \in C^0\big (\overline {\Omega }\times [0,T]\big )\cap C^{2,1}\big (\overline {\Omega }\times (0,T]\big ),\\ &v_\varepsilon \in \bigcap \limits _{p\gt 2}C^0\big ([0,T];\; W^{1,p}(\overline {\Omega })\big )\cap C^{2,1}\big (\overline {\Omega }\times (0,T]\big ), \end {split} \right . \end{equation*}
such that
![]() $(u_\varepsilon,v_\varepsilon )$
solves the approximate problem (17) classically in
$(u_\varepsilon,v_\varepsilon )$
solves the approximate problem (17) classically in
![]() $\Omega \times [0,\infty )$
. Moreover, we have
$\Omega \times [0,\infty )$
. Moreover, we have
and
for some
![]() $C\gt 0$
, independent of
$C\gt 0$
, independent of
![]() $\varepsilon$
.
$\varepsilon$
.
Proof. Similar to [Reference Aida, Osaka, Tsujikawa and Mimura2, Reference Freitag11, Reference Rodríguez and Bertozzi28, Reference Winkler43], the well-known strategy invoking the contraction mapping principle presents that for each
![]() $\varepsilon \in (0,1)$
and any
$\varepsilon \in (0,1)$
and any
![]() $\chi \gt 0$
, there exist a time
$\chi \gt 0$
, there exist a time
![]() $T_{\max,\varepsilon }\in (0,\infty ]$
and a unique pair
$T_{\max,\varepsilon }\in (0,\infty ]$
and a unique pair
![]() $(u_\varepsilon,v_\varepsilon )$
of positive functions with the properties that for any
$(u_\varepsilon,v_\varepsilon )$
of positive functions with the properties that for any
![]() $p\gt 2$
$p\gt 2$
 \begin{equation*} \left \{ \begin {split} &u_\varepsilon \in C^0\big (\overline {\Omega }\times [0,T_{\max,\varepsilon })\big )\cap C^{2,1}\big (\overline {\Omega }\times (0,T_{\max,\varepsilon })\big ),\\ &v_\varepsilon \in C^0\big ([0,T_{\max,\varepsilon });\; W^{1,p}(\overline {\Omega })\big )\cap C^{2,1}\big (\overline {\Omega }\times (0,T_{\max,\varepsilon })\big ) \end {split} \right . \end{equation*}
\begin{equation*} \left \{ \begin {split} &u_\varepsilon \in C^0\big (\overline {\Omega }\times [0,T_{\max,\varepsilon })\big )\cap C^{2,1}\big (\overline {\Omega }\times (0,T_{\max,\varepsilon })\big ),\\ &v_\varepsilon \in C^0\big ([0,T_{\max,\varepsilon });\; W^{1,p}(\overline {\Omega })\big )\cap C^{2,1}\big (\overline {\Omega }\times (0,T_{\max,\varepsilon })\big ) \end {split} \right . \end{equation*}
such that
![]() $(u_\varepsilon,v_\varepsilon )$
solves the approximate problem (17) classically in
$(u_\varepsilon,v_\varepsilon )$
solves the approximate problem (17) classically in
![]() $\Omega \times [0,T_{\max,\varepsilon })$
. Moreover, if
$\Omega \times [0,T_{\max,\varepsilon })$
. Moreover, if
![]() $T_{\max,\varepsilon }\lt \infty$
, then for any
$T_{\max,\varepsilon }\lt \infty$
, then for any
![]() $p\gt 2$
$p\gt 2$
To show that
![]() $T_{\max,\varepsilon }=\infty$
, let us start with the pointwise lower bound for the solution component
$T_{\max,\varepsilon }=\infty$
, let us start with the pointwise lower bound for the solution component
![]() $v_\varepsilon$
. Indeed, we can apply the comparison principle for the Neumann problem associated with the heat equation to the variation-of-constants formula for
$v_\varepsilon$
. Indeed, we can apply the comparison principle for the Neumann problem associated with the heat equation to the variation-of-constants formula for
![]() $v_\varepsilon$
, namely
$v_\varepsilon$
, namely
and get
due to the facts that
![]() $h_2\geq 0$
and
$h_2\geq 0$
and
![]() $u_\varepsilon, v_\varepsilon \gt 0$
. We can also apply the properties of the Neumann heat semigroup (cf. [Reference Winkler42, Lemma 1.3], [Reference Cao7, Lemma 2.1]) to (22) and get that for any
$u_\varepsilon, v_\varepsilon \gt 0$
. We can also apply the properties of the Neumann heat semigroup (cf. [Reference Winkler42, Lemma 1.3], [Reference Cao7, Lemma 2.1]) to (22) and get that for any
![]() $q\gt 2$
$q\gt 2$
Since
![]() $\frac{u_\varepsilon v_\varepsilon }{1+\varepsilon u_\varepsilon v_\varepsilon }\leq \varepsilon ^{-1}$
and
$\frac{u_\varepsilon v_\varepsilon }{1+\varepsilon u_\varepsilon v_\varepsilon }\leq \varepsilon ^{-1}$
and
![]() $-\frac 12-(\frac 12-\frac 1q)=-1+\frac 1q\gt -1$
, it follows from (11) that for any
$-\frac 12-(\frac 12-\frac 1q)=-1+\frac 1q\gt -1$
, it follows from (11) that for any
![]() $q\gt 2$
$q\gt 2$
We now establish the bound of
![]() $\|u_\varepsilon \|_{L^1}$
by integrating the first equation in (17) over
$\|u_\varepsilon \|_{L^1}$
by integrating the first equation in (17) over
![]() $\Omega$
$\Omega$
which, integrating over
![]() $[0,t]$
, implies that
$[0,t]$
, implies that
We next estimate
![]() $\|u_\varepsilon \|_{L^\infty }$
by applying the properties of the Neumann heat semigroup (cf. [Reference Winkler42, Lemma 1.3], [Reference Cao7, Lemma 2.1]) to the variation-of-constants formula for
$\|u_\varepsilon \|_{L^\infty }$
by applying the properties of the Neumann heat semigroup (cf. [Reference Winkler42, Lemma 1.3], [Reference Cao7, Lemma 2.1]) to the variation-of-constants formula for
![]() $u_\varepsilon$
, denoted by
$u_\varepsilon$
, denoted by
and, due to the maximum principle and the non-negativity of
![]() $\kappa u_\varepsilon v_\varepsilon$
, conclude that for
$\kappa u_\varepsilon v_\varepsilon$
, conclude that for
![]() $r\in (2,q)$
$r\in (2,q)$
 \begin{align} \|u_\varepsilon (\cdot,t)\|_{L^\infty } &\le \|u_0\|_{L^\infty }+C \int _0^t\left (1+(t-s)^{-\frac 12-\frac 1r}\right )e^{-(t-s)}\|u_\varepsilon \nabla \ln v_\varepsilon \|_{L^r}ds\nonumber \\ &\quad +C\int _0^t\left (1+(t-s)^{-\frac{q-r}{qr}}\right )e^{-(t-s)}\|u_\varepsilon +h_1\|_{L^{\frac{qr}{q-r}}}ds. \end{align}
\begin{align} \|u_\varepsilon (\cdot,t)\|_{L^\infty } &\le \|u_0\|_{L^\infty }+C \int _0^t\left (1+(t-s)^{-\frac 12-\frac 1r}\right )e^{-(t-s)}\|u_\varepsilon \nabla \ln v_\varepsilon \|_{L^r}ds\nonumber \\ &\quad +C\int _0^t\left (1+(t-s)^{-\frac{q-r}{qr}}\right )e^{-(t-s)}\|u_\varepsilon +h_1\|_{L^{\frac{qr}{q-r}}}ds. \end{align}
In view of Hölder’s inequality, (23) and (24), we have
By means of the interpolation inequality and (26), we obtain
Substituting (29) and (30) into (28), and using (11) we arrive at for
![]() $t\in (0,T_{\max,\varepsilon })$
$t\in (0,T_{\max,\varepsilon })$
Letting
![]() $K(T)\;:\!=\;\sup _{t\in (0, T)}\|u_\varepsilon (\cdot, t)\|_{L^\infty }$
for any
$K(T)\;:\!=\;\sup _{t\in (0, T)}\|u_\varepsilon (\cdot, t)\|_{L^\infty }$
for any
![]() $T\in (0, T_{\max,\varepsilon })$
, it follows that
$T\in (0, T_{\max,\varepsilon })$
, it follows that
Since
![]() $0\lt 1-\frac{q-r}{qr}\lt 1$
, an application of Young’s inequality entails that
$0\lt 1-\frac{q-r}{qr}\lt 1$
, an application of Young’s inequality entails that
![]() $K(T)\le C_\varepsilon (T)$
. Hence for any
$K(T)\le C_\varepsilon (T)$
. Hence for any
![]() $T\in (0,T_{\max,\varepsilon })$
, we infer that
$T\in (0,T_{\max,\varepsilon })$
, we infer that
This, combined with (24) and (23), establishes a contradiction to (21) and thereby ensures that actually we must have
![]() $T_{\max,\varepsilon }=\infty$
.
$T_{\max,\varepsilon }=\infty$
.
Finally, using (23) and (26) with
![]() $T_{\max,\varepsilon }=\infty$
, we can get (18) and (19). After an integration in time, we infer from the second equation in (17) that for any
$T_{\max,\varepsilon }=\infty$
, we can get (18) and (19). After an integration in time, we infer from the second equation in (17) that for any
![]() $t\gt 0$
$t\gt 0$
which, together with (11) and (19), ensures (20).
At the end of this section, we also note a useful consequence of the dominated convergence theorem (see [Reference Winkler45, Lemma A.4]).
Lemma 2.2.
Let
![]() $M \subset \mathbb{R}^n$
with
$M \subset \mathbb{R}^n$
with
![]() $n \geq 1$
be measurable, and suppose that
$n \geq 1$
be measurable, and suppose that
![]() $(w_j)_{j\in N}\subset L^\infty (M)$
and
$(w_j)_{j\in N}\subset L^\infty (M)$
and
![]() $\left (z_j\right )_{j \in \mathbb{N}}\subset L^2(M)$
are such that
$\left (z_j\right )_{j \in \mathbb{N}}\subset L^2(M)$
are such that
![]() $\left |w_j\right | \leq C$
in
$\left |w_j\right | \leq C$
in
![]() $M$
for all
$M$
for all
![]() $j \in \mathbb{N}$
and
$j \in \mathbb{N}$
and
![]() $w_j \rightarrow w$
a.e. in
$w_j \rightarrow w$
a.e. in
![]() $M$
as well as
$M$
as well as
for some
![]() $C\gt 0, w \in L^{\infty }(M)$
, and
$C\gt 0, w \in L^{\infty }(M)$
, and
![]() $z \in L^2(M)$
. Then,
$z \in L^2(M)$
. Then,
3. Global generalised solutions
To construct the global existence of the generalised solution, we will seek some uniform in
![]() $\varepsilon$
estimates on the approximate solutions
$\varepsilon$
estimates on the approximate solutions
![]() $(u_\varepsilon,v_\varepsilon )$
given in Lemma 2.1. To this end, we begin with deriving the spatio-temporal integrability of
$(u_\varepsilon,v_\varepsilon )$
given in Lemma 2.1. To this end, we begin with deriving the spatio-temporal integrability of
![]() $\nabla \ln v_\varepsilon$
and some regularity features of the time derivatives.
$\nabla \ln v_\varepsilon$
and some regularity features of the time derivatives.
Lemma 3.1.
Let
![]() $(u_\varepsilon,v_\varepsilon )$
be given in Lemma 2.1. For any
$(u_\varepsilon,v_\varepsilon )$
be given in Lemma 2.1. For any
![]() $T\gt 0$
, there exists
$T\gt 0$
, there exists
![]() $C(T)\gt 0$
, independent of
$C(T)\gt 0$
, independent of
![]() $\varepsilon$
, with the property that
$\varepsilon$
, with the property that
Proof. Testing the second equation in (17) by
![]() $\frac{\varphi }{v_\varepsilon }$
with
$\frac{\varphi }{v_\varepsilon }$
with
![]() $\varphi (x)\in C^\infty (\overline{\Omega })$
, for
$\varphi (x)\in C^\infty (\overline{\Omega })$
, for
![]() $t\gt 0$
we have
$t\gt 0$
we have
 \begin{align} \int _\Omega \varphi \partial _t\ln v_\varepsilon dx=&\int _\Omega \frac{\varphi }{v_\varepsilon }\left (\Delta v_\varepsilon -v_\varepsilon +\frac{u_\varepsilon v_\varepsilon }{1+\varepsilon u_\varepsilon v_\varepsilon }+h_2\right )\nonumber \\ =&\int _\Omega \frac{\varphi |\nabla v_\varepsilon |^2}{v_\varepsilon ^2}dx-\int _\Omega \frac{\nabla \varphi \cdot \nabla v_\varepsilon }{v_\varepsilon }dx-\int _\Omega \varphi dx+\int _\Omega \frac{u_\varepsilon \varphi }{1+\varepsilon u_\varepsilon v_\varepsilon }dx+\int _\Omega \frac{\varphi h_2}{v_\varepsilon }dx. \end{align}
\begin{align} \int _\Omega \varphi \partial _t\ln v_\varepsilon dx=&\int _\Omega \frac{\varphi }{v_\varepsilon }\left (\Delta v_\varepsilon -v_\varepsilon +\frac{u_\varepsilon v_\varepsilon }{1+\varepsilon u_\varepsilon v_\varepsilon }+h_2\right )\nonumber \\ =&\int _\Omega \frac{\varphi |\nabla v_\varepsilon |^2}{v_\varepsilon ^2}dx-\int _\Omega \frac{\nabla \varphi \cdot \nabla v_\varepsilon }{v_\varepsilon }dx-\int _\Omega \varphi dx+\int _\Omega \frac{u_\varepsilon \varphi }{1+\varepsilon u_\varepsilon v_\varepsilon }dx+\int _\Omega \frac{\varphi h_2}{v_\varepsilon }dx. \end{align}
By taking
![]() $\varphi \equiv 1$
in (36) and using
$\varphi \equiv 1$
in (36) and using
![]() $u_\varepsilon, h_2\gt 0$
, we arrive at
$u_\varepsilon, h_2\gt 0$
, we arrive at
which on integration in time implies
Since
![]() $\ln \zeta \leq \zeta$
for any
$\ln \zeta \leq \zeta$
for any
![]() $\zeta \gt 0$
, it follows that
$\zeta \gt 0$
, it follows that
Note that (10) ensures
Hence, it follows from (20) that
with
![]() $C\gt 0$
independent of
$C\gt 0$
independent of
![]() $\varepsilon$
. In addition, let
$\varepsilon$
. In addition, let
![]() $\eta (t)\;:\!=\;e^{-t}\inf _{x \in \overline{\Omega }} v_{0}(x)$
; then, we have
$\eta (t)\;:\!=\;e^{-t}\inf _{x \in \overline{\Omega }} v_{0}(x)$
; then, we have
![]() $\eta ^{-1}(t)v_\varepsilon \geq 1$
owing to (18). Thus, from the fact that
$\eta ^{-1}(t)v_\varepsilon \geq 1$
owing to (18). Thus, from the fact that
![]() $\frac 12\ln ^2\zeta \leq \zeta$
for any
$\frac 12\ln ^2\zeta \leq \zeta$
for any
![]() $\zeta \geq 1$
and (20) we infer that
$\zeta \geq 1$
and (20) we infer that
Consequently, we have
This, combined with (37), entails (32).
Meanwhile, based on (37) and (18), we also have
and
 \begin{align*} \int _0^t\left \|\nabla v_\varepsilon ^{-1}(\cdot,s)\right \|_{L^2}^2ds=&\int _0^t\left \|-v_\varepsilon ^{-1}(\cdot,s)\nabla \ln v_\varepsilon (\cdot,s)\right \|_{L^2}^2ds\\ \le & \int _0^t\left \|v_\varepsilon ^{-1}(\cdot,s)\right \|_{L^\infty }^2\left \|\nabla \ln v_\varepsilon (\cdot,s)\right \|_{L^2}^2ds\\ \le & C(1+t)e^{2t},\,\,t\gt 0, \end{align*}
\begin{align*} \int _0^t\left \|\nabla v_\varepsilon ^{-1}(\cdot,s)\right \|_{L^2}^2ds=&\int _0^t\left \|-v_\varepsilon ^{-1}(\cdot,s)\nabla \ln v_\varepsilon (\cdot,s)\right \|_{L^2}^2ds\\ \le & \int _0^t\left \|v_\varepsilon ^{-1}(\cdot,s)\right \|_{L^\infty }^2\left \|\nabla \ln v_\varepsilon (\cdot,s)\right \|_{L^2}^2ds\\ \le & C(1+t)e^{2t},\,\,t\gt 0, \end{align*}
these immediately entail (33) as desired.
On the other hand, taking
![]() $\varphi \equiv g(x)\in C^\infty (\overline{\Omega })$
with
$\varphi \equiv g(x)\in C^\infty (\overline{\Omega })$
with
![]() $\|g\|_{H^2}\le 1$
in (36), it follows Hölder’s inequality that
$\|g\|_{H^2}\le 1$
in (36), it follows Hölder’s inequality that
 \begin{align*} \left |\int _\Omega g\partial _t\ln v_{\varepsilon }dx\right |\leq &\|\nabla \ln v_\varepsilon \|_{L^2}^2\|g\|_{L^\infty }+\|\nabla \ln v_\varepsilon \|_{L^2}\|\nabla g\|_{L^2}+\|g\|_{L^1}\\ &+\|u_\varepsilon \|_{L^1}\|g\|_{L^\infty }+ \|h_2\|_{L^\infty }\|g\|_{L^1}\|v_\varepsilon ^{-1}\|_{L^\infty }, \end{align*}
\begin{align*} \left |\int _\Omega g\partial _t\ln v_{\varepsilon }dx\right |\leq &\|\nabla \ln v_\varepsilon \|_{L^2}^2\|g\|_{L^\infty }+\|\nabla \ln v_\varepsilon \|_{L^2}\|\nabla g\|_{L^2}+\|g\|_{L^1}\\ &+\|u_\varepsilon \|_{L^1}\|g\|_{L^\infty }+ \|h_2\|_{L^\infty }\|g\|_{L^1}\|v_\varepsilon ^{-1}\|_{L^\infty }, \end{align*}
which, with the help of Young’s inequality and Sobolev’s embedding theorem, ensures
By means of (37), (19), (38), and (11), it in turn ensures (34). Similarly, in view of
by the same procedure of the proof of (34), we obtain
 \begin{align*} \left |\int _\Omega g\partial _t v_{\varepsilon }^{-1}dx\right |=&\left |\int _\Omega -2v_{\varepsilon }^{-1}|\nabla \ln v_{\varepsilon }|^2g+v_{\varepsilon }^{-1}\nabla g\cdot \nabla \ln v_{\varepsilon }+v_{\varepsilon }^{-1}g-\frac{u_\varepsilon v_\varepsilon ^{-1}g}{1+\varepsilon u_\varepsilon v_\varepsilon }- v_\varepsilon ^{-2}h_2g\right |\\ \leq &2\|v_{\varepsilon }^{-1}\|_{L^\infty }\|\nabla \ln v_\varepsilon \|_{L^2}^2\|g\|_{L^\infty }+\|v_{\varepsilon }^{-1}\|_{L^\infty }\|\nabla \ln v_\varepsilon \|_{L^2}\|\nabla g\|_{L^2}+\|v_{\varepsilon }^{-1}\|_{L^\infty }\|g\|_{L^1}\\ &+\|u_\varepsilon \|_{L^1}\|v_{\varepsilon }^{-1}\|_{L^\infty }\|g\|_{L^\infty }+ \|h_2\|_{L^\infty }\|v_{\varepsilon }^{-2}\|_{L^\infty }\|g\|_{L^1},\\ \le &C\|v_{\varepsilon }^{-1}\|_{L^\infty }\left (\|\nabla \ln v_\varepsilon \|_{L^2}^2+1 +\|u_\varepsilon \|_{L^1}+ \|h_2\|_{L^\infty }\|v_{\varepsilon }^{-1}\|_{L^\infty }\right )\|g\|_{H^2}, \end{align*}
\begin{align*} \left |\int _\Omega g\partial _t v_{\varepsilon }^{-1}dx\right |=&\left |\int _\Omega -2v_{\varepsilon }^{-1}|\nabla \ln v_{\varepsilon }|^2g+v_{\varepsilon }^{-1}\nabla g\cdot \nabla \ln v_{\varepsilon }+v_{\varepsilon }^{-1}g-\frac{u_\varepsilon v_\varepsilon ^{-1}g}{1+\varepsilon u_\varepsilon v_\varepsilon }- v_\varepsilon ^{-2}h_2g\right |\\ \leq &2\|v_{\varepsilon }^{-1}\|_{L^\infty }\|\nabla \ln v_\varepsilon \|_{L^2}^2\|g\|_{L^\infty }+\|v_{\varepsilon }^{-1}\|_{L^\infty }\|\nabla \ln v_\varepsilon \|_{L^2}\|\nabla g\|_{L^2}+\|v_{\varepsilon }^{-1}\|_{L^\infty }\|g\|_{L^1}\\ &+\|u_\varepsilon \|_{L^1}\|v_{\varepsilon }^{-1}\|_{L^\infty }\|g\|_{L^\infty }+ \|h_2\|_{L^\infty }\|v_{\varepsilon }^{-2}\|_{L^\infty }\|g\|_{L^1},\\ \le &C\|v_{\varepsilon }^{-1}\|_{L^\infty }\left (\|\nabla \ln v_\varepsilon \|_{L^2}^2+1 +\|u_\varepsilon \|_{L^1}+ \|h_2\|_{L^\infty }\|v_{\varepsilon }^{-1}\|_{L^\infty }\right )\|g\|_{H^2}, \end{align*}
which, together with (37), (19), (38) and (11), yields (35) as desired.
Similar to Lemma 3.1, we focus on deriving the spatio-temporal integrability of
![]() $\nabla \ln (u_\varepsilon +1)$
.
$\nabla \ln (u_\varepsilon +1)$
.
Lemma 3.2.
Let
![]() $(u_\varepsilon,v_\varepsilon )$
be given in Lemma 2.1. For any
$(u_\varepsilon,v_\varepsilon )$
be given in Lemma 2.1. For any
![]() $T\gt 0$
, there exists
$T\gt 0$
, there exists
![]() $C(T)\gt 0$
, independent of
$C(T)\gt 0$
, independent of
![]() $\varepsilon$
, with the property that
$\varepsilon$
, with the property that
Proof. Multiplying the first equation in (17) by
![]() $\frac{\varphi }{1+u_\varepsilon }$
with
$\frac{\varphi }{1+u_\varepsilon }$
with
![]() $\varphi (x)\in C^\infty (\overline{\Omega })$
and using the integration by parts, we arrive at
$\varphi (x)\in C^\infty (\overline{\Omega })$
and using the integration by parts, we arrive at
 \begin{align} \int _\Omega \varphi \partial _t\ln (1+u_\varepsilon )dx =& \int _{\Omega } \frac{\left |\nabla u_{\varepsilon }\right |^{2}\varphi }{\left (u_{\varepsilon }+1\right )^{2}}dx-\int _{\Omega }\frac{\nabla \varphi \cdot \nabla u_\varepsilon }{1+u_\varepsilon }dx-\chi \int _{\Omega } \frac{u_{\varepsilon }\varphi \nabla u_{\varepsilon } \cdot \nabla \ln v_{\varepsilon }}{\left (u_{\varepsilon }+1\right )^{2}}dx\nonumber \\[5pt] &+\chi \int _\Omega \frac{u_\varepsilon \nabla \varphi \cdot \nabla \ln v_\varepsilon }{1+u_\varepsilon }dx-\kappa \int _\Omega \frac{\varphi u_\varepsilon v_\varepsilon }{1+u_\varepsilon }dx+\int _\Omega \frac{h_1\varphi }{1+u_\varepsilon }dx. \end{align}
\begin{align} \int _\Omega \varphi \partial _t\ln (1+u_\varepsilon )dx =& \int _{\Omega } \frac{\left |\nabla u_{\varepsilon }\right |^{2}\varphi }{\left (u_{\varepsilon }+1\right )^{2}}dx-\int _{\Omega }\frac{\nabla \varphi \cdot \nabla u_\varepsilon }{1+u_\varepsilon }dx-\chi \int _{\Omega } \frac{u_{\varepsilon }\varphi \nabla u_{\varepsilon } \cdot \nabla \ln v_{\varepsilon }}{\left (u_{\varepsilon }+1\right )^{2}}dx\nonumber \\[5pt] &+\chi \int _\Omega \frac{u_\varepsilon \nabla \varphi \cdot \nabla \ln v_\varepsilon }{1+u_\varepsilon }dx-\kappa \int _\Omega \frac{\varphi u_\varepsilon v_\varepsilon }{1+u_\varepsilon }dx+\int _\Omega \frac{h_1\varphi }{1+u_\varepsilon }dx. \end{align}
By taking
![]() $\varphi \equiv 1$
in (41), thanks to
$\varphi \equiv 1$
in (41), thanks to
![]() $h_1\geq 0$
, an application of Young’s inequality yields that
$h_1\geq 0$
, an application of Young’s inequality yields that
 \begin{align*} \frac 12\int _{\Omega } \frac{\left |\nabla u_{\varepsilon }\right |^{2}}{\left (u_{\varepsilon }+1\right )^{2}}dx\leq &\frac{d}{dt}\int _\Omega \ln (1+u_\varepsilon )dx+\frac{\chi ^2}{2}\int _{\Omega } \frac{u_{\varepsilon }^{2}}{\left (u_{\varepsilon }+1\right )^{2}}\left |\nabla \ln v_{\varepsilon }\right |^{2}dx\\[5pt] &+\int _\Omega \frac{\kappa u_\varepsilon v_\varepsilon }{1+u_\varepsilon }dx-\int _\Omega \frac{h_1}{1+u_\varepsilon }dx\\[5pt] \leq &\frac{d}{dt}\int _\Omega \ln (1+u_\varepsilon )dx+\frac{\chi ^2}{2}\int _{\Omega }\left |\nabla \ln v_{\varepsilon }\right |^{2}dx+\kappa \int _\Omega v_\varepsilon dx. \end{align*}
\begin{align*} \frac 12\int _{\Omega } \frac{\left |\nabla u_{\varepsilon }\right |^{2}}{\left (u_{\varepsilon }+1\right )^{2}}dx\leq &\frac{d}{dt}\int _\Omega \ln (1+u_\varepsilon )dx+\frac{\chi ^2}{2}\int _{\Omega } \frac{u_{\varepsilon }^{2}}{\left (u_{\varepsilon }+1\right )^{2}}\left |\nabla \ln v_{\varepsilon }\right |^{2}dx\\[5pt] &+\int _\Omega \frac{\kappa u_\varepsilon v_\varepsilon }{1+u_\varepsilon }dx-\int _\Omega \frac{h_1}{1+u_\varepsilon }dx\\[5pt] \leq &\frac{d}{dt}\int _\Omega \ln (1+u_\varepsilon )dx+\frac{\chi ^2}{2}\int _{\Omega }\left |\nabla \ln v_{\varepsilon }\right |^{2}dx+\kappa \int _\Omega v_\varepsilon dx. \end{align*}
In view of the non-negativity of
![]() $\ln (1+u_\varepsilon )$
, on integration in time gives us
$\ln (1+u_\varepsilon )$
, on integration in time gives us
Note that
![]() $\zeta \geq \ln (1+\zeta )\geq 0$
for any
$\zeta \geq \ln (1+\zeta )\geq 0$
for any
![]() $\zeta \geq 0$
. This, together with (19), leads to
$\zeta \geq 0$
. This, together with (19), leads to
On the basis of this, we infer from (20) and (37) that there exists
![]() $C\gt 0$
, independent of
$C\gt 0$
, independent of
![]() $\varepsilon$
, such that for any
$\varepsilon$
, such that for any
![]() $t\gt 0$
$t\gt 0$
On the other hand, since
![]() $\frac 12\ln ^2(1+\zeta )\leq \zeta$
for any
$\frac 12\ln ^2(1+\zeta )\leq \zeta$
for any
![]() $\zeta \geq 0$
, it follows from (19) that there exists
$\zeta \geq 0$
, it follows from (19) that there exists
![]() $C\gt 0$
, independent of
$C\gt 0$
, independent of
![]() $\varepsilon$
, such that
$\varepsilon$
, such that
Combining with the above two inequalities, we obtain (39) as desired.
Now, let
![]() $\varphi \in C^\infty (\overline{\Omega })$
with
$\varphi \in C^\infty (\overline{\Omega })$
with
![]() $\|\varphi \|_{H^2}\le 1$
in (41), Hölder’s inequality and Young’s inequality imply that
$\|\varphi \|_{H^2}\le 1$
in (41), Hölder’s inequality and Young’s inequality imply that
 \begin{align*} \left |\int _\Omega \varphi \partial _t\ln (1+u_\varepsilon )dx\right |\leq &\|\varphi \|_{L^\infty }\|\nabla \ln (1+u_\varepsilon )\|_{L^2}^2+\chi \|\nabla \ln (1+u_\varepsilon )\|_{L^2}\|\nabla \ln v_\varepsilon \|_{L^2}\|\varphi \|_{L^\infty } \\[5pt] &+\|\nabla \ln (1+u_\varepsilon )\|_{L^2}\|\nabla \varphi \|_{L^2} +\chi \|\nabla \ln v_\varepsilon \|_{L^2}\|\nabla \varphi \|_{L^2}\\[5pt] &+\kappa \|v_\varepsilon \|_{L^1}\|\varphi \|_{L^\infty }+\|h_1\|_{L^\infty }\|\varphi \|_{L^1}\\[5pt] \leq &C\|\varphi \|_{H^2}\left (\|\nabla \ln (1+u_\varepsilon )\|_{L^2}^2+\|\nabla \ln v_\varepsilon \|_{L^2}^2+\kappa \|v_\varepsilon \|_{L^1}+\|h_1\|_{L^\infty }+1\right ). \end{align*}
\begin{align*} \left |\int _\Omega \varphi \partial _t\ln (1+u_\varepsilon )dx\right |\leq &\|\varphi \|_{L^\infty }\|\nabla \ln (1+u_\varepsilon )\|_{L^2}^2+\chi \|\nabla \ln (1+u_\varepsilon )\|_{L^2}\|\nabla \ln v_\varepsilon \|_{L^2}\|\varphi \|_{L^\infty } \\[5pt] &+\|\nabla \ln (1+u_\varepsilon )\|_{L^2}\|\nabla \varphi \|_{L^2} +\chi \|\nabla \ln v_\varepsilon \|_{L^2}\|\nabla \varphi \|_{L^2}\\[5pt] &+\kappa \|v_\varepsilon \|_{L^1}\|\varphi \|_{L^\infty }+\|h_1\|_{L^\infty }\|\varphi \|_{L^1}\\[5pt] \leq &C\|\varphi \|_{H^2}\left (\|\nabla \ln (1+u_\varepsilon )\|_{L^2}^2+\|\nabla \ln v_\varepsilon \|_{L^2}^2+\kappa \|v_\varepsilon \|_{L^1}+\|h_1\|_{L^\infty }+1\right ). \end{align*}
After an integration in time, we infer from (11), (20), (32), and (39) that (40) holds as desired.
With the help of Lemmas 2.1, 3.1 and 3.2, we can find a candidate
![]() $(u,v)$
for a generalised solution by standard compactness arguments.
$(u,v)$
for a generalised solution by standard compactness arguments.
Lemma 3.3.
Let
![]() $(u_\varepsilon,v_\varepsilon )$
be taken from Lemma 2.1. Then, there exist
$(u_\varepsilon,v_\varepsilon )$
be taken from Lemma 2.1. Then, there exist
![]() $u\geq 0$
and
$u\geq 0$
and
![]() $v\gt 0$
defined on
$v\gt 0$
defined on
![]() $\Omega \times (0,T)$
for any
$\Omega \times (0,T)$
for any
![]() $T\gt 0$
and a sequence
$T\gt 0$
and a sequence
![]() $\{\varepsilon _j\}_{j=1}^\infty \subset (0,1)$
such that
$\{\varepsilon _j\}_{j=1}^\infty \subset (0,1)$
such that
![]() $\varepsilon _j\rightarrow 0$
as
$\varepsilon _j\rightarrow 0$
as
![]() $j\rightarrow \infty$
, with the properties that for any
$j\rightarrow \infty$
, with the properties that for any
![]() $T\gt 0$
, as
$T\gt 0$
, as
![]() $\varepsilon =\varepsilon _j\rightarrow 0$
,
$\varepsilon =\varepsilon _j\rightarrow 0$
,
Proof. Thanks to (32) and (34), the Aubin-Lions compactness theorem [Reference Simon36] implies that there exist a subsequence of
![]() $\{\varepsilon _j\}_{j=1}^\infty$
(still expressed as
$\{\varepsilon _j\}_{j=1}^\infty$
(still expressed as
![]() $\{\varepsilon _j\}_{j=1}^\infty$
) and a function
$\{\varepsilon _j\}_{j=1}^\infty$
) and a function
![]() $w\in L^2(0,T;\; H^1(\Omega ))$
, with the property that as
$w\in L^2(0,T;\; H^1(\Omega ))$
, with the property that as
![]() $\varepsilon =\varepsilon _j\rightarrow 0$
,
$\varepsilon =\varepsilon _j\rightarrow 0$
,
and by Sobolev’s inequality
which, in particular, ensures
On the basis of these, setting
![]() $v=e^w$
, we conclude that (42)–(44) hold as desired. Similarly, according to (33) and (35), we can obtain (46). Furthermore, along the lines of the proof of [Reference Winkler46, Lemma 2.8] we can establish the uniform integrability of
$v=e^w$
, we conclude that (42)–(44) hold as desired. Similarly, according to (33) and (35), we can obtain (46). Furthermore, along the lines of the proof of [Reference Winkler46, Lemma 2.8] we can establish the uniform integrability of
![]() $\{v_\varepsilon \}_{\varepsilon \in (0,1)}$
. In view of the Vitali convergence theorem, this together with (44) ensures the validity of (45).
$\{v_\varepsilon \}_{\varepsilon \in (0,1)}$
. In view of the Vitali convergence theorem, this together with (44) ensures the validity of (45).
Meanwhile, the assertions (47)–(50) immediately follow from the bounds (19), (39), and (40) and the Sobolev embedding theorem by using a standard subsequence extraction procedure and resorting to the Aubin-Lions compactness theorem [Reference Simon36].
Up to now, our knowledge on approximation of
![]() $(u,v)$
by
$(u,v)$
by
![]() $(u_\varepsilon,v_\varepsilon )$
is enough to pass to the limit
$(u_\varepsilon,v_\varepsilon )$
is enough to pass to the limit
![]() $\varepsilon =\varepsilon _j\rightarrow 0$
in a manner of (8) in Definition 1.
$\varepsilon =\varepsilon _j\rightarrow 0$
in a manner of (8) in Definition 1.
Lemma 3.4.
Let
![]() $u$
and
$u$
and
![]() $v$
be given in Lemma 3.3. For any
$v$
be given in Lemma 3.3. For any
![]() $T\gt 0$
, the inequality (8) in Definition 1 is valid for any non-negative
$T\gt 0$
, the inequality (8) in Definition 1 is valid for any non-negative
![]() $\varphi (x,t)\in C_0^\infty (\overline{\Omega }\times [0,T))$
.
$\varphi (x,t)\in C_0^\infty (\overline{\Omega }\times [0,T))$
.
Proof. Note that for any non-negative
![]() $\varphi (x,t)\in C_0^\infty (\overline{\Omega }\times [0,T))$
the identity (36) is also valid. Based on it and using the integration by parts, we have
$\varphi (x,t)\in C_0^\infty (\overline{\Omega }\times [0,T))$
the identity (36) is also valid. Based on it and using the integration by parts, we have
 \begin{align} -\int _\Omega \ln v_0\varphi |_{t=0}dx =&\int _0^T\int _\Omega \ln v_\varepsilon \varphi _tdx+\int _0^T\int _\Omega \frac{\varphi |\nabla v_\varepsilon |^2}{v_\varepsilon ^2}dxds-\int _0^T\int _\Omega \frac{\nabla \varphi \cdot \nabla v_\varepsilon }{v_\varepsilon }dxds\nonumber \\[5pt] &-\int _0^T\int _\Omega \varphi dxds+\int _0^T\int _\Omega \frac{u_\varepsilon \varphi }{(1+\varepsilon u_\varepsilon v_\varepsilon )}dxds+\int _0^T\int _\Omega \frac{\varphi h_2}{v_\varepsilon }dxds. \end{align}
\begin{align} -\int _\Omega \ln v_0\varphi |_{t=0}dx =&\int _0^T\int _\Omega \ln v_\varepsilon \varphi _tdx+\int _0^T\int _\Omega \frac{\varphi |\nabla v_\varepsilon |^2}{v_\varepsilon ^2}dxds-\int _0^T\int _\Omega \frac{\nabla \varphi \cdot \nabla v_\varepsilon }{v_\varepsilon }dxds\nonumber \\[5pt] &-\int _0^T\int _\Omega \varphi dxds+\int _0^T\int _\Omega \frac{u_\varepsilon \varphi }{(1+\varepsilon u_\varepsilon v_\varepsilon )}dxds+\int _0^T\int _\Omega \frac{\varphi h_2}{v_\varepsilon }dxds. \end{align}
It follows from (43) that there exists a subsequence of
![]() $\{\varepsilon _j\}_{j=1}^\infty$
(still expressed as
$\{\varepsilon _j\}_{j=1}^\infty$
(still expressed as
![]() $\{\varepsilon _j\}_{j=1}^\infty$
) such that for any
$\{\varepsilon _j\}_{j=1}^\infty$
) such that for any
![]() $T\gt 0$
, as
$T\gt 0$
, as
![]() $\varepsilon =\varepsilon _j\rightarrow 0$
,
$\varepsilon =\varepsilon _j\rightarrow 0$
,
and from (42) that
On the other hand, similar to the proof of [Reference Li and Xie19, Lemma 3.4] we can infer from the Moser-Trudinger inequality that
 \begin{align*} \int _\Omega \left (1+\frac{u_\varepsilon }{1+\varepsilon u_\varepsilon v_\varepsilon } \right )^2dx\leq & \int _\Omega \left (1+u_\varepsilon \right )^2dx\\[5pt] \leq &C_1\exp \left \{C_2\int _\Omega |\nabla \ln (1+u_\varepsilon )|^2dx+C_3\int _\Omega \ln (1+u_\varepsilon )dx\right \}, \end{align*}
\begin{align*} \int _\Omega \left (1+\frac{u_\varepsilon }{1+\varepsilon u_\varepsilon v_\varepsilon } \right )^2dx\leq & \int _\Omega \left (1+u_\varepsilon \right )^2dx\\[5pt] \leq &C_1\exp \left \{C_2\int _\Omega |\nabla \ln (1+u_\varepsilon )|^2dx+C_3\int _\Omega \ln (1+u_\varepsilon )dx\right \}, \end{align*}
which, in view of (19) and the fact that
![]() $\ln (1+\varsigma )\leq \varsigma$
for any
$\ln (1+\varsigma )\leq \varsigma$
for any
![]() $\varsigma \geq 0$
, leads to
$\varsigma \geq 0$
, leads to
 \begin{align*} \ln \left \{\frac{1}{|\Omega |}\int _\Omega \left (1+\frac{u_\varepsilon }{1+\varepsilon u_\varepsilon v_\varepsilon } \right )^2dx\right \}\leq &\ln \frac{C_1}{|\Omega |}+C_2\int _\Omega |\nabla \ln (1+u_\varepsilon )|^2dx+C_4(1+t),\quad t\gt 0. \end{align*}
\begin{align*} \ln \left \{\frac{1}{|\Omega |}\int _\Omega \left (1+\frac{u_\varepsilon }{1+\varepsilon u_\varepsilon v_\varepsilon } \right )^2dx\right \}\leq &\ln \frac{C_1}{|\Omega |}+C_2\int _\Omega |\nabla \ln (1+u_\varepsilon )|^2dx+C_4(1+t),\quad t\gt 0. \end{align*}
Integrating it in time and using (39), for any
![]() $T\gt 0$
we can find
$T\gt 0$
we can find
![]() $\widehat{C}=\widehat{C}(T)$
such that
$\widehat{C}=\widehat{C}(T)$
such that
 \begin{align*} \int _0^T\ln \left \{\frac{1}{|\Omega |}\int _\Omega \left (1+\frac{u_\varepsilon }{1+\varepsilon u_\varepsilon v_\varepsilon } \right )^2dxds\right \}\leq \widehat{C}. \end{align*}
\begin{align*} \int _0^T\ln \left \{\frac{1}{|\Omega |}\int _\Omega \left (1+\frac{u_\varepsilon }{1+\varepsilon u_\varepsilon v_\varepsilon } \right )^2dxds\right \}\leq \widehat{C}. \end{align*}
Invoking this, using (19) again and proceeding along the lines of the proof of [Reference Winkler46, Lemma 2.8], for fixed
![]() $\eta \gt 0$
, we can find
$\eta \gt 0$
, we can find
![]() $\delta \gt 0$
suitably small such that given an arbitrary measurable
$\delta \gt 0$
suitably small such that given an arbitrary measurable
![]() $\mathcal{E}\subset \Omega \times (0,T)$
with
$\mathcal{E}\subset \Omega \times (0,T)$
with
![]() $|\mathcal{E}|\lt \delta$
,
$|\mathcal{E}|\lt \delta$
,
Since we already know from (44) and (49) that
along with the Vitali theorem this shows that in fact
and thereby ensures that
Similarly, in view of (46), we have
Moreover, invoking (32) and (43), the weak lower semicontinuity of the norm ensures
Substituting these into (51), the functions
![]() $u$
and
$u$
and
![]() $v$
obtained in Lemma 3.3 satisfy the inequality (8) in Definition 1.
$v$
obtained in Lemma 3.3 satisfy the inequality (8) in Definition 1.
To show the validity of (7) in Definition 1, we need the following (weak) convergence.
Lemma 3.5.
Let
![]() $(u_\varepsilon,v_\varepsilon )$
be described in Lemma 2.1 and let
$(u_\varepsilon,v_\varepsilon )$
be described in Lemma 2.1 and let
![]() $u$
and
$u$
and
![]() $v$
be established in Lemma 3.3. Then, for
$v$
be established in Lemma 3.3. Then, for
![]() $p\geq 1$
and
$p\geq 1$
and
![]() $q\geq 2$
there exists a subsequence of
$q\geq 2$
there exists a subsequence of
![]() $\{\varepsilon _j\}_{j=1}^\infty$
(still expressed as
$\{\varepsilon _j\}_{j=1}^\infty$
(still expressed as
![]() $\{\varepsilon _j\}_{j=1}^\infty$
) such that for any
$\{\varepsilon _j\}_{j=1}^\infty$
) such that for any
![]() $T\gt 0$
, as
$T\gt 0$
, as
![]() $\varepsilon =\varepsilon _j\rightarrow 0$
,
$\varepsilon =\varepsilon _j\rightarrow 0$
,
Proof. Thanks to (44) and (49); for any
![]() $\alpha,\beta \ge 0$
, there exists a subsequence of
$\alpha,\beta \ge 0$
, there exists a subsequence of
![]() $\{\varepsilon _j\}_{j=1}^\infty$
(still expressed as
$\{\varepsilon _j\}_{j=1}^\infty$
(still expressed as
![]() $\{\varepsilon _j\}_{j=1}^\infty$
) such that for any
$\{\varepsilon _j\}_{j=1}^\infty$
) such that for any
![]() $T\gt 0$
, as
$T\gt 0$
, as
![]() $\varepsilon =\varepsilon _j\rightarrow 0$
,
$\varepsilon =\varepsilon _j\rightarrow 0$
,
which, in particular, ensures that for any
![]() $p\geq 1$
and
$p\geq 1$
and
![]() $q\geq 2$
$q\geq 2$
 \begin{align*} v_\varepsilon ^{-q+1}(u_{\varepsilon }+1)^{-p}\rightarrow v^{-q+1}(u+1)^{-p} \quad a.e.\,\,\,\mathrm{in}\quad \Omega \times (0,T),\\[5pt] v_\varepsilon ^{-q+1}(u_{\varepsilon }+1)^{-p-1}u_\varepsilon \rightarrow v^{-q+1}(u+1)^{-p-1}u \quad a.e.\,\,\,\mathrm{in}\quad \Omega \times (0,T). \end{align*}
\begin{align*} v_\varepsilon ^{-q+1}(u_{\varepsilon }+1)^{-p}\rightarrow v^{-q+1}(u+1)^{-p} \quad a.e.\,\,\,\mathrm{in}\quad \Omega \times (0,T),\\[5pt] v_\varepsilon ^{-q+1}(u_{\varepsilon }+1)^{-p-1}u_\varepsilon \rightarrow v^{-q+1}(u+1)^{-p-1}u \quad a.e.\,\,\,\mathrm{in}\quad \Omega \times (0,T). \end{align*}
In addition, we can infer from (38) that
which implies that
Hence, invoking (46) with
![]() $\sigma =2$
and Lemma 2.2, for
$\sigma =2$
and Lemma 2.2, for
![]() $p\geq 1$
and
$p\geq 1$
and
![]() $q\geq 2$
we get that, as
$q\geq 2$
we get that, as
![]() $\varepsilon =\varepsilon _j\rightarrow 0$
,
$\varepsilon =\varepsilon _j\rightarrow 0$
,
This, together with (48), entails that, as
![]() $\varepsilon =\varepsilon _j\rightarrow 0$
,
$\varepsilon =\varepsilon _j\rightarrow 0$
,
Moreover, by means of (38) and (39), for any
![]() $T\gt 0$
there exists
$T\gt 0$
there exists
![]() $C(T)\gt 0$
, independent of
$C(T)\gt 0$
, independent of
![]() $\varepsilon$
, such that
$\varepsilon$
, such that
which, combined with (56), implies (52) as desired. Similarly, employing (38), (44), (50), (46), Lemma 2.2, and (32), we conclude that (53) and (54) also hold.
By means of Lemma 3.5, we present the validity of (7) in Definition 1.
Lemma 3.6.
Let
![]() $u$
and
$u$
and
![]() $v$
be given in Lemma 3.3. For
$v$
be given in Lemma 3.3. For
![]() $p$
and
$p$
and
![]() $q$
taken from Lemma 3.5 which satisfy
$q$
taken from Lemma 3.5 which satisfy
![]() $\frac{p(p+1)\chi ^2}{4}\lt q+\frac{q^2}{p+1}$
, the inequality (
7
) in Definition
1
is valid for any non-negative
$\frac{p(p+1)\chi ^2}{4}\lt q+\frac{q^2}{p+1}$
, the inequality (
7
) in Definition
1
is valid for any non-negative
![]() $\varphi (x,t)\in C_0^\infty (\overline{\Omega }\times [0,T))$
.
$\varphi (x,t)\in C_0^\infty (\overline{\Omega }\times [0,T))$
.
Proof. By virtue of (18) and the non-negativity of
![]() $u_\varepsilon$
, for
$u_\varepsilon$
, for
![]() $p$
and
$p$
and
![]() $q$
taken from Lemma 3.5 and any
$q$
taken from Lemma 3.5 and any
![]() $0\leq \varphi \in C_0^\infty (\overline{\Omega }\times [0,T))$
, we have
$0\leq \varphi \in C_0^\infty (\overline{\Omega }\times [0,T))$
, we have
 \begin{align*} &\frac{d}{dt}\int _\Omega (u_\varepsilon +1)^{-p}v_\varepsilon ^{-q}\varphi dx-\int _\Omega (u_\varepsilon +1)^{-p}v_\varepsilon ^{-q}\varphi _t dx\\[5pt] &\quad=-p\int _\Omega \varphi (u_\varepsilon +1)^{-p-1}v_\varepsilon ^{-q}\partial _tu_\varepsilon dx-q\int _\Omega \varphi (u_\varepsilon +1)^{-p}v_\varepsilon ^{-q-1}\partial _tv_\varepsilon dx\\[5pt] &\quad=-p\int _\Omega (u_\varepsilon +1)^{-p-1}v_\varepsilon ^{-q}\left (\Delta u_\varepsilon -\chi \nabla \cdot \left ( u_\varepsilon \nabla \ln v_\varepsilon \right )-\kappa u_\varepsilon v_\varepsilon +h_1\right )\varphi dx\\[5pt] &\qquad-q\int _\Omega (u_\varepsilon +1)^{-p}v_\varepsilon ^{-q-1}\left (\Delta v_\varepsilon - v_\varepsilon +\frac{u_\varepsilon v_\varepsilon }{1+\varepsilon u_\varepsilon v_\varepsilon }+h_2 \right )\varphi dx, \end{align*}
\begin{align*} &\frac{d}{dt}\int _\Omega (u_\varepsilon +1)^{-p}v_\varepsilon ^{-q}\varphi dx-\int _\Omega (u_\varepsilon +1)^{-p}v_\varepsilon ^{-q}\varphi _t dx\\[5pt] &\quad=-p\int _\Omega \varphi (u_\varepsilon +1)^{-p-1}v_\varepsilon ^{-q}\partial _tu_\varepsilon dx-q\int _\Omega \varphi (u_\varepsilon +1)^{-p}v_\varepsilon ^{-q-1}\partial _tv_\varepsilon dx\\[5pt] &\quad=-p\int _\Omega (u_\varepsilon +1)^{-p-1}v_\varepsilon ^{-q}\left (\Delta u_\varepsilon -\chi \nabla \cdot \left ( u_\varepsilon \nabla \ln v_\varepsilon \right )-\kappa u_\varepsilon v_\varepsilon +h_1\right )\varphi dx\\[5pt] &\qquad-q\int _\Omega (u_\varepsilon +1)^{-p}v_\varepsilon ^{-q-1}\left (\Delta v_\varepsilon - v_\varepsilon +\frac{u_\varepsilon v_\varepsilon }{1+\varepsilon u_\varepsilon v_\varepsilon }+h_2 \right )\varphi dx, \end{align*}
which, by the integration by parts, leads to
 \begin{align*} &\frac{d}{dt}\int _\Omega (u_\varepsilon +1)^{-p}v_\varepsilon ^{-q}\varphi dx-\int _\Omega (u_\varepsilon +1)^{-p}v_\varepsilon ^{-q}\varphi _t dx\\[5pt] &\quad=-p(p+1)\int _\Omega (u_\varepsilon +1)^{-p-2}v_\varepsilon ^{-q}\varphi |\nabla u_\varepsilon |^2dx\\[5pt] &\qquad+\int _\Omega \left (p(p+1)\chi \frac{u_\varepsilon }{u_\varepsilon +1}-2pq\right )(u_\varepsilon +1)^{-p-1}v_\varepsilon ^{-q-1}\varphi \nabla u_\varepsilon \cdot \nabla v_\varepsilon dx\\[5pt] &\qquad+\int _\Omega \left (\chi pq\frac{u_\varepsilon }{u_\varepsilon +1}-q(q+1)\right )(u_\varepsilon +1)^{-p}v_\varepsilon ^{-q-2}\varphi |\nabla v_\varepsilon |^2dx\\[5pt] &\qquad-p\int _\Omega (u_\varepsilon +1)^{-p-1}v_\varepsilon ^{-q}\left (-\kappa u_\varepsilon v_\varepsilon +h_1\right )\varphi dx\\[5pt] &\qquad-q\int _\Omega (u_\varepsilon +1)^{-p}v_\varepsilon ^{-q-1}\left (- v_\varepsilon +\frac{u_\varepsilon v_\varepsilon }{1+\varepsilon u_\varepsilon v_\varepsilon }+h_2 \right )\varphi dx\\[5pt] &\qquad+p\int _\Omega (u_\varepsilon +1)^{-p-1}v_\varepsilon ^{-q}\nabla u_\varepsilon \cdot \nabla \varphi dx-p\chi \int _\Omega (u_\varepsilon +1)^{-p-1}v_\varepsilon ^{-q-1}u_\varepsilon \nabla v_\varepsilon \cdot \nabla \varphi dx \\[5pt] &\qquad+q\int _\Omega (u_\varepsilon +1)^{-p}v_\varepsilon ^{-q-1}\nabla v_\varepsilon \cdot \nabla \varphi dx\\[5pt] &\quad\;=\!:\;\int _\Omega \sum _{i=1}^8P_i^\varepsilon (\cdot,t)dx. \end{align*}
\begin{align*} &\frac{d}{dt}\int _\Omega (u_\varepsilon +1)^{-p}v_\varepsilon ^{-q}\varphi dx-\int _\Omega (u_\varepsilon +1)^{-p}v_\varepsilon ^{-q}\varphi _t dx\\[5pt] &\quad=-p(p+1)\int _\Omega (u_\varepsilon +1)^{-p-2}v_\varepsilon ^{-q}\varphi |\nabla u_\varepsilon |^2dx\\[5pt] &\qquad+\int _\Omega \left (p(p+1)\chi \frac{u_\varepsilon }{u_\varepsilon +1}-2pq\right )(u_\varepsilon +1)^{-p-1}v_\varepsilon ^{-q-1}\varphi \nabla u_\varepsilon \cdot \nabla v_\varepsilon dx\\[5pt] &\qquad+\int _\Omega \left (\chi pq\frac{u_\varepsilon }{u_\varepsilon +1}-q(q+1)\right )(u_\varepsilon +1)^{-p}v_\varepsilon ^{-q-2}\varphi |\nabla v_\varepsilon |^2dx\\[5pt] &\qquad-p\int _\Omega (u_\varepsilon +1)^{-p-1}v_\varepsilon ^{-q}\left (-\kappa u_\varepsilon v_\varepsilon +h_1\right )\varphi dx\\[5pt] &\qquad-q\int _\Omega (u_\varepsilon +1)^{-p}v_\varepsilon ^{-q-1}\left (- v_\varepsilon +\frac{u_\varepsilon v_\varepsilon }{1+\varepsilon u_\varepsilon v_\varepsilon }+h_2 \right )\varphi dx\\[5pt] &\qquad+p\int _\Omega (u_\varepsilon +1)^{-p-1}v_\varepsilon ^{-q}\nabla u_\varepsilon \cdot \nabla \varphi dx-p\chi \int _\Omega (u_\varepsilon +1)^{-p-1}v_\varepsilon ^{-q-1}u_\varepsilon \nabla v_\varepsilon \cdot \nabla \varphi dx \\[5pt] &\qquad+q\int _\Omega (u_\varepsilon +1)^{-p}v_\varepsilon ^{-q-1}\nabla v_\varepsilon \cdot \nabla \varphi dx\\[5pt] &\quad\;=\!:\;\int _\Omega \sum _{i=1}^8P_i^\varepsilon (\cdot,t)dx. \end{align*}
Integrating it in time arrives at
A straightforward rearrangement entails
 \begin{align*} \sum _{i=1}^3P_i^\varepsilon (x, t)=&-p(p+1)\left |(u_\varepsilon +1)^{-\frac p2-1}v_\varepsilon ^{-\frac{q}{2}}\nabla u_\varepsilon -\frac 12\left (\frac{\chi u_\varepsilon }{u_\varepsilon +1}-\frac{2q}{p+1}\right )(u_\varepsilon +1)^{-\frac{p}{2}}v_\varepsilon ^{-\frac{q}{2}-1}\nabla v_\varepsilon \right |^2\varphi \\[5pt] &+\left (\frac{p(p+1)\chi ^2 u_\varepsilon ^2}{4(u_\varepsilon +1)^2}+\frac{pq^2}{p+1}-q(q+1)\right )(u_\varepsilon +1)^{-p}v_\varepsilon ^{-q-2}|\nabla v_\varepsilon |^2\varphi . \end{align*}
\begin{align*} \sum _{i=1}^3P_i^\varepsilon (x, t)=&-p(p+1)\left |(u_\varepsilon +1)^{-\frac p2-1}v_\varepsilon ^{-\frac{q}{2}}\nabla u_\varepsilon -\frac 12\left (\frac{\chi u_\varepsilon }{u_\varepsilon +1}-\frac{2q}{p+1}\right )(u_\varepsilon +1)^{-\frac{p}{2}}v_\varepsilon ^{-\frac{q}{2}-1}\nabla v_\varepsilon \right |^2\varphi \\[5pt] &+\left (\frac{p(p+1)\chi ^2 u_\varepsilon ^2}{4(u_\varepsilon +1)^2}+\frac{pq^2}{p+1}-q(q+1)\right )(u_\varepsilon +1)^{-p}v_\varepsilon ^{-q-2}|\nabla v_\varepsilon |^2\varphi . \end{align*}
Note that the assumption
![]() $\frac{p(p+1)\chi ^2}{4}\lt q+\frac{q^2}{p+1}$
implies that
$\frac{p(p+1)\chi ^2}{4}\lt q+\frac{q^2}{p+1}$
implies that
thus, it follows that
 \begin{equation*} -\int _0^T\int _\Omega \sum _{i=1}^3P_i^\varepsilon (t)dxdt=\left \|\sqrt {-\sum _{i=1}^3P_i^\varepsilon }\right \|_{L^2(\Omega \times (0, T))}^2. \end{equation*}
\begin{equation*} -\int _0^T\int _\Omega \sum _{i=1}^3P_i^\varepsilon (t)dxdt=\left \|\sqrt {-\sum _{i=1}^3P_i^\varepsilon }\right \|_{L^2(\Omega \times (0, T))}^2. \end{equation*}
Subsequently, based on Lemmas 3.3 and 3.5, a lower semicontinuity argument entails that there exists a subsequence of
![]() $\{\varepsilon _j\}_{j=1}^\infty$
(still expressed as
$\{\varepsilon _j\}_{j=1}^\infty$
(still expressed as
![]() $\{\varepsilon _j\}_{j=1}^\infty$
) such that for any
$\{\varepsilon _j\}_{j=1}^\infty$
) such that for any
![]() $T\gt 0$
, as
$T\gt 0$
, as
![]() $\varepsilon =\varepsilon _j\rightarrow 0$
,
$\varepsilon =\varepsilon _j\rightarrow 0$
,
 \begin{align*} &\liminf _{\varepsilon =\varepsilon _{j} \rightarrow 0} \int _0^T\int _\Omega -\sum _{i=1}^3P_i^\varepsilon dxdt\\[5pt] &\quad\ge p(p+1)\int _0^T\int _\Omega (u+1)^{-p-2}v^{-q}\varphi |\nabla u|^2dxdt\\[5pt] &\qquad-\int _0^T\int _\Omega \left (p(p+1)\chi \frac{u}{u+1}-2pq\right )(u+1)^{-p-1}v^{-q-1}\varphi \nabla u\cdot \nabla v dxdt\\[5pt] &\qquad-\int _0^T\int _\Omega \left (\chi pq\frac{u}{u+1}-q(q+1)\right )(u+1)^{-p}v^{-q-2}\varphi |\nabla v|^2dxdt. \end{align*}
\begin{align*} &\liminf _{\varepsilon =\varepsilon _{j} \rightarrow 0} \int _0^T\int _\Omega -\sum _{i=1}^3P_i^\varepsilon dxdt\\[5pt] &\quad\ge p(p+1)\int _0^T\int _\Omega (u+1)^{-p-2}v^{-q}\varphi |\nabla u|^2dxdt\\[5pt] &\qquad-\int _0^T\int _\Omega \left (p(p+1)\chi \frac{u}{u+1}-2pq\right )(u+1)^{-p-1}v^{-q-1}\varphi \nabla u\cdot \nabla v dxdt\\[5pt] &\qquad-\int _0^T\int _\Omega \left (\chi pq\frac{u}{u+1}-q(q+1)\right )(u+1)^{-p}v^{-q-2}\varphi |\nabla v|^2dxdt. \end{align*}
In addition, similar to (55), we can prove that, as
![]() $\varepsilon =\varepsilon _j\rightarrow 0$
.
$\varepsilon =\varepsilon _j\rightarrow 0$
.
and
Hence, there exists a subsequence of
![]() $\{\varepsilon _j\}_{j=1}^\infty$
(still expressed as
$\{\varepsilon _j\}_{j=1}^\infty$
(still expressed as
![]() $\{\varepsilon _j\}_{j=1}^\infty$
) such that for any
$\{\varepsilon _j\}_{j=1}^\infty$
) such that for any
![]() $T\gt 0$
, as
$T\gt 0$
, as
![]() $\varepsilon =\varepsilon _j\rightarrow 0$
,
$\varepsilon =\varepsilon _j\rightarrow 0$
,
Similarly, we have
and
Finally, in view of Lemma 3.5, we obtain
 \begin{align*} \int _0^T\int _\Omega \sum _{i=6}^8P_i^\varepsilon dxdt\rightarrow &p\int _0^T\int _\Omega (u+1)^{-p-1}v^{-q}\nabla u \cdot \nabla \varphi dxdt\\[5pt] &-p\chi \int _0^T\int _\Omega (u+1)^{-p-1}v^{-q-1}u\nabla v\cdot \nabla \varphi dxdt\\[5pt] &+q\int _0^T\int _\Omega (u+1)^{-p}v^{-q-1}\nabla v\cdot \nabla \varphi dxdt. \end{align*}
\begin{align*} \int _0^T\int _\Omega \sum _{i=6}^8P_i^\varepsilon dxdt\rightarrow &p\int _0^T\int _\Omega (u+1)^{-p-1}v^{-q}\nabla u \cdot \nabla \varphi dxdt\\[5pt] &-p\chi \int _0^T\int _\Omega (u+1)^{-p-1}v^{-q-1}u\nabla v\cdot \nabla \varphi dxdt\\[5pt] &+q\int _0^T\int _\Omega (u+1)^{-p}v^{-q-1}\nabla v\cdot \nabla \varphi dxdt. \end{align*}
Hence, by collecting these (7) holds as desired.
We are now able to proceed to the proof of Theorem 1.1.
Proof of Theorem 1.1. Invoking Lemmas 3.6 and 3.4, we only need to verify the validity of (5) and (6). In fact, according to (25) we have
for any
![]() $t\gt 0$
and each
$t\gt 0$
and each
![]() $\varepsilon \in (0,1)$
. Hence, (5) is a consequence from (44), (49) and Fatou’s lemma. Moreover, combined with (31) and (57), we arrive at
$\varepsilon \in (0,1)$
. Hence, (5) is a consequence from (44), (49) and Fatou’s lemma. Moreover, combined with (31) and (57), we arrive at
which, together with (44), (49) and Fatou’s lemma, ensures that (6) holds as desired. Therefore,
![]() $(u,v)$
is a global generalised solution to the initial-boundary value problem (3) in the sense of Definition 1. This finishes the proof of Theorem 1.1.
$(u,v)$
is a global generalised solution to the initial-boundary value problem (3) in the sense of Definition 1. This finishes the proof of Theorem 1.1.
4. Large-time behaviour
This section is devoted to the large-time behaviour of the generalised solution
![]() $(u,v)$
determined in Theorem 1.1, under the additional assumptions (12)–(14). We start with the result on the solvability of the boundary value problem (2), which directly follows from [Reference Ladyzhenskaya and Ural’tseva17].
$(u,v)$
determined in Theorem 1.1, under the additional assumptions (12)–(14). We start with the result on the solvability of the boundary value problem (2), which directly follows from [Reference Ladyzhenskaya and Ural’tseva17].
Lemma 4.1.
For any given
![]() $h_{2,\infty }\in C^1(\overline{\Omega })$
, the problem (2) possesses a unique classical solution
$h_{2,\infty }\in C^1(\overline{\Omega })$
, the problem (2) possesses a unique classical solution
![]() $v_\infty$
fulfilling that
$v_\infty$
fulfilling that
![]() $v_\infty \in C^{2+\theta }(\overline{\Omega })$
for some
$v_\infty \in C^{2+\theta }(\overline{\Omega })$
for some
![]() $\theta \in (0,1)$
.
$\theta \in (0,1)$
.
We are also concerned with the decay in a linear differential inequality, which is an extended version of [Reference Espejo and Winkler10, Lemma 4.6] (see also [Reference Li and Xie20, Lemma 2.5], [Reference Li and Xie21, Lemma 2.6]).
Lemma 4.2.
Let
![]() $\varepsilon \gt 0$
,
$\varepsilon \gt 0$
,
![]() $y_\varepsilon \in C^1([0,\infty ))$
be non-negative functions satisfying
$y_\varepsilon \in C^1([0,\infty ))$
be non-negative functions satisfying
with some positive constant
![]() $m$
independent of
$m$
independent of
![]() $\varepsilon$
. If there exist a positive constant
$\varepsilon$
. If there exist a positive constant
![]() $\mu$
and a non-negative function
$\mu$
and a non-negative function
![]() $g_\varepsilon (t)\in C([0, \infty ))\cap L^\infty ([0,\infty ))$
which satisfy
$g_\varepsilon (t)\in C([0, \infty ))\cap L^\infty ([0,\infty ))$
which satisfy
and
such that for each
![]() $\varepsilon \gt 0$
and some
$\varepsilon \gt 0$
and some
![]() $\lambda \gt 0$
,
$\lambda \gt 0$
,
then
Proof. Based on (58), an integration of (61) shows that
Therefore, we only need to show that
Similar to [Reference Espejo and Winkler10, Lemma 4.6], thanks to (60), for any
![]() $\varsigma \gt 0$
we may fix some
$\varsigma \gt 0$
we may fix some
![]() $k$
(independent of
$k$
(independent of
![]() $\varepsilon$
) enough large such that
$\varepsilon$
) enough large such that
![]() $\frac{\mu e^{-ak}}{a}\lt \frac{\varsigma }2$
. For such
$\frac{\mu e^{-ak}}{a}\lt \frac{\varsigma }2$
. For such
![]() $k$
, we further take
$k$
, we further take
![]() $\sigma \gt 0$
(independent of
$\sigma \gt 0$
(independent of
![]() $\varepsilon$
) fulfilling that
$\varepsilon$
) fulfilling that
![]() $k\sigma \lt \frac \varsigma 2$
. Subsequently, due to (59) we can find
$k\sigma \lt \frac \varsigma 2$
. Subsequently, due to (59) we can find
![]() $t_0$
, independent of
$t_0$
, independent of
![]() $\varepsilon$
, sufficiently large in the sense that
$\varepsilon$
, sufficiently large in the sense that
Consequently, we have
 \begin{align*} e^{-at}\int _0^te^{as}g_\varepsilon (s)ds&=e^{-at}\int _0^{t-k}e^{as}g_\varepsilon (s)ds+e^{-at}\sum _{j=0}^{j=k-1}\int _{t-k+j}^{t-k+j+1}e^{as}g_\varepsilon (s)ds\\[5pt] &\le \frac{\mu e^{-ak}}{a}+k\sigma \\[5pt] &\lt \varsigma, \quad t\gt t_0. \end{align*}
\begin{align*} e^{-at}\int _0^te^{as}g_\varepsilon (s)ds&=e^{-at}\int _0^{t-k}e^{as}g_\varepsilon (s)ds+e^{-at}\sum _{j=0}^{j=k-1}\int _{t-k+j}^{t-k+j+1}e^{as}g_\varepsilon (s)ds\\[5pt] &\le \frac{\mu e^{-ak}}{a}+k\sigma \\[5pt] &\lt \varsigma, \quad t\gt t_0. \end{align*}
Hence, we have (63) as a desired result and (62) has been established simultaneously.
Next, we focus on the pointwise lower bound for the solution component
![]() $v_\varepsilon$
, which plays a key role in the sequel.
$v_\varepsilon$
, which plays a key role in the sequel.
Lemma 4.3.
Let
![]() $(u_\varepsilon,v_\varepsilon )$
come from Lemma 2.1, and let (
12
) be in force. Under the additional assumption that
$(u_\varepsilon,v_\varepsilon )$
come from Lemma 2.1, and let (
12
) be in force. Under the additional assumption that
![]() $\Omega$
is convex, then there exists
$\Omega$
is convex, then there exists
![]() $c_1\gt 0$
, independent of
$c_1\gt 0$
, independent of
![]() $t$
and
$t$
and
![]() $\varepsilon$
, fulfilling that
$\varepsilon$
, fulfilling that
Proof. Thanks to the convexity of
![]() $\Omega$
, a slight adaptation of the proof of [Reference Li and Xie20, Corollary 3.1] is easy to show that (64) holds as desired.
$\Omega$
, a slight adaptation of the proof of [Reference Li and Xie20, Corollary 3.1] is easy to show that (64) holds as desired.
A straightforward consequence of Lemma 4.3 is the following
![]() $L^1$
-decay on the component
$L^1$
-decay on the component
![]() $u_\varepsilon$
.
$u_\varepsilon$
.
Lemma 4.4. Let (12)–(13) hold, and let all assumptions in Lemma 4.3 be fulfilled. Then, the solution
![]() $(u_\varepsilon,v_\varepsilon )$
fulfils that for some
$(u_\varepsilon,v_\varepsilon )$
fulfils that for some
![]() $C\gt 0$
independent of
$C\gt 0$
independent of
![]() $(\varepsilon,t)$
$(\varepsilon,t)$
and that
and
Proof. If (12) holds, invoking (25) and (64), we obtain
This, invoking (11) and a standard ODE technique, ensures that for some
![]() $C\gt 0$
independent of
$C\gt 0$
independent of
![]() $(\varepsilon,t)$
$(\varepsilon,t)$
In addition, thanks to (13) and Lemma 4.2, using (68) again we infer that the decay (66) holds as desired.
We now integrate (68) over
![]() $[t,t+1]$
to get
$[t,t+1]$
to get
Recalling (13) and (66), we arrive at (67); moreover, due to (69) and (11), using (69) again, we obtain (65).
In the sequel, we will track the time evolution of
![]() $\|v_\varepsilon (\cdot,t)-v_\infty (\!\cdot\!)\|_{L^1}$
, where
$\|v_\varepsilon (\cdot,t)-v_\infty (\!\cdot\!)\|_{L^1}$
, where
![]() $v_\infty$
is the classical solution of the boundary value problem (2). For convenience, we set
$v_\infty$
is the classical solution of the boundary value problem (2). For convenience, we set
![]() $\widehat{v}_\varepsilon \;:\!=\;v_\varepsilon -v_\infty$
. Thanks to (2) and (17), it is clear that for
$\widehat{v}_\varepsilon \;:\!=\;v_\varepsilon -v_\infty$
. Thanks to (2) and (17), it is clear that for
![]() $(u_\varepsilon,v_\varepsilon )$
given in Lemma 2.1, the initial-boundary value problem
$(u_\varepsilon,v_\varepsilon )$
given in Lemma 2.1, the initial-boundary value problem
 \begin{equation} \left \{ \begin{split} &\widehat{v}_{\varepsilon t}=\Delta \widehat{v}_\varepsilon -\widehat{v}_\varepsilon +\frac{u_\varepsilon v_\varepsilon }{1+\varepsilon u_\varepsilon v_\varepsilon }+h_2-h_{2,\infty },&x\in \Omega,\,\,t\gt 0,\\[5pt] &\nabla \widehat{v}_\varepsilon \cdot \nu =0,&x\in \partial \Omega,\,\,t\gt 0,\\[5pt] &\widehat{v}_\varepsilon (x,0)=v_0(x)-v_\infty (x),&x\in \Omega \end{split} \right . \end{equation}
\begin{equation} \left \{ \begin{split} &\widehat{v}_{\varepsilon t}=\Delta \widehat{v}_\varepsilon -\widehat{v}_\varepsilon +\frac{u_\varepsilon v_\varepsilon }{1+\varepsilon u_\varepsilon v_\varepsilon }+h_2-h_{2,\infty },&x\in \Omega,\,\,t\gt 0,\\[5pt] &\nabla \widehat{v}_\varepsilon \cdot \nu =0,&x\in \partial \Omega,\,\,t\gt 0,\\[5pt] &\widehat{v}_\varepsilon (x,0)=v_0(x)-v_\infty (x),&x\in \Omega \end{split} \right . \end{equation}
admits a unique classical solution
![]() $\widehat{v}_\varepsilon$
.
$\widehat{v}_\varepsilon$
.
Lemma 4.5. Let all assumptions in Theorem 1.2 be in force. Then, we have
where
![]() $\widehat{v}_\varepsilon$
is a unique classical solution of (70).
$\widehat{v}_\varepsilon$
is a unique classical solution of (70).
Proof. For any
![]() $\sigma \gt 0$
, we multiply the first equation in (70) by
$\sigma \gt 0$
, we multiply the first equation in (70) by
![]() $\frac{\widehat{v}_\varepsilon }{\sqrt{\sigma +|\widehat{v}_\varepsilon |^2}}$
and integrate by parts to obtain
$\frac{\widehat{v}_\varepsilon }{\sqrt{\sigma +|\widehat{v}_\varepsilon |^2}}$
and integrate by parts to obtain
 \begin{align*} &\frac{d}{dt}\int _\Omega \sqrt{\sigma +|\widehat{v}_\varepsilon |^2}dx+\int _\Omega \frac{|\nabla \widehat{v}_\varepsilon |^2}{\sqrt{\sigma +|\widehat{v}_\varepsilon |^2}}dx-\int _\Omega \frac{|\nabla \widehat{v}_\varepsilon |^2|\widehat{v}_\varepsilon |^2}{(\sigma +|\widehat{v}_\varepsilon |^2)^{\frac 32}}dx\\[5pt] &\quad=-\int _\Omega \frac{|\widehat{v}_\varepsilon |^2}{\sqrt{\sigma +|\widehat{v}_\varepsilon |^2}}dx+ \int _\Omega \frac{u_\varepsilon v_\varepsilon \widehat{v}_\varepsilon }{(1+\varepsilon u_\varepsilon v_\varepsilon )\sqrt{\sigma +|\widehat{v}_\varepsilon |^2}}dx+\int _\Omega \frac{\widehat{v}_\varepsilon (h_2-h_{2,\infty })}{\sqrt{\sigma +|\widehat{v}_\varepsilon |^2}}dx. \end{align*}
\begin{align*} &\frac{d}{dt}\int _\Omega \sqrt{\sigma +|\widehat{v}_\varepsilon |^2}dx+\int _\Omega \frac{|\nabla \widehat{v}_\varepsilon |^2}{\sqrt{\sigma +|\widehat{v}_\varepsilon |^2}}dx-\int _\Omega \frac{|\nabla \widehat{v}_\varepsilon |^2|\widehat{v}_\varepsilon |^2}{(\sigma +|\widehat{v}_\varepsilon |^2)^{\frac 32}}dx\\[5pt] &\quad=-\int _\Omega \frac{|\widehat{v}_\varepsilon |^2}{\sqrt{\sigma +|\widehat{v}_\varepsilon |^2}}dx+ \int _\Omega \frac{u_\varepsilon v_\varepsilon \widehat{v}_\varepsilon }{(1+\varepsilon u_\varepsilon v_\varepsilon )\sqrt{\sigma +|\widehat{v}_\varepsilon |^2}}dx+\int _\Omega \frac{\widehat{v}_\varepsilon (h_2-h_{2,\infty })}{\sqrt{\sigma +|\widehat{v}_\varepsilon |^2}}dx. \end{align*}
Thanks to the non-negativity of
![]() $u_\varepsilon v_\varepsilon$
and the fact that
$u_\varepsilon v_\varepsilon$
and the fact that
we arrive at
Integrating it over
![]() $[t,t+1]$
, we have
$[t,t+1]$
, we have
 \begin{align*} &\int _\Omega \sqrt{\sigma +|\widehat{v}_\varepsilon |^2}(\cdot,t+1)dx-\int _\Omega \sqrt{\sigma +|\widehat{v}_\varepsilon |^2}(\cdot,t)dx+\int _t^{t+1}\int _\Omega \frac{|\widehat{v}_\varepsilon |^2}{\sqrt{\sigma +|\widehat{v}_\varepsilon |^2}}dxds\\[5pt] &\quad\leq \int _t^{t+1}\int _\Omega u_\varepsilon v_\varepsilon dxds+\int _t^{t+1}\int _\Omega |h_2-h_{2,\infty }|dxds. \end{align*}
\begin{align*} &\int _\Omega \sqrt{\sigma +|\widehat{v}_\varepsilon |^2}(\cdot,t+1)dx-\int _\Omega \sqrt{\sigma +|\widehat{v}_\varepsilon |^2}(\cdot,t)dx+\int _t^{t+1}\int _\Omega \frac{|\widehat{v}_\varepsilon |^2}{\sqrt{\sigma +|\widehat{v}_\varepsilon |^2}}dxds\\[5pt] &\quad\leq \int _t^{t+1}\int _\Omega u_\varepsilon v_\varepsilon dxds+\int _t^{t+1}\int _\Omega |h_2-h_{2,\infty }|dxds. \end{align*}
Using the Beppo Levi theorem, as
![]() $\sigma \rightarrow 0$
, it follows that
$\sigma \rightarrow 0$
, it follows that
A straightforward calculation shows that
which leads to that, as
![]() $\sigma \rightarrow 0$
,
$\sigma \rightarrow 0$
,
Collecting these, we conclude that
 \begin{align*} &\int _\Omega |\widehat{v}_\varepsilon |(\cdot,t+1)dx-\int _\Omega |\widehat{v}_\varepsilon |(\cdot,t)dx+\int _t^{t+1}\int _\Omega |\widehat{v}_\varepsilon | dxds\\[5pt] &\quad\leq \int _t^{t+1}\int _\Omega u_\varepsilon v_\varepsilon dxds+\int _t^{t+1}\int _\Omega |h_2-h_{2,\infty }|dxds. \end{align*}
\begin{align*} &\int _\Omega |\widehat{v}_\varepsilon |(\cdot,t+1)dx-\int _\Omega |\widehat{v}_\varepsilon |(\cdot,t)dx+\int _t^{t+1}\int _\Omega |\widehat{v}_\varepsilon | dxds\\[5pt] &\quad\leq \int _t^{t+1}\int _\Omega u_\varepsilon v_\varepsilon dxds+\int _t^{t+1}\int _\Omega |h_2-h_{2,\infty }|dxds. \end{align*}
By setting
![]() $z_\varepsilon (t)\;:\!=\;\int _t^{t+1}\int _\Omega |\widehat{v}_\varepsilon | dxds$
, we have
$z_\varepsilon (t)\;:\!=\;\int _t^{t+1}\int _\Omega |\widehat{v}_\varepsilon | dxds$
, we have
and thereby obtain
To use Lemma 4.2, we shall need to verify that
![]() $g_\varepsilon (t)$
is uniformly in
$g_\varepsilon (t)$
is uniformly in
![]() $(\varepsilon,t)$
bounded and that
$(\varepsilon,t)$
bounded and that
![]() $\int _t^{t+1}g_\varepsilon (s)ds$
uniformly in
$\int _t^{t+1}g_\varepsilon (s)ds$
uniformly in
![]() $\varepsilon$
converges to
$\varepsilon$
converges to
![]() $0$
, as
$0$
, as
![]() $t\rightarrow \infty$
. In fact,
$t\rightarrow \infty$
. In fact,
which, together with (65) and (11), entails
for some
![]() $C\gt 0$
independent of
$C\gt 0$
independent of
![]() $(\varepsilon,t)$
. Thanks to the non-negativity of
$(\varepsilon,t)$
. Thanks to the non-negativity of
![]() $g_\varepsilon (t)$
, this is enough to present the uniform in
$g_\varepsilon (t)$
, this is enough to present the uniform in
![]() $\varepsilon$
bound of
$\varepsilon$
bound of
![]() $\|g_\varepsilon (t)\|_{L^\infty (0,\infty )}$
. On the other hand, due to the definition of
$\|g_\varepsilon (t)\|_{L^\infty (0,\infty )}$
. On the other hand, due to the definition of
![]() $g_\varepsilon (t)$
we arrive at
$g_\varepsilon (t)$
we arrive at
which, combined with (14) and (67), implies that
![]() $\int _t^{t+1}g_\varepsilon (s)ds\rightarrow 0$
as
$\int _t^{t+1}g_\varepsilon (s)ds\rightarrow 0$
as
![]() $t\rightarrow \infty$
uniformly in
$t\rightarrow \infty$
uniformly in
![]() $\varepsilon \in (0,1)$
. Hence, it follows from Lemma 4.2 that
$\varepsilon \in (0,1)$
. Hence, it follows from Lemma 4.2 that
This finishes the proof.
As a consequence of Lemmas 4.4 and 4.5, the large-time behaviour of the generalised solution featured in Theorem 1.2 is now almost immediate.
Proof of Theorem 1.2. On the basis of Lemma 3.3 and the Fubini-Tonelli theorem, there evidently exist
![]() $(\varepsilon _j)_{j\in N}\subset (0,1)$
and a null set
$(\varepsilon _j)_{j\in N}\subset (0,1)$
and a null set
![]() $\mathcal{N}\subset (0,\infty )$
such that
$\mathcal{N}\subset (0,\infty )$
such that
![]() $\varepsilon _j\rightarrow 0$
as
$\varepsilon _j\rightarrow 0$
as
![]() $j\rightarrow \infty$
and
$j\rightarrow \infty$
and
as
![]() $\varepsilon =\varepsilon _j\rightarrow 0$
. This, by virtue of Fatou’s lemma and Lemmas 4.4 and 4.5, gives us the desired large-time behaviour of the generalised solution in Theorem 1.2.
$\varepsilon =\varepsilon _j\rightarrow 0$
. This, by virtue of Fatou’s lemma and Lemmas 4.4 and 4.5, gives us the desired large-time behaviour of the generalised solution in Theorem 1.2.
Acknowledgements
The authors are very grateful to the referees for their detailed comments and valuable suggestions, which greatly improved the manuscript.
Financial support
The research of BL is supported by Natural Science Foundation of Ningbo Municipality (No. 2022J147). The research of LX is supported by Chongqing Science and Technology Commission Project (No. CSTB2023NSCQ-MSX0411) and Research Project of Chongqing Education Commission (No. CXQT21014).
Competing interests
None.