Hostname: page-component-586b7cd67f-rdxmf Total loading time: 0 Render date: 2024-11-22T18:32:05.809Z Has data issue: false hasContentIssue false
  • English
  • Français

Fast magneto-acoustic wave turbulence and the Iroshnikov–Kraichnan spectrum

Published online by Cambridge University Press:  31 March 2023

Sébastien Galtier Open the ORCID record for Sébastien Galtier [Opens in a new window]
Sébastien Galtier*
Affiliation:
Laboratoire de Physique des Plasmas, École polytechnique, F-91128 Palaiseau CEDEX, France Université Paris-Saclay, IPP, CNRS, Observatoire Paris, Meudon, France Institut universitaire de France
*
†Email address for correspondence: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

An analytical theory of wave turbulence is developed for pure compressible magnetohydrodynamics in the small $\beta$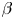 limit. In contrast to previous works where the multiple scale method was not mentioned and slow magneto-acoustic waves were included, we present here a theory for fast magneto-acoustic waves for which only an asymptotic closure is possible in three dimensions. We introduce the compressible Elsässer fields (canonical variables) and show their linear relationship with the mass density and the compressible velocity. The kinetic equations of wave turbulence for three-wave interactions are obtained and the detailed conservation is shown for the two invariants, energy and momentum (cross-helicity). An exact stationary solution (Kolmogorov-Zakharov spectrum) exists only for the energy. We find a $k^{-3/2}$ 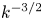energy spectrum compatible with the Iroshnikov–Kraichnan (IK) phenomenological prediction; this leads to a mass density spectrum with the same scaling. Despite the presence of a relatively strong uniform magnetic field, this turbulence is characterized by an energy spectrum with a power index that is independent of the angular direction; its amplitude, however, shows an angular dependence. We prove the existence of the IK solution using the locality condition, show that the energy flux is positive and hence the cascade direct and find the Kolmogorov constant. This theory offers a plausible explanation for recent observations in the solar wind at small $\beta$ 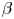where isotropic spectra with a $-3/2$ 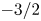power-law index are found and associated with fast magneto-acoustic waves. This theory may also be used to explain the IK spectrum often observed near the Sun. Besides, it provides a rigorous theoretical basis for the well-known phenomenological IK spectrum, which coincides with the Zakharov–Sagdeev spectrum for acoustic wave turbulence.

Keywords

astrophysical plasmasspace plasma physicsplasma nonlinear phenomena
Type
Research Article
Information
Journal of Plasma Physics , Volume 89 , Issue 2 , April 2023 , 905890205
Check for updates
Copyright
Copyright © The Author(s), 2023. Published by Cambridge University Press

1. Introduction

1.1. Solar wind turbulence

The solar wind has been studied for many years and despite its proximity and the fact that spacecraft have been launched to discover its turbulent properties, several questions remain open (Goldstein & Roberts Reference Goldstein and Roberts1999; Bruno & Carbone Reference Bruno and Carbone2013; Sahraoui, Hadid & Huang Reference Sahraoui, Hadid and Huang2020). However, it would be wrong to think that solar wind turbulence is not understood at all as we have made significant progress in this area over the last few decades. For example, the existence of a finite inertial range for the applicability of magnetohydrodynamics (MHD) is now well established, as is the fact that this turbulence consists of Alfvén waves and is anisotropic (Matthaeus Reference Matthaeus2021). To interpret the anisotropy at 1 AU, the critical balance phenomenology (Higdon Reference Higdon1984; Goldreich & Sridhar Reference Goldreich and Sridhar1995; Oughton & Matthaeus Reference Oughton and Matthaeus2020) is often used. This simple model of strong incompressible MHD turbulence predicts, for the energy spectrum in the direction transverse to the local mean magnetic field, a power-law index $\alpha = -5/3$, which is often observed for the magnetic fluctuation spectrum (Podesta, Roberts & Goldstein Reference Podesta, Roberts and Goldstein2007). However, this interpretation has limitations since the power-law index observed for the velocity fluctuation spectrum is $\alpha = -3/2$. If we want to better understand sub-MHD scales, it is also recognized that the MHD approximation must be improved with, in particular, the introduction of new nonlinear effects such as the Hall effect (Galtier Reference Galtier2006; Passot & Sulem Reference Passot and Sulem2019). The higher resolution observations provided by Cluster/ESA (Bale et al. Reference Bale, Kellogg, Mozer, Horbury and Reme2005; Kiyani, Osman & Chapman Reference Kiyani, Osman and Chapman2015) have led us to propose new theories for plasma turbulence. As far as we are concerned, we can mention the generalization of the exact (MHD) Kolmogorov law (Kolmogorov Reference Kolmogorov1941; Politano & Pouquet Reference Politano and Pouquet1998; Galtier Reference Galtier2008) for compressible turbulence, first in the case of isothermal hydrodynamics (Galtier & Banerjee Reference Galtier and Banerjee2011) and then to MHD (with different descriptions of closures and/or scales) (Banerjee & Galtier Reference Banerjee and Galtier2013; Andrés, Galtier & Sahraoui Reference Andrés, Galtier and Sahraoui2018; Ferrand, Galtier & Sahraoui Reference Ferrand, Galtier and Sahraoui2021; Simon & Sahraoui Reference Simon and Sahraoui2022). Second, the extensive use of these (compressible) laws as a solar wind model has led to a better estimate of the turbulent transfer and thus of the local heating, although we still do not know precisely by what mechanism this small-scale heating occurs (Sorriso-Valvo et al. Reference Sorriso-Valvo, Marino, Carbone, Noullez, Lepreti, Veltri, Bruno, Bavassano and Pietropaolo2007; Osman et al. Reference Osman, Wan, Matthaeus, Weygand and Dasso2011; Banerjee et al. Reference Banerjee, Hadid, Sahraoui and Galtier2016; Hadid, Sahraoui & Galtier Reference Hadid, Sahraoui and Galtier2017; Bandyopadhyay et al. Reference Bandyopadhyay, Sorriso-Valvo, Chasapis, Hellinger, Matthaeus, Verdini, Landi, Franci, Matteini and Giles2020; Marino & Sorriso-Valvo Reference Marino and Sorriso-Valvo2023).

The most remarkable recent solar wind observations come from PSP/NASA (Parker Solar Probe): they reveal a universal behaviour of the solar wind near the Sun (${\sim }0.1$ AU) with identical power-law indices $\alpha = -3/2$ for the velocity and magnetic fluctuation spectra (Chen et al. Reference Chen, Bale, Bonnell, Borovikov, Bowen, Burgess, Case, Chandran, de Wit and Goetz2020; Shi et al. Reference Shi, Velli, Panasenco, Tenerani, Réville, Bale, Kasper, Korreck, Bonnell and Dudok de Wit2021; Zhao et al. Reference Zhao, Zank, Telloni, Stevens, Kasper and Bale2022a). The mass density spectrum measured by PSP is also roughly compatible with this (Moncuquet et al. Reference Moncuquet, Meyer-Vernet, Issautier, Pulupa, Bonnell, Bale, Dudok de Wit, Goetz, Griton and Harvey2020; Zank et al. Reference Zank, Zhao, Adhikari, Telloni, Kasper, Stevens, Rahmati and Bale2022). This new property is certainly related to the plasma $\beta$ (ratio of thermodynamic pressure to magnetic pressure) which is often close to unity at 1 AU but smaller than one at ${\sim }0.1$ AU. A recent solar wind study at 1 AU and low $\beta$, reveals the singular role played by fast magneto-acoustic waves (Zhao et al. Reference Zhao, Yan, Liu, Liu and Wang2022b): it is shown that this part of turbulence is isotropic with $\alpha = -3/2$. Interestingly, this is a feature that we will demonstrate analytically in the context of fast magneto-acoustic wave turbulence. Since the intensity of the mean magnetic field is expected to be stronger near the Sun, it is natural to think that the wave turbulence regime can provide a relevant description of the young solar wind.

1.2. Wave turbulence in MHD

In incompressible MHD, the Alfvén wave turbulence theory involves three-wave interactions and leads to a strong anisotropy with a cascade only in the direction perpendicular to the uniform magnetic field ${\boldsymbol {B}_{\boldsymbol {0}}} = B_0 {\boldsymbol {e}_\parallel }$ (Galtier et al. Reference Galtier, Nazarenko, Newell and Pouquet2000; Galtier & Chandran Reference Galtier and Chandran2006). The energy spectrum, which is an exact solution of the equations, scales in the simplest case as $k_\perp ^{-2}$, and it is expected that MHD turbulence becomes strong at small perpendicular scales (Meyrand, Galtier & Kiyani Reference Meyrand, Galtier and Kiyani2016). This regime is expected in the solar corona (Rappazzo et al. Reference Rappazzo, Velli, Einaudi and Dahlburg2007; Bigot, Galtier & Politano Reference Bigot, Galtier and Politano2008), observed in the Jupiter magnetosphere (Saur et al. Reference Saur, Politano, Pouquet and Matthaeus2002), but not in the solar wind.

A theory of compressible turbulence for MHD is much more difficult to derive because, in particular, one has to deal with three waves: Alfvén (A), fast (F) and slow (S) magneto-acoustic waves (see Galtier, Nazarenko & Newell (Reference Galtier, Nazarenko and Newell2001) for a study of the resonance conditions). A first theory has been proposed in the limit of small $\beta$ and where the main nonlinear mechanism considered is the resonance scattering of (high frequency) A and F waves on (low frequency) S waves (Kuznetsov Reference Kuznetsov2001). Therefore, this theory involves non-local interactions in time scale (or frequency). The author found anisotropic spectra for each type of wave, and in particular for F waves, which are not compatible with isotropic spectra found in observations of the solar wind (Zhao et al. Reference Zhao, Yan, Liu, Liu and Wang2022b) or in direct numerical simulations (Cho & Lazarian Reference Cho and Lazarian2002; Makwana & Yan Reference Makwana and Yan2020). A second theory has been proposed, in the small $\beta$ limit, but where the S-wave contribution is neglected (Chandran Reference Chandran2005). However, an additional non-physical assumption has also been made on the mass density which has been taken to be constant (it will not be the case in this paper). To be consistent with the energy conservation, the momentum equation was then artificially modified. As a result, the initial equations used are not the original MHD equations, which limits the significance of the predictions. Finally, a third theory has been proposed, again in the small $\beta$ limit, to describe three-wave interactions between A, F and S waves, in the presence of extra terms to model collisionless damping (Chandran Reference Chandran2008). The presence of this effect justifies the absence of three-wave interactions involving only S waves. However, the complexity of the equations does not allow for exact predictions, especially for F waves for which an anisotropic spectrum is expected (the reduced case involving only F waves is mentioned but reference is made to Chandran (Reference Chandran2005) where, as explained above, the predictions prove to be limited).

The aim of this paper is to present a self-consistent and pedagogical theory for compressible MHD turbulence in the small $\beta$ limit, where A and S waves are neglected (thus retaining only local time scale interactions, with high frequency fluctuations). Note that this type of approximation has been used for incompressible Hall MHD to derive a theory of wave turbulence where left and right polarized waves have been studied separately (Galtier Reference Galtier2006); the direct numerical simulations show that indeed, at main order, the dynamics between the two types of fluctuations is decoupled (Meyrand et al. Reference Meyrand, Kiyani, Gürcan and Galtier2018). It is believed that the exact results obtained with this sub-system can serve as a basis for a better understanding of compressible MHD turbulence, which is a very complex subject. This complexity is underlined by recent direct numerical simulations of subsonic MHD turbulence where a wide range of situations is found, depending in particular on the forcing used. For example, it is shown that F and S waves become non-negligible compared with A waves when a compressible forcing is applied instead of an incompressible one (Andrés et al. Reference Andrés, Clark di Leoni, Mininni, Dmitruk, Sahraoui and Matthaeus2017; Makwana & Yan Reference Makwana and Yan2020; Gan et al. Reference Gan, Li, Fu and Du2022). The role of these compressible waves can certainly be increased if, instead, a wave forcing is applied as it is usually done in wave turbulence (Le Reun, Favier & Le Bars Reference Le Reun, Favier and Le Bars2020). Moreover, the frequency–wavenumber spectra reveal that at small $\beta$ the fluctuations corresponding to S waves are limited to low frequencies, leaving a large frequency domain for a dynamics driven possibly by fast magneto-acoustic wave turbulence (Andrés et al. Reference Andrés, Clark di Leoni, Mininni, Dmitruk, Sahraoui and Matthaeus2017; Brodiano, Andrés & Dmitruk Reference Brodiano, Andrés and Dmitruk2021).

We will see in this paper that the complexity of the kinetic equations of fast magneto-acoustic wave turbulence are relatively limited. This apparent simplicity is linked to the semi-dispersive nature of F waves with the dispersion relation $\omega \propto k = \sqrt {k_\perp ^2 + k_\parallel ^2}$. A priori, this leads to some analytical difficulties for the asymptotic closure because we are dealing with three-wave interactions and, in this case, the resonance condition corresponds to collinear wavevectors (note that this constraint does not exist for four-wave interactions – see e.g. the case of gravitational wave turbulence Galtier & Nazarenko Reference Galtier and Nazarenko2017). It turns out that this problem is similar to acoustic wave turbulence (Zakharov & Sagdeev Reference Zakharov and Sagdeev1970) for which it was shown that the uniformity of the asymptotic development is broken in one or two dimensions, but can eventually be restored in three dimensions (Benney & Saffman Reference Benney and Saffman1966; Newell & Aucoin Reference Newell and Aucoin1971; L'vov et al. Reference L'vov, L'vov, Newell and Zakharov1997). This mathematical property fully justifies the use of the derived wave kinetic equations in this paper, even if a slight correction might be necessary, which can take the form of a broadening of the resonance loci (in our case, rays).

1.3. The case of semi-dispersive waves

The theory of wave turbulence describes a sea of random waves interacting in a weakly nonlinear manner (Galtier Reference Galtier2023). The great achievement of this theory is the discovery of the existence of a natural asymptotic closure induced by the separation of time scales between the linear and nonlinear times (Benney & Saffman Reference Benney and Saffman1966; Benney Reference Benney1967). It is natural because it does not assume anything about the statistical distributions of the field such as joint Gaussianity (Newell, Nazarenko & Biven Reference Newell, Nazarenko and Biven2001). This represents a breakthrough compared with previous work where the usual procedure was to invoke an ad hoc statistical assumption in order to close the hierarchy of moment equations (Hasselmann Reference Hasselmann1962). A necessary ingredient for this success that uses the multiple scale method, is a sufficient degree of decoupling of the initial correlations by the linear response of the system. In simple terms, the reason of the closure is that the cumulant (or moment) evolution separates into two processes. On short time scale, of the order of the wave period (which is $\mathcal {O} (1)$), there is a phase mixing which leads to the decoupling of the correlations initially present and to a statistics that is close to Gaussianity, as expected from the central limit theorem. On a longer time scale (for three-wave interactions, it is $\mathcal {O} (1/\epsilon ^2)$, with $\epsilon$ the amplitude of the waves), the nonlinear coupling – weak over short time – becomes non-negligible because of the resonance mechanism. This coupling leads to a regeneration of the cumulants via the product of lower-order cumulants. It is these contributions that are at the origin of the energy transfer mechanism.

It is often thought that the dispersive nature of the waves is a necessary ingredient for achieving an asymptotic closure. The argument is that for non-dispersive waves, all disturbances travel at the same speed and therefore initial correlations between the phases of the waves persist, whereas for dispersive waves any initial correlations are quickly lost as different waves travel with different speeds. However, several comments must be made to nuance this statement. First, the analysis is done for three-wave interactions. In this case, the resonance condition leads to rays in Fourier space along which correlations can be preserved. For four-wave interactions, the situation is different because the solutions of the resonance condition are not necessarily confined along rays (Nazarenko Reference Nazarenko2011; Galtier & Nazarenko Reference Galtier and Nazarenko2017; Hassaini et al. Reference Hassaini, Mordant, Miquel, Krstulovic and Düring2019). Second, for three-wave interactions, the loss of correlation depends on the dimension of the problem. It was shown by Benney & Saffman (Reference Benney and Saffman1966) that, in one dimension, a natural closure for acoustic wave turbulence is indeed not possible because the initial correlation is preserved, which leads to an energy transfer on a time scale shorter than $\mathcal {O} (1/\epsilon ^2)$. Physically, we know that for one-dimensional compressible flow, shocks are formed in a finite time. What is true in one dimension is not necessarily true in a multidimensional space. Indeed, the fact that many wave packets carrying statistically independent information pass through a given direction can lead to a state close to Gaussianity. Therefore, the central limit theorem can again be operative and a natural closure occur. However, these phenomenological arguments must be checked carefully. This has been done for acoustic wave turbulence in two dimensions by Newell & Aucoin (Reference Newell and Aucoin1971) and in three dimensions by L'vov et al. (Reference L'vov, L'vov, Newell and Zakharov1997). The conclusion is that in two dimensions the uniformity of the development seems difficult to achieve because of the fast growth of secular terms, however, in three dimensions the growth is much weaker (logarithmic) and a natural closure may be obtained. Although a complete demonstration (involving higher-order terms) is still lacking, the study of L'vov et al. (Reference L'vov, L'vov, Newell and Zakharov1997) gives the expression of the renormalized frequency needed to restore the uniformity of the development, as well as the generalized kinetic equation which differs from the original equation derived by Zakharov & Sagdeev (Reference Zakharov and Sagdeev1970) by the $\delta$ functions which are replaced by Lorenz functions. Interestingly, this generalized equation has the same Kolmogorov–Zakharov solution as the original but, in addition, it allows local angular transfer between adjacent rays.

The problem studied here, which involves semi-dispersive waves, is similar to acoustic wave turbulence. Therefore, one can assume that the previous development for tri-dimensional acoustic wave turbulence can be directly applied here. In other words, we will assume that a given wave packet travelling in a fixed direction is crossed by a sufficient number of F-wave packets (carrying statistically independent information) to break its initial correlation. This number is sufficient in three dimensions, but not in two dimensions. This physically explains why the uniformity of the asymptotic development can be preserved for three-dimensional F-wave turbulence, and why the Kolmogorov–Zakharov spectrum that will be derived is indeed a relevant solution of the problem. In figure 1, a phenomenological interpretation of this discussion is given with collisions between semi-dispersive wave packets in one, two and three dimensions.

Figure 1. Propagation of wave packets of amplitude $\epsilon$, with $\omega \propto k$, in one dimension (left), two dimensions (middle) and three dimensions (right). In one dimension, the (nonlinear) interaction between wave packets (1) and (2) becomes quickly strong because they are moving in the same direction at the same speed, and thus the initial correlations between the phases of the wave packets persist; collisions between wave packet (1) and those propagating in the opposite direction, which carry statistically independent information, cannot change the situation; therefore, turbulence cannot be weak. In two dimensions, the number of collisions between wave packet (1) and the others moving in different directions is higher than in one dimension but still not enough to change the conclusion. In three dimensions, this number is sufficient to randomize the phases of wave packet (1) and turbulence can eventually be weak. In pure compressible MHD at $\beta \ll 1$, this explanation applies well for F waves for which $\omega \propto k$ (semi-dispersive wave). For S waves where $\omega \propto k_\parallel$ (non-dispersive wave), whatever the dimension, the situation reduces to the one-dimensional case with propagation of wave packets along the strong uniform magnetic field; therefore, turbulence of S waves cannot be weak and can produce shocks.

1.4. Phenomenology of compressible MHD wave turbulence

A recent study carried out at 1 AU (Zhao et al. Reference Zhao, Yan, Liu, Liu and Wang2022b) reveals that when the plasma $\beta$ is small, solar wind turbulence can be composed of Alfvénic fluctuations following the critical balance phenomenology, and of fast magneto-acoustic fluctuations with an isotropic $k^{-3/2}$ energy spectrum. This observation can be understood with the help of simple phenomenological arguments. Assuming the existence of a relatively strong uniform magnetic field (written ${\boldsymbol {b}_{\boldsymbol {0}}}$ in velocity units) and considering the small $\beta$ limit, we obtain the Alfvén time

(1.1)\begin{equation} \tau_A \sim \frac{1}{\omega_A} \sim \frac{1}{k_\parallel b_0} , \end{equation}

with $k_\parallel$ the wavenumber component along ${\boldsymbol {b}_{\boldsymbol {0}}}$, and the fast magneto-acoustic time

(1.2)\begin{equation} \tau_F \sim \frac{1}{\omega_F} \sim \frac{1}{k b_0} . \end{equation}

If we assume that the dynamics is mainly governed by Alfvén waves, an anisotropic cascade develops (whatever the regime, weak or strong) with energy mainly located at $k_\perp \gg k_\parallel$. Then, the nonlinear time reads

(1.3)\begin{equation} \tau_{{\rm NL}} \sim \frac{1}{k b_\ell} \sim \frac{1}{k_\perp b_\ell} , \end{equation}

where $b_\ell$ represents the fluctuations of the magnetic field at a given length scale $\ell$ (for simplicity, we assume equipartition between the velocity and the magnetic field fluctuations). We deduce the following time ratios:

(1.4a,b)\begin{equation} \chi^A = \frac{\tau_A}{\tau_{{\rm NL}}} \sim \frac{k_\perp b_\ell}{k_\parallel b_0} \quad {\rm{and}} \quad \chi^F = \frac{\tau_F}{\tau_{{\rm NL}}} \sim \frac{b_\ell}{b_0} . \end{equation}

If the Alfvénic fluctuations follow the critical balance regime as often claimed (Horbury, Forman & Oughton Reference Horbury, Forman and Oughton2008), then $\chi ^A \sim 1$ and necessarily we have $\chi ^F \ll 1$, which is synonymous with weak F-wave turbulence. Therefore, at any location where the critical balance regime is observed for A waves (strong wave turbulence), if the plasma is compressible and $\beta$ small, we should find the regime of (weak) F-wave turbulence. Note that signatures of the coexistence of strong and weak wave turbulence in a plasma have already been observed in three-dimensional direct numerical simulations of incompressible Hall MHD where left and right circularly polarized waves are present, the former being in the strong turbulence regime and the latter in the weak turbulence regime (Meyrand et al. Reference Meyrand, Kiyani, Gürcan and Galtier2018).

Using phenomenological arguments for three-wave interactions, we can also find a prediction for the energy spectrum corresponding to fast magneto-acoustic wave turbulence. We introduce the mean rate of energy transfer (or energy flux) $\varepsilon$ in the inertial range, the transfer (or cascade) time $\tau _{{\rm tr}}$ and the isotropic energy spectrum $E_k$ (we anticipate that this turbulence is isotropic) such that

(1.5)\begin{equation} \varepsilon \sim \frac{b^2_\ell}{\tau_{tr}} \sim \frac{kE_k}{\omega_F \tau_{{\rm NL}}^2} \sim \frac{k^2 E_k b^2_\ell}{b_0} \sim \frac{k^3 E^2_k}{b_0} , \end{equation}

which gives the one-dimensional energy spectrum

(1.6)\begin{equation} E_k \sim \sqrt{b_0 \varepsilon} k^{{-}3/2} . \end{equation}

This is the well-known Iroshnikov–Kraichnan (IK) isotropic spectrum (Iroshnikov Reference Iroshnikov1964; Kraichnan Reference Kraichnan1965) often cited in incompressible MHD (with the same type of phenomenology – or dimensional analysis – a $k^{-3/2}$ energy spectrum can also be found in acoustic wave turbulence Zakharov & Sagdeev Reference Zakharov and Sagdeev1970). However, it is known that this weak isotropic turbulence phenomenology is not well adapted to this situation where anisotropy is expected in the presence of Alfvén waves (Galtier et al. Reference Galtier, Nazarenko, Newell and Pouquet2000). This phenomenology is also not relevant for slow magneto-acoustic waves since we cannot build a theory of weak turbulence. In conclusion, the IK phenomenology of weak turbulence is much better suited to fast magneto-acoustic wave turbulence. Note that the IK spectrum is precisely what was observed by Zhao et al. (Reference Zhao, Yan, Liu, Liu and Wang2022b) in the solar wind. In this paper, we will show that this isotropic spectrum is in fact an exact solution of fast magneto-acoustic wave turbulence.

1.5. Plan of the paper

This paper is organized as follows. In § 2, we present the leading-order compressible MHD equations and the compressible Elsässer fields. In § 3, the wave amplitude equations for the canonical variables are derived. In § 4, we introduce the wave turbulence formalism and derive the kinetic equations for fast magneto-acoustic wave turbulence. In § 5, the properties of the kinetic equations are given with the detailed conservation of energy and momentum. We derive the exact stationary solutions (Kolmogorov–Zakharov spectra), find the locality domain, the sign of the flux and the Kolmogorov constant. In the last section, a conclusion is proposed with a discussion on the relevance of this wave turbulence theory for the solar wind.

2. Compressible MHD

2.1. Leading-order equations

Neglecting the dissipative (and forcing) terms, the three-dimensional compressible MHD equations write (Galtier Reference Galtier2016)

(2.1)\begin{gather} {\partial \rho \over \partial t} + \boldsymbol{\nabla} \boldsymbol{\cdot} (\rho {\boldsymbol{u}}) = 0 , \end{gather}
(2.2)\begin{gather}\rho \left({\partial {\boldsymbol{u}} \over \partial t} + {\boldsymbol{u}} \boldsymbol{\cdot} \boldsymbol{\nabla} {\boldsymbol{u}} \right) ={-} \boldsymbol{\nabla} P + {1 \over \mu_0}(\boldsymbol{\nabla} \times {\boldsymbol{B}}) \times {\boldsymbol{B}} , \end{gather}
(2.3)\begin{gather}{\partial {\boldsymbol{B}} \over \partial t} = \boldsymbol{\nabla} \times ({\boldsymbol{u}} \times {\boldsymbol{B}}) , \end{gather}
(2.4)\begin{gather}\boldsymbol{\nabla}\boldsymbol{\cdot} {\boldsymbol{B}} = 0 , \end{gather}

where $\rho$ is the mass density, ${\boldsymbol {u}}$ the velocity, $P$ the pressure, $\mu _0$ the permeability of free space and ${\boldsymbol {B}}$ the magnetic field. Hereafter, we will consider small mass density fluctuations $\rho _1$ over a uniform density $\rho _0$, namely $\rho \equiv \rho _0 + \rho _1$ with $\rho _1 \ll \rho _0$. We will also neglect the pressure compared with the magnetic pressure (small $\beta$ limit). We introduce the normalized magnetic field ${\boldsymbol {b}} \equiv {\boldsymbol {B}} / \sqrt {\mu _0 \rho _0}$ and a uniform (normalized) magnetic field along the parallel direction ${\boldsymbol {b}}_0 = b_0 {\boldsymbol {e}_\parallel }$ such that $\vert {\boldsymbol {b}} \vert \equiv b \ll b_0$. Under these considerations, the system (2.1)–(2.3) reads at leading order

(2.5)\begin{gather} {\partial \rho_1 \over \partial t} + \rho_0 \boldsymbol{\nabla} \boldsymbol{\cdot} {\boldsymbol{u}} ={-} \boldsymbol{\nabla} \boldsymbol{\cdot} (\rho_1 {\boldsymbol{u}}) , \end{gather}
(2.6)\begin{gather}{\partial {\boldsymbol{u}} \over \partial t} - b_0 \left(\partial_\parallel {\boldsymbol{b}} - \boldsymbol{\nabla} b_\parallel \right) ={-} ({\boldsymbol{u}} \boldsymbol{\cdot}\boldsymbol{\nabla}) {\boldsymbol{u}} - \boldsymbol{\nabla} \left(\frac{{\boldsymbol{b}}^2}{2} \right) + ({\boldsymbol{b}} \boldsymbol{\cdot} \boldsymbol{\nabla}) {\boldsymbol{b}} + \frac{b_0}{\rho_0} \rho_1 \left( \partial_\parallel {\boldsymbol{b}} - \boldsymbol{\nabla} b_\parallel \right) , \end{gather}
(2.7)\begin{gather}{\partial {\boldsymbol{b}} \over \partial t} - b_0 \partial_\parallel {\boldsymbol{u}} + {\boldsymbol{b}}_0 (\boldsymbol{\nabla} \boldsymbol{\cdot} {\boldsymbol{u}}) = ({\boldsymbol{b}} \boldsymbol{\cdot} \boldsymbol{\nabla}) {\boldsymbol{u}} - ({\boldsymbol{u}} \boldsymbol{\cdot}\boldsymbol{\nabla}) {\boldsymbol{b}} - {\boldsymbol{b}} (\boldsymbol{\nabla} \boldsymbol{\cdot} {\boldsymbol{u}}) , \end{gather}

where the quadratic nonlinear contributions are written in the right-hand side and the linear terms in the left-hand side.

The primary vector fields will be decomposed into toroidal ($\psi ^{u,b}$), poloidal ($\phi ^{u,b}$) and compressible ($\xi$) scalar fields in the following manner:

(2.8)\begin{gather} {\boldsymbol{u}} = \boldsymbol{\nabla} \times (\psi^u {\boldsymbol{e}_\parallel}) + \boldsymbol{\nabla} \times (\boldsymbol{\nabla} \times (\phi^u {\boldsymbol{e}_\parallel}) ) + \boldsymbol{\nabla} \xi , \end{gather}
(2.9)\begin{gather}{\boldsymbol{b}} = \boldsymbol{\nabla} \times (\psi^b {\boldsymbol{e}_\parallel}) + \boldsymbol{\nabla} \times (\boldsymbol{\nabla} \times (\phi^b {\boldsymbol{e}_\parallel}) ) . \end{gather}

Since shear-Alfvén waves will be filtered out, we impose $\psi ^u = \psi ^b = 0$. Then, in Fourier space, we obtain the decomposition

(2.10)\begin{gather} \hat{{\boldsymbol{u}}}({\boldsymbol{k}}) \equiv \hat{{\boldsymbol{u}}}_k = \hat{\phi}^u_k (k^2 {\boldsymbol{e}_\parallel} - k_{{\parallel}} {\boldsymbol{k}}) + {\rm i} \hat{\xi}_k {\boldsymbol{k}} , \end{gather}
(2.11)\begin{gather}\hat{{\boldsymbol{b}}}({\boldsymbol{k}}) \equiv \hat{{\boldsymbol{b}}}_k = \hat{\phi}^b_k (k^2 {\boldsymbol{e}_\parallel} - k_{{\parallel}} {\boldsymbol{k}}) , \end{gather}

where the symbol $\hat.$ means the Fourier transform and ${\boldsymbol {k}}$ is a wavevector.

2.2. Compressible Elsässer variables

The linearization of (2.1)–(2.3) gives

(2.12)\begin{gather} {\partial \hat{\rho}_k \over \partial t} ={-} {\rm i} \rho_0 {\boldsymbol{k}} \boldsymbol{\cdot} \hat{{\boldsymbol{u}}}_k , \end{gather}
(2.13)\begin{gather}{\partial \hat{{\boldsymbol{u}}}_k \over \partial t} = {\rm i} k_{{\parallel}} b_0 {\hat{{\boldsymbol{b}}}}_k - {\rm i} b_0 {\boldsymbol{k}} {\hat{b}}_{{\parallel} k} , \end{gather}
(2.14)\begin{gather}{\partial \hat{{\boldsymbol{b}}}_k \over \partial t} = {\rm i} k_{{\parallel}} b_0 \hat{{\boldsymbol{u}}}_k - {\rm i} {\boldsymbol{b}}_0 ({\boldsymbol{k}} \boldsymbol{\cdot} \hat{{\boldsymbol{u}}}_k) , \end{gather}

which becomes with the decomposition (to simplify the notation, we write $\hat {\rho }_k \equiv \widehat {\rho _1}_k$)

(2.15)\begin{gather} {\partial \hat{\rho}_k \over \partial t} = \rho_0 k^2 \hat{\xi}_k , \end{gather}
(2.16)\begin{gather}{\partial \hat{\xi}_k \over \partial t} ={-} b_0 k_{{\perp}}^2 \hat{\phi}^b_k , \end{gather}
(2.17)\begin{gather}{\partial \hat{\phi}^u_k \over \partial t} = {\rm i} b_0 k_{{\parallel}} \hat{\phi}^b_k , \end{gather}
(2.18)\begin{gather}{\partial \hat{\phi}^b_k \over \partial t} = {\rm i} b_0 k_{{\parallel}} \hat{\phi}^u_k + b_0 \hat{\xi}_k . \end{gather}

It is straightforward to show that the dispersion relation is (with our convention $\omega > 0$)

(2.19)\begin{equation} \omega_k = b_0 k . \end{equation}

From (2.15)–(2.18), one finds the canonical variables $A_k^s$ (the compressible Elsässer fields)

(2.20)\begin{equation} A^s ({\boldsymbol{k}}) \equiv A_k^s \equiv \frac{k^2 k_{{\perp}}}{k_{{\parallel}}} \left( \hat{\phi}^u_k - s \frac{k_{{\parallel}}}{k} \hat{\phi}^b_k \right) , \end{equation}

with $s=\pm$ the directional polarity. Interestingly, we find the linear relationships

(2.21)\begin{equation} \hat{\xi}_k = {\rm i} \frac{k_{{\perp}}^2}{k_{{\parallel}}} \hat{\phi}^u_k , \end{equation}

and

(2.22)\begin{equation} \hat{\rho}_k = \frac{\rho_0}{b_0} k_{{\perp}}^2 \hat{\phi}^b_k . \end{equation}

This means that the canonical variables have several writings. The choice (2.20) seems, however, the most natural since its form is similar to the incompressible Elsässer fields that involve only ${\boldsymbol {u}}$ and ${\boldsymbol {b}}$ (Galtier Reference Galtier2016). Another interesting comment is that very often the parallel component of the magnetic field is used to evaluate the compressibility at MHD scales (Zank et al. Reference Zank, Zhao, Adhikari, Telloni, Kasper, Stevens, Rahmati and Bale2022). Relation (2.21) demonstrates that here it is not a good proxy.

2.3. Energy and momentum conservation

We assume that the field components have a zero mean value. Then, at leading order and in the small $\beta$ limit, the energy conservation reads

(2.23)\begin{equation} E = \tfrac{1}{2} \rho_0 \left\langle {\boldsymbol{u}}^2 + {\boldsymbol{b}}^2 \right\rangle , \end{equation}

where $\langle \rangle$ means the spatial average (hereafter, $\langle \rangle$ will be also used as the ensemble average). Note that the fact that the mass density field $\rho _1$ does not appear explicitly in this formula does not mean that it has no effect on the (nonlinear) dynamics. In Fourier space, the energy becomes

(2.24)\begin{align} E({\boldsymbol{k}}) & = \tfrac{1}{2} \rho_0 \left\langle \hat{{\boldsymbol{u}}}_k \boldsymbol{\cdot} \hat{{\boldsymbol{u}}}_k^* + \hat{{\boldsymbol{b}}}_k \boldsymbol{\cdot} \hat{{\boldsymbol{b}}}_k^* \right\rangle = \tfrac{1}{2} \rho_0 \left\langle k_{{\perp}}^2 k^2 \left( \vert \hat{\phi}^u_k \vert^2 + \vert \hat{\phi}^b_k \vert^2 \right) + k^2 \vert \hat{\xi}_k \vert^2 \right\rangle \nonumber\\ & = \tfrac{1}{4} \rho_0 \left\langle \vert A_k^+ \vert^2 + \vert A_k^- \vert^2 \right\rangle . \end{align}

As will be proved later, the second invariant is the momentum (or cross-helicity)

(2.25)\begin{equation} H = \tfrac{1}{2} \rho_0 \left\langle {\boldsymbol{u}} \boldsymbol{\cdot} {\boldsymbol{b}} \right\rangle . \end{equation}

In Fourier space, it reads

(2.26)\begin{align} H({\boldsymbol{k}}) & = \frac{1}{2} \rho_0 \left\langle \hat{{\boldsymbol{u}}}_k \boldsymbol{\cdot} \hat{{\boldsymbol{b}}}_k^* + \hat{{\boldsymbol{b}}}_k \boldsymbol{\cdot} \hat{{\boldsymbol{u}}}_k^* \right\rangle = \frac{1}{2} \rho_0 \left\langle k_{{\perp}}^2 k^2 \left[\hat{\phi}^u_k (\hat{\phi}^b_k)^* + (\hat{\phi}^u_k)^* \hat{\phi}^b_k \right] \right\rangle \nonumber\\ & ={-} \frac{1}{4} \rho_0 \frac{k_{{\parallel}}}{k} \left\langle \vert A_k^+ \vert^2 - \vert A_k^- \vert^2 \right\rangle . \end{align}

3. Fundamental equation

With the introduction of the canonical variables, one can derive the equation for the F-wave amplitude variation. Its form is

(3.1)\begin{equation} {\partial A_k^s \over \partial t} + {\rm i} s \omega_k A_k^s = {\mathcal{N}}_k , \end{equation}

with ${\mathcal {N}}_k$ the nonlinear contribution in spectral space. A little calculation leads to the following expressions:

(3.2)\begin{align} {\partial \hat{\phi}^u_k \over \partial t} & = {\rm i} b_0 k_{{\parallel}} \hat{\phi}^b_k \nonumber\\ & \quad +\frac{{\rm i} k_{{\parallel}}}{2 k_{{\perp}}^2 k^2} \int_{\mathbb{R}^6} \left[ \frac{p^2 q^2 k_{{\perp}}^2}{p_{{\parallel}} q_{{\parallel}}} ({\boldsymbol{p}_{{\perp}}} \boldsymbol{\cdot} {\boldsymbol{q}_{{\perp}}}) \hat{\phi}_p^u \hat{\phi}_q^u + 2 k_{{\parallel}} p_{{\parallel}} q^2 ({\boldsymbol{p}} \boldsymbol{\cdot} {\boldsymbol{q}} - p_{{\parallel}}^2) \hat{\phi}_p^b \hat{\phi}_q^b \right] \delta_{{\boldsymbol{k}},{\boldsymbol{p}}{\boldsymbol{q}}} \,\mathrm{d} {\boldsymbol{p}} \,\mathrm{d} {\boldsymbol{q}} , \end{align}

and

(3.3)\begin{equation} {\partial \hat{\phi}^b_k \over \partial t} = \frac{{\rm i} {b}_0 k^2}{k_{{\parallel}}} \hat{\phi}^u_k + \frac{{\rm i}}{k_{{\perp}}^2} \int_{\mathbb{R}^6} \frac{ p_{{\perp}}^2 q^2}{q_{{\parallel}}} \left[ {\boldsymbol{p}} \boldsymbol{\cdot} {\boldsymbol{q}} + q_{{\perp}}^2-p_{{\parallel}} q_{{\parallel}} \right] \hat{\phi}_p^b \hat{\phi}_q^u \delta_{{\boldsymbol{k}},{\boldsymbol{p}}{\boldsymbol{q}}} \,\mathrm{d} {\boldsymbol{p}} \,\mathrm{d} {\boldsymbol{q}} , \end{equation}

where $\delta _{{\boldsymbol {k}},{\boldsymbol {p}}{\boldsymbol {q}}} \equiv \delta ({\boldsymbol {k}}-{\boldsymbol {p}}-{\boldsymbol {q}})$. To derive these expressions, we have used relations (2.21) and (2.22). The canonical variables can be introduced by noticing the relations

(3.4)\begin{gather} \hat{\phi}^u_k = \frac{k_{{\parallel}}}{2k_{{\perp}} k^2} \sum_s A_k^s , \end{gather}
(3.5)\begin{gather}\hat{\phi}^b_k ={-}\frac{1}{2k_{{\perp}} k} \sum_s s A_k^s . \end{gather}

We obtain

(3.6)\begin{align} {\partial \hat{\phi}^u_k \over \partial t} & = {\rm i} b_0 k_{{\parallel}} \hat{\phi}^b_k\nonumber\\ & \quad + \frac{{\rm i} k_{{\parallel}}}{8 k_{{\perp}}^2 k^2} \int_{\mathbb{R}^6} \sum_{s_p s_q} \left[ \frac{k_{{\perp}}^2}{p_{{\perp}} q_{{\perp}}} ({\boldsymbol{p}_{{\perp}}} \boldsymbol{\cdot} {\boldsymbol{q}_{{\perp}}}) + \frac{2 s_p s_q k_{{\parallel}} p_{{\parallel}} q}{pp_{{\perp}} q_{{\perp}}} ({\boldsymbol{p}} \boldsymbol{\cdot} {\boldsymbol{q}} - p_{{\parallel}}^2) \right] A_p^{s_p} A_q^{s_q} \delta_{{\boldsymbol{k}},{\boldsymbol{p}}{\boldsymbol{q}}} \,\mathrm{d} {\boldsymbol{p}} \,\mathrm{d} {\boldsymbol{q}} , \end{align}

and

(3.7)\begin{equation} {\partial \hat{\phi}^b_k \over \partial t} = \frac{{\rm i} b_0 k^2}{k_{{\parallel}}} \hat{\phi}^u_k - \frac{{\rm i}}{4 k_{{\perp}}^2} \int_{\mathbb{R}^6} \sum_{s_p s_q} \frac{s_p p_{{\perp}}}{pq_{{\perp}}} \left[ {\boldsymbol{p}} \boldsymbol{\cdot} {\boldsymbol{q}} + q_{{\perp}}^2-p_{{\parallel}} q_{{\parallel}} \right] A_p^{s_p} A_q^{s_q} \delta_{{\boldsymbol{k}},{\boldsymbol{p}}{\boldsymbol{q}}} \,\mathrm{d} {\boldsymbol{p}} \,\mathrm{d} {\boldsymbol{q}} . \end{equation}

Finally, a combination of the two last expressions gives

(3.8)\begin{align} {\partial A_k^s \over \partial t} + {\rm i} s \omega_k A_k^s & = \frac{{\rm i}}{8 k_{{\perp}}} \int_{\mathbb{R}^6} \sum_{s_p s_q} \left[ \frac{k_{{\perp}}^2}{p_{{\perp}} q_{{\perp}}} ({\boldsymbol{p}_{{\perp}}} \boldsymbol{\cdot} {\boldsymbol{q}_{{\perp}}}) + \frac{2s_ps_qk_{{\parallel}} p_{{\parallel}} q}{pp_{{\perp}} q_{{\perp}}} ({\boldsymbol{p}} \boldsymbol{\cdot} {\boldsymbol{q}} - p_{{\parallel}}^2)\right.\nonumber\\ & \quad \left. +\, \frac{2s s_p k p_{{\perp}}}{pq_{{\perp}}} ({\boldsymbol{p}} \boldsymbol{\cdot} {\boldsymbol{q}} + q_{{\perp}}^2-p_{{\parallel}} q_{{\parallel}})\right] A_p^{s_p} A_q^{s_q} \delta_{{\boldsymbol{k}},{\boldsymbol{p}}{\boldsymbol{q}}} \,\mathrm{d} {\boldsymbol{p}} \,\mathrm{d} {\boldsymbol{q}} , \end{align}

which can also be written in a symmetric form

(3.9)\begin{align} & {\partial A_k^s \over \partial t} + {\rm i} s \omega_k A_k^s \nonumber\\ & \quad= \frac{{\rm i}}{8 k_{{\perp}}} \int_{\mathbb{R}^6} \sum_{s_p s_q} \left[ \frac{k_{{\perp}}^2}{p_{{\perp}} q_{{\perp}}} ({\boldsymbol{p}_{{\perp}}} \boldsymbol{\cdot} {\boldsymbol{q}_{{\perp}}}) + \frac{k_{{\parallel}} s_ps_q}{p_{{\perp}} q_{{\perp}} pq} \left( p_{{\parallel}} q^2 ({\boldsymbol{p}} \boldsymbol{\cdot} {\boldsymbol{q}} - p_{{\parallel}}^2) + q_{{\parallel}} p^2 ({\boldsymbol{p}} \boldsymbol{\cdot} {\boldsymbol{q}} - q_{{\parallel}}^2) \right) \right.\nonumber\\ & \qquad \left. +\, \frac{sk}{p_{{\perp}} q_{{\perp}} pq} \left( s_p p_{{\perp}}^2q ({\boldsymbol{p}_{{\perp}}} \boldsymbol{\cdot} {\boldsymbol{q}_{{\perp}}} + q_{{\perp}}^2) + s_q q_{{\perp}}^2 p ({\boldsymbol{p}_{{\perp}}} \boldsymbol{\cdot} {\boldsymbol{q}_{{\perp}}} + p_{{\perp}}^2) \right)\right] A_p^{s_p} A_q^{s_q} \delta_{{\boldsymbol{k}},{\boldsymbol{p}}{\boldsymbol{q}}} \,\mathrm{d} {\boldsymbol{p}} \,\mathrm{d} {\boldsymbol{q}} . \end{align}

The form of the wave amplitude equation is non-trivial, however, several simplifications are possible. First, we shall use the interaction representation and consider a wave of small amplitude ($0 < \epsilon \ll 1$)

(3.10)\begin{equation} A_k^s = \epsilon a_k^s \exp({-{\rm i}s\omega_kt}) , \end{equation}

which leads to

(3.11)\begin{align} {\partial a_k^s \over \partial t} & = \frac{{\rm i} \epsilon}{8 k_{{\perp}}} \int_{\mathbb{R}^6} \sum_{s_p s_q} \left[ \frac{k_{{\perp}}^2}{p_{{\perp}} q_{{\perp}}} ({\boldsymbol{p}_{{\perp}}} \boldsymbol{\cdot} {\boldsymbol{q}_{{\perp}}}) + \frac{k_{{\parallel}} s_ps_q}{p_{{\perp}} q_{{\perp}} pq} \left( p_{{\parallel}} q^2 ({\boldsymbol{p}} \cdot {\boldsymbol{q}} - p_{{\parallel}}^2) + q_{{\parallel}} p^2 ({\boldsymbol{p}} \cdot {\boldsymbol{q}} - q_{{\parallel}}^2) \right) \right.\nonumber\\ & \quad \left. +\,\frac{sk}{p_{{\perp}} q_{{\perp}} pq} \left( s_p p_{{\perp}}^2q ({\boldsymbol{p}_{{\perp}}} \boldsymbol{\cdot} {\boldsymbol{q}_{{\perp}}} + q_{{\perp}}^2) + s_q q_{{\perp}}^2 p ({\boldsymbol{p}_{{\perp}}} \boldsymbol{\cdot} {\boldsymbol{q}_{{\perp}}} + p_{{\perp}}^2) \right) \right] \nonumber\\ & \quad \times a_p^{s_p} a_q^{s_q} \exp({{\rm i}\varOmega_{k,pq} t}) \delta_{{\boldsymbol{k}},{\boldsymbol{p}}{\boldsymbol{q}}} \,\mathrm{d} {\boldsymbol{p}} \,\mathrm{d} {\boldsymbol{q}} , \end{align}

with $\varOmega _{k,pq} \equiv s\omega _k - s_p\omega _p - s_q\omega _q$. Second, we will anticipate the consequence of the resonance condition that the kinetic equations must satisfy. This condition

(3.12)\begin{gather} sk = s_pp + s_qq , \end{gather}
(3.13)\begin{gather}{\boldsymbol{k}} = {\boldsymbol{p}} + {\boldsymbol{q}} , \end{gather}

leads to collinear wavevectors and thus to the relations ${\boldsymbol {p}} \boldsymbol {\cdot } {\boldsymbol {q}} = s_p s_q pq$ and ${\boldsymbol {p}_{\perp }} \boldsymbol {\cdot } {\boldsymbol {q}_{\perp }} = s_p s_q p_{\perp } q_{\perp }$. We also have $p_{\perp }^2q_{\parallel }^2=q_{\perp }^2 p_{\parallel }^2$. With this information, the wave amplitude equation reduces to

(3.14)\begin{align} {\partial a_k^s \over \partial t} & = \frac{{\rm i} \epsilon}{8 k_{{\perp}}} \int_{\mathbb{R}^6} \sum_{s_p s_q} \left[ s_p s_q k_{{\perp}}^2 + \frac{k_{{\parallel}}}{pq} \left( p_{{\parallel}} q^2 + q_{{\parallel}} p^2 \right) \right.\nonumber\\ & \quad \left. +\, \frac{sks_ps_q}{pq} \left( skp_{{\perp}}q_{{\perp}} + s_p p_{{\perp}}^2q + s_q q_{{\perp}}^2 p \right) \right] a_p^{s_p} a_q^{s_q} \exp({{\rm i}\varOmega_{k,pq} t}) \delta_{{\boldsymbol{k}},{\boldsymbol{p}}{\boldsymbol{q}}} \,\mathrm{d} {\boldsymbol{p}} \,\mathrm{d} {\boldsymbol{q}} . \end{align}

A last simplification can be made by introducing $\theta$, the angle between ${\boldsymbol {k}}$ and ${\boldsymbol {e}_\parallel }$ and, thus, the relations $k_{\parallel } = k \cos \theta _k$, $p_\parallel =s s_p p \cos \theta _k$ and $q_\parallel =s s_q q \cos \theta _k$. We also have $k_{\perp } = k \sin \theta _k$, $p_\perp = p \sin \theta _k$ and $q_\perp = q \sin \theta _k$. Since the wavevectors ${\boldsymbol {k}}$, ${\boldsymbol {p}}$ and ${\boldsymbol {q}}$ are collinear, we arrive at

(3.15)\begin{equation} {\partial a_k^s \over \partial t} = {\rm i} \epsilon \int_{\mathbb{R}^6} \sum_{s_p s_q} \left(\frac{1 + 2 \sin^2 \theta_k}{8 \sin \theta_k}\right) k s_p s_q a_p^{s_p} a_q^{s_q} \exp({{\rm i}\varOmega_{k,pq} t}) \delta_{{\boldsymbol{k}},{\boldsymbol{p}}{\boldsymbol{q}}} \,\mathrm{d} {\boldsymbol{p}} \,\mathrm{d} {\boldsymbol{q}} . \end{equation}

The presence of $\sin \theta _k$ in the denominator cannot lead to a divergence because by definition the canonical variable is null for $\theta _k = 0$. Note that in the small $\beta$ limit, the displacement vectors of the fast waves are almost transverse to ${\boldsymbol {e}_\parallel }$, which is the opposite limit $\theta _k \simeq {\rm \pi}/2$ (Galtier Reference Galtier2016). Equation (3.15) is the fundamental equation of our problem and its form is classical for three-wave interactions. As expected, we see that the nonlinear terms are of order $\epsilon$. This means that weak nonlinearities will only change the amplitude of the F waves slowly over time. The nonlinearities contain an exponentially oscillating term that is essential for the asymptotic closure. Indeed, the theory of wave turbulence deals with variations of spectral densities at very large times, i.e. for a nonlinear transfer time much larger than the F-wave period: in other words, we have a time scale separation between the fast oscillations of the waves (due to the phase variations in the exponential) and the slow variations of the wave amplitudes. As a consequence, most of the nonlinear terms are destroyed and only a few of them, the resonance terms, for which $\varOmega _{k,pq} =0$, survive (Benney & Saffman Reference Benney and Saffman1966; Benney Reference Benney1967; Benney & Newell Reference Benney and Newell1967). From (3.15), we finally see that, contrary to incompressible MHD, there are no exact solutions to the nonlinear problem. The origin of such a difference is that in incompressible MHD the nonlinear term implies Alfvén waves moving only in opposite directions (Galtier et al. Reference Galtier, Nazarenko, Newell and Pouquet2000) whereas in purely compressible MHD this constraint does not exist (we have a summation over $s_p$ and $s_q$). In other words, if one type of wave is not present in incompressible MHD then the nonlinear term cancels out whereas in the present problem this is not the case.

Note that it is legitimate to wonder whether a derivation based on the other variables ($\hat {\rho }_k, \hat {\xi }_k$) could lead to another expression that would invalidate our initial choice of canonical variables. A similar calculation based on the equations (2.15)–(2.16) including the nonlinear terms leads to the same expression as (3.15), thus proving the consistency of the present derivation. Hereafter, we shall introduce the following variable $c_k^s \equiv a_k^s /\sqrt {\omega _k}$ (linked to the action) that will facilitate the derivation of the kinetic equations. We obtain

(3.16)\begin{equation} {\partial c_k^s \over \partial t} = {\rm i} \epsilon \int_{\mathbb{R}^6} \sum_{s_p s_q} L_{{-}kpq}^{{-}ss_ps_q} c_p^{s_p} c_q^{s_q} \exp({{\rm i}\varOmega_{k,pq} t}) \delta_{{\boldsymbol{k}},{\boldsymbol{p}}{\boldsymbol{q}}} \,\mathrm{d} {\boldsymbol{p}} \,\mathrm{d} {\boldsymbol{q}} , \end{equation}

where the interaction coefficient

(3.17)\begin{equation} L_{kpq}^{ss_ps_q} \equiv \sqrt{b_0} \left(\frac{1 + 2 \sin^2 \theta_k}{8 \sin \theta_k}\right) s_p s_q \sqrt{kpq} , \end{equation}

satisfies the following symmetries:

(3.18)\begin{gather} L_{kpq}^{ss_{p}s_{q}} = L_{kqp}^{ss_{q}s_{p}} , \end{gather}
(3.19)\begin{gather}L_{0pq}^{ss_{p}s_{q}} = 0 , \end{gather}
(3.20)\begin{gather}L_{{-}k-p-q}^{ss_{p}s_{q}} = L_{kpq}^{ss_{p}s_{q}} , \end{gather}
(3.21)\begin{gather}L_{kpq}^{{-}s-s_{p}-s_{q}} = L_{kpq}^{ss_{p}s_{q}} , \end{gather}
(3.22)\begin{gather}ss_{q} L_{qpk}^{s_{q}s_{p}s} = L_{kpq}^{ss_{p}s_{q}} , \end{gather}
(3.23)\begin{gather}ss_{p} L_{pkq}^{s_{p}ss_{q}} = L_{kpq}^{ss_{p}s_{q}} . \end{gather}

4. Derivation of the kinetic equations

We now move on to a statistical description. We use the ensemble average $\langle \rangle$ and define the following spectral correlators (cumulants) for homogeneous turbulence (we will also assume $\langle c^s_k \rangle =0$):

(4.1)\begin{gather} \langle c^s_k c^{s'}_{k'} \rangle = q^{ss'}_{kk'}({\boldsymbol{k}},{\boldsymbol{k}}') \delta({\boldsymbol{k}}+{\boldsymbol{k}}') , \end{gather}
(4.2)\begin{gather} \langle c^s_k c^{s'}_{k'} c^{s''}_{k''} \rangle = q^{ss's''}_{kk'k''}({\boldsymbol{k}},{\boldsymbol{k}}',{\boldsymbol{k}}'') \delta({\boldsymbol{k}}+{\boldsymbol{k}}'+{\boldsymbol{k}}'') , \end{gather}
(4.3)\begin{align} \langle c^s_k c^{s'}_{k'} c^{s''}_{k''} c^{s'''}_{k'''} \rangle & = q^{ss's''s'''}_{kk'k''k'''}({\boldsymbol{k}},{\boldsymbol{k}}',{\boldsymbol{k}}'',{\boldsymbol{k}}''') \delta({\boldsymbol{k}}+{\boldsymbol{k}}'+{\boldsymbol{k}}''+{\boldsymbol{k}}''') \nonumber\\ & \quad + q^{ss'}_{kk'}({\boldsymbol{k}},{\boldsymbol{k}}') q^{s''s'''}_{k''k'''}({\boldsymbol{k}}'',{\boldsymbol{k}}''') \delta({\boldsymbol{k}}+{\boldsymbol{k}}') \delta({\boldsymbol{k}}''+{\boldsymbol{k}}''') \nonumber\\ & \quad + q^{ss''}_{kk''}({\boldsymbol{k}},{\boldsymbol{k}}'') q^{s's'''}_{k'k'''}({\boldsymbol{k}}',{\boldsymbol{k}}''') \delta({\boldsymbol{k}}+{\boldsymbol{k}}'') \delta({\boldsymbol{k}}'+{\boldsymbol{k}}''') \nonumber\\ & \quad + q^{ss'''}_{kk'''}({\boldsymbol{k}},{\boldsymbol{k}}''') q^{s's''}_{k'k''}({\boldsymbol{k}}',{\boldsymbol{k}}'') \delta({\boldsymbol{k}}+{\boldsymbol{k}}''') \delta({\boldsymbol{k}}'+{\boldsymbol{k}}'') . \end{align}

From the fundamental equation (3.16), we get

(4.4)\begin{align} \frac{\partial \langle c^s_k c^{s'}_{k'} \rangle}{\partial t} & = \left\langle \frac{\partial c^s_k}{\partial t} c^{s'}_{k'} \right\rangle + \left\langle c^s_k \frac{\partial c^{s'}_{k'}}{\partial t} \right\rangle \nonumber\\ & = {\rm i} \epsilon \int_{{\mathbb{R}}^{6}} \sum_{s_{p} s_{q}} L_{{-}kpq}^{{-}ss_{p}s_{q}} \langle c^{s'}_{k'} c^{s_{p}}_{p} c^{s_{q}}_{q} \rangle \exp({{\rm i} \varOmega_{k,pq} t}) \delta_{k,pq} \,\mathrm{d} {\boldsymbol{p}}\, \mathrm{d} {\boldsymbol{q}} \nonumber\\ & \quad + {\rm i} \epsilon \int_{{\mathbb{R}}^{6}} \sum_{s_{p} s_{q}} L_{{-}k'pq}^{{-}s's_{p}s_{q}} \langle c^s_k c^{s_{p}}_{p} c^{s_{q}}_{q} \rangle \exp({{\rm i}\varOmega_{k',pq} t}) \delta_{k',pq} \,\mathrm{d} {\boldsymbol{p}}\, \mathrm{d} {\boldsymbol{q}} . \end{align}

At the next order we have

(4.5)\begin{align} \frac{\partial \langle c^s_k c^{s'}_{k'} c^{s''}_{k''} \rangle}{\partial t} & = \left\langle \frac{\partial c^s_k}{\partial t} c^{s'}_{k'} c^{s''}_{k''} \right\rangle + \left\langle c^s_k \frac{\partial c^{s'}_{k'}}{\partial t} c^{s''}_{k''} \right\rangle + \left\langle c^s_k c^{s'}_{k'} \frac{\partial c^{s''}_{k''}}{\partial t} \right\rangle \nonumber\\ & = {\rm i} \epsilon \int_{{\mathbb{R}}^{6}} \sum_{s_{p} s_{q}} L_{{-}kpq}^{{-}ss_{p}s_{q}} \langle c^{s'}_{k'} c^{s''}_{k''} c^{s_{p}}_{p} c^{s_{q}}_{q} \rangle \exp({{\rm i} \varOmega_{k,pq} t}) \delta_{k,pq} \,\mathrm{d} {\boldsymbol{p}} \,\mathrm{d} {\boldsymbol{q}} \nonumber\\ & \quad + {\rm i} \epsilon \int_{{\mathbb{R}}^{6}} \sum_{s_{p} s_{q}} L_{{-}k'pq}^{{-}s's_{p}s_{q}} \langle c^s_k c^{s''}_{k''} c^{s_{p}}_{p} c^{s_{q}}_{q} \rangle \exp({{\rm i} \varOmega_{k',pq} t}) \delta_{k',pq} \,\mathrm{d} {\boldsymbol{p}} \,\mathrm{d} {\boldsymbol{q}} \nonumber\\ & \quad + {\rm i} \epsilon \int_{{\mathbb{R}}^{6}} \sum_{s_{p} s_{q}} L_{{-}k''pq}^{{-}s''s_{p}s_{q}} \langle c^s_k c^{s'}_{k'} c^{s_{p}}_{p} c^{s_{q}}_{q} \rangle \exp({{\rm i} \varOmega_{k'',pq} t}) \delta_{k'',pq} \,\mathrm{d} {\boldsymbol{p}} \,\mathrm{d} {\boldsymbol{q}} . \end{align}

Here, we face the classic problem of closure: a hierarchy of statistical equations of increasingly higher order emerges (see discussion in § 1.3). In contrast to the strong turbulence regime, in the weak wave turbulence regime we can use the scale separation in time to achieve a natural closure of the system (Benney & Saffman Reference Benney and Saffman1966). Expressions (4.1)–(4.3) are introduced into (4.5)

(4.6)\begin{align} & \frac{\partial q^{ss's''}_{kk'k''}({\boldsymbol{k}},{\boldsymbol{k}}',{\boldsymbol{k}}'')}{\partial t} \delta({\boldsymbol{k}}+{\boldsymbol{k}}'+{\boldsymbol{k}}'') \nonumber\\ & \quad = {\rm i} \epsilon \int_{{\mathbb{R}}^{6}} \sum_{s_{p} s_{q}} L_{{-}kpq}^{{-}ss_{p}s_{q}} \left[ q^{s's''s_{s_{p}}s_{s_{q}}}_{k'k''pq}({\boldsymbol{k}}',{\boldsymbol{k}}'',{\boldsymbol{p}},{\boldsymbol{q}}) \delta({\boldsymbol{k}}'+{\boldsymbol{k}}''+{\boldsymbol{p}}+{\boldsymbol{q}}) \right. \nonumber\\ & \qquad + q^{s's''}_{k'k''}({\boldsymbol{k}}',{\boldsymbol{k}}'') q^{s_{p}s_{q}}_{pq}({\boldsymbol{p}},{\boldsymbol{q}}) \delta({\boldsymbol{k}}'+{\boldsymbol{k}}'') \delta({\boldsymbol{p}}+{\boldsymbol{q}}) \nonumber\\ & \qquad + q^{s's_{p}}_{k'p}({\boldsymbol{k}}',{\boldsymbol{p}}) q^{s''s_{q}}_{k''q}({\boldsymbol{k}}'',{\boldsymbol{q}}) \delta({\boldsymbol{k}}'+{\boldsymbol{p}}) \delta({\boldsymbol{k}}''+{\boldsymbol{q}}) \nonumber\\ & \qquad \left. +\, q^{s's_{q}}_{k'q}({\boldsymbol{k}}',{\boldsymbol{q}}) q^{s''s_{p}}_{k''p}({\boldsymbol{k}}'',{\boldsymbol{p}}) \delta({\boldsymbol{k}}'+{\boldsymbol{q}}) \delta({\boldsymbol{k}}''+{\boldsymbol{p}}) \right] \exp({{\rm i} \varOmega_{k,pq} t}) \delta_{k,pq} \,\mathrm{d} {\boldsymbol{p}} \,\mathrm{d} {\boldsymbol{q}} \nonumber\\ & \qquad + {\rm i} \epsilon \int_{{\mathbb{R}}^{6}} \left\{ ({\boldsymbol{k}},s) \leftrightarrow ({\boldsymbol{k}}',s') \right\} \mathrm{d} {\boldsymbol{p}} \,\mathrm{d} {\boldsymbol{q}} \nonumber\\ & \qquad + {\rm i} \epsilon \int_{{\mathbb{R}}^{6}} \left\{ ({\boldsymbol{k}},s) \leftrightarrow ({\boldsymbol{k}}'',s'') \right\} \mathrm{d} {\boldsymbol{p}} \, \mathrm{d} {\boldsymbol{q}} , \end{align}

where the last two lines correspond to the exchange at the notation level between ${\boldsymbol {k}}$, $s$ in the expanded expression and ${\boldsymbol {k}}'$, $s'$ (penultimate line), then ${\boldsymbol {k}}''$, $s''$ (last line).

We are now going to integrate expression (4.6) both on ${\boldsymbol {p}}$ and ${\boldsymbol {q}}$, and on time, by considering a long integrated time compared with the reference time (the F-wave period). The presence of several Dirac functions leads to the conclusion that the second term on the right (in the main expression) makes no contribution since it corresponds to $k=0$ for which the interaction coefficient is null. It is a property of statistical homogeneity. The last two terms on the right (always in the main expression) lead to a strong constraint on wavevectors ${\boldsymbol {p}}$ and ${\boldsymbol {q}}$ which must be equal to $-{\boldsymbol {k}}'$ or $-{\boldsymbol {k}}''$. For the fourth-order cumulant, the constraint is much less strong since only the sum of ${\boldsymbol {p}}$ and ${\boldsymbol {q}}$ is imposed. A consequence (of the multiple scale analysis) is that for long times this term will not contribute (at this order) to the nonlinear dynamics (Galtier Reference Galtier2023). Finally, for long times the second-order cumulants are only relevant when the associated polarities have different signs. In order to understand this, it is necessary to go back to the definition of the moment, $\langle A^s_k A^{s'}_{k'} \rangle = \epsilon ^{2} \langle a_k^s a_{k'}^{s'} \rangle \exp (-{\rm i}(s\omega _{k}+s'\omega _{k'})t)$, from which we see that in the limit of large time a non-zero contribution is possible for homogeneous turbulence (${\boldsymbol {k}}=-{\boldsymbol {k}}'$) only if $s=-s'$ (then the coefficient of the exponential is cancelled). We finally get

(4.7)\begin{align} & q^{ss's''}_{kk'k''}({\boldsymbol{k}},{\boldsymbol{k}}',{\boldsymbol{k}}'') \delta({\boldsymbol{k}}+{\boldsymbol{k}}'+{\boldsymbol{k}}'') \nonumber\\ & \quad = {\rm i} \epsilon \varDelta(\varOmega_{kk'k''}) \delta({\boldsymbol{k}}+{\boldsymbol{k}}'+{\boldsymbol{k}}'') \left\{ \left[ L_{{-}k-k'-k''}^{{-}s-s'-s''} + L_{{-}k-k''-k'}^{{-}s-s''-s'} \right] q^{s''-s''}_{k''-k''}({\boldsymbol{k}}'',-{\boldsymbol{k}}'') q^{s'-s'}_{k'-k'}({\boldsymbol{k}}',-{\boldsymbol{k}}') \right. \nonumber\\ & \qquad +\left[ L_{{-}k'-k-k''}^{{-}s'-s-s''} + L_{{-}k'-k''-k}^{{-}s'-s''-s} \right] q^{s''-s''}_{k''-k''}({\boldsymbol{k}}'',-{\boldsymbol{k}}'') q^{s-s}_{k-k}({\boldsymbol{k}},-{\boldsymbol{k}}) \nonumber\\ & \qquad \left. + \left[ L_{{-}k''-k'-k}^{{-}s''-s'-s} + L_{{-}k''-k-k'}^{{-}s''-s-s'} \right] q^{s-s}_{k-k}({\boldsymbol{k}},-{\boldsymbol{k}}) q^{s'-s'}_{k'-k'}({\boldsymbol{k}}',-{\boldsymbol{k}}') \right\} , \end{align}

with

(4.8)\begin{equation} \varDelta(\varOmega_{kk'k''}) = \int_0^{t\gg1/\omega} \exp({{\rm i} \varOmega_{kk'k''}t^\prime}) \,{\rm d}t^\prime = {\exp({{\rm i} \varOmega_{kk'k''}t}) - 1 \over {\rm i} \varOmega_{kk'k''} } . \end{equation}

We can now write without ambiguity: $q^{s-s}_{k-k}({\boldsymbol {k}},-{\boldsymbol {k}}) = q^s_k({\boldsymbol {k}})$. Using the symmetry relations of the interaction coefficient, we obtain

(4.9)\begin{align} q^{ss's''}_{kk'k''}({\boldsymbol{k}},{\boldsymbol{k}}',{\boldsymbol{k}}'') \delta({\boldsymbol{k}}+{\boldsymbol{k}}'+{\boldsymbol{k}}'') & ={-} 2 {\rm i} \epsilon \varDelta(\varOmega_{kk'k''}) \delta({\boldsymbol{k}}+{\boldsymbol{k}}'+{\boldsymbol{k}}'') \left[ L_{kk'k''}^{ss's''} q^{s''}_{k''}({\boldsymbol{k}}'') q^{s'}_{k'}({\boldsymbol{k}}') \right.\nonumber\\ & \quad \left.+\, L_{k'kk''}^{s'ss''} q^{s''}_{k''}({\boldsymbol{k}}'') q^{s}_{k}({\boldsymbol{k}}) + L_{k''k'k}^{s''s's} q^{s}_{k}({\boldsymbol{k}}) q^{s'}_{k'}({\boldsymbol{k}}') \right] , \end{align}

and then

(4.10)\begin{align} q^{ss's''}_{kk'k''}({\boldsymbol{k}},{\boldsymbol{k}}',{\boldsymbol{k}}'') \delta({\boldsymbol{k}}+{\boldsymbol{k}}'+{\boldsymbol{k}}'') & ={-} 2 {\rm i} \epsilon \varDelta(\varOmega_{kk'k''}) \delta({\boldsymbol{k}}+{\boldsymbol{k}}'+{\boldsymbol{k}}'') L_{kk'k''}^{ss's''} \left[ q^{s''}_{k''}({\boldsymbol{k}}'') q^{s'}_{k'}({\boldsymbol{k}}') \right.\nonumber\\ & \quad \left. +\, ss' q^{s''}_{k''}({\boldsymbol{k}}'') q^{s}_{k}({\boldsymbol{k}}) + ss'' q^{s}_{k}({\boldsymbol{k}}) q^{s'}_{k'}({\boldsymbol{k}}') \right] . \end{align}

The effective long time limit (which introduces irreversibility) gives us (Riemann–Lebesgue's lemma)

(4.11)\begin{equation} \varDelta(x) \to {\rm \pi}\delta(x) + {\rm i} {\mathcal{P}} (1/x) , \end{equation}

with ${\mathcal {P}}$ the principal value integral.

The so-called kinetic equation is obtained by injecting expression (4.10) in the long time limit, into (4.4) and integrating on ${\boldsymbol {k}}'$ (with the relation $q^{-s}_{-k}(-{\boldsymbol {k}})=q^{s}_{k}({\boldsymbol {k}})$)

(4.12)\begin{align} \frac{\partial q^{s}_{k}({\boldsymbol{k}})}{\partial t} & = 2 \epsilon^{2} \int_{{\mathbb{R}}^{6}} \sum_{s_{p} s_{q}} \vert L_{{-}kpq}^{{-}ss_{p}s_{q}} \vert^2 ({\rm \pi} \delta(\varOmega_{{-}kpq}) + i {\mathcal{P}} (1/\varOmega_{{-}kpq})) \exp({{\rm i}\varOmega_{k,pq} t}) \delta_{k,pq} \nonumber\\ & \quad\times s_{p}s_{q} \left[ s_{p}s_{q} q^{s_{q}}_{q}({\boldsymbol{q}}) q^{s_{p}}_{p}({\boldsymbol{p}}) - ss_{q} q^{s_{q}}_{q}({\boldsymbol{q}}) q^{s}_{k}({\boldsymbol{k}})- ss_{p} q^{s}_{k}({\boldsymbol{k}}) q^{s_{p}}_{p}({\boldsymbol{p}}) \right] \mathrm{d} {\boldsymbol{p}} \,\mathrm{d} {\boldsymbol{q}} \nonumber\\ & \quad + 2 \epsilon^{2} \int_{{\mathbb{R}}^{6}} \sum_{s_{p} s_{q}} \vert L_{kpq}^{ss_{p}s_{q}} \vert^2 ({\rm \pi} \delta(\varOmega_{kpq}) + {\rm i} {\mathcal{P}} (1/\varOmega_{kpq})) \exp({{\rm i}\varOmega_{kpq} t}) \delta_{kpq} \nonumber\\ & \quad\times s_{p}s_{q} \left[ s_{p}s_{q} q^{s_{q}}_{q}({\boldsymbol{q}}) q^{s_{p}}_{p}({\boldsymbol{p}}) + ss_{q} q^{s_{q}}_{q}({\boldsymbol{q}}) q^{s}_{k}({\boldsymbol{k}}) + ss_{p} q^{s}_{k}({\boldsymbol{k}}) q^{s_{p}}_{p}({\boldsymbol{p}}) \right] \mathrm{d} {\boldsymbol{p}} \,\mathrm{d} {\boldsymbol{q}} . \end{align}

By changing the sign of the (dummy) variables ${\boldsymbol {p}}$ and ${\boldsymbol {q}}$ of integration, and the associated polarities, the principal values are eliminated. Using the symmetries of the interaction coefficient, we finally arrive at the following expression after simplification:

(4.13)\begin{align} \frac{\partial q^{s}_{k}({\boldsymbol{k}})}{\partial t} & = \frac{{\rm \pi} \epsilon^{2} b_0}{16} \int_{{\mathbb{R}}^{6}} \sum_{s_{p} s_{q}} \left(\frac{1 + 2 \sin^2 \theta_k}{\sin \theta_k}\right)^2 kpq \delta(\varOmega_{kpq}) \delta({\boldsymbol{k}}+{\boldsymbol{p}}+{\boldsymbol{q}}) \nonumber\\ & \quad \times s_{p}s_{q} \left[ s_{p}s_{q} q^{s_{q}}_{q}({\boldsymbol{q}}) q^{s_{p}}_{p}({\boldsymbol{p}}) + ss_{q} q^{s_{q}}_{q}({\boldsymbol{q}}) q^{s}_{k}({\boldsymbol{k}}) + ss_{p} q^{s}_{k}({\boldsymbol{k}}) q^{s_{p}}_{p}({\boldsymbol{p}}) \right] \mathrm{d} {\boldsymbol{p}} \,\mathrm{d} {\boldsymbol{q}} . \end{align}

Expression (4.13) is the kinetic equation of fast magneto-acoustic wave turbulence. The presence of the small parameter $\epsilon \ll 1$ means that the amplitude of the quadratic nonlinearities is weak and that, consequently, the characteristic time over which we place ourselves to measure these effects is of the order of $1/\epsilon ^2$ (the reference time being the wave period $1/\omega$).

5. Properties of F-wave turbulence

5.1. Detailed conservation

A remarkable property verified by the kinetic equation (4.13) is the detailed conservation of the invariants (energy and momentum for three-wave interactions). To demonstrate this result, the kinetic equation must be rewritten for the polarized energy spectrum

(5.1)\begin{equation} e^s({\boldsymbol{k}}) \equiv \omega_{k} q^{s}_{k}({\boldsymbol{k}}) . \end{equation}

One notices in particular that, $e^s({\boldsymbol {k}})=e^{-s}(-{\boldsymbol {k}})$. After a few manipulations, we get

(5.2)\begin{align} \frac{\partial e^s({\boldsymbol{k}})}{\partial t} & = \frac{{\rm \pi} \epsilon^{2}}{16 b_0^2} \int_{{\mathbb{R}}^{6}} \sum_{s_{p} s_{q}} \left(\frac{1 + 2 \sin^2 \theta_k}{\sin \theta_k}\right)^2 \delta(\varOmega_{kpq}) \delta({\boldsymbol{k}}+{\boldsymbol{p}}+{\boldsymbol{q}}) \nonumber\\ & \quad\times s \omega_{k} \left[ \frac{s\omega_{k}}{e^s({\boldsymbol{k}})} + \frac{s_{p} \omega_{p}}{e^{s_{p}}({\boldsymbol{p}})} + \frac{s_{q} \omega_{q}}{e^{s_{q}}({\boldsymbol{q}})} \right] e^{s}({\boldsymbol{k}}) e^{s_{p}}({\boldsymbol{p}}) e^{s_{q}}({\boldsymbol{q}}) \,\mathrm{d} {\boldsymbol{p}} \,\mathrm{d} {\boldsymbol{q}} . \end{align}

By considering the integral in ${\boldsymbol {k}}$ of the total energy spectrum, $E({\boldsymbol {k}}) \equiv \sum _s e^s({\boldsymbol {k}})$, we find

(5.3)\begin{align} \frac{\partial \displaystyle\int\nolimits_{{\mathbb{R}}^{3}} E({\boldsymbol{k}}) \,{\rm d}{\boldsymbol{k}}}{\partial t} & = \frac{{\rm \pi} \epsilon^{2}}{16 b_0^2} \int_{{\mathbb{R}}^{9}} \sum_{s s_{p} s_{q}} \left(\frac{1 + 2 \sin^2 \theta_k}{\sin \theta_k}\right)^2 \delta(\varOmega_{kpq}) \delta({\boldsymbol{k}}+{\boldsymbol{p}}+{\boldsymbol{q}}) (s \omega_k +s_p \omega_p +s_q \omega_q) \nonumber\\ & \quad\times\left[ \frac{s\omega_{k}}{e^s({\boldsymbol{k}})} + \frac{s_{p} \omega_{p}}{e^{s_{p}}({\boldsymbol{p}})} + \frac{s_{q} \omega_{q}}{e^{s_{q}}({\boldsymbol{q}})} \right] e^{s}({\boldsymbol{k}}) e^{s_{p}}({\boldsymbol{p}}) e^{s_{q}}({\boldsymbol{q}}) \,\mathrm{d} {\boldsymbol{k}} \,\mathrm{d} {\boldsymbol{p}} \,\mathrm{d} {\boldsymbol{q}} = 0 . \end{align}

This means that energy is conserved by triadic interaction: the redistribution of energy takes place within a triad satisfying the resonance condition.

The second invariant is the momentum also called cross-helicity in MHD (see § 2.3). The polarized cross-helicity spectrum is defined as

(5.4)\begin{equation} h^s({\boldsymbol{k}}) \equiv \frac{k_{{\parallel}}}{k} e^s({\boldsymbol{k}}) . \end{equation}

After a few manipulations, we find

(5.5)\begin{align} \frac{\partial h^s({\boldsymbol{k}})}{\partial t} & = \frac{{\rm \pi} \epsilon^2}{16} \int_{{\mathbb{R}}^{6}} \sum_{s_{p} s_{q}} \left(\frac{1 + 2 \sin^2 \theta_k}{\sin \theta_k}\right)^2 \delta(\varOmega_{kpq}) \delta({\boldsymbol{k}}+{\boldsymbol{p}}+{\boldsymbol{q}}) \nonumber\\ & \quad \times\frac{kpq}{k_{\parallel} p_{{\parallel}}q_{{\parallel}}} s k_{{\parallel}} \left[ \frac{sk_{{\parallel}}}{h^s({\boldsymbol{k}})} + \frac{s_{p} p_{{\parallel}}}{h^{s_{p}}({\boldsymbol{p}})} + \frac{s_{q} q_{{\parallel}}}{h^{s_{q}}({\boldsymbol{q}})} \right] h^{s}({\boldsymbol{k}}) h^{s_{p}}({\boldsymbol{p}}) h^{s_{q}}({\boldsymbol{q}}) \,\mathrm{d} {\boldsymbol{p}} \,\mathrm{d} {\boldsymbol{q}} . \end{align}

By introducing the total cross-helicity spectrum $H({\boldsymbol {k}}) \equiv \sum _s s h^s({\boldsymbol {k}})$, we obtain

(5.6)\begin{align} \frac{\partial \displaystyle\int\nolimits_{{\mathbb{R}}^{3}} H({\boldsymbol{k}}) \,{\rm d}{\boldsymbol{k}}}{\partial t} & = \frac{{\rm \pi} \epsilon^{2}}{16} \int_{{\mathbb{R}}^{9}} \sum_{s s_{p} s_{q}} \left(\frac{1 + 2 \sin^2 \theta_k}{\sin \theta_k}\right)^2\delta(\varOmega_{kpq}) \delta({\boldsymbol{k}}+{\boldsymbol{p}}+{\boldsymbol{q}}) \frac{kpq}{k_{\parallel} p_{{\parallel}}q_{{\parallel}}} (k_{{\parallel}}+p_{{\parallel}}+q_{{\parallel}}) \nonumber\\ & \quad \times\left[ \frac{sk_{{\parallel}}}{h^s({\boldsymbol{k}})} + \frac{s_{p} p_{{\parallel}}}{h^{s_{p}}({\boldsymbol{p}})} + \frac{s_{q} q_{{\parallel}}}{h^{s_{q}}({\boldsymbol{q}})} \right] h^{s}({\boldsymbol{k}}) h^{s_{p}}({\boldsymbol{p}}) h^{s_{q}}({\boldsymbol{q}}) \,\mathrm{d} {\boldsymbol{k}} \,\mathrm{d} {\boldsymbol{p}} \,\mathrm{d} {\boldsymbol{q}} = 0 . \end{align}

This means that cross-helicity is conserved by triadic interaction and its redistribution takes place within a triad satisfying the resonance condition.

5.2. Angular anisotropic spectra

For discussion purposes, it is best to rewrite the kinetic equation for energy as follows:

(5.7)\begin{align} \frac{\partial e^s({\boldsymbol{k}})}{\partial t} & = \left(\frac{1 + 2 \sin^2 \theta_k}{\sin \theta_k}\right)^2 \frac{{\rm \pi} \epsilon^{2}}{16} \int_{{\mathbb{R}}^{6}} \sum_{s_{p} s_{q}} \delta(\varOmega_{kpq}) \delta({\boldsymbol{k}}+{\boldsymbol{p}}+{\boldsymbol{q}}) \nonumber\\ & \quad \times s k \left[ sk e^{s_p}({\boldsymbol{p}}) e^{s_q}({\boldsymbol{q}}) + s_p p e^s({\boldsymbol{k}}) e^{s_q}({\boldsymbol{q}}) + s_q q e^s({\boldsymbol{k}}) e^{s_p}({\boldsymbol{p}}) \right] \mathrm{d} {\boldsymbol{p}} \,\mathrm{d} {\boldsymbol{q}} , \end{align}

where the dependence in $\theta _k$ has been placed outside the integral since it depends only on ${\boldsymbol {k}}$. Before deriving the exact power-law solutions of the kinetic equation, we will use a property deduced from the resonant condition. We know (and have already used) that the wavevectors are aligned, which means that the energy cascade develops along rays and thus each spectrum within the integral has the same angular dependence. However, the coefficient in front of the integral depends on $\theta _k$: in particular, the smaller $\theta _k$ is, the larger the coefficient is, and therefore the smaller the transfer time is. This property is compatible with the phenomenology introduced in § 1.4: the cascade tends to be stronger along the parallel direction. Note that, for acoustic wave turbulence, there is no such angular dependence, so the problem is more isotropic than in MHD (Zakharov & Sagdeev Reference Zakharov and Sagdeev1970).

From the previous remark, we introduce the reduced spectrum

(5.8)\begin{equation} k^2 e^s({\boldsymbol{k}})= k^2 e^s(k,\theta_k,\phi_k) = f(\theta_k,\phi_k) E^s(k) = f(\theta_k,\phi_k) E^s_k . \end{equation}

The function $f(\theta _k,\phi _k) \geqslant 0$ depends on the initial condition: once given, it will not change by the turbulence cascade because there is no redistribution of energy in $\theta _k$ or $\phi _k$. This leads to

(5.9)\begin{align} \frac{\partial E^s_k}{\partial t} & = \left(\frac{1 + 2 \sin^2 \theta_k}{\sin \theta_k}\right)^2 f(\theta_k,\phi_k) \frac{{\rm \pi} \epsilon^{2}}{16} \int_{{\mathbb{R}}^{6}} \sum_{s_{p} s_{q}} \delta(\varOmega_{kpq}) \delta({\boldsymbol{k}}+{\boldsymbol{p}}+{\boldsymbol{q}}) \nonumber\\ & \quad\times \frac{s k}{p^2q^2} \left[ sk^3 E^{s_p}_p E^{s_q}_q + s_p p^3 E^s_k E^{s_q}_q + s_q q^3 E^s_k E^{s_p}_p \right] \mathrm{d} {\boldsymbol{p}} \,\mathrm{d} {\boldsymbol{q}} . \end{align}

Since there is no angular dependence in the integral except for the delta function, we can perform angular averaging and use the following relationship (Zakharov, L'Vov & Falkovich Reference Zakharov, L'Vov and Falkovich1992):

(5.10)\begin{equation} \langle \delta({\boldsymbol{k}}+{\boldsymbol{p}}+{\boldsymbol{q}}) \rangle_{\rm angle} = \int_{{\mathbb{R}}^{4}} \delta({\boldsymbol{k}}+{\boldsymbol{p}}+{\boldsymbol{q}}) \,\mathrm{d} \cos \theta_p \,\mathrm{d} \cos \theta_q \,\mathrm{d} \phi_p \,\mathrm{d} \phi_q = \frac{1}{2kpq} . \end{equation}

We obtain

(5.11)\begin{equation} \frac{\partial E^s_k}{\partial t} = \frac{{\rm \pi} \epsilon^{2} K_{\theta,\phi}}{32b_0} \int_{\varDelta_\perp} \sum_{s_{p} s_{q}} \delta(sk+s_pp+s_qq)\frac{s}{pq} \left[ sk^3 E^{s_p}_p E^{s_q}_q + s_p p^3 E^s_k E^{s_q}_q + s_q q^3 E^s_k E^{s_p}_p \right] \mathrm{d} p \,\mathrm{d} q , \end{equation}

with $\varDelta _\perp$ the integration domain (infinitely long band) and by definition

(5.12)\begin{equation} K_{\theta,\phi} = \left(\frac{1 + 2 \sin^2 \theta_k}{\sin \theta_k}\right)^2 f(\theta_k,\phi_k) . \end{equation}

We recall that, by construction, the canonical variables (2.20) cancel for $\theta _k=0$ (as does the spectrum), so we will not consider this limit in the following. The exact solutions can now be derived using the Zakharov transform. It will provide power-law spectra at given angles $(\theta _k, \phi _k)$. Therefore, this problem is anisotropic but of a very special type because it does not imply different power laws in parallel and perpendicular directions as is usually found in plasma physics (Galtier & Bhattacharjee Reference Galtier and Bhattacharjee2003; Galtier Reference Galtier2006,  Reference Galtier2014; Galtier & Meyrand Reference Galtier and Meyrand2015). An exception is the case of incompressible MHD (Galtier et al. Reference Galtier, Nazarenko, Newell and Pouquet2000) where no cascade is possible along the parallel direction (a function $f(k_{\parallel })$ is then introduced whose form depends on the initial condition). Note that a similar qualitative dependence in $\theta _k$ (but not in $\phi _k$) has been reported by Chandran (Reference Chandran2005) but, as explained in the introduction, the compressible MHD equations have been artificially modified to satisfy energy conservation with a constant mass density. Unlike Chandran (Reference Chandran2005), the mass density spectrum can be predicted here (see below).

From expression (5.11) we can deduce the kinetic equations for energy and momentum, which are respectively

(5.13)\begin{align} \frac{\partial E_k}{\partial t} & = \frac{{\rm \pi} \epsilon^{2} K_{\theta,\phi}}{128 b_0} \int_{\varDelta_\perp} \sum_{ss_{p} s_{q}} \delta(sk+s_pp+s_qq)\frac{s}{pq} \left[ sk^3 \left( E_p E_q + H_p H_q / \cos^2 \theta_k \right) \right.\nonumber\\ & \quad \left. +\, s_p p^3 \left(E_k E_q + H_k H_q/ \cos^2 \theta_k \right) + s_q q^3 \left(E_k E_p + H_k H_p/ \cos^2 \theta_k \right) \right] \mathrm{d} p \,\mathrm{d} q , \end{align}

and

(5.14)\begin{align} \frac{\partial H_k}{\partial t} & = \frac{{\rm \pi} \epsilon^{2} K_{\theta,\phi}}{128 b_0} \int_{\varDelta_\perp} \sum_{ss_{p} s_{q}} \delta(sk+s_pp+s_qq)\frac{1}{pq}\left[ k^3 \left( E_p H_q + E_q H_p \right) \right.\nonumber\\ & \quad \left. +\, p^3 \left(E_k H_q + E_q H_k \right) + q^3 \left(E_k H_p + E_p H_k \right) \right] \mathrm{d} p \,\mathrm{d} q , \end{align}

with (see § 2.3) $E_k \equiv E_k^+ + E_k^-$ and $H_k \equiv - (k_\parallel / k) (E_k^+ - E_k^-)$.

5.3. Kolmogorov–Zakharov spectra

In this section, we shall derive the exact power-law solutions of the kinetic equations (5.13)–(5.14). We introduce

(5.15a,b)\begin{equation} E_k \equiv C_E k^x \quad {\rm and} \quad H_k \equiv C_H k^y , \end{equation}

and the dimensionless wavenumbers $\tilde {p} \equiv p/k$ and $\tilde {q} \equiv q/k$; $C_E$ and $C_H$ are two constants such that $C_E \in {\mathbb {R}}^+$ and $C_H \in {\mathbb {R}}$, leading to

(5.16)\begin{align} \frac{\partial E_k}{\partial t} & = \frac{{\rm \pi} \epsilon^{2} K_{\theta,\phi}}{128 b_0} k^{2+2x} \int_{\varDelta_\perp} \sum_{ss_{p} s_{q}} \delta(s+s_p \tilde{p}+s_q \tilde{q})\frac{s}{\tilde{p} \tilde{q}} \left[ C_E^2 \left( s {\tilde{p}}^x {\tilde{q}}^x + s_p {\tilde{p}}^3 {\tilde{q}}^x + s_q {\tilde{p}}^x {\tilde{q}}^3 \right) \right. \nonumber\\ & \quad + \left. C_H^2 \left( s{\tilde{p}}^y {\tilde{q}}^y + s_p{\tilde{p}}^3 {\tilde{q}}^y + s_q{\tilde{p}}^y {\tilde{q}}^3 \right) k^{2y-2x} / \cos^2 \theta_k \right] \mathrm{d} {\tilde{p}} \,\mathrm{d} {\tilde{q}} , \end{align}

and

(5.17)\begin{align} \frac{\partial H_k}{\partial t} & = \frac{{\rm \pi} \epsilon^{2} K_{\theta,\phi}}{128 b_0} k^{x+y+2} C_E C_H \int_{\varDelta_\perp} \sum_{ss_{p} s_{q}} \delta(s+s_p \tilde{p}+s_q \tilde{q})\frac{1}{\tilde{p} \tilde{q}} \left[ {\tilde{p}}^x {\tilde{q}}^y + {\tilde{p}}^y {\tilde{q}}^x \right.\nonumber\\ & \quad \left. + {\tilde{p}}^3 {\tilde{q}}^y + {\tilde{p}}^3 {\tilde{q}}^x + {\tilde{p}}^y {\tilde{q}}^3 + {\tilde{p}}^x {\tilde{q}}^3 \right] \mathrm{d} \tilde{p} \,\mathrm{d} \tilde{q} . \end{align}

The Zakharov transform (Zakharov et al. Reference Zakharov, L'Vov and Falkovich1992) consists of splitting the kinetic equations into three parts and applying to two of them the following change of variables:

(5.18a,b)\begin{equation} \tilde{p} \to \frac{1}{\tilde{p}} , \quad \tilde{q} \to \frac{\tilde{q}}{\tilde{p}} , \end{equation}

and

(5.19a,b)\begin{equation} \tilde{p} \to \frac{\tilde{p}}{\tilde{q}} , \quad \tilde{q} \to \frac{1}{\tilde{q}} . \end{equation}

We obtain for the energy

(5.20)\begin{align} \frac{\partial E_k}{\partial t} & = \frac{{\rm \pi} \epsilon^{2} K_{\theta,\phi}}{384 b_0} k^{2+2x} \int_{\varDelta_\perp} \sum_{ss_{p} s_{q}} \delta(s+s_p \tilde{p}+s_q \tilde{q})\frac{1}{\tilde{p} \tilde{q}}\nonumber\\ & \quad \times\left\{ C_E^2 \left[ s \left( s {\tilde{p}}^x {\tilde{q}}^x + s_p {\tilde{p}}^3 {\tilde{q}}^x + s_q {\tilde{p}}^x {\tilde{q}}^3 \right) + s_p {\tilde{p}} \left( s_p {\tilde{p}}^{{-}2x} {\tilde{q}}^x + s {\tilde{p}}^{{-}3-x} {\tilde{q}}^x + s_q {\tilde{p}}^{{-}3-x} {\tilde{q}}^3 \right) \right. \right.\nonumber\\ & \quad \left. +\, s_q {\tilde{q}} \left( s_q {\tilde{p}}^{x} {\tilde{q}}^{{-}2x} + s_p {\tilde{p}}^3 {\tilde{q}}^{{-}3-x} + s {\tilde{p}}^x {\tilde{q}}^{{-}3-x} \right) \right]\nonumber\\ & \quad + \frac{k^{2y-2x} C_H^2}{\cos^2 \theta_k} \left[ s \left( s{\tilde{p}}^y {\tilde{q}}^y + s_p {\tilde{p}}^3 {\tilde{q}}^y + s_q {\tilde{p}}^y {\tilde{q}}^3 \right) + s_p {\tilde{p}} \left( s_p {\tilde{p}}^{{-}2y} {\tilde{q}}^y + s {\tilde{p}}^{{-}3-y} {\tilde{q}}^y + s_q {\tilde{p}}^{{-}3-y} {\tilde{q}}^3 \right) \right.\nonumber\\ & \quad + \left. \left. s_q {\tilde{q}} \left( s_q {\tilde{p}}^y {\tilde{q}}^{{-}2y} + s_p {\tilde{p}}^3 {\tilde{q}}^{{-}3-y} + s {\tilde{p}}^y {\tilde{q}}^{{-}3-y} \right) \right] \right\} \mathrm{d} {\tilde{p}} \,\mathrm{d} {\tilde{q}} , \end{align}

which can be written in a compact form as

(5.21)\begin{align} \frac{\partial E_k}{\partial t} & = \frac{{\rm \pi} \epsilon^{2} K_{\theta,\phi}}{384 b_0} k^{2+2x} \int_{\varDelta_\perp} \sum_{ss_{p} s_{q}} \delta(s+s_p \tilde{p}+s_q \tilde{q})\nonumber\\ & \quad \times\left[\vphantom{\left. + \frac{k^{2y-2x}C_H^2}{ \cos^2 \theta_k} {\tilde{p}}^{y-1} {\tilde{q}}^{y-1} \left( s+ s_p{\tilde{p}}^{{-}2y-2} + s_q{\tilde{q}}^{{-}2y-2} \right) \left(s+ s_p{\tilde{p}}^{3-y} + s_q{\tilde{q}}^{3-y} \right) \right]} C_E^2 {\tilde{p}}^{x-1} {\tilde{q}}^{x-1} \left(s+s_p {\tilde{p}}^{{-}2x-2} +s_q {\tilde{q}}^{{-}2x-2} \right) \left(s+s_p {\tilde{p}}^{3-x} +s_q {\tilde{q}}^{3-x} \right) \right.\nonumber\\ & \quad \left. +\, \frac{k^{2y-2x}C_H^2}{ \cos^2 \theta_k} {\tilde{p}}^{y-1} {\tilde{q}}^{y-1} \left( s+ s_p{\tilde{p}}^{{-}2y-2} + s_q{\tilde{q}}^{{-}2y-2} \right) \left(s+ s_p{\tilde{p}}^{3-y} + s_q{\tilde{q}}^{3-y} \right) \right] \mathrm{d} {\tilde{p}} \,\mathrm{d} {\tilde{q}} . \end{align}

We can find exact stationary solutions. First, we have $x=y=2$ as a spectrum with zero energy flux: this is the thermodynamic solution for which we have no cascade. The other (more interesting) solution corresponds to $x=y=-3/2$: it is the Kolmogorov-Zakharov spectrum for which the energy flux is finite. In the two cases, the helicity spectrum is associated with an energy flux; in other words, its dynamics is driven by the energy cascade.

The Zakharov transform applied to the momentum (cross-helicity) gives

(5.22)\begin{align} \frac{\partial H_k}{\partial t} & = \frac{{\rm \pi} \epsilon^{2} K_{\theta,\phi}}{384 b_0} k^{x+y+2} C_E C_H \int_{\varDelta_\perp} \sum_{ss_{p} s_{q}} \delta(s+s_p \tilde{p}+s_q \tilde{q})\frac{1}{\tilde{p} \tilde{q}}\nonumber\\ & \quad \times \left[ {\tilde{p}}^x {\tilde{q}}^y + {\tilde{p}}^y {\tilde{q}}^x + {\tilde{p}}^3 {\tilde{q}}^y +{\tilde{p}}^3 {\tilde{q}}^x + {\tilde{p}}^y {\tilde{q}}^3 + {\tilde{p}}^x {\tilde{q}}^3 \right.\nonumber\\ & \quad + \tilde{p} ({\tilde{p}}^{{-}x-y} {\tilde{q}}^y + {\tilde{p}}^{{-}x-y} {\tilde{q}}^x + {\tilde{p}}^{{-}3-y} {\tilde{q}}^y + {\tilde{p}}^{{-}3-x} {\tilde{q}}^x + {\tilde{p}}^{{-}3-y} {\tilde{q}}^3 + {\tilde{p}}^{{-}3-x} {\tilde{q}}^3)\nonumber\\ & \quad \left. +\, \tilde{q} ({\tilde{p}}^x {\tilde{q}}^{{-}x-y} + {\tilde{p}}^y {\tilde{q}}^{{-}x-y} + {\tilde{p}}^{3} {\tilde{q}}^{{-}3-y} + {\tilde{p}}^3 {\tilde{q}}^{{-}3-x} + {\tilde{p}}^y {\tilde{q}}^{{-}3-y} + {\tilde{p}}^x {\tilde{q}}^{{-}3-x}) \right] \mathrm{d} {\tilde{p}} \,\mathrm{d} {\tilde{q}} , \end{align}

which can be written in a compact form as

(5.23)\begin{align} \frac{\partial H_k}{\partial t} & = \frac{{\rm \pi} \epsilon^{2} K_{\theta,\phi}}{384 b_0} k^{x+y+2} C_E C_H \int_{\varDelta_\perp} \sum_{ss_{p} s_{q}} \delta(s+s_p \tilde{p}+s_q \tilde{q})\frac{1}{\tilde{p} \tilde{q}} \left( 1+ {\tilde{p}}^{{-}x-y-2} + {\tilde{q}}^{{-}x-y-2} \right) \nonumber\\ & \quad\times \left[ {\tilde{p}}^x {\tilde{q}}^y \left(1+ {\tilde{p}}^{3-x} + {\tilde{q}}^{3-y} \right) + {\tilde{p}}^y {\tilde{q}}^x \left(1+ {\tilde{p}}^{3-y} + {\tilde{q}}^{3-x} \right) \right] \mathrm{d} {\tilde{p}} \,\mathrm{d} {\tilde{q}} . \end{align}

We see that in this case no stationary solution is possible. The finite cross-helicity flux solution $x+y=-3$ (first line) gives the coefficient $1+ {\tilde {p}} + {\tilde {q}}$ that does cancel on the resonance manifold. For the thermodynamic solution, $x=y=2$, we arrive at the same conclusion.

In conclusion, the most relevant exact solution for fast magneto-acoustic wave turbulence is the one-dimensional Kolmogorov–Zakharov energy spectrum

(5.24)\begin{equation} E_k = C_E k^{{-}3/2} , \end{equation}

characterized by a finite energy flux. Interestingly, this is the well-known IK spectrum (Iroshnikov Reference Iroshnikov1964; Kraichnan Reference Kraichnan1965) proposed many years ago for incompressible MHD. This is also the exact solution for acoustic wave turbulence (Zakharov & Sagdeev Reference Zakharov and Sagdeev1970), however, a difference exists between the two problems because, unlike acoustic waves, here the spectrum depends on the angle $\theta _k$ between the wavevector and the direction of the applied magnetic field. As we will see, this anisotropy appears in the amplitude $C_E$ of the energy spectrum, with a modulation of its amplitude.

As explained above, the constant energy flux solutions lead also to a cross-helicity spectrum $H_k \sim k^{-3/2}$. Using the definition of the canonical variables (2.20) and relation (2.22), we find dimensionally

(5.25)\begin{equation} E^{\rho}_k \sim k^{{-}3/2} , \end{equation}

where $E^{\rho }_k$ is the one-dimensional spectrum of density fluctuations. Although a Kolmogorov-type spectrum in $k^{-5/3}$ is often found at 1 AU in the solar wind (Chen et al. Reference Chen, Sorriso-Valvo, Šafránková and Němeček2014), near the Sun this spectrum is slightly less steep (Moncuquet et al. Reference Moncuquet, Meyer-Vernet, Issautier, Pulupa, Bonnell, Bale, Dudok de Wit, Goetz, Griton and Harvey2020). This difference can be interpreted as an evolution of the turbulence regime, from weak to strong as the solar wind expands.

5.4. Locality condition

The Kolmogorov–Zakharov energy spectrum (5.24) found previously is an exact solution of the problem which is only relevant if it satisfies the locality condition. This condition consists in checking the convergence of the integrals in the case of strongly non-local interactions (it will be done in the case $C_H=0$). Physically, the convergence ensures that the solution is independent of the physics at large and small scales where forcing and dissipation are dominant. This calculation must be done before the application of the Zakharov transformation. Therefore, we consider the expression (hereafter, the small parameter $\epsilon$ is removed since it is a measure of the time scale)

(5.26)\begin{equation} \frac{\partial E_k}{\partial t} = \frac{{\rm \pi} K_{\theta,\phi} C_E^2 k^{2+2x}}{128 b_0} \sum_{ss_{p} s_{q}} \int_{\varDelta_\perp} \delta(s+s_p \tilde{p}+s_q \tilde{q})\frac{s}{\tilde{p} \tilde{q}} \left( s {\tilde{p}}^x {\tilde{q}}^x + s_p {\tilde{p}}^3 {\tilde{q}}^x + s_q {\tilde{p}}^x {\tilde{q}}^3 \right) \mathrm{d} {\tilde{p}} \,\mathrm{d} {\tilde{q}} , \end{equation}

that we integrate once; one finds

(5.27)\begin{equation} \frac{\partial E_k}{\partial t} = \frac{{\rm \pi} K_{\theta,\phi} C_E^2 k^{2+2x}}{32b_0} \sum_{ss_{p} s_{q}} I^{ss_ps_q}(x) , \end{equation}

with

(5.28)\begin{equation} I^{ss_ps_q}(x) = \frac{1}{4}\int_0^{+\infty} \left[ ({\tilde{p}}^{x-1} + s s_p{\tilde{p}}^2)({-}ss_q -s_ps_q \tilde{p})^{x-1} +ss_q {\tilde{p}}^{x-1} (s+s_p\tilde{p})^2 \right] \mathrm{d} {\tilde{p}} . \end{equation}

For a question of convergence, it is relevant to rewrite this sum of integrals as a single integral. First, we apply the following change of variables: $y=1/{\tilde {p}}$ for $I^{+-+}$, $y=1/ ({\tilde {p}}+1)$ for $I^{++-}$ and $y={\tilde {p}}$ for $I^{+--}$; we obtain ($s=s_p=s_q$ being not allowed)

(5.29)\begin{align} G(x) & = \sum_{ss_{p} s_{q}} I^{ss_ps_q}(x) \nonumber\\ & = {1 \over 2} \int_0^{1} \left[ (1-y)^{x-1} (y^{x-1}-y^2+2y^{{-}2x}-2y^{{-}x-3}) + (1-y)^2 (2y^{{-}3-x}-y^{x-1}) \right] \mathrm{d} y . \end{align}

Then, we split the integral in two parts ($\int _0^{1/2} + \int _{1/2}^{1}$) and get after modification of the second integral (with a change of variable $y \to 1-y$)

(5.30)\begin{align} G(x) & = \int_0^{1/2} \left[ (1-y)^{x-1} (y^{x-1}-y^2+y^{{-}2x}-y^{{-}x-3}) \right. \nonumber\\ & \quad \left. +\, (1-y)^2(y^{{-}3-x}-y^{x-1}) + y^{x-1} \left[(1-y)^{{-}2x}-(1-y)^{{-}x-3}\right] + y^2(1-y)^{{-}3-x} \right] \mathrm{d} y . \end{align}

The condition of convergence must be studied only when $y \to 0$. A detailed calculation leads to the following condition:

(5.31)\begin{equation} -2 < x <{-}1 , \end{equation}

which justifies the relevance of the Kolmogorov–Zakharov energy spectrum. As very often, the power-law index found for the constant flux solution is placed exactly in the middle of the convergence domain. The variation of $G(x)$ is shown in figure 2.

Figure 2. Variation of $G(x)$ for $x \in [-2,-1]$. A divergence of the integral is clearly observed close to $-2$ and $-1$. Inset: as expected, we see that the power-law index $x=-3/2$ (Kolmogorov–Zakharov spectrum) cancels the integral.

5.5. Direction of the cascade

The next analytical result of this paper is about the direction of the energy cascade. We can prove that this cascade is direct. We introduce the isotropic energy flux $\varPi _{k}$ such that

(5.32)\begin{equation} \frac{\partial E_k}{\partial t} ={-} \frac{\partial \varPi_k} {\partial k} = \frac{{\rm \pi} K_{\theta,\phi} C_E^2 k^{2+2x}}{32b_0} I(x) , \end{equation}

where

(5.33)\begin{align} I(x) & = \frac{1}{12} \int_{\varDelta_\perp} \sum_{ss_{p} s_{q}} {\tilde{p}}^{x-1} {\tilde{q}}^{x-1} \left(s+s_p {\tilde{p}}^{3-x} +s_q {\tilde{q}}^{3-x} \right) \left(s+s_p {\tilde{p}}^{{-}2x-2} +s_q {\tilde{q}}^{{-}2x-2} \right) \nonumber\\ & \quad \times\delta(s+s_p \tilde{p}+s_q \tilde{q}) \,\mathrm{d} {\tilde{p}} \,\mathrm{d} {\tilde{q}} . \end{align}

Here, we use expression (5.21) obtained after applying the Zakharov transformation. We get

(5.34)\begin{equation} \varPi_k ={-} \frac{{\rm \pi} K_{\theta,\phi} C_E^2 k^{3+2x}}{32b_0} \frac{I(x)}{3+2x} . \end{equation}

The direction of the cascade will be given by the sign of the energy flux when $x=-3/2$ (Kolmogorov–Zakharov spectrum), but in this limit, the numerator and denominator cancel out. The use of L’Hopital's rule leads to the relation

(5.35)\begin{align} \lim_{x \to -3/2} \varPi_k \equiv \varepsilon & ={-} \frac{{\rm \pi} K_{\theta,\phi} C_E^2}{32b_0} \lim_{x \to -3/2} \frac{I(x)}{3+2x} \end{align}
(5.36)\begin{align} & ={-} \frac{{\rm \pi} K_{\theta,\phi} C_E^2}{32b_0} \frac{\partial I(x)/\partial x\vert_{x={-}3/2}}{2} = \frac{{\rm \pi} K_{\theta,\phi} C_E^2}{32b_0} J , \end{align}

with

(5.37)\begin{equation} J = \frac{1}{12} \sum_{ss_{p} s_{q}} J^{ss_ps_q}, \end{equation}

and

(5.38)\begin{align} J^{ss_ps_q} & = \int_{\varDelta_\perp} {\tilde{p}}^{{-}5/2} {\tilde{q}}^{{-}5/2} \left(s+s_p {\tilde{p}}^{9/2} +s_q {\tilde{q}}^{9/2} \right) \left(s_p {\tilde{p}} \ln {\tilde{p}} +s_q {\tilde{q}} \ln {\tilde{q}} \right)\nonumber\\ & \quad\times \delta(s+s_p \tilde{p}+s_q \tilde{q}) \,\mathrm{d} {\tilde{p}} \,\mathrm{d} {\tilde{q}} . \end{align}

After a few manipulations, $J$ can be written as a one-dimensional integral. To find this integral, we first use the following change of variables: ${\tilde {q}} = {\tilde {p}} +1$ for $J^{++-}$, ${\tilde {q}} = {\tilde {p}} -1$ for $J^{+-+}$ and ${\tilde {q}} = 1-{\tilde {p}}$ for $J^{+--}$, which leads to

(5.39)\begin{gather} J^{+{+}-} = \int_0^{+\infty} x^{{-}5/2} (1+x)^{{-}5/2} \left(1+x^{9/2} - (1+x)^{9/2} \right) \left(x \ln x - (1+x) \ln (1+x) \right) \mathrm{d} x , \end{gather}
(5.40)\begin{gather}J^{+{-}+} = J^{+{+}-} \end{gather}

and

(5.41)\begin{equation} J^{+{-}-} ={-} \int_0^{1} x^{{-}5/2} (1-x)^{{-}5/2} \left(1-x^{9/2} - (1-x)^{9/2} \right) \left(x \ln x + (1-x) \ln (1-x) \right) \mathrm{d} x . \end{equation}

Then, we introduce the change of variable $y = 1/(x+1)$ for $J^{++-}$ which becomes equal to $J^{+--}$. This leads after summation to

(5.42)\begin{equation} J = \frac{1}{2} \int_0^1 y^{{-}5/2} (1-y)^{{-}5/2} \left(y^{9/2} + (1-y)^{9/2} -1 \right) \left(y \ln y + (1-y) \ln (1-y) \right) \mathrm{d} y . \end{equation}

The integrand of $J$ is always positive (see figure 3), therefore the energy flux is positive (because $K_{\theta,\phi } \geqslant 0$) and the energy cascade direct.

Figure 3. Variation of the integrand of $J$ in expression (5.42).

5.6. Kolmogorov constant

The last result of this paper is the numerical evaluation of the universal (Kolmogorov) constant $C_K$ of this problem. From the previous expression and the definition (5.15a,b), we deduce the analytical expression

(5.43)\begin{equation} E_k = \sqrt{\frac{b_0 \varepsilon}{K_{\theta,\phi}}} C_K k^{{-}3/2} \quad {\rm with} \ C_K \equiv \sqrt{\frac{32}{{\rm \pi} J}} . \end{equation}

A numerical evaluation of $J$ (5.42) leads to the Kolmogorov constant

(5.44)\begin{equation} C_K \simeq 0.623 . \end{equation}

The one-dimensional energy spectrum is not universal since it depends on $K_{\theta,\phi }$, thus on the anisotropic nature of the system (and also the initial condition). Note that if initially the spectrum is isotropic, then $f(\theta _k,\phi _k) = 4 {\rm \pi}$ and the expression simplifies. In this case, we can define the Kolmogorov constant as $C'_K = C_K / \sqrt {4 {\rm \pi}} \simeq 0.176$.

With the definition of $K_{\theta,\phi }$, the energy spectrum tends to zero when $\theta _k \to 0$, which is consistent with the idea that the contribution of fast waves becomes negligible in this limit. However, when a measurement is made in the solar wind, the spectrum may be affected by the change in direction of ${\boldsymbol {e}_\parallel }$ such that only a mean value around a cone of angle $\theta _0 \ll {\rm \pi}$ is accessible. This effect can be evaluated by introducing $\theta _0$ and the following functions:

(5.45)\begin{gather} g(\theta_k) = \frac{\sin \theta_k}{1+2 \sin^2 \theta_k} , \end{gather}
(5.46)\begin{gather}\bar{g}(\theta_0) = \frac{1}{\theta_0} \int_0^{\theta_0} g(\theta_k) \,{\rm d}\theta = \frac{1}{\sqrt{24}\theta_0} \left( \ln \left( \frac{\sqrt{3}+\sqrt{2}}{\sqrt{3}-\sqrt{2}} \right) - \ln \left( \frac{\sqrt{3}+\sqrt{2} \cos \theta_0}{\sqrt{3}-\sqrt{2} \cos \theta_0} \right) \right) . \end{gather}

With $\theta _0 = {\rm \pi}/18$ ($10^o$), we get $\bar g({\rm \pi} /18) \simeq 0.085$ and $g({\rm \pi} /18)=0.164$ (note that $g({\rm \pi} /2)=1/3$). Therefore, we see that $g$ saturates at a relatively high value with $\bar {g}({\rm \pi} /18) / g({\rm \pi} /18) \simeq 52\,\%$. This remark can explain the observations where the variation in amplitude of the spectrum does not change very much with the angle $\theta _k$ (Zhao et al. Reference Zhao, Yan, Liu, Liu and Wang2022b).

6. Conclusion and discussion

In this paper, an analytical theory of wave turbulence is derived for compressible MHD in the small $\beta$ limit for which slow magneto-acoustic waves and Alfvén waves are neglected. Then, the nonlinear dynamics is reduced to three-wave interactions between fast magneto-acoustic waves. We find the canonical variables – the compressible Elsässer fields: this is a non-trivial combination of the poloidal components of the velocity and magnetic field. These variables are linearly related to the compressible velocity and mass density, respectively. In particular, this means that the parallel component of the magnetic field is not a good proxy to estimate the compressibility. We show that the kinetic equations of wave turbulence possess two quadratic invariants, energy and momentum, which are conserved in detail. However, a relevant exact power-law solution (Kolmogorov–Zakharov spectrum) exists only for the energy: it is the well-known one-dimensional isotropic IK spectrum in $k^{-3/2}$ which finds here a rigorous justification. Interestingly, the mass density spectrum follows also the same scaling. We prove rigorously that this solution is local and corresponds to a direct cascade. The analytical expression of the Kolmogorov constant is also obtained and a numerical estimate is given. Unlike acoustic waves (Zakharov & Sagdeev Reference Zakharov and Sagdeev1970), fast magneto-acoustic wave turbulence is not isotropic in the sense that the amplitude of the spectrum depends on the angle between the wavevector and the direction of the applied uniform magnetic field.

It is often believed that a theory of wave turbulence is only possible for dispersive waves. The argument is that for non-dispersive waves, all disturbances move at the same speed and therefore initial correlations between the wave phases persist and lead, over a long period of time, to strong turbulence, whereas for dispersive waves, any initial correlations are quickly lost as different waves travel with different speeds. However, this statement should be taken with caution for several reasons. First, it is implicitly assumed that we have three-wave interactions: in this case, the resonance condition implies solutions along rays, which means that interacting waves are indeed propagating in the same direction. But for four-wave interactions, the situation is different because the solutions of the resonance condition are not necessarily confined along rays (see e.g. elastic waves in Hassaini et al. (Reference Hassaini, Mordant, Miquel, Krstulovic and Düring2019) or gravitational waves in Galtier & Nazarenko Reference Galtier and Nazarenko2017). Second, even for three-wave interactions, one can find exceptions. A well-known example is given by Alfvén waves for which $\omega \propto k_\parallel$ and for which nonlinear interactions occur only between waves propagating in opposite directions. Therefore, there is no cumulative effect and a theory of wave turbulence can be developed (Galtier et al. Reference Galtier, Nazarenko, Newell and Pouquet2000). Third, a $\omega \propto k$ relation is non-dispersive only in one dimension. In two or three dimensions, it is semi-dispersive. By semi-dispersive we physically mean that a wave packet moving in a fixed direction interacts with many other wave packets carrying statistically independent information. It turns out that in three dimensions, this number of interactions can be sufficient to break the initial correlation; we then find ourselves in the same situation as for dispersive waves (but with some particularities). From a mathematical point of view, it was recognized very early that a theory of acoustic wave turbulence is not feasible in one dimension because the uniformity of the development is not guaranteed (Benney & Saffman Reference Benney and Saffman1966). The same problem seems inevitable in two dimensions but not in three dimensions (Newell & Aucoin Reference Newell and Aucoin1971; L'vov et al. Reference L'vov, L'vov, Newell and Zakharov1997), justifying a posteriori the results obtained by Zakharov & Sagdeev (Reference Zakharov and Sagdeev1970). A recent three-dimensional direct numerical simulation shows for the first time the existence of the regime of acoustic wave turbulence with, as expected, an energy spectrum in $k^{-3/2}$ (Kochurin & Kuznetsov Reference Kochurin and Kuznetsov2022). The similarity between acoustic and fast magneto-acoustic waves fully justifies the development of a wave turbulence theory and the use of the exact solutions (Kolmogorov–Zakharov spectrum) as signature of this regime. Note that, for acoustic waves, a small dispersion is sometimes introduced to justify the existence of the wave turbulence regime. In MHD, such a dispersion can be played naturally by the Hall effect which leads to a correction at small MHD scales (Galtier Reference Galtier2006). In the particular case of three-wave interactions between dispersive kinetic Alfvén waves, an angular distribution of energy is found with a reduction of the cascade along the uniform magnetic field (Galtier Reference Galtier2023).

Interestingly, recent observations made by PSP reveal a more universal solar wind near the Sun (${\sim }0.1$ AU) than near the Earth in that the power-law index found for the kinetic and magnetic energies is $-3/2$ (Chen et al. Reference Chen, Bale, Bonnell, Borovikov, Bowen, Burgess, Case, Chandran, de Wit and Goetz2020; Shi et al. Reference Shi, Velli, Panasenco, Tenerani, Réville, Bale, Kasper, Korreck, Bonnell and Dudok de Wit2021; Zhao et al. Reference Zhao, Zank, Telloni, Stevens, Kasper and Bale2022a). In light of the present study, it is not surprising that at the same time $\beta$ is generally much less than one. For the future, it would be interesting to extend the study by Zhao et al. (Reference Zhao, Yan, Liu, Liu and Wang2022b) to other data and also check whether the mass density spectrum is consistent with the $-3/2$ power-law index (Moncuquet et al. Reference Moncuquet, Meyer-Vernet, Issautier, Pulupa, Bonnell, Bale, Dudok de Wit, Goetz, Griton and Harvey2020; Zank et al. Reference Zank, Zhao, Adhikari, Telloni, Kasper, Stevens, Rahmati and Bale2022) (whereas it seems rather compatible with $-5/3$ at 1 AU Montgomery, Brown & Matthaeus Reference Montgomery, Brown and Matthaeus1987; Coles & Harmon Reference Coles and Harmon1989; Hnat, Chapman & Rowlands Reference Hnat, Chapman and Rowlands2005). It seems also interesting to consider fast magneto-acoustic wave turbulence as a relevant regime to study the heating of the solar corona (Galtier & Pouquet Reference Galtier and Pouquet1998; Chandran Reference Chandran2005).

Acknowledgements

Editor Thierry Passot thanks the referees for their advice in evaluating this article.

Funding

This research received no specific grant from any funding agency, commercial or not-for-profit sectors.

Declaration of interests

The author reports no conflict of interest.

References

Andrés, N., Clark di Leoni, P., Mininni, P.D., Dmitruk, P., Sahraoui, F. & Matthaeus, W.H. 2017 Interplay between Alfvén and magnetosonic waves in compressible magnetohydrodynamics turbulence. Phys. Plasmas 24 (10), 102314.CrossRefGoogle Scholar
Andrés, N., Galtier, S. & Sahraoui, F. 2018 Exact law for homogeneous compressible Hall magnetohydrodynamics turbulence. Phys. Rev. E 97 (1), 013204.CrossRefGoogle ScholarPubMed
Bale, S.D., Kellogg, P.J., Mozer, F.S., Horbury, T.S. & Reme, H. 2005 Measurement of the electric fluctuation spectrum of magnetohydrodynamic turbulence. Phys. Rev. Lett. 94 (21), 215002.CrossRefGoogle ScholarPubMed
Bandyopadhyay, R., Sorriso-Valvo, L., Chasapis, A., Hellinger, P., Matthaeus, W., Verdini, A., Landi, S., Franci, L., Matteini, L., Giles, B., et al. 2020 In situ observation of Hall magnetohydrodynamic cascade in space plasma. Phys. Rev. Lett. 124 (22), 225101.CrossRefGoogle ScholarPubMed
Banerjee, S. & Galtier, S. 2013 Exact relation with two-point correlation functions and phenomenological approach for compressible MHD turbulence. Phys. Rev. E 87 (1), 013019.CrossRefGoogle Scholar
Banerjee, S., Hadid, L., Sahraoui, F. & Galtier, S. 2016 Scaling of compressible magnetohydrodynamic turbulence in the fast solar wind. Astrophys. J. Lett. 829 (2), L27.CrossRefGoogle Scholar
Benney, D. 1967 Asymptotic behavior of nonlinear dispersive waves. J. Maths Phys. 46 (2), 115–132.CrossRefGoogle Scholar
Benney, D. & Newell, A. 1967 Sequential time closures for interacting random waves. J. Maths Phys. 46 (4), 363–392.CrossRefGoogle Scholar
Benney, D. & Saffman, P. 1966 Nonlinear interactions of random waves in a dispersive medium. Proc. R. Soc. Lond. A 289 (1418), 301–320.Google Scholar
Bigot, B., Galtier, S. & Politano, H. 2008 An anisotropic turbulent model for solar coronal heating. Astron. Astrophys. 490, 325–337.CrossRefGoogle Scholar
Brodiano, M., Andrés, N. & Dmitruk, P. 2021 Spatiotemporal analysis of waves in compressively driven magnetohydrodynamics turbulence. Astrophys. J. 922 (2), 240.CrossRefGoogle Scholar
Bruno, R. & Carbone, V. 2013 The solar wind as a turbulence laboratory. Living Rev. Solar Phys. 10 (1), 2.CrossRefGoogle Scholar
Chandran, B. 2005 Weak compressible magnetohydrodynamic turbulence in the solar corona. Phys. Rev. Lett. 95, 265004.CrossRefGoogle ScholarPubMed
Chandran, B. 2008 Weakly turbulent magnetohydrodynamic waves in compressible low-${\beta }$ plasmas. Phys. Rev. Lett. 101 (23), 235004.CrossRefGoogle ScholarPubMed
Chen, C.H.K., Bale, S.D., Bonnell, J.W., Borovikov, D., Bowen, T.A., Burgess, D., Case, A.W., Chandran, B.D.G., de Wit, T.D., Goetz, K., et al. 2020 The evolution and role of solar wind turbulence in the inner heliosphere. Astrophys. J. Suppl. 246 (2), 53.CrossRefGoogle Scholar
Chen, C.H.K., Sorriso-Valvo, L., Šafránková, J. & Němeček, Z. 2014 Intermittency of solar wind density fluctuations from ion to electron scales. Astrophys. J. Lett. 789 (1), L8.CrossRefGoogle Scholar
Cho, J. & Lazarian, A. 2002 Compressible sub-Alfvénic MHD turbulence in low-${\beta }$ plasmas. Phys. Rev. Lett. 88 (24), 245001.CrossRefGoogle ScholarPubMed
Coles, W. & Harmon, J. 1989 Propagation observations of the solar wind near the Sun. Astrophys. J. 337, 1023.CrossRefGoogle Scholar
Ferrand, R., Galtier, S. & Sahraoui, F. 2021 A compact exact law for compressible isothermal Hall magnetohydrodynamic turbulence. J. Plasma Phys. 87 (2), 905870220.CrossRefGoogle Scholar
Galtier, S. 2006 Wave turbulence in incompressible Hall magnetohydrodynamics. J. Plasma Phys. 72, 721–769.CrossRefGoogle Scholar
Galtier, S. 2008 von Kármán–Howarth equations for Hall magnetohydrodynamic flows. Phys. Rev. E 77 (1), 015302.CrossRefGoogle ScholarPubMed
Galtier, S. 2014 Weak turbulence theory for rotating magnetohydrodynamics and planetary flows. J. Fluid Mech. 757, 114–154.CrossRefGoogle Scholar
Galtier, S. 2016 Introduction to Modern Magnetohydrodynamics. Cambridge University Press.CrossRefGoogle Scholar
Galtier, S. 2023 Physics of Wave Turbulence. Cambridge University Press.Google Scholar
Galtier, S. & Banerjee, S. 2011 Exact relation for correlation functions in compressible isothermal turbulence. Phys. Rev. Lett. 107 (13), 134501.CrossRefGoogle ScholarPubMed
Galtier, S. & Bhattacharjee, A. 2003 Anisotropic weak whistler wave turbulence in electron magnetohydrodynamics. Phys. Plasmas 10, 3065–3076.CrossRefGoogle Scholar
Galtier, S. & Chandran, B.D.G. 2006 Extended spectral scaling laws for shear-Alfvén wave turbulence. Phys. Plasmas 13 (11), 114505.CrossRefGoogle Scholar
Galtier, S. & Meyrand, R. 2015 Entanglement of helicity and energy in kinetic Alfvén wave/whistler turbulence. J. Plasma Phys. 81 (1), 325810106.CrossRefGoogle Scholar
Galtier, S. & Nazarenko, S. 2017 Turbulence of weak gravitational waves in the early Universe. Phys. Rev. Lett. 119, 221101.CrossRefGoogle ScholarPubMed
Galtier, S., Nazarenko, S., Newell, A. & Pouquet, A. 2000 A weak turbulence theory for incompressible magnetohydrodynamics. J. Plasma Phys. 63, 447–488.CrossRefGoogle Scholar
Galtier, S., Nazarenko, S.V. & Newell, A.C. 2001 On wave turbulence in MHD. Nonlinear Process. Geophys. 8 (3), 141–150.CrossRefGoogle Scholar
Galtier, S. & Pouquet, A. 1998 Solar flare statistics with a one-dimensional MHD model. Solar Phys. 179 (1), 141–165.CrossRefGoogle Scholar
Gan, Z., Li, H., Fu, X. & Du, S. 2022 On the existence of fast modes in compressible magnetohydrodynamic turbulence. Astrophys. J. 926 (2), 222.CrossRefGoogle Scholar
Goldreich, P. & Sridhar, S. 1995 Toward a theory of interstellar turbulence. 2: strong alfvenic turbulence. Astrophys. J. 438, 763–775.CrossRefGoogle Scholar
Goldstein, M. & Roberts, D. 1999 Magnetohydrodynamic turbulence in the solar wind. Phys. Plasmas 6 (11), 4154–4160.CrossRefGoogle Scholar
Hadid, L., Sahraoui, F. & Galtier, S. 2017 Energy cascade rate in compressible fast and slow solar wind turbulence. Astrophys. J. 838 (1), 9.CrossRefGoogle Scholar
Hassaini, R., Mordant, N., Miquel, B., Krstulovic, G. & Düring, G. 2019 Elastic weak turbulence: from the vibrating plate to the drum. Phys. Rev. E 99 (3), 033002.CrossRefGoogle Scholar
Hasselmann, K. 1962 On the non-linear energy transfer in a gravity-wave spectrum. Part 1. General theory. J. Fluid Mech. 12, 481–500.CrossRefGoogle Scholar
Higdon, J. 1984 Density fluctuations in the interstellar medium: evidence for anisotropic magnetogasdynamic turbulence. I – model and astrophysical sites. Astrophys. J. 285, 109–123.CrossRefGoogle Scholar
Hnat, B., Chapman, S. & Rowlands, G. 2005 Compressibility in solar wind plasma turbulence. Phys. Rev. Lett. 94 (20), 204502.CrossRefGoogle ScholarPubMed
Horbury, T., Forman, M. & Oughton, S. 2008 Anisotropic scaling of magnetohydrodynamic turbulence. Phys. Rev. Lett. 101 (17), 175005.CrossRefGoogle ScholarPubMed
Iroshnikov, P. 1964 Turbulence of a conducting fluid in a strong magnetic field. Sov. Astron. 7, 566–571.Google Scholar
Kiyani, K., Osman, K. & Chapman, S. 2015 Dissipation and heating in solar wind turbulence: from the macro to the micro and back again. Phil. Trans. R. Soc. Lond. A 373 (2041), 1–10.Google Scholar
Kochurin, E.A. & Kuznetsov, E.A. 2022 Direct numerical simulation of acoustic turbulence: Zakharov–Sagdeev spectrum. JETP Lett. 116, 1–12.CrossRefGoogle Scholar
Kolmogorov, A. 1941 Dissipation of energy in locally isotropic turbulence. Dokl. Akad. Nauk SSSR 32, 16–18.Google Scholar
Kraichnan, R. 1965 Inertial-range spectrum of hydromagnetic turbulence. Phys. Fluids 8, 1385–1387.CrossRefGoogle Scholar
Kuznetsov, E. 2001 Weak magnetohydrodynamic turbulence of a magnetized plasma. Sov. J. Expl Theor. Phys. 93 (5), 1052–1064.CrossRefGoogle Scholar
Le Reun, T., Favier, B. & Le Bars, M. 2020 Evidence of the Zakharov–Kolmogorov spectrum in numerical simulations of inertial wave turbulence. Europhys. Lett. 132 (6), 64002.CrossRefGoogle Scholar
L'vov, V., L'vov, Y., Newell, A. & Zakharov, V. 1997 Statistical description of acoustic turbulence. Phys. Rev. E 56 (1), 390–405.CrossRefGoogle Scholar
Makwana, K.D. & Yan, H. 2020 Properties of magnetohydrodynamic modes in compressively driven plasma turbulence. Phys. Rev. X 10 (3), 031021.Google Scholar
Marino, R. & Sorriso-Valvo, L. 2023 Scaling laws for the energy transfer in space plasma turbulence. Phys. Rep. 1006, 1–144.CrossRefGoogle Scholar
Matthaeus, W.H. 2021 Turbulence in space plasmas: who needs it? Phys. Plasmas 28 (3), 032306.CrossRefGoogle Scholar
Meyrand, R., Galtier, S. & Kiyani, K. 2016 Direct evidence of the transition from weak to strong magnetohydrodynamic turbulence. Phys. Rev. Lett. 116 (10), 105002.CrossRefGoogle ScholarPubMed
Meyrand, R., Kiyani, K., Gürcan, O. & Galtier, S. 2018 Coexistence of weak and strong wave turbulence in incompressible Hall magnetohydrodynamics. Phys. Rev. X 8 (3), 031066.Google Scholar
Moncuquet, M., Meyer-Vernet, N., Issautier, K., Pulupa, M., Bonnell, J.W., Bale, S., Dudok de Wit, T., Goetz, K., Griton, L., Harvey, P., et al. 2020 First in situ measurements of electron density and temperature from quasi-thermal noise spectroscopy with Parker solar probe/Fields. Astrophys. J. Suppl. 246 (2), 44.CrossRefGoogle Scholar
Montgomery, D., Brown, M.R. & Matthaeus, W.H. 1987 Density fluctuation spectra in magnetohydrodynamic turbulence. J. Geophys. Res. 92 (A1), 282–284.CrossRefGoogle Scholar
Nazarenko, S. 2011 Wave Turbulence. Lecture Notes in Physics. Springer.CrossRefGoogle Scholar
Newell, A. & Aucoin, P. 1971 Semi-dispersive wave systems. J. Fluid Mech. 49, 593–609.CrossRefGoogle Scholar
Newell, A., Nazarenko, S. & Biven, L. 2001 Wave turbulence and intermittency. Physica D 152, 520–550.CrossRefGoogle Scholar
Osman, K., Wan, M., Matthaeus, W., Weygand, J. & Dasso, S. 2011 Anisotropic third-moment estimates of the energy cascade in solar wind turbulence using multispacecraft data. Phys. Rev. Lett. 107 (16), 165001.CrossRefGoogle ScholarPubMed
Oughton, S. & Matthaeus, W. 2020 Critical balance and the physics of magnetohydrodynamic turbulence. Astrophys. J. 897 (1), 37.CrossRefGoogle Scholar
Passot, T. & Sulem, P.L. 2019 Imbalanced kinetic Alfvén wave turbulence: from weak turbulence theory to nonlinear diffusion models for the strong regime. J. Plasma Phys. 85 (3), 905850301.CrossRefGoogle Scholar
Podesta, J., Roberts, D. & Goldstein, M. 2007 Spectral exponents of kinetic and magnetic energy spectra in solar wind turbulence. Astrophys. J. 664, 543–548.CrossRefGoogle Scholar
Politano, H. & Pouquet, A. 1998 von Kármán–Howarth equation for magnetohydrodynamics and its consequences on third-order longitudinal structure and correlation functions. Phys. Rev. E 57, 21.CrossRefGoogle Scholar
Rappazzo, A., Velli, M., Einaudi, G. & Dahlburg, R. 2007 Coronal heating, weak MHD turbulence, and scaling laws. Astrophys. J. Lett. 657, L47–L51.CrossRefGoogle Scholar
Sahraoui, F., Hadid, L. & Huang, S. 2020 Magnetohydrodynamic and kinetic scale turbulence in the near-Earth space plasmas: a (short) biased review. Rev. Mod. Plasma Phys. 4 (1), 4.CrossRefGoogle Scholar
Saur, J., Politano, H., Pouquet, A. & Matthaeus, W. 2002 Evidence for weak MHD turbulence in the middle magnetosphere of Jupiter. Astrophys. Astron. 386, 699–708.CrossRefGoogle Scholar
Shi, C., Velli, M., Panasenco, O., Tenerani, A., Réville, V., Bale, S.D., Kasper, J., Korreck, K., Bonnell, J.W., Dudok de Wit, T., et al. 2021 Alfvénic versus non-Alfvénic turbulence in the inner heliosphere as observed by Parker Solar Probe. Astron. Astrophys. 650, A21.CrossRefGoogle Scholar
Simon, P. & Sahraoui, F. 2022 Exact law for compressible pressure-anisotropic MHD turbulence: toward linking energy cascade and instabilities. Phys. Rev. E 105 (5), 055111.CrossRefGoogle Scholar
Sorriso-Valvo, L., Marino, R., Carbone, V., Noullez, A., Lepreti, F., Veltri, P., Bruno, R., Bavassano, B. & Pietropaolo, E. 2007 Observation of inertial energy cascade in interplanetary space plasma. Phys. Rev. Lett. 99 (11), 115001.CrossRefGoogle ScholarPubMed
Zakharov, V., L'Vov, V. & Falkovich, G. 1992 Kolmogorov Spectra of Turbulence I: Wave Turbulence. Springer Series in Nonlinear Dynamics. Springer.CrossRefGoogle Scholar
Zakharov, V. & Sagdeev, R. 1970 Spectrum of acoustic turbulence. Sov. Phys. Dokl. 15, 439.Google Scholar
Zank, G., Zhao, L.-L., Adhikari, L., Telloni, D., Kasper, J., Stevens, M., Rahmati, A. & Bale, S. 2022 Turbulence in the sub-Alfvénic solar wind. Astrophys. J. Lett. 926 (2), L16.CrossRefGoogle Scholar
Zhao, L.-L., Zank, G., Telloni, D., Stevens, M., Kasper, J. & Bale, S. 2022 a The turbulent properties of the sub-Alfvénic solar wind measured by the Parker Solar Probe. Astrophys. J. Lett. 928 (2), L15.CrossRefGoogle Scholar
Zhao, S., Yan, H., Liu, T., Liu, M. & Wang, H. 2022 b Multispacecraft analysis of the properties of MHD fluctuations in sub-Alfvénic solar wind turbulence at 1 AU. Astrophys. J. 937 (2), 102.CrossRefGoogle Scholar
Figure 0

Figure 1. Propagation of wave packets of amplitude $\epsilon$, with $\omega \propto k$, in one dimension (left), two dimensions (middle) and three dimensions (right). In one dimension, the (nonlinear) interaction between wave packets (1) and (2) becomes quickly strong because they are moving in the same direction at the same speed, and thus the initial correlations between the phases of the wave packets persist; collisions between wave packet (1) and those propagating in the opposite direction, which carry statistically independent information, cannot change the situation; therefore, turbulence cannot be weak. In two dimensions, the number of collisions between wave packet (1) and the others moving in different directions is higher than in one dimension but still not enough to change the conclusion. In three dimensions, this number is sufficient to randomize the phases of wave packet (1) and turbulence can eventually be weak. In pure compressible MHD at $\beta \ll 1$, this explanation applies well for F waves for which $\omega \propto k$ (semi-dispersive wave). For S waves where $\omega \propto k_\parallel$ (non-dispersive wave), whatever the dimension, the situation reduces to the one-dimensional case with propagation of wave packets along the strong uniform magnetic field; therefore, turbulence of S waves cannot be weak and can produce shocks.

Figure 1

Figure 2. Variation of $G(x)$ for $x \in [-2,-1]$. A divergence of the integral is clearly observed close to $-2$ and $-1$. Inset: as expected, we see that the power-law index $x=-3/2$ (Kolmogorov–Zakharov spectrum) cancels the integral.

Figure 2

Figure 3. Variation of the integrand of $J$ in expression (5.42).