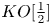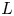1. Introduction
For an oriented family of manifolds $\pi : E \to B$![]() , a family signature theorem is an equation between two classes in the (generalized) cohomology of $B$
, a family signature theorem is an equation between two classes in the (generalized) cohomology of $B$![]() . The first should be local in the total space $E$
. The first should be local in the total space $E$![]() , and arise as the image under a fibre-integration map of a class on $E$
, and arise as the image under a fibre-integration map of a class on $E$![]() which is locally defined. The second should depend only on the local coefficient system on $B$
which is locally defined. The second should depend only on the local coefficient system on $B$![]() given by the middle cohomology of the fibres, equipped with its intersection (or linking) form. When the fibres have dimension $4k$
given by the middle cohomology of the fibres, equipped with its intersection (or linking) form. When the fibres have dimension $4k$![]() and $B$
and $B$![]() is a point, it should reduce to Hirzebruch's signature theorem.
is a point, it should reduce to Hirzebruch's signature theorem.
We will discuss several implementations of this idea, in increasing levels of sophistication: firstly in rational cohomology, then in real $K$![]() -theory localized away from 2, and finally in symmetric $L$
-theory localized away from 2, and finally in symmetric $L$![]() -theory of the integers. Our main contribution is to do so in what we feel is the correct generality, by interpreting ‘family of manifolds’ to mean ‘topological block bundle’, i.e. block bundles with topological manifold fibres. Under more restrictive conditions the results are (well) known: for smooth fibre bundles the rational cohomology statement is due to Atiyah [Reference Atiyah4, eq. (4.3)], and for PL fibre bundles the $L$
-theory of the integers. Our main contribution is to do so in what we feel is the correct generality, by interpreting ‘family of manifolds’ to mean ‘topological block bundle’, i.e. block bundles with topological manifold fibres. Under more restrictive conditions the results are (well) known: for smooth fibre bundles the rational cohomology statement is due to Atiyah [Reference Atiyah4, eq. (4.3)], and for PL fibre bundles the $L$![]() -theory statement was given by Lück and Ranicki [Reference Lück and Ranicki34, p. 184] and its proof outlined. As the statement for smooth block bundles in rational cohomology has seen some recent use [Reference Ebert and Reinhold13], and the author will soon need the statement for topological fibre bundles in $L$
-theory statement was given by Lück and Ranicki [Reference Lück and Ranicki34, p. 184] and its proof outlined. As the statement for smooth block bundles in rational cohomology has seen some recent use [Reference Ebert and Reinhold13], and the author will soon need the statement for topological fibre bundles in $L$![]() -theory [Reference Galatius and Randal-Williams18], it seems appropriate to give a detailed stand-alone account.
-theory [Reference Galatius and Randal-Williams18], it seems appropriate to give a detailed stand-alone account.
The highlights are: the three forms of the Family Signature Theorem (theorems 2.6, 3.1, 4.1); triviality of the family signature for families of odd-dimensional manifolds (corollary 5.3); multiplicativity of the signature modulo 4 for local systems over topological manifolds (corollary 2.3) and for fibrations of Poincaré complexes (corollary 6.4); an analysis of the (non)multiplicativity of the de Rham invariant (§ 6.3).
2. Meyer
We first give an exposition of the work of Meyer [Reference Meyer35], and use it to prove a form of the family signature theorem for topological block bundles in rational cohomology. We also use it to prove the multiplicativity of the signature modulo 4 for local systems of $(-1)^n$![]() -symmetric forms over a topological manifold.
-symmetric forms over a topological manifold.
2.1 Twisted signatures
Suppose that $n \in \mathbb {N}$![]() , $H_\mathbb {R}$
, $H_\mathbb {R}$![]() is a real vector space and $\lambda : H_\mathbb {R} \otimes H_\mathbb {R} \to \mathbb {R}$
is a real vector space and $\lambda : H_\mathbb {R} \otimes H_\mathbb {R} \to \mathbb {R}$![]() is a $(-1)^n$
is a $(-1)^n$![]() -symmetric bilinear form which is nondegenerate, i.e. such that the adjoint map $\lambda ^\mathrm {ad} : H_\mathbb {R} \to \mathrm {Hom}_\mathbb {R}(H_\mathbb {R},\, \mathbb {R})$
-symmetric bilinear form which is nondegenerate, i.e. such that the adjoint map $\lambda ^\mathrm {ad} : H_\mathbb {R} \to \mathrm {Hom}_\mathbb {R}(H_\mathbb {R},\, \mathbb {R})$![]() is an isomorphism. Let $\mathrm {Aut}(H_\mathbb {R},\, \lambda ) \leq GL(H_\mathbb {R})$
is an isomorphism. Let $\mathrm {Aut}(H_\mathbb {R},\, \lambda ) \leq GL(H_\mathbb {R})$![]() denote the subgroup of those automorphisms of $H_\mathbb {R}$
denote the subgroup of those automorphisms of $H_\mathbb {R}$![]() which preserve the form $\lambda$
which preserve the form $\lambda$![]() , considered as a discrete group. There is a corresponding flat vector bundle, or local coefficient system, $\mathcal {H}_\mathbb {R} \to B\mathrm {Aut}(H_\mathbb {R},\, \lambda )$
, considered as a discrete group. There is a corresponding flat vector bundle, or local coefficient system, $\mathcal {H}_\mathbb {R} \to B\mathrm {Aut}(H_\mathbb {R},\, \lambda )$![]() , equipped with a nondegenerate $(-1)^n$
, equipped with a nondegenerate $(-1)^n$![]() -symmetric fibrewise bilinear form.
-symmetric fibrewise bilinear form.
If $M^{4k-2n}$![]() is an oriented closed manifold and $f : M \to B\mathrm {Aut}(H_\mathbb {R},\, \lambda )$
is an oriented closed manifold and $f : M \to B\mathrm {Aut}(H_\mathbb {R},\, \lambda )$![]() is a map, then the bilinear form
is a map, then the bilinear form

is symmetric because the cup product and $\lambda$![]() are either both symmetric or both antisymmetric. We may therefore take its signature
are either both symmetric or both antisymmetric. We may therefore take its signature
and Meyer proves that this depends only on the oriented cobordism class of the map $f : M^{4k-2n} \to B\mathrm {Aut}(H_\mathbb {R},\, \lambda )$![]() . This is the twisted signature of $(M;f)$
. This is the twisted signature of $(M;f)$![]() .
.
2.2 Meyer's formula for twisted signatures
Given the flat vector bundle $\mathcal {H}_\mathbb {R} \to B\mathrm {Aut}(H_\mathbb {R},\, \lambda )$![]() and the nondegenerate $(-1)^n$
and the nondegenerate $(-1)^n$![]() -symmetric fibrewise bilinear form induced by $\lambda$
-symmetric fibrewise bilinear form induced by $\lambda$![]() , we may choose a Riemannian metric $\langle -,\, - \rangle$
, we may choose a Riemannian metric $\langle -,\, - \rangle$![]() on this bundle and hence define a fibrewise operator $A$
on this bundle and hence define a fibrewise operator $A$![]() by $\lambda (x,\,y) = \langle x,\, A y \rangle$
by $\lambda (x,\,y) = \langle x,\, A y \rangle$![]() satisfying $A^* = (-1)^n A$
satisfying $A^* = (-1)^n A$![]() , and use this to form a complex $K$
, and use this to form a complex $K$![]() -theory class $\xi \in K^0(B\mathrm {Aut}(H_\mathbb {R},\, \lambda ))$
-theory class $\xi \in K^0(B\mathrm {Aut}(H_\mathbb {R},\, \lambda ))$![]() as follows (see [Reference Meyer35, §1], [Reference Atiyah and Singer2, pp. 478-9]):
as follows (see [Reference Meyer35, §1], [Reference Atiyah and Singer2, pp. 478-9]):
(i) If $n$
 is even then $A$
is even then $A$ is self-adjoint and its positive and negative eigenspaces give a decomposition $\mathcal {H}_\mathbb {R}^+ \oplus \mathcal {H}_\mathbb {R}^-$
is self-adjoint and its positive and negative eigenspaces give a decomposition $\mathcal {H}_\mathbb {R}^+ \oplus \mathcal {H}_\mathbb {R}^-$ of $\mathcal {H}_\mathbb {R}$
of $\mathcal {H}_\mathbb {R}$ , and we set
\[ \xi := (\mathcal{H}_\mathbb{R}^+{-} \mathcal{H}_\mathbb{R}^-) \otimes \mathbb{C} \in K^0(B\mathrm{Aut}(H_\mathbb{R}, \lambda)). \]
, and we set
\[ \xi := (\mathcal{H}_\mathbb{R}^+{-} \mathcal{H}_\mathbb{R}^-) \otimes \mathbb{C} \in K^0(B\mathrm{Aut}(H_\mathbb{R}, \lambda)). \]
(ii) If $n$
 is odd then $A$
is odd then $A$ is skew-adjoint and $J := A/\sqrt {A A^*}$
is skew-adjoint and $J := A/\sqrt {A A^*}$ , formed using the positive square root of $AA^*$
, formed using the positive square root of $AA^*$ , determines a complex structure on $\mathcal {H}_\mathbb {R}$
, determines a complex structure on $\mathcal {H}_\mathbb {R}$ , and we set
\[ \xi := \overline{\mathcal{H}}_\mathbb{R} - \mathcal{H}_\mathbb{R} \in K^0(B\mathrm{Aut}(H_\mathbb{R}, \lambda)), \]where $\overline {\mathcal {H}}_\mathbb {R}$
, and we set
\[ \xi := \overline{\mathcal{H}}_\mathbb{R} - \mathcal{H}_\mathbb{R} \in K^0(B\mathrm{Aut}(H_\mathbb{R}, \lambda)), \]where $\overline {\mathcal {H}}_\mathbb {R}$
 denotes the complex conjugate bundle.
denotes the complex conjugate bundle.
As the Riemannian metric is not adapted to the flat structure of $\mathcal {H}_\mathbb {R}$![]() , these virtual vector bundles need not be flat and can have interesting Chern classes. For $f : M \to B\mathrm {Aut}(H_\mathbb {R},\, \lambda )$
, these virtual vector bundles need not be flat and can have interesting Chern classes. For $f : M \to B\mathrm {Aut}(H_\mathbb {R},\, \lambda )$![]() with $M$
with $M$![]() an oriented smooth manifold Meyer establishes the following formula
an oriented smooth manifold Meyer establishes the following formula
by applying the index theorem to the signature operator of $M$![]() twisted in a certain way by the bundle $f^*\mathcal {H}_\mathbb {R}$
twisted in a certain way by the bundle $f^*\mathcal {H}_\mathbb {R}$![]() , using its nondegenerate $(-1)^n$
, using its nondegenerate $(-1)^n$![]() -symmetric fibrewise bilinear form. Here $\mathrm {ch}$
-symmetric fibrewise bilinear form. Here $\mathrm {ch}$![]() denotes the Chern character, $\psi ^2$
denotes the Chern character, $\psi ^2$![]() denotes the second Adams operation, and $\mathcal {L}$
denotes the second Adams operation, and $\mathcal {L}$![]() denotes the Hirzebruch $L$
denotes the Hirzebruch $L$![]() -class.
-class.
Remark 2.1 For later use, we observe that the complex $K$![]() -theory classes $\xi$
-theory classes $\xi$![]() have refinements to real $K$
have refinements to real $K$![]() -theory classes $\xi _\mathbb {R}$
-theory classes $\xi _\mathbb {R}$![]() . Namely
. Namely
(i) If $n$
 is even then $\xi$
is even then $\xi$ is visibly the complexification of
\[ \xi_\mathbb{R} := \mathcal{H}_\mathbb{R}^+{-} \mathcal{H}_\mathbb{R}^-{\in} KO^{0}(B\mathrm{Aut}(H_\mathbb{R}, \lambda)). \]
is visibly the complexification of
\[ \xi_\mathbb{R} := \mathcal{H}_\mathbb{R}^+{-} \mathcal{H}_\mathbb{R}^-{\in} KO^{0}(B\mathrm{Aut}(H_\mathbb{R}, \lambda)). \]
(ii) If $n$
 is odd then writing $c : KO^i(-) \to K^i(-)$
is odd then writing $c : KO^i(-) \to K^i(-)$ and $r : K^i(-) \to KO^i(-)$
and $r : K^i(-) \to KO^i(-)$ for the complexification and realification maps, and $b \in K^{-2}(*)$
for the complexification and realification maps, and $b \in K^{-2}(*)$ for the Bott class, we have $b \cdot \xi = c(r(b \cdot \overline {\mathcal {H}}_\mathbb {R}))$
for the Bott class, we have $b \cdot \xi = c(r(b \cdot \overline {\mathcal {H}}_\mathbb {R}))$ , so $b \cdot \xi$
, so $b \cdot \xi$ is the complexification of
\[ \xi_\mathbb{R} := r(b \cdot \overline{\mathcal{H}}_\mathbb{R}) \in KO^{{-}2}(B\mathrm{Aut}(H_\mathbb{R}, \lambda)). \]
is the complexification of
\[ \xi_\mathbb{R} := r(b \cdot \overline{\mathcal{H}}_\mathbb{R}) \in KO^{{-}2}(B\mathrm{Aut}(H_\mathbb{R}, \lambda)). \]
2.3 Divisibility and multiplicativity of the signature
It does not seem to be well-known that the discussion so far can be used to establish multiplicativity of the signature modulo 4, for example recovering and in fact strengthening the main theorem of [Reference Hambleton, Korzeniewski and Ranicki19]. Although this is not our main goal, we take a brief excursion in this and the following subsection to explain how. Related ideas will arise in § 5.3 where we investigate the delicate 2-local structure of the $L$![]() -theoretic family signature theorem.
-theoretic family signature theorem.
Lemma 2.2 The identity (2.1) holds even if $M$![]() is an oriented topological manifold.
is an oriented topological manifold.
Proof. Interpreting $\mathcal {L}(TM)$![]() as the topological Hirzebruch $L$
as the topological Hirzebruch $L$![]() -class the two sides define homomorphisms $MSTop_{4k-2n}(B\mathrm {Aut}(H_\mathbb {R},\, \lambda )) \to \mathbb {Q}$
-class the two sides define homomorphisms $MSTop_{4k-2n}(B\mathrm {Aut}(H_\mathbb {R},\, \lambda )) \to \mathbb {Q}$![]() , which are equal when precomposed with $MSO_{4k-2n}(B\mathrm {Aut}(H_\mathbb {R},\, \lambda )) \to MSTop_{4k-2n}(B\mathrm {Aut}(H_\mathbb {R},\, \lambda ))$
, which are equal when precomposed with $MSO_{4k-2n}(B\mathrm {Aut}(H_\mathbb {R},\, \lambda )) \to MSTop_{4k-2n}(B\mathrm {Aut}(H_\mathbb {R},\, \lambda ))$![]() . But the latter map is an isomorphism after rationalizing, as $BSO \to BSTop$
. But the latter map is an isomorphism after rationalizing, as $BSO \to BSTop$![]() is a rational equivalence, by [Reference Kirby and Siebenmann28, p. 246 eq. (5)] and the finiteness of the groups $\Theta _n$
is a rational equivalence, by [Reference Kirby and Siebenmann28, p. 246 eq. (5)] and the finiteness of the groups $\Theta _n$![]() of homotopy $n$
of homotopy $n$![]() -spheres for $n \geq 5$
-spheres for $n \geq 5$![]() .
.
Corollary 2.3 If $(H_\mathbb {R},\, \lambda )$![]() is a nondegenerate $(-1)^n$
is a nondegenerate $(-1)^n$![]() -symmetric bilinear form and $f : M^{4k-2n} \to B\mathrm {Aut}(H_\mathbb {R},\, \lambda )$
-symmetric bilinear form and $f : M^{4k-2n} \to B\mathrm {Aut}(H_\mathbb {R},\, \lambda )$![]() is a map from an oriented topological manifold, then
is a map from an oriented topological manifold, then
Proof. We rely on the formula (2.1), which holds in this situation by the previous lemma. If the manifold $M$![]() is smooth the the polynomials exhibiting $\mathcal {L}_i(TM)$
is smooth the the polynomials exhibiting $\mathcal {L}_i(TM)$![]() in terms of the integral cohomology classes $p_j(TM)$
in terms of the integral cohomology classes $p_j(TM)$![]() are defined over the 2-local integers $\mathbb {Z}_{(2)}$
are defined over the 2-local integers $\mathbb {Z}_{(2)}$![]() , as the coefficients of the power series $x/\mathrm {tanh}(x)$
, as the coefficients of the power series $x/\mathrm {tanh}(x)$![]() lie in this ringFootnote 1 , and so we have refinements $\mathcal {L}_i(TM) \in H^{4i}(M;\mathbb {Z}_{(2)})$
lie in this ringFootnote 1 , and so we have refinements $\mathcal {L}_i(TM) \in H^{4i}(M;\mathbb {Z}_{(2)})$![]() . If $M$
. If $M$![]() is a topological manifold then we cannot make this argument, but its conclusion is nonetheless true by work of Morgan and Sullivan [Reference Morgan and Sullivan37] (see section 7, and the remark at the end of that section). As the classes $\mathcal {L}_i(TM)$
is a topological manifold then we cannot make this argument, but its conclusion is nonetheless true by work of Morgan and Sullivan [Reference Morgan and Sullivan37] (see section 7, and the remark at the end of that section). As the classes $\mathcal {L}_i(TM)$![]() are 2-integral, and as $\mathrm {ch}_0(\psi ^2(f^*\xi )) = f^*\mathrm {ch}_0(\xi ) = \sigma (H_\mathbb {R},\, \lambda )$
are 2-integral, and as $\mathrm {ch}_0(\psi ^2(f^*\xi )) = f^*\mathrm {ch}_0(\xi ) = \sigma (H_\mathbb {R},\, \lambda )$![]() if $n$
if $n$![]() is even, to conclude the argument it suffices to show that $\mathrm {ch}_i(\psi ^2(\xi ))$
is even, to conclude the argument it suffices to show that $\mathrm {ch}_i(\psi ^2(\xi ))$![]() are 2-integral and 2-integrally divisible by 4 for all $i>0$
are 2-integral and 2-integrally divisible by 4 for all $i>0$![]() .
.
For any complex vector bundle $V$![]() we have
we have
where $\bar {p}_i$![]() is the polynomial over $\mathbb {Z}$
is the polynomial over $\mathbb {Z}$![]() expressing the power sum polynomial $t_1^i + t_2^i + t_3^i + \cdots$
expressing the power sum polynomial $t_1^i + t_2^i + t_3^i + \cdots$![]() in terms of elementary symmetric polynomials. By Legendre's formula $\tfrac {2^i}{i!}$
in terms of elementary symmetric polynomials. By Legendre's formula $\tfrac {2^i}{i!}$![]() is 2-integral and 2-integrally divisible by 2. There are now cases depending on the parity of $n$
is 2-integral and 2-integrally divisible by 2. There are now cases depending on the parity of $n$![]() . If $n$
. If $n$![]() is odd then $\mathrm {ch}_i(\xi ) = \mathrm {ch}_i(\overline {\mathcal {H}}_\mathbb {R} - \mathcal {H}_\mathbb {R}) = (1-(-1)^i) \mathrm {ch}_i(\overline {\mathcal {H}}_\mathbb {R})$
is odd then $\mathrm {ch}_i(\xi ) = \mathrm {ch}_i(\overline {\mathcal {H}}_\mathbb {R} - \mathcal {H}_\mathbb {R}) = (1-(-1)^i) \mathrm {ch}_i(\overline {\mathcal {H}}_\mathbb {R})$![]() which vanishes for $i$
which vanishes for $i$![]() even and is $2\mathrm {ch}_i(\overline {\mathcal {H}}_\mathbb {R})$
even and is $2\mathrm {ch}_i(\overline {\mathcal {H}}_\mathbb {R})$![]() for $i$
for $i$![]() odd. As $\mathrm {ch}_i(\overline {\mathcal {H}}_\mathbb {R})$
odd. As $\mathrm {ch}_i(\overline {\mathcal {H}}_\mathbb {R})$![]() is 2-integrally divisible by 2 by the previous paragraph, this finishes the argument in this case.
is 2-integrally divisible by 2 by the previous paragraph, this finishes the argument in this case.
If $n$![]() is even then $2c_i(\xi )=0$
is even then $2c_i(\xi )=0$![]() for $i$
for $i$![]() odd, as $\xi$
odd, as $\xi$![]() is the complexification of a real vector bundle. This implies that $2\bar {p}_i(c_1(\xi ),\, c_2(\xi ),\, \ldots,\, c_i(\xi ))$
is the complexification of a real vector bundle. This implies that $2\bar {p}_i(c_1(\xi ),\, c_2(\xi ),\, \ldots,\, c_i(\xi ))$![]() is zero for $i$
is zero for $i$![]() odd, as then each monomial much contain some odd Chern class, and we will now show that $2\bar {p}_{2i}(c_1(\xi ),\, c_2(\xi ),\, \ldots,\, c_{2i}(\xi ))$
odd, as then each monomial much contain some odd Chern class, and we will now show that $2\bar {p}_{2i}(c_1(\xi ),\, c_2(\xi ),\, \ldots,\, c_{2i}(\xi ))$![]() is 2-integrally divisible by 4. Writing $2i = 2^r \cdot s$
is 2-integrally divisible by 4. Writing $2i = 2^r \cdot s$![]() with $r \geq 1$
with $r \geq 1$![]() and $s$
and $s$![]() odd, we have
odd, we have
and so $2\bar {p}_{2i}(c_1(\xi ),\, c_2(\xi ),\, \ldots,\, c_{2i}(\xi )) \equiv 2\bar {p}_s(c_1(\xi ),\, c_2(\xi ),\, \ldots,\, c_{2i}(\xi ))^{2^r} \mod 4$![]() . But as $s$
. But as $s$![]() is odd the right-hand side vanishes by the case discussed above, which finishes the argument in this case.
is odd the right-hand side vanishes by the case discussed above, which finishes the argument in this case.
2.4 Signatures of fibrations of Poincaré complexes
We consider Poincaré complexes in the sense of Wall [Reference Wall52], i.e. finitely-dominated CW-complexes enjoying Poincaré duality with respect to a twisted integral fundamental class and all systems of local coefficients. Suppose that $F^{d} \to E \to B^{4k-d}$![]() is a fibration of finitely-dominated spaces with Poincaré base and fibre (and hence Poincaré total space too [Reference Klein25, Corollary F], [Reference Gottlieb17]), which is oriented in the sense that $B$
is a fibration of finitely-dominated spaces with Poincaré base and fibre (and hence Poincaré total space too [Reference Klein25, Corollary F], [Reference Gottlieb17]), which is oriented in the sense that $B$![]() is oriented, $F$
is oriented, $F$![]() is orientable, and the local coefficient system $\mathcal {H}^d(F;\mathbb {Z})$
is orientable, and the local coefficient system $\mathcal {H}^d(F;\mathbb {Z})$![]() is trivialized: this induces an orientation of $E$
is trivialized: this induces an orientation of $E$![]() . Let
. Let
denote the Serre spectral sequence for this fibration. If $d=2n$![]() then there is a map
then there is a map
given by the action of the fundamental groupoid of $B$![]() on the middle cohomology of the fibres, which preserves the $(-1)^n$
on the middle cohomology of the fibres, which preserves the $(-1)^n$![]() -symmetric form $\lambda$
-symmetric form $\lambda$![]() given by cup product. The definition of the twisted signature above did not really use that $M$
given by cup product. The definition of the twisted signature above did not really use that $M$![]() is a manifold, only that it has Poincaré duality with all systems of local coefficients: thus we can define $\sigma (B; \phi )$
is a manifold, only that it has Poincaré duality with all systems of local coefficients: thus we can define $\sigma (B; \phi )$![]() in the same way. Meyer shows that there is an identity
in the same way. Meyer shows that there is an identity

Remark 2.4 Combining (2.2) with corollary 2.3 shows that $\sigma (E) \equiv \sigma (B) \cdot \sigma (F) \mod 4$![]() as long as $B$
as long as $B$![]() is homotopy equivalent to a topological manifold, generalizing the main theorem of [Reference Hambleton, Korzeniewski and Ranicki19]. This result also follows from Korzeniewski's thesis [Reference Korzeniewski27, theorem 7.2], which allows the base to be a finite Poincaré complex having trivial Whitehead torsion (and a topological manifold is an example of this). We will give a further strengthening of this result as corollary 6.4, which allows $B$
is homotopy equivalent to a topological manifold, generalizing the main theorem of [Reference Hambleton, Korzeniewski and Ranicki19]. This result also follows from Korzeniewski's thesis [Reference Korzeniewski27, theorem 7.2], which allows the base to be a finite Poincaré complex having trivial Whitehead torsion (and a topological manifold is an example of this). We will give a further strengthening of this result as corollary 6.4, which allows $B$![]() to be an arbitrary Poincaré complex.
to be an arbitrary Poincaré complex.
Meyer proves (2.2) in two steps: Firstly $\sigma (E)$![]() is related to the signature of $E_2^{*,*}$
is related to the signature of $E_2^{*,*}$![]() taken with respect to the form
taken with respect to the form
where the latter map denotes the projection to $E_2^{4k-d,d} = H^{4k-d}(B ; \mathcal {H}^d(F;\mathbb {R})) = \mathbb {R}$![]() . This is done by (i) showing that the signature is unchanged by passing from one page of the spectral sequence to the next, so is the same as the signature of $E_\infty ^{*,*}$
. This is done by (i) showing that the signature is unchanged by passing from one page of the spectral sequence to the next, so is the same as the signature of $E_\infty ^{*,*}$![]() with the analogous form (this is [Reference Meyer35, Satz I.1.4]), (ii) observing that the signature of $E_\infty ^{*,*}$
with the analogous form (this is [Reference Meyer35, Satz I.1.4]), (ii) observing that the signature of $E_\infty ^{*,*}$![]() is identified with $\sigma (E)$
is identified with $\sigma (E)$![]() , as signatures are unchanged under passing to associated grades. Secondly, by recognizing $L := \bigoplus _{q > d/2} E_2^{*, q}$
, as signatures are unchanged under passing to associated grades. Secondly, by recognizing $L := \bigoplus _{q > d/2} E_2^{*, q}$![]() as a sublagrangian of $E_2^{*,*}$
as a sublagrangian of $E_2^{*,*}$![]() with $L^\perp = \bigoplus _{q \geq d/2} E_2^{*, q}$
with $L^\perp = \bigoplus _{q \geq d/2} E_2^{*, q}$![]() , this signature is the same as that of the induced form on $L^\perp /L$
, this signature is the same as that of the induced form on $L^\perp /L$![]() , which is trivial if $d$
, which is trivial if $d$![]() is odd and is the form described above on $H^{2k-d/2}(B; \mathcal {H}^{d/2}(F;\mathbb {R}))$
is odd and is the form described above on $H^{2k-d/2}(B; \mathcal {H}^{d/2}(F;\mathbb {R}))$![]() if $d$
if $d$![]() is even.
is even.
Remark 2.5 Meyer assumes various additional hypotheses, most notably that $B$![]() and $F$
and $F$![]() are homology manifolds. This is because he wishes to allow (non locally constant) sheaf coefficients. For locally constant coefficients being Poincaré complexes suffices for his argument to go through.
are homology manifolds. This is because he wishes to allow (non locally constant) sheaf coefficients. For locally constant coefficients being Poincaré complexes suffices for his argument to go through.
2.5 The family signature theorem over $\mathbb {Q}$
We may rationalize the twisted signature map $\sigma : \Omega _*^{\mathrm {fr}}(B\mathrm {Aut}(H_\mathbb {R},\, \lambda )) \to \mathbb {Z}$![]() on framed bordism, then use that rational framed bordism is naturally isomorphic to rational homology, and that rational cohomology is dual to rational homology, to define rational cohomology classes
on framed bordism, then use that rational framed bordism is naturally isomorphic to rational homology, and that rational cohomology is dual to rational homology, to define rational cohomology classes
In other words, if $f : W^{4k-2n} \to B\mathrm {Aut}(H_\mathbb {R},\, \lambda )$![]() is a map from a stably framed manifold, then $\sigma (W; f) = \int _W f^* \sigma _{4k-2n}$
is a map from a stably framed manifold, then $\sigma (W; f) = \int _W f^* \sigma _{4k-2n}$![]() . It follows from (2.1), applied to all maps $f : W^{4k-2n} \to B\mathrm {Aut}(H_\mathbb {R},\, \lambda )$
. It follows from (2.1), applied to all maps $f : W^{4k-2n} \to B\mathrm {Aut}(H_\mathbb {R},\, \lambda )$![]() from stably framed manifolds (which have $\mathcal {L}(TW)=1$
from stably framed manifolds (which have $\mathcal {L}(TW)=1$![]() ), that
), that
The family signature theorem—in the generality we wish to discuss it in this note—concerns oriented topological block bundles $\pi : E \to |K|$![]() with $d$
with $d$![]() -dimensional fibres, as described in [Reference Hebestreit, Land, Lück and Randal-Williams20, section 2.3]. There the base $|K|$
-dimensional fibres, as described in [Reference Hebestreit, Land, Lück and Randal-Williams20, section 2.3]. There the base $|K|$![]() is taken to be the realization of a simplicial complex, but one can equally well take it to be the realization of a semi-simplicial set. This notion then includes the universal block bundle described in [Reference Hebestreit, Land, Lück and Randal-Williams20, definition 2.3.1] and the proceeding discussion. In [Reference Hebestreit, Land, Lück and Randal-Williams20, section 2.4] it is shown that there is an associated stable vertical tangent microbundle, given by a map
is taken to be the realization of a simplicial complex, but one can equally well take it to be the realization of a semi-simplicial set. This notion then includes the universal block bundle described in [Reference Hebestreit, Land, Lück and Randal-Williams20, definition 2.3.1] and the proceeding discussion. In [Reference Hebestreit, Land, Lück and Randal-Williams20, section 2.4] it is shown that there is an associated stable vertical tangent microbundle, given by a map
and we write $\mathcal {L}_k(T_\pi ^s E)$![]() for the pullback of the $k$
for the pullback of the $k$![]() th Hirzebruch $L$
th Hirzebruch $L$![]() -class along this map. An oriented block bundle also has an associated fibre-integration, or Gysin, map $\int _\pi : H^*(E) \to H^{*-d}(|K|)$
-class along this map. An oriented block bundle also has an associated fibre-integration, or Gysin, map $\int _\pi : H^*(E) \to H^{*-d}(|K|)$![]() as discussed in [Reference Hebestreit, Land, Lück and Randal-Williams20, section 4.1], and the family signature theorem is then as follows.
as discussed in [Reference Hebestreit, Land, Lück and Randal-Williams20, section 4.1], and the family signature theorem is then as follows.
Theorem 2.6 (Family signature theorem over $\mathbb {Q}$ )
)
Let $\pi : E \to |K|$![]() be an oriented topological block bundle with fibre $F^d$
be an oriented topological block bundle with fibre $F^d$![]() . If $d=2n$
. If $d=2n$![]() let $\phi : |K| \to B\mathrm {Aut}(H^n(F;\mathbb {R}),\, \lambda )$
let $\phi : |K| \to B\mathrm {Aut}(H^n(F;\mathbb {R}),\, \lambda )$![]() classify the local coefficient system $\mathcal {H}^{n}(F;\mathbb {R})$
classify the local coefficient system $\mathcal {H}^{n}(F;\mathbb {R})$![]() over $|K|$
over $|K|$![]() with the $(-1)^n$
with the $(-1)^n$![]() -symmetric fibrewise bilinear form given by cup product. Then
-symmetric fibrewise bilinear form given by cup product. Then

Proof. As rational cohomology is dual to rational framed bordism, by naturality it is enough to consider the case where $|K|=B^{4k-d}$![]() is a stably framed smooth manifold of dimension $4k-d$
is a stably framed smooth manifold of dimension $4k-d$![]() , where the cohomology classes in question are top-dimensional and are hence determined by their integrals over $B$
, where the cohomology classes in question are top-dimensional and are hence determined by their integrals over $B$![]() .
.
As $B$![]() is a stably framed smooth manifold then by [Reference Hebestreit, Land, Lück and Randal-Williams20, lemma 2.5.2] $E$
is a stably framed smooth manifold then by [Reference Hebestreit, Land, Lück and Randal-Williams20, lemma 2.5.2] $E$![]() is a topological manifold and its stable tangent microbundle satisfies
is a topological manifold and its stable tangent microbundle satisfies
so $\mathcal {L}_k(T_\pi ^s E) = \mathcal {L}_k(T E)$![]() by multiplicativity of the total $L$
by multiplicativity of the total $L$![]() -class, and hence
-class, and hence
by the defining property of the (topological) Hirzebruch $L$![]() -classes. A block bundle determines a fibration with homotopy equivalent fibre, total space, and base, so by (2.2) we have $\sigma (E)=0$
-classes. A block bundle determines a fibration with homotopy equivalent fibre, total space, and base, so by (2.2) we have $\sigma (E)=0$![]() if $d$
if $d$![]() is odd and $\sigma (E) = \sigma (B; \phi )$
is odd and $\sigma (E) = \sigma (B; \phi )$![]() if $d$
if $d$![]() is even. To obtain the first identity observe that as $B$
is even. To obtain the first identity observe that as $B$![]() is stably framed the definition of $\sigma _{4k-d}$
is stably framed the definition of $\sigma _{4k-d}$![]() gives $\sigma (B; \phi ) = \int _B \phi ^*(\sigma _{4k-d})$
gives $\sigma (B; \phi ) = \int _B \phi ^*(\sigma _{4k-d})$![]() . The second identity then follows from (2.3).
. The second identity then follows from (2.3).
3. Sullivan
We now explain how Meyer's work can be combined with ideas of Sullivan [Reference Sullivan50] to obtain a $\mathbb {Z}[\tfrac {1}{2}]$![]() -integral form of the family signature theorem, formulated not in ordinary cohomology but in the generalized cohomology theory $KO[\tfrac {1}{2}]$
-integral form of the family signature theorem, formulated not in ordinary cohomology but in the generalized cohomology theory $KO[\tfrac {1}{2}]$![]() , real $K$
, real $K$![]() -theory localized away from 2. Useful later references for these ideas are [Reference Morgan and Sullivan37] (especially section 1) and [Reference Madsen and Milgram36] (especially chapter 4.B).
-theory localized away from 2. Useful later references for these ideas are [Reference Morgan and Sullivan37] (especially section 1) and [Reference Madsen and Milgram36] (especially chapter 4.B).
3.1 Cobordism, coefficients and $K$ -theory
-theory
Coefficients in an abelian group $A$![]() can be introduced into the generalized homology theory represented by a spectrum $\mathrm {E}$
can be introduced into the generalized homology theory represented by a spectrum $\mathrm {E}$![]() by the device of smashing with the Moore spectrum $\mathrm {M}A$
by the device of smashing with the Moore spectrum $\mathrm {M}A$![]() , i.e. setting $E_*(-;A) := E_*(\mathrm {M}A \wedge -) = \pi _*(\mathrm {E} \wedge \mathrm {M}A \wedge -)$
, i.e. setting $E_*(-;A) := E_*(\mathrm {M}A \wedge -) = \pi _*(\mathrm {E} \wedge \mathrm {M}A \wedge -)$![]() . There is a corresponding cohomology theory, represented by $\mathrm {E} \wedge \mathrm {M}A$
. There is a corresponding cohomology theory, represented by $\mathrm {E} \wedge \mathrm {M}A$![]() . When $A$
. When $A$![]() is a localization of $\mathbb {Z}$
is a localization of $\mathbb {Z}$![]() , i.e. a subring of $\mathbb {Q}$
, i.e. a subring of $\mathbb {Q}$![]() , the construction of $\mathrm {M}A$
, the construction of $\mathrm {M}A$![]() as a mapping telescope shows that $E_*(-;A) = E_*(-) \otimes _\mathbb {Z} A$
as a mapping telescope shows that $E_*(-;A) = E_*(-) \otimes _\mathbb {Z} A$![]() , and similarly for the cohomology theory on finite complexes (but not in general).
, and similarly for the cohomology theory on finite complexes (but not in general).
Write $\mathrm {KO}[\tfrac {1}{2}] := \mathrm {KO} \wedge \mathrm {M} \mathbb {Z}[\tfrac {1}{2}]$![]() for the spectrum representing real $K$
for the spectrum representing real $K$![]() -theory localized away from 2, with homotopy ring $\pi _*(\mathrm {KO}[\tfrac {1}{2}]) = \pi _*(\mathrm {KO}) \otimes \mathbb {Z}[\tfrac {1}{2}] = \mathbb {Z}[\tfrac {1}{2}][a^{\pm 1}]$
-theory localized away from 2, with homotopy ring $\pi _*(\mathrm {KO}[\tfrac {1}{2}]) = \pi _*(\mathrm {KO}) \otimes \mathbb {Z}[\tfrac {1}{2}] = \mathbb {Z}[\tfrac {1}{2}][a^{\pm 1}]$![]() , for $a$
, for $a$![]() the class of degree 4 which under the complexification map is sent to $b^2$
the class of degree 4 which under the complexification map is sent to $b^2$![]() with $b \in \pi _2(\mathrm {K}[\tfrac {1}{2}])$
with $b \in \pi _2(\mathrm {K}[\tfrac {1}{2}])$![]() the Bott class. There is an orientation ([Reference Sullivan50, p. 201])
the Bott class. There is an orientation ([Reference Sullivan50, p. 201])
whose Pontrjagin character satisfies $\mathrm {ph}(\Delta ) = \mathcal {L}^{-1} \cdot u \in H^*(\mathrm {MSO};\mathbb {Q})$![]() , where $u$
, where $u$![]() is the cohomological Thom class and $\mathcal {L} \in H^*(BSO;\mathbb {Q})$
is the cohomological Thom class and $\mathcal {L} \in H^*(BSO;\mathbb {Q})$![]() is the total Hirzebruch $L$
is the total Hirzebruch $L$![]() -class. These conventions are arranged so that on homotopy groups the map
-class. These conventions are arranged so that on homotopy groups the map
is given by $\Delta _*([M^{4k}]) = \sigma (M) \cdot a^k$![]() . Sullivan shows, using the results of Conner–Floyd, that the induced map $MSO_*(-) \otimes _{MSO_*}\mathbb {Z}[\tfrac {1}{2}][a^{\pm 1}] \to KO[\tfrac {1}{2}]_*(-)$
. Sullivan shows, using the results of Conner–Floyd, that the induced map $MSO_*(-) \otimes _{MSO_*}\mathbb {Z}[\tfrac {1}{2}][a^{\pm 1}] \to KO[\tfrac {1}{2}]_*(-)$![]() is an isomorphism of generalized homology theories. This can also be deduced from Landweber's exact functor theorem [Reference Landweber29, example 3.4]. Using the way we have introduced coefficients, and re-writing slightly, it follows that there is an isomorphism
is an isomorphism of generalized homology theories. This can also be deduced from Landweber's exact functor theorem [Reference Landweber29, example 3.4]. Using the way we have introduced coefficients, and re-writing slightly, it follows that there is an isomorphism
for any $A$![]() .
.
Sullivan applies this to show that for $X$![]() a finite complex, the data of a class $\Phi \in KO^0(X ; \mathbb {Z}[\tfrac {1}{2}])$
a finite complex, the data of a class $\Phi \in KO^0(X ; \mathbb {Z}[\tfrac {1}{2}])$![]() is equivalent to the data of morphisms $\phi _\mathbb {Q}$
is equivalent to the data of morphisms $\phi _\mathbb {Q}$![]() and $\phi _k$
and $\phi _k$![]() for each odd $k$
for each odd $k$![]() such that
such that

commutes, the $\phi _k$![]() are compatible under divisibility, and such that $\phi _\mathbb {Q}$
are compatible under divisibility, and such that $\phi _\mathbb {Q}$![]() and $\phi _k$
and $\phi _k$![]() satisfy
satisfy
for all $[W,\,f] \in MSO_{4*}(X)$![]() . Here one thinks of $\mathbb {Q}/\mathbb {Z}$
. Here one thinks of $\mathbb {Q}/\mathbb {Z}$![]() as given by $\operatorname *{colim}_{\text {all }k} \mathbb {Z}/k$
as given by $\operatorname *{colim}_{\text {all }k} \mathbb {Z}/k$![]() . A $\Phi$
. A $\Phi$![]() determines such maps $\phi$
determines such maps $\phi$![]() by applying (3.1) and then evaluating the resulting $KO[\tfrac {1}{2}]$
by applying (3.1) and then evaluating the resulting $KO[\tfrac {1}{2}]$![]() -homology class on $\Phi$
-homology class on $\Phi$![]() . By replacing $X$
. By replacing $X$![]() by its suspensions, we get a similar description of elements of $KO^d(X;\mathbb {Z}[\tfrac {1}{2}])$
by its suspensions, we get a similar description of elements of $KO^d(X;\mathbb {Z}[\tfrac {1}{2}])$![]() .
.
3.2 Signatures of $\mathbb {Z}/k$ -manifolds
-manifolds
Oriented cobordism with $\mathbb {Z}/k$![]() -coefficients, $MSO_n(X;\mathbb {Z}/k)$
-coefficients, $MSO_n(X;\mathbb {Z}/k)$![]() , has an interpretation as cobordism classes of smooth $n$
, has an interpretation as cobordism classes of smooth $n$![]() -dimensional singular $\mathbb {Z}/k$
-dimensional singular $\mathbb {Z}/k$![]() -manifolds over $X$
-manifolds over $X$![]() [Reference Morgan and Sullivan37, §1]. An oriented $\mathbb {Z}/k$
[Reference Morgan and Sullivan37, §1]. An oriented $\mathbb {Z}/k$![]() -manifold is the data of a compact oriented $n$
-manifold is the data of a compact oriented $n$![]() -manifold $\overline {W}$
-manifold $\overline {W}$![]() , a closed oriented $(n-1)$
, a closed oriented $(n-1)$![]() -manifold $\beta W$
-manifold $\beta W$![]() and an oriented identification $b: \partial \overline {W} \overset {\sim }\to \beta W \times \mathbb {Z}/k$
and an oriented identification $b: \partial \overline {W} \overset {\sim }\to \beta W \times \mathbb {Z}/k$![]() . We then write $W$
. We then write $W$![]() for the space obtained by identifying the $k$
for the space obtained by identifying the $k$![]() copies of $\beta W$
copies of $\beta W$![]() , and call $\overline {W}$
, and call $\overline {W}$![]() its resolution. This may be done in the category of smooth, PL or topological manfolds. In the smooth case the data $(\overline {W},\, \beta W,\, b,\, f : W \to X)$
its resolution. This may be done in the category of smooth, PL or topological manfolds. In the smooth case the data $(\overline {W},\, \beta W,\, b,\, f : W \to X)$![]() represents a class in $MSO_n(X;\mathbb {Z}/k)$
represents a class in $MSO_n(X;\mathbb {Z}/k)$![]() . The notion of cobordism of $\mathbb {Z}/k$
. The notion of cobordism of $\mathbb {Z}/k$![]() -manifolds, and of maps out of them, is evident.
-manifolds, and of maps out of them, is evident.
A $4n$![]() -dimensional oriented manifold with boundary $(V,\, \partial V)$
-dimensional oriented manifold with boundary $(V,\, \partial V)$![]() still has a signature $\sigma (V) \in \mathbb {Z}$
still has a signature $\sigma (V) \in \mathbb {Z}$![]() defined algebraically as the signature of the (possibly degenerate) symmetric form
defined algebraically as the signature of the (possibly degenerate) symmetric form
The invariant $\sigma (W) := \sigma (\overline {W}) \mod k$![]() of a $\mathbb {Z}/k$
of a $\mathbb {Z}/k$![]() -manifold $W$
-manifold $W$![]() is a cobordism invariant [Reference Morgan and Sullivan37, proposition 1.3], as a consequence of Novikov's additivity theorem for the signature and the usual cobordism invariance of the signature.
is a cobordism invariant [Reference Morgan and Sullivan37, proposition 1.3], as a consequence of Novikov's additivity theorem for the signature and the usual cobordism invariance of the signature.
3.3 The Sullivan orientation
Let $MSPL_n$![]() be the $n$
be the $n$![]() th space in the oriented $PL$
th space in the oriented $PL$![]() cobordism spectrum, i.e. the Thom space of the universal bundle over $BSPL(n)$
cobordism spectrum, i.e. the Thom space of the universal bundle over $BSPL(n)$![]() . Then by PL transversality, $MSO_{n+4i}(MSPL_n)$
. Then by PL transversality, $MSO_{n+4i}(MSPL_n)$![]() may be interpreted as cobordism classes of pairs $(M^{4i+n} \supset W^{4i})$
may be interpreted as cobordism classes of pairs $(M^{4i+n} \supset W^{4i})$![]() of an oriented smooth manifold and an oriented $PL$
of an oriented smooth manifold and an oriented $PL$![]() -submanifold, and assigning to this the signature $\sigma (W^{4i})$
-submanifold, and assigning to this the signature $\sigma (W^{4i})$![]() gives a map
gives a map
The $MSO_*$![]() -module structure is given by $[X] \cdot [M^{4i+n} \subset W^{4i}] = [X \times M^{4i+n} \subset X \times W^{4i}]$
-module structure is given by $[X] \cdot [M^{4i+n} \subset W^{4i}] = [X \times M^{4i+n} \subset X \times W^{4i}]$![]() , so $\phi _\mathbb {Q}$
, so $\phi _\mathbb {Q}$![]() satisfies (3.2). Similarly, $MSO_{n+4i}(MSPL_n ; \mathbb {Z}/k)$
satisfies (3.2). Similarly, $MSO_{n+4i}(MSPL_n ; \mathbb {Z}/k)$![]() may be interpreted as cobordism classes of pairs $(M^{4i+n} \supset W^{4i})$
may be interpreted as cobordism classes of pairs $(M^{4i+n} \supset W^{4i})$![]() of a smooth $\mathbb {Z}/k$
of a smooth $\mathbb {Z}/k$![]() -manifold and a $PL$
-manifold and a $PL$![]() $\mathbb {Z}/k$
$\mathbb {Z}/k$![]() -submanifold, and assigning to this the signature $\sigma (W^{4i})$
-submanifold, and assigning to this the signature $\sigma (W^{4i})$![]() as defined above gives a map
as defined above gives a map
These maps are compatible, and determine a homotopy class of maps of spectra
(a priori only well-defined up to phantom maps, as $\mathrm {MSPL}$![]() is not finite, but in fact unique [Reference Madsen and Milgram36, §5.D]). By the same discussion with $\mathrm {MSPL}$
is not finite, but in fact unique [Reference Madsen and Milgram36, §5.D]). By the same discussion with $\mathrm {MSPL}$![]() replaced by $\mathrm {MSO}$
replaced by $\mathrm {MSO}$![]() , $\Delta _{PL}$
, $\Delta _{PL}$![]() restricts to $\Delta$
restricts to $\Delta$![]() . Furthermore, as the fibre of $BPL \to BTop$
. Furthermore, as the fibre of $BPL \to BTop$![]() is a $K(\mathbb {Z}/2,\,3)$
is a $K(\mathbb {Z}/2,\,3)$![]() [Reference Kirby and Siebenmann28, p. 246], it follows that the fibre of $\mathrm {MSPL} \to \mathrm {MSTop}$
[Reference Kirby and Siebenmann28, p. 246], it follows that the fibre of $\mathrm {MSPL} \to \mathrm {MSTop}$![]() is 2-local, and so $\Delta _{PL}$
is 2-local, and so $\Delta _{PL}$![]() canonically extends to a $\Delta _{Top} : \mathrm {MSTop} \to \mathrm {KO}[\tfrac {1}{2}]$
canonically extends to a $\Delta _{Top} : \mathrm {MSTop} \to \mathrm {KO}[\tfrac {1}{2}]$![]() . (Alternatively one can repeat the construction using topological transversality, but we can avoid this for now.)
. (Alternatively one can repeat the construction using topological transversality, but we can avoid this for now.)
3.4 Twisted signatures
Returning to a nondegenerate $(-1)^n$![]() -symmetric bilinear form $(H_\mathbb {R},\, \lambda )$
-symmetric bilinear form $(H_\mathbb {R},\, \lambda )$![]() , if $f : W^{4i-2n} \to B\mathrm {Aut}(H_\mathbb {R},\, \lambda )$
, if $f : W^{4i-2n} \to B\mathrm {Aut}(H_\mathbb {R},\, \lambda )$![]() is a map from a smooth $\mathbb {Z}/k$
is a map from a smooth $\mathbb {Z}/k$![]() -manifold then there is an associated symmetric bilinear form
-manifold then there is an associated symmetric bilinear form
given by cup product, applying $\lambda$![]() , then capping with the fundamental class, whose signature we call $\sigma (W; f)$
, then capping with the fundamental class, whose signature we call $\sigma (W; f)$![]() . This number taken modulo $k$
. This number taken modulo $k$![]() is again $\mathbb {Z}/k$
is again $\mathbb {Z}/k$![]() -cobordism invariant, replacing Novikov additivity and cobordism invariance of the signature with the analogues [Reference Meyer35, Sätze I.3.1, I.3.2] for twisted signatures proved by Meyer. The assignment $[W,\, f] \mapsto \sigma (W;f)$
-cobordism invariant, replacing Novikov additivity and cobordism invariance of the signature with the analogues [Reference Meyer35, Sätze I.3.1, I.3.2] for twisted signatures proved by Meyer. The assignment $[W,\, f] \mapsto \sigma (W;f)$![]() defines a map
defines a map
and these are easily checked to be compatible with each other under divisibility, and compatible with the analogue $\mathrm {sign}_\mathbb {Q} = \sigma : MSO_{4i-2n}(B\mathrm {Aut}(H_\mathbb {R},\, \lambda )) \to \mathbb {Z}$![]() for closed manifolds.
for closed manifolds.
Furthermore, if $N^{4j}$![]() is a smooth oriented closed manifold then we can form the map $W \times N \overset {\pi _W}\to W \overset {f}\to B\mathrm {Aut}(H_\mathbb {R},\, \lambda )$
is a smooth oriented closed manifold then we can form the map $W \times N \overset {\pi _W}\to W \overset {f}\to B\mathrm {Aut}(H_\mathbb {R},\, \lambda )$![]() . By the Künneth theorem we have
. By the Künneth theorem we have
and the sum $L$![]() of those terms with $b>2j$
of those terms with $b>2j$![]() is a sublagrangian with $L^\perp$
is a sublagrangian with $L^\perp$![]() given by the sum of those terms with $b \geq 2j$
given by the sum of those terms with $b \geq 2j$![]() along with the radical, and so with
along with the radical, and so with
We therefore have $\sigma (W \times N; f \circ \pi _W) = \sigma (W; f) \cdot \sigma (N)$![]() . Similarly for closed manifolds.
. Similarly for closed manifolds.
By the discussion in § 3.1, this data corresponds to a map
well-defined up to homotopy and phantom maps.
3.5 The family signature theorem over $\mathrm {KO}[\tfrac {1}{2}]$
As we have already mentioned in § 2.5, a topological block bundle $\pi : E \to |K|$![]() with $d$
with $d$![]() -dimensional fibres has a stable vertical tangent microbundle $T^s_\pi E$
-dimensional fibres has a stable vertical tangent microbundle $T^s_\pi E$![]() of virtual dimension $d$
of virtual dimension $d$![]() , and so a stable vertical normal microbundlebundle $\nu _\pi$
, and so a stable vertical normal microbundlebundle $\nu _\pi$![]() of virtual dimension $-d$
of virtual dimension $-d$![]() , given by [Reference Hebestreit, Land, Lück and Randal-Williams20, section 2.4]. If the block bundle is oriented, then these two microbundles obtain orientations. Using the constructions in that sectionFootnote 2 there is a Pontrjagin–Thom, or Gysin, map $\pi _! : |K| \to \Omega ^\infty \mathrm {Th}(\nu _\pi \to E)$
, given by [Reference Hebestreit, Land, Lück and Randal-Williams20, section 2.4]. If the block bundle is oriented, then these two microbundles obtain orientations. Using the constructions in that sectionFootnote 2 there is a Pontrjagin–Thom, or Gysin, map $\pi _! : |K| \to \Omega ^\infty \mathrm {Th}(\nu _\pi \to E)$![]() and hence, Thomifying the map $E \to BSTop$
and hence, Thomifying the map $E \to BSTop$![]() classifying $\nu _\pi$
classifying $\nu _\pi$![]() , a map
, a map
Theorem 3.1 (Family signature theorem over ${\mathrm {KO}[\tfrac {1}{2}]}$ )
)
Let $\pi : E \to |K|$![]() be an oriented topological block bundle with fibre $F^d$
be an oriented topological block bundle with fibre $F^d$![]() . If $d=2n$
. If $d=2n$![]() let $\phi : |K| \to B\mathrm {Aut}(H^n(F;\mathbb {R}),\, \lambda )$
let $\phi : |K| \to B\mathrm {Aut}(H^n(F;\mathbb {R}),\, \lambda )$![]() classify the local coefficient system $\mathcal {H}^{n}(F;\mathbb {R})$
classify the local coefficient system $\mathcal {H}^{n}(F;\mathbb {R})$![]() over $|K|$
over $|K|$![]() with the $(-1)^n$
with the $(-1)^n$![]() -symmetric bilinear form given by cup product. Then the square
-symmetric bilinear form given by cup product. Then the square

commutes up to homotopy and phantom maps.
Proof. The two ways around the square give two elements of $KO^d(|K| ; \mathbb {Z}[\tfrac {1}{2}])$![]() , which we must compare. By the discussion in § 3.1 each of these corresponds to compatible maps $MSO_{4i-d}(|K|) \to \mathbb {Z}[\tfrac {1}{2}]$
, which we must compare. By the discussion in § 3.1 each of these corresponds to compatible maps $MSO_{4i-d}(|K|) \to \mathbb {Z}[\tfrac {1}{2}]$![]() and $MSO_{4i-d}(|K| ; \mathbb {Z}/k) \to \mathbb {Z}/k$
and $MSO_{4i-d}(|K| ; \mathbb {Z}/k) \to \mathbb {Z}/k$![]() , and so we shall compare these.
, and so we shall compare these.
That the maps $MSO_{4i-d}(|K|) \to \mathbb {Z}[\tfrac {1}{2}]$![]() obtained by going the two ways around the square agree follows from theorem 2.6 (it is the same as saying that the square commutes after rationalizing ${\Omega ^{\infty +d} KO[\tfrac {1}{2}]}$
obtained by going the two ways around the square agree follows from theorem 2.6 (it is the same as saying that the square commutes after rationalizing ${\Omega ^{\infty +d} KO[\tfrac {1}{2}]}$![]() , whereupon the top composition is the collection of the $\int _\pi \mathcal {L}_i(T_\pi ^s E)$
, whereupon the top composition is the collection of the $\int _\pi \mathcal {L}_i(T_\pi ^s E)$![]() and the bottom composition is the collection of the $\phi ^*\sigma _{4i-d}$
and the bottom composition is the collection of the $\phi ^*\sigma _{4i-d}$![]() ), so it remains to compare the two maps $MSO_{4i-d}(|K|;\mathbb {Z}/k) \to \mathbb {Z}/k$
), so it remains to compare the two maps $MSO_{4i-d}(|K|;\mathbb {Z}/k) \to \mathbb {Z}/k$![]() .
.
Let $f : W^{4i-d} \to |K|$![]() be a map from a $\mathbb {Z}/k$
be a map from a $\mathbb {Z}/k$![]() -manifold; we may homotope it to be simplicial with respect to some triangulation of $W$
-manifold; we may homotope it to be simplicial with respect to some triangulation of $W$![]() , giving a topological block bundle $f^* E \to W$
, giving a topological block bundle $f^* E \to W$![]() , whose total space $f^*E$
, whose total space $f^*E$![]() is a topological $\mathbb {Z}/k$
is a topological $\mathbb {Z}/k$![]() -manifold. We would like to say that the top composition $\Omega ^{\infty +d}\Delta _{Top} \circ \alpha$
-manifold. We would like to say that the top composition $\Omega ^{\infty +d}\Delta _{Top} \circ \alpha$![]() assigns to $(W,\, f)$
assigns to $(W,\, f)$![]() the signature $\sigma (f^*E)$
the signature $\sigma (f^*E)$![]() of the topological $\mathbb {Z}/k$
of the topological $\mathbb {Z}/k$![]() -manifold $f^* E$
-manifold $f^* E$![]() , which we have defined to be the signature of the (possibly degenerate) intersection form on the resolution $\overline {f^* E}$
, which we have defined to be the signature of the (possibly degenerate) intersection form on the resolution $\overline {f^* E}$![]() , taken modulo $k$
, taken modulo $k$![]() . This is true, but as the map $\Delta _{Top}$
. This is true, but as the map $\Delta _{Top}$![]() was obtained by obstruction theory from the more meaningful map $\Delta _{PL} : \mathrm {MSPL} \to \mathrm {KO}[\tfrac {1}{2}]$
was obtained by obstruction theory from the more meaningful map $\Delta _{PL} : \mathrm {MSPL} \to \mathrm {KO}[\tfrac {1}{2}]$![]() , it requires a small argument. Namely, as $\mathrm {MSPL} \to \mathrm {MSTop}$
, it requires a small argument. Namely, as $\mathrm {MSPL} \to \mathrm {MSTop}$![]() is a $\mathbb {Z}[\tfrac {1}{2}]$
is a $\mathbb {Z}[\tfrac {1}{2}]$![]() -equivalence there is an $N \gg 1$
-equivalence there is an $N \gg 1$![]() such that the element $2^N \alpha _*(W,\, f)$
such that the element $2^N \alpha _*(W,\, f)$![]() lifts to $\Omega ^{\infty +d}\mathrm {MSPL}$
lifts to $\Omega ^{\infty +d}\mathrm {MSPL}$![]() . In other words, the disjoint union of $2^N$
. In other words, the disjoint union of $2^N$![]() copies of the topological $\mathbb {Z}/k$
copies of the topological $\mathbb {Z}/k$![]() -manifold $f^* E$
-manifold $f^* E$![]() is topologically cobordant to a $PL$
is topologically cobordant to a $PL$![]() $\mathbb {Z}/k$
$\mathbb {Z}/k$![]() -manifold $E'$
-manifold $E'$![]() , and $\Delta _{Top}$
, and $\Delta _{Top}$![]() assigns to this $\sigma (E') = 2^N \sigma (f^*E)$
assigns to this $\sigma (E') = 2^N \sigma (f^*E)$![]() : as we work with $2$
: as we work with $2$![]() inverted, $\Delta _{Top}$
inverted, $\Delta _{Top}$![]() assigns $\sigma (f^*E)$
assigns $\sigma (f^*E)$![]() to $\alpha _*(W,\, f)$
to $\alpha _*(W,\, f)$![]() . (If $\Delta _{Top}$
. (If $\Delta _{Top}$![]() is defined using topological transversality then we can of course omit this step.)
is defined using topological transversality then we can of course omit this step.)
The block bundle $\overline {f^* E} \to \overline {W}$![]() has a relative Serre spectral sequence
has a relative Serre spectral sequence
In parallel to the discussion in § 2.4, by [Reference Meyer35, Satz I.1.5] the signature of the form on $E_2^{*,*}$![]() is the same as that of $E_\infty ^{*,*}$
is the same as that of $E_\infty ^{*,*}$![]() , and the latter is the same as the signature of $\overline {f^* E}$
, and the latter is the same as the signature of $\overline {f^* E}$![]() . Furthermore $L := \bigoplus _{q > (4i-d)/2} E_2^{*, q}$
. Furthermore $L := \bigoplus _{q > (4i-d)/2} E_2^{*, q}$![]() is again a sublagrangian of $E_2^{*,*}$
is again a sublagrangian of $E_2^{*,*}$![]() , and as in § 3.4 we have $L^\perp = \bigoplus _{q \geq (4i-d)/2} E_2^{*, q} + \text {radical}$
, and as in § 3.4 we have $L^\perp = \bigoplus _{q \geq (4i-d)/2} E_2^{*, q} + \text {radical}$![]() and so
and so
In particular, if $d$![]() is odd then this is radical so has signature 0, and if $d=2n$
is odd then this is radical so has signature 0, and if $d=2n$![]() then this has signature $\mathrm {sign}_k(W,\, \phi )$
then this has signature $\mathrm {sign}_k(W,\, \phi )$![]() . This is tautologically what the composition $\mathrm {sign} \circ \phi$
. This is tautologically what the composition $\mathrm {sign} \circ \phi$![]() assigns to $(W,\, f)$
assigns to $(W,\, f)$![]() too, as required.
too, as required.
3.6 A formula for twisted signatures
For applications we also want to know how to evaluate the map $\mathrm {sign} : B\mathrm {Aut}(H_\mathbb {R},\, \lambda ) \to \Omega ^{\infty +2n} \mathrm {KO}[\tfrac {1}{2}]$![]() in concrete terms: in other words, to have an analogue of Meyer's formula (2.1). Such an analogue is as follows, where $\xi \in K^0(B\mathrm {Aut}(H_\mathbb {R},\, \lambda ))$
in concrete terms: in other words, to have an analogue of Meyer's formula (2.1). Such an analogue is as follows, where $\xi \in K^0(B\mathrm {Aut}(H_\mathbb {R},\, \lambda ))$![]() is the class constructed in § 2.2 which appears in Meyer's formula.
is the class constructed in § 2.2 which appears in Meyer's formula.
Theorem 3.2 The square

commutes up to homotopy and phantom maps.
Proof. We first argue that the map $\mathrm {sign}$![]() factors canonically (up to phantom maps) as
factors canonically (up to phantom maps) as
through the classifying space of the topologized variant

This is certainly necessary, since the lower composition factors over this space, by replacing $\xi$![]() by the construction of § 2.2 applied to the non-flat universal bundle $\mathcal {H}_\mathbb {R}$
by the construction of § 2.2 applied to the non-flat universal bundle $\mathcal {H}_\mathbb {R}$![]() over $B\mathrm {Aut}(H_\mathbb {R},\, \lambda )^{top}$
over $B\mathrm {Aut}(H_\mathbb {R},\, \lambda )^{top}$![]() .
.
The map $\mathrm {sign}_\mathbb {Q}$![]() can be interpreted as assigning to a manifold $W^{4i-2n}$
can be interpreted as assigning to a manifold $W^{4i-2n}$![]() and a flat vector bundle $V := f^* \mathcal {H}_\mathbb {R} \to W$
and a flat vector bundle $V := f^* \mathcal {H}_\mathbb {R} \to W$![]() with a nondegenerate $(-1)^n$
with a nondegenerate $(-1)^n$![]() -symmetric bilinear form the index of the operator constructed by Meyer in the proof of [Reference Meyer35, Satz II.4.1], but the definition of this operator does not require $V$
-symmetric bilinear form the index of the operator constructed by Meyer in the proof of [Reference Meyer35, Satz II.4.1], but the definition of this operator does not require $V$![]() to be flat so $\mathrm {sign}_\mathbb {Q}$
to be flat so $\mathrm {sign}_\mathbb {Q}$![]() factors through a $\mathrm {sign}'_\mathbb {Q} : MSO_{4i-2n}(B\mathrm {Aut}(H_\mathbb {R},\, \lambda )^{top}) \to \mathbb {Z}$
factors through a $\mathrm {sign}'_\mathbb {Q} : MSO_{4i-2n}(B\mathrm {Aut}(H_\mathbb {R},\, \lambda )^{top}) \to \mathbb {Z}$![]() . Similarly, making use of index theory for $\mathbb {Z}/k$
. Similarly, making use of index theory for $\mathbb {Z}/k$![]() -manifolds (as in [Reference Freed and Melrose14], see also [Reference Rosenberg46]) we recognize $\mathrm {sign}_k(W; f)$
-manifolds (as in [Reference Freed and Melrose14], see also [Reference Rosenberg46]) we recognize $\mathrm {sign}_k(W; f)$![]() as the index of the signature operator on the manifold with boundary $\overline {W}$
as the index of the signature operator on the manifold with boundary $\overline {W}$![]() twisted, in the same way as by Meyer, by the flat vector bundle $f^* \mathcal {H}_\mathbb {R}$
twisted, in the same way as by Meyer, by the flat vector bundle $f^* \mathcal {H}_\mathbb {R}$![]() with its $(-1)^n$
with its $(-1)^n$![]() -symmetric structure. This operator is considered with the same Atiyah–Patodi–Singer boundary conditions on each of the $k$
-symmetric structure. This operator is considered with the same Atiyah–Patodi–Singer boundary conditions on each of the $k$![]() copies of $\beta W$
copies of $\beta W$![]() forming its boundary, and having done so its index is well-defined modulo $k$
forming its boundary, and having done so its index is well-defined modulo $k$![]() . As above, forming this index does not use the flatness of the vector bundle, so $\mathrm {sign}_k$
. As above, forming this index does not use the flatness of the vector bundle, so $\mathrm {sign}_k$![]() factors through a $\mathrm {sign}'_k : MSO_{4i-2n}(B\mathrm {Aut}(H_\mathbb {R},\, \lambda )^{top};\mathbb {Z}/k) \to \mathbb {Z}/k$
factors through a $\mathrm {sign}'_k : MSO_{4i-2n}(B\mathrm {Aut}(H_\mathbb {R},\, \lambda )^{top};\mathbb {Z}/k) \to \mathbb {Z}/k$![]() , in total giving the claimed factorization.
, in total giving the claimed factorization.
Claim. Maps

are determined by their rationalizations, i.e. by their Pontrjagin character.
Proof of claim. This may be deduced from the Atiyah–Segal completion theorem as follows (see [Reference Madsen and Milgram36, theorem 4.29] for a similar argument). We first reduce to the same statement for $\mathrm {K}[\tfrac {1}{2}]$![]() and the Chern character, as $\mathrm {KO}[\tfrac {1}{2}]$
and the Chern character, as $\mathrm {KO}[\tfrac {1}{2}]$![]() is a retract of $\mathrm {K}[\tfrac {1}{2}]$
is a retract of $\mathrm {K}[\tfrac {1}{2}]$![]() , and then by Bott periodicity we can remove the $\Omega ^{2n}$
, and then by Bott periodicity we can remove the $\Omega ^{2n}$![]() . Writing $G$
. Writing $G$![]() for $U(g)$
for $U(g)$![]() or $O(p) \times O(q)$
or $O(p) \times O(q)$![]() , $R(G)$
, $R(G)$![]() for its complex representation ring, $I(G)$
for its complex representation ring, $I(G)$![]() for the augmentation ideal, and $BG^{(n)}$
for the augmentation ideal, and $BG^{(n)}$![]() for a $n$
for a $n$![]() -skeleton of $BG$
-skeleton of $BG$![]() , by [Reference Atiyah and Segal3, theorem 2.1] the maps
, by [Reference Atiyah and Segal3, theorem 2.1] the maps
induce an isomorphism of pro-rings, and $K^{-1}(BG^{(n)})$![]() is pro-zero (and hence Mittag–Leffler). Using Milnor's $\lim ^1$
is pro-zero (and hence Mittag–Leffler). Using Milnor's $\lim ^1$![]() -sequence in $\mathrm {K}[\tfrac {1}{2}]$
-sequence in $\mathrm {K}[\tfrac {1}{2}]$![]() -theory we therefore have
-theory we therefore have
The claim now follows by direct calculation with a presentation of the representation rings involved (the fact that $O(p) \times O(q)$![]() is not connected is ameliorated by our working with 2 inverted).
is not connected is ameliorated by our working with 2 inverted).
By the index theorem applied to Meyer's signature operator twisted by a non-necessarily flat vector bundle with a nondegenerate $(-1)^n$![]() -symmetric bilinear form, we have $\mathrm {ph}(\mathrm {sign}') = \mathrm {ch}(\psi ^2(\xi ))$
-symmetric bilinear form, we have $\mathrm {ph}(\mathrm {sign}') = \mathrm {ch}(\psi ^2(\xi ))$![]() . At this point we invoke the real forms of $\xi$
. At this point we invoke the real forms of $\xi$![]() discussed in remark 2.1: if $n$
discussed in remark 2.1: if $n$![]() is even then $\xi = c(\xi _\mathbb {R})$
is even then $\xi = c(\xi _\mathbb {R})$![]() and if $n$
and if $n$![]() is odd then $\xi = b^{-1} \cdot c(\xi _\mathbb {R})$
is odd then $\xi = b^{-1} \cdot c(\xi _\mathbb {R})$![]() . In either case we have $b^n \xi = c(a^{\lfloor n/2 \rfloor } \cdot \xi _\mathbb {R})$
. In either case we have $b^n \xi = c(a^{\lfloor n/2 \rfloor } \cdot \xi _\mathbb {R})$![]() and so using that $\psi ^2(b) = 2b$
and so using that $\psi ^2(b) = 2b$![]() and that Adams operations commute with complexification and realification [Reference Karoubi23, proposition IV.7.40] we have
and that Adams operations commute with complexification and realification [Reference Karoubi23, proposition IV.7.40] we have

and so $\mathrm {ch}(\psi ^2 ( \xi )) = \mathrm {ph}(\tfrac {1}{2} r(b^n \psi ^2\xi ))$![]() . Thus $\mathrm {ph}(\mathrm {sign}') = \mathrm {ph}(\tfrac {1}{2} r(b^n \psi ^2\xi ))$
. Thus $\mathrm {ph}(\mathrm {sign}') = \mathrm {ph}(\tfrac {1}{2} r(b^n \psi ^2\xi ))$![]() and so $\mathrm {sign}' \simeq \tfrac {1}{2} r(b^n \psi ^2\xi )$
and so $\mathrm {sign}' \simeq \tfrac {1}{2} r(b^n \psi ^2\xi )$![]() .
.
4. Ranicki
We now explain the strongest formulation of the family signature theorem for topological block bundles, as an equation in the generalized cohomology theory given by the symmetric $L$![]() -theory of the integers, using Ranicki's ideas on $L$
-theory of the integers, using Ranicki's ideas on $L$![]() -theory and algebraic surgery (a vast literature, but in particular [Reference Ranicki45]). Ranicki's work in this direction was visionary, but his specific technical implementation is not ideal for our purposes (see remark 4.9). Instead, we will use the recent framework of Calmès, Dotto, Harpaz, Hebestreit, Land, Moi, Nardin, Nikolaus and Steimle [Reference Calmès, Dotto, Harpaz, Hebestreit, Land, Moi, Nardin, Nikolaus and Steimle10–Reference Calmès, Dotto, Harpaz, Hebestreit, Land, Moi, Nardin, Nikolaus and Steimle12].
-theory and algebraic surgery (a vast literature, but in particular [Reference Ranicki45]). Ranicki's work in this direction was visionary, but his specific technical implementation is not ideal for our purposes (see remark 4.9). Instead, we will use the recent framework of Calmès, Dotto, Harpaz, Hebestreit, Land, Moi, Nardin, Nikolaus and Steimle [Reference Calmès, Dotto, Harpaz, Hebestreit, Land, Moi, Nardin, Nikolaus and Steimle10–Reference Calmès, Dotto, Harpaz, Hebestreit, Land, Moi, Nardin, Nikolaus and Steimle12].
4.1 The family signature theorem over $\mathrm {L}^s(\mathbb {Z})$
Let $\pi : E \to |K|$![]() be an oriented topological block bundle with fibre $F^d$
be an oriented topological block bundle with fibre $F^d$![]() . If $d=2n$
. If $d=2n$![]() then $H^n(F;\mathbb {Z})/tors$
then $H^n(F;\mathbb {Z})/tors$![]() is equipped with its intersection form $\lambda$
is equipped with its intersection form $\lambda$![]() , which is nondegenerate and $(-1)^n$
, which is nondegenerate and $(-1)^n$![]() -symmetric, and the monodromy of this family gives a map
-symmetric, and the monodromy of this family gives a map
If $d=2n+1$![]() then $tors\, H^{n+1}(F;\mathbb {Z})$
then $tors\, H^{n+1}(F;\mathbb {Z})$![]() is equipped with its linking form $\ell$
is equipped with its linking form $\ell$![]() , which is nondegenerate and $(-1)^{n+1}$
, which is nondegenerate and $(-1)^{n+1}$![]() -symmetric, and the monodromy of this family gives a map
-symmetric, and the monodromy of this family gives a map
Writing $\mathrm {L}^s(\mathbb {Z})$![]() for the symmetric $L$
for the symmetric $L$![]() -theory spectrum of the integers, and writing $\sigma : \mathrm {MSTop} \to \mathrm {L}^s(\mathbb {Z})$
-theory spectrum of the integers, and writing $\sigma : \mathrm {MSTop} \to \mathrm {L}^s(\mathbb {Z})$![]() for the Ranicki orientation (as in [Reference Ranicki42, proposition 15.8], [Reference Ranicki43, p. 287], [Reference Ranicki45, proposition 16.1], [Reference Kühl, Macko and Mole26, proposition 7.10], [Reference Laures and McClure32]; we will give our own definition in § 4.6), our main result is as follows.
for the Ranicki orientation (as in [Reference Ranicki42, proposition 15.8], [Reference Ranicki43, p. 287], [Reference Ranicki45, proposition 16.1], [Reference Kühl, Macko and Mole26, proposition 7.10], [Reference Laures and McClure32]; we will give our own definition in § 4.6), our main result is as follows.
Theorem 4.1 (Family signature theorem over $\mathrm {L}^s(\mathbb {Z})$ )
)
Let $\pi : E \to |K|$![]() be an oriented topological block bundle with fibre $F^d$
be an oriented topological block bundle with fibre $F^d$![]() . Then the square
. Then the square

commutes up to homotopy.
The bottom map $inc$![]() in this diagram arises from considering isomorphisms of (linking) forms as being cobordisms. We will construct this map in § 4.7, and construct the Ranicki orientation in § 4.6. Our proof of this theorem uses only formal properties of symmetric $L$
in this diagram arises from considering isomorphisms of (linking) forms as being cobordisms. We will construct this map in § 4.7, and construct the Ranicki orientation in § 4.6. Our proof of this theorem uses only formal properties of symmetric $L$![]() -theory. In § 5 we will explain how the result can be somewhat improved, and interpreted, using non-formal results about the homotopy type of $\mathrm {L}^s(\mathbb {Z})$
-theory. In § 5 we will explain how the result can be somewhat improved, and interpreted, using non-formal results about the homotopy type of $\mathrm {L}^s(\mathbb {Z})$![]() and its relation with Grothendieck–Witt theory.
and its relation with Grothendieck–Witt theory.
We will obtain theorem 4.1 as the combination of two results, each of which holds for a class of families $\pi : E \to |K|$![]() more general than oriented topological block bundles. Firstly, when $\pi : E \to |K|$
more general than oriented topological block bundles. Firstly, when $\pi : E \to |K|$![]() is a Poincaré mock bundle (defined in § 4.4) we will define a family signature map $|K| \to \Omega ^{\infty +d} \mathrm {L}^s(\mathbb {Z})$
is a Poincaré mock bundle (defined in § 4.4) we will define a family signature map $|K| \to \Omega ^{\infty +d} \mathrm {L}^s(\mathbb {Z})$![]() . Secondly, when $\pi$
. Secondly, when $\pi$![]() is in fact a manifold mock bundle (defined in § 4.2) we shall explain why the family signature map factors as $\Omega ^{\infty +d} \sigma \circ \alpha : |K| \to \Omega ^{\infty +d} \mathrm {MSTop} \to \Omega ^{\infty +d} \mathrm {L}^s(\mathbb {Z})$
is in fact a manifold mock bundle (defined in § 4.2) we shall explain why the family signature map factors as $\Omega ^{\infty +d} \sigma \circ \alpha : |K| \to \Omega ^{\infty +d} \mathrm {MSTop} \to \Omega ^{\infty +d} \mathrm {L}^s(\mathbb {Z})$![]() . Thirdly, when the Poincaré mock bundle $\pi$
. Thirdly, when the Poincaré mock bundle $\pi$![]() comes from a fibration with Poincaré fibre (and in fact even something slightly more general) we will prove that the family signature map factors as $inc \circ \phi$
comes from a fibration with Poincaré fibre (and in fact even something slightly more general) we will prove that the family signature map factors as $inc \circ \phi$![]() . Hence when all these conditions hold, such as for topological block bundles, we obtain the conclusion of theorem 4.1.
. Hence when all these conditions hold, such as for topological block bundles, we obtain the conclusion of theorem 4.1.
4.2 Manifold mock bundles
We shall describe a model for $\Omega ^{\infty +d} \mathrm {MSTop}$![]() as the classifying space for (oriented, topological, codimension $-d$
as the classifying space for (oriented, topological, codimension $-d$![]() ) mock bundles in the sense of [Reference Buoncristiano, Rourke and Sanderson8, §II]. The construction is similar to the ‘ad theories’ of [Reference Laures and McClure32, Reference Quinn41], but we spell things out explicitly.
) mock bundles in the sense of [Reference Buoncristiano, Rourke and Sanderson8, §II]. The construction is similar to the ‘ad theories’ of [Reference Laures and McClure32, Reference Quinn41], but we spell things out explicitly.
Write $\Delta ^{p-1}_i \subset \Delta ^p$![]() for the $(p-1)$
for the $(p-1)$![]() -simplex spanned by all vertices except the $i$
-simplex spanned by all vertices except the $i$![]() th, and $\Delta ^p_i(\varepsilon ) := \{(t_0,\, t_1,\, \ldots,\, t_p) \in \Delta ^p \, | \, 0 \leq t_i < \varepsilon \}$
th, and $\Delta ^p_i(\varepsilon ) := \{(t_0,\, t_1,\, \ldots,\, t_p) \in \Delta ^p \, | \, 0 \leq t_i < \varepsilon \}$![]() , with the projection map
, with the projection map

The following is parallel to [Reference Hebestreit, Land, Lück and Randal-Williams20, definition 2.3.1].
Definition 4.2 For $d \in \mathbb {Z}$![]() , let $\mathrm {Mock}(d,\,n)$
, let $\mathrm {Mock}(d,\,n)$![]() be the semi-simplicial set with $p$
be the semi-simplicial set with $p$![]() -simplices given by locally flat compact topological $(d+p)$
-simplices given by locally flat compact topological $(d+p)$![]() -dimensional oriented submanifolds $E \subset \Delta ^p \times \mathbb {R}^n$
-dimensional oriented submanifolds $E \subset \Delta ^p \times \mathbb {R}^n$![]() such that for each $i=0,\,1,\,\ldots,\, p$
such that for each $i=0,\,1,\,\ldots,\, p$![]() ,
,
(i) $E$
 is topologically transverse to each $\Delta ^{p-1}_i \times \mathbb {R}^n$
is topologically transverse to each $\Delta ^{p-1}_i \times \mathbb {R}^n$ ,
,(ii) there is an $\varepsilon >0$
 such that
\[ E \cap (\Delta^p_i(\varepsilon) \times \mathbb{R}^n) = (\pi_i(\varepsilon) \times \mathbb{R}^n)^{{-}1}(E \cap (\Delta^{p-1}_i \times \mathbb{R}^n)), \]
such that
\[ E \cap (\Delta^p_i(\varepsilon) \times \mathbb{R}^n) = (\pi_i(\varepsilon) \times \mathbb{R}^n)^{{-}1}(E \cap (\Delta^{p-1}_i \times \mathbb{R}^n)), \]
(iii) $\partial E = E \cap (\partial \Delta ^p \times \mathbb {R}^n)$
 .
.
Define face maps $d_i : \mathrm {Mock}(d,\,n)_p \to \mathrm {Mock}(d,\,n)_{p-1}$![]() by restricting $E$
by restricting $E$![]() to the $i$
to the $i$![]() th face $\Delta _i^{p-1} \subset \Delta ^p$
th face $\Delta _i^{p-1} \subset \Delta ^p$![]() , and giving it the induced orientation. Let $\mathrm {Mock}(d) := \operatorname *{colim}\limits _{n \to \infty } \mathrm {Mock}(d,\,n)$
, and giving it the induced orientation. Let $\mathrm {Mock}(d) := \operatorname *{colim}\limits _{n \to \infty } \mathrm {Mock}(d,\,n)$![]() .
.
This semi-simplicial set is Kan, by the same discussion as the paragraph after [Reference Hebestreit, Land, Lück and Randal-Williams20, definition 2.3.1]. The space $|\mathrm {Mock}(d)|$![]() carries a tautological family of manifolds. Let
carries a tautological family of manifolds. Let
and $\pi (d)_p : {E}(d)_p \to \mathrm {Mock}(d)_p \times \Delta ^p$![]() denote the projection map. The maps $\pi (d)_p$
denote the projection map. The maps $\pi (d)_p$![]() assemble to a map
assemble to a map
where ${E}(d) := (\bigsqcup _{p \geq 0} {E}(d)_p){/\sim }$![]() with
with
This family is tautological in the sense that $\pi (d)^{-1}(\{E\} \times \Delta ^p) = \{E\} \times E$![]() . If $\phi : K \to \mathrm {Mock}(d)$
. If $\phi : K \to \mathrm {Mock}(d)$![]() is a semi-simplicial map then we can form the pullback
is a semi-simplicial map then we can form the pullback
this is an (oriented, topological, codimension $-d$![]() ) mock bundle over $|K|$
) mock bundle over $|K|$![]() .
.
We wish to explain why the spaces $|\mathrm {Mock}(d)|$![]() arise as the $d$
arise as the $d$![]() th spaces of an $\Omega$
th spaces of an $\Omega$![]() -spectrum.
-spectrum.
Definition 4.3 Let $\mathrm {Mock}_\partial (d+1,\, n)$![]() have $p$
have $p$![]() -simplices given by a $(d+1+p)$
-simplices given by a $(d+1+p)$![]() -manifold $E^{d+1+p} \subset \Delta ^p \times \mathbb {R}^{n} \times [0,\,\infty )$
-manifold $E^{d+1+p} \subset \Delta ^p \times \mathbb {R}^{n} \times [0,\,\infty )$![]() satisfying (i) and (ii) from definition 4.2 as well as
satisfying (i) and (ii) from definition 4.2 as well as
(i’) $E$
 is topologically transverse to $\Delta ^p \times \mathbb {R}^{n} \times \{0\}$
is topologically transverse to $\Delta ^p \times \mathbb {R}^{n} \times \{0\}$ , and writing $\partial _v E := E \cap \Delta ^p \times \{0\}$
, and writing $\partial _v E := E \cap \Delta ^p \times \{0\}$ there is a $\delta >0$
there is a $\delta >0$ such that $E \cap (\Delta ^p \times \mathbb {R}^{n} \times [0,\,\delta )) = \partial _v E \times [0,\,\delta )$
such that $E \cap (\Delta ^p \times \mathbb {R}^{n} \times [0,\,\delta )) = \partial _v E \times [0,\,\delta )$ , and $\partial E = (E \cap (\partial \Delta ^p \times \mathbb {R}^{n+1})) \cup \partial _v E$
, and $\partial E = (E \cap (\partial \Delta ^p \times \mathbb {R}^{n+1})) \cup \partial _v E$ .
.
Let $\mathrm {Mock}_\partial (d+1) := \operatorname *{colim}\limits _{n \to \infty } \mathrm {Mock}_\partial (d+1,\, n)$![]() .
.
As above this semi-simplicial set is Kan, and carries a tautological family ${E}_\partial (d+1) \to |\mathrm {Mock}_\partial (d+1)|$![]() of $(d+1)$
of $(d+1)$![]() -manifolds with boundary, whose boundaries assemble into a family $\partial _v {E}_\partial (d+1) \to |\mathrm {Mock}_\partial (d+1)|$
-manifolds with boundary, whose boundaries assemble into a family $\partial _v {E}_\partial (d+1) \to |\mathrm {Mock}_\partial (d+1)|$![]() of $d$
of $d$![]() -manifolds. Intersecting with $\Delta ^p \times \mathbb {R}^{n} \times \{0\}$
-manifolds. Intersecting with $\Delta ^p \times \mathbb {R}^{n} \times \{0\}$![]() gives a semi-simplicial map
gives a semi-simplicial map
which is a Kan fibration, and classifies the family $\partial _v {E}_\partial (d+1)$![]() . The fibre of this map over the empty manifold is isomorphic to $\mathrm {Mock}(d+1)$
. The fibre of this map over the empty manifold is isomorphic to $\mathrm {Mock}(d+1)$![]() (via a choice of homeomorphism $(0,\,\infty ) \cong \mathbb {R}$
(via a choice of homeomorphism $(0,\,\infty ) \cong \mathbb {R}$![]() ). One verifies that the connecting map $\partial : \pi _{i}(\mathrm {Mock}(d)) \to \pi _{i-1}(\mathrm {Mock}(d+1))$
). One verifies that the connecting map $\partial : \pi _{i}(\mathrm {Mock}(d)) \to \pi _{i-1}(\mathrm {Mock}(d+1))$![]() is an isomorphism, as both sides are identified with cobordism classes of oriented topological $(d+i)$
is an isomorphism, as both sides are identified with cobordism classes of oriented topological $(d+i)$![]() -manifolds and this map corresponds to the identity map. Thus there are equivalences
-manifolds and this map corresponds to the identity map. Thus there are equivalences
(and $|\mathrm {Mock}_\partial (d+1)| \simeq *$![]() ), and so an $\Omega$
), and so an $\Omega$![]() -spectrum $\mathrm {Mock}$
-spectrum $\mathrm {Mock}$![]() with $\Omega ^{\infty +d} \mathrm {Mock} \simeq |\mathrm {Mock}(d)|$
with $\Omega ^{\infty +d} \mathrm {Mock} \simeq |\mathrm {Mock}(d)|$![]() .
.
4.3 Topological transversality
There is a variant $\mathrm {Mock}'(d,\,n)$![]() of $\mathrm {Mock}(d,\,n)$
of $\mathrm {Mock}(d,\,n)$![]() in which simplices $E \subset \Delta ^p \times \mathbb {R}^n$
in which simplices $E \subset \Delta ^p \times \mathbb {R}^n$![]() are equipped with a choice of tubular neighbourhood (i.e. a $\mathbb {R}^{n-d}$
are equipped with a choice of tubular neighbourhood (i.e. a $\mathbb {R}^{n-d}$![]() -bundle over $E$
-bundle over $E$![]() with a homeomorphism to an open neighbourhood of $E$
with a homeomorphism to an open neighbourhood of $E$![]() , both compatible with the collar structure given by (ii)) and the forgetful and Pontrjagin–Thom collapse maps give a zig-zag
, both compatible with the collar structure given by (ii)) and the forgetful and Pontrjagin–Thom collapse maps give a zig-zag
In the limit as $n\to \infty$![]() the leftwards map is an equivalence (by the stable existence and uniqueness of normal microbundles [Reference Kirby and Siebenmann28, p. 204] and the Kister–Mazur theorem [Reference Kirby and Siebenmann28, p. 159]), and the right-hand side is the space $\Omega ^{\infty +d} \mathrm {MSTop}$
the leftwards map is an equivalence (by the stable existence and uniqueness of normal microbundles [Reference Kirby and Siebenmann28, p. 204] and the Kister–Mazur theorem [Reference Kirby and Siebenmann28, p. 159]), and the right-hand side is the space $\Omega ^{\infty +d} \mathrm {MSTop}$![]() , giving a homotopy class of map
, giving a homotopy class of map
It follows from topological transversality ([Reference Kirby and Siebenmann28, p. 85], [Reference Freedman and Quinn16, §9.6]) that this map is a homotopy equivalence. Furthermore this discussion identifies the spectrum $\mathrm {Mock}$![]() with $\mathrm {MSTop}$
with $\mathrm {MSTop}$![]() , by comparing the analogue of the map (4.1) for manifolds in $\mathbb {R}^{n} \times [0,\,\infty )$
, by comparing the analogue of the map (4.1) for manifolds in $\mathbb {R}^{n} \times [0,\,\infty )$![]() with the path-fibration over $\Omega ^n \mathrm {Th}(\gamma _{n-d} \to BSTop(n-d))$
with the path-fibration over $\Omega ^n \mathrm {Th}(\gamma _{n-d} \to BSTop(n-d))$![]() .
.
4.4 Poincaré mock bundles
If $\tau$![]() is a simplex, $E \subset \tau \times \mathbb {R}^\infty$
is a simplex, $E \subset \tau \times \mathbb {R}^\infty$![]() is a closed subset, and $\sigma$
is a closed subset, and $\sigma$![]() is a face of $\tau$
is a face of $\tau$![]() , write $E_\sigma := (\sigma \times \mathbb {R}^\infty ) \cap E$
, write $E_\sigma := (\sigma \times \mathbb {R}^\infty ) \cap E$![]() . Write $E_{\partial \tau } = \cup _{\sigma < \tau } E_\sigma$
. Write $E_{\partial \tau } = \cup _{\sigma < \tau } E_\sigma$![]() , the union over all proper faces.
, the union over all proper faces.
Definition 4.4 For $d \in \mathbb {Z}$![]() , let $\mathrm {Mock}^P(d)$
, let $\mathrm {Mock}^P(d)$![]() be the semi-simplicial set with $p$
be the semi-simplicial set with $p$![]() -simplices given by pairs of a closed subset $E \subset \Delta ^p \times \mathbb {R}^\infty$
-simplices given by pairs of a closed subset $E \subset \Delta ^p \times \mathbb {R}^\infty$![]() and a singular chain $[E_\sigma ] \in C_{d+|\sigma |}(E_\sigma ;\mathbb {Z})$
and a singular chain $[E_\sigma ] \in C_{d+|\sigma |}(E_\sigma ;\mathbb {Z})$![]() for each face $\sigma$
for each face $\sigma$![]() of $\Delta ^p$
of $\Delta ^p$![]() , such that
, such that
(i) each $E_\sigma$
 is homotopy equivalent to a finite CW-complex,
is homotopy equivalent to a finite CW-complex,(ii) $d[E_\sigma ] = \sum _{i=0}^{|\sigma |} (-1)^i [E_{d_i \sigma }] \in C_{d+|\sigma |-1}(E_\sigma ;\mathbb {Z})$
 , so that in particular $[E_\sigma ]$
, so that in particular $[E_\sigma ]$ is a cycle in $C_{d+|\sigma |}(E_\sigma,\, E_{\partial \sigma };\mathbb {Z})$
is a cycle in $C_{d+|\sigma |}(E_\sigma,\, E_{\partial \sigma };\mathbb {Z})$ ,
,(iii) the maps
\begin{align*} & -{\frown} [E_\sigma] : H^*(E_\sigma ; \mathbb{Z}) \longrightarrow H_{d+|\sigma|-*}(E_\sigma, E_{\partial \sigma}; \mathbb{Z})\\ & -{\frown} d[E_\sigma] : H^*(E_{\partial \sigma} ; \mathbb{Z}) \longrightarrow H_{d-1+|\sigma|-*}(E_{\partial \sigma}; \mathbb{Z}) \end{align*}are isomorphisms.
Define face maps $d_i : \mathrm {Mock}^P(d)_p \to \mathrm {Mock}^P(d)_{p-1}$![]() by restricting $E$
by restricting $E$![]() to the $i$
to the $i$![]() th face $\Delta _i^{p-1} \subset \Delta ^p$
th face $\Delta _i^{p-1} \subset \Delta ^p$![]() , and taking those $[E_\sigma ]$
, and taking those $[E_\sigma ]$![]() with $\sigma \leq \Delta _i^{p-1}$
with $\sigma \leq \Delta _i^{p-1}$![]() .
.
Remark 4.5 It is worth emphasizing that such $E$![]() 's are not Poincaré complexes (or -ads) in the sense of [Reference Wall53, Section 2]—and so in the sense we have used earlier in this paper—as we are only asking for duality with $\mathbb {Z}$
's are not Poincaré complexes (or -ads) in the sense of [Reference Wall53, Section 2]—and so in the sense we have used earlier in this paper—as we are only asking for duality with $\mathbb {Z}$![]() -coefficients rather than with all local coefficients. This is deliberate!
-coefficients rather than with all local coefficients. This is deliberate!
Similarly to the case of mock bundles, the semi-simplicial set $\mathrm {Mock}^P(d)$![]() is Kan (the evident analogues of [Reference Wall52, lemma 1.2, theorem 2.1 Addendum] for duality with $\mathbb {Z}$
is Kan (the evident analogues of [Reference Wall52, lemma 1.2, theorem 2.1 Addendum] for duality with $\mathbb {Z}$![]() -coefficients are used for verifying this) and the space $|\mathrm {Mock}^P(d)|$
-coefficients are used for verifying this) and the space $|\mathrm {Mock}^P(d)|$![]() carries a tautological family, given by defining
carries a tautological family, given by defining
and letting $\pi (d)_p : {E}^P(d)_p \to \mathrm {Mock}^P(d)_p \times \Delta ^p$![]() denote the projection maps, which assemble to $\pi (d) : {E}^P(d) \longrightarrow |\mathrm {Mock}^P(d)|$
denote the projection maps, which assemble to $\pi (d) : {E}^P(d) \longrightarrow |\mathrm {Mock}^P(d)|$![]() . This tautological family can be pulled back along a semi-simplicial map $\phi : K \to \mathrm {Mock}^P(d)$
. This tautological family can be pulled back along a semi-simplicial map $\phi : K \to \mathrm {Mock}^P(d)$![]() to obtain a Poincaré mock bundle over $|K|$
to obtain a Poincaré mock bundle over $|K|$![]() .
.
Just as in the last section, one introduces the evident analogue $\mathrm {Mock}^P_\partial (d+1)$![]() (see the proof of lemma 4.8 below for a definition), to obtain equivalences $\Omega |\mathrm {Mock}^P(d)| \overset {\sim }\to |\mathrm {Mock}^P(d+1)|$
(see the proof of lemma 4.8 below for a definition), to obtain equivalences $\Omega |\mathrm {Mock}^P(d)| \overset {\sim }\to |\mathrm {Mock}^P(d+1)|$![]() and so an associated $\Omega$
and so an associated $\Omega$![]() -spectrum $\mathrm {Mock}^P$
-spectrum $\mathrm {Mock}^P$![]() .
.
Remark 4.6 The spectrum $\mathrm {Mock}^P$![]() is equivalent to Levitt's [Reference Levitt31] Poincaré bordism spectrum. In particular, there is a Pontrjagin–Thom map $\mathrm {Mock}^P \to \mathrm {MSG}$
is equivalent to Levitt's [Reference Levitt31] Poincaré bordism spectrum. In particular, there is a Pontrjagin–Thom map $\mathrm {Mock}^P \to \mathrm {MSG}$![]() but it is not an equivalence (its fibre is the 0-connected cover of quadratic $L$
but it is not an equivalence (its fibre is the 0-connected cover of quadratic $L$![]() -theory, cf. [Reference Ranicki45, remark 19.9], explicated in [Reference Land30, remark 2.3]). The comparison with Levitt's theory uses the fact that the present naive definition of Poincaré complexes still have Spivak normal fibrations [Reference Browder7], which is Levitt's definition of a Poincaré complex.
-theory, cf. [Reference Ranicki45, remark 19.9], explicated in [Reference Land30, remark 2.3]). The comparison with Levitt's theory uses the fact that the present naive definition of Poincaré complexes still have Spivak normal fibrations [Reference Browder7], which is Levitt's definition of a Poincaré complex.
Compact oriented topological manifolds with boundary admit fundamental chains with respect to which they have Poincaré–Lefschetz duality. We may choose such chains by induction over the skeleta of $\mathrm {Mock}(d)$![]() as follows. For each $0$
as follows. For each $0$![]() -simplex $E \in \mathrm {Mock}(d)_0$
-simplex $E \in \mathrm {Mock}(d)_0$![]() we choose a fundamental cycle for the oriented $d$
we choose a fundamental cycle for the oriented $d$![]() -manifold $E$
-manifold $E$![]() . Supposing such chains have been chosen for all simplices of $\mathrm {Mock}(d)$
. Supposing such chains have been chosen for all simplices of $\mathrm {Mock}(d)$![]() of dimension $< p$
of dimension $< p$![]() , then for each $p$
, then for each $p$![]() -simplex $E \in \mathrm {Mock}(d)_p$
-simplex $E \in \mathrm {Mock}(d)_p$![]() we have a fundamental chain
we have a fundamental chain

for $E_{\partial \Delta ^p}$![]() , which is trivial in homology as this is the boundary of $E$
, which is trivial in homology as this is the boundary of $E$![]() so we can take $[E] \in C_{d+p}(E;\mathbb {Z})$
so we can take $[E] \in C_{d+p}(E;\mathbb {Z})$![]() to be a chain with boundary the above, and which also restricts to a fundamental cycle on any closed components of $E$
to be a chain with boundary the above, and which also restricts to a fundamental cycle on any closed components of $E$![]() . This gives (using also that compact topological manifolds are homotopy equivalent to finite CW-complexes) a map $\mathrm {Mock}(d) \longrightarrow \mathrm {Mock}^P(d)$
. This gives (using also that compact topological manifolds are homotopy equivalent to finite CW-complexes) a map $\mathrm {Mock}(d) \longrightarrow \mathrm {Mock}^P(d)$![]() , unique up to homotopy because at each stage we have chosen a top-dimensional chain of $E$
, unique up to homotopy because at each stage we have chosen a top-dimensional chain of $E$![]() which is unique up to a boundary. These maps assemble into a map of spectra
which is unique up to a boundary. These maps assemble into a map of spectra
and hence give a map $\mathrm {MSTop} \to \mathrm {Mock}^P$![]() .
.
4.5 Categorical preliminaries
In subsections 4.5–4.8 we will make extensive use of the definitions and constructions of [Reference Calmès, Dotto, Harpaz, Hebestreit, Land, Moi, Nardin, Nikolaus and Steimle10–Reference Calmès, Dotto, Harpaz, Hebestreit, Land, Moi, Nardin, Nikolaus and Steimle12]. We will give references for all results that we use, but the reader will need to be familiar with the general set-up of those papers, which we will not review.
For a semi-simplicial set $K$![]() , we will often work in the stable $\infty$
, we will often work in the stable $\infty$![]() -category
-category
of functors from the (opposite of the) poset of simplices of $K$![]() to the derived $\infty$
to the derived $\infty$![]() -category $\mathcal {D}^p(\mathbb {Z})$
-category $\mathcal {D}^p(\mathbb {Z})$![]() of perfect $\mathbb {Z}$
of perfect $\mathbb {Z}$![]() -modules. On $\mathcal {D}^p(\mathbb {Z})$
-modules. On $\mathcal {D}^p(\mathbb {Z})$![]() we have the symmetric hermitian structure $\unicode{x03D8} = \unicode{x03D8} ^s$
we have the symmetric hermitian structure $\unicode{x03D8} = \unicode{x03D8} ^s$![]() given by $\unicode{x03D8} (X) := \mathrm {Hom}_\mathbb {Z}(X \otimes X,\, \mathbb {Z})^{hC_2}$
given by $\unicode{x03D8} (X) := \mathrm {Hom}_\mathbb {Z}(X \otimes X,\, \mathbb {Z})^{hC_2}$![]() , whose underlying bilinear functor is $B(X,\, Y) = \mathrm {Hom}_{\mathbb {Z}}(X \otimes Y,\, \mathbb {Z})$
, whose underlying bilinear functor is $B(X,\, Y) = \mathrm {Hom}_{\mathbb {Z}}(X \otimes Y,\, \mathbb {Z})$![]() which is perfect with associated duality $D(X) = \mathrm {Hom}_\mathbb {Z}(X,\, \mathbb {Z})$
which is perfect with associated duality $D(X) = \mathrm {Hom}_\mathbb {Z}(X,\, \mathbb {Z})$![]() . The discussion in [Reference Calmès, Dotto, Harpaz, Hebestreit, Land, Moi, Nardin, Nikolaus and Steimle12, construction 6.3.1] shows that $\unicode{x03D8}$
. The discussion in [Reference Calmès, Dotto, Harpaz, Hebestreit, Land, Moi, Nardin, Nikolaus and Steimle12, construction 6.3.1] shows that $\unicode{x03D8}$![]() induces a hermitian functor $\unicode{x03D8} _K$
induces a hermitian functor $\unicode{x03D8} _K$![]() on the cotensoring $\mathsf {C}$
on the cotensoring $\mathsf {C}$![]() , and writing $\underline {\mathbb {Z}}$
, and writing $\underline {\mathbb {Z}}$![]() for the constant functor we can express this as
for the constant functor we can express this as
where the tensor product in $\mathsf {C}$![]() is formed objectwise. By [Reference Calmès, Dotto, Harpaz, Hebestreit, Land, Moi, Nardin, Nikolaus and Steimle12, proposition 6.3.2] its underlying bilinear functor is $B_K(X,\,Y) = \mathrm {Hom}_\mathsf {C}(X \otimes Y,\, \underline {\mathbb {Z}})$
is formed objectwise. By [Reference Calmès, Dotto, Harpaz, Hebestreit, Land, Moi, Nardin, Nikolaus and Steimle12, proposition 6.3.2] its underlying bilinear functor is $B_K(X,\,Y) = \mathrm {Hom}_\mathsf {C}(X \otimes Y,\, \underline {\mathbb {Z}})$![]() , and as $((\mathsf {Simp}(K)^{op})_{\sigma /})^{op}$
, and as $((\mathsf {Simp}(K)^{op})_{\sigma /})^{op}$![]() is finite (it is the poset of simplices of a fixed simplex $\sigma$
is finite (it is the poset of simplices of a fixed simplex $\sigma$![]() ) this bilinear functor is nondegenerate with associated duality
) this bilinear functor is nondegenerate with associated duality
It is elementary to check that this duality is perfect (alternatively, observe that this may be checked for each simplex $K$![]() , and appeal to [Reference Calmès, Dotto, Harpaz, Hebestreit, Land, Moi, Nardin, Nikolaus and Steimle12, proposition 6.6.1] for the finite simplicial complex given by a single simplex), making $(\mathsf {C},\, \unicode{x03D8} _K)$
, and appeal to [Reference Calmès, Dotto, Harpaz, Hebestreit, Land, Moi, Nardin, Nikolaus and Steimle12, proposition 6.6.1] for the finite simplicial complex given by a single simplex), making $(\mathsf {C},\, \unicode{x03D8} _K)$![]() a Poincaré category.
a Poincaré category.
4.6 The Ranicki orientation
The Ranicki orientation is a certain map of spectra $\sigma : \mathrm {MSTop} \to \mathrm {L}^s(\mathbb {Z})$![]() . Its construction was outlined in [Reference Ranicki42, proposition 15.8] (for PL, rather than topological, manifolds), but the first rigorous implementation seems to not have been until [Reference Laures and McClure32], where it is constructed as a map of $E_1$
. Its construction was outlined in [Reference Ranicki42, proposition 15.8] (for PL, rather than topological, manifolds), but the first rigorous implementation seems to not have been until [Reference Laures and McClure32], where it is constructed as a map of $E_1$![]() -rings. We will give our own construction of this map, intuitively the same as Ranicki's but using the definition of the symmetric $L$
-rings. We will give our own construction of this map, intuitively the same as Ranicki's but using the definition of the symmetric $L$![]() -theory spectrum from [Reference Calmès, Dotto, Harpaz, Hebestreit, Land, Moi, Nardin, Nikolaus and Steimle10, section 4.4]. In fact we will construct a map $\sigma ^P : \mathrm {Mock}^P \to \mathrm {L}^s(\mathbb {Z})$
-theory spectrum from [Reference Calmès, Dotto, Harpaz, Hebestreit, Land, Moi, Nardin, Nikolaus and Steimle10, section 4.4]. In fact we will construct a map $\sigma ^P : \mathrm {Mock}^P \to \mathrm {L}^s(\mathbb {Z})$![]() , which may be precomposed with $\mathrm {MSTop} \to \mathrm {Mock}^P$
, which may be precomposed with $\mathrm {MSTop} \to \mathrm {Mock}^P$![]() to obtain $\sigma$
to obtain $\sigma$![]() .
.
For any semi-simplicial set $K$![]() and semi-simplicial map $\phi : K \to \mathrm {Mock}^P(d)$
and semi-simplicial map $\phi : K \to \mathrm {Mock}^P(d)$![]() we can form the pullback
we can form the pullback
a Poincaré mock bundle over $|K|$![]() . For a simplex $\sigma$
. For a simplex $\sigma$![]() of $K$
of $K$![]() we write $E_\sigma := f(\sigma )$
we write $E_\sigma := f(\sigma )$![]() . This defines a functor
. This defines a functor
by $C(\sigma ) := C^*(E_\sigma ; \mathbb {Z})$![]() , i.e. an object of the category $\mathsf {C}$
, i.e. an object of the category $\mathsf {C}$![]() described above.
described above.
We first explain how $C$![]() has the structure of a Poincaré object in $(\mathsf {C},\, \unicode{x03D8} ^{[-d]}_K)$
has the structure of a Poincaré object in $(\mathsf {C},\, \unicode{x03D8} ^{[-d]}_K)$![]() .
.
Lemma 4.7 There is a canonical morphism $[{E}] : C \to S^{-d} \otimes \underline {\mathbb {Z}},$![]() a ‘fibrewise fundamental chain’.
a ‘fibrewise fundamental chain’.
Proof. By adjunction a morphism as indicated is the same as a morphism
in $\mathcal {D}^p(\mathbb {Z})$![]() , which is a morphism $S^d \to \operatorname *{holim}\limits _{\sigma \in \mathsf {Simp}(K)^{op}} \mathrm {Hom}_\mathbb {Z}(C(\sigma ),\, \mathbb {Z})$
, which is a morphism $S^d \to \operatorname *{holim}\limits _{\sigma \in \mathsf {Simp}(K)^{op}} \mathrm {Hom}_\mathbb {Z}(C(\sigma ),\, \mathbb {Z})$![]() . As $C(\sigma ) = C^*(E_\sigma ; \mathbb {Z}) = \mathrm {Hom}(C_*(E_\sigma ;\mathbb {Z}) ,\, \mathbb {Z})$
. As $C(\sigma ) = C^*(E_\sigma ; \mathbb {Z}) = \mathrm {Hom}(C_*(E_\sigma ;\mathbb {Z}) ,\, \mathbb {Z})$![]() and $C_*(E_\sigma ;\mathbb {Z})$
and $C_*(E_\sigma ;\mathbb {Z})$![]() is perfect, this is equivalent to a morphism
is perfect, this is equivalent to a morphism
The data of the compatible fundamental chains $\{[E_\sigma ]\}_{\sigma \in K}$![]() precisely gives such a $d$
precisely gives such a $d$![]() -cycle in this homotopy limit.
-cycle in this homotopy limit.
Using this morphism we may form $q : C \otimes C \overset {-\smile -}\to C \overset {[{E}]}\to S^{-d} \otimes \underline {\mathbb {Z}}$![]() , which, as the multiplication on $C$
, which, as the multiplication on $C$![]() is commutative, determines a Hermitian form
is commutative, determines a Hermitian form
To see that this is nondegenerate, note that its adjoint $q_\sharp : C \to S^{-d} \otimes D_K(C)$![]() evaluated at $\sigma$
evaluated at $\sigma$![]() is the map
is the map
given by cap product with the chain $[E_\sigma ]$![]() and evaluation. There is an equivalence $C_*(E_\tau ;\mathbb {Z}) \overset {\sim }\to \mathrm {Hom}_\mathbb {Z}(C^*(E_\tau ;\mathbb {Z}),\, \mathbb {Z})$
and evaluation. There is an equivalence $C_*(E_\tau ;\mathbb {Z}) \overset {\sim }\to \mathrm {Hom}_\mathbb {Z}(C^*(E_\tau ;\mathbb {Z}),\, \mathbb {Z})$![]() given by evaluation, which identifies this map with the map
given by evaluation, which identifies this map with the map
given by cap product with the chain $[E_\sigma ]$![]() , and this is an equivalence by the definition of Poincaré mock bundle. Thus $(C,\, q)$
, and this is an equivalence by the definition of Poincaré mock bundle. Thus $(C,\, q)$![]() is indeed a Poincaré object in $(\mathsf {C},\, \unicode{x03D8} ^{[-d]}_K)$
is indeed a Poincaré object in $(\mathsf {C},\, \unicode{x03D8} ^{[-d]}_K)$![]() .
.
Let us briefly recall how the $L$![]() -theory space $\mathcal {L}(\mathbb {Z},\, \unicode{x03D8} ^{[-d]})$
-theory space $\mathcal {L}(\mathbb {Z},\, \unicode{x03D8} ^{[-d]})$![]() is defined in [Reference Calmès, Dotto, Harpaz, Hebestreit, Land, Moi, Nardin, Nikolaus and Steimle10, section 4.4]. It is the geometric realization of the simplicial space with $p$
is defined in [Reference Calmès, Dotto, Harpaz, Hebestreit, Land, Moi, Nardin, Nikolaus and Steimle10, section 4.4]. It is the geometric realization of the simplicial space with $p$![]() -simplices given by the space(=$\infty$
-simplices given by the space(=$\infty$![]() -groupoid) of Poincaré objects in the Poincaré category $\rho _p(\mathcal {D}^p(\mathbb {Z}),\, \unicode{x03D8} ^{[-d]}) := (\mathsf {Fun}(\mathsf {Simp}(\Delta ^p)^{op},\, \mathcal {D}^p(\mathbb {Z})),\, \unicode{x03D8} ^{[-d]}_{\Delta ^p})$
-groupoid) of Poincaré objects in the Poincaré category $\rho _p(\mathcal {D}^p(\mathbb {Z}),\, \unicode{x03D8} ^{[-d]}) := (\mathsf {Fun}(\mathsf {Simp}(\Delta ^p)^{op},\, \mathcal {D}^p(\mathbb {Z})),\, \unicode{x03D8} ^{[-d]}_{\Delta ^p})$![]() .
.
We may then apply the following ‘coassembly’ construction to $(C,\, q)$![]() . For each $p$
. For each $p$![]() -simplex $\sigma : \Delta ^p \to K$
-simplex $\sigma : \Delta ^p \to K$![]() we obtain a Poincaré object in $\rho _p(\mathcal {D}^p(\mathbb {Z}),\, \unicode{x03D8} ^{[-d]})$
we obtain a Poincaré object in $\rho _p(\mathcal {D}^p(\mathbb {Z}),\, \unicode{x03D8} ^{[-d]})$![]() by pullback: the underlying object is the functor
by pullback: the underlying object is the functor
given by restriction of $C$![]() , and it is made into a Poincaré object via the restriction $\sigma ^*q$
, and it is made into a Poincaré object via the restriction $\sigma ^*q$![]() of $q$
of $q$![]() . Applying this construction levelwise defines a map
. Applying this construction levelwise defines a map
We call this the family signature of the Poincaré mock bundle $\pi : E \to |K|$![]() . In particular, for the universal example $K=\mathrm {Mock}^P(d)$
. In particular, for the universal example $K=\mathrm {Mock}^P(d)$![]() with associated Poincaré object $(C_d,\, q_d)$
with associated Poincaré object $(C_d,\, q_d)$![]() this construction defines a map
this construction defines a map
The symmetric $L$![]() -theory spectrum $\mathrm {L}^s(\mathbb {Z})$
-theory spectrum $\mathrm {L}^s(\mathbb {Z})$![]() as described in the discussion after [Reference Calmès, Dotto, Harpaz, Hebestreit, Land, Moi, Nardin, Nikolaus and Steimle10, corollary 4.4.5] has $(-d)$
as described in the discussion after [Reference Calmès, Dotto, Harpaz, Hebestreit, Land, Moi, Nardin, Nikolaus and Steimle10, corollary 4.4.5] has $(-d)$![]() th space equivalent to $\mathcal {L}(\mathbb {Z},\, \unicode{x03D8} ^{[-d]})$
th space equivalent to $\mathcal {L}(\mathbb {Z},\, \unicode{x03D8} ^{[-d]})$![]() by [Reference Calmès, Dotto, Harpaz, Hebestreit, Land, Moi, Nardin, Nikolaus and Steimle10, corollary 4.4.5], and the spectrum $\mathrm {Mock}^P$
by [Reference Calmès, Dotto, Harpaz, Hebestreit, Land, Moi, Nardin, Nikolaus and Steimle10, corollary 4.4.5], and the spectrum $\mathrm {Mock}^P$![]() has $(-d)$
has $(-d)$![]() -th space $|\mathrm {Mock}^P(d)|$
-th space $|\mathrm {Mock}^P(d)|$![]() , so the maps $\Phi _{d}$
, so the maps $\Phi _{d}$![]() can in principle arise from a map of spectra. They do:
can in principle arise from a map of spectra. They do:
Lemma 4.8 The $\Phi _d$![]() arise as $\Omega ^{\infty +d}\sigma ^P$
arise as $\Omega ^{\infty +d}\sigma ^P$![]() for a spectrum map $\sigma ^P : \mathrm {Mock}^P \to \mathrm {L}^s(\mathbb {Z})$
for a spectrum map $\sigma ^P : \mathrm {Mock}^P \to \mathrm {L}^s(\mathbb {Z})$![]() .
.
We define the composition
to be the Ranicki orientation. The construction is conceptually the same as the map constructed in [Reference Laures and McClure32], though implemented differently. It is also conceptually the same as the maps constructed in [Reference Ranicki42, proposition 15.7], [Reference Ranicki43, p. 289], [Reference Ranicki45, proposition 16.1] and [Reference Kühl, Macko and Mole26, proposition 7.10 (1)], though see remark 4.9.
Proof. We must establish a compatibility between the $\Phi _d$![]() 's, and to do so we give a precise definition of $\mathrm {Mock}_\partial ^P(d+1)$
's, and to do so we give a precise definition of $\mathrm {Mock}_\partial ^P(d+1)$![]() . For a simplex $\tau$
. For a simplex $\tau$![]() , a face $\sigma \leq \tau$
, a face $\sigma \leq \tau$![]() , and a closed subset $E \subset \tau \times \mathbb {R}^\infty \times [0,\,\infty )$
, and a closed subset $E \subset \tau \times \mathbb {R}^\infty \times [0,\,\infty )$![]() , write $\partial _v E_\sigma := (\sigma \times \mathbb {R}^\infty \times \{0\}) \cap E$
, write $\partial _v E_\sigma := (\sigma \times \mathbb {R}^\infty \times \{0\}) \cap E$![]() . Let $\mathrm {Mock}_\partial ^P(d+1)$
. Let $\mathrm {Mock}_\partial ^P(d+1)$![]() have $p$
have $p$![]() -simplices given by a closed subset $E \subset \Delta ^p \times \mathbb {R}^{\infty } \times [0,\,\infty )$
-simplices given by a closed subset $E \subset \Delta ^p \times \mathbb {R}^{\infty } \times [0,\,\infty )$![]() and a singular chain $[E_\sigma ] \in C_{d+1+|\sigma |}(E_\sigma ;\mathbb {Z})$
and a singular chain $[E_\sigma ] \in C_{d+1+|\sigma |}(E_\sigma ;\mathbb {Z})$![]() for each face $\sigma$
for each face $\sigma$![]() of $\Delta ^p$
of $\Delta ^p$![]() , such that
, such that
(i’) each $E_\sigma$
 and $\partial _v E_\sigma$
and $\partial _v E_\sigma$ is homotopy equivalent to a finite CW-complex,
is homotopy equivalent to a finite CW-complex,(ii’) the chain $[\partial _v E_\sigma ] := d[E_\sigma ] - \sum _{i=0}^{|\sigma |} [E_{d_i \sigma }] \in C_{d+|\sigma |}(E_\sigma ; \mathbb {Z})$
 lies in the subgroup $C_{d+|\sigma |}(\partial _v E_\sigma ; \mathbb {Z})$
lies in the subgroup $C_{d+|\sigma |}(\partial _v E_\sigma ; \mathbb {Z})$ , so $[E_\sigma ]$
, so $[E_\sigma ]$ is a cycle in $C_{d+1+|\sigma |}(E_\sigma,\, \partial _v E_\sigma \cup E_{\partial \sigma } ; \mathbb {Z})$
is a cycle in $C_{d+1+|\sigma |}(E_\sigma,\, \partial _v E_\sigma \cup E_{\partial \sigma } ; \mathbb {Z})$ ,
,(iii’) the maps
\begin{align*} & -{\frown} [E_\sigma] : H^*(E_\sigma ; \mathbb{Z}) \longrightarrow H_{d+1+|\sigma|-*}(E_\sigma, \partial_v E_\sigma \cup E_{\partial \sigma}; \mathbb{Z})\\ & -{\frown} d[E_\sigma] : H^*(\partial_v E_\sigma \cup E_{\partial \sigma} ; \mathbb{Z}) \longrightarrow H_{d+|\sigma|-*}(\partial_v E_\sigma \cup E_{\partial \sigma}; \mathbb{Z}) \end{align*}are isomorphisms.
Assigning to $(E,\, \{[E_\sigma ]\})$![]() the data $(\partial _v E,\, \{[\partial _v E_\sigma ]\})$
the data $(\partial _v E,\, \{[\partial _v E_\sigma ]\})$![]() , where the $[\partial _v E_\sigma ]$
, where the $[\partial _v E_\sigma ]$![]() are given by (ii’), defines a semi-simplicial map
are given by (ii’), defines a semi-simplicial map
which is furthermore a Kan fibration. (The key calculation is to show that the maps $- \frown [\partial _v E_\sigma ] : H^*(\partial _v E_\sigma ; \mathbb {Z}) \to H_{d+|\sigma |-*}(\partial _v E_\sigma,\, \partial _v E_{\partial \sigma };\mathbb {Z})$![]() , and $- \frown d[\partial _v E_\sigma ] :H^*(\partial _v E_{\partial \sigma };\mathbb {Z}) \to H_{d-1+|\sigma |-*}(\partial _v E_{\partial \sigma };\mathbb {Z})$
, and $- \frown d[\partial _v E_\sigma ] :H^*(\partial _v E_{\partial \sigma };\mathbb {Z}) \to H_{d-1+|\sigma |-*}(\partial _v E_{\partial \sigma };\mathbb {Z})$![]() are isomorphisms, which follows by repeatedly using [Reference Wall52, lemma 1.2 and theorem 2.1 Addendum].) The space $|\mathrm {Mock}_\partial ^P(d+1)|$
are isomorphisms, which follows by repeatedly using [Reference Wall52, lemma 1.2 and theorem 2.1 Addendum].) The space $|\mathrm {Mock}_\partial ^P(d+1)|$![]() carries a tautological family ${E}^P_\partial (d+1)$
carries a tautological family ${E}^P_\partial (d+1)$![]() and the map $res$
and the map $res$![]() classifies the associated family $\partial _v {E}^P_\partial (d+1)$
classifies the associated family $\partial _v {E}^P_\partial (d+1)$![]() given by intersecting with $\mathbb {R}^\infty \times \{0\}$
given by intersecting with $\mathbb {R}^\infty \times \{0\}$![]() . The fibre of the map $res$
. The fibre of the map $res$![]() over the basepoint (which is the empty space) is isomorphic to $\mathrm {Mock}^P(d+1)$
over the basepoint (which is the empty space) is isomorphic to $\mathrm {Mock}^P(d+1)$![]() (via a choice of homeomorphism $(0,\,\infty ) \cong \mathbb {R}$
(via a choice of homeomorphism $(0,\,\infty ) \cong \mathbb {R}$![]() ).
).
We wish to establish a commutative diagram

in which the rows are homotopy fibre sequences. The lower sequence comes from the metabolic Poincaré–Verdier sequence [Reference Calmès, Dotto, Harpaz, Hebestreit, Land, Moi, Nardin, Nikolaus and Steimle10, example 1.2.5] and the fact that $\mathcal {L}(-)$![]() is Verdier-localizing and bordism-invariant [Reference Calmès, Dotto, Harpaz, Hebestreit, Land, Moi, Nardin, Nikolaus and Steimle10, theorem 4.4.2]. The two middle spaces are contractible so this will give the desired compatibility.
is Verdier-localizing and bordism-invariant [Reference Calmès, Dotto, Harpaz, Hebestreit, Land, Moi, Nardin, Nikolaus and Steimle10, theorem 4.4.2]. The two middle spaces are contractible so this will give the desired compatibility.
To obtain the middle vertical map in this diagram observe that $\mathrm {Coass}(C_d) \circ |res|$![]() is the construction from above applied with $K = \mathrm {Mock}_{\partial }^P(d+1)$
is the construction from above applied with $K = \mathrm {Mock}_{\partial }^P(d+1)$![]() and $\phi =res$
and $\phi =res$![]() , the map that classifies the family $\partial _v {E}^P_\partial (d+1) \to |\mathrm {Mock}_\partial ^P(d+1)|$
, the map that classifies the family $\partial _v {E}^P_\partial (d+1) \to |\mathrm {Mock}_\partial ^P(d+1)|$![]() . Recall that Poincaré objects in $\mathrm {Met}(\mathcal {D}^p(\mathbb {Z}),\, \unicode{x03D8} ^{[-d]})$
. Recall that Poincaré objects in $\mathrm {Met}(\mathcal {D}^p(\mathbb {Z}),\, \unicode{x03D8} ^{[-d]})$![]() encode Poincaré objects in $(\mathcal {D}^p(\mathbb {Z}),\, \unicode{x03D8} ^{[-d]})$
encode Poincaré objects in $(\mathcal {D}^p(\mathbb {Z}),\, \unicode{x03D8} ^{[-d]})$![]() equipped with a lagrangian, so we must equip the Poincaré object $(res)^*(C_d,\, q_d)$
equipped with a lagrangian, so we must equip the Poincaré object $(res)^*(C_d,\, q_d)$![]() associated to $\partial _v {E}^P_\partial (d+1) \to |\mathrm {Mock}_\partial ^P(d+1)|=|K|$
associated to $\partial _v {E}^P_\partial (d+1) \to |\mathrm {Mock}_\partial ^P(d+1)|=|K|$![]() with a lagrangian.
with a lagrangian.
This of course comes from the fact that $\partial _v {E}^P_\partial (d+1)$![]() is canonically the boundary of the family ${E}_\partial ^P(d+1) \to |\mathrm {Mock}_\partial ^P(d+1)|$
is canonically the boundary of the family ${E}_\partial ^P(d+1) \to |\mathrm {Mock}_\partial ^P(d+1)|$![]() . Define a morphism $f : L \to (res)^*C_d$
. Define a morphism $f : L \to (res)^*C_d$![]() in $\mathsf {C}$
in $\mathsf {C}$![]() by the restriction map
by the restriction map
and choose the nullhomotopy of $f^*q_d$![]() given by the nullhomotopy of the composition $L \overset {f}\to (res)^*C_d \overset {[\partial _v {E}^P_\partial (d+1)]}\to S^{-d} \otimes \underline {\mathbb {Z}}$
given by the nullhomotopy of the composition $L \overset {f}\to (res)^*C_d \overset {[\partial _v {E}^P_\partial (d+1)]}\to S^{-d} \otimes \underline {\mathbb {Z}}$![]() provided by a fibrewise fundamental chain $[{E}^P_\partial (d+1)]$
provided by a fibrewise fundamental chain $[{E}^P_\partial (d+1)]$![]() of the family ${E}^P_\partial (d+1) \to |\mathrm {Mock}^P_\partial (d+1)|$
of the family ${E}^P_\partial (d+1) \to |\mathrm {Mock}^P_\partial (d+1)|$![]() extending $[\partial _v {E}^P_\partial (d+1)]$
extending $[\partial _v {E}^P_\partial (d+1)]$![]() , constructed as in lemma 4.7. This gives the middle vertical map, and as we chose a fundamental chain, on $(d+1)$
, constructed as in lemma 4.7. This gives the middle vertical map, and as we chose a fundamental chain, on $(d+1)$![]() -manifolds without boundary it restricts to a map homotopic to $\mathrm {Coass}(C_{d+1})$
-manifolds without boundary it restricts to a map homotopic to $\mathrm {Coass}(C_{d+1})$![]() .
.
4.7 The map $inc$
Recall that $\mathcal {L}(\mathbb {Z},\, \unicode{x03D8} ^{[-d]})$![]() is defined as the geometric realization of the simplicial space $[p] \mapsto \mathrm {Pn} \rho _p(\mathcal {D}^p(\mathbb {Z}),\, \unicode{x03D8} ^{[-d]})$
is defined as the geometric realization of the simplicial space $[p] \mapsto \mathrm {Pn} \rho _p(\mathcal {D}^p(\mathbb {Z}),\, \unicode{x03D8} ^{[-d]})$![]() , whose space of 0-simplices is $\mathrm {Pn}(\mathcal {D}^p(\mathbb {Z}),\, \unicode{x03D8} ^{[-d]})$
, whose space of 0-simplices is $\mathrm {Pn}(\mathcal {D}^p(\mathbb {Z}),\, \unicode{x03D8} ^{[-d]})$![]() , the space(=$\infty$
, the space(=$\infty$![]() -groupoid) of Poincaré objects in the Poincaré category $(\mathcal {D}^p(\mathbb {Z}),\, \unicode{x03D8} ^{[-d]})$
-groupoid) of Poincaré objects in the Poincaré category $(\mathcal {D}^p(\mathbb {Z}),\, \unicode{x03D8} ^{[-d]})$![]() .
.
Suppose first that $(H,\, \lambda )$![]() is a free $\mathbb {Z}$
is a free $\mathbb {Z}$![]() -module $H$
-module $H$![]() with a $(-1)^n$
with a $(-1)^n$![]() -symmetric bilinear form $\lambda : H \otimes H \to \mathbb {Z}$
-symmetric bilinear form $\lambda : H \otimes H \to \mathbb {Z}$![]() which is nondegenerate, i.e. the adjoint $\lambda ^\mathrm {ad} : H \to \mathrm {Hom}_\mathbb {Z}(H,\, \mathbb {Z})$
which is nondegenerate, i.e. the adjoint $\lambda ^\mathrm {ad} : H \to \mathrm {Hom}_\mathbb {Z}(H,\, \mathbb {Z})$![]() is an isomorphism. Then there is a Poincaré object in $(\mathcal {D}^p(\mathbb {Z}),\, \unicode{x03D8} ^{[-2n]})$
is an isomorphism. Then there is a Poincaré object in $(\mathcal {D}^p(\mathbb {Z}),\, \unicode{x03D8} ^{[-2n]})$![]() given by $H[-n]$
given by $H[-n]$![]() equipped with the symmetric form
equipped with the symmetric form
As $H[-n]$![]() is concentrated in a single degree, the space of automorphisms of $(H[-n],\, q_\lambda )$
is concentrated in a single degree, the space of automorphisms of $(H[-n],\, q_\lambda )$![]() in the $\infty$
in the $\infty$![]() -groupoid $\mathrm {Pn}(\mathcal {D}^p(\mathbb {Z}),\, \unicode{x03D8} ^{[-2n]})$
-groupoid $\mathrm {Pn}(\mathcal {D}^p(\mathbb {Z}),\, \unicode{x03D8} ^{[-2n]})$![]() is homotopy-discrete, and is equivalent to $\mathrm {Aut}(H,\, \lambda )$
is homotopy-discrete, and is equivalent to $\mathrm {Aut}(H,\, \lambda )$![]() : thus the path-component of $(H[-n],\, q_\lambda )$
: thus the path-component of $(H[-n],\, q_\lambda )$![]() in $\mathrm {Pn}(\mathcal {D}^p(\mathbb {Z}),\, \unicode{x03D8} ^{[-2n]})$
in $\mathrm {Pn}(\mathcal {D}^p(\mathbb {Z}),\, \unicode{x03D8} ^{[-2n]})$![]() is equivalent to $B\mathrm {Aut}(H,\, \lambda )$
is equivalent to $B\mathrm {Aut}(H,\, \lambda )$![]() . This yields a map
. This yields a map
Suppose now that $(T,\, \ell )$![]() is a finite $\mathbb {Z}$
is a finite $\mathbb {Z}$![]() -module $T$
-module $T$![]() with a $(-1)^n$
with a $(-1)^n$![]() -symmetric linking form $\ell : T \otimes T \to \mathbb {Q}/\mathbb {Z}$
-symmetric linking form $\ell : T \otimes T \to \mathbb {Q}/\mathbb {Z}$![]() which is nondegenerate, i.e. the adjoint $\ell ^\mathrm {ad} : T \to \mathrm {Hom}_\mathbb {Z}(T,\, \mathbb {Q}/\mathbb {Z})$
which is nondegenerate, i.e. the adjoint $\ell ^\mathrm {ad} : T \to \mathrm {Hom}_\mathbb {Z}(T,\, \mathbb {Q}/\mathbb {Z})$![]() is an isomorphism, then there is a Poincaré object in $(\mathcal {D}^p(\mathbb {Z}),\, \unicode{x03D8} ^{[-(2n-1)]})$
is an isomorphism, then there is a Poincaré object in $(\mathcal {D}^p(\mathbb {Z}),\, \unicode{x03D8} ^{[-(2n-1)]})$![]() given by $T[-n]$
given by $T[-n]$![]() equipped with the symmetric form
equipped with the symmetric form
where the first map is the truncation and the last is the universal Bockstein. (Before now we have been working in $\mathcal {D}^p(\mathbb {Z})$![]() and all tensor products have been implicitly derived: here we indicate that the first is derived and the second is not.) Again, as $T[-n]$
and all tensor products have been implicitly derived: here we indicate that the first is derived and the second is not.) Again, as $T[-n]$![]() is concentrated in a single degree the space of automorphisms of $(T[-n],\, q_\ell )$
is concentrated in a single degree the space of automorphisms of $(T[-n],\, q_\ell )$![]() is equivalent to the discrete group $\mathrm {Aut}(T,\, \ell )$
is equivalent to the discrete group $\mathrm {Aut}(T,\, \ell )$![]() , which as above yields a map
, which as above yields a map
4.8 Surgery above the middle dimension
Suppose now that $\pi : {E} \to |K|$![]() is an oriented Poincaré mock bundle of dimension $d$
is an oriented Poincaré mock bundle of dimension $d$![]() which has the property that the inclusions $E_\tau \subset E_\sigma$
which has the property that the inclusions $E_\tau \subset E_\sigma$![]() are $\mathbb {Z}$
are $\mathbb {Z}$![]() -homology equivalences whenever $\tau \subset \sigma$
-homology equivalences whenever $\tau \subset \sigma$![]() . (For example, $\pi$
. (For example, $\pi$![]() could be a block bundle.) Then the associated functor
could be a block bundle.) Then the associated functor
has the property that it sends each morphism to an equivalence. Write $\mathsf {C}_{loc} \subset \mathsf {C}$![]() for the full subcategory of those functors sending each morphism to an equivalence. It inherits a hermitian structure $\unicode{x03D8} _{K, loc}$
for the full subcategory of those functors sending each morphism to an equivalence. It inherits a hermitian structure $\unicode{x03D8} _{K, loc}$![]() from $\unicode{x03D8} _{K}$
from $\unicode{x03D8} _{K}$![]() by restriction, and the associated bilinear functor is still perfect, with duality $D_{K, loc}$
by restriction, and the associated bilinear functor is still perfect, with duality $D_{K, loc}$![]() still given by the formula for $D_K$
still given by the formula for $D_K$![]() in (4.2), as this duality preserves the subcategory $\mathsf {C}_{loc}$
in (4.2), as this duality preserves the subcategory $\mathsf {C}_{loc}$![]() . Furthermore, on this subcategory the duality simplifies to
. Furthermore, on this subcategory the duality simplifies to
because the homotopy limit in (4.2) is over a (homotopically) constant diagram.
We will make use of this to do algebraic surgery on $(C,\, q) \in (\mathsf {C}_{loc},\, \unicode{x03D8} _{K, loc}^{[-d]})$![]() , using the conveniently-packaged result of [Reference Calmès, Dotto, Harpaz, Hebestreit, Land, Moi, Nardin, Nikolaus and Steimle11, section 1.3].
, using the conveniently-packaged result of [Reference Calmès, Dotto, Harpaz, Hebestreit, Land, Moi, Nardin, Nikolaus and Steimle11, section 1.3].
If $d=2n$![]() then we consider the usual $t$
then we consider the usual $t$![]() -structure on $\mathcal {D}^p(\mathbb {Z})$
-structure on $\mathcal {D}^p(\mathbb {Z})$![]() . The duality $D(-) = \mathrm {Hom}_\mathbb {Z}(-,\, \mathbb {Z})$
. The duality $D(-) = \mathrm {Hom}_\mathbb {Z}(-,\, \mathbb {Z})$![]() associated to the symmetric Poincaré structure satisfies $D(\mathcal {D}^p(\mathbb {Z})_{\leq 0}) \subset \mathcal {D}^p(\mathbb {Z})_{\geq -1}$
associated to the symmetric Poincaré structure satisfies $D(\mathcal {D}^p(\mathbb {Z})_{\leq 0}) \subset \mathcal {D}^p(\mathbb {Z})_{\geq -1}$![]() , as $\mathbb {Z}$
, as $\mathbb {Z}$![]() has global dimension 1, as well as $D(\mathcal {D}^p(\mathbb {Z})_{\geq 0}) \subset \mathcal {D}^p(\mathbb {Z})_{\leq 0}$
has global dimension 1, as well as $D(\mathcal {D}^p(\mathbb {Z})_{\geq 0}) \subset \mathcal {D}^p(\mathbb {Z})_{\leq 0}$![]() . Applied objectwise, this yields a $t$
. Applied objectwise, this yields a $t$![]() -structure on $\mathsf {C}_{loc}$
-structure on $\mathsf {C}_{loc}$![]() , and the duality $D_{K, loc}$
, and the duality $D_{K, loc}$![]() satisfies $D_{K, loc}((\mathsf {C}_{loc})_{\leq 0}) \subset (\mathsf {C}_{loc})_{\geq -1}$
satisfies $D_{K, loc}((\mathsf {C}_{loc})_{\leq 0}) \subset (\mathsf {C}_{loc})_{\geq -1}$![]() and $D_{K, loc}((\mathsf {C}_{loc})_{\geq 0}) \subset (\mathsf {C}_{loc})_{\leq 0}$
and $D_{K, loc}((\mathsf {C}_{loc})_{\geq 0}) \subset (\mathsf {C}_{loc})_{\leq 0}$![]() , as the expression (4.3) shows that this duality is performed objectwise.Footnote 3 We apply the algebraic surgery move of [Reference Calmès, Dotto, Harpaz, Hebestreit, Land, Moi, Nardin, Nikolaus and Steimle11, proposition 1.3.1] to the Poincaré object $(C,\,q) \in (\mathsf {C}_{loc},\, \unicode{x03D8} _{K, loc}^{[-2n]})$
, as the expression (4.3) shows that this duality is performed objectwise.Footnote 3 We apply the algebraic surgery move of [Reference Calmès, Dotto, Harpaz, Hebestreit, Land, Moi, Nardin, Nikolaus and Steimle11, proposition 1.3.1] to the Poincaré object $(C,\,q) \in (\mathsf {C}_{loc},\, \unicode{x03D8} _{K, loc}^{[-2n]})$![]() , using this $t$
, using this $t$![]() -structure, $r=\infty$
-structure, $r=\infty$![]() , and $a=0$
, and $a=0$![]() , to obtain a cobordism to a $(C',\, q')$
, to obtain a cobordism to a $(C',\, q')$![]() where $C'$
where $C'$![]() is $(-n)$
is $(-n)$![]() -connective. As $S^{-2n} \otimes D_{K, loc}(C') \simeq C'$
-connective. As $S^{-2n} \otimes D_{K, loc}(C') \simeq C'$![]() , it follows that $C'$
, it follows that $C'$![]() is also $(-n)$
is also $(-n)$![]() -truncated, so it is an $n$
-truncated, so it is an $n$![]() -fold desuspension of an object in the heart of this $t$
-fold desuspension of an object in the heart of this $t$![]() -structure, i.e. a local coefficient system on $K$
-structure, i.e. a local coefficient system on $K$![]() . Contemplating the surgery move of [Reference Calmès, Dotto, Harpaz, Hebestreit, Land, Moi, Nardin, Nikolaus and Steimle11, proposition 1.3.1] shows that $H_{-n}(C')$
. Contemplating the surgery move of [Reference Calmès, Dotto, Harpaz, Hebestreit, Land, Moi, Nardin, Nikolaus and Steimle11, proposition 1.3.1] shows that $H_{-n}(C')$![]() is the local coefficient system $\sigma \mapsto H^n(E_\sigma ; \mathbb {Z})/tors$
is the local coefficient system $\sigma \mapsto H^n(E_\sigma ; \mathbb {Z})/tors$![]() , and the symmetric form $q'$
, and the symmetric form $q'$![]() on it is that given by cup product and evaluation against the fundamental class of a fibre.
on it is that given by cup product and evaluation against the fundamental class of a fibre.
If $d=2n+1$![]() then we will proceed similarly, but use a modified $t$
then we will proceed similarly, but use a modified $t$![]() -structure. Define a $t$
-structure. Define a $t$![]() -structure on $\mathcal {D}^p(\mathbb {Z})$
-structure on $\mathcal {D}^p(\mathbb {Z})$![]() by declaring that $X \in \mathcal {D}^p(\mathbb {Z})_{\geq 0}$
by declaring that $X \in \mathcal {D}^p(\mathbb {Z})_{\geq 0}$![]() if $H_i(X)=0$
if $H_i(X)=0$![]() for $i<-1$
for $i<-1$![]() and $H_{-1}(X)$
and $H_{-1}(X)$![]() is torsion, and that $X \in \mathcal {D}^p(\mathbb {Z})_{\leq 0}$
is torsion, and that $X \in \mathcal {D}^p(\mathbb {Z})_{\leq 0}$![]() if $H_i(X)=0$
if $H_i(X)=0$![]() for $i>0$
for $i>0$![]() and $H_0(X)$
and $H_0(X)$![]() is torsionfree. This is easily checked to define a $t$
is torsionfree. This is easily checked to define a $t$![]() -structure, and the duality $D(-) = \mathrm {Hom}_\mathbb {Z}(-,\, \mathbb {Z})$
-structure, and the duality $D(-) = \mathrm {Hom}_\mathbb {Z}(-,\, \mathbb {Z})$![]() associated to the symmetric Poincaré structure satisfies $D(\mathcal {D}^p(\mathbb {Z})_{\leq 0}) \subset \mathcal {D}^p(\mathbb {Z})_{\geq 0}$
associated to the symmetric Poincaré structure satisfies $D(\mathcal {D}^p(\mathbb {Z})_{\leq 0}) \subset \mathcal {D}^p(\mathbb {Z})_{\geq 0}$![]() . Applied objectwise, this yields a $t$
. Applied objectwise, this yields a $t$![]() -structure on $\mathsf {C}_{loc}$
-structure on $\mathsf {C}_{loc}$![]() , and as above the duality $D_{K, loc}$
, and as above the duality $D_{K, loc}$![]() satisfies $D_{K, loc}((\mathsf {C}_{loc})_{\leq 0}) \subset (\mathsf {C}_{loc})_{\geq 0}$
satisfies $D_{K, loc}((\mathsf {C}_{loc})_{\leq 0}) \subset (\mathsf {C}_{loc})_{\geq 0}$![]() . We apply the algebraic surgery move of [Reference Calmès, Dotto, Harpaz, Hebestreit, Land, Moi, Nardin, Nikolaus and Steimle11, proposition 1.3.1] to the Poincaré object $(C,\,q) \in (\mathsf {C}_{loc},\, \unicode{x03D8} _{K, loc}^{[-(2n+1)]})$
. We apply the algebraic surgery move of [Reference Calmès, Dotto, Harpaz, Hebestreit, Land, Moi, Nardin, Nikolaus and Steimle11, proposition 1.3.1] to the Poincaré object $(C,\,q) \in (\mathsf {C}_{loc},\, \unicode{x03D8} _{K, loc}^{[-(2n+1)]})$![]() , using this $t$
, using this $t$![]() -structure, $r=\infty$
-structure, $r=\infty$![]() , and $a=-1$
, and $a=-1$![]() , to obtain a cobordism to a $(C',\, q')$
, to obtain a cobordism to a $(C',\, q')$![]() where $C'$
where $C'$![]() is $(-n)$
is $(-n)$![]() -connective with respect to this $t$
-connective with respect to this $t$![]() -structure. That is, each chain complex $C'(\sigma )$
-structure. That is, each chain complex $C'(\sigma )$![]() has $H_i(C'(\sigma ))=0$
has $H_i(C'(\sigma ))=0$![]() for $i < -n-1$
for $i < -n-1$![]() and $H_{-n-1}(C'(\sigma ))$
and $H_{-n-1}(C'(\sigma ))$![]() torsion. By the Universal Coefficient Theorem we then have $H_i(D(C'(\sigma ))) = 0$
torsion. By the Universal Coefficient Theorem we then have $H_i(D(C'(\sigma ))) = 0$![]() for $i > n$
for $i > n$![]() , and as $q'$
, and as $q'$![]() induces equivalences $S^{-(2n+1)} \otimes D(C'(\sigma )) \simeq C'(\sigma )$
induces equivalences $S^{-(2n+1)} \otimes D(C'(\sigma )) \simeq C'(\sigma )$![]() , it follows that each $C'(\sigma )$
, it follows that each $C'(\sigma )$![]() only has homology in degree $-(n+1)$
only has homology in degree $-(n+1)$![]() . Thus the $(n+1)$
. Thus the $(n+1)$![]() -fold suspension of $C'$
-fold suspension of $C'$![]() is in the heart of the ordinary $t$
is in the heart of the ordinary $t$![]() -structure, i.e. is a local coefficient system on $K$
-structure, i.e. is a local coefficient system on $K$![]() . Contemplating the surgery move of [Reference Calmès, Dotto, Harpaz, Hebestreit, Land, Moi, Nardin, Nikolaus and Steimle11, proposition 1.3.1] shows that $H_{-(n+1)}(C')$
. Contemplating the surgery move of [Reference Calmès, Dotto, Harpaz, Hebestreit, Land, Moi, Nardin, Nikolaus and Steimle11, proposition 1.3.1] shows that $H_{-(n+1)}(C')$![]() is the local coefficient system $\sigma \mapsto tors H^{n+1}(E_\sigma ; \mathbb {Z})$
is the local coefficient system $\sigma \mapsto tors H^{n+1}(E_\sigma ; \mathbb {Z})$![]() , and the symmetric form $q'$
, and the symmetric form $q'$![]() on it is that given by the linking form.
on it is that given by the linking form.
In both cases, the coassembly of the cobordism from $(C,\, q)$![]() to $(C',\, q')$
to $(C',\, q')$![]() produces a homotopy $\mathrm {Coass}(C,\, q) \simeq \mathrm {Coass}(C',\, q') : |K| \to \mathcal {L}(\mathbb {Z},\, \unicode{x03D8} ^{[-d]})$
produces a homotopy $\mathrm {Coass}(C,\, q) \simeq \mathrm {Coass}(C',\, q') : |K| \to \mathcal {L}(\mathbb {Z},\, \unicode{x03D8} ^{[-d]})$![]() , and if $F$
, and if $F$![]() is a typical fibre of $\pi : E \to |K|$
is a typical fibre of $\pi : E \to |K|$![]() then the discussion above identifies $\mathrm {Coass}(C',\, q')$
then the discussion above identifies $\mathrm {Coass}(C',\, q')$![]() with the composition
with the composition

This identifies the family signature $\mathrm {Coass}(C,\, q)$![]() with the lower composition in the statement of theorem 4.1.
with the lower composition in the statement of theorem 4.1.
4.9 Proof of theorem 4.1
Suppose now that $\pi : E \to |K|$![]() is a block bundle, or more generally a mock bundle such that the inclusions $E_\tau \subset E_\sigma$
is a block bundle, or more generally a mock bundle such that the inclusions $E_\tau \subset E_\sigma$![]() are $\mathbb {Z}$
are $\mathbb {Z}$![]() -homology equivalences whenever $\tau \subset \sigma$
-homology equivalences whenever $\tau \subset \sigma$![]() , classified by $f : |K| \to |\mathrm {Mock}(d)|$
, classified by $f : |K| \to |\mathrm {Mock}(d)|$![]() . There is a diagram
. There is a diagram

in which each region commutes (up to homotopy) tautologically, and by the discussion in the last section the anticlockwise composition agrees with $inc \circ \phi$![]() , proving theorem 4.1.
, proving theorem 4.1.
Remark 4.9 The main difficulty in implementing the above in the framework of [Reference Ranicki45] is that Ranicki only considers bounded chain complexes of finitely-generated free (or projective) modules, and (co)chains on a manifold is never equal to such a thing. The usual solution to this issue seems to have been to pretend otherwise, or to change definitions but assume that Ranicki's results are unchanged, or to restrict to PL manifolds and use simplicial chains for some choice of PL-triangulation instead.
5. Twisted signature formulas in $L$ -theory
-theory
We consider theorem 4.1 to be the most natural formulation of the Family Signature Theorem, but for applications we must also provide tools for understanding the bottom map $inc$![]() , just as we did in § 3.6 for the $KO[\tfrac {1}{2}]$
, just as we did in § 3.6 for the $KO[\tfrac {1}{2}]$![]() -theory formulation. This will require significantly more external machinery than the discussion so far. In particular it relies extensively on the relation between $L$
-theory formulation. This will require significantly more external machinery than the discussion so far. In particular it relies extensively on the relation between $L$![]() -theory and Grothendieck–Witt theory developed in [Reference Calmès, Dotto, Harpaz, Hebestreit, Land, Moi, Nardin, Nikolaus and Steimle10–Reference Calmès, Dotto, Harpaz, Hebestreit, Land, Moi, Nardin, Nikolaus and Steimle12], and we must now assume more familiarity with these papers.
-theory and Grothendieck–Witt theory developed in [Reference Calmès, Dotto, Harpaz, Hebestreit, Land, Moi, Nardin, Nikolaus and Steimle10–Reference Calmès, Dotto, Harpaz, Hebestreit, Land, Moi, Nardin, Nikolaus and Steimle12], and we must now assume more familiarity with these papers.
5.1 The symmetric $L$ -theory spectrum
-theory spectrum
Following Hebestreit, Land and Nikolaus [Reference Hebestreit, Land and Nikolaus21], the symmetric $L$![]() -theory spectrum of the integers may be described as follows: there is a fibration sequence
-theory spectrum of the integers may be described as follows: there is a fibration sequence
where $\pi _*(\mathrm {L}^s(\mathbb {R})) = \mathbb {Z}[x^{\pm 1}]$![]() with $|x|=4$
with $|x|=4$![]() and $\pi _i(\mathrm {dR})$
and $\pi _i(\mathrm {dR})$![]() is $\mathbb {Z}/2$
is $\mathbb {Z}/2$![]() if $i \equiv 1 \mod 4$
if $i \equiv 1 \mod 4$![]() and is zero otherwise. The homotopy groups in degrees $4i$
and is zero otherwise. The homotopy groups in degrees $4i$![]() detect the signature, and those in degrees $4i+1$
detect the signature, and those in degrees $4i+1$![]() detect the de Rham invariant.
detect the de Rham invariant.
There are equivalences $\mathrm {L}^s(\mathbb {Z})[\tfrac {1}{2}] \simeq \mathrm {L}^s(\mathbb {R})[\tfrac {1}{2}] \simeq \mathrm {KO}[\tfrac {1}{2}]$![]() , and we would like to say that theorem 3.1 is obtained from theorem 4.1 by inverting 2 and using such an equivalence. In order for the Sullivan orientation $\Delta _{Top}$
, and we would like to say that theorem 3.1 is obtained from theorem 4.1 by inverting 2 and using such an equivalence. In order for the Sullivan orientation $\Delta _{Top}$![]() to agree (up to phantom maps) with the Ranicki orientation $\sigma$
to agree (up to phantom maps) with the Ranicki orientation $\sigma$![]() under such an equivalence, it suffices (by construction of $\Delta _{Top}$
under such an equivalence, it suffices (by construction of $\Delta _{Top}$![]() ) to choose an equivalence inducing the ring map $a \mapsto x : \mathbb {Z}[\tfrac {1}{2}][a^{\pm 1}] = \pi _*(\mathrm {KO}[\tfrac {1}{2}]) \to \pi _*(\mathrm {L}^s(\mathbb {R})[\tfrac {1}{2}]) = \mathbb {Z}[\tfrac {1}{2}][x^{\pm 1}]$
) to choose an equivalence inducing the ring map $a \mapsto x : \mathbb {Z}[\tfrac {1}{2}][a^{\pm 1}] = \pi _*(\mathrm {KO}[\tfrac {1}{2}]) \to \pi _*(\mathrm {L}^s(\mathbb {R})[\tfrac {1}{2}]) = \mathbb {Z}[\tfrac {1}{2}][x^{\pm 1}]$![]() on homotopy groups. Choosing this isomorphism between their homotopy groups we obtain an isomorphism of generalized homology theories
on homotopy groups. Choosing this isomorphism between their homotopy groups we obtain an isomorphism of generalized homology theories
as the right-hand map can be shown to be an isomorphism using the Landweber exact functor theorem [Reference Landweber29, example 3.4] just as the left-hand map is. This gives an equivalence of representing spectra $\mathrm {KO}[\tfrac {1}{2}] \simeq \mathrm {L}^s(\mathbb {R})[\tfrac {1}{2}]$![]() inducing the required map on homotopy groups.
inducing the required map on homotopy groups.
At the prime 2, following Taylor and Williams [Reference Taylor and Williams51, Section 2] one can use that $\mathrm {MSO}_{(2)}$![]() is a generalized Eilenberg–MacLane spectrum to deduce that any module spectrum over it is too. This applies to $\mathrm {L}^s(\mathbb {Z})_{(2)}$
is a generalized Eilenberg–MacLane spectrum to deduce that any module spectrum over it is too. This applies to $\mathrm {L}^s(\mathbb {Z})_{(2)}$![]() and $\mathrm {L}^s(\mathbb {R})_{(2)}$
and $\mathrm {L}^s(\mathbb {R})_{(2)}$![]() via the map of homotopy ringFootnote 4 spectra $\mathrm {MSO} \to \mathrm {MSTop} \overset {\sigma }\to \mathrm {L}^s(\mathbb {Z})$
via the map of homotopy ringFootnote 4 spectra $\mathrm {MSO} \to \mathrm {MSTop} \overset {\sigma }\to \mathrm {L}^s(\mathbb {Z})$![]() , and hence to $\mathrm {dR} = \mathrm {dR}_{(2)}$
, and hence to $\mathrm {dR} = \mathrm {dR}_{(2)}$![]() using (5.1). Taylor and Williams produce specific maps
using (5.1). Taylor and Williams produce specific maps

which combine to give an equivalence. Pulled back along the Ranicki orientation they behave as follows. The class $\sigma ^*L$![]() corresponds under the Thom isomorphism with Morgan and Sullivan's class $\mathscr {L} \in H^*(BSTop ; \mathbb {Z}_{(2)})$
corresponds under the Thom isomorphism with Morgan and Sullivan's class $\mathscr {L} \in H^*(BSTop ; \mathbb {Z}_{(2)})$![]() constructed in [Reference Morgan and Sullivan37, section 7], which is in turn characterized by restricting to the inverse of the Hirzebruch $L$
constructed in [Reference Morgan and Sullivan37, section 7], which is in turn characterized by restricting to the inverse of the Hirzebruch $L$![]() -class when rationalized, and the square of the total Wu classFootnote 5 $V$
-class when rationalized, and the square of the total Wu classFootnote 5 $V$![]() when reduced modulo 2. The class $\sigma ^*r$
when reduced modulo 2. The class $\sigma ^*r$![]() corresponds under the Thom isomorphism with $\sum _{i \geq 0}V_{2i} \cdot \mathrm {Sq}^1V_{2i}$
corresponds under the Thom isomorphism with $\sum _{i \geq 0}V_{2i} \cdot \mathrm {Sq}^1V_{2i}$![]() , which is the well-known characteristic class measuring the de Rham invariant [Reference Lusztig, Milnor and Peterson33]. The composition $\mathrm {dR} \to \mathrm {L}^s(\mathbb {Z}) \to \mathrm {L}^s(\mathbb {Z})_{(2)} \overset {r}\to \bigoplus _{j \in \mathbb {Z}} \mathrm {H} \mathbb {Z}/ 2[4j+1]$
, which is the well-known characteristic class measuring the de Rham invariant [Reference Lusztig, Milnor and Peterson33]. The composition $\mathrm {dR} \to \mathrm {L}^s(\mathbb {Z}) \to \mathrm {L}^s(\mathbb {Z})_{(2)} \overset {r}\to \bigoplus _{j \in \mathbb {Z}} \mathrm {H} \mathbb {Z}/ 2[4j+1]$![]() is necessarily an equivalence, which gives a splitting $\mathrm {L}^s(\mathbb {Z}) \simeq \mathrm {L}^s(\mathbb {R}) \oplus \mathrm {dR}$
is necessarily an equivalence, which gives a splitting $\mathrm {L}^s(\mathbb {Z}) \simeq \mathrm {L}^s(\mathbb {R}) \oplus \mathrm {dR}$![]() such that $\mathrm {L}^s(\mathbb {R}) \to \mathrm {L}^s(\mathbb {Z}) \to \mathrm {L}^s(\mathbb {Z})_{(2)} \overset {L}\to \bigoplus _{i \in \mathbb {Z}} \mathrm {H} \mathbb {Z}_{(2)}[4i]$
such that $\mathrm {L}^s(\mathbb {R}) \to \mathrm {L}^s(\mathbb {Z}) \to \mathrm {L}^s(\mathbb {Z})_{(2)} \overset {L}\to \bigoplus _{i \in \mathbb {Z}} \mathrm {H} \mathbb {Z}_{(2)}[4i]$![]() is a 2-local equivalence.
is a 2-local equivalence.
A more structured approach is also possible. Hebestreit, Land and Nikolaus describe [Reference Hebestreit, Land and Nikolaus21, section 3] an $E_1$![]() -algebra map $\mathrm {H} \mathbb {Z}_{(2)} \to \mathrm {MSO}_{(2)}$
-algebra map $\mathrm {H} \mathbb {Z}_{(2)} \to \mathrm {MSO}_{(2)}$![]() , which then endows any $\mathrm {MSO}_{(2)}$
, which then endows any $\mathrm {MSO}_{(2)}$![]() -module with a canonical $\mathrm {H} \mathbb {Z}_{(2)}$
-module with a canonical $\mathrm {H} \mathbb {Z}_{(2)}$![]() -module structure. Using [Reference Hebestreit, Land and Nikolaus21, corollary 3.8] it follows that there are unique equivalences of $\mathrm {H} \mathbb {Z}_{(2)}$
-module structure. Using [Reference Hebestreit, Land and Nikolaus21, corollary 3.8] it follows that there are unique equivalences of $\mathrm {H} \mathbb {Z}_{(2)}$![]() -modules
-modules
inducing the identity on homotopy groups. They also show [Reference Hebestreit, Land and Nikolaus21, corollary 4.3] that there is a unique splitting $\mathrm {L}^s(\mathbb {R}) \to \mathrm {L}^s(\mathbb {Z})$![]() of $E_1$
of $E_1$![]() -algebras which 2-locally is a splitting of $\mathrm {H} \mathbb {Z}_{(2)}$
-algebras which 2-locally is a splitting of $\mathrm {H} \mathbb {Z}_{(2)}$![]() -algebras.
-algebras.
Remark 5.1 We do not assert anything about any compatibility between the splittings of the previous paragraph and those obtained using the maps $L$![]() and $r$
and $r$![]() above. Using the discussion in [Reference Taylor and Williams51, section 2] it seems that this kind of question comes down to whether the class $\mathscr {L} \in H^*(BSO;\mathbb {Z}_{(2)})$
above. Using the discussion in [Reference Taylor and Williams51, section 2] it seems that this kind of question comes down to whether the class $\mathscr {L} \in H^*(BSO;\mathbb {Z}_{(2)})$![]() is trivial on the bundle classified by $\eta : \tau _{\geq 2}\Omega ^2 S^3 \to BSO$
is trivial on the bundle classified by $\eta : \tau _{\geq 2}\Omega ^2 S^3 \to BSO$![]() .
.
5.2 Odd dimensions
In § 4.7 we have explained how a nondegenerate $(-1)^n$![]() -symmetric linking form $(T,\,\ell )$
-symmetric linking form $(T,\,\ell )$![]() yields a Poincaré object $(T[-n],\, q_\ell )$
yields a Poincaré object $(T[-n],\, q_\ell )$![]() and hence a map
and hence a map
Theorem 5.2 The map (5.3) is homotopic to a constant map.Footnote 6
Proof. Firstly, there is a canonical decomposition $T = \bigoplus _{p \text { prime}} T_p$![]() of $T$
of $T$![]() into its Sylow subgroups, which is orthogonal with respect to $\ell$
into its Sylow subgroups, which is orthogonal with respect to $\ell$![]() . This gives a corresponding decomposition of $\mathrm {Aut}(T,\,\ell )$
. This gives a corresponding decomposition of $\mathrm {Aut}(T,\,\ell )$![]() , meaning that we may assume that $T$
, meaning that we may assume that $T$![]() is a $p$
is a $p$![]() -group.
-group.
Secondly, if $(T,\,\ell )$![]() is a nondegenerate $(-1)^{n}$
is a nondegenerate $(-1)^{n}$![]() -symmetric linking form on a $p$
-symmetric linking form on a $p$![]() -group then consider the subgroup $L := (p \cdot T) \cap ([p](T))$
-group then consider the subgroup $L := (p \cdot T) \cap ([p](T))$![]() of $p$
of $p$![]() -divisible and $p$
-divisible and $p$![]() -torsion elements of $T$
-torsion elements of $T$![]() . The restriction of $\ell$
. The restriction of $\ell$![]() to $L$
to $L$![]() vanishes, as if $x = p \cdot \bar {x},\, y \in L$
vanishes, as if $x = p \cdot \bar {x},\, y \in L$![]() then $\ell (x,\, y) = \ell (p \bar {x},\, y) = \ell (\bar {x},\, py)=0$
then $\ell (x,\, y) = \ell (p \bar {x},\, y) = \ell (\bar {x},\, py)=0$![]() as $y$
as $y$![]() is $p$
is $p$![]() -torsion. Thus we may do algebraic surgery to $(T[-n],\, q_\ell )$
-torsion. Thus we may do algebraic surgery to $(T[-n],\, q_\ell )$![]() along the map $L[-n] \to T[-n]$
along the map $L[-n] \to T[-n]$![]() , the result of which is the Poincaré object associated to the linking form $(T',\, \ell ')$
, the result of which is the Poincaré object associated to the linking form $(T',\, \ell ')$![]() with
with
and $\ell '$![]() the linking form induced by $\ell$
the linking form induced by $\ell$![]() . This is functorial, giving a map $B\mathrm {Aut}(T,\, \ell ) \to B\mathrm {Aut}(T',\, \ell ')$
. This is functorial, giving a map $B\mathrm {Aut}(T,\, \ell ) \to B\mathrm {Aut}(T',\, \ell ')$![]() , and furthermore the algebraic surgery between these forms is functorial, giving a homotopy between the two maps into $\Omega ^{\infty +2n-1} \mathrm {L}^s(\mathbb {Z})$
, and furthermore the algebraic surgery between these forms is functorial, giving a homotopy between the two maps into $\Omega ^{\infty +2n-1} \mathrm {L}^s(\mathbb {Z})$![]() . If $L \neq 0$
. If $L \neq 0$![]() then $T'$
then $T'$![]() is strictly smaller than $T$
is strictly smaller than $T$![]() , so continuing in this way we may assume that $(T,\,\ell )$
, so continuing in this way we may assume that $(T,\,\ell )$![]() is such that $L=0$
is such that $L=0$![]() , i.e. $T$
, i.e. $T$![]() is an elementary abelian $p$
is an elementary abelian $p$![]() -group.
-group.
When $(T,\,\ell )$![]() is such that $T$
is such that $T$![]() is an elementary abelian $p$
is an elementary abelian $p$![]() -group, $\ell$
-group, $\ell$![]() takes values in the subgroup of $\mathbb {Q}/\mathbb {Z}$
takes values in the subgroup of $\mathbb {Q}/\mathbb {Z}$![]() generated by $\tfrac {1}{p}$
generated by $\tfrac {1}{p}$![]() , and identifying this subgroup with $\mathbb {F}_p$
, and identifying this subgroup with $\mathbb {F}_p$![]() we may consider $\ell : T \otimes T \to \mathbb {F}_p$
we may consider $\ell : T \otimes T \to \mathbb {F}_p$![]() as a nondegenerate $(-1)^n$
as a nondegenerate $(-1)^n$![]() -symmetric form on an $\mathbb {F}_p$
-symmetric form on an $\mathbb {F}_p$![]() -module. Thus $\mathrm {Aut}(T,\, \ell )$
-module. Thus $\mathrm {Aut}(T,\, \ell )$![]() is a symplectic or orthogonal group over $\mathbb {F}_p$
is a symplectic or orthogonal group over $\mathbb {F}_p$![]() , and there is a factorization
, and there is a factorization
where the latter is the map arising in the localization-dévissage sequence
Thirdly, suppose that $p$![]() is odd. We will argue that $\partial _p : \Sigma ^{-1} \mathrm {L}^s(\mathbb {F}_p) \to \mathrm {L}^s(\mathbb {Z})$
is odd. We will argue that $\partial _p : \Sigma ^{-1} \mathrm {L}^s(\mathbb {F}_p) \to \mathrm {L}^s(\mathbb {Z})$![]() is nullhomotopic. As $\partial _p$
is nullhomotopic. As $\partial _p$![]() has a canonical nullhomotopy when mapped to $\mathrm {L}^s(\mathbb {Q})$
has a canonical nullhomotopy when mapped to $\mathrm {L}^s(\mathbb {Q})$![]() it also does when mapped to $\mathrm {L}^s(\mathbb {R})$
it also does when mapped to $\mathrm {L}^s(\mathbb {R})$![]() , giving a canonical lift $\partial _p' : \Sigma ^{-1} \mathrm {L}^s(\mathbb {F}_p) \to \mathrm {dR}$
, giving a canonical lift $\partial _p' : \Sigma ^{-1} \mathrm {L}^s(\mathbb {F}_p) \to \mathrm {dR}$![]() which we wish to show is nullhomotopic.
which we wish to show is nullhomotopic.
The target of this map is 2-local, so we can localize all spectra involved at 2 and make use of the canonical $H\mathbb {Z}_{(2)}$![]() -module structure on $\mathrm {L}^s(\mathbb {Z})_{(2)}$
-module structure on $\mathrm {L}^s(\mathbb {Z})_{(2)}$![]() -modules discussed in § 5.1. We have already discussed how the terms in (5.1) obtain $H\mathbb {Z}_{(2)}$
-modules discussed in § 5.1. We have already discussed how the terms in (5.1) obtain $H\mathbb {Z}_{(2)}$![]() -module structures, in particular giving an equivalence $\mathrm {dR} \simeq \bigoplus _{i \in \mathbb {Z}} \mathrm {H} \mathbb {Z}/2 [4i+1]$
-module structures, in particular giving an equivalence $\mathrm {dR} \simeq \bigoplus _{i \in \mathbb {Z}} \mathrm {H} \mathbb {Z}/2 [4i+1]$![]() of $H\mathbb {Z}_{(2)}$
of $H\mathbb {Z}_{(2)}$![]() -modules. On the other hand the fibre sequence (5.4) endows $\Sigma ^{-1} \mathrm {L}^s(\mathbb {F}_p)$
-modules. On the other hand the fibre sequence (5.4) endows $\Sigma ^{-1} \mathrm {L}^s(\mathbb {F}_p)$![]() with a $\mathrm {L}^s(\mathbb {Z})$
with a $\mathrm {L}^s(\mathbb {Z})$![]() -module structure (potentially different from that given by $\mathrm {L}^s(\mathbb {Z}) \to \mathrm {L}^s(\mathbb {F}_p)$
-module structure (potentially different from that given by $\mathrm {L}^s(\mathbb {Z}) \to \mathrm {L}^s(\mathbb {F}_p)$![]() , though experts tell me it is in fact not) making $\partial _p$
, though experts tell me it is in fact not) making $\partial _p$![]() into an $\mathrm {L}^s(\mathbb {Z})$
into an $\mathrm {L}^s(\mathbb {Z})$![]() -module map. As $p$
-module map. As $p$![]() is odd we have
is odd we have

where $W(F_p)$![]() is the Witt group of $\mathbb {F}_p$
is the Witt group of $\mathbb {F}_p$![]() and is either $\mathbb {Z}/4$
and is either $\mathbb {Z}/4$![]() or $\mathbb {Z}/2 \oplus \mathbb {Z}/2$
or $\mathbb {Z}/2 \oplus \mathbb {Z}/2$![]() [Reference Ranicki44, proposition 4.3.2]. In either case it follows that $\Sigma ^{-1} \mathrm {L}^s(\mathbb {F}_p)$
[Reference Ranicki44, proposition 4.3.2]. In either case it follows that $\Sigma ^{-1} \mathrm {L}^s(\mathbb {F}_p)$![]() is 2-local and with the $\mathrm {H}\mathbb {Z}_{(2)}$
is 2-local and with the $\mathrm {H}\mathbb {Z}_{(2)}$![]() -module structure given by (5.4) it is equivalent to $\bigoplus _{j \in \mathbb {Z}} \mathrm {H} W(\mathbb {F}_p)[4j-1]$
-module structure given by (5.4) it is equivalent to $\bigoplus _{j \in \mathbb {Z}} \mathrm {H} W(\mathbb {F}_p)[4j-1]$![]() . As the nullhomotopy of $\partial _p$
. As the nullhomotopy of $\partial _p$![]() into $\mathrm {L}^s(\mathbb {R})$
into $\mathrm {L}^s(\mathbb {R})$![]() can be taken to be one of $\mathrm {L}^s(\mathbb {Z})$
can be taken to be one of $\mathrm {L}^s(\mathbb {Z})$![]() -modules, via (5.4), the map $\partial _p' : \Sigma ^{-1} \mathrm {L}^s(\mathbb {F}_p) \to \mathrm {dR}$
-modules, via (5.4), the map $\partial _p' : \Sigma ^{-1} \mathrm {L}^s(\mathbb {F}_p) \to \mathrm {dR}$![]() is one of $\mathrm {H}\mathbb {Z}_{(2)}$
is one of $\mathrm {H}\mathbb {Z}_{(2)}$![]() -modules with the module structures just described. But
-modules with the module structures just described. But

so $\partial '_p$![]() is null.
is null.
Fourthly, suppose that $p=2$![]() . In this case the map $\partial _2'$
. In this case the map $\partial _2'$![]() is not trivial, and we instead argue that the map $B\mathrm {Aut}(T,\, \ell ) \to \Omega ^{\infty +2n} \mathrm {L}^s(\mathbb {F}_2)$
is not trivial, and we instead argue that the map $B\mathrm {Aut}(T,\, \ell ) \to \Omega ^{\infty +2n} \mathrm {L}^s(\mathbb {F}_2)$![]() is homotopic to a constant map, so that its composition with $\Omega ^{\infty +2n} \mathrm {L}^s(\mathbb {F}_2) \to \Omega ^{\infty +2n-1} \mathrm {dR}$
is homotopic to a constant map, so that its composition with $\Omega ^{\infty +2n} \mathrm {L}^s(\mathbb {F}_2) \to \Omega ^{\infty +2n-1} \mathrm {dR}$![]() is too. As we start with actual automorphisms of a symmetric form over $\mathbb {F}_2$
is too. As we start with actual automorphisms of a symmetric form over $\mathbb {F}_2$![]() , this map factors through the Grothendieck–Witt space $\Omega ^\infty \mathrm {GW}(\mathbb {F}_2 ; \unicode{x03D8} )$
, this map factors through the Grothendieck–Witt space $\Omega ^\infty \mathrm {GW}(\mathbb {F}_2 ; \unicode{x03D8} )$![]() , via the map
, via the map
where the latter identification holds because $\mathrm {L}^s(\mathbb {F}_2)$![]() is 2-periodic. (Here $\unicode{x03D8} = \unicode{x03D8} ^s$
is 2-periodic. (Here $\unicode{x03D8} = \unicode{x03D8} ^s$![]() is the symmetric structure.) By [Reference Calmès, Dotto, Harpaz, Hebestreit, Land, Moi, Nardin, Nikolaus and Steimle11, proposition 3.1.4] the map
is the symmetric structure.) By [Reference Calmès, Dotto, Harpaz, Hebestreit, Land, Moi, Nardin, Nikolaus and Steimle11, proposition 3.1.4] the map
is an equivalence but by Quillen's calculation [Reference Quillen39] of the $K$![]() -theory of finite fields, the truncation map $\mathrm {K}(\mathbb {F}_2 ; \unicode{x03D8} ) \to \mathrm {H} \mathbb {Z}$
-theory of finite fields, the truncation map $\mathrm {K}(\mathbb {F}_2 ; \unicode{x03D8} ) \to \mathrm {H} \mathbb {Z}$![]() is a 2-local equivalence, so $\Omega ^\infty \mathrm {GW}(\mathbb {F}_2 ; \unicode{x03D8} )$
is a 2-local equivalence, so $\Omega ^\infty \mathrm {GW}(\mathbb {F}_2 ; \unicode{x03D8} )$![]() is 2-locally equivalent to the discrete space $\mathbb {Z}$
is 2-locally equivalent to the discrete space $\mathbb {Z}$![]() . As the target of (5.5) is 2-local, it follows that (5.5) is homotopic to a constant map as required.
. As the target of (5.5) is 2-local, it follows that (5.5) is homotopic to a constant map as required.
Corollary 5.3 Let $\pi : E \to |K|$![]() be an oriented topological block bundle with $d$
be an oriented topological block bundle with $d$![]() -dimensional fibre, and $d$
-dimensional fibre, and $d$![]() odd. Then the composition
odd. Then the composition
is homotopic to a constant map.
5.3 Even dimensions
With the choice of equivalence $\mathrm {L}^s(\mathbb {R})[\tfrac {1}{2}] \simeq \mathrm {KO}[\tfrac {1}{2}]$![]() explained in § 5.1, the composition
explained in § 5.1, the composition
agrees (up to phantom maps) with the map $\mathrm {sign}$![]() constructed in § 3.4, because it has the same interpretation in terms of signatures on $\mathbb {Z}/k$
constructed in § 3.4, because it has the same interpretation in terms of signatures on $\mathbb {Z}/k$![]() -bordism.
-bordism.
The new information in theorem 4.1 is therefore at the prime $2$![]() . By the discussion in § 5.1, there is a splitting $\mathrm {L}^s(\mathbb {Z}) \simeq \mathrm {L}^s(\mathbb {R}) \oplus \mathrm {dR}$
. By the discussion in § 5.1, there is a splitting $\mathrm {L}^s(\mathbb {Z}) \simeq \mathrm {L}^s(\mathbb {R}) \oplus \mathrm {dR}$![]() induced by the composition $\mathrm {dR} \to \mathrm {L}^s(\mathbb {Z}) \overset {r}\to \bigoplus _{j \in \mathbb {Z}} \mathrm {H} \mathbb {Z}/2[4j+1]$
induced by the composition $\mathrm {dR} \to \mathrm {L}^s(\mathbb {Z}) \overset {r}\to \bigoplus _{j \in \mathbb {Z}} \mathrm {H} \mathbb {Z}/2[4j+1]$![]() being an equivalence, and this induces an equivalence $\mathrm {L}^s(\mathbb {R})_{(2)} \simeq \bigoplus _{i \in \mathbb {Z}} \mathrm {H} \mathbb {Z}_{(2)}[4i]$
being an equivalence, and this induces an equivalence $\mathrm {L}^s(\mathbb {R})_{(2)} \simeq \bigoplus _{i \in \mathbb {Z}} \mathrm {H} \mathbb {Z}_{(2)}[4i]$![]() such that the composition
such that the composition
corresponds under the Thom isomorphism to Morgan and Sullivan's class $\mathscr {L}$![]() . The following theorem is the analogue of theorem 3.2, and stating it requires a preparatory lemma.
. The following theorem is the analogue of theorem 3.2, and stating it requires a preparatory lemma.
Lemma 5.4 There are unique classes $\widetilde {\mathrm {ph}}_i \in H^{4i}(BO;\mathbb {Z}_{(2)})$![]() rationalizing to $2^{2i} \mathrm {ph}_i$
rationalizing to $2^{2i} \mathrm {ph}_i$![]() and for $i>0$
and for $i>0$![]() reducing to zero modulo 2.
reducing to zero modulo 2.
Furthermore, for $i>0$![]() these classes are in fact divisible by 4.
these classes are in fact divisible by 4.
Proof. As the integral cohomology of $BO$![]() only has $\mathbb {Z}/2$
only has $\mathbb {Z}/2$![]() -torsion the uniqueness is clear. For existence, as in corollary 2.3 we use that $2^j/j!$
-torsion the uniqueness is clear. For existence, as in corollary 2.3 we use that $2^j/j!$![]() is 2-integral and even 2-integrally divisible by 2 so that $\widetilde {\mathrm {ch}}_j = 2^j \mathrm {ch}_j$
is 2-integral and even 2-integrally divisible by 2 so that $\widetilde {\mathrm {ch}}_j = 2^j \mathrm {ch}_j$![]() is a 2-integral cohomology class on $BU$
is a 2-integral cohomology class on $BU$![]() which reduces to zero modulo 2. Pulling $\widetilde {\mathrm {ch}}_{2i}$
which reduces to zero modulo 2. Pulling $\widetilde {\mathrm {ch}}_{2i}$![]() back to $BO$
back to $BO$![]() gives the required classes $\mathrm {ph}_i$
gives the required classes $\mathrm {ph}_i$![]() . The second part follows identically to the case $n$
. The second part follows identically to the case $n$![]() even of the proof of corollary 2.3.
even of the proof of corollary 2.3.
To state the following, we use the real form $\xi _\mathbb {R}$![]() of $\xi$
of $\xi$![]() from remark 2.1.
from remark 2.1.
Theorem 5.5 If $(H_\mathbb {R},\, \lambda )$![]() is a nondegenerate $(-1)^n$
is a nondegenerate $(-1)^n$![]() -symmetric bilinear form then the square
-symmetric bilinear form then the square

commutes up to homotopy and phantom maps.
Proof. We can verify this after inverting 2, and after completing at 2. After inverting 2 we are working rationally, and the equivalence
obtained by further localizing the equivalences $\mathrm {L}^s(\mathbb {R})[\tfrac {1}{2}] \simeq \mathrm {KO}[\tfrac {1}{2}]$![]() and $\mathrm {L}^s(\mathbb {R})_{(2)} \simeq \bigoplus _{i \in \mathbb {Z}} \mathrm {H} \mathbb {Z}_{(2)}[4i]$
and $\mathrm {L}^s(\mathbb {R})_{(2)} \simeq \bigoplus _{i \in \mathbb {Z}} \mathrm {H} \mathbb {Z}_{(2)}[4i]$![]() sends $a^k \in \pi _{4k}(\mathrm {KO})_{(0)}$
sends $a^k \in \pi _{4k}(\mathrm {KO})_{(0)}$![]() to $1 \in \pi _{4k}(\bigoplus _{i \in \mathbb {Z}} \mathrm {H} \mathbb {Q}[4i])$
to $1 \in \pi _{4k}(\bigoplus _{i \in \mathbb {Z}} \mathrm {H} \mathbb {Q}[4i])$![]() . As $a$
. As $a$![]() was chosen to map to the square of the Bott class $b^2 \in \pi _4(\mathrm {K})$
was chosen to map to the square of the Bott class $b^2 \in \pi _4(\mathrm {K})$![]() under complexification, and the Chern character takes the value 1 on $b$
under complexification, and the Chern character takes the value 1 on $b$![]() , it follows that the equivalence (5.6) is induced by the Pontrjagin character. By theorem 3.2 the clockwise composition is then rationally $\mathrm {ph}(\tfrac {1}{2}r(b^n \psi ^2 \xi ))$
, it follows that the equivalence (5.6) is induced by the Pontrjagin character. By theorem 3.2 the clockwise composition is then rationally $\mathrm {ph}(\tfrac {1}{2}r(b^n \psi ^2 \xi ))$![]() which is calculated in the proof of that theorem to be $\mathrm {ch}(\psi ^2 \xi )$
which is calculated in the proof of that theorem to be $\mathrm {ch}(\psi ^2 \xi )$![]() which is the same as $\widetilde {\mathrm {ph}}(\xi _\mathbb {R})$
which is the same as $\widetilde {\mathrm {ph}}(\xi _\mathbb {R})$![]() .
.
To deal with the 2-complete case we use the fact that, up to a translation of path-components, the maps $inc$![]() and $\xi _\mathbb {R}$
and $\xi _\mathbb {R}$![]() commute with the map $B\mathrm {Aut}(H_\mathbb {R},\, \lambda ) \to B\mathrm {Aut}(H_\mathbb {R} \oplus H'_\mathbb {R},\, \lambda \oplus \lambda ')$
commute with the map $B\mathrm {Aut}(H_\mathbb {R},\, \lambda ) \to B\mathrm {Aut}(H_\mathbb {R} \oplus H'_\mathbb {R},\, \lambda \oplus \lambda ')$![]() given by stabilizing by a form $(H'_\mathbb {R},\, \lambda ')$
given by stabilizing by a form $(H'_\mathbb {R},\, \lambda ')$![]() . As the square does commute at the level of $\pi _0$
. As the square does commute at the level of $\pi _0$![]() by the previous case, by choosing $(H'_\mathbb {R},\, \lambda ')$
by the previous case, by choosing $(H'_\mathbb {R},\, \lambda ')$![]() to have large rank (and opposite signature to $(H_\mathbb {R},\, \lambda )$
to have large rank (and opposite signature to $(H_\mathbb {R},\, \lambda )$![]() if $n$
if $n$![]() is even) this allows us to assume that $(H_\mathbb {R},\, \lambda )$
is even) this allows us to assume that $(H_\mathbb {R},\, \lambda )$![]() is a hyperbolic form of arbitrarily large rank. Then, by a version [Reference Karoubi24, p. 260] of the stable Milnor conjecture for the groups $\mathrm {Sp}_{2g}(\mathbb {R})$
is a hyperbolic form of arbitrarily large rank. Then, by a version [Reference Karoubi24, p. 260] of the stable Milnor conjecture for the groups $\mathrm {Sp}_{2g}(\mathbb {R})$![]() orFootnote 7 $\mathrm {O}_{g,g}(\mathbb {R})$
orFootnote 7 $\mathrm {O}_{g,g}(\mathbb {R})$![]() the map
the map

induces an isomorphism on cohomology with all finite coefficients in a range of cohomological degrees tending to $\infty$![]() with $g$
with $g$![]() . It therefore also induces an isomorphism with 2-adic coefficients in such a range.
. It therefore also induces an isomorphism with 2-adic coefficients in such a range.
If $n$![]() is odd it follows that in each degree in the stable range $H^*(B\mathrm {Aut}(H_\mathbb {R},\, \lambda ) ; \mathbb {Z}_2)$
is odd it follows that in each degree in the stable range $H^*(B\mathrm {Aut}(H_\mathbb {R},\, \lambda ) ; \mathbb {Z}_2)$![]() is a finitely-generated free $\mathbb {Z}_2$
is a finitely-generated free $\mathbb {Z}_2$![]() -module, so by the Bockstein sequence the map
-module, so by the Bockstein sequence the map
is injective. As the diagram in the statement of the theorem commutes over $\mathbb {Q}$![]() it also does over $\mathbb {Q}_2$
it also does over $\mathbb {Q}_2$![]() , and by this injectivity it also does over $\mathbb {Z}_2$
, and by this injectivity it also does over $\mathbb {Z}_2$![]() .
.
If $n$![]() is even it follows that in the stable range $H^*(B\mathrm {Aut}(H_\mathbb {R},\, \lambda ) ; \mathbb {Z}_2)$
is even it follows that in the stable range $H^*(B\mathrm {Aut}(H_\mathbb {R},\, \lambda ) ; \mathbb {Z}_2)$![]() is a sum of a finitely-generated free $\mathbb {Z}_2$
is a sum of a finitely-generated free $\mathbb {Z}_2$![]() -module and a finite $\mathbb {Z}/2$
-module and a finite $\mathbb {Z}/2$![]() -module. Elements are therefore detected by their images with $\mathbb {Q}_2$
-module. Elements are therefore detected by their images with $\mathbb {Q}_2$![]() - and $\mathbb {Z}/2$
- and $\mathbb {Z}/2$![]() -coefficients. With $\mathbb {Q}_2$
-coefficients. With $\mathbb {Q}_2$![]() -coefficients we proceed as above. With $\mathbb {Z}/2$
-coefficients we proceed as above. With $\mathbb {Z}/2$![]() -coefficients the composition $\Omega ^{1-(-1)^n} \widetilde {\mathrm {ph}} \circ \xi _\mathbb {R}$
-coefficients the composition $\Omega ^{1-(-1)^n} \widetilde {\mathrm {ph}} \circ \xi _\mathbb {R}$![]() is trivial, as the classes $\widetilde {\mathrm {ph}}_i$
is trivial, as the classes $\widetilde {\mathrm {ph}}_i$![]() are trivial modulo 2. To show the other composition is trivial, we use that
are trivial modulo 2. To show the other composition is trivial, we use that
is an isomorphism in the stable range, and that this is detected on the subgroup
given by acting by a sign in each basis vector, in some basis given by bases for a choice of positive and negative definite subspaces. As the map $inc$![]() is additive with respect to orthogonal sum of forms, this reduces us to considering
is additive with respect to orthogonal sum of forms, this reduces us to considering
or its negative-definite analogue, which can be treated similarly. To evaluate this we can use the family signature theorem, because the complex conjugation involution on $\mathbb {CP}^2$![]() gives a splitting $BC_2 \to B\mathrm {Diff}^+(\mathbb {CP}^2) \overset {\phi } \to B\mathrm {Aut}(\mathbb {R},\, (1))$
gives a splitting $BC_2 \to B\mathrm {Diff}^+(\mathbb {CP}^2) \overset {\phi } \to B\mathrm {Aut}(\mathbb {R},\, (1))$![]() and so we may apply theorem 4.1 to say that the map in question is homotopic to
and so we may apply theorem 4.1 to say that the map in question is homotopic to

where the first map is the parameterized Pontrjagin–Thom map for the smooth oriented fibre bundle $\pi : E:= EC_2 \times _{C_2} \mathbb {CP}^2 \to BC_2$![]() , and the second is given by Thomifying the map $E \to BSTop$
, and the second is given by Thomifying the map $E \to BSTop$![]() classifying $-T_\pi E$
classifying $-T_\pi E$![]() . As the reduction of $\sigma ^*(L)$
. As the reduction of $\sigma ^*(L)$![]() modulo 2 corresponds under the Thom isomorphism to the square of the total Wu class, as a spectrum cohomology class on $\mathrm {Th}(-T_\pi E \to E)$
modulo 2 corresponds under the Thom isomorphism to the square of the total Wu class, as a spectrum cohomology class on $\mathrm {Th}(-T_\pi E \to E)$![]() it corresponds to $u_{-T_\pi E} \cdot V(-T_\pi E)^2$
it corresponds to $u_{-T_\pi E} \cdot V(-T_\pi E)^2$![]() . This satisfies
. This satisfies

This cohomology class is supported in degrees $\leq 0$![]() , so when pulled back to $\Sigma ^\infty _+ BC_2$
, so when pulled back to $\Sigma ^\infty _+ BC_2$![]() along the adjoint of the parameterized Pontrjagin–Thom map it only has a component of degree 0 (namely, the characteristic number $\int _{\mathbb {CP}^2} w_4(T\mathbb {CP}^2) = 1$
along the adjoint of the parameterized Pontrjagin–Thom map it only has a component of degree 0 (namely, the characteristic number $\int _{\mathbb {CP}^2} w_4(T\mathbb {CP}^2) = 1$![]() ). But as $\mathrm {Sq}$
). But as $\mathrm {Sq}$![]() is invertible, the pullback of $u_{-T_\pi E} \cdot V(-T_\pi E)^2$
is invertible, the pullback of $u_{-T_\pi E} \cdot V(-T_\pi E)^2$![]() to $\Sigma ^\infty _+ BC_2$
to $\Sigma ^\infty _+ BC_2$![]() must also be trivial in positive degrees, as required.
must also be trivial in positive degrees, as required.
The remaining information at the prime 2 concerns the de Rham invariant map $r : \mathrm {L}^s(\mathbb {Z}) \to \bigoplus _{j \in \mathbb {Z}} \mathrm {H}\mathbb {Z}/2[4j+1]$![]() . We have already mentioned that $r \circ \sigma$
. We have already mentioned that $r \circ \sigma$![]() corresponds, under the Thom isomorphism, with the class $\sum _{i \geq 0} V_{2i} \cdot \mathrm {Sq}^1 V_{2i}$
corresponds, under the Thom isomorphism, with the class $\sum _{i \geq 0} V_{2i} \cdot \mathrm {Sq}^1 V_{2i}$![]() . Theorem 5.6 below determines the corresponding cohomology classes on the intersection form side. During the proof we will explain that $H^3(BSp_\infty (\mathbb {Z});\mathbb {Z}/2) = \mathbb {Z}/2$
. Theorem 5.6 below determines the corresponding cohomology classes on the intersection form side. During the proof we will explain that $H^3(BSp_\infty (\mathbb {Z});\mathbb {Z}/2) = \mathbb {Z}/2$![]() and the unique nontrivial element $r_3$
and the unique nontrivial element $r_3$![]() of this group provides, by stabilizing, a characteristic class for all local systems of skew-symmetric lattices. Relatedly, we will explain why the function $r_1 : \mathrm {Aut}(H_\mathbb {Z},\, \lambda ) \to \mathbb {Z}/2$
of this group provides, by stabilizing, a characteristic class for all local systems of skew-symmetric lattices. Relatedly, we will explain why the function $r_1 : \mathrm {Aut}(H_\mathbb {Z},\, \lambda ) \to \mathbb {Z}/2$![]() , which assigns to an automorphism $\phi$
, which assigns to an automorphism $\phi$![]() the number $\dim _{\mathbb {Z}/2} (\mathbb {Z}/2 \otimes tors\tfrac {H_\mathbb {Z}}{(\mathrm {Id}-\phi )H_\mathbb {Z}})$
the number $\dim _{\mathbb {Z}/2} (\mathbb {Z}/2 \otimes tors\tfrac {H_\mathbb {Z}}{(\mathrm {Id}-\phi )H_\mathbb {Z}})$![]() modulo 2, is a homomorphism.
modulo 2, is a homomorphism.
Theorem 5.6 If $n$![]() is even so $(H_\mathbb {Z},\, \lambda )$
is even so $(H_\mathbb {Z},\, \lambda )$![]() is symmetric then
is symmetric then

is the cohomology class given by $r_1$![]() in degree 1, and is trivial in all other degrees.
in degree 1, and is trivial in all other degrees.
If $n$![]() is odd so $(H_\mathbb {Z},\, \lambda )$
is odd so $(H_\mathbb {Z},\, \lambda )$![]() is skew-symmetric then
is skew-symmetric then

is the cohomology class $r_3$![]() in degree 3, and is trivial in all other degrees.
in degree 3, and is trivial in all other degrees.
To begin the proof of this theorem, the map $inc$![]() tautologically factors over ($\Omega ^\infty$
tautologically factors over ($\Omega ^\infty$![]() of) the map
of) the map
so it suffices to analyse the map

which is an infinite loop map. The following lemma shows that there are not so many such maps which refine to infinite loop maps.
Lemma 5.7 The cohomology suspension map
has trivial image in degrees congruent to $1 - 2n \mod 4,$![]() except for degree 1 if $n$
except for degree 1 if $n$![]() is even or degree 3 if $n$
is even or degree 3 if $n$![]() is odd.
is odd.
Proof. Berrick and Karoubi [Reference Berrick and Karoubi5] establish a 2-adically cartesian square

where the left-hand terms are (the 0-connected covers of) the classical symmetric Grothendieck–Witt spectra. There is a zig-zag
whose left-hand map is an equivalence by [Reference Calmès, Dotto, Harpaz, Hebestreit, Land, Moi, Nardin, Nikolaus and Steimle11, 1.3.15] (using [Reference Hebestreit and Steimle22, theorem A]), and whose right-hand map is a 2-adic equivalence by [Reference Calmès, Dotto, Harpaz, Hebestreit, Land, Moi, Nardin, Nikolaus and Steimle11, 3.1.11]. Combined with theorems IV.2.4 and IV.5.4 of [Reference Fiedorowicz and Priddy15] this gives fibre sequences of (implicitly 2-completed) spectra
where the right-hand maps are $bo \oplus bo \overset +\to bo \overset {\psi ^3-1}\to bso$![]() and $bu \to bsp \overset {\psi ^3-1}\to bsp$
and $bu \to bsp \overset {\psi ^3-1}\to bsp$![]() respectively. These spectra are the deloopings of $BO$
respectively. These spectra are the deloopings of $BO$![]() , $BSO$
, $BSO$![]() , $BU$
, $BU$![]() and $BSp$
and $BSp$![]() , and their $\mathbb {Z}/2$
, and their $\mathbb {Z}/2$![]() -cohomology as left modules over the Steenrod algebra $\mathcal {A}$
-cohomology as left modules over the Steenrod algebra $\mathcal {A}$![]() follows from the calculations of [Reference Stong49], as
follows from the calculations of [Reference Stong49], as

where $\iota _r$![]() denotes a class of degree $r$
denotes a class of degree $r$![]() , and here and in the rest of this proof all cohomology is taken with $\mathbb {Z}/2$
, and here and in the rest of this proof all cohomology is taken with $\mathbb {Z}/2$![]() -coefficients.
-coefficients.
The map $\psi ^3-1 : bsp \to bsp$![]() induces multiplication by 8($=3^2-1$
induces multiplication by 8($=3^2-1$![]() ) on the lowest homotopy group $\pi _4(bsp) = \mathbb {Z}_2$
) on the lowest homotopy group $\pi _4(bsp) = \mathbb {Z}_2$![]() , so by the above it induces the zero map on $\mathbb {Z}/2$
, so by the above it induces the zero map on $\mathbb {Z}/2$![]() -cohomology.
-cohomology.
The based map $BO(1) \overset {L-1}\to BO \overset {\psi ^3-1}\to BSO$![]() , where $L$
, where $L$![]() is the tautological real line bundle over $BO(1)$
is the tautological real line bundle over $BO(1)$![]() , is nullhomotopic as $\psi ^3(L) = L^{\otimes 3} = L$
, is nullhomotopic as $\psi ^3(L) = L^{\otimes 3} = L$![]() . Thus the adjoint $\Sigma ^\infty BO(1) \to bo \overset {\psi ^3-1}\to bso$
. Thus the adjoint $\Sigma ^\infty BO(1) \to bo \overset {\psi ^3-1}\to bso$![]() is nullhomotopic too, but the first map sends the generator $\iota _1 \in H^1(bo)$
is nullhomotopic too, but the first map sends the generator $\iota _1 \in H^1(bo)$![]() to $w_1(L) \in H^1(BO(1))$
to $w_1(L) \in H^1(BO(1))$![]() and so sends $H^2(bo) = \mathbb {Z}/2\{\mathrm {Sq}^1 \iota _1\}$
and so sends $H^2(bo) = \mathbb {Z}/2\{\mathrm {Sq}^1 \iota _1\}$![]() isomorphically to $H^2(BO(1)) = \mathbb {Z}/2\{w_1(L)^2\}$
isomorphically to $H^2(BO(1)) = \mathbb {Z}/2\{w_1(L)^2\}$![]() . Thus the map $\psi ^3-1 : bo \to bso$
. Thus the map $\psi ^3-1 : bo \to bso$![]() is zero on $H^2(-)$
is zero on $H^2(-)$![]() , and so on all $\mathbb {Z}/2$
, and so on all $\mathbb {Z}/2$![]() -cohomology.
-cohomology.
We obtain extensions of $\mathcal {A}$![]() -modules
-modules

and so find that $H^*(\tau _{\geq 0} \mathrm {GW}^{s}(\mathbb {Z}; +))$![]() is generated as an $\mathcal {A}$
is generated as an $\mathcal {A}$![]() -module by three elements of degree 1, and $H^*(\tau _{\geq 0} \mathrm {GW}^{s}(\mathbb {Z}; -))$
-module by three elements of degree 1, and $H^*(\tau _{\geq 0} \mathrm {GW}^{s}(\mathbb {Z}; -))$![]() is generated as an $\mathcal {A}$
is generated as an $\mathcal {A}$![]() -module by an element of degree 2 and an element of degree 3.
-module by an element of degree 2 and an element of degree 3.
In the second case the right-hand term vanishes in total degree 3, so there is a unique lift $\bar {\iota }_3$![]() of the generator $\iota _3$
of the generator $\iota _3$![]() of the left-hand term. This must satisfy either $\mathrm {Sq}^1(\bar {\iota }_3)=0$
of the left-hand term. This must satisfy either $\mathrm {Sq}^1(\bar {\iota }_3)=0$![]() or $\mathrm {Sq}^1(\bar {\iota }_3)= \mathrm {Sq}^2 (\iota _2)$
or $\mathrm {Sq}^1(\bar {\iota }_3)= \mathrm {Sq}^2 (\iota _2)$![]() . The latter can be ruled out by assuming that this is the case and then using the Adams spectral sequence to calculate $\pi _3(\mathrm {GW}^{s}(\mathbb {Z}; -))$
. The latter can be ruled out by assuming that this is the case and then using the Adams spectral sequence to calculate $\pi _3(\mathrm {GW}^{s}(\mathbb {Z}; -))$![]() , which one finds to be $\mathbb {Z}/4$
, which one finds to be $\mathbb {Z}/4$![]() . But it is in fact seen to be $\mathbb {Z}/16$
. But it is in fact seen to be $\mathbb {Z}/16$![]() by calculating with (5.7) (cf. the corresponding table in [Reference Calmès, Dotto, Harpaz, Hebestreit, Land, Moi, Nardin, Nikolaus and Steimle11, section 3.2]). Writing $uns M$
by calculating with (5.7) (cf. the corresponding table in [Reference Calmès, Dotto, Harpaz, Hebestreit, Land, Moi, Nardin, Nikolaus and Steimle11, section 3.2]). Writing $uns M$![]() for the unstable quotient of an $\mathcal {A}$
for the unstable quotient of an $\mathcal {A}$![]() -module $M$
-module $M$![]() , we therefore find that
, we therefore find that

In the first case a basis for $uns \mathcal {A}\{\iota _1\}$![]() is given by those $\mathrm {Sq}^{i_1} \cdots \mathrm {Sq}^{i_r} {\iota }_1$
is given by those $\mathrm {Sq}^{i_1} \cdots \mathrm {Sq}^{i_r} {\iota }_1$![]() which are admissible and have excess $\leq 1$
which are admissible and have excess $\leq 1$![]() , i.e. the $\mathrm {Sq}^{2^{i}} \cdots \mathrm {Sq}^{2} \mathrm {Sq}^1 {\iota }_1$
, i.e. the $\mathrm {Sq}^{2^{i}} \cdots \mathrm {Sq}^{2} \mathrm {Sq}^1 {\iota }_1$![]() , having degrees $1+1+2+2^2 + \cdots + 2^i$
, having degrees $1+1+2+2^2 + \cdots + 2^i$![]() . This is only congruent to 1 modulo 4 for the class $\iota _1$
. This is only congruent to 1 modulo 4 for the class $\iota _1$![]() itself. The same goes for the summands generated by $\iota _1'$
itself. The same goes for the summands generated by $\iota _1'$![]() and $\iota ''_1$
and $\iota ''_1$![]() .
.
In the second case, $uns \mathcal {A}\{\iota _2\}/(\mathrm {Sq}^1 \iota _2)$![]() has basis given by those $\mathrm {Sq}^{i_1} \cdots \mathrm {Sq}^{i_r} {\iota }_2$
has basis given by those $\mathrm {Sq}^{i_1} \cdots \mathrm {Sq}^{i_r} {\iota }_2$![]() which are admissible, have excess $\leq 2$
which are admissible, have excess $\leq 2$![]() , and have $i_r \geq 2$
, and have $i_r \geq 2$![]() , i.e. the $\mathrm {Sq}^{2^{i}} \cdots \mathrm {Sq}^{2^2} \mathrm {Sq}^2 {\iota }_2$
, i.e. the $\mathrm {Sq}^{2^{i}} \cdots \mathrm {Sq}^{2^2} \mathrm {Sq}^2 {\iota }_2$![]() . These all have even degree. On the other hand $uns \mathcal {A}\{\bar {\iota }_3\}/(\mathrm {Sq}^1 \bar {\iota }_3)$
. These all have even degree. On the other hand $uns \mathcal {A}\{\bar {\iota }_3\}/(\mathrm {Sq}^1 \bar {\iota }_3)$![]() has basis given by those $\mathrm {Sq}^{i_1} \cdots \mathrm {Sq}^{i_r} {\iota }_2$
has basis given by those $\mathrm {Sq}^{i_1} \cdots \mathrm {Sq}^{i_r} {\iota }_2$![]() which are admissible, have excess $\leq 3$
which are admissible, have excess $\leq 3$![]() , and have $i_r \geq 2$
, and have $i_r \geq 2$![]() . These have the form $\mathrm {Sq}^{2^j(2^i+1)} \cdots \mathrm {Sq}^{2(2^i+1)} \mathrm {Sq}^{2^i+1} \mathrm {Sq}^{2^{i-1}} \cdots \mathrm {Sq}^{2} {\iota }_3$
. These have the form $\mathrm {Sq}^{2^j(2^i+1)} \cdots \mathrm {Sq}^{2(2^i+1)} \mathrm {Sq}^{2^i+1} \mathrm {Sq}^{2^{i-1}} \cdots \mathrm {Sq}^{2} {\iota }_3$![]() for some $i \geq 1$
for some $i \geq 1$![]() and $j \geq -1$
and $j \geq -1$![]() (correctly interpreted), and some checking of cases shows that such elements have degree congruent to 3 modulo 4 only in the case of ${\iota }_3$
(correctly interpreted), and some checking of cases shows that such elements have degree congruent to 3 modulo 4 only in the case of ${\iota }_3$![]() itself.
itself.
Lemma 5.8 If $n$![]() is even, so $(H_\mathbb {Z},\, \lambda )$
is even, so $(H_\mathbb {Z},\, \lambda )$![]() is symmetric, then on $\pi _1$
is symmetric, then on $\pi _1$![]() the map
the map
assigns to an automorphism $\phi$![]() of $(H_\mathbb {Z},\, \lambda )$
of $(H_\mathbb {Z},\, \lambda )$![]() the number $\dim _{\mathbb {Z}/2} (\mathbb {Z}/2 \otimes tors \tfrac {H_\mathbb {Z}}{(\mathrm {Id}-\phi )H_\mathbb {Z}})$
the number $\dim _{\mathbb {Z}/2} (\mathbb {Z}/2 \otimes tors \tfrac {H_\mathbb {Z}}{(\mathrm {Id}-\phi )H_\mathbb {Z}})$![]() modulo 2. In particular this function $r_1$
modulo 2. In particular this function $r_1$![]() is a homomorphism, and the map in question is the cohomology class given by $r_1$
is a homomorphism, and the map in question is the cohomology class given by $r_1$![]() .
.
Proof. Given a $\phi \in \mathrm {Aut}(H_\mathbb {Z},\, \lambda )$![]() , we are required to evaluate the de Rham invariant of the algebraic mapping torus $T_\phi$
, we are required to evaluate the de Rham invariant of the algebraic mapping torus $T_\phi$![]() of $\phi : H_\mathbb {Z}[-n] \to H_{\mathbb {Z}}[-n]$
of $\phi : H_\mathbb {Z}[-n] \to H_{\mathbb {Z}}[-n]$![]() . Fortunately the value of this invariant does not depend on the symmetric structure but only on the underlying chain complex $T_\phi \simeq ( H_\mathbb {Z}[-n] \xrightarrow {1-\phi } H_\mathbb {Z}[-n-1] )$
. Fortunately the value of this invariant does not depend on the symmetric structure but only on the underlying chain complex $T_\phi \simeq ( H_\mathbb {Z}[-n] \xrightarrow {1-\phi } H_\mathbb {Z}[-n-1] )$![]() , and is given by
, and is given by
Remark 5.9 Using the first fibration in (5.7) and the calculation of the groups $H^1(\tau _{>0}\mathrm {GW}^s(\mathbb {Z} ; +) ;\mathbb {Z}/2)$![]() from the proof of lemma 5.7, we find that
from the proof of lemma 5.7, we find that
We may describe this as follows.
Negation gives automorphisms $i_+$![]() and $i_-$
and $i_-$![]() of $(\mathbb {Z},\, (1))$
of $(\mathbb {Z},\, (1))$![]() and $(\mathbb {Z},\, (-1))$
and $(\mathbb {Z},\, (-1))$![]() respectively, and there is an automorphism $i_{rot}$
respectively, and there is an automorphism $i_{rot}$![]() of the positive definite form $\left (\mathbb {Z}^2,\, \left (\begin {smallmatrix} 1 & 0 \\ 0 & 1 \end {smallmatrix}\right )\right )$
of the positive definite form $\left (\mathbb {Z}^2,\, \left (\begin {smallmatrix} 1 & 0 \\ 0 & 1 \end {smallmatrix}\right )\right )$![]() given by the rotation $\left (\begin {smallmatrix} 0 & -1 \\ 1 & 0 \end {smallmatrix}\right )$
given by the rotation $\left (\begin {smallmatrix} 0 & -1 \\ 1 & 0 \end {smallmatrix}\right )$![]() . In parallel we have the maps
. In parallel we have the maps
which assign to an automorphism of a symmetric form the sign of the determinant of the induced map on positive and negative definite subspaces of its realification, as well as the de Rham invariant $r_1 : H_1(\Omega ^\infty _0 \mathrm {GW}^s(\mathbb {Z} ; +);\mathbb {Z}) \to \mathbb {Z}/2$![]() as described in the proof of Lemma 5.8. It is easy to check that $r_1$
as described in the proof of Lemma 5.8. It is easy to check that $r_1$![]() is nontrivial on each of $i_+,\, i_-,\, i_{rot}$
is nontrivial on each of $i_+,\, i_-,\, i_{rot}$![]() , and that ${\det }^+(i_+)$
, and that ${\det }^+(i_+)$![]() and ${\det }^-(i_-)$
and ${\det }^-(i_-)$![]() are nontrivial but all other values of ${\det }^\pm$
are nontrivial but all other values of ${\det }^\pm$![]() on $i_+,\, i_-,\, i_{rot}$
on $i_+,\, i_-,\, i_{rot}$![]() are trivial. Thus $i_+,\, i_-,\, i_{rot}$
are trivial. Thus $i_+,\, i_-,\, i_{rot}$![]() give a basis for the left-hand side of (5.8), and ${\det }^+,\, {\det }^-,\, r_1$
give a basis for the left-hand side of (5.8), and ${\det }^+,\, {\det }^-,\, r_1$![]() give a dual basis for it.
give a dual basis for it.
The following lemma finishes the proof of theorem 5.6.
Lemma 5.10 If $n$![]() is odd then the composition
is odd then the composition

given by projecting to the lowest degree summand is the unique nontrivial element of $H^3(\Omega ^\infty _0 \mathrm {GW}^s(\mathbb {Z}; -);\mathbb {Z}/2) = H^3(BSp_\infty (\mathbb {Z});\mathbb {Z}/2)$![]() .
.
Proof. We implicitly 2-complete everywhere, and work in $\mathbb {Z}/2$![]() -cohomology. Firstly, taking infinite loop spaces of the second fibration in (5.7) and looping it up gives a fibration
-cohomology. Firstly, taking infinite loop spaces of the second fibration in (5.7) and looping it up gives a fibration
which is pulled back from a fibration $Sp \to \Omega ^\infty _0 \mathrm {GW}^s(\mathbb {F}_3; -) \to BSp$![]() . By [Reference Fiedorowicz and Priddy15, proposition I.4.2] the Serre spectral sequence for the latter fibration collapses, so that of the former does too. It follows that $H^3(\Omega ^\infty _0 \mathrm {GW}^s(\mathbb {Z}; -)) = \mathbb {Z}/2$
. By [Reference Fiedorowicz and Priddy15, proposition I.4.2] the Serre spectral sequence for the latter fibration collapses, so that of the former does too. It follows that $H^3(\Omega ^\infty _0 \mathrm {GW}^s(\mathbb {Z}; -)) = \mathbb {Z}/2$![]() , and in terms of the notation introduced in the proof of lemma 5.7 it is generated by $\Omega ^\infty \bar {\iota }_3$
, and in terms of the notation introduced in the proof of lemma 5.7 it is generated by $\Omega ^\infty \bar {\iota }_3$![]() . We need to show that the map in the statement of the lemma is the nontrivial element of this group.
. We need to show that the map in the statement of the lemma is the nontrivial element of this group.
By the Main Theorem of [Reference Calmès, Dotto, Harpaz, Hebestreit, Land, Moi, Nardin, Nikolaus and Steimle10] (and that fact that $\pi _1(\Sigma ^{-2n}\mathrm {L}^s(\mathbb {Z}))=0$![]() ) there is a homotopy fibre sequence of 0-connected covers
) there is a homotopy fibre sequence of 0-connected covers
where $\sigma$![]() denotes the sign representation of $C_2$
denotes the sign representation of $C_2$![]() . On cohomology the right-hand map has the form
. On cohomology the right-hand map has the form
in degrees $\leq 3$![]() , and in terms of the calculations in the proof of lemma 5.7 we must have $\iota _2 \mapsto A \iota _2$
, and in terms of the calculations in the proof of lemma 5.7 we must have $\iota _2 \mapsto A \iota _2$![]() and $\iota _3 \mapsto B\bar {\iota }_3$
and $\iota _3 \mapsto B\bar {\iota }_3$![]() for some $A,\, B \in \mathbb {Z}/2$
for some $A,\, B \in \mathbb {Z}/2$![]() . We need to show that $B=1$
. We need to show that $B=1$![]() , which we shall do by analysing the cohomology of $\tau _{>0}((S^{2\sigma -2} \otimes \mathrm {K}(\mathbb {Z}))_{hC_2})$
, which we shall do by analysing the cohomology of $\tau _{>0}((S^{2\sigma -2} \otimes \mathrm {K}(\mathbb {Z}))_{hC_2})$![]() in low degrees.
in low degrees.
The unit map $\mathrm {S} \to \mathrm {K}(\mathbb {Z})$![]() induces an isomorphism on homotopy groups in degrees $\leq 2$
induces an isomorphism on homotopy groups in degrees $\leq 2$![]() , and induces an injection $\mathbb {Z}/24 = \pi _3(\mathrm {S}) \to \pi _3(\mathrm {K}(\mathbb {Z})) = \mathbb {Z}/48$
, and induces an injection $\mathbb {Z}/24 = \pi _3(\mathrm {S}) \to \pi _3(\mathrm {K}(\mathbb {Z})) = \mathbb {Z}/48$![]() . Thus the map $(S^{2\sigma -2})_{hC_2} \to (S^{2\sigma -2} \otimes \mathrm {K}(\mathbb {Z}))_{hC_2}$
. Thus the map $(S^{2\sigma -2})_{hC_2} \to (S^{2\sigma -2} \otimes \mathrm {K}(\mathbb {Z}))_{hC_2}$![]() has fibre $\mathrm {F}$
has fibre $\mathrm {F}$![]() which is 1-connected and has $\pi _2(\mathrm {F})=\mathbb {Z}/2$
which is 1-connected and has $\pi _2(\mathrm {F})=\mathbb {Z}/2$![]() . Taking 0-connected covers gives a fibration sequence
. Taking 0-connected covers gives a fibration sequence
By the Thom isomorphism we have
with $\mathcal {A}$![]() -module structure determined by $\mathrm {Sq}(u) = w(2\sigma -2) \cdot u = (1+x^2) \cdot u$
-module structure determined by $\mathrm {Sq}(u) = w(2\sigma -2) \cdot u = (1+x^2) \cdot u$![]() , the Cartan formula, and the usual action of Steenrod operations on $H^*(BC_2) = \mathbb {Z}/2[x]$
, the Cartan formula, and the usual action of Steenrod operations on $H^*(BC_2) = \mathbb {Z}/2[x]$![]() . In degrees $\leq 3$
. In degrees $\leq 3$![]() this means that the only nontrivial operations are
this means that the only nontrivial operations are
Using the fibre sequence $\tau _{>0}((S^{2\sigma -2})_{hC_2}) \to (S^{2\sigma -2})_{hC_2} \to \mathrm {H}\mathbb {Z}$![]() we deduce that $H^i(\tau _{>0}((S^{2\sigma -2})_{hC_2}))$
we deduce that $H^i(\tau _{>0}((S^{2\sigma -2})_{hC_2}))$![]() is trivial for $i=0$
is trivial for $i=0$![]() and 1-dimensional for $i=1,\,2$
and 1-dimensional for $i=1,\,2$![]() . Combined with (5.10), we find that $H^i(\tau _{>0}((S^{2\sigma -2} \otimes \mathrm {K}(\mathbb {Z}))_{hC_2}))$
. Combined with (5.10), we find that $H^i(\tau _{>0}((S^{2\sigma -2} \otimes \mathrm {K}(\mathbb {Z}))_{hC_2}))$![]() is trivial for $i=0$
is trivial for $i=0$![]() , 1-dimensional for $i=1$
, 1-dimensional for $i=1$![]() , and at most 1-dimensional for $i=2$
, and at most 1-dimensional for $i=2$![]() . Returning to (5.9), as $H^1(\tau _{>0}((S^{2\sigma -2} \otimes \mathrm {K}(\mathbb {Z}))_{hC_2}))=\mathbb {Z}/2$
. Returning to (5.9), as $H^1(\tau _{>0}((S^{2\sigma -2} \otimes \mathrm {K}(\mathbb {Z}))_{hC_2}))=\mathbb {Z}/2$![]() it follows that $A=0$
it follows that $A=0$![]() , but then we have an exact sequence
, but then we have an exact sequence
and as $H^2(\tau _{>0}((S^{2\sigma -2} \otimes \mathrm {K}(\mathbb {Z}))_{hC_2}))$![]() has dimension at most 1 it follows that $B=1$
has dimension at most 1 it follows that $B=1$![]() , as required.
, as required.
The following lemma shows that the de Rham invariants vanish in the presence of a quadratic structure.
Lemma 5.11 If $(H_\mathbb {Z},\, \lambda )$![]() is a nondegenerate $(-1)^n$
is a nondegenerate $(-1)^n$![]() -symmetric form and $\mu : H_\mathbb {Z} \to \mathbb {Z}/(1-(-1)^n)$
-symmetric form and $\mu : H_\mathbb {Z} \to \mathbb {Z}/(1-(-1)^n)$![]() is a quadratic refinement of it, then the composition
is a quadratic refinement of it, then the composition

is nullhomotopic.
Proof. The composition of the first two maps agrees with
but by [Reference Taylor and Williams51, eq. (1.10)] the composition $\mathrm {L}^q(\mathbb {Z}) \to \mathrm {L}^s(\mathbb {Z}) \overset {r}\to \bigoplus _{j \in \mathbb {Z}} \mathrm {H}\mathbb {Z}/2[4j+1]$![]() is null.
is null.
6. Examples and applications
6.1 Multiplicativity of the signature
Normal $L$![]() -theory $\mathrm {L}^n(\mathbb {Z})$
-theory $\mathrm {L}^n(\mathbb {Z})$![]() fits into a fibration sequence
fits into a fibration sequence
where the first map encodes the forgetful map from quadratic to symmetric $L$![]() -theory. Its homotopy groups are therefore
-theory. Its homotopy groups are therefore

It is in fact a ring spectrum and $\mathrm {L}^s(\mathbb {Z}) \to \mathrm {L}^n(\mathbb {Z})$![]() is a ring map, which may be seen by tracing through the definitions in [Reference Ranicki42, p. 384]; as it is 2-local, it follows as in § 5.1 that $\mathrm {L}^n(\mathbb {Z})$
is a ring map, which may be seen by tracing through the definitions in [Reference Ranicki42, p. 384]; as it is 2-local, it follows as in § 5.1 that $\mathrm {L}^n(\mathbb {Z})$![]() is an Eilenberg–MacLane spectrum. Taylor and Williams produce specific maps
is an Eilenberg–MacLane spectrum. Taylor and Williams produce specific maps

and $\Sigma k : \mathrm {L}^n(\mathbb {Z}) \to \bigoplus _{k \in \mathbb {Z}} \mathrm {H}\mathbb {Z}/2[4k+2]$![]() exhibiting it as an Eilenberg–MacLane spectrum, whose precompositions with $\mathrm {L}^s(\mathbb {Z}) \to \mathrm {L}^n(\mathbb {Z})$
exhibiting it as an Eilenberg–MacLane spectrum, whose precompositions with $\mathrm {L}^s(\mathbb {Z}) \to \mathrm {L}^n(\mathbb {Z})$![]() are $L \mod 8$
are $L \mod 8$![]() , $r$
, $r$![]() , and 0 respectively.
, and 0 respectively.
Ranicki has constructed [Reference Ranicki42, p. 385] a normal signature map $\sigma ^n$![]() such that
such that

commutes up to homotopy; here $\mathrm {MSG}$![]() is the Thom spectrum of the universal spherical fibration over $BSG$
is the Thom spectrum of the universal spherical fibration over $BSG$![]() , and is a model for the cobordism theory given by Quinn's normal spaces [Reference Quinn38, Reference Quinn40]. Furthermore, Taylor and Williams construct $\hat {L}$
, and is a model for the cobordism theory given by Quinn's normal spaces [Reference Quinn38, Reference Quinn40]. Furthermore, Taylor and Williams construct $\hat {L}$![]() so that $\hat {L} \circ \sigma ^n$
so that $\hat {L} \circ \sigma ^n$![]() corresponds under the Thom isomorphism to the characteristic class of stable spherical fibrations $l \in H^{4*}(BSG ; \mathbb {Z}/8)$
corresponds under the Thom isomorphism to the characteristic class of stable spherical fibrations $l \in H^{4*}(BSG ; \mathbb {Z}/8)$![]() constructed by Brumfiel–Morgan [Reference Brumfiel and Morgan6, §8]. Using this we can apply the results of the previous section to oriented fibrations with finite Poincaré fibre as follows. (It is likely that this can be extended to Poincaré fibres which are merely finitely-dominated, but we do not pursue this here.)
constructed by Brumfiel–Morgan [Reference Brumfiel and Morgan6, §8]. Using this we can apply the results of the previous section to oriented fibrations with finite Poincaré fibre as follows. (It is likely that this can be extended to Poincaré fibres which are merely finitely-dominated, but we do not pursue this here.)
Proposition 6.1 If $F^d \to E \overset {\pi } \to B$![]() is an oriented fibration with finite Poincaré fibre and finitely-dominated base then it has a fibrewise Spivak normal fibration $\nu _\pi,$
is an oriented fibration with finite Poincaré fibre and finitely-dominated base then it has a fibrewise Spivak normal fibration $\nu _\pi,$![]() and
and

Proof. By pulling back to a finite CW-complex dominating $B$![]() we may assume without loss of generality that $B = |K|$
we may assume without loss of generality that $B = |K|$![]() is the realization of a finite semi-simplicial set. By induction on the simplices of $K$
is the realization of a finite semi-simplicial set. By induction on the simplices of $K$![]() we may construct a $U \subset |K| \times \mathbb {R}^N$
we may construct a $U \subset |K| \times \mathbb {R}^N$![]() and compatible maps
and compatible maps
for each simplex $\sigma$![]() of $K$
of $K$![]() , such that each $U\vert _\sigma \subset \sigma \times \mathbb {R}^N$
, such that each $U\vert _\sigma \subset \sigma \times \mathbb {R}^N$![]() is a codimension 0 compact submanifold with boundary $\partial (U\vert _\sigma ) = (U\vert _{\partial \sigma }) \cup \partial _0(U\vert _\sigma )$
is a codimension 0 compact submanifold with boundary $\partial (U\vert _\sigma ) = (U\vert _{\partial \sigma }) \cup \partial _0(U\vert _\sigma )$![]() . The inclusions $U\vert _\tau \to U\vert _\sigma$
. The inclusions $U\vert _\tau \to U\vert _\sigma$![]() for $\tau \leq \sigma$
for $\tau \leq \sigma$![]() are equivalences, as $E\vert _\tau \to E\vert _\sigma$
are equivalences, as $E\vert _\tau \to E\vert _\sigma$![]() are, and it follows from Poincaré duality and induction over simplices that (for $N$
are, and it follows from Poincaré duality and induction over simplices that (for $N$![]() large enough) the inclusions $\partial _0(U\vert _\tau ) \to \partial _0(U\vert _\sigma )$
large enough) the inclusions $\partial _0(U\vert _\tau ) \to \partial _0(U\vert _\sigma )$![]() are equivalences too. As the inclusions $\partial _0(U\vert _\sigma ) \to U\vert _\sigma$
are equivalences too. As the inclusions $\partial _0(U\vert _\sigma ) \to U\vert _\sigma$![]() have homotopy fibre a $(N-d-1)$
have homotopy fibre a $(N-d-1)$![]() -sphere when $\sigma$
-sphere when $\sigma$![]() is a 0-simplex, by Spivak's theorem [Reference Spivak48, proposition 4.6], it follows that the same is true for all simplices. Then
is a 0-simplex, by Spivak's theorem [Reference Spivak48, proposition 4.6], it follows that the same is true for all simplices. Then
also has homotopy fibre a $(N-d-1)$![]() -sphere so gives the required oriented spherical fibration $\nu _\pi$
-sphere so gives the required oriented spherical fibration $\nu _\pi$![]() . Collapsing the complement of $U$
. Collapsing the complement of $U$![]() gives a Pontrjagin–Thom collapse map
gives a Pontrjagin–Thom collapse map
which can be composed with the Thomification of the map $E \to BSG$![]() classifying the oriented spherical fibration $\nu _\pi$
classifying the oriented spherical fibration $\nu _\pi$![]() to obtain $\alpha : |K| \to \Omega ^{\infty +d} \mathrm {MSG}$
to obtain $\alpha : |K| \to \Omega ^{\infty +d} \mathrm {MSG}$![]() . The manifolds $U\vert _\sigma \subset \sigma \times \mathbb {R}^N$
. The manifolds $U\vert _\sigma \subset \sigma \times \mathbb {R}^N$![]() can inductively be equipped with singular chains representing $(\psi \vert _\sigma )^{-1}_*[E\vert _\sigma,\, E\vert _{\partial \sigma }] \in H_{d + \mathrm {dim}(\sigma )}(U\vert _\sigma,\, U\vert _{\partial \sigma } ; \mathbb {Z})$
can inductively be equipped with singular chains representing $(\psi \vert _\sigma )^{-1}_*[E\vert _\sigma,\, E\vert _{\partial \sigma }] \in H_{d + \mathrm {dim}(\sigma )}(U\vert _\sigma,\, U\vert _{\partial \sigma } ; \mathbb {Z})$![]() in order to define a semi-simplicial map $f : K \to \mathrm {Mock}^P(d)$
in order to define a semi-simplicial map $f : K \to \mathrm {Mock}^P(d)$![]() .
.
We can then form the diagram

in which all regions commute up to homotopy tautologically, apart from the leftmost trapezium, which commutes up to homotopy by surgery below the middle dimension as explained in § 4.8. The claimed formula then follows by combining this diagram with theorem 5.5.
Remark 6.2 The fibrewise Spivak fibration $\nu _\pi$![]() exists without assuming that the fibre is finite; constructions are given in [Reference Quinn38, proposition 1.8] and [Reference Klein25, Addendum C].
exists without assuming that the fibre is finite; constructions are given in [Reference Quinn38, proposition 1.8] and [Reference Klein25, Addendum C].
Remark 6.3 Taylor and Williams do not settle what characteristic class $\hat {r} \circ \sigma ^n$![]() corresponds to in $H^{4*+1}(BSG;\mathbb {Z}/2)$
corresponds to in $H^{4*+1}(BSG;\mathbb {Z}/2)$![]() under the Thom isomorphism, but if we call it $\rho$
under the Thom isomorphism, but if we call it $\rho$![]() for now then there is a corresponding identity for $\int _\pi \rho (\nu _\pi )$
for now then there is a corresponding identity for $\int _\pi \rho (\nu _\pi )$![]() . It would be interesting to determine what this $\rho$
. It would be interesting to determine what this $\rho$![]() is.
is.
As a consequence we obtain the following generalization of the result explained in remark 2.4. It generalizes [Reference Korzeniewski27, theorem 7.2] in that the base can be an arbitrary Poincaré complex, not necessarily simple.
Corollary 6.4 Let $F^d \to E^{4k} \overset {\pi }\to B^{4k-d}$![]() be an oriented fibration of oriented Poincaré complexes with finite fibre. Then
be an oriented fibration of oriented Poincaré complexes with finite fibre. Then
Proof. Writing $\nu _X$![]() for the Spivak normal fibration of a Poincaré complex $X$
for the Spivak normal fibration of a Poincaré complex $X$![]() , and $\nu _\pi$
, and $\nu _\pi$![]() for the fibrewise Spivak normal fibration of $\pi$
for the fibrewise Spivak normal fibration of $\pi$![]() , there is an identity $\nu _E \simeq \pi ^*(\nu _B) * \nu _\pi$
, there is an identity $\nu _E \simeq \pi ^*(\nu _B) * \nu _\pi$![]() (see [Reference Klein25, theorem I]). Using the properties of the characteristic class $l$
(see [Reference Klein25, theorem I]). Using the properties of the characteristic class $l$![]() given in [Reference Brumfiel and Morgan6, theorem I] we calculate
given in [Reference Brumfiel and Morgan6, theorem I] we calculate

but by proposition 6.1 and the last part of lemma 5.4 we have $\int _\pi l(\nu _\pi ) \equiv \sigma (F) \mod 4$![]() and so the above becomes $\sigma (B) \cdot \sigma (F) \mod 4$
and so the above becomes $\sigma (B) \cdot \sigma (F) \mod 4$![]() .
.
This line of reasoning will give, in principle, information about $\sigma (E) - \sigma (B) \cdot \sigma (F) \mod 8$![]() . There will be additional terms coming from (i) the characteristic class $l$
. There will be additional terms coming from (i) the characteristic class $l$![]() not exactly being multiplicative modulo 8 [Reference Brumfiel and Morgan6, theorem I (iii)], and (ii) the classes $\widetilde {\mathrm {ph}}_i$
not exactly being multiplicative modulo 8 [Reference Brumfiel and Morgan6, theorem I (iii)], and (ii) the classes $\widetilde {\mathrm {ph}}_i$![]() not necessarily vanishing mod 8. It would be interesting to compare this with the formula of [Reference Rovi47].
not necessarily vanishing mod 8. It would be interesting to compare this with the formula of [Reference Rovi47].
6.2 Fibrewise Stiefel–Whitney classes
As a further application of proposition 6.1 we have the following vanishing result for fibre integrals of fibrewise Stiefel–Whitney classes.
Corollary 6.5 If $F \to E \overset {\pi }\to B$![]() is an oriented fibration with finite Poincaré fibre, then
is an oriented fibration with finite Poincaré fibre, then

This is obvious for fibre bundles, as the vertical tangent bundle has dimension $d$![]() and so $w_i(-\nu _\pi )$
and so $w_i(-\nu _\pi )$![]() vanishes for $i>d$
vanishes for $i>d$![]() . But for fibrations with Poincaré fibre it does not seem obvious.
. But for fibrations with Poincaré fibre it does not seem obvious.
Proof. The Brumfiel–Morgan class $l$![]() reduces modulo 2 to the square of the Wu class [Reference Brumfiel and Morgan6, theorem I (ii)], so as the $\widetilde {\mathrm {ph}}_i$
reduces modulo 2 to the square of the Wu class [Reference Brumfiel and Morgan6, theorem I (ii)], so as the $\widetilde {\mathrm {ph}}_i$![]() reduce to zero modulo 2 for $i>0$
reduce to zero modulo 2 for $i>0$![]() we obtain from proposition 6.1 the identity $\int _\pi V(\nu _\pi )^2 \equiv \sigma (F) \mod 2$
we obtain from proposition 6.1 the identity $\int _\pi V(\nu _\pi )^2 \equiv \sigma (F) \mod 2$![]() which is also $\chi (F) \mod 2$
which is also $\chi (F) \mod 2$![]() . As in the proof of theorem 5.5 we take the total Steenrod square of this to obtain
. As in the proof of theorem 5.5 we take the total Steenrod square of this to obtain
as required.
6.3 Multiplicativity of the de Rham invariant
We can make a similar analysis of the de Rham invariant $d$![]() , though it turns out to not be multiplicative in general: however, the failure to be multiplicative gives an interpretation of the cohomology classes $r_1$
, though it turns out to not be multiplicative in general: however, the failure to be multiplicative gives an interpretation of the cohomology classes $r_1$![]() and $r_3$
and $r_3$![]() appearing in theorem 5.6. See [Reference Alexander1] for a special case, and [Reference Becker and Schultz9] for a related result on the $\mathbb {R}$
appearing in theorem 5.6. See [Reference Alexander1] for a special case, and [Reference Becker and Schultz9] for a related result on the $\mathbb {R}$![]() -semicharacteristic.
-semicharacteristic.
Proposition 6.6 Let $F^d \to E^{4k+1} \overset {\pi }\to B^{4k+1-d}$![]() be an oriented block bundle of oriented topological manifolds. If $d$
be an oriented block bundle of oriented topological manifolds. If $d$![]() is odd then $d(E)=\sigma (B) \cdot d(F)$
is odd then $d(E)=\sigma (B) \cdot d(F)$![]() . If $d$
. If $d$![]() is even with monodromy $\phi : B \to B\mathrm {Aut}(H^{d/2}(F;\mathbb {Z})/tors,\, \lambda )$
is even with monodromy $\phi : B \to B\mathrm {Aut}(H^{d/2}(F;\mathbb {Z})/tors,\, \lambda )$![]() then
then
Proof. We have $V(\nu _E) = 1 + V_2(\nu _E) + V_4(\nu _E) + \cdots + V_{2k}(\nu _E)$![]() , so
, so
The stable isomorphism $TE \cong _s \pi ^* TB \oplus T_\pi ^s E$![]() gives $V(\nu _E) = \pi ^*V(\nu _B) \cdot V(\nu _\pi )$
gives $V(\nu _E) = \pi ^*V(\nu _B) \cdot V(\nu _\pi )$![]() , using which we can rewrite this as
, using which we can rewrite this as

As in the proof of corollary 6.5 we have $\int _\pi V(\nu _\pi )^2 \equiv \sigma (F) \mod 2$![]() and so the first term simplifies to $d(B) \cdot \sigma (F)$
and so the first term simplifies to $d(B) \cdot \sigma (F)$![]() (which is trivial unless $d \equiv 0 \mod 4$
(which is trivial unless $d \equiv 0 \mod 4$![]() ). Abbreviating $V_i := V_i(\nu _\pi )$
). Abbreviating $V_i := V_i(\nu _\pi )$![]() we have
we have

and so the second term in the above equation can be written as

The latter term is zero, as $E$![]() is by assumption oriented so $\mathrm {Sq}^1$
is by assumption oriented so $\mathrm {Sq}^1$![]() into its top cohomology is zero. Furthermore $\int _\pi \sum _{i} V_{2i} \cdot \mathrm {Sq}^1 V_{2i}$
into its top cohomology is zero. Furthermore $\int _\pi \sum _{i} V_{2i} \cdot \mathrm {Sq}^1 V_{2i}$![]() is the family de Rham class, so is equal to the scalar $d(F)$
is the family de Rham class, so is equal to the scalar $d(F)$![]() if $d$
if $d$![]() is odd by theorem 5.2, and is equal to the class $r_1$
is odd by theorem 5.2, and is equal to the class $r_1$![]() or $r_3$
or $r_3$![]() if $d$
if $d$![]() is even by theorem 5.6. Combining this with the fact that $\int _B V(\nu _B)^2 \equiv \sigma (B) \mod 2$
is even by theorem 5.6. Combining this with the fact that $\int _B V(\nu _B)^2 \equiv \sigma (B) \mod 2$![]() if $B$
if $B$![]() is even-dimensional, and with $\int _B V(\nu _B) \cdot - = \int _B \mathrm {Sq}(-)$
is even-dimensional, and with $\int _B V(\nu _B) \cdot - = \int _B \mathrm {Sq}(-)$![]() , gives the claimed formulas.
, gives the claimed formulas.
Example 6.7 Let $\mathbb {CP}^2 \to E^{4k+1} \overset {\pi }\to \mathbb {RP}^{4k-3}$![]() be the standard fibering of the Dold manifold, i.e. $E = S^{4k-3} \times _{C_2} \mathbb {CP}^2$
be the standard fibering of the Dold manifold, i.e. $E = S^{4k-3} \times _{C_2} \mathbb {CP}^2$![]() where the involution acts antipodally on $S^{4k-3}$
where the involution acts antipodally on $S^{4k-3}$![]() and by complex conjugation on $\mathbb {CP}^2$
and by complex conjugation on $\mathbb {CP}^2$![]() . The generator of $\pi _1(\mathbb {RP}^{4k-3}) = \mathbb {Z}/2$
. The generator of $\pi _1(\mathbb {RP}^{4k-3}) = \mathbb {Z}/2$![]() acts on the intersection form $(\mathbb {Z},\, (1))$
acts on the intersection form $(\mathbb {Z},\, (1))$![]() of $\mathbb {CP}^2$
of $\mathbb {CP}^2$![]() by a sign, so it follows as in remark 5.9 that $\phi ^* r_1 = x \in \mathbb {Z}/2[x]/(x^{4k-2}) = H^*(\mathbb {RP}^{4k-3};\mathbb {Z}/2)$
by a sign, so it follows as in remark 5.9 that $\phi ^* r_1 = x \in \mathbb {Z}/2[x]/(x^{4k-2}) = H^*(\mathbb {RP}^{4k-3};\mathbb {Z}/2)$![]() . We have
. We have
and so $d(E) = d(\mathbb {RP}^{4k-3})\cdot \sigma (\mathbb {CP}^2)+1 = 1$![]() , as $\mathbb {RP}^{4k-3}$
, as $\mathbb {RP}^{4k-3}$![]() has de Rham invariant 0.
has de Rham invariant 0.
In contradistinction with this example, the following shows that for topological fibre bundles with fibres of dimension $2 \mod 4$![]() the invariant $\phi ^*r_3$
the invariant $\phi ^*r_3$![]() is trivial (so e.g. the de Rham invariant is multiplicative for such bundles, by proposition 6.6).
is trivial (so e.g. the de Rham invariant is multiplicative for such bundles, by proposition 6.6).
Proposition 6.8 If $F^{4k+2} \to E \overset {\pi }\to B$![]() is an oriented topological fibre bundle, with $\phi : B \to BSp_{2g}(\mathbb {Z})$
is an oriented topological fibre bundle, with $\phi : B \to BSp_{2g}(\mathbb {Z})$![]() classifying the associated local system of symplectic forms, then $\phi ^*r_3=0 \in H^3(B;\mathbb {Z}/2)$
classifying the associated local system of symplectic forms, then $\phi ^*r_3=0 \in H^3(B;\mathbb {Z}/2)$![]() .
.
Proof. Writing $V(\nu _\pi ) = 1 + {V}_2 + {V}_4 + V_6 + \cdots$![]() , by theorem 5.6 and the Family Signature Theorem we have $\phi ^*r_3 = \int _\pi V_{2k+2} \cdot \mathrm {Sq}^1 V_{2k+2}$
, by theorem 5.6 and the Family Signature Theorem we have $\phi ^*r_3 = \int _\pi V_{2k+2} \cdot \mathrm {Sq}^1 V_{2k+2}$![]() . Without loss of generality we may suppose that $B$
. Without loss of generality we may suppose that $B$![]() is a (not necessarily orientable) 3-manifold, whereupon we wish to show that $\int _B \phi ^*r_3 = \int _E V_{2k+2} \cdot \mathrm {Sq}^1 V_{2k+2}$
is a (not necessarily orientable) 3-manifold, whereupon we wish to show that $\int _B \phi ^*r_3 = \int _E V_{2k+2} \cdot \mathrm {Sq}^1 V_{2k+2}$![]() vanishes.
vanishes.
The Wu class of $B$![]() has the form $V(\nu _B) = 1 + x$
has the form $V(\nu _B) = 1 + x$![]() for $x$
for $x$![]() of degree 1, so writing $V(\nu _E) = 1 + \bar {V}_1 + \bar {V}_2 + \cdots + \bar {V}_{2k+2}$
of degree 1, so writing $V(\nu _E) = 1 + \bar {V}_1 + \bar {V}_2 + \cdots + \bar {V}_{2k+2}$![]() the identity $V(\nu _E) = V(\nu _B) \cdot V(\nu _\pi )$
the identity $V(\nu _E) = V(\nu _B) \cdot V(\nu _\pi )$![]() implies that $\bar {V}_{2i} = V_{2i}$
implies that $\bar {V}_{2i} = V_{2i}$![]() and $\bar {V}_{2i+1} = x \cdot V_{2i}$
and $\bar {V}_{2i+1} = x \cdot V_{2i}$![]() , so in particular $V_{2i}=0$
, so in particular $V_{2i}=0$![]() for $i>k+1$
for $i>k+1$![]() . Thus
. Thus
and as $T_\pi E$![]() has dimension $4k+2$
has dimension $4k+2$![]() it follows that $0= w_{4k+3}(T_\pi E) = \mathrm {Sq}^{2k+1} V_{2k+2}$
it follows that $0= w_{4k+3}(T_\pi E) = \mathrm {Sq}^{2k+1} V_{2k+2}$![]() . Using the Adem relation
. Using the Adem relation

and instability, we deduce that $\mathrm {Sq}^{2k+2} \mathrm {Sq}^1 V_{2k+2}=0$![]() too. But then by definition of the Wu classes of $E$
too. But then by definition of the Wu classes of $E$![]() and the relation $\bar {V}_{2k+2}={V}_{2k+2}$
and the relation $\bar {V}_{2k+2}={V}_{2k+2}$![]() we find that
we find that
as required.
6.4 Integrality
For an oriented topological block bundle $\pi : E \to |K|$![]() with $d$
with $d$![]() -dimensional fibres the discussion in § 5.3 shows that there is a 2-integral refinement $\mathcal {L}(T_\pi ^s E) \in H^{*}(E ; \mathbb {Z}_{(2)})$
-dimensional fibres the discussion in § 5.3 shows that there is a 2-integral refinement $\mathcal {L}(T_\pi ^s E) \in H^{*}(E ; \mathbb {Z}_{(2)})$![]() of the Hirzebruch $L$
of the Hirzebruch $L$![]() -class, and that its fibre integral satisfies
-class, and that its fibre integral satisfies

At odd primes $p$![]() a similar result is available in a range of degrees: for this we can work either with $\mathrm {KO}[\tfrac {1}{2}]$
a similar result is available in a range of degrees: for this we can work either with $\mathrm {KO}[\tfrac {1}{2}]$![]() or $\mathrm {L}^s(\mathbb {Z})$
or $\mathrm {L}^s(\mathbb {Z})$![]() ; lets take the former for concreteness. As the first torsion in $\pi _*(S_{(p)})$
; lets take the former for concreteness. As the first torsion in $\pi _*(S_{(p)})$![]() is in degree $2p-3$
is in degree $2p-3$![]() , it follows from the Atiyah–Hirzebruch spectral sequence that there is a unique homotopy class
, it follows from the Atiyah–Hirzebruch spectral sequence that there is a unique homotopy class

which on homotopy groups sends $a^k$![]() to 1 for $0 \leq k \leq \lfloor (2p-4)/4 \rfloor$
to 1 for $0 \leq k \leq \lfloor (2p-4)/4 \rfloor$![]() . Pulled back along the Sullivan orientation $\Delta _{Top}$
. Pulled back along the Sullivan orientation $\Delta _{Top}$![]() these cohomology classes correspond under the Thom isomorphism to canonical $p$
these cohomology classes correspond under the Thom isomorphism to canonical $p$![]() -local classes $\mathcal {L}_k \in H^{4k}(BSTop ; \mathbb {Z}_{(p)})$
-local classes $\mathcal {L}_k \in H^{4k}(BSTop ; \mathbb {Z}_{(p)})$![]() defined for $4k < 2p-3$
defined for $4k < 2p-3$![]() , whose rationalizations are the usual topological $L$
, whose rationalizations are the usual topological $L$![]() -classes. If $d=2n$
-classes. If $d=2n$![]() then looped $2n$
then looped $2n$![]() times and pulled back along $\mathrm {sign} : B\mathrm {Aut}(H_\mathbb {R},\, \lambda ) \to \Omega ^{\infty +2n} \mathrm {KO}_{(p)}$
times and pulled back along $\mathrm {sign} : B\mathrm {Aut}(H_\mathbb {R},\, \lambda ) \to \Omega ^{\infty +2n} \mathrm {KO}_{(p)}$![]() these classes correspond to $2^{2k-n} \mathrm {ch}_{2k-n}(\xi )$
these classes correspond to $2^{2k-n} \mathrm {ch}_{2k-n}(\xi )$![]() by theorem 3.2 and its proof (note that $(2k-n)!$
by theorem 3.2 and its proof (note that $(2k-n)!$![]() is a $p$
is a $p$![]() -local unit as $2k < p-1$
-local unit as $2k < p-1$![]() , so $\mathrm {ch}_{2k-n}$
, so $\mathrm {ch}_{2k-n}$![]() is indeed defined $p$
is indeed defined $p$![]() -integrally). Theorem 3.1 then gives the $p$
-integrally). Theorem 3.1 then gives the $p$![]() -integral identity
-integral identity

for $4k < 2p-3$![]() .
.
Acknowledgements
I would like to thank J. Ebert, F. Hebestreit and especially M. Land for useful discussions, and the anonymous referee for their helpful remarks. I have been supported by the ERC under the European Union's Horizon 2020 research and innovation programme (grant agreement No. 756444) and by a Philip Leverhulme Prize from the Leverhulme Trust.