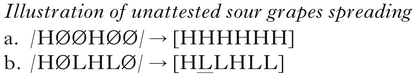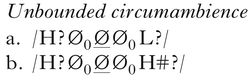1 Introduction
Jardine (Reference Jardine2016) points out an interesting shared formal property of two types of phonological pattern, termed ‘unbounded plateauing’ and ‘sour grapes’: for a given segment, whether or not it undergoes a featural change can only be determined by examining potentially unbounded strings both before and after that segment. He shows that in Formal Language Theory (FLT) this property places them outside of the class of weakly deterministic maps, which contains all phonological processes previously studied in these terms (Heinz & Lai Reference Heinz, Lai, Kornai and Kuhlmann2013, Chandlee Reference Chandlee2014).
Building on Hyman's (Reference Hyman and Goldsmith2011) observations about asymmetries between tonal and non-tonal features, Jardine claims that unbounded plateauing and sour grapes-like patterns occur in tonal systems, but rarely, if ever, in processes involving other phonological features. He goes on to argue (2016: 278) that the FLT treatment of this typological distinction (i.e. the statement that tone systems are more formally complex) is superior to any available treatment in Optimality Theory (OT; Prince & Smolensky Reference Prince and Smolensky2004), since OT would rule out sour grapes and unbounded plateauing for non-tonal phonology using distinct theoretical restrictions, unlike the unified statement allowed by FLT.
In this short paper, I point out that Jardine's tonal sour grapes example, Copperbelt Bemba unbounded tonal spreading (Kula & Bickmore Reference Kula and Bickmore2015), is in crucial respects unlike the hypothetical pattern that Baković (Reference Bakovi«2000: 217ff), Wilson (Reference Wilson2003), McCarthy (2011) and others have pointed out is generally unattested in unbounded spreading. It appears that ‘true’ sour grapes is just as much unattested for tone as it is for other features. The generalisations that only the sour grapes-like pattern in Copperbelt Bemba is attested, and that it is attested only for tone, can be captured by OT, but not by FLT as presented in Jardine (Reference Jardine2016). This is because OT, unlike FLT, provides a means for the development of substantive theories of constraints. One may be able to place substantive restrictions on the patterns generated by an FLT system, but it remains to be shown that this can be done in a way that yields results comparable to those obtained with OT's constraint interaction. Furthermore, the fact that true sour grapes is unattested for tone as well as for other features undermines Jardine's argument for FLT over OT, since it weakens the motivation for capturing the set of weakly deterministic processes as a class. I conclude that FLT is best understood not as an alternative to OT, as it is treated in Jardine's paper, but instead as a more general tool for the formalisation and comparison of theories.
2 Sour grapes: Copperbelt Bemba
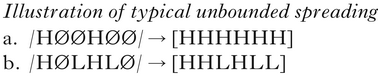
Unbounded spreading refers to the extension of the span of a feature from its underlying segmental host over a potentially unbounded number of segments. It can be bounded by the size of the spreading domain (e.g. a morphological or prosodic constituent, such as stem or prosodic word), and can also be limited by the intervention of blocking segments or morphemes, which fail to undergo assimilation, and stop spreading from extending any further in the domain. Unbounded spreading is well attested in tonal systems, and for many other features, including ATR and RTR, height, nasality, and backness and rounding (see Rose & Walker Reference Rose, Walker and Goldsmith2011 for an overview). As an illustration, consider the abstract tonal case in (1). Tone-bearing units (TBUs) specified as High are notated with H, Low TBUs with L, and ones with no specification with Ø.
-
(1)

In (1a), the H tones spread from their underlying position rightward to the end of the domain, changing unspecified TBUs to H. Depending on the analysis, the final representation could have various degrees of one-to-many linkage of tones to TBUs. In (1b), the Hs spread until they reach a specified L, and the final tone is L by default.
The unattested sour grapes pattern is shown in (2). Here, a H spreads when it can reach the end of the domain (2a), but not at all when it would be blocked by a following L, as in (2b). (Sour grapes: ‘If I can't spread all the way, I won't spread at all!’.) As Wilson (Reference Wilson2003) and McCarthy (Reference McCarthy, Goldsmith, Hume and Wetzels2010) point out, this pattern can be produced by an Agree constraint (Baković Reference Bakovi«2000) that demands that adjacent segments have the same value for a feature when it interacts with a faithfulness constraint that penalises changes to each segment's underlying specification. The desired optimum [HHLHLL] has the same number of disagreeing sequences that violate Agree as does the problematic outcome in (2b), as well as an extra violation of faithfulness. Here, the relevant faithfulness constraint would be one that penalises the change from Ø to H; other changes, in particular L to H, or H to L, would be penalised by a different constraint, ranked above Agree. In addition, the default realisation of Ø as L would have to incur a lower cost than Ø to H (which could also result from the markedness of H, as in Kula & Bickmore Reference Kula and Bickmore2015).
-
(2)

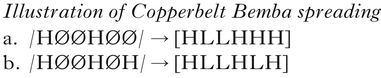
The Copperbelt Bemba unbounded spreading pattern that Jardine (Reference Jardine2016) labels ‘sour grapes-like’ can be abstractly illustrated as in (3). The rightmost H in a phrase-final word spreads unboundedly to the right edge, as in (3a). As shown in (3b), when there is a final H, there is no unbounded spreading – I abstract from the bounded spreading pattern that occurs instead. According to Kula & Bickmore's OT analysis, spreading fails to apply in (3b) because there is already a H tone in final position that satisfies the relevant constraint.
-
(3)

In terms of Jardine's FLT treatment, (2) and (3) have the same distinguishing formal property, which he terms unbounded cirumambience: the determination of whether a potential target is affected by the process requires examination of a string of potentially unbounded length in both directions. That is, to determine whether the underlined unspecified TBUs in (4) will surface as H requires looking potentially unboundedly far to the left to see if there is a trigger for harmony, indicated as H? (Ø0 indicates a string of zero or more unspecified TBUs), and potentially unboundedly far to the right to see if there is a blocking L for sour grapes (4a), and a final H for the Copperbelt Bemba pattern (4b).
-
(4)

3 Sour grapes vs. Copperbelt Bemba in OT
We would like a theory of phonological typology that captures the relationship between the special nature of Copperbelt Bemba's spreading pattern and the fact that it displays a kind of look-ahead that other unbounded spreading processes, tonal and non-tonal, do not. In this section, I discuss how such a theory can be constructed in OT. This discussion is based on previously published proposals, and many of the details are irrelevant to the general point I want to make, so I do not provide a specific theory of unbounded assimilation in OT, nor do I provide many analytic details.
In Kula & Bickmore's (Reference Kula and Bickmore2015) OT analysis, Copperbelt Bemba's unbounded spreading is motivated not by a spreading constraint per se, like Agree, but by a constraint that requires phrases to end in a H tone, which I will label φfin-H. When there is an underlying final H tone, as in (3b), there is no motivation for spreading, so φfin-H would incur fatal faithfulness violations. When there is no final H, but there is one earlier in the word, as in (3a), spreading from the rightmost H satisfies φfin-H without requiring the insertion of a non-underlying tone. Highs further to the left do not spread (modulo the separate bounded spreading process) because there is again no motivation for them to do so when the final position is already occupied by a H tone.
Most OT theories of unbounded spreading (see again Rose & Walker Reference Rose, Walker and Goldsmith2011 for an overview) do not produce sour grapes, the exception being the Agree theory already mentioned. Given one of those theories, along with Kula & Bickmore's φfin-H-based analysis of Copperbelt Bemba, we can generate regular unbounded spreading for all features, and the sour grapes-like pattern only for tone. It is worth noting that look-ahead similar to that seen in Copperbelt Bemba is possible with other features when the motivating constraint is a licensing constraint, rather than a spreading constraint. A case in point is Central Veneto metaphony, as analysed in Walker (Reference Walker2005, Reference Walker2010) and Kimper (Reference Kimper2012). Post-tonic [high] spreads into the stressed syllable, raising [e] and [o], but not [a]. Notably, a sequence [ˈe…e…i] becomes [ˈi…i…i], with spreading onto the intervening mid vowel, while [ˈa…e…i] surfaces faithfully, with no spreading at all. Thus spreading from the final [i] to the intervening [e] looks ahead to see if there is an eligible target in the stressed syllable. This differs from the Copperbelt Bemba pattern only in that longer instances of spreading are unattested, given the position of stress. Like the Copperbelt Bemba pattern, it is produced by a constraint requiring a feature in a particular prominent position, rather than by a constraint demanding the extension of a feature's domain into both prominent and non-prominent positions.
In Kula & Bickmore's proposal, there is no formal reason why counterparts of φfin-H targeting non-tonal features do not exist. Instead, the restriction is a substantive one, presumably related to the shared phonetic substance of lexical tone and phrasal intonation. Stipulations about the contents of a universal constraint set may or may not ultimately be the best way to account for substantive differences in the behaviour of different features. For example, Hyman (Reference Hyman and Goldsmith2011) often simply makes direct reference to the production and perception of tones in suggesting explanations for their special behaviour, with an apparently implicit understanding that phonologisation (Hyman Reference Hyman and Yu2013) yields the phonological skews. The point is that OT allows those stipulations to be made. This allows OT to function at the very least as a formally explicit heuristic in understanding and explaining phonological typology. It's worth emphasising that OT is just like other theories of generative phonology in placing substantive restrictions on its formal devices – Vergnaud (Reference Vergnaud and Vago1980: 61) has this to say about his ‘formal theory of vowel harmony’: ‘we see that the notation we have discussed … is adequate not because it restricts significantly the class of possible grammars, but because it permits us to formulate a theory that restricts the latter class’. This highlights an ambiguity of the word ‘substance’ in this paper, and elsewhere in the literature. A ‘substantive restriction’, as I've just used the phrase, is a restriction on combinations of formal primitives that permits other combinations of the same or greater formal complexity. The other sense is being used when we refer to the phonetic substance of phonology (see e.g. Hyman Reference Hyman and Yu2013). ‘Substance’ in the title of this paper is intended to be ambiguous.
4 Conclusions
FLT makes theoretically well-motivated formal divisions in the space of possible languages, but the cut does not seem to be in the right place here, since it conflates the unattested true sour grapes pattern with the attested Copperbelt Bemba pattern. The unelaborated statement that tonal patterns are more formally complex than non-tonal ones leaves open the possibility of true sour grapes for tone, which seems unattested. I have explained how Kula & Bickmore's OT analysis links special properties of Copperbelt Bemba unbounded spreading (that it targets the rightmost high only, and only spreads to phrase-final position) with its unbounded look-ahead. I have also pointed out that combining Kula & Bickmore's theory of Copperbelt Bemba's special unbounded spreading with a theory of regular unbounded spreading would yield the desired typology in OT. Finally, I have noted that OT can generate the desired typology because it places substantive restrictions on the constraint set.
Jardine argues for FLT over OT because it allows Copperbelt Bemba and unbounded plateauing to be grouped together under the shared property of being inexpressible by a weakly deterministic system, thus giving a general characterisation of the special nature of tonal phonology, a general characterisation that is unavailable in OT. I have pointed out that the general characterisation is in fact undesirable, insofar as it admits true sour grapes into the set of predicted tonal processes. Moreover, I have suggested that the difference between tonal and non-tonal systems with respect to the presence of the Copperbelt Bemba pattern is due to substantive factors, rather than to a difference in formal complexity. It is worth noting that the formal complexity statement leaves completely unaddressed why tonal systems should be more complex. In the substance-based account sketched above, the features shared between word-level tone and phrase-level intonation are taken as the basis for why a Copperbelt Bemba-like pattern is unattested for non-tonal features.
In my view, none of this argues for OT over FLT as a framework for typological study – I prefer the conclusion that they are incommensurable, pace Jardine's (Reference Jardine2016) comparison. FLT allows us to make general statements about the formal power needed to capture different aspects of natural language, in a way that is orthogonal to distinctions between various rule-based and constraint-based theories. Moreover, it allows us to formalise those theories so as to more precisely understand their predictions – see Hulden (Reference Hulden2017) and the work cited there. While there are good reasons to use FLT in the phonological enterprise, I think it is a mistake to conceive of FLT as an alternative to OT (and other theories), and this reply points out one reason why: it provides no obvious way of stating the kinds of substantive restrictions on phonological systems that are needed to delimit phonological typology.