1. Introduction
There has been a surge in the macroeconomics literature on aggregate uncertainty post global financial crisis (GFC) of 2008–2009. Bloom (Reference Bloom2009) was the first paper to show how an increase in the aggregate uncertainty affected firms’ behavior of hiring and investment and led to a fall in the industrial production up to 1% in the US. Later, Gourio et al. (Reference Gourio, Siemer and Verdelhan2013) showed a similar result for G7 countries. Recent literature including Bloom et al. (Reference Bloom, Floetotto, Jaimovich, Saporta-Eksten and Terry2018), Basu and Bundick (Reference Basu and Bundick2017), and Ravn and Sterk (Reference Ravn and Sterk2017) have focused on the role of uncertainty shocks in amplifying the adverse effects of GFC for the advanced economies (AEs). While related literature for the emerging market economies (EMEs) is still growing, Carriere-Swallow and Cespedes (Reference Carriere-Swallow and Cespedes2013) was the first paper to argue that the global uncertainty shocks impact EMEs more severely than the AEs. The authors showed that the consumption (private) and investment in the EMEs are affected more quantitatively than the AEs. Furthermore, the EMEs take more time to recover from such shocks due to incomplete financial markets. Recently, Bonciani and Ricci (Reference Bonciani and Ricci2020) created an alternate global financial risk and uncertainty index and studied its impact on the AEs and the EMEs. Similar to Carriere-Swallow and Cespedes (Reference Carriere-Swallow and Cespedes2013), the authors also found that the EMEs are more severely impacted than the AEs. Additionally, the effect of such shocks is severe for the group of countries that have a higher economic openness and weaker institutions. Bhattarai et al. (Reference Bhattarai, Chatterjee and Park2020) identified heterogeneous monetary policy responses of the Latin American EMEs and the rest of the EMEs to the global uncertainty shocks; which the authors explain is due to the heterogeneous spillover effects of these shocks on these groups of the economies.Footnote 1 While Bhattarai et al. (Reference Bhattarai, Chatterjee and Park2020) emphasize on the trade-offs faced by the policymakers at the central bank of EMEs between financial stability objective versus output and inflation stabilization under inflation-targeting, in the presence of high global uncertainty, they did not go further to analyze an alternate monetary policy that can improve the real outcomes and reduce welfare losses. This paper addresses this gap. To the best of our knowledge, the role of monetary policy in offsetting the adverse effects of global uncertainty shock in an EME and its link with the exchange rates is not explored in the literature. Our analysis shows that the current monetary policy framework of using Taylor type interest rate rules (IRRs) in a floating exchange rate regime is ineffective in stabilizing an EME from global uncertainty shocks. We also find that the standard results hold when the economy is hit with the first-moment shocks. To be precise, the domestic inflation-based Taylor IRR is a welfare dominating rule with a standard first-moment shock but not in the presence of global uncertainty shocks or second-moment shocks.
Open economy macroeconomics literature has time and again emphasized on the importance of the flexibility of exchange rates in stabilizing the domestic economy from a foreign shock going back to Friedman (Reference Friedman1953). Floating exchange rates leave interest rates to be determined by the policymakers as an instrument to stabilize the economy. Gali and Monacelli (Reference Galí and Monacelli2005) through a small open economy (SOE) framework showed that a domestic inflation-based Taylor rule with floating exchange rates is a welfare dominating rule. Recently, Corsetti et al. (Reference Corsetti, Kuester and Muller2017) while revisiting this issue under zero lower bound (ZLB), concludes that the floating exchange rates dominate the PEG rules when a SOE experiences a negative demand shocks from abroad. This happens as the floating exchange rate allows for the domestic currency depreciation and thus it acts as a shock absorber. On the contrary, we find that the flexibility of exchange rates can amplify the real effects of the global uncertainty shocks. The difference is primarily driven by the source of disturbance to the economy. While the above mentioned papers are analyzed with the level or first-moment shocks, the present paper considers global uncertainty shocks which are time-varying volatility shocks or second-moment shocks (Schmitt-Grohé and Uribe (Reference Schmitt-Grohé and Uribe2004); Benigno et al. (Reference Benigno, Benigno and Nisticò2013); Benigno et al. (Reference Benigno, Benigno and Nisticò2012); Fernández-Villaverde et al. (Reference Fernández-Villaverde, Guerrón-Quintana, Rubio-Ramírez and Uribe2011)).
Similar to Bhattarai et al. (Reference Bhattarai, Chatterjee and Park2020) and Bonciani and Ricci (Reference Bonciani and Ricci2020) in our empirical exercise, we strongly observe that the exchange rate movements are significant in EMEs vis-a-vis AEs when global uncertainty rises. To be specific, the data distinctly shows that the exchange rates, both nominal as well real, depreciate strongly during the periods of high global uncertainty. This happens because capital moves out of the EMEs as an immediate response to a higher global uncertainty. Typically when the global risks are high, investors move their risky asset portfolio into safer assets like US treasury bills and that’s why EMEs experience a net portfolio outflow. This is consistent with the flight-to-safety hypothesis. When global risks were high during the GFC, Fratzscher (Reference Fratzscher2012) finds a strong empirical evidence showing a significant net portfolio outflow from EMEs. The author also argues that the global risks have been a key “push factor” driving capital flows from EMEs. The capital outflow from these EMEs during high global uncertainty leads to depreciation of the currency. A depreciating currency in an EME does not lead to an expansion of output, as explained by the expenditure switching via trade channel, because increase in the global uncertainty contracts the world output too. Instead, the depreciating currency is contractionary here. This follows from the existing literature which has emphasized on the contractionary effect of a depreciating currency in EMEs through the financial channel (Avdjiev et al. (Reference Avdjiev, Bruno, Koch and Shin2019); Kearns and Patel (Reference Kearns and Patel2016); Banerjee et al. (Reference Banerjee, Hofmann and Mehrotra2020); Caldara et al. (Reference Caldara, Fuentes-Albero, Gilchrist and Zakrajsek2016); Caballero et al. (Reference Caballero, Fernandez and Park2019); Cook (Reference Cook2004); Korinek (Reference Korinek2018)). The main reason argued in this literature is worsening of the balance sheets of the firms in EMEs, as most of the external debt held by the firms is denominated in dominant currencies such as the US dollar. Caballero et al., (Reference Caballero, Fernandez and Park2019) find that foreign borrowing of corporate in the EMEs have increased from 600 billion US dollars in early 2000s to 2.4 trillion US dollars by the end of 2014. A depreciation (both nominal and real) of the currency would worsens the balance sheets of firms and these firms hit a borrowing/ credit constraint. This can make things worse if the currency depreciates further with capital moving out of the country. This point has also been emphasized in Carriere-Swallow and Cespedes (Reference Carriere-Swallow and Cespedes2013) to explain a longer recovery time period for a fall in investment in emerging markets when hit with a global uncertainty shock.
Further, due to a currency depreciation, domestic consumer prices increase due to an increase in the import prices in the EMEs. As a response to increasing inflationary expectations, the central bank in EMEs increases the nominal interest rate.Footnote 2 Other possible reasons for increasing interest rates could be to put a check on the outflow of capital. Our stylized facts show that emerging markets grapple with a fall in private consumption and investment during episodes of increasing uncertainty, as shown in Carriere-Swallow and Cespedes (Reference Carriere-Swallow and Cespedes2013). An increase in the nominal interest rate can further destabilize a contracting SOE by reinforcing the adverse real effects of the uncertainty shocks. A monetary policy, implemented using Taylor type IRRs, is thus faced with a strong trade-offs in inflation and output stabilization, and between financial stability and output stabilization.
A link between global uncertainty and floating exchange rate regime can be detrimental to the economy for two important reasons. Firstly, as discussed above in the presence of high global uncertainty, investments in the EMEs starts drying up and depreciation further aggravates the issue. Secondly, an independent monetary policy followed by the central bank of EMEs becomes trivial or ineffective as the uncovered interest rate parity (UIP) does not hold. Benigno et al. (Reference Benigno, Benigno and Nisticò2012) argue that when an uncertainty shock hits an economy, fluctuations in the exchange rates are guided by a hedging motive. Under such a scenario, UIP does not hold and time-varying risk premiums are generated.Footnote 3 The left chart of Figure 1 summarizes how key macroeconomic variables are connected in a SOE. Furthermore, when an economy deviates from UIP the link between nominal interest rates (monetary policy instrument) and the nominal exchange rate breaks down. Thus, any attempt to stabilize the nominal exchange rate movement and the economy through an independent monetary policy rule or IRR is unsuccessful.Footnote 4 Stabilization of exchange rates is imperative here as it amplifies the contractionary effect of global uncertainty shocks in an EME and an IRR fails to do so.

Figure 1. In presense of global uncertainty shock (a) Monetary policy using nominal interest rates as instrument (left); (b) Monetary policy using nominal exchange rates as instrument (right).
In the present paper, we consider response of the economy under alternate monetary policy instruments, since IRRs are ineffective here.Footnote 5 To look for a monetary policy rule which minimizes the welfare loss, we build a SOE new Keynesian DSGE model with an uncertainty shock to the world demand and examine the response of real macroeconomic variables under a variety of monetary policy rules. A most obvious alternate policy to be considered here is a fixed exchange rate regime. Cook (Reference Cook2004) has argued that a fixed exchange rate regime (PEG) offers a greater stability than an IRR (or floating exchange rate regime) when currency depreciation destabilizes the business cycle. We find that, while fixed exchange rate regime does better than an IRR in terms of welfare losses, it brings high variability to other nominal variables in the economy like consumer price inflation (CPI), which adjusts more. Although, the PEG rule performs poorly with respect to inflation volatility, the fixed exchange rates does give a higher consumption level than floating exchange rates on impact of the second-moment shocks and a lower variability to consumption in the long-run. This result is different from papers which consider level/ moment shock like Corsetti et al. (Reference Corsetti, Kuester and Muller2017) as UIP is satisfied there. Since floating exchange rate regimes are associated with higher risk premiums than PEG, the latter performs better under high global uncertainty for certain variables.
We find that a monetary policy rule that gives a lowest welfare loss, when a SOE is hit with a global uncertainty shock, is an exchange rate rule (ERR) followed by a PEG rule. When a monetary policy uses the exchange rate as an instrument, the exchange rate follows a rule and is guided by key fundamentals governing the domestic economy, like inflation and output. The Monetary Authority of Singapore (MAS) has been successfully following this rule since 1981 (McCallum (2006)). ERR allows an economy not to choose from corner solutions as dictated by a fixed exchange rates and floating exchange rates (Heiperzt et al. (Reference Heiperzt, Mihov and Santacreu2017)). Since the exchange rate follows a rule with ERR and does not float freely, the hedging/ flight-to-safety motive mentioned above is weakened. Thus, nominal exchange rates are stabilized and welfare losses are reduced significantly. The right chart in Figure 1 shows how a link between monetary policy, exchange rates and key macroeconomic variables like inflation and output is restored when ERRs are followed. This rule restores the lost connection between monetary policy, exchange rates, inflation and output, thus making monetary policy rules much effective in stabilizing the economy. The risk premiums associated with ERRs are also lower due to a lower hedging motive. Due to ERRs association with lower risk premiums the precautionary motive to save and thus consume less, is also weak. This reduces the transmission of uncertainty shocks on the real economy through the aggregate demand channel. ERRs not only reduce welfare losses but also reduce the variability of nominal exchange rates, consumption, and inflation remarkably from the baseline case of IRR. Heiperzt et al. (Reference Heiperzt, Mihov and Santacreu2017) derive an analytical solution to show that the ERRs have lower risk premiums then Taylor rules and smoothing economic fluctuations in SOEs using first-moment shocks. Our results are different from Heiperzt et al. (Reference Heiperzt, Mihov and Santacreu2017) as we do not find that ERRs perform better for a first-moment shock. It is only when the economy is hit with a time-varying second-moment shock the standard results do not hold.
1.1. Empirical evidence
In this section, we do empirical analysis to study the effects of global uncertainty shocks on AEs and EMEs as already done in Bhattarai et al. (Reference Bhattarai, Chatterjee and Park2020) and Bonciani and Ricci (Reference Bonciani and Ricci2020). We redo this exercise because of two reasons. Firstly, besides updating the series for recent years, we use datasets available in the public domain so that the results can be replicated. Due to this, we work with the available quarterly series for the variables in our analysis, unlike the monthly series used in the papers mentioned above.Footnote 6 Secondly, two parameters related to the uncertainty shock process in the model are set to match the impulse response functions of the nominal interest rate from the model with the empirical counterpart. This matching is similar to Basu and Bundick (Reference Basu and Bundick2017). For the empirical strategy, we use a local projection method proposed by Jorda (Reference Jorda2005) to look into the effects of global uncertainty shocks on a wide variety of variables for both AEs and EMEs.Footnote 7 To capture global uncertainty we use the VXO index series as proxied in Bloom (Reference Bloom2009) and Carriere-Swallow and Cespedes (Reference Carriere-Swallow and Cespedes2013). For the VXO series, we use the CBOE S&P 100 Volatility Index’s daily series accessed from the Federal Reserve Bank of St. Louis database from 1996 to 2019.Footnote 8 We also consider VIX volatility index for robustness check and find that the results are consistent. For further analysis, we create a quarterly panel dataset for 14 economies from 1996:Q1 to 2019:Q4. We consider seven AEs (US, UK, Canada, Japan, Australia, South Korea, and Sweden) and seven EMEs (Brazil, Chile, Indonesia, India, Mexico, Russia, and South Africa).Footnote 9 The primary source for most of the macroeconomic series is the quarterly national accounts data compiled by the Organization for Economic Cooperation and Development (OECD (2021)). The macroeconomic series we consider are: real GDP, real consumption, real investment, trade balance, nominal exchange rate, REER, short-term interest rates, consumer price index (CPI), and the net portfolio investment. We also create the net portfolio investment series for Chile, Indonesia, and Mexico using International Monetary Fund’s International Financial Statistics (IFS (2021)). A detailed data description is provided in the Data Appendix A.1.
We estimate panel local projections for horizon,
![]() $h=0,1,2,3,4,5,6,7,8$
as described below,
$h=0,1,2,3,4,5,6,7,8$
as described below,
Here, for country
![]() $i,$
$i,$
![]() $\varsigma _{i,t+h}$
is the projection residual,
$\varsigma _{i,t+h}$
is the projection residual,
![]() $\alpha _{i,h},$
$\alpha _{i,h},$
![]() $\theta _{i,h}$
and
$\theta _{i,h}$
and
![]() $\beta _{i,h}^{q}$
are the projection coefficients. The vector
$\beta _{i,h}^{q}$
are the projection coefficients. The vector
![]() $Y_{t}$
is a set of response variables including real GDP, real consumption, real investment, trade balance, nominal exchange rate, REER, net portfolio investment, inflation, and short-term interest rates. The vector
$Y_{t}$
is a set of response variables including real GDP, real consumption, real investment, trade balance, nominal exchange rate, REER, net portfolio investment, inflation, and short-term interest rates. The vector
![]() $X_{t}$
is a set of control variables including lagged dependent variables and policy variables. The local projection impulse response of
$X_{t}$
is a set of control variables including lagged dependent variables and policy variables. The local projection impulse response of
![]() $Y_{t}$
with respect to
$Y_{t}$
with respect to
![]() $vxo_{t}$
at horizon
$vxo_{t}$
at horizon
![]() $h$
for country
$h$
for country
![]() $i$
is given by
$i$
is given by
![]() $\left \{ \theta _{i,h}\right \}$
for
$\left \{ \theta _{i,h}\right \}$
for
![]() $h\succeq 0.$
The lag of control variables,
$h\succeq 0.$
The lag of control variables,
![]() $q,$
is set to up to four periods. We control for the country fixed effects in our panel regression. It is worth mentioning that since
$q,$
is set to up to four periods. We control for the country fixed effects in our panel regression. It is worth mentioning that since
![]() $vxo_{t}$
captures the volatility in the stock prices in the US economy (AE), for EMEs it is an exogenous shock variable.Footnote 10
$vxo_{t}$
captures the volatility in the stock prices in the US economy (AE), for EMEs it is an exogenous shock variable.Footnote 10
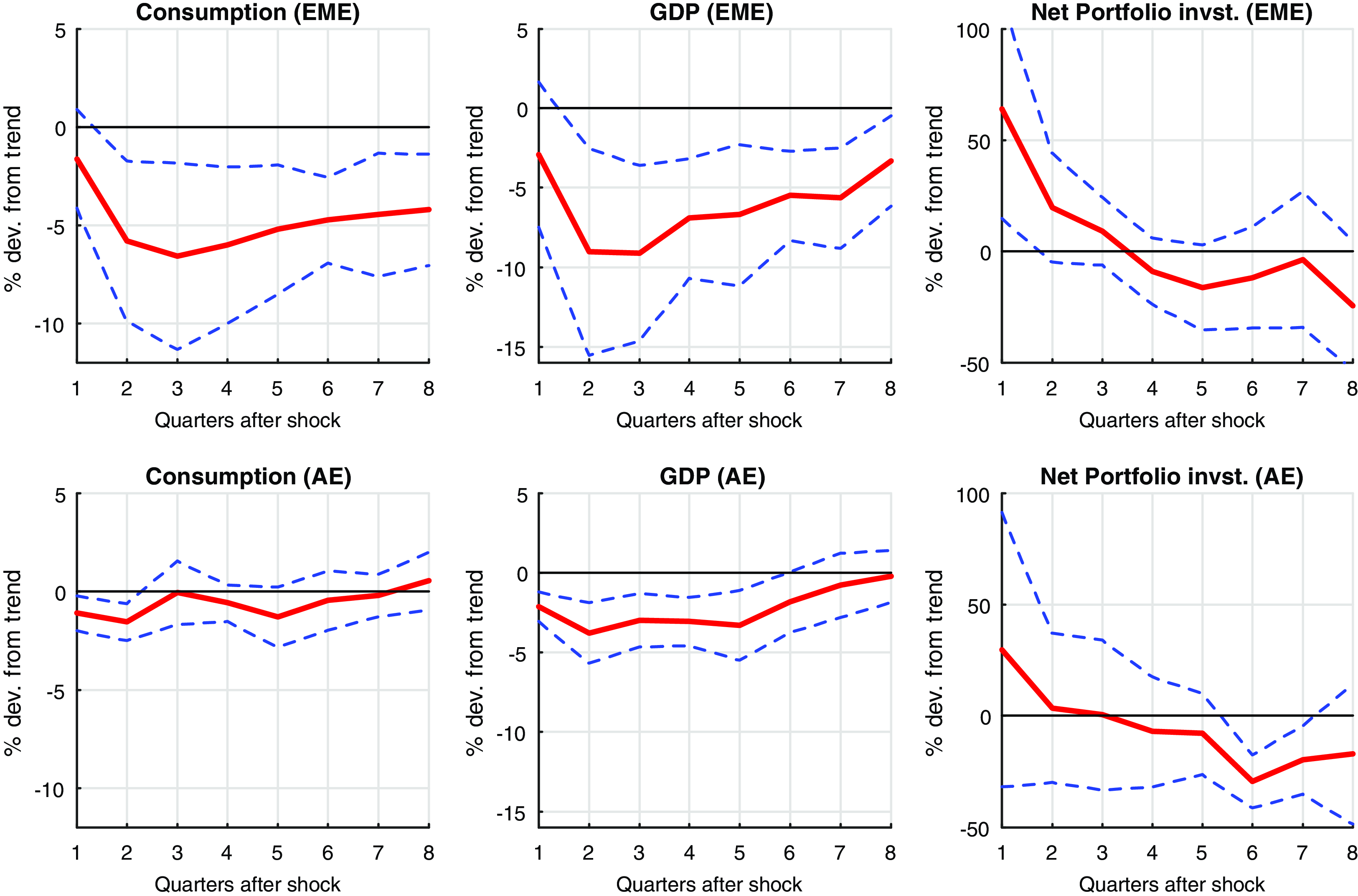
Figure 2. Local projection responses for (col 1) Real GDP; (col 2) Real Consumption; (col 3) Net Portfolio Invt. with VXO impulse [95% CI].
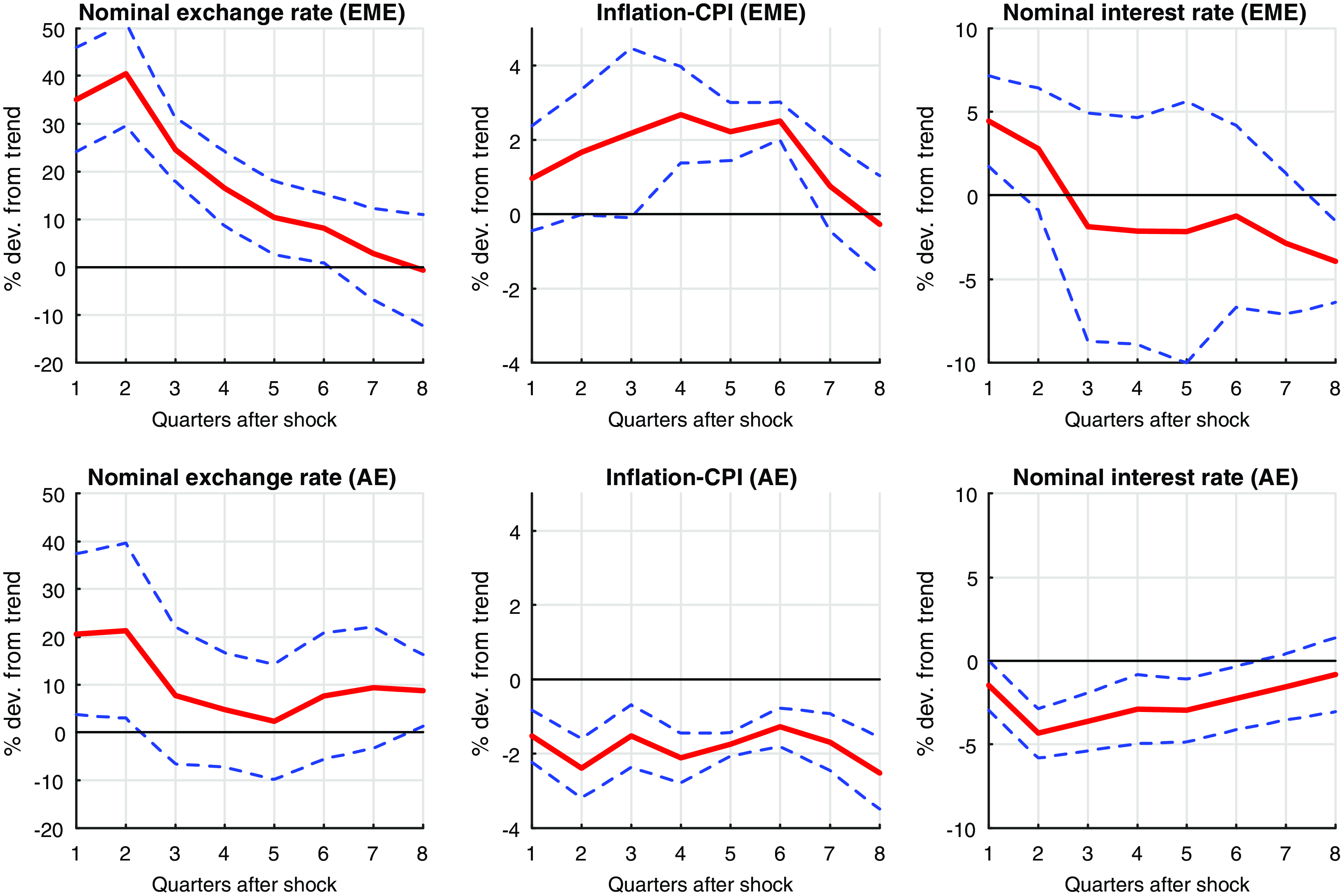
Figure 3. Local projection responses for (col 1) Nominal Exchange Rate; (col 2) Consumer price index; (col 3) Nominal interest rates with VXO impulse [95% CI].
Figures 2 and 3 show local projection responses using OLS for eight quarters after the shock to global uncertainty of 1% from its trend. We plot impulse response functions with 95% confidence bands. Figures 2 shows that the GDP and private consumption decrease in both EMEs and AEs, but the decrease is much higher (up to 10% from the trend) in EMEs compared to the AEs.Footnote 11 These results are consistent with the empirical facts observed in Carriere-Swallow and Cespedes (Reference Carriere-Swallow and Cespedes2013), Forbes and Warnock (Reference Forbes and Warnock2012), Bonciani and Ricci (Reference Bonciani and Ricci2020), and Bhattarai et al. (Reference Bhattarai, Chatterjee and Park2020). The net portfolio investment outflows from the EMEs immediately after the shock. About 50% increase in the net portfolio investment from it’s trend provides a strong evidence of capital outflows in EMEs when global uncertainty increases. AEs do not experience a significant change in there capital movement as compared to the EMEs. The literature has identified high global risk as one of the most important push factor in determining capital outflows from EMEs (Fratzscher (Reference Fratzscher2012); Forbes and Warnock (Reference Forbes and Warnock2012); Caldara et al. (Reference Caldara, Fuentes-Albero, Gilchrist and Zakrajsek2016)). As a result of capital outflows, the domestic currency (nominal exchange rate) in EMEs depreciates by 40% from the trend on impact and remains depreciated upto six quarters after the shock (Figure 3: col 1).Footnote 12 We also see significant exchange rate depreciation in the first quarter after the shock in the group of AEs consider quarters but subsequently the movement is not significant as compared to EMEs. A sustained real or nominal depreciation of the currency amplifies the reduction in real activity and brings instability to the business cycle in EMEs as argued in the literature.Footnote 13 Kido (Reference Kido2016) finds a strong link between US economic policy uncertainty and exchange rates.
Currency depreciation in EMEs leads to a rise in inflation due to a rise in the import goods prices (Figure 3: col 2). For the countries and time periods we consider in our empirical analysis, we find strong evidence of the CPI increasing when the EMEs are hit with an exogenous
![]() $vxo_{t}$
uncertainty shock. Intuitively, multiple channels are working in opposite directions. While demand reduction (both global and domestic) will push down the prices, depreciation and supply-side disturbances will increase the prices. There is ample evidence on how the depreciation tightens the financial conditions of the firms and as a response, the supply gets affected (Caballero et al. (Reference Caballero, Fernandez and Park2019); Caldara et al. (Reference Caldara, Fuentes-Albero, Gilchrist and Zakrajsek2016); Carriere-Swallow and Cespedes (Reference Carriere-Swallow and Cespedes2013)). The depreciation/ supply channel dominates in our empirical exercise as the consumer prices rise for the EMEs.Footnote 14 We do perform the sensitivity analysis by dropping each country one by one but the results do not change significantly. AEs on the other hand, experience a fall in consumer prices as their aggregate demand falls. Bhattarai et al. (Reference Bhattarai, Chatterjee and Park2020) showed that the response of consumer prices varies for the Latin American EMEs and the rest of the EMEs.Footnote 15 Bonciani and Ricci (Reference Bonciani and Ricci2020) found that the consumer prices fall in both the AEs and the EMEs but the price fall in the EMEs is much lower and not significant.Footnote 16
$vxo_{t}$
uncertainty shock. Intuitively, multiple channels are working in opposite directions. While demand reduction (both global and domestic) will push down the prices, depreciation and supply-side disturbances will increase the prices. There is ample evidence on how the depreciation tightens the financial conditions of the firms and as a response, the supply gets affected (Caballero et al. (Reference Caballero, Fernandez and Park2019); Caldara et al. (Reference Caldara, Fuentes-Albero, Gilchrist and Zakrajsek2016); Carriere-Swallow and Cespedes (Reference Carriere-Swallow and Cespedes2013)). The depreciation/ supply channel dominates in our empirical exercise as the consumer prices rise for the EMEs.Footnote 14 We do perform the sensitivity analysis by dropping each country one by one but the results do not change significantly. AEs on the other hand, experience a fall in consumer prices as their aggregate demand falls. Bhattarai et al. (Reference Bhattarai, Chatterjee and Park2020) showed that the response of consumer prices varies for the Latin American EMEs and the rest of the EMEs.Footnote 15 Bonciani and Ricci (Reference Bonciani and Ricci2020) found that the consumer prices fall in both the AEs and the EMEs but the price fall in the EMEs is much lower and not significant.Footnote 16
All countries considered for the present analysis have an inflation-targeting mandate with interest rates as a monetary policy instrument. Interest rates thus fall in AEs as a policy response to a contracting economy and deflation (see Figure 3: col 3). For EMEs, the interest rates increase as a response to an increase in the inflation rate (see Figure 3: col 3). Although for EMEs a contracting economy would suggest a reduction in the interest rates (expansionary monetary policy), and an increase in consumer prices with exchange rate depreciation would suggest an increase in the interest rates (contractionary monetary policy).Footnote 17 Furthermore, as the central bank gives more weight to stabilizing inflation in a Taylor type IRR, we observe an increase in the interest rates in the EMEs by up to 5% (Figure 3: col 3). Another reason for the increased interest rates would be to put a check on the outflow of capital flows or financial stability, as discussed in Bhattarai et al. (Reference Bhattarai, Chatterjee and Park2020) as well. Policymakers in the EMEs are thus faced with the trade-offs between inflation and output stabilization and between financial sector stability versus real sector stabilization. Bhattarai et al. (Reference Bhattarai, Chatterjee and Park2020) did a discussion on the strong trade-offs that central bankers in EMEs face while implementing the inflation-targeting regime and explain the heterogeneous monetary policy response between the Latin American EMEs and the rest of the EMEs. None of the papers in the literature mentioned above highlight the limitation/ ineffectiveness of the IRRs and study how monetary policy response can be improved with an alternate monetary policy instrument. We thus attempt to answer two research questions that emerge from the empirical observations. First, to analyze the trade-offs that arise due to the global uncertainty shocks for the policymakers in the EMEs. Secondly, to study the role of monetary policy and compare alternate monetary policy regimes in the presence of such shocks for the EMEs. We answer both these questions using a theoretical NK-DSGE open economy model featuring a second-moment shock to the demand.Footnote 18
1.2. Summary of the stylized facts
The empirical observations explained above can be summarized as following stylized facts:
Fact 1: An increase in global uncertainty reduces real activity in both AEs as well as EMEs. EMEs experience a greater fall in real GDP, real private consumption, and real investment compared to AEs and also take more time to recover from the shock.
Fact 2: An increase in global uncertainty pulls capital (net portfolio investment) out from EMEs. The trade balances deteriorates initially before improving due to an exchange rate depreciation.
Fact 3: The capital outflow from EMEs leads to a currency (both nominal and real exchange rates) depreciation. As has been emphasized in the literature, an exchange rate depreciation worsens the balance sheets of firms, which is followed by foreign investors pulling out capital further and thus amplifying the effect of the shock on the real economy.
Fact 4: Consumer prices in EMEs increase due to a depreciation, and monetary policy responds by increasing interest rates. A rise in interest rates can thus reinforce the adverse effects of global uncertainty shock on the real economy.
To explain these facts and understand the role of monetary policy, we build a SOE NK-DSGE model with uncertainty shocks. The basic framework of the model is adapted from the two country model (foreign and domestic country) discussed in Benigno et al. (Reference Benigno, Benigno and Nisticò2012). While we characterize the domestic economy as a SOE, the foreign economy is an approximation to the world economy. The uncertainty is present in the preference/ demand shock of households in the foreign economy. We calibrate a SOE and the world economy to a prototypical EME and AE, respectively.
2. Model
Our model is a two-country (domestic and foreign) open economy model in a new Keynesian DSGE setup. The domestic country represents an EME, which is modeled here as a SOE, and the foreign country represents an AE. The idea of calibrating a SOE to an EME in essence captures the limited ability of the EMEs in influencing the global economy, although they do get heavily impacted due to global shocks. The basic framework of the model is adapted from Benigno et al. (Reference Benigno, Benigno and Nisticò2012) with the following modifications. First, in our model the domestic economy is characterized as a SOE and the foreign economy is thus an approximation to the world economy.Footnote 19 Second, we consider a second-moment shock (uncertainty shock) on the demand process of the foreign/ world economy only. We do this because the foreign economy represents the world due to its size, and we are interested in analyzing effects of global uncertainty shocks on a SOE. Third, we follow Fernández-Villaverde et al. (Reference Fernández-Villaverde, Guerrón-Quintana, Rubio-Ramírez and Uribe2011)and take a third-order approximation of the model to solve it. Benigno et al. (Reference Benigno, Benigno and Nisticò2012) follows an approach discussed in Benigno et al. (Reference Benigno, Benigno and Nisticò2013) and take a second-order approximation to solve the model and capture the effects of second-moment shocks. Note that the present model does not have capital and capital borrowings across the countries as we keep the model simple.
2.1. Households
The world is assumed to consist of two countries, domestic
![]() $(D)$
and foreign
$(D)$
and foreign
![]() $(F).$
We assume the size of the domestic economy to be
$(F).$
We assume the size of the domestic economy to be
![]() $n$
relative to the world economy, which is modeled as a foreign economy.Footnote 20 A continuum of domestic households exist over
$n$
relative to the world economy, which is modeled as a foreign economy.Footnote 20 A continuum of domestic households exist over
![]() $[ 0,n]$
, while foreign households from
$[ 0,n]$
, while foreign households from
![]() $(n,1],$
where
$(n,1],$
where
![]() $n\in ( 0,1) .$
An agent in each country is both a consumer and a producer, producing a single differentiated good and consuming all the goods produced in both countries. Also, the population size in each country is set equal to the range of goods produced in that country, such that domestic firms produce goods on
$n\in ( 0,1) .$
An agent in each country is both a consumer and a producer, producing a single differentiated good and consuming all the goods produced in both countries. Also, the population size in each country is set equal to the range of goods produced in that country, such that domestic firms produce goods on
![]() $[0,n]$
, and foreign firms produce goods on
$[0,n]$
, and foreign firms produce goods on
![]() $(n,1]$
. The preferences for both domestic and foreign households is assumed to be recursive following Epstein and Zin (Reference Epstein and Zin1989) framework. The Epstein–Zin preferences are assumed similar to Benigno et al. (Reference Benigno, Benigno and Nisticò2012) and Basu and Bundick (Reference Basu and Bundick2017) as these preferences are risk-sensitive and are able to generate variations in the variables comparable to the empirical counterpart.Footnote 21 Following this a representative household in domestic country is captured by the following recursive utility function,Footnote 22
$(n,1]$
. The preferences for both domestic and foreign households is assumed to be recursive following Epstein and Zin (Reference Epstein and Zin1989) framework. The Epstein–Zin preferences are assumed similar to Benigno et al. (Reference Benigno, Benigno and Nisticò2012) and Basu and Bundick (Reference Basu and Bundick2017) as these preferences are risk-sensitive and are able to generate variations in the variables comparable to the empirical counterpart.Footnote 21 Following this a representative household in domestic country is captured by the following recursive utility function,Footnote 22
 \begin{align} V_{D,t}=\left ( U(C_{t},H_{D,t})^{1-\eta }+\beta \left ( E_{t}\left (V_{D,t+1}\right ) ^{1-\gamma }\right ) ^{\frac{\left ( 1-\eta \right ) }{\left ( 1-\gamma \right ) }}\right ) ^{\frac{1}{\left ( 1-\eta \right ) }}. \end{align}
\begin{align} V_{D,t}=\left ( U(C_{t},H_{D,t})^{1-\eta }+\beta \left ( E_{t}\left (V_{D,t+1}\right ) ^{1-\gamma }\right ) ^{\frac{\left ( 1-\eta \right ) }{\left ( 1-\gamma \right ) }}\right ) ^{\frac{1}{\left ( 1-\eta \right ) }}. \end{align}
Here
![]() $C_{t}$
denotes the aggregate consumption index,
$C_{t}$
denotes the aggregate consumption index,
![]() $H_{D,t}$
denotes hours worked by the representative domestic household,
$H_{D,t}$
denotes hours worked by the representative domestic household,
![]() $\eta$
is a measure of the inverse of the intertemporal elasticity of substitution,
$\eta$
is a measure of the inverse of the intertemporal elasticity of substitution,
![]() $\gamma$
is the measure of risk aversion, and
$\gamma$
is the measure of risk aversion, and
![]() $\beta \in (0,1)$
is the discount factor. The utility flow
$\beta \in (0,1)$
is the discount factor. The utility flow
![]() $U(.)$
is represented by a Cobb–Douglas function of aggregate consumption index,
$U(.)$
is represented by a Cobb–Douglas function of aggregate consumption index,
![]() $C_{t}$
and leisure
$C_{t}$
and leisure
![]() $\left (1-H_{D,t}\right ),$
$\left (1-H_{D,t}\right ),$
where
![]() $\nu$
is the weight on consumption over leisure in the utility flow function. The aggregate consumption index,
$\nu$
is the weight on consumption over leisure in the utility flow function. The aggregate consumption index,
![]() $C_{t}$
, is defined as:
$C_{t}$
, is defined as:
 \begin{align} C_{t}=\left [ (\mu _{D})^{1/\xi _{D}}\left ( C_{D,t}\right ) ^{\frac{\xi _{D}-1}{\xi _{D}}}+\left ( 1-\mu _{D}\right ) ^{1/\xi _{D}}\left ( C_{F,t}\right ) ^{\frac{\xi _{D}-1}{\xi _{D}}}\right ] ^{\frac{\xi _{D}}{\xi _{D}-1}} \end{align}
\begin{align} C_{t}=\left [ (\mu _{D})^{1/\xi _{D}}\left ( C_{D,t}\right ) ^{\frac{\xi _{D}-1}{\xi _{D}}}+\left ( 1-\mu _{D}\right ) ^{1/\xi _{D}}\left ( C_{F,t}\right ) ^{\frac{\xi _{D}-1}{\xi _{D}}}\right ] ^{\frac{\xi _{D}}{\xi _{D}-1}} \end{align}
where
![]() $C_{D,t}$
and
$C_{D,t}$
and
![]() $C_{F,t}$
denotes the consumption index of domestic goods and foreign goods of domestic households, respectively.
$C_{F,t}$
denotes the consumption index of domestic goods and foreign goods of domestic households, respectively.
![]() $\xi _{D}\gt 0$
is the elasticity of substitution between domestic goods and foreign goods for domestic households and
$\xi _{D}\gt 0$
is the elasticity of substitution between domestic goods and foreign goods for domestic households and
![]() $\mu _{D}\in (0,1)$
is the weight given to domestic goods in the aggregate consumption basket,
$\mu _{D}\in (0,1)$
is the weight given to domestic goods in the aggregate consumption basket,
![]() $C_{t}.$
Footnote 23 Analogous to equation (1), the utility function for a representative household in a foreign country is given by:
$C_{t}.$
Footnote 23 Analogous to equation (1), the utility function for a representative household in a foreign country is given by:
 \begin{align} V_{F,t}=\left ( \Gamma _{F,t}U(C_{t}^{\ast },H_{F,t})^{1-\eta }+\beta \left ( E_{t}\left ( V_{F,t+1}\right ) ^{1-\gamma }\right ) ^{\frac{\left ( 1-\eta \right ) }{\left ( 1-\gamma \right ) }}\right ) ^{\frac{1}{\left ( 1-\eta \right ) }} \end{align}
\begin{align} V_{F,t}=\left ( \Gamma _{F,t}U(C_{t}^{\ast },H_{F,t})^{1-\eta }+\beta \left ( E_{t}\left ( V_{F,t+1}\right ) ^{1-\gamma }\right ) ^{\frac{\left ( 1-\eta \right ) }{\left ( 1-\gamma \right ) }}\right ) ^{\frac{1}{\left ( 1-\eta \right ) }} \end{align}
where
![]() $C_{t}^{\ast }$
denotes the aggregate consumption index,
$C_{t}^{\ast }$
denotes the aggregate consumption index,
![]() $H_{F,t}$
denotes hours worked and
$H_{F,t}$
denotes hours worked and
![]() $\Gamma _{F,t}$
is the preference/ demand shock process. The utility flow function is given by:
$\Gamma _{F,t}$
is the preference/ demand shock process. The utility flow function is given by:
The aggregate consumption bundle
![]() $C_{t}^{\ast }$
is given by:
$C_{t}^{\ast }$
is given by:
 \begin{align} C_{t}^{\ast }=\left [ (\mu _{F})^{1/\xi _{F}}\left ( C_{D,t}^{\ast }\right ) ^{\frac{\xi _{F}-1}{\xi _{F}}}+\left ( 1-\mu _{F}\right ) ^{1/\xi _{F}}\left ( C_{F,t}^{\ast }\right ) ^{\frac{\xi _{F}-1}{\xi _{F}}}\right ] ^{\frac{\xi _{F}}{\xi _{F}-1}} \end{align}
\begin{align} C_{t}^{\ast }=\left [ (\mu _{F})^{1/\xi _{F}}\left ( C_{D,t}^{\ast }\right ) ^{\frac{\xi _{F}-1}{\xi _{F}}}+\left ( 1-\mu _{F}\right ) ^{1/\xi _{F}}\left ( C_{F,t}^{\ast }\right ) ^{\frac{\xi _{F}-1}{\xi _{F}}}\right ] ^{\frac{\xi _{F}}{\xi _{F}-1}} \end{align}
where
![]() $\mu _{F}\in (0,1)$
is weight given to domestic goods in the aggregate consumption basket,
$\mu _{F}\in (0,1)$
is weight given to domestic goods in the aggregate consumption basket,
![]() $C_{t}^{\ast }$
. Following Benigno et al. (Reference Benigno, Benigno and Nisticò2012), the weights mentioned in the aggregate consumption bundles equations (2) and (4) are related to country sizes through:
$C_{t}^{\ast }$
. Following Benigno et al. (Reference Benigno, Benigno and Nisticò2012), the weights mentioned in the aggregate consumption bundles equations (2) and (4) are related to country sizes through:
Here,
![]() $\chi \in (0,1)$
is the (common) degree of openness between the domestic and foreign country. When
$\chi \in (0,1)$
is the (common) degree of openness between the domestic and foreign country. When
![]() $\chi =0,$
there is no trade of either goods or assets happening across the two countries and it represents an autarky case.
$\chi =0,$
there is no trade of either goods or assets happening across the two countries and it represents an autarky case.
![]() $\chi =1$
, represents a case of complete free trade of both goods and assets between the two countries. Consumption bundles,
$\chi =1$
, represents a case of complete free trade of both goods and assets between the two countries. Consumption bundles,
![]() $C_{D,t}$
,
$C_{D,t}$
,
![]() $C_{F,t},C_{D,t}^{\ast }$
, and
$C_{F,t},C_{D,t}^{\ast }$
, and
![]() $C_{F,t}^{\ast }$
are Dixit–Stiglitz aggregates of differentiated goods produced in two countries and are defined as:
$C_{F,t}^{\ast }$
are Dixit–Stiglitz aggregates of differentiated goods produced in two countries and are defined as:
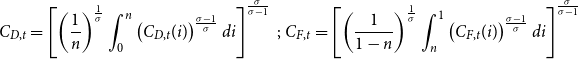 \begin{align} C_{D,t} =\left [ \left ( \frac{1}{n}\right ) ^{\frac{1}{\sigma }}\int _{0}^{n}\left ( C_{D,t}(i) \right ) ^{\frac{\sigma -1}{\sigma }}di\right ] ^{\frac{\sigma }{\sigma -1}}\text{ ; }C_{F,t}=\left [ \left ( \frac{1}{1-n}\right ) ^{\frac{1}{\sigma }}\int _{n}^{1}\left ( C_{F,t}(i) \right ) ^{\frac{\sigma -1}{\sigma }}di\right ] ^{\frac{\sigma }{\sigma -1}} \end{align}
\begin{align} C_{D,t} =\left [ \left ( \frac{1}{n}\right ) ^{\frac{1}{\sigma }}\int _{0}^{n}\left ( C_{D,t}(i) \right ) ^{\frac{\sigma -1}{\sigma }}di\right ] ^{\frac{\sigma }{\sigma -1}}\text{ ; }C_{F,t}=\left [ \left ( \frac{1}{1-n}\right ) ^{\frac{1}{\sigma }}\int _{n}^{1}\left ( C_{F,t}(i) \right ) ^{\frac{\sigma -1}{\sigma }}di\right ] ^{\frac{\sigma }{\sigma -1}} \end{align}
 \begin{align} C_{D,t}^{\ast } &=\left [ \left ( \frac{1}{n}\right ) ^{\frac{1}{\sigma }}\int _{0}^{n}\left ( C_{D,t}^{\ast }(i) \right ) ^{\frac{\sigma -1}{\sigma }}di\right ] ^{\frac{\sigma }{\sigma -1}}\text{ ; }C_{F,t}^{\ast }=\left [ \left ( \frac{1}{1-n}\right ) ^{\frac{1}{\sigma }}\int _{n}^{1}\left ( C_{F,t}^{\ast }(i) \right ) ^{\frac{\sigma -1}{\sigma }}di\right ] ^{\frac{\sigma }{\sigma -1}}. \end{align}
\begin{align} C_{D,t}^{\ast } &=\left [ \left ( \frac{1}{n}\right ) ^{\frac{1}{\sigma }}\int _{0}^{n}\left ( C_{D,t}^{\ast }(i) \right ) ^{\frac{\sigma -1}{\sigma }}di\right ] ^{\frac{\sigma }{\sigma -1}}\text{ ; }C_{F,t}^{\ast }=\left [ \left ( \frac{1}{1-n}\right ) ^{\frac{1}{\sigma }}\int _{n}^{1}\left ( C_{F,t}^{\ast }(i) \right ) ^{\frac{\sigma -1}{\sigma }}di\right ] ^{\frac{\sigma }{\sigma -1}}. \end{align}
Here,
![]() $\sigma$
is the elasticity of substitution between the varieties, where a variety is indexed by
$\sigma$
is the elasticity of substitution between the varieties, where a variety is indexed by
![]() $i\in [ 0,1] .$
The demand for each variety of a differentiated domestic and foreign good by each country’s household is given as follows:
$i\in [ 0,1] .$
The demand for each variety of a differentiated domestic and foreign good by each country’s household is given as follows:
 \begin{align} C_{D,t}^{\ast }(i) =\left ( \frac{1}{n}\right ) \left ( \frac{P_{D,t}^{\ast }(i) }{P_{D,t}^{\ast }}\right ) ^{-\sigma }C_{D,t}^{\ast }\text{ ; }C_{F,t}^{\ast }(i) =\left ( \frac{1}{1-n}\right ) \left ( \frac{P_{F,t}^{\ast }(i) }{P_{F,t}^{\ast }}\right ) ^{-\sigma }C_{F,t}^{\ast } \end{align}
\begin{align} C_{D,t}^{\ast }(i) =\left ( \frac{1}{n}\right ) \left ( \frac{P_{D,t}^{\ast }(i) }{P_{D,t}^{\ast }}\right ) ^{-\sigma }C_{D,t}^{\ast }\text{ ; }C_{F,t}^{\ast }(i) =\left ( \frac{1}{1-n}\right ) \left ( \frac{P_{F,t}^{\ast }(i) }{P_{F,t}^{\ast }}\right ) ^{-\sigma }C_{F,t}^{\ast } \end{align}
where
![]() $P_{D,t}(i)$
and
$P_{D,t}(i)$
and
![]() $P_{D,t}^{\ast }(i)$
are prices of a variety
$P_{D,t}^{\ast }(i)$
are prices of a variety
![]() $i$
of a good produced in the domestic country in domestic and foreign currency, respectively. Similarly,
$i$
of a good produced in the domestic country in domestic and foreign currency, respectively. Similarly,
![]() $P_{F,t}(i),$
and
$P_{F,t}(i),$
and
![]() $P_{F,t}^{\ast }(i)$
are prices of a variety
$P_{F,t}^{\ast }(i)$
are prices of a variety
![]() $i$
of a good produced in the foreign country in domestic and foreign currency, respectively.
$i$
of a good produced in the foreign country in domestic and foreign currency, respectively.
![]() $P_{D,t},$
$P_{D,t},$
![]() $P_{F,t},$
$P_{F,t},$
![]() $P_{D,t}^{\ast }$
, and
$P_{D,t}^{\ast }$
, and
![]() $P_{F,t}^{\ast }$
are the price aggregates of the aggregate consumption baskets,
$P_{F,t}^{\ast }$
are the price aggregates of the aggregate consumption baskets,
![]() $C_{D,t},$
$C_{D,t},$
![]() $C_{F,t},$
$C_{F,t},$
![]() $C_{D,t}^{\ast }$
, and
$C_{D,t}^{\ast }$
, and
![]() $C_{F,t}^{\ast },$
, respectively, and are defined as follows:
$C_{F,t}^{\ast },$
, respectively, and are defined as follows:
 \begin{align} P_{D,t} =\left [ \left ( \frac{1}{n}\right ) \int _{0}^{n}P_{D,t}(i) ^{1-\sigma }di\right ] ^{\frac{1}{1-\sigma }}\text{ ; }P_{F,t}=\left [ \left ( \frac{1}{1-n}\right ) \int _{n}^{1}P_{F,t}(i) ^{1-\sigma }di\right ] ^{\frac{1}{1-\sigma }} \end{align}
\begin{align} P_{D,t} =\left [ \left ( \frac{1}{n}\right ) \int _{0}^{n}P_{D,t}(i) ^{1-\sigma }di\right ] ^{\frac{1}{1-\sigma }}\text{ ; }P_{F,t}=\left [ \left ( \frac{1}{1-n}\right ) \int _{n}^{1}P_{F,t}(i) ^{1-\sigma }di\right ] ^{\frac{1}{1-\sigma }} \end{align}
 \begin{align} P_{D,t}^{\ast } =\left [ \left ( \frac{1}{n}\right ) \int _{0}^{n}P_{D,t}^{\ast }(i) ^{1-\sigma }di\right ] ^{\frac{1}{1-\sigma }}\text{ ; }P_{F,t}^{\ast }=\left [ \left ( \frac{1}{1-n}\right ) \int _{n}^{1}P_{F,t}^{\ast }(i) ^{1-\sigma }di\right ] ^{\frac{1}{1-\sigma }} \end{align}
\begin{align} P_{D,t}^{\ast } =\left [ \left ( \frac{1}{n}\right ) \int _{0}^{n}P_{D,t}^{\ast }(i) ^{1-\sigma }di\right ] ^{\frac{1}{1-\sigma }}\text{ ; }P_{F,t}^{\ast }=\left [ \left ( \frac{1}{1-n}\right ) \int _{n}^{1}P_{F,t}^{\ast }(i) ^{1-\sigma }di\right ] ^{\frac{1}{1-\sigma }} \end{align}
The law of one price is assumed to hold across all individual goods, such that,
![]() $P_{D,t}(i) =X_{t}P_{D,t}^{\ast }(i),$
and
$P_{D,t}(i) =X_{t}P_{D,t}^{\ast }(i),$
and
![]() $P_{F,t}(i) =X_{t}P_{F,t}^{\ast }(i),$
where
$P_{F,t}(i) =X_{t}P_{F,t}^{\ast }(i),$
where
![]() $X_{t}$
is the nominal exchange rate (price of foreign currency in terms of domestic currency). Using this relation with the price aggregates in equations (10) and (11) we also get,
$X_{t}$
is the nominal exchange rate (price of foreign currency in terms of domestic currency). Using this relation with the price aggregates in equations (10) and (11) we also get,
![]() $P_{D,t}=X_{t}P_{D,t}^{\ast }$
and
$P_{D,t}=X_{t}P_{D,t}^{\ast }$
and
![]() $P_{F,t}=X_{t}P_{F,t}^{\ast }.$
Demand functions for the consumption aggregates,
$P_{F,t}=X_{t}P_{F,t}^{\ast }.$
Demand functions for the consumption aggregates,
![]() $C_{D,t},$
$C_{D,t},$
![]() $C_{F,t},$
$C_{F,t},$
![]() $C_{D,t}^{\ast }$
and
$C_{D,t}^{\ast }$
and
![]() $C_{F,t}^{\ast }$
are as follows:
$C_{F,t}^{\ast }$
are as follows:
where
![]() $P_{t}$
and
$P_{t}$
and
![]() $P_{t}^{\ast }$
are the aggregate consumer price indices (CPI) in the domestic and foreign country, in domestic and foreign currency, respectively, and are defined as:
$P_{t}^{\ast }$
are the aggregate consumer price indices (CPI) in the domestic and foreign country, in domestic and foreign currency, respectively, and are defined as:
It can be seen that due to a heterogeneous preference structure across the two countries, purchasing power parity (PPP) does not hold at the aggregate price levels, such that
![]() $P_{t}\neq X_{t}P_{t}^{\ast }.$
PPP holds only when
$P_{t}\neq X_{t}P_{t}^{\ast }.$
PPP holds only when
![]() $\mu _{D}=\mu _{F}$
and
$\mu _{D}=\mu _{F}$
and
![]() $\xi _{D}=\xi _{F}.$
Benigno et al. (Reference Benigno, Benigno and Nisticò2012) assume
$\xi _{D}=\xi _{F}.$
Benigno et al. (Reference Benigno, Benigno and Nisticò2012) assume
![]() $\mu _{D}\neq \mu _{F},$
such that PPP does not hold in their model too. Any deviations from PPP are measured through the real exchange rate, which is defined as the ratio of consumer price indices in the two countries in terms of domestic prices and is given by:
$\mu _{D}\neq \mu _{F},$
such that PPP does not hold in their model too. Any deviations from PPP are measured through the real exchange rate, which is defined as the ratio of consumer price indices in the two countries in terms of domestic prices and is given by:
Rewriting equation (16) gives us the following relationship between CPI in the domestic and foreign country:
Here, CPI in the foreign country and domestic country are defined as
![]() $\pi _{t}^{\ast }=\frac{P_{t}^{\ast }}{P_{t-1}^{\ast }}$
and
$\pi _{t}^{\ast }=\frac{P_{t}^{\ast }}{P_{t-1}^{\ast }}$
and
![]() $\pi _{t}=\frac{P_{t}}{P_{t-1}}$
, respectively. Also, the change in the nominal exchange rate is defined as
$\pi _{t}=\frac{P_{t}}{P_{t-1}}$
, respectively. Also, the change in the nominal exchange rate is defined as
![]() $\pi _{X,t}=\frac{X_{t}}{X_{t-1}}.$
The terms of trade is defined as a ratio of foreign prices to domestic prices, where both price indices are denominated in domestic currency and is given by:
$\pi _{X,t}=\frac{X_{t}}{X_{t-1}}.$
The terms of trade is defined as a ratio of foreign prices to domestic prices, where both price indices are denominated in domestic currency and is given by:
where we define relative price ratios,
![]() $T_{D,t}=\frac{P_{D,t}}{P_{t}}$
and
$T_{D,t}=\frac{P_{D,t}}{P_{t}}$
and
![]() $T_{F,t}=\frac{P_{F,t}}{P_{t}}$
. Using these definitions of relative price ratios with equation (14), we get the following relation,
$T_{F,t}=\frac{P_{F,t}}{P_{t}}$
. Using these definitions of relative price ratios with equation (14), we get the following relation,
 \begin{align} T_{F,t}=\left [ \frac{1-\mu _{D}\left ( T_{D,t}\right ) ^{1-\xi _{D}}}{1-\mu _{D}}\right ] ^{\frac{1}{1-\xi _{D}}}. \end{align}
\begin{align} T_{F,t}=\left [ \frac{1-\mu _{D}\left ( T_{D,t}\right ) ^{1-\xi _{D}}}{1-\mu _{D}}\right ] ^{\frac{1}{1-\xi _{D}}}. \end{align}
Similarly, equation (15) can be re-written in terms of gross foreign inflation
![]() $\left (\pi _{F,t}^{\ast }\right ),$
foreign CPI
$\left (\pi _{F,t}^{\ast }\right ),$
foreign CPI
![]() $\left (\pi _{t}^{\ast }\right ),$
and the terms of trade as:
$\left (\pi _{t}^{\ast }\right ),$
and the terms of trade as:
 \begin{align} \pi _{t}^{\ast }=\pi _{F,t}^{\ast }\left [ \frac{\mu _{F}\left ( T_{t}\right ) ^{\xi _{F}-1}+\left ( 1-\mu _{F}\right ) }{\mu _{F}\left ( T_{t-1}\right ) ^{\xi _{F}-1}+\left ( 1-\mu _{F}\right ) }\right ] ^{\frac{1}{1-\xi _{F}}} \end{align}
\begin{align} \pi _{t}^{\ast }=\pi _{F,t}^{\ast }\left [ \frac{\mu _{F}\left ( T_{t}\right ) ^{\xi _{F}-1}+\left ( 1-\mu _{F}\right ) }{\mu _{F}\left ( T_{t-1}\right ) ^{\xi _{F}-1}+\left ( 1-\mu _{F}\right ) }\right ] ^{\frac{1}{1-\xi _{F}}} \end{align}
where
![]() $\pi _{F,t}^{\ast }=\frac{P_{F,t}^{\ast }}{P_{F,t-1}^{\ast }}.$
For the above described preferences, the total demand for each variety
$\pi _{F,t}^{\ast }=\frac{P_{F,t}^{\ast }}{P_{F,t-1}^{\ast }}.$
For the above described preferences, the total demand for each variety
![]() $i$
of the domestic produce is given by
$i$
of the domestic produce is given by
![]() $Y_{D,t}(i) =nC_{D,t}(i) +\left ( 1-n\right ) C_{D,t}^{\ast }(i)$
, where
$Y_{D,t}(i) =nC_{D,t}(i) +\left ( 1-n\right ) C_{D,t}^{\ast }(i)$
, where
![]() $nC_{D,t}(i)$
and
$nC_{D,t}(i)$
and
![]() $(1-n) C_{D,t}^{\ast }(i)$
is the aggregate demand of all households in the domestic and foreign country, respectively, for variety
$(1-n) C_{D,t}^{\ast }(i)$
is the aggregate demand of all households in the domestic and foreign country, respectively, for variety
![]() $i$
of the domestic produce. Using the demand functions described in (8) and (9), we get
$i$
of the domestic produce. Using the demand functions described in (8) and (9), we get
where aggregate demand for domestic good (all varieties) is given by
![]() $Y_{D,t}=$
$Y_{D,t}=$
![]() $C_{D,t}+\left ( \frac{1-n}{n}\right ) C_{D,t}^{\ast }.$
Further, using (12) and (13) in equation (21), we can re-write
$C_{D,t}+\left ( \frac{1-n}{n}\right ) C_{D,t}^{\ast }.$
Further, using (12) and (13) in equation (21), we can re-write
![]() $Y_{D,t}$
in terms of aggregate consumption bundles in the two countries, as given by:
$Y_{D,t}$
in terms of aggregate consumption bundles in the two countries, as given by:
Similar to the domestic country, aggregate demand for a variety
![]() $i$
of the foreign good is given by:
$i$
of the foreign good is given by:
where aggregate demand for the foreign good (all varieties),
![]() $Y_{F,t}=\frac{n}{\left ( 1-n\right ) }C_{F,t}+C_{F,t}^{\ast }.$
Aggregate demand,
$Y_{F,t}=\frac{n}{\left ( 1-n\right ) }C_{F,t}+C_{F,t}^{\ast }.$
Aggregate demand,
![]() $Y_{F,t},$
can be rewritten in terms of aggregate consumption bundles in the two countries as:
$Y_{F,t},$
can be rewritten in terms of aggregate consumption bundles in the two countries as:
Households in the domestic and foreign country maximize (1) and (3) subject to the following flow budget constraints,
respectively. Here
![]() $W_{D,t}$
and
$W_{D,t}$
and
![]() $W_{F,t}$
are nominal wages in the domestic and foreign country, respectively. The nominal wages are decided in a common labor market in each country. Also,
$W_{F,t}$
are nominal wages in the domestic and foreign country, respectively. The nominal wages are decided in a common labor market in each country. Also,
![]() $\varpi _{D,t}$
and
$\varpi _{D,t}$
and
![]() $\varpi _{F,t}$
are the nominal profits which households receive from owning monopolistically competitive firms in the domestic and foreign country, respectively. Each household in each country holds equal shares in all firms and there is no trade in firm shares. The asset markets are assumed to be complete both at domestic and at international levels. Households trade in state-contingent nominal securities denominated in the domestic currency.
$\varpi _{F,t}$
are the nominal profits which households receive from owning monopolistically competitive firms in the domestic and foreign country, respectively. Each household in each country holds equal shares in all firms and there is no trade in firm shares. The asset markets are assumed to be complete both at domestic and at international levels. Households trade in state-contingent nominal securities denominated in the domestic currency.
![]() $B_{D,t+1}$
is the state-contingent payoff at time
$B_{D,t+1}$
is the state-contingent payoff at time
![]() $t+1$
of a portfolio of state-contingent nominal securities held by a household in the domestic country at the end of period
$t+1$
of a portfolio of state-contingent nominal securities held by a household in the domestic country at the end of period
![]() $t$
. The value of this portfolio can be written as
$t$
. The value of this portfolio can be written as
![]() $E_{t}\left \{ B_{D,t+1}M_{t,t+1}\right \},$
where
$E_{t}\left \{ B_{D,t+1}M_{t,t+1}\right \},$
where
![]() $M_{t,t+1}$
is the nominal stochastic discount factor for discounting wealth denominated in the domestic currency.
$M_{t,t+1}$
is the nominal stochastic discount factor for discounting wealth denominated in the domestic currency.
Households in the foreign country also trade in state-contingent securities denominated in the domestic currency. Let
![]() $B_{t+1}$
be the state-contingent payoff (denominated in domestic currency) in period
$B_{t+1}$
be the state-contingent payoff (denominated in domestic currency) in period
![]() $t+1$
of the state-contingent portfolio held by foreign households at the end of period
$t+1$
of the state-contingent portfolio held by foreign households at the end of period
![]() $t.$
The payoff in the foreign currency in period
$t.$
The payoff in the foreign currency in period
![]() $t+1$
is given by
$t+1$
is given by
![]() $B_{F,t+1}=\frac{B_{t+1}}{X_{t+1}}.$
Also the value of the portfolio today in foreign currency in period
$B_{F,t+1}=\frac{B_{t+1}}{X_{t+1}}.$
Also the value of the portfolio today in foreign currency in period
![]() $t$
is given by
$t$
is given by
![]() $\frac{E_{t}\left \{ B_{t+1}M_{t,t+1}\right \} }{X_{t}}=\frac{E_{t}\left \{ B_{F,t+1}X_{t+1}M_{t,t+1}\right \} }{X_{t}}.$
The nominal stochastic discount factor for discounting wealth denominated in the foreign currency can thus be defined as:
$\frac{E_{t}\left \{ B_{t+1}M_{t,t+1}\right \} }{X_{t}}=\frac{E_{t}\left \{ B_{F,t+1}X_{t+1}M_{t,t+1}\right \} }{X_{t}}.$
The nominal stochastic discount factor for discounting wealth denominated in the foreign currency can thus be defined as:
The first order conditions for maximizing utility functions (1) and (3) for consumption
![]() $\left ( C_{t},C_{t}^{\ast }\right )$
, labor
$\left ( C_{t},C_{t}^{\ast }\right )$
, labor
![]() $(H_{D,t},H_{F,t})$
and asset holdings
$(H_{D,t},H_{F,t})$
and asset holdings
![]() $(B_{D,t+1,}B_{F,t+1})$
subject to the flow budget constraints (25) and (26), respectively, are given by the following Euler’s equations and labor supply equations:
$(B_{D,t+1,}B_{F,t+1})$
subject to the flow budget constraints (25) and (26), respectively, are given by the following Euler’s equations and labor supply equations:
 \begin{align} \text{ }\left ( D\right ) :\,{\small E}_{t}\left \{ M_{t,t+1}\right \}{\small =}{\small \beta }\left ( \frac{E_{t}\left ( V_{t+1}\right ) ^{1-\gamma }}{\left ( V_{t+1}\right ) ^{1-\gamma }}\right ) ^{\frac{\left ( \gamma -\eta \right ) }{\left ( 1-\gamma \right ) }}\left ( \frac{U_{D,t+1}}{U_{D,t}}\right ) ^{1-\eta }\left ( \frac{C_{t}}{C_{t+1}}\right ) \left ( \frac{1}{E_{t}\left \{ \pi _{t+1}\right \} }\right ) \end{align}
\begin{align} \text{ }\left ( D\right ) :\,{\small E}_{t}\left \{ M_{t,t+1}\right \}{\small =}{\small \beta }\left ( \frac{E_{t}\left ( V_{t+1}\right ) ^{1-\gamma }}{\left ( V_{t+1}\right ) ^{1-\gamma }}\right ) ^{\frac{\left ( \gamma -\eta \right ) }{\left ( 1-\gamma \right ) }}\left ( \frac{U_{D,t+1}}{U_{D,t}}\right ) ^{1-\eta }\left ( \frac{C_{t}}{C_{t+1}}\right ) \left ( \frac{1}{E_{t}\left \{ \pi _{t+1}\right \} }\right ) \end{align}
 \begin{align} (F) \,:\,E_{t}\left \{ M_{t,t+1}^{\ast }\right \} =\beta \left ( \frac{\Gamma _{F,t+1}}{\Gamma _{F,t}}\right ) \left ( \frac{E_{t}\left ( V_{t+1}^{\ast }\right ) ^{1-\gamma }}{\left ( V_{t+1}^{\ast }\right ) ^{1-\gamma }}\right ) ^{\frac{\left ( \gamma -\eta \right ) }{\left ( 1-\gamma \right ) }}\left ( \frac{U_{F,t+1}}{U_{F,t}}\right ) ^{1-\eta }\left ( \frac{C_{t}^{\ast }}{C_{t+1}^{\ast }}\right ) \left ( \frac{1}{E_{t}\left \{ \pi _{t+1}^{\ast }\right \} }\right ) \end{align}
\begin{align} (F) \,:\,E_{t}\left \{ M_{t,t+1}^{\ast }\right \} =\beta \left ( \frac{\Gamma _{F,t+1}}{\Gamma _{F,t}}\right ) \left ( \frac{E_{t}\left ( V_{t+1}^{\ast }\right ) ^{1-\gamma }}{\left ( V_{t+1}^{\ast }\right ) ^{1-\gamma }}\right ) ^{\frac{\left ( \gamma -\eta \right ) }{\left ( 1-\gamma \right ) }}\left ( \frac{U_{F,t+1}}{U_{F,t}}\right ) ^{1-\eta }\left ( \frac{C_{t}^{\ast }}{C_{t+1}^{\ast }}\right ) \left ( \frac{1}{E_{t}\left \{ \pi _{t+1}^{\ast }\right \} }\right ) \end{align}
Here, the gross nominal interest rate in domestic country is given by
![]() $\left ( 1+R_{t}\right ) =\frac{1}{E_{t}\left \{ M_{t,t+1}\right \} }$
and the gross nominal interest rate in foreign country is given by
$\left ( 1+R_{t}\right ) =\frac{1}{E_{t}\left \{ M_{t,t+1}\right \} }$
and the gross nominal interest rate in foreign country is given by
![]() $\left (1+R_{t}^{\ast }\right ) =\frac{1}{E_{t}\left \{ M_{t,t+1}^{\ast }\right \} }$
. Real wages in the domestic and foreign country are defined, respectively, as
$\left (1+R_{t}^{\ast }\right ) =\frac{1}{E_{t}\left \{ M_{t,t+1}^{\ast }\right \} }$
. Real wages in the domestic and foreign country are defined, respectively, as
![]() $w_{D,t}=\frac{W_{D,t}}{P_{D,t}}$
and
$w_{D,t}=\frac{W_{D,t}}{P_{D,t}}$
and
![]() $w_{F,t}=\frac{W_{F,t}}{P_{F,t}}$
. Combining the Euler equation from equation (28) and (29) with equation (27), we get the following complete asset market condition:
$w_{F,t}=\frac{W_{F,t}}{P_{F,t}}$
. Combining the Euler equation from equation (28) and (29) with equation (27), we get the following complete asset market condition:
 \begin{align} \left ( \frac{V_{t+1}^{1-\gamma }E_{t}V_{t+1}^{\ast 1-\gamma }}{V_{t+1}^{\ast 1-\gamma }E_{t}V_{t+1}^{1-\gamma }}\right ) ^{\frac{\left ( \eta -\gamma \right ) }{\left ( 1-\gamma \right ) }}\left ( \frac{U\left ( C_{t+1},H_{D,t+1}\right ) }{U\left ( C_{t+1}^{\ast },H_{F,t+1}\right ) }\right ) ^{1-\eta }\left ( \frac{C_{t+1}^{\ast }}{C_{t+1}}\right ) Q_{t+1}=\left ( \frac{U\left ( C_{t},H_{D,t}\right ) }{U\left ( C_{t}^{\ast },H_{F,t}\right ) }\right ) ^{1-\eta }\left ( \frac{C_{t}^{\ast }}{C_{t}}\right ) Q_{t} \end{align}
\begin{align} \left ( \frac{V_{t+1}^{1-\gamma }E_{t}V_{t+1}^{\ast 1-\gamma }}{V_{t+1}^{\ast 1-\gamma }E_{t}V_{t+1}^{1-\gamma }}\right ) ^{\frac{\left ( \eta -\gamma \right ) }{\left ( 1-\gamma \right ) }}\left ( \frac{U\left ( C_{t+1},H_{D,t+1}\right ) }{U\left ( C_{t+1}^{\ast },H_{F,t+1}\right ) }\right ) ^{1-\eta }\left ( \frac{C_{t+1}^{\ast }}{C_{t+1}}\right ) Q_{t+1}=\left ( \frac{U\left ( C_{t},H_{D,t}\right ) }{U\left ( C_{t}^{\ast },H_{F,t}\right ) }\right ) ^{1-\eta }\left ( \frac{C_{t}^{\ast }}{C_{t}}\right ) Q_{t} \end{align}
Re-writing the above gives us,
 \begin{align*} \kappa _{t+1}=\kappa _{t}\left ( \frac {V_{t+1}^{1-\gamma }E_{t}V_{t+1}^{\ast 1-\gamma }}{V_{t+1}^{\ast 1-\gamma }E_{t}V_{t+1}^{1-\gamma }}\right ) ^{\frac {\left ( \eta -\gamma \right ) }{\left ( 1-\gamma \right ) }} \end{align*}
\begin{align*} \kappa _{t+1}=\kappa _{t}\left ( \frac {V_{t+1}^{1-\gamma }E_{t}V_{t+1}^{\ast 1-\gamma }}{V_{t+1}^{\ast 1-\gamma }E_{t}V_{t+1}^{1-\gamma }}\right ) ^{\frac {\left ( \eta -\gamma \right ) }{\left ( 1-\gamma \right ) }} \end{align*}
where
![]() $\kappa _{t}=\left ( \frac{U\left ( C_{t},H_{D,t}\right ) }{U\left ( C_{t}^{\ast },H_{F,t}\right ) }\right ) ^{1-\eta }\left ( \frac{C_{t}^{\ast }}{C_{t}}\right ) Q_{t}.$
We estimate the initial value
$\kappa _{t}=\left ( \frac{U\left ( C_{t},H_{D,t}\right ) }{U\left ( C_{t}^{\ast },H_{F,t}\right ) }\right ) ^{1-\eta }\left ( \frac{C_{t}^{\ast }}{C_{t}}\right ) Q_{t}.$
We estimate the initial value
![]() $\kappa _{0}$
from the data as the ratio of marginal utilities of nominal income across countries in the initial period. Equation (27) when combined with definitions of nominal stochastic discount factors that is,
$\kappa _{0}$
from the data as the ratio of marginal utilities of nominal income across countries in the initial period. Equation (27) when combined with definitions of nominal stochastic discount factors that is,
![]() $E_{t}\left \{ M_{t,t+1}\right \} =\frac{1}{\left ( 1+R_{t}\right ) }$
and
$E_{t}\left \{ M_{t,t+1}\right \} =\frac{1}{\left ( 1+R_{t}\right ) }$
and
![]() $E_{t}\left \{ M_{t,t+1}^{\ast }\right \} =\frac{1}{\left ( 1+R_{t}^{\ast }\right ) },$
gives the following uncovered interest rate parity
$E_{t}\left \{ M_{t,t+1}^{\ast }\right \} =\frac{1}{\left ( 1+R_{t}^{\ast }\right ) },$
gives the following uncovered interest rate parity
![]() $(UIP)$
condition (log-linearized):
$(UIP)$
condition (log-linearized):
where
![]() $r_{t},$
$r_{t},$
![]() $r_{t}^{\ast }$
and
$r_{t}^{\ast }$
and
![]() $E_{t}\left \{ \Delta e_{t+1}\right \}$
are logs of
$E_{t}\left \{ \Delta e_{t+1}\right \}$
are logs of
![]() $\left (1+R_{t}\right ),$
$\left (1+R_{t}\right ),$
![]() $\left (1+R_{t}^{\ast }\right )$
and
$\left (1+R_{t}^{\ast }\right )$
and
![]() $E_{t}\left \{ \frac{X_{t+1}}{X_{t}}\right \},$
respectively. Following Menkhoff et al. (Reference Menkhoff, Sarno, Schmeling and Schrimpf2012), Backus et al. (Reference Backus, Gavazzoni, Telmer and Zin2010) and Benigno et al. (Reference Benigno, Benigno and Nisticò2012), we define time-varying risk premiums as deviations from the UIP condition, mentioned in equation (32). The log-linearized time-varying risk premiums,
$E_{t}\left \{ \frac{X_{t+1}}{X_{t}}\right \},$
respectively. Following Menkhoff et al. (Reference Menkhoff, Sarno, Schmeling and Schrimpf2012), Backus et al. (Reference Backus, Gavazzoni, Telmer and Zin2010) and Benigno et al. (Reference Benigno, Benigno and Nisticò2012), we define time-varying risk premiums as deviations from the UIP condition, mentioned in equation (32). The log-linearized time-varying risk premiums,
![]() $rp_{t},$
are excess returns on holding domestic currency and written as follows:
$rp_{t},$
are excess returns on holding domestic currency and written as follows:
2.2. Firms
The domestic country produces goods on the interval
![]() $\left [ 0,n\right ]$
and the foreign country on
$\left [ 0,n\right ]$
and the foreign country on
![]() $(n,1].$
A firm producing variety
$(n,1].$
A firm producing variety
![]() $i$
of a good in the domestic and foreign country follows a production function linear in labor as given by:
$i$
of a good in the domestic and foreign country follows a production function linear in labor as given by:
respectively. Here,
![]() $A_{D,t}$
and
$A_{D,t}$
and
![]() $A_{F,t}$
are the productivity levels (common) following exogenous processes. We will keep the productivity level of both the firms at the steady state level (
$A_{F,t}$
are the productivity levels (common) following exogenous processes. We will keep the productivity level of both the firms at the steady state level (
![]() $\overline{A}_{D}$
and
$\overline{A}_{D}$
and
![]() $\overline{A}_{F})$
as in the present paper we are focusing on the second-moment shocks to the global demand shocks. Also,
$\overline{A}_{F})$
as in the present paper we are focusing on the second-moment shocks to the global demand shocks. Also,
![]() $\overline{A}_{D}=\overline{A}_{F}=1,$
at the steady state.
$\overline{A}_{D}=\overline{A}_{F}=1,$
at the steady state.
![]() $H_{D,t}(i)$
and
$H_{D,t}(i)$
and
![]() $H_{F,t}(i)$
are composites of all the differentiated labor supplied by household
$H_{F,t}(i)$
are composites of all the differentiated labor supplied by household
![]() $h$
in each country as given by:
$h$
in each country as given by:
where
![]() $H_{D,t}^{h}(i)$
and
$H_{D,t}^{h}(i)$
and
![]() $H_{F,t}^{h}(i)$
are the labor supplied by household
$H_{F,t}^{h}(i)$
are the labor supplied by household
![]() $h$
to firm
$h$
to firm
![]() $i$
in the domestic and foreign country, respectively.
$i$
in the domestic and foreign country, respectively.
2.2.1. Price setting
In the benchmark model we assume that firms in both the countries have nominal price rigidities in the form of price stickiness. We follow Calvo (Reference Calvo1983) to capture price stickiness here. In each period only
![]() $(1-\alpha _{D})$
fraction of firms in the domestic country can reset their prices independent of whether they had a chance to reset them in the last period. A firm
$(1-\alpha _{D})$
fraction of firms in the domestic country can reset their prices independent of whether they had a chance to reset them in the last period. A firm
![]() $i$
which gets a chance to reset its prices,
$i$
which gets a chance to reset its prices,
![]() $\overline{P}_{D,t}(i),$
maximizes a discounted sum of current and future expected values of profit, given by
$\overline{P}_{D,t}(i),$
maximizes a discounted sum of current and future expected values of profit, given by
 \begin{align} \max _{\overline{P}_{D,t}(i)}\sum \limits _{k=0}^{\infty }\alpha _{D}^{k}M_{t,t+k}\left ( \overline{P}_{D,t}(i)Y_{D,t_{+k}}(i)-MC_{D,t+k}Y_{D,t_{+k}}(i)\right ) \end{align}
\begin{align} \max _{\overline{P}_{D,t}(i)}\sum \limits _{k=0}^{\infty }\alpha _{D}^{k}M_{t,t+k}\left ( \overline{P}_{D,t}(i)Y_{D,t_{+k}}(i)-MC_{D,t+k}Y_{D,t_{+k}}(i)\right ) \end{align}
where
![]() $MC_{D,t+k}$
is the nominal marginal cost of domestic firms in period
$MC_{D,t+k}$
is the nominal marginal cost of domestic firms in period
![]() $t+k$
and is the same for all firms as the nominal wage is decided in a common labor market and all firms face a common productivity level realization. The demand function
$t+k$
and is the same for all firms as the nominal wage is decided in a common labor market and all firms face a common productivity level realization. The demand function
![]() $Y_{D,t+k}(i),$
for each firm
$Y_{D,t+k}(i),$
for each firm
![]() $i$
in period
$i$
in period
![]() $t+k$
is given by:
$t+k$
is given by:
The optimal price chosen by firms resetting prices is given by:
 \begin{align} \overline{P}_{D,t}(i)=\frac{\sigma }{\sigma -1}\frac{\sum \limits _{k=0}^{\infty }\alpha _{D}^{k}M_{t,t+k}MC_{D,t+k}Y_{D,t+k}(i)}{\sum \limits _{k=0}^{\infty }\alpha _{D}^{k}M_{t,t+k}Y_{D,t+k}(i)} \end{align}
\begin{align} \overline{P}_{D,t}(i)=\frac{\sigma }{\sigma -1}\frac{\sum \limits _{k=0}^{\infty }\alpha _{D}^{k}M_{t,t+k}MC_{D,t+k}Y_{D,t+k}(i)}{\sum \limits _{k=0}^{\infty }\alpha _{D}^{k}M_{t,t+k}Y_{D,t+k}(i)} \end{align}
where
![]() $\frac{\sigma }{\sigma -1}$
is the constant markup charged by firms. As can be seen from equation (38), the optimal price today depends on not just current but future marginal costs, and also demand conditions in the economy. A firm
$\frac{\sigma }{\sigma -1}$
is the constant markup charged by firms. As can be seen from equation (38), the optimal price today depends on not just current but future marginal costs, and also demand conditions in the economy. A firm
![]() $i$
, which does not reset its price is assumed to keep the prices same as last year’s prices,
$i$
, which does not reset its price is assumed to keep the prices same as last year’s prices,
![]() $P_{D,t-1}(i).$
Thus, the law of motion for the aggregate producer’s price index (PPI) in the domestic country for Calvo’s model can be written as:
$P_{D,t-1}(i).$
Thus, the law of motion for the aggregate producer’s price index (PPI) in the domestic country for Calvo’s model can be written as:
Using the domestic household’s optimization problem we can write the stochastic discount factor
![]() $M_{t,t+k}$
as:
$M_{t,t+k}$
as:
 \begin{align} E_{t}\left \{ M_{t,t+k}\right \} =\beta ^{k}\left ( \frac{E_{t}V_{D,t+k}}{V_{D,t+k}^{1-\gamma }}^{1-\gamma }\right ) ^{\frac{\left ( \gamma -\eta \right ) }{\left ( 1-\gamma \right ) }}\left ( \frac{V_{D,t}}{V_{D,t+k}}\right ) ^{\eta }\frac{\lambda _{D,t+k}}{\lambda _{D,t}}\frac{P_{t}}{P_{t+k}} \end{align}
\begin{align} E_{t}\left \{ M_{t,t+k}\right \} =\beta ^{k}\left ( \frac{E_{t}V_{D,t+k}}{V_{D,t+k}^{1-\gamma }}^{1-\gamma }\right ) ^{\frac{\left ( \gamma -\eta \right ) }{\left ( 1-\gamma \right ) }}\left ( \frac{V_{D,t}}{V_{D,t+k}}\right ) ^{\eta }\frac{\lambda _{D,t+k}}{\lambda _{D,t}}\frac{P_{t}}{P_{t+k}} \end{align}
where
![]() $\lambda _{D,t}=\nu \frac{V_{t}^{\eta }U_{D,t}^{1-\eta }}{C_{t}}$
is the Lagrangian multiplier denoting the marginal utility of income. Combined with equation (40), the price setting equation (38) can be written recursively as:
$\lambda _{D,t}=\nu \frac{V_{t}^{\eta }U_{D,t}^{1-\eta }}{C_{t}}$
is the Lagrangian multiplier denoting the marginal utility of income. Combined with equation (40), the price setting equation (38) can be written recursively as:
where
![]() $X_{D,t}$
and
$X_{D,t}$
and
![]() $Z_{D,t}$
are defined as follows:
$Z_{D,t}$
are defined as follows:
 \begin{align} X_{D,t} =\lambda _{D,t}Y_{D,t}mc_{D,t}T_{D,t}+\alpha _{D}\beta \left ( \pi _{D,t+1}\right ) ^{\sigma }\left ( \frac{E_{t}\left ( V_{t+1}\right ) }{\left ( V_{t+1}\right ) ^{1-\gamma }}^{1-\gamma }\right ) ^{\frac{\left ( \gamma -\eta \right ) }{\left ( 1-\gamma \right ) }}\left ( \frac{1}{V_{t+1}}\right ) ^{\eta }E_{t}\left \{ X_{D,t+1}\right \} \end{align}
\begin{align} X_{D,t} =\lambda _{D,t}Y_{D,t}mc_{D,t}T_{D,t}+\alpha _{D}\beta \left ( \pi _{D,t+1}\right ) ^{\sigma }\left ( \frac{E_{t}\left ( V_{t+1}\right ) }{\left ( V_{t+1}\right ) ^{1-\gamma }}^{1-\gamma }\right ) ^{\frac{\left ( \gamma -\eta \right ) }{\left ( 1-\gamma \right ) }}\left ( \frac{1}{V_{t+1}}\right ) ^{\eta }E_{t}\left \{ X_{D,t+1}\right \} \end{align}
 \begin{align} Z_{D,t} =\lambda _{D,t}Y_{D,t}T_{D,t+k}+\alpha _{D}\beta \left ( \pi _{D,t+1}\right ) ^{\sigma -1}\left ( \frac{E_{t}\left ( V_{t+k}\right ) }{\left ( V_{t+1}\right ) ^{1-\gamma }}^{1-\gamma }\right ) ^{\frac{\left ( \gamma -\eta \right ) }{\left ( 1-\gamma \right ) }}\left ( \frac{1}{V_{t+1}}\right ) ^{\eta }E_{t}\left \{ Z_{D,t+1}\right \} \end{align}
\begin{align} Z_{D,t} =\lambda _{D,t}Y_{D,t}T_{D,t+k}+\alpha _{D}\beta \left ( \pi _{D,t+1}\right ) ^{\sigma -1}\left ( \frac{E_{t}\left ( V_{t+k}\right ) }{\left ( V_{t+1}\right ) ^{1-\gamma }}^{1-\gamma }\right ) ^{\frac{\left ( \gamma -\eta \right ) }{\left ( 1-\gamma \right ) }}\left ( \frac{1}{V_{t+1}}\right ) ^{\eta }E_{t}\left \{ Z_{D,t+1}\right \} \end{align}
Here, the reset domestic price inflation is defined as
![]() $\overline{\pi }_{D,t}=\frac{\overline{P}_{D,t}}{P_{D,t-1}},$
and domestic price inflation is defined as
$\overline{\pi }_{D,t}=\frac{\overline{P}_{D,t}}{P_{D,t-1}},$
and domestic price inflation is defined as
![]() $\pi _{D,t}=\frac{P_{D,t}}{P_{D,t-1}}.$
The real marginal cost for domestic firms in terms of domestic prices is given by
$\pi _{D,t}=\frac{P_{D,t}}{P_{D,t-1}}.$
The real marginal cost for domestic firms in terms of domestic prices is given by
![]() $mc_{D,t}=\frac{MC_{D,t}}{P_{D,t}}.$
The law of motion for the domestic producer’s prices in equation (39) can be written in terms of inflation as follows:
$mc_{D,t}=\frac{MC_{D,t}}{P_{D,t}}.$
The law of motion for the domestic producer’s prices in equation (39) can be written in terms of inflation as follows:
Since labor is the only input into production, the real marginal cost for domestic firms,
![]() $mc_{D,t},$
in terms of domestic prices would then be
$mc_{D,t},$
in terms of domestic prices would then be
where
![]() $w_{D,t}=\frac{w_{D,t}}{P_{D,t}}$
are real wages in the domestic country.
$w_{D,t}=\frac{w_{D,t}}{P_{D,t}}$
are real wages in the domestic country.
The price setting behavior of firms in the foreign country is similar to the price setting behavior of firms in the domestic country, as described from equation (37)–(60). In the foreign country,
![]() $(1-\alpha _{F})$
proportion of the firms reset their prices to
$(1-\alpha _{F})$
proportion of the firms reset their prices to
![]() $\overline{P}_{F,t}$
and the rest
$\overline{P}_{F,t}$
and the rest
![]() $\alpha _{F}$
proportion keep it the same as last year prices,
$\alpha _{F}$
proportion keep it the same as last year prices,
![]() $P_{F,t-1}^{\ast }.$
Maximizing the current and future stream of profits by firms in the foreign country yields the following equation on reset foreign inflation, similar to equation (41)
$P_{F,t-1}^{\ast }.$
Maximizing the current and future stream of profits by firms in the foreign country yields the following equation on reset foreign inflation, similar to equation (41)
where
![]() $X_{F,t}$
and
$X_{F,t}$
and
![]() $Z_{F,t}$
are defined as follows:
$Z_{F,t}$
are defined as follows:
 \begin{align} X_{F,t} =\lambda _{F,t}Y_{F,t}mc_{F,t}T_{F,t}+\alpha _{F}\beta \left ( \pi _{F,t+1}^{\ast }\right ) ^{\sigma }\left ( \frac{E_{t}\left ( V_{t+1}^{\ast }\right ) }{\left ( V_{t+1}^{\ast }\right ) ^{1-\gamma }}^{1-\gamma }\right ) ^{\frac{\left ( \gamma -\eta \right ) }{\left ( 1-\gamma \right ) }}\left ( \frac{1}{V_{t+1}^{\ast }}\right ) ^{\eta }E_{t}\left \{ X_{F,t+1}\right \} \end{align}
\begin{align} X_{F,t} =\lambda _{F,t}Y_{F,t}mc_{F,t}T_{F,t}+\alpha _{F}\beta \left ( \pi _{F,t+1}^{\ast }\right ) ^{\sigma }\left ( \frac{E_{t}\left ( V_{t+1}^{\ast }\right ) }{\left ( V_{t+1}^{\ast }\right ) ^{1-\gamma }}^{1-\gamma }\right ) ^{\frac{\left ( \gamma -\eta \right ) }{\left ( 1-\gamma \right ) }}\left ( \frac{1}{V_{t+1}^{\ast }}\right ) ^{\eta }E_{t}\left \{ X_{F,t+1}\right \} \end{align}
 \begin{align} Z_{F,t} =\lambda _{F,t}Y_{F,t}T_{F,t}+\alpha _{F}\beta \left ( \pi _{F,t+1}^{\ast }\right ) ^{\sigma -1}\left ( \frac{E_{t}\left ( V_{t+k}^{\ast }\right ) }{\left ( V_{t+1}^{\ast }\right ) ^{1-\gamma }}^{1-\gamma }\right ) ^{\frac{\left ( \gamma -\eta \right ) }{\left ( 1-\gamma \right ) }}\left ( \frac{1}{V_{t+1}^{\ast }}\right ) ^{\eta }E_{t}\left \{ Z_{F,t+1}\right \} \end{align}
\begin{align} Z_{F,t} =\lambda _{F,t}Y_{F,t}T_{F,t}+\alpha _{F}\beta \left ( \pi _{F,t+1}^{\ast }\right ) ^{\sigma -1}\left ( \frac{E_{t}\left ( V_{t+k}^{\ast }\right ) }{\left ( V_{t+1}^{\ast }\right ) ^{1-\gamma }}^{1-\gamma }\right ) ^{\frac{\left ( \gamma -\eta \right ) }{\left ( 1-\gamma \right ) }}\left ( \frac{1}{V_{t+1}^{\ast }}\right ) ^{\eta }E_{t}\left \{ Z_{F,t+1}\right \} \end{align}
Here, the reset foreign price inflation is defined as
![]() $\overline{\pi }_{F,t}=\frac{\overline{P}_{F,t}}{P_{F,t}^{\ast }},$
and the foreign price inflation is defined as
$\overline{\pi }_{F,t}=\frac{\overline{P}_{F,t}}{P_{F,t}^{\ast }},$
and the foreign price inflation is defined as
![]() $\pi _{F,t}^{\ast }=\frac{P_{F,t}^{\ast }}{P_{F,t-1}^{\ast }}$
. The real marginal cost for the foreign firms in terms of foreign prices is given by
$\pi _{F,t}^{\ast }=\frac{P_{F,t}^{\ast }}{P_{F,t-1}^{\ast }}$
. The real marginal cost for the foreign firms in terms of foreign prices is given by
![]() $mc_{F,t}=\frac{MC_{F,t}}{P_{F,t}}.$
The law of motion for the foreign producer’s inflation is given by:
$mc_{F,t}=\frac{MC_{F,t}}{P_{F,t}}.$
The law of motion for the foreign producer’s inflation is given by:
The real marginal cost for the foreign firms,
![]() $mc_{F,t},$
in terms of foreign prices would be
$mc_{F,t},$
in terms of foreign prices would be
where
![]() $w_{F,t}=\frac{w_{F,t}}{P_{F,t}}$
denotes real wages in the foreign country.
$w_{F,t}=\frac{w_{F,t}}{P_{F,t}}$
denotes real wages in the foreign country.
The terms of trade equation (18) can be written as
![]() $T_{t}=\frac{X_{t}P_{F,t}^{\ast }}{P_{D,t}}.$
Rewriting this gives us the following relation between the terms of trade, the nominal exchange rate change and producer price inflation between the two countries:
$T_{t}=\frac{X_{t}P_{F,t}^{\ast }}{P_{D,t}}.$
Rewriting this gives us the following relation between the terms of trade, the nominal exchange rate change and producer price inflation between the two countries:
Under a flexible price equilibrium,
![]() $\alpha _{D}=$
$\alpha _{D}=$
![]() $\alpha _{F}=0$
, such that all firms reset their prices in each period. This would imply,
$\alpha _{F}=0$
, such that all firms reset their prices in each period. This would imply,
![]() $P_{D,t}=\overline{P}_{D,t}$
,
$P_{D,t}=\overline{P}_{D,t}$
,
![]() $P_{F,t}^{\ast }=\overline{P}_{F,t}$
and
$P_{F,t}^{\ast }=\overline{P}_{F,t}$
and
![]() $Disp_{D,t}=Disp_{F,t}=1.$
The reset price in each period would simply be a markup over marginal cost in both the countries that is,
$Disp_{D,t}=Disp_{F,t}=1.$
The reset price in each period would simply be a markup over marginal cost in both the countries that is,
![]() $P_{D,t}=\frac{\sigma }{\sigma -1}MC_{D,t}$
and
$P_{D,t}=\frac{\sigma }{\sigma -1}MC_{D,t}$
and
![]() $P_{F,t}=\frac{\sigma }{\sigma -1}MC_{F,t}.$
$P_{F,t}=\frac{\sigma }{\sigma -1}MC_{F,t}.$
2.3. Equilibrium
2.3.1. Aggregate goods market equilibrium in a SOE
In this section we will describe the equilibrium for the benchmark case of the SOE. To characterize the SOE we follow Benigno and Paoli (Reference Benigno and De Paoli2010) and limit
![]() $n\rightarrow 0,$
such that
$n\rightarrow 0,$
such that
![]() $1-\mu _{D}$
$1-\mu _{D}$
![]() $\rightarrow \chi$
and
$\rightarrow \chi$
and
![]() $\mu _{F}\rightarrow 0$
from equation (5). It can be seen that the share of domestic goods in the consumption basket of domestic households,
$\mu _{F}\rightarrow 0$
from equation (5). It can be seen that the share of domestic goods in the consumption basket of domestic households,
![]() $\mu _{D},$
now depends only upon the degree of openness (inversely), while the share of domestic goods in the consumption basket of foreign households,
$\mu _{D},$
now depends only upon the degree of openness (inversely), while the share of domestic goods in the consumption basket of foreign households,
![]() $\mu _{F},$
is negligible.Footnote 24 The real exchange rate in equation (16) is now given by:
$\mu _{F},$
is negligible.Footnote 24 The real exchange rate in equation (16) is now given by:
(since
![]() $P_{t}^{\ast }=P_{F,t}^{\ast }$
under the limit
$P_{t}^{\ast }=P_{F,t}^{\ast }$
under the limit
![]() $n\rightarrow 0$
in CPI equation (15)). The demand function equations (12) and (13), aggregate demand equations (22) and (24), relative price and inflation relations in equations (19) and (20) reduce to the following, respectively:
$n\rightarrow 0$
in CPI equation (15)). The demand function equations (12) and (13), aggregate demand equations (22) and (24), relative price and inflation relations in equations (19) and (20) reduce to the following, respectively:
 \begin{align} T_{F,t} =\left [ \frac{1-\left ( 1-\chi \right ) \left ( T_{D,t}\right ) ^{1-\xi _{D}}}{\chi }\right ] ^{\frac{1}{1-\xi _{D}}} \end{align}
\begin{align} T_{F,t} =\left [ \frac{1-\left ( 1-\chi \right ) \left ( T_{D,t}\right ) ^{1-\xi _{D}}}{\chi }\right ] ^{\frac{1}{1-\xi _{D}}} \end{align}
2.3.2. Aggregate labor market equilibrium
Equilibrium in the labor market would require aggregate labor supply to be equal to aggregate labor demand. For the domestic country, labor is aggregated as follows:
 \begin{align*} H_{D,t}=\frac {1}{n}\int \limits _{0}^{n}H_{D,t}(i) di \end{align*}
\begin{align*} H_{D,t}=\frac {1}{n}\int \limits _{0}^{n}H_{D,t}(i) di \end{align*}
Using labor demand of a firm
![]() $i,$
$i,$
![]() $H_{D,t}(i),$
from equation (34), and demand for the firms’s output,
$H_{D,t}(i),$
from equation (34), and demand for the firms’s output,
![]() $Y_{D,t}(i),$
from equation (21), we re-write equilibrium in labor market as:
$Y_{D,t}(i),$
from equation (21), we re-write equilibrium in labor market as:
is the recursive form of price dispersion term,
![]() $Disp_{D,t}=\frac{1}{n}\int \limits _{0}^{n}\left ( \frac{P_{D,t}(i) }{P_{D,t}}\right ) ^{-\sigma }di$
. Analogously, equilibrium in the foreign labor market implies,
$Disp_{D,t}=\frac{1}{n}\int \limits _{0}^{n}\left ( \frac{P_{D,t}(i) }{P_{D,t}}\right ) ^{-\sigma }di$
. Analogously, equilibrium in the foreign labor market implies,
is the recursive form of the price dispersion term,
![]() $Disp_{F,t}=\frac{1}{1-n}\int \limits _{n}^{1}\left ( \frac{P_{F,t}^{\ast }(i) }{P_{F,t}^{\ast }}\right ) ^{-\sigma }di.$
For a given wages and prices, labor supply equations (30) along with labor demand equations (59) and (61) determines the labor market equilibrium.
$Disp_{F,t}=\frac{1}{1-n}\int \limits _{n}^{1}\left ( \frac{P_{F,t}^{\ast }(i) }{P_{F,t}^{\ast }}\right ) ^{-\sigma }di.$
For a given wages and prices, labor supply equations (30) along with labor demand equations (59) and (61) determines the labor market equilibrium.
2.3.3. Trade balance and welfare
The trade balance is captured through net exports (net trade of goods) in domestic and foreign country. The value of net exports for the domestic country in terms of domestic consumer prices,
![]() $NX_{D,t},$
is defined as the value of total imports (in domestic consumer prices) subtracted from the value of total exports (in domestic consumer prices) and is given by:
$NX_{D,t},$
is defined as the value of total imports (in domestic consumer prices) subtracted from the value of total exports (in domestic consumer prices) and is given by:
Similarly, the value of net exports for the foreign country in terms of foreign consumer prices (foreign currency),
![]() $NX_{F,t},$
is defined as the value of total imports (in foreign consumer prices) subtracted from the value of total exports (in foreign consumer prices) and is given by:
$NX_{F,t},$
is defined as the value of total imports (in foreign consumer prices) subtracted from the value of total exports (in foreign consumer prices) and is given by:
A positive and a negative net exports are referred to as trade surplus and trade deficit, respectively. The utility-based welfare criterion defines welfare as an expected lifetime utility of a representative household.Footnote 25 The welfare function in the domestic/ foreign country would thus be a following lifetime utility of a representative household, described in equation (1)/(3):
where
![]() $i=D$
or
$i=D$
or
![]() $F.$
We define welfare losses in the domestic country and foreign country as
$F.$
We define welfare losses in the domestic country and foreign country as
![]() $-Welfare_{D,t}$
and
$-Welfare_{D,t}$
and
![]() $-Welfare_{F,t}$
, respectively.
$-Welfare_{F,t}$
, respectively.
2.4. Monetary policy rules
2.4.1. Simple taylor rule: Baseline policy rule
In the baseline case we assume that the central banks in both the domestic and the foreign country set a monetary policy rule on the nominal interest rates using a simple Taylor rule (Taylor (Reference Taylor1993)). Here the central bank attempts to stabilize both inflation and output. In this case, we assume that the measure of inflation targeted by a central bank targets is the CPI in their respective countries. The rules are given by:
for the domestic and foreign country, respectively. Here,
![]() $\overline{R}=\frac{1}{\beta }$
and
$\overline{R}=\frac{1}{\beta }$
and
![]() $\overline{R}^{\ast }=\frac{1}{\beta }$
are the steady state values of nominal interest rate,
$\overline{R}^{\ast }=\frac{1}{\beta }$
are the steady state values of nominal interest rate,
![]() $R_{t},$
and
$R_{t},$
and
![]() $R_{t}^{\ast },$
respectively. We get these steady state values from Euler equations (28) and (29). Here,
$R_{t}^{\ast },$
respectively. We get these steady state values from Euler equations (28) and (29). Here,
![]() $\overline{\pi }$
and
$\overline{\pi }$
and
![]() $\overline{\pi }^{\ast }$
are the steady state values of CPI, in the domestic and foreign country, respectively. The parameters
$\overline{\pi }^{\ast }$
are the steady state values of CPI, in the domestic and foreign country, respectively. The parameters
![]() $(\phi _{\pi },\text{ }\phi _{y})$
and
$(\phi _{\pi },\text{ }\phi _{y})$
and
![]() $(\phi _{\pi }^{\ast },\text{ }\phi _{y}^{\ast })$
capture the responsiveness of the interest rates to the deviation of inflation from its steady state level and deviation of output from its flexible price level counterpart in the respective countries. We will estimate the
$(\phi _{\pi }^{\ast },\text{ }\phi _{y}^{\ast })$
capture the responsiveness of the interest rates to the deviation of inflation from its steady state level and deviation of output from its flexible price level counterpart in the respective countries. We will estimate the
![]() $\phi _{\pi },$
$\phi _{\pi },$
![]() $\phi _{y}$
to match the IRFs of model with that of the data for the baseline case in a SOE. Thus, TR-CPI with usual calibration will also be part of the alternate monetary policy rules.
$\phi _{y}$
to match the IRFs of model with that of the data for the baseline case in a SOE. Thus, TR-CPI with usual calibration will also be part of the alternate monetary policy rules.
2.4.2. Alternate monetary policy rules
For comparative analysis, we only vary the monetary policy rule in the domestic economy/ SOE. The monetary policy rule for the foreign economy is assumed to be a simple Taylor rule as described in equation (66) for all the alternative monetary policy cases we consider for the domestic economy. The Taylor rule we consider in the baseline case, as described in equation (65) is a CPI-based rule. The first alternate rule we consider is a Taylor rule with PPI as given by:
Here,
![]() $\pi _{D,t}$
is producer price inflation in the domestic country and
$\pi _{D,t}$
is producer price inflation in the domestic country and
![]() $\overline{\pi }_{D}$
is it’s steady state value. This is an interesting case because it has been shown in Gali and Monacelli (Reference Galí and Monacelli2005) that under a floating exchange regime it is optimal for the central bank of a SOE to target producer price inflation. Later, Engel (Reference Engel2011) showed that under local currency pricing, exchange rate flexibility does not matter and the optimal policy for a central bank is to completely stabilize CPI.Footnote 26
$\overline{\pi }_{D}$
is it’s steady state value. This is an interesting case because it has been shown in Gali and Monacelli (Reference Galí and Monacelli2005) that under a floating exchange regime it is optimal for the central bank of a SOE to target producer price inflation. Later, Engel (Reference Engel2011) showed that under local currency pricing, exchange rate flexibility does not matter and the optimal policy for a central bank is to completely stabilize CPI.Footnote 26
As argued in Calvo and Reinhart (Reference Calvo and Reinhart2002) and Reinhart (Reference Reinhart2000), EMEs use their foreign exchange reserves and monetary policy with interest rates as an instrument to stabilize exchange rate movements in a floating exchange rate regime. There also exists empirical evidence showing that central banks in emerging markets consider exchange rate movements while setting their monetary policy (Cuevas and Topak (Reference Cuevas and Topak2008); Aizenman et al. (Reference Aizenman and Noy2011)). Given this, the next set of rules we consider are Taylor rules (both CPI and PPI) with nominal exchange rates, as given by
Here,
![]() $\frac{X_{t}}{X_{t-1}}$
denotes a change in the nominal exchange rate and the policy rate responds positively to a positive change in the nominal exchange rate. This is because a depreciation of currency would imply an increase in expected future inflation (due to a rise in import prices) and an increase in output (because of a higher demand for exports and import substitution). A rise (fall) in the interest rate is thus required to stabilize the economy from the effects of the depreciation (appreciation).
$\frac{X_{t}}{X_{t-1}}$
denotes a change in the nominal exchange rate and the policy rate responds positively to a positive change in the nominal exchange rate. This is because a depreciation of currency would imply an increase in expected future inflation (due to a rise in import prices) and an increase in output (because of a higher demand for exports and import substitution). A rise (fall) in the interest rate is thus required to stabilize the economy from the effects of the depreciation (appreciation).
From the empirical evidence shown in Section 1.1, it is evident that the movement of the exchange rates (both nominal as well as real) is high and significant in emerging markets in presence of global uncertainty shocks. We also observed that the nominal interest rates increase as a response to an increase in global uncertainty and thus can reinforce the adverse effects of uncertainty shock. At the same time the interest rates do not seem to stabilize exchange rates. Aizenman et al. (Reference Aizenman and Noy2011) showed that when monetary policy is geared to stabilize inflation, output and exchange rates, exchange rates are not much stabilized as a part of mixed strategy in an IT (inflation-targeting) regime. Given the inability of IRRs to absorb the effect of the shock under consideration, we examine, an alternative instrument for conducting monetary policy, namely, exchange rates. This puts a rule on exchange rates directly and does not let them float freely. These set of rules are called ERR where a central bank manages exchange rates to target inflation and output. The Monetary Authority of Singapore (MAS) has been following this rule since 1981 (McCallum (2006)). We consider a simple ERR as described in Heiperzt et al. (Reference Heiperzt, Mihov and Santacreu2017):
Here,
![]() $\phi _{y}^{e}$
and
$\phi _{y}^{e}$
and
![]() $\phi _{\pi }^{e}$
are the response parameters of nominal exchange to the change in output and inflation. Note that the exchange rate responds negatively to an increase in inflation and output to stabilize the economy. This is because increase in inflation and output can be stabilized when nominal exchange rates fall (an appreciation). An appreciation reduces inflation (by reducing the price of imports) and also reduces output (by reducing the foreign demand for domestic goods and reducing the domestic good’s demand by domestic households). We also consider an extreme case of a fixed exchange rule (PEG) where the central bank completely stabilizes the nominal exchange rate, as given by
$\phi _{\pi }^{e}$
are the response parameters of nominal exchange to the change in output and inflation. Note that the exchange rate responds negatively to an increase in inflation and output to stabilize the economy. This is because increase in inflation and output can be stabilized when nominal exchange rates fall (an appreciation). An appreciation reduces inflation (by reducing the price of imports) and also reduces output (by reducing the foreign demand for domestic goods and reducing the domestic good’s demand by domestic households). We also consider an extreme case of a fixed exchange rule (PEG) where the central bank completely stabilizes the nominal exchange rate, as given by
When,
![]() $\phi _{y}^{e}\rightarrow 0$
and
$\phi _{y}^{e}\rightarrow 0$
and
![]() $\phi _{\pi }^{e}\rightarrow 0,$
the ERR (70) approaches a PEG rule in (71). As values of
$\phi _{\pi }^{e}\rightarrow 0,$
the ERR (70) approaches a PEG rule in (71). As values of
![]() $\phi _{y}^{e}$
and
$\phi _{y}^{e}$
and
![]() $\phi _{\pi }^{e}$
increase, the exchange rate adjusts more to stabilize the economy. Note that interest rates are endogenously determined in the economy under ERR and PEG rule.
$\phi _{\pi }^{e}$
increase, the exchange rate adjusts more to stabilize the economy. Note that interest rates are endogenously determined in the economy under ERR and PEG rule.
2.5. Exogenous shock processes
We followed Basu and Bundick (Reference Basu and Bundick2017) and Fernández-Villaverde et al., (Reference Fernández-Villaverde, Guerrón-Quintana, Rubio-Ramírez and Uribe2011) to describe the shock processes with uncertainty shocks. For the global uncertainty shocks we assume a shock to the second-moment of a foreign country’s preference/ demand process as mentioned above. The demand shock process in equation (3) take the following form,
where
![]() $\varepsilon _{F,t}$
is shock to the first-moment of demand shock. The standard deviation
$\varepsilon _{F,t}$
is shock to the first-moment of demand shock. The standard deviation
![]() $v_{F,t-1}$
in the foreign demand are not constant and are described by the following AR
$v_{F,t-1}$
in the foreign demand are not constant and are described by the following AR
![]() $(1)$
processes,
$(1)$
processes,
Here,
![]() $\vartheta _{F,t}$
is shock to the second-moment or an uncertainty shock to the underlying demand. In other words, uncertainty shocks here refer to the shocks to standard deviation of the underlying process. It is assumed that the stochastic shocks,
$\vartheta _{F,t}$
is shock to the second-moment or an uncertainty shock to the underlying demand. In other words, uncertainty shocks here refer to the shocks to standard deviation of the underlying process. It is assumed that the stochastic shocks,
![]() $\varepsilon _{F,t}$
and
$\varepsilon _{F,t}$
and
![]() $\vartheta _{F,t},$
are independent and normally distributed random variables.
$\vartheta _{F,t},$
are independent and normally distributed random variables.
2.6. Solution method
We are interested in looking at the effects of shocks to the second moments (or uncertainty shocks) of the demand/ preference levels of the foreign country on a SOE (domestic country). To capture the complete effect of the second-moment shocks on the endogenous variables of the model, we need to take the third order approximation of the model equations as explained in Fernández-Villaverde et al., (Reference Fernández-Villaverde, Guerrón-Quintana, Rubio-Ramírez and Uribe2011) and later also applied in Basu and Bundick (Reference Basu and Bundick2017). Following this, we do a third order Taylor series approximation of the model using the Dynare software package in MATLAB to find a solution to our benchmark model.Footnote 27 All the approximations are done around the stochastic steady state.
2.7. Calibration
In this section we attempt to calibrate the SOE to a prototypical EME and the foreign country, which comprises the world, to an AE. We estimate the degree of openness parameter,
![]() $\chi,$
to be 0.6, as the average trade share to GDP of EMEs. To get this we use World Bank’s country level trade data for year 2015 (World Bank (Reference Bank2018)). The value of
$\chi,$
to be 0.6, as the average trade share to GDP of EMEs. To get this we use World Bank’s country level trade data for year 2015 (World Bank (Reference Bank2018)). The value of
![]() $\kappa$
, which is the initial parameter in the asset market condition is estimated to be 3.8. We calculate this using the OECD database on national accounts (OECD (2019)). Details on the calculation of
$\kappa$
, which is the initial parameter in the asset market condition is estimated to be 3.8. We calculate this using the OECD database on national accounts (OECD (2019)). Details on the calculation of
![]() $\chi$
and
$\chi$
and
![]() $\kappa$
is provided in the Data Appendix A.1. The value of intertemporal elasticity of substitution varies from 0.2 to 0.5 following Fernández-Villaverde et al. (Reference Fernández-Villaverde, Guerrón-Quintana, Rubio-Ramírez and Uribe2011) and Benigno et al. (Reference Benigno, Benigno and Nisticò2012), respectively. The elasticity of intertemporal of substitution here is set to 0.33 such that the inverse of the intertemporal elasticity of substitution parameter,
$\kappa$
is provided in the Data Appendix A.1. The value of intertemporal elasticity of substitution varies from 0.2 to 0.5 following Fernández-Villaverde et al. (Reference Fernández-Villaverde, Guerrón-Quintana, Rubio-Ramírez and Uribe2011) and Benigno et al. (Reference Benigno, Benigno and Nisticò2012), respectively. The elasticity of intertemporal of substitution here is set to 0.33 such that the inverse of the intertemporal elasticity of substitution parameter,
![]() $\eta,$
for the domestic and the foreign country, is 3. For the value of the elasticity of substitution between domestic and foreign goods,
$\eta,$
for the domestic and the foreign country, is 3. For the value of the elasticity of substitution between domestic and foreign goods,
![]() $\xi _{D}$
and
$\xi _{D}$
and
![]() $\xi _{F},$
we use 1.5 as calculated in Benigno et al. (Reference Benigno, Benigno and Nisticò2012). The values are kept same for both the foreign as well domestic country due to lack of any data evidence on EMEs for the same. The goods are thus assumed to be relatively substitutable in the benchmark calibration for both the countries. The discount factor,
$\xi _{F},$
we use 1.5 as calculated in Benigno et al. (Reference Benigno, Benigno and Nisticò2012). The values are kept same for both the foreign as well domestic country due to lack of any data evidence on EMEs for the same. The goods are thus assumed to be relatively substitutable in the benchmark calibration for both the countries. The discount factor,
![]() $\beta$
is assumed to be the same in both the countries and is set to 0.994 following Basu and Bundick (Reference Basu and Bundick2017). We use standard value for the weight on the consumption over leisure that is, 1/3 as also calibrated in Benigno et al. (Reference Benigno, Benigno and Nisticò2012). The parameter for the elasticity of substitution between varieties,
$\beta$
is assumed to be the same in both the countries and is set to 0.994 following Basu and Bundick (Reference Basu and Bundick2017). We use standard value for the weight on the consumption over leisure that is, 1/3 as also calibrated in Benigno et al. (Reference Benigno, Benigno and Nisticò2012). The parameter for the elasticity of substitution between varieties,
![]() $\theta$
, is set to 6 following Benigno et al. (Reference Benigno, Benigno and Nisticò2012) such that the steady state markup for a firm is 20%. In the baseline calibration we fix the value of stickiness parameter for the foreign country,
$\theta$
, is set to 6 following Benigno et al. (Reference Benigno, Benigno and Nisticò2012) such that the steady state markup for a firm is 20%. In the baseline calibration we fix the value of stickiness parameter for the foreign country,
![]() $\alpha _{F},$
to be 0.66 following Sbordone (Reference Sbordone2002) and Gali et al. (Reference Gali and Lopez-Salido2001). These papers provide empirical evidence for stickiness parameter for the US and Europe, respectively. For the domestic country/SOE the parameter for stickiness,
$\alpha _{F},$
to be 0.66 following Sbordone (Reference Sbordone2002) and Gali et al. (Reference Gali and Lopez-Salido2001). These papers provide empirical evidence for stickiness parameter for the US and Europe, respectively. For the domestic country/SOE the parameter for stickiness,
![]() $\alpha _{D}$
is set slightly higher to 0.75 such that domestic firms revise prices in 4 quarters.Footnote 28 We also compare our baseline sticky price calibration results to a completely flexible price calibration, where
$\alpha _{D}$
is set slightly higher to 0.75 such that domestic firms revise prices in 4 quarters.Footnote 28 We also compare our baseline sticky price calibration results to a completely flexible price calibration, where
![]() $\alpha _{D}=0$
and
$\alpha _{D}=0$
and
![]() $\alpha _{F}=0$
. The preference shock parameters for the foreign country at first-order and second-order are partially calibrated from Basu and Bundick (Reference Basu and Bundick2017)
$\alpha _{F}=0$
. The preference shock parameters for the foreign country at first-order and second-order are partially calibrated from Basu and Bundick (Reference Basu and Bundick2017)
![]() $,$
such that we set persistence shock parameter
$,$
such that we set persistence shock parameter
![]() $\delta _{F}=0.94$
and the steady state values for the demand shock,
$\delta _{F}=0.94$
and the steady state values for the demand shock,
![]() $\overline{\Gamma }_{F}=1.$
The rest of the shocks parameters namely, the persistence to the uncertainty shock parameter,
$\overline{\Gamma }_{F}=1.$
The rest of the shocks parameters namely, the persistence to the uncertainty shock parameter,
![]() $\delta _{\sigma _{F}}=0.62,$
the steady state values its standard deviation of demand,
$\delta _{\sigma _{F}}=0.62,$
the steady state values its standard deviation of demand,
![]() $\overline{v}_{F}=0.085$
and the scaling parameter for the uncertainty shock
$\overline{v}_{F}=0.085$
and the scaling parameter for the uncertainty shock
![]() $\varpi =0.45$
are set to match the impulse response function of the nominal interest rates with the empirical counterpart as shown in Figure 4. The response of the rest of the economy is put for an assessment. This is how we take the IRFs generated by the model to the IRFs generated using data in the empirical section.
$\varpi =0.45$
are set to match the impulse response function of the nominal interest rates with the empirical counterpart as shown in Figure 4. The response of the rest of the economy is put for an assessment. This is how we take the IRFs generated by the model to the IRFs generated using data in the empirical section.
Figure 4. Interest rate response before and after IRF matching for Taylor parameter
![]() $ \phi _{y}.$
$ \phi _{y}.$
For the baseline calibration of the Taylor rule as described in equations (65) and (66), for both the countries, we set the weight on inflation to be
![]() $\phi _{\pi }=\phi _{\pi }^{\ast }=1.5$
. These are the standard values used in the literature (Taylor (Reference Taylor1993)). While the weight on output growth for the foreign country,
$\phi _{\pi }=\phi _{\pi }^{\ast }=1.5$
. These are the standard values used in the literature (Taylor (Reference Taylor1993)). While the weight on output growth for the foreign country,
![]() $\phi _{y}^{\ast }$
is set to its standard value
$\phi _{y}^{\ast }$
is set to its standard value
![]() $0.5$
, for the domestic country we estimate the weight to match the impulse response in data and find
$0.5$
, for the domestic country we estimate the weight to match the impulse response in data and find
![]() $\phi _{y}=0.1$
. In other words, the response of the EMEs to the output change is muted in presence of uncertainty shock. We also consider models with alternate monetary policies. The parameter for Taylor rules with an exchange rate where weight on the exchange rate change,
$\phi _{y}=0.1$
. In other words, the response of the EMEs to the output change is muted in presence of uncertainty shock. We also consider models with alternate monetary policies. The parameter for Taylor rules with an exchange rate where weight on the exchange rate change,
![]() $\phi _{X}$
, is set to 0.05 uses estimates from Cuevas and Topak (Reference Cuevas and Topak2008). The ERR parameters,
$\phi _{X}$
, is set to 0.05 uses estimates from Cuevas and Topak (Reference Cuevas and Topak2008). The ERR parameters,
![]() $\phi _{\pi }^{e},$
that is, weight on the inflation gap, and
$\phi _{\pi }^{e},$
that is, weight on the inflation gap, and
![]() $\phi _{y}^{e},$
that is, weight on the output gap are set to 0.30 and 0.02, respectively, similar estimates from Parrado (Reference Parrado2004) and Heiperzt et al. (Reference Heiperzt, Mihov and Santacreu2017). We also show the impulse response functions for ERRs with varying value of inflation sensitivity parameter,
$\phi _{y}^{e},$
that is, weight on the output gap are set to 0.30 and 0.02, respectively, similar estimates from Parrado (Reference Parrado2004) and Heiperzt et al. (Reference Heiperzt, Mihov and Santacreu2017). We also show the impulse response functions for ERRs with varying value of inflation sensitivity parameter,
![]() $\phi _{\pi }^{e},$
to 0.60 and 0.16, respectively. The parameters are summarized in Table 1.
$\phi _{\pi }^{e},$
to 0.60 and 0.16, respectively. The parameters are summarized in Table 1.
Table 1. Summary of parameter values
3. Results
3.1. IRFs to an uncertainty shock to global demand
This section discusses the macroeconomic effects of a one standard deviation shock to the uncertainty in demand of the foreign households as described in the equation (73) to compare responses with the data. Figure 5 (row 1, column 1) shows that two exogenous shocks to the economic system: shock to VXO in the data and shock to second-moment of demand in the model closely follow each other, especially from the second quarter. This may not be the best comparison to make but we exploit the fact that global uncertainty shocks are exogenous to SOEs/ EMEs, so that they are comparable. For the quantitative comparison between the empirical and model outcomes for other variables it is observed that on impact consumption and output fall much more strongly in the model than in the data but from the second quarter it is within the 95% confidence interval. For the net exports, CPI, and the interest rates the responses to the shock from the model are well within the 95% confidence interval band.
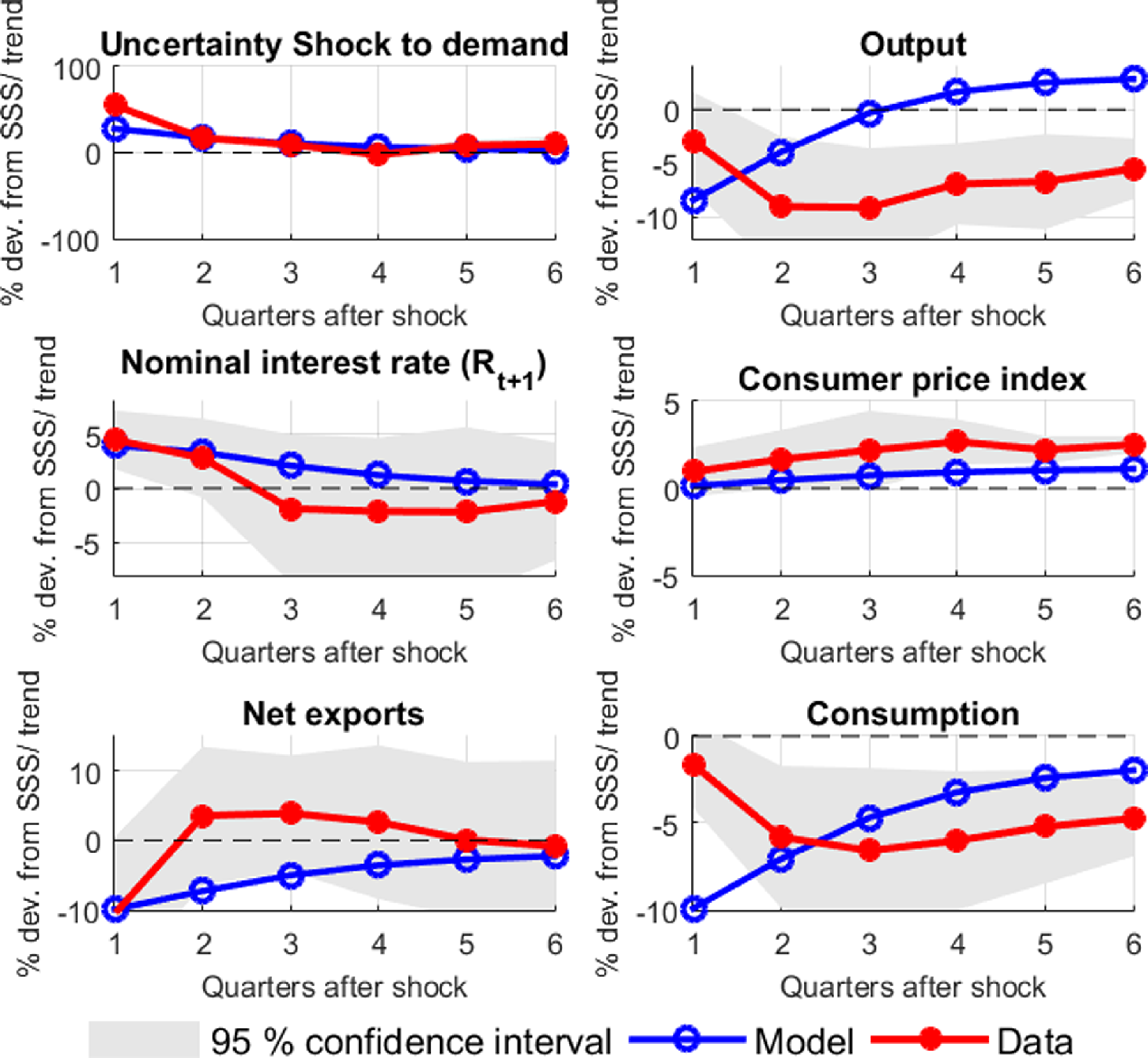
Figure 5. Comparison of IRFs from model and empirical excercise.

Figure 6. IRFs comparing the sticky price and flexible price allocation for a one standard deviation shock to uncertainty in foreign demand.
To understand the transmission of uncertainty shocks to the domestic economy consider Figure 6 comparing the response of the economy under sticky price (red line) and flexible price (green line) scenarios. The case of sticky price is the baseline case here. While we find that the model fits qualitatively well to the data, we also find a good quantitative match for variables including consumption, nominal interest rates, CPI, output, and net exports. On impact, with increase in the global uncertainty the domestic country experiences a sudden outflow of capital and the nominal exchange rate depreciates in the model like in the data (Figure 6, Subplot (1,1)). Although, the extent of the rise observed in data is more than the it is observed in the model this result is consistent with fact 3. Due to an uncertain future demand, households in the domestic economy too save more (precautionary savings) and consume less today because of which consumption demand falls (Subplot (2,1)).Footnote 29 The average fall in the consumption over the first six quarters is about 5–6% from data as well as the model. This is consistent with the stylized fact 1 we observe in the data, and the model. Note that both domestic as well as the foreign economy have a new Keynesian feature of nominal rigidities in the form of price stickiness and thus output is demand determined in the present model.
The prices fall in the foreign economy due to contracting demand, while in the EMEs prices rise due to an increase in import prices due to high depreciation (Subplot (1,3)). The sensitivity of domestic prices to depreciation depends on the degree of openness as shown in equation (53.2). Following this, the nominal interest rate increases under inflation-targeting regime (Subplot(1,2)).Footnote 30 This result too quantitatively matches empirical fact 4 we observe in the data (Figure 4). The real interest rates also increase here as the rise in nominal interest rates is higher than the increase in CPI. Due to this the consumption remains depressed for longer periods in the EMEs. The net export falls because of a fall in the real foreign demand for goods by 10% on impact as we observe in data (Subplot (1,2)). This result is in line with empirical facts 1 and 2, although in the data we observe that the trade balance to GDP ratio improves after one quarter due to positive depreciation effect but it is insignificant. The welfare in the domestic economy is negative because of the adverse real effects of the shock.
Figure 6 also shows how the response to the economy varies under flexible price scenario. Figure 6 clearly shows that the response of the real variables to the global uncertainty is muted when the price movement is completely flexible. Infact, change in the exchange movement is also less due to which the inflation actually falls instead of rising; considering that the uncertainty actually leads to a fall aggregate demand in the economy. These results are consistent with Basu and Bundick (Reference Basu and Bundick2017).Footnote 31 Due to lower real effects of uncertainty shocks under flexible price then sticky prices, the welfare losses are less under the former.

Figure 7. Welfare loss responses in a SOE under different monetary policy rules to one standard deviation shock to uncertainty in foreign demand.
3.2. Role of monetary policy
In the baseline model calibration we have assumed that the central bank of a SOE (domestic country) follows a simple Taylor rule (TR-CPI) described in equation (65) with weight on the output gap being 0.1. In Figure 4 the IRF matching with the empirical observation indicates that the weight on output gap is as low as 0.1 instead of its standard value of 0.5. As discussed earlier a positive response of an IRR in the EMEs amplifies the contractionary effect of an uncertainty shock on the real economy. In this section we consider alternate monetary policy rules to ascertain the role of monetary policy in determining the post shock (uncertainty shock) equilibrium. For a comparative analysis we set TR-CPI
![]() $(\phi _{\pi }=1.5$
;
$(\phi _{\pi }=1.5$
;
![]() $\phi _{y}=0.1)$
as the baseline case. The other monetary policy rules we consider for comparison can broadly be grouped into two categories. The first category correspond to the modified Taylor rules. We consider a TR-CPI with standard weight on the output movements that is, TR-CPI
$\phi _{y}=0.1)$
as the baseline case. The other monetary policy rules we consider for comparison can broadly be grouped into two categories. The first category correspond to the modified Taylor rules. We consider a TR-CPI with standard weight on the output movements that is, TR-CPI
![]() $(\phi _{\pi }=1.5$
;
$(\phi _{\pi }=1.5$
;
![]() $\phi _{y}=0.5)$
. Other rules include Taylor rule with PPI (TR-PPI), a CPI Taylor rule with an exchange rate mandate (TR-CPI-ER), a PPI Taylor rule with an exchange rate mandate (TR-CPI-ER), as specified in equations (67), (68), and (69), respectively. In all the above mentioned cases, we have a free movement of assets across countries and an independent monetary policy. Following the impossible trinity, the exchange rate is completely flexible. The second category is a different class of monetary policy rules where the exchange rate is a monetary policy instrument. Here we consider a very simple ERR and an extreme case of fixed exchange rates (PEG), as specified in equations (70) and (71), respectively. A detailed description of the alternate monetary policy rules is given in Section 2.4.
$\phi _{y}=0.5)$
. Other rules include Taylor rule with PPI (TR-PPI), a CPI Taylor rule with an exchange rate mandate (TR-CPI-ER), a PPI Taylor rule with an exchange rate mandate (TR-CPI-ER), as specified in equations (67), (68), and (69), respectively. In all the above mentioned cases, we have a free movement of assets across countries and an independent monetary policy. Following the impossible trinity, the exchange rate is completely flexible. The second category is a different class of monetary policy rules where the exchange rate is a monetary policy instrument. Here we consider a very simple ERR and an extreme case of fixed exchange rates (PEG), as specified in equations (70) and (71), respectively. A detailed description of the alternate monetary policy rules is given in Section 2.4.
Figure 7 compares the impulse response functions for welfare losses (left-side) and risk premiums (right-side) under the above described monetary policy rules, in presence of a global uncertainty shock. The figure clearly shows that the welfare losses and risk-premiums are highest in the baseline case. The lowest welfare losses are given by the ERRs followed by the PEG rule. Infact, both these rules give a positive welfare in contrast to the other rules. Similarly, the risk premiums on holding foreign bonds are highest in the baseline case followed by TR-CPI rules. The risk premium change associated with the PEG rule is zero. However, the ERRs and TR-PPI lead to fall in risk premiums. This implies that under these rules the capital does not outflows from the domestic country due to flight to safe but we observe capital inflow and the exchange rates appreciates as shown in Figure 8 (Subplot 1,1). Although, the volatility is more in case of TR-PPI rules as compared to ERR, among the Taylor rules considered here, TR-PPI is performs the best for the given calibration. It is to be noted that adding exchange rate to the Taylor rules does not significantly affect the outcomes. Quantitatively, the welfare losses are 350% less under the ERR regime as compared to the baseline case. This happens because in the presence of uncertainty, the link between exchange rate and the monetary policy through interest rates (UIP condition) breaks down and the risk premiums are positive, with higher-order moment shocks. On the contrary, ERRs restores the broken link between monetary policy, exchange rates, and other real variables in the domestic economy like inflation and output as shown in the equation (70). Alternatively, ERRs anchor the market beliefs on future exchange rate movement and prevent sudden capital outflows during uncertain economic times from EMEs.
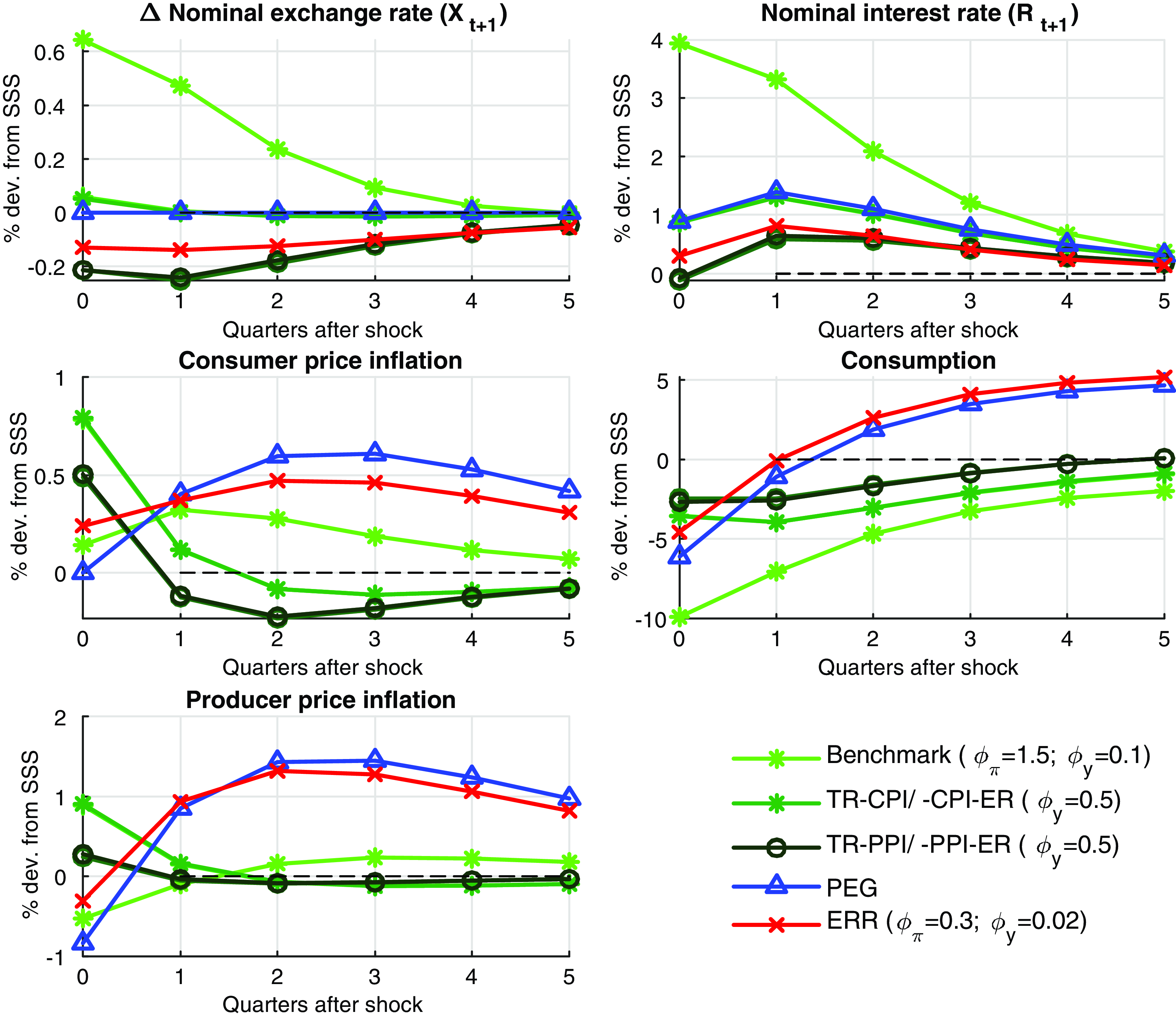
Figure 8. IRFs for a SOE under different monetary policy rules to a one standard deviation shock to uncertainty in foreign demand.
Table 2 compares the welfare losses on impact in the presence of first-moment/ level demand shock and the time-varying second-moment/ uncertainty demand shock. The ranking between Taylor rules and ERRs completely reverses. While the Taylor rules minimize the welfare losses in the presence of the standard first-moment/ level shock, they perform the worst in presence of uncertainty shocks. We get very similar results for the PEG rules. This implies that the choice of instrument for monetary policy clearly depends on the source and type of the shock affecting an economy. This result is different from Heiperzt et al. (Reference Heiperzt, Mihov and Santacreu2017), as the authors there find that the ERRs perform better even with the first-moment shocks.
Table 2. Comparing welfare losses with first-moment vs second-moment demand shocks
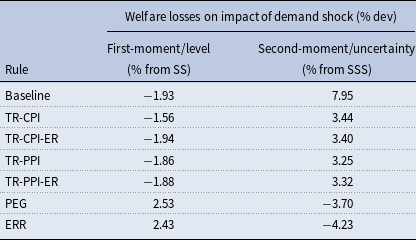
Figure 8 compares the impulse response functions for nominal exchange rate, inflation (both PPI and CPI) and consumption. The nominal exchange rate depreciates quite steeply under the baseline case as compared to other TR-CPI rules which show slight depreciation. As a result of this jump in the nominal exchange rates the CPI increases here despite the fall in consumption demand. As the interest rate in the baseline case responds to the change in inflation, we observe that the nominal interest rates rises to an extend that the real interest rates are positive. Furthermore, we observe a higher and more persistent fall in the consumption. Compared to the IRRs, the ERR, and the PEG rules results in a positive level of consumption for five quarters after falling in the first quarter. The inflation both PPI and CPI is increased due to this rise the demand. Moreover, the real interest rates actually fall in this case compared to the Taylor rules considered as IRRs. It is also to be noticed that with the policy response in ERR, the inflation and demand does not face any trade-offs as we observe in the case for the baseline case and other Taylor rules. Both ERR and PEG rules perform better then the Taylor rules which is consistent with the welfare loss differences we observed in Figure 7. Taylor rules with CPI as inflation measure performs poorly then TR-PPI rules. This is consistent with the literature which shows that with producer currency pricing, a Taylor rule with CPI brings more inefficiency (Gali and Monacelli (Reference Galí and Monacelli2005); Engel (Reference Engel2011); Devereux and Engel (Reference Devereux and Engel2003)). Taylor rules with an exchange rate mandate perform slightly better than those without it but they do not significantly reduce welfare losses.
Figure 9 compares the impulse responses with change in the inflation sensitivity parameter of ERR. As the inflation sensitivity parameter,
![]() $\phi _{\pi }^{e}$
is doubled, from 0.30 to 0.60, the policy response of exchange rate appreciation is more aggressive and inflation is much more stabilized. The real interest rates fall more as a result. The increase in consumption is also muted for all the periods and as a result the welfare losses are higher. The opposite is observed in the case when sensitivity parameter is reduced by half that is, from 0.30 to 0.16. As the sensitivity parameter to inflation is reduced, we observe the rise inflation is higher. The real interest rates reduces, which increases the consumption for all periods reducing the welfare losses. With ERRs there exists a trade-off in stabilizing the inflation and nominal exchange rate and it depends on the coefficient of inflation sensitivity. Further, we do not observe any trade-offs in stabilizing output and inflation as we do in the case of Taylor rules (IRRs). The choice of
$\phi _{\pi }^{e}$
is doubled, from 0.30 to 0.60, the policy response of exchange rate appreciation is more aggressive and inflation is much more stabilized. The real interest rates fall more as a result. The increase in consumption is also muted for all the periods and as a result the welfare losses are higher. The opposite is observed in the case when sensitivity parameter is reduced by half that is, from 0.30 to 0.16. As the sensitivity parameter to inflation is reduced, we observe the rise inflation is higher. The real interest rates reduces, which increases the consumption for all periods reducing the welfare losses. With ERRs there exists a trade-off in stabilizing the inflation and nominal exchange rate and it depends on the coefficient of inflation sensitivity. Further, we do not observe any trade-offs in stabilizing output and inflation as we do in the case of Taylor rules (IRRs). The choice of
![]() $\phi _{\pi }^{e}$
by a central bank should thus depends on the weight it puts on the variability of the nominal exchange rates and inflation in its objective function. Welfare losses reduce by 13% when
$\phi _{\pi }^{e}$
by a central bank should thus depends on the weight it puts on the variability of the nominal exchange rates and inflation in its objective function. Welfare losses reduce by 13% when
![]() $\phi _{\pi }^{e}$
increases from 0.30 to 0.60 due to more stabilized CPI and output. The higher value of
$\phi _{\pi }^{e}$
increases from 0.30 to 0.60 due to more stabilized CPI and output. The higher value of
![]() $\phi _{\pi }^{e}$
ensures that exchange rates respond more to the change in key fundamental variables governing the domestic economy.
$\phi _{\pi }^{e}$
ensures that exchange rates respond more to the change in key fundamental variables governing the domestic economy.
Table 3. Comparing second empirical moments for different monetary policy rules

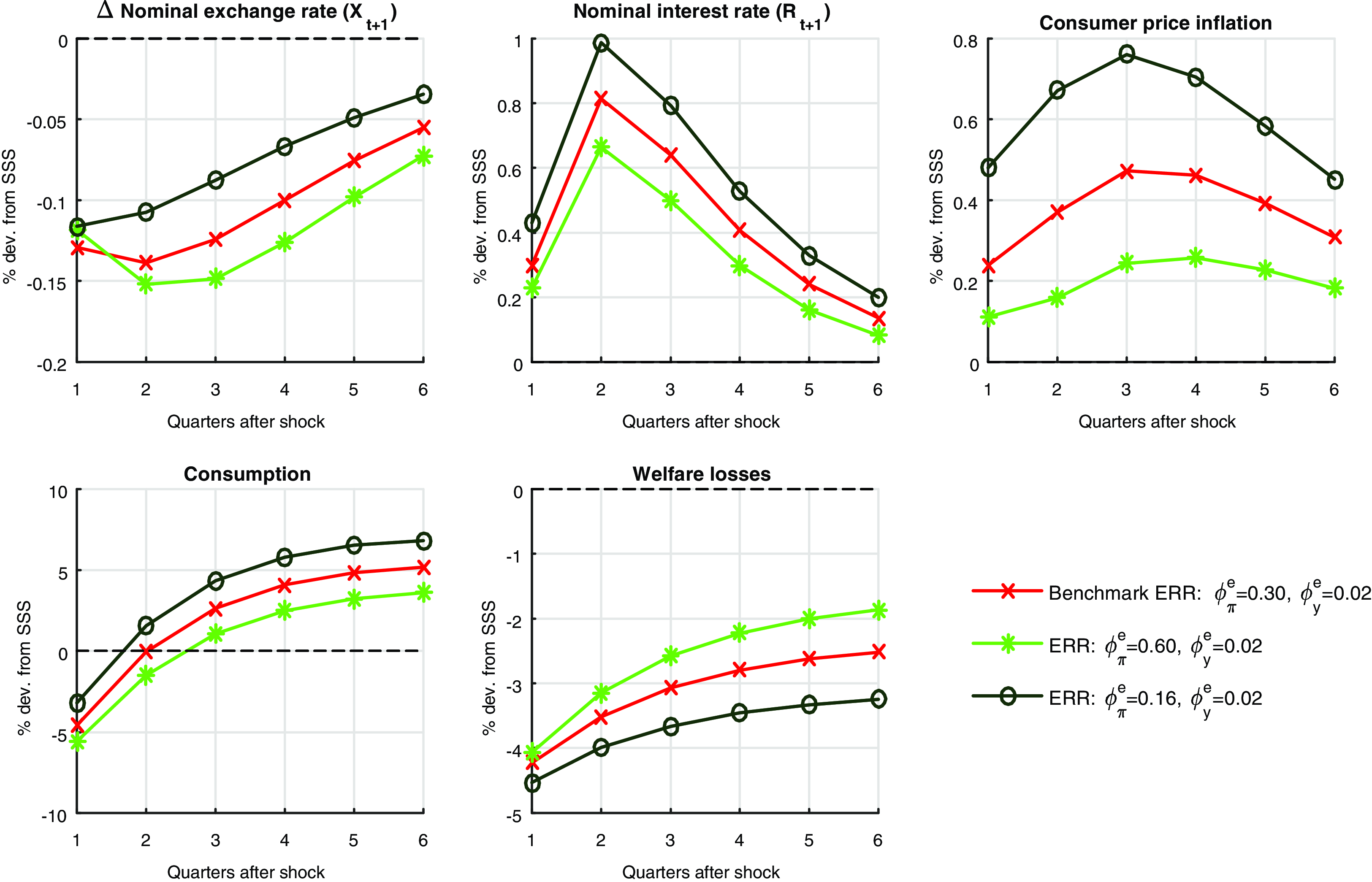
Figure 9. IRFs for a SOE under exchange rate rules with varying sensitivity to inflation
![]() $(\phi _{\pi }^{e})$
for a one standard deviation shock to uncertainty in foreign demand.
$(\phi _{\pi }^{e})$
for a one standard deviation shock to uncertainty in foreign demand.
The above impulse responses are only capturing response to the economy for a one time uncertainty shock. We investigate how the economy responds in the long run when the economy is hit with the global uncertainty shock in every period under different monetary policy rules. We simulate the data from the model for 100 quarter periods (or 25 years) under the considered monetary policy rules.Footnote 32 Table 3 compares the coefficient of variation that is, standard deviation adjusted for the mean of each variable under different monetary policy rules. The results we get are mixed. Comparing the rules according to the variation in welfare function of the households, we find that the ranking remains the same as we observed earlier. We find that the utility over time is stabilized the most in case of ERR followed by PEG and then IRRs. Among the IRRs, baseline case performs the worst followed by TR-CPI rules and then TR-PPI rules. Note that over the long-run the Taylor rules with exchange rates (TR-CPI-ER and TR-PPI-ER) perform quite similar to the simple Taylor rules (TR-CPI and TR-PPI), though the simple rules have less variation to the welfare. While ERRs are able to stabilize the inflation and nominal exchange rates better as compared to IRRs, the PEG performs the worst in stabilizing the inflation rates (both CPI and PPI ). This is quite intuitive as nominal price variables like the inflation adjusts more when the nominal exchange rates are fixed.
Despite the exchange rates being the policy instrument with ERR (column 6), we do not see high standard deviation of nominal exchange rates. This is in contrast to the baseline case where the policy instrument that is, interest rates show high volatility in attempt to stabilize the economy. The coefficient of variation of the interest rates for the baseline case is around 90% more than the ERR. We can also see that consumption is much more volatile in the baseline than with ERR and the PEG rule. Both inflation measures (PPI and CPI) are stabilized the best with ERR then any other rule. The variation in CPI and PPI is reduced by upto 28% and 39%, respectively, with ERR as compared to the baseline case. Among the Taylor rules, again the TR-PPI rules performs the best and for consumption stabilization, even better then ERRs. But considering that inflation and the lifetime utility is much more stable with ERRs, it is very important that we study these rules which gives us alternate to using interest rates as a policy instrument. Since we get mixed results for the use of PEG rule over a long horizon it is difficult to conclude whether we are consistent with Cook (Reference Cook2004), where the author argues that the fixed exchange rate regimes offer greater stability than IRRs. Studying the second-moment, we can conclude that ERRs offer a promising alternate to IRRs under the global uncertainty shocks.
4. Conclusion
Current monetary policy framework in most central banks of EMEs follow a flexible inflation-targeting regime with IRR as an instrument. The present literature also support the use of IRRs with floating exchange rate as the welfare dominating monetary policy. This paper attempts to show that this approach of using IRRs with floating exchange rate is not effective in the presence of high global uncertainty. We also find that the standard approach works well in the presence of first-moment shocks. Furthermore, a strong empirical evidence of capital outflow and currency depreciation in the EMEs is found, when economy is hit with a global uncertainty shock. During these uncertain times, the movements of the capital flows and the foreign exchange rates is primarily driven by hedging or flight-to-safety motives rather than fundamentals of the economy. Our analysis shows that monetary policy using IRRs is ineffective in the presence of high global uncertainty for two reasons: firstly, any change in interest rates would be ineffective in stabilizing the exchange rate movement as UIP does not hold and non-zero risk premiums are generated. Secondly, interest rates face strong trade-offs between inflation and output stabilization. To study alternate monetary policy rules, we build a model with Epstein–Zin preferences to quantitatively fit the stylized facts from the data. We analyze the effects of an uncertainty shock in a SOE NK-DSGE framework with an emphasis on exploring alternate monetary policy instrument. The SOE is calibrated to a prototypical EME.
It is observed that a monetary policy using an exchange rate as an instrument to stabilize price and output in an economy, under flexible inflation-targeting regime, reduces the welfare losses up to 350%. The long-run simulations from the model also show that the ERRs reduce the variability of nominal and real variables in an economy significantly, as compared to the baseline case. To be specific, the second-order moments from the model show that the variability of consumption, CPI, and nominal interest rate is reduced by 69%, 28% and 47%, respectively, when ERRs are followed instead of the baseline Taylor rule. One way of implementing an ERR is using a managed float regime of a basket, band, and crawl (BBC), as followed by Singapore. BBC regime allows for a dynamic band for exchange rate to float where slope, width, and mean of the band are policy parameters. During uncertain times anchoring market beliefs to an optimistic future is a key to prevent capital outflows from EMEs especially the portfolio investment flows. If the policymakers at a central bank can effectively communicate to the market about the future expected path of exchange rates during such times, the rapid flight movement of capital for hedging/ safety motive can be prevented from the EMEs. Moreover, there is a substantial evidence in the literature suggesting that EMEs intervene to stabilize foreign exchange rates despite claiming to have a floating exchange rates (Calvo and Reinhart (Reference Calvo and Reinhart2002); Reinhart (Reference Reinhart2000)). These measures are mostly corrective in nature rather then being preventive of sudden capital flows. As Mishkin (Reference Mishkin2004) has emphasized increased transparency of the monetary policy strategy through communication with the public and the markets about the plans, objectives, and decisions of the monetary authorities’ is one of the important elements to have an effective inflation-targeting regime in EMEs. A monetary policy rule like ERR with effective and transparent communication not only stabilizes the domestic economy but can act as a shock absorber to global uncertainty shocks.
While the present paper questions the efficacy of the current monetary policy framework, it limits itself to considering alternate instruments of monetary policy to improve the welfare. Moreover, considering that the instruments available with the central banks are limited, the future research agenda includes looking at the role of macroprudential regulation, within this framework, in stabilizing an EME during periods of high global uncertainty. The model framework of SOE presented here has minimal structure and yet the results are intriguing and insightful. For future research, we believe that adding the following features to the model can make the framework richer:
![]() $(1)$
introducing foreign borrowing by domestic firms as working capital loans, this way external debt in major currencies can be introduced.
$(1)$
introducing foreign borrowing by domestic firms as working capital loans, this way external debt in major currencies can be introduced.
![]() $(2)$
having heterogeneous firms with financial frictions especially in EMEs;
$(2)$
having heterogeneous firms with financial frictions especially in EMEs;
![]() $(3)$
adding a trend inflation rate to a small open economy (EME). This would allow us to analyze the case of a ZLB in the AE leaving the EME unconstrained (i.e., no ZLB).
$(3)$
adding a trend inflation rate to a small open economy (EME). This would allow us to analyze the case of a ZLB in the AE leaving the EME unconstrained (i.e., no ZLB).
Acknowledgements
I thank Susanto Basu, V.V. Chari, Chetan Ghate, Morten O. Ravn, Chetan Subramanian, Martin Uribe, seminar participants at the 7 Delhi Macroeconomics Workshop (Indian Statistical Institute-Delhi Oct. 2018), 14 Annual Conference on Economic Growth and Development (Delhi- Dec. 2018), Conference on Economic Theory and Policy (Ambedkar University, Delhi-Mar 2019), Reserve Bank of India, Mumbai (Aug. 2019), Delhi School of Economics-CDE Seminar (Sep. 2019), IGIDR Mumbai-Seminar (Oct. 2019), IISER-Bhopal- seminar (Nov. 2020), 12 International Research Conference (Central Bank of Sri Lanka) (Nov. 2019); Winter School-DSE, Delhi (November); IMRDC IIM-Bangalore (Dec. 2019); Ashoka University, Sonipat (Sep. 2020) ; anonymous referees for their extremely helpful comments. This paper is part of my Ph.D. thesis submitted at Indian Statistical Institute, Delhi-India.
Competing interests
None.
Supplementary material
To view supplementary material for this article, please visit https://doi.org/10.1017/ S1365100524000178. The replication folder on Mendeley data repository can be found at the following link https://data.mendeley.com/datasets/txmybjt36t/1.
















