Introduction

Powder snow avalanches (PSAs) engulf massive amounts of material from the underlying snow cover by erosion mechanisms that are not fully understood. Despite their diversity, PSAs have recognizable flow features: they are fast, reaching frontal speed ˜60ms^-1, and they develop a tall, low-density powder cloud of considerable volume (Reference Turnbull, McElwaine and AnceyVallet and others, 2004). In the frontal region with length on the order of cloud height, PSA dynamics crucially depend on entrainment from the snow cover and, because oscillations of the air/cloud interface develop slowly from the nose (Reference Carroll, Turnbull and LougeCarroll and others, 2012), to a lesser extent on incorporation of ambient air at the air/cloud interface (Reference AnceyAncey, 2004). Not far behind the front, a layer of light, cold and cohesionless snow is rapidly entrained, creating a turbulent, stratified head (Reference Simpson and BritterSovilla and others, 2006). Fast and localized entrainment of deeper and warmer snow layers may also occur well behind the front, where stratification can become more pronounced.

Although PSAs resemble gravity currents (Reference RankineSimpson and Britter, 1979), their rapid frontal injection of snow produces markedly different head dynamics. Conscious of the role played by such material input, Reference Carroll, Turnbull and LougeCarroll and others (2012) modeled the frontal region as an ‘eruption current’. In that model, the depression created by the material injection induces pore pressure gradients fluidizing the snowpack (Reference d'AlembertLouge and others, 2011), and entrains part of the weakened material into the head from a relatively narrow traveling source. Conscious of the complex dynamics arising far behind the front, Reference Carroll, Louge and TurnbullCarroll and others (in press) focused their model exclusively on the head, which they defined as the region where the pressure gradient along the interface remains negative. For tractability, they also ignored interface air entrainment and regarded head density as homogeneous. The model then predicted that eruption currents begin with an unstable mass balance but rapidly reach a stable acceleration that is crucially affected by the width that topography allows them to adopt.

Surprisingly, gravity current acceleration is insensitive to local slope (Reference Britter and LindenBritter and Linden, 1980; Reference Turnbull and McElwaineTurnbull and McElwaine, 2008). Observations suggest that the frontal speed of PSAs shares the same insensitivity (Reference Simpson and BritterSovilla and others, 2006). Reference Carroll, Louge and TurnbullCarroll and others (in press) attributed this observation to the insignificant role played by deviatoric stresses, which rapid turbulent mixing renders small compared to hydrostatic pressure contributions in the head (Reference d'AlembertLouge and others, 2011). Recognizing this insignificance, Reference d'AlembertLouge and others (2011) exploited the convenient mathematical framework of potential flow theory to derive pressure fields in the head, from which they deduced pore pressure within the snow cover that feeds it, as well as fluidization limits restricting the likelihood that a dense and cohesive snowpack will ignite into a powder cloud. Reference Carroll, Louge and TurnbullCarroll and others (in press) then calculated analytical relations among frontal speed, cloud height, snow scouring depth, mixed-mean density and impact pressure when the cloud head reaches a stable growth rate. Finally, they derived a dynamical equation for the head, predicted the runout distance necessary for its density to reach its stable value and, underlining the role of avalanche width in frontal dynamics, discussed mechanisms for cloud collapse.

Although Reference Carroll, Louge and TurnbullCarroll and others (in press) focused exclusively on frontal dynamics, we outline here a simple model of the tail that exploits their analysis for insight into growth rate of the powder cloud. Doing so, we contrast processes controlling frontal speed with those setting volume growth in the tail. This approach complements the analysis of Reference Turnbull and McElwaineTurnbull and others (2007) who, by modeling a powder cloud as an elliptical body, could not explicitly predict growth rate in the tail. We show that, although a substantial part of volume growth can be attributed to frontal snow injection, late incorporation of air at the interface, or perhaps entrainment of more snow by subsequent avalanches, should add to such growth.

Background

Reference Carroll, Louge and TurnbullCarroll and others (in press) modeled the dynamics of the head of dilute powder snow avalanches as an eruption current sustained by massive frontal blow-out arising as a weakly cohesive snow cover is fluidized by the very pore pressure gradients that the avalanche induces within the snowpack. The part of fluidized material erupting just behind the front acts as a source of denser fluid thrust into a uniform ambient airflow of density at high Reynolds number (Reference d'AlembertLouge and others, 2011). Using potential flow theory inspired by the classical calculation of Reference PrandtlRankine (1864), Reference Carroll, Louge and TurnbullCarroll and others (in press) calculated the pressure gradient along the interface between cloud and ambient air and located the back of the head at an exit plane perpendicular to the slope where this gradient becomes positive (i.e. adverse) at the polar angle θ_f ⋍ 13π/20, beyond which large interface oscillations engulf the tail (Fig. 1). In such an eruption current, Reference d'AlembertLouge and others (2011) calculated that fluidization depth is the inverse power a ₁ of a bulk Richardson number

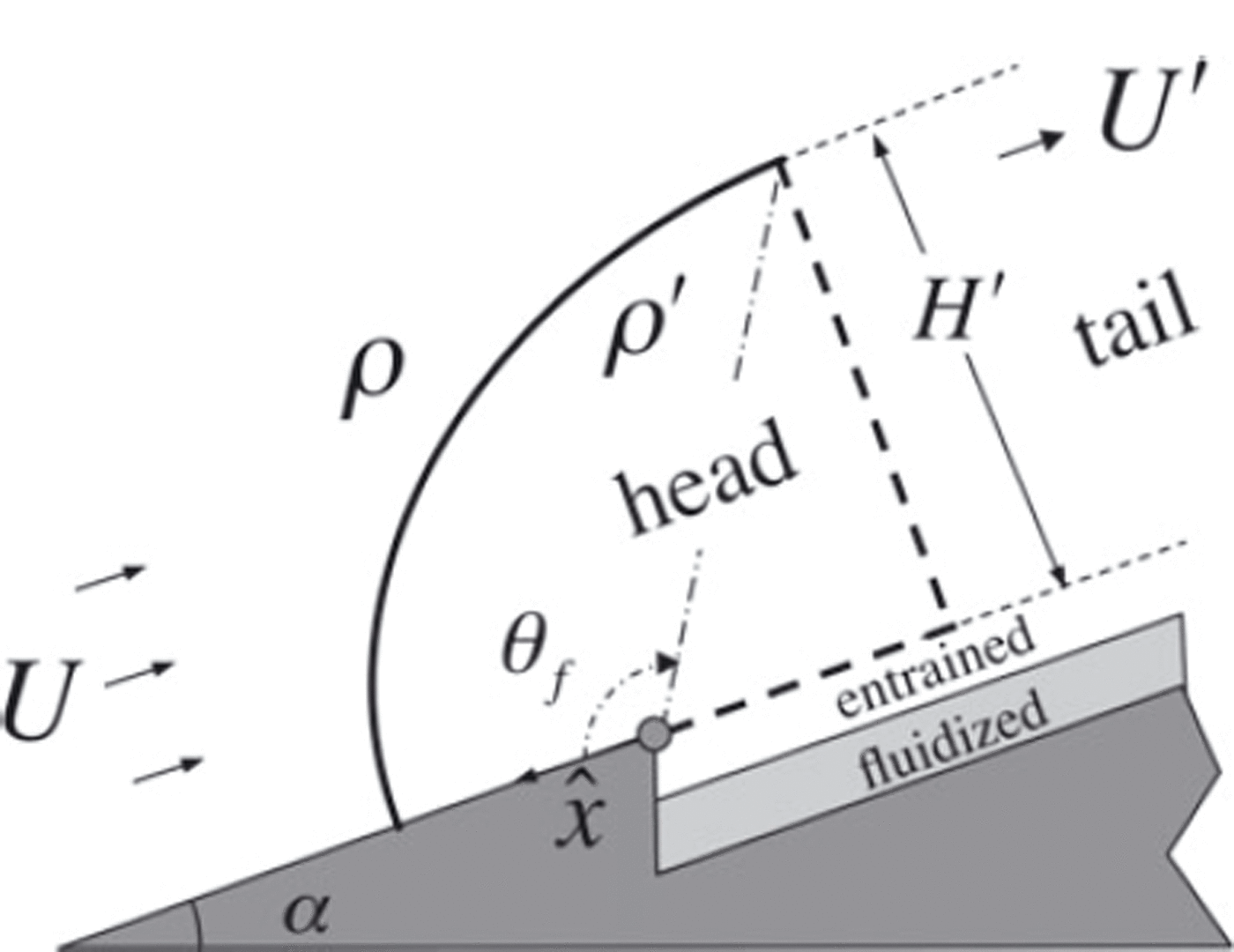
Fig. 1. Model of the avalanche head with origin at the traveling source of entrained snow. The head is delimited by the air/cloud interface (solid curve) and virtual planes (dashed lines).

where p is density, g is gravitational acceleration, H' is head height and U' is the asymptotic tail value. Reference Carroll, Turnbull and LougeCarroll and others (2012) then showed that any mixed-mean suspension density > swells the head and reduces velocities within the cloud from the front speed U to the asymptotic tail value U' = Uδ, where

and ζ=1-p/p'. In this framework, the behavior of an eruption current is determined by two parameters (Ri,ζ).

An advantage of this approach is that the rate of material eruption from the snow cover can be calculated explicitly without resorting to a model of frontal entrainment. Instead, Reference Carroll, Louge and TurnbullCarroll and others (in press) wrote a mass balance involving snow cover and powder cloud relating avalanche height and mixed-mean density. By determining which solution of the mass balance is stable, they found that avalanches achieve steady growth (denoted by the subscript n) when [Ri,ζ] = [Ri _n ,ζ_n ] = [2a ₁ /(1-2a ₁),2a ₁], i.e. at a mixed-mean density p' _n = p'/(1-2a ₁). (In this expression, a ₁ a¹ ⋍ 0.42 is the power exponent relating fluidization depth and bulk Richardson number that Reference d'AlembertLouge and others (2011) had calculated.) At that state, they deduced from a momentum balance on the head that the avalanche front accelerates at a rate

where δ_n = 1-2a ₁, W is cloud head width and x is distance along the avalanche path. As Eqn (3) shows, a spreading cloud (dW/dx>0) weakens acceleration, as extra momentum must be supplied to uptake new material into the head. Because turbulent, dilute, homogeneous powder clouds have negligible deviatoric stresses, they reach a constant effective inclination angle (Reference Carroll, Louge and TurnbullCarroll and others, in press)

thus achieving a dynamics nearly independent of slope, like some gravity currents (Reference Britter and LindenBritter and Linden, 1980; Reference Turnbull and McElwaineTurnbull and McElwaine, 2008). In Eqn (3), the constants a_A ≡ {(1-2a ₁)^-1+[(a_μ/a_V )-(a_M/a_V )]}^-1, a_V ⋍ 3.0, a_M ⋍ 3.3 and a_μ ⋍ πθ_f ²/4 are exact. Reference Carroll, Louge and TurnbullCarroll and others (in press) estimated ϖ ⋍ 0.84 by analogy with the Reference Louge, Carroll and TurnbullPrandtl (1927) resolution of the d'Alembert (1752) paradox for the cylinder in cross-flow.

The main benefit of this analysis is to capture the rate of frontal erosion without invoking fitted parameters or an empirical model of material entrainment. For instance, as soon as the head reaches a stable equilibirum at [Ri _n ,ζ_n ], its dynamics only depends on evolution of frontal width, which is chiefly imposed by local topography. Although this analysis assumed, rather crudely, that the head has uniform density, it captured well the observations of Reference Simpson and BritterSovilla and others (2006) at Vallée de la Sionne, Switzerland.

Volume Growth

We now discuss how frontal dynamics and air entrainment in the tail affect growth of total avalanche volume. Because Reference Carroll, Louge and TurnbullCarroll and others (in press) confine all material eruption to the traveling source, while ignoring sedimentation, interface air entrainment and particle resuspension from the snow cover, they imply that total cloud volume V grows at a rate related to the mass_s input in a unit of time by the source,

If the powder cloud started from rest at (Ri _n ,ζ_n ), reached stable conditions (Ri _n ,ζ_n ) instantly and proceeded with invariant width, integration of Eqns (3–5) would yield

implying a growth rate d ln V/dt = 4/t roughly consistent with observations (Reference Sovilla, Burlando and BarteltTurnbull and McElwaine, 2007).

However, because cloud width W and density p'' appear explicitly in Eqn(5), we must account for variations of these parameters to integrate it. To that end, like Reference Carroll, Louge and TurnbullCarroll and others (in press), we assume that the cloud progressively densifies after reaching Ri = Ri _n instantly. Then, using their eqn (46), we find

We integrate it numerically with two equations governing dynamics and mass conservation that Reference Carroll, Louge and TurnbullCarroll and others (in press) derived (their eqns (52-53)). The result is shown as a dashed line in Figure 2. Clearly, Eqn(5) under-predicts total volume growth.

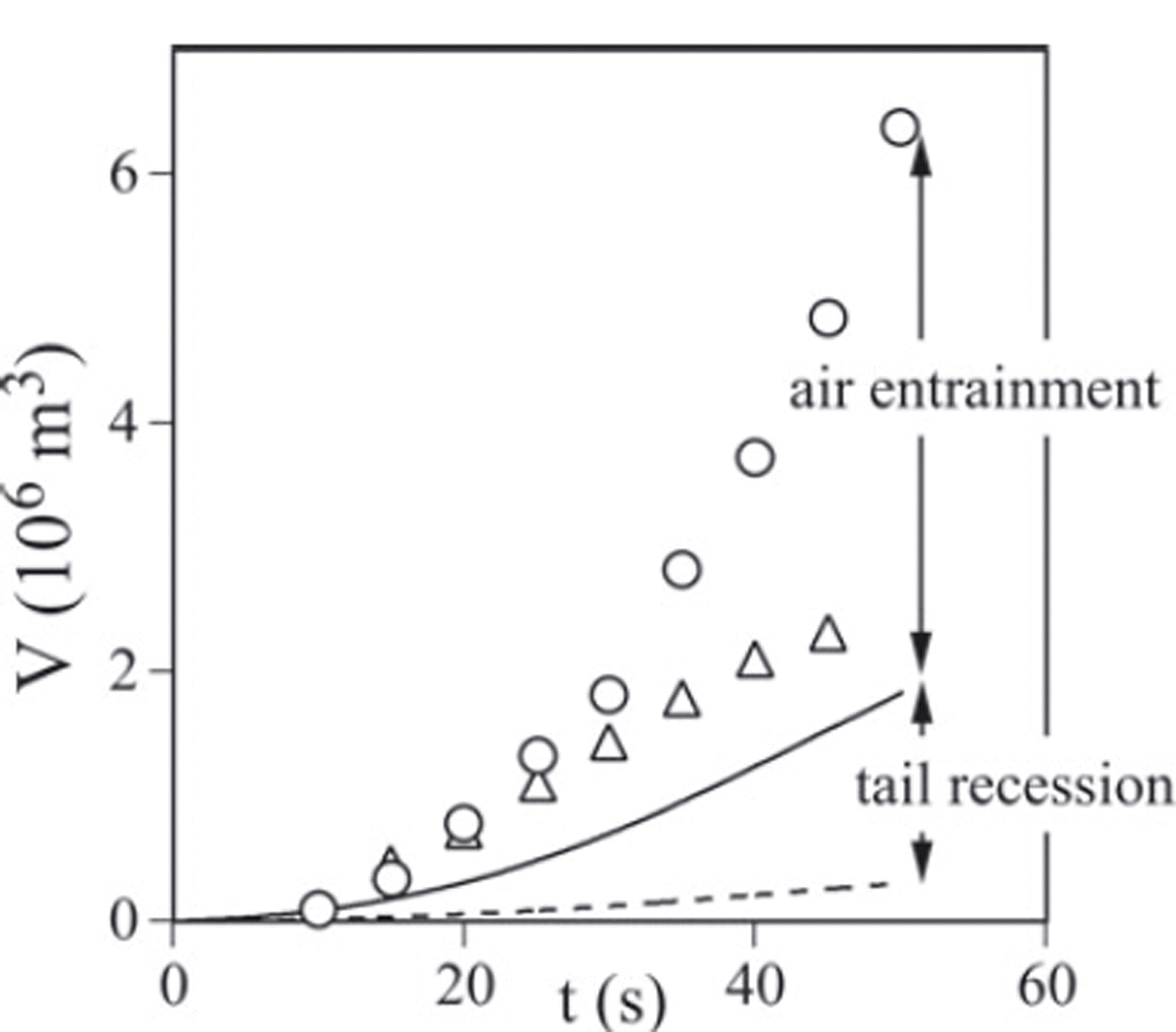
Fig. 2. Time history of total cloud volume V of avalanche 509. Circles are data of Reference Turnbull, McElwaine and AnceyVallet and others (2004) from videogrammetry. Triangles represent trapezoid integration ∫ H'WU dt of width and speed from Reference Simpson and BritterSovilla and others (2006) and height from Reference Turnbull, McElwaine and AnceyVallet and others (2004). The dashed line is the prediction of Eqn (7) coupled to ODEs for mass and momentum balance in the head (Reference Carroll, Louge and TurnbullCarroll and others, in press). The solid line is a prediction of Eqn (8).

The principal reason for this discrepancy is associated with flow in the tail, which the frontal analysis of Reference Carroll, Louge and TurnbullCarroll and others (in press) eschewed entirely. Rather than developing an ab initio model of the tail on par with their approach, we first note that the tail, rather than moving forward in the mountain frame at the velocity that the potential theory framework predicts, is in fact nearly stopped upon incorporation of stagnant air by entrainment at its interface. This apparent tail ‘recession’ is similar to the prompt arrest of a smoke jet spewed upward from the steam engine of a moving locomotive. Blindly adopting the equations governing frontal dynamics implicitly ignores this effect, wrongly implying that the tail moves rapidly forward, thus artificially reducing total volume growth. If instead the tail was completely stopped, then it would move at in the cloud reference frame, rather than This faster recession of the tail away from the source would produce a larger volume growth given, to a good approximation, by dV/dt ⋍ H'WU instead of Eqn (5) or, equivalently,

Predictions of Eqn (8) based on the model of Reference Carroll, Louge and TurnbullCarroll and others (in press) for (H'WU) are shown as a solid line in Figure 2. Although smaller than the same integral (triangles) calculated from the frontal data of Reference Turnbull, McElwaine and AnceyVallet and others (2004) for H', and Reference Simpson and BritterSovilla and others (2006) for U and W, Eqn (8) captures the growth of that integral better, suggesting that the tail is more likely arrested than moving rapidly downslope.

Further inspection of data reveals that other mechanisms conspire to grow cloud volume in the tail beyond prescriptions of Eqn (8), which strictly involves frontal data. While consistent with the total volume that Reference Turnbull, McElwaine and AnceyVallet and others (2004) measured in the first 30s of avalanche 509 (circles), Eqn (8) under-predicts V in the last 20 s. This later discrepancy among data may betray in part how interface air entrainment progressively swells the tail height, as is apparent in most powder clouds. (Sedimentation of snow particles should also play a role on longer timescales.) In this mechanism, the tail swells by considerable entrainment of ambient air, unlike the relatively short head, where fluid exchange across the cloud interface is small (Reference Carroll, Turnbull and LougeCarroll and others, 2012). If this interpretation has merit, predictions of total volume will require accurate models of interface air entrainment in the tail, perhaps by invoking plume theory (Reference Sovilla, Burlando and BarteltTurnbull and McElwaine, 2007). Existing information on entrainment is limited. Interpreting experiments of Reference Beghin, Hopfinger and BritterBeghin and others (1981), Reference AnceyAncey (2004) calculated that the rate of air mass entrained into the entire cloud on a slope α scales as ϕ _vpV^1/2 W ^1/2 U, where ϕ _v is a two-piece function of a bulk Richardson number Ri _A ≡Riδ ²cosα/[2(1-ζ)] with ϕ _v ⋍ 1-0.2Ri² _A for Ri _A<1 and ϕ _v ⋍ 0.2/Ri _A otherwise. Another explanation for the late discrepancy in volume data is that subsequent avalanches, facilitated by weakening of the snow cover by deep frontal fluidization, may have entrained further material into the cloud. Avalanche 509 did include such subsequent slides trailing far behind the front.

Conclusions

We showed that recession of an arrested tail in the mountain reference frame increases the tail’s contribution to total volume growth of a powder cloud. However, such effect is not enough to explain greater cloud swelling late in the avalanche. We suggested that incorporation of ambient air into the tail, or additional entrainment from the snow cover by subsequent slides, might explain additional volume growth far behind the front. Because the model of Reference Carroll, Louge and TurnbullCarroll and others (in press) ignores air entrainment and restricts attention to the head, it is not surprising that its strict application to total volume prediction in Eqn (5) would fail. Nonetheless, repairing the theory by posing that the tail comes to rest produces total volume predictions consistent with early data. Better agreement will require an analysis of air entrainment, sedimentation rate and avalanche dynamics in the tail.