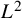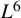1 Introduction
The question of obtaining scattering, global in time solutions for one-dimensional dispersive flows with quadratic/cubic nonlinearities has attracted a lot of attention in recent years, and many global well-posedness results have been proved for a number of models under the assumption that the initial data is both small and localized; without being exhaustive, see, for instance, [Reference Hayashi and Naumkin12, Reference Hayashi and Naumkin13, Reference Lindblad and Soffer21, Reference Kato and Pusateri18, Reference Ifrim and Tataru14]. The nonlinearities in these models are primarily cubic, though the analysis has also been extended via normal form methods to problems which also have nonresonant quadratic interactions; several such examples are [Reference Alazard and Delort1, Reference Ifrim and Tataru15, Reference Delort9, Reference Ifrim and Tataru16, Reference Lindblad, Lührmann and Soffer20]; see also further references therein.
In this article, we consider instead the much more difficult case where the initial data is just small but without any localization assumption. Here, it is natural to restrict the analysis to defocusing problems, as focusing one-dimensional cubic nonlinear Schrödinger (NLS) type problems typically admit small solitons, and thus, generically, the solutions do not scatter at infinity. Then one may formulate the following broad conjecture:
Conjecture. One-dimensional dispersive flows with cubic defocusing nonlinearities, and small initial data have global in time, scattering solutions.
The goal of this article is to prove the first global in time well-posedness result of this type. As part of our results, we also prove that our global solutions are scattering at infinity in a very precise, quantitative way, in the sense that they satisfy both
![]() $L^6$
Strichartz estimates and bilinear
$L^6$
Strichartz estimates and bilinear
![]() $L^2$
bounds. This is despite the fact that the nonlinearity is nonperturbative on large time scales.
$L^2$
bounds. This is despite the fact that the nonlinearity is nonperturbative on large time scales.
1.1 Cubic NLS problems in one space dimension
One of the fundamental one-dimensional dispersive flows in one space dimension is the cubic NLS flow,
Depending on the choice of signs, this comes in a defocusing (+) and a focusing (-) flavor. Both of these equations are important, not only by themselves but also as model problems for more complex one-dimensional dispersive flows, both semilinear and quasilinear.
The above cubic NLS flow is globally well-posed in
![]() $L^2$
both in the focusing and in the defocusing case, though the global behavior differs in the two cases.
$L^2$
both in the focusing and in the defocusing case, though the global behavior differs in the two cases.
Precisely, the focusing problem admits small solitons, so the solutions cannot in general scatter at infinity. If in addition the initial data is localized, then one expects the solution to resolve into a superposition of (finitely many) solitons and a dispersive part; this is called the soliton resolution conjecture and is known to hold in a restrictive setting, via the method of inverse scattering; see, for example, [Reference Borghese, Jenkins and McLaughlin2].
In the defocusing case, the inverse scattering approach also allows one to treat the case of localized data and show that global solutions scatter at infinity; see, for instance, [Reference Deift and Zhou8]. This can also be proved in a more robust way, without using inverse scattering, under the assumption that the initial data is small and localized; see [Reference Ifrim and Tataru14] and references therein. Much less is known in terms of scattering for nonlocalized
![]() $L^2$
data. However, if more regularity is assumed for the data, then we have the following estimate due to Planchon–Vega [Reference Planchon and Vega22]; see also the work of Colliander–Grillakis–Tzirakis [Reference Colliander, Grillakis and Tzirakis3]:
$L^2$
data. However, if more regularity is assumed for the data, then we have the following estimate due to Planchon–Vega [Reference Planchon and Vega22]; see also the work of Colliander–Grillakis–Tzirakis [Reference Colliander, Grillakis and Tzirakis3]:
This allows one to estimate the
![]() $L^6$
Strichartz norm of the solution, that is, to prove some type of scattering or dispersive decay.
$L^6$
Strichartz norm of the solution, that is, to prove some type of scattering or dispersive decay.
Because of the above considerations, our interest in this paper is in defocusing cubic problems. Precisely, we will consider a cubic nonlinear Schrödinger equation (NLS) type model in one space dimension
where u is a complex valued function,
![]() $u:\mathbb {R}\times \mathbb {R}\rightarrow \mathbb {C}$
. Here C is a trilinear translation invariant form, whose symbol
$u:\mathbb {R}\times \mathbb {R}\rightarrow \mathbb {C}$
. Here C is a trilinear translation invariant form, whose symbol
![]() $c(\xi _1,\xi _2,\xi _3)$
can always be assumed to be symmetric in
$c(\xi _1,\xi _2,\xi _3)$
can always be assumed to be symmetric in
![]() $\xi _1,\xi _3$
; see Section 2.3 for an expanded discussion of multilinear forms. The arguments
$\xi _1,\xi _3$
; see Section 2.3 for an expanded discussion of multilinear forms. The arguments
![]() $u,\bar u$
and u of C are chosen so that our equation (1.3) has the phase rotation symmetry,
$u,\bar u$
and u of C are chosen so that our equation (1.3) has the phase rotation symmetry,
![]() $u \to u e^{i\theta }$
, as it is the case in most examples of interest. The symbol
$u \to u e^{i\theta }$
, as it is the case in most examples of interest. The symbol
![]() $c(\xi _1,\xi _2,\xi _3)$
will be required to satisfy a minimal set of assumptions:
$c(\xi _1,\xi _2,\xi _3)$
will be required to satisfy a minimal set of assumptions:
-
(H1) Bounded and regular:
(1.4) $$ \begin{align} |\partial_{\xi}^{\alpha} c(\xi_1,\xi_2,\xi_3)| \leq c_{\alpha}, \qquad \xi_1,\xi_2,\xi_3 \in {\mathbb R},\, \mbox{ for every multi-index } \alpha. \end{align} $$
$$ \begin{align} |\partial_{\xi}^{\alpha} c(\xi_1,\xi_2,\xi_3)| \leq c_{\alpha}, \qquad \xi_1,\xi_2,\xi_3 \in {\mathbb R},\, \mbox{ for every multi-index } \alpha. \end{align} $$
-
(H2) Conservative:
(1.5) $$ \begin{align} \Im c(\xi,\xi,\eta) = 0, \qquad \xi,\eta \in {\mathbb R}, \mbox { where } \Im z=\mbox{imaginary part of } z\in \mathbb{C}. \end{align} $$
$$ \begin{align} \Im c(\xi,\xi,\eta) = 0, \qquad \xi,\eta \in {\mathbb R}, \mbox { where } \Im z=\mbox{imaginary part of } z\in \mathbb{C}. \end{align} $$
-
(H3) Defocusing:
(1.6) $$ \begin{align} c(\xi,\xi,\xi) \geq c> 0, \qquad \xi \in {\mathbb R} \mbox{ and } c \in \mathbb{R^+}. \end{align} $$
$$ \begin{align} c(\xi,\xi,\xi) \geq c> 0, \qquad \xi \in {\mathbb R} \mbox{ and } c \in \mathbb{R^+}. \end{align} $$
In selecting these assumptions, we have tried to strike a balance between the generality of the result on one hand and a streamlined exposition on the other hand.
The simplest example of such a trilinear form C is of course
![]() $C = 1$
, which corresponds to the classical one-dimensional cubic NLS problem. But this problem is of course completely integrable and thus has infinitely many conservation laws. In particular, global well-posedness is straightforward, though our
$C = 1$
, which corresponds to the classical one-dimensional cubic NLS problem. But this problem is of course completely integrable and thus has infinitely many conservation laws. In particular, global well-posedness is straightforward, though our
![]() $L^6$
Strichartz and bilinear
$L^6$
Strichartz and bilinear
![]() $L^2$
bounds are new even for this problem in the
$L^2$
bounds are new even for this problem in the
![]() $L^2$
data setting. By contrast, the assumptions we impose on our model do not guarantee any exact conservation law at the
$L^2$
data setting. By contrast, the assumptions we impose on our model do not guarantee any exact conservation law at the
![]() $L^2$
level or at any other regularity level.
$L^2$
level or at any other regularity level.
At the other end, both our use of the linear Schrödinger operator and the boundedness condition (H1) are nonoptimal, and we hope to relax both of these restrictions in subsequent work. However, using these restrictions brings the major expository advantage that our model has a Galilean invariance, in the sense that a Galilean transformation yields a problem that is in the same class, even though it is not exactly the same. This allows us to provide cleaner, shorter proofs for our results and to keep the focus on the main ideas.
1.2 The main result
Our main result asserts that global well-posedness holds for our problem for small
![]() $L^2$
data. In addition, our solutions not only satisfy uniform
$L^2$
data. In addition, our solutions not only satisfy uniform
![]() $L^2$
but also global space-time
$L^2$
but also global space-time
![]() $L^6$
estimates, as well as bilinear
$L^6$
estimates, as well as bilinear
![]() $L^2$
bounds, as follows:
$L^2$
bounds, as follows:
Theorem 1. Under the above assumptions (H1), (H2) and (H3) on the symbol of the cubic form C, small initial data
yields a unique global solution u for equation (1.3), which satisfies the following bounds:
-
(i) Uniform
 $L^2$
bound: (1.7)
$L^2$
bound: (1.7) $$ \begin{align} \| u \|_{L^{\infty}_t L^2_x} \lesssim \epsilon. \end{align} $$
$$ \begin{align} \| u \|_{L^{\infty}_t L^2_x} \lesssim \epsilon. \end{align} $$
-
(ii) Strichartz bound:
(1.8) $$ \begin{align} \| u \|_{L^6_{t,x}} \lesssim \epsilon^{\frac23}. \end{align} $$
$$ \begin{align} \| u \|_{L^6_{t,x}} \lesssim \epsilon^{\frac23}. \end{align} $$
-
(iii) Bilinear Strichartz bound:
(1.9) $$ \begin{align} \| \partial_x (u \bar u(\cdot+x_0))\|_{L^2_t H_x^{-\frac12}} \lesssim \epsilon^2, \qquad x_0 \in {\mathbb R}. \end{align} $$
$$ \begin{align} \| \partial_x (u \bar u(\cdot+x_0))\|_{L^2_t H_x^{-\frac12}} \lesssim \epsilon^2, \qquad x_0 \in {\mathbb R}. \end{align} $$
Here, we note that in the case
![]() $x_0 = 0$
the last bound gives
$x_0 = 0$
the last bound gives
which is the more classical formulation of the bilinear
![]() $L^2$
bound. However, making this bound uniform with respect to the
$L^2$
bound. However, making this bound uniform with respect to the
![]() $x_0$
translation captures the natural separate translation invariance of this bound and is also quite useful in our proofs.
$x_0$
translation captures the natural separate translation invariance of this bound and is also quite useful in our proofs.
We also remark that all the bounds above are indeed Galilean invariant. As noted earlier, our main equation is not Galilean invariant, but the class of equations we are considering is. The estimates in the theorem do not represent the full strength of what we actually prove but are merely a simple but relevant sample. Our actual proof yields stronger frequency envelope bounds associated to a decomposition of the solution u on a unit frequency scale (rather than the more traditional dyadic decomposition); see Theorem 5 in Section 6.
Applied to the model cubic NLS problem (1.1), by scaling we have the following result which applies to the large data problem:
Theorem 2. Consider the defocusing 1-d cubic NLS problem (1.1)(+) with
![]() $L^2$
initial data
$L^2$
initial data
![]() $\mathfrak {u}_0$
. Then the global solution u satisfies the following bounds:
$\mathfrak {u}_0$
. Then the global solution u satisfies the following bounds:
-
(i) Uniform
 $L^2$
bound: (1.11)
$L^2$
bound: (1.11) $$ \begin{align} \| u \|_{L^{\infty}_t L^2_x} \lesssim \|\mathfrak{u}_0\|_{L^2_x}. \end{align} $$
$$ \begin{align} \| u \|_{L^{\infty}_t L^2_x} \lesssim \|\mathfrak{u}_0\|_{L^2_x}. \end{align} $$
-
(ii) Strichartz bound:
(1.12) $$ \begin{align} \| u \|_{L^6_{t,x}} \lesssim \|\mathfrak{u}_0\|_{L^2_x}. \end{align} $$
$$ \begin{align} \| u \|_{L^6_{t,x}} \lesssim \|\mathfrak{u}_0\|_{L^2_x}. \end{align} $$
-
(iii) Bilinear Strichartz bound:
(1.13) $$ \begin{align} \| \partial_x |u|^2\|_{L^2_t (\dot H_x ^{-\frac12} + c L^2_x) } \lesssim \|\mathfrak{u}_0\|_{L^2}^2, \qquad c = \| \mathfrak{u}_0\|_{L^2}. \end{align} $$
$$ \begin{align} \| \partial_x |u|^2\|_{L^2_t (\dot H_x ^{-\frac12} + c L^2_x) } \lesssim \|\mathfrak{u}_0\|_{L^2}^2, \qquad c = \| \mathfrak{u}_0\|_{L^2}. \end{align} $$
One may compare the above
![]() $L^6$
bound with the Planchon–Vega estimate (1.2), see [Reference Planchon and Vega22], which applies only to
$L^6$
bound with the Planchon–Vega estimate (1.2), see [Reference Planchon and Vega22], which applies only to
![]() $H^1$
solutions.
$H^1$
solutions.
There are several ideas which play key roles in our analysis, all of which are used in a nonstandard fashion in the present work:
1. Energy estimates via density-flux identities. This is a classical idea in partial differential equations (PDEs), and particularly in the study of conservation laws, namely that the density-flux identities play a more fundamental role than just energy identities. The new twist in our context is that this analysis is carried out in a nonlocal setting, where both the densities and the fluxes involve translation invariant multilinear forms.
2. The use of energy corrections. This is an idea originally developed in the context of the so-called I-method [Reference Colliander, Keel, Staffilani, Takaoka and Tao4] or more precisely the second generation I-method [Reference Colliander, Keel, Staffilani, Takaoka and Tao7], whose aim was to construct more accurate almost conserved quantities. Here, we implement this idea at the level of density-flux identities, in a form closer to [Reference Koch and Tataru19].
3. Interaction Morawetz bounds. These were originally developed in the context of the three-dimensional NLS problems by Colliander–Keel–Stafillani–Takaoka-Tao in [Reference Colliander, Keel, Staffilani, Takaoka and Tao5] and have played a fundamental role in the study of many nonlinear Schrödinger flows (see, for example, [Reference Colliander, Keel, Staffilani, Takaoka and Tao6, Reference Ryckman and Visan23]) and also for one-dimensional quintic flows in the work of Dodson [Reference Dodson10, Reference Dodson11]. Our take on this is somewhat closer to the one-dimensional approach of Planchon–Vega [Reference Planchon and Vega22], though recast in the setting and language of nonlocal multilinear forms.
4. Tao’s frequency envelope method. This is used as a way to accurately track the evolution of the energy distribution across frequencies. Unlike the classical implementation relative to dyadic Littlewood–Paley decompositions, here we adapt and refine this notion for lattice decompositions instead. This is also very convenient as a bootstrap tool (see, e.g., Tao [Reference Tao24], [Reference Tao25]) but with the added twist of also bootstrapping bilinear Strichartz bounds, as in the authors’ paper [Reference Ifrim and Tataru17].
1.3 An outline of the paper
In the next section, we begin by setting up the notations for function spaces and multilinear forms. More importantly, we also introduce our class of admissible frequency envelopes associated to lattice decompositions; this is based on the maximal function.
In Section 3, we carry our a preliminary step in the proof of our main result, namely we prove the small data local well-posedness result. This is independent of the global result and uses a contraction argument in a well-chosen function space defined via a wave packet type decomposition.
The goal of Section 4 is to recast energy identities for the mass and the momentum in density-flux form. We supplement this with two additional steps, where we first consider frequency localized mass and momentum densities, and then we improve their accuracy by adding a well chosen quartic correction.
In Section 5, we begin with the classical idea of Interaction Morawetz identities for the linear Schrödinger flow, and then we use our density-flux identities for the sharp frequency localized mass and momentum in order to obtain a set of refined Interaction Morawetz identities for our problem. For clarity of exposition, we consider separately the diagonal case, where the Interaction of equal frequency components is considered and the transversal case, which corresponds to separated frequency ranges.
The proof of our global result uses a complex bootstrap argument, involving both energy, Strichartz and bilinear
![]() $L^2$
bounds in a frequency localized setting and based on frequency envelopes. The bootstrap set-up is laid out in Section 6, which also contains a sharper, frequency envelope version of our result in Theorem 5. Our main estimates closing the bootstrap argument are carried out in Section 7, using the density-flux and Interaction Morawetz identities previously obtained.
$L^2$
bounds in a frequency localized setting and based on frequency envelopes. The bootstrap set-up is laid out in Section 6, which also contains a sharper, frequency envelope version of our result in Theorem 5. Our main estimates closing the bootstrap argument are carried out in Section 7, using the density-flux and Interaction Morawetz identities previously obtained.
Finally, in the last section of the paper we return from frequency localized bounds to global bounds in order to complete the proof of our main global result.
2 Notations and preliminaries
2.1 Lattice frequency decompositions
For our analysis, it will be convenient to localize functions in (spatial) frequency on the unit scale. For this, we consider a partition of unity
where
![]() $p_k$
are smooth bump functions localized in
$p_k$
are smooth bump functions localized in
![]() $[k-1,k+1]$
. Correspondingly, our solution u will be decomposed as
$[k-1,k+1]$
. Correspondingly, our solution u will be decomposed as
The main estimates we will establish for our solution u will be linear and bilinear estimates for the functions
![]() $u_k$
.
$u_k$
.
For a larger interval
![]() $A \subset {\mathbb Z}$
, we denote
$A \subset {\mathbb Z}$
, we denote
2.2 Frequency envelopes
This is a tool which allows us to more accurately track the distribution of energy at various frequencies for the solutions to nonlinear evolution equations. In the present paper, they play a key bookkeeping role in the proof of the linear and bilinear bounds for our solutions in the context of a complex bootstrap argument. In brief, given some standard decomposition of, say, an
![]() $L^2$
function
$L^2$
function
a frequency envelope for u is a sequence
![]() $\{c_k\}$
with the property that
$\{c_k\}$
with the property that
In addition, one also limits how rapidly the sequence
![]() $\{c_k\}$
is allowed to vary. As originally introduced in work of Tao (see, e.g., [Reference Tao24]), in the context of dyadic Littlewood–Paley decompositions, one assumes that the sequence
$\{c_k\}$
is allowed to vary. As originally introduced in work of Tao (see, e.g., [Reference Tao24]), in the context of dyadic Littlewood–Paley decompositions, one assumes that the sequence
![]() $\{c_k\}$
is slowly varying, in the sense that
$\{c_k\}$
is slowly varying, in the sense that
Here, we will instead work with a uniform lattice decomposition on the unit frequency scale. This requires a major revision of the above notion of ‘slowly varying’, which turns out to be far too weak for our purposes.
Instead, we want to strengthen this property in order to say that
![]() $c \approx Mc$
(the maximal function):
$c \approx Mc$
(the maximal function):
Definition 2.1. A lattice frequency envelope
![]() $\{c_k\}$
is said to have the maximal property if
$\{c_k\}$
is said to have the maximal property if
where
![]() $Mc$
represents the maximal function of c,
$Mc$
represents the maximal function of c,
 $$\begin{align*}(Mc)_k = \sup_{j \geq 0} \frac{1}{2j+1} \sum_{l=k-j}^{k+j} c_l. \end{align*}$$
$$\begin{align*}(Mc)_k = \sup_{j \geq 0} \frac{1}{2j+1} \sum_{l=k-j}^{k+j} c_l. \end{align*}$$
Here, C is a universal constant.
Frequency envelopes that have this property will be called admissible. An important observation is that admissible envelopes can always be found:
Lemma 2.2. Any
![]() $\ell ^2$
frequency envelope
$\ell ^2$
frequency envelope
![]() $c^0$
can be placed under a comparable maximal frequency envelope c, that is,
$c^0$
can be placed under a comparable maximal frequency envelope c, that is,
Proof. We will use two properties of the maximal function:
(i)
![]() $\|Mf\|_{L^2} \leq C \|f\|_{L^2}$
.
$\|Mf\|_{L^2} \leq C \|f\|_{L^2}$
.
(ii)
![]() $M(f+g) \leq Mf + Mg$
.
$M(f+g) \leq Mf + Mg$
.
Given
![]() $c^0$
, we define c as
$c^0$
, we define c as
 $$\begin{align*}c = \sum_{k=0}^{\infty} (2C)^{-k} M^k c^0. \end{align*}$$
$$\begin{align*}c = \sum_{k=0}^{\infty} (2C)^{-k} M^k c^0. \end{align*}$$
By property (i), this series converges in
![]() $\ell ^2$
, with
$\ell ^2$
, with
Then by property (ii), we have
The proof is concluded.
For an interval
![]() $A \subset {\mathbb Z}$
, we denote
$A \subset {\mathbb Z}$
, we denote
Also for a dyadic integer n, we set
Also given a translation invariant function space X, we denote by
![]() $X_c$
the associated frequency envelope controlled norm
$X_c$
the associated frequency envelope controlled norm
2.3 Multilinear forms and symbols
A key notion which is used throughout the paper is that of multilinear form. All our multilinear forms are invariant with respect to translations and have as arguments either complex valued functions or their complex conjugates.
For an integer
![]() $k \geq 2$
, we will use translation invariant k-linear forms
$k \geq 2$
, we will use translation invariant k-linear forms
where the nonconjugated and conjugated entries are alternating.
Such a form is uniquely described by its symbol
![]() $\ell (\xi _1,\xi _2, \cdots ,\xi _{k})$
via
$\ell (\xi _1,\xi _2, \cdots ,\xi _{k})$
via
 $$\begin{align*}\begin{aligned} L(u_1,{\bar u}_2,\cdots)(x) = (2\pi)^{-k} & \int e^{i(x-x_1)\xi_1} e^{-i(x-x_2)\xi_2} \cdots \ell(\xi_1,\cdots,\xi_{k}) \\ & \qquad u_1(x_1) {\bar u}_2(x_2) \cdots dx_1 \cdots dx_{k} d\xi_1\cdots d\xi_k \end{aligned} \end{align*}$$
$$\begin{align*}\begin{aligned} L(u_1,{\bar u}_2,\cdots)(x) = (2\pi)^{-k} & \int e^{i(x-x_1)\xi_1} e^{-i(x-x_2)\xi_2} \cdots \ell(\xi_1,\cdots,\xi_{k}) \\ & \qquad u_1(x_1) {\bar u}_2(x_2) \cdots dx_1 \cdots dx_{k} d\xi_1\cdots d\xi_k \end{aligned} \end{align*}$$
or equivalently on the Fourier side
where, with alternating signs,
They can also be described via their kernel
where K is defined in terms of the Fourier transform of
![]() $\ell $
$\ell $
All the symbols in this article will be assumed to be smooth, bounded and with bounded derivatives.
We remark that our notation is slightly nonstandard because of the alternation of complex conjugates, which is consistent with the setup of this paper. Another important remark is that, for k-linear forms, the cases of odd k, respectively, even k play different roles here, as follows:
i) The
![]() $2k+1$
multilinear forms will be thought of as functions, for example, those which appear in some of our evolution equations.
$2k+1$
multilinear forms will be thought of as functions, for example, those which appear in some of our evolution equations.
ii) The
![]() $2k$
multilinear forms will be thought of as densities, for example, which appear in some of our density-flux pairs.
$2k$
multilinear forms will be thought of as densities, for example, which appear in some of our density-flux pairs.
Correspondingly, to each
![]() $2k$
-linear form L we will associate a
$2k$
-linear form L we will associate a
![]() $2k$
-linear functional
$2k$
-linear functional
![]() $\mathbf {L}$
defined by
$\mathbf {L}$
defined by
which takes real or complex values. This may be alternatively expressed on the Fourier side as
where, with alternating signs, the diagonal
![]() $D_0$
is given by
$D_0$
is given by
Note that in order to define the multilinear functional
![]() $\mathbf {L}$
we only need to know the symbol
$\mathbf {L}$
we only need to know the symbol
![]() $\ell $
on
$\ell $
on
![]() $D_0$
. There will be, however, more than one possible smooth extension of
$D_0$
. There will be, however, more than one possible smooth extension of
![]() $\ell $
outside
$\ell $
outside
![]() $D_0$
. This will play a role in our story later on.
$D_0$
. This will play a role in our story later on.
2.4 Cubic Interactions in Schrödinger flows
Given three input frequencies
![]() $\xi _1, \xi _2,\xi _3$
for our cubic nonlinearity, the output will be at frequency
$\xi _1, \xi _2,\xi _3$
for our cubic nonlinearity, the output will be at frequency
This relation can be described in a more symmetric fashion as
This is a resonant Interaction if and only if we have a similar relation for the associated time frequencies, namely
Hence, we define the resonant set in a symmetric fashion as
It is easily seen that this set may be characterized as
2.5 The Galilean symmetry
Here, we investigate how the equation (1.3) changes if we apply a Galilean transformation. In particular, we will justify our claim in the introduction that the transformed equation is of the same type.
We first recall the linear case. Suppose u solves the linear Schrödinger equation
Given a frequency k, its Galilean transform v is defined by
and solves the linear Schrödinger equation
where
Now, suppose that u solves equation(1.3). Then the above computation shows that v will solve a similar equation,
where
This allows us to compute the symbol of
![]() $\tilde C$
as
$\tilde C$
as
This translated symbol is easily seen to have exactly the same properties as c.
3 Local well-posedness
Before approaching the global problem, an initial step is to establish local in time well-posedness. Since we only assume boundedness and smoothness on the symbol C, this is not an entirely straightforward matter. Our main result can be summarily stated as follows:
Theorem 3. The evolution (1.3) is locally well-posed for small data in
![]() $L^2$
.
$L^2$
.
Here, we need to clarify the meaning of well-posedness. For this problem, we will establish a semilinear type of well-posedness result. Precisely, for each initial data
![]() $\mathfrak {u}_0$
which is small in
$\mathfrak {u}_0$
which is small in
![]() $L^2$
a unique solution exists in
$L^2$
a unique solution exists in
![]() $C([0,1];L^2)$
, with Lipschitz dependence on the initial data.
$C([0,1];L^2)$
, with Lipschitz dependence on the initial data.
However, as it is often the case in the dispersive realm, we will not try to prove unconditional uniqueness and contend ourselves with having both existence and uniqueness of solutions in a ball in a restricted space
![]() $X \subset C([0,1];L^2)$
.
$X \subset C([0,1];L^2)$
.
A natural follow-up question here would be whether the same result holds for large data in our context. The answer is indeed affirmative; however, in this article we have chosen to only consider small data because this is all we need on one hand, and a large data result would require a more complex choice of the space X mentioned above, as well as a correspondingly more complex proof, on the other hand.
Another related question is whether a standard scaling argument could be used here. The scaling transformation would be the standard one for the cubic NLS problem,
For the initial data, this corresponds to
It is then easy to see that
![]() $u_{\lambda }$
solves an equation of the same type as equation (1.3) but with the rescaled symbol
$u_{\lambda }$
solves an equation of the same type as equation (1.3) but with the rescaled symbol
This satisfies the bound (1.4) uniformly only for
![]() $\lambda \geq 1$
, so it cannot be used to reduce the large data problem to the small data problem. However, it can be used to obtain better life-span bounds for small data:
$\lambda \geq 1$
, so it cannot be used to reduce the large data problem to the small data problem. However, it can be used to obtain better life-span bounds for small data:
Corollary 3.1. Assume that the initial data
![]() $\mathfrak {u}_0$
for equation (1.3) satisfies
$\mathfrak {u}_0$
for equation (1.3) satisfies
![]() $\|\mathfrak {u}_0\|_{L^2} \leq \epsilon $
. Then the solution u exists on
$\|\mathfrak {u}_0\|_{L^2} \leq \epsilon $
. Then the solution u exists on
![]() $[0, T_{\epsilon }]$
with
$[0, T_{\epsilon }]$
with
![]() $T_{\epsilon } :=c \epsilon ^{-2}$
, with similar bounds.
$T_{\epsilon } :=c \epsilon ^{-2}$
, with similar bounds.
The rest of this section is devoted to the proof of Theorem 3. The first step in our proof is to construct a suitable function space X where we seek the solutions.
Given a function u in
![]() $[0,1] \times {\mathbb R}$
, we start with a decomposition
$[0,1] \times {\mathbb R}$
, we start with a decomposition
![]() $u = \sum _{k \in {\mathbb Z}} u_k$
on the unit frequency scale and then a partition of unity in the physical space, also on the unit scale,
$u = \sum _{k \in {\mathbb Z}} u_k$
on the unit frequency scale and then a partition of unity in the physical space, also on the unit scale,
 $$\begin{align*}1 = \sum_{j \in {\mathbb Z}} \chi_j(x). \end{align*}$$
$$\begin{align*}1 = \sum_{j \in {\mathbb Z}} \chi_j(x). \end{align*}$$
Finally, we define the norm of the space X for solutions
 $$ \begin{align} \| u \|_{X}^2 = \sum_{k \in {\mathbb Z}} \| u_k\|_{X_k}^2, \qquad \|u_k\|_{X_k}^2= \sum_{j \in {\mathbb Z}} \| \chi_j (t, x-2t k) u_k \|_{L^{\infty}_t L^2_x}^2. \end{align} $$
$$ \begin{align} \| u \|_{X}^2 = \sum_{k \in {\mathbb Z}} \| u_k\|_{X_k}^2, \qquad \|u_k\|_{X_k}^2= \sum_{j \in {\mathbb Z}} \| \chi_j (t, x-2t k) u_k \|_{L^{\infty}_t L^2_x}^2. \end{align} $$
Here, the second argument of
![]() $\chi _j$
is consistent with the group velocity of frequency k waves. Indeed, if u were an
$\chi _j$
is consistent with the group velocity of frequency k waves. Indeed, if u were an
![]() $L^2$
solution to the homogeneous Schrödinger equation, then this would be nothing but a wave packet decomposition of u on the unit time scale. It is easily seen that we have the embedding
$L^2$
solution to the homogeneous Schrödinger equation, then this would be nothing but a wave packet decomposition of u on the unit time scale. It is easily seen that we have the embedding
Remark 3.2. Due to the unit frequency localization of
![]() $u_k$
and Bernstein’s inequality, we may freely replace the
$u_k$
and Bernstein’s inequality, we may freely replace the
![]() $L^{\infty }_t L^2_x$
norm in equation (3.1) by
$L^{\infty }_t L^2_x$
norm in equation (3.1) by
![]() $L^{\infty }_{t,x}$
.
$L^{\infty }_{t,x}$
.
Correspondingly, we define a similar space Y for the source term in a linear Schrödinger equation, namely
 $$ \begin{align} \| f \|_{Y}^2 = \sum_{k \in {\mathbb Z}} \| f_k\|_{Y_k}^2, \qquad \| f_k\|_{Y_k}^2 = \sum_{j\in Z} \| \chi_j (t, x-2t k) f_k \|_{L^1_t L^2_x}^2 \end{align} $$
$$ \begin{align} \| f \|_{Y}^2 = \sum_{k \in {\mathbb Z}} \| f_k\|_{Y_k}^2, \qquad \| f_k\|_{Y_k}^2 = \sum_{j\in Z} \| \chi_j (t, x-2t k) f_k \|_{L^1_t L^2_x}^2 \end{align} $$
so that we have the duality relation
with equivalent norms.
Then for the small data local well-posedness result in X it suffices to establish the following two properties. The first is a linear mapping property:
Lemma 3.3. The solution to the linear Schrödinger equation
in the time interval
![]() $[0,1]$
satisfies
$[0,1]$
satisfies
The second is an estimate for the nonlinearity:
Lemma 3.4. For the cubic nonlinearity C, we have the bound
Once we have these two lemmas, the proof of the local well-posedness result follows in a standard manner using the contraction principle in a small ball in X. However, for later use we also need to have a more precise, frequency envelope version of Theorem 3. This is as follows:
Theorem 4. For each small initial data
there exists a unique solution u to equation (1.3) which is small in X. In addition, suppose
![]() $c_k$
is an
$c_k$
is an
![]() $\ell ^2$
normalized admissible frequency envelope so that
$\ell ^2$
normalized admissible frequency envelope so that
Then the solution u satisfies
This requires stronger, frequency envelope versions of Lemmas 3.3, 3.4:
Lemma 3.5. The solution to the linear Schrödinger equation
in the time interval
![]() $[0,1]$
satisfies
$[0,1]$
satisfies
The second is an estimate for the nonlinearity:
Lemma 3.6. Let
![]() $c_k$
be an
$c_k$
be an
![]() $\ell ^2$
normalized admissible frequency envelope. Then for the cubic nonlinearity C we have the bound
$\ell ^2$
normalized admissible frequency envelope. Then for the cubic nonlinearity C we have the bound
Proof of Lemmas 3.3, 3.5
We can freely localize on the unit scale in frequency and reduce the problem to the frequency localized estimate
We can further reduce the problem by applying a Galilean transformation by setting
Here, the functions
![]() $v,\mathfrak {v}_0,g$
are now localized at frequency
$v,\mathfrak {v}_0,g$
are now localized at frequency
![]() $0$
and solve
$0$
and solve
whereas the bound (3.10) reduces to
Inserting a harmless frequency localization
![]() $P_0$
, we represent v as
$P_0$
, we represent v as
 $$\begin{align*}v(t) = e^{it \partial_x^2} P_0 \mathfrak{v}_0 -i \int_0^t e^{i(t-s) \partial_x^2} P_0 g\, ds. \end{align*}$$
$$\begin{align*}v(t) = e^{it \partial_x^2} P_0 \mathfrak{v}_0 -i \int_0^t e^{i(t-s) \partial_x^2} P_0 g\, ds. \end{align*}$$
Here, by a slight abuse a notation, we allow
![]() $P_0$
to have slightly larger support. Finally, we localize spatially at both ends,
$P_0$
to have slightly larger support. Finally, we localize spatially at both ends,
 $$\begin{align*}\chi_j v(t) = \sum_{l \in {\mathbb Z}} \left( \chi_j e^{it \partial_x^2} P_0 \chi_l \mathfrak{v}_0 + \int_0^t \chi_j e^{i(t-s) \partial_x^2} P_0 \chi_l g \, ds\right). \end{align*}$$
$$\begin{align*}\chi_j v(t) = \sum_{l \in {\mathbb Z}} \left( \chi_j e^{it \partial_x^2} P_0 \chi_l \mathfrak{v}_0 + \int_0^t \chi_j e^{i(t-s) \partial_x^2} P_0 \chi_l g \, ds\right). \end{align*}$$
Here, the kernels for
![]() $e^{it \partial _x^2} P_0$
are uniformly Schwartz for
$e^{it \partial _x^2} P_0$
are uniformly Schwartz for
![]() $t \in [0,1]$
, so we get an
$t \in [0,1]$
, so we get an
![]() $L^2$
bound with off-diagonal decay,
$L^2$
bound with off-diagonal decay,
This implies that
which in view of the off-diagonal decay implies the bound (3.11).
Proof of Lemmas 3.4, 3.6
Here, the second lemma implies the first. We need to prove the estimate
By duality, this reduces to the integral bound
Without any restriction in generality, we may assume that
We use the unit scale frequency decomposition to separate the above integral as
 $$\begin{align*}I = \sum_{k_1-k_2+k_3=k} \int C_{k_1k_2k_3}(u_{k_1},{\bar u}_{k_2},u_{k_3}) {\bar v}_{k} \, dx dt, \end{align*}$$
$$\begin{align*}I = \sum_{k_1-k_2+k_3=k} \int C_{k_1k_2k_3}(u_{k_1},{\bar u}_{k_2},u_{k_3}) {\bar v}_{k} \, dx dt, \end{align*}$$
where we have also localized the kernel of C near frequencies
![]() $k_1$
,
$k_1$
,
![]() $k_2$
,
$k_2$
,
![]() $k_3$
on the unit scale. The symbol of
$k_3$
on the unit scale. The symbol of
![]() $C_{k_1k_2k_3}$
is smooth and bounded on the unit scale, so the above summands are essentially like products and may be indeed thought of as products via separation of variables. For bilinear products, we have the estimate
$C_{k_1k_2k_3}$
is smooth and bounded on the unit scale, so the above summands are essentially like products and may be indeed thought of as products via separation of variables. For bilinear products, we have the estimate
 $$ \begin{align} \| u_{k_1} v_{k_2}\|_{L^2_{x,t}} \lesssim \frac{1}{\langle k_1-k_2\rangle^{\frac12}} \| u_{k_1}\|_{X_{k_1}} \|v_{k_2}\|_{X_{k_2}}. \end{align} $$
$$ \begin{align} \| u_{k_1} v_{k_2}\|_{L^2_{x,t}} \lesssim \frac{1}{\langle k_1-k_2\rangle^{\frac12}} \| u_{k_1}\|_{X_{k_1}} \|v_{k_2}\|_{X_{k_2}}. \end{align} $$
This is obtained simply by examining the intersection of the supports of the bump functions traveling with speeds
![]() $2k_1$
, respectively
$2k_1$
, respectively
![]() $2k_2$
.
$2k_2$
.
Denoting
![]() $\delta k^{hi} = \max |k_i - k_j|$
, the relation
$\delta k^{hi} = \max |k_i - k_j|$
, the relation
![]() $k_1+k_3 = k_2+k$
insures that we can group the four frequencies into two pairs at distance
$k_1+k_3 = k_2+k$
insures that we can group the four frequencies into two pairs at distance
![]() $\delta k^{hi}$
. Then, using twice the above bilinear estimate, we have
$\delta k^{hi}$
. Then, using twice the above bilinear estimate, we have
 $$\begin{align*}|I| \lesssim \sum_{k_1-k_2+k_3-k= 0} \frac{1}{\langle \delta k^{hi}\rangle} c_{k_1} c_{k_2} c_{k_3}. \end{align*}$$
$$\begin{align*}|I| \lesssim \sum_{k_1-k_2+k_3-k= 0} \frac{1}{\langle \delta k^{hi}\rangle} c_{k_1} c_{k_2} c_{k_3}. \end{align*}$$
Let n represent the dyadic size of
![]() $\delta k^{hi}$
. Without loss of generality, by relabeling, suppose that
$\delta k^{hi}$
. Without loss of generality, by relabeling, suppose that
Then using the Cauchy–Schwartz inequality for the pair
![]() $(k_2,k_3)$
for fixed
$(k_2,k_3)$
for fixed
![]() $k_1$
we estimate
$k_1$
we estimate
 $$\begin{align*}|I| \lesssim \sum_{n} \frac{1}{n}\sum_{|k_1-k| \lesssim n} c_{k_1} c_{n}^2, \qquad c_n^2:= \sum_{|j-k|\approx n} c_j^2. \end{align*}$$
$$\begin{align*}|I| \lesssim \sum_{n} \frac{1}{n}\sum_{|k_1-k| \lesssim n} c_{k_1} c_{n}^2, \qquad c_n^2:= \sum_{|j-k|\approx n} c_j^2. \end{align*}$$
Now, we use the maximal function inequality for c, which gives
 $$\begin{align*}\frac{1}{n} \sum_{|k_1-k| \lesssim n} c_{k_1} \lesssim c_{k}. \end{align*}$$
$$\begin{align*}\frac{1}{n} \sum_{|k_1-k| \lesssim n} c_{k_1} \lesssim c_{k}. \end{align*}$$
We obtain
Thus, equation (3.12) is proved.
For later use, we note that the frequency envelope bounds for u together with the bilinear
![]() $L^2$
bound (3.13) imply the following.
$L^2$
bound (3.13) imply the following.
Corollary 3.7. Let u be a solution for equation (1.3) in
![]() $[0,1]$
as in Theorem 4. Then the following bounds hold:
$[0,1]$
as in Theorem 4. Then the following bounds hold:
4 Energy estimates and conservation laws
4.1 Conservation laws for the linear problem
We begin our discussion with the linear Schrödinger equation
For this, we consider the following three conserved quantities, the mass
the momentum
as well as the energy
To these quantities, we associate corresponding densities
The choice of densities here is not entirely straightforward. Symmetry is clearly a criterion, but further motivation is provided by the conservation law computation,
The symbols of these densities viewed as bilinear forms are
More generally, we can start start with a symbol
![]() $a(\xi ,\eta )$
which is symmetric, in the sense that
$a(\xi ,\eta )$
which is symmetric, in the sense that
and then define an associated weighted mass density by
We also define corresponding momentum and energy symbols
![]() $p_a$
and
$p_a$
and
![]() $e_a$
by
$e_a$
by
Then a direct computation yields the density-flux relations
4.2 Nonlinear density-flux identities for the mass and momentum
Here, we develop the counterpart of the linear analysis above for the nonlinear problem (1.3).
4.2.1 The modified mass
To motivate what follows, we begin with a simpler computation for the
![]() $L^2$
norm of a solution u of equation (1.3):
$L^2$
norm of a solution u of equation (1.3):
A priori the symbol of the quartic form
![]() $C^4_m$
, defined on the diagonal
$C^4_m$
, defined on the diagonal
![]() $\Delta ^4 \xi = 0$
, is given by
$\Delta ^4 \xi = 0$
, is given by
However, we can further symmetrize and replace it by
In particular, we are interested in the behavior of
![]() $c^4_m(\xi _1,\xi _2,\xi _3,\xi _4)$
on the resonant set
$c^4_m(\xi _1,\xi _2,\xi _3,\xi _4)$
on the resonant set
On this set, we compute
 $$\begin{align*}\begin{aligned} c^4_m(\xi_1,\xi_1,\xi_3,\xi_3) = & \ \frac{i}2 \left( - c(\xi_1,\xi_1,\xi_3) - c(\xi_1,\xi_3,\xi_3)+ \bar c(\xi_1,\xi_3,\xi_3)+ \bar c(\xi_1,\xi_1,\xi_3) \right) \\ = & \ \Im( c(\xi_1,\xi_1,\xi_3) + c(\xi_1,\xi_3,\xi_3)). \end{aligned} \end{align*}$$
$$\begin{align*}\begin{aligned} c^4_m(\xi_1,\xi_1,\xi_3,\xi_3) = & \ \frac{i}2 \left( - c(\xi_1,\xi_1,\xi_3) - c(\xi_1,\xi_3,\xi_3)+ \bar c(\xi_1,\xi_3,\xi_3)+ \bar c(\xi_1,\xi_1,\xi_3) \right) \\ = & \ \Im( c(\xi_1,\xi_1,\xi_3) + c(\xi_1,\xi_3,\xi_3)). \end{aligned} \end{align*}$$
Then we observe that our (H2) assumption on C shows that this expression vanishes. One might wonder here if we could not weaken this assumption by requiring that the sum of the two terms is zero, rather than each of them separately. This would indeed be the case if all we were interested in is the almost conservation of mass. However, we will later add localization weights which will act differently on the two terms.
The fact that
![]() $c^4_m$
vanishes on the resonant set
$c^4_m$
vanishes on the resonant set
![]() $\mathcal {R}$
implies (see Lemma 4.1 below) that we can smoothly divide
$\mathcal {R}$
implies (see Lemma 4.1 below) that we can smoothly divide
 $$\begin{align*}b^4_m(\xi_1,\xi_2,\xi_3,\xi_4) = - \frac{i c^4_m(\xi_1,\xi_2,\xi_3,\xi_4)}{\Delta^4 \xi^2} \end{align*}$$
$$\begin{align*}b^4_m(\xi_1,\xi_2,\xi_3,\xi_4) = - \frac{i c^4_m(\xi_1,\xi_2,\xi_3,\xi_4)}{\Delta^4 \xi^2} \end{align*}$$
on
![]() $\Delta ^4 \xi = 0$
. We now use
$\Delta ^4 \xi = 0$
. We now use
![]() $\mathbf B^4_m$
as an energy correction. Then we obtain the modified energy relation
$\mathbf B^4_m$
as an energy correction. Then we obtain the modified energy relation
where
![]() $\mathbf R^6_m$
is a symmetric
$\mathbf R^6_m$
is a symmetric
![]() $6$
-linear form. Here, the left-hand side may be viewed as a modified energy, while the right-hand side can potentially be estimated using the
$6$
-linear form. Here, the left-hand side may be viewed as a modified energy, while the right-hand side can potentially be estimated using the
![]() $L^6_{t,x}$
norm of u.
$L^6_{t,x}$
norm of u.
4.2.2 The modified mass and momentum density-flux pairs
The key idea here is that, corresponding to the above modified mass, we also want to write a conservation law for an associated mass density
However, when doing this, we remark that the symbol of
![]() $B^4_m$
was previously defined only on the diagonal
$B^4_m$
was previously defined only on the diagonal
![]() $\Delta ^4 \xi = 0$
, whereas in order for the above expression to be well defined we need to extend it everywhere. For the purpose of this computation, we simply assume that we have chosen some smooth extension. A more careful choice will be considered later in Lemma 4.1.
$\Delta ^4 \xi = 0$
, whereas in order for the above expression to be well defined we need to extend it everywhere. For the purpose of this computation, we simply assume that we have chosen some smooth extension. A more careful choice will be considered later in Lemma 4.1.
Now, we compute
By the choice of
![]() $ B^4_m$
, the symbol of the quartic term above
$ B^4_m$
, the symbol of the quartic term above
![]() $c^4_m + i \Delta ^4 \xi ^2 b^4_m$
vanishes on the diagonal
$c^4_m + i \Delta ^4 \xi ^2 b^4_m$
vanishes on the diagonal
![]() $\{\Delta ^4 \xi = 0\}$
; therefore, we can express it smoothly in the form
$\{\Delta ^4 \xi = 0\}$
; therefore, we can express it smoothly in the form
Hence, the above relation can be written in the better form
One may view here the relation (4.5) as a division problem, where
![]() $c^4_m$
vanishes on the resonant set
$c^4_m$
vanishes on the resonant set
![]() $\mathcal {R}$
. The symbols
$\mathcal {R}$
. The symbols
![]() $b^4_m$
and
$b^4_m$
and
![]() $r^4_m$
are not uniquely determined by the relation (4.5), as we can change them by
$r^4_m$
are not uniquely determined by the relation (4.5), as we can change them by
for any smooth q. However, this is the only ambiguity. In particular
![]() $r_m^4$
is uniquely determined on the set
$r_m^4$
is uniquely determined on the set
![]() $\Delta ^4 \xi ^2 = 0$
, while
$\Delta ^4 \xi ^2 = 0$
, while
![]() $b_m^4$
is uniquely determined on the set
$b_m^4$
is uniquely determined on the set
![]() $\Delta ^4 \xi = 0$
.
$\Delta ^4 \xi = 0$
.
One could carry out a similar computation for the momentum, where the starting point is the relation
Precisely, the symbol of
![]() $C^4_p$
is initially given by
$C^4_p$
is initially given by
However, we can further symmetrize it exactly as in the case of
![]() $C_m^4$
. Then it also vanishes on the resonant set
$C_m^4$
. Then it also vanishes on the resonant set
![]() $\mathcal {R}$
, so it admits a (nonunique) representation of the form
$\mathcal {R}$
, so it admits a (nonunique) representation of the form
Hence, as in the case of the mass, we define a quartic correction for the momentum density
This satisfies a conservation law of the form
4.3 The choice for the density-flux corrections
Here, we consider the division problem in equation (4.5) and ask what should be a good balance between the symbols
![]() $B_m^4$
and
$B_m^4$
and
![]() $R_m^4$
. We recall that
$R_m^4$
. We recall that
![]() $b_m^4$
is uniquely determined on the diagonal
$b_m^4$
is uniquely determined on the diagonal
![]() $\Delta ^4 \xi = 0$
, but we can choose it freely away from the diagonal.
$\Delta ^4 \xi = 0$
, but we can choose it freely away from the diagonal.
To move away from the diagonal, it is useful to do it in a Galilean invariant fashion. The expression
![]() $\Delta ^4 \xi ^2$
is not Galilean invariant, but we do have a suitable replacement, namely the expression
$\Delta ^4 \xi ^2$
is not Galilean invariant, but we do have a suitable replacement, namely the expression
This is easily seen to be invariant with respect to translations. To measure the size of both
![]() $\Delta ^4 \xi $
and
$\Delta ^4 \xi $
and
![]() ${\tilde {\Delta }}^4 \xi ^2$
, we introduce two parameters,
${\tilde {\Delta }}^4 \xi ^2$
, we introduce two parameters,
 $$ \begin{align} \begin{aligned} {\delta \xi^{\text{hi}}} := & \ \max \{|\xi_1 - \xi_{2}|+|\xi_3-\xi_4|, |\xi_1 - \xi_{4}|+|\xi_3-\xi_2| \}, \\ {\delta \xi^{\text{med}}} :=& \ \min \{|\xi_1 - \xi_{2}|+|\xi_3-\xi_4|, |\xi_1 - \xi_{4}|+|\xi_3-\xi_2| \}, \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} {\delta \xi^{\text{hi}}} := & \ \max \{|\xi_1 - \xi_{2}|+|\xi_3-\xi_4|, |\xi_1 - \xi_{4}|+|\xi_3-\xi_2| \}, \\ {\delta \xi^{\text{med}}} :=& \ \min \{|\xi_1 - \xi_{2}|+|\xi_3-\xi_4|, |\xi_1 - \xi_{4}|+|\xi_3-\xi_2| \}, \end{aligned} \end{align} $$
where
![]() ${\delta \xi ^{\text {hi}}}$
measures the diameter of the full set of
${\delta \xi ^{\text {hi}}}$
measures the diameter of the full set of
![]() $\xi $
’s whereas
$\xi $
’s whereas
![]() ${\delta \xi ^{\text {med}}}$
measures the distance of the sets
${\delta \xi ^{\text {med}}}$
measures the distance of the sets
![]() $\{\xi _1,\xi _3\}$
and
$\{\xi _1,\xi _3\}$
and
![]() $\{\xi _2,\xi _4\}$
. With these notations, we have bounds from above as follows:
$\{\xi _2,\xi _4\}$
. With these notations, we have bounds from above as follows:
We will think of the symbol
![]() $\Delta ^4 \xi $
as being elliptic where approximate equality holds in the first relation and of
$\Delta ^4 \xi $
as being elliptic where approximate equality holds in the first relation and of
![]() ${\tilde {\Delta }}^4 \xi ^2$
as being elliptic where approximate equality holds in the second relation. Based on this, we will decompose the phase space into three overlapping regions which can be separated using cutoff functions which are smooth on the unit scale:
${\tilde {\Delta }}^4 \xi ^2$
as being elliptic where approximate equality holds in the second relation. Based on this, we will decompose the phase space into three overlapping regions which can be separated using cutoff functions which are smooth on the unit scale:
-
i) The full division region,
which represents a full unit size neighbourhood of the resonant set $$\begin{align*}\Omega_1 = \{ {\delta \xi^{\text{med}}} \lesssim 1 \}, \end{align*}$$
$$\begin{align*}\Omega_1 = \{ {\delta \xi^{\text{med}}} \lesssim 1 \}, \end{align*}$$
 $\mathcal {R}$
.
$\mathcal {R}$
.
-
ii) The region
where $$\begin{align*}\Omega_2 = \{ 1+ |\Delta^4 \xi| \ll {\delta \xi^{\text{med}}} \}, \end{align*}$$
$$\begin{align*}\Omega_2 = \{ 1+ |\Delta^4 \xi| \ll {\delta \xi^{\text{med}}} \}, \end{align*}$$
 ${\tilde {\Delta }}^4 \xi ^2$
must be elliptic,
${\tilde {\Delta }}^4 \xi ^2$
must be elliptic,
 $|{\tilde {\Delta }}^4 \xi ^2| \approx {\delta \xi ^{\text {hi}}} {\delta \xi ^{\text {med}}}$
, and thus we will favor division by the symbol
$|{\tilde {\Delta }}^4 \xi ^2| \approx {\delta \xi ^{\text {hi}}} {\delta \xi ^{\text {med}}}$
, and thus we will favor division by the symbol
 ${\tilde {\Delta }}^4 \xi ^2$
.
${\tilde {\Delta }}^4 \xi ^2$
.
-
iii) The region
we will instead divide by $$\begin{align*}\Omega_3 = \{ 1 \ll {\delta \xi^{\text{med}}} \lesssim |\Delta^4 \xi| \}, \end{align*}$$
$$\begin{align*}\Omega_3 = \{ 1 \ll {\delta \xi^{\text{med}}} \lesssim |\Delta^4 \xi| \}, \end{align*}$$
 $\Delta ^4 \xi $
; this is compensated by the relatively small size of this region.
$\Delta ^4 \xi $
; this is compensated by the relatively small size of this region.
This decomposition leads us to the following division lemma:
Lemma 4.1. Let
![]() $c^4$
be a bounded symbol which is smooth on the unit scale and which vanishes on
$c^4$
be a bounded symbol which is smooth on the unit scale and which vanishes on
![]() $\mathcal {R}$
. Then it admits a representation
$\mathcal {R}$
. Then it admits a representation
where
![]() $\tilde r^4$
and
$\tilde r^4$
and
![]() $b^4$
are also smooth on the unit scale, with the following properties:
$b^4$
are also smooth on the unit scale, with the following properties:
-
i) Size
(4.12) $$ \begin{align} \begin{aligned} |\partial^{\alpha} \tilde r^4| \lesssim & \ \frac{1}{\langle {\delta \xi^{\text{med}}} \rangle} , \\ |\partial^{\alpha} b^4| \lesssim & \ \frac{1}{\langle{\delta \xi^{\text{hi}}}\rangle \langle{\delta \xi^{\text{med}}}\rangle}. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} |\partial^{\alpha} \tilde r^4| \lesssim & \ \frac{1}{\langle {\delta \xi^{\text{med}}} \rangle} , \\ |\partial^{\alpha} b^4| \lesssim & \ \frac{1}{\langle{\delta \xi^{\text{hi}}}\rangle \langle{\delta \xi^{\text{med}}}\rangle}. \end{aligned} \end{align} $$
-
ii) Support:
 $b^4$
is supported in
$b^4$
is supported in
 $\Omega _1 \cup \Omega _2$
and
$\Omega _1 \cup \Omega _2$
and
 $\tilde r^4$
is supported in
$\tilde r^4$
is supported in
 $\Omega _1 \cup \Omega _3$
.
$\Omega _1 \cup \Omega _3$
.
Here and later in the paper, by ‘smooth on the unit scale’ we mean that the above functions and all their derivatives are bounded, with bounds as in equation (4.12), and where the implicit constant is allowed to depend on
![]() $\alpha $
, but not on anything else. As usual, only finitely many derivatives are needed on our analysis, but we do not take the extra step of determining how many.
$\alpha $
, but not on anything else. As usual, only finitely many derivatives are needed on our analysis, but we do not take the extra step of determining how many.
To return to
![]() $\Delta ^4\xi $
, we have the following straightforward observation:
$\Delta ^4\xi $
, we have the following straightforward observation:
Remark 4.2. Later, we will need similar decompositions but with
![]() ${\tilde {\Delta }}^4 \xi ^2$
replaced by
${\tilde {\Delta }}^4 \xi ^2$
replaced by
![]() $\Delta ^4 \xi ^2$
,
$\Delta ^4 \xi ^2$
,
This is easily done via the substitution
But in doing this, we loose the above bound for
![]() $\tilde r^4$
unless
$\tilde r^4$
unless
![]() $|\xi _{avg}| \lesssim {\delta \xi ^{\text {hi}}}$
. Precisely, we obtain instead
$|\xi _{avg}| \lesssim {\delta \xi ^{\text {hi}}}$
. Precisely, we obtain instead
 $$ \begin{align} |\partial^{\alpha} r^4| \lesssim \frac{1}{\langle {\delta \xi^{\text{med}}} \rangle} \left( 1+ \frac{|\xi_{avg}|}{\langle {\delta \xi^{\text{hi}}} \rangle}\right). \end{align} $$
$$ \begin{align} |\partial^{\alpha} r^4| \lesssim \frac{1}{\langle {\delta \xi^{\text{med}}} \rangle} \left( 1+ \frac{|\xi_{avg}|}{\langle {\delta \xi^{\text{hi}}} \rangle}\right). \end{align} $$
Proof. Using a partition of unity which is smooth on the unit scale, we can reduce the problem to the case when
![]() $c^4$
is supported in exactly one of the regions
$c^4$
is supported in exactly one of the regions
![]() $\Omega _1$
,
$\Omega _1$
,
![]() $\Omega _2$
and
$\Omega _2$
and
![]() $\Omega _3$
. We consider each of these cases separately.
$\Omega _3$
. We consider each of these cases separately.
i)
![]() $c^4$
is supported in
$c^4$
is supported in
![]() $\Omega _1$
. To simplify notations here, we introduce new linear coordinates
$\Omega _1$
. To simplify notations here, we introduce new linear coordinates
![]() $(\eta _1,\eta _2,\eta _3,\eta _4)$
, where
$(\eta _1,\eta _2,\eta _3,\eta _4)$
, where
For
![]() $\eta _4$
, we can choose in a symmetric fashion
$\eta _4$
, we can choose in a symmetric fashion
though this does not play any role in the sequel.
In these coordinates, we have
where
 $$\begin{align*}\begin{aligned} & \Omega_{11} := \left\{|\eta_1| + |\eta_2|+ |\eta_3| \lesssim 1\right\}, \qquad \Omega_{12} := \left\{ |\eta_1|+ |\eta_2| \lesssim 1 \lesssim |\eta_3| \right\}, \\ & \qquad \qquad \Omega_{13} := \left\{|\eta_1|+ |\eta_3| \lesssim 1 \lesssim |\eta_2| \right\}. \end{aligned} \end{align*}$$
$$\begin{align*}\begin{aligned} & \Omega_{11} := \left\{|\eta_1| + |\eta_2|+ |\eta_3| \lesssim 1\right\}, \qquad \Omega_{12} := \left\{ |\eta_1|+ |\eta_2| \lesssim 1 \lesssim |\eta_3| \right\}, \\ & \qquad \qquad \Omega_{13} := \left\{|\eta_1|+ |\eta_3| \lesssim 1 \lesssim |\eta_2| \right\}. \end{aligned} \end{align*}$$
Using another partition of unity which is smooth on the unit scale, the problem reduces to separately considering the case when
![]() $c^4$
is supported in each of these three sets.
$c^4$
is supported in each of these three sets.
Within the set
![]() $\Omega _{12}$
, we have
$\Omega _{12}$
, we have
![]() $c^4(0,0,\eta _3,\eta _4) = 0$
; therefore, we can easily represent
$c^4(0,0,\eta _3,\eta _4) = 0$
; therefore, we can easily represent
where the first difference may be smoothly divided by
![]() $\eta _1$
and the second by
$\eta _1$
and the second by
![]() $\eta _2$
, with the quotients contributing to
$\eta _2$
, with the quotients contributing to
![]() $\tilde r^4$
, respectively
$\tilde r^4$
, respectively
![]() $b^4$
. The set
$b^4$
. The set
![]() $\Omega _{13}$
can be dealt with in a similar fashion.
$\Omega _{13}$
can be dealt with in a similar fashion.
It remains to consider
![]() $\Omega _{11}$
, where we know that
$\Omega _{11}$
, where we know that
![]() $c^4 = 0$
in
$c^4 = 0$
in
![]() $\eta _1 = \eta _2 \eta _3 = 0$
. Here, we write
$\eta _1 = \eta _2 \eta _3 = 0$
. Here, we write
Now, the first difference can be smoothly divided by
![]() $\eta _1$
, while the last term can be successively and smoothly divided by
$\eta _1$
, while the last term can be successively and smoothly divided by
![]() $\eta _2$
and
$\eta _2$
and
![]() $\eta _3$
.
$\eta _3$
.
ii)
![]() $c^4$
is supported in
$c^4$
is supported in
![]() $\Omega _2$
. Here we set
$\Omega _2$
. Here we set
 $$\begin{align*}b^4 = \frac{c^4}{{\tilde{\Delta}}^4 \xi^2}, \qquad \tilde r^4 = 0, \end{align*}$$
$$\begin{align*}b^4 = \frac{c^4}{{\tilde{\Delta}}^4 \xi^2}, \qquad \tilde r^4 = 0, \end{align*}$$
and we observe that
 $$\begin{align*}\left|\partial^{\alpha}\frac{1}{{\tilde{\Delta}}^4 \xi^2}\right| \lesssim \frac{1}{{\delta \xi^{\text{med}}} {\delta \xi^{\text{hi}}}}. \end{align*}$$
$$\begin{align*}\left|\partial^{\alpha}\frac{1}{{\tilde{\Delta}}^4 \xi^2}\right| \lesssim \frac{1}{{\delta \xi^{\text{med}}} {\delta \xi^{\text{hi}}}}. \end{align*}$$
iii)
![]() $c^4$
is supported in
$c^4$
is supported in
![]() $\Omega _3$
. Here, we set
$\Omega _3$
. Here, we set
 $$\begin{align*}b^4 = 0, \qquad \tilde r^4 = -\frac{c^4}{\Delta^4 \xi}, \end{align*}$$
$$\begin{align*}b^4 = 0, \qquad \tilde r^4 = -\frac{c^4}{\Delta^4 \xi}, \end{align*}$$
and we observe that
 $$\begin{align*}\left|\partial^{\alpha}\frac{1}{\Delta^4 \xi}\right| \lesssim \frac{1}{{\delta \xi^{\text{med}}}}. \\[-42pt]\end{align*}$$
$$\begin{align*}\left|\partial^{\alpha}\frac{1}{\Delta^4 \xi}\right| \lesssim \frac{1}{{\delta \xi^{\text{med}}}}. \\[-42pt]\end{align*}$$
4.4 The Galilean invariance
While the assumptions (H1–3) on the cubic nonlinearity C are Galilean invariant, our density-flux identities are not. In order to rectify that, suppose heuristically that we are looking at linear waves concentrated around a frequency
![]() $\xi _0$
. This corresponds to a linear group velocity of
$\xi _0$
. This corresponds to a linear group velocity of
![]() $2 \xi _0$
, so in the density-flux identities it would be natural to replace the operator
$2 \xi _0$
, so in the density-flux identities it would be natural to replace the operator
![]() $\partial _t$
by
$\partial _t$
by
![]() $\partial _t + 2 \xi _0 \partial _x$
. At the linear level, this is done by recentering the energy and momentum densities at
$\partial _t + 2 \xi _0 \partial _x$
. At the linear level, this is done by recentering the energy and momentum densities at
![]() $\xi _0$
,
$\xi _0$
,
 $$ \begin{align} \begin{aligned} p_{\xi_0}(\xi_1,\xi_2) = & \ - \xi_1 -\xi_2 + 2 \xi_0 = p + 2 \xi_0 m, \\ e_{\xi_0}(\xi_1,\xi_2) = & \ (\xi_1+\xi_2 - 2 \xi_0)^2 = e + 4 \xi_0 p + 4 \xi_0^2 m. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} p_{\xi_0}(\xi_1,\xi_2) = & \ - \xi_1 -\xi_2 + 2 \xi_0 = p + 2 \xi_0 m, \\ e_{\xi_0}(\xi_1,\xi_2) = & \ (\xi_1+\xi_2 - 2 \xi_0)^2 = e + 4 \xi_0 p + 4 \xi_0^2 m. \end{aligned} \end{align} $$
Then the density-flux identities (4.2) become
Next, we consider the nonlinear setting. There
![]() $M^{\sharp }$
is the same as before, but
$M^{\sharp }$
is the same as before, but
![]() $P^{\sharp }_{\xi _0}$
is
$P^{\sharp }_{\xi _0}$
is
where the symbol for
![]() $B^4_{p,\xi _0}$
is given by
$B^4_{p,\xi _0}$
is given by
Then our density-flux identities have the form
where the symbols for
![]() $R^4_{m,\xi _0}$
and
$R^4_{m,\xi _0}$
and
![]() $R^4_{p,\xi _0}$
are defined by
$R^4_{p,\xi _0}$
are defined by
4.5 Localized density-flux identities for mass and momentum
In our analysis later on, we will not use density-flux pairs for global estimates, but instead we will use them only in a frequency localized setting.
Here, we begin our discussion with a symmetric bilinear symbol
![]() $a(\xi ,\eta )$
. We are assuming it generates a real valued quadratic form
$a(\xi ,\eta )$
. We are assuming it generates a real valued quadratic form
![]() $A(u,\bar u)$
, that is, that
$A(u,\bar u)$
, that is, that
and that its symbol is bounded and uniformly smooth. Later, we will use such symbols a to localize our analysis to intervals I in frequency, either of unit size or larger.
Corresponding to such a, we define corresponding quadratic localized mass, momentum and energy by
A direct computation yields the relation
where the symbol
![]() $C_{m,a}^4$
is given by
$C_{m,a}^4$
is given by
 $$\begin{align*}\begin{aligned} c_{m,a}^4(\xi_1,\xi_2,\xi_3,\xi_4) = -\frac{i}{2} [ & \ c(\xi_1,\xi_2,\xi_3) m_a(\xi_1-\xi_2 +\xi_3,\xi_4) +c(\xi_1,\xi_4,\xi_3) m_a(\xi_1-\xi_4 +\xi_3,\xi_2) \\ & - \bar{c}(\xi_2,\xi_3,\xi_4) m_a(\xi_3, \xi_2-\xi_3+\xi_4) - \bar{c}(\xi_2,\xi_1,\xi_4) m_a(\xi_3, \xi_2-\xi_1+\xi_4)]. \end{aligned} \end{align*}$$
$$\begin{align*}\begin{aligned} c_{m,a}^4(\xi_1,\xi_2,\xi_3,\xi_4) = -\frac{i}{2} [ & \ c(\xi_1,\xi_2,\xi_3) m_a(\xi_1-\xi_2 +\xi_3,\xi_4) +c(\xi_1,\xi_4,\xi_3) m_a(\xi_1-\xi_4 +\xi_3,\xi_2) \\ & - \bar{c}(\xi_2,\xi_3,\xi_4) m_a(\xi_3, \xi_2-\xi_3+\xi_4) - \bar{c}(\xi_2,\xi_1,\xi_4) m_a(\xi_3, \xi_2-\xi_1+\xi_4)]. \end{aligned} \end{align*}$$
A similar identity applies in the case of the localized momentum, where we simply replace the symbol
![]() $m_a$
by
$m_a$
by
![]() $p_a$
.
$p_a$
.
As before, this symbol vanishes on the resonant set
![]() $\mathcal {R}$
, so we can represent it as in the division relation (4.5),
$\mathcal {R}$
, so we can represent it as in the division relation (4.5),
as well as
Then, defining
![]() $M^{\sharp }_a$
and
$M^{\sharp }_a$
and
![]() $P^{\sharp }_a$
as before,
$P^{\sharp }_a$
as before,
we obtain density-flux identities akin to equation (4.6), namely
and
We will consider these relations together with their Galilean shifts obtaining relations of the form
respectively
These correspond to the algebraic division relations
respectively
where
 $$ \begin{align} \begin{aligned} c_{p,a,\xi_0}^4(\xi_1,\xi_2,\xi_3,\xi_4) = & -\frac{i}{2} [ c(\xi_1,\xi_2,\xi_3) p_{a,\xi_0}(\xi_1-\xi_2 +\xi_3,\xi_4) +c(\xi_1,\xi_4,\xi_3) p_{a,\xi_0}(\xi_1-\xi_4 +\xi_3,\xi_2) \\ & - \bar{c}(\xi_2,\xi_3,\xi_4) p_{a,\xi_0}(\xi_1, \xi_2-\xi_3+\xi_4) - \bar{c}(\xi_2,\xi_1,\xi_4) p_{a,\xi_0}(\xi_3, \xi_2-\xi_1+\xi_4)]. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} c_{p,a,\xi_0}^4(\xi_1,\xi_2,\xi_3,\xi_4) = & -\frac{i}{2} [ c(\xi_1,\xi_2,\xi_3) p_{a,\xi_0}(\xi_1-\xi_2 +\xi_3,\xi_4) +c(\xi_1,\xi_4,\xi_3) p_{a,\xi_0}(\xi_1-\xi_4 +\xi_3,\xi_2) \\ & - \bar{c}(\xi_2,\xi_3,\xi_4) p_{a,\xi_0}(\xi_1, \xi_2-\xi_3+\xi_4) - \bar{c}(\xi_2,\xi_1,\xi_4) p_{a,\xi_0}(\xi_3, \xi_2-\xi_1+\xi_4)]. \end{aligned} \end{align} $$
The symbols above are connected in the obvious way. Precisely, we have
and
and finally
To use these density-flux relations we need to have appropriate bounds for our symbols:
Proposition 4.3. Let
![]() $J \subset {\mathbb R}$
be an interval of length r and
$J \subset {\mathbb R}$
be an interval of length r and
![]() $d(\xi _0,J) \lesssim r$
. Assume that a is supported in
$d(\xi _0,J) \lesssim r$
. Assume that a is supported in
![]() $J \times J$
, with bounded and uniformly smooth symbol. Then the relations (4.28) and (4.29) hold with symbols
$J \times J$
, with bounded and uniformly smooth symbol. Then the relations (4.28) and (4.29) hold with symbols
![]() $b^{4}_{m,a}$
,
$b^{4}_{m,a}$
,
![]() $b^{4}_{p,a,\xi _0}$
,
$b^{4}_{p,a,\xi _0}$
,
![]() $r^4_{m,a,\xi _0}$
and
$r^4_{m,a,\xi _0}$
and
![]() $r^4_{p,a,\xi _0}$
which can be chosen to have the following properties:
$r^4_{p,a,\xi _0}$
which can be chosen to have the following properties:
-
i) Support: They are all supported in the region where at least one of the frequencies is in J.
-
ii) Size:
(4.34) $$ \begin{align} |b^{4}_{m,a}| \lesssim \frac{1}{\langle {\delta \xi^{\text{hi}}} \rangle \langle {\delta \xi^{\text{med}}} \rangle }, \qquad |b^{4}_{p,a,\xi_0}| \lesssim \frac{r}{\langle {\delta \xi^{\text{hi}}} \rangle \langle {\delta \xi^{\text{med}}} \rangle }, \end{align} $$
(4.35)
$$ \begin{align} |b^{4}_{m,a}| \lesssim \frac{1}{\langle {\delta \xi^{\text{hi}}} \rangle \langle {\delta \xi^{\text{med}}} \rangle }, \qquad |b^{4}_{p,a,\xi_0}| \lesssim \frac{r}{\langle {\delta \xi^{\text{hi}}} \rangle \langle {\delta \xi^{\text{med}}} \rangle }, \end{align} $$
(4.35) $$ \begin{align} \begin{aligned} |r^{4}_{m,a,\xi_0}| \lesssim & \ \frac{1}{\langle {\delta \xi^{\text{med}}} \rangle } 1_{\Omega_1 \cup \Omega_3} + \frac{r}{\langle {\delta \xi^{\text{hi}}} \rangle \langle {\delta \xi^{\text{med}}} \rangle } 1_{\Omega_1 \cup \Omega_2}, \\ |R^{4}_{p,a,\xi_0}| \lesssim & \ \frac{r}{\langle {\delta \xi^{\text{med}}} \rangle } 1_{\Omega_1 \cup \Omega_3} + \frac{r^2}{\langle {\delta \xi^{\text{hi}}} \rangle \langle {\delta \xi^{\text{med}}} \rangle } 1_{\Omega_1 \cup \Omega_2}. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} |r^{4}_{m,a,\xi_0}| \lesssim & \ \frac{1}{\langle {\delta \xi^{\text{med}}} \rangle } 1_{\Omega_1 \cup \Omega_3} + \frac{r}{\langle {\delta \xi^{\text{hi}}} \rangle \langle {\delta \xi^{\text{med}}} \rangle } 1_{\Omega_1 \cup \Omega_2}, \\ |R^{4}_{p,a,\xi_0}| \lesssim & \ \frac{r}{\langle {\delta \xi^{\text{med}}} \rangle } 1_{\Omega_1 \cup \Omega_3} + \frac{r^2}{\langle {\delta \xi^{\text{hi}}} \rangle \langle {\delta \xi^{\text{med}}} \rangle } 1_{\Omega_1 \cup \Omega_2}. \end{aligned} \end{align} $$
-
iii) Regularity: Similar bounds hold for all derivatives.
5 Interaction Morawetz identities
5.1 The linear Schrodinger equation
The Interaction Morawetz inequality aims to capture the fact that the momentum moves to the right faster than the mass. Here, the left/right symmetry is broken due to the sign choice which is implicit in the choice of the momentum.
5.1.1 A global computation
To warm up, we start with two solutions u and v for the linear Schrödinger equation. To these we associate the Interaction functional
 $$\begin{align*}\mathbf{I}(u,v) = \int_{x> y} M(u)(x) P(v)(y) - P(u)(x) M(v)(y) \,dx dy \end{align*}$$
$$\begin{align*}\mathbf{I}(u,v) = \int_{x> y} M(u)(x) P(v)(y) - P(u)(x) M(v)(y) \,dx dy \end{align*}$$
and compute
![]() $d\mathbf {I}/dt$
using the conservation laws (4.2). We have
$d\mathbf {I}/dt$
using the conservation laws (4.2). We have
 $$\begin{align*}\begin{aligned} \frac{d}{dt} \mathbf{I}(u,v) = & \ \int_{x> y} \partial_x P(u)(x) P(v)(y) + M(u)(x) \partial_y E(v)(y) \\ & \ \ \ \ -\partial_x E(u)(x) M(v)(y) - P(u)(x) \partial_y P(v)(y)\, dx dy \\ = & \int M(u) E(v) + M(v) E(u) - 2 P(u)P(v) \,dx:= \int J^4(u,{\bar u},v,{\bar v})\, dx .\end{aligned} \end{align*}$$
$$\begin{align*}\begin{aligned} \frac{d}{dt} \mathbf{I}(u,v) = & \ \int_{x> y} \partial_x P(u)(x) P(v)(y) + M(u)(x) \partial_y E(v)(y) \\ & \ \ \ \ -\partial_x E(u)(x) M(v)(y) - P(u)(x) \partial_y P(v)(y)\, dx dy \\ = & \int M(u) E(v) + M(v) E(u) - 2 P(u)P(v) \,dx:= \int J^4(u,{\bar u},v,{\bar v})\, dx .\end{aligned} \end{align*}$$
Here,
![]() $J^4$
can be chosenFootnote 2 to have symbol
$J^4$
can be chosenFootnote 2 to have symbol
This is because of the following computation on the diagonal
![]() $\Delta ^4 \xi = 0$
:
$\Delta ^4 \xi = 0$
:
Thus, we have the positivity
The above computation is classically done using integration by parts; see [Reference Planchon and Vega22]. However, it is more interesting to do it at the symbol level because we want to apply it in a more general context. Classically, this is done with
![]() $u=v$
, but here we find it convenient to break the symmetry. Primarily, our v’s will be spatial translations of u.
$u=v$
, but here we find it convenient to break the symmetry. Primarily, our v’s will be spatial translations of u.
5.1.2 A frequency localized bound
Here, we start with a symbol a which is localized on the unit scale near some frequency
![]() $\xi _0$
, and consider the Interaction Morawetz functional
$\xi _0$
, and consider the Interaction Morawetz functional
 $$ \begin{align} \mathbf{I}_a(u,v) = \int_{x> y} M_a(u)(x) P_a(v)(y) - P_a(u) (x) M_a(v)(y) \, dx dy. \end{align} $$
$$ \begin{align} \mathbf{I}_a(u,v) = \int_{x> y} M_a(u)(x) P_a(v)(y) - P_a(u) (x) M_a(v)(y) \, dx dy. \end{align} $$
As above, its time derivative is
where
![]() $J_a^4$
has symbol
$J_a^4$
has symbol
This no longer has obvious positivity. However, if a has separated variables
then
![]() $J_a$
is nonnegative,
$J_a$
is nonnegative,
where
![]() $K_a$
has symbol
$K_a$
has symbol
![]() $(\xi -\eta ) a_0(\xi ) a_0(\eta )$
, that is,
$(\xi -\eta ) a_0(\xi ) a_0(\eta )$
, that is,
where
![]() $A_0$
is the multiplier associated to the symbol
$A_0$
is the multiplier associated to the symbol
![]() $a_0$
.
$a_0$
.
5.1.3 Interaction Morawetz for separated velocities
Here, we instead take two symbols a and b localized to two frequency intervals A and B so that
![]() $|A|,|B| \lesssim r$
and A and B have separation r (say A is to the left of B). Then we take the Interaction functional
$|A|,|B| \lesssim r$
and A and B have separation r (say A is to the left of B). Then we take the Interaction functional
 $$\begin{align*}\mathbf{I}_{AB} = \int_{x> y} M_A(u)(x) P_B(v)(y) - P_A(u)(x) M_B(v)(y) \, dx dy , \end{align*}$$
$$\begin{align*}\mathbf{I}_{AB} = \int_{x> y} M_A(u)(x) P_B(v)(y) - P_A(u)(x) M_B(v)(y) \, dx dy , \end{align*}$$
or equivalently
 $$\begin{align*}\mathbf{I}_{AB} = \int_{x> y} M_A(x) P_{B,\xi_0} (y) - P_{A,\xi_0}(x) M_B(y) \,dx dy , \end{align*}$$
$$\begin{align*}\mathbf{I}_{AB} = \int_{x> y} M_A(x) P_{B,\xi_0} (y) - P_{A,\xi_0}(x) M_B(y) \,dx dy , \end{align*}$$
where
![]() $\xi _0$
is arbitrary but can be chosen more efficiently at distance
$\xi _0$
is arbitrary but can be chosen more efficiently at distance
![]() $O(r)$
from both A and B.
$O(r)$
from both A and B.
Then we compute
where
![]() $\mathbf {J}^4_{AB}$
has symbol
$\mathbf {J}^4_{AB}$
has symbol
Assuming that
we can write
![]() $\mathbf {J}^4_{AB}$
as
$\mathbf {J}^4_{AB}$
as
where
Now, the differences
![]() $(\xi _1-\xi _4)$
and
$(\xi _1-\xi _4)$
and
![]() $(\xi _2-\xi _3)$
have size r so this leads to a bilinear
$(\xi _2-\xi _3)$
have size r so this leads to a bilinear
![]() $L^2$
bound for
$L^2$
bound for
![]() $A_0 u \cdot \overline {B_0 u}$
,
$A_0 u \cdot \overline {B_0 u}$
,
5.2 Nonlinear Interaction Morawetz estimates
Here, we consider the same Interaction Morawetz functional as above but now apply it to (two) solutions for the nonlinear equation (1.3).
5.2.1 A simple case
As a starting point, here we consider density-flux pairs as in equations (4.6), (4.8) to which we associate the nonlinear Interaction functional
 $$ \begin{align} \mathbf{I}(u,v) = \iint_{x> y} M^{\sharp}(u)(x) P^{\sharp}(v)(y) - P^{\sharp}(u)(x) M^{\sharp}(v)(y) \, dx dy. \end{align} $$
$$ \begin{align} \mathbf{I}(u,v) = \iint_{x> y} M^{\sharp}(u)(x) P^{\sharp}(v)(y) - P^{\sharp}(u)(x) M^{\sharp}(v)(y) \, dx dy. \end{align} $$
Using the density-flux relations, we obtain
where
![]() $\mathbf {J}^4$
is the same as above, while
$\mathbf {J}^4$
is the same as above, while
![]() $\mathbf {J}^6$
and
$\mathbf {J}^6$
and
![]() $\mathbf {J}^8$
are given by
$\mathbf {J}^8$
are given by
 $$ \begin{align} \begin{aligned} \mathbf{J}^6(u,v) = \int & \ M(u) R^4_{p}(v)+ B^4_m(u) E(v) - P(u)B^4_p(v)- R^4_m(u)P(v) + \\ & \ M(v) R^4_{p}(u)+ B^4_m(v) E(u) - P(v)B^4_p(u)- R^4_m(v)P(u)\, dx , \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \mathbf{J}^6(u,v) = \int & \ M(u) R^4_{p}(v)+ B^4_m(u) E(v) - P(u)B^4_p(v)- R^4_m(u)P(v) + \\ & \ M(v) R^4_{p}(u)+ B^4_m(v) E(u) - P(v)B^4_p(u)- R^4_m(v)P(u)\, dx , \end{aligned} \end{align} $$
respectively
Finally, we are also left with the double integral
 $$ \begin{align} \begin{aligned} \mathbf{K}^8 &= \iint_{x> y} M^{\sharp}(u)(x) R^6_{p}(v)(y) + P^{\sharp}(v)(y) R^6_{m}(u)(x) \, dx dy \\ \quad &- \iint_{x > y} M^{\sharp}(v)(y) R^6_{p}(u)(x) + P^{\sharp}(u)(x) R^6_{m}(v)(y) \, dx dy, \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \mathbf{K}^8 &= \iint_{x> y} M^{\sharp}(u)(x) R^6_{p}(v)(y) + P^{\sharp}(v)(y) R^6_{m}(u)(x) \, dx dy \\ \quad &- \iint_{x > y} M^{\sharp}(v)(y) R^6_{p}(u)(x) + P^{\sharp}(u)(x) R^6_{m}(v)(y) \, dx dy, \end{aligned} \end{align} $$
whose leading part has order
![]() $8$
but also contains terms of order
$8$
but also contains terms of order
![]() $10$
, but we will treat it all perturbatively later.
$10$
, but we will treat it all perturbatively later.
It is instructive to consider the case of the cubic defocusing NLS. There
![]() $B^4_m= 0$
,
$B^4_m= 0$
,
![]() $B^4_p=0$
and thus
$B^4_p=0$
and thus
![]() $R^6_m= 0$
,
$R^6_m= 0$
,
![]() $R^6_p=0$
. Further,
$R^6_p=0$
. Further,
![]() $R^4_{m} = 0$
but
$R^4_{m} = 0$
but
![]() $R^4_p = 1$
. Thus, in particular we get
$R^4_p = 1$
. Thus, in particular we get
This is where the focusing/defocusing type of the equation comes in, as it determines the sign of
![]() $\mathbf {J}^6$
(relative to the sign of
$\mathbf {J}^6$
(relative to the sign of
![]() $\mathbf {J}^4$
).
$\mathbf {J}^4$
).
5.2.2 Nonlinear Interaction Morawetz: the localized diagonal case
Here, we use the frequency localized mass density-flux identity (4.17) and the corresponding momentum density-flux identity (4.18) in order to produce a localized Interaction Morawetz estimate. We consider a smooth symbol a as in equation (5.2), where
![]() $a_0$
is localized around a frequency
$a_0$
is localized around a frequency
![]() $\xi _0$
on the unit scale.
$\xi _0$
on the unit scale.
Correspondingly, we have the localized mass and momentum densities
which satisfy the conservation laws
For these, we define the Interaction Morawetz functional
 $$ \begin{align} \mathbf{I}_{a}(u,v) = \iint_{x> y} M^{\sharp}_a(u)(x) P^{\sharp}_{a,\xi_0}(v) (y) - P^{\sharp}_{a,\xi_0}(u)(x) M^{\sharp}_{a}(v) (y) \, dx dy, \end{align} $$
$$ \begin{align} \mathbf{I}_{a}(u,v) = \iint_{x> y} M^{\sharp}_a(u)(x) P^{\sharp}_{a,\xi_0}(v) (y) - P^{\sharp}_{a,\xi_0}(u)(x) M^{\sharp}_{a}(v) (y) \, dx dy, \end{align} $$
where, by writing it in a symmetric fashion, we have completely eliminated its dependence on
![]() $\xi _0$
.
$\xi _0$
.
The time derivative of
![]() $\mathbf {I}_{a}$
is
$\mathbf {I}_{a}$
is
where all the terms are independent of
![]() $\xi _0$
.
$\xi _0$
.
Here, the quartic contribution
![]() $\mathbf {J}^4_{a}$
is the same as in the linear case,
$\mathbf {J}^4_{a}$
is the same as in the linear case,
The sixth-order term
![]() $\mathbf {J}^6_{a}$
has the form
$\mathbf {J}^6_{a}$
has the form
 $$ \begin{align} \begin{aligned} \mathbf{J}^6_a(u,v) = \int & \ M_a(u) R^4_{p,a,\xi_0}(v)+ B^4_{m,a}(u) E_{a,\xi_0}(v) - P_{a,\xi_0}(u)B^4_{p,a,\xi_0}(v)- R^4_{m,a,\xi_0}(u)P_{a,\xi_0}(v) \\ & \ + M_a(v) R^4_{p,a,\xi_0}(u)+ B^4_{m,a}(v) E_{a,\xi_0}(u) - P_{a,\xi_0}(v)B^4_{p,a,\xi_0}(u)- R^4_{m,a,\xi_0}(v)P_{a,\xi_0}(u)\, dx. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \mathbf{J}^6_a(u,v) = \int & \ M_a(u) R^4_{p,a,\xi_0}(v)+ B^4_{m,a}(u) E_{a,\xi_0}(v) - P_{a,\xi_0}(u)B^4_{p,a,\xi_0}(v)- R^4_{m,a,\xi_0}(u)P_{a,\xi_0}(v) \\ & \ + M_a(v) R^4_{p,a,\xi_0}(u)+ B^4_{m,a}(v) E_{a,\xi_0}(u) - P_{a,\xi_0}(v)B^4_{p,a,\xi_0}(u)- R^4_{m,a,\xi_0}(v)P_{a,\xi_0}(u)\, dx. \end{aligned} \end{align} $$
Next, we have
 $$ \begin{align} &\mathbf{J}^8_{a}(u,v) = \\&\quad\int B^4_{m,a}(u) R^4_{p,a,\xi_0}(v) - R^4_{m,a,\xi_0}(u) B^4_{p,a,\xi_0}(v) + B^4_{m,a}(v) R^4_{p,a,\xi_0}(u) - R^4_{m,a,\xi_0}(v) B^4_{p,a,\xi_0}(u) \, dx.\nonumber \end{align} $$
$$ \begin{align} &\mathbf{J}^8_{a}(u,v) = \\&\quad\int B^4_{m,a}(u) R^4_{p,a,\xi_0}(v) - R^4_{m,a,\xi_0}(u) B^4_{p,a,\xi_0}(v) + B^4_{m,a}(v) R^4_{p,a,\xi_0}(u) - R^4_{m,a,\xi_0}(v) B^4_{p,a,\xi_0}(u) \, dx.\nonumber \end{align} $$
Finally, the
![]() $8$
-linear term
$8$
-linear term
![]() $\mathbf {K}^8_{a}$
has the form
$\mathbf {K}^8_{a}$
has the form
 $$ \begin{align} \begin{aligned} \mathbf{K}^8_a(u,v) = \iint_{x> y} & \ M^{\sharp}_a(u)(x) R^6_{p,a,\xi_0}(v)(y) + P^{\sharp}_{a,\xi_0}(v)(y) R^6_{m,a}(u)(x) \\ & \ - M^{\sharp}_a(v)(y) R^6_{p,a,\xi_0}(u)(x) - P^{\sharp}_{a,\xi_0}(u)(x) R^6_{m,a}(v)(y) \, dx dy. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \mathbf{K}^8_a(u,v) = \iint_{x> y} & \ M^{\sharp}_a(u)(x) R^6_{p,a,\xi_0}(v)(y) + P^{\sharp}_{a,\xi_0}(v)(y) R^6_{m,a}(u)(x) \\ & \ - M^{\sharp}_a(v)(y) R^6_{p,a,\xi_0}(u)(x) - P^{\sharp}_{a,\xi_0}(u)(x) R^6_{m,a}(v)(y) \, dx dy. \end{aligned} \end{align} $$
This also includes a
![]() $10$
-linear term.
$10$
-linear term.
Importantly, here we compute the symbol of
![]() $\mathbf {J}^6_{a,\xi _0}$
on the diagonal
$\mathbf {J}^6_{a,\xi _0}$
on the diagonal
![]() $\xi _1 = \xi _2=\xi _3=\xi _4=\xi _5=\xi _6:=\xi $
. This will be essential later on in order to obtain bounds for the
$\xi _1 = \xi _2=\xi _3=\xi _4=\xi _5=\xi _6:=\xi $
. This will be essential later on in order to obtain bounds for the
![]() $L^6$
Strichartz norm.
$L^6$
Strichartz norm.
Lemma 5.1. The diagonal trace of the symbol
![]() $j^6_{a}$
is
$j^6_{a}$
is
Proof. Since our symbol does not actually depend on
![]() $\xi _0$
, it suffices to compute it at
$\xi _0$
, it suffices to compute it at
![]() $\xi = \xi _0$
. The advantage is that
$\xi = \xi _0$
. The advantage is that
![]() $p_{a,\xi _0}(\xi _0) = e_{a,\xi _0}(\xi _0)=0$
, so we are left with the simpler expression
$p_{a,\xi _0}(\xi _0) = e_{a,\xi _0}(\xi _0)=0$
, so we are left with the simpler expression
For
![]() $r^4_{p,a,\xi _0}$
, we have the relation
$r^4_{p,a,\xi _0}$
, we have the relation
We differentiate with respect to
![]() $\xi _1$
and then set all
$\xi _1$
and then set all
![]() $\xi $
’s equal to obtain
$\xi $
’s equal to obtain
It remains to compute the
![]() $\xi _1$
derivative of
$\xi _1$
derivative of
![]() $c^4_{p,a,\xi _0}$
on the diagonal. This is a direct computation using the formula (4.30). Recalling that
$c^4_{p,a,\xi _0}$
on the diagonal. This is a direct computation using the formula (4.30). Recalling that
it follows that
where we recall that c is real on the diagonal. Therefore,
as needed.
5.2.3 Nonlinear Interaction Morawetz: the transversal case
Here, we return to the setting of Section 5.1.3 where we have two frequency intervals
![]() $A,B$
with size at most M and separation also M and two smooth and bounded symbols
$A,B$
with size at most M and separation also M and two smooth and bounded symbols
![]() $a,b$
which are localized in the two intervals. Our Interaction Morawetz functional is given by
$a,b$
which are localized in the two intervals. Our Interaction Morawetz functional is given by
 $$ \begin{align} \mathbf{I}_{AB} = \int_{x> y} M^{\sharp}_a(u)(x) P^{\sharp}_{b,\xi_0}(v)(y) - P^{\sharp}_{a,\xi_0}(u)(x) M^{\sharp}_b(v)(y)\, dx dy , \end{align} $$
$$ \begin{align} \mathbf{I}_{AB} = \int_{x> y} M^{\sharp}_a(u)(x) P^{\sharp}_{b,\xi_0}(v)(y) - P^{\sharp}_{a,\xi_0}(u)(x) M^{\sharp}_b(v)(y)\, dx dy , \end{align} $$
and we observe as before that this does not depend on
![]() $\xi _0$
.
$\xi _0$
.
Using again the frequency localized mass density-flux identity (4.17) and the corresponding momentum density-flux identity (4.18) we produce a localized Interaction Morawetz estimate,
Here, the quartic contribution
![]() $\mathbf {J}^4_{AB}$
is the same as in the linear case
$\mathbf {J}^4_{AB}$
is the same as in the linear case
and captures the bilinear
![]() $L^2$
bound.
$L^2$
bound.
The sixth-order term
![]() $\mathbf {J}^6_{AB}$
has the form
$\mathbf {J}^6_{AB}$
has the form
where in the symmetric part we interchange both the indices
![]() $a,b$
and the functions
$a,b$
and the functions
![]() $u,v$
.
$u,v$
.
Next, we have
Finally, the
![]() $8$
-linear term
$8$
-linear term
![]() $\mathbf {K}^8_{a,\xi _0}$
has the form
$\mathbf {K}^8_{a,\xi _0}$
has the form
 $$\begin{align*}\mathbf{K}^8_{AB} = \iint_{x> y} M^{\sharp}_a(x) R^6_{p,b,\xi_0} + P^{\sharp}_{b,\xi_0} R^6_{m,a,\xi_0} - \text{symmetric} \, dx dy. \end{align*}$$
$$\begin{align*}\mathbf{K}^8_{AB} = \iint_{x> y} M^{\sharp}_a(x) R^6_{p,b,\xi_0} + P^{\sharp}_{b,\xi_0} R^6_{m,a,\xi_0} - \text{symmetric} \, dx dy. \end{align*}$$
As before, this also includes a
![]() $10$
-linear term.
$10$
-linear term.
6 Frequency envelopes and the bootstrap argument
The primary goal of the proof of our main result in Theorem 1 is to establish a global
![]() $L^{\infty }_t L^2_x$
bound for small data solutions; by the local well-posedness result in Section 3, this implies the desired global well-posedness result. However, along the way, we will also establish bilinear
$L^{\infty }_t L^2_x$
bound for small data solutions; by the local well-posedness result in Section 3, this implies the desired global well-posedness result. However, along the way, we will also establish bilinear
![]() $L^2$
and Strichartz bounds for the solutions. These will both play an essential role in the proof of Theorem 1 and will also establish the scattering properties of our global solutions.
$L^2$
and Strichartz bounds for the solutions. These will both play an essential role in the proof of Theorem 1 and will also establish the scattering properties of our global solutions.
Since the proof of our estimates loops back in a complex manner, it is most convenient to establish the bilinear
![]() $L^2$
and the
$L^2$
and the
![]() $L^6$
Strichartz bounds in the setting of a bootstrap argument, where we already assume that the desired bilinear and Strichartz estimates hold but with weaker constants.
$L^6$
Strichartz bounds in the setting of a bootstrap argument, where we already assume that the desired bilinear and Strichartz estimates hold but with weaker constants.
The setup for the bootstrap is most conveniently described using the language of frequency envelopes. This was originally introduced in work of Tao; see, for example, [Reference Tao24], but in the context of dyadic Littlewood–Paley decompositions. But here instead we work with a uniform decomposition on the unit scale, which requires a substantial revision of the notion of ‘slowly varying’, which we replace by the new notion of ‘maximal property’ introduced in Section 2.2.
To start with, we assume that the initial data is small size,
We consider a frequency decomposition for the initial data on a unit spatial scale,
Then we place the initial data components under an admissible frequency envelope on the unit scale,
where the envelope
![]() $\{c_k\}$
is not too large,
$\{c_k\}$
is not too large,
Our goal will be to establish the following frequency envelope bounds for the solution:
Theorem 5. Let
![]() $u \in C([0,T];L^2)$
be a solution for the equation (1.3) with initial data
$u \in C([0,T];L^2)$
be a solution for the equation (1.3) with initial data
![]() $\mathfrak {u}_0$
which has
$\mathfrak {u}_0$
which has
![]() $L^2$
size at most
$L^2$
size at most
![]() $\epsilon $
. Let
$\epsilon $
. Let
![]() $\{\epsilon c_k\}$
be an admissible frequency envelope for the initial data in
$\{\epsilon c_k\}$
be an admissible frequency envelope for the initial data in
![]() $L^2$
, with
$L^2$
, with
![]() $c_k$
normalized in
$c_k$
normalized in
![]() $\ell ^2$
. Then the solution u satisfies the following bounds:
$\ell ^2$
. Then the solution u satisfies the following bounds:
-
(i) Uniform frequency envelope bound:
(6.1) $$ \begin{align} \| u_k \|_{L^{\infty}_t L^2_x} \lesssim \epsilon c_k, \end{align} $$
$$ \begin{align} \| u_k \|_{L^{\infty}_t L^2_x} \lesssim \epsilon c_k, \end{align} $$
-
(ii) Localized Strichartz bound:
(6.2) $$ \begin{align} \| u_k \|_{L_{t,x}^6} \lesssim (\epsilon c_k)^{\frac23}, \end{align} $$
$$ \begin{align} \| u_k \|_{L_{t,x}^6} \lesssim (\epsilon c_k)^{\frac23}, \end{align} $$
-
(iii) Localized Interaction Morawetz:
(6.3) $$ \begin{align} \| \partial_x |u_k|^2 \|_{L^2_{t,x}} \lesssim \epsilon^2 c_k^2, \end{align} $$
$$ \begin{align} \| \partial_x |u_k|^2 \|_{L^2_{t,x}} \lesssim \epsilon^2 c_k^2, \end{align} $$
-
(iv) Transversal bilinear
 $L^2$
bound: (6.4)for all
$L^2$
bound: (6.4)for all $$ \begin{align} \| \partial_x(u_{A} {\bar u}_B(\cdot+x_0)) \|_{L^2_{t,x}} \lesssim \epsilon^2 c_A c_B\, \langle dist(A,B)\rangle^{\frac12}, \end{align} $$
$$ \begin{align} \| \partial_x(u_{A} {\bar u}_B(\cdot+x_0)) \|_{L^2_{t,x}} \lesssim \epsilon^2 c_A c_B\, \langle dist(A,B)\rangle^{\frac12}, \end{align} $$
 $x_0 \in {\mathbb R}$
whenever
$x_0 \in {\mathbb R}$
whenever
 $|A| + |B| \lesssim \langle dist(A,B)\rangle $
.
$|A| + |B| \lesssim \langle dist(A,B)\rangle $
.
Here, equation (6.3) can be seen as a particular case of equation (6.4) when
![]() $A=B$
have unit length; we stated it separately in order to ease comparison with earlier work on Interaction Morawetz estimates.
$A=B$
have unit length; we stated it separately in order to ease comparison with earlier work on Interaction Morawetz estimates.
To prove this theorem, we make a bootstrap assumption where we assume the same bounds but with a worse constant C, as follows:
-
(i) Uniform frequency envelope bound,
(6.5) $$ \begin{align} \| u_k \|_{L^{\infty}_t L^2_x} \lesssim C \epsilon c_k, \end{align} $$
$$ \begin{align} \| u_k \|_{L^{\infty}_t L^2_x} \lesssim C \epsilon c_k, \end{align} $$
-
(ii) Localized Strichartz bound,
(6.6) $$ \begin{align} \| u_k \|_{L^6_{t,x}} \lesssim C(\epsilon c_k)^{\frac23}, \end{align} $$
$$ \begin{align} \| u_k \|_{L^6_{t,x}} \lesssim C(\epsilon c_k)^{\frac23}, \end{align} $$
-
(iii) Localized Interaction Morawetz,
(6.7) $$ \begin{align} \| \partial_x |u_k|^2 \|_{L^2_{t,x}} \lesssim C\epsilon^2 c_k^2, \end{align} $$
$$ \begin{align} \| \partial_x |u_k|^2 \|_{L^2_{t,x}} \lesssim C\epsilon^2 c_k^2, \end{align} $$
-
(iv) Transversal Interaction Morawetz,
(6.8)uniformly for all $$ \begin{align} \| \partial_x (u_{k_1} \bar u_{k_2}(\cdot+x_0)) \|_{L^2_{t,x}} \lesssim C \epsilon^2 c_{k_1} c_{k_2} \langle k_1-k_2\rangle^{\frac12} \end{align} $$
$$ \begin{align} \| \partial_x (u_{k_1} \bar u_{k_2}(\cdot+x_0)) \|_{L^2_{t,x}} \lesssim C \epsilon^2 c_{k_1} c_{k_2} \langle k_1-k_2\rangle^{\frac12} \end{align} $$
 $x_0 \in {\mathbb R}$
.
$x_0 \in {\mathbb R}$
.
Then we seek to improve the constant in these bounds. The gain will come from the fact that the C’s will always come paired with extra
![]() $\epsilon $
s.
$\epsilon $
s.
We remark that the bootstrap hypothesis for the transversal bilinear
![]() $L^2$
bound (6.8) only requires unit size localization, unlike the corresponding conclusion (6.4). On one hand, this simplifies the continuity argument closing the bootstrap. On another hand, this is related to the fact that closing the bootstrap argument for global well-posedness only requires equation (6.4) for unit size sets. The full bound (6.4) is only used in the last section in order to obtain the global Strichartz and bilinear
$L^2$
bound (6.8) only requires unit size localization, unlike the corresponding conclusion (6.4). On one hand, this simplifies the continuity argument closing the bootstrap. On another hand, this is related to the fact that closing the bootstrap argument for global well-posedness only requires equation (6.4) for unit size sets. The full bound (6.4) is only used in the last section in order to obtain the global Strichartz and bilinear
![]() $L^2$
bounds, which are of course very interesting but secondary to the proof of the global result.
$L^2$
bounds, which are of course very interesting but secondary to the proof of the global result.
We also remark on the need to add translations to the bilinear
![]() $L^2$
estimates. This is because, unlike the linear bounds (6.5) and (6.6) which are inherently invariant with respect to translations, bilinear estimates are not invariant with respect to separate translations for the two factors. One immediate corollary of equation (6.8) is that for any multipliers
$L^2$
estimates. This is because, unlike the linear bounds (6.5) and (6.6) which are inherently invariant with respect to translations, bilinear estimates are not invariant with respect to separate translations for the two factors. One immediate corollary of equation (6.8) is that for any multipliers
![]() $L_1$
and
$L_1$
and
![]() $L_2$
with smooth and bounded symbols we have
$L_2$
with smooth and bounded symbols we have
This is essentially the only way we will use this translation invariance in our proofs.
For the rest of this section, we provide the continuity argument which shows that it suffices to prove Theorem 5 under the bootstrap assumptions (6.5)–(6.8).
For this, we denote by T the maximal time for which the bounds (6.5)–(6.8) hold in
![]() $[0,T]$
. By the local well-posedness result, we have
$[0,T]$
. By the local well-posedness result, we have
![]() $T \geq 1$
. Assume by contradiction that T is finite. Then the bootstrap version of the theorem implies that the bounds (6.1)–(6.4) hold in
$T \geq 1$
. Assume by contradiction that T is finite. Then the bootstrap version of the theorem implies that the bounds (6.1)–(6.4) hold in
![]() $[0,T]$
. In particular,
$[0,T]$
. In particular,
![]() $u(T)$
will also be controlled by the same maximal envelope
$u(T)$
will also be controlled by the same maximal envelope
![]() $c_j$
coming from the initial data. By the local well-posedness result, this implies in turn that the bounds (6.5)–(6.8) hold in
$c_j$
coming from the initial data. By the local well-posedness result, this implies in turn that the bounds (6.5)–(6.8) hold in
![]() $[T,T+1]$
with
$[T,T+1]$
with
![]() $C \approx 1$
. Adding this to the bounds (6.1)–(6.4) in
$C \approx 1$
. Adding this to the bounds (6.1)–(6.4) in
![]() $[0,T]$
, it follows that (6.5)–(6.8) hold in
$[0,T]$
, it follows that (6.5)–(6.8) hold in
![]() $[0,T+1]$
, thereby contradicting the maximality of T.
$[0,T+1]$
, thereby contradicting the maximality of T.
7 The frequency envelope bounds
The aim of this section is to prove the frequency envelope bounds in Theorem 5, given the bootstrap assumptions (6.5)–(6.8). In the proof, we will rely on our modified energy and momentum functionals, whose components we estimate first. The frequency localized energy estimate (6.1) will be an immediate consequence of these bounds. For the Strichartz and
![]() $L^2$
bilinear bounds, we will then use the Interaction Morawetz identities, first in a localized diagonal setting and then in a transversal setting.
$L^2$
bilinear bounds, we will then use the Interaction Morawetz identities, first in a localized diagonal setting and then in a transversal setting.
7.1 Spatial and space-time
 $L^1$
bounds
$L^1$
bounds
Here, we consider the corrections
![]() $B^4_{m,a}$
and errors
$B^4_{m,a}$
and errors
![]() $R^6_{m,a}$
and their momentum counterparts associated to a smooth bump function a selecting a frequency interval
$R^6_{m,a}$
and their momentum counterparts associated to a smooth bump function a selecting a frequency interval
![]() $A \subset {\mathbb Z}$
. For
$A \subset {\mathbb Z}$
. For
![]() $B^4_{m,a}$
, we will prove a fixed time
$B^4_{m,a}$
, we will prove a fixed time
![]() $L^1$
bound, while for
$L^1$
bound, while for
![]() $R^6_{m,a}$
we will prove a space-time
$R^6_{m,a}$
we will prove a space-time
![]() $L^1$
bound. These bounds will be repeatedly used in each of the following subsections, first in the case when A has unit size and then in the case when A has a larger size. We begin with the
$L^1$
bound. These bounds will be repeatedly used in each of the following subsections, first in the case when A has unit size and then in the case when A has a larger size. We begin with the
![]() $B^4_{m,a}$
bound.
$B^4_{m,a}$
bound.
Lemma 7.1. Assume that the bootstrap bound (6.5) holds. Then we have the fixed time estimate
The corresponding bound for the momentum follows as a corollary once we add an additional assumption in order to fix the momentum size:
Corollary 7.2. Assume that the bootstrap bound (6.5) holds. Let
![]() $\xi _0 \in {\mathbb R}$
, and
$\xi _0 \in {\mathbb R}$
, and
Then we have the fixed time estimate
Proof. The bounds (7.1) and (7.2) are similar, the only difference arises from the additional n factor in the size of the symbol
![]() $p_A$
. So we will prove the first bound. Using our partition of unity in frequency on the unit scale, we expand
$p_A$
. So we will prove the first bound. Using our partition of unity in frequency on the unit scale, we expand
Here, we will separately estimate each term in
![]() $L^1_x$
based on the size of the symbol. By Proposition 4.3, for frequencies within a unit neighbourhood of
$L^1_x$
based on the size of the symbol. By Proposition 4.3, for frequencies within a unit neighbourhood of
![]() $[k]=(k_1,k_2,k_3,k_4)$
the symbol
$[k]=(k_1,k_2,k_3,k_4)$
the symbol
![]() $b^4_{m,a}$
and its derivatives can be estimated by
$b^4_{m,a}$
and its derivatives can be estimated by
In addition, its support is contained in the region
![]() $\Omega _1 \cup \Omega _2$
, where at least one frequency is in A. The region
$\Omega _1 \cup \Omega _2$
, where at least one frequency is in A. The region
![]() $\Omega _1 \cup \Omega _2$
can be described as the set of those quadruples
$\Omega _1 \cup \Omega _2$
can be described as the set of those quadruples
![]() $[k]$
so that
$[k]$
so that
Without loss in generality, we assume that
![]() $k_1 \in A$
. Then, using the above properties, we can estimate the
$k_1 \in A$
. Then, using the above properties, we can estimate the
![]() $L^1_x$
bound in the lemma as
$L^1_x$
bound in the lemma as
 $$\begin{align*}\| B^4_{m,a}(u) \|_{L^1_x} \lesssim \epsilon^4 \sum_{k_1 \in A} \sum_{[k] \in \Omega_1 \cup \Omega_2} \frac{1}{\langle \delta k^{hi}\rangle \langle \delta k^{med}\rangle} c_{k_1} c_{k_2} c_{k_3} c_{k_4}. \end{align*}$$
$$\begin{align*}\| B^4_{m,a}(u) \|_{L^1_x} \lesssim \epsilon^4 \sum_{k_1 \in A} \sum_{[k] \in \Omega_1 \cup \Omega_2} \frac{1}{\langle \delta k^{hi}\rangle \langle \delta k^{med}\rangle} c_{k_1} c_{k_2} c_{k_3} c_{k_4}. \end{align*}$$
Fixing
![]() $k_1 \in A$
, it suffices to show that
$k_1 \in A$
, it suffices to show that
 $$ \begin{align} S_{k_1} := \sum_{k_2,k_3,k_4} \frac{1}{\langle \delta k^{hi}\rangle \langle \delta k^{med}\rangle} c_{k_2} c_{k_3} c_{k_4} \lesssim c_{k_1}. \end{align} $$
$$ \begin{align} S_{k_1} := \sum_{k_2,k_3,k_4} \frac{1}{\langle \delta k^{hi}\rangle \langle \delta k^{med}\rangle} c_{k_2} c_{k_3} c_{k_4} \lesssim c_{k_1}. \end{align} $$
This no longer has anything to do with the set A. For later use we have also removed the restriction
![]() $[k] \in \Omega _1 \cup \Omega _2$
.
$[k] \in \Omega _1 \cup \Omega _2$
.
To discuss the possible configurations for
![]() $[k]$
, we denote by
$[k]$
, we denote by
![]() $n_1 \leq n_2$
the dyadic size of
$n_1 \leq n_2$
the dyadic size of
![]() $\delta k^{med}$
, respectively
$\delta k^{med}$
, respectively
![]() $\delta k^{hi}$
. By Galilean invariance, we set
$\delta k^{hi}$
. By Galilean invariance, we set
![]() $k_1=0$
, and then the rest of the indices may be reordered so that
$k_1=0$
, and then the rest of the indices may be reordered so that
Then we have
 $$\begin{align*}S \lesssim \sum_{n_1 \leq n_2} \sum_{|k_2| \lesssim n_1} \sum_{|k_4| \approx n_2} \sum_{|k_3-k_4| \lesssim n_1} \frac{1}{n_1 n_2} c_{k_2} c_{k_3} c_{k_4}. \end{align*}$$
$$\begin{align*}S \lesssim \sum_{n_1 \leq n_2} \sum_{|k_2| \lesssim n_1} \sum_{|k_4| \approx n_2} \sum_{|k_3-k_4| \lesssim n_1} \frac{1}{n_1 n_2} c_{k_2} c_{k_3} c_{k_4}. \end{align*}$$
Here, we use twice the envelope maximal function bound to write
 $$\begin{align*}\frac{1}{n_1} \sum_{|k_2| \lesssim n_1} c_{k_2} \lesssim c_0, \qquad \frac{1}{n_1} \sum_{|k_3-k_4| \lesssim n_1} c_{k_3} \lesssim c_{k_4}. \end{align*}$$
$$\begin{align*}\frac{1}{n_1} \sum_{|k_2| \lesssim n_1} c_{k_2} \lesssim c_0, \qquad \frac{1}{n_1} \sum_{|k_3-k_4| \lesssim n_1} c_{k_3} \lesssim c_{k_4}. \end{align*}$$
This gives
 $$\begin{align*}S \lesssim c_0 \sum_{n_1 \leq n_2} \frac{n_1}{n_2} \sum_{|k_4| \approx n_2} c_{k_4}^2 \approx c_0 \sum_{n_2} \sum_{|k_4| \approx n_2} c_{k_4}^2\lesssim c_0. \end{align*}$$
$$\begin{align*}S \lesssim c_0 \sum_{n_1 \leq n_2} \frac{n_1}{n_2} \sum_{|k_4| \approx n_2} c_{k_4}^2 \approx c_0 \sum_{n_2} \sum_{|k_4| \approx n_2} c_{k_4}^2\lesssim c_0. \end{align*}$$
This concludes the proof of equation (7.4) and therefore the proof of the lemma.
Next, we turn our attention to
![]() $R^6_{m,a}$
, which we estimate as follows:
$R^6_{m,a}$
, which we estimate as follows:
Lemma 7.3. Under our bootstrap assumptions (6.5)–(6.8), we have the space-time bound
As above, we also have a similar bound for the momentum:
Corollary 7.4. Assume that the bootstrap bounds (6.5)–(6.8) hold. Let
![]() $\xi _0 \in {\mathbb R}$
, and
$\xi _0 \in {\mathbb R}$
, and
Then we have the space-time bound
Proof. As in the case of the earlier fixed time bound, we will focus on equation (7.5), as the proof of equation (7.6) is essentially the same. We recall
![]() $R^6_{m,a}$
is obtained from the cubic terms in the time derivative of
$R^6_{m,a}$
is obtained from the cubic terms in the time derivative of
![]() $B^4_{m,a}$
. We denote the four frequencies in
$B^4_{m,a}$
. We denote the four frequencies in
![]() $B^4_{m,a}$
by
$B^4_{m,a}$
by
![]() $k_0,k_1,k_2,k_3$
, where the
$k_0,k_1,k_2,k_3$
, where the
![]() $k_0$
factor gets differentiated in time. One of these four frequencies, call it
$k_0$
factor gets differentiated in time. One of these four frequencies, call it
![]() $k_A$
, must be in A.
$k_A$
, must be in A.
With
![]() $k_A$
as above, we expand
$k_A$
as above, we expand
Then it suffices to establish the bound
Here, by Galilean invariance we can set
![]() $k_A=0$
. We also drop the index A, as no localization associated to the set A will be used in the sequel. In particular, we replace
$k_A=0$
. We also drop the index A, as no localization associated to the set A will be used in the sequel. In particular, we replace
![]() $B^4_{m,a}$
by
$B^4_{m,a}$
by
![]() $B^4_{m,0}$
to emphasize that one of the frequencies in
$B^4_{m,0}$
to emphasize that one of the frequencies in
![]() $B^4$
is assumed to be near zero.
$B^4$
is assumed to be near zero.
To describe the size and localization of the symbol
![]() $b^4_{m,0}$
, we introduce as before the notations
$b^4_{m,0}$
, we introduce as before the notations
![]() $\delta k^{med}$
and
$\delta k^{med}$
and
![]() $\delta k^{hi}$
for the distances between
$\delta k^{hi}$
for the distances between
![]() $k_0,k_1,k_2,k_3$
,
$k_0,k_1,k_2,k_3$
,
![]() $n_1 < n_2$
for the dyadic size of
$n_1 < n_2$
for the dyadic size of
![]() $\delta k^{med}$
and
$\delta k^{med}$
and
![]() $\delta k^{hi}$
, and
$\delta k^{hi}$
, and
![]() $\Delta ^4 k$
associated to the same indices. In the support of
$\Delta ^4 k$
associated to the same indices. In the support of
![]() $b^4_{m,0}$
, we must have
$b^4_{m,0}$
, we must have
In this region, the symbol of
![]() $b^4_{m,0}$
as well as its derivatives have size
$b^4_{m,0}$
as well as its derivatives have size
The time differentiation is producing three additional frequencies
![]() $k_4,k_5, k_6$
so that
$k_4,k_5, k_6$
so that
Then equation (7.8) translates to
relative to the indices
![]() $k_1,\cdots , k_6$
.
$k_1,\cdots , k_6$
.
Overall, for
![]() $R^{6}_{m,0}$
we have the decomposition
$R^{6}_{m,0}$
we have the decomposition
where
![]() $\Gamma $
describes the set of indices satisfying equations (7.8) and (7.10). To bound this sum in
$\Gamma $
describes the set of indices satisfying equations (7.8) and (7.10). To bound this sum in
![]() $L^1_{t,x}$
, we consider several cases:
$L^1_{t,x}$
, we consider several cases:
A. If all six frequencies are near
![]() $0$
, then we use the localized
$0$
, then we use the localized
![]() $L^6$
bound to obtain
$L^6$
bound to obtain
which suffices.
B. Otherwise, we denote by
![]() $1 \ll n$
the minimal dyadic size of the interval containing all six k indices. Clearly, we have
$1 \ll n$
the minimal dyadic size of the interval containing all six k indices. Clearly, we have
![]() $n_1 \leq n_2 \leq n$
. Also, due to equation (7.11) we must also have
$n_1 \leq n_2 \leq n$
. Also, due to equation (7.11) we must also have
![]() $|\Delta ^6 k| \ll n$
. This implies that within the set
$|\Delta ^6 k| \ll n$
. This implies that within the set
![]() $(k_1,\cdots ,k_6)$
there must be at least two disjoint pairs of frequencies at distance comparable to n. Applying two bilinear
$(k_1,\cdots ,k_6)$
there must be at least two disjoint pairs of frequencies at distance comparable to n. Applying two bilinear
![]() $L^2$
estimates and
$L^2$
estimates and
![]() $L^{\infty }$
bounds for the other two factors, we can bound
$L^{\infty }$
bounds for the other two factors, we can bound
 $$ \begin{align} \|R^{6}_{m,0}(u)\|_{L^1_{t,x}} \lesssim \epsilon^6 C^4 S, \qquad S := \sum_{n_1 \leq n_2} \sum_{k_{0-6} \in \Gamma} \frac{1}{n_1 n_2 n} c_{k_1} c_{k_2}c_{k_3} c_{k_4} c_{k_5} c_{k_6}. \end{align} $$
$$ \begin{align} \|R^{6}_{m,0}(u)\|_{L^1_{t,x}} \lesssim \epsilon^6 C^4 S, \qquad S := \sum_{n_1 \leq n_2} \sum_{k_{0-6} \in \Gamma} \frac{1}{n_1 n_2 n} c_{k_1} c_{k_2}c_{k_3} c_{k_4} c_{k_5} c_{k_6}. \end{align} $$
It remains to bound the above sum S by
There are several cases to consider:
B1.
![]() $k_0 = 0$
. Relabeling, we may assume that
$k_0 = 0$
. Relabeling, we may assume that
We distinguish further cases by comparing
![]() $n_2$
and n.
$n_2$
and n.
B1a.
![]() $n \gg n_2$
. Then we may assume that
$n \gg n_2$
. Then we may assume that
For fixed
![]() $k_4$
, we can apply the Cauchy–Schwarz inequality for the pair of indices
$k_4$
, we can apply the Cauchy–Schwarz inequality for the pair of indices
![]() $(k_5,k_6)$
, and also for
$(k_5,k_6)$
, and also for
![]() $(k_2,k_3)$
. We obtain
$(k_2,k_3)$
. We obtain
 $$\begin{align*}S \lesssim \sum_{n_1 \leq n_2 \ll n} \sum_{|k_1| \approx n_1, |k_4| \lesssim n} \frac{1}{n_2 n} c_{k_1} c_{k_4} c_{n_2}^2 c_{n}^2 = \sum_{n_2 \ll n} \sum_{|k_1| \leq n_2, |k_4| \lesssim n} \frac{1}{n_2 n} c_{k_1} c_{k_4} c_{n_2}^2 c_{n}^2. \end{align*}$$
$$\begin{align*}S \lesssim \sum_{n_1 \leq n_2 \ll n} \sum_{|k_1| \approx n_1, |k_4| \lesssim n} \frac{1}{n_2 n} c_{k_1} c_{k_4} c_{n_2}^2 c_{n}^2 = \sum_{n_2 \ll n} \sum_{|k_1| \leq n_2, |k_4| \lesssim n} \frac{1}{n_2 n} c_{k_1} c_{k_4} c_{n_2}^2 c_{n}^2. \end{align*}$$
Now, we use twice the envelope maximal bound for the
![]() $k_1$
, respectively
$k_1$
, respectively
![]() $k_4$
summation to get
$k_4$
summation to get
B1b.
![]() $k_0 = 0$
,
$k_0 = 0$
,
![]() $n \approx n_2$
. In this case, we can introduce another dyadic parameter
$n \approx n_2$
. In this case, we can introduce another dyadic parameter
![]() $n_3 \leq n$
so that, after relabeling,
$n_3 \leq n$
so that, after relabeling,
Then applying Cauchy–Schwarz inequality exactly as above we arrive at
 $$\begin{align*}S \lesssim \sum_{n_3 \leq n_2} \sum_{|k_1| \leq n_2, |k_4| < n_3} \frac{1}{n_2^2} c_{k_1} c_{k_4} c_{n_2}^2 c_{n_3}^2, \end{align*}$$
$$\begin{align*}S \lesssim \sum_{n_3 \leq n_2} \sum_{|k_1| \leq n_2, |k_4| < n_3} \frac{1}{n_2^2} c_{k_1} c_{k_4} c_{n_2}^2 c_{n_3}^2, \end{align*}$$
where we can conclude again by applying twice the envelope maximal bound for the
![]() $k_1$
, respectively the
$k_1$
, respectively the
![]() $k_4$
summation relative to
$k_4$
summation relative to
![]() $0$
.
$0$
.
B2.
![]() $k_1 = 0$
,
$k_1 = 0$
,
![]() $|k_0| \approx n_1$
. In this case, we must also have
$|k_0| \approx n_1$
. In this case, we must also have
Again, we compare n and
![]() $n_2$
:
$n_2$
:
B2a.
![]() $n \gg n_2$
. Here, we can assume again that equation (7.15) holds. As in case B1a, we apply the Cauchy–Schwarz inequality for the pair of indices
$n \gg n_2$
. Here, we can assume again that equation (7.15) holds. As in case B1a, we apply the Cauchy–Schwarz inequality for the pair of indices
![]() $(k_5,k_6)$
and also for
$(k_5,k_6)$
and also for
![]() $(k_3,k_2)$
, with the difference that now the difference
$(k_3,k_2)$
, with the difference that now the difference
![]() $k_5-k_6$
is no longer fixed, instead it varies in an
$k_5-k_6$
is no longer fixed, instead it varies in an
![]() $n_1$
range. Thus, we lose two
$n_1$
range. Thus, we lose two
![]() $n_1$
factors, obtaining
$n_1$
factors, obtaining
 $$\begin{align*}S \lesssim c_{0} \sum_{n_1 \leq n_2 \ll n} \sum_{|k_4| < n} \frac{n_1}{n_2 n} c_{k_4} c_{n_2}^2 c_{n}^2. \end{align*}$$
$$\begin{align*}S \lesssim c_{0} \sum_{n_1 \leq n_2 \ll n} \sum_{|k_4| < n} \frac{n_1}{n_2 n} c_{k_4} c_{n_2}^2 c_{n}^2. \end{align*}$$
The
![]() $n_1$
summation is trivial now, and for the
$n_1$
summation is trivial now, and for the
![]() $k_4$
summation we use the envelope maximal bound to obtain
$k_4$
summation we use the envelope maximal bound to obtain
B2b.
![]() $n \approx n_2$
. Here, we take two subcases.
$n \approx n_2$
. Here, we take two subcases.
B2b(i). If
then we use the Cauchy–Schwarz inequality for the pair
![]() $(k_2,k_3)$
to obtain
$(k_2,k_3)$
to obtain
 $$\begin{align*}S \lesssim c_0 \sum_{n_1 \leq n_2} \frac{1}{n_2^2} c_{n_2}^2 \sum_{|k_4|+|k_5|+|k_6| \lesssim n_1} c_{k_4} c_{k_5} c_{k_6}. \end{align*}$$
$$\begin{align*}S \lesssim c_0 \sum_{n_1 \leq n_2} \frac{1}{n_2^2} c_{n_2}^2 \sum_{|k_4|+|k_5|+|k_6| \lesssim n_1} c_{k_4} c_{k_5} c_{k_6}. \end{align*}$$
Finally, we use the envelope maximal bound for the
![]() $k_4$
summation relative to
$k_4$
summation relative to
![]() $0$
and for
$0$
and for
![]() $k_5$
relative to
$k_5$
relative to
![]() $k_6$
to get
$k_6$
to get
 $$\begin{align*}S \lesssim c_0^2 \sum_{n_1 \leq n_2} \frac{n_1^2}{n_2^2} c_{n_2}^2 c_{\leq n_1}^2 \lesssim c_0^2 \sum_{ n_2} c_{n_2}^2 c_{\leq n_2}^2 \lesssim c_0^2, \end{align*}$$
$$\begin{align*}S \lesssim c_0^2 \sum_{n_1 \leq n_2} \frac{n_1^2}{n_2^2} c_{n_2}^2 c_{\leq n_1}^2 \lesssim c_0^2 \sum_{ n_2} c_{n_2}^2 c_{\leq n_2}^2 \lesssim c_0^2, \end{align*}$$
which suffices.
B2b(ii). If instead
then we can introduce
![]() $n_3$
as in equation (7.16), with
$n_3$
as in equation (7.16), with
![]() $ n_1 \ll n_3 \leq n_2$
. Applying the Cauchy–Schwarz inequality for the pair of indices
$ n_1 \ll n_3 \leq n_2$
. Applying the Cauchy–Schwarz inequality for the pair of indices
![]() $(k_5,k_6)$
, and
$(k_5,k_6)$
, and
![]() $(k_2,k_3)$
yields
$(k_2,k_3)$
yields
 $$\begin{align*}S \lesssim c_0 \sum_{n_1 \ll n_3 \leq n_2} \sum_{|k_4| < n_3} \frac{n_1}{n_2^2} c_{k_4} c_{n_2}^2 c_{n_3}^2 \approx c_0 \sum_{n_3 \leq n_2} \sum_{|k_4| < n_3} \frac{n_3}{n_2^2} c_{k_4} c_{n_2}^2 c_{n_3}^2. \end{align*}$$
$$\begin{align*}S \lesssim c_0 \sum_{n_1 \ll n_3 \leq n_2} \sum_{|k_4| < n_3} \frac{n_1}{n_2^2} c_{k_4} c_{n_2}^2 c_{n_3}^2 \approx c_0 \sum_{n_3 \leq n_2} \sum_{|k_4| < n_3} \frac{n_3}{n_2^2} c_{k_4} c_{n_2}^2 c_{n_3}^2. \end{align*}$$
At this stage, we complete the argument by using the envelope maximal bound for the
![]() $k_4$
summation.
$k_4$
summation.
B3.
![]() $k_1 = 0$
,
$k_1 = 0$
,
![]() $|k_0| \approx n_2 \gg n_1$
. In this case, we may assume that
$|k_0| \approx n_2 \gg n_1$
. In this case, we may assume that
Next, we compare
![]() $n_2$
and n:
$n_2$
and n:
B3a.
![]() $n_2 \ll n$
. Retaining
$n_2 \ll n$
. Retaining
![]() $k_0$
as a summation index, we first apply the Cauchy–Schwarz inequality for the pair
$k_0$
as a summation index, we first apply the Cauchy–Schwarz inequality for the pair
![]() $(k_5,k_6)$
to obtain
$(k_5,k_6)$
to obtain
 $$\begin{align*}\begin{aligned} S \lesssim & \ c_0 \sum_{n_1 \ll n_2 \ll n} \sum_{|k_0| \approx n_2} \sum_{|k_2| \approx n_1} \sum_{|k_0 - k_3| \approx n_1} \sum_{|k_4| \lesssim n} \frac{1}{n_1 n_2 n}c_{k_2} c_{k_3} c_{k_4} c_n^2 \\ \lesssim & \ c_0 \sum_{n_1 \ll n_2 \ll n} \sum_{|k_3| \approx n_2} \sum_{|k_2| \approx n_1} \sum_{|k_4| \lesssim n} \frac{1}{ n_2 n}c_{k_2} c_{k_3} c_{k_4}c_n^2 \\ = & \ c_0 \sum_{n_2 \ll n} \sum_{|k_3| \approx n_2} \sum_{|k_2| \ll n_2} \sum_{|k_4| \lesssim n} \frac{1}{ n_2 n} c_{k_2} c_{k_3} c_{k_4}c_n^2. \end{aligned} \end{align*}$$
$$\begin{align*}\begin{aligned} S \lesssim & \ c_0 \sum_{n_1 \ll n_2 \ll n} \sum_{|k_0| \approx n_2} \sum_{|k_2| \approx n_1} \sum_{|k_0 - k_3| \approx n_1} \sum_{|k_4| \lesssim n} \frac{1}{n_1 n_2 n}c_{k_2} c_{k_3} c_{k_4} c_n^2 \\ \lesssim & \ c_0 \sum_{n_1 \ll n_2 \ll n} \sum_{|k_3| \approx n_2} \sum_{|k_2| \approx n_1} \sum_{|k_4| \lesssim n} \frac{1}{ n_2 n}c_{k_2} c_{k_3} c_{k_4}c_n^2 \\ = & \ c_0 \sum_{n_2 \ll n} \sum_{|k_3| \approx n_2} \sum_{|k_2| \ll n_2} \sum_{|k_4| \lesssim n} \frac{1}{ n_2 n} c_{k_2} c_{k_3} c_{k_4}c_n^2. \end{aligned} \end{align*}$$
Now, we use the envelope maximal bound for
![]() $k_4$
relative to
$k_4$
relative to
![]() $0$
and for
$0$
and for
![]() $k_2$
relative to
$k_2$
relative to
![]() $k_3$
. This yields
$k_3$
. This yields
 $$\begin{align*}S \lesssim c_0^2 \sum_{n_2 \ll n} \sum_{|k_3| \approx n_2} c_{k_3}^2 c_n^2 \approx c_0^2. \end{align*}$$
$$\begin{align*}S \lesssim c_0^2 \sum_{n_2 \ll n} \sum_{|k_3| \approx n_2} c_{k_3}^2 c_n^2 \approx c_0^2. \end{align*}$$
B3b.
![]() $n = n_2$
. In this case, we dispense with
$n = n_2$
. In this case, we dispense with
![]() $k_0$
as a summation index, retaining instead the relation
$k_0$
as a summation index, retaining instead the relation
At least one of the frequencies
![]() $k_4,k_5,k_6$
must have size
$k_4,k_5,k_6$
must have size
![]() $n_2$
, say
$n_2$
, say
![]() $|k_6| \approx n_2$
. Then we use the Cauchy–Schwarz inequality for the
$|k_6| \approx n_2$
. Then we use the Cauchy–Schwarz inequality for the
![]() $(k_3,k_6)$
pair, losing an
$(k_3,k_6)$
pair, losing an
![]() $n_1$
factor due to the relation above, and arriving at
$n_1$
factor due to the relation above, and arriving at
 $$\begin{align*}S \lesssim c_0 \sum_{n_1 \leq n_2 } \sum_{|k_2| \approx n_1} \sum_{|k_4|,|k_5| \leq n_2} \frac{1}{n_2^2}c_{k_2} c_{k_4} c_{k_5} c_{n_2}^2 \approx c_0 \sum_{|k_2|,|k_4|,|k_5| \leq n_2} \frac{1}{n_2^2}c_{k_2} c_{k_4} c_{k_5} c_{n_2}^2. \end{align*}$$
$$\begin{align*}S \lesssim c_0 \sum_{n_1 \leq n_2 } \sum_{|k_2| \approx n_1} \sum_{|k_4|,|k_5| \leq n_2} \frac{1}{n_2^2}c_{k_2} c_{k_4} c_{k_5} c_{n_2}^2 \approx c_0 \sum_{|k_2|,|k_4|,|k_5| \leq n_2} \frac{1}{n_2^2}c_{k_2} c_{k_4} c_{k_5} c_{n_2}^2. \end{align*}$$
Finally, we use the envelope maximal bound for
![]() $k_2$
relative to
$k_2$
relative to
![]() $0$
and for
$0$
and for
![]() $k_4$
relative to
$k_4$
relative to
![]() $k_5$
to obtain
$k_5$
to obtain
This concludes the proof of the lemma.
B4.
![]() $k_2=0$
. Here, we can assume that
$k_2=0$
. Here, we can assume that
but the size of
![]() $k_0$
is both not set and not needed. Instead, we will simply rely on equation (7.11) and consider two subcases.
$k_0$
is both not set and not needed. Instead, we will simply rely on equation (7.11) and consider two subcases.
B4a.
![]() $n_2 \ll n$
, where we can assume that equation (7.15) holds. Here, we first use the maximal function for
$n_2 \ll n$
, where we can assume that equation (7.15) holds. Here, we first use the maximal function for
![]() $c_{k_1}$
to estimate
$c_{k_1}$
to estimate
 $$\begin{align*}S \leq c_0^2 \sum_{n_1 \leq n_2 \ll n} \frac{1}{n_2n} c_{k_3} c_{k_4} c_{k_5} c_{k_6}, \end{align*}$$
$$\begin{align*}S \leq c_0^2 \sum_{n_1 \leq n_2 \ll n} \frac{1}{n_2n} c_{k_3} c_{k_4} c_{k_5} c_{k_6}, \end{align*}$$
where we retain the constraint relative to
![]() $k_3,k_4,k_5,k_6$
,
$k_3,k_4,k_5,k_6$
,
Here, we can fix
![]() $\Delta ^4 k$
at the expense of another
$\Delta ^4 k$
at the expense of another
![]() $n_1$
factor. Then fixing
$n_1$
factor. Then fixing
![]() $k_3$
and
$k_3$
and
![]() $k_4$
fixes the difference
$k_4$
fixes the difference
![]() $k_5-k_6$
, so applying the Cauchy–Schwarz inequality with respect to
$k_5-k_6$
, so applying the Cauchy–Schwarz inequality with respect to
![]() $k_5$
,
$k_5$
,
![]() $k_6$
we arrive at
$k_6$
we arrive at
Finally, using Hölder’s inequality for
![]() $k_3$
and
$k_3$
and
![]() $k_4$
, which have size
$k_4$
, which have size
![]() $n_2$
, respectively
$n_2$
, respectively
![]() $\leq h$
yields
$\leq h$
yields
B4b.
![]() $n_2 \approx n$
. Here, the case
$n_2 \approx n$
. Here, the case
![]() $n_1 \approx n_2$
is straightforward, as we can directly apply once the Cauchy–Schwartz inequality for two size n frequencies, twice Hölder’s inequality and once the maximal function bound for the three remaining frequencies of size
$n_1 \approx n_2$
is straightforward, as we can directly apply once the Cauchy–Schwartz inequality for two size n frequencies, twice Hölder’s inequality and once the maximal function bound for the three remaining frequencies of size
![]() $\lesssim n$
. We are left with the more interesting case when
$\lesssim n$
. We are left with the more interesting case when
![]() $n_1 \ll n$
. There, using again the maximal function for
$n_1 \ll n$
. There, using again the maximal function for
![]() $c_{k_1}$
we estimate
$c_{k_1}$
we estimate
 $$\begin{align*}S \leq c_0^2 \sum_{n_1 \leq n_2 \ll n} \frac{1}{n^2} c_{k_3} c_{k_4} c_{k_5} c_{k_6}, \end{align*}$$
$$\begin{align*}S \leq c_0^2 \sum_{n_1 \leq n_2 \ll n} \frac{1}{n^2} c_{k_3} c_{k_4} c_{k_5} c_{k_6}, \end{align*}$$
where for the four remaining indices we have
![]() $|\Delta ^4 k| \lesssim n_1 \ll n$
. Here,
$|\Delta ^4 k| \lesssim n_1 \ll n$
. Here,
![]() $|k_3| \approx n$
, so there must be at least one other frequency of size n. Then, as in the previous case, we apply once the Cauchy–Schwartz inequality for the two size n frequencies, and twice Hölder’s inequality for the two remaining frequencies of size
$|k_3| \approx n$
, so there must be at least one other frequency of size n. Then, as in the previous case, we apply once the Cauchy–Schwartz inequality for the two size n frequencies, and twice Hölder’s inequality for the two remaining frequencies of size
![]() $\lesssim n$
. This concludes the proof of the lemma.
$\lesssim n$
. This concludes the proof of the lemma.
7.2 The energy estimate
Our objective here is to prove the bound (6.1). We remark that once this is proved, we may drop the
![]() $C^4$
factor in Lemma 7.1. By the Galilean invariance, it suffices to prove the desired bound (6.1) at
$C^4$
factor in Lemma 7.1. By the Galilean invariance, it suffices to prove the desired bound (6.1) at
![]() $k = 0$
. For this, we consider a symbol
$k = 0$
. For this, we consider a symbol
![]() $a(\xi _1,\xi _2)$
of the form
$a(\xi _1,\xi _2)$
of the form
with
![]() $a_0$
localized near frequency
$a_0$
localized near frequency
![]() $0$
on the unit scale. Then
$0$
on the unit scale. Then
and we need to bound this quantity uniformly in time,
For this, we use the density-flux relation (4.26) with
![]() $\xi _0 = 0$
, which yields
$\xi _0 = 0$
, which yields
where
To prove equation (7.20), we integrate the above density-flux relation in
![]() $t,x$
to obtain:
$t,x$
to obtain:
 $$ \begin{align} \left. \int M_a(u) + B^4_{m,a}(u) \, dx \right|{}_0^T = \int_{0}^T \int_{\mathbb R} R^6_{m,a}(u) \ dx dt. \end{align} $$
$$ \begin{align} \left. \int M_a(u) + B^4_{m,a}(u) \, dx \right|{}_0^T = \int_{0}^T \int_{\mathbb R} R^6_{m,a}(u) \ dx dt. \end{align} $$
Finally, we can estimate the contributions of
![]() $B^4_{m,a}$
and
$B^4_{m,a}$
and
![]() $R^6_{m,a}$
using Lemma 7.1, respectively Lemma 7.3.
$R^6_{m,a}$
using Lemma 7.1, respectively Lemma 7.3.
Remark 7.5. For later use, we observe that once the energy bounds (6.1) have been established, then they can be used instead of the bootstrap assumption (6.5) in the proof of Lemma 7.1. This leads to a stronger form of equations (7.1), (7.2), with the constant C removed:
7.3 The localized Interaction Morawetz
Our objective here is to prove the bounds (6.2) and (6.3) using our bootstrap assumptions. By the Galilean invariance, it suffices to do this at
![]() $k=0$
. This will be achieved using our Interaction Morawetz identity (5.9) with
$k=0$
. This will be achieved using our Interaction Morawetz identity (5.9) with
![]() $v=u$
and with a localized at frequency
$v=u$
and with a localized at frequency
![]() $0$
, exactly as in equation (7.19). For such a, we can simply set
$0$
, exactly as in equation (7.19). For such a, we can simply set
![]() $\xi _0=0$
. It will suffice to estimate the quantities in equation (5.9) as follows:
$\xi _0=0$
. It will suffice to estimate the quantities in equation (5.9) as follows:
 $$ \begin{align} \int_0^T \mathbf{J}^6_a(u,u)\, dt \approx \| A_0(D)^{\frac23} u\|_{L^6_{t,x}}^6 + O(\epsilon^5 C^6 c_0^4) , \end{align} $$
$$ \begin{align} \int_0^T \mathbf{J}^6_a(u,u)\, dt \approx \| A_0(D)^{\frac23} u\|_{L^6_{t,x}}^6 + O(\epsilon^5 C^6 c_0^4) , \end{align} $$
 $$ \begin{align} \int_0^T \mathbf{J}^8_a(u,u)\, dt = O(\epsilon^5 C^6 c_0^4), \end{align} $$
$$ \begin{align} \int_0^T \mathbf{J}^8_a(u,u)\, dt = O(\epsilon^5 C^6 c_0^4), \end{align} $$
 $$ \begin{align} \int_0^T\mathbf{K}^8_a(u,u)\, dt = O(\epsilon^5 C^8 c_0^4). \end{align} $$
$$ \begin{align} \int_0^T\mathbf{K}^8_a(u,u)\, dt = O(\epsilon^5 C^8 c_0^4). \end{align} $$
This allows us to estimate the localized Interaction Morawetz term, as well as the localized
![]() $L^6$
norm as in equations (6.2) and (6.3), provided that
$L^6$
norm as in equations (6.2) and (6.3), provided that
![]() $\epsilon $
is small enough. There is nothing to do for
$\epsilon $
is small enough. There is nothing to do for
![]() $\mathbf {J}^4_{a}$
, so we consider the remaining contributions:
$\mathbf {J}^4_{a}$
, so we consider the remaining contributions:
7.3.1 The
 $\mathbf {I}_a$
bound
$\mathbf {I}_a$
bound
The Interaction Morawetz functional
![]() $\mathbf {I}_a$
is as in equation (5.8), with
$\mathbf {I}_a$
is as in equation (5.8), with
![]() $\xi _0=0$
,
$\xi _0=0$
,
 $$ \begin{align} \mathbf{I}_{a} = \iint_{x> y} M^{\sharp}_a(u)(x) P^{\sharp}_{a}(v) (y) - P^{\sharp}_{a}(u)(x) M^{\sharp}_{a}(v) (y)\, dx dy \end{align} $$
$$ \begin{align} \mathbf{I}_{a} = \iint_{x> y} M^{\sharp}_a(u)(x) P^{\sharp}_{a}(v) (y) - P^{\sharp}_{a}(u)(x) M^{\sharp}_{a}(v) (y)\, dx dy \end{align} $$
with
For
![]() $B^4_{m,a}$
and
$B^4_{m,a}$
and
![]() $B^4_{p,a}$
, we have the
$B^4_{p,a}$
, we have the
![]() $L^{\infty }_tL^1_x$
bound (7.22). For
$L^{\infty }_tL^1_x$
bound (7.22). For
![]() $M_a(u)$
and
$M_a(u)$
and
![]() $P_a(u)$
, we have the straightforward uniform in time bounds
$P_a(u)$
, we have the straightforward uniform in time bounds
Combining this with equation (7.22), the estimate (7.23) immediately follows.
7.3.2 The
 $\mathbf {J}^6_a$
bound
$\mathbf {J}^6_a$
bound
This is a
![]() $6$
-linear expression whose expression we recall from equation (5.10),
$6$
-linear expression whose expression we recall from equation (5.10),
where again we have set
![]() $\xi _0 = 0$
.
$\xi _0 = 0$
.
We first discuss the symbol localization properties for
![]() $\mathbf {J}^6_a$
with respect to the six entries at frequencies
$\mathbf {J}^6_a$
with respect to the six entries at frequencies
![]() $k_1$
,
$k_1$
,
![]() $k_2$
,
$k_2$
,
![]() $k_3$
,
$k_3$
,
![]() $k_4$
,
$k_4$
,
![]() $k_5$
and
$k_5$
and
![]() $k_6$
. Here, we a priori have two frequencies close to
$k_6$
. Here, we a priori have two frequencies close to
![]() $0$
, say
$0$
, say
![]() $k_5 = k_6=0$
, namely those arising from
$k_5 = k_6=0$
, namely those arising from
![]() $M_a$
,
$M_a$
,
![]() $P_a$
and
$P_a$
and
![]() $E_a$
, all of which have smooth and bounded symbols. In the symbols for
$E_a$
, all of which have smooth and bounded symbols. In the symbols for
![]() $B^4_a$
and
$B^4_a$
and
![]() $R^4_a$
, on the other hand, we have at least one frequency equal to zero, say
$R^4_a$
, on the other hand, we have at least one frequency equal to zero, say
![]() $k_1=0$
, and the near-diagonal property
$k_1=0$
, and the near-diagonal property
![]() $\Delta ^4 k= 0$
.
$\Delta ^4 k= 0$
.
Next, we consider the size of the symbols, where we use Proposition 4.3. This gives the following symbol bounds regardless of the p or m index:
and similarly for their derivatives. We split the analysis in two cases, depending on whether all frequencies are equal (i.e.,
![]() $\delta k^{hi} \lesssim 1$
) or not.
$\delta k^{hi} \lesssim 1$
) or not.
A. The case of separated frequencies,
![]() $\delta k^{hi} \gg 1$
. To fix the notations, suppose that
$\delta k^{hi} \gg 1$
. To fix the notations, suppose that
![]() $|k_2| \approx \delta k^{med} \approx n_1$
and
$|k_2| \approx \delta k^{med} \approx n_1$
and
![]() $|k_3| \approx |k_4|\approx \delta k^{hi} \approx n_2$
, where
$|k_3| \approx |k_4|\approx \delta k^{hi} \approx n_2$
, where
![]() $n_1 \leq n_2$
represent dyadic scales. Then we can apply two bilinear
$n_1 \leq n_2$
represent dyadic scales. Then we can apply two bilinear
![]() $L^2$
bounds (6.7) for the frequency pairs
$L^2$
bounds (6.7) for the frequency pairs
![]() $(k_1=0,k_4)$
and
$(k_1=0,k_4)$
and
![]() $(k_2,k_3)$
and simply estimate the
$(k_2,k_3)$
and simply estimate the
![]() $k_5$
and
$k_5$
and
![]() $k_6$
factors in
$k_6$
factors in
![]() $L^{\infty }$
by Bernstein’s inequality. This yields the bound for the corresponding portion of
$L^{\infty }$
by Bernstein’s inequality. This yields the bound for the corresponding portion of
![]() $J^6_a$
$J^6_a$
 $$\begin{align*}\left|\int _0^T\mathbf{J}^{6,unbal}_a(u)\, dt \right| \lesssim \epsilon^6 C^6 c_0^3 \sum_{k_2,k_3,k_4} \frac{1}{n_1 n_2} c_{k_2} c_{k_3} c_{k_4}. \end{align*}$$
$$\begin{align*}\left|\int _0^T\mathbf{J}^{6,unbal}_a(u)\, dt \right| \lesssim \epsilon^6 C^6 c_0^3 \sum_{k_2,k_3,k_4} \frac{1}{n_1 n_2} c_{k_2} c_{k_3} c_{k_4}. \end{align*}$$
Since
![]() $k_4-k_3=k_2$
, for fixed
$k_4-k_3=k_2$
, for fixed
![]() $k_2$
we can apply the Cauchy–Schwartz inequality with respect to the
$k_2$
we can apply the Cauchy–Schwartz inequality with respect to the
![]() $k_3$
and
$k_3$
and
![]() $k_4$
indices to obtain
$k_4$
indices to obtain
 $$\begin{align*}\left|\int_0^T\mathbf{J}^{6,unbal}_a(u)\, dt \right| \lesssim \epsilon^6 C^6 c_0^3 \sum_{|k_2| \approx n_1 \leq n_2} \frac{1}{n_1 n_2} c_{k_2} c_{n_2}^2. \end{align*}$$
$$\begin{align*}\left|\int_0^T\mathbf{J}^{6,unbal}_a(u)\, dt \right| \lesssim \epsilon^6 C^6 c_0^3 \sum_{|k_2| \approx n_1 \leq n_2} \frac{1}{n_1 n_2} c_{k_2} c_{n_2}^2. \end{align*}$$
Finally, using the maximal function property for
![]() $c_{k_2}$
we arrive at
$c_{k_2}$
we arrive at
 $$\begin{align*}\left|\int_0^T\mathbf{J}^{6,unbal}_a(u)\, dt\right| \lesssim \epsilon^6 C^6 c_0^4 \sum_{n_2} \frac{\log n_2}{ n_2} c_{n_2}^2, \end{align*}$$
$$\begin{align*}\left|\int_0^T\mathbf{J}^{6,unbal}_a(u)\, dt\right| \lesssim \epsilon^6 C^6 c_0^4 \sum_{n_2} \frac{\log n_2}{ n_2} c_{n_2}^2, \end{align*}$$
which suffices.
B. The case of equal frequencies,
![]() $\delta k^{hi} \lesssim 1$
. Here, we have
$\delta k^{hi} \lesssim 1$
. Here, we have
![]() $|k_j| \lesssim 1$
for all j, and the symbol of
$|k_j| \lesssim 1$
for all j, and the symbol of
![]() $j^6_a$
is smooth and bounded. The important feature here is the symbol of the 6-linear form
$j^6_a$
is smooth and bounded. The important feature here is the symbol of the 6-linear form
![]() $J^6_0$
on the diagonal
$J^6_0$
on the diagonal
which we would like to be positive. But we know this by equation (5.13), which shows that this equals
It follows that we can write the symbol
![]() $j^6_a$
in the form
$j^6_a$
in the form
where
![]() $b_0(\xi ) = a_0(\xi )^{\frac 23} c(\xi , \xi , \xi )^{\frac 16}$
and
$b_0(\xi ) = a_0(\xi )^{\frac 23} c(\xi , \xi , \xi )^{\frac 16}$
and
![]() $j^{6,rem}_0$
vanishes when all
$j^{6,rem}_0$
vanishes when all
![]() $\xi $
’s are equal. Then we can write
$\xi $
’s are equal. Then we can write
![]() $j^{6,rem}_0$
as a linear combination of terms
$j^{6,rem}_0$
as a linear combination of terms
![]() $\xi _{even} -\xi _{odd}$
with smooth coefficients. The first term yields the desired
$\xi _{even} -\xi _{odd}$
with smooth coefficients. The first term yields the desired
![]() $L^6$
norm,
$L^6$
norm,
On the other hand the contribution
![]() $\mathbf {J}^{6,rem}_a$
of the second term be estimated using a bilinear
$\mathbf {J}^{6,rem}_a$
of the second term be estimated using a bilinear
![]() $L^2$
bound (6.7), three
$L^2$
bound (6.7), three
![]() $L^6$
bounds (6.6) and one
$L^6$
bounds (6.6) and one
![]() $L^{\infty }$
via Bernstein’s inequality,
$L^{\infty }$
via Bernstein’s inequality,
 $$\begin{align*}\left|\int_0^T\mathbf{J}^{6,rem}_a(u)\, dt \right| \lesssim \|J^{6,rem}_a(u)\|_{L^1_{t,x}} \lesssim (C \epsilon^2 c_0^2) C^3(\epsilon c_0)^2 C \epsilon c_0 = C^5 \epsilon^5 c_0^5, \end{align*}$$
$$\begin{align*}\left|\int_0^T\mathbf{J}^{6,rem}_a(u)\, dt \right| \lesssim \|J^{6,rem}_a(u)\|_{L^1_{t,x}} \lesssim (C \epsilon^2 c_0^2) C^3(\epsilon c_0)^2 C \epsilon c_0 = C^5 \epsilon^5 c_0^5, \end{align*}$$
which suffices.
7.3.3 The bound for
 $\mathbf {J}^8_0$
$\mathbf {J}^8_0$
We recall that
![]() $\mathbf {J}^8_0$
has an expression of the form
$\mathbf {J}^8_0$
has an expression of the form
see equation (5.11) where we set
![]() $\xi _0 = 0$
. For this, we need to show that
$\xi _0 = 0$
. For this, we need to show that
 $$\begin{align*}\left| \int_0^T\mathbf{J}^8_a\, dt\right| \lesssim \epsilon^6 c_0^4. \end{align*}$$
$$\begin{align*}\left| \int_0^T\mathbf{J}^8_a\, dt\right| \lesssim \epsilon^6 c_0^4. \end{align*}$$
This is an
![]() $8$
-linear term which has two factors, both of which are
$8$
-linear term which has two factors, both of which are
![]() $4$
-linear terms with output at frequency
$4$
-linear terms with output at frequency
![]() $0$
and one factor at frequency
$0$
and one factor at frequency
![]() $0$
. But the symbols are not the same, that is, we have more decay in
$0$
. But the symbols are not the same, that is, we have more decay in
![]() $B^4_a$
than in
$B^4_a$
than in
![]() $R^4_a$
.
$R^4_a$
.
As usual, we localize the entries of
![]() $\mathbf {J}^8_a$
on the unit frequency scale and estimate each term separately. We denote the four frequencies in
$\mathbf {J}^8_a$
on the unit frequency scale and estimate each term separately. We denote the four frequencies in
![]() $B^4_a$
by
$B^4_a$
by
![]() $k_1,k_2,k_3.k_4$
with
$k_1,k_2,k_3.k_4$
with
![]() $k_1 = 0$
and the four frequencies in
$k_1 = 0$
and the four frequencies in
![]() $R^4_a$
by
$R^4_a$
by
![]() $l_1,l_2,l_3,l_4$
with
$l_1,l_2,l_3,l_4$
with
![]() $l_1=0$
. These are constrained by the relations
$l_1=0$
. These are constrained by the relations
![]() $\Delta ^4 k = 0$
,
$\Delta ^4 k = 0$
,
![]() $\Delta ^4 l=0$
. In addition, their symbols are bounded, along with their derivatives, as follows:
$\Delta ^4 l=0$
. In addition, their symbols are bounded, along with their derivatives, as follows:
We consider several cases:
A) All eight frequencies are close to zero. Then we use six
![]() $L^6_{t,x}$
Strichartz bounds as in equation (6.6) and two
$L^6_{t,x}$
Strichartz bounds as in equation (6.6) and two
![]() $L^{\infty }$
bounds obtained from the energy via Bernstein’s inequality.
$L^{\infty }$
bounds obtained from the energy via Bernstein’s inequality.
B) Some frequencies are away from zero. Denote by
![]() $n_1 \leq n_2$
the dyadic separations for the
$n_1 \leq n_2$
the dyadic separations for the
![]() $k_j$
frequencies in
$k_j$
frequencies in
![]() $B_4$
, and by
$B_4$
, and by
![]() $o_1 \leq o_2$
the dyadic separations for the
$o_1 \leq o_2$
the dyadic separations for the
![]() $l_j$
frequencies in
$l_j$
frequencies in
![]() $R_4$
. We consider two cases depending on how
$R_4$
. We consider two cases depending on how
![]() $n_2$
and
$n_2$
and
![]() $o_2$
compare.
$o_2$
compare.
B1)
![]() $n_2 \lesssim o_2$
. Then the
$n_2 \lesssim o_2$
. Then the
![]() $R^4$
frequencies are in two
$R^4$
frequencies are in two
![]() $o_2$
separated clusters with distance below
$o_2$
separated clusters with distance below
![]() $o_1$
within each cluster. We use two bilinear
$o_1$
within each cluster. We use two bilinear
![]() $L^2$
bounds there, and
$L^2$
bounds there, and
![]() $L^{\infty }$
bounds for all the
$L^{\infty }$
bounds for all the
![]() $B^4_a$
factors to estimate
$B^4_a$
factors to estimate
 $$\begin{align*}\left|\int_0^T \mathbf{J}^8_a(u)\, dt\right| \lesssim \epsilon^8 C^6 c_0^2 \sum \frac{1}{n_1 n_2} c_{k_2} c_{k_3} c_{k_4} \frac{1}{o_1 o_2} c_{l_2} c_{l_3} c_{l_4}. \end{align*}$$
$$\begin{align*}\left|\int_0^T \mathbf{J}^8_a(u)\, dt\right| \lesssim \epsilon^8 C^6 c_0^2 \sum \frac{1}{n_1 n_2} c_{k_2} c_{k_3} c_{k_4} \frac{1}{o_1 o_2} c_{l_2} c_{l_3} c_{l_4}. \end{align*}$$
Suppose
![]() $k_2$
and
$k_2$
and
![]() $l_2$
are the smaller frequencies in each group so that
$l_2$
are the smaller frequencies in each group so that
![]() $|k_2| \approx n_1$
and
$|k_2| \approx n_1$
and
![]() $|l_2| \approx o_1$
. For fixed
$|l_2| \approx o_1$
. For fixed
![]() $k_2$
, respectively
$k_2$
, respectively
![]() $l_2$
, we apply the Cauchy–Schwarz inequality for the pairs
$l_2$
, we apply the Cauchy–Schwarz inequality for the pairs
![]() $(k_3,k_4)$
, respectively
$(k_3,k_4)$
, respectively
![]() $(l_3,l_4)$
. We obtain
$(l_3,l_4)$
. We obtain
 $$\begin{align*}\left|\int_0^T \mathbf{J}^8_a(u)\, dt\right| \lesssim \epsilon^8 C^6 c_0^2 \sum \frac{1}{n_1 n_2} c_{k_2} c_{n_2}^2 \frac{1}{o_1 o_2} c_{l_2} c_{o_2}^2. \end{align*}$$
$$\begin{align*}\left|\int_0^T \mathbf{J}^8_a(u)\, dt\right| \lesssim \epsilon^8 C^6 c_0^2 \sum \frac{1}{n_1 n_2} c_{k_2} c_{n_2}^2 \frac{1}{o_1 o_2} c_{l_2} c_{o_2}^2. \end{align*}$$
Now, we use the maximal function to also fix
![]() $k_2$
and
$k_2$
and
![]() $l_2$
,
$l_2$
,
 $$\begin{align*}\left|\int_0^T \mathbf{J}^8_a(u)\, dt\right| \lesssim \epsilon^8 C^6 c_0^4 \sum_{n_2 \leq o_2} \frac{\log n_2}{ n_2} c_{n_2}^2 \frac{\log o_2}{ o_2} c_{o_2}^2 \lesssim \epsilon^8 C^6 c_0^4. \end{align*}$$
$$\begin{align*}\left|\int_0^T \mathbf{J}^8_a(u)\, dt\right| \lesssim \epsilon^8 C^6 c_0^4 \sum_{n_2 \leq o_2} \frac{\log n_2}{ n_2} c_{n_2}^2 \frac{\log o_2}{ o_2} c_{o_2}^2 \lesssim \epsilon^8 C^6 c_0^4. \end{align*}$$
B2)
![]() $o_2 \ll n_2$
. Here, we proceed exactly as before but using instead two bilinear
$o_2 \ll n_2$
. Here, we proceed exactly as before but using instead two bilinear
![]() $L^2$
bounds in
$L^2$
bounds in
![]() $B^4_a$
. Following the same steps, we arrive at
$B^4_a$
. Following the same steps, we arrive at
 $$\begin{align*}\left|\int_0^T\mathbf{J}^8_a(u)\, dt \right| \lesssim \epsilon^8 C^6 c_0^4 \sum_{o_2 \leq n_2} \frac{\log n_2}{ n_2^2} c_{n_2}^2 \log o_2 c_{o_2}^2 \lesssim \epsilon^8 C^6 c_0^4. \end{align*}$$
$$\begin{align*}\left|\int_0^T\mathbf{J}^8_a(u)\, dt \right| \lesssim \epsilon^8 C^6 c_0^4 \sum_{o_2 \leq n_2} \frac{\log n_2}{ n_2^2} c_{n_2}^2 \log o_2 c_{o_2}^2 \lesssim \epsilon^8 C^6 c_0^4. \end{align*}$$
Here, the denominators are unbalanced compared to the previous case but in a favourable way.
7.3.4 The bound for
 $\mathbf {K}^8_a$
$\mathbf {K}^8_a$
We recall that
![]() $\mathbf {K}^8_a$
has the form
$\mathbf {K}^8_a$
has the form
 $$ \begin{align} \begin{aligned} \mathbf{K}^8_a(u) = \iint_{x> y} &\ M^{\sharp}_a(u)(x) R^6_{p,a}(u)(y) + P^{\sharp}_{a}(u)(y) R^6_{m,a}(u)(x) \\ & \ - M^{\sharp}_a(u)(y) R^6_{p,a}(u)(x) - P^{\sharp}_{a}(u)(x) R^6_{m,a}(u)(y) \, dx dy. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \mathbf{K}^8_a(u) = \iint_{x> y} &\ M^{\sharp}_a(u)(x) R^6_{p,a}(u)(y) + P^{\sharp}_{a}(u)(y) R^6_{m,a}(u)(x) \\ & \ - M^{\sharp}_a(u)(y) R^6_{p,a}(u)(x) - P^{\sharp}_{a}(u)(x) R^6_{m,a}(u)(y) \, dx dy. \end{aligned} \end{align} $$
The time integral of
![]() $\mathbf {K}^8_a(u)$
is estimated directly using the
$\mathbf {K}^8_a(u)$
is estimated directly using the
![]() $L^1_{t,x}$
bound for
$L^1_{t,x}$
bound for
![]() $R^6$
in Lemma 7.3 and the uniform
$R^6$
in Lemma 7.3 and the uniform
![]() $L^1_x$
bound for
$L^1_x$
bound for
![]() $M^{\sharp }$
and
$M^{\sharp }$
and
![]() $P^{\sharp }$
, provided by Lemma 7.1 together with the simpler bound (7.29).
$P^{\sharp }$
, provided by Lemma 7.1 together with the simpler bound (7.29).
7.4 Near parallel interactions
Here, we briefly discuss the bilinear
![]() $L^2$
bound (6.4) in the case when the sets A and B are of size
$L^2$
bound (6.4) in the case when the sets A and B are of size
![]() $\lesssim 1$
and at distance
$\lesssim 1$
and at distance
![]() $\lesssim 1$
. This can be viewed on one hand as a slight generalization of the argument in the previous subsection, where instead of
$\lesssim 1$
. This can be viewed on one hand as a slight generalization of the argument in the previous subsection, where instead of
![]() $v = u$
we take
$v = u$
we take
![]() $v = u(\cdot +x_0)$
. The only difference in the proof is that, because of the translations, we can no longer use the defocusing property to control the sign of the diagonal
$v = u(\cdot +x_0)$
. The only difference in the proof is that, because of the translations, we can no longer use the defocusing property to control the sign of the diagonal
![]() $\mathbf {J}^{6}$
contribution. However, this is not a problem because the localized
$\mathbf {J}^{6}$
contribution. However, this is not a problem because the localized
![]() $L^6$
norm of
$L^6$
norm of
![]() $u_k$
has already been estimated in the previous subsection.
$u_k$
has already been estimated in the previous subsection.
7.5 The transversal bilinear
 $L^2$
estimate
$L^2$
estimate
Here, we prove the bilinear
![]() $L^2$
bound (6.4). This repeats the same analysis as before but using the Interaction Morawetz functional associated to two separated frequency intervals A and B, of size at most n and with n separation. Here, we no longer take
$L^2$
bound (6.4). This repeats the same analysis as before but using the Interaction Morawetz functional associated to two separated frequency intervals A and B, of size at most n and with n separation. Here, we no longer take
![]() $v = u$
, and instead we let
$v = u$
, and instead we let
![]() $v = u(\cdot +x_0)$
. The parameter
$v = u(\cdot +x_0)$
. The parameter
![]() $x_0 \in {\mathbb R}$
is arbitrary and the estimates are uniform in
$x_0 \in {\mathbb R}$
is arbitrary and the estimates are uniform in
![]() $x_0$
.
$x_0$
.
Since
![]() $x_0$
does not play any role in the analysis, we simply drop it from our notations. To further simplify the notations in what follows, we take advantage of the Galilean invariance to translate the problem in frequency so that
$x_0$
does not play any role in the analysis, we simply drop it from our notations. To further simplify the notations in what follows, we take advantage of the Galilean invariance to translate the problem in frequency so that
![]() $0$
is roughly halfway between the intervals A and B. This will allow us to set
$0$
is roughly halfway between the intervals A and B. This will allow us to set
![]() $\xi _0=0$
in equation (5.14), and to assume that both A and B are within distance n from the origin. We consider mass
$\xi _0=0$
in equation (5.14), and to assume that both A and B are within distance n from the origin. We consider mass
![]() $m_a$
,
$m_a$
,
![]() $m_b$
and momentum forms
$m_b$
and momentum forms
![]() $p_a$
,
$p_a$
,
![]() $p_b$
, where a and b are bump functions, smooth on the unit scale, selecting the sets A and B.
$p_b$
, where a and b are bump functions, smooth on the unit scale, selecting the sets A and B.
The Interaction functional takes the form (see equation (5.14))
 $$ \begin{align} \mathbf{I}_{AB}(u,v) = \iint_{x> y} M^{\sharp}_a(u)(x) P^{\sharp}_{b}(v)(y) - P^{\sharp}_{a}(u)(x) M^{\sharp}_b(v)(y) \,dx dy. \end{align} $$
$$ \begin{align} \mathbf{I}_{AB}(u,v) = \iint_{x> y} M^{\sharp}_a(u)(x) P^{\sharp}_{b}(v)(y) - P^{\sharp}_{a}(u)(x) M^{\sharp}_b(v)(y) \,dx dy. \end{align} $$
Its time derivative is given (see equation (5.9)) by
Following the same pattern as in the earlier case of the localized Interaction Morawetz case, we will estimate each of these terms as follows:
 $$ \begin{align} \left|\int_0^T\mathbf{J}^6_{AB}\, dt \right| \lesssim n (\epsilon^6 C^6 + \epsilon^4) c_A^2 c_B^2 , \end{align} $$
$$ \begin{align} \left|\int_0^T\mathbf{J}^6_{AB}\, dt \right| \lesssim n (\epsilon^6 C^6 + \epsilon^4) c_A^2 c_B^2 , \end{align} $$
 $$ \begin{align} \left|\int _0^T\mathbf{J}^8_{AB}\, dt\right| \lesssim n \epsilon^8 C^8 c_A^2 c_B^2 , \end{align} $$
$$ \begin{align} \left|\int _0^T\mathbf{J}^8_{AB}\, dt\right| \lesssim n \epsilon^8 C^8 c_A^2 c_B^2 , \end{align} $$
 $$ \begin{align} \left| \int_0^T \mathbf{K}^8_{AB}\, dt \right| \lesssim n \epsilon^6 C^8 c_A^2 c_B^2. \end{align} $$
$$ \begin{align} \left| \int_0^T \mathbf{K}^8_{AB}\, dt \right| \lesssim n \epsilon^6 C^8 c_A^2 c_B^2. \end{align} $$
7.5.1 The fixed time estimate for
 $\mathbf {I}_{AB}$
$\mathbf {I}_{AB}$
Here, we prove the bound (7.35), which is a consequence of fixed time
![]() $L^1$
estimates for the energy densities, namely
$L^1$
estimates for the energy densities, namely
and the similar estimates with a replaced by b and u replaced by v. This is obvious for the quadratic part of the above densities, where we note that the n factor for the momentum bound arises due to the distance
![]() $o(n)$
between the set A and the origin. It remains to consider the quartic terms, where we can use Lemma 7.1 together with Corollary 7.2.
$o(n)$
between the set A and the origin. It remains to consider the quartic terms, where we can use Lemma 7.1 together with Corollary 7.2.
7.5.2 The bound for
 $\mathbf {J}^6_{AB}$
$\mathbf {J}^6_{AB}$
Here, we prove the bound for
![]() $\mathbf {J}^6_{AB}$
in equation (7.37). We recall that
$\mathbf {J}^6_{AB}$
in equation (7.37). We recall that
![]() $\mathbf {J}^6_{AB}$
has the form
$\mathbf {J}^6_{AB}$
has the form
where the symmetric term is obtained by interchanging the indices a and b and also u and v. The symbols for the M, P and E factors have size
![]() $1$
, n and
$1$
, n and
![]() $n^2$
, respectively, with a similar balance between the
$n^2$
, respectively, with a similar balance between the
![]() $B^4_m$
and
$B^4_m$
and
![]() $B^4_p$
terms, respectively the
$B^4_p$
terms, respectively the
![]() $R^4_m$
and
$R^4_m$
and
![]() $R^4_p$
terms. So it suffices to consider one
$R^4_p$
terms. So it suffices to consider one
![]() $R^4$
term and one
$R^4$
term and one
![]() $B^4$
term.
$B^4$
term.
A) The
![]() $B^4$
term
$B^4$
term
![]() $B^4_{m,a}(u) E_b(v)$
. Here, we denote by
$B^4_{m,a}(u) E_b(v)$
. Here, we denote by
![]() $l_1,l_2$
the
$l_1,l_2$
the
![]() $E_b$
frequencies and by
$E_b$
frequencies and by
![]() $k_1,k_2,k_3, k_4$
the
$k_1,k_2,k_3, k_4$
the
![]() $B^4_{m,a}$
frequencies, where
$B^4_{m,a}$
frequencies, where
The symbol for
![]() $E_b$
has size
$E_b$
has size
![]() $n^2$
, with both frequencies in B. The symbol for
$n^2$
, with both frequencies in B. The symbol for
![]() $B^4_{m,a}(u)$
has size
$B^4_{m,a}(u)$
has size
![]() $( \langle \delta k^{med}\rangle \langle \delta k^{hi}\rangle )^{-1}$
and support in the region, where
$( \langle \delta k^{med}\rangle \langle \delta k^{hi}\rangle )^{-1}$
and support in the region, where
![]() $|\Delta ^4 k| \ll 1 + k^{med}$
, and at least one of the frequencies is in A. We denote the dyadic sizes of
$|\Delta ^4 k| \ll 1 + k^{med}$
, and at least one of the frequencies is in A. We denote the dyadic sizes of
![]() $k^{med}$
and
$k^{med}$
and
![]() $k^{hi}$
by
$k^{hi}$
by
![]() $n_1 \leq n_2$
. Without any loss in generality, we may assume that
$n_1 \leq n_2$
. Without any loss in generality, we may assume that
![]() $k_1,k_2,k_3,k_4$
are chosen so that
$k_1,k_2,k_3,k_4$
are chosen so that
Depending on the size of n relative to
![]() $n_1,n_2$
, we consider two cases:
$n_1,n_2$
, we consider two cases:
A1)
![]() $ n_2 \ll n$
. Since A and B are n-separated, within the set of six frequencies we can find two pairs of n -separated frequencies. Then we can apply twice the bilinear
$ n_2 \ll n$
. Since A and B are n-separated, within the set of six frequencies we can find two pairs of n -separated frequencies. Then we can apply twice the bilinear
![]() $L^2$
bound and estimate the remaining factors in
$L^2$
bound and estimate the remaining factors in
![]() $L^{\infty }$
. We arrive at the frequency envelope bound
$L^{\infty }$
. We arrive at the frequency envelope bound
 $$\begin{align*}\left|\int_0^T\mathbf{J}^6_{AB}\, dt\right| \lesssim \epsilon^6 C^6 n \sum \frac{1}{n_1 n_2} c_{l_1} c_{l_2} c_{k_1} c_{k_2} c_{k_3} c_{k_4}, \end{align*}$$
$$\begin{align*}\left|\int_0^T\mathbf{J}^6_{AB}\, dt\right| \lesssim \epsilon^6 C^6 n \sum \frac{1}{n_1 n_2} c_{l_1} c_{l_2} c_{k_1} c_{k_2} c_{k_3} c_{k_4}, \end{align*}$$
where the summation indices are restricted as discussed above. Then, applying the Cauchy–Schwarz inequality for the pair
![]() $(l_1,l_2)$
we obtain
$(l_1,l_2)$
we obtain
 $$\begin{align*}\begin{aligned} \left|\int_0^T\mathbf{J}^6_{AB}\, dt \right| \lesssim & \ \epsilon^6 C^6 n \sum \frac{1}{n_1 n_2} \sum_{|\Delta^4 k| < n_1} c_{k_1} c_{k_2} c_{k_3} c_{k_4} \sum_{l_1,l_2 \in B}^{\Delta l =- \Delta^4 k} c_{l_1} c_{l_2} \\ \lesssim & \ \epsilon^6 n C^6 c_B^2 \sum \frac{1}{ n_1 n_2} \sum_{|\Delta^4 k| < n_1} c_{k_1} c_{k_2} c_{k_3} c_{k_4}. \end{aligned}. \end{align*}$$
$$\begin{align*}\begin{aligned} \left|\int_0^T\mathbf{J}^6_{AB}\, dt \right| \lesssim & \ \epsilon^6 C^6 n \sum \frac{1}{n_1 n_2} \sum_{|\Delta^4 k| < n_1} c_{k_1} c_{k_2} c_{k_3} c_{k_4} \sum_{l_1,l_2 \in B}^{\Delta l =- \Delta^4 k} c_{l_1} c_{l_2} \\ \lesssim & \ \epsilon^6 n C^6 c_B^2 \sum \frac{1}{ n_1 n_2} \sum_{|\Delta^4 k| < n_1} c_{k_1} c_{k_2} c_{k_3} c_{k_4}. \end{aligned}. \end{align*}$$
Hence, it remains to estimate the last sum above as follows:
 $$ \begin{align} S_A: = \sum_{n_1 < n_2} \frac{1}{ n_1 n_2} \sum_{D} c_{k_1} c_{k_2} c_{k_3} c_{k_4} \lesssim c_A^2, \end{align} $$
$$ \begin{align} S_A: = \sum_{n_1 < n_2} \frac{1}{ n_1 n_2} \sum_{D} c_{k_1} c_{k_2} c_{k_3} c_{k_4} \lesssim c_A^2, \end{align} $$
where the summation set D is described by equation (7.3). In this estimate, the parameter n no longer appears. Recalling that
![]() $k_1 \in A$
, we fix
$k_1 \in A$
, we fix
![]() $k_1$
and split
$k_1$
and split
 $$\begin{align*}S_A = \sum_{k_1 \in A} c_{k_1} S_{k_1}, \qquad S_{k_1}:=\sum_{D}\sum_{n_1 < n_2} \frac{1}{ n_1 n_2} \sum_{D} c_{k_2} c_{k_3} c_{k_4}. \end{align*}$$
$$\begin{align*}S_A = \sum_{k_1 \in A} c_{k_1} S_{k_1}, \qquad S_{k_1}:=\sum_{D}\sum_{n_1 < n_2} \frac{1}{ n_1 n_2} \sum_{D} c_{k_2} c_{k_3} c_{k_4}. \end{align*}$$
Then it suffices to show that
which is exactly the bound (7.4) proved earlier.
A2)
![]() $ n_2 \gtrsim n$
. This time, within the set of four k frequencies we can find two pairs of
$ n_2 \gtrsim n$
. This time, within the set of four k frequencies we can find two pairs of
![]() $n_2$
-separated frequencies. Applying twice the bilinear
$n_2$
-separated frequencies. Applying twice the bilinear
![]() $L^2$
bound and estimating the remaining factors in
$L^2$
bound and estimating the remaining factors in
![]() $L^{\infty }$
, we arrive at
$L^{\infty }$
, we arrive at
 $$\begin{align*}\left|\int_0^T\mathbf{J}^6_{AB}\, dt\right| \lesssim \epsilon^6 C^6 n^2 \sum \frac{1}{n_1 n_2^2} c_{l_1} c_{l_2} c_{k_1} c_{k_2} c_{k_3} c_{k_4}, \end{align*}$$
$$\begin{align*}\left|\int_0^T\mathbf{J}^6_{AB}\, dt\right| \lesssim \epsilon^6 C^6 n^2 \sum \frac{1}{n_1 n_2^2} c_{l_1} c_{l_2} c_{k_1} c_{k_2} c_{k_3} c_{k_4}, \end{align*}$$
Applying the Cauchy–Schwarz inequality for the pair
![]() $(l_1,l_2)$
now yields
$(l_1,l_2)$
now yields
 $$\begin{align*}\begin{aligned} \left|\int_0^T\mathbf{J}^6_{AB}\, dt \right| \lesssim & \ \epsilon^6 C^6 n^2 c_B^2 \sum \frac{1}{n_1 n_2^2} \sum_{|\Delta^4 k| < n} c_{k_1} c_{k_2} c_{k_3} c_{k_4} \end{aligned}\!\!\!\!\!\!. \end{align*}$$
$$\begin{align*}\begin{aligned} \left|\int_0^T\mathbf{J}^6_{AB}\, dt \right| \lesssim & \ \epsilon^6 C^6 n^2 c_B^2 \sum \frac{1}{n_1 n_2^2} \sum_{|\Delta^4 k| < n} c_{k_1} c_{k_2} c_{k_3} c_{k_4} \end{aligned}\!\!\!\!\!\!. \end{align*}$$
Since
![]() $n \lesssim n_2$
, we can conclude again using the bound (7.42) which was already proved in (A1).
$n \lesssim n_2$
, we can conclude again using the bound (7.42) which was already proved in (A1).
B. The
![]() $R^4$
terms are also all similar, so to fix the notations we will discuss the expression
$R^4$
terms are also all similar, so to fix the notations we will discuss the expression
![]() $P_b(u) R^4_{m,a}(u)$
. We denote again the six frequencies by
$P_b(u) R^4_{m,a}(u)$
. We denote again the six frequencies by
![]() $l_1,l_2$
for
$l_1,l_2$
for
![]() $P_b$
, respectively by
$P_b$
, respectively by
![]() $k_1,k_2,k_3, k_4$
for
$k_1,k_2,k_3, k_4$
for
![]() $B^4_{m,a}$
. The symbol of
$B^4_{m,a}$
. The symbol of
![]() $p_B$
is supported in
$p_B$
is supported in
![]() $B \times B$
and has size n. The symbol
$B \times B$
and has size n. The symbol
![]() $R^4_{m,a}$
has size
$R^4_{m,a}$
has size
 $$\begin{align*}|r^4_{m,a}([k])| \lesssim \frac{n + \delta k^{hi}}{ \langle \delta k^{med}\rangle \langle\delta k^{hi}\rangle}. \end{align*}$$
$$\begin{align*}|r^4_{m,a}([k])| \lesssim \frac{n + \delta k^{hi}}{ \langle \delta k^{med}\rangle \langle\delta k^{hi}\rangle}. \end{align*}$$
The bound for the portion containing the n term in the denominator is identical to the one in case A, so in the sequel we dismiss this term and simplify the above bound to
Retaining the notations
![]() $n_1 \leq n_2 $
for the dyadic sizes of
$n_1 \leq n_2 $
for the dyadic sizes of
![]() $\delta k^{med}$
and
$\delta k^{med}$
and
![]() $\delta k^{hi}$
, we may also restrict our analysis to the case when
$\delta k^{hi}$
, we may also restrict our analysis to the case when
![]() $n_2 \gg n$
. This is similar to case A above. We get the better
$n_2 \gg n$
. This is similar to case A above. We get the better
![]() $n_2^{-1}$
factor from the bilinear
$n_2^{-1}$
factor from the bilinear
![]() $L^2$
bounds, which allows us to reduce the problem to proving exactly the bound (7.42), but for a larger set of indices
$L^2$
bounds, which allows us to reduce the problem to proving exactly the bound (7.42), but for a larger set of indices
But this still follows from equation (7.4).
7.5.3 The bound for
 $\mathbf {J}^8_{AB}$
$\mathbf {J}^8_{AB}$
Here, we prove the bound (7.38). We recall that
![]() $\mathbf {J}^8_{AB}$
has the form
$\mathbf {J}^8_{AB}$
has the form
All terms here are similar, so it suffices to consider the first one. To avoid a lengthy proof which would largely repeat the arguments in the proof of equation (7.37), we make a simple observation, namely that the proof of the bound for this term becomes a corollary of the previous bound if we can establish a representation
so that, for each k which is M-separated from
![]() $l_2$
, the function
$l_2$
, the function
![]() $w_{l_2}$
satisfies a bilinear
$w_{l_2}$
satisfies a bilinear
![]() $L^2$
bound of the form
$L^2$
bound of the form
If that is true, then
![]() $w_{l_2}$
would play exactly the role of
$w_{l_2}$
would play exactly the role of
![]() $u_{l_2}$
in the
$u_{l_2}$
in the
![]() $\mathbf {J}^6_{AB}$
estimate.
$\mathbf {J}^6_{AB}$
estimate.
Indeed, we may represent
Here, the symbol for
![]() $B^4_{m,a}$
and its derivatives have size
$B^4_{m,a}$
and its derivatives have size
![]() $\lesssim \dfrac {1}{n_1 n_2}$
in a unit region around frequency
$\lesssim \dfrac {1}{n_1 n_2}$
in a unit region around frequency
![]() $(l_1,k_2,k_3,k_4)$
. Hence, we may separate variables and represent
$(l_1,k_2,k_3,k_4)$
. Hence, we may separate variables and represent
![]() $B^4_{m,a}(u_{l_1},u_{k_2},u_{k_3}, u_{k_4})$
as the sum of a rapidly convergent series
$B^4_{m,a}(u_{l_1},u_{k_2},u_{k_3}, u_{k_4})$
as the sum of a rapidly convergent series
where the symbols for
![]() $D^j$
, respectively
$D^j$
, respectively
![]() $B^{4,j}_{m,a} $
have unit size, respectively
$B^{4,j}_{m,a} $
have unit size, respectively
![]() $\lesssim \frac {1}{n_1 n_2}$
with rapid decay in j. Then it remains to prove the estimate (7.44) for the functions
$\lesssim \frac {1}{n_1 n_2}$
with rapid decay in j. Then it remains to prove the estimate (7.44) for the functions
![]() $w^j_{l_2}$
.
$w^j_{l_2}$
.
Indeed, at least one of the k’s must be M-separated from k, so using a bilinear
![]() $L^2$
bound we have
$L^2$
bound we have
 $$\begin{align*}\| w^j_{l_2} u_k \|_{L^2} \lesssim M^{-\frac12} \epsilon^4 C^4 c_{k} j^{-10} \sum_{k_2 - k_3+k_4 = l_2} \frac{1}{n_1 n_2} c_{k_2} c_{k_3} c_{k_4}. \end{align*}$$
$$\begin{align*}\| w^j_{l_2} u_k \|_{L^2} \lesssim M^{-\frac12} \epsilon^4 C^4 c_{k} j^{-10} \sum_{k_2 - k_3+k_4 = l_2} \frac{1}{n_1 n_2} c_{k_2} c_{k_3} c_{k_4}. \end{align*}$$
It remains to estimate the last sum. Suppose
![]() $k_2$
is within distance
$k_2$
is within distance
![]() $n_1$
from
$n_1$
from
![]() $l_2$
, then we use the maximal function to estimate
$l_2$
, then we use the maximal function to estimate
 $$\begin{align*}\sum_{k_2 - k_3+k_4 = l_2} \frac{1}{n_1 n_2} c_{k_2} c_{k_3} c_{k_4} \lesssim c_{l_2} \sup_{k_2} \sum_{k_2 - k_3+k_4 = l_2} \frac{1}{n_2} c_{k_3} c_{k_4} \lesssim c_{l_2}, \end{align*}$$
$$\begin{align*}\sum_{k_2 - k_3+k_4 = l_2} \frac{1}{n_1 n_2} c_{k_2} c_{k_3} c_{k_4} \lesssim c_{l_2} \sup_{k_2} \sum_{k_2 - k_3+k_4 = l_2} \frac{1}{n_2} c_{k_3} c_{k_4} \lesssim c_{l_2}, \end{align*}$$
as needed.
8 Global bilinear and Strichartz estimates
Our objective in this last section is to supplement the unit frequency scale bilinear
![]() $L^2$
and Strichartz estimates with their more global counterparts:
$L^2$
and Strichartz estimates with their more global counterparts:
Theorem 6. The global small data solutions u for equation (1.3) in Theorem 5 satisfy the following bounds:
-
• Strichartz estimate:
(8.1) $$ \begin{align} \| u\|_{L^6_{t,x}}^6 \lesssim \epsilon^4, \end{align} $$
$$ \begin{align} \| u\|_{L^6_{t,x}}^6 \lesssim \epsilon^4, \end{align} $$
-
• Bilinear
 $L^2$
bound: (8.2)
$L^2$
bound: (8.2) $$ \begin{align} \|\partial_x |u|^2 \|_{L^2_t H^{-\frac12}_x}^2 \lesssim \epsilon^4. \end{align} $$
$$ \begin{align} \|\partial_x |u|^2 \|_{L^2_t H^{-\frac12}_x}^2 \lesssim \epsilon^4. \end{align} $$
Proof. We successively consider the two estimates:
A. The global
![]() $L^6$
bound. We prove the global
$L^6$
bound. We prove the global
![]() $L^6$
bound using the previous localized estimates. We aim to estimate the integral
$L^6$
bound using the previous localized estimates. We aim to estimate the integral
by taking a suitable frequency decomposition. Given six unit frequency regions indexed by
![]() $k_1$
,
$k_1$
,
![]() $k_2$
,
$k_2$
,
![]() $k_3$
,
$k_3$
,
![]() $k_4$
,
$k_4$
,
![]() $k_5$
and
$k_5$
and
![]() $k_6$
, they can only contribute to the above integral iff
$k_6$
, they can only contribute to the above integral iff
![]() $\Delta ^6 k = 0$
. We divide them as follows:
$\Delta ^6 k = 0$
. We divide them as follows:
-
1. The diagonal case
 $|k_i - k_j| \lesssim 1$
.
$|k_i - k_j| \lesssim 1$
. -
2. The nondiagonal case. we index these frequencies by the dyadic size
 $n \gg 1$
of the set of frequencies, that is, so that
$n \gg 1$
of the set of frequencies, that is, so that  $$\begin{align*}\max |k_i-k_j| \approx n. \end{align*}$$
$$\begin{align*}\max |k_i-k_j| \approx n. \end{align*}$$
Within this range, we organize frequencies in intervals
 $A_1, \cdots A_6$
of size
$A_1, \cdots A_6$
of size
 $n/100$
. Of these intervals, at least two pairs must be n-separated in order to contribute to the above integral.
$n/100$
. Of these intervals, at least two pairs must be n-separated in order to contribute to the above integral.
Based on this, we split I as
where
 $$\begin{align*}I_0 = \sum_{|k_i - k_j| \lesssim 1 } \iint u_{k_1} {\bar u}_{k_2} u_{k_3} {\bar u}_{k_4} u_{k_5} {\bar u}_{k_6} \, dx dt, \end{align*}$$
$$\begin{align*}I_0 = \sum_{|k_i - k_j| \lesssim 1 } \iint u_{k_1} {\bar u}_{k_2} u_{k_3} {\bar u}_{k_4} u_{k_5} {\bar u}_{k_6} \, dx dt, \end{align*}$$
and
where the last sum is indexed over the sets
![]() $A_j$
of size
$A_j$
of size
![]() $n/100$
, with largest distance
$n/100$
, with largest distance
![]() $\approx n$
and at least two distances
$\approx n$
and at least two distances
![]() $\geq n/10$
.
$\geq n/10$
.
For the diagonal part, we use the
![]() $L^6$
bound (6.2) to estimate
$L^6$
bound (6.2) to estimate
which suffices.
For the off-diagonal part we apply two bilinear
![]() $L^2$
bounds for the separated intervals (gaining
$L^2$
bounds for the separated intervals (gaining
![]() $n^{-\frac 12}$
each time) and two
$n^{-\frac 12}$
each time) and two
![]() $L^{\infty }$
bounds via Bernstein’s inequality (losing
$L^{\infty }$
bounds via Bernstein’s inequality (losing
![]() $n^{\frac 12}$
each time) to bound the corresponding term by
$n^{\frac 12}$
each time) to bound the corresponding term by
We retain only the separated parts and apply the Cauchy–Schwarz inequality to estimate
Then summation over n yields
which again suffices.
B. The global bilinear
![]() $L^2$
bound. Here, we prove the estimate (8.2). Expanding relative to the dyadic difference n of the two input frequencies, we have
$L^2$
bound. Here, we prove the estimate (8.2). Expanding relative to the dyadic difference n of the two input frequencies, we have
where
 $$\begin{align*}w_n = \sum_{|A_1|,|A_2| \approx n}^{d(A_1,A_2) \approx n} u_{A_1} {\bar u}_{A_2}. \end{align*}$$
$$\begin{align*}w_n = \sum_{|A_1|,|A_2| \approx n}^{d(A_1,A_2) \approx n} u_{A_1} {\bar u}_{A_2}. \end{align*}$$
We use equation (6.3) to estimate
![]() $w_0$
as
$w_0$
as
On the other hand, for
![]() $w_n$
we get
$w_n$
we get
 $$\begin{align*}\|\partial_x w_n \|_{L^2_t H^{-\frac12}_x}^2 \lesssim n \sum_{|A_1|,|A_2| \approx n}^{d(A_1,A_2) \approx n} \sum_{|A_3|,|A_4| \approx n}^{d(A_3,A_4) \approx n} \int u_{A_1} {\bar u}_{A_2}u_{A_3} {\bar u}_{A_4} \, dx. \end{align*}$$
$$\begin{align*}\|\partial_x w_n \|_{L^2_t H^{-\frac12}_x}^2 \lesssim n \sum_{|A_1|,|A_2| \approx n}^{d(A_1,A_2) \approx n} \sum_{|A_3|,|A_4| \approx n}^{d(A_3,A_4) \approx n} \int u_{A_1} {\bar u}_{A_2}u_{A_3} {\bar u}_{A_4} \, dx. \end{align*}$$
Denoting by
![]() $n_0 \geq n$
the largest distance between two
$n_0 \geq n$
the largest distance between two
![]() $A_j$
’s, we have two pairs of intervals with separation
$A_j$
’s, we have two pairs of intervals with separation
![]() $O(n_0)$
; therefore, applying twice the bilinear
$O(n_0)$
; therefore, applying twice the bilinear
![]() $L^2$
bound we obtain
$L^2$
bound we obtain
 $$\begin{align*}\|\partial_x w_n \|_{H^{-\frac12}}^2 \lesssim \epsilon^4 \sum_{n_0 \geq n} \frac{n}{n_0} \sum_{|A_1|,|A_2| \approx n}^{d(A_1,A_2) \approx n} \sum_{|A_3|,|A_4| \approx n}^{d(A_3,A_4) \approx n} c_{A_1} c_{A_2} c_{A_3} c_{A_4}. \end{align*}$$
$$\begin{align*}\|\partial_x w_n \|_{H^{-\frac12}}^2 \lesssim \epsilon^4 \sum_{n_0 \geq n} \frac{n}{n_0} \sum_{|A_1|,|A_2| \approx n}^{d(A_1,A_2) \approx n} \sum_{|A_3|,|A_4| \approx n}^{d(A_3,A_4) \approx n} c_{A_1} c_{A_2} c_{A_3} c_{A_4}. \end{align*}$$
We separate the cases when
![]() $n_0 \approx n$
and
$n_0 \approx n$
and
![]() $n_0 \gg n$
. In the first, diagonal case we simply bound the corresponding part of the sum by
$n_0 \gg n$
. In the first, diagonal case we simply bound the corresponding part of the sum by
 $$\begin{align*}\epsilon^4 \sum_{|A_1|,|A_2| \approx n}^{d(A_1,A_2) \approx n} c_{A_1}^2 c_{A_2}^2. \end{align*}$$
$$\begin{align*}\epsilon^4 \sum_{|A_1|,|A_2| \approx n}^{d(A_1,A_2) \approx n} c_{A_1}^2 c_{A_2}^2. \end{align*}$$
In the off-diagonal case, we apply the Cauchy–Schwarz inequality separately for the pairs
![]() $A_1,A_2$
and
$A_1,A_2$
and
![]() $A_3,A_4$
to obtain a bound
$A_3,A_4$
to obtain a bound
 $$\begin{align*}\epsilon^4 \frac{n}{n_0} \sum_{|B_1|,|B_2| \approx n_0}^{d(B_1,B_2) \approx n_0} c_{B_1}^2 c_{B_2}^2. \end{align*}$$
$$\begin{align*}\epsilon^4 \frac{n}{n_0} \sum_{|B_1|,|B_2| \approx n_0}^{d(B_1,B_2) \approx n_0} c_{B_1}^2 c_{B_2}^2. \end{align*}$$
Incorporating the first case into the second, we arrive at
 $$\begin{align*}\|\partial_x w_n \|_{L^2_t H^{-\frac12}_x}^2 \lesssim \epsilon^4 \sum_{n_0 \geq n} \frac{n}{n_0}\sum_{|B_1|,|B_2| \approx n_0}^{d(B_1,B_2) \approx n_0} c_{B_1}^2 c_{B_2}^2. \end{align*}$$
$$\begin{align*}\|\partial_x w_n \|_{L^2_t H^{-\frac12}_x}^2 \lesssim \epsilon^4 \sum_{n_0 \geq n} \frac{n}{n_0}\sum_{|B_1|,|B_2| \approx n_0}^{d(B_1,B_2) \approx n_0} c_{B_1}^2 c_{B_2}^2. \end{align*}$$
Finally, using orthogonality in frequency we have
 $$\begin{align*}\begin{aligned} \|\sum_n \partial_x w_n \|_{L^2_t H^{-\frac12}_x}^2 \lesssim & \ \epsilon^4 \sum_n \sum_{n_0 \geq n} \frac{n}{n_0}\sum_{|B_1|,|B_2| \approx n_0}^{d(B_1,B_2) \approx n_0} c_{B_1}^2 c_{B_2}^2 \\ \lesssim & \ \epsilon^4 \sum_{n_0} \sum_{|B_1|,|B_2| \approx n_0}^{d(B_1,B_2) \approx n_0} c_{B_1}^2 c_{B_2}^2 \\ \lesssim & \ \epsilon^4. \end{aligned} \end{align*}$$
$$\begin{align*}\begin{aligned} \|\sum_n \partial_x w_n \|_{L^2_t H^{-\frac12}_x}^2 \lesssim & \ \epsilon^4 \sum_n \sum_{n_0 \geq n} \frac{n}{n_0}\sum_{|B_1|,|B_2| \approx n_0}^{d(B_1,B_2) \approx n_0} c_{B_1}^2 c_{B_2}^2 \\ \lesssim & \ \epsilon^4 \sum_{n_0} \sum_{|B_1|,|B_2| \approx n_0}^{d(B_1,B_2) \approx n_0} c_{B_1}^2 c_{B_2}^2 \\ \lesssim & \ \epsilon^4. \end{aligned} \end{align*}$$
The proof of the theorem is concluded.
Acknowledgements
The authors also wish to thank the anonymous referee for the careful reading of the manuscript and for the very useful corrections and suggestions.
Competing interest
The authors have no competing interest to declare.
Funding statement
The first author was supported by a Luce Professorship, by the Sloan Foundation and by an NSF CAREER grant DMS-1845037. The second author was supported by the NSF grant DMS-2054975 as well as by a Simons Investigator grant from the Simons Foundation. Some of this work was carried out while both authors were participating in the MSRI program ‘Mathematical Problems in Fluid Dynamics’ during spring 2021.