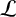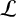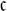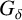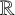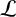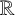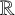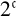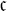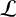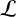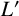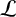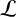1 Introduction
It has been known for over 175 years that every Liouville number is transcendental and for 120 years that the set
![]() $\mathcal {L}$
of Liouville numbers is uncountable. Notwithstanding this, the set
$\mathcal {L}$
of Liouville numbers is uncountable. Notwithstanding this, the set
![]() $\mathcal {L}$
is known to have Lebesgue measure zero. So in this sense,
$\mathcal {L}$
is known to have Lebesgue measure zero. So in this sense,
![]() $\mathcal {L}$
is very small. Therefore, it is surprising that each real number equals the sum of two Liouville numbers. It is reasonable to ask if
$\mathcal {L}$
is very small. Therefore, it is surprising that each real number equals the sum of two Liouville numbers. It is reasonable to ask if
![]() $\mathcal {L}$
is the smallest set, in some sense, with this property. In this paper, it is proved that there is an uncountable number of sets smaller than
$\mathcal {L}$
is the smallest set, in some sense, with this property. In this paper, it is proved that there is an uncountable number of sets smaller than
![]() $\mathcal {L}$
which have this property. Indeed, there are
$\mathcal {L}$
which have this property. Indeed, there are
![]() $2^{\mathfrak {c}}$
such subsets of
$2^{\mathfrak {c}}$
such subsets of
![]() $\mathcal {L}$
no two of which are homeomorphic as subspaces of
$\mathcal {L}$
no two of which are homeomorphic as subspaces of
![]() $\mathbb {R}$
.
$\mathbb {R}$
.
2 Preliminaries
Remark 2.1. In 1844, Joseph Liouville proved the existence of transcendental numbers [Reference Angell2, Reference Baker3]. He introduced the set
![]() $\mathcal L$
of real numbers, now known as Liouville numbers, and showed that they are all transcendental. A real number x is said to be a Liouville number if for every positive integer n, there exists a pair of integers
$\mathcal L$
of real numbers, now known as Liouville numbers, and showed that they are all transcendental. A real number x is said to be a Liouville number if for every positive integer n, there exists a pair of integers
![]() $(p,q)$
with
$(p,q)$
with
![]() $q>1$
such that
$q>1$
such that
 $$ \begin{align*} 0< \bigg\lvert x-\frac{p}{q}\bigg\rvert<\frac{1}{q^n}. \end{align*} $$
$$ \begin{align*} 0< \bigg\lvert x-\frac{p}{q}\bigg\rvert<\frac{1}{q^n}. \end{align*} $$
This definition of a Liouville number can be reformulated as follows. For a given irrational x, let
![]() $p_k/q_k=p_k(x)/q_k(x)$
, where
$p_k/q_k=p_k(x)/q_k(x)$
, where
![]() $q_k(x)>0$
, denote the sequence of convergents of the continued fraction expansion of x; then for every
$q_k(x)>0$
, denote the sequence of convergents of the continued fraction expansion of x; then for every
![]() $n\in \mathbb {N}$
, there are infinitely many k such that
$n\in \mathbb {N}$
, there are infinitely many k such that
![]() $q_{k+1}>q_k^n$
. A more restrictive class of Liouville numbers is obtained by requiring this inequality to hold for every
$q_{k+1}>q_k^n$
. A more restrictive class of Liouville numbers is obtained by requiring this inequality to hold for every
![]() $k> N=N(n)\in \mathbb {N}$
. Such numbers are called strong Liouville numbers.
$k> N=N(n)\in \mathbb {N}$
. Such numbers are called strong Liouville numbers.
In 1962, Erdős [Reference Erdős8] proved that every real number is the sum of two Liouville numbers (and also the product of two Liouville numbers). He gave two proofs. One was a constructive proof. The other proof used the fact that the set
![]() $\mathcal {L}$
of all Liouville numbers is a dense
$\mathcal {L}$
of all Liouville numbers is a dense
![]() $G_{\delta }$
-set in
$G_{\delta }$
-set in
![]() $\mathbb {R}$
and showed that every dense
$\mathbb {R}$
and showed that every dense
![]() $G_{\delta }$
-set in
$G_{\delta }$
-set in
![]() $\mathbb {R}$
has this property.
$\mathbb {R}$
has this property.
Definition 2.2. A set W of complex numbers is said to have the Erdős property if every real number is a sum of two numbers in W.
Remark 2.3. Recall that if A and B are subsets of the set
![]() $\mathbb {C}$
of all complex numbers, then the sum-set is defined to be
$\mathbb {C}$
of all complex numbers, then the sum-set is defined to be
![]() $A+B=\{a+b:a\in A, b\in B\}$
. So the subset W of
$A+B=\{a+b:a\in A, b\in B\}$
. So the subset W of
![]() $\mathbb {C}$
has the Erdős property if the sum-set
$\mathbb {C}$
has the Erdős property if the sum-set
![]() $W+W$
contains the set
$W+W$
contains the set
![]() $\mathbb {R}$
. (See [Reference Brown, Yin, Pollington and Moran4, Reference Pollington, Pollington and Moran13].)
$\mathbb {R}$
. (See [Reference Brown, Yin, Pollington and Moran4, Reference Pollington, Pollington and Moran13].)
Remark 2.4. By the theorem proved by Erdős mentioned above, the set
![]() $\mathcal {L}$
of all Liouville numbers has the Erdős property.
$\mathcal {L}$
of all Liouville numbers has the Erdős property.
Remark 2.5. If W is a set with the Erdős property, then every set containing W also has the Erdős property.
Definition 2.6. A set W is said to be an Erdős–Liouville set if it has the Erdős property and is a dense subset of the set
![]() $\mathcal {L}$
of Liouville numbers.
$\mathcal {L}$
of Liouville numbers.
Remark 2.7. It is not immediately obvious that there exist any Erdős–Liouville sets other than the set
![]() $\mathcal {L}$
itself. It is known that some sets of positive Lebesgue measure have the Erdős property, but they are not subsets of
$\mathcal {L}$
itself. It is known that some sets of positive Lebesgue measure have the Erdős property, but they are not subsets of
![]() $\mathcal {L}$
as the set
$\mathcal {L}$
as the set
![]() $\mathcal {L}$
is known to have measure zero. (See, for example, [Reference Chalebgwa and Morris5].) According to Petruska, [Reference Petruska12], Erdős asked if the set of strong Liouville numbers has the Erdős property. However, Petruska [Reference Petruska12] proved that it does not. He did this by showing that the sum of two strong Liouville numbers is either a Liouville number or a rational number. Hence, the sum of two strong Liouville numbers cannot equal any irrational number other than a Liouville number. However, it is proved in [Reference Conman and Poletsky7], in the text following Corollary 1.4 and in Section 3, that there does exist another Erdős–Liouville set. In [Reference Marques and Moreira10], the set of ultra-Liouville numbers is introduced and it is shown that this set is a dense
$\mathcal {L}$
is known to have measure zero. (See, for example, [Reference Chalebgwa and Morris5].) According to Petruska, [Reference Petruska12], Erdős asked if the set of strong Liouville numbers has the Erdős property. However, Petruska [Reference Petruska12] proved that it does not. He did this by showing that the sum of two strong Liouville numbers is either a Liouville number or a rational number. Hence, the sum of two strong Liouville numbers cannot equal any irrational number other than a Liouville number. However, it is proved in [Reference Conman and Poletsky7], in the text following Corollary 1.4 and in Section 3, that there does exist another Erdős–Liouville set. In [Reference Marques and Moreira10], the set of ultra-Liouville numbers is introduced and it is shown that this set is a dense
![]() $G_{\delta }$
-subset of
$G_{\delta }$
-subset of
![]() $\mathcal {L}$
which is therefore an Erdős–Liouville set.
$\mathcal {L}$
which is therefore an Erdős–Liouville set.
Remark 2.8. In the literature, there are various strengthenings of the Erdős result on Liouville numbers. We mention explicitly [Reference Alniaçik and Saias1, Reference Rieger14, Reference Schwarz15]. The paper [Reference Kumar, Thangadurai and Waldschmidt9] shows that the set of Liouville numbers has a property stronger than the Erdős property. Though we do not study such properties, we record here that the
![]() $\mathfrak {c}$
Erdős–Liouville sets we produce in Theorem 4.6 also possess this stronger property, while Theorem 3.6 and the proof of Theorem 4.6 show that there are only
$\mathfrak {c}$
Erdős–Liouville sets we produce in Theorem 4.6 also possess this stronger property, while Theorem 3.6 and the proof of Theorem 4.6 show that there are only
![]() $\mathfrak {c}$
dense
$\mathfrak {c}$
dense
![]() $G_{\delta }$
subsets of
$G_{\delta }$
subsets of
![]() $\mathbb {R}$
. The relevant theorem from [Reference Kumar, Thangadurai and Waldschmidt9] describing this stronger property is the following result.
$\mathbb {R}$
. The relevant theorem from [Reference Kumar, Thangadurai and Waldschmidt9] describing this stronger property is the following result.
Theorem 2.9. Let G be a dense
![]() $G_{\delta }$
-subset of
$G_{\delta }$
-subset of
![]() $\mathbb {R}$
, I an interval in
$\mathbb {R}$
, I an interval in
![]() $\mathbb {R}$
with nonempty interior, and f a continuous function from I to
$\mathbb {R}$
with nonempty interior, and f a continuous function from I to
![]() $\mathbb {R}$
which is nowhere locally constant. (This means that f is not constant on any nonempty open subinterval of I.) Then there exists an
$\mathbb {R}$
which is nowhere locally constant. (This means that f is not constant on any nonempty open subinterval of I.) Then there exists an
![]() $x\in G\cap I$
such that
$x\in G\cap I$
such that
![]() $f(x)\in G$
. Indeed, there is an uncountable number of such x.
$f(x)\in G$
. Indeed, there is an uncountable number of such x.
If we put
![]() $f(x)=r-x$
, for
$f(x)=r-x$
, for
![]() $r,x\in \mathbb {R}$
and
$r,x\in \mathbb {R}$
and
![]() $I=\mathbb {R}$
, we see that f satisfies the conditions of the theorem and thus G has the Erdős property. However, as observed in [Reference Kumar, Thangadurai and Waldschmidt9], if we put
$I=\mathbb {R}$
, we see that f satisfies the conditions of the theorem and thus G has the Erdős property. However, as observed in [Reference Kumar, Thangadurai and Waldschmidt9], if we put
![]() $I=(0,\sqrt {r})$
and
$I=(0,\sqrt {r})$
and
![]() $f(x) = \sqrt {r-x^2}$
, we see that for every Erdős–Liouville set G, every positive real number is the sum of two squares of numbers in G. Also, the argument in [Reference Kumar, Thangadurai and Waldschmidt9, pages 63–64] with
$f(x) = \sqrt {r-x^2}$
, we see that for every Erdős–Liouville set G, every positive real number is the sum of two squares of numbers in G. Also, the argument in [Reference Kumar, Thangadurai and Waldschmidt9, pages 63–64] with
![]() $L^1= \{\exp (\alpha ): \alpha \in \mathcal {L}\}$
leads to the observation that
$L^1= \{\exp (\alpha ): \alpha \in \mathcal {L}\}$
leads to the observation that
![]() $L^1\cap {\mathcal {L}}$
is an Erdős–Liouville set. Although it was not explicitly mentioned in [Reference Kumar, Thangadurai and Waldschmidt9], it follows by induction that if
$L^1\cap {\mathcal {L}}$
is an Erdős–Liouville set. Although it was not explicitly mentioned in [Reference Kumar, Thangadurai and Waldschmidt9], it follows by induction that if
![]() $L^n= L^{n-1}\cap \mathcal {L}$
, for
$L^n= L^{n-1}\cap \mathcal {L}$
, for
![]() $n\in \mathbb {N}$
,
$n\in \mathbb {N}$
,
![]() $n>1$
, then each
$n>1$
, then each
![]() $L^n$
is an Erdős–Liouville set. However, we do not know if the sets
$L^n$
is an Erdős–Liouville set. However, we do not know if the sets
![]() $L^n$
are distinct from each other and distinct from
$L^n$
are distinct from each other and distinct from
![]() $\mathcal {L}$
.
$\mathcal {L}$
.
Proposition 2.10. Let S be a set of real numbers such that
![]() $W_1\supset S\supset W_2$
, where
$W_1\supset S\supset W_2$
, where
![]() $W_1$
and
$W_1$
and
![]() $W_2$
are Erdős–Liouville sets. Then S is an Erdős–Liouville set.
$W_2$
are Erdős–Liouville sets. Then S is an Erdős–Liouville set.
Proof. As
![]() $S\supset W_2$
, by Remark 2.5, it has the Erdős property. Also as
$S\supset W_2$
, by Remark 2.5, it has the Erdős property. Also as
![]() $W_2$
is dense in
$W_2$
is dense in
![]() $\mathbb {R}$
, so too is S. Finally, as
$\mathbb {R}$
, so too is S. Finally, as
![]() $S\subset W_1$
, it is a subset of
$S\subset W_1$
, it is a subset of
![]() $\mathcal {L}$
. Therefore, S is an Erdős–Liouville set.
$\mathcal {L}$
. Therefore, S is an Erdős–Liouville set.
3 Some topology
Before proving the existence of an uncountable number of Erdős–Liouville sets, we need to record some topology, some of which was laid bare in [Reference Chalebgwa and Morris5, Reference Chalebgwa and Morris6, Reference Morris11].
Definition 3.1. A topological space X is said to be topologically complete (or completely metrisable) if the topology of X is the same as the topology induced by a complete metric on X.
Of course, every complete metric space is topologically complete.
We denote by
![]() $\mathbb {P}$
the set of all irrational real numbers with the topology it inherits as a subspace of the euclidean space
$\mathbb {P}$
the set of all irrational real numbers with the topology it inherits as a subspace of the euclidean space
![]() $\mathbb {R}$
.
$\mathbb {R}$
.
A beautiful characterisation of the topological space
![]() $\mathbb {P}$
is given in [Reference van Mill16, Theorem 1.9.8].
$\mathbb {P}$
is given in [Reference van Mill16, Theorem 1.9.8].
Theorem 3.2. The space of all irrational real numbers
![]() $\mathbb {P}$
is topologically the unique nonempty, separable, metrisable, topologically complete, nowhere locally compact, and zero-dimensional space.
$\mathbb {P}$
is topologically the unique nonempty, separable, metrisable, topologically complete, nowhere locally compact, and zero-dimensional space.
![]() $\Box $
$\Box $
This has a Corollary 3.3, [Reference van Mill16, Corollary 1.9.9], which is often proved using continued fractions.
Corollary 3.3. The space
![]() $\mathbb {P}$
is homeomorphic to the Tychonoff product
$\mathbb {P}$
is homeomorphic to the Tychonoff product
![]() $\mathbb {N}^{\aleph _0}$
of a countably infinite number of homeomorphic copies of the discrete space
$\mathbb {N}^{\aleph _0}$
of a countably infinite number of homeomorphic copies of the discrete space
![]() $\mathbb {N}$
of positive integers. Hence,
$\mathbb {N}$
of positive integers. Hence,
![]() $\mathbb {P}\times \mathbb {P}$
is homeomorphic to
$\mathbb {P}\times \mathbb {P}$
is homeomorphic to
![]() $\mathbb {P}$
. Indeed,
$\mathbb {P}$
. Indeed,
![]() $\mathbb {P}$
is homeomorphic to
$\mathbb {P}$
is homeomorphic to
![]() $\mathbb {P}^{\aleph _0}$
.
$\mathbb {P}^{\aleph _0}$
.
Remark 3.4. Recall that a subset X of a topological space Y is said to be a
![]() $G_{\delta }$
-set if it is a countable intersection of open sets in Y while X is said to be an
$G_{\delta }$
-set if it is a countable intersection of open sets in Y while X is said to be an
![]() $F_{\sigma }$
-set if it is a countable union of closed sets in Y. Obviously, a subset X of a topological space Y is a
$F_{\sigma }$
-set if it is a countable union of closed sets in Y. Obviously, a subset X of a topological space Y is a
![]() $G_{\delta }$
-set if and only if its complement is an
$G_{\delta }$
-set if and only if its complement is an
![]() $F_{\sigma }$
-set. We see immediately that in a metric space such as
$F_{\sigma }$
-set. We see immediately that in a metric space such as
![]() $\mathbb {R}$
, the set
$\mathbb {R}$
, the set
![]() $\mathcal {T}$
of all transcendental real numbers is a
$\mathcal {T}$
of all transcendental real numbers is a
![]() $G_{\delta }$
-set as its complement is the countably infinite set
$G_{\delta }$
-set as its complement is the countably infinite set
![]() $\mathbb {A}$
of all real algebraic numbers.
$\mathbb {A}$
of all real algebraic numbers.
Now we connect the notion of
![]() $G_{\delta }$
-set in
$G_{\delta }$
-set in
![]() $\mathbb {R}$
to the property of being topologically complete.
$\mathbb {R}$
to the property of being topologically complete.
Theorem 3.5 [Reference van Mill16, Theorem A.63].
A subset of a separable metric topologically complete space is a
![]() $G_{\delta }$
-set in that space if and only if it is topologically complete.
$G_{\delta }$
-set in that space if and only if it is topologically complete.
Using Theorems 3.2, 3.5 and Corollary 3.3, we obtain the following result.
Theorem 3.6. Every
![]() $G_{\delta }$
subset of the set
$G_{\delta }$
subset of the set
![]() $\mathbb {P}$
of all irrational real numbers is homeomorphic to
$\mathbb {P}$
of all irrational real numbers is homeomorphic to
![]() $\mathbb {P}$
and to
$\mathbb {P}$
and to
![]() $\mathbb {N}^{\aleph _0}$
. In particular, the space
$\mathbb {N}^{\aleph _0}$
. In particular, the space
![]() $\mathcal {T}$
of all real transcendental numbers and the space
$\mathcal {T}$
of all real transcendental numbers and the space
![]() $\mathcal {L}$
of all Liouville numbers, with their subspace topologies from
$\mathcal {L}$
of all Liouville numbers, with their subspace topologies from
![]() $\mathbb {R}$
, are both homeomorphic to
$\mathbb {R}$
, are both homeomorphic to
![]() $\mathbb {P}$
and to
$\mathbb {P}$
and to
![]() $\mathbb {N}^{\aleph _0}$
.
$\mathbb {N}^{\aleph _0}$
.
These results and a similar one [Reference van Mill16, Theorem 1.9.6] characterising the space
![]() $\mathbb {Q}$
of all rational numbers with its euclidean topology, are used in [Reference Chalebgwa and Morris6, Reference Morris11] to describe transcendental groups and topological transcendental fields.
$\mathbb {Q}$
of all rational numbers with its euclidean topology, are used in [Reference Chalebgwa and Morris6, Reference Morris11] to describe transcendental groups and topological transcendental fields.
4 The existence of
 $2^{\mathfrak {c}}$
Erdős–Liouville sets
$2^{\mathfrak {c}}$
Erdős–Liouville sets
Theorem 4.1. Let X be a topological space homeomorphic to
![]() $\mathbb {P}$
. Then X has a dense
$\mathbb {P}$
. Then X has a dense
![]() $G_{\delta }$
-set Y which is homeomorphic to
$G_{\delta }$
-set Y which is homeomorphic to
![]() $\mathbb {P}$
such that the cardinality of the set
$\mathbb {P}$
such that the cardinality of the set
![]() $X\setminus Y$
is
$X\setminus Y$
is
![]() $\mathfrak {c}$
, the cardinality of the continuum.
$\mathfrak {c}$
, the cardinality of the continuum.
Proof. Consider the topological space
![]() $\mathcal {T}$
of all real transcendental numbers and the topological space
$\mathcal {T}$
of all real transcendental numbers and the topological space
![]() $\mathcal {L}$
of all Liouville numbers. We saw in Corollary 2.6 and Remark 2.1 that
$\mathcal {L}$
of all Liouville numbers. We saw in Corollary 2.6 and Remark 2.1 that
![]() $\mathcal {L}$
is a dense
$\mathcal {L}$
is a dense
![]() $G_{\delta }$
-set, and
$G_{\delta }$
-set, and
![]() $\mathcal {T}$
and
$\mathcal {T}$
and
![]() $\mathcal {L}$
are homeomorphic to
$\mathcal {L}$
are homeomorphic to
![]() $\mathbb {P}$
. Further, the cardinality of the set
$\mathbb {P}$
. Further, the cardinality of the set
![]() $\mathcal {T}\setminus \mathcal {L}$
is
$\mathcal {T}\setminus \mathcal {L}$
is
![]() $\mathfrak {c}$
. As the properties of being a dense
$\mathfrak {c}$
. As the properties of being a dense
![]() $G_{\delta }$
-set and having cardinality
$G_{\delta }$
-set and having cardinality
![]() $\mathfrak {c}$
are preserved by homeomorphisms, the theorem is proved.
$\mathfrak {c}$
are preserved by homeomorphisms, the theorem is proved.
By Theorem 4.1 and Remark 2.1, we have the following corollary.
Corollary 4.2. The space
![]() $\mathcal {L}$
of all Liouville numbers has a dense
$\mathcal {L}$
of all Liouville numbers has a dense
![]() $G_{\delta }$
-set
$G_{\delta }$
-set
![]() $L_1 $
homeomorphic to
$L_1 $
homeomorphic to
![]() $\mathcal {L}$
. Further,
$\mathcal {L}$
. Further,
![]() $L_1$
is an Erdős–Liouville set.
$L_1$
is an Erdős–Liouville set.
Theorem 4.3. If L is any Erdős–Liouville set homeomorphic to
![]() $\mathbb {P}$
, then it has a proper subset
$\mathbb {P}$
, then it has a proper subset
![]() $L_1$
which is an Erdős–Liouville set homeomorphic to
$L_1$
which is an Erdős–Liouville set homeomorphic to
![]() $\mathbb {P}$
. Therefore, there is no minimal Erdős–Liouville set homeomorphic to
$\mathbb {P}$
. Therefore, there is no minimal Erdős–Liouville set homeomorphic to
![]() $\mathbb {P}$
.
$\mathbb {P}$
.
![]() $\Box $
$\Box $
Our next theorem follows immediately from Corollary 4.2 and Theorem 4.1.
Theorem 4.4. There exist Erdős–Liouville sets
![]() $L_1, L_2,\ldots , L_n, \ldots, $
for
$L_1, L_2,\ldots , L_n, \ldots, $
for
![]() $n\in \mathbb {N}$
, such that
$n\in \mathbb {N}$
, such that
with each
![]() $L_n\setminus L_{n+1}$
having cardinality
$L_n\setminus L_{n+1}$
having cardinality
![]() $\mathfrak {c}$
and each
$\mathfrak {c}$
and each
![]() $L_{n+1}$
a
$L_{n+1}$
a
![]() $G_{\delta }$
-set in
$G_{\delta }$
-set in
![]() $L_n$
which is homeomorphic to
$L_n$
which is homeomorphic to
![]() $\mathbb {P}$
.
$\mathbb {P}$
.
![]() $\Box $
$\Box $
Theorem 4.5. There exist
![]() $2^{\mathfrak {c}}$
Erdős–Liouville sets no two of which are homeomorphic.
$2^{\mathfrak {c}}$
Erdős–Liouville sets no two of which are homeomorphic.
Proof. First, we note that there are precisely
![]() $2^{\mathfrak {c}}$
subsets of the set
$2^{\mathfrak {c}}$
subsets of the set
![]() $\mathcal {L}$
of all Liouville numbers as
$\mathcal {L}$
of all Liouville numbers as
![]() $\mathcal {L}$
has cardinality
$\mathcal {L}$
has cardinality
![]() $\mathfrak {c}$
. So the cardinality of the set of Erdős–Liouville sets is not greater than
$\mathfrak {c}$
. So the cardinality of the set of Erdős–Liouville sets is not greater than
![]() $2^{\mathfrak {c}}$
.
$2^{\mathfrak {c}}$
.
Using the notation of Theorem 4.4, let W be any subset of
![]() $\mathcal {L}\setminus L_1$
. As
$\mathcal {L}\setminus L_1$
. As
![]() $L_1$
is an Erdős–Liouville set and
$L_1$
is an Erdős–Liouville set and
![]() $L_1\subset \mathcal {L}$
, Remark 2.5 implies that
$L_1\subset \mathcal {L}$
, Remark 2.5 implies that
![]() $L_1\cup W$
is an Erdős–Liouville set. As there are
$L_1\cup W$
is an Erdős–Liouville set. As there are
![]() $2^{\mathfrak {c}}$
subsets W of the set
$2^{\mathfrak {c}}$
subsets W of the set
![]() $\mathcal {L}\setminus L_1$
, it follows that there are
$\mathcal {L}\setminus L_1$
, it follows that there are
![]() $2^{\mathfrak {c}}$
distinct Erdős–Liouville sets. So it remains to show only that amongst these, there are
$2^{\mathfrak {c}}$
distinct Erdős–Liouville sets. So it remains to show only that amongst these, there are
![]() $2^{\mathfrak {c}}$
no two of which are homeomorphic.
$2^{\mathfrak {c}}$
no two of which are homeomorphic.
By the Laverentieff theorem, [Reference van Mill16, Theorem A8.5], there are at most
![]() $\mathfrak {c}$
subspaces of
$\mathfrak {c}$
subspaces of
![]() $\mathbb {R}$
which are homeomorphic. As there are
$\mathbb {R}$
which are homeomorphic. As there are
![]() $2^{\mathfrak {c}}$
distinct Erdős–Liouville sets, it follows that there are
$2^{\mathfrak {c}}$
distinct Erdős–Liouville sets, it follows that there are
![]() $2^{\mathfrak {c}}$
Erdős–Liouville sets no two of which are homeomorphic, as required.
$2^{\mathfrak {c}}$
Erdős–Liouville sets no two of which are homeomorphic, as required.
Theorem 4.6. There exist
![]() $\mathfrak {c}$
Erdős–Liouville sets each of which is homeomorphic to
$\mathfrak {c}$
Erdős–Liouville sets each of which is homeomorphic to
![]() $\mathcal {L}$
with its subspace topology. So each is homeomorphic to
$\mathcal {L}$
with its subspace topology. So each is homeomorphic to
![]() $\mathbb {P}$
.
$\mathbb {P}$
.
Proof. Using the notation of Theorem 4.4,
![]() $\mathcal {L}\supset L_1$
, and the set
$\mathcal {L}\supset L_1$
, and the set
![]() $\mathcal {L}\setminus L_1$
has cardinality
$\mathcal {L}\setminus L_1$
has cardinality
![]() $\mathfrak {c}$
. Let
$\mathfrak {c}$
. Let
![]() $S= \{s_1, s_2, \ldots , s_n, \ldots \}$
be any countably infinite subset of
$S= \{s_1, s_2, \ldots , s_n, \ldots \}$
be any countably infinite subset of
![]() $\mathcal {L}\setminus L_1$
. As
$\mathcal {L}\setminus L_1$
. As
![]() $\mathcal {L}\setminus L_1$
has cardinality
$\mathcal {L}\setminus L_1$
has cardinality
![]() $\mathfrak {c}$
, there are
$\mathfrak {c}$
, there are
![]() $\mathfrak {c}$
distinct such subsets S. Then,
$\mathfrak {c}$
distinct such subsets S. Then,
![]() $\mathcal {L}\setminus S= \bigcap _{i=1}^\infty (\mathcal {L}\setminus \{s_i\})$
.
$\mathcal {L}\setminus S= \bigcap _{i=1}^\infty (\mathcal {L}\setminus \{s_i\})$
.
Observing that
![]() $\mathcal {L}\supset \mathcal {L}\setminus S\supset L_1$
, Proposition 2.10 implies that each
$\mathcal {L}\supset \mathcal {L}\setminus S\supset L_1$
, Proposition 2.10 implies that each
![]() $\mathcal {L}\setminus S$
is an Erdős–Liouville set.
$\mathcal {L}\setminus S$
is an Erdős–Liouville set.
Noting that
![]() $\mathcal {L}$
is a
$\mathcal {L}$
is a
![]() $G_{\delta }$
-set in
$G_{\delta }$
-set in
![]() $\mathbb {R}$
, and each
$\mathbb {R}$
, and each
![]() $\mathcal {L}\setminus \{s_i\}$
is an open set in
$\mathcal {L}\setminus \{s_i\}$
is an open set in
![]() $\mathcal {L}$
, it follows that
$\mathcal {L}$
, it follows that
![]() $\mathcal {L}\setminus S$
is a
$\mathcal {L}\setminus S$
is a
![]() $G_{\delta }$
-set. By Theorem 3.6, each of the
$G_{\delta }$
-set. By Theorem 3.6, each of the
![]() $\mathfrak {c}$
sets
$\mathfrak {c}$
sets
![]() $\mathcal {L}\setminus S$
is therefore homeomorphic to
$\mathcal {L}\setminus S$
is therefore homeomorphic to
![]() $ \mathcal {L}$
and
$ \mathcal {L}$
and
![]() $\mathbb {P}$
.
$\mathbb {P}$
.