Published online by Cambridge University Press: 23 April 2024
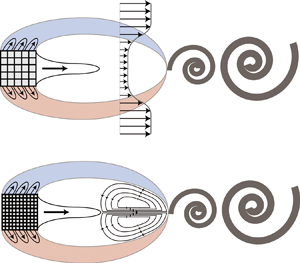
This study experimentally investigates the wake structure of a porous square cylinder in terms of permeability over two decades of  $Da$ (i.e.
$Da$ (i.e.  $2.4 \times 10^{-5} < Da < 2.9 \times 10^{-3}$). The porous cylinder, featuring a simple cubic lattice structure, was fabricated using an additive manufacturing technique. This unique method, combined with a periodic and scalable lattice structure, effectively isolates permeability from porosity, making it suitable for an in-depth parametric study. The key parameter, permeability, was directly estimated by measuring the pressure drop and superficial velocity for each porous case in an open-loop pipe flow system. The downstream flow fields were obtained using standard planar particle image velocimetry measurements in an open-loop wind tunnel. Based on the experimental data, structural modifications in the near wake were examined in relation to permeability, leading to the identification of four distinct flow regimes depending on
$2.4 \times 10^{-5} < Da < 2.9 \times 10^{-3}$). The porous cylinder, featuring a simple cubic lattice structure, was fabricated using an additive manufacturing technique. This unique method, combined with a periodic and scalable lattice structure, effectively isolates permeability from porosity, making it suitable for an in-depth parametric study. The key parameter, permeability, was directly estimated by measuring the pressure drop and superficial velocity for each porous case in an open-loop pipe flow system. The downstream flow fields were obtained using standard planar particle image velocimetry measurements in an open-loop wind tunnel. Based on the experimental data, structural modifications in the near wake were examined in relation to permeability, leading to the identification of four distinct flow regimes depending on  $Da$. Additionally, the downstream flow adjustment length (
$Da$. Additionally, the downstream flow adjustment length ( $L_i$) was assessed by introducing a permeability-based source term into the momentum equation, facilitating the development of an analytical model for
$L_i$) was assessed by introducing a permeability-based source term into the momentum equation, facilitating the development of an analytical model for  $L_i$. The present experimental data support this analytical model, and our results further confirmed that
$L_i$. The present experimental data support this analytical model, and our results further confirmed that  $L_i$ plays a crucial role as a characteristic length scale in the near wake.
$L_i$ plays a crucial role as a characteristic length scale in the near wake.