Since gas hydrates were admitted to the last ice conference as legitimate forms of ice there has been substantial progress in some areas of their study. There is space here only for a brief survey. (For infrared results, see the paper by Othen and others (1978) in the present symposium.)
New Hydrates
Twenty-six clathrate hydrates (Table I) have been identified since the publication of the last compilation (Davidson, 1973). With one exception, these are cubic forms of von Stackelberg’s structure I or structure II. The structure formed is primarily determined by the size of the hydrate-forming molecule and its ability to fit into the clathrate cages of the appropriate structure (Fig. I). All the new hydrates (Ripmeester and Davidson, 1977) are formed by molecules too large to occupy the 12-hedral cages which occur in both structures and owe their stability to almost complete occupancy of the 14-hedra (structure I) or 16-hedra (structure II). Ethylene sulphide is of intermediate size and may form either structure under suitable conditions.
Table I. New Clathrate Hydrates (Ripmeester and Davidson, 1977)


Fig. 1. Polyhedral cages of water molecules in clathrate ices of structures I and II. Circles represent oxygen atoms and lines the hydrogen bonds between them.
The structure II aldehyde hydrates are unstable, presumably because of the gradual conversion of aldehyde into gem-diol: RCHO + H2O → RCH(OH)2 (Davidson and others, 1976). Ethanal and propanal were once thought (Cohen and van der Horst, 1938) to promote the formation of an unstable cubic form of ice (“ice VIII”) in aqueous solutions. As in the case of acetone, this particular “ice VIII” is a clathrate ice,
Of particular interest is the low-temperature hydrate formed by dimethyl ether (Miller and others, 1977). This appears to be a tetragonal clathrate in which the ether molecules occupy 15-hcdral (Fig. 2) as well as 14-hedral cages. The size and shape requirements for molecules to form this structure are so severe that the only other known example is bromine hydrate.Footnote * In contrast, 38 molecules are now known to form structure I hydrates and 55 molecules structure II.

Fig. 2. Dimethyl ether encaged in the 14- and 15-hedron of the tetragonal structure. The ether molecule is represented by the van der Waals outlines of the oxygen atom and rotating methyl groups.
Deuteron Quadrupole Coupling Constants
The quadrupole coupling constants of the structure II D2O hydrates of p-dioxane (e 2 qQ/h = 217 kHz, η = 0.10 at 63 K (Ripmeester, 1977)) and tetrahydrofuran (215 kHz, 0.11 at 37 K) are very nearly the same as for hexagonal ice (213.2 kHz, 0.100 for D in OD bonds parallel to c-axis, 216.4 kHz for remaining D’s, at 263 K. (Waldstein and others, 1964) ; 213.4 kHz, 0.112 for polycrystalline ice at 77 K (Edmonds and MacKay, 1975)). According to this sensitive electric field-gradient criterion, the hydrogen-bonded OD bond lengths in the D2O lattices of ice Ih and structure II are thus practically identical.
Thermodynamic Properties
The degree of validity of the assumptions on which the ideal solid-solution thermodynamic theory of clathrate ices is based (van der Waals and Platteeuw, 1959) has proven difficult to define. The fundamental result that the μ-potential of water in the hydrate is related to the degree of occupany θ i of the cages by
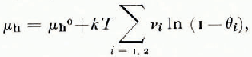
where i distinguishes small and large cages, and v i is the number of cages of type i per lattice water molecule, does not uniquely define the composition of hydrate in equilibrium with ice (μ h = μ ice) if both θ 1 and θ 2 are finite, as is common for structure I hydrates. For simple structure II hydrates only the large 16-hedral cages are occupied and the composition is fixed by
Here, however, θ L is so near to 1 that no composition has yet been measured with sufficient accuracy to yield a reliable value of △μ = μ ice — μ h 0 (Gough and Davidson, 1971). Dyadin and others (1976) have used this apparent stoichiometry to argue that these hydrates are not solid solutions. In their view the results of Glew and Rath (1966), which clearly defined a change in composition of the structure I hydrate of ethylene oxide with the activity of ethylene oxide in the aqueous solution from which it was prepared, may be attributed to complete occupancy of the 14-hedra together with variable occupancy of the 12-hedra. This position is not supported by the compositions of such structure I hydrates as those of cyclopropane, CH2ClF, and CH3Br, all of which correspond to less than complete occupancy of the 14-hcdra even if the 12-hedra are empty. Nor does there appear to be any thermodynamic reason why stability should depend on the degree of occupancy of large and small cages in a qualitatively different way.
Carbonnel, Rosso, and collaborators (Kaloustian and others, 1976, and references given there) found that the hydrates formed by the relatively large molecules of m- and p-dioxane, isoxazole, isothiazole, CH2Cl2, CHCl3, and CCl4 are structure II hydrates with only half the 16-hedra occupied. This contention, which would confound the solid-solution model, is not supported by composition data obtained by other workers (for summary, see Davidson and others, 1977[b]).
Some progress has been made in the calculation of the partition functions of encaged molecules. These determine the Langmuir constants which in the solid-solution model relate the degree of cage occupancy to the pressure of the encageable gas. Parrish and Prausnitz (1972) assumed a Kihara spherical-core potential function for the interaction between guest and cage water molecules, the latter being treated as a spherical continuum. The rotational part of the partition function was thus taken to be the same as for the gas. This method was applied to the calculation of the stability conditions of mixed hydrates, the potential parameters being fitted to the dissociation pressures of hydrates of single encageable components. Ng and Robinson (1976) obtained improved dissociation pressures of hydrates of binary gases by multiplying △μ in the Prausnitz–Parrish method by the factor 1 + 3(α— 1) y 1 2—2 (α — 1) y 1 3 where α is a constant of the order of unity for a given binary pair and y 1 is the mole fraction of the more volatile component of the gas. This empirical correction factor, although “to be used only for gas mixtures”, is greatest at y 1 = 1, which suggests that the departure of α from 1 in large part merely measures experimental inconsistencies between dissociation pressures measured for hydrates of the single- and two-component gases.
Tester and others (1972) employed pair-wise interaction potentials between the guest molecule and individual (isotropic) water molecules. They used Monte Carlo techniques of sampling these interactions at many positions and orientations of the guest molecules. A non-spherical hard-core Kihara potential was found suitable for the structure I hydrates of N2, O2 and CO2. Again the adequacy of the model could not be independently estimated because the experimental dissociation pressures were used to fix the Kihara interaction parameters.
It appears that substantial progress in testing the statistical thermodynamic theory will require more accurate knowledge of compositions and heats of encagement. There have been no proper calorimetric measurements.
Motion of the Water Molecules
The reorientation of water molecules has been studied dielectrically in a considerable number of clathrate hydrates (Table II). For structure II hydrates the characteristic dielectric behaviour (e.g. Fig. 3) is now well established. The static permittivity is given by ε 0 = ε 02 + 14 900/T, where ε 02 (= ε ∞1) is the permittivity measured (or calculated) to the high-frequency side of the water-dispersion region.
Table II. Reorientation of Water Molecules in Clathrate Hydrates


Fig. 3. Cole–Cole pole of the complex permittivity of p-dioxane hydrate in the water-molecule relaxation region.
The shape of the complex permittivity locus may be described within experimental error in terms of two discrete relaxation processes, the slower (by a factor of about two near — 60°C) contributing about twice as much to the permittivity as the faster. The “mean” reorientation times τ 0 (given in Table II as reciprocals of the angular frequencies of maximum dielectric absorption) are quite sensitive to the nature of the encaged molecule. Thus for non-polar guest molecules like SF6 and Xe the water-molecule reorientation times and activation energies are not much smaller than those of ice Ih (τ 0 = 1 420 μs at — 4.0°C, E A = 13.3 kcal/mol = 56 kJ/mol), whereas for guest molecules which are ethers or ketones the reorientation times are three or four orders of magnitude smaller and the activation energies as little as half as great. It is natural to imagine that oxygen-bearing molecules are able to inject Bjerrum defects of the L type into the lattice through formation of occasional hydrogen bonds with water molecules of the cage. Indeed, one can make some sense of the order of the relaxation times of the structure II hydrates on the basis of the geometric ability of oxygen atoms in the guest molecules to approach and hydrogen-bond with cage water molecules.
It is well known that the intrinsic relaxation of ice Ih at temperatures of — 40°C and below is difficult to measure because of the catalysing effects of impurities and lattice imperfections such as intercrystalline interfaces on the relaxation rate. The experimental problem is accentuated for those clathrate ices whose intrinsic relaxation is slow by the difficulty in growing good crystals in a system in which the hydrate-forming component is only sparingly-soluble. Such hydrates are normally prepared in polycrystalline form from finely powdered ice or by vigorous agitation and pressed into discs for dielectric study. Such samples are adequate for study of the motion of the encaged molecules but not, in many cases, for study of the slow relaxation of the water lattice: the results tend to be variable and the dielectric absorption to be broad. Nevertheless it is possible to infer that for the halogenated hydrocarbon hydrates which have been measured, the reorientation rates at —40°C are within about an order of magnitude of the reorientation rate in ice Ih and therefore that these guest species are much less effective than ethers in promoting orientational relaxation of the lattice.
The first information about the translational diffusion of water molecules in clathrates has been revealed by recent NMR studies. The second moment of the proton absorption line of the hydrate of perdeuterated ethylene oxide (Fig. 4) shows two distinct regions of line narrowing (Garg and others, 1977). That at lower temperature is associated with reorientation of the water molecules since it starts close to the temperature (indicated by the arrow) where the dielectric relaxation time is 10-4 s, a rate just sufficient to cause line narrowing. The second narrowing process, which is centred at 260 K and which ultimately reduces the second moment to zero, is diffusion of the water molecules. Spin-lattice relaxation time measurements in the rotating frame (T 1ρ ) of the same hydrate (Fig. 5) show two minima corresponding to the same two motional processes (Ripmeester, 1976). Analysis of these data, as well as of similar data for the structure II hydrate of tetrahydrofuran-d8 (Garg and others, 1974), yields the parameters given in Table III, where the diffusional activation parameters are of limited accuracy. For these two hydrates there is no doubt that diffusion of water molecules is considerably slower than reorientation, the reverse of the case in ice Ih.

Fig. 4. Proton second moments (mean-square widths of the proton NMR lines) of a number of structure I hydrates.

Fig. 5. Proton spin–lattice relaxation times in the rotating frame of ethylene oxide-d4 hydrate. H1 is the amplitude of the radio-frequency magnetic field.
Table 3. Reorientational and Translational Correlation Times of Water Molecules from T1ρ Measurements

For other clathrate hydrates, the onset of narrowing of the proton resonance line for the water molecule correlates quite well with reorientation, even when this is relatively slow (e.g. type I Xe and cyclopropane hydrates (Fig. 4) and type II SF6 hydrate (Majid and others, 1968)). In these latter cases diffusion is almost certainly slower than in hexagonal ice in which diffusion appears to occur via a lattice-vacancy (Schottky-defect) mechanism. If this is also the dominant mechanism in clathrate ices it is rather surprising that the slightly weaker hydrogen bonding and the presence of unoccupied cages do not promote faster diffusion. The effect of the guest molecule on the diffusion rate appears to be less than on reorientation. No direct measurements of diffusion coefficients have been reported.
Reorientation of Guest Molecules
Much information has now accumulated from NMR and dielectric studies of the re-orientational motions of individual enclathrated molecules (Davidson, 1973; Gough and others, 1973, 1975; Garg and others, 1974, 1975; Davidson and others, 1977[b]). Since these are perhaps of limited interest to those primarily concerned with ice, we mention here only certain features connected with the disorder of the water lattices.
The reorientation rates of guest molecules are exceptionally fast for molecules in the solid stale. Another characteristic feature is the presence of extremely broad distributions of NMR correlation times and dielectric relaxation times. These generally reflect the occurrence of several preferred orientations of different energy in individual cages as well as differences in these preferred orientations in different cages.
Although the second moments of the 1H or 19F resonance lines of D2O hydrates of guest molecules containing these nuclei first begin to fall, as expected, at temperatures near to those at which the 10 kHz dielectric loss is maximum, the fall in second moment in the great majority of cases extends over a very wide range of temperature to above 200 K, where the second moment frequently is still larger than that calculated for isotropic reorientation of the guest molecules. Some examples of this residual motional anisotropy will be shown below (cf. Fig. 8). The only exceptions which have been found to this behaviour involve guest molecules of cubic point-group symmetries.
Figure 6 shows the proton second moment of neopentane (2,2-dimethyl propane) a tetrahedral molecule, in the 16-hedral cages of the D2S–D2O double hydrate. There is a broad region of line narrowing centred at 24 K. By about 50 K the second moment has reached the value expected for isotropic reorientation (0.26 G2) and remains unchanged to 200 K. Between about 6 and 50 K the resonance line (cf. Fig. 7) consists of a superposition of the broad, structured, low-temperature component and a narrow component 1.2 G wide, the second increasing in intensity with rise of temperature until it is the only component observed. This is an example of the Resing apparent-phase-change effect associated with a very broad distribution of correlation times (Resing, 1965). In effect, at a temperature within the transition region, practically all the correlation times lie in the ranges lying above and below the correlation times which give components of intermediate shape.

Fig. 6. Temperature dependence of the proton second moment of neopentane-D2S double deuterohydrate.
To understand why molecules of neopentane appear to be rotating isotropically or not at all, it is sufficient only to consider the tetrahedral symmetry of this molecule. Since the rotational symmetry number is 12, any rotational process which exchanges the 12 energetically indistinguishable orientations of the molecule at any site in the cage sufficiently fast averages the directions of the internuclear magnetic fields in the molecule to zero. It is immaterial how many distinguishable preferred sites in the cage are populated: one will suffice. The distribution of correlation times in this case results from wide differences in the correlation times in different cages. This in turn can only be due to the orientational disorder of the water molecules which constitute the cages and to a dependence of reorientation rate on the positions of the hydrogen atoms in the hydrogen bonds.
The temperature dependence of the second moment of encaged neopentane may be represented, within the experimental accuracy, by correlation times τ c = 10-12 exp (E A/RT) with a Gaussian distribution of activation energies G(EA) =
The curve drawn for neopentane in Figure 6 was derived from the parameters given in Table IV, which includes corresponding values for other guest molecules of tetrahedral (CF4) and octahedral symmetry (SF6, SeF6). These also show the Resing effect clearly, along with isotropic second moments at temperatures above the transition. There is nothing unique about a log-normal representation of the distribution of correlation times, which was chosen for its simplicity. However, the values of A provide some idea of the relatively large spreads of the energies with which the molecules are held in preferred orientations in different cages.

Fig. 7. Proton NMR line shapes of neopentane-D2S deuterohydrate at a number of temperatures.
Table 4. Reorientational Correlation time Parameters derived from the Resing Effect in Hydrates of Symmetrical Molecules

For less symmetrical guests, second moments appreciably exceed the isotropic values to above 200 K. For the four structure II deuterohydrates of Figure 8, for example, the isotropic second moments are 0.14 to 0.16 G2 (Gough and others, 1977), The case of SF6 has already been considered. The second moments of the other three molecules fall to their isotropic values rather abruptly at temperatures between 180 and 220 K. This is the temperature range where the reorientation rate of the D2O molecules becomes fast enough to average out the local fields of the deuterons, but the direct effect of this on the proton second moment is much too small (? 0.02 G2) to account for the observed changes. The major effect is an indirect one due to change in the effective symmetry of the 16-hedral cage.

Fig. 8. Proton (19F for SF6) second moments of a number of structure II deuterohydrates above 100 K.
The X-ray crystallographic symmetry of the 16-hedral cage is 4 3m. This is of course a space, and, at relatively high temperatures, a time average over the disordered orientations of the water molecules. The drop in second moment to the value expected for isotropic rotation is due to the rapid reorientation of guest molecules in cages which themselves are changing their configurations rapidly enough (> 100 kHz) at 220 K, as a result of reorientation of D2O molecules, to realize the full time-averaged tetrahedral symmetry. About half the remaining second moment at this temperature is contributed by interactions with the deuterons of the D2O lattice. The disappearance of this contribution as self-diffusion of D2O molecules becomes sufficiently fast may be recognized at temperatures near 250 K.
The effect of time-averaging of the cage symmetry is particularly well illustrated by the deuteron resonance spectra of deuterated guest molecules in H2O clathrates. Figure 9 illustrates the deuteron line widths of the structure I hydrate of ethylene oxide-d4 (Ripmeester, 1976) and the structure 11 hydrate of tetrahydrofuran-d8. The width parameter plotted was derived from the widths of quadrupole echo signals at some temperatures and from the free induction decay curves at others. It represents mainly the root-mean-square value of the deuteron splitting frequency as represented by

Fig. 9. Effective deuterium quadrupole splitting frequencies (as

Fig. 10. Low-temperature dielectric absorption in p-dioxane hydrate.
p-dioxane exists exclusively in the non-dipolar chair form at low temperatures. Nevertheless the hydrate of this molecule shows measurable dielectric absorption and dispersion (Fig. 10) which, from the correspondence with the value of the nuclear relaxation time T 1 determined by NMR, is associated with reorientation of the dioxane molecule (Gough and others, 1975). The charge distribution in p-dioxane is roughly representable by the opposed dipoles associated with the two C–O–C groups. The magnitude of the dielectric absorption, that of an apparent molecular dipole moment of about 0.2 debye, may be satisfactorily accounted for by the sum of the dipole moments induced in the 28 water molecules of the 16-hedral cage by the two ether-group moments.
Orientational Disorder of the Water Molecules
The degree to which the configurational disorder of the water lattices of clathrate ices approaches completeness (the half-hydrogen model) is uncertain. The recent neutron diffraction study by Hollander and Jeffrey (1977) of ethylene oxide deuterohydrate at 80 K, while giving for the eight distinct D–O–D angles at the three crystallographically distinct water-molecule sites average values ranging from 107.4 to 115.0°, gave no evidence of departure from the half-hydrogen assumption. The observation of narrow distributions of dielectric relaxation times for the water molecules in hydrates of both structures does not distinguish between differences in the stability of different orientations at individual sites and differences between water molecules at different sites. In both lattices it is possible to account for the distribution by differences in the rate of diffusion of Bjerrum defects along different paths in the lattice.
Even completely disordered lattices will have residual configurational entropies somewhat smaller than those of ice Ih because of the increased correlations imposed by the presence of five-membered rings of water molecules. These outnumber six-membered rings by 8:1 in structure I and 9 : 1 in structure II.
Structural Properties of Encaged Molecules
Clathrate ices may be used to advantage in various matrix-isolation studies. In particular, low-temperature NMR studies of guest molecules enclathrated in D2O yield quite well-resolved rigid-lattice line shapes characteristic of the arrangement of mangnetic nuclei (e.g. 1H, 19F) in the guest molecules. In a hitherto largely negelected method of studying molecular geometry, powder-averaged spectra are being calculated for guest molecules containing up to eight magnetic nuclei. It has been established, for example, that 1,2-dichloroethane is encaged in a gauche configuration (unpublished work by S. K. Garg and J. A. Ripmeester).
This method has proved particularly useful in providing good line shapes for the study of methyl group tunnelling at low temperatures (cf. for example, the 2.4 K spectrum of Figure 7). Encageable CH3-containing molecules cover most of the range of line shapes between the fast and slow tunnelling limits. In some cases (e.g. CH3CD2Br), interactions between the methyl group and the cage lead to distributions of tunnelling frequencies and to a kind of Resing effect which again arises from disorder of the water molecules.
Natural Gas Hydrates
It is now quite certain that clathrate ices of natural gas occur in substantial quantities at relatively shallow depths below the Earth’s surface in northern areas which roughly coincide with the presence of permafrost (Makogon, 1974; Bily and Dick, 1974). Clathrate ices thus become the only polymorphs of ice in addition to ordinary hexagonal ice known to exits in Nature.
As much as 1.5 × 1013 standard m3 of natural gas in hydrate form in the Soviet Union has been estimated (Chersky and Makogon, 1970). This value may have been somewhat exaggerated because of failure to recognize the existence of natural gas hydrates of two structures, of winch only the form (structure I) with the narrower stability range is likely to prove and important reservoir of gas. (The presence of propane and isobutane promotes the stabler structure II.) For Canada, present estimates, based on the conservative use of the stability conditions of structure I methane hydrate, are ? 1011 m3 for the Mackenzie Delta region, with further appreciable quantities anticipated for the Arctic Archipelago and adjacent seas.
There is considerable evidence that natural gas hydrates also occur in the sedimentary deposits on the ocean floor, although it is certainly premature to conclude (Trofimuk and others, 1975) that they occur almost everywhere where there are such sedimentary accumulation in amounts which, in toto, contain much more gas than the world’s supply of conventional gas.
Natural gas hydrates have also assumed a new importance because of the hazards their presence may present. A number of blow-outs of varying seventy have occurred in both the Soviet Union and Canada during the drilling of hydrate-bearing sands
Although the general nature of many of the physical property of natural-gas hydrate may be predicted from their structures, there have been few actual measurements of properties other than those related to their thermodynamic stability. A study of the dielectric and NMR characteristics ?f the hydrates formed by the major components of natural gas has recently been undertaken (Davidson and others, 1977[a]).
Dielectric absorption from reorienting guests in the structure I hydrates formed by methane and ethane does not occur. The dipole moments of propane and isobutane m structure II are, however, large enough (? 0.1 debye) to give rise to finite absorption (Fig. 11), as is that of n-butane (Fig. 12). The latter does not form a stable hydrate by itself, but does so in the presence of H2S or CH4 which stabilize the structure II lattice by occupying some of the small (12-hedral) cages. The rise in loss to a peak below 2 K in Figure 12 arises from very rapid reorientation of H2S molecules, as is shown by independent measurements of H2S hydrate itself. Although the non-dipolar trans form of n-butane is the stabler form in the gas, it is clear from the presence of dielectric absorption and size considerations that n-butane is encaged as a gauche isomer.

Fig. 11. Dielectric absorption and dispersion in propane and isobutane hydrates.

Fig. 12. Dielectric absorption and dispersion in n-butane-H2S double hydrate.

Fig. 13. Proton NMR line shapes of propane and isobutane. hydrates.
The NMR spectra of hydrates of methane, ethane, propane, and isobutane show that the presence of a natural gas H2O hydrate may be recognized by the superposition of a relatively narrow line (3 to 4 G wide) on a broad line from the water lattice, at all temperatures between about 50 and 200 K (cf. Fig, 13). The narrow line due to methane persists to below 2 K while the lines from ethane in structure I and propane and isobutane in structure II broaden at low temperatures, reaching half their rigid-lattice second moments at
Discussion
G. NOLL: What kind of interaction have you assumed for the calculation of the correlation times of reorientation and diffusion derived from T 1ρ ?
D. W. DAVIDSON: The interactions assumed were the magnetic dipole interactions. Part of these interactions contributes to each T lρ process in
J. BERTIE: Which guest molecules reorient most rapidly in their clathrate hydrate cages?
DAV IDSON: CH4 shows hardly any change in second moment from its isotropic value down to below 1.8 K. This behaviour is likely to have been strongly affected by proton tunnelling at low temperatures.
BERTIE: How rapidly docs H2S reorient in its clathrate hydrate?
DAVIDSON: H2S has a reorientation rate in its hydrate that corresponds to a maximum dielectric absorption at 1 MHz which recurs below 1.8 K. This makes it the dipolar guest molecule with the fastest reorientation rate as far as is known.



















