Introduction
Over the last few decades, research in cognitive archaeology on early mathematical thought was dominated by what one might call a ‘quest for the first numbers’, or indeed for more sophisticated numerical notations and astronomical devices such as calendars (e.g. Frolov Reference Frolov and Emmanuel1970; Marshack Reference Marshack1972; Rouillon Reference Rouillon2006). In more recent publications, however, scholars have begun to look instead (and perhaps less spectacularly) for the ‘precursors’ of numbers and have sought to gain an insight into how numbers and numerical thinking might have emerged relatively seamlessly from proto- or even non-numerical practices (d’Errico et al. Reference d'Errico, Doyon and Colagé2018; Overmann Reference Overmann, Overmann and Coolidge2019). Of special interest in this context is the question of how ‘numerosity’—that is, the innate capacity to grasp and deal with small quantities (Coolidge & Overmann Reference Coolidge and Overmann2012), a capacity humans seem to share with other animals—was transformed into practices of counting and, eventually, into mathematical thinking.
This first shift in approaches to prehistoric mathematics is closely connected with a second one of equal importance. Traditional approaches in cognitive archaeology have tended to regard material artefacts as mere ‘expressions’, or passive material witnesses, of mental capacities, which were believed—implicitly or explicitly—to have developed and existed independently of these material devices. Contrary to this, new approaches—not least among them Material Engagement Theory (Malafouris Reference Malafouris2013)—propose that we ascribe an active role to material culture with a view to providing an account of how it may have contributed to the emergence of cognition. The possible roles played by material culture range from its being a mere catalyst for biological and cultural evolution to its constituting an active component of cognition in the sense of extended cognition. Thanks to this twofold shift in approach, we now possess the first detailed and refined (though admittedly still quite speculative) accounts of how numerical thinking may have evolved during prehistory prior to the invention of writing (e.g. d’Errico et al. Reference d'Errico, Doyon and Colagé2018; Overmann Reference Overmann2018; Reference Overmann, Overmann and Coolidge2019). The basic idea is that artefacts possess structural, unintended properties which can become significant in contexts other than those of their original purpose (McLaughlin Reference McLaughlin2014). Overmann (Reference Overmann, Wynn and Coolidge2017, 107) calls this process ‘repurposing’ while other authors speak of ‘exaptation’ (de Beaune Reference de Beaune2008b, 83; d’Errico et al. Reference d'Errico, Doyon and Colagé2018; Haidle Reference Haidle2012), a term taken from evolutionary biology (Gould & Vrba Reference Gould and Vrba1982).
This approach can be regarded as occurring in the tradition of Leroi-Gourhan's claim that inventionsFootnote 1 should be explained as phenomena that emerge from a ‘milieu favorable’, i.e. the coincidence of opportune circumstances (Leroi-Gourhan Reference Leroi-Gourhan1945) in which, as he put it later, ‘spontaneous innovation has become possible’ (Leroi-Gourhan Reference Leroi-Gourhan1964, 222). Sophie A. de Beaune interpreted this to mean that inventions should be explained as ‘the result of the combination of preexisting elements rather than creations ex nihilo’ (de Beaune Reference de Beaune2004, 149). Leroi-Gourhan's (perhaps slightly outdated) example is the emergence of hot metallurgy as it appeared in the sixth millennium bc. In a culture that, due to its former experiences with pottery, has already learned how to maintain fires of high temperature, and in which metal oxides are present for other reasons such as painting, the invention of hot metallurgy becomes an objective possibility and can be understood as resulting from the simple combination of existing elements (Leroi-Gourhan Reference Leroi-Gourhan1965, 210).Footnote 2 Contemporary approaches in cognitive archaeology broadly rely on the same model of invention, but apply it to invention and change at the level of cognitive capacities and conceptual content. As I will discuss later in more detail, Overmann (Reference Overmann, Wynn and Coolidge2017) and Wynn et al. (Reference Wynn, Overmann, Coolidge, Janulis, Wynn and Coolidge2017) point to the fact that strings of beads (unintentionally) instantiate features such as one-dimensional series, stable order, or plus-one, which later informed the way we think about numbers. In this way, material culture is held to provide a ‘scaffold’ for cognitive developments.
If we accept this proposition, then an important issue arises: it can generally be assumed that cultural artefacts such as beads were highly significant—in social, aesthetic and spiritual terms—and that this significance occluded their non-intentional, subjacent properties and thus prevented them from developing their conceptual potential. Under what circumstances might the overtly evident properties of such artefacts retreat into the background, permitting the less evident ones to shift to the centre of attention, as required by the accounts of Overmann and Wynn et al.? This is the question I will discuss in the present paper. In order to do so I will introduce the idea of ‘tokenization’, based on the type–token distinction which, though common in the philosophy of language, seems to be absent in the archaeological literature. This conceptual device has recently come to play a larger role in the philosophy of mathematics, a field that is currently beginning to pay more attention to the material and practical aspects of mathematics (Dutilh Novaes Reference Dutilh Novaes2012; Reference Dutilh Novaes2013; Hutchins Reference Hutchins1995).
In the present article, I will begin by describing how I understand the task of identifying the origins of mathematical thought in prehistoric culture (section 2). I will then introduce the notions of token and tokenization and show how they relate to the kind of abstraction which is characteristic for mathematics understood as a symbolic practice (section 3). I will go through a number of examples from prehistoric culture in order to identify some possible triggers of tokenization (section 4) and will explain how tokenization relates to the emergence of numbers (section 5). In conclusion (section 6), I will discuss how these findings fit into current models of the emergence of numbers.
Mind and matter, or how to look for the origins of mathematics
In Colin Renfrew's definition (Reference Renfrew, Renfrew and Zubrow1994, 3), cognitive archaeology is ‘the study of past ways of thought as inferred from material remains’. It might seem trivial but is actually important to note that archaeology in general starts from material remains not because it attaches special importance to them, but merely because they are the only things that remain from the ancient world. Archaeologists simply have no choice, and if they had a choice, they would probably choose otherwise. Or, as Knappett put it, the archaeologist can easily find herself in ‘the unhappy state of being a frustrated mentalist condemned to materialism’ (quoted in Malafouris Reference Malafouris2013, 229). A cursory overview of the abundant classical literature on prehistoric art and use of symbols does indeed reveal a sort of antinomy in archaeological research on this matter. On the one hand, it seems impossible not to raise questions about the meaning of the art works, be they figurative paintings or marks and strokes; on the other hand, however, it is equally impossible, due to the lack of corroboratory evidence, to give a definitive answer to such questions. Every possible answer, no matter how plausible it might seem, remains speculative, i.e. unverifiable. In the quest for the origins of mathematics, the debate about Marshack's hypotheses of notational systems and lunar calendars is a classic case.Footnote 3 Schmandt-Besserat's (Reference Schmandt-Besserat1992, 160) Solomonic verdict on Marshack's hypothesis illustrates the fundamental problem well: ‘This interpretation cannot be proven or disproven nor can it be ignored.’ The problem is that the ‘meaning’ of the paintings, figures, and symbols—if there ever was one, and given a traditional understanding of meaning—has disappeared irretrievably along with the prehistoric artists who created them, or at least so it seems.
Is there any way out of this antinomy? One strategy is to look for contemporary substitutes for the unavailable prehistoric agents. These may be contemporary societies of hunter-gatherers (Overmann Reference Overmann2013; Reference Overmann2014) or individuals from modern societies, placed in an experimental setting (d’Errico et al. Reference d'Errico, Doyon and Colagé2018; Majkic et al. Reference Majkić, Evans, Stepanchuk, Tsvelykh and d'Errico2017). Both approaches are of limited use, though. The validity of ‘uniformitarist’ comparisons between past and present societies of hunter-gatherers has always been hotly debated (Binford Reference Binford1967; Ebert Reference Ebert1978; Hayter Reference Hayter1994; Hodder Reference Hodder1982, 13). The experimental approach, in turn, can be used to prove only the intentional character of prehistoric artefacts: it says nothing about their meaning.
Other scholars, well aware of these difficulties, have suggested that we should stop asking about the meaning of artefacts at all. We should instead ‘examine the ways in which symbols were used’ (Renfrew Reference Renfrew, Renfrew and Zubrow1994, 6). One empirically feasible possibility lies in the study of syntactical structures which can be examined by means of classification and statistics (d’Errico Reference d'Errico1995; Dutkiewicz & Conard Reference Dutkiewicz, Conard, Cleyet-Merlye, Geneste and Man-Estier2016; Dutkiewicz et al. Reference Dutkiewicz, Wolf and Conard2018; Leroi-Gourhan Reference Leroi-Gourhan1966; Sauvet Reference Sauvet and Clottes1990; Reference Sauvet1993; Sauvet et al. Reference Sauvet, Sauvet and Wlodarczyk1977). However, while these syntactical structures are empirically accessible, there remains a gap between syntax and semantics—a gap which will probably always remain, given a traditional conceptual framing that posits an opposition between syntax and semantics, operation and intention, materiality and meaning. As long as this gap is not bridged convincingly, it is a mistake to believe that even the most complete knowledge of a symbolic system's syntactical structure will bring us any closer to its meaning. Our impressively detailed knowledge of, say, the manufacture of the La Marche antler, provided by d’Errico (Reference d'Errico1995), who was able to determine the number of tools and techniques used to carve the marks and the number of times the person who crafted it had to turn the object in his or her hands, poses a striking contrast to our absolute lack of knowledge about its actual use and meaning. De Beaune (Reference de Beaune2008a, 23–4) reminded us that crimped bone or antler artefacts might just as well have been musical instruments (Fig. 1)!

Figure 1. Artefact from Abri Cellier (© Logan Museum of Anthropology, Beloit College, with kind permission). A mathematical notation (Overmann Reference Overmann2013)—or a musical instrument (de Beaune & Balzeau Reference de Beaune and Balzeau2009, 187)?
This standoff has caused some students of prehistoric culture to distrust the traditional conceptual setting and to try to overcome the underlying dichotomy of ‘matter and mind’ and its declensions such as syntax and semantics. Malafouris’ (Reference Malafouris2013) theory of ‘material engagement’, based on the notion of embodiment in the cognitive sciences, is a recent eloquent candidate for such an endeavour. Instead of treating artefacts as mere ‘expressions’ of a human thought deemed to exist independently of them, Malafouris (Reference Malafouris2013, 11) suggests that we analyse the active role the artefacts ‘might have played in bringing about these cognitive capacities and processes or in changing them over the long term’. Applied to semiotics, this amounts to the claim that syntactical structures do not simply provide a basis for expressing pre-existing content but actively shape meaning and enable certain forms of reasoning. Malafouris (Reference Malafouris, Morley and Renfrew2010) has already suggested applying this approach to the question of the origin of mathematics, and Overmann (Reference Overmann2013; Reference Overmann2014; Reference Overmann2015; Reference Overmann, Wynn and Coolidge2017; Reference Overmann, Overmann and Coolidge2019) has generated interesting insights from taking it further. Overmann recently expressed her findings in this way: ‘embodied interactivity with materiality has the potential to generate concepts’ (Overmann Reference Overmann, Overmann and Coolidge2019, 437).
This fundamental problem with interpretation is reinforced in the case of numbers by certain doubts surrounding the claim that they first emerged as early as the Upper or even Middle Palaeolithic. The emergence of numeric symbols in Mesopotamia some 5000 years bp has been studied extensively (Nissen et al. Reference Nissen, Damerow and Englund1993; Proust Reference Proust2008; Schmandt-Besserat Reference Schmandt-Besserat1992; etc.). These studies suggest that the first numbers arose in conjunction with a range of complex socio-cultural activities which were most likely absent in the societies of the Upper Palaeolithic. At the same time, however, we know that the first abstract symbols existed during this period. As recent studies have shown, the claim that these symbols lacked systematic structure can hardly be sustained any longer. Dutkiewicz & Conard (Reference Dutkiewicz, Conard, Cleyet-Merlye, Geneste and Man-Estier2016, 150 & 160) speak of a ‘symbolic “language”’ in the Aurignacian of the Swabian Jura and provide evidence of an ‘inner logic of a semiotic system’. Prior to this Sauvet (Reference Sauvet and Clottes1990, 95) had already spoken of a ‘formalised graphic set’ that constituted a ‘champ symbolique’. It thus seems that, in their pioneering work on the development of mathematics from pre-arithmetical quantification to concept-based arithmetic, Damerow and others underestimated the symbolic resources of the Upper Palaeolithic (Damerow Reference Damerow1999; Damerow et al. Reference Damerow, Englund and Nissen1988; Nissen et al. Reference Nissen, Damerow and Englund1993). This causes one to hesitate with regard to Nissen et al.'s (Reference Nissen, Damerow and Englund1993, 125) assumption that in the societies of the Middle or Late Palaeolithic numerical judgements were confined to the oral language and relied on purely qualitative terms for an appreciation of quantities that were intuitively understood (such as ‘a single’, ‘both’, ‘a couple’, ‘a lot’, ‘many’, ‘all’ in modern languages). Is it realistic to posit, following Damerow (Reference Damerow1999, 27–8), the complete absence of socially transmitted standards for the construction of one-to-one correspondences, structured sequences for counting, tally systems such as finger counting, counting notches and counting knots, and arithmetic operations such as the construction of numbers through the repetition of units? The uneven preservation of artefacts may lead us to underestimate the relevant material resources of that time. But even if we restrict ourselves to the known finds, the coexistence of a rudimentary linguistic mastering of quantities on the one hand and a fairly developed, though non-arithmetic, symbolic system on the other raises questions about their mutual influence in subsequent times.
This approach is also of interest in the wider context of interdisciplinary research on the emergence of counting and mathematical thinking, a process to which various factors contribute: neurological (Coolidge & Overmann Reference Coolidge and Overmann2012; Nieder Reference Nieder2019), linguistic (Bender & Beller Reference Bender and Beller2011; Overmann Reference Overmann2015; Pagel & Meade Reference Pagel and Meade2017; Wiese Reference Wiese2003), the use of the body, e.g. fingers (Bender & Beller Reference Bender and Beller2012; Moeller et al. Reference Moeller, Fischer, Link, Wasner, Huber, Cress and Nuerk2012; Morrissey et al. Reference Morrissey, Liu, Kang, Hallett and Wang2016; Overmann Reference Overmann2014) and, finally, material culture (d’Errico et al. Reference d'Errico, Doyon and Colagé2018; Malafouris Reference Malafouris, Morley and Renfrew2010; Núñez Reference Núñez2017; Overmann Reference Overmann2013). While some authors appear still to seek reductive, monocausal explanations, there is a growing consensus that the complete picture involves an interaction between all these factors (cf. e.g. Overmann Reference Overmann, Wynn and Coolidge2017). Archaeologists are, in principle, well placed to highlight the importance of material culture and the active role it may well have played in the cultural evolution of humankind. However, in focusing too hastily on the meaning of artefacts, they reduce them to passive witnesses of previously developed cognitive capacities and thus forfeit the opportunity to understand the contribution made by artefacts to the emergence of these very capacities.
Type, token and tokenization
The distinction between type and token was drawn by Charles Sanders Peirce, who introduced it in the context of linguistic signs (Peirce Reference Peirce1931–1958, vol. 4, §4.537):
There will ordinarily be about twenty the's on a page, and of course they count as twenty words. In another sense of the word ‘word,’ however, there is but one word ‘the’ in the English language; […] Such a definitely significant Form, I propose to term a Type. […] A Single event which happens once […], such as this or that word on a single line of a single page of a single copy of a book, I will venture to call a Token. […] In order that a Type may be used, it has to be embodied in a Token which shall be a sign of the Type, and thereby of the object the Type signifies. I propose to call such a Token of a Type an Instance of the Type.
Note that ‘type’ refers to something like a pattern or a form. A character can be written in different sizes and different colours, but the form is fixed (within certain limits). One can call the type abstract and the token concrete if one wants to, but one must not confuse type with other things commonly referred to as abstract, such as meaning or abstract numbers. Such entities are absent from the conceptual framework of tokens. As we shall shortly see, the advantage of the notion of tokens and tokenization is that it permits us to appreciate cultural artefacts without raising questions about their meaning.
The distinction between type and token applies to any symbolic context and even beyond to non-symbolic practices (one might think, for example, of swimming as the instantiation of a swimming pattern such as breast stroke or crawl). Beyond this, however, it has special relevance for mathematics, as has become clear in recent debates in the philosophy of mathematics. In the wake of a ‘practical turn’ (Giardino Reference Giardino2017) quite similar to recent developments in cognitive archaeology, some scholars have come to consider mathematics not as a purely intellectual or mental activity, but as ‘thinking on paper’, i.e. as an activity which depends crucially on the ‘material means of thought’ (Hutchins Reference Hutchins1995) and, in particular, on the existence of external symbolic representations (Dutilh Novaes Reference Dutilh Novaes2013, 48 & 53).
If we pursue this idea of mathematical thought as ‘thinking on paper’—taken in the broader sense of ‘thinking using a material aid’, be it drawings in the sand or strokes on a bone—we are led to think of mathematics not simply as the use of, but more precisely as an operation that uses symbols, i.e. as a sort of calculus. Stated in abstract terms, a calculus consists in a set of signs and a set of rules for manipulating these signs (Whitehead Reference Whitehead1898, 4). The signs are typically made of basic signs in an iterative routine such as successively adding strokes to ‘I’, resulting in complex signs such as ‘II’ and ‘III’ and so on. The calculus may also contain a concatenation rule that permits us to put signs together such as ‘II’ and ‘III’ to ‘IIIII’.
It has recently been suggested by philosophers of mathematics that the signs in such a calculus work as tokens (Heinzmann Reference Heinzmann2013, 55). This, they argue, distinguishes mathematics from other symbolic techniques such as writing and figurative painting. Let me explain. A linguistic phrase like ‘the man who sold the world’ has two occurrences (tokens) of the word (type) ‘the’. While this is true, it is of no importance to the way the linguistic symbolism works. What counts here is the semantic content of the words. The situation is different in mathematics. In expressions like ‘III’ or ‘II + III’ anything can be substituted for the stroke, provided it is a token (symbol or icon, but also objects like stones or beads). ‘the the the’ makes no sense as a linguistic utterance. As mathematics, however, it does. ‘the the the’ is a legitimate sign of calculus set up using the basic sign ‘the’. This means that mathematics is a symbolic practice which not only uses signs—as language does—but uses signs as mere signs, irrespective of their meaning, i.e. as tokens. And if the meaning does not matter, the signs are reduced to mere instantiations of a type, i.e. to tokens. This reduction of meaningful cultural items to tokens I will call ‘tokenization’.
From a logical point of view, we can conclude that tokens and tokenization are essential for mathematics understood as ‘thinking on paper’, i.e. ‘thinking using a material aid’. Now, why is this interesting for historical inquiry in general and for the study of prehistoric artefacts with a view to understanding the origins of numbers and mathematics in particular? The answer is straightforward. Generally speaking, the phenomenon of tokenization is interesting because tokens fall outside the ‘closed and compartmentalized semantic universe’ as it is often implicitly presupposed in the archaeological literature (Fig. 2). According to this notion, artefacts can be sorted into three jointly exhaustive and mutually exclusive kinds of meaningful entities: (a) tools and marks with utilitarian meaning, fixed by use; (b) signs with an iconic, symbolic or indexical meaning, fixed by resemblance, convention or correlation; and (c) aesthetic and spiritual entities, fixed by the corresponding human emotional needs.Footnote 4
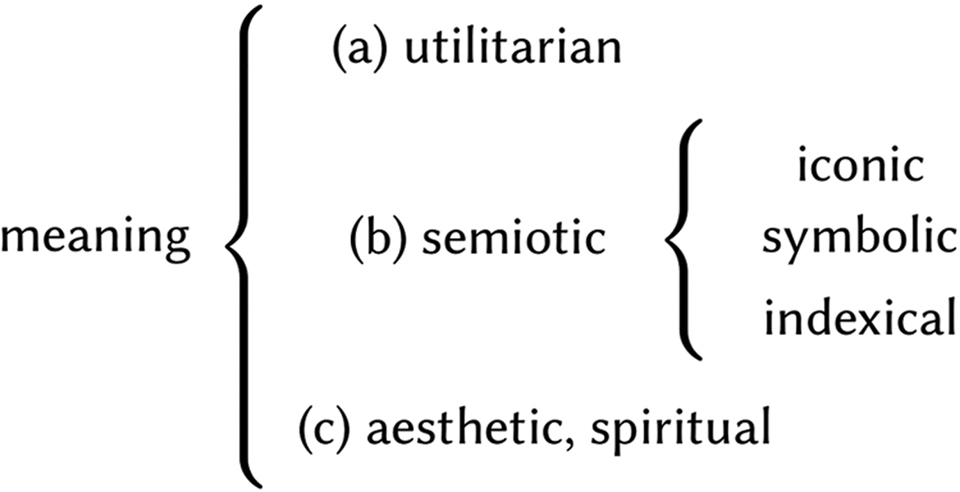
Figure 2. A closed, compartmentalized semantic universe as it is often implicitly presupposed in the archaeological literature.
Tokens, however, do not fit into this picture. The emergence of numbers involves utilitarian and semiotic artefacts which, through aesthetic use, say, are tokenized and might later reappear as symbols with genuine numerical meaning. We have thus to deal with dynamics which cut across the fixed categories of the semantic universe.Footnote 5
The consequences of this for the study of prehistoric remains are significant. First, in this perspective the difficult question of whether the Abri Cellier artefact referred to above (Fig. 1) is a musical instrument or a counting device becomes less important. Instead, we can ask ourselves whether the marks on its surface are tokenized in such a way that they may have played a role in the emergence of numerical thinking. The notion of tokenization thus turns our attention away from the quest for ‘meaning’ and invites us instead to study how the making and the use of symbolic or utilitarian artefacts may have influenced cognitive developments such as mathematical abstraction.
A second consequence which we can draw from the importance of tokenization is that this phenomenon hints at a basic layer of mathematical thinking below the level of numbers. Studying this layer, as we will do in the next sections, might prove helpful in understanding the emergence of numbers.
Third and finally, tokenization is a plausible catalysing mechanism for cultural change as explained in the Introduction above: tokenization pushes the overtly evident properties of cultural artefacts into the background and permits less evident ones to emerge.
If we pursue this line of inquiry, the challenge will be to understand tokenization in terms of material practices, i.e. as a highly behavioural and material process. This is how I suggest that we render more tangible, for the case of mathematical thought, Malafouris’ claim that the quest for a ‘meaning’ of prehistoric marks should be replaced by the question ‘What did the activity of mark making do for the ancient mind?’ (Malafouris Reference Malafouris2013, 190). Our question will be: Did mark making or other symbolic practices engage the prehistoric artist in an activity in which symbols were reduced to tokens? If the answer to this question is ‘yes’, then we are dealing with a practice which might have impacted the evolution of numbers.
Did prehistoric art induce tokenization?
The question formulated at the end of the last section can be tackled straightforwardly. Do we encounter anywhere in prehistoric art—symbols, cave paintings, portable art, ornamental decoration of tools—circumstances appropriate for inducing tokenization?
Let us tackle this question first from the negative standpoint: consider any specimen of Upper Palaeolithic cave art that shows a sole animal, such as a ‘Chinese horse’ from Lascaux, a bison from Altamira, or a bear from the Chauvet cave. Surely these paintings do not possess a mathematical dimension. But why not? Perhaps the answer can be found in Peirce, when he comments on his notion of ‘icon’ (Peirce Reference Peirce1931–1958, vol. 3, §3.362):
[I]n contemplating a painting, there is a moment when we lose the consciousness that it is not the thing, the distinction of the real and the copy disappears, and it is for the moment a pure dream—not any particular existence, and yet not general. At that moment we are contemplating an icon.
This comment is helpful, for now we understand that tokenization will not set in as long as the contemplator is absorbed by the painting in the way described by Peirce. We need an additional element which ‘disenchants’ the painting, as it were, and reduces it to a token. This alone is an interesting insight. Applying the theory of material engagement to the problem of the symbol, Malafouris advises us to stop asking what a symbol meant and instead to ask ‘how a sign emerges and acquires symbolic force’ (Malafouris Reference Malafouris2013, 96). For the case of mathematical thought, this functional account takes a paradoxical form: becoming a mathematical symbol (e.g. a stroke in our calculus) does not mean that a drawing or engraving somehow becomes loaded with a special mathematical kind of meaning. On the contrary, tokenization consists in an artefact/a symbol ‘discarding’ its iconic content, described so impressively by Peirce in the above quotation, and becoming a mere token.
As a consequence, we need not necessarily understand the emergence of mathematics as the creation ex nihilo of a symbolic system with a completely new meaning, a process which indeed would be highly implausible. Instead, we can take into account existing symbolic and artistic techniques and ask—in order to render the question formulated at the end of section 2 more precise—whether the prehistoric artist ever engaged in an activity in which signs cast off their iconic, symbolic, or utilitarian meaning and function as mere tokens?
Let us first ask how we can understand the process of ‘de-iconization’ or ‘de-symbolization’, or even ‘de-utilization’, leading from an icon or symbol or a utilitarian mark to a token. Under what circumstances would such a process take place? A valuable pointer to this can be found in Sauvet's (Reference Sauvet and Clottes1990) classification of engravings on portable art objects. Commenting on the geometric form of such engravings, Sauvet stresses the importance of ‘repetitiveness’ (répétitivité), which is characteristic for some of them. He writes: ‘Such a repetitiveness […] suggests that we are dealing with symbols in the exact sense defined above’, i.e. a ‘graphic unit, showing formal characteristics that are stable enough across its occurrences to allow us to presume that the graphic unit was associated with one or several signified’ (Sauvet Reference Sauvet and Clottes1990, 93 & 84). What is interesting for us here is less Sauvet's notion of a symbol (which remains akin to de Saussure's definition of the sign) than the fact that he takes repetitiveness as evidence of a type–token distinction, as his ‘graphic units’ are indeed types. Leroi-Gourhan made a similar proposition when interpreting engravings on portable art objects, the famous marques de chasse that appeared in the late Mousterian. He rejected debatable semantic interpretations (counting devices, calendars) and drew our attention to what he called the ‘rhythmicity’ (rythmicité) of the marks: ‘they show intentional repetition and thus rhythm’ (Leroi-Gourhan Reference Leroi-Gourhan1965, 217; cf. also Reference Leroi-Gourhan1964, 262–6).
Can repetitiveness or rhythmicity, then, be considered a possible mechanism for tokenization? The idea behind Sauvet's proposition seems to be that repetitiveness redirects the maker's attention from the artefact's meaning to an exact reproduction of its shape. Repetitiveness may thus shatter the iconic illusion described by Peirce. Leroi-Gourhan refers (see latter quotation above) to ‘intentional repetition’ and hence to something like a conscious effort to repeat the same shape and to avoid variation. If we want to retain the idea that repetition is a possible trigger of tokenization, i.e. that the material activity of repetition reduces meaningful cultural items to tokens, we would have to identify a mode of repetition in which at least the exactness of the repetition (i.e. repeating not just ‘something’ but the ‘same thing’) does not stem from a conscious intention but is imposed by the material constraints of the symbolic technique.
Are there any candidates for such material constraints? Repetitiveness is a common trait in prehistoric culture. We find it in cave paintings, in marks on portable objects or in the use of beads. I will discuss some obvious examples, beginning with repetitiveness as a stylistic device in cave paintings. We find repetitiveness in particular in the depiction of animals during the Upper Palaeolithic in the Franco-Cantabrian region. One might recall the ‘swimming stags’ of Lascaux (frise des cerfs nageant, Fig. 3), or the horses panel, the lion panel and the rhinoceros panel in the Chauvet cave, all of them showing a number of similar specimens of the same species in a staggered arrangement (Fig. 4). In addition, we know that cave paintings often followed the relief of the caves’ walls (cf. Brot Reference Brot2005, for an overview, and Pigeaud et al. Reference Pigeaud, Berrouet, Bougard, Paitier, Pommier and Bonic2012, for a recent detailed case study). Fritz and Tosello (Reference Fritz and Tosello2015, 305) speak of the artists adopting an ‘opportunistic’ stance vis-à-vis the surface of the walls. Cave painting, then, is definitely a symbolic practice with regard to material constraints.

Figure 3. ‘Swimming stags/La frise des cerfs nageant’ from Lascaux (Dordogne). (© N. Aujoulat/Centre National de la Préhistoire/Ministère de la Culture.)

Figure 4. ’Panneau des Chevaux’ from Chauvet-Pont-d'Arc (Ardèche). (© J. Clottes/Ministère de la Culture.)
However, although repetitiveness is striking in all these cases, these panels are not plausible candidates for a source of tokenization, because variation plays an equally important role in them. The artists depicted slight variations in size (in some cases a paradoxical arrangement involving increasing size with increasing distance), but first and foremost subtle variation in the posture, e.g. in the inclination of the heads, which evokes a vivid impression of dynamics. The panels often give the impression that they seek to depict a motion-based sequence (Azéma Reference Azéma2008). At least for the modern contemplator, this aspect contributes significantly to the appreciation of the artistic quality of the paintings, and the mastery demonstrated in the execution of the figures leaves no doubt as to the intentional character of these variations. This type of varied repetition does not lead to de-iconization but rather contributes, as an organic whole rather than as an aggregation of similar elements, to creating a new icon of a more abstract kind, e.g. the representation of motion-based patterns, or the cycle of life and of the seasons (Testart Reference Testart2016, 52–4).Footnote 6
Another striking case of repetitiveness and rhythmicity in cave paintings is of course hand imprints, both positive and negative, found not only in the Franco-Cantabrian region but all over the world (e.g. at Sulawesi, Borneo, Indonesia, dating from 40,000 to 35,000 bp: cf. Aubert et al. Reference Aubert, Brumm and Ramli2014; Reference Aubert, Setiawan and Oktaviana2018, and in the Cueva de las Manos in Argentina, dating from 13,000 to 9000 bp: Gradin et al. Reference Gradin, Aschero and Aguerre1976). Series of handprints meet the requirements defined above insofar as the exactness of the repetition need not be intentional but simply due to the identity of the hand thus impressed. Sauvet et al. (Reference Sauvet, Sauvet and Wlodarczyk1977, 555) stressed the ambiguous character of such imprints: due to their perfect mutual resemblance in shape they are realist representations par excellence, but due to the stereotypical repetition they also acquire the status of conventional signs. According to this interpretation, repetition would lead directly to de-iconization! Nevertheless, again I do not think that we have a case in point. First, it is possible that we are dealing with ‘organic wholes’, where the whole shape created out of the individual imprints may have a symbolic meaning which its parts lack (Fig. 5). And even if we can plausibly argue that the patterns of handprints are mere aggregates of single imprints, the identity of the impressed hand does not really constitute the kind of material constraint we are looking for, as it ensures the exactness of the tokens rather than stipulating it. The exactness is achieved without effort (indeed it would require effort to deviate from it), and thus it is not clear how this symbolic activity could have led to hand imprints striking the artist or the contemplator as tokens. I am thus reluctant to accept panels of hand printings as sources of mathematical thinking.
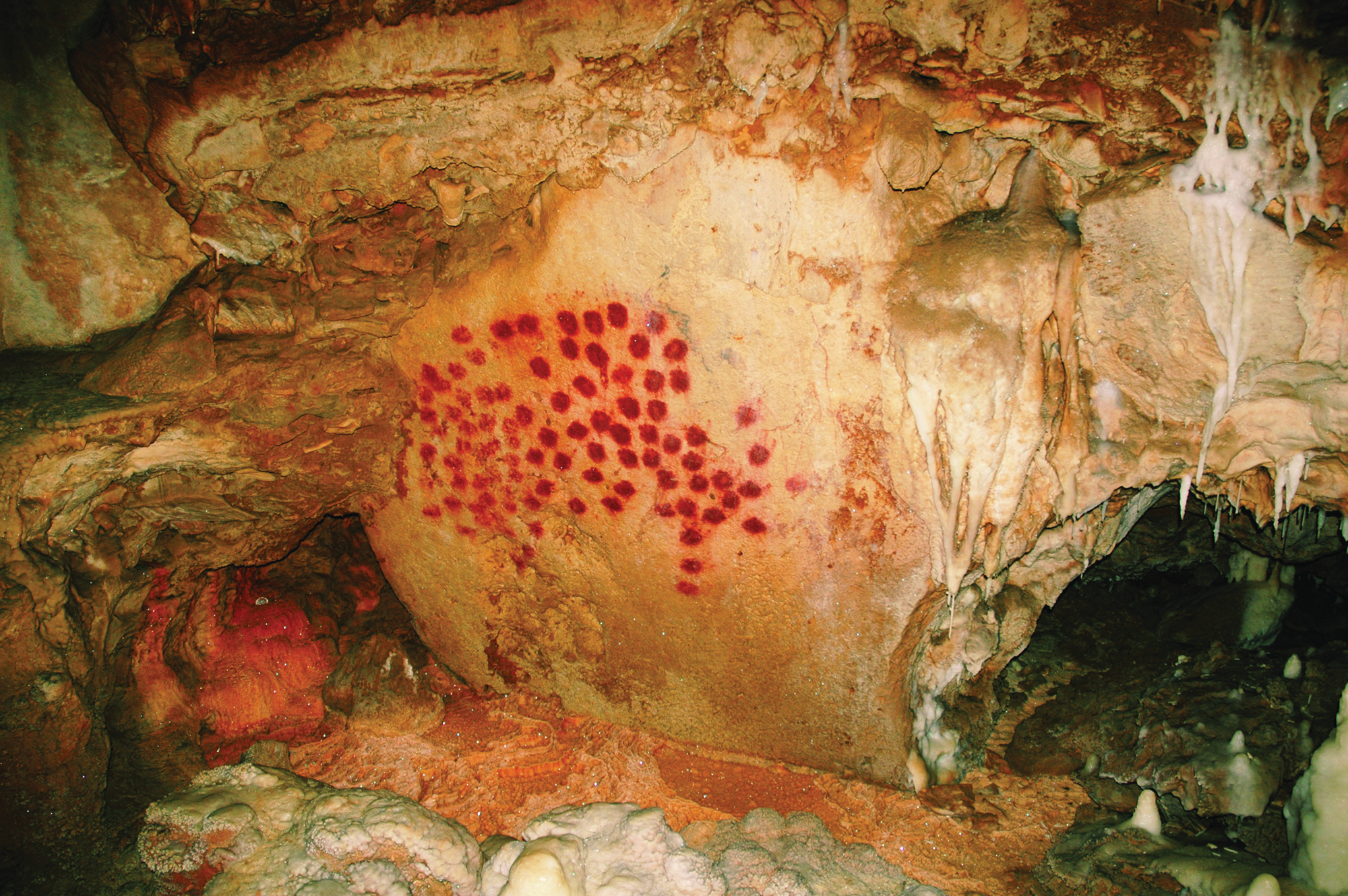
Figure 5. Repetitiveness in hand imprints: positive imprints of the palm of the hand from Chauvet cave, 36,000 bp, ‘Grand panneau des Points-paumes’. (© V. Feruglio/Ministère de la Culture.)
What we are looking for, then, is a case where the exactness of repetition is not automatically induced by the material constraints, but where these constraints impose a norm of exactness of repetition on the acting individual. I have found two examples in the literature which meet this requirement. The first consists of engraved depictions of animals on portable objects such as a batôn percé from l'Abri de la Madeleine, France, conserved at the Musée d'Archéologie Nationale, showing a fragmentary series of similar horsesFootnote 7 (Fig. 6). The artist who created this object was free, of course, to choose the motifs, and we have no reason to doubt that it was his or her conscious will to draw the same animal again in the same position. The case is nevertheless interesting because the exactness of the repetition regarding the size of the animals is imposed by the decorated object itself, which hardly varies in its width. ‘The material (the elongated shape of the bones and tools, spear-thrower or pierced stick) naturally leads to engraving a line of horses, a line of lions, etc.’, comments Testart (Reference Testart2016, 54, my translation). The exact repetition might therefore have been the outcome of the artist's intention and the ‘material's will’, or of a ‘dialogue’ between the two, to use Leroi-Gourhan's words (Reference Leroi-Gourhan1965, 132, cf. Malafouris Reference Malafouris2013, 177). The artist may have been ‘seduced’ by the material to adopt a technique which, once performed, induces tokenization. This loss of meaning through tokenization may also explain the tendency to geometrize the signs, a phenomenon observed by Leroi-Gourhan (Reference Leroi-Gourhan1965, 233).
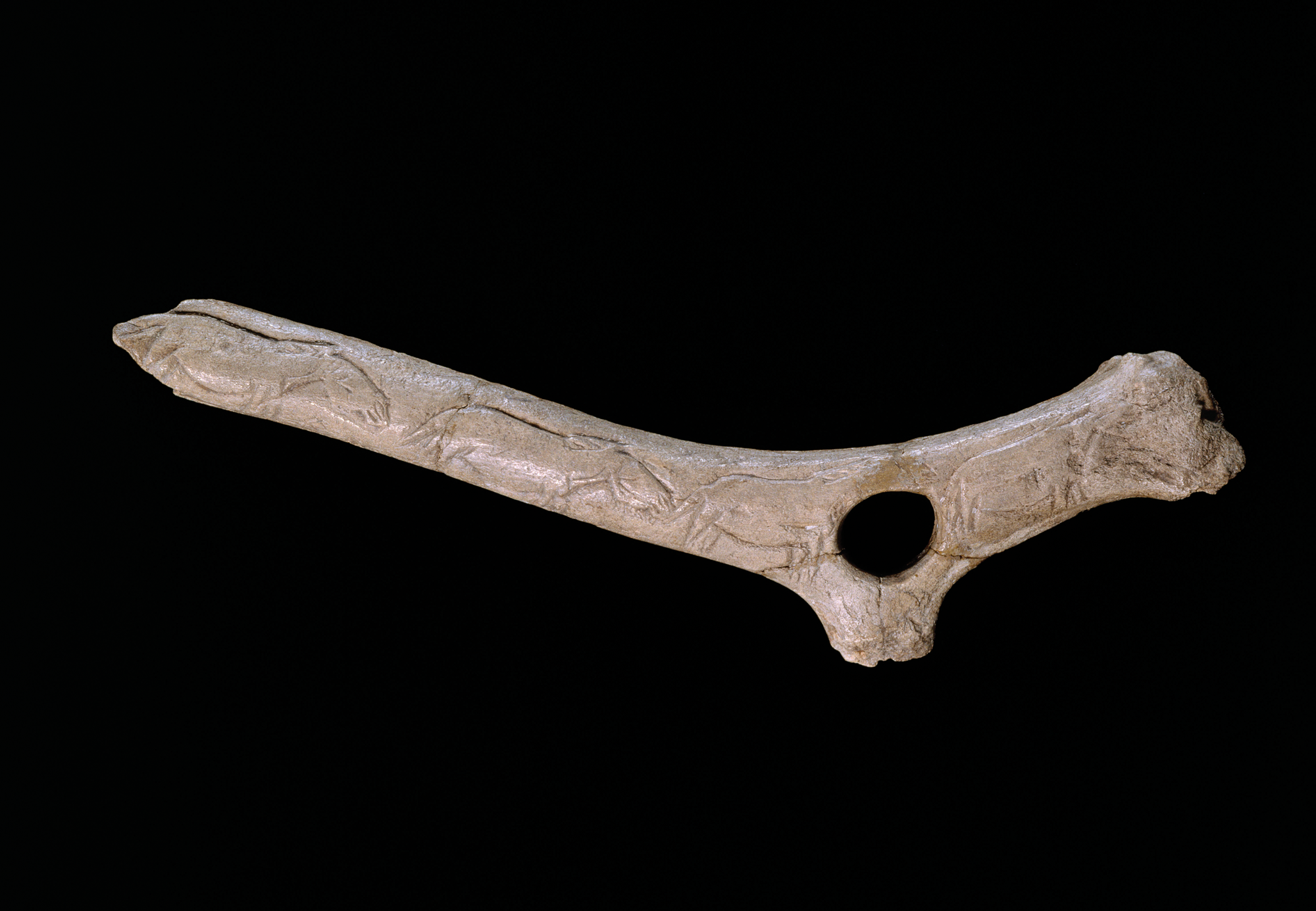
Figure 6. ‘Batôn perforé avec une file de chevaux gravés’ (Upper Palaeolithic), Abri de la Madeleine, Dordogne, France. (Musée d'Archéologie nationale et domaine national de Saint-Germain-en-Laye, © bpk/RMN – Grand Palais/Loïc Hamon.)
Sauvet, to whom we already owe the notion of repetitiveness, provides us with a second, perhaps even more convincing example. In their classification of engravings on portable objects, Sauvet et al. (Reference Sauvet, Sauvet and Wlodarczyk1977, 551) identified a pattern which they called the ‘spatial combination’, ‘concatenation’ and ‘juxtaposition’ of symbols. For example, small crosses are combined to form a check or diamond pattern (Fig. 7). One might also think of engraved pieces of ochre, familiar from the Blombos cave, dating from 75,000 bp (Henshilwood et al. Reference Henshilwood, d'Errico and Watts2009), and engraved ostrich eggshells from Diepkloof rock-shelter, dating from 60,000 bp (Texier et al. Reference Texier, Porraz, Parkington, Rigaud, Poggenpoel and Tribolo2013), shown in Figures 8 and 9. These artefacts also show geometrical patterns in which the ‘fit’ of the strokes requires exact repetition. These cases of concatenated symbols are interesting because the exactness of the repetition here is indeed required, but is not automatically imposed. This means that we do need not to ascribe to the artist an intention to repeat the same sign exactly, only an intention to produce a complex pattern of symbols that match each other. The act of producing this pattern appears as a form of material engagement that requires exactness of repetition and thus ‘compels’ the artist to fulfil this requirement.

Figure 7. Examples of the repetition of strokes on portable objects from Sauvet (Reference Sauvet and Clottes1990). (Reprinted by kind permission of the author.)

Figure 8. Engraved pieces of ochre, Blombos cave, 75,000 bp. (Reprinted from Henshilwood et al. Reference Henshilwood, d'Errico and Watts2009, 35, with permission.)

Figure 9. Engraved ostrich eggshells, Diepkloof Rock Shelter, 60,000 bp. (Reprinted from Texier et al. Reference Texier, Porraz, Parkington, Rigaud, Poggenpoel and Tribolo2013, 3420, with permission.)
Both cases, the repetition of icons on an object and the construction of a pattern of matching strokes, can be described as processes of ‘ornamentalization’. In this reading, the ornamentalization of icons and symbols can be suggested as a plausible source of tokenization, as it is constitutive of mathematical thought, as already argued. Does this mean that regularity or exactness of repetition can be taken as unambiguous evidence of proto-mathematical notation? D'Errico et al. (Reference d'Errico, Doyon and Colagé2018), by contrast, take regularity to be evidence of aesthetic value. Commenting on sequentially marked bones, they write:
Apparently, the Neanderthal was interested in producing marks that could be perceived as identical but not in creating a visual pattern relying on equidistance and, for a subset, parallelism. This suggests that the aim of the markings was not that of producing decoration visually striking for its regularity […]; rather, the aim seems to have been that of recording in a single session homologous units of information. (d’Errico et al. Reference d'Errico, Doyon and Colagé2018, 7)
This interpretation takes irregularity as evidence of information content and thus seems to contradict my hypothesis. I think, however, that the conflict can be solved. The thesis of tokenization through ornamentalization only suggests that ornamentalization is a plausible origin of tokenization, because concentrating on exact repetition may empty the signs of meaning and reduce them to mere tokens. Once this cognitive step is achieved, however, regularity is no longer necessary for notational systems like marques de chasse. We thus have to distinguish between two periods, before and after the achievement of tokenization and the emergence of the first notations. Before, regularity may have led to tokenization. After, regularity is no longer necessary, and d'Errico et al. may therefore be perfectly justified in taking it as evidence of a purely ornamental character. A striking insight from his study is that the Neanderthal had already achieved a fundamental level of symbolic notation.
Before concluding, I wish briefly to discuss, from the point of view of my hypothesis, a sophisticated case which has been brought up in recent studies, namely, strings of beads (Fig. 10).

Figure 10. Strings of beads, reconstructed for wear experiments, South Africa, c. 76,000 bp. Scale bar = 1 cm. (Reprinted from Vanhaeren et al. Reference Vanhaeren, d'Errico, van Niekerk, Henshilwood and Erasmus2013, 503, with permission.)
The use of beads for personal ornamentation appears at least 76,000 bp in South Africa (Vanhaeren et al. Reference Vanhaeren, d'Errico, van Niekerk, Henshilwood and Erasmus2013). Overmann (Reference Overmann, Wynn and Coolidge2017, 107) draws our attention to numerically relevant aspects of strings of beads:
Stringed beads, although generally made and used for ornamentation, have affordances that may (in comparison to other artefacts) increase their likelihood of being repurposed from ornamentation to counting [… A]s beads are slid along a string, they instantiate stable-order, plus-one, accumulative relations and are analogous in this regard to other initial counting technologies like fingers and tallies.
In the same volume, Wynn et al. (Reference Wynn, Overmann, Coolidge, Janulis, Wynn and Coolidge2017, 203) explain that strings of beads instantiate three relevant phenomena: ‘a one-dimensional series, individuation of items, and an invariant sequence’. These qualities, they stress, are inherent to the structure of a string rather than intentionally incorporated into it. Stringing beads thus ‘enables [a person] to notice and […] think about’ ordinality.
What can be said about this case from the point of view of tokenization? In particular, when Wynn et al. talk about the ‘individuation of items’, do they mean tokens? I think what they are hinting at is a more sophisticated and less fundamental notion, namely, a position in a sequence. There is a kind of abstraction involved here, but not exactly the one I am interested in. ‘Items’ are beads that are reduced to ‘the next one (in a series)’, whereas tokens are objects that are reduced to ‘just the same (as the foregoing one)’. Of course, these notions might overlap when, as it appears to be the case in strings of beads, ‘the next one’ is at once ‘the next of the same sort’. (In order to disentangle these notions, we might think of counting with reference to body parts where ‘the next one’, e.g. the forearm following the palm of the hand, is not of the same sort.) On the one hand, then, it is not clear whether stringing beads is a plausible trigger for tokenization. This would be otherwise if there were evidence that the beads were sorted according to size or colour (but see d’Errico et al. Reference d'Errico, Vanhaeren, Van Niekerk, Henshilwood and Erasmus2015). On the other hand, however, tokenization may be an essential ingredient of the story Overmann and Wynn et al. are telling. Indeed, if making strings of beads involves tokenization—i.e. casting off overtly evident cultural meaning—it becomes plausible how non-evident features such as invariant sequence, plus-one etc. may have started to attract attention.
From tokens to numbers
So far, I have argued that tokens, though themselves not numerical, are essential for mathematics, understood as a calculus, and that it seems reasonable to assume that tokenization occurs in prehistoric art. How, then, is tokenization related to the emergence of numbers? It would go beyond the scope of this paper to describe in detail how tokenization contributes cognitively, psychologically and culturally to the emergence of numbers. Nonetheless, I will try to identify a few elements from which the relevance of tokenization in this context should become clear, and also why I have called tokens ‘proto-‘ or ‘sub-numerical’.
What can reasonably be said is that tokenization, resulting from repetition and concatenation, transforms the meaning not only of the individual elements but of the entire arrangement depicted. I argued above that what the two examples in Figures 3 and 4 show are not ‘five stags’ and ‘four horses’, but rather groups of these animals or even something more abstract, such as a motion-based pattern or a life cycle. Tokenization, as it seems to occur in the examples given in Figures 6 and 7, not only strips the individual elements of meaning, but breaks down meaningful, complex entities such as ‘groups’ or ‘wholes’ into sets. By a ‘set’ I mean a mere repetition of the same type, a collection of discrete, separable, individually identifiable and similar elements. Unlike a group, a set has a cardinality, can be reconstructed by an operation of ‘plus-one’ and can thus be counted. I do not mean to say that a group cannot be counted. But it has to be transformed into a set or be understood according to the model of a set in order to be subjected to the operation of counting.
In general, ‘groups’ or ‘wholes’ are meaningful entities that occur in our natural environment and are suggested to us by passive perception. There is no reason why such occurrences should turn into countable sets on their own. Tokenization, by contrast, occurs in artefacts and as a result of our actions. It transforms our perception and affects our intentionality. It seems plausible to assume that tokenized artefacts provide what we might call, with Renn et al. (Reference Renn, Damerow, Schemmel, Lehner, Valleriani, Feldhay, Renn, Schemmel and Valleriani2018), a mental model for transforming natural groups or wholes into countable sets (where ‘mental model’ should not be understood in a mentalistic way—mental models are instruments for the mind, not in the mind).
Counting, then, consists in mapping a set onto numerals. From a logical point of view, and probably also from a historical one, this is a second, independent step, and tokenization as I described it in this paper is proto-numerical. Tokenization is still relevant here, however, insofar as numerals themselves are nothing other than a standardized set of tokens. In the technique of ‘body counting’, i.e. in the use of the body parts as a tallying device, Sof'ya Yanovskaya once argued (Reference Yanovskaya and Yanovskaya1936) that the names of the body parts lose their original meaning—i.e. become tokenized—and little by little turn into numerals which eventually (perhaps only in ancient Greece) are understood as names for abstract numbers. Of particular interest is also the fact that tokenization is induced on the level of syntax, that is, through compositional rules of repetition and concatenation, but it then has semantic consequences, for it prepares the way for the emergence of numbers as a new semantic field. Tokenization thus bridges syntax and semantics and shows how syntactical studies of prehistoric symbolism can be relevant to issues of semantics.
Conclusion
In this paper I have discussed some of the structural conditions in prehistoric art and symbolism that may have contributed to the tokenization of meaningful cultural items and which may thus have contributed to the emergence of mathematical thought at a sub-numerical level. I argued that ornamentalization is a good candidate because it brings forth signs which actually function as mere signs (tokens) and hence open up the possibility of perceiving relational properties relevant for the development of numerical thinking.
D'Errico et al. (Reference d'Errico, Doyon and Colagé2018, 5) recently presented a model for the gradual development of numbers, starting with the accidental production of cut marks and proceeding in five exaptative steps:

It is interesting to see how the hypothesis elaborated in this paper fits into this picture. I think that it agrees with both the general pattern and the idea of understanding the emergence of numbers as a series of exaptations. However, in light of the considerations presented in this paper, I suggest two modifications concerning levels 1–2 and 3–5.
Starting out from the notion of tokenization, we have seen, first, that there is no reason to focus solely on carved marks or strokes. Any cultural item can constitute the starting point of tokenization. We recall here that a mathematical calculus can be constructed using any basic sign or object whatsoever. From a purely logical point of view, the stroke ‘I’ is no more or less appropriate than the word ‘the’. As a consequence, there is no reason to privilege apparently meaningless carved strokes and points on portable objects or geometric patterns in cave paintings over figurative cave paintings or meaningful de Saussurian symbols! It is perfectly conceivable that a mathematical symbol acquires its symbolic force by casting off its iconicity or conventional meaning. There is also nothing reprehensible about looking for the origins of an epistemic activity like mathematics in the aesthetic domain of painting, because both forms of expression are anachronistic and hence of only limited value when applied to prehistoric civilizations. ‘The primitive order is generalized. A clear differentiation of spheres into social and economic does not appear there’, Marshall Sahlins once wrote (Reference Sahlins1972, 182); we can probably take this as a general rule for pre-Neolithic cultures. Spheres which we are accustomed to consider separate might actually have been interwoven. We should not think of cultural practices like cave painting purely as the domain of aesthetics (the more so as archaeologists tend to consider everything as aesthetic which has no obvious utilitarian value), but rather as a sort of common matrix from which the epistemic, the aesthetic, the spiritual and so on could gradually have emerged.
The second modification concerns steps 3–5. We have seen that the emergence of mathematical patterns does not require the attribution of a special mathematical meaning to previously meaningless items. Quite the contrary, tokens emerge from symbols by discarding previous meanings. D'Errico et al.'s formulation of steps 3–5 suggests a kind of bottom-up construction of numerical thinking, i.e. the construction of something entirely new from scratch. Tokenization, by contrast, renders plausible how such a process might have unfolded through, or have been catalysed by, existing cultural resources.
If this hypothesis can be substantiated, it would invite us to speculate about the further development of mathematical thought. According to this hypothesis, the situation in the Upper Palaeolithic would be such that a spoken language possessing at least qualitative terms for the expression of intuitively grasped quantities (‘a single’, ‘both’, ‘some’, ‘many’, ‘all’, etc.) coexisted side-by-side with fairly complex symbolic systems which in particular may have induced tokenization. These symbolic systems thus objectively contain the arithmetic operation of the construction of numbers by means of the repetition of units, even if this objective possibility was not grasped subjectively. This coexistence, however, makes it plausible that both elements began to act the one on the other and to transform each other. We can therefore formulate the hypothesis that the emergence of calculi-like, tokenized symbols in prehistoric art contributed towards the transformation of existing linguistic proto-numerical expressions into fully fledged numerical ones, relying on objective and socially shared standards for the construction of one-to-one correspondences. Tokenized symbolic notations could thus have transformed the qualitative appreciations of quantities into true quantitative ones, and language could in turn have infused the symbolic notations with numerical meaning.
Acknowledgements
The author is indebted to Ewa Dutkiewicz, Miriam Haidle, Karenleigh Overmann, Georges Sauvet, the editor and two anonymous reviewers for helpful comments.












