1. Introduction
This paper is a follow-up to [Reference Hayes and Kunnawalkam Elayavalli32]. We are once again interested in approximate homomorphisms of groups. Recall that approximate homomorphisms are sequences of maps
![]() $\sigma _{n}\colon G\to H_{n}$
where
$\sigma _{n}\colon G\to H_{n}$
where
![]() $G,H_{n}$
are groups, each
$G,H_{n}$
are groups, each
![]() $H_{n}$
has a bi-invariant metric
$H_{n}$
has a bi-invariant metric
![]() $d_{n}$
, and the sequence satisfies
$d_{n}$
, and the sequence satisfies
In our previous article, we studied automorphic conjugacy of sofic approximations. In this article, we are interested in when approximation homomorphisms with values in permutation groups are asymptotically conjugate via a sequence of permutations.
One motivation for the study of asymptotic conjugacy of approximate homomorphisms of groups is the notion of stability. Stability of homomorphisms dates back to the 1940s via work of Hyers [Reference Hyers33] (answering a question of Ulam), and asks when approximate homomorphisms can be perturbed to a sequence of honest homomorphisms. For example, we say a group is permutation stable if every sequence of approximate homomorphisms of the group with values in permutation groups is pointwise close to a sequence of honest homomorphisms. See [Reference Arzhantseva and Păunescu4, Reference Arzhantseva and Păunescu5, Reference Becker, Lubotzky and Thom7, Reference Eckhardt and Shulman23, Reference Eilers, Shulman and Sørensen24, Reference Hadwin and Shulman30, Reference Ioana34] for work in this direction. The notion of stability gives a potential approach to proving the existence of a non-sofic group [Reference Arzhantseva and Păunescu4, Reference Bowen and Burton11, Reference Glebsky and Rivera29], and has connections to cohomology [Reference Dadarlat19–Reference De Chiffre, Glebsky, Lubotzky and Thom21] and to operator algebras [Reference Atkinson and Kunnawalkam Elayavalli6, Reference Carrión and Dadarlat13, Reference Dadarlat18, Reference Hadwin and Shulman31].
While not immediate, there is a natural connection between stability and asymptotic conjugacy. For example, one could consider a modification of permutation stability where we only demand that every sofic approximation (instead of every approximate homomorphism) is close to an honest homomorphism (this concept is introduced in [Reference Arzhantseva and Păunescu4] under the name weak stability). When the group is amenable, then as shown in [Reference Arzhantseva and Păunescu4, Theorem 1.1], the Kerr–Li [Reference Kerr and Li36, Lemma 4.5] and Elek–Szabo [Reference Elek and Szabó27] uniqueness theorems imply that this modified version of permutation stability is equivalent to residual finiteness.
The situation for permutation stability of general asymptotic homomorphisms of amenable groups was fully classified by Becker, Lubotzky, and Thom [Reference Becker, Lubotzky and Thom7, Theorem 1.3] who showed that an amenable group G is permutation stable if and only if every invariant random subgroup of G is a limit of IRSs coming from actions on finite sets. Invariant random subgroups arose from the works [Reference Abért, Glasner and Virág2, Reference Bergeron and Gaboriau9, Reference Stuck and Zimmer47, Reference Vershik49], we recall the definition in Definition 2.1. A different proof of this was given in [Reference Arzhantseva and Păunescu5, Theorem 3.12], which reformulates the results in terms of traces.
Given a sequence
![]() $(\sigma _{n})_{n}$
of approximate homomorphisms and a free ultrafilter
$(\sigma _{n})_{n}$
of approximate homomorphisms and a free ultrafilter
![]() $\omega $
, one can naturally produce an invariant random subgroup associated to
$\omega $
, one can naturally produce an invariant random subgroup associated to
![]() $(\sigma _{n})_{n},\omega $
which we denote by
$(\sigma _{n})_{n},\omega $
which we denote by
![]() $\operatorname {\mathrm {IRS}}(\sigma _{\omega })$
(see Definition 2.4). Given an invariant random subgroup
$\operatorname {\mathrm {IRS}}(\sigma _{\omega })$
(see Definition 2.4). Given an invariant random subgroup
![]() $\Theta $
of G, following [Reference Abért, Glasner and Virág2, Proposition 13], we can construct a generalized Bernoulli shift action
$\Theta $
of G, following [Reference Abért, Glasner and Virág2, Proposition 13], we can construct a generalized Bernoulli shift action
![]() $G \,{\curvearrowright }\, (X_{\Theta },\mu _{\Theta })$
associated to
$G \,{\curvearrowright }\, (X_{\Theta },\mu _{\Theta })$
associated to
![]() $\Theta $
. Let
$\Theta $
. Let
![]() ${\mathcal R}_{G,X_{\Theta }}$
be the orbit equivalence relation of this action. We show that for every sequence of asymptotic homomorphisms of G whose given IRS is
${\mathcal R}_{G,X_{\Theta }}$
be the orbit equivalence relation of this action. We show that for every sequence of asymptotic homomorphisms of G whose given IRS is
![]() $\Theta $
, we may extend the asymptotic homomorphism to a sofic approximation (in the sense of [Reference Elek and Lippner26]) of
$\Theta $
, we may extend the asymptotic homomorphism to a sofic approximation (in the sense of [Reference Elek and Lippner26]) of
![]() ${\mathcal R}_{G,X_{\Theta }}$
. This extension result holds for any countable group G.
${\mathcal R}_{G,X_{\Theta }}$
. This extension result holds for any countable group G.
Theorem 1.1. Let G be a group, and let
![]() $(\sigma _{n})_{n=1}^{\infty }$
be a sequence of approximate homomorphisms of G and
$(\sigma _{n})_{n=1}^{\infty }$
be a sequence of approximate homomorphisms of G and
![]() $\omega $
a free ultrafilter on
$\omega $
a free ultrafilter on
![]() ${\mathbb N}$
. Let
${\mathbb N}$
. Let
![]() $\sigma _{\omega }$
be the ultraproduct of this sequence. Let
$\sigma _{\omega }$
be the ultraproduct of this sequence. Let
![]() $\Theta $
be the IRS of
$\Theta $
be the IRS of
![]() $(\sigma _{\omega })$
and let
$(\sigma _{\omega })$
and let
![]() ${\mathcal R}_{G,X_{\Theta }}$
be the orbit equivalence relation of the
${\mathcal R}_{G,X_{\Theta }}$
be the orbit equivalence relation of the
![]() $\Theta $
-Bernoulli shift over G with base
$\Theta $
-Bernoulli shift over G with base
![]() $[0,1]$
. Then
$[0,1]$
. Then
![]() $\sigma _{\omega }$
extends to a sofic approximation of
$\sigma _{\omega }$
extends to a sofic approximation of
![]() ${\mathcal R}_{G,X_{\Theta }}$
.
${\mathcal R}_{G,X_{\Theta }}$
.
In the case where
![]() $\Theta $
is
$\Theta $
is
![]() $\delta _{\{1\}}$
, our result says that any sofic approximation of G extends to a sofic approximation of any Bernoulli shift over G. This was previously proved in [Reference Bowen10, Reference Elek and Lippner26, Reference Păunescu42, Reference Popa44] (in fact, [Reference Popa44] proves that the generalized Bernoulli shift
$\delta _{\{1\}}$
, our result says that any sofic approximation of G extends to a sofic approximation of any Bernoulli shift over G. This was previously proved in [Reference Bowen10, Reference Elek and Lippner26, Reference Păunescu42, Reference Popa44] (in fact, [Reference Popa44] proves that the generalized Bernoulli shift
![]() ${\mathcal R}_{G\,{\curvearrowright }\, (X,\mu )^{G/H}}$
is sofic if G is sofic, H is amenable, and
${\mathcal R}_{G\,{\curvearrowright }\, (X,\mu )^{G/H}}$
is sofic if G is sofic, H is amenable, and
![]() $(X,\mu )$
is any probability space). The proof of the case
$(X,\mu )$
is any probability space). The proof of the case
![]() $\Theta =\delta _{\{1\}}$
given in [Reference Elek and Lippner26, Proposition 7.1] (see also [Reference Cavaleri, Munteanu and Păunescu14, Theorem 3.1] and [Reference Bowen10, Theorem 8.1]) provided inspiration for the proof we give of Theorem 1.1.
$\Theta =\delta _{\{1\}}$
given in [Reference Elek and Lippner26, Proposition 7.1] (see also [Reference Cavaleri, Munteanu and Păunescu14, Theorem 3.1] and [Reference Bowen10, Theorem 8.1]) provided inspiration for the proof we give of Theorem 1.1.
In the context of Theorem 1.1, if G is amenable, then
![]() ${\mathcal R}_{G,X_{\Theta }}$
is hyperfinite by [Reference Ornstein and Weiss40], [Reference Ornstein and Weiss41, II §3] (see [Reference Connes, Feldman and Weiss15] for more general results), and thus any two sofic approximations of
${\mathcal R}_{G,X_{\Theta }}$
is hyperfinite by [Reference Ornstein and Weiss40], [Reference Ornstein and Weiss41, II §3] (see [Reference Connes, Feldman and Weiss15] for more general results), and thus any two sofic approximations of
![]() ${\mathcal R}_{G,X_{\Theta }}$
are conjugate [Reference Păunescu42, Proposition 1.20]. Using this conjugacy fact, the results of [Reference Arzhantseva and Păunescu5, Theorem 3.12], [Reference Becker, Lubotzky and Thom7, Theorem 1.3] are corollaries of Theorem 1.1. This again illustrates the utility of approximate conjugacy results in the context of stability.
${\mathcal R}_{G,X_{\Theta }}$
are conjugate [Reference Păunescu42, Proposition 1.20]. Using this conjugacy fact, the results of [Reference Arzhantseva and Păunescu5, Theorem 3.12], [Reference Becker, Lubotzky and Thom7, Theorem 1.3] are corollaries of Theorem 1.1. This again illustrates the utility of approximate conjugacy results in the context of stability.
1.1. Comments on some applications
To demonstrate the utility of Theorem 1.1, we recover, with separate proof ideas, some results characterizing conjugacy for almost representations of amenable group appearing in [Reference Arzhantseva and Păunescu4, Reference Becker, Lubotzky and Thom7, Reference Elek25, Reference Newman and Sohler39]. Namely, those results are proved via usage of the asymptotic combinatorial notation of hyperfinite graphs, and on Benjamini–Schramm convergence. Our proof is in some sense more ‘continuous’, and is based purely in ergodic theory and probabilistic arguments. In particular, we do not need the combinatorial notion of hyperfiniteness of graph sequences or Benjamini–Schramm convergence. In some sense, one can view ergodic theory as a limit of combinatorics, and so our methods can be viewed as a limiting version of those in [Reference Arzhantseva and Păunescu5, Reference Becker, Lubotzky and Thom7, Reference Elek25, Reference Newman and Sohler39]. Both the combinatorial and continuous approaches have their utility. We believe one benefit of our approach is that it reveals that one can work directly with the limiting object, and does not always have to resort to working with combinatorics at the finitary level and taking limits.
1.2. Organization of the paper
We begin in §2 by recalling some background on metric groups and approximate homomorphisms. We also give the definition of the IRS of a sequence of approximate homomorphisms here and restate Theorem 1.1 in these terms. In §3, we recall the background on orbit equivalence relations and their sofic approximations we need, and state Theorem 1.1 in these terms. In §5, we deduce [Reference Arzhantseva and Păunescu5, Theorem 3.12] from Theorem 1.1, and also deduce [Reference Becker, Lubotzky and Thom7, Theorem 1.3] from Theorem 1.1. We also explain the connection between action traces and IRSs in this section. In §4, we prove Theorem 1.1.
2. Preliminaries
Throughout, we consider G to be a countable group. Let
![]() ${\operatorname {Sym}}(n)$
denote the finite symmetric group of rank n. The normalized Hamming distance, which is a bi-invariant metric on
${\operatorname {Sym}}(n)$
denote the finite symmetric group of rank n. The normalized Hamming distance, which is a bi-invariant metric on
![]() ${\operatorname {Sym}}(n)$
, is given by
${\operatorname {Sym}}(n)$
, is given by
Recall the following.
Definition 2.1. A sequence of maps
![]() $\sigma _{n}\colon G\to {\operatorname {Sym}}(d_{n})$
are said to be approximate homomorphisms if for all
$\sigma _{n}\colon G\to {\operatorname {Sym}}(d_{n})$
are said to be approximate homomorphisms if for all
![]() $g,h\in G$
, we have
$g,h\in G$
, we have
Let
![]() $\omega $
be a free ultrafilter on
$\omega $
be a free ultrafilter on
![]() $\mathbb {N}$
. Let
$\mathbb {N}$
. Let
![]() $(G_n,d_n)$
be countable groups with bounded bi-invariant metrics. Denote by
$(G_n,d_n)$
be countable groups with bounded bi-invariant metrics. Denote by
Observe that by the bi-invariance property of the metrics
![]() $d_n$
, the subgroup
$d_n$
, the subgroup
![]() $\{(g_n): \lim _{n\to \omega } d_n(g_n,1_n)=0\}$
is a normal subgroup. If
$\{(g_n): \lim _{n\to \omega } d_n(g_n,1_n)=0\}$
is a normal subgroup. If
![]() $(g_{n})_{n}\in \prod _{n}G_{n},$
we let
$(g_{n})_{n}\in \prod _{n}G_{n},$
we let
![]() $(g_{n})_{n\to \omega }$
denote its image in the ultraproduct. In the above context, a sequence of approximate homomorphisms
$(g_{n})_{n\to \omega }$
denote its image in the ultraproduct. In the above context, a sequence of approximate homomorphisms
![]() $\sigma _{n}\colon G\to {\operatorname {Sym}}(d_{n})$
naturally produces a homomorphism into
$\sigma _{n}\colon G\to {\operatorname {Sym}}(d_{n})$
naturally produces a homomorphism into
![]() $\prod _{n\to \omega }({\operatorname {Sym}}(d_{n}),d_{\operatorname {\mathrm {Hamm}}})$
by
$\prod _{n\to \omega }({\operatorname {Sym}}(d_{n}),d_{\operatorname {\mathrm {Hamm}}})$
by
For a non-negative integer k, we use
![]() $[k]=\{1,\ldots ,k\}$
. We also set
$[k]=\{1,\ldots ,k\}$
. We also set
![]() $[0]=\varnothing $
.
$[0]=\varnothing $
.
Suppose that X is a compact, metrizable space. Assume
![]() $(Y,\nu )$
is a standard probability space and that we have a Borel map
$(Y,\nu )$
is a standard probability space and that we have a Borel map
![]() $Y\to \operatorname {\mathrm {Prob}}(X)$
given by
$Y\to \operatorname {\mathrm {Prob}}(X)$
given by
![]() $y\mapsto \mu _{y}$
. Then by the Riesz representation theorem, we can define
$y\mapsto \mu _{y}$
. Then by the Riesz representation theorem, we can define
![]() $\int _{Y}\mu _{y}\,d\nu (y)$
to be the unique probability measure
$\int _{Y}\mu _{y}\,d\nu (y)$
to be the unique probability measure
![]() $\eta $
satisfying
$\eta $
satisfying
for all
![]() $f\in C(X)$
.
$f\in C(X)$
.
2.1. Preliminaries on IRSs
Given a sequence of approximate homomorphisms
![]() $\sigma _{n}\colon G\to {\operatorname {Sym}}(d_{n})$
, define
$\sigma _{n}\colon G\to {\operatorname {Sym}}(d_{n})$
, define
![]() $S_{\sigma _{n}}\colon [d_{n}]\to \{0,1\}^{G}$
by
$S_{\sigma _{n}}\colon [d_{n}]\to \{0,1\}^{G}$
by
![]() $(S_{\sigma _{n}})(j)(g)=1_{\{j\}}(\sigma _{n}(g)(j))$
. Throughout the paper, for a finite set E, we use
$(S_{\sigma _{n}})(j)(g)=1_{\{j\}}(\sigma _{n}(g)(j))$
. Throughout the paper, for a finite set E, we use
![]() $u_{E}$
for the uniform measure on E and we typically use
$u_{E}$
for the uniform measure on E and we typically use
![]() $u_{d}$
instead of
$u_{d}$
instead of
![]() $u_{[d]}$
. Set
$u_{[d]}$
. Set
![]() $\Theta _{n}=(S_{\sigma _{n}})_{*}(u_{d_{n}})$
. It turns out that subsequential limits of
$\Theta _{n}=(S_{\sigma _{n}})_{*}(u_{d_{n}})$
. It turns out that subsequential limits of
![]() $\Theta _{n}$
can be nicely described in terms of well-known objects.
$\Theta _{n}$
can be nicely described in terms of well-known objects.
Definition 2.2. Let G be a countable, discrete group. We let
![]() $\operatorname {\mathrm {Sub}}(G)$
be the set of subgroups of G, which we regard as a subspace of
$\operatorname {\mathrm {Sub}}(G)$
be the set of subgroups of G, which we regard as a subspace of
![]() $\{0,1\}^{G}$
by identifying a subgroup with its indicator function. We equip
$\{0,1\}^{G}$
by identifying a subgroup with its indicator function. We equip
![]() $\operatorname {\mathrm {Sub}}(G)$
with the topology induced from this inclusion. Then
$\operatorname {\mathrm {Sub}}(G)$
with the topology induced from this inclusion. Then
![]() $\operatorname {\mathrm {Sub}}(G)$
is a closed subset of
$\operatorname {\mathrm {Sub}}(G)$
is a closed subset of
![]() $\{0,1\}^{G}$
and is thus compact in the induced topology. We let
$\{0,1\}^{G}$
and is thus compact in the induced topology. We let
![]() $\operatorname {\mathrm {IRS}}(G)$
be the set of probability measures on
$\operatorname {\mathrm {IRS}}(G)$
be the set of probability measures on
![]() $\operatorname {\mathrm {Sub}}(G)$
which are invariant under the conjugation action of G given by
$\operatorname {\mathrm {Sub}}(G)$
which are invariant under the conjugation action of G given by
![]() $g\cdot H=gHg^{-1}$
for all
$g\cdot H=gHg^{-1}$
for all
![]() $g\in G, H\in \operatorname {\mathrm {Sub}}(G)$
.
$g\in G, H\in \operatorname {\mathrm {Sub}}(G)$
.
We equip
![]() $\operatorname {\mathrm {Prob}}(\{0,1\}^{G})$
with the weak
$\operatorname {\mathrm {Prob}}(\{0,1\}^{G})$
with the weak
![]() $^{*}$
-topology (viewing complex Borel measures on
$^{*}$
-topology (viewing complex Borel measures on
![]() $\{0,1\}^{G}$
as the dual of
$\{0,1\}^{G}$
as the dual of
![]() $C(\{0,1\}^{G})$
). We often regard
$C(\{0,1\}^{G})$
). We often regard
![]() $\operatorname {\mathrm {Prob}}(\operatorname {\mathrm {Sub}}(G))$
as a closed subset of
$\operatorname {\mathrm {Prob}}(\operatorname {\mathrm {Sub}}(G))$
as a closed subset of
![]() $\operatorname {\mathrm {Prob}}(\{0,1\}^{G})$
by identifying
$\operatorname {\mathrm {Prob}}(\{0,1\}^{G})$
by identifying
![]() $\operatorname {\mathrm {Prob}}(\operatorname {\mathrm {Sub}}(G))$
with the probability measures which assign
$\operatorname {\mathrm {Prob}}(\operatorname {\mathrm {Sub}}(G))$
with the probability measures which assign
![]() $\operatorname {\mathrm {Sub}}(G)$
total mass one. In [Reference Abért, Glasner and Virág2, Proposition 13], it is shown that
$\operatorname {\mathrm {Sub}}(G)$
total mass one. In [Reference Abért, Glasner and Virág2, Proposition 13], it is shown that
![]() $\Theta \in \operatorname {\mathrm {IRS}}(G)$
if and only if there is a probability measure-preserving action
$\Theta \in \operatorname {\mathrm {IRS}}(G)$
if and only if there is a probability measure-preserving action
![]() $G\,{\curvearrowright }\, (X,\mu )$
so that
$G\,{\curvearrowright }\, (X,\mu )$
so that
![]() $\Theta ={\operatorname {Stab}}_{*}(\mu )$
, where
$\Theta ={\operatorname {Stab}}_{*}(\mu )$
, where
![]() ${\operatorname {Stab}}\colon X\to \operatorname {\mathrm {Sub}}(G)$
is given by
${\operatorname {Stab}}\colon X\to \operatorname {\mathrm {Sub}}(G)$
is given by
![]() ${\operatorname {Stab}}(x)=\{g\in G:gx=x\}$
. So IRSs are a naturally occurring construction when considering general (that is, not assumed essentially free) probability measure-preserving actions. One can think of a sofic approximation as a sequence of almost free almost actions on finite sets. From this perspective, it is reasonable to expect IRSs to arise when one considers more general almost actions (that is, asymptotic homomorphisms) that are not asymptotically free almost actions. The following lemma explains exactly how IRSs arise from approximate homomorphisms.
${\operatorname {Stab}}(x)=\{g\in G:gx=x\}$
. So IRSs are a naturally occurring construction when considering general (that is, not assumed essentially free) probability measure-preserving actions. One can think of a sofic approximation as a sequence of almost free almost actions on finite sets. From this perspective, it is reasonable to expect IRSs to arise when one considers more general almost actions (that is, asymptotic homomorphisms) that are not asymptotically free almost actions. The following lemma explains exactly how IRSs arise from approximate homomorphisms.
Lemma 2.3. Let G be a countable, discrete group and
![]() $\sigma _{n}\colon G\to {\operatorname {Sym}}(d_{n})$
approximate homomorphisms. For every free ultrafilter
$\sigma _{n}\colon G\to {\operatorname {Sym}}(d_{n})$
approximate homomorphisms. For every free ultrafilter
![]() $\omega \in \beta {\mathbb N}\setminus {\mathbb N}$
, we have that
$\omega \in \beta {\mathbb N}\setminus {\mathbb N}$
, we have that
Proof. Let
![]() $G\,{\curvearrowright }\, \{0,1\}^{G}$
be given by
$G\,{\curvearrowright }\, \{0,1\}^{G}$
be given by
![]() $(g\cdot x)(h)=x(g^{-1}hg)$
. We use
$(g\cdot x)(h)=x(g^{-1}hg)$
. We use
![]() $\alpha $
for the induced action on functions:
$\alpha $
for the induced action on functions:
![]() $(\alpha _{g}f)(x)=f(g^{-1}\cdot x)$
for all
$(\alpha _{g}f)(x)=f(g^{-1}\cdot x)$
for all
![]() $f\colon \{0,1\}^{G}\to {\mathbb C}$
Borel and all
$f\colon \{0,1\}^{G}\to {\mathbb C}$
Borel and all
![]() $g\in G$
. Note that if
$g\in G$
. Note that if
![]() $F\subset G$
is finite, then we can find a sequence
$F\subset G$
is finite, then we can find a sequence
![]() $\Omega _{n}\subseteq [d_{n}]$
(depending upon F) with
$\Omega _{n}\subseteq [d_{n}]$
(depending upon F) with
![]() $u_{d_{n}}(\Omega _{n})\to 1$
so that for all
$u_{d_{n}}(\Omega _{n})\to 1$
so that for all
![]() $j\in \Omega _{n}$
, all
$j\in \Omega _{n}$
, all
![]() $1\leq k\leq (2023)!$
, all
$1\leq k\leq (2023)!$
, all
![]() $g_{1},\ldots ,g_{k}\in F\cup F^{-1}\cup \{e\}$
, and all
$g_{1},\ldots ,g_{k}\in F\cup F^{-1}\cup \{e\}$
, and all
![]() $s_{1},\ldots ,s_{k}\in \{\pm 1\}$
, we have
$s_{1},\ldots ,s_{k}\in \{\pm 1\}$
, we have
Then if
![]() $g,h\in F$
and
$g,h\in F$
and
![]() $j\in \Omega _{n}$
, we have
$j\in \Omega _{n}$
, we have
This shows that
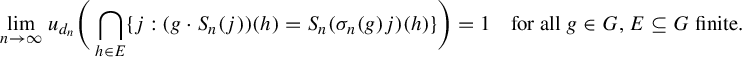 $$ \begin{align} \lim_{n\to\infty}u_{d_{n}}\bigg(\bigcap_{h\in E}\{j:(g\cdot S_{n}(j))(h)=S_{n}(\sigma_{n}(g)j)(h)\}\bigg)=1 \quad \text{for all } g\in G,E\subseteq G \text{ finite}. \end{align} $$
$$ \begin{align} \lim_{n\to\infty}u_{d_{n}}\bigg(\bigcap_{h\in E}\{j:(g\cdot S_{n}(j))(h)=S_{n}(\sigma_{n}(g)j)(h)\}\bigg)=1 \quad \text{for all } g\in G,E\subseteq G \text{ finite}. \end{align} $$
For a finite
![]() $E\subseteq G$
, let
$E\subseteq G$
, let
![]() $A_{E}=\{f\circ \pi _{E}:f\in C(\{0,1\}^{E\vphantom {E^{1^{1}}}})\}$
, where
$A_{E}=\{f\circ \pi _{E}:f\in C(\{0,1\}^{E\vphantom {E^{1^{1}}}})\}$
, where
![]() $\pi _{E}\colon \{0,1\}^{G}\to \{0,1\}^{E}$
is given by
$\pi _{E}\colon \{0,1\}^{G}\to \{0,1\}^{E}$
is given by
![]() $\pi _{E}(x)=x|_{E}$
. It follows from equation (2.1) and permutation invariance of
$\pi _{E}(x)=x|_{E}$
. It follows from equation (2.1) and permutation invariance of
![]() $u_{d_{n}}$
that
$u_{d_{n}}$
that
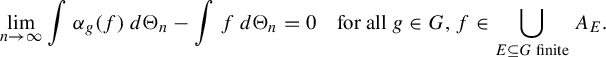 $$ \begin{align*} \lim_{n\to\infty}\int \alpha_{g}(f)\,d\Theta_{n}-\int f\,d\Theta_{n}=0\quad \text{for all } g\in G, f\in \bigcup_{E\subseteq G \text{ finite}}A_{E}. \end{align*} $$
$$ \begin{align*} \lim_{n\to\infty}\int \alpha_{g}(f)\,d\Theta_{n}-\int f\,d\Theta_{n}=0\quad \text{for all } g\in G, f\in \bigcup_{E\subseteq G \text{ finite}}A_{E}. \end{align*} $$
Thus,
for all
![]() $g\in G,f\in \bigcup _{E}A_{E}$
. Stone and Weierstrass imply that
$g\in G,f\in \bigcup _{E}A_{E}$
. Stone and Weierstrass imply that
![]() $\bigcup _{E}A_{E}$
is norm dense in
$\bigcup _{E}A_{E}$
is norm dense in
![]() $C(\{0,1\}^{G})$
and so by the Riesz representation theorem, we have shown that
$C(\{0,1\}^{G})$
and so by the Riesz representation theorem, we have shown that
![]() $\Theta _{\omega }$
is invariant under the conjugation action of G.
$\Theta _{\omega }$
is invariant under the conjugation action of G.
It thus suffices to show that
![]() $\Theta _{\omega }$
is supported on the space of subgroups of G. For
$\Theta _{\omega }$
is supported on the space of subgroups of G. For
![]() ${g,h\in G}$
, let
${g,h\in G}$
, let
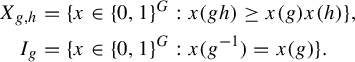 $$ \begin{align*} X_{g,h}&=\{x\in \{0,1\}^{G}:x(gh)\geq x(g)x(h)\},\\ I_{g}&=\{x\in \{0,1\}^{G}:x(g^{-1})=x(g)\}. \end{align*} $$
$$ \begin{align*} X_{g,h}&=\{x\in \{0,1\}^{G}:x(gh)\geq x(g)x(h)\},\\ I_{g}&=\{x\in \{0,1\}^{G}:x(g^{-1})=x(g)\}. \end{align*} $$
Then
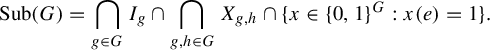 $$ \begin{align*}\operatorname{\mathrm{Sub}}(G)=\bigcap_{g\in G}I_{g}\cap \bigcap_{g,h\in G}X_{g,h}\cap \{x\in \{0,1\}^{G}:x(e)=1\}.\end{align*} $$
$$ \begin{align*}\operatorname{\mathrm{Sub}}(G)=\bigcap_{g\in G}I_{g}\cap \bigcap_{g,h\in G}X_{g,h}\cap \{x\in \{0,1\}^{G}:x(e)=1\}.\end{align*} $$
Since G is countable, it suffices to show that
![]() $\Theta _{\omega }$
assigns each set in this intersection measure
$\Theta _{\omega }$
assigns each set in this intersection measure
![]() $1$
. By the Portmanteau theorem [Reference Dudley22, Theorem 11.1.1], for each
$1$
. By the Portmanteau theorem [Reference Dudley22, Theorem 11.1.1], for each
![]() $g,h\in G$
,
$g,h\in G$
,
 $$ \begin{align*} &\Theta_{\omega}(\{x\in \{0,1\}^{G}:x(gh)\geq x(g)x(h)\})\\ &\quad \geq\lim_{n\to\omega}u_{d_{n}}(\{j:1_{\{j\}}(\sigma_{n}(gh)(j))\geq 1_{\{j\}}(\sigma_{n}(g)(j))1_{\{j\}}(\sigma_{n}(h)(j))\})\\ &\quad\geq \lim_{n\to\omega}u_{d_{n}}(\{j:\sigma_{n}(gh)(j)=\sigma_{n}(g)\sigma_{n}(h)(j)\})=1. \end{align*} $$
$$ \begin{align*} &\Theta_{\omega}(\{x\in \{0,1\}^{G}:x(gh)\geq x(g)x(h)\})\\ &\quad \geq\lim_{n\to\omega}u_{d_{n}}(\{j:1_{\{j\}}(\sigma_{n}(gh)(j))\geq 1_{\{j\}}(\sigma_{n}(g)(j))1_{\{j\}}(\sigma_{n}(h)(j))\})\\ &\quad\geq \lim_{n\to\omega}u_{d_{n}}(\{j:\sigma_{n}(gh)(j)=\sigma_{n}(g)\sigma_{n}(h)(j)\})=1. \end{align*} $$
The proofs that
![]() $\Theta _{\omega }$
assigns measure
$\Theta _{\omega }$
assigns measure
![]() $1$
to
$1$
to
![]() $I_{g}$
and
$I_{g}$
and
![]() $\{x\in \{0,1\}^{G}:x(e)=1\}$
are similar.
$\{x\in \{0,1\}^{G}:x(e)=1\}$
are similar.
We are thus able to make the following definition.
Definition 2.4. Let G be a countable, discrete group and
![]() $\sigma _{n}\colon G\to {\operatorname {Sym}}(d_{n})$
approximate homomorphisms. Define
$\sigma _{n}\colon G\to {\operatorname {Sym}}(d_{n})$
approximate homomorphisms. Define
![]() $\Theta _{n}$
as was done before Definition 2.2. Given
$\Theta _{n}$
as was done before Definition 2.2. Given
![]() $\omega \in \beta {\mathbb N}\setminus {\mathbb N}$
, we define
$\omega \in \beta {\mathbb N}\setminus {\mathbb N}$
, we define
![]() $\operatorname {\mathrm {IRS}}(\sigma _{\omega })=\lim _{n\to \omega }\Theta _{n}$
.
$\operatorname {\mathrm {IRS}}(\sigma _{\omega })=\lim _{n\to \omega }\Theta _{n}$
.
We remark on an alternate construction of
![]() $\operatorname {\mathrm {IRS}}(\sigma _{\omega })$
. One can take an ultraproduct of the measure spaces
$\operatorname {\mathrm {IRS}}(\sigma _{\omega })$
. One can take an ultraproduct of the measure spaces
![]() $(\{1,\ldots ,d_{n}\},u_{d_{n}})$
to obtain a probability space
$(\{1,\ldots ,d_{n}\},u_{d_{n}})$
to obtain a probability space
![]() $({\mathcal L},u_{\omega })$
called the Loeb measure space [Reference Loeb38]. The actions
$({\mathcal L},u_{\omega })$
called the Loeb measure space [Reference Loeb38]. The actions
![]() ${\operatorname {Sym}}(d_{n})\,{\curvearrowright }\, \{1,\ldots ,d_{n}\}$
along with the approximate homomorphisms
${\operatorname {Sym}}(d_{n})\,{\curvearrowright }\, \{1,\ldots ,d_{n}\}$
along with the approximate homomorphisms
![]() $\sigma _{n}$
will induce a probability measure-preserving action on
$\sigma _{n}$
will induce a probability measure-preserving action on
![]() $({\mathcal L},u_{\omega })$
in a natural way. Under this action, one can show that
$({\mathcal L},u_{\omega })$
in a natural way. Under this action, one can show that
![]() $\operatorname {\mathrm {IRS}}(\sigma _{\omega })$
is
$\operatorname {\mathrm {IRS}}(\sigma _{\omega })$
is
![]() ${\operatorname {Stab}}_{*}(u_{\omega })$
, where
${\operatorname {Stab}}_{*}(u_{\omega })$
, where
![]() ${{\operatorname {Stab}}\colon {\mathcal L}\to \operatorname {\mathrm {Sub}}(G)}$
is given by
${{\operatorname {Stab}}\colon {\mathcal L}\to \operatorname {\mathrm {Sub}}(G)}$
is given by
![]() ${\operatorname {Stab}}(z)=\{g\in G:gz=z\}$
. However, we will not need this fact and thus will not prove it. If
${\operatorname {Stab}}(z)=\{g\in G:gz=z\}$
. However, we will not need this fact and thus will not prove it. If
![]() $\operatorname {\mathrm {IRS}}(\sigma _{\omega })$
does not depend upon
$\operatorname {\mathrm {IRS}}(\sigma _{\omega })$
does not depend upon
![]() $\omega ,$
then
$\omega ,$
then
![]() $\lim _{n\to \infty }\Theta _{n}$
exists. In this case, we call
$\lim _{n\to \infty }\Theta _{n}$
exists. In this case, we call
![]() $\lim _{n\to \infty }\Theta _{n}$
the stabilizer type of
$\lim _{n\to \infty }\Theta _{n}$
the stabilizer type of
![]() $\sigma _{n}$
. For example,
$\sigma _{n}$
. For example,
![]() $\lim _{n\to \infty }\Theta _{n}=\delta _{\{1\}}$
if and only if
$\lim _{n\to \infty }\Theta _{n}=\delta _{\{1\}}$
if and only if
![]() $\sigma _{n}$
is a sofic approximation.
$\sigma _{n}$
is a sofic approximation.
3. Background on orbit equivalence relations and Theorem 1.1
To extend approximate homomorphisms to sofic approximations of relations, we need the following construction (appearing first in [Reference Abért, Glasner and Virág2]) of an action associated to an IRS, say
![]() $\Theta $
. The intention is that the action is ‘Bernoulli as possible’ while still having
$\Theta $
. The intention is that the action is ‘Bernoulli as possible’ while still having
![]() $\Theta $
as its IRS. For technical reasons, the action will not always have
$\Theta $
as its IRS. For technical reasons, the action will not always have
![]() $\Theta $
as its IRS, but under mild conditions (which we state precisely after the definition), it will, and we think it is still worth stating the general construction.
$\Theta $
as its IRS, but under mild conditions (which we state precisely after the definition), it will, and we think it is still worth stating the general construction.
Definition 3.1. Let G be a countable, discrete group and let
![]() $\Theta \in \operatorname {\mathrm {IRS}}(G)$
. Let X be a compact metrizable space and
$\Theta \in \operatorname {\mathrm {IRS}}(G)$
. Let X be a compact metrizable space and
![]() $\nu $
a Borel probability measure on G. Let
$\nu $
a Borel probability measure on G. Let
Observe that Y is a closed subset of
![]() $\operatorname {\mathrm {Sub}}(G)\times X^{G}$
. For
$\operatorname {\mathrm {Sub}}(G)\times X^{G}$
. For
![]() $H\in \operatorname {\mathrm {Sub}}(G)$
, let
$H\in \operatorname {\mathrm {Sub}}(G)$
, let
![]() $G/H$
be the space of right cosets of H in G and regard
$G/H$
be the space of right cosets of H in G and regard
![]() $\nu ^{\otimes G/H}$
as a probability measure on
$\nu ^{\otimes G/H}$
as a probability measure on
![]() $X^{G}$
which is supported on the
$X^{G}$
which is supported on the
![]() $x\in X^{G}$
which are constant on right H-cosets. Let
$x\in X^{G}$
which are constant on right H-cosets. Let
![]() $\mu _{\Theta }$
be the measure
$\mu _{\Theta }$
be the measure
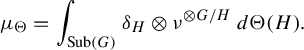 $$ \begin{align*}\mu_{\Theta}=\int_{\operatorname{\mathrm{Sub}}(G)}\delta_{H}\otimes \nu^{\otimes G/H}\,d\Theta(H).\end{align*} $$
$$ \begin{align*}\mu_{\Theta}=\int_{\operatorname{\mathrm{Sub}}(G)}\delta_{H}\otimes \nu^{\otimes G/H}\,d\Theta(H).\end{align*} $$
We sometimes denote
![]() $(Y,\mu _{\Theta })$
as
$(Y,\mu _{\Theta })$
as
![]() $\operatorname {\mathrm {Bern}}(X,\nu ,\Theta )$
. We let
$\operatorname {\mathrm {Bern}}(X,\nu ,\Theta )$
. We let
![]() $G\,{\curvearrowright }\, X^{G}$
by
$G\,{\curvearrowright }\, X^{G}$
by
Note that
![]() $G\,{\curvearrowright }\, Y$
by
$G\,{\curvearrowright }\, Y$
by
We call
![]() $G\,{\curvearrowright }\, (Y,\mu _{\Theta })$
the
$G\,{\curvearrowright }\, (Y,\mu _{\Theta })$
the
![]() $\Theta $
-Bernoulli action with base
$\Theta $
-Bernoulli action with base
![]() $(X,\nu )$
.
$(X,\nu )$
.
Suppose that
![]() $\nu $
is not a dirac mass, and choose
$\nu $
is not a dirac mass, and choose
![]() $b\in [0,1)$
so that
$b\in [0,1)$
so that
![]() $\nu (\{x\})\in [0,b]$
for
$\nu (\{x\})\in [0,b]$
for
![]() $x\in X$
. Suppose that
$x\in X$
. Suppose that
![]() $H\in \operatorname {\mathrm {Sub}}(G)$
and
$H\in \operatorname {\mathrm {Sub}}(G)$
and
![]() $F\subseteq G/H$
is finite with
$F\subseteq G/H$
is finite with
![]() $H\in F$
, then by Fubini and Tonelli,
$H\in F$
, then by Fubini and Tonelli,
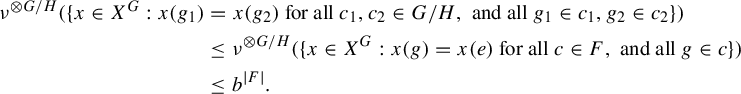 $$ \begin{align*} \nu^{\otimes G/H}(\{x\in X^{G}:x(g_{1})&=x(g_{2}) \text{ for all } c_{1},c_{2}\in G/H, \text{ and all } g_{1}\in c_{1},g_{2}\in c_{2}\}) \\ &\leq \nu^{\otimes G/H}(\{x\in X^{G}:x(g)=x(e) \text{ for all } c\in F, \text{ and all } g\in c\})\\ &\leq b^{|F|}. \end{align*} $$
$$ \begin{align*} \nu^{\otimes G/H}(\{x\in X^{G}:x(g_{1})&=x(g_{2}) \text{ for all } c_{1},c_{2}\in G/H, \text{ and all } g_{1}\in c_{1},g_{2}\in c_{2}\}) \\ &\leq \nu^{\otimes G/H}(\{x\in X^{G}:x(g)=x(e) \text{ for all } c\in F, \text{ and all } g\in c\})\\ &\leq b^{|F|}. \end{align*} $$
Since
![]() $b<1$
, and the above inequality is true for every finite
$b<1$
, and the above inequality is true for every finite
![]() $F\subseteq G$
, we deduce that if either:
$F\subseteq G$
, we deduce that if either:
-
•
 $\nu $
is atomless; or
$\nu $
is atomless; or -
• H is infinite index in G almost surely,
then for
![]() $\mu _{\Theta }$
-almost every
$\mu _{\Theta }$
-almost every
![]() $(H,x)$
with
$(H,x)$
with
![]() $H\ne G$
, we have
$H\ne G$
, we have
![]() ${\operatorname {Stab}}((H,x))=H$
. Note that
${\operatorname {Stab}}((H,x))=H$
. Note that
![]() ${\operatorname {Stab}}((G,x))$
=G. So, under either of the above bulleted conditions, the action
${\operatorname {Stab}}((G,x))$
=G. So, under either of the above bulleted conditions, the action
![]() $G\,{\curvearrowright }\, (Y,\mu _{\Theta })$
has IRS equal to
$G\,{\curvearrowright }\, (Y,\mu _{\Theta })$
has IRS equal to
![]() $\Theta .$
This construction first appears in [Reference Abért, Glasner and Virág1, Proposition 13] (see [Reference Creutz and Peterson17, §§3.2–3.3] for the locally compact case, as well as a proof of the fact that if
$\Theta .$
This construction first appears in [Reference Abért, Glasner and Virág1, Proposition 13] (see [Reference Creutz and Peterson17, §§3.2–3.3] for the locally compact case, as well as a proof of the fact that if
![]() $\Theta $
is ergodic, then we can modify the above construction to get an ergodic action). See [Reference Seward46], [Reference Tucker-Drob48, §5] for further applications of this construction.
$\Theta $
is ergodic, then we can modify the above construction to get an ergodic action). See [Reference Seward46], [Reference Tucker-Drob48, §5] for further applications of this construction.
The classical Bernoulli shift with base
![]() $(X,\nu )$
is the case when
$(X,\nu )$
is the case when
![]() $\Theta =\delta _{\{1\}}$
. It is of great importance in ergodic theory, via its connections to probability (it is the sample space for independent and identically distributed X-valued random variables
$\Theta =\delta _{\{1\}}$
. It is of great importance in ergodic theory, via its connections to probability (it is the sample space for independent and identically distributed X-valued random variables
![]() $(\Upsilon _{g})_{g\in G}$
). It also has many desirable properties such as being mixing ([Reference Petersen43, §2.5] and [Reference Kerr and Li37, §2.3]), complete positive entropy [Reference Kerr35, Reference Rudolph and Weiss45], Koopman representation being an infinite direct sum of the left regular [Reference Kerr and Li37, §2.3], and being a free action when the acting group is infinite (proved above). It is also canonically associated to any group. We refer the reader to [Reference Walters50, §4.9], [Reference Petersen43, §§6.4 and 6.5], and [Reference Kerr and Li37, §2.3] for more details and information on the classical Bernoulli shift. For our purposes, we will only need that the
$(\Upsilon _{g})_{g\in G}$
). It also has many desirable properties such as being mixing ([Reference Petersen43, §2.5] and [Reference Kerr and Li37, §2.3]), complete positive entropy [Reference Kerr35, Reference Rudolph and Weiss45], Koopman representation being an infinite direct sum of the left regular [Reference Kerr and Li37, §2.3], and being a free action when the acting group is infinite (proved above). It is also canonically associated to any group. We refer the reader to [Reference Walters50, §4.9], [Reference Petersen43, §§6.4 and 6.5], and [Reference Kerr and Li37, §2.3] for more details and information on the classical Bernoulli shift. For our purposes, we will only need that the
![]() $\Theta $
-Bernoulli shift retains a residue of freeness, in that under the above conditions, it has
$\Theta $
-Bernoulli shift retains a residue of freeness, in that under the above conditions, it has
![]() $\Theta $
as its IRS.
$\Theta $
as its IRS.
We will need the notion of an orbit equivalence relation.
Definition 3.2. A discrete, probability measuring preserving equivalence relation is a tuple
![]() $(X,\nu ,{\mathcal R})$
where
$(X,\nu ,{\mathcal R})$
where
![]() $(X,\nu )$
is a standard probability space,
$(X,\nu )$
is a standard probability space,
![]() ${\mathcal R}\subseteq X\times X$
is Borel, and so that the following hold:
${\mathcal R}\subseteq X\times X$
is Borel, and so that the following hold:
-
• (equivalence relation) the relation
 $x\thicksim y$
given by
$x\thicksim y$
given by
 $(x,y)\in {\mathcal R}$
is an equivalence relation;
$(x,y)\in {\mathcal R}$
is an equivalence relation; -
• (discreteness) for almost every
 $x\in X$
, we have is countable;
$x\in X$
, we have is countable; $$ \begin{align*}[x]_{{\mathcal R}}=\{y\in X:(x,y)\in {\mathcal R}\}\end{align*} $$
$$ \begin{align*}[x]_{{\mathcal R}}=\{y\in X:(x,y)\in {\mathcal R}\}\end{align*} $$
-
• (pmp) for every Borel
 $f\colon {\mathcal R}\to [0,+\infty ]$
, we have
$f\colon {\mathcal R}\to [0,+\infty ]$
, we have  $$ \begin{align*}\int \sum_{y\in [x]_{{\mathcal R}}}f(x,y)\,d\nu(x)=\int \sum_{y\in [x]_{{\mathcal R}}}f(y,x)\,d\nu(x).\end{align*} $$
$$ \begin{align*}\int \sum_{y\in [x]_{{\mathcal R}}}f(x,y)\,d\nu(x)=\int \sum_{y\in [x]_{{\mathcal R}}}f(y,x)\,d\nu(x).\end{align*} $$
The last item can be recast as follows: define a Borel measure
![]() $\overline {\nu }$
on
$\overline {\nu }$
on
![]() ${\mathcal R}$
by
${\mathcal R}$
by
Then the map
![]() $(x,y)\mapsto (y,x)$
preserves the measure if and only if the last item holds. This implies, for example, that if
$(x,y)\mapsto (y,x)$
preserves the measure if and only if the last item holds. This implies, for example, that if
![]() ${\mathcal R}$
is a discrete, probability measure-preserving equivalence relation on
${\mathcal R}$
is a discrete, probability measure-preserving equivalence relation on
![]() $(X,\nu )$
and if
$(X,\nu )$
and if
![]() $f\in L^{1}({\mathcal R})$
, then
$f\in L^{1}({\mathcal R})$
, then
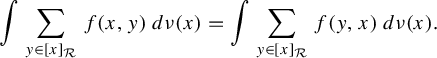 $$ \begin{align*}\int \sum_{y\in [x]_{{\mathcal R}}}f(x,y)\,d\nu(x)=\int \sum_{y\in [x]_{{\mathcal R}}}f(y,x)\,d\nu(x).\end{align*} $$
$$ \begin{align*}\int \sum_{y\in [x]_{{\mathcal R}}}f(x,y)\,d\nu(x)=\int \sum_{y\in [x]_{{\mathcal R}}}f(y,x)\,d\nu(x).\end{align*} $$
If G is a countable discrete group and
![]() $G\,{\curvearrowright }\, (X,\nu )$
is a probability measure-preserving action, we then have a discrete, probability-measure relation given as the orbit equivalence relation
$G\,{\curvearrowright }\, (X,\nu )$
is a probability measure-preserving action, we then have a discrete, probability-measure relation given as the orbit equivalence relation
All discrete, probability measure-preserving equivalence relations arise this way [Reference Feldman and Moore28].
As mentioned before, we will extend approximate homomorphisms to sofic approximations of equivalence relations. To define a sofic approximation of an equivalence relation, we use tracial von Neumann algebras.
Definition 3.3. Let
![]() ${\mathcal H}$
be a Hilbert space. A unital
${\mathcal H}$
be a Hilbert space. A unital
![]() $*$
-subalgebra M of
$*$
-subalgebra M of
![]() $\mathbb {B}(\mathcal {H})$
is said to be a von Neumann algebra if it is closed in the weak operator topology given by the convergence
$\mathbb {B}(\mathcal {H})$
is said to be a von Neumann algebra if it is closed in the weak operator topology given by the convergence
![]() $T_n\to T$
if
$T_n\to T$
if
![]() $\langle (T_n-T)v, w\rangle \to 0$
for all
$\langle (T_n-T)v, w\rangle \to 0$
for all
![]() $v,w\in \mathcal {H}$
. A projection in M is an element
$v,w\in \mathcal {H}$
. A projection in M is an element
![]() $p\in M$
with
$p\in M$
with
![]() $p=p^{*}=p^{2}$
. We let
$p=p^{*}=p^{2}$
. We let
![]() $\operatorname {\mathrm {Proj}}(M)$
be the set of projections in M. A normal homomorphism between von Neumann algebras
$\operatorname {\mathrm {Proj}}(M)$
be the set of projections in M. A normal homomorphism between von Neumann algebras
![]() $M,N$
is a linear
$M,N$
is a linear
![]() $\pi \colon M\to N$
which preserves products and adjoints, and such that
$\pi \colon M\to N$
which preserves products and adjoints, and such that
![]() $\pi |_{\{x\in M:\|x\|\leq 1\}}$
is weak operator topology continuous. Such maps are automatically norm continuous [Reference Conway16, Proposition 1.7(e)]. We say that
$\pi |_{\{x\in M:\|x\|\leq 1\}}$
is weak operator topology continuous. Such maps are automatically norm continuous [Reference Conway16, Proposition 1.7(e)]. We say that
![]() $\pi $
is an isomorphism if is bijective, it is then automatic that
$\pi $
is an isomorphism if is bijective, it is then automatic that
![]() $\pi ^{-1}$
is a normal homomorphism [Reference Conway16, Proposition 46.6]. A pair
$\pi ^{-1}$
is a normal homomorphism [Reference Conway16, Proposition 46.6]. A pair
![]() $(M,\tau )$
is a tracial von Neumann algebra if M is a von Neumann algebra and
$(M,\tau )$
is a tracial von Neumann algebra if M is a von Neumann algebra and
![]() $\tau $
is a trace, meaning that
$\tau $
is a trace, meaning that
![]() $\tau : M\to {\mathbb C}$
satisfies:
$\tau : M\to {\mathbb C}$
satisfies:
-
•
 $\tau $
is linear;
$\tau $
is linear; -
•
 $\tau (x^{*}x)\geq 0$
and
$\tau (x^{*}x)\geq 0$
and
 $\tau (x^{*}x)>0$
if
$\tau (x^{*}x)>0$
if
 $x\ne 0$
;
$x\ne 0$
; -
•
 $\tau (ba)=\tau (ab)$
for all
$\tau (ba)=\tau (ab)$
for all
 $a,b\in M$
;
$a,b\in M$
; -
•
 $\tau (1)=1$
;
$\tau (1)=1$
; -
•
 $\tau |_{\{x\in M:\|x\|\leq 1\}}$
is weak operator topology continuous.
$\tau |_{\{x\in M:\|x\|\leq 1\}}$
is weak operator topology continuous.
Given a Hilbert space
![]() ${\mathcal H}$
and
${\mathcal H}$
and
![]() $E\subseteq B({\mathcal H})$
, we let
$E\subseteq B({\mathcal H})$
, we let
![]() $W^{*}(E)$
be the von Neumann algebra generated by E.
$W^{*}(E)$
be the von Neumann algebra generated by E.
For a tracial von Neumann algebra
![]() $(M,\tau )$
and
$(M,\tau )$
and
![]() $x\in M$
, we set
$x\in M$
, we set
![]() $\|x\|_{2}=\tau (x^{*}x)^{1/2}$
. A simple example of a tracial von Neumann algebra is the following. For
$\|x\|_{2}=\tau (x^{*}x)^{1/2}$
. A simple example of a tracial von Neumann algebra is the following. For
![]() $k\in {\mathbb N}$
, define
$k\in {\mathbb N}$
, define
![]() $\operatorname {\mathrm {tr}}\colon M_{k}({\mathbb C})\to {\mathbb C}$
by
$\operatorname {\mathrm {tr}}\colon M_{k}({\mathbb C})\to {\mathbb C}$
by
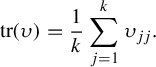 $$ \begin{align*}\operatorname{\mathrm{tr}}(\upsilon)=\frac{1}{k}\sum_{j=1}^{k}\upsilon_{jj}.\end{align*} $$
$$ \begin{align*}\operatorname{\mathrm{tr}}(\upsilon)=\frac{1}{k}\sum_{j=1}^{k}\upsilon_{jj}.\end{align*} $$
Then
![]() $(M_{k}({\mathbb C}),\operatorname {\mathrm {tr}})$
is a tracial von Neumann algebra. The following is folklore, but we highlight it because we will use it explicitly. This can be proved, e.g. by following the discussion in [Reference Bekka8, §Reference Abért, Glasner and Virág2].
$(M_{k}({\mathbb C}),\operatorname {\mathrm {tr}})$
is a tracial von Neumann algebra. The following is folklore, but we highlight it because we will use it explicitly. This can be proved, e.g. by following the discussion in [Reference Bekka8, §Reference Abért, Glasner and Virág2].
Lemma 3.4. Let
![]() $(M_{j},\tau _{j}), j=1,2$
be tracial von Neumann algebras. Suppose that
$(M_{j},\tau _{j}), j=1,2$
be tracial von Neumann algebras. Suppose that
![]() $N\subseteq M_{1}$
is a weak operator topology dense
$N\subseteq M_{1}$
is a weak operator topology dense
![]() $*$
-subalgebra, and that
$*$
-subalgebra, and that
![]() $\pi \colon N\to M_{2}$
is a
$\pi \colon N\to M_{2}$
is a
![]() $*$
-homomorphism with
$*$
-homomorphism with
![]() $\tau _{2}\circ \pi =\tau _{1}|_{N}$
. Then
$\tau _{2}\circ \pi =\tau _{1}|_{N}$
. Then
![]() $\pi $
extends uniquely to a trace-preserving, normal
$\pi $
extends uniquely to a trace-preserving, normal
![]() $*$
-homomorphism from
$*$
-homomorphism from
![]() $M_{1}\to M_{2}$
.
$M_{1}\to M_{2}$
.
Given a discrete, probability measure-preserving equivalence relation
![]() ${\mathcal R}$
on
${\mathcal R}$
on
![]() $(X,\nu )$
, we let
$(X,\nu )$
, we let
![]() $[{\mathcal R}]$
be the group of all bimeasurable bijections
$[{\mathcal R}]$
be the group of all bimeasurable bijections
![]() $\gamma \colon X_{0}\to Y_{0}$
, where
$\gamma \colon X_{0}\to Y_{0}$
, where
![]() $X_{0},Y_{0}$
are conull subsets of X and with
$X_{0},Y_{0}$
are conull subsets of X and with
![]() $\gamma (x)\in [x]_{{\mathcal R}}$
for almost every
$\gamma (x)\in [x]_{{\mathcal R}}$
for almost every
![]() $x\in X$
. As usual, we identify two such maps if they agree off a set of measure zero. The group
$x\in X$
. As usual, we identify two such maps if they agree off a set of measure zero. The group
![]() $[{\mathcal R}]$
is called the full group of
$[{\mathcal R}]$
is called the full group of
![]() ${\mathcal R}$
. We let
${\mathcal R}$
. We let
![]() $[[{\mathcal R}]]$
be the set of all bimeasurable bijections
$[[{\mathcal R}]]$
be the set of all bimeasurable bijections
![]() $\gamma \colon B_{1}\to B_{2}$
(where
$\gamma \colon B_{1}\to B_{2}$
(where
![]() $B_{1},B_{2}$
are measurable subsets of X) which satisfy that
$B_{1},B_{2}$
are measurable subsets of X) which satisfy that
![]() $\gamma (x)\in [x]_{{\mathcal R}}$
for almost every
$\gamma (x)\in [x]_{{\mathcal R}}$
for almost every
![]() $x\in B_{1}$
. As usual, we identify two such maps if they agree off a set of measure zero. We usually use
$x\in B_{1}$
. As usual, we identify two such maps if they agree off a set of measure zero. We usually use
![]() $\operatorname {\mathrm {dom}}(\gamma ),\operatorname {\mathrm {ran}}(\gamma )$
for
$\operatorname {\mathrm {dom}}(\gamma ),\operatorname {\mathrm {ran}}(\gamma )$
for
![]() $B_{1},B_{2}$
above. We define maps
$B_{1},B_{2}$
above. We define maps
![]() $\vartheta \colon L^{\infty }(X,\nu )\to B(L^{2}({\mathcal R},\overline {\nu }))$
and
$\vartheta \colon L^{\infty }(X,\nu )\to B(L^{2}({\mathcal R},\overline {\nu }))$
and
![]() $\unicode{x3bb} \colon [[{\mathcal R}]]\to \mathcal {U}(L^{2}({\mathcal R},\overline {\nu }))$
by
$\unicode{x3bb} \colon [[{\mathcal R}]]\to \mathcal {U}(L^{2}({\mathcal R},\overline {\nu }))$
by
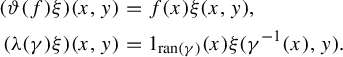 $$ \begin{align*} (\vartheta(f)\xi)(x,y)&=f(x)\xi(x,y),\\ (\unicode{x3bb}(\gamma)\xi)(x,y)&=1_{\operatorname{\mathrm{ran}}(\gamma)}(x)\xi(\gamma^{-1}(x),y). \end{align*} $$
$$ \begin{align*} (\vartheta(f)\xi)(x,y)&=f(x)\xi(x,y),\\ (\unicode{x3bb}(\gamma)\xi)(x,y)&=1_{\operatorname{\mathrm{ran}}(\gamma)}(x)\xi(\gamma^{-1}(x),y). \end{align*} $$
We define the von Neumann algebra of the equivalence relation to be
Note that if
![]() $B\subseteq X$
is measurable, then we have an element
$B\subseteq X$
is measurable, then we have an element
![]() $\operatorname {\mathrm {id}}_{B}\in [[{\mathcal R}]]$
with
$\operatorname {\mathrm {id}}_{B}\in [[{\mathcal R}]]$
with
![]() $\operatorname {\mathrm {dom}}(\operatorname {\mathrm {id}}_{B})=E=\operatorname {\mathrm {ran}}(\operatorname {\mathrm {id}}_{B})$
and
$\operatorname {\mathrm {dom}}(\operatorname {\mathrm {id}}_{B})=E=\operatorname {\mathrm {ran}}(\operatorname {\mathrm {id}}_{B})$
and
![]() $\operatorname {\mathrm {id}}_{B}(x)=x$
for all
$\operatorname {\mathrm {id}}_{B}(x)=x$
for all
![]() $x\in B$
. Moreover,
$x\in B$
. Moreover,
![]() $\unicode{x3bb} (\operatorname {\mathrm {id}}_{B})=\vartheta (1_{B})$
. Since simple functions are dense in
$\unicode{x3bb} (\operatorname {\mathrm {id}}_{B})=\vartheta (1_{B})$
. Since simple functions are dense in
![]() $L^{\infty }(X,\nu )$
, this implies that
$L^{\infty }(X,\nu )$
, this implies that
The von Neumann algebra
![]() $L({\mathcal R})$
is equipped with a trace
$L({\mathcal R})$
is equipped with a trace
where
![]() $\Lambda =\{(x,x):x\in X\}$
. We typically identify
$\Lambda =\{(x,x):x\in X\}$
. We typically identify
![]() $L^{\infty }(X,\nu )$
and
$L^{\infty }(X,\nu )$
and
![]() $[[{\mathcal R}]]$
as subsets of
$[[{\mathcal R}]]$
as subsets of
![]() $L({\mathcal R})$
and do not make explicit reference to the maps
$L({\mathcal R})$
and do not make explicit reference to the maps
![]() $\unicode{x3bb} ,\vartheta .$
$\unicode{x3bb} ,\vartheta .$
Another example of a tracial von Neumann algebra is the ultraproduct of tracial von Neumann algebras. Let
![]() $\omega $
be a free ultrafilter on
$\omega $
be a free ultrafilter on
![]() $\mathbb {N}$
. Suppose
$\mathbb {N}$
. Suppose
![]() $(N_k, \tau _k)$
are tracial von Neumann algebras. Denote the ultraproduct by
$(N_k, \tau _k)$
are tracial von Neumann algebras. Denote the ultraproduct by
If
![]() $(x_{k})_{k}\in \prod _{k}N_{k}$
with
$(x_{k})_{k}\in \prod _{k}N_{k}$
with
![]() $\sup _{k}\|x_{k}\|<+\infty ,$
we use
$\sup _{k}\|x_{k}\|<+\infty ,$
we use
![]() $(x_{k})_{k\to \omega }$
for its image in
$(x_{k})_{k\to \omega }$
for its image in
![]() $\prod _{k\to \omega }(N_{k},\tau _{k})$
. By the proof of [Reference Brown and Ozawa12, Lemma A.9], the ultraproduct is a tracial von Neumann algebra and is equipped with a canonical trace
$\prod _{k\to \omega }(N_{k},\tau _{k})$
. By the proof of [Reference Brown and Ozawa12, Lemma A.9], the ultraproduct is a tracial von Neumann algebra and is equipped with a canonical trace
![]() $\tau ((x_n)_{\omega })= \lim _{n\to \omega }\tau _n(x_n)$
.
$\tau ((x_n)_{\omega })= \lim _{n\to \omega }\tau _n(x_n)$
.
For a sequence of integers
![]() $d_{n}$
, set
$d_{n}$
, set
We let
and
View
![]() $\ell ^{\infty }(d_{n})\subseteq M_{d_{n}}({\mathbb C})$
by identifying each function with the diagonal matrix whose entries are
$\ell ^{\infty }(d_{n})\subseteq M_{d_{n}}({\mathbb C})$
by identifying each function with the diagonal matrix whose entries are
![]() $(f(1),\ldots ,f(d_{n}))$
, and identify each permutation with its corresponding permutation matrix. In this way, we can identify
$(f(1),\ldots ,f(d_{n}))$
, and identify each permutation with its corresponding permutation matrix. In this way, we can identify
![]() $L^{\infty }({\mathcal L},u_{\omega })$
as a subalgebra of
$L^{\infty }({\mathcal L},u_{\omega })$
as a subalgebra of
![]() ${\mathcal M}$
, and
${\mathcal M}$
, and
![]() ${\mathcal S}_{\omega }$
as a subgroup of the unitary group of
${\mathcal S}_{\omega }$
as a subgroup of the unitary group of
![]() ${\mathcal M}$
.
${\mathcal M}$
.
Definition 3.5. Let
![]() $(X,\nu ,{\mathcal R})$
be a discrete, probability measure-preserving equivalence relation. We say that
$(X,\nu ,{\mathcal R})$
be a discrete, probability measure-preserving equivalence relation. We say that
![]() ${\mathcal R}$
is sofic if there is a free ultrafilter
${\mathcal R}$
is sofic if there is a free ultrafilter
![]() $\omega $
, a sequence of positive integers
$\omega $
, a sequence of positive integers
![]() $(d_{n})_{n}$
, and maps
$(d_{n})_{n}$
, and maps
 $$ \begin{align*} \rho\colon L^{\infty}(X,\nu)\to L^{\infty}({\mathcal L},u_{\omega}) &:=\prod_{n\to\omega}(\ell^{\infty}(d_{n}),u_{d_{n}}),\\ \sigma\colon [{\mathcal R}]\to {\mathcal S}_{\omega}&:=\prod_{n\to\omega}({\operatorname{Sym}}(d_{n}),d_{\operatorname{\mathrm{Hamm}}}) \end{align*} $$
$$ \begin{align*} \rho\colon L^{\infty}(X,\nu)\to L^{\infty}({\mathcal L},u_{\omega}) &:=\prod_{n\to\omega}(\ell^{\infty}(d_{n}),u_{d_{n}}),\\ \sigma\colon [{\mathcal R}]\to {\mathcal S}_{\omega}&:=\prod_{n\to\omega}({\operatorname{Sym}}(d_{n}),d_{\operatorname{\mathrm{Hamm}}}) \end{align*} $$
so that:
-
•
 $\rho $
is a normal
$\rho $
is a normal
 $*$
-homomorphism;
$*$
-homomorphism; -
•
 $\sigma $
is a homomorphism;
$\sigma $
is a homomorphism; -
•
 $\tau _{\omega }(\rho (f)\sigma (\gamma ))=\int _{\{x\in X:\gamma (x)=x\}}f\,d\nu $
for every
$\tau _{\omega }(\rho (f)\sigma (\gamma ))=\int _{\{x\in X:\gamma (x)=x\}}f\,d\nu $
for every
 $f\in L^{\infty }(X,\nu ),\gamma \in [{\mathcal R}]$
;
$f\in L^{\infty }(X,\nu ),\gamma \in [{\mathcal R}]$
; -
•
 $\sigma (\gamma )\rho (f)\sigma (\gamma )^{-1}=\rho (f\circ \gamma ^{-1})$
for every
$\sigma (\gamma )\rho (f)\sigma (\gamma )^{-1}=\rho (f\circ \gamma ^{-1})$
for every
 $f\in L^{\infty }(X,\nu ),\gamma \in [{\mathcal R}]$
.
$f\in L^{\infty }(X,\nu ),\gamma \in [{\mathcal R}]$
.
Since
![]() $[{\mathcal R}],L^{\infty }(X,\nu )$
are uncountable, this definition can be a bit unwieldy. We give a few equivalent definitions of soficity below for the readers convenience. Essentially, all of this is either folklore or due to Elek and Lippner (see the proof [Reference Elek and Lippner26, Theorem 2]) or [Reference Păunescu42]; therefore, we do not claim originality for these results.
$[{\mathcal R}],L^{\infty }(X,\nu )$
are uncountable, this definition can be a bit unwieldy. We give a few equivalent definitions of soficity below for the readers convenience. Essentially, all of this is either folklore or due to Elek and Lippner (see the proof [Reference Elek and Lippner26, Theorem 2]) or [Reference Păunescu42]; therefore, we do not claim originality for these results.
Proposition 3.6. Let
![]() ${\mathcal R}$
be a discrete, probability measure-preserving relation over a standard probability space
${\mathcal R}$
be a discrete, probability measure-preserving relation over a standard probability space
![]() $(X,\nu )$
. View
$(X,\nu )$
. View
![]() $L^{\infty }(X,\nu )$
and
$L^{\infty }(X,\nu )$
and
![]() $[[{\mathcal R}]]$
as subsets of
$[[{\mathcal R}]]$
as subsets of
![]() $L({\mathcal R})$
.
$L({\mathcal R})$
.
-
(i) Let
 $\rho \colon L^{\infty }(X,\nu )\to L^{\infty }({\mathcal L},u_{\omega })$
,
$\rho \colon L^{\infty }(X,\nu )\to L^{\infty }({\mathcal L},u_{\omega })$
,
 $\sigma \colon [{\mathcal R}]\to {\mathcal S}_{\omega }$
be a sofic approximation. Then there is a trace-preserving
$\sigma \colon [{\mathcal R}]\to {\mathcal S}_{\omega }$
be a sofic approximation. Then there is a trace-preserving
 $*$
-homomorphism
$*$
-homomorphism
 $\pi \colon L({\mathcal R})\to \prod _{k\to \omega }(M_{k}({\mathbb C}),\operatorname {\mathrm {tr}})$
so that
$\pi \colon L({\mathcal R})\to \prod _{k\to \omega }(M_{k}({\mathbb C}),\operatorname {\mathrm {tr}})$
so that
 $\pi |_{L^{\infty }(X)}=\rho $
,
$\pi |_{L^{\infty }(X)}=\rho $
,
 $\pi |_{[{\mathcal R}]}=\sigma $
.
$\pi |_{[{\mathcal R}]}=\sigma $
. -
(ii) Conversely, suppose that
 $\pi \colon L({\mathcal R})\to \prod _{k\to \omega }(M_{k}({\mathbb C}),\operatorname {\mathrm {tr}})$
is a trace-preserving
$\pi \colon L({\mathcal R})\to \prod _{k\to \omega }(M_{k}({\mathbb C}),\operatorname {\mathrm {tr}})$
is a trace-preserving
 $*$
-homomorphism with
$*$
-homomorphism with
 $\pi (L^{\infty }(X))\subseteq L^{\infty }({\mathcal L},u_{\omega })$
and
$\pi (L^{\infty }(X))\subseteq L^{\infty }({\mathcal L},u_{\omega })$
and
 $\pi ([{\mathcal R}])\subseteq {\mathcal S}_{\omega }$
. Then the pair
$\pi ([{\mathcal R}])\subseteq {\mathcal S}_{\omega }$
. Then the pair
 $(\rho ,\sigma )$
given by
$(\rho ,\sigma )$
given by
 $\rho =\pi |_{L^{\infty }(X,\nu )}$
,
$\rho =\pi |_{L^{\infty }(X,\nu )}$
,
 $\sigma =\pi |_{[{\mathcal R}]}$
is a sofic approximation.
$\sigma =\pi |_{[{\mathcal R}]}$
is a sofic approximation. -
(iii) Let
 $D\subseteq L^{\infty }(X,\nu )$
be a subset which is closed under products, and
$D\subseteq L^{\infty }(X,\nu )$
be a subset which is closed under products, and
 $G\subseteq [{\mathcal R}]$
a countable subgroup. Suppose that D is G-invariant, that
$G\subseteq [{\mathcal R}]$
a countable subgroup. Suppose that D is G-invariant, that
 $\operatorname {\mathrm {span}}(D)$
is weak
$\operatorname {\mathrm {span}}(D)$
is weak
 $^{*}$
-dense in
$^{*}$
-dense in
 $L^{\infty }(X)$
, and that
$L^{\infty }(X)$
, and that
 $Gx=[x]_{{\mathcal R}}$
for almost every
$Gx=[x]_{{\mathcal R}}$
for almost every
 $x\in X$
. Suppose that
$x\in X$
. Suppose that
 $\rho _{0}\colon D\to L^{\infty }({\mathcal L},u_{\omega })$
and
$\rho _{0}\colon D\to L^{\infty }({\mathcal L},u_{\omega })$
and
 $\sigma _{0}\colon G\to {\mathcal S}_{\omega }$
are such that:
$\sigma _{0}\colon G\to {\mathcal S}_{\omega }$
are such that:-
•
 $\rho _{0}(f_{1}f_{2})=\rho _{0}(f_{1})\rho _{0}(f_{2})$
for every
$\rho _{0}(f_{1}f_{2})=\rho _{0}(f_{1})\rho _{0}(f_{2})$
for every
 $f_{1},f_{2}\in D$
;
$f_{1},f_{2}\in D$
; -
•
 $\sigma _{0}(\gamma )\rho _{0}(f)\sigma _{0}(\gamma )^{-1}=\rho _{0}(f\circ \gamma ^{-1})$
for every
$\sigma _{0}(\gamma )\rho _{0}(f)\sigma _{0}(\gamma )^{-1}=\rho _{0}(f\circ \gamma ^{-1})$
for every
 $f\in D,\gamma \in G$
;
$f\in D,\gamma \in G$
; -
•
 $\tau _{\omega }(\rho _{0}(f)\sigma _{0}(\gamma ))=\int _{\{x\in X:\gamma (x)=x\}}f\,d\nu $
for all
$\tau _{\omega }(\rho _{0}(f)\sigma _{0}(\gamma ))=\int _{\{x\in X:\gamma (x)=x\}}f\,d\nu $
for all
 $f\in D,\gamma \in G$
.
$f\in D,\gamma \in G$
.
Then there is a unique sofic approximation
 $(\rho ,\sigma )$
of
$(\rho ,\sigma )$
of
 ${\mathcal R}$
so that
${\mathcal R}$
so that
 $\rho |_{D}=\rho _{0}, \sigma |_{G}=\sigma _{0}$
.
$\rho |_{D}=\rho _{0}, \sigma |_{G}=\sigma _{0}$
. -
-
(iv) Let
 ${\mathcal A}$
be an algebra of measurable sets in X, and let G be a countable subgroup of
${\mathcal A}$
be an algebra of measurable sets in X, and let G be a countable subgroup of
 $[{\mathcal R}]$
with
$[{\mathcal R}]$
with
 $Gx=[x]_{{\mathcal R}}$
for almost every
$Gx=[x]_{{\mathcal R}}$
for almost every
 $x\in X$
. Assume that
$x\in X$
. Assume that
 ${\mathcal A}$
is G-invariant and that the complete sigma-algebra generated by
${\mathcal A}$
is G-invariant and that the complete sigma-algebra generated by
 ${\mathcal A}$
is the algebra of all
${\mathcal A}$
is the algebra of all
 $\nu $
-measurable sets. Suppose that
$\nu $
-measurable sets. Suppose that
 $\rho _{0}\colon {\mathcal A}\to \operatorname {\mathrm {Proj}}(L^{\infty }({\mathcal L},u_{\omega }))$
and
$\rho _{0}\colon {\mathcal A}\to \operatorname {\mathrm {Proj}}(L^{\infty }({\mathcal L},u_{\omega }))$
and
 $\sigma _{0}\colon G\to {\mathcal S}_{\omega }$
satisfies:
$\sigma _{0}\colon G\to {\mathcal S}_{\omega }$
satisfies:-
•
 $\rho _{0}(B_{1}\cap B_{2})=\rho _{0}(B_{1})\rho _{0}(B_{2})$
and
$\rho _{0}(B_{1}\cap B_{2})=\rho _{0}(B_{1})\rho _{0}(B_{2})$
and
 $u_{\omega }(\rho _{0}(B_{1}))=\nu (B_{1})$
for every
$u_{\omega }(\rho _{0}(B_{1}))=\nu (B_{1})$
for every
 $B_{1},B_{2}\in {\mathcal A}$
;
$B_{1},B_{2}\in {\mathcal A}$
; -
•
 $\sigma _{0}$
is a homomorphism and
$\sigma _{0}$
is a homomorphism and
 $\tau (\rho _{0}(B)\sigma _{0}(\gamma ))=\nu (\{x\in B:\gamma (x)= x\})$
for every
$\tau (\rho _{0}(B)\sigma _{0}(\gamma ))=\nu (\{x\in B:\gamma (x)= x\})$
for every
 $\gamma \in G$
,
$\gamma \in G$
,
 $B\in {\mathcal A}$
;
$B\in {\mathcal A}$
; -
•
 $\sigma _{0}(\gamma )\rho _{0}(E)\sigma _{0}(\gamma )^{-1}=\rho _{0}(\gamma (B))$
for every
$\sigma _{0}(\gamma )\rho _{0}(E)\sigma _{0}(\gamma )^{-1}=\rho _{0}(\gamma (B))$
for every
 $\gamma \in G,B\in {\mathcal A}$
.
$\gamma \in G,B\in {\mathcal A}$
.
Then there is a unique sofic approximation
 $\rho \colon L^{\infty }(X,\nu )\to L^{\infty }({\mathcal L},u_{\omega })$
,
$\rho \colon L^{\infty }(X,\nu )\to L^{\infty }({\mathcal L},u_{\omega })$
,
 $\sigma \colon [{\mathcal R}]\to S_{\omega }$
so that
$\sigma \colon [{\mathcal R}]\to S_{\omega }$
so that
 $\rho |_{{\mathcal A}}=\rho _{0}$
,
$\rho |_{{\mathcal A}}=\rho _{0}$
,
 $\sigma |_{G}=\sigma _{0}$
.
$\sigma |_{G}=\sigma _{0}$
. -
Proof. Throughout, set
![]() $({\mathcal M},\tau _{\omega })=\prod _{k\to \omega }(M_{k}({\mathbb C}),\operatorname {\mathrm {tr}}).$
$({\mathcal M},\tau _{\omega })=\prod _{k\to \omega }(M_{k}({\mathbb C}),\operatorname {\mathrm {tr}}).$
(i) Let
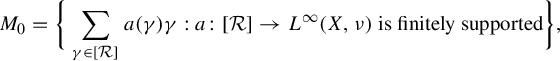 $$ \begin{align*} M_{0}=\bigg\{\sum_{\gamma\in [{\mathcal R}]}a(\gamma)\gamma:a\colon[{\mathcal R}]\to L^{\infty}(X,\nu) \text{ is finitely supported}\bigg\}, \end{align*} $$
$$ \begin{align*} M_{0}=\bigg\{\sum_{\gamma\in [{\mathcal R}]}a(\gamma)\gamma:a\colon[{\mathcal R}]\to L^{\infty}(X,\nu) \text{ is finitely supported}\bigg\}, \end{align*} $$
then
![]() $M_{0}$
is weak operator topology dense in
$M_{0}$
is weak operator topology dense in
![]() $L({\mathcal R})$
by definition. Moreover, for all
$L({\mathcal R})$
by definition. Moreover, for all
![]() $f_{1},\ldots ,f_{n}\in L^{\infty }(X,\nu ),\gamma _{1},\ldots ,\gamma _{n}\in [{\mathcal R}]$
, we have by the axioms of a sofic approximation:
$f_{1},\ldots ,f_{n}\in L^{\infty }(X,\nu ),\gamma _{1},\ldots ,\gamma _{n}\in [{\mathcal R}]$
, we have by the axioms of a sofic approximation:
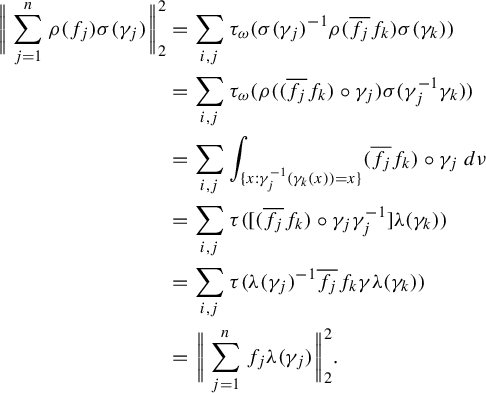 $$ \begin{align*} \bigg\|\sum_{j=1}^{n}\rho(f_{j})\sigma(\gamma_{j})\bigg\|_{2}^{2} &= \sum_{i,j}\tau_{\omega}(\sigma(\gamma_{j})^{-1}\rho(\overline{f_{j}}f_{k})\sigma(\gamma_{k}))\\ &=\sum_{i,j}\tau_{\omega}(\rho((\overline{f_{j}}f_{k})\circ \gamma_{j})\sigma(\gamma_{j}^{-1}\gamma_{k})) \\ &=\sum_{i,j}\int_{\{x:\gamma_{j}^{-1}(\gamma_{k}(x))=x\}}(\overline{f_{j}}f_{k})\circ \gamma_{j}\,d\nu\\&=\sum_{i,j}\tau([(\overline{f_{j}}f_{k})\circ \gamma_{j}\gamma_{j}^{-1}]\unicode{x3bb}(\gamma_{k}))\\ &=\sum_{i,j}\tau(\unicode{x3bb}(\gamma_{j})^{-1}\overline{f_{j}}f_{k}\gamma\unicode{x3bb}(\gamma_{k}))\\ &=\bigg\|\sum_{j=1}^{n}f_{j}\unicode{x3bb}(\gamma_{j})\bigg\|_{2}^{2}. \end{align*} $$
$$ \begin{align*} \bigg\|\sum_{j=1}^{n}\rho(f_{j})\sigma(\gamma_{j})\bigg\|_{2}^{2} &= \sum_{i,j}\tau_{\omega}(\sigma(\gamma_{j})^{-1}\rho(\overline{f_{j}}f_{k})\sigma(\gamma_{k}))\\ &=\sum_{i,j}\tau_{\omega}(\rho((\overline{f_{j}}f_{k})\circ \gamma_{j})\sigma(\gamma_{j}^{-1}\gamma_{k})) \\ &=\sum_{i,j}\int_{\{x:\gamma_{j}^{-1}(\gamma_{k}(x))=x\}}(\overline{f_{j}}f_{k})\circ \gamma_{j}\,d\nu\\&=\sum_{i,j}\tau([(\overline{f_{j}}f_{k})\circ \gamma_{j}\gamma_{j}^{-1}]\unicode{x3bb}(\gamma_{k}))\\ &=\sum_{i,j}\tau(\unicode{x3bb}(\gamma_{j})^{-1}\overline{f_{j}}f_{k}\gamma\unicode{x3bb}(\gamma_{k}))\\ &=\bigg\|\sum_{j=1}^{n}f_{j}\unicode{x3bb}(\gamma_{j})\bigg\|_{2}^{2}. \end{align*} $$
Since
![]() $\|\cdot \|_{2}$
is a norm, the above calculation implies that
$\|\cdot \|_{2}$
is a norm, the above calculation implies that
![]() $\sum _{j}\rho (f_{j})\sigma (\gamma _{j})=0$
if and only if
$\sum _{j}\rho (f_{j})\sigma (\gamma _{j})=0$
if and only if
![]() $\sum _{j}f_{j}\unicode{x3bb} (\gamma _{j)}=0$
. This implies that the map
$\sum _{j}f_{j}\unicode{x3bb} (\gamma _{j)}=0$
. This implies that the map
![]() $\pi _{0}\colon M_{0}\to \prod _{k\to \omega }(M_{k}({\mathbb C}),\operatorname {\mathrm {tr}})$
given by
$\pi _{0}\colon M_{0}\to \prod _{k\to \omega }(M_{k}({\mathbb C}),\operatorname {\mathrm {tr}})$
given by
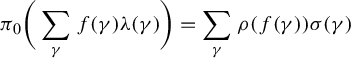 $$ \begin{align*}\pi_{0}\bigg(\sum_{\gamma}f(\gamma)\unicode{x3bb}(\gamma)\bigg) = \sum_{\gamma}\rho(f(\gamma))\sigma(\gamma)\end{align*} $$
$$ \begin{align*}\pi_{0}\bigg(\sum_{\gamma}f(\gamma)\unicode{x3bb}(\gamma)\bigg) = \sum_{\gamma}\rho(f(\gamma))\sigma(\gamma)\end{align*} $$
is a well-defined linear map. It is direct to check from the definition of a sofic approximation that it is a trace-preserving
![]() $*$
-homomorphism. Lemma 3.4 implies that
$*$
-homomorphism. Lemma 3.4 implies that
![]() $\pi _{0}$
has a unique extension to trace-preserving normal
$\pi _{0}$
has a unique extension to trace-preserving normal
![]() $*$
-homomorphism
$*$
-homomorphism
![]() $\pi $
.
$\pi $
.
(ii) This is an exercise in understanding the definitions.
(iii) Let
![]() $A=\operatorname {\mathrm {span}}(D)$
so that A is a weak operator topology dense
$A=\operatorname {\mathrm {span}}(D)$
so that A is a weak operator topology dense
![]() $*$
-subalgebra of
$*$
-subalgebra of
![]() $L^{\infty }(X,\nu )$
. Let
$L^{\infty }(X,\nu )$
. Let
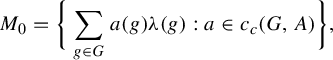 $$ \begin{align*} M_{0}=\bigg\{\sum_{g\in G}a(g)\unicode{x3bb}(g):a\in c_{c}(G,A)\bigg\}, \end{align*} $$
$$ \begin{align*} M_{0}=\bigg\{\sum_{g\in G}a(g)\unicode{x3bb}(g):a\in c_{c}(G,A)\bigg\}, \end{align*} $$
then
![]() $M_{0}$
is
$M_{0}$
is
![]() $*$
-subalgebra of
$*$
-subalgebra of
![]() $L({\mathcal R})$
. As in item (i), we know there is a unique function
$L({\mathcal R})$
. As in item (i), we know there is a unique function
![]() $\pi _{0}\colon M_{0}\to {\mathcal M}$
satisfying
$\pi _{0}\colon M_{0}\to {\mathcal M}$
satisfying
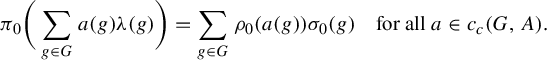 $$ \begin{align*} \pi_{0}\bigg(\sum_{g\in G}a(g)\unicode{x3bb}(g)\bigg)=\sum_{g\in G}\rho_{0}(a(g))\sigma_{0}(g)\quad \text{for all } a\in c_{c}(G,A). \end{align*} $$
$$ \begin{align*} \pi_{0}\bigg(\sum_{g\in G}a(g)\unicode{x3bb}(g)\bigg)=\sum_{g\in G}\rho_{0}(a(g))\sigma_{0}(g)\quad \text{for all } a\in c_{c}(G,A). \end{align*} $$
Our hypothesis implies that
![]() $\pi _{0}$
is a trace-preserving
$\pi _{0}$
is a trace-preserving
![]() $*$
-homomorphism. Thus, by Lemma 3.4 and items (i), (ii), it suffices to show that
$*$
-homomorphism. Thus, by Lemma 3.4 and items (i), (ii), it suffices to show that
![]() $M_{0}$
is weak
$M_{0}$
is weak
![]() $^{*}$
-dense in
$^{*}$
-dense in
![]() $L({\mathcal R})$
. Let M be the weak operator topology closure of
$L({\mathcal R})$
. Let M be the weak operator topology closure of
![]() $M_{0}$
. Then
$M_{0}$
. Then
Since
![]() $Gx=[x]_{{\mathcal R}}$
for almost every
$Gx=[x]_{{\mathcal R}}$
for almost every
![]() $x\in X$
, given
$x\in X$
, given
![]() $\gamma \in [[{\mathcal R}]]$
, we may find (not necessarily unique) disjoint sets
$\gamma \in [[{\mathcal R}]]$
, we may find (not necessarily unique) disjoint sets
![]() $(B_{g})_{g\in G}$
so that
$(B_{g})_{g\in G}$
so that
![]() $B_{g}\subseteq \{x\in \operatorname {\mathrm {dom}}(\gamma ):\gamma (x)=gx\}$
and with
$B_{g}\subseteq \{x\in \operatorname {\mathrm {dom}}(\gamma ):\gamma (x)=gx\}$
and with
 $$ \begin{align*}\nu\bigg(\operatorname{\mathrm{dom}}(\gamma)\Delta \bigsqcup_{g\in G}B_{g}\bigg)=0.\end{align*} $$
$$ \begin{align*}\nu\bigg(\operatorname{\mathrm{dom}}(\gamma)\Delta \bigsqcup_{g\in G}B_{g}\bigg)=0.\end{align*} $$
We leave it as an exercise to check that
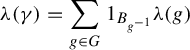 $$ \begin{align*}\unicode{x3bb}(\gamma)=\sum_{g\in G}1_{B_{g^{-1}}}\unicode{x3bb}(g)\end{align*} $$
$$ \begin{align*}\unicode{x3bb}(\gamma)=\sum_{g\in G}1_{B_{g^{-1}}}\unicode{x3bb}(g)\end{align*} $$
with the sum converging in the strong operator topology. Since we have already shown that
![]() $L^{\infty }(X,\nu )\subseteq M$
, it follows that
$L^{\infty }(X,\nu )\subseteq M$
, it follows that
![]() $[[{\mathcal R}]]\subseteq M$
. Hence,
$[[{\mathcal R}]]\subseteq M$
. Hence,
(iv) Let
![]() $D=\{1_{E}:E\in {\mathcal A}\}$
, then
$D=\{1_{E}:E\in {\mathcal A}\}$
, then
![]() $\operatorname {\mathrm {span}}(D)$
is weak
$\operatorname {\mathrm {span}}(D)$
is weak
![]() $^{*}$
-dense in
$^{*}$
-dense in
![]() $L^{\infty }(X)$
since
$L^{\infty }(X)$
since
![]() ${\mathcal A}$
is generating. Now apply item (iii).
${\mathcal A}$
is generating. Now apply item (iii).
Because Proposition 3.6 gives several equivalent definitions of soficity, we will often use the term sofic approximation to any one of the kinds of maps in each item of this proposition. For example, a map
![]() $\pi \colon L({\mathcal R})\to \prod _{k\to \omega }(M_{k}({\mathbb C}),\tau )$
satisfying the hypotheses of item (i) will be called a sofic approximation.
$\pi \colon L({\mathcal R})\to \prod _{k\to \omega }(M_{k}({\mathbb C}),\tau )$
satisfying the hypotheses of item (i) will be called a sofic approximation.
Additionally, item (iv) suggest a sequential version of a sofic approximation of an equivalence relation. Namely, we can consider sequences
![]() $\rho _{n}\colon {\mathcal A}\to \mathcal {P}(\{1,\ldots ,d_{n}\})$
and
$\rho _{n}\colon {\mathcal A}\to \mathcal {P}(\{1,\ldots ,d_{n}\})$
and
![]() $\sigma _{n}\colon G\to {\operatorname {Sym}}(d_{n})$
so that:
$\sigma _{n}\colon G\to {\operatorname {Sym}}(d_{n})$
so that:
-
•
 $\sigma _{n}$
is an asymptotic homomorphism;
$\sigma _{n}$
is an asymptotic homomorphism; -
•
 $u_{d_{n}}(\rho _{n}(B_{1}\cap B_{2})\Delta (\rho _{n}(B_{1})\cap \rho _{n}(B_{2})))\to _{n\to \infty }0$
for all
$u_{d_{n}}(\rho _{n}(B_{1}\cap B_{2})\Delta (\rho _{n}(B_{1})\cap \rho _{n}(B_{2})))\to _{n\to \infty }0$
for all
 $B_{1},B_{2}\in {\mathcal A}$
;
$B_{1},B_{2}\in {\mathcal A}$
; -
•
 $u_{d_{n}}(\{j\in \rho _{n}(B):\sigma _{n}(g)(j)=j\})\to _{n\to \infty } \nu (\{x\in E:gx=x\})$
for all
$u_{d_{n}}(\{j\in \rho _{n}(B):\sigma _{n}(g)(j)=j\})\to _{n\to \infty } \nu (\{x\in E:gx=x\})$
for all
 $B\in {\mathcal A}$
,
$B\in {\mathcal A}$
,
 $g\in G$
;
$g\in G$
; -
•
 $u_{d_{n}}(\rho _{n}(gB)\Delta (\sigma _{n}(g)\rho _{n}(B)\sigma _{n}(g)^{-1}))\to _{n\to \infty }0$
for all
$u_{d_{n}}(\rho _{n}(gB)\Delta (\sigma _{n}(g)\rho _{n}(B)\sigma _{n}(g)^{-1}))\to _{n\to \infty }0$
for all
 $g\in G$
,
$g\in G$
,
 $B\in {\mathcal A}$
.
$B\in {\mathcal A}$
.
This is sometimes taken as the definition of soficity. Our definition has the advantage of being canonical and not requiring a choice of
![]() $G,{\mathcal A}$
. However, this alternate definition is typically how one would check soficity of relations in specific examples, whereas ours is more abstract. Similarly, item (iii) suggests a different definition of soficity. One could require a sequence of maps
$G,{\mathcal A}$
. However, this alternate definition is typically how one would check soficity of relations in specific examples, whereas ours is more abstract. Similarly, item (iii) suggests a different definition of soficity. One could require a sequence of maps
![]() $\rho _{n}\colon D\to \ell ^{\infty }(d_{n})$
,
$\rho _{n}\colon D\to \ell ^{\infty }(d_{n})$
,
![]() $\sigma _{n}\colon G\to {\operatorname {Sym}}(d_{n})$
so that:
$\sigma _{n}\colon G\to {\operatorname {Sym}}(d_{n})$
so that:
-
•
 $\|\rho _{n}(f_{1}f_{2})-\rho _{n}(f_{1})\rho _{n}(f_{2})\|_{2}\to _{n\to \infty }0$
for all
$\|\rho _{n}(f_{1}f_{2})-\rho _{n}(f_{1})\rho _{n}(f_{2})\|_{2}\to _{n\to \infty }0$
for all
 $f_{1},f_{2}\in D$
;
$f_{1},f_{2}\in D$
; -
•
 $\sigma _{n}$
is an asymptotic homomorphism;
$\sigma _{n}$
is an asymptotic homomorphism; -
•
 ${1}/{d_{n}} \sum _{j:\sigma _{n}(g)(j)=j}\rho _{n}(f)(j)\to _{n\to \infty }\int _{\{x\in X:gx=x\}}f\,d\nu $
for all
${1}/{d_{n}} \sum _{j:\sigma _{n}(g)(j)=j}\rho _{n}(f)(j)\to _{n\to \infty }\int _{\{x\in X:gx=x\}}f\,d\nu $
for all
 $f\in D,g\in G$
;
$f\in D,g\in G$
; -
•
 $\|\rho _{n}(f)\circ \sigma _{n}(g)^{-1}-\rho _{n}(\alpha _{g}(f))\|_{2}\to _{n\to \infty } 0$
for every
$\|\rho _{n}(f)\circ \sigma _{n}(g)^{-1}-\rho _{n}(\alpha _{g}(f))\|_{2}\to _{n\to \infty } 0$
for every
 $f\in D,g\in G$
.
$f\in D,g\in G$
.
Here, the
![]() $\|\cdot \|_{2}$
-norms are with respect to the uniform measure and
$\|\cdot \|_{2}$
-norms are with respect to the uniform measure and
![]() $\alpha _{g}(f)(x)=f(g^{-1}x)$
. We will refer to either of these as a sofic approximation sequence.
$\alpha _{g}(f)(x)=f(g^{-1}x)$
. We will refer to either of these as a sofic approximation sequence.
We now rephrase Theorem 1.1. We use m for the Lebesgue measure on
![]() $[0,1]$
.
$[0,1]$
.
Theorem 3.7. (Theorem 1.1)
Let G be countable, discrete group and let
![]() $\sigma _{n}\colon G\to {\operatorname {Sym}}(d_{n})$
be a sequence of asymptotic homomorphisms. Fix
$\sigma _{n}\colon G\to {\operatorname {Sym}}(d_{n})$
be a sequence of asymptotic homomorphisms. Fix
![]() $\omega \in \beta {\mathbb N}\setminus {\mathbb N}$
and set
$\omega \in \beta {\mathbb N}\setminus {\mathbb N}$
and set
![]() ${\Theta =\operatorname {\mathrm {IRS}}(\sigma _{\omega })}$
. Let
${\Theta =\operatorname {\mathrm {IRS}}(\sigma _{\omega })}$
. Let
![]() ${\mathcal R}$
be the orbit equivalence relation of the
${\mathcal R}$
be the orbit equivalence relation of the
![]() $\Theta $
-Bernoulli action with base
$\Theta $
-Bernoulli action with base
![]() $([0,1],m)$
. Let
$([0,1],m)$
. Let
![]() $\Xi \colon G\to [{\mathcal R}]$
be given by
$\Xi \colon G\to [{\mathcal R}]$
be given by
![]() $\Xi (g)(x)=gx$
. Then there is a sofic approximation
$\Xi (g)(x)=gx$
. Then there is a sofic approximation
![]() $(\rho ,\widehat {\sigma })$
of
$(\rho ,\widehat {\sigma })$
of
![]() ${\mathcal R}$
so that
${\mathcal R}$
so that
![]() $\widehat {\sigma }\circ \Xi =\sigma _{\omega }$
.
$\widehat {\sigma }\circ \Xi =\sigma _{\omega }$
.
4. Proof of Theorem 3.7
We now proceed to prove Theorem 3.7. We remark that one can use [Reference Tucker-Drob48, Theorem 1.5] to prove Theorem 3.7. The essential idea behind such a proof is that given a sequence of approximate homomorphisms with IRS
![]() $\Theta $
, the induced action on the Loeb measure space
$\Theta $
, the induced action on the Loeb measure space
![]() $G\,{\curvearrowright }\, ({\mathcal L},u_{\omega })$
also has IRS
$G\,{\curvearrowright }\, ({\mathcal L},u_{\omega })$
also has IRS
![]() $\Theta $
. One can use the Löwenheim–Skolem theorem in continuous model theory to build an action on a standard probability space which is a factor of this action and which still has IRS
$\Theta $
. One can use the Löwenheim–Skolem theorem in continuous model theory to build an action on a standard probability space which is a factor of this action and which still has IRS
![]() $\Theta $
. Being an action on a standard probability space, such a factor is weakly contained in a
$\Theta $
. Being an action on a standard probability space, such a factor is weakly contained in a
![]() $\Theta $
-Bernoulli shift by [Reference Tucker-Drob48, Theorem 1.5]. This implies that the
$\Theta $
-Bernoulli shift by [Reference Tucker-Drob48, Theorem 1.5]. This implies that the
![]() $\Theta $
-Bernoulli shift action
$\Theta $
-Bernoulli shift action
![]() $G\,{\curvearrowright }\, (X_{\Theta },\mu _{\Theta })$
with base
$G\,{\curvearrowright }\, (X_{\Theta },\mu _{\Theta })$
with base
![]() $[0,1]$
(equipped with Lebesgue measure) is weakly contained in
$[0,1]$
(equipped with Lebesgue measure) is weakly contained in
![]() $G\,{\curvearrowright }\, ({\mathcal L},u_{\omega })$
. Since
$G\,{\curvearrowright }\, ({\mathcal L},u_{\omega })$
. Since
![]() $G\,{\curvearrowright }\, ({\mathcal L},u_{\omega })$
is an ultraproduct action, if
$G\,{\curvearrowright }\, ({\mathcal L},u_{\omega })$
is an ultraproduct action, if
![]() $G\,{\curvearrowright }\, (X_{\Theta },\mu _{\Theta })$
is weakly contained in
$G\,{\curvearrowright }\, (X_{\Theta },\mu _{\Theta })$
is weakly contained in
![]() $G\,{\curvearrowright }\, ({\mathcal L},u_{\omega })$
, it must actually be a factor of this action. Putting this altogether shows that any sequences of approximate homomorphisms extend to a sofic approximation of the
$G\,{\curvearrowright }\, ({\mathcal L},u_{\omega })$
, it must actually be a factor of this action. Putting this altogether shows that any sequences of approximate homomorphisms extend to a sofic approximation of the
![]() $\Theta $
-Bernoulli shift.
$\Theta $
-Bernoulli shift.
For the sake of concreteness, we have instead elected to give a direct probabilistic argument for the proof of Theorem 3.7. The following is the main technical probabilistic lemma we need and is inspired by the proof of [Reference Bowen10, Theorem 8.1]. Bowen’s purpose in [Reference Bowen10] for such a result was to prove that the sofic entropy of Bernoulli shifts is the Shannon entropy of the base space. In this regard, our proof should be compared with [Reference Seward46, Theorem 9.1] which also says, in some sense, that the
![]() $\Theta $
-Bernoulli shift with base
$\Theta $
-Bernoulli shift with base
![]() $(X,\nu )$
is the ‘largest entropy’ action whose IRS is
$(X,\nu )$
is the ‘largest entropy’ action whose IRS is
![]() $\Theta $
and which is generated by the translates of an X-valued random variable with distribution
$\Theta $
and which is generated by the translates of an X-valued random variable with distribution
![]() $\nu $
.
$\nu $
.
For ease of notation, if X is a compact, metrizable space,
![]() $\nu \in \operatorname {\mathrm {Prob}}(X)$
, and
$\nu \in \operatorname {\mathrm {Prob}}(X)$
, and
![]() ${f\colon X\to {\mathbb C}}$
is bounded and Borel, we often use
${f\colon X\to {\mathbb C}}$
is bounded and Borel, we often use
![]() $\nu (f)$
for
$\nu (f)$
for
![]() $\int f\,d\nu $
. Suppose I is a set and
$\int f\,d\nu $
. Suppose I is a set and
![]() $(X_{i})_{i\in I}$
are compact Hausdorff spaces. If
$(X_{i})_{i\in I}$
are compact Hausdorff spaces. If
![]() $E\subseteq I$
is finite and
$E\subseteq I$
is finite and
![]() $(f_{i})_{i\in E}\in \prod _{i\in E}C(X_{i}),$
we define
$(f_{i})_{i\in E}\in \prod _{i\in E}C(X_{i}),$
we define
![]() $\bigotimes _{i\in E}f_{i}\in C(\prod _{i\in I}X_{i})$
by
$\bigotimes _{i\in E}f_{i}\in C(\prod _{i\in I}X_{i})$
by
 $$ \begin{align*} \bigg(\bigotimes_{i\in E}f_{i}\bigg)(x)=\prod_{i\in E}f_{i}(x_{i})\quad \text{if } x=(x_{i})_{i\in I}\in \prod_{i\in I}X_{i}. \end{align*} $$
$$ \begin{align*} \bigg(\bigotimes_{i\in E}f_{i}\bigg)(x)=\prod_{i\in E}f_{i}(x_{i})\quad \text{if } x=(x_{i})_{i\in I}\in \prod_{i\in I}X_{i}. \end{align*} $$
For a finite
![]() $F\subseteq G$
, we define
$F\subseteq G$
, we define
![]() ${\mathcal E}_{F}\in C(\{0,1\}^{G}$
) by
${\mathcal E}_{F}\in C(\{0,1\}^{G}$
) by
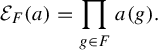 $$ \begin{align*} {\mathcal E}_{F}(a)=\prod_{g\in F}a(g). \end{align*} $$
$$ \begin{align*} {\mathcal E}_{F}(a)=\prod_{g\in F}a(g). \end{align*} $$
Viewing
![]() $\operatorname {\mathrm {Sub}}(G)\subseteq \{0,1\}^{G}$
, we have
$\operatorname {\mathrm {Sub}}(G)\subseteq \{0,1\}^{G}$
, we have
![]() ${\mathcal E}_{F}|_{\operatorname {\mathrm {Sub}}(G)}$
is the indicator function of
${\mathcal E}_{F}|_{\operatorname {\mathrm {Sub}}(G)}$
is the indicator function of
![]() $\{H:F\subseteq H\}$
. If Y is a compact, metrizable space, we often slightly abuse notation and regard
$\{H:F\subseteq H\}$
. If Y is a compact, metrizable space, we often slightly abuse notation and regard
![]() ${{\mathcal E}_{F}\in C(\{0,1\}^{G}\times Y)}$
via the embedding
${{\mathcal E}_{F}\in C(\{0,1\}^{G}\times Y)}$
via the embedding
![]() $C(\{0,1\}^{G})\to C(\{0,1\}^{G}\times Y)$
given by
$C(\{0,1\}^{G})\to C(\{0,1\}^{G}\times Y)$
given by
Lemma 4.1. Let
![]() $\sigma _{n}\colon G\to {\operatorname {Sym}}(d_{n})$
be a sequence of asymptotic homomorphisms and
$\sigma _{n}\colon G\to {\operatorname {Sym}}(d_{n})$
be a sequence of asymptotic homomorphisms and
![]() $\omega \in \beta {\mathbb N}\setminus {\mathbb N}$
. Set
$\omega \in \beta {\mathbb N}\setminus {\mathbb N}$
. Set
![]() $\Theta =\operatorname {\mathrm {IRS}}(\sigma _{\omega })$
. Let
$\Theta =\operatorname {\mathrm {IRS}}(\sigma _{\omega })$
. Let
![]() $\mu _{\Theta }$
be the
$\mu _{\Theta }$
be the
![]() $\Theta $
-Bernoulli measure on
$\Theta $
-Bernoulli measure on
![]() $\operatorname {\mathrm {Sub}}(G)\times [0,1]^{G}$
as in Definition 3.1. View
$\operatorname {\mathrm {Sub}}(G)\times [0,1]^{G}$
as in Definition 3.1. View
![]() $\operatorname {\mathrm {Sub}}(G)\times [0,1]^{G}\subseteq (\{0,1\}\times [0,1])^{G}$
by identifying each subgroup with its indicator function. For
$\operatorname {\mathrm {Sub}}(G)\times [0,1]^{G}\subseteq (\{0,1\}\times [0,1])^{G}$
by identifying each subgroup with its indicator function. For
![]() $x\in [0,1]^{d_{n}}$
, define
$x\in [0,1]^{d_{n}}$
, define
![]() $\phi _{x}\colon [d_{n}]\to (\{0,1\}\times [0,1])^{G}$
by
$\phi _{x}\colon [d_{n}]\to (\{0,1\}\times [0,1])^{G}$
by
Then, we have the following items.
-
(i) in the weak
 $^{*}$
-topology,
$^{*}$
-topology,  $$ \begin{align*} \lim_{n\to\omega}\int_{[0,1]^{d_{n}}}(\phi_{x})_{*}(u_{d_{n}})\,dx = \mu_{\Theta}. \end{align*} $$
$$ \begin{align*} \lim_{n\to\omega}\int_{[0,1]^{d_{n}}}(\phi_{x})_{*}(u_{d_{n}})\,dx = \mu_{\Theta}. \end{align*} $$
-
(ii) Given
 $f\in C(\{0,1\}^{G}\times [0,1]^{G})$
, set
$f\in C(\{0,1\}^{G}\times [0,1]^{G})$
, set
 $J_{n,f}=\int _{[0,1]^{d_{n}}}(\phi _{x})_{*}(u_{d_{n}})(f)\,dx$
. Then
$J_{n,f}=\int _{[0,1]^{d_{n}}}(\phi _{x})_{*}(u_{d_{n}})(f)\,dx$
. Then  $$ \begin{align*} \lim_{n\to\infty}\int_{[0,1]^{d_{n}}}|(\phi_{x})_{*}(u_{d_{n}})(f)-J_{n,f}|^{2}\,dx=0. \end{align*} $$
$$ \begin{align*} \lim_{n\to\infty}\int_{[0,1]^{d_{n}}}|(\phi_{x})_{*}(u_{d_{n}})(f)-J_{n,f}|^{2}\,dx=0. \end{align*} $$
-
(iii) For
 $g\in G$
, define
$g\in G$
, define
 $\alpha _{g}\in B(C((\{0,1\}\times [0,1])^{G}))$
by
$\alpha _{g}\in B(C((\{0,1\}\times [0,1])^{G}))$
by
 $(\alpha _{g}(f))(H,x)= f(g^{-1}Hg, g^{-1}x)$
. Then for any
$(\alpha _{g}(f))(H,x)= f(g^{-1}Hg, g^{-1}x)$
. Then for any
 $f\in C(\{0,1\}\times [0,1])^{G})$
,
$f\in C(\{0,1\}\times [0,1])^{G})$
,
 $g\in G$
,
$g\in G$
,  $$ \begin{align*}\lim_{n\to\infty}\sup_{x\in [0,1]^{d_{n}}}\|f\circ \phi_{x}\circ \sigma_{n}(g)^{-1}-\alpha_{g}(f)\circ \phi_{x}\|_{\ell^{2}(u_{d_{n}})}=0.\end{align*} $$
$$ \begin{align*}\lim_{n\to\infty}\sup_{x\in [0,1]^{d_{n}}}\|f\circ \phi_{x}\circ \sigma_{n}(g)^{-1}-\alpha_{g}(f)\circ \phi_{x}\|_{\ell^{2}(u_{d_{n}})}=0.\end{align*} $$
Proof. Throughout, we use
![]() $G/H$
for the space of right cosets of H in G. For
$G/H$
for the space of right cosets of H in G. For
![]() $F\subseteq G$
finite, we set
$F\subseteq G$
finite, we set
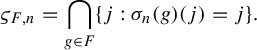 $$ \begin{align*}\varsigma_{F,n}=\bigcap_{g\in F}\{j:\sigma_{n}(g)(j)=j\}.\end{align*} $$
$$ \begin{align*}\varsigma_{F,n}=\bigcap_{g\in F}\{j:\sigma_{n}(g)(j)=j\}.\end{align*} $$
(i) By the Riesz representation theorem, we can define
![]() $\eta \in \operatorname {\mathrm {Prob}}((\{0,1\}\times [0,1])^{G})$
by
$\eta \in \operatorname {\mathrm {Prob}}((\{0,1\}\times [0,1])^{G})$
by
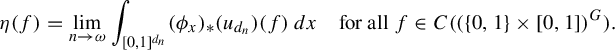 $$ \begin{align*} \eta(f)=\lim_{n\to\omega}\int_{[0,1]^{d_{n}}}(\phi_{x})_{*}(u_{d_{n}})(f)\,dx\quad \text{for all } f\in C((\{0,1\}\times [0,1])^{G}). \end{align*} $$
$$ \begin{align*} \eta(f)=\lim_{n\to\omega}\int_{[0,1]^{d_{n}}}(\phi_{x})_{*}(u_{d_{n}})(f)\,dx\quad \text{for all } f\in C((\{0,1\}\times [0,1])^{G}). \end{align*} $$
Let
 $$ \begin{align*} \digamma=\bigg\{\bigg(\bigotimes_{g\in E}f_{g}\bigg){\mathcal E}_{F}:E, F\subseteq G \text{ are finite}, (f_{g})_{g\in E}\in C([0,1])^{E},f_{g}\geq 0 \text{ for all } g\in E\bigg\}. \end{align*} $$
$$ \begin{align*} \digamma=\bigg\{\bigg(\bigotimes_{g\in E}f_{g}\bigg){\mathcal E}_{F}:E, F\subseteq G \text{ are finite}, (f_{g})_{g\in E}\in C([0,1])^{E},f_{g}\geq 0 \text{ for all } g\in E\bigg\}. \end{align*} $$
By Stone and Weierstrass,
![]() $\operatorname {\mathrm {span}}(\digamma )$
is norm dense in
$\operatorname {\mathrm {span}}(\digamma )$
is norm dense in
![]() $C((\{0,1\}\times [0,1])^{G})$
, and by the Riesz representation theorem to show that
$C((\{0,1\}\times [0,1])^{G})$
, and by the Riesz representation theorem to show that
![]() $\eta =\mu _{\Theta }$
, it suffices to show that they have the same integral against any element of
$\eta =\mu _{\Theta }$
, it suffices to show that they have the same integral against any element of
![]() $\digamma $
. Fix
$\digamma $
. Fix
![]() $f=(\bigotimes _{g\in E}f_{g}){\mathcal E}_{F}\in \digamma $
. Let
$f=(\bigotimes _{g\in E}f_{g}){\mathcal E}_{F}\in \digamma $
. Let
![]() $\Omega _{n}$
be the set of
$\Omega _{n}$
be the set of
![]() $j\in [d_{n}]$
so that for all
$j\in [d_{n}]$
so that for all
![]() $1\leq k\leq (2023)!$
and for all
$1\leq k\leq (2023)!$
and for all
![]() $g_{1},\ldots ,g_{k}\in E$
and all
$g_{1},\ldots ,g_{k}\in E$
and all
![]() $s_{1},\ldots ,s_{k}\in \{-1,1\}$
, we have that
$s_{1},\ldots ,s_{k}\in \{-1,1\}$
, we have that
Since
![]() $\sigma _{n}$
is an approximate homomorphism,
$\sigma _{n}$
is an approximate homomorphism,
![]() $u_{d_{n}}(\Omega _{n})\to 1$
. Hence,
$u_{d_{n}}(\Omega _{n})\to 1$
. Hence,
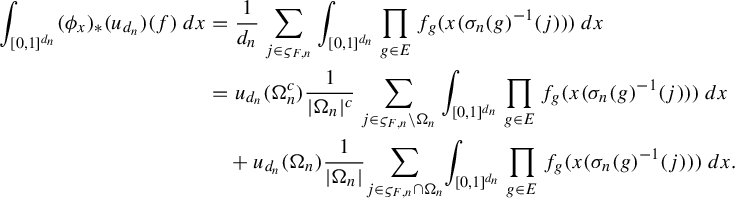 $$ \begin{align*} \int_{[0,1]^{d_{n}}}(\phi_{x})_{*}(u_{d_{n}})(f)\,dx&=\frac{1}{d_{n}}\sum_{j\in \varsigma_{F,n}}\int_{[0,1]^{d_{n}}}\prod_{g\in E}f_{g}(x(\sigma_{n}(g)^{-1}(j)))\,dx\\ &=u_{d_{n}}(\Omega_{n}^{c})\frac{1}{|\Omega_{n}|^{c}}\sum_{j\in \varsigma_{F,n}\setminus \Omega_{n}}\int_{[0,1]^{d_{n}}}\prod_{g\in E}f_{g}(x(\sigma_{n}(g)^{-1}(j)))\,dx\\ &\quad +u_{d_{n}}(\Omega_{n})\frac{1}{|\Omega_{n}|}\!\sum_{j\in \varsigma_{F,n}\cap \Omega_{n}}\!\int_{[0,1]^{d_{n}}}\prod_{g\in E}f_{g}(x(\sigma_{n}(g)^{-1}(j)))\,dx. \end{align*} $$
$$ \begin{align*} \int_{[0,1]^{d_{n}}}(\phi_{x})_{*}(u_{d_{n}})(f)\,dx&=\frac{1}{d_{n}}\sum_{j\in \varsigma_{F,n}}\int_{[0,1]^{d_{n}}}\prod_{g\in E}f_{g}(x(\sigma_{n}(g)^{-1}(j)))\,dx\\ &=u_{d_{n}}(\Omega_{n}^{c})\frac{1}{|\Omega_{n}|^{c}}\sum_{j\in \varsigma_{F,n}\setminus \Omega_{n}}\int_{[0,1]^{d_{n}}}\prod_{g\in E}f_{g}(x(\sigma_{n}(g)^{-1}(j)))\,dx\\ &\quad +u_{d_{n}}(\Omega_{n})\frac{1}{|\Omega_{n}|}\!\sum_{j\in \varsigma_{F,n}\cap \Omega_{n}}\!\int_{[0,1]^{d_{n}}}\prod_{g\in E}f_{g}(x(\sigma_{n}(g)^{-1}(j)))\,dx. \end{align*} $$
Since
![]() $u_{d_{n}}(\Omega _{n})\to 1$
and the
$u_{d_{n}}(\Omega _{n})\to 1$
and the
![]() $f_{g}$
are bounded, the first term tends to zero. It thus remains to analyze the second term. For
$f_{g}$
are bounded, the first term tends to zero. It thus remains to analyze the second term. For
![]() $j\in \Omega _{n}$
,
$j\in \Omega _{n}$
,
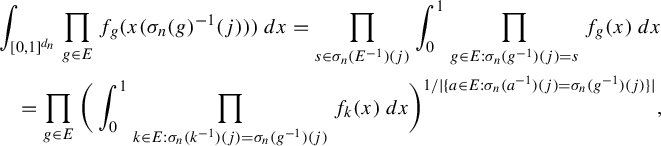 $$ \begin{align*} &\int_{[0,1]^{d_{n}}}\prod_{g\in E}f_{g}(x(\sigma_{n}(g)^{-1}(j)))\,dx=\prod_{s\in \sigma_{n}(E^{-1})(j)}\int_{0}^{1}\prod_{g\in E:\sigma_{n}(g^{-1})(j)=s}f_{g}(x)\,dx \\ &\quad =\prod_{g\in E}\bigg(\int_{0}^{1}\prod_{k\in E:\sigma_{n}(k^{-1})(j)=\sigma_{n}(g^{-1})(j)}f_{k}(x)\,dx\bigg)^{{1}/{|\{a\in E:\sigma_{n}(a^{-1})(j)=\sigma_{n}(g^{-1})(j)\}|}}, \end{align*} $$
$$ \begin{align*} &\int_{[0,1]^{d_{n}}}\prod_{g\in E}f_{g}(x(\sigma_{n}(g)^{-1}(j)))\,dx=\prod_{s\in \sigma_{n}(E^{-1})(j)}\int_{0}^{1}\prod_{g\in E:\sigma_{n}(g^{-1})(j)=s}f_{g}(x)\,dx \\ &\quad =\prod_{g\in E}\bigg(\int_{0}^{1}\prod_{k\in E:\sigma_{n}(k^{-1})(j)=\sigma_{n}(g^{-1})(j)}f_{k}(x)\,dx\bigg)^{{1}/{|\{a\in E:\sigma_{n}(a^{-1})(j)=\sigma_{n}(g^{-1})(j)\}|}}, \end{align*} $$
where in the last step, we use that
![]() $f_{g}\geq 0$
to make sense of the fractional power (which is there to account for over-counting). Because
$f_{g}\geq 0$
to make sense of the fractional power (which is there to account for over-counting). Because
![]() $j\in \Omega _{n}$
,
$j\in \Omega _{n}$
,
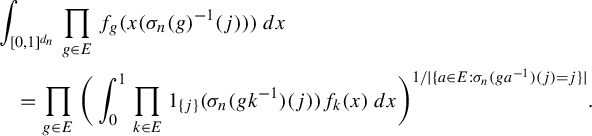 $$ \begin{align*} &\int_{[0,1]^{d_{n}}}\prod_{g\in E}f_{g}(x(\sigma_{n}(g)^{-1}(j)))\,dx\\ &\quad =\prod_{g\in E}\bigg(\int_{0}^{1}\prod_{k\in E}1_{\{j\}}(\sigma_{n}(gk^{-1})(j))f_{k}(x)\,dx\bigg)^{{1}/{|\{a\in E:\sigma_{n}(ga^{-1})(j)=j\}|}}. \end{align*} $$
$$ \begin{align*} &\int_{[0,1]^{d_{n}}}\prod_{g\in E}f_{g}(x(\sigma_{n}(g)^{-1}(j)))\,dx\\ &\quad =\prod_{g\in E}\bigg(\int_{0}^{1}\prod_{k\in E}1_{\{j\}}(\sigma_{n}(gk^{-1})(j))f_{k}(x)\,dx\bigg)^{{1}/{|\{a\in E:\sigma_{n}(ga^{-1})(j)=j\}|}}. \end{align*} $$
Since
![]() $u_{d_{n}}(\Omega _{n})\to 1$
, we have altogether shown that
$u_{d_{n}}(\Omega _{n})\to 1$
, we have altogether shown that
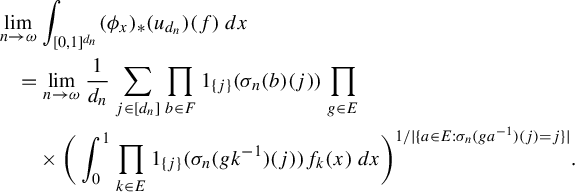 $$ \begin{align*} &\lim_{n\to\omega}\int_{[0,1]^{d_{n}}}(\phi_{x})_{*}(u_{d_{n}})(f)\,dx\\ &\quad =\lim_{n\to\omega}\frac{1}{d_{n}}\sum_{j\in [d_{n}]}\prod_{b\in F}1_{\{j\}}(\sigma_{n}(b)(j))\prod_{g\in E}\\ &\qquad\times \bigg(\int_{0}^{1}\prod_{k\in E}1_{\{j\}}(\sigma_{n}(gk^{-1})(j))f_{k}(x)\,dx\bigg)^{{1}/{|\{a\in E:\sigma_{n}(ga^{-1})(j)=j\}|}}. \end{align*} $$
$$ \begin{align*} &\lim_{n\to\omega}\int_{[0,1]^{d_{n}}}(\phi_{x})_{*}(u_{d_{n}})(f)\,dx\\ &\quad =\lim_{n\to\omega}\frac{1}{d_{n}}\sum_{j\in [d_{n}]}\prod_{b\in F}1_{\{j\}}(\sigma_{n}(b)(j))\prod_{g\in E}\\ &\qquad\times \bigg(\int_{0}^{1}\prod_{k\in E}1_{\{j\}}(\sigma_{n}(gk^{-1})(j))f_{k}(x)\,dx\bigg)^{{1}/{|\{a\in E:\sigma_{n}(ga^{-1})(j)=j\}|}}. \end{align*} $$
It is direct to verify that the function
![]() $\Phi _{f}\colon \{0,1\}^{G}\to [0,+\infty )$
given by
$\Phi _{f}\colon \{0,1\}^{G}\to [0,+\infty )$
given by
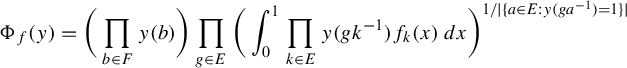 $$ \begin{align*}\Phi_{f}(y)=\bigg(\prod_{b\in F}y(b)\bigg)\prod_{g\in E}\bigg(\int_{0}^{1}\prod_{k\in E}y(gk^{-1})f_{k}(x)\,dx\bigg)^{{1}/{|\{a\in E:y(ga^{-1})=1\}|}}\end{align*} $$
$$ \begin{align*}\Phi_{f}(y)=\bigg(\prod_{b\in F}y(b)\bigg)\prod_{g\in E}\bigg(\int_{0}^{1}\prod_{k\in E}y(gk^{-1})f_{k}(x)\,dx\bigg)^{{1}/{|\{a\in E:y(ga^{-1})=1\}|}}\end{align*} $$
is continuous (in fact, it is locally constant). The definition of
![]() $\operatorname {\mathrm {IRS}}(\sigma _{\omega })$
thus proves that
$\operatorname {\mathrm {IRS}}(\sigma _{\omega })$
thus proves that
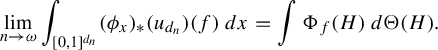 $$ \begin{align*}\lim_{n\to\omega}\int_{[0,1]^{d_{n}}}(\phi_{x})_{*}(u_{d_{n}})(f)\,dx= \int \Phi_{f}(H)\,d\Theta(H).\end{align*} $$
$$ \begin{align*}\lim_{n\to\omega}\int_{[0,1]^{d_{n}}}(\phi_{x})_{*}(u_{d_{n}})(f)\,dx= \int \Phi_{f}(H)\,d\Theta(H).\end{align*} $$
By definition,
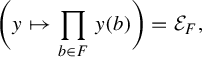 $$ \begin{align*}\bigg(y\mapsto \prod_{b\in F}y(b)\bigg)={\mathcal E}_{F},\end{align*} $$
$$ \begin{align*}\bigg(y\mapsto \prod_{b\in F}y(b)\bigg)={\mathcal E}_{F},\end{align*} $$
moreover, if
![]() $H\in \operatorname {\mathrm {Sub}}(G)$
, then
$H\in \operatorname {\mathrm {Sub}}(G)$
, then
![]() $1_{H}(ga^{-1})=1$
if and only if
$1_{H}(ga^{-1})=1$
if and only if
![]() $Ha=Hg$
. Thus, viewing
$Ha=Hg$
. Thus, viewing
![]() $\operatorname {\mathrm {Sub}}(G)\subseteq \{0,1\}^{G}$
, we have
$\operatorname {\mathrm {Sub}}(G)\subseteq \{0,1\}^{G}$
, we have
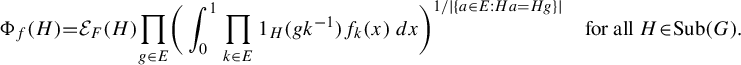 $$ \begin{align*} \Phi_{f}(H)\!=\!{\mathcal E}_{F}(H)\!\prod_{g\in E}\!\bigg(\int_{0}^{1}\prod_{k\in E}1_{H}(gk^{-1})f_{k}(x)\,dx\bigg)^{{1}/{|\{a\in E:Ha=Hg\}|}}\quad \text{for all } H\!\in\! \operatorname{\mathrm{Sub}}(G). \end{align*} $$
$$ \begin{align*} \Phi_{f}(H)\!=\!{\mathcal E}_{F}(H)\!\prod_{g\in E}\!\bigg(\int_{0}^{1}\prod_{k\in E}1_{H}(gk^{-1})f_{k}(x)\,dx\bigg)^{{1}/{|\{a\in E:Ha=Hg\}|}}\quad \text{for all } H\!\in\! \operatorname{\mathrm{Sub}}(G). \end{align*} $$
So
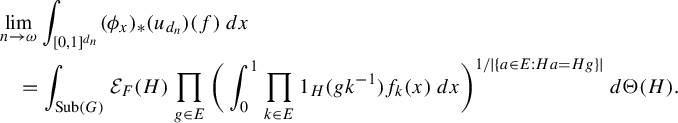 $$ \begin{align*} &\lim_{n\to\omega}\int_{[0,1]^{d_{n}}}(\phi_{x})_{*}(u_{d_{n}})(f)\,dx\\ &\quad =\int_{\operatorname{\mathrm{Sub}}(G)}{\mathcal E}_{F}(H)\prod_{g\in E}\bigg(\int_{0}^{1}\prod_{k\in E}1_{H}(gk^{-1})f_{k}(x)\,dx\bigg)^{{1}/{|\{a\in E:Ha=Hg\}|}}\,d\Theta(H). \end{align*} $$
$$ \begin{align*} &\lim_{n\to\omega}\int_{[0,1]^{d_{n}}}(\phi_{x})_{*}(u_{d_{n}})(f)\,dx\\ &\quad =\int_{\operatorname{\mathrm{Sub}}(G)}{\mathcal E}_{F}(H)\prod_{g\in E}\bigg(\int_{0}^{1}\prod_{k\in E}1_{H}(gk^{-1})f_{k}(x)\,dx\bigg)^{{1}/{|\{a\in E:Ha=Hg\}|}}\,d\Theta(H). \end{align*} $$
Note that
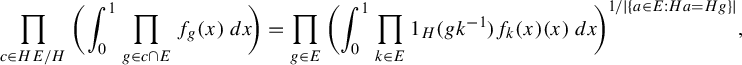 $$ \begin{align*}\prod_{c\in HE/H}\bigg(\!\kern1.2pt\int_{0}^{1}\prod_{g\in c\cap E}f_{g}(x)\,dx\!\bigg) = \prod_{g\in E}\bigg(\!\int_{0}^{1}\prod_{k\in E}1_{H}(gk^{-1})f_{k}(x)(x)\,dx\!\bigg)^{{1}/{|\{a\in E:Ha=Hg\}|}},\end{align*} $$
$$ \begin{align*}\prod_{c\in HE/H}\bigg(\!\kern1.2pt\int_{0}^{1}\prod_{g\in c\cap E}f_{g}(x)\,dx\!\bigg) = \prod_{g\in E}\bigg(\!\int_{0}^{1}\prod_{k\in E}1_{H}(gk^{-1})f_{k}(x)(x)\,dx\!\bigg)^{{1}/{|\{a\in E:Ha=Hg\}|}},\end{align*} $$
with the last step following because the inverse image of g under the map
![]() $E\mapsto G/H, g\mapsto Hg$
has cardinality
$E\mapsto G/H, g\mapsto Hg$
has cardinality
![]() $|\{a\in E:Ha=Hg\}|.$
Thus,
$|\{a\in E:Ha=Hg\}|.$
Thus,
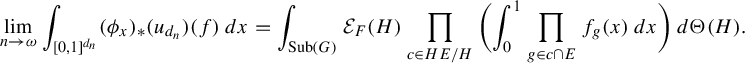 $$ \begin{align*} \lim_{n\to\omega}\int_{[0,1]^{d_{n}}}(\phi_{x})_{*}(u_{d_{n}})(f)\,dx=\int_{\operatorname{\mathrm{Sub}}(G)}{\mathcal E}_{F}(H)\prod_{c\in HE/H}\bigg(\!\int_{0}^{1}\prod_{g\in c\cap E}f_{g}(x)\,dx\bigg)\,d\Theta(H). \end{align*} $$
$$ \begin{align*} \lim_{n\to\omega}\int_{[0,1]^{d_{n}}}(\phi_{x})_{*}(u_{d_{n}})(f)\,dx=\int_{\operatorname{\mathrm{Sub}}(G)}{\mathcal E}_{F}(H)\prod_{c\in HE/H}\bigg(\!\int_{0}^{1}\prod_{g\in c\cap E}f_{g}(x)\,dx\bigg)\,d\Theta(H). \end{align*} $$
Note that for
![]() $H\in \operatorname {\mathrm {Sub}}(G)$
, we have that
$H\in \operatorname {\mathrm {Sub}}(G)$
, we have that
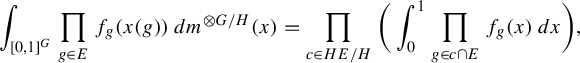 $$ \begin{align*}\int_{[0,1]^{G}}\prod_{g\in E}f_{g}(x(g))\,dm^{\otimes G/H}(x)=\prod_{c\in HE/H}\bigg(\int_{0}^{1}\prod_{g\in c\cap E}f_{g}(x)\,dx\bigg),\end{align*} $$
$$ \begin{align*}\int_{[0,1]^{G}}\prod_{g\in E}f_{g}(x(g))\,dm^{\otimes G/H}(x)=\prod_{c\in HE/H}\bigg(\int_{0}^{1}\prod_{g\in c\cap E}f_{g}(x)\,dx\bigg),\end{align*} $$
where we view
![]() $m^{\otimes G/H}$
as a probability measure on
$m^{\otimes G/H}$
as a probability measure on
![]() $[0,1]^{G}$
that is supported on the
$[0,1]^{G}$
that is supported on the
![]() $x\in [0,1]^{G}$
that are constant on right H-cosets. So
$x\in [0,1]^{G}$
that are constant on right H-cosets. So
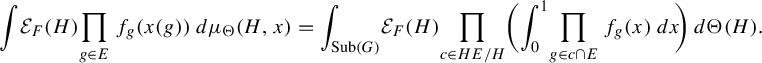 $$ \begin{align*} \int\! {\mathcal E}_{F}(H)\!\prod_{g\in E}f_{g}(x(g))\,d\mu_{\Theta}(H,x)=\int_{\operatorname{\mathrm{Sub}}(G)}\!{\mathcal E}_{F}(H)\!\prod_{c\in HE/H}\!\bigg(\!\int_{0}^{1}\!\prod_{g\in c\cap E}f_{g}(x)\,dx\!\bigg)\,d\Theta(H). \end{align*} $$
$$ \begin{align*} \int\! {\mathcal E}_{F}(H)\!\prod_{g\in E}f_{g}(x(g))\,d\mu_{\Theta}(H,x)=\int_{\operatorname{\mathrm{Sub}}(G)}\!{\mathcal E}_{F}(H)\!\prod_{c\in HE/H}\!\bigg(\!\int_{0}^{1}\!\prod_{g\in c\cap E}f_{g}(x)\,dx\!\bigg)\,d\Theta(H). \end{align*} $$
Altogether, this shows that
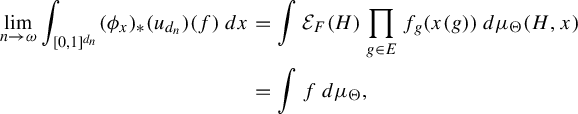 $$ \begin{align*} \lim_{n\to\omega}\int_{[0,1]^{d_{n}}}(\phi_{x})_{*}(u_{d_{n}})(f)\,dx&=\int {\mathcal E}_{F}(H)\prod_{g\in E}f_{g}(x(g))\,d\mu_{\Theta}(H,x)\\ &=\int f\,d\mu_{\Theta}, \end{align*} $$
$$ \begin{align*} \lim_{n\to\omega}\int_{[0,1]^{d_{n}}}(\phi_{x})_{*}(u_{d_{n}})(f)\,dx&=\int {\mathcal E}_{F}(H)\prod_{g\in E}f_{g}(x(g))\,d\mu_{\Theta}(H,x)\\ &=\int f\,d\mu_{\Theta}, \end{align*} $$
as desired.
(ii) Define
![]() $T_{n}\colon C((\{0,1\}\times [0,1])^{G})\to L^{2}([0,1]^{d_{n}})$
by
$T_{n}\colon C((\{0,1\}\times [0,1])^{G})\to L^{2}([0,1]^{d_{n}})$
by
Giving
![]() $C((\{0,1\}\times [0,1])^{G})$
the supremum norm, we have the operator norm of
$C((\{0,1\}\times [0,1])^{G})$
the supremum norm, we have the operator norm of
![]() $T_{n}$
satisfies
$T_{n}$
satisfies
![]() $\|T_{n}\|\leq 2$
. This uniform estimate implies that
$\|T_{n}\|\leq 2$
. This uniform estimate implies that
![]() $\{\zeta \in C((\{0,1\}\times [0,1])^{G}):\|T_{n}\zeta \|_{2}\to _{n\to \omega }0\}$
is a closed, linear subspace. So as in item (i), it suffices to verify the desired statement for
$\{\zeta \in C((\{0,1\}\times [0,1])^{G}):\|T_{n}\zeta \|_{2}\to _{n\to \omega }0\}$
is a closed, linear subspace. So as in item (i), it suffices to verify the desired statement for
![]() $f=(\bigotimes _{g\in E}f_{g}){\mathcal E}_{F}\in B$
, where
$f=(\bigotimes _{g\in E}f_{g}){\mathcal E}_{F}\in B$
, where
![]() $(f_{g})_{g\in E}\in C([0,1])^{G}$
and
$(f_{g})_{g\in E}\in C([0,1])^{G}$
and
![]() $E,F\subseteq G$
are finite. By direct computation,
$E,F\subseteq G$
are finite. By direct computation,
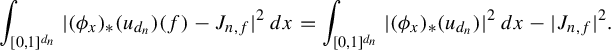 $$ \begin{align} \int_{[0,1]^{d_{n}}}|(\phi_{x})_{*}(u_{d_{n}})(f)-J_{n,f}|^{2}\,dx = \int_{[0,1]^{d_{n}}}|(\phi_{x})_{*}(u_{d_{n}})|^{2}\,dx-|J_{n,f}|^{2}. \end{align} $$
$$ \begin{align} \int_{[0,1]^{d_{n}}}|(\phi_{x})_{*}(u_{d_{n}})(f)-J_{n,f}|^{2}\,dx = \int_{[0,1]^{d_{n}}}|(\phi_{x})_{*}(u_{d_{n}})|^{2}\,dx-|J_{n,f}|^{2}. \end{align} $$
Moreover,
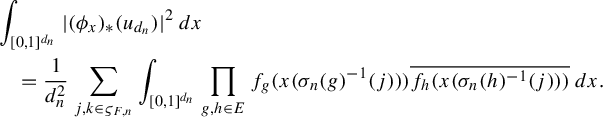 $$ \begin{align*} &\int_{[0,1]^{d_{n}}}|(\phi_{x})_{*}(u_{d_{n}})|^{2}\,dx\\ &\quad =\frac{1}{d_{n}^{2}}\sum_{j,k\in \varsigma_{F,n}}\int_{[0,1]^{d_{n}}}\prod_{g,h\in E}f_{g}(x(\sigma_{n}(g)^{-1}(j)))\overline{f_{h}(x(\sigma_{n}(h)^{-1}(j)))}\,dx. \end{align*} $$
$$ \begin{align*} &\int_{[0,1]^{d_{n}}}|(\phi_{x})_{*}(u_{d_{n}})|^{2}\,dx\\ &\quad =\frac{1}{d_{n}^{2}}\sum_{j,k\in \varsigma_{F,n}}\int_{[0,1]^{d_{n}}}\prod_{g,h\in E}f_{g}(x(\sigma_{n}(g)^{-1}(j)))\overline{f_{h}(x(\sigma_{n}(h)^{-1}(j)))}\,dx. \end{align*} $$
We can rewrite this as
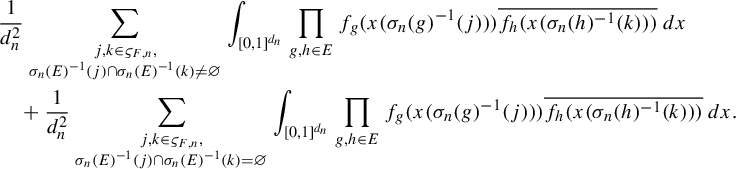 $$ \begin{align} &\frac{1}{d_{n}^{2}}\sum_{\substack{j,k\in \varsigma_{F,n},\\ \sigma_{n}(E)^{-1}(j)\cap \sigma_{n}(E)^{-1}(k)\ne \varnothing}}\int_{[0,1]^{d_{n}}}\prod_{g,h\in E}f_{g}(x(\sigma_{n}(g)^{-1}(j)))\overline{f_{h}(x(\sigma_{n}(h)^{-1}(k)))}\,dx\notag\\ &\quad +\frac{1}{d_{n}^{2}}\sum_{\substack{j,k\in \varsigma_{F,n},\\ \sigma_{n}(E)^{-1}(j)\cap \sigma_{n}(E)^{-1}(k)= \varnothing}}\int_{[0,1]^{d_{n}}}\prod_{g,h\in E}f_{g}(x(\sigma_{n}(g)^{-1}(j)))\overline{f_{h}(x(\sigma_{n}(h)^{-1}(k)))}\,dx. \end{align} $$
$$ \begin{align} &\frac{1}{d_{n}^{2}}\sum_{\substack{j,k\in \varsigma_{F,n},\\ \sigma_{n}(E)^{-1}(j)\cap \sigma_{n}(E)^{-1}(k)\ne \varnothing}}\int_{[0,1]^{d_{n}}}\prod_{g,h\in E}f_{g}(x(\sigma_{n}(g)^{-1}(j)))\overline{f_{h}(x(\sigma_{n}(h)^{-1}(k)))}\,dx\notag\\ &\quad +\frac{1}{d_{n}^{2}}\sum_{\substack{j,k\in \varsigma_{F,n},\\ \sigma_{n}(E)^{-1}(j)\cap \sigma_{n}(E)^{-1}(k)= \varnothing}}\int_{[0,1]^{d_{n}}}\prod_{g,h\in E}f_{g}(x(\sigma_{n}(g)^{-1}(j)))\overline{f_{h}(x(\sigma_{n}(h)^{-1}(k)))}\,dx. \end{align} $$
For a fixed j, the set of k for which
![]() $\sigma _{n}(E)^{-1}(j)\cap \sigma _{n}(E)^{-1}(k)\ne \varnothing $
has cardinality at most
$\sigma _{n}(E)^{-1}(j)\cap \sigma _{n}(E)^{-1}(k)\ne \varnothing $
has cardinality at most
![]() $|E|^{2}$
. So the first term is bounded by
$|E|^{2}$
. So the first term is bounded by
 $$ \begin{align*}\frac{1}{d_{n}}|E|^{2}\prod_{g\in E}\|f_{g}\|_{\infty}^{2}\to_{n\to\omega}0.\end{align*} $$
$$ \begin{align*}\frac{1}{d_{n}}|E|^{2}\prod_{g\in E}\|f_{g}\|_{\infty}^{2}\to_{n\to\omega}0.\end{align*} $$
For
![]() $n\in {\mathbb N}$
, define
$n\in {\mathbb N}$
, define
![]() $\Psi _{n,f}\colon \{1,\ldots ,d_{n}\}\to {\mathbb R}$
by
$\Psi _{n,f}\colon \{1,\ldots ,d_{n}\}\to {\mathbb R}$
by
 $$ \begin{align*} \Psi_{n,f}(j)=\int_{[0,1]^{d_{n}}}\prod_{g\in E}f_{g}(x(\sigma_{n}(g)^{-1}(j)))\,dx. \end{align*} $$
$$ \begin{align*} \Psi_{n,f}(j)=\int_{[0,1]^{d_{n}}}\prod_{g\in E}f_{g}(x(\sigma_{n}(g)^{-1}(j)))\,dx. \end{align*} $$
The second term in equation (4.2) is
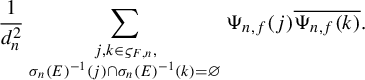 $$ \begin{align*} \frac{1}{d_{n}^{2}}\sum_{\substack{j,k\in \varsigma_{F,n},\\ \sigma_{n}(E)^{-1}(j)\cap \sigma_{n}(E)^{-1}(k)= \varnothing}}\Psi_{n,f}(j)\overline{\Psi_{n,f}(k)}. \end{align*} $$
$$ \begin{align*} \frac{1}{d_{n}^{2}}\sum_{\substack{j,k\in \varsigma_{F,n},\\ \sigma_{n}(E)^{-1}(j)\cap \sigma_{n}(E)^{-1}(k)= \varnothing}}\Psi_{n,f}(j)\overline{\Psi_{n,f}(k)}. \end{align*} $$
Thus,
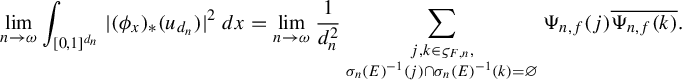 $$ \begin{align} \lim_{n\to\omega}\int_{[0,1]^{d_{n}}}|(\phi_{x})_{*}(u_{d_{n}})|^{2}\,dx=\lim_{n\to\omega} \frac{1}{d_{n}^{2}}\sum_{\substack{j,k\in \varsigma_{F,n},\\ \sigma_{n}(E)^{-1}(j)\cap \sigma_{n}(E)^{-1}(k)=\varnothing}}\Psi_{n,f}(j)\overline{\Psi_{n,f}(k)}. \end{align} $$
$$ \begin{align} \lim_{n\to\omega}\int_{[0,1]^{d_{n}}}|(\phi_{x})_{*}(u_{d_{n}})|^{2}\,dx=\lim_{n\to\omega} \frac{1}{d_{n}^{2}}\sum_{\substack{j,k\in \varsigma_{F,n},\\ \sigma_{n}(E)^{-1}(j)\cap \sigma_{n}(E)^{-1}(k)=\varnothing}}\Psi_{n,f}(j)\overline{\Psi_{n,f}(k)}. \end{align} $$
By another direct computation,
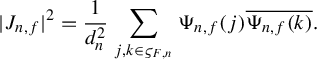 $$ \begin{align*}|J_{n,f}|^{2}=\frac{1}{d_{n}^{2}}\sum_{j,k\in \varsigma_{F,n}}\Psi_{n,f}(j)\overline{\Psi_{n,f}(k)}.\end{align*} $$
$$ \begin{align*}|J_{n,f}|^{2}=\frac{1}{d_{n}^{2}}\sum_{j,k\in \varsigma_{F,n}}\Psi_{n,f}(j)\overline{\Psi_{n,f}(k)}.\end{align*} $$
By the same estimates as above,
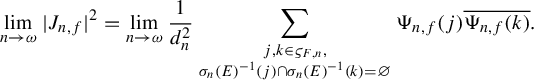 $$ \begin{align*}\lim_{n\to\omega}|J_{n,f}|^{2}=\lim_{n\to\omega}\frac{1}{d_{n}^{2}}\sum_{\substack{j,k\in \varsigma_{F,n},\\ \sigma_{n}(E)^{-1}(j)\cap \sigma_{n}(E)^{-1}(k)=\varnothing}}\Psi_{n,f}(j)\overline{\Psi_{n,f}(k)}.\end{align*} $$
$$ \begin{align*}\lim_{n\to\omega}|J_{n,f}|^{2}=\lim_{n\to\omega}\frac{1}{d_{n}^{2}}\sum_{\substack{j,k\in \varsigma_{F,n},\\ \sigma_{n}(E)^{-1}(j)\cap \sigma_{n}(E)^{-1}(k)=\varnothing}}\Psi_{n,f}(j)\overline{\Psi_{n,f}(k)}.\end{align*} $$
Combining this with equations (4.1), (4.3) shows that
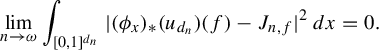 $$ \begin{align*}\lim_{n\to\omega}\int_{[0,1]^{d_{n}}}| (\phi_{x})_{*}(u_{d_{n}})(f)-J_{n,f}|^{2}\,dx=0.\end{align*} $$
$$ \begin{align*}\lim_{n\to\omega}\int_{[0,1]^{d_{n}}}| (\phi_{x})_{*}(u_{d_{n}})(f)-J_{n,f}|^{2}\,dx=0.\end{align*} $$
Since this is true for every free ultrafilter, we have proven item (ii).
(iii) Since f is continuous, we can find a
![]() $C\geq 0$
with
$C\geq 0$
with
![]() $|f|\leq C$
. View
$|f|\leq C$
. View
![]() $\{0,1\}\times [0,1]\subseteq {\mathbb R}^{2}$
and give
$\{0,1\}\times [0,1]\subseteq {\mathbb R}^{2}$
and give
![]() ${\mathbb R}^{2}$
the norm
${\mathbb R}^{2}$
the norm
![]() $\|(t,s)\|=\sqrt {t^{2}+s^{2}}$
. Given
$\|(t,s)\|=\sqrt {t^{2}+s^{2}}$
. Given
![]() $\varepsilon>0$
, compactness of
$\varepsilon>0$
, compactness of
![]() $(\{0,1\}\times [0,1])^{G}$
and continuity of f imply that we may find a finite
$(\{0,1\}\times [0,1])^{G}$
and continuity of f imply that we may find a finite
![]() $E\subseteq G$
and a
$E\subseteq G$
and a
![]() $\delta>0$
so that if
$\delta>0$
so that if
![]() $x,y\in (\{0,1\}\times [0,1])^{G}$
and
$x,y\in (\{0,1\}\times [0,1])^{G}$
and
then
Then, for any
![]() $x\in [0,1]^{d_{n}}$
, we have
$x\in [0,1]^{d_{n}}$
, we have
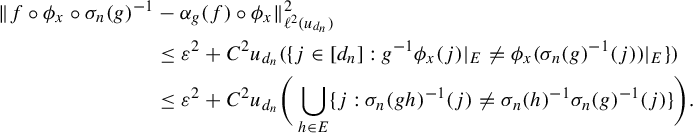 $$ \begin{align*}\|f\circ \phi_{x}\circ \sigma_{n}(g)^{-1}&-\alpha_{g}(f)\circ \phi_{x}\|_{\ell^{2}(u_{d_{n}})}^{2}\\ &\leq\varepsilon^{2}+C^{2}u_{d_{n}}(\{j\in [d_{n}]:g^{-1}\phi_{x}(j)|_{E}\ne \phi_{x}(\sigma_{n}(g)^{-1}(j))|_{E}\})\\ &\leq \varepsilon^{2}+C^{2}u_{d_{n}}\bigg(\bigcup_{h\in E}\{j:\sigma_{n}(gh)^{-1}(j)\ne \sigma_{n}(h)^{-1}\sigma_{n}(g)^{-1}(j)\}\bigg). \end{align*} $$
$$ \begin{align*}\|f\circ \phi_{x}\circ \sigma_{n}(g)^{-1}&-\alpha_{g}(f)\circ \phi_{x}\|_{\ell^{2}(u_{d_{n}})}^{2}\\ &\leq\varepsilon^{2}+C^{2}u_{d_{n}}(\{j\in [d_{n}]:g^{-1}\phi_{x}(j)|_{E}\ne \phi_{x}(\sigma_{n}(g)^{-1}(j))|_{E}\})\\ &\leq \varepsilon^{2}+C^{2}u_{d_{n}}\bigg(\bigcup_{h\in E}\{j:\sigma_{n}(gh)^{-1}(j)\ne \sigma_{n}(h)^{-1}\sigma_{n}(g)^{-1}(j)\}\bigg). \end{align*} $$
Since
![]() $\sigma _{n}$
is an asymptotic homomorphism, the second term tends to zero as
$\sigma _{n}$
is an asymptotic homomorphism, the second term tends to zero as
![]() $n\to \infty $
.
$n\to \infty $
.
While technical, Lemma 4.1 has all the tools to prove Theorem 3.7. Indeed, as we now show, Lemma 4.1 essentially says that a random choice of
![]() $x\in [0,1]^{d_{n}}$
will produce a sofic approximation of the appropriate equivalence relation.
$x\in [0,1]^{d_{n}}$
will produce a sofic approximation of the appropriate equivalence relation.
Proof of Theorem 3.7
For notation, define
![]() $S\colon [d_{n}]\to \{0,1\}^{G}$
by
$S\colon [d_{n}]\to \{0,1\}^{G}$
by
![]() $S(j)(g)= 1_{\{j\}}(\sigma _{n}(g)(j)).$
Set
$S(j)(g)= 1_{\{j\}}(\sigma _{n}(g)(j)).$
Set
![]() $\Theta _{n}=S_{*}(u_{d_{n}}).$
For
$\Theta _{n}=S_{*}(u_{d_{n}}).$
For
![]() $n\in {\mathbb N},f\in C((\{0,1\}\times [0,1])^{G})$
, let
$n\in {\mathbb N},f\in C((\{0,1\}\times [0,1])^{G})$
, let
![]() $J_{n,f}=\int _{[0,1]^{d_{n}}} (\phi _{x})_{*}(u_{d_{n}})(f)\,dx$
. Fix a countable, dense set
$J_{n,f}=\int _{[0,1]^{d_{n}}} (\phi _{x})_{*}(u_{d_{n}})(f)\,dx$
. Fix a countable, dense set
![]() $D\subseteq C((\{0,1\}\times [0,1])^{G})$
which is closed under products and is G-invariant. Write
$D\subseteq C((\{0,1\}\times [0,1])^{G})$
which is closed under products and is G-invariant. Write
![]() $D=\bigcup _{k=1}^{\infty }D_{k}$
and
$D=\bigcup _{k=1}^{\infty }D_{k}$
and
![]() $G=\bigcup _{n=1}^{\infty }F_{k}$
where
$G=\bigcup _{n=1}^{\infty }F_{k}$
where
![]() $D_{k},F_{k}$
are increasing sequences of finite sets. For
$D_{k},F_{k}$
are increasing sequences of finite sets. For
![]() $k\in {\mathbb N}$
, let
$k\in {\mathbb N}$
, let
![]() $L_{k}$
be the set of
$L_{k}$
be the set of
![]() $n\in {\mathbb N}$
so that:
$n\in {\mathbb N}$
so that:
-
•
 $n\geq k$
;
$n\geq k$
; -
•
 $\sum _{f\in D_{k},g\in F_{k}}|\mu _{\Theta }(f{\mathcal E}_{g})-J_{n,f{\mathcal E}_{g}}|<2^{-k}$
;
$\sum _{f\in D_{k},g\in F_{k}}|\mu _{\Theta }(f{\mathcal E}_{g})-J_{n,f{\mathcal E}_{g}}|<2^{-k}$
; -
•
 $\sum _{f\in D_{k},g\in F_{k}}(\int _{[0,1]^{d_{n}}}|(\phi _{x})_{*}(u_{d_{n}})(f{\mathcal E}_{g})-J_{n,f{\mathcal E}_{g}}|^{2}\,dx)^{1/2}<2^{-k}$
;
$\sum _{f\in D_{k},g\in F_{k}}(\int _{[0,1]^{d_{n}}}|(\phi _{x})_{*}(u_{d_{n}})(f{\mathcal E}_{g})-J_{n,f{\mathcal E}_{g}}|^{2}\,dx)^{1/2}<2^{-k}$
; -
•
 $\sup _{x\in [0,1]^{d_{n}}}\sum _{g\in F_{k},f\in D_{k}}\|f\circ \phi _{x}\circ \sigma _{n}(g)^{-1}-\alpha _{g}(f)\circ \phi _{x}\|_{\ell ^{2}(u_{d_{n}})}<2^{-k}.$
$\sup _{x\in [0,1]^{d_{n}}}\sum _{g\in F_{k},f\in D_{k}}\|f\circ \phi _{x}\circ \sigma _{n}(g)^{-1}-\alpha _{g}(f)\circ \phi _{x}\|_{\ell ^{2}(u_{d_{n}})}<2^{-k}.$
Then
![]() $L_{k}$
is a decreasing sequence of sets and Lemma 4.1 implies that
$L_{k}$
is a decreasing sequence of sets and Lemma 4.1 implies that
![]() $L_{k}\in \omega $
for all
$L_{k}\in \omega $
for all
![]() $k\in {\mathbb N}$
, and
$k\in {\mathbb N}$
, and
![]() $\bigcap _{k}L_{k}=\varnothing $
by the first bullet point. Set
$\bigcap _{k}L_{k}=\varnothing $
by the first bullet point. Set
![]() $L_{0}={\mathbb N}\setminus L_{1}$
. For
$L_{0}={\mathbb N}\setminus L_{1}$
. For
![]() $n\in {\mathbb N}$
, let
$n\in {\mathbb N}$
, let
![]() $k(n)$
be such that
$k(n)$
be such that
![]() $n\in L_{k(n)}\setminus L_{k(n)+1}$
. For
$n\in L_{k(n)}\setminus L_{k(n)+1}$
. For
![]() $n\in {\mathbb N}$
, let
$n\in {\mathbb N}$
, let
![]() $\Omega _{n}$
be the set of
$\Omega _{n}$
be the set of
![]() $x\in [0,1]^{d_{n}}$
so that
$x\in [0,1]^{d_{n}}$
so that
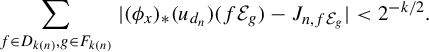 $$ \begin{align}\sum_{f\in D_{k(n)},g\in F_{k(n)}}|(\phi_{x})_{*}(u_{d_{n}})(f{\mathcal E}_{g})-J_{n,f{\mathcal E}_{g}}|<2^{-k/2}. \end{align} $$
$$ \begin{align}\sum_{f\in D_{k(n)},g\in F_{k(n)}}|(\phi_{x})_{*}(u_{d_{n}})(f{\mathcal E}_{g})-J_{n,f{\mathcal E}_{g}}|<2^{-k/2}. \end{align} $$
Then for
![]() $n\in L_{k}$
, we have
$n\in L_{k}$
, we have
![]() $m^{\otimes d_{n}}(\Omega _{n}^{c})\leq 2^{-k/2}$
. Hence, if
$m^{\otimes d_{n}}(\Omega _{n}^{c})\leq 2^{-k/2}$
. Hence, if
![]() $k\geq (2023)!$
and
$k\geq (2023)!$
and
![]() $n\in L_{k}$
, we may choose an
$n\in L_{k}$
, we may choose an
![]() $x_{n}\in \Omega _{n}$
. Let
$x_{n}\in \Omega _{n}$
. Let
![]() $x_{n}$
be defined arbitrarily for
$x_{n}$
be defined arbitrarily for
![]() $n\in {\mathbb N}\setminus L_{(2023)!}$
. Define
$n\in {\mathbb N}\setminus L_{(2023)!}$
. Define
by
![]() $\rho _{0}(f)=(f\circ \phi _{x_{k(n)}})_{n\to \omega }$
. Then
$\rho _{0}(f)=(f\circ \phi _{x_{k(n)}})_{n\to \omega }$
. Then
![]() $\rho _{0}$
preserves products. Recall that we view
$\rho _{0}$
preserves products. Recall that we view
![]() $\ell ^{\infty }(d_{n})$
as a subalgebra of
$\ell ^{\infty }(d_{n})$
as a subalgebra of
![]() $M_{d_{n}}({\mathbb C})$
by identifying each function with the corresponding diagonal matrix. Let
$M_{d_{n}}({\mathbb C})$
by identifying each function with the corresponding diagonal matrix. Let
![]() $f\in D,g\in G$
. By the fact that
$f\in D,g\in G$
. By the fact that
![]() $\sigma _{n}$
is an asymptotic homomorphism and the fourth bullet point above, we know that
$\sigma _{n}$
is an asymptotic homomorphism and the fourth bullet point above, we know that
By our choice of
![]() $x_{n}$
,
$x_{n}$
,
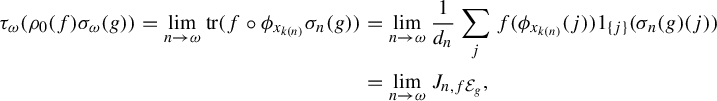 $$ \begin{align*} \tau_{\omega}(\rho_{0}(f)\sigma_{\omega}(g))=\lim_{n\to\omega}\operatorname{\mathrm{tr}}(f\circ \phi_{x_{k(n)}}\sigma_{n}(g))&=\lim_{n\to\omega}\frac{1}{d_{n}}\sum_{j}f(\phi_{x_{k(n)}}(j))1_{\{j\}}(\sigma_{n}(g)(j))\\ &=\lim_{n\to\omega}J_{n,f{\mathcal E}_{g}}, \end{align*} $$
$$ \begin{align*} \tau_{\omega}(\rho_{0}(f)\sigma_{\omega}(g))=\lim_{n\to\omega}\operatorname{\mathrm{tr}}(f\circ \phi_{x_{k(n)}}\sigma_{n}(g))&=\lim_{n\to\omega}\frac{1}{d_{n}}\sum_{j}f(\phi_{x_{k(n)}}(j))1_{\{j\}}(\sigma_{n}(g)(j))\\ &=\lim_{n\to\omega}J_{n,f{\mathcal E}_{g}}, \end{align*} $$
where in the last step, we use equation (4.4). By Lemma 4.1, this last limit is
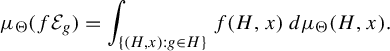 $$ \begin{align*}\mu_{\Theta}(f{\mathcal E}_{g})=\int_{\{(H,x):g\in H\}}f(H,x)\,d\mu_{\Theta}(H,x).\end{align*} $$
$$ \begin{align*}\mu_{\Theta}(f{\mathcal E}_{g})=\int_{\{(H,x):g\in H\}}f(H,x)\,d\mu_{\Theta}(H,x).\end{align*} $$
Since
![]() $([0,1],m)$
is atomless and G is countable,
$([0,1],m)$
is atomless and G is countable,
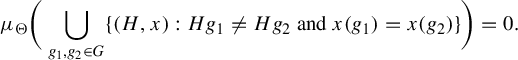 $$ \begin{align*} \mu_{\Theta}\bigg(\bigcup_{g_{1},g_{2}\in G}\{(H,x):Hg_{1}\ne Hg_{2} \text{ and } x(g_{1})=x(g_{2})\}\bigg)=0. \end{align*} $$
$$ \begin{align*} \mu_{\Theta}\bigg(\bigcup_{g_{1},g_{2}\in G}\{(H,x):Hg_{1}\ne Hg_{2} \text{ and } x(g_{1})=x(g_{2})\}\bigg)=0. \end{align*} $$
Thus, for every
![]() $g\in G$
,
$g\in G$
,
So
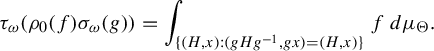 $$ \begin{align*} \tau_{\omega}(\rho_{0}(f)\sigma_{\omega}(g))=\int_{\{(H,x):(gHg^{-1},gx)=(H,x)\}}f\,d\mu_{\Theta}. \end{align*} $$
$$ \begin{align*} \tau_{\omega}(\rho_{0}(f)\sigma_{\omega}(g))=\int_{\{(H,x):(gHg^{-1},gx)=(H,x)\}}f\,d\mu_{\Theta}. \end{align*} $$
Thus, Proposition 3.6(iii) implies that there is a unique sofic approximation
![]() ${\pi \colon L({\mathcal R})\to \prod _{n\to \omega }(M_{d_{n}}({\mathbb C}),\operatorname {\mathrm {tr}})}$
so that
${\pi \colon L({\mathcal R})\to \prod _{n\to \omega }(M_{d_{n}}({\mathbb C}),\operatorname {\mathrm {tr}})}$
so that
![]() $\pi \circ \Xi =\sigma _{\omega }$
and
$\pi \circ \Xi =\sigma _{\omega }$
and
![]() $\pi |_{D}=\rho _{0}$
. Set
$\pi |_{D}=\rho _{0}$
. Set
![]() $\rho =\pi |_{L^{\infty }(X)}$
and
$\rho =\pi |_{L^{\infty }(X)}$
and
![]() $\widehat {\sigma }=\pi |_{[{\mathcal R}]}$
. By Proposition 3.6(ii), we have that
$\widehat {\sigma }=\pi |_{[{\mathcal R}]}$
. By Proposition 3.6(ii), we have that
![]() $(\rho ,\widehat {\sigma })$
is a sofic approximation. The fact that
$(\rho ,\widehat {\sigma })$
is a sofic approximation. The fact that
![]() $\widehat {\sigma }\circ \Xi =\sigma _{\omega }$
is true by construction.
$\widehat {\sigma }\circ \Xi =\sigma _{\omega }$
is true by construction.
5. Applications of Theorem 1.1
One of the applications of the theorem we wish to highlight is the following result which is a reformulation of the Newman–Sohler theorem [Reference Newman and Sohler39] (see [Reference Elek25, Theorem 5] for a statement of the Newman–Sohler theorem which is closer to our language).
Theorem 5.1. Let G be an amenable group, and
![]() $\sigma _{n},\psi _{n}\colon G\to {\operatorname {Sym}}(d_{n})$
two sequences of approximate homomorphisms. Let
$\sigma _{n},\psi _{n}\colon G\to {\operatorname {Sym}}(d_{n})$
two sequences of approximate homomorphisms. Let
![]() $\omega \in \beta {\mathbb N}\setminus {\mathbb N}$
. Then
$\omega \in \beta {\mathbb N}\setminus {\mathbb N}$
. Then
![]() $\sigma _{\omega }$
is conjugate to
$\sigma _{\omega }$
is conjugate to
![]() $\psi _{\omega }$
if and only if
$\psi _{\omega }$
if and only if
![]() $\operatorname {\mathrm {IRS}}(\sigma _{\omega })=\operatorname {\mathrm {IRS}}(\psi _{\omega })$
.
$\operatorname {\mathrm {IRS}}(\sigma _{\omega })=\operatorname {\mathrm {IRS}}(\psi _{\omega })$
.
Proof. Let
![]() $\Theta =\operatorname {\mathrm {IRS}}(\sigma _{\omega })=\operatorname {\mathrm {IRS}}(\psi _{\omega })$
and let
$\Theta =\operatorname {\mathrm {IRS}}(\sigma _{\omega })=\operatorname {\mathrm {IRS}}(\psi _{\omega })$
and let
![]() ${\mathcal R}$
be the orbit equivalence relation of the
${\mathcal R}$
be the orbit equivalence relation of the
![]() $\Theta $
-Bernoulli shift with base
$\Theta $
-Bernoulli shift with base
![]() $([0,1],m)$
. Let
$([0,1],m)$
. Let
![]() $\Xi $
be given as in Theorem 3.7. By Theorem 3.7, we can find sofic approximations
$\Xi $
be given as in Theorem 3.7. By Theorem 3.7, we can find sofic approximations
![]() $(\rho _{j},\widehat {\sigma }_{j}),j=1,2$
so that
$(\rho _{j},\widehat {\sigma }_{j}),j=1,2$
so that
![]() $\widehat {\sigma }_{1}\circ \Xi =\sigma _{\omega }$
,
$\widehat {\sigma }_{1}\circ \Xi =\sigma _{\omega }$
,
![]() $\widehat {\sigma }_{2}\circ \Xi =\psi _{\omega }$
. Since G is amenable, we know by [Reference Ornstein and Weiss40], [Reference Ornstein and Weiss41, II §3] (see also [Reference Connes, Feldman and Weiss15]) that
$\widehat {\sigma }_{2}\circ \Xi =\psi _{\omega }$
. Since G is amenable, we know by [Reference Ornstein and Weiss40], [Reference Ornstein and Weiss41, II §3] (see also [Reference Connes, Feldman and Weiss15]) that
![]() ${\mathcal R}$
is hyperfinite. Thus, by [Reference Păunescu42, Proposition 1.20], there is a
${\mathcal R}$
is hyperfinite. Thus, by [Reference Păunescu42, Proposition 1.20], there is a
![]() $\chi \in {\mathcal S}_{\omega }$
with
$\chi \in {\mathcal S}_{\omega }$
with
In particular,
for all
![]() $g\in G$
.
$g\in G$
.
We remark that Theorem 5.1 recovers the result of Kerr and Li [Reference Kerr and Li36, Lemma 4.5] and Elek and Szabo [Reference Elek and Szabó27] on uniqueness of sofic approximations of amenable groups up to asymptotic conjugacy. Indeed, sofic approximations correspond to the cases
![]() ${\operatorname {\mathrm {IRS}}(\sigma _{\omega })=\operatorname {\mathrm {IRS}}(\psi _{\omega })=\{1\}}$
. Another reformulation of this result is as follows.
${\operatorname {\mathrm {IRS}}(\sigma _{\omega })=\operatorname {\mathrm {IRS}}(\psi _{\omega })=\{1\}}$
. Another reformulation of this result is as follows.
Corollary 5.2. [Reference Arzhantseva and Păunescu5, Theorem 3.12]
Let G be an amenable group and
![]() $\psi _{n},\sigma _{n}\colon G\to {\operatorname {Sym}}(d_{n})$
be approximate homomorphisms, and fix a free ultrafilter
$\psi _{n},\sigma _{n}\colon G\to {\operatorname {Sym}}(d_{n})$
be approximate homomorphisms, and fix a free ultrafilter
![]() $\omega \in \beta {\mathbb N}\setminus {\mathbb N}$
.
$\omega \in \beta {\mathbb N}\setminus {\mathbb N}$
.
-
(1) Then
 $(\psi _{\omega }),(\sigma _{\omega })$
are conjugate if and only if for all finite
$(\psi _{\omega }),(\sigma _{\omega })$
are conjugate if and only if for all finite
 $F\subseteq G$
,
$F\subseteq G$
,  $$ \begin{align*}\lim_{n\to\omega}u_{d_{n}}\bigg(\bigcap_{g\in F}\{j:\psi_{n}(g)(j)=j\}\bigg)=\lim_{n\to\omega}u_{d_{n}}\bigg(\bigcap_{g\in F}\{j:\sigma_{n}(g)(j)=j\}\bigg).\end{align*} $$
$$ \begin{align*}\lim_{n\to\omega}u_{d_{n}}\bigg(\bigcap_{g\in F}\{j:\psi_{n}(g)(j)=j\}\bigg)=\lim_{n\to\omega}u_{d_{n}}\bigg(\bigcap_{g\in F}\{j:\sigma_{n}(g)(j)=j\}\bigg).\end{align*} $$
-
(2) In particular,
 $(\sigma _{n}),(\psi _{n})_{n}$
are asymptotically conjugate as
$(\sigma _{n}),(\psi _{n})_{n}$
are asymptotically conjugate as
 $n\to \infty $
if and only if for all finite
$n\to \infty $
if and only if for all finite
 $F\subseteq G$
,
$F\subseteq G$
,  $$ \begin{align*} \lim_{n\to\infty}\!\bigg|\frac{1}{d_{n}}|\{j:\sigma_{n}(g)(j)=j \text{ for all } g\!\in\! F\} |-\frac{1}{d_{n}}|\{j:\psi_{n}(g)(j)=\!j \text{ for all } g\!\in\! F\}|\bigg|=0. \end{align*} $$
$$ \begin{align*} \lim_{n\to\infty}\!\bigg|\frac{1}{d_{n}}|\{j:\sigma_{n}(g)(j)=j \text{ for all } g\!\in\! F\} |-\frac{1}{d_{n}}|\{j:\psi_{n}(g)(j)=\!j \text{ for all } g\!\in\! F\}|\bigg|=0. \end{align*} $$
Proof. (1) The forward implication is an exercise. For the reverse, let
![]() $\Theta _{1}=\operatorname {\mathrm {IRS}}(\sigma _{\omega }), \Theta _{2}=\operatorname {\mathrm {IRS}}(\psi _{\omega })$
. For every finite
$\Theta _{1}=\operatorname {\mathrm {IRS}}(\sigma _{\omega }), \Theta _{2}=\operatorname {\mathrm {IRS}}(\psi _{\omega })$
. For every finite
![]() $F\subseteq G$
, we have
$F\subseteq G$
, we have
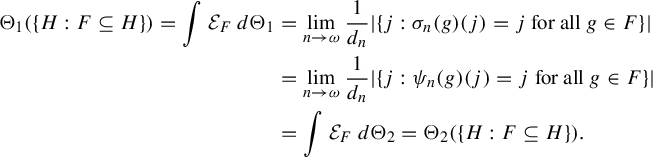 $$ \begin{align*} \Theta_{1}(\{H:F\subseteq H\})=\int {\mathcal E}_{F}\,d\Theta_{1}&=\lim_{n\to\omega}\frac{1}{d_{n}}|\{j:\sigma_{n}(g)(j)=j \text{ for all } g\in F\}| \\ &=\lim_{n\to\omega}\frac{1}{d_{n}}|\{j:\psi_{n}(g)(j)=j \text{ for all } g\in F\}|\\ &=\int {\mathcal E}_{F}\,d\Theta_{2}=\Theta_{2}(\{H:F\subseteq H\}). \end{align*} $$
$$ \begin{align*} \Theta_{1}(\{H:F\subseteq H\})=\int {\mathcal E}_{F}\,d\Theta_{1}&=\lim_{n\to\omega}\frac{1}{d_{n}}|\{j:\sigma_{n}(g)(j)=j \text{ for all } g\in F\}| \\ &=\lim_{n\to\omega}\frac{1}{d_{n}}|\{j:\psi_{n}(g)(j)=j \text{ for all } g\in F\}|\\ &=\int {\mathcal E}_{F}\,d\Theta_{2}=\Theta_{2}(\{H:F\subseteq H\}). \end{align*} $$
The
![]() $*$
-subalgebra
$*$
-subalgebra
![]() $A_{0}=\operatorname {\mathrm {span}}\{\mathcal {E}_{F}:F\subseteq G\text { is finite}\}$
of
$A_{0}=\operatorname {\mathrm {span}}\{\mathcal {E}_{F}:F\subseteq G\text { is finite}\}$
of
![]() $C(\operatorname {\mathrm {Sub}}(G))$
contains
$C(\operatorname {\mathrm {Sub}}(G))$
contains
![]() $1$
and separates points, and is thus dense by Stone and Weierstrass. It follows by the density and the Riesz representation theorem that
$1$
and separates points, and is thus dense by Stone and Weierstrass. It follows by the density and the Riesz representation theorem that
![]() $\Theta _{1}=\Theta _{2}$
. The result now follows by Theorem 5.1.
$\Theta _{1}=\Theta _{2}$
. The result now follows by Theorem 5.1.
(2) The forward implication is an exercise. For the reverse, suppose that
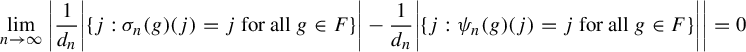 $$ \begin{align*} \lim_{n\to\infty}\bigg|\frac{1}{d_{n}}\bigg|\{j:\sigma_{n}(g)(j)=j \text{ for all } g\in F\}\bigg| - \frac{1}{d_{n}}\bigg|\{j:\psi_{n}(g)(j)=j \text{ for all } g\in F\}\bigg|\bigg|=0 \end{align*} $$
$$ \begin{align*} \lim_{n\to\infty}\bigg|\frac{1}{d_{n}}\bigg|\{j:\sigma_{n}(g)(j)=j \text{ for all } g\in F\}\bigg| - \frac{1}{d_{n}}\bigg|\{j:\psi_{n}(g)(j)=j \text{ for all } g\in F\}\bigg|\bigg|=0 \end{align*} $$
for every finite
![]() $F\subseteq G$
. To show that
$F\subseteq G$
. To show that
![]() $\psi _{n},\sigma _{n}$
are conjugate, it suffices by a diagonal argument to show that for every finite
$\psi _{n},\sigma _{n}$
are conjugate, it suffices by a diagonal argument to show that for every finite
![]() $E\subseteq G$
,
$E\subseteq G$
,
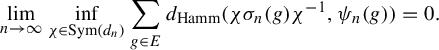 $$ \begin{align*}\lim_{n\to\infty}\inf_{\chi\in {\operatorname{Sym}}(d_{n})}\sum_{g\in E}d_{\operatorname{\mathrm{Hamm}}}(\chi\sigma_{n}(g)\chi^{-1},\psi_{n}(g))=0.\end{align*} $$
$$ \begin{align*}\lim_{n\to\infty}\inf_{\chi\in {\operatorname{Sym}}(d_{n})}\sum_{g\in E}d_{\operatorname{\mathrm{Hamm}}}(\chi\sigma_{n}(g)\chi^{-1},\psi_{n}(g))=0.\end{align*} $$
If this does not hold, then there is an increasing sequence
![]() $n_{1}<n_{2}<\cdots $
and an
$n_{1}<n_{2}<\cdots $
and an
![]() $\varepsilon>0$
with
$\varepsilon>0$
with
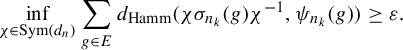 $$ \begin{align*}\inf_{\chi\in {\operatorname{Sym}}(d_{n})}\sum_{g\in E}d_{\operatorname{\mathrm{Hamm}}}(\chi\sigma_{n_{k}}(g)\chi^{-1},\psi_{n_{k}}(g))\geq \varepsilon.\end{align*} $$
$$ \begin{align*}\inf_{\chi\in {\operatorname{Sym}}(d_{n})}\sum_{g\in E}d_{\operatorname{\mathrm{Hamm}}}(\chi\sigma_{n_{k}}(g)\chi^{-1},\psi_{n_{k}}(g))\geq \varepsilon.\end{align*} $$
Let
![]() $\omega \in \beta {\mathbb N}\setminus {\mathbb N}$
with
$\omega \in \beta {\mathbb N}\setminus {\mathbb N}$
with
![]() $\{n_{k}:k\in {\mathbb N}\}\in \omega .$
By Corollary 5.2 and our hypothesis, we see
$\{n_{k}:k\in {\mathbb N}\}\in \omega .$
By Corollary 5.2 and our hypothesis, we see
![]() $(\sigma _{\omega }),(\psi _{\omega })$
are conjugate. Then there is a
$(\sigma _{\omega }),(\psi _{\omega })$
are conjugate. Then there is a
![]() $\chi =(\chi _{n})_{n\to \omega }\in \prod _{n\to \omega }({\operatorname {Sym}}(d_{n}),d_{\operatorname {\mathrm {Hamm}}})$
so that
$\chi =(\chi _{n})_{n\to \omega }\in \prod _{n\to \omega }({\operatorname {Sym}}(d_{n}),d_{\operatorname {\mathrm {Hamm}}})$
so that
![]() $\chi \sigma _{\omega }(g)\chi ^{-1}=\psi _{\omega }(g)$
for all
$\chi \sigma _{\omega }(g)\chi ^{-1}=\psi _{\omega }(g)$
for all
![]() $g\in G$
.
$g\in G$
.
In particular,
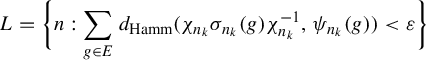 $$ \begin{align*}L=\bigg\{n:\sum_{g\in E}d_{\operatorname{\mathrm{Hamm}}}(\chi_{n_{k}}\sigma_{n_{k}}(g)\chi_{n_{k}}^{-1},\psi_{n_{k}}(g))<\varepsilon\bigg\}\end{align*} $$
$$ \begin{align*}L=\bigg\{n:\sum_{g\in E}d_{\operatorname{\mathrm{Hamm}}}(\chi_{n_{k}}\sigma_{n_{k}}(g)\chi_{n_{k}}^{-1},\psi_{n_{k}}(g))<\varepsilon\bigg\}\end{align*} $$
is in
![]() $\omega $
and by our choice of
$\omega $
and by our choice of
![]() $n_{k},\omega $
, it follows that
$n_{k},\omega $
, it follows that
![]() $L\in \omega ^{c}$
. This contradicts
$L\in \omega ^{c}$
. This contradicts
![]() $\omega $
being a filter.
$\omega $
being a filter.
We remark that our proof of item (1) goes through the fact that for a group G, any
![]() $\Theta \in \operatorname {\mathrm {IRS}}(G)$
is uniquely determined by
$\Theta \in \operatorname {\mathrm {IRS}}(G)$
is uniquely determined by
thus the data of the IRS and those of the action trace as given in [Reference Arzhantseva and Păunescu5] are the same.
At this stage, we need the following two propositions for additional applications. Recall that if
![]() $\sigma _{n}\colon G\to {\operatorname {Sym}}(d_{n})$
is a sofic approximation and there is a
$\sigma _{n}\colon G\to {\operatorname {Sym}}(d_{n})$
is a sofic approximation and there is a
![]() $\Theta \in \operatorname {\mathrm {Sub}}(G)$
with
$\Theta \in \operatorname {\mathrm {Sub}}(G)$
with
![]() $\operatorname {\mathrm {IRS}}(\sigma _{\omega })=\Theta $
for all
$\operatorname {\mathrm {IRS}}(\sigma _{\omega })=\Theta $
for all
![]() $\omega \in \beta {\mathbb N}\setminus {\mathbb N}$
, then we say that
$\omega \in \beta {\mathbb N}\setminus {\mathbb N}$
, then we say that
![]() $(\sigma _{n})_{n}$
has stabilizer type
$(\sigma _{n})_{n}$
has stabilizer type
![]() $\Theta $
. Recall that we do not define stabilizer type if
$\Theta $
. Recall that we do not define stabilizer type if
![]() $\operatorname {\mathrm {IRS}}(\sigma _{\omega })$
is different for different choices of
$\operatorname {\mathrm {IRS}}(\sigma _{\omega })$
is different for different choices of
![]() $\omega $
.
$\omega $
.
Proposition 5.3. Let G be a sofic group and
![]() $\sigma _{n}\colon G\to {\operatorname {Sym}}(d_{n})$
approximate homomorphisms with stabilizer type
$\sigma _{n}\colon G\to {\operatorname {Sym}}(d_{n})$
approximate homomorphisms with stabilizer type
![]() $\Theta \in \operatorname {\mathrm {IRS}}(G)$
.
$\Theta \in \operatorname {\mathrm {IRS}}(G)$
.
-
(i) If
 $\widetilde {\sigma }_{n}\colon G\to {\operatorname {Sym}}(d_{n})$
are maps so that then
$\widetilde {\sigma }_{n}\colon G\to {\operatorname {Sym}}(d_{n})$
are maps so that then $$ \begin{align*}\lim_{n\to\infty}d_{\operatorname{\mathrm{Hamm}}}(\sigma_{n}(g),\widetilde{\sigma}_{n}(g))=0,\quad \text{for all } g\in G,\end{align*} $$
$$ \begin{align*}\lim_{n\to\infty}d_{\operatorname{\mathrm{Hamm}}}(\sigma_{n}(g),\widetilde{\sigma}_{n}(g))=0,\quad \text{for all } g\in G,\end{align*} $$
 $\widetilde {\sigma }_{n}$
are approximate homomorphisms with stabilizer type
$\widetilde {\sigma }_{n}$
are approximate homomorphisms with stabilizer type
 $\Theta $
.
$\Theta $
.
-
(ii) If
 $(q_{n})_{n=1}^{\infty }$
is any sequence of integers, then given by
$(q_{n})_{n=1}^{\infty }$
is any sequence of integers, then given by $$ \begin{align*}\sigma_{n}^{\oplus q_{n}}\colon G\to {\operatorname{Sym}}(\{1,\ldots,d_{n}\}\times \{1,\ldots, q_{n}\})\end{align*} $$
$$ \begin{align*}\sigma_{n}^{\oplus q_{n}}\colon G\to {\operatorname{Sym}}(\{1,\ldots,d_{n}\}\times \{1,\ldots, q_{n}\})\end{align*} $$
 $\sigma _{n}^{\oplus q_{n}}(g)(j,r)=(\sigma _{n}(g)(j),r)$
are approximate homomorphisms with stabilizer type
$\sigma _{n}^{\oplus q_{n}}(g)(j,r)=(\sigma _{n}(g)(j),r)$
are approximate homomorphisms with stabilizer type
 $\Theta $
.
$\Theta $
.
-
(iii) If
 $(r_{n})_{n}$
is any sequence of integers so that
$(r_{n})_{n}$
is any sequence of integers so that
 $({r_{n}}/{d_{n}})\to 0$
, define
$({r_{n}}/{d_{n}})\to 0$
, define
 $\sigma _{n}\oplus t_{r_{n}}\colon G\to {\operatorname {Sym}}(d_{n}+r_{n})$
by then
$\sigma _{n}\oplus t_{r_{n}}\colon G\to {\operatorname {Sym}}(d_{n}+r_{n})$
by then $$ \begin{align*} (\sigma_{n}\oplus t_{r_{n}})(g)(j)=\begin{cases} \sigma_{n}(g)(j) \text{ if } 1\leq j\leq d_{n}\\ j \text{ if } d_{n}+1\leq j\leq d_{n}+r_{n}\!\!\! \end{cases}\!\!\!{,} \end{align*} $$
$$ \begin{align*} (\sigma_{n}\oplus t_{r_{n}})(g)(j)=\begin{cases} \sigma_{n}(g)(j) \text{ if } 1\leq j\leq d_{n}\\ j \text{ if } d_{n}+1\leq j\leq d_{n}+r_{n}\!\!\! \end{cases}\!\!\!{,} \end{align*} $$
 $\sigma _{n}\oplus t_{r_{n}}$
are approximate homomorphisms with stabilizer type
$\sigma _{n}\oplus t_{r_{n}}$
are approximate homomorphisms with stabilizer type
 $\Theta $
.
$\Theta $
.
-
(iv) If
 $s\colon {\mathbb N}\to {\mathbb N}$
is any function so that then
$s\colon {\mathbb N}\to {\mathbb N}$
is any function so that then $$ \begin{align*}\lim_{n\to\infty}s(n)=+\infty,\end{align*} $$
$$ \begin{align*}\lim_{n\to\infty}s(n)=+\infty,\end{align*} $$
 $\sigma _{s(n)}$
are approximate homomorphisms with stabilizer type
$\sigma _{s(n)}$
are approximate homomorphisms with stabilizer type
 $\Theta $
.
$\Theta $
.
Proof. These are all exercises.
We also need the following analogue of [Reference Arzhantseva and Păunescu4, Proposition 6.1], which is proved exactly as in [Reference Becker, Lubotzky and Thom7, Lemma 7.6] using Proposition 5.3.
Proposition 5.4. Let G be a countable discrete group and
![]() $\Theta \in \operatorname {\mathrm {IRS}}(G)$
. Suppose there is a sequence of integers
$\Theta \in \operatorname {\mathrm {IRS}}(G)$
. Suppose there is a sequence of integers
![]() $k_{n}$
with
$k_{n}$
with
![]() $k_{n}\to \infty $
and approximate homomorphisms
$k_{n}\to \infty $
and approximate homomorphisms
![]() $\psi _{n}\colon G\to {\operatorname {Sym}}(k_{n})$
with stabilizer type
$\psi _{n}\colon G\to {\operatorname {Sym}}(k_{n})$
with stabilizer type
![]() $\Theta $
. Then for any sequence of integers
$\Theta $
. Then for any sequence of integers
![]() $d_{n}\to \infty $
, there are approximate homomorphisms
$d_{n}\to \infty $
, there are approximate homomorphisms
![]() $\sigma _{n}\colon G\to {\operatorname {Sym}}(d_{n})$
with stabilizer type
$\sigma _{n}\colon G\to {\operatorname {Sym}}(d_{n})$
with stabilizer type
![]() $\Theta $
.
$\Theta $
.
We now have the tools to explain why Theorem 5.1 implies [Reference Becker, Lubotzky and Thom7, Theorem 1.3].
Corollary 5.5. [Reference Becker, Lubotzky and Thom7, Theorem 1.3]
Let G be an amenable group. Then G is permutation stable if and only if for every
![]() $\Theta \in \operatorname {\mathrm {IRS}}(G)$
, there is a sequence of positive integers
$\Theta \in \operatorname {\mathrm {IRS}}(G)$
, there is a sequence of positive integers
![]() $(d_{n})_{n}$
and a sequence of homomorphism
$(d_{n})_{n}$
and a sequence of homomorphism
![]() $\kappa _{n}\colon G\to {\operatorname {Sym}}(d_{n})$
with
$\kappa _{n}\colon G\to {\operatorname {Sym}}(d_{n})$
with
![]() $({\operatorname {Stab}}_{\kappa _{n}})_{*}(u_{d_{n}})\to _{n\to \infty }\Theta $
in the weak
$({\operatorname {Stab}}_{\kappa _{n}})_{*}(u_{d_{n}})\to _{n\to \infty }\Theta $
in the weak
![]() $^{*}$
-topology. Here
$^{*}$
-topology. Here
![]() ${\operatorname {Stab}}_{\kappa _{n}}$
is the map
${\operatorname {Stab}}_{\kappa _{n}}$
is the map
![]() $j\mapsto \{g\in G:\kappa _{n}(g)(j)=j\}$
.
$j\mapsto \{g\in G:\kappa _{n}(g)(j)=j\}$
.
Proof. First suppose that for every
![]() $\Theta \in \operatorname {\mathrm {IRS}}(G)$
, there is a sequence of positive integers
$\Theta \in \operatorname {\mathrm {IRS}}(G)$
, there is a sequence of positive integers
![]() $(d_{n})_{n}$
and a sequence of homomorphisms
$(d_{n})_{n}$
and a sequence of homomorphisms
![]() $\kappa _{n}\colon G\to {\operatorname {Sym}}(d_{n})$
with
$\kappa _{n}\colon G\to {\operatorname {Sym}}(d_{n})$
with
![]() $({\operatorname {Stab}}_{\kappa _{n}})_{*}(u_{d_{n}})\to _{n\to \infty }\Theta $
in the weak
$({\operatorname {Stab}}_{\kappa _{n}})_{*}(u_{d_{n}})\to _{n\to \infty }\Theta $
in the weak
![]() $^{*}$
-topology. Let
$^{*}$
-topology. Let
![]() $\sigma _{n}\colon G\to {\operatorname {Sym}}(k_{n})$
be asymptotic homomorphisms, and fix
$\sigma _{n}\colon G\to {\operatorname {Sym}}(k_{n})$
be asymptotic homomorphisms, and fix
![]() $\omega \in \beta {\mathbb N}\setminus {\mathbb N}$
. Let
$\omega \in \beta {\mathbb N}\setminus {\mathbb N}$
. Let
![]() $\Theta =\operatorname {\mathrm {IRS}}(\sigma _{\omega })$
. By assumption, we can find a sequence of homomorphisms
$\Theta =\operatorname {\mathrm {IRS}}(\sigma _{\omega })$
. By assumption, we can find a sequence of homomorphisms
![]() $\kappa _{n}\colon G\to {\operatorname {Sym}}(d_{n})$
with
$\kappa _{n}\colon G\to {\operatorname {Sym}}(d_{n})$
with
![]() $({\operatorname {Stab}}_{\kappa _{n}})_{*}(u_{d_{n}})\to _{n\to \infty }\Theta $
in the weak
$({\operatorname {Stab}}_{\kappa _{n}})_{*}(u_{d_{n}})\to _{n\to \infty }\Theta $
in the weak
![]() $^{*}$
-topology. By Proposition 5.4, we may assume that
$^{*}$
-topology. By Proposition 5.4, we may assume that
![]() $d_{n}=k_{n}$
. Set
$d_{n}=k_{n}$
. Set
![]() $\kappa _{\omega }=(\kappa _{n})_{n\to \omega }$
. Then by Theorem 5.1,
$\kappa _{\omega }=(\kappa _{n})_{n\to \omega }$
. Then by Theorem 5.1,
![]() $\sigma _{\omega },\kappa _{\omega }$
are conjugate. Since
$\sigma _{\omega },\kappa _{\omega }$
are conjugate. Since
![]() $\omega $
was arbitrary, this implies that there is a sequence of permutations
$\omega $
was arbitrary, this implies that there is a sequence of permutations
![]() $\chi _{n}\in {\operatorname {Sym}}(d_{n})$
with
$\chi _{n}\in {\operatorname {Sym}}(d_{n})$
with
Since
![]() $g\mapsto \chi _{n}\kappa _{n}(g)\chi _{n}^{-1}$
are homomorphisms, this proves that G is permutation stable.
$g\mapsto \chi _{n}\kappa _{n}(g)\chi _{n}^{-1}$
are homomorphisms, this proves that G is permutation stable.
Now suppose that G is permutation stable. Let
![]() $\Theta \in \operatorname {\mathrm {IRS}}(G)$
, and choose an action
$\Theta \in \operatorname {\mathrm {IRS}}(G)$
, and choose an action
![]() $G\,{\curvearrowright }\, (X,\nu )$
with
$G\,{\curvearrowright }\, (X,\nu )$
with
![]() ${\operatorname {Stab}}_{*}(\nu )=\Theta $
(e.g. the
${\operatorname {Stab}}_{*}(\nu )=\Theta $
(e.g. the
![]() $\Theta $
-Bernoulli action of G with base
$\Theta $
-Bernoulli action of G with base
![]() $([0,1],m)$
). Let
$([0,1],m)$
). Let
![]() ${\mathcal R}$
be the orbit equivalence relation of
${\mathcal R}$
be the orbit equivalence relation of
![]() $G\,{\curvearrowright }\, (X,\nu )$
. Since G is amenable, [Reference Ornstein and Weiss40], [Reference Ornstein and Weiss41, II §3] (see also [Reference Connes, Feldman and Weiss15]) imply that
$G\,{\curvearrowright }\, (X,\nu )$
. Since G is amenable, [Reference Ornstein and Weiss40], [Reference Ornstein and Weiss41, II §3] (see also [Reference Connes, Feldman and Weiss15]) imply that
![]() ${\mathcal R}$
is hyperfinite and thus sofic (see e.g. [Reference Păunescu42, Proposition 3.4]). By Proposition 3.6, this implies that for every free ultrafilter
${\mathcal R}$
is hyperfinite and thus sofic (see e.g. [Reference Păunescu42, Proposition 3.4]). By Proposition 3.6, this implies that for every free ultrafilter
![]() $\omega $
, we may find a trace-preserving homomorphism
$\omega $
, we may find a trace-preserving homomorphism
such that
![]() $\pi (L^{\infty }(X))\subseteq L^{\infty }({\mathcal L})$
and
$\pi (L^{\infty }(X))\subseteq L^{\infty }({\mathcal L})$
and
![]() $\pi ([{\mathcal R}])\subseteq {\mathcal S}$
. For
$\pi ([{\mathcal R}])\subseteq {\mathcal S}$
. For
![]() $g\in G$
, let
$g\in G$
, let
![]() $p_{g}=1_{\operatorname {\mathrm {Fix}}(g)}\in L^{\infty }(X)$
and apply [Reference Anantharaman Delaroche and Popa3, Lemma 5.4.2(i)] to find
$p_{g}=1_{\operatorname {\mathrm {Fix}}(g)}\in L^{\infty }(X)$
and apply [Reference Anantharaman Delaroche and Popa3, Lemma 5.4.2(i)] to find
![]() $B_{g,n}\subseteq \{1,\ldots ,d_{n}\}$
with
$B_{g,n}\subseteq \{1,\ldots ,d_{n}\}$
with
![]() $\pi (p_{g})=(1_{B_{g,n}})_{n\to \omega }$
. For
$\pi (p_{g})=(1_{B_{g,n}})_{n\to \omega }$
. For
![]() $g\in G$
, let
$g\in G$
, let
![]() $\pi (\unicode{x3bb} (g))=(\sigma _{n}(g))_{n\to \omega }$
. We first note the following.
$\pi (\unicode{x3bb} (g))=(\sigma _{n}(g))_{n\to \omega }$
. We first note the following.
Claim.
![]() $u_{d_{n}}(B_{g,n}\Delta \operatorname {\mathrm {Fix}}(\sigma _{n}(g)))\to _{n\to \omega }0$
for every
$u_{d_{n}}(B_{g,n}\Delta \operatorname {\mathrm {Fix}}(\sigma _{n}(g)))\to _{n\to \omega }0$
for every
![]() $g\in G$
. To prove the claim, note that
$g\in G$
. To prove the claim, note that
Let
![]() $p_{g,n}=1_{B_{g,n}}\in \ell ^{\infty }(d_{n})$
which we view as a subset of
$p_{g,n}=1_{B_{g,n}}\in \ell ^{\infty }(d_{n})$
which we view as a subset of
![]() $M_{n}({\mathbb C}).$
Thus,
$M_{n}({\mathbb C}).$
Thus,
the last part following as
![]() $\sigma _{n}$
is a sofic approximation and
$\sigma _{n}$
is a sofic approximation and
![]() $\unicode{x3bb} (g)p_{g}=p_{g}$
. However,
$\unicode{x3bb} (g)p_{g}=p_{g}$
. However,
the second-to-last part following as
![]() $\sigma _{n}$
is a sofic approximation. This proves the claim.
$\sigma _{n}$
is a sofic approximation. This proves the claim.
For
![]() $F\subseteq G$
, let
$F\subseteq G$
, let
![]() $\mathcal {E}_{F}\in C(\operatorname {\mathrm {Sub}}(G))$
be the indicator function of
$\mathcal {E}_{F}\in C(\operatorname {\mathrm {Sub}}(G))$
be the indicator function of
![]() $\{H:F\subseteq H\}$
. The claim similarly implies that for
$\{H:F\subseteq H\}$
. The claim similarly implies that for
![]() $F\subseteq G$
is finite if
$F\subseteq G$
is finite if
![]() $\pi ({\mathcal E}_{F})=(1_{B_{F,n}})_{n\to \omega }$
, then
$\pi ({\mathcal E}_{F})=(1_{B_{F,n}})_{n\to \omega }$
, then
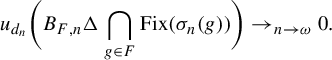 $$ \begin{align*}u_{d_{n}}\bigg(B_{F,n}\Delta\bigcap_{g\in F}\operatorname{\mathrm{Fix}}(\sigma_{n}(g))\bigg)\to_{n\to\omega}0.\end{align*} $$
$$ \begin{align*}u_{d_{n}}\bigg(B_{F,n}\Delta\bigcap_{g\in F}\operatorname{\mathrm{Fix}}(\sigma_{n}(g))\bigg)\to_{n\to\omega}0.\end{align*} $$
Setting
![]() $\varsigma _{F,n}=\bigcap _{g\in F}\operatorname {\mathrm {Fix}}(\sigma _{n}(g))$
, we then have
$\varsigma _{F,n}=\bigcap _{g\in F}\operatorname {\mathrm {Fix}}(\sigma _{n}(g))$
, we then have
![]() $\pi ({\mathcal E}_{F})=(1_{\varsigma _{F,n}})_{n\to \omega }$
. Since G is permutation stable, we may find honest homomorphisms
$\pi ({\mathcal E}_{F})=(1_{\varsigma _{F,n}})_{n\to \omega }$
. Since G is permutation stable, we may find honest homomorphisms
![]() $\kappa _{n}\colon G\to {\operatorname {Sym}}(n)$
so that
$\kappa _{n}\colon G\to {\operatorname {Sym}}(n)$
so that
![]() $\sigma \circ \Xi =(\kappa _{n})_{n\to \omega }$
, where
$\sigma \circ \Xi =(\kappa _{n})_{n\to \omega }$
, where
![]() $\Xi \colon G\to [{\mathcal R}]$
is the map
$\Xi \colon G\to [{\mathcal R}]$
is the map
![]() $\Xi (g)(x)=gx$
. So for any finite
$\Xi (g)(x)=gx$
. So for any finite
![]() $F\subseteq G$
,
$F\subseteq G$
,
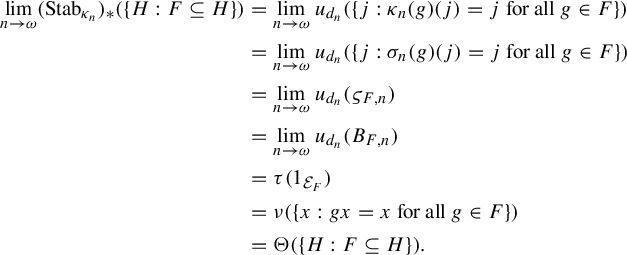 $$ \begin{align*} \lim_{n\to\omega}({\operatorname{Stab}}_{\kappa_{n}})_{*}(\{H:F\subseteq H\})&=\lim_{n\to\omega}u_{d_{n}}(\{j:\kappa_{n}(g)(j)=j \text{ for all } g\in F\})\\ &=\lim_{n\to\omega}u_{d_{n}}(\{j:\sigma_{n}(g)(j)=j \text{ for all } g\in F\})\\ &=\lim_{n\to\omega}u_{d_{n}}(\varsigma_{F,n})\\ &=\lim_{n\to\omega}u_{d_{n}}(B_{F,n})\\ &=\tau(1_{{\mathcal E}_{F}})\\ &=\nu(\{x:gx=x \text{ for all } g\in F\})\\ &=\Theta(\{H:F\subseteq H\}). \end{align*} $$
$$ \begin{align*} \lim_{n\to\omega}({\operatorname{Stab}}_{\kappa_{n}})_{*}(\{H:F\subseteq H\})&=\lim_{n\to\omega}u_{d_{n}}(\{j:\kappa_{n}(g)(j)=j \text{ for all } g\in F\})\\ &=\lim_{n\to\omega}u_{d_{n}}(\{j:\sigma_{n}(g)(j)=j \text{ for all } g\in F\})\\ &=\lim_{n\to\omega}u_{d_{n}}(\varsigma_{F,n})\\ &=\lim_{n\to\omega}u_{d_{n}}(B_{F,n})\\ &=\tau(1_{{\mathcal E}_{F}})\\ &=\nu(\{x:gx=x \text{ for all } g\in F\})\\ &=\Theta(\{H:F\subseteq H\}). \end{align*} $$
As in Corollary 5.2, this implies that
![]() $\lim _{n\to \omega }({\operatorname {Stab}}_{\kappa _{n}})_{*}(u_{n})=\Theta .$
Since this holds for all
$\lim _{n\to \omega }({\operatorname {Stab}}_{\kappa _{n}})_{*}(u_{n})=\Theta .$
Since this holds for all
![]() $\omega $
, we may find a sequence of honest homomorphisms
$\omega $
, we may find a sequence of honest homomorphisms
![]() $\kappa _{n}\colon G\to {\operatorname {Sym}}(n)$
with
$\kappa _{n}\colon G\to {\operatorname {Sym}}(n)$
with
The proof of the reverse implication given above is similar to that in [Reference Arzhantseva and Păunescu5, Proposition 3.15].
Acknowledgements
The authors thank Andreas Thom and Liviu Păunescu for helpful comments on an earlier version of this paper. B.H. gratefully acknowledges support from the NSF grant DMS-2144739. S.K.E. gratefully acknowledges support from the Simons Postdoctoral Fellowship. Both authors thank the anonymous referee for their numerous comments, which greatly improved the paper.









