Article contents
Conformal blocks for Galois covers of algebraic curves
Published online by Cambridge University Press: 29 August 2023
Abstract
We study the spaces of twisted conformal blocks attached to a 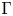 $\Gamma$-curve
$\Gamma$-curve 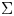 $\Sigma$ with marked
$\Sigma$ with marked 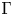 $\Gamma$-orbits and an action of
$\Gamma$-orbits and an action of 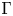 $\Gamma$ on a simple Lie algebra
$\Gamma$ on a simple Lie algebra  $\mathfrak {g}$, where
$\mathfrak {g}$, where 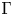 $\Gamma$ is a finite group. We prove that if
$\Gamma$ is a finite group. We prove that if 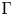 $\Gamma$ stabilizes a Borel subalgebra of
$\Gamma$ stabilizes a Borel subalgebra of 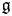 $\mathfrak {g}$, then the propagation theorem and factorization theorem hold. We endow a flat projective connection on the sheaf of twisted conformal blocks attached to a smooth family of pointed
$\mathfrak {g}$, then the propagation theorem and factorization theorem hold. We endow a flat projective connection on the sheaf of twisted conformal blocks attached to a smooth family of pointed 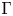 $\Gamma$-curves; in particular, it is locally free. We also prove that the sheaf of twisted conformal blocks on the stable compactification of Hurwitz stack is locally free. Let
$\Gamma$-curves; in particular, it is locally free. We also prove that the sheaf of twisted conformal blocks on the stable compactification of Hurwitz stack is locally free. Let 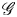 $\mathscr {G}$ be the parahoric Bruhat–Tits group scheme on the quotient curve
$\mathscr {G}$ be the parahoric Bruhat–Tits group scheme on the quotient curve 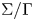 $\Sigma /\Gamma$ obtained via the
$\Sigma /\Gamma$ obtained via the 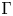 $\Gamma$-invariance of Weil restriction associated to
$\Gamma$-invariance of Weil restriction associated to 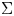 $\Sigma$ and the simply connected simple algebraic group
$\Sigma$ and the simply connected simple algebraic group 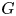 $G$ with Lie algebra
$G$ with Lie algebra 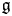 $\mathfrak {g}$. We prove that the space of twisted conformal blocks can be identified with the space of generalized theta functions on the moduli stack of quasi-parabolic
$\mathfrak {g}$. We prove that the space of twisted conformal blocks can be identified with the space of generalized theta functions on the moduli stack of quasi-parabolic 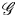 $\mathscr {G}$-torsors on
$\mathscr {G}$-torsors on 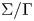 $\Sigma /\Gamma$ when the level
$\Sigma /\Gamma$ when the level 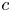 $c$ is divisible by
$c$ is divisible by  $|\Gamma |$ (establishing a conjecture due to Pappas and Rapoport).
$|\Gamma |$ (establishing a conjecture due to Pappas and Rapoport).
Keywords
MSC classification
- Type
- Research Article
- Information
- Copyright
- © 2023 The Author(s). The publishing rights in this article are licensed to Foundation Compositio Mathematica under an exclusive licence
References
- 3
- Cited by



