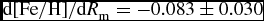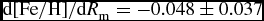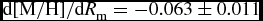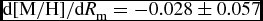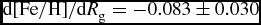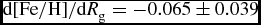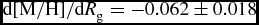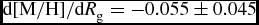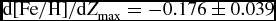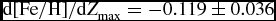1 INTRODUCTION
Metallicity gradient is one of the tools used for understanding the structure, formation, and evolution of the Milky Way Galaxy. Systematic sky surveys, which use photometric, astrometric, and spectroscopic observations, are needed to reveal the metallicity gradients of the Milky Way. These surveys are used to determine the atmospheric model parameters and kinematic properties of a large number of objects simultaneously. Specifically, Genova-Copenhagen Survey (GCS; Nordström et al., Reference Nordström2004), RAdial Velocity Experiment (RAVE; Steinmetz et al., Reference Steinmetz2006), Sloan Extension for Galactic Understanding and Exploration (SEGUE; Yanny et al., Reference Yanny2009), the Large Sky Area Multi-Object Fiber Spectroscopic Telescope (LAMOST; Deng et al., Reference Deng2012; Zhao et al., Reference Zhao, Zhao, Chu, Jing and Deng2012), and the Gaia-ESO Spectroscopic Survey (Gilmore et al., Reference Gilmore2012) are among the most useful systematic sky surveys. In order to estimate the metallicity gradient in any direction, distances of the objects in question must be known. Different objects such as F and G type main-sequence stars (dwarfs), red clump stars, open and globular clusters, and cepheids have been used for this purpose, for which the distances can be accurately estimated. The metallicity gradients are estimated either vertically or in the Galactocentric radial direction. The radial metallicity gradients, 
$\text{d}[\text{M}/\text{H}]/\text{d}{R}$, in different vertical distance (z) intervals from the Galactic plane have been presented in the previous studies. A metallicity gradient often indicates the inward-outside formation of the Galactic part in question, such as the thin disc (Matteucci & Francois, Reference Matteucci and Francois1989; Chiappini, Matteucci, & Gratton, Reference Chiappini, Matteucci and Gratton1997; Cescutti et al., Reference Cescutti, Matteucci, Francois and Chiappini2007; Pilkington et al., Reference Pilkington2012). However, Schönrich & Binney (Reference Schönrich and Binney2009) showed that an inward-outside formation is not necessary for a metallicity gradient.
The vertical and radial distances of a star sample can be estimated for its observed position, or they can be obtained from its possible Galactic orbit as determined using the Milky Way potential (Section 2). Usually, we use the z and R symbols for the observed vertical and radial distances, respectively, while Z max, Z min, and 
$R_{\text{m}}$ are the maximum and minimum distances of a star to the Galactic plane, and the mean Galactocentric radial distance, respectively. R m is defined as R m = (R p + R a)/2, where R p and R a are the perigalactic and apogalactic distances, respectively. The scale of the R distances for the objects such as giants can be used in the metallicity gradient evaluations. However, this parameter as well as Z may not represent the birth place of a star, due to its large orbital eccentricity. For dwarfs, the orbital parameters Z max and R m had to be used in order to extend the scale in the vertical and radial distances. However, in this case, we cannot avoid a bias as explained below: Only stars with large orbital eccentricities among a sample of small R m distances can reach to the solar circle. But, such stars are metal-poor relative to the ones on the circular orbits with the same R m radial distances which cannot reach to the solar circle. Thus, the number of the metal-rich stars at the solar circle decreases. This is a bias against metal-rich stars with small R m radial distances (Boeche et al., Reference Boeche2014).
The researchers found iron metallicities in the range 
$-0.17\le \text{d}[\text{Fe}/\text{H}]/\text{d}R\le -0.06$ dex kpc−1 for the Galactic thin disc. The value at the left is estimated by Sestito et al. (Reference Sestito, Bragaglia, Randich, Pallavicini, Andrievsky and Korotin2008) with open clusters, while the right one—corresponds to the cepheids—appeared in Luck & Lambert (Reference Luck and Lambert2011). An iron metallicity gradient close to 
$\text{d}[\text{Fe}/\text{H}]/\text{d}R=-0.06$ dex kpc−1 can be found in recent studies which are based on the data from large surveys such as RAVE and SEGUE, i.e. Cheng et al. (Reference Cheng2012) and Boeche et al. (Reference Boeche2013, Reference Boeche2014). The radial metallicity gradients in these recent studies are given in different Z max intervals. In these studies, the radial metallicity gradient becomes less negative with increasing Z max and approach to zero or even to a positive value at the terminal vertical distance. It is assumed that the different numerical values of the radial metallicity gradient at large vertical distances are due to the different structure of the thick disc, i.e. the metallicity gradient of the thick disc is almost zero, if it exists (Ruchti et al., Reference Ruchti2011; Cheng et al., Reference Cheng2012; Coşkunoǧlu et al., Reference Coşkunoǧlu, Ak, Bilir, Karaali, Önal, Yaz, Gilmore and Seabroke2012; Bilir et al., Reference Bilir, Karaali, Ak, Önal, Daǧtekin, Yontan, Gilmore and Seabroke2012). Stars at different ages exhibit substantial differences in radial metallicity gradient (Schönrich & Binney, Reference Schönrich and Binney2009; Minchev, Chiappini, & Martig, Reference Minchev, Chiappini and Martig2013, Reference Minchev, Chiappini and Martig2014); hence, investigation of the metallicity gradients in narrow Z max intervals plays a limiting role on these differences. Actually, thin-disc stars concentrate close to the Galactic mid-plane as compared to the farther thick-disc stars, which are older than the thin-disc stars. We wish to refer the recent results on gradients from the SDSS APOGEE, as reported in Hayden et al. (Reference Hayden2014) and Anders et al. (Reference Anders2014). Hayden et al. (Reference Hayden2014) observed radial gradients as a function of |z| for a variation of sub-samples including low-α and high-α stars, while Anders et al. (Reference Anders2014) give a metallicity gradient of 
$\text{d}[\text{M}/\text{H}]/\text{d}{R}=-0.082\pm 0.002$ dex kpc−1 for their sample.
As stated above, different objects, which represent the structure of the interstellar gas at the time they were formed, are used in metallicity estimations. These objects therefore correspond to different metallicity gradients. However, the situation is not so simple as explained in the following text. Some processes such as the spiral structure, molecular clouds, or small aggregations causes a dynamical heating of the Galaxy which change the orbits of the objects in question (cf. Cheng et al., Reference Cheng2012). Radial mixing is another constraint which changes the original positions of the objects used in metallicity gradient estimations. The main processes related this constraint are the irregularities in the Galactic potential (Wielen, Reference Wielen1977; Wielen, Fuchs, & Dettbarn, Reference Wielen, Fuchs and Dettbarn1996; Haywood, Reference Haywood2008) and the passage of spiral patterns (Sellwood & Binney, Reference Sellwood and Binney2002; De Simone, Wu, & Tremaine, Reference De Simone, Wu and Tremaine2004; Minchev & Quillen, Reference Minchev and Quillen2006). As a result of the radial mixing, super metallicity stars (
$[\text{Fe}/\text{H}]>0.2$ dex) migrate from the inner part of the disc to the solar circle, while the metal-poor ones (
$-0.7<[\text{Fe}/\text{H}]<-0.3$ dex) change their formation place outside of the disc to the solar circle. Additionally, details about this constraint can be found in Haywood (Reference Haywood2008).
There are substantial differences between the kinematic and spectroscopic parameters of thin and thick discs. Although the observed parameters for the two types of discs are local records and do not cover the regions at remote distances, these differences have been used by researchers as clues to propose a different formation history for the thick disc. The zero (or close to this value) radial metallicity gradient for the thick disc is also an indication of a different formation scenario for the thick disc.
In this study, our main purpose is to investigate the metallicity gradients of the thin disc in two directions, i.e. vertically and in the Galactocentric direction. Two constraints are used to construct a thin-disc star sample: (i) we restrict the vertical distances of the sample stars with Z max ⩽ 825 pc, and (ii) we use only the stars with planar eccentricities e p ⩽ 0.10. The value Z max = 825 pc corresponds to the vertical distance where the space densities for the thin and thick discs are compatible, and by adopting a planar eccentricity less than 0.10 we aim to base our estimation on the stars at the solar circle. Thus, we expect less contamination from the thick-disc stars and from the stars migrated from the inner or outward regions of the disc. Eccentricity plays an effective role in discrimination of the thin and thick discs; in addition, it may vary within either of these populations with age. We investigated the metallicity gradient for stars on elongated orbits as well for comparison purposes. The paper is designed follows: Section 2 is devoted to the data, while the results and discussion are presented in Sections 3 and 4, respectively.
2 THE DATA
2.1 The sample
The sample consists of F and G type dwarfs selected from the recent RAVE Data Release 4 (DR4) database (Kordopatis et al., Reference Kordopatis2013) which are identified as explained. The temperature scale is limited to 5310 ⩽ T eff(K) ⩽ 7310 (Cox, Reference Cox and Cox2000). The surface gravities of the star sample are identified by the zero-age main sequence (ZAMS) and the terminal-age main sequence (TAMS) lines via mass tracks in the 
$\log T_{\text{eff}}$–logg plane as taken from Ekström et al. (Reference Ekström2012), who adopted the solar abundance as Z ⊙ = 0.014 (Figure 1). We assumed that stars satisfying the stated conditions are F and G type dwarfs. We omitted the stars with |b| ⩽ 10° to avoid high extinction. We used the E(B − V) colour excesses taken from Schlafly & Finkbeiner (Reference Schlafly and Finkbeiner2011) using IPACFootnote 1, which are more reliable than the RAVE ones for de-reddening the colours and magnitudes of the sample stars. The near-infrared (JHKs) magnitudes of the Two-Micron All Sky Survey (2MASS; Skrutskie et al., Reference Skrutskie2006) were taken from the 2MASS All-Sky Catalogue of Point Sources (Cutri et al., Reference Cutri2003). Next, we used the procedure in Bilir et al. (Reference Bilir, Karaali, Ak, Yaz, Cabrera-Lavers and Coşkunoǧlu2008) to estimate their MJ absolute magnitudes, which provide distances in combination with the true apparent J 0 magnitudes. The (J − H)0 vs. MJ colour-absolute magnitude diagram of the star sample (15 373 stars in total) thus obtained is given in Figure 2. The range and the median value of the colour excess for the star sample is 0 ⩽ E(B − V) ⩽ 0.25 and E(B − V) = 0.023 mag, respectively. The errors estimated for the apparent—and absolute—magnitudes are ΔJ ⩽ ±0.04 and ΔMJ = ±0.19 mag, respectively, which result an error of Δμ ~ ±0.20 mag in (J − MJ)o distance modulus.
Figure 1. The logT eff–logg diagram for the F and G type dwarfs identified by means of the mass tracks of Ekström et al. (Reference Ekström2012). Lower and upper bounds indicate the positions of ZAMS and TAMS.
Figure 2. (J − H)0 vs. MJ colour-absolute magnitude diagram of 15 373 F and G type dwarfs identified by means of the mass tracks of Ekström et al. (Reference Ekström2012).
The radial velocities (γ) of the sample stars are taken from the RAVE DR4 database. The radial velocities of about three dozen stars with an 
$\text{SNR}\sim$14 (signal-to-noise ratio) are rather large; hence, these stars were discarded from the sample. In addition, we also removed the stars beyond the ± 3σ (i.e. |γ| > 115 km s−1) limit of the radial velocities. Thus, the number of the sample stars was reduced to 14 927 with 
$\text{SNR}\ge 14$. The proper motions of the sample stars are those published in the RAVE DR4 database which contains the data in Tycho-2 (Hog et al., Reference Hog2000), UCAC2, UCAC3, UCAC4 (Zacharias et al., Reference Zacharias2004, Reference Zacharias2010, Reference Zacharias2013), PPMX, PPMXL (Roeser et al., Reference Roeser, Schilbach, Schwan, Kharchenko, Piskunov and Scholz2008; Roeser, Demleitner, & Schilbach, Reference Roeser, Demleitner and Schilbach2010), and SPM4 (Girard et al., Reference Girard2011).
The temperature scale of the sample stars, F and G dwarfs, is limited to 
$5310\le T_{\text{eff}}(\text{K})\le 7310$ (Cox, Reference Cox and Cox2000) and their surface gravities are identified by ZAMS and TAMS lines via mass tracks in the 
$\log T_{\text{eff}}\text{--}\log g$ plane, taken from Ekström et al. (Reference Ekström2012). We tested any probable bias in metallicity by comparing the metallicity distribution for the stars in our sample with the distribution for all dwarf stars in the effective temperature range 
$5\,310\le T_{{\rm eff}}(\text{K})\le 7\,310$ and surface gravity 4 ⩽ logg ⩽ 5. Our sample consists of 14 927 dwarfs, while the number of stars in the second sample, which are identified without any restriction for mass tracks, is 30 500. Our research indicated that the metallicity distributions in the two samples are Gaussian with compatible medians, 
$[\text{Fe}/\text{H}]= -0.04$ dex and 
$[\text{Fe}/\text{H}]=-0.02$ dex for our sample and for the second one, respectively, and their standard deviations are exactly equal at σ = 0.25 dex. Based on these results, we believe that there is no any significant metallicity bias in our sample.
Another argument that our sample is metallicity un-biased is that metallicity is weakly temperature dependent. Since distances of stars in our data set are not more than 800 pc (see Section 2.2), we conclude that the RAVE DR4 data in this study include the thin-disc main-sequence stars in the solar vicinity. Thus, the number of metal poor stars in the sample is negligible.
2.2 Space velocities and Galactic orbits
We combined the distances, radial velocities and proper motions detailed in Section 2.1 and applied the standard algorithms and transformation matrices of Johnson & Soderblom (Reference Johnson and Soderblom1987) to obtain their Galactic space velocity components, U, V and W. The procedure is explained in detail in Coşkunoǧlu et al. (Reference Coşkunoǧlu2011, Reference Coşkunoǧlu, Ak, Bilir, Karaali, Önal, Yaz, Gilmore and Seabroke2012). Here, we will give only the results we obtained. Correction for differential Galactic rotation is necessary for accurate determination of U, V, and W velocity components. We applied the procedure of Mihalas & Binney (Reference Mihalas and Binney1981) to the distribution of the sample stars and estimated the first-order Galactic differential corrections for the U and V velocity components of the sample stars. The velocity component W is not affected by Galactic differential rotation (Mihalas & Binney, Reference Mihalas and Binney1981). The range of the corrections is 
$-19.28\le \text{d}U\le 10.95$ and 
$-1.25\le \text{d}V\le 1.58$ km s−1 for U and V space velocity components, respectively.
The uncertainties in the space-velocity components U err, V err, and W err were computed by propagating the uncertainties in the proper motions, distances, and radial velocities via an algorithm described by Johnson & Soderblom (Reference Johnson and Soderblom1987). The median values and the standard deviations for the errors of the velocity components are (Ũerr, Ṽerr, 
err)=(1.82 ± 0.98, 1.85 ± 0.99, 1.82 ± 0.86) km s−1. Next, the error for the total space motion of a star follows from the equation:
$$\begin{equation}
S_{{\rm err}}^{2}=U_{{\rm err}}^{2}+V_{{\rm err}}^{2}+W_{{\rm err}}^{2}.
\end{equation}$$
err = 3.37 and σ = 2.67 km s−1, respectively. We applied a final constraint to obtain to the space velocity error to determine the stars with high precision. We rejected stars with errors beyond median value plus 2σ of the total space velocity error, err ⩾ 8.71 km s−1, reducing the sample to 14 361 stars which is 96% of the former sample size. The median values of the rectangular solar centred coordinates of the sample stars are X = Y = Z = 0 pc. Although the distances of the sample stars lie up to about 900 pc, the number of distant stars is small and the median of the whole sample is only 276 pc (Figure 3).
Figure 3. Distance histogram for the final 14361 dwarfs where (a) shows cumulative sample and (b) the number of stars.
To determine a possible orbit for a given sample star, we performed test-particle integration in a Milky Way potential consisting of three components: halo, disc, and bulge potentials. We used MWpotential2014 code of Bovy (Reference Bovy2015) to calculate the Galactic orbit parameters of the sample stars. The parameters and properties of the Galactic components were taken from the Table 1 of Bovy (Reference Bovy2015). The orbital parameters used in this study are Z max: maximum distance to the Galactic plane, 
$R_{\text{a}}$ and 
$R_{\text{p}}$: apogalactic and perigalactic radial distances, $R_{\text{m}}$: the arithmetic mean of $R_{\text{a}}$ and $R_{\text{p}}$, 
$R_{\text{m}}=(R_{\rm a}+R_{\rm p})/2$, and e p: the planar eccentricity defined as e p = (R a − R p)/(R a + R p). The orbital parameters of the sample stars were calculated within the integration time of 3 Gyr. This integration time corresponds to about 15 revolutions around the Galactic centre, so that the average orbital parameters can be determined reliably.
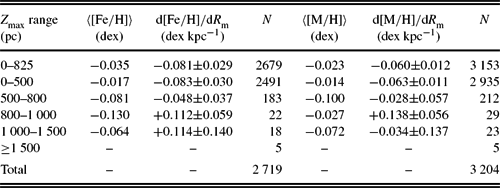
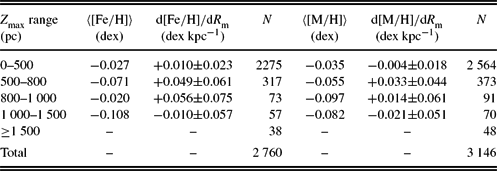
Table 1. Radial iron and metallicity gradients for the F and G type dwarfs on circular orbits, e p ⩽ 0.10, for different Z max intervals. N indicates the number of stars. Signal to noise ratio is 
$\text{S/N}\ge 40$.
2.3 Population types of the sample stars
We adopted the procedure detailed in Ak et al. (Reference Ak, Bilir, Özdönmez, Soydugan, Soydugan, Püsküllü, Ak and Eker2015) to separate the sample stars into different populations. Thus, stars with Z max ⩽ 825 pc are assumed to be thin-disc stars, while those with Z max > 825 pc are categorised as thick disc or perhaps halo stars. The above procedure is based on the Monte Carlo simulations with a wide range of a set of Galactic model parameters, i.e. local space density of the thick disc 
$0\le n_{\text{TK}} \le 15\%$, and exponential scale height of the thin and thick discs 200 
$\le H_{\text{TN}}\le$ 350 pc and 500 
$\le H_{\text{TK}}\le$ 1 500 pc, respectively. The numerical value Z max = 825 pc is in agreement with the those previously appeared in the related research, (i.e. Ojha et al., Reference Ojha, Bienaymé, Mohan and Robin1999; Siegel et al., Reference Siegel, Majewski, Reid and Thompson2002; Karaali, Bilir, & Hamzaoğlu, Reference Karaali, Bilir and Hamzaoğlu2004; Bilir, Karaali, & Gilmore, Reference Bilir, Karaali and Gilmore2006); hence, it is robust. We are aware that there is some discussion in the literature whether a distinct two-component disc is a good description of our Galaxy. In any case, stars close to the Galactic mid-plane belong to the thin disc defined in situ via the spatial distribution of the Galactic components. However, we do not exclude the possibility of contamination of the thick-disc stars at metallicities typical of the thin disc in this region.
3 RESULTS
3.1 Metallicity gradient for dwarfs on circular orbits
We restricted our sample with $\text{S/N}\ge 40$ (7935 stars) to obtain the best-quality data and applied the constraint related to the planar eccentricity, e p ⩽ 0.10, to limit the sample stars with circular orbits. This sample lie at the solar circle, 7 ⩽ R m ⩽ 9 kpc. The number of stars for which 
$[\text{M}/\text{H}]$ metallicity were determined is 3 204, while 2 719 indicated iron abundance 
$[\text{Fe}/\text{H}]$. We estimated metallicity gradients for the two sub-samples for a set of Z max intervals, 0 < Z max ⩽ 825, 0 < Z max ⩽ 500, 500 < Z max ⩽ 800, 800 < Z max ⩽ 1000, and 1000 < Z max ⩽ 1500 pc, which are presented in Table 1. The reason for estimation gradients for two sub-samples is that the number of stars with available $[\text{M}/\text{H}]$ metallicity is larger than the stars with iron abundance (for which we expect more accurate result) while iron gradients give us the chance to compare our results with those previously appeared in research literature. The value Z max = 800 pc is close to 825 pc, which is stated as an upper limit for the thin disc in the vertical distance.
The iron gradients for the intervals 0 < Z max ⩽ 500 and 500 < Z max ⩽ 800 pc are 
$\text{d}[\text{Fe}/\text{H}]/\text{d}R_{\rm m}=-0.083\pm 0.030$ and 
$\text{d}[\text{Fe}/\text{H}]/\text{d}R_{\rm m}=-0.048\pm 0.037$ dex kpc−1, while for the two later intervals they are 
$\text{d}[\text{Fe}/\text{H}]/\text{d}R_{\rm m}=+0.112\pm 0.059$ and 
$\text{d}[\text{Fe}/\text{H}]/\text{d}R_{\rm m}=+0.114\pm 0.140$ dex kpc−1. Radial iron gradients close to zero or positive values at relatively high vertical distances are common in related research literature. However, we should also note that number of stars which cover the mentioned Z max intervals are only 22 and 18, respectively. We could not estimate any iron gradient for the interval Z max > 1500 pc due to a sample size of only five stars in this interval. The range of the mean iron abundances in four Z max intervals in Table 1 is 
$-0.13<[\text{Fe}/\text{H}]<-0.01$ dex, which indicates that all the stars in these intervals are thin-disc stars. The radial iron gradient for the interval 0 < Z max ⩽ 825 pc, i.e. 
$\text{d}[\text{Fe}/\text{H}]/\text{d}R_{\rm m}=-0.081\pm 0.029$ dex kpc−1, is rather close to the one for 0 < Z max ⩽ 500 pc.
A metallicity gradient distribution could be observed for $[\text{M}/\text{H}]$ similar to $[\text{Fe}/\text{H}]$ in Table 1. The radial metallicity gradients 
$\text{d}[\text{M}/\text{H}]/dR_{\rm m}=-0.063\pm 0.011$ dex kpc−1 and 
$\text{d}[\text{M}/\text{H}]/\text{d}R_{\rm m}=-0.028\pm 0.057$ dex kpc−1 are compatible with the iron gradients in the same vertical distance intervals, 0 < Z max ⩽ 500 and 500 < Z max ⩽ 800 pc. The same case holds true also for the third Z max interval, 800 < Z max ⩽ 1000 pc. However, the error for the metallicity gradient for the last Z max interval is large, ±0.137. Therefore, there would be no meaning in comparing the metallicity gradient in this interval with the one corresponding to the iron metallicity, whose error is also large at ±0.140. We should note that the large gradient errors are due to the small number of stars in those samples. The uncertainties in the derived gradients were determined via regression analysis. The metallicity gradients for two sub-samples are plotted in Figure 4.
Figure 4. Radial iron and metallicity distributions (left and right panels, respectively) for the F and G type dwarfs on circular orbits, e p ⩽ 0.10, or different Z max intervals.
We used both iron and metallicity abundances in deriving gradients in our study. Thus, we were able to compare the gradients estimated here with those previously appearing in the literature for either type of abundance (
$\text{d}[\text{Fe}/\text{H}]/\text{d}R$ or 
$\text{d}[\text{M}/\text{H}]/\text{d}{R}$). All abundances (iron or metallicity) are taken from the same source, the RAVE DR4 database. The metallicity gradients have the advantage of a larger corresponding number of stars than those used for the iron gradients: 3 204 and 2 719, respectively. However, as one can see in Tables 1 and 5, the iron gradients are (absolutely) larger than the metallicity ones. The iron originates in binary couples via the SN Ia process in a longer timescale, (t ⩽ 8.5 Gyr), meanwhile, the metallicity symbol “M” indicates the combination of a large number of metals including the α-elements whose timescale is, 5.5 ⩽ t ⩽ 10 Gyr (Brook et al., Reference Brook2012), as well as their formation process, SN II, are different than the former ones. Calcium element (Ca) which dominates the overall metal abundance in RAVE survey is an α-process product (although some Ca element could be produced by SN Ia as stated by Chiappini, Matteucci, & Romano (Reference Chiappini, Matteucci and Romano2001)). Hence, different gradients between iron and metallicity abundances is due to these differences just mentioned.
3.2 Metallicity gradient for dwarfs on elongated orbits
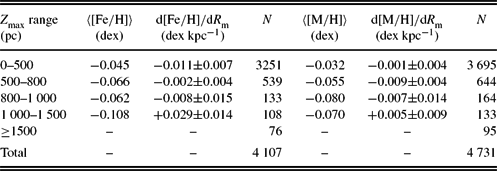
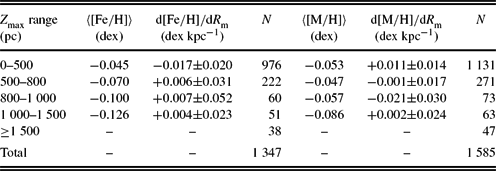
We chose the dwarfs with planar eccentricities e p > 0.10 in the final sample (14 361 stars) and limited them with $\text{S/N}\ge 40$ to obtain an alternative sub-sample for investigation of a metallicity gradient. The number of stars on elongated orbits used for estimation of the 
$\text{d}[\text{Fe}/\text{H}]/\text{d}R_{\rm m}$ and 
$\text{d}[\text{M}/\text{H}]/\text{d}R_{\rm m}$ gradients are 4107 and 4731, respectively (Table 2). These stars occupy a larger radial distance interval than the sub-sample in Section 3.1, i.e. 5 < R m < 12 kpc. We estimated radial metallicity gradients for the same Z max intervals given in the preceding section. The 
$\text{d}[\text{Fe}/\text{H}]/\text{d}R_{\rm m}$ iron gradients and the 
$\text{d}[\text{M}/\text{H}]/dR_{\rm m}$ metallicity gradients for the three consecutive Z max intervals, 0 < Z max ⩽ 500, 500 < Z max ⩽ 800 and 800 < Z max ⩽ 1000 pc, are negative and close to zero, ~ −0.01 dex kpc−1, while both gradients for the interval 1000 < Z max ⩽ 1500 pc are small positive numbers. The iron and metallicity abundances for the stars in this sub-sample, 
$-0.11<[\text{Fe}/\text{H}]<-0.04$ and 
$-0.08<[\text{M}/\text{H}]<-0.03$ dex correspond to the thin-disc population at least for those at small Z max distances (i.e. 0 < Z max < 800 pc) where their number is much larger than those at larger Z max distances.
Table 2. Radial iron and metallicity gradients for the F and G type dwarfs on elongated orbits, e p > 0.10, for different Z max intervals. N indicates the number of stars. Signal to noise ratio is $\text{S/N}\ge 40$. The gradients are not significant (see the text).
The results are plotted in Figure 5. There is a noticeable deficiency-slit of stars at the radial distance R m ~ 8 kpc, which is the solar distance where the stars with circular orbits are concentrated (Section 3.1). We separated the stars subject in this section into two categories based on their radial distances and investigated metallicity gradients for both categories. The first category consists of stars with R m ⩽ 8 kpc, while the second one covers the stars with R m > 8 kpc. The results for the first category are presented in Table 3 and Figure 6. All the iron and metallicity gradients are small positive or negative numbers. The positive gradients for small Z max distances from the Galactic plane have not appeared in related research literature until now. The case is similar for the iron and metallicity gradients estimated for the stars with R m > 8 kpc on elongated orbits (Table 4 and Figure 7). That is, the insignificant iron and metallicity gradients for stars on elongated orbits are not radial distance dependent.
Figure 5. Radial iron and metallicity distributions (left and right panels, respectively) for the F and G type dwarfs on elongated orbits, e p > 0.10, for different Z max intervals.
Figure 6. Radial iron and metallicity distributions (left and right panels, respectively) for the F and G type dwarfs with radial distances R m ⩽ 8 kpc on elongated orbits, e p > 0.10, for different Z max intervals.
Figure 7. Radial iron and metallicity distributions (left and right panels, respectively) for the F and G type dwarfs with radial distances R m > 8 kpc on elongated orbits, e p > 0.10, for different Z max intervals.
Table 3. Radial iron and metallicity gradients for the F and G type dwarfs with radial distances R m ⩽ 8 kpc, on elongated orbits, e p > 0.10 (a sub-sample of stars in Table 2). N indicates the number of stars. Signal to noise ratio is $\text{S/N}\ge 40$.
Table 4. Radial iron and metallicity gradients for the F and G type dwarfs with radial distances R m > 8 kpc, on elongated orbits, e p > 0.10 (the complement sub-sample of the one in Table 3). N indicates the number of stars. Signal to noise ratio is $\text{S/N}\ge 40$.
3.3 Metallicity gradient for stars in the vertical direction
We also estimated vertical metallicity gradients for both $[\text{Fe}/\text{H}]$ and $[\text{M}/\text{H}]$. We restricted our sub-sample to stars on circular orbits and $\text{S/N}\ge 40$. The results are displayed in Figures 8 and 9, for the iron and metallicity abundances, respectively. The iron gradient, 
$\text{d}[\text{Fe}/\text{H}]/\text{d}Z_{{\rm max}}$, is − 0.176 ± 0.039 dex kpc−1 for Z max ⩽ 825 pc (upper panel) while it is − 0.119 ± 0.036 dex kpc−1 for Z max ⩽ 1500 pc (lower panel). The metallicity gradients, 
$\text{d}[\text{M}/\text{H}]/\text{d}Z_{{\rm max}}$, in Figure 9 are compatible with the corresponding ones in Figure 8, i.e. − 0.155 ± 0.035 dex kpc−1 for Z max ⩽ 825 pc and − 0.126 ± 0.048 dex kpc−1 for Z max ⩽ 1500 pc. There is a noticeable flattening of the vertical gradient with the height above the Galactic mid-plane, which is a common result in previous research literature.
Figure 8. Vertical iron distributions for two distance intervals: Z max ⩽ 825 pc (upper panel) and Z max ⩽ 1500 pc (lower panel).
Figure 9. Vertical metallicity distributions for two distance intervals: Z max ⩽ 825 pc (upper panel) and Z max ⩽ 1500 pc (lower panel).
4 DISCUSSION
We estimated iron and metallicity gradients in the radial and vertical directions with F and G type dwarfs selected from the recent RAVE DR4 database (Kordopatis et al., Reference Kordopatis2013). We restricted the data with $\text{S/N}\ge 40$ to obtain the probable best results. We also applied two constraints to obtain a limited sample of F and G dwarfs and estimated iron and metallicity gradients for the stars in this sample. The constraints are as follows: (i) Z max ⩽ 825 pc and (ii) e p ⩽ 0.10. The first parameter was first used by Ak et al. (Reference Ak, Bilir, Özdönmez, Soydugan, Soydugan, Püsküllü, Ak and Eker2015), while the second appeared in Huang et al. (Reference Huang, Liu, Yuan, Xiang, Huo, Chen, Zhang and Hou2015), who used the range e p < 0.13 to separate the cold thin-disc stars from the thick-disc stars. The vertical distance Z max = 825 pc is the place where space densities of the thin and thick discs are compatible. The second parameter, e p = 0.10, is the mode of e p estimated in our sample. That is, our constraints define a thin disc with F and G type dwarfs on circular orbits. If some thick-disc stars contaminate our sample, the resulting metallicity distribution will not be different than a pure thin-disc metallicity distribution. Because, the metallicity of the thick disc stars in question would be compatible to that of the thin-disc stars. We used the stars with Z max ⩽ 825 pc and e p ⩽ 0.10 to estimate iron and metallicity gradients with respect to R m radius. However, we also estimated radial iron and metallicity gradients beyond the vertical distance Z max = 825 pc for comparison purposes.
We adopted the vertical distance intervals as 0 < Z max ⩽ 500, 500 < Z max ⩽ 800, 800 < Z max ⩽ 1000, and 1000 < Z max ⩽ 1500 pc in our calculations. Thus, we decreased the Z max distance in the first constraint by 25 pc. The iron and metallicity gradients for the intervals 0 < Z max ⩽ 500, 500 < Z max ⩽ 800 pc, for the most likely thin disc thus defined, are compatible with each other and they are at the level of the radial iron gradients previously appearing in related research. Actually 
$\text{d}[\text{Fe}/\text{H}]/\text{d}R_{\rm m}=-0.083\pm 0.030$ and 
$\text{d}[\text{Fe}/\text{H}]/\text{d}R_{\rm m}=-0.048\pm 0.037$ dex kpc−1 in our study (Table 1) are generally compatible with the ones in Boeche et al. (Reference Boeche2013), i.e. 
$\text{d}[\text{Fe}/\text{H}]/\text{d}R_{\rm g}=-0.059\pm 0.005$ dex kpc−1, estimated for the interval 0.4 < Z max ⩽ 0.8 kpc, and in Cheng et al. (Reference Cheng2012), 
$\text{d}[\text{Fe}/\text{H}]/\text{d}R=-0.055$ dex kpc−1, estimated for the interval 0.25 < |Z| ⩽ 0.50 kpc, where R g and R are the guiding and Galactocentric radii, respectively. The range of the mean iron abundances for the dwarfs in question is 
$-0.064\le [\text{Fe}/\text{H}]\le -0.017$ dex which indicates that dwarfs subject to the aforementioned radial iron (metallicity) gradient are thin disc stars. The Toomre diagram in Figure 10 confirms our argument kinematically. The 
$V_{\text{LSR}}$ and 
$\scriptstyle\sqrt{U^{2}_{\text{LSR}}+W^{2}_{\text{LSR}}}$ velocity components of the stars in question lie in a circle with radius 50 km s−1. That is, F and G type dwarfs with Z max ⩽ 800 pc on circular orbits are thin-disc stars and exhibit a notable radial metallicity gradient. The radial distance range of these stars is 7 ⩽ R m ⩽ 9 kpc, indicating that they lie at the solar circle.
Figure 10. Toomre diagram for the F and G type dwarfs on circular orbits, e p ⩽ 0.10, for different Z max intervals: 0 < Z max ⩽ 500 pc, 500 < Z max ⩽ 800 pc, 800 < Z max ⩽ 1000 pc, and 1000 < Z max ⩽ 1500 pc.
The iron (and metallicity) gradients for F and G dwarfs in the intervals 800 < Z max ⩽ 1000 and 1000 < Z max ⩽ 1500 pc consist of three small positive values, 
$\text{d}[\text{Fe}/\text{H}]/\text{d}R_{\rm m}=+0.112\pm 0.059$, 
$\text{d}[\text{Fe}/\text{H}]/\text{d}R_{\rm m}=+0.114\pm 0.140$ and 
$\text{d}[\text{M}/\text{H}]/\text{d}R_{\rm m}=+0.138\pm 0.056$ dex kpc−1 (Table 1), in agreement with the corresponding values in the literature (cf. Cheng et al., Reference Cheng2012; Boeche et al., Reference Boeche2013), along with one negative value with large error, 
$\text{d}[\text{M}/\text{H}]/\text{d}R_{\rm m}=-0.034\pm 0.137$ dex kpc−1. We should note that the number of stars corresponding with each gradient just cited is not greater than 30. According to the arguments in the literature, zero or even positive radial gradients are due to the effect of the thick-disc stars at relatively large vertical distances. The metallicity range of these stars is almost the same as the range for the stars with 0 < Z max ⩽ 800 pc, as investigated in the preceding paragraph. That is, they should be thin-disc stars, if we use only the metallicity parameter to determine their population types. However, their velocity components are a bit different than the ones discussed in the preceding paragraph. These stars lie at the outermost part of the velocity circle with a radius of 50 km s−1 (Figure 10).
We also investigated the iron and metallicity gradients for the F and G type dwarfs on elongated orbits, e p > 0.10. Again, we chose the data with S/N ⩾ 40 to obtain the probable best results. Significant metallicity gradients could not be derived for four Z max intervals for this sample (Table 2 and Figure 5). The range of the mean iron and metal abundances of the stars in this sample are 
$-0.11<[\text{Fe}/\text{H}]<-0.04$ and 
$-0.08\le [\text{M}/\text{H}]<-0.03$ dex, respectively. Stars with these metallicities and short Z max distances probably belong to the thin-disc population. However, the metal-poor ends of these abundance intervals may include some thick-disc stars. We separated this sample into two sub-samples by means of their radial distance, R m ⩽ 8 and R m > 8 kpc, and estimated iron and metallicity gradients for each sub-sample. Neither for the sub-sample stars with R m ⩽ 8 kpc, nor for those with R m > 8 kpc could any significant iron or metallicity gradient be detected. This indicates that the insignificance for the F and G type dwarfs on elongated orbits is due to planar eccentricity, and that radial distance does not have any constraint on such small (positive or negative) gradients.
We compared the Toomre diagrams of the two sub-samples to reveal any differences in kinematics. Figure 11 shows that space velocity components for these two sub-samples are much larger than the F and G type dwarfs on the circular orbits (Figure 10). However, there are some noticeable differences between the space velocity components of stars in the two sub-samples as well: the range of the velocity components and the absolute value of a given space velocity component for stars with R m ⩽ 8 kpc are both larger than the corresponding values for stars with R m > 8 kpc. The diagrams in Figure 11 indicate that both sub-samples are probably a mixture of thin- and thick-disc stars with different percentages. However, as stated above, the range of the iron and metallicity abundances of the stars in these two sub-samples favours a sub-sample of thin-disc population. The solution to this conflict is to assume that the thick-disc stars in two sub-samples should be the metal-rich tail of the thick-disc population.
Figure 11. Toomre diagram for the F and G type dwarfs with radial distances R m ⩽ 8 and R m > 8 kpc on elongated orbits, e p > 0.10, for different Z max intervals: 0 < Z max ⩽ 500 pc, 500 < Z max ⩽ 800 pc, 800 < Z max ⩽ 1000 pc, and 1000 < Z max ⩽ 1500 pc.
The vertical iron gradient 
$\text{d}[\text{Fe}/\text{H}]/\text{d}Z_{{\rm max}}=-0.176\pm 0.039$ dex kpc−1 in our work is compatible with the one found by Boeche et al. (Reference Boeche2014), 
$\text{d}[\text{Fe}/\text{H}]/\text{d}Z_{{\rm max}}=-0.112\pm 0.007$ dex kpc−1, estimated for the red clump stars with z ⩽ 2 kpc. Our vertical metallicity gradient, 
$\text{d}[\text{M}/\text{H}]/\text{d}Z_{{\rm max}}=-0.155\pm 0.035$ dex kpc−1 is also compatible with the corresponding values appearing in the literature which are estimated for stars with different vertical distances and Galactic latitudes, i.e. 
$\text{d}[\text{M}/\text{H}]/\text{d}z=-0.16\pm 0.02$ dex kpc−1 for z ⩽ 3 kpc and b = +45°, (Ak et al., Reference Ak, Bilir, Karaali and Buser2007a); 
$\text{d}[\text{M}/\text{H}]/\text{d}z=-0.22\pm 0.03$ dex kpc−1 for z ⩽ 3 kpc and b = +60°, (Ak et al., Reference Ak, Bilir, Karaali, Buser and Cabrera-Lavers2007b); 
$\text{d}[\text{M}/\text{H}]/\text{d}Z_{{\rm max}}=-0.167\pm 0.011$ dex kpc−1 for Z max ⩽ 1.5 kpc, (Bilir et al., Reference Bilir, Karaali, Ak, Önal, Daǧtekin, Yontan, Gilmore and Seabroke2012).
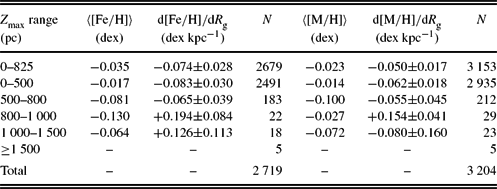
In recent years, metallicity gradient estimations have been based on the guiding radius R g (cf. Boeche et al., Reference Boeche2013, Reference Boeche2014). In our study, we estimated the metallicity gradients using mean radius R m and compared our results with the ones estimated with R g in previous research. We calculated the metallicity gradients of the sub-samples in Table 1 according to the guiding radius R g. Results are listed in Table 5. There are clear negative metallicity and iron gradients for the Z max intervals below 800 pc, while there are positive gradients above this Z max value. It is clear that the results in Tables 1 and 5 are in good agreement. Thus, we conclude that both R g and R m can be used in the estimation of the radial metallicity gradients.
Table 5. Radial iron and metallicity gradients with R g radii for the F and G type dwarfs on circular orbits, e p ⩽ 0.10, for different Z max intervals. N indicates the number of stars. Signal to noise ratio is $\text{S/N}\ge 40$.
Small differences in the two different studies are always expected due to different types of radii such as mean radius (R m) and guiding radius (R g), different Galactic potential and different procedures for distance estimation. In our study, we used R m distances, the recent MWpotential2014 code of Bovy (Reference Bovy2015), a different procedure for distance estimation (Bilir et al., Reference Bilir, Karaali, Ak, Yaz, Cabrera-Lavers and Coşkunoǧlu2008, Reference Bilir, Karaali, Ak, Coşkunoǧlu, Yaz and Cabrera-Lavers2009), and another for identifying the F and G type dwarfs. Despite these differences, we obtained iron and metallicity gradients compatible with those in previously published research.
Another agreement holds between the iron and metallicity gradients estimated in Anders et al. (Reference Anders2014) with respect to two different radial distances, i.e. guiding radius R g (their Table 3) and Galactocentric radius R (their Figure A.1, upper-left panel), and our iron and metallicity gradients based on the data of stars on circular orbits (Table 1). It is interesting that the metallicity gradient with respect to the Galactocentric radius in Anders et al. (Reference Anders2014), 
$\text{d}[\text{M}/\text{H}]/\text{d}{R}=-0.082\pm 0.002$ dex kpc−1 is rather close to the iron gradient with respect to the R m radius, 
$\text{d}[\text{Fe}/\text{H}]/\text{d}R_{\rm m}=-0.083\pm 0.030$ dex kpc−1 in our study. Different gradients cited above can be attributed to different star categories in the Galactic disc. For example, different components of the disc, such as thin disc and thick disc, could have different gradients and even gradients in a single component could be a function of age. It is most likely that the lower gradient observed in stars of higher eccentricity corresponds to a flatter gradient for older stars.
We mentioned in the introduction that there is a bias against metal-rich stars if one uses R m distances, i.e. only stars with large orbital eccentricities among a sample with small R m distances can reach the solar circle. But such stars are metal-poor relative to the ones on circular orbits with the same R m radial distances which cannot reach to the solar circle. Thus, the number of metal-rich stars at the solar circle decreases. However, in our case stars with large orbital eccentricities were removed by applying the constraint e p ⩽ 0.1. Hence, the effects of the bias in question have been minimized.
5 CONCLUSION
Two constraints, Z max ⩽ 825 pc and e p ⩽ 0.1, provide a sample of thin-disc stars at the solar circle with radial iron and metallicity gradients in the vertical distance intervals, 0 < Z max ⩽ 500 and 500 < Z max ⩽ 800 pc. Negative or positive small gradients at further vertical distances probably originate from the mixture of two Galactic disc populations; i.e. thin and thick discs. The metallicity gradients could not be detected for stars on elongated orbits, e p > 0.1. Vertical iron and metallicity gradients estimated for the thin-disc sample are compatible with the ones in previous research.
ACKNOWLEDGEMENTS
Authors are grateful to the anonymous referee for his/her considerable contributions to improve the paper. The authors are very grateful to Mrs Shannon Darling Oflaz for her careful and meticulous reading of the English manuscript. This study has been supported in part by the Scientific and Technological Research Council (TÜBİTAK) 114F347. Part of this work was supported by the Research Fund of the University of Istanbul, Project Numbers: 39170, 39742, and 48027.
