1. Introduction
Most of the permanent GPS receivers in Greenland are on bedrock, near the ice-sheet margin (Reference BevisBevis and others, 2012). A few, though, have been installed on the ice-sheet surface. Reference Zwally, Abdalati, Herring, Larson, Saba and SteffenZwally and others (2002) placed a continuous GPS receiver on the ice at Swiss Camp, ∼30 km inside the western margin, and left it in place for ∼3 years in the late 1990s. Since then there have been various, largely independent experiments where continuously operating GPS receivers have been left on the ice for a few years or longer. In these cases the primary objective has usually been to monitor horizontal motion of the ice.
Here we discuss additional ways in which continuous GPS measurements on the ice-sheet surface can be useful for glaciological applications. We show how GPS observations of vertical displacements can provide information about the densification of snow as it moves downward through the firn layer (the layer of snow above the ice) and about the downward motion of the ice below the firn. And we show how GPS signal-to-noise ratio (SNR) measurements can be used to monitor the ‘reflector height’: the distance between the GPS antenna and the surface of the snow beneath the antenna. The reflector height changes as snow accumulates on the surface and as the antenna anchor moves downward through the firn layer. Both types of measurements can be used to assess output from surface accumulation and firn densification models, which in turn are useful for constructing ice-sheet mass-balance estimates.
There are other, non-satellite-based methods for monitoring the distance between the snow surface and a reference pole anchored in the firn (Reference Steffen and BoxSteffen and Box, 2001), as well as techniques that combine in situ measurements and campaign GPS surveys (Reference Hamilton and WhillansHamilton and Whillans, 2000). One advantage of using GPS is that by combining the GPS reflector height measurements with vertical positioning results from the same GPS receiver, it is possible to monitor changes in the geocentric elevation of the snow surface. This is the quantity detected by satellite altimeters, and so these GPS results offer a means of assessing future altimeter measurements.
In the following sections we describe the GPS sites installed on the surface of the Greenland ice sheet and how position and snow reflector heights were estimated from the GPS data. We then provide general descriptions of the relation between GPS vertical positioning measurements and the firn density profile. We apply these ideas to the position and snow reflector height data, and compare the results with model predictions.
2. GPS Network
The GPS data used in this study are part of the GLISN (Greenland Ice Sheet Monitoring Network) project. The goals of GLISN are to detect, locate and characterize glacial earthquakes (Reference ClintonClinton and others, 2014). At three of the GLISN seismic sites, dual-frequency geodetic-quality GPS instruments were installed in June–August 2011: GLS1, GLS2 and GLS3 (Fig. 1; Table 1), located at the Dye-2, Ice South Station and NEEM field camps respectively. The GPS receivers are dual-frequency carrier phase receivers (Trimble NetR9), and have a patch antenna/ground plane. Each receiver was operated at a sampling rate of 30 s. Each antenna is placed atop a 4.57 m pole with a diameter of 0.076 m. That pole is placed on a 0.6 m × 0.6 m plywood base; the base of the pole is set ∼1.5 m below the snow surface in summer (i.e. ∼3 m of the pole is above the snow surface after installation; Fig. 2a). The GPS data are telemetered on an hourly or daily basis via Iridium satellite modems to a central facility in Boulder, Colorado.

Fig. 1. Map of Greenland showing the GPS sites (plus signs). Reference Herron and LangwayHerron and Langway (1980) provide ice-core parameter values to use in their analytical expression for snow density, at the locations (in red) denoted by the circles.

Fig. 2. (a) Direct and reflected signals with respect to the satellite elevation angle e for a GPS antenna set above a planar surface for GPS site GLS2. The reflector height is derived from the interference of the direct and reflected GPS signals. (b, c) Signal-to-noise ratio (SNR) data for two dates, so as to contrast the large frequency changes that occurred when the monument was extended in height in spring 2013. Gray traces show the approximate direct signal component.
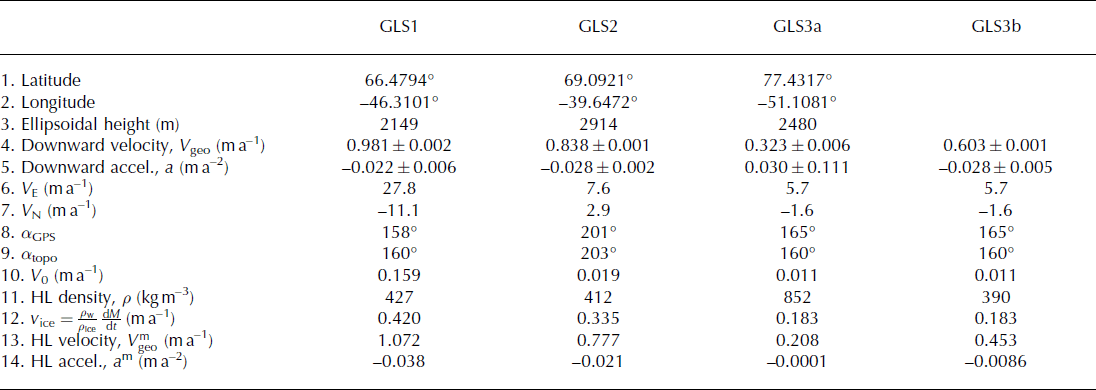
Table 1. Velocities and model predictions at the GPS sites. GLS1, GLS2 and GLS3 (approximate coordinates in rows 1–3) were installed on 13 August, 7 June and 21 July 2011. GLS3a and GLS3b represent GLS3 before and after the antenna was re-anchored. Rows 4 and 5: GPS solutions, with their 2σ uncertainties, for the geocentric downward velocity and acceleration; 6 and 7: GPS solutions for the eastward and northward velocities. In each case the 2σ uncertainty is <0.005 m a−1; 8 and 9: directions of the horizontal motion and of the downward topographic gradient, expressed as the angles α GPS and α topo counterclockwise from eastward; 10: downward geocentric velocity of points on the outer surface due to the downhill flow of the ice sheet; 11: firn density at the mean anchor depth, inferred from HL’s model; 12: downward velocity at the ice/firn interface, computed using the long-term accumulation rate, dM/dt, from the RACMO2 regional atmospheric climate model; 13 and 14: solutions for the downward velocity and acceleration, computed using HL’s density profiles and the V 0 and v ice values in rows 10 and 12
The GLISN GPS monuments were designed so that the poles can be extended as they sink into the snow. For example, the GLS2 antenna was extended by ∼2 m on 25 May 2013; the horizontal position of the antenna was not disturbed. To date, the GLS1 site has not been reset horizontally or vertically. The situation at GLS3 is more complex. GLS3 was initially mounted on a borehole that extended 90 m into the firn; the GPS antenna remained there until 17 July 2012. At that time it was moved to the standard GLISN mount, i.e. the pole was set ∼1.5 m into the snow. Unfortunately, there was a significant data outage (37 days) before that time, making it difficult to unambiguously determine the offset between the new and old monuments.
We use the GPS data produced by these sites in two distinct ways, one traditional and one non-traditional. The traditional use of a GPS receiver is to calculate three-dimensional (3-D) positions. As with previous GPS studies from the Greenland ice sheet, those coordinates are derived from the GPS carrier phase data, precise GPS orbits and sophisticated atmospheric delay models (Reference Zwally, Abdalati, Herring, Larson, Saba and SteffenZwally and others, 2002). Here the GIPSY (GPS inferred positioning system) point positioning software was used and the coordinates and orbits are defined in the ITRF2008 reference frame (Reference Altamimi, Collilieux and MétivierAltamimi and others, 2011; NGL, 2014). Daily Cartesian positions are then translated into local coordinates (east, north, vertical) with respect to a stable North American Reference Frame (Reference Blewitt, Plag, Bar-Sever, Kreemer, Hammond and GoldfarbBlewitt and others, 2013).
In the past 5 years, studies have shown that the same GPS receiver used to calculate 3-D positions can also be used to estimate the vertical distance, or reflector height, between the GPS antenna and the land or water surfaces beneath the antenna (Reference Larson, Small, Gutmann, Bilich, Braun and ZavorotnyLarson and others, 2008, Reference Larson, Gutmann, Zavorotny, Braun, Williams and Nievinski2009, Reference Larson, Ray, Nievinski and Freymueller2013). This method uses the SNR data; these are included in the same GPS data file used to compute position. The GPS reflection technique is driven by geometry and dielectric characteristics of the surface surrounding the GPS antenna. The reflected GPS signal travels farther than the direct signal; the two signals interfere at the antenna (Fig. 2a). This effectively turns the GPS receiver into an interferometer. The interference pattern varies as a GPS satellite rises or sets, i.e. as its elevation angle (e) changes, and the SNR is then

The amplitude A depends on the transmitted GPS signal power, the antenna gain pattern, and composition/roughness of the reflecting surface. The frequency of the SNR data depends explicitly on the ratio of the reflector height R and the GPS wavelength λ, which is 19 and 24.4 cm for the L1 and L2 frequencies, respectively. The phase offset φ is constant during a given satellite track, and is not used in this analysis.
For all positioning applications, reflections are a source of noise, and in principle the antenna gain pattern used by GLISN has been optimized to suppress reflections. This goal is somewhat accomplished in that reflection effects are rarely seen in data for satellite elevation angles >25°. However, below this elevation angle, reflections from most natural surfaces (soil, snow, water, ice) can clearly be observed if the surface is planar and smooth enough. While layers of snow surfaces of different density will produce distinct reflections as the signal penetrates the snow (Reference Cardellach, Fabra, Rius, Pettinato and D’AddioCardellach and others, 2012), the reflection contrast, and thus the interference effect, is greatest at the surface.
Recall that the frequency of the interference pattern observed in SNR data is 2R/λ, where the independent variable is sine of the satellite elevation angle. The SNR data shown in Figure 2b and c have been chosen to emphasize the dependence of frequency on R. In Figure 2b the antenna was ∼1.1 m above the snow. The maintenance crew subsequently extended the antenna pole ∼2 m, resulting in the higher-frequency SNR oscillations seen in Figure 2c. Small variations in terrain slope have little impact on the observed SNR reflection frequency, and can be ignored for slopes <2° (Reference Larson and NievinskiLarson and Nievinski, 2013). The amplitude of the interference pattern depends primarily on the dielectric constant and roughness of the surface, and on the antenna gain pattern. Roughness of the surface (at GPS wavelengths) is a significant restriction, so reflections from the surface of outlet glaciers are much more difficult to resolve than those from snow surface variations in the Greenland interior as are shown here.
The small gray trend shown in Figure 2b and c is unrelated to snow; instead, it is driven by the transmitted signal power and the antenna gain pattern (Reference Nievinski and LarsonNievinski and Larson, 2014). In this study it is removed by a second-order polynomial fit. As described earlier, the oscillations observed in the SNR data are created by the interference of the direct and reflected signals. The frequency of the oscillations for the SNR data will be a constant for a given rising or setting satellite track. Because that frequency depends on sine of elevation angle and not on time, we extract the dominant frequency using the Lomb–Scargle periodogram (LSP; Reference Press, Teukolsky, Vetterling and FlanneryPress and others, 1996). To report a significant reflector height, we require that a satellite track have at least 75 SNR observations and that the peak amplitude be >1.5 dB Hz. An oversampling factor of 50 is used to produce a LSP resolution of ∼0.05 m. LSP reflector heights smaller than 0.5 m are not allowed, as retrievals smaller than twice the GPS wavelength are poorly resolved (Reference Larson and NievinskiLarson and Nievinski, 2013). Although previous GPS snow studies have relied on the new public code on the L2 frequency data (Reference Larson, Gutmann, Zavorotny, Braun, Williams and NievinskiLarson and others, 2009; Reference Gutmann, Larson, Williams, Nievinski and ZavorotnyGutmann and others, 2012; Reference Larson and NievinskiLarson and Nievinski, 2013), only one-third of GPS satellites currently transmit this code. Here we opt to use the public signal on the L1 frequency, known as the C/A code. This offers the advantage that we can use data from all 30+ satellites.
Figure 3a shows successful reflector height retrievals for a single year at station GLS2. Retrievals are color-coded by quadrant (northwest, northeast, etc.) to check for signs of bias. Approximately 30% more retrievals are derived from the southern tracks than from the northern tracks. However, estimated snow levels show roughly the same behavior in each quadrant. On each day an average reflector height value is calculated and values >3σ from the mean are discarded. For the retrievals shown in Figure 3, 1.5% of the reflector heights are removed, resulting in a normal distribution with an average reflector height precision of 0.01 m.

Fig. 3. (a) Reflector height retrievals for station GLS2 in 2012. Retrievals are plotted by sector (northeast, southeast, southwest, northwest). The daily reflector height retrieval is the arithmetic mean of all successful retrievals on a given day. (b) Map view of reflection points (defined as H/tan(e)) for satellite elevation angles <25°. The horizontal axis represents west to east, and the vertical axis represents south to north.
Many in situ snow measurement systems, such as ultrasonic sensors, have small footprints, ∼1 m2 (Reference Ryan, Doesken and FassnachtRyan and others, 2008). This intrinsically limits how well an ultrasonic sensor can characterize snow levels over larger areas. The GPS snow technique has a footprint that varies azimuthally depending on which satellite track is used; it varies in length depending on how high the GPS antenna is above the reflecting surface. Figure 3b shows each satellite track’s reflection point for a GLISN antenna that is 2 m above the snow. As a rule of thumb, the full sensing footprint for each satellite track is an ellipse which is ∼2× the distance to the reflection point in length and ∼4 m across. This results in a circle of diameter ∼60 m, area 2800 m2. To increase the size of the GPS snow footprint, a user can simply raise the antenna. While here we emphasize variations in the daily average reflector height, there is no intrinsic reason that sub-daily reflector heights could not also be estimated.
3. GPS Data and Firn Density
3.1. Relation between GPS verticals and firn density
The GPS receivers considered here are located near ice divides, where the ice is covered year-round with a firn layer. The firn is composed of snow that has accumulated during previous years, and that is compressing into ice as more snow is added to the surface. Snow densities typically vary from ∼350 kg m−3 near the outer surface, to 917 kg m−3 (the density of ice) at the bottom of the firn layer.
Figure 4 shows a GPS antenna permanently anchored in the firn. The red box on the left side outlines a volume of mass at time t A, where the top coincides with the location of the anchor, a depth z beneath the surface, and the bottom is at the firn/ice interface, at a depth of z ice. This entire region of the ice sheet is flowing downhill to the right.

Fig. 4. Cartoon showing a firn/ice column (bounded by the vertical green lines) at initial time t A and later time t B. The column moves to the right, carried by the downhill flow of the ice, which causes the column to subside relative to the geocenter by the distance H. The red box outlines a portion of this column, defined at t A so that the GPS antenna (purple) is anchored to the snow at the top of the box, and the bottom of the box is at the firn/ice boundary. At t A the upper and lower levels of the box are at depths z and z ice below the surface. As time progresses, new snow is added to the top of the column. The bottom of the box moves downward relative to the surface due to flow in the underlying ice sheet, and this subsidence carries the entire box with it. Particles in the firn subside further due to compaction of the snow beneath those particles. At time t B the top and bottom levels of the box have moved downward relative to the outer surface by h and h 2. The dashed parallelogram in the box at time t A has compressed into the dashed parallelogram shown at t B, which means the downward velocity of the firn at the bottom of the parallelogram is smaller than the velocity at the top. This implies the downward velocity field in the firn decreases with depth, so that the downward velocity of the GPS antenna decreases with time.
The right side of the figure shows the same column at a later time, t B. The top is a distance H closer to the geocenter, because of the downhill flow. All the particles that were in the column at t A have moved downward relative to the surface, and new snow has accumulated at the top. The red box contains the same particles at times t A and t B, and so has the same mass at those times. The top and bottom of the box have subsided relative to the surface by the amounts h and h 2.
Suppose the firn is in steady state, so that at any fixed depth beneath the surface, neither the density nor the velocity change with time. Then at time t B the mass in the white area between z and z + h will equal the mass in the red area between z ice and z ice + h 2. The material between z ice and z ice +h 2 is ice, with uniform density ρ ice. Suppose the displacement, h, is small enough during this time that the difference in density between depths z and z + h is negligible, so the density everywhere between z and z + h is ρ(z). Then the requirement that the box have the same mass at both times reduces to
Taking the time-derivative of Eqn (2), and defining v(z) =dh/dt and v ice = dh 2/dt as the downward velocities, relative to the outer surface, of the anchor and the particles at the firn/ice interface, Eqn (2) implies
The geocentric velocity of the anchor, as determined by a GPS receiver, is V geo(z) = v(z) + dH/dt. Defining V0 = dH/dt as the downward geocentric velocity due to the downslope flow of the ice sheet, Eqn (3) becomes
This result, Eqn (4), implies that densities at depths z a and z b within the same firn column are related by

If the ice sheet is nearly flat in the vicinity of a GPS site, then V 0 is much smaller than V geo(z). In that case, Eqn (5) shows that for steady-state conditions the geocentric downward velocity at any level within the firn is nearly inversely proportional to the density at that level.
For a steady-state ice sheet, v
ice can be related to the long-term accumulation rate. Suppose we had drawn the top level of the red box in the left-hand column of Figure 4 so that it extended all the way to the surface. Then, to conserve mass the mass in the white region that opens up above the box by time t
B (the accumulation between t
A and t
B) would equal the mass in the part of the box that subsides below z
ice. We denote the mass/area of the accumulation as ρ
w
M, where M is the accumulated mass and ρ
w is the density of water (1000 kg m−3). The mass/area in the bottom part of the box is ![]() . Setting these two masses equal, dividing by ρ
ice and taking the time derivative gives
. Setting these two masses equal, dividing by ρ
ice and taking the time derivative gives
Equation (4) can be used to predict the geocentric, vertical position of the GPS anchor as a function of time, using models of the accumulation rate (to determine v ice using Eqn (6)), the density and V 0. The predictions can be compared against the observed GPS results to help assess those models. Let z(t) be the depth of the anchor below the surface at time t. A short time δt later, that depth is

This result allows us to numerically propagate z(t) from its starting depth to its value at any later time. Once we have found a time series for z(t), we compute the geocentric vertical position of the anchor (defined to be positive upward, corresponding to the usual sign of GPS verticals) as
where we have assumed that V 0 does not change with time, and where the geocentric vertical position and the negative of the depth below the surface are defined to be equal at t = 0.
If the antenna is anchored above the ice layer, then the density at the anchor, ρ(z), is smaller than the density of ice, ρ ice. In that case, Eqn (3) shows that the downward velocity of the antenna relative to the surface, v(z), is larger than the downward velocity of the ice, v ice. This is expected, since v(z) includes a contribution from the compacting snow beneath the anchor, that does not affect v ice. Since the density increases with depth, the downward velocity of the GPS anchor will decrease with time as the anchor moves deeper into the firn: the velocity at the bottom of the dashed parallelogram in the left-hand side of Figure 4 must be less than the velocity at the top of the parallelogram, because compression causes the parallelogram thickness to decrease with time. This causes a deceleration of the GPS verticals.
This deceleration can be related to the vertical gradient of the density by taking the time-derivative of Eqn (4). Assuming that V0, dM/dt and ρ ice do not change with time during the observation period, the downward GPS acceleration is

where ρ = ρ(z), v = v(z) and V geo = V geo(z).
3.2. Monitoring the snow surface using GPS
Suppose the rate of accumulated snow is constant over long time periods, so that the ice sheet is in steady state. Then the thickness of a firn column would not change with time, as shown in Figure 4 where the z = 0 and z = z ice surfaces are straight, parallel lines. The geocentric elevation of a point on the surface will still decrease with time, because of the downhill flow of the ice. If there were no downhill flow then the antenna would move toward the surface at the same rate it moves toward the geocenter, and so the rates of change of the reflector height and the geocentric vertical position would be the same. Downhill flow causes the geocentric vertical position to decrease more quickly than the reflector height, by the rate V 0 = dH/dt.
Suppose, though, the accumulation rate is not constant, so that the ice sheet is not in steady state. In a year where the accumulation is, say, smaller than the long-term mean, the surface grows more slowly than the downward motion of particles at the firn/ice boundary, and the firn thins. This causes an additional decrease in the geocentric elevation of the outer surface. In this case, the reflector height, R, decreases even more slowly than the geocentric vertical position: i.e. the difference in rates is larger than V 0.
In general, the geocentric elevation, E, of the surface at the location of the GPS antenna is
In the steady-state case, E(t) = −V 0 t.
Satellite and airborne altimeters are used to monitor changes in elevation of the ice-sheet surface. GPS surface elevation estimates could thus be useful for assessing altimeter measurements. E(t) computed using Eqn (10) describes changes in elevation at a point that is being carried downhill by the horizontal flow of the ice sheet. But an altimeter measures changes in elevation at locations that are fixed to geocentric latitude/longitude coordinates (Eulerian coordinates), rather than to coordinates that move with the ice (Lagrangian coordinates). Thus, altimeter results do not include the −V 0 t contribution, and should be compared instead to
which is the GPS-based estimate of elevations at a fixed Eulerian point whose coordinates coincide with the initial coordinates of the GPS antenna. The simple V
0
t approximation for the effects of downhill flow becomes less accurate if the time span is long enough that V
0 can no longer be assumed to be constant. Then V
0
t should be replaced by ![]() . Also, the assertion that Eqn (11) represents elevation changes at the initial latitude/longitude point assumes the snow accumulation is sufficiently uniform that it is the same at the fixed Eulerian point as at the GPS antenna, which is gradually moving away from that fixed point.
. Also, the assertion that Eqn (11) represents elevation changes at the initial latitude/longitude point assumes the snow accumulation is sufficiently uniform that it is the same at the fixed Eulerian point as at the GPS antenna, which is gradually moving away from that fixed point.
4. Application to Greenland GPS Data
4.1. GPS positioning results
4.1.1. Vertical displacements
The black lines in Figure 5a–c show GPS vertical positions, after offsets at the times described above are fit and removed. The results are dominated by a near-steady rate of subsidence, of many tens of cm a−1. There is a significant increase in the slope at GLS3 after the May 2012 antenna change, which is consistent with the antenna being re-anchored much higher in the firn at that time: points higher in the firn subside more quickly than deeper points because of compaction of the intervening snow. There is also a discernible change in the GLS1 slope between mid-2012 and early 2013. This is associated with refreezing of meltwater from the large melting event that occurred during summer 2012, and is discussed below.

Fig. 5. The black lines in the top row show the GPS verticals at (a) GLS1, (b) GLS2 and (c) GLS3. Offsets, including a large ∼May 2012 discontinuity at GLS3 caused by raising and resetting the antenna anchor (vertical blue line in (c)), have been fit and removed. The orange lines show predictions based on HL’s density model, and on the mean accumulation rate inferred from the RACMO2 atmospheric model. The dashed green lines show results from the dynamic firn model. The black lines in the bottom row show the residual GPS verticals after removing the best-fitting linear term, for (d) GLS1, (e) GLS2 and (f) GLS3. The blue lines show the quadratic terms obtained from the fit to the GPS data. The orange lines in (d–f) show predictions based on HL’s density model, after removing the best-fitting linear term.
To obtain quantitative estimates of the slopes and how they change with time, we simultaneously fit a constant, a linear term, a quadratic (t 2/2) term, and cosine and sine of a once-per-year variation, to the verticals at each site. (The seasonal terms are included in the fit to make sure they do not contaminate the linear and quadratic results.) For GLS3 we fit two sets of terms, one before and one after the May 2012 antenna change. We refer to the pre- and post-May 2012 solutions as GLS3a and GLS3b. Results for the corresponding downward velocity (V geo; the negative of the linear term) and downward acceleration (a; the negative of the quadratic term), along with their 2σ formal uncertainty intervals, are shown in Table 1. All velocity solutions differ from zero by far more than their uncertainties. This is not surprising given the strong linear nature of the data shown in Figure 5a–c. This is also true of the acceleration solutions for GLS1, GLS2 and GLS3b. But for GLS3a the acceleration values are not significantly different from zero.
Evidence of the accelerations can be seen in Figure 5d–f. The black lines show the residuals obtained by subtracting the sum of the constant and linear terms from the GPS data. The blue lines show the best-fitting quadratic terms. The GLS2 and GLS3b residuals show clear concave-upward signals, implying a decreasing downward velocity. This is consistent with the numerical results in Table 1, that show the acceleration values are negative and differ significantly from zero in those two cases.
For GLS3a there is a dramatic concave-downward component in the residuals (the black pre-May 2012 results in Fig. 5f). This implies an increasing, rather than decreasing, downward velocity. The quadratic solution at GLS3a (shown in blue) does not capture this concave-downward component, because we have included annually varying terms in the fit and those terms have absorbed most of the concave-downward behavior. This is also why the uncertainty in the Table 1 GLS3a acceleration value is larger than the value itself. The GLS3a time span is <1 year, which makes it difficult to separate the t 2/2 term from an annual cycle, and this is reflected in the large uncertainty.
Still, whether the concave signal in the GLS3a residuals is due to an annual cycle or to a steady acceleration, the results suggest the GLS3a anchor was moving downward more quickly in early 2012 than in late 2011. It is not clear what mechanism could cause that behavior. A seasonally varying component would be expected, due to seasonal variations in surface accumulation. But seasonal variability at the other sites, and at GLS3 after the antenna change, is no larger than the concave-downward signal at GLS3a. This is surprising given the much greater anchor depth for GLS3a than for the other antennas. We suspect, instead, that there are seasonal contributions to the GLS3a positioning data that are not caused by dynamic processes in the ice sheet. One possibility is that this apparent increase in velocity is due to thermal contraction of the 90 m pipe to which the GPS antenna was anchored prior to May 2012. If that pipe contracted by just 0.025% during the 2012 winter, it would have caused an apparent 2 cm subsidence, consistent with Figure 5f.
The GLS1 residuals (Fig. 5d) show that there was a significantly larger total subsidence rate between mid-2012 and early 2013 than during the preceding and subsequent time periods. Because of this large signal, our 2σ formal uncertainty estimate for the GLS1 t 2/2 solution is largely irrelevant and our result for the GLS1 acceleration is not meaningful.
This systematic signal in the GLS1 residuals is likely a consequence of the unprecedented surface melting that occurred across Greenland during summer 2012 (e.g. Reference TedescoTedesco and others, 2013). The GPS reflector height results discussed below suggest there was considerable melting of near-surface snow at GLS1 during the 2012 summer. GLS1 is more likely to experience melting than GLS2 and GLS3, because of its lower latitude and lower elevation. It is probable that most of the resulting meltwater infiltrated into the firn, where it refroze. The latent heat released during refreezing would warm the snow and increase its density (e.g. Reference Braithwaite, Laternser and PfefferBraithwaite and others, 1994), thus causing increased subsidence of the overlying firn. We hypothesize that some of the 2012 summer meltwater percolated far enough into the firn that, when it refroze, the latent heat penetrated below the GPS antenna anchor, thus causing the dramatic mid-2012 to early-2013 subsidence evident in Figure 5d.
4.1.2. Horizontal displacements
We simultaneously fit a constant and a linear (i.e. a velocity) term to the eastward and northward components of position at each GPS site, after fitting and removing offsets at the times noted above. The velocity solutions are shown in Table 1. Uncertainties are not given, but for each component at every site the 2σ formal uncertainty is <0.005 m a−1, far smaller than the velocity values. The velocities are on the order of many m a−1, much larger than any likely secular errors.
Figure 6 shows the direction of each horizontal velocity vector superimposed on local surface elevation maps extracted from the GIMP Greenland elevation dataset (Reference Howat, Negrete and SmithHowat and others, 2014). In each case, the velocity vector is directed downslope, as is expected for flowing ice. Columns 6 and 7 of Table 1 show that at each site the directions of the velocity and the downslope gradient agree to within a few degrees.

Fig. 6. Maps of the ice-sheet surface topography, determined from the GIMP dataset, centered around each GPS site. The numbers along the edges of each box are distances in km. The color contours are m of elevation, where the [−80…60] legend applies to GLS1, and the [−30…30] legend to GLS2 and GLS3. The topographic gradients are about twice as large near GLS1 as near the other two sites. The circles denote the locations of the antennas, and the lines point outward from the circles in the direction of motion as determined from the GPS horizontal positions.
The slopes of the GIMP topography (vertical drop per horizontal distance) averaged over ±15 km of each GPS site are 0.0053, 0.0023 and 0.0019 at GLS1, GLS2 and GLS3 respectively. By combining these slopes with the horizontal velocity values, we obtain estimates of V 0, the downward vertical velocity of the surface caused by the downhill flow of the ice sheet, shown in row 10 of Table 1. Both the horizontal velocity amplitude and the surface slope are much larger at GLS1 than at the other sites, causing the GLS1 V 0 value to be far larger than those at GLS2 and GLS3.
4.2. GPS reflector height measurements
The blue lines in Figure 7a–f show the GPS reflector heights at the three sites. In Figure 7d–f, the black lines show the vertical positions, and the orange lines show the geocentric, Eulerian surface elevations, E eul(t), computed by subtracting the reflector heights from the vertical positions and correcting for the downhill flow of the ice sheet (Eqn (11)).

Fig. 7. Blue lines show the GPS reflector heights at GLS1 (a, d), GLS2 (b, e) and GLS3 (c, f). In (a), the purple line shows reflector height observations from an ultrasonic snow sensor located ∼2 km from GLS1 (Reference Steffen and BoxSteffen and Box, 2001). The dashed green lines in (a–c) show results for the reflector heights predicted by the dynamic firn model. The black lines in (d–f) show the GPS geocentric vertical positions, and the orange lines show the geocentric, Eulerian snow surface elevations, E eul, obtained by subtracting the GPS reflector heights from the GPS vertical positioning results, and correcting for the downhill flow of the ice sheet. The dashed green lines in (d–f) show results for the geocentric, Eulerian surface elevations predicted by the dynamic firn model.
At both GLS2 and GLS3, the reflector height and the vertical position are steadily decreasing at about the same rate. (The reflector height shows more short-term variability, presumably because accumulation occurs episodically.) E eul(t) shows some year-to-year variability at those two sites: the elevation rose rapidly at GLS2 before summer 2012, and less rapidly afterwards; while at GLS3 there was a slight elevation decrease leading up to summer 2012, followed by a steady increase. Starting in summer 2012, E eul(t) has been steadily increasing by 0.05–0.10 m a−1 at GLS2 and 0.10–0.15 m a−1 at GLS3.
At GLS1, though, there is a striking difference between the reflector heights and the vertical positions. Until the start of summer 2012, the reflector height was decreasing at about the same rate as the geocentric GPS elevation (E eul(t) was only slightly increasing). But during the 2012 summer the reflector height increased abruptly, so that by the end of the summer the reflector height was even larger than it had been at the end of the 2011 summer. This suggests that the snow that had accumulated between the start of the GPS time span and the end of the 2011/12 winter, plus some of the snow that was in place at the start of that time span, melted during the 2012 summer. This is consistent with photographs taken of the site (personal communication from D. Childs, 2013). This caused the geocentric surface elevation to drop by ∼1.5m over a 3–4 month period. Since then, the GLS1 surface elevation has remained near constant.
The GPS reflector height at GLS1 can be compared with results from an ultrasonic snow sensor operating ∼2 km from the GPS antenna (Reference Steffen and BoxSteffen and Box, 2001). The ultrasonic snow sensor is mounted on a pole that was anchored 3 m into the firn in 1996. That anchor has subsided by 12 m since then, so that it was at a depth of ∼15 m during the June 2011–March 2014 time span of the GLS1 GPS data (personal communication from K. Steffen, 2014). The sensor is thus moving downward more slowly than the GPS antenna, since the latter was anchored at ∼2 m depth at its June 2011 installation. To remove this bias, we modify the post-June 2011 snow sensor results to be consistent with what would have been observed had the pole been anchored at 2 m depth in June 2011. We use Eqn (5) to estimate the downward velocity, V(z a), of the 15m snow sensor anchor, using values of the observed velocity (V(z b)) of the 2 m GPS anchor, the velocity (V 0) caused by the downslope flow of the ice sheet, and the density ratio (ρ(z a)/ρ(z b)) inferred from the density model of Reference Herron and LangwayHerron and Langway (1980) discussed below. This modification increases the downward slope of the snow sensor reflector height by 0.22 m a−1.
The purple line in Figure 7a shows the snow sensor reflector height after applying this modification for the 15 m anchor depth. The results are in good agreement with the GPS reflector heights. This is especially encouraging because the GPS antenna and the ultrasonic sensors have different sensing zones and are not exactly collocated.
In principle, GPS geocentric, Eulerian surface elevation results (Eqn (11)) could be used to compare with geocentric elevations obtained with satellite altimetry. This is a potential advantage of working with reflector height results obtained from GPS measurements. In fact, the ∼60 m resolution of the GPS results is roughly equal to the resolution of the ICESat (Ice, Cloud and land Elevation Satellite) and ICESat-2 laser altimeters (Reference AbdalatiAbdalati and others, 2010), though it is smaller than the 380 m along-track resolution of the CryoSat-2 radar altimeter (Reference BouzinacBouzinac, 2012).
4.3. Models of firn density and accumulation rates
We compare our GPS measurements with two sets of model predictions. For one set, we use an analytical expression for the depth-dependent firn density, ρ(z). We assume the density profile is steady-state, and use that density profile in Eqn (7), along with an atmospheric model estimate of dM/dt, to find v ice (Eqn (6)), to predict the anchor depth as a function of time. We use those results in Eqn (8), together with our estimate of V 0, to obtain the geocentric vertical position. The other set of predictions comes from a fully dynamic firn model, driven by surface mass-balance and temperature values. We describe both these models in this subsection.
4.3.1. Steady-state density model
GLS1 and GLS3 are located at coring sites: GLS1 at Dye-2, and GLS3 at NEEM. Reference Steen-LarsenSteen-Larsen and others (2011) found that the depth-dependent density at NEEM is well represented by the analytical firn density model of Reference Herron and LangwayHerron and Langway (1980; denoted below as HL), so we use that model in the computations below.
HL parameterize their density model in terms of the density (ρ 0) of the surface snow layer, the density of ice (917 kg m−3), the annual mean temperature at 10 m depth and the annual mean accumulation rate. These parameters vary from one location to another, and HL provide values at several Greenland locations, indicated by the circles in Figure 1. For our three GPS sites, parameter values are given only at GLS1. For the other two sites we use values from nearby locations given by HL. For GLS2 we use parameters for both ‘Milcent’ and ‘Crete’, roughly 225 km and 240 km from GLS2. And for GLS3 we use parameters for ‘Site 2’, ∼130 km from GLS3, though we follow Steen-Larsen and others in using ρ 0 = 340 kg m−3 at this site (we use HL’s value of ρ 0 = 360 kg m−3 at the other locations). Row 11 of Table 1 gives the model density at the anchor depths, which we assume are the mean depths of the anchors during the time span. We obtain the mean depth by using the observed GPS velocity to compute how far downward the anchor moved during half the observing period, and add that to the starting depth.
4.3.2. Dynamic firn model
The other set of predictions comes from a dynamic firn model that computes surface height changes as a result of accumulation, wind erosion, sublimation, melt and compaction (Reference Ligtenberg, Helsen and Van den BroekeLigtenberg and others, 2011; Reference Kuipers Munneke, Ligtenberg, Van den Broeke, Van Angelen and ForsterKuipers Munneke and others, 2014). It also computes the evolution of vertical profiles of firn density and temperature. Density can be modified by firn compaction, and by refreezing of percolating meltwater. The densification expressions in the model are a modified version of the semi-empirical relations by Reference Arthern, Vaughan, Rankin, Mulvaney and ThomasArthern and others (2010), and depend on temperature and on the mean accumulation rate. The temperature evolution within the snowpack is influenced by diffusion and advection of the surface temperature, and by the release of latent heat upon refreezing of percolated meltwater. At the firn/ice boundary, a value for v ice is prescribed as discussed below. Dynamic firn model results are presented through 31 December 2012 because no atmospheric input data were available after that date.
4.3.3. Atmospheric model
Output from an atmospheric model is required to find the mean accumulation rates to use with both models, and to drive the dynamic firn model. For both applications, we use output from the regional atmospheric climate model RACMO2 (Reference Van den BroekeVan den Broeke and others, 2009; Reference Van AngelenVan Angelen and others, 2012). RACMO2’s accumulation values represent the effects of snowfall, sublimation and surface melting (with possible subsequent refreezing). To find the mean accumulation rate, dM/dt, we average RACMO2’s monthly accumulation values over the entire 1960–2012 model time span. The results, after transforming into v ice by multiplying by ρ w/ρ ice, are given in row 12 of Table 1.
RACMO2 fails to simulate the correct surface mass balance at GLS1. Reference Pfeffer, Meier and IllangasekarePfeffer and others (1991) argue that there can be no firn layer at a location where the long-term ratio of refrozen meltwater to snowfall is >0.7. This is the value at which the meltwater fills all the pore spaces in the unmelted snow. RACMO2 predicts a long-term ratio of 0.83 at GLS1. Thus, when the RACMO2 output fields are used to force the dynamic firn model, the model concludes there is no firn layer at GLS1. In reality a firn layer does exist there. RACMO2’s overestimate of the ratio can probably be attributed to overestimates of both the melt flux and the fraction of meltwater that refreezes. The dynamic firn model thus predicts a density at the GLS1 anchor that is close to the ice density and so is much too high. For high densities, the compaction velocity is lower, so the vertical movement of the GLS1 antenna due to firn compaction is underestimated.
4.4. GPS/model comparisons
4.4.1. Vertical position comparison
Geocentric vertical positions inferred from the HL density model are shown as orange lines in Figure 7d–f. We simultaneously fit constant, linear, quadratic and annually varying terms to the model results, just as we do for the GPS estimates. We identify the solutions for the linear and quadratic terms as the model geocentric downward velocity, ![]() , and acceleration, a
m, and give the results in Table 1. For the orange lines in Figure 7d–f, the best-fitting trend has been removed, to be consistent with the GPS residuals shown in black.
, and acceleration, a
m, and give the results in Table 1. For the orange lines in Figure 7d–f, the best-fitting trend has been removed, to be consistent with the GPS residuals shown in black.
Figure 7a–c show that the model predictions of the velocities are in good agreement with the GPS velocities at GLS1 and GLS2, but that the model underestimates the velocities at GLS3. A comparison of the GPS and model solutions for V
geo and ![]() (Table 1) shows the model agrees with the observed velocities to better than 10% for GLS1 and GLS2; but that it underestimates the observed velocities by 36% for GLS3a and 25% for GLS3b.
(Table 1) shows the model agrees with the observed velocities to better than 10% for GLS1 and GLS2; but that it underestimates the observed velocities by 36% for GLS3a and 25% for GLS3b.
For the accelerations, there is good agreement between the model and GPS results for GLS2, as can be seen by comparing the blue and orange curves in Figure 7e, and the a and a m values in Table 1. For GLS3b, however, the model acceleration is one-third of the GPS value. Model/GPS acceleration comparisons for GLS1 and GLS3a are not useful, because of the complications described in Section 4.1.1. We discuss possible explanations for the velocity and acceleration discrepancies in Section 5.
Predictions from the dynamic firn model are shown as the dashed green lines in Figure 7a–c. Because the results from the firn model stop at the end of 2012, we have not fit linear or other terms to the results, and so have not included results from this model in Figure 7d–f or Table 1. We note from Figure 7a–c, though, that where they overlap, the velocities predicted by the HL density model and by the dynamic firn model are in good agreement for GLS2 and GLS3. For GLS1, the dynamic firn model gives a much lower velocity than the steady-state density model, because of the problems with the firn model input data from RACMO2 discussed above.
4.4.2. Reflector height and surface elevation comparison
For the reflector height and surface elevation results, we compare the GPS estimates with predictions from the dynamic firn model. Results from the model are shown as dashed green lines in Figure 7a–c for the reflector heights, and in Figure 7d–f for the geocentric, Eulerian snow surface elevations. We note that the reflector heights are simulated well at all locations, although the trend in reflector height seems somewhat underestimated and dampened by the firn model at GLS1 and GLS2. In large part, both the reflector height and the surface elevation changes are caused directly by variability of accumulation and melt. A good representation of these processes in the RACMO2 climate data will lead to a good simulation of the reflector and surface heights. A secondary cause of reflector and surface height changes is the compaction rate. We address two issues related to the compaction rate that could explain the underestimated trends simulated by the model. First, the compaction rate at GLS1 is underestimated as discussed above. This can explain the lower surface elevation changes in the model. Second, the compaction in the firn model depends on the mean accumulation rate dM/dt for the period 1960–2012. This is an empirical approximation to the fact that in reality the densification rate of a firn layer depends on the overburden pressure from the layers above it. From year to year, the overburden pressure in the upper few meters varies much more strongly than is captured by the mean densification rate. The observed response of surface and reflector height at GLS1 and GLS2 could therefore be larger in amplitude than simulated by the model.
Another type of dynamic firn compaction model (e.g. Reference Barnola, Pimienta, Raynaud and KorotkevichBarnola and others, 1991) uses an empirical formulation based on the overburden pressure from overlying firn layers. These models assume that compaction occurs mainly because of plastic deformation of the firn grains, which is dependent on the overburden pressure. These empirical relations could be improved by observational constraints on the relation between overburden pressure and compaction, especially in the uppermost part of the firn column. Future comparisons between GPS-observed surface elevation changes and firn models could help to improve these representations of firn compaction.
5. Summary and Discussion
We have described how data from a continuously operating GPS receiver installed in the firn layer of an ice sheet can be used to learn about the density and vertical velocity profiles of the firn, and changes in surface elevation. We have focused on two types of GPS measurements: the geocentric vertical position of the antenna and the distance between the antenna and the snow/ice surface (the ‘reflector height’). The recovery of reflector heights is a new application of GPS data in Greenland, and we have discussed the methodology in some detail. Both types of measurements can help to assess firn densification and surface accumulation models. The two measurements can be combined to help validate surface elevation results obtained using satellite altimetry.
We have illustrated some of the ways in which these observations can be useful, by considering data from three permanent GPS sites installed in the interior of the Greenland ice sheet. Here we summarize and discuss our results.
5.1. Positioning results
The GLISN GPS antennas are attached to anchors buried in the firn, and the positioning measurements reflect motion of those anchors. The general characteristics of the positioning results agree qualitatively with expectations:
-
1. At each location the anchor subsides relative to the geocenter. Since vertical motion near the surface is caused by a combination of (i) downhill flow of the ice sheet, (ii) downward motion of the ice at the top of the firn/ice layer as it replaces ice flowing horizontally out of the column below, and (iii) downward displacements within the firn as snow is compacted by the weight of newly accumulated snow, then the anchor should be moving downward, as observed.
-
2. At each site the anchor moves horizontally in a direction compatible with the downward surface topographic gradient to within a few degrees, consistent with standard models that show ice flow is largely driven by stress imbalance caused by the slope of surface topography.
-
3. The subsidence rate at GLS3 increased notably when the anchor was raised from 90 m to 2 m depth. At GLS2 and GLS3b (the GLS3 measurements after the anchor had been raised), the downward velocity decreases with time. These results are consistent with the fact that much of the downward motion is caused by compaction of the part of the firn column lying below the anchor. When the anchor is lower in the firn, there is less firn beneath the anchor to compact. Thus, the compaction contribution decreases as the anchor moves lower. The downward motion for the other two cases, GLS1 and GLS3a (the GLS3 results before the anchor was raised), was affected by additional factors that complicate attempts to interpret the observed velocity variations, i.e. the GLS1 displacements were impacted by the unprecedented surface melting in summer 2012, and displacements at GLS3a could have been affected by thermal contraction of the pipe to which the GPS antenna was attached.
We used a model of the depth-dependent firn density, combined with the steady-state assumption and with estimates of long-term surface accumulation rates, to estimate downward velocities and accelerations to compare with the GPS results. For GLS1 and GLS2 the modeled and observed velocities agree to better than 10%. At GLS3 the modeled velocity underestimates the observed velocity before and after the May 2012 antenna change by 36% and 25%, respectively.
One possible explanation for the GLS3 discrepancy is that the value of v ice used in Eqn (7) could be too small. The velocity of the anchor relative to the surface is proportional to v ice (Eqn (3)), so an inaccurate v ice estimate would map directly into an error in the predicted downward velocity. One way to partially assess this possibility at GLS3 is to use Eqn (5) to see if the velocity change that occurred when the anchor was moved from 90 m to 2 m depth is consistent with the model predictions. Let z a and z b be the anchor depths before and after May 2012. Using GLS3a and GLS3b velocity values from Table 1,

From HL’s model, the ratio of densities at those two depths is

From Eqn (5), the results (Eqns (12) and (13)) should be equal. They differ here by ∼15%, which is significantly smaller than the differences for the two cases individually (36% for GLS3a and 25% for GLS3b). So the model/GPS agreement is much better for the velocity ratio (which does not depend on v ice) than it is for the velocities themselves (which do).
This possibility is further supported by the good agreement between the GLS3 velocities predicted by the HL density model and the dynamic firn model, evident by comparing the orange and green curves in Figure 7c. Figure 7b shows that there is similarly good agreement for GLS2. (The poor agreement at GLS1 is due to problems with the firn model predictions at GLS1 noted above.) These two models use the same values of v ice, but predict the firn compaction velocities using independent methods. The fact that they agree so well for GLS3 (and GLS2) gives us increased confidence that the explanation for the model/GPS discrepancy at GLS3 is that the modeled value of v ice is too small.
Errors in v
ice of this size could arise either because RACMO2 underestimates the mean accumulation rate, or because the assumption that the present-day velocity at the firn/ice boundary is in steady-state equilibrium with the mean accumulation rate over the past 50 years is incorrect. We are not able to use the GPS results to differentiate between these possibilities. We note, though, that Reference BuizertBuizert and others (2012) use measurements from the NEEM (i.e. GLS3) core to estimate a value of v
ice = 0.216 m a−1. If we scale our GLS3b HL model results by the ratio of this value to the v
ice = 0.183 m a−1 value inferred from RACMO2, we obtain ![]() , which agrees with the GPS result (0.603 m a−1) to within 12%. The use of Buizert and others’ v
ice value increases the model estimate at GLS3a to
, which agrees with the GPS result (0.603 m a−1) to within 12%. The use of Buizert and others’ v
ice value increases the model estimate at GLS3a to ![]() , which is still 24% smaller than the GPS value (0.323 m a−1).However, the short GPS record at GLS3a makes us less confident in our estimate of the trend there.
, which is still 24% smaller than the GPS value (0.323 m a−1).However, the short GPS record at GLS3a makes us less confident in our estimate of the trend there.
This discussion suggests the HL density model provides realistic values for the densification contributions to the velocity. The residuals shown in Figure 7d–f allow us to also compare the model and GPS accelerations, though this can only be done meaningfully for GLS2 and GLS3b because of the complications in the GLS1 and GLS3a GPS signals noted above. For both GLS2 and GLS3b, the HL model underestimates the observed acceleration. For GLS2, the underestimate is modest, but for GLS3b the model acceleration is only about one-third of the observed acceleration. Some of this disagreement could be due to the underestimate of v
ice hypothesized above. But, the v
ice underestimate is not likely to be larger than ∼30% (compare the GLS3b values of ![]() and V
geo given in Table 1), which is not nearly large enough to explain the massive GLS3b discrepancy.
and V
geo given in Table 1), which is not nearly large enough to explain the massive GLS3b discrepancy.
Perhaps some of the discrepancy is due to meltwater from the 2012 melt event, percolating into the firn and releasing latent heat when refreezing. This mechanism probably caused the anomalous motion at GLS1 seen in Figure 7d. Figure 7f shows that GLS3b also experienced clear downward motion in mid- to late 2012 relative to later times, which is similar to (though much smaller than) what is seen at GLS1. This downward feature in the GPS time series could have skewed the GLS3b acceleration solution.
There are other issues that could cause errors in our estimates from the HL density model. We assume the firn density profile is in steady state, and that it is accurately represented by HL’s model. These assumptions are particularly suspect at the shallow depths of the GLS1, GLS2 and GLS3b anchors. For example, the steady-state assumption, that the density at any depth is the same at all times, is violated by the deep meltwater percolation and refreezing discussed above for GLS1 and GLS3b.
Other factors can lead to violations of the steady-state assumption. Inter- and intra-annual variations in accumulation and meltwater generation cause near-surface layering in the firn, and those layers move downward through the firn in subsequent years. Thus, the density at a fixed depth changes with time as those distinct layers move through that depth, which violates the steady-state assumption.
This is more apt to be a problem for estimating the acceleration than the velocity; and we have shown that the HL-based densification results are probably quite accurate for the velocity. The rate of compaction at any depth is reflected in the density gradient at that depth. The velocity is determined by the rate of compaction of the entire underlying firn column, so the model only needs to capture the average density gradient through the entire column to provide an accurate velocity estimate. However, the acceleration averaged over a GPS time period of just 2–3 years depends on the density gradient only at the mean depth of the anchor (Eqn (9)). The predictions of a steady-state model are likely to be less accurate for a local density gradient than for the average gradient through the column. This would be less of a problem for a deeply anchored GPS antenna, since the layers become less distinct as depth increases, and so are better represented by a smoothly varying density model, such as that described by HL.
5.2. Reflector heights
The reflector height changes as the GPS antenna moves downward through the firn layer, and as snow accumulates and melts at the surface. We have described a method of recovering temporal variations in reflector height that uses GPS SNR measurements. The method provides estimates of the distance to the snow surface averaged over a disc of diameter ∼60 m centered at the GPS antenna. We obtain good agreement with measurements from a nearby ultrasonic snow sensor at the one GPS location where we could conduct a meaningful comparison.
One advantage GPS offers over non-satellite-based methods of determining reflector heights is that the GPS results can be combined with vertical positions provided by that same GPS receiver to obtain estimates of changes in the geocentric elevation of the surface beneath the antenna. These elevation results can be corrected for the downhill flow of the ice sheet (which can be estimated from the GPS horizontal position measurements) to obtain estimates of variations in the geocentric snow surface elevation at a fixed latitude/longitude location: the location, for example, that has the coordinates of the GPS antenna at the start of the time span. These latter (Eulerian) surface elevation estimates, computed using Eqn (11), could be used to assess future altimeter elevation measurements.
If the ice sheet is in steady-state equilibrium, then although the Eulerian surface elevation results could have short-term fluctuations caused by episodic accumulation events, there would be no long-term trends. Our three GPS sites have been returning data for a little less than 3 years, which is not yet long enough to study long-term variability. The results do show yearly changes in surface elevation on the order of 0.1 m at GLS2 and GLS3, and the widespread summer 2012 melting event shows up clearly at GLS1 as a ∼1.5 m drop in elevation. There is a suggestion of a similar feature at GLS2, though with a much smaller drop of ∼0.3 m.
Measurements of the reflector height, whether obtained using GPS or by other means, are made to the surface surrounding the pole that holds the sensor off the snow. An underlying assumption of the types of comparisons described here is that elevation changes of this local patch of surface are representative of changes over broader scales. In practice, there could be complicating factors. Nearby instruments or structures could impact the local wind pattern in ways that cause the snow surface beneath the pole to have a different elevation than the surface away from camp (e.g. Reference Larsen, Hvidberg, Dahl-Jensen and BuchardtLarsen and others, 2014). The pole could conceivably impact the underlying snow surface, either through its effect on the wind pattern or on the surface melting at its base. People walking or standing around the pole could compress the snow, lowering the surface elevation and increasing the reflector height. Snow that is shoveled around a sagging pole to stabilize the base would raise the surface elevation and so decrease the reflector height.
For GPS reflector heights we would expect very local effects to be tempered by the fact that GPS senses the surface across a reasonably broad region (∼60 m diameter). But we have found that sudden offsets do occasionally occur that complicate attempts to interpret the results. At GLS3, there is an abrupt change (∼8 cm) in both reflector height and vertical position in December 2011. This vertical change can be explained by a snow layer on top of the antenna, which produces a height error in the GPS position analysis (Reference Jaldehag, Johansson, Davis and ElóseguiJaldehag and others, 1996). There is also an abrupt change in the GLS1 reflector height in July 2013, but this has been confirmed by the field crew at Dye-2 to have been at the time of an unusual summer snowstorm. The fairly rapid variation in reflector height observed after that offset is associated with the summer melt season.
Still, the results of this trial study suggest that the use of continuous GPS measurements on an ice sheet to monitor both the vertical position of the antenna and the reflector height can provide useful constraints on models of snow accumulation and firn densification. Furthermore, subtracting the reflector height from the vertical position provides results for the geocentric elevation of the snow surface which could be useful for assessing altimeter estimates of surface elevations.
Acknowledgements
This study was partially supported by the US National Science Foundation (NSF EAR-1144221), by funds from NASA’s solid Earth and cryospheric programs, and by NWO/ALW (Netherlands Organization of Scientific Research, Earth and Life Sciences division) grant 866.10.112. Felipe Nievinski translated the digital elevation models for us from a file provided by The Ohio State University. We particularly thank David Shean, Ian Joughin, Stefan Ligtenberg, Eric Larour, Nicole-Jean Schlegel, Philippe Huybrechts and Waleed Abdalati for providing feedback. IRIS (Incorporated Research Institutions for Seismology) maintains the GLISN sites; Dean Childs was particularly helpful in providing information to us about the sites. Major funding for GLISN is provided by the NSF; the Geological Survey of Denmark and Greenland; the Swiss Science Foundation; the Helmholtz Centre Potsdam Geo-ForschungsZentrum, Germany; Centre National de la Recherche Scientifique (CNRS) and the French Ministry of Research; the Japan Society for the Promotion of Science; and the Korea Polar Research Institute. GLISN GPS data are archived at the University Navstar Consortium (UNAVCO). Snow depth data for Dye-2 were provided by the Greenland Climate Network. We thank Koni Steffen and Jason Box for providing additional information about the GCN sites. RAMCO2 data were provided by Brice Noël and Michiel van den Broeke (IMAU).










