Introduction
Natural arsenates constitute a large, chemically and structurally variable group of minerals (Drahota and Filippi, Reference Drahota and Filippi2009; Majzlan et al., Reference Majzlan, Fillipi, Drahota, Bowell, Alpers, Jamieson, Kirk Nordstrom and Majzlan2014). They can accommodate many divalent metals in various structural types. The vivianite-group arsenates, for example, have the general formula M 3(AsO4)2⋅8H2O, where M = Ni, Co, Zn, Mg, Mn, Fe and Cu (Sejkora et al., Reference Sejkora, Bureš and Hykš2014; Plášil et al., Reference Plášil, Škácha, Sejkora, Škoda, Novák, Veselovský and Hloušek2017; Ciesielczuk et al., Reference Ciesielczuk, Janeczek and Szełęg2018; Siuda and Macioch, Reference Siuda and Macioch2018; Dumańska-Słowik et al., Reference Dumańska-Słowik, Pieczka, Natkaniec-Nowak, Kunecki, Gaweł, Heflik, Smoliński and Kozub-Budzyń2018). Natural members of this group are mostly Ni or Co rich. The olivenite group with the general formula M 2(AsO4)OH includes members with M = Cu, Zn or Mn, although only the Cu- and Zn-rich compositions are more common in Nature (Southwood et al., Reference Southwood, Števko and Carr2020). Minerals of the roselite and fairfieldite group with the general formula Ca2M(AsO4)2⋅2H2O are less common and include members with M = Co, Mn, Zn, Cu, Ni and Mg (Fleck et al., Reference Fleck, Kolitsch and Hertweck2002). The krautite group, the subject of this work, hosts M(AsO3OH)⋅H2O minerals with M = Mn, Zn, Co, Mg and Ca. The group is not structurally homogeneous. The structures contain heteropoly-hedral sheets with similar, but not identical topology. The sheets must accommodate the coordination requirements of the different divalent cations.
The selection of the phases and their metals is controlled by a combination of geochemical parameters (composition of the primary minerals), physico-chemical properties of the aqueous fluids (e.g. pH) and thermodynamics of the solids. The relative importance of such variables can be judged by detailed investigations of mineral-rich, classical localities, such as Jáchymov in the Czech Republic (Škácha et al., Reference Škácha, Plášil and Horák2019), associated solutions (e.g. Majzlan et al., Reference Majzlan, Plášil, Dachs, Benisek, Mangold, Škoda and Abrosimova2020) and thermodynamic measurements. Zinc and cobalt for such minerals are released by weathering of primary ore minerals. Manganese, on the other hand, could be released from minerals of ore deposits (Holtstam et al., Reference Holtstam, Bindi, Förster, Karlsson and Gatedal2022; Cámara et al., Reference Cámara, Biagioni, Ciriotti, Bosi, Kolitsch, Paar, Hålenius, Lepore, Blass and Bittarello2023) but could have other sources in the environment (e.g. Gatuingt et al., Reference Gatuingt, Rossano, Mertz, Fourdrin, Rozenbaum, Lemasson, Reguer, Trcera and Lanson2021).
This work focuses on thermodynamic properties and crystal structures on selected synthetic equivalents of the minerals in the krautite group. Enthalpies of formation and entropies were measured by acid-solution and relaxation calorimetry, respectively. The data set was augmented by previously acquired data for some of the krautite-group phases (Plumhoff et al., Reference Plumhoff, Dachs, Benisek, Plášil, Sejkora, Števko and Majzlan2020; Majzlan et al., Reference Majzlan, Plášil, Dachs, Benisek, Mangold, Škoda and Abrosimova2020) and estimates for some phases. Phase diagrams document the stability fields of these minerals and their formation conditions. Single-crystal X-ray diffraction experiments were used to determine the position of all atoms (including the H atoms) in these structures and to understand hydrogen bonding schemes in these phases.
Materials
Synthetic krautite was prepared by a method outlined in Buckley et al. (Reference Buckley, Bramwell and Day1990), specified already by Catti and Franchini-Angela (Reference Catti and Franchini-Angela1979) and Deiss (Reference Deiss1914). One solution was prepared by mixing and dissolving 4.5 g KH2AsO4 in 20 mL water. Another solution was prepared with 4.95 g MnCl2⋅4H2O and 20 mL water. The arsenical solution was heated slightly to dissolve the solid completely. The two solutions were mixed rapidly and turned immediately to a thick gel. Aggregates of pink krautite crystals grew in the gel. After two months, parts of the gel started to turn to liquid and released some of the aggregates (Fig. 1a). They were picked up with tweezers, dried with a paper towel and examined under binocular microscope for morphology or colour that deviate from that of krautite.

Fig. 1. Aggregates of synthetic (a) krautite, (b) koritnigite and (c) cobaltkoritnigite.
Koritnigite was synthesised by the same procedure, taking 3.41 g ZnCl2 instead of the manganese chloride. Again, thick gel formed and turned slowly to liquid. In this case, even after one year, more than half of the volume still consisted of gel, however a sufficient number of crystals (Fig. 1b) were available for all analyses.
A similar synthesis was attempted with CoCl2⋅6H2O but the gel remained thick and essentially unchanged for more than one year. No crystals were seen in the purple, compact gel. Therefore, cobaltkoritnigite was prepared by the procedure described by Zettler et al. (Reference Zettler, Riffel, Hess and Keller1979). As specified therein, 0.33 g As2O5 and 1.4 g CoSO4⋅7H2O were mixed with 5 mL water and maintained in a Teflon-lined pressure bomb at 150°C for six days. Afterwards, the bomb was allowed to cool slowly to room temperature and the crystals (Fig. 1c) were filtered from the remaining liquid.
Methods
Selected single crystals were investigated by a Rigaku SuperNova single-crystal diffractometer equipped with the Atlas S2 detector and using the mirror-monochromatised MoKα radiation (λ = 0.71073 Å) from a micro-focus X-ray tube. Correction for background, Lorentz effect and polarisation, as well as the empirical (multi-scan) absorption correction were applied to the data during reduction in the CrysAlis package (Rigaku v.2018). The structure has been solved independently from previous structure investigations (Catti and Franchini-Angela, Reference Catti and Franchini-Angela1979; Keller et al., Reference Keller, Hess and Riffel1980) using an intrinsic-phasing algorithm of the program SHELXT (Sheldrick, Reference Sheldrick2015) and subsequently treated by the least-squares refinement in Jana2020 (Petříček et al., Reference Petříček, Dušek and Palatinus2020).
The aggregates of crystals used for calorimetry were ground to powder and tested for their purity with a Bruker D8 ADVANCE powder X-ray diffractometer with DAVINCI design, and with CuKα radiation, Ni filter and a Lynxeye 1D detector. A step size of 0.02°2θ and a 0.25 s per step were used. Lattice parameters were refined using JANA2006 (Petříček et al., Reference Petříček, Dušek and Palatinus2014).
Acid-solution calorimetry and relaxation calorimetry were used to measure enthalpies of dissolution in 5 N HCl and low-temperature heat capacities, respectively. Both methods were used in an identical fashion as in our previous work (e.g. Majzlan et al., Reference Majzlan, Plášil, Dachs, Benisek, Mangold, Škoda and Abrosimova2020). The details on acid-solution calorimetry of secondary minerals are summarised by Majzlan (Reference Majzlan2017). The principles of relaxation calorimetry, the accuracy and precision of the method have been described and evaluated by Dachs and Benisek (Reference Dachs and Benisek2011) and Kennedy et al. (Reference Kennedy, Stancescu, Marriott and White2007).
Results
Crystal structure of koritnigite
A prismatic large, 0.140 × 0.099 × 0.023 mm, fragment of synthetic koritnigite crystal (also used for calorimetric study) was investigated. The structure solution revealed nearly all atomic positions except those of the H atoms. Those were localised subsequently from the difference-Fourier maps and refined keeping soft constraints of 1.00 Å on the O–H distances as well as H–O–H angles, 105° within the H2O molecules, and with the U iso of each H set to 1.2 times that of the donor O atom. The final refinement including 265 parameters, 12 restraints and 12 constraints, converged to R = 0.0270 and wR = 0.0663 for 3330 unique observed reflections, of I > 3σ(I), with goodness of fit = 1.37. The structure was modelled as twinned due to reticular merohedry (see Petříček et al., Reference Petříček, Dušek and Plášil2016) as a two-component twin (Table 1). Crystallographic details, data collection and refinement parameters are given in Table 1. The bond-valence analysis (after Brown Reference Brown2002) is provided in Supplementary Table S1, based on the refined interatomic distances (Supplementary Table S2) and the bond-valence parameters given by Gagné and Hawthorne (Reference Gagné and Hawthorne2015). Hydrogen-bond geometry is summarised in Supplementary Table S3. The crystallographic information file has been deposited with the Principal Editor of Mineralogical Magazine and is available as Supplementary material (see below).
Table 1. Crystal data, collection and refinement parameters for synthetic koritnigite and krautite.

Crystal structure of krautite
A short-prismatic, 0.093 × 0.054 × 0.007 mm, fragment of synthetic krautite crystal (also used for calorimetric study) was investigated. The structure solution revealed nearly all atomic positions except those of the H atoms. The structure is non-centrosymmetric, of the space-group P21; the absolute structure has been refined (as an inversion-twin). Afterwards, the positions of all H atoms have been successfully localised from the difference-Fourier maps corrected for the F 2 from the second twin-domain contribution (Petříček et al., Reference Petříček, Dušek and Plášil2016). H atoms were refined keeping soft constraints of 1.00 Å on the O–H distances as well as H–O–H angles, 105° within the H2O molecules, and with the U iso of each H set to 1.2 times that of the donor O atom. The final refinement including 284 parameters, 15 restraints and 19 constraints, converged to R = 0.0338 and wR = 0.0666 for 3895 unique observed reflections, of I > 3σ(I ), with goodness of fit = 1.24. Crystallographic details, data collection and refinement parameters are given in Table 1. The bond-valence analysis (after Brown, Reference Brown2002) is provided in Supplementary Table S4, based on the refined interatomic distances (Supplementary Table S5) and the bond-valence parameters given by Gagné and Hawthorne (Reference Gagné and Hawthorne2015). The hydrogen-bond geometry is summarised in Supplementary Table S6. The crystallographic information file and the structure factors list have been deposited with the Principal Editor of Mineralogical Magazine and are available as Supplementary material (see below).
Thermodynamic measurements
Apart from the title compounds, additional phases must be measured in order to convert the dissolution enthalpies to enthalpies of formation. These additional phases, so-called reference phases, were ZnO, MnO, CoSO4⋅7H2O, KH2AsO4, HCl⋅9.96H2O, H2O and KCl. The enthalpies of dissolution of all these phases in 5 N HCl are given in Table 2, together with an appropriate thermochemical cycle. The calculated enthalpies of formation are listed in Table 3.
Table 2. Thermochemical cycle and the enthalpies of the individual reactions used in this work. The bottom portion of the table lists the equations needed for the calculation of formation enthalpies of the arsenates of the krautite group.

Table 3. Summary of the thermodynamic data for the minerals of the krautite group.
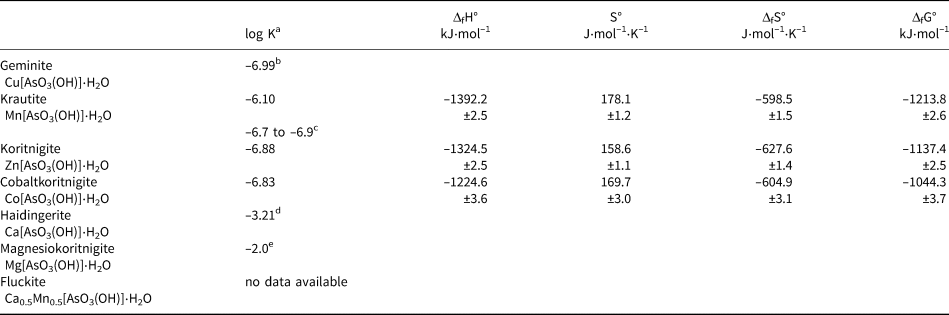
a All log K sp values refer to a dissolution reaction M[AsO3(OH)]⋅H2O → M 2+ + HAsO42– + H2O
b Plumhoff et al. (Reference Plumhoff, Dachs, Benisek, Plášil, Sejkora, Števko and Majzlan2020)
c calculated from Tournassat et al. (Reference Tournassat, Charlet, Bosbach and Manceau2002)
d Majzlan et al. (Reference Majzlan, Plášil, Dachs, Benisek, Mangold, Škoda and Abrosimova2020)
e estimated, see text
The low-temperature heat capacities (Fig. 2a) were measured and integrated for koritnigite (Supplementary Tables S7, S8) and krautite (Supplementary Tables S9, S10). Thermodynamic functions calculated from the smoothed C p data are presented in Supplementary Tables S8 and S10. Both data sets show anomalies at very low temperatures. In the data for koritnigite, there is a very weak, broad C p anomaly at 3 K. The nature of this anomaly is unclear but its contribution to overall C p and S is negligible.

Fig. 2. Experimentally measured heat capacity of koritnigite and krautite. The panel (a) shows the full data sets and (b) shows a detail at low temperatures.
In the data for krautite, there is a sharp lambda-shaped anomaly at 3 K (Fig. 2b). This anomaly can be assigned to the magnetic ordering below this temperature. The position of the anomaly is in excellent agreement with magnetic-susceptibility data of Bramwel et al. (Reference Bramwell, Buckley, Visser and Day1988). They determined that synthetic krautite is antiferromagnetic, with a Curie temperature of 3.2 K.
The presence of the anomalies complicated the fitting necessary to extract entropies for the two phases. There are no appropriate functions for the fitting of the lambda-shaped anomalies (e.g. Shapiro et al., Reference Shapiro, Woodfield, Stevens and Boerio-Goates1999). Both data sets were fitted with a series of polynomials that have no physical meaning. The polynomials were joined at temperatures where the differences in smoothed C p and their slopes were minimal. These polynomial segments were then used to calculate thermodynamic functions between 0 and 300 K and the results are listed in Tables S8 and S10.
The calculated entropies were converted to entropies of formation, using the entropies of pure elements in their standard state from Robie and Hemingway (Reference Robie and Hemingway1995). Enthalpies and entropies of formation were then used to calculate the Gibbs free energies of formation (Table 3) and the solubility products, using auxiliary data from Robie and Hemingway (Reference Robie and Hemingway1995) and Nordstrom et al. (Reference Nordstrom, Königsberger, Majzlan, Bowell, Alpers, Jamieson, Kirk Nordstrom and Majzlan2014).
Entropy estimate for cobaltkoritnigite
In the absence of low-temperature heat capacity data for Co[AsO3(OH)]⋅H2O, its entropy can be estimated from solid-state reactions:
where M′ and M″ are two different divalent metals. We have chosen oxides MO because of their simple structures and accurately known entropies. Because all phases that participate in this reaction are solids, it could be assumed that the entropy change associated with this reaction (ΔrS) is 0 J⋅mol–1⋅K–1. This assumption can be tested for M' = Zn and M'' = Mn with the data from this work and entropies for simple oxides from Robie and Hemingway (Reference Robie and Hemingway1995). The calculated ΔrSZn–Mn = 3.0±1.7 J⋅mol–1⋅K–1, a small entropy value. The reason for the small difference could be a different structural type for MnO (halite) and ZnO (wurtzite). For the estimate for cobaltkoritnigite, pairs of MnO–CoO (both halite structures) and ZnO–CoO (different structure types) can be tested. Assuming that ΔrSZn–Co and ΔrSMn–Co are both 0 J⋅mol–1⋅K–1, the entropy of Co[AsO3(OH)]⋅H2O can be estimated as 168.2 and 171.2 J⋅mol–1⋅K–1, respectively. Hence, even though there is a structural difference between ZnO and CoO, the entropy estimate is similar to that obtained from the calculation with the MnO–CoO pair. We adopted the average value 169.7 J⋅mol–1⋅K–1, with a conservative error estimate of ±3.0 J⋅mol–1⋅K–1.
Discussion
Role of H2O in the crystal structures of solids
To analyse and evaluate the role of molecular water in the structures of solids, a useful scheme was introduced in the literature by Frank Hawthorne and co-workers (Hawthorne, Reference Hawthorne1992, Reference Hawthorne2012; Hawthorne and Schindler, Reference Hawthorne and Schindler2008; Hawthorne and Sokolova, Reference Hawthorne and Sokolova2012; Schindler and Hawthorne, Reference Schindler and Hawthorne2008). Generally, there are several types of H2O moieties in crystal structures and each of them play a distinct role in structure bonding. Particular types of H2O can be distinguished based on the coordination number of O atoms in these H2O groups. In the structures of oxysalts, in general, there are ‘transformer’, ‘non-transformer’ and ‘inverse’ transformer H2O groups with [3], [4] and [5]-fold coordinated O atoms, respectively. Their role is generally to transfer the bond-valence from cations (Lewis acids) to anions (Lewis bases), keeping the structure together, as the strengths of these components are equal or similarly matching, following the valence-matching principle of the bond-valence theory (Brown, Reference Brown2002, Reference Brown2009; Hawthorne Reference Hawthorne2012).
Symmetry of the structures of krautite and koritnigite
In this work, the crystal structure of krautite was refined in the monoclinic space group P21, in agreement with the earlier (Catti and Franchini-Angela, Reference Catti and Franchini-Angela1979) or newer (Weil et al., Reference Weil, Kolitsch and Stürzer2022) models. On the other hand, other M[AsO3(OH)]⋅H2O structures with M = Co, Cu, Zn and Mg are triclinic (Keller et al., Reference Keller, Hess and Riffel1980; Cooper and Hawthorne, Reference Cooper and Hawthorne1995; Kampf et al., Reference Kampf, Nash, Dini and Donoso2013). The most recent addition to this group is a triclinic polymorph of Mn[AsO3(OH)]⋅H2O (Weil et al., Reference Weil, Kolitsch and Stürzer2022), not known from Nature so far. The differences between the monoclinic and triclinic structures in this group of phases are subtle and seem to be related to the hydrogen-bonding scheme in these structures. Our refinements confirmed the choice of symmetry for krautite and koritnigite. There were no indications that the symmetry should be changed.
Crystal structure and hydrogen-bonding network of koritnigite
The structure of koritnigite has been determined first by Keller et al. (Reference Keller, Hess and Riffel1980). It contains four Zn sites, four As sites, twenty O sites and twelve H sites. In the general view, the structure consists of zig-zag edge-sharing chains of ZnO5(H2O) octahedra that run parallel to [10$\bar{1}$![]() ]. They are joined by corner-sharing with AsO3(OH) tetrahedra to form sheets parallel to {010} (Fig. 3). Two of the four vertices of each of the AsO3(OH) tetrahedra are O atoms of Zn-octahedra, while the other two are unlinked, except by hydrogen bonding. The sheets are linked in the [010] direction only by hydrogen bonds (Fig. 3). The Zn1 and Zn4 octahedra form one set of chains linked into a sheet centred at 0 along b and the Zn2 and Zn3 octahedra form another set of chains linked into a sheet centred at ½ along b.
]. They are joined by corner-sharing with AsO3(OH) tetrahedra to form sheets parallel to {010} (Fig. 3). Two of the four vertices of each of the AsO3(OH) tetrahedra are O atoms of Zn-octahedra, while the other two are unlinked, except by hydrogen bonding. The sheets are linked in the [010] direction only by hydrogen bonds (Fig. 3). The Zn1 and Zn4 octahedra form one set of chains linked into a sheet centred at 0 along b and the Zn2 and Zn3 octahedra form another set of chains linked into a sheet centred at ½ along b.

Fig. 3. Hydrogen-bonding in the structure of koritnigite. (a) {ZnO5(H2O)AsO3(OH)}∞ sheets, stacked perpendicular to b, are linked via loose H-bonds only, whereas (b) the intrasheet H-bonding network is denser (shown is a single layer). Zn is in violet colour, As is green, blue dashed are H-bonds, H atoms are whitish. Unit-cell edges are outlined in black lines. (c) a detail of the intrasheet H-bonding network. Zn is in pale-green colour, As is green, pale-green dashed are H-bonds.
The structure of koritnigite contains four symmetrically independent OH groups and four symmetrically independent H2O molecules. Each of those H2O molecules participates in the bonding within the single ZnO5(H2O) octahedron. Those linked to Zn3 and Zn4 (O20 and O17 respectively; see Table S1) are transformer H2O groups with the 3-coordinated O atom. On the other hand, the O15 and O11 that are linked to Zn1 and Zn2, respectively, seem to be non-transformer H2O groups, as each of them accepts one additional weak H-bond from the interlayer. These findings are consistent with observations and predictions made by Keller et al. (Reference Keller, Hess and Riffel1980) for koritnigite and by Kampf et al. (Reference Kampf, Nash, Dini and Donoso2013) for magnesiokoritnigite. Nevertheless, neither of these papers found H atoms from the diffraction data and were based only on the crystal-chemical considerations. The geometry of hydrogen bonds in the crystal structure of synthetic koritnigite is summarised in Supplementary Table S3. The structural formula of synthetic koritnigite is Zn4(H2[3]O)2[AsO3(OH)]4(H2[4]O)2, Z = 2, D calc. = 3.5956 g cm–3.
Crystal structure and hydrogen-bonding network of krautite
The structure of krautite has been first determined by Catti and Franchini-Angela (Reference Catti and Franchini-Angela1979). It contains four Mn, four As and twenty O sites. Furthermore, it hosts twelve H atoms, associated with OH and H2O, which have not been found in previous work. The structure consists of (010) layers composed of chains of Mnφ6 octahedra running in the [101] direction (Fig. 4). These chains are interconnected by the As tetrahedra. Each of the four independent arsenate tetrahedra attaches to the octahedral chains via three oxygen atoms; the fourth oxygen is protonated, staggered towards the interlayer, and it participates in hydrogen-bonding between the layers (Fig. 4). Adjacent layers are held together only by hydrogen bonds resulting in the excellent (010) cleavage of krautite. The layers are stacked along and related by the screw 21 axis.

Fig. 4. Hydrogen-bonding in the structure of krautite. (a) {MnO5(H2O)AsO3(OH)}∞ sheets, stacked perpendicular to b, are linked via loose H-bonds only, whereas (b) the intrasheet H-bonding network (detail only displayed) is dense and strong. Mn is light-pink colour, As is green, blue dashed are H bonds, labels in red belong to O2– and blue to H2O/OH. Unit-cell edges are outlined in black lines.
The structure of krautite contains four symmetrically independent OH groups and four symmetrically independent H2O molecules in the asymmetric part of the unit cell. Similarly to koritnigite, each of those H2O participates in the bonding within the single MnO5(H2O) octahedron. Nevertheless, based on the current structure refinement it is likely that three H2O groups within the krautite structure, O10 (Mn2), O13 (Mn3) and O20 (Mn4) (see Table S4), are transformer H2O groups with a 3-coordinated O atom. The O7 atom seems to be a part of a non-transformer H2O group with a fourfold coordinated O atom. The geometry of hydrogen bonds in the crystal structure of synthetic krautite is summarised in Table S6. The structural formula of synthetic krautite is Mn4(H2[3]O)3[AsO3(OH)]4(H2[4]O), Z = 2, D calc. = 3.2739 g cm–3.
The structural models of synthetic krautite from this work and that of Bramwell et al. (Reference Bramwell, Buckley, Rosseinsky and Day1994) are very similar. The calculated arithmetic mean (dav) of the equivalent atoms distances is 0.1331 Å. The measure of similarity (Δ) (after Bergerhoff et al., Reference Bergerhoff, Berndt, Brandenburg and Degen1999) is 0.012, which is a function of the differences in atomic positions, weighted by the multiplicities of the sites, and the ratios of the corresponding lattice parameters of the structures. The maximum difference in those two structures has been found for the atom H1O10 and is 0.6609 Å. This difference is seen as reasonable as we are comparing X-ray diffraction (this work) and neutron diffraction (Bramwell et al., Reference Bramwell, Buckley, Rosseinsky and Day1994) techniques.
Stability and formation conditions of koritnigite, krautite and related phases
The thermodynamic data acquired in this work allow for quantitative assessment of the stability of the M[AsO3(OH)]⋅H2O, including krautite, koritnigite and cobaltkoritnigite, and comparison of these phases to the chemically related geminite [Cu[AsO3(OH)]⋅H2O] and haidingerite [Ca[AsO3(OH)]⋅H2O]. Given the presence of the acidic AsO3(OH) group in their structures, it is not surprising that they are predicted to crystallise from acidic solutions (Figs 5, 6). Another property, not obvious from their composition, is their relatively high solubility. Hence, in general, these phases precipitate from oxidised acidic (acid mine drainage) solutions with high metal and arsenic concentrations.

Fig. 5. pH–pɛ diagrams for the system (a) ZnO–As2O5–H2O–S and (b) Cu–O2–S–As2O5–H2O. Constructed for log a[Zn(II)] or log a[Cu(II)] = –1, log a[As(V)] = –1, log a(S) = –3 and T = 298.15 K.
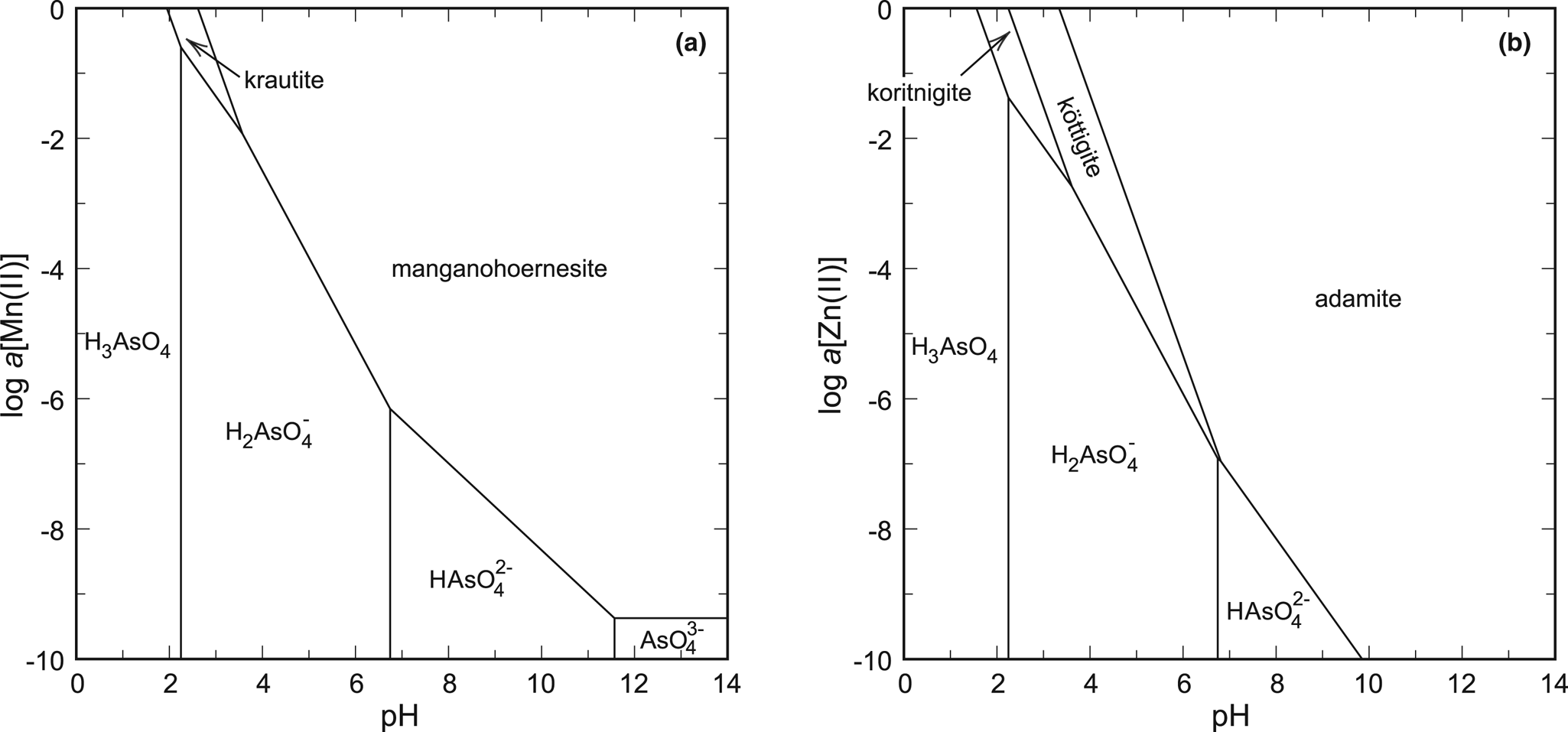
Fig. 6. pH-activity phase diagrams for the systems (a) MnO–As2O5–H2O and (b) ZnO–As2O5–H2O. Constructed for log a[As(V)] = –1 and T = 298.15 K.
The best example is the system ZnO–As2O5–H2O, with the phases koritnigite, köttigite [vivianite group, Zn3(AsO4)2⋅8H2O] and adamite [olivenite group, Zn2(AsO4)(OH)]. Thermodynamic data for köttigite were taken from Lee and Nriagu (Reference Lee and Nriagu2007) and those for adamite from Magalhães et al. (Reference Magalhães, De Jesus and Williams1988). A phase diagram that represents only an oxidised solution (Fig. 5a, 6b) shows the relationships between the three zinc arsenates. The stability field of koritnigite is restricted to low pH values and high Zn and As concentrations. The greatest stability field belongs to adamite, a Zn arsenate that is much more common than koritnigite.
The evaluation in the system MnO–As2O5–H2O is more difficult. The data for manganohörnesite [vivianite group, Mn3(AsO4)2⋅8H2O] from Johnston and Singer (Reference Johnston and Singer2007) are uncertain and there are no thermodynamic data for eveite [olivenite group, Mn2(AsO4)(OH)], to our best knowledge. There is another datum for the solubility product of krautite available (Tournassat et al., Reference Tournassat, Charlet, Bosbach and Manceau2002). Converting their data to the reaction used in this present work (see footnote in Table 3), their value of log K sp is –6.7 to –6.9, comparing fairly well to our datum of –6.10. Calculations suggest that manganohörnesite is stable over most of the diagram (Fig. 6a). We have to emphasise that the thermodynamic data for eveite are not known and this phase, similarly to adamite in the system with zinc, could displace much of the stability field of manganohörnesite. A small field for krautite appears under low pH and high aqueous ion concentrations.
The system CuO–As2O5–H2O is complex because of the number of phases, resulting from the flexibility of coordination of Cu2+ in their structures. The stable phase in the system is olivenite [Cu2(AsO4)(OH)], the mineral structurally very similar to adamite and eveite. The structural analogue of köttigite and manganohörnesite is the rare mineral babánekite [vivianite group, Cu3(AsO4)2⋅8H2O] (Plášil et al., Reference Plášil, Škácha, Sejkora, Škoda, Novák, Veselovský and Hloušek2017) for which no thermodynamic data are available. Lide (Reference Lide2005) gave a solubility product for Cu3(AsO4)2, suggesting that it may perhaps relate to a phase such as babánekite, but implying that such a phase would be quite stable. Such stability is in stark contrast with the rare occurrence of such a phase. Suppressing olivenite from the calculations, a small geminite field appears at low pH and high Cu and As concentrations (Fig. 5b), as expected. These predictions agree with the occurrence and assemblages of geminite as a relatively abundant secondary mineral in Jáchymov (Škácha et al., Reference Škácha, Plášil and Horák2019; Majzlan et al., Reference Majzlan, Plášil, Dachs, Benisek, Mangold, Škoda and Abrosimova2020).
Limited natural observations on aqueous solutions that precipitate M[AsO3(OH)]⋅H2O minerals support our findings. Recently, we have described solutions that precipitate cobaltkoritnigite [(Co,Zn)[AsO3(OH)]⋅H2O] in underground spaces in Jáchymov, Czech Republic (Majzlan et al., Reference Majzlan, Plášil, Dachs, Benisek, Mangold, Škoda and Abrosimova2020, their tables 2 and 3). The pH of these two solutions were 2.41 and 2.96. Calculations with PHREEQC (Parkhurst and Appelo, Reference Parkhurst and Appelo1999; LLNL database) returned saturation indices for koritnigite of –0.48 and +0.78. This result proves that a koritnigite-like phase is near equilibrium with these aqueous solutions, in good agreement with the active precipitation of cobaltkoritnigite at this site.
Haidingerite [Ca[AsO3(OH)]⋅H2O] and the chemically related pharmacolite [Ca[AsO3(OH)]⋅2H2O] are predicted to crystallise from Ca- and As-rich solutions (Majzlan et al., Reference Majzlan, Plášil, Dachs, Benisek, Mangold, Škoda and Abrosimova2020). In this case, however, their solubility is higher than for the M[AsO3(OH)]⋅H2O with M 2+ = Cu, Zn or Mn. Because of the much larger ionic radius of Ca2+ (in comparison to Cu2+, Zn2+ or Mn2+), there are limited structural relationships between the systems CaO–As2O5–H2O and those with CuO, ZnO, or MnO.
In the system MgO–As2O5–H2O, the mineral magnesiokoritnigite [Mg[AsO3(OH)]⋅H2O] was described recently by Kampf et al. (Reference Kampf, Nash, Dini and Donoso2013). It occurs together with anhydrite, halite, lavendulan, quartz and scorodite at the Torrecillas mine in the Atacama Desert in Chile. The association with scorodite and lavendulan suggests precipitation from acidic solutions and the presence of anhydrite implies low activity of H2O, elevated formation temperature, low relative air humidity, or combination of such factors. The Atacama Desert is dry but not particularly hot (McKay et al., Reference McKay, Friedmann, Gómez-Silva, Cáceres-Villanueva, Andersen and Landheim2003), with average temperatures of 16–17°C and air humidity of 25%. The humidity of the air and soil could occasionally increase during the rare rain events. Having recently derived a thermodynamic data set for brassite [Mg[AsO3(OH)]⋅4H2O] and rösslerite [Mg[AsO3(OH)]⋅7H2O] (Majzlan et al., Reference Majzlan, Plášil, Dachs, Benisek, Mangold, Škoda and Abrosimova2020), we can estimate roughly the thermodynamic properties of magnesiokoritnigite. Considering the reaction:
If these phases are in equilibrium at 25°C and relative air humidity (RH) of 25%, the calculation gives ΔfG°(magnesiokoritnigite) of –1418 kJ⋅mol–1 and the solubility product of –2.0. The equilibrium may lie at even lower air humidities and in that case, the solubility product would be higher. For example, if RH = 10%, then log K sp = –0.9. We adopt log K sp of –2.0 as a rough estimate and compare this value to the log K sp values for other minerals in this group.
Field observations of assemblages with koritnigite and krautite
Our field observations in underground spaces in Jáchymov showed that precipitation of cobaltkoritnigite and koritnigite is connected to strongly acidic solutions (Majzlan et al., Reference Majzlan, Plášil, Dachs, Benisek, Mangold, Škoda and Abrosimova2020). They are derived from oxidative weathering of nickelskutterudite or krutovite in the absence of carbonate gangue minerals which could serve as a pH buffer. Cobaltkoritnigite seems much scarcer than koritnigite, in agreement with the general prevalence of Ni over Co in the ores in Jáchymov. As there are no carbonates as potential sources of Ca or Mn, haidingerite (which otherwise can precipitate under similar pH conditions as koritnigite) has never been observed together with koritnigite and its occurrences are linked to other locations in the mines.
Koritnigite and cobaltkoritnigite are rarely associated with the vivianite-group minerals köttigite and erythrite. The latter minerals should form from mildly acidic or neutral solutions and grow centimetres to decimetres away from the koritnigite and cobaltkoritnigite aggregates. Such associations document strong pH gradients over short distances that could be driven only by neutralisation by primary carbonates in specific local environments.
Krautite occurs in the same parts of the galleries of the Geschieber vein in the Svornost mine as koritnigite and cobaltkoritnigite. The source of Mn is probably a small amount of the gangue carbonates. This notion could be supported by the fact that unlike cobaltkoritnigite/koritnigite, which occur without any directly associated secondary phases, krautite usually grows on gypsum crystals. Therefore, both Ca and Mn can be derived from the dissolved carbonates. Calcium reacts preferably with sulfate in the solution to form gypsum, whereas Mn, and probably also Zn and Co, prefer the arsenates structures of the krautite-type.
Acknowledgements
We appreciate the comments of two anonymous reviewers who helped to improve the manuscript. This work was supported financially by a Deutsche Forschungsgemeinschaft grant MA 3927/42-1. The support to J.P. through the Operational Programme of the MEYS CR (Project No. SOLID21 CZ.02. 1.01/0.0/0.0/16_019/0000760) is acknowledged.
Supplementary material
To view supplementary material for this article, please visit https://doi.org/10.1180/mgm.2022.140
Competing interests
The authors declare none.











