Thickness and volume

In 1994 the MG surface elevation, bed topography and ice thickness were estimated based on monopulse radio-echo soundings (Reference Knudsen and HasholtKnudsen and Hasholt, 1999). The mean MG ice thickness (115 m) was derived from measurements at 450 positions, spaced ∼100 m apart along profiles running across the glacier, and ∼300 m apart along the flowline with a vertical spacing of 50 m (two such profiles are illustrated in Fig. 2). The error in measured ice thickness was estimated to be less than ±5 m (Reference Knudsen and HasholtKnudsen and Hasholt, 1999), giving a relative uncertainty of <5% for the mean 1994 ice thickness (115 m).

Fig. 2. A comparison between the 2011 calculated mean MG thickness and the 2011 and 1994 monopulse radio-echo sounding estimated mean thicknesses at two cross-section locations in the ablation area: (a) at ∼300 m a.s.l.; (b) at ∼400 m a.s.l. Approximate locations of the cross sections are shown in Figure 7c.

In 1995 a glacier observation program was initiated to measure MG’s annual SMB and to map changes in ice thickness. A network of stakes (Fig. 1) was used to measure summer ablation (Fig. 3) based on the direct glaciological method (Reference Østrem and BrugmanØstrem and Brugman, 1991; Reference MernildMernild and others, 2011a). The vertical accuracy of observed annual stake mass-balance measurements has been estimated to be within 5 cm, or <±10% (Reference Østrem and StanleyØstrem and Stanley, 1969). Measurements were obtained at 59 stakes covering 16.3 km² of MG, excluding the crevassed area in the southeastern part of the glacier (this omission is not likely to bias the results, since the surface of the crevassed area follows the general hypsometric distribution in the upper part of MG (Reference Mernild, Liston, Hasholt and KnudsenMernild and others, 2006, Reference Mernild, Liston, Kane, Hasholt and Knudsen2008b)). Since its establishment, the stake network has moved slowly down-glacier by 50–275 m (based on calculations, this movement has an insignificant impact on estimates of the mean annual surface velocity). The winter balance was calculated as the difference between the net annual balance and the summer balance. The mass-balance observations are accurate within ±15% for the entire MG (Fig. 3) (Reference Knudsen and HasholtKnudsen and Hasholt, 2004), which is within the uncertainty range suggested by Reference Cogley and AdamsCogley and Adams (1998) for these methods.

Fig. 3. Annual mass-balance distributions and changes at MG: (a) mean winter mass balance and annual change (blue-red shades); (b) mean summer mass balance and annual change; and (c) net annual mass balance and annual change for 1996/97 through 2010/11. The white bold lines (in the right-side panels) indicate the margin for significant annual trends in winter, summer and net mass balances, where values below are significant. The white area has no data, and the margin is based on Landsat 7 ETM+ Mosaic imagery, 1 August 2009 and 14 August 2011.

The MG ice volume was calculated for 1986, 1999 and 2011 and based on the satellite-derived glacier extent (from Landsat imagery) multiplied by the mean ice thickness (Reference Mernild, Malmros, Yde and KnudsenMernild and others, 2012). The mean ice thicknesses for 1999 and 2011 were calculated from the observed 1994 mean thickness and the cumulative observed mass balance. To assess the accuracy of the calculations, we compared the 2011 calculated MG thickness against thickness measured in 2011 by monopulse radio-echo sounding along two cross-section profiles (both located in the ablation zone) (Fig. 2). The mean difference in ice thickness between the calculations and radio-echo soundings was on average 2 m (seven stakes, root mean square (rms) = 3 m) (Fig. 2).

The 1986 mean ice thickness was estimated by adding the cumulative mass balance during 1986–94, based on modeled MG annual mass-balance data from Reference Mernild, Kane, Hansen, Jakobsen, Hasholt and KnudsenMernild and others (2008c), to the 1994 mean thickness (Fig. 4). The calculated MG annual mass balance was compared against observed mass balance for a control period 1995/96 to 2003/04, indicating an r ² value of 0.71 (significant, p < 0.01) and a difference less than 0.01 m between observed and calculated mass-balance values. The 1986–94 calculation method was extended back to 1981, at which point the mean calculated surface elevation was compared to a 1981 map (1 : 20 000) of digitized mean surface topography (Reference Knudsen and HasholtKnudsen and Hasholt, 1999), indicating an average difference of 2–4 m (rms = 3 m) (not shown).

Fig. 4. Time series of estimated mean thickness (line), area (diamonds; Reference Mernild, Malmros, Yde and KnudsenMernild and others, 2012) and volume (circles) for MG. The dashed time series is estimated based on MG net mass-balance calculations (Reference Mernild, Kane, Hansen, Jakobsen, Hasholt and KnudsenMernild and others, 2008c). The percent of 1986 MG mean height, area and volume (the 1986 values were set to 100%) are shown in parentheses.

The MG surface slope was calculated for both 1996 and 2011 for the longitudinal profile along stakes 31, 40, 50, 60, 70, 80, 107, 110, 120, 130 and 140 (Figs 1 and 5).

Fig. 5. (a) Longitudinal surface elevation for 1994 and 2011, where the 2011 elevation was calculated with and without vertical velocity (w _e), showing the positions of stakes 31–140; and (b) longitudinal mean surface slope for 1996 and 2011, SMB, w _e and dh/dt including uncertainty bars.

Surface ice velocity and thickness changes

Each stake position (Fig. 1) was measured annually, varying from 47 stakes in 1998 and 2001 to 18 stakes for the years 2008–11. Eighteen stakes were measured continuously throughout the period 1995/96–2010/11. Before 2004, the horizontal stake positions were measured by topographic surveys using a theodolite (Kern) with an Electro-optical Distance Meter, having a horizontal uncertainty of less than ±1 m. After 2004, stake position was based on a portable single-frequency GPS (Garmin GPS 12 XL) with a relative horizontal uncertainty (std dev.) of about ±2–3 m (similar to a relative uncertainty of approximately ±10% for maximum annual velocity, and ±25% for mean velocity). The horizontal ±2–3 m value is based on long time repeated fixed station measurements with the same instrument during several years. The annual stake positions were used to calculate the spatial mean surface velocity field.

Also, a continuous ice surface velocity time series was obtained from a dual-frequency GPS receiver (Javad Laxon GGD160T, operated by the Geological Survey of Denmark and Greenland) positioned near the center of MG (Fig. 1). This time series was used to determine the seasonal variability in ice surface velocity. However, we have access to data only from May 2004 through July 2005 (when the GPS receiver was located at elevations from 462 to 455 m a.s.l.) and from March 2009 through August 2010 (513–509 m a.s.l.). The horizontal and vertical uncertainties in the GPS time series were on average around 3 and 6 mm, respectively.

Thickness changes, dh/dt, at a point on the glacier are a combination of SMB and vertical strain and can be described by continuity (Cuffey and Patterson, 2010) approximately as

where b is the SMB, u _s is the horizontal surface velocity, α is the surface slope and w _s is the vertical velocity of a fixed point on the glacier (e.g. the top of a stake). However, our surveys measured the position of the ice surface at each stake, so our observed vertical velocity includes the SMB. Thus, we calculate thickness changes as

where w _obs is the observed vertical velocity measured as the height difference between two successive surveys of the ice surface elevation at the position of a stake. We separate the component of thickness change due to vertical strain rate (emergence velocity, w _e) as

To assess how much of the deceleration in surface velocity can be explained by changes in thickness, the theoretical surface velocity due to deformation at the beginning and end of the study period was calculated using the shallow ice approximation (SIA; Reference HutterHutter 1983):

where A is the flow law rate factor, taken as 2.1 × 10⁻¹⁶ a⁻¹ Pa ⁻³ for isothermal ice at 0°C (Reference Cuffey and PatersonCuffey and Paterson, 2010), ρ is 900 kgm⁻³, g is acceleration due to gravity, 9.81 m s⁻², dS/dx is the surface slope and H is the ice thickness. We apply Eqn (4) within the ablation area along the longitudinal profile from stake 31 through stake 80, performing the calculation midway between stake locations, based on the values of thickness, slope and observed velocity averaged between the two adjacent stake locations. This provides a flowline average over ∼3–5 ice thicknesses, which compensates somewhat for the fact that the SIA ignores longitudinal and lateral stresses that may be important for a mountain glacier. A shape factor is not used because MG is wide relative to its depth (half-width/thickness ≈ 10).

Spatial surface mass-balance and thickness changes

Figure 3 illustrates the mean spatial variations in winter, summer and annual net mass balances. The mean winter balance shows less accumulation at low elevations (0.3 m w.e.a⁻¹) than at higher elevations (>1.4 m w.e. a⁻¹) (Fig. 3a), with a mean orographic gradient of ∼0 m w.e. a⁻¹ per 100 m increase in elevation (1995/96–2007/08). Figure 3a also illustrates the spatial distribution of the annual change in winter balance, showing that the terminus, the marginal areas at high elevations, and areas near mountain ridges had the smallest decrease, while other areas had an increasing winter balance (0.04 m w.e. a⁻²). The largest changes (−0.20 m w.e. a ⁻²) occurred along the center line of the glacier and at higher elevations, most pronounced at ∼500 m a.s.l., where significant trends below −0.07 m w.e.a⁻² occurred (Fig. 3a).

The summer balance shows more ablation at low elevations, and decreasing mass loss towards higher elevations (Fig. 3b), as expected. The summer mass balance varied from −3.6 m w.e. a⁻¹ at low elevations to −1.4 m w.e.a⁻¹ at high elevations, giving a mean gradient of 0.3 m w.e. a⁻¹ per 100 m increase in elevation (1995/96–2007/08). Figure 3b illustrates the spatial distribution of the annual change in summer balance, showing the largest change towards the margins, and most pronounced in the southern part of the glacier (−0.22 m w.e.a⁻²). Significant trends occurred where the annual trend in summer balance was less than −0.06 m w.e. a⁻² (Fig. 3b). A possible explanation for the spatial pattern in summer mass-balance change is that the surface albedo was reduced as the margins receded, for example due to aeolian- and englacially transported debris exposed at the ice surface. Additionally, enhanced melting along the margins may have been due to increasing convection of heat from the surrounding areas. Towards the center of the glacier the energy balance will be less affected by these processes.

The net mass balance shows the combined effects of changes in winter and summer balances. The net mass balance shows the lowest values at low elevations (−3.0 m w.e.a⁻¹) and highest values at higher elevations (−0.4 m w.e.a⁻¹) (Fig. 3c). The mean net mass-balance gradient was 0.5 m w.e.a⁻¹ per 100 m (1995/96–2010/11). The annual change in net mass balance is inhomogeneous, with the largest changes in the marginal area in the south (−0.24 m w.e. a ⁻²) and along the center line (around −0.16 m w.e. a ⁻²) (Fig. 3c). A significant trend occurred below −0.08 m w.e. a⁻².The mass loss at ∼500 m a.s.l. likely reflects that more ice has recently been exposed in that area as the snow and firn cover receded up-glacier. Due to the increased ice exposure, a change in surface albedo has occurred from 0.8–0.9 for snow to around 0.4 for bare ice, highly reinforcing the surface melt of MG, especially at mid-to high elevations.

Surface elevation and ice thickness decreased across the glacier from 1995 to 2011 (Fig. 5a and b). Surface elevation changes (dh/dt calculated from Eqn (2)) for the longitudinal MG profile are −5.7 ± 2.0 to −37.9 ± 13.3 m w.e. (averaging −23.3 ± 8.2 m w.e.) on the lower part of the glacier at stakes 31, 40, 50, 60 and 70, and −1.4 ± 0.5 to −2.3 ± 0.8 m w.e. (averaging −1.8 ± 0.6 m w.e.) on the upper part at stakes 110, 120, 130 and 140 (Fig. 5b, green line). The surface elevation change due to SMB alone was more negative than the total elevation changes: −25.0 ± 2.5 to −43.5 ± 4.4 m w.e. (averaging −37.5 ± 3.8 m w.e.) in the lower part and −5.5 ± 0.6 to −11.8 ± 1.2 m w.e. (averaging −7.8 ± 0.8 m w.e.) in the upper part (Fig. 5b, red line). Vertical strain was able to compensate for ∼60% of the elevation change due to SMB in the lower part, ∼25% in the upper part, and overall on average ∼50% for the longitudinal profile. If the glacier were in equilibrium with climate, vertical strain would be equal, and of opposite sign, to SMB; the large discrepancy in the magnitudes of the two processes is an indicator of the disequilibrium of MG. The vertical strain was unevenly distributed along the longitudinal profile (Fig. 5b, blue line), with the greatest compensation of thinning due to SMB at central elevations at stake 80 (w _e = 20 m) where the mean surface velocity was greatest, and decreasing towards high and low elevations. That vertical strain is strongly positive throughout the region profiled suggests that the accumulation zone must be thinning strongly because the accumulation rates there are low and unlikely to be able to compensate for the transfer of mass to the ablation zone. Due to logistical constraints with working in the accumulation zone, we are unable to measure thinning there, but we are able to document thinning (elevation lowering) at a single point at the upper part of MG (Fig. 6; the nunatak location is illustrated in Fig. 1). Based on repeated markings of the ice margin position, the surface lowered 24 m between 1994 and 2010 at this specific location.

Fig. 6. Observed surface elevation lowering from 1994 through 2010 at a nunatak in the upper part of MG (the location of the nunatak, close to the northwestern margin, is marked with a black square in Fig. 1). The lines corresponding to the MG margin location were marked with spray-paint on the nunatak during the indicated summers. The photograph was taken looking south, and the distance from where the photo was taken to the glacier margin (the 2010 line) was approximately 12–13 m (photographs: S. H. Mernild, August 2010).

Volume changes

The glacier-covered area is one of the easiest glacier morphometric quantities to measure (e.g. Reference Bahr, Singh, Singh and HaritashyaBahr, 2011). The surface area of MG was estimated for the years 1986, 1999 and 2011 based on satellite imagery, and the area changed by −18% during this period (Reference Mernild, Malmros, Yde and KnudsenMernild and others 2012). For the same period, the estimated mean ice thickness changed by −15%, from 115 ± 17 m (1986) to 110 ± 17 m (1999) to 97 ± 15 m (2011) (where the uncertainties are assumed equal to the mass-balance method uncertainty of 115%). Based on observed changes in area cover and mean thickness, the mean volume diminished by 1.1 km³ (30%) (Fig. 4), from 3.7 ± 0.5 km³ (1986) to 3.3 ± 0.5 km³ (1999) to 2.6 ± 0.4 km³ (2011). This change in volume occurred contemporaneously with highly significant observed changes in mean annual air temperature (MAAT) of 0.09°Ca⁻¹ (r ² = 0.51; p<0.01), mean summer air temperature (June–August) of 0.09°Ca⁻¹ (r ² = 0.60; p<0.01) and in mean annual (uncorrected) precipitation of −8 m m w.e. a⁻² (r ² =0.08; p<0.10) (1986–2011) at the nearby DMI station in Tasiilaq (Reference Carstensen and JørgensenCarstensen and Jørgensen, 2011). Climate records from other meteorological stations in southeast Greenland show significant increases in MAAT and mean summer air temperature since the early 1980s in the ranges 0.05–0.08°Ca⁻¹ and 0.02–0.08°Ca⁻¹, respectively, suggesting that the MG trends are not merely a local phenomenon but are indicative of glacier changes in the broader region (Reference MernildMernild and others, 2011a). Such changes at the broader regional scale have been illustrated by Reference BjørkBjørk and others (2012), highlighting widespread retreat along the southeastern margin of Greenland over the past 80 years, where major retreat occurred not only during the recent warming, but also during and after warming in the early 20th century.

Surface velocity changes

The surface velocity of MG has been observed since 1996/97 at the stake locations (Fig. 1). Mean surface velocity has a maximum of 22 m a⁻¹ near the center of the glacier (shown in red in Fig. 7a), and a spatial average of 8 m a⁻¹ . The velocity at the lateral margins consistent with drag from the valley walls and thinner ice (e.g. Reference Cuffey and PatersonCuffey and Paterson, 2010) was ∼3–5 m a⁻¹. The highest surface velocities are observed where the ice is thickest, and at the two cirques to the south of MG. In this context it has to be emphasized that the estimation of the spatial surface velocity field is likely to have a higher degree of uncertainty towards the crevassed parts of the glacier where no direct measurements of velocity are available.

Fig. 7. Mittivakkat Gletscher: (a, b) Mean annual surface velocity (a) and mean surface velocity change (b) from 1996/97 to 2010/11. The white bold lines indicate the margin for significant annual trends in surface velocity, where values below are significant. (c) Ice thickness based on radar observations in 1994 (Reference Knudsen and HasholtKnudsen and Hasholt, 1999) including the location of the longitudinal profile (white circles) (illustrated in (a, b)) and the two cross-section profiles (illustrated in Fig. 2). The locations of stakes 31 and 140 are marked. No observations were made in the southeastern part of the glacier since this is a heavily crevassed area. The white area has no data, and the margin in (a) and (b) is based on Landsat 7 ETM+ Mosaic imagery 1 August 2009 and 14 August 2011, and in (c) is derived from GPS observations.

Over the 15 year period (1996/97–2010/11), surface velocity has decelerated across the glacier, by >50% in much of the ablation area. However, the change in annual surface velocity has been unevenly distributed across the glacier (Fig. 7b). The greatest deceleration, ∼0.6 m a ⁻², is observed on the lower part of the glacier near the margins (a significant deceleration trend occurred below 0.38 m a ⁻²; Fig. 7b), where the greatest thinning has also occurred (Fig. 3c).

The decelerating change in annual surface velocity observed across MG is likely related to the glacier thinning, which will decrease both deformation and sliding (Reference Cuffey and PatersonCuffey and Paterson, 2010), and slow the transfer of ice to lower elevations, which might buffer the retreat to some extent. An alternative explanation for the reduction in velocity is that changes in subglacial hydrology from increased surface melting over the study period have led to an earlier and more extensive development of channelized drainage and subsequent decrease in sliding each summer (e.g. Reference SchoofSchoof, 2010; Reference Sundal, Shepherd, Nienow, Hanna, Palmer and HuybrechtsSundal and others, 2011).

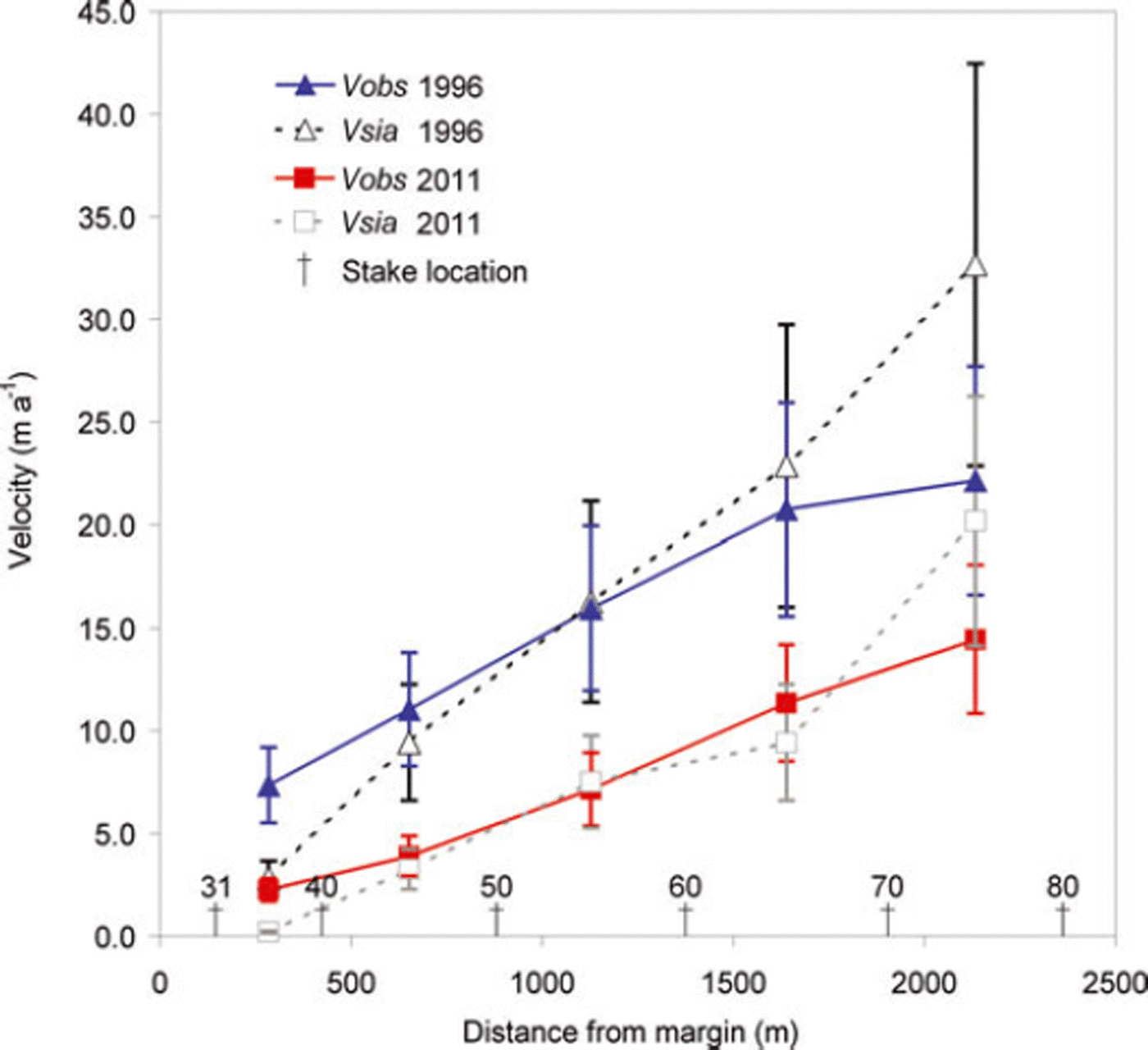
We assess the deceleration in the theoretical surface velocity that can be explained by changes in thickness, though the calculation of v _sia (Eqn (4)) has a high degree of uncertainty due to uncertainty in the flow rate factor and the lack of higher-order stresses. The calculations indicate that the observed changes in surface velocity can largely be explained by the thickness changes over the study period (Fig. 8). Our calculation of v _sia does not include a contribution to surface velocity from sliding, which is typically a large component on temperate glaciers (Reference WeertmanWeertman, 1957; Reference Cuffey and PatersonCuffey and Paterson, 2010). However, sliding velocity is commonly assumed to vary with ice thickness to a power of 1–3 (Reference BindschadlerBindschadler, 1983; Reference ClarkeClarke, 2005; Reference Cuffey and PatersonCuffey and Paterson, 2010), and, allowing a component of surface velocity due to sliding (e.g. by lowering A) with powers that range from 1 to 3, we find that the change in thickness can still explain most of the change in observed velocity without requiring changes in sliding related to hydrology since thickness changes affect sliding in a similar fashion to deformation.

Fig. 8. Observed (V _obs) and calculated (V _sia; Eqn (4)) surface velocities including uncertainty bars for 1996 and 2011 along a longitudinal profile (Fig. 7c) through the ablation zone. Each point is midway between two stake locations which are identified by dagger symbols.

The alternative hypothesis is that the observed surface velocity is due to a reduction in basal sliding associated with changing hydrology. Though meltwater draining to the beds of glaciers can increase sliding initially, once subglacial hydrologic systems adjust to the input, sliding can decrease with sustained meltwater input (Reference Bartholomaus, Anderson and AndersonBartholomaus and others, 2008; Reference SchoofSchoof, 2010), potentially leading to lower average summer velocity (Reference Truffer, Harrison and MarchTruffer and others, 2005; Reference Vincent, Soruco, Six and Le MeurVincent and others, 2009; Reference Sundal, Shepherd, Nienow, Hanna, Palmer and HuybrechtsSundal and others, 2011). Summer mass balance (and by association, melt) has become increasingly negative across MG during the study period (Fig. 3b). However, changes in melt appear to have only a minor impact on surface velocity at the seasonal scale. Summer mass balance and mean June–August (JJA) temperatures, both proxies for melt, are only weakly correlated with mean annual surface velocity (r ² = 0.15, insignificant at p<0.25, and r ² = 0.30, significant at p<0.025, respectively), while thickness is relatively strongly positively correlated with surface velocity (r ² = 0.64, significant at p<0.01; Fig. 9). Thus changes to summer melt are relatively unimportant, compared with thickness changes, for changes in velocity.

Fig. 9. Linear relationship between MG mean annual surface velocity and mean ice thickness (black diamonds) estimated from stake observations, observed summer mass balance (dark gray circles) and observed mean JJA air temperature at station Nunatak (light-gray triangles) from 1996 to 2011.

Based on these analyses, we conclude that the observed 15 year slowdown was caused by decreasing ice deformation (and possibly sliding) resulting from glacier thinning, whereas changes to hydrology during that time do not seem to be important. This is consistent with previous studies which found that time periods of decadal lengths are necessary to observe the dynamic effects of thinning. Reference Vincent, Soruco, Six and Le MeurVincent and others (2009) recorded 20 years of thickening and speed-up followed by 30 years of thinning and slowdown at Glacier d’Argentière, France. In contrast, Reference Müller and IkenMüller and Iken (1973) found small (∼1 m) thickness changes inadequate to explain annual velocity changes over a 2–3 year period on White Glacier, Arctic Canada.

Seasonal velocity variations

Daily MG surface velocity was observed during two periods (May 2004 through July 2005, and March 2009 through August 2010) (Fig. 10a) (see Fig. 1 for locations of the GPS stations), illustrating variations in speed at short timescales. For the summer (JJA) the mean ice surface velocity varied between 0.061 ± 0.01 and 0.066 ± 0.02 m d⁻¹, with a maximum observed daily velocity of 0.10 m d⁻¹ (26 June 2005). For the winter (September–May) the velocity varied between 0.038 ± 0.01 and 0.043 ± 0.01 m d⁻¹.The summer values are 50–60% higher than the winter background values, and up to 160% higher for peak events (Fig. 10a and b). Similar seasonal patterns in ice surface velocity were observed at Flade Isblink ice cap (the largest ice cap in Greenland), northeast Greenland (Reference Palmer, Shepherd, Sundal, Rinne and NienowPalmer and others, 2010), at John Evans Glacier, Nunavut, Canada (Reference Bingham, Nienow and SharpBingham and others, 2003), and at the western land-terminating margin of the Greenland ice sheet, where the peak summer velocity was up to 220% above the winter background velocity (Reference Bartholomew, Nienow, Mair, Hubbard, King and SoleBartholomew and others, 2010; Reference Hoffman, Catania, Neumann, Andrews and RumrillHoffman and others, 2011). There is some evidence that increases in water storage are associated with increases in sliding. MG peak velocity events were typically accompanied by uplift of a few centimeters. Similar uplift has been observed for mountain glaciers (e.g. Reference Iken, Röthlisberger, Flotron and HaeberliIken and others 1983; Reference Bartholomaus, Anderson and AndersonBartholomaus and others, 2008; Reference Howat, Tulaczyk, Waddington and BjörnssonHowat and others, 2008) and the Greenland ice sheet (e.g. Reference Bartholomew, Nienow, Mair, Hubbard, King and SoleBartholomew and others, 2010; Reference Hoffman, Catania, Neumann, Andrews and RumrillHoffman and others, 2011; Reference SoleSole and others, 2011) during speed-up events.

Fig. 10. (a) Observed MG seasonal surface velocity at the GPS station. Between 2005 and 2009 the GPS station was moved to a higher elevation on the glacier (see black and white diamonds in Fig. 1 for locations). The mean seasonal surface velocities are also shown, for the winter (September–May; marked with light blue at the top of the figure) and summer (June–August; marked with red). (b) Observed air temperature at station Nunatak and observed precipitation (uncorrected) at station Tasiilaq.

The seasonal pattern in the daily surface velocity demonstrates the spring speed-up, which is common on temperate mountain glaciers, in which the onset of summer melt results in a large increase in velocity that is short-lived despite continued melt throughout the summer (e.g. Reference Iken, Röthlisberger, Flotron and HaeberliIken and others, 1983; Reference Nienow, Sharp and WillisNienow and others, 1998; Reference AndersonAnderson and others, 2004). At the beginning of each summer, velocity increase follows increasing air temperature, peaking in early to mid-June. After this initial speed-up, velocity has little clear relationship with air temperature until the end of summer when air temperatures fall to and remain well below 0°C (Fig. 10). This behavior is consistent with transient speed-up when subglacial water storage is increasing in spring and water inputs encounter an undeveloped drainage system (e.g. Reference Truffer, Harrison and MarchTruffer and others 2005; Reference Bartholomaus, Anderson and AndersonBartholomaus and others 2008). The periods 25 July to 5 August 2004, 30 June to 19 July 2009, and 13 June to 18 July 2010 are examples of multi-week periods of increasing temperatures during midsummer accompanied by a slowdown in surface velocity (Fig. 10a), suggestive of the presence of an efficient subglacial hydrologic system by midsummer. Despite these complex variations in sliding during summer, changes to hydrology over the 15 year study period do not appear to be the primary cause of the observed long-term deceleration (Section 4.3).