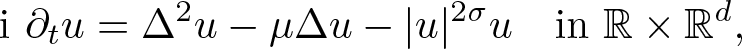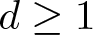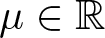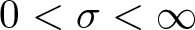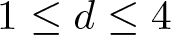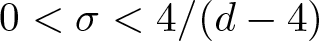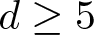1. Introduction
In this paper, we are concerned with blowup of cylindrically symmetric solutions to the Cauchy problem for the following biharmonic nonlinear Schrödinger equation NLS,
where ![]() $d \geq 1$,
$d \geq 1$, ![]() $\mu \in \mathbb{R}$ and
$\mu \in \mathbb{R}$ and ![]() $0 \lt \sigma \lt \infty$ if
$0 \lt \sigma \lt \infty$ if ![]() $1 \leq d \leq 4$ and
$1 \leq d \leq 4$ and ![]() $0 \lt \sigma \lt 4/(d-4)$ if
$0 \lt \sigma \lt 4/(d-4)$ if ![]() $d \geq 5$. The first study of biharmonic NLS traces back to Karpman [Reference Karpman14] and Karpman–Shagalov [Reference Karpman and Shagalov15], where the authors investigated the regularization and stabilization effect of the fourth-order dispersion. Later, Fibich et al. [Reference Fibich, Ilan and Papanicolaou11] carried out a rigorous survey to biharmonic NLS from mathematical point of views and proved global existence in time of solutions to the Cauchy problem for (1.1). During recent years, there is a large number of literature mainly devoted to the study of well-posedness and scattering of solutions to the Cauchy problem for (1.1), see for example [Reference Dinh9, Reference Guo13, Reference Miao, Xu and Zhao17–Reference Pausader and Xia21] and references therein. In [Reference Boulenger and Lenzmann8], Boulenger and Lenzmann rigorously and completely discussed the existence of blowup solutions to the Cauchy problem for (1.1) with radially symmetric initial data, which in turn confirms a series of numerical studies conducted in [Reference Baruch and Fibich1–Reference Bellazzini and Forcella4]. We also refer to the readers to the papers due to Bonheure et al. [Reference Bonheure, Castéras, Gou and Jeanjean6, Reference Bonheure, Castéras, Gou and Jeanjean7] with respect to orbital instability of radially symmetric standing waves to (1.1). Inspired by the aforementioned works, the aim of the present paper is to investigate blowup of solutions to the Cauchy problem for (1.1) with cylindrically symmetric initial data, i.e. initial data belong to
$d \geq 5$. The first study of biharmonic NLS traces back to Karpman [Reference Karpman14] and Karpman–Shagalov [Reference Karpman and Shagalov15], where the authors investigated the regularization and stabilization effect of the fourth-order dispersion. Later, Fibich et al. [Reference Fibich, Ilan and Papanicolaou11] carried out a rigorous survey to biharmonic NLS from mathematical point of views and proved global existence in time of solutions to the Cauchy problem for (1.1). During recent years, there is a large number of literature mainly devoted to the study of well-posedness and scattering of solutions to the Cauchy problem for (1.1), see for example [Reference Dinh9, Reference Guo13, Reference Miao, Xu and Zhao17–Reference Pausader and Xia21] and references therein. In [Reference Boulenger and Lenzmann8], Boulenger and Lenzmann rigorously and completely discussed the existence of blowup solutions to the Cauchy problem for (1.1) with radially symmetric initial data, which in turn confirms a series of numerical studies conducted in [Reference Baruch and Fibich1–Reference Bellazzini and Forcella4]. We also refer to the readers to the papers due to Bonheure et al. [Reference Bonheure, Castéras, Gou and Jeanjean6, Reference Bonheure, Castéras, Gou and Jeanjean7] with respect to orbital instability of radially symmetric standing waves to (1.1). Inspired by the aforementioned works, the aim of the present paper is to investigate blowup of solutions to the Cauchy problem for (1.1) with cylindrically symmetric initial data, i.e. initial data belong to ![]() $\Sigma_d$ defined by
$\Sigma_d$ defined by
 \begin{equation*}
\Sigma_d :=\left\{u \in H^2(\mathbb{R}^d) : u(y, x_d) =u(|y|, x_d), x_d u \in L^2(\mathbb{R}^d)\right\},
\end{equation*}
\begin{equation*}
\Sigma_d :=\left\{u \in H^2(\mathbb{R}^d) : u(y, x_d) =u(|y|, x_d), x_d u \in L^2(\mathbb{R}^d)\right\},
\end{equation*} where ![]() $x=(y, x_d) \in \mathbb{R}^d$ and
$x=(y, x_d) \in \mathbb{R}^d$ and ![]() $y=(x_1, \cdots, x_{d-1}) \in \mathbb{R}^{d-1}$.
$y=(x_1, \cdots, x_{d-1}) \in \mathbb{R}^{d-1}$.
For further clarifications, we shall fix some notation. Let us define
 \begin{equation*}
s_c:=\frac d 2 -\frac {2}{\sigma}.
\end{equation*}
\begin{equation*}
s_c:=\frac d 2 -\frac {2}{\sigma}.
\end{equation*} We refer to the cases ![]() $s_c \lt 0$,
$s_c \lt 0$, ![]() $s_c=0$ and
$s_c=0$ and ![]() $s_c \gt 0$ as mass subcritical, critical and supercritical, respectively. The end case
$s_c \gt 0$ as mass subcritical, critical and supercritical, respectively. The end case ![]() $s_c=2$ is energy critical. Note that the cases
$s_c=2$ is energy critical. Note that the cases ![]() $s_c=0$ and
$s_c=0$ and ![]() $s_c=2$ correspond to the exponents
$s_c=2$ correspond to the exponents ![]() $\sigma=4/d$ and
$\sigma=4/d$ and ![]() $\sigma=4/(d-4)$, respectively. For
$\sigma=4/(d-4)$, respectively. For ![]() $1 \leq p \lt \infty$, we denote by
$1 \leq p \lt \infty$, we denote by ![]() $L^q(\mathbb{R}^{d})$ the usual Lebesgue space with the norm
$L^q(\mathbb{R}^{d})$ the usual Lebesgue space with the norm
 \begin{equation*}
\|u\|_p:=\left( \int_{\mathbb{R}^d} |u|^p \,\mathrm{d}x \right)^{\frac 1p}.
\end{equation*}
\begin{equation*}
\|u\|_p:=\left( \int_{\mathbb{R}^d} |u|^p \,\mathrm{d}x \right)^{\frac 1p}.
\end{equation*} The Sobolev space ![]() $H^2(\mathbb{R}^d)$ is equipped with the standard norm
$H^2(\mathbb{R}^d)$ is equipped with the standard norm
In addition, we denote by ![]() $Q \in H^2(\mathbb{R}^d)$ a ground state to the following nonlinear elliptic equation,
$Q \in H^2(\mathbb{R}^d)$ a ground state to the following nonlinear elliptic equation,
The main results of the present paper read as follows, which gives blowup criteria for solutions to the Cauchy problem for (1.1) with cylindrically symmetric data.
Theorem 1.1.
(Blowup for Mass-Supercritical Case) Let ![]() $d \geq 5$,
$d \geq 5$, ![]() $\mu \in \mathbb{R}$ and
$\mu \in \mathbb{R}$ and ![]() $0 \lt s_c \lt 2$ with
$0 \lt s_c \lt 2$ with ![]() $0 \lt \sigma \leq 1$. Suppose that
$0 \lt \sigma \leq 1$. Suppose that ![]() $u_0 \in \Sigma_d$ satisfies one of the following conditions.
$u_0 \in \Sigma_d$ satisfies one of the following conditions.
(i) If µ ≠ 0, we assume that
 \begin{align*}
E[u_0] \lt \left\{
\begin{aligned}
&0, \quad &\text{for} \,\, \mu \gt 0, \\
&-\chi \mu^2 M[u_0], \quad &\text{for} \,\, \mu \lt 0,
\end{aligned}
\right.
\end{align*}
\begin{align*}
E[u_0] \lt \left\{
\begin{aligned}
&0, \quad &\text{for} \,\, \mu \gt 0, \\
&-\chi \mu^2 M[u_0], \quad &\text{for} \,\, \mu \lt 0,
\end{aligned}
\right.
\end{align*}with some constant
 $\chi=\chi(d, \sigma) \gt 0$.
$\chi=\chi(d, \sigma) \gt 0$.(ii) If µ = 0, we assume that either
 $E[u_0] \lt 0$ or if
$E[u_0] \lt 0$ or if  $E[u_0] \geq 0$, we suppose that
$E[u_0] \geq 0$, we suppose that
 \begin{equation*}
E[u_0]^{s_c}M[u_0]^{2-s_c} \lt E[Q]^{s_c}M[Q]^{2-s_c}
\end{equation*}
\begin{equation*}
E[u_0]^{s_c}M[u_0]^{2-s_c} \lt E[Q]^{s_c}M[Q]^{2-s_c}
\end{equation*}and
 \begin{equation*}
\|\Delta u_0\|_2^2 \|u_0\|_2^{2-s_c} \gt \|\Delta Q\|_2^2 \|Q\|_2^{2-s_c}.
\end{equation*}
\begin{equation*}
\|\Delta u_0\|_2^2 \|u_0\|_2^{2-s_c} \gt \|\Delta Q\|_2^2 \|Q\|_2^{2-s_c}.
\end{equation*}Then the solution
 $u \in C([0, T), H^2(\mathbb{R}^d))$ to the Cauchy problem for (1.1) with initial datum u 0 blows up in finite time, i.e.
$u \in C([0, T), H^2(\mathbb{R}^d))$ to the Cauchy problem for (1.1) with initial datum u 0 blows up in finite time, i.e.  $0 \lt T \lt +\infty$ and
$0 \lt T \lt +\infty$ and  $\lim_{t \to T^-} \|\Delta u\|_2=+\infty$.
$\lim_{t \to T^-} \|\Delta u\|_2=+\infty$.
Remark 1.1. The extra restriction on σ comes from the use of the well-known radial Sobolev inequality in ![]() $\mathbb{R}^{d-1}$. Note that if
$\mathbb{R}^{d-1}$. Note that if ![]() $4/d \lt \sigma \leq 1$, then
$4/d \lt \sigma \leq 1$, then ![]() $d \geq 5$. This is the reason that we need to assume that
$d \geq 5$. This is the reason that we need to assume that ![]() $d \geq 5$.
$d \geq 5$.
Theorem 1.2.
(Blowup for Mass-Critical Case) Let ![]() $d \geq 4$,
$d \geq 4$, ![]() $\mu \geq 0$ and
$\mu \geq 0$ and ![]() $s_c=0$. Let
$s_c=0$. Let ![]() $u_0 \in \Sigma_d$ be such that
$u_0 \in \Sigma_d$ be such that ![]() $E(u_0) \lt 0$. Then the solution
$E(u_0) \lt 0$. Then the solution ![]() $u \in C([0, T), H^2(\mathbb{R}^d))$ to the Cauchy problem for (1.1) satisfies the following.
$u \in C([0, T), H^2(\mathbb{R}^d))$ to the Cauchy problem for (1.1) satisfies the following.
(i) If µ > 0, then u(t) blows up in finite time.
(ii) If µ = 0, then u(t) either blows up in finite time or u(t) blows up in infinite time.
To prove Theorems 1.1 and 1.2, the essential argument is to deduce the evolution of the localized virial quantity ![]() $M_{\varphi_R}[u(t)]$ defined by (2.2) along time, see Lemma 2.2. To this end, we shall make use of ideas from [Reference Boulenger and Lenzmann8, Reference Martel16]. It is worth mentioning [Reference Bellazzini and Forcella4, Reference Bellazzini, Forcella and Georgiev5, Reference Dinh and Forcella10, Reference Forcella12], where blowup of solutions to NLS for cylindrically symmetric data has been investigated. Comparing with the existing works, we deal with the evolution of the localized virial quantity to biharmonic NLS for cylindrically symmetric data and extra treatments are needed in the cylindrically symmetric context, because of the presence of the biharmonic term. For cylindrically symmetric solutions, the radial Sobolev inequality is only applicable in
$M_{\varphi_R}[u(t)]$ defined by (2.2) along time, see Lemma 2.2. To this end, we shall make use of ideas from [Reference Boulenger and Lenzmann8, Reference Martel16]. It is worth mentioning [Reference Bellazzini and Forcella4, Reference Bellazzini, Forcella and Georgiev5, Reference Dinh and Forcella10, Reference Forcella12], where blowup of solutions to NLS for cylindrically symmetric data has been investigated. Comparing with the existing works, we deal with the evolution of the localized virial quantity to biharmonic NLS for cylindrically symmetric data and extra treatments are needed in the cylindrically symmetric context, because of the presence of the biharmonic term. For cylindrically symmetric solutions, the radial Sobolev inequality is only applicable in ![]() $\mathbb{R}^{d-1}$, which is different from the radially symmetric case handled in [Reference Boulenger and Lenzmann8], we shall take advantage of ingredients in [Reference Martel16] to estimate error terms due to the nonlinearity in the process of discussion of the evolution of the localized virial quantity.
$\mathbb{R}^{d-1}$, which is different from the radially symmetric case handled in [Reference Boulenger and Lenzmann8], we shall take advantage of ingredients in [Reference Martel16] to estimate error terms due to the nonlinearity in the process of discussion of the evolution of the localized virial quantity.
Remark 1.2. It seems possible to remove the condition that ![]() $x_d u_0 \in L^2(\mathbb{R}^d)$ to study blowup of solutions to (1.1) for cylindrically symmetric data in the spirit of work due to Martel [Reference Martel16]. In this case, more restrictive conditions should be imposed on σ. This shall be discussed in forthcoming publications.
$x_d u_0 \in L^2(\mathbb{R}^d)$ to study blowup of solutions to (1.1) for cylindrically symmetric data in the spirit of work due to Martel [Reference Martel16]. In this case, more restrictive conditions should be imposed on σ. This shall be discussed in forthcoming publications.
2. Proofs of main results
In this section, we are going to prove Theorems 1.1 and 1.2. To do this, we first need to introduce a localized virial quantity, which is inspired by [Reference Boulenger and Lenzmann8] and [Reference Martel16]. For ![]() $d \geq 2$, let
$d \geq 2$, let ![]() $\psi : \mathbb{R}^{d-1} \to \mathbb{R}$ be a radially symmetric and smooth function such that
$\psi : \mathbb{R}^{d-1} \to \mathbb{R}$ be a radially symmetric and smooth function such that ![]() $|\nabla \psi^j| \in L^{\infty}(\mathbb{R}^{d-1})$ for
$|\nabla \psi^j| \in L^{\infty}(\mathbb{R}^{d-1})$ for ![]() $1 \leq j \leq 6$ and
$1 \leq j \leq 6$ and
 \begin{align*}
\psi(r):=\left\{
\begin{aligned}
&\frac{r^2}{2} &\quad \text{for} \,\, r \leq 1,\\
&\mathrm{const.} &\quad \text{for} \,\, r \geq 10,
\end{aligned}
\right.
\quad \psi''(r) \leq 1 \,\, \text{for}\,\, r \geq 0.
\end{align*}
\begin{align*}
\psi(r):=\left\{
\begin{aligned}
&\frac{r^2}{2} &\quad \text{for} \,\, r \leq 1,\\
&\mathrm{const.} &\quad \text{for} \,\, r \geq 10,
\end{aligned}
\right.
\quad \psi''(r) \leq 1 \,\, \text{for}\,\, r \geq 0.
\end{align*} For R > 0 given, we define a radial function ![]() $\psi_R : \mathbb{R}^{d-1} \to \mathbb{R}$ by
$\psi_R : \mathbb{R}^{d-1} \to \mathbb{R}$ by
 \begin{equation*}
\psi_R(r):= R^2 \varphi\left(\frac{r}{R}\right).
\end{equation*}
\begin{equation*}
\psi_R(r):= R^2 \varphi\left(\frac{r}{R}\right).
\end{equation*}It follows from (3.3) in [Reference Boulenger and Lenzmann8] that
 \begin{align}
1-\psi_R''(r) \geq 0, \quad 1-\frac{\psi'_R(r)}{r} \geq 0, \quad d-1-\Delta \psi_R(r) \geq 0, \quad r \geq 0.
\end{align}
\begin{align}
1-\psi_R''(r) \geq 0, \quad 1-\frac{\psi'_R(r)}{r} \geq 0, \quad d-1-\Delta \psi_R(r) \geq 0, \quad r \geq 0.
\end{align}Let
 \begin{equation*}
\varphi_R(x):=\psi_R(r) + \frac{x_d^2}{2}, \quad x=(y, x_d) \in \mathbb{R}^{d-1} \times \mathbb{R}, \,\, r=|y|.
\end{equation*}
\begin{equation*}
\varphi_R(x):=\psi_R(r) + \frac{x_d^2}{2}, \quad x=(y, x_d) \in \mathbb{R}^{d-1} \times \mathbb{R}, \,\, r=|y|.
\end{equation*}Define
 \begin{align}
\mathcal{M}_{\varphi_R}[u]:=2 \text{Im } \int_{\mathbb{R}^d} \overline{u} \left(\nabla \varphi_R \cdot \nabla u \right) \,\mathrm{d}x.
\end{align}
\begin{align}
\mathcal{M}_{\varphi_R}[u]:=2 \text{Im } \int_{\mathbb{R}^d} \overline{u} \left(\nabla \varphi_R \cdot \nabla u \right) \,\mathrm{d}x.
\end{align} It is simple see that ![]() $\mathcal{M}_{\varphi_R}[u]$ is well-defined for any
$\mathcal{M}_{\varphi_R}[u]$ is well-defined for any ![]() $u \in \Sigma_d$. For later use, we shall give the well-known radial Sobolev’s inequality in [Reference Strauss22]. For every radial function
$u \in \Sigma_d$. For later use, we shall give the well-known radial Sobolev’s inequality in [Reference Strauss22]. For every radial function ![]() $f \in H^1(\mathbb{R}^{d-1})$ with
$f \in H^1(\mathbb{R}^{d-1})$ with ![]() $d \geq 3$, then
$d \geq 3$, then
 \begin{align}
|y|^{\frac{d-2}{2}} |f(y)| \leq 2 \|f\|_{2}^{\frac 12} \|\nabla f\|_{2}^{\frac 12}, \quad y\neq 0.
\end{align}
\begin{align}
|y|^{\frac{d-2}{2}} |f(y)| \leq 2 \|f\|_{2}^{\frac 12} \|\nabla f\|_{2}^{\frac 12}, \quad y\neq 0.
\end{align} We also present the well-known Gagliardo–Nirenberg’s inequality in one dimension. For any ![]() $f \in H^1(\mathbb{R})$ and p > 2, then
$f \in H^1(\mathbb{R})$ and p > 2, then
 \begin{align}
\|f\|_{p} \leq C_p \|f'\|_2^{\alpha} \|f\|_2^{1-\alpha}, \quad \alpha=\frac{p-2}{2p}.
\end{align}
\begin{align}
\|f\|_{p} \leq C_p \|f'\|_2^{\alpha} \|f\|_2^{1-\alpha}, \quad \alpha=\frac{p-2}{2p}.
\end{align} Let ![]() $f : \mathbb{R}^{d-1} \to \mathbb{C}$ be a radial and smooth function, then
$f : \mathbb{R}^{d-1} \to \mathbb{C}$ be a radial and smooth function, then
 \begin{align}
\partial_{kl}^2 f=\left(\delta_{kl}-\frac{x_kx_l}{r^2}\right) \frac{\partial_r f}{r} +\frac{x_kx_l}{r^2} \partial^2_rf.
\end{align}
\begin{align}
\partial_{kl}^2 f=\left(\delta_{kl}-\frac{x_kx_l}{r^2}\right) \frac{\partial_r f}{r} +\frac{x_kx_l}{r^2} \partial^2_rf.
\end{align} Next we present the well-posedness of solutions to the Cauchy problem for (1.1) in ![]() $H^2(\mathbb{R}^d)$, which was established by Pausader [Reference Pausader18].
$H^2(\mathbb{R}^d)$, which was established by Pausader [Reference Pausader18].
Lemma 2.1. [Reference Pausader18, Proposition 4.1] Let ![]() $d \geq 1$,
$d \geq 1$, ![]() $\mu \in \mathbb{R}$ and
$\mu \in \mathbb{R}$ and ![]() $s_c \lt 2$. Then, for any
$s_c \lt 2$. Then, for any ![]() $u_0 \in H^2(\mathbb{R}^d)$, there exist a constant T > 0 and a unique solution
$u_0 \in H^2(\mathbb{R}^d)$, there exist a constant T > 0 and a unique solution ![]() $u \in C([0, T), H^2(\mathbb{R}^d))$ to the Cauchy problem for (1.1) with initial datum u 0. The solution has conserved mass and energy in the sense that
$u \in C([0, T), H^2(\mathbb{R}^d))$ to the Cauchy problem for (1.1) with initial datum u 0. The solution has conserved mass and energy in the sense that
where
 \begin{equation*}
M[u]:=\int_{\mathbb{R}^d} |u|^2 \,\mathrm{d}x
\end{equation*}
\begin{equation*}
M[u]:=\int_{\mathbb{R}^d} |u|^2 \,\mathrm{d}x
\end{equation*}and
 \begin{equation*}
E[u]=\frac 12 \int_{\mathbb{R}^d} |\Delta u|^2 \,\mathrm{d}x + \frac{\mu}{2} \int_{\mathbb{R}^d} |\nabla u|^2 \,\mathrm{d}x -\frac{1}{2 \sigma +2} \int_{\mathbb{R}^d} |u|^{2 \sigma +2} \,\mathrm{d}x.
\end{equation*}
\begin{equation*}
E[u]=\frac 12 \int_{\mathbb{R}^d} |\Delta u|^2 \,\mathrm{d}x + \frac{\mu}{2} \int_{\mathbb{R}^d} |\nabla u|^2 \,\mathrm{d}x -\frac{1}{2 \sigma +2} \int_{\mathbb{R}^d} |u|^{2 \sigma +2} \,\mathrm{d}x.
\end{equation*} Moreover, blowup alternative holds, i.e. either ![]() $T = + \infty $ or
$T = + \infty $ or ![]() $\|u(t)\|_{H^2}= +\infty$ as
$\|u(t)\|_{H^2}= +\infty$ as ![]() $t\to T^-$. The solution map
$t\to T^-$. The solution map
is continuous.
In the following, we give the evolution of ![]() $\mathcal{M}[u(t)]$ along time, which is the key argument to prove Theorems 1.1 and 1.2.
$\mathcal{M}[u(t)]$ along time, which is the key argument to prove Theorems 1.1 and 1.2.
Lemma 2.2. Let ![]() $d \geq 3$, R > 0 and
$d \geq 3$, R > 0 and ![]() $0 \lt \sigma \leq 1$. Suppose that
$0 \lt \sigma \leq 1$. Suppose that ![]() $u \in C([0, T); H^2(\mathbb{R}^d))$ is the solution to the Cauchy problem for (1.1) with initial datum
$u \in C([0, T); H^2(\mathbb{R}^d))$ is the solution to the Cauchy problem for (1.1) with initial datum ![]() $u_0 \in \Sigma_d$. Then, for any
$u_0 \in \Sigma_d$. Then, for any ![]() $t \in [0, T)$, there holds that
$t \in [0, T)$, there holds that
 \begin{align*}
\frac{\mathrm{d}}{\mathrm{d}t}\mathcal{M}_R[u(t)] &\leq 8 \int_{\mathbb{R}^d} |\Delta u|^2 \,\mathrm{d}x+4 \mu \int_{\mathbb{R}^d} \left|\nabla u\right|^2 \,\mathrm{d}x -\frac{2 \sigma d}{\sigma+1} \int_{\mathbb{R}^d} |u|^{2 \sigma +2} \,\mathrm{d}x + X_{\mu}[u] \\
& \quad + \mathcal{O}\left(R^{-4} +R^{-2} \|\nabla u\|_2^2 + R^{-\sigma(d-2)} \|\nabla u\|_2^{2\sigma} + |\mu|R^{-2}\right) \\
&=4d\sigma E(u_0)-(2d \sigma -8)\|\Delta u\|^2_2 -\mu (2d \sigma -4)\|\nabla u\|^2_2 + X_{\mu}[u]\\
& \quad +\mathcal{O}\left(R^{-4} +R^{-2} \|\nabla u\|_2^2 + R^{-\sigma(d-2)} \|\nabla u\|_2^{2\sigma} + |\mu|R^{-2}\right),
\end{align*}
\begin{align*}
\frac{\mathrm{d}}{\mathrm{d}t}\mathcal{M}_R[u(t)] &\leq 8 \int_{\mathbb{R}^d} |\Delta u|^2 \,\mathrm{d}x+4 \mu \int_{\mathbb{R}^d} \left|\nabla u\right|^2 \,\mathrm{d}x -\frac{2 \sigma d}{\sigma+1} \int_{\mathbb{R}^d} |u|^{2 \sigma +2} \,\mathrm{d}x + X_{\mu}[u] \\
& \quad + \mathcal{O}\left(R^{-4} +R^{-2} \|\nabla u\|_2^2 + R^{-\sigma(d-2)} \|\nabla u\|_2^{2\sigma} + |\mu|R^{-2}\right) \\
&=4d\sigma E(u_0)-(2d \sigma -8)\|\Delta u\|^2_2 -\mu (2d \sigma -4)\|\nabla u\|^2_2 + X_{\mu}[u]\\
& \quad +\mathcal{O}\left(R^{-4} +R^{-2} \|\nabla u\|_2^2 + R^{-\sigma(d-2)} \|\nabla u\|_2^{2\sigma} + |\mu|R^{-2}\right),
\end{align*}where
 \begin{align*}
X_{\mu}[u]\lesssim \left\{
\begin{aligned}
&0, &\quad \text{for} \,\, \mu \geq 0,\\
&|\mu| \|\nabla u\|_2^2 , &\quad \text{for} \,\, \mu \lt 0.
\end{aligned}
\right.
\end{align*}
\begin{align*}
X_{\mu}[u]\lesssim \left\{
\begin{aligned}
&0, &\quad \text{for} \,\, \mu \geq 0,\\
&|\mu| \|\nabla u\|_2^2 , &\quad \text{for} \,\, \mu \lt 0.
\end{aligned}
\right.
\end{align*}Proof. To achieve this, we shall adapt some elements from [Reference Boulenger and Lenzmann8] and [Reference Martel16]. In view of Step 1 of the proof of [Reference Boulenger and Lenzmann8, Lemma 3.1], we first have that
 \begin{align*}
\frac{\mathrm{d}}{\mathrm{d}t}\mathcal{M}_R[u(t)]&=8\sum_{k,l,m=1}^d\left\langle u, \partial_{kl}^2\left(\partial_{lm}^2\varphi_R \right) \partial_{mk}^2 u \right\rangle +4\sum_{k,l=1}^d\left\langle u, \partial_k \left(\partial_{kl}\Delta \varphi_R \right) \partial_l u\right\rangle \\
& \quad +2\sum_{k=1}^d\left\langle u, \partial_k \left(\Delta^2 \varphi_R \right) \partial_l u\right\rangle +\left\langle u, \left(\Delta^3 \varphi_R \right) u\right\rangle \\
& \quad -4\mu\sum_{k,l=1}^d\left\langle u, \partial_k \left(\partial_{kl}^2\varphi_R \right) \partial_l u\right\rangle -\mu\left\langle u, \left(\Delta^2 \varphi_R \right) u\right\rangle -\\ & \qquad \left \langle u, [|u|^{2 \sigma}, \nabla \varphi_R \cdot \nabla + \nabla \cdot \nabla \varphi_R] u\right\rangle,\\
&=: \mathcal{A}_R^{(1)}[u] +\mathcal{A}_R^{(2)}[u] +\mathcal{B}_R[u].
\end{align*}
\begin{align*}
\frac{\mathrm{d}}{\mathrm{d}t}\mathcal{M}_R[u(t)]&=8\sum_{k,l,m=1}^d\left\langle u, \partial_{kl}^2\left(\partial_{lm}^2\varphi_R \right) \partial_{mk}^2 u \right\rangle +4\sum_{k,l=1}^d\left\langle u, \partial_k \left(\partial_{kl}\Delta \varphi_R \right) \partial_l u\right\rangle \\
& \quad +2\sum_{k=1}^d\left\langle u, \partial_k \left(\Delta^2 \varphi_R \right) \partial_l u\right\rangle +\left\langle u, \left(\Delta^3 \varphi_R \right) u\right\rangle \\
& \quad -4\mu\sum_{k,l=1}^d\left\langle u, \partial_k \left(\partial_{kl}^2\varphi_R \right) \partial_l u\right\rangle -\mu\left\langle u, \left(\Delta^2 \varphi_R \right) u\right\rangle -\\ & \qquad \left \langle u, [|u|^{2 \sigma}, \nabla \varphi_R \cdot \nabla + \nabla \cdot \nabla \varphi_R] u\right\rangle,\\
&=: \mathcal{A}_R^{(1)}[u] +\mathcal{A}_R^{(2)}[u] +\mathcal{B}_R[u].
\end{align*} In what follows, we are going to estimate the terms  $\mathcal{A}_R^{(1)}[u]$,
$\mathcal{A}_R^{(1)}[u]$,  $\mathcal{A}_R^{(2)}[u]$ and
$\mathcal{A}_R^{(2)}[u]$ and ![]() $\mathcal{B}_R[u]$. The estimates of dispersive terms
$\mathcal{B}_R[u]$. The estimates of dispersive terms  $\mathcal{A}_R^{(1)}[u]$ and
$\mathcal{A}_R^{(1)}[u]$ and  $\mathcal{A}_R^{(2)}[u]$ are inspired by the proof of [Reference Boulenger and Lenzmann8, Lemma 3.1]. Let us begin with treating the term
$\mathcal{A}_R^{(2)}[u]$ are inspired by the proof of [Reference Boulenger and Lenzmann8, Lemma 3.1]. Let us begin with treating the term  $ \mathcal{A}_R^{(1)}[u]$. Using integration by parts and the definition of φR, we are able to derive that
$ \mathcal{A}_R^{(1)}[u]$. Using integration by parts and the definition of φR, we are able to derive that
 \begin{align}
\begin{split}
\sum_{k,l,m=1}^d\left\langle u, \partial_{kl}^2\left(\partial_{lm}^2\varphi_R \right) \partial_{mk}^2 u \right\rangle
&=\sum_{k,l,m=1}^d \int_{\mathbb{R}^d}\left(\partial_{kl}^2 \overline{u}\right)\left(\partial_{lm}^2\varphi_R \right) \left(\partial_{mk}^2 u \right) \,\mathrm{d}x \\
&=\sum_{k,l,m=1}^{d-1} \int_{\mathbb{R}^d}\left(\partial_{kl}^2 \overline{u}\right)\left(\partial_{lm}^2\psi_R \right) \left(\partial_{mk}^2 u \right) \,\mathrm{d}x \\
& \quad + \sum_{l,m=1}^{d-1}\int_{\mathbb{R}^d}\left(\partial_{dl}^2 \overline{u}\right)\left(\partial_{lm}^2\psi_R \right) \left(\partial_{md}^2 u \right) \,\mathrm{d}x \\
& \quad + \sum_{k=1}^{d-1} \int_{\mathbb{R}^d}\left(\partial_{kd}^2 \overline{u}\right)\left(\partial_{dk}^2 u \right) \,\mathrm{d}x+ \int_{\mathbb{R}^d}\left|\partial_{dd}^2 u\right|^2 \,\mathrm{d}x.
\end{split}
\end{align}
\begin{align}
\begin{split}
\sum_{k,l,m=1}^d\left\langle u, \partial_{kl}^2\left(\partial_{lm}^2\varphi_R \right) \partial_{mk}^2 u \right\rangle
&=\sum_{k,l,m=1}^d \int_{\mathbb{R}^d}\left(\partial_{kl}^2 \overline{u}\right)\left(\partial_{lm}^2\varphi_R \right) \left(\partial_{mk}^2 u \right) \,\mathrm{d}x \\
&=\sum_{k,l,m=1}^{d-1} \int_{\mathbb{R}^d}\left(\partial_{kl}^2 \overline{u}\right)\left(\partial_{lm}^2\psi_R \right) \left(\partial_{mk}^2 u \right) \,\mathrm{d}x \\
& \quad + \sum_{l,m=1}^{d-1}\int_{\mathbb{R}^d}\left(\partial_{dl}^2 \overline{u}\right)\left(\partial_{lm}^2\psi_R \right) \left(\partial_{md}^2 u \right) \,\mathrm{d}x \\
& \quad + \sum_{k=1}^{d-1} \int_{\mathbb{R}^d}\left(\partial_{kd}^2 \overline{u}\right)\left(\partial_{dk}^2 u \right) \,\mathrm{d}x+ \int_{\mathbb{R}^d}\left|\partial_{dd}^2 u\right|^2 \,\mathrm{d}x.
\end{split}
\end{align}We now compute each term in the right hand side of (2.6). Utilizing (2.5), we can derive that
 \begin{align}
\begin{split}
&\sum_{k,l,m=1}^{d-1} \int_{\mathbb{R}^d}\left(\partial_{kl}^2 \overline{u}\right)\left(\partial_{lm}^2\psi_R \right) \left(\partial_{mk}^2 u \right) \,\mathrm{d}x \\
&=\sum_{k,l,m=1}^{d-1} \int_{\mathbb{R}}\int_{\mathbb{R}^{d-1}}\left(\partial_{kl}^2 \overline{u}\right)\left(\partial_{lm}^2\psi_R \right) \left(\partial_{mk}^2 u \right) \,\mathrm{d}y \mathrm{d}x_d \\
&=\int_{\mathbb{R}}\int_{\mathbb{R}^{d-1}} \left(\partial_r^2 \psi_R |\partial_r^2 u|^2 + \frac{d-2}{r^2} \frac{\partial_r \psi_R}{r} |\partial_r u|^2 \right)\,\mathrm{d}y\mathrm{d}x_d \\
&=\int_{\mathbb{R}^d} |\Delta_y u|^2-\left(1-\partial_r^2 \psi_R\right)|\partial_r^2 u|^2 -\left(1-\frac{\partial_r \psi_R}{r}\right)\frac{d-2}{r^2}|\partial_r u|^2\,\mathrm{d}x
\end{split}
\end{align}
\begin{align}
\begin{split}
&\sum_{k,l,m=1}^{d-1} \int_{\mathbb{R}^d}\left(\partial_{kl}^2 \overline{u}\right)\left(\partial_{lm}^2\psi_R \right) \left(\partial_{mk}^2 u \right) \,\mathrm{d}x \\
&=\sum_{k,l,m=1}^{d-1} \int_{\mathbb{R}}\int_{\mathbb{R}^{d-1}}\left(\partial_{kl}^2 \overline{u}\right)\left(\partial_{lm}^2\psi_R \right) \left(\partial_{mk}^2 u \right) \,\mathrm{d}y \mathrm{d}x_d \\
&=\int_{\mathbb{R}}\int_{\mathbb{R}^{d-1}} \left(\partial_r^2 \psi_R |\partial_r^2 u|^2 + \frac{d-2}{r^2} \frac{\partial_r \psi_R}{r} |\partial_r u|^2 \right)\,\mathrm{d}y\mathrm{d}x_d \\
&=\int_{\mathbb{R}^d} |\Delta_y u|^2-\left(1-\partial_r^2 \psi_R\right)|\partial_r^2 u|^2 -\left(1-\frac{\partial_r \psi_R}{r}\right)\frac{d-2}{r^2}|\partial_r u|^2\,\mathrm{d}x
\end{split}
\end{align}and
 \begin{align}
\sum_{l,m=1}^{d-1}\int_{\mathbb{R}^d}\left(\partial_{dl}^2 \overline{u}\right)\left(\partial_{lm}^2\psi_R \right) \left(\partial_{md}^2 u \right) \,\mathrm{d}x &= \sum_{k=1}^{d-1}\int_{\mathbb{R}^d}\left(\partial_{r}^2\psi_R \right) \left|\partial_{kd}^2 u \right|^2 \,\mathrm{d}x \nonumber\\
&=\sum_{k=1}^{d-1}\int_{\mathbb{R}^d}\left|\partial_{kd}^2 u \right|^2-\left(1-\partial_r^2 \psi_R\right)\left|\partial_{kd}^2 u \right|^2\,\mathrm{d}x\nonumber\\
&= \sum_{k=1}^{d-1} \int_{\mathbb{R}^d}\left(\partial_{kd}^2 \overline{u}\right)\left(\partial_{dk}^2 u \right) -\left(1-\partial_r^2 \psi_R\right)\left|\partial_{kd}^2 u \right|^2\,\mathrm{d}x.
\end{align}
\begin{align}
\sum_{l,m=1}^{d-1}\int_{\mathbb{R}^d}\left(\partial_{dl}^2 \overline{u}\right)\left(\partial_{lm}^2\psi_R \right) \left(\partial_{md}^2 u \right) \,\mathrm{d}x &= \sum_{k=1}^{d-1}\int_{\mathbb{R}^d}\left(\partial_{r}^2\psi_R \right) \left|\partial_{kd}^2 u \right|^2 \,\mathrm{d}x \nonumber\\
&=\sum_{k=1}^{d-1}\int_{\mathbb{R}^d}\left|\partial_{kd}^2 u \right|^2-\left(1-\partial_r^2 \psi_R\right)\left|\partial_{kd}^2 u \right|^2\,\mathrm{d}x\nonumber\\
&= \sum_{k=1}^{d-1} \int_{\mathbb{R}^d}\left(\partial_{kd}^2 \overline{u}\right)\left(\partial_{dk}^2 u \right) -\left(1-\partial_r^2 \psi_R\right)\left|\partial_{kd}^2 u \right|^2\,\mathrm{d}x.
\end{align}In addition, applying integration by parts, we have that
 \begin{align}
\int_{\mathbb{R}^d}\left(\partial_{kd}^2 \overline{u}\right)\left(\partial_{dk}^2 u \right) \,\mathrm{d}x =\int_{\mathbb{R}^d}\left(\partial_{kk}^2 \overline{u}\right)\left(\partial_{dd}^2 u \right) \,\mathrm{d}x.
\end{align}
\begin{align}
\int_{\mathbb{R}^d}\left(\partial_{kd}^2 \overline{u}\right)\left(\partial_{dk}^2 u \right) \,\mathrm{d}x =\int_{\mathbb{R}^d}\left(\partial_{kk}^2 \overline{u}\right)\left(\partial_{dd}^2 u \right) \,\mathrm{d}x.
\end{align}As a consequence, coming back to (2.6) and using (2.1), (2.6), (2.7), (2.8) and (2.9), we now conclude that
 \begin{align}
\sum_{k,l,m=1}^d\left\langle u, \partial_{kl}^2\left(\partial_{lm}^2\varphi_R \right) \partial_{mk}^2 u \right\rangle \leq \int_{\mathbb{R}^d} |\Delta u|^2 \,\mathrm{d}x.
\end{align}
\begin{align}
\sum_{k,l,m=1}^d\left\langle u, \partial_{kl}^2\left(\partial_{lm}^2\varphi_R \right) \partial_{mk}^2 u \right\rangle \leq \int_{\mathbb{R}^d} |\Delta u|^2 \,\mathrm{d}x.
\end{align}Furthermore, by the definitions of φR and ψR, there holds that
 \begin{equation*}
\sum_{k,l=1}^d\left|\left\langle u, \partial_k \left(\partial_{kl}\Delta \varphi_R \right) \partial_l u\right\rangle \right| =\sum_{k,l=1}^{d-1}\left|\left\langle u, \partial_k \left(\partial_{kl}\Delta \psi_R\right) \partial_l u\right\rangle \right|\lesssim R^{-2} \|\nabla u\|_2^2,
\end{equation*}
\begin{equation*}
\sum_{k,l=1}^d\left|\left\langle u, \partial_k \left(\partial_{kl}\Delta \varphi_R \right) \partial_l u\right\rangle \right| =\sum_{k,l=1}^{d-1}\left|\left\langle u, \partial_k \left(\partial_{kl}\Delta \psi_R\right) \partial_l u\right\rangle \right|\lesssim R^{-2} \|\nabla u\|_2^2,
\end{equation*} \begin{equation*}
\sum_{k, l=1}^d\left|\left\langle u, \partial_k \left(\Delta^2 \varphi_R \right) \partial_l u\right\rangle \right| = \sum_{k, l=1}^{d-1}\left|\left\langle u, \partial_k \left(\Delta^2 \psi_R \right) \partial_l u\right\rangle \right|\lesssim R^{-2} \|\nabla u\|_2^2,
\end{equation*}
\begin{equation*}
\sum_{k, l=1}^d\left|\left\langle u, \partial_k \left(\Delta^2 \varphi_R \right) \partial_l u\right\rangle \right| = \sum_{k, l=1}^{d-1}\left|\left\langle u, \partial_k \left(\Delta^2 \psi_R \right) \partial_l u\right\rangle \right|\lesssim R^{-2} \|\nabla u\|_2^2,
\end{equation*}and
 \begin{equation*}
\left|\left\langle u, \left(\Delta^3 \varphi_R \right) u\right\rangle \right| =\left|\left\langle u, \left(\Delta^3 \psi_R \right) u\right\rangle \right| \lesssim R^{-4} \|u\|_2^2.
\end{equation*}
\begin{equation*}
\left|\left\langle u, \left(\Delta^3 \varphi_R \right) u\right\rangle \right| =\left|\left\langle u, \left(\Delta^3 \psi_R \right) u\right\rangle \right| \lesssim R^{-4} \|u\|_2^2.
\end{equation*}This along with (2.10) and the conservation of mass implies that
 \begin{equation*}
\mathcal{A}_R^{(1)}[u] \leq 8 \int_{\mathbb{R}^d} |\Delta u|^2 \,\mathrm{d}x + \mathcal{O} \left(R^{-4} + R^{-2}\|\nabla u\|_2^2\right).
\end{equation*}
\begin{equation*}
\mathcal{A}_R^{(1)}[u] \leq 8 \int_{\mathbb{R}^d} |\Delta u|^2 \,\mathrm{d}x + \mathcal{O} \left(R^{-4} + R^{-2}\|\nabla u\|_2^2\right).
\end{equation*} We next deal with the term  $\mathcal{A}_R^{(2)}[u]$. In virtue of integration by parts, the definition of φR and (2.5), we can show that
$\mathcal{A}_R^{(2)}[u]$. In virtue of integration by parts, the definition of φR and (2.5), we can show that
 \begin{align*}
\mathcal{A}_R^{(2)}[u(t)]&=4 \mu \sum_{k, l=1}^d\int_{\mathbb{R}^d} \left(\partial_k \overline{u}\right) \left(\partial_{kl}^2 \varphi_R\right) \left(\partial_l u\right) \,\mathrm{d}x -\mu \int_{\mathbb{R}^d} \left(\Delta^2 \varphi_R\right) |u|^2 \,\mathrm{d}x \\
&=4 \mu \sum_{k, l=1}^{d-1}\int_{\mathbb{R}}\int_{\mathbb{R}^{d-1}} \left(\partial_k \overline{u}\right) \left(\partial_{kl}^2 \psi_R\right) \left(\partial_l u\right) \,\mathrm{d}y\mathrm{d}x_d +4 \mu \int_{\mathbb{R}^d}\left |\partial_d u\right|^2 \,\mathrm{d}x\\ & \qquad -\mu \int_{\mathbb{R}^d} \left(\Delta^2 \psi_R\right) |u|^2 \,\mathrm{d}x \\
&=4 \mu \int_{\mathbb{R}}\int_{\mathbb{R}^{d-1}} \left(\partial_r^2 \psi_R\right) \left|\partial_r u\right|^2 \,\mathrm{d}y\mathrm{d}x_d +4 \mu \int_{\mathbb{R}^d}\left |\partial_d u\right|^2 \,\mathrm{d}x -\mu \int_{\mathbb{R}^d} \left(\Delta^2 \psi_R\right) |u|^2 \,\mathrm{d}x \\
&=4 \mu \int_{\mathbb{R}^d} \left|\nabla_y u\right|^2 \,\mathrm{d}x + X_{\mu}[u]+4 \mu \int_{\mathbb{R}^d}\left |\partial_d u\right|^2 \,\mathrm{d}x-\mu \int_{\mathbb{R}^d} \left(\Delta^2 \psi_R\right) |u|^2 \,\mathrm{d}x \\
&=4 \mu \int_{\mathbb{R}^d} \left|\nabla u\right|^2 \,\mathrm{d}x + X_{\mu}[u]-\mu \int_{\mathbb{R}^d} \left(\Delta^2 \psi_R\right) |u|^2 \,\mathrm{d}x
\end{align*}
\begin{align*}
\mathcal{A}_R^{(2)}[u(t)]&=4 \mu \sum_{k, l=1}^d\int_{\mathbb{R}^d} \left(\partial_k \overline{u}\right) \left(\partial_{kl}^2 \varphi_R\right) \left(\partial_l u\right) \,\mathrm{d}x -\mu \int_{\mathbb{R}^d} \left(\Delta^2 \varphi_R\right) |u|^2 \,\mathrm{d}x \\
&=4 \mu \sum_{k, l=1}^{d-1}\int_{\mathbb{R}}\int_{\mathbb{R}^{d-1}} \left(\partial_k \overline{u}\right) \left(\partial_{kl}^2 \psi_R\right) \left(\partial_l u\right) \,\mathrm{d}y\mathrm{d}x_d +4 \mu \int_{\mathbb{R}^d}\left |\partial_d u\right|^2 \,\mathrm{d}x\\ & \qquad -\mu \int_{\mathbb{R}^d} \left(\Delta^2 \psi_R\right) |u|^2 \,\mathrm{d}x \\
&=4 \mu \int_{\mathbb{R}}\int_{\mathbb{R}^{d-1}} \left(\partial_r^2 \psi_R\right) \left|\partial_r u\right|^2 \,\mathrm{d}y\mathrm{d}x_d +4 \mu \int_{\mathbb{R}^d}\left |\partial_d u\right|^2 \,\mathrm{d}x -\mu \int_{\mathbb{R}^d} \left(\Delta^2 \psi_R\right) |u|^2 \,\mathrm{d}x \\
&=4 \mu \int_{\mathbb{R}^d} \left|\nabla_y u\right|^2 \,\mathrm{d}x + X_{\mu}[u]+4 \mu \int_{\mathbb{R}^d}\left |\partial_d u\right|^2 \,\mathrm{d}x-\mu \int_{\mathbb{R}^d} \left(\Delta^2 \psi_R\right) |u|^2 \,\mathrm{d}x \\
&=4 \mu \int_{\mathbb{R}^d} \left|\nabla u\right|^2 \,\mathrm{d}x + X_{\mu}[u]-\mu \int_{\mathbb{R}^d} \left(\Delta^2 \psi_R\right) |u|^2 \,\mathrm{d}x
\end{align*}where
 \begin{equation*}
X_{\mu}[u]:=-4 \mu \int_{\mathbb{R}^d} \left(1-\partial_r^2 \psi_R\right) |\partial_r u|^2 \,\mathrm{d}x.
\end{equation*}
\begin{equation*}
X_{\mu}[u]:=-4 \mu \int_{\mathbb{R}^d} \left(1-\partial_r^2 \psi_R\right) |\partial_r u|^2 \,\mathrm{d}x.
\end{equation*} Due to ![]() $\|\Delta^2 \psi_R\|_{\infty} \lesssim R^{-2}$, then
$\|\Delta^2 \psi_R\|_{\infty} \lesssim R^{-2}$, then
 \begin{align*}
\mathcal{A}_R^{(2)}[u(t)]&=4 \mu \int_{\mathbb{R}^d} \left|\nabla u\right|^2 \,\mathrm{d}x + X_{\mu}[u]+\mathcal{O}(|\mu|R^{-2}).
\end{align*}
\begin{align*}
\mathcal{A}_R^{(2)}[u(t)]&=4 \mu \int_{\mathbb{R}^d} \left|\nabla u\right|^2 \,\mathrm{d}x + X_{\mu}[u]+\mathcal{O}(|\mu|R^{-2}).
\end{align*} We now turn to handle the term ![]() $\mathcal{B}_{R}[u]$. Here we need some special treatments. Applying integration by parts and the definition of φR, we first derive that
$\mathcal{B}_{R}[u]$. Here we need some special treatments. Applying integration by parts and the definition of φR, we first derive that
 \begin{align*}
\mathcal{B}_{R}[u] =2 \int_{\mathbb{R}^d} |u|^2 \nabla \varphi_R \cdot \nabla \left(|u|^{2 \sigma}\right) &=-\frac{2 \sigma }{\sigma+1} \int_{\mathbb{R}^d} \left(\Delta \varphi_R\right) |u|^{2 \sigma +2} \,\mathrm{d}x \\
&=-\frac{2 \sigma }{\sigma+1} \int_{\mathbb{R}^d} \left(\Delta \psi_R \right) |u|^{2 \sigma +2} \,\mathrm{d}x\\
& \qquad - \frac{2 \sigma }{\sigma+1} \int_{\mathbb{R}^d} |u|^{2 \sigma +2} \,\mathrm{d}x\\
&=-\frac{2 \sigma d}{\sigma+1} \int_{\mathbb{R}^d} |u|^{2 \sigma +2} \,\mathrm{d}x\\ & \qquad -\frac{2 \sigma }{\sigma+1} \int_{\mathbb{R}^d}\left(\Delta \psi_R -d+1\right) |u|^{2 \sigma +2} \,\mathrm{d}x.
\end{align*}
\begin{align*}
\mathcal{B}_{R}[u] =2 \int_{\mathbb{R}^d} |u|^2 \nabla \varphi_R \cdot \nabla \left(|u|^{2 \sigma}\right) &=-\frac{2 \sigma }{\sigma+1} \int_{\mathbb{R}^d} \left(\Delta \varphi_R\right) |u|^{2 \sigma +2} \,\mathrm{d}x \\
&=-\frac{2 \sigma }{\sigma+1} \int_{\mathbb{R}^d} \left(\Delta \psi_R \right) |u|^{2 \sigma +2} \,\mathrm{d}x\\
& \qquad - \frac{2 \sigma }{\sigma+1} \int_{\mathbb{R}^d} |u|^{2 \sigma +2} \,\mathrm{d}x\\
&=-\frac{2 \sigma d}{\sigma+1} \int_{\mathbb{R}^d} |u|^{2 \sigma +2} \,\mathrm{d}x\\ & \qquad -\frac{2 \sigma }{\sigma+1} \int_{\mathbb{R}^d}\left(\Delta \psi_R -d+1\right) |u|^{2 \sigma +2} \,\mathrm{d}x.
\end{align*} In virtue of the definition of ψR and (2.5), then there holds that ![]() $\Delta \psi_R(r) -d+1=0$ for
$\Delta \psi_R(r) -d+1=0$ for ![]() $0 \leq r \leq R$. This further implies that
$0 \leq r \leq R$. This further implies that
 \begin{align}
\mathcal{B}_{R}[u]=-\frac{2 \sigma d}{\sigma+1} \int_{\mathbb{R}^d} |u|^{2 \sigma +2} \,\mathrm{d}x -\frac{2 \sigma }{\sigma+1} \int_{\mathbb{R}}\int_{|y| \geq R} \left(\Delta \psi_R -d+1\right) |u|^{2 \sigma +2} \,\mathrm{d}y\mathrm{d}x_d.
\end{align}
\begin{align}
\mathcal{B}_{R}[u]=-\frac{2 \sigma d}{\sigma+1} \int_{\mathbb{R}^d} |u|^{2 \sigma +2} \,\mathrm{d}x -\frac{2 \sigma }{\sigma+1} \int_{\mathbb{R}}\int_{|y| \geq R} \left(\Delta \psi_R -d+1\right) |u|^{2 \sigma +2} \,\mathrm{d}y\mathrm{d}x_d.
\end{align}In the following, we shall estimate the second term in the right hand side of (2.11). Observe first that
 \begin{align}
\int_{\mathbb{R}} \int_{|y| \geq R} |u|^{2 \sigma +2} \,\mathrm{d}y\mathrm{d}x_d \leq \int_{\mathbb{R}} \|u\|^{2 \sigma}_{L^{\infty}(|y| \geq R)} \|u\|_{L^2_y}^2 \,\mathrm{d}x_d.
\end{align}
\begin{align}
\int_{\mathbb{R}} \int_{|y| \geq R} |u|^{2 \sigma +2} \,\mathrm{d}y\mathrm{d}x_d \leq \int_{\mathbb{R}} \|u\|^{2 \sigma}_{L^{\infty}(|y| \geq R)} \|u\|_{L^2_y}^2 \,\mathrm{d}x_d.
\end{align}To proceed the proof, we first consider the case that σ = 1. In this case, by (2.3), Hölder’s inequality and the conservation of mass, then
 \begin{align}
\begin{split}
\int_{\mathbb{R}}\|u\|^2_{L^{\infty}(|y| \geq R)} \,\mathrm{d}x_d &\lesssim R^{-(d-2)}\int_{\mathbb{R}} \|u\|_{L^2_y} \|\nabla_y u\|_{L^2_y} \,\mathrm{d}x_d \\
&\leq R^{-(d-2)} \|u\|_2 \|\nabla _y u\|_2 \lesssim R^{-(d-2)} \|\nabla _y u\|_2.
\end{split}
\end{align}
\begin{align}
\begin{split}
\int_{\mathbb{R}}\|u\|^2_{L^{\infty}(|y| \geq R)} \,\mathrm{d}x_d &\lesssim R^{-(d-2)}\int_{\mathbb{R}} \|u\|_{L^2_y} \|\nabla_y u\|_{L^2_y} \,\mathrm{d}x_d \\
&\leq R^{-(d-2)} \|u\|_2 \|\nabla _y u\|_2 \lesssim R^{-(d-2)} \|\nabla _y u\|_2.
\end{split}
\end{align}On the other hand, by Hölder’s inequality and the conservation of mass, we know that
 \begin{align}
\begin{split}
\|u\|^2_{L^{\infty}(\mathbb{R}, {L^2_y}(\mathbb{R}^{d-1}))}&=\sup_{x_d \in \mathbb{R}} \int_{\mathbb{R}^{d-1}} |u|^2 \,\mathrm{d}y = \sup_{x_d \in \mathbb{R}} \int_{\mathbb{R}^{d-1}} \int_{-\infty}^{x_d} \partial_{d}\left(|u|^2\right) \,\mathrm{d}y\mathrm{d}x_d \\
&= 2 \text{Re }\sup_{x_d \in \mathbb{R}} \int_{\mathbb{R}^{d-1}} \int_{-\infty}^{x_d} \overline{u}\left(\partial_{d} u \right) \,\mathrm{d}y\mathrm{d}x_d \leq 2 \|u\|_2 \|\partial_d u\|_2 \lesssim \|\partial_d u\|_2.
\end{split}
\end{align}
\begin{align}
\begin{split}
\|u\|^2_{L^{\infty}(\mathbb{R}, {L^2_y}(\mathbb{R}^{d-1}))}&=\sup_{x_d \in \mathbb{R}} \int_{\mathbb{R}^{d-1}} |u|^2 \,\mathrm{d}y = \sup_{x_d \in \mathbb{R}} \int_{\mathbb{R}^{d-1}} \int_{-\infty}^{x_d} \partial_{d}\left(|u|^2\right) \,\mathrm{d}y\mathrm{d}x_d \\
&= 2 \text{Re }\sup_{x_d \in \mathbb{R}} \int_{\mathbb{R}^{d-1}} \int_{-\infty}^{x_d} \overline{u}\left(\partial_{d} u \right) \,\mathrm{d}y\mathrm{d}x_d \leq 2 \|u\|_2 \|\partial_d u\|_2 \lesssim \|\partial_d u\|_2.
\end{split}
\end{align}Consequently, going back to (2.12) and using (2.13) and (2.14), we derive that
 \begin{align}
\int_{\mathbb{R}}\int_{|y| \geq R} |u|^4 \,\mathrm{d}y\mathrm{d}x_d \lesssim R^{-(d-2)} \|\nabla_y u\|_2 \|\partial_d u\|_2 \lesssim R^{-(d-2)} \|\nabla u\|_2^2.
\end{align}
\begin{align}
\int_{\mathbb{R}}\int_{|y| \geq R} |u|^4 \,\mathrm{d}y\mathrm{d}x_d \lesssim R^{-(d-2)} \|\nabla_y u\|_2 \|\partial_d u\|_2 \lesssim R^{-(d-2)} \|\nabla u\|_2^2.
\end{align} We next consider the case that ![]() $0 \lt \sigma \lt 1$. In this case, from (2.12) and Hölder’s inequality, it follows that
$0 \lt \sigma \lt 1$. In this case, from (2.12) and Hölder’s inequality, it follows that
 \begin{align}
\begin{split}
\int_{\mathbb{R}}\int_{|y| \geq R} |u|^{2 \sigma +2} \,\mathrm{d}x \leq \left(\int_{\mathbb{R}} \|u\|_{L^{\infty}(|y| \geq R)}^2\,\mathrm{d}x_d \right)^{\sigma} \left(\int_{\mathbb{R}}\|u\|^{\frac{2}{1-\sigma}}_{L^2_y} \,\mathrm{d}x_d \right)^{1-\sigma}.
\end{split}
\end{align}
\begin{align}
\begin{split}
\int_{\mathbb{R}}\int_{|y| \geq R} |u|^{2 \sigma +2} \,\mathrm{d}x \leq \left(\int_{\mathbb{R}} \|u\|_{L^{\infty}(|y| \geq R)}^2\,\mathrm{d}x_d \right)^{\sigma} \left(\int_{\mathbb{R}}\|u\|^{\frac{2}{1-\sigma}}_{L^2_y} \,\mathrm{d}x_d \right)^{1-\sigma}.
\end{split}
\end{align}In view of (2.4) and the conservation of mass, we get that
 \begin{align}
\begin{split}
\int_{\mathbb{R}}\|u\|^{\frac{2}{1-\sigma}}_{L^2_y} \,\mathrm{d}x_d &\leq \left(\int_{\mathbb{R}} \left|\partial_d \left(\|u\|_{L^2_y}\right) \right|^2\,\mathrm{d}x_d\right)^{\frac{\sigma}{2(1-\sigma)}} \left(\int_{\mathbb{R}}\|u\|^2_{{L^2_y}} \,\mathrm{d}x\right)^{\frac{2-\sigma}{2(1-\sigma)}} \\
&\lesssim \left(\int_{\mathbb{R}} \left|\partial_d \left(\|u\|_{L^2_y}\right) \right|^2\,\mathrm{d}x_d\right)^{\frac{\sigma}{2(1-\sigma)}}.
\end{split}
\end{align}
\begin{align}
\begin{split}
\int_{\mathbb{R}}\|u\|^{\frac{2}{1-\sigma}}_{L^2_y} \,\mathrm{d}x_d &\leq \left(\int_{\mathbb{R}} \left|\partial_d \left(\|u\|_{L^2_y}\right) \right|^2\,\mathrm{d}x_d\right)^{\frac{\sigma}{2(1-\sigma)}} \left(\int_{\mathbb{R}}\|u\|^2_{{L^2_y}} \,\mathrm{d}x\right)^{\frac{2-\sigma}{2(1-\sigma)}} \\
&\lesssim \left(\int_{\mathbb{R}} \left|\partial_d \left(\|u\|_{L^2_y}\right) \right|^2\,\mathrm{d}x_d\right)^{\frac{\sigma}{2(1-\sigma)}}.
\end{split}
\end{align}Furthermore, notice that
 \begin{align*}
\left|\partial_d \left(\|u\|_{L^2_y}\right) \right|\|u\|_{L^2_y}=\frac 12 \left|\partial_d \left(\|u\|^2_{L^2_y}\right) \right|=\frac 12 \left| \text{Re } \int_{\mathbb{R}^{d-1}} \overline{u} \left(\partial_{d} u\right) \,\mathrm{d}y\right| \leq \frac 12 \|\partial_d u\|_{L^2_y}\|u\|_{L^2_y}.
\end{align*}
\begin{align*}
\left|\partial_d \left(\|u\|_{L^2_y}\right) \right|\|u\|_{L^2_y}=\frac 12 \left|\partial_d \left(\|u\|^2_{L^2_y}\right) \right|=\frac 12 \left| \text{Re } \int_{\mathbb{R}^{d-1}} \overline{u} \left(\partial_{d} u\right) \,\mathrm{d}y\right| \leq \frac 12 \|\partial_d u\|_{L^2_y}\|u\|_{L^2_y}.
\end{align*}This means that
 \begin{align}
\left|\partial_d \left(\|u\|_{L^2_y}\right) \right| \leq \frac 12 \|\partial_d u\|_{L^2_y}.
\end{align}
\begin{align}
\left|\partial_d \left(\|u\|_{L^2_y}\right) \right| \leq \frac 12 \|\partial_d u\|_{L^2_y}.
\end{align}As a result, via (2.17), we obtain that
 \begin{align}
\int_{\mathbb{R}}\|u\|^{\frac{2}{1-\sigma}}_{L^2_y} \,\mathrm{d}x_d \lesssim \left(\int_{\mathbb{R}}\|\partial_d u\|_{L^2_y}^2 \,\mathrm{d}x_d \right)^{\frac{\sigma}{2(1-\sigma)}}=\|\partial_d u\|_2^{\frac{\sigma}{1-\sigma}}.
\end{align}
\begin{align}
\int_{\mathbb{R}}\|u\|^{\frac{2}{1-\sigma}}_{L^2_y} \,\mathrm{d}x_d \lesssim \left(\int_{\mathbb{R}}\|\partial_d u\|_{L^2_y}^2 \,\mathrm{d}x_d \right)^{\frac{\sigma}{2(1-\sigma)}}=\|\partial_d u\|_2^{\frac{\sigma}{1-\sigma}}.
\end{align}Using (2.13) and (2.19), we then obtain from (2.16) that
 \begin{align}
\int_{\mathbb{R}}\int_{|y| \geq R} |u|^{2 \sigma +2} \,\mathrm{d}x \lesssim R^{-\sigma(d-2) } \|\nabla _y u\|_2^{\sigma} \|\partial_d u\|_2^{\sigma} \lesssim R^{-\sigma(d-2)}\|\nabla u\|_2^{2\sigma}.
\end{align}
\begin{align}
\int_{\mathbb{R}}\int_{|y| \geq R} |u|^{2 \sigma +2} \,\mathrm{d}x \lesssim R^{-\sigma(d-2) } \|\nabla _y u\|_2^{\sigma} \|\partial_d u\|_2^{\sigma} \lesssim R^{-\sigma(d-2)}\|\nabla u\|_2^{2\sigma}.
\end{align}To sum up, it then follows from (2.11), (2.15) and (2.20) that
 \begin{align*}
\mathcal{B}_{R}[u] \lesssim -\frac{2 \sigma d}{\sigma+1} \int_{\mathbb{R}^d} |u|^{2 \sigma +2} \,\mathrm{d}x +R^{-\sigma(d-2)}\|\nabla u\|_2^{2\sigma}.
\end{align*}
\begin{align*}
\mathcal{B}_{R}[u] \lesssim -\frac{2 \sigma d}{\sigma+1} \int_{\mathbb{R}^d} |u|^{2 \sigma +2} \,\mathrm{d}x +R^{-\sigma(d-2)}\|\nabla u\|_2^{2\sigma}.
\end{align*} Accordingly, applying the estimates to  $\mathcal{A}_R^{(1)}[u]$,
$\mathcal{A}_R^{(1)}[u]$,  $\mathcal{A}_R^{(2)}[u]$ and
$\mathcal{A}_R^{(2)}[u]$ and ![]() $\mathcal{B}_{R}[u]$ and the conservation of energy, we finally derive that
$\mathcal{B}_{R}[u]$ and the conservation of energy, we finally derive that
 \begin{align*}
\frac{\mathrm{d}}{\mathrm{d}t}\mathcal{M}_R[u(t)] & \leq 8 \int_{\mathbb{R}^d} |\Delta u|^2 \,\mathrm{d}x+4 \mu \int_{\mathbb{R}^d} \left|\nabla u\right|^2 \,\mathrm{d}x -\frac{2 \sigma d}{\sigma+1} \int_{\mathbb{R}^d} |u|^{2 \sigma +2} \,\mathrm{d}x + X_{\mu}[u] \\
& + \mathcal{O}\left(R^{-4} +R^{-2} \|\nabla u\|_2^2 + R^{-\sigma(d-2)} \|\nabla u\|_2^{2\sigma} + |\mu|R^{-2}\right) \\
&=4d\sigma E(u_0)-(2d \sigma -8)\|\Delta u\|^2_2 -\mu (2d \sigma -4)\|\nabla u\|^2_2 + X_{\mu}[u]\\
&+\mathcal{O}\left(R^{-4} +R^{-2} \|\nabla u\|_2^2 + R^{-\sigma(d-2)} \|\nabla u\|_2^{2\sigma} + |\mu|R^{-2}\right).
\end{align*}
\begin{align*}
\frac{\mathrm{d}}{\mathrm{d}t}\mathcal{M}_R[u(t)] & \leq 8 \int_{\mathbb{R}^d} |\Delta u|^2 \,\mathrm{d}x+4 \mu \int_{\mathbb{R}^d} \left|\nabla u\right|^2 \,\mathrm{d}x -\frac{2 \sigma d}{\sigma+1} \int_{\mathbb{R}^d} |u|^{2 \sigma +2} \,\mathrm{d}x + X_{\mu}[u] \\
& + \mathcal{O}\left(R^{-4} +R^{-2} \|\nabla u\|_2^2 + R^{-\sigma(d-2)} \|\nabla u\|_2^{2\sigma} + |\mu|R^{-2}\right) \\
&=4d\sigma E(u_0)-(2d \sigma -8)\|\Delta u\|^2_2 -\mu (2d \sigma -4)\|\nabla u\|^2_2 + X_{\mu}[u]\\
&+\mathcal{O}\left(R^{-4} +R^{-2} \|\nabla u\|_2^2 + R^{-\sigma(d-2)} \|\nabla u\|_2^{2\sigma} + |\mu|R^{-2}\right).
\end{align*}This completes the proof.
Proof of Theorem 1.1
Noting that ![]() $0 \lt \sigma \leq 1$ and applying Lemma 2.2, then the proof can be completed by closely following the one of [Reference Boulenger and Lenzmann8, Theorem 1].
$0 \lt \sigma \leq 1$ and applying Lemma 2.2, then the proof can be completed by closely following the one of [Reference Boulenger and Lenzmann8, Theorem 1].
Proof of Theorem 1.2
If µ > 0, using Lemma 2.2 and arguing as the proof of [Reference Boulenger and Lenzmann8, Theorem 3], we can get the desired result. To complete the proof, we only need to consider the case that µ = 0. In this case, we need to conduct a more refined analysis to the evolution of ![]() $\mathcal{M}[u(t)]$ along time. From the proof of Lemma 2.2, (2.1) and (2.5), we first have that
$\mathcal{M}[u(t)]$ along time. From the proof of Lemma 2.2, (2.1) and (2.5), we first have that
 \begin{align}
\begin{split}
\frac{\mathrm{d}}{\mathrm{d}t}\mathcal{M}_R[u(t)] &\leq 16 E(u_0)-8\int_{\mathbb{R}^d}\left(1-\partial_r^2 \psi_R\right)|\partial_r^2 u|^2 \,\mathrm{d}x + \int_{\mathbb{R}^d} \left(\Delta^3 \psi_R \right)|u|^2 \,\mathrm{d}x \\
& \quad -\int_{\mathbb{R}^d} A_R |\partial_r u|^2 \,\mathrm{d}x + \int_{\mathbb{R}^N} B_R |u|^{2+ \frac 8 d} \,\mathrm{d}x ,
\end{split}
\end{align}
\begin{align}
\begin{split}
\frac{\mathrm{d}}{\mathrm{d}t}\mathcal{M}_R[u(t)] &\leq 16 E(u_0)-8\int_{\mathbb{R}^d}\left(1-\partial_r^2 \psi_R\right)|\partial_r^2 u|^2 \,\mathrm{d}x + \int_{\mathbb{R}^d} \left(\Delta^3 \psi_R \right)|u|^2 \,\mathrm{d}x \\
& \quad -\int_{\mathbb{R}^d} A_R |\partial_r u|^2 \,\mathrm{d}x + \int_{\mathbb{R}^N} B_R |u|^{2+ \frac 8 d} \,\mathrm{d}x ,
\end{split}
\end{align}where
 \begin{equation*}
A_R:=4 \partial_r^2 \Delta \psi_R +2 \Delta^2 \psi_R(r), \quad B_R:=\frac{8}{d+4} \left(d-1-\Delta \psi_R\right).
\end{equation*}
\begin{equation*}
A_R:=4 \partial_r^2 \Delta \psi_R +2 \Delta^2 \psi_R(r), \quad B_R:=\frac{8}{d+4} \left(d-1-\Delta \psi_R\right).
\end{equation*}Thereinafter, we shall estimate the last two terms in the right hand side of (2.21). Using (7.7) in [Reference Boulenger and Lenzmann8] and the conservation of mass, we can derive that
 \begin{align*}
\left|\int_{\mathbb{R}^d} A_R |\partial_r u|^2 \,\mathrm{d}x \right| =\left|\int_{\mathbb{R}}\int_{\mathbb{R}^{d-1}} A_R |\partial_r u|^2 \,\mathrm{d}y\mathrm{d}x_d \right|
&\lesssim 8 \eta R^4 \int_{\mathbb{R}} \|A_R \partial_r^2 u\|_{L^2_y}^2 \,\mathrm{d}x_d\\ & \qquad + \eta^{-1}R^{-4} \int_{\mathbb{R}} \|u\|_{L^2_y}^2 \,\mathrm{d}x_d \\
&=8 \eta R^4 \|A_R \partial_r^2 u\|_2^2 + \eta^{-1}R^{-4},
\end{align*}
\begin{align*}
\left|\int_{\mathbb{R}^d} A_R |\partial_r u|^2 \,\mathrm{d}x \right| =\left|\int_{\mathbb{R}}\int_{\mathbb{R}^{d-1}} A_R |\partial_r u|^2 \,\mathrm{d}y\mathrm{d}x_d \right|
&\lesssim 8 \eta R^4 \int_{\mathbb{R}} \|A_R \partial_r^2 u\|_{L^2_y}^2 \,\mathrm{d}x_d\\ & \qquad + \eta^{-1}R^{-4} \int_{\mathbb{R}} \|u\|_{L^2_y}^2 \,\mathrm{d}x_d \\
&=8 \eta R^4 \|A_R \partial_r^2 u\|_2^2 + \eta^{-1}R^{-4},
\end{align*}where η > 0 is an arbitrary constant. We now treat the other term. To do this, we first consider the case that d = 4. In this case, we have that
 \begin{align}
\left|\int_{\mathbb{R}^d} B_R |u|^4 \,\mathrm{d}x\right|=\left|\int_{\mathbb{R}}\int_{|y| \geq R} B_R |u|^4\,\mathrm{d}y\mathrm{d}x_d \right| &\leq \int_{\mathbb{R}} \|u\|^2_{L^2_y} \|B_R^{\frac 12} u\|_{L^{\infty}(|y| \geq R)}^2 \,\mathrm{d}x_d \nonumber\\
&\leq \|u\|^2_{L^{\infty}(R, {L^2_y}(\mathbb{R}^{N-1}))}\nonumber\\ & \quad \int_{\mathbb{R}} \|B_R^{\frac 12} u\|_{L^{\infty}(|y| \geq R)}^2 \,\mathrm{d}x_d,
\end{align}
\begin{align}
\left|\int_{\mathbb{R}^d} B_R |u|^4 \,\mathrm{d}x\right|=\left|\int_{\mathbb{R}}\int_{|y| \geq R} B_R |u|^4\,\mathrm{d}y\mathrm{d}x_d \right| &\leq \int_{\mathbb{R}} \|u\|^2_{L^2_y} \|B_R^{\frac 12} u\|_{L^{\infty}(|y| \geq R)}^2 \,\mathrm{d}x_d \nonumber\\
&\leq \|u\|^2_{L^{\infty}(R, {L^2_y}(\mathbb{R}^{N-1}))}\nonumber\\ & \quad \int_{\mathbb{R}} \|B_R^{\frac 12} u\|_{L^{\infty}(|y| \geq R)}^2 \,\mathrm{d}x_d,
\end{align} because of ![]() $B_R=0$ for
$B_R=0$ for ![]() $0 \leq r \leq R$. In view of (2.3) with d = 4 and the definition of BR, we are able to infer that
$0 \leq r \leq R$. In view of (2.3) with d = 4 and the definition of BR, we are able to infer that
 \begin{align}
\begin{split}
\int_{\mathbb{R}}\|B_R^{\frac 12} u\|_{L^{\infty}(|y| \geq R)}^2 \,\mathrm{d}x_d &\lesssim R^{-2}\int_{\mathbb{R}}\|B_R^{\frac 12} u\|_{L^2_y}\|\nabla_y (B_R^{\frac 12} u)\|_{L^2_y} \,\mathrm{d}x_d \\
&\lesssim R^{-2}\int_{\mathbb{R}}\|u\|_{L^2_y}\|\nabla_y (B_R^{\frac 12 } u)\|_{L^2_y} \,\mathrm{d}x_d.
\end{split}
\end{align}
\begin{align}
\begin{split}
\int_{\mathbb{R}}\|B_R^{\frac 12} u\|_{L^{\infty}(|y| \geq R)}^2 \,\mathrm{d}x_d &\lesssim R^{-2}\int_{\mathbb{R}}\|B_R^{\frac 12} u\|_{L^2_y}\|\nabla_y (B_R^{\frac 12} u)\|_{L^2_y} \,\mathrm{d}x_d \\
&\lesssim R^{-2}\int_{\mathbb{R}}\|u\|_{L^2_y}\|\nabla_y (B_R^{\frac 12 } u)\|_{L^2_y} \,\mathrm{d}x_d.
\end{split}
\end{align}It follows from (7.9) with d = 4 in [Reference Boulenger and Lenzmann8] that
 \begin{equation*}
\|\nabla_y (B_R^{\frac 12} u)\|_{L^2_y}^2 \lesssim \left(\eta^{-\frac 14} + R^{-2}\right) \|u\|_{L^2_y}^2 + 8 \eta^{\frac 14} \|B_R \partial_r^2 u\|_{L^2_y}^2.
\end{equation*}
\begin{equation*}
\|\nabla_y (B_R^{\frac 12} u)\|_{L^2_y}^2 \lesssim \left(\eta^{-\frac 14} + R^{-2}\right) \|u\|_{L^2_y}^2 + 8 \eta^{\frac 14} \|B_R \partial_r^2 u\|_{L^2_y}^2.
\end{equation*}By means of (2.23), the conservation of mass and Hölder’s inequality, we then get that
 \begin{align}
\int_{\mathbb{R}}\|B_R^{\frac 1 2} u\|_{L^{\infty}(|y| \geq R)}^{2} \,\mathrm{d}x_d &\lesssim R^{-2} \left(\eta^{-\frac 14} + R^{-2}\right) + 8R^{-2} \eta^{\frac 14} \int_{\mathbb{R}^d} \|u\|_{L^2_y} \|B_R \partial_r^2 u\|_{L^2_y} \,\mathrm{d}x_d \nonumber\\
& \lesssim R^{-2} \left(\eta^{-\frac 14} + R^{-2}\right) + 8 R^{-2} \eta^{\frac 14} \|B_R \partial_r^2 u\|_2.
\end{align}
\begin{align}
\int_{\mathbb{R}}\|B_R^{\frac 1 2} u\|_{L^{\infty}(|y| \geq R)}^{2} \,\mathrm{d}x_d &\lesssim R^{-2} \left(\eta^{-\frac 14} + R^{-2}\right) + 8R^{-2} \eta^{\frac 14} \int_{\mathbb{R}^d} \|u\|_{L^2_y} \|B_R \partial_r^2 u\|_{L^2_y} \,\mathrm{d}x_d \nonumber\\
& \lesssim R^{-2} \left(\eta^{-\frac 14} + R^{-2}\right) + 8 R^{-2} \eta^{\frac 14} \|B_R \partial_r^2 u\|_2.
\end{align}Going back to (2.22) and using (2.14) and (2.24), we then get that
 \begin{align*}
\left|\int_{\mathbb{R}^N} B_R |u|^4 \,\mathrm{d}x \right| &\lesssim R^{-2} \left(\eta^{-\frac 14} + R^{-2}\right) \|\partial_d u\|_2 +8R^{-2} \eta^{\frac 14} \|B_R\partial_r^2 u\|_2 \|\partial_d u\|_2 \\
& \leq R^{-2} \left(\eta^{-\frac 14} + R^{-2}\right) \|\partial_d u\|_2 +R^{-4} \eta^{-\frac 12} \|\partial_d u\|_2^2 + 8 \eta \|B_R \partial_r^2 u\|_2^2.
\end{align*}
\begin{align*}
\left|\int_{\mathbb{R}^N} B_R |u|^4 \,\mathrm{d}x \right| &\lesssim R^{-2} \left(\eta^{-\frac 14} + R^{-2}\right) \|\partial_d u\|_2 +8R^{-2} \eta^{\frac 14} \|B_R\partial_r^2 u\|_2 \|\partial_d u\|_2 \\
& \leq R^{-2} \left(\eta^{-\frac 14} + R^{-2}\right) \|\partial_d u\|_2 +R^{-4} \eta^{-\frac 12} \|\partial_d u\|_2^2 + 8 \eta \|B_R \partial_r^2 u\|_2^2.
\end{align*} Taking into account (2.21) and noting that ![]() $\|\Delta^2 \varphi_R\|_{\infty} \lesssim R^{-2}$, we then obtain that
$\|\Delta^2 \varphi_R\|_{\infty} \lesssim R^{-2}$, we then obtain that
 \begin{align}
\begin{split}
\frac{\mathrm{d}}{\mathrm{d}t}\mathcal{M}_R[u(t)] &\leq 16 E(u_0)-8\int_{\mathbb{R}^d}\left(1-\partial_r^2 \psi_R-\eta \left(R^4 A_R^2 +B_R^2\right)\right)|\partial_r^2 u|^2 \,\mathrm{d}x \\
&+ R^{-2} \left(\eta^{-\frac 14} + R^{-2}\right) \|\partial_d u\|_2 +R^{-4} \eta^{-\frac 12} \|\partial_d u\|_2^2 +\eta^{-1}R^{-4} + R^{-2}.
\end{split}
\end{align}
\begin{align}
\begin{split}
\frac{\mathrm{d}}{\mathrm{d}t}\mathcal{M}_R[u(t)] &\leq 16 E(u_0)-8\int_{\mathbb{R}^d}\left(1-\partial_r^2 \psi_R-\eta \left(R^4 A_R^2 +B_R^2\right)\right)|\partial_r^2 u|^2 \,\mathrm{d}x \\
&+ R^{-2} \left(\eta^{-\frac 14} + R^{-2}\right) \|\partial_d u\|_2 +R^{-4} \eta^{-\frac 12} \|\partial_d u\|_2^2 +\eta^{-1}R^{-4} + R^{-2}.
\end{split}
\end{align} Next we consider the case that ![]() $d \geq 5$. In this case, by Hölder’s inequality and the definition of BR, we can obtain that
$d \geq 5$. In this case, by Hölder’s inequality and the definition of BR, we can obtain that
 \begin{align}
\begin{split}
\left|\int_{\mathbb{R}^N} B_R |u|^{2 +\frac 8 d} \,\mathrm{d}x \right| &=\left|\int_{\mathbb{R}} \int_{|y| \geq R} B_R |u|^{2 +\frac 8 d} \,\mathrm{d}y\mathrm{d}x_d \right|
\leq \!\int_{\mathbb{R}} \|B_R^{\frac 12} u\|_{L^{\infty}_y(|y| \geq R)}^{\frac 8 d} \|B_R^{\frac 1 2-\frac 2d} u\|_{L^2_y}^2\,\mathrm{d}x_d \\
& \leq \left(\int_{\mathbb{R}} \|B_R^{\frac 12} u\|_{L^{\infty}_y(|y| \geq R)}^2 \,\mathrm{d}x_d \right)^{\frac 4 d} \left(\int_{\mathbb{R}}\|u\|_{L^2_y}^{\frac{2d}{d-4}} \,\mathrm{d}x_d\right)^{\frac{d-4}{d}}.
\end{split}
\end{align}
\begin{align}
\begin{split}
\left|\int_{\mathbb{R}^N} B_R |u|^{2 +\frac 8 d} \,\mathrm{d}x \right| &=\left|\int_{\mathbb{R}} \int_{|y| \geq R} B_R |u|^{2 +\frac 8 d} \,\mathrm{d}y\mathrm{d}x_d \right|
\leq \!\int_{\mathbb{R}} \|B_R^{\frac 12} u\|_{L^{\infty}_y(|y| \geq R)}^{\frac 8 d} \|B_R^{\frac 1 2-\frac 2d} u\|_{L^2_y}^2\,\mathrm{d}x_d \\
& \leq \left(\int_{\mathbb{R}} \|B_R^{\frac 12} u\|_{L^{\infty}_y(|y| \geq R)}^2 \,\mathrm{d}x_d \right)^{\frac 4 d} \left(\int_{\mathbb{R}}\|u\|_{L^2_y}^{\frac{2d}{d-4}} \,\mathrm{d}x_d\right)^{\frac{d-4}{d}}.
\end{split}
\end{align}As an application of (2.4) leads to
 \begin{align}
\int_{\mathbb{R}}\|u\|_{L^2_y}^{\frac{2d}{d-4}} \,\mathrm{d}x_d \lesssim \left(\int_{\mathbb{R}^d} \left|\partial_d \left(\|u\|_{L^2_y}\right)\right|^2\,\mathrm{d}x_d\right)^{\frac{2}{d-4}} \left(\int_{\mathbb{R}} \|u\|_{L^2_y}^2 \,\mathrm{d}x_d\right)^{\frac{d-2}{d-4}}.
\end{align}
\begin{align}
\int_{\mathbb{R}}\|u\|_{L^2_y}^{\frac{2d}{d-4}} \,\mathrm{d}x_d \lesssim \left(\int_{\mathbb{R}^d} \left|\partial_d \left(\|u\|_{L^2_y}\right)\right|^2\,\mathrm{d}x_d\right)^{\frac{2}{d-4}} \left(\int_{\mathbb{R}} \|u\|_{L^2_y}^2 \,\mathrm{d}x_d\right)^{\frac{d-2}{d-4}}.
\end{align}It then follows from (2.18), (2.27) and the conservation of mass that
 \begin{align}
\int_{\mathbb{R}}\|u\|_{L^2_y}^{\frac{2d}{d-4}} \,\mathrm{d}x_d \lesssim \left(\int_{\mathbb{R}^d} \|\partial_d u\|_{L^2_y}^2\,\mathrm{d}x_d\right)^{\frac{2}{d-4}}=\|\partial_d u\|_2^{\frac{4}{d-4}}.
\end{align}
\begin{align}
\int_{\mathbb{R}}\|u\|_{L^2_y}^{\frac{2d}{d-4}} \,\mathrm{d}x_d \lesssim \left(\int_{\mathbb{R}^d} \|\partial_d u\|_{L^2_y}^2\,\mathrm{d}x_d\right)^{\frac{2}{d-4}}=\|\partial_d u\|_2^{\frac{4}{d-4}}.
\end{align}Therefore, coming back to (2.26) and using (2.24) and (2.28), we derive that
 \begin{align*}
\left|\int_{\mathbb{R}^N} B_R |u|^{2 +\frac 8 d} \,\mathrm{d}x \right| &\lesssim \left(\int_{\mathbb{R}} \|B_R^{\frac 12} u\|_{L^{\infty}_y(|y| \geq R)}^2 \,\mathrm{d}x_d\right)^{\frac 4 d}\|\partial_d u\|_2^{\frac 4 d} \\
& \lesssim R \int_{\mathbb{R}} \|B_R^{\frac 12} u\|_{L^{\infty}_y(|y| \geq R)}^2 \,\mathrm{d}x_d + R^{-\frac{4}{d-4}} \|\partial_d u\|_2^{\frac{4}{d-4}} \\
& \leq R^{-1} \left(\eta^{-\frac 14} + R^{-2}\right)\|\partial_d u\|_2 + 8 R^{-1} \eta^{\frac 14} \|B_R \partial_r^2 u\|_2\\ & \quad + R^{-\frac{4}{d-4}} \|\partial_d u\|_2^{\frac{4}{d-4}} \\
& \lesssim R^{-1} \left(\eta^{-\frac 14} + R^{-2}\right)\|\partial_d u\|_2 + 8 \eta \|B_R \partial_r^2 u\|_2^2 + \\ & \qquad R^{-\frac{4}{d-4}} \|\partial_d u\|_2^{\frac{4}{d-4}} + R^{-2} \eta^{-\frac 12}.
\end{align*}
\begin{align*}
\left|\int_{\mathbb{R}^N} B_R |u|^{2 +\frac 8 d} \,\mathrm{d}x \right| &\lesssim \left(\int_{\mathbb{R}} \|B_R^{\frac 12} u\|_{L^{\infty}_y(|y| \geq R)}^2 \,\mathrm{d}x_d\right)^{\frac 4 d}\|\partial_d u\|_2^{\frac 4 d} \\
& \lesssim R \int_{\mathbb{R}} \|B_R^{\frac 12} u\|_{L^{\infty}_y(|y| \geq R)}^2 \,\mathrm{d}x_d + R^{-\frac{4}{d-4}} \|\partial_d u\|_2^{\frac{4}{d-4}} \\
& \leq R^{-1} \left(\eta^{-\frac 14} + R^{-2}\right)\|\partial_d u\|_2 + 8 R^{-1} \eta^{\frac 14} \|B_R \partial_r^2 u\|_2\\ & \quad + R^{-\frac{4}{d-4}} \|\partial_d u\|_2^{\frac{4}{d-4}} \\
& \lesssim R^{-1} \left(\eta^{-\frac 14} + R^{-2}\right)\|\partial_d u\|_2 + 8 \eta \|B_R \partial_r^2 u\|_2^2 + \\ & \qquad R^{-\frac{4}{d-4}} \|\partial_d u\|_2^{\frac{4}{d-4}} + R^{-2} \eta^{-\frac 12}.
\end{align*}As a consequence, invoking (2.21), we finally derive that
 \begin{align}
\begin{split}
\frac{\mathrm{d}}{\mathrm{d}t}\mathcal{M}_R[u(t)] &\leq 16 E(u_0)-8\int_{\mathbb{R}^d}\left(1-\partial_r^2 \psi_R-\eta \left(R^4 A_R^2 +B_R^2\right)\right)|\partial_r^2 u|^2 \,\mathrm{d}x \\
&\quad + R^{-1} \left(\eta^{-\frac 14} + R^{-2}\right) \|\partial_d u\|_2 +R^{-4} \eta^{-\frac 12} \|\partial_d u\|_2^2 \\
& \quad+ R^{-\frac{4}{d-4}} \|\partial_d u\|_2^{\frac{4}{d-4}} + R^{-2} \eta^{-\frac 12}+\eta^{-1}R^{-4} + R^{-2}.
\end{split}
\end{align}
\begin{align}
\begin{split}
\frac{\mathrm{d}}{\mathrm{d}t}\mathcal{M}_R[u(t)] &\leq 16 E(u_0)-8\int_{\mathbb{R}^d}\left(1-\partial_r^2 \psi_R-\eta \left(R^4 A_R^2 +B_R^2\right)\right)|\partial_r^2 u|^2 \,\mathrm{d}x \\
&\quad + R^{-1} \left(\eta^{-\frac 14} + R^{-2}\right) \|\partial_d u\|_2 +R^{-4} \eta^{-\frac 12} \|\partial_d u\|_2^2 \\
& \quad+ R^{-\frac{4}{d-4}} \|\partial_d u\|_2^{\frac{4}{d-4}} + R^{-2} \eta^{-\frac 12}+\eta^{-1}R^{-4} + R^{-2}.
\end{split}
\end{align}At this point, using (2.25) and (2.29) and reasoning as the proof of [Reference Boulenger and Lenzmann8, Theorem 3], we are able to finish the proof. This completes the proof.
Funding statement
The author was supported by the National Natural Science Foundation of China (No. 12101483) and the Postdoctoral Science Foundation of China.
Competing interests
Statements and declarations. The author declares that there are no conflict of interests.