1. Introduction
The paper treats the propagation of the anisotropic Gabor wave front set for a class of continuous linear operators.
Hörmander [Reference Hörmander9] introduced in 1991 the Gabor wave front set of a tempered distribution as a closed conic subset of the phase space ![]() $T^* {\mathbf R}^{d} \setminus 0$. It consists of directions in
$T^* {\mathbf R}^{d} \setminus 0$. It consists of directions in ![]() $T^* {\mathbf R}^{d} \setminus 0$ of global singularities, in no neighbourhood of which the short-time Fourier transform decays superpolynomially. The Gabor wave front set is empty precisely when the tempered distribution is a Schwartz function, so it records smoothness and decay at infinity simultaneously.
$T^* {\mathbf R}^{d} \setminus 0$ of global singularities, in no neighbourhood of which the short-time Fourier transform decays superpolynomially. The Gabor wave front set is empty precisely when the tempered distribution is a Schwartz function, so it records smoothness and decay at infinity simultaneously.
Recent works [Reference Carypis and Wahlberg1, Reference Cordero and Rodino4, Reference Pravda-Starov, Rodino and Wahlberg15, Reference Rodino and Wahlberg17, Reference Schulz and Wahlberg20, Reference Wahlberg22, Reference Wahlberg23] treat the Gabor wave front set and similar concepts. The Gabor wave front set is identical to Nakamura’s homogeneous wave front set [Reference Nakamura13, Reference Schulz and Wahlberg20]. Hörmander’s original paper [Reference Hörmander9] contains results on the action of a linear continuous operator on the Gabor wave front set. Propagation of the Gabor wave front set for the solution to evolution equations with quadratic Hamiltonian with non-negative real part is treated in [Reference Pravda-Starov, Rodino and Wahlberg15, Reference Wahlberg23]. The singular space of such a quadratic form, introduced by Hitrik and Pravda–Starov [Reference Hitrik and Pravda–Starov7], then plays a crucial role.
We have defined and studied an anisotropic version of the Gabor wave front set, which is parametrized by s > 0, in [Reference Rodino and Wahlberg19]. The new feature is to replace the superpolynomial decay along straight lines in phase space ![]() $T^* {\mathbf R}^{d} \setminus 0$, characteristic to the Gabor wave front set, by decay along curves of the form:
$T^* {\mathbf R}^{d} \setminus 0$, characteristic to the Gabor wave front set, by decay along curves of the form:
where ![]() $(x,\xi) \in T^* {\mathbf R}^{d} \setminus 0$. The resulting wave front set is baptized to the anisotropic s-Gabor wave front set, and it is denoted
$(x,\xi) \in T^* {\mathbf R}^{d} \setminus 0$. The resulting wave front set is baptized to the anisotropic s-Gabor wave front set, and it is denoted  $\mathrm{WF}_{\rm g}^s (u) \subseteq T^* {\mathbf R}^{d} \setminus 0$ for a tempered distribution
$\mathrm{WF}_{\rm g}^s (u) \subseteq T^* {\mathbf R}^{d} \setminus 0$ for a tempered distribution ![]() $u \in \mathscr{S}'({\mathbf R}^{d})$. If s = 1, we recover the standard Gabor wave front set.
$u \in \mathscr{S}'({\mathbf R}^{d})$. If s = 1, we recover the standard Gabor wave front set.
In [Reference Rodino and Wahlberg19], we develop pseudodifferential calculus and microlocal analysis for the anisotropic s-Gabor wave front set, inspired by e.g. [Reference Cappiello, Gramchev and Rodino2, Reference Cappiello, Gramchev, Pilipovic and Rodino3] which treat anisotropic partial differential operators with polynomial coefficients. This means that we study pseudodifferential calculus with symbol classes that are anisotropic modifications of the standard Shubin symbols. The anisotropic symbols [Reference Shubin21] satisfy estimates of the form:
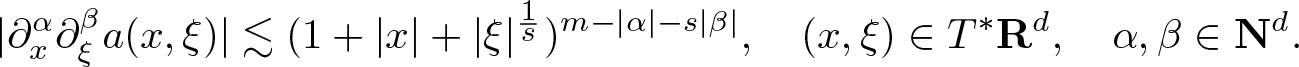 \begin{equation*}
|\partial_{x}^{\alpha} \partial_{\xi}^{\beta} a(x,\xi)|
\lesssim ( 1 + |x| + |\xi|^{\frac1s} )^{m - |\alpha| - s |\beta|}, \quad (x,\xi) \in T^* {\mathbf R}^{d}, \quad \alpha, \beta \in {\mathbf N}^{d}.
\end{equation*}
\begin{equation*}
|\partial_{x}^{\alpha} \partial_{\xi}^{\beta} a(x,\xi)|
\lesssim ( 1 + |x| + |\xi|^{\frac1s} )^{m - |\alpha| - s |\beta|}, \quad (x,\xi) \in T^* {\mathbf R}^{d}, \quad \alpha, \beta \in {\mathbf N}^{d}.
\end{equation*}It also means results on microlocality and microellipticity in the anisotropic framework.
For this purpose, we benefit from ideas and techniques from papers on microlocal analysis that is anisotropic in the dual (frequency) variables only (see, e.g., [Reference Parenti and Rodino14]), as opposed to our anisotropy, which refers to the space and frequency variables comprehensively. An overall summary of [Reference Rodino and Wahlberg19] is an anisotropic version of Shubin’s calculus of pseudodifferential operators [Reference Shubin21].
The anisotropic s-Gabor wave front describes accurately the global singularities of oscillatory functions of chirp type [Reference Rodino and Wahlberg19, Theorem 7.1]. These are exponentials with real polynomial phase functions.
In this paper, the chief result concerns propagation of the anisotropic s-Gabor wave front set by a continuous linear operator ![]() $\mathscr{K}: \mathscr{S}({\mathbf R}^{d}) \to \mathscr{S}'({\mathbf R}^{d})$ defined by a Schwartz kernel
$\mathscr{K}: \mathscr{S}({\mathbf R}^{d}) \to \mathscr{S}'({\mathbf R}^{d})$ defined by a Schwartz kernel ![]() $K \in \mathscr{S}'({\mathbf R}^{2d})$. Suppose that the s-Gabor wave front set of K contains no points of the form
$K \in \mathscr{S}'({\mathbf R}^{2d})$. Suppose that the s-Gabor wave front set of K contains no points of the form ![]() $(x, 0, \xi, 0) \in T^* \mathbf R^{2d} \setminus 0$ nor of the form
$(x, 0, \xi, 0) \in T^* \mathbf R^{2d} \setminus 0$ nor of the form ![]() $(0, y, 0, -\eta) \in T^* \mathbf R^{2d} \setminus 0$, with
$(0, y, 0, -\eta) \in T^* \mathbf R^{2d} \setminus 0$, with ![]() $x, y, \xi, \eta \in {\mathbf R}^{d}$. (Roughly speaking, this amounts to that
$x, y, \xi, \eta \in {\mathbf R}^{d}$. (Roughly speaking, this amounts to that ![]() $\mathrm{WF}_{\rm g}^s (K)$ resembles the graph of an invertible matrix.) Then
$\mathrm{WF}_{\rm g}^s (K)$ resembles the graph of an invertible matrix.) Then ![]() $\mathscr{K}: \mathscr{S}({\mathbf R}^{d}) \to \mathscr{S}({\mathbf R}^{d})$ acts continuously and extends uniquely to a sequentially continuous linear operator
$\mathscr{K}: \mathscr{S}({\mathbf R}^{d}) \to \mathscr{S}({\mathbf R}^{d})$ acts continuously and extends uniquely to a sequentially continuous linear operator ![]() $\mathscr{K}: \mathscr{S}'({\mathbf R}^{d}) \to \mathscr{S}'({\mathbf R}^{d})$, and for
$\mathscr{K}: \mathscr{S}'({\mathbf R}^{d}) \to \mathscr{S}'({\mathbf R}^{d})$, and for ![]() $u \in \mathscr{S}'({\mathbf R}^{d})$, we have
$u \in \mathscr{S}'({\mathbf R}^{d})$, we have
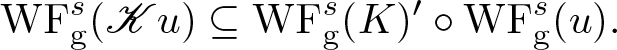 \begin{equation}
\mathrm{WF}_{\rm g}^s (\mathscr{K} u) \subseteq \mathrm{WF}_{\rm g}^s (K)' \circ \mathrm{WF}_{\rm g}^s (u).
\end{equation}
\begin{equation}
\mathrm{WF}_{\rm g}^s (\mathscr{K} u) \subseteq \mathrm{WF}_{\rm g}^s (K)' \circ \mathrm{WF}_{\rm g}^s (u).
\end{equation}Here, we use the notation
for ![]() $A \subseteq \mathbf R^{4d}$ and
$A \subseteq \mathbf R^{4d}$ and ![]() $B \subseteq \mathbf R^{2d}$.
$B \subseteq \mathbf R^{2d}$.
The inclusion (1.1) is conceptually similar to propagation results for other types of wave front sets, local [Reference Hörmander8], or global [Reference Carypis and Wahlberg1, Reference Pravda-Starov, Rodino and Wahlberg15, Reference Wahlberg22].
As an application of the inclusion (1.1), we study propagation of the anisotropic s-Gabor wave front set for the initial value Cauchy problem for an evolution equation of the form
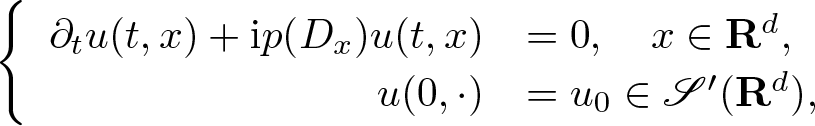 \begin{equation*}
\left\{
\begin{array}{rl}
\partial_t u(t,x) + \mathrm{i} p(D_x) u (t,x) & = 0, \quad x \in {\mathbf R}^{d}, \\
u(0,\cdot) & = u_0 \in \mathscr{S}'({\mathbf R}^{d}),
\end{array}
\right.
\end{equation*}
\begin{equation*}
\left\{
\begin{array}{rl}
\partial_t u(t,x) + \mathrm{i} p(D_x) u (t,x) & = 0, \quad x \in {\mathbf R}^{d}, \\
u(0,\cdot) & = u_0 \in \mathscr{S}'({\mathbf R}^{d}),
\end{array}
\right.
\end{equation*} where ![]() $p: {\mathbf R}^{d} \to \mathbf R$ is a polynomial with real coefficients of order
$p: {\mathbf R}^{d} \to \mathbf R$ is a polynomial with real coefficients of order ![]() $m \geqslant 2$. This generalizes the Schrödinger equation for the free particle where m = 2 and
$m \geqslant 2$. This generalizes the Schrödinger equation for the free particle where m = 2 and ![]() $p(\xi) = |\xi|^2$.
$p(\xi) = |\xi|^2$.
Provided  $s = \frac{1}{m-1}$, we show that
$s = \frac{1}{m-1}$, we show that ![]() $\mathrm{WF}_{\rm g}^s$ of the solution at time
$\mathrm{WF}_{\rm g}^s$ of the solution at time ![]() $t \in \mathbf R$ equals
$t \in \mathbf R$ equals ![]() $\mathrm{WF}_{\rm g}^s (u_0)$ transported by the Hamilton flow χt with respect to the principal part pm of
$\mathrm{WF}_{\rm g}^s (u_0)$ transported by the Hamilton flow χt with respect to the principal part pm of ![]() $p(\xi)$, that is
$p(\xi)$, that is
The conclusion is again conceptually similar to other results on propagation of singularities [Reference Carypis and Wahlberg1, Reference Hörmander8, Reference Wahlberg22], and generalizes known results when p is a homogeneous quadratic form and s = 1 [Reference Pravda-Starov, Rodino and Wahlberg15].
The article [Reference Wahlberg24] contains results similar to those of this paper but in the functional framework of Gelfand–Shilov spaces and their ultradistribution dual spaces.
The article is organized as follows. Notations and definitions are collected in § 2. Section 3 recalls the definition of the anisotropic s-Gabor wave front set, and a result on tensorization is proved as well as a characterization of the anisotropic s-Gabor wave front set in terms of characteristic sets of symbols. Then, § 4 is devoted to a proof of the main result on propagation of the anisotropic s-Gabor wave front set. Finally, § 5 treats an application to a class of evolution equations of Schrödinger type.
2. Preliminaries
The unit sphere in ![]() ${\mathbf R}^{d}$ is denoted
${\mathbf R}^{d}$ is denoted ![]() $\mathbf S^{d-1} \subseteq {\mathbf R}^{d}$. A ball of radius r > 0 centred in
$\mathbf S^{d-1} \subseteq {\mathbf R}^{d}$. A ball of radius r > 0 centred in ![]() $x \in {\mathbf R}^{d}$ is denoted
$x \in {\mathbf R}^{d}$ is denoted ![]() ${\rm B}_r (x)$, and
${\rm B}_r (x)$, and ![]() ${\rm B}_r(0) = {\rm B}_r$. The transpose of a matrix
${\rm B}_r(0) = {\rm B}_r$. The transpose of a matrix ![]() $A \in \mathbf R^{d \times d}$ is denoted
$A \in \mathbf R^{d \times d}$ is denoted ![]() $A^\mathrm{T}$, and the inverse transpose of
$A^\mathrm{T}$, and the inverse transpose of ![]() $A \in {\rm GL}(d,\mathbf R)$ is
$A \in {\rm GL}(d,\mathbf R)$ is ![]() $A^{\mathrm{-T}}$. We write
$A^{\mathrm{-T}}$. We write ![]() $f (x) \lesssim g (x)$ provided there exists C > 0 such that
$f (x) \lesssim g (x)$ provided there exists C > 0 such that ![]() $f (x) \leqslant C \, g(x)$ for all x in the domain of f and of g. If
$f (x) \leqslant C \, g(x)$ for all x in the domain of f and of g. If ![]() $f (x) \lesssim g (x) \lesssim f(x)$, then we write
$f (x) \lesssim g (x) \lesssim f(x)$, then we write ![]() $f \asymp g$. We use the bracket
$f \asymp g$. We use the bracket  $\langle x\rangle = (1 + |x|^2)^{\frac12}$ for
$\langle x\rangle = (1 + |x|^2)^{\frac12}$ for ![]() $x \in {\mathbf R}^{d}$. Peetre’s inequality with optimal constant [Reference Rodino and Wahlberg18, Lemma 2.1] is
$x \in {\mathbf R}^{d}$. Peetre’s inequality with optimal constant [Reference Rodino and Wahlberg18, Lemma 2.1] is
 \begin{equation}
\langle x+y\rangle^s \leqslant \left( \frac{2}{\sqrt{3}} \right)^{|s|} \langle x\rangle^s\langle y\rangle^{|s|}\qquad x,y \in {\mathbf R}^{d}, \quad s \in \mathbf R.
\end{equation}
\begin{equation}
\langle x+y\rangle^s \leqslant \left( \frac{2}{\sqrt{3}} \right)^{|s|} \langle x\rangle^s\langle y\rangle^{|s|}\qquad x,y \in {\mathbf R}^{d}, \quad s \in \mathbf R.
\end{equation}The normalization of the Fourier transform is
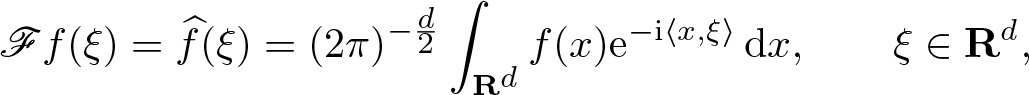 \begin{equation*}
\mathscr{F} f (\xi )= \widehat f(\xi ) = (2\pi )^{-\frac d2} \int _{{\mathbf R}^{d}} f(x)\mathrm{e}^{-\mathrm{i}\langle x,\xi\rangle } \, \mathrm {d} x, \qquad \xi \in {\mathbf R}^{d},
\end{equation*}
\begin{equation*}
\mathscr{F} f (\xi )= \widehat f(\xi ) = (2\pi )^{-\frac d2} \int _{{\mathbf R}^{d}} f(x)\mathrm{e}^{-\mathrm{i}\langle x,\xi\rangle } \, \mathrm {d} x, \qquad \xi \in {\mathbf R}^{d},
\end{equation*} for ![]() $f\in \mathscr{S}({\mathbf R}^{d})$ (the Schwartz space), where
$f\in \mathscr{S}({\mathbf R}^{d})$ (the Schwartz space), where ![]() $\langle \, \cdot \, , \, \cdot \,\rangle $ denotes the scalar product on
$\langle \, \cdot \, , \, \cdot \,\rangle $ denotes the scalar product on ![]() ${\mathbf R}^{d}$. The conjugate linear action of a distribution u on a test function ϕ is written
${\mathbf R}^{d}$. The conjugate linear action of a distribution u on a test function ϕ is written ![]() $(u,\phi)$, consistent with the L 2 inner product
$(u,\phi)$, consistent with the L 2 inner product ![]() $(\, \cdot \, ,\, \cdot \, ) = (\, \cdot \, ,\, \cdot \, )_{L^2}$ which is conjugate linear in the second argument.
$(\, \cdot \, ,\, \cdot \, ) = (\, \cdot \, ,\, \cdot \, )_{L^2}$ which is conjugate linear in the second argument.
Denote translation by ![]() $T_x f(y) = f( y-x )$ and modulation by
$T_x f(y) = f( y-x )$ and modulation by ![]() $M_\xi f(y) = \mathit{e}^{\mathit{i} \langle y, \xi\rangle} f(y)$ for
$M_\xi f(y) = \mathit{e}^{\mathit{i} \langle y, \xi\rangle} f(y)$ for ![]() $x,y,\xi \in {\mathbf R}^{d}$, where f is a function or distribution defined on
$x,y,\xi \in {\mathbf R}^{d}$, where f is a function or distribution defined on ![]() ${\mathbf R}^{d}$. The composed operator is denoted
${\mathbf R}^{d}$. The composed operator is denoted ![]() $\Pi(x,\xi) = M_\xi T_x$. Let
$\Pi(x,\xi) = M_\xi T_x$. Let ![]() $\varphi \in \mathscr{S}({\mathbf R}^{d}) \setminus \{0\}$. The short-time Fourier transform (STFT) of a tempered distribution
$\varphi \in \mathscr{S}({\mathbf R}^{d}) \setminus \{0\}$. The short-time Fourier transform (STFT) of a tempered distribution ![]() $u \in \mathscr{S}'({\mathbf R}^{d})$ is defined by
$u \in \mathscr{S}'({\mathbf R}^{d})$ is defined by
 \begin{equation*}
V_\varphi u (x,\xi) = (2\pi )^{-\frac d2} (u, M_\xi T_x \varphi) = \mathscr{F} (u T_x \overline \varphi)(\xi), \quad x,\xi \in {\mathbf R}^{d}.
\end{equation*}
\begin{equation*}
V_\varphi u (x,\xi) = (2\pi )^{-\frac d2} (u, M_\xi T_x \varphi) = \mathscr{F} (u T_x \overline \varphi)(\xi), \quad x,\xi \in {\mathbf R}^{d}.
\end{equation*} Then, ![]() $V_\varphi u$ is smooth and polynomially bounded [Reference Gröchenig6, Theorem 11.2.3], that is there exists
$V_\varphi u$ is smooth and polynomially bounded [Reference Gröchenig6, Theorem 11.2.3], that is there exists ![]() $k \geqslant 0$ such that
$k \geqslant 0$ such that
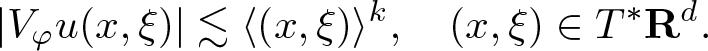 \begin{equation}
|V_\varphi u (x,\xi)| \lesssim \langle (x,\xi)\rangle^{k}, \quad (x,\xi) \in T^* {\mathbf R}^{d}.
\end{equation}
\begin{equation}
|V_\varphi u (x,\xi)| \lesssim \langle (x,\xi)\rangle^{k}, \quad (x,\xi) \in T^* {\mathbf R}^{d}.
\end{equation} We have ![]() $u \in \mathscr{S}({\mathbf R}^{d})$ if and only if
$u \in \mathscr{S}({\mathbf R}^{d})$ if and only if
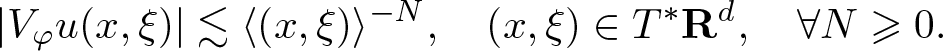 \begin{equation}
|V_\varphi u (x,\xi)| \lesssim \langle (x,\xi)\rangle^{-N}, \quad (x,\xi) \in T^* {\mathbf R}^{d}, \quad \forall N \geqslant 0.
\end{equation}
\begin{equation}
|V_\varphi u (x,\xi)| \lesssim \langle (x,\xi)\rangle^{-N}, \quad (x,\xi) \in T^* {\mathbf R}^{d}, \quad \forall N \geqslant 0.
\end{equation}The inverse transform is given by
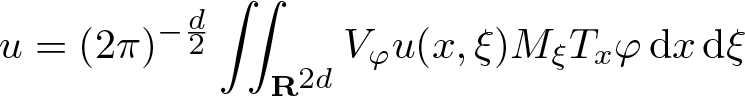 \begin{equation}
u = (2\pi )^{-\frac d2} \iint_{\mathbf R^{2d}} V_\varphi u (x,\xi) M_\xi T_x \varphi \, \mathrm {d} x \, \mathrm {d} \xi
\end{equation}
\begin{equation}
u = (2\pi )^{-\frac d2} \iint_{\mathbf R^{2d}} V_\varphi u (x,\xi) M_\xi T_x \varphi \, \mathrm {d} x \, \mathrm {d} \xi
\end{equation} provided ![]() $\| \varphi \|_{L^2} = 1$, with action under the integral understood, that is
$\| \varphi \|_{L^2} = 1$, with action under the integral understood, that is
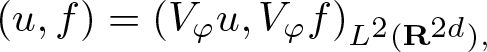 \begin{equation}
(u, f) = (V_\varphi u, V_\varphi f)_{L^2(\mathbf R^{2d}),}
\end{equation}
\begin{equation}
(u, f) = (V_\varphi u, V_\varphi f)_{L^2(\mathbf R^{2d}),}
\end{equation} for ![]() $u \in \mathscr{S}'({\mathbf R}^{d})$ and
$u \in \mathscr{S}'({\mathbf R}^{d})$ and ![]() $f \in \mathscr{S}({\mathbf R}^{d})$, cf. [Reference Gröchenig6, Theorem 11.2.5].
$f \in \mathscr{S}({\mathbf R}^{d})$, cf. [Reference Gröchenig6, Theorem 11.2.5].
By [Reference Gröchenig6, Corollary 11.2.6], the topology for ![]() $\mathscr{S} ({\mathbf R}^{d})$ can be defined by the collection of seminorms
$\mathscr{S} ({\mathbf R}^{d})$ can be defined by the collection of seminorms
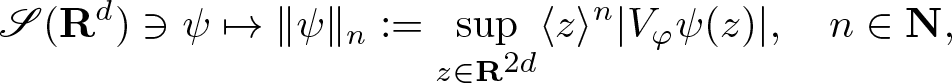 \begin{equation}
\mathscr{S}({\mathbf R}^{d}) \ni \psi \mapsto \| \psi \|_n := \sup_{z \in {\mathbf R}^{2d}} \langle z\rangle^n |V_\varphi \psi (z)|, \quad n \in \mathbf N,
\end{equation}
\begin{equation}
\mathscr{S}({\mathbf R}^{d}) \ni \psi \mapsto \| \psi \|_n := \sup_{z \in {\mathbf R}^{2d}} \langle z\rangle^n |V_\varphi \psi (z)|, \quad n \in \mathbf N,
\end{equation} for any ![]() $\varphi \in \mathscr{S}({\mathbf R}^{d}) \setminus 0$.
$\varphi \in \mathscr{S}({\mathbf R}^{d}) \setminus 0$.
2.1. s-conic subsets
We will use subsets of ![]() $T^* {\mathbf R}^{d} \setminus 0$ that are s-conic, that is closed under the operation
$T^* {\mathbf R}^{d} \setminus 0$ that are s-conic, that is closed under the operation ![]() $T^* {\mathbf R}^{d} \setminus 0 \ni (x,\xi) \mapsto ( \lambda x, \lambda^s \xi)$ for all λ > 0.
$T^* {\mathbf R}^{d} \setminus 0 \ni (x,\xi) \mapsto ( \lambda x, \lambda^s \xi)$ for all λ > 0.
Let s > 0 be fixed. We need the following simplified version of a tool taken from [Reference Parenti and Rodino14] and its references. Given ![]() $(x,\xi) \in \mathbf R^{2d} \setminus 0$, there is a unique
$(x,\xi) \in \mathbf R^{2d} \setminus 0$, there is a unique ![]() $\lambda = \lambda(x,\xi) = \lambda_s (x,\xi) \gt 0$ such that
$\lambda = \lambda(x,\xi) = \lambda_s (x,\xi) \gt 0$ such that
Then, ![]() $(x,\xi) \in \mathbf S^{2d-1}$ if and only if
$(x,\xi) \in \mathbf S^{2d-1}$ if and only if ![]() $\lambda (x,\xi) = 1$. By the implicit function theorem, the function
$\lambda (x,\xi) = 1$. By the implicit function theorem, the function ![]() $\lambda: \mathbf R^{2d} \setminus 0 \to \mathbf R_+$ is smooth [Reference Krantz and Parks11]. We have [Reference Rodino and Wahlberg19, Eq. (3.1)]
$\lambda: \mathbf R^{2d} \setminus 0 \to \mathbf R_+$ is smooth [Reference Krantz and Parks11]. We have [Reference Rodino and Wahlberg19, Eq. (3.1)]
The projection ![]() $\pi_s(x,\xi)$ of
$\pi_s(x,\xi)$ of ![]() $(x,\xi) \in \mathbf R^{2d} \setminus 0$ along the curve
$(x,\xi) \in \mathbf R^{2d} \setminus 0$ along the curve ![]() $\mathbf R_+ \ni \mu \mapsto (\mu x, \mu^s \xi)$ onto
$\mathbf R_+ \ni \mu \mapsto (\mu x, \mu^s \xi)$ onto ![]() $\mathbf S^{2d-1}$ is defined as
$\mathbf S^{2d-1}$ is defined as
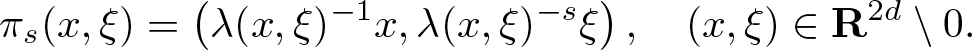 \begin{equation}
\pi_s(x,\xi) = \left( \lambda(x,\xi)^{-1} x, \lambda(x,\xi)^{-s} \xi \right), \quad (x,\xi) \in \mathbf R^{2d} \setminus 0.
\end{equation}
\begin{equation}
\pi_s(x,\xi) = \left( \lambda(x,\xi)^{-1} x, \lambda(x,\xi)^{-s} \xi \right), \quad (x,\xi) \in \mathbf R^{2d} \setminus 0.
\end{equation} Then, ![]() $\pi_s(\mu x, \mu^s \xi) = \pi_s(x, \xi)$ does not depend on µ > 0. The function
$\pi_s(\mu x, \mu^s \xi) = \pi_s(x, \xi)$ does not depend on µ > 0. The function ![]() $\pi_s: \mathbf R^{2d} \setminus 0 \to \mathbf S^{2d-1}$ is smooth since
$\pi_s: \mathbf R^{2d} \setminus 0 \to \mathbf S^{2d-1}$ is smooth since ![]() $\lambda \in C^\infty(\mathbf R^{2d} \setminus 0)$ and
$\lambda \in C^\infty(\mathbf R^{2d} \setminus 0)$ and ![]() $\lambda(x,\xi) \gt 0$ for all
$\lambda(x,\xi) \gt 0$ for all ![]() $(x,\xi) \in \mathbf R^{2d} \setminus 0$.
$(x,\xi) \in \mathbf R^{2d} \setminus 0$.
From [Reference Parenti and Rodino14], or by straightforward arguments, we have the bounds
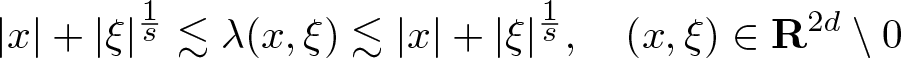 \begin{equation}
|x| + |\xi|^{\frac1s}
\lesssim \lambda(x,\xi) \lesssim |x| + |\xi|^{\frac1s}, \quad (x,\xi) \in \mathbf R^{2d} \setminus 0
\end{equation}
\begin{equation}
|x| + |\xi|^{\frac1s}
\lesssim \lambda(x,\xi) \lesssim |x| + |\xi|^{\frac1s}, \quad (x,\xi) \in \mathbf R^{2d} \setminus 0
\end{equation}and
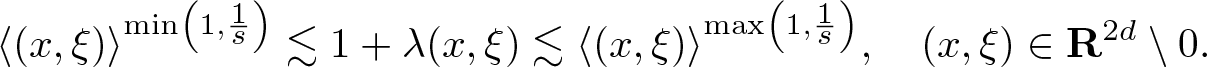 \begin{equation}
\langle (x,\xi) \rangle^{\min \left( 1, \frac1s \right)}
\lesssim 1 + \lambda(x,\xi)
\lesssim \langle (x,\xi)\rangle^{\max \left( 1, \frac1s \right)}, \quad (x,\xi) \in \mathbf R^{2d} \setminus 0.
\end{equation}
\begin{equation}
\langle (x,\xi) \rangle^{\min \left( 1, \frac1s \right)}
\lesssim 1 + \lambda(x,\xi)
\lesssim \langle (x,\xi)\rangle^{\max \left( 1, \frac1s \right)}, \quad (x,\xi) \in \mathbf R^{2d} \setminus 0.
\end{equation}We will use two types of s-conic neighbourhoods. The first type is defined as follows.
Definition 2.1. Suppose ![]() $s, \varepsilon \gt 0$ and
$s, \varepsilon \gt 0$ and ![]() $z_0 \in \mathbf S^{2d-1}$. Then,
$z_0 \in \mathbf S^{2d-1}$. Then,
 \begin{equation*}
\Gamma_{s, z_0, \varepsilon}
= \{ (x,\xi) \in \mathbf R^{2d} \setminus 0, \ | z_0 - \pi_s(x,\xi) | \lt \varepsilon \}
\subseteq T^* {\mathbf R}^{d} \setminus 0.
\end{equation*}
\begin{equation*}
\Gamma_{s, z_0, \varepsilon}
= \{ (x,\xi) \in \mathbf R^{2d} \setminus 0, \ | z_0 - \pi_s(x,\xi) | \lt \varepsilon \}
\subseteq T^* {\mathbf R}^{d} \setminus 0.
\end{equation*} We write ![]() $\Gamma_{z_0, \varepsilon} = \Gamma_{s, z_0, \varepsilon}$ when s is fixed and understood from the context. If ɛ > 2 then
$\Gamma_{z_0, \varepsilon} = \Gamma_{s, z_0, \varepsilon}$ when s is fixed and understood from the context. If ɛ > 2 then  $\Gamma_{z_0, \varepsilon} = T^* {\mathbf R}^{d} \setminus 0$ so we usually restrict to
$\Gamma_{z_0, \varepsilon} = T^* {\mathbf R}^{d} \setminus 0$ so we usually restrict to ![]() $\varepsilon \leqslant 2$.
$\varepsilon \leqslant 2$.
The second type of s-conic neighbourhood is defined as follows.
Definition 2.2. Suppose ![]() $s, \varepsilon \gt 0$ and
$s, \varepsilon \gt 0$ and ![]() $(x_0, \xi_0) \in \mathbf S^{2d-1}$. Then
$(x_0, \xi_0) \in \mathbf S^{2d-1}$. Then
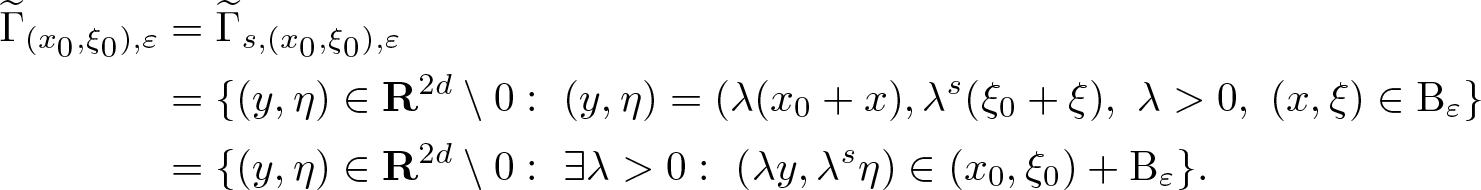 \begin{align*}
\widetilde \Gamma_{(x_0,\xi_0),\varepsilon}
& = \widetilde \Gamma_{s,(x_0,\xi_0),\varepsilon} \\
& = \{ (y,\eta) \in \mathbf R^{2d} \setminus 0: \ (y,\eta) = (\lambda (x_0 + x), \lambda^s (\xi_0 + \xi), \ \lambda \gt 0, \ (x,\xi) \in {\rm B}_\varepsilon \} \\
& = \{ (y,\eta) \in \mathbf R^{2d} \setminus 0: \ \exists \lambda \gt 0: \ (\lambda y, \lambda^s \eta) \in (x_0,\xi_0) + {\rm B}_\varepsilon \}.
\end{align*}
\begin{align*}
\widetilde \Gamma_{(x_0,\xi_0),\varepsilon}
& = \widetilde \Gamma_{s,(x_0,\xi_0),\varepsilon} \\
& = \{ (y,\eta) \in \mathbf R^{2d} \setminus 0: \ (y,\eta) = (\lambda (x_0 + x), \lambda^s (\xi_0 + \xi), \ \lambda \gt 0, \ (x,\xi) \in {\rm B}_\varepsilon \} \\
& = \{ (y,\eta) \in \mathbf R^{2d} \setminus 0: \ \exists \lambda \gt 0: \ (\lambda y, \lambda^s \eta) \in (x_0,\xi_0) + {\rm B}_\varepsilon \}.
\end{align*} By [Reference Rodino and Wahlberg19, Lemma 3.7], the two types of s-conic neighbourhoods are topologically equivalent. This means that if ![]() $z_0 \in \mathbf S^{2d-1}$ then for each ɛ > 0 there exists δ > 0 such that
$z_0 \in \mathbf S^{2d-1}$ then for each ɛ > 0 there exists δ > 0 such that  $\Gamma_{z_0, \delta} \subseteq \widetilde \Gamma_{z_0,\varepsilon}$ and
$\Gamma_{z_0, \delta} \subseteq \widetilde \Gamma_{z_0,\varepsilon}$ and  $\widetilde \Gamma_{z_0, \delta} \subseteq \Gamma_{z_0,\varepsilon}$.
$\widetilde \Gamma_{z_0, \delta} \subseteq \Gamma_{z_0,\varepsilon}$.
2.2. Pseudodifferential operators and anisotropic Shubin symbols
We need some elements from the calculus of pseudodifferential operators [Reference Folland5, Reference Hörmander8, Reference Nicola and Rodino12, Reference Shubin21]. Let ![]() $a \in C^\infty (\mathbf R^{2d})$,
$a \in C^\infty (\mathbf R^{2d})$, ![]() $m \in \mathbf R$ and
$m \in \mathbf R$ and ![]() $0 \leqslant \rho \leqslant 1$. Then, a is a Shubin symbol of order m and parameter ρ, denoted
$0 \leqslant \rho \leqslant 1$. Then, a is a Shubin symbol of order m and parameter ρ, denoted ![]() $a\in G_\rho^m$, if for all
$a\in G_\rho^m$, if for all ![]() $\alpha,\beta \in {\mathbf N}^{d}$, there exists a constant
$\alpha,\beta \in {\mathbf N}^{d}$, there exists a constant ![]() $C_{\alpha,\beta} \gt 0$ such that
$C_{\alpha,\beta} \gt 0$ such that
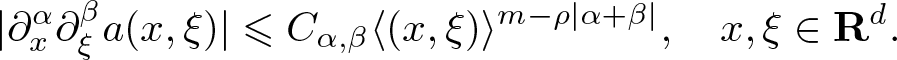 \begin{equation}
|\partial_x^\alpha \partial_\xi^\beta a(x,\xi)| \leqslant C_{\alpha,\beta} \langle (x,\xi)\rangle^{m - \rho|\alpha + \beta|}, \quad x,\xi \in {\mathbf R}^{d}.
\end{equation}
\begin{equation}
|\partial_x^\alpha \partial_\xi^\beta a(x,\xi)| \leqslant C_{\alpha,\beta} \langle (x,\xi)\rangle^{m - \rho|\alpha + \beta|}, \quad x,\xi \in {\mathbf R}^{d}.
\end{equation} The Shubin symbols ![]() $G_\rho^m$ form a Fréchet space where the seminorms are given by the smallest possible constants in (2.11). We write
$G_\rho^m$ form a Fréchet space where the seminorms are given by the smallest possible constants in (2.11). We write ![]() $G_1^m = G^m$.
$G_1^m = G^m$.
For ![]() $a \in G_\rho^m$ and
$a \in G_\rho^m$ and ![]() $t \in \mathbf R$, a pseudodifferential operator in the t-quantization is defined by
$t \in \mathbf R$, a pseudodifferential operator in the t-quantization is defined by
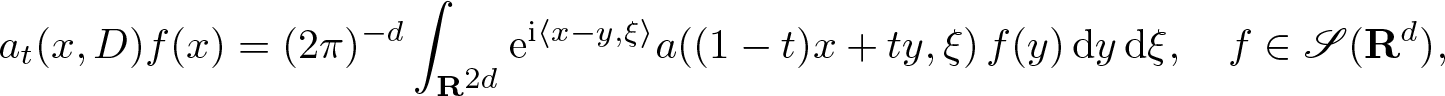 \begin{equation}
a_t(x,D) f(x)
= (2\pi)^{-d} \int_{\mathbf R^{2d}} \mathrm{e}^{\mathrm{i} \langle x-y, \xi \rangle} a ( (1-t) x + t y,\xi ) \, f(y) \, \mathrm {d} y \, \mathrm {d} \xi, \quad f \in \mathscr{S}({\mathbf R}^{d}),
\end{equation}
\begin{equation}
a_t(x,D) f(x)
= (2\pi)^{-d} \int_{\mathbf R^{2d}} \mathrm{e}^{\mathrm{i} \langle x-y, \xi \rangle} a ( (1-t) x + t y,\xi ) \, f(y) \, \mathrm {d} y \, \mathrm {d} \xi, \quad f \in \mathscr{S}({\mathbf R}^{d}),
\end{equation} when ![]() $m \lt -d$. The definition extends to
$m \lt -d$. The definition extends to ![]() $m \in \mathbf R$ if the integral is viewed as an oscillatory integral. If t = 0, we get the Kohn–Nirenberg quantization
$m \in \mathbf R$ if the integral is viewed as an oscillatory integral. If t = 0, we get the Kohn–Nirenberg quantization ![]() $a_0(x,D)$ and if
$a_0(x,D)$ and if  $t = \frac12$ we get the Weyl quantization
$t = \frac12$ we get the Weyl quantization ![]() $a_{1/2}(x,D) = a^w(x,D)$. The Weyl product is the product of symbols corresponding to operator composition (when well defined):
$a_{1/2}(x,D) = a^w(x,D)$. The Weyl product is the product of symbols corresponding to operator composition (when well defined): ![]() $( a {\#} b)^w(x,D) = a^w(x,D) b^w (x,D)$.
$( a {\#} b)^w(x,D) = a^w(x,D) b^w (x,D)$.
Anisotropic versions of the Shubin classes are defined as follows [Reference Rodino and Wahlberg19, Definition 3.1].
Definition 2.3. Let s > 0 and ![]() $m \in \mathbf R$. The space of (s-)anisotropic Shubin symbols
$m \in \mathbf R$. The space of (s-)anisotropic Shubin symbols ![]() $G^{m,s}$ of order m consists of functions
$G^{m,s}$ of order m consists of functions ![]() $a \in C^\infty(\mathbf R^{2d})$ that satisfy the estimates
$a \in C^\infty(\mathbf R^{2d})$ that satisfy the estimates
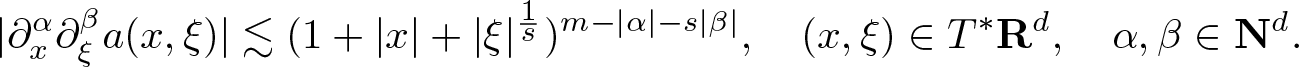 \begin{equation*}
|\partial_{x}^{\alpha} \partial_{\xi}^{\beta} a(x,\xi)|
\lesssim ( 1 + |x| + |\xi|^{\frac1s} )^{m - |\alpha| - s |\beta|}, \quad (x,\xi) \in T^* {\mathbf R}^{d}, \quad \alpha, \beta \in {\mathbf N}^{d}.
\end{equation*}
\begin{equation*}
|\partial_{x}^{\alpha} \partial_{\xi}^{\beta} a(x,\xi)|
\lesssim ( 1 + |x| + |\xi|^{\frac1s} )^{m - |\alpha| - s |\beta|}, \quad (x,\xi) \in T^* {\mathbf R}^{d}, \quad \alpha, \beta \in {\mathbf N}^{d}.
\end{equation*}We have
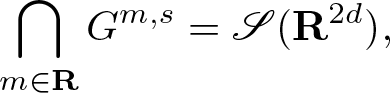 \begin{equation*}
\bigcap_{m \in \mathbf R} G^{m,s} = \mathscr{S}(\mathbf R^{2d}),
\end{equation*}
\begin{equation*}
\bigcap_{m \in \mathbf R} G^{m,s} = \mathscr{S}(\mathbf R^{2d}),
\end{equation*} and ![]() $G^{m,1} = G^m = G_1^m$, that is the usual Shubin class, but we cannot embed
$G^{m,1} = G^m = G_1^m$, that is the usual Shubin class, but we cannot embed ![]() $G_\rho^m$ in a space
$G_\rho^m$ in a space ![]() $G^{n,s}$ unless
$G^{n,s}$ unless ![]() $\rho = s = 1$. Using (2.9) and (2.10), the embedding
$\rho = s = 1$. Using (2.9) and (2.10), the embedding
where ![]() $m_0 = \max(m, m/s)$ and
$m_0 = \max(m, m/s)$ and ![]() $\rho = \min(s, 1/s)$ can be confirmed. Thus, the Shubin calculus [Reference Nicola and Rodino12, Reference Shubin21] applies to the anisotropic Shubin symbols. However, there is a more subtle anisotropic subcalculus adapted to the anisotropic Shubin symbols
$\rho = \min(s, 1/s)$ can be confirmed. Thus, the Shubin calculus [Reference Nicola and Rodino12, Reference Shubin21] applies to the anisotropic Shubin symbols. However, there is a more subtle anisotropic subcalculus adapted to the anisotropic Shubin symbols ![]() $G^{m,s}$, for each fixed s > 0. In fact by [Reference Rodino and Wahlberg19, Proposition 3.3], the symbol classes
$G^{m,s}$, for each fixed s > 0. In fact by [Reference Rodino and Wahlberg19, Proposition 3.3], the symbol classes ![]() $G^{m,s}$ are invariant under a change of the quantization parameter
$G^{m,s}$ are invariant under a change of the quantization parameter ![]() $t \in \mathbf R$ in (2.12), and the Weyl product
$t \in \mathbf R$ in (2.12), and the Weyl product ![]() ${\#}: G^{m,s} \times G^{n,s} \to G^{m+n,s}$ is continuous.
${\#}: G^{m,s} \times G^{n,s} \to G^{m+n,s}$ is continuous.
The following two definitions are taken from [Reference Rodino and Wahlberg19, Definitions 3.8 and 6.1]. The anisotropic weight is denoted
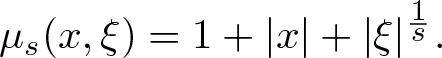 \begin{equation*}
\mu_s(x,\xi) = 1 + |x| + |\xi|^{\frac1s}.
\end{equation*}
\begin{equation*}
\mu_s(x,\xi) = 1 + |x| + |\xi|^{\frac1s}.
\end{equation*}Definition 2.4. Let s > 0, ![]() $z_0 \in \mathbf R^{2d} \setminus 0$ and
$z_0 \in \mathbf R^{2d} \setminus 0$ and ![]() $a \in G^{m,s}$. Then, z 0 is called non-characteristic of order
$a \in G^{m,s}$. Then, z 0 is called non-characteristic of order ![]() $m_1 \leqslant m$,
$m_1 \leqslant m$, ![]() $z_0 \notin {\rm char}_{s,m_1} (a)$, if there exists ɛ > 0 such that, with
$z_0 \notin {\rm char}_{s,m_1} (a)$, if there exists ɛ > 0 such that, with ![]() $\Gamma = \Gamma_{s,\pi_s(z_0),\varepsilon}$,
$\Gamma = \Gamma_{s,\pi_s(z_0),\varepsilon}$,
 \begin{align}
|a( x, \xi )| & \geqslant C \mu_s(x,\xi)^{m_1}, \quad (x,\xi) \in \Gamma \quad, \quad |x| + |\xi|^{\frac1s} \geqslant R,
\end{align}
\begin{align}
|a( x, \xi )| & \geqslant C \mu_s(x,\xi)^{m_1}, \quad (x,\xi) \in \Gamma \quad, \quad |x| + |\xi|^{\frac1s} \geqslant R,
\end{align} \begin{align}
|\partial_{x}^{\alpha} \partial_{\xi}^{\beta} a(x,\xi)| &\lesssim |a(x,\xi)| \mu_s(x,\xi)^{- |\alpha| - s |\beta|}, \quad \alpha, \beta \in {\mathbf N}^{d}, \quad (x,\xi) \in \Gamma, \quad |x| + |\xi|^{\frac1s} \geqslant R,
\end{align}
\begin{align}
|\partial_{x}^{\alpha} \partial_{\xi}^{\beta} a(x,\xi)| &\lesssim |a(x,\xi)| \mu_s(x,\xi)^{- |\alpha| - s |\beta|}, \quad \alpha, \beta \in {\mathbf N}^{d}, \quad (x,\xi) \in \Gamma, \quad |x| + |\xi|^{\frac1s} \geqslant R,
\end{align} for suitable ![]() $C, R \gt 0$.
$C, R \gt 0$.
If ![]() $m_1 = m$, we write
$m_1 = m$, we write ![]() ${\rm char}_{s,m} (a) = {\rm char}_{s} (a)$, and then the condition (2.15) is redundant. Note that
${\rm char}_{s,m} (a) = {\rm char}_{s} (a)$, and then the condition (2.15) is redundant. Note that ![]() ${\rm char}_{s,m_1} (a)$ is a closed s-conic subset of
${\rm char}_{s,m_1} (a)$ is a closed s-conic subset of ![]() $T^* {\mathbf R}^{d} \setminus 0$ and
$T^* {\mathbf R}^{d} \setminus 0$ and ![]() ${\rm char}_{s,m_1} (a) \subseteq {\rm char}_{s,m_2} (a)$ if
${\rm char}_{s,m_1} (a) \subseteq {\rm char}_{s,m_2} (a)$ if ![]() $m_1 \leqslant m_2 \leqslant m$.
$m_1 \leqslant m_2 \leqslant m$.
Definition 2.5. Suppose s > 0, ![]() $a \in G^{m,s}$ and let πs be the projection (2.8). The s-conical support
$a \in G^{m,s}$ and let πs be the projection (2.8). The s-conical support ![]() ${\rm conesupp}_{s} (a) \subseteq T^* {\mathbf R}^{d} \setminus 0$ of a is defined as follows. A point
${\rm conesupp}_{s} (a) \subseteq T^* {\mathbf R}^{d} \setminus 0$ of a is defined as follows. A point ![]() $z_0 \in T^* {\mathbf R}^{d} \setminus 0$ satisfies
$z_0 \in T^* {\mathbf R}^{d} \setminus 0$ satisfies ![]() $z_0 \notin {\rm conesupp}_{s} (a)$ if there exists ɛ > 0 such that
$z_0 \notin {\rm conesupp}_{s} (a)$ if there exists ɛ > 0 such that
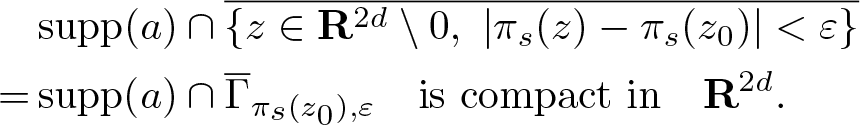 \begin{align*}
& \, {\rm supp} (a) \cap \overline{ \{ z \in \mathbf R^{2d} \setminus 0, \ | \pi_s(z) - \pi_s(z_0) | \lt \varepsilon \} } \\
= & \, {\rm supp} (a) \cap \overline{ \Gamma }_{\pi_s (z_0), \varepsilon}
\quad \mbox{is compact in} \quad \mathbf R^{2d}.
\end{align*}
\begin{align*}
& \, {\rm supp} (a) \cap \overline{ \{ z \in \mathbf R^{2d} \setminus 0, \ | \pi_s(z) - \pi_s(z_0) | \lt \varepsilon \} } \\
= & \, {\rm supp} (a) \cap \overline{ \Gamma }_{\pi_s (z_0), \varepsilon}
\quad \mbox{is compact in} \quad \mathbf R^{2d}.
\end{align*} Clearly, ![]() ${\rm conesupp}_{s} (a) \subseteq T^* {\mathbf R}^{d} \setminus 0$ is s-conic. Note that for any
${\rm conesupp}_{s} (a) \subseteq T^* {\mathbf R}^{d} \setminus 0$ is s-conic. Note that for any ![]() $a \in G^{m,s}$ and any
$a \in G^{m,s}$ and any ![]() $m_1 \leqslant m$, we have
$m_1 \leqslant m$, we have
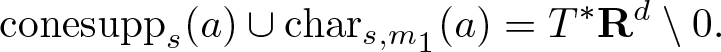 \begin{equation*}
{\rm conesupp}_{s} (a) \cup {\rm char}_{s,m_1} (a) = T^* {\mathbf R}^{d} \setminus 0.
\end{equation*}
\begin{equation*}
{\rm conesupp}_{s} (a) \cup {\rm char}_{s,m_1} (a) = T^* {\mathbf R}^{d} \setminus 0.
\end{equation*}3. Anisotropic Gabor wave front sets
The following definition is inspired by Zhu [Reference Zhu25, Definition 1.3] of a quasi-homogeneous wave front set defined by two non-negative parameters. Zhu uses a semiclassical formulation, whereas we use the STFT. As far as we know it is an open question to determine if the concepts coincide.
Given a parameter s > 0, we define the s-Gabor wave front set  $\mathrm{WF}_{\rm g}^{s} ( u ) \subseteq T^* {\mathbf R}^{d} \setminus 0$ of
$\mathrm{WF}_{\rm g}^{s} ( u ) \subseteq T^* {\mathbf R}^{d} \setminus 0$ of ![]() $u \in \mathscr{S}'({\mathbf R}^{d})$.
$u \in \mathscr{S}'({\mathbf R}^{d})$.
Definition 3.1. Suppose ![]() $u \in \mathscr{S}'({\mathbf R}^{d})$,
$u \in \mathscr{S}'({\mathbf R}^{d})$, ![]() $\varphi \in \mathscr{S}({\mathbf R}^{d}) \setminus 0$ and s > 0. A point
$\varphi \in \mathscr{S}({\mathbf R}^{d}) \setminus 0$ and s > 0. A point ![]() $z_0 = (x_0,\xi_0) \in T^* {\mathbf R}^{d} \setminus 0$ satisfies
$z_0 = (x_0,\xi_0) \in T^* {\mathbf R}^{d} \setminus 0$ satisfies ![]() $z_0 \notin \mathrm{WF_{g}^{\it s}} ( u )$ if there exists an open set
$z_0 \notin \mathrm{WF_{g}^{\it s}} ( u )$ if there exists an open set ![]() $U \subseteq T^* {\mathbf R}^{d}$ such that
$U \subseteq T^* {\mathbf R}^{d}$ such that ![]() $z_0 \in U$ and
$z_0 \in U$ and
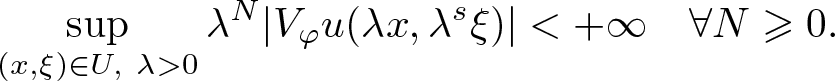 \begin{equation}
\sup_{(x,\xi) \in U, \ \lambda \gt 0} \lambda^N |V_\varphi u (\lambda x, \lambda^s \xi)| \lt + \infty \quad \forall N \geqslant 0.
\end{equation}
\begin{equation}
\sup_{(x,\xi) \in U, \ \lambda \gt 0} \lambda^N |V_\varphi u (\lambda x, \lambda^s \xi)| \lt + \infty \quad \forall N \geqslant 0.
\end{equation} If s = 1, we have  $\mathrm{WF}_{\rm g}^{1} ( u ) = \mathrm{WF_{\rm g}} (u)$ which denotes the usual Gabor wave front set [Reference Hörmander9, Reference Rodino and Wahlberg17]. We call
$\mathrm{WF}_{\rm g}^{1} ( u ) = \mathrm{WF_{\rm g}} (u)$ which denotes the usual Gabor wave front set [Reference Hörmander9, Reference Rodino and Wahlberg17]. We call ![]() $\mathrm{WF_{g}^{\it s}} ( u )$ the s-Gabor wave front set or the anisotropic Gabor wave front set. It is clear that
$\mathrm{WF_{g}^{\it s}} ( u )$ the s-Gabor wave front set or the anisotropic Gabor wave front set. It is clear that ![]() $\mathrm{WF_{g}^{\it s}} ( u )$ is s-conic. In Definition 3.1, we may therefore assume that
$\mathrm{WF_{g}^{\it s}} ( u )$ is s-conic. In Definition 3.1, we may therefore assume that ![]() $(x_0,\xi_0) \in \mathbf S^{2d-1}$.
$(x_0,\xi_0) \in \mathbf S^{2d-1}$.
Referring to (2.2) and (2.3), we see that ![]() $\mathrm{WF}_{\rm g}^s ( u )$ records curves
$\mathrm{WF}_{\rm g}^s ( u )$ records curves ![]() $0 \lt \lambda \mapsto (\lambda x, \lambda^s \xi)$ where
$0 \lt \lambda \mapsto (\lambda x, \lambda^s \xi)$ where ![]() $V_\varphi u$ does not behave like the STFT of a Schwartz function. We have
$V_\varphi u$ does not behave like the STFT of a Schwartz function. We have ![]() $\mathrm{WF_{g}^{\it s}} ( u ) = \emptyset$ if and only if
$\mathrm{WF_{g}^{\it s}} ( u ) = \emptyset$ if and only if ![]() $u \in \mathscr{S} ({\mathbf R}^{d})$ [Reference Rodino and Wahlberg19, Section 4].
$u \in \mathscr{S} ({\mathbf R}^{d})$ [Reference Rodino and Wahlberg19, Section 4].
If s > 0, then (2.9) and (2.10) give the bounds
 \begin{equation}
\langle (x,\xi) \rangle^{\min \left( 1, \frac1s \right)}
\lesssim 1 + |x| + |\xi|^{\frac1s}
\lesssim \langle (x,\xi)\rangle^{\max \left( 1, \frac1s \right)}, \quad (x,\xi) \in \mathbf R^{2d} \setminus 0.
\end{equation}
\begin{equation}
\langle (x,\xi) \rangle^{\min \left( 1, \frac1s \right)}
\lesssim 1 + |x| + |\xi|^{\frac1s}
\lesssim \langle (x,\xi)\rangle^{\max \left( 1, \frac1s \right)}, \quad (x,\xi) \in \mathbf R^{2d} \setminus 0.
\end{equation} If  $(y,\eta) \in \widetilde \Gamma_{(x_0,\xi_0), \varepsilon}$ for
$(y,\eta) \in \widetilde \Gamma_{(x_0,\xi_0), \varepsilon}$ for ![]() $0 \lt \varepsilon \lt 1$, then for some λ > 0 and
$0 \lt \varepsilon \lt 1$, then for some λ > 0 and ![]() $(x,\xi) \in {\rm B}_\varepsilon$, we have
$(x,\xi) \in {\rm B}_\varepsilon$, we have ![]() $(y,\eta) = (\lambda (x_0+x), \lambda^s (\xi_0+\xi))$. Thus,
$(y,\eta) = (\lambda (x_0+x), \lambda^s (\xi_0+\xi))$. Thus,  $|y| + |\eta|^{\frac1s} \asymp \lambda$, so combining with (3.2), we obtain the following equivalent criterion to the condition (3.1) in Definition 3.1. The point
$|y| + |\eta|^{\frac1s} \asymp \lambda$, so combining with (3.2), we obtain the following equivalent criterion to the condition (3.1) in Definition 3.1. The point ![]() $(x_0,\xi_0) \in \mathbf S^{2d-1}$ satisfies
$(x_0,\xi_0) \in \mathbf S^{2d-1}$ satisfies ![]() $(x_0,\xi_0) \notin \mathrm{WF_{g}^{\it s}} (u)$ if and only if for some ɛ > 0 we have
$(x_0,\xi_0) \notin \mathrm{WF_{g}^{\it s}} (u)$ if and only if for some ɛ > 0 we have
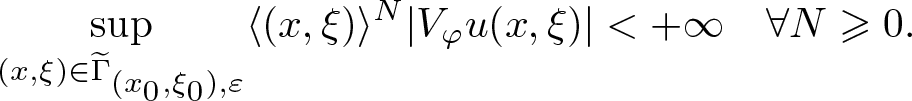 \begin{equation}
\sup_{(x,\xi) \in \widetilde \Gamma_{(x_0,\xi_0), \varepsilon}} \langle (x,\xi)\rangle^N |V_\varphi u (x,\xi)| \lt + \infty \quad \forall N \geqslant 0.
\end{equation}
\begin{equation}
\sup_{(x,\xi) \in \widetilde \Gamma_{(x_0,\xi_0), \varepsilon}} \langle (x,\xi)\rangle^N |V_\varphi u (x,\xi)| \lt + \infty \quad \forall N \geqslant 0.
\end{equation} We will need the following result on the anisotropic Gabor wave front set of a tensor product. The corresponding result for the Gabor wave front set is [Reference Hörmander9, Proposition 2.8]. Here, we use the notation ![]() $x=(x',x'') \in \mathbf R^{m+n}$,
$x=(x',x'') \in \mathbf R^{m+n}$, ![]() $x' \in {\mathbf R}^{m}$,
$x' \in {\mathbf R}^{m}$, ![]() $x'' \in {\mathbf R}^{n}$.
$x'' \in {\mathbf R}^{n}$.
Proposition 3.2. If s > 0, ![]() $u \in \mathscr{S}'({\mathbf R}^{m})$, and
$u \in \mathscr{S}'({\mathbf R}^{m})$, and ![]() $v \in \mathscr{S}'({\mathbf R}^{n})$ then
$v \in \mathscr{S}'({\mathbf R}^{n})$ then
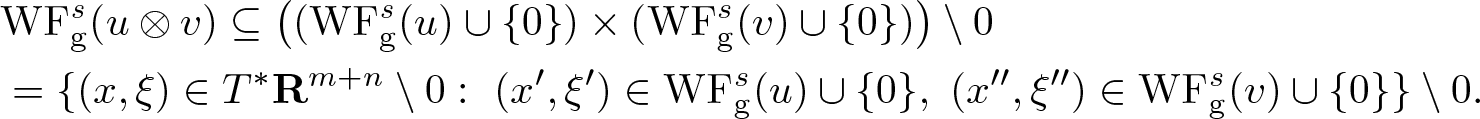 \begin{align*}
& \mathrm{WF_{g}^{\it s}} (u \otimes v) \subseteq \left( ( \mathrm{WF_{g}^{\it s}}(u) \cup \{0\} ) \times ( \mathrm{WF_{g}^{\it s}}(v) \cup \{0\} ) \right)\setminus 0 \\
& = \{ (x,\xi) \in T^* \mathbf R^{m+n} \setminus 0: \ (x',\xi') \in \mathrm{WF_{g}^{\it s}}(u) \cup \{ 0 \}, \ (x'',\xi'') \in \mathrm{WF_{g}^{\it s}}(v) \cup \{ 0 \} \} \setminus 0.
\end{align*}
\begin{align*}
& \mathrm{WF_{g}^{\it s}} (u \otimes v) \subseteq \left( ( \mathrm{WF_{g}^{\it s}}(u) \cup \{0\} ) \times ( \mathrm{WF_{g}^{\it s}}(v) \cup \{0\} ) \right)\setminus 0 \\
& = \{ (x,\xi) \in T^* \mathbf R^{m+n} \setminus 0: \ (x',\xi') \in \mathrm{WF_{g}^{\it s}}(u) \cup \{ 0 \}, \ (x'',\xi'') \in \mathrm{WF_{g}^{\it s}}(v) \cup \{ 0 \} \} \setminus 0.
\end{align*}Proof. Let ![]() $\varphi \in \mathscr{S}({\mathbf R}^{m}) \setminus 0$ and
$\varphi \in \mathscr{S}({\mathbf R}^{m}) \setminus 0$ and ![]() $\psi \in \mathscr{S}({\mathbf R}^{n}) \setminus 0$. Suppose
$\psi \in \mathscr{S}({\mathbf R}^{n}) \setminus 0$. Suppose ![]() $(x_0,\xi_0) \in T^* \mathbf R^{m+n} \setminus 0$ does not belong to the set on the right-hand side. Then, either
$(x_0,\xi_0) \in T^* \mathbf R^{m+n} \setminus 0$ does not belong to the set on the right-hand side. Then, either ![]() $(x_0',\xi_0') \notin \mathrm{WF_{g}^{\it s}}(u) \cup \{ 0 \}$ or
$(x_0',\xi_0') \notin \mathrm{WF_{g}^{\it s}}(u) \cup \{ 0 \}$ or ![]() $(x_0'',\xi_0'') \notin \mathrm{WF_{g}^{\it s}}(v) \cup \{ 0 \}$. For reasons of symmetry, we may assume
$(x_0'',\xi_0'') \notin \mathrm{WF_{g}^{\it s}}(v) \cup \{ 0 \}$. For reasons of symmetry, we may assume ![]() $(x_0',\xi_0') \notin \mathrm{WF_{g}^{\it s}}(u) \cup \{ 0 \}$.
$(x_0',\xi_0') \notin \mathrm{WF_{g}^{\it s}}(u) \cup \{ 0 \}$.
Thus, there exists ɛ > 0 such that
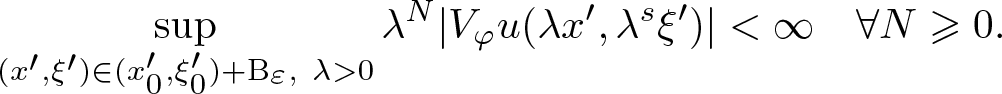 \begin{equation*}
\sup_{(x',\xi') \in (x_0',\xi_0') + {\rm B}_\varepsilon, \ \lambda \gt 0} \lambda^N |V_\varphi u( \lambda x', \lambda^s \xi')| \lt \infty \quad \forall N \geqslant 0.
\end{equation*}
\begin{equation*}
\sup_{(x',\xi') \in (x_0',\xi_0') + {\rm B}_\varepsilon, \ \lambda \gt 0} \lambda^N |V_\varphi u( \lambda x', \lambda^s \xi')| \lt \infty \quad \forall N \geqslant 0.
\end{equation*} Let ![]() $(x',\xi') \in (x_0',\xi_0') + {\rm B}_\varepsilon$,
$(x',\xi') \in (x_0',\xi_0') + {\rm B}_\varepsilon$, ![]() $(x'',\xi'') \in (x_0'',\xi_0'') + {\rm B}_\varepsilon$, let
$(x'',\xi'') \in (x_0'',\xi_0'') + {\rm B}_\varepsilon$, let ![]() $N \in \mathbf N$ be arbitrary and let
$N \in \mathbf N$ be arbitrary and let ![]() $\lambda \geqslant 1$. We obtain using (2.2), for some
$\lambda \geqslant 1$. We obtain using (2.2), for some ![]() $k \in \mathbf N$
$k \in \mathbf N$
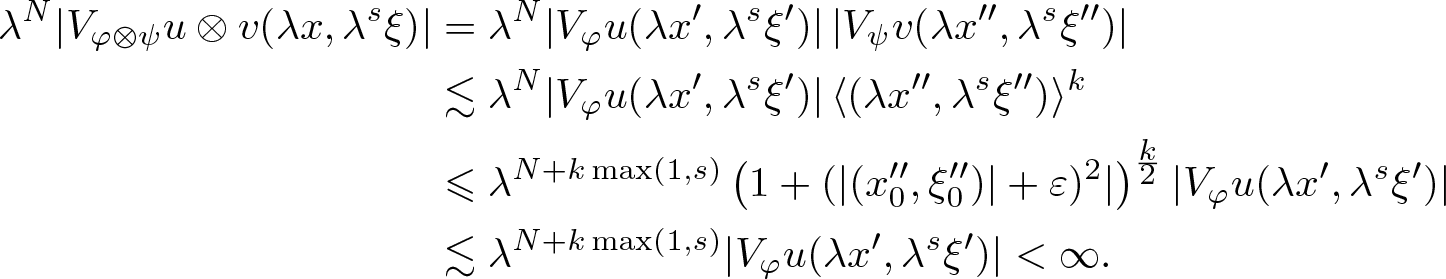 \begin{align*}
\lambda^N |V_{\varphi \otimes \psi} u \otimes v (\lambda x, \lambda^s \xi)|
& = \lambda^N |V_\varphi u ( \lambda x', \lambda^s \xi')| \, |V_\psi v (\lambda x'', \lambda^s \xi'')| \\
& \lesssim \lambda^N |V_\varphi u ( \lambda x', \lambda^s \xi')| \, \langle (\lambda x'', \lambda^s \xi'' )\rangle^k \\
& \leqslant \lambda^{N+ k \max(1,s) }
\left( 1 + ( |(x_0'', \xi_0'')| + \varepsilon)^2 | \right)^{\frac{k}{2}} |V_\varphi u ( \lambda x', \lambda^s \xi')| \\
& \lesssim \lambda^{N+ k \max(1,s) } |V_\varphi u ( \lambda x', \lambda^s \xi')| \lt \infty.
\end{align*}
\begin{align*}
\lambda^N |V_{\varphi \otimes \psi} u \otimes v (\lambda x, \lambda^s \xi)|
& = \lambda^N |V_\varphi u ( \lambda x', \lambda^s \xi')| \, |V_\psi v (\lambda x'', \lambda^s \xi'')| \\
& \lesssim \lambda^N |V_\varphi u ( \lambda x', \lambda^s \xi')| \, \langle (\lambda x'', \lambda^s \xi'' )\rangle^k \\
& \leqslant \lambda^{N+ k \max(1,s) }
\left( 1 + ( |(x_0'', \xi_0'')| + \varepsilon)^2 | \right)^{\frac{k}{2}} |V_\varphi u ( \lambda x', \lambda^s \xi')| \\
& \lesssim \lambda^{N+ k \max(1,s) } |V_\varphi u ( \lambda x', \lambda^s \xi')| \lt \infty.
\end{align*} It follows that ![]() $(x_0,\xi_0) \notin \mathrm{WF_{g}^{\it s}} (u \otimes v)$.
$(x_0,\xi_0) \notin \mathrm{WF_{g}^{\it s}} (u \otimes v)$.
For the next result, we need the following lemma to construct functions in ![]() $a \in G^{m,s}$ such that
$a \in G^{m,s}$ such that ![]() ${\rm char}_{s,m} (a) = \emptyset$.
${\rm char}_{s,m} (a) = \emptyset$.
Lemma 3.3. If s > 0 and ![]() $m \in \mathbf R$, then there exists
$m \in \mathbf R$, then there exists ![]() $a \in G^{m,s}$ such that
$a \in G^{m,s}$ such that ![]() ${\rm char}_{s,m} (a) = \emptyset$.
${\rm char}_{s,m} (a) = \emptyset$.
Proof. Let ![]() $g \in C^\infty(\mathbf R)$ satisfy
$g \in C^\infty(\mathbf R)$ satisfy ![]() $0 \leqslant g \leqslant 1$,
$0 \leqslant g \leqslant 1$, ![]() $g(x) = 0$ if
$g(x) = 0$ if  $x \leqslant \frac12$ and
$x \leqslant \frac12$ and ![]() $g(x) = 1$ if
$g(x) = 1$ if ![]() $x \geqslant 1$. Set
$x \geqslant 1$. Set
and
Note that (3.4) can be written as
and it follows that ![]() $\psi \in C^\infty( \mathbf R^{2d} \setminus 0 )$, and thus
$\psi \in C^\infty( \mathbf R^{2d} \setminus 0 )$, and thus ![]() $a \in C^\infty (\mathbf R^{2d})$.
$a \in C^\infty (\mathbf R^{2d})$.
If ![]() $(x,\xi) \in \mathbf R^{2d} \setminus 0$ and λ > 0, then by (2.7)
$(x,\xi) \in \mathbf R^{2d} \setminus 0$ and λ > 0, then by (2.7)
This gives
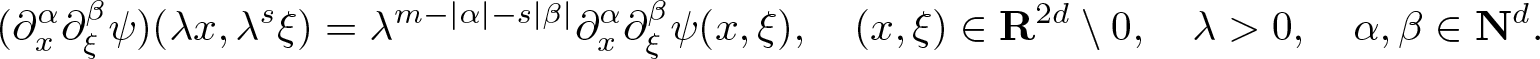 \begin{equation}
(\partial_{x}^{\alpha} \partial_{\xi}^{\beta} \psi) (\lambda x, \lambda^s \xi)
= \lambda^{m-|\alpha| - s |\beta|} \partial_{x}^{\alpha} \partial_{\xi}^{\beta} \psi( x, \xi ), \quad (x,\xi) \in \mathbf R^{2d} \setminus 0,
\quad \lambda \gt 0, \quad \alpha, \beta \in {\mathbf N}^{d}.
\end{equation}
\begin{equation}
(\partial_{x}^{\alpha} \partial_{\xi}^{\beta} \psi) (\lambda x, \lambda^s \xi)
= \lambda^{m-|\alpha| - s |\beta|} \partial_{x}^{\alpha} \partial_{\xi}^{\beta} \psi( x, \xi ), \quad (x,\xi) \in \mathbf R^{2d} \setminus 0,
\quad \lambda \gt 0, \quad \alpha, \beta \in {\mathbf N}^{d}.
\end{equation} Let ![]() $(y,\eta) \in \mathbf R^{2d} \setminus {\rm B}_1$. Then
$(y,\eta) \in \mathbf R^{2d} \setminus {\rm B}_1$. Then ![]() $(y,\eta) = (\lambda x, \lambda^s \xi)$ for a unique
$(y,\eta) = (\lambda x, \lambda^s \xi)$ for a unique ![]() $(x,\xi) \in \mathbf S^{2d-1}$ and
$(x,\xi) \in \mathbf S^{2d-1}$ and ![]() $\lambda = \lambda_s (y,\eta) \geqslant 1$. Combining
$\lambda = \lambda_s (y,\eta) \geqslant 1$. Combining
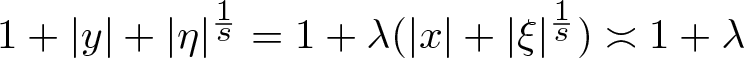 \begin{equation*}
1 + |y| + |\eta|^{\frac1s} = 1 + \lambda ( |x| + |\xi|^{\frac1s} ) \asymp 1+ \lambda
\end{equation*}
\begin{equation*}
1 + |y| + |\eta|^{\frac1s} = 1 + \lambda ( |x| + |\xi|^{\frac1s} ) \asymp 1+ \lambda
\end{equation*} with (3.6), we obtain for any ![]() $\alpha, \beta \in {\mathbf N}^{d}$
$\alpha, \beta \in {\mathbf N}^{d}$
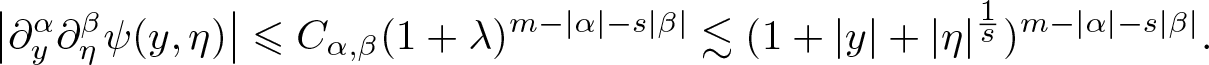 \begin{equation*}
\left| \partial_{y}^{\alpha} \partial_{\eta}^{\beta} \psi (y, \eta) \right|
\leqslant C_{\alpha,\beta} (1+\lambda)^{m -|\alpha| - s |\beta|}
\lesssim ( 1 + |y| + |\eta|^{\frac1s} )^{m -|\alpha| - s |\beta|}.
\end{equation*}
\begin{equation*}
\left| \partial_{y}^{\alpha} \partial_{\eta}^{\beta} \psi (y, \eta) \right|
\leqslant C_{\alpha,\beta} (1+\lambda)^{m -|\alpha| - s |\beta|}
\lesssim ( 1 + |y| + |\eta|^{\frac1s} )^{m -|\alpha| - s |\beta|}.
\end{equation*} Referring to (3.5), we may conclude that ![]() $a \in G^{m,s}$.
$a \in G^{m,s}$.
For the same reason, we have
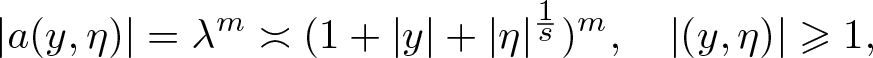 \begin{equation*}
\left| a (y, \eta) \right|
= \lambda^m
\asymp ( 1 + |y| + |\eta|^{\frac1s} )^m, \quad |(y,\eta)| \geqslant 1,
\end{equation*}
\begin{equation*}
\left| a (y, \eta) \right|
= \lambda^m
\asymp ( 1 + |y| + |\eta|^{\frac1s} )^m, \quad |(y,\eta)| \geqslant 1,
\end{equation*} which shows that ![]() ${\rm char}_{s,m} (a) = \emptyset$.
${\rm char}_{s,m} (a) = \emptyset$.
Remark 3.4. The proof of Lemma 3.3 gives a correction of the slightly erroneous argument in the proof of [Reference Rodino and Wahlberg19, Lemma 3.5]. More precisely [Reference Rodino and Wahlberg19, Eq. (3.16)] is not well motivated. But the conclusion ![]() $\chi \in G^{0,s}$ follows from a homogeneity argument as above.
$\chi \in G^{0,s}$ follows from a homogeneity argument as above.
The following result generalizes [Reference Rodino and Wahlberg17, Definitions 2.6 and 3.1 combined with Theorems 4.1 and 4.2] and is a characterization of the s-Gabor wave front set which is conceptually similar to characterizations of other types of wave front sets [Reference Hörmander8].
Proposition 3.5. If s > 0, ![]() $m \in \mathbf R$ and
$m \in \mathbf R$ and ![]() $u \in \mathscr{S}'({\mathbf R}^{d})$, then
$u \in \mathscr{S}'({\mathbf R}^{d})$, then
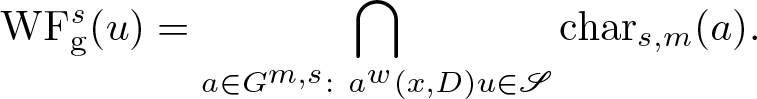 \begin{equation*}
\mathrm{WF_{g}^{\it s}} (u) = \bigcap_{a \in G^{m,s}: \ a^w(x,D) u \in \mathscr{S}} {\rm char}_{s,m} (a).
\end{equation*}
\begin{equation*}
\mathrm{WF_{g}^{\it s}} (u) = \bigcap_{a \in G^{m,s}: \ a^w(x,D) u \in \mathscr{S}} {\rm char}_{s,m} (a).
\end{equation*}Proof. First, we show
 \begin{equation}
\mathrm{WF_{g}^{\it s}} (u) \subseteq \bigcap_{a \in G^{m,s}: \ a^w(x,D) u \in \mathscr{S}} {\rm char}_{s,m} (a).
\end{equation}
\begin{equation}
\mathrm{WF_{g}^{\it s}} (u) \subseteq \bigcap_{a \in G^{m,s}: \ a^w(x,D) u \in \mathscr{S}} {\rm char}_{s,m} (a).
\end{equation} Suppose ![]() $a \in G^{m,s}$,
$a \in G^{m,s}$, ![]() $a^w(x,D) u \in \mathscr{S}$,
$a^w(x,D) u \in \mathscr{S}$, ![]() $z_0 \in T^* {\mathbf R}^{d} \setminus 0$ and
$z_0 \in T^* {\mathbf R}^{d} \setminus 0$ and ![]() $z_0 \notin {\rm char}_{s,m} (a)$. We may assume that
$z_0 \notin {\rm char}_{s,m} (a)$. We may assume that ![]() $| z_0 | = 1$. Let ɛ > 0 be small enough to guarantee
$| z_0 | = 1$. Let ɛ > 0 be small enough to guarantee ![]() $\Gamma_{z_0, 2\varepsilon} \cap {\rm char}_{s,m} (a) = \emptyset$. By [Reference Rodino and Wahlberg19, Lemma 3.5], there exists for any ρ > 0 an s-conic cutoff function
$\Gamma_{z_0, 2\varepsilon} \cap {\rm char}_{s,m} (a) = \emptyset$. By [Reference Rodino and Wahlberg19, Lemma 3.5], there exists for any ρ > 0 an s-conic cutoff function ![]() $\chi \in G^{0,s}$ such that
$\chi \in G^{0,s}$ such that ![]() $0 \leqslant \chi \leqslant 1$,
$0 \leqslant \chi \leqslant 1$, ![]() ${\rm supp} \chi \subseteq \Gamma_{z_0, 2\varepsilon} \setminus {\rm B}_{\rho/2}$ and
${\rm supp} \chi \subseteq \Gamma_{z_0, 2\varepsilon} \setminus {\rm B}_{\rho/2}$ and  $\chi |_{\Gamma_{z_0, \varepsilon} \setminus \overline {\rm B}_{\rho} } \equiv 1$.
$\chi |_{\Gamma_{z_0, \varepsilon} \setminus \overline {\rm B}_{\rho} } \equiv 1$.
If ρ > 0 is sufficiently large, then by [Reference Rodino and Wahlberg19, Lemma 6.3], there exists ![]() $b \in G^{-m,s}$ and
$b \in G^{-m,s}$ and ![]() $r \in \mathscr{S}(\mathbf R^{2d})$ such that
$r \in \mathscr{S}(\mathbf R^{2d})$ such that
Thus, we may write
where ![]() $r^w(x,D) u \in \mathscr{S}$ since
$r^w(x,D) u \in \mathscr{S}$ since ![]() $r^w(x,D): \mathscr{S}' \to \mathscr{S}$ is regularizing, and
$r^w(x,D): \mathscr{S}' \to \mathscr{S}$ is regularizing, and ![]() $b^w(x,D) a^w(x,D) u \in \mathscr{S}$ since
$b^w(x,D) a^w(x,D) u \in \mathscr{S}$ since ![]() $a^w(x,D) u \in \mathscr{S}$ and
$a^w(x,D) u \in \mathscr{S}$ and ![]() $b^w(x,D): \mathscr{S} \to \mathscr{S}$ is continuous [Reference Shubin21, Section 23.2]. It follows that
$b^w(x,D): \mathscr{S} \to \mathscr{S}$ is continuous [Reference Shubin21, Section 23.2]. It follows that ![]() $\mathrm{WF_{g}^{\it s}} (u) = \mathrm{WF_{g}^{\it s}} ( (1-\chi)^w(x,D) u )$, and finally [Reference Rodino and Wahlberg19, Proposition 6.2] yields
$\mathrm{WF_{g}^{\it s}} (u) = \mathrm{WF_{g}^{\it s}} ( (1-\chi)^w(x,D) u )$, and finally [Reference Rodino and Wahlberg19, Proposition 6.2] yields
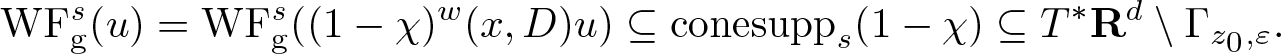 \begin{equation*}
\mathrm{WF_{g}^{\it s}} (u) = \mathrm{WF_{g}^{\it s}} ( (1-\chi)^w(x,D) u ) \subseteq {\rm conesupp}_{s} ( 1-\chi ) \subseteq T^* {\mathbf R}^{d} \setminus \Gamma_{z_0, \varepsilon}.
\end{equation*}
\begin{equation*}
\mathrm{WF_{g}^{\it s}} (u) = \mathrm{WF_{g}^{\it s}} ( (1-\chi)^w(x,D) u ) \subseteq {\rm conesupp}_{s} ( 1-\chi ) \subseteq T^* {\mathbf R}^{d} \setminus \Gamma_{z_0, \varepsilon}.
\end{equation*} It follows that ![]() $z_0 \notin \mathrm{WF_{g}^{\it s}} (u)$, so we have proved (3.7).
$z_0 \notin \mathrm{WF_{g}^{\it s}} (u)$, so we have proved (3.7).
It remains to show
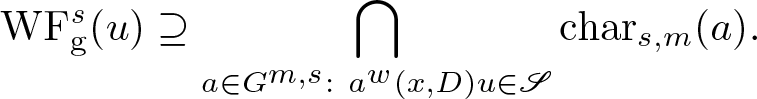 \begin{equation}
\mathrm{WF_{g}^{\it s}} (u) \supseteq \bigcap_{a \in G^{m,s}: \ a^w(x,D) u \in \mathscr{S}} {\rm char}_{s,m} (a).
\end{equation}
\begin{equation}
\mathrm{WF_{g}^{\it s}} (u) \supseteq \bigcap_{a \in G^{m,s}: \ a^w(x,D) u \in \mathscr{S}} {\rm char}_{s,m} (a).
\end{equation} Suppose ![]() $z_0 \in T^* {\mathbf R}^{d} \setminus 0$,
$z_0 \in T^* {\mathbf R}^{d} \setminus 0$, ![]() $z_0 \notin \mathrm{WF_{g}^{\it s}} (u)$ and
$z_0 \notin \mathrm{WF_{g}^{\it s}} (u)$ and ![]() $| z_0 | = 1$. Let ɛ > 0 be small enough to guarantee
$| z_0 | = 1$. Let ɛ > 0 be small enough to guarantee ![]() $\Gamma_{z_0, 2\varepsilon} \cap \mathrm{WF_{g}^{\it s}} (u) = \emptyset$. Let ρ > 0 and let
$\Gamma_{z_0, 2\varepsilon} \cap \mathrm{WF_{g}^{\it s}} (u) = \emptyset$. Let ρ > 0 and let ![]() $\chi \in G^{0,s}$ satisfy
$\chi \in G^{0,s}$ satisfy ![]() $0 \leqslant \chi \leqslant 1$,
$0 \leqslant \chi \leqslant 1$, ![]() ${\rm supp} \chi \subseteq \Gamma_{z_0, 2\varepsilon} \setminus {\rm B}_{\rho/2}$ and
${\rm supp} \chi \subseteq \Gamma_{z_0, 2\varepsilon} \setminus {\rm B}_{\rho/2}$ and  $\chi |_{\Gamma_{z_0, \varepsilon} \setminus \overline {\rm B}_{\rho} } \equiv 1$. Using Lemma 3.3, we let
$\chi |_{\Gamma_{z_0, \varepsilon} \setminus \overline {\rm B}_{\rho} } \equiv 1$. Using Lemma 3.3, we let ![]() $b \in G^{m,s}$ satisfy
$b \in G^{m,s}$ satisfy ![]() ${\rm char}_{s,m} (b) = \emptyset$, and we set
${\rm char}_{s,m} (b) = \emptyset$, and we set ![]() $a = b \chi \in G^{m,s}$. Then,
$a = b \chi \in G^{m,s}$. Then, ![]() $z_0 \notin {\rm char}_{s,m} ( a )$.
$z_0 \notin {\rm char}_{s,m} ( a )$.
We have ![]() ${\rm conesupp}_{s} ( a ) \subseteq \Gamma_{z_0, 2\varepsilon}$, and by the microlocal inclusion [Reference Rodino and Wahlberg19, Proposition 5.1], we have
${\rm conesupp}_{s} ( a ) \subseteq \Gamma_{z_0, 2\varepsilon}$, and by the microlocal inclusion [Reference Rodino and Wahlberg19, Proposition 5.1], we have ![]() $\mathrm{WF_{g}^{\it s}} ( a^w (x,D) u) \subseteq \mathrm{WF_{g}^{\it s}} (u)$. Combining with [Reference Rodino and Wahlberg19, Proposition 6.2] this implies
$\mathrm{WF_{g}^{\it s}} ( a^w (x,D) u) \subseteq \mathrm{WF_{g}^{\it s}} (u)$. Combining with [Reference Rodino and Wahlberg19, Proposition 6.2] this implies
It follows that ![]() $a^w (x,D) u \in \mathscr{S}$, which means that we have proved (3.8).
$a^w (x,D) u \in \mathscr{S}$, which means that we have proved (3.8).
4. Propagation of anisotropic Gabor wave front sets
Define for ![]() $K \in \mathscr{S}'(\mathbf R^{2d})$
$K \in \mathscr{S}'(\mathbf R^{2d})$
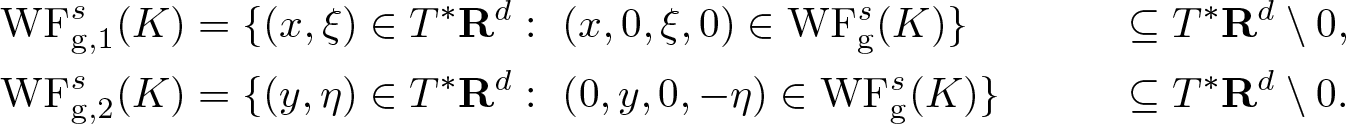 \begin{align*}
\mathrm{WF}_{\rm g,1}^s(K) & = \{ (x,\xi) \in T^* {\mathbf R}^{d}: \ (x, 0, \xi, 0) \in \mathrm{WF_{g}^{\it s}} (K) \} & \subseteq T^* {\mathbf R}^{d} \setminus 0, \\
\mathrm{WF}_{\rm g,2}^s(K) & = \{ (y,\eta) \in T^* {\mathbf R}^{d}: \ (0, y, 0, -\eta) \in \mathrm{WF_{g}^{\it s}} (K) \} & \subseteq T^* {\mathbf R}^{d} \setminus 0.
\end{align*}
\begin{align*}
\mathrm{WF}_{\rm g,1}^s(K) & = \{ (x,\xi) \in T^* {\mathbf R}^{d}: \ (x, 0, \xi, 0) \in \mathrm{WF_{g}^{\it s}} (K) \} & \subseteq T^* {\mathbf R}^{d} \setminus 0, \\
\mathrm{WF}_{\rm g,2}^s(K) & = \{ (y,\eta) \in T^* {\mathbf R}^{d}: \ (0, y, 0, -\eta) \in \mathrm{WF_{g}^{\it s}} (K) \} & \subseteq T^* {\mathbf R}^{d} \setminus 0.
\end{align*}We will use the assumption
We note that the condition (4.1) appears in several other works for various global isotropic [Reference Carypis and Wahlberg1, Reference Hörmander9, Reference Pravda-Starov, Rodino and Wahlberg15, Reference Wahlberg22] and anisotropic [Reference Wahlberg24] wave front sets. The following lemma is a version of [Reference Wahlberg24, Lemma 5.1] for tempered distributions and the s-Gabor wave front set (cf. [Reference Carypis and Wahlberg1, Lemma 6.1]).
Lemma 4.1. If s > 0, ![]() $K \in \mathscr{S}'(\mathbf R^{2d})$ and (4.1) holds, then there exists c > 1 such that
$K \in \mathscr{S}'(\mathbf R^{2d})$ and (4.1) holds, then there exists c > 1 such that
 \begin{equation}
\mathrm{WF}_{\rm g}^s (K) \subseteq
\Gamma_1 := \left\{ (x,y,\xi,\eta) \in T^* \mathbf R^{2d}: \ c^{-1} \left( |x| + |\xi|^{\frac1s} \right) \lt |y| + |\eta|^{\frac1s} \lt c \left( |x| + |\xi|^{\frac1s} \right) \right\}.
\end{equation}
\begin{equation}
\mathrm{WF}_{\rm g}^s (K) \subseteq
\Gamma_1 := \left\{ (x,y,\xi,\eta) \in T^* \mathbf R^{2d}: \ c^{-1} \left( |x| + |\xi|^{\frac1s} \right) \lt |y| + |\eta|^{\frac1s} \lt c \left( |x| + |\xi|^{\frac1s} \right) \right\}.
\end{equation}Proof. Suppose that
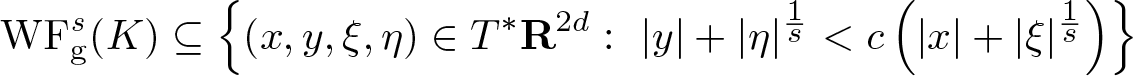 \begin{equation*}
\mathrm{WF_{g}^{\it s}} (K) \subseteq \left\{ (x,y,\xi,\eta) \in T^* \mathbf R^{2d}: \ |y| + |\eta|^{\frac1s} \lt c \left( |x| + |\xi|^{\frac1s} \right) \right\}
\end{equation*}
\begin{equation*}
\mathrm{WF_{g}^{\it s}} (K) \subseteq \left\{ (x,y,\xi,\eta) \in T^* \mathbf R^{2d}: \ |y| + |\eta|^{\frac1s} \lt c \left( |x| + |\xi|^{\frac1s} \right) \right\}
\end{equation*} does not hold for any c > 0. Then, for each ![]() $n \in \mathbf N$, there exists
$n \in \mathbf N$, there exists ![]() $(x_n,y_n,\xi_n,\eta_n) \in \mathrm{WF_{g}^{\it s}} (K)$ such that
$(x_n,y_n,\xi_n,\eta_n) \in \mathrm{WF_{g}^{\it s}} (K)$ such that
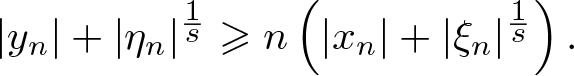 \begin{equation}
|y_n| + |\eta_n|^{\frac1s} \geqslant n \left( |x_n| + |\xi_n|^{\frac1s} \right).
\end{equation}
\begin{equation}
|y_n| + |\eta_n|^{\frac1s} \geqslant n \left( |x_n| + |\xi_n|^{\frac1s} \right).
\end{equation} By rescaling ![]() $(x_n,y_n,\xi_n,\eta_n)$ as
$(x_n,y_n,\xi_n,\eta_n)$ as ![]() $(x_n,y_n,\xi_n,\eta_n) \mapsto ( \lambda x_n, \lambda y_n, \lambda^{s} \xi_n, \lambda^{s} \eta_n)$, we obtain for a unique
$(x_n,y_n,\xi_n,\eta_n) \mapsto ( \lambda x_n, \lambda y_n, \lambda^{s} \xi_n, \lambda^{s} \eta_n)$, we obtain for a unique ![]() $\lambda = \lambda (x_n,y_n,\xi_n,\eta_n) \gt 0$ a vector in
$\lambda = \lambda (x_n,y_n,\xi_n,\eta_n) \gt 0$ a vector in  $\mathrm{WF_{g}^{\it s}} (K) \cap \mathbf S^{4d-1}$, cf. § 2.1. This s-conic rescaling leaves (4.3) invariant. Abusing notation we still denote the rescaled vector
$\mathrm{WF_{g}^{\it s}} (K) \cap \mathbf S^{4d-1}$, cf. § 2.1. This s-conic rescaling leaves (4.3) invariant. Abusing notation we still denote the rescaled vector  $(x_n,y_n,\xi_n,\eta_n) \in \mathrm{WF_{g}^{\it s}} (K) \cap \mathbf S^{4d-1}$.
$(x_n,y_n,\xi_n,\eta_n) \in \mathrm{WF_{g}^{\it s}} (K) \cap \mathbf S^{4d-1}$.
From (4.3), it follows that ![]() $(x_n,\xi_n) \rightarrow 0$ as
$(x_n,\xi_n) \rightarrow 0$ as ![]() $n \rightarrow \infty$. Passing to a subsequence (without change of notation) and using the closedness of
$n \rightarrow \infty$. Passing to a subsequence (without change of notation) and using the closedness of ![]() $\mathrm{WF_{g}^{\it s}} (K)$ gives
$\mathrm{WF_{g}^{\it s}} (K)$ gives
for some ![]() $(y,\eta) \in \mathbf S^{2d-1}$. This implies
$(y,\eta) \in \mathbf S^{2d-1}$. This implies ![]() $(y,-\eta) \in \mathrm{WF}_{\rm{g}, 2}^s(K)$, which is a contradiction.
$(y,-\eta) \in \mathrm{WF}_{\rm{g}, 2}^s(K)$, which is a contradiction.
Similarly, one shows
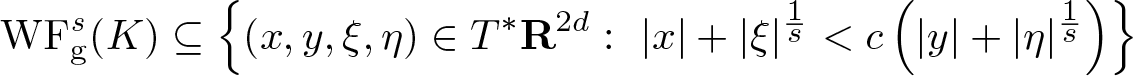 \begin{equation*}
\mathrm{WF_{g}^{\it s}} (K) \subseteq \left\{ (x,y,\xi,\eta) \in T^* \mathbf R^{2d}: \ |x| + |\xi|^{\frac1s} \lt c \left( |y| + |\eta|^{\frac1s} \right) \right\}
\end{equation*}
\begin{equation*}
\mathrm{WF_{g}^{\it s}} (K) \subseteq \left\{ (x,y,\xi,\eta) \in T^* \mathbf R^{2d}: \ |x| + |\xi|^{\frac1s} \lt c \left( |y| + |\eta|^{\frac1s} \right) \right\}
\end{equation*} for some c > 0 using ![]() $\mathrm{WF}_{\rm g,1}^s(K) = \emptyset$.
$\mathrm{WF}_{\rm g,1}^s(K) = \emptyset$.
The set ![]() $\Gamma_1 \subseteq \mathbf R^{4d} \setminus 0$ in (4.2) is open and s-conic in the sense that it is closed with respect to
$\Gamma_1 \subseteq \mathbf R^{4d} \setminus 0$ in (4.2) is open and s-conic in the sense that it is closed with respect to ![]() $(x,y,\xi,\eta) \mapsto ( \lambda x, \lambda y, \lambda^s \xi, \lambda^s \eta )$ for any λ > 0. Hence,
$(x,y,\xi,\eta) \mapsto ( \lambda x, \lambda y, \lambda^s \xi, \lambda^s \eta )$ for any λ > 0. Hence, ![]() $(\mathbf R^{4d} \setminus \Gamma_1)$ is s-conic and
$(\mathbf R^{4d} \setminus \Gamma_1)$ is s-conic and ![]() $(\mathbf R^{4d} \setminus \Gamma_1) \cap \mathbf S^{4d-1}$ is compact. From (3.3), we then obtain if
$(\mathbf R^{4d} \setminus \Gamma_1) \cap \mathbf S^{4d-1}$ is compact. From (3.3), we then obtain if ![]() $\Phi \in \mathscr{S}(\mathbf R^{2d}) \setminus 0$
$\Phi \in \mathscr{S}(\mathbf R^{2d}) \setminus 0$
From (4.2) and (2.10), it follows that
 \begin{equation}
(x,y,\xi, - \eta) \in \Gamma_1 \quad \Longrightarrow \quad
\langle (y,\eta)\rangle^{\min \left( s, \frac1s\right)}
\lesssim \langle (x,\xi)\rangle
\lesssim \langle (y,\eta)\rangle^{\max \left( s, \frac1s\right)}.
\end{equation}
\begin{equation}
(x,y,\xi, - \eta) \in \Gamma_1 \quad \Longrightarrow \quad
\langle (y,\eta)\rangle^{\min \left( s, \frac1s\right)}
\lesssim \langle (x,\xi)\rangle
\lesssim \langle (y,\eta)\rangle^{\max \left( s, \frac1s\right)}.
\end{equation} A tempered distribution ![]() $K \in \mathscr{S}'(\mathbf R^{2d})$ defines a continuous linear map
$K \in \mathscr{S}'(\mathbf R^{2d})$ defines a continuous linear map ![]() $\mathscr{K}: \mathscr{S} ({\mathbf R}^{d}) \to \mathscr{S}'({\mathbf R}^{d})$ by
$\mathscr{K}: \mathscr{S} ({\mathbf R}^{d}) \to \mathscr{S}'({\mathbf R}^{d})$ by
The following result says that the condition (4.1) implies continuity of ![]() $\mathscr{K}$ on
$\mathscr{K}$ on ![]() $\mathscr{S}({\mathbf R}^{d})$ and a unique extension to a continuous operator on
$\mathscr{S}({\mathbf R}^{d})$ and a unique extension to a continuous operator on ![]() $\mathscr{S}'({\mathbf R}^{d})$. This is the basis for the forthcoming result on propagation of the s-Gabor wave front sets Theorem 4.4. In the proof, we use the conventional notation (cf. [Reference Hörmander9, Reference Hörmander10]) for the reflection operator in the fourth
$\mathscr{S}'({\mathbf R}^{d})$. This is the basis for the forthcoming result on propagation of the s-Gabor wave front sets Theorem 4.4. In the proof, we use the conventional notation (cf. [Reference Hörmander9, Reference Hörmander10]) for the reflection operator in the fourth ![]() ${\mathbf R}^{d}$ coordinate in
${\mathbf R}^{d}$ coordinate in ![]() ${\mathbf R}^{4d}$
${\mathbf R}^{4d}$
Proposition 4.2. Let s > 0 and let ![]() $\mathscr{K}: \mathscr{S}({\mathbf R}^{d}) \to \mathscr{S}'({\mathbf R}^{d})$ be the continuous linear operator (4.6) defined by the Schwartz kernel
$\mathscr{K}: \mathscr{S}({\mathbf R}^{d}) \to \mathscr{S}'({\mathbf R}^{d})$ be the continuous linear operator (4.6) defined by the Schwartz kernel ![]() $K \in \mathscr{S}'(\mathbf R^{2d})$. If (4.1) holds, then
$K \in \mathscr{S}'(\mathbf R^{2d})$. If (4.1) holds, then
(1)
 $\mathscr{K}: \mathscr{S}({\mathbf R}^{d}) \to \mathscr{S}({\mathbf R}^{d})$ is continuous;
$\mathscr{K}: \mathscr{S}({\mathbf R}^{d}) \to \mathscr{S}({\mathbf R}^{d})$ is continuous;(2)
 $\mathscr{K}$ extends uniquely to a sequentially continuous linear operator
$\mathscr{K}$ extends uniquely to a sequentially continuous linear operator  $\mathscr{K}: \mathscr{S}' ({\mathbf R}^{d}) \to \mathscr{S}' ({\mathbf R}^{d})$;
$\mathscr{K}: \mathscr{S}' ({\mathbf R}^{d}) \to \mathscr{S}' ({\mathbf R}^{d})$;(3) if
 $\varphi \in \mathscr{S}({\mathbf R}^{d})$,
$\varphi \in \mathscr{S}({\mathbf R}^{d})$,  $\| \varphi \|_{L^2} = 1$,
$\| \varphi \|_{L^2} = 1$,  $\Phi = \varphi \otimes \varphi \in \mathscr{S}({\mathbf R}^{2d})$,
$\Phi = \varphi \otimes \varphi \in \mathscr{S}({\mathbf R}^{2d})$,  $u \in \mathscr{S}'({\mathbf R}^{d})$ and
$u \in \mathscr{S}'({\mathbf R}^{d})$ and  $\psi \in \mathscr{S}({\mathbf R}^{d})$, then
(4.8)
$\psi \in \mathscr{S}({\mathbf R}^{d})$, then
(4.8) \begin{equation}
(\mathscr{K} u, \psi)
= \int_{\mathbf R^{4d}} V_\Phi K(x,y,\xi,-\eta) \, \overline{V_\varphi \psi (x,\xi)} \, V_{\overline \varphi} u(y,\eta) \, \mathrm {d} x \, \mathrm {d} y \, \mathrm {d} \xi \, \mathrm {d} \eta.
\end{equation}
\begin{equation}
(\mathscr{K} u, \psi)
= \int_{\mathbf R^{4d}} V_\Phi K(x,y,\xi,-\eta) \, \overline{V_\varphi \psi (x,\xi)} \, V_{\overline \varphi} u(y,\eta) \, \mathrm {d} x \, \mathrm {d} y \, \mathrm {d} \xi \, \mathrm {d} \eta.
\end{equation}
Proof. By [Reference Wahlberg22, Lemma 5.1], the formula (4.8) holds for ![]() $u,\psi \in \mathscr{S}({\mathbf R}^{d})$.
$u,\psi \in \mathscr{S}({\mathbf R}^{d})$.
Let ![]() $\varphi \in \mathscr{S}({\mathbf R}^{d})$ satisfy
$\varphi \in \mathscr{S}({\mathbf R}^{d})$ satisfy ![]() $\| \varphi \|_{L^2} = 1$ and set
$\| \varphi \|_{L^2} = 1$ and set ![]() $\Phi = \varphi \otimes \varphi \in \mathscr{S}({\mathbf R}^{2d})$. Since
$\Phi = \varphi \otimes \varphi \in \mathscr{S}({\mathbf R}^{2d})$. Since
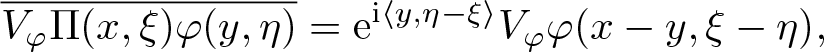 \begin{equation*}
\overline{V_\varphi \Pi(x,\xi) \varphi (y,\eta)} = \mathrm{e}^{\mathrm{i} \langle y, \eta - \xi \rangle} V_\varphi \varphi ( x-y, \xi - \eta),
\end{equation*}
\begin{equation*}
\overline{V_\varphi \Pi(x,\xi) \varphi (y,\eta)} = \mathrm{e}^{\mathrm{i} \langle y, \eta - \xi \rangle} V_\varphi \varphi ( x-y, \xi - \eta),
\end{equation*} we get from (4.8) for ![]() $u \in \mathscr{S} ({\mathbf R}^{d})$ and
$u \in \mathscr{S} ({\mathbf R}^{d})$ and ![]() $(x,\xi) \in T^* {\mathbf R}^{d}$
$(x,\xi) \in T^* {\mathbf R}^{d}$
 \begin{align}
& V_\varphi(\mathscr{K} u) (x, \xi)
= (2 \pi)^{-\frac{d}{2}} (\mathscr{K} u, \Pi(x,\xi) \varphi)\nonumber \\
& = (2 \pi)^{-\frac{d}{2}} \int_{\mathbf R^{4d}} \mathrm{e}^{\mathrm{i} \langle y,\eta -\xi \rangle} V_\Phi K (y,z,\eta,-\theta) V_\varphi \varphi (x-y,\xi-\eta) \, V_{\overline \varphi} u(z,\theta) \, \mathrm {d} y \, \mathrm {d} z \, \mathrm {d} \eta \, \mathrm {d} \theta
\end{align}
\begin{align}
& V_\varphi(\mathscr{K} u) (x, \xi)
= (2 \pi)^{-\frac{d}{2}} (\mathscr{K} u, \Pi(x,\xi) \varphi)\nonumber \\
& = (2 \pi)^{-\frac{d}{2}} \int_{\mathbf R^{4d}} \mathrm{e}^{\mathrm{i} \langle y,\eta -\xi \rangle} V_\Phi K (y,z,\eta,-\theta) V_\varphi \varphi (x-y,\xi-\eta) \, V_{\overline \varphi} u(z,\theta) \, \mathrm {d} y \, \mathrm {d} z \, \mathrm {d} \eta \, \mathrm {d} \theta
\end{align}which gives
 \begin{equation}
|V_\varphi(\mathscr{K} u) (x, \xi)|
\lesssim \int_{\mathbf R^{4d}} | V_\Phi K (y,z,\eta,-\theta) | \, | V_\varphi \varphi (x-y,\xi-\eta)| \, | V_{\overline \varphi} u(z,\theta)| \, \mathrm {d} y \, \mathrm {d} z \, \mathrm {d} \eta \, \mathrm {d} \theta.
\end{equation}
\begin{equation}
|V_\varphi(\mathscr{K} u) (x, \xi)|
\lesssim \int_{\mathbf R^{4d}} | V_\Phi K (y,z,\eta,-\theta) | \, | V_\varphi \varphi (x-y,\xi-\eta)| \, | V_{\overline \varphi} u(z,\theta)| \, \mathrm {d} y \, \mathrm {d} z \, \mathrm {d} \eta \, \mathrm {d} \theta.
\end{equation} We use the seminorms (2.6) for ![]() $\mathscr{S}({\mathbf R}^{d})$. Let
$\mathscr{S}({\mathbf R}^{d})$. Let ![]() $n \in \mathbf N$ and consider first the right-hand side integral in (4.10) over
$n \in \mathbf N$ and consider first the right-hand side integral in (4.10) over ![]() $(y,z,\eta,-\theta) \in \mathbf R^{4d} \setminus \Gamma_1$ where Γ1 is defined by (4.2) with c > 1 chosen so that
$(y,z,\eta,-\theta) \in \mathbf R^{4d} \setminus \Gamma_1$ where Γ1 is defined by (4.2) with c > 1 chosen so that ![]() $\mathrm{WF_{g}^{\it s}} (K) \subseteq \Gamma_1$. By Lemma 4.1, we may use the estimates (4.4). Using (2.1) and (2.3), we obtain for any
$\mathrm{WF_{g}^{\it s}} (K) \subseteq \Gamma_1$. By Lemma 4.1, we may use the estimates (4.4). Using (2.1) and (2.3), we obtain for any ![]() $m \in \mathbf N$
$m \in \mathbf N$
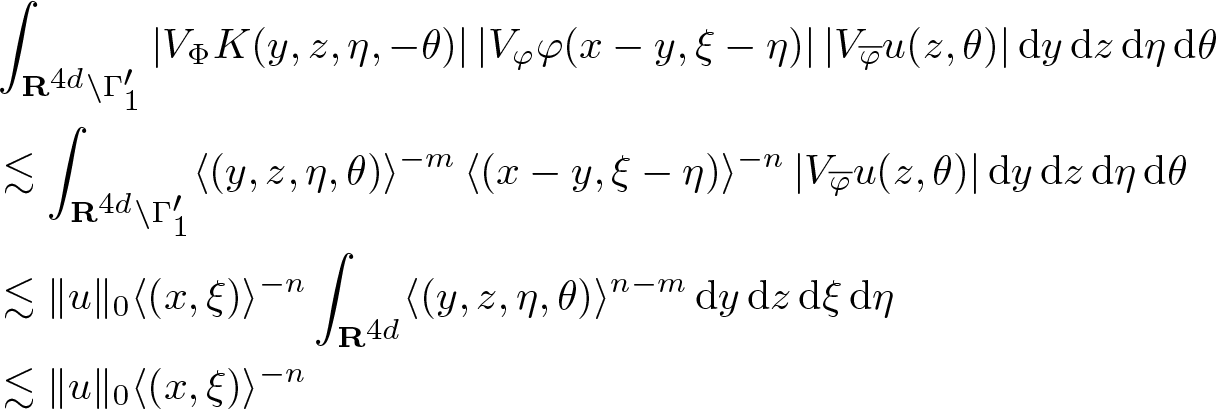 \begin{equation}
\begin{aligned}
& \int_{\mathbf R^{4d} \setminus \Gamma_1'}
|V_\Phi K(y,z,\eta,-\theta)| \, | V_\varphi \varphi (x-y,\xi-\eta)| \, |V_{\overline \varphi} u (z,\theta)| \, \mathrm {d} y \, \mathrm {d} z \, \mathrm {d} \eta \, \mathrm {d} \theta \\
& \lesssim
\int_{\mathbf R^{4d} \setminus \Gamma_1'}
\langle (y,z,\eta,\theta)\rangle^{-m} \, \langle (x-y,\xi-\eta)\rangle^{-n} \, |V_{\overline \varphi} u (z,\theta)| \, \mathrm {d} y \, \mathrm {d} z \, \mathrm {d} \eta \, \mathrm {d} \theta \\
& \lesssim
\| u \|_0 \langle (x,\xi)\rangle^{-n}
\int_{\mathbf R^{4d}} \langle (y,z,\eta,\theta)\rangle^{n-m}\, \mathrm {d} y \, \mathrm {d} z \, \mathrm {d} \xi \, \mathrm {d} \eta \\
& \lesssim \| u \|_0 \langle (x,\xi)\rangle^{-n}
\end{aligned}
\end{equation}
\begin{equation}
\begin{aligned}
& \int_{\mathbf R^{4d} \setminus \Gamma_1'}
|V_\Phi K(y,z,\eta,-\theta)| \, | V_\varphi \varphi (x-y,\xi-\eta)| \, |V_{\overline \varphi} u (z,\theta)| \, \mathrm {d} y \, \mathrm {d} z \, \mathrm {d} \eta \, \mathrm {d} \theta \\
& \lesssim
\int_{\mathbf R^{4d} \setminus \Gamma_1'}
\langle (y,z,\eta,\theta)\rangle^{-m} \, \langle (x-y,\xi-\eta)\rangle^{-n} \, |V_{\overline \varphi} u (z,\theta)| \, \mathrm {d} y \, \mathrm {d} z \, \mathrm {d} \eta \, \mathrm {d} \theta \\
& \lesssim
\| u \|_0 \langle (x,\xi)\rangle^{-n}
\int_{\mathbf R^{4d}} \langle (y,z,\eta,\theta)\rangle^{n-m}\, \mathrm {d} y \, \mathrm {d} z \, \mathrm {d} \xi \, \mathrm {d} \eta \\
& \lesssim \| u \|_0 \langle (x,\xi)\rangle^{-n}
\end{aligned}
\end{equation} provided ![]() $m \gt n + 4 d$.
$m \gt n + 4 d$.
Next, we consider the right-hand side integral (4.10) over ![]() $(y,z,\eta,-\theta) \in \Gamma_1$. Then, we may use (4.5). From (2.2) and (2.3), we obtain for some
$(y,z,\eta,-\theta) \in \Gamma_1$. Then, we may use (4.5). From (2.2) and (2.3), we obtain for some ![]() $m \geqslant 0$ and any
$m \geqslant 0$ and any ![]() $k \geqslant 0$
$k \geqslant 0$
 \begin{align}
& \int_{\Gamma_1'}
|V_\Phi K(y,z,\eta,-\theta)| \, | V_\varphi \varphi (x-y,\xi-\eta)| \, |V_{\overline \varphi} u (z,\theta)| \, \mathrm {d} y \, \mathrm {d} z \, \mathrm {d} \eta \, \mathrm {d} \theta\nonumber\\
& \lesssim
\| u \|_k
\langle (x,\xi)\rangle^{-n}
\int_{\Gamma_1'}
\langle (y,z,\eta,\theta)\rangle^{m+4d+1-4d-1} \, \langle (y,\eta)\rangle^{n} \,\langle (z,\theta)\rangle^{-k} \, \mathrm {d} x \, \mathrm {d} y \, \mathrm {d} \xi \, \mathrm {d} \eta \nonumber\\
& \lesssim
\| u \|_k \langle (x,\xi)\rangle^{-n}\nonumber\\
& \qquad\qquad \int_{\Gamma_1'}
\langle (y,z,\eta,\theta)\rangle^{-4d-1} \langle (z,\theta)\rangle^{(m+4d+1) \left(1 + \max \left( s, \frac1s \right) \right) + n \max \left( s, \frac1s \right)^{-k}}{\mathrm {d} x \, \mathrm {d} y \, \mathrm {d} \xi \, \mathrm {d} \eta} \nonumber\\
& \lesssim
\| u \|_k \langle (x,\xi)\rangle^{-n}
\end{align}
\begin{align}
& \int_{\Gamma_1'}
|V_\Phi K(y,z,\eta,-\theta)| \, | V_\varphi \varphi (x-y,\xi-\eta)| \, |V_{\overline \varphi} u (z,\theta)| \, \mathrm {d} y \, \mathrm {d} z \, \mathrm {d} \eta \, \mathrm {d} \theta\nonumber\\
& \lesssim
\| u \|_k
\langle (x,\xi)\rangle^{-n}
\int_{\Gamma_1'}
\langle (y,z,\eta,\theta)\rangle^{m+4d+1-4d-1} \, \langle (y,\eta)\rangle^{n} \,\langle (z,\theta)\rangle^{-k} \, \mathrm {d} x \, \mathrm {d} y \, \mathrm {d} \xi \, \mathrm {d} \eta \nonumber\\
& \lesssim
\| u \|_k \langle (x,\xi)\rangle^{-n}\nonumber\\
& \qquad\qquad \int_{\Gamma_1'}
\langle (y,z,\eta,\theta)\rangle^{-4d-1} \langle (z,\theta)\rangle^{(m+4d+1) \left(1 + \max \left( s, \frac1s \right) \right) + n \max \left( s, \frac1s \right)^{-k}}{\mathrm {d} x \, \mathrm {d} y \, \mathrm {d} \xi \, \mathrm {d} \eta} \nonumber\\
& \lesssim
\| u \|_k \langle (x,\xi)\rangle^{-n}
\end{align}provided k > 0 is sufficiently large.
Combining (4.11) and (4.12), we obtain from (4.10) ![]() $\| \mathscr{K} u \|_n \lesssim \| u \|_k$, which proves claim (1).
$\| \mathscr{K} u \|_n \lesssim \| u \|_k$, which proves claim (1).
To show claims (2) and (3), let ![]() $u \in \mathscr{S}'({\mathbf R}^{d})$ and set for
$u \in \mathscr{S}'({\mathbf R}^{d})$ and set for ![]() $N \in \mathbf N$
$N \in \mathbf N$
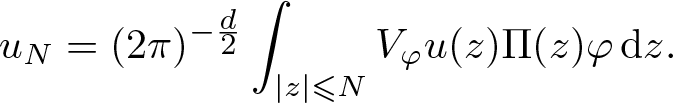 \begin{equation*}
u_N = (2 \pi)^{-\frac{d}{2}} \int_{|z| \leqslant N} V_\varphi u(z) \Pi(z) \varphi \, \mathrm {d} z.
\end{equation*}
\begin{equation*}
u_N = (2 \pi)^{-\frac{d}{2}} \int_{|z| \leqslant N} V_\varphi u(z) \Pi(z) \varphi \, \mathrm {d} z.
\end{equation*} From (2.2) for some ![]() $k \geqslant 0$ and (2.3), we obtain for any
$k \geqslant 0$ and (2.3), we obtain for any ![]() $n \geqslant 0$
$n \geqslant 0$
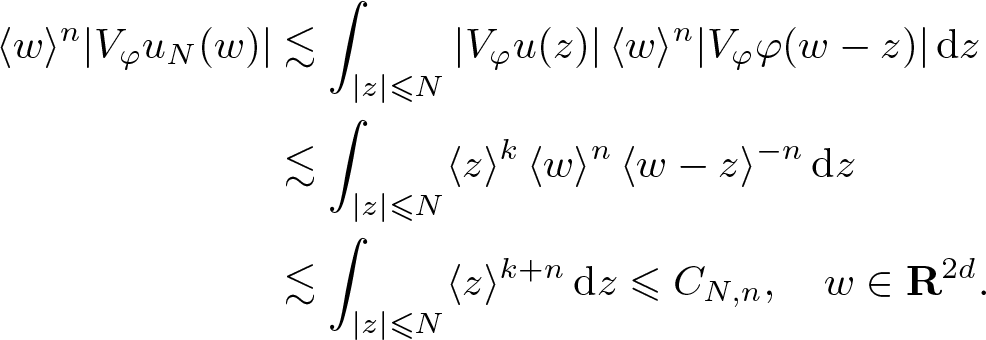 \begin{align*}
\langle w\rangle^n |V_\varphi u_N (w)|
& \lesssim \int_{|z| \leqslant N} |V_\varphi u(z)| \, \langle w\rangle^n |V_\varphi \varphi(w-z)| \, \mathrm {d} z \\
& \lesssim \int_{|z| \leqslant N} \langle z\rangle^k \, \langle w\rangle^n \, \langle w-z\rangle^{-n} \, \mathrm {d} z \\
& \lesssim \int_{|z| \leqslant N} \langle z\rangle^{k+n} \, \mathrm {d} z
\leqslant C_{N,n}, \quad w \in \mathbf R^{2d}.
\end{align*}
\begin{align*}
\langle w\rangle^n |V_\varphi u_N (w)|
& \lesssim \int_{|z| \leqslant N} |V_\varphi u(z)| \, \langle w\rangle^n |V_\varphi \varphi(w-z)| \, \mathrm {d} z \\
& \lesssim \int_{|z| \leqslant N} \langle z\rangle^k \, \langle w\rangle^n \, \langle w-z\rangle^{-n} \, \mathrm {d} z \\
& \lesssim \int_{|z| \leqslant N} \langle z\rangle^{k+n} \, \mathrm {d} z
\leqslant C_{N,n}, \quad w \in \mathbf R^{2d}.
\end{align*} Referring to the seminorms (2.6) shows that ![]() $u_N \in \mathscr{S}({\mathbf R}^{d})$ for
$u_N \in \mathscr{S}({\mathbf R}^{d})$ for ![]() $N \in \mathbf N$. The fact that
$N \in \mathbf N$. The fact that ![]() $u_N \to u$ in
$u_N \to u$ in ![]() $\mathscr{S}'({\mathbf R}^{d})$ as
$\mathscr{S}'({\mathbf R}^{d})$ as ![]() $N \to \infty$ is a consequence of (2.5), (2.2), (2.3) and dominated convergence.
$N \to \infty$ is a consequence of (2.5), (2.2), (2.3) and dominated convergence.
We also need the estimate (cf. [Reference Gröchenig6, Eq. (11.29)])
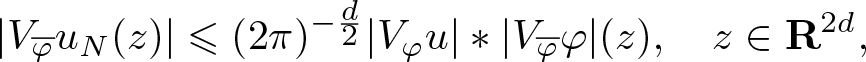 \begin{equation*}
|V_{\overline{\varphi}} u_N (z)| \leqslant (2 \pi)^{-\frac{d}{2}} |V_\varphi u| * |V_{\overline{\varphi}} \varphi| (z), \quad z \in \mathbf R^{2d},
\end{equation*}
\begin{equation*}
|V_{\overline{\varphi}} u_N (z)| \leqslant (2 \pi)^{-\frac{d}{2}} |V_\varphi u| * |V_{\overline{\varphi}} \varphi| (z), \quad z \in \mathbf R^{2d},
\end{equation*}which in view of (2.2) and (2.3) gives the bound
 \begin{equation}
|V_{\overline{\varphi}} u_N (z)| \lesssim \langle z\rangle^{k + 2d + 1}, \quad z \in \mathbf R^{2d}, \quad N \in \mathbf N,
\end{equation}
\begin{equation}
|V_{\overline{\varphi}} u_N (z)| \lesssim \langle z\rangle^{k + 2d + 1}, \quad z \in \mathbf R^{2d}, \quad N \in \mathbf N,
\end{equation} that holds uniformly over ![]() $N \in \mathbf N$, for some
$N \in \mathbf N$, for some ![]() $k \in \mathbf N$.
$k \in \mathbf N$.
We are now in a position to assemble the ingredients into a proof of formula (4.8) for ![]() $u \in \mathscr{S}'({\mathbf R}^{d})$ and
$u \in \mathscr{S}'({\mathbf R}^{d})$ and ![]() $\psi \in \mathscr{S}({\mathbf R}^{d})$. Set
$\psi \in \mathscr{S}({\mathbf R}^{d})$. Set
 \begin{equation}
\begin{aligned}
(\mathscr{K} u, \psi)
& = \lim_{N \to \infty} (\mathscr{K} u_N, \psi) \\
& = \lim_{N \to \infty}
\int_{\mathbf R^{4d}} V_\Phi K(x,y,\xi,-\eta) \, \overline{V_\varphi \psi (x,\xi)} \, V_{\overline \varphi} u_N (y,\eta) \, \mathrm {d} x \, \mathrm {d} y \, \mathrm {d} \xi \, \mathrm {d} \eta.
\end{aligned}
\end{equation}
\begin{equation}
\begin{aligned}
(\mathscr{K} u, \psi)
& = \lim_{N \to \infty} (\mathscr{K} u_N, \psi) \\
& = \lim_{N \to \infty}
\int_{\mathbf R^{4d}} V_\Phi K(x,y,\xi,-\eta) \, \overline{V_\varphi \psi (x,\xi)} \, V_{\overline \varphi} u_N (y,\eta) \, \mathrm {d} x \, \mathrm {d} y \, \mathrm {d} \xi \, \mathrm {d} \eta.
\end{aligned}
\end{equation} Since ![]() $V_{\overline \varphi} u_N(y,\eta) \to V_{\overline \varphi} u(y,\eta)$ as
$V_{\overline \varphi} u_N(y,\eta) \to V_{\overline \varphi} u(y,\eta)$ as ![]() $N \to \infty$ for all
$N \to \infty$ for all ![]() $(y,\eta) \in \mathbf R^{2d}$, the formula (4.8) follows from dominated convergence if we can show that the modulus of the integrand in (4.14) is bounded by an integrable function that does not depend on
$(y,\eta) \in \mathbf R^{2d}$, the formula (4.8) follows from dominated convergence if we can show that the modulus of the integrand in (4.14) is bounded by an integrable function that does not depend on ![]() $N \in \mathbf N$, which we now set out to do.
$N \in \mathbf N$, which we now set out to do.
Consider first the right-hand side integral over ![]() $(x,y,\xi,-\eta) \in \mathbf R^{4d} \setminus \Gamma_1$, where Γ1 is defined by (4.2) with c > 1 again chosen so that
$(x,y,\xi,-\eta) \in \mathbf R^{4d} \setminus \Gamma_1$, where Γ1 is defined by (4.2) with c > 1 again chosen so that ![]() $\mathrm{WF_{g}^{\it s}} (K) \subseteq \Gamma_1$. By Lemma 4.1, we may use the estimates (4.4). Using (4.13), we obtain for any
$\mathrm{WF_{g}^{\it s}} (K) \subseteq \Gamma_1$. By Lemma 4.1, we may use the estimates (4.4). Using (4.13), we obtain for any ![]() $m \in \mathbf N$
$m \in \mathbf N$
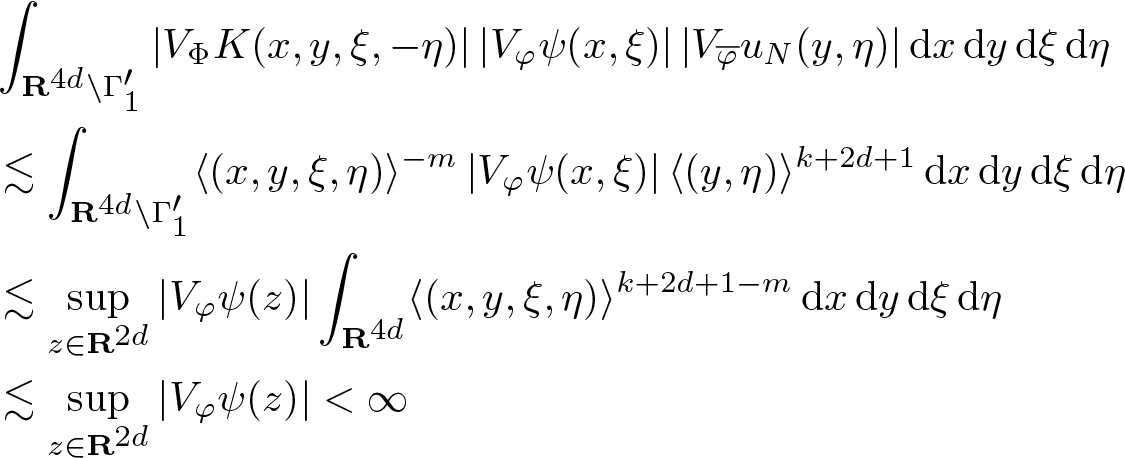 \begin{equation}
\begin{aligned}
& \int_{\mathbf R^{4d} \setminus \Gamma_1'}
|V_\Phi K(x,y,\xi,-\eta)| \, |V_\varphi \psi (x,\xi)| \, |V_{\overline \varphi} u_N (y,\eta)| \, \mathrm {d} x \, \mathrm {d} y \, \mathrm {d} \xi \, \mathrm {d} \eta \\
& \lesssim
\int_{\mathbf R^{4d} \setminus \Gamma_1'}
\langle (x,y,\xi,\eta)\rangle^{-m} \, |V_\varphi \psi (x,\xi)| \, \langle (y,\eta)\rangle^{k + 2 d + 1} \, \mathrm {d} x \, \mathrm {d} y \, \mathrm {d} \xi \, \mathrm {d} \eta \\
& \lesssim \sup_{z \in \mathbf R^{2d}} |V_\varphi \psi (z)|
\int_{\mathbf R^{4d}} \langle (x,y,\xi,\eta)\rangle^{k + 2 d + 1 - m} \, \mathrm {d} x \, \mathrm {d} y \, \mathrm {d} \xi \, \mathrm {d} \eta \\
& \lesssim \sup_{z \in \mathbf R^{2d}} |V_\varphi \psi (z)| \lt \infty
\end{aligned}
\end{equation}
\begin{equation}
\begin{aligned}
& \int_{\mathbf R^{4d} \setminus \Gamma_1'}
|V_\Phi K(x,y,\xi,-\eta)| \, |V_\varphi \psi (x,\xi)| \, |V_{\overline \varphi} u_N (y,\eta)| \, \mathrm {d} x \, \mathrm {d} y \, \mathrm {d} \xi \, \mathrm {d} \eta \\
& \lesssim
\int_{\mathbf R^{4d} \setminus \Gamma_1'}
\langle (x,y,\xi,\eta)\rangle^{-m} \, |V_\varphi \psi (x,\xi)| \, \langle (y,\eta)\rangle^{k + 2 d + 1} \, \mathrm {d} x \, \mathrm {d} y \, \mathrm {d} \xi \, \mathrm {d} \eta \\
& \lesssim \sup_{z \in \mathbf R^{2d}} |V_\varphi \psi (z)|
\int_{\mathbf R^{4d}} \langle (x,y,\xi,\eta)\rangle^{k + 2 d + 1 - m} \, \mathrm {d} x \, \mathrm {d} y \, \mathrm {d} \xi \, \mathrm {d} \eta \\
& \lesssim \sup_{z \in \mathbf R^{2d}} |V_\varphi \psi (z)| \lt \infty
\end{aligned}
\end{equation}provided m > 0 is sufficiently large.
Next, we consider the right-hand side integral (4.14) over ![]() $(x,y,\xi,-\eta) \in \Gamma_1$, where we may use (4.5). Again, from (2.2), we obtain for some
$(x,y,\xi,-\eta) \in \Gamma_1$, where we may use (4.5). Again, from (2.2), we obtain for some ![]() $m \geqslant 0$
$m \geqslant 0$
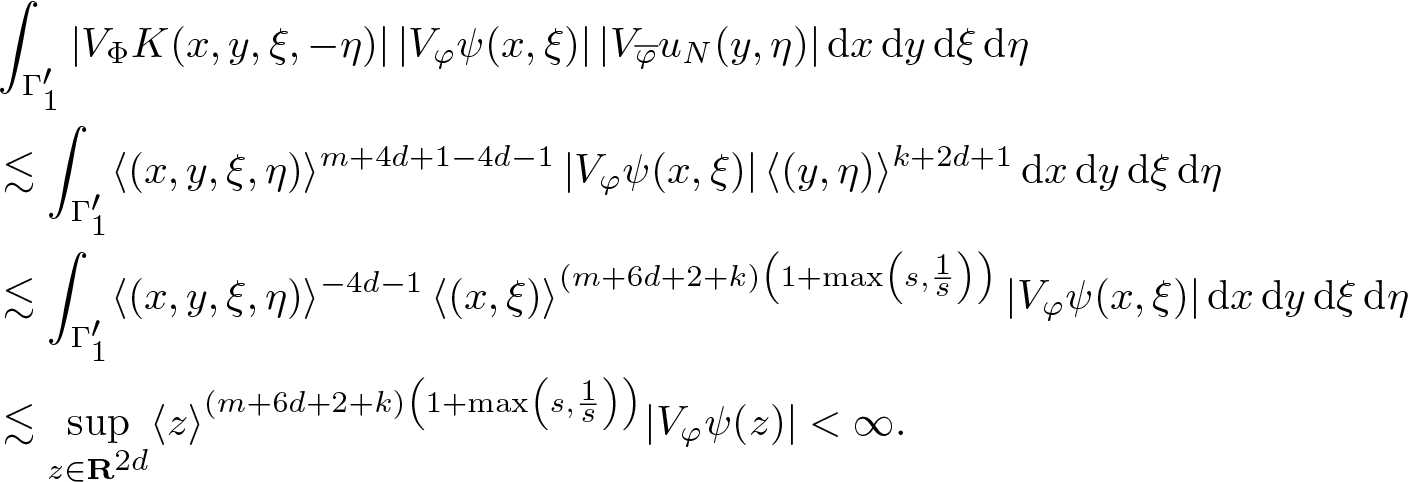 \begin{equation}
\begin{aligned}
& \int_{\Gamma_1'}
|V_\Phi K(x,y,\xi,-\eta)| \, |V_\varphi \psi (x,\xi)| \, |V_{\overline \varphi} u_N (y,\eta)| \, \mathrm {d} x \, \mathrm {d} y \, \mathrm {d} \xi \, \mathrm {d} \eta \\
& \lesssim
\int_{\Gamma_1'}
\langle (x,y,\xi,\eta)\rangle^{m+4d+1-4d-1} \, |V_\varphi \psi (x,\xi)| \, \langle (y,\eta)\rangle^{k + 2 d + 1} \, \mathrm {d} x \, \mathrm {d} y \, \mathrm {d} \xi \, \mathrm {d} \eta \\
& \lesssim
\int_{\Gamma_1'}
\langle (x,y,\xi,\eta)\rangle^{-4d-1} \, \langle (x,\xi)\rangle^{(m+6d+2+k) \left(1 + \max \left( s, \frac1s \right)\right)} \, |V_\varphi \psi (x,\xi)| \, \mathrm {d} x \, \mathrm {d} y \, \mathrm {d} \xi \, \mathrm {d} \eta \\
& \lesssim \sup_{z \in \mathbf R^{2d}} \langle z\rangle^{ (m+6d+2+k) \left(1 + \max \left( s, \frac1s \right)\right) } |V_\varphi \psi (z)| \lt \infty.
\end{aligned}
\end{equation}
\begin{equation}
\begin{aligned}
& \int_{\Gamma_1'}
|V_\Phi K(x,y,\xi,-\eta)| \, |V_\varphi \psi (x,\xi)| \, |V_{\overline \varphi} u_N (y,\eta)| \, \mathrm {d} x \, \mathrm {d} y \, \mathrm {d} \xi \, \mathrm {d} \eta \\
& \lesssim
\int_{\Gamma_1'}
\langle (x,y,\xi,\eta)\rangle^{m+4d+1-4d-1} \, |V_\varphi \psi (x,\xi)| \, \langle (y,\eta)\rangle^{k + 2 d + 1} \, \mathrm {d} x \, \mathrm {d} y \, \mathrm {d} \xi \, \mathrm {d} \eta \\
& \lesssim
\int_{\Gamma_1'}
\langle (x,y,\xi,\eta)\rangle^{-4d-1} \, \langle (x,\xi)\rangle^{(m+6d+2+k) \left(1 + \max \left( s, \frac1s \right)\right)} \, |V_\varphi \psi (x,\xi)| \, \mathrm {d} x \, \mathrm {d} y \, \mathrm {d} \xi \, \mathrm {d} \eta \\
& \lesssim \sup_{z \in \mathbf R^{2d}} \langle z\rangle^{ (m+6d+2+k) \left(1 + \max \left( s, \frac1s \right)\right) } |V_\varphi \psi (z)| \lt \infty.
\end{aligned}
\end{equation} The estimates (4.15) and (4.16) prove our claim that the modulus of the integrand in right-hand side of (4.14) is bounded by an ![]() $L^1(\mathbf R^{4d})$ function uniformly over
$L^1(\mathbf R^{4d})$ function uniformly over ![]() $N \in \mathbf N$. Thus, (4.14) extends the domain of
$N \in \mathbf N$. Thus, (4.14) extends the domain of ![]() $\mathscr{K}$ from
$\mathscr{K}$ from ![]() $\mathscr{S}({\mathbf R}^{d})$ to
$\mathscr{S}({\mathbf R}^{d})$ to ![]() $\mathscr{S}'({\mathbf R}^{d})$. We have shown claim (3).
$\mathscr{S}'({\mathbf R}^{d})$. We have shown claim (3).
From (4.15) and (4.16), we also see that ![]() $\mathscr{K}$ extended to the domain
$\mathscr{K}$ extended to the domain ![]() $\mathscr{S}'({\mathbf R}^{d})$ satisfies
$\mathscr{S}'({\mathbf R}^{d})$ satisfies ![]() $\mathscr{K} u \in \mathscr{S}'({\mathbf R}^{d})$ when
$\mathscr{K} u \in \mathscr{S}'({\mathbf R}^{d})$ when ![]() $u \in \mathscr{S}'({\mathbf R}^{d})$. To prove claim (2), it remains to show the sequential continuity of the extension (4.14) on
$u \in \mathscr{S}'({\mathbf R}^{d})$. To prove claim (2), it remains to show the sequential continuity of the extension (4.14) on ![]() $\mathscr{S}'({\mathbf R}^{d})$. The uniqueness of the extension is a consequence of the continuity.
$\mathscr{S}'({\mathbf R}^{d})$. The uniqueness of the extension is a consequence of the continuity.
Let ![]() $(u_n)_{n = 1}^\infty \subseteq \mathscr{S}'({\mathbf R}^{d})$ be a sequence such that
$(u_n)_{n = 1}^\infty \subseteq \mathscr{S}'({\mathbf R}^{d})$ be a sequence such that ![]() $u_n \to 0$ in
$u_n \to 0$ in ![]() $\mathscr{S}'({\mathbf R}^{d})$ as
$\mathscr{S}'({\mathbf R}^{d})$ as ![]() $n \to \infty$. Then,
$n \to \infty$. Then, ![]() $V_{\overline \varphi} u_n(y,\eta) \to 0$ as
$V_{\overline \varphi} u_n(y,\eta) \to 0$ as ![]() $n \to \infty$ for all
$n \to \infty$ for all ![]() $(y,\eta) \in \mathbf R^{2d}$. By the Banach–Steinhaus theorem [Reference Reed and Simon16, Theorem V.7],
$(y,\eta) \in \mathbf R^{2d}$. By the Banach–Steinhaus theorem [Reference Reed and Simon16, Theorem V.7], ![]() $(u_n)_{n = 1}^\infty$ is equicontinuous. This means that there exists
$(u_n)_{n = 1}^\infty$ is equicontinuous. This means that there exists ![]() $m \in \mathbf N$ such that
$m \in \mathbf N$ such that
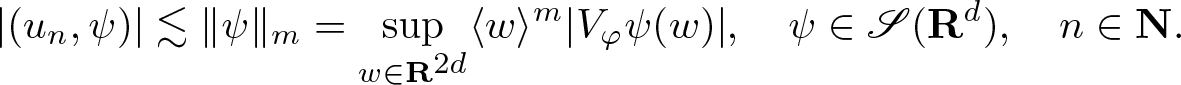 \begin{equation*}
|(u_n, \psi)|
\lesssim \| \psi \|_m
= \sup_{w \in \mathbf R^{2d}} \langle w\rangle^m |V_\varphi \psi (w)|, \quad \psi \in \mathscr{S}({\mathbf R}^{d}), \quad n \in \mathbf N.
\end{equation*}
\begin{equation*}
|(u_n, \psi)|
\lesssim \| \psi \|_m
= \sup_{w \in \mathbf R^{2d}} \langle w\rangle^m |V_\varphi \psi (w)|, \quad \psi \in \mathscr{S}({\mathbf R}^{d}), \quad n \in \mathbf N.
\end{equation*}Hence,
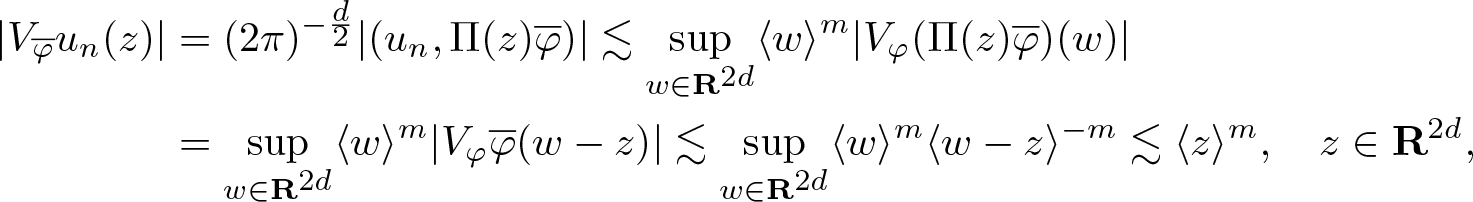 \begin{align*}
|V_{\overline \varphi} u_n(z)|
& = (2 \pi)^{- \frac{d}{2}} |(u_n, \Pi(z) \overline \varphi )|
\lesssim \sup_{w \in \mathbf R^{2d}} \langle w\rangle^m |V_\varphi (\Pi(z) \overline \varphi) (w)| \\
& = \sup_{w \in \mathbf R^{2d}} \langle w\rangle^m |V_\varphi \overline \varphi (w-z) |
\lesssim \sup_{w \in \mathbf R^{2d}} \langle w\rangle^m \langle w-z\rangle^{-m}
\lesssim \langle z\rangle^m, \quad z \in \mathbf R^{2d},
\end{align*}
\begin{align*}
|V_{\overline \varphi} u_n(z)|
& = (2 \pi)^{- \frac{d}{2}} |(u_n, \Pi(z) \overline \varphi )|
\lesssim \sup_{w \in \mathbf R^{2d}} \langle w\rangle^m |V_\varphi (\Pi(z) \overline \varphi) (w)| \\
& = \sup_{w \in \mathbf R^{2d}} \langle w\rangle^m |V_\varphi \overline \varphi (w-z) |
\lesssim \sup_{w \in \mathbf R^{2d}} \langle w\rangle^m \langle w-z\rangle^{-m}
\lesssim \langle z\rangle^m, \quad z \in \mathbf R^{2d},
\end{align*} uniformly for all ![]() $n \in \mathbf N$. From (4.8), the estimates (4.15), (4.16) and dominated convergence, it follows that
$n \in \mathbf N$. From (4.8), the estimates (4.15), (4.16) and dominated convergence, it follows that ![]() $(\mathscr{K} u_n, \psi) \to 0$ as
$(\mathscr{K} u_n, \psi) \to 0$ as ![]() $n \to \infty$ for all
$n \to \infty$ for all ![]() $\psi \in \mathscr{S}({\mathbf R}^{d})$, that is
$\psi \in \mathscr{S}({\mathbf R}^{d})$, that is ![]() $\mathscr{K} u_n \to 0$ in
$\mathscr{K} u_n \to 0$ in ![]() $\mathscr{S}'({\mathbf R}^{d})$. This finally proves claim (2).
$\mathscr{S}'({\mathbf R}^{d})$. This finally proves claim (2).
Now, we start to prepare for the main result Theorem 4.4. We need the relation mapping between a subset ![]() $A \subseteq X \times Y$ of the Cartesian product of two sets X, Y, and a subset
$A \subseteq X \times Y$ of the Cartesian product of two sets X, Y, and a subset ![]() $B \subseteq Y$,
$B \subseteq Y$,
When ![]() $X = Y = \mathbf R^{2d}$, we use the convention
$X = Y = \mathbf R^{2d}$, we use the convention
Note that there is a swap of the second and third variables.
If we denote by
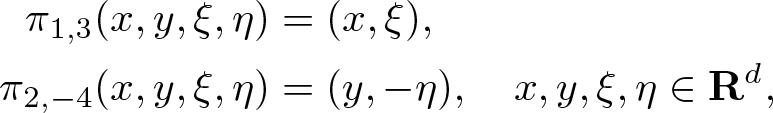 \begin{align*}
\pi_{1,3}(x,y,\xi,\eta) & = (x,\xi), \\
\pi_{2,-4}(x,y,\xi,\eta) & = (y,-\eta), \quad x,y,\xi, \eta \in {\mathbf R}^{d},
\end{align*}
\begin{align*}
\pi_{1,3}(x,y,\xi,\eta) & = (x,\xi), \\
\pi_{2,-4}(x,y,\xi,\eta) & = (y,-\eta), \quad x,y,\xi, \eta \in {\mathbf R}^{d},
\end{align*} the projections ![]() $\mathbf R^{4d} \rightarrow \mathbf R^{2d}$ onto the first and the third
$\mathbf R^{4d} \rightarrow \mathbf R^{2d}$ onto the first and the third ![]() ${\mathbf R}^{d}$ coordinate and onto the second and the fourth
${\mathbf R}^{d}$ coordinate and onto the second and the fourth ![]() ${\mathbf R}^{d}$ coordinate with a change of sign in the latter, respectively, then we may write
${\mathbf R}^{d}$ coordinate with a change of sign in the latter, respectively, then we may write
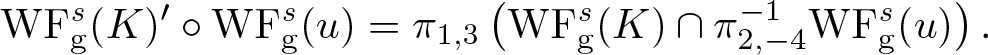 \begin{equation}
\mathrm{WF_{g}^{\it s}} (K)' \circ \mathrm{WF_{g}^{\it s}} (u)
= \pi_{1,3} \left( \mathrm{WF_{g}^{\it s}} (K) \cap \pi_{2,-4}^{-1} \mathrm{WF_{g}^{\it s}} (u) \right).
\end{equation}
\begin{equation}
\mathrm{WF_{g}^{\it s}} (K)' \circ \mathrm{WF_{g}^{\it s}} (u)
= \pi_{1,3} \left( \mathrm{WF_{g}^{\it s}} (K) \cap \pi_{2,-4}^{-1} \mathrm{WF_{g}^{\it s}} (u) \right).
\end{equation}We need a lemma which is similar to [Reference Wahlberg24, Lemma 5.1].
Lemma 4.3. If s > 0, ![]() $K \in \mathscr{S}'(\mathbf R^{2d})$, (4.1) holds and
$K \in \mathscr{S}'(\mathbf R^{2d})$, (4.1) holds and ![]() $u \in \mathscr{S}'({\mathbf R}^{d})$ then
$u \in \mathscr{S}'({\mathbf R}^{d})$ then
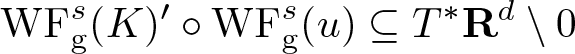 \begin{equation*}
\mathrm{WF}_{\rm g}^s (K)' \circ \mathrm{WF}_{\rm g}^s (u) \subseteq T^* {\mathbf R}^{d} \setminus 0
\end{equation*}
\begin{equation*}
\mathrm{WF}_{\rm g}^s (K)' \circ \mathrm{WF}_{\rm g}^s (u) \subseteq T^* {\mathbf R}^{d} \setminus 0
\end{equation*} is s-conic and closed in ![]() $T^* {\mathbf R}^{d} \setminus 0$.
$T^* {\mathbf R}^{d} \setminus 0$.
Proof. Let ![]() $(x,\xi) \in \mathrm{WF_{g}^{\it s}} (K)' \circ \mathrm{WF_{g}^{\it s}} (u)$. Then, there exists
$(x,\xi) \in \mathrm{WF_{g}^{\it s}} (K)' \circ \mathrm{WF_{g}^{\it s}} (u)$. Then, there exists ![]() $(y,\eta) \in \mathrm{WF_{g}^{\it s}} (u)$ such that
$(y,\eta) \in \mathrm{WF_{g}^{\it s}} (u)$ such that ![]() $(x,y,\xi,-\eta) \in \mathrm{WF_{g}^{\it s}} (K)$. Let λ > 0. Since
$(x,y,\xi,-\eta) \in \mathrm{WF_{g}^{\it s}} (K)$. Let λ > 0. Since ![]() $\mathrm{WF_{g}^{\it s}} (K)$ and
$\mathrm{WF_{g}^{\it s}} (K)$ and ![]() $\mathrm{WF_{g}^{\it s}} (u)$ are s-conic, we have
$\mathrm{WF_{g}^{\it s}} (u)$ are s-conic, we have ![]() $( \lambda x, \lambda y, \lambda^s \xi,- \lambda^s \eta) \in \mathrm{WF_{g}^{\it s}} (K)$ and
$( \lambda x, \lambda y, \lambda^s \xi,- \lambda^s \eta) \in \mathrm{WF_{g}^{\it s}} (K)$ and ![]() $(\lambda y, \lambda^s \eta) \in \mathrm{WF_{g}^{\it s}} (u)$. It follows that
$(\lambda y, \lambda^s \eta) \in \mathrm{WF_{g}^{\it s}} (u)$. It follows that ![]() $(\lambda x, \lambda^s \xi) \in \mathrm{WF_{g}^{\it s}} (K)' \circ \mathrm{WF_{g}^{\it s}} (u)$ which shows that
$(\lambda x, \lambda^s \xi) \in \mathrm{WF_{g}^{\it s}} (K)' \circ \mathrm{WF_{g}^{\it s}} (u)$ which shows that ![]() $\mathrm{WF_{g}^{\it s}} (K)' \circ \mathrm{WF_{g}^{\it s}} (u)$ is s-conic.
$\mathrm{WF_{g}^{\it s}} (K)' \circ \mathrm{WF_{g}^{\it s}} (u)$ is s-conic.
Next, we assume that ![]() $(x_n,\xi_n) \in \mathrm{WF_{g}^{\it s}} (K)' \circ \mathrm{WF_{g}^{\it s}} (u)$ for
$(x_n,\xi_n) \in \mathrm{WF_{g}^{\it s}} (K)' \circ \mathrm{WF_{g}^{\it s}} (u)$ for ![]() $n \in \mathbf N$ and
$n \in \mathbf N$ and ![]() $(x_n, \xi_n) \to (x,\xi) \neq 0$ as
$(x_n, \xi_n) \to (x,\xi) \neq 0$ as ![]() $n \to +\infty$. For each
$n \to +\infty$. For each ![]() $n \in \mathbf N$, there exists
$n \in \mathbf N$, there exists ![]() $(y_n,\eta_n) \in \mathrm{WF_{g}^{\it s}} (u)$ such that
$(y_n,\eta_n) \in \mathrm{WF_{g}^{\it s}} (u)$ such that ![]() $(x_n,y_n,\xi_n,-\eta_n) \in \mathrm{WF_{g}^{\it s}} (K)$.
$(x_n,y_n,\xi_n,-\eta_n) \in \mathrm{WF_{g}^{\it s}} (K)$.
Since the sequence ![]() $\{ (x_n, \xi_n)_n \} \subseteq T^* {\mathbf R}^{d}$ is bounded it follows from Lemma 4.1 that also the sequence
$\{ (x_n, \xi_n)_n \} \subseteq T^* {\mathbf R}^{d}$ is bounded it follows from Lemma 4.1 that also the sequence ![]() $\{ (y_n, \eta_n)_n \} \subseteq T^* {\mathbf R}^{d}$ is bounded. Passing to a subsequence (without change of notation), we get convergence
$\{ (y_n, \eta_n)_n \} \subseteq T^* {\mathbf R}^{d}$ is bounded. Passing to a subsequence (without change of notation), we get convergence
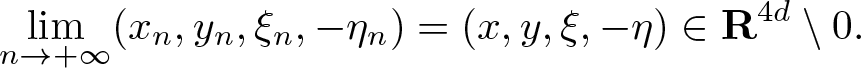 \begin{equation*}
\lim_{n \to +\infty} (x_n,y_n,\xi_n,-\eta_n)
= (x,y,\xi,-\eta) \in \mathbf R^{4d} \setminus 0.
\end{equation*}
\begin{equation*}
\lim_{n \to +\infty} (x_n,y_n,\xi_n,-\eta_n)
= (x,y,\xi,-\eta) \in \mathbf R^{4d} \setminus 0.
\end{equation*} Here, ![]() $(x,y,\xi,-\eta) \in \mathrm{WF_{g}^{\it s}} (K)$ since
$(x,y,\xi,-\eta) \in \mathrm{WF_{g}^{\it s}} (K)$ since  $\mathrm{WF_{g}^{\it s}} (K) \subseteq T^* \mathbf R^{2d} \setminus 0$ is closed and
$\mathrm{WF_{g}^{\it s}} (K) \subseteq T^* \mathbf R^{2d} \setminus 0$ is closed and ![]() $(y,\eta) \neq 0$ due to the assumption
$(y,\eta) \neq 0$ due to the assumption ![]() $\mathrm{WF}_{\rm g,1}^{s} (K) = \emptyset$. Moreover,
$\mathrm{WF}_{\rm g,1}^{s} (K) = \emptyset$. Moreover, ![]() $(y,\eta) \in \mathrm{WF_{g}^{\it s}} (u)$ since
$(y,\eta) \in \mathrm{WF_{g}^{\it s}} (u)$ since  $\mathrm{WF_{g}^{\it s}} (u) \subseteq T^* {\mathbf R}^{d} \setminus 0$ is closed. We have proved that
$\mathrm{WF_{g}^{\it s}} (u) \subseteq T^* {\mathbf R}^{d} \setminus 0$ is closed. We have proved that ![]() $(x,\xi) \in \mathrm{WF_{g}^{\it s}} (K)' \circ \mathrm{WF_{g}^{\it s}} (u)$ which shows that
$(x,\xi) \in \mathrm{WF_{g}^{\it s}} (K)' \circ \mathrm{WF_{g}^{\it s}} (u)$ which shows that ![]() $\mathrm{WF_{g}^{\it s}} (K)' \circ \mathrm{WF_{g}^{\it s}} (u)$ is closed in
$\mathrm{WF_{g}^{\it s}} (K)' \circ \mathrm{WF_{g}^{\it s}} (u)$ is closed in ![]() $T^* {\mathbf R}^{d} \setminus 0$.
$T^* {\mathbf R}^{d} \setminus 0$.
Finally, we may state and prove our main result on propagation of singularities.
Theorem 4.4. Let s > 0 and let ![]() $\mathscr{K}: \mathscr{S}({\mathbf R}^{d}) \to \mathscr{S}'({\mathbf R}^{d})$ be the continuous linear operator (4.6) defined by the Schwartz kernel
$\mathscr{K}: \mathscr{S}({\mathbf R}^{d}) \to \mathscr{S}'({\mathbf R}^{d})$ be the continuous linear operator (4.6) defined by the Schwartz kernel ![]() $K \in \mathscr{S}'(\mathbf R^{2d})$, and suppose that (4.1) holds. Then, for
$K \in \mathscr{S}'(\mathbf R^{2d})$, and suppose that (4.1) holds. Then, for ![]() $u \in \mathscr{S}'({\mathbf R}^{d})$, we have
$u \in \mathscr{S}'({\mathbf R}^{d})$, we have
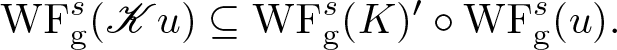 \begin{equation*}
\mathrm{WF}_{\rm g}^s (\mathscr{K} u) \subseteq \mathrm{WF}_{\rm g}^s (K)' \circ \mathrm{WF}_{\rm g}^s (u).
\end{equation*}
\begin{equation*}
\mathrm{WF}_{\rm g}^s (\mathscr{K} u) \subseteq \mathrm{WF}_{\rm g}^s (K)' \circ \mathrm{WF}_{\rm g}^s (u).
\end{equation*}Proof. By Proposition 4.2, ![]() $\mathscr{K}: \mathscr{S} ({\mathbf R}^{d}) \to \mathscr{S}({\mathbf R}^{d})$ is continuous and extends uniquely to a continuous linear operator
$\mathscr{K}: \mathscr{S} ({\mathbf R}^{d}) \to \mathscr{S}({\mathbf R}^{d})$ is continuous and extends uniquely to a continuous linear operator ![]() $\mathscr{K}: \mathscr{S}' ({\mathbf R}^{d}) \to \mathscr{S}'({\mathbf R}^{d})$.
$\mathscr{K}: \mathscr{S}' ({\mathbf R}^{d}) \to \mathscr{S}'({\mathbf R}^{d})$.
Let ![]() $\varphi \in \mathscr{S}({\mathbf R}^{d})$ satisfy
$\varphi \in \mathscr{S}({\mathbf R}^{d})$ satisfy ![]() $\| \varphi \|_{L^2} = 1$ and set
$\| \varphi \|_{L^2} = 1$ and set ![]() $\Phi = \varphi \otimes \varphi \in \mathscr{S}({\mathbf R}^{2d})$. Proposition 4.2, (4.8) and (4.9) give for
$\Phi = \varphi \otimes \varphi \in \mathscr{S}({\mathbf R}^{2d})$. Proposition 4.2, (4.8) and (4.9) give for ![]() $u \in \mathscr{S}' ({\mathbf R}^{d})$ and
$u \in \mathscr{S}' ({\mathbf R}^{d})$ and ![]() $(x,\xi) \in T^* {\mathbf R}^{d}$ and λ > 0
$(x,\xi) \in T^* {\mathbf R}^{d}$ and λ > 0
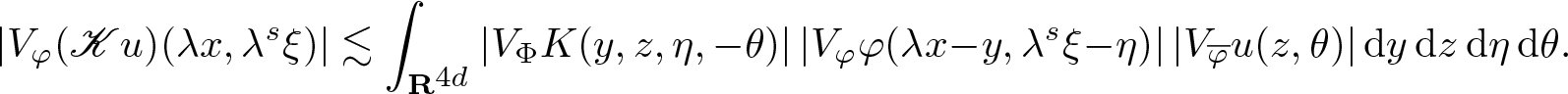 \begin{equation}
| V_\varphi(\mathscr{K} u) ( \lambda x, \lambda^s \xi) |
\lesssim \int_{\mathbf R^{4d}} | V_\Phi K (y,z,\eta,-\theta) | \, |V_\varphi \varphi ( \lambda x-y, \lambda^s \xi-\eta) | \, | V_{\overline \varphi} u(z,\theta) | \, \mathrm {d} y \, \mathrm {d} z \, \mathrm {d} \eta \, \mathrm {d} \theta.
\end{equation}
\begin{equation}
| V_\varphi(\mathscr{K} u) ( \lambda x, \lambda^s \xi) |
\lesssim \int_{\mathbf R^{4d}} | V_\Phi K (y,z,\eta,-\theta) | \, |V_\varphi \varphi ( \lambda x-y, \lambda^s \xi-\eta) | \, | V_{\overline \varphi} u(z,\theta) | \, \mathrm {d} y \, \mathrm {d} z \, \mathrm {d} \eta \, \mathrm {d} \theta.
\end{equation} Suppose ![]() $z_0 = (x_0,\xi_0) \in T^* {\mathbf R}^{d} \setminus 0$ and
$z_0 = (x_0,\xi_0) \in T^* {\mathbf R}^{d} \setminus 0$ and
 \begin{equation}
z_0 \notin \mathrm{WF_{g}^{\it s}} (K)' \circ \mathrm{WF_{g}^{\it s}} (u).
\end{equation}
\begin{equation}
z_0 \notin \mathrm{WF_{g}^{\it s}} (K)' \circ \mathrm{WF_{g}^{\it s}} (u).
\end{equation} To prove the theorem, we will show ![]() $z_0\notin \mathrm{WF_{g}^{\it s}} (\mathscr{K} u)$.
$z_0\notin \mathrm{WF_{g}^{\it s}} (\mathscr{K} u)$.
By Lemma 4.3, the set ![]() $\mathrm{WF_{g}^{\it s}} (K)' \circ \mathrm{WF_{g}^{\it s}} (u)$ is s-conic and closed. Thus, we may assume that
$\mathrm{WF_{g}^{\it s}} (K)' \circ \mathrm{WF_{g}^{\it s}} (u)$ is s-conic and closed. Thus, we may assume that ![]() $z_0 \in \mathbf S^{2d-1}$. Moreover, with
$z_0 \in \mathbf S^{2d-1}$. Moreover, with  $\widetilde \Gamma_{z_0,2 \varepsilon} = \widetilde \Gamma_{s, z_0, 2 \varepsilon}$, there exists ɛ > 0 such that
$\widetilde \Gamma_{z_0,2 \varepsilon} = \widetilde \Gamma_{s, z_0, 2 \varepsilon}$, there exists ɛ > 0 such that
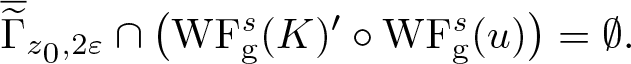 \begin{equation*}
\overline{\widetilde \Gamma}_{z_0,2 \varepsilon} \cap \left( \mathrm{WF_{g}^{\it s}} (K)' \circ \mathrm{WF_{g}^{\it s}} (u) \right)= \emptyset.
\end{equation*}
\begin{equation*}
\overline{\widetilde \Gamma}_{z_0,2 \varepsilon} \cap \left( \mathrm{WF_{g}^{\it s}} (K)' \circ \mathrm{WF_{g}^{\it s}} (u) \right)= \emptyset.
\end{equation*} Here,  $\overline{\widetilde \Gamma}_{z_0,2 \varepsilon}$ denotes the closure of
$\overline{\widetilde \Gamma}_{z_0,2 \varepsilon}$ denotes the closure of  $\widetilde \Gamma_{z_0,2 \varepsilon}$ in
$\widetilde \Gamma_{z_0,2 \varepsilon}$ in ![]() $T^* {\mathbf R}^{d} \setminus 0$. Using (4.17), we may write this as
$T^* {\mathbf R}^{d} \setminus 0$. Using (4.17), we may write this as
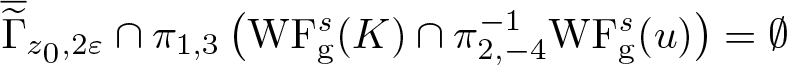 \begin{equation*}
\overline{\widetilde \Gamma}_{z_0,2 \varepsilon} \cap \pi_{1,3} \left( \mathrm{WF_{g}^{\it s}} (K) \cap \pi_{2,-4}^{-1} \mathrm{WF_{g}^{\it s}} (u) \right)= \emptyset
\end{equation*}
\begin{equation*}
\overline{\widetilde \Gamma}_{z_0,2 \varepsilon} \cap \pi_{1,3} \left( \mathrm{WF_{g}^{\it s}} (K) \cap \pi_{2,-4}^{-1} \mathrm{WF_{g}^{\it s}} (u) \right)= \emptyset
\end{equation*}or equivalently
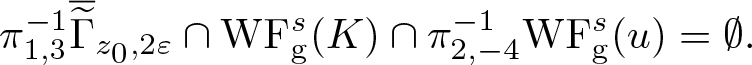 \begin{equation*}
\pi_{1,3}^{-1} \overline{\widetilde \Gamma}_{z_0,2 \varepsilon} \cap \mathrm{WF_{g}^{\it s}} (K) \cap \pi_{2,-4}^{-1} \mathrm{WF_{g}^{\it s}} (u) = \emptyset.
\end{equation*}
\begin{equation*}
\pi_{1,3}^{-1} \overline{\widetilde \Gamma}_{z_0,2 \varepsilon} \cap \mathrm{WF_{g}^{\it s}} (K) \cap \pi_{2,-4}^{-1} \mathrm{WF_{g}^{\it s}} (u) = \emptyset.
\end{equation*}Due to assumption (4.1), we may strengthen this into
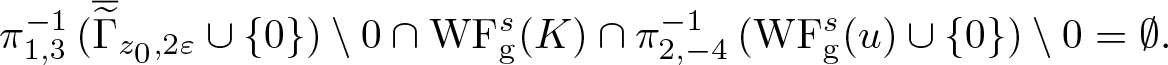 \begin{equation*}
\pi_{1,3}^{-1} \, (\overline{\widetilde \Gamma}_{z_0,2 \varepsilon} \cup \{ 0 \} ) \setminus 0 \cap \mathrm{WF_{g}^{\it s}} (K) \cap \pi_{2,-4}^{-1} \, (\mathrm{WF_{g}^{\it s}} (u) \cup \{ 0 \} ) \setminus 0 = \emptyset.
\end{equation*}
\begin{equation*}
\pi_{1,3}^{-1} \, (\overline{\widetilde \Gamma}_{z_0,2 \varepsilon} \cup \{ 0 \} ) \setminus 0 \cap \mathrm{WF_{g}^{\it s}} (K) \cap \pi_{2,-4}^{-1} \, (\mathrm{WF_{g}^{\it s}} (u) \cup \{ 0 \} ) \setminus 0 = \emptyset.
\end{equation*} Note that  $\pi_{1,3}^{-1} \, (\overline{\widetilde \Gamma}_{z_0,2 \varepsilon} \cup \{ 0 \} ) \setminus 0$,
$\pi_{1,3}^{-1} \, (\overline{\widetilde \Gamma}_{z_0,2 \varepsilon} \cup \{ 0 \} ) \setminus 0$, ![]() $\mathrm{WF_{g}^{\it s}} (K)$, and
$\mathrm{WF_{g}^{\it s}} (K)$, and  $\pi_{2,-4}^{-1} \, (\mathrm{WF_{g}^{\it s}} (u) \cup \{ 0 \} ) \setminus 0$ are all closed and s-conic subsets of
$\pi_{2,-4}^{-1} \, (\mathrm{WF_{g}^{\it s}} (u) \cup \{ 0 \} ) \setminus 0$ are all closed and s-conic subsets of ![]() $T^* \mathbf R^{2d} \setminus 0$.
$T^* \mathbf R^{2d} \setminus 0$.
Now, [Reference Wahlberg24, Lemma 5.4] gives the following conclusion. There exists open s-conic subsets ![]() $\Gamma_1 \subseteq T^* \mathbf R^{2d} \setminus 0$ and
$\Gamma_1 \subseteq T^* \mathbf R^{2d} \setminus 0$ and ![]() $\Gamma_2 \subseteq T^* {\mathbf R}^{d} \setminus 0$ such that
$\Gamma_2 \subseteq T^* {\mathbf R}^{d} \setminus 0$ such that
and
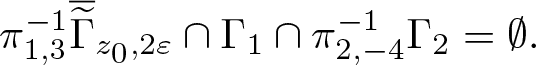 \begin{equation}
\pi_{1,3}^{-1} \overline{\widetilde \Gamma}_{z_0,2 \varepsilon}
\cap \Gamma_1 \cap \pi_{2,-4}^{-1} \Gamma_2 = \emptyset.
\end{equation}
\begin{equation}
\pi_{1,3}^{-1} \overline{\widetilde \Gamma}_{z_0,2 \varepsilon}
\cap \Gamma_1 \cap \pi_{2,-4}^{-1} \Gamma_2 = \emptyset.
\end{equation}By intersecting Γ1 with the set Γ1 defined in (4.2), we may by Lemma 4.1 assume that (4.2) holds true.
We will now start to estimate the integral (4.18) when ![]() $(x,\xi) \in (x_0, \xi_0) + {\rm B}_\varepsilon$ for some
$(x,\xi) \in (x_0, \xi_0) + {\rm B}_\varepsilon$ for some  $0 \lt \varepsilon \leqslant \frac12$ and
$0 \lt \varepsilon \leqslant \frac12$ and ![]() $\lambda \geqslant 1$.
$\lambda \geqslant 1$.
We split the domain ![]() $\mathbf R^{4d}$ of the integral (4.18) into three pieces. First, we integrate over
$\mathbf R^{4d}$ of the integral (4.18) into three pieces. First, we integrate over ![]() $\mathbf R^{4d} \setminus \Gamma_1'$ where we may use (4.4). Combined with (2.2) and (2.3), this gives if
$\mathbf R^{4d} \setminus \Gamma_1'$ where we may use (4.4). Combined with (2.2) and (2.3), this gives if ![]() $(x,\xi) \in (x_0, \xi_0) + {\rm B}_\varepsilon$ for some
$(x,\xi) \in (x_0, \xi_0) + {\rm B}_\varepsilon$ for some ![]() $k \in \mathbf N$ and any
$k \in \mathbf N$ and any ![]() $n,N \in \mathbf N$
$n,N \in \mathbf N$
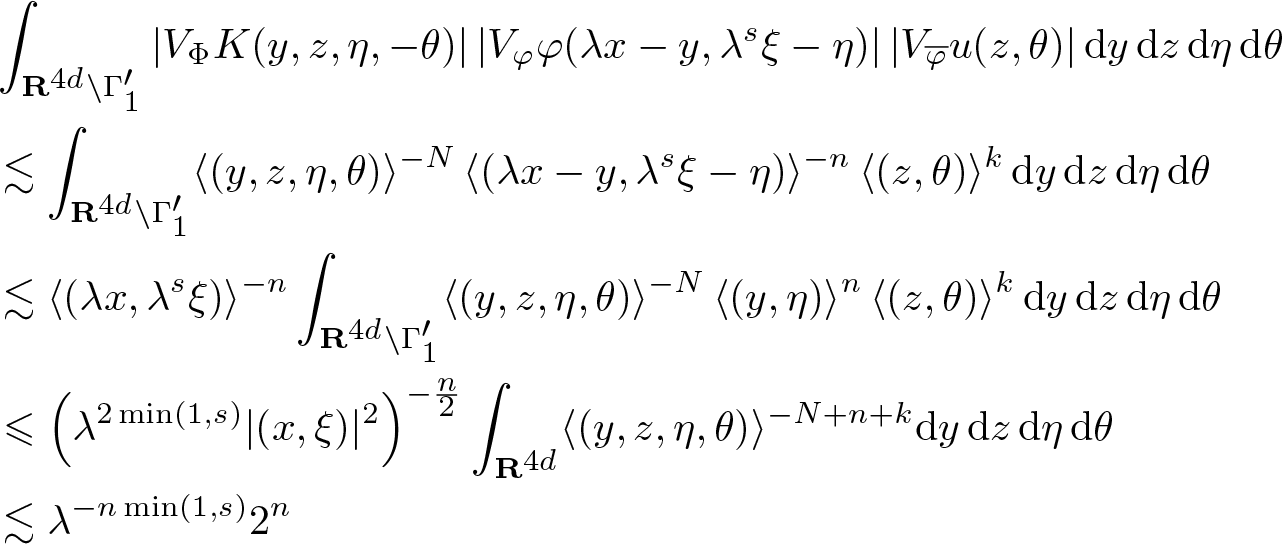 \begin{equation}
\begin{aligned}
& \int_{\mathbf R^{4d} \setminus \Gamma_1'} | V_\Phi K (y,z,\eta,-\theta) | \, |V_\varphi \varphi ( \lambda x-y, \lambda^s \xi-\eta) | \, | V_{\overline \varphi} u(z,\theta) | \, \mathrm {d} y \, \mathrm {d} z \, \mathrm {d} \eta \, \mathrm {d} \theta \\
& \lesssim \int_{\mathbf R^{4d} \setminus \Gamma_1'} \langle (y,z,\eta,\theta)\rangle^{-N} \, \langle (\lambda x-y, \lambda^s \xi-\eta) \rangle^{-n} \, \langle (z,\theta) \rangle^k \, \mathrm {d} y \, \mathrm {d} z \, \mathrm {d} \eta \, \mathrm {d} \theta \\
& \lesssim \langle (\lambda x, \lambda^s \xi) \rangle^{-n} \int_{\mathbf R^{4d} \setminus \Gamma_1'} \langle (y,z,\eta,\theta)\rangle^{-N} \, \langle (y,\eta) \rangle^{n} \, \langle (z,\theta) \rangle^{k} \, \mathrm {d} y \, \mathrm {d} z \, \mathrm {d} \eta \, \mathrm {d} \theta \\
& \leqslant \left( \lambda^{2 \min(1,s)} |(x,\xi)| ^2 \right)^{-\frac{n}{2}} \int_{\mathbf R^{4d}} \langle (y,z,\eta,\theta)\rangle^{-N+ n + k} \mathrm {d} y \, \mathrm {d} z \, \mathrm {d} \eta \, \mathrm {d} \theta \\
& \lesssim \lambda^{- n \min(1,s)} 2^{n}
\end{aligned}
\end{equation}
\begin{equation}
\begin{aligned}
& \int_{\mathbf R^{4d} \setminus \Gamma_1'} | V_\Phi K (y,z,\eta,-\theta) | \, |V_\varphi \varphi ( \lambda x-y, \lambda^s \xi-\eta) | \, | V_{\overline \varphi} u(z,\theta) | \, \mathrm {d} y \, \mathrm {d} z \, \mathrm {d} \eta \, \mathrm {d} \theta \\
& \lesssim \int_{\mathbf R^{4d} \setminus \Gamma_1'} \langle (y,z,\eta,\theta)\rangle^{-N} \, \langle (\lambda x-y, \lambda^s \xi-\eta) \rangle^{-n} \, \langle (z,\theta) \rangle^k \, \mathrm {d} y \, \mathrm {d} z \, \mathrm {d} \eta \, \mathrm {d} \theta \\
& \lesssim \langle (\lambda x, \lambda^s \xi) \rangle^{-n} \int_{\mathbf R^{4d} \setminus \Gamma_1'} \langle (y,z,\eta,\theta)\rangle^{-N} \, \langle (y,\eta) \rangle^{n} \, \langle (z,\theta) \rangle^{k} \, \mathrm {d} y \, \mathrm {d} z \, \mathrm {d} \eta \, \mathrm {d} \theta \\
& \leqslant \left( \lambda^{2 \min(1,s)} |(x,\xi)| ^2 \right)^{-\frac{n}{2}} \int_{\mathbf R^{4d}} \langle (y,z,\eta,\theta)\rangle^{-N+ n + k} \mathrm {d} y \, \mathrm {d} z \, \mathrm {d} \eta \, \mathrm {d} \theta \\
& \lesssim \lambda^{- n \min(1,s)} 2^{n}
\end{aligned}
\end{equation}provided N is sufficiently large.
It remains to estimate the integral (4.18) over ![]() $(y,z,\eta, - \theta) \in \Gamma_1$ where we may use (4.5). By (4.20), we have
$(y,z,\eta, - \theta) \in \Gamma_1$ where we may use (4.5). By (4.20), we have
where
 \begin{equation*}
\Omega_0 = \Gamma_1 \setminus \pi_{1,3}^{-1} \overline{\widetilde \Gamma}_{z_0,2 \varepsilon}, \quad
\Omega_2 = \Gamma_1 \setminus \pi_{2,-4}^{-1} \Gamma_2.
\end{equation*}
\begin{equation*}
\Omega_0 = \Gamma_1 \setminus \pi_{1,3}^{-1} \overline{\widetilde \Gamma}_{z_0,2 \varepsilon}, \quad
\Omega_2 = \Gamma_1 \setminus \pi_{2,-4}^{-1} \Gamma_2.
\end{equation*} First, we estimate the integral over ![]() $(y,z,\eta, - \theta) \in \Omega_2$. Then,
$(y,z,\eta, - \theta) \in \Omega_2$. Then, ![]() $(z,\theta) \in \mathbf R^{2d} \setminus \Gamma_2$ which is a closed s-conic set. By the compactness of
$(z,\theta) \in \mathbf R^{2d} \setminus \Gamma_2$ which is a closed s-conic set. By the compactness of ![]() $\mathbf S^{2d-1} \setminus \Gamma_2$ and (3.3), we obtain the estimates
$\mathbf S^{2d-1} \setminus \Gamma_2$ and (3.3), we obtain the estimates
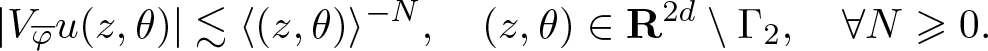 \begin{equation*}
|V_{\overline \varphi} u (z,\theta)|
\lesssim \langle (z,\theta)\rangle^{-N}, \quad (z,\theta) \in \mathbf R^{2d} \setminus \Gamma_2, \quad \forall N \geqslant 0.
\end{equation*}
\begin{equation*}
|V_{\overline \varphi} u (z,\theta)|
\lesssim \langle (z,\theta)\rangle^{-N}, \quad (z,\theta) \in \mathbf R^{2d} \setminus \Gamma_2, \quad \forall N \geqslant 0.
\end{equation*} Together with (4.5), (2.2) and (2.3), this gives if ![]() $(x,\xi) \in (x_0, \xi_0) + {\rm B}_\varepsilon$ for some
$(x,\xi) \in (x_0, \xi_0) + {\rm B}_\varepsilon$ for some ![]() $m \in \mathbf N$ and any
$m \in \mathbf N$ and any ![]() $n \in \mathbf N$
$n \in \mathbf N$
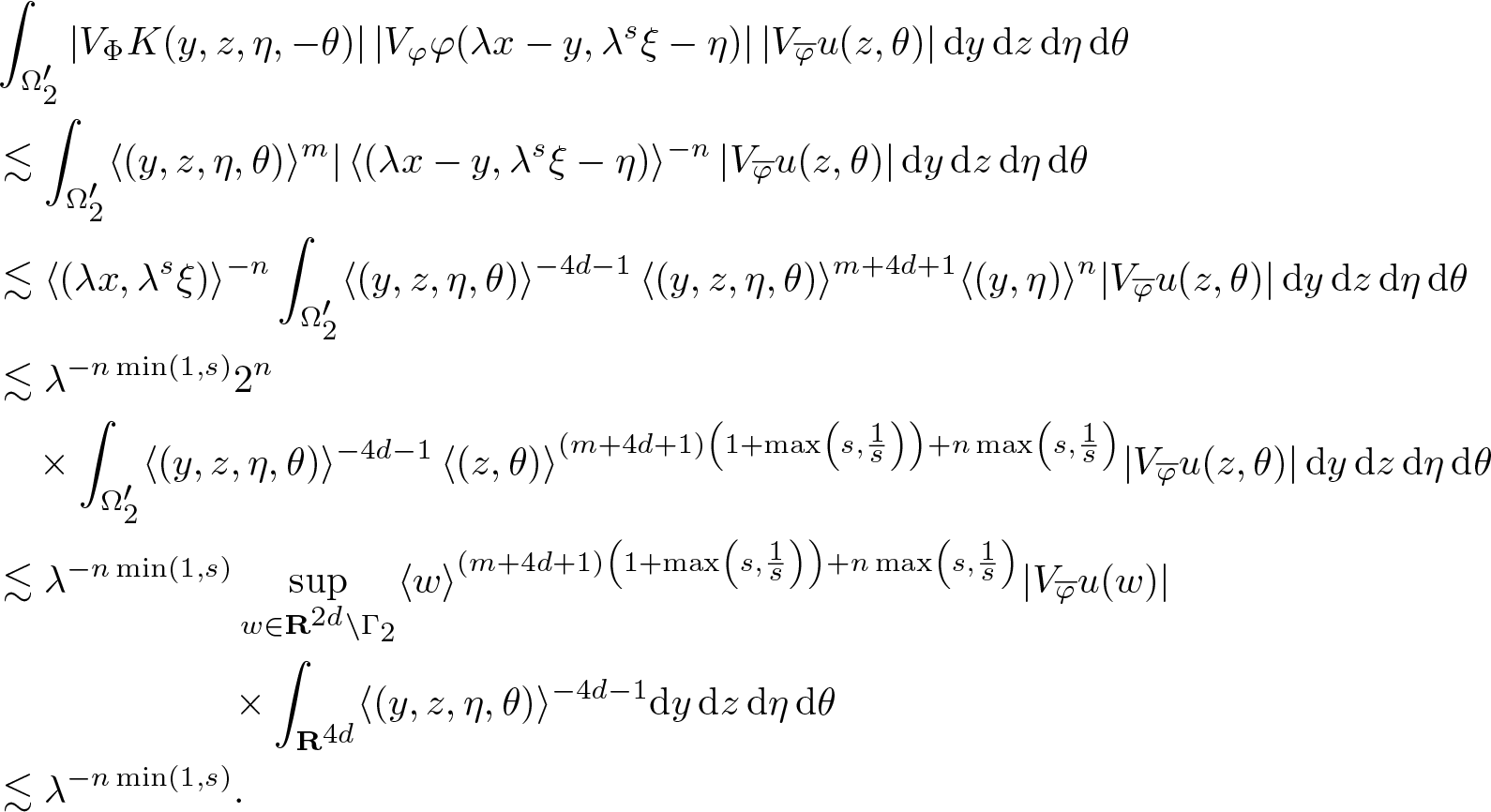 \begin{equation}
\begin{aligned}
& \int_{\Omega_2'} | V_\Phi K (y,z,\eta,-\theta) | \, |V_\varphi \varphi ( \lambda x-y, \lambda^s \xi-\eta) | \, | V_{\overline \varphi} u(z,\theta) | \, \mathrm {d} y \, \mathrm {d} z \, \mathrm {d} \eta \, \mathrm {d} \theta \\
& \lesssim \int_{\Omega_2'} \langle (y,z,\eta,\theta)\rangle^{m} | \, \langle (\lambda x-y, \lambda^s \xi-\eta) \rangle^{-n} \, | V_{\overline \varphi} u(z,\theta) | \, \mathrm {d} y \, \mathrm {d} z \, \mathrm {d} \eta \, \mathrm {d} \theta \\
& \lesssim \langle (\lambda x, \lambda^s \xi) \rangle^{-n} \int_{\Omega_2'} \langle (y,z,\eta,\theta)\rangle^{- 4 d - 1} \,
\langle (y,z,\eta,\theta)\rangle^{m + 4 d + 1}
\langle (y,\eta)\rangle^n | V_{\overline \varphi} u(z,\theta) | \, \mathrm {d} y \, \mathrm {d} z \, \mathrm {d} \eta \, \mathrm {d} \theta \\
& \lesssim
\lambda^{- n \min(1,s)} 2^{n} \\
& \quad \times \int_{\Omega_2'} \langle (y,z,\eta,\theta)\rangle^{- 4 d - 1} \,
\langle (z,\theta)\rangle^{(m + 4 d + 1) \left( 1 + \max \left( s,\frac1s \right) \right) + n \max \left( s,\frac1s \right) } | V_{\overline \varphi} u(z,\theta) | \, \mathrm {d} y \, \mathrm {d} z \, \mathrm {d} \eta \, \mathrm {d} \theta \\
& \lesssim
\lambda^{- n \min(1,s)}
\sup_{w \in \mathbf R^{2d} \setminus \Gamma_2} \langle w\rangle^{ (m + 4 d + 1) \left( 1 + \max \left( s,\frac1s \right) \right) + n \max \left( s,\frac1s \right) } | V_{\overline \varphi} u(w) | \\
& \qquad \qquad \qquad \times \int_{\mathbf R^{4d}} \langle (y,z,\eta,\theta)\rangle^{- 4 d - 1} \mathrm {d} y \, \mathrm {d} z \, \mathrm {d} \eta \, \mathrm {d} \theta \\
& \lesssim \lambda^{- n \min(1,s)}.
\end{aligned}
\end{equation}
\begin{equation}
\begin{aligned}
& \int_{\Omega_2'} | V_\Phi K (y,z,\eta,-\theta) | \, |V_\varphi \varphi ( \lambda x-y, \lambda^s \xi-\eta) | \, | V_{\overline \varphi} u(z,\theta) | \, \mathrm {d} y \, \mathrm {d} z \, \mathrm {d} \eta \, \mathrm {d} \theta \\
& \lesssim \int_{\Omega_2'} \langle (y,z,\eta,\theta)\rangle^{m} | \, \langle (\lambda x-y, \lambda^s \xi-\eta) \rangle^{-n} \, | V_{\overline \varphi} u(z,\theta) | \, \mathrm {d} y \, \mathrm {d} z \, \mathrm {d} \eta \, \mathrm {d} \theta \\
& \lesssim \langle (\lambda x, \lambda^s \xi) \rangle^{-n} \int_{\Omega_2'} \langle (y,z,\eta,\theta)\rangle^{- 4 d - 1} \,
\langle (y,z,\eta,\theta)\rangle^{m + 4 d + 1}
\langle (y,\eta)\rangle^n | V_{\overline \varphi} u(z,\theta) | \, \mathrm {d} y \, \mathrm {d} z \, \mathrm {d} \eta \, \mathrm {d} \theta \\
& \lesssim
\lambda^{- n \min(1,s)} 2^{n} \\
& \quad \times \int_{\Omega_2'} \langle (y,z,\eta,\theta)\rangle^{- 4 d - 1} \,
\langle (z,\theta)\rangle^{(m + 4 d + 1) \left( 1 + \max \left( s,\frac1s \right) \right) + n \max \left( s,\frac1s \right) } | V_{\overline \varphi} u(z,\theta) | \, \mathrm {d} y \, \mathrm {d} z \, \mathrm {d} \eta \, \mathrm {d} \theta \\
& \lesssim
\lambda^{- n \min(1,s)}
\sup_{w \in \mathbf R^{2d} \setminus \Gamma_2} \langle w\rangle^{ (m + 4 d + 1) \left( 1 + \max \left( s,\frac1s \right) \right) + n \max \left( s,\frac1s \right) } | V_{\overline \varphi} u(w) | \\
& \qquad \qquad \qquad \times \int_{\mathbf R^{4d}} \langle (y,z,\eta,\theta)\rangle^{- 4 d - 1} \mathrm {d} y \, \mathrm {d} z \, \mathrm {d} \eta \, \mathrm {d} \theta \\
& \lesssim \lambda^{- n \min(1,s)}.
\end{aligned}
\end{equation} Finally, we need to estimate the integral over ![]() $(y,z,\eta, - \theta) \in \Omega_0$. Then,
$(y,z,\eta, - \theta) \in \Omega_0$. Then,  $(y,\eta) \in \mathbf R^{2d} \setminus \overline{\widetilde \Gamma}_{z_0, 2 \varepsilon}$. Hence,
$(y,\eta) \in \mathbf R^{2d} \setminus \overline{\widetilde \Gamma}_{z_0, 2 \varepsilon}$. Hence,
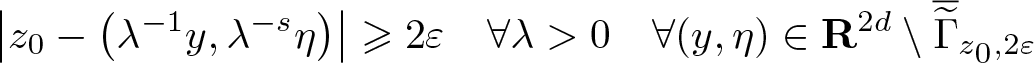 \begin{equation*}
\left| z_0 - \left( \lambda^{-1} y, \lambda^{-s} \eta \right) \right| \geqslant 2 \varepsilon \quad \forall \lambda \gt 0 \quad \forall (y,\eta) \in \mathbf R^{2d} \setminus \overline{\widetilde \Gamma}_{z_0, 2 \varepsilon}
\end{equation*}
\begin{equation*}
\left| z_0 - \left( \lambda^{-1} y, \lambda^{-s} \eta \right) \right| \geqslant 2 \varepsilon \quad \forall \lambda \gt 0 \quad \forall (y,\eta) \in \mathbf R^{2d} \setminus \overline{\widetilde \Gamma}_{z_0, 2 \varepsilon}
\end{equation*} and we have for ![]() $(x,\xi) \in z_0 + {\rm B}_\varepsilon$
$(x,\xi) \in z_0 + {\rm B}_\varepsilon$
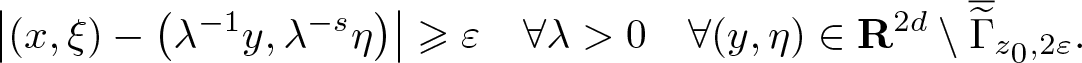 \begin{equation*}
\left| (x,\xi) - \left( \lambda^{-1} y, \lambda^{-s} \eta \right) \right| \geqslant \varepsilon \quad \forall \lambda \gt 0 \quad \forall (y,\eta) \in \mathbf R^{2d} \setminus \overline{\widetilde \Gamma}_{z_0, 2 \varepsilon}.
\end{equation*}
\begin{equation*}
\left| (x,\xi) - \left( \lambda^{-1} y, \lambda^{-s} \eta \right) \right| \geqslant \varepsilon \quad \forall \lambda \gt 0 \quad \forall (y,\eta) \in \mathbf R^{2d} \setminus \overline{\widetilde \Gamma}_{z_0, 2 \varepsilon}.
\end{equation*} It follows that for ![]() $\lambda \geqslant 1$,
$\lambda \geqslant 1$, ![]() $(x,\xi) \in z_0 + {\rm B}_\varepsilon$ and
$(x,\xi) \in z_0 + {\rm B}_\varepsilon$ and  $(y,\eta) \in \mathbf R^{2d} \setminus \overline{\widetilde \Gamma}_{z_0, 2 \varepsilon}$ we have
$(y,\eta) \in \mathbf R^{2d} \setminus \overline{\widetilde \Gamma}_{z_0, 2 \varepsilon}$ we have
 \begin{align*}
\left| ( \lambda x, \lambda^s \xi) - (y,\eta) \right|^2
& = \lambda^2 | x - \lambda^{-1} y |^2 + \lambda^{2s} | \xi - \lambda^{-s} \eta |^2 \\
& \geqslant \lambda^{2 \min (1,s)} \varepsilon^2.
\end{align*}
\begin{align*}
\left| ( \lambda x, \lambda^s \xi) - (y,\eta) \right|^2
& = \lambda^2 | x - \lambda^{-1} y |^2 + \lambda^{2s} | \xi - \lambda^{-s} \eta |^2 \\
& \geqslant \lambda^{2 \min (1,s)} \varepsilon^2.
\end{align*} Together with (4.5), (2.2) and (2.3), this gives if ![]() $(x,\xi) \in (x_0, \xi_0) + {\rm B}_\varepsilon$ for some
$(x,\xi) \in (x_0, \xi_0) + {\rm B}_\varepsilon$ for some ![]() $m,k \in \mathbf N$ and any
$m,k \in \mathbf N$ and any ![]() $n,N \in \mathbf N$
$n,N \in \mathbf N$
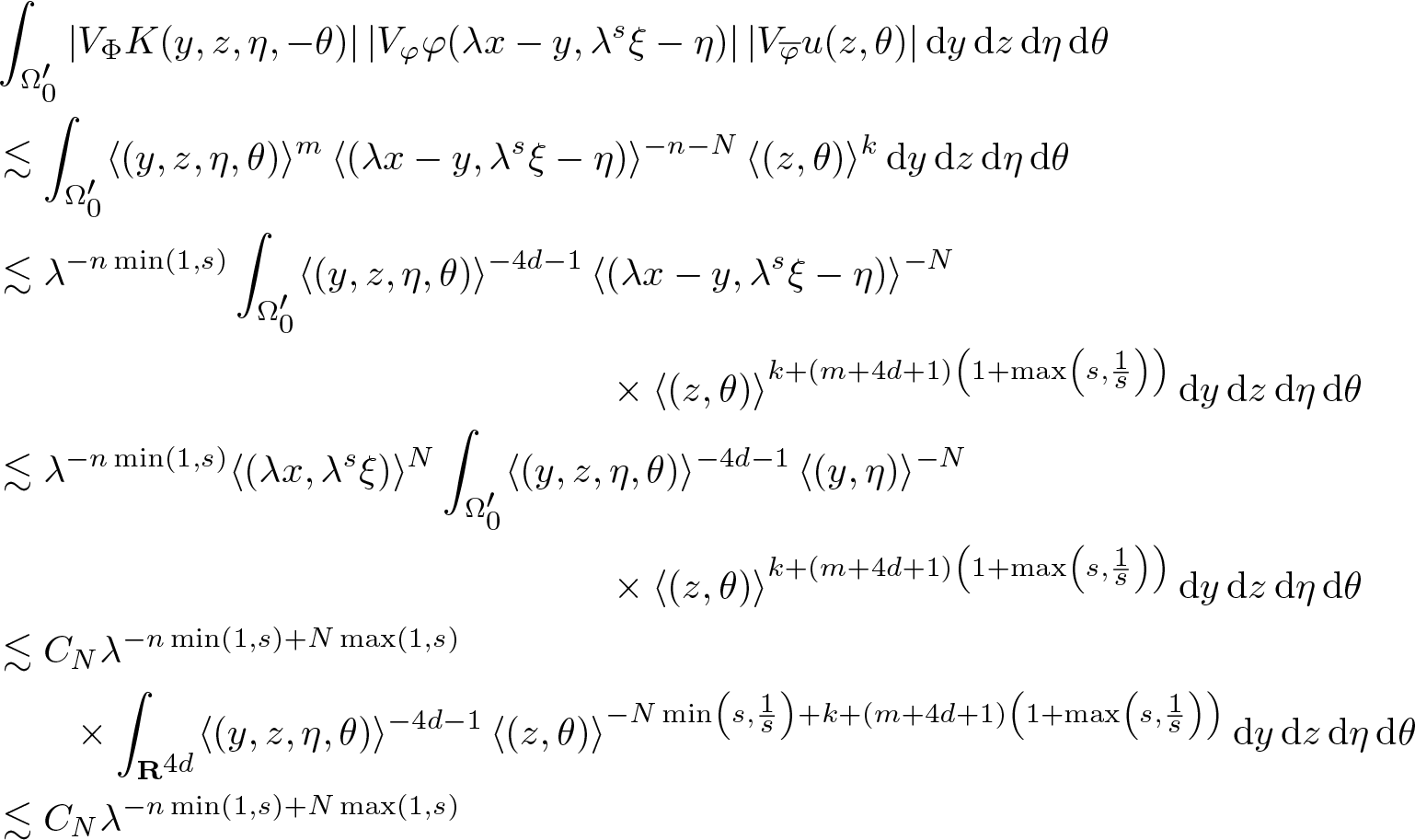 \begin{equation}
\begin{aligned}
& \int_{\Omega_0'} | V_\Phi K (y,z,\eta,-\theta) | \, |V_\varphi \varphi ( \lambda x-y, \lambda^s \xi-\eta) | \, | V_{\overline \varphi} u(z,\theta) | \, \mathrm {d} y \, \mathrm {d} z \, \mathrm {d} \eta \, \mathrm {d} \theta \\
& \lesssim \int_{\Omega_0'} \langle (y,z,\eta,\theta)\rangle^{m} \, \langle (\lambda x-y, \lambda^s \xi-\eta) \rangle^{-n-N} \,
\langle (z,\theta)\rangle^k
\, \mathrm {d} y \, \mathrm {d} z \, \mathrm {d} \eta \, \mathrm {d} \theta \\
& \lesssim
\lambda^{- n \min(1,s)}
\int_{\Omega_0'} \langle (y,z,\eta,\theta)\rangle^{- 4 d - 1} \,
\langle (\lambda x-y, \lambda^s \xi-\eta) \rangle^{-N} \\
& \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \times
\langle (z,\theta)\rangle^{ k + (m + 4 d + 1) \left( 1 + \max \left( s,\frac1s \right) \right) }
\, \mathrm {d} y \, \mathrm {d} z \, \mathrm {d} \eta \, \mathrm {d} \theta \\
& \lesssim
\lambda^{- n \min(1,s)}
\langle (\lambda x, \lambda^s \xi) \rangle^{N}
\int_{\Omega_0'} \langle (y,z,\eta,\theta)\rangle^{- 4 d - 1} \, \langle (y, \eta) \rangle^{-N} \\
& \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \times
\langle (z,\theta)\rangle^{ k + (m + 4 d + 1) \left( 1 + \max \left( s,\frac1s \right) \right) }
\, \mathrm {d} y \, \mathrm {d} z \, \mathrm {d} \eta \, \mathrm {d} \theta \\
& \lesssim
C_N \lambda^{- n \min(1,s) + N \max(1,s) } \\
& \qquad \times
\int_{\mathbf R^{4d}} \langle (y,z,\eta,\theta)\rangle^{- 4 d - 1} \,
\langle (z,\theta)\rangle^{- N \min \left( s,\frac1s \right) + k + (m + 4 d + 1) \left( 1 + \max \left( s,\frac1s \right) \right)}
\, \mathrm {d} y \, \mathrm {d} z \, \mathrm {d} \eta \, \mathrm {d} \theta \\
& \lesssim
C_N \lambda^{- n \min(1,s) + N \max(1,s) }
\end{aligned}
\end{equation}
\begin{equation}
\begin{aligned}
& \int_{\Omega_0'} | V_\Phi K (y,z,\eta,-\theta) | \, |V_\varphi \varphi ( \lambda x-y, \lambda^s \xi-\eta) | \, | V_{\overline \varphi} u(z,\theta) | \, \mathrm {d} y \, \mathrm {d} z \, \mathrm {d} \eta \, \mathrm {d} \theta \\
& \lesssim \int_{\Omega_0'} \langle (y,z,\eta,\theta)\rangle^{m} \, \langle (\lambda x-y, \lambda^s \xi-\eta) \rangle^{-n-N} \,
\langle (z,\theta)\rangle^k
\, \mathrm {d} y \, \mathrm {d} z \, \mathrm {d} \eta \, \mathrm {d} \theta \\
& \lesssim
\lambda^{- n \min(1,s)}
\int_{\Omega_0'} \langle (y,z,\eta,\theta)\rangle^{- 4 d - 1} \,
\langle (\lambda x-y, \lambda^s \xi-\eta) \rangle^{-N} \\
& \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \times
\langle (z,\theta)\rangle^{ k + (m + 4 d + 1) \left( 1 + \max \left( s,\frac1s \right) \right) }
\, \mathrm {d} y \, \mathrm {d} z \, \mathrm {d} \eta \, \mathrm {d} \theta \\
& \lesssim
\lambda^{- n \min(1,s)}
\langle (\lambda x, \lambda^s \xi) \rangle^{N}
\int_{\Omega_0'} \langle (y,z,\eta,\theta)\rangle^{- 4 d - 1} \, \langle (y, \eta) \rangle^{-N} \\
& \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \times
\langle (z,\theta)\rangle^{ k + (m + 4 d + 1) \left( 1 + \max \left( s,\frac1s \right) \right) }
\, \mathrm {d} y \, \mathrm {d} z \, \mathrm {d} \eta \, \mathrm {d} \theta \\
& \lesssim
C_N \lambda^{- n \min(1,s) + N \max(1,s) } \\
& \qquad \times
\int_{\mathbf R^{4d}} \langle (y,z,\eta,\theta)\rangle^{- 4 d - 1} \,
\langle (z,\theta)\rangle^{- N \min \left( s,\frac1s \right) + k + (m + 4 d + 1) \left( 1 + \max \left( s,\frac1s \right) \right)}
\, \mathrm {d} y \, \mathrm {d} z \, \mathrm {d} \eta \, \mathrm {d} \theta \\
& \lesssim
C_N \lambda^{- n \min(1,s) + N \max(1,s) }
\end{aligned}
\end{equation}if N is large enough.
Combining (4.21), (4.23) and (4.24) and taking into account (4.22), we have by (4.18) shown
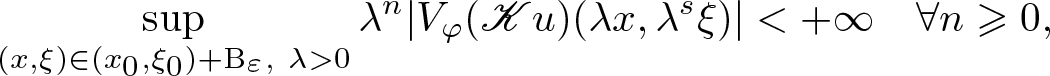 \begin{equation*}
\sup_{(x,\xi) \in (x_0, \xi_0) + {\rm B}_\varepsilon, \ \lambda \gt 0} \lambda^n | V_\varphi(\mathscr{K} u) ( \lambda x, \lambda^s \xi) | \lt + \infty \quad \forall n \geqslant 0,
\end{equation*}
\begin{equation*}
\sup_{(x,\xi) \in (x_0, \xi_0) + {\rm B}_\varepsilon, \ \lambda \gt 0} \lambda^n | V_\varphi(\mathscr{K} u) ( \lambda x, \lambda^s \xi) | \lt + \infty \quad \forall n \geqslant 0,
\end{equation*} which finally proves the claim ![]() $z_0 \notin \mathrm{WF}_{\rm g}^s (\mathscr{K} u)$.
$z_0 \notin \mathrm{WF}_{\rm g}^s (\mathscr{K} u)$.
5. Propagation of the s-Gabor wave front set for certain evolution equations
In [Reference Rodino and Wahlberg18, Remark 4.7], we discuss the initial value Cauchy problem for the evolution equation in dimension d = 1
 \begin{equation}
\left\{
\begin{array}{rl}
\partial_t u(t,x) + \mathrm{i} D_x^{m} u (t,x) & = 0, \quad m \in \mathbf N \setminus 0, \quad x \in \mathbf R, \quad t \in \mathbf R, \\
u(0,\cdot) & = u_0.
\end{array}
\right.
\end{equation}
\begin{equation}
\left\{
\begin{array}{rl}
\partial_t u(t,x) + \mathrm{i} D_x^{m} u (t,x) & = 0, \quad m \in \mathbf N \setminus 0, \quad x \in \mathbf R, \quad t \in \mathbf R, \\
u(0,\cdot) & = u_0.
\end{array}
\right.
\end{equation}It is a generalization of the Schrödinger equation for the free particle where m = 2.
Here, we generalize this equation into
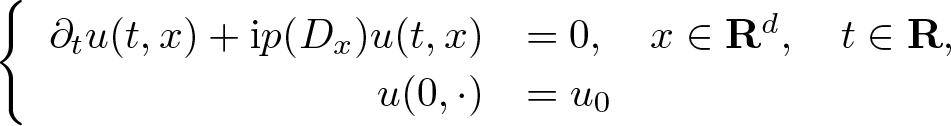 \begin{equation}
\left\{
\begin{array}{rl}
\partial_t u(t,x) + \mathrm{i} p(D_x) u (t,x) & = 0, \quad x \in {\mathbf R}^{d}, \quad t \in \mathbf R, \\
u(0,\cdot) & = u_0
\end{array}
\right.
\end{equation}
\begin{equation}
\left\{
\begin{array}{rl}
\partial_t u(t,x) + \mathrm{i} p(D_x) u (t,x) & = 0, \quad x \in {\mathbf R}^{d}, \quad t \in \mathbf R, \\
u(0,\cdot) & = u_0
\end{array}
\right.
\end{equation} where ![]() $p: {\mathbf R}^{d} \to \mathbf R$ is a polynomial with real coefficients of order
$p: {\mathbf R}^{d} \to \mathbf R$ is a polynomial with real coefficients of order ![]() $m \geqslant 2$, that is
$m \geqslant 2$, that is
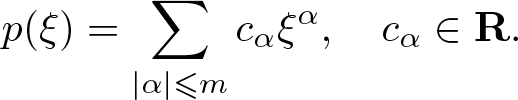 \begin{equation}
p (\xi) = \sum_{|\alpha| \leqslant m} c_\alpha \xi^\alpha, \quad c_\alpha \in \mathbf R.
\end{equation}
\begin{equation}
p (\xi) = \sum_{|\alpha| \leqslant m} c_\alpha \xi^\alpha, \quad c_\alpha \in \mathbf R.
\end{equation}The principal part is
 \begin{equation}
p_m (\xi) = \sum_{|\alpha| = m} c_\alpha \xi^\alpha,
\end{equation}
\begin{equation}
p_m (\xi) = \sum_{|\alpha| = m} c_\alpha \xi^\alpha,
\end{equation} and there exists ![]() $\alpha \in {\mathbf N}^{d}$ such that
$\alpha \in {\mathbf N}^{d}$ such that ![]() $|\alpha| = m$ and
$|\alpha| = m$ and ![]() $c_\alpha \neq 0$.
$c_\alpha \neq 0$.
The Hamiltonian is ![]() $p(\xi)$, and the Hamiltonian flow of the principal part
$p(\xi)$, and the Hamiltonian flow of the principal part ![]() $p_m(\xi)$ is given by
$p_m(\xi)$ is given by
The explicit solution to (5.2) is
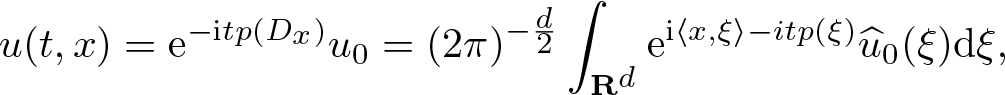 \begin{equation}
u (t,x)
= \mathrm{e}^{- \mathrm{i} t p(D_x)} u_0
= (2 \pi)^{- \frac{d}{2}} \int_{{\mathbf R}^{d}} \mathrm{e}^{\mathrm{i} \langle x, \xi \rangle - i t p(\xi)} \widehat u_0 (\xi) \mathrm {d} \xi,
\end{equation}
\begin{equation}
u (t,x)
= \mathrm{e}^{- \mathrm{i} t p(D_x)} u_0
= (2 \pi)^{- \frac{d}{2}} \int_{{\mathbf R}^{d}} \mathrm{e}^{\mathrm{i} \langle x, \xi \rangle - i t p(\xi)} \widehat u_0 (\xi) \mathrm {d} \xi,
\end{equation} for ![]() $u_0 \in \mathscr{S}({\mathbf R}^{d})$. Thus,
$u_0 \in \mathscr{S}({\mathbf R}^{d})$. Thus, ![]() $u (t,x) = \mathscr{K}_t u_0(x)$ where
$u (t,x) = \mathscr{K}_t u_0(x)$ where ![]() $\mathscr{K}_t$ is the operator with Schwartz kernel
$\mathscr{K}_t$ is the operator with Schwartz kernel
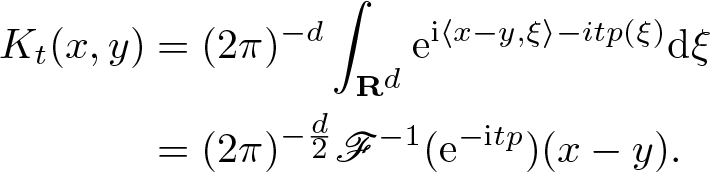 \begin{align*}
K_t (x,y) & = (2 \pi)^{-d} \int_{{\mathbf R}^{d}} \mathrm{e}^{\mathrm{i} \langle x-y, \xi \rangle - i t p(\xi)} \mathrm {d} \xi \\
& = (2 \pi)^{- \frac{d}{2}} \mathscr{F}^{-1} (\mathrm{e}^{- \mathrm{i} t p}) (x-y).
\end{align*}
\begin{align*}
K_t (x,y) & = (2 \pi)^{-d} \int_{{\mathbf R}^{d}} \mathrm{e}^{\mathrm{i} \langle x-y, \xi \rangle - i t p(\xi)} \mathrm {d} \xi \\
& = (2 \pi)^{- \frac{d}{2}} \mathscr{F}^{-1} (\mathrm{e}^{- \mathrm{i} t p}) (x-y).
\end{align*} The propagator ![]() $\mathscr{K}_t$ is a convolution operator with kernel
$\mathscr{K}_t$ is a convolution operator with kernel
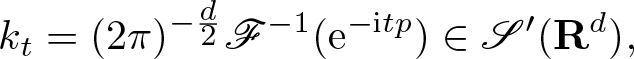 \begin{equation}
k_t = (2 \pi)^{- \frac{d}{2}} \mathscr{F}^{-1} (\mathrm{e}^{- \mathrm{i} t p}) \in \mathscr{S}'({\mathbf R}^{d}),
\end{equation}
\begin{equation}
k_t = (2 \pi)^{- \frac{d}{2}} \mathscr{F}^{-1} (\mathrm{e}^{- \mathrm{i} t p}) \in \mathscr{S}'({\mathbf R}^{d}),
\end{equation}and we may write
where ![]() $\kappa \in \mathbf R^{2d \times {2d}}$ is the matrix defined by
$\kappa \in \mathbf R^{2d \times {2d}}$ is the matrix defined by ![]() $\kappa(x,y) = (x+\frac{y}{2}, x - \frac{y}{2})$ for
$\kappa(x,y) = (x+\frac{y}{2}, x - \frac{y}{2})$ for ![]() $x,y \in {\mathbf R}^{d}$.
$x,y \in {\mathbf R}^{d}$.
It follows from (5.6) that ![]() $\mathscr{K}_t: \mathscr{S}({\mathbf R}^{d}) \to \mathscr{S}({\mathbf R}^{d})$ is continuous, invertible with inverse
$\mathscr{K}_t: \mathscr{S}({\mathbf R}^{d}) \to \mathscr{S}({\mathbf R}^{d})$ is continuous, invertible with inverse ![]() $\mathscr{K}_{-t}$, and
$\mathscr{K}_{-t}$, and ![]() $\mathscr{K}_{-t} = \mathscr{K}_t^*$ which denotes the adjoint. Defining for
$\mathscr{K}_{-t} = \mathscr{K}_t^*$ which denotes the adjoint. Defining for ![]() $u \in \mathscr{S}'({\mathbf R}^{d})$,
$u \in \mathscr{S}'({\mathbf R}^{d})$,
gives a unique continuous extension ![]() $\mathscr{K}_t: \mathscr{S}'({\mathbf R}^{d}) \to \mathscr{S}'({\mathbf R}^{d})$.
$\mathscr{K}_t: \mathscr{S}'({\mathbf R}^{d}) \to \mathscr{S}'({\mathbf R}^{d})$.
As we will see now the continuity of ![]() $\mathscr{K}_t$ on
$\mathscr{K}_t$ on ![]() $\mathscr{S}({\mathbf R}^{d})$ and the unique extension to a continuous operator on
$\mathscr{S}({\mathbf R}^{d})$ and the unique extension to a continuous operator on ![]() $\mathscr{S}'({\mathbf R}^{d})$ may alternatively be proved as a consequence of
$\mathscr{S}'({\mathbf R}^{d})$ may alternatively be proved as a consequence of ![]() $\mathrm{WF}_{\rm g,1}^s(K_t) = \mathrm{WF}_{\rm g,2}^s(K_t) = \emptyset$ and Proposition 4.2.
$\mathrm{WF}_{\rm g,1}^s(K_t) = \mathrm{WF}_{\rm g,2}^s(K_t) = \emptyset$ and Proposition 4.2.
The next result shows that ![]() $\mathscr{K}_t$ propagates the anisotropic s-Gabor wave front set along the Hamiltonian flow of pm if
$\mathscr{K}_t$ propagates the anisotropic s-Gabor wave front set along the Hamiltonian flow of pm if  $s = \frac{1}{m-1}$, whereas the anisotropic s-Gabor wave front set is invariant if
$s = \frac{1}{m-1}$, whereas the anisotropic s-Gabor wave front set is invariant if  $s \lt \frac{1}{m-1}$. In the proof, we use the symplectic matrix
$s \lt \frac{1}{m-1}$. In the proof, we use the symplectic matrix
 \begin{equation*}
\mathcal{J} =
\left(
\begin{array}{cc}
0 & I_d \\
-I_d & 0
\end{array}
\right) \in \mathbf R^{2d \times 2d}.
\end{equation*}
\begin{equation*}
\mathcal{J} =
\left(
\begin{array}{cc}
0 & I_d \\
-I_d & 0
\end{array}
\right) \in \mathbf R^{2d \times 2d}.
\end{equation*}Theorem 5.1. Let ![]() $m \geqslant 2$ and let p be defined by (5.3), (5.4) and denote by (5.5) the Hamiltonian flow of the principal part pm. Suppose
$m \geqslant 2$ and let p be defined by (5.3), (5.4) and denote by (5.5) the Hamiltonian flow of the principal part pm. Suppose ![]() $\mathscr{K}_t : \mathscr{S}({\mathbf R}^{d}) \to \mathscr{S}({\mathbf R}^{d})$ is the continuous linear operator with Schwartz kernel (5.8) where kt is defined by (5.7). Then, if
$\mathscr{K}_t : \mathscr{S}({\mathbf R}^{d}) \to \mathscr{S}({\mathbf R}^{d})$ is the continuous linear operator with Schwartz kernel (5.8) where kt is defined by (5.7). Then, if  $0 \lt s \leqslant \frac{1}{m-1}$, we have for
$0 \lt s \leqslant \frac{1}{m-1}$, we have for ![]() $u \in \mathscr{S}' ({\mathbf R}^{d})$ and
$u \in \mathscr{S}' ({\mathbf R}^{d})$ and ![]() $t \in \mathbf R$
$t \in \mathbf R$
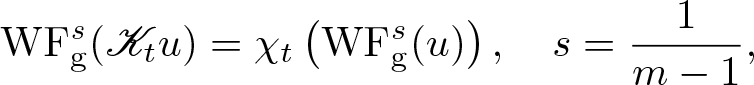 \begin{align}
& \mathrm{WF_{g}^{\it s}} ( \mathscr{K}_t u) = \chi_t \left( \mathrm{WF_{g}^{\it s}} (u) \right), \quad s = \frac{1}{m-1},
\end{align}
\begin{align}
& \mathrm{WF_{g}^{\it s}} ( \mathscr{K}_t u) = \chi_t \left( \mathrm{WF_{g}^{\it s}} (u) \right), \quad s = \frac{1}{m-1},
\end{align} \begin{align}
& \mathrm{WF_{g}^{\it s}} ( \mathscr{K}_t u) = \mathrm{WF_{g}^{\it s}} (u), \quad s \lt \frac{1}{m-1}.
\end{align}
\begin{align}
& \mathrm{WF_{g}^{\it s}} ( \mathscr{K}_t u) = \mathrm{WF_{g}^{\it s}} (u), \quad s \lt \frac{1}{m-1}.
\end{align}Proof. First let  $s = \frac{1}{m-1}$. By [Reference Rodino and Wahlberg19, Theorem 7.1], we have
$s = \frac{1}{m-1}$. By [Reference Rodino and Wahlberg19, Theorem 7.1], we have
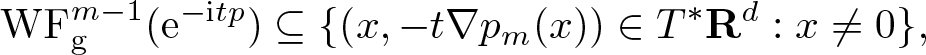 \begin{equation*}{\mathrm W\mathrm F}_{\mathrm g}^{m-1}(\mathrm e^{-\mathrm itp})\subseteq\{(x,-t\nabla p_m(x))\in T^\ast\mathbf R^d: x\neq0\},\end{equation*}
\begin{equation*}{\mathrm W\mathrm F}_{\mathrm g}^{m-1}(\mathrm e^{-\mathrm itp})\subseteq\{(x,-t\nabla p_m(x))\in T^\ast\mathbf R^d: x\neq0\},\end{equation*}and from [Reference Rodino and Wahlberg19, Eq. (4.6) and Proposition 4.3 (i)], we obtain
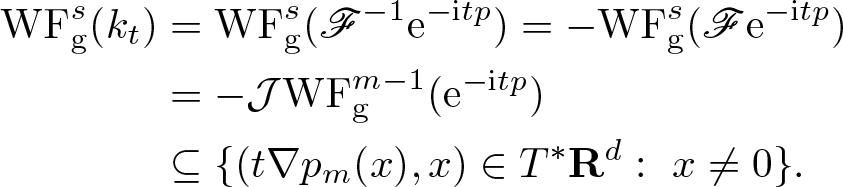 \begin{align*}
\mathrm{WF}_{\rm g}^{s} ( k_t )
& = \mathrm{WF}_{\rm g}^{s} ( \mathscr{F}^{-1} \mathrm{e}^{- \mathrm{i} t p} )
= - \mathrm{WF}_{\rm g}^{s} ( \mathscr{F} \mathrm{e}^{- \mathrm{i} t p} ) \\
& = - \mathcal{J} \mathrm{WF}_{\rm g}^{m-1} ( \mathrm{e}^{- \mathrm{i} t p} ) \\
& \subseteq \{ ( t \nabla p_m(x) , x) \in T^* {\mathbf R}^{d}: \ x \neq 0 \}.
\end{align*}
\begin{align*}
\mathrm{WF}_{\rm g}^{s} ( k_t )
& = \mathrm{WF}_{\rm g}^{s} ( \mathscr{F}^{-1} \mathrm{e}^{- \mathrm{i} t p} )
= - \mathrm{WF}_{\rm g}^{s} ( \mathscr{F} \mathrm{e}^{- \mathrm{i} t p} ) \\
& = - \mathcal{J} \mathrm{WF}_{\rm g}^{m-1} ( \mathrm{e}^{- \mathrm{i} t p} ) \\
& \subseteq \{ ( t \nabla p_m(x) , x) \in T^* {\mathbf R}^{d}: \ x \neq 0 \}.
\end{align*}Now, (5.8), [Reference Rodino and Wahlberg19, Proposition 4.3 (ii)], Proposition 3.2 and [Reference Rodino and Wahlberg19, Proposition 5.3 (iii)] yield
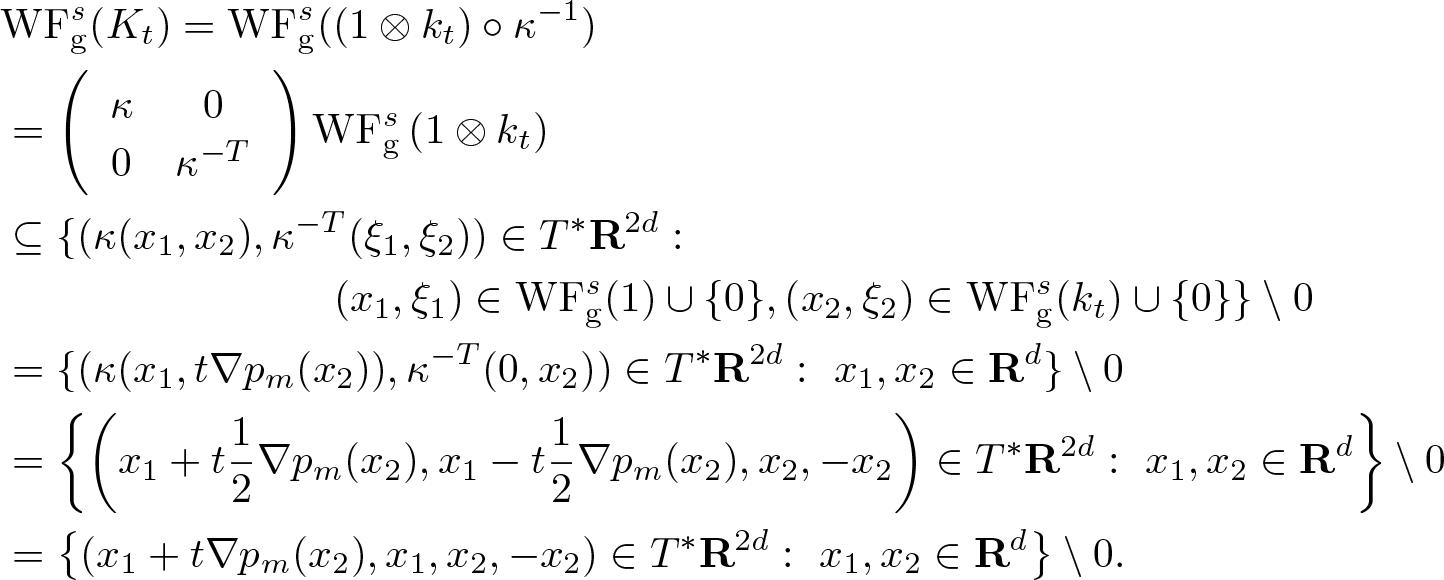 \begin{align*}
& \mathrm{WF_{g}^{\it s}} (K_t)
= \mathrm{WF_{g}^{\it s}} ( \left( 1 \otimes k_t \right) \circ \kappa^{-1} ) \\
& =
\left(
\begin{array}{cc}
\kappa & 0 \\
0 & \kappa^{-T}
\end{array}
\right)
\mathrm{WF_{g}^{\it s}} \left( 1 \otimes k_t \right) \\
& \subseteq \{ ( \kappa( x_1, x_2), \kappa^{-T}(\xi_1, \xi_2) ) \in T^* \mathbf R^{2d}: \\
& \qquad \qquad \qquad \qquad (x_1, \xi_1) \in \mathrm{WF_{g}^{\it s}} (1) \cup \{ 0 \},
(x_2, \xi_2) \in \mathrm{WF_{g}^{\it s}} (k_t) \cup \{ 0 \} \} \setminus 0 \\
& = \{ ( \kappa( x_1, t \nabla p_m(x_2) ), \kappa^{-T} (0, x_2) ) \in T^* \mathbf R^{2d}: \ x_1, x_2 \in {\mathbf R}^{d} \} \setminus 0 \\
& = \left\{ \left( x_1 + t \frac12 \nabla p_m(x_2), x_1 - t \frac12 \nabla p_m(x_2), x_2, - x_2 \right) \in T^* \mathbf R^{2d}: \ x_1, x_2 \in {\mathbf R}^{d} \right\} \setminus 0 \\
& = \left\{ \left( x_1 + t \nabla p_m(x_2), x_1, x_2, - x_2 \right) \in T^* \mathbf R^{2d}: \ x_1, x_2 \in {\mathbf R}^{d} \right\} \setminus 0.
\end{align*}
\begin{align*}
& \mathrm{WF_{g}^{\it s}} (K_t)
= \mathrm{WF_{g}^{\it s}} ( \left( 1 \otimes k_t \right) \circ \kappa^{-1} ) \\
& =
\left(
\begin{array}{cc}
\kappa & 0 \\
0 & \kappa^{-T}
\end{array}
\right)
\mathrm{WF_{g}^{\it s}} \left( 1 \otimes k_t \right) \\
& \subseteq \{ ( \kappa( x_1, x_2), \kappa^{-T}(\xi_1, \xi_2) ) \in T^* \mathbf R^{2d}: \\
& \qquad \qquad \qquad \qquad (x_1, \xi_1) \in \mathrm{WF_{g}^{\it s}} (1) \cup \{ 0 \},
(x_2, \xi_2) \in \mathrm{WF_{g}^{\it s}} (k_t) \cup \{ 0 \} \} \setminus 0 \\
& = \{ ( \kappa( x_1, t \nabla p_m(x_2) ), \kappa^{-T} (0, x_2) ) \in T^* \mathbf R^{2d}: \ x_1, x_2 \in {\mathbf R}^{d} \} \setminus 0 \\
& = \left\{ \left( x_1 + t \frac12 \nabla p_m(x_2), x_1 - t \frac12 \nabla p_m(x_2), x_2, - x_2 \right) \in T^* \mathbf R^{2d}: \ x_1, x_2 \in {\mathbf R}^{d} \right\} \setminus 0 \\
& = \left\{ \left( x_1 + t \nabla p_m(x_2), x_1, x_2, - x_2 \right) \in T^* \mathbf R^{2d}: \ x_1, x_2 \in {\mathbf R}^{d} \right\} \setminus 0.
\end{align*} Since ![]() $m \geqslant 2$, we have
$m \geqslant 2$, we have ![]() $\nabla p_m(0) = 0$ and
$\nabla p_m(0) = 0$ and ![]() $\mathrm{WF}_{\rm g,1}^s(K_t) = \mathrm{WF}_{\rm g,2}^s(K_t) = \emptyset$ follows. By Proposition 4.2, we thus obtain an alternative proof of the already known fact that
$\mathrm{WF}_{\rm g,1}^s(K_t) = \mathrm{WF}_{\rm g,2}^s(K_t) = \emptyset$ follows. By Proposition 4.2, we thus obtain an alternative proof of the already known fact that ![]() $\mathscr{K}_t$ is continuous on
$\mathscr{K}_t$ is continuous on ![]() $\mathscr{S}({\mathbf R}^{d})$ and extends uniquely to be continuous on
$\mathscr{S}({\mathbf R}^{d})$ and extends uniquely to be continuous on ![]() $\mathscr{S}'({\mathbf R}^{d})$. Invertibility also follows since
$\mathscr{S}'({\mathbf R}^{d})$. Invertibility also follows since ![]() $\mathscr{K}_t^{-1} = \mathscr{K}_{-t}$. Moreover, we may apply Theorem 4.4 which gives for
$\mathscr{K}_t^{-1} = \mathscr{K}_{-t}$. Moreover, we may apply Theorem 4.4 which gives for ![]() $u \in \mathscr{S}'({\mathbf R}^{d})$
$u \in \mathscr{S}'({\mathbf R}^{d})$
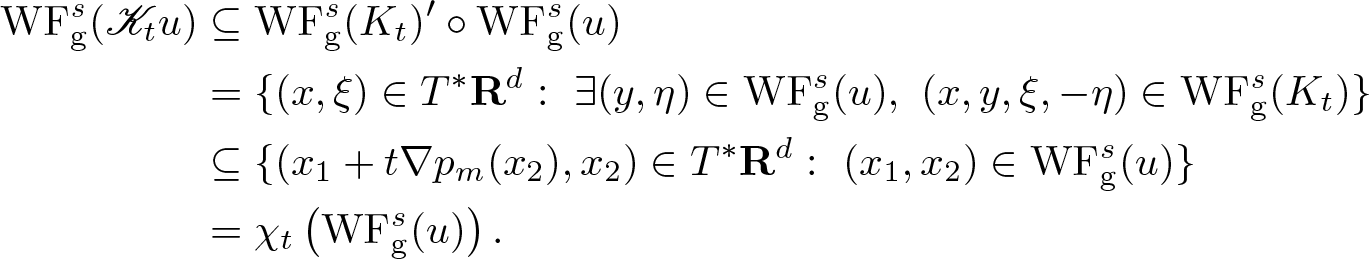 \begin{align*}
\mathrm{WF_{g}^{\it s}}( \mathscr{K}_t u)
& \subseteq \mathrm{WF_{g}^{\it s}} (K_t)' \circ \mathrm{WF_{g}^{\it s}} (u) \\
& = \{ (x,\xi) \in T^* {\mathbf R}^{d}: \ \exists (y,\eta) \in \mathrm{WF_{g}^{\it s}} (u), \ (x,y, \xi, - \eta) \in \mathrm{WF_{g}^{\it s}} (K_t) \} \\
& \subseteq \{ ( x_1 + t \nabla p_m(x_2) , x_2) \in T^* {\mathbf R}^{d}: \ (x_1,x_2) \in \mathrm{WF_{g}^{\it s}} (u) \} \\
& = \chi_t \left( \mathrm{WF_{g}^{\it s}} (u) \right).
\end{align*}
\begin{align*}
\mathrm{WF_{g}^{\it s}}( \mathscr{K}_t u)
& \subseteq \mathrm{WF_{g}^{\it s}} (K_t)' \circ \mathrm{WF_{g}^{\it s}} (u) \\
& = \{ (x,\xi) \in T^* {\mathbf R}^{d}: \ \exists (y,\eta) \in \mathrm{WF_{g}^{\it s}} (u), \ (x,y, \xi, - \eta) \in \mathrm{WF_{g}^{\it s}} (K_t) \} \\
& \subseteq \{ ( x_1 + t \nabla p_m(x_2) , x_2) \in T^* {\mathbf R}^{d}: \ (x_1,x_2) \in \mathrm{WF_{g}^{\it s}} (u) \} \\
& = \chi_t \left( \mathrm{WF_{g}^{\it s}} (u) \right).
\end{align*} The opposite inclusion follows from ![]() $\mathscr{K}_{t}^{-1} = \mathscr{K}_{-t}$,
$\mathscr{K}_{t}^{-1} = \mathscr{K}_{-t}$,
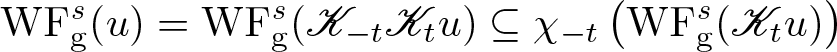 \begin{equation*}
\mathrm{WF_{g}^{\it s}}( u)
= \mathrm{WF_{g}^{\it s}}( \mathscr{K}_{-t} \mathscr{K}_t u) \\
\subseteq \chi_{-t} \left( \mathrm{WF_{g}^{\it s}} ( \mathscr{K}_t u) \right)
\end{equation*}
\begin{equation*}
\mathrm{WF_{g}^{\it s}}( u)
= \mathrm{WF_{g}^{\it s}}( \mathscr{K}_{-t} \mathscr{K}_t u) \\
\subseteq \chi_{-t} \left( \mathrm{WF_{g}^{\it s}} ( \mathscr{K}_t u) \right)
\end{equation*} and ![]() $\chi_{-t} = \chi_t^{-1}$. We have proved (5.9).
$\chi_{-t} = \chi_t^{-1}$. We have proved (5.9).
It remains to consider the case  $s \lt \frac1{m-1}$. By [Reference Rodino and Wahlberg19, Theorem 7.2], we have
$s \lt \frac1{m-1}$. By [Reference Rodino and Wahlberg19, Theorem 7.2], we have
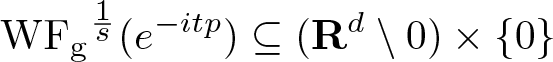 \begin{equation*}
\mathrm{WF_{\rm g}}^{\frac1{s}} ( e^{- i t p} )
\subseteq ( {\mathbf R}^{d} \setminus 0 ) \times \{ 0 \}
\end{equation*}
\begin{equation*}
\mathrm{WF_{\rm g}}^{\frac1{s}} ( e^{- i t p} )
\subseteq ( {\mathbf R}^{d} \setminus 0 ) \times \{ 0 \}
\end{equation*}and from [Reference Rodino and Wahlberg19, Eq. (4.6) and Proposition 4.3 (i)], we obtain
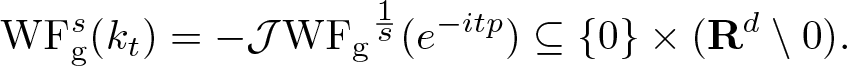 \begin{equation*}
\mathrm{WF_{g}^{\it s}} ( k_t )
= - \mathcal{J} \mathrm{WF_{\rm g}}^{\frac1{s}} ( e^{- i t p} ) \\
\subseteq \{ 0 \} \times ( {\mathbf R}^{d} \setminus 0 ).
\end{equation*}
\begin{equation*}
\mathrm{WF_{g}^{\it s}} ( k_t )
= - \mathcal{J} \mathrm{WF_{\rm g}}^{\frac1{s}} ( e^{- i t p} ) \\
\subseteq \{ 0 \} \times ( {\mathbf R}^{d} \setminus 0 ).
\end{equation*}Again, (5.8), [Reference Rodino and Wahlberg19, Propositions 4.3 (ii) and 5.3 (iii)] and Proposition 3.2 yield
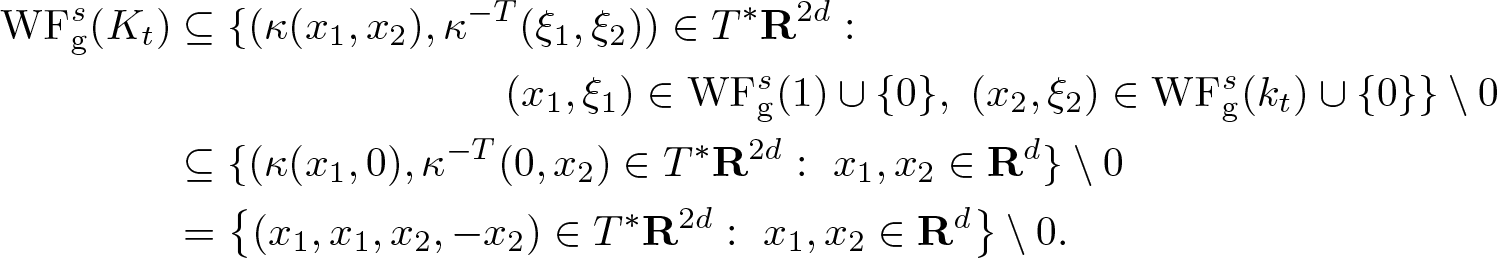 \begin{align*}
\mathrm{WF_{g}^{\it s}} (K_t)
& \subseteq \{ ( \kappa( x_1, x_2), \kappa^{-T}(\xi_1, \xi_2) ) \in T^* \mathbf R^{2d}: \\
& \qquad \qquad \qquad \qquad (x_1, \xi_1) \in \mathrm{WF_{g}^{\it s}} (1) \cup \{ 0 \},
\ (x_2, \xi_2) \in \mathrm{WF_{g}^{\it s}} (k_t) \cup \{ 0 \} \} \setminus 0 \\
& \subseteq \{ ( \kappa( x_1, 0 ), \kappa^{-T}(0, x_2) \in T^* \mathbf R^{2d}: \ x_1, x_2 \in {\mathbf R}^{d} \} \setminus 0 \\
& = \left\{ \left( x_1 , x_1, x_2, - x_2 \right) \in T^* \mathbf R^{2d}: \ x_1, x_2 \in {\mathbf R}^{d} \right\} \setminus 0.
\end{align*}
\begin{align*}
\mathrm{WF_{g}^{\it s}} (K_t)
& \subseteq \{ ( \kappa( x_1, x_2), \kappa^{-T}(\xi_1, \xi_2) ) \in T^* \mathbf R^{2d}: \\
& \qquad \qquad \qquad \qquad (x_1, \xi_1) \in \mathrm{WF_{g}^{\it s}} (1) \cup \{ 0 \},
\ (x_2, \xi_2) \in \mathrm{WF_{g}^{\it s}} (k_t) \cup \{ 0 \} \} \setminus 0 \\
& \subseteq \{ ( \kappa( x_1, 0 ), \kappa^{-T}(0, x_2) \in T^* \mathbf R^{2d}: \ x_1, x_2 \in {\mathbf R}^{d} \} \setminus 0 \\
& = \left\{ \left( x_1 , x_1, x_2, - x_2 \right) \in T^* \mathbf R^{2d}: \ x_1, x_2 \in {\mathbf R}^{d} \right\} \setminus 0.
\end{align*} Again, we have ![]() $\mathrm{WF}_{\rm g,1}^s(K_t) = \mathrm{WF}_{\rm g,2}^s(K_t) = \emptyset$, and Proposition 4.2 gives continuity on
$\mathrm{WF}_{\rm g,1}^s(K_t) = \mathrm{WF}_{\rm g,2}^s(K_t) = \emptyset$, and Proposition 4.2 gives continuity on ![]() $\mathscr{S} ({\mathbf R}^{d})$ and on
$\mathscr{S} ({\mathbf R}^{d})$ and on ![]() $\mathscr{S}' ({\mathbf R}^{d})$; the invertibility also follows since
$\mathscr{S}' ({\mathbf R}^{d})$; the invertibility also follows since ![]() $\mathscr{K}_t^{-1} = \mathscr{K}_{-t}$. Now, Theorem 4.4 gives for
$\mathscr{K}_t^{-1} = \mathscr{K}_{-t}$. Now, Theorem 4.4 gives for ![]() $u \in \mathscr{S}'({\mathbf R}^{d})$
$u \in \mathscr{S}'({\mathbf R}^{d})$
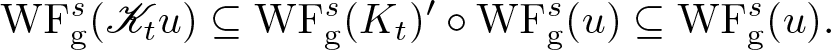 \begin{equation*}
\mathrm{WF_{g}^{\it s}} ( \mathscr{K}_t u)
\subseteq \mathrm{WF_{g}^{\it s}} (K_t)' \circ \mathrm{WF_{g}^{\it s}} (u)
\subseteq \mathrm{WF_{g}^{\it s}} (u).
\end{equation*}
\begin{equation*}
\mathrm{WF_{g}^{\it s}} ( \mathscr{K}_t u)
\subseteq \mathrm{WF_{g}^{\it s}} (K_t)' \circ \mathrm{WF_{g}^{\it s}} (u)
\subseteq \mathrm{WF_{g}^{\it s}} (u).
\end{equation*} The opposite inclusion again follows from ![]() $\mathscr{K}_{t}^{-1} = \mathscr{K}_{-t}$ and
$\mathscr{K}_{t}^{-1} = \mathscr{K}_{-t}$ and ![]() $\chi_{-t} = \chi_t^{-1}$. We have proved (5.10).
$\chi_{-t} = \chi_t^{-1}$. We have proved (5.10).
Remark 5.2. If  $s \gt \frac1{m-1}$ and
$s \gt \frac1{m-1}$ and ![]() $p_m (x) \neq 0$ for all
$p_m (x) \neq 0$ for all ![]() $x \in {\mathbf R}^{d} \setminus 0$, then by [Reference Rodino and Wahlberg19, Theorem 7.3]
$x \in {\mathbf R}^{d} \setminus 0$, then by [Reference Rodino and Wahlberg19, Theorem 7.3]
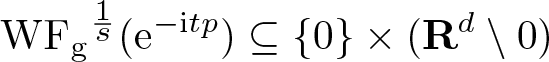 \begin{equation*}
\mathrm{WF_{\rm g}}^{\frac1{s}} ( \mathrm{e}^{- \mathrm{i} t p} )
\subseteq \{ 0 \} \times ( {\mathbf R}^{d} \setminus 0 )
\end{equation*}
\begin{equation*}
\mathrm{WF_{\rm g}}^{\frac1{s}} ( \mathrm{e}^{- \mathrm{i} t p} )
\subseteq \{ 0 \} \times ( {\mathbf R}^{d} \setminus 0 )
\end{equation*}so [Reference Rodino and Wahlberg19, Eq. (4.6) and Proposition 4.3 (i)] give
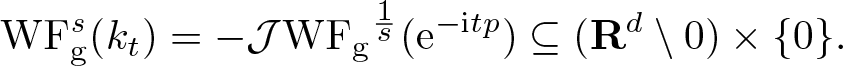 \begin{equation*}
\mathrm{WF_{g}^{\it s}} ( k_t )
= - \mathcal{J} \mathrm{WF_{\rm g}}^{\frac1{s}} ( \mathrm{e}^{- \mathrm{i} t p} ) \\
\subseteq ( {\mathbf R}^{d} \setminus 0 ) \times \{ 0 \}.
\end{equation*}
\begin{equation*}
\mathrm{WF_{g}^{\it s}} ( k_t )
= - \mathcal{J} \mathrm{WF_{\rm g}}^{\frac1{s}} ( \mathrm{e}^{- \mathrm{i} t p} ) \\
\subseteq ( {\mathbf R}^{d} \setminus 0 ) \times \{ 0 \}.
\end{equation*}Again (5.8), [Reference Rodino and Wahlberg19, Propositions 4.3 (ii) and 5.3 (iii)], and Proposition 3.2 yield
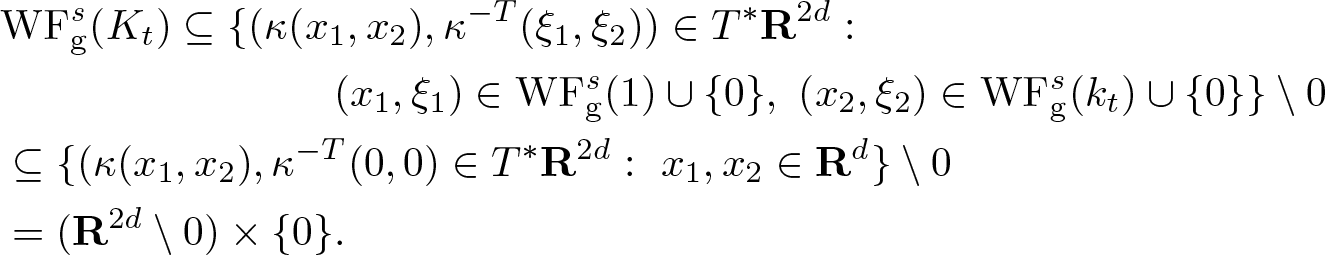 \begin{align*}
& \mathrm{WF_{g}^{\it s}} (K_t)
\subseteq \{ ( \kappa( x_1, x_2), \kappa^{-T}(\xi_1, \xi_2) ) \in T^* \mathbf R^{2d}: \\
& \qquad \qquad \qquad \qquad (x_1, \xi_1) \in \mathrm{WF_{g}^{\it s}} (1) \cup \{ 0 \},
\ (x_2, \xi_2) \in \mathrm{WF_{g}^{\it s}} (k_t) \cup \{ 0 \} \} \setminus 0 \\
& \subseteq \{ ( \kappa( x_1, x_2 ), \kappa^{-T}(0,0) \in T^* \mathbf R^{2d}: \ x_1, x_2 \in {\mathbf R}^{d} \} \setminus 0 \\
& = ( \mathbf R^{2d} \setminus 0 ) \times \{ 0 \}.
\end{align*}
\begin{align*}
& \mathrm{WF_{g}^{\it s}} (K_t)
\subseteq \{ ( \kappa( x_1, x_2), \kappa^{-T}(\xi_1, \xi_2) ) \in T^* \mathbf R^{2d}: \\
& \qquad \qquad \qquad \qquad (x_1, \xi_1) \in \mathrm{WF_{g}^{\it s}} (1) \cup \{ 0 \},
\ (x_2, \xi_2) \in \mathrm{WF_{g}^{\it s}} (k_t) \cup \{ 0 \} \} \setminus 0 \\
& \subseteq \{ ( \kappa( x_1, x_2 ), \kappa^{-T}(0,0) \in T^* \mathbf R^{2d}: \ x_1, x_2 \in {\mathbf R}^{d} \} \setminus 0 \\
& = ( \mathbf R^{2d} \setminus 0 ) \times \{ 0 \}.
\end{align*} In this case, we cannot conclude that ![]() $\mathrm{WF}_{\rm g,1}^s(K_t)$ and
$\mathrm{WF}_{\rm g,1}^s(K_t)$ and ![]() $\mathrm{WF}_{\rm g,2}^s(K_t)$ are empty.
$\mathrm{WF}_{\rm g,2}^s(K_t)$ are empty.
Thus, we cannot conclude any statement on propagation of the anisotropic s-Gabor wave front set from Theorem 4.4 when  $s \gt \frac1{m-1}$.
$s \gt \frac1{m-1}$.
Acknowledgements
This work was partially supported by the MIUR project ‘Dipartimenti di Eccellenza 2018-2022’ (CUP E11G18000350001).




