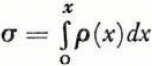Sir,
The depth-density curve presented by Langway Reference Langway 1 in this Journal cannot be represented by an exponential relation between depth and density.
When the data extended only to 47.5 m., Landauer Reference Bader 2 fitted an empirical curve to them. It was a simple exponential relation and fitted the existing data very well; but, as he pointed out, it did not satisfy the boundary conditions because density increased without limit with depth (the curve was asymptotic to a line with slope 5.26×10−3 gm. cm.−3 m.−1). In an attempt to find an analytic expression, I have used load rather than depth as the independent variable; and, in place of firn density as the dependent variable, its reciprocal (specific volume) is used.Reference Benson 3
As a first approximation it is assumed that melt is negligible and the only cause of densification is the load of overlying snow and firn applied at a constant rate. No assumptions are made regarding the mechanics of deformation of ice; in particular, the effect of time in producing deformation by creep at constant load is neglected. The assumptions are that: (1) the ice in a firn sample remains at constant density, (2) the change of volume produced by load is solely due to the elimination of pore space, and (3) the rate at which pore space is eliminated with increasing load is proportional to the pore space itself. These assumptions are expressed in equation (1)
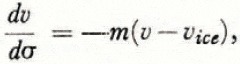

Equation (1) may readily be solved for v in terms of σ:

When Landauer’s depth-density data are expressed in terms of specific volume and load they agree with equation (2) except in the top 10 meters where the rate of densification is much higher.
The more rapid rate of densification in the top so meters is attributed to processes which operate in addition to the compressive action of the load. Among these is the sudden collapse of low-density layers which are common in the top 6 to 10 meters, but not below. Another factor in the upper layers is the annual variation of temperature which has an amplitude of 1° C. to a depth of nearly 10 m. A more complete discussion of these points is presented by Benson.Reference Benson 3
If good depth-density data are available to a depth of 30 m. it is possible to determine the constants m and v o in equation (2). For Landauer’s data m = 4·3 × 10−4 cm.2 gm.−1, and v o = 2·0 cm.3 gm.−1. Then, because the function