1. Introduction

Most of the West Antarctic ice sheet rests on rock that is below sea-level. As such it may be unstable (Reference WeertmanWeertman 1974) and may become decoupled from its bed by a variety of processes (Hughes 1973). Grounding-line retreat of the large fast-flowing ice streams which drain the interior may be the most important mechanism whereby collapse of the ice sheet could occur (Reference HughesHughes 1977). Since the position of the grounding line is determined by the condition of hydrostatic equilibrium, it will advance outwards if the ice thickness increases or if sea-level falls, ultimately to the edge of the continental shelf if conditions allow. Conversely it is argued (Reference HughesHughes 1977) that if the ice thins or sea-level rises, icestream grounding lines may retreat over low sills into the heart of the West Antarctic ice sheet. Grounding-line retreat will be halted if a high bedrock sill is reached or i f an ice shelf forms and restrains the flow of ice across the grounding line. Thus the Ronne, Filchner, and Ross ice shelves are probably impeding flow of most of the ice streams which drain the present West Antarctic ice sheet, thereby tending to render the ice sheet stable (Reference Thomas and BentleyThomas and Bentley 1978)

The CLIMAP ice-sheet disintegration model (Reference Stuiver, Denton, Hughes, Fastook, Denton and HughesStuiver and others 1981) indicates that Pine Island Bay in the Amundsen Sea may be the area mostlikely to control any collapse of the West Antarctic ice sheet both in the Holocene and also today. Two large ice streams, which drain the interior of West Antarct ica, Pine Island Glacier, and Thwaites Glacier, calve directly into the bay without the restraining effect of an ice shelf. Reference Stuiver, Denton, Hughes, Fastook, Denton and HughesStuiver and others (1981) suggest that, provided that no high bedrock sill exists, the grounding line of Pine Island Glacier in particular could retreat along the Bentley Subglacial Trench and across the base of the Antarctic Peninsula. A similar retreat could take place up Rutford Ice Stream (Reference Stuiver, Denton, Hughes, Fastook, Denton and HughesStuiver and others 1981) and ultimately the collapse of the ice sheet would lead to the expansion of Pine Island Bay and/or Ronne Ice Shelf into the Byrd Subglacial Basin.

Clearly, field data on the ice thickness and bedrock topography of this region are crucial to the argument. In February 1981 the British Antarctic Survey carried out radio echo-sounding in Ellsworth Land as part of ajoint project with IWD Dalziel of Lamont-Doherty Geological Observatory to investigate the geological relationship between Greater and Lesser Antarctica. Based at the US National Science Foundation's (NSF) unoccupied Ellsworth Mountains field camp a total of 16 000 km was flown using fuelleft by NSF the previous year. Aflight on 6 February crossed Pine Island Glacier from northeast to south-west, returning to the middle of the glacier and turning upstream from there. On 9 February the entire length of the glacier was sounded and a transverse line flown close to the ice front. These flights are shown superimposed on a Landsat image of Pine Island Glacier (Fig. l).

Fig.1. Landsat image of Pine Island Glacier showing flight lines of 6 February (dashed line) and 9 February 1981 (solid line). The dotted line shows the position of the inferred grounding line.

2. Profiles

Figure 2(a) shows a longitudinal profile of the surface and bottom elevations and Figure 3 shows two transverse profiles. Surface elevations were obtained from pressure altimetry, allowing for terrain clearance. The difference in radio altimeter readings crossing the ice front gave the glacier elevation a.s.l. and provided control for the pressure readings. Surface elevations should be within ±10 m. Ice thicknesses were measured from the radio echo film and should be within ±30 m; the velocity of radio waves in ice was taken as 169 mμs⁻¹.

Fig.2. Longitudinal profiles of Pine Island Glacier. (Letters refer to Fig.1.) (a) Surface and bottom elevations of Pine Island Glacier. The dashed lines are the profile of 6 February, the solid lines from the flight of 9 February. The dotted lines indicate the thickness of ice needed to float in hydrostatic equilibrium. They follow the bottom profiles up to a point of sudden divergence, indicating the position of the grounding line (see text). (b) Thickness profiles of Pine Island Glacier. The solid line shows the profile as measured on the flight of 9 February 1981, the dashed line as derived from the model.

Fig.3. Surface and bottom elevations across Pine Island Glacier. (Letters refer to Fig.1.) (a) Near the ice front (there is a break in the radio echo between the glacier and ice shelf to the west). (b) About 20 km down-stream from the grounding line.

By using measured values of surface elevation and ice thickness, the average ice density was calculated on the assumption that the glacier was floating in hydrostatic equilibrium on sea-water of density 1.028 Mg m⁻³. Where the glacier was floating, the average density was approximately constant at around 0.89 Mg m⁻³. Going up-stream, there was a sharp reduction in the apparent average density coinciding with a prominent break in slope of the surface, suggesting that the glacier was aground. To confirm the position of the grounding line, the surface elevation data were used to calculate the thickness of ice of average density 0.89 Mg m⁻³ that would float in hydrostatic equilibrium with sea-water. Where the glacier is aground the “equilibrium” thickness was of course greater than the measured thickness (Fig.2). In this way the position of the grounding line was found to within ±1 km

By comparing the position of the ice front on three Landsat images taken over a two-year period between 1973 and 1975 the average velocity at the ice front was found to be 2.1±0.2 km a⁻¹. This compares with an independent estimate, using the same data, of 2.2 km a⁻¹ (RS Williams personal communication to C W M Swithinbank). The shape of the ice front is basically unchanged, indicating that there were no major calving events during this period.

The position of the ice front in February 1981 was close to where a large rift was seen to run across the glacier in a 1973 Landsat image. With an average velocity of more than 2 km a⁻¹ the ice front should have been at least 16 km further forward by 1981. The ice front must calve periodically, maintaining the same approximate position.

The longitudinal profile can be modelled by using aslightly modified version of the procedure described by Reference SandersonSanderson (1979) for calculating equilibrium profiles of ice shelves. The general equation for the thickness profile of an ice shelf confined in a bay with non-parallel sides (Reference SandersonSanderson 1979: equation 27) is

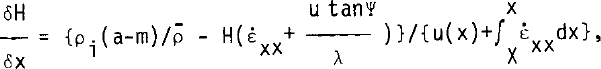
where H is the ice thickness, x the horizontal axis (originat the grounding line and positive in the direction of ice movement), ρ_i the density of pure ice,ρ̄ the average ice density over a vertical column, a the accumulation rate, and m the melt rate (positive for melting), both expressed in metres of pure ice per unit time; u(x) is the horizontal veloc it λ the half-width of the bay, ψ the angle of the bay wall to the centre line, X the total length of the ice shelf, and ε⋅_xx the longitudinal strainrate given by

where g is acceleration due to gravity, B and n are parameters in the flow law for ice, written in the_form ε⋅= (τ/B)ⁿ, and B ̄ is the average over depth of B; τ_S is the shear stress at the bay sides, ρ_w the density of sea-water, and d is a parameter in the expression describing the variations of snow density with depth z below the surface

where b is a constant.

Sanderson (1979) derived Equation (1) using the principle of continuity of mass. Equation (1) cannot be solved analytically, but may be readily solved numerically by calculating the incremental change in the thickness δH for a small horizontal step δx. The method which Sanderson used to obtain profiles was to integrate backwards towards the hinge zone from boundary conditions set up at the ice front. This was done because of the form of the integral in Equation (2), where the strain-rate is a function of the horizontal distance from the ice front. By considering the overall mass balance of the ice shelf for given conditions of bay geometry, net accumulation, length along a flow line, ice thickness, and velocity at the grounding line, there is just one degree of freedom in choice of boundary conditions at the ice front: choosing the thickness H(X) determines the velocity u(X). Sanderson's method therefore was to choose a value for H(X) (or u(X)) and integrate backwards. A tedious process of trial and error was required to find the value of H(X) which fitted the required grounding-line parameters.

An alternative method, allowing integration forwards from the hinge zone towards the ice front, can be found by considering the meaning of the awkward integral in Equation (2). If we assume for simplicity at this moment that the half-width λ of the ice shelf is constant, then the integral I reduces to

which can be w r i t t en as H̄(X - x)/λ, where H is the average ice thickness between the ice front and a point at distance (X - x) from the ice front. The expression H̄(X - x) is just the total area of iceshelf side wall down-stream from the point at distance (X - x) from the ice front. If instead of choosing an initial value for the length X of the ice shelf, we choose a value for the integral I, then, although we do not know the form of the thickness over x (which we are tryingtocalculate), we have still constrained the total length X, but it is unknown until the full profile has been calculated.

We have made no more assumptions than before and have no more degrees of freedom (i.e. adjustable parameters) than in the backward integration method. All that has been done is to replace an initial boundary condition for the ice-shelf length by a similar condition for the total ice-shelf side-wall area.

The effect of pinning by ice rises or locally grounded areas which exert an up-stream restraining force Fr is allowed for (Reference SandersonSanderson 1979) by changing Equation (2) to

where

Pine Island Glacier was modelled using Equation (1) and (3). Initial conditions were thickness and velocity at the grounding line, bay geometry, values for (a-m), ρ _a, B̄,τ̄ and F_r. and a value asr for the integral

Figure 2 shows the thickness profile obtained by using the values of the parameters given in Table I. Ice thickness at the grounding line was taken from the radio echo results. The bay geometry was inter preted from Landsat images but it was difficultto decide how to define the margins of Pine Island Glacier in regions where there is extensive shear crevassing. The grounding line is not easy to delineate and, as with the Rutford Ice Stream (Reference Stephenson and DoakeStephenson and Doake 1982), it may curve tortuously between ill-defined side walls. The value of pe was almost constant for ρ̄ and d varying over_a large range of reasonable values. The value for B̄ was equivalent to an average temperature of -14°C (Reference ThomasThomas 1973). The profiles were little affected by accumulation and melting rates of the order of magnitude considered here. The limiting shear stress τ̄_S was allowed to fall from 90 to 40 kN m⁻² on the assumption that a preferred crystal orientation might be established at the glacier sides by the fast flow of the ice (Reference Thomas and BentleyThomas and Bentley 1978). The restraining force Fr was necessary in the converging bay over the first 16 km in order to make the modelf it the measured profile. The physical explanation is that even i f the shear stress at the sides was zero, the ice shelf would still feel a restraint owing to the convergence of the side walls. A somewhat analogous situation is that of a glacier sliding over a wavy bed, where there is a net up-stream force exerted by the traction normal to the glacier bed even where there is no frict i on (Reference MorlandMoriand 1976). The convergent lateral strainrate is an order of magnitude less than the longitudinal strain-rate and so does not invalidate the derivation of Equation (2). By knowing the velocity and thickness at the ice front, a simple mass-balance calculation gave an approximate figure for the veloc ity at the grounding line. The value of the integral

was then adjusted so that the computed length corresponded with that measured (84 km).

The interaction between the parameters in the model is complex, but to gain some idea about the sensitivity of the profiles to changes in values of the parameters, Table I also shows the approximate percentage change required to vary the ice-front position, velocity, or thickness by 10%.

Because of large uncertainties in the values of most of the parameters the model is unconstrained. The degree to which the model can be made to f i t the measured profile depends on how much the input data varies with position. For the example shown here the only changes in the input data occurred where the bay geometry also changed. The biggest discrepancy between modelled and measured profiles, of 200 m at 32 km, can be reduced by introducing another, but arbitrary, “break point”in the data and allowing Fr or xs to change there. However, this procedure can soon degenerate to curve fitting with little gain in physical insight. It is worth noting that Equation (3) can be written in the form

where

is an effective shear stress restraining the motion. Thus practically any profile could be modelled by allowing τ_eff t0 vary ln a sufficiently complicated way with distance. For Pine Island Glacier values for τeff would only have to fluctuate between 160 and 0 kN m⁻² in order to fit the profile. These values seem reasonable but it is difficult to understand why they should fluctuate quickly.

It was difficult to make the model fit the thin ice near the ice front. Features on the Landsat image (Fig.l) suggest that the flight did not follow a flow line for about the last 20 km. The transverse profile at the ice front (Fig.3) shows that the average thickness is nearly 500 m, in much better agreement with model results. The model ice front velocity was 2.21 km a⁻¹.

3. Stability of pine island glacier

A model developed from a steady-state assumption can successfully reproduce the measured thickness profile and ice-front velocity. However, because of the insensitivity of the model to non-steady-state behaviour, it is not possible to determine whether the glacier is in an equilibrium state or not. Nonsteady- state behaviour might be simulated by allowing aδH/δt term to be incorporated with the netaccumulation terms. As Table I shows, however, the profile is relatively insensitive to small changes in net accumulation, implying that thinning or thickening rates as high as a few ma⁻¹ would have little direct effect on the profiles. They would, however, eventually change the thickness at the grounding line, which would cause the position of the grounding line to migrate. Both of these effects would change the longitudinal profile.

The position of the grounding line may also oscillate in response to conditions near the terminus. At present the grounding line is held on a rock bar 200 m high. In one profile the grounding line is near the top of the bar while on the other profile it is at the bottom. The rock bar is likely to be continuous between the two profiles and it lies parallel to and just up-stream from a prominent feature on the Landsat Image (Fig.l). With this limited information It is difficult to decide whether or not the rock bar plays a crucial role in controlling the position of the grounding line and hence the possible stability of the ice sheet.

4. Mass balance

From the surface-elevation data obtained on flights during February 1981 and from radio echosounding from Siple station in January 1975 (Reference SwithinbankSwithlnbank 1977) the map in Figure 4 has been drawn up, showing Ice-sheet elevation to within ±50 m. The drainage basin of Pine Island Glacier has an area of 214 000±20 000 km²Taking an average figure for accumulation 1n t h i s area of 0.40±0.1 Mg m-2 a ⁻¹ (Reference Bull and QuamBull 1971, Giovinetto 1964) the total input to the glacier system 1s 86±30 Gt a⁻¹. Mass flux at the ice front Is 25±6 Gt a⁻¹ based on an average velocity of 2.1+0.2 km a⁻¹, an average thickness of 0.5±0.03 km and a width of 26±2.5 km. Therefore, the minimum possible input of 56 Gt a⁻¹ is roughly twice the maximum possible output and it may be inferred that the ice in the drainage basin Is building up.

Fig.4. The surface form of the ice sheet as determined by pressure altlmetry during radio echo-sounding flights (thin dashed lines) and Tropical Wind, Energy Conversion and Reference Level Experiment (TWERLE) balloon data (Levanon personal communication). The estimated drainage basins of Pine Island Glacier and Rutford Ice Stream are shown by the heavy dashed line.

A similar Inference i s made by Allison (1979) for the Lambert Glacier basin. With an input of 60 Gt a⁻¹ and losses to the Amery Ice Shelf and by ablation of 18 Gt a⁻¹, he suggests that the ice level is currently rising, possibly undergoing a post-surge build-up. Also, Reference Shimizu and MellorShimizu and others (1978) show that the Shirase Glacier drainage basin is not in equilibrium but thickening. Input to the Shirase system is 12.7 Gt a⁻¹ and losses total 7.4 Gt a⁻¹.

In all three cases input exceeds output by 1.5 to 3 times. But because of the uncertainty surrounding accumulation rates and the magnitude of the errors quoted by some authors, conclusions about ice-sheet build-up can only be tentative. The accumulation rate of 0.404 Mg m⁻² a⁻¹ cited by Reference Bull and QuamBull (1971) and Reference Giovinetto and MellorGiovinetto (1964) for the area of the Pine Island Glacier catchment i s based on stratigraphy from the Ellsworth Highland traverse by Reference Shimizu and MellorShimizu (1964) whose stated opinion i s that "stratigraphic interpretation is subjective, especially in coastal regions of Antarctica". Allison's (1979) budget surplus of 42 Gt a⁻¹ for the Lambert Glacier basin is subject to estimated limits of +9 and +89 Gt a⁻¹ so that, while positive, the actual mass balance may leave only a small surplus. The figure of 12.7 Gt a"1 quoted as input for the Shirase Glacier basin is based on calculations by Reference Yamada and WatanabeYamada and Watanabe (1978) who attach maximum and minimum values of 20.8 and 4.6 Gt a⁻¹. The minimum accumulation i s actually lower than the discharge figure quoted by Reference Shimizu, Watanabe, Kobayashi, Yamada, Naruse and AgetaShimizu and others (1978) for the Shirase Glacier.

An interesting comparison may be made between Pine Island Glacier and the Rutford Ice Stream which drains that part of Ellsworth Land which lies to the east of the Pine Island Glacier basin. The drainage basin of the Rutford Ice Stream is smaller, 40 500±4 000 km2 and annual accumulation is probably around 0.30 Mg m⁻² a⁻¹ (Reference Stephenson and DoakeStephenson and Doake (1982). Mass flux at the grounding line is 18.5±2.0 Gt a⁻¹ using values of 0.40 km a-1 for velocity, 1.7 km for ice thickness, and 30 km for ice-stream width. Applying an estimated error of 25% to the accumulation rate, accumulation over the basin is 12.2 Gt a⁻¹, with minimum and maximum values of 7.9 and 16.5 Gt a⁻¹. There would thus appear to be a negative mass balance in the system. This comparison between Pine Island Glacier and Rutford Ice Stream also assumes a change in accumulation from 0.4 to 0.3 Mg m⁻² a⁻¹ at the Ice ice divide and further illustrates the problems of deriving, with any confidence, input measurements from scanty and possibly erroneous accumulation data.

Conclusion

Radio echo thickness measurements on Pine Island Glacier have been made along longitudinal and transverse profiles. The results show that the grounding Tine is on a rock bar between 1200 and 1300 m below sea-level. The longitudinal profile of the floating part of the glacier showed an abrupt thinning about 16 km down-stream from the grounding lin e, coinciding with a change In bay geometry from converging to nearly parallel sides. Using the velocity at the ice front deduced from satellite Imagery, the longitudinal thickness profile has been successfully modelled assuming steady-state conditions. However, this cannot be taken as evidence that the glacier is necessarily in an equilibrium state

Mass-balance calculations suggest that the drainage basin may be building up, as appears to be the case with some other major Antarctic 1ce streams. However, accumulation data are so scarce and possible errors so large that any such conclusions should be regarded as tentative.