It has been proposed that a small mean difference can be magnified when continuous data are transformed to categorical data (e.g. response or remission). Reference Moncrieff and Kirsch1 This apparent discrepancy between continuous and response/remission measures implies that the rating scale scores are not normally distributed, which is a violation of the assumptions underlying the analysis of covariance (ANCOVA) model. Hence, it is also an indication that not all patients benefit from the intervention. This issue has important implications with respect to understanding the clinical significance of antidepressant medications, as some have argued that the small mean differences in symptom scores (compared with placebo) observed in meta-analyses of randomised controlled trials (RCTs) of newer generation antidepressants indicate that the utility of these treatments falls below the threshold of clinical significance for all but the most severely depressed patients. Reference Kirsch, Deacon, Huedo-Medina, Scoboria, Moore and Johnson2–Reference Fournier, DeRubeis, Hollon, Dimidjian, Amsterdam and Shelton4
There are various ways in which continuous parameters, such as total scores on a depression rating scale, can change as a result of an intervention. For example, one intervention can move the whole distribution, indicating an improvement for all patients, whereas another intervention might improve scores in only some patients. These different patterns of improvement can result in the same mean change in the study population. Although data can be analysed using ANCOVA, assuming that all patients benefit from the intervention in terms of improvement on a rating scale, models that address the latter pattern of improvement have not been explored using data from RCTs of antidepressants. The analysis reported here was undertaken to determine whether it is possible to distinguish between these two patterns by pooling data from a comprehensive data-set of placebo-controlled RCTs in major depressive disorder. Specifically, we aimed to determine whether the distribution of post-treatment scores shifts laterally from baseline to the end of treatment or, conversely, whether the shape of the distribution changes. Thus, we applied the mixture model, which includes the ANCOVA as a special case, in an attempt to improve the description of the observed score distribution while preserving a relatively simple interpretation of the effect of the intervention.
Method
Data were pooled from all five of the trials of escitalopram sponsored by Forest and Lundbeck. Reference Lepola, Loft and Reines5–Reference Alexopoulos, Gordon and Zhang9 These were randomised placebo-controlled trials in which it was possible to receive escitalopram at a dose of 20 mg per day (Table 1). Khan et al have shown that antidepressant–placebo differences are greater in patients with severe depression than in those with moderate depression, Reference Khan, Leventhal, Khan and Brown10,Reference Khan, Brodhead, Kolts and Brown11 and Bech et al have demonstrated that 20 mg is a more effective daily dose of escitalopram than 10 mg for treatment of patients with severe depression, Reference Bech, Andersen and Wade12 defined as those with a baseline score of 30 or above on the Montgomery–Åsberg Depression Rating Scale (MADRS). Reference Montgomery and Åsberg13 Thus, in order to have as large a signal-to-noise ratio as possible, only patients with a baseline MADRS score of 30 or over were included in the initial
Table 1 Summary data for studies included in pooled analysis

| Study | Duration weeks | Dose mg/day | All patients n | Patients with severe MDD a n | Mean age years |
|---|---|---|---|---|---|
| Lepola et al 20035 | 8 | Placebo | 154 | 58 | 43 |
| Escitalopram 10–20 | 155 | 69 | 43 | ||
| Citalopram 20–40 | 159 | 69 | 44 | ||
| Burke et al 20026 | 8 | Placebo | 119 | 59 | 39 |
| Escitalopram 10 b | 118 | 42 | 40 | ||
| Escitalopram 20 | 123 | 51 | 40 | ||
| Citalopram 40 | 125 | 60 | 41 | ||
| Rapaport et al 20047 | 8 | Placebo | 125 | 49 | 42 |
| Escitalopram 10–20 | 124 | 49 | 41 | ||
| Citalopram 20–40 | 119 | 42 | 42 | ||
| Ninan et al 20038 | 8 | Placebo | 151 | 88 | 39 |
| Escitalopram 10–20 | 143 | 89 | 38 | ||
| Alexopoulos et al 20049 | 8 | Placebo | 132 | 78 | 41 |
| Escitalopram 10–20 | 131 | 77 | 40 | ||
| Sertraline 50–200 | 135 | 70 | 40 | ||
| Total | Placebo 681 | Placebo 332 | |||
| Escitalopram 676 | Escitalopram 335 | ||||
MDD, major depressive disorder.
a Baseline score on the Montgomery–Åsberg Depression Rating Scale ≥30.
b These patients are not included in the analyses since escitalopram 10 mg/day has not shown any robust effect in patients with severe depression.
analyses. After validating the analyses in the more severe subset, analyses were repeated for the overall study group, as well as the subset with less severe depression.
Details of the individual studies have been published elsewhere; Reference Lepola, Loft and Reines5–Reference Alexopoulos, Gordon and Zhang9 no unpublished study was excluded. Analyses are based on the full-analysis set, comprising all patients who took at least one dose of study medication, and had at least one valid post-baseline MADRS assessment. Data are from week 8, using the method of last observation carried forward (LOCF). Although we are aware of the limitations of this conservative approach to account for the data of participants who drop out of the study (see, for example, papers by Lavori and Mallinckrodt et al), Reference Lavori14,Reference Mallinckrodt, Clark and David15 we used LOCF because it was used in several of the meta-analyses that support the contention that antidepressants have small effects. Reference Kirsch, Deacon, Huedo-Medina, Scoboria, Moore and Johnson2–Reference Fournier, DeRubeis, Hollon, Dimidjian, Amsterdam and Shelton4 Remission was defined as a MADRS score of ≤10 or ≤12 and response as a 50% or greater decrease from baseline in MADRS total score.
Statistical analysis
The mixture model, a parametric, group-based approach, Reference McLachlan and Peel16 was used to identify patient subgroups and to directly model the skewness of the observed MADRS scores at week 8. By using a mixture of probability distributions that are suitably specified to describe the data, this modelling strategy explicitly recognises uncertainty in group membership and assumes no single factor as necessary and sufficient in determining group membership. Reference Zhang, Mitchell, Bambauer, Jones and Prigerson17 It was assumed that both treatment groups (placebo or escitalopram) consisted of two subgroups (i.e. two latent classes, Reference Larsen18 or mixture components): one comprising patients who benefited from treatment and the other comprising patients who did not. The MADRS score at week 8 was assumed to be normally distributed within each of the subgroups regardless of treatment group. Hence, the distribution of the scores among patients who benefit from the treatment was assumed to be the same for the two treatment groups and the same assumption was made for patients who did not benefit. So, a difference in the distribution of MADRS scores at week 8 between treatment groups would be attributed to different proportions of patients benefiting from the treatment, rather than a shift in a single distribution as in the ANCOVA model. This leads to three types of patients: those who benefit from either of the treatments (placebo benefiters), those who benefit from neither treatment (escitalopram non-benefiters) and those who benefit from escitalopram but not placebo. It is noted that the case with no placebo benefiters, no escitalopram non-benefiters and equal variance in the benefiter and non-benefiter groups is identical to the standard ANCOVA. In this sense, the mixture model is a generalisation of the ANCOVA.
It is not directly known to which subgroup each specific patient belongs, and class assignment is done implicitly during the estimation of the parameters of the model, although individual probabilities of the likelihood of a patient belonging to the benefiter group can be obtained. Our focus here is on finding a model that fits the data better than the ANCOVA, while keeping an intuitive clinical interpretation of the treatment effect. To this end, the mixture model allows for a flexible shape of the distribution of the observed MADRS scores at week 8, including bimodal or just skewed distributions. Based on the above assumptions, the model for the MADRS score at week 8 (MADRSW8) included the effect (β) of the baseline MADRS score (MADRSBL) and an intercept (αSTUDY), which varied between the five studies:
where GROUP is a dichotomous latent class variable taking the value 0 for patients who benefit from treatment and 1 for patients who do not benefit from treatment, and λ is the mean difference in the MADRS score at week 8 between non-benefiters and benefiters (which is the same for both treatment groups). The last term (ε) is the error, which is assumed to be normally distributed with a mean of zero and a variance that differs between benefiters and non-benefiters; in other words, the populations of benefiters and non-benefiters are assumed to be normally distributed with a variance of σ0 2 and σ1 2 respectively. The effect of treatment (placebo or escitalopram) enters the equation indirectly, as the probability of a patient being in group 0 (the benefiter group) depends on treatment. Thus, the difference in mean MADRS score at week 8 between treatment groups is due to different proportions of benefiters in the two treatment groups.
All parameters including λ, σ0 2 and σ1 2 were estimated jointly by the maximum likelihood principle using a program written in R (http://www.r-project.org). Although the ANCOVA model is statistically nested within the mixture model (the ANCOVA is obtained from the mixture model by restricting the probabilities of being a benefiter to 1 in the escitalopram group and 0 in the placebo group and setting σ0 2 equal to σ1 2), a formal test comparing these models is not possible, and Akaike’s information criterion was used instead. Reference Akaike, Petrov and Csaki19 The primary criterion for judging the fit of the model was the fit to the observed distribution of MADRS scores observed at week 8. The predictions of the observed response and remission rates were compared between the ANCOVA and mixture model to investigate whether the mixture model is a substantial improvement.
Results
There was no significant difference between treatment groups at baseline (Table 2). For all patients (n = 1357) the mean baseline MADRS total score was 29.6 (s.d. = 4.5), the mean age was 41 (s.d. = 12) years and 61.5% of patients were women. Using a median split, patients with MADRS scores below 30 were classified as less severely depressed and those scoring 30 or higher were classified as more severely depressed. Among the subset with more severe depression, 335 patients were treated with escitalopram and 332 with placebo.
Table 2 Patient characteristics at baseline

| Less severe depression a | More severe depression b | |||
|---|---|---|---|---|
| Escitalopram | Placebo | Escitalopram | Placebo | |
| Patients treated, n | 341 | 349 | 335 | 332 |
| Gender: female, n | 211 | 224 | 196 | 204 |
| Age, years: | ||||
| Mean (s.d.) | 40.9 (12.0) | 41.5 (12.1) | 39.7 (11.1) | 40.5 (11.6) |
| Range | 18–73 | 18–76 | 19–71 | 18–70 |
| ≥65 years, n | 5 | 5 | 1 | 2 |
| MADRS score: mean (s.d.) | 25.9 (2.3) | 26.1 (2.3) | 33.1 (2.6) | 33.4 (3.2) |
MADRS, Montgomery–Åsberg Depression Rating Scale.
a Baseline MADRS score <30.
b Baseline MADRS score ≥30.
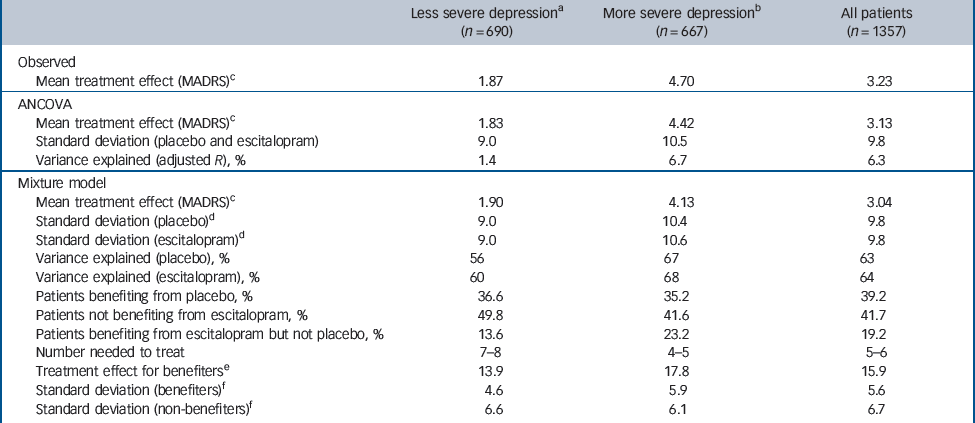
Table 3 Treatment effect and participants benefiting from treatment at week 8
| Less severe depression a (n = 690) | More severe depression b (n = 667) | All patients (n = 1357) | |
|---|---|---|---|
| Observed | |||
| Mean treatment effect (MADRS) c | 1.87 | 4.70 | 3.23 |
| ANCOVA | |||
| Mean treatment effect (MADRS) c | 1.83 | 4.42 | 3.13 |
| Standard deviation (placebo and escitalopram) | 9.0 | 10.5 | 9.8 |
| Variance explained (adjusted R), % | 1.4 | 6.7 | 6.3 |
| Mixture model | |||
| Mean treatment effect (MADRS) c | 1.90 | 4.13 | 3.04 |
| Standard deviation (placebo) d | 9.0 | 10.4 | 9.8 |
| Standard deviation (escitalopram) d | 9.0 | 10.6 | 9.8 |
| Variance explained (placebo), % | 56 | 67 | 63 |
| Variance explained (escitalopram), % | 60 | 68 | 64 |
| Patients benefiting from placebo, % | 36.6 | 35.2 | 39.2 |
| Patients not benefiting from escitalopram, % | 49.8 | 41.6 | 41.7 |
| Patients benefiting from escitalopram but not placebo, % | 13.6 | 23.2 | 19.2 |
| Number needed to treat | 7–8 | 4–5 | 5–6 |
| Treatment effect for benefiters e | 13.9 | 17.8 | 15.9 |
| Standard deviation (benefiters) f | 4.6 | 5.9 | 5.6 |
| Standard deviation (non-benefiters) f | 6.6 | 6.1 | 6.7 |
ANCOVA, analysis of covariance; MADRS, Montgomery–Åsberg Depression Rating Scale.
a Baseline MADRS score <30.
b Baseline MADRS score ≤30.
c Escitalopram minus placebo (mean MADRS points).
d Residual error standard deviation.
e Mean MADRS change from baseline.
f Standard deviation of MADRS total scores at week 8.
Conventional analyses
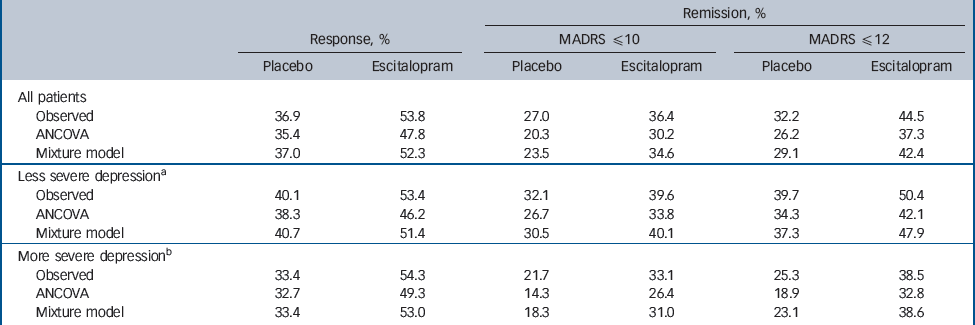
For all patients (n = 1357) the observed mean treatment difference (escitalopram v. placebo) from baseline after 8 weeks of treatment (LOCF) was 3.2 (s.d. = 9.5) MADRS points (Table 3), with observed response rates of 53.8% (escitalopram) and 36.9% (placebo), and remission rates (MADRS≤12) of 44.5% (escitalopram) and 32.2% (placebo) (Table 4). These values correspond to number-needed-to-treat (NNT) values of 6 for response and 8 for remission. For more severely depressed patients (MADRS≥30, n = 667) estimated MADRS means at last visit were 16.8 (s.d. = 10.5) for escitalopram treatment and 21.5 (s.d. = 10.9) for placebo, with an estimated mean treatment difference from baseline of 4.7 (s.d. = 10.7) (see Table 3). Response rates were 54.3% (escitalopram) and 33.4% (placebo), and remission rates (MADRS≤12) were 38.5% (escitalopram) and 25.3% (placebo) (Table 4). These values correspond to an NNT of 5 (100/20.9) for response and 8 (100/13.2) for remission. Corresponding values for the less severely depressed patients are also shown in Tables 3 and 4.
Mixture model v. ANCOVA
The distributions of MADRS total scores (LOCF) after 8 weeks of treatment with escitalopram or placebo are shown in Fig. 1.
Table 4 Response and remission rates
| Remission, % | ||||||
|---|---|---|---|---|---|---|
| Response, % | MADRS ≤10 | MADRS ≤12 | ||||
| Placebo | Escitalopram | Placebo | Escitalopram | Placebo | Escitalopram | |
| All patients | ||||||
| Observed | 36.9 | 53.8 | 27.0 | 36.4 | 32.2 | 44.5 |
| ANCOVA | 35.4 | 47.8 | 20.3 | 30.2 | 26.2 | 37.3 |
| Mixture model | 37.0 | 52.3 | 23.5 | 34.6 | 29.1 | 42.4 |
| Less severe depression a | ||||||
| Observed | 40.1 | 53.4 | 32.1 | 39.6 | 39.7 | 50.4 |
| ANCOVA | 38.3 | 46.2 | 26.7 | 33.8 | 34.3 | 42.1 |
| Mixture model | 40.7 | 51.4 | 30.5 | 40.1 | 37.3 | 47.9 |
| More severe depression b | ||||||
| Observed | 33.4 | 54.3 | 21.7 | 33.1 | 25.3 | 38.5 |
| ANCOVA | 32.7 | 49.3 | 14.3 | 26.4 | 18.9 | 32.8 |
| Mixture model | 33.4 | 53.0 | 18.3 | 31.0 | 23.1 | 38.6 |
ANCOVA, analysis of covariance; MADRS, Montgomery–Åsberg Depression Rating Scale.
a Baseline MADRS score <30.
b Baseline MADRS score ≥30.
Inspection of the six graphs shows that the mixture model substantially improves the fit of the histograms compared with the ANCOVA, which assumes just one bell-shaped curve. Akaike’s information criterion strongly supported this in the entire population (a difference of 106.78 points in favour of the mixture model) as well as in both subgroups (differences of 74.03 points in severe depression and 48.98 points in moderate depression). Whereas the ANCOVA model explains about 6% of the variance, the mixing component of the mixture model accounts for about 60% (see Table 3). A bimodal distribution of outcomes is evident in five of the six panels, with the curve on the left capturing patients who benefited from treatment (‘responders’, characterised by low MADRS scores at week 8), whereas that on the right captures patients who did not benefit from treatment (‘non-responders’, characterised by high MADRS scores at week 8).
Distribution of MADRS scores at week 8
All patients
The distribution of MADRS total scores after 8 weeks of treatment is shown for all patients in Fig. 1(a,b). The treatment difference for those who benefited was 15.9 (95% CI 15.2–16.6) MADRS points (Table 3). The mean MADRS scores decreased from approximately 30 at baseline to approximately 10 at week 8 for patients benefiting from treatment (whether treated with placebo or escitalopram) and to approximately 25 at week 8 for patients who did not benefit from treatment. The proportion of patients who benefited from placebo was 39.2%, whereas 41.7% of patients did not benefit from treatment with escitalopram (see Table 3). The difference in proportions of patients who benefited from escitalopram v. placebo treatment (58.3%–39.2%) was 19.1% (95% CI 13.1–25.3; P<0.001). The mean treatment difference was therefore 3.0 MADRS points (19.2% of 15.9 points) and the NNT was 5 (100/19.2). Among those who did not benefit from treatment was a small group of patients whose scores increased. Specifically, depression worsened in 6.3% (n = 43) of patients given escitalopram and 10.3% (n = 70) of patients given placebo.
Less severely depressed patients
For patients with less severe depression at baseline, the distribution of MADRS total scores after 8 weeks of treatment is shown in Fig. 1(c,d). The mean scores decreased from approximately 26 at baseline to approximately 9 at week 8 for patients benefiting from treatment (whether treated with escitalopram or placebo) and to 22 at week 8 for patients who did not benefit from treatment. The treatment difference for those who benefited was 13.9 (95% CI 12.7–15.2; P<0.001) MADRS points (see Table 3). The proportion of patients who benefited from placebo was 36.6%, whereas the proportion of patients who benefited from escitalopram was 50.2%. Thus, the absolute difference was 13.6% (95% CI 4.2–23.1), with a mean treatment difference of 1.9 MADRS points (13.6% of 13.9 points) and an NNT of 7 (100/13.6). Depression became worse in 8.8% (n = 30) of escitalopram-treated patients and in 10.3% (n = 36) of placebo-treated patients.
More severely depressed patients
For patients with more severe depression at baseline, the distribution of MADRS total scores after 8 weeks of treatment is shown in Fig. 1(e,f). The mean scores decreased from approximately 33 at baseline to approximately 10 at week 8 for patients benefiting from treatment (either escitalopram or placebo) and to approximately 27 at week 8 for patients who did not benefit from treatment. The treatment difference for those who benefited was 17.8 (95% CI 16.7–18.7) MADRS points (see Table 3). A higher percentage of patients treated with escitalopram benefited compared with those receiving placebo (difference 23.2%, P<0.001).
Patients who benefited from placebo treatment (35.2%) could be regarded as patients who would benefit regardless of treatment (i.e. the easiest to treat). Patients who did not benefit from escitalopram treatment (41.6%) could likewise be regarded as those who are more difficult to treat (i.e. they would also not have responded to placebo). The difference in the proportions of patients benefiting from escitalopram (58.4%) v. placebo (35.2%) was 23.2% (95% CI 14.8–1.6). The estimated mean treatment difference was therefore 4.1 MADRS points (23.2% of 17.8 points) and the NNT was 5 (100/23.2). Depression became worse in 3.9% (n = 13) of escitalopram-treated patients and in 10.2% (n = 34) of placebo-treated patients.
To test the robustness of the mixture model, it was applied to a single study in elderly depressed patients in which the treatment difference between escitalopram (n = 170) and placebo (n = 180) of 0.03 MADRS points was not statistically significant. Reference Kasper, de Swart and Andersen20 The treatment effect of 11.9 (s.d. = 4.7) MADRS points for participants who benefited was similar to that found for moderately depressed patients in the pooled analyses (13.9, s.d. = 4.6; see Table 3). The predicted benefiter rates were 33.9% for escitalopram and 30.8% for placebo, with a non-significant difference of 3.1% (P = 0.85).

Fig. 1 Distribution of Montgomery–Åsberg Depression Rating Scale (MADRS) total scores at week 8 (last observation carried forward); (a) all patients treated with placebo (n = 681); (b) all patients treated with 10–20 mg/day escitalopram (n = 676); (c) patients with less severe depression (baseline MADRS score <30) treated with placebo (n = 349); (d) patients with less severe depression treated with 10–20 mg/day escitalopram (n = 341); (e) patients with more severe depression (baseline MADRS score ≥30) treated with placebo (n = 332); (f) patients with more severe depression treated with 10–20 mg/day escitalopram (n = 335).
Prediction of response and remission
The response and remission rates predicted by the ANCOVA and mixture model are shown in Table 4 with the observed rates. The mixture model performs consistently better than the ANCOVA in terms of the predicted rates being close to the observed rates (in all of the three criteria in each of the treatment groups and severity subgroups).
Discussion
We used a mixture model to identify two groups of patients: those who benefited from treatment and those who did not. In the total population we found that approximately 39% of patients benefited and 42% failed to benefit, regardless of treatment. We found that approximately 19% of the total would benefit from treatment with escitalopram but not with placebo. Consistent with earlier studies, we found that the percentage of patients who benefited specifically from treatment with the active antidepressant was higher among the subgroup with more severe depressive symptoms (23%) than it was for the subset with less severe symptoms (14%), corresponding to an NNT of 5 and 7 respectively.
It has been argued that the large sample sizes available in meta-analyses that use individual patient data can show statistical significance even when the clinical difference between two treatment groups is small. Reference Thase21 Mayer gives as an example a difference of 6.5 points in pain perception on a visual analogue scale of 0–100. Reference Mayer22 If another study had shown that patients could not discriminate a difference of less than 13 points on this scale, he argues that the difference, although statistically significant, would not be clinically important. In this case, the difference for a group of patients is compared with an individual patient, and assumes that all patients responded (i.e. a single distribution) and showed the same, relatively small, mean difference. The same argument was recently made following a meta-analysis of RCTs of antidepressants, which observed a mean difference of about 2 points v. placebo. Reference Kirsch, Moore, Scoboria and Nicholls23 Our analyses using the mixture model indicate that a difference from placebo of 1 MADRS point corresponds to a difference of 5 percentage points in the proportion of benefiters, calculated as (52.3–37.0) / 3.04, which is close to the value of 5.2, calculated as (53.8–36.9) / 3.23, in the proportion of observed responder rates for all patients.
The mixture model is a substantial improvement on the standard ANCOVA in fitting the empirical distribution of the MADRS score at week 8. This is supported by the test criterion (Akaike’s information criterion) and the graphical fit of the week 8 MADRS scores, as well as the prediction of response and remission rates. Scrutinising the graphs, one may argue that the mixture model – although vastly improving the ANCOVA fit – still has problems capturing the floor effect, as there tends to be a ‘piling up’ of patients with a very low score. However, we consider this as a minor misfit, and it should come as no surprise, as the mixture model comprises components of the normal distributions. With the risk of over-interpretation, the distribution of patients with less severe depression receiving placebo looks multimodal (i.e. more complex than bimodal). As this pattern is not present in any of the three other subgroups, we interpret this as artefactual. In any case the number of patients is probably too small to draw valid conclusions based on a more elaborate model, although one could argue that there might be three or more classes of outcomes. More classes would allow for a slightly better fit to the empirical distribution, but would require more data. Three classes might correspond clinically to ‘remitters’ (patients with very low final scores), ‘responders’ (patients who benefit but who have too many residual symptoms to be classified as ‘well’) and ‘non-responders’ (patients who obtain less than 20% improvement from baseline). An obvious next step would be to use the mixture model approach on longitudinal data from major depressive disorder trials, using a strategy similar to that of Uher et al. Reference Uher, Muthén, Souery, Mors, Jaracz and Placentino24
The ANCOVA model systematically underestimated the proportion of ‘responders’ and ‘remitters’, whereas the mixture model did not, and was closer to the observed rates in both treatment groups and in more and less severely affected patient subgroups. This might be because the mixture model is richer in terms of the number of parameters, but neither model was tailored specifically to capture the response and remission rates. Therefore, we believe that the superior prediction of the response/remission rates in the mixture model is because it better captures the distribution of MADRS scores at week 8.
The National Institute for Health and Clinical Evidence (NICE) has concluded that although there is evidence suggesting a statistically significant difference favouring selective serotonin reuptake inhibitors (SSRIs) over placebo on reducing depression symptoms as measured by the Hamilton Rating Scale for Depression (HRSD; N = 16, n = 2223; random effects standardised mean difference effect size –0.34, 95% CI –0.47 to –0.22), the size of this mean difference is unlikely to be of clinical significance. 25 For patients with severe depression, they concluded that there is evidence to support a clinically significant difference favouring SSRIs over placebo on reducing depression symptoms as measured by the HRSD (N =4, n = 344; effect size –0.61, 95% CI –0.83 to –0.4). Thus, a standardised mean difference effect size of 0.61 is considered clinically relevant, whereas 0.34 is not. The basis for this is that 0.5 is considered to be a ‘medium’ effect size (Cohen), although it should be noted that Cohen also stated, ‘The values chosen had no more reliable a basis than my own intuition’. Reference Cohen26 Meta-analyses by Kirsch et al and Fournier et al, Reference Kirsch, Deacon, Huedo-Medina, Scoboria, Moore and Johnson2,Reference Fournier, DeRubeis, Hollon, Dimidjian, Amsterdam and Shelton4 using a mean drug v. placebo difference of 3 points on the HRSD as the criterion of clinical significance, likewise reached a similar conclusion, namely that antidepressants conveyed a significant advantage over inert placebos only for patients with relatively severe depressive episodes. Our findings indicate that what appears to be a modest effect in the grouped data – on the boundary of clinical significance, as suggested above – is actually a very large effect for a subset of patients who benefited more from escitalopram than from placebo treatment. This subset ranged from 14% to 23% for milder and more severe depression respectively, and in both cases the NNT values derived from these analyses were above accepted thresholds of clinical significance. Said another way, a relatively small mean difference in grouped data can obscure a large difference in benefit in a clinically meaningful proportion of patients.
Limitations of the study
Our analysis has several limitations. First, the model is based on data from patients with major depressive disorder who were recruited on the basis of strict inclusion and exclusion criteria and who provided informed consent for participation in placebo-controlled RCTs. Second, our analysis was limited to studies of a single antidepressant, escitalopram, and was further limited to studies that permitted use of the maximum approved daily dose of that medication (20 mg). As escitalopram at this dose may be particularly effective, Reference Kennedy, Andersen and Thase27,Reference Cipriani, Furukawa, Salanti, Geddes, Higgins and Churchill28 it is possible that analyses of other antidepressants at other doses might have resulted in smaller estimates of drug v. placebo differences. Third, the model tested here assumed that the fourth cell in the theoretical 2 × 2 table (i.e. patients who did not respond to escitalopram but would have responded to placebo) was empty. It is likely that a small percentage of those who did not respond to escitalopram did so because they either were made worse by the medication or withdrew early because of intolerable side-effects; such patients might have responded had they been allocated to placebo. However, as attrition due to intolerable side-effects was relatively small in the escitalopram group (approximately 6.8% v. 2.2% in the placebo group) and the placebo response rate was 37%, it is plausible that the hypothetical proportion of benefiters in our data-set was underestimated by about 3%. Finally, it is worth remembering that ‘Essentially, all models are wrong, but some are useful’. Reference Box and Draper29
Implications of the study
These analyses indicate that small mean differences obscure large and clinically meaningful responses for a subgroup of people with depression. Specifically, the use of a mixture model indicates that the modest mean difference favouring the group receiving the active antidepressant is actually explained by a large and clinically relevant effect of 14–18 points on the MADRS among the subgroup of depressed patients who specifically benefited from active treatment. This subgroup, in turn, represented between 14% (less severe) and 23% (more severe) of the patients who consented to double-blind therapy. Application of the mixture model to this pooled data-set gave a considerably better fit to the data than one in which all patients were assumed to benefit from treatment.
Funding
The original studies were sponsored by H. Lundbeck A/S or Forest Pharmaceuticals, Inc.
Acknowledgements
We thank David Simpson, PhD, for assistance in the preparation of the manuscript. Dr Simpson is an employee of H. Lundbeck A/S.








eLetters
No eLetters have been published for this article.