1. Introduction
Attention was drawn to Thwaites Glacier and its neighbour Pine Island Glacier by Reference HughesHughes (1973, Reference Hughes1975, Reference Hughes1977, Reference Hughes1981) as the sector of the West Antarctic ice sheet he considered to be most prone to instability and perhaps collapse. He inferred this because these glaciers drain vast areas of high accumulation at high velocities, are not restrained by large, buttressing ice shelves and rest on bedrock below sea level and which deepens inland. This bed configuration is, according to Reference WeertmanWeertman (1974), unstable and could yield an irreversible retreat of the glacier, independent of climatic change. Reference HughesHughes (1973) and Reference Thomas, Sanderson and RoseThomas and others (1979) went as far as to suggest that those ice streams could be in a process of collapse today, with obvious consequences for the future of the West Antarctic ice sheet and contemporaneous changes in global sea level. Until recently, however, little reliable glacio-logical data had been collected in this sector of Antarctica to verify their prediction.
An interferometric synthetic aperture radar (InSAR) analysis of Pine Island Glacier was presented in Reference RignotRignot (1998a). It showed that the basin feeding Pine Island Glacier was losing mass at a rate of 7 ± 10% (or 5 ± 7 km ice a−1) of its total yearly flux. In addition, the grounding line was retreating by 4.8 ± 1.2 km between 1992 and 1996, which implied that the glacier was thinning 3.5 ± 0.9 m ice a−1 at the center and less near the sides. The InSAR results suggested that Pine Island Glacier could be in a state of rapid retreat. In this paper, a similar analysis of remote-sensing data is applied to Thwaites Glacier.
Reference Lindstrom and HughesLindstrom and Hughes (1984) estimated the output mass flux of Thwaites Glacier at 44.4 Gt a−1, which was nearly in balance with an estimated mass accumulation of 48.9 Gt a−1. In all likelihood, however, the gate Reference Lindstrom and HughesLindstrom and Hughes (1984) used to obtain the flux was actually on floating ice, well downstream of the grounding line. At that location, the ice velocity is high (3.1 km a−1), but the mean ice thickness is low (325 m), probably due to pronounced basal melting from the glacier base. Drainage-basin boundaries were determined with limited precision from the surface elevation data available at the time. Ice velocity was remeasured by Reference Lucchitta, Rosanova and MullinsLucchitta and others (1995), but mostly on the ice tongue, and the precise location of the grounding line was not known. As a result, no reliable estimate of mass balance has been obtained.
In this study, a high-resolution, vector map of the ice velocity on Thwaites Glacier, near and above its grounding line, is derived from InSAR data. Estimates of its output mass flux are obtained both across the Scott Polar Research Institute (SPRI)/U.S. National Science Foundation (NSF)/Technical University of Denmark (TUD) ice-sounding radar profile collected in 1978/79 (Reference DrewryDrewry, 1983) (hereafter referred to as the SPRI ice-sounding radar profile), and across the interferometrically derived glacier grounding line, where an ice thickness is deduced from ice-shelf hydro-static equilibrium. These output fluxes are compared with the mass accumulation calculated from a prior map of mean surface mass balance of Antarctica to deduce the glacier mass balance. InSAR data are also employed to measure the glacier grounding-line migration between 1992, 1994 and 1996 and estimate the corresponding rate of glacier thinning/thickening at the grounding line. Finally, other evidence of the state of stability of Thwaites floating tongue is examined. The results are summarized to discuss the state of mass balance of this sector of West Antarctica.
2. Study area
Thwaites Glacier is located at about 75° S, between 105° W and 110° W (Fig. 1), in Marie Byrd Land. Discovered in 1946/47 during the U.S. Navy Operation Highjump (Reference ByrdByrd, 1947), it is known for its floating glacier tongue which projects >100 km into the ocean. The glacier tongue broke away to form Thwaites Iceberg Tongue in 1967, which remained in front of the glacier until 1986 (Reference Lucchitta, Smith, Bowell and MullinsLucchitta and others, 1994). The ice tongue moves at 3.4 km a−1, one of the largest ice velocities recorded in Antarctica, while the grounded part moves 1 km a−1 slower. Reference Ferrigno, Lucchitta, Mullins, Allison, Allen and GouldFerrigno and others (1993) detected an increase in velocity of the floating tongue between 1972–84 and 1984–90, confirmed with European Remote-sensing Satellites (ERS) data acquired in the 1990s (Reference Rosanova, Lucchitta and FerrignoRosanova and others, 1998). The increase in velocity of the floating tongue, however, is of no relevance to the grounded part of the ice stream, for which there is no detected change (increase nor decrease) in ice velocity (Reference Rosanova, Lucchitta and FerrignoRosanova and others, 1999).
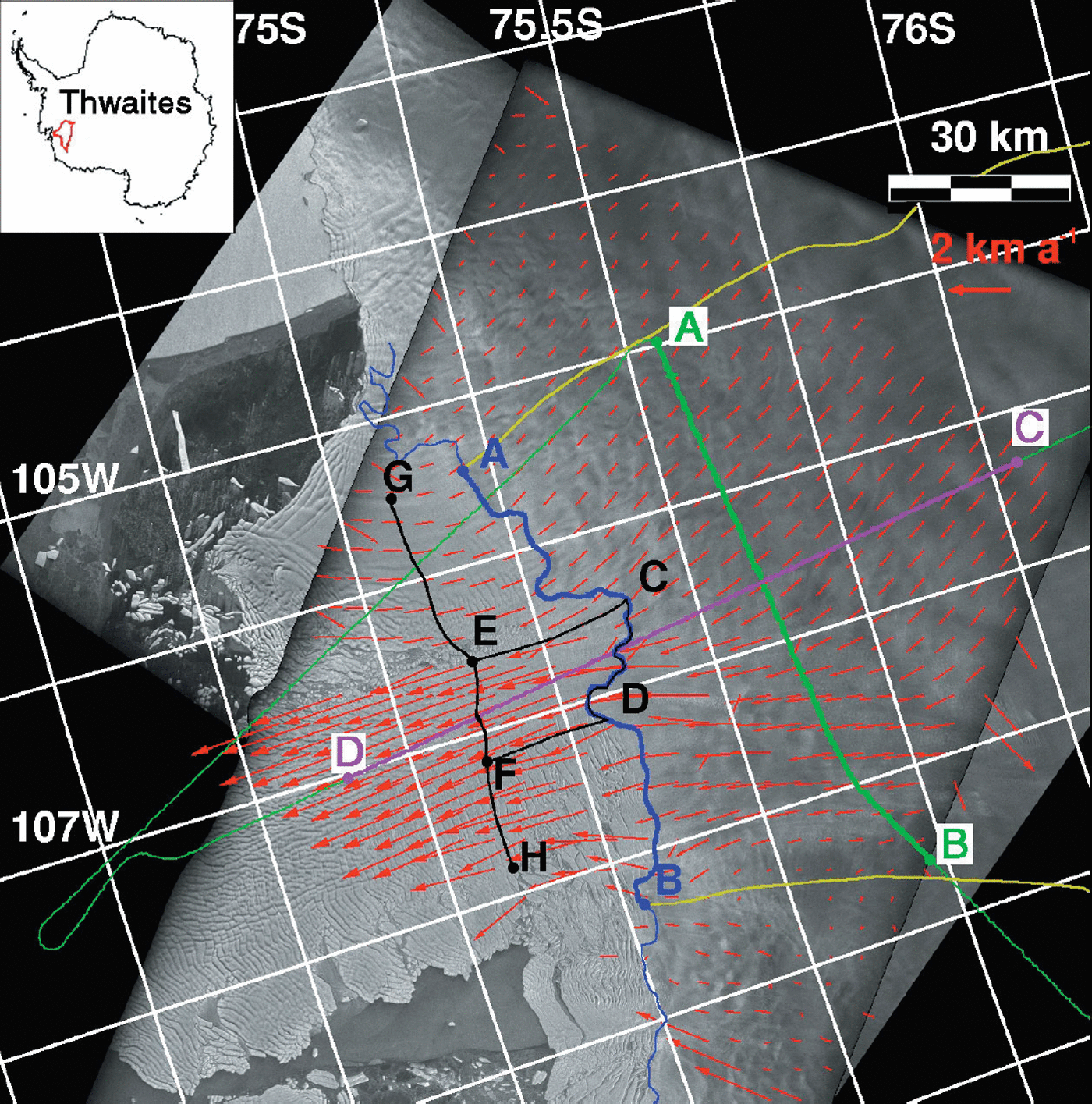
Fig. 1. ERS-1 mosaic image of Thwaites Glacier acquired in early 1996 (see inset for location of Thwaites basin in the Antarctic). Orbit 22557 of ERS-1 is used for descending track, and orbit 23885 of ERS-1 for ascending track. The fading radar brightness at the edges of the SAR scenes is due to the fading of antenna pattern correction beyond a certain range of the ERS swath. The glacier grounding line derived from 1994 data is shown in blue. The SPRI profile is green. The gates of calculation of the ice flux at the grounding line and at the SPRI gate are shown in thick blue and green, respectively, between A and B, which are marked with a dot. The limits of the drainage basin are shown in yellow. The location of the thickness profile discussed in Figure 4 is shown in purple between C and D. Ice-velocity vectors derived from ascending and descending tracks are shown in red. Ice fluxes employed to estimate basal melting in the first 20 km of floating ice are calculated at A–B and G–H for the whole glacier width, and C–D and E–F for the central ice tongue. All locations are marked by a dot. © European Space Agency 1999.
The glacier grounding line, shown in blue in Figure 1, as inferred from InSAR (see below), is close to the line along which prominent crevasses form at the surface of the glacier, if not at the initiation of iceberg break-up along the westernmost sector of the glacier, which is the region where ice velocity is the highest. This situation contrasts with the case of Pine Island Glacier which develops a 70 km long floating ice section with no major line of rupture close to the grounding line (Reference RignotRignot, 1998a). From the distribution of crevasses revealed by the SAR imagery (Fig. 1) and the deformation pattern of ice blocks and rafts measured with InSAR (Fig. 2), the present-day Thwaites ice tongue does not resemble an ice shelf but rather an ensemble of broken-up icebergs glued together with an ice melange (Reference Rignot and MacAyealRignot and MacAyeal, 1998), and grounded on a few subglacial shoals (Fig. 2). In contrast, the eastern side of the glacier flows into a more compact, smaller-sized ice shelf, which abuts a large ice rise (Fig. 2).
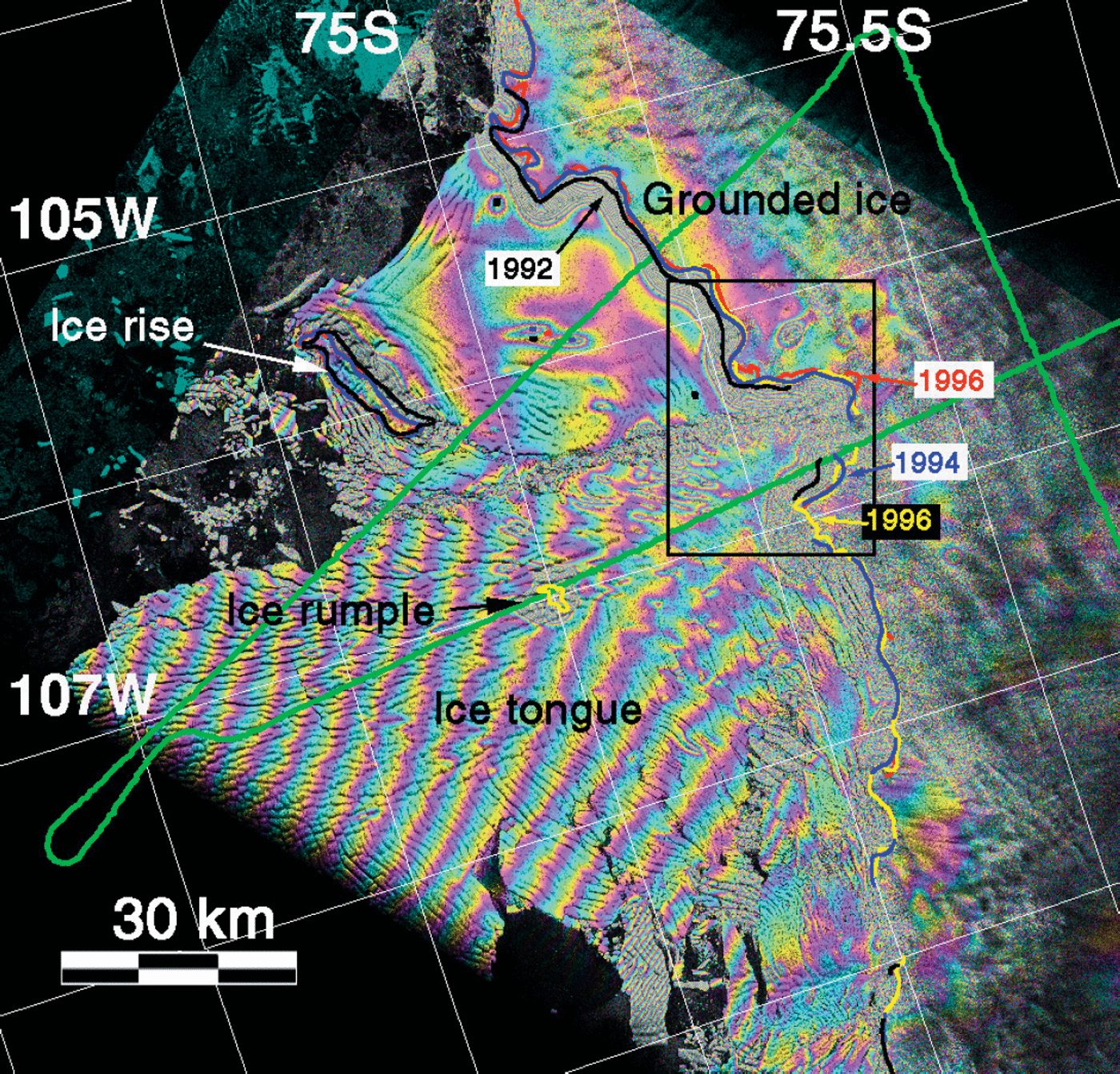
Fig. 2. InSAR image of tidal motion of Thwaites Glacier from 1994 showing the location of the 1992 (black line), 1994 (blue line), 1996a (red line) and 1996b (yellow line) grounding line inferred from InSAR. Each color cycle (from blue to purple, yellow, and blue again) represents a 31 mm increment in vertical displacement of the glacier surface. An ice rumple, about 40 km downstream of the grounding-line center, a few km in diameter, is indicated with an arrow, at 75° S, 107° W The less active eastern sector of the ice shelf is restrained by a large ice rise, as indicated by an arrow, at 74.8.5° S, 106° W. The regular fringe pattern observed on Thwaites ice tongue is caused by the slow, solid-block, horizontal rotation of the ice tongue under the action of tidal currents. The black square in the middle of the scene identifies the location of data shown in Figure 3. The SPRI line is shown in green.
3. Methods and results
3.1. Ice-velocity vector mapping
A combination of ascending and descending interferometric pairs (Table 1) is employed to map the velocity of Thwaites Glacier in vector form (Reference Joughin, Kwok and FahnestockJoughin and others, 1998). It is assumed that ice flows parallel to the ice surface, which is a reasonable assumption when surface ablation is negligible and the glacier is close to steady-state conditions (i.e. not thinning nor thickening). The ice sheet topography, which complicates the two interferograms, is removed using the 5 km spacing Antarctic digital elevation model (DEM) described in Reference Bamber and BindschadlerBamber and Bindschadler (1997).
Table 1. ERS interferometric data employed in this study
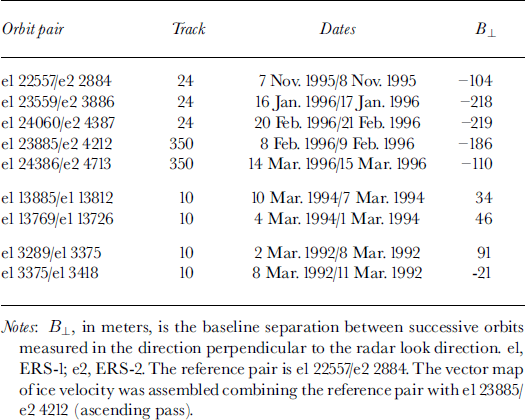
Phase noise in the interferogram is typically a couple of millimeters, which translates into a velocity uncertainty of a few meters per year. Additional uncertainty results from phase unwrapping errors (the process of counting interferometric fringes from an area believed to be moving only slowly, using the algorithm of Reference Goldstein, Zebker and WernerGoldstein and others (1988)) in areas of high phase noise (e.g. a high density of interferometric fringes caused by high strain rates), and residual tilts in the velocity map due to second-order errors in interferometric baseline estimation or uncertainties in absolute velocity. Tilts are in principle removed using non-moving sectors of the ice sheet, here at scene corners of the SAR imagery. Phase unwrapping errors are limited to small areas, which do not limit the precision of calculation of ice fluxes, but yield occasionally contaminated flow vectors in Figure 1. Elsewhere, the flow vectors are well aligned with flow features in the SAR imagery. The precision of the ice-velocity mapping is typically better than 1–2% of the glacier velocity (in km a−1 in the grounding-line region).
As shown in Table 1, ice velocity was measured from data spanning several months. If the glacier velocity had changed over that time period, we would have observed residual deformation fringes on grounded ice in the quadruple-difference interferogram used to map the glacier grounding-line position, which was not the case. Hence, the glacier velocity was stable during that short time period, within an uncertainty of a few meters per year. Although year-to-year fluctuations in ice velocity are not to be excluded (a possibility that will be examined in future studies), the 1996 ice velocity is thereby assumed to represent a reasonable estimate of the long-term glacier velocity.
The floating tongue of Thwaites Glacier flows faster (3.4 km a−1) than the ice shelf in front of Pine Island Glacier (2.6 km a−1) (Reference Rosanova, Lucchitta and FerrignoRosanova and others, 1998). The velocity of Thwaites Glacier at its grounding line, however, is only 2.2 km a−1, which is similar to, if not lower than, that of Pine Island Glacier at its grounding line.
3.2. Deformation velocity
The deformation velocity, V d, associated with creep deformation with no slip, is given by (Reference PatersonPaterson, 1994)
where n is the flow-rate factor, α is surface slope, ρ i is the column-averaged density of ice, g is the acceleration of gravity, B is the deformation constant of ice integrated along the ice column, H is ice thickness, and zero ice velocity is assumed at the bed. This formula is used at the grounding-line center, with n = 3, α = −0.9% calculated over a 5 km distance, ρ i = 917 kg m−3, g = 9.81 m s−2, B = 540 kPa a1/3 for ice at −20°C, and H = 1160 m, to find V d = 96 m a−1. This value is one order magnitude less than the InSAR velocity at the glacier center. Hence, the glacier flows almost entirely through basal sliding in the vicinity of the grounding line. This conclusion probably applies to the area 20 km upstream where ice thickness was measured in 1978 as well.
3.3. Tidal displacements
To measure the ice-tongue tidal displacements, two tandem ERS-1/-2 interferometric pairs (spanning a 1 day time interval), acquired 35 days apart in 1996, are co-registered and double differenced (Table 2). The phase signal associated with the ice-sheet topography is removed from the double-difference interferogram using the Antarctic DEM. The resulting quadruple-difference interferogram measures changes in the glacier tidal displacement between four instances of imaging, plus noise (Reference RignotRignot, 1996). The grounding line is located in the vicinity of the inner limit of the zone of tidal flexing.
Table 2. Double-difference pairs employed for hinge-line mapping
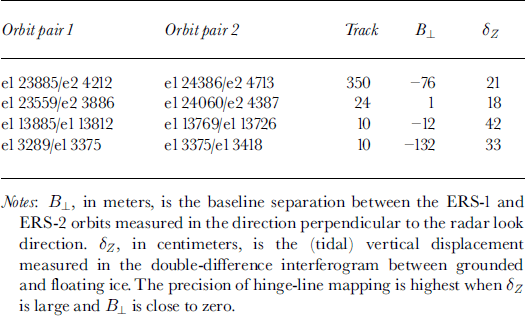
The tidal fringes of Thwaites Glacier (Fig. 2) are complex compared to other glaciers because the high deformation rates of the ice in the vicinity of the grounding line yield a high fringe density. Ice flowing over and around topographic bumps and hollows (several km wide and several tens of meters high) generates a complex pattern of “bull’s-eye” sets of interferometric fringes overlaid on the larger-scale deformation regime of the glacier. Ice also rifts and calves close to the grounding line so that the observation of tidal fringes becomes difficult. The glacier grounding line is here mostly mapped by hand, with a precision no better than 50–100 m, based on prior experience with other glaciers (Reference Rignot, Gogineni, Krabill and EkholmRignot and others, 1997; Reference RignotRignot, 1998a, Reference Rignotb, Reference Rignotc) (Figs 2 and 3).
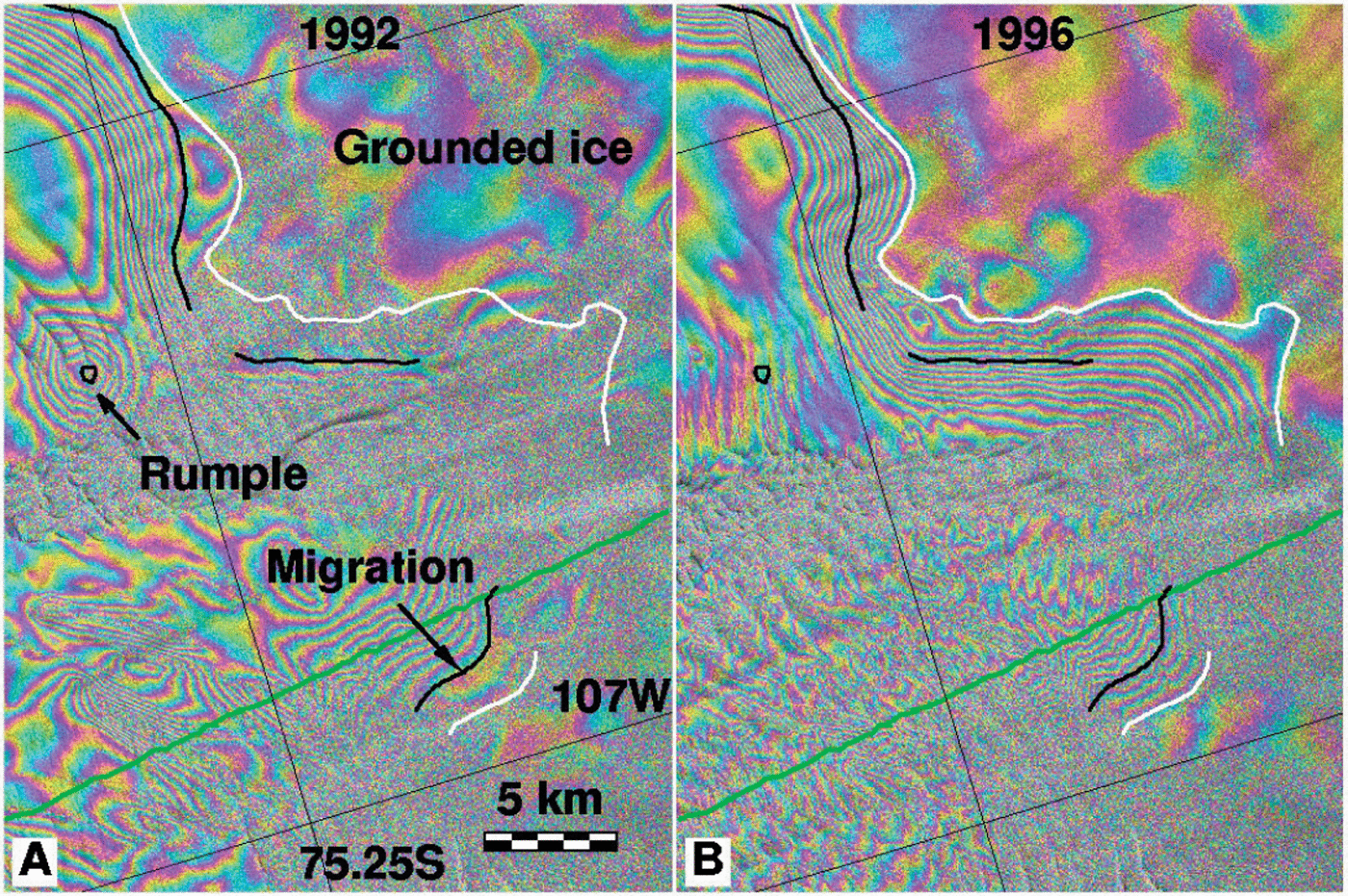
Fig. 3. Details of the grounding-line retreat of Thwaites Glacier at the glacier center. (a) 1992 quadruple-difference interferogram showing the tidal motion of the glacier (each color cycle represents a 31 mm increment in vertical displacement); (b) the same for 1996 data. White and black lines indicate, respectively, the 1992 and 1996 grounding-line positions in (a) and (b). The grounding line migration quoted in the text of 1.4 km in 4 years is measured over a 5 km long segment, identified in (a) with a black arrow and the label “migration”. On the eastern, slow-moving ice-shelf the grounding-line retreat along a 15 km long segment varies between 0.5 and 2 km. An ice rumple detected in 1992 on the slow-moving ice shelf, indicated by an arrow and the label “rumple” in (a), is no longer present in 1996.
The regular train of fringes observed on the ice tongue is perpendicular to the satellite track. The satellite is here looking to its right, and moving from the top left to the bottom right of Figure 2. This fringe pattern indicates a solid-block rotation of the ice tongue about a vertical axis (Reference Peltzer, Hudnut and FeiglPeltzer and others, 1994; Reference Rignot and MacAyealRignot and MacAyeal, 1998). The fringe pattern does not provide information on the position of the vertical axis. The 392 mm displacement measured in the quadruple-difference interferogram (about 14 fringes, each contributing a 28 mm displacement in the radar looking direction, over a distance of 64 km) corresponds to a rotation angle of 0.13° a−1. A similar fringe pattern was observed in single interferograms of the flanks of Hemmen Ice Rise, in the Ronne Ice Shelf (Reference Rignot and MacAyealRignot and MacAyeal, 1998), but not in quadruple-difference interferograms of the same area. This meant that the solid-block rotation of ice blocks measured on the flanks of Hemmen Ice Rise was caused by flow deformation alone, and not by tidal currents. Here, the situation is reversed, as the regular set of fringes is observed only in the tidal interferograms. This means that the ice-block rotation of the Thwaites floating tongue is of tidal origin (e.g. due to ice friction with tidal currents). No reliable tidal data are available in this sector, however, to compare the InSAR results with in situ data.
3.4. Ice thickness
Ice thickness was estimated by the SPRI ice-sounding radar system in 1978/79 (Reference DrewryDrewry, 1983) (Figs 1 and 2 in green). The radar profile is assumed to reflect present-day thickness conditions, despite possible thinning/thickening trends. The positional uncertainty of the data is ±5 km (D. G. Vaughan (personal communication, 2000) quotes a 10 km uncertainty).
At the grounding line, ice-shelf elevations are converted into ice thicknesses using a multiplicative factor of 9.11. Ice-shelf elevation is obtained from the Antarctic DEM (Reference Bamber and BindschadlerBamber and Bindschadler, 1997), referenced to sea level using the OSU 91 geoid model, minus a 10 m height offset. The conversion factor of 9.11 corresponds to an ice density ρ i = 917 kg m−3 and a sea-water density of ρ w = 1030 kg m−3. The 10 m height offset presumably reflects residual errors in the geoid model, combined with a firn correction. The height offset is necessary to obtain a reasonable agreement between inferred and measured thicknesses on the ice tongue and at the interferometric grounding line.
In a 15 km long segment below the grounding line, the ice elevation is 20 ± 10 m below buoyancy. It is not possible to remove this difference by changing the conversion factor or the height offset, or by accounting for a 10 km positional uncertainty of the SPRI profile. Figure 2 shows, however, that this 15 km segment experiences tidal flexure (denoted by the presence of interferometric fringes in the quadruple-difference interferogram), which suggests that ice in this region has not yet reached full hydrostatic ice (about 9 km in Fig. 2) because the SPRI profile crosses the flexure zone at an angle in this area. Another possibility explaining this pattern, combined with the effect of tidal flexure, is that the grounding line of Thwaites Glacier was at a more advanced position in 1978.
3.5. Grounding-line migration
By repeating the grounding-line mapping at different epochs, in a self-consistent fashion, and co-registering the data with sub-pixel precision to a reference interferometric pair (the first pair in Table 1, with the smallest B ⊥, and best for velocity mapping), the grounding-line migration of Thwaites Glacier is detected with a precision of 100–200 m (each position is determined with a precision of 50–100 m) (see Fig. 3 for a comparison between the 1992 and 1996 grounding-line positions at the glacier center). The 1992, 1994 and 1996 data were acquired 3, 6 and 1 day apart, respectively, so the strategy of combining the data to measure tidal deformation was slightly different in each case (Table 2).
To register the various interferograms together with precision, two sets of image features are employed: (1) areas of stagnant ice on the glacier sides or near grounded shoals; (2) irregularities (bumps and hollows) in ice-sheet topography (and hence in radar brightness) in the ice-sheet interior, which are assumed to be stationary with time, similar to the assumption made by Reference Bindschadler and ScambosBindschadler and Scambos (1991) to measure the ice velocity of Antarctic ice streams from Landsat imagery. No control points are used where ice velocity was high or where there are no stable image features. Overall, the precision of registration is about one pixel (here 50 m).
The results show that the grounding line of Thwaites Glacier retreated 1.4 ± 0.2 km in 3.9 years at the glacier center (Fig. 3). The retreat is less pronounced along the easternmost part of the glacier, which abuts a large ice rise, and difficult to estimate along its western side where ice calves before it reaches full hydrostatic equilibrium.
The retreat measured between 1994 and 1996 is less than between 1992 and 1994 (Fig. 2). The same pattern (high retreat in 1992–94 and lower retreat in 1994–96) was observed on Pine Island Glacier (Reference RignotRignot, 1998a), which suggests that the retreat varies from year to year. The retreat rate measured between 1992 and 1996 may not necessarily reflect the longer-term glacier trend.
Surface slope, α, measured at the grounding line from the Antarctic DEM over a 5 km × km wide area is −0.91 ± 0.05% (see Fig. 4, α positive upwards). Bedrock slope, β (measured positive upwards), along the SPRI profile varies from −0.2% at the 2 km scale, +1% at the 5 km scale, to −0.9% at the 20 km scale, meaning that the value of β to be used to convert grounding-line retreat into thinning rate could be anywhere between −1% and +1% (Fig. 4). The ice-thinning rate,
![]() , is deduced from the retreat rate
, is deduced from the retreat rate
![]() , using (Reference Thomas and BentleyThomas and Bentley, 1978)
, using (Reference Thomas and BentleyThomas and Bentley, 1978)
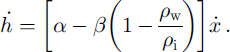
Using ρ
i = 900 kg m−3 and ρ
w = 1027.5 kg m−3, yields
![]() at the glacier center. The thinning rate is comparatively less near the glacier side margins. Varying β by ± 1% only changes
at the glacier center. The thinning rate is comparatively less near the glacier side margins. Varying β by ± 1% only changes
![]() by 0.4 m ice a−1, because the multiplicative factor in front of β in Equation (2) is small, which increases the uncertainty in estimated thinning to ±0.6 m ice a−1.
by 0.4 m ice a−1, because the multiplicative factor in front of β in Equation (2) is small, which increases the uncertainty in estimated thinning to ±0.6 m ice a−1.

Fig. 4. SPRI ice-sounding radar profile (between C and D in Fig. 1, color purple) acquired in 1978/79 across the grounding line of Thwaites Glacier (distance 0 on horizontal axis). Negative distances are seaward; positive distances are on grounded ice. Surface slope, α, calculated from the Antarctic DEM, is indicated. Bedrock slope, β, not represented in the figure, is anywhere between −1% and +1% at the grounding line. Ice thickness deduced from ice-shelf hydrostatic equilibrium is shown by thick black line.
The tidal amplitudes in Pine Island Bay are not known. Examination of tidal interferograms of Thwaites Glacier in 1992, 1994 and 1996 (see δZ in Table 2) suggests that the tidal amplitudes should not exceed ±80 cm in this sector. Using α = −0.91% and β = 0, this means that the interferometrically derived grounding line should not deviate more than ±90 m from its mean-sea-level position. This level of uncertainty is less than the precision of the grounding-line mapping.
Complex interactions between the rough seabed beneath Thwaites Glacier and oceanic tides cannot be excluded, however, which could yield migration rates of several hundred meters if β were to reach several per cent locally (and hence favor water infiltration beneath the glacier at high tide). Most likely, however, the grounding line would migrate either inland or seaward from its mean-sea-level position, and only an exceptional configuration of oceanic tides would yield the consistent grounding-line retreat detected between 1992, 1994 and 1996.
3.6. Drainage basin
Drainage boundaries are drawn automatically from the end-points of the two gates of calculation of the output fluxes, following the lines of steepest slope obtained from the Antarctic SPRI (Fig. 5). The gate of calculation of the grounding-line ice flux is matched to flowlines that extend from the end-points of the SPRI profile (Fig. 1) so that the two estimates could be compared if accumulation in between the two gates is subtracted from the total. Surface slope is calculated from the Antarctic DEM smoothed using a 30 × 30 averaging box (hence smoothing elevations over ≈20 ice thicknesses), followed by a 5 × 5 median filtering of surface slope to remove residual noise.
Fig. 5. Drainage basin of Thwaites Glacier inferred from a DEM of Antarctica, overlaid on an Advanced Very High Resolution Radiometer mosaic of Antarctica (Reference MersonMerson, 1989 and http://terraweb.wr.usgs.gov/web-cgi/webvista.cgi). The drainage basins of Pine Island Glacier (Reference RignotRignot, 1998a), Rutford Ice Stream and Carlson Inlet (Reference RignotRignot, 1998c) and Evans Ice Stream are also shown.
At low elevation, the lines of steepest slope are consistent with flowline features visible in the SAR imagery, except in the southwest sector of the glacier (Fig. 1). There, flowline features were used instead of surface slope to define the drainage basin. Changing the degree of smoothing of the DEM did not change the results significantly. The total accumulation area above the grounding line is 166 500 km2 after correction for the area distortion inherent in the polar stereographic projection (Fig. 5). The inferred drainage basin is known with a precision of ±2 km along its boundary, or ±4000 km2 (2%).
3.7. Balance flux
A map of surface mass balance of Antarctica was compiled on a 50 km grid by Reference Giovinetto and ZwallyGiovinetto and Zwally (2000) and a 10 km grid by Reference Vaughan, Bamber, Giovinetto, Russell and CooperVaughan and others (1999). Both maps use the same field data, yet with different data selection and rejection procedures and different interpolation/extrapolation schemes. Mass accumulation is known from these maps with a precision of 10%, so the balance flux of Thwaites Glacier should be known with 10% precision, or ±5 Gt a−1.
The total mass input to the grounding line of Thwaites Glacier is 53 ± 5 Gt a−1 (or 58 ± 6 km3 ice a−1) with Giovinetto and Zwally’s (2000) map and 57 ± 5 Gt a−1 (or 62 ± 6 km3 ice a−1) with Reference Vaughan, Bamber, Giovinetto, Russell and CooperVaughan and others’ (1999) map (see Table 3). This gives a mean value for the balance flux of Thwaites Glacier of 55 ± 5 Gt a−1, or 60 ± 6 km3 ice a−1 (an ice density of 917 kg m−3 is used throughout the paper to convert volume fluxes into mass fluxes). Total accumulation in between the two gates averages to 1.6 ± 0.2 Gt a−1, or 1.8 ± 0.2 km ice a−1, from the two accumulation maps.
Table 3. Mass accumulation and discharge of Thwaites Glacier at two flux gates: the SPRI ice-sounding radar profile (Fig. 1) and the grounding line (GL). Ice density is 917 kg m3

An independent calculation of the balance flux of Thwaites Glacier, using similar data and methods (personal communication from D. G. Vaughan, 2000) but a narrower output flux gate at the coast, gives a drainage basin of 154 000 km2 and a net accumulation of 52 Gt a−1.
3.8. Ice discharge
Ice discharge is calculated as the integrated product of ice thickness and ice velocity normal to the gate. No attempt is made to correct for the vertical velocity profile at the flux gates. The correction is likely negligible at the grounding line (it is zero on the ice shelf) and at the SPRI gate. Corrections employed for calculating mass discharge at the 2000 m contour elevation in Greenland, where sliding is even less likely to dominate, were, for reference, <5% (Reference Thomas, Csathó, Gogineni, Jezek and KuivinenThomas and others, 1998).
To account for a ±5 km uncertainty in location of the SPRI profile, the ice flux is calculated with a profile displaced ±5 km in the upstream and downstream and across the flow direction and averaging the resulting fluxes.
Ice thickness along the SPRI profile is assumed to be accurate to ±100 m (or 7%), much of this uncertainty resulting from the position uncertainty. At the grounding line, where ice thickness is determined by hydrostatic equilibrium, the uncertainty is ±100 m, most of which arises from uncertainties in the geoid model. Ice velocity is known with a precision of 1–2%. The precision in ice discharge should be 10% at both gates.
At the SPRI gate, the ice flux is 70 ± 7 Gt a−1 (or 76 ± 8 km3 ice a−1). At the grounding line, the flux is 71 ± 7 Gt a−1 (or 77 ± 8 km3 ice a−1). These values are in reasonable agreement, which is expected since accumulation is only 1.6 Gt a−1 in between the two gates. More important, both ice fluxes significantly exceed mass accumulation in the interior, by about 30% of the total accumulation, i.e. well beyond the ±15% uncertainty of the calculation. This means that the glacier is likely losing mass to the ocean and thinning at present.
3.9. Basal melting
To estimate the glacier net balance on floating ice, the ice flux is measured at two gates separated by 20 km along flow-lines. The difference in ice flux between the two gates divided by the ice-shelf area in between represents the net loss of ice experienced by the glacier. If the glacier is in steady state, the net loss of ice on the floating tongue is due to basal melting because surface ablation and accumulation are negligible compared to, say, 1 m ice a−1 in this sector (Reference Jenkins, Vaughan, Jacobs, Hellmer and KeysJenkins and others, 1997).
A comparison of the grounding-line flux (A–B in Fig. 1) with a flux estimated 20 km downstream (G–H in Fig. 1) indicates that basal melting over the 1683 km ice-shelf area must average 12 ± 5 m ice a−1 in order to maintain the present thickness (Table 4). The same calculation performed along the most active and thicker part of the glacier (profiles C–D and E–F) yields a balance basal melt rate of 31 ± 9 m ice a−1. A higher melt rate is expected on the thicker part of the floating tongue because of the pressure dependence of the melting point of ice. Ice thickness is 650 ± 100 m on the eastern ice shelf vs 1100 ± 150 m at the glacier center.
Table 4. Mass fluxes of Thwaites ice tongue along the profiles shown in figure 1, and corresponding rates of basal melting. Ice density is 917 kg m−3
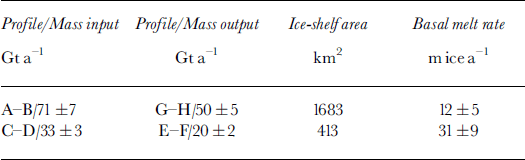
Despite the several meter per year uncertainty of the calculation, the inferred basal melt rates are significantly higher than those reported elsewhere in Antarctica (Reference Jacobs, Hellmer, Doake, Jenkins and FrolichJacobs and others, 1992), but lower than those recorded for Pine Island Glacier (Reference RignotRignot, 1998a). The interpretation of the Pine Island Glacier result was that the continental shelf is invaded by warm circumpolar ocean waters that fuel high basal melting (Reference Jacobs, Hellmer and JenkinsJacobs and others, 1996; Reference Jenkins, Vaughan, Jacobs, Hellmer and KeysJenkins and others, 1997). This study suggests that warm ocean waters probably also affect Thwaites Glacier, although basal melting is somewhat less efficient there than beneath Pine Island Glacier.
3.10. Ice-shelf back pressure
Ice shelves deform under the influence of gravity and are restrained by the action of ice rises and lateral shearing along the side margins. Reference ThomasThomas (1973) calculated an expression for the rate of longitudinal spreading of an ice shelf,
![]() (where the x axis is parallel to the flow direction, and oriented downflow), and the back-pressure force resulting from compression along ice rises and shearing of the shear margins, F, as
(where the x axis is parallel to the flow direction, and oriented downflow), and the back-pressure force resulting from compression along ice rises and shearing of the shear margins, F, as

where h is the ice-shelf surface elevation, and the parameter θ is
With n = 3, α∊ = 0 and β∊ = 0 (which is a reasonable approximation at the glacier center line; see Reference ThomasThomas, 1973), the total ice-shelf back pressure, F, exerted on the inland ice by the ice shelf is
The first term on the righthand side of the equation corresponds to the action of sea-water pressure; the second term corresponds to the action of the ice-shelf longitudinal spreading. The back pressure F was calculated on Thwaites and Pine Island Glaciers, and compared with that obtained on Rutford Ice Stream by Reference Stephenson and DoakeStephenson and Doake (1982) using the same equation.
The results show that the ice-shelf back pressure exerted on Pine Island Glacier is 2 times less than on Rutford Ice Stream (Table 5). The ice-shelf back pressure on Thwaites Glacier is 14 times less than on Rutford Ice Stream. Side shearing of the floating tongue of Thwaites Glacier is limited to a small sector of floating ice because deep crevasses and rifts form almost immediately past the grounding line to decouple the main ice tongue from the surrounding ice (Figs 1 and 2). Only one local area of grounding, about 40 km downstream of the grounding line and 5 km in diameter, is found to restrain longitudinal spreading of the ice tongue within the area covered by Figure 1. It is therefore not surprising to find that Thwaites floating tongue exerts nearly no back pressure on the inland ice at present.
Table 5. Ice-shelf back-pressure force per unit width of ice shelf, F, for three West Antarctic glaciers (RIS, Rutford Ice Stream; PIG, Pine Island Glacier; TWG, Thwaites Glacier)

3.11. Critical thickness for stability
Reference Thomas, Hansen and TakahashiThomas (1984) calculated a critical grounding-line thickness to insure stability of an ice stream based on a model combining total upstream accumulation, width of the grounding line, and parameters defining the flow and sliding of ice (Reference Thomas and BentleyThomas and Bentley, 1978). For Thwaites Glacier, the critical depth of a bedrock sill capable of supporting an ice shelf in equilibrium was estimated at 400–550 m. In Figure 4, the bed elevation is 1027 m below sea level at the grounding line, well below the 500 m theoretical limit. If Thomas’ theory is correct, Thwaites Glacier is unstable and there is a high risk of retreat in the area.
4. Discussion
The mass-budget method applied along both the SPRI profile and the grounding line suggests a significant negative mass balance for Thwaites Glacier. The uncertainties in mass accumulation and drainage basin are unlikely to account for the calculated mass imbalance. The reasonable agreement obtained between the SPRI flux and the grounding-line flux provides some confidence that the mass outflow from Thwaites Glacier is estimated correctly. Confirmation of this result, however, awaits the collection of modern ice-sounding radar data with precise navigation.
The glacier grounding line retreated 1.4 km in 4 years near the glacier center, which suggests mass loss at the grounding line. If the retreat rate were confirmed over a longer time period, it would mean that the glacier is thinning rapidly, at a rate of several meters of ice per year. Ice thinning of that magnitude cannot be explained by temporal changes in accumulation, and implies that the glacier is thinning dynamically.
The variability in retreat rate between 1992, 1994 and 1996 indicates that the 1992–96 retreat may not reflect the longer-term glacier trend (e.g. the 1992–94 rapid retreat may be the result of unusual circumstances). A longer-time period of observations is needed to confirm the state of retreat of the grounding line and obtain more precise information on ice thinning.
The mass deficit of Thwaites Glacier calculated from the mass-budget method at the grounding line is 16 ± 9 Gt a−1, or 17 ± 10 km3 ice a−1. If this mass deficit were to be distributed evenly over the entire drainage basin, the ice surface elevation would drop by 10 cm a−1. This value is comparable to the signal measured by satellite radar altimetry over this area (11.7 cm a−1 in Reference Wingham, Ridout, Scharroo, Arthern and ShumWingham and others (1998) for segment H–G in Fig. 1). If the thinning is due to dynamic changes in the basin then, most likely, thinning is larger nearer to the coast, where ice flow is more developed and creep rates are higher, than in the ice-sheet deep interior. The decrease in ice thinning with increasing elevation is not apparent in the radar altimetry data of Reference Wingham, Ridout, Scharroo, Arthern and ShumWingham and others (1998) because changes near the coast are not detected due to limitations in radar altimetry processing.
While satellite radar altimetry data indicate no significant thinning/thickening trend of the interior of the Antarctic ice sheet, except for the Thwaites/Pine Island sector, important changes may be taking place along the coast that remain undetected. No estimate of mass loss/gain from the Antarctic ice sheet should be considered reliable until all coastal regions are included.
Rapid ice flow is the most likely source of ice thinning on Thwaites Glacier. One possibility is that the glacier discharge velocity, though nearly constant at present, significantly exceeds the balance velocity that would maintain the glacier in steady state, in which case the glacier is slowly depleting its ice supply and is thinning as a result. A second possibility is that ice flow is accelerating at present, in which case extending stresses associated with the flow acceleration would cause ice to thin by creep. Sufficient conditions for rapid or accelerated ice flow include enhanced bed lubrication, softening of ice at the margins, or reduction in ice-shelf buttressing caused by ice-shelf retreat. Basal resistance may be reduced if more basal meltwater becomes available at a pressure that exceeds the ice-overburden pressure. Ice-shelf retreat may be caused by enhanced basal melting in Pine Island Bay. At present, there is not sufficient information on these processes to determine the origin of the mass imbalance of Thwaites Glacier.
Conclusions
The results from the 1996 InSAR analysis suggest that Thwaites Glacier is thinning. The combination of InSAR with satellite radar altimetry indicates that ice thinning may affect the entire basin. The coastal changes detected with InSAR are unlikely to be caused by temporal changes in accumulation/ablation (which was the proposed explanation for the satellite radar altimetry record), and must be due to the glacier flow dynamics instead. Similar conclusions apply to Pine Island Glacier, suggesting that this entire sector of West Antarctica may be undergoing significant changes at present. Detailed studies of this part of West Antarctica are timely.
Acknowledgements
This work was performed at the Jet Propulsion Laboratory, California Institute of Technology, under a contract with the National Aeronautics and Space Administration, Polar Program. The European Space Agency acquired and distributed the radar data employed in this study. R. H. Thomas, D. G. Vaughan, R. A. Bindschadler and two anonymous reviewers are gratefully acknowledged for providing stimulating and constructive comments on the manuscript.












