INTRODUCTION

Viewed physically, the startup dynamics of a snow avalanche is likely to be controlled by different processes from those of later high-speed motion. Avalanche release zones usually show well defined slope-normal boundaries and a smooth lower slip surface, allowing the released snow slab to accelerate in a near rigid-body configuration. However, as motion proceeds the snow slab breaks up, blocks tumble and fragment, and eventually the moving mass transforms into a granular aggregate. Thus, special attention may rightfully be given to avalanche startup dynamics. However, recognizing that minimal data exist on high-speed flow, much less on startup dynamics, the problem has been virtually ignored in recent developments of computer analysis methods For modeling avalanche motion. But Shoda and associates (1965) over two decades of studying short, steep avalanche runouts in central Japan, provide sufficient data on snow material properties and kinematical information to allow at least an initial effort toward defining the startup dynamics. Upwards of 22 avalanches were initiated and recorded by Shoda, of which three ran full track and have sufficient documentation from which leading edge displacement-time profiles could be constructed. Three computer codes were used to analyze separately the startup and later high-speed dynamics of these avalanches. From these evaluations, the following information was sought. 1), the deviation of the startup part of the avalanche motion from the high speed part, and 2), the degree of modification of the empirical coefficients in the computer codes in order to model startup motion.

THE AVALANCHE SITES

The three avalanche paths, Takahira, Mitsumata, and Myoko, are located near the west coast of central Honshu, south of the city of Nagaoka, in Niigata Prefecture, Japan (Figure 1). Mt Takahira and the Mitsumata slope are westerly facing, and border on a major railroad and highway, respectively. Mt Myoko is southeasterly facing. The three sites are exposed to prevailing winds from the Sea of Japan, and have a coastal environment. In these experiments deep snow releases were obtained by use of explosives. Prior to artificial release, the snow slopes were in stable condition, so that extensive measurements were made of snow depth and distribution, stratification and density, air and snow temperatures, and other related properties. Pit data taken at each site on the day of avalanche release, and in proximity to the release zones, indicate that the snow was isothermal and wet (Figure 2). The pit data do not correlate with the actual slab release depths, which were difficult to determine from field data, and some personal communications were necessary to establish approximate values. Following the snow pit investigations, marker flags were placed at 20 m intervals along the paths, so that advance of the released snow could be determined from 16 mm film monitoring of the runout. This provided data points on early motion which characterizes the kinematics of startup. A few seconds of startup motion were shrouded by the explosion powder cloud, but this does not detract significantly from the measurements that depict the startup transient.

Fig. 1. Location of Avalanche test slopes - central Honshu Island.

Mt Takahira, 62 km from the coast of the Sea of Japan, has an average avalanche slope of 34°, extending from 600 to 900 m elevation (Figure 3). On 6 March 1961 a 1.3 m average depth wet snow avalanche was released at the summit of the path (elevation 870 to 890 m). The avalanche followed the dashed line path of Figure 3, terminating just beyond two barriers in the path after a 38.5 s run. Snow pit and kinematical data of the leading edge are published by Shoda (1965), numbered experiment 12b.

Fig. 2. Pit data for the three avalanche paths. Granular now indicated with white circles is snow which usually settled Of smaller grains and without melting stage. That shown in solid circles is snow of larger grains, sometimes melting.

The Mitsumata slope, located on Mt Higashiya, is 8 km west of Mt Takahira, and 58 km from the Sea of Japan. This avalanche path extends from 700 m to 1280 m; however, the experimental avalanches were released below a bench at elevation 925 m (Figure 4). On 3 March 1967 a wet snow avalanche of nominal 2.0 m deep snow slab ran to the base of the average 32° slope. Kinematics of the flow of this avalanche are reported by Nakamura and others (1983) from reduction of experimental data, National Highway (1971).

Fig. 3. Mt Takahira avalanche path.

Fig. 4. Mitsumata avalanche path.

Fig. 5. Mt Myoko contour map and avalanche path.

The Myoko test slope, located 23 km from the Sea of Japan, extends from 800 m to 100 m (34° average slope), on which a 2.0 m average depth avalanche was initiated on 18 February 1966 (Figure 5). For this avalanche, position versus time of the avalanche leading edge was measured by three techniques, namely by a series of stereographic photographs, by stop watch, and by 16 mm movie film, Kawasaki (1966). The displacemenMime plot and the slope profile used in the computer modeling are shown in Figure 6.

NUMERICAL ANALYSIS PROGRAMS

Three computer programs were used to analyze the Shoda avalanches, Program AVALNCH (Lang, Dawson, Martinelli 1979) with an updated material biviscous modeling of snow flow (Dent, Lang 1983) was used to model the flows as transient 2-D motion of a viscous boundary layer type fluid. The modified program, designated BIAV herein, uses one of two possible values of material viscosity depending upon the magnitude of shear stress in the flowing material. By this mechanism the locking property of snow at low shear stress is approximated. With the viscosity corresponding to material locking taken as a multiple of the viscosity of normal (high speed) flow, only the normal flow kinematic viscosity, v, can be varied in this code to model the startup dynamics.

Fig. 6. Slope profile and position-time plots of Mt Myoko avalanche of IS February 1966.

A second computer program ACCEL (Cheng and Perla 1979) is based upon the equation of uniform hydrodynamics, since change in depth of flow is precluded by the solution algorithm, for which the particle acceleration equation of motion is:

(1)

Here, gravity, g, is driving on a slope of angle θ, and two dissipative mechanisms resist the motion. One is dry friction with coefficient μ, and the second is dynamic viscosity, with coefficient D/M, treated as a single parameter. In application to snow this form of equation was first introduced by Voellmy (1955). The two coefficients of flow resistance may be varied in modeling the startup dynamics. Since the original program ACCEL was modified somewhat, the program is designated ACEL herein.

A third program BIEQ (Lang and others 1984), also based upon an equation applicable to uniform flow hydrodynamics since flow depth is not allowed to vary in the solution algorithm, incorporates a mechanism for material locking that is introduced by re-definition of the viscous drag coefficient to incorporate variable viscosity. The governing particle equation is:

(2)

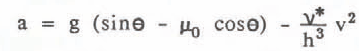
Here μ_o is the friction coefficient, h is the average depth of the release snow, and

(3)

which is the viscous parameterization for different flow speeds. Viscosity v₀ is the high speed viscosity. Coefficients C and α were determined numerically to have values of 500 and 1.25, respectively, in order to best fit the startup dynamics of the avalanches. With these values of the coefficients, viscosity v* → v₀ for flow speeds greater than 8.0 ms^-1, and v* > v₀ at flow speeds less than 8.0 ms^-1. This increase in viscosity at the lower flow speeds simulates material lockup.

For these programs, the three avalanche paths were divided into 10 m long straight line segments as shown for the Mt Myoko path in Figure 6. The procedure then followed in using these programs was to select viscous and/or frictional coefficients in the codes in order to match the high-speed motion of each avalanche. This solution was then extended back to the point of release on a position-time plot to determine the mismatch between the computed and experimental curves (Figure 7 - Mt Myoko case). In all cases, a well-defined mismatch was obtained. The coefficients in the programs were then modified until the computer and experimental startup curves came into approximate correspondence (Figure 7). In programs with both frictional and viscous coefficients, initial adjustment was made to the frictional coefficients, with the idea that frictional effects would have greater influence at startup.

Fig. 7. Comparison between computed and experimental avalanche trajectories for Mt Myoko.

SUMMARY OF RESULTS

A summary of starting zone geometric characteristics, and of coefficient intensifications for each program, in order to match the startup dynamics, is given in Table 1. Results obtained indicate that the mechanics of motion initiation or startup of snow avalanches is different from that of later high speed motion. Viewed physically, during startup the motion is primarily sliding, until the large blocks of snow rotate and break up, and for granularized snow to accumulate at the lower boundary of movement. In the case of artificial release by explosives, as considered herein, initial fragmentation and block breakup is likely to occur faster than with natural releases. Thus, the startup zone in natural avalanche releases may be longer than for these artificial releases.

For Mt Takahira, with a starting zone of approximately 150 m, program BIAV, based upon transient fluid dynamics, required increase in viscosity by a factor of 2.4 in four segments within the avalanche release zone, and in two 10 m segments downslope of the release zone in order for the computer results to match the experimental data. Programs BIEQ and ACEL, based upon equilibrium hydrodynamics, needed starting zone corrections over 120 m with the locking shear stress and friction coefficients increased by factors of 5.5 and 7.0 respectively. This resulted in friction coefficient values in the range 0.30 to 0.35, which falls into the range reported for sliding snow blocks by Inaho (1941). In the high speed range the coefficients were μ ₀ = 0.055 and μ ₀ = 0.05, values lower than what is usually associated with avalanche motion. If viscosity is changed instead of friction in program BIEQ, the coefficient must be increased by a factor of 2.7, and must extend for seven 10 m segments ahead of the release zone. The trend shown by these results is that viscous correction for startup is of smaller magnitude and extends over shorter distances than corresponding friction coefficients, which confirms the viscous fluid character of avalanching snow.

Table I. SUMMARY OF A V ALANCHE PROPERTIES AND COMPUTER PROGRAM PARAMETERIZATION TO MODEL STARTUP TRANSIENTS OF A VALANCHE FLOW.

For the Mitsumata and Myoko avalanches the BIAV correction for startup is in the same range as for Mt Takahira. However, with programs BIEQ and ACEL the changes in the coefficients remain at factors of 5 or so, but the increase is over only 3 or 4 segments compared to the 12 for Mt Takahira. This situation could not be reconciled until it was recognized that the Mt Takahira path is convex in the starting zone and the other two paths are concave. For a concave slope, if parameters are increased in order to slow down the startup, then the decreasing slope encountered by the advancing avalanche will tend to keep the acceleration down. However, for a convex slope, the increasing slope will tend to increase acceleration as the material moves forward. So with programs BIEQ and ACEL a longer zone of coefficient intensification can be expected with the Mt Takahira case, compared to the others. In the case of program BIAV, which is a transient fluid code, depth of the avalanching snow can change as the snow advances. On a convex slope the depth of flow would tend to decrease thus slowing down the motion, while on a concave slope the depth would increase, thereby speeding up the motion. Since depth of flow is the single most sensitive parameter affecting avalanche speed (Lang and others 1979), these trends in depth change apparently moderate the differences between the different starting zones. Thus, the shape of the starting zone has an effect on the srtatup dynamics, particularly with the uniform hydrodynamic flow computer codes like BIEQ and ACEL.

Another significant factor from these startup studies is the necessity to use lower friction values than is usually the case with avalanche flow. This suggests that dry friction has a decreased role in avalanche motion when viscosity of snow is modelled according to its characteristic as a thixotropic material, for which the locking representation is an approximation. To add perspective to the relative importance of the startup transient, it should be noted that the time mismatch between the high speed solution and actual startup is largest at 7 seconds for Mt Takahira, which ran for 38.5 seconds. Thus, startup is 18% of the total runout time for this short duration avalanche. For longer duration avalanches, which may run for 2 minutes or longer, account of startup is probably negligible.