I. INTRODUCTION
High dynamic range (HDR) images are diffusing in many fields: photography, computer graphics, on-vehicle cameras, medical imaging, and more. They have wider dynamic range of pixel values than standard low dynamic range (LDR) images. In contrast, display devices which can express the pixel values of HDR images are not popular yet. Therefore, the importance of a tone mapping operation (TMO) which generates an LDR image from an HDR image by compressing its dynamic range is growing.
Various research works on tone mapping have so far been done [Reference Reinhard, Stark, Shirley and Ferwerda1–Reference Ward and Simmons9]. Many of these are focused on compression techniques or quality of tone mapped images. Unlike these research works, our method proposes to reduce resources such as computational and memory cost during a TMO.
In general, reducing computational and memory cost is an important issue in image processing. HDR images are generally expressed in floating-point data formats such as the OpenEXR [Reference Kainz, Bogart and Hess10] and the RGBE [Reference Ward11]. Because of this, a TMO is executed with floating-point arithmetic, and it requires large computational and memory cost. Specifically, embedded systems often have only limited resources: low-memory or low-performance processor without a floating-point unit (FPU). Furthermore, real-time processing, such as an HDR video, requires speeding-up or parallelization of computing. For these reasons, reducing computational and memory cost regarding a TMO is an important issue.
To reduce the computational cost, fixed-point arithmetic is effective. Fixed-point arithmetic is often utilized in image processing and embedded systems because of the advantages such as low-power consumption, the small circuit size and high-speed computing [Reference Viitanen, Jaaskelainen, Esko and Takala12–Reference Marrot and Bourennane16]. However, executing a TMO with fixed-point arithmetic is difficult due to the wide range value of HDR images. On the other hand, fast tone mapping functions were proposed in [Reference Shen, Jin and Sun17–Reference Thakur, Sivasubramanian, Nallaperumal, Marappan and Vishwanath20]. The authors in [Reference Shen, Jin and Sun17, Reference Shen, Fang, Zhao, Jin and Sun18] focus on speeding up of the trilateral filter-based HDR tone mapping technique. However, it still takes a long time for processing because the trilateral filter-based technique itself is heavy. In [Reference Duan and Qiu19, Reference Thakur, Sivasubramanian, Nallaperumal, Marappan and Vishwanath20], visibility and contrast are simply controlled with a single parameter. Nevertheless, it does not directly contribute to reducing resources, and tone mapping functions for this approach is limited to a specific one. Moreover, the tone mapping function is only one process out of many processes in a TMO. The proposed method considers the whole process of a TMO, and focuses on global tone mapping [Reference Reinhard, Stark, Shirley and Ferwerda1, Reference Reinhard, Ward, Pattanaik, Debevec, Heidrich and Myszkowski2].
Unlike the lightweight tone mapping approach, an integer TMO, which deals with resource reduction was proposed in [Reference Murofushi, Iwahashi and Kiya21, Reference Dobashi, Murofushi, Iwahashi and Kiya22]. Considering not only a function itself, but also the whole process of a TMO, this method tries to resolve the essential problem on high demand of resources. In these methods, any kind of global tone mapping functions can be used. The method in [Reference Murofushi, Iwahashi and Kiya21] treats a floating-point number as two 8-bit integer numbers, which correspond to a exponent part and a mantissa part, and applies tone mapping to these integer numbers separately. The method reduces the memory cost using 8-bit integer data instead of 64-bit floating-point data. Moreover, using 8-bit integer data facilitates executing calculations with fixed-point arithmetic because it eases the limitation of the bit length. The method in [Reference Dobashi, Murofushi, Iwahashi and Kiya22] executes the integer TMO with fixed-point arithmetic, and therefore it reduces the computational cost as well.
The proposed method is based on [Reference Murofushi, Iwahashi and Kiya21, Reference Dobashi, Murofushi, Iwahashi and Kiya22]. The integer TMO [Reference Murofushi, Iwahashi and Kiya21, Reference Dobashi, Murofushi, Iwahashi and Kiya22] is designed for the RGBE format; if using for other formats, it is necessary to design a new algorithm dedicated to each format. The method introduces an intermediate format to relieve the limitation of the input HDR image format, and expands the integer TMO for the intermediate format. The proposed integer TMO can be applied for multiple HDR image formats by converting the input image to the intermediate format. The method can conduct all the calculations of the TMO with only fixed-point arithmetic. By these features, the method can be executed under limited resources, such as processors without a FPU or low-memory. The experiments and evaluation confirmed that the proposed method reduces the computational cost and the memory cost, and keeps the quality of tone mapped images, compared to the conventional method with floating-point arithmetic [Reference Reinhard, Stark, Shirley and Ferwerda1].
II. PRELIMINARIES
This section describes widely used HDR image formats and the conventional TMO.
A) HDR image formats
1) THE RGBE FORMAT
Figure 1 shows the bit allocation of the RGBE format [Reference Ward11]. Each pixel is 32 bits long in this format. It consists of 8-bit common exponent and 8-bit mantissa for each RGB channel. The relation among a real number F 1, the exponent part F 1E and the mantissa part F 1M is given as

Fig. 1. Bit allocation of the RGBE format.
2) THE OPENEXR FORMAT
Figure 2 shows the bit allocation of the OpenEXR format [Reference Kainz, Bogart and Hess10]. Each pixel is 48 bits long in this format. This format has two expressions: the normalized numbers and the denormalized numbers. The range of the normalized numbers is restricted as shown in Table 1. The denormalized numbers are used to express the small absolute values which cannot be expressed in the normalized numbers. Therefore, the OpenEXR format has two different encoding processes and decoding processes, respectively. The relation among a real number F 2, the sign s 2 ∈ {0, 1}, the exponent part F 2E and the mantissa part F 2M in the decoding process for a normalized number is given as
On the other hand, the relation for a denormalized number is described as
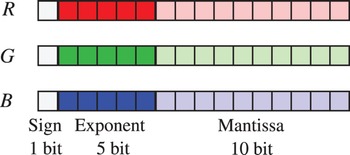
Fig. 2. Bit allocation of the OpenEXR format.
Table 1. The range of the normalized number and the denormalized number in the OpenEXR format.

3) THE IEEE754 FORMAT
The IEEE754 format is a standard specification which is used for calculation of floating-point number [23]. The processor with a FPU can perform high-speed processing for this format. Figure 3 shows the bit allocation of the IEEE754 single precision format. The relation among a real number F 3, the sign s 3 ∈ {0, 1}, the exponent part F 3E and the mantissa part F 3M is given as

Fig. 3. Bit allocation of the IEEE754 single precision format.
B) Global TMO
A procedure of the conventional TMO [Reference Reinhard, Stark, Shirley and Ferwerda1] is described in this section. A TMO generates an LDR image expressed in integer from an HDR image expressed in floating-point. There are two types of a TMO: global tone mapping and local tone mapping; this paper deals with global tone mapping. Figure 4 shows “Photographic Tone Reproduction” which is one of the well-known global TMOs [Reference Reinhard, Stark, Shirley and Ferwerda1]. Each step in this figure is described as follows.
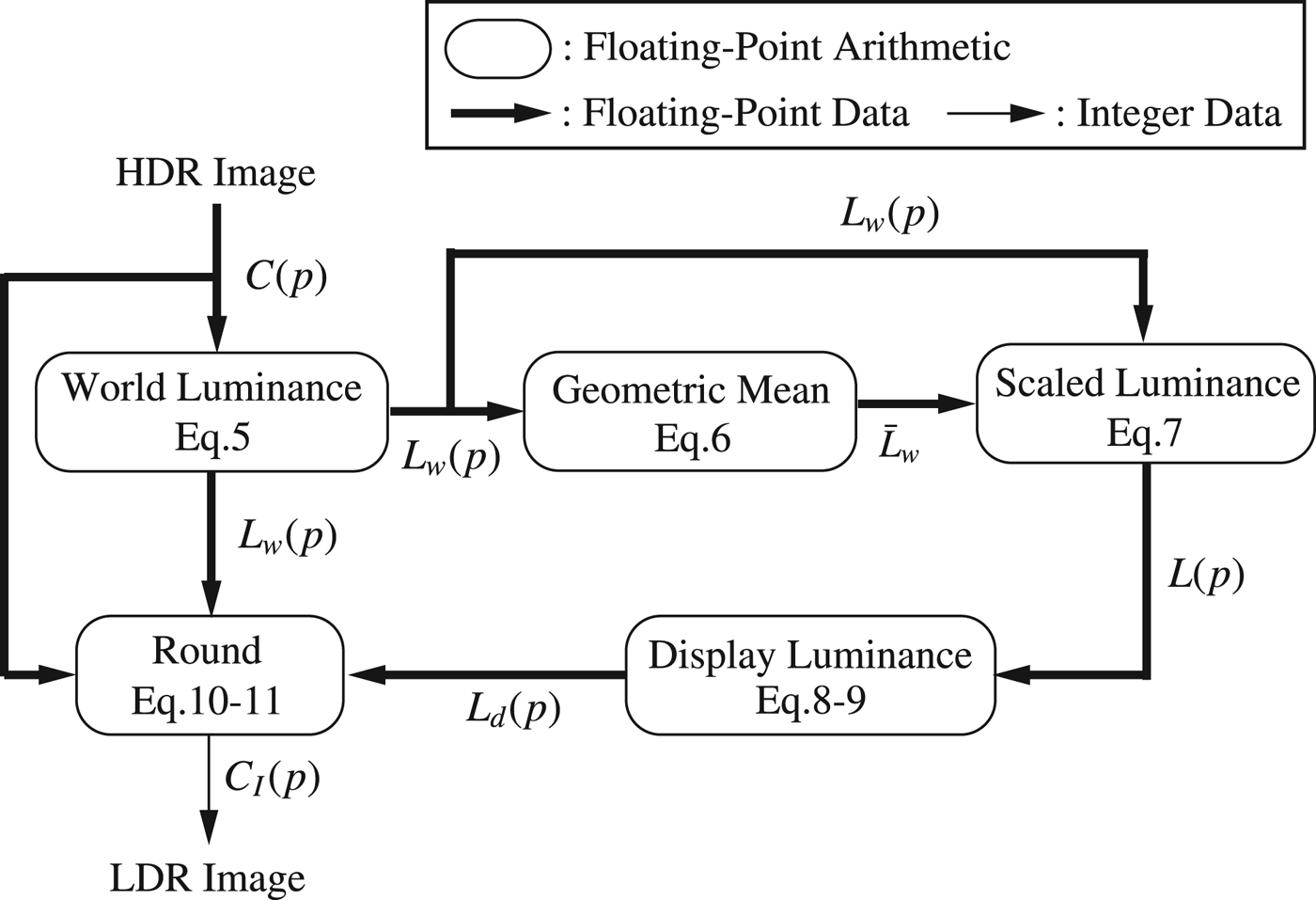
Fig. 4. Outline of the photographic tone reproduction [1].
First, the world luminance L w (p) of the HDR image is calculated from RGB pixel values of the HDR image,
where R(p), G(p), and B(p) are floating-point RGB pixel values of the HDR image, respectively.
Next, the geometric mean
![]() $\bar{L}_{w}$
of the world luminance L
w
(p) is calculated as follows:
$\bar{L}_{w}$
of the world luminance L
w
(p) is calculated as follows:
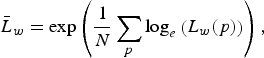 $$\bar{L}_w = \exp \left({1 \over N} \sum_p \log_e \left(L_w\lpar p\rpar \right)\right)\comma \;$$
$$\bar{L}_w = \exp \left({1 \over N} \sum_p \log_e \left(L_w\lpar p\rpar \right)\right)\comma \;$$
where N is the total number of pixels in the input HDR image. Note that equation (6) has the singularity due to zero value of L w (p). It is avoided by introducing a small value as shown in [Reference Reinhard, Stark, Shirley and Ferwerda1]. However, its affection is not negligible for pixel values in a resulting LDR image because a typical HDR image format such as the RGBE can express a small pixel value. Therefore, only non-zero values are used in this calculation.
Then, the scaled luminance L(p) is calculated as
where k ∈ [0, 1] is the parameter called “key value”.
Next, the display luminance L d (p) is calculated using a tone mapping function y() as follows:
The Reinhard's global operator [Reference Reinhard, Stark, Shirley and Ferwerda1] which is one of the well-known tone mapping functions is defined as
Finally, the floating-point pixel values C F (p) of the LDR image is calculated as follows:
where C(p) ∈ {R(p), G(p), B(p)} is the floating-point RGB value of the input HDR image, and C F (p) ∈ {R F (p), G F (p), B F (p)}.
The 24-bit color RGB values C I (p) of the LDR image is derived from
where round (x) rounds x to its nearest integer value, and C I (p) ∈ {R I (p), G I (p), B I (p)}.
Despite the resulting LDR image is integer data, the data and arithmetic in the above procedure are both floating-point. Large computational and memory cost is required from this.
The integer TMO [Reference Murofushi, Iwahashi and Kiya21, Reference Dobashi, Murofushi, Iwahashi and Kiya22] implements a global TMO with integer data and fixed-point arithmetic. Using integer data and fixed-point arithmetic reduces the memory cost and the computational cost. However, this method works on only the RGBE format; its performance is not guaranteed for other formats such as the OpenEXR.
The proposed method is an extended version of [Reference Murofushi, Iwahashi and Kiya21, Reference Dobashi, Murofushi, Iwahashi and Kiya22]. The method introduces the intermediate format to relieve the limitation of the input HDR image format, and expands the integer TMO for the intermediate format.
III. PROPOSED METHOD
This section describes an intermediate format, an integer TMO for the intermediate format, and the way to execute the integer TMO with fixed-point arithmetic. Sections IIIA and IIIB contain extensions of [Reference Murofushi, Iwahashi and Kiya21, Reference Dobashi, Murofushi, Iwahashi and Kiya22], and Section IIIC belongs to [Reference Dobashi, Murofushi, Iwahashi and Kiya22].
A) Intermediate format
An input HDR image is converted to the intermediate format (Fig. 5) at the first step of the proposed method. The proposed integer TMO can be applied for multiple HDR image formats by converting the input image to the intermediate format. This format can be applied for the RGBE, the OpenEXR, and the IEEE754. Figure 5 shows the bit allocation of the intermediate format. Unlike the RGBE format, the exponent part of each RGB channel in this format is independent, and it reduces the error of the format conversion. As an example, this section describes the case of 8-bit mantissa and 8-bit exponent; the bit length of the intermediate format will be discussed in the later section. The encode functions that yield the exponent part F E and the mantissa part F M of each RGB channel F are defined as
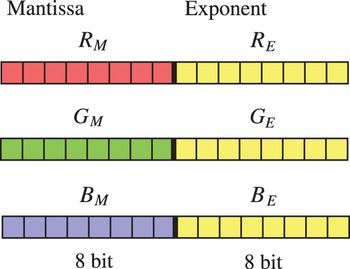
Fig. 5. The bit allocation of the proposed intermediate format.
where ⌈x⌉ rounds x to the nearest integer greater than or equal to x, and ⌊x⌋ rounds x to the nearest integer less than or equal to x. On the other hand, the decode function which yields the original RGB value from the intermediate format is defined as
B) Integer TMO for the intermediate format
The integer TMO converts input and output data of each process to two 8-bit integer data. Using 8-bit integer data facilitates executing calculations with fixed-point arithmetic because it eases the limitation of the bit length. Figure 6 shows the difference between the conventional method [Reference Reinhard, Stark, Shirley and Ferwerda1] and the proposed integer TMO. The integer TMO defines new processes and replaces each tone mapping process by them. These new processes are composite functions shown in Fig. 7. Each process of the proposed method is described as follows.
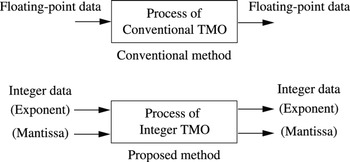
Fig. 6. The difference between the conventional method [1] and the proposed integer TMO.
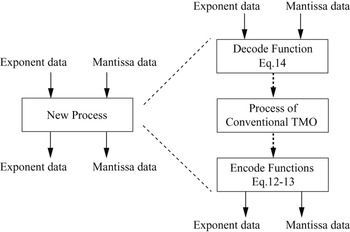
Fig. 7. A new process defined in the proposed integer TMO.
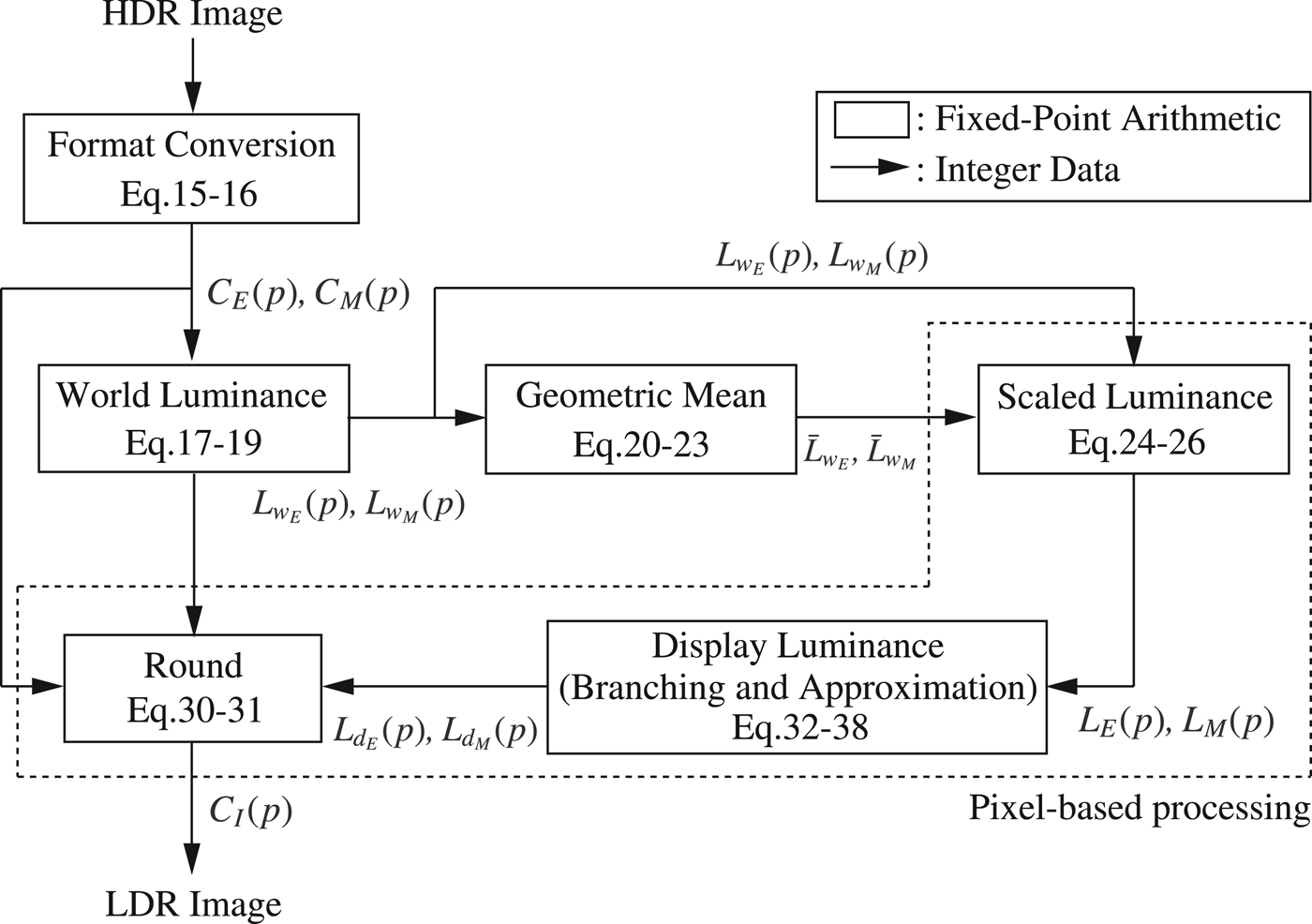
Fig. 8. The outline of the proposed method.
The proposed integer TMO converts RGB values C(p) into the intermediate format described in Section IIIA at the first step. The exponent parts C E (p) ∈ {R E (p), G E (p), B E (p)}, and the mantissa parts C M (p) ∈ {R M (p), G M (p), B M (p)} are calculated as
Then, the exponent part
![]() $L_{w_{E}}\lpar p\rpar $
and the mantissa part
$L_{w_{E}}\lpar p\rpar $
and the mantissa part
![]() $L_{w_{M}}\lpar p\rpar $
of the world luminance L
w
(p) of the HDR image are calculated as
$L_{w_{M}}\lpar p\rpar $
of the world luminance L
w
(p) of the HDR image are calculated as
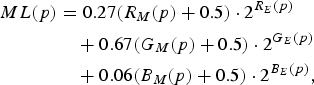 $$\eqalign{ML\lpar p\rpar &= 0.27 \lpar R_M\lpar p\rpar +0.5\rpar \cdot 2^{R_E\lpar p\rpar } \cr &\quad +0.67 \lpar G_M\lpar p\rpar + 0.5\rpar \cdot 2^{G_E\lpar p\rpar } \cr &\quad +0.06 \lpar B_M\lpar p\rpar +0.5\rpar \cdot 2^{B_E\lpar p\rpar }\comma \; }$$
$$\eqalign{ML\lpar p\rpar &= 0.27 \lpar R_M\lpar p\rpar +0.5\rpar \cdot 2^{R_E\lpar p\rpar } \cr &\quad +0.67 \lpar G_M\lpar p\rpar + 0.5\rpar \cdot 2^{G_E\lpar p\rpar } \cr &\quad +0.06 \lpar B_M\lpar p\rpar +0.5\rpar \cdot 2^{B_E\lpar p\rpar }\comma \; }$$
where
![]() $0 \le L_{w_{E}}\lpar p\rpar \le 255$
and
$0 \le L_{w_{E}}\lpar p\rpar \le 255$
and
![]() $0 \le L_{w_{M}}\lpar p\rpar \le 255$
. The method sets
$0 \le L_{w_{M}}\lpar p\rpar \le 255$
. The method sets
![]() $L_{w_{E}}\lpar p\rpar = L_{w_{M}}\lpar p\rpar = 0$
if C
E
(p) = 0, and the method sets
$L_{w_{E}}\lpar p\rpar = L_{w_{M}}\lpar p\rpar = 0$
if C
E
(p) = 0, and the method sets
![]() $L_{w_{M}}\lpar p\rpar = 255$
if
$L_{w_{M}}\lpar p\rpar = 255$
if
![]() $L_{w_{M}}\lpar p\rpar = 256$
.
$L_{w_{M}}\lpar p\rpar = 256$
.
Next, the exponent part
![]() $\bar{L}_{w_{E}}$
and the mantissa part
$\bar{L}_{w_{E}}$
and the mantissa part
![]() $\bar{L}_{w_{M}}$
of the geometric mean
$\bar{L}_{w_{M}}$
of the geometric mean
![]() $\bar{L}_{w}$
of the HDR image are calculated as
$\bar{L}_{w}$
of the HDR image are calculated as
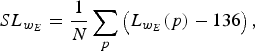 $$SL_{w_E} = {1 \over N} \sum_p \left(L_{w_E}\lpar p\rpar - 136 \right)\comma \;$$
$$SL_{w_E} = {1 \over N} \sum_p \left(L_{w_E}\lpar p\rpar - 136 \right)\comma \;$$
 $$SL_{w_M} = {1 \over N} \sum_p \log_2 \left(L_{w_M}\lpar p\rpar + 0.5 \right)\comma \;$$
$$SL_{w_M} = {1 \over N} \sum_p \log_2 \left(L_{w_M}\lpar p\rpar + 0.5 \right)\comma \;$$
where
![]() $0 \le \bar{L}_{w_{E}} \le 255$
and
$0 \le \bar{L}_{w_{E}} \le 255$
and
![]() $0 \le \bar{L}_{w_{M}} \le 255$
. Here,
$0 \le \bar{L}_{w_{M}} \le 255$
. Here,
![]() $\bar{L}_{w_{E}}$
and
$\bar{L}_{w_{E}}$
and
![]() $\bar{L}_{w_{M}}$
are computed using only non-zero
$\bar{L}_{w_{M}}$
are computed using only non-zero
![]() $L_{w_{E}}\lpar p\rpar $
's.
$L_{w_{E}}\lpar p\rpar $
's.
Then, the exponent part L E (p) and the mantissa part L M (p) of the scaled luminance L(p) of the HDR image are calculated as
The method sets L E (p) = L M (p) = 0 if L E (p) < 0, and L E (p) = L M (p) = 255 if L E (p) > 255. That is, 0 ≤ L E (p) ≤ 255, 0 ≤ L M (p) ≤ 255.
Next, the method calculates the exponent part
![]() $L_{d_E}\lpar p\rpar $
and the mantissa part
$L_{d_E}\lpar p\rpar $
and the mantissa part
![]() $L_{d_M}\lpar p\rpar $
of the display luminance L
d
(p). This calculation depends on tone mapping functions. Here, the tone mapping function of equation (9) is used as an example,
$L_{d_M}\lpar p\rpar $
of the display luminance L
d
(p). This calculation depends on tone mapping functions. Here, the tone mapping function of equation (9) is used as an example,
The method sets
![]() $L_{d_{E}}\lpar p\rpar = L_{d_{M}}\lpar p\rpar = 0$
, if
$L_{d_{E}}\lpar p\rpar = L_{d_{M}}\lpar p\rpar = 0$
, if
![]() $L_{d_{E}}\lpar p\rpar \lt 0$
, and
$L_{d_{E}}\lpar p\rpar \lt 0$
, and
![]() $L_{d_{E}}\lpar p\rpar = L_{d_{M}}\lpar p\rpar = 255$
if
$L_{d_{E}}\lpar p\rpar = L_{d_{M}}\lpar p\rpar = 255$
if
![]() $L_{d_{E}}\lpar p\rpar \gt 255$
. That is,
$L_{d_{E}}\lpar p\rpar \gt 255$
. That is,
![]() $0 \le L_{d_{E}}\lpar p\rpar \le 255\comma \; 0 \le L_{d_{M}}\lpar p\rpar \le 255$
.
$0 \le L_{d_{E}}\lpar p\rpar \le 255\comma \; 0 \le L_{d_{M}}\lpar p\rpar \le 255$
.
Finally, the 24-bit RGB pixel values C I (p) of the LDR image is obtained as
In the above processes, the input and output data of each calculation are all 8-bit integer data. The next section describes fixed-point arithmetic in the proposed method.
C) Fixed-point arithmetic
In the integer TMO, only the data are converted to integer, and the memory cost is reduced. However, the internal arithmetic of the integer TMO is still with floating-point. The proposed method introduces fixed-point arithmetic to reduce the computational cost as well. This section describes the way to execute the internal arithmetic with fixed-point arithmetic. Most of equations can be calculated with fixed-point arithmetic because each variable is expressed in 8-bit integer [Reference Dobashi, Murofushi, Iwahashi and Kiya22]. Nevertheless, equation (29) is difficult to be calculated without floating-point arithmetic because the range of value of the denominator is very wide. Because of this, the method deforms equation (29) as follows:
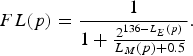 $$FL\lpar p\rpar = {1 \over 1 + {2^{136 - L_E\lpar p\rpar } \over L_M\lpar p\rpar + 0.5}}.$$
$$FL\lpar p\rpar = {1 \over 1 + {2^{136 - L_E\lpar p\rpar } \over L_M\lpar p\rpar + 0.5}}.$$
Furthermore, the method branches equation (32) into three cases and approximates it based on the power of two in the denominator as follows.
Case 1: If 136 − L E (p) > 15 in equation (32), “1” in the denominator can be ignored because the right part of the denominator is very large, and so it is approximated as
Case 2: If 136 − L E (p) < −8 in equation (32), the right part of the denominator can be ignored because it is very small, and so it is approximated as
Case 3: Otherwise, it can be calculated with fixed-point arithmetic.
In addition, the method uses pre-calculated tables for calculations of 2 x (in equation (21)) and log 2 (in equation (23)). Each table consists of 16 × 256 bits. In equation (15)–(38), division operations are simply done by division, not right shift. Moreover, 2 x and log 2 are conducted using simple bit shift operation except equations (21) and (23). The method can calculate all equations of the TMO with only fixed-point arithmetic by these branching, approximation, and tables. Note that the conventional method [Reference Reinhard, Stark, Shirley and Ferwerda1] consists of floating-point data and floating-point arithmetic. In contrast, the proposed method consists of integer data and fixed-point arithmetic.
IV. EXPERIMENTAL AND EVALUATION RESULTS
The proposed method introduces the intermediate format to relieve the limitation of formats. Moreover, the computational cost of the TMO is reduced using fixed-point arithmetic instead of floating-point arithmetic in the proposed method. However, errors can occur by these format conversion and fixed-point arithmetic. To confirm the efficacy of the proposed method and the errors involved with it, the experiments and evaluation were carried out. These experiments and evaluation consist of measurements of peak signal-to-noise ratio (PSNR) of the resulting LDR images and processing time of the TMO, and evaluation of memory usage. Figure 9 shows the block diagram of these experiments. The HDR images in the RGBE format and the OpenEXR format were used as input images. Figure 10 shows examples of these images. The input HDR image is converted to IEEE754 floating-point format in the conventional method [Reference Reinhard, Stark, Shirley and Ferwerda1] at the first step. On the other hand, it is converted to the proposed intermediate format in the proposed method. Negative values in the OpenEXR format were set to zero. Both the proposed method and the conventional method [Reference Reinhard, Stark, Shirley and Ferwerda1] were implemented in C-language. The proposed method was compared with [Reference Reinhard, Stark, Shirley and Ferwerda1] in Sections IVB–IVD, and with the other conventional methods [Reference Thakur, Sivasubramanian, Nallaperumal, Marappan and Vishwanath20–Reference Dobashi, Murofushi, Iwahashi and Kiya22] in Section IVE.
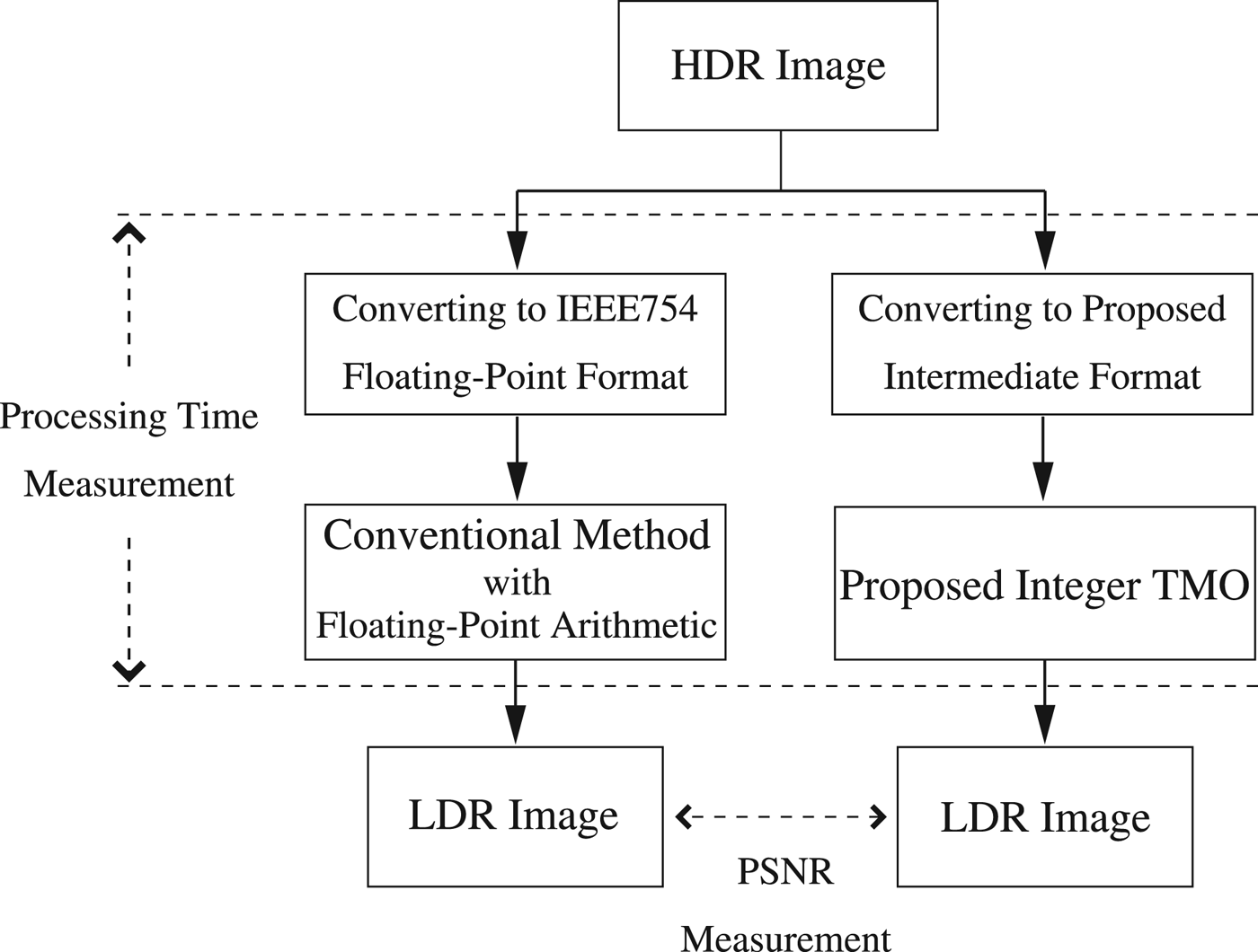
Fig. 9. The block diagram of the experiments.

Fig. 10. The examples of HDR images used in the experiments.
A) The relation between the bit length and the tone mapped LDR image quality
This experiment was carried out to examine the relation between the bit length of the intermediate format and the tone mapped LDR image quality. In this experiment, 32 images in the RGBE format and 42 images in the OpenEXR format were used. Figure 11 shows the relation between the bit length of the intermediate format and the average PSNR, where the exponent part and the mantissa part have same bit length. It indicates that the PSNR values get better with increase in the bit length, and they can be a little <60 dB at 8-bit. Therefore, the other experiments and evaluation used the intermediate format with 8-bit exponent part and 8-bit mantissa part.
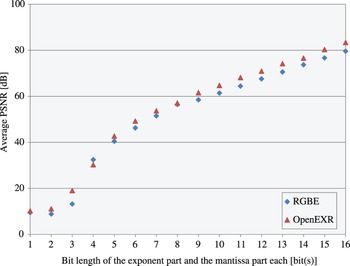
Fig. 11. The relation between the bit length of the intermediate format and the average PSNR. The exponent part and the mantissa part have same bit length.
B) Comparison of tone mapped LDR images
This experiment applied tone mapping for 32 HDR images in the RGBE format and 42 images in the OpenEXR format using the proposed method and the conventional method [Reference Reinhard, Stark, Shirley and Ferwerda1], and measured the PSNR of the tone mapped LDR images. Table 2 shows that condition of this experiment. The parameter k was set to 0.5.

Fig. 12. LDR images comparison (OpenEXR).

Fig. 13. LDR images comparison (RGBE).
Table 2. The conditions in the experiments and the evaluation.

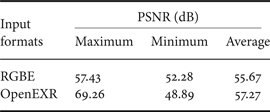
Tables 3 and 4 show the PSNR of each LDR image. Table 5 shows the maximum, minimum, and average PSNR. In all cases, high PSNR values were obtained in the proposed method. The proposed method involves many rounding operations; however, the PSNR results still indicated high values. Therefore, the errors with accumulative rounding do not significantly affect the resulting LDR images. Figures 12 and 13 show LDR images obtained by the proposed method and the conventional method [Reference Reinhard, Stark, Shirley and Ferwerda1]. It indicates that it is impossible for human eyes to distinguish these two images. From the above results, it was confirmed that the proposed method can execute the TMO with high accuracy, even though it involves the format conversion and the fixed-point arithmetic.
Table 3. The PSNR between the proposed and the conventional methods [Reference Reinhard, Stark, Shirley and Ferwerda1] (RGBE).
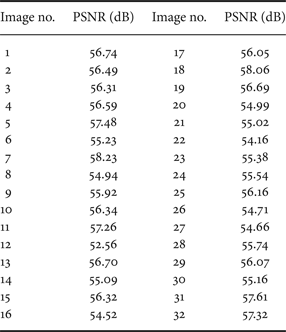
Table 4. The PSNR between the proposed and the conventional methods [Reference Reinhard, Stark, Shirley and Ferwerda1] (OpenEXR).
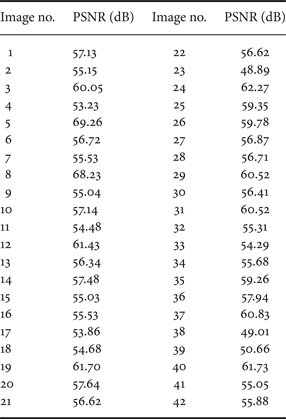
Table 5. The maximum, minimum, and average PSNR between the proposed and the conventional methods [Reference Reinhard, Stark, Shirley and Ferwerda1].
C) Comparison of the processing time
This experiment applied tone mapping for HDR images with 393216 pixels in the IEEE754, the OpenEXR, and the RGBE format using the proposed method and the conventional method [Reference Reinhard, Stark, Shirley and Ferwerda1], and measured the processing time of the methods. The experimental environment was with Marvell PXA270 ARM Processor 624MHz and 128MB RAM. Note that this processor does not have a FPU. The proposed method used 32-bit fixed-point arithmetic, and the conventional method [Reference Reinhard, Stark, Shirley and Ferwerda1] used 64-bit floating-point arithmetic in this experiment. Table 2 shows that condition of this experiment.
Figure 14 compares the processing time of the proposed method and the conventional method [Reference Reinhard, Stark, Shirley and Ferwerda1]. The proposed method was 7.26, 10.44, and 17.13 times faster than the conventional method when the input HDR image formats were the IEEE754, the OpenEXR, and the RGBE, respectively. Therefore, this experiment confirmed that the proposed method reduced the computational cost using fixed-point arithmetic.
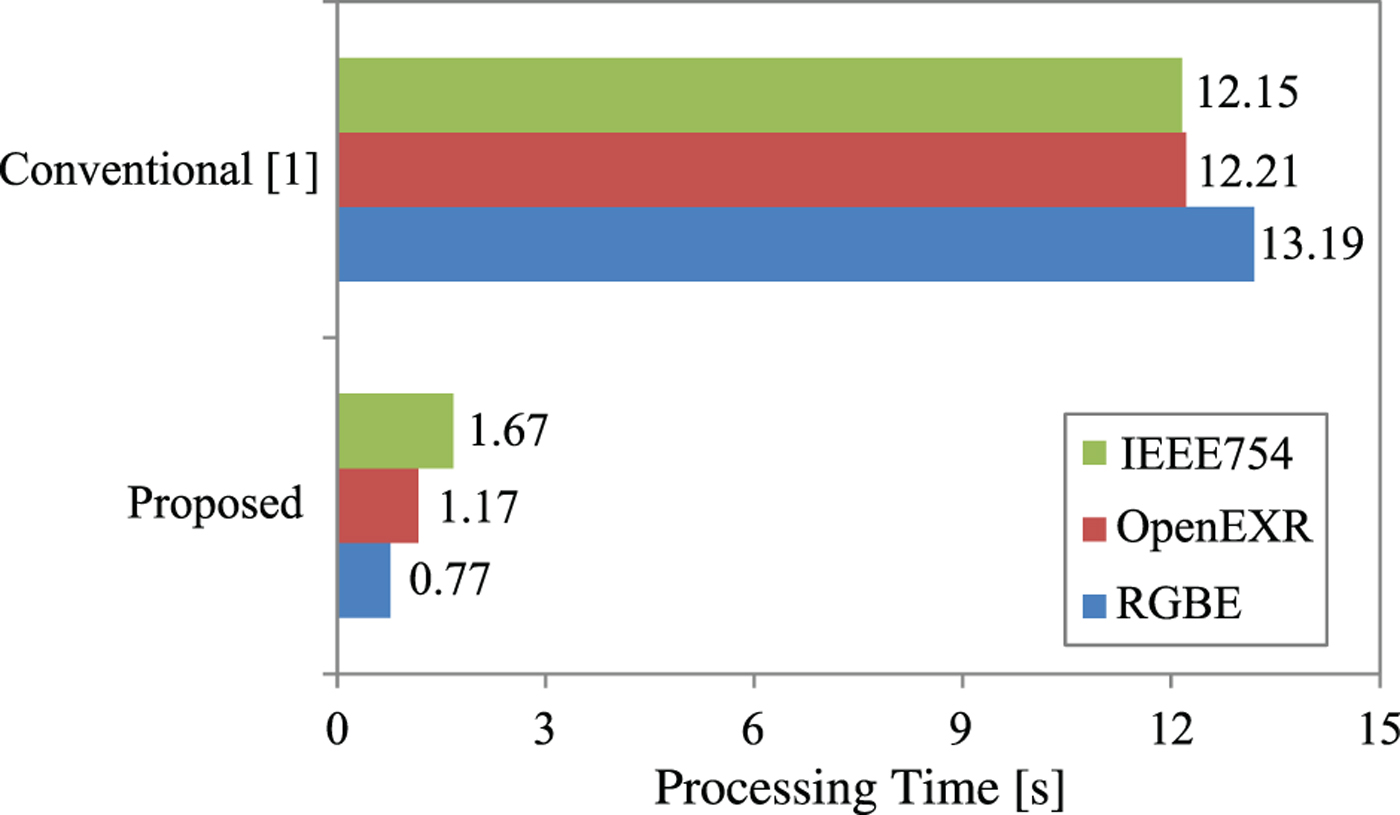
Fig. 14. The processing time of the proposed method and the conventional method [1].
D) Comparison of the memory usage
Table 6 shows the memory usage of each calculation when the size of the input HDR image is A × B pixels. The rest of calculations which is not included this table can be conducted per pixel, and it is indicated in Fig. 8. The memory usage which depends on the image size is reduced by 75.0% in the proposed method. The method uses two pre-calculated tables, and each table consists of 16 × 256 bits. Therefore, the total memory usage of the proposed method which includes the tables is A × B × 64 + 8208 bits. The 8208 bits are canceled out if the size of the input HDR image is larger than 42 pixels.
Table 6. The memory usage of the conventional method [Reference Reinhard, Stark, Shirley and Ferwerda1] and the proposed method.

E) Comparison with the other conventional methods
The proposed method was compared with the other conventional methods [Reference Thakur, Sivasubramanian, Nallaperumal, Marappan and Vishwanath20–Reference Dobashi, Murofushi, Iwahashi and Kiya22].
1) COMPARISON OF THE PROCESSING TIME
The processing times of the proposed method and [Reference Thakur, Sivasubramanian, Nallaperumal, Marappan and Vishwanath20–Reference Dobashi, Murofushi, Iwahashi and Kiya22] during tone mapping for HDR image (393216 pixels) were 0.77, 0.47, 78.42, and 0.55 s, respectively. Note that the CPUs used for the proposed method and [Reference Murofushi, Iwahashi and Kiya21, Reference Dobashi, Murofushi, Iwahashi and Kiya22] were PXA270 ARM processor 624 MHz, and that of [Reference Thakur, Sivasubramanian, Nallaperumal, Marappan and Vishwanath20] was Pentium4 1800 MHz. The processing speed of [Reference Murofushi, Iwahashi and Kiya21] was very slow without FPU because it used floating-point for its internal arithmetic. The same in [Reference Dobashi, Murofushi, Iwahashi and Kiya22] gave high-speed processing because it is designed for the RGBE format exclusive use. The proposed method was a little slower than [Reference Dobashi, Murofushi, Iwahashi and Kiya22]; however, it can be applied for various formats. Moreover, considering the performance of CPUs, it is expected that the proposed method can be processed faster than [Reference Thakur, Sivasubramanian, Nallaperumal, Marappan and Vishwanath20].
2) COMPARISON OF THE PSNR VALUES
The [Reference Murofushi, Iwahashi and Kiya21, Reference Dobashi, Murofushi, Iwahashi and Kiya22] are basis methods of the proposed method, and these methods are designed for the RGBE format. The experiment in this section applied tone mapping for 32 HDR images in the RGBE format, and compared the average PSNRs between these methods and the conventional method [Reference Reinhard, Stark, Shirley and Ferwerda1]. The PSNR values of the proposed method, [Reference Murofushi, Iwahashi and Kiya21, Reference Dobashi, Murofushi, Iwahashi and Kiya22] were 55.67 dB, 58.78, and 56.18 dB, respectively. The proposed method and [Reference Dobashi, Murofushi, Iwahashi and Kiya22] used fixed-point arithmetic. On the other hand, [Reference Murofushi, Iwahashi and Kiya21] used floating-point arithmetic. Errors occurred using fixed-point arithmetic instead of floating-point arithmetic, and it was cause of PSNR drop. Comparing with [Reference Dobashi, Murofushi, Iwahashi and Kiya22], the PSNR dropped a little because a part of internal process of the proposed method was changed in order to adapt to the intermediate format. However, the average PSNR still maintained over 55 dB, and it is sufficiently high value.
V. CONCLUSION
This paper proposed a TMO with fixed-point arithmetic and low-memory. The proposed method can apply the TMO for multiple HDR image formats using an intermediate format. Using the intermediate format, the method can apply the tone mapping to two 8-bit integer numbers, which correspond to the exponent part and the mantissa part, separately. The method reduces the memory cost using 8-bit integer numbers instead of a 64-bit floating-point number. Furthermore, the method performs the TMO with only fixed-point arithmetic to reduce the computational cost. As a result, the method is effective on a computer with low-memory and a low-performance processor. The experimental results confirmed that the proposed method can execute the TMO with high accuracy, even though it is with fixed-point arithmetic and integer data. The future work is applying the method to local TMOs.
Toshiyuki Dobashi received his B. Eng. and M. Eng. degrees from Tokyo Metropolitan University, Japan in 2012 and 2014, respectively. He joined Canon Inc. in 2014. His research interests include image processing.
Atsushi Tashiro received his B. Eng. degree from Tokyo Metropolitan University, Japan in 2014. He joined Hitachi Co., Ltd. in 2014. His research interests include image processing.
Masahiro Iwahashi received his B.Eng., M.Eng., and D.Eng. degrees in Electrical Engineering from Tokyo Metropo-litan University in 1988, 1990, and 1996, respectively. In 1990, he joined Nippon Steel Co. Ltd. From 1991 to 1992, he was dispatched to Graphics Communication Technology Co. Ltd. In 1993, he joined Nagaoka University of Technology, where he is currently a Professor of Department of Electrical Engineering, Faculty of Technology. From 1995 to 2001, he served concurrently as a lecturer of Nagaoka Technical College. From 1998 to 2001, he was dispatched to Thammasat University, Thailand, and to the Electronic Engineering Polytechnic Institute of Surabaya, Indonesia, as a JICA expert. His research interests are in the area of digital signal processing, multi-rate systems, and image compression. He served as an editorial committee member of the transaction on fundamentals of IEICE from 2007 to 2011.
Hitoshi Kiya received his B.Eng. and M.Eng. degrees from Nagaoka University of Technology, Japan, in 1980 and 1982, respectively, and his D.Eng. degree from Tokyo Metropolitan University in 1987. In 1982, he joined Tokyo Metropolitan University as an Assistant Professor, where he became a Full Professor in 2000. From 1995 to 1996, he attended the University of Sydney, Australia as a Visiting Fellow. He currently serves as the Chair of IEEE SPS Japan Chapter, an Associate Editor for IEEE Trans. Image Processing and IEEE Trans. Information Forensics and Security, respectively. He also served as the President of IEICE Engineering Sciences Society (ESS), an Associate Editor of IEEE Trans. Signal Processing, the Editor-in-Chief for IEICE Fundamentals Review, a Vice President of APSIPA, a Member of the Board of Governors of APSIPA, and the Editor-in-Chief for IEICE ESS publications. His research interests are in the area of signal and image processing including multirate signal processing, wavelets, video coding, compressed-domain video{} manipulation, and security for multimedia. He received the IWAIT Best Paper Award in 2014, the ITE Niwa-Takayanagi Best Paper Award in 2012, the Telecommunications Advancement Foundation Award in 2011, the IEICE ESS Contribution Award in 2010, and the IEICE Best Paper Award in 2008. He is a Fellow Member of the IEICE and the ITE, and a Senior Member of the IEEE.






















